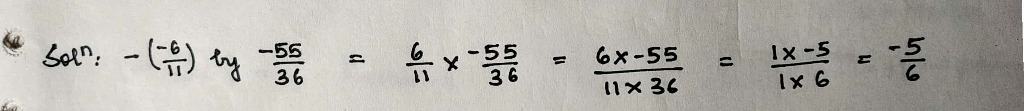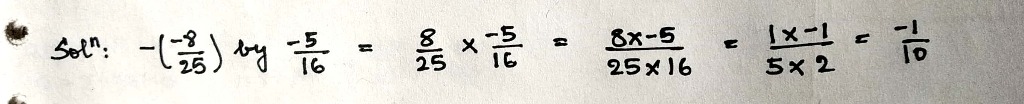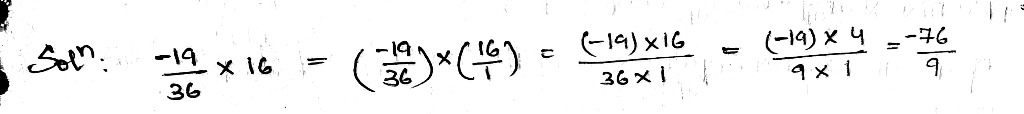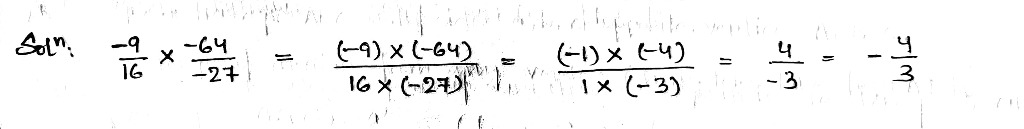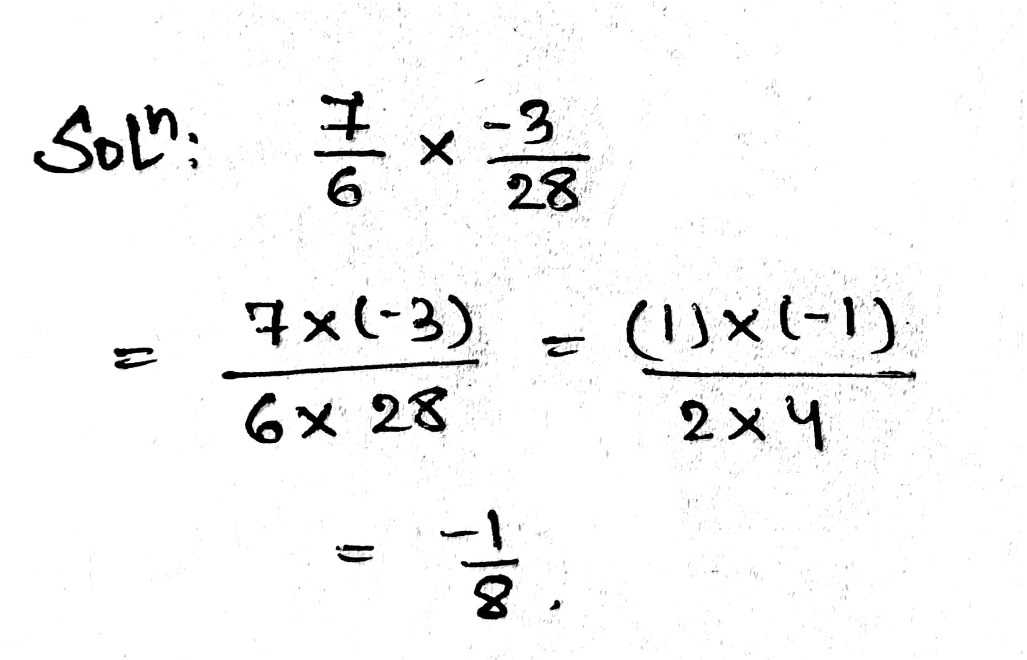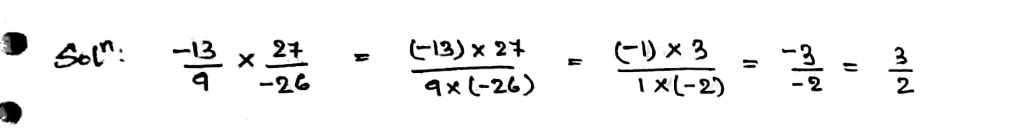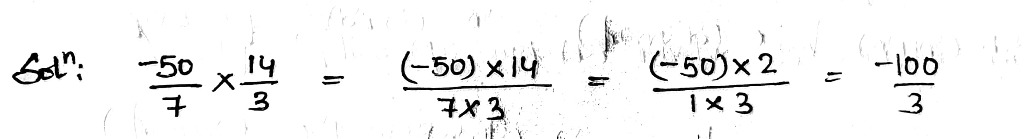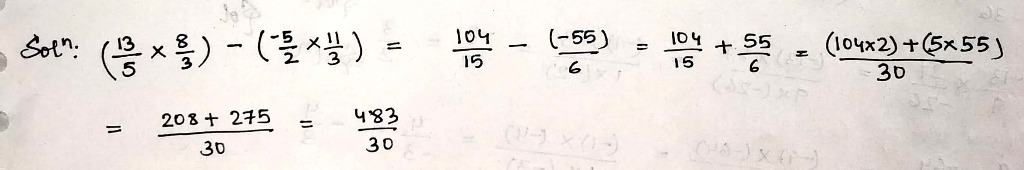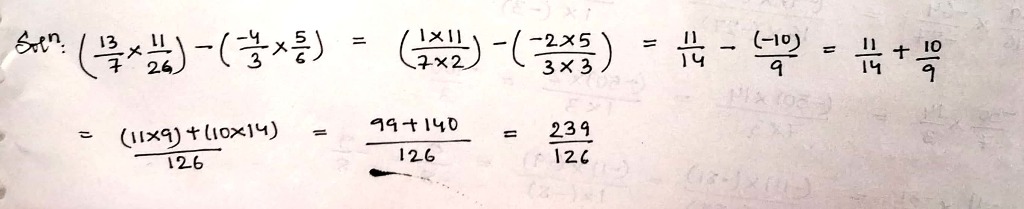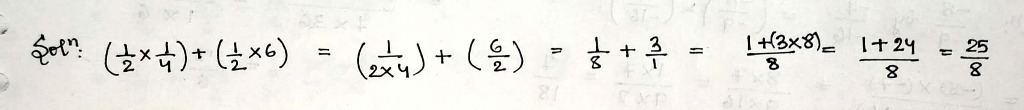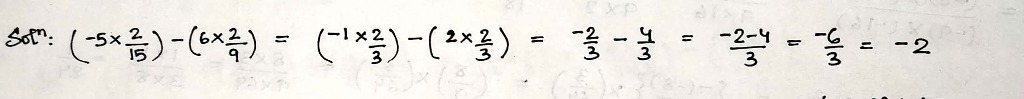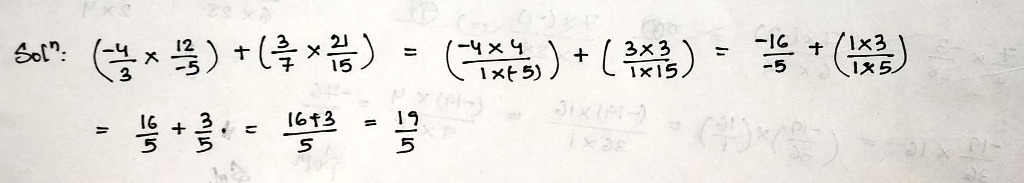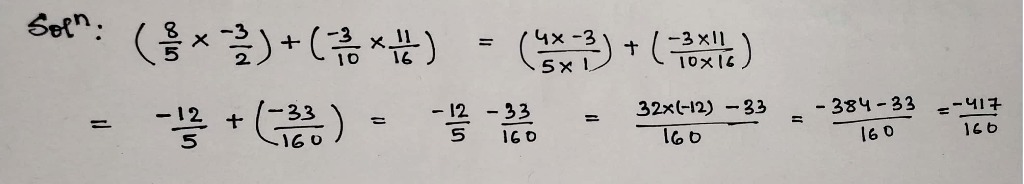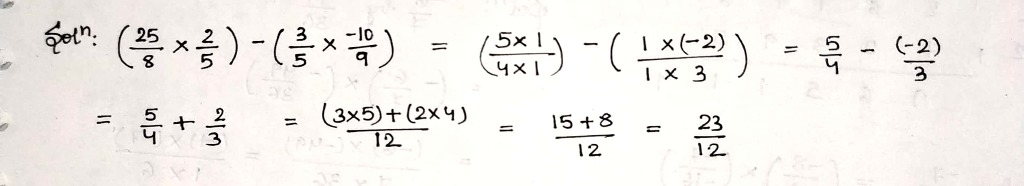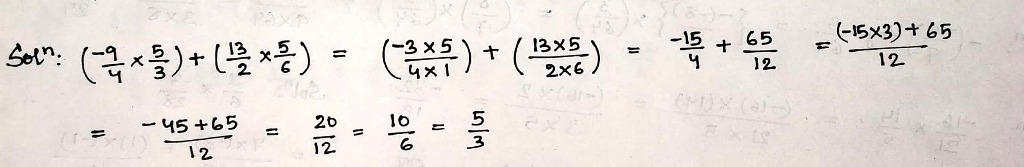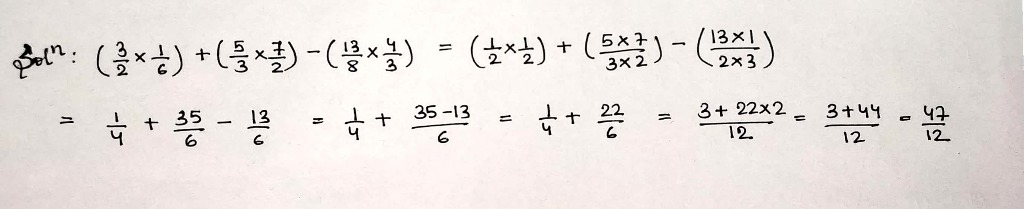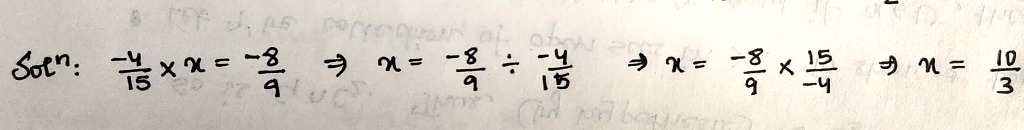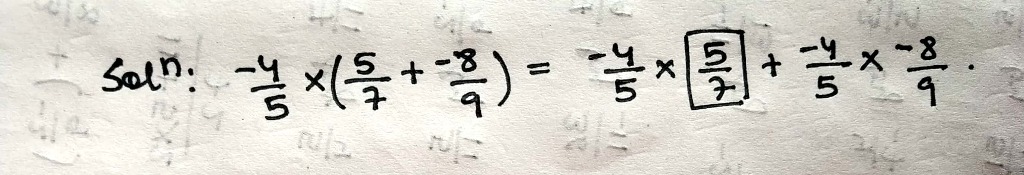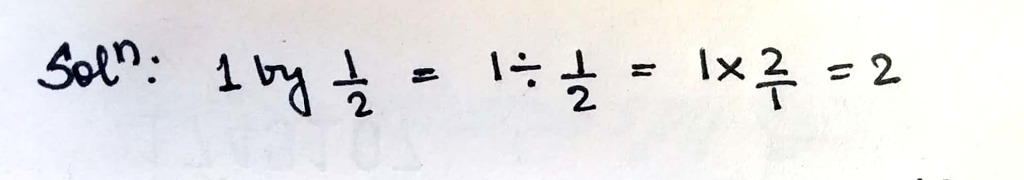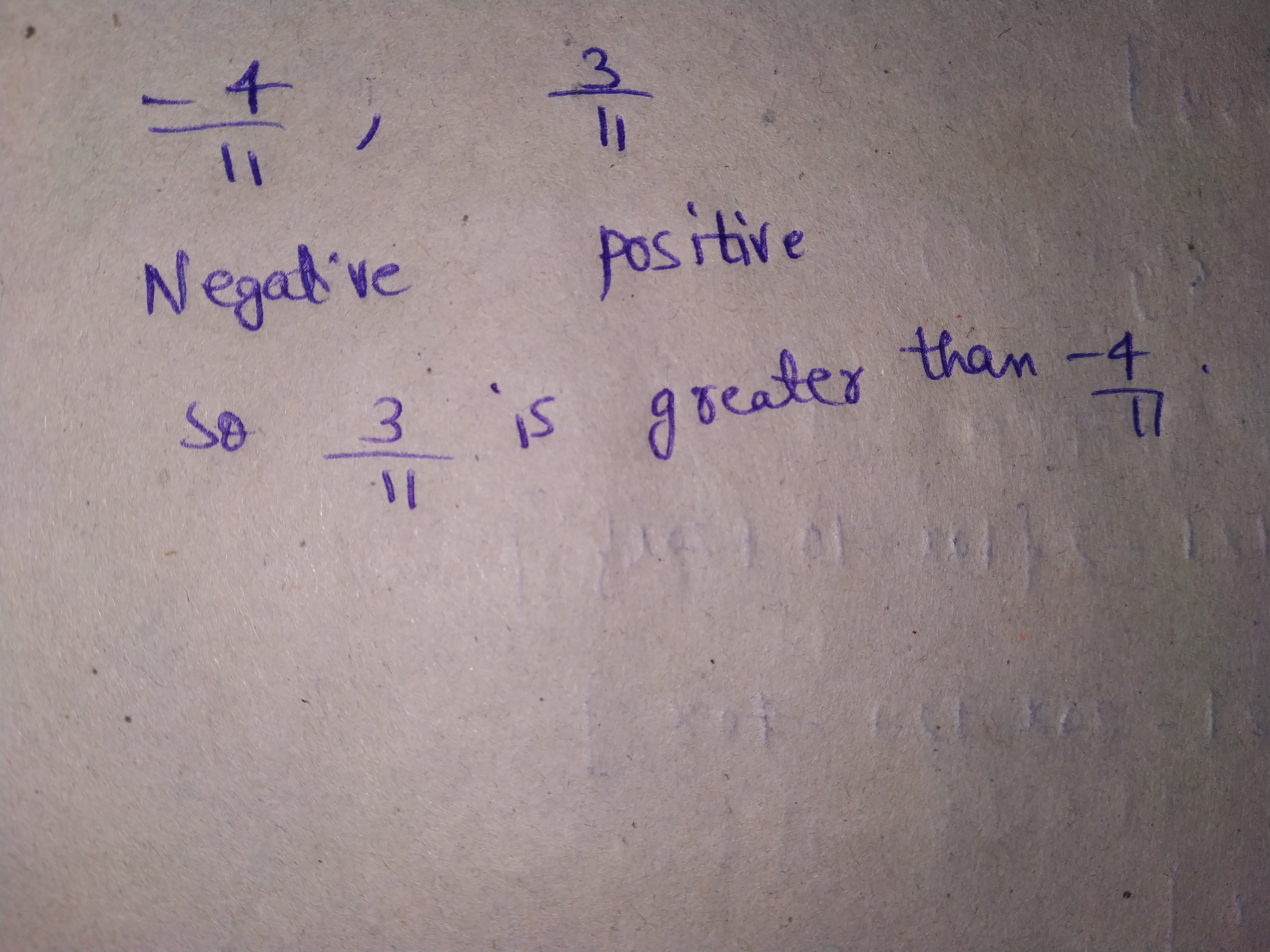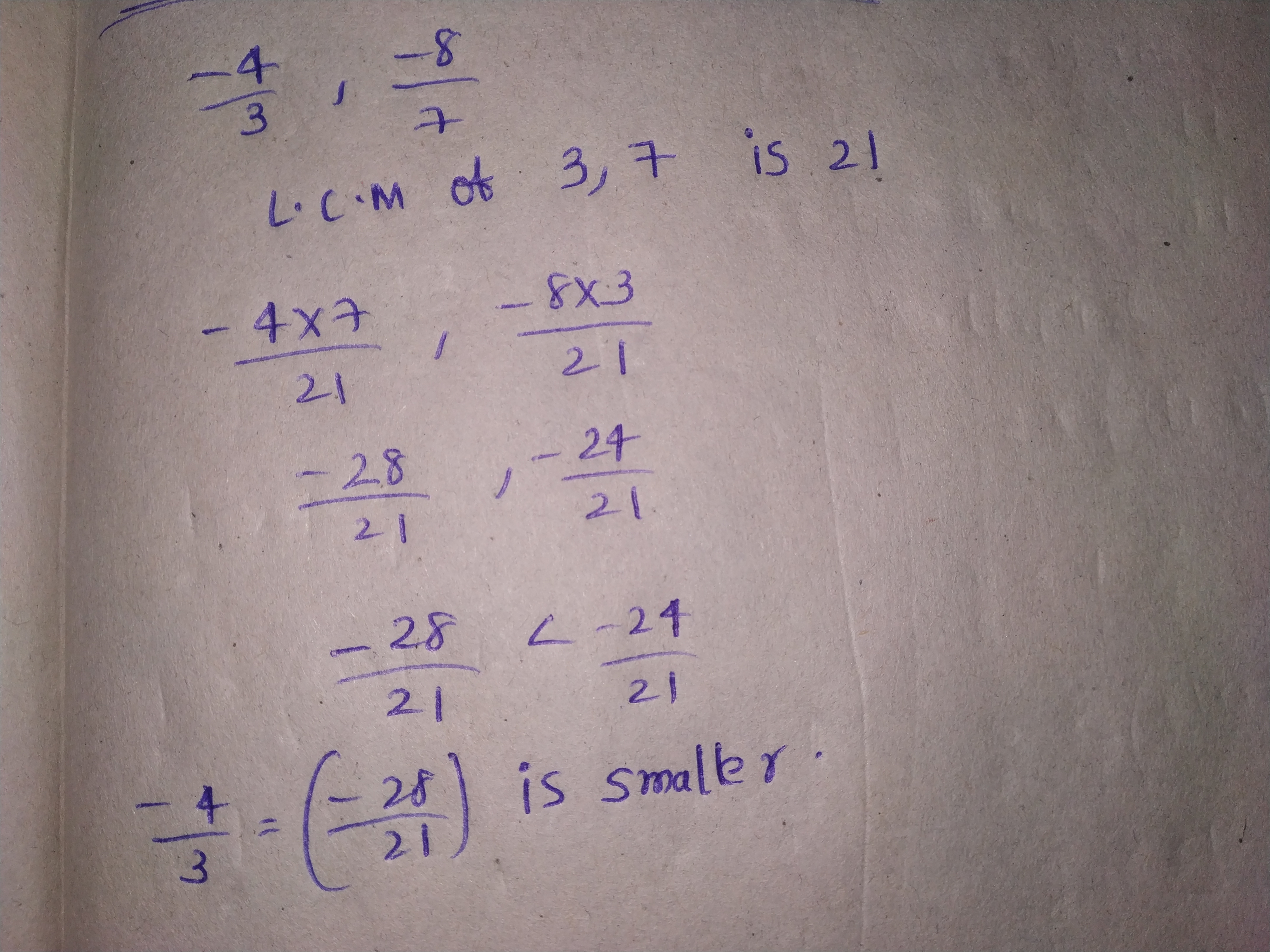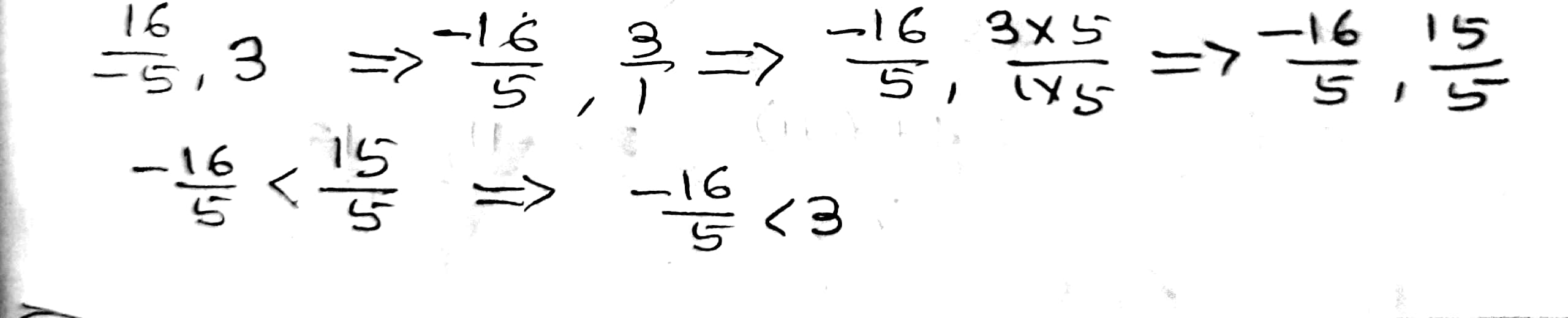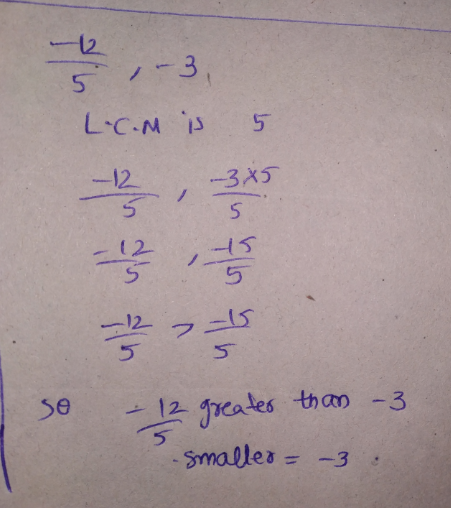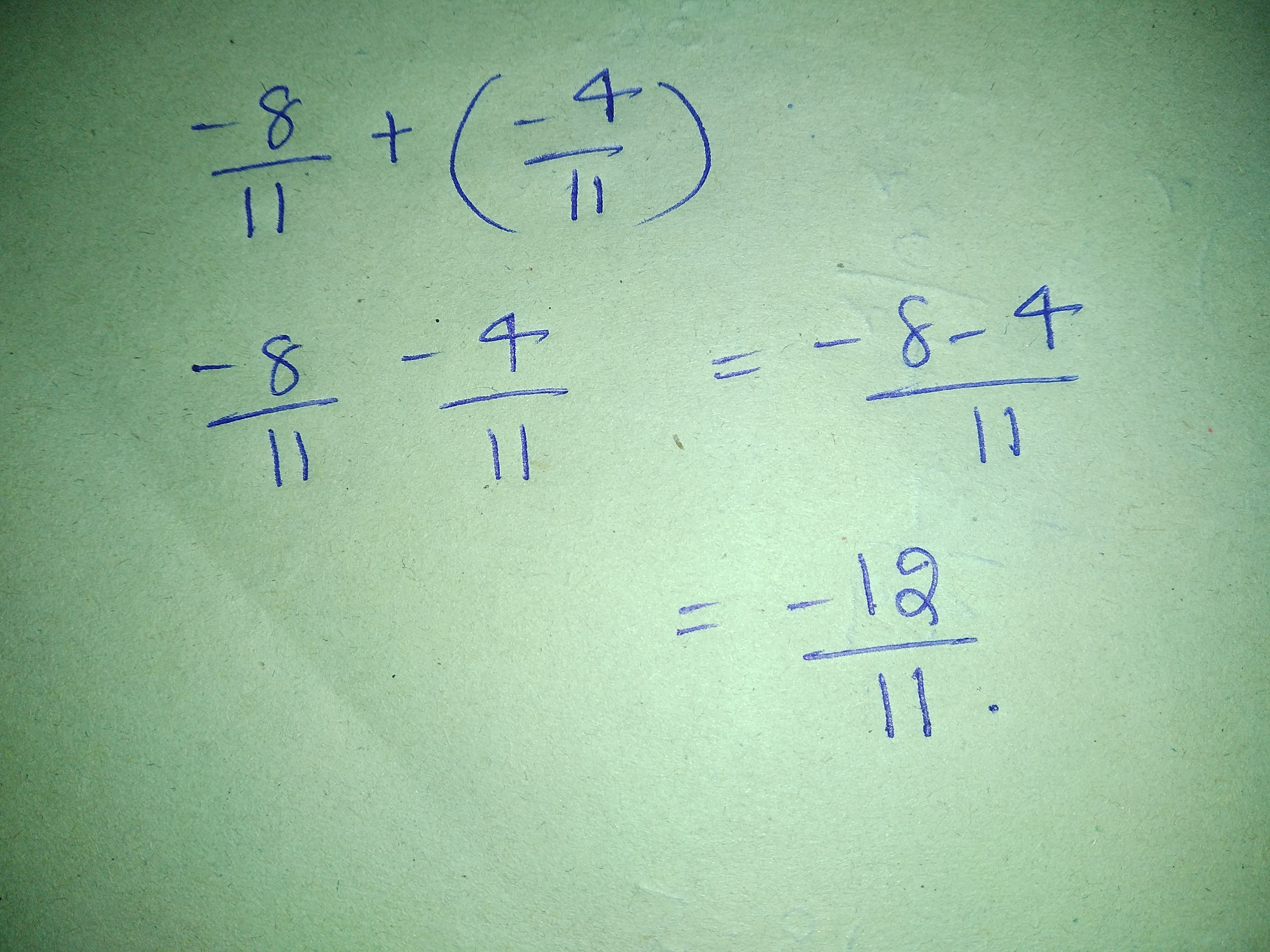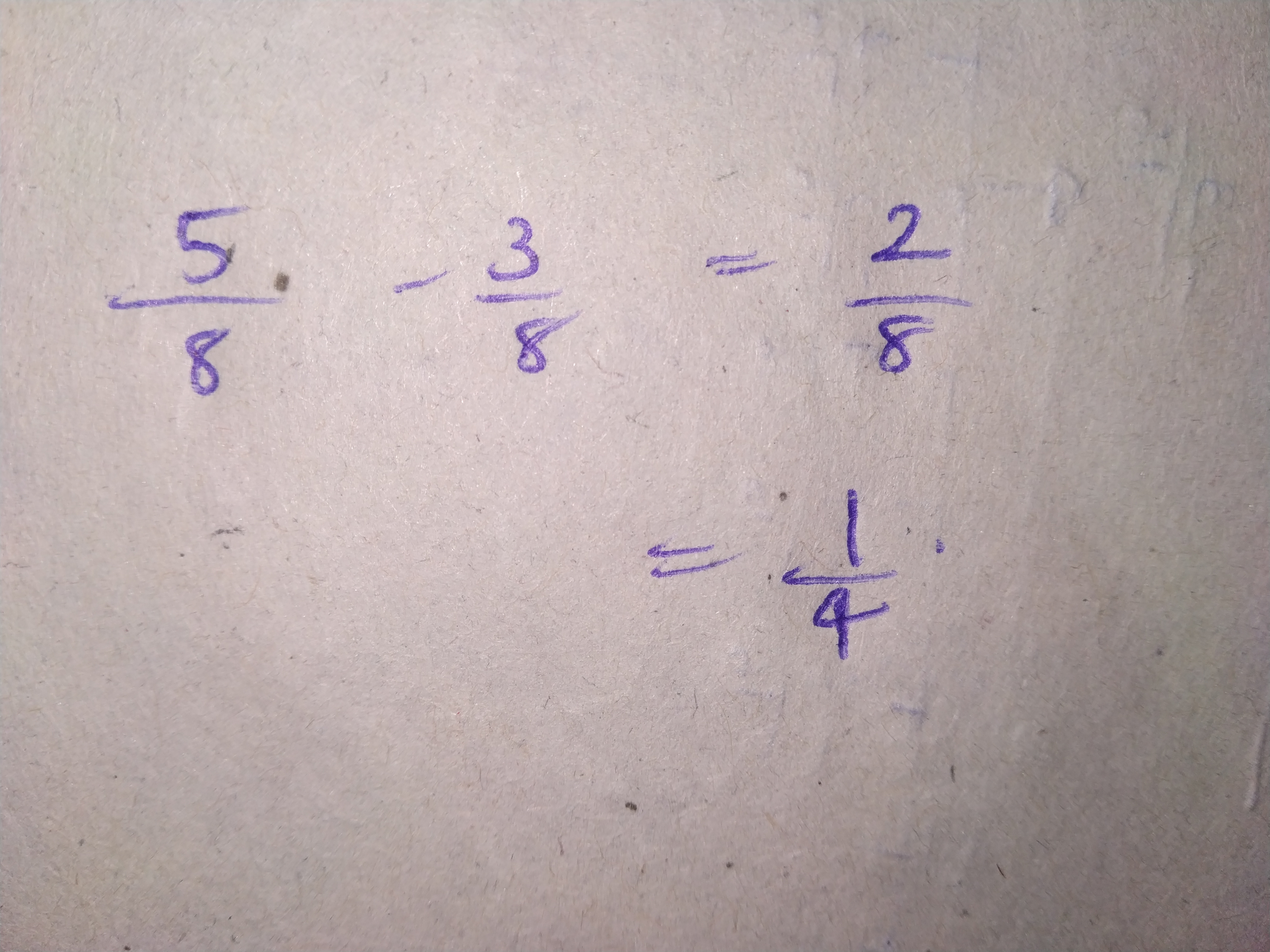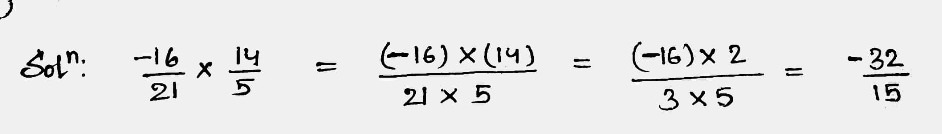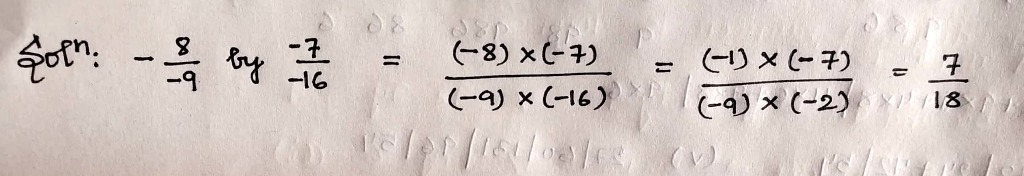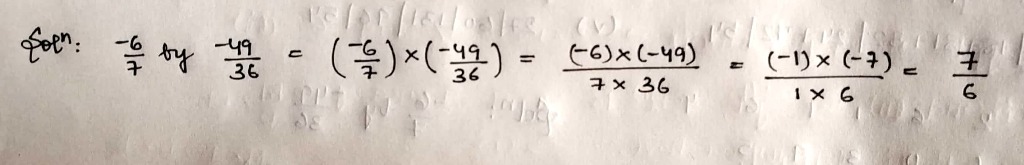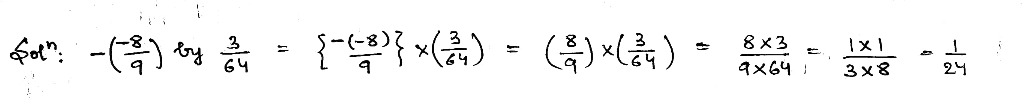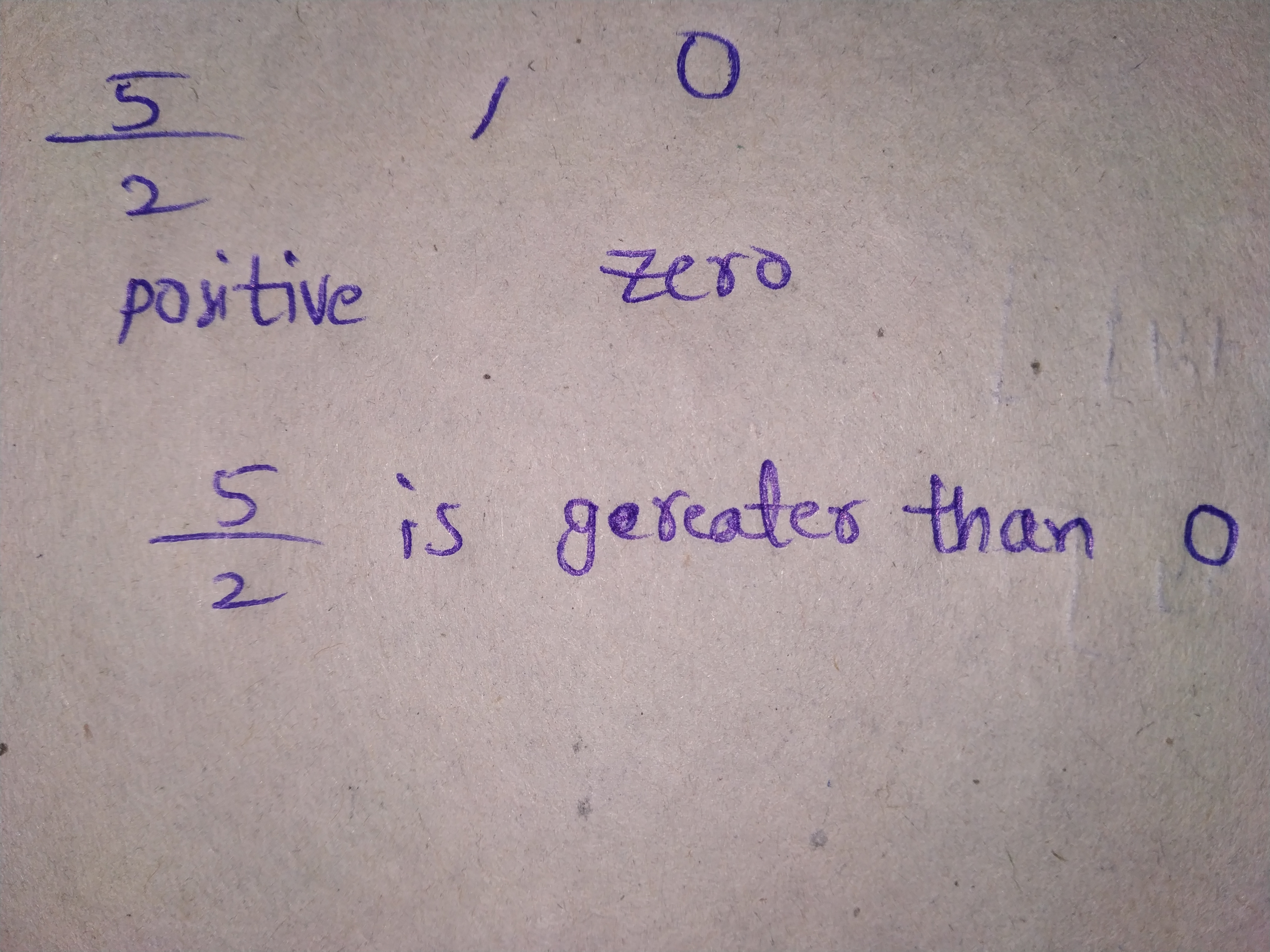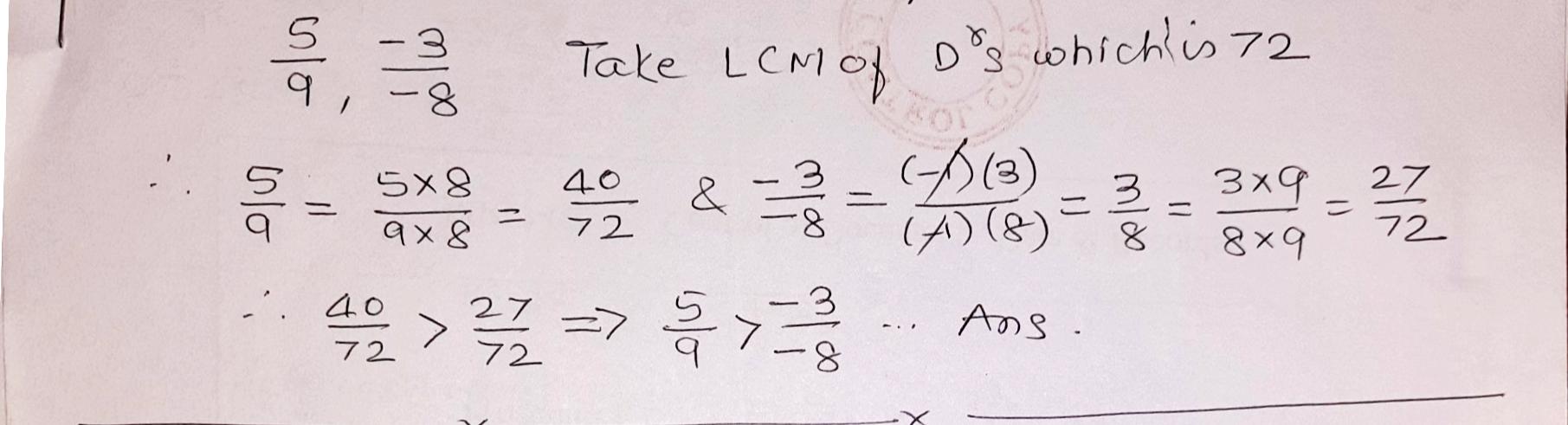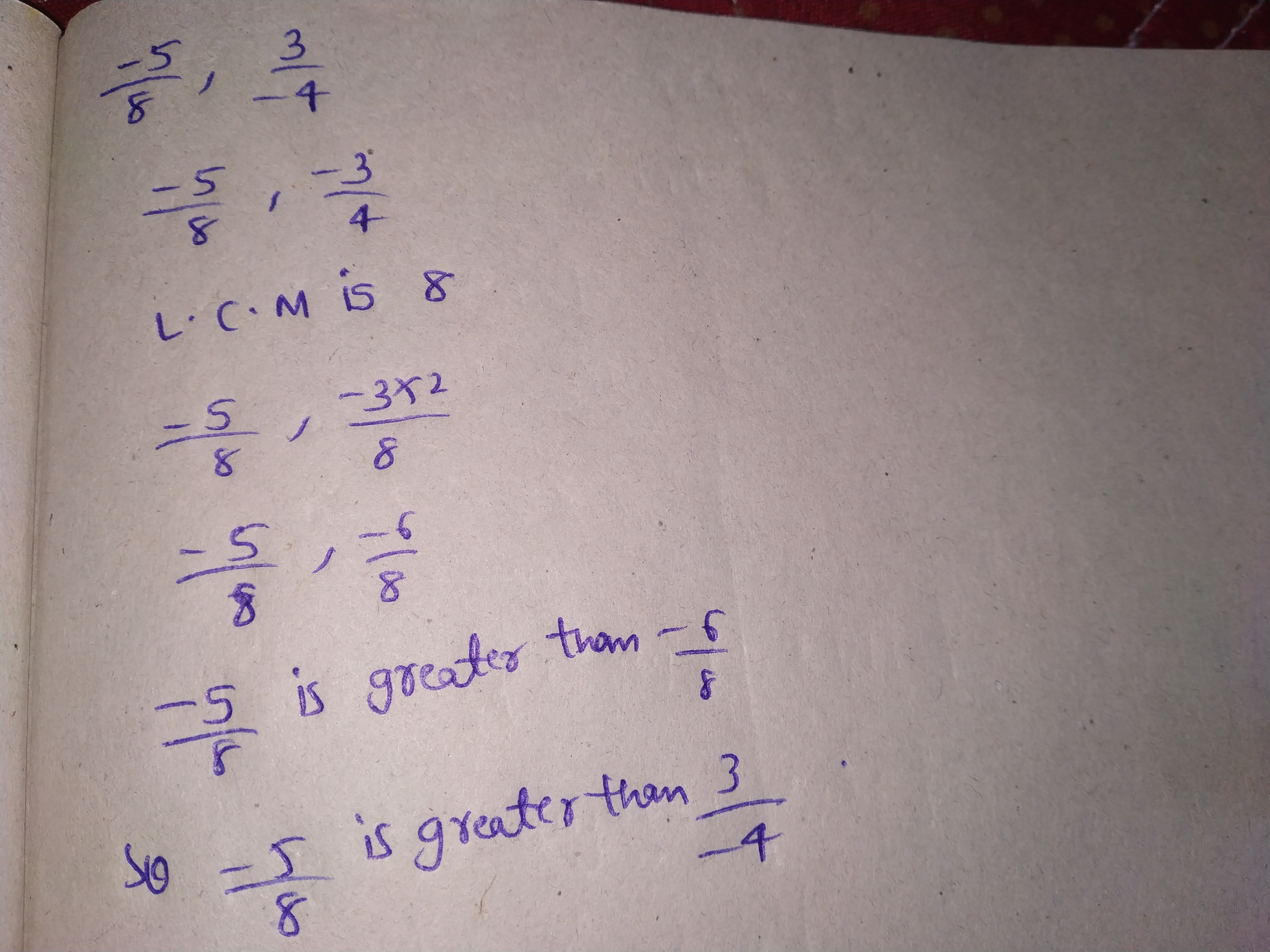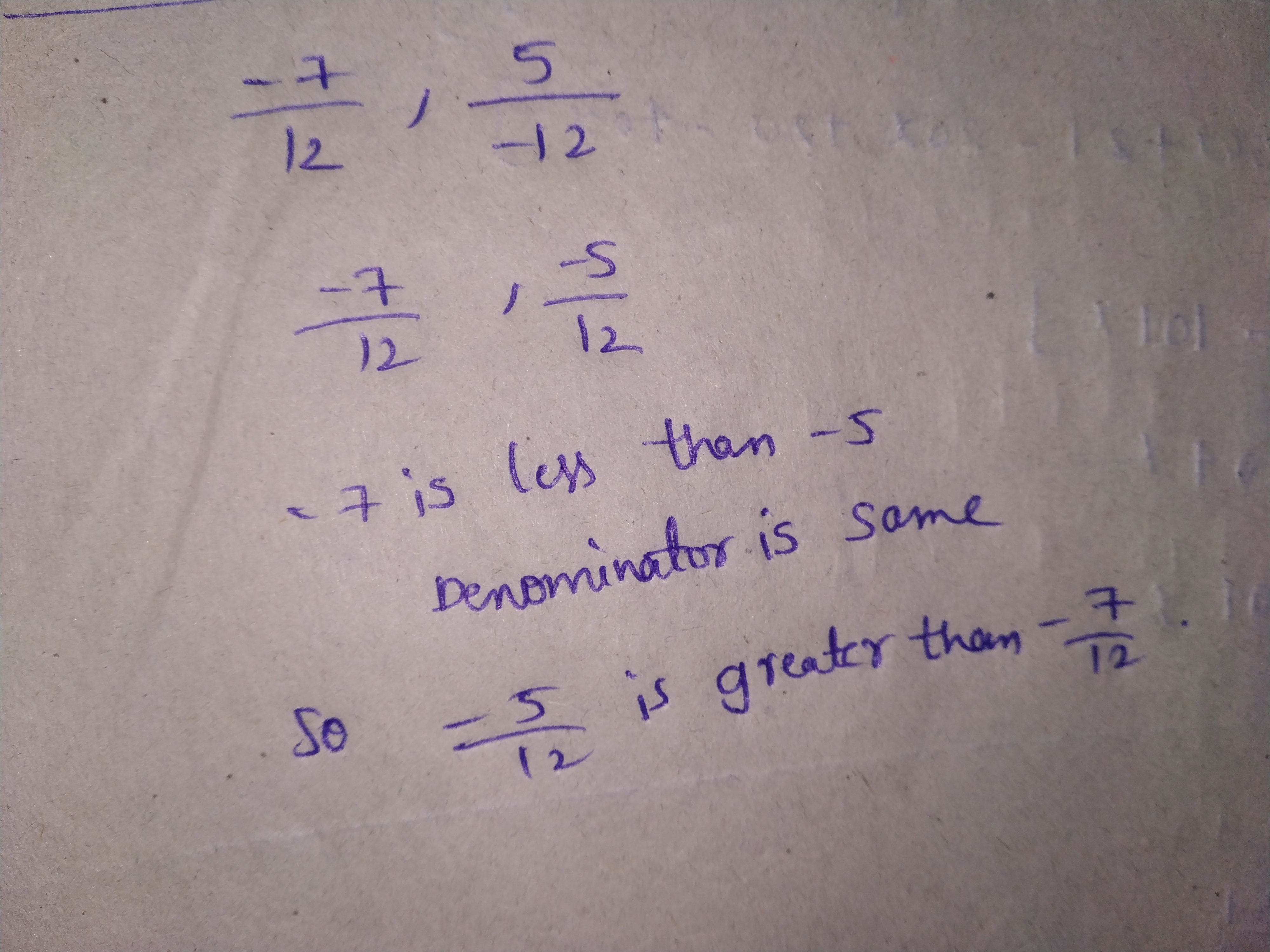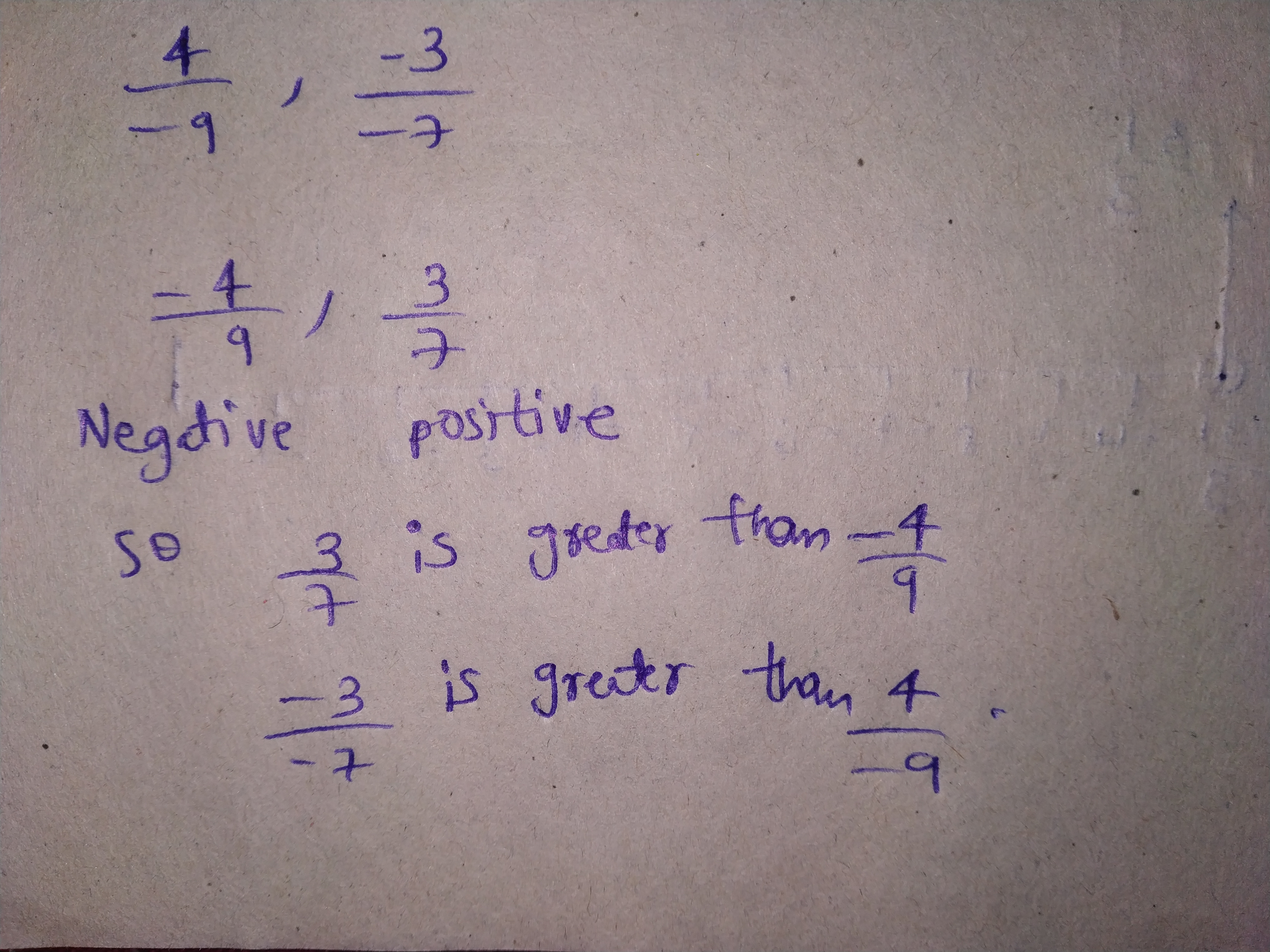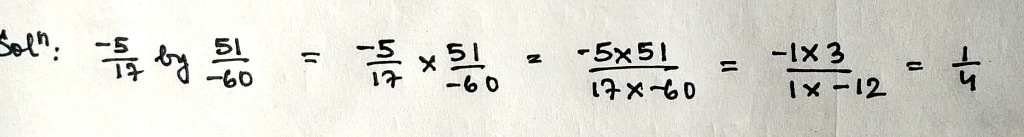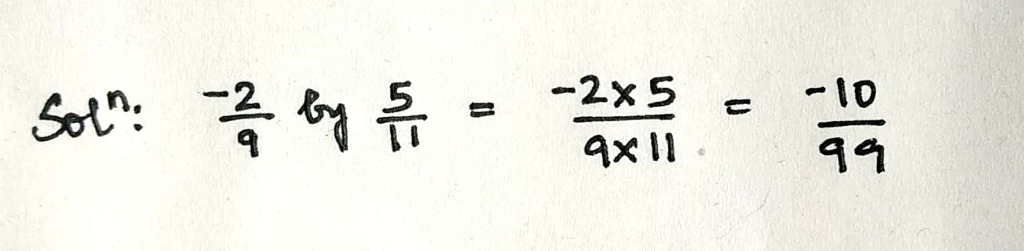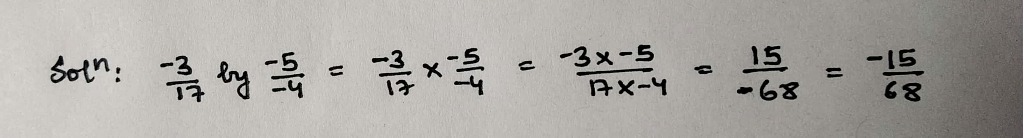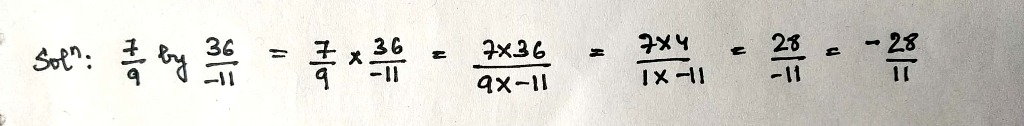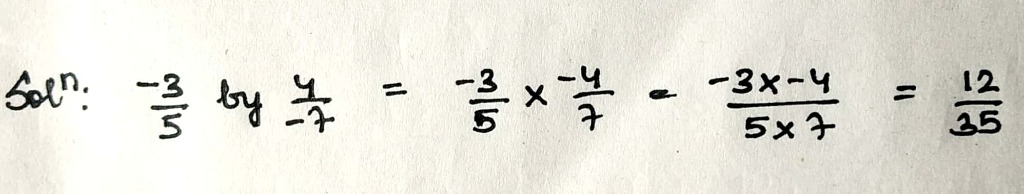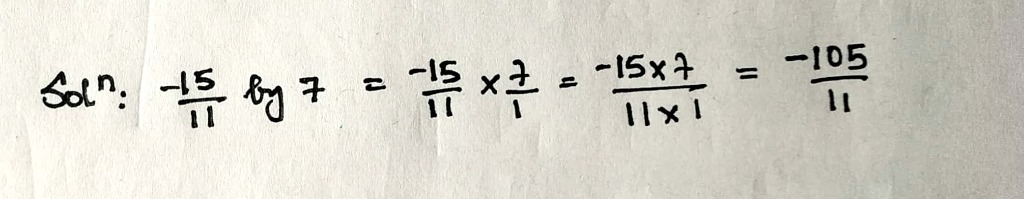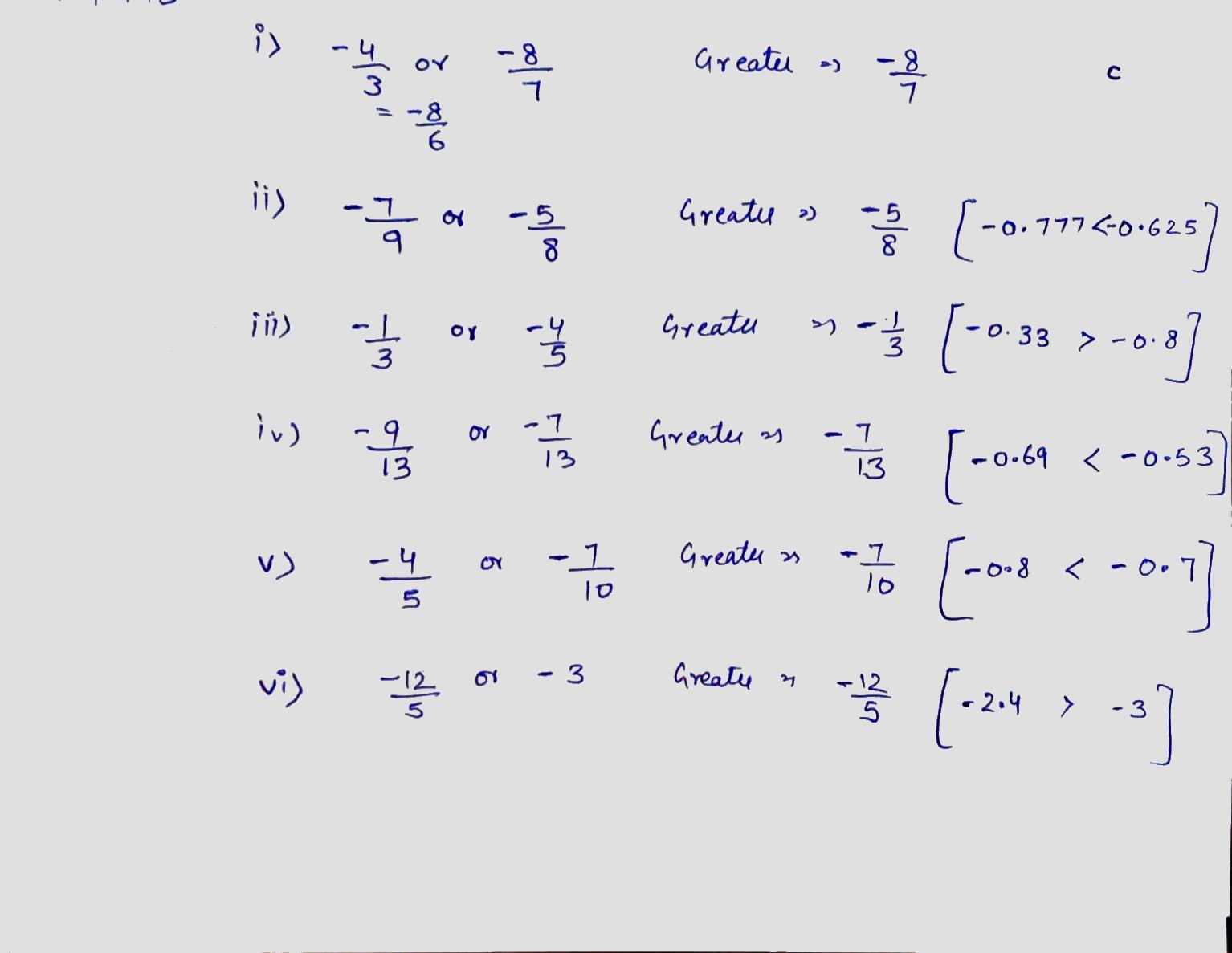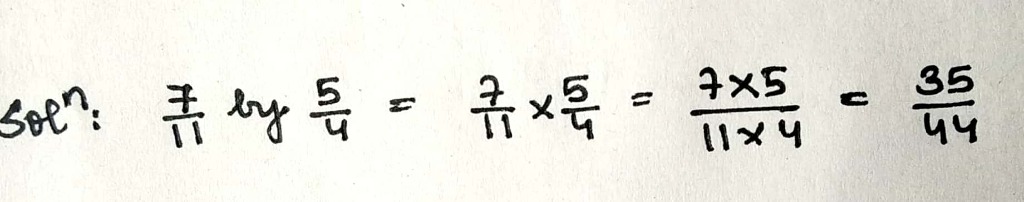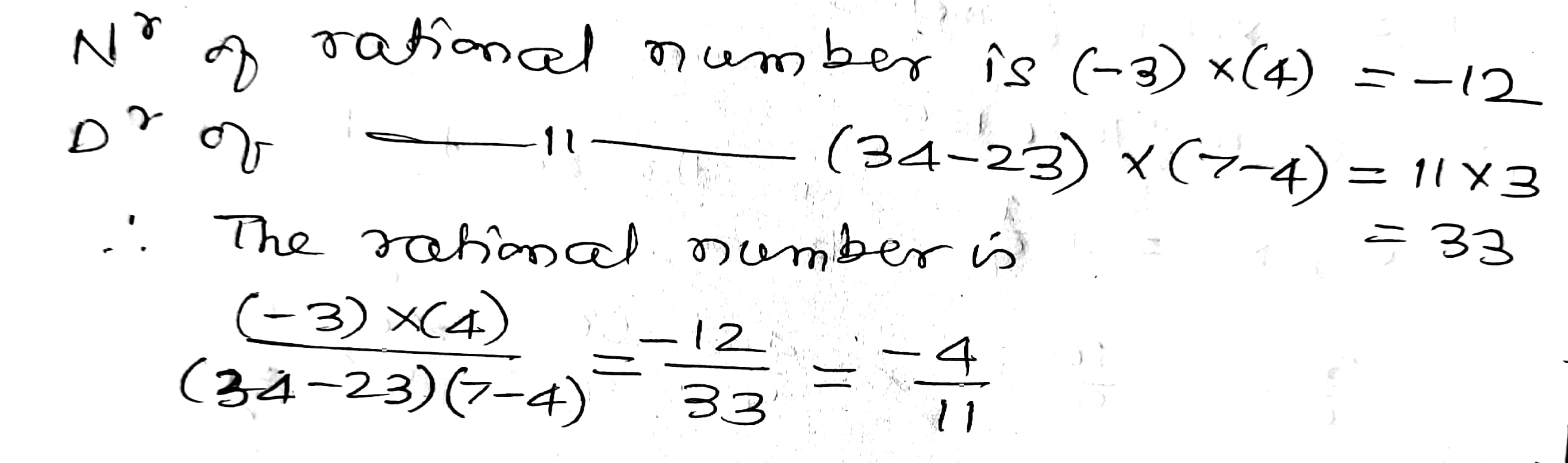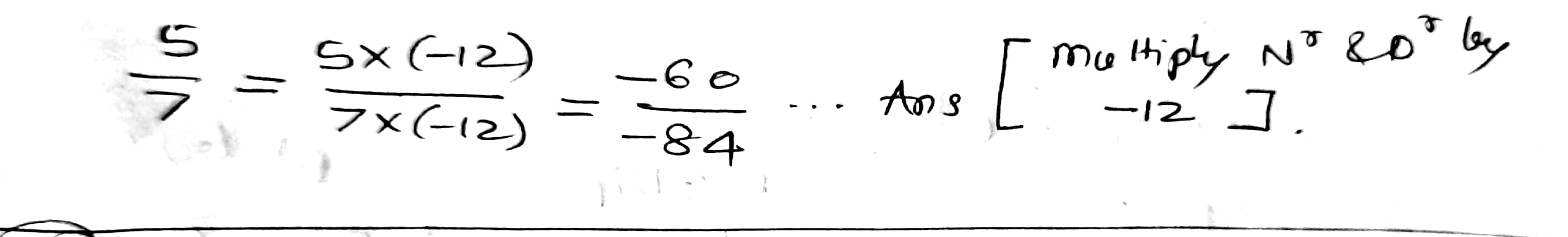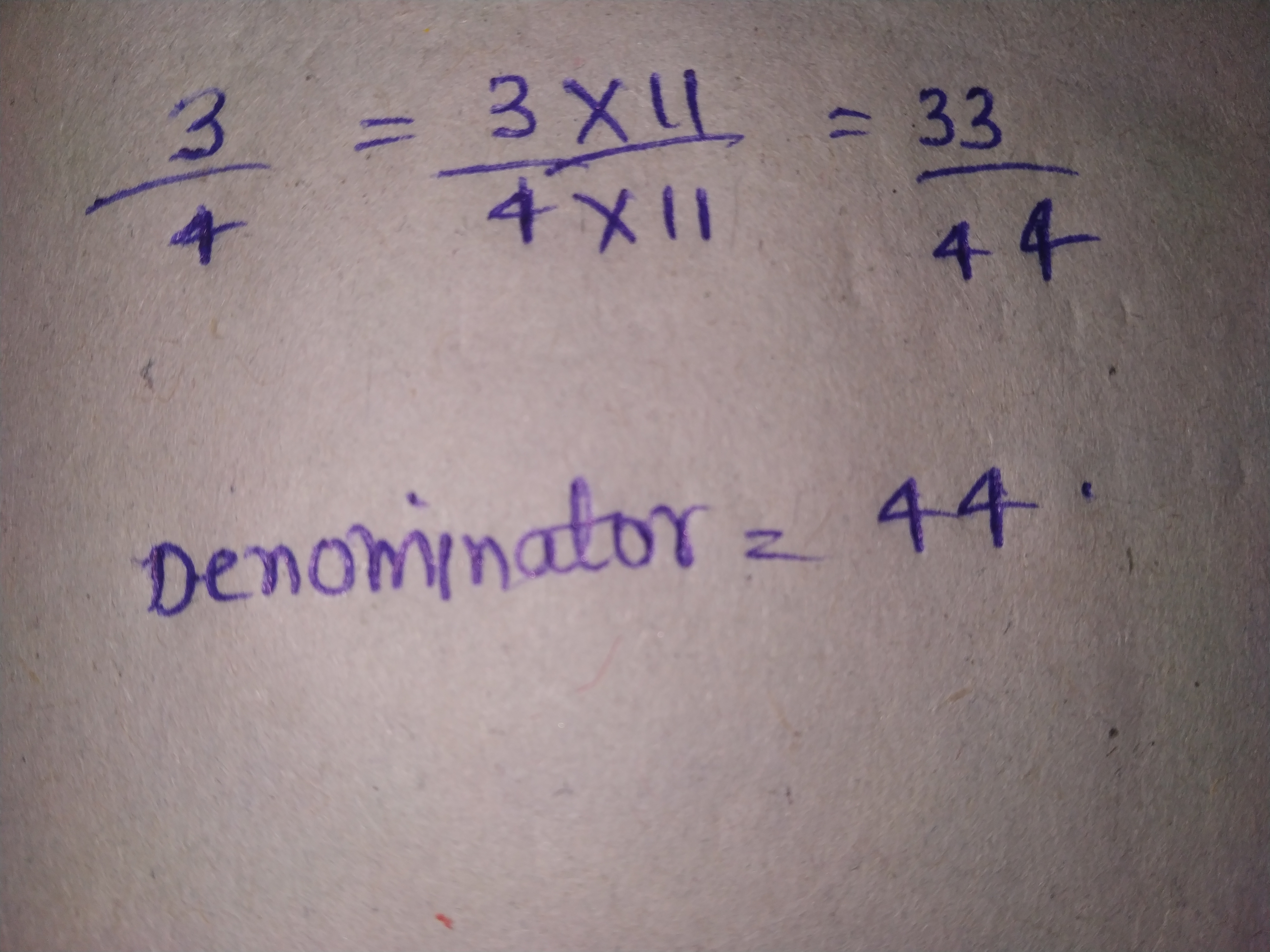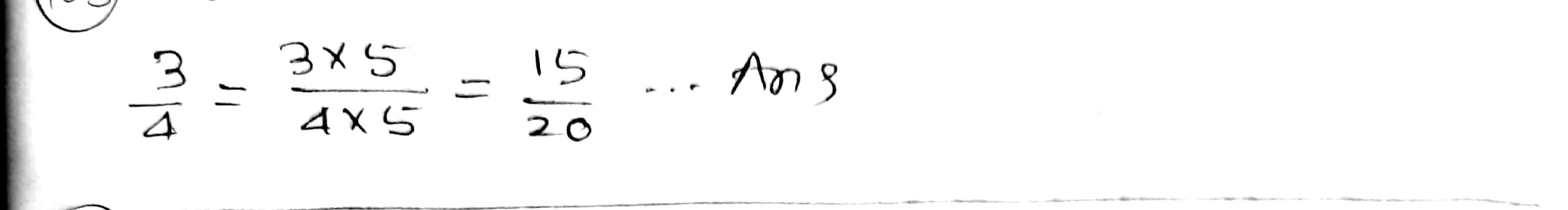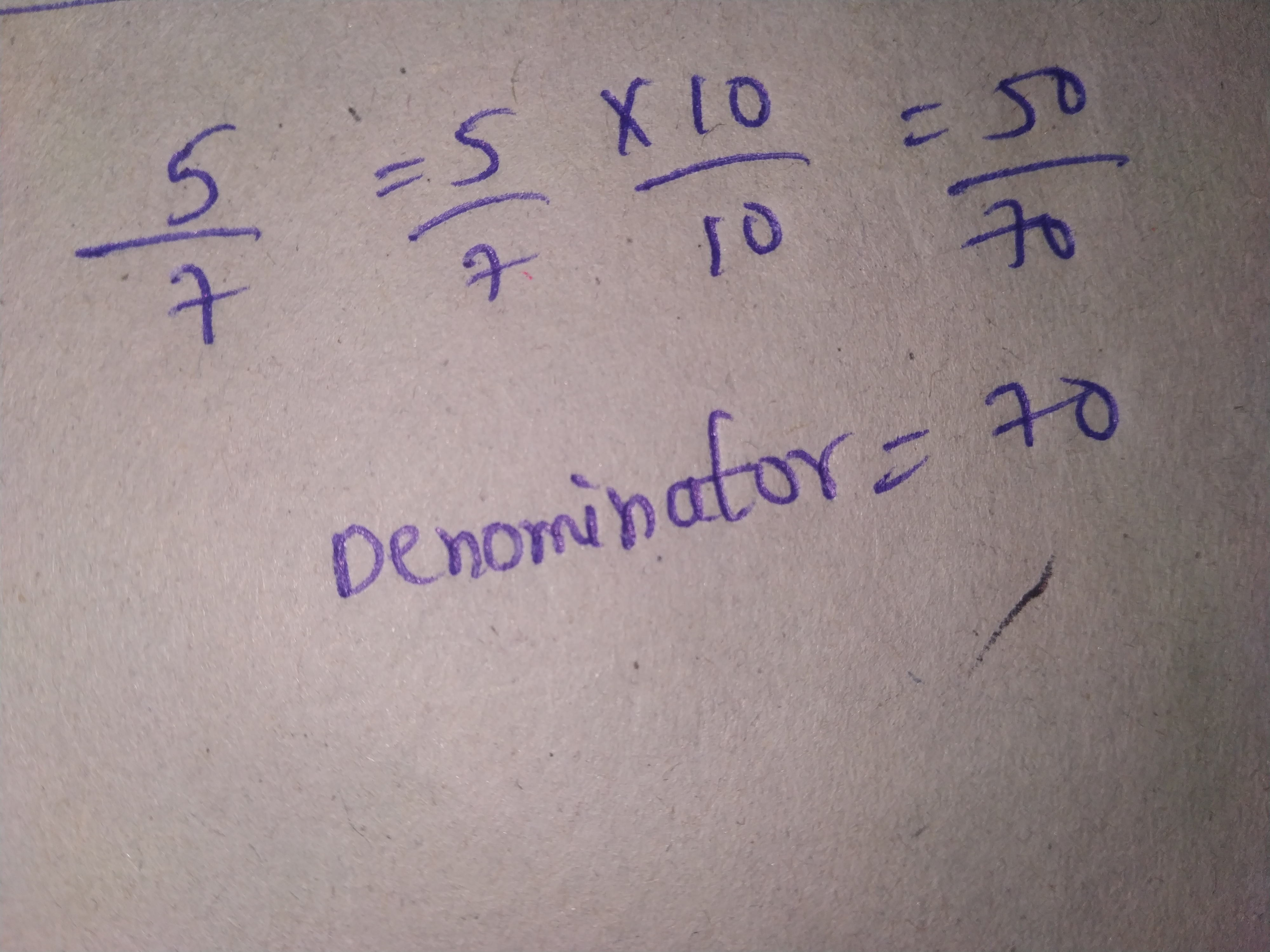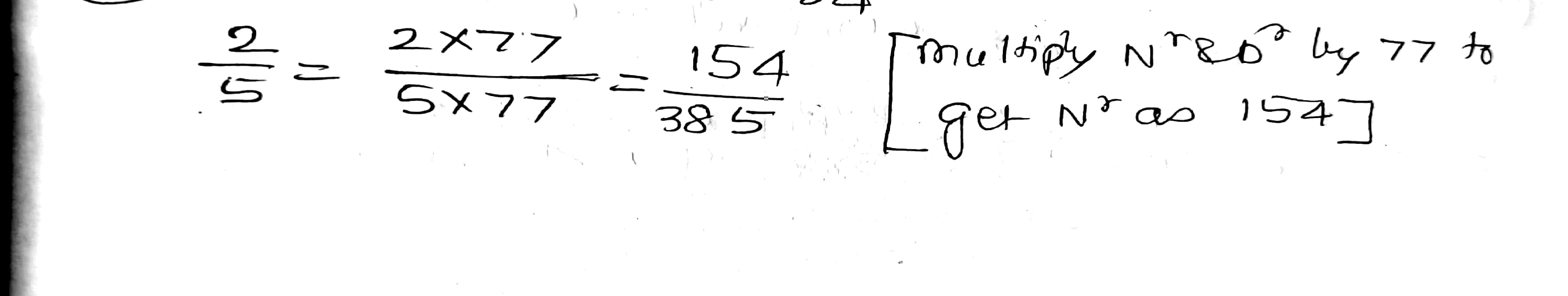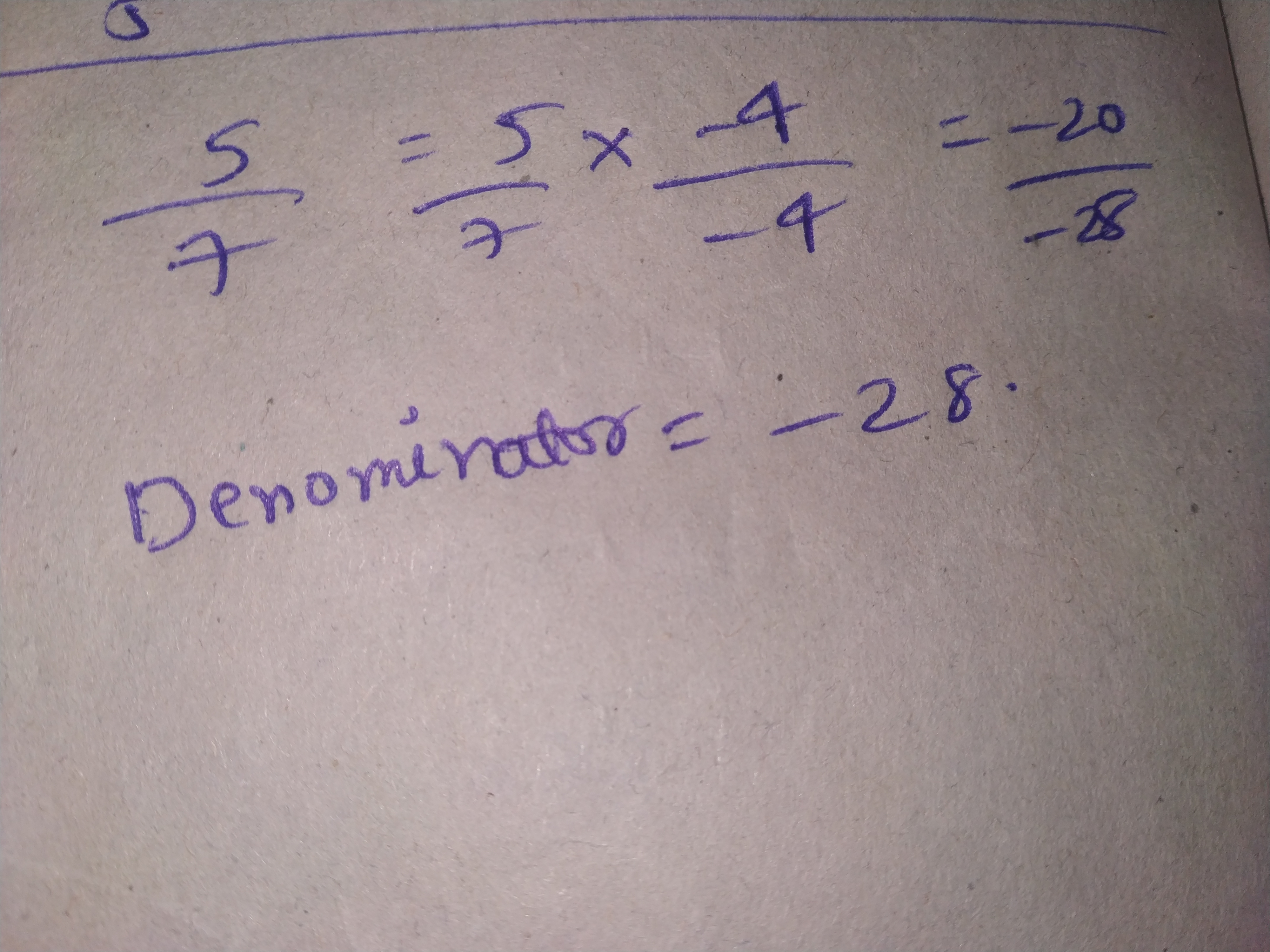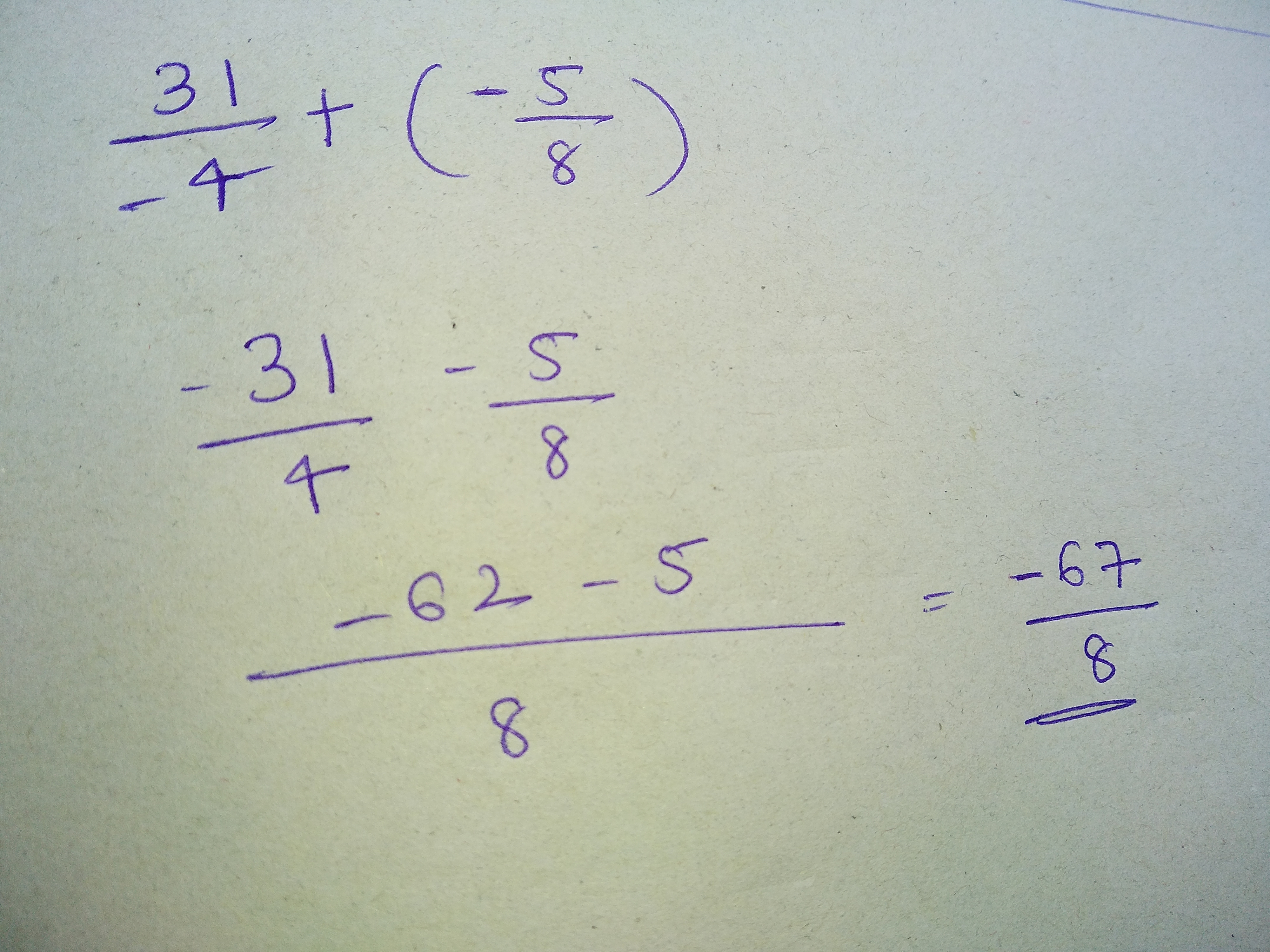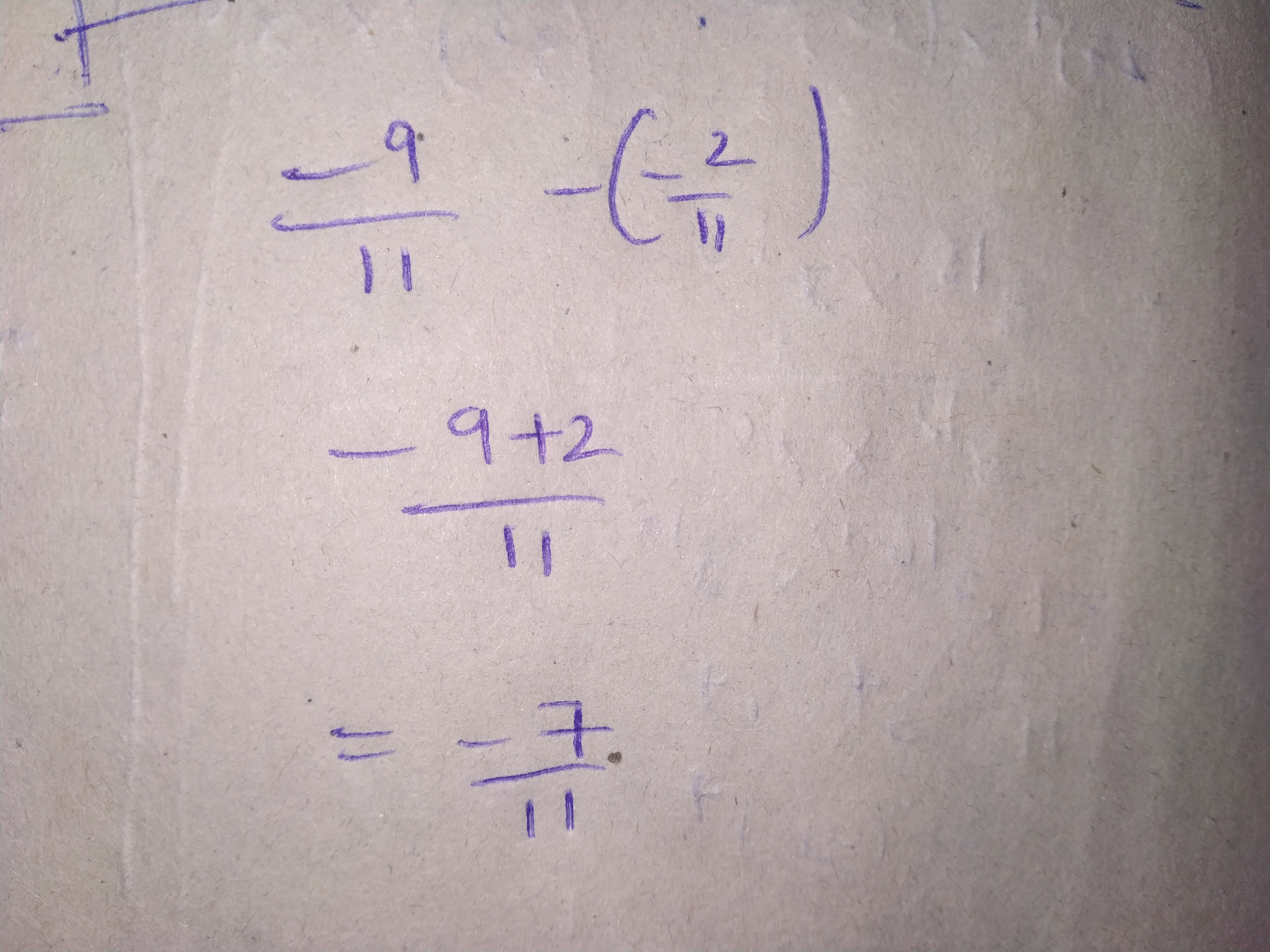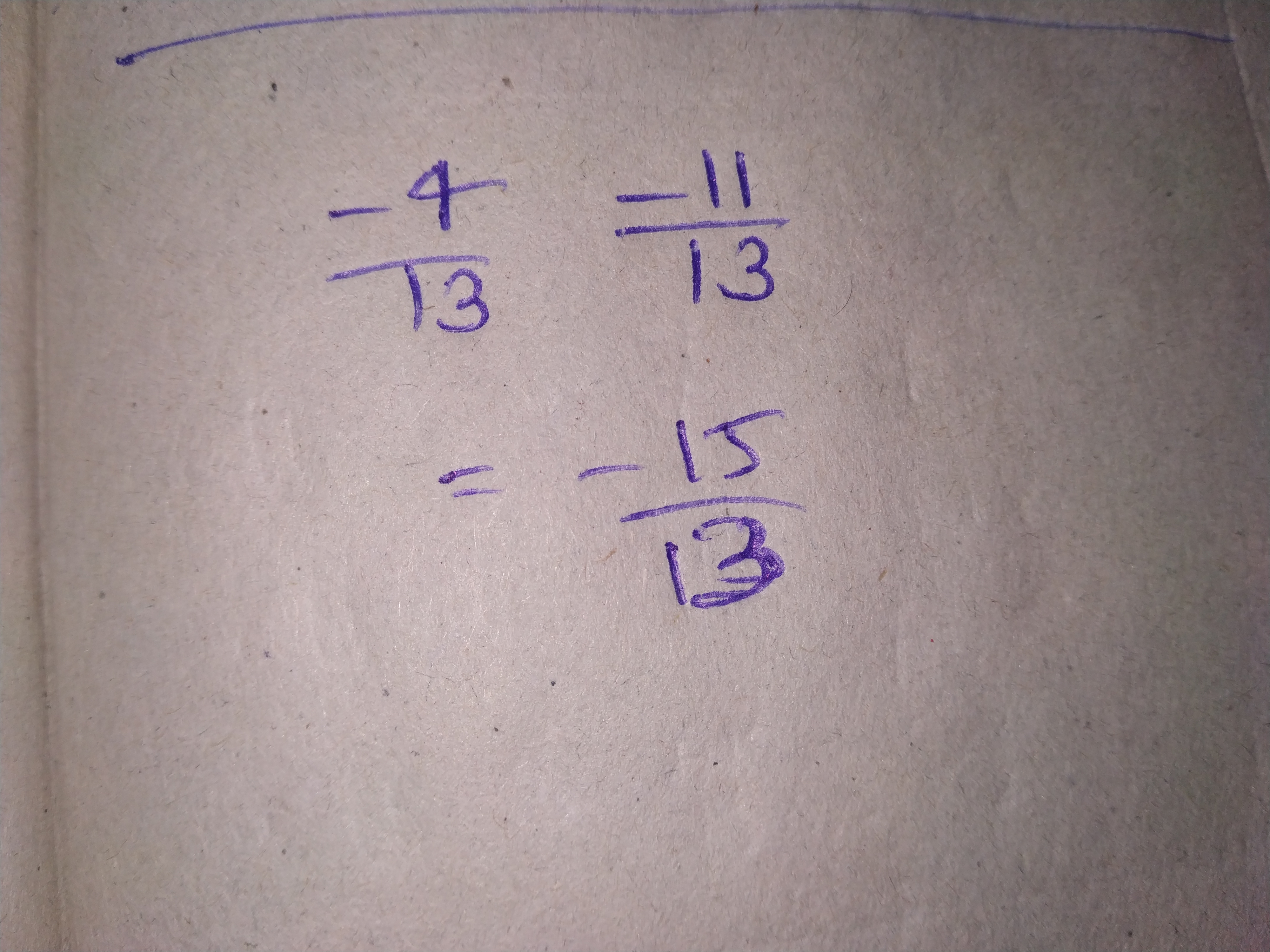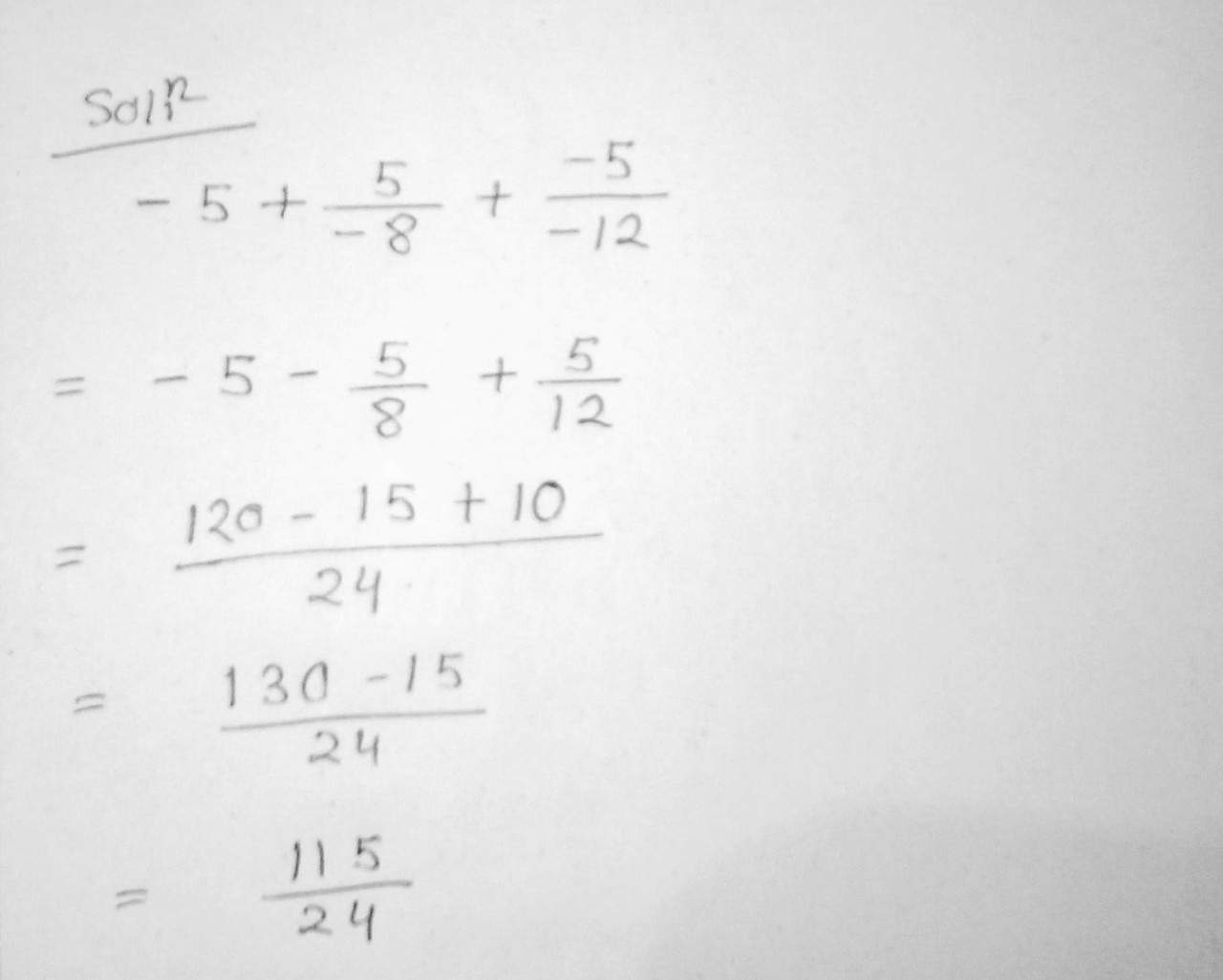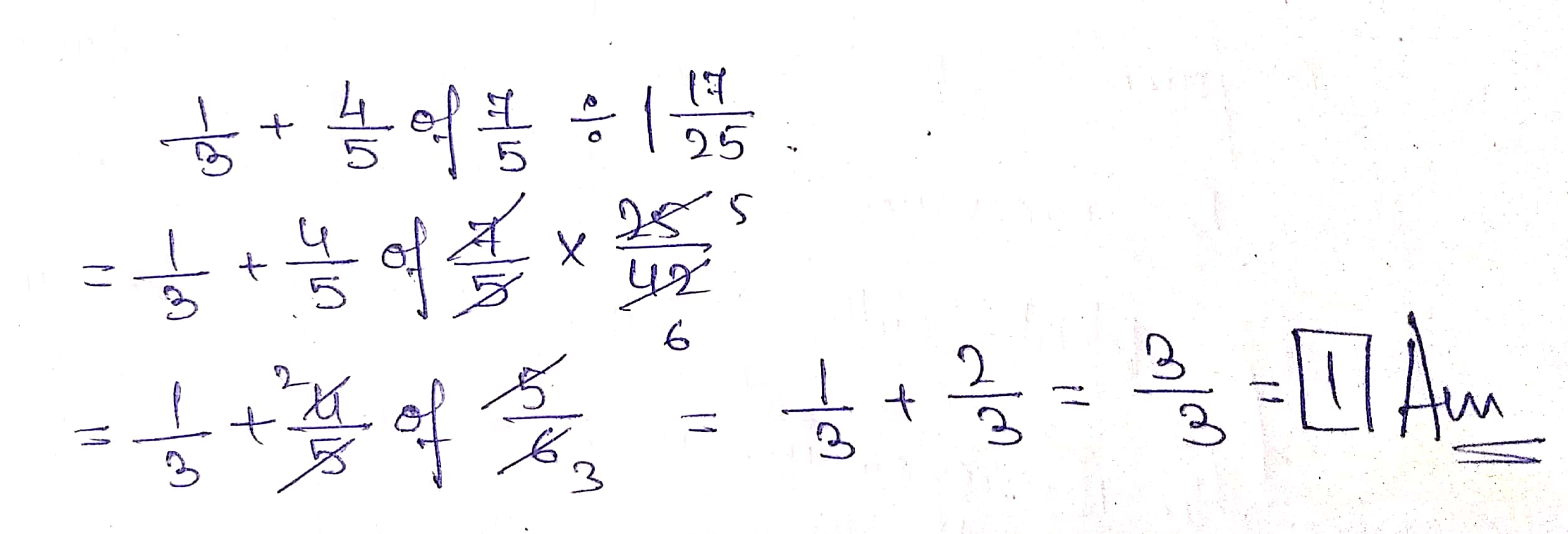Rational Numbers - Class 7 Maths - Extra Questions
Does the following pairs represent the same rational number:
$$\dfrac {-16}{20}$$ and $$\dfrac {20}{-25}$$
Does the following pairs represent the same rational number:
$$\dfrac {-2}{-3}$$ and $$\dfrac {2}{3}$$
Which of the following pairs represent the same rational numbers?
$$\dfrac {8}{-5}$$ and $$\dfrac {-24}{15}$$
Multiply:
$$-\dfrac{-6}{11}$$ by $$\dfrac{-55}{36}.$$
If the answer is $$\dfrac ab$$, then the value of $$(a+b)$$ is
So comparing with $$\dfrac ab$$ mentioned in question, the value of (a+b) becomes 1.
Multiply:
$$-\dfrac{-8}{25}$$ by $$\dfrac{-5}{16}$$
Simplify:
$$\dfrac{-19}{36}\times 16$$
Simplify:
$$\dfrac{-9}{16}\times \dfrac{-64}{-27}$$
Simplify:
$$\dfrac{7}{6}\times \dfrac{-3}{28}$$
Simplify:
$$\dfrac{-13}{9}\times \dfrac{27}{-26}$$
Simplify and express the result as a rational number in standard form, and find the value of $$a$$
$$\dfrac{-50}{7}\times \dfrac{14}{3}=\dfrac{-a}{b}$$
Simplify:
$$\dfrac{-5}{9}\times \dfrac{72}{-5}$$
Simplify:
$$\left(\dfrac{13}{5}\times \dfrac{8}{3}\right)-\left(\dfrac{-5}{2}\times \dfrac{11}{3}\right)$$
Simplify:
$$\left(\dfrac{13}{7}\times \dfrac{11}{26}\right)-\left(\dfrac{-4}{3}\times \dfrac{5}{6}\right)$$
Simplify:
$$\left(\dfrac{1}{2}\times \dfrac{1}{4}\right)+\left(\dfrac{1}{2}\times 6\right)$$
Simplify:
$$\left(-5\times \dfrac{2}{15}\right)-\left(6\times \dfrac{2}{9}\right)$$
Simplify:
$$\left(\dfrac{-4}{3}\times \dfrac{12}{-5}\right)+\left(\dfrac{3}{7}\times \dfrac{21}{15}\right)$$
Simplify:
$$\left(\dfrac{8}{5}\times \dfrac{-3}{2}\right)+\left(\dfrac{-3}{10}\times \dfrac{11}{16}\right)$$
Simplify:
$$\left(\dfrac{25}{8}\times \dfrac{2}{5}\right)-\left(\dfrac{3}{5}\times \dfrac{-10}{9}\right)$$.
If the answer will be $$\dfrac ab$$, then the value of $$a+b$$ will be
So comparing with $$\dfrac ab$$ mentioned in question, the value of (a+b) becomes 35.
Simplify:
$$\left(\dfrac{-9}{4}\times \dfrac{5}{3}\right)+\left(\dfrac{13}{2}\times \dfrac{5}{6}\right)$$
If $$\left(\dfrac{3}{2}\times \dfrac{1}{6}\right)+\left(\dfrac{5}{3}\times \dfrac{7}{2}\right)-\left(\dfrac{13}{8}\times \dfrac{4}{3}\right)=\dfrac{47}{4 \times a}$$, then what is the value of $$a?$$
The product of two rational numbers is $$\dfrac{-8}{9}$$. If one of the numbers is $$\dfrac{-4}{15}$$ then find the other.
Fill in the blank:
The product of a rational number and its reciprocal is _____.1
Fill in the blank:
The number $$0$$ is ____ the reciprocal of any number.
Fill in the blank:
The reciprocal of a negative rational number is _____.
Fill in the blank:
Reciprocal of $$\dfrac{1}{a}\ ,\ a\neq 0$$ is .........
Fill in the blank:
$$\dfrac{-4}{5}\times \left(\dfrac{5}{7}+\dfrac{-8}{9}\right)=\left(\dfrac{-4}{5}\times ........\right)+\dfrac{-4}{5}\times \dfrac{-8}{9}$$
Fill in the blank:
Zero has _____ reciprocal.
Divide:
$$1$$ by $$\dfrac{1}{2}$$
Fill in the blank:
The reciprocal of a positive rational number is _____.
Simplify the following:
$$\sqrt{24}/8 + \sqrt{54}/9$$
Compare :
$$ -1 \dfrac{1}{2} $$ and $$0$$
Compare :
$$ \dfrac{-7}{2} $$ and $$ \dfrac{5}{2} $$
Compare :
$$ -3 $$ and $$ 2\dfrac{3}{4} $$
Compare :
$$ \dfrac{1}{4} $$ and $$0$$
Compare :
$$0$$ and $$ \dfrac{3}{4} $$
Write the following rational numbers in ascending order:
$$\cfrac{1}{3}$$, $$\cfrac{-2}{9}$$, $$\cfrac{-4}{3}$$
Which of the two rational numbers in each of the following pairs of rational numbers is greater?
$$\dfrac{-4}{11}, \dfrac{3}{11}$$
Which of the two rational numbers in each of the following pairs of rational numbers is greater?
$$\dfrac{-3}{8}, 0$$
Which of the two rational numbers in each of the following pairs of rational numbers is smaller?
$$\dfrac{-4}{3}, \dfrac{8}{-7}$$
Which of the two rational numbers in each of the following pairs of rational numbers is smaller?
$$\dfrac{16}{-5}, 3$$
Which of the two rational numbers in each of the following pairs of rational numbers is smaller?
$$\dfrac{-12}{5}, -3$$
Which of the two rational numbers in each of the following pairs of rational numbers is smaller?
$$\dfrac{-6}{-13}, \dfrac{7}{13}$$
Which of the two rational numbers in each of the following pairs of rational numbers is greater?
$$\dfrac{5}{-8}, \dfrac{-7}{12}$$
Add the following rational numbers:
$$\dfrac{-8}{11}$$ and $$\dfrac{-4}{11}$$
Add the following rational numbers:
$$\dfrac{-5}{7}$$ and $$\dfrac{3}{7}$$
Add the following rational numbers:
$$\dfrac{6}{13}$$ and $$\dfrac{-9}{13}$$
Add the following rational numbers:
$$\dfrac{-7}{27}$$ and $$\dfrac{11}{18}$$
Subtract the first rational number from the second in each of the following:
$$\dfrac{3}{8}, \dfrac{5}{8}$$
Fill in the blanks:
$$\dfrac {-16}{7} + ... = ... + \dfrac {-16}{7} = \dfrac {-16}{7}$$.
Which of the two rational numbers is greater in each of the following pairs?
$$\cfrac79$$ or $$\cfrac{-5}9$$
Simplify:
$$\dfrac{6}{5}\times\dfrac{3}{7}-\dfrac{1}{5}\times\dfrac{3}{7}$$
Solve
$$\dfrac{5}{13}-\dfrac{-8}{26}$$
Multiply:
$$ -24 $$ and $$ \dfrac{5}{16} $$
Fill in the following blanks:
The number _______ and _____ are their own reciprocals.
Simplify:
$$1+\dfrac{-4}{5}$$
Simplify:
$$0+\dfrac{-3}{5}$$
Simplify:
$$\dfrac{-16}{21}\times \dfrac{14}{5}$$
Multiply:
$$-\dfrac{8}{-9}$$ by $$\dfrac{-7}{-16}$$
Multiply:
$$-\dfrac{6}{7}$$ by $$\dfrac{-49}{36}$$
Multiply:
$$-\dfrac{-8}{9}$$ by $$\dfrac{3}{64}$$
solve
$$2\frac{1}{3} + 1\frac{1}{4} + 2\frac{5}{6} + 3\frac{7}{{12}}$$
Find the rational number that should be subtracted from $$\dfrac{-5}{7}$$ to get $$-1$$?
Subtract :
$$ 0 $$ from $$ \dfrac{-3}{8} $$
Which of the two rational numbers in each of the following pairs of rational numbers is greater?
$$\dfrac{5}{2}, 0$$
Which of the two rational numbers in each of the following pairs of rational numbers is greater?
$$\dfrac{5}{9}, \dfrac{-3}{-8}$$
Which of the two rational numbers in each of the following pairs of rational numbers is greater?
$$\dfrac{-5}{8}, \dfrac{3}{-4}$$
Which of the two rational numbers in each of the following pairs of rational numbers is greater?
$$\dfrac{-7}{12}, \dfrac{5}{-12}$$
Which of the two rational numbers in each of the following pairs of rational numbers is greater?
$$\dfrac{4}{-9}, \dfrac{-3}{-7}$$
Fill in the blanks:
$$-9 + \dfrac {-21}{8} = (...) + (-9)$$.
Give four rational numbers equivalent to $$\dfrac {4}{9}$$
Arrange $$\displaystyle \frac{5}{8}, \frac{3}{16}, -\frac{1}{4}$$ and $$\displaystyle \frac{17}{32}$$ in descending order of their magnitudes.Identify the largest rational number.
Multiply $$\dfrac{6}{13}$$ by the reciprocal of $$\dfrac{-7}{16}$$.
Does the following pair represents the same rational number:
$$\dfrac {-7}{21}$$ and $$\dfrac {3}{9}$$
The sum of two rational numbers is $$\dfrac{-4}{5}$$.If one of them is $$\dfrac{-11}{20}$$, find the other
Rewrite the following rational numbers in the simplest form:
$$\cfrac{-8}{6}$$
Rewrite the following rational numbers in the simplest form:
$$\cfrac{-44}{72}$$
Rewrite the following rational number in the simplest form:
$$\cfrac{25}{45}$$
Simplify:
$$\dfrac{-13}{8}+\dfrac{5}{36}$$
Add the following rational numbers:
$$\dfrac{6}{13}$$ and $$\dfrac{-9}{13}$$.
Simplify:
$$\dfrac{-16}{9}+\dfrac{-5}{12}=\dfrac{-39.5 \times a}{36}$$
What is the value of $$'a'?$$
Add the following rational numbers:
$$\dfrac{5}{-9}$$ and $$\dfrac{7}{3}$$
Simplify:
$$\dfrac{7}{9}+\dfrac{3}{-4}$$
Add the following rational numbers:
$$\dfrac {7}{-18}$$ and $$\dfrac {8}{27}$$
Rewrite the following rational numbers in the simplest form:
$$\cfrac{-8}{10}$$
Simplify:
$$\dfrac{1}{-12}+\dfrac{2}{15}$$
Add the following rational numbers:
$$\dfrac{3}{4}$$ and $$\dfrac{-5}{8}$$
Multiply:
$$-\dfrac{-5}{17}$$ by $$\dfrac{51}{-60}$$
Multiply:
$$\dfrac{-2}{9}$$ by $$\dfrac{5}{11}$$
Multiply:
$$\dfrac{-3}{17}$$ by $$\dfrac{-5}{-4}$$
Multiply:
$$\dfrac{7}{9}$$ by $$\dfrac{36}{-11}$$
Multiply:
$$\dfrac{5}{7}$$ by $$\dfrac{-3}{4}$$
Multiply:
$$\dfrac{-11}{13}$$ by $$\dfrac{-21}{7}$$
Multiply:
$$-\dfrac{3}{5}$$ by $$-\dfrac{4}{7}$$
Multiply:
$$-\dfrac{15}{11}$$ by $$7$$
By what number should we multiply $$\dfrac{-1}{6}$$ so that the product may be $$\dfrac{-23}{9}$$ ?
Add the following rational numbers:
$$0$$ and $$\dfrac {-2}{5}$$.
Add the following rational numbers:
$$\dfrac {-7}{3}$$ and $$\dfrac {1}{3}$$.
Add the following rational numbers:
$$\dfrac {5}{6}$$ and $$\dfrac {-1}{6}$$.
Add the following rational numbers:
$$\dfrac {-11}{8}$$ and $$\dfrac {5}{8}$$.
Add the following rational numbers:
$$\dfrac {-6}{11}$$ and $$\dfrac {-4}{11}$$.
Add the following rational numbers:
$$\dfrac {-2}{5}$$ and $$\dfrac {4}{5}$$.
Write $$ \dfrac{5}{6} $$ as a fraction with numerator $$ 60 $$.
A reciprocal of a fraction is obtained by
inverting it upside down.
Fill in the boxes with the correct symbol 0 , > , < or =.
$$\dfrac{3}{7} \square \dfrac{-5}{6}$$
1 is the only number which is its own reciprocal.
Write the following number in the form $$\dfrac{p}{q}$$, where p and q are integers.
Reciprocal of $$1$$
Write the following as rational number in their standard forms:
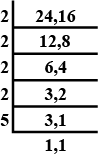
$$240÷(-840)$$
Given that $$\dfrac{p}{q}$$ and $$\dfrac{r}{s}$$ are two rational numbers with different denominators and both of them are in standard form. To compare these rational numbers we say that:
$$\dfrac{\square}{\square}<\dfrac{\square}{\square},$$if $$p\times s<r\times q$$
Which is greater in the following?
$$-3\dfrac{5}{7},3\dfrac{1}{9}$$
Write the following as a rational number in their standard forms:
$$115÷207$$
Find the reciprocal of the following:
$$\dfrac{3}{13}\div \dfrac{-4}{64}$$
Taking $$x=\dfrac{-4}{9},y=\dfrac{5}{12}$$ and $$z=\dfrac{7}{18},$$ find:
the sum of reciprocals of $$x$$ and $$y $$.
Find the value of the following:
$$4\dfrac {5}{8} \div (-4/9)$$.
Taking
$$x=\dfrac{-4}{9},y=\dfrac{5}{12}$$ and $$z=\dfrac{7}{18},$$ find:
$$(xy)\times z$$
Taking
$$x=\dfrac{-4}{9},y=\dfrac{5}{12}$$ and $$z=\dfrac{7}{18},$$ find:
$$x-(y+z)$$
Taking
$$x=\dfrac{-4}{9},y=\dfrac{5}{12}$$ and $$z=\dfrac{7}{18},$$ find:
the reciprocal of $$x+y.$$
What should be divided by $$\dfrac{1}{2}$$ to obtain the greatest negative integer?
Taking
$$x=\dfrac{-4}{9},y=\dfrac{5}{12}$$ and $$z=\dfrac{7}{18},$$ find:
$$x÷(y÷z)$$
Taking
$$x=\dfrac{-4}{9},y=\dfrac{5}{12}$$ and $$z=\dfrac{7}{18},$$ find:
$$x+(y+z)$$
Find.
$$\dfrac{1}{3} \times \dfrac{-5}{7} \times \dfrac{-21}{10}$$
Insert $$3$$ equivalent rational numbers between
$$0$$ and $$-10$$
Fill in the blanks to make the statement true:
The reciprocal of $$\dfrac{-5}{7}$$ is .............
'a' and 'b' are two different numbers taken from the numbers 1-What is the largest value that $$\dfrac{a-b}{a+b}$$ can have? What is the largest value that $$\left(\dfrac{a+b}{a-b}\right)$$ can have?
Simplify :
$$\dfrac {2\sqrt {3}}{3} - \dfrac {\sqrt {3}}{6}$$.
A body floats $$\dfrac{2}{9}$$ of its volume above the surface.What is the ratio of the body-submerged volume to its exposed volume? Re-write it as a rational number.
Subtract:
$$-4/9$$ and $$3\dfrac {5}{8}$$.
Two rational numbers are
called equivalent if they have ________ value
Using appropriate properties of addition, find the following:
$$3/7 + 4/9 + (-5/21) + (2/3)$$.
Using appropriate properties of addition, find the following:
$$4/5 + 11/7 + (-7/5) + (-2/7)$$.
Simplify:
$$-4/9 + 2\dfrac {12}{13}$$.
Fill in the blanks:
$$(-4/9) + (2/7)$$ is a ______ number.
Fill in the following blanks:
$$2/3\times -4/5$$ is a ______ number.
Verify the following and name the property also:
$$3/5\times (-4/7 \times -8/9) = (3/5 \times - 4/7) \times -8/9$$.
Multiply and express the result in the lowest form:
$$ - \dfrac{6}{7} \times \dfrac{{14}}{{30}}$$
Subtract:
$$-3\dfrac {1}{5}$$ from $$-4\dfrac {7}{9}$$.
Sum of two rational numbers is $$3/5$$. If one of them is $$-2/7$$, find the other.
Fill in the following blanks:
$$16/23 \times$$ _____ $$= 0$$.
Multiply and express the result in the lowest form:
$$25/-9\times -3/10$$.
What rational number should be subtracted from $$-4\dfrac {3}{5}$$ to get $$-3\dfrac {1}{2}$$?
What rational number should be added to $$-5/11$$ to get $$-7/8$$.
Multiply and express the result in the lowest form:
$$6\dfrac {2}{3}\times 1\dfrac {2}{7}$$.
Find the value of the following:
$$-8/9\div -3/5$$.
The product of two rational number is $$-11/12$$. If one of them is $$2\dfrac {4}{9}$$ find the other.
Fill in the following blanks:
The product of a non-zero rational number and its reciprocal is ______.
Find the value of the following:
$$-3/7\div 4$$.
By what rational number should $$-3$$ is divided to get $$-9/13$$?
By what rational number should $$-7/12$$ be multiplied to get the product as $$5/14$$?
Compare :
$$ \dfrac{-3}{8} $$ and $$ \dfrac{2}{5} $$
Arrange $$\displaystyle -\frac{5}{9}, \frac{7}{12}, -\frac{2}{3}$$ and $$\displaystyle \frac{11}{18}$$ in ascending order of their magnitudes. Identify the smallest
Write down ten positive rational numbers such that the sum of the numerator and the denominator of each is $$11$$. Write them in decreasing order
Write down ten positive rational numbers such that numerator - denominator for each of them is $$-2$$. Write them in increasing order
Write the following rational numbers in ascending order:
$$\dfrac {3}{4}, \dfrac {7}{12}, \dfrac {15}{11}, \dfrac {22}{19}, \dfrac {101}{100}, \dfrac {-4}{5}, \dfrac {-102}{81}, \dfrac {-13}{7}$$
Which of the rational number is greater in the given pair?
(i) $$\frac{-4}{3}$$ or $$\frac{-8}{7}$$
(ii)$$\frac{7}{-9}$$ or $$\frac{-5}{8}$$
(iii)$$\frac{-1}{3}$$ or $$\frac{4}{-5}$$
(iv)$$\frac{9}{-13}$$ or $$\frac{7}{-12}$$
(v)$$\frac{4}{-5}$$ or $$\frac{-7}{10}$$
(vi)$$\frac{-12}{5}$$ or $$-3$$
Give four rational numbers equivalent to:
i) $$\dfrac{-2}{7}$$ ii) $$\dfrac{5}{-3}$$
Which of the following pairs represent the same rational number?
$$\dfrac {-7}{21}$$ and $$\dfrac {3}{9}$$
Are $$\dfrac{-1}{2}$$ and $$\dfrac{-3}{6}$$ represented by the same point on the number line?
Write $$5$$ equivalent rational numbers to:-$$(i)\ \ \dfrac{5}{2}$$
$$(ii)\ -\dfrac{7}{9}$$
$$(iii)-\dfrac{3}{7}$$
$$(ii)\ -\dfrac{7}{9}$$
$$(iii)-\dfrac{3}{7}$$
Which of the following pairs represent the same rational number?
$$\dfrac {-2}{-3}$$ and $$\dfrac {2}{3}$$
Which of the following pairs represent the same rational number?
$$\dfrac {-16}{20}$$ and $$\dfrac {20}{-25}$$
Give four rational numbers equivalent to:
$$\dfrac {-2}{7}$$
Solve $$\dfrac{-3}{5}+\dfrac{-12}{20}$$
The product of two integers is $$105$$.If one of them is $$-7$$, then find the other.
What should be subtracted from thrice the rational number $$\dfrac{-8}{3}$$ to get $$\dfrac{5}{2}$$.
The product of two rational numbers is $$\dfrac{-28}{75}$$.If one of the numbers is $$\dfrac{14}{25}$$.Find the other.
Give four rational numbers equivalent to:
$$\dfrac {5}{-3}$$
Find the sum of the rational numbers $$\dfrac{-4}{9},\,\dfrac{15}{12}$$ and $$\dfrac{-7}{18}$$
Out of the rational numbers $$\cfrac { -5 }{ 11 } ,\cfrac { -5 }{ 12 }, \cfrac { -5 }{ 17 } $$ which is smallest.
Write the following rational numbers in ascending order:
$$\cfrac{-3}{7}$$, $$\cfrac{-3}{2}$$, $$\cfrac{-3}{4}$$
Check if the following pair represent the same rational number:
$$\cfrac{1}{3}$$ and $$\cfrac{-3}{9}$$
Add the following rational numbers:
$$\dfrac{-7}{27}$$ and $$\dfrac{11}{18}$$
Add the rational numbers
$$\dfrac {-5}{16}$$ and $$\dfrac {7}{24}$$
Add the following rational numbers:
$$\dfrac{31}{-4}$$ and $$\dfrac{-5}{8}$$
Simplify:
$$\dfrac{5}{26}+\dfrac{11}{-39}$$
Add the following rational numbers:
$$\dfrac {5}{8}$$ and $$\dfrac {-7}{12}$$.
$$\dfrac{-8}{11}$$ + $$\dfrac{-4}{11}=\dfrac{p}{11}$$
then
$$p=?$$
Simplify:
$$\dfrac{-8}{19}+\dfrac{-4}{57}$$
Add the following rational numbers:
$$\dfrac{-15}{4}$$ and $$\dfrac{7}{4}$$
Multiply:
$$\dfrac{7}{11}$$ by $$\dfrac{5}{4}$$.
If the answer is $$\dfrac ab$$, then the value of $$(a+b)$$ will be:-
So comparing with $$\dfrac ab$$ mentioned in question, the value of (a+b) becomes 79.
What should be subtracted from $$\left(\dfrac{3}{4}-\dfrac{2}{3}\right)$$ to get $$\dfrac{-1}{6}$$? Hence, find the sum of numerator and denominator.
Find the value of $$p+q$$
$$\dfrac{-11}{9}\times \dfrac{-81}{-88}=\,\dfrac{-p}{q}$$
where $$\dfrac{-p}{q}$$ is in lowest form
Select those rational numbers which can be written as a rational number with numerator $$6$$:
$$\displaystyle \frac{1}{22}, \frac{2}{3}, \frac{3}{4}, \frac{4}{-5}, \frac{5}{6}, \frac{-6}{7}, \frac{-7}{8}$$
Verify commutativity of addition of rational number for each of the following pairs of rational numbers:
$$4$$ and $$\dfrac{-3}{5}$$
Write down the rational number whose numerator is $$(-3) \times 4$$, and whose denominator is $$(34-23) \times (7-4)$$.
What number should be subtracted from $$\dfrac{-5}{3}$$ to get $$\dfrac{5}{6}$$ ?
Number should be subtracted from $$\dfrac{3}{7}$$ to get $$\dfrac{5}{4}$$ is $$\dfrac{-23}{x}$$ .Find 'x'.
Express $$\dfrac{3}{5}$$ as a rational number with numerator:
$$6$$
Express $$\dfrac{5}{7}$$ as a rational number with denominator:
$$-14$$
Express $$\dfrac{5}{7}$$ as a rational number with denominator:
$$-84$$
Express $$\dfrac{3}{4}$$ as a rational number with denominator:
$$44$$
Express $$\dfrac{3}{5}$$ as a rational number with numerator:
$$21$$
Express $$\dfrac{3}{4}$$ as a rational number with denominator:
$$20$$
Express $$\dfrac{3}{4}$$ as a rational number with denominator:
$$36$$
Express $$\dfrac{5}{7}$$ as a rational number with denominator:
$$70$$
Express $$\dfrac{2}{5}$$ as a rational number with numerator :
$$154$$
Express $$\dfrac{5}{7}$$ as a rational number with denominator:
$$-28$$
Express $$\dfrac{3}{5}$$ as a rational number with numerator:
$$-15$$
Fill in the blanks to make the statement true:
Two rational numbers are said to be equal, if they have the same _____ form.
Fill in the blanks so as to make the statement true:
Two rational numbers with different numerators are equal, if their numerators are in the same ______ as their denominators.
Add the following rational numbers:
$$\dfrac {3}{4}$$ and $$\dfrac {-3}{5}$$.
Add the following rational numbers:
$$\dfrac{-15}{4}$$ and $$\dfrac{7}{4}$$
Add the following rational numbers:
$$-3$$ and $$\dfrac{3}{5}$$
Add the following rational numbers:
$$\dfrac{31}{-4}$$ and $$\dfrac{-5}{8}$$
Find the value and express as a rational number in standard form:
$$\dfrac{2}{5} \div \dfrac{26}{15}$$
Subtract the first rational number from the second in each of the following:
$$\dfrac{-2}{11}, \dfrac{-9}{11}$$
State whether the given statement is true or false.
(i) the sum of two rationals is always rational.
(ii) the product of two rational is always rational.
(iii) The sum of two irrational is always an irrational.
(iv) the product of two irrational is always an irrational.
(v) the sum of a rational and an irrational is irrational.
(vi) The product of a rational and an irrational is irrational.
Subtract the first rational number from the second in each of the following:
$$\dfrac{11}{13}, \dfrac{-4}{13}$$
Subtract the first rational number from the second in each of the following:
$$\dfrac{-7}{9}, \dfrac{4}{9}$$
The product of two rational numbers is $$\dfrac{-8}{9}$$. If one of the numbers is $$\dfrac{-4}{15}$$, find the other.
Express $$\dfrac {-3}{5}$$ as a rational number whose denominators are $$35$$.
Express $$\dfrac {-48}{60}$$ as a rational number whose denominator is $$5$$.
Express $$\dfrac {-42}{98}$$ as a rational number whose denominator is $$7$$.
Express $$\dfrac {-3}{5}$$ as a rational number whose denominators is $$20$$.
Express $$\dfrac {-3}{5}$$ as a rational number whose denominator is $$-40$$.
Express $$\dfrac {-3}{5}$$ as a rational number whose denominator is $$-30$$.
Fill in the blanks:
$$\left (\dfrac {-8}{13} + \dfrac {3}{7}\right ) + \left (\dfrac {-13}{4}\right ) = (....) + \left [\dfrac {3}{7} + \left (\dfrac {-13}{4}\right )\right ]$$.
Add the following rational numbers:
$$\dfrac {-8}{9}$$ and $$\dfrac {11}{6}$$.
Add the following rational numbers:
$$\dfrac {1}{-12}$$ and $$\dfrac {2}{-15}$$.
Add the following rational numbers:
$$2$$ and $$\dfrac {-5}{4}$$.
Add the following rational numbers:
$$\dfrac {-17}{15}$$ and $$\dfrac {-1}{15}$$.
Add the following rational numbers:
$$-1$$ and $$\dfrac {3}{4}$$.
Verify the following:
$$3 + \dfrac {-7}{12} = \dfrac {-7}{12} + 3$$.
Verify the following:
$$\left (\dfrac {3}{4} + \dfrac {-2}{5}\right ) + \dfrac {-7}{10} = \dfrac {3}{4} + \left (\dfrac {-2}{5} + \dfrac {-7}{10}\right )$$.
Verify the following:
$$\dfrac {-5}{8} + \dfrac {-9}{13} = \dfrac {-9}{13} + \dfrac {-5}{8}$$.
Verify the following:
$$\dfrac {-12}{5} + \dfrac {2}{7} = \dfrac {2}{7} + \dfrac {-12}{5}$$.
Fill in the blanks:
$$\left (\dfrac {-13}{17}\right ) + \left (\dfrac {-12}{5}\right ) = \left (\dfrac {-12}{5}\right ) + (.....)$$.
Verify the following:
$$\left (\dfrac {-7}{11} + \dfrac {2}{-5}\right ) + \dfrac {-13}{22} = \dfrac {-7}{11} + \left (\dfrac {2}{-5} + \dfrac {-13}{22}\right )$$.
Verify the following:
$$-1 + \left (\dfrac {-2}{3} + \dfrac {-3}{4}\right ) = \left (-1 + \dfrac {-2}{3}\right ) + \dfrac {-3}{4}$$.
Verify the following:
$$\dfrac {2}{-7} + \dfrac {12}{-35} = \dfrac {12}{-35} + \dfrac {2}{-7}$$.
The sum of two rational numbers is $$\dfrac {-1}{2}$$. If one the number is $$\dfrac {5}{6}$$, find the other.
The sum of two rational numbers is $$-2$$. If one of the numbers is $$\dfrac {-14}{5}$$, find the other.
Fill in the blanks:
$$\dfrac {19}{-5} + \left (\dfrac {-3}{11} + \dfrac {-7}{8}\right ) = \left \{\dfrac {19}{-5} + (....)\right \} + \dfrac {-7}{8}$$.
Fill in the blanks:
$$-12 + \left (\dfrac {7}{12} + \dfrac {-9}{11}\right ) = \left (12 + \dfrac {7}{12}\right ) + (....)$$.
Which of the two rational number is greater in each of the following pairs?
$$\cfrac7{-9}$$ or $$\cfrac{-5}8$$
Which of the two rational numbers is greater in each of the following pairs?
$$\cfrac{-15}4$$ or $$\cfrac{-17}4$$
Which of the two rational number is greater in each of the following pairs?
$$\cfrac{9}{-13}$$ or $$\cfrac{7}{-12}$$
Which of the two rational numbers is greater in each of the following pairs?
$$\cfrac{-6}{11}$$ or $$\cfrac5{11}$$
Which of the two rational numbers is greater in each of the following pairs?
$$\cfrac 58$$ or $$\cfrac38$$
Which of the two rational numbers is greater in the following pair?
$$\cfrac{4}{-3}$$ or $$\cfrac{-8}{7}$$
Which of the two rational number is greater in each of the following pairs?
$$\cfrac{4}{-5}$$ or $$\cfrac{-7}{8}$$
Fill in the blanks with the correct symbol out of $$> , <$$ and $$=$$
$$\cfrac{-3}{7} ....\cfrac{6}{-13}$$
Which of the two rational number is greater in each of the following pairs?
$$\cfrac59$$ or $$\cfrac{-3}8$$
Fill in the blanks with the correct symbol out of $$> , <$$ and $$=$$
$$-2...\cfrac{13}5$$
Fill in the blanks with the correct symbol out of $$> , <$$ and $$=$$
$$\cfrac{5}{-13}$$ _____ $$\cfrac{-35}{91}$$
Add the following rational numbers:
$$\cfrac{12}7$$ and $$\cfrac37$$
Fill in the blanks with the correct symbol out of $$> , <$$ and $$=$$
$$0...\cfrac{-3}{-15}$$
Fill in the blanks with the correct symbol out of $$> , <$$ and $$=$$
$$\cfrac{-8}{9}...\cfrac{-9}{10}$$
Fill in the blanks with the correct symbol out of $$> , <$$ and $$=$$ :-
$$\cfrac{-2}{3}.... \cfrac{5}{-8}$$
Add the following rational numbers:
$$\cfrac{-2}5$$ and $$\cfrac15$$
Add the following rational numbers:
$$\cfrac{-3}{7}\ and \ \cfrac{5}{-7}$$
Add the following rational numbers:
$$\cfrac{-2}9$$ and $$\cfrac{-5}9$$
Add the following rational numbers:
$$-4$$ and $$\cfrac12$$
Add the following rational numbers:
$$\cfrac{-5}{11}$$ and $$\cfrac{7}{-11}$$
Add the following rational numbers:
$$\cfrac{9}{-13}\ and \ \cfrac{-11}{-13}$$
Add the following rational numbers:
$$\cfrac3{-8}$$ and $$\cfrac18$$
Express $$\cfrac58$$ as a rational number with numerator $$15$$
Add the following rational numbers:
$$\cfrac{-2}5$$ and $$\cfrac 34$$
Add the following rational numbers:
$$\cfrac{-5}{9}\ and \ \cfrac{2}{3}$$
Add the following rational numbers:
$$\cfrac{-17}9$$ and $$\cfrac{-11}9$$
Write each of the following rational numbers with positive denominators: $$\dfrac{5}{-8}, \dfrac{15}{-28}, \dfrac{-17}{-13}$$
Subtract:
$$\cfrac{-8}{9}$$ from $$\cfrac{-3}{5}$$
Add the following rational numbers:
$$\cfrac{27}{-4}$$ and $$\cfrac{-15}8$$
Subtract:
$$\cfrac{-9}{7}$$ from $$-1$$
Add the following rational numbers:
$$\cfrac{-7}{27}$$ and $$\cfrac5{18}$$
Add the following rational numbers:
$$\cfrac{-9}{24}$$ and $$\cfrac{-1}{18}$$
Add the following rational numbers:
$$\cfrac{-5}{36}$$ and $$\cfrac{-7}{12}$$
Subtract:
$$\cfrac{-18}{11}$$ from $$1$$
Subtract:
$$\cfrac{-5}{6}$$ from $$\cfrac13$$
Subtract:
$$\cfrac{3}{4}$$ from $$\cfrac{1}{3}$$
Write the next three rational numbers to complete the pattern:
$$\dfrac{4}{-5},\dfrac{8}{-10},\dfrac{12}{-15},\dfrac{16}{-20},$$ , ____ , ____ , ____.
Add the following rational numbers:
$$\cfrac1{-9}$$ and $$\cfrac4{-27}$$
Subtract:
$$\cfrac{5}{1}$$ from $$\cfrac{-3}{5}$$
Evaluate:
$$\cfrac{3}{4}$$ $$-\left(\cfrac{4}{5}\right)$$
Evaluate:
$$\cfrac{7}{24}$$ $$-\left(\cfrac{19}{36}\right)$$
Subtract:
$$\cfrac{5}{9}$$ from $$\cfrac{-2}{3}$$
Subtract:
$$7$$ from $$\cfrac{-4}{7}$$
Evaluate:
$$\cfrac{4}{9}$$ $$-\left(\cfrac{2}{-3}\right)$$
Subtract:
$$\cfrac{-32}{13}$$ from $$\cfrac{-6}{5}$$
Find the sum of
$$\dfrac{8}{13}$$ and $$\dfrac{3}{11}$$
Evaluate:
$$\cfrac{14}{15}$$ $$-\left(\cfrac{13}{20}\right)$$
Evaluate:
$$-3-\left(\cfrac{-4}{7}\right)$$
Subtract:
$$\cfrac{-13}9$$ from $$0$$
Evaluate:
$$\cfrac{-5}{-8}$$ $$-\left(\cfrac{-3}{4}\right)$$
Evaluate the following.
$$ | 5 - 13 | $$
Subtract the sum of $$\cfrac{-36}{11}$$ and $$\cfrac{49}{22}$$ from the sum of $$\cfrac{33}{8}$$ and $$\cfrac{-19}{4}$$
The sum of two rational numbers is $$(-3)$$ . If one of them is $$(-15/7)$$, find the other.
The sum of two rational number is $$(-3/8)$$. If one of them is $$(3/16)$$, find the other.
Evaluate:
$$\cfrac{7}{11}$$ $$-\left(\cfrac{-4}{-11}\right)$$
Evaluate the following.
$$ |-8| + |-6| $$
Evaluate the following.
$$ | -11 | + | 9 | $$
Evaluate:
$$\cfrac{-5}{14}-\left(\cfrac{-2}{7}\right)$$
$$\dfrac{-3}{7}
\div \dfrac{-7}{3}=$$ __________
The sum of two rational number is $$(4/21)$$. If one of them is $$(5/7)$$, find the other.
Evaluate the following.
$$ |-19| - |-13| $$
Evaluate :
$$ |35 - 41| - |7 - (-2)| $$
Evaluate the following.
$$ |7| - |-3| $$
Evaluate :
$$ |-13| - |-15| $$
Fill in the blanks to make the statements true.
$$\dfrac{-2}{9}-\dfrac{7}{9}= $$ ________
Fill in the blanks to make the statements true.
$$\dfrac{-3}{5}+\dfrac{2}{5}=$$ ________.
Fill in the boxes with the correct symbol 0 , > , < or =.
$$\dfrac{5}{8}\square \dfrac{8}{4}$$
Fill in the blanks to make the statements true.
$$\dfrac{-3}{4}\times\left( \dfrac{-2}{3}\right)= $$ ________.
Fill in the blanks to make the statements true.
$$\dfrac{-5}{6}+\dfrac{-1}{6}=$$________.
Fill in the boxes with the correct symbol 0 , > , < or =.
$$\dfrac{7}{-8} \square \dfrac{8}{9}$$
Fill in the boxes with the correct symbol 0 , > , < or =.
$$\dfrac{-9}{7}\square \dfrac{4}{-7}$$
Fill in the boxes with the correct symbol 0 , > , < or =.
$$\dfrac{8}{8}\square \dfrac{2}{2}$$
Fill in the blanks to make the statements true.
$$-\dfrac{1}{2}$$ is ________ than $$\dfrac{1}{5}$$.
Fill in the blanks to make the statements true.
$$\dfrac{-27}{45}$$ and $$\dfrac{-3}{5}$$ represent ________ rational numbers.
Fill in the blanks to make the statements true.
The reciprocal of 1 is ______.
Fill in the blanks to make the statements true.
The reciprocal of ______ does not exist.
Fill in the blanks to make the statements true.
If m is a common divisor of a and b, then $$\dfrac{a}{b}=\dfrac{am}{}$$
Fill in the blanks to make the statements true.
$$\dfrac{-3}{7} ÷ \left(\dfrac{-7}{3}\right)=$$______.
Write the next three rational numbers to complete the pattern:
$$\dfrac{-8}{7},\dfrac{-16}{14},\dfrac{-24}{21},\dfrac{-32}{28},$$ , ____ , ____ , ____.
Which is greater in the following?
$$\dfrac{3}{4},\dfrac{7}{8}$$
Simplify:
$$\dfrac{13}{11}\times \dfrac{-14}{5}+\dfrac{13}{11}\times \dfrac{-7}{5}+\dfrac{-13}{11}\times \dfrac{34}{5} $$
Find the product of:
$$\dfrac{-22}{11}$$ and $$\dfrac{-21}{11}$$
Find the sum of
$$\dfrac{7}{3}$$ and $$\dfrac{-4}{3}$$
Find the product of:
$$\dfrac{-4}{5}$$and $$\dfrac{-5}{12}$$
Solve:
$$\dfrac{29}{4}-\dfrac{30}{7}$$
Given that $$\dfrac{p}{q}$$ and $$\dfrac{r}{s}$$ are two rational numbers with different denominators and both of them are in standard form. To compare these rational numbers we say that:
$$\dfrac{p}{q}=\dfrac{r}{s},$$ if ______ = ______
Taking $$x=\dfrac{-4}{9},y=\dfrac{5}{12}$$ and $$z=\dfrac{7}{18},$$ find:
the rational number which subtracted from y gives z.
Find the reciprocal of the following:
$$\left(\dfrac{1}{2}\times \dfrac{1}{4}\right)+\left(\dfrac{1}{2}\times 6\right)$$
Complete the following table by finding the sums:
| + | $$-\dfrac{1}{9}$$ | $$\dfrac{4}{11}$$ | $$\dfrac{-5}{6}$$ |
| $$\dfrac{2}{3}$$ | |||
| $$-\dfrac{5}{4}$$ | $$-\dfrac{39}{44}$$ | ||
| $$-\dfrac{1}{3}$$ |
Taking $$x=\dfrac{-4}{9},y=\dfrac{5}{12}$$ and $$z=\dfrac{7}{18},$$ find the rational number which when added to x gives y.
Taking
$$x=\dfrac{-4}{9},y=\dfrac{5}{12}$$ and $$z=\dfrac{7}{18},$$ find:
$$(x-y)+z$$
Fill in the blanks to make the statement true:
Between the numbers $$\dfrac{15}{20}$$ and $$\dfrac{34}{40},$$ the greater number is .........
What should be added $$\dfrac{-1}{2}$$ to obtain the nearest natural number?
Divide the sum of $$8/3$$ and $$4/7$$ by the product of $$-3/7$$ and $$14/9$$.
Taking $$ x=\dfrac{-4}{9},y=\dfrac{5} {12}$$ and $$z=\dfrac{7}{18},$$ find:
the rational number which when added to z gives us x.
What should be subtracted from $$\dfrac{-2}{3}$$ to obtain nearest integer?
Fill in the blanks to make the statement true:
$$\dfrac{-5}{7}$$ is ............. than $$-3.$$
Verify $$- (-x) = x$$ for $$x = \dfrac{-7}{9}$$
Simplify-
$$\dfrac{7}{8} + \dfrac{1}{16} - \dfrac{1}{12}$$
A train travels $$\dfrac{1445}{2}$$ km in $$\dfrac{17}{2}$$ hours. Find the speed of the train in km/h.
The product of two rational numbers is $$\dfrac{-14}{27}.$$ If one of the numbers be $$\dfrac{7}{9},$$ find the other.
By what numbers should we multiply $$\dfrac{-15}{20}$$ so that the product may be $$\dfrac{-5}{7}$$ ?
Simplify-
$$\dfrac{32}{5} + \dfrac{23}{11} \times \dfrac{22}{15}$$
Simplify
$$\dfrac{3}{7} \times \dfrac{28}{15} \div \dfrac{14}{5}$$
Verify $$- (-x) = x$$ for $$x = \dfrac{13}{-15}$$
The table shows the portion of some common materials that are recycled.
| Material | Recycled |
| Paper | $$\dfrac{5}{11}$$ |
| Aluminium Cans | $$\dfrac{5}{8}$$ |
| Glass | $$\dfrac{2}{5}$$ |
| Scap | $$\dfrac{3}{4}$$ |
(b) Which items have a recycled amount less than $$\dfrac{1}{2}$$ ?
(c) Is the quantity of aluminium cans recycled more (or less) than half of the quantity of aluminium cans ?
(d) Arrange the rate of recycling the materials from the greatest to the smallest.
Which of the
following pairs represent the same rational number?
(i) $$-\dfrac{7}{21},
\dfrac{3}{9}$$
(ii) $$\dfrac{-16}{20},
\dfrac{20}{-25}$$
(iii) $$\dfrac{-3}{5},
\dfrac{-12}{20}$$
(iv) $$\dfrac{8}{-5},
\dfrac{-24}{15}$$
Which of the
following pairs of rational numbers are equal?
(i) $$\dfrac{-3}{-7}$$
and $$\dfrac{15}{35}$$
(ii) $$\dfrac{-6}{8}$$
and $$\dfrac{10}{-15}$$
(iii) $$\dfrac{6}{-10}$$
and $$\dfrac{-12}{20}$$
Fill the blanks to make the statement true:
The denominator of a rational number is greater than the numerator by $$10$$. If the numerator is increased by $$1$$ and denominator is decreased by $$1$$, then expression for new denominator is _________.
Add the
following pairs of rational numbers
(i) $$\dfrac{3}{11},
\dfrac{-5}{11}$$
(ii) $$\dfrac{4}{9},
\dfrac{5}{-9}$$
(iii) $$\dfrac{5}{-7},
\dfrac{-2}{-7}$$
(iv) $$\dfrac{-2}{5},
\dfrac{3}{4}$$
The sum of two rational
numbers is $$\dfrac{2}{5}$$ if one of them is $$\dfrac{-4}{7}$$, find the other
What
rational number should be added to $$\dfrac{-5}{12}$$ to get $$\dfrac{-7}{8} ?$$
Which of the
two rational numbers is greater in each of the following pairs?
(i) $$\dfrac{-4}{7},
0$$
(ii) $$\dfrac{5}{-9},
\dfrac{3}{7}$$
(iii) $$\dfrac{-9}{-5},
0$$
$$(i v) \dfrac{7}{-5},
\dfrac{-21}{-23}$$
What
rational number should be subtracted from $$\dfrac{-2}{3}$$ to get $$\dfrac{-5}{6}
?$$
Subtract:
(i) $$\dfrac{-6}{13}$$
from $$\dfrac{4}{13}$$
(ii) $$\dfrac{-1}{2}$$
from $$\dfrac{-2}{3}$$
(iii) $$\dfrac{5}{9}$$
from $$\dfrac{-2}{3}$$
Compare :
$$ \dfrac{-7}{8} $$ and $$ \dfrac{5}{-6} $$
Add:
$$ \dfrac{-4}{9} $$ and $$ \dfrac{2}{9} $$
Find:
(i) $$\dfrac{5}{63}-\left(\dfrac{-6}{21}\right)$$
(ii) $$\dfrac{-6}{13}-\left(\dfrac{-7}{15}\right)$$
$$(\text {
in }) 3 \dfrac{1}{8}-\left(-1 \dfrac{5}{6}\right)$$
Find the
sum:
(i) $$\dfrac{27}{-4}+\dfrac{-15}{8}$$
(ii) $$\dfrac{-1}{18}+\dfrac{-3}{8}$$
$$(i i i)-3
\dfrac{1}{6}+2 \dfrac{3}{8}$$
$$(i v)-2 \dfrac{4}{5}+4
\dfrac{3}{10}$$
Find the
product:
(i) $$\dfrac{2}{3}
\times \dfrac{-7}{8}$$
(ii) $$\dfrac{-6}{7}
\times \dfrac{5}{7}$$
(iii) $$\dfrac{-2}{9}
\times(-5)$$
$$(i v) \dfrac{-5}{11}
\times\left(\dfrac{11}{-5}\right)$$
(v) $$\dfrac{8}{35}
\times \dfrac{21}{-32}$$
$$(v i) \dfrac{-105}{128}
\times\left(-1 \dfrac{29}{35}\right)$$
Subtract:
(i) $$\dfrac{-11}{24}$$ from $$\dfrac{-5}{36}$$
(ii) $$\dfrac{-8}{15}$$ from $$-1 \dfrac{2}{5}$$
$$(i i i)-2 \dfrac{2}{9}$$ from $$-3 \dfrac{5}{12}$$
Find the
reciprocal of the following:
(i) $$\dfrac{3}{13}
\div \dfrac{-4}{65}$$
$$(i
i)\left(-5 \times \dfrac{12}{15}\right)-\left(-3 \times \dfrac{2}{9}\right)$$
Find the sum:
(i) $$\dfrac{-2}{3}+\left(\dfrac{5}{-7}\right)$$
$$(i i)-1 \dfrac{1}{12}+\dfrac{-5}{9}$$
$$(i i i) 2 \dfrac{2}{5}+\left(-4 \dfrac{3}{10}\right)$$
The product of two
rational numbers is $$\dfrac{18}{35}$$ If one of them is $$\dfrac{-2}{5}$$,
find the other.
Subtract the sum of $$-\dfrac57$$ and $$-\dfrac83$$ from the sum of $$\dfrac52$$ and $$-\dfrac{11}{12}$$.
If $$p = \dfrac{-3}{2},\ q = \dfrac 45$$ and $$r = \dfrac{-7}{12},$$ then verify that $$(p\div q)\div r\neq p\div (q\div r)$$
Express $$ \dfrac{3}{5} $$ as a rational number with denominator :
$$ -20$$
Express $$ \dfrac{3}{5} $$ as a rational number with denominator :
$$ 25 $$
Express each of the following integers as a rational number with denominator $$7$$ :
$$0$$
Express $$ \dfrac{3}{5} $$ as a rational number with denominator :
$$-35$$
Express each of the following integers as a rational number with denominator $$7$$ :
$$-16$$
Express each of the following integers as a rational number with denominator $$7$$ :
$$-8$$
Express each of the following integers as a rational number with denominator $$7$$ :
$$7$$
Express $$ \dfrac{3}{5} $$ as a rational number with denominator :
$$ 45$$
Express each of the following integers as a rational number with denominator $$7$$ :
$$5$$
Compare :
$$ \dfrac{5}{-9} $$ and $$ \dfrac{-5}{-9} $$
Add:
$$ \dfrac{7}{5} $$ and $$ \dfrac{2}{5} $$
Compare :
$$ \dfrac{-5}{8} $$ and $$ \dfrac{7}{-12} $$
Compare :
$$ \dfrac{3}{5} $$ and $$ \dfrac{5}{7} $$
Compare :
$$ \dfrac{2}{7} $$ and $$ \dfrac{-3}{-8} $$
Add:
$$ \dfrac{-5}{6}$$ and $$ \dfrac{4}{9} $$
Add:
$$ \dfrac{4}{-15} $$ and $$ \dfrac{-7}{-15} $$
Add:
$$ \dfrac{-2}{5} $$ and $$ \dfrac{3}{7} $$
Add:
$$ \dfrac{-7}{26} $$ and $$ \dfrac{7}{-26} $$
Add:
$$ \dfrac{-7}{25} $$ and $$ \dfrac{9}{-25} $$
Add:
$$ \dfrac{1}{-18} $$ and $$ \dfrac{5}{-27} $$
Add:
$$ \dfrac{-7}{24} $$ and $$ \dfrac{-5}{48} $$
Add:
$$ \dfrac{5}{-12} $$ and $$ \dfrac{1}{12} $$
Add :
$$ \dfrac{-5}{9} $$ and $$ \dfrac{7}{18} $$
Add :
$$ -3$$ and $$ \dfrac{2}{3} $$
Evaluate :
$$ -2 + \dfrac{2}{5} + \dfrac{-2}{15} $$
Evaluate :
$$ \dfrac{-7}{6} + \dfrac{4}{-15} + \dfrac{-4}{-30} $$
Evaluate :
$$ \dfrac{5}{-24} + \dfrac{-1}{8} + \dfrac{3}{16} $$
Add :
$$ \dfrac{13}{-16} $$ and $$ \dfrac{-11}{24} $$
Evaluate :
$$ \dfrac{-2}{5} + \dfrac{3}{5} + \dfrac{-1}{5} $$
Evaluate :
$$ \dfrac{-11}{12} + \dfrac{5}{16} + \dfrac{-3}{8} $$
Add:
$$ \dfrac{-9}{-16} $$ and $$ \dfrac{-11}{8} $$
Add :
$$ \dfrac{-9}{25} $$ and $$ \dfrac{1}{-75} $$
Evaluate :
$$ \dfrac{-11}{18} + \dfrac{-3}{9} + \dfrac{2}{-3} $$
Evaluate :
$$ \dfrac{-8}{9} + \dfrac{4}{9} + \dfrac{-2}{9} $$
Subtract :
$$ \dfrac{5}{8} $$ from $$ \dfrac{-5}{16} $$
Evaluate :
$$ \dfrac{-2}{3} + \dfrac{5}{2} + 2 $$
Subtract :
$$ \dfrac{2}{9} $$ from $$ \dfrac{5}{9} $$
Subtract :
$$ \dfrac{-2}{15} $$ from $$ \dfrac{-8}{15} $$
Subtract :
$$ \dfrac{-3}{10} $$ from $$ \dfrac{1}{5} $$
Subtract :
$$ \dfrac{-4}{11} $$ from $$-2$$
Subtract :
$$ \dfrac{-6}{11} $$ from$$ \dfrac{-3}{-11} $$
Subtract :
$$ \dfrac{11}{18} $$ from $$ \dfrac{-5}{18} $$
Evaluate :
$$ -5 + \dfrac{5}{-8} + \dfrac{-5}{-12} $$
Evaluate :
$$ \dfrac{-9}{4} + \dfrac{13}{3} + \dfrac{25}{6} $$
Evaluate :
$$ 5 + \dfrac{-3}{4} + \dfrac{-5}{8} $$
The sum of two rational numbers is $$ \dfrac{-7}{12} $$. If one of them is $$ \dfrac{13}{24} $$, find the other.
Subtract :
$$ -2 $$ from $$ \dfrac{-3}{10} $$
The sum of two rational number is $$ \dfrac{11}{24} $$. If one of them is $$ \dfrac{3}{8} $$ , find the other.
Subtract :
$$ \dfrac{-6}{25} $$ from $$ \dfrac{-8}{5} $$
Subtract :
$$ 4$$ from $$ \dfrac{-3}{13} $$
Subtract :
$$ \dfrac{-16}{21} $$ from $$1$$
Subtract :
$$ \dfrac{-7}{4} $$ from $$ -2 $$
Subtract :
$$ \dfrac{-8}{15} $$ from $$0$$
The sum of two numbers is $$ \dfrac{-6}{5} $$. If one of them is $$-2$$ , find the other.
Evaluate :
$$ \dfrac{-12}{5} \times \dfrac{10}{-3} $$
Evaluate :
$$ \dfrac{-45}{39} \times \dfrac{-13}{15} $$
What should be subtracted from $$ \dfrac{-4}{5} $$ to get $$1$$ ?
Evaluate :
$$ \dfrac{2}{3} \times \dfrac{-6}{7} $$
Evaluate :
$$ \dfrac{5}{4} \times \dfrac{3}{7} $$
What should be added to $$ \dfrac{-7}{12} $$ to get $$ \dfrac{3}{8} $$ ?
What should be added to $$ \dfrac{-3}{5} $$ to get $$2$$ ?
What should be added to $$ \dfrac{-3}{16} $$ to get $$ \dfrac{11}{24} $$
What should be subtracted from $$ \dfrac{5}{9} $$ to get $$ \dfrac{9}{5} $$ ?
Multiply :
$$ \dfrac{3}{25} $$ and $$ \dfrac{4}{5} $$
Evaluate :
$$ 3\dfrac{1}{8} \times \left ( -2 \dfrac{2}{5} \right) $$
Multiply:
$$35$$ and $$ \dfrac{-18}{25} $$
Multiply:
$$ 1\dfrac{1}{6} $$ and $$18$$
Multiply:
$$ 2 \dfrac{1}{14} $$ and $$-7$$
Evaluate :
$$ 2\dfrac{14}{25} \times \dfrac{-5}{16} $$
Multiply:
$$ 3\dfrac{3}{5} $$ and $$-10$$
Evaluate :
$$ \dfrac{-8}{9} \times \dfrac{-3}{16} $$
Multiply:
$$ 5 \dfrac{1}{8} $$ and $$ -16$$
Evaluate :
$$ \dfrac{5}{-27} \times \dfrac{-9}{20} $$
The sum of two rational numbers is $$-5$$. If one of them is $$ \dfrac{-52}{25} $$ , find the other.
What rational number should be added to $$ \dfrac{-3}{16} $$ to get $$ \dfrac{11}{24} $$ ?
It is given that
Sum of two rational numbers $$ = \dfrac{11}{24} $$
One rational number $$ = \dfrac{-3}{16} $$
Other number $$=x$$
$$\dfrac{-3}{4}+x=\dfrac{11}{24}$$
$$x = \dfrac{11}{24} - \left ( \dfrac{-3}{16} \right ) $$
It can be written as
$$ = \dfrac{11}{24} + \dfrac{3}{16} $$
Here LCM of $$16$$ and $$24$$ is $$48$$
$$ = \dfrac{11 \times 2}{24 \times 2} + \dfrac{3 \times 3}{16 \times 3} $$
By further calculation
$$ \dfrac{22 + 9}{48} $$
$$ = \dfrac{31}{48} $$
Sum of two rational numbers $$ = \dfrac{11}{24} $$
One rational number $$ = \dfrac{-3}{16} $$
Other number $$=x$$
$$\dfrac{-3}{4}+x=\dfrac{11}{24}$$
$$x = \dfrac{11}{24} - \left ( \dfrac{-3}{16} \right ) $$
It can be written as
$$ = \dfrac{11}{24} + \dfrac{3}{16} $$
Here LCM of $$16$$ and $$24$$ is $$48$$
$$ = \dfrac{11 \times 2}{24 \times 2} + \dfrac{3 \times 3}{16 \times 3} $$
By further calculation
$$ \dfrac{22 + 9}{48} $$
$$ = \dfrac{31}{48} $$
What rational number should be added to $$ \dfrac{-3}{5} $$ to get $$2$$ ?
The product of two numbers is $$14$$ . If one of the numbers is $$ \dfrac{-8}{7} $$, find the other.
Multiply:
$$ \dfrac{27}{28} $$ and $$ -14 $$
What rational number should be subtracted from $$ \dfrac{-5}{12} $$ to get $$ \dfrac{5}{24} $$ ?
Required rational number $$=x$$
$$ = \dfrac{-5}{12} - x=\dfrac{5}{24} $$
$$x=\dfrac{-5}{12}-\dfrac{5}{24}$$
Here the LCM of $$12$$ and $$24$$ is $$24$$
$$ = \dfrac{-5 \times 2}{12 \times 2} - \dfrac{5 \times 1}{24 \times 1} $$
By further calculation
$$ = \dfrac{-10 - 5}{24} $$
So we get
$$ = \dfrac{-15}{24} $$
$$ = \dfrac{-5}{8} $$
$$ = \dfrac{-5}{12} - x=\dfrac{5}{24} $$
$$x=\dfrac{-5}{12}-\dfrac{5}{24}$$
Here the LCM of $$12$$ and $$24$$ is $$24$$
$$ = \dfrac{-5 \times 2}{12 \times 2} - \dfrac{5 \times 1}{24 \times 1} $$
By further calculation
$$ = \dfrac{-10 - 5}{24} $$
So we get
$$ = \dfrac{-15}{24} $$
$$ = \dfrac{-5}{8} $$
Evaluate :
$$ -1 + \dfrac{2}{-3} + \dfrac{5}{6} $$
$$ -1 + \dfrac{2}{-3} + \dfrac{5}{6} $$
Here LCM of $$3$$ and $$6$$ is $$6$$
So we get
$$ = \dfrac{-1 \times 6}{1 \times 6} - \dfrac{2 \times 2}{3 \times 2} + \dfrac{5 \times 1}{6 \times 1} $$
By further calculation
$$ = \dfrac{-6 -4 + 5}{6} $$
We get
$$ = \dfrac{-10 + 5}{6} $$
$$ = \dfrac{-5}{6} $$
Here LCM of $$3$$ and $$6$$ is $$6$$
So we get
$$ = \dfrac{-1 \times 6}{1 \times 6} - \dfrac{2 \times 2}{3 \times 2} + \dfrac{5 \times 1}{6 \times 1} $$
By further calculation
$$ = \dfrac{-6 -4 + 5}{6} $$
We get
$$ = \dfrac{-10 + 5}{6} $$
$$ = \dfrac{-5}{6} $$
Evaluate :
$$ \dfrac{-2}{3} - \left (\dfrac{-5}{7} \right) $$
$$ \dfrac{-2}{3} - \left (\dfrac{-5}{7} \right) $$
It can be written as
$$ = \dfrac{-2}{3} + \dfrac{5}{7} $$
Here LCM of $$3$$ and $$7$$ is $$21$$
So we get
$$ = \dfrac{-2 \times 7}{3 \times 7} + \dfrac{5 \times 3}{7 \times 3} $$
By further calculation
$$ = \dfrac{-14 + 15}{21} $$
$$ = \dfrac{1}{21} $$
It can be written as
$$ = \dfrac{-2}{3} + \dfrac{5}{7} $$
Here LCM of $$3$$ and $$7$$ is $$21$$
So we get
$$ = \dfrac{-2 \times 7}{3 \times 7} + \dfrac{5 \times 3}{7 \times 3} $$
By further calculation
$$ = \dfrac{-14 + 15}{21} $$
$$ = \dfrac{1}{21} $$
By what number should $$ \dfrac{-3}{8} $$ be multiplied so that the product is $$ \dfrac{-9}{16} $$ ?
What rational number should be subtracted from $$ \dfrac{5}{8} $$ to get $$ \dfrac{8}{5} $$ ?
Rational number $$=x$$
$$ = \dfrac{5}{8} - x=\dfrac{8}{5} $$
$$x=\dfrac{5}{8}-\dfrac{8}{5}$$
Here LCM of $$8$$ and $$5$$ is $$40$$
$$ = \dfrac{5 \times 5}{8 \times 5} - \dfrac{8 \times 8}{5 \times 8} $$
By further calculation
$$ = \dfrac{25 - 64}{40} $$
$$ = \dfrac{-39}{40} $$
$$ = \dfrac{5}{8} - x=\dfrac{8}{5} $$
$$x=\dfrac{5}{8}-\dfrac{8}{5}$$
Here LCM of $$8$$ and $$5$$ is $$40$$
$$ = \dfrac{5 \times 5}{8 \times 5} - \dfrac{8 \times 8}{5 \times 8} $$
By further calculation
$$ = \dfrac{25 - 64}{40} $$
$$ = \dfrac{-39}{40} $$
The product of two rational numbers is $$24$$. If one of them is $$ \dfrac{-36}{11} $$, find the other.
By what rational number should we multiply $$ \dfrac{20}{-9} $$, so that the product may be $$ \dfrac{-5}{9} $$ ?
$$\dfrac{1}{3}+\dfrac{4}{5}$$ of $$\dfrac{7}{5}\div 1\dfrac{17}{25}$$.
Class 7 Maths Extra Questions
- Algebraic Expressions Extra Questions
- Comparing Quantities Extra Questions
- Data Handling Extra Questions
- Exponents And Powers Extra Questions
- Fractions And Decimals Extra Questions
- Integers Extra Questions
- Lines And Angles Extra Questions
- Perimeter And Area Extra Questions
- Practical Geometry Extra Questions
- Rational Numbers Extra Questions
- Simple Equations Extra Questions
- Symmetry Extra Questions
- The Triangle And Its Properties Extra Questions
- Visualising Solid Shapes Extra Questions