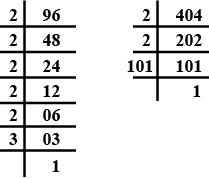
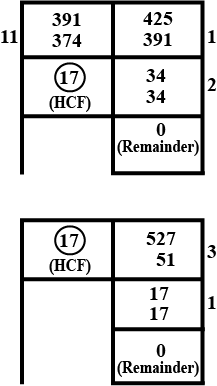
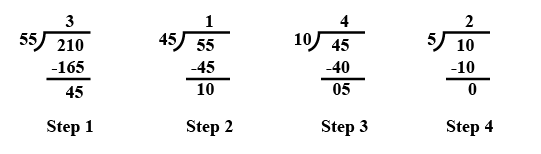
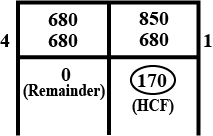
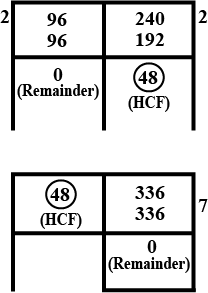
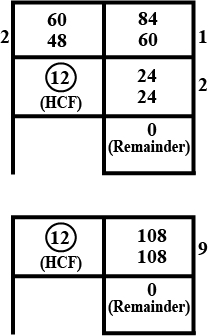
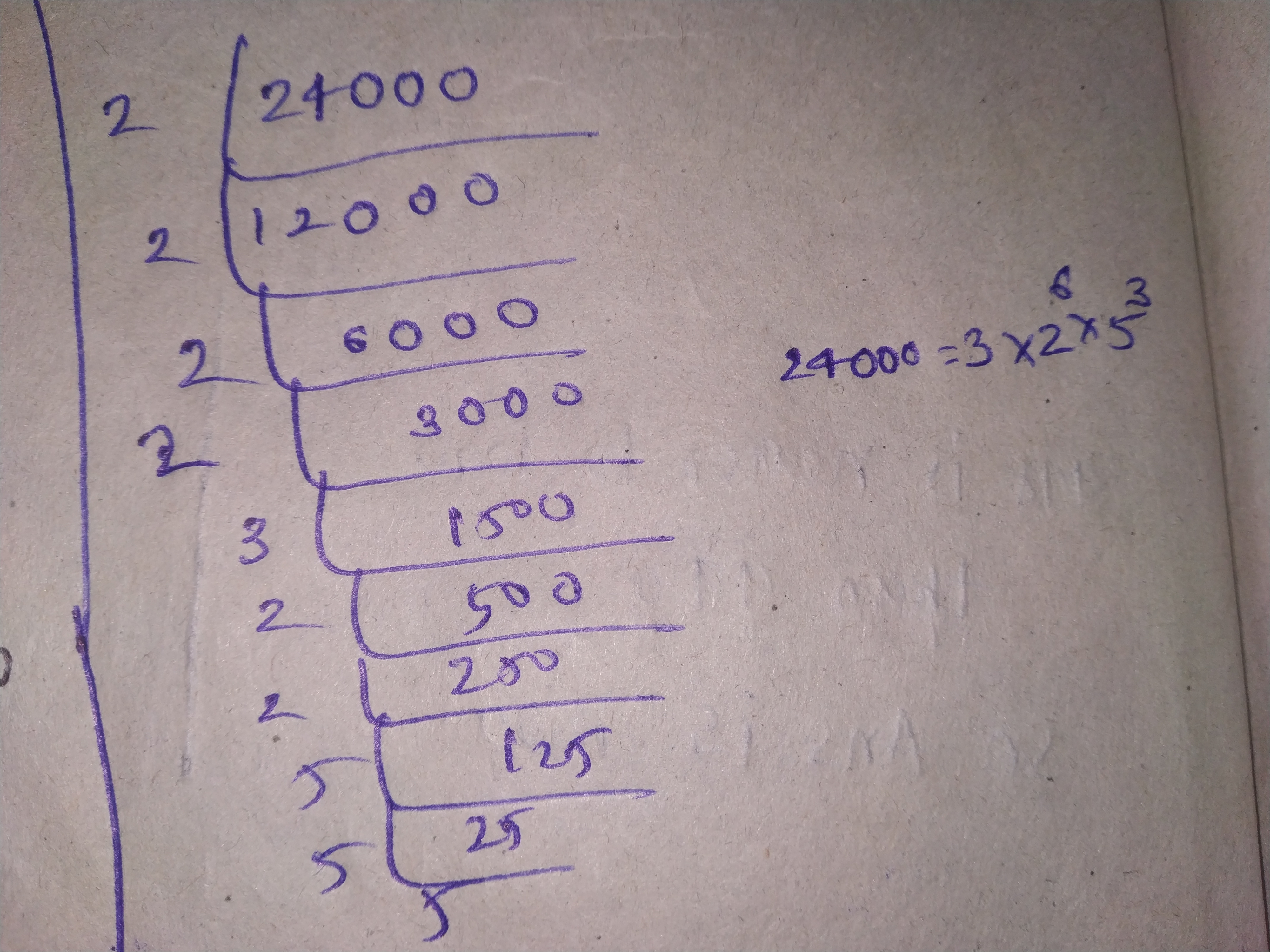
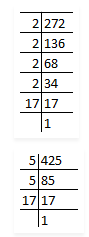
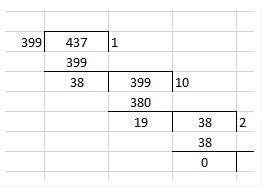
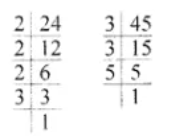
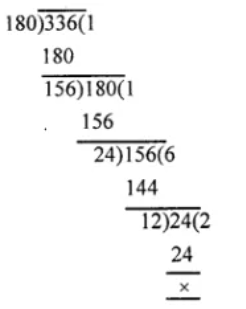
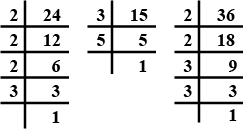
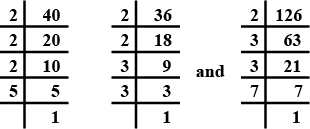
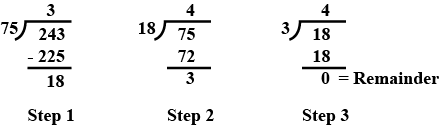
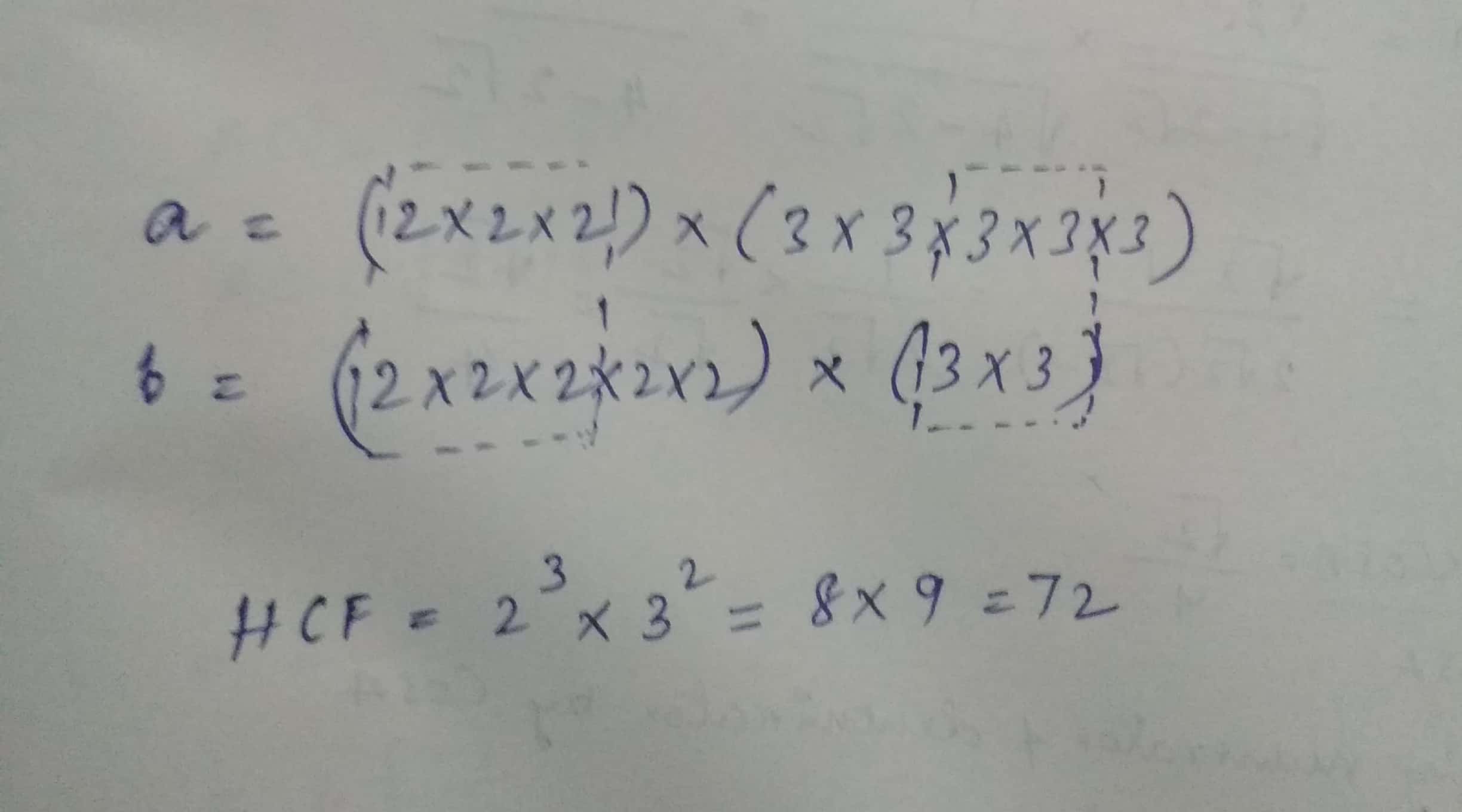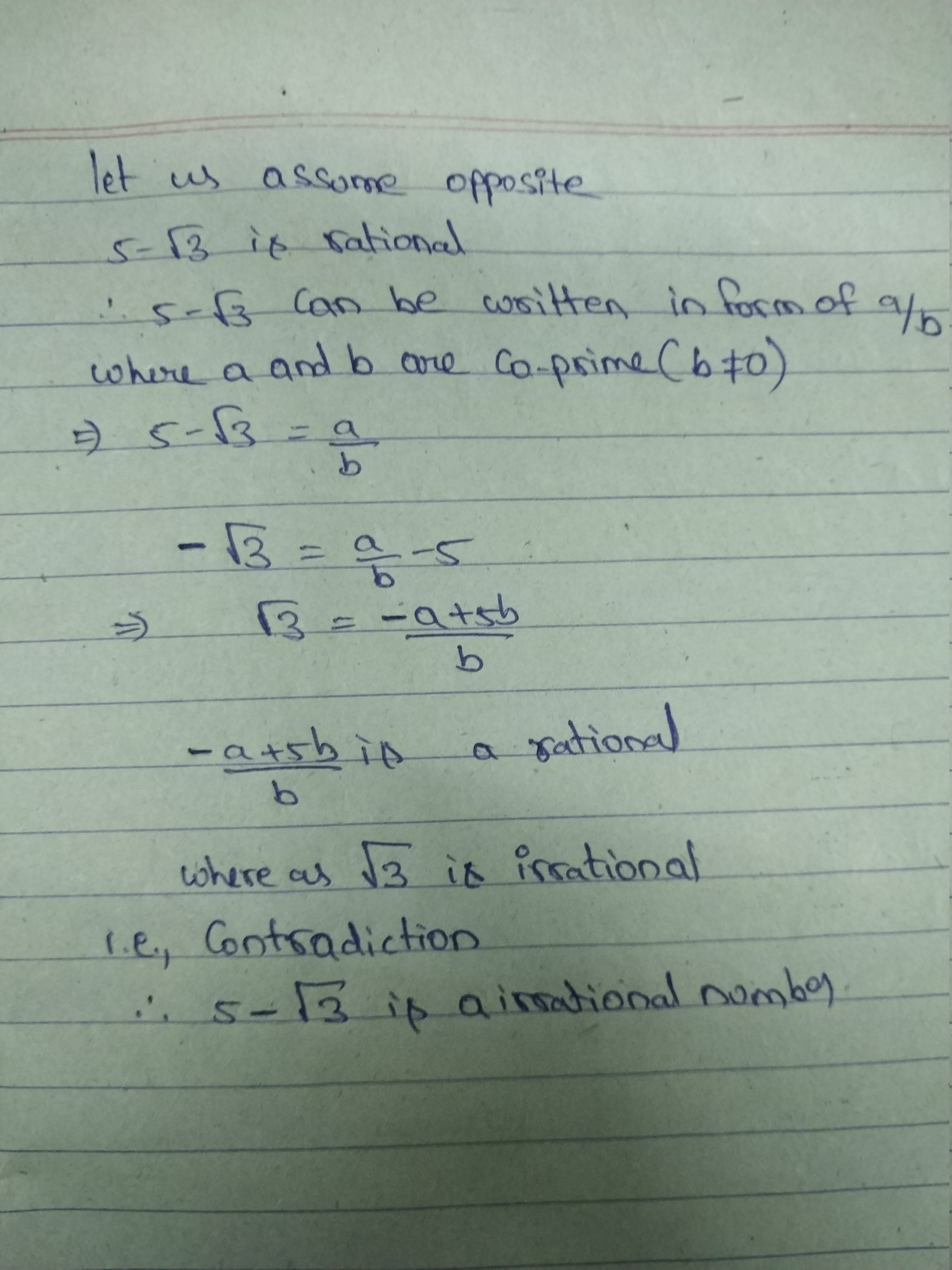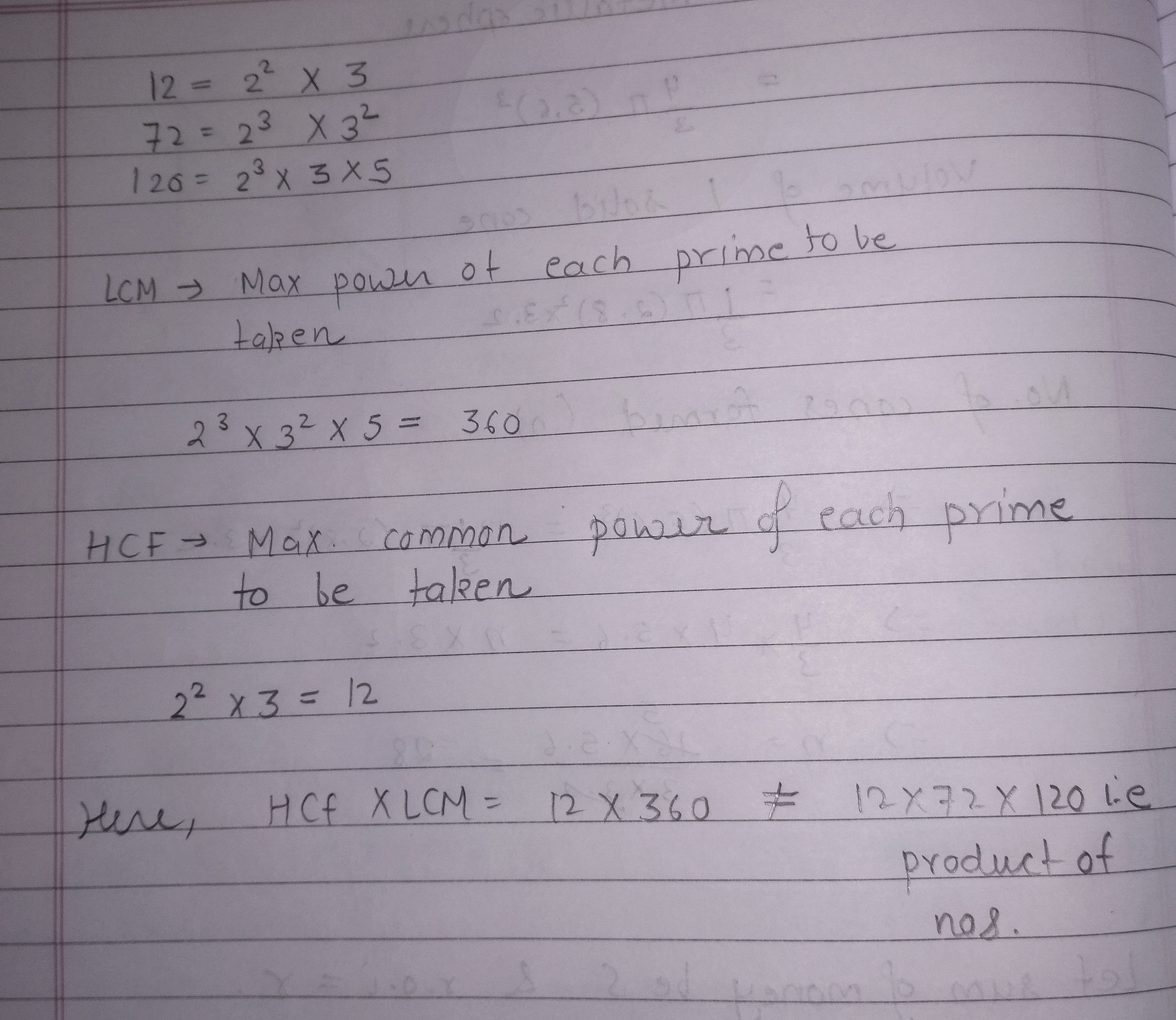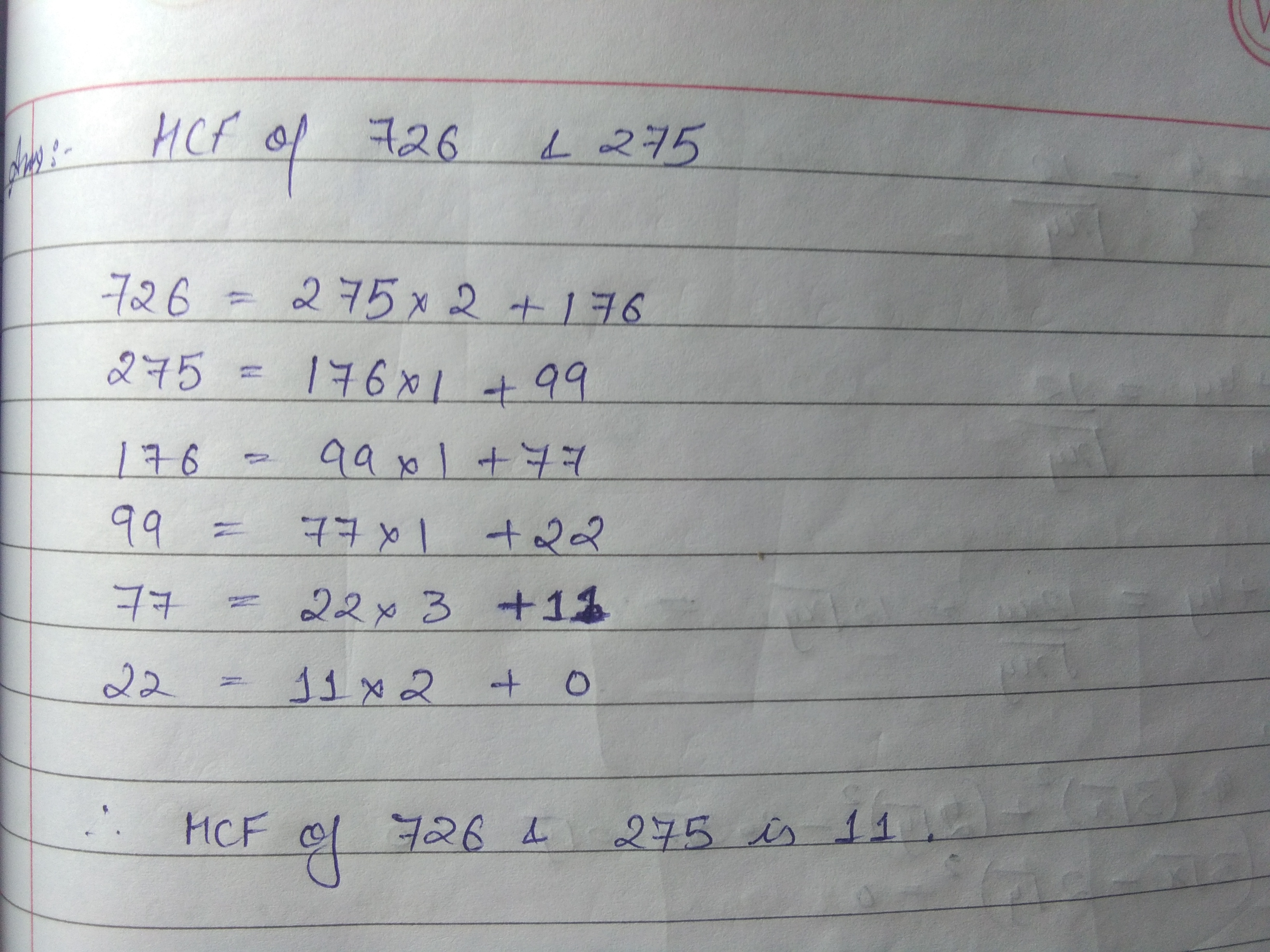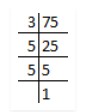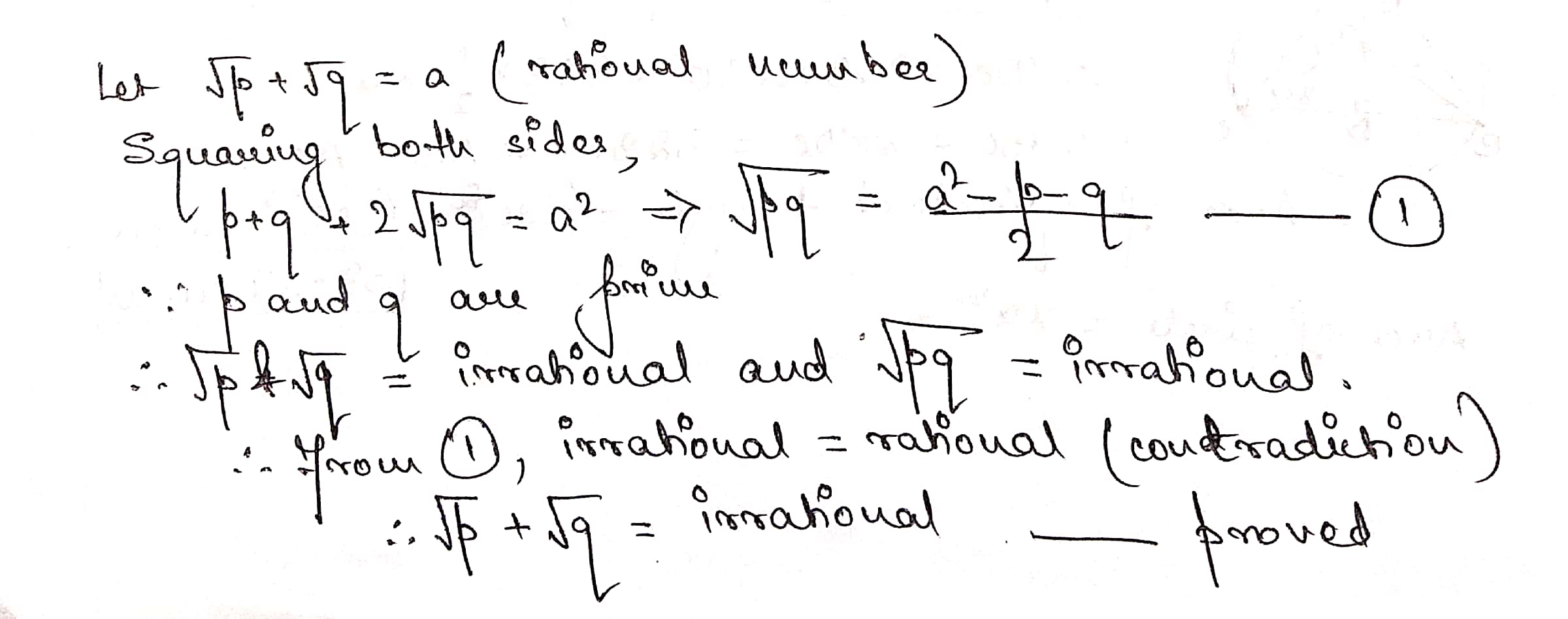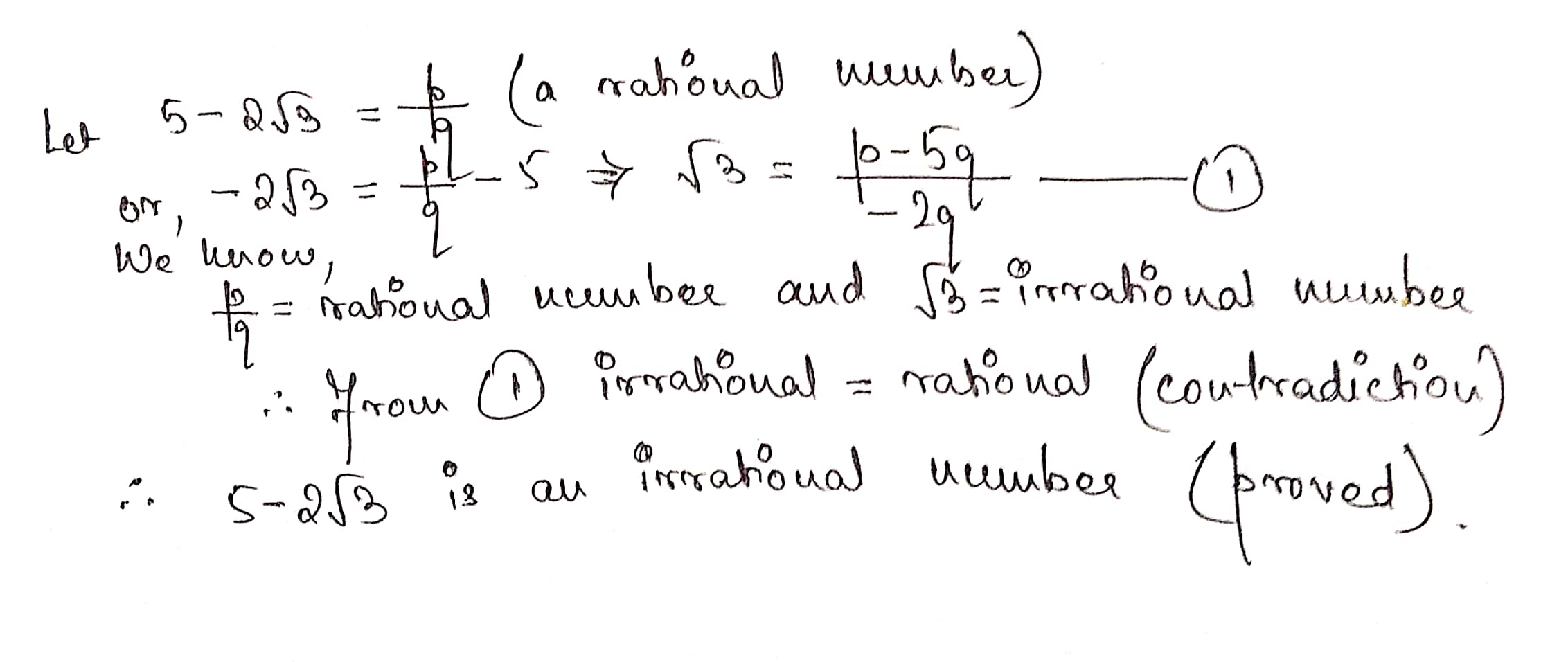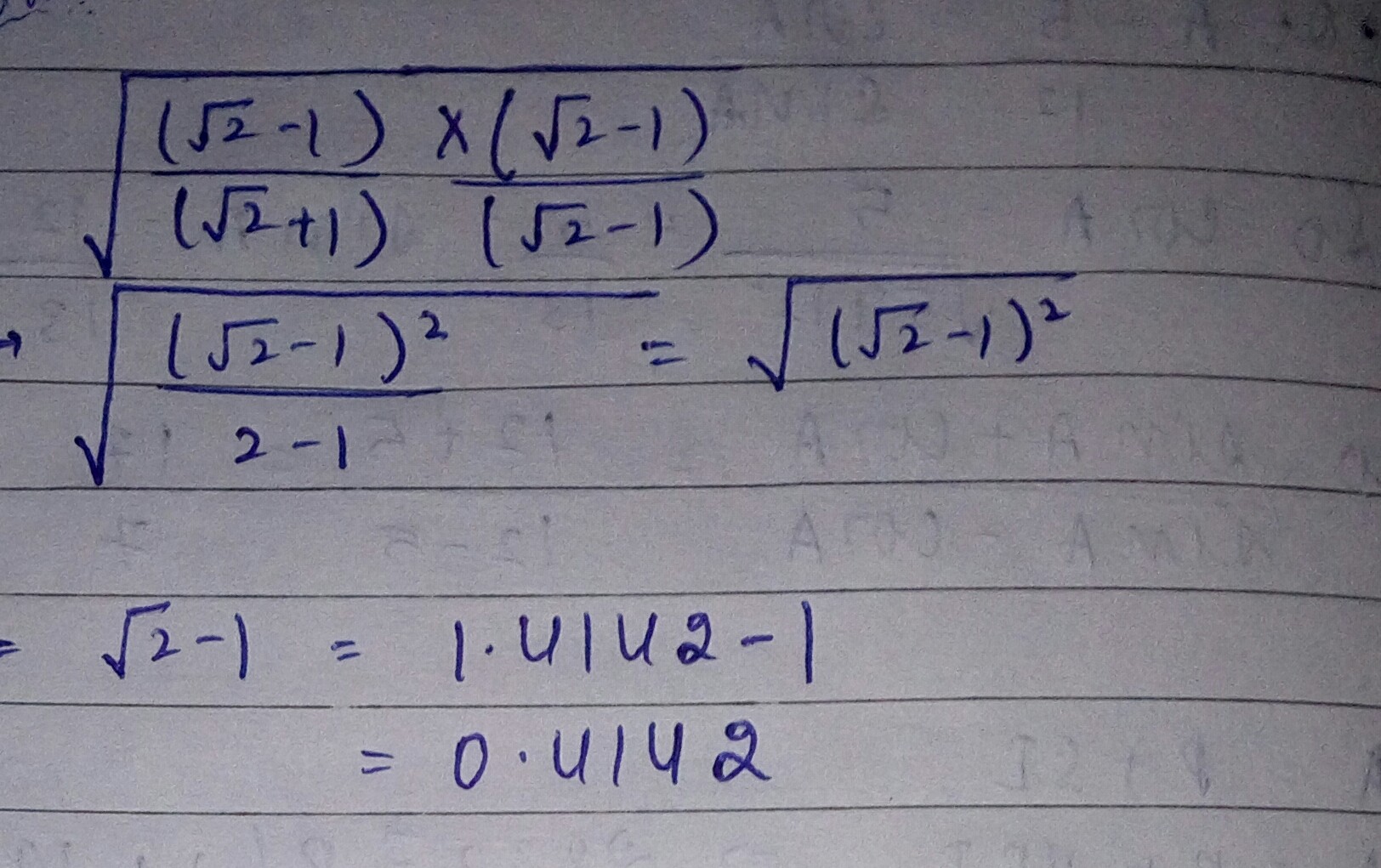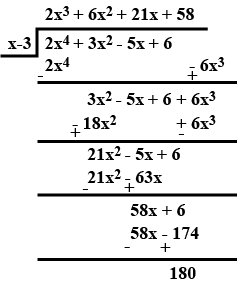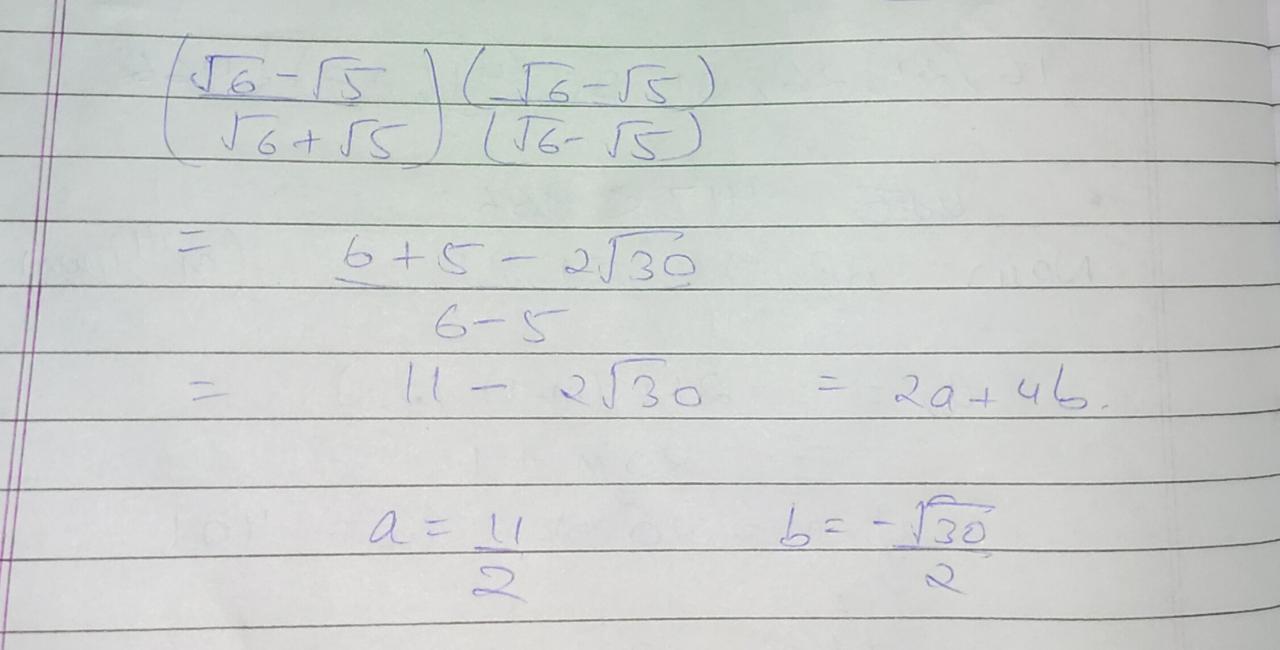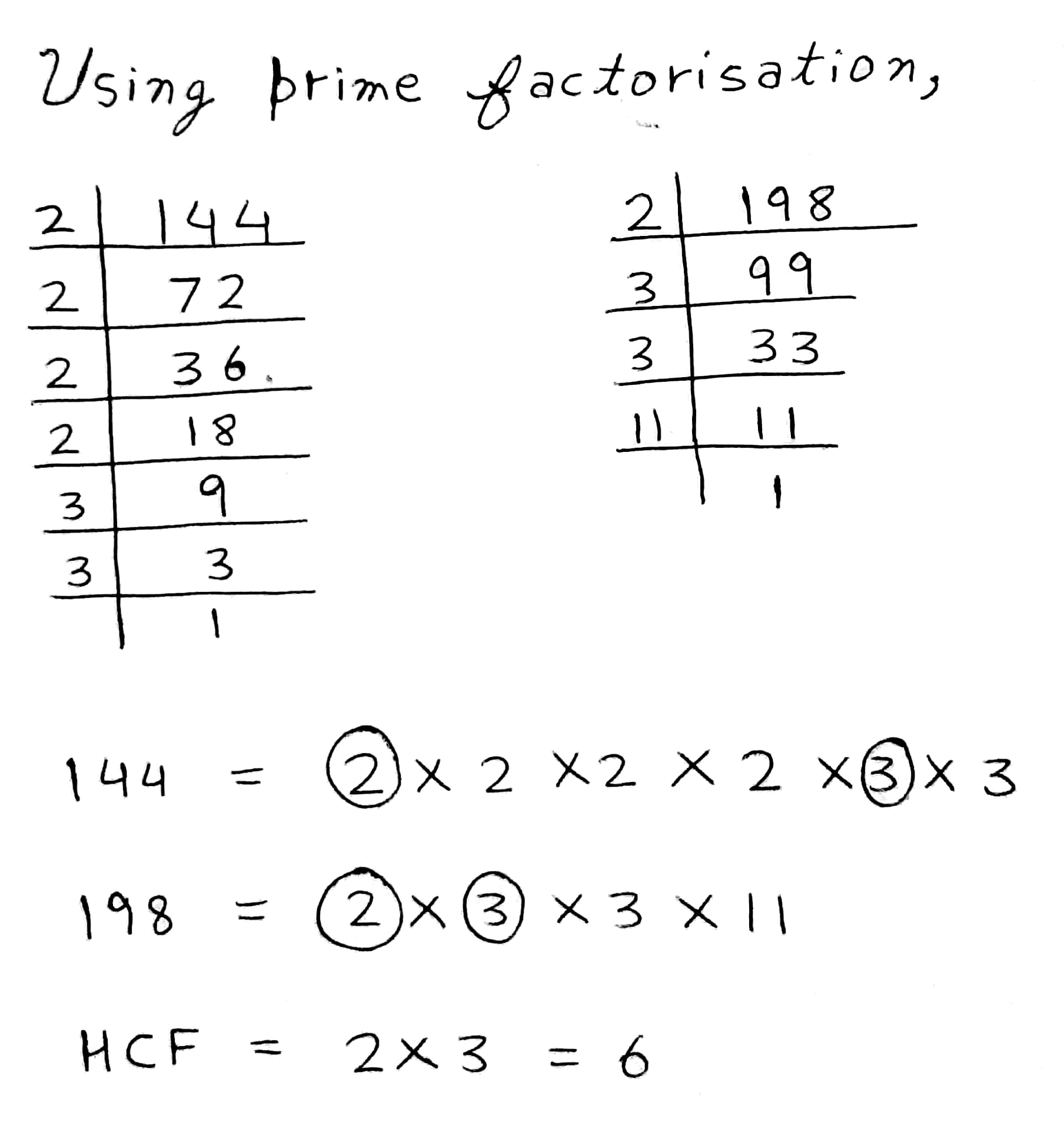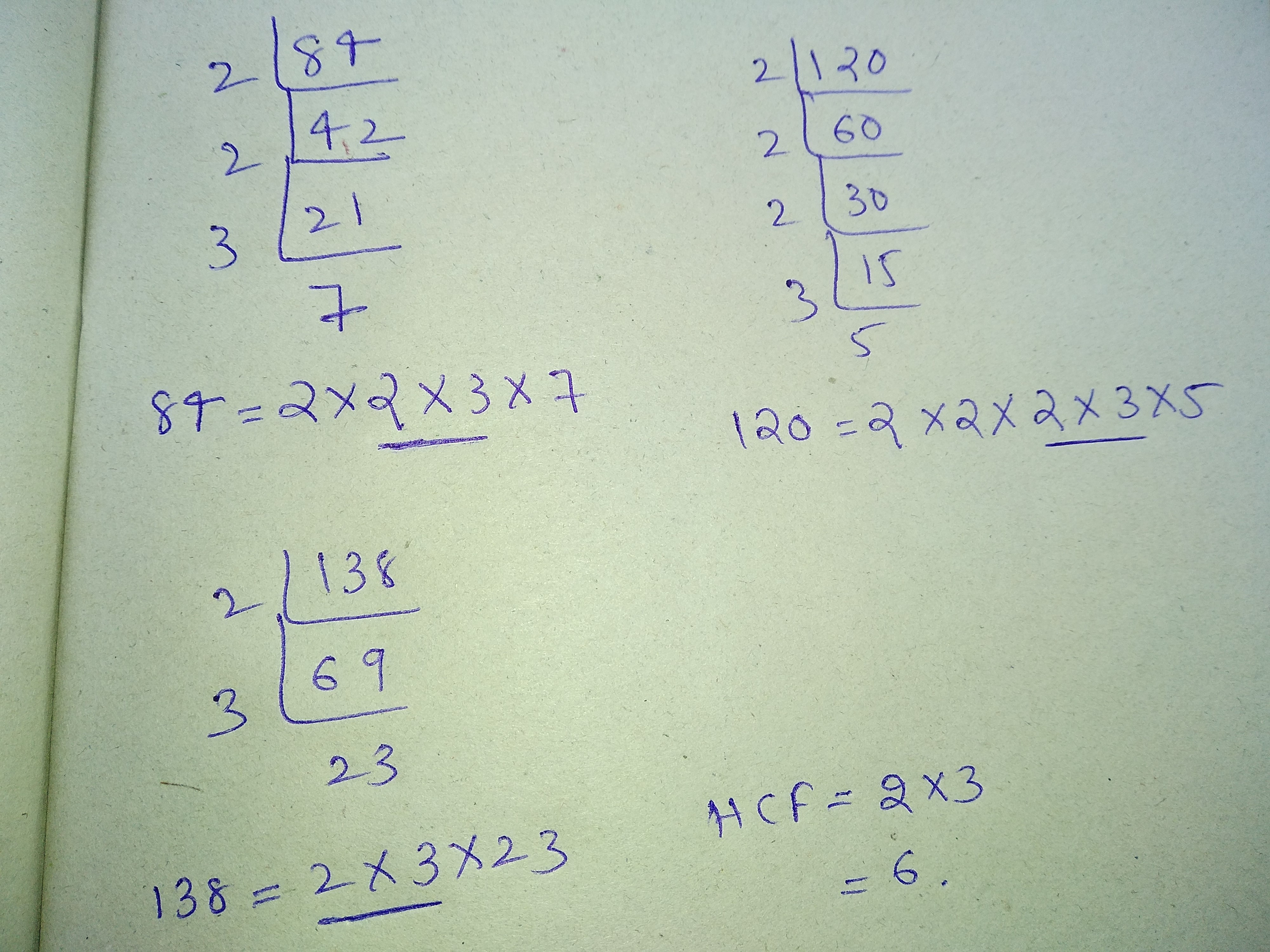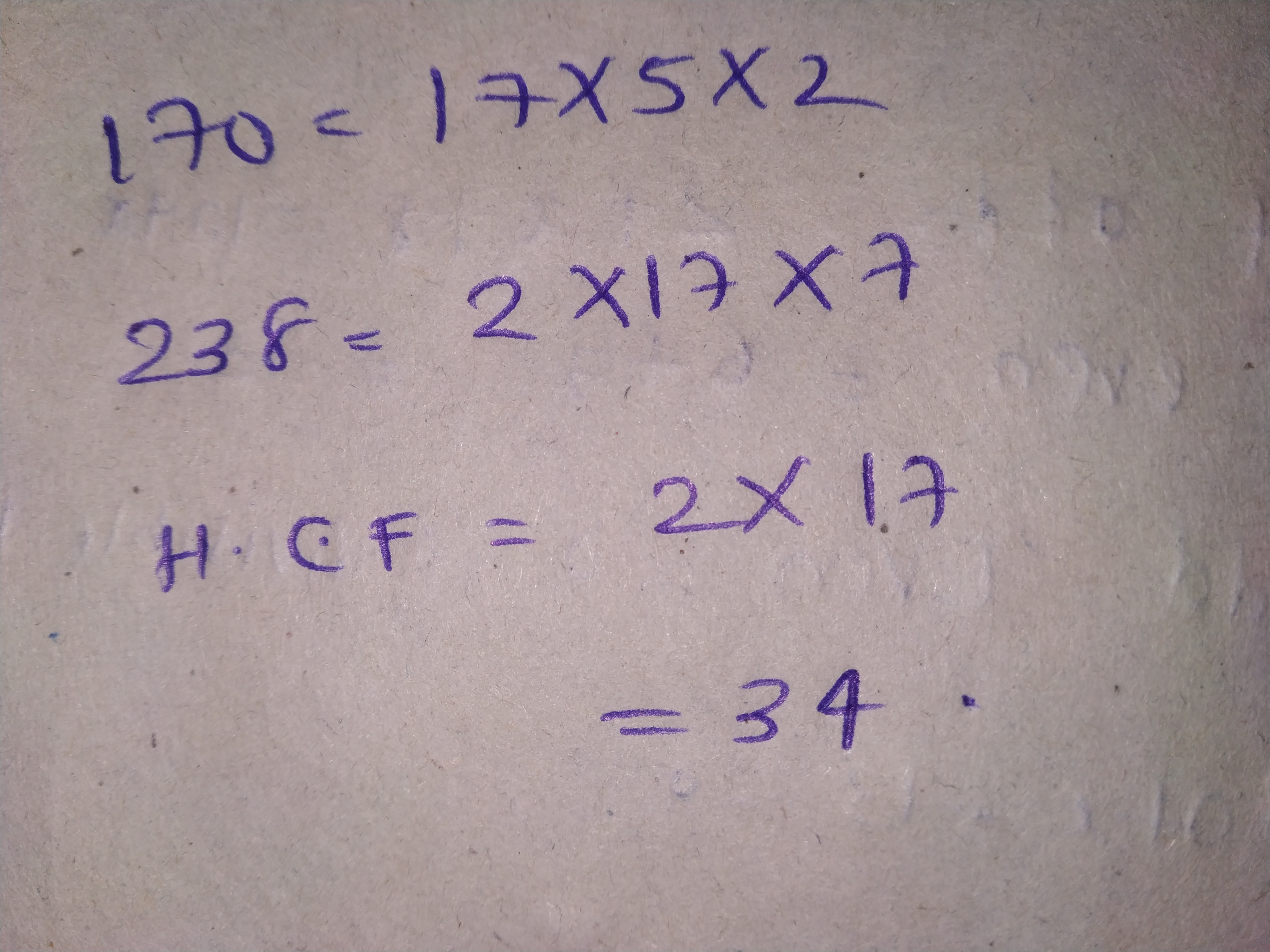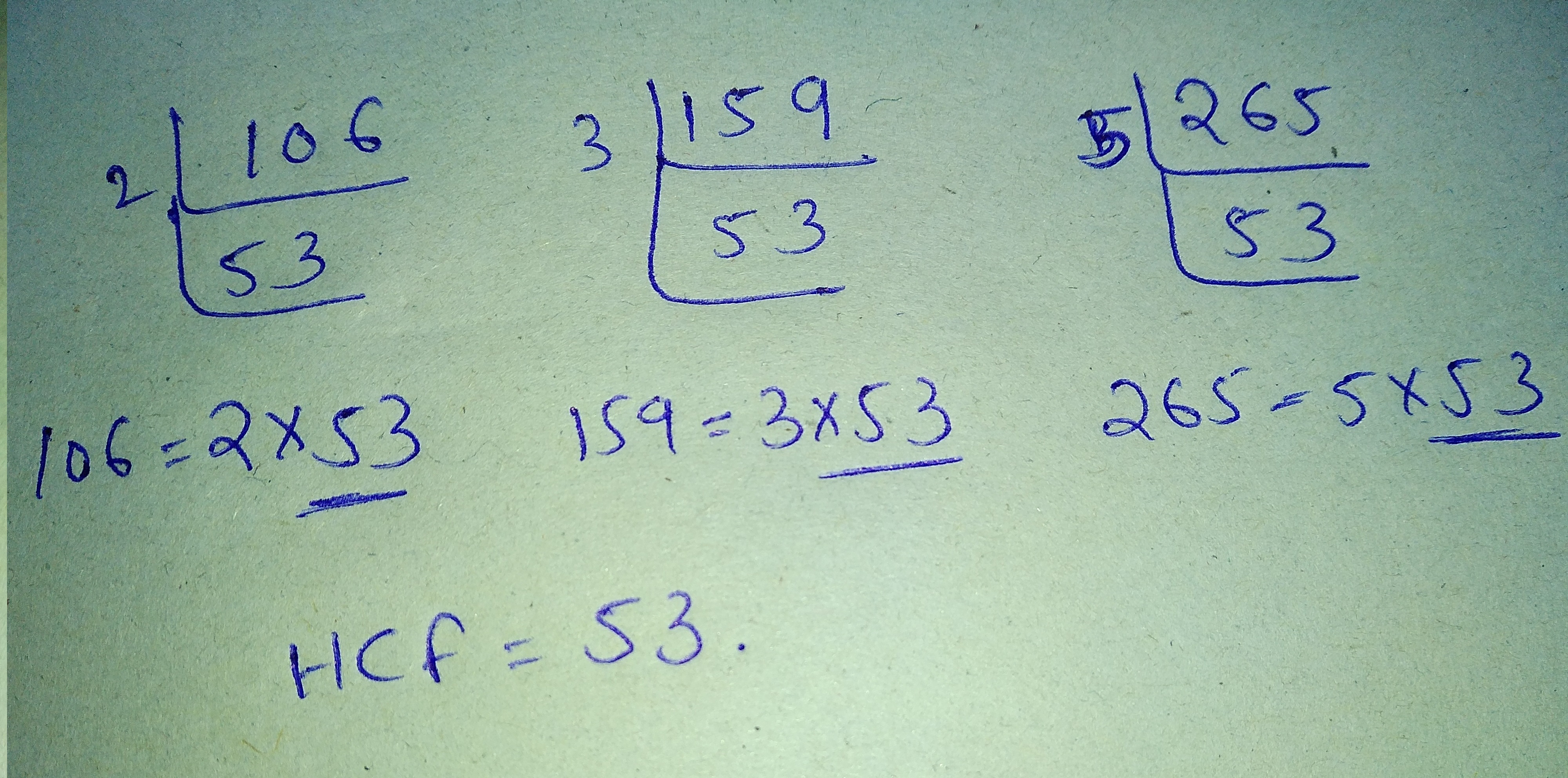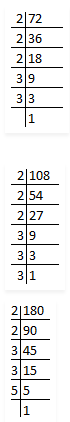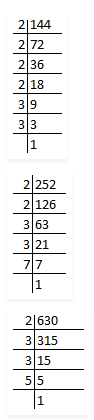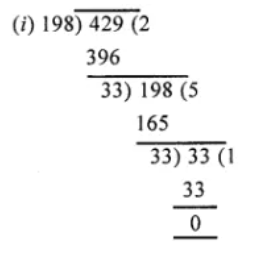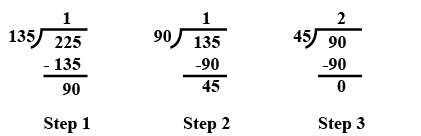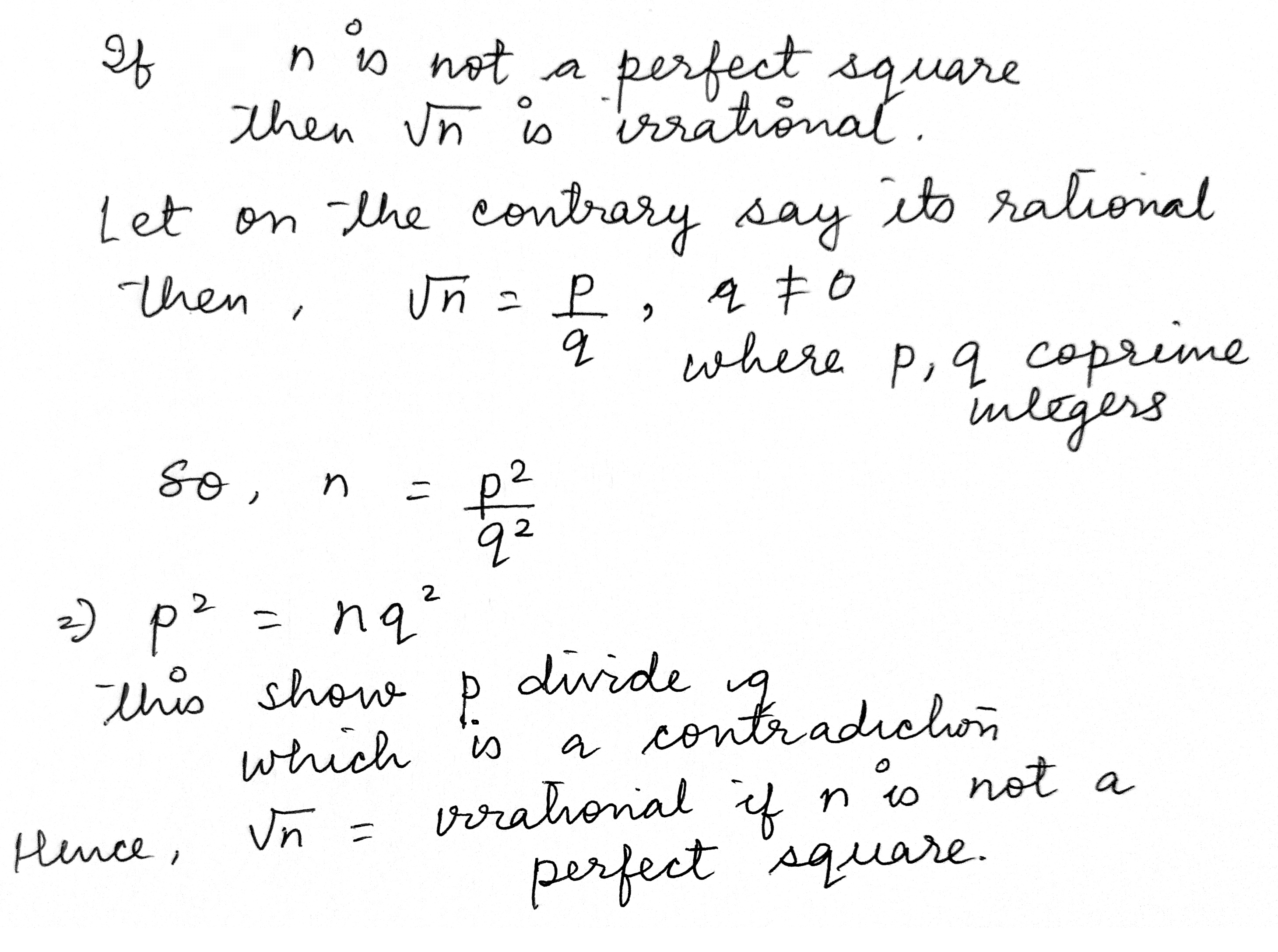Class 10 Maths - Real Numbers

Real Numbers - Class 10 Maths - Extra Questions

Prove that $\sqrt 2+\sqrt 3$ is irrational

Let us assume that

$\sqrt{2}+\sqrt{3}$ is a rational number
Then. there exist coprime integers

$p$ ,

$q$ ,

$q\neq 0$ such that

$\sqrt{2}+\sqrt{3}=\dfrac{p}{q}$

$=>\dfrac{p}{q}-\sqrt{3}=\sqrt{2}$
Squaring on both sides, we get

$=>(\dfrac{p}{q}-\sqrt{3})^2=(\sqrt{2})^2$

$=>\dfrac{p^2}{q^2}-2\dfrac{p}{q}\sqrt{3}+(\sqrt{3})^2=2$

$=>\dfrac{p^2}{q^2}-2\dfrac{p}{q}\sqrt{3}+3=2$

$=>\dfrac{p^2}{q^2}+1=2\dfrac{p}{q}\sqrt{3}$

$=>\dfrac{p^2+q^2}{q^2}\times \dfrac{q}{2p}=\sqrt{3}$

$=>\dfrac{p^2+q^2}{2pq}=\sqrt{3}$
Since,

$p$ ,

$q$ are integers,

$\dfrac{p^2+q^2}{2pq}$ is a rational number.

$=>\sqrt{3}$ is a rational number.
This contradicts the fact that

$\sqrt{3}$ is irrational.
Thus, our assumption is incorrect.
Therefore,

$\sqrt{2}+\sqrt{3}$ is a irrational.

$3- \sqrt5$ is an irrational number
If true then enter $1$ and if false then enter $0$

Let assume that on the contrary that

$3- \sqrt5$ is rational. Then, there exist co-prime positive integers a and b such that,

$3- \sqrt5 = \displaystyle \frac{a}{b}$

$\Rightarrow 3- \displaystyle \frac{a}{b} = \sqrt5$

$\Rightarrow \displaystyle \frac{3b-a}{b} = \sqrt5$

$\Rightarrow \sqrt 5$ is rational

$[\because$ ab, b are integer

$\therefore \displaystyle \frac{3b-a}{b}$ is a rational number]
This contradicts the fact that

$\sqrt5$ is irrational
Hence,

$3- \sqrt5$ is an irrational number

$144$ cartons of coke cans and $90$ cartons of pepsi cans are to be stacked in a canteen. If each stack is of same height and is to contain cartons of the same drink, what would be the greatest number of cartons each stack would have?

In order to arrange the cartons of the same drink in the same stack, we have to find the greatest number that divides

$144$ and

$90$ exactly.

Using Euclid's division algorithm, to find the H.C.F. of

$144$ and

$90$ .

$144=90$

$\times$

$1+54$

$90 =54$

$\times$

$1 + 36$

$54 =36$

$\times$

$1 +18$

$36 =18$

$\times$

$2 + 0$

So, the H.C.F. of

$144$ and

$90$ is

$18$ .

Number of cartons in each stack

$= 18.$

Use Euclid's division algorithm to find the H.C.F. of $196$ and $38318$

While applying Euclid's division lemma for finding H.C.F. of say

$c$ &

$d$ we proceed through the following steps:

1. Find whole numbers

$q$ and

$r$ such that

$c=dq+r$ ..............

$0\leq r<d$

2. If

$r=0$ , then

$d$ is

$H.C.F.$
If

$r \neq 0$ , then continue division until remainder or

$r$ becomes

$0$ , thus divisor or

$d$ becoming

$H.C.F.$

Applying Euclid’s division lemma to

$196$ and

$38318.$

$38318 = 196 \times 195 + 98$

$196 = 98 × 2 + 0$

The remainder at the second stage is zero

$(0)$

So, the H.C.F. of

$38318$ and

$196$ is

$98.$

Classify the following numbers as rational or irrational.
$30.2323422345...$

Given number

$30.2323422345.........$

The decimal expression of above number is non terminating , non repeating.

So number

$30.2323422345.......$ is an irrational number

Classify the following numbers as rational or irrational.
$2\pi$

$2\pi$ , 2 is a rational number and

$\pi$ is a irrational number.

So product of a non zero rational number with an irrational number is also irrational number.

Then

$2\pi$ is an irrational number

Without actually dividing find if $\dfrac {13}{20}$ is terminating decimal.

Given

$\dfrac{13}{20}$

The

$\dfrac{p}{q}$ is terminating if

(i) P & Q are co-prime and

(ii) q is of the form

$2^{n}5^{m}$ where n & m are non negative

$\dfrac{13}{20}$

The denominator is 20 from of

$20=2\times 2\times 5=2^{2}5^{1}$

Then

$\dfrac{13}{20}$ is the terminating decimal

Find the largest positive integer that will divide $150, 187$ and leaving remainders $6, 7$ and $11$ respectively.

It is given that on dividing

$150$ by the required number, the remainder will be

$6$ .

$\implies 150 - 6 = 144$ , will be exactly divisible by the required largest positive integer.
Hence, the required number is a factor of

$144$ .

Similarly, required positive integer is a factor of

$187 - 7=180$ and

$203 - 11 =192$ .

Hence, the required positive integer is the HCF of

$144, 180$ and

$192$

.
By prime factorization:

$144 = 2^4 \times 3^2$

$180 = 2^2 \times 3^2 \times 5$

$192 =2^6 \times 3$

$\therefore \text{HCF} (144, 180, 192) = 2^2 \times 3 = 12$

Hence, the required positive integer is

$12$ .

$\therefore$

$12$ is the largest positive integer that will divide

$150, 187$ and

$203$ leaving remainders

$6, 7$ and

$11$ respectively.

Classify the following numbers as rational or irrational.
$\dfrac {1}{\sqrt {3}}$

$\dfrac{1}{\sqrt{3}}$ , '1'

$(1\neq 0)$ is a rational number but

$\sqrt{3}$ is an irrational number

We know that the quotient of rational and irrational number is an irrational number

$\dfrac{1}{\sqrt{3}}$ is an irrational number

Prove that $5-\sqrt{3}$ is an irrational number.

Let us assume,

$5-\sqrt{3}$ is a rational number

$\Rightarrow 5-\sqrt{3}=\dfrac{p}{q}$ , where

$p, q \in z, q \neq 0$

$5-\dfrac{p}{q}=\sqrt{3}$

$\Rightarrow \dfrac{5q-p}{q}=\sqrt{3}$

$\Rightarrow \sqrt{3}$ is a rational number

$\because \dfrac{5q-p}{q}$ is rational
but

$\sqrt{3}$ is not a rational number.
This gives us a contradiction.

$\therefore$ our assumption that

$5 -\sqrt{3}$ is a rational number is wrong

$\Rightarrow 5-\sqrt{3}$ is an irrational number.

Classify the following numbers as rational or irrational.
$\sqrt {441}$

A rational number is part of a whole expressed as a fraction, decimal or a percentage. ... It is a number that cannot be written as a ratio of two integers (or cannot be expressed as a fraction). For example, the square root of 2 is an irrational number because it cannot be written as a ratio of two integers.

Given number

$\sqrt{441}$

Then

$\sqrt{441}=\sqrt{2\times 2\times 7\times 7}=21$ is the perfect square

$\sqrt{441}$ is the rational number

In the following equations, find whether variables $x, y, z$ etc. represent rational or irrational numbers
$x^{2} = 7$

Given,

$x^{2}=7$

$\Rightarrow x=\sqrt{7}$

The number

$\sqrt{7}$ is an irrational number.

Hence,

$x$ is an irrational number.

Find HCF:
$15, 25$ and $35$ .

Factorization of the following.

$15 = 1 \times 3 \times 5$

$25 = 1 \times 5 \times 5$

$35 = 1 \times 7 \times 5$

Hence, The common factor is

$1,5$ . This implies that

$HCF=5$

Check whether $21 + \sqrt {3}$ are irrational numbers are not?

$21+\sqrt{3}$

$\sqrt{2}=1.4142....,\sqrt{3}=1.7320.....,\pi 3.1415.....$

Here 21 is a rational number but

$\sqrt{2}$ is an irrational number

The sum of rational and irrational number is an irrational number

$21+\sqrt{2}=21+1.4142....=22.4142....$ is an irrational number

Check whether $\pi + 3$ are irrational numbers or not?

$\pi +3$

$\sqrt{2}=1.4142....\sqrt{3}=1.7320...,\pi =3.1415....$

$\pi +3=3.1415...+3=6.1415.......$

All there are non-terminating, non-recurring decimals.

Thus

$\pi +3$ is an irrational numbers.

Check whether $5\sqrt {2}$ is an irrational numbers are not?

Here

$5$ is a rational number.

But

$\sqrt{2}=1.4142\dots,$ is an irrational number.

The product of an irrational and rational number is also an irrational number.

So,

$5\sqrt{2}=5\times 1.4142\dots=7.0710\dots$ is an irrational number.

Prove that $2 + \sqrt {5}$ is an irrational number.

If possible, let us assume

$2 + \sqrt {5}$ is a rational number.

$2 + \sqrt {5} = \dfrac {p}{q}$ where

$p, q\in z, q\neq 0$

$2 - \dfrac {p}{q} = -\sqrt {5}$

$\dfrac {2q - p}{q} = -\sqrt {5}$

$\Rightarrow -\sqrt {5}$ is a rational number

$\because \dfrac {2q - p}{q}$ is a rational number
But

$-\sqrt {5}$ is not a rational number.

$\therefore$ Our supposition

$2 + \sqrt {5}$ is a rational number is wrong.

$\Rightarrow 2 + \sqrt {5}$ is an irrational number.

Prove that the following are irrational.
$\displaystyle\frac{1}{\sqrt{2}}$ .

To prove

$\dfrac{1}{\sqrt{2}}$ is irrational

Let us assume that

$\sqrt{2}$ is irrational

$\dfrac{1}{\sqrt{2}} = \dfrac{p}{q}$ (where

$p$ and

$q$ are co prime)

$\dfrac{q}{p} = \sqrt{2}$

$q = \sqrt{2}p$

Squaring both sides

$q^2 = 2p^2$ .....................(1)

By theorem - If

$p$ is a prime no. and

$p$ divides

$a^2$ , then

$p$ divides

$a$ also, where

$a$ is a positive integer}

$q$ is divisible by

$2$

$\therefore q = 2c$ (where

$c$ is an integer)

Putting the value of q in equitation (1)

$2p^2 = q^2 = 4c^2$

$p^2 =\dfrac{4c^2}{2} =2c^2$

$\dfrac{p^2}{2} = c^2$

$p$ is also divisible by

$2$

But

$p$ and

$q$ are coprime

This is a contradiction which has arisen due to our wrong assumption

$\dfrac{1}{\sqrt{2}}$ is irrational

Prove that $6+\sqrt{2}$ is irrational.

Let us assume

$6+\sqrt{2}$ is rational. Then it can be expressed in the form

$\dfrac{p}{q}$ , where

$p$ and

$q$ are co-prime

Then,

$6+\sqrt{2}=\dfrac{p}{q}$

$\sqrt{2}=\dfrac{p}{q}-6$

$\sqrt{2}=\dfrac{p-6q}{q}$ -----(

$p,q,-6$ are integers)

$\dfrac{p-6q}{q}$ is rational

But,

$\sqrt{2}$ is irrational.

This contradiction is due to our incorrect assumption that

$6+\sqrt{2}$ is rational

Hence,

$6+\sqrt{2}$ is irrational

For any positive real number $x$ , prove that there exists an irrational number $y$ such that $0 < y < x$ .

$X$ can be a rational number or irrational number . So let us consider two cases

1) if

$X$ is irrational then

$\dfrac{X}{2}$ is also an irrational number which satisfies the hypothesis.

2) if

$X$ is rational then

$\dfrac{X}{2}\times {\sqrt2}$ is also an irrational number which satisfies the hypothesis.

Show that $3\sqrt{2}$ is irrational.

Let us assume, to the contrary, that

$3\sqrt{2}$ is rational.

That is, we can find co-prime a and b

$(b\neq 0)$ such that

$3\sqrt{2}=\displaystyle\frac{a}{b}$ .

Rearranging, we get

$\sqrt{2}=\displaystyle\frac{a}{3b}$ .

Since

$3$ , a and b are integers,

$\displaystyle\frac{a}{3b}$ is rational,

and so

$\sqrt{2}$ is rational.

But this contradicts the fact that

$\sqrt{2}$ is irrational.

So, we conclude that

$3\sqrt{2}$ is irrational.

Given that $\sqrt{2}$ is irrational, prove that $(5+3\sqrt{2})$ is an irrational number.

Given that

$\sqrt2$ is irrational.

We know that the theorem "The product of any irrational number with a rational number is irrational".

So, since we know

$3$ is a rational number,

$3\sqrt2$ is irrational.

$\left(3=\dfrac{3}{1}\quad;1\neq0\right)$

Now we know that

$3\sqrt2$ is irrational.

$Theorem:$ The sum of a rational number with an irrational number is irrational.

So, since we know

$5$ is a rational number,

$5+3\sqrt2$ is irrational.

$\left(5=\dfrac{5}{1}\quad;1\neq0\right)$

Thus we proved that

$5+3\sqrt2$ is an irrational number.

Prove that $\sqrt { 3 }$ is a irrational number.

Let us assume

$\sqrt 3$ is rational

So that we can find two integers

$a$ and

$b$ such that

$\sqrt { 3 } =\frac { a }{ b }$

Suppose

$a$ and

$b$ has a common factor other than

$1$ and assume that

$a$ and

$b$ are co prime

$\sqrt { 3 } b=a\\ \Rightarrow 3{ b }^{ 2 }={ a }^{ 2 }$

Therefore

${a}^{2}$ is divisible

$3$

Hence

$a$ is also divisible by

$3$

$\Rightarrow a=3c$

$\Rightarrow 3{ b }^{ 2 }={ (3c) }^{ 2 }\\ \Rightarrow { b }^{ 2 }=3{ c }^{ 2 }$

$b$ is also divisible by

$3$

$a$ and

$b$ has a factor

$3$ in common.

which contradicts our assumption.

hence proved that

$\sqrt3$ is irrational.

Prove that $\displaystyle \sqrt{2} +\, \sqrt{3}$ is an irrational number.

First we prove that

$\sqrt { 2 }$ is irrational.

for that we assume that

$\sqrt { 2 }$ is rational. And as rational number can be written as

$\dfrac { p }{ q }$ form.

where we assume that p and q have no common factor. Squaring in both side. After that

$2 = \dfrac { { p }^{ 2 } }{ { q }^{ 2 } }$

which implies that

${ p }^{ 2 }=2{ q }^{ 2 }$

thus

${ p }^{ 2 }$ is even. The only way this can be true is that

$p$ itself is even. But then

${ p }^{ 2 }$ is actually divisible by

$4$ . Hence

${ q }^{ 2 }$ and therefore q must be even. So

$p$ and

$q$ are both even which is a contradiction to our assumption that they have no common factors. The square root of

$2$ cannot be rational.

and we similarly prove for

$\sqrt { 3 }$ .

And as we know that sum of two irrational no. is always irrational.

If $a={2}^{3}{3}^{5},b={3}^{2}{2}^{5}$ , then find the $HCF$ of $a$ and $b$ .

$\displaystyle a =2^33^5 =(2\times2\times2) \times (3\times3\times3\times3\times3)$

$\displaystyle b= 2^53^2 =(2\times2\times2\times2\times2) \times (3\times3)$

$\displaystyle HCF(a,b) = (2\times 2\times 2\times)( 3\times 3) = 2^3 \times 3^2 = 8 \times 9 = 72$

1042390_1038012_ans_40559a4719524652ae50c084e93878ff.jpg

Prove that $5 -\sqrt 3$ is irrational

Let us assume the given number be rational and we will write the given number in p/q form

$\Rightarrow 5-\sqrt {3}=\dfrac {p} {q}$

$\Rightarrow \sqrt {3}=\dfrac {5q-p}{q}$

We observe that LHS is irrational and RHS is rational, which is not possible.

This is contradiction.

Hence our assumption that given number is rational is false

$\Rightarrow 5-\sqrt {3}$ is irrational

Prove the following are irrational.
$\sqrt {3} + \sqrt {5}$

Let us assume that

$\sqrt{3} +\sqrt{5}$ is rational.

That is, we can find two integers

$a$ and

$b (b\neq0)$ such that,

$\sqrt{3} +\sqrt{5} =\dfrac{a}{b}$ where

$a$ and

$b$ are co-prime integers.

$\therefore \sqrt{5} = \dfrac{a}{b} - \sqrt{3}$

Squaring on both sides we get,

$\implies 5 = \dfrac{a^2}{b^2} + 3 - \dfrac{2a}{b}\sqrt{3}$

$\implies \dfrac{2a}{b}\sqrt{3} = \dfrac{a^2}{b^2} -2 =\dfrac{a^2 -2b^2}{b^2}$

$\implies \sqrt{3} = \dfrac{a^2 -2b^2}{2ab}$

Since,

$a$ and

$b$ are integers, thus

$\dfrac{a^2 - 2b^2}{2ab}$ is rational. So,

$\sqrt{3}$ is also rational.

But, this contradicts the fact that

$\sqrt{3}$ is irrational.

Thus, our assumption is wrong that

$\sqrt{3}+\sqrt{5}$ is rational.

Hence,

$\sqrt{3}+\sqrt{5}$ is an irrational.

Prove the following are irrational.
$6+\sqrt {2}$

Let contrary that

$6+ \sqrt 2$ be a rational number

Then we can write

$6+\sqrt 2 =\cfrac{a}{b}$ , where

$a$ &

$b$

are co-primw integers &

$b \ne 0$

$\Rightarrow \sqrt 2= \cfrac{a}{b}-6$

$\Rightarrow \sqrt 2 =\cfrac{a-6}{b}$

Since

$a$ &

$b$ are integers

$\cfrac{a-6}{b}$ is rational

$\Rightarrow \sqrt 2$ is rational

this contradict the fact that

$\sqrt 2$ is irrational

Therefore our assumption is wrong

Hence

$6+ \sqrt 2$ is an irrational number (Proved)

Prove that $\sqrt{5}$ is irrational and hence prove that $(2-\sqrt{5})$ is also irrational.

Let's prove this by the method of contradiction-

Say, √5 is a rational number. ∴ It can be expressed in the form p/q where p,q are co-prime integers.

⇒√5=p/q

⇒5=p²/q² {Squaring both the sides}

⇒5q²=p² (1)

⇒p² is a multiple of 5. {Euclid's Division Lemma}

⇒p is also a multiple of 5. {Fundamental Theorm of arithmetic}

⇒p=5m

⇒p²=25m² (2)

From equations (1) and (2), we get,

5q²=25m²

⇒q²=5m²

⇒q² is a multiple of 5. {Euclid's Division Lemma}

⇒q is a multiple of 5.{Fundamental Theorm of Arithmetic}

Hence, p,q have a common factor 5. this contradicts that they are co-primes. Therefore, p/q is not a rational number. This proves that √5 is an irrational number.

For the second query, as we've proved √5 irrational. Therefore 2-√5 is also irrational because difference of a rational and an irrational number is always an irrational number.

Find the $HCF$ of $81$ and $237$ and express it as a linear combination of $81$ and $237.$

Given integers are

$81$ and

$237$ such that

$81<237$ .

Applying division lemma to

$81$ and

$237$ , we get

$237=81\times 2+75$
Since the remainder

$75\neq0$ . So, consider the divisor

$81$ and the remainder

$75$ arndapply division lemma to get

$81=75\times1+6$
We consider the new divisor

$75$ and the new remainder

$6$ and apply division lemma to get

$75=6\times12+3$
We consider the new divisor

$6$ and the new remainder

$3$ and apply division lemma to get

$6=3\times2+0$
The remainder at this stage is zero. So, the divisor at this stage or the remainder at the earlier stage i.e.

$3$ is the

$HCF$ of

$81$ and

$237$ .

To represent the

$HCF$ as a linear combination of the given two numbers, we start from the last but one step and successively eliminate the previous remainder as follows:
From

$(iii)$ , we have

$3=75-6\times12$

$\Rightarrow 3=75-\left( 81-75\times 1 \right) \times 12$

$\Rightarrow 3=75-12\times 81+12\times75$

$\Rightarrow 3=13\times 75-12\times 81$

$\Rightarrow 3=13 \times (237-81\times 2)-12\times 81$

$\Rightarrow 3=13 \times 237-26\times 81-12 \times 81$

$\Rightarrow 3=13 \times 237-38 \times 81$

$\Rightarrow 3=237x+81y$ , where

$x=13$ and

$y=-38$ .

Now the

$HCF$ (say d) of two positive integers

$a$ and

$b$ can be expressed as a linear combination of

$a$ and

$b$ i.e.,

$d=xa+yb$ for some integers

$x$ and

$y$ .

Also, this representation is not unique. Because,

$d=xa+yb$

$\Rightarrow d=xa+yb+ab-ab$

$\Rightarrow d=(x+b)a+(y-a)b$

In the above example, we had

$3=13\times 237-38 \times 81$

$\Rightarrow 3=13\times 237-38 \times 81+237 \times 81-237 \times 81$

$\Rightarrow 3=\left( 13\times 237+237\times 81 \right) +\left( -38\times 81-237\times 81 \right)$

$\Rightarrow 3=\left( 13+81 \right) \times 237+\left( -38-237 \right) \times 81$

$\Rightarrow 3=94\times 237-275\times 81$

$\Rightarrow 3=94\times 237+\left( -275 \right) \times 81$

Find the $HCF$ of $65$ and $117$ and express it in the form $65\ m + 117\ n.$

Given integers are

$65$ and

$117$ such that

$117>65$

Applying division lemma to

$65$ and

$117$ , we get

$117=65\times1+52$
Since the remainder

$52\neq0$ . So, apply the division lemma to the divisor

$65$ and the remainder

$52$ to get

$65=52\times1+13$

We consider the new divisor

$52$ and the new remainder

$13$ and apply division lemma, to get

$52=13\times4+0$

At this stage the remainder is zero. So, that last divisor or the non-zero remainder at the earlier stage i.e.

$13$ is the

$HCF$ of

$65$ and

$117$ .

From

$(ii)$ , we have

$13=65-52 \times 1$

$\Rightarrow\quad 13=65-( 117-65\times 1)$

$\Rightarrow\quad 13=65-117+65\times 1$

$\Rightarrow\quad 13=65\times 2+117 \times(-1)$

$\Rightarrow\quad 13=65m+117n$ , where

$m=2$ and

$n=-1$ .

Somu says " $\dfrac{\sqrt{3}}{1}$ is a rational number" do you agree with Somu? Give reasons.

No ,

$\dfrac{\sqrt{3}}{1}$ is not a rational number

Because

$\dfrac{\sqrt{3}}{1}=\sqrt{3}$

$\sqrt{3}$ is an irrational number

$\dfrac{\sqrt{3}}{1}$ is an irrational number

Show that $\sqrt{5} + 3\sqrt{5}$ is irrational.

Let us assume

$5+3\sqrt{5}$ is rational.

$5+3\sqrt{5}=\dfrac{a}{b}$

$3\sqrt{5}=\dfrac{a}{b}-5$

$\sqrt{5}=\dfrac{a}{3b}-\dfrac{5}{3}$

Here

$\sqrt{5}$ is irrational &

$\dfrac{a}{3b}-\dfrac{5}{3}$ is rational.

i.e., which contradicts the statement

$\therefore 5+3\sqrt{5}$ is irrational.

Hence proved.

Prove the following are irrational.
$3+2\sqrt {5}$

Let us assume that

$3+2\sqrt{5}$ is rational.

That is, we can find two integers

$a$ and

$b (b\neq0)$ such that,

$3+2\sqrt{5} =\dfrac{a}{b}$ , where

$a$ and

$b$ are co-prime integers.

$\therefore 2\sqrt{5} = \dfrac{a}{b} -3$

$\implies \sqrt{5} =\dfrac{a - 3b}{2b}$

Since,

$a$ and

$b$ are integers, thus

$\dfrac{a - 3b}{2b}$ is rational.

So,

$\sqrt{5}$ is also rational.

But, this contradicts the fact that

$\sqrt{5}$ is irrational.

Thus, our assumption is wrong that

$3+2\sqrt{5}$ is rational.

Hence,

$3+2\sqrt{5}$ is an irrational.

Check whether $\dfrac{6}{{200}}$ has terminating or non terminating repeating decimal expansion.

$\dfrac{6}{200}=\dfrac{3}{100}=0.03$ , which is a terminating decimal

Hence,

$\dfrac{6}{{200}}$ has a terminating decimal expansion.

Without actually performing the long deviation, state whether the following rational number will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
$\dfrac {77}{210}$

Let

$\dfrac{77}{210}=\dfrac{11}{30}$

$\frac{p}{q}$ is terminating if ,

$11$ and

$30$ have no common factor,

Therefore,

$11$ and

$30$ are co prime.

For denominator

$=30=2 \times 3 \times 5$

Denominator is not of the form

$2^n5^m$

Thus

$\dfrac{11}{30},\dfrac{77}{210}$ is not terminating repeating decimal.

Find the H.C.F. of 18 and 48 in division method.

Factors of given numbers are:

$18:(2*3)*3\\48:(2*3)*2*2*2$

we can see that common multiples are

$2*3$

Hence, Highest common Factor of

$18$ and

$48$ is

$6$

Find H.C.F. of $25$ and $40$

$25 = 5 \times 5=5^2$

$40 = 2 \times 2\times 2 \times 5=2^3\times 5$

$\therefore$ H.C.F. of $25$ and $40$ is $5$

Prove that : $4 - 5\sqrt 3$ is irrational.

Let us assume that

$4-5\sqrt3$ be rational

$\implies 4-5\sqrt3 = \cfrac{a}{b}$ where

$a,b \epsilon Z$

$\implies -5\sqrt3 = \cfrac{a}{b}-4$

$\implies \sqrt3 = \cfrac{4}{5} - \cfrac{a}{b}$

L.H.S = irrational number as

$\sqrt3$ is a irrational number.

R.H.S = rational number

$as \space RHS \neq LHS$

Hence, our assumption is wrong and

$4-5\sqrt3$ is a irrational number.

State whether the following statement is True or False? Justify your answer.
$= \dfrac{\sqrt{3}}{7}$ is a rational number.

False.

$\dfrac{\sqrt{3}}{7}$ is an irrational number

A rational number is one which can be expressed as a fraction where both the numerator & the denominator are whole numbers.

For example:

$1.5$ which can be expressed as

$\dfrac{3}{2}$

Evidently

$\sqrt{3}$ is an irrational number, because it cannot be expressed as a fraction with a whole number numerator & denominator.

Hence

$\dfrac{\sqrt{3}}{7}$ is also irrational.

Show that $4\sqrt{2}$ is an irrational number.

Assume that,

$4\sqrt{2}$ is a rational number.

Then, there exists coprime positive integers p & q such that

$4\sqrt{2}=\dfrac{p}{q}$

$\sqrt{2}=\dfrac{p}{4q}$ (

$\because$ p & q are integers)

$\Rightarrow \dfrac{p}{4q}$ is rational

$\Rightarrow \sqrt{2}$ is rational

This contradict the fact that

$\sqrt{2}$

is irrational. so our assumption is incorrect.

Hence

$4\sqrt{2}$ is irritational.

Classify the numbers as rational or irrational : $7.478478$

$7.478478=7.\overline {478}$

It is a non-terminating & repeating decimal therefore, it is a

$\textbf{rational}$ number.

Note:

A decimal number can either be terminating and other is non-terminating.

When a decimal digit is terminating than it is a rational number.

When a decimal digit is non-terminating then again there are two cases:

1. First when decimal digits are non-terminating and recurring then it is a rational number.

2. Other case is when decimal digits are non-terminating and non-recurring then it is irrational.

Classify the numbers as rational or irrational : $1.101001000100001...$

Since the decimal expansion is non-terminating and non-recurring.

Hence,

$1.101001000100001...$ is an irrational number.

Prove that $5-\sqrt{3}$ is an irrational number.

Let us assume opposite

$5-\sqrt{3}$ is rational

$\therefore 5-\sqrt{3}$ can be written in from of a/b

where a and b are co-prime

$(b \neq 0)$

$\Rightarrow 5-\sqrt{3} = \dfrac{a}{b}$

$-\sqrt{3}=\dfrac{a}{b}-5$

$\Rightarrow \sqrt{3}=\dfrac{-a+5b}{b}$

$\dfrac{-a+5b}{b}$ is a rational

where as

$\sqrt{3}$ is irrational

i.e; contradiction

$\therefore 5-\sqrt{3}$ is a irrational number

1162333_1068941_ans_633c420a316f48b9a4ea348eede7b2d4.jpg

Find the $HCF$ of $510$ and $92$ .

First step is to write

$510$ and

$92$ as product of its prime factors,

$510=2\times 3\times 5\times 17$

$92=2\times 2\times 23$

So,

$2$ is the only common factor of

$510$ and

$92$ so, the

$HCF$ of the given two numbers is equal to

$2$ .

Classify the numbers as rational or irrational : $\sqrt {225}$

$\sqrt{225}=\sqrt{15\times 15}=15$

Hence, The number is

$rational$ as well as real.

Classify the number as rational or irrational : $\sqrt {23}$

Let

$\sqrt{23}$ be rational number

$\Rightarrow \sqrt{23} = \dfrac{p}{q} [p \in 2, q \in 2, q \neq 0 \,\, HCF \, of \, p \, \&\, q = 1]$

$\Rightarrow (\sqrt{23})^2 = \left(\dfrac{p}{q}\right)^2 [sbs]$

$\Rightarrow 23 = \dfrac{p^2}{q^2}$

$\Rightarrow 23 q^2 = p^2$

$\Rightarrow p^2 = 23 q^2$

$\Rightarrow 23$ is a factor of

$p^2$

$\Rightarrow 23$ is also a factor of

$p$ .....I

Let

$p^2 = 23 n$

$\Rightarrow (p)^2 = (23 n)^2 [sbs]$

$\Rightarrow p^2 = 529 n$

$\Rightarrow 23 q^2 = 529 n \, [\therefore p^2 = 23 q^2]$

$\Rightarrow q^2 = \dfrac{529}{23}$

$\Rightarrow q^2 = 23 n$

$\Rightarrow 23$ is a factor of

$q^2$

$\Rightarrow 23$ is also a factor of

$q$ ......II

From this, I & II equations we got

$23$ as a common factor of

$p$ &

$q$ .

so, one assumption is wrong

$\Rightarrow \sqrt{23}$ is not a rational number.

$\Rightarrow \sqrt{23}$ is an irrational number

What is the condition for decimals expansion of a rational numbers to terminate. Explain with example.

Let

$x=p/q$ be a rational number such that the prime factorization of q is of the form

$2^m5^n$ , where n, m are positive integers.

Then x has a decimal expansion which terminates.

Example:

$\dfrac{49}{500}\times \dfrac{49}{2^2\times 5^3}$

Since the denominator is of the form

$2^m\times 5^n$ , the rational number has a terminating decimal expansion.

Find $GCD$ of $736$ and $85$ by using Euclid's algorithm.

Given, the numbers

$736,85$ .

Using Euclid's algorithm,

$736=85\times 8+56\\ \;\;85=56\times 1+29\\ \;\;56=29\times 1+27\\ \;\;29=27\times 1+2\\ \;\;27=2\times 13+1\\ \quad2=\boxed{ 1}\times 2+0$

Hence,

$GCD$ of

$736$ and

$85$ is

$1.$

Prove that $7 - 4\sqrt 2$ is irrational.

Since, ${{\left( 7-4\sqrt{2} \right)}^{2}}$

$=49-32-56\sqrt{2}$

$=17-56\sqrt{2}$

$\sqrt{2}$ is irrational ,so is $17-56\sqrt{2}$ and so is . $\left( 7-4\sqrt{2} \right)$

Rationalise the denominators of the following :
$\dfrac{1}{{\sqrt 7 }}$
$\dfrac{1}{{\sqrt 7 - \sqrt 6 }}$
$\dfrac{1}{{\sqrt 5 + \sqrt 2 }}$
$\dfrac{1}{{\sqrt 7 - \sqrt 2 }}$

1092226_1179806_ans_32b7e030e08b459ba62ea587302581ac.png

Classify the following numbers as rational or irrational.
$\dfrac { 1 }{ \sqrt { 2 } }$

Here

$\sqrt2$ is not the perfect square,

So,

$\dfrac{1}{\sqrt2}$ is an irrational number

Classify the following numbers as rational or irrational.
$2-\sqrt{5}$

Here,

$\sqrt5$ is not any perfect square,

Hence,

$2-\sqrt5$ is an irrational number

Find the $HCF$ of by prime factorisation. $48$ , $144$

Prime factorization of

$48$ is

$\Rightarrow 2\times 2\times 2\times 2\times 3$

$\Rightarrow 2^4\times 3$

and

Prime factorization of

$144$ is

$\Rightarrow 2\times 2\times 2\times 2\times 3\times 3$

$\Rightarrow 2^4\times 3^2$

Highest common factor is

$\Rightarrow 2^4\times 3=48$

Use prime factorisation method to determine the HCF of 520 and 1430.

Given numbers are

$520$ and

$1430$ .

To find out: The HCF of the given numbers.

We can represent the given numbers as the product of their prime factors as:

$520=2\times 2\times 2\times 5\times 13$

$1430=2\times 5\times 11\times 13$

Now, the HCF of the numbers is the product of the prime factors common between them.

$\therefore\ HCF(520,\ 1430)=2\times 5\times 13=130$

Hence, the HCF of

$520$ and

$1430$ is

$130$ .

Without actually performing the long division,state whether the following rational number will have a terminating decimal expansion or a non terminating repeating decimal expansion:
$\dfrac{129}{2^25^77^5}$

A simplified fraction of the form

$\dfrac{p}{q}$ has a terminating decimal expansion if and only if all the prime factors of

$q$ are either 2 or 5.

Given:

$q=2^25^77^5$

As the given denominator has

$7$ as a prime factor, the decimal expansion will be non-terminating.

Show that $2+\sqrt {6}$ is a irrational number.

1230215_1227339_ans_6a8fa43dc50249b68172dc8598803351.jpg

Find H.C.F of $847$ and $1650$ .

Find the prime factors of

$847$ and

$1650$

$847=7\times 11\times 11$

$1650=2\times 3\times 5\times 5\times 11$

$\therefore$ Highest common factor of

$847$ and

$1650$ is

$11$

Thus H.C.F. of these two numbers is

$1$ .

Find the $LCM$ and $HCF$ of $12,72$ and $120$ using fundamental theorem of arithmetic. Also show that $HCF$ $\times LCM$ is not equal to the product of three given numbers.

1112599_1205727_ans_fdcf8bf327f14e0191f9ceff845c0680.jpg

Without actually performing the long division,state whether the following rational number will have a terminating decimal expansion or a non terminating repeating decimal expansion:
$\dfrac{23}{2^35^2}$

A simplified fraction of the form

$\dfrac{p}{q}$ has a terminating decimal expansion if and only if all the prime factors of

$q$ are either 2 or 5.

Given:

$q=2^35^2$

As the only prime factors of the denominator are

$2$ and

$5$ , the decimal expansion will be terminating.

Find the $\text{HCF}$ of $180,252$ and $354$ using prime factorization method.

Consider given numbers,

$\Rightarrow 180,252,354$

Now,

$180=2\times 2\times 3\times 3\times 5$

$252=2\times 2\times 3\times 3\times 7$

$354=2\times 3\times 59$

H.C.F of $180,252,354$ is _{= $2\times 3=6$}

Hence, this is the answer.

Find the LCM and HCF of 12,72 and 120 using fundamental theorem of arithmetic. Also show that HCF $\times LCM$ is not equal to the product of three given numbers.

1111844_1205728_ans_e397fc69197047299186bffdef95238d.jpg

Prove that $2 - 3 \sqrt { 5 }$ is an irrational no.

Let

$x=2-3\sqrt{5}$ be a rational number.

$3\sqrt{5}=2-x$

$\sqrt{5}=\frac{2-x}{3}$

Since x is rational, 2-x is rational and hence

$\frac{2-x}{3}$ is also rational number

$\Rightarrow \sqrt{5}$ is a rational numbers, which is a contradiction.

Hence

$2-3\sqrt{5}$ must be an irrational number.

Find the $HCF$ of the following
$27,63$

$27 = 3 \times 3 \times 3 = {3}^{3}$

$63 = 3 \times 3 \times 7 = {3}^{2} \times 7$

Highest common factor-

$HCF \left( 27, 63 \right) = {3}^{2} = 9$

Find the $HCF$ of the following
$70,105,175$

$70 = 2 \times 5 \times 7$

$105 = 3 \times 5 \times 7$

$175 = 5 \times 5 \times 7$

Highest common factor-

$HCF \left( 70, 105, 175 \right) = 7$

Classify the following number as Rational or Irrational:

$\sqrt {23}$

$\sqrt {23}$

Since, 23 is not a perfect square,

$\sqrt {23}$ is an irrational number.

Find the $HCF$ of the following
$36,84$

$36 = 2 \times 2 \times 3 \times 3 = {2}^{2} \times {3}^{2}$

$84 = 2 \times 2 \times 3 \times 7 = {2}^{2} \times 3 \times 7$

Highest common factor-

$HCF \left( 36, 84 \right) = {2}^{2} \times 3 = 12$

Show that ${ \left( \sqrt { 3 } +\sqrt { 5 } \right) }^{ 2 }$ is an irrational no.

Let us assume to the contrary that (√3+√5)² is a rational number,then there exists a and b co-prime integers such that,

(√3+√5)²=a/b

3+5+2√15=a/b

8+2√15=a/b

2√15=(a/b)-8

2√15=(a-8b)/b

√15=(a-8b)/2b

(a-8b)/2b is a rational number.

Then √15 is also a rational number

But as we know √15 is an irrational number.

This is a contradiction.

This contradiction has arisen as our assumption is wrong.

Hence (√3+√5)² is an irrational number.

Prove $6+3\sqrt{5}$ is irrational

Let us assume that is

$6 + 3\sqrt 5$ rational .

So, we can write it as:

$6 + 3\sqrt 5 = \left( {\frac{a}{b}} \right)$ . [

$a$ and

$b$ are integers,

$b \ne 0,a$ and

$b$ are co- primes]

$\begin{array}{l} \Rightarrow 3\sqrt { 5 } =\frac { a }{ b } -6 \\ \Rightarrow 3\sqrt { 5 } =\frac { { \left( { a-6b } \right) } }{ b } \\ \Rightarrow \sqrt { 5 } =\frac { { \left( { a-6b } \right) } }{ { 3b } } \end{array}$

$\therefore \frac{{\left( {a - 6b} \right)}}{{3b}}$ is a ration number.

So,

$\sqrt 5$ should also be rational number.

But

$\sqrt 5$ is irrational.

Which contradicts our assumption is wrong.

Therefore,

$\therefore 6 + 3\sqrt 5$ is irrational number.

Find the $HCF$ of the following
$18,54,81$

Write the numbers as product of their prime factors,

$18 = 2 \times 3 \times 3$

$54 = 2 \times 3 \times 3 \times 3$

$81 = 3 \times 3 \times 3 \times 3$

Hence,

$HCF \left( 18, 54, 81 \right) = {3}\times3$

$= 9$

Prove that $\dfrac { 1 } { 2 - \sqrt { 5 } }$ is a irrational number

1192761_1310010_ans_b2b68a331e33490e89a402526fb571a4.jpg

Prove that following is inrrational number :
i) $3-\sqrt{2}$

If possible, let

$3-\sqrt{2}$ be rational. Then,

$(3-\sqrt{2})$ is rational, 3 is rational

$\implies {(3-\sqrt{2})-3}$ is rational [Difference of rationals is rational]

$\implies \sqrt{2}$ is rational.

$\sqrt{2}$ is rational, let its simplest form be

$\dfrac{a}{b}$ .

Then, a and b are integers having no common factor other than 1, and b

$\neq$ 0.

Now,

$\sqrt{2} = \dfrac{a}{b}$

$2b^{2}=a^{2}$

2 divides a

$^{2}$ . [2 divides 2b

$^{2}$ ]

2 divides a.

Let a = 2c for some integer c.

Therefore,

$2b^{2}=4c^{2}$

$b^{2}=2c^{2}$

2 divides b

$^{2}$ . [2 divides 2c

$^{2}$ ]

2 divides b.

Thus, 2 is a common factor of a and b.

But this contradicts the fact that a and b have no common factor other than 1.

Hence,

$\sqrt{2}$ is irrational.

Hence,

$3-\sqrt{2}$ is irrational.

Use Euclid's Division Algorithm to find the HCF of $726$ and $275$

HCF of 726 & 275

$726 = 275 \times 2 + 176$

$275 = 176 \times 1 + 99$

$176 = 99 \times 1 + 77$

$99 = 77 \times 1 + 22$

$77 = 22 \times 3 + 11$

$22 = 11 \times 2 + 0$

$\therefore$ HCF of 726 & 275 is 11

1212516_1363726_ans_4791d6e5a183444085944a756e64776f.jpg

Prove that $3+2\sqrt {5}$ is an irrational numbers

Let us assume on contrary that

$3+2\sqrt{5}$ is rational. Then there exists

co-prime positive integers a and b such that

$3+2\sqrt{5} = \dfrac{a}{b}$

$2\sqrt{5} = \dfrac{a}{b}-3$

$\sqrt{5} = \dfrac{a-3b}{3b}$

$\implies \sqrt{5}$ is rational.

$\sqrt{5}$ is rational then, there exist co-prime positive integers a and b such that

$\sqrt{5}=\dfrac{a}{b}$

$5b^{2}=a^{2}$

$5|a^{2}$

$[ 5|5b^{2}]$

$5|a$ ....(1)

$a=5c$ for some positive integer c.

$a^{2}=25c^{2}$

$5b^{2}=25c^{2}$

$b^{2}=5c^{2}$

$5|b^{2}$

$5|b$ .....(2)

From equations 1 & 2, we find that a and b have at least 5 as a common factor.

This contradicts the fact that and b are co-prime.

Hence,

$\sqrt{5}$ is irrational.

So, our assumption is wrong and

$3+2\sqrt{5}$ is irrational.

Find the H.C.F of $3,9,81,27$

Factors of

$3=3\times 1$

Factors of

$9=3\times 3$

Factors of

$81=3\times 3\times 3\times 3$

Factors of

$27=3\times 3\times 3$

H.C.F

$=3$

Find HCF of $45$ and $72$

$45=3\times 3\times 5\\72=2\times 2\times 2\times 3\times3\\HCF=3\times 3=9$

Verify whether the rational expression $\dfrac{x^2-1}{(2x+1)(x+2)}$ is in its lowest terms.

The given rational expression can be written as

$\dfrac{(x+1)(x-1)}{(2x+1)(x+2)}$ and clearly HCF of numerator and denominator of the given expression is 1.

Therefore, it is in its lowest terms.

Find $HCF$ of $81$ and $243$

$81=3\times3\times3\times3\\$

$243=3\times3\times 3\times 3\times 3\\$

$HCF=3\times3\times3\times3=81$

Find the H.C.F of $2,8,32,10$

Let's first find the prime factorization of each of the given numbers

$2=2^1$

$8=2\times 2\times 2=2^3$

$32=2\times 2\times 2\times 2\times 2=2^5$

$10=2\times 5$

So common factor is

$2$

and the lowest power of common factor is

$1$

$\therefore$ H.C.F

$=2^1=2$

Prove that the following are irrational.
$\sqrt{3}+\sqrt{5}$

Let √3 + √5 be a rational number , say r

then √3 + √5 = r

On squaring both sides,

(√3 + √5)² = r²

3 + 2 √15 + 5 = r²

8 + 2 √15 = r²

2 √15 = r² - 8

√15 = (r²- 8) / 2

Now (r² - 8) / 2 is a rational number and √15 is an irrational number .

Since a rational number cannot be equal to an irrational number . Our assumption that √3 + √5 is rational wrong .

If $n$ is an odd integer then show that ${n^2} - 1$ is divisible by 8

Any odd positive integer is in the form of 4p+1 & 4p+3 for n=4p+1

$(n^{2}-1)=(1p+1)^{2}-1=16p^{2}+8p+1=16p^{2}+8p=8p(2p+1)$

$=(n^{2}-1)$ is divisible by 8.

$(n^{2}-1)=(4p+3)^{2}-1=8(2p^{2}+3p+1)$

$\Rightarrow n^{2}-1$ is divisible by 8

$n^{2}-1$ is divisible by 8

1212964_1404805_ans_77bc6b03634e4f8fb38837551eaadc15.jpg

Prove that : $\frac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}$

$\dfrac{\sqrt{3}-1}{\sqrt{3}+1}=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\times \dfrac{\sqrt{3}-1}{\sqrt{3}-1}=\dfrac{(\sqrt{3}-1)^2}{(\sqrt{3})^2-1^2}=\dfrac{(\sqrt{3})^2+(1)^2-2\sqrt{3}}{3-1}=\dfrac{4-2\sqrt{3}}{2}=2-\sqrt{3}$

Write pair of irrational numbers whose sum is irrational

${\textbf{Step - 1: Writing any pair of irrational number}}{\text{.}}$

${\text{We will get an irrational number if two numbers do not cancel each other}}{\text{.}}$

${\text{As we know that the sum of irrational numbers }}$

${\text{can be both rational and irrational numbers,}}$

${\text{so carefully choose the pair of number}}{\text{.}}$

${\text{ We can write any pair of irrational with same sign}}$

$\sqrt 2 + 2\sqrt 2 = 3\sqrt 2$

${\textbf{Hence, A pair of irrational numbers whose sum irrational is }}\sqrt 2 + 2\sqrt 2 = 3\sqrt 2 \;$

Find the $H.C.F$ of $3,6,9.$

Factors of

$3$ are,

$3=3\times 1$

Factors of

$6$ are,

$6=3\times 2$

Factors of

$9$ are,

$9=3\times 3$

Hence, only

$3$ is the common factor of

$3,6,9$ hence,

$H.C.F(3,6,9)=3.$

Find the highest common factor of the monomial.
$6a^{2}b^{2}c$ and $27 abc^{3}$

Factors of

$6{a}^{2}{b}^{2}c=2\times 3\times a\times a\times b\times b\times c$

Factors of

$27ab{c}^{3}=3\times 3\times 3\times a\times b\times c\times c\times c$

Common factors

$=3\times a\times b\times c$

$\therefore$ H.C.F

$=3abc$

Find the H.C.F of $4,7,8$

H.C.F of

$4,7,8$

Factors of

$4=2\times 2 \times 1$

Factors of

$7=7\times 1$

Factors of

$8=2\times 2\times 2 \times 1$

H.C.F

$=1$

Write the rational number $13.\overline {514}$ in $\dfrac{p}{q}$ form.

Let

$x=13.514514$ …

$\Rightarrow 1000x=13514.514$

$1000x-x=|350|$

$\Rightarrow 999x=|350|$

$\Rightarrow x=\dfrac{|350|}{999}$ .

1207994_1392605_ans_3fe7e99c825043fea545f5f40bc5bbfd.jpg

Find the H.C.F of $7,14,3$ .

To find: H.C.F of

$7,14,3$

Factors of

$7=7\times 1$

Factors of

$14=7\times 2 \times 1$

Factors of

$3=3\times 1$

H.C.F

$=1$ as there is no common prime factor except

$1$ .

Find the H.C.F of the given numbers by prime factorisation method :
$105 , 140 , 175$

Prime factorisation of given numbers are :

$105 = 3 \times 5 \times 7$

$140 = 2 \times 2 \times 5 \times 7$

$165 = 5 \times 5 \times 7$
Notice that

$5$ occurs as a common prime factor at least factor one time and

$7$ one time in given numbers.

$\therefore \,$ H.C.F

$= 5 \times 7 = 35$

Find the HCF of 96 and 404 by prime factorization method.

$96 = 2 \times 2 \times 2 \times 2 \times 2 \times 3$

$404 = 2 \times 2 \times 101$
Common prime factor for both the number is 2

$\therefore$ H.C.F

$= 2 \times 2 = 4$ .
1849629_1588280_ans_3cf96e721d654e92a8563fd2bbfa755a.png

Find the HCF of the following.
$8$ and $12$ .

$8=2\times2\times2$

$12=2\times2\times3$

HCF is

$2$

Prove that $\sqrt{2}$ is an irrational number. Hence show that $3 - \sqrt{2}$ is irrational.

Let us consider $\sqrt{2}$ be a rational number, then

$\sqrt{2} = p/q$ , where ‘p’ and ‘q’ are integers, $q \neq 0$ and p, q have no common factors (except 1).

So,

$2 = p^2 / q^2$

$p^2 = 2q^2$ …. (1)

As we know, ‘ $2$ ’ divides $2q^2$ , so ‘ $2$ ’ divides $p^2$ as well. Hence, ‘ $2$ ’ is prime.

So $2$ divides p

Now, let $p = 2k$ , where ‘k’ is an integer

Square on both sides, we get

$p^2 = 4k^2$

$2q^2 = 4k^2$ [Since, $p^2 = 2q^2$ , from equation (1)]

$q^2 = 2k^2$

As we know, ‘ $2$ ’ divides $2k^2$ , so ‘ $2$ ’ divides $q^2$ as well. But ‘ $2$ ’ is prime.

So $2$ divides q

Thus, p and q have a common factor of $2$ . This statement contradicts that ‘p’ and ‘q’ has no common factors (except 1).

We can say that $\sqrt{2}$ is not a rational number.

$\sqrt{2}$ is an irrational number.

Now, let us assume $3 -\sqrt{2}$ be a rational number, ‘r’

So, $3 -\sqrt{2}= r$

$3 – r = \sqrt{2}$

We know that, ‘r’ is rational, ‘ $3- r$ ’ is rational, so ‘ $\sqrt{2}$ ’ is also rational.

This contradicts the statement that $\sqrt{2}$ is irrational.

So, $3- \sqrt{2}$ is an irrational number.

Hence proved.

Prove that $\dfrac{1}{\sqrt{11}}$ is an irrational number.

Let us consider $1/\sqrt{11}$ be a rational number, then

$1/\sqrt{11} = p/q$ , where ‘p’ and ‘q’ are integers, $$q \neq 0$$ and p, q have no common factors (except 1).

So,

$1/11 = p^2 / q^2$

$q^2 = 11p^2$ …. (1)

As we know, ‘ $11$ ’ divides $11p^2$ , so ‘ $11$ ’ divides $q^2$ as well. Hence, ‘ $11$ ’ is prime.

So $11$ divides q

Now, let $q = 11k$ , where ‘k’ is an integer

Square on both sides, we get

$q^2 = 121k^2$

$11p^2 = 121k^2$ [Since, $q^2 = 11p^2$ , from equation (1)]

$p^2 = 11k^2$

As we know, ‘ $11$ ’ divides $11k^2$ , so ‘ $11$ ’ divides $p^2$ as well. But ‘ $11$ ’ is prime.

So $11$ divides p

Thus, p and q have a common factor of $11$ . This statement contradicts that ‘p’ and ‘q’ has no common factors (except 1).

We can say that $1/\sqrt{11}$ is not a rational number.

$1/\sqrt{11}$ is an irrational number.

Hence proved.

Find the $HCF$ of $28$ and $126$ by prime factor method.

Prime factorization of

$28$

$28 = 2 \times 2 \times 7 = {2}^{2} \times {7}^{1}$

Prime factorization of

$126$

$126 = 2 \times 3 \times 3 \times 7 = {2}^{1} \times {3}^{2} \times {7}^{1}$

Therefore,

$HCF{\left( 28, 126 \right)} = {2}^{1} \times {3}^{0} \times {7}^{1} = 14$

The HCF of two or more given numbers is the highest of their common ______,

The HCF of two or more given numbers is the highest of their common Factor

Find the H.C.F of the given numbers by prime factorisation method :
$54 , 72 , 90$

Prime factorisation of the given numbers are :

$54 = 2 \times 3 \times 3 \times 3$

$72 = 2 \times 2 \times 2 \times 3 \times 3$

$90 = 2 \times 3 \times 3 \times 5$
Notice that

$2$ occurs as a common prime factor at least one times and

$3$ at least two times in given numbers.

$\therefore \,$ H.C.F

$= 2 \times 3 \times 3 = 18$

What is the HCF of two consecutive numbers?

HCF of two consecutive numbers is always 1 .

explanation : Take two consecutive numbers as 9 and 10. between these two numbers there is no common factor other than 1.

Take two consecutive numbers as 17 and 18. These two numbers do not have any factor common in them other than 1.

Prove that $7-\sqrt{5}$ is an irrational number.

Let

$7 - \sqrt{5}$ is a rational number.

$7 + \sqrt{5} = \dfrac{a}{b} , b \neq 0$ ..........(i)
Where a and b co-prime integer number.
Equation (i) can be written as

$\sqrt{5} = \dfrac{a}{b} - 7$

or

$\sqrt{5} = \dfrac{a - 7b}{b}$ .........(ii)

Since, a and b are integers. So

$\dfrac{a - 7b}{b}$ will be rational number, so from equation (ii) we find that

$\sqrt{5}$ is a rational number. But we know that

$\sqrt{5}$ is a irrational number.
So this result is contradicted.
So our hypothesis is wrong.
Hence,

$7 + \sqrt{5}$ is a rational number.
Hence proved.

Prove that the following numbers are irrational: $\sqrt{2} + \sqrt{5}$

$\sqrt{2} + \sqrt{5}$

Now, let us assume $\sqrt{2} + \sqrt{5}$ be a rational number, ‘r’

So, $\sqrt{2} + \sqrt{5} = r$

$\sqrt{5} = r – \sqrt{2}$

Square on both sides,

$(\sqrt{5})2 = (r – \sqrt{2})2$

$5 = r^2 + (\sqrt{2})2 – 2r\sqrt{2}$

$5 = r^2 + 2 – 2\sqrt{2}r$

$5 – 2 = r^2 – 2\sqrt{2}r$

$r^2 – 3 = 2\sqrt{2}r$

$(r^2 – 3)/2r = \sqrt{2}$

We know that ‘r’ is rational, ‘ $(r^2 – 3)/2r$ ’ is rational, so ‘ $\sqrt{2}$ ’ is also rational.

This contradicts the statement that $\sqrt 2$ is irrational.

So, $\sqrt{2} +\sqrt{5}$ is an irrational number.

Prove that the following numbers are irrational: $2\sqrt{3} 7$

$2\sqrt{3} – 7$

Now, let us assume $2\sqrt{3} – 7$ be a rational number, ‘r’

So, $2\sqrt{3} – 7 = r$

$2\sqrt{3} = r + 7$

$\sqrt{3} = (r + 7)/2$

We know that ‘r’ is rational, ‘ $(r + 7)/2$ ’ is rational, so ‘ $\sqrt{3}$ ’ is also rational.

This contradicts the statement that $\sqrt{3}$ is irrational.

So, $2\sqrt{3} – 7$ is an irrational number.

Without actually performing the king division, State whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion: $\dfrac{23}{75}$

$$23/75$$ hence NON-terminating.

denominator is NOT multiple of $2^{m}\times 5^{n}$ hence NON-terminating.

It is a non-terminating repeating decimal.

1722298_1810519_ans_cddcab0f3ac84c23bf44ccbb6687e067.jpg

Without actually performing the king division, State whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion: $\dfrac{6}{15}$

Let us divide both numerator and denominator by $3$

$6/15=(6\div 3)/(15 \div 3)$

$= 2/5$

Since the denominator is $5$ .

It is a terminating decimal.

State which of the following are irrational numbers.
$3/\sqrt 3$

$3/\sqrt 3$

Let us simplify,

By rationalizing, we get

$3/\sqrt 3=3\sqrt{3}/(\sqrt 3 \times \sqrt 3)$

= $3\sqrt 3/3$

$= \sqrt 3$

Hence, it is an irrational number

Prove that the following numbers are irrational: $3 5\sqrt{3}$

$3 – 5\sqrt{3}$

Now, let us assume $3 – 5\sqrt{3}$ be a rational number, ‘r’

So, $3 – 5\sqrt{3} = r$

$3 – r = 5\sqrt{3}$

$(3 – r)/5 = \sqrt{3}$

We know that ‘r’ is rational, ‘ $(3 – r)/5$ ’ is rational, so ‘ $\sqrt{3}$ ’ is also rational.

This contradicts the statement that $\sqrt{3}$ is irrational.

So, $3 – 5\sqrt{3}$ is an irrational number.

State whether number is irrational or rational.
$-\dfrac{2}{3} + \sqrt[3]{2}$

$-\dfrac{2}{3} + \sqrt[3]{2}$

Let us simplify,

$-\dfrac{2}{3} + \sqrt[3]2 = -\dfrac{2}{3} + 2^{\dfrac{1}{3}}$

Since, $2$ is not a perfect cube.

Hence it is an irrational number.

Classify the numbers as rational or irrational :
$345.0\overline{456}$

Let $x = 345.0456456$

Multiplying by $10$ on both sides, we get

$10x = 3450.456456$

Since there is three repeating digit after the decimal point,

Multiplying by $1000$ on both sides, we get

$1000x = 3450456.456456$ …

Now, subtract both the values,

$10000x – 10x = 3450456 – 345$

$9990x = 3450111$

$x = 3450111/9990$

Since it is a non-terminating repeating decimal.

$345.0\overline{456}$ is a rational number.

State which of the following are rational or irrational decimals.
$-\sqrt{(2/49)}, 3/200, \sqrt{(25/3)}, -\sqrt{(49/16)}$

$-\sqrt{(2/49)}, 3/200, \sqrt{(25/3)}, -\sqrt{(49/16)}$

$-\sqrt{(2/49)} = -\sqrt 2/7$

$3/200 = 3/200$

$\sqrt{(25/3)} = 5/\sqrt 3$

$-\sqrt{(49/16)} = -7/4$

So,

$-\sqrt{2}/7$ and $5/\sqrt 3$ are irrational decimals.

$3/200$ and $-7/4$ are rational decimals.

State which of the following are irrational numbers.
$3 \sqrt{(7/25)}$

$3 – \sqrt{(7/25)}$

Let us simplify,

$3 – \sqrt{(7/25)} = 3 – \sqrt 7/\sqrt {25}$

$= 3 – \sqrt 7/5$

Hence, $3 – \sqrt 7/5$ is an irrational number.

Using the prime factor method, find the $H.C.F.$ of:
$5$ and $8$

(i) The prime factors of

$5$ and

$8$ are as follows:

$P_5 = 5$

$P_8 = 2 \times 2 \times 2$
No common prime factors between

$5$ and

$8$
Hence,

$H.C.F.$ of

$5$ and

$8 = 1$

Using the prime factor method, find the $H.C.F.$ of:
$40, 60$ and $80$

The prime factors of

$40, 60$ and

$80$ are as follows:

$P_{40} = 2 \times 2 \times 2 \times 5$

$P_{60} = 2 \times 2 \times 3 \times 5$

$P_{80} = 2 \times 2 \times 2 \times 2 \times 5$
Common prime factors between

$40, 60$ and

$80$

$=2 \times 2 \times 5$
Hence,

$H.C.F.$ of

$40, 60$ and

$80 = 20$

Using the prime factor method, find the $H.C.F.$ of:
$24$ and $49$

The prime factors of

$24$ and

$49$ are as follows:

$P_{24} = 2 \times 2 \times 2 \times 3$

$P_{49} = 7 \times 7$
No common prime factors between

$24$ and

$49$
Hence,

$H.C.F.$ of

$24$ and

$49 = 1$

Prove the following are irrational numbers.
$\sqrt[3]3$

$\sqrt[3]3$

We know that $\sqrt[3]3 = 3^{1/3}$

Let us consider $3^{1/3} = p/q$ , where p, q are integers, q>0.

p and q have no common factors (except 1).

So,

$3^{1/3} = p/q$

$3 = p^3/q^3$

$p^3 = 3q^3$ ….. (1)

We know that $3$ divides $3q^3$ then $3$ divides $p^3$

So, $3$ divides p

Now, let us consider $p = 3k$ , where k is an integer

Substitute the value of p in (1), we get

$p^3 = 3q^3$

$(3k)^3 = 3q^3$

$9k^3 = 3q^3$

$3k^3 = q^3$

We know that, $3$ divides $9k^3$ then $3$ divides $q^3$

So, $3$ divides q

Thus p and q have a common factor ‘3’.

This contradicts the statement, p and q have no common factor (except 1).

Hence, $∛3$ is an irrational number.

State which of the following are irrational numbers.
$$(3 + \sqrt 5)^2$$

$(3 + \sqrt 5)^2$

Let us simplify,

By using $(a + b)^2 = a^2 + b^2 + 2ab$

$(3 + \sqrt 5)^2 = 3^2 + (\sqrt 5)^2 + 2.3.\sqrt 5$

$= 9 + 5 + 6\sqrt 5$

$= 14 + 6\sqrt 5$

Hence, it is an irrational number.

Prove the following are irrational numbers. $\sqrt[3]{2}$

$\sqrt[3]2$

We know that $\sqrt[3]2 = 2^{1/3}$

Let us consider $2^{1/3} = p/q$ , where p, q are integers, q>0.

p and q have no common factors (except 1).

So,

$2^{1/3} = p/q$

$2 = p^3/q^3$

$p^3 = 2q^3$ ….. (1)

We know that $2$ divides $2q^3$ then $2$ divides $p^3$

So, $2$ divides p

Now, let us consider $p = 2k$ , where k is an integer

Substitute the value of p in (1), we get

$p^3 = 2q^3$

$(2k)^3 = 2q^3$

$8k^3 = 2q^3$

$4k^3 = q^3$

We know that, $2$ divides $4k^3$ then $2$ divides $q^3$

So, $2$ divides q

Thus p and q have a common factor ‘2’.

This contradicts the statement, p and q have no common factor (except 1).

Hence, $\sqrt[3]2$ is an irrational number.

State which of the following are irrational numbers.
$(2/5 \sqrt{7})^2$

$(2/5 \sqrt 7)^2$

Let us simplify,

$(2/5 \sqrt 7)^2 = (2/5 \sqrt 7) \times (2/5 \sqrt 7)$

$= 4/ (25 \times 7)$

$= 4/175$

Hence it is a rational number.

State which of the following are irrational numbers.
$-2/7 \sqrt[3] 5$

$-2/7 \sqrt[3] 5$

Let us simplify,

$-2/7 \sqrt[3] 5 = -2/7 (5)^{1/3}$

Since $5$ is not a perfect cube.

Hence it is an irrational number.

Prove the following are irrational numbers.
$\sqrt[4]5$

We know that $\sqrt[4]5 = 5^{1/4}$

Let us consider $5^{1/4} = p/q$ , where p, q are integers, q>0.

p and q have no common factors (except 1).

So,

$5^{1/4} = p/q$

$5 = p^4/q^4$

$P^4 = 5q^4$ ….. (1)

We know that $5$ divides $5q^4$ then $5$ divides $p^4$

So, $5$ divides p

Now, let us consider $p = 5k$ , where k is an integer

Substitute the value of p in (1), we get

$P^4 = 5q^4$

$(5k)^4 = 5q^4$

$625k^4 = 5q^4$

$125k^4 = q^4$

We know that, $5$ divides $125k^4$ then $5$ divides $q^4$

So, $5$ divides q

Thus p and q have a common factor ‘ $5$ ’.

This contradicts the statement, p and q have no common factor (except 1).

Hence, $\sqrt[4]5$ is an irrational number.

State which of the following are irrational numbers.
$(2 \sqrt 3) (2 + \sqrt 3)$

$(2 – \sqrt 3) (2 + \sqrt 3)$

Let us simplify,

By using the formula,

$(a + b) (a – b) = (a)^2 -(b)^2$

$(2 – \sqrt 3) (2 + \sqrt 3) = (2)^2 – (\sqrt 3)^2$

$= 4 – 3$

$= 1$

Hence, it is a rational number.

Prove that each of the following numbers is irrational:
$\sqrt{3}+\sqrt{2}$

$\sqrt{3}+\sqrt{2}$
Let

$\sqrt{3}+\sqrt{2}$ be a rational number.

$\Rightarrow \sqrt{3}+\sqrt{2}=x$
Squaring on both the sides, we get

$(\sqrt{3}+\sqrt{2})^{2}=x^{2}$

$\Rightarrow 3+2+2 \times \sqrt{3} \times \sqrt{2}=x^{2}$

$\Rightarrow x^{2}-5=2 \sqrt{6}$

$\Rightarrow \sqrt{6}=\dfrac{x^{2}-5}{2}$
Here,

$\mathrm{x}$ is a rational number.

$\Rightarrow \mathrm{x}^{2}$ is a rational number.

$\Rightarrow \mathrm{x}^{2}-5$ is a rational number.

$\Rightarrow \dfrac{x^{2}-5}{2}$ is also a rational number.

$\Rightarrow \dfrac{x^{2}-5}{2}=\sqrt{6}$ is a rational number.
But

$\sqrt{6}$ is an irrational number.

$\Rightarrow \dfrac{x^{2}-5}{2}$ is an irrational number.

$\Rightarrow \mathrm{x}^{2}-5$ is an irrational number.

$\Rightarrow \mathrm{x}^{2}$ is an irrational number.

$\Rightarrow \mathrm{x}$ is an irrational number.
But we have assume that

$x$ is a rational number.

$\therefore$ we arrive at a contradiction. So, our assumption that

$\sqrt{3}+\sqrt{2}$ is a rational number is wrong.

$\therefore \sqrt{3}+\sqrt{2}$ is an irrational number.

Use a method of your own choice to find the $H.C.F.$ of:
$30, 60, 90,$ and $105$

$30, 60, 90,$ and

$105$
The prime factors

$30, 60, 90$ and

$105$ are as follows:

${30} = 2 \times 3 \times 5$

${60} = 2 \times 2 \times 3 \times 5$

${90} = 2 \times 3 \times 3 \times 5$

${105} = 3 \times 5 \times 7$
The common factors of

$30, 60, 90$ and

$105 = 3 \times 5$

$∴ H.C.F.$ of

$30, 60, 90$ and

$105 = 15$

Using the prime factor method, find the $H.C.F.$ of:
$12, 16$ and $28$

The prime factors of

$12, 16$ and

$28$ are as follows:

$P_{12} = 2 \times 2 \times 3$

$P_{16} = 2 \times 2 \times 2 \times 2$

$P_{28} = 2 \times 2 \times 7$
Common prime factors between

$12, 16$ and

$28 = 2 \times 2$
Hence,

$H.C.F.$ of

$12, 16$ and

$28 = 2 \times 2 = 4$

Use a method of your own choice to find the H.C.F. of:
$45, 75$ and $135$

$45, 75$ and

$135$
The prime factors of

$45, 75$ and

$135$ are as follows:

${45} = 3 \times 3 \times 5$

${75} = 3 \times 5 \times 5$

${135} = 3 \times 3 \times 3 \times 5$
The common factors of

$45, 75$ and

$135 = 3 \times 5$

$∴ H.C.F.$ of

$45, 75$ and

$135 = 15$

Write the denominators of the following rational number in $2^{n}5^{m}$ form where $n$ and $m$ are non-negative integers and then write them in their decimal form.
$\dfrac{80}{100}$

$\dfrac{80}{100}=\dfrac{80}{2^{2}*5^{2}}=\dfrac{80}{10^{2}}=0.80$ .

$\therefore$ The decimal form of

$\dfrac{80}{100}=0.8$ .

Use method of contradiction to show that $\sqrt{3}$ and $\sqrt{5}$ are irrational.

Let us suppose that

$\sqrt{3}$ and

$\sqrt{5}$ are rational numbers

$\sqrt{3}=\dfrac{a}{b} \quad$ and

$\sqrt{5}=\dfrac{x}{y} \quad($ Where

$a, b \in 7$ and

$b, y \neq 0 x, y)$
Squaring both sides

$3=\dfrac{a^{2}}{b^{2}} \quad, 5=\dfrac{x^{2}}{y^{2}}$

$\left.3 b^{2}=a^{2} \quad, 5 y^{2}=x^{2}\right\} \quad \ldots(*)$

$\Rightarrow \mathrm{a}^{2}$ and

$\mathrm{x}^{2}$ are odd as

$3 \mathrm{b}^{2}$ and

$5 \mathrm{y}^{2}$ are odd

$\Rightarrow \mathrm{a}$ and

$\mathrm{x}$ are odd.... (1)
Let

$a=3 c, x=5 z$

$a^{2}=9 c^{2}, x^{2}=25 z^{2}$

$3 b^{2}=9 c^{2}, 5 y^{2}=25 z^{2}\left(\right.$ From equation

$\left(^{*}\right)$

$\Rightarrow b^{2}=3 c^{2}, y^{2}=5 z^{2}$

$\Rightarrow \mathrm{b}^{2}$ and

$\mathrm{y}^{2}$ are odd as

$3 \mathrm{c}^{2}$ and

$5 \mathrm{z}^{2}$ are odd

$\Rightarrow \mathrm{b}$ and

$\mathrm{y}$ are

$\operatorname{odd} \ldots(2)$
From equation (1) and (2) we get a, b,

$x, y$ are odd integers.
i.e.,

$a, b,$ and

$x, y$ have common factors 3 and 5 this contradicts our assumption that

$\dfrac{a}{b}$ and

$\dfrac{x}{y}$ are rational i.e,

$a, b$ and

$x, y$ do not have any common factors other than.

$\Rightarrow \dfrac{a}{b}$ and

$\dfrac{x}{y}$ is not rational

$\Rightarrow \sqrt{3}$ and

$\sqrt{5}$ are irrational.

Using the prime factor method, find the $H.C.F.$ of:
$48, 84$ and $88$

The prime factors of 48, 84 and 88 are as follows:

$P_{48} = 2 \times 2 \times 2 \times 2 \times 3$

$P_{84} = 2 \times 2 \times 3 \times 7$

$P_{88} = 2 \times 2 \times 2 \times 11$
Common prime factors between

$48, 84$ and

$88$

$= 2 \times 2$
Hence,

$H.C.F.$ of

$48, 84$ and

$88$

$= 2 \times 2 = 4$

Use a method of your own choice to find the $H.C.F.$ of:
$24, 36, 60$ and $132$

$24, 36, 60$ and

$132$
The prime factors of

$24, 36, 60$ and

$132$ are as follows:

${24} = 2 \times 2 \times 2 \times 3$

${36} = 2 \times 2 \times 3 \times 3$

${60} = 2 \times 2 \times 3 \times 5$

${132} = 2 \times 2 \times 3 \times 11$
The common factors of

$24, 36, 60$ and

$132 = 2 \times 2 \times 3$

$∴ H.C.F.$ of

$24, 36, 60$ and

$132 = 12$

Use a method of your own choice to find the H.C.F. of:
$48, 36$ and $96$

$48, 36$ and

$96$
The prime factors of

$48, 36$ and

$96$ are as follows:

${48} = 2 \times 2 \times 2 \times 2 \times 3$

${36} = 2 \times 2 \times 3 \times 3$

${96} = 2 \times 2 \times 2 \times 2 \times 2 \times 3$
The common factors of

$48, 36$ and

$96 = 2 \times 2 \times 3$

$∴ H.C.F.$ of

$48, 36$ and

$96 = 12$

Use a method of your own choice to find the H.C.F. of:
$66, 33$ and $132$

$66, 33$ and

$132$
The prime factors of

$66, 33$ and

$132$ are as follows:

${66} = 2 \times 3 \times 11$

${33} = 3 \times 11$

${132} = 2 \times 2 \times 3 \times 11$
The common factors of

$66, 33$ and

$132 = 3 \times 11$

$∴ H.C.F.$ of

$66, 33$ and

$132 = 33$

Using Euclid's algorithm, find the HCF of 2048 and 960.

If the HCF of 408 and 1032 will be written using Euclid's algorithm,

$2048=960\times 2+128$

$960=128\times 7+64$

$128=64\times 2+0$
Now, the remainder becomes

$0$ .
Therefore, the HCF of 2048 and 960 is 64.

Show that $x$ is rational if:
$x^{2}=0.0004$

$x^{2}=0.0004$

$\Rightarrow x=\sqrt{0.0004}=\sqrt{\dfrac{4}{10000}}=\dfrac{2}{100}=0.02,$ which is rational.

Classify the following numbers as rational or irrational:
$\sqrt{23}$

$\sqrt{23}=4.795831523..........$
The decimal expansion is non terminating non-recurring.

$\therefore \sqrt{23}$ is a irrational number.

Classify the following numbers as rational or irrational:
$0.3796$

$0.3796$ is the decimal expansion is terminating.
So

$0.3796$ is a rational number.

Prove that each of the following numbers is irrational:
$\sqrt{5}-2$

$\sqrt{5}−2$
Let

$\sqrt{5}−2$ be a rational number.

$\Rightarrow \sqrt{5}−2=x$
Squaring on both the sides, we get

$(\sqrt{5}−2)^2=x^2$

$\Rightarrow 5+4−2\times2\times \sqrt{5}=x^2$

$\Rightarrow 9−x^2=4\sqrt{5}$

$\Rightarrow \sqrt{5}=\dfrac{9−x^2}{4}$

Here,

$x$ is a rational number.

$x^2$ is a rational number.

$\Rightarrow 9−x^2$ is a rational number.

$\Rightarrow \dfrac{9−x^2}{4}$ is also a rational number

$\Rightarrow \sqrt{2}=\dfrac{11−x^2}{6}$ is a rational number

But

$\sqrt{2}$ is an irrational number.

$\Rightarrow \sqrt{5}=\dfrac{9−x^2}{4}$ is an irrational number.

$\Rightarrow 9−x^2$ is an irrational number.

$\Rightarrow x^2$ is an irrational number.

$\Rightarrow x$ is an irrational number.
But we have assume that

$x$ is a rational number.
We arrive at a contradiction. So, our assumption that

$\sqrt{5}−2$ is a rational number is wrong.

$\because \sqrt{5}−2$ is an irrational number.

Show that $x$ is irrational if $x^{2}=27$

Given:

$x^{2}=27$

$\Rightarrow x=\sqrt{27}$

$=5.1961 ...$

Here,

$5.1961...$ is an irrational number, so

$x$ is an irrational number.

Use Euclids division algorithm to find the HCF of $441, 567, 693.$

The Euclidean Algorithm for finding HCF $(A,B)$ is as follows:

If $A = 0$ then HCF $(A,B)=B,$ since the HCF $(0,B)=B,$ and we can stop.

If $B = 0$ then HCF $(A,B)=A,$ since the HCF $(A,0)=A,$ and we can stop.

Write $A$ in quotient remainder form $(A = BQ + R)$

Find HCF $(B,R)$ using the Euclidean Algorithm since

HCF $(A,B) = HCF(B,R)$

Here, HCF of $441$ and $567$ can be found as follows:-

$567=441\times 1+126$

$\Rightarrow$ $441=126\times 3+63$

$\Rightarrow$ $126=63\times 2 + 0$

Since remainder is $0$ , therefore,

H.C.F of $\left( 441,567 \right)$ is $=63$

Now H.C.F of $63$ and $693$ is

$693=63\times11 +0$

Therefore, H.C.F of $\left( 63,693 \right) =63$

Thus, H.C.F of $\left( 441,567,693 \right) =63.$

State whether the following number is rational, If rational then enter $1$ and if false then enter $0$ .
$\displaystyle \left ( 2+\sqrt{2} \right )^{2}$

$\quad \\ (2+\sqrt { 2 } )^ 2=4+4\sqrt{2}+2 \quad....... \quad {(a+b)}^2 = a^2 +2ab+ b^2$

$\:As \quad \sqrt { 2 } \quad being\quad irrational,$

$\text {which is not in the form of} \frac {p}{q},\text {where p and q are integers and $$ q }\neq 0 .$

$\therefore$

$\text { the given number is irrational}$ .

State, whether the following number is rational,
If rational then enter $1$ and if false then enter $0$ .
$\displaystyle \left ( 5+\sqrt{5} \right )\left ( 5-\sqrt{5} \right )$

$\quad \\ \\ (5+\sqrt { 5 } )(5-\sqrt { 5 } )=25-5=20 \quad ......... (a-b)(a+b)= a^2-b^2\\ \text As \quad20 \quad is \quad rational \quad number \quad, \text {which is of the form} \frac {p}{q},\text {where p and q are integers and $$ q }\neq 0 .$

$\\ \therefore\quad Given \quad number \quad is\quad a\quad rational\quad number.\\$

State whether the following number is rational,
If rational then enter $1$ and if false then enter $0$ .
$\displaystyle \left ( 3-\sqrt{3} \right )^{2}$

$\quad \\ (3-\sqrt { 3 } )^ 2\ =9-6\sqrt{3}+3 \quad......(a-b)^2 = a^2 -2ab +b^2\\ As\quad \sqrt { 3 } \quad being\quad irrational, \text {which is not in the form of } \frac {p}{q},\text {where p and q are integers and $$ q }\neq 0 .$

$the\quad given\quad number\quad is\quad irrational.\\$

Use method of contradiction to show that $\displaystyle \sqrt{3}$ is irrational number.

Suppose for the sake of contradicton that

$\sqrt {3}$ is rational.
We know that rational

numbers are those numbers which can be expressed in the form

$\frac {p}{q}$ , where p and q are integers and

$q \neq 0$

Hence,

$\sqrt {3} = \frac {p}{q}$

where p and q are integers with no factor in common.

Squaring both sides,

$3 = \frac{{p}^{2}}{{q}^{2}}$

${p}^{2} = 3{q}^{2}$ -- (1)

That is, since

${p}^{2} = 3{q}^{2}$ , which is multiple of 3, means p itself must be a multiple of 3 such as

$p = 3n$ .

Now we have that

${ p }^{ 2 }=({ 3n) }^{ 2 }=9{ n }^{ 2 }$ ---- (2)

From (1) and (2),

$9{n}^{2} =3{q}^{2}$

$=> 3{n}^{2} ={q}^{2}$
This means, q is also a multiple of 3, contradicting the fact that p and q had no common

factors.

Hence,

$\sqrt {3}$ is an irrational number.

1128 $and$ 1464$$.

According to the definition of Euclid's theorem,

$a = b \times q + r$ where

$0 \leq r < b .$

Using Euclid's Method

$1464= 1128 \times 1+336$

$1128 = 336 \times3+120$

$336 = 120 \times 2+96$

$120 = 96\times 1+24$

$96 = 24\times 4 +0$

Hence H.C.F

$=24$

Prove that $7+\sqrt 2$ is irrational

Let us assume that

$7+\sqrt{2}$ is a rational number
Then. there exist coprime integers

$p$ ,

$q$ ,

$q\neq 0$ such that

$7+\sqrt{2}=\frac{p}{q}$

$=> \sqrt {2}=\frac {p}{q}-7$
Here,

$\frac {p}{q}-7$ is a rational number, but

$\sqrt{2}$ is a irrational number.
But, a irrational cannot be equal to a rational number.This is a contradiction.
Thus, our assumption is wrong.
Therefore

$7+\sqrt{2}$ is a irrational number.

Use Euclid's algorithm to find the HCF of $4052$ and $12576$ .

According to the definition of Euclid's theorem,

$a = b \times q + r$ where

$0 \leq r < b .$

Using euclid's algorithm

$12576 = 4052\times 3+420$

$4052 = 420 \times 9+272$

$420 = 272\times 1+148$

$272 = 148\times1+124$

$124 = 24\times 5+4$

$24=4\times6+0$

Therefore 4 is the H.C.F of 4052 and 12576

Use Euclid's division lemma to find the HCF of $13281$ and $15844$ .

The given numbers are

$13281$ and

$15844$

Using Euclid algorithm

$15844 = 13281\times 1+2563$

$13281 = 2563 \times 5 +466$

$2563= 466 \times 5+233$

$466 = 233\times 2 +0$

Hence H.C.F

$=233$

Find the HCF of 861 and 1353, using Euclid's algorithm

Using euclid's algorithm

$1353 = 861\times 1 +492$

$861 = 492\times1+369$

$492 = 369 \times 1+123$

$369 = 123\times 3+0$

Prove that $3-\sqrt 5$ is irrational

Let us assume that

$3-\sqrt{5}$ is a rational number
Then. there exist coprime integers

$p$ ,

$q$ ,

$q\neq 0$ such that

$3-\sqrt{5}=\dfrac{p}{q}$

$=> \sqrt 5=3-\dfrac {p}{q}$
Here,

$3-\dfrac {p}{q}$ is a rational number, but

$\sqrt 5$ is a irrational number.
But, a irrational cannot be equal to a rational number.
This is a contradiction.
Thus, our assumption is wrong.
Therefore

$3-\sqrt{5}$ is an irrational number.

Prove that $3-\sqrt 3$ is irrational

Let us assume that

$3-\sqrt{3}$ is a rational number
Then. there exist coprime integers

$p$ ,

$q$ ,

$q\neq 0$ such that

$3-\sqrt{3}=\dfrac{p}{q}$

$=> \sqrt {3}=3-\dfrac {p}{q}$
Here,

$3-\dfrac {p}{q}$ is a rational number, but

$\sqrt{3}$ is an irrational number.
But, an irrational cannot be equal to a rational number.This is a contradiction.
Thus, our assumption is wrong.
Therefore

$3-\sqrt{3}$ is an irrational number.

Use Euclid's division lemma to find th HCF of 10524 and 12752.

Using Euclid algorithm

$12752 = 10524 \times 1+2228$

$10524 = 2228\times4 +1612$

$2228 = 1612 \times 1 +616$

$1612 = 616 \times 2 +380$

$616 = 380\times 1+236$

$380 = 236 \times 1+144$

$236 = 144\times 1+92$

$144 = 92\times 1+52$

$92 = 52 \times 1 +40$

$52 = 40 \times 1 +12$

$40 = 12 \times 3+4$

$12 = 4 \times 3+0$

As there is 0 remainder,so deviser 4 is HCF

Hence H.C.F

$= 4$ .

Show that there is no positive integer n for which $\sqrt {n-1}+\sqrt {n+1}$ is rational.

Suppose there exists a positive integer

$n$ for which is a rational number.
Where p and q positive integers and

$q \neq 0$

$\Rightarrow \dfrac{q}{p}= \dfrac{1}{\sqrt{n-1}+ \sqrt{n+1}}$

$\Rightarrow \dfrac{q}{p} = \dfrac{\sqrt{n-1} - \sqrt{n+1}}{ \left(n-1\right) -\left(n+1\right)} = \dfrac{\sqrt{n-1}-\sqrt{n+1}}{-2}$

$\Rightarrow \dfrac{2q}{p} = \sqrt{n+1} -\sqrt{n-1}$

$\left(\sqrt{n-1}+\sqrt{n+1}\right)+\left(\sqrt{n+1}-\sqrt{n-1}\right) = \dfrac{p}{q} +\dfrac{2q}{p}$

$\Rightarrow 2\sqrt{n+1} = \dfrac{p^2 +2q^2}{pq}$

$\Rightarrow \sqrt{n+1} = \dfrac{p^2+2q^2}{2pq}$ .....(1)

$\left(\sqrt{n-1}+\sqrt{n+1}\right)-\left(\sqrt{n+1}-\sqrt{n-1}\right) = \dfrac{p}{q} -\dfrac{2q}{p}$

$\Rightarrow 2\sqrt{n-1} = \dfrac{p^2 -2q^2}{pq}$

$\Rightarrow \sqrt{n-1} = \dfrac{p^2-2q^2}{2pq}$ .....(2)

From eq1 and eq 2

$\sqrt{n+1} and \sqrt{n-1} \ are\ rational$

$\because p\ and \ q \ are \ integers \Rightarrow \dfrac{p^2+2q^2}{2pq} and \dfrac{p^2-2q^2}{2pq}$

$\Rightarrow n+1 \ and \ n-1 \ perfect \ square \ of \ positive \ integers$ .

Now

$\sqrt(n+1) - \sqrt(n-1) = 2$ which is not possible since any two perfect squares differ by at least

$3$ .

Hence there is no positive integer

$n$ for which is a rational number.

Prove that $\sqrt 7$ is irrational

Let us assume that

$\sqrt{7}$ is rational
It can be written as

$\sqrt{7}=\frac{a}{b}$ where

$a$ and

$b$ are integers in the lowest terms and

$b\neq 0$

$a$ and

$b$ are integers in the lowest terms, it means that donot share any common factors.
So, our equation can be written as

$7=\frac{a^2}{b^2}$ (by squaring both sides)

$=>7b^2=a^2$

Since, both sides are equal, if

$7$ divides the L.H.S., then it must also divide R.H.S. So we can rewrite '

$a$ ' as

$7k$ , where

$k$ is some integer and

$k\neq0$

$=>7b^2=(7k)^2$

$=>7b^2=49k^2$

$=>b^2=7k^2$

Similarly,

$b$ is also divisible by

$7$

Thus,

$a$ and

$b$ are divisible by

$7$
But,

$a$ and

$b$ are in the lowest terms and donot share any common factors.

Thus, we have a contradiction which means our assumption is wrong.
Therefore,

$\sqrt{7}$ is irrational

Find the greatest length which can be contained exactly in $10$ m $5$ dm $2$ cm $4$ mm and $12$ m $7$ dm $5$ cm $2$ mm.

$10\ m\ 5\ dm\ 2 \ cm\ 4 \ mm = 10524\ mm$

$1\ 2m\ 7\ dm\ 5cm\ 2mm = 12752\ mm$
The greatest length required is G.C.F of

$10524\ and \ 12752$
Using Euclid algorithm

$12752 = 10524 \times 1+2228$

$10524 = 2228\times4 +1612$

$2228 = 1612 \times 1 +616$

$1612 = 616 \times 2 +380$

$616 = 380\times 1+236$

$380 = 236 \times 1+144$

$236 = 144\times 1+92$

$144 = 92\times 1+52$

$92 = 52 \times 1 +40$

$52 = 40 \times 1 +12$

$40 = 12 \times 3+4$

$12 = 4 \times 3+0$
Hence G.C.F

$= 4mm$

Use Euclid's division algorithm to find the HCF of:
(i) $135$ and $225$ (ii) $196$ and $38220$ (iii) $867$ and $255$ .
Find the highest HCF among them.

(i) By Euclid's division lemma,

$225 = 135 \times 1 + 90$

$r = 90 \ne 0$

$135 = 90 \times 1 + 45$

$r = 45 \ne 0$

$90 = 45 \times 2 + 0$

$r = 0$

So,H.C.F of

$135$ and

$225$ is

$45$

(ii) By Euclid's division lemma,

$38220 = 196 \times 195 + 0$

$r = 0$

So, H.C.F of

$38220$ and

$196$ is

$196$

(iii) By Euclid's division lemma,

$867 = 255 \times 3 + 102$

$r = 102 \ne 0$

$255 = 102 \times 2 + 51$

$r = 51 \ne 0$

$102 = 51 \times 2 + 0$

$r = 0$

So, H.C.F of

$867$ and

$255$ is

$51$

The highest HCF among the three is

$196$ .

Find H.C.F of $81$ and $237$ .
Also express it as a linear combination of $81$ and $237$ i.e, H.C.F of $81,237 = 81x + 237 y$ for some $x, y$ .
[Note: Values of $x$ and $y$ are not unique]

According to the definition of Euclid's theorem,

$a = b \times q + r$ where

$0 \leq r < b .$

Since

$81 < 237$ , let us apply division algorithm to these numbers.

$81 |237|2$

$|162|$

$\overline {|75|}$

$\therefore 237=81\times 2+75$ ..... (1)
Since the remainder

$75\neq 0$

$\therefore$ we consider the divisor

$81$ and the remainder

$75$ .

Again by division algorithm,

$75\overline{)81(}1$

$\underline {75}$

$\underline {6}$

$\therefore 81=75\times 1+6$ .... (2)

Again consider divisor

$75$ and new remainder

$=6$ ,

$6\overline {)75(}12$

$\underline {75}$

$\underline {3}$ ... (3)

Again consider divisor

$6$ and new remainder

$= 3$ ,
By division algorithm,

$3\overline {)6(}2$

$\underline 6$

$\underline 0$

$\therefore 6=3\times 2+0$ ..... (4)

$\therefore$ The remainder

$=0$

$\therefore H.C.F.=3$

In order to write

$H.C.F.$ in form of

$81$ &

$237$ , we have

$3=75-6\times 12=75-(81-75\times 1)\times 12$

$=75-12\times 81+12\times 75=13\times 75-12\times 81$

$=13\times (237-81\times 2)-12\times 81$

$=13\times 237-26\times 81-12\times 81$

$=13\times 237-38\times 81$
Thus

$3=237y+81x$ where

$y=13$ and

$x=-38$

Prove that $(3-\sqrt 5)$ is an irrational number

If possible, suppose

$3-\sqrt 5$ is rational

$\Rightarrow 3-\sqrt 5=\frac {p}{q}$ , p and q are co-prime and

$q\neq 0$ .

$\Rightarrow \sqrt 5=3-\frac {p}{q}$

$\Rightarrow$ irrational number = rational - rational

$\Rightarrow$ irrational number = rational number
which is not possible

$\therefore$ Our supposition is wrong.
Hence,

$3-\sqrt 5$ is an irrational number.

Write the condition to be satisfied by $q$ so that a rational number $\dfrac {p}{q}$ has a terminating decimal expansion.

The rational number

$\dfrac {p}{q}$ where p and q are co-prime q will have a ferminating decimal expansion only if the prime factorisation of q is of the form

$2^n. 5^m$ , where n and m are non-negative integers.

If the H.C.F of $657$ and $963$ is expressible in the form $657 x -(963 \times 15)$ , find $x$ .

Using Euclid's division

$a=bq+r$

$963=657\times 1+306$

$657=306\times 2+45$

$306=45\times 6+36$

$45=36\times 1+9$

$36=9\times 4+0$

$\therefore$ H.C.F

$=9$

$\therefore 9=657x-(963\times 15)$

$657x=14454$

$x=22$

Use Euclid's division algorithm to find the H.C.F. of $6265$ and $76254$ .

H.C.F. of

$6265$ and

$76254$

$76254 = 6265 \times 12 + 1074$

$6265 = 1074 \times 5+895$

$1074=895 \times 1+179$

$895 =179 \times 5+0$
Hence, the H.C.F. of

$6265$ and

$76254$ is

$179$ .

Check if the rational number has terminating or non-terminating decimal expansion.
$\cfrac{211}{{2}^{5}\times {5}^{0}}$

Given rational number is

$\cfrac{211}{{2}^{5}\times {5}^{0}}$

We know that, a rational number has terminating decimal expansion only when its denominator is of the form

${2}^{m}\times {5}^{n}$ .

The given rational number has denominator

${2}^{5}\times {5}^{0}$ , which is of the form

${2}^{m}\times {5}^{n}$ .

Hence, the given rational number will have a terminating decimal expansion.

Check if $\dfrac{131}{{2}^{3}\times {5}^{4}}$ have terminating or non-terminating decimal expansion

If yes then answer $1$ , if no the answer $0$

$\cfrac{131}{{2}^{3}\times {5}^{4}}$ has terminating decimal expansion.

Expressing the denominator in the form of prime factorization in

$2$ and

$5$ .

$2\times2\times2\times5\times5\times5\times5$

We know that denominators that are expressed only in

$2$ and

$5$ have terminating decimal expansion.

Since the denominator does have it so it has terminating decimal expansion

Check if the rational number have terminating or non-terminating decimal expansion.

$\cfrac{23}{343}$

$\cfrac{23}{343}=\cfrac{23}{{7}^{3}}$ , so denominator is not of the form of

${2}^{m}\times {5}^{n}$
so its decimal expansion is non-terminating.

Classify the following numbers as rational or irrational:
(i) $\sqrt{23}$
(ii) $\sqrt{225}$
(iii) $0.3796$
(iv) $7.478478...$
(v) $1.101001000100001...$

Solve the given expressions

(1)

$\sqrt{23}=4.795831523..........$

The decimal expansion is non terminating non recurring.

$\therefore \sqrt{23}$ is a irrational number.

(2)

$\sqrt{225}=15$

$\therefore \sqrt{225}$ is a rational number.

(3)

$0.3796$ is the decimal expansion is terminating.

$0.3796$ is a rational number.

(4)

$7.478478......=7.\overline{478}$ is the decimal expansion is non termination and recurring.

$7.478478......$ is a rational number.

(5)

$1.101001000100001......$ is the decimal expansion is non termination and non recurring.

$71.101001000100001......$ is a irrational number.

Recall, $\pi$ is defined as the ratio of the circumference(say c) of a circle to its diameter(say d). That is, $\pi=\displaystyle\frac{c}{d}$ . This seems to contradict the fact that $\pi$ is irrational. How will you resolve this contradiction?

Here,

$\pi = \dfrac{22}{7}$

Now, it is in the form of

$\dfrac pq$ , which is a rational number, but this is an approximate value of

$\pi$ .

If you divide

$22$ by

$7$ , the quotient

$(3.14\cdots)$ is a non-terminating number i.e. it is irrational.

Approximate fractions include (in order of increasing accuracy)

$\dfrac{22}7, \dfrac{333}{106},\dfrac{355}{113}, \cdots$

If we divide anyone of these we get, the quotient

$(3.14\cdots)$ is a non-terminating number. i.e. it is irrational.

So,

There is no contradiction as either

$c$ or

$d$ irrational and

hence

$\pi$ is a irrational number.

State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form $\sqrt{m}$ , where $m$ is a natural number.
(iii) Every real number is an irrational number.

(i) True: Real numbers are any number which can we think.

Thus, every irrational number is a real number.

(ii) False: A number line may have negative or positive number.

Since, no negative can be the square root of a natural number, thus every point the the number line cannot be in the form of

$\sqrt{m}$ , where

$m$ is a natural number.

(iii) False: All numbers are real number and non terminating numbers are irrational number.

For example

$2, 3, 4,$ etc. are some example of real numbers and these are not irrational.

Look at several examples of rational numbers in the form $\displaystyle\frac{p}{q}(q\neq 0)$ , where $p$ and $q$ are integers with no common factors other than $1$ and having terminating decimal representaions (expansions). Can you guess what property $q$ must satisfy?

The property that

$q$ must satisfy in order that the rational numbers in the

from

$\dfrac{p}{q}$ , where

$p$ and

$q$ are integers with no

common factor other than

$1$ , have maintaining decimal representation is

prime factorization of

$q$ has only powers of

$2$ or power of

$5$ or both .

i.e

$2^{m}\times 5^{n}$ , where

$m=1,2,3,\cdots$ or

$n=1,2,3,\cdots$

Prove that $\displaystyle 4+5\sqrt { 3 }$ is an irrational number.

An irrational number can be written as a decimal, but not as a fraction.

An irrational number has endless non-repeating digits to the right of the decimal point.

$4+5\sqrt{3}=4+5(1.732050.....)=4+8.66025....=12.66025...$

As per definition

$4+5\sqrt{3}$ is an irrational number

The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational and of the form $p$ , you say about the prime factors of $q$ ?
(i) $43.123456789$ (ii) $0.. .$ (iii) $43.\overline{123456789}$

(i) 43.123456789

It has certain number of digits, so they can be represented in form of

$\dfrac{p}{q}$ .

Hence they are rational number.

As they have certain number of digits and the number which has certain

number of digits is always terminating number and for terminating number

denominator has prime factor

$2$ and

$5$ only.

(ii) 0.120120012000120000. . .

Here the prime factor of denominator Q will has a value which is not equal to

$2$ or

$5$ .

So, it is an irrational number as it is non-terminating and non-repeating.

(iii) $43.\overline{123456789}$

Here the prime factor of denominator Q will has a value which is apart from

$2$ or

$5$ , some other factor also.

So, it is an rational number,

$0.123456789$ repeating again and again. It is non- terminating.

Prove that $\sqrt{3}$ is an irrational number. Hence, show that $7+2\sqrt{3}$ is also an irrational number.

Solution:

If possible , let

$\sqrt3$ be a rational number and its simplest form be

$\cfrac ab$ then,

$a$ and

$b$ are integers having no common factor

other than

$1$ and

$b\neq0.$

Now,

$\sqrt3=\cfrac ab\Longrightarrow3=\cfrac{a^2}{b^2}$ (On squaring both sides )

or,

$3b^2=a^2$ .......(i)

$\Longrightarrow 3$ divides

$a^2$

$(\because 3$ divides

$3b^2)$

$\Longrightarrow 3$ divides

$a$

Let

$a=3c$ for some integer

$c$

Putting

$a=3c$ in (i), we get

or,

$3b^2=9c^2\Longrightarrow b^2=3c^2$

$\Longrightarrow 3$ divides

$b^2$

$(\because 3$ divides

$3c^2)$

$\Longrightarrow 3$ divides

$a$

Thus

$3$ is a common factor of

$a$ and

$b$

This contradicts the fact that

$a$ and

$b$ have no common factor other than

$1.$

The contradiction arises by assuming

$\sqrt3$ is a rational.

Hence,

$\sqrt3$ is irrational.

$2^{nd}$ part

If possible, Let

$(7+2\sqrt3)$ be a rational number.

$\Longrightarrow 7-(7+2\sqrt3)$ is a rational

$\therefore$

$-2\sqrt3$ is a rational.

This contradicts the fact that

$-2\sqrt3$ is an irrational number.

Since, the contradiction arises by assuming

$7+2\sqrt3$ is a rational.

Hence,

$7+2\sqrt3$ is irrational.

Proved.

Prove that the following are irrational:
(i) $\dfrac{1}{\sqrt{2}}$ (ii) $7\sqrt{5}$ (iii) $6+\sqrt{2}$

(i) $\dfrac{1}{\sqrt{2}}$

Let us assume

$\dfrac{1}{\sqrt{2}}$ is rational.

So we can write this number as

$\dfrac{1}{\sqrt{2}} = \dfrac{a}{b}$ ---- (1)

Here,

$a$ and

$b$ are two co-prime numbers and

$b$ is not equal to zero.

Simplify the equation (1) multiply by

$\sqrt{2}$ both sides, we get

$1 = \dfrac{a\sqrt{2}}{b}$

Now, divide by

$b$ , we get

$b = a\sqrt{2}$ or

$\dfrac{b}{a}= \sqrt{2}$

Here,

$a$ and

$b$ are integers so,

$\dfrac{b}{a}$ is a rational number,

$\sqrt{2}$ should be a rational number.

But

$\sqrt{2}$ is a irrational number, so it is contradictory.

Therefore,

$\dfrac{1}{\sqrt{2}}$ is irrational number.

(ii) $7\sqrt{5}$

Let us assume

$7\sqrt{5}$ is rational.

So, we can write this number as

$7\sqrt{5} = \dfrac{a}{b}$ ---- (1)

Here,

$a$ and

$b$ are two co-prime numbers and

$b$ is not equal to zero.

Simplify the equation (1) divide by 7 both sides, we get

$\sqrt{5} = \dfrac{a}{7b}$

Here,

$a$ and

$b$ are integers, so

$\dfrac{a}{7b}$ is a rational

number, so

$\sqrt{5}$ should be a rational number.

But

$\sqrt{5}$ is a irrational number, so it is contradictory.

Therefore,

$7\sqrt{5}$ is irrational number.

(iii) $6+\sqrt{2}$

Let us assume

$6+\sqrt{2}$ is rational.

So we can write this number as

$6+\sqrt{2} = \dfrac{a}{b}$ ---- (1)

Here,

$a$ and

$b$ are two co-prime number and

$b$ is not equal to zero.

Simplify the equation (1) subtract 6 on both sides, we get

$\sqrt{2} = \dfrac{a}{b}-6$

$\sqrt{2} = \dfrac{a-6b}{b}$

Here,

$a$ and

$b$ are integers so,

$\dfrac{a-6b}{b}$ is a rational

number, so

$\sqrt{2}$ should be a rational number.

But

$\sqrt{2}$ is a irrational number, so it is contradictory.

Therefore,

$6+\sqrt{2}$ is irrational number.

Use Euclids division lemma to show that the square of any positive integer is either of the form $3m$ or $3m + 1$ for some integer $m$ .

Using Euclid division algorithm, we know that

$a = bq + r,$

$0 \leq r < b$ .......(1)

Let

$a$ be any positive integer, and

$b = 3.$

After substituting

$b = 3$ in equation

$(i),$

$a = 3q + r$ where

$0 \leq r < 3$

$r = 0, 1, 2/$

$r = 0$ and

$a = 3q,$

On squaring we get,

$a^2 = 3(3q^2)$

$a^2 = 3m$ , where

$m=3q^2$

$r = 1$ and

$a = 3q + 1,$

On squaring we get,

$a^2 = 3(3q^2 + 2q) + 1$

$a^2=3m+1$ , where

$m=3q^2+2q$

$r = 2$ and

$a = 3q + 2,$

On squaring we get,

$a^2 = 3(3q^2 + 4q + 1)+1$

$a^2=3m+1$ , where

$m=3q^2+4q+1$

Hence, proved square of any positive integer is either of the forms

$3m$ or

$3m + 1$ for some integer

$m.$

Prove that $3+2\surd{5}$ is irrational.

Let us assume

$3+2\sqrt{5}$ + is rational.

So we can write this number as

$3+2\sqrt{5} = \dfrac{a}{b}$ ---- (1)

Here a and b are two co-prime number and b is not equal to zero.
Simplify the equation (1) subtract 3 both sides, we get

$2\sqrt{5} = \dfrac{a}{b}-3$

$2\sqrt{5} = \dfrac{a-3b}{b}$

Now divide by 2 we get

$\sqrt{5} = \dfrac{a - 3b}{2b}$

Here a and b are integer so

$\dfrac{a - 3b}{2b}$ is a rational number, so

$\sqrt{5}$ should be a rational number.

But

$\sqrt{5}$ is a irrational number, so it is contradict.

Therefore,

$3+2\sqrt{5}$ is irrational number.

$867$ and $225$

867 is grater than 225

867 = 225 × 3 + 192

225 = 192 × 1 + 33

192 = 33 × 5 + 27

33 = 27 × 1 + 6

27 = 6 × 4 + 3

6 = 3 × 2 + 0

The HCF of (867 and 225) is 3.

Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i) $\dfrac{13}{3125}$ (ii) $\dfrac{17}{8}$ (iii) $\dfrac{64}{455}$ (iv) $\dfrac{15}{1600}$ (v) $\dfrac{29}{343}$

(vi) $\dfrac{23}{2^{3}5^{2}}$ (vii) $\dfrac{129}{2^{2}5^{7}7^{5}}$ (viii) $\dfrac{6}{15}$ (ix) $\dfrac{35}{50}$ (x) $\dfrac{77}{210}$

Theorem: Let

$x = \dfrac{p}{q}$ be a rational number, such that the prime factorisation of q is of the form

$2^{n}5^{m}$ , where n, m are non-negative integers. Then,

$x$ has a decimal expansion which terminates.

(i) $\dfrac{13}{3125}$

Factorise the denominator, we get

$3125 = 5 \times 5 \times 5 \times 5 \times 5 = 5^5$
So, denominator is in form of

$5^m$ so,

$\dfrac{13}{3125}$ is terminating.

(ii) $\dfrac{17}{8}$

Factorise the denominator, we get

$8 = 2 \times 2 \times 2 = 2^3$
So, denominator is in form of

$2^n$ so,

$\dfrac{17}{8}$ is terminating.

(iii) $\dfrac{64}{455}$

Factorise the denominator, we get

$455 = 5 \times 7 \times 13$
So, denominator is not in form of

$2^{n} 5^{m}$ so,

$\dfrac{64}{455}$ is not terminating.

(iv) $\dfrac{15}{1600}$

Factorise the denominator, we get

$1600 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 5 \times 5 = 2^{6} 5^{2}$
So, denominator is in form of

$2^{n}5^{m}$ so,

$\dfrac{15}{1600}$ is terminating.

(v) $\dfrac{29}{343}$

Factorise the denominator, we get

$343 = 7 \times 7 \times 7 = 7^{3}$
So, denominator is not in form of

$2^{n}5^{m}$ so,

$\dfrac{29}{343}$ is not terminating.

(vi) $\dfrac{23}{2^{3}5^{2}}$

Here, the denominator is in form of

$2^{n}5^{m}$ so,

$\dfrac{23}{2^{3}5^{2}}$ is terminating.

(vii) $\dfrac{129}{2^{2}5^{7}7^{5}}$

Here, the denominator is not in form of

$2^{n}5^{m}$ so,

$\dfrac{129}{2^{2}5^{7}7^{5}}$ is not terminating.

(viii) $\dfrac{6}{15}$

Divide nominator and denominator both by 3 we get

$\dfrac{3}{15}$
So, denominator is in form of

$5^{m}$ so,

$\dfrac{6}{15}$ is terminating.

(ix) $\dfrac{35}{50}$

Divide nominator and denominator both by 5 we get

$\dfrac{7}{10}$
Factorise the denominator, we get

$10 = 2 \times 5$
So, denominator is in form of

$2^{n}5^{m}$ so,

$\dfrac{35}{50}$ is terminating.

(x) $\dfrac{77}{210}$

Divide nominator and denominator both by 7 we get

$\dfrac{11}{30}$
Factorise the denominator, we get

$30 = 2 \times 3 \times 5$

So, denominator is not in the form of

$2^{n}5^{m}$ so

$\dfrac{6}{15}$ is not terminating.

(ii) 196 and 38220

Step 1: First find which integer is larger.

$38220 > 196$

Step 2: Then apply the Euclid's division algorithm to 38220 and 196 to obtain

$38220 = 196 \times 195 + 0$
Since the remainder is zero, we cannot proceed further.

Step 3: Hence, the divisor at the last process is 196.
So, the H.C.F. of

$196$ and

$38220$ is

$196.$

Use Euclid's division algorithm to find the HCF of the following number: 305 and 793

Since

$793 > 305$ , we apply the division lemma to

$793$ and

$305$ to obtain:

$793=305\times 2+183$

Since remainder

$183 ≠ 0$ , we apply the division lemma to

$305$ and

$183$ to obtain:

$305=183\times 1+122$

We consider the new divisor

$183$ and new remainder

$122$ , and apply the division lemma to obtain

$183=122\times 1+61$

Now, the new divisor is

$122$ and new remainder is

$61$ , and apply the division lemma to obtain

$122=61\times 2+0$

Since the remainder is zero, the process stops.

Also, the divisor at this stage is

$61$ ,

Hence, the

$HCF$ of

$793$ and

$305$ is

$61$ .

Prove that $2\sqrt{3}$ is an irrational number.

Let us assume that

$\sqrt { 3 }$ is a rational number which can be expressed in the form of

$\dfrac {p}{q}$ , where

$p$ and

$q$ are integers,

$q\neq 0$ and

$p$ and

$q$ are co prime that is

$HCF(p,q)=1$ .

We have,

$\sqrt { 3 } =\dfrac { p }{ q } \\ \Rightarrow \sqrt { 3 } q=p......(1)\\ \Rightarrow 3{ q }^{ 2 }=p^{ 2 }\quad \quad \quad \quad (squaring\quad both\quad sides)$

$\Rightarrow p^{ 2 }$ is divisible by

$3$

$\Rightarrow p$ is divisible by

$3$

$......(2)$

Therefore, for an integer

$r$ ,

$p=3r\\ \Rightarrow \sqrt { 3 } q=3r\quad \quad \quad (from\quad (1))\\ \Rightarrow 3q^{ 2 }=9r^{ 2 }\quad \quad \quad (squaring\quad both\quad sides)\\ \Rightarrow q^{ 2 }=\dfrac { 9 }{ 3 } r^{ 2 }\\ \Rightarrow q^{ 2 }=3r^{ 2 }$

$\Rightarrow q^{ 2 }$ is divisible by

$3$

$\Rightarrow q$ is divisible by

$3$

$......(3)$

From equations 2 and 3, we get that

$3$ is the common factor of

$p$ and

$q$ which contradicts that

$p$ and

$q$ are co prime. This means that our assumption was wrong.

Thus

$\sqrt { 3 }$ is an irrational number.

Now, since multiplication of a rational number with an irrational number is an irrational number.

Hence

$2\sqrt { 3 }$ is an irrational number.

Prove that the square of real number is always non-negative.

Suppose

$a$ is real number.

Then either

$a > 0$ or

$a=0$ or

$a < 0$ and only one of these is true.

Suppose

$a > 0$ .

Then

$a\times a > 0 \times a$ , since we are multiplying by a positive real number.

Hence

$a^2 > 0$ .

$a = 0$ , then

$a^2 = 0$ .

Suppose

$a < 0$ .

Then

$a \times a > 0 \times a$ , as the inequality changes when multiplied by a negative number.

Again we obtain

$a^2 > 0$ .

We can conclude that

$a^2 > 0$ when

$a$ is either positive or negative; and

$a^2=0$ when

$a=0$ .

Thus

$a^2 \ge 0$ for any real number

$a$ .

So, the square of a real number is always non-negative.

Use Euclid's division algorithm to find the HCF of the following numbers: $55$ and $210$

Since

$210 > 55$ , we apply the division lemma to

$210$ and

$55$ to obtain:

$210=55\times 3+45$

Since remainder

$45 ≠ 0$ , we apply the division lemma to

$55$ and

$45$ to obtain:

$55=45\times 1+10$

Since, the remainder

$10\ne0$ ,we consider the new divisor

$45$ and new remainder

$10$ , and apply the division lemma to obtain

$45=10\times 4+5$

Since remainder

$5 ≠ 0$ , now, taking the new divisor

$10$ and new remainder

$5$ , and apply the division lemma to obtain

$10=5\times 2+0$

Since the remainder is zero, the process stops.

The divisor at last stage is

$5$ ,

Hence, the

$HCF$ of

$210$ and

$55$ is

$5$ .

Use Euclid's division algorithm to find the HCF of the following number: 65 and 117

Since

$117 > 65$ , we apply the division lemma to

$117$ and

$65$ to obtain:

$117=65\times 1+52$

Since remainder

$52 ≠ 0$ , we apply the division lemma to

$65$ and

$52$ to obtain:

$65=52\times 1+13$

We consider the new divisor

$52$ and new remainder

$13$ , and apply the division lemma to obtain

$52=13\times 4+0$

Since the remainder is zero, the process stops.

Also, the divisor at this stage is

$13$ ,

Hence, the

$HCF$ of

$117$ and

$65$ is

$13$ .

Use Euclid's division algorithm to find the $HCF$ of the following number: $237$ and $81$

Since

$237 > 81$ , we apply the division lemma to

$237$ and

$81$ to obtain:

$237=81\times 2+75$

Since remainder

$75 ≠ 0$ , we apply the division lemma to

$81$ and

$75$ to obtain:

$81=75\times 1+6$

We consider the new divisor

$75$ and new remainder

$6$ , and apply the division lemma to obtain

$75=6\times 12+3$

Now, the new divisor is

$6$ and new remainder is

$3$ , and apply the division lemma to obtain

$6=3\times 2+0$

Since the remainder is zero, the process stops.

Also, the divisor at this stage is

$3$ ,

Hence, the

$HCF$ of

$237$ and

$81$ is

$3$ .

Prove that $3+\sqrt{5}$ is an irrational number.

Let us assume that

$\sqrt { 5 }$ is a rational number which can be expressed in the form of

$\dfrac {p}{q}$ , where

$p$ and

$q$ are integers,

$q\neq 0$ and

$p$ and

$q$ are co prime that is

$HCF(p,q)=1$ .

We have,

$\sqrt {5 } =\dfrac { p }{ q } \\ \Rightarrow \sqrt { 5 } q=p......(1)\\ \Rightarrow 5{ q }^{ 2 }=p^{ 2 }\quad \quad \quad \quad (squaring\quad both\quad sides)$

$\Rightarrow p^{ 2 }$ is divisible by

$5$

$\Rightarrow p$ is divisible by

$5$

$......(2)$

Therefore, for an integer

$r$ ,

$p=5r\\ \Rightarrow \sqrt { 5 } q=5r\quad \quad \quad (from\quad (1))\\ \Rightarrow 5q^{ 2 }=25r^{ 2 }\quad \quad \quad (squaring\quad both\quad sides)\\ \Rightarrow q^{ 2 }=\dfrac { 25 }{ 5 } r^{ 2 }\\ \Rightarrow q^{ 2 }=5r^{ 2 }$

$\Rightarrow q^{ 2 }$ is divisible by

$5$

$\Rightarrow q$ is divisible by

$5$

$......(3)$

From equations 2 and 3, we get that

$5$ is the common factor of

$p$ and

$q$ which contradicts that

$p$ and

$q$ are co prime. This means that our assumption was wrong.

Thus

$\sqrt { 5 }$ is an irrational number.

Now, since addition of a rational number to an irrational number is an irrational number.

Hence

$3+\sqrt { 5 }$ is an irrational number.

Show that $\sqrt{2}$ is not a rational number

Solution:

If possible , let

$\sqrt2$ be a rational number and its simplest form be

$\cfrac ab$ then,

$a$ and

$b$ are integers having no common factor other than

$1$ and

$b\neq0.$

Now,

$\sqrt2=\cfrac ab\Longrightarrow2=\cfrac{a^2}{b^2}$ (On squaring both sides )

or,

$2b^2=a^2$ .......(i)

$\Longrightarrow 2$ divides

$a^2$

$(\because 2$ divides

$2b^2)$

$\Longrightarrow 2$ divides

$a$

Let

$a=2c$ for some integer

$c$

Putting

$a=3c$ in (i), we get

or,

$2b^2=4c^2\Longrightarrow b^2=2c^2$

$\Longrightarrow 2$ divides

$b^2$

$(\because 2$ divides

$2c^2)$

$\Longrightarrow 2$ divides

$a$

Thus

$2$ is a common factor of

$a$ and

$b$

This contradicts the fact that

$a$ and

$b$ have no common factor other than

$1.$

The contradiction arises by assuming

$\sqrt2$ is a rational.

Hence,

$\sqrt2$ is irrational.

Show that every positive even integer is of the form $2q$ and every positive odd integer is of the form $2q + 1$ , where q is a whole number.

(i) Let '

$a$ ' be an even positive integer.
Apply division algorithm with a and b, where

$b = 2$

$a = (2 \times q)+r$ where

$0\le r < 2$

$a = 2q + r$ where

$r = 0$ or

$r = 1$
since '

$a$ ' is an even positive integer, 2 divides '

$a$ '.

$\therefore r= 0\Rightarrow a= 2q+ 0 = 2q$
Hence,

$a = 2q$ when '

$a$ ' is an even positive integer.
(ii) Let '

$a$ ' be an odd positive integer.
apply division algorithm with

$a$ and

$b$ , where

$b = 2$

$a = (2 \times q)+r$ where

$0\le r < 2$

$a = 2q+ r$ where

$r= 0$ or 1
Here

$r \neq 0$ (

$\because a$ is not even)

$\Rightarrow r= 1$

$\therefore a = 2q + 1$
Hence,

$a = 2q + 1$ when '

$a$ ' is an odd positive integer.

Prove that, if x and y are odd positive integers, then $x^2 + y^2$ is even but not divisible by 4.

We know that any odd positive integer is of the form

$2q + 1$ , where

$q$ is an integer.

So, let

$x = 2m + 1$ and

$y = 2n + 1$ , for some integers m and n.

we have

$x^2 + y^2$

$x^2 + y^2 = (2m + 1)^2 + (2n + 1)^2$

$x^2 + y^2 = 4m^2 + 1 + 4m + 4n^2 + 1 + 4n = 4m^2 + 4n^2 + 4m + 4n + 2$

$x^2+ y^2 = 4(m^2 + n^2) + 4(m + n) + 2 = 4\{(m^2 + n^2) + (m + n)\}+ 2$

$x^2 + y2 = 4q + 2$ , when

$q = (m^2 + n^2)+(m + n)$

$x^2 + y^2$ is even and leaves remainder 2 when divided by 4.

$x^2 + y^2$ is even but not divisible by 4.

A book seller has 28 Kannada and 72 English books. The books are of the same size. These books are to be packed in separate bundles and each bundle must contain the same number of books. Find the least number of bundles which can be made and also the number of books in each bundle.

Number of Kannada books

$= 28$ Number of English books

$= 72$
We have to find the HCF of 28 and 72 by Euclid's lemma.

$72 = (28 \times 2) + 16$

$28 = (16 \times 1) + 12$

$16 = (12 \times 1) + 04$

$12 = (4 \times 3) + 0$

$\therefore$ HCF of 28 and

$72 = 4$

$\therefore$ Each bundle contains 4 books.
No. of bundles of Kannada books

$=\dfrac{28}{4}= 7$ , No. of bundles of English books

$=\dfrac{72}{4}=18$

Prove that $2\sqrt{3}-4$ is an irrational number.

Let us assume that

$\sqrt { 3 }$ be a rational number which can be expressed in the form of

$\dfrac {p}{q}$ where

$p$ and

$q$ are integers,

$q\neq 0$ and

$p$ and

$q$ are co prime that is

$HCF(p,q)=1$ .

We have,

$\sqrt { 3 } =\dfrac { p }{ q } \\ \Rightarrow \sqrt { 3 } q=p.....(1)\\ \Rightarrow 3q^{ 2 }=p^{ 2 }\quad \quad \quad (squaring\quad both\quad sides)$

$\Rightarrow p^{ 2 }$ is divisible by

$3$

$\Rightarrow p$ is divisible by

$3$

$......(2)$

Now, for any integer

$r$ ,

$Let,\ p=3r\\ \Rightarrow \sqrt { 3 } q=3r\quad \quad \quad (from\quad (1))\\ \Rightarrow 3q^{ 2 }=9r^{ 2 }\quad \quad \quad \quad (squaring\quad both\quad sides)\\ \Rightarrow q^{ 2 }=\dfrac { 9 }{ 3 } r^{ 2 }\\ \Rightarrow q^{ 2 }=3r^{ 2 }$

$\Rightarrow q^{ 2 }$ is divisible by

$3$

$\Rightarrow q$ is divisible by

$3$

$......(3)$

From equation

$(2)$ and

$(3)$ , we get that

$3$ is the common factor of

$p$ and

$q$ which contradicts that

$p$ and

$q$ are co prime. This means that our assumption was wrong.

Thus

$\sqrt { 3 }$ is an irrational number which implies that

$2\sqrt { 3 }$ is also an irrational number.

We know that the subtraction of an irrational number and a rational number is an irrational number.

Hence

$2\sqrt { 3 }-4$ is an irrational number.

Classify the following numbers as rational or irrational.
$7.484848...$

Given number

$7.484848.....$

The decimal expression of above number is non terminating recurring

So number

$7.484848........$ is a rational number

Prove that $\sqrt{2}+\sqrt{5}$ is an irrational number.

Let us assume that

$\sqrt { 2 }$ be a rational number which can be expressed in the form of

$\dfrac {p}{q}$ where

$p$ and

$q$ are integers,

$q\neq 0$ and

$p$ and

$q$ are co prime that is

$HCF(p,q)=1$ .

We have,

$\sqrt { 2 } =\dfrac { p }{ q } \\ \Rightarrow \sqrt { 2 } q=p.....(1)\\ \Rightarrow 2q^{ 2 }=p^{ 2 }\quad \quad \quad (squaring\quad both\quad sides)$

$\Rightarrow p^{ 2 }$ is divisible by

$2$

$\Rightarrow p$ is divisible by

$2$

$......(2)$

Therefore, for any integer

$r$ ,

$p=2r\\ \Rightarrow \sqrt { 2 } q=2r\quad \quad \quad (from\quad (1))\\ \Rightarrow 2q^{ 2 }=4r^{ 2 }\quad \quad \quad \quad (squaring\quad both\quad sides)\\ \Rightarrow q^{ 2 }=\dfrac { 4 }{ 2 } r^{ 2 }\\ \Rightarrow q^{ 2 }=2r^{ 2 }$

$\Rightarrow q^{ 2 }$ is divisible by

$2$

$\Rightarrow q$ is divisible by

$2$

$......(3)$

From equation 2 and 3, we get that

$2$ is the common factor of

$p$ and

$q$ which is a contradicts that

$p$ and

$q$ are co prime. This means that our assumption was wrong.

Thus

$\sqrt { 2 }$ is an irrational number.

Similarly, we can prove that

$\sqrt { 5 }$ is an irrational number.

We know that the sum of two irrational numbers is an irrational number.

Hence

$\sqrt { 2 } +\sqrt { 5 }$ is an irrational number.

Find the largest number that divides $455$ and $42$ with the help of division algorithm.

i) Start with the larger integer

$, 455$

$42)455 (10 \rightarrow$ quotient
420

$35\rightarrow$ remainder

$\therefore 455 = (42 \times 10) + 35$ (By Euclid's lemma)

ii) Consider

$42 \div 35$ iii) Consider

$35 \div 7$

$35)42(1$

$7)35(5$
35 35
7 00

$\therefore 42 = (35 \times 1) + 7$

$\therefore 35 = (7 \times 5) + 0$

$\Rightarrow HCF (455, 42) = HCF (42, 35) = HCF (35, 7) = 7$

$\therefore 7$ is the largest number that divides

$455$ and

$42$ .

Without actually dividing find if $3.12\overline {7}$ is terminating decimal.

Given fraction

$\dfrac{3}{25}$

The

$\dfrac{p}{q}$ is terminating decimal if

(i) p & q are co-prime and

(ii) q is in the form

$2^{n}5^{m}$

Here 3 and 25 are co-prime

And

$25=2^{0}\times 5^{2}$

$\dfrac{3}{25}$ is terminating decimal (yes)

Classify the following numbers as rational or irrational.
$11.2132435465$

Given number 11.2132435465

The decimal expression of above number is non terminating.

So number 11.2132435465 is a rational number

Without actually dividing find if $\dfrac {41}{42}$ is terminating decimal.

Given

$\dfrac{41}{42}$

The

$\dfrac{p}{q}$ is terminating if

(i) P & Q are co-prime and

(ii) q is of the form

$2^{n}5^{m}$ where n & m are non negative

$\dfrac{41}{42}$

The denominator 42 is not from of

$2^{n}5^{m}$

Then

$\dfrac{41}{42}$ is not the terminating decimal

In the following equations, find whether variables $x, y, z$ etc. represent rational or irrational numbers
$z^{2} = 0.02$

Given,

$z^{2}=0.02$

$\Rightarrow z=\sqrt{0.02}$

The number

$\sqrt{0.02}$ is an irrational number.

Hence,

$z$ is an irrational number.

In the following equations, find whether variables $w$ represent rational or irrational numbers
$w^{2} = 27$

$w^{2}=27$

$\Rightarrow w=\sqrt{27}$

The number

$\sqrt{27}$ is an irrational number.

Hence,

$w$ represents an irrational number.

In the following equations, find whether variables $x, y, z$ etc. represent rational or irrational numbers
$y^{2} = 16$

$y^{2}=16$

$\Rightarrow y=4$

Here 4 is a rational number

$y$ is a rational number

Prove that $\sqrt 2$ is an irrational number.

Assume that

$\sqrt2$ =

$\dfrac{p}{q}$ (rational number)

squaring on both the sides,

$2$ =

$\dfrac{p^2}{q^2}$

$p^2= 2q^2$ ---

$(1)$

$p^2$ is a perfect square number which can be even or odd.

But

$2q^2$ is only even number.

So,

$p^2$ is not necessarily equal to

$2q^2$ which is contradictory to the equation

$(1)$ .

So, our assumption was incorrect.

Hence, root is an irrational number.

Classify the following numbers as rational or irrational.
$0.3030030003.....$

Given number

$0.3030030003......$

The decimal expression of above number is non terminating , non repeating.

So number

$0.3030030003........$ is an irrational number

The ratio of circumference to the diameter of a circle $\dfrac {c}{d}$ is represented by $\pi$ . But we say that $\pi$ is an irrational number. Why?

$\pi =\dfrac{c}{d}$ is a rational number

When c & d both are rational numbers

But the c & d we calculated is not exactly a rational number and either c or d or both can be irrational numbers

Since quotient of rational and irrational number is an irrational number .

$\pi$ is an irrational number

In the following equations, find whether variables $u$ represents rational or irrational numbers
$u^{2} = \dfrac {17}{4}$

$u^{2}=\frac{17}{4}$

$\Rightarrow u=\sqrt{\frac{17}{4}}$

$\Rightarrow u=\frac{\sqrt{17}}{2}=\frac{1}{2}\times \sqrt{17}$

Here

$\frac{1}{2}$ is a rational number and

$\sqrt{17}$ is an irrational number

We know that the product of rational with irrational number is an irrational number

Hence,

$u$ represents an irrational number.

Prove that $\sqrt 6$ is an irrational number

The following proof is a proof by contradiction.

Let us assume that

$\sqrt 6$ is rational number.

Then it can be represented as fraction of two integers.

Let the lowest terms representation be:

$\sqrt 6 = \cfrac{a}{b}$ where

$b \neq 0$

Note that this representation is in lowest terms and hence,

$a$ and

$b$ have no common factors

$a^2 = 6 b^2$

From above

$a^2$ is even. If

$a^2$ is even, then

$a$ should also be even.

$\implies a = 2c$

$4c^2 = 6b^2$

$2c^2 = 3b^2$

From above

$3b^2$ is even. If

$3b^2$ is even, then

$b^2$ should also be even and again

$b$ is even.

But

$a$ and

$b$ were in lowest form and both cannot be even. Hence, assumption was wrong and hence,

$\sqrt 6$ is an irrational number.

In the following equation, find whether variable $t$ represents rational or irrational number:
$t^{4} = 256$

The given equation is

$t^{4}=256$

$\Rightarrow t^4=(\pm4)^4$

$\Rightarrow t=\pm4$

$4$ and

$-4$ both are rational numbers.

Hence,

$t$ represents rational numbers.

Check whether $\dfrac {5}{\sqrt {2}}$ are irrational numbers

Given number is

$\dfrac{5}{\sqrt{2}}$ .

Clearly,

$5$ is a rational number and

$\sqrt2$ is an irrational number.

We know that, a rational number divided by an irrational number is an irrational number.

Here,

$5$ is divided by

$\sqrt2$

Hence,

$\dfrac{5}{\sqrt{2}}$ is an irrational number.

If $7$ is a prime number, then prove that $\sqrt 7$ is irrational.

Let us assume,

$\sqrt 7$ is a rational number.
Let,

$\sqrt 7 = \dfrac{a}{b}$ , where HCF

$(a, b)$

$= 1; a \varepsilon N, b \varepsilon N$

Now,

$\sqrt 7 = \dfrac{a}{b}$

$\Rightarrow a= \sqrt{7}b$

$\Rightarrow a^2 = 7b^2$ ........ (1)

So,

$a^2$ is divisible by

$7$

$\therefore a$ is divisible by

$7$

Let,

$a = 7k$ , where

$k$

$\varepsilon$

$N$

From (1),

$\Rightarrow (7k)^2 = 7b^2$

$\Rightarrow 49 k^2 = 7b^2$

$\Rightarrow b^2 = 7k^2$

So,

$b^2$ is divisible by

$7$

$\therefore b$ is divisible by

$7$

Thus,

$a$ and

$b$ both are divisible by

$7$ .
This is a contradiction, because HCF

$(a, b) = 1$ .

Thus, our assumption is wrong .
Hence,

$\sqrt 7$ is irrational.

Without actual division, classify the decimal expansion of the following numbers as terminating or non-terminating and recurring.
(i) $\displaystyle\frac{7}{16}$
(ii) $\displaystyle\frac{13}{150}$
(iii) $\displaystyle\frac{-11}{75}$
(iv) $\displaystyle\frac{17}{200}$

(i)

$16=2^4$

$\displaystyle\frac{7}{16}=\frac{7}{2^4}=\frac{7}{2^4\times 5^0}$ . So,

$\displaystyle\frac{7}{16}$ has a terminating decimal expansion.
(ii)

$150=2\times 3\times 5^2$

$\displaystyle\frac{13}{150}=\frac{13}{2\times 3\times 5^2}$
Since it is not in the form

$\displaystyle\frac{p}{2^m\times 5^n}, \frac{13}{150}$ has a non-terminating and recurring decimal expansion.
(iii)

$\displaystyle\frac{-11}{75}=\frac{-11}{3\times 5^2}$
Since it is not in the form

$\displaystyle\frac{p}{2^m\times 5^n}. \frac{-11}{75}$ has a non-terminating and recurring decimal expansion.
(iv)

$\displaystyle\frac{17}{200}=\frac{17}{8\times 25}=\frac{17}{2^3\times 5^2}$ . So

$\displaystyle\frac{17}{200}$ has a terminating decimal expansion.

Prove that $3+2\sqrt { 5 }$ is an irrational number.

Let take that

$3 + 2\sqrt { 5 }$ is a rational number.

So we can write this number as

$3 + 2\sqrt { 5 }$ =

$\dfrac{a}{b}$

Here

$a$ and

$b$ are two co prime number and

$b$ is not equal to

$0$

Subtract

$3$ both sides we get

$2\sqrt { 5 }$ =

$\dfrac{a}{b}-3$

$2\sqrt { 5 }$ =

$\dfrac{a-3b}{b}$

Now divide by

$2$ , we get

$\sqrt { 5 }$ =

$\dfrac{a-3b}{2b}$

Here a and b are integer so

$\dfrac{a-3b}{2b}$ is a rational number so

$\sqrt { 5 }$ should be a rational number but

$\sqrt { 5 }$ irrational

number so it contradicts.

Hence,

$3 + 2\sqrt { 5 }$ is a irrational number.

Prove that $3+\sqrt { 5 }$ is an irrational number.

Solution:

If possible, let us suppose

$3+\sqrt5$ be a rational number.

$\Longrightarrow 3+\sqrt5=\cfrac pq$ where,

$p,q\in Z,\quad q\neq 0.$

$\Longrightarrow \sqrt5=\cfrac pq-3$

$\sqrt5=\cfrac{p-3q}{q}$ which is rational.

This leads to contradiction because

$\sqrt5$ is irrational.

$\therefore$

$3+\sqrt5$ is an irrational number.

Identify whether $\sqrt{32}$ is rational or irrational.

$\sqrt{32}=\sqrt{16\times 2}=4\sqrt{2}$

$4$ is a rational number and

$\sqrt{2}$ is an irrational number.

$\therefore 4\sqrt{2}$ is an irrational number and hence

$\sqrt{32}$ is an irrational number.

Prove that $\sqrt 5$ is irrational by the method of Contradiction.

Let

$\sqrt5$ be a rational number.

then it must be in form of

$\dfrac pq$ where,

$q\neq0$ (

$p$ and

$q$ are co-prime)

$\sqrt5=\dfrac pq$

$\sqrt5 \times q=p$

Suaring on both sides,

$5{q}^2{}={p}^{2}$ --------------(1)

${p}^{2}$ is divisible by

$5$ .

So,

$p$ is divisible by

$5$ .

$p=5c$

Suaring on both sides,

${p}^{2}=25{c}^{2}$ --------------(2)

Put

${p}^{2}$ in eqn.(1)

$5{q}^{2}=25(c)^{2}$

${q}^{2}=5 c^{2}$

So,

$q$ is divisible by

$5$ .

Thus

$p$ and

$q$ have a common factor of

$5$ .

So, there is a contradiction as per our assumption.

We have assumed

$p$ and

$q$ are co-prime but here they a common factor of

$5$ .

The above statement contradicts our assumption.

Therefore,

$\sqrt5$ is an irrational number.

Show that $\left (5 - \sqrt {3} \right )$ is irrational.

We Have to prove that

$5-\sqrt{3}$ is irrational.

We will prove it by Contradiction method.

Let us assume the opposite, i.e,

$5-\sqrt{3}$ is rational

As we know that any rational no. can be written in the form of

$\dfrac{p}{q}$

where

$p$ and

$q (q \neq 0)$ are co-prime (no common factor other than

$1$ ).

Hence,

$5 - \sqrt{3} = \dfrac{p}{q}$

$-\sqrt{3}= \dfrac{p}{q} -5$

$-\sqrt{3} = \dfrac{p-5q}{q}$

$\sqrt{3} =-\dfrac{p-5q}{q}$

$\sqrt{3} =\dfrac{5q-p}{q}$

Here,

$\dfrac{5q-p}{q}$ is rational.

But

$\sqrt{3}$ is irrartional.

Since, Rational

$\neq$ Irrational

This is contradiction.

$\therefore$ Our assumption is incorrect.

Hence,

$5-\sqrt{3}$ is irrational.

Hence Proved.

Identify whether the following numbers are rational or irrational.
(i) $3+\sqrt{3}$
(ii) $(4+\sqrt{2})-(4-\sqrt{3})$
(iii) $\displaystyle \frac{\sqrt{18}}{2\sqrt{2}}$
(iv) $\sqrt{19}-(2+\sqrt{19})$
(v) $\displaystyle \frac{2}{\sqrt{3}}$
(vi) $\sqrt{12}\times \sqrt{3}$ .

(i)

$3+\sqrt{3}$

$3$ is a rational number and

$\sqrt{3}$ is irrational. Hence,

$3+\sqrt{3}$ is irrational.
(ii)

$(4+\sqrt{2})-(4-\sqrt{3})$

$=4+\sqrt{2}-4+\sqrt{3}=\sqrt{2}+\sqrt{3}$ , is irrational.
(iii)

$\displaystyle\frac{\sqrt{18}}{2\sqrt{2}}=\frac{\sqrt{9\times 2}}{2\sqrt{2}}=\frac{\sqrt{9}\times \sqrt{2}}{2\sqrt{2}}=\frac{3}{2}$ , is rational.
(iv)

$\sqrt{19}-(2+\sqrt{19})=\sqrt{19}-2-\sqrt{19}=-2,$ is rational.
(v)

$\displaystyle\frac{2}{\sqrt{3}}$ here

$2$ is rational and

$\sqrt{3}$ is irrational. Hence,

$\displaystyle\frac{2}{\sqrt{3}}$ is irrational.
(vi)

$\sqrt{12}\times \sqrt{3}=\sqrt{12\times 3}=\sqrt{36}=6$ , is rational.

Prove that $\sqrt{3}$ is irrational.

Let us assume, to the contrary, that

$\sqrt{3}$ is rational.

That is, we can find integers a and b

$(\neq 0)$ such that

$\sqrt{3}=\displaystyle\frac{a}{b}$ .

Suppose a and b have a common factor other than

$1$ , then we can divide by the common factor, and assume that a and b are coprime.

So,

$b\sqrt{3}=a$ .

Squaring on both sides, and rearranging, we get

$3b^2=a^2$ .

Therefore,

$a^2$ is divisible by

$3$ , and by Theorem

$1.3$ , it follows

that a is also divisible by

$3$ .

So, we can write a

$=3c$ for some integer c.

Substituting for a, we get

$3b^2=9c^2$ , that is,

$b^2=3c^2$ .

This means that

$b^2$ is divisible by

$3$ , and so b is also divisible by

$3$ (using Theorem

$1.3$ with

$p=3$ ).

Therefore, a and b have at least

$3$ as a common factor.

But this contradicts the fact that a and b are coprime.

This contradiction has arisen because of our incorrect assumption that

$\sqrt{3}$ is rational. So, we conclude that

$\sqrt{3}$ is irrational.

Prove that $5 \sqrt{3}$ is an irrational number.

$\textbf{Step 1: Use the definition of rational number and prove p is divisible by 3.}$

$\text{Let}\;5\sqrt{3}\;\text{is a rational number.}$

$\therefore 5\sqrt{3}=\dfrac{p}{q},$

$\text{where p and q are some integer and HCF(p,q)=1}$

$--(1)$

$\Rightarrow{5\sqrt{3}.q=p}$

$\quad \quad \textbf{[Squaring on both sides.]}$

$\Rightarrow{(5\sqrt{3}.q)^2=p^2}$

$\Rightarrow{3(25q^2)=p^2}$

$\Rightarrow{p^2}$

$\text{is divisible by 3}$

$\Rightarrow{p}$

$\text{is divisible by 3}$

$--(2)$

$\textbf{Step 2: Prove q is divisible by 3.}$

$\text{Let}\;p=3m,$

$\text{where m is some integer.}$

$\Rightarrow{5\sqrt{3}.q=3m}$

$\quad \quad \textbf{[Squaring on both sides.]}$

$\Rightarrow{(5\sqrt{3}.q)^2}=(3m)^2$

$\Rightarrow{3(25q^2)=9m^2}$

$\Rightarrow{25q^2}={3m^2}$

$\Rightarrow{q^2}$

$\text{is divisible by 3}$

$\Rightarrow{q}$

$\text{is divisible by 3}$

$--(3)$

$\text{From (2) and (3), there is a common factor for p and q, which contradicts (1).}$

$\textbf{Hence,}$

$\bf{5\sqrt{3}}$

$\textbf{is an irrational number proved.}$

Every surd is an irrational, but every irrational need not be a surd. Justify your answer.

By definition , a surd is an irrational root of a rational number. So now we know that surds are always irrational and they are always roots.

For example , square root of

$2$ i.e.

$\sqrt{2}$ is a surd since

$2$ is rational and square root of

$2$ is irrational.

Similarly, cube root of

$9$ is also a surd since

$9$ is rational and cube root of

$9$ is irrational.

On the other hand,

$\pi$ and

$e$ are not surds even though they are irrational, because they are not the roots of any algebraic expression.

Find the HCF of the following pair of integers and express it as a linear combination of them.
$963$ and $657$

We can use Euclid division linear to find

$HCF$ of

$963$ and

$657$

$963 = 657 \times 1 + 306$

$657 = 306 \times 2 + 45$

$306 = 45 \times 6 + 36$

$45 = 36 \times 1 + 9$

$36 = 9 \times 4 + 0$

Since Remainder

$= 0$

$\therefore HCF (963 , 657) = 9$

Now, we do backward calculation

$\Rightarrow$

$9 = 45 - 36$

$9 = 45 - (306 - 45 \times 6)$

$9 = 45 \times 7 - 306$

$9 = (657 - 306 \times 2) \times 7 - 306$

$9 = 657 \times 7 - 306 \times 15$

$9 = 657 \times 7 - (963 - 657) \times 15$

$9 = 657 \times 22 - 963 \times 15$

$\therefore 9 = 657 \times 22 - 963 \times 15$

$HCF (657$ ,

$963)$ as their linear combination

Prove that $\sqrt { 5 } +\sqrt { 3 }$ is irrational.

Assume that $\sqrt 5 + \sqrt 3$ is rational. So,

$\sqrt 5 + \sqrt 3 = \dfrac{p}{q}$

$5 + 3 + 2\sqrt {15} = \dfrac{{{p^2}}}{{{q^2}}}$

$\sqrt {15} = \dfrac{1}{2}\left( {\dfrac{{{p^2}}}{{{q^2}}} - 8} \right)$

Since the RHS of the above equation is rational but $\sqrt {15}$ is an irrational number, so the assumption is wrong.

Therefore, $\sqrt 5 + \sqrt 3$ is irrational.

Verify by the method of contradiction $P:\sqrt { 7 }$ is irrational.

Let

$\sqrt {7}$ be rational

It must in the form of (a/b) where a, b have no common factor

Let

$\sqrt {7}=\dfrac {a} {b}$ (a, b have no common factor)

$\Rightarrow 7=\dfrac {a^{2}}{b^{2}}$

$\Rightarrow a^{2}=7b^{2}$

$\Rightarrow$

$7$ divide

$a$

$\Rightarrow$ Therefore there exists an integer

$'c'$ such that

$a=7c$

$\Rightarrow a^{2}=49c^{2}$

$\Rightarrow 49c^{2}=7b^{2}$

$\Rightarrow b^{2}=7c^{2}$

$\Rightarrow$

$7$ also divides

$b$

$\Rightarrow$ we got that

$7$ divides both

$'a'\ and\ 'b'$

But we assumed that

$a, b$ have no common factor

This is a contradiction and what we assumed is incorrect

$\therefore \sqrt {7}$ is irrational

Show that the number $\dfrac { 1 }{ \sqrt { 2 } }$ is irrational.

If possible, let

$\dfrac { 1 }{ \sqrt { 2 } }$ be rational. Then, there exist positive co-primes

$a$ and

$b$ such that

$\dfrac { 1 }{ \sqrt { 2 } } =\dfrac { a }{ b }$

$\Rightarrow 2{ a }^{ 2 }={ b }^{ 2 }\qquad \left[ \because 2|2{ a }^{ 2 } \right] \\$

$\Rightarrow 2|{ b }^{ 2 }\\$

$\Rightarrow 2|{ b }\\$

$\Rightarrow b=2c\\$ for some positive integer

$c$

$\therefore 2{ a }^{ 2 }={ b }^{ 2 }\Rightarrow 2{ a }^{ 2 }=4{ c }^{ 2 }\Rightarrow { a }^{ 2 }=2{ c }^{ 2 }\Rightarrow 2|{ a }^{ 2 }\qquad \left[ \because 2|2{ c }^{ 2 } \right] \\$

$\Rightarrow 2|{ a }$

This is a contradiction to the fact that

$a,\ b$ are co-primes.

Hence,

$\dfrac { 1 }{ \sqrt { 2 } }$ is irrational.

What can you say about the prime factorisations of the denominators of the following rationals:

(i) 43.123456789 (ii) $43.\overline { 123456789 }$ (iii) $27.\overline { 142857 }$ (iv) 0.120120012000120000 ....

Given,

(i)

$43.123456789$

it is terminating

$=\dfrac{43.123456789}{10^9}$

$=\dfrac{43.123456789}{2^9 \times 5^9}$

as 43.123456789 is in form of p/q

q is of form

$2^n5^m$

prime factors of q will be

$2,5$

(ii)

$43.\bar{123456789}$

it is not terminating, but repeating

$=\dfrac{43.\bar{123456789}}{10^9}$

$=\dfrac{43.\bar{123456789}}{2^9 \times 5^9}$

$43.\bar{123456789}$ is in form of p/q

q is of form

$2^n5^m$

prime factors of q will be

$2,5$

(iii)

$27.\bar{142857}$

it is not terminating, but repeating

$=\dfrac{27.\bar{142857}}{10^6}$

$=\dfrac{27.\bar{142857}}{2^6 \times 5^6}$

$27.\bar{142857}$ is in form of p/q

q is of form

$2^n5^m$

prime factors of q will be

$2,5$

(iii)

$0.120120012000120000 ....$

as this is non terminanting and non repeating,

so, it is not a rational number

Prove that for any prime positive integer $p$ , $\sqrt { p }$ is an irrational number.

Let us assume on the contrary that

$\sqrt {p}$ is rational. Then, there exist positive co-primes

$a$ and

$b$ such that

$\sqrt {p} = \dfrac {a}{b}$

$\therefore p = \dfrac {a^{2}}{b^{2}}$

$\therefore b^{2} p = a^{2}$

$\Rightarrow p\ | \ { a }^{ 2 }\qquad \left[ \because p\ |\ { b }^{ 2 }p \right]$

$\therefore p\ | \ { a }$

$\therefore a = pc$ for some positive integer

$c$ .

Now,

$b^{2} p = a^{2}$

$\therefore b^{2} p = p^{2}c^{2} \qquad \left[ \because a=pc \right]$

$\therefore b^{2} = p c^{2}$

$\Rightarrow p\ | \ { b }^{ 2 }\qquad \left[ \because p\ | \ p{ c }^{ 2 } \right]$

$\Rightarrow p\ |\ { b }$

$\therefore p\ |\ { a }$ and

$p\ |\ { b }$

This contradicts that

$a$ and

$b$ are co-primes.

Hence,

$\sqrt {p}$ is irrational

Evaluate $\sqrt{11\sqrt{11\sqrt{11\sqrt{11.......\infty}}}}$

Let,

$y=\sqrt{11\sqrt{11\sqrt{11\sqrt{11.......\infty}}}}$

$\Rightarrow y=\sqrt{11.y}$

$\Rightarrow y^2=11y$

$\Rightarrow y(y-11)=0$

$\Rightarrow y=0,11$

But

$y$ cann't be

$0$ .

$\therefore y=11$

Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.

(i) $\dfrac { 23 }{ 8 }$ (ii) $\dfrac { 125 }{ 441 }$ (iii) $\dfrac { 35 }{ 50 }$ (iv) $\dfrac { 77 }{ 210 }$ (v) $\dfrac { 129 }{ { 2 }^{ 2 }\times { 5 }^{ 7 }\times { 7 }^{ 17 } }$

$1)$ Denominator is

$8$ ,so the rational has a non-terminating decimal expansion

$2)$ Denominator is a multiple of

$3,7$ so the rational number has a terminating decimal expansion

$3)\dfrac{35}{50}=\dfrac{7}{10}$ Denominator is

$10$ ,so the rational has a non-terminating decimal expansion

$4)\dfrac{77}{210}=\dfrac{11}{30}$ Denominator is a multiple of

$3$ ,so the rational has a terminating decimal expansion

$5)$ Denominator is a multiple of

$7$ ,so the rational has a terminating decimal expansion

Is this number ${ 7\sqrt { 5 } }$ is irrational or rational?

Let

$7\sqrt{5}$ be rational

$7\sqrt{5}=\dfrac{p}{q} \left(\dfrac{p}{q} \text{is a rational }\right)$

$\sqrt{5}=\left(\dfrac{p}{q}\right)\times \dfrac{1}{7}$

here

$\sqrt{5}$ is irrational

but it is equal to a rational number this contradicts that

$7\sqrt{5}$ is a rational number.

hence

$7\sqrt5$ is a irrational number

Show that the number $3-\sqrt { 5 }$ is irrational.

Let

$3-\sqrt { 5 }$ be a rational equal to

$\dfrac {a}{b}$ Then,

$\Rightarrow 3-\sqrt { 5 } = \dfrac {a}{b}$

$\Rightarrow \sqrt {5} = 3 - \dfrac {a}{b}$

$\Rightarrow \sqrt {5} = \dfrac {3b-a}{b}$

$\Rightarrow \sqrt {5}$ is rational.

This is a contradiction.

Hence,

$3-\sqrt { 5 }$ is irrational.

Is $\pi$ a rational number? Justify your answer.

$\pi$ is not a rational number because the value of

$\pi$ is

$3.141592653589793238$ And it is non-terminating and non repeating.

Prove that $\log\,_2 \ 3$ is an irrational number.

Suppose, if possible, that

$log_2 \, 3$ is rational.
So we assume,

$log_2 \, 3 \, = \, \dfrac{p}{q}$
where

$p$ and

$q$ are positive integers having no factor in common. Then

$3 \, = \, 2^{p/q} \, or \, 3^q \, = \, 2^p$
which is impossible since

$3^q$ is odd and

$2^p$ is even. Hence

$log_2 \, 3$ cannot be rational, that is it is irrational.

Find the largest number that divides $2053$ and $967$ and leaves a remainder of $5$ and $7$ respectively.

Given that on dividing

$2053$ , there is a remainder of

$5$ .
This means that

$2053 - 5 = 2048$ is exactly divisible by the required number.
Similarly,

$967 - 7 = 960$ is exactly divisible by the required number.

$2048 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2$

$= 2^{11}$
and

$960 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 5$

$= 2^{6} \times 3 \times 5$
The smallest common power in both prime factorization

$= 2^{6}$ .

$= 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 64$
So, H.C.F

$= 64$ .

924162_1008055_ans_a5626762f1bd4c6b9b80383953fd6f62.PNG

prove that $\sqrt 5$ is not a rational number. Hence, prove that 2 - $\sqrt 5$ is also irrational.

Let us suppose that

$\sqrt 5$ is a rational number.

Hence,

$\sqrt 5$ can be written as

$\dfrac ab$

where both

$a\ and \ b$ are co-primes.

$\sqrt 5 = \dfrac{a}{b}$

$\Rightarrow\sqrt 5 b = a$

$\Rightarrow 5b^{2} = a^2$

$\therefore \ \dfrac{a^2}{5} = b^2$ .........

$1$

We know that, if a number

$p$ divides

$q^2$ , it will divide

$q$ as well.

Here,

$5$ divides

$a^2$ . Hence, it must divide

$a$ as well.

$\therefore \ \dfrac{a}{5} = c$ (

$c=$ any integer)

$a=5c$ .....

$2$

From

$1$ and

$2$ , we get:

$25c^2= 5b^2$

$b^2 = 5c^2$

$\dfrac{b^2}{5} = c^2$

Again,

$5$ divides

$b^2$ . Hence, it will also divide

$b$ .

Hence,

$5$ is a factor of both

$a$ and

$b$ .

Therefore

$a$ and

$b$ are not co-primes.

So, what we assumed is not true.

Hence,

$\sqrt 5$ is irrational.

Now, according to the properties of irrational numbers, the sum or difference of a rational number and an irrational number is always an irrational number.

Hence,

$(2-\sqrt 5)$ is also irrational.

Find the largest number that will divide $398,\ 436$ and $542$ leaving remainders $7,\ 11$ and $15$ respectively.

Clearly, the required number is the

$HCF$ of the numbers

$398-7=391,436-11=425,$ and,

$542-15=527$ .

First we find the

$HCF$ of

$391$ and

$425$ by Euclids algorithm as given below.

Clearly,

$H.C.F.$ of

$391$ and

$425$ is

$17$ .
Let us now the

$HCF$ of

$17$ and the third number

$527$ by Euclids algorithm:

The

$HCF$ of

$17$ and

$527$ is

$17$ . Hence,

$HCF$ of

$391,4250$ and

$527$ is

$17$ .
Hence, the required number is

$17$ .

1055728_1008057_ans_437f7c5f58264e83aba45c538e4a2ec0.png

Use Euclid's division algorithm to find the $HCF$ of $4052$ and $12576.$

Since 12576 > 4052

12576 = 4052 × 3 + 420

Since the remainder 420 ≠ 0

4052 = 420 × 9 + 272

Consider the new divisor 420 and the new remainder 272

420 = 272 × 1 + 148

Consider the new divisor 272 and the new remainder 148

272 = 148 × 1 + 124

Consider the new divisor 148 and the new remainder 124

148 = 124 × 1 + 24

Consider the new divisor 124 and the new remainder 24

124 = 24 × 5 + 4

Consider the new divisor 24 and the new remainder 4

24 = 4 × 6 + 0

The remainder has now become zero, so procedure stops. Since the divisor at this stage is 4, the HCF of 12576 and 4052 is 4.

If the $HCF$ of $210$ and $55$ is expressible in the form $210 \times 5 + 55y,$ find $y.$

Let us first find the

$HCF$ of

$210$ and

$55$ .

Applying Euclids division lemma on

$210$ and

$55$ , we get

$210=55\times 3+45$

Since the remainder

$45\neq0$ . So, we now apply division lemma on the divisor

$55$ and the remainder

$45$ to get

$55=45\times1+10$

We consider the divisor

$45$ and the remainder

$10$ and apply division lemma to get

$45=4\times10+5$

We consider the divisor

$10$ and the remainder

$5$ and apply division lemma to get

$10=5\times2+0$

We observe that the remainder at this stage is zero. So, that last divisor i.e.

$5$ is the

$HCF$ of

$210$ and

$55$ .

$\therefore\quad 5=210\times 5+55y$

$\Rightarrow\quad 55y=5-210 \times 5=5-1050$

$\Rightarrow\quad 55y=-1045$

$\Rightarrow\quad y=\dfrac { -1045 }{ 55 } =-19$

If $d$ is the $HCF$ of $56$ and $72,$ find $x,\ y$ satisfying $d=56x+72y.$ Also, show that $x$ and $y$ are not unique.

Applying Euclids division lemma to

$56$ and

$72$ , we get

$72=56\times1+16$

Since the remainder

$16\neq0$ . So, we consider the divisor

$56$ and remainder

$16$ and apply division lemma to get

$56=16\times3+8$ ..........

$(ii)$

We consider the divisor

$16$ and the remainder

$8$ and apply division algorithm to get

$16=8\times2+0$

We observe that the remainder at this stage is zero. Therefore, last divisor

$8$ (or the remainder at the earlier stage) is the

$HCF$ of

$56$ and

$72$ .

From

$(ii)$ , we get

$8=56-16 \times 3$

$\Rightarrow\quad 8=56-(72-56 \times 1)\times 3$

$\Rightarrow\quad 8=56-3\times72+56 \times 3$

$\Rightarrow\quad 8=56\times4+(-3) \times72$

$\therefore \quad x=4$ and

$y=-3$ .

Now,

$\quad8=56\times 4+\left( -3 \right) \times 72$

$\Rightarrow\quad 8=56\times 4+\left( -3 \right) \times 72-56\times 72+56\times 72$

$\Rightarrow\quad 8=56\times 4-56\times 72+\left( -3 \right) \times 72+56\times 72$

$\Rightarrow\quad 8=56\times \left( 4-72 \right) +\left\{ \left( -3 \right) +56 \right\} \times 72$

$\Rightarrow\quad 8=56\times \left( -68 \right) +\left( 53 \right) \times 72$

$\therefore\quad x=-68$ and

$y=53$ .

Hence

$x$ and

$y$ are not unique.

Use Euclid's division algorithm to find the $HCF$ of $210$ and $55.$

Step 1 : Given integers are

$210$ and

$55$ such as

$210 > 55$
By Euclid division lemma

$210 = 55 \times 3 + 45$ ..........(i)

Step 2 : Since remainder

$45 \neq 0$ . So for divisor

$55$ and remainder

$45$
By Euclid division lemma

$55 = 45 \times 1 + 10$ ......(ii)
Remainder

$\neq 0$

Step 3 : For division

$45$ and remainder

$10$ by Euclid division lemma

$45 = 10 \times 4 + 5$ ......(iii)
Remainder

$\neq 0$

Step 4 : For new divisor

$10$ and remainder

$5$ by Euclid division lemma

$10 = 5 \times 2 + 0$ ........(iv)
Hence remainder

$= 0$
So, HCF of

$210 , 55$ is

$5$

1029331_1008012_ans_d51c101b88db466084d945c2ba885460.PNG

Find the largest number which divides $245$ and $1029$ leaving remainder $5$ in each case.

It is given that the required number when divides

$245$ and

$1029$ , the remainder is

$5$ in each case, This means that

$245-5=240$ and

$1029-5=1024$ are completely divisible by the required number.

It follows from this that the required number is a common factor of

$240$ and

$1024$ . It is also given that the required number is the largest number satisfying the given property. Therefore, it is the

$HCF$ of

$240$ and

$1024$ .

Let us now find the

$HCF$ of

$240$ and

$1024$ by Prime factorization method(refer above image).
Clearly,

$HCF$ of

$240$ and

$1024$ is common divisor i.e.,

$2\times2\times2\times2=16$ .
Hence, required number

$=16$ .

924157_1008054_ans_4d570b11cb9e475ba75ff46a32e13ca3.jpg

Two tankers contain $850\ litres$ and $680\ litres$ of petrol respectively. Find the maximum capacity of a container which can measure the petrol of either tanker in exact number of times.

Clearly, the maximum capacity of the container is the

$HCF$ of

$850$ and

$680$ in litres.

So, Let us find the

$HCF$ of

$850$ and

$680$ by Euclids algorithm.

Clearly,

$HCF$ of

$850$ and

$680$ is

$170$ .

Hence, capacity of the container must be

$170$ litres.

1055736_1008064_ans_f04e9f68df134d298983121bef1779c5.png

Three sets of English, Hindi and Mathematics books have to be stacked in such a way that all the books are stored topic-wise and the height of each stack is the same. The number of English books is $96,$ the number of Hindi books is $240$ and the number of Mathematics books is $336.$ Assuming that the books are of the same thickness, determine the number of stacks of English, Hindi and Mathematics books.

In order to arrange the books as required, we have to find the largest number that divides

$96,240$ and

$336$ exactly. Clearly, such a number is their

$HCF$ Computation of

$HCF$ of

$96$ and

$240$ :
Clearly,

$HCF$ of

$96$ and

$240$ is

$48$ .
Computation of

$HCF$ of

$48$ and

$336$ :
Thus,

$HCF$ of

$96,240$ and

$336$ is

$48$ .
Hence, there must be

$48$ books in each stack.
Now, Number of stacks of English books

$=\dfrac { Number\ of\ English\ books }{ Number\ of\ books\ in\ each\ stack } =\dfrac { 96 }{ 48 } =2$
Number of stacks of Hindi books

$=\dfrac { Number\ of\ Hindi\ books }{ Number\ of\ books\ in\ each\ stack }$

$=\dfrac { 240 }{ 48 } =5$
and, Number of stacks of Mathematics books

$=\dfrac { Number\ of\ Mathematics\ books\ }{ No.\ of\ books\ in\ each\ stack } =\dfrac { 336 }{ 48 } =7$
1035703_1008067_ans_be4f82ca263b4a9c9244e09df393e8e7.png

Prove that $\sqrt {3}$ is an irrational number.

Let us assume on the contrary that

$\sqrt {3}$ is a rational number.

Then, there exist positive integers

$a$ and

$b$ such that

$\sqrt { 3 } =\dfrac { a }{ b }$ where,

$a$ and

$b$ , are co-prime i.e. their

$HCF$ is

$1$
Now,

$\sqrt { 3 } =\dfrac { a }{ b }$

$\Rightarrow \quad 3=\dfrac { { a }^{ 2 } }{ { b }^{ 2 } }$

$\Rightarrow \quad 3{ b }^{ 2 }={ a }^{ 2 }$

$\Rightarrow \quad 3$ divides

${ a }^{ 2 }\quad \quad \left[ \because 3 \ \text{divides}\ 3{ b }^{ 2 } \right]$

$\Rightarrow \quad 3$ divides

$a\quad \quad ...\left( i \right)$

$\Rightarrow \quad a=3c$ for some integer

$c$

$\Rightarrow \quad { a }^{ 2 }=9{ c }^{ 2 }$

$\Rightarrow \quad 3{ b }^{ 2 }={ 9c }^{ 2 }\quad \quad \left[ \because { a }^{ 2 }=3{ b }^{ 2 } \right]$

$\Rightarrow \quad { b }^{ 2 }={ 3c }^{ 2 }$

$\Rightarrow \quad 3$ divides

${ b }^{ 2 }\quad \quad \left[ \because 3 \ \text{divides}\ 3{ c }^{ 2 } \right]$

$\Rightarrow \quad 3$ divides

$b\quad \quad ...\left( ii \right)$

From

$(i)$ and

$(ii),$ we observe that

$a$ and

$b$ have at least

$3$ as a common factor. But, this contradicts the fact that

$a$ and

$b$ are co-prime. This means that our assumption is not correct.

Hence,

$\sqrt {3}$ is an irrational number.

Prove that $\sqrt {2}$ is an irrational number.

Let us assume on the contrary that

$\sqrt {2}$ is a rational number. Then, there exist positive integers

$a$ and

$b$ such that

$\sqrt { 2 } =\dfrac { a }{ b }$ where,

$a$ and

$b$ , are co-prime i.e. their

$HCF$ is

$1$

$\Rightarrow \quad { \left( \sqrt { 2 } \right) }^{ 2 }={ \left( \dfrac { a }{ b } \right) }^{ 2 }$

$\Rightarrow \quad 2=\dfrac { { a }^{ 2 } }{ { b }^{ 2 } }$

$\Rightarrow \quad 2{ b }^{ 2 }={ a }^{ 2 }$

$\Rightarrow \quad 2|{ a }^{ 2 }\quad \quad \left[ \because 2|2{ b }^{ 2 }\ and\ 2{ b }^{ 2 }={ a }^{ 2 } \right]$

$\Rightarrow \quad 2|a\quad \quad ...\left( i \right)$

$\Rightarrow \quad a=2c$ for some integer

$c$

$\Rightarrow \quad { a }^{ 2 }=4{ c }^{ 2 }$

$\Rightarrow \quad 2{ b }^{ 2 }={ 4c }^{ 2 }\quad \quad \left[ \because 2{ b }^{ 2 }={ a }^{ 2 } \right]$

$\Rightarrow \quad { b }^{ 2 }={ 2c }^{ 2 }$

$\Rightarrow \quad 2|{ b }^{ 2 }\quad \quad \left[ \because 2|2{ c }^{ 2 } \right]$

$\Rightarrow \quad 2|b\quad \quad ...\left( ii \right)$
From

$(i)$ and

$(ii),$ we obtain that

$2$ is a common factor of

$a$ and

$b$ . But, this contradicts the fact that

$a$ and

$b$ have no common factor other than

$1$ . This means that our supposition is wrong.
Hence,

$\sqrt {2}$ is an irrational number.

In a seminar, the number of participants in Hindi, English and Mathematics are $60,\ 84$ and $108$ respectively. Find the number of rooms required if in each room the same number of participants are to be seated and all of them being in the same subject.

The number of participants in each room must be the

$HCF$ of

$60,84$ and

$108$ .

In order to find the

$HCF$ of

$60,84$ and

$108$ , we first the

$HCF$ of

$60$ and

$84$ by Euclids division algorithm:
Clearly,

$HCF$ of

$60$ and

$84$ is

$12$ .

Now, we find the

$HCF$ of

$12$ and

$108$
Clearly,

$HCF$ of

$12$ and

$108$ is

$12$ .
Hence, the

$HCF$ of

$60,84$ and

$108$ is

$12$ .

Therefore, in each room maximum

$12$ participants can be seated.
Wehave,

Total number of participants

$=60+84+108=252$

$\therefore \quad$ Number of rooms required

$=\dfrac { 252 }{ 12 } =21$ .

924180_1008065_ans_8b65ba944dd548ac9721d3fa12188862.png

Show that there is no positive integer $n$ for which $\sqrt { n-1 } +\sqrt { n+1 }$ is rational.

If possible, let there be a positive integer

$n$ for which

$\sqrt { n-1 } +\sqrt { n+1 }$ is rational, which is equal to

$\dfrac { a }{ b }$ (say), where

$a, b$ are positive integers.

Then,

$\dfrac { a }{ b } =\sqrt { n-1 } +\sqrt { n+1 }$ ..... (1)

$\Rightarrow \quad$

$\dfrac { b }{ a } =\dfrac { 1 }{ \sqrt { n-1 } +\sqrt { n+1 } }$

$\Rightarrow \quad$

$\dfrac { b }{ a } =\dfrac { \sqrt { n+1 } -\sqrt { n-1 } }{ \left\{ \sqrt { n+1 } +\sqrt { n-1 } \right\} \left\{ \sqrt { n+1 } -\sqrt { n-1 } \right\} }$

$\Rightarrow \dfrac{b}{a}=\dfrac { \sqrt { n } +1-\sqrt { n-1 } }{ \left( n+1 \right) -\left( n-1 \right) }$

$\Rightarrow \dfrac{b}{a}=\dfrac { \sqrt { n+1 } -\sqrt { n-1 } }{ 2 }$

$\Rightarrow \quad$

$\dfrac { 2b }{ a } =\sqrt { n+1 } -\sqrt { n-1 }$ ..... (2)

Adding (1) and (2), we get

$2\sqrt { n+1 } =\dfrac { a }{ b } +\dfrac { 2b }{ a }$

Subtracting (2) from (1), we get

$2\sqrt { n-1 } =\dfrac { a }{ b } -\dfrac { 2b }{ a }$

$\Rightarrow \quad$

$\sqrt { n+1 } =\dfrac { { a }^{ 2 }+2{ b }^{ 2 } }{ 2ab }$ and

$\sqrt { n-1 } =\dfrac { { a }^{ 2 }-2{ b }^{ 2 } }{ 2ab }$

$\Rightarrow \quad \sqrt { n+1 }$ and

$\sqrt { n-1 }$ are rationals

$[$

$\because a,b$ are integers

$\therefore \dfrac { { a }^{ 2 }+{ b }^{ 2 } }{ 2ab }$ and

$\dfrac { { a }^{ 2 }-2{ b }^{ 2 } }{ 2ab }$ are rationals

$]$

$\Rightarrow \quad (n+1)$ and

$(n-1)$ are perfect square of positive integers.

Now,

$(n+1)-(n-1)=2$ which is not possible as any two perfect squares differ at least by

$3$ .

Hence, there is no positive integer

$n$ for which

$(\sqrt { n-1 } +\sqrt { n+1 })$ is rational.

Prove that $3 + 2\sqrt {5}$ is an irrational.

Assume that $3 + 2\sqrt 5$ is rational. Then,

$3 + 2\sqrt 5 = \dfrac{a}{b}$

$\sqrt 5 = \dfrac{{a - 3b}}{{2b}}$

This gives that $\dfrac{{a - 3b}}{{2b}}$ is rational but $\sqrt 5$ is an irrational number, therefore, the assumption is wrong.

Hence, $3 + 2\sqrt 5$ is irrational.

Find the largest positive integer that will divide $398,\ 436$ and $542$ leaving remainders $7,\ 11$ and $15$ respectively.

It is given that on dividing

$398$ by the required number, there is a remainder of

$7$ .
This means that

$398-7=391$ is exactly divisible by the required number. In other words required number is a factor of

$391$ .

Similarly, required positive integer is a factor of

$436-11=425$ and

$542-15=527$ .
Clearly, required number is the

$HCF$ of

$391,425$ and

$527$ .
Using the factor theorem the prime factorizations of

$391,425$ and

$527$ are as follows:

$391=17\times 23,425={5}^{2}\times 17$ and

$527=17\times 31$

$\therefore\ HCF$ of

$391,425$ and

$527$ is

$17$
Hence, required number

$=17$

Prove that $3\sqrt { 2 }$ is irrational.

Let us assume, to the contrary, that

$3 \sqrt {2}$ is

rational. Then, there exist co-prime positive integers

$a$ and

$b$ such that

$3\sqrt { 2 } =\cfrac { a }{ b }$

$\Rightarrow$

$\sqrt { 2 } =\cfrac { a }{ 3b }$

$\Rightarrow$

$\sqrt {2}$ is rational ...

$[$

$\because 3,a$ and

$b$ are integers

$\therefore \cfrac { a }{ 3b }$ is a rational number

$]$

This contradicts the fact that

$\sqrt {2}$ is irrational.

So, our assumption is not correct.

Hence,

$3 \sqrt {2}$ is an irrational number.

In a seminar, the number of participants in Hindi, English and Mathematics are $60,\ 84$ and $108$ respectively. Find the minimum number of rooms required if in each room the same number of participants are to be seated and all of them being in the same subject.

The Number of room will be minimum if each room accomodates maximum

number of participants. Since in each room the same number of participants

are to be seated and all of them must be of the same subject. Therefore, the

number of participants in each room must be the

$HCF$ of

$60,84$ and

$108$ . The prime factorisations of

$60,84$ and

$108$ are as under.

$60={2}^{2}\times 3\times 5,84={2}^{2}\times 3\times 7$ and

$108={2}^{2}\times {3}^{3}$

$\therefore\ HCF$ of

$60,84$ and

$108$ is

${2}^{2}\times 3=12$
Therefore, in each room

$12$ participants can be seated.

$\therefore\ Number\ of\ rooms\ required =\dfrac { Total\ number\ of\ participants }{ 12 }$

$=\dfrac { 60+84+108 }{ 12 } =\dfrac { 252 }{ 12 } =21$

Prove that $5 - \sqrt {3}$ is an irrational number.

Let us assume on the contrary that

$5-\sqrt {3}$ is
rational. Then, there exist prime positive integers

$a$
and

$b$ such that

$5-\sqrt { 3 } =\dfrac { a }{ b }$

$\Rightarrow \quad$

$5-\dfrac { a }{ b } =\sqrt { 3 }$

$\Rightarrow \quad$

$\sqrt {3}$ is rational

$[$

$\because a,b$ are integers

$\therefore \dfrac { 5b-a }{ b }$ is a rational number

$]$

This contradicts the fact that

$\sqrt {3}$ is irrational.
So, our assumption is incorrect. Hence,

$5-\sqrt {3}$ is
an irrational number.

Without actually performing the long division, state whether the following rational number will have terminating decimal expansion or a non-terminating repeating decimal expansion. Also, find the numbers of places of decimals after which the decimal expansion terminates.
$\dfrac { 17 }{ 8 }$

We have,

$\dfrac { 17 }{ 8 } =\dfrac { 17 }{ { 2 }^{ 3 }\times { 5 }^{ 0 } }$

So, the denominator 8 of the given rational number is of the form

$2^m \times 5^n$ , where m,n are non-negative integers.

Hence

$\frac{17}{8}$ has terminating decimal expansion. the decimal expansion of

$\frac { 17 }{ 8 }$ terminates after

$\text{max}(3,0)=3$ places of decimals.

$\frac{p - 5q}{3q}$ is rational, So is $\sqrt{2}$ , but this contradicts the fact that $\sqrt{2}$ is irrational. Hence, we conclude $5 + 3\sqrt{2}$ is irrational.

1316996_1010009_ans_b3ecc17d35e641f7a6b6df79e7629346.jpg

Find the HCF of $1656$ and $4025$ by Euclids division theorem

HCF of

$1656$ and

$4025$ by Euclids division method .

$4025=1656\times 2+713$

$1656=713\times 2+230$

$713=230\times 3+23$

$230=23\times 10+0$

we divide until we get remainder 0.

$\therefore$ HCF of

$1656$ and

$4025$ is

$23$

Without actually performing the long division, state whether the following rational number will have terminating decimal expansion or a non-terminating repeating decimal expansion. Also, find the numbers of places of decimals after which the decimal expansion terminates.
$\dfrac { 15 }{ 1600 }$

we have,

$\dfrac { 15 }{ 1600 } =\dfrac { 3 }{ 320 } =\dfrac { 3 }{ { 2 }^{ 6 }\times { 5 }^{ 2 } }$

this means that the prime factrorization of the denominator of

$\dfrac{15}{1600}$ s of the form

$2^m \times 5^n$ .

hence, it has terminating decimal expansion which terminates after

$max(6,2)=6$ places of decimals.

Without actually performing the long division, state whether the following rational number will have terminating decimal expansion or a non-terminating repeating decimal expansion. Also, find the numbers of places of decimals after which the decimal expansion terminates.
$\dfrac { 64 }{ 455 }$

We have

$\dfrac { 64 }{ 455 } =\dfrac { 64 }{ 5\times 7\times 13 }$

Clearly

$455$ is not of the form

$2^m \times 5^n$

If it is not of the above mentioned form then, the decimal expansion is non-terminating

$\Rightarrow \dfrac{64}{455}$ is non -terminating repeating.

Prove that $\sqrt {5}$ is an irrational number.

Let us assume that

$√5$ is a rational number.

we know that the rational numbers are in the form of p/q form where p,q are coprime numbers.

so,

$\sqrt5 = \dfrac{p}{q}$

$p = \sqrt(5)q$

we know that 'p' is a rational number. so

$\sqrt(5)$ q must be rational since it equals to p

but it doesnt occurs with

$\sqrt(5)q$ since its not an integer

therefore, p is not equal to

$\sqrt(5)q$

this contradicts the fact that

$\sqrt(5)$ is an irrational number

hence our assumption is wrong and

$\sqrt(5)$ is an irrational number

Without actual division find whether ${\dfrac{17} {68}}$ has terminating of non-terminating recurring decimal expansion?

$68=2\times2\times17=2^2\times17$

Since Denominator has

$17$ and as well as numerator has

$17$ so,

$\cfrac{17}{68}$ will terminate as non repeating decimal.

Without actually performing the long division, state whether the following rational number will have terminating decimal expansion or a non-terminating repeating decimal expansion. Also, find the numbers of places of decimals after which the decimal expansion terminates.
$\dfrac { 29 }{ 343 }$

Given fraction can be rewritten as,

$\dfrac { 29 }{ 343 } =\dfrac { 29 }{ 7^3 }$

Clearly

$343$ is not of the form

$2^m \times 5^n.$

Therefore the decimal expansion of

$\dfrac{29}{343}$ is non -terminating repeating.

Without actually performing the long division, state whether the following rational numbers will have terminating decimal expansion or a non-terminating repeating decimal expansion. Also, find the numbers of places of decimals after which the decimal expansion terminates.
$\dfrac { 23 }{ { 2 }^{ 3 }{ 5 }^{ 2 } }$

clearly ,the prime factorisation of the denominator of

$\dfrac{23}{2^3 \times 5^2}$ is of the form

$2^m \times 5^n$ . so it has terminating decimal expansion which terminates after

$max( 3,2)=3$ places of decimals.

The prime factorization method to determine the HCF of each of the following.
$520,1430$

$HCF$ of

$520$ and

$1430$

By prime factorization Method

$\Rightarrow 520=2^{2}\times 5\times 13$

$\Rightarrow 1430=2\times 5\times 13\times 11$

Thus

$HCF (520,1430)=5\times 13\times 2=130$

The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational or not. If they are rational, and of them $\dfrac{p}{q}$ , what can you say about the prime factors of $q$ ?

i) $43.123456789$

ii) $0.120120012000120000....$

iii) $43.\overline {123456789}$

$43.123456789$ is terminating or rational

$43.123456789=\dfrac{43123456789}{1000000000}=\dfrac{43123456789}{10^9}=\dfrac{43123456789}{(2\times5)^9}=\dfrac{43123456789}{2^9 \times5^9}$

This is in the form of

$\dfrac{p}{q}$ , and the prime factors of

$q$ are in terms of

$2$ and

$5$ .

ii)

$0.120120012000120000....$ is non-terminating and non-repeating, it is irrational. Hence cannot be expressed in the form of

$\dfrac{p}{q}$

iii)

$43. \overline{123456789}$ is non-terminating but repeating. So, it would be rational.

Let

$x=43. \overline{123456789}$

$\dots(1)$

$1000000000x=43123456789,\overline{123456789}$

$\dots(2)$

$(2)-(1)\Rightarrow 999999999x=43123456746\Rightarrow x=\dfrac{43123456746}{999999999}=\dfrac{43123456746}{3^4 \times 37^1 \times 333667^1}$

In a non-termination repeating expansion of

$\dfrac{p}{q}$ ,

$q$ will have factors

$3,37,333667$ .

Prove that $\sqrt{5}-\sqrt{3}$ is not a rational number.

Let

$\sqrt 5-\sqrt 3$ be a rational number of form

$\frac{a}{b}$ ,where

$b\neq 0$

Squaring on both sides

$(\sqrt 5- \sqrt 3)^2=(\dfrac{a}{b})^2$

$(\sqrt 5)^2+(\sqrt 3)^2- 2(\sqrt 5)(\sqrt 3)=\dfrac{a^2}{b^2}$

$5+3+2\sqrt 15=\dfrac{a^2}{b^2}$

$8+2\sqrt 15=\dfrac{a^2}{b^2}$

$2\sqrt 15=\dfrac{a^2}{b^2}-8$

$\sqrt 15=\dfrac{a^2-8b^2}{2b^2}$

since

$\sqrt 15$ is irrational ,

$\dfrac{a^2-8b^2}{2b^2}$ is rational

Since LHS

$\neq$ RHS, contradiction arises,

Therefore

$\sqrt 5-\sqrt 3$ is irrational

Prove that $\sqrt {7}$ is an irrational number.

Let us assume that

$\sqrt{7}$ is rational. Then, there exist co-prime positive integers

$a$ and

$b$ such that

$\sqrt{7} = \dfrac{a}{b}$

$\implies a = b\sqrt{7}$

Squaring on both sides, we get

$a^2 = 7b^2$

Therefore,

$a^2$ is divisible by

$7$ and hence,

$a$ is also divisible by

$7$

so, we can write

$a = 7p,$ for some integer

$p.$

Substituting for

$a$ , we get

$49p^2 = 7b^2 \implies b^2 = 7p^2.$

This means,

$b^2$ is also divisible by

$7$ and so,

$b$ is also divisible by

$7$ .

Therefore,

$a$ and

$b$ have at least one common factor, i.e.,

$7$ .

But, this contradicts the fact that

$a$ and

$b$ are co-prime.

Thus, our supposition is wrong.

Hence,

$\sqrt{7}$ is irrational.

144, 280 and 360 - Find HCF of these three numbers

$144=2^4\times3^2\\280=2^3\times5\times7\\360=2^3\times3^2\times5$

So, HCF

$(144,280,360)=2^3=8$

Check $\frac{2\sqrt{45} + 3\sqrt{20}}{2\sqrt{5}}$ is rational number and irrational number?

$\dfrac{2\sqrt{45}+3\sqrt{20}}{2\sqrt{5}}$

$=\dfrac{2\sqrt{(3.3).5}+3\sqrt{(2.2).5}}{2\sqrt{5}}$

$=\dfrac{2.3\sqrt{5}+3.2\sqrt{5}}{2\sqrt{5}}$

$=\dfrac{6\sqrt{5}+6\sqrt{5}}{2\sqrt{5}}$

$=\dfrac{12\sqrt{5}}{2\sqrt{5}}$

$=6$

Hence, it is a rational number.

Prove the following are irrational.
$\sqrt {5}$

Assume that $\sqrt 5$ be a rational number. So,

$\sqrt 5 = \dfrac{p}{q}$ , where $p$ and $q$ are co prime.

$5 = \dfrac{{{p^2}}}{{{q^2}}}$

$5{q^2} = {p^2}$ (1)

This shows that ${p^2}$ is divisible by 5, then $p$ is divisible by 5, then for any positive integer $c$ , it can be said that $p = 5c$ , ${p^2} = 25{c^2}$ .

Then equation (1) can be written as,

$5{q^2} = 25{c^2}$

${q^2} = 5{c^2}$

This gives that $q$ is divisible by 5.

So, $p$ and $q$ has a common factor 5 which is a contradiction to the assumption that they are co prime.

Hence, $\sqrt 5$ is an irrational number.

Prove the following number is irrational.
$\dfrac {1}{\sqrt {2}}$

Le us consider that the

$\dfrac{1}{\sqrt2}$ is rational.

Now we write it in the form of

$\dfrac{a}{b}$

where

$a$ and

$b$ are co-prime

Therefore,

$\dfrac{1}{\sqrt2}=\dfrac{a}{b}$

Hence,

$\dfrac{b}{a}=\sqrt2$

where

$\dfrac{b}{a}$ is rational,

$\sqrt 2$ is irrational.

i.e.

$Rational \ne Irrational$

which is a contradiction,

and our consideration is incorrect.

Therefore

$\dfrac{1}{\sqrt 2}$ is irrational.

Prove that $\sqrt {2}$ is on irrational number and also prove that $3+5\sqrt {2}$ is irrational number.

Consider the problem

$\sqrt 2$ is non terminating, repeating terms so

$\sqrt 2$ is irrational.

For

$3+5\sqrt 2$

Let us consider that the

$3+5\sqrt 2$ is rational

$3+5\sqrt 2$ is rational. it must be in the form of

$\frac{p}{q}$

Then

$3+5\sqrt 2=\frac{p}{q}$

$5\sqrt 2=\frac{p}{q}-3$

$\sqrt 2=\frac{p-3q}{5}$ ,

And

$\sqrt 2$ irrational

Therefore,

$3+5\sqrt 2$ is irrational.

Prove that $5-\frac{2}{7}\sqrt3$ is irrational number.

1158945_1052167_ans_514822e1fbc6440889122b6342eb2710.jpg

Show that $(\sqrt{3} + \sqrt{5})^{2}$ is an irrational.

$(\sqrt{3}+\sqrt{5})^2=(\sqrt{3})^2 + (\sqrt{5})^2 + 2\sqrt{3}\sqrt{5}$

$=3+5+2\sqrt{15}$

$=8+2\sqrt{15}$ which is an irrational number

Without actually performing the long deviation, state whether the following rational number will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
$\dfrac {13}{3125}$

Let us consider factor of denominator

$3125=5 \times 5 \times 5 \times 5 \times 5=5^5$

Denominator

$=5^5=2^0 \times 5^5=2^0 \times 5^5$

in the form

$2^n5^m$

Where

$m=0,n=5$

Thus they are terminating decimal .

Find the greatest number which can divide $257$ and $329$ so as to leave a remainder $5$ in each case.

Let

$x=257$

$y=329$

Given

$R=5$

$\Rightarrow x-5=257-5\\= 252$

$\Rightarrow y-5=329-5\\= 324$

Factorize

$252$ and

$324$

$252=2^2\times 3^2\times 7$

$324=2^2\times 3^4$

Required number will be the HCF of

$324$ and

$252$

$HCF= 2^2\times 3^2\\=4\times 9\\=36$ .

The decimal expansion of the rational no. $\dfrac{43}{2^45^3}$ will terminate after how many of decimals?

Solution:-

If the denominator of a rational number is of the form

${2}^{n}{5}^{m}$ , then it will terminate after

$n$ places, if

$n > m$ or

$m$ places, if

$m > n$ .

The given rational number is

$\cfrac{43}{{2}^{4}{5}^{3}}$

As the denominator is of the form

${2}^{n} {5}^{m}$ , where as

$n \left( = 4 \right) > m \left( = 3 \right)$

Hence, the given rational number will terminate after n places, i.e., 4 places.

Hence, the correct answer is 4.

Prove that $\sqrt{2}$ is irrational and hence prove that $\dfrac{5- 3\sqrt{2}}{7}$ is irrational.

Let us assume that

$\sqrt{2}$ is a rational. Then there exist co-prime positive integers

$a$ and

$b$ such that,

$\sqrt{2} = \dfrac{a}{b}$

$\implies a = b\sqrt{2}$

Squaring on both sides, we get

$a^2 = 2b^2$

Therefore,

$a^2$ is divisible by

$2$ and hence

$a$ is also divisible by

$2$

So, we can write

$a = 2p$ , for some integer

$p$

substituting for

$a$ , we get

$4p^2 = 2b^2 \implies b^2 = 2p^2$

This means,

$b^2$ is divisible by

$2$ and so,

$b$ is also divisible by

$2$ .

Therefore,

$a$ and

$b$ have at least one common factor, i.e,

$2$

But, this contradicts the fact that

$a$ and

$b$ are co-primes.

Thus, our supposition is wrong.

Hence,

$\sqrt{2}$ is an irrational.

$\sqrt{2}$ is an irrational ,

$5-3\sqrt{2}$ is an irrational,

And

$\dfrac{5-3\sqrt{2}}{7}$ is also an irrational.

Show that $\sqrt{2}+\sqrt{3}$ is an irrational number.

Assume that $\sqrt 2 + \sqrt 3$ is a rational number. Then,

$\sqrt 2 + \sqrt 3 = \frac{p}{q}$

Where $p$ and $q$ are co-prime numbers and $q \ne 0$ .

Squaring both sides,

$2 + 3 + 2\sqrt 3 = \frac{{{p^2}}}{{{q^2}}}$

$5 + 2\sqrt 3 = \frac{{{p^2}}}{{{q^2}}}$

$2\sqrt 3 = \frac{{{p^2}}}{{{q^2}}} - 5$

$2\sqrt 3 = \frac{{{p^2} - 5{q^2}}}{{{q^2}}}$

$\sqrt 3 = \frac{{{p^2} - 5{q^2}}}{{2{q^2}}}$

It can be observed that $\frac{{{p^2} - 5{q^2}}}{{2{q^2}}}$ is a rational number but $\sqrt 3$ is an irrational number which cannot be possible.

Therefore, the assumption is wrong.

Hence, $\sqrt 2 + \sqrt 3$ is an irrational number.

Show that $5 + 3\sqrt{5}$ is irrational.

Let us assume

$5+3\sqrt{5}$ is rational

$5+3\sqrt{5}=\dfrac{a}{b}$

$3\sqrt{5}=\dfrac{a}{b}-5$

$\sqrt{5}=\dfrac{a}{3b}-\dfrac{5}{3}$

here

$\sqrt{5}$ is lrrational

$\dfrac{a}{3b}-\dfrac{5}{5}$ is rational

i,e which condradicts the statement

$\therefore$

$5+3\sqrt{5}$ is irrational

Hence proved

Without actually performing the long deviation, state whether the following rational number will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
$\dfrac {15}{1600}$

$\begin{array}{l} \dfrac { { 15 } }{ { 1600 } } \\ =\dfrac { { 15 } }{ { { 2^{ 6 } }\times { 5^{ 2 } } } } \end{array}$

Since prime factorization of the denominator is of the form

${2^n}{5^m}$ where m,n are whole numbers

therefore it has terminating decimal.

Show that $3\sqrt{2}$ is an irrational number.

Consider that $3\sqrt 2$ is a rational number. Then,

$3\sqrt 2 = \frac{p}{q}$

Where $p$ and $q$ are co-prime numbers and $q \ne 0$ .

Squaring both sides,

$18 = \frac{{{p^2}}}{{{q^2}}}$

$18{q^2} = {p^2}$ (1)

This shows that ${p^2}$ is divisible by 18 and thus $p$ is divisible by 18. Therefore,

$p = 18k$

${p^2} = 324{k^2}$ (2)

From equation (1) and (2),

$18{q^2} = 324{k^2}$

${q^2} = 18{k^2}$

It can be observed that $p$ and $q$ both are divisible by 18 which is a contradiction to the fact that $p$ and $q$ are co-primes.

Therefore, the assumption is wrong.

Hence, $3\sqrt 2$ is an irrational number.

Show that $\sqrt{3}$ is an irrational number.

Consider that $\sqrt 3$ is a rational number. Then,

$\sqrt 3 = \frac{p}{q}$

Where $p$ and $q$ are co-prime numbers and $q \ne 0$ .

Squaring both sides,

$3 = \frac{{{p^2}}}{{{q^2}}}$

$3{q^2} = {p^2}$ (1)

This shows that ${p^2}$ is divisible by 3 and thus $p$ is divisible by 3. Therefore,

$p = 3k$

${p^2} = 9{k^2}$ (2)

From equation (1) and (2),

$3{q^2} = 9{k^2}$

${q^2} = 3{k^2}$

It can be observed that $p$ and $q$ both are divisible by 3 which is a contradiction to the fact that $p$ and $q$ are co-primes.

Therefore, the assumption is wrong.

Hence, $\sqrt 3$ is an irrational number.

Show that $5-\sqrt{3}$ is an irrational number.

Assume that $5 - \sqrt 3$ is a rational number. Then it can be expressed as a fraction,

$5 - \sqrt 3 = \frac{p}{q}$

$5 - \frac{p}{q} = \sqrt 3$

Where $p$ and $q$ are co-prime numbers and $q \ne 0$ .

$\dfrac{{5q - p}}{q} = \sqrt 3$

It can be observed that $\dfrac{{5q - p}}{q}$ is a rational number because adding or subtracting two rational numbers gives a rational number but $\sqrt 3$ is an irrational number which cannot be possible.

Therefore, the assumption is wrong.

Hence, $5 - \sqrt 3$ is an irrational number.

Without actually performing the long deviation, state whether the following rational number will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
$\dfrac {35}{50}$

Let,

$\dfrac{35}{50}=\dfrac{7}{10}$

Cheking co-prime

$7$ and

$10$ have no common factor

Therefore,

$7$ and

$10$ are co-prime.

For denominator

$=10=2^1 \times 5^1$

Therefore,

denominator is of the form

$2^n5^m$

Where

$m=1.n=1$

Hence the

$\dfrac{7}{10}$ and

$\dfrac{35}{50}$ are the terminating decimal.

Without performing division check whether the following rational numbers will have a terminating decimal from or none-terminating repeating decimal form.(RP)
i) $\dfrac {11}{12}$

ii) $\dfrac {15}{1600}$

$\dfrac{p}{q}$ is terminating if

a) p and q are co-primes

and

b) q is of the form

$2^m\times 5^n$ ,where m and n are non negative integers

$\dfrac{11}{12}$

$11$ and

$12$ have no common factors ,so

$11$ and

$12$ are co-primes

$12 =$

$2^2\times 3^1$

Denominator

$12$ is not of the form

$2^m\times 5^n$

Hence

$\dfrac{11}{12}$ is a non-terminating repeating decimal

ii)

$\dfrac{15}{1600}$

$=\dfrac{3}{320}$

Here,

$3$ and

$320$ have no common factors ,so

$3$ and

$320$ are co-primes

$320 =$

$2^6\times 5^1$

Denominator

$320$ is of the form

$2^m\times 5^n$ where,

$m= 6$ and

$n= 1$ where, m and n are non negative integers

Hence

$\dfrac{15}{1600}$ is a terminating decimal

Without actually performing the long deviation, state whether the following rational number will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
$\dfrac {6}{15}$

Let,

$\dfrac{6}{15}=\dfrac{2}{5}$

Checking co-prime

$2$ and

$5$ are no factor

Therefore

$2$ and

$5$ are co prime

For denominator

$=5=2^0 \times 5^1$

in the form of

$2^n5^m$ where

$m=1,n=0$

Hence they are terminating decimal

Raghu's mother wants to pack $88$ sweets, $66$ pencils and $44$ erases into boxed for his birthday to give as return gifts to his friends. The sweets, pencils and erasers should be equally distributed among the boxes. Find the maximum number of boxes that can be packed and the number of sweets, pencils and erasers that can be packed in each box.

To find the max number of boxes to be packed we need to find the HCF.

$88=2\times 2\times 2\times 11\\66=2\times 3\times 11\\44=2\times 2\times 11\\HCF=2\times 11=22$

$22$ no . of boxes are needed to be packed.

No .of sweets in each box

$\dfrac {88}{22}=4$

No .of pencils in each box

$\dfrac {66}{22}=3$

No .of erasers in each box

$\dfrac {44}{22}=2$

If $p$ and $q$ are the positive prime number, then prove that $\sqrt p + \sqrt q$ is an irrational number.

Let us asume

$\sqrt{p}+\sqrt{q}$ are rational.

Given that

$p$ and

$q$ are prime positive integers.

$\sqrt{p}+\sqrt{q}=\dfrac{a}{b}$

Squaring on both sides, we get

$p+q+2\sqrt{pq}=\left(\dfrac{a}{b}\right)^{2}$

$\sqrt{pq}=\dfrac{1}{2}\left[\left(\dfrac{a}{b}\right)^{2}-p-q\right] - (i)$

We know that

$p$ &

$q$ are prime positive numbers

$\Rightarrow \sqrt{p}$ ,

$\sqrt{q}$ and

$\sqrt{pq}$ are irrational

So our assumption

$\sqrt{p}+\sqrt{q}$ are rational is incorrect.

$\Rightarrow\ \sqrt p+\sqrt q$ is a irrational number if

$p,q$ are prime positive numbers

prove that $3 + \sqrt 5$ is an irrational number.

Let us assume that

$3+\sqrt{5}$ is a rational number.

Now,

$3+\sqrt{5}=\dfrac{a}{b}$ [Here a and b are co-prime numbers]

$\sqrt{5} =\left [ \left ( \dfrac{a}{b} \right )-3 \right ]$

$\sqrt{5} =\left [ \left ( \dfrac{a-3b}{b} \right ) \right ]$

Here,

$\left [ \left ( \dfrac{a-3b}{b} \right ) \right ]$ is a rational number.

But we know that

$\sqrt{5}$ is an irrational number.

So,

$\left [ \left ( \dfrac{a-3b}{b} \right ) \right ]$ is also a irrational number.

So, our assumption is wrong.

$3+\sqrt{5}$ is an irrational number.

Hence, proved.

Prove the following number is an irrational number
$\cfrac{1}{2+\sqrt{3}}$

1132318_1093401_ans_5ed25bdcc6dd45618e13a189835da300.jpg

Show that $\sqrt{7}$ is irrational.

1298824_1096185_ans_5c80abbc586c46059382a0639133dcc1.jpg

Find the $LCM$ and $HCF$ of the following itegers by applying the prime factorization method.
$17,23$ and $29$

$17,23,29$ are prime numbers.they have only two factors i.e 1 and itself
$f(17)={1,17}$
$f(23)={1,23}$
$f(29)={1,29}$

hcf of prime numbers =1
hcf $(17,23,29)=1$

lcm of prime numbers= product of the numbers

hcf $(8,9,25)=1$ (1 is common factor of each number)
$lcm =17*29*23=11339$

Prove the following are irrational numbers
$3+\sqrt{5}$

Let us assume

$3 + (5)^{1/2}$ is a rational number

we know that 3 is a rational number.

Now subtract 3 from

$3+(5)^{1/2}$ and we know that the difference of two rational number is also a rational number

That means,

$3+(5)^{1/2}-3=(5)^{1/2}$ should be a rational number but it is not

This means that

$3+(5)^{1/2}$ is an irrational number.

Hence Proved!!

Find the HCF of the following numbers by prime factorisation method ?
i) $18, 27, 36$
ii) $106, 159, 265$
iii) $10, 35, 40$
iv) $32, 64, 96, 128$

$(i) \ 18,27,36$

The three numbers can be represented as the product of their prime factors, as

$3^{2}\times 2,\ \ 3^{3} \text{ and } 3^{2}\times 2^{2}$ respectively.

The product of the lowest powers of the common factors among the three numbers is

$2^1\times 3^2$

$\therefore \ HCF=2 \times 3^{2}=18$

$(ii) \, 106,159,165$

The three numbers can be represented as the product of their prime factors, as

$2\times 53 , \, 3\times 53\text{ and } 5\times 53$ respectively.

The product of the lowest powers of the common factors among the three numbers is

$53^1$

$\therefore \ HCF= 53$

$(iii) \, 10,35,40$

The three numbers can be represented as the product of their prime factors, as

$5\times 2, \,5\times 7, \text{ and } 2^{3} \times 5$ respectively.

The product of the lowest powers of the common factors among the three numbers is

$5^1$

$\therefore \ HCF = 5$

$(iv) \,32,64,96,128$

The three numbers can be represented as the product of their prime factors, as

$2^{5},\, 2^{6}, \, 2^{5}\times 3\text{ and } 2^{7}$ respectively.

The product of the lowest powers of the common factors among the three numbers is

$2^5$

$\therefore \ HCF = 2^{5}=32$

The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational and of the from $\dfrac{p}{q}$ , what can you say about the prime factors of $q$ ?
i) $43.123456789$

$43.123456789$ is terminating

So, it would be a rational number

$43.123456789=\dfrac{43.123456789}{1000000000}$

$=\dfrac{43.123456789}{10^9}$

$=\dfrac{43.123456789}{(2 \times 5)^9}$

$=\dfrac{43.123456789}{2^9 \times 5^9}$

Hence

$43.123456789$ is now in the form

$\dfrac{p}{q}$

And the prime factors of q are in terms of

$2$ and

$5$

What is the $HCF$ of $2^{3}\times 5$ and $2^{2}\times 5^{2}$

We know that

$HCF$ is equal to the product of the common prime factors with the smallest exponent.

Hence,

$HCF = 2^2\times5^1$

$= 4\times5$

$=20$

Show that $\sqrt { 2 }$ is irrational.

Let

$\sqrt { 2 }$ is an rational number.

So,

$\sqrt { 2 } =\dfrac { p }{ q }$ (where p and q are co-prime number and q is not equal to 0)

Squaring both Sides,

$2=\dfrac { p^{ 2 } }{ q^{ 2 } }$

Cross Multiplying,

$q^{ 2 }=2p^{ 2 }\Longrightarrow (1)$

So,We can say that

$q^{ 2 }$ is divisible by

$2$ and

$q$ is also divisible by

$2$ .

Let

$q=2r$

Squaring both Sides,

$q^{ 2 }=4r^{ 2 }\Longrightarrow (2)$

From Eq.1 and 2,

$2p^{ 2 }=4r^{ 2 }$

Dividing both Sides by

$2$ ,

$p^{ 2 }=2r^{ 2 }$

So,We can say that

$p^{ 2 }$ is divisible by

$2$ and

$p$ is also divisible by

$2$ .

From this, we have reached a conclusion that

$p$ and

$q$ both divisible by

$2$ .

It contradicts the fact that

$p$ and

$q$ are co-prime numbers. So, Our Supposition is wrong.

Hence,we can say that

$\sqrt { 2 }$ is an irrational number.

We also use $1.732$ instead of $\sqrt {3}$ , so, can we consider that $\sqrt 3$ is a rational number? Note your opinion.

1121722_1093778_ans_e1d0613077924e648aab75a478be1531.jpg

Without finding the decimal representation, state whether the following rational numbers are terminating decimal or non-terminating decimals.
$\dfrac {1}{12}$

Given that

$\cfrac{1}{12}$

Here

$1$ and

$12$ have no common factors and

$1$ and

$12$ are co-prime

For denominator

$12$

$={2}^{2}\times 3$

$\therefore$ the denominator is not of the form

${2}^{n}.{5}^{m}$

Thus

$\cfrac{1}{12}$ has a non terminating decimals.

Without finding the decimal representation, state whether the following rational numbers are terminating decimal or non-terminating decimals.
$\dfrac {18}{30}$

Given that

$\cfrac{30}{18}=\cfrac{5}{3}$

Here,

$5$ and

$3$ have no common factors and

$3,5$ are co prime factor.

Denominator

$=3$

So, the denominator is not of the form

${2}^{n}.{5}^{m}$

Thus

$\cfrac{30}{18}$ has a non terminating decimals.

Without finding the decimal representation, state whether the following rational numbers are terminating decimal or non-terminating decimals.
$-\dfrac {5}{10}$

Given that

$-\cfrac{5}{10}=-\cfrac{1}{2}$

Formula:

$\cfrac{p}{q}$ is terminating if

(i)

$p$ and

$q$ are co-prime and

(ii)

$q$ is of the form

${2}^{n}.{5}^{m}$

where

$n$ and

$m$ are non-negative integers

Here

$1$ and

$2$ have no common factors

so,

$1$ and

$2$ are co-prime

for denominator

$=2$

$={2}^{1}\times {5}^{0}$

where

$n=1,m=0$

$\therefore$

$-\cfrac{5}{10}=-\cfrac{1}{2}$ is a terminating decimal

Find the HCF using Euclids Algorithm. 136,170,255.

Consider the problem

Euclid division

$a=bq+r$

$0 \le r < b$

First we find the HCF of

$255$ and

$170$

$\begin{array}{l} 255=170\left( 1 \right) +85 \\ 170=85\left( 2 \right) +0 \end{array}$

So, HCF of

$255$ and

$170$ is

$85$

Now, find the HCF of

$136$ and

$85$

$\begin{array}{l} 136=85\left( 1 \right) +51 \\ 85=51\left( 1 \right) +34 \\ 51=34\left( 1 \right) +17 \\ 34=17\left( 2 \right) +0 \end{array}$

HCF of

$136$ and

$85$ is

$17$

Therefore,

$HCF\left( {136,170,255} \right) = 17$

Given that $\sqrt{3} \ and\ \sqrt{5}$ are irrational numbers, prove that $\sqrt{3}+\sqrt{5}$ is an irrational number.

$\sqrt{3}$ &

$\sqrt{5}$ are irrational [given]

To prove:

$\sqrt{3}+\sqrt{5}$ is irrational

Let us assume

$\sqrt{3}+\sqrt{5}$ is rational

Now

$\sqrt{3}+\sqrt{5} = \dfrac{a}{b},$ where a & b are coprime

integers as

$b\neq o$

$\sqrt{3}+\sqrt{5} = \dfrac{a}{b}$

$\sqrt{3} = \dfrac{a}{b}-\sqrt{5}$

$\Rightarrow \dfrac{a-\sqrt{5}b}{b}$ is a form of

$\dfrac{a}{b}$ then

it is rational number

$\dfrac{a-\sqrt{5}b}{b}$ is a rational number

then

$\sqrt{3}$ is also rational numbers

which is not true

$\therefore$ our assumption is false

$\sqrt{3}+\sqrt{5}$ is an irrational number

Without actually performing the long division,state whether the following rational numbers will have a terminating decimal expansion or a non terminating repeating decimal expansion:
$\dfrac{77}{210}$

A simplified fraction of the form

$\dfrac{p}{q}$ has a terminating decimal expansion if and only if all the prime factors of

$q$ are either

$2$ or

$5$ .

$\dfrac{77}{210}=\dfrac{11}{30}$

Given:

$q=30=2\cdot3\cdot5$

As the given denominator has

$3$ as a prime factor, the decimal expansion will be non-terminating.

Without finding the decimal representation, state whether the following rational numbers are terminating decimal or non-terminating decimals.
$-\dfrac {33}{20}$

Given that

$-\cfrac{33}{20}$

Here

$3$ and

$20$ have no common factors and

$33$ and

$20$ are co-prime

for denominator

$=20$

$=5\times 4$

$={2}^{2}.{5}^{1}$

Here

$n=2,m=1$

$\therefore$ the denominator is form of

${2}^{n}.{5}^{m}$

$\therefore$

$-\cfrac{33}{20}$ is a terminating decimal

Without actually performing the long division,state whether the following rational numbers will have a terminating decimal expansion or a non terminating repeating decimal expansion:
$\dfrac{13}{3125}$

A simplified fraction of the form

$\dfrac{p}{q}$ has a terminating decimal expansion if and only if all the prime factors of

$q$ are either 2 or 5.

Given:

$q=3125=5^5$

As the only prime factor of the denominator is

$5$ , the decimal expansion will be terminating.

Prove that $\sqrt {p} + \sqrt {q}$ is irrational , where p , q are primes .

1292980_1254673_ans_abbc4a0f04cc43f8ad7e7512dd20b9b7.jpg

Without finding the decimal representation, state whether the following rational numbers are terminating decimal or non-terminating decimals.
$-\dfrac {13}{27}$

Here

$13$ and

$27$ has no common factor.

So,

$13$ and

$27$ are co-prime.

Denominator

$27=7\times 3$

Here, denominator is not of the form

${2}^{n}\times {5}^{m}.$

Hence,

$-\cfrac{13}{27}$ is non terminating decimals.

Without actual division, check whether $\dfrac { 47 } { 14 }$ is terminating or not.

If the denominator can be in the powers of either

$2$ or

$5$ or both, then it will be a terminating decimal, otherwise non-terminating.

But the denominator of the given fraction is

$14$ and

$14$ can be rewritten as

$2\times7$ , i.e. not in the form

$2^m\times5^n$ ; where

$n,m$ are non-negative.

Hence, the rational number is non-terminating.

Show that $3\sqrt{7}$ is an irrational number.

1231053_1249335_ans_e3191ac0e3f644e381d32839a0539a05.JPG

Prove that $3+2\sqrt {5}$ is irrational.

Prove

$3+2\sqrt{5}$ is irrational.

$\rightarrow$ let take that

$3+2\sqrt{5}$ is rational number

$\rightarrow$ so, we can write this answer as

$\Rightarrow$

$3+2\sqrt{5} = \dfrac ab$

Here

$a$ &

$b$ use two coprime number and

$b \neq 0.$

$\Rightarrow$

$2\sqrt{5} = \dfrac{a}{b}-3$

$\Rightarrow$

$2\sqrt{5} = \dfrac{a-3b}{b}$

$\therefore \sqrt{5} = \dfrac{a-3b}{2b}$

Here

$a$ and

$b$ are integer so

$\dfrac{a-3b}{2b}$ is a rational number so

$\sqrt{5}$ should be rational number but

$\sqrt{5}$ is a irrational number so it is contradict

- Hence

$3+2\sqrt{5}$ is irrational.

Without finding the decimal representation, state whether the following rational numbers are terminating decimal or non-terminating decimals.
$\dfrac {71}{75}$

Given that

$\cfrac{71}{75}$

Here

$71$ and

$75$ have no common factors so

$71$ and

$75$ are co-prime

denominator

$=75={5}^{2}=3$

$\therefore$ the denominator is not a form of

${2}^{n}.{5}^{m}$

$\therefore$

$\cfrac{71}{75}$ is non terminating decimals

Prove that $5-2\sqrt{3}$ is an irrational number.

1292985_1256966_ans_2bf2dafb50e443678004d621c0d1c35d.jpg

Without finding the decimal representation, state whether the following rational numbers are terminating decimal or non-terminating decimals.
$\dfrac {19}{45}$

Given that

$\cfrac{19}{45}$

Here

$19$ and

$45$ have no common factors

$19$ and

$45$ are co prime

denominator

$=45=9\times 5$

$\therefore$ the denominator is of the form of

${2}^{n}.{5}^{m}$

$\therefore$

$\cfrac{19}{45}$ is non terminating decimal

Show that $2+\sqrt{5}$ is an irrational number.

Let

$2 + \sqrt{5}$ is a rational number such that

$2 + \sqrt{5} = \cfrac{p}{q}$

Where

$p$ and

$q$ are co-prime.

Therefore,

$2 + \sqrt{5} = \cfrac{p}{q}$

$\sqrt{5} = \cfrac{p}{q} - 2$

$\Rightarrow \sqrt{5} = \cfrac{p - 2q}{q}$

$\sqrt{5}$ is an irrational number and

$\cfrac{p-2q}{q}$ is a rational number.

$\because$ Rational

$\ne$ Irrational.

Thus

$2 + \sqrt{5}$ is not a rational number.

Hence

$2 + \sqrt{5}$ is an irrational number.

Hence proved.

Prove that $(2\sqrt { 3 } +\sqrt { 5 } )$ is an irrational number. Also check whether $(2\sqrt { 3 } +\sqrt { 5 } )(2\sqrt { 3 } -\sqrt { 5 } )$ is rational or irrational

a) Let us assume that

$2\sqrt{3}+\sqrt{5}$ is rational number.

Let

$P=2\sqrt{3}+\sqrt{5}$ is rational

on squaring both sides we get

$P^2=(2\sqrt{3}+\sqrt{5})^2=(2\sqrt{3})^2+(\sqrt{5})^2+2\times 2\sqrt{3}\times \sqrt{5}$

$P^2=12+5+4\sqrt{15}$

$P^2=17+4\sqrt{15}$

$\dfrac{P^2-17}{4}=\sqrt{15}$ ………..

$(1)$

Since

$P$ is rational no. therefore

$P^2$ is also rational &

$\dfrac{P^2-17}{4}$ is also rational.

But

$\sqrt{15}$ is irrational & in equation

$(1)$

$\dfrac{P^2-17}{4}=\sqrt{15}$

Rational

$\neq$ irrational

Hence our assumption is incorrect &

$2\sqrt{3}+\sqrt{5}$ is irrational number.

$P=(2\sqrt{3}+\sqrt{5})(2\sqrt{3}-\sqrt{5})$

$P=12-5=7$

Hence P is rational as

$\dfrac{p}{q}=\dfrac{7}{1}$ & both

$p$ &

$q$ are coprime numbers.

What is the exponent of $3$ in the prime factorization of $864$ .

$\Rightarrow 864=2^5\times 3^3$

$\Rightarrow$ Exponent of

$3=3.$

Hence, the answer is

$3.$

Prove that $5-\sqrt { 3 }$ is a irrational numbers.

Let

$5 - \sqrt{3}$ is a rational number.
We have to find out two integers a and b such as

$5 - \sqrt{3} = \dfrac{a}{b}$

$- \sqrt{3} = \dfrac{a}{b} - 5$

$\sqrt{3} = 5 - \dfrac{a}{b}$

$\sqrt{3} = \dfrac{5b - a}{b}$

$a , b$ and

$5$ all are integers

$\dfrac{5b - a}{b}$ is a rational number.

$\sqrt{3}$ will be also rational number.
But this contradicts the fact that

$\sqrt{3}$ is an irrational number.
So our hypothesis is wrong.
Hence,

$5 - \sqrt{3}$ is an irrational number.
Hence proved.

Prove that $\sqrt { 3 } +\sqrt { 8 }$ is an irrational number.

Let

$\sqrt{8}$ be a rational number

Then

$\sqrt{8}=\dfrac{m}{n}$ where m, n are integers and m, n are coprimes and

$n\neq 0$

$\Rightarrow m=\sqrt{8}n$

Squaring both sides we get

$m^2=8n^2$

$\Rightarrow \dfrac{m^2}{8}=n^2$ ……………(iv)

$\Rightarrow 8$ divides

$m^2$ i.e.,

$8$ divides m

Then m can be written as

$m=8$ k for some integer k.

Substituting value of m in (iv) we get

$\Rightarrow \dfrac{(8k)^2}{3}=n^2$

$\Rightarrow 8k^2=n^2$

$\Rightarrow k^2=\dfrac{n^2}{8}$

$\Rightarrow 8$ divides

$n^2$ i.e.,

$8$ divides n

Thus we get that

$8$ is a common factor of m and n but m and n are co-primes which is a contradiction to our assumption.

Hence

$\sqrt{8}$ is an irrational number.

Now consider

$\sqrt{3}+\sqrt{8}$ to be an rational number

Then

$\sqrt{3}+\sqrt{8}=\dfrac{a}{b}$ where a, b are integers, co-primes and

$b\neq 0$

$\Rightarrow \sqrt{3}=\dfrac{a}{b}-\sqrt{8}$

Squaring both sides we get

$\Rightarrow 3=\dfrac{a^2}{b^2}+(\sqrt{8})^2-2\dfrac{a}{b}\sqrt{8}$

$\Rightarrow 3=\dfrac{a^2}{b^2}+8-\dfrac{2a}{b}\sqrt{8}$

$\Rightarrow 3-\dfrac{a^2}{b^2}-8=-\dfrac{2a}{b}\sqrt{8}$

$\Rightarrow \dfrac{3b^2-a^2-8b^2}{b^2}=\dfrac{-2a}{b}\sqrt{8}$

$\Rightarrow \sqrt{8}=\dfrac{(3b^2-a^2-8b^2)}{-2ab}$

$\Rightarrow \sqrt{8}=\dfrac{a^2+8b^2-3b^2}{2ab}$

$\Rightarrow \sqrt{8}=\dfrac{a^2+5b^2}{2ab}$

Where

$a^2+5b^2$ is an integer and

$2ab$ is also an integer, but

$\sqrt{8}$ is an irrational number, which is a contradiction.

Hence

$\sqrt{3}+\sqrt{8}$ is an irrational number.

If the HCF of $152$ and $272$ is expressible in the form of $272 \times 8 + 152 x,$ then find $x.$

$\textbf{Step 1: Using Euclid's Division Lemma for given numbers}$

$\text{On applying the Euclid's division lemma to find HCF of}$

$152,272$ , we get,

$\textbf{Refer image, 1}$

$272=152\times 1+120$

$\text{Here the remainder = 0}$

$\text{Using Euclid's division lemma to find the HCF of }$

$152$

$\text{and}$

$120$

$\text{, we get,}$

$152=120\times 1+32$

$\text{Again the remainder = 0}$

$\text{Using division lemma to find the HCF of 120 and 32, we get}$

$\textbf{Refer image, 2}$

$32=24\times 1+8$

$24=8\times 3+0$

$\text{HCF of 272 and 152 is 8}$

$\textbf{Step 2: Solve the Linear Equation.}$

$272\times 8+152x=H.C.F$

$\text{of the numbers}$

$[\textbf{Given, }]$

$\Rightarrow 8=272\times 8+152x$

$\Rightarrow 8-272\times 8=152x$

$\Rightarrow 8(1-272)=152x$

$\Rightarrow x=\dfrac{-271}{19}$

$\textbf{Hence, } \boldsymbol{x=\dfrac{-271}{19}.}$

2153108_1324999_ans_90965356459d4dd99fe05ccedfc6d7c5.JPG

Given that $\sqrt{3}$ is an irrational number, prove that $(2+\sqrt{3})$ is an irrational number.

Given

$\sqrt{3}$ is irrational number

Let

$2 + \sqrt{3}$ is rational number.

then

$2+ \sqrt{3} = \dfrac{p}{q}$

$\sqrt{3} = \dfrac{p-2q}{q}$

Since

$\sqrt{3}$ is irrational number but

$\dfrac{p-2q}{q}$ is rational it mean

irrational = rational

which contradict,

$\therefore$ our assumption is wrong and

$2+\sqrt{3}$ is irrational number.

State where $\left( {\sqrt 6 + \sqrt 9 } \right)$ is rational or not.

Given number is

$\sqrt6+\sqrt9$

$\sqrt9=3$

Hence, the number is

$\sqrt6+3$

We know that

$\sqrt6$ is an irrational number while

$3$ is a rational number.

We also know that, the sum of a rational number and an irrational number is always an irrational number.

Hence,

$\sqrt6+\sqrt9$ is an irrational number.

If $\sqrt {2}=1.4142$ then $\sqrt {\dfrac {\sqrt {2}-1}{\sqrt {2}+1}}=$

$\frac{\sqrt{\frac{(\sqrt{2}-1)}{(\sqrt{2}+1)}\times \frac{(\sqrt{2}-1)}{(\sqrt{2}-1)}}}{\sqrt{\frac{(\sqrt{2}-1)^{2}}{2-1}}}=\sqrt{(\sqrt{2}-1)^{2}}$

$= \sqrt{2} - 1 = 1.4.42 - 1$

= 0.4142

1189495_1354505_ans_77a9b11c1ea54cb985d440ace70947c8.jpg

Show by long deviation method that is $x-3$ factor of $2x^{4}+3x^{2}-5x+6$ or not.

Since remainder is not zero,

$(x-3)$ is not a factor of

$2x^4+3x^2-5x+6$

2035333_1346938_ans_dd7e9ae4cc7542d2a7a523bd4ea59f54.png

Square root of $\sqrt{13-4\sqrt{3}}$ .

Let

$\sqrt{13-4\sqrt{3}}=\sqrt{x}-\sqrt{y}$

$\Rightarrow 13-4\sqrt{3},x+y-2\sqrt{xy}$

$\Rightarrow x+y=13,xy=12$

$\Rightarrow x^2+y^2=169-24=145$

$\Rightarrow \left( x-y\right)^2=145-24=121\Rightarrow x-y=11$

$\therefore x=12,y=1$

$\therefore \sqrt{13-4\sqrt{3}}=\sqrt{12}=1$

$\therefore \sqrt{\sqrt{13-4\sqrt{3}}}=\sqrt{\sqrt{12}-1}$

Hence, solved.

Is $\pi$ an irrational number? Why?

$\pi$ is ratio of circumference to the

diameter of any circle. It is a

transcended number which cannot be

expressed in decimals so,

$\pi$ is an irrational number.

1211218_1340738_ans_86216640c6a7454c997f596799a0f873.jpg

Prove that $5\sqrt{2}+3$ is an irrational number.

Assume,

$5\sqrt{2}+3$ is a rational number.

Then it should be represented in the form of

$\dfrac{p}{q}$ .

$\Rightarrow 5\sqrt{2}+3=\dfrac{p}{q}$

$5\sqrt{2}=\dfrac{p}{q}-3$

$\sqrt{2}=\dfrac{a-3b}{5b}$

$\sqrt{2}$ is irrational.

$\dfrac{a-3b}{5b}$ is rational.

Irrational number can't be equated to rational number.

$\therefore 5\sqrt{2}+3$ is an irrational number.

Prove that $4-3\sqrt { 2 }$ is an irrational.

If possible, let

$4-3\sqrt{2}$ be rational.

Then,

$4-3\sqrt{2}$ is rational and

$4$ is rational.

$[(4-3\sqrt{2})-4]$ is rational. [Difference of two rationals is rational]

$-3\sqrt{2}$ is rational.

$\sqrt{2}$ is rational.

Let the simplest form of

$\sqrt{2}$ be

$\dfrac{a}{b}$ .

Then, a and b are integers having no common factor other than 1, and b

$\neq$ 0.

Now,

$\sqrt{2}=\dfrac{a}{b}$

$2b^{2}=a^{2}$

$2$ divides a

$^{2}$ . [2 divides 2b

$^{2}$ ]

$2$ divides

$a$

Let

$a=2c$ for some integer

$c$ .

Therefore,

$2b^{2}=4c^{2}$

$b^{2}=2c^{2}$

$2$ divides b

$^{2}$ [

$2$ divides 2c

$^{2}$ ]

$2$ divides

$b$

Thus,

$2$ is a common factor of

$a$ and

$b.$

This contradicts the fact that

$a$ and

$b$ have no common factor other than

$1.$

So,

$\sqrt{2}$ is irrational.

Hence,

$4-3\sqrt{2}$ is irrational.

Prove that $5+\surd{2}$ is an irrational number,

To prove

$5+\sqrt{2}$ is irrational,

Let us assume

$\sqrt{2}$ is rational

$\Rightarrow \sqrt{2}=\dfrac{a}{b}$

$(a$ and

$b$ has no common factors except

$1$ )

$\Rightarrow$

$2=\dfrac{a^2}{b^2}$

$\Rightarrow$

$2b^2=a^2$

Hence

$a$ is even ...(1)

Let

$a=2k$

$\Rightarrow 2b^2=\left( 2k\right)^2$

$\Rightarrow b^2=2k^2$

Hence

$b$ is also even ...(2)

This contradicts our assumptions as both

$a$ and

$b$ are even because they have

$2$ as the common factor.

Hence,

$\sqrt{2}$ is irrational.

Hence, proved.

Prove that $\sqrt{5}$ is irrrational

Assume that

$\sqrt{5}$ is rational.

Hence,

$\sqrt{5}$ can be written in the form of

$\dfrac{a}{b}$ where

$a$ and

$b$ are co-prime and

$b\neq 0$

Hence

$\sqrt{5}=\dfrac{a}{b}$

$\Rightarrow a=b\sqrt{5}$

$\Rightarrow {a}^{2}=5{b}^{2}$ by squaring on both sides

$\Rightarrow \dfrac{{a}^{2}}{5}={b}^{2}$

Hence

$5$ divides

${a}^{2}$

By theorem,if

$p$ is a prime number,and

$p$ divided

${a}^{2}$ , then

$p$ divides

$a$ , where

$a$ is a positive number.

So,

$5$ shall divide

$a$ also. ......

$(1)$

Hence, we can say

$\dfrac{a}{5}=c$ where

$c$ is some integer.

So,

$a=5c$

Now we know that

${a}^{2}=5{b}^{2}$

Put

$a=5c$ we get

$25{c}^{2}=5{b}^{2}$

$\Rightarrow {b}^{2}=5{c}^{2}$

$\Rightarrow \dfrac{{b}^{2}}{5}={c}^{2}$

Hence,

$5$ divides

${b}^{2}$

So,

$5$ divides

$b$ also. ......

$(2)$

$(1)$ and

$(2)$

$5$ divides both

$a$ and

$b$

Hence

$5$ is a factor of

$a$ and

$b$

So,

$a$ and

$b$ have a factor

$5$

$\therefore,a$ and

$b$ are not co-prime.

Hence, our assumption is wrong.

$\therefore$ by contradiction,

$\sqrt{5}$ is irrational.

Find the greatest possible length which can be used to measure exactly the lengths $7$ m $, 3$ m $, 85$ m $, 12$ m $95$ cm.

The three given lengths are

$7$ m

$= 700$ cm

$3$ m

$85$ cm

$= 385$ cm and

$12$ m

$95$ m

$= 1295$ cm

now the required length is HCF of

$700 , 385$ and

$1295.$

$700 = 2^2 \times 5^2 \times 7$

$385 = 5 \times 7 \times 11$

$1295 = 5 \times 7 \times 37$
HCF

$(700 , 385$ and

$1295 ) = 5 \times 7 = 35$
The greatest possible length is 35 cm

Prove that $5\sqrt { 3 }$ is an irrational.

If possible, let

$5\sqrt{3}$ is rational.

Let its simplest form be

$5\sqrt{3}=\dfrac{a}{b}$ , where a and b are positive integers having no common factor other than 1.Then,

$5\sqrt{3}=\dfrac{a}{b}$

$\sqrt{3}=\dfrac{a}{5b}$

Since,

$a$ and

$5b$ are non-zero integers, so

$\dfrac{a}{5b}$ is rational.

Thus,

$\sqrt{3}$ is rational.

Let simplest form of

$\sqrt{3}$ be

$\dfrac{a}{b}$ .

Then, a and b are integers having no common factor other than 1, and b

$\neq$ 0.

Now,

$\sqrt{3}=\dfrac{a}{b}$

$3b^{2}=a^{2}$

3 divides a

$^{2}$ . [3 divides 3b

$^{2}$ ]

$3$ divides

$a$ .

Let

$a = 3c$ for some integer

$c$ .

Therefore,

$3b^{2}=9c^{2}$

$b^{2}=3c^{2}$

$3$ divides b

$^{2}$ . [3 divides 3c

$^{2}$ ]

$3$ divides

$b$ .

Thus,

$3$ is a common factor of

$a$ and

$b$ .

But this contradicts the fact that

$a$ nad

$b$ have no common factor other than 1.

Thus,

$\sqrt{3}$ is irrational.

Hence,

$5\sqrt{3}$ is irrational.

Prove that 7 $\sqrt { 5 }$ is irrationals number.

Let us assume that

$7\sqrt{5}$ is rational number

Hence

$7\sqrt{5}$ can be written in the form of

$\dfrac{a}{b}$ where

$a,b(b\ne 0)$ are co-prime

$\implies 7\sqrt{5}=\dfrac{a}{b}$

$\implies \sqrt{5}=\dfrac{a}{7 b}$

But here

$\sqrt{5}$ is irrational and

$\dfrac{a}{7 b}$ is rational

$\mathrm{Rational\ne Irrational}$

This is a contradiction

$7\sqrt{5}$ is a irrational number

Use Euclid's division algorithm to find the $HCF$ of $196$ and $38220$ .

Since

$38220 > 196$ , we apply the division lemma to

$38220$ and

$196$ to obtain HCF

$38220 = 196 \times 195 + 0$

Since the remainder is zero, the process stops.

Since the divisor at this stage is

$196$ ,

$\therefore$ , HCF of

$196$ and

$38220$ is

$196$ .

Find the H.C.F of $\left(x+1\right)\left({x}^{2}-4\right)$ and $\left({x}^{2}-1\right)\left(x-2\right)$

Let

$p\left(x\right)=\left(x+1\right)\left({x}^{2}-4\right)=\left(x+1\right)\left(x+2\right)\left(x-2\right)$

and

$q\left(x\right)=\left({x}^{2}-1\right)\left(x-2\right)=\left(x+1\right)\left(x-1\right)\left(x-2\right)$

The common factor of

$p\left(x\right)$ and

$q\left(x\right)$ is

$=\left(x+1\right)\left(x-2\right)$

$\therefore$ H.C.F of

$p\left(x\right)$ and

$q\left(x\right)$

$=\left(x+1\right)\left(x-2\right)$

Convert the recurring decimal $0.\overline {35}$ to fraction

Let

$x=0.\overline{35}$

$100x=35.\overline{35}$

$100x=35+0.\overline{35}$

$100x=35+x$

$99x=35$

$x=\dfrac{35}{99}$

Evaluate $\dfrac { 15 }{ \sqrt { 10 } +\sqrt { 20 } +\sqrt { 40 } -\sqrt { 5 } -\sqrt { 80 } }$

$\dfrac { 15 }{ \sqrt { 10 } +\sqrt { 20 } +\sqrt { 40 } -\sqrt { 5 } -\sqrt { 80 } }$

$=\dfrac{15}{\sqrt{10}+2\sqrt{5}+2\sqrt{10}-\sqrt{5}-4\sqrt{5}}$

$=\dfrac{15}{3\sqrt{10}-3\sqrt{5}}$

$=\dfrac{5}{\sqrt{10}-\sqrt{5}}$

$=\dfrac{\sqrt{5}}{(\sqrt{2}-1)}$

$=\dfrac{\sqrt{5} (\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)}$

$=\sqrt{10}+\sqrt{5}$

Prove that $\sqrt { 2 }$ is irrational.

Let us assume that

$\sqrt{2}$ is rational. So, we can find integers

$p$ and

$q(\neq 0)$ such that,

$\sqrt{2}=\dfrac{p}{q}$
Suppose

$p$ and

$q$ have a common factor other than

$1$ .

Then, we divide by the common factor to get

$\sqrt{2}=\dfrac{a}{b}$ , where

$a$ and

$b$ are co-prime.
So,

$b\sqrt{2}=a$
Squaring on both sides, we get

$2b^{2}=a^{2}$
Therefore,

$2$ divides

$a^{2}$
Now, we know that, if a prime number,

$p$ divides

$a^{2}$ , then

$p$ divides

$a$ , where

$a$ is a positive integer.
Hence,

$2$ divides

$a$ .

So, we can write

$a=2c$ for some integer

$c$ .
Substituting for

$a$ , we get

$2b^{2}=4c^{2}$

$\Rightarrow b^{2}=2c^{2}$
This means that

$2$ divides

$b^{2}$ and so,

$2$ divides

$b$ .

Therefore,

$a$ and

$b$ have at least

$2$ as a common factor.
But, this contradicts the fact that

$a$ and

$b$ have no common factors other than

$1$ .

This contradiction is because of our incorrect assumption that

$\sqrt2$ is rational.

So, we can conclude that

$\sqrt{2}$ is irrational.

$\quad [Hence\ proved]$

Is pie an irrational number?

$\pi \simeq \dfrac { 22 }{ 7 } =3.14285714......$

It is non terminating non recurring decimal. And its approximate value is

$\dfrac { 22 }{ 7 }$ . But it is not exact value.

Hence

$\pi$ is irrational.

Prove that $3 + 2 \sqrt { 5 }$ is irrational .

$Let\space us\space assume\space that\space$

$3 + 2 \sqrt { 5 }$

$is\space a\space rational\space number.$

$Here,$

$p, q, ∈ z, q \neq 0$

$3 + 2 \sqrt { 5 }=\dfrac{p}{q}$

$2 \sqrt { 5 }=\dfrac{p}{q}-3$

$\sqrt { 5 }=\dfrac{p-3q}{2q}$

$\sqrt {5}$

$is\space an \space irrational\space number.$

$Since \space p,q \space are \space integers\space hence\dfrac{p-3q}{2q}$

$is \space rational \space number$

$But$

$\sqrt { 5 }$

$is\space not\space a\space rational\space number.$

$This\space contradicts\space the\space fact\space that,$

$\therefore\,3 + 2 \sqrt { 5 }$

$is\space an\space irrational\space number.$

Show that the square of any integer is either of the form $4q$ or $4q+1$ for some integer $q.$

By Euclid's division algorithm ,

$a = bq + r$ where

$a , b , q , r$ are non-negative integers and

$0 \leq r < b$ .

On putting

$b = 4$ we get

$a = 4q + r$ ....(i)

When

$r = 0 , a = 4q$

Squaring both sides, we get

$a^2= (4q )^2$

$= 4(4q^2 )$

$= 4m$ is perfect square for

$m = 4q^2$

When

$r = 1 , a = 4q + 1$

Squaring both sides, we get

$a^2= (4q + 1)^2$

$= (4q)^2 + (1)^2 + 2(4q)$

$= 4(4q^2 + 2q ) + 1$

$= 4m + 1$ is perfect square for

$m = 4q^2 + 2q$

When

$r = 2 , a = 4q + 2$

Squaring both sides, we get

$a^2= (4q + 2)^2$

$= (4q)^2 + (2)^2 + 2(4q)(2)$

$= 4(4q^2 + 4q + 1 )$

$= 4m$ is perfect square for

$m = 4q^2 + 4q +1$

When

$r = 3 , a = 4q + 3$

Squaring both sides, we get

$a^2=(4q + 3)^2$

$= (4q)^2 + (3)^2 + 2(4q) (3)$

$= 16q^2 + 9 + 24q$

$= 16q^2 + 24q + 8 + 1$

$= 4(4q^2 \,6q + 2) + 1$

$= 4m + 1$ is perfect square for some value of

$m$ .

Hence, the square on any integer is either of the form

$4q$ or

$(4q+1)$ for some integer

$q$ .

Prove that $\sqrt 3 + \sqrt 5$ is irrational.

To prove :

$\sqrt{3}+\sqrt{5}$ is irrational.

Let us assume it to be a rational number.

Rational numbers are the ones that can be expressed in

$\dfrac p q$ form where

$p,q$ are integers and

$q$ isn't equal to zero.

$\sqrt{3}+\sqrt{5}=\dfrac p q\\$

$\sqrt{3}=\dfrac p q-\sqrt{5}\\$

squaring on both sides,

$3= \dfrac {p^{2}}{q^{2}}-2.\sqrt{5} \left(\dfrac {p} {q}\right)+5$

$\Rightarrow \dfrac{(2\sqrt{5}p)}{q}=5-3+\left(\dfrac {p^2} {q^2}\right)$

$\Rightarrow \dfrac{(2\sqrt{5}p)}{q}= \dfrac {2q^{2}- {p^2}} {q^2}$

$\Rightarrow \sqrt{5}= \dfrac {2q^{2}- {p^2}} {q^2}. \dfrac {q}{2p}\\$

$\Rightarrow \sqrt{5}=\dfrac {(2q^{2}-p^{2})} {2pq}\\$

$p$ and

$q$ are integers RHS is also rational.

As RHS is rational LHS is also rational i.e

$\sqrt{5}$ is rational.

But this contradicts the fact that

$\sqrt{5}$ is irrational.

This contradiction arose because of our false assumption.

so,

$\sqrt{3}+\sqrt{5}$ irrational.

Prove that $4-\sqrt { 3 }$ is an irrational number.

Let us assume the contrary, that

$4-\sqrt{3}$ is rational.

That is, we can find co-prime a and b

$(b\neq 0)$ such that

$4-\sqrt{3} = \dfrac a b$ .

Therefore

$4-\dfrac ab=\sqrt{3}.$

Rearranging this equation, we get

$\sqrt{3}=4-\dfrac a b$

$\dfrac{4b-a}{b}$

Since a and b are integers, we get

$\dfrac{4b-a}{b}$ is rational, and so

$\sqrt{3}$ is rational.

But this contradicts the fact that

$\sqrt{3}$ is irrational,

This contradicts the fact that

$\sqrt{3}$ is irrational.

This contradiction has arisen because of our incorrect assumption that 4-

$\sqrt{3}$ is rational.

so, we conclude that 4

$-\sqrt{3}$ is irrational.

Prove that $5+\sqrt { 3 }$ is irrational.

$5+\sqrt{3}$ , the number

$\sqrt{3}$ is an irrational number.

Also,

$5$ is a rational number.

We know, the sum of a rational number and an irrational number is always an irrational number.

Therefore, since

$\sqrt{3}$ is an irrational number,

$5+\sqrt{3}$ is also an irrational number.

$\therefore$ Hence proved.

Calculate the HCF of $3 ^ { 3 } \times 5$ and $3 ^ { 2 } \times 5 ^ { 2 }$

1298568_1533327_ans_7978a5727b2a43cdb2fe441ecfb73384.jpg

Use Euclid's algorithm to find HCF of $1190$ and $1445$ . Express the HCF in the form $1190m+1445n.$

1670453_1459364_ans_b13eac64c60e48329eecba3dec0e1d45.jpg

Prove that $5-3\sqrt{2}$ is an irrational number.

We know that,

$\sqrt{2}$ has non-terminating, non-repeating decimal expansion.

Hence it is an irrational number.

Using the properties of irrational numbers, we can say that the product of a non-zero rational number and an irrational number is always an irrational number.

Hence,

$3\sqrt{2}$ is an irrational number.

Further, we know that the difference of a rational number and an irrational number is always an irrational number.

Therefore,

$5-3\sqrt{2}$ is also an irrational number.

$[\text{Hence proved}]$

Write whether the square of any positive integer can be of the form $3m+2$ , where $m$ is a natural number. Justify your answer.

By Euclid's division lemma,

$b = aq + r$

where

$a, b, q, r$ are

$+ve$ integers and here

$a=3$ then

$b = 3q + r$ then

$0 \le r < 3$ or

$r= 0, 1, 2$ so

$b$ becomes

$b = 3q, 3q + 1, 3q+2$ ,

$b= 3q$

$\Rightarrow (b)^2 = (3q)^22$

$\Rightarrow b^2 = 3 . 3q^2 = 3m$ where,

$3q^2 = m$

So, as

$b^2$ is perfect square so

$3m$ will also be perfect square.

when

$r = 1, b= 3q+1$

$\Rightarrow (b)^2 = (3q+1)^2$

$\Rightarrow b^2 = 9q^2 + 1 + 2 \times 3q$

$\Rightarrow b^2 = 3[3q^2 + q] + 1$

$\Rightarrow b^2 = 3m + 1$ and

$m= 3q^2 + 2q$

So,

$b^2$ is perfect square or a number of the form

$3m+1$ is perfect square.

when

$r = 2, b= 3q+2$

$\Rightarrow b^2 = 9q^2 + 4 + 2. 3q . 2$

$= 9q^2 + 3 + 3 \times 4q + 1$

$= 3[3q^2 + 1 + 4q] + 1$

$\Rightarrow b^2 = 3m + 1$

Again, a number of the form

$3m + 1$ is perfect square.

Hence, a number of the

$(3m+2)cm$ never be perfect square. But a number of the form

$3m$ , and

$3m+1$ are perfect squares.

Without actually performing the long division, state whether the following rational numbers will have the terminating decimal expansion or a non-terminating repeating decimal expansion. Also, find the numbers of places of decimals after which the decimal expansion terminates.
$\dfrac { 77 }{ 210 }$

$77/210=(77\div 7)/(210 \div 7)$

Let us divide both numerator and denominator by $7$

$77/210$

$= 11/30$

$30 = 2 \times 3 \times 5$ = $.3\bar{6}$

Prime factor of $30 = 2, 3, 5$

denominator isnot multiple of $2^{m}\times 5^{n}$ hence non-terminating.

It is a non-terminating repeating decimal.

Find the value of the following.
$(2\sqrt{2}+2\sqrt{3})+\sqrt{2}-3\sqrt{3}$ .

$(2\sqrt{2}+2\sqrt{3})+\sqrt{2}-3\sqrt{3}$

$=3\sqrt{2}-\sqrt{3}$ .

A positive integer is of the form $3q+1, q$ being a natural number. Can you write its square in any form other than $3m+1$ i.e., $3m$ or $3m+2$ for some integer $m$ ? Justify your answer.

By Euclid's division algorithm ,

$a = bq + r$ where

$a , b , q , r$ are non-negative integers and

$0 \leq r < b$ .

On putting

$b = 3$ and

$r=1$ we get

$a = 3q + 1$

Squaring both sides

$\Rightarrow a^2= (3q + 1)^2$

$\Rightarrow a^2 = (3q)^2 + (1)^2 + 2(3q)$

$\Rightarrow a^2 = 3(3q^2 + 2q ) + 1$

$\Rightarrow a^2= 3m + 1$ , where $$ m = 4q^2 + 2q $ is any integer.

Hence, the square of a positive integer iof the form

$3q+1$ can not be written in any form other than

$3m+1$

Calculate the HCF of $3^{3}\times 5$ an $3^{2}\times 5^{2}$

Given numbers are

$3^3\times 5,3^2\times 5^2$

$HCF$ will be least powers

$HCF=3^2\times 5^1=9\times 5=45$

Prove that $\sqrt{2}$ is an irrational number.

Let us assume

$\sqrt{2}$ is a rational number then there exist positive integers a , b such that

$\Rightarrow \sqrt{2} = \dfrac{a}{b}$ (where, a & b are co-prime)

$\Rightarrow 2 = \dfrac{a^2}{b^2}$

$\Rightarrow a^2 = 2b^2$ ___(1)

Here

$a^2$ is even, means a is also an even number.

So,

$a = 2c$ for some integer c.

$\Rightarrow a^2 = 4c^2$

$\Rightarrow 2b^2 = 4c^2$ from (1)

$\Rightarrow b^2 = 2c^2$

Here,

$b^2$ is even, means b is also an even number from above calculation, we get that a & b are even number i.e, a & b have a common factor 2.

This contradicts that a & b have no other factor than 1.

Hence, our supposition is wrong &

$\sqrt{2}$ is an irrational number.

Find the value of $a$ & $b$ if $\displaystyle{{\sqrt 6 - \sqrt 5 } \over {\sqrt 6 + \sqrt 5 }} = 2a + 4b$ .

1313711_1535514_ans_1483980b303d4ba9b1e5acf43958dbfc.jpeg

Show that $5-\sqrt3$ is an irrational number.

$5-\sqrt{3}$ , the number

$\sqrt{3}$ is an irrational number.

Also,

$5$ is a rational number.

We know, the difference of a rational number and an irrational number is always an irrational number.

Therefore, since

$\sqrt{3}$ is an irrational number,

$5-\sqrt{3}$ is also an irrational number.

$\therefore$ Hence proved.

Find the largest number which divides $438$ and $606$ , leaving remainder $6$ in each case.

The largest number divided

$438$ and

$606 ,$ leaving remainder

$6$ is the largest number divides

$432( i.e. 438 - 6 = 432)$ and

$600 ( i.e. 606 -6 = 600)$

HCF of

$432$ and

$600$ gives the required number.

To find : HCF of

$432$ and

$600$

HCF of

$432$ and

$600$ using prime factorization

$432 =2^4 \times 3^3$

$600 = 2^3 \times 3 \times 5^2$
HCF =

$2^3 \times 3 = 24$
therefore , the required number is

$24.$

Identify the following as rational or irrational number. Give the decimal representation rational number.
$3\sqrt{8}$ .

First we will rewrite the given number,

$\begin{aligned}{}3\sqrt 8 & = 3\sqrt {4 \times 2} \\ &= 3 \times 2\sqrt 2 \\& = 6\sqrt 2 \end{aligned}$

$\sqrt2$ is irrational then

$6\sqrt2$ or

$3\sqrt8$ is irrational as well.

Now,

$\begin{aligned}{}\sqrt 2 &= 1.414213562\\ &\approx 1.41\end{aligned}$

So,

$\begin{aligned}{}3\sqrt 8& = 6\sqrt 2 \\& = 6 \times 1.41\\ &= 8.46\end{aligned}$

Find the H.C.F. of the following numbers using prime factorization method.
$540, 980$ .

1502715_1659165_ans_cd784a285483485097b35bc1687a59e7.jpg

Find the H.C.F. of the following numbers using prime factorization method.
$150, 140, 210$ .

1502803_1659166_ans_527eaf63c51942f88169bd673782773f.jpg

Find the H.C.F of the following numbers using prime factorization method.
$144, 198$ .

1575285_1659158_ans_450d35f90f474c38b9e7d7d5cb4d115f.jpg

Find the HCF of $12, 16$ and $28.$

$12=2\times2\times3$

$16=2\times2\times2\times2$

$28=2\times2\times7$

common factor

$3$ numbers

$=2\times2$

HCF is

$2$

Find the H.C.F. of the following numbers using prime factorisation method:
$84, 98$

1575288_1659162_ans_28609ef6d0d64c3a80280574c2b84a6a.jpg

Find the $HCF$ of the following numbers using the prime factorization method.
$81, 117$

Let us write th given numbers as product of their prime factors,

$81 = 3\times 3\times 3\times 3$

$117 = 3\times 3 \times 13$

So,

$HCF\left( {81,117} \right)= 3\times 3$

$= 9$

Find the H.C.F. of the following numbers using prime factorization method.
$84, 120, 138$ .

1502805_1659167_ans_cbf3d0c695424ed2b6300c4027b0c4ce.jpg

Find the H.C.F. of the following numbers using prime factorization method.
$225, 450$ .

1575293_1659163_ans_b5428fb586164fc1a8c553d093c7232a.jpg

Find the H.C.F. of the following numbers using prime factorization method.
$170, 238$ .

1505125_1659164_ans_4b152f52174144c7a14b814486bb010e.jpg

Given that $\sqrt{3}$ is an irrational number, show that $(5 + 2\sqrt{3})$ is an irrational number.

Given

$\sqrt{3}$ is an irrational number

Let

$5 + 2\sqrt{3}$ is a rational number

$\therefore$ we can write

$5 + 2\sqrt{3} = \dfrac{p}{q}$ , where

$p$ and

$q$ are integers

$\Rightarrow 2\sqrt{3} = \dfrac{p}{q} - 5 = \dfrac{p - 5q}{q}$

$\sqrt{3} = \dfrac{p - 5q}{2q}$

Here,

$\dfrac{p-5q}{2q}$ is a rational number

So,

$\sqrt{3}$ is also a rational number.

But it is given that

$\sqrt{3}$ is irrational number.

$\Rightarrow$ our assumption was wrong

$\Rightarrow 5 +2 \sqrt{3}$ is an irrational number.

What do you mean by Euclid's division lemma ?

As per Euclid's division lemma, for any two positive integers, say

$a$ and

$b$ , there exists unique integers

$q$ and

$r$ , such that

$a =bq+ r$ ; where

$0 \le r < b$ .
It is also written as :

$\text{Dividend}= \text{(Divisor} \times \text{quotient)} +\text{Remainder}$ .

Using Euclid's algorithm, find HCF of $504$ and $1188$

Step 1 : choose bigger number :

$1188 > 504$
On dividing

$1188$ by

$504 ,$ we get
Quotient = 2 and remainder = 180

$\Rightarrow 1188 = 504 \times 2 +180$

Step 2: on dividing 504 by 180

Quotient = 2 and remainder = 144

$\Rightarrow 504 = 180 \times 2 +144$

Step 3 : on dividing 180 by 144
quotient = 1 and remainder = 36

$\Rightarrow 180 = 144 \times 1 +36$

Step 4 : On dividing 144 by 36
quotient = 4 and remainder =0

$\Rightarrow 144 = 36 \times 4 +0$
Since remainder is zero, stop the process

therefore, HCF of

$1188$ and

$504$ is

$36.$

Using Euclid's algorithm, find HCF of $405$ and $2520$

(i) Step 1 : choose bigger number :

$2520 >405$
On dividing 2520 by 405 , we get
quotient = 6 , remainder = 90

$\Rightarrow$

$2520= (405 \times 6) +90$

Step 2 : On dividing 405 by 90 , we get
Quotient =4 and remanider= 45

$\Rightarrow$

$405 = 90 \times 4 + 45$

Step 3: On dividing 90 by 45 , we get
quotient = 2 and remainder = 0

$\Rightarrow$

$90 = 45 \times 2 + 0$

Step 4 : Since remainder is zero, stop the process
therefore , HCF of

$405$ and

$2520$ is

$45.$

Find the H.C.F. of the following numbers using prime factorization method.
$106, 159, 265$ .

1502807_1659168_ans_1ac5f3d320b14737976a9be712aa0246.jpg

Express the following number as product of powers of prime factors:
$24000$

1516263_1676200_ans_e0f696eaa2af4d9aa5ba8191dbe74d42.jpg

Determine the H.C.F. of the following numbers by using Euclid's algorithm.
$1045, 1520$ .

Since

$1520>1045$ , we apply the division lemma to

$1520$ and

$1045$ to obtain:

$1520=1045\times 1+475$

Since remainder

$475\neq 0$ , we apply the division lemma to

$1045$ and

$475$ to obtain:

$1045=475\times 2+95$

We consider the new divisor

$475$ and new remainder

$95$ , and apply the division lemma to obtain

$475=95\times 5+0$

Since the remainder is zero, the process stops.

Also, the divisor at this stage is

$95$ ,

Hence, the HCF of

$1520$ and

$1045$ is

$95$ .

Using Euclid's algorithm, find HCF of $960$ and $1575$

(iii) Step 1: Choose bigger number :

$1575 > 960$

On dividing

$1575$ by

$90$ , we have
quotient

$= 1$ remainder

$= 615$

$\Rightarrow$ 1575 = 960

$\times$ 1 +615

Step 2 : on Dividing

$960$ by

$615$ , we have

Quotient

$= 1$ and remainder

$=345$

$\Rightarrow 960= 615 \times 1 +345$

Step 3 :on dividing

$615$ by

$345$
quotient

$1$ and remainder

$= 270$

$\Rightarrow 615 = 345 \times 1 +270$

Step 4 : On dividing

$345$ by

$270$ , we have

quotient

$= 1$ and remainder

$= 75$

$\Rightarrow 345 = 270 \times 1 +75$

Step 5 : dividing

$270$ by

$75$ , we get
Quotient

$= 3$ , remainder

$= 30$

$\Rightarrow 270 = 75 \times +45$

Step 6 : Dividing

$75$ by

$45$ we get

Quotient

$= 1$ , remainder

$= 30$

$\Rightarrow 75 = 45 \times 1 +30$

Step 7: Dividing

$45$ by

$30$ , we get

quotient

$= 1$ and remainder

$= 15$

$\Rightarrow 45 = 30 \times 1 +15$

Step 8 : Dividing

$30$ by

$15$ , we get

quotient

$= 2$ and remainder

$= 0$

Since remainder is zero, stop the process

Therefore , HCF of

$1575$ and

$960$ is

$15.$

Determine the H.C.F. of the following numbers by using Euclid's algorithm.
$300, 450$ .

1575325_1659173_ans_c8222b7dd8cf443bbe323929b36600fc.jpg

Find the greatest number that will divide that will divide 43, 91 and 183 so as to leave the same remainder in each case.

Given numbers are

$43, 91$ and

$183.$
Subtract smallest number from both the highest numbers.

we have three cases :

$183 > 43$ ;

$183 >91$ and

$91 > 43$

$183 -43 = 140$

$183-91 = 92$ and

$91-43 = 48$

Now , we have three new numbers :

$140 , 48$ and

$92$

For HCF of

$140 , 48$ and

$92$ using prime factorization method, we get
HCF

$( 140, 48$ and

$92 ) = 4$

the highest number that divide

$183 ,91$ and

$43$ and leave the same remainder is

$4.$

Using Prime factorization , find the HCF and LCM of $24 , 36, 40$

Prime factors of

$24 , 36, 40$

$24 = 2 \times 2 \times 2 \times 3 =2^3 \times 3$

$36 = 2 \times 2 \times 3 \times =2^2 \times 3^2$

$40 =2 \times 2 \times 2 \times 2 \times 5 = 2^3 \times 5$

HCF (24,36,40) =

$2^2 = 4$
LCM ( 24, 36, 40) =

$2^2 \times 3^2 \times 5 = 360$

Using Prime factorization , find the HCF and LCM of $8, 9, 25$

prime factors of

$8, 9, 25$

$8 = 2 \times 2 \times 2 = 2^3$

$9 = 3 \times 3=3^2$

$25 = 5 \times 5 =5^2$

$HCF(8,9,25) = 1$

$LCM ( 8,9,25)=$

$2^3 \times 3^2 \times 5^2 = 1800$

Using prime factorization , find the HCF and LCM of : $36, 84$ in each case , verify that $HCF \times LCM$ = product of given numbers.

$36 = 2 \times 2 \times 3 \times 3$

$84 = 2 \times 2 \times 3 \times 7$

$LCM (36, 84)= 2\times 2 \times 3 \times 3 \times 7 = 252$

$HCF (36, 84 ) = 2 \times 2 \times 3 = 12$

verification :

$HCF \times LCF = 12 \times 252 \\= 3024$
product of given numbers

$= 36 \times 84$

$= 3024$

$\Rightarrow HCF \times LCM =$ product of given numbers
verified

Find the largest number which when divided by 20, 25, 35 and 40 leaves remainder as 14, 19 ,29 and 34 respectively.

First LCM of

$20 , 25, 35$ and

$40 ,$ using prime factorization method

$20 = 2 \times 2 \times 5$

$25 = 5 \times 5$

$35 = 5 \times 7$

$40 = 2 \times 2 \times 2 \times 5$

LCM

$( 20,25,35,40) = 1400$

as per given statement we have to find the greatest number which when divided by

$20, 25, 35$ and

$40$ leaves remainder as

$14 ,19,29$ and

$34$ respectively.

i.e. less than Divisor in each case .
Required number

$= 1400-6= 1394......................(20-14=25-19=35-29=40-34=6)$

$1394$ is the required number.

Without actual division , show that each of the following rational numbers is non -terminating repeating decimal : $\dfrac {73}{( 2^2 \times 3^3 \times 5)}$

$\dfrac {73}{( 2^2 \times 3^3 \times 5)}$

2 or 3 and 5 is not factor of 73 so fraction is in its simplest form.
and,

$(2^2 \times 3^3 \times 5 ) \neq (2^m \times 5^n )$ in denominator

hence given fraction is non -terminating repeating decimal.

Using prime factorization , find the HCF and LCM of $396 , 1080$
in each case , verify that $HCF \times LCM$ = product of given numbers.

$396 = 2^2 \times 3^2 \times 11$

$1080 = 2^3 \times 3^3 \times 5$

LCM (396 , 1080 ) =

$2^3 \times 3^3 \times 5 \times 11= 11880$
HCF ( 396, 1080) =

$2^2 \times 3^2 = 36$

verification :

$HCF \times LCM = 11880 \times 36 = 427680$
Product of given numbers =

$396 \times 1080 = 427680$

$\Rightarrow HCF \times LCM$ = product given numbers.

verified.

Using prime factorization , find the HCF and LCM of $96, 404$
in each case , verify that $HCF \times LCM$ = product of given numbers.

$96 = 2 \times 2 \times 2 \times 2 \times 2 \times 3$

$404 =2 \times 2 \times 101$

LCM (96 and 404 ) =

$2^5 \times 3 \times 101 = 9696$
HCF ( 96 and 404 )=

$2^2= 4$

Verification :

$HCF \times LCM = 9696 \times 4 = 38784$
product of given numbers

$= 96 \times 404 = 38784$

$\Rightarrow HCF \times LCM =$ Product of given numbers
verified.

Find the largest four-digit number which when divided by 4, 7 and 13 leaves a remainder of 3 in each case.

Prime factors of

$4, 7$ and

$13$

$4 = 2 \times 2$

$7$ and

$13$ are prime numbers
LCM

$( 4, 7 , 13)= 364$

we know that, the largest

$4$ digit number is

$9999.$

Step 1 : divide

$9999$ by

$364 ,$ we get

$\dfrac {9999} {364} = 171$

Step 2: subtract

$171$ from

$9999$

$9999-171 = 9828$

Since a remainder of

$3$ is to be left

$9282 +3 = 9831$

therefore

$9831$ is the number.

Without actual division , show that each of the following rational numbers is non -terminating repeating decimal $\dfrac {11}{ (2^3 \times 3)}$

$\dfrac {11}{(2^3 \times 3)}$

$2$ or

$3$ are not the factors of

$11$ so fraction is in its simplest form.
and,

$(2^3 \times 3) \neq (2^m \times 5^n )$

hence given fraction is non -terminating repeating decimal.

Prove that the following number is irrational : $( 3 + \sqrt {2} )$

$( 3 + \sqrt {2} )$

Let us assume that

$( 3 + \sqrt {2} )$
is rational

Subtract given numbers from 3, considering 3 is rational number as we know,difference of two rational numbers is rational.

So

$( 3 + \sqrt {2} )$ is rational
but,

$\sqrt {2}$ is irrational
Which is contradictory to our assumption.

So

$( 3 + \surd {2} )$ is an irrational.

Prove that the following number is irrational $( 2+ \sqrt {5})$

$( 2+ \sqrt {5})$

Let us assume that

$( 2+ \sqrt {5})$
is rational

Subtract given numbers from 2, considering 2 is rational number as we know,difference of two rational numbers is rational.

$( 2+ \sqrt {5})$ is rational

but

$\sqrt {5}$ is irrational
Which is contradictory to our assumption.

So

$( 2+ \sqrt {5})$ is an irrational.

Without actual division, show that the following rational number is non-terminating repeating decimal:
$\dfrac {129}{(2^2 \times 5^3 \times 7^2 )}$

$2,5$ or

$7$ is not a factor of

$129$ so the fraction is in its simplest form. But for a rational number to be terminating decimal, its decimal should be in the form

$(2^m \times 5^n )$ but here the denominator is

$(2^2 \times 5^7 \times 7^5 )$ that is why given fraction is non -terminating repeating decimal.

Without doing actual division , show that the following rational number has a non-terminating repeating decimal expansion :
$\dfrac {29} {343}$

The given number is

$\dfrac{29}{343}.$

Now,

$\dfrac {29} {343}=\dfrac{29}{7 \times 7 \times 7}=\dfrac{29}{7^3}$

$7$ is not a factor of

$29,$ so the given fraction is in its simplest form.

Here, the denominator is not in the form

$(2^m \times 5^n )$

$\because (7^3 ) \neq (2^m \times 5^n )$

Hence, given rational number has a non-terminating repeating decimal expansion.

Without actual division , show that the following rational number is non-terminating repeating decimal : $\dfrac {64} {455}$

Given rational number is

$\dfrac {64} {455}$

Prime factorization of the denominator of the given rational number is

$455=5 \times 7 \times 13$

If the prime factorization of the denominator of any rational number is of the form

$2^m\times 5^n$ where

$m$ and

$n$ are non-negative integers, then the decimal expansion of the given number is terminating else non-terminating repeating

$(5 \times 7 \times 13 )$ is not of the form

$(2^m \times 5^n )$
Hence given fraction has non -terminating repeating decimal expansion.

Prove that each of the following numbers in irrational
(ii) $( 2 - \sqrt {3} )$

1961091_1713844_ans_793ea4b6e7a24152a89df636a1f117dd.jpg

Prove that the following number is irrational $( 5 +\sqrt [3]{2} )$

$( 5 +\sqrt [3]{2} )$

Let assume that

$( 5 +\sqrt [3]{2} )$ is irrational
Subtract 5 from given number, considering 5 is rational number .as we know , Difference of two rational numbers is a rational.

$( 5 +\sqrt [3]{2} )-5$ is rational

$\Rightarrow \sqrt [3]{2}$ is rational.
(product of two rational numbers is rational)

but,

$\sqrt [3]{2}$ is irrational
which is contradictory to our assumption.

So

$( 5 +\sqrt [3]{2} )$ is irrational.

Without actual division , show that each of the following rational numbers is non -terminating repeating decimal : $\dfrac {9} {35}$

$\dfrac {9} { 35}=\dfrac {9} { 5 \times 7}$

5 or 7 is not factor of 9 so fraction is in its simplest form.
and,

$(5 \times 7 ) \neq (2^m \times 5^n )$ in denominator

hence given fraction is non -terminating repeating decimal.

Prove that each of the following numbers in irrational : $\sqrt {6}$

$\sqrt {6}$
let us suppose that

$\surd {6}$ is rational number.

There exist two co-prime numbers , say p and q
So

$\sqrt6 = \dfrac p q$

Squaring both sides , we get

$6 =\dfrac{p^2}{q^2}$ ..(1)

Which shows that ,

$p^2$ is divisible by 6
this implies ,

$p$ is divisible by

$6$
Let

$p = 6a$ for some integer

$a$

Equation (1) implies =

$6q^2 = 36a^2$

$\Rightarrow q^2 = 6a^2$

$q^2$ is also divisible by 6

$\Rightarrow q$ is divisible by 6

$6$ is common factors of

$p$ and

$q$
but this contradicts the fact that

$p$ and

$q$ have no common factor.
our assumption is wrong thus

$\sqrt {6}$ is irrational

Without actual division , show that each of the following rational numbers is non -terminating repeating decimal : $\dfrac {77} { 210}$

$\dfrac {77}{ 210}=\dfrac {77}{ 3 \times 5 \times 2 \times 7}=\dfrac {11}{ 3 \times 5 \times 2 }$

2, 3 or 5 is not factor of 11 so given fraction is in its simplest form.
and,

$(2 \times 3 \times 5 ) \neq (2^m \times 5^n )$

hence given fraction is non -terminating repeating decimal.

Prove that the following number is irrational $( 2 - 3 \sqrt {5})$

(viii)

$( 2 - 3 \sqrt {5})$
Let us assume that

$( 2 - 3 \sqrt {5})$ is rational.

subtract given numbers from 2 , considering 2 is rational number.
as we know , difference of two rational numbers is rational

$2- ( 2 - 3 \sqrt {5})$ is rational.

$\Rightarrow 3 \surd{5}$ is rational

above result is possible if 3is rational and

$\surd {5}$ is rational.
Because , product of two rational numbers is rational.

but the fact is

$\surd {5}$ is an irrational .

Our assumption is wrong, and

$( 2 - 3 \sqrt {5})$ is irrational

Prove that $\dfrac {2}{ \sqrt {7}}$ is irrational.

Let us assume that

$\dfrac {2}{ \sqrt {7}}$ is rational number.

$\dfrac {2} {\sqrt {7}} \times \dfrac {\sqrt {7}} {\sqrt{7}} = \dfrac {2 \sqrt 7}{7}$ is rational number .

which is only possible is

$\dfrac {2 \sqrt7}7$ is rational and

$\surd {7}$ is rational.

But the fact is

$\sqrt {7}$ is an irrational.

which contradicts to our assumption.

$$ \dfrac {2}{ \sqrt {7}}$ is an irrational number. hence proved.

Prove that $( 4 - 5 \sqrt {2})$ is an irrational number.

Let us assume that

$( 4 - 5 \sqrt {2})$ is rational .

Subtract given number from

$4 ,$ considering

$4$ is rational number. as we know difference of two rational numbers is rational.

$4 - ( 4 - 5 \sqrt {2} )$ is rational

$\Rightarrow 5 \sqrt{2}$ is rational

which is only possible if

$5$ is rational and

$\sqrt {2}$ is rational.

As we know prouduct of two rational number s rational
But the fact is

$\sqrt {2}$ is an irrational.

Which is contradictory to our assumption.

Hence,

$4 - 5 \sqrt {2}$ is irrational . hence proved.

Prove that $( 5 - 2 \sqrt {3} )$ is an irrational number.

Let us assume that

$( 5 - 2 \sqrt {3} )$ is a rational.

Subtract given number from

$5,$ considering

$5$ is a rational number.

as we know Difference of two rational number is rational.

$\Rightarrow 5 - ( 5 - 2 \sqrt{3} )$ is rational

$\Rightarrow 2 \sqrt {3}$ is rational

Which is only possible if

$2$ is rational and

$\sqrt{3}$ is rational.

As we know the product of two rational number is rational.

But the fact is

$\sqrt {3}$ is an irrational

which is contradictory to our assumption

$(5 - 2 \sqrt {3} )$ is an irrational number.

Prove that $5 \sqrt {2}$ is irrational.

Let us assume that

$5 \sqrt {2}$ is a rational number.

This is only possible if

$5$ is rational and

$\sqrt {2}$ is rational.

We know that product of two rational numbers is rational.

But we know that is

$\sqrt {2}$ is an irrational.

This contradicts our assumption that

$5 \sqrt {2}$ is a rational number.

$\therefore\ \ 5 \sqrt{2}$ is an irrational number.

Prove that $\dfrac { 1} { \sqrt {3}}$ is irrational

Let us assume that

$\dfrac { 1} { \sqrt {3}}$ is rational

$\Rightarrow \dfrac { 1} { \sqrt {3}} \times \dfrac { \sqrt 3} { \sqrt {3}} = \dfrac { \sqrt 3} { {3}}$ is rational

which is only possible if

$\dfrac 13$ is rational and

$\sqrt {3}$ is rational. as we know that, product of two rational numbers is rational.

But the fact is

$\sqrt {3}$ is an irrational

Which is contradictory to our assumption.

which implies

$\dfrac { 1} { \sqrt {3}}$ is irrational. hence proved.

Prove that the following number is irrational $3 \sqrt {7}$

$3 \sqrt {7}$

let us assume that

$3 \sqrt {7}$ is rational.

as we know, product of two rational numbers is rational.

but

$\surd {7}$ is irrational , which is contradictory to our assumption.

SO

$3 \sqrt {7}$ is irrational.

Prove that the following number is irrational $( \sqrt {3} + \sqrt {5})$

$( \sqrt {3} + \sqrt {5})$

Let us assume that

$( \sqrt {3} + \sqrt {5})$ is rational
On squaring , we get

$( \sqrt {3} + \sqrt {5})$ is rational

$\Rightarrow 3 + 2 \sqrt {3} \times \sqrt {5} + 5$ is rational

$\Rightarrow 8 + 2 \sqrt{15}$ is rational

Subtract 8 from above result , considering 8 is a rational number.
as we know , difference of two national numbers is a rational.

$\Rightarrow 8 + 2 \sqrt {15} -8$ is rational

$\Rightarrow 2 \sqrt {15}$ is rational

Which is only possible if 2 is rational and

$\sqrt {15}$ is rational .
The fact is

$\sqrt {15}$ is not a rational number.

Our assumption is wrong, and

$( \sqrt {3} + \sqrt {5} )$ is irrational

Prove that the following number is irrational $\dfrac {3}{ \sqrt {5} }$

$\dfrac {3}{ \surd {5} }$

Let asuume that

$\dfrac {3}{ \sqrt {5} }$ is rartional

$\dfrac {3}{ \sqrt {5} } \times \dfrac {\sqrt {5} } {\sqrt{5}} = \dfrac {3 \sqrt{5}} 5$

where

$\dfrac {3 \sqrt{5}} 5$ is rational.

which shows that

$\dfrac35$ is rational and

$\surd {5}$ is rational

but the fact is

$\surd {5}$ is an irrational.

our assumption is wrong, and

$\dfrac {3} {\sqrt {5}}$ is irrational.

Prove that $( 2 \sqrt {3} -1)$ is an irrational number .

Let us assume that

$( 2 \surd {3} - 1)$ is rational .
add

$1$ to be above number, considering 1 is rational number.

as we know , sum of two rational numbers is rational.
Sum =

$2 \sqrt 3 -1 + 1 = 2 \surd {3}$

which is only possible if 2 is rational and

$\surd {3}$ is rational.

But the fact is

$\surd {3}$ is an irrational number which contradicts to our assumption .

So,

$( 2 \sqrt {3} - 1 )$ is an irrational.

Without actual division, state whether the following rational number is termining decimal or not.
$\dfrac{7}{24}$ .

$\dfrac{7}{24}=\dfrac{7}{2\times 2\times 2\times 3}=\dfrac{7}{2^3\times 3}$

The denominator has the prime factors

$2$ and

$3$ then

$\dfrac{7}{24}$ is not a terminating decimal.

Without actual division, state whether the following rational number is terminating decimal or not.
$\dfrac{16}{125}$ .

$\dfrac{16}{125}=\dfrac{16}{5\times 5\times 5}=\dfrac{16}{5^3}$ .

The denominator prime factor has

$5$ thus we can consider

$\dfrac{16}{125}$ as a terminating decimal.

Without actual division, state whether the following rational number is terminating decimal or not.
$\dfrac{31}{375}$ .

$\dfrac{31}{375}=\dfrac{31}{3\times 5\times 5\times 5}=\dfrac{3}{3\times 5^3}$

The denominator is not in the form of

$2^p$ then

$\dfrac{31}{375}$ is not a terminating decimal.

Without actual division, state whether the following rational number is terminating decimal or not.
$\dfrac{5}{12}$ .

$\dfrac{5}{12}=\dfrac{5}{2\times 2\times 3}=\dfrac{5}{2^2\times 3}$

$\dfrac{5}{12}$ Has the prime factors in the denominator as

$2$ and

$3$ .

Thus

$\dfrac{5}{12}$ is not a terminating decimal.

If a and b are two prime numbers, then find HCF (a,b) .

HCF of two primes is always

$1.$
HCF

$(a,b) = 1$

Without actual division, state whether the following rational number is terminating decimal or not.
$\dfrac{13}{80}$ .

We can write

$\dfrac{13}{80}$ as

$\dfrac{13}{80}=\dfrac{13}{2\times 2\times 2\times 2\times 5}=\dfrac{13}{2^4\times 5}$

If the denominator has prime factors as

$2$ or

$5$ then we can consider the rational number as a terminating Decimal.

$\dfrac{13}{80}$ is considered a terminating decimal as we have

$2$ and

$5$ as prime factors for

$80$ .

State Euclid's division lemma and give some examples.

${\textbf{State Euler's division lemma and give some examples}}$

${\textbf{Step -1: Stating Euler's division lemma}}$

${\text{According to Euler's division lemma, if we have two positive integers a and b, then there exist unique}}$

${\text{integers q and r which satisfies the condition a = bq + r where 0}} \leqslant {\text{r < b}}$

${\textbf{Step -2: Writing some examples}}$

${\text{Consider two numbers 78 and 980,}}$

${\text{We have, 980 = 78}} \times {\text{12 + 44}}$

$\therefore {\text{ Here, a = 980, b = 78, q = 12, r = 44}}$

${\text{Similarly, a = 675 and b = 81}}$

$\Rightarrow {\text{ 675 = 81}} \times {\text{8 + 27}}$

$\textbf{Hence, Euclid's division lemma is stated.}$

Express why 0.15015001500015... is an irrational number.

As we know , irrational numbers are non -terminating non -recurring decimals.
Thus

$, 0.15015001500015 ...$ is a irrational number.

Write the following in decimal form and say what kind of decimal expansion has.
$\dfrac{261}{400}$ .

1669843_1714942_ans_32c99c96956f49f9acb2fc6db852b57e.jpg

Write the following in decimal form and say what kind of decimal expansion has.
$\dfrac{231}{625}$ .

1669846_1714947_ans_607712bf6ddc464ea6faefd7c58064b3.jpg

Classify the following number as rational and irrational. Give reasons to support your answer.
$\sqrt{21}$ .

As we know

$21$ is not a perfect square.

Therefore,

$\sqrt{21}$ is irrational.

Examine whether the following number is rational or irrational.
$\sqrt{7}-2$ .

As we know that the subtraction of a rational and irrational number is irrational then

$\sqrt{7}-2$ is irrational.

Classify the following number as rational and irrational. Give reasons to support your answer.
$6.834834....$ .

$6.834834....=6.\overline{834}$ .

The number

$6.834834....$ is a non-terminating recurring decimal and hence called as a rational number.

Classify the following number as rational and irrational. Give reasons to support your answer.
$3.040040004....$ .

$3.040040004....$ is a non-terminating and non-recurring decimal and hence considered as an irrational number.

Examine whether the following number is rational or irrational.
$3+\sqrt{3}$ .

We know that the sum of rational and irrational number is an irrational number.
Thus,

$3+\sqrt{3}$ is an irrational number.

Classify the following number as rational and irrational.
$\sqrt{\dfrac{3}{81}}$ .

$\sqrt{\dfrac{3}{81}}=\dfrac{\sqrt{3}}{9}=\dfrac{1}{3\sqrt{3}}$ .

It is an irrational number.

Classify the following number as rational and irrational. Give reasons to support your answer.
$\dfrac{22}{7}$ .

$\dfrac{22}{7}=3.\overline{142857}$

$\dfrac{22}{7}$ is a non-terminating decimal and is considered as a rational number.

Classify the following number as rational and irrational. Give reasons to support your answer.
$1.232332333....$ .

$1.232332333$ .... is a non-recurring and non-terminating decimal.

Thus,

$1.232332333....$ is irrational.

Classify the following number as rational and irrational. Give reasons to support your answer.
$\dfrac{2}{3}\sqrt{6}$ .

We have a rational number

$\dfrac{2}{3}$ and irrational number

$\sqrt{6}$ .

As per the theorem the product of both rational and irrational number is an irrational number.
Thus,

$\dfrac{2}{3}\sqrt{6}$ is irrational.

Classify the following number as rational and irrational. Give reasons to support your answer.
$4.1276$ .

$4.1276$ is basically a terminating decimal.

Therefore, it is rational.

Find the HCF of the following numbers, using the prime factorization method:
$272, 425$

The prime factors of

$272 = 2^4 \times 17$
The prime factors of

$425 = 5^2 \times 17$

$\therefore HCF = 17$
1632009_1777674_ans_a3f51500eb94460e8d2346f448f4c97a.png

Show that the square of $\dfrac{(\sqrt{26 - 15\sqrt{3}})}{(5\sqrt{2} - \sqrt{38 + 5\sqrt{3}})}$ is a rational number.

Given,

$x = \dfrac{\sqrt{26 - 15\sqrt{3}}}{5\sqrt{2} - \sqrt{38 + 5\sqrt{3}}}$

$x^2 = \dfrac{26 - 15\sqrt{3}}{50 + 38 + 5\sqrt{3} - 10\sqrt{76 + 10\sqrt{3}}}$

$\Rightarrow x^2 = \dfrac{26 - 15\sqrt{3}}{88 + 5\sqrt{3} - 10\sqrt{75 + 1 + 10\sqrt{3}}}$

$\Rightarrow x^2 = \dfrac{26 - 15\sqrt{3}}{88 + 5\sqrt{3} - 10\sqrt{(5\sqrt{3} + 1)^2}}$

$\Rightarrow x^2 = \dfrac{26 - 15\sqrt{3}}{88 + 5\sqrt{3} - 10( 5\sqrt{3} + 1)}$

$\Rightarrow x^2 = \dfrac{26 - 15\sqrt{3}}{3(26 - 15\sqrt{3})} = \dfrac{1}{3}$ which is a rational number.

Find the HCF of the following numbers, using the prime factorization method:
$504, 980$

The prime factors of

$980 = 2^2 \times 5 \times 7^2$

$\therefore HCF = 2^2 \times 7 = 28$
1631979_1777667_ans_0abad999bcf84a18aa2fb331e12c4f99.png

Find the HCF of the following numbers, using the prime factorization method:
$106, 159, 371$

The prime factors of

$106 = 2 \times 53$
The prime factors of

$159 = 3 \times 53$
The prime factors of

$371 = 7 \times 53$

HCF is the product of all common factors

$\therefore HCF = 53$

Find the $H.C.F$ of the following numbers, using the prime factorization method:
$72, 108, 180$

The prime factors of

$72 = 2^3 \times 3^2$
The prime factors of

$108 = 2^3 \times 3$
The prime factors of

$180 = 2^2 \times 3^2 \times 5$

$\therefore HCF = 2^2 \times 3^2 = 36$

1631991_1777669_ans_597c4df29d74448b868f21d68cccdc22.png

Find the HCF of the following numbers, using the prime factorization method:
$144, 252, 630$

The prime factors of

$144 = 2^4 \times 3^2$
The prime factors of

$252 = 2^2 \times 3^2 \times 7$
The prime factors of

$630 = 2 \times 3^2 \times 5$

$\therefore HCF = 18$
1632018_1777676_ans_8d54b561717e48a9bd14409e2f885b84.png

Examine whether the following number is rational or irrational.
$\sqrt{8}\times \sqrt{2}$ .

$\sqrt{8}\times \sqrt{2}=\sqrt{4\times 2}\times \sqrt{2}$

$=2\sqrt{2}\times \sqrt{2}$

$=4$ .

It is a rational number.

Find the HCF of the following numbers, using the prime factorization method:
$1197, 5320, 4389$

The prime factors of

$1197 = 3^2 \times 7 \times 19$
The prime factors of

$5320 = 2^3 \times 5 \times 7 \times 19$
The prime factors of

$4389 = 3 \times 7 \times 11 \times 19$

$\therefore HCF = 133$
1632040_1777678_ans_1d59c31e9c9b49c9be5c606abb75ce09.png

Find the HCF of the following numbers, using the division method:
$399, 437$

$\therefore$ The common factor of

$399, 437 = 19$
1632744_1777684_ans_86b2f04a633a404c9595333fdd4054c6.png

Show that the following primes are co-primes:
$512, 945$

$512 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2$

$= 2^9$

$945 = 3 \times 3 \times 3 \times 5 \times 7$

$= 3^3 \times 5 \times 7$
Here common factor

$= 1$

$HCF = 1$
Hence the given numbers are co primes

Show that the following primes are co-primes:
$343, 432$

$343 = 7 \times 7 \times 7$

$= 7^3 \times 1$

$432 = 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3$

$= 2^4 \times 3^3 \times 1$
Here common factor

$= 1$

$HCF = 1$
Hence the given numbers are co primes

Show that the following primes are co-primes:
$385, 621$

$385 = 5 \times 7 \times 11 \times 1$

$621 = 3 \times 3 \times 3 \times 23 \times 1$

$= 3^3 \times 23$
Here common factor

$= 1$

$HCF = 1$
Hence the given numbers are co primes

Show that the following primes are co-primes:
$161, 192$

$161 = 7 \times 23$

$192 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3$

$= 2^6 \times 3 \times 1$
Here common factor

$= 1$

$HCF = 1$
Hence the given numbers are co primes

Without actually performing the long division, find if $\dfrac{987}{10500}$ will have terminating or non-terminating repeating decimal expansion. Give reason for your answer.

$\textbf{Checking of }$

$\dfrac{987}{10500}$

$\textbf{ is terminating or non-terminating decimal expansion.}$

$\textbf{Step 1 : converts given fraction into lowest form }$

$\dfrac{987}{10500}$

$= \dfrac{47}{500}$

$\textbf{Step 2 : Factorisation of denominator }$

$\dfrac{47}{500}$

$=\dfrac{47}{2^2\times 5^3}$

Since, the denominator has only 2 and 5 as its prime divisors.

thus, it is a terminating decimal expansion.

$\textbf{Hence,} \dfrac{987}{10500} \textbf{ is a terminating decimal expansion.}$

Show that the following primes are co-primes:
$847, 1014$

$847 = 7 \times 11 \times 11 \times 1$

$= 7 \times 11^2 \times 1$

$1014 = 2 \times 3 \times 13^2 \times 1$
Here common factor

$= 1$

$HCF = 1$
Hence the given numbers are co primes

Fill in the blanks:
The bigger number from the numbers $57,631$ and $57,361$ is ...................

The bigger number from the numbers

$57,631$ and

$57,361$ is

$57,631.$

Use Euclid's division algorithm to find the HCF of:
(i) $960$ and $432$
(ii) $4052$ and $12576$

$(i)$

$\begin{aligned}{}960 &= 432 \times 2 + 96\\432& = 96 \times 4 + 48\\96 &= 48 \times 2 + 0\end{aligned}$

Hence,

$HCF$ of

$960$ and

$432$ is

$48.$

$(ii)$

$\begin{aligned}{}12576 &= 4052 \times 3 + 420\\4052 &= 420 \times 9 + 272\\420& = 272 \times 1 + 148\\272& = 148 \times 1 + 124\\148& = 124 \times 1 + 24\\124&=24\times 5+4\\24&=4\times 6+0\end{aligned}$

Hence,

$HCF$ of

$4052$ and

$12576$ is

$4.$

Find the largest number that will divide 623, 729 and 841, leaving remainders 3, 9 and 1 respectively.

The given numbers are

$623,\ 729\ and\ 841$ .

We need to find the highest number which will leave remainders

$3,\ 9\ and\ 1$ respectively, when we divide the given numbers by it.

On subtracting the remainders from the respective numbers, we get:

$623-3=620$

$729-9=720$

$841-1=840$

Now, the largest number that can divide the three obtained numbers will be the

$HCF$ of the numbers.

Hence, let's find the

$HCF$ of these numbers.

The numbers can be represented as the product of their prime factors, as:

$620=2\times 2\times 5\times 31$

$720=2\times 2\times 2\times 2\times 3\times 3\times 5$

$840=2\times 2\times 2\times 3\times 5\times 7$

We know that, the

$HCF$ of two or more numbers is the product of all the factors common between them.

Hence,

$HCF(620,\ 720,\ 840)=2\times 2\times 5$

$=20$

Hence,

$20$ is the largest number that will divide

$623,\ 729$ and

$841$ , leaving remainders

$3,\ 9$ and

$1$ , respectively.

Find the H.C.F of the given numbers by division method :
$198 , 429$

Last remainder

$= 0$ , stop here

$\therefore \,$

$H.C.F$ of

$198,429= 33$ (Last divisor)
1752219_1789143_ans_3f69eeca43f340f28e206c1c41369649.png

Find the G.C.D of the given numbers by prime factorisation method :
$24 , 45$

$24 , 45$

$24 = 2 \times 2 \times 2 \times 3$

$45 = 3 \times 3 \times 5$

The greatest common factor is

$3$ .

G.C.D =

$3$

1759371_1789443_ans_5db83815612749648f6b808805847734.PNG

Identify the rational number that does not belong with the other three. Explain your reasoning $\dfrac{-5}{6}, \dfrac{-1}{2}, \dfrac{-4}{9}, \dfrac{-7}{3}$

$\dfrac{-1}{2}$ does not belong to these because, the value

$0.5$ is non-recurring while the others are recurring

Here,

$\dfrac{-5}{11} = 0.\overline{45}, \quad\dfrac{4}{9} = 0.\overline4,\quad \dfrac{-7}{3} = 2.\overline3\quad$ are recurring.

And ,

$\dfrac{-1}2=0.5\quad$ is terminating.

Find the greatest $3$ -digit number which is exactly divisible by $8 , 20$ and $24$ .

First we have to find the LCM of

$8 , 20$ and

$24$

$\therefore \,$ LCM of given numbers

$= 2 \times 2 \times \times 2 \times 3 \times 5 = 120$
Greatest number of

$3$ digit is

$999$
We divide

$999$ by

$120$ and find the remainder
According to given condition , we need a greatest

$3$ -digit number which is exactly divisible by

$120$

$\therefore \,$ The required number

$= 999 - 39 = 960$
1759221_1789212_ans_7a1c1172505643eab94a6a2d956df844.PNG

Find the common factors of :
$10 , 30$ and $45$

$10 , 30$ and

$45$

The factor of

$10$ are :

$1 , 2 , 5 , 10$

The factor of

$30$ are :

$1 , 2 , 3 , 5 , 10 , 15 , 30$

The factor of

$45$ are :

$1 , 3 , 5 , 9 , 15 , 45$

The common factors of

$10 , 30 , 45$ are

$1 , 5$

Find the greatest number which divides $2706 , 7, 41$ and $8250$ leaving remainder $6 , 21$ and $42$ respectively.

When

$2706$ is divided by the required number ,

$6$ is left as a remainder . So ,

$2706 - 6 = 2700$ i.e.,

$2700$ is exactly divisible by that number.

Similarly ,

$7041 - 21 = 7020$ is exactly divisible by that number.

Similarly, also ,

$8250 - 42 = 8208$ is exactly divisible by that number.

Therefore ,

$2700 , 7020$ and

$8208$ are divisible by that number.

Thus , required number is the H.C.F of

$2700 , 7020$ and

$8208$

First , we find H.C.F of

$2700$ and

$7020$ .

$\therefore \,$ The H.C.F of

$2700 , 7020$ and

$8208$ is

$108$ .

Hence the required number is

$108$

1759382_1789456_ans_17f49c4b512a48b7a860ee373653b05a.PNG

Find the HCF of $180$ and $336$ . Hence , find their LCM.

Division method : HCF of

$180$ and

$336$

$\therefore \,$ HCF of

$180$ and

$336 = 12$

Products of numbers LCM of

$180$ and

$336 = \dfrac{{\text{Products of numbers}}}{{\text{their H.C.F}}}$

$= \dfrac{180 \times 336}{12} = 15 \times 336 = 5040$

1759228_1789232_ans_65855cf8663e48a4ac582e357ced660b.PNG

Find the H.C.F of the given numbers by prime factorisation method:
$28 , 36$

The given numbers are

$28,\ 36$ .

The prime factorisation of the given numbers will be as follows:

$28 = 2 \times 2 \times 7$

$36 = 2 \times 2 \times 3 \times 3$

We know that, the

$HCF$ of two or more numbers is the product of all the prime factors common between them.

$\therefore \, HCF(28,\ 36) = 2 \times 2$

$= 4$

Hence, the

$HCF$ of

$28,\ 36$ is

$4$ .

Classify the following number as rational or irrational with justification:
$-\sqrt {0.4}$ .

Rational number is a number which can be written in form

$\cfrac pq$ , where

$p,q$ are both integers.

$-\sqrt {0.4} =-\sqrt{\cfrac{4}{10}}= -\dfrac {2}{\sqrt {10}}$

So,

$-\sqrt {0.4}$ cannot be written in a form

$\cfrac pq$ , with

$p,q$ both integers.

So, it is a irrational number.

Find what number variable $x$ denotes and find whether it is rational or irrational:
$x^{2} = 5$ .

Rational number is a number which can be written in a form

$\cfrac pq$ , where

$p,q$ are both integers.

$x^{2} = 5\Rightarrow x =\pm \sqrt {5}$

It cannot be written in form

$\cfrac pq$ , with

$p,q$ both integers.

So, it is irrational number.

Classify the following number as rational or irrational with justification:
$\sqrt {196}$ .

Rational number is a number which can be written in form

$\cfrac pq$ , where

$p,q$ are both integers.

$\sqrt {196} = 14=\cfrac{14}{1}$ , which follows rule of rational number.

So,

$\sqrt{196}$ is a rational number.

Classify the following number as rational or irrational with justification:
$10.124124...$ .

In decimals if decimals are terminating then it is rational number

OR if decimals are non terminating but they are recurring (repeating same pattern again and again) then that number is also a rational number.

Here,

$10.124124...$ is a decimal expansion which is non-terminating but recurring.

Hence, it is a rational number.

Classify the following number as rational or irrational with justification:
$3\sqrt {18}$ .

Rational number is a number which can be written in form

$\cfrac pq$ , where

$p,q$ are both integers.

$3\sqrt {18} = 3\sqrt {9\times 2} = 3\times 3\sqrt {2} = 9\sqrt {2}$ .

So, it cannot be written in a form

$\cfrac pq$ , with

$p,q$ both integers.

Hence,

$3\sqrt {18}$ is an irrational number.

Show that the cube of any positive integer is either of the form $4m , 4m + 1$ or $4m + 3$ for some integer $m$ .

By Euclid's division algorithm , corresponding to the positive integer

$a$ and

$4$

$a = 4q + r \quad$ ...(i)

where

$a , q , r$ are non-negative integers and

$0 \leqslant r < 4$ i.e.,

$r = 0, 1 , 2 , 3$

Now , at

$r = 0 , a = 4q + 0\quad$ [From(i)]

$\Rightarrow \, a^3 = (4q)^3 \quad$ [Cubing both sides]

$\Rightarrow \, a^3 = 4 \cdot (16q^3)$

$\Rightarrow \, a^3 = 4m$ , where

$m = 16q^3$

$\because \,a^3$ is perfect cube so

$4m$ will also be perfect cube for some specified value of

$m$ .

Now , at

$r = 1 , a = 4q + 1$

$\Rightarrow \,a^3 = (4q + 1)^3 \quad$ [Cubing both sides]

$\Rightarrow \, a^3 = (4q)^3 + (1)^3 + 3(4q^2)(1) + 3(4q)(1)^2$

$\Rightarrow \, a^3=4\cdot16q^3 + 1 + 4\cdot12q^2 + 4\cdot3q$

$\Rightarrow \ a^3= 4(16q^3 + 12q^2 + 3q) + 1$

$\Rightarrow \,a^3 = 4m + 1$ , where

$m = 16q^3 + 12q^2 + 3q$

$\because \, a^3$ is perfect cube so

$4m + 1$ will also be a perfect cube for some specified value of

$m$ .

$r = 2 , a = 4q + 2\quad$ [From (i)]

$\Rightarrow \,a^3 = (4q + 2)^3 \quad$ [Cubing both sides]

$\Rightarrow \,a^3 = (4q)^3 +(2)^3 + 3(4q)^2(2) + 3(4q)(2)^2$

$\Rightarrow \,a^3= 4 \cdot 16q^3 + 8 + 4\cdot 24q^2 + 4 \cdot 12q$

$\Rightarrow \,a^3= 4 ( 16q^3 + 2 + 24q^2 + 12q)$

$\Rightarrow \, a^3 = 4m$ , where

$m = 16q^3 + 24q^2 + 12q + 2$

$a^3$ is perfect cube so,

$4m$ is also a perfect cube for some value of positive integer

$m$ .

$r = 3 , a = 4q + 3 \quad$ [From(i)]

$\Rightarrow \,a^3 =(4q +3)^3 \quad$ [Cubing both sides]

$\Rightarrow \,a^3 =(4 q)^3 + (3)^3 + 3(4q)^2 (3) + 3(4q)(3)^2$

$\Rightarrow \, a^3 = 4 \cdot 16q^3 + 27 + 4 \cdot 36q^2 + 4q \cdot 27$

$\Rightarrow \,a^3 = 4 \cdot 16q^3 + 24 + 3 + 4 \cdot 36 \cdot q^2 + 4 \cdot 27q$

$\Rightarrow \,a^3= 4(16q^3 + 6 + 36q^2 + 27q) + 3$

$\Rightarrow \,a^3 = 4m + 3$ , where

$m = 16q^3 + 36q^2 + 27 + 6$

Hence , a number of the form

$4m , 4m + 1$ and

$4m + 3$ is perfect cube for specified natural value of

$m$ .

Classify the following number as rational or irrational with justification:
$1.010010001...$ .

In decimals if decimals are terminating then it is rational number

OR if decimals are non terminating but they are recurring (repeating same pattern again and again) then that number is also a rational number.

Here,

$1.010010001...$ is a decimal expansion which is non-terminating and also non-recurring.

Hence, it is an irrational number.

Classify the following number as rational or irrational with justification:
$0.5918$ .

Rational number is a number which can be written in form

$\cfrac pq$ , where

$p,q$ are both integers.

$0.5918=\cfrac{0.5918\times 10000}{1\times 10000}=\cfrac{5918}{10000}$

So,

$0.5918$ can be written in a form

$\cfrac pq$ , with

$p,q$ both integers.

So, it is a rational number.

Classify the following number as rational or irrational with justification:
$(1 + \sqrt {5}) - (4 + \sqrt {5})$ .

Rational number is a number which can be written in form

$\cfrac pq$ , where

$p,q$ are both integers.

$(1 + \sqrt {5}) - (4 + \sqrt {5}) = -3=\cfrac{-3}{1}$

So,

$(1 + \sqrt {5}) - (4 + \sqrt {5})$ can be written in a form

$\cfrac pq$ , with

$p,q$ both integers.

So, it is a rational number.

Prove that $\sqrt{5}$ is an irrational number. Hence, show that $-3 + 2\sqrt{5}$ is an irrational number.

Let us consider $\sqrt{5}$ be a rational number, then

$\sqrt{5}= p/q$ , where ‘p’ and ‘q’ are integers, $q \neq 0$ and p, q have no common factors (except 1).

So,

$5 = p^2 / q^2$

$p^2 = 5q^2$ …. (1)

As we know, ‘ $5$ ’ divides $5q^2$ , so ‘ $5$ ’ divides $p^2$ as well. Hence, ‘ $5$ ’ is prime.

So $5$ divides p

Now, let $p = 5k$ , where ‘k’ is an integer

Square on both sides, we get

$p^2 = 25k^2$

$5q^2 = 25k^2$ [Since, $p^2 = 5q^2$ , from equation (1)]

$q^2 = 5k^2$

As we know, ‘ $5$ ’ divides $5k^2$ , so ‘ $5$ ’ divides $q^2$ as well. But ‘ $5$ ’ is prime.

So $5$ divides q

Thus, p and q have a common factor of $5$ . This statement contradicts that ‘p’ and ‘q’ has no common factors (except 1).

We can say that $\sqrt{5}$ is not a rational number.

$\sqrt{5}$ is an irrational number.

Now, let us assume $-3 + 2\sqrt{5}$ be a rational number, ‘r’

So, $-3 + 2\sqrt{5} = r$

$-3 – r = 2\sqrt{5}$

$(-3 – r)/2 = \sqrt{5}$

We know that, ‘r’ is rational, ‘ $(-3 – r)/2$ ’ is rational, so ‘ $\sqrt{5}$ ’ is also rational.

This contradicts the statement that √5 is irrational.

So, $-3 + 2\sqrt{5}$ is irrational number.

Hence proved.

Write the denominator of the rational number $257/5000$ in the form $2^m \times 5^n$ where m, n is non-negative integers. Hence, write its decimal expansion on without actual division.

The fraction $257/5000$

Since the denominator is $5000$ ,

The factors for $5000$ are:

$5000 = 2 \times 2 \times 2 \times 5 \times 5 \times 5 \times 5$

$= 23 \times 54$

$257/5000 = 257/(23 \times 54)$

It is a terminating decimal.

So,

Let us multiply both numerator and denominator by $2$ , we get

$257/5000=(257 \times 2)/(5000\times 2)$

$= 514/10000$

$= 0.0514$

Using Euclid's division algorithm, find the HCF of $156$ and $504$ .

Given numbers are

$156$ and

$504$

Euclid's division algorithm states that,

$a=b\times q+r$ , where

$0\le r<b$

Here,

$504>156$

By using Euclid's division algorithm, we get

$504=156\times3+36$

Here,

$r=36\neq 0$

On taking

$156$ as dividend and

$36$ as the divisor and applying Euclid's division algorithm again , we get

$156=36\times4+12$

Here,

$r=12\neq 0$

So, on taking

$36$ as dividend and

$12$ as the divisor and again applying Euclid's division algorithm, we get

$36=12\times 3+0$

The remainder has now become

$0$ , so our procedure stops.

Here, the divisor at this last stage is

$12$ .

Hence, the HCF of

$156$ and

$504$ is

$12$ .

State which of the following are rational or irrational decimals.
$\sqrt{(4/9)}, -3/70, \sqrt{(7/25)}, \sqrt{(16/5)}$

$\sqrt{(4/9)}, -3/70, \sqrt{(7/25)}, \sqrt{(16/5)}$

$\sqrt{(4/9)} = 2/3$

$-3/70 = -3/70$

$\sqrt{(7/25)} = \sqrt{7}/5$

$\sqrt{(16/5)} = 4/\sqrt 5$

So,

$\sqrt{7}/5$ and $4/\sqrt{5}$ are irrational decimals.

$2/3$ and $-3/70$ are rational decimals.

Using Euclid's division algorithm, find the HCF of $135$ and $225$ .

Step 1 : For given integer

$135$ and

$225$

$225 > 135$
By Euclid division lemma

$225 = 135 \times 1 + 90$

Step 2 : Here remainder is not zero.
So, for divisor

$135$ and remainder

$90$ .

$135 = 90 \times 1 + 45$

Step 3 : Here remainder is not zero. So for divisor

$18$ and remainder

$3$ .

$90 = 45 \times 2 + 0$
Remainder

$= 0$
Hence HCF of

$135$ and

$225 = 45$

1789044_1814118_ans_2ddd87846d1644f3a13fe5a6834747a8.PNG

Using Euclid's division algorithm, find the HCF of $445$ and $42$ .

Given numbers are

$445$ and

$42$

Here,

$445>42$

So, we divide

$445$ by

$42$

By using Euclid's division lemma, we get

$445=42*10+35$

Here,

$r=35\neq 0$

On taking

$42$ as dividend and

$35$ as the divisor and we apply Euclid's divison lemma, we get

$42=35*1+7$

Here,

$r=7\neq 0$

So, on taking

$35$ as dividend and

$7$ as the divisor and again we apply Euclid's division lemma, we get

$35=7*5+0$

The remainder has now become

$0$ , so our procedure stops.

Since the divisor at this last stage is

$7$ , the HCF of

$445$ and

$42$ is

$7$ .

Show that the cube of a positive integer of the form $(6q + r)$ where $q$ is an integer and $r = 0 , 1 , 2, 3 , 4$ and $5$ is also of the form $(6m + r)$ .

By Euclid's division algorithm,

$a = 6q + r$ ..... (i)

where

$a , q$ and

$r$ are non-negative integers

$0 \leq r < 6$ i.e.,

$r = 0 , 1 , 2 , 3 , 4 , 5$ .

Cubing (i) both sides , we get

$(a)^3 = (6q + r)^3$

$\Rightarrow \,a^3 = (6q)^3 + (r)^3 + 3(6q)^2 (r) + 3(6q) (r)^2$

$\Rightarrow \,a^3= 6^3q^3 + r^3 + 3 (6)^2q^2r + 6 \times 3qr^2$

$\Rightarrow \,a^3 = 6[36q^3 + 18q^2r + 3qr^2] + r^3$ ....(ii)

When

$r = 0$

$a^3 = 6[36q^3 + 18q^2 \times 0 + 3q 0^2] + 0^3$ [From (ii)]

$\Rightarrow \,a^3= 6[36q^3]$

$\Rightarrow \,a^3 = 6m$ is perfect cube for some integer

$m$ such that

$m = 36q^2$

When

$r = 1$

$a^3 = 6[36q^3 + 18q^2 \times 1 + 3q 1^2] + 1^3$

$\Rightarrow \,a^3 = 6[36q^3 + 18q^2 \times 1 + 3q ] + 1$

$\Rightarrow \,a^3 = 6m + 1$ is perfect cube for some integer

$m$ such that

$m = (36q^2 + 18q^2 + 3q)$

When

$r = 2$

$a^3 = 6[36q^3 + 18q^2 \times 2 + 3q \times 2^2] + 2^3$ [From(ii)]

$\Rightarrow \,a^3 = 6[36q^3 + 36q^2 + 12q] + 6 + 2$

$\Rightarrow \,a^3= 6[36q^3 + 36q^2 + 12q + 1] + 2$

$\Rightarrow \,a^3 = 6m + 2$ is perfect cube for some integer

$m$ such that

$m = 36q^3 + 36q^2 + 12q + 1$

When

$r = 3$

$a^3 = 6[36q^3 + 18q^2 \times 3 + 3q \times 3^2] + 3^3$ [From(ii)]

$\Rightarrow \,a^3 = 6[36q^3 + 54q^2 + 27q] + 24 + 3$

$\Rightarrow \,a^3 = 6[36q^3 + 54q^2 + 27q + 4] + 3$

$\Rightarrow \,a^3 = 6m + 3$

So ,

$(6m + 3)$ is perfect cube for some integer

$m$ such that

$m = 36q^2 + 54q^2 + 27q + 4$

When

$r = 4$

$a^3 = 6[36q^3 + 18q^2(4) + 3q4^2] + 4^3$ [From(ii)]

$\Rightarrow \,a^3 = 6 [36q^3 + 72q^2 + 48q] + 60 + 4$

$\Rightarrow \,a^3 = 6 [36q^3 + 72q^2 + 48q + 10] + 4$

$\Rightarrow \,a^3 = 6m + 4$

So ,

$(6m + 4)$ is perfect cube for some integer

$m$ such that

$m = 36q^3 + 72q^2 + 48q + 10$

When

$r = 5$

$a^3 = 6[36q^3 + 18q^2(5) + 3q(5)^2] +(5)^3$ [From(ii)]

$\Rightarrow \,a^3 = 6[36q^3 + 90q^2 + 75q ] + 120 + 5$

$\Rightarrow \,a^3= 6[36q^3 + 90q^2 75q + 20] + 5$

$\Rightarrow \,a^3 = 6m + 5$

So,

$,(6m + 5)$ is perfect cube for some integer of

$m = 36q^3 + 90q^2 + 75q + 20$

Hence , cubes of positive integers of the form

$(6q+r)$ is also of the form

$(6m + r)$ where

$m$ is a specified integer and

$r = 0, 1 , 2 , 3 , 4 , 5$ .

Prove that, $\sqrt{3}$ is an irrational number. Hence, show that $2/5 \times \sqrt{3}$ is an irrational number.

Let us consider $\sqrt{3}$ be a rational number, then

$\sqrt{3} = p/q$ , where ‘p’ and ‘q’ are integers, $q \neq 0$ and p, q have no common factors (except 1).

So,

$3 = p^2 / q^2$

$p^2 = 3q^2$ …. (1)

As we know, ‘ $3$ ’ divides $3q^2$ , so ‘ $3$ ’ divides $p^2$ as well. Hence, ‘ $3$ ’ is prime.

So $3$ divides p

Now, let $p = 3k$ , where ‘k’ is an integer

Square on both sides, we get

$p^2 = 9k^2$

$3q^2 = 9k^2$ [Since, $p^2 = 3q^2$ , from equation (1)]

$q^2 = 3k^2$

As we know, ‘ $3$ ’ divides $3k^2$ , so ‘ $3$ ’ divides $q^2$ as well. But ‘ $3$ ’ is prime.

So $3$ divides q

Thus, p and q have a common factor of $3$ . This statement contradicts that ‘p’ and ‘q’ has no common factors (except 1).

We can say that $\sqrt{3}$ is not a rational number.

$\sqrt{3}$ is an irrational number.

Now, let us assume $(2/5)\sqrt{3}$ be a rational number, ‘r’

So, $(2/5)\sqrt{3} = r$

$5r/2 = \sqrt{3}$

We know that, ‘r’ is rational, ‘ $5r/2$ ’ is rational, so ‘ $\sqrt{3}$ ’ is also rational.

This contradicts the statement that $\sqrt{3}$ is irrational.

So, $(2/5)\sqrt{3}$ is an irrational number.

Hence proved.

Show that the square of any positive integer cannot be of the form $(6m + 2)$ or $(6m + 5)$ for any integer $m$ .

By Euclid's division algorithm , we have

$a = 6q + r$ , where ,

$0 \leq r < 6$

$r = 0 , 1 , 2 , 3 , 4 , 5$

Now squaring both sides of

$a = 6q + r$

$\Rightarrow \, a^3 = (6q)^2 + (r(^2 + 2(6q)(r)$

$\Rightarrow \, a^2 = 6[6q^2 + 2qr] + r^2$ .....(i)

$r = 0$

$a^2 = 6[6q^2 + 2q \times 0] + 0^2$ [From (i)]

$\Rightarrow \, a^2 = 36q^2$

$\Rightarrow \,a^2 = 6m$ , where

$m = 6q^2$

$r = 1$

$a^2 = 6[6q^2 + 2q \times 1] + 1^2$ [From (i)]

$\Rightarrow \, a^2 = 6[6q^2 + 2q] + 1$

$\Rightarrow \, a^2 = 6m + 1$ , where

$m = 6q^2 + 2q$

$r = 2$

$a^2 = 6[6q^2 + 2q \cdot 2] + 2^2$ [From(i)]

$\Rightarrow \, a^2 = 6m + 4$ , where

$m = (6q^2 + 4q)$

$r = 3$

$a^2 = 6[6q^2 + 2q \cdot 3] + 3^2$ [From (i)]

$\Rightarrow \, a^2 = 6[6q^2 + 6q] + 6 + 3$

$\Rightarrow \, a^2 = 6[6q^2 + 6q + 1] + 3$

$\Rightarrow \,a^2 = 6m + 3$ , where

$m = 6q^2 + 6q + 1$

$r = 4$

$a^2 = 6[6q^2 + 2q \cdot 4] + 4^2$

$\Rightarrow \, a^2 = 6[6q^2 + 8q] + 12 + 4$

$\Rightarrow \, a^2 = 6[6q^2 + 8q + 2] + 4$

$\Rightarrow \, a^2 = 6m + 4$ , where

$m = 6q^4 + 8q + 2$

$r = 5 , a^2 = 6[6q^2 + 2q \cdot 5 ] + 5^2$ [From(i)]

$\Rightarrow \,a^2 = 6[6q^2 + 10q] + 24 + 1$

$= 6[6q^2 + 10q + 4] + 1$

$\Rightarrow \,a^2 = 6m + 1$ , where

$m = 6q^2 + 10q + 4$

Hence , the number of the form

$6m , (6m + 1) , (6m + 3)$ and

$(6m + 4)$ are perfect squares and

$(6m + 2)$ and ,

$(6m + 5)$ are not perfect square for some value of

$m$ .

Show that the square on any odd integer is of the form $(4q + 1)$ for some integer $q$ .

By Euclid's division algorithm ,

$a = bq + r$ where

$a , b , q , r$ are non-negative integers and

$0 \leq r < b$ .

On putting

$b = 4$ we get

$a = 4q + r$ ....(i)

When

$r = 0 , a = 4q$ which is even (as it is divisible by

$2$ )

When

$r = 1 , a = 4q + 1$ which is odd (as it is not divisible by

$2$ )

Squaring the odd number

$(4q + 1)$ , we get

$a^2= (4q + 1)^2$

$= (4q)^2 + (1)^2 + 2(4q)$

$= 4[4q^2 + 2q ] + 1$

$= 4m + 1$ is perfect square for

$m = 4q^2 + 2q$

When

$r = 2 , a = 4q + 2$ [From(i)]

$\Rightarrow \,a = 2(2q + 1)$ which is even (as it is divisible by

$2$ )

When

$r = 3 , a = 4q + 3 = 4q + 2 + 1$

$= 2[2q + 1] + 1$ which is odd (as it is not divisible by

$2$ )

Squaring the odd number

$(4q + 3)$ , we get

$a^2=(4q + 3)^2 = (4q)^2 + (3)^2 + 2(4q) (3)$

$= 16q^2 + 9 + 24q$

$= 16q^2 + 24q + 8 + 1$

$= 4[4q^2 \,6q + 2] + 1$

$= 4m + 1$ is perfect square for some value of

$m$ .

Hence, the square on any odd integer is of the form

$(4q+1)$ for some integer

$q$ .

Using the Euclid's division algorithm, find the HCF of $3318$ and $4661$ .

Given numbers are

$3318$ and

$4661$

Here,

$4661>3318$

So, we divide

$4661$ by

$3318$

By using Euclid's division lemma, we get

$4661=3318*1+1343$

Here,

$r=1343\neq 0$

On taking

$3318$ as dividend and

$1343$ as the divisor and we apply Euclid's divison lemma, we get

$3318=1343*2+632$

Here,

$r=632\neq 0$

So, on taking

$1343$ as dividend and

$632$ as the divisor and again we apply Euclid's division lemma, we get

$1343=632*2+79$

Here,

$r=79\neq0$

On taking

$632$ as dividend and

$79$ as the divisor and we apply Euclid's division lemma, we get

$632=79*8+0$

The remainder has now become

$0$ , so our procedure stops.

Since the divisor at this last stage is

$79$ , the HCF of

$3318$ and

$4661$ is

$79$ .

Using Euclid's division algorithm, find the HCF of $4407,2938$ and $1469$ .

Given numbers are

$4407,2938$ and

$1469$ .

$\therefore 4407>2938>1469$

On applying Euclid's division lemma for

$4407$ and

$2938$ , we get

$4407=2938*1+1469$

Here,

$r=1469\neq 0$

So, again applying Euclid's division lemma with new dividend

$2938$ and new divisor

$1469$ , we get

$2938=1469*2+0$

The remainder has now become

$0$ , so our procedure stops.

Since the divisor at this stage is

$1469$ , the HCF of

$4407$ and

$2938$ is

$1469$ .

Now, applying Euclid's division lemma for

$1469$ and

$1469$ , we get

$1469=1469*1+0$

Here remainder =

$0$

So, HCF of

$4407,2938$ and

$1469$ is

$1469$ .

Using Euclid's division algorithm, find the HCF of $4052$ and $12576$ .

Given numbers are

$4052$ and

$12576$

Here,

$12576>4052$

So, we divide

$12576$ by

$4052$

By using Euclid's division lemma, we get

$12576=4052*3+420$

Here,

$r=420\neq 0$

On taking

$4052$ as dividend and

$420$ as the divisor and we apply Euclid's divison lemma, we get

$4052=420*9+272$

Here,

$r=272\neq 0$

So, on taking

$420$ as dividend and

$272$ as the divisor and again we apply Euclid's division lemma, we get

$420=272*1+148$

Here,

$r=148\neq0$

On taking

$272$ as dividend and

$148$ as the divisor and we apply Euclid's division lemma, we get

$272=148*1+124$

Here,

$r=124\neq 0$

So, on taking

$148$ as dividend and

$124$ as the divisor and we apply Euclid's divison lemma, we get

$148=124*1+24$

Here,

$r=24\neq 0$

So, on taking

$124$ as dividend and

$24$ as the divisor and agin we apply Euclid's division lemma we get

$124=24*5+4$

Here,

$r=4\neq 0$

So, on taking

$24$ as dividend and

$4$ as the divisor and again Euclid's division lemma, we get

$24=4*6+0$

The remainder has now become

$0$ , so our procedure stops.

Since the divisor at this last stage is

$4$ , the HCF of

$4052$ and

$12576$ is

$4$ .

Using Euclid's division algorithm, find the $HCF$ of $8840$ and $23120$

Given numbers are

$8840$ and

$23120.$

Here,

$23120>8840$

So, we divide

$23120$ by

$8840$

By using Euclid's division lemma, we get

$23120=8840\times2+5440$

Here,

$r=5440\neq 0$

On taking

$8840$ as dividend and

$5440$ as the divisor and we apply Euclid's division lemma, we get

$8840=5440\times1+3400$

Here,

$r=3400\neq 0$

So, on taking

$5440$ as dividend and

$3400$ as the divisor and again we apply Euclid's division lemma, we get

$5440=3400\times1+2040$

Here,

$r=2040\neq0$ \

On taking

$3400$ as dividend and

$2040$ as the divisor and we apply Euclid's division lemma, we get

$3400=2040\times1+1360$

Here,

$r=1360\neq 0$

So, on taking

$2040$ as dividend and

$2040$ as the divisor and we apply Euclid's division lemma, we get

$2040=1360\times1+680$

Here,

$r=680\neq 0$

So, on taking

$1360$ as dividend and

$680$ as the divisor and again we apply Euclid's division lemma we get

$1360=680\times2+0$

The remainder has now become

$0$ , so our procedure stops.

Since the divisor at this last stage is

$680$ , the

$HCF$ of

$8840$ and

$23120$ is

$680$ .

Find the LCM and HCF of the following integers by applying the prime factorization method: $26$ and $91$ .

Given numbers are

$26$ and

$91$ .
The prime factorization of

$26$ and

$91$ gives:
1789445_1814414_ans_6cedc3db7b0f446ca36f0e99caebad7a.PNG

If $6370=2^{m}.5^{n}.7^{k}.13^{p}$ , then find $m+n+k+p$ .

We have to factorize the

$6370$ to find the value of

$m,n,k$ and

$p$ factorization of

$6370$ is

$m+n+k+p=1+1+2+1=5$

1789086_1814374_ans_3ebf72b8dc224e4f92e4e923ae30ecbf.PNG

Find the LCM and HCF of the following integers by applying the prime factorization method: $1485$ and $4356$ .

Given numbers are

$1485$ and

$4356$ .
The prime factorization of

$1485$ and

$4356$ gives:
1789456_1814425_ans_5ed96dfed21942cabad658c934fdf834.PNG

Find the LCM and HCF of the following integers by applying the prime factorization method: $96$ and $404$ .

Given numbers are

$96$ and

$404$ .
The prime factorization of

$96$ and

$404$ gives:
1789429_1814409_ans_64ff5ffa9b754737b55792221eafa9a8.PNG

Using Euclid's division algorithm, find the HCF of $250,175$ and $425$ .

Given numbers are

$250,175$ and

$425$ .

$\therefore 425>250>175$

On applying Euclid's division lemma for

$425$ and

$250$ , we get

$425=250*1+175$

Here,

$r=175\neq 0$

So, again applying Euclid's division lemma with new dividend

$250$ and new divisor

$175$ , we get

$250=175*1+75$

Here,

$r=75\neq 0$

So, on taking

$175$ as dividend and

$75$ as divisor and again we apply Euclid division lemma, we get

$175=75*2+25$

Here,

$r=25\neq 0$

So, again applying Euclid's division lemma with new dividend

$75$ and new divisor

$25$ , we get

$75=25*3+0$

Here,

$r=0$ and divisor is

$25$ .

So, HCF of

$425$ and

$225$ is

$25$ .

Now, applying Euclid's division lemma for

$175$ and

$25$ , we get

$175=25*7+0$

Here remainder =

$0$

So, HCF of

$250,175$ and

$425$ is

$25$ .

Find the LCM and HCF of the following integers by applying the prime factorization method: $1095$ and $1168$ .

Given numbers are

$1095$ and

$1168$ .
The prime factorization of

$1095$ and

$1168$ gives:
1789459_1814426_ans_096917898cbc4b72801b15d1f3cc11a7.PNG

Prove that following numbers are irrational: $6+\sqrt{2}$

Let us assume

$6+\sqrt{2}$ is rational.

$\Rightarrow 6+\sqrt{2}$ can be written in the form

$\frac{a}{b}$ where

$a$ and

$b$ are co-prime.

Hence,

$6+\sqrt{2}=\frac{a}{b}$

$\sqrt{2}=\frac{a}{b}-6$

$\sqrt{2}=\frac{a-6b}{b}$

$\sqrt{2}=\left ( \frac{a-6b}{b} \right )$

$\sqrt{2}(irrational)=\left ( \frac{a-6b}{b} \right )(rational)$

Since,

$rational\neq irrational$

This is contradiction.

$\therefore$ Our assumption is incorrect.

Hence,

$6+\sqrt{2}$ is irrational.

Find the LCM and HCF of the following pair of integers and verify that LCM * HCF = product of two numbers: $32$ and $80$ .

Given numbers are

$32$ and

$80$
The prime factorization of

$32$ and

$80$ gives:

$32=2^{5}$ and

$80=2^{4}*5$
Therefore, the HCF of these two integers =

$2^{4}=16$
Now, the LCM of

$32$ and

$80=5*2^{5}=160$
Now, we have to verify,
[LCM

$(a,b)$ * HCF

$(a,b)$ = product of two numbers

$(a*b)$ ]
LHS = LCM * HCF =

$160*16=2560$
RHS = Product of two numbers =

$32*80=2560$
Hence, LHS=RHS
So, the product of two numbers is equal to the product of their HCF and LCM.

Find LCM and HCF of the following integers by using prime factorization method: $48,72$ and $108$ .

Given numbers are

$48,72$ and

$108$
Factorization of

$48,72$ and

$108$

1789513_1814495_ans_3725d7be7a9d4c3198c8bed8363ca647.PNG

Find the LCM and HCF of the following integers by applying the prime factorization method: $6$ and $21$ .

Given numbers are

$6$ and

$21$ .
The prime factorization of

$6$ and

$21$ gives:
1789466_1814430_ans_1359e8dab85545028e8560de8f424c97.PNG

Find LCM and HCF of the following integers by using prime factorization method: $42,63$ and $140$ .

Given numbers are

$42,63$ and

$140$
Factorization of

$42,63$ and

$140$

1789509_1814488_ans_02b7dff769224c648e4dfb116ffa6679.PNG

Prove that following numbers are irrational: $5-\sqrt{3}$

Let us assume

$5-\sqrt{3}$ is rational.

$\Rightarrow 5-\sqrt{3}$ can be written in the form

$\frac{a}{b}$ where

$a$ and

$b$ are co-prime.

Hence,

$5-\sqrt{3}=\frac{a}{b}$

$-\sqrt{3}=\frac{a}{b}-5$

$-\sqrt{3}=\frac{a-5b}{b}$

$\sqrt{3}=-\left ( \frac{a-3b}{b} \right )$

$\sqrt{3}(irrational)=\left ( \frac{5b-a}{b} \right )(rational)$

Since,

$rational\neq irrational$

This is a contradiction.

$\therefore$ Our assumption is incorrect.

Hence,

$5-\sqrt{3}$ is irrational.

Find the LCM and HCF of the following pair of integers and verify that LCM * HCF = product of two numbers: $36$ and $64$ .

Given numbers are

$36$ and

$64$
The prime factorization of

$36$ and

$64$ gives:

$36=2*2*3*3$ and

$64=2^{6}$
Therefore, the HCF of these two integers =

$2*2=4$
Now, the LCM of

$36$ and

$64=3*3*2^{6}=576$
Now, we have to verify,
[LCM

$(a,b)$ * HCF

$(a,b)$ = product of two numbers

$(a*b)$ ]
LHS = LCM * HCF =

$576*4=2304$
RHS = Product of two numbers =

$36*64=2304$
Hence, LHS=RHS
So, the product of two numbers is equal to the product of their HCF and LCM.

Prove that following numbers are irrational: $2+\sqrt{2}$

Let us assume

$2+\sqrt{2}$ is rational,

$\Rightarrow 2+\sqrt{2}$ can be written in the form

$\frac{a}{b}$ where

$a$ and

$b$ are co-prime.

Hence,

$2+\sqrt{2}=\frac{a}{b}$

$\sqrt{2}=\frac{a}{b}-2$

$\sqrt{2}=\frac{a-2b}{b}$

$\sqrt{2}=\left ( \frac{a-2b}{b} \right )$

$\sqrt{2}(irrational)=\left ( \frac{a-2b}{b} \right )(rational)$

Since,

$rational\neq irrational$

This is a contradiction.

$\therefore$ Our assumption is incorrect.

Hence,

$2+\sqrt{2}$ is irrational.

Find LCM and HCF of the following integers by using prime factorization method: $6,72$ and $120$ .

Given numbers are

$6,72$ and

$120$
Factorization of

$6,72$ and

$120$

1789474_1814464_ans_2b291ecebd314c09843b5c0b6b34adf5.PNG

Find LCM and HCF of the following integers by using prime factorization method: $36,45$ and $72$ .

Given numbers are

$36,45$ and

$72$

Factorization of

$36,45$ and

$72$

1789503_1814481_ans_db52e04ae39c4df490482af90eb8cf7b.PNG

Prove that following numbers are not rational: $3\sqrt{3}$

Let us assume that

$3\sqrt{3}$ be a rational number.

Then, it will be of the form

$\frac{a}{b}$ where

$a$ and

$b$ are co-prime and

$b\neq 0$

Now,

$\frac{a}{b}=3\sqrt{3}$

$\Rightarrow \frac{a}{3b}=\sqrt{3}$

Since,

$a$ is an integer and

$3b$ is also an integer

$(3b\neq 0)$

So,

$\frac{a}{3b}$ is a rational number.

$\Rightarrow \sqrt{3}$ is a rational number.

But this is contradiction to the fact that

$\sqrt{3}$ is an irrational number.

Therefore, our assumption is wrong.

Hence,

$3\sqrt{3}$ is an irrational number.

Without actually performing the long division, state whether the following rational number has terminating or non-terminating repeating (recurring) decimal expansion: $\dfrac{29}{343}$

Given rational number is

$\dfrac{29}{343}$

$\dfrac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ where

$n$ and

$m$ are non-negative integers.

Firstly we check co-prime.

$29=29*1$

$343=7*7*7$

$\Rightarrow 29$ and

$343$ have no common factors.

Therefore,

$29$ and

$343$ are co-prime.

Now, we have to check that

$q$ is in the form of

$2^{n}5^{m}$ .

$343=7^{3}$

So, the denominator is not of the form

$2^{n}5^{m}$ .

Thus,

$\frac{29}{343}$ is a non-terminating repeating decimal.

Without actually performing the long division, state whether the following rational number have terminating or non-terminating repeating (recurring) decimal expansion: $\dfrac{13}{125}$

Given rational number is

$\dfrac{13}{125}$

We know,

$\dfrac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ , where

$n$ and

$m$ are non-negative integers.

Firstly we check for co-prime.

$13=13\times 1$

$125=5\times 5\times 5\times 1$

$\Rightarrow 13$ and

$125$ have no common factors except

$1$ .

Therefore,

$13$ and

$125$ are co-prime.

Now, we have to check whether,

$q$ is in the form of

$2^{n}5^{m}$ or not.

$125=5^{3}$

$=1\times5^{3}$

$=2^{0}\times 5^{3}$

So, denominator is of the form

$2^{n}5^{m}$ , where

$n=0$ and

$m=3$ .

Thus,

$\dfrac{13}{125}$ is a terminating decimal.

Without actually performing the long division, state whether the following rational number have terminating or non-terminating repeating (recurring) decimal expansion: $\frac{3}{8}$

Given rational number is

$\frac{3}{8}$

$\frac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ where

$n$ and

$m$ are non-negative integers.

Firstly we check co-prime.

$3=3*1$

$8=2*2*2$

$\Rightarrow 3$ and

$8$ have no common factors.

Therefore,

$3$ and

$8$ are co-prime.

Now, we have to check that

$q$ is in the form of

$2^{n}5^{m}$ .

$8=2^{3}$

$=1*2^{3}$

$=5^{0}*2^{3}$

So, denominator is of the form

$2^{n}5^{m}$ where

$n=3$ and

$m=0$ .

Thus,

$\frac{3}{8}$ is a terminating decimal.

Prove that the following numbers are not rational: $5\sqrt{3}$

Let us assume that

$5\sqrt{3}$ be a rational number.

Then it will be of the form

$\frac{a}{b}$ where

$a$ and

$b$ are co-prime and

$b\neq 0$

Now,

$\frac{a}{b}=5\sqrt{3}$

$\Rightarrow \frac{a}{5b}=\sqrt{3}$

Since,

$a$ is an integer and

$3b$ is also an integer

$(5b\neq 0)$

So,

$\frac{a}{5b}$ is a rational number.

$\Rightarrow \sqrt{3}$ is a rational number.

But this contradicts to the fact that

$\sqrt{3}$ is an irrational number.

Therefore, our assumption is wrong.

Hence,

$5\sqrt{3}$ is an irrational number.

Prove that $\frac{1}{\sqrt{5}}$ is irrational.

Let us assume that

$\frac{1}{\sqrt{5}}$ be a rational number.

Then, it will be of the form

$\frac{a}{b}$ wher

$a$ and

$b$ are co-prime and

$b\neq 0$ .

Now,

$\frac{a}{b}=\frac{1}{\sqrt{5}}$

$\Rightarrow \frac{a}{b}=\frac{1*\sqrt{5}}{\sqrt{5*\sqrt{5}}}$

$\Rightarrow \frac{5a}{b}=\sqrt{5}$

Since,

$5a$ is an integer and

$b$ is also an integer.

$\frac{5a}{b}$ is a rational number.

$\Rightarrow \sqrt{5}$ is a rational number.

But this contradicts to the fact that

$\sqrt{5}$ is an irrational number.

Therefore, our assumption is wrong.

Hence,

$\frac{1}{\sqrt{5}}$ is an irrational number.

Prove that following numbers are irrational: $\sqrt{7}-\sqrt{5}$

Let us assume

$\sqrt{7}-\sqrt{5}$ is rational

Let,

$\sqrt{7}-\sqrt{5}=\frac{a}{b}$

Squaring both sides, we get

$(\sqrt{7}-\sqrt{5})^{2}=\frac{a^{2}}{b^{2}}$

$12-2\sqrt{35}=\frac{a^{2}}{b^{2}}$

$2\sqrt{35}=\frac{a^{2}}{b^{2}}-12$

$2\sqrt{35}=\left ( \frac{a^{2}-12b^{2}}{b^{2}} \right )$

$\sqrt{35}=\left ( \frac{a^{2}-12b^{2}}{2b^{2}} \right )$

$\sqrt{35}(irrational)=\left ( \frac{a^{2}-12b^{2}}{2b^{2}} \right )(Rational)$

Since,

$rational\neq irrational$

This is a contradiction.

$\therefore$ Our assumption is incorrect.

Hence

$\sqrt{7}-\sqrt{5}$ is irrational.

Prove that following numbers are irrational: $\sqrt{3}-\sqrt{2}$

Let us assume

$\sqrt{3}-\sqrt{2}$ is rational,

Let

$\sqrt{3}-\sqrt{2}=\frac{a}{b}$

Squaring both sides, we get

$(\sqrt{3}-\sqrt{2})^{2}=\frac{a^{2}}{b^{2}}$

$5-2\sqrt{6}=\frac{a^{2}}{b^{2}}$

$2\sqrt{6}=\frac{a^{2}}{b^{2}}-5$

$2\sqrt{6}=\frac{a^{2}-5b^{2}}{b^{2}}$

$\sqrt{6}=\left ( \frac{a^{2}-5b^{2}}{2b^{2}} \right )$

$\sqrt{6}(irrational)=\left ( \frac{a^{2}-5b^{2}}{2b^{2}} \right )(rational)$

Since

$rational\neq irrational$

This is contradiction.

$\therefore$ Our assumption is incorrect.

Hence,

$\sqrt{3}-\sqrt{2}$ is irrational.

Without actually performing the long division, state whether the following rational number have terminating or non-terminating repeating (recurring) decimal expansion: $\frac{27}{8}$

Given rational number is

$\frac{27}{8}$

$\frac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ where

$n$ and

$m$ are non-negative integers.

Firstly we check co-prime.

$27=3*3*3$

$8=2*2*2$

$\Rightarrow 27$ and

$8$ have no common factors.

Therefore,

$27$ and

$8$ are co-prime.

Now, we have to check that

$q$ is in the form of

$2^{n}5^{m}$ .

$8=2^{3}$

$=1*2^{3}$

$=5^{0}*2^{3}$

So, denominator is of the form

$2^{n}5^{m}$ where

$n=3$ and

$m=0$ .

Thus,

$\frac{27}{8}$ is a terminating decimal.

Prove that following numbers are irrational: $3+\sqrt{5}$

Let us assume

$3+\sqrt{5}$ is rational.

$\Rightarrow 3+\sqrt{5}$ can be written in the form

$\frac{a}{b}$ where

$a$ and

$b$ are co-prime.

Hence,

$3+\sqrt{5}=\frac{a}{b}$

$\sqrt{5}=\frac{a}{b}-3$

$\sqrt{5}=\frac{a-3b}{b}$

$\sqrt{5}=\left ( \frac{a-3b}{b} \right )$

$\sqrt{5}(irrational)=\left ( \frac{a-3b}{b} \right )(rational)$

Since,

$rational\neq irrational$

This is contradiction.

$\therefore$ Our assumption is incorrect.

Hence

$3+\sqrt{5}$ is irrational.

Use Euclid's algorithm to find the HCF of $900$ and $270$ .

$900$ and

$270$ ,
The given integers are

$900$ and

$270$ ,
Since

$270<900$ ,
Apply Euclid's division algorithm to find HCF of

$900$ and

$270$ ,

$900=(270*3)+90$
Since the remainder

$90\neq 0$ .
Apply Euclid's division algorithm to

$270$ and

$90$ ,

$270=(90*3)+0$
Since the remainder is zero.

$\therefore$ HCF of

$900$ and

$270$ is

$90$ .

Without actually performing the long division, state whether the following rational number has terminating or non-terminating repeating (recurring) decimal expansion: $\dfrac{129}{2^{2}5^{7}7^{5}}$

Given rational number is

$\dfrac{129}{2^{2}*5^{7}*7^{5}}$

$\dfrac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ where

$n$ and

$m$ are non-negative integers.

Firstly we check co-prime.

$129=3*43$

Denominator =

$2^{2}*5^{7}*7^{5}$

$\Rightarrow 129$ and

$2^{2}*5^{7}*7^{5}$ have no common factors.

Therefore,

$129$ and

$2^{2}*5^{7}*7^{5}$ are co-prime.

Now, we have to check that

$q$ is in the form of

$2^{n}5^{m}$ .

Denominator =

$2^{2}*5^{7}*7^{5}$

So, the denominator is not of the form

$2^{n}5^{m}$ .

Thus,

$\frac{129}{2^{2}*5^{7}*7^{5}}$ is a non-terminating repeating decimal.

Without actually performing the long division, state whether the following rational number has terminating or non-terminating repeating (recurring) decimal expansion: $\dfrac{29}{243}$

Given rational number is

$\dfrac{29}{243}$

$\dfrac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ where

$n$ and

$m$ are non-negative integers.

Firstly we check co-prime.

$29=29*1$

$243=3^{5}$

$\Rightarrow 29*$ and

$243$ have no common factors.

Therefore,

$29$ and

$243$ are co-prime.

Now, we have to check that

$q$ is in the form of

$2^{n}5^{m}$ .

$243=3^{5}$

So, the denominator is not of the form

$2^{n}5^{m}$ .

Thus,

$\frac{29}{243}$ is a non-terminating repeating decimal.

Without actually performing the long division, state whether the following rational number have terminating or non-terminating repeating (recurring) decimal expansion: $\frac{64}{455}$

Given rational number is

$\frac{64}{455}$

$\frac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ where

$n$ and

$m$ are non-negative integers.

Firstly we check co-prime,

$64=2^{6}$

$455=5*7*13$

$\Rightarrow 64$ and

$455$ have no common factors.

Therefore,

$64$ and

$455$ are co-prime.

Now, we have to check that

$q$ is in the form of

$2^{n}5^{m}$ .

$455=5*7*13$

So, denominator is not of the form

$2^{n}5^{m}$ .

Thus,

$\frac{64}{455}$ is a non-terminating repeating decimal.

Without actually performing the long division, state whether the following rational number have terminating or non-terminating repeating (recurring) decimal expansion: $\frac{6}{15}$

Given rational number is

$\dfrac{6}{15}=\dfrac{2}{5}$

$\dfrac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ where

$n$ and

$m$ are non-negative integers.

Firstly we check co-prime.

$\Rightarrow 2$ and

$5$ have no common factors.

Therefore,

$2$ and

$5$ are co-prime.

Now, we have to check that

$q$ is in the form of

$2^{n}5^{m}$ .

$5=5^{1}*1$

$=5^{1}*2^{0}$

So, denominator is of the form

$2^{n}5^{m}$ where

$n=0$ and

$m=1$

Thus,

$\dfrac{6}{15}$ is a terminating decimal.

Without actually performing the long division, state whether the following rational number have terminating or non-terminating repeating (recurring) decimal expansion: $\frac{35}{50}$

Given rational number is

$\frac{35}{50}=\frac{7}{10}$

$\frac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ where

$n$ and

$m$ are non-negative integers.

Firstly we check co-prime.

$7=1*7$

$10=2*5$

$\Rightarrow 7$ and

$10$ have no common factors.

Therefore,

$7$ and

$10$ are co-prime.

Now, we have to check that

$q$ is in the form of

$2^{n}5^{m}$ .

$10=5^{1}*2^{1}$

So, denominator is of the form

$2^{n}5^{m}$ where

$n=1$ and

$m=1$ .

Thus,

$\frac{35}{50}$ is a terminating decimal.

Without actually performing the long division, state whether the following rational number has terminating or non-terminating repeating (recurring) decimal expansion: $\dfrac{2^{2}*7}{5^{4}}$

Given rational number is

$\dfrac{2^{2}*7}{5^{4}}$

$\dfrac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ where

$n$ and

$m$ are non-negative integers.

Firstly we check co-prime.

$28=7*2^{2}$

$625=5^{4}$

$\Rightarrow 28$ and

$625$ have no common factors.

Therefore,

$28$ and

$625$ are co-prime.

Now, we have to check that

$q$ is in the form of

$2^{n}5^{m}$ .

$625=5^{4}*1$

$=5^{4}*2^{0}$

So, denominator is of the form

$2^{n}5^{m}$ where

$n=0$ and

$m=4$ .

Thus,

$\dfrac{2^{2}*7}{5^{4}}$ is a terminating decimal.

Use Euclid's algorithm to find the HCF of $1651$ and $2032$ .

$1651$ and

$2032$ ,
The given integers are

$1651$ and

$2032$ ,
Since

$1651<2032$ ,
Apply Euclid's division algorithm to find HCF of

$1651$ and

$2032$

$2032=(1651*1)+381$
Since the remainder

$381\neq 0$

Apply Euclid's division algorithm to find HCF of

$1651$ and

$381$

$1651=(381*4*1)+127$
Since the remainder

$127\neq 0$
Apply Euclid's division algorithm to

$381$ and

$127$

$381=(127*3)+0$
Since the remainder is zero.

$\therefore$ HCF of

$1651$ and

$2032$ is

$127$ .

Use Euclid's algorithm to find the HCF of $196$ and $38220$ .

$196$ and

$38220$ ,
The given integers are

$196$ and

$38220$ ,
Since

$196<38220$ ,
Apply Euclid's division algorithm to find HCF of

$196$ and

$38220$ ,

$38220=(196*195)+0$
Since the remainder is zero.

$\therefore$ HCF of

$196$ and

$38220$ is

$196$ .

Without actually performing the long division, state whether the following rational number have terminating or non-terminating repeating (recurring) decimal expansion: $\dfrac{7}{80}$

Given rational number is

$\dfrac{7}{80}$

$\dfrac{p}{q}$ is terminating if

$p$ and

$q$ are co-prime and

$q$ is of the form of

$2^{n}5^{m}$ where

$n$ and

$m$ are non-negative integers.

Firstly we check co-prime.

$7=7*1$

$80=2*2*2*2*5$

$\Rightarrow 7$ and

$80$ have no common factors.

Therefore,

$7$ and

$80$ are co-prime.

Now, we have to check that

$q$ is in the form of

$2^{n}5^{m}$ .

$80=2^{4}*5$

So, denominator is of the form

$2^{n}5^{m}$ where

$n=4$ and

$m=1$ .

Thus,

$\dfrac{7}{80}$ is a terminating decimal.

Write the following rational number in their decimal form and also state if it is terminating or non terminating, repeating decimal $\dfrac{3}{8}$ .

$\dfrac{3}{8}=\dfrac{3}{2^{3}}$

Multiplying and dividing

$5^3$

$\dfrac{3\times5^{3}}{2^{3}\times5^{3}}$

$=\dfrac{3\times125}{10^{3}}=\dfrac{375}{1000}=0.375$ .

$\therefore \dfrac{3}{8}$ is a terminating decimal form.

Write the following rational numbers in their decimal form and also state which are terminating and which are non terminating, repeating decimal.
$\dfrac{2}{11}$ .

$\dfrac{2}{11}$
The denominator

$11$ can not be written in the form

$2^{n}5^{m}$ ,

$\dfrac{2}{11}=0.181818..........$

$\therefore \dfrac{2}{11}$ has a non terminating, repeating decimal form.

Without performing division, state whether the following rational numbers will have a terminating decimal form or a non terminating, repeating decimal form.
$\dfrac{129}{2^{2}.5^{7}.7^{5}}$ .

$\dfrac{129}{2^{2}.5^{7}.7^{5}}$

$\therefore$ The denominator can not be written in the form

$2^{n}5^{m}$ .

$\therefore \dfrac{129}{2^{2}.5^{7}.7^{5}}$ has a non terminating, repeating decimal form.

Without performing division, state whether the following rational numbers will have a terminating decimal form or a non terminating, repeating decimal form.
$\dfrac{36}{100}$ .

$\dfrac{36}{100}=\dfrac{36}{10^{2}}=\dfrac{36}{2^{2}*5^{2}}$

$\therefore$ The denominator can be written in the form

$2^{n}5^{m}$ .

$\therefore \dfrac{36}{100}$ has a terminating decimal form.

Without performing actual division, state whether the following rational number will have a terminating decimal form or a non terminating, repeating decimal form.
$\dfrac{13}{3125}$

$\dfrac{13}{3125}=\dfrac{13}{5\times 5\times 5\times 5\times 5}=\dfrac{13}{5^{5}}$

Since the denominator can be written in the form

$5^{m}$ .

$\therefore \dfrac{13}{3125}$ has a terminating decimal form.

Write the following rational numbers in their decimal form and also state which are terminating and which are non terminating, repeating decimal.
$4\dfrac{1}{5}$ .

$4\dfrac{1}{5}=\dfrac{21}{5}=\dfrac{21*2}{5*2}=\dfrac{42}{10}=4.2$

$\therefore 4\dfrac{1}{5}$ has a terminating decimal form.

Find the $LCM$ and $HCF$ of the following integers by the prime factorization method:
$8,9$ and $25$ .

From the above figure,

$8 = 2 \times 2 \times 2$

$= 2^{3}$

$9 = 3 \times 3$

$= 3^{2}$

$25 = 5 \times 5$

$= 5^{2}$

For

$HCF$ common factor is

$1.$

For

$LCM,$ taking maximum power of prime factors,

$LCM = 2^{3} \times 3^{2} \times 5^{2}$

$= 8 \times 9 \times 25$

$= 1800$

So,

$HCF = 1$ and

$LCM = 180.$

1760276_1835321_ans_48d19e877ae94cc3961d31f37d1fe132.png

Find the LCM and HCF of the following integers by the prime factorization method: $12,15$ and $21$ .

$12,15$ and

$21$

$12=2*6=2*2*3=2^{2}*3^{1}$ ,

$15=3*5=3^{1}*5^{1}$ ,

$21=3*7=3^{1}*7^{1}$ .

$\therefore$ HCF of

$12,15$ and

$21=3^{1}=3$ .

$\therefore$ LCM of

$12,15$ and

$21=2^{2}*3^{1}*5^{1}*7^{1}=420$ .

Find the $LCM$ and $HCF$ of the following integers by the prime factorization method:
$72$ and $108$ .

$72$ and

$108$

$72=2*36$ ,

$=2*2*18$ ,

$=2*2*2*9$ ,

$=2*2*2*3*3=2^{3}*3^{2}$ .

$108=2*54$ ,

$=2*2*27$ ,

$=2*2*3*9$ ,

$=2*2*3*3*3=2^{2}*3^{3}$ .

$\therefore$ HCF of

$72$ and

$108=3^{2}*2^{2}=36$ .

$\therefore$ LCM of

$72$ and

$108=2^{3}*3^{3}=216$ .

Without performing division, state whether the following rational numbers will have a terminating decimal form or a non terminating, repeating decimal form.
$\dfrac{64}{455}$ .

$\dfrac{64}{455}=\dfrac{64}{5*7*13}$

$\therefore$ The denominator can not be written in the form

$2^{n}5^{m}$ .

$\therefore \dfrac{64}{455}$ has a non terminating repeating decimal form.

Can you find the HCF of $1.2$ and $0.12$ ? Justify your answer.

${\textbf{Step -1: Make both number in equal digit and convert to whole number}}{\text{.}}$

${\text{So now,}}$

${\text{1}}{\text{.2 can be written as 1}}{\text{.20}}$

${\text{0}}{\text{.12 stays as 0}}{\text{.12}}$

${\text{Next, you should convert both the numbers to whole numbers of the same ratio}}{\text{.}}$

${\text{So 1}}{\text{.20 will be equal to 120}}\;{\text{and 0}}{\text{.12 will be equal to 12}}$

${\textbf{Step -2: Find HCF}}$

${\text{Now, find the HCF of 120 and 12}}{\text{.}}$

${\text{HCF of 120 and 12 = 12}}$

${\text{As we multiplied both 1}}{\text{.20 and 0}}{\text{.12 by 100, }}$

${\text{the HCF}}\left( {{\text{which is now in whole number form}}} \right){\text{ should be divided by 100}}$

$\Rightarrow \dfrac{12}{100} {{ = 0}}{\text{.12}}$

${\text{The HCF of 1}}{\text{.2 and 0}}{\text{.12 = 0}}{\text{.12}}$

${\textbf{Hence, the HCF is 0}}{\textbf{.12}}{\textbf{.}}$

Find the HCF of the following by using Euclid algorithm.
$300$ and $550$ .

Euclid algorithm

$a=bq+r$

$a>b$ and

$0\leqslant r<b$ .

$300$ and

$550$
The positive integers are

$300$ and

$550$ ,

$550>300$
Apply Euclid's algorithm to

$550$ and

$300$ ,

$\therefore 550=(300*1)+250$
The remainder is

$250$ .
Apply Euclid's algorithm to

$300$ and

$250$ ,

$\therefore 300=(250*1)+50$
The remainder is

$50$ .
Apply Euclid's algorithm to

$250$ and

$50$

$\therefore 250=(50*5)+0$
The remainder is zero.

$\therefore$ HCF of

$300$ and

$550$ is

$50$ .

Find the HCF of the following by using Euclid algorithm.
$1860$ and $2015$ .

Euclid algorithm

$a=bq+r$

$a>b$ and

$0\leqslant r<b$ .

$1860$ and

$2015$
The positive integers are

$1860$ and

$2015$ ,

$2015>1860$
Apply Euclid's algorithm to

$2015$ and

$1860$

$\therefore 2015=(1860*1)+155$
The remainder is

$155$ .
Apply Euclid's algorithm to

$1860$ and

$155$

$\therefore 1860=(155*12)+0$
The remainder is zero.

$\therefore$ HCF of

$1860$ and

$2015$ is

$156$ .

Find the HCF and LCM of the following given pairs of numbers by prime factorization method.
$120,90$ .

$120,90$

$120=2*2*2*3*5$

$=2^{3}*3^{1}*5^{1}$

$90=2*3*3*5$

$=2^{1}*3^{2}*5^{1}$

$\therefore$ HCF

$=2^{1}*3^{1}*5^{1}=30$ .

$\therefore$ LCM

$=2^{3}*3^{2}*5=360$ .

Find the HCF and LCM of the following pair of numbers by prime factorization method:
$37,49$ .

Given numbers are

$37,49$

$37=1\times37$

$49=1\times7\times7$

$\therefore$ HCF

$=1$ .

$\therefore$ LCM

$=37\times7\times7=1813$

Write the following rational numbers as decimal form and find out the block of repeating digit $n$ the quotient.
$\dfrac{10}{13}$

$\dfrac{10}{13}=0.769230769230...$
The block of digits, repeating in the quotient are

$769230$ .

Write the following rational numbers as decimal form and find out the block of repeating digit $n$ the quotient.
$\dfrac{2}{7}$

$\dfrac{2}{7}=0.285714285714....$
The block of digit, repeating in the quotient are

$285714$ .

Write the following rational number in decimal form and find out the block of repeating digits in the quotient.
$\dfrac{5}{11}$

Given rational number is

$\dfrac{5}{11}$

To find out: Its decimal form and the block of repeating digits.

We will divide

$5$ by

$11$ for converting the given rational number to its equivalent decimal form.

$\therefore \ \dfrac{5}{11}=0.454545....$

The block of digits, repeating in the quotient is

$45$ .

Hence, the decimal form of the given rational number is

$0.45454545...$ and the block of repeating digits is

$45$ .

Find the HCF of the following by using Euclid algorithm.
$50$ and $70$ .

Euclid algorithm

$a=bq+r$

$a>B$ and

$0\leqslant r<b$

$50$ and

$70$
The positive integers are

$50$ and

$70$

$70>50$
Apply Euclid algorithm to

$70$ and

$50$

$\therefore 70=(50*1)+20$
The remainder is

$20$
Apply Euclid algorithm to

$50$ and

$20$

$\therefore 50=(20*2)+10$
The remainder is

$10$ .
Apply Euclid algorithm to

$20$ and

$10$

$\therefore 20=(10*2)+0$
The remainder is zero.

$\therefore$ HCF of

$70$ and

$50$ is

$10$ .

Find the HCF of the following by using Euclid algorithm.
$96$ and $72$ .

Euclid algorithm

$a=bq+r$

$a>b$ and

$0\leqslant r<b$ .

$96$ and

$72$
The positive integers are

$96$ and

$72$ ,

$96>72$
Apply Euclid algorithm to

$96$ and

$72$ ,

$\therefore 96=(72*1)+24$
The remainder is

$24$ .
Apply Euclid's algorithm to

$72$ and

$24$ ,

$\therefore 72=(24*3)+0$
The remainder is zero.

$\therefore$ HCF of

$96$ and

$72$ is

$24$ .

Write the denominators of the following rational number in $2^{n}5^{m}$ form where $n$ and $m$ are non negative integers and then write them in their decimal form.
$\frac{3}{4}$

$\dfrac{3}{4}=\dfrac{3}{2^{2}}=\dfrac{3*5^{2}}{2^{2}*5^{2}}=\dfrac{3*25}{10^{2}}=\dfrac{75}{100}=0.75$

$\therefore$ The decimal form of

$\dfrac{3}{4}=0.75$ .

Write the denominators of the following rational number in $2^{n}5^{m}$ form where $n$ and $m$ are non-negative integers and then write them in their decimal form.
$\dfrac{7}{25}$

$\dfrac{7}{5}=\dfrac{7}{5^{2}}=\dfrac{7*2^{2}}{5^{2}*2^{2}}=\dfrac{28}{10^{2}}=\dfrac{28}{100}=0.28$

$\therefore$ The decimal form of

$\dfrac{7}{25}=0.28$ .

Prove that the following are irrational:
$\frac{1}{\sqrt{2}}$ .

$\frac{1}{\sqrt{2}}$
Let us assume that

$\frac{1}{\sqrt{2}}$ is a rational.
That is, we can find coprimes

$a$ and

$b$ ,

$b\neq 0$ ,
Such that

$\frac{1}{\sqrt{2}}=\frac{a}{b}\Rightarrow \sqrt{2}=\frac{b}{a}$

$\frac{b}{a}$ is a rational number as

$a$ and

$b$ are integers.

$\therefore \sqrt{2}$ is a rational number.
But this contradicts the fact that

$\frac{1}{\sqrt{2}}$ is a irrational number.

$\therefore$ Our assumption is wrong.

$\therefore \frac{1}{\sqrt{2}}$ is irrational number.

Write the denominators of the following rational number in $2^{n}5^{m}$ form where $n$ and $m$ are non-negative integers and then write them in their decimal form.
$\dfrac{51}{64}$

$\dfrac{51}{64}=\dfrac{51}{2^{6}}=\dfrac{51*5^{6}}{2^{6}*5^{6}}=\dfrac{796875}{10^{6}}=0.796875$ .

$\therefore$ The decimal form of

$\dfrac{51}{64}=0.796875$ .

Prove that the following are irrational:
$3+2\sqrt{5}$

$3+2\sqrt{5}$
Let us assume that

$3+2\sqrt{5}$ is a rational.
That is, we can find coprimes

$a$ and

$b$ ,

$b\neq 0$
Such that

$3+2\sqrt{5}=\frac{a}{b}$

$\Rightarrow 2\sqrt{5}=\frac{a}{b}-3\Rightarrow \sqrt{5}=\frac{1}{2}\left ( \frac{a}{b}-3 \right )$
Since

$a$ and

$b$ are integers.

$\frac{1}{2}\left ( \frac{a}{b}-3 \right )$ is a rational number and

$\sqrt{5}$ is also a rational number.
But this contradicts the fact that

$\sqrt{5}$ is an irrational number.

$\therefore$ Our assumption is wrong.

$\therefore 3+2\sqrt{5}$ is an irrational number.

Prove that the following are irrational:
$6+\sqrt{2}$ .

$6+\sqrt{2}$
Let us assume that

$6+\sqrt{2}$ is a rational.
That is, we can find coprimes

$a$ and

$b$ ,

$b\neq 0$
Such that

$6+\sqrt{2}=\frac{a}{b}$

$\Rightarrow \sqrt{2}=\frac{a}{b}-6$
Since

$a$ and

$b$ are integers,

$\frac{a}{b}-6$ is a rational number and

$\sqrt{2}$ is also a rational number.
But this contradicts the fact that

$\sqrt{2}$ is an irrational number.

$\therefore$ Our assumption is wrong.

$\therefore 6+\sqrt{2}$ is an irrational number.

Prove that the following are irrational:
$\sqrt{3}+\sqrt{5}$ .

$\sqrt{3}+\sqrt{5}$
Let us assume that

$\sqrt{3}+\sqrt{5}$ is a rational.
That is, we can find coprimes

$a$ and

$b$ ,

$b\neq 0$ ,
Such that

$\sqrt{3}+\sqrt{5}=\dfrac{a}{b}$

$\Rightarrow \sqrt{3}=\dfrac{a}{b}-\sqrt{5}$
Square on both sides,

$(\sqrt{3})^{2}=\left ( \dfrac{a}{b}-\sqrt{5} \right )^{2}\Rightarrow 3=\dfrac{a^{2}}{b^{2}}+5-\dfrac{2a\sqrt{5}}{b}=3$

$\Rightarrow \dfrac{a^{2}}{b^{2}}+5-\dfrac{2a\sqrt{5}}{b}=3$

$\Rightarrow \dfrac{a^{2}}{b^{2}}+5-3=\dfrac{2a\sqrt{5}}{b}$

$\Rightarrow \dfrac{a^{2}}{b^{2}}+2=\dfrac{2a\sqrt{5}}{b}$

$\Rightarrow \dfrac{a^{2}+2b^{2}}{b^{2}}=\dfrac{2a\sqrt{5}}{b}$

$\Rightarrow \dfrac{a^{2}+2b^{2}}{b^{2}}.\dfrac{b}{2a}=\sqrt{5}\Rightarrow \dfrac{a^{2}+2b^{2}}{2ab}=\sqrt{5}$
Since

$a$ and

$b$ are integers,

$\dfrac{a^{2}+2b^{2}}{2ab}$ is rational.

$\therefore \sqrt{5}$ is a rational number.
But this contradicts the fact that

$\sqrt{3}+\sqrt{5}$ is an irrational number.

$\therefore$ Our assumption is wrong.

$\sqrt{3}+\sqrt{5}$ is an irrational number.

Prove that the following are irrational:
$\sqrt{5}$ .

$\sqrt{5}$
Let us assume that

$\sqrt{5}$ is a rational.
That is we can find coprimes

$a$ and

$b$ ,

$b\neq 0$ ,
Such that

$\sqrt{5}=\dfrac{a}{b}\Rightarrow a=\sqrt{5}b$
Let

$a$ and

$b$ have a common factor opther than

$1$ .
Square both sides,

$a^{2}=5b^{2}$

$a^{2}$ is divisible by

$5$ .

$\therefore a$ is also divisible by

$5$ .
Let

$a=5k$ where

$k$ is an integer.

$a^{2}=5b^{2}\Rightarrow (5k)^{2}=5b^{2}\Rightarrow 25k^{2}=5b^{2}$

$\Rightarrow b^{2}=\dfrac{25k^{2}}{5}=5k^{2}$

$b^{2}$ is divisible by

$5$ .

$\therefore b$ is also divisible by

$5$ . This means that both

$a$ and

$b$ are coprimes.
This contradiction has arisen because of our assumption that

$\sqrt{5}$ is a rational number.

$\therefore$ Our assumption is wrong.
So,

$\sqrt{5}$ is a irrational number.

Prove that $(2\sqrt{3}+\sqrt{5})$ is an irrational number. Also check whether $(2\sqrt{3}+\sqrt{5})(2\sqrt{3}-\sqrt{5})$ is rational or irrational.

Let us suppose

$(2\sqrt{3}+\sqrt{5})$ is an irrational i.e, we can find coprimes

$a$ and

$b$ .

$(b\neq 0)$ such that

$(2\sqrt{3}+\sqrt{5})=\dfrac{a}{b}$

$\Rightarrow 2\sqrt{3}=\dfrac{a}{b}-\sqrt{5}$
Square on both sides

$(2\sqrt{3})^{2}=\left ( \dfrac{a}{b}-\sqrt{5} \right )^{2}$

$\Rightarrow 12=\dfrac{a^{2}}{b^{2}}+5-2\sqrt{5}\dfrac{a}{b}$

$\Rightarrow 12-5=\dfrac{a^{2}}{b^{2}}-2\sqrt{5}\dfrac{a}{b}$

$\Rightarrow 2\sqrt{5}\dfrac{a}{b}=\dfrac{a^{2}}{b^{2}}-7$

$\Rightarrow 2\sqrt{5}\dfrac{a}{b}=\dfrac{a^{2}-7b^{2}}{b^{2}}$

$\Rightarrow \sqrt{5}=\dfrac{a^{2}-7b^{2}}{b^{2}}*\dfrac{b}{2a}$

$\Rightarrow \sqrt{5}=\dfrac{a^{2}-7b^{2}}{2ab}$
Since

$a$ and

$b$ are integers,

$\dfrac{a^{2}-7b^{2}}{2ab}$ is a rational.
So,

$\sqrt{5}$ is a rational.
This contradicts the fact that

$\sqrt{5}$ is irrational.

$2\sqrt{3}+\sqrt{5}$ is irrational.

$(2\sqrt{3}+\sqrt{5})(2\sqrt{3}-\sqrt{5})=12-5=7$ . This is a rational number.

Write the denominators of the following rational number in $2^{n}5^{m}$ form where $n$ and $m$ are non-negative integers and then write them in their decimal form.
$\dfrac{14}{25}$

$\dfrac{14}{25}=\dfrac{14}{5^{2}}=\dfrac{14*2^{2}}{5^{2}*2^{2}}=\dfrac{56}{10^{2}}=0.56$

$\therefore$ The decimal form of

$\dfrac{14}{25}=0.56$ .

Prove that $\sqrt{p}+\sqrt{q}$ is an irrational, where $p,q$ are primes.

$\sqrt{p}+\sqrt{q}$ where,

$p,q$ are primes.

Let us assume that

$\sqrt{p}+\sqrt{q}$ is a rational number.

That is, we can find coprime

$a$ and

$b$ ,

$b\neq 0$ ,

Such that

$\sqrt{p}+\sqrt{q}=\dfrac{a}{b}$

Square on both sides

$\begin{aligned}{}{\left( {\sqrt p + \sqrt q } \right)^2} &= {\left( {\frac{a}{b}} \right)^2}\\{p^2} + 2\sqrt {pq} + {q^2}& = \frac{{{a^2}}}{{{b^2}}}\\2\sqrt {pq} & = \frac{{{a^2}}}{{{b^2}}} - {p^2} - {q^2}\\\sqrt {pq} &= \frac{1}{2}\left( {\frac{{{a^2}}}{{{b^2}}} - {p^2} - {q^2}} \right)\end{aligned}$

Since

$a$ and

$b$ are integers,

$\dfrac{1}{2}\left ( \dfrac{a^{2}}{b^{2}}-p^{2}-q^{2} \right )$ is a rational number but

$\sqrt{pq}$ is an irrational number.

This contradict our assumption hence,

$\sqrt{p}+\sqrt{q}$ is an irrational number.

Show that $x$ is irrational if:
$x^{2}=6$

$x^{2}=6$

$\Rightarrow x=\sqrt{6}=2.449 ......$ which is irrational.

Prove that the following number is irrational:
$3-\sqrt{2}$

Let

$3-\sqrt{2}$ be a rational number.

$\Rightarrow 3-\sqrt{2}=x$
Squaring on both the sides, we get

$(3-\sqrt{2})^{2}=x^{2}$

$\Rightarrow 9+2-2 \times 3 \times \sqrt{2}=x^{2}$

$\Rightarrow 11-x^{2}=6 \sqrt{2}$

$\Rightarrow \sqrt{2}=\dfrac{11-x^{2}}{6}$
Here,

$\mathrm{x}$ is a rational number.

$\Rightarrow \mathrm{x}^{2}$ is a rational number.

$\Rightarrow 11-\mathrm{x}^{2}$ is a rational number.

$\Rightarrow \dfrac{11-x^{2}}{6}$ is also a rational number.

$\Rightarrow \sqrt{2}=\dfrac{11-x^{2}}{6}$ is a rational number.
But

$\sqrt{2}$ is an irrational number.

$\Rightarrow \dfrac{11-x^{2}}{6}=\sqrt{2}$ is an irrational number.

$\Rightarrow 11-\mathrm{x}^{2}$ is an irrational number.

$\Rightarrow \mathrm{x}^{2}$ is an irrational number.

$\Rightarrow \mathrm{x}$ is an irrational number
But we have assume that x is a rational number.

$\therefore$ we arrive at a contradiction. So, our assumption that

$3-\sqrt{2}$ is a rational number is wrong.

$\therefore 3-\sqrt{2}$ is an irrational number.

Show that $x$ is irrational if:
$x^{2}=0.009$

Given that

$x^{2}=0.009$

So,

$\Rightarrow x=\sqrt{0.009}=0.0948 ......$ (which is irrational.)

Find the HCF of the following numbers :
$18,60$

$18 , 60$

$18 = 1,2,3,6,9,18$

$60= 1,2,3,4,6,10,12,15,30,60$
Common factors =

$1, 2, 3, 6$

$\therefore$ H.C.F. of

$18$ &

$60$ is

$\boxed {6}$

Find the HCF of the following numbers :
$91,112,49$

$91, 112 , 49$

$91 = \underline {1} ,\underline {7} , 13 ,91$

$112 = \underline {1} , 2 , 4, \underline {7} , 8, 14,16 ,28 ,56 , 112$

$49 = \underline {1}, \underline {7}, {49}$

$\therefore$ Common Factors =

$1, 7$

$\therefore$ H.C.F. of

$91 , 112 , 49$ is

$7$

Find the HCF of the following numbers :
$12,45,75$

$12,45,75$

$12 = \underline {1} , 2, 3, 4, 6, 12$

$45 = \underline {1} , 3, 5, 9, 15, 45$

$75 = \underline {1} , 3, 5, 15 , 26 , 75$

$\therefore$ Common factors

$1, 3$

$\therefore$ H.C.F. of

$12, 45, 75$ is

$3$

Find the HCF of the following numbers :
$30,42$

$30, 42$

$30 = 1,2,3,5,6,10,15,30$

$42 = 1,2,3,4,6,7,14,21,42$
Common factors =

$1,2,3,6$

$\therefore$ H.C.F. = $$ \boxed { 6 }

\therefore

$H.C.F. of$ 30

$and$ 42 is

${6}$

Find the $H.C.F$ of the following numbers :
$34,102$

$34$ &

$102$

$34 = 1,2,17,34$

$102 = 1,2,3,6,17,34,51, 102$

$\therefore$ common factors

$= 1,2,17,34$

$\therefore$ H.C.F. of

$34$ &

$102$ is

$34$ .

Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion :
$\dfrac{35}{50}$

$\dfrac{35}{50}$

$=\dfrac{5 \times 7}{5 \times 10}=\dfrac{7}{10}=0.7$

$\therefore$ This is terminating decimal expansion.

What is HCF of two consecutive
(a) Numbers ?
(b) Even numbers ?
(c) Odd numbers ?
Find the HCF of the following :
$8$ and $12$

(a) HCF will be 1

(b) HCF will be 2 only common dividing value

HCF of 8 and 12 is 4

What is HCF of two consecutive
(a) Numbers ?
(b) Even numbers ?
(c) Odd numbers ?

$\textbf{Step-1: Apply the concept of H.C.F.}$

$\text{(a) Let the consecutive numbers be 2 and 3 }$

$2 = 1 \times 2$

$3 = 1 \times 3$

$\text{We know that H.C.F. = Highest Common Factor}$

$\text{Common factor of 2 and 3 =1 }$

$\text{Therefore, HCF of two consecutive numbers is 1}$

$\text{(b) Let the consecutive even numbers be 2 and 4 }$

$2 = 1 \times 2$

$4 = 2 \times 2$

$\text{We know that H.C.F. = Highest Common Factor}$

$\text{Common factor of 2 and 4 = 2 }$

$\text{Therefore, HCF of two consecutive even numbers is 2}$

$\text{(c) Let the consecutive odd numbers be 3 and 5 }$

$3 = 1 \times 3$

$5 = 1 \times 5$

$\text{We know that H.C.F. = Highest Common Factor}$

$\text{Common factor of 3 and 5 =1 }$

$\text{Therefore, HCF of two consecutive odd numbers is 1}$

$\textbf{Hence, the HCF of given numbers is obtained.}$

Classify the following numbers as rational or irrational.
$2 - \sqrt5$

$2 - \sqrt5 = 2 - 2.2360679........$

$= -0.2360679$
This is non-terminating, non-recurring decimal.

$\therefore$ This is an irrational number.

Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion :
$\dfrac{6}{15}$

$\dfrac{6}{15}$

$=\dfrac{6}{15}=\dfrac{3 \times 2}{3 \times 5}=\dfrac{2}{5} \times \dfrac{2}{2}=\dfrac{4}{10}$

$\therefore$ This is terminating decimal expansion.

Prove that $\sqrt{5}$ is irrational.

$Let\space us\space assume\space, to\space the\space contrary\space, that\space$

$\sqrt{5}$

$is\space rational$ .

$\therefore \sqrt{5}=\dfrac{a}{b}$

$\therefore \sqrt{5} \times b=a$

$By\space Squaring\space on\space both\space sides,$

$5b^2 = a^2$

$…………. (i)$

$\therefore 5\,divides\,a^2$

$5$

$divides\space a$ .

$Substituting\space the\space value\space of\space ‘a’ in\space eqn$ .

$(i),$

$5b^2 = (5c)^2 = 25c^2$

$b^2=5c^2$

$It\space means\space$

$5$

$divides$

$b^2$ .

$\therefore$

$5$

$divides$

$b$ .

$\therefore$

$‘a’\space and\space ‘b’\space have\space at\space least$

$5$

$as\space a \space common\space factor.$

$But\space this\space contradicts\space the\space fact\space that\space a’\space and \space ‘b’\space are\space prime\space numbers.$

$\therefore$

$\sqrt{5}$

$is\space an\space irrational\space number.$

Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion :
$\dfrac{129}{2^2\,5^7\,7^5}$

$\dfrac{129}{2^2\,5^7\,7^5}$

Here, the denominator is not in form of

$2^n5^m$ .

$\therefore$ This is a non-terminating repeating expansion.

Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion :
$\dfrac{23}{2^3\,5^2}$

$\dfrac{23}{2^3\,5^2}$

$=\dfrac{23 \times 5^1}{2^3 \times 5^2\times 5^1}=\dfrac{115}{10^3}$

$=\dfrac{115}{1000}=0.115$

$\therefore$ This is terminating decimal expansion.

Look at several examples of rational numbers in the form $\frac{p}{q} (q \neq 0)$ , where $p$ and $q$ are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?

Rational numbers in the form

$\frac{p}{q} (q \neq 0)$ where

$P$ and

$q$ are integers with no common factors.

$q$ has factors 2 or 5 or both.

$i.e,$

$q=2^m5^n$ where

$m,n\ge0$

Classify the following numbers as rational or irrational :
(i) $\sqrt{23}$
(ii) $\sqrt{225}$
(iii) $0.3796$
(iv) $7.478478$
(v) $1.101001000100001...$

$\sqrt{23} = 4.7958.......$ This is not terminating or non-recurring decimal.

$\therefore \ \sqrt{23}$ is an irrational number.
ii)

$\sqrt{225} = 15$ this is a rational number.
iii)

$0.3796$ This is rational number, because terminating decimal has expansion.
iv)

$0.478478...$ This is rational number, because decimal expansion is recurring.
v)

$0.101001000100001...$ This is an irrational number because termianting or recruring decimal has no expansion.

Find the HCF and LCM of the following integers by applying the prime factorization method
$24 , 15$ and $36$

$24, 15$ and

$36$

$24 = 2 \times 2 \times 2 \times 3 = 2^{3} \times 3$

$15 = 3 \times 5$
and

$36 = 2 \times 2 \times 3 \times 3 = 2^{2} \times 3^{2}$
For HCF, taking minimum power of common prime factor
H.C.F

$= (3)^{1} = 3$
For LCM, taking maximum power of prime factor
L.C.M

$= 2^{3} \times 3^{2} \times 5^{1} = 8 \times 9 \times 5 = 360$
So H.C.F

$= 3$
L.C.M =

$360$

1853201_1875010_ans_b1d8925e79544034b89bb668ad847d57.png

Prove that following numbers are irrational
$3 \sqrt{2}$

Let

$3 \sqrt{2}$ is a rational number we find two integers a and b such as

$3 \sqrt{2} = \dfrac{a}{b}$ (where

$a$ and

$b$ co-prime integers)

$\Rightarrow \sqrt{2} = \dfrac{a}{3b}$

$\Rightarrow a , b$ and

$3$ are integers

$\dfrac{a}{3b}$ is a rational number

$\sqrt{2}$ is a rational number

$3 \sqrt{2}$ will be also a rational numbers.
But this contradicts the fact that

$\sqrt{2}$ is an irrational number.
So our hypothesis is wrong.
So,

$3 \sqrt{2}$ is an irrational number.
Hence proved.

Find the HCF and LCM of the following integers by applying the prime factorization method
$40 , 36$ and $126$

$40 = 2 \times 2 \times 2 \times 5 = 2^{3} \times 5$

$36 = 2 \times 2 \times 3 \times 3 = 2^{2} \times 3^{2}$
and

$126 = 2 \times 3 \times 3 \times 7 = 2 \times 3^{2} \times 7$
For H.C.F taking minimum power of common factor
H.C.F

$= (2)^{1} = 2$
For L.C.M, taking maximum power of prime factors
L.C.M

$= 2^{3} \times 3^{2} \times 5 \times 7 = 8 \times 9 \times 5 \times 7 = 2520$
Hence, H.C.F

$=2$
L.C.M

$= 2520$

1853219_1875020_ans_5b845047afe044f89faf916cfb1f524b.png

Without actually performing the long division method, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
$\dfrac{17}{6}$

$\dfrac{17}{6} =\dfrac{17}{2\times3}$

Denominator is not of the form

$2^{m} \times 5^{n}$ .

Hence,

$\dfrac{17}{6}$ has non-terminating repeating decimal expansion.

Classify the following numbers as rational or irrational.
$(3 + \sqrt{23}) - \sqrt{23}$

$(3 + \sqrt{23}) - \sqrt{23}$

$= 3 + \sqrt{23} - \sqrt{23}$

$= 3$

$\Rightarrow \ \ \frac{3}{1}$ . This can be written in the form of

$\frac{p}{q}$ .

$\therefore$ This is a rational number.

Classify the following numbers as rational or irrational.
$\frac{2\sqrt7}{7\sqrt7}$

$\displaystyle \frac { 2\sqrt { 7 } }{ 7\sqrt { 7 } } =\frac { 2 }{ 7 }$

This number can be written in the form of

$\displaystyle \frac{p}{q}$

$\therefore$ This is rational number.

If HCF of or numbers $408$ and $1032$ is expressed in the form of $1032x - 408 \times 5$ , then find the value of $x$ .

Step 1 : For a number

$408$ and

$1032$ as

$1032 > 408$
Using Euclid division lemma

$1032 = 408 \times 2 + 216$ .......(i)

Step 2 : Remainder

$\neq 0$
For divisor

$408$ and remainder

$216$
Using Euclid division lemma

$408 = 216 \times 1 + 192$ ..........(ii)

Step 3 : Remainder

$\neq 0$
For divisor

$216$ and remainder

$192$
Using Euclid division lemma

$216 = 192 \times 1 + 24$ .......(iii)

Step 4 : Remainder

$\neq 0$
For division

$192$ and remainder

$24$
Using Euclid division lemma

$192 = 24 \times 8 + 0$ ........(iv)
Hence, remainder

$= 0$
Hence , HCF of

$408$ and

$1032 = 24$
H.C.F

$= 1032x - 408 \times 5$

$\Rightarrow\ 24 = 1032x - 408 \times 5 (\therefore H.C.F = 24)$

$\Rightarrow\ 1032 x = 24 + 408 \times 5$

$\Rightarrow\ 1032x = 24 + 2040$

$\Rightarrow\ 1032 x = 2064$

$\Rightarrow\ x = 2$
Hence, the value of

$x = 2$ .

1851312_1874932_ans_191a5834de5a4e1ba0d9747b3566ac19.png

Use Euclid's division algorithm to find the HCF of $75 , 243$

Step 1 : For given integer

$75$ and

$243$

$243 > 75$
By Euclid division lemma

$243 = 75 \times 3 + 18$ ........(i)

Step 2 : Here remainder

$\neq 0$
So using Euclid division lemma for divisor

$75$ and remainder

$18$ .

$75 = 18 \times 4 + 3$ .........(ii)

Step 3 : Here remainder

$\neq 0$

So using Euclid division lemma for divisor

$18$ and remainder

$3$

$18 = 3 \times 6 + 0$ ..........(iii)
Since remainder

$= 0$
Hence, H.C.F of

$75$ and

$243 = 3$

1851239_1874921_ans_8a1a7438eaad472fac7e7993f78d9c5f.png

Classify the following numbers as rational or irrational.
$2\pi$

$2\pi$

$= 2 \times 3.1415.....$

$= 6.2830.....$
This is non-terminating, non-recurring decimal.

$\therefore$ This is an irrational number.

Without actually performing the long division method, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
$\dfrac{35}{50}$

$\dfrac{35}{50} = \dfrac{5 \times 7}{2 \times 5 \times 5} = \dfrac{7}{2 \times 5}$

$= \dfrac{7}{2^1 \times 5^1}$

$\because$ Denominator is of the form

$2^m \times 5^n$ .
Hence,

$\dfrac{35}{50}$ is the terminating decimal expansion.

Prove that following numbers are irrational numbers
$4 + \sqrt{2}$

Let

$4 + \sqrt{2}$ is rational number.

$\therefore$ Now we find two integers

$a$ and

$b$ such as

$4 + \sqrt{2} = \dfrac{a}{b}$

$\Rightarrow$

$\sqrt{2} = \dfrac{a}{b} - 4$

$\Rightarrow$

$\sqrt{2} = \dfrac{a - 4b}{b}$

$a , b , ab$ and

$4$ are all integers.

$\dfrac{a - 4b}{b}$ is a rational number.

$\sqrt{2}$ will be a rational number.

But

$\sqrt{2}$ is not rational number.
This contradicts.
Our hypothesis is wrong.
So,

$4 + \sqrt{2}$ is an irrational number.
Hence proved.

Prove that following numbers are irrational numbers
$5 \sqrt{2}$

Let

$5 \sqrt{2}$ is a rational number.

$\therefore \, 5 \sqrt{2} = \dfrac{a}{b} , b\neq 0$ , (where

$a , b$ are co-prime numbers)

or

$\sqrt{2} = \dfrac{a}{5b}$ .............(i)

Since,

$a , b$ are integer.

So,

$\dfrac{a}{5b}$ is a rational number.

It is clear that from equation (i)

$\sqrt{2}$ is a rational number which is contradict statement,

since we know that

$\sqrt{2}$ is a irrational number.

So our hypothesis is wrong.

Hence,

$5 \sqrt{2}$ is a irrational number.

Prove that following numbers are irrational numbers
$\dfrac{3}{2 \sqrt{5}}$

Let

$\dfrac{3}{2 \sqrt{7}}$ is a rational number.

We find two integers such as

$\dfrac{3}{2 \sqrt{5}} = \dfrac{a}{b} (b \neq 0)$ Where

$a$ and

$b$ are co-prime.

$\dfrac{1}{\sqrt{5}} = \dfrac{2a}{3b}$

$\therefore a$ and

$b$ integer

$r$ .

$\therefore \dfrac{2a}{3b}$ is a rational number.

$\Rightarrow \dfrac{1}{\sqrt{5}}$ will be also a rational number.

But

$\dfrac{1}{\sqrt{5}}$ is not rational number. It is a irrational number. This is contradict.
So, our hypothesis is wrong.
Hence

$\dfrac{3}{2 \sqrt{5}}$ is a irrational number.
Hence proved.

Prove that following numbers are irrational numbers
$\dfrac{2}{\sqrt{7}}$

Let

$\dfrac{2}{\sqrt{7}}$ is a rational number.
We find two integers such as

$\dfrac{2}{\sqrt{7}} = \dfrac{a}{b} (b \neq 0)$ where a and b are co-prime.

$\dfrac{1}{\sqrt{7}} = \dfrac{a}{2b}$

$\because a$ and

$b$ is integers.

$\therefore\ \dfrac{a}{2b}$ is a rational number.

$\Rightarrow\ \dfrac{1}{\sqrt{7}}$ also a rational number.

But

$\Rightarrow\ \dfrac{1}{\sqrt{7}}$ is not rational number. This is contradict.

Hence,

$\dfrac{2}{\sqrt{7}}$ is a irrational number.
Hence proved.

Use Euclid's division lemma to show that the square of any positive integer is either of the form $3m$ or $3m+1$ for some integer m, but not of the form $3m+2$ .

Let

$a$ be the positive integer and

$b=3$ .

We know

$a=bq+r$ ,

$0 ≤ r < b$

Now,

$a=3q+r$ ,

$0 ≤ r < 3$

The possibilities of remainder is

$0,1,$ or

$2$ .

Case 1 : When

$a=3q$

$a^2 = (3q)^2=9q^2=3q\times 3q=3m$ where

$m = 3q^2$

Case 2 : When

$a = 3q+1$

$a^{ 2 }=(3q+1)^{ 2 }=(3q)^{ 2 }+(2×3q×1)+(1)^{ 2 }=3q(3q+2)+1=3m+1$ where

$m= q(3q+2)$

Case 3: When

$a= 3q+2$

$a^{ 2 }=(3q+2)^2=(3q)^{ 2 }+(2×3q×2)+(2)^{ 2 }=9q^{ 2 }+12q+4=9q^{ 2 }+12q+3+1=3(3q^{ 2 }+4q+1)+1=3m+1$

where

$m= 3q^2+4q+1$

Hence, from all the above cases, it is clear that square of any positive integer is of the form

$3m$ or

$3m+1$ .

Use Euclids division lemma to show that the cube of any positive integer is of the form $9m, 9m + 1$ or $9m + 8.$

Using Euclid division algorithm, we know that

$a = bq + r,$

$0 \leq r \leq b$

$----(1)$

Let a be any positive integer, and

$b = 3.$

Substitute

$b = 3$ in equation

$(1)$

$a = 3q + r$ where

$0 \leq r \leq 3,$

$r = 0, 1, 2$

$r = 0, a = 3q$

Cube the value, we get

$a^3 = 27q^3$

$a^3 = 9(3q^3)$ , where m =

$3q^3$

$--- (2)$

$r = 1, a = 3q + 1$

Cube the value, we get

$a^3 = (3q + 1)^3$

$a^3 = (27q^3 + 27q^2+9q+1)$

$a^3 = 9(3q^3 + 3q^2 + 1) + 1$ , where m =

$3q^3 + 3q^2 + q$

$---(3)$

$r = 2, a = 3q + 2$

Cube the value, we get

$a^3 = (3q+2)^3$

$a^3 = (27q^3+53q^2+36q+8)$

$a^3 = 9(3q^3 + 6q^2 + 4q) + 8$ , where m =

$3q^3 + 6q^2 + 4q$

$---- (4)$

From equation

$2, 3$ and

$4,$

The cube of any positive integer is of the form

$9m, 9m + 1$ or

$9m + 8.$

The length and breadth of a rectangular field is 110 m and 30 m respectively. Calculate the length of the longest rod which can measure the length and breath of the field exactly.

Given that the length and breadth of a rectangular field is

$110$ m and

$30$ m respectively.

The length of the longest rod that can measure both the length and breadth of the field exactly will be the highest common factor

$(HCF)$ of the length and breadth.

Therefore, factorise

$110$ as follows:

$110=2×5×11$

Now, factorise

$30$ as follows:

$30=2×3×5$

We know that

$HCF$ is the highest common factor.

Since the common factor between the numbers

$110$ and

$30$ is

$2\times 5=10$ .

Hence, the length of the longest rod which can measure the length and breadth of the field exactly, is

$10\ m$

Show that any positive even integer is of the form $4q$ or $4q+2$ , where $q$ is a whole number.

Let

$a$ be any positive integer and

$b=4$ , then by Euclid's algorithm,

$a=4q+r$ , for some integer

$q\ge 0$ and

$r=0,1,2,3$

So,

$a=4q$ or

$4q+1$ or

$4q+2$ or

$4q+3$ because

$0 ≤ r < 4$ .

Now,

$4q$ that is

$(2\times 2q)$ is an even number.

Therefore,

$4q+1$ is an odd number.

Now,

$4q+2$ that is

$2(2q+1)$ which is also an even number.

Therefore,

$(4q+2)+1=4q+3$ is an odd number.

Hence, we can say that any even integer can be written in the form of

$4q$ or

$4q+2$ where

$q$ is a whole number.

There are 75 rose and 45 lily flowers. These are to be made into bouquets containing both the flowers. All the bouquets should contain the same number of flowers. Find the number of bouquets with maximum number of flowers that can be formed and the number of flowers in them.

Since it is given that there are

$75$ rose and

$45$ lily flowers. Therefore,

Factorise

$75$ as follows:

$75=3×5×5$

Now, factorise

$45$ as follows:

$45=3×3×5$

We know that

$HCF$ is the highest common factor.

Since the common factor between the numbers

$75$ and

$45$ is

$3\times 5=15$ .

Hence, the number of banquets that can be formed is

$15$ and total number of flowers are

$5+3=8$ .

Express $3825$ as a product of prime factors

Factorise

$3825$ as follows:

$3825=3×3×5×5×17=3^{ 2 }×5^{ 2 }×17$

Since,

$3,5$ and

$17$ are prime numbers as these are the numbers that are only divisible by themselves.

Hence,

$3825=3^{ 2 }×5^{ 2 }×17$

Use Euclids division algorithm to find the HCF of:
(i) $135$ and $225$
(ii) $196$ and $38220$
(iii) $867$ and $225$

(i) $135$ and $225$

Step 1: First find which integer is larger.

$225 > 135$

Step 2: Then apply the Euclid's division algorithm to

$225$ and

$135$ to obtain

$225 = 135 \times 1 + 90$

Repeat the above step until you will get remainder as zero.

Step 3: Now consider the divisor

$135$ and the remainder

$90,$ and apply the division lemma to get

$135 = 90 \times 1 + 45$

$90 = 2 \times 45 + 0$

Since the remainder is zero, we cannot proceed further.

Step 4: Hence, the divisor at the last process is

$45$

So, the H.C.F. of

$135$ and

$225$ is

$45.$

(ii)

$196$ and

$38220$

Step 1: First find which integer is larger.

$38220 > 196$

Step 2: Then apply the Euclid's division algorithm to 38220 and 196 to obtain

$38220 = 196 \times 195 + 0$

Since the remainder is zero, we cannot proceed further.

Step 3: Hence, the divisor at the last process is 196.

So, the H.C.F. of

$196$ and

$38220$ is

$196.$

(iii)

$867$ and

$225$

Step 1: First find which integer is larger.

$867 > 255$

Step 2: Then apply the Euclid's division algorithm to

$867$ and

$255$ to obtain

$867 = 255 \times 3 + 102$

Repeat the above step until you will get remainder as zero.

Step 3: Now consider the divisor

$225$ and the remainder

$102,$ and apply the division lemma to get

$255 = 102 \times 2 + 51$

$102 = 51 \times 2 = 0$

Since the remainder is zero, we cannot proceed further.

Step 4: Hence the divisor at the last process is 51.

So, the H.C.F. of

$867$ and

$255$ is

$51.$

Show that any positive odd integer is of the form $6q + 1$ , or $6q + 3$ , or $6q + 5$ , where $q$ is some integer.

Using Euclid division algorithm, we know that

$a = bq + r,$

$0 \leq r \leq b$ ----(1)

Let

$a$ be any positive integer and

$b = 6$ .

Then, by Euclid’s algorithm,

$a = 6q + r$ for some integer

$q\geq 0$ , and

$r = 0, 1, 2, 3, 4, 5$ ,

$\:or$

$0 ≤ r < 6$ .

Therefore,

$a = 6q \:or\: 6q + 1 \:or\: 6q + 2 \:or\: 6q + 3 \:or\: 6q + 4 \:or\: 6q + 5$

$6q+0: 6$ is divisible by

$2$ , so it is an even number.

$6q+1: 6$ is divisible by

$2$ , but

$1$ is not divisible by

$2$ so it is an odd number.

$6q+2: 6$ is divisible by

$2$ , and

$2$ is divisible by

$2$ so it is an even number.

$6q+3: 6$ is divisible by

$2$ , but

$3$ is not divisible by

$2$ so it is an odd number.

$6q+4: 6$ is divisible by

$2$ , and

$4$ is divisible by

$2$ so it is an even number.

$6q+5: 6$ is divisible by

$2$ , but

$5$ is not divisible by

$2$ so it is an odd number.

And therefore, any odd integer can be expressed in the form

$6q + 1\:or\: 6q + 3\; or\: 6q + 5$

Prove that the product of three consecutive positive integers is divisible by 6.

Let the three consecutive positive integers be

$n$ ,

$n+1$ and

$n+2$ .

Whenever a number is divided by

$3$ , the remainder obtained is either

$0,1$ or

$2$ .

Therefore,

$n=3p$ or

$3p+1$ or

$3p+2$ , where

$p$ is some integer.

$n=3p$ , then

$n$ is divisible by

$3$ .

$n=3p+1$ , then

$n+2=3p+1+2=3p+3=3(p+1)$ is divisible by

$3$ .

$n=3p+2$ , then

$n+1=3p+2+1=3p+3=3(p+1)$ is divisible by

$3$ .

So, we can say that one of the numbers among

$n, n+1$ and

$n+2$ is always divisible by

$3$ that is:

$n(n+1)(n+2)$ is divisible by

$3$ .

Similarly, whenever a number is divided by

$2$ , the remainder obtained is either

$0$ or

$1$ .

Therefore,

$n=2q$ or

$2q+1$ , where

$q$ is some integer.

$n=2q$ , then

$n$ and

$n+2=2q+2=2(q+1)$ is divisible by

$2$ .

$n=2q+1$ , then

$n+1=2q+1+1=2q+2=2(q+1)$ is divisible by

$2$ .

So, we can say that one of the numbers among

$n$ ,

$n+1$ and

$n+2$ is always divisible by

$2$ .

Since,

$n(n+1)(n+2)$ is divisible by

$2$ and

$3$ .

Hence,

$n(n+1)(n+2)$ is divisible by

$6$ .

Find least positive value of $a+b$ where $a,b$ are positive integers such that $11 \left| a+13b\quad and\quad 13 \right| a+11b$

We have $13|a+11b$

$\Rightarrow 13|a-2b$ and hence $13|6a-12b$ this implies $13|6a+b$

Similarly,

$11|a+13b\Rightarrow 11|a+2b\\ \Rightarrow 11|6a+12b \Rightarrow 11|6a+b$

Since $\text{G.C.D}(11,13)=1$

We conclude $143|6a+b$

Thus we may write $6a+b=143k$ for some integer $k$

Hence, $6a+6b=143k+5b=144k+6b-(k+b)$

This shows that $6|k+b$ and hence $k+b\geq 6$

We therefore obtain

$6(a+b)=143k+5b\\ \qquad \quad\ \ =138k+5(k+b)\geq 138+(5\times 6)=168$

It follows that $a+b\geq 28$

Taking $a=23$ and $b=5$

we see that the conditions of the problem satisfied. Thus the minimum value of $a+b$ is $28$

Show that $\sqrt{2}$ is an irrational number.

$\textbf{Step 1: Use the definition of rational number and prove the required result}$

$\text{Consider}$

$\sqrt 2$

$\text{as a rational number.}$

$\text{We know that, a rational number can be expressed in the form $\dfrac{p}{q} \\$ where p, q are co-prime integers.}$

$\Rightarrow \sqrt2 = \dfrac{p}{q}$

$\text{Squaring on both side we get}$

$\Rightarrow 2 = \dfrac{p^2}{q^2}$

$\Rightarrow 2q^2 = p^2$ $\ldots(i)$

$\text{Eqaution (i), can be written as}$ $q^2 = \dfrac{p^2}{2}$

$\text{This shows, p is divisible by 2. It can be expressed as p=2m}$

$\text{Squaring on both sides}$

${p^2=(2m)^2\Rightarrow p^2=4m^2 }$

$\ldots(ii)$

$\text{Substitute equation (ii) in eqaution (i) we get}$

${2q^2=4m^2\Rightarrow q^2=2m^2}$

$\text{Clearly , 2 is a factor of q}$

$\text{Thus we see that both p and q have comman factor 2 which is a contradiction that $\\$ H.C.F of (p,q)=1}$

$\textbf{Hence,}$

$\boldsymbol{ \sqrt 2}$

$\textbf{ is not a rational number therefore is an irrational number. }$

Express $6762$ as a product of prime factors

Factorise

$6762$ as follows:

$6762=2×3×7×7×23=2×3×7^{ 2 }×23$

Since,

$2,3,7$ and

$23$ are prime numbers as these are the numbers that are only divisible by themselves.

Hence,

$6762=2×3×7^{ 2 }×23$

Use Euclid's division algorithm to find the HCF of
$\left ( 1 \right )135\ and \ 225$
$\left ( 2 \right )196 \ and\ 38220$
$\left ( 3 \right )867 \ and \ 255$

$A)\ HCF$ of

$135$ and

$225$

$15\times 9, 15\times 15$

$HCF$ is

$15$

$B)\ HCF$ of

$196$ and

$38220$

$196, 196\times 195$

$\therefore \ HCF$ of

$867$ and

$255$

$17\times 17\times 3$ and

$17\times 15$

$HCF$ is

$17$

Express $32844$ as a product of prime factors

Given number is

$32844$ .

We can represent

$32844$ as a product of its prime factors as follows:

$32844=2×2×3×7×17×23$

$=2^{ 2 }×3×7×17×23$

Hence,

$32844=2^{ 2 }×3×7×17×23$

Prove that $\frac{\sqrt{7}}{4}$ is an irrational number.

Let us assume that

$\sqrt { 7 }$ is a rational number which can be expressed in the form of

$\dfrac {p}{q}$ , where

$p$ and

$q$ are integers,

$q\neq 0$ and

$p$ and

$q$ are co prime that is

$HCF(p,q)=1$ .

We have,

$\sqrt { 7 } =\dfrac { p }{ q } \\ \Rightarrow \sqrt { 7 } q=p......(1)\\ \Rightarrow 7{ q }^{ 2 }=p^{ 2 }\quad \quad \quad \quad (squaring\quad both\quad sides)$

$\Rightarrow p^{ 2 }$ is divisible by

$7$

$\Rightarrow p$ is divisible by

$7$

$......(2)$

Therefore, for an integer

$r$ ,

$p=7r\\ \Rightarrow \sqrt { 7 } q=7r\quad \quad \quad (from\quad (1))\\ \Rightarrow 7q^{ 2 }=49r^{ 2 }\quad \quad \quad (squaring\quad both\quad sides)\\ \Rightarrow q^{ 2 }=\dfrac { 49 }{ 7 } r^{ 2 }\\ \Rightarrow q^{ 2 }=7r^{ 2 }$

$\Rightarrow q^{ 2 }$ is divisible by

$7$

$\Rightarrow q$ is divisible by

$7$

$......(3)$

From equations 2 and 3, we get that

$7$ is the common factor of

$p$ and

$q$ which contradicts that

$p$ and

$q$ are co prime. This means that our assumption was wrong.

Thus

$\sqrt { 7 }$ is an irrational number.

Now, since division of a rational number to an irrational number is an irrational number.

Hence

$\dfrac {\sqrt { 7 }}{4}$ is an irrational number.

Find the HCF of 105 and 1515 by prime factorisation method and hence find its LCM.

The given integers

$105$ and

$1515$ can be factorised as follows:

$105=3×5×7\\ 1515=5×3×101$

$3,5,7$ and

$101$ are prime numbers as these are the numbers that are only divisible by themselves.

We know that

$HCF$ is the highest common factor, therefore, the

$HCF$ of

$105$ and

$1515$ is:

$HCF=3\times 5=15$

Also, the

$LCM$ is the least common multiple, therefore, the

$LCM$ of

$105$ and

$1515$ is:

$LCM=3×5×7×101=10605$

Hence, the

$HCF$ is

$15$ and

$LCM$ is

$10605$ .

If $25025 = p_1^{x_1}.p_2^{x_2}.p_3^{x_3}.p_4^{x_4}$ find the value of $p_1, p_2, p_3, p_4$ and $x_1, x_2, x_3, x_4$ .

Given that,

$25025={ p }_{ 1 }^{ { x }_{ 1 } }×{ p }_{ 2 }^{ { x }_{ 2 } }×{ p }_{ 3 }^{ { x }_{ 3 } }×{ p }_{ 4 }^{ { { x }_{ 4 } } }$

To find out,

The values of

$p_1,\ p_2,\ p_3,\ p_4,\ x_1,\ x_2,\ x_3$ and

$x_4$

$25025$ can be represented as the product of its prime factors as:

$25025=5×5×7×11×13$

$\Rightarrow 25025=5^{ 2 }×7^{ 1 }×11^{ 1 }×13^{ 1\quad \quad \quad\quad \quad \quad }...............(1)$

It is given that,

$25025={ p }_{ 1 }^{ { x }_{ 1 } }×{ p }_{ 2 }^{ { x }_{ 2 } }×{ p }_{ 3 }^{ { x }_{ 3 } }×{ p }_{ 4 }^{ { { x }_{ 4 } } }\quad ...............(2)$

Comparing

$(1)$ and

$(2)$ , we get,

$p_1=5,\ p_2=7,\ p_3=11,\ p_4=13,\ x_1=2,\ x_2=1,\ x_3=1$ and

$x_4=1$

Hence,

$p_1=5,\ p_2=7,\ p_3=11,\ p_4=13,\ x_1=2,\ x_2=1,\ x_3=1$ and

$x_4=1$ .

If $\sqrt{2}=1.4142$ check whether $3+\sqrt{2}$ is rational or irrational? Give reason.

$\sqrt { 2 } =1.4142$ then,

$3+\sqrt { 2 } =3.14142$ .so if

$\sqrt { 2 }$ is irrational then

$3+\sqrt { 2 }$ will also be and if

$\sqrt { 2 }$ is rational then

$3+\sqrt { 2 }$ is also rational.they both will be same.

Use Euclid's division lemma to show that the cube of any positive integer is of the form $9m,9m+1$ or $9m+8$

Let x be any positive integer. Then, it is of the form 3q or, 3q + 1 or, 3q + 2.

So, we have the following cases :

Case I : When x = 3q.

then, x³ = (3q)³ = 27q³ = 9 (3q³) = 9m, where m = 3q³.

Case II : When x = 3q + 1

then, x³ = (3q + 1)³

= 27q³ + 27q² + 9q + 1

= 9 q (3q² + 3q + 1) + 1

= 9m + 1, where m = q (3q² + 3q + 1)

Case III. When x = 3q + 2

then, x³ = (3q + 2)³

= 27 q³ + 54q² + 36q + 8

= 9q (3q² + 6q + 4) + 8

= 9 m + 8, where m = q (3q² + 6q + 4)

Hence, x³is either of the form 9 m or 9 m + 1 or, 9 m + 8.

Show that $\sqrt 5$ is an irrational number.

We have to show that

$\sqrt{5}$ is irrational.

We will prove this via the method of contradiction.

So let's assume

$\sqrt{5}$ is rational.

Hence, we can write

$\sqrt{5}$ in the form

$\dfrac{a}{b},$ where

$a$ and

$b$ are co-prime numbers such that

$a,b, \in R$ and

$b\neq 0.$

$\therefore \sqrt{5}=\dfrac{a}{b}$

squaring both sides we have

$\Rightarrow 5=\dfrac{a^2}{b^2}$

$\Rightarrow 5b^2=a^2$

$\Rightarrow \dfrac{a^2}{5}=b^2$

Hence, 5 divides

$a^2$

Now, a theorem tells that if 'P' is a prime number and P divides

$a^2$ then P should divide 'a', where

$a$ is a positive number.

Hence, 5 divides a

$......\left(1\right)$

$\therefore$ we can say that

$\dfrac{a}{5}=c$

we already know that

$\Rightarrow 5b^2=a^2$

From

$\left( 2\right),$ we know

$a=5c$ substituting that in the above equation we get,

$\Rightarrow 5b^2=25c^2$

$\Rightarrow b^2=5c^2$

$\Rightarrow \dfrac{b^2}{5}=c^2$

Hence, 5 divides

$b^2.$ And by the above mentioned theorem we can say that

$5$ divides

$b$ as well.

hence,

$5$ divides

$b$

$.........\left(3\right)$

So from

$\left(2\right)$ and

$\left(3\right)$ we can see that both a and b have a common factor

$5.$ Therefore

$a\;\&\;b$ are no co-prime. Hence our assumption is wrong.

$\therefore$ by contradiction

$\sqrt{5}$ is irrational.

Hence, solved.

Classify the following number as rational and irrational.
$\sqrt{1.44}$ .

1670360_1715010_ans_ded3fab1193841789f6d040b418b7b71.jpg

Prove that $\sqrt n$ is not a rational number, if n is not perfect square.

2043828_1538065_ans_ba63a7eef9ff4f809f9db9cba8edd6f5.png

Prove that $5-2\sqrt{3}$ is an irrational number.

1294730_1559863_ans_1872108855774989b8355ccb117fd6b4.jpg

If $\dfrac {p}{q}$ is a rational number $(q\neq 0)$ , what is the condition on $q$ so that the decimal representation of $\dfrac {p}{q}$ is terminating?

For a rational number, if the denominator of that rational number is of form

$2^m\cdot5^n$

then it will be terminating.

It means that q should be factor of 2 and 5 both or only 2 or only 5.

Then it will be terminating.

Class 10 Maths Extra Questions

Real Numbers - Class 10 Maths - Extra Questions

Prove that √2+√3\sqrt 2+\sqrt 3 is irrational

3−√53- \sqrt5 is an irrational numberIf true then enter 11 and if false then enter 00

144144 cartons of coke cans and 9090 cartons of pepsi cans are to be stacked in a canteen. If each stack is of same height and is to contain cartons of the same drink, what would be the greatest number of cartons each stack would have?

Use Euclid's division algorithm to find the H.C.F. of 196196 and 3831838318

Classify the following numbers as rational or irrational.30.2323422345...30.2323422345...

Classify the following numbers as rational or irrational.2\pi2\pi

Without actually dividing find if \dfrac {13}{20}\dfrac {13}{20} is terminating decimal.

Find the largest positive integer that will divide 150, 187150, 187 and leaving remainders 6, 76, 7 and 1111 respectively.

Classify the following numbers as rational or irrational.\dfrac {1}{\sqrt {3}}\dfrac {1}{\sqrt {3}}

Prove that 5-\sqrt{3}5-\sqrt{3} is an irrational number.

Classify the following numbers as rational or irrational.\sqrt {441}\sqrt {441}

In the following equations, find whether variables x, y, zx, y, z etc. represent rational or irrational numbersx^{2} = 7x^{2} = 7

Find HCF:15, 2515, 25 and 3535.

Check whether 21 + \sqrt {3}21 + \sqrt {3} are irrational numbers are not?

Check whether \pi + 3\pi + 3 are irrational numbers or not?

Check whether 5\sqrt {2}5\sqrt {2} is an irrational numbers are not?

Prove that 2 + \sqrt {5}2 + \sqrt {5} is an irrational number.

Prove that the following are irrational.\displaystyle\frac{1}{\sqrt{2}}\displaystyle\frac{1}{\sqrt{2}}.

Prove that 6+\sqrt{2}6+\sqrt{2} is irrational.

For any positive real number xx, prove that there exists an irrational number yy such that 0 < y < x0 < y < x.

Show that 3\sqrt{2}3\sqrt{2} is irrational.

Given that \sqrt{2}\sqrt{2} is irrational, prove that (5+3\sqrt{2})(5+3\sqrt{2}) is an irrational number.

Prove that \sqrt { 3 } \sqrt { 3 } is a irrational number.

Prove that \displaystyle \sqrt{2} +\, \sqrt{3}\displaystyle \sqrt{2} +\, \sqrt{3} is an irrational number.

If a={2}^{3}{3}^{5},b={3}^{2}{2}^{5}a={2}^{3}{3}^{5},b={3}^{2}{2}^{5}, then find the HCFHCF of aa and bb.

Prove that 5 -\sqrt 3 5 -\sqrt 3 is irrational

Prove the following are irrational.\sqrt {3} + \sqrt {5}\sqrt {3} + \sqrt {5}

Prove the following are irrational.6+\sqrt {2}6+\sqrt {2}

Prove that \sqrt{5}\sqrt{5} is irrational and hence prove that (2-\sqrt{5})(2-\sqrt{5}) is also irrational.

Find the HCFHCF of 8181 and 237237 and express it as a linear combination of 8181 and 237.237.

Find the HCFHCF of 6565 and 117117 and express it in the form 65\ m + 117\ n.65\ m + 117\ n.

Somu says "\dfrac{\sqrt{3}}{1}\dfrac{\sqrt{3}}{1} is a rational number" do you agree with Somu? Give reasons.

Show that \sqrt{5} + 3\sqrt{5}\sqrt{5} + 3\sqrt{5} is irrational.

Prove the following are irrational.3+2\sqrt {5}3+2\sqrt {5}

Check whether \dfrac{6}{{200}}\dfrac{6}{{200}} has terminating or non terminating repeating decimal expansion.

Without actually performing the long deviation, state whether the following rational number will have a terminating decimal expansion or a non-terminating repeating decimal expansion:\dfrac {77}{210}\dfrac {77}{210}

Find the H.C.F. of 18 and 48 in division method.

Find H.C.F. of 2525 and 4040

Prove that : 4 - 5\sqrt 3 4 - 5\sqrt 3 is irrational.

State whether the following statement is True or False? Justify your answer.= \dfrac{\sqrt{3}}{7}= \dfrac{\sqrt{3}}{7} is a rational number.

Show that 4\sqrt{2}4\sqrt{2} is an irrational number.

Classify the numbers as rational or irrational : 7.4784787.478478

Classify the numbers as rational or irrational : 1.101001000100001...1.101001000100001...

Prove that 5-\sqrt{3}5-\sqrt{3} is an irrational number.

Find the HCFHCF of 510510 and 9292.

Classify the numbers as rational or irrational : \sqrt {225} \sqrt {225}

Classify the number as rational or irrational : \sqrt {23} \sqrt {23}

What is the condition for decimals expansion of a rational numbers to terminate. Explain with example.

Find GCDGCD of 736736 and 8585 by using Euclid's algorithm.

Prove that 7 - 4\sqrt 2 7 - 4\sqrt 2 is irrational.

Rationalise the denominators of the following :\dfrac{1}{{\sqrt 7 }}\dfrac{1}{{\sqrt 7 }}\dfrac{1}{{\sqrt 7 - \sqrt 6 }}\dfrac{1}{{\sqrt 7 - \sqrt 6 }}\dfrac{1}{{\sqrt 5 + \sqrt 2 }}\dfrac{1}{{\sqrt 5 + \sqrt 2 }}\dfrac{1}{{\sqrt 7 - \sqrt 2 }}\dfrac{1}{{\sqrt 7 - \sqrt 2 }}

Classify the following numbers as rational or irrational.\dfrac { 1 }{ \sqrt { 2 } } \dfrac { 1 }{ \sqrt { 2 } }

Classify the following numbers as rational or irrational.2-\sqrt{5}2-\sqrt{5}

Find the HCFHCF of by prime factorisation. 4848, 144144

Use prime factorisation method to determine the HCF of 520 and 1430.

Without actually performing the long division,state whether the following rational number will have a terminating decimal expansion or a non terminating repeating decimal expansion: \dfrac{129}{2^25^77^5}\dfrac{129}{2^25^77^5}

Show that 2+\sqrt {6}2+\sqrt {6} is a irrational number.

Find H.C.F of 847847 and 16501650.

Find the LCMLCM and HCFHCF of 12,7212,72 and 120120 using fundamental theorem of arithmetic. Also show that HCFHCF \times LCM\times LCM is not equal to the product of three given numbers.

Without actually performing the long division,state whether the following rational number will have a terminating decimal expansion or a non terminating repeating decimal expansion: \dfrac{23}{2^35^2}\dfrac{23}{2^35^2}

Find the \text{HCF}\text{HCF} of 180,252180,252 and 354354 using prime factorization method.

Find the LCM and HCF of 12,72 and 120 using fundamental theorem of arithmetic. Also show that HCF \times LCM\times LCM is not equal to the product of three given numbers.

Prove that 2 - 3 \sqrt { 5 }2 - 3 \sqrt { 5 } is an irrational no.

Find the HCFHCF of the following 27,6327,63

Find the HCFHCF of the following 70,105,17570,105,175

Classify the following number as Rational or Irrational: \sqrt {23} \sqrt {23}

Find the HCFHCF of the following 36,8436,84

Show that { \left( \sqrt { 3 } +\sqrt { 5 } \right) }^{ 2 }{ \left( \sqrt { 3 } +\sqrt { 5 } \right) }^{ 2 } is an irrational no.

Prove 6+3\sqrt{5}6+3\sqrt{5} is irrational

Find the HCFHCF of the following 18,54,8118,54,81

Prove that \dfrac { 1 } { 2 - \sqrt { 5 } }\dfrac { 1 } { 2 - \sqrt { 5 } } is a irrational number

Prove that following is inrrational number :i) 3-\sqrt{2}3-\sqrt{2}

Use Euclid's Division Algorithm to find the HCF of 726726 and 275275

Prove that 3+2\sqrt {5}3+2\sqrt {5} is an irrational numbers

Find the H.C.F of 3,9,81,273,9,81,27

Find HCF of 4545 and 7272

Verify whether the rational expression \dfrac{x^2-1}{(2x+1)(x+2)}\dfrac{x^2-1}{(2x+1)(x+2)} is in its lowest terms.

Find HCFHCF of 8181 and 243243

Find the H.C.F of 2,8,32,102,8,32,10

Prove that $\sqrt 2+\sqrt 3$ is irrational

$3- \sqrt5$ is an irrational number
If true then enter $1$ and if false then enter $0$

$144$ cartons of coke cans and $90$ cartons of pepsi cans are to be stacked in a canteen. If each stack is of same height and is to contain cartons of the same drink, what would be the greatest number of cartons each stack would have?

Use Euclid's division algorithm to find the H.C.F. of $196$ and $38318$

Classify the following numbers as rational or irrational.
$30.2323422345...$

Classify the following numbers as rational or irrational.
$2\pi$

Without actually dividing find if $\dfrac {13}{20}$ is terminating decimal.

Find the largest positive integer that will divide $150, 187$ and leaving remainders $6, 7$ and $11$ respectively.

Classify the following numbers as rational or irrational.
$\dfrac {1}{\sqrt {3}}$

Prove that $5-\sqrt{3}$ is an irrational number.

Classify the following numbers as rational or irrational.
$\sqrt {441}$

In the following equations, find whether variables $x, y, z$ etc. represent rational or irrational numbers
$x^{2} = 7$

Find HCF:
$15, 25$ and $35$ .

Check whether $21 + \sqrt {3}$ are irrational numbers are not?

Check whether $\pi + 3$ are irrational numbers or not?

Check whether $5\sqrt {2}$ is an irrational numbers are not?

Prove that $2 + \sqrt {5}$ is an irrational number.

Prove that the following are irrational.
$\displaystyle\frac{1}{\sqrt{2}}$ .

Prove that $6+\sqrt{2}$ is irrational.

For any positive real number $x$ , prove that there exists an irrational number $y$ such that $0 < y < x$ .

Show that $3\sqrt{2}$ is irrational.

Given that $\sqrt{2}$ is irrational, prove that $(5+3\sqrt{2})$ is an irrational number.

Prove that $\sqrt { 3 }$ is a irrational number.

Prove that $\displaystyle \sqrt{2} +\, \sqrt{3}$ is an irrational number.

If $a={2}^{3}{3}^{5},b={3}^{2}{2}^{5}$ , then find the $HCF$ of $a$ and $b$ .

Prove that $5 -\sqrt 3$ is irrational

Prove the following are irrational.
$\sqrt {3} + \sqrt {5}$

Prove the following are irrational.
$6+\sqrt {2}$

Prove that $\sqrt{5}$ is irrational and hence prove that $(2-\sqrt{5})$ is also irrational.

Find the $HCF$ of $81$ and $237$ and express it as a linear combination of $81$ and $237.$

Find the $HCF$ of $65$ and $117$ and express it in the form $65\ m + 117\ n.$

Somu says " $\dfrac{\sqrt{3}}{1}$ is a rational number" do you agree with Somu? Give reasons.

Show that $\sqrt{5} + 3\sqrt{5}$ is irrational.

Prove the following are irrational.
$3+2\sqrt {5}$

Check whether $\dfrac{6}{{200}}$ has terminating or non terminating repeating decimal expansion.

Without actually performing the long deviation, state whether the following rational number will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
$\dfrac {77}{210}$

Find H.C.F. of $25$ and $40$

Prove that : $4 - 5\sqrt 3$ is irrational.

State whether the following statement is True or False? Justify your answer.
$= \dfrac{\sqrt{3}}{7}$ is a rational number.

Show that $4\sqrt{2}$ is an irrational number.

Classify the numbers as rational or irrational : $7.478478$

Classify the numbers as rational or irrational : $1.101001000100001...$

Prove that $5-\sqrt{3}$ is an irrational number.

Find the $HCF$ of $510$ and $92$ .

Classify the numbers as rational or irrational : $\sqrt {225}$

Classify the number as rational or irrational : $\sqrt {23}$

Find $GCD$ of $736$ and $85$ by using Euclid's algorithm.

Prove that $7 - 4\sqrt 2$ is irrational.

Rationalise the denominators of the following :
$\dfrac{1}{{\sqrt 7 }}$
$\dfrac{1}{{\sqrt 7 - \sqrt 6 }}$
$\dfrac{1}{{\sqrt 5 + \sqrt 2 }}$
$\dfrac{1}{{\sqrt 7 - \sqrt 2 }}$

Classify the following numbers as rational or irrational.
$\dfrac { 1 }{ \sqrt { 2 } }$

Classify the following numbers as rational or irrational.
$2-\sqrt{5}$

Find the $HCF$ of by prime factorisation. $48$ , $144$

Without actually performing the long division,state whether the following rational number will have a terminating decimal expansion or a non terminating repeating decimal expansion:
$\dfrac{129}{2^25^77^5}$

Show that $2+\sqrt {6}$ is a irrational number.

Find H.C.F of $847$ and $1650$ .

Find the $LCM$ and $HCF$ of $12,72$ and $120$ using fundamental theorem of arithmetic. Also show that $HCF$ $\times LCM$ is not equal to the product of three given numbers.

Without actually performing the long division,state whether the following rational number will have a terminating decimal expansion or a non terminating repeating decimal expansion:
$\dfrac{23}{2^35^2}$

Find the $\text{HCF}$ of $180,252$ and $354$ using prime factorization method.

Find the LCM and HCF of 12,72 and 120 using fundamental theorem of arithmetic. Also show that HCF $\times LCM$ is not equal to the product of three given numbers.

Prove that $2 - 3 \sqrt { 5 }$ is an irrational no.

Find the $HCF$ of the following
$27,63$

Find the $HCF$ of the following
$70,105,175$

Classify the following number as Rational or Irrational:

$\sqrt {23}$

Find the $HCF$ of the following
$36,84$

Show that ${ \left( \sqrt { 3 } +\sqrt { 5 } \right) }^{ 2 }$ is an irrational no.

Prove $6+3\sqrt{5}$ is irrational

Find the $HCF$ of the following
$18,54,81$

Prove that $\dfrac { 1 } { 2 - \sqrt { 5 } }$ is a irrational number

Prove that following is inrrational number :
i) $3-\sqrt{2}$

Use Euclid's Division Algorithm to find the HCF of $726$ and $275$

Prove that $3+2\sqrt {5}$ is an irrational numbers

Find the H.C.F of $3,9,81,27$

Find HCF of $45$ and $72$

Verify whether the rational expression $\dfrac{x^2-1}{(2x+1)(x+2)}$ is in its lowest terms.

Find $HCF$ of $81$ and $243$

Find the H.C.F of $2,8,32,10$

Prove that the following are irrational.
$\sqrt{3}+\sqrt{5}$

If $n$ is an odd integer then show that ${n^2} - 1$ is divisible by 8

Prove that : $\frac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}$

Find the $H.C.F$ of $3,6,9.$