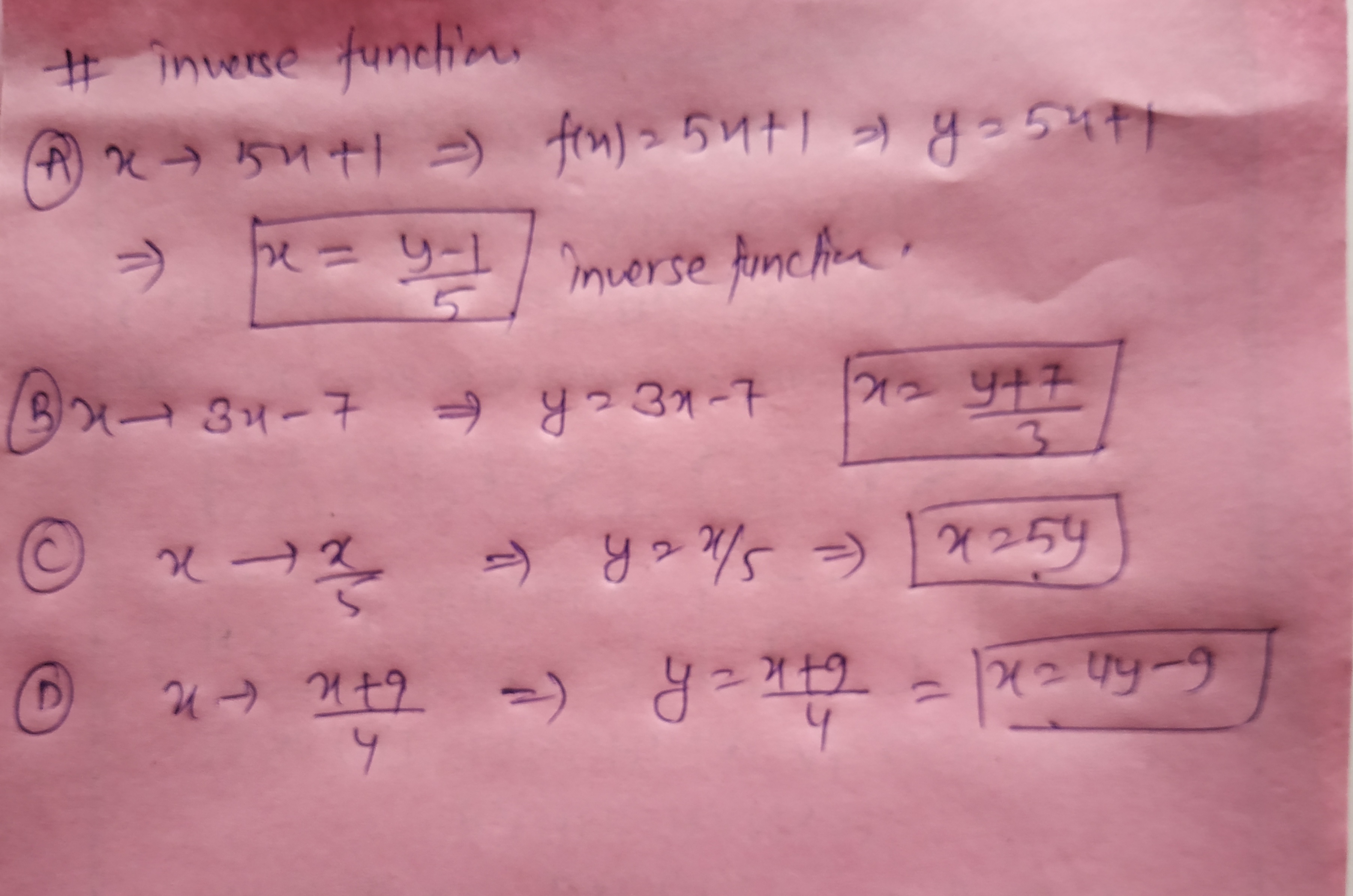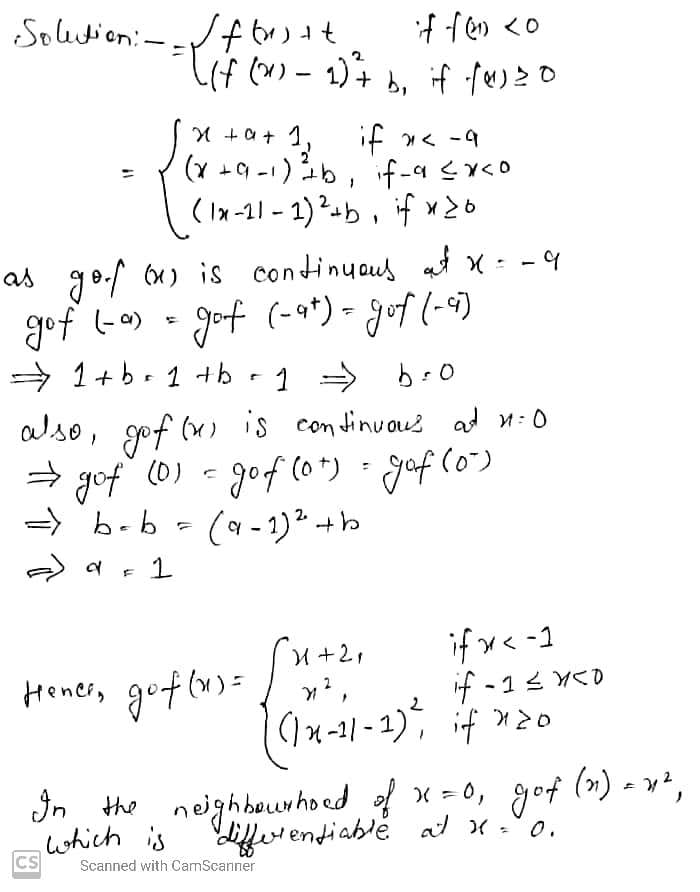Relations And Functions - Class 12 Engineering Maths - Extra Questions

Show that if $$f:A\rightarrow B$$ and $$g:B\rightarrow C$$ are one-one, then $$g\circ f:A\rightarrow C$$ is also one-one.

Given $$f:A\rightarrow B$$ is one one 
$${ a }_{ i }\in A,{ b }_{ i }\in B$$
$$f({ a }_{ i })={ b }_{ i }$$
$$g:A\rightarrow B$$ is one one 
$${ b }_{ i }\in B,{ c }_{ i }\in C$$
$$g({ b }_{ i })={ c }_{ i }$$ for all $${ b }_{ i }$$
$$g(f({ a }_{ i }))={ c }_{ i }$$ for all $${ a }_{ i }$$ only one $${ c }_{ i }$$
$$g(f(x))$$ is one one.



Let $$f:R\rightarrow R$$ be defined by $$f(x)={x}^{3}+5$$ then find $${f}^{-1}(x)$$

let $$f(x)=x^3+5=y$$
$$y-5=x^3$$
$$x=(y-5)^{\dfrac{1}{3}}$$
so therefore $$f^{-1}(x)=(x-5)^{\dfrac{1}{3}}$$


If the function $$ f:[1,\infty)\rightarrow [1,\infty)$$ is defined by $$ f(x)=2^{x(x-1)}$$,then find $$ f^{-1}(4)$$

$$y=2^{x(x-1)}$$

$$log_{2}(y)=x^{2}-x$$

$$log_{2}(y)=(x-\dfrac{1}{2})^{2}-\dfrac{1}{4}$$

$$\dfrac{4log_{2}(y)+1}{4}=(x-\dfrac{1}{2})^{2}$$

$$x-\dfrac{1}{2}=\dfrac{\pm\sqrt{4log_{2}(y)+1}}{2}$$
Since the range of f(x) is $$R^{+}$$
hence
$$x-\dfrac{1}{2}=\dfrac{\sqrt{4log_{2}(y)+1}}{2}$$

$$x=\dfrac{1+\sqrt{4log_{2}(y)+1}}{2}$$
Replacing x and y

$$f^{-1}(x)=\dfrac{1+\sqrt{4log_{2}(x)+1}}{2}$$
Therefore
$$f^{-1}(4)=\dfrac{1+\sqrt{8+1}}{2}$$

$$=\dfrac{4}{2}$$

$$=2$$


Let $$f: R\rightarrow R$$ be defined as $$f(s) = 10x + 7$$. Find the function $$g: R\rightarrow R$$ such that $$gof = fog = 1_{R}$$

Step:1
$$f\left( x \right)=10x+7\\ Let\quad f\left( x \right)=y\\ y=10x+7\\ y-7=10x\\ \therefore 10x=y-7\quad where\quad g:Y\rightarrow N\\ x=\cfrac { y-7 }{ 10 } \\ Let\quad g\left( y \right)=\cfrac { y-7 }{ 10 } \\ $$
Step:2
$$gof=g\left( f\left( x \right) \right)=g\left( 10x+7 \right)\\ =\cfrac { (10x+7)-7 }{ 10 } =\cfrac { 10x }{ 10 } =x={ I }_{ R }$$
Step:3
$$fog=f\left( g\left( y \right) \right)=f[\cfrac { y-7 }{ 10 } ]=10(\cfrac { y-7 }{ 10 } )+y\\ =y+0=y={ I }_{ R }\\ $$
Since,$$gof=fog={ I }_{ R }$$
$$f $$ is invertible.
and inverse of $$f=g\left( y \right)=\cfrac { y-3 }{ 4 } $$


Let $$f:R\rightarrow R$$ be defined by $$f(x)=2x+3$$, find $${f}^{-1}(4)$$.

Given that:
$$f(x)=2x+3$$
To find:
$$f^{-1}(4)=?$$
Solution:
A function is one-to=one for which every element of the range of the function corresponds to exactly one element of the domain.
Since, $$f$$ is a linear function, we can say $$f$$ is one-to-one and hence $$f^{-1}$$ exits.
Let $$y=f(x)=2x+3$$
or, $$y-3=2x$$
or, $$\dfrac {y-3}2=x$$
or, $$y=\dfrac{x-3}2$$  (Interchange $$x$$ and $$y$$)
or, $$\therefore f^{-1}(x)=y=\dfrac{x-3}2$$
or, $$f^{-1}(4)=\dfrac{4-3}2$$
or, $$f^{-1}(4)=\dfrac12$$


Consider $$f:R - \left\{ - \dfrac{4}{3} \right \} \rightarrow R - \left\{ \dfrac{4}{3} \right \}$$ given by $$f(x) = \dfrac{4x + 3}{3x + 4}$$. Show that $$f$$ is bijective. Find the inverse of $$f$$ and hence if the value of $$f^{-1}(0)$$ is $$A$$ and $$x$$ is $$B$$ such that $$f^{-1} (x) = 2$$, then find $$(A+B)\times100$$.

Given $$f(x)=\cfrac{4x+3}{3x+4}$$
For one-one function, we have
 $$f(x_1) = f(x_2)\implies x_1=x_2$$ 
Thus, consider $$f(x_1) = f(x_2)$$
$$\implies \cfrac{4x_1+3}{3x_1+4}=$$ $$\cfrac{4x_2+3}{3x_2+4}$$
$$\implies 12x_1x_2+16x_1+9x_2+12=12x_1x_2+9x_1+16x_2+12$$
$$\implies 7x_1=7x_2$$
$$\implies x_1=x_2$$
$$\therefore \ f(x)$$ is one-one function.

For onto function:
Let $$f(x)=y $$
$$\implies \cfrac{4x+3}{3x+4} =y$$ 
$$\implies x =$$ $$\cfrac{3-4y}{3y-4}$$
Domain of the above function is $$R-\{ \frac{4}{3}\}$$, which is range of function $$f(x)$$. 
So, given function $$f(x)$$ is onto.
Hence, given function $$f(x)$$ is bijective.

Now, let us find the inverse of $$f(x)$$
Let the given function $$f(x)$$ be $$y$$
$$\Rightarrow f(x)=\cfrac{4x+3}{3x+4}=y$$
So we get $$f^{-1}{(y)}=x=\cfrac{3-4y}{3y-4}$$
So the inverse of function $$f$$ is $$f^{-1}{(x)}=\cfrac{3-4x}{3x-4}$$

Also, $$A = f^{-1}{(0)}$$
$$\Rightarrow A =  f^{-1}{(0)}=-\cfrac{3}{4}$$
Given that $$f^{-1}{(x)}=\cfrac{3-4x}{3x-4}=2$$
$$\Rightarrow 3-4x=6x-8$$
$$\Rightarrow B = x=\cfrac{11}{10}$$

$$\therefore 100\times (A+B) = 35$$


If $$f(x)=\dfrac{(4x+3)}{(6x-4)}$$, $$x\neq \dfrac{2}{3}$$, show that $$fof(x)=x$$, for all $$x\neq\dfrac{2}{3}$$. What is the inverse of f?

$$f(x)=\cfrac{4x+3}{6x-4}$$
$$fof(x)=\cfrac{4(\cfrac{4x+3}{6x-4})+3}{6(\cfrac{4x+3}{6x-4})-4}$$
$$=\cfrac{16x+12+18x-12}{24x+18-24+16}$$
$$=\cfrac{34x}{34}=x.$$
$$y=\cfrac{4x+3}{6x-4} $$
$$6xy-4y=4x+3$$
$$6xy-4x=4y+3$$
$$x=\cfrac{4y+3}{6y-4} $$
$$\therefore f(x)=\cfrac{4x+3}{6x-4} $$


Let $$f: N\rightarrow Y$$ be a function defined as $$f(x)=4x+3$$, where, $$Y=\{y\in N : y=4x+3\ for\ some\ x\in N\}$$, Show that f is invertible. Find the inverse.

$$f(x)=4x+3$$
$$\rightarrow$$ let $$f(x_{1})=f(x_{2}), x_{1}x_{2}\in N$$
$$4x_{1}+3=4x_{2}+3$$
$$\therefore 4x_{1}=4x_{2}$$
$$\therefore x_{1}=x_{2}$$
Thus $$f(x_{1})=f(x_{2})\Rightarrow x_{1}=x_{2}$$ Hence the $$fx$$ is one-one.
Let $$y\in y$$ be a number of the form $$y=4k+3$$
$$y=f(x)$$
$$\therefore 4k+3=4x+3$$
$$\therefore k=x$$
$$\rightarrow$$ This corresponding to any $$y\in y$$ we have $$x\in N$$
The function is onto
the function being both one one and onto is invertible 
$$y=4x+3$$
$$\therefore y-3=4x$$
$$\therefore x=\dfrac{y-3}{4}$$
$$\therefore f(x)=\dfrac{x-3}{4}$$ or $$g(y)=\dfrac{4-3}{4}$$ is inverse function.


Let $$f:N\rightarrow N$$ be a function defined as $$f(x)=4{x}^{2}+12x+15$$. Show that $$f:N\rightarrow S$$ is invertible. Find the inverse of $$f$$ and hence find $${f}^{-1}(31)$$ and $${f}^{-1}(87)$$ .  

$$y={4x}^{2}+12x+15$$
$$y-15={4x}^{2}+12x$$
$${4x}^{2}+12x+15-y=0$$
$$x=\cfrac { -12\pm \sqrt { 144-4(15-y) } \times 4 }{ 8 } $$
$$=\cfrac { -12\pm \sqrt { 144-(60-4y)\times 4 } }{ 8 } $$
$$=\cfrac { -12\pm \sqrt { 144-240-{16y}^{2}} }{ 8 } $$
$$=\cfrac { -12\pm \sqrt { {16y}^{2}-6 } }{ 8 } $$
$$=\cfrac { -3\pm \sqrt { {y}^{2}-6 } }{ 2 } $$
$${f}^{-1}(31)$$ $$=\cfrac { -3\pm \sqrt { {31}^{2}-6 } }{ 2 }\\=\cfrac{-3\pm30.90}{2}\\=\cfrac{27.9}{2} \text{ or } \cfrac{-33.90}{2}\\=13.95 \text{ or }-16.95$$

$${f}^{-1}(87)$$ $$=\cfrac{-3\pm \sqrt{{87}^{2}-6}}{2}\\ =\cfrac{-3\pm 86.96}{2}\\=41.98 \text{ or }-44.98$$

$$\therefore $$ $${f}^{-1}(31)=13.95$$ or $$-16.95,$$ $${f}^{-1}(87)=41.98$$ or $$-44.98$$. 


Show that $$f:\left[ -1,1 \right] \rightarrow R$$, given by $$f\left( x \right) =\dfrac { x }{ \left( x+2 \right)  } $$ is one-one. Find the inverse of the function $$f:\left[ -1,1 \right] \rightarrow Range\ f.$$

Given $$f:[-1, 1]\to R$$
$$f(x)=\dfrac {x}{x+2}$$
To show, one-one we have to show , if two different element of Domain gives same, then they are equal 
Let $$x, y \in [-1, 1]$$
Let $$f(x)=f(y)$$
$$\Rightarrow \ \dfrac {x}{x+2}=\dfrac {y}{y+2}$$
$$\Rightarrow \ xy+2x=xy+2y$$
$$\Rightarrow \ 2x=2y$$
$$\Rightarrow \ x=y$$
Hence they function is one-one
Now let $$y=\dfrac {x}{x+2}\ \Rightarrow \ yx+2y=x$$
$$\Rightarrow \ x(y-1)=-2y$$
$$\Rightarrow \ x=\dfrac {2y}{1-y}$$
$$x=f^{-1} \left (\dfrac {x}{x+2}\right)=\dfrac {2y}{1-y}$$


Work out the inverse function for each mapping.

$$x \rightarrow 5 x + 1$$

$$x \rightarrow 3 x - 7$$

$$x \rightarrow \dfrac { x } { 5 } $$

$$x \rightarrow \dfrac { x + 9 } { 4 }$$


1099715_1175669_ans_96bbd1139f8b46ad981b48ed516d6527.jpg


Let $$f$$ be any real function and let $$g$$ be a function given by $$g(x)=2x$$. Prove that $$g\circ f=f+f$$.

$$f:R\rightarrow R$$......... [ Given ]
Since, $$g(x)=2x$$ is a polynomial, $$g:R\rightarrow R$$
Clearly, $$g\circ f:R\rightarrow R$$ and $$f+f:R\rightarrow R$$
So, domains of $$g\circ f$$ and $$f+f$$ are the same.

$$\Rightarrow$$  $$(g\circ f)(x)=g[f(x)]$$
                         $$=2f(x)$$......... [ Since, $$g(x)=2x$$ ]

$$\Rightarrow$$  $$f+f)(x)=f(x)+f(x)$$
                         $$=2f(x)$$

We can see that,
$$\Rightarrow$$  $$(g\circ f)(x)=(f+f)(x),$$  $$\forall\,x\in R$$
$$\therefore$$  $$g\circ f=f+f$$


If $$f:\left (-\dfrac {\pi}{2},\dfrac {\pi}{2}\right)\rightarrow R$$ and $$g:[-1,1]\rightarrow R$$ be defined as $$f(x)=\tan x$$ and $$g(x)=\sqrt{1-{x}^{2}}$$ respectively. Describe $$f\circ g$$ and $$g\circ f$$.

$$f:\left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\rightarrow R$$ and $$g:[-1,1]\rightarrow R$$ defined as $$f(x)=\tan x$$ and $$g(x)=\sqrt{1-x^2}$$

Range of $$f:$$ 
Let $$y=f(x)$$
$$\Rightarrow$$  $$y=\tan x$$
$$\Rightarrow$$  $$x=\tan^{-1}y$$

Since, $$x\in\left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right),\,y\in(-\infty,\infty)$$
$$\therefore$$  Range of $$f$$ is subset of domain $$g=[-1,1]$$
$$\therefore$$  $$g\circ f$$ exists.

By similar argument $$f\circ g$$ exists.
$$\Rightarrow$$  $$f\circ g(x)=f[g(x)]$$

                      $$=f(\sqrt{1-x^2})$$......... [ Since, $$g(x)=\sqrt{1-x^2}$$ ]

                      $$=\tan\sqrt{1-x^2}$$......... [ Since, $$f(x)=\tan x$$ ]

$$\Rightarrow$$  $$g\circ f(x)=g[f(x)]$$

                     $$=g(\tan x)$$ ......... [ Since, $$f(x)=\tan x$$ ]

                     $$=\sqrt{1-\tan^2x}$$.........  [ Since, $$g(x)=\sqrt{1-x^2}$$ ]


If $$f(x)=2x+5$$ and $$g(x)={x}^{2}+1$$ be two real functions, then describe given functions:
(i) $$f\circ g$$
(ii) $$g\circ f$$
(iii) $$f\circ f$$
(iv) $${f}^{2}$$
Also, show that $$f\circ f\ne {f}^{2}$$.

$$f\circ g$$ means $$g(x)$$ function is in $$f(x)$$ function. 
 $$g\circ f$$ means $$f(x)$$ function is in $$g(x)$$ function.

$$f(x)$$ and $$g(x)$$ are polynomials.
$$\Rightarrow$$ $$f:R\rightarrow R$$ and $$g:R\rightarrow R.$$
So, $$f\circ g:R\rightarrow R,$$ and $$g\circ f:R\rightarrow R$$

$$(i)$$  $$(f\circ g)(x)=f[g(x)]$$
                         $$=f(x^2+1)$$.........  [ Since, $$g(x)=x^2+1$$ ]
                         $$=2(x^2+1)+5$$.........  [ Since, $$f(x)=2x+5$$ ]
                         $$=2x^2+2+5$$
                         $$=2x^2+7$$

$$(ii)$$  $$(g\circ f)(x)=g[f(x)]$$
                            $$=g(2x+5)$$ .........  [ Since, $$f(x)=2x+5$$ ]
                            $$=g(2x+5)^2+1$$ .........  [ Since, $$g(x)=x^2+1$$ ]
                            $$=4x^2+20x+26$$

$$(iii)$$  $$(f\circ f)(x)=f[f(x)]$$
                             $$=f(2x+5)$$ ......... [ Since, $$f(x)=2x+5$$ ]
                             $$=2(2x+5)+5$$
                             $$=4x+10+5$$
                             $$=4x+15$$              ---- ( 1 )

$$(iv)$$  $$f^2(x)=f(x)\times f(x)$$
                    $$=(2x+5)(2x+5)$$
                    $$=(2x+5)^2$$
                    $$=4x^2+20x+25$$              ----- ( 2 )

From ( 1 ) and ( 2 ),
$$\Rightarrow$$  $$(f\circ f)(x)\ne f^2(x)$$
$$\therefore$$  $$f\circ f\ne f^2$$


If $$f(x)=\sqrt{1-x}$$ and $$g(x)=\log _{ e }{ x } $$ are two real functions, then describe functions $$f\circ g$$ and $$g\circ f$$.

$$f(x)=\sqrt{1-x}$$
For domain, $$1-x\ge 0$$
$$\Rightarrow$$  $$x\le 1$$
$$\Rightarrow$$  Domain of $$f=(-\infty , 1]$$
$$\Rightarrow$$  $$f:(\infty , 1]\rightarrow (0,\infty)$$
$$g(x)=\log_e x$$

Clearly, the range of $$g$$ is not a subset of the domain of $$f$$.
So, we need to compute the domain of $$f\circ g.$$

$$\Rightarrow$$ Domain $$(f\circ g)=(0,e)\rightarrow R$$
$$\Rightarrow$$  $$(f\circ g)(x)=f[g(x)]$$
                         $$=f(\log_e x)$$
                         $$=\sqrt{1-\log_e x}$$

The range of $$f$$ is a subset of the domain of $$g.$$
$$\Rightarrow$$  $$g\circ f:(-\infty , 1]\rightarrow R$$
$$\Rightarrow$$  $$(g\circ f)(x)=g[f(x)]$$
                         $$=g(\sqrt{1-x})$$
                         $$=\log_e(1-x)^{\frac{1}{2}}$$
                         $$=\dfrac{1}{2}\log_e(1-x)$$


If $$f,g:R\rightarrow R$$ be two functions defined as $$f(x)=\left| x \right| +x$$ and $$g(x)=\left| x \right| -x$$ for all $$x\in R$$. Then, find $$f\circ g$$ and $$g\circ f$$. Hence, find $$f\circ g(-3)$$, $$f\circ g (5)$$ and $$g\circ f(-2)$$.

$$f(x)=|x|+x$$......... [ Given ]
$$g(x)=|x|-x,$$  $$\forall x\in R$$
$$\Rightarrow$$  $$f\circ g=f[g(x)]$$
               $$=f(|x|-x)$$  .........  [ Since, $$g(x)=|x|-x$$  ]
               $$=||x|-x||+(|x|-x)$$.........  [ Since, $$f(x)=|x|+x$$ ]

$$\Rightarrow$$  $$f(g(x))=\begin{cases}0&x\ge 0\\4x& x<0\end{cases}$$
$$\Rightarrow$$  $$f(g(x))=\begin{cases}4x& x>0\\ 0& x\ge 0\end{cases}$$

$$\Rightarrow$$  $$g\circ f=g(f(x))$$
                $$=g(|x|+x)$$.........  [ Since, $$f(x)=|x|+x$$ ]
                $$=||x|+x|-(|x|+x)$$.........  [ Since, $$g(x)=|x|-x$$  ]

$$\Rightarrow$$  $$g(f(x))=\begin{cases}0&x\ge 0\\0& x<0\end{cases}$$
$$\therefore$$  $$g(f(x))=g\circ f=0$$

$$\Rightarrow$$  $$f\circ g(-3)=4(-3)=-12$$.........  [ Since, $$f\circ g=4$$ for $$x<0$$ ]

$$\Rightarrow$$  $$f\circ g(5)=0$$  .........  [ Since, $$f\circ g=0$$ for $$x\ge 0$$ ]

$$\Rightarrow$$  $$g\circ f(-2)=0$$.........  [ Since, $$g\circ f=0$$ for $$x< 0$$ ]


If $$f(x)=\sqrt{x+3}$$ and $$g(x)={x}^{2}+1$$ be two real functions, then find $$f\circ g$$ and $$g\circ f$$.

$$f(x)=\sqrt{x+3}$$
For domain, $$x+3\ge 0$$
$$\Rightarrow$$  $$x\ge -3$$
Domain of $$f=[-3,\infty)$$
Range of $$f=(-3,\infty)$$
Similarly, range of $$g=(1,\infty)$$

Then, rangle of f is subset of domain $$g$$ and range of $$g$$ is subset of $$f$$.
$$\therefore$$  $$f\circ g$$ and $$g\circ f$$ exist.

$$\Rightarrow$$  $$f\circ g(x)=f[g(x)]$$
                     $$=f(x^2+1)$$  ......... [ Since, $$g(x)^2+1$$ ]
                     $$=\sqrt{x^2+1+3}$$ ......... [ Since, $$f(x)=\sqrt{x+3}$$ ]
                     $$=\sqrt{x^2+4}$$

$$\Rightarrow$$  $$g\circ f(x)=g[f(x)]$$
                      $$=g(\sqrt{x+3})$$.........  [ Since, $$f(x)=\sqrt{x+3}$$ ]
                      $$=(\sqrt{x+3})^2+1$$......... [ Since, $$g(x)^2+1$$ ]
                      $$=x+3+1$$
                      $$=x+4$$


Let $$A=\left\{ x\in R|-1\le x\le 1 \right\} $$ and let $$f:A\rightarrow A,g:A\rightarrow A$$ be two functions defined by $$f(x)={x}^{2}$$ and $$g(x)=\sin \cfrac { \pi x }{ 2 } $$.Show that $${g}^{-1}$$ exists but $${f}^{-1}$$ does not exist. Also find $${g}^{-1}$$.

$$f$$ is not one-one because $$f\left(-1\right)={\left(-1\right)}^{2}=1$$
and $$f\left(1\right)={\left(1\right)}^{2}=1$$
$$\Rightarrow\,-1$$ and $$1$$ have the same image under $$f$$
$$\Rightarrow\,f$$ is not a bijection.
So,$${f}^{-1}$$ does not exist.
Injectivity of $$g$$
Let $$x$$ and $$y$$ be any two elements in the domain of $$A$$ such that
$$g\left(x\right)=g\left(y\right)$$
$$\Rightarrow\,\sin{\dfrac{\pi x}{2}}=\sin{\dfrac{\pi y}{2}}$$
$$\Rightarrow\,\dfrac{\pi x}{2}=\dfrac{\pi y}{2}$$
$$\Rightarrow\,x=y$$
So,$$g$$ is one-one.
Surjectivity of $$g:$$
Range of $$g=\left[\sin{\left(-\dfrac{\pi}{2}\right),\sin{\dfrac{\pi}{2}}}\right]=\left[-1,1\right]=A$$(co-domain of $$g$$)
$$\Rightarrow\,g$$ is onto
$$\Rightarrow\,g$$ is a bijection.
So,$${g}^{-1}$$ exists.
Also,
Let $${g}^{-1}{\left(x\right)}=y$$        .......$$(1)$$
$$\Rightarrow\,g\left(y\right)=x$$
$$\Rightarrow\,\sin{\dfrac{\pi y}{2}}=x$$
$$\Rightarrow\,y=\dfrac{2}{\pi}{\sin}^{-1}{x}$$
$$\Rightarrow\,{g}^{-1}{\left(x\right)}=\dfrac{2}{\pi}{\sin}^{-1}{x}$$ from $$(1)$$



Let $$f:\rightarrow R$$, $$g:R\rightarrow R$$ be two functions defined by $$f(x)={x}^{2}+x+1$$ and $$g(x)=1-{x}^{2}$$. Write $$f\circ g(-2)$$.

$$f\circ g$$ means $$g(x)$$ function is in $$f(x)$$ function. 

$$\Rightarrow$$  $$(f\circ g)(x)=f[g(x)]$$
                         $$=f(1-x^2)$$
                         $$=(1-x^2)^2+(1-x^2)+1$$

$$\Rightarrow$$  $$(f\circ g)(x)=(1-x^2)^2+(1-x^2)+1$$

$$\Rightarrow$$  $$(f\circ g)(-2)=[1-(-2)^2]^2+[1-(-2)^2]+1$$
                            $$=[1-4]^2+[1-4]+1$$
                            $$=[-3]^2-3+1$$
                            $$=9-3+1$$
                            $$=7$$


If $$f:\left\{ 5,6 \right\} \rightarrow \left\{ 2,3 \right\} $$ and $$g:\left\{ 2,3 \right\} \rightarrow \left\{ 5,6 \right\} $$ are given by $$f=\left\{ \left( 5,2 \right) ,\left( 6,3 \right)  \right\} $$ and $$g=\left\{ \left( 2,5 \right) ,\left( 3,6 \right)  \right\} $$, find $$f\circ g$$.

$$f\circ g$$ means $$g(x)$$ function is in $$f(x)$$ function.
 
$$f:\{5,6\}\rightarrow \{2,3\}$$ and $$g:\{2,3\}\rightarrow \{5,6\}$$ given by 
$$f=\{(5,2),(6,3)\}$$ and $$g=\{(2,5),(3,6)\}$$

$$\Rightarrow$$  $$f\circ g(2)=f[g(2)]$$
                     $$=f(5)$$
                     $$=2$$

$$\Rightarrow$$  $$f\circ g(3)=f[g(3)]$$
                     $$=f(6)$$
                     $$=3$$

So, $$f\circ g:\{2,3\}\rightarrow \{2,3\}$$ is defined as
$$\Rightarrow$$  $$f\circ g=\{(2,2),(3,3)\}$$


Let f(x) be a continuous and g(x) is a discontinuous function then prove that f(x)+g(x) is discontinuous at x=a 

Given that f(x) is a continuous function and g(x) is a discontinuous function then for some arbitrary real number a we must have 
$$\underset{x\rightarrow a}{\lim}f(x)=f(a)$$

and $$\underset{x\rightarrow a}{\lim}g(x)\neq g(a)$$

Now,
$$\underset{x\rightarrow a}{lim}[f(x)+g(x)]$$ $$=\underset{x\rightarrow a}{lim}f(x)+\underset{x\rightarrow a}{lim}g(x)\neq f(a)+g(a)$$ [Using equations (1) and(2)] 
$$\Rightarrow $$ $$f(x)+g(x)$$ is discontinuous


If  $$f$$  is an invertible function, define as  $$f\left ( x \right )=\cfrac{3x-4}{5}$$, write  $$f^{-1}\left ( x \right )$$.

let,$$f(x)=y=\cfrac{3x-4}{5}$$
So, to find inverse of $$f(x)$$ we need $$x$$ in terms of $$y$$ which is $$f^{-1}(x)$$
$$\therefore y=\cfrac{3x-4}{5}$$
$$\Rightarrow 5y=3x-4$$
$$\Rightarrow 5y+4=3x$$
$$\Rightarrow x=\cfrac{5y+4}{3}$$
$$\therefore f^{-1}(y)=\cfrac{5y+4}{3}$$
$$\therefore f^{-1}(x)=\cfrac{5x+4}{3}$$         ......$$\{$$ replacing $$y$$ with $$x\}$$



If $$A=\left\{a,b,c,d \right\}$$ and $$f=\left\{(a,b),(b,d),(c,a),(d,c)\right\}$$, show that $$f$$ is one-one from $$A$$ onto $$A$$. Find $$f^{-1}$$

For $$f^{-1}$$ to exist the function should be one-one and onto.
Here, $$f$$ is one=one since each element of $$A$$ is assigned to distinct element of the set $$A$$. Also, $$f$$ is onto since $$f (A)=A$$.
Moreover, $$f^{-1}=\left\{(b,a),(d,b),(a,c),(c,d)\right\} $$


Let $$f:R\to R$$ be the function defined by $$f(x)=4x-3\forall x\in R$$. Then write $$f^{-1}$$.

Given that $$f(x)=4x-3=y(say)$$, then
To find the $$f^{-1}$$ we must represent $$x$$ in terms of the variable $$y$$.
So,
$$4x=y+3$$
$$\Rightarrow \ x=\dfrac {y+3}{4}$$
Hence $$f^{-1}(y)=\dfrac {y+3}{4}\Rightarrow f^{-1}(x)=\dfrac {x+3}{4}$$


Show that $$f;[-1,1]\rightarrow R$$, given by $$f(x)=\dfrac{x}{(x+2)}$$ is one-one. Find the inverse of the function $$f;[-1,1]\rightarrow $$ Range $$f$$.
(Hint: For $$y\in $$ Range, $$f, y=f(x)=\dfrac{x}{x+2}$$ for some $$x$$ in $$[-1,1]$$
$$x=\dfrac{2y}{(1-y)}$$

Let $$x_{1}, x_{2}\in D_{f}$$
$$f(x_{1})=f(x_{2})\rightarrow \dfrac{x_{1}}{x_1+2}=\dfrac{x_2}{x_2+2}$$
$$\Rightarrow x_1(x_2+2)=x_2(x_1+2)$$
$$\Rightarrow x_1x_2+2x_1=x_1x_2+2x_2$$
$$\Rightarrow x_1=x_2$$
hence $$f$$ is one-one
let $$y=\dfrac{x}{x+2}\Rightarrow xy+2y=x$$
$$\Rightarrow xy-x=-2y$$
$$\Rightarrow x(1-y(|)=2y$$
$$\Rightarrow x=\dfrac{2y}{1-y}$$
$$\forall\ y\ \in\ R, \exists\ x\ \in\ D_f$$ such that
$$f\left(\dfrac{2y}{1-y}\right)=y$$, hence $$f$$ is onto
$$\therefore$$ Inverse exist
$$\therefore f^{-1}(x)=\dfrac{2x}{1-x}\forall\ x\ \in\ D_{f-1}=R_f=R-\left\{1\right\}$$


Consider $$f:R\rightarrow R$$ given by $$f(x)=4x+3$$. Show that $$f$$ is invertible. Find the inverse of $$f$$.

Let $$x_1, x_2\in R$$
$$f(x_1)=f(x_2)\Rightarrow 4x_1+3=4x_2+3$$
$$\Rightarrow x_1=x_2$$
hence $$f$$ is one-one
let $$y=4x+3\Rightarrow y-3=4x$$
$$\Rightarrow x=\dfrac{y-3}{4}$$
$$\forall\ y\ \in\ R\ \exists\ x\ \in\ R$$ such that
$$f\left(\dfrac{y-3}{4}\right)=\dfrac{4(y-3)}{4}+3=y$$
hence inverse exist. And
$$f^{-1}:R\rightarrow R$$ such that $$f^{-1}(y)=\dfrac{y-3}{4}$$.


Consider $$f : R - \left \{ -\dfrac{4}{3} \right \} \rightarrow R - \left \{ \dfrac{4}{3} \right \}$$ given by $$f(x) = \dfrac{4x + 3}{3x + 4}.$$ Show that f is
bijective. Find the inverse of f and hence find $$f^{-1} (0)$$ and x such that $$f^{-1}(x) = 2.$$

Let $$x_1 , x_2 \in R - \left\{\dfrac{-4}{3}\right\} $$ and $$f(x_1) = f(x_2)$$

$$\therefore \dfrac{4x_1 + 3}{3x_1 + 4} = \dfrac{4x_2 + 3}{3x_2 + 4} \Rightarrow (4x_1 + 3)( 3x_1 + 4) = (4x_2 + 3)(3x_1 + 4)$$

$$\Rightarrow 12x_1 x_2 + 16x_1 + 9x_2 + 12 = 12x_1 x_2 + 16x_2 + 9 x_2 + 12$$

$$\Rightarrow 16(x_1 - x_2) - 9 (x_1 - x_2) = 0 = 7(x_1 - x_2) = 0$$

$$\Rightarrow x_1 - x_2 = 0 \Rightarrow x_1 = x_2$$

$$\Rightarrow f$$ is a one one function.

Let $$y = \dfrac{4x + 3}{3x + 4} $$ for $$y \in R - \left\{\dfrac{4}{3}\right\}$$

$$\Rightarrow 3xy + 4y = 4x + 3 \Rightarrow 4x - 3xy = 4y - 3 \Rightarrow x(4 - 3y) = 4y - 3$$

$$\Rightarrow x = \dfrac{4y - 3}{4 - 3y} \Rightarrow \forall  y \in R - \left\{\dfrac{4}{3}\right\}, x \ \in \ R - \left\{-\dfrac{4}{3} \right\}$$

$$\Rightarrow f$$ is onto function and hence it is bijective.

Now,

$$\because x = \dfrac{4y - 3}{4 - 3y} \Rightarrow f^{-1} (x) = \dfrac{4x - 3}{4 - 3x}$$

for $$f^{-1} (x) = 2 , \dfrac{4x - 3}{4 - 3x} = 2 \Rightarrow 4x - 3 = 8 - 6x$$

$$\Rightarrow 10x = 11 \Rightarrow x = \dfrac{11}{10}$$


Prove that the function $$f : N \to N, $$ defined by $$f(x) = x^2 + x + 1$$ is one-one but not onto. Find inverse of $$f : N \to S$$, where $$S$$ is range of $$f$$. 

$$f(x)=x^2+x+1;\,\,f:N\rightarrow N$$ (Given)

Let $$x_1,x_2\,\epsilon \,D_f$$ and $$f(x_1)=f(x_2)$$

$$\Rightarrow x^2_1+x_1+1=x^2_2+x_2+1\Rightarrow x^2_1-x^2_2+x_1-x_2=0$$

$$\Rightarrow (x_1-x_2)(x_1+x_2)+(x_1-x_2)=0\Rightarrow (x_1+x_2+1)(x_1-x_2)=0$$

$$\Rightarrow x_1-x_2=0\,\,[\because x_1+x_2+1\neq 0\,for\,any\,x\epsilon N]$$

$$\Rightarrow x_1=x_2\Rightarrow f$$ is one-one function.

Now,
$$f(x)=x^2+x+1=x^2+x+\left(\dfrac{1}{2}\right)^2+1-\left(\dfrac{1}{2}\right)^2=\left(x+\dfrac{1}{2}\right)^2+1-\dfrac{1}{4}$$

$$\Rightarrow f(x)=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}$$........increasing function.

$$\because f(1)=3\Rightarrow f(x)\ge 3$$ for energy $$x\epsilon N$$

$$\Rightarrow f(x)$$ will not assume the values $$1$$ and $$2$$ 

$$\Rightarrow f$$ is not onto function.

Now, let $$y=x^2+x+1\Rightarrow x^2+x+1-y=0$$

$$\Rightarrow x=\dfrac{-1\pm \sqrt{1-4(1-y)}}{2}$$ [Using Discriminant rule]

$$x=\dfrac{-1\pm \sqrt{4y-3}}{2}\Rightarrow f^{-1}(x)=\dfrac{-1\pm \sqrt{4x-3}}{2}$$

$$\Rightarrow f^{-1}(x)=\dfrac{-1+\sqrt{4x-3}}{2}\,\,[\because f(1)=3\Rightarrow f^{-1}(3)=1]$$


Let $$g$$ be a real valued differentiable function on $$R$$ such that $$g(x) = 3e^{x-2}+4\displaystyle\int_{2}^{x}\sqrt{2t^{2}+6t+5}dt \quad\forall x \in  R$$ and let $$g^{-1}$$ be the inverse function of $$g$$. If $$(g^{-1})' (3)$$ is equal to $$\dfrac{p}{q}$$ where $$p$$ and $$q$$ are relatively prime, then find $$\dfrac{p+q}{6}$$

$$g\left( x \right) =3{ e }^{ x-2 }+4\int _{ 2 }^{ x }{ \sqrt { 2{ t }^{ 2 }+6t+5 }  } dt\\ g\left( x \right) =y\\ \Rightarrow g^{ -1 }\left( y \right) =x$$ 

Differentiating the above equation w.r.t $$x$$ gives
$$g^{ { -1 }^{ ' } }\left( g\left( x \right)  \right) g^{ ' }\left( x \right) =1$$

$$\Rightarrow g^{ { -1 }^{ ' } }\left( g\left( x \right)  \right) =\dfrac { 1 }{ g^{ ' }\left( x \right)  }$$
When $$\displaystyle x=2,\quad g\left( x \right) =3{ e }^{ 2-2 }+4\int _{ 2 }^{ 2 }{ \sqrt { 2{ t }^{ 2 }+6t+5 }  } dt= 3+0=3$$

$$g'\left( x \right) =3{ e }^{ x-2 }+4\sqrt { 2{ x }^{ 2 }+6x+5 }$$
$$g'(2) = 23$$
$$x=2        g(x)=3$$    implies  $$ (g)^{-1}(3)=2$$
Now, 
$$g^{-1'}(g(x)) = g^{-1'}(3) = \dfrac1{g'(2)}$$

$$g^{ { -1 }^{ ' } }\left( 3 \right) =\dfrac { 1 }{ g^{ ' }\left( 2 \right)  } =\dfrac { 1 }{ 23 } =\dfrac { p }{ q }$$

$$\therefore p+q=24\ (componendo)
\therefore \dfrac { p+q }{ 6 } =4\\ \quad \quad \quad \quad $$


Let $$A = R - \left \{3\right \}$$ and $$B = R - \left \{1\right \}$$. Consider the function $$f: A\rightarrow B$$ defined by $$f(x) = \left (\dfrac {x - 2}{x - 3}\right )$$ Show that f is one-one and onto and hence find $$f^{-1}$$

Let $$x_1, x_2 \epsilon A$$.
Now, $$f(x_1)=f(x_2)\Rightarrow \dfrac{x_1-2}{x_1-3}=\dfrac{x_2-2}{x_2-3}$$
$$(x_1-2)(x_2-3)=(x_1-3)(x_2-2)$$
$$x_1x_2-3x_1-2x_2+6=x_1x_2-2x_1-3x_2+6$$
$$-3x_1-2x_2=-2x_1-3x_2$$
$$-x_1=-x_2\Rightarrow x_1=x_2$$
Hence f is one-one function.
For Onto:
Let $$y=\dfrac{x-2}{x-3}$$
$$xy-3y=x-2\Rightarrow xy-x=3y-2$$
$$x(y-1)=3y-2$$
$$x=\dfrac{3y-2}{y-1}$$--- (1)
From above it is obviously that $$\forall$$ y except 1, i.e.,$$\forall y \epsilon B=R-[1]\exists x\epsilon A$$.
Hence f is onto function.
Thus f is one-one function.
It $$f^{-1}$$ is inverse of f then $$f^{-1}(y)=\dfrac{3y-2}{y-1}$$ [from (1)].



Let $$f$$ be a real function given by $$f(x)=\sqrt{x-2}$$. Find the following.
(i) $$f\circ f$$  (ii) $$f\circ f\circ f$$  (iii) $$(f\circ f\circ f)(38)$$   (iv) $${f}^{2}$$
Also, show that $$f\circ f\ne {f}^{2}$$.

$$f(x)=\sqrt{x-2}$$
For domain,
$$\Rightarrow$$  $$x-2\ge 0$$
$$\Rightarrow$$  $$x\ge 2$$
Domain of $$f=[2,\infty)$$
Since, $$f$$ is a square root function, range of $$f=(0,\infty)$$
So, $$f:[2,\infty)\rightarrow (0,\infty)$$

$$(i)$$  $$f\circ f$$
Range of $$f$$ is not a subset of the domain of $$f$$.
$$\Rightarrow$$  Domain $$(f\circ f)=\{x:x:\in[2,\infty)\,and\,\sqrt{x-2}\in[2,\infty)\}$$
                                 $$=\{x:x\in [2,\infty)\,and\,\sqrt{x-2}\ge 2\}$$
                                 $$=\{x:x:\in[2\infty)\,and\,x-2\ge 4\}$$
                                 $$=\{x:x\in[2,\infty)\,and\,x\ge 6\}$$
                                 $$=[6,\infty)$$
$$\Rightarrow$$  $$(f\circ f)(x)=f(f(x))$$
                        $$=f(\sqrt{x-2})$$
                        $$=\sqrt{\sqrt{x-2}-2}$$

$$(ii)$$  $$f\circ f\circ f=(f\circ f)\circ f$$
$$f(x)=\sqrt{x-2}$$
We have $$f:[2,\infty)\rightarrow (0,\infty)$$ and $$f\circ f:[6,\infty)\rightarrow R$$
$$\Rightarrow$$  Range of $$f$$ is not a subset of the domain of $$f\circ f.$$
$$\Rightarrow$$  Domain $$((f\circ f)\circ f)=\{x:x\in$$ Domain of $$f$$ and $$f(x)\in $$ Domain of $$f\circ f\}$$
                                           $$=\{x:x\in [2,\infty)\,and\,\sqrt{x-2}\in[6,\infty)\}$$
                                           $$=\{x:x\in[2,\infty)\,and\,\sqrt{x-2}\ge 6\}$$
                                           $$=\{x:x\in[2,\infty)\,and\,x-2\ge 36\}$$
                                           $$=\{x:x\in[2,\infty)\,and\,x\ge 38\}$$
                                           $$=\{x:x\ge 38\}$$
                                           $$=[38,\infty)$$ 
 
$$\Rightarrow$$  $$f\circ f:[38,\infty)\rightarrow R$$
$$\Rightarrow$$  $$f\circ f\circ f(x)=(f\circ f)\circ f(x)$$
                      $$=(f\circ f)(\sqrt{x-2})$$
                      $$=f(\sqrt{\sqrt{x-2}-2})$$
                      $$=\sqrt{\sqrt{\sqrt{x-2}-2}-2}$$

$$(iii)$$ $$(f\circ f\circ f)(x)$$ $$=\sqrt{\sqrt{\sqrt{x-2}-2}-2}$$
So, $$(f\circ f\circ f)(38)$$ $$=\sqrt{\sqrt{\sqrt{38-2}-2}-2}$$
                                 $$=\sqrt{\sqrt{\sqrt{36}-2}-2}$$
                                 $$=\sqrt{\sqrt{6-2}-2}$$
                                 $$=\sqrt{2-2}$$
                                 $$=0$$

$$(iv)$$  We hae, $$f\circ f=\sqrt{\sqrt{x-2}-2}$$
$$f^2(x)=f(x)\times f(x)=\sqrt{x-2}\times \sqrt{x-2}=x-2$$

$$\therefore$$ from $$(i)$$ and $$(iv)$$ we can say that,
$$\therefore$$  $$f\circ f\ne f^2$$


If $$f:R\rightarrow R$$ be defined by $$f(x)={x}^{3}-3$$, then prove that $${f}^{-1}$$ exists and find a formula for $${f}^{-1}$$. Hence, find $${f}^{-1}(24)$$ and $${f}^{-1}(5)$$.

$$one-one$$ test of $$f:$$
Let $$x$$ and $$y$$ be two elements in domain $$(R),$$
Such that, $$f(x)=f(y)$$
$$\Rightarrow$$  $$x^3-3=y^3-3$$
$$\Rightarrow$$  $$x^3=y^3$$
$$\Rightarrow$$  $$x=y$$
$$\therefore$$  $$f$$ is one-one.

$$onto$$ test for $$f:$$
Let $$y$$ be in the co-domain $$(R)$$, such that $$f(x)=y$$
$$\Rightarrow$$  $$x^3-3=y$$
$$\Rightarrow$$  $$x^3=y+3$$
$$\Rightarrow$$  $$x=\sqrt[3]{y+3}\in R$$
Since, $$f$$ is one-one and onto, then it is bijective.
$$\therefore$$  $$f$$ is invertible.

Find $$f^{-1}:$$
Let $$f^{-1}(x)=y$$            ---- ( 1 )
$$\Rightarrow$$  $$x=f(y)$$
$$\Rightarrow$$  $$x=y^3-3$$
$$\Rightarrow$$  $$x+3=y^3$$

$$y=\sqrt[3]{x+3}$$

From ( 1 ),
$$f^{-1}=\sqrt[3]{x+3}$$
$$\Rightarrow$$  Now, $$f^{-1}(24)=\sqrt[3]{24+3}$$
                                $$=\sqrt[3]{27}$$
                                $$=3$$

$$\Rightarrow$$  Now, $$f^{-1}(5)=\sqrt[3]{5+3}$$
                             $$=\sqrt[3]{8}$$
                             $$=2$$


Let $$f:N\rightarrow N$$ be a function defined as $$f(x)=9{x}^{2}+6x-5$$. Show that $$f:N\rightarrow S$$, where $$S$$ is the range of $$f$$, is invertible. Find the inverse of $$f$$ and hence find $${f}^{-1}(43)$$ and $${f}^{-1}(163)$$.

$$f:N\rightarrow N$$ is a function defined as $$f(x)=9x^2+6x-5$$

Let $$y=f(x)=9x^2+6x-5$$
$$\Rightarrow$$  $$y-9x^2+6x-5$$
$$\Rightarrow$$  $$y=9x^2+6x+1-1-5$$
$$\Rightarrow$$  $$y=(9x^2+6x+1)-6$$
$$\Rightarrow$$  $$y=(3x+1)^2-6$$
$$\Rightarrow$$  $$y+6=(3x+1)^2$$
$$\Rightarrow$$  $$\sqrt{y+6}=3x+1$$          $$(\because y\in N)$$
$$\Rightarrow$$  $$\sqrt{y+6}-1=3x$$

$$\Rightarrow$$  $$x=\dfrac{\sqrt{y+6}-1}{3}$$
Let $$x=g(y)$$
$$\Rightarrow$$  $$g(y)=\dfrac{\sqrt{y+6}-1}{3}$$     
       
Now, $$f\circ g(y)=f[g(y)]$$

                        $$=f\left(\dfrac{\sqrt{y+6}-1}{3}\right)$$

                        $$=9\left(\dfrac{\sqrt{y+6}-1}{3}\right)^2+6\left(\dfrac{\sqrt{y+6}-1}{3}\right)-5$$

                        $$=9\left(\dfrac{y+6-2\sqrt{y+6}+1}{9}\right)-5$$

                        $$=9\left(\dfrac{y+6-2\sqrt{y+6}+1}{9}\right)+2(\sqrt{y+6}-1)-5$$
 
                        $$=y+6-2\sqrt{y+6}+1+2\sqrt{y+6}-2-5$$
                        $$=y$$
                        $$=I_y,$$ Identify function

$$\Rightarrow$$  $$g\circ f(x)=g[f(x)]$$

                      $$=g(9x^2+6x-5)$$

                      $$=\dfrac{\sqrt{(9x^2+6x-5)+6}-1}{3}$$

                      $$=\dfrac{\sqrt{(9x^2+6x+1)}-1}{3}$$

                      $$=\dfrac{\sqrt{(3x+1)^2}-1}{3}$$

                      $$=\dfrac{(3x+1)-1}{3}$$
   
                      $$=\dfrac{3x}{3}$$
                      $$=x$$
                      $$=I_x$$, Indenfity function.

Since, $$f\circ g(y)$$ and $$g(g\circ f(x)$$ are identify function.
$$\therefore$$  $$f$$ is invertible.
So, $$f^{-1}(x)=g(x)=\dfrac{\sqrt{x+6}-1}{3}$$
Now,
$$\Rightarrow$$  $$f^{-1}(43)=\dfrac{\sqrt{43+6}-1}{3}$$
                      $$=\dfrac{\sqrt{46}-1}{3}$$

                      $$=\dfrac{7-1}{3}$$

                      $$=\dfrac{6}{3}$$

                      $$=2$$.
$$\Rightarrow$$  $$f^{-1}(163)=\dfrac{\sqrt{163+6}-1}{3}$$
 
                        $$=\dfrac{\sqrt{169}-1}{3}$$

                        $$=\dfrac{13-1}{3}$$
 
                        $$=\dfrac{12}{3}$$

                        $$=4$$


Let $$f(x) =\left\{\begin{matrix} x+a & \text{if} \ x < 0 \\ |x-1| & \text{if} \ x \ge 0 \end{matrix}\right.$$ and
$$g(x) = \left\{\begin{matrix} x+1 & \text{if} \ x < 0\\ (x-1)^2+b & \text{if} \ x \ge 0, \end{matrix}\right.$$
Where a and b are non-negative real number. Determine the composite function g o f. if is continuous for all real x, determine the Values of a and b. Further for these values of a and b is g o f differentiable at x=0? Justify your answer 


1976015_1752592_ans_3a0fce8756e44abb997fb60f2f98f4df.jpeg


Class 12 Engineering Maths Extra Questions