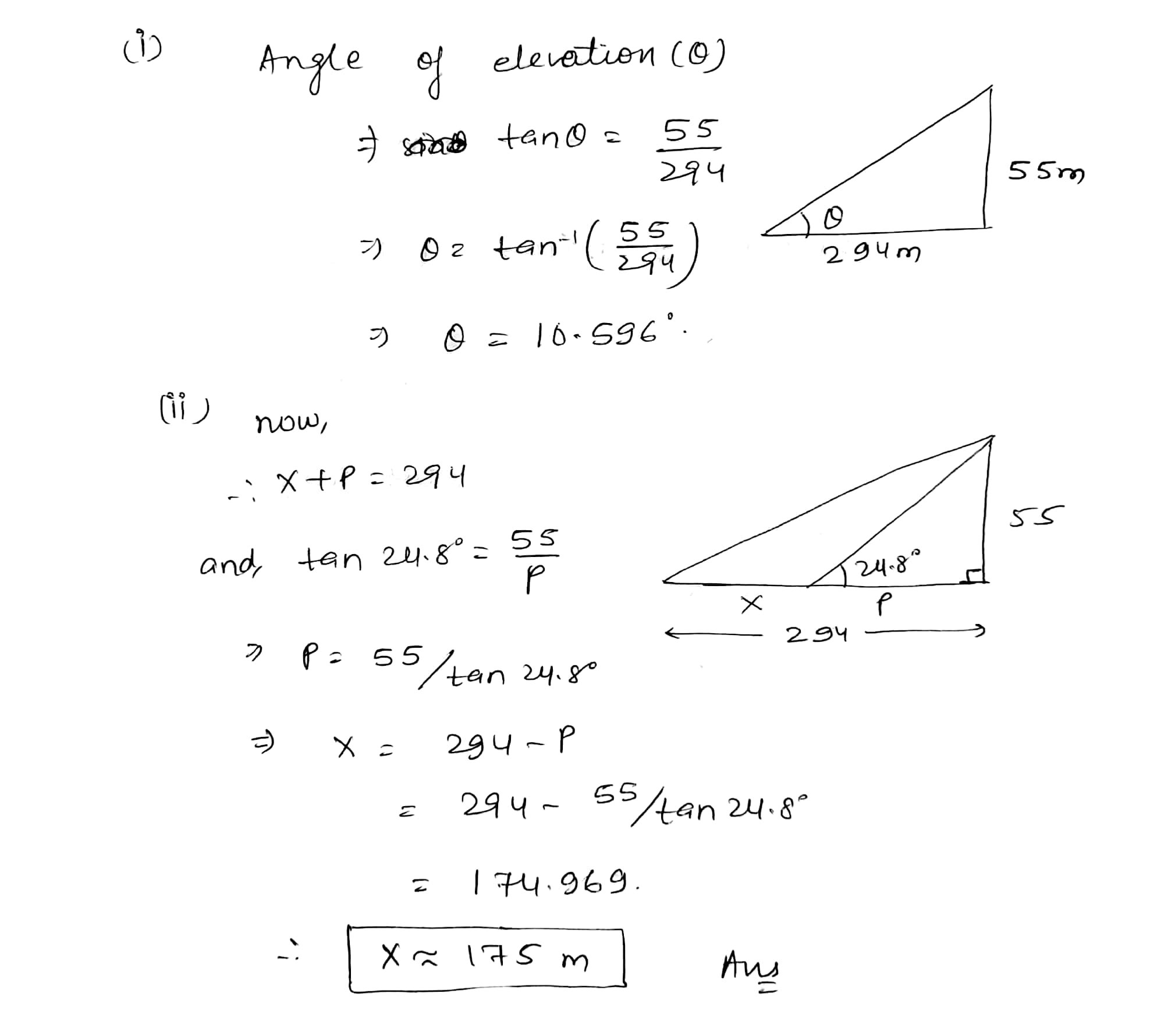
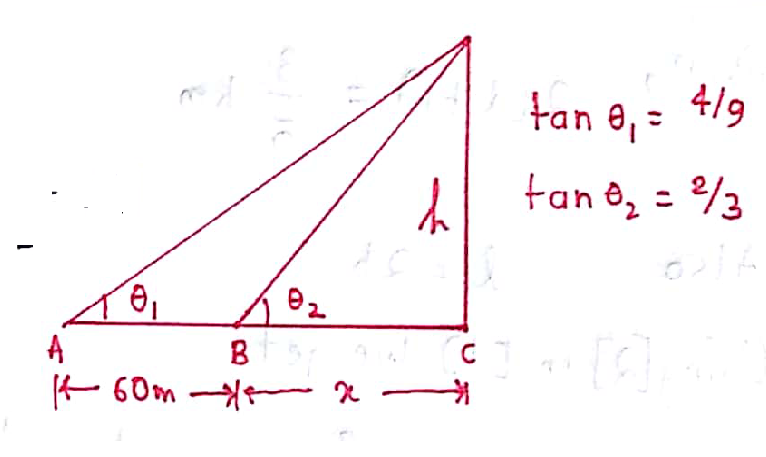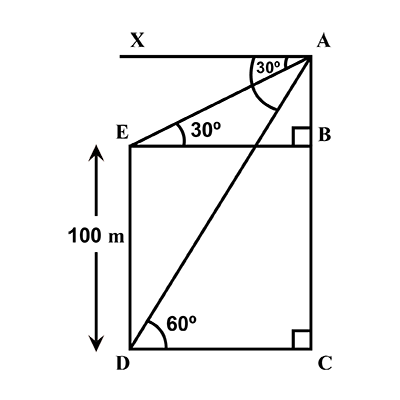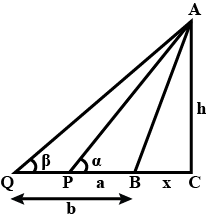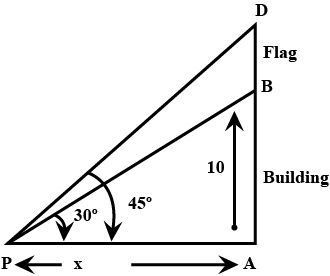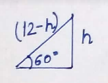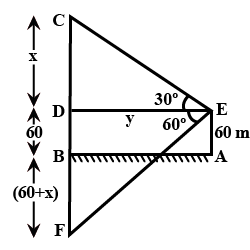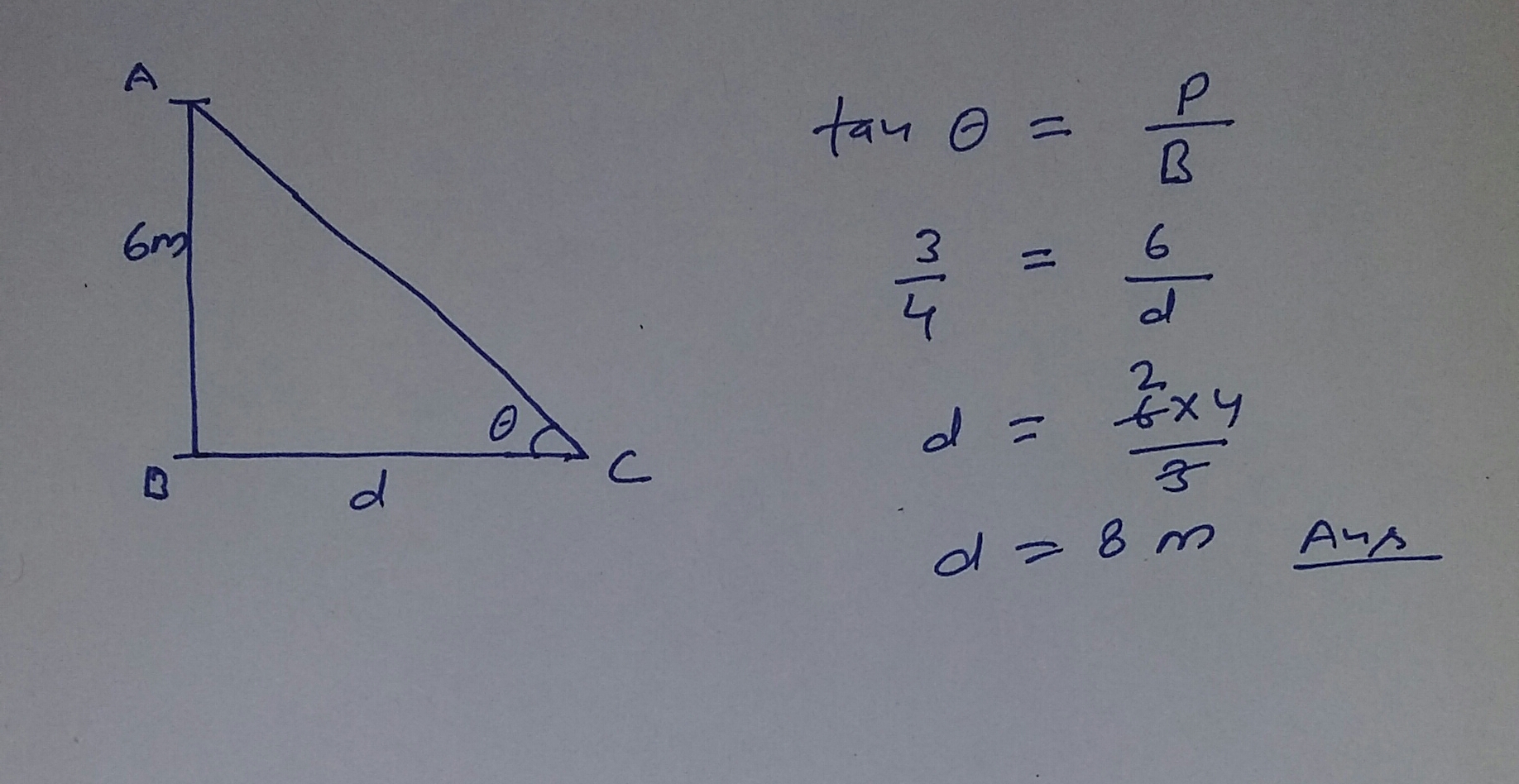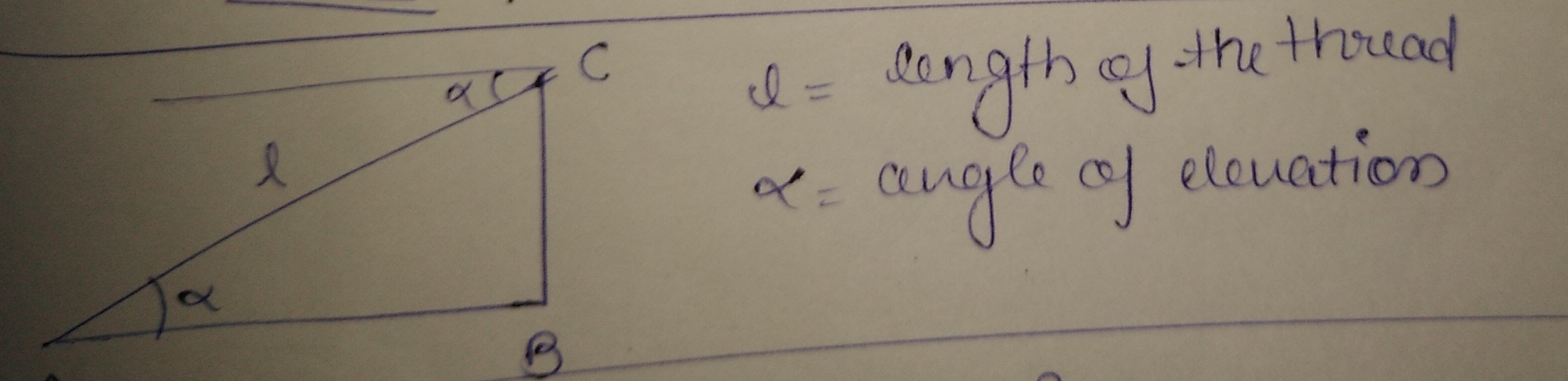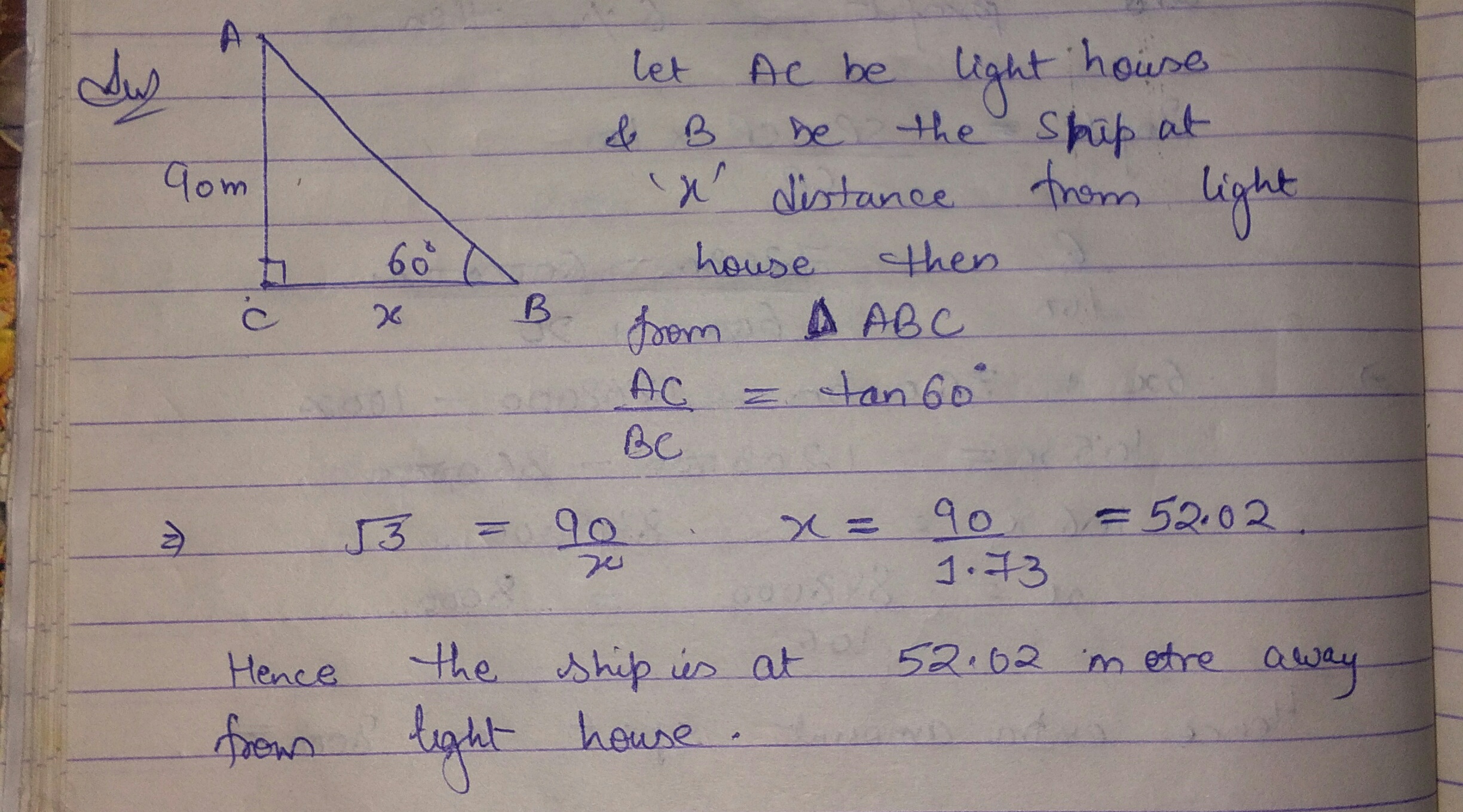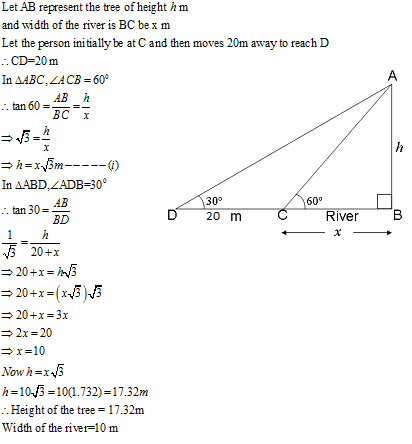Some Applications Of Trigonometry - Class 10 Maths - Extra Questions
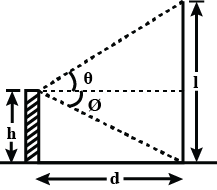
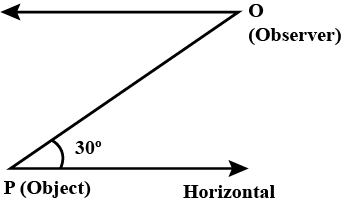
In the adjoining figure, the positions of observer and object are marked. The angle of depression is ______ .
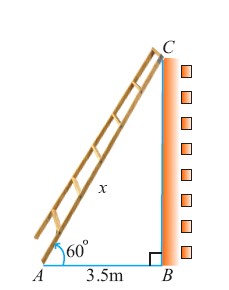
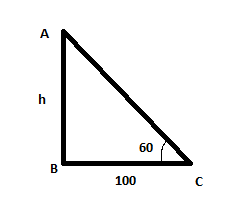
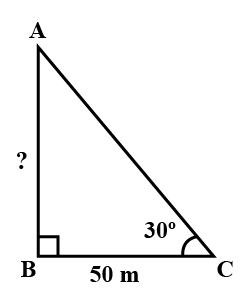
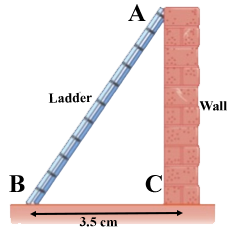
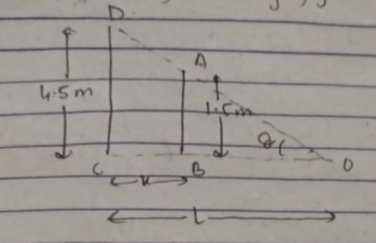
A ladder leaning against a vertical wall, makes an angle of $$60^{\circ}$$ with the ground. The foot of the ladder is $$3.5$$m away from the wall. Find the length of the ladder.
Let $$AC$$ denote the ladder and $$B$$ be foot of the wall.
Let the length of the ladder $$AC$$ be $$x$$ metres.
Given that $$\angle CAB=60^{\circ}$$ and $$AB=3.5$$m
In the right $$\displaystyle \bigtriangleup CAB , \cos60^{\circ}=\frac{AB}{AC}$$
$$\displaystyle \Rightarrow AC=\frac{AB}{\cos 60^{\circ}}$$
$$\therefore x=2\times 3.5=7$$m
Thus, the length of the ladder is $$7$$m.
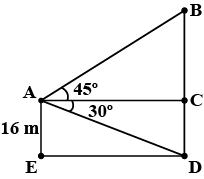
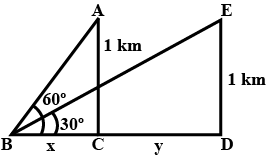
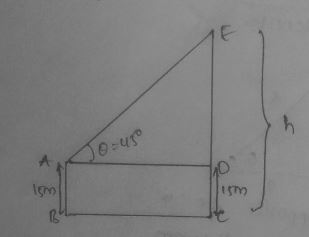
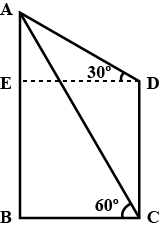
A man on the deck of a ship is 16 m above water level. He observes that the angle of elevation of the top of a cliff is 45$$^o$$ and the angle of depression of the base is 30$$^o$$. Calculate the distance of the cliff front the ship and the height of the cliff.
$$tan45=1$$
=> $$\dfrac{BC}{AC}=1$$
=> $$BC=AC= x(let)$$
Now $$CD=AE=16m$$
$$tan30=\dfrac{CD}{AE}$$
=>$$\dfrac{1}{\sqrt{(3)}}=\dfrac{16}{x}$$
=> $$x=16\sqrt{3}$$ $$=$$distance of the cliff from the ship$$=$$height of cliff
The angle of elevation from a point P of the top of a tower QR, $$50$$cm high is $$60^o$$ and that of the tower PT from a point Q is $$30^o$$. Find the height of the tower PT, correct to the nearest metre.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle $${60}^{o}$$ with it. The distance between the foot of the tree to the point where the top touches the ground is $$3m$$. Find the height of the tree.
$$\tan { { 60 }^{ \circ } } =\dfrac { OA }{ OB } \\ \sqrt { 3 } =\dfrac { OA }{ 3 } \\ \Rightarrow OA=\sqrt { 3 } \\ \sin { { 60 }^{ \circ } } =\dfrac { OA }{ AB } \\ \dfrac { \sqrt { 3 } }{ 2 } =\dfrac { \sqrt { 3 } }{ AB } \\ \Rightarrow AB=2$$
Height of tree $$=OA+AB=\sqrt { 3 } +2$$
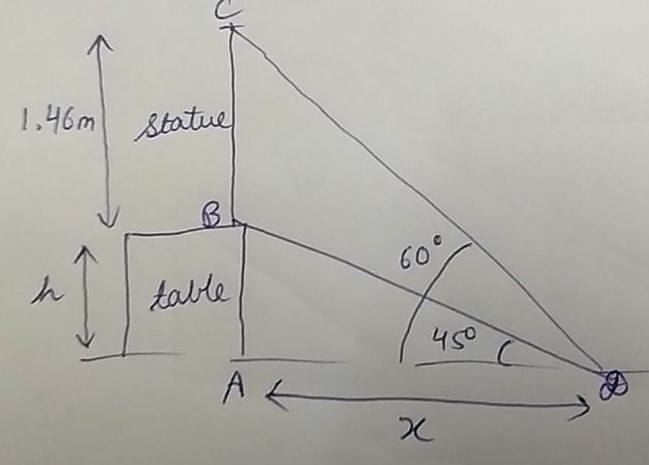
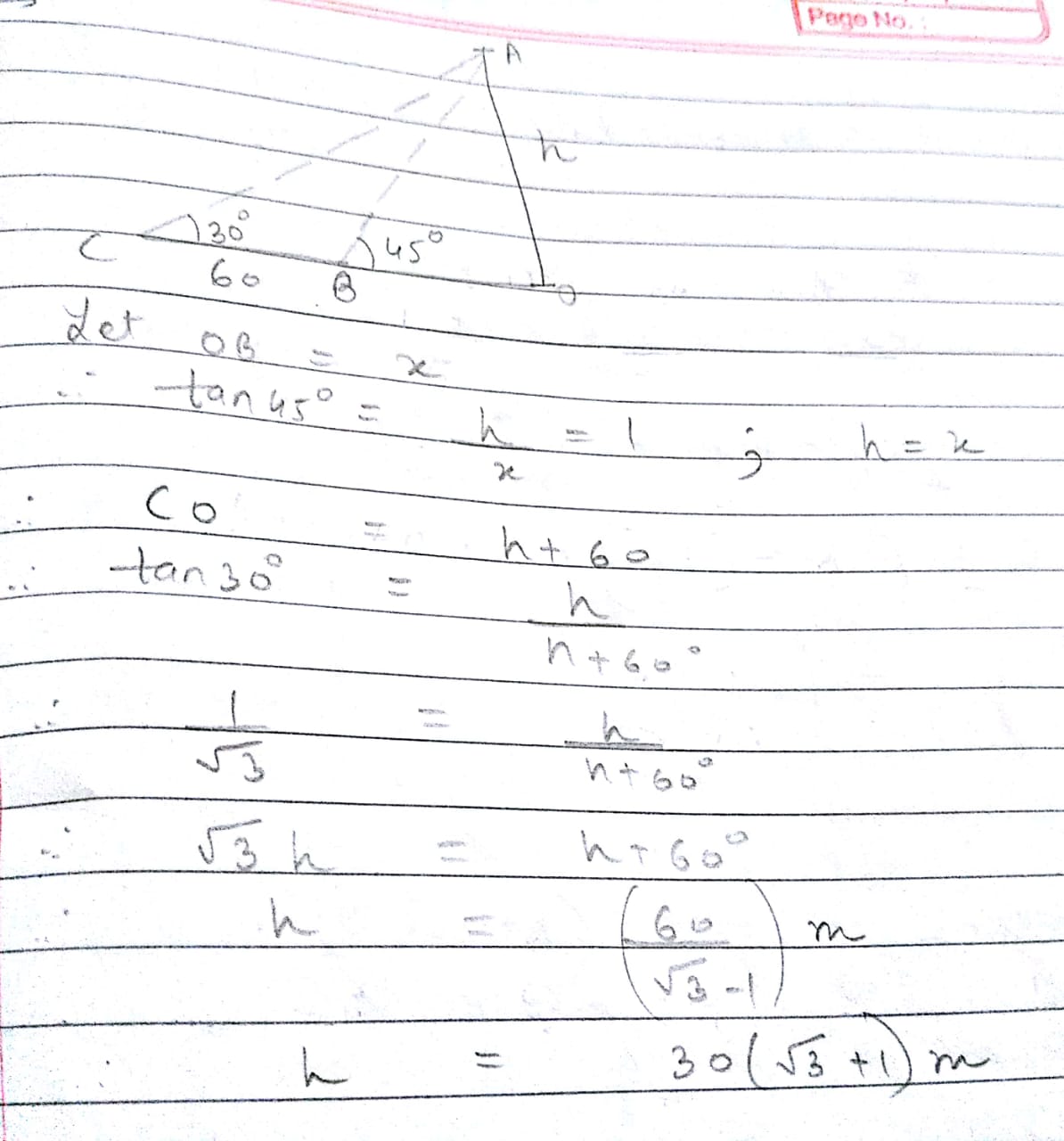
To statue of height $$1.46\ m$$ is placed on a table of certain height. The angle of elevation of the top of the statue from the point on the ground is $$60^{\circ}$$ and that of the top of the table is $$45^{\circ}$$. Find the height of the table.
Given:Height of the statue$$=BC=1.46m$$
Angle of elevation of the top of the statue from a point on the ground$$=\angle ADB=60^{\circ}$$
Angle of elevation of the top of the table from a point on the ground$$=\angle ADB=45^{\circ}$$
$$\tan(\angle ADB)=\dfrac{AB}{AD}$$
$$\tan 45^{\circ}=\dfrac{h}{x}$$
$$1=\dfrac{h}{x}$$ (1)
$$\tan(\angle ADC)=\dfrac{AC}{AD}$$
$$\tan 60^{\circ}=\dfrac{h+1.46}{x}$$
$$\sqrt{3}=\dfrac{h+1.46}{x}$$(2)
Substituting value of x from (1) in (2)
$$\sqrt{3}=\dfrac{h+1.46}{h}$$
$$\sqrt{3}-1=\dfrac{1.46}{h}$$
$$h=1.994m\approx 2m$$
Hence, the height of the table $$=2m$$.
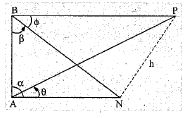
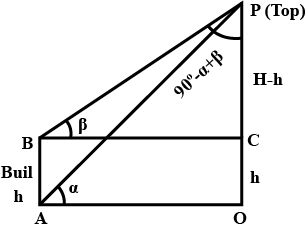
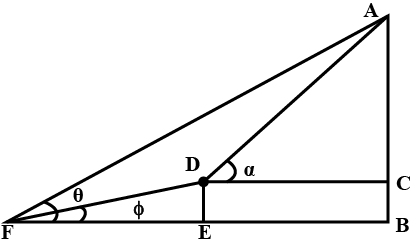
If top P of a mountain is observed from A and B at the sea level. If N is the point vertically below P and $$\angle NAB = \alpha$$,
$$\angle NBA = \beta, \angle NAP = \theta, \angle NBP = \phi$$ then show that $$cot \phi sin \beta = cot \theta sin \alpha$$.
Let PN = h, Then $$AN = h cot \theta$$ and $$BN = h cot \phi$$
Now from $$\Delta ABN$$, we get
$$\dfrac{AN}{sin \beta} = \dfrac{BN}{sin \alpha}$$
or $$AN sin \alpha = BN sin \beta$$
or $$h cot \theta sin \alpha = h cot \phi sin \beta$$
or $$cot \theta sin \alpha = cot \phi sin \beta$$.
Now from $$\Delta ABN$$, we get
$$\dfrac{AN}{sin \beta} = \dfrac{BN}{sin \alpha}$$
or $$AN sin \alpha = BN sin \beta$$
or $$h cot \theta sin \alpha = h cot \phi sin \beta$$
or $$cot \theta sin \alpha = cot \phi sin \beta$$.
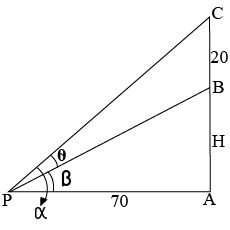
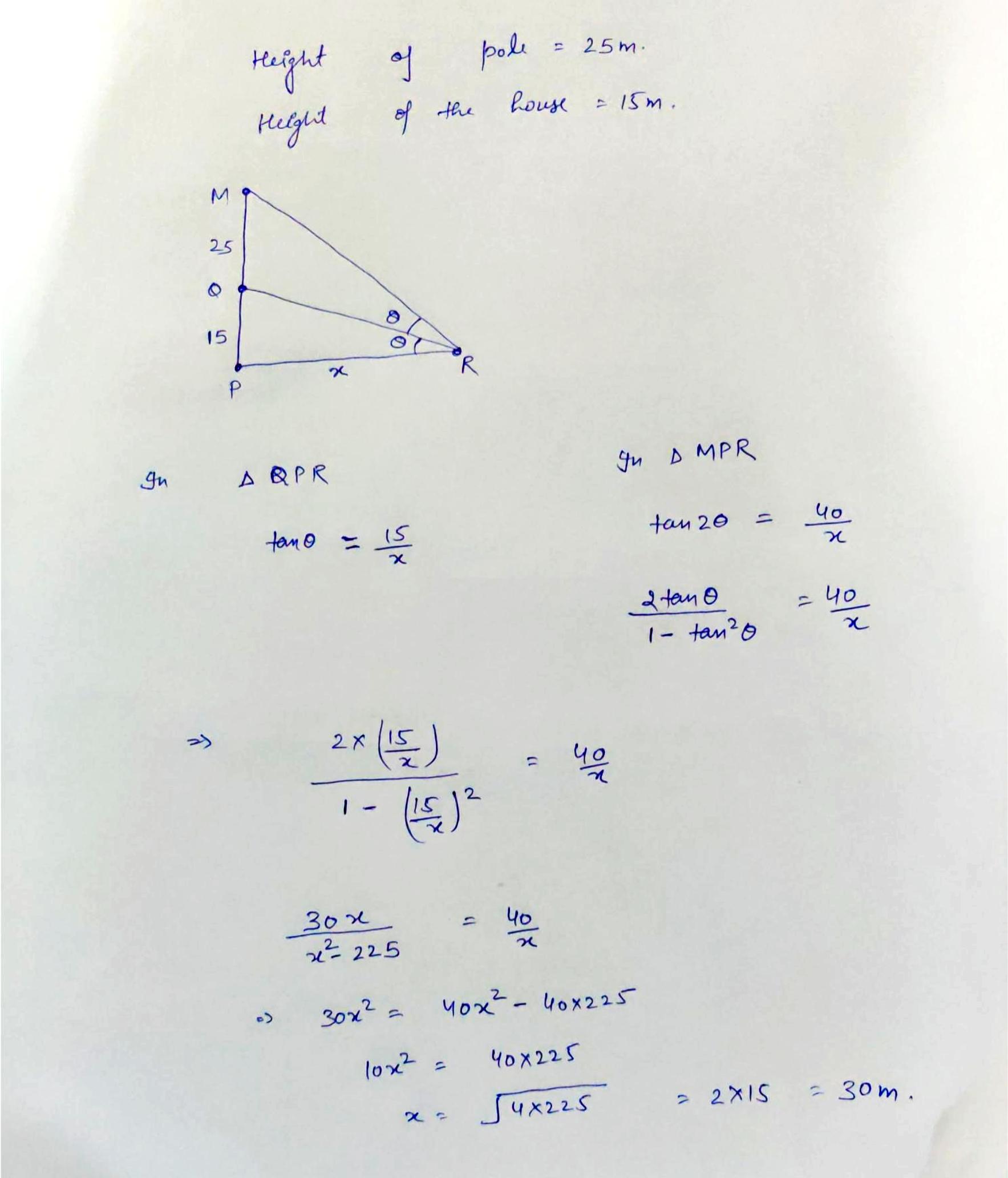
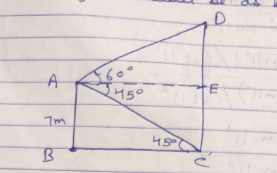
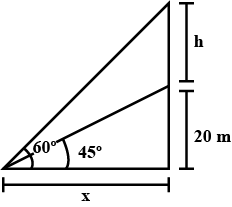
A straight pillar $$PQ$$ stands at a point $$P$$, the points $$A$$ and $$B$$ are situated due south and east of P respectively. $$M$$ is the mid-point of $$AB$$. $$PAM$$ is an equilateral triangle and $$N$$ is the foot of the perpendicular from $$P$$ on $$AB$$. Suppose $$AN = 20$$ metre and the angle of elevation of the top of the pillar at $$N$$ is $$tan^{-1} 2$$. Find the height of the pillar and the angles of elevation of its top at $$A$$ and $$B$$.
PQ is a vertical pillar. The points A and B are respectively due south and due east of the point P so that $$\angle APB = 90^o$$, M is the mid-point of AB and N is the foot of perpendicular from P on AB where AN = 20 metres.
N is mid-point of AM as $$\Delta PAM$$ is equilateral
$$\therefore AM =2AN= 40$$ ...(1)
$$AB = 2AM = 80$$ ...(2)
Also $$\angle PAM = \angle MPA = 60^o$$, since the $$\Delta PAM$$ is equilateral. Elevation of Q as seen from N is $$\alpha$$ where $$tan \alpha =2.$$
If PQ = h, then
$$PN = h cot \alpha =AN tan 60^o = 20\sqrt{3}$$
$$h . \left( \dfrac{1}{2} \right) = 20\sqrt{3}$$ so that $$ h = 40 \sqrt{3}$$.
To find the elevations of A and B, we first find PA and PB. We have
$$PA = AM = 40$$ by (1) as $$\Delta PAM$$ is equilateral
$$\therefore PB = \sqrt{AB^2 - PA^2} = \sqrt{80^2 - 40^2}$$
$$= 40 \sqrt{3}$$ metre. by (1) and (2)
$$tan \beta = \dfrac{PQ}{PA} = \dfrac{40 \sqrt{3}}{40} = \sqrt{3}$$ so that $$\beta = 60^o$$
$$tan \gamma = \dfrac{PQ}{PB} = \dfrac{40 \sqrt{3}}{40 \sqrt{(3)}} = 1$$ and so $$\gamma = 45^o$$
N is mid-point of AM as $$\Delta PAM$$ is equilateral
$$\therefore AM =2AN= 40$$ ...(1)
$$AB = 2AM = 80$$ ...(2)
Also $$\angle PAM = \angle MPA = 60^o$$, since the $$\Delta PAM$$ is equilateral. Elevation of Q as seen from N is $$\alpha$$ where $$tan \alpha =2.$$
If PQ = h, then
$$PN = h cot \alpha =AN tan 60^o = 20\sqrt{3}$$
$$h . \left( \dfrac{1}{2} \right) = 20\sqrt{3}$$ so that $$ h = 40 \sqrt{3}$$.
To find the elevations of A and B, we first find PA and PB. We have
$$PA = AM = 40$$ by (1) as $$\Delta PAM$$ is equilateral
$$\therefore PB = \sqrt{AB^2 - PA^2} = \sqrt{80^2 - 40^2}$$
$$= 40 \sqrt{3}$$ metre. by (1) and (2)
$$tan \beta = \dfrac{PQ}{PA} = \dfrac{40 \sqrt{3}}{40} = \sqrt{3}$$ so that $$\beta = 60^o$$
$$tan \gamma = \dfrac{PQ}{PB} = \dfrac{40 \sqrt{3}}{40 \sqrt{(3)}} = 1$$ and so $$\gamma = 45^o$$
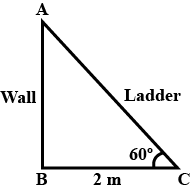
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is $$2$$ m away from the wall and the ladder is making an angle of $$60^o$$ with the level of the ground. Determine the height of the wall.
$$\Rightarrow$$ Here $$AC$$ is a ladder and $$AB$$ is the height of wall.
$$\Rightarrow$$ $$BC=2\,m$$
$$\Rightarrow$$ Now, $$\tan\,60^o=\dfrac{AB}{BC}$$
$$\Rightarrow$$ $$\sqrt{3}=\dfrac{AB}{2}$$
$$\therefore$$ $$AB=2\sqrt{3}\,m$$
$$\therefore$$ Height of the wall is $$2\sqrt{3}\,m$$.
$$PQ$$ is a tower standing on a horizontal plane, $$Q$$ being its foot. Two points $$A$$ and $$B$$ are taken on the plane such that $$AB=32$$ and $$\angle QAB$$ is a right angle. It is found that $$\cot { PAQ } =2/5$$ and $$\cot { PBQ } =3/5$$, the height of the tower is
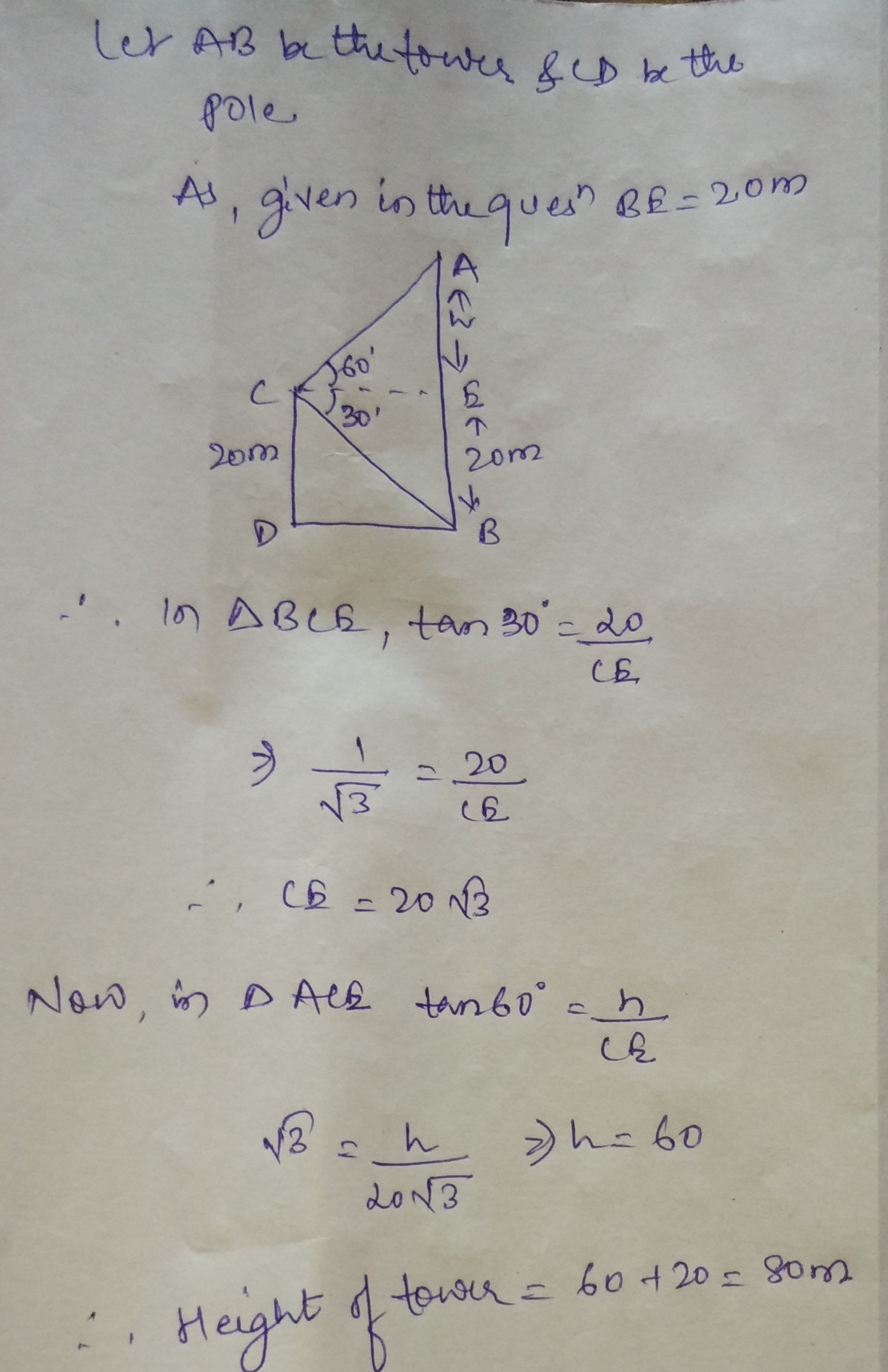
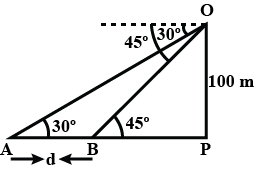
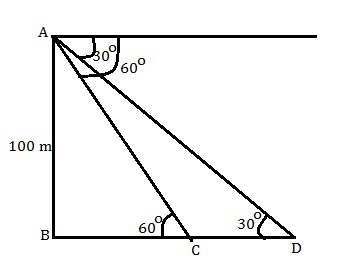
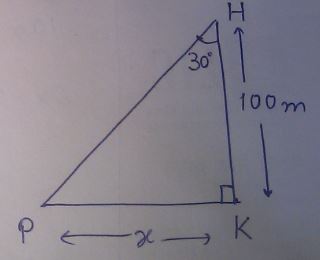
From top of a tower the angle of depression of top and bottom of a multistored building are $$30^o$$ and $$60^o$$ respectively. If the height of the building is 100m. find the height if a tower.
Let $$AB=$$height of the building$$=100m$$
$$DE=AC=AB+BC=h=$$ height of the tower
$$\angle ADC=60^{\circ}$$
$$\angle BDC=60^{\circ}$$
Now
$$\tan 30^{\circ}=\dfrac{CB}{CD}=\dfrac{x}{d}$$
$$\dfrac{1}{\sqrt{3}}=\dfrac{x}{d}$$ (1)
$$\tan 60^{\circ}=\dfrac{CA}{CD}=\dfrac{x+100}{d}$$
$$\sqrt{3}=\dfrac{x+100}{d}$$ (2)
From (1)
$$d=\sqrt{3}x$$ (3)
Substituting (3) in (2)
$$\sqrt{3}=\dfrac{(x+100)}{\sqrt{3}x}$$
$$3x=x+100$$
$$2x=100$$
$$x=50$$
Height of the tower$$=DE=h=AB+CB=100m+x=100m+50m=150m$$
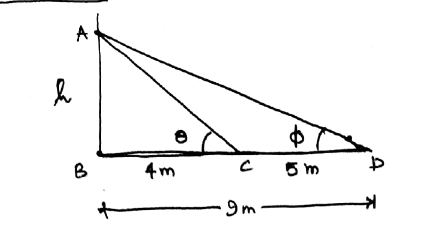
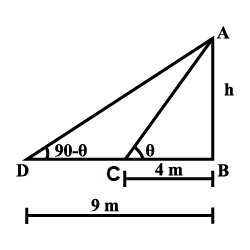
The angles of elevation of a tower from two points at a distance of $$4\ m$$ and $$9\ m$$ from the base of the tower and in the same straight line with it are complimentary. Prove that the height of the tower is $$6m.$$
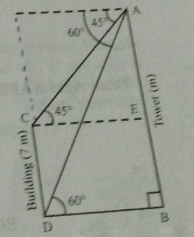
The angles of depression of the top and the bottom of a $$7\ m$$ tall building from the top of a tower are $$45^o$$ and $$60^o$$, respectively. Find the height of the tower.
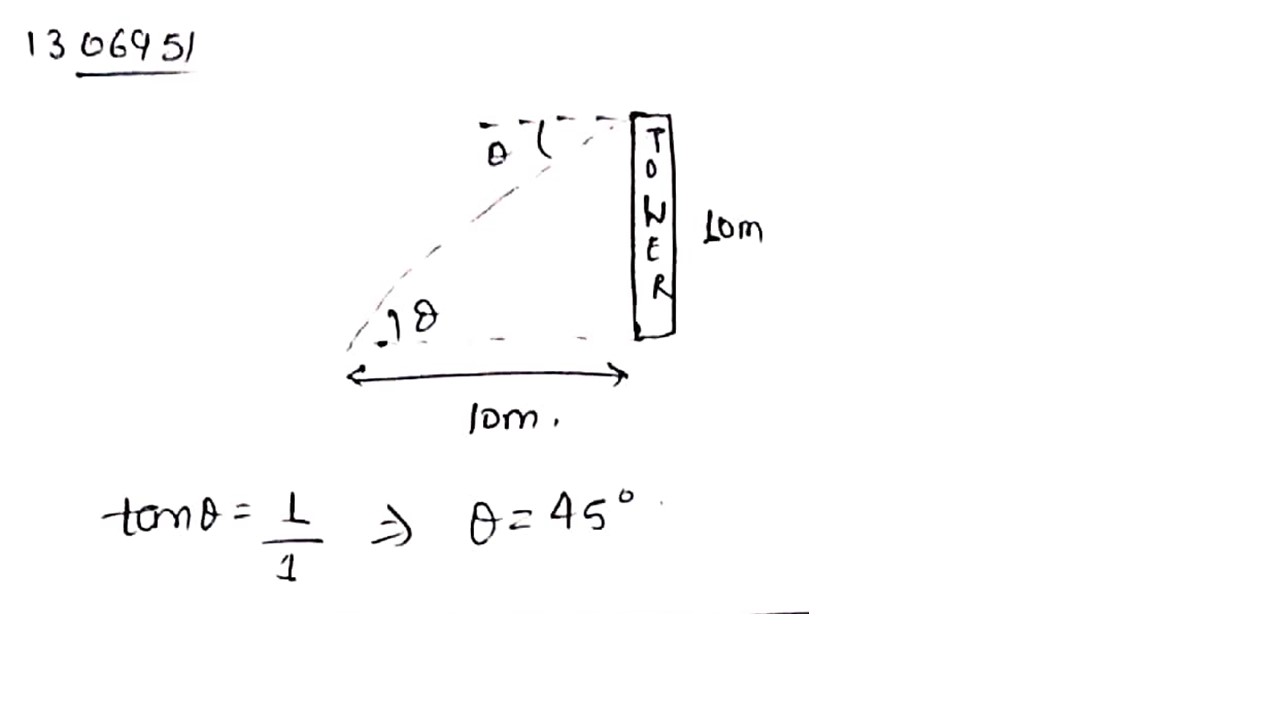
A man standing at a point $$P$$ is watching the top of a tower 10 m in height, which makes an angle of elevation of $$30^o$$ with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation $$45^o$$. What is the distance between the base of the tower and the point $$P$$?
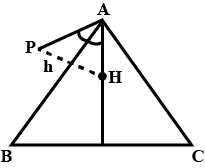
A tower HP standing vertically at the orthocentre H of a triangle ABC subtends an angle A at the vertex A of the triangle. The height of the tower is....
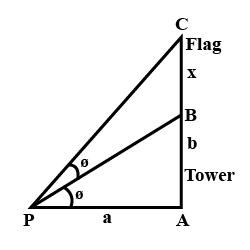
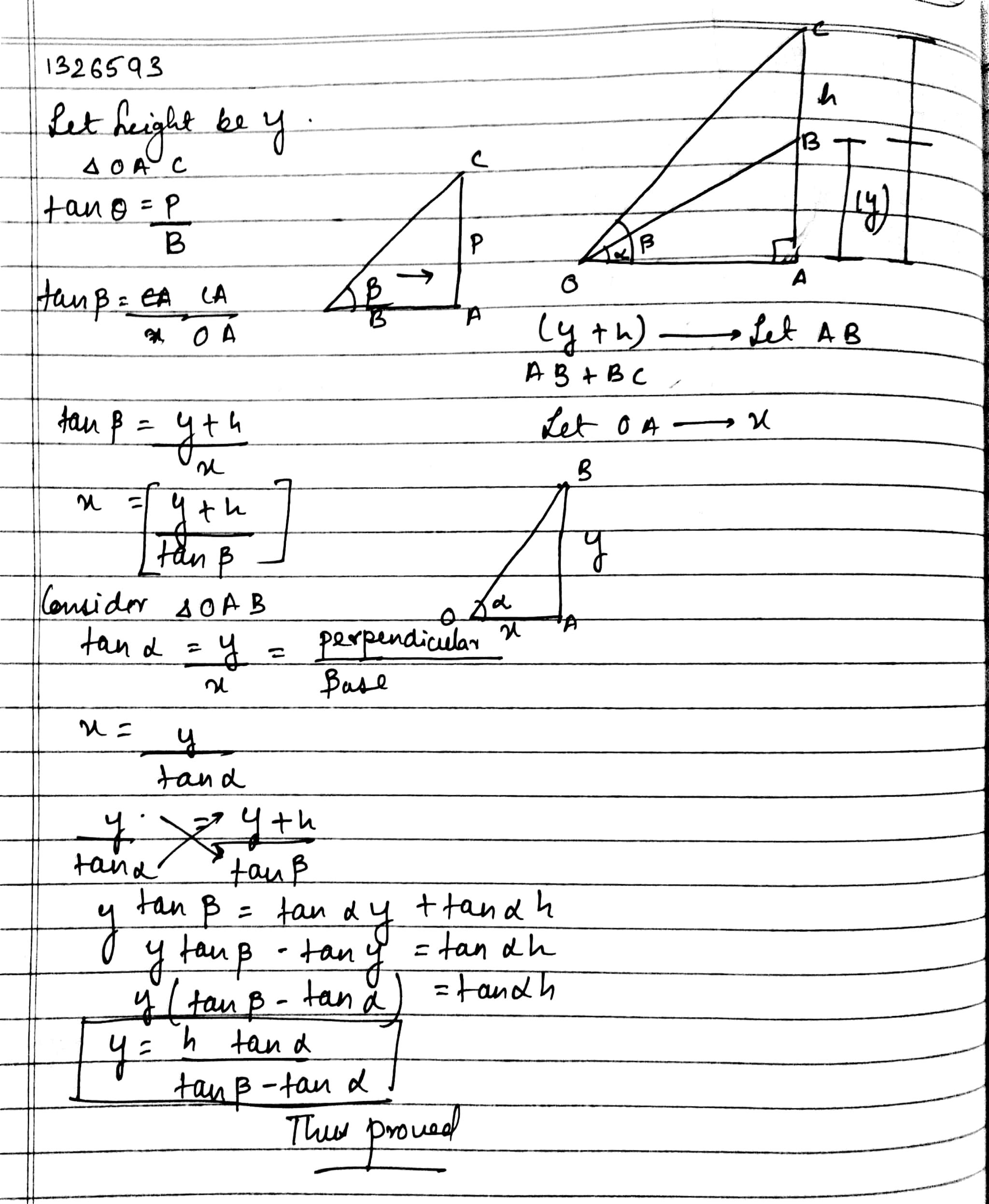
A vertices tower stands on a horizontal plan and is surrounding by a vertices flag staff of a height h . At a point on the plane , the angle of elevation pf the bottom and the top of the flag staff are the $$ \alpha \, and \, \beta $$ respectively. Prove that the height of the tower is $$ \dfrac {h \, \tan \, \alpha }{\tan \, \beta \, - \, \tan \, \alpha } $$
At apoint on the ground yhe angle of elevations of a tower is such that its tangents is $$\dfrac{4}{9}$$. On walking $$60m$$ towards the tower, the tangent of the angle of elevation changes to $$\dfrac{2}{3}$$. find the height of the tower.
$$AB=60$$m $$BC=x$$m (say)
$$\tan { { \theta }_{ 1 } } =\cfrac { h }{ 60+x } =\cfrac { 4 }{ 9 } \quad \quad \Rightarrow 9h=240+4x\quad -(i)\\ \tan { { \theta }_{ 2 } } =\cfrac { h }{ x } =\cfrac { 2 }{ 3 } \quad \Rightarrow 3h=2x\quad -(ii)$$
Using $$(ii)$$ in $$(i)$$ we get
$$9h=240+6h$$
$$ \Rightarrow h=80$$m
$$x=120$$m
$$\therefore$$ Height of the tower is $$80$$m.
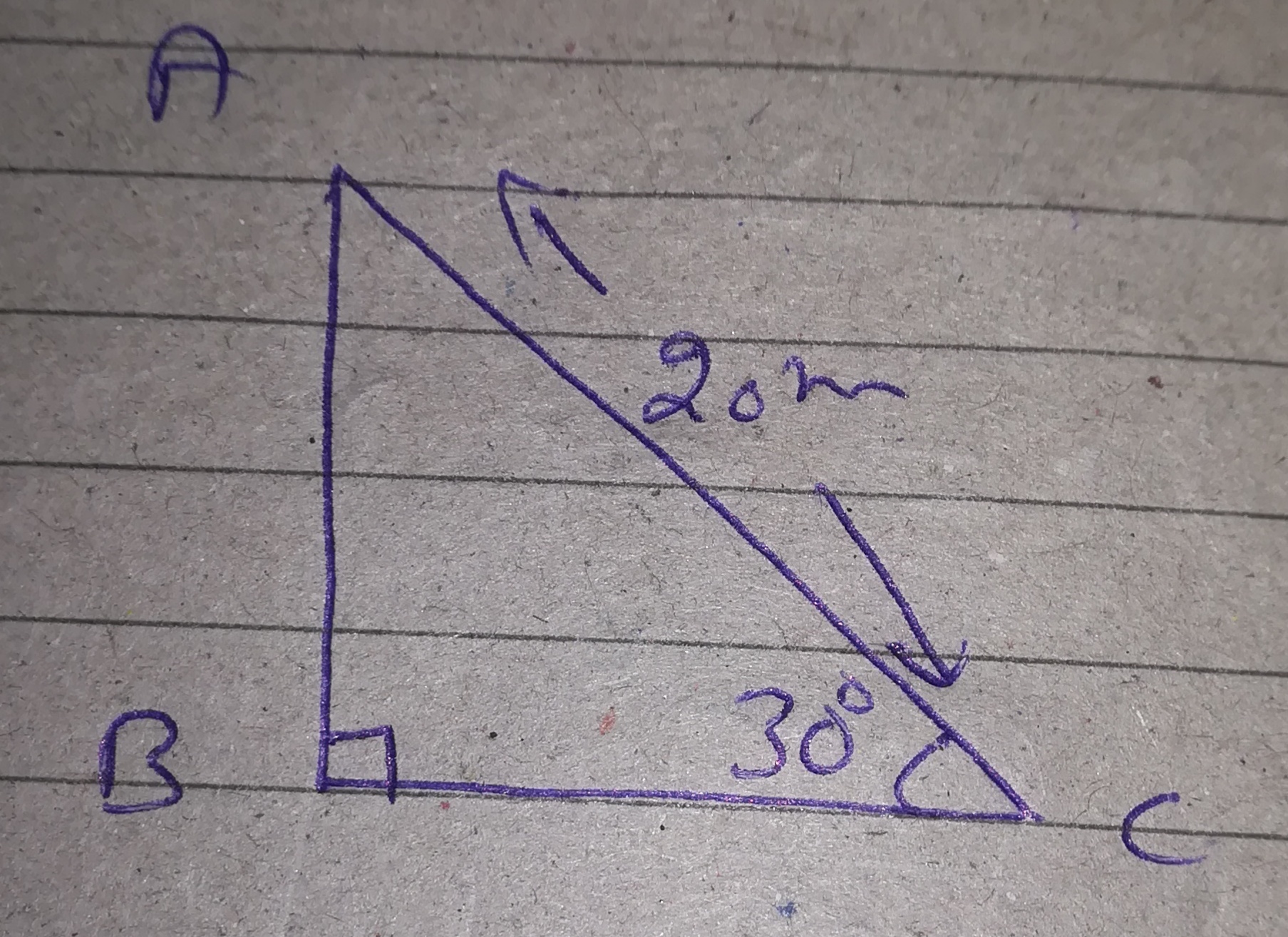
A circuit artist is climbing a $$20\ m$$ long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is $$30^{o}$$.
Let $$AB$$ be the pole and $$Ac$$ be the rope making angle $${30^ \circ }$$
In
I$$\begin{array}{l} \Delta ABC \\ \dfrac { { AB } }{ { AC } } =\sin 30^{ \circ } \\ \Rightarrow \dfrac { { AB } }{ { 20 } } =\dfrac { 1 }{ 2 } \\ \Rightarrow AB=\dfrac { { 20 } }{ 2 } \\ \Rightarrow AB=10m \end{array}$$
Therefore, height of the Pole is $$10 m$$.
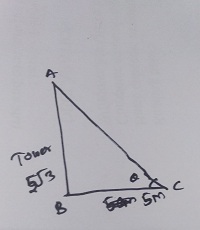
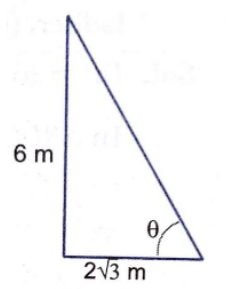
A tower is $$5\sqrt { 3 }$$ meters height. Find the angle of elevation of its top from a point $$5$$ meter away from its foot.
Solution:
$$\tan \theta=\dfrac{opp}{adj}$$
$$\tan \theta=\dfrac{5\sqrt 3}{5}$$
$$\tan \theta=\sqrt 3$$
$$tan {60}^{\circ}=\sqrt 3$$
$$\theta ={60}^{\circ}$$
A vertically straight tree, 15 m high , is broken by the wind in such a way that its top touch the ground and makes an angle of 30$$^{\circ}$$ with the ground . At what height from the ground did the tree break?
Angle ($$ \theta $$) is not given. Incomplete Question. Refer attached image, if angle is given, then height (x) can be determined using below formula:
$$ Sin\theta \quad =\quad \frac { x }{ 15-x } $$
$$ Sin30\quad =\quad \frac { x }{ 15-x } $$
$$\frac{1}{\sqrt{2}}$$ = $$\frac{x}{15-x}$$
X = $$\frac{15}{\sqrt{2}+1}$$
A 1.6 m tall boy spots an object moving with the wind in a horizontal line at a height of 88.6 m from the ground . the angle of elevation reduces to $${30^ \circ }$$ . find the distance travelled by the object during the interval .
The angles of elevation of the top of a tower from two pointsat a distance of $$4m$$ and $$9m$$ from the base of the tower and in the same straight line with it are complementry. Prove that the height of the tower is $$6m$$.
A flag-staff stands on the top of a $$5 m$$ high tower. From a point on the ground, the angle of elevation of the top of the flag-staff is $$60^\circ $$ and from the same point, the angle of elevation of the top of the tower is $$45^\circ $$. Find the height of the flag-staff.
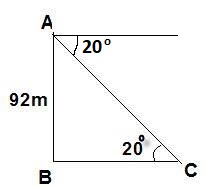
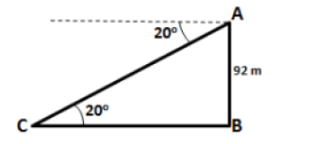
From the top of a cliff of $$92m$$ height, the angle of depression of a buoy is $$20^{\circ}$$. Calculate to the nearest meter, the distance of the buoy from the foot of the cliff. {Use $$\tan 20^o = 0.36 $$}
Let AB be the height of the Cliff and C be the buoy.
$$ \begin{array}{l} \tan { 20^{ \circ } } =\dfrac { { AB } }{ { BC } } =\dfrac { { 92 } }{ x } \\ \\ \Rightarrow 0.36=\dfrac { { 92 } }{ x } \\ \\ x=255.55\, m \end{array}$$
Therefore, the distance of buoy from foot $$=$$ 255.55 m
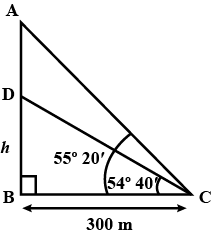
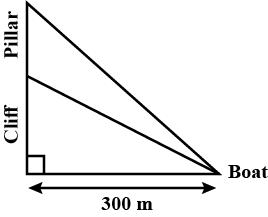
From a boat $$300$$ metres away from a vertical cliff, the angles of elevation of the top and the foot of a vertical concrete pillar at the edge of the cliff are $${55^ \circ } 40'$$ and $${54^ \circ } 20'$$ respectively. Find the height of the pillar correct to the nearest metre.
Let the height of the cliff be $$h$$ metres
and the height of the pillar is $$x$$ metres.
Then, in $$\triangle BDC,$$
$$\tan {54^\circ}20'=\dfrac{BD}{BC}$$
$$\Rightarrow \tan {54^\circ 20'} = \dfrac{h} {300}$$
$$\Rightarrow 1.37 = \dfrac{h }{300}$$
$$ \Rightarrow h = 411\ m$$
Now in $$\triangle ABC,$$
$$\tan {55^0}40' = {\dfrac{x + h}{300}}$$
$$ \Rightarrow 1.42 = {\dfrac {x + 411} {300}}$$
$$ \Rightarrow 426 = x + 411$$
$$ \Rightarrow x = 15$$
Height of pillar $$ = 15\ m$$
From a point on the ground, the angles of elevation of the bottom and the top transmission tower fixed at the top off a $$20\ m$$ high building are $${ 45 }^{ 0 }$$ and $${ 45 }^{ 0 }$$ respectively .Find the height of the tower.
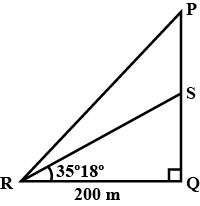
In the given $$\Delta PQR, \angle Q = 90^o. \, S$$ is a point on $$PQ$$ such that $$\angle SRQ= 35^o\, 18^o$$ and $$\angle PRS = 3^o 30^o$$. If $$QR - 200m$$, find the length of $$PS$$.
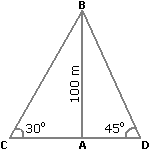
As observed from the top of a light-house, $$100$$ $$m$$ high above sea level, the angle of depression of a ship, sailing directly towards it, changes from $$30 ^ { \circ } $$ to $$60 ^ { \circ }$$ . Determine the distance travelled by the ship during the period of observation.$$(Use \sqrt { 3 } = 1.732 )$$
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is same as the angle of depression from the tree to the man if the height of tree is $$200m$$ find the width of the river .
$$\theta =45^o$$
$$\Rightarrow r=200$$m.
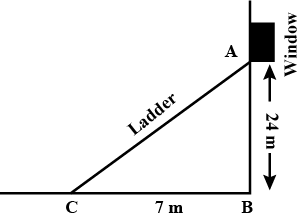
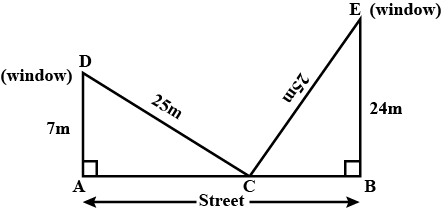
A ladder $$25m$$ long reaches a window which is $$7m$$ above the ground. on one side of the street. Keeping its foot at the same point, the ladder is turned t the other side of the street to reach a window a height of $$24m$$. Find the width (in metre) of the street.
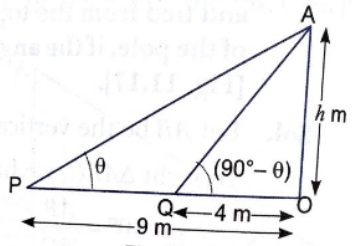
From a point P on level ground, the angle of elevation of the top of a tower is $$30^{0}$$. If the tower is 100 m high, how far is p from the foot of the tower ?
As we know that,
$$\tan{\theta} = \dfrac{\text{Perpendicular}}{\text{Base}}$$
Let $$AB$$ be the tower.Therefore, from fig.,
$$AB = 100 \; m$$
Now,
$$\tan{30°} = \dfrac{AB}{BP}$$
$$\dfrac{1}{\sqrt{3}} = \dfrac{100}{BP}$$
$$\Rightarrow BP = 100 \sqrt{3} = 173.2 \; m \; \left( \because \sqrt{3} = 1.732 \right)$$
Hence the point $$P$$ is $$173.2 \; m$$ away from the foot of tower.
A vertical pole and a vertical tower are on the same level ground. From the top of the pole, the angle of elevation of the top of the tower is $$60^{o}$$ and the angle of depression of the foot of the tower is $$30^{o}$$. Find the height of the tower if the height of the pole is $$20m$$.
REF.Image.
Let AB be the tower & CD be the
pole
As, given in the question BE = 20 m
$$ \therefore $$ In $$ \triangle BCE, tan30^{\circ} = \dfrac{20}{CE}$$
$$ \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{20}{CE}$$
$$ \therefore CE = 20\sqrt{3}$$
Now, in $$ \triangle ACE \,tan60^{\circ} = \dfrac{h}{CE}$$
$$ \sqrt{3} = \dfrac{h}{20\sqrt{3}} \Rightarrow h = 60$$
$$ \therefore $$ Height of tower = 60+20 = 80 m
The height of tower is $$80m$$The angle of elevation from a point $$50m$$ away from tower is
The shadow of a flagpost $$25m$$ height is $$25\sqrt { 3 } m ,$$ find the angle of elevation of the sun.
REF.Image
$$\Delta ABC$$
$$tan \theta =\frac{BC}{AB}$$
$$=\frac{25\sqrt{3}}{25}$$
$$tan\theta =\sqrt{3}$$
$$tan \theta = tan 60^{\circ}$$
$$\theta =60^{\circ}$$
A tower of height $$100$$ as its shadow as $$75$$ cm when the angle of sun rays with ground is.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree . Find the original
Let $$A’CB$$ be the tree before it broken at the point C and let the top $$A'$$ touches the ground at A after it broke$$.$$ Then $$ΔABC$$ is a right angled triangle$$,$$ at $$B.$$
$$AB = 12\ m$$ and $$BC = 5\ m$$
Using Pythagoras theorem$$,$$
In $$ΔABC$$
$$(AC)^2=(AB)^2+(BC)^2$$
$$(AC)^2=(12)^2+(5)^2$$
$$(AC)^2=144+25$$
$$(AC)^2=169$$
$$AC = \sqrt {169}$$
$$AC= 13\ m$$
Hence$$,$$ the total height of the tree$$(A'B)$$ $$= A'C + CB = 13 + 5 = 18 m.$$
a ladder is placed against a well such that it just reaches the top of the wall.the foot of the ladder is 1.5 m metere away from the wall and the ladder is inclined at an angle of$${ 60 }^{ \circ }$$ with the ground .find the height of the wall
The distance of tower and observer is $$40m$$. The angle of elevation is $$30^{\circ}$$ Find the height of the tower.
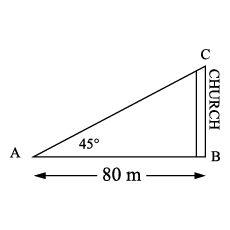
For a person standing at a distance of $$80m$$ from a church. The angle of elevation of its top is of measure $$45 ^ { \circ } .$$ Find the height of the church.
Let $$BC$$ be the height of the church
consider person's height is negligible
In $$ \Delta ABC $$
$$ tan 45^o = \dfrac{BC}{AB} \Rightarrow \dfrac{Perpendicular}{Base}$$
$$ 1 = \dfrac{BC}{80}$$
$$ BC = 80 m $$
The length of the shadow of a tree is $$\sqrt{3}$$ times its height, then find the angle of elevation of the sun at the same time.
R.E.F image
Let AC be tree and AB be its shadow.
Given: AB =$$\sqrt{3}h$$ ---(1)
then,
In $$ \bigtriangleup ABC $$,
$$\frac{AC}{AB}= tan\theta $$
$$\frac{h}{\sqrt{3}h}=tan\theta $$
$$ tan\theta = \frac{1}{\sqrt{3}}\Rightarrow [\theta =30^{\circ}]$$
$$\therefore $$ Angle of elevation of sun is $$ 30^{\circ}$$
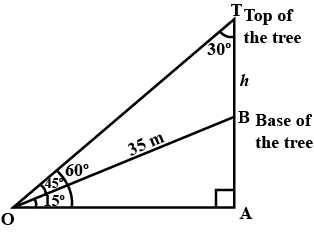
A tree stands vertically on a hill side which makes an angle of $${ 15 }^{ \circ }$$ with the horizontal. From a point on the ground $$35$$ m down the from the base of the tree, the angle of elevation of the tree is $${ 60 }^{ \circ }$$. Find the height of the tree.
In $$\triangle OBT$$
$$\dfrac{h}{\sin 45^o}=\dfrac{35}{\sin 30^o}$$
$$\Rightarrow h=\dfrac{35.\left(\dfrac{1}{\sqrt{2}}\right)}{\dfrac{1}{2}}$$
$$=35\sqrt{2}\ m$$
$$\dfrac{h}{\sin 45^o}=\dfrac{35}{\sin 30^o}$$
$$\Rightarrow h=\dfrac{35.\left(\dfrac{1}{\sqrt{2}}\right)}{\dfrac{1}{2}}$$
$$=35\sqrt{2}\ m$$
Write about angle of elevation.
Surface area of a cone is 188.4 sq cm and its slant heigh is 10 cm. Find its perpendicular height $$(\pi =3.14)$$
An idol $$30 \,m$$ tall stands on a pillar $$15 \,m$$ high. Find the angle in degrees which the idol subtends at a point distant $$15 \sqrt{3} \,m$$ from the base of the pillar.
Let AB be the idol and BC be the pillar
So, $$AB = 30 \,m$$ and $$BC = 15 \,m$$
Distance from the base of pillar $$= 15 \sqrt{3}m$$
Now, In right $$\Delta ACD,$$ we have
$$\tan x = \dfrac{CD}{AC}$$
$$\Rightarrow \tan x = \dfrac{15 \sqrt 3}{30 + 15}$$
$$\Rightarrow \tan x = \dfrac{15\sqrt 3}{45}$$
$$\Rightarrow \tan x = \dfrac{\sqrt 3}{3}$$
$$\Rightarrow \tan x = \dfrac{1}{\sqrt 3}$$
$$\Rightarrow \tan x = \tan 30^\circ$$
$$\Rightarrow x = 30^\circ$$
Hence, the angles subtends from the base of the pillar is $$30^\circ$$
So, $$AB = 30 \,m$$ and $$BC = 15 \,m$$
Distance from the base of pillar $$= 15 \sqrt{3}m$$
Now, In right $$\Delta ACD,$$ we have
$$\tan x = \dfrac{CD}{AC}$$
$$\Rightarrow \tan x = \dfrac{15 \sqrt 3}{30 + 15}$$
$$\Rightarrow \tan x = \dfrac{15\sqrt 3}{45}$$
$$\Rightarrow \tan x = \dfrac{\sqrt 3}{3}$$
$$\Rightarrow \tan x = \dfrac{1}{\sqrt 3}$$
$$\Rightarrow \tan x = \tan 30^\circ$$
$$\Rightarrow x = 30^\circ$$
Hence, the angles subtends from the base of the pillar is $$30^\circ$$
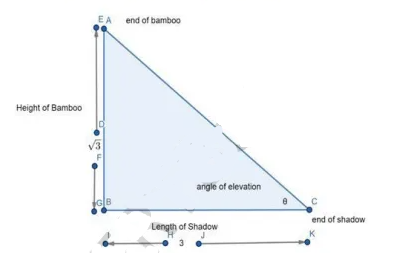
The length of the shadow of a $$\sqrt{3}m$$ high bamboo tree is $$3 \,m,$$ then will be the angle of elevation of the top of the bamboo tree at the end of the shadow.
Drawing the given diagram so that we get a better understanding of the problem,
We have to find the angle of elevation of the end of bamboo from the end of the shadow with the horizontal as the reference line from which the angle is measured.
We know that from trigonometric ratios that,
$$tan\theta = \dfrac{perpendicular}{hypotenuse}$$
Therefore, using this ratio in this problem,
$$tan\theta = \dfrac{perpendicular}{hypotenuse} = \dfrac{AB}{BC}$$
$$tan\theta = \dfrac{height \,of \,bamboo}{length \,of \,shadow} = \dfrac{\sqrt 3}{3} = \dfrac{1}{\sqrt 3}$$
$$\theta = \tan ^{-1}(\dfrac{1}{\sqrt 3})$$
$$\theta = 30^\circ$$
Therefore, the angle of elevation is $$30^\circ.$$
We have to find the angle of elevation of the end of bamboo from the end of the shadow with the horizontal as the reference line from which the angle is measured.
We know that from trigonometric ratios that,
$$tan\theta = \dfrac{perpendicular}{hypotenuse}$$
Therefore, using this ratio in this problem,
$$tan\theta = \dfrac{perpendicular}{hypotenuse} = \dfrac{AB}{BC}$$
$$tan\theta = \dfrac{height \,of \,bamboo}{length \,of \,shadow} = \dfrac{\sqrt 3}{3} = \dfrac{1}{\sqrt 3}$$
$$\theta = \tan ^{-1}(\dfrac{1}{\sqrt 3})$$
$$\theta = 30^\circ$$
Therefore, the angle of elevation is $$30^\circ.$$
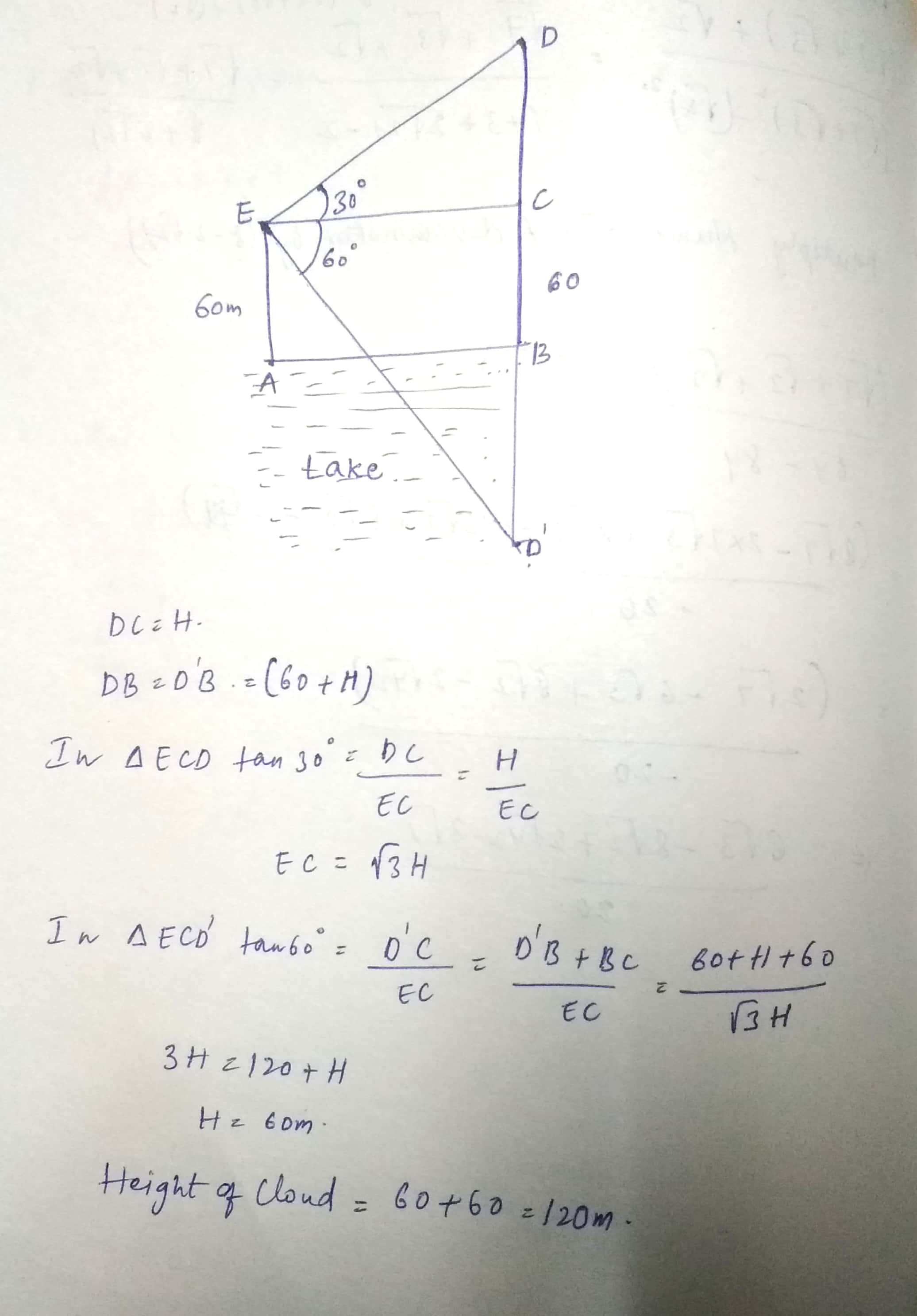
The angle of elevation of a cloud from a point $$P$$, $$60\ m$$ above the surface of a lake is $${ 30 }^{ 0 }$$ and the angle of depression of the reflection of the cloud in the lake at $$P$$ is $${ 60 }^{ 0 }$$. Find the height of the cloud from the surface of the lake.
Let AO= H
CD= OB = 60 m
A'B=AB=(60+H)m
In $$\Delta AOB,tan 30^{\circ}=\frac{OA}{OD}=\frac{H}{OD}$$
$$H=\frac{OD}{\sqrt{3}}, OD =\sqrt{3}H$$
$$\Delta AOD, tan 60^{\circ}=\frac{OA}{OD}=\frac{(OB+BA)}{OD}$$
$$\sqrt{3}=\frac{(60+60+H)}{\sqrt{3}H}\Rightarrow \frac{120 H}{\sqrt{3}H}$$
$$\Rightarrow 1200+H=3H\Rightarrow 2H=120\Rightarrow H=60 m$$
Height of the cloud above the lake = AB+A'B= 60+60 = 120 m
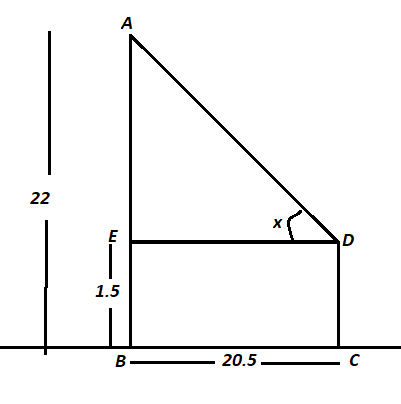
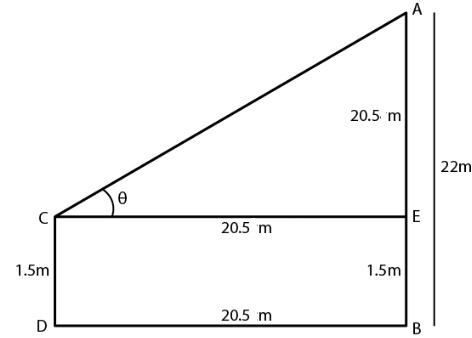
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
As the height of the Observer is $$1.5$$
$$AE=22-1.5=20.5$$
In $$\triangle AED$$
$$\tan\theta=\dfrac{AE}{ED}=\dfrac{20.5}{20.5}=1\Rightarrow \theta=45^o$$
Therefore, answer is $$45^o$$
Find the angle of elevation in degrees of the sun when the shadow of a pole h metres high is $$\sqrt{3} h$$ meters long.
Let opposite to angle $$=$$ $$h$$ ....(pole height)
Adjusted to angle $$=$$ $$h\sqrt{3}$$ ....(length of the shadow)
Hence, $$\tan\theta=\dfrac{h}{h\sqrt{3}}$$
$$\Rightarrow \tan\theta=\dfrac{1}{\sqrt{3}}$$
$$\Rightarrow \theta=30^\circ$$
Adjusted to angle $$=$$ $$h\sqrt{3}$$ ....(length of the shadow)
Hence, $$\tan\theta=\dfrac{h}{h\sqrt{3}}$$
$$\Rightarrow \tan\theta=\dfrac{1}{\sqrt{3}}$$
$$\Rightarrow \theta=30^\circ$$
State true(1) or false(0):If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
The angle of elevation $$\theta$$ can be expressed as $$ \tan { \theta =\cfrac { \text{height of the tower} }{ \text {length of the shadow} } } $$.
$$ \therefore \tan { \theta}$$ will decrease as the length of the shadow increases i.e $$\theta$$ will decrease.
So, the given assertion is false.
The angle of elevation of the top of a tower $$30$$ m high from the foot of another tower in the same plane is $$60^0$$ and the angle of elevation of the top of the second tower from the foot of the first tower is $$30^0$$. Find the height of the other tower.
Let $$h=$$ height of second tower, d=distance between two towers
height of first tower $$=$$ $$30$$ m
From given data,
$$\dfrac{30}{d}=\tan60^\circ=\sqrt{3}$$
$$\dfrac{h}{d}=\tan30^\circ=\dfrac{1}{\sqrt{3}}$$
$$\sqrt{3}h=d,30=d\sqrt{3}$$
$$h=10$$ m, $$d=10\sqrt{3}$$ m
height of first tower $$=$$ $$30$$ m
From given data,
$$\dfrac{30}{d}=\tan60^\circ=\sqrt{3}$$
$$\dfrac{h}{d}=\tan30^\circ=\dfrac{1}{\sqrt{3}}$$
$$\sqrt{3}h=d,30=d\sqrt{3}$$
$$h=10$$ m, $$d=10\sqrt{3}$$ m
Therefore, height of the other tower is $$10$$ m.
The top of a building from a fixed point is observed at an angle of elevation $$60^o$$ and the distance from the foot of the building to the point is $$100\ m$$. The height of the building is $$100\sqrt{a}\ m$$, then
$$ a$$ is _____ .
$$ Let\quad the\quad height\quad of\quad the\quad building\quad be\quad h\quad m.\\ In\quad \triangle ABC,\\ \tan { { 60 }^{ \circ }=\frac { AB }{ BC } } \\ \sqrt { 3 } =\frac { h }{ 100 } \\ h=100\sqrt { 3 } m $$
A vertical pole of height $$5.60\ m$$ casts a shadow of length $$3.20\ m$$ on the horizontal earth surface. Under the similar conditions and at the same time, find the length of the shadow cast by another vertical pole of height $$10.5\ m$$.
For a person standing at a distance of 80 m from a church, the angle of elevation of it stop is of measure $$45^{\circ}$$. Find the height of the church.
The angles of depressions of the top and bottom of $$8\ m$$ tall building from the top of a multistoried building are $$\displaystyle 30^{o} $$ and $$\displaystyle 45^{o} $$ respectively. Find the height of multistoried building and the distance between the two buildings.
Let AB be the multistoried building of height h and let the distance between two buildings be x meters
$$\displaystyle \angle XAC=\angle ACB=45^{\circ}$$ [Alternate angles $$\displaystyle \because$$ AX || DE]
$$\displaystyle \angle XAD=\angle ADE=30^{\circ}$$ [Alternate angles $$\displaystyle \because$$ AX || BC]
In $$\displaystyle \Delta ADE$$
$$\displaystyle \tan 30^{\circ}=\frac{AE}{ED}$$
$$\displaystyle \Rightarrow \frac{1}{\sqrt{3}}=\frac{h-8}{x}$$ ($$\displaystyle \because $$ CB = DE = x)
$$\displaystyle \Rightarrow x=\sqrt{3}\left ( h-8 \right )$$ .......(i)
$$\displaystyle \Delta ACB$$
$$\displaystyle \tan 45^{\circ}=\frac{h}{x}$$
$$\displaystyle \Rightarrow 1=\frac{h}{x}$$
$$\displaystyle \Rightarrow $$ $$x = h$$ .......(ii)
From (i) and (ii)
$$\displaystyle \sqrt{3}\left ( h-8 \right )=h$$
$$\displaystyle \Rightarrow \sqrt{3}h-8\sqrt{3}=h $$
$$\displaystyle \Rightarrow \sqrt{3}h-h=8\sqrt{3} $$
$$\displaystyle \Rightarrow h\left ( \sqrt{3}-1 \right )=8\sqrt{3} $$
$$\displaystyle \Rightarrow h=\frac{8\sqrt{3}}{\sqrt{3}-1}\times \frac{\left ( \sqrt{3}+1 \right )}{\sqrt{3}+1} $$
$$\displaystyle \Rightarrow h=\frac{8\sqrt{3}\left ( \sqrt{3}+1 \right )}{2}$$
$$\displaystyle \Rightarrow h=4\sqrt{3}\left ( \sqrt{3}+1 \right )$$
$$\displaystyle \Rightarrow h=4\left ( 3+\sqrt{3} \right )meters $$
Form (ii) $$x = h$$
So, $$x =$$ $$\displaystyle 4\left ( 3+\sqrt{3} \right )meters $$
Hence, height of multistoried bulding $$=$$ $$\displaystyle 4\left ( 3+\sqrt{3} \right )m $$
Distance between two building $$=$$ $$\displaystyle 4\left ( 3+\sqrt{3} \right )m $$
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of $$\displaystyle 30^{\circ}$$ Another boy is standing on the roof of a 10 m high building and is flying his kite at an elevation of $$\displaystyle 45^{\circ}$$ Both the boys are on opposite sides of both the kites Find the length of the string that the second boy must have so that the two kites meet
Let the length of second string be $$x$$ m
In $$\displaystyle \Delta ABC$$
$$\displaystyle \sin 30^{\circ}=\frac{AC}{AB}$$
$$\displaystyle \frac{1}{2}=\frac{AC}{100}\Rightarrow AC=50m$$
In $$\displaystyle \Delta AEF$$
$$\displaystyle \sin 45^{\circ}=\frac{AF}{AE}$$
$$\displaystyle \frac{1}{\sqrt{2}}=\frac{AC-FC}{x}$$
$$\displaystyle \frac{1}{\sqrt{2}}=\frac{50-10}{x}$$ [$$\displaystyle \because $$ AC = 50 m, FC = ED = 10 m]
$$\displaystyle \frac{1}{\sqrt{2}}=\frac{40}{x} $$
$$x=\displaystyle 40\sqrt{2}$$ m
$$\therefore$$ the length of string that the second boy must have so that the two kites meet = $$\displaystyle 40\sqrt{2}$$ m
If the height of a pole is $$\displaystyle 2\sqrt{3}$$ meters and the length of its shadow is $$2$$ meters, then find the angle of elevation of the sun.
Let A be the pole and AC be its shadow
Let angle of elevation $$\displaystyle \angle ACB=\theta $$
Then $$\displaystyle AB=2\sqrt{3}m,AC=2m$$
$$\displaystyle \tan \theta =\frac{AB}{AC}=\frac{2\sqrt{3}}{2}=\sqrt{3}$$
$$\displaystyle \Rightarrow \theta =60^{0}$$
So the angle of elevation is $$\displaystyle 60^{0}$$
Let angle of elevation $$\displaystyle \angle ACB=\theta $$
Then $$\displaystyle AB=2\sqrt{3}m,AC=2m$$
$$\displaystyle \tan \theta =\frac{AB}{AC}=\frac{2\sqrt{3}}{2}=\sqrt{3}$$
$$\displaystyle \Rightarrow \theta =60^{0}$$
So the angle of elevation is $$\displaystyle 60^{0}$$
The angle of elevation of the top of a tower at a point on the ground is $$\displaystyle 30^{0}$$ On walking $$24$$ m towards the tower, the angle of elevation becomes $$\displaystyle 60^{0}$$ Find the height of the tower
In $$\triangle ABD,$$
$$\displaystyle \frac{AB}{AD}=\tan 60^{0}=\sqrt{3}$$
$$\Rightarrow AD=\dfrac{AB}{\sqrt{3}}=\dfrac{h}{\sqrt{3}}$$
In $$\triangle ABC,$$
$$\displaystyle \frac{AB}{AC}=\tan 30^{0}=\frac{1}{\sqrt{3}}$$
$$\Rightarrow AC=AB\times \sqrt{3}=h\sqrt{3}$$
Now, $$\displaystyle CD=\left ( AC-AD \right )=\left ( h\sqrt{3}-\frac{h}{\sqrt{3}} \right )$$
$$\displaystyle \therefore\ h\sqrt{3}-\frac{h}{\sqrt{3}}=24$$
$$\Rightarrow h=12\sqrt{3}$$
$$=\left ( 12\times 1.73 \right )$$
$$\displaystyle =20.76m$$
Hence the height of the tower is $$20.76\ m$$
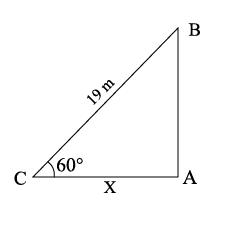
A ladder leaning against a wall makes an angle of $$\displaystyle 60^{0}$$ with the ground.If the length of the ladder is $$19 m$$ ,find the distance of the foot of the ladder from the wall
Let AB be the wall and BC be the ladder
Then $$\displaystyle \angle ACB=60^{0}$$ and $$\displaystyle BC=19m$$
Let $$\displaystyle AC=X$$ meters
$$\displaystyle \frac{AC}{BC}=\cos 60^{0}$$
Then $$\displaystyle \angle ACB=60^{0}$$ and $$\displaystyle BC=19m$$
Let $$\displaystyle AC=X$$ meters
$$\displaystyle \frac{AC}{BC}=\cos 60^{0}$$
$$\Rightarrow \frac{X}{19}=\frac{1}{2}$$
$$\displaystyle \Rightarrow X=\frac{19}{2}=9.5$$
$$\displaystyle \therefore $$ Distance of the foot of the ladder from the wall
$$\displaystyle =9.5m$$
$$\displaystyle \Rightarrow X=\frac{19}{2}=9.5$$
$$\displaystyle \therefore $$ Distance of the foot of the ladder from the wall
$$\displaystyle =9.5m$$
The angles of elevation of the top of a tower from two points at a distance of $$4$$ m and $$9$$ m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is $$6$$ m.
$$\angle C$$ and $$\angle D$$ are complementary .....given
In $$\triangle ABD, \dfrac{AB}{BD}=\tan(90-Q)$$
$$\dfrac{AB}{9}=\cot Q$$ ...(ii)
$$\dfrac{AB}{9}=\dfrac{1}{\tan Q}\quad and \quad \tan Q = \dfrac{7}{AB}$$
Put value of $$\tan Q$$ in eqn (ii)
$$\therefore \dfrac{AB}{BC}=\dfrac{9}{AB}$$
$$AB^2=9BC$$
$$ AB=\sqrt{36}=6$$
Height of tower $$= 6$$m
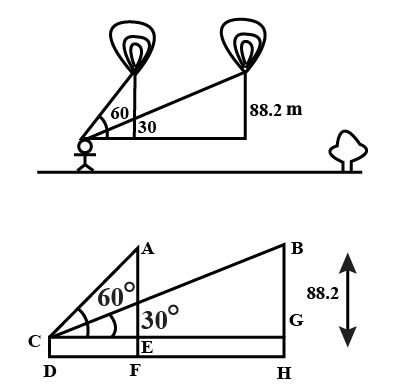
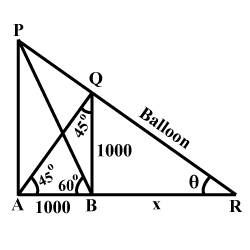
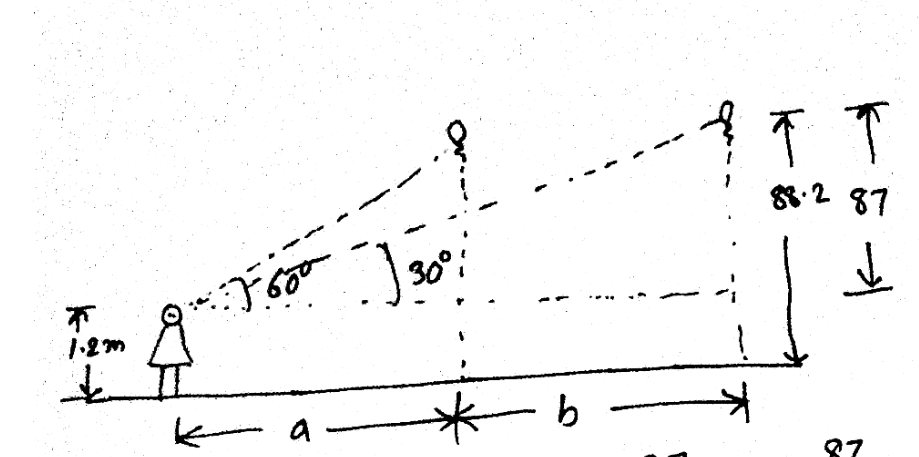
A $$1.2$$ m tall girl spots a balloon moving with the wind in a horizontal line at a height of $$88.2$$ m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is $$\displaystyle { 60 }^{ \circ }$$. After some time, the angle of elevation reduces to $$\displaystyle { 30 }^{ \circ }$$. (see Fig.). Find the distance travelled by the balloon during the interval.
$$\dfrac{88.2-1.2}{CE} = \sqrt{3}$$
$$CE=29\sqrt{3}$$
In $$\triangle BCD , \dfrac{BG}{CG}=\tan30^o$$
$$\dfrac{88.2-1.2}{CG}=\dfrac{1}{\sqrt{3}}$$
$$CG=87\sqrt{3}$$m
Balloon traveled distance $$=EG=GC-EC$$
$$=57\sqrt{3}-22\sqrt{3}$$
$$=58\sqrt{3}$$m
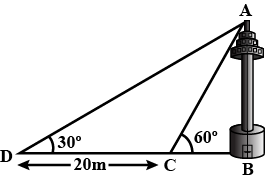
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is $$\displaystyle { 60 }^{ \circ }$$. From another point $$20$$ m away from this point on the line joing this point to the foot of the tower, the angle of elevation of the top of the tower is $$\displaystyle { 30 }^{ \circ }$$ (see Fig.). Find the height of the tower and the width of the canal.
In the figure, let $$AB$$ be the tower and $$AC$$ be the canal. $$C$$ is the point on the other side of the canal directly opposite the tower.
Let $$AB=h, CA=x$$ and $$CD=20$$
From right $$\triangle BAC$$.
$$\cot 60^o=x/h$$
$$1/\sqrt 3=x/h$$
$$x=h/ \sqrt 3$$....(1)
From right $$\triangle BAD$$:
$$\cot 30^o=AD/AB$$
$$\sqrt 3=(x+20)/h$$
$$x=h\sqrt 3 -20$$....(2)
$$h=10\sqrt 3$$
From (1): $$x=(10\sqrt 3)/\sqrt 3=10$$
Therefore, the width of the canal is $$10\ m$$ and height of the canal is $$10\sqrt 3\ m$$.
Let $$AB=h, CA=x$$ and $$CD=20$$
From right $$\triangle BAC$$.
$$\cot 60^o=x/h$$
$$1/\sqrt 3=x/h$$
$$x=h/ \sqrt 3$$....(1)
From right $$\triangle BAD$$:
$$\cot 30^o=AD/AB$$
$$\sqrt 3=(x+20)/h$$
$$x=h\sqrt 3 -20$$....(2)
$$h=10\sqrt 3$$
From (1): $$x=(10\sqrt 3)/\sqrt 3=10$$
Therefore, the width of the canal is $$10\ m$$ and height of the canal is $$10\sqrt 3\ m$$.
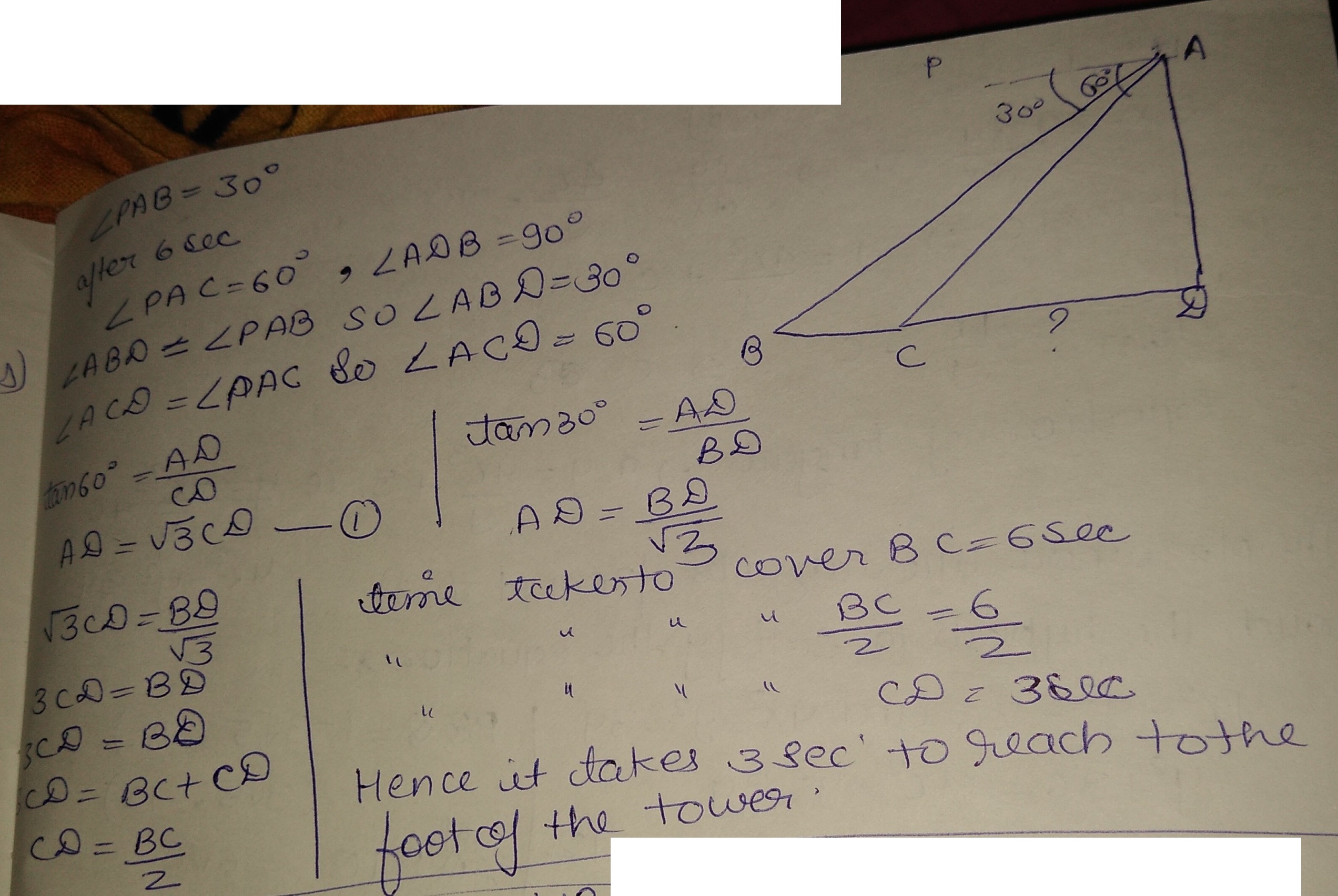
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of $$\displaystyle { 30 }^{ o }$$, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be $$\displaystyle { 60 }^{ o }$$. Find the time taken by the car to reach the foot of the tower from this point.
In $$\triangle ABD, \tan 60=\dfrac{AB}{DB}=\sqrt{3}$$
$$DB=\dfrac{AB}{\sqrt{3}}$$
In $$\triangle ABC, \dfrac{AB}{BC} = \tan 30$$
$$\dfrac{AB}{BD+DC}=\dfrac{1}{\sqrt{3}}$$
$$AB\sqrt{3}=\dfrac{AB}{\sqrt{3}}+DC$$
$$DC=AB\sqrt{3}-\dfrac{AB}{\sqrt{3}}=AD(B-\dfrac{1}{\sqrt{3}})$$
$$DC=\dfrac{2AB}{\sqrt{3}}$$
$$\dfrac{2AB}{\sqrt{3}} = 6$$
Time $$\Rightarrow \dfrac{AB}{\sqrt{3}} = \dfrac{6}{2\dfrac{AB}{\sqrt{3}}}\times \dfrac{AB}{\sqrt{3}}=3 sec.$$
From the top of a $$7$$ m high building, the angle of elevation of the top of a cable tower is $$\displaystyle { 60 }^{ \circ }$$ and the angle of depression of its foot is $$\displaystyle { 45 }^{ \circ }$$. Determine the height of the tower.
$$CD=AB=7\ \text{m}$$ and $$BC=AD$$
In $$\triangle ABC$$,
$$\tan 45^{\circ}=\dfrac {AB}{BC}=\dfrac{CD}{AD}$$
$$BC=7\times 1\ \text{m}$$ $$=AD=7\ \text{m}$$
$$AD=CD=7\ \text{m} $$
In $$\triangle ADE$$,
$$\tan 60^{\circ}=\dfrac{DE}{AD}=\dfrac{DE}{CD}$$
$$DE=7\sqrt{3}\ \text{m}$$
Height of tower $$= EC = DE+CD$$
$$=(7\sqrt{3}+7)\ \text{m}$$
$$=7(\sqrt{3}+1)\ \text{m}$$
As observed from the top of a $$75$$ m high lighthouse from the sea-level, the angles of depression of two ships are $$\displaystyle { 30 }^{ \circ }$$ and $$\displaystyle { 45 }^{ \circ }$$. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
$$\dfrac{AB}{BC} = \tan 45^o, BC=75$$m
In $$\triangle ABD$$,
$$\dfrac{AB}{BD} = \tan 30^o$$
$$\Rightarrow \dfrac{75}{BC+CD}=\dfrac{1}{\sqrt{3}}$$
$$\Rightarrow \dfrac{75}{75+CD}=\dfrac{1}{\sqrt{3}}$$
$$\therefore CD=[75(\sqrt{3}-1)]$$m
The angle of elevation of a tower from a point $$150\text{ m}$$ away from foot of tower is $$60^{\circ}$$. Find the height of tower.
The angle of elevation $$60^{\circ}$$
Distance from tower $$=BC=150\text{ m}$$
Height of tower $$=AB=h$$
Height of tower $$=AB=h$$
$$\tan 60^\circ=\dfrac{AB}{BC}=\dfrac{\text{Height}}{\text{Distance}}\\$$
$$\tan 60^{\circ}=\dfrac{h}{150}\\$$
$$h=\sqrt3\times 150\\$$
$$h=150\sqrt3 \text{ m}$$
Two poles of equal heights are standing opposite each other on either side of the roads, which is $$ 80\ m$$ wide. From a point between them on the road, the angles of elevation of the top of the poles are $$60^o$$ and $$30^o$$ respectively. Find the height of the poles and the distances of the point from the poles.
Let the height of the poles be $$h$$
Then $$AB=ED=h$$
$$BD =80\,m$$ [given]
Let the given point be $$C$$ such that $$BC=x$$ and $$CD =80-x$$
In $$\triangle ABC,$$
$$\tan 30^\circ=\dfrac{AB}{BC}$$
$$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h}{x}$$
$$\Rightarrow x=\sqrt{3}h$$
In $$\triangle ECD,$$
$$\tan 60^{0}=\dfrac{ED}{CD}$$
$$\Rightarrow \sqrt{3}=\dfrac{h}{80-x}$$
$$\Rightarrow h=(80-x)\sqrt{3}$$
Put the value $$x=\sqrt { 3 }h$$
we get $$h=(80-\sqrt{3}h)\sqrt{3}$$
$$\Rightarrow h=80\sqrt{3}-3h$$
$$\Rightarrow 4h=80\sqrt{3}$$
$$\Rightarrow h=20\sqrt{3}$$
Then, height of poles $$\ h=20\sqrt{3}\,m$$
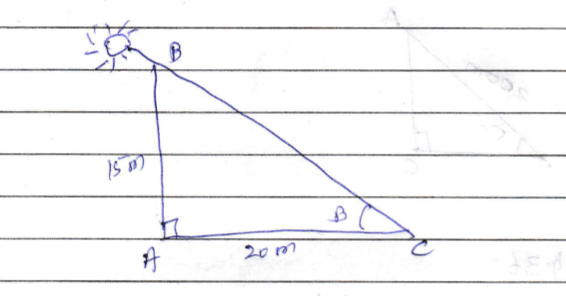
In the following figure, a tower AB is $$20$$ m high and its shadow BC on the ground is $$20 \sqrt{3}$$ m long. Find the distance of the tip of the tower from point $$C$$.
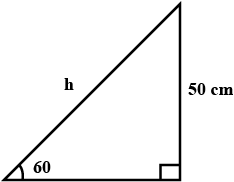
A ladder leaning against a wall makes an angle of $$\displaystyle { 60 }^{ \circ }$$ with the horizontal. If the foot of the ladder is $$2.5$$ m away from the wall, find the length of the ladder.
Let AC be a ladder, AB is the wall and BC is the ground as shown in the figure.
We know that
$$cos 60^o = \dfrac{BC}{AC}$$
$$\dfrac{1}{2}=\dfrac{2.5}{AC}$$
$$AC = 5 \ m$$
Therefore, the length of ladder is $$5 \ m.$$
The angle of elevation from an observer at ground level to a vertically ascending rocket measures $${ 55 }^{ o }$$. If the observer is located $$5$$ miles from the lift-off point of the rocket, what is the altitude of the rocket?
From the top of a building $$50\sqrt{3}m$$ high, the angle of depression of an object on the ground is observed to be $${45}^{o}$$. Find the distance of the object from the building.
Let $$\triangle ABC$$ be a right angled triangle where $$\angle B={ 90 }^{ 0 }$$ and $$\angle DAC={ 45 }^{ 0 }$$ as shown in the above figure.
Let $$x$$ be the distance of object from the building.
Since $$AD||BC$$, therefore,
$$\angle DAC=\angle BCA=45^0$$ (Alternate angles)
We know that $$\tan { \theta } =\dfrac { Opposite\quad side }{ Adjacent\quad side } =\dfrac { AB }{ BC }$$
Here, $$\theta ={ 45 }^{ 0 }$$, $$BC=x$$ m and $$AB=50\sqrt { 3 }$$ m, therefore,
$$\tan { \theta } =\dfrac { AB }{ BC } \\ \Rightarrow \tan { 45^{ 0 } } =\dfrac { 50\sqrt { 3 } }{ x } \\ \Rightarrow 1=\dfrac { 50\sqrt { 3 } }{ x } \quad \quad \quad \quad \quad \quad \left( \because \quad \tan { 45^{ 0 } } =1 \right) \quad \quad \quad \quad \quad \quad \\ \Rightarrow x=50\sqrt { 3 }$$
Hence, the distance of the object from the building is $$50\sqrt { 3 }$$ m.
A boy is standing on the ground and flying a kite with 75 m of string at an elevation of 45$$^o$$. Another boy is standing on the roof of a 25 m high building and is flying his kite at an elevation of 30$$^o$$. Both the boys are on opposite sides of the two kites. Find the length of the string that the second boy must have so that the two kites meet.
Let $$AB$$ be the length of string of first boy's kite and $$AD$$ be the length of string of second boy's kite.
In $$\triangle ADC$$
$$\tan30^o=\dfrac{AC}{CD}$$=>$$\dfrac{AC}{CD}=\dfrac{1}{\sqrt{3}}$$
=>Let $$AC=x, CD=x\sqrt{3}$$
$$AE=AC+CE=x+25$$
In $$\triangle AEB$$
$$\sin45^o=\dfrac{1}{\sqrt{2}}=\dfrac{AE}{AB}$$
=>$$\dfrac{x+25}{75}=\dfrac{1}{\sqrt{2}}$$
=> $$x=\dfrac{75\sqrt{2}-50}{2}=28.03\ m$$
=> $$AC=28.03\ m, CD= 48.54\ m$$
$$AD=\sqrt{AC^2+CD^2}=\sqrt{28.03^2+48.54^2} =\sqrt{785.6809+2356.1316}=\sqrt{3141.8125}=56.05\ m$$
From the top of a building $$50\sqrt { 3 }m$$ high the angle of depression of a car on the ground is observed to be $${ 60 }^{ o }$$. Find the distance of the car from the building.
Let $$QR$$ be the distance of the car from the building.
Now, In $$\triangle PQR$$
$$\Rightarrow \tan { 60° } =\dfrac { PQ }{ QR } =\dfrac { 50\sqrt { 3 } }{ QR } $$
$$\Rightarrow \sqrt { 3 } =\dfrac { 50\sqrt { 3 } }{ QR } $$
$$\Rightarrow QR=50m$$
$$\therefore$$ The car is at $$50m$$ distant from the building.
Hence, the answer is $$50m.$$
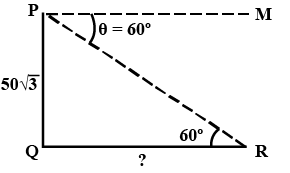
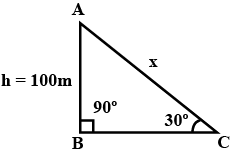
A tower stands vertically on the ground. From a point on the ground, which is $$50 \text{ m}$$ away from the foot of the tower, the angle of elevation to the top of the tower is $${30}^{\circ}$$. Find the height of the tower.
Draw a figure to represent the given information.
Let $$AB$$ be the height $$\left(h\right)$$ of the tower, and $$BC$$ is the distance between the tower and the point of the viewer.
In $$\triangle ABC$$, $$\angle ACB = {30}^{o}$$ $$\tan{\theta} = \dfrac{AB}{BC}$$
$$\tan { { 30 }^{ o } } =\dfrac { h }{ 50 } \Rightarrow \dfrac { 1 }{ \sqrt { 3 } } =\dfrac { h }{ 50 } $$
$$\therefore h=\dfrac { 50 }{ \sqrt { 3 } } \text{m}$$
In $$\triangle ABC$$, $$\angle ACB = {30}^{o}$$ $$\tan{\theta} = \dfrac{AB}{BC}$$
$$\tan { { 30 }^{ o } } =\dfrac { h }{ 50 } \Rightarrow \dfrac { 1 }{ \sqrt { 3 } } =\dfrac { h }{ 50 } $$
$$\therefore h=\dfrac { 50 }{ \sqrt { 3 } } \text{m}$$
A wire extends from the top of a $$50$$ foot vertical pole to a stake in the ground. If the wire makes an angle of $${ 55 }^{ o }$$ with the ground, find the length of the wire.
Find the angle of elevation if an object is at a height of $$50 m$$ on the tower and the distance between the observer and the foot of the tower is $$50 m$$.
Let the angle of elevation be $$'\theta'$$
Now, In $$\triangle ABC,$$
$$\Rightarrow \tan { \theta } =\dfrac { AB }{ BC } =\dfrac { 50 }{ 50 } $$
$$\Rightarrow \tan { \theta } =1$$
$$\therefore \theta = 45°$$
Hence, the answer is $$45°.$$
The angle of elevation of a cliff from a fixed point is $$\theta$$. After going up a distance of k metres towards the top of the cliff at an angle of $$\phi$$, it is found that the angle of elevation is $$\alpha$$. Show that the height of the cliff is
$$\displaystyle \frac{k(cos \phi - sin \phi cot \alpha)}{cot \theta - cot \alpha}$$ metres.
Height of the cliff$$= AB$$
In triangle EFC,
$$EC=k$$
=> $$EF=ksin\phi, CF=kcos\phi=BD$$
In triangle ABC, Let $$AB=x$$
=>$$AC=xcosec\theta ; BC=xcot\theta$$
$$FB= BC-CF= xcot\theta-kcos\phi=ED$$
$$AD=EDtan\alpha=tan\alpha(xcot\theta-kcos\phi)$$
$$AD= AB-BD= x-ksin\phi$$
=>$$tan\alpha=\dfrac{x-ksin\alpha}{xcot\theta-kcos\phi}$$
From the top of lighthouse, an observer looks at a ship and finds the angle of depression to be $$60^\circ$$. If the height of the lighthouse is $$90$$ metres, then find how far is that ship from the lighthouse? $$(\sqrt{3}=1.7.3)$$
Let $$AB = 90\ m$$ represents the height of lighthouse. Point $$C$$ represents the position of the ship.
Draw ray $$AM\, \parallel$$ seg $$BC$$
$$\angle ACB$$ is the angle of depression,
$$\angle MAC = 60^o$$
Also, $$\angle ACB \simeq \angle MAC $$ (Alernate angles)
$$\angle ACB = 60^o$$
Let the distance of ship from the light-house be $$x$$ metres.
In right angled $$\Delta ABC$$,
$$\tan 60^o = \dfrac{90}{x}$$
$$\Rightarrow x = \dfrac{90}{\sqrt 3} \times \dfrac{\sqrt 3}{\sqrt 3}$$
$$= \dfrac{90 \sqrt 3}{3}$$
$$= 30 \sqrt 3$$
$$= 30 \times 1.73 = 51.9$$
$$\therefore$$ Distance of the ship from the lighthouse is $$51.9\ m.$$
Draw ray $$AM\, \parallel$$ seg $$BC$$
$$\angle ACB$$ is the angle of depression,
$$\angle MAC = 60^o$$
Also, $$\angle ACB \simeq \angle MAC $$ (Alernate angles)
$$\angle ACB = 60^o$$
Let the distance of ship from the light-house be $$x$$ metres.
In right angled $$\Delta ABC$$,
$$\tan 60^o = \dfrac{90}{x}$$
$$\Rightarrow x = \dfrac{90}{\sqrt 3} \times \dfrac{\sqrt 3}{\sqrt 3}$$
$$= \dfrac{90 \sqrt 3}{3}$$
$$= 30 \sqrt 3$$
$$= 30 \times 1.73 = 51.9$$
$$\therefore$$ Distance of the ship from the lighthouse is $$51.9\ m.$$
Find the angle of depression if an observer $$150 cm$$ tall looks at the tip of his shadow which is $$150\sqrt{3} cm$$ from his foot.
Let $$\theta$$ be the angle of depression, AB be the height of the observer, CB be the length of the shadow and C be the tip of the shadow.
From the above figure, it is clear that $$BC||AD$$, therefore,
$$\angle DAC=\angle ACB=\theta$$ (Alternate angles)
We know that,
$$\tan { \theta } =\dfrac { AB }{ BC }$$
In $$\triangle ABC,$$ $$\angle B={ 90 }^{ 0 }$$ and $$\angle C=\theta$$.
Here, $$BC=150\sqrt {3}m$$ and $$AB=150m$$, therefore,
$$\tan { \theta } =\dfrac { AB }{ BC } \\ \Rightarrow \tan { \theta } =\dfrac { 150 }{ 150\sqrt { 3 } } \\ \Rightarrow \tan { \theta } =\dfrac { 1 }{ \sqrt { 3 } } \quad \quad \quad \quad \quad \\ \Rightarrow \tan { \theta } =\tan { 30^{ 0 } } \quad \quad \quad \quad \quad \left( \because \quad \tan { 30^{ 0 } } =\dfrac { 1 }{ \sqrt { 3 } } \right) \quad \\ \Rightarrow \theta =30^{ 0 }$$
Hence, the angle of depression is $$30^0$$.
A ship of height $$24 m$$ is sighted from a lighthouse. From the top of the lighthouse, the angles of depression to the top of the mast and base of the ship are $${30}^{o}$$ and $${45}^{o}$$ respectively. How far is the ship from the lighthouse? $$\left(\sqrt{3}=1.73\right)$$
Let $$AB$$ be the lighthouse and $$CD$$ be the ship. Let the height of the lighthouse be '$$h$$' and let the distance from the ship of the lighthouse is '$$x$$' $$m$$. The height of the ship is $$24 m$$. The angle of depression to the top of the mast is $${ 30 }^{ o }$$ and the angle of depression to the base of the ship is $${ 45 }^{ o }$$.
$$CE \perp AB$$.
In $$\Delta ABD$$,
$$\tan { { 45 }^{ o } } =\dfrac { h }{ x }$$
$$1=\dfrac { h }{ x } $$
$$\therefore h=x$$ ....(i)
In $$\Delta AEC$$,
$$\tan { { 30 }^{ o } } =\dfrac { AE }{ EC } =\dfrac { h-24 }{ x } $$
$$\dfrac { 1 }{ \sqrt { 3 } } =\dfrac { h-24 }{ x }$$
$$ h-24=\dfrac { x }{ \sqrt { 3 } }$$ ...(ii)
From equations (i) and (ii), we get
$$x-24=\dfrac { x }{ \sqrt { 3 } } $$
$$x-\dfrac { x }{ \sqrt { 3 } } =24$$
$$\left( \sqrt { 3 } -1 \right) x=24\sqrt { 3 } $$
$$x=\dfrac { 24\sqrt { 3 } }{ \sqrt { 3 } -1 } $$
$$=\dfrac { 24\sqrt { 3 } \left( \sqrt { 3 } +1 \right) }{ \left( \sqrt { 3 } -1 \right) \left( \sqrt { 3 } +1 \right) } $$
$$=\dfrac { 24\left( 3+\sqrt { 3 } \right) }{ 3-1 } $$
$$=12\left( 3+\sqrt { 3 } \right) $$
$$=12\left( 3+1.73 \right) $$
$$=12\times 4.73$$
$$=56.76$$
$$\therefore$$ The ship is at a distance of $$ 56.76m$$ from the lighthouse.
$$CE \perp AB$$.
In $$\Delta ABD$$,
$$\tan { { 45 }^{ o } } =\dfrac { h }{ x }$$
$$1=\dfrac { h }{ x } $$
$$\therefore h=x$$ ....(i)
In $$\Delta AEC$$,
$$\tan { { 30 }^{ o } } =\dfrac { AE }{ EC } =\dfrac { h-24 }{ x } $$
$$\dfrac { 1 }{ \sqrt { 3 } } =\dfrac { h-24 }{ x }$$
$$ h-24=\dfrac { x }{ \sqrt { 3 } }$$ ...(ii)
From equations (i) and (ii), we get
$$x-24=\dfrac { x }{ \sqrt { 3 } } $$
$$x-\dfrac { x }{ \sqrt { 3 } } =24$$
$$\left( \sqrt { 3 } -1 \right) x=24\sqrt { 3 } $$
$$x=\dfrac { 24\sqrt { 3 } }{ \sqrt { 3 } -1 } $$
$$=\dfrac { 24\sqrt { 3 } \left( \sqrt { 3 } +1 \right) }{ \left( \sqrt { 3 } -1 \right) \left( \sqrt { 3 } +1 \right) } $$
$$=\dfrac { 24\left( 3+\sqrt { 3 } \right) }{ 3-1 } $$
$$=12\left( 3+\sqrt { 3 } \right) $$
$$=12\left( 3+1.73 \right) $$
$$=12\times 4.73$$
$$=56.76$$
$$\therefore$$ The ship is at a distance of $$ 56.76m$$ from the lighthouse.
A person standing at a distance of $$80$$ m away from a church making the angle of elevation with its top is $${45}^{o}$$. Find the height of the church.
Let, $$ab$$ be the height of the church.
Given, $$\angle acb={ 45 }^{ o },bc=80\ m$$Let the height of the church be $$x$$ metres.
$$\therefore$$ $$ab=x$$ metres
In right angled $$\triangle {abc}$$, we have,
$$\tan { { 45 }^{ o } } =\cfrac { ab }{ bc } $$
$$\Rightarrow 1=\cfrac{x}{80}$$
$$\Rightarrow$$ $$x=80$$
Thus, the height of the church is $$80\ m$$.
Find the angular elevation (angle of elevation from the ground level) of the sun when the length of the shadow of a $$30$$ m long pole is $$10\sqrt { 3 } $$ m.
Two men on either side of a temple of $$30\ m$$ height observe its top at the angles of elevation $${30}^{\circ}$$ and $${60}^{\circ}$$ respectively. Find the distance between the two men.
Let $$AB$$ be the height of the temple and $$P$$ and $$Q$$ are the two men on either side of the temple.
Given that,
$$AB=30\ m$$, $$\angle APB={30}^{\circ}, \angle AQB={60}^{\circ}$$
In $$\triangle ABP,$$
$$\tan(\angle APB)=\dfrac{AB}{PB}$$
$$\tan{30}^{\circ}=\dfrac{30\ m}{PB}$$
$$PB=30\sqrt{3}\ m$$
In $$\triangle ABP,$$
$$\tan(\angle AQB)=\dfrac{AB}{QB}$$
$$\tan{60}^{\circ}=\dfrac{30\ m}{QB}$$
$$QB=\dfrac{30}{\sqrt{3}\ m}$$
$$QB=10\sqrt{3}\ m$$
Now, $$PQ = PB + QB = 30\sqrt{3}\ m + 10\sqrt3\ m $$
So, $$PQ=40\sqrt3\ m$$
Therefore, distance between two men, i.e. $$PQ=40\sqrt3\ m$$
A body observed the top of an electric pole at an angle of elevation of $${60}^{\circ}$$, when the observation point is $$8$$ metres away from the foot of the pole. Find the height of the pole.
Let $$PQ$$ be the electric pole.
Angle of elevation $$=\angle QOP={60}^{\circ}$$
In right angle $$\triangle PQO,$$
$${\tan}{(\angle QOP)}=\dfrac {PQ}{QO}$$
or, $${\tan}\,{60}^{\circ}=\dfrac{PQ}{8\,m}$$
or, $$PQ=8\times \sqrt{3}\,m$$
or, $$PQ=13.86\, m$$
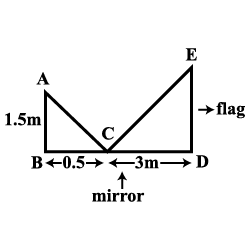
A student wants to determine the height of a flagpole. He placed a small mirror on the ground so that he can see the reflection of the top of the flagpole. The distance of the mirror from him is $$0.5\ m$$ and the distance of the flagpole from the mirror is $$3\ m$$. If his eyes are $$1.5\ m$$ above the ground level, then find the height of the flagpole. (The foot of student, mirror and the foot of flagpole lie along a straight line)
Let $$C$$ is point of reflection in $$\triangle ABC$$ and $$\triangle EDC$$
$$\angle ABC = \angle EDC (90^{\circ})$$
$$\angle ACB = \angle ECD$$ (reflexive angle)
By $$AA$$ symmetry
$$\triangle ABC \sim \triangle EDC$$
$$\dfrac {AB}{ED} = \dfrac {BC}{DC}$$
$$\dfrac {1.5\times 3}{0.5} = ED$$
$$ED = 9$$
So height of pole is $$9\ m$$
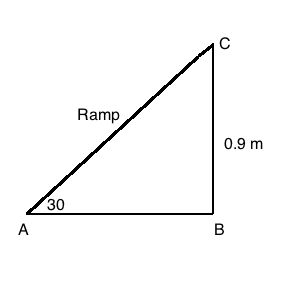
A ramp for unloading a moving truck has an angle of elevation of $$30^{\circ}$$. If the top of the ramp is $$0.9\ m$$ above the ground level, then find the length of the ramp.
From diagram
we have to find AC.
Since, ABC is right angled triangle.
$$\Rightarrow \dfrac{BC}{AC}=\sin 30^0$$
$$\Rightarrow \dfrac{0.9}{AC}=0.5$$
$$\Rightarrow AC=\dfrac{0.9}{0.5}$$
$$\Rightarrow AC=1.8 $$m
we have to find AC.
Since, ABC is right angled triangle.
$$\Rightarrow \dfrac{BC}{AC}=\sin 30^0$$
$$\Rightarrow \dfrac{0.9}{AC}=0.5$$
$$\Rightarrow AC=\dfrac{0.9}{0.5}$$
$$\Rightarrow AC=1.8 $$m
A ladder leaning against a vertical wall makes an angle of $${60}^{o}$$ with the ground. The foot of the ladder is $$3.5$$ m away from the wall. Find the length of the ladder.
Let $$AB$$ be the length of the ladder and $$CA$$ be the wall.
The ladder makes an angle of $${60}^{\circ}$$ with the horizontal.
$$\therefore\,\triangle{ABC}$$ is $${30}^{\circ}-{60}^{\circ}-{90}^{\circ}$$ ,right triangle
We have $$\tan{{60}^{\circ}}=\dfrac{AC}{BC}$$
$$\Rightarrow\,AC=3.5\times \tan{{60}^{\circ}}$$
$$\Rightarrow\,AC=3.5\times \sqrt{3}$$m
From Pythagoras theorem, we have
$${AB}^{2}={BC}^{2}+{CA}^{2}$$
$$\Rightarrow\,{AB}^{2}={\left(3.5\right)}^{2}+{\left(3.5\times \sqrt{3}\right)}^{2}$$
$$\Rightarrow\,{AB}^{2}=12.25+36.75$$
$$\Rightarrow\,{AB}^{2}=49$$
$$\therefore\,AB=7m$$
Hence,length of the ladder$$=7m$$
The upper part of a tree, broken by wind in two parts, makes an angle of $$30^{\circ}$$ with the ground. The top of the tree touches the ground at a distance of $$20\ \text{m}$$ from the foot of the tree. Find the height of the tree before it was broken
Let $$AC$$ is the broken part of the tree and $$AB$$ is standing part.
Given that:
$$BC=20\ \text{m}$$ and $$\angle ACB={30}^{\circ}$$
Solution:
In $$\triangle ABC$$
$$\tan (\angle ACB)=\cfrac{AB}{BC}$$
or, $$\tan {30}^{\circ}=\cfrac {AB}{20\ \text{m}}$$
or, $$AB=20\ \text{m}\times\cfrac1{\sqrt3}=\cfrac{20}{\sqrt3} \text{m}$$
Similarly,
$$\cos {30}^{\circ}=\cfrac{BC}{AC}$$
or, $$AC=\cfrac{20\ \text{m}}{\cos {30}^{\circ}}$$
or, $$AC=\cfrac{20\ \text{m}\times2}{\sqrt3}$$
or, $$AC=\cfrac{40}{\sqrt3} \text{m}$$
Total length of the tree $$=AB+AC=\cfrac{20}{\sqrt3} \text{m}+\cfrac{40}{\sqrt3} \text{m}=\cfrac{60}{\sqrt3} \text{m}=20\sqrt3 \text{ m}$$
Therefore, total length of the tree$$ =20\sqrt3\ \text{m}=34.64\ \text{m}$$
Length of the shadow of a $$15$$ meter high pole is $$5\sqrt{3}$$ meters at 7'o clock in the morning. Then what is the angle of elevation of the Sun rays with the ground at that time?
Length of pole is $$XY=15\ m$$
Shadow of pole is $$=YZ=5\sqrt { 3 } $$
angle of elevation of sun with ground is $$\phi $$ as shown in figure.
Here in a right angled triangle,
$$\tan(90^\circ-\phi )=\cfrac { YZ }{ XY } =\cfrac { 5\sqrt { 3 } }{ 15 } =\cfrac { 1 }{ \sqrt { 3 } } \\ \Rightarrow\tan(90^{ \circ }-\phi )=\dfrac { 1 }{ \sqrt { 3 } } \\ \Rightarrow 90^\circ - \phi = 60^\circ\\ \Rightarrow \phi =30^\circ$$
Elevation is $$30^\circ$$
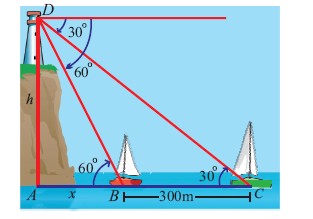
A girl standing on a lighthouse built on a cliff near the seashore, observes two boats due East of the lighthouse. The angles of depression of the two boats are $$30^{\circ}$$ and $$60^{\circ}$$. The distance between the boats is 300 m. Find the distance of the top of the lighthouse from the sea level. (Boats and foot of the lighthouse are in a straight line.)
Let $$A$$ and $$D$$ denote the foot of the cliff and the top of the lighthouse respectively.
Let $$B$$ and $$C$$ denote the two boats.
Let $$h$$ metres be the distance of the top of the lighthouse from the sea level.
Let $$AB=x$$ metres.
Given that $$\angle ABD=60^{\circ},\angle ACD=30^{\circ}$$
In the right angled $$\bigtriangleup ABD$$,
Let $$B$$ and $$C$$ denote the two boats.
Let $$h$$ metres be the distance of the top of the lighthouse from the sea level.
Let $$AB=x$$ metres.
Given that $$\angle ABD=60^{\circ},\angle ACD=30^{\circ}$$
In the right angled $$\bigtriangleup ABD$$,
$$\displaystyle \tan60^{\circ}=\frac{AD}{AB}$$
$$\displaystyle \Rightarrow AB=\frac{AD}{\tan60^{\circ}}$$
Thus, $$\displaystyle x=\frac{h}{\sqrt{3}}$$ ..........(1)
Also, in the right angled $$\bigtriangleup ACD$$, we have
$$\displaystyle \tan30^{\circ}=\frac{AD}{AC}$$
$$\displaystyle \Rightarrow AC=\frac{AD}{\tan30^{\circ}}\Rightarrow x+300=\frac{h}{\left ( \frac{1}{\sqrt{3}} \right )}$$
Thus, $$\displaystyle x+300=h\sqrt{3}$$ ........ (2)
Using (1) in (2), we get:
$$\displaystyle \frac{h}{\sqrt{3}}+300=h\sqrt{3}$$
$$\Rightarrow h\sqrt{3}-\frac{h}{\sqrt{3}}=300$$
$$\therefore 2h=300\sqrt{3}$$.
$$\therefore \ h=150\sqrt{3}\ m$$.
Hence, the height of the lighthouse from the sea level is $$150\sqrt{3}\ m$$.
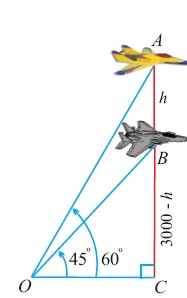
A jet fighter at a height of $$3000$$ m from the ground, passes directly over another jet fighter at an instance when their angles of elevation from the same observation point are $$60^{\circ}$$ and $$45^{\circ}$$ respectively. Find the distance of the first jet fighter from the second jet at that instant. $$(\sqrt{3}=1.732)$$
Let $$O$$ be the point of observation.
Let $$A$$ and $$B$$ be the positions of the two jet fighters at the given instant when one is directly above the other.
Let $$C$$ be the point on the ground such that $$AC=3000m$$.
Given: $$\angle AOC=60^{\circ}$$ and $$\angle BOC=45^{\circ}$$
Let $$h$$ denote the distance between the jets at the instant.
Therefore, $$BC=3000-h$$.
In the right angled $$\displaystyle \bigtriangleup BOC$$,
$$\tan 45^{\circ}=\frac{BC}{OC}$$
$$\Rightarrow OC=BC $$ $$(\because\tan 45^{\circ}=1)$$
Thus, $$OC=3000-h$$ .....(1)
In the right angled $$\displaystyle \bigtriangleup AOC , $$
$$\tan 60^{\circ}=\frac{AC}{OC}$$
$$\displaystyle \Rightarrow OC=\frac{AC}{\tan 60^{\circ}}=\frac{3000}{\sqrt{3}}$$
$$\displaystyle =\frac{3000}{\sqrt{3}}\times\frac{\sqrt{3}}{\sqrt{3}}=1000\sqrt{3}$$ ...... (2)
From (1) and (2), we get,
$$3000-h =1000\sqrt{3}$$
$$\Rightarrow h=3000-1000\times 1.732=1268$$m
The distance of the first jet fighter from the second jet at that instant is $$1268$$ m.
The angle of elevation of the a tower as seen by an observer is $$30^{\circ}$$. The observer is at a distance of $$30\sqrt{3}$$m from the tower. If the eye level of the observer is $$1.5$$ m above the ground level, then find the height of the tower.
Let $$BD$$ be the height of the tower and $$AE$$ be the distance of the eye level of the observer from the ground level.
Draw $$EC$$ parallel to $$AB$$ such that $$AB=EC$$.
Given $$AB=EC=30\sqrt{3}\text{ m}$$ and $$AE=BC=1.5\text{ m}$$
In right angled $$\bigtriangleup DEC$$,
$$\displaystyle \tan30^{\circ}=\frac{CD}{EC}$$
$$\displaystyle \Rightarrow CD=EC\tan 30^{\circ}=\frac{30\sqrt{3}}{\sqrt{3}}$$
$$\therefore CD=30\text{ m}$$
Thus, the height of the tower, $$BD=BC+CD$$
$$=1.5+30=31.5\text{ m}$$.
The angle of elevation of an aeroplane from a point $$A$$ on the ground is $$60^{\circ}$$. After a flight of $$15$$ seconds horizontally, the angle of elevation changes to $$30^{\circ}$$. If the aeroplane is flying at a speed of $$200$$ m/s, then find the constant height at which the aeroplane is flying.
Let $$A$$ be the point of observation.
Let $$E$$ and $$D$$ be positions of the aeroplane initially and after $$15$$ seconds respectively.
Let $$BE$$ and $$CD$$ denote the constant height at which the aeroplane is flying.
Given that $$\angle DAC=30^{\circ}, \angle EAB=60^{\circ} $$.
Let $$BE=CD=h$$ metres.
The distance covered in $$15$$ seconds,
$$ED=200\times15=3000$$m ( distance travelled = speed $$\times$$ time )
Thus, $$BC=3000$$m.
In the right angled $$\bigtriangleup DAC$$,
$$\displaystyle \tan30^{\circ}=\frac{CD}{AC}$$
$$\Rightarrow CD=AC\tan30^{\circ}$$
Thus, $$\displaystyle h=\left ( x+3000 \right )\frac{1}{\sqrt{3}}$$. (1)
In the right angled $$\bigtriangleup EAB$$,
$$\displaystyle \tan60^{\circ}=\frac{BE}{AB}$$
$$\Rightarrow BE=AB\tan60^{\circ}\Rightarrow h=\sqrt{3}x$$ (2)
From (1) and (2), we have $$\displaystyle \Rightarrow \sqrt{3}x=\frac{1}{\sqrt{3}}\left ( x+3000 \right )$$
$$\Rightarrow 3x=x+3000\Rightarrow x=1500$$.
Thus, from (2) it follows that $$h=1500\sqrt{3}$$m.
The constant height at which the aeroplane is flying, is $$1500\sqrt{3}m$$.
Let $$E$$ and $$D$$ be positions of the aeroplane initially and after $$15$$ seconds respectively.
Let $$BE$$ and $$CD$$ denote the constant height at which the aeroplane is flying.
Given that $$\angle DAC=30^{\circ}, \angle EAB=60^{\circ} $$.
Let $$BE=CD=h$$ metres.
The distance covered in $$15$$ seconds,
$$ED=200\times15=3000$$m ( distance travelled = speed $$\times$$ time )
Thus, $$BC=3000$$m.
In the right angled $$\bigtriangleup DAC$$,
$$\displaystyle \tan30^{\circ}=\frac{CD}{AC}$$
$$\Rightarrow CD=AC\tan30^{\circ}$$
Thus, $$\displaystyle h=\left ( x+3000 \right )\frac{1}{\sqrt{3}}$$. (1)
In the right angled $$\bigtriangleup EAB$$,
$$\displaystyle \tan60^{\circ}=\frac{BE}{AB}$$
$$\Rightarrow BE=AB\tan60^{\circ}\Rightarrow h=\sqrt{3}x$$ (2)
From (1) and (2), we have $$\displaystyle \Rightarrow \sqrt{3}x=\frac{1}{\sqrt{3}}\left ( x+3000 \right )$$
$$\Rightarrow 3x=x+3000\Rightarrow x=1500$$.
Thus, from (2) it follows that $$h=1500\sqrt{3}$$m.
The constant height at which the aeroplane is flying, is $$1500\sqrt{3}m$$.
The angle of elevation of the top of a hill from the foot of a tower is $$60^{\circ}$$ and the angle of elevation of the top of the tower from the foot of the hill is $$30^{\circ}$$. If the tower is $$50$$m high, then find the height of the hill.
Let $$AD$$ be the height of tower and $$BC$$ be the height of the hill.
Given $$\angle CAB = 60^{\circ}, \angle ABD=30^{\circ}$$ and $$AD=50$$m.
Let $$BC=h$$ metres.
Now, in the right angled $$\displaystyle \bigtriangleup DAB, \tan 30^{\circ}=\frac{AD}{AB}$$
$$\displaystyle \Rightarrow AB=\frac{AD}{\tan30^{\circ}}$$
$$\therefore AB=50\sqrt{3}$$m (1)
Also, in the right angled $$\displaystyle \bigtriangleup CAB, \tan 60^{\circ}=\frac{BC}{AB}$$
$$\Rightarrow BC=AB\tan 60^{\circ}$$
Thus, using (1) we get $$ h=BC=(50\sqrt{3})\sqrt{3}=150$$m
Hence, the height of the hill is $$150$$m.
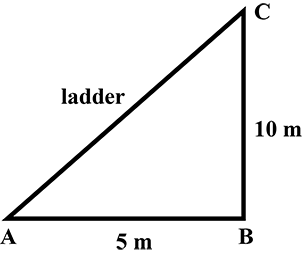
A ladder is at a distance of $$5m$$ from the foot of the wall and it touches a window which is at a height of $$10$$ from the ground then find the length of ladder.
$$In:\triangle ABC$$, side $$BC$$ represents the vertical distance of window from base and $$AC$$ represents the ladder.
Given :
$$BC=10m$$
$$AB=5m$$
To find: $$AC$$
Now, $$In:\triangle ABC$$, we have
$${ AB }^{ 2 }+{ BC }^{ 2 }={ AC }^{ 2 }$$ (using pythagoras theorem)
$${ 5 }^{ 2 }+{ 10 }^{ 2 }={ AC }^{ 2 }$$
$${ AC }^{ 2 }=25+100\\=125$$
$$\Rightarrow AC=5\sqrt { 5 } m$$
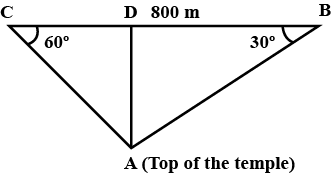
A bridge across a valley is $$800$$ metres long. There is a temple in the valley directly below the bridge. The angle of depression of the top of the temple from the two ends of the bridge have measure 30$$^o$$ and 60$$^o$$.
Find the height of the bridge above the top of the temple.
In the above figure, $$BC$$ represents the length of the bridge.
$$AD = h$$
Let $$CD = x, BD = 800 - x$$
In $$\Delta ADC$$,
$$\tan 60^o = \dfrac{AD}{CD}$$
$$\therefore \tan 60^o = \dfrac{h}{x}$$
$$\therefore \sqrt 3 = \dfrac{h}{x}$$
$$\therefore x = \dfrac{h}{\sqrt 3}$$ ......... $$(i)$$
In $$\Delta ADB$$,
$$\tan 30^o = \dfrac{AD}{BD}$$
$$\therefore \tan 30^o = \dfrac{h}{800 - x}$$
$$\therefore \dfrac{1}{\sqrt 3} = \dfrac{h}{800 - x}$$
$$\therefore 800 - x = h \sqrt 3$$
$$\therefore x = 800 - h \sqrt 3$$ ....... $$(ii)$$
From $$(i)$$ and $$(ii)$$,
$$\therefore \dfrac{h}{\sqrt 3} = 800 - h \sqrt 3$$
$$\therefore h = 800 \sqrt 3 - 3h$$
$$\therefore 4h = 800 \sqrt 3$$
$$\therefore h = 200 \sqrt 3$$
$$\therefore$$ Height of the bridge above the temple $$= 200 \sqrt 3m$$
From the top of a tower, the angle of depression of the top and bottom of a multistoreyed building are 30$$^o$$ and 60$$^o$$ respectively. If the height of the building is 100m. Find the height of a tower.
Let $$AC = h$$ be the height of the tower.
and $$ED$$ be the multi-storeyed building, where $$ED = 100m$$
So, $$ED = BC = 100 m$$
So, $$AB = (h - 100) m$$
In $$\Delta ABE$$,
$$tan 30^o = \dfrac{AB}{EB}$$
$$\Rightarrow \dfrac{1}{\sqrt 3} = \dfrac{h - 100}{EB}$$
$$\Rightarrow EB = \sqrt 3 (h - 100)$$ .... (i)
So, $$DC = EB = \sqrt 3 (h - 100)$$
In $$\Delta ADC$$,
$$tan 60^o = \dfrac{AC}{DC}$$
$$= \sqrt 3 = \dfrac{h}{\sqrt 3 (h - 100)}$$
$$\Rightarrow 3(h - 100) = h$$
$$\Rightarrow 3h - 300 = h$$
$$\Rightarrow 2h = 300$$
$$\Rightarrow h = 150 \ metres$$
Thus, the height of the tower is $$150 \ m.$$
and $$ED$$ be the multi-storeyed building, where $$ED = 100m$$
So, $$ED = BC = 100 m$$
So, $$AB = (h - 100) m$$
In $$\Delta ABE$$,
$$tan 30^o = \dfrac{AB}{EB}$$
$$\Rightarrow \dfrac{1}{\sqrt 3} = \dfrac{h - 100}{EB}$$
$$\Rightarrow EB = \sqrt 3 (h - 100)$$ .... (i)
So, $$DC = EB = \sqrt 3 (h - 100)$$
In $$\Delta ADC$$,
$$tan 60^o = \dfrac{AC}{DC}$$
$$= \sqrt 3 = \dfrac{h}{\sqrt 3 (h - 100)}$$
$$\Rightarrow 3(h - 100) = h$$
$$\Rightarrow 3h - 300 = h$$
$$\Rightarrow 2h = 300$$
$$\Rightarrow h = 150 \ metres$$
Thus, the height of the tower is $$150 \ m.$$
A vertical tower stands on a horizontal plane and is surmounted by a flag-staff of height $$7m$$ from a point on the plane, the angle of elevation of the bottom and the top of flag-staff are $${30}^{o}$$ and $${45}^{o}$$ respectively. Find the height of the tower.
$$In \triangle OBA$$,
$$\tan { 30^o } =\dfrac { x }{ OA } $$
$$OA=\sqrt { 3 } x$$
$$In \triangle OCA$$,
$$\tan { 45^o } =\dfrac { x+7 }{ OA } =\dfrac { x+7 }{ \sqrt { 3 } x } $$
$$\sqrt { 3 } x=x+7$$
$$x=\dfrac { 7 }{ \sqrt { 3 } -1 } $$m is the height of tower
If a tower $$30\ m$$ high, cause a shadow $$10\sqrt{3}\ m$$ long on the ground, then what is the angle of elevation of the sun?
Let $$AB$$ be the height of the tower
and $$BC$$ be the length of its shadow on the ground.
Let, $$\theta$$ is the angle of elevation.
so, $$\angle ACB=\theta$$
From $$\triangle ABC$$,
$$\Rightarrow \tan\theta =\dfrac{AB}{BC} $$
$$\Rightarrow \tan\theta= \dfrac{30}{10\sqrt{3}}$$
$$\Rightarrow \tan\theta = \sqrt{3}$$
$$\Rightarrow \tan\theta = \tan 60^o$$
$$\Rightarrow \theta = 60^o$$
Hence, the angle of elevation of the sun is $$60^o$$.
A man observed from the top of the electric pole, the angle of depression of a point on the ground is $${60}^{o}$$. If the distance of a point from the foot of the electric pole is $$25m$$, then find the height of the electric pole.
Let $$AB$$ be the pole, $$C$$ be the point from where the man observes the pole.
In $$\triangle ABC, \angle B = 90^\circ$$
$$\tan { 60 } =\dfrac { AB }{ BC } $$
$$=\dfrac { AB }{ 25 } $$
$$AB=25\sqrt { 3 } m$$
Therefore height of the pole $$= 25\sqrt { 3 } m$$
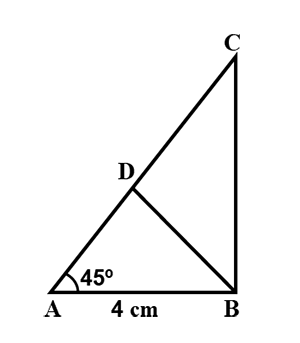
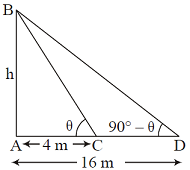
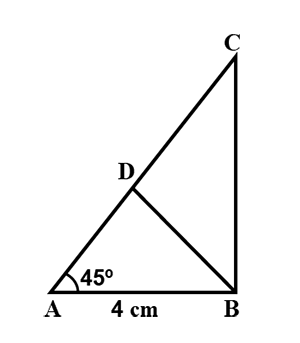
In the figure $$ABC$$ is a right angled triangle, $$AB = 4cm, \angle A = 45^{\circ}$$ and $$D$$ is midpoint of $$AC$$.Then find the length of $$BC, AC$$ and $$BD$$.
From the figure, we have
$$\cos 45^{\circ} = \dfrac {AB}{AC}$$
$$\Rightarrow AC = \dfrac {AB}{\cos 45^{\circ}} = \dfrac {4}{1\sqrt {2}} = 4\sqrt {2}cm$$
Now, $$\sin 45^{\circ} = \dfrac {BC}{AC}$$
$$\Rightarrow BC = AC \times \sin 45^{\circ} = 4\sqrt {2}\times \dfrac {1}{\sqrt {2}} = 4\ cm$$
Also, $$\sin 45^{\circ} = \dfrac {BD}{AB}$$
$$\Rightarrow BD = AB \times \sin 45^{\circ} = 4\times \dfrac {1}{\sqrt {2}} = 2\sqrt {2} cm$$.
$$\cos 45^{\circ} = \dfrac {AB}{AC}$$
$$\Rightarrow AC = \dfrac {AB}{\cos 45^{\circ}} = \dfrac {4}{1\sqrt {2}} = 4\sqrt {2}cm$$
Now, $$\sin 45^{\circ} = \dfrac {BC}{AC}$$
$$\Rightarrow BC = AC \times \sin 45^{\circ} = 4\sqrt {2}\times \dfrac {1}{\sqrt {2}} = 4\ cm$$
Also, $$\sin 45^{\circ} = \dfrac {BD}{AB}$$
$$\Rightarrow BD = AB \times \sin 45^{\circ} = 4\times \dfrac {1}{\sqrt {2}} = 2\sqrt {2} cm$$.
The angles of the depression from the top of a $$60\ m$$ high building to the base and top of a tower are $$45^{\circ}$$ and $$30^{\circ}$$ respectively. Find the height of the tower.
$$AB\to $$ Building $$\to $$ som
$$DC\to $$ Towen $$\to $$?
In $$\triangle ABC$$
$$\dfrac {AB}{BC}=\tan 45=1$$
$$\Rightarrow \ BC=60\ m\quad (ED=BC\Rightarrow ED=60\ m)$$
In $$\triangle AED$$
$$\dfrac {AE}{ED}=\tan 30=\dfrac {1}{\sqrt 3}$$
$$\Rightarrow \ AE=30\sqrt 3\ m$$
$$DC=AB-AE$$
$$=60-30\sqrt 3$$
$$=30(2-\sqrt 3)m$$
A tower is standing on one side of a road of $$12m$$ breadth and a house is on the other side of it. From the foot of the house the angle of elevation of the top of tower is $${60}^{o}$$ and from the top of the tower the angle of depression of the top of house is $${45}^{o}$$. Find the heights of the tower and the house.
From the figure,
Let CE be the house and AD be the tower,
Given Angle of elevation $$=\angle AED = 60^\circ$$, angle of depression $$\angle CAF=\angle ACB=45^\circ$$(alt angle)
Now, In $$\triangle ABC$$,
$$tan 45^\circ=\dfrac{AB}{BC} = \dfrac{AB}{12}$$
$$ \implies 1= \dfrac{AB}{12}$$ [$$\because tan \space 45^\circ=1]$$
$$\implies AB=12 m$$
In $$\triangle ADE$$,
$$ tan \space 60^\circ=\dfrac{AD}{DE}$$
$$\implies \sqrt{3}=\dfrac{AD}{12}$$ [$$tan\space 60^\circ=\sqrt3]$$
$$\implies AD=12 \sqrt3$$
$$= 12\times 1.73=20.76m$$
$$\therefore$$ Height of tower = $$20.76 m$$
Height of house= $$AD-AB=BD=CE=$$
$$=20.76-12=8.76m$$
A $$1.6\ m$$ tall girl stands at a distance of $$3.2\ m$$ from a lamp-post and casts a shadow of $$4.8\ m$$ on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
$$(i)$$ Using trigonometric ratios.
Let $$AB$$ be the height of lamp post.
Now, in right $$\triangle CDE, $$
$$\Rightarrow \tan { \theta } =\dfrac { ED }{ DC } =\dfrac { 1.6 }{ 4.8 } =\dfrac { 1 }{ 3 }\longrightarrow \left( 1 \right) $$
In , $$\triangle ACB,$$
$$\Rightarrow \tan { \theta } =\dfrac { AB }{ BC } =\dfrac { AB }{ 3.2+4.8 } =\dfrac { AB }{ 8 } \longrightarrow \left( 2 \right) $$
From $$(1)\;\&\;(2)$$ we get
$$\Rightarrow \dfrac{1}{3}=\dfrac{AB}{8}$$
$$\Rightarrow AB=\dfrac{8}{3}=2.67m$$
$$\therefore $$ Height of the lamp post $$=2.67m$$
$$(ii)$$ Using similar triangles :
In $$\triangle CDE\;\&\;\triangle CBA$$
$$i)\angle CDE=\angle CBA=90°$$
$$ii)\angle DCE=\angle BCA$$ (Common)
$$\therefore \triangle CDE\sim \triangle CBA$$ ( By AA similarities )
Hence, $$\dfrac { DE }{ AB } =\dfrac { CD }{ BC } $$
$$\Rightarrow AB=\dfrac{DE\times BC}{CD}$$
$$=\dfrac{1.6\times 8 }{4.8}$$
$$=\dfrac{8}{3}$$
$$=2.67m$$
$$\therefore$$ Height of lamp post $$=2.67m.$$
Hence, the answer is $$2.67.$$
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complimentary. Prove that the height of the tower is 6 m.
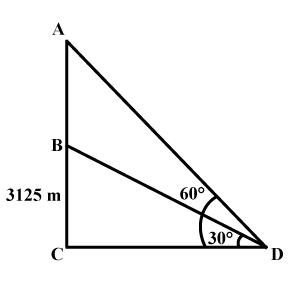
An aeroplane when flying at a height of $$3125\ m$$ from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are $$30^{o}$$ and $$60^{o}$$ respectively. Find the distance between the two planes at that instant.
In $$\triangle BCD,$$
$$\Rightarrow \tan { 30° } =\dfrac { BC }{ CD } =\dfrac { 3125 }{ CD } $$
$$\Rightarrow \dfrac { 1 }{ \sqrt { 3 } } =\dfrac { 3125 }{ CD } $$
$$\Rightarrow CD=3125\sqrt { 3 } m\longrightarrow \left( 1 \right) $$
In $$\triangle ADC,$$
$$\Rightarrow \tan { 60° } =\dfrac { AC }{ CD } =\dfrac { AB+BC }{ CD } $$
$$\Rightarrow \sqrt { 3 } =\dfrac { AB+3125 }{ CD } $$
$$\Rightarrow CD=\dfrac { AB+3125 }{ \sqrt { 3 } } \longrightarrow \left( 2 \right) $$
From $$(1)\;\&\;(2)$$ we get
$$\Rightarrow 3125\sqrt { 3 } =\dfrac { \left( AB+3125 \right) }{ \sqrt { 3 } } $$
$$\Rightarrow AB=\left( 3125\times 3 \right) -3125$$
$$\Rightarrow AB=3125\times 2$$
$$\Rightarrow AB=6250m$$
$$\therefore$$ Distance between the two planes is $$6250m$$
Hence, the answer is $$6250.$$
A girl of height $$90 \text{ cm}$$ is walking away from the base of a lamp-post at a speed at $$1.2\text{ m/sec}$$. If the lamp is $$3.6 \text{ m}$$ above the ground, find the length of her shadow after $$4$$ seconds.
Given,
- Girl is walking away from the base of the lamp-post and let the girl be at point D after $$4$$ seconds
- speed $$=1.2\text{ m/sec}$$
- time $$=4\text{ sec}$$
$$\text{speed}=\dfrac{\text{distance}}{\text{time}}$$
$$\implies 1.2=\dfrac{\text{distance}}{4}$$
$$\implies \text{distance}=AD=12\times 4=4.8\text{ m}$$
Consider $$\triangle ABC$$ and $$\triangle DBE$$
$$\angle CAB=\angle EDB=90^{\circ}$$
$$\angle CBA=\angle EDB$$ (common angle)
So by $$AA$$ similarity, $$\triangle ABC\sim \triangle DBE$$
Hence, $$\dfrac{AC}{DE}=\dfrac{AB}{DB}$$
$$\implies \dfrac{AC}{DE}=\dfrac{AD+DB}{DB}$$
$$\implies \dfrac{3.6}{0.9}=\dfrac{4.8+DB}{DB}$$
$$\implies 4DB=4.8+DB$$
$$\implies 3DB=4.8$$
$$\implies DB=1.6$$
Hence the length of the shadow $$1.6\text{ m}$$
An electric pole is $$10$$ m high. A steel wire tied to top of the pole is affixed at a point on the ground to keep the pole up right. If the wire makes an angle of $$45^o$$ with the horizontal through the foot of the pole, find the length of the wire.
Let $$AB=10=$$ Height of Pole
and $$AD $$ be the length of the wire
From $$\triangle ABD$$
$$\sin 45^o=\dfrac{AB}{AD}\Rightarrow \dfrac{1}{\sqrt2}=\dfrac{10}{AD}\Rightarrow AD=10\sqrt2$$
$$\Rightarrow 10\times1.414 \ $$ $$ (Take \sqrt2=1.414) $$
$$=14.14\ m$$
A vertical stick of length 6 m casts a shadow 4 m long on the ground and the same time a tower casts a shadow 28 m long. Find the height of the tower.
Length of shadow of vertical stick $$=4m$$
Length of shadow of tower $$=28m$$
Considering $$\triangle ABC$$ and $$\triangle DEF$$
$$\angle ABC=\angle DEF=90^{\circ}$$
$$\angle ACB=\angle DFE$$ (angle of elevation same as shadows casted at same time)
So by $$AA$$, $$\triangle ABC\sim \triangle DEF$$
Hence $$\dfrac{AB}{BC}=\dfrac{DE}{EF}$$
$$\dfrac{6}{4}=\dfrac{DE}{28}$$
$$DE=7\times 6$$
$$DE=42m$$
So, Height of the tower $$ =42m$$
A vertical stick $$10$$ cm long casts a shadow $$8$$ cm long. At the same time, a tower long casts a shadow $$30$$ cm long. Determine the height of the tower.
Let the height of the tower be $$x\,cm$$
Since the two triangles are similar by $$AA$$ similarity criterion, we have
$$\Rightarrow$$ $$\dfrac{x}{10}=\dfrac{30}{8}$$
$$\therefore$$ $$x=\dfrac{30\times 10}{8}$$
$$\therefore$$ $$x=37.5\,cm$$
Hence, the height of the tower be $$37.5\,cm$$
The angle of elevation of a ladder leaning against a wall is $$60^o$$ and the foot of the ladder is $$9.5$$ m away from the wall. Find the length of the ladder.
Here, $$AC$$ is a length of ladder.
$$\Rightarrow$$ $$BC=9.5\,m$$
$$\Rightarrow$$ Now, $$\cos\,60^o=\dfrac{BC}{AC}$$ [ $$\cos\theta=\dfrac{Adjacent\,side}{Hypotenuse}$$ ]
$$\Rightarrow$$ $$\dfrac{1}{2}=\dfrac{9.5}{AC}$$
$$\therefore$$ $$AC=9.5\times 2$$
$$\therefore$$ $$AC=19\,m$$
$$\therefore$$ Length of the ladder is $$19\,m$$.
A guy-wire attached to a vertical pole of height $$18$$ m is $$24$$ m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so the wire will be tight?
Let $$AB$$ be the pole and $$AC$$ be the wire.
By Pythagoras theorem,
$$AC^2 = AB^2 + BC^2$$
$$(24)^2 = (18)^2 + (BC)^2$$
$$(BC)^2 = 576 - 324$$
$$(BC)^2 = 252$$
$$BC = 6\sqrt{7}m$$
Therefore, the distance from the base is $$6\sqrt{7}m$$
A tower stands vertically one the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is $$60^o$$. What is the height of the tower?
Here, $$AB$$ is the height of a tower.
$$\Rightarrow$$ $$CB=20\,m$$
$$\Rightarrow$$ Now, $$\tan\,60^o=\dfrac{AB}{CB}$$
$$\Rightarrow$$ $$\sqrt{3}=\dfrac{AB}{20}$$
$$\therefore$$ $$AB=20\sqrt{3}\,m$$
$$\therefore$$ Height of a tower is $$20\sqrt{3}\,m$$.
The horizontal distance between two trees of different height is $$60$$ m. The angle of depression of the top of the first tree when seen from the top of the second tree is $$45^\circ$$. If the height of the second tree is $$80$$ m, find the length of the first tree.
Let $$AE$$ be the height of first tree and $$BD$$ be the height of second tree.
$$\Rightarrow\ AE=CB$$ and $$AB=EC=60\ m$$
$$\Rightarrow$$ In $$\triangle DEC,\,\tan\,45^\circ=\dfrac{DC}{EC}$$
$$\Rightarrow$$ $$1=\dfrac{DC}{60}$$
$$\therefore$$ $$DC=60\,m$$
Now,
$$\Rightarrow$$ $$DB=DC+CB$$
$$\Rightarrow$$ $$80=60+CB$$
$$\therefore$$ $$CB=20\,m$$
Hence $$AE=20\,m$$
$$\Rightarrow$$ Length of the first tree is $$20\,m$$
An aeroplane flying horizontal $$1$$ km above the ground is observed at an elevation of $$60^\circ$$. After $$10$$ seconds, its elevation is observed to be $$30^\circ$$. Find the speed of the aeroplane in km/hr.
Let $$AC$$ be the height of the aeroplane above the ground
$$\tan\,60^\circ=\dfrac{AC}{BC}$$
$$\Rightarrow$$ $$\sqrt{3}=\dfrac{1}{x}$$
$$\therefore$$ $$x=\dfrac{1}{\sqrt{3}}$$ $$...(1)$$
Now, In $$\triangle BED,$$
$$\tan\,30^o=\dfrac{ED}{BD}$$
$$\Rightarrow$$ $$\dfrac{1}{\sqrt{3}}=\dfrac{1}{x+y}$$
$$\Rightarrow$$ $$1=\dfrac{\sqrt{3}}{\dfrac{1}{\sqrt{3}}+y}$$ [From $$( 1 )$$]
$$\Rightarrow$$ $$\dfrac{1}{\sqrt{3}}+y=\sqrt{3}$$
$$\therefore$$ $$y=\dfrac{2}{\sqrt{3}}\ km$$
$$\Rightarrow$$ $$\mathrm{Speed}=\dfrac{\mathrm{Distance}}{\mathrm{Time}}$$
$$=\dfrac{\dfrac{2}{\sqrt{3}}\ km}{10\ \mathrm{seconds}}$$
$$=\dfrac{\dfrac{2}{\sqrt 3}\ km}{\dfrac{10}{60\times 60}\ hr}$$
$$=\dfrac{2\times 60\times 60}{10 \times \sqrt 3}$$
$$=\dfrac{720}{\sqrt{3}}$$ $$(\mathrm{Take}\ \sqrt3=1.73)$$
$$=415.69\,\dfrac{km}{hr}$$
There are two temples, one on each bank of a river, just opposite to each other. One temple is $$50$$ m high. From the top of this temple, the angle of depression of the top and the foot of the other temple are $$30^0$$ and $$60^0$$ respectively. Find the width of the river and the height of the other temple.
$$AB=50\,m$$
$$\Rightarrow$$ In $$\triangle ABC,\,\tan\,60^o=\dfrac{AB}{BC}$$
$$\Rightarrow$$ $$\sqrt{3}=\dfrac{50}{BC}$$
$$\Rightarrow$$ $$BC=\dfrac{50}{\sqrt{3}}=\dfrac{50\sqrt{3}}{3}=28.867\,m$$ $$(Take \sqrt3=1.73)$$
$$\Rightarrow$$ In $$\triangle AED,\,\tan\,30^o=\dfrac{AE}{ED}$$
$$\Rightarrow$$ $$\dfrac{1}{\sqrt{3}}=\dfrac{AB-BE}{BC}=\dfrac{AB-DC}{BC}$$
$$\therefore$$ $$\dfrac{1}{\sqrt{3}}=\dfrac{50-DC}{\dfrac{50}{\sqrt{3}}}$$
$$\therefore$$ $$\dfrac{50}{3}=50-DC$$
$$\Rightarrow$$ $$DC=50-\dfrac{50}{3}=\dfrac{150-50}{3}=\dfrac{100}{3}=33.33\,m$$
$$\therefore$$ The width of the river is $$28.867\,m$$ and height of the temple is $$33.33\,m$$
A kite is flying at a height of $$75$$ meters from the ground level, attached to a string inclined at $$60^o$$ to the horizontal. Find the length of the string nearest to the ground.
Let $$AB=75=$$ Height of Pole
and $$AD $$ be the length of the wire
From $$\triangle ABD$$
$$\sin 60^o=\dfrac{AB}{AD}\Rightarrow \dfrac{\sqrt3}{2}=\dfrac{75}{AD}\Rightarrow AD=\dfrac{150}{\sqrt3}$$
and $$AD $$ be the length of the wire
From $$\triangle ABD$$
$$\sin 60^o=\dfrac{AB}{AD}\Rightarrow \dfrac{\sqrt3}{2}=\dfrac{75}{AD}\Rightarrow AD=\dfrac{150}{\sqrt3}$$
$$\Rightarrow \dfrac{150} {1.73}$$ $$(Take \sqrt3=1.73$$)
$$=86.6 \ m$$
From the top of a $$50$$ m high tower, the angles of depression of the top and bottom of a pole are observed to be $$45^\circ$$ and $$60^\circ$$ respectively. Find the height of the pole.
In $$\triangle CDB$$, $$\tan\,60^o=\dfrac{CD}{BC}$$
$$\sqrt{3}=\dfrac{50}{BC}$$
$$BC=\dfrac{50}{\sqrt{3}}\,m$$
$$AE=BC$$
$$\therefore$$ $$AE=\dfrac{50}{\sqrt{3}}m$$
In $$\triangle ADE,\,\tan\,45^o=\dfrac{DE}{AE}$$
$$\Rightarrow$$ $$1=\dfrac{DE}{\dfrac{50}{\sqrt{3}}}$$
$$\therefore$$ $$DE=\dfrac{50}{\sqrt{3}}m$$
$$\therefore$$ Height of the pole is $$\dfrac{50}{\sqrt{3}}m$$
The length of a string between a kite and a point on the ground is $$90$$ meters. If the string makes an angles $$\theta$$ with the ground level such that $$\tan \theta = \dfrac{15}{8}$$, how high is the kite? Assume that there is no slack in the string.
Let the length of the String be $$AD$$
and $$AB$$ be the Height
In $$\triangle ABD$$
$$\tan \theta=\dfrac{AB}{BD}\Rightarrow \dfrac{15}{8}=\dfrac{AB}{BD}$$
$$\Rightarrow AB=\dfrac{15}{8}BD..................(1)$$
Also applying Pythagoras Theorem
$$AB^2+BD^2=AD^2$$
$$\Rightarrow \dfrac{225}{64}BD^2+BD^2=90^2$$
$$\Rightarrow \dfrac{289}{64}BD^2=8100$$
$$\Rightarrow \dfrac{17}{8}BD=90\Rightarrow BD=42.35$$
Now, from $$(1)$$
$$AB=\dfrac{15}{8}\times42.35=79.40$$
A vertical tower stands on a horizontal plane is surmounted by a vertical flagstaff. At a point on the plane $$70$$ meters away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively $$60^o$$ and $$45^o$$. Find the height of the flagstaff and that of the tower.
Given that the distance of the observer from the Tower $$=x=70 \ m$$
Now, Let the Height of the Tower be $$q$$
and Height of Flagstaff be $$p$$
From $$\triangle ABC$$
$$\tan 60^o=\dfrac{p+q}{70}\Rightarrow p+q=70\sqrt3..........(1)$$
and
From $$\triangle DBC$$
$$\tan 45^o=\dfrac{q}{70}\Rightarrow q=70................(2)$$
From (1) and (2)
$$p+70=70\sqrt3$$
$$\Rightarrow p=70(\sqrt3-1)=51.24\ m$$ $$(Take \sqrt3=1.73)$$
Therefore, Height of Tower $$=70\ m$$
and Height of Flagstaff $$=51.24\ m$$
The angle of elevation of the top point $$P$$ of a vertical tower $$PQ$$ of height $$h$$ from a point $$A$$ on the ground is $$45^\circ$$ and from point $$B$$ is $$60^\circ$$, where $$B$$ is a point at a distance $$30$$ meters from the point $$A$$ measured along the line $$AB$$ which makes an angle $$30^\circ$$ with $$AQ$$. Find the height of the tower.
The angle of elevation of an aeroplane from a point on the ground is $$45^o$$. After a flight of $$15$$ seconds, the elevation changes to $$30^o$$. If the aeroplane is flying at a height of $$2500\ m$$, find the speed of the aeroplane.
$$(\sqrt{3}=1.732).$$
$$\Rightarrow$$ $$AD=CB=3\,km$$
$$\Rightarrow$$ In $$\triangle PAD,\,\tan\,45^o=\dfrac{AD}{AP}$$
$$\Rightarrow$$ $$1=\dfrac{3}{AP}$$
$$\Rightarrow$$ $$AP=3\,km$$
$$\Rightarrow$$ In $$\triangle PBC,\,\tan\,30^o=\dfrac{BC}{PB}$$
$$\Rightarrow$$ $$\dfrac{1}{\sqrt{3}}=\dfrac{3}{PB}$$
$$\therefore$$ $$PB=3\sqrt{3}\,km$$
$$\Rightarrow$$ Now, $$ AB=PB-AP$$
$$\Rightarrow$$ $$AB=3\sqrt{3}-3=3(\sqrt{3}-1)km$$
$$\therefore$$ $$AD=CD=3(\sqrt{3}-1)km$$
$$\Rightarrow$$ Time taken to move from $$C$$ to $$D=15\,sec=\dfrac{15}{60\times 60}=\dfrac{15}{3600}hours$$
$$\Rightarrow$$ So, $$Speed=\dfrac{Distance}{Time}=\dfrac{CD}{Time}$$
$$\Rightarrow$$ $$Speed=\dfrac{3(\sqrt{3}-1)}{\dfrac{15}{3600}}$$
$$\Rightarrow$$ $$Speed=\dfrac{3(\sqrt{3}-1)\times 3600}{15}$$
$$\Rightarrow$$ $$Speed=720(\sqrt{3}-1)=527.076\,km/hr$$ $$(Take \sqrt3=1.73)$$
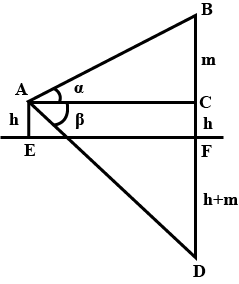
A tree standing on a horizontal plane is leaning towards east. At two points situated at distance $$a$$ and $$b$$ exactly due west on it, the angles of elevation of the top are respectively $$\alpha$$ and $$ \beta$$. Prove that the height of the top from the ground is $$\dfrac { \left( b-a \right) \tan { \alpha \tan { \beta } } }{ \tan { \alpha -\tan { \beta } } }$$.
Draw $$AC$$ perpendicular to the ground.
Here, $$BP=a,\,BQ=b$$
Let $$AC=h$$ and $$BC=x$$
$$\Rightarrow$$ In $$\triangle ACP,\,\tan\alpha=\dfrac{AC}{PC}$$
$$\Rightarrow$$ $$\tan\alpha=\dfrac{h}{x+a}$$
$$\therefore$$ $$x+a=\dfrac{h}{\tan\alpha}$$
$$\therefore$$ $$x=\dfrac{h}{\tan\alpha}-a$$ -------- ( 1 )
Similarly, in $$\triangle ACQ,\,\tan\beta=\dfrac{AC}{QC}$$
$$\Rightarrow$$ $$\tan\beta=\dfrac{h}{x+b}$$
$$\therefore$$ $$x+b=\dfrac{h}{\tan\beta}$$
$$\therefore$$ $$x=\dfrac{h}{\tan\beta}-b$$ --------- ( 2 )
$$\Rightarrow$$ $$\dfrac{h}{\tan\alpha}-a=\dfrac{h}{\tan\beta}-b$$ [ Comparing ( 1 ) and ( 2 ) ]
$$\therefore$$ $$\dfrac{h}{\tan\alpha}-\dfrac{h}{\tan\beta}=-b+a$$
$$\therefore h\left(\dfrac{\tan\beta-\tan\alpha}{\tan\alpha\times\tan\beta}\right)=-(b-a)$$
$$\therefore$$ $$h=-(b-a)\times \dfrac{\tan\alpha\times\tan\beta}{\tan\beta-\tan\alpha}$$
$$\therefore$$ $$h=\dfrac{(b-a)\tan\alpha\times \tan\beta}{\tan\alpha-\tan\beta}$$ [ Hence proved ]
PQ is a post of given height , and AB is a tower at some distance. If $$\alpha$$ and $$\beta$$ are the angles of elevation from the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
Let the height of the tower be $$h$$.
$$PQ=AR=a$$
$$\therefore$$ $$BR=AB-AR=h-a$$
$$\therefore$$ $$BR=AB-AR=h-a$$
In Right angled $$\triangle BAP$$,
$$\tan\alpha=\dfrac{AB}{AP}$$
$$\therefore$$ $$\tan\alpha=\dfrac{h}{AP}$$
$$\Rightarrow$$ $$AP=\dfrac{h}{\tan\alpha}$$ ------ ( 1 )
In right angled $$\triangle BRQ,$$
$$\tan\beta=\dfrac{BR}{QR}$$
$$\therefore$$ $$\tan\beta=\dfrac{h-a}{AP}$$ [ Since, $$AP=RQ$$ ]
$$\Rightarrow$$ $$AP=\dfrac{h-a}{\tan\beta}$$ ------- ( 2 )
$$\Rightarrow$$ $$\dfrac{h-a}{\tan\beta}=\dfrac{h}{\tan\alpha}$$ [ From ( 1 ) and ( 2 ) ]
$$\Rightarrow$$ $$h\tan\alpha-a\tan\alpha=h\tan\beta$$
$$\Rightarrow$$ $$h(\tan\alpha-\tan\beta)=a\tan\alpha$$
$$\Rightarrow$$ $$h=\dfrac{a\tan\alpha}{\tan\alpha-\tan\beta}$$
$$\therefore$$ Height of the tower $$=\dfrac{a\tan\alpha}{\tan\alpha-\tan\beta}$$
$$\therefore$$ $$AP=\dfrac{h}{\tan\alpha}=\dfrac{\dfrac{a\tan\alpha}{\tan\alpha-\tan\beta}}{\tan\alpha}$$
$$\therefore$$ $$AP=\dfrac{a}{\tan\alpha-\tan\beta}$$
$$\therefore$$ Distance of the tower from post is $$\dfrac{a}{\tan\alpha-\tan\beta}$$
A ladder rests against a wall at an angle αα.
In right angled $$\triangle ABC$$, we have
$$\sin\alpha=\dfrac{AB}{BC}=\dfrac{AE+EB}{BC}$$
$$\sin\alpha=\dfrac{AE+b}{BC}$$
But, $$AE=\sin\beta\times ED$$ [ In $$\triangle AED$$ ]
So, replacing $$AE$$ by $$ED$$ $$\sin\beta$$, we get
$$\Rightarrow$$ $$\sin\alpha=\dfrac{ED\sin\beta+b}{BC}$$
$$\Rightarrow$$ $$b=BC\sin\alpha-ED\sin\beta$$
As, $$BC$$ and $$ED$$ both represents the same ladder.
$$BC=ED$$ [ Length of the ladder does not change ]
$$\Rightarrow$$ $$BC\sin\alpha-BC\sin\beta=b$$
$$\Rightarrow$$ $$BC(\sin\alpha-\sin\beta)=b$$ ------ ( 1 )
Similarly, in right-angled $$\triangle AED$$, we have
$$\cos\beta=\dfrac{AD}{ED}=\dfrac{AC+CD}{ED}$$
$$\cos\beta=\dfrac{AC+a}{ED}$$
But, In $$\triangle ABC$$, $$AC=BC\cos\alpha$$
So, by replacing $$AC$$ by $$BC\cos\alpha$$, we get,
$$cos\beta=\dfrac{BC\cos\alpha+a}{ED}$$
$$\therefore$$ $$BC(\cos\beta-cos\alpha)=a$$ ------ ( 2 ) [ $$ED=BC$$ ]
(From 1 and 2)
$$\dfrac{a}{b}=\dfrac{\cos\beta-cos\alpha}{\sin\alpha-sin\beta}$$
By arranging we get,
$$\Rightarrow$$ $$\dfrac{a}{b}=\dfrac{\cos\alpha-cos\beta}{\sin\beta-sin\alpha}$$ [ Hence, proved ]
A boy is standing on the ground and flying a kite with $$150\ m$$ of string at an elevation of $$30^0$$. Another boy is standing on a roof of a $$25\ m$$ high building and is flying his kite at an elevation $$45^\circ$$. Both the boys are on opposite sides of both the kites. Find the length of the string (in meters), that the second boy must have so that the two kites meet.
Let the length of the string (CD) with second boy be $$x\,meters.$$
In $$\triangle ABC,\,\sin\,30^o=\dfrac{BC}{AC}$$
$$\Rightarrow$$ $$\dfrac{1}{2}=\dfrac{BC}{100}$$
$$\therefore$$ $$BC=\dfrac{100}{2}=50\,m$$
Now, $$CF=BC-BF=50\,m-10\,m=40\,m$$
In $$\triangle CFD,\,\sin\,45^o=\dfrac{CF}{CD}$$
$$\Rightarrow$$ $$\dfrac{1}{\sqrt{2}}=\dfrac{40}{x}$$
$$\therefore$$ $$x=40\sqrt{2}\,m=40\times1.414=56.56 \ m$$ $$(Take \sqrt2=1.414)$$
Hence, the length of the string second by must-have is $$56.56 \,m$$.
A carpenter makes stools for electronics with a square top of side $$0.5$$ m and at a height of $$1.5$$ m above the ground. Also each leg is inclined at an angle of $$60^0$$ to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
Let $$AB$$ be the one side of the top of the stool.
$$\therefore$$ $$AB=0.5\,m$$
Let $$CD$$ be the surface of the ground.
Let $$AC$$ be the length of the leg.
$$AC$$ is inclined at an angle of $$60^o$$.
$$\Rightarrow$$ In $$\triangle ACL,\,\tan\,60^o=\dfrac{AL}{CL}$$
$$\Rightarrow$$ $$\sqrt{3}=\dfrac{1.5}{CL}$$
$$\Rightarrow$$ $$CL=\dfrac{1.5}{\sqrt{3}}=\dfrac{1.5}{\sqrt{3}}\times \dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{1.5}{3}\sqrt{3}$$
$$\Rightarrow$$ $$CL=0.5\sqrt{3}=0.5\times 1.732=0.866\,m$$.
$$\Rightarrow$$ $$\sin\,60^o=\dfrac{AL}{AC}$$
$$\Rightarrow$$ $$\dfrac{\sqrt{3}}{2}=\dfrac{1.5}{AC}$$
$$\therefore$$ $$AC=\dfrac{2\times 1.5}{\sqrt{3}}=\dfrac{3}{\sqrt{3}}=\sqrt{3}\,m$$
$$\Rightarrow$$ $$AC=1.732\,m$$
From the diagram the length of the steps are $$GH$$ and $$EF$$. Steps are put such that $$AP=PR=RL$$
$$\therefore$$ $$\triangle AGP\sim\triangle ACL$$
$$\Rightarrow$$ $$\dfrac{AP}{AL}=\dfrac{GP}{CL}$$
$$\Rightarrow$$ $$\dfrac{AP}{3AP}=\dfrac{GP}{0.866}$$
$$\Rightarrow$$ $$GP=\dfrac{0.866}{3}m=0.2887\,m$$
$$\Rightarrow$$ Length of the steps $$GH=GP+PQ+OH=GP+AB+GP$$ [ $$QH=GP$$ by symmetry ]
$$GH=2GP+AB=2\times 0.2887+0.5=1.077\,m$$
$$\Rightarrow$$ Similarly, $$ER=\dfrac{2}{3}CL=\dfrac{2}{3}\times 0.866=0.577\,m$$
$$\Rightarrow$$ Length of the steps
$$EF=ER+RS+SF=ER+AB+ER=2ER+AB$$
$$EF=2\times 0.5773+0.5=1.6546\,m$$
The angle of elevation of a stationery cloud from a point $$2500$$ m above a lake is $$15^\circ$$ and the angle of depression of its reflection in the lake is $$45^\circ$$. What is the height of the cloud above the lake level? $$\left (Use \tan { 15^\circ } =0.268 \right)$$.
Let $$BD=x$$
Then $$DQ=AP=2500 \ m$$ and $$QC=BQ=BD+DQ=2500+x$$
Also $$DC=DQ+QC=2500+x$$
Also $$DC=DQ+QC=2500+2500+x=5000+x$$
$$\Rightarrow$$ In $$\triangle ADC,\,\tan\,45^o=\dfrac{DC}{AD}$$
$$\Rightarrow$$ $$1=\dfrac{5000+x}{AD}$$
$$\Rightarrow$$ $$AD=5000+x$$ ------ ( 1 )
$$\Rightarrow$$ In $$\triangle ABD,\,\tan\,15^o=\dfrac{BD}{AD}$$
$$\Rightarrow$$ $$0.268=\dfrac{x}{5000+x}$$
$$\Rightarrow$$ $$0.268(5000+x)=x$$
$$\Rightarrow$$ $$1340+0.268x=x$$
$$\Rightarrow$$ $$0.732x=1340$$
$$\therefore$$ $$x=1830.60$$
$$\Rightarrow$$ $$ BQ=BD+DQ=x+2500$$
$$\Rightarrow$$ $$BQ=1830.60+2500$$
$$\therefore$$ $$BQ=4330.6\,$$
$$\therefore$$ The height of the cloud above the lake level is $$4330.6\,m$$
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive mile stones on opposite sides of the aeroplane are observed to be $$\alpha$$ and $$\beta$$. Show that the height in miles of aeroplane above the road is given by
$$\dfrac { \tan\ \alpha \ \tan\ \beta }{ \tan\ \alpha \ +\ \tan\ \beta }$$
$$\therefore$$ $$BC=BD+CD=1\,miles$$
Let the height of the aeroplane $$AD=H\,miles$$
$$\Rightarrow$$ In $$\triangle ABD,\,\tan\,\alpha=\dfrac{AD}{BD}$$ ........ $$tan(\Theta ) = \dfrac {Opposite}{Adjacent}$$
$$\Rightarrow$$ $$\tan\,\alpha=\dfrac{h}{BD}$$
$$\Rightarrow$$ $$BD=\dfrac{h}{\tan\,\alpha}$$ -------- ( 1 )
$$\Rightarrow$$ In $$\triangle ACD,\,\tan\,\beta=\dfrac{AD}{CD}$$
$$\Rightarrow$$ $$\tan\beta=\dfrac{h}{CD}$$ .......... $$tan(\Theta ) = \dfrac {Opposite}{Adjacent}$$
$$\Rightarrow$$ $$CD=\dfrac{h}{\tan\beta}$$ -------- ( 2 )
$$\Rightarrow$$ $$BC=BD+CD=\dfrac{h}{\tan\alpha}+\dfrac{h}{\tan\beta}$$
$$\Rightarrow$$ $$BC=h\left(\dfrac{1}{\tan\alpha}+\dfrac{1}{\tan\beta}\right)$$
$$\Rightarrow$$ $$1=h\left(\dfrac{\tan\alpha+\tan\beta}{\tan\alpha \tan\beta}\right)$$
$$\therefore$$ $$h=\dfrac{\tan\alpha\tan\beta}{\tan\alpha+\tan\beta}$$
$$\Rightarrow$$ Hence, height of the aeroplane is $$\dfrac{\tan\alpha\tan\beta}{\tan\alpha+\tan\beta}$$
A tower subtends an angle $$\alpha$$ at a point A in the plane of its base and the angle of depression of the foot of the tower at a point $$b$$ metres just above A is $$\beta$$. Prove that the height of the tower is $$b\tan { \alpha } \cot { \beta }$$.
In $$\triangle ABC,\,\tan\beta=\dfrac{AB}{AC}$$
$$\Rightarrow$$ $$\tan\beta=\dfrac{b}{AC}$$
$$\therefore$$ $$AC=\dfrac{b}{\tan\beta}$$
$$\therefore$$ $$AC=b\cot\beta$$ ------ ( 1 )
In $$\triangle ACD,\,\tan\alpha=\dfrac{CD}{AC}$$
$$\Rightarrow$$ $$CD=\tan\alpha\times AC$$
$$\Rightarrow$$ $$CD=\tan\alpha\times b\cot\beta$$ [ From ( 1 ) ]
$$\therefore$$ $$CD=b\tan\alpha\cot\beta$$ [ Hence proved ]
From the top light house, the angles of the depression of two ship on the opposite side of it are observed to be $$\alpha$$ and $$\beta$$. If the height of the light house be h metres and the line joining the ship passes through the foot of the light house, show that the distance between the ship is $$\dfrac { h\left( \tan { \alpha } +\tan { \beta } \right) }{ \tan { \alpha } \tan { \beta } }$$ meters.
$$\Rightarrow$$ In $$\triangle APB,\,\tan\alpha=\dfrac{AB}{PB}$$
$$\Rightarrow$$ $$\tan\alpha=\dfrac{h}{PB}$$
$$\therefore$$ $$PB=\dfrac{h}{\tan\alpha}$$ ---- ( 1 )
$$\Rightarrow$$ In $$\triangle ABQ,\,\tan\beta=\dfrac{AB}{BQ}$$
$$\Rightarrow$$ $$\tan\beta=\dfrac{h}{BQ}$$
$$\therefore$$ $$BQ=\dfrac{h}{\tan\beta}$$ ------ ( 2 )
Now the distance between two ships $$PQ=PB+BQ$$
$$\Rightarrow$$ $$PQ=\dfrac{h}{\tan\alpha}+\dfrac{h}{\tan\beta}$$ [ From ( 1 ) and ( 2 )]
$$\Rightarrow$$ $$PQ=\dfrac{h\tan\beta+h\tan\alpha}{\tan\alpha\tan\beta}=\dfrac{h(\tan\beta+\tan\alpha)}{\tan\alpha\tan\beta}\,m$$
An observer, $$1.5$$ m tall, is $$28.5$$ m away from a tower $$30$$ m high. Determine the angle of elevation of the top of the tower from his eye.
Given the Height of the Tower $$=AE=30\ m$$
and Distance between the Tower and the Observer $$CD=EF=28.5\ m$$
and Height of Man $$=DF=1.5\ m$$
Now, we can see that CDEF is a rectangle
so, $$CE=DF=1.5$$
Now, in $$\triangle ACD$$
$$\tan\theta=\dfrac{AC}{CD}=\dfrac{AE-CE}{CD}=\dfrac{30-1.5}{28.5}=1\Rightarrow \tan\theta=1\Rightarrow \theta=45^o$$
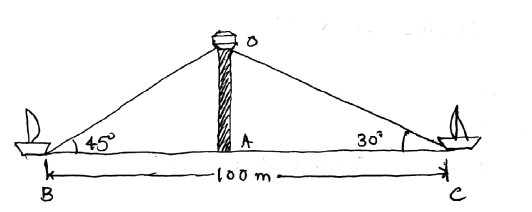
Two boats approach a lighthouse in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from the two boats are $$30^0$$ and $$60^0$$ respectively. If the distance between two boats is $$100$$ m, then find the height of the lighthouse.
$$\Rightarrow$$ Here, $$CD$$ is the height of the lighthouse of height $$h$$ and $$A$$ and $$B$$ are the two boats $$100m$$ far from each other.
$$\Rightarrow $$ let say $$x$$ be the distance between $$A$$ and lighthouse, then $$100-x$$ would be the distance between $$B$$ and the lighthouse.
$$\Rightarrow$$ In $$\triangle ACD,\,\tan\,30^o=\dfrac{CD}{AD}$$
$$\Rightarrow$$ $$\dfrac{1}{\sqrt{3}}=\dfrac{h}{x}$$
$$\Rightarrow$$ $$x=\sqrt{3}h\,m$$ ----- ( 1 )
$$\Rightarrow$$ In $$\triangle BCD,\,\tan\,60^o=\dfrac{CD}{BD}$$
$$\Rightarrow$$ $$\sqrt{3}=\dfrac{h}{100-x}$$
$$\Rightarrow$$ $$h=\sqrt{3}(100-x)$$
$$\Rightarrow$$ $$h=\sqrt{3}(100-\sqrt{3}h)$$ { from (1) }
$$\Rightarrow$$ $$h+3h=100\sqrt{3}$$
$$\Rightarrow$$ $$4h=100\sqrt{3}$$
$$\therefore$$ $$h=25\sqrt{3}\,m$$
$$\therefore$$ $$h=43.30\,m$$ $$(Take \sqrt3=1.73)$$
From the top of a spire, the angles of depression of the top and bottom of a tower of height $$h$$ are $$\theta$$ and $$\phi$$. show that the height of the spire and its horizontal distance from the tower are respectively
$$h.\dfrac{ \cos \theta \sin \phi }{ \sin(\phi-\theta) }$$ and $$\dfrac{ h \cos \theta \cos \phi }{ \sin (\phi-\theta) }$$
$$y-h=x \tan { \theta },$$ from $$\triangle BQR.$$$$y=x \tan { \phi },$$ from $$\triangle BPA$$.
$$\therefore \quad \dfrac { y-h }{ y } =\dfrac { \tan { \theta } }{ \tan { \phi } } =\dfrac { \sin { \theta } \cos { \phi } }{ \cos { \theta } \sin { \phi } }$$
$$\therefore \quad 1-\dfrac { h }{ y } =\dfrac { \sin { \theta } \cos { \phi } }{ \cos { \theta } \sin { \phi } }$$
or $$\dfrac { \sin { \phi } \cos { \theta } -\cos { \phi \sin { \theta } \quad } }{ \sin { \phi } \cos { \theta } } =\dfrac { h }{ y }$$
$$\therefore \quad y=\dfrac { h\sin { \phi } \cos { \theta } }{ \sin { \left( \phi -\theta \right) } }$$
Again $$y=x\tan { \phi }$$
or $$\dfrac { h\sin { \phi } \cos { \theta } }{ \sin { \left( \phi -\theta \right) } } =x\dfrac { \sin { \phi } }{ \cos { \phi } }$$
$$\therefore \quad x=h\dfrac { \cos { \theta } \cos { \phi } }{ \sin { \left( \phi -\theta \right) } }$$
Note : You can prove it by sine rule on triangle $$BQR$$ and $$BQP$$ and eliminating $$BQ$$. This man also be done by $$m-n$$ theorem on $$\triangle BPR$$.
$$\alpha =\phi -\theta ,\beta =\theta ,\theta \rightarrow 90-\theta$$.
A vertical tower $$50\ ft$$. high stands on a sloping ground. The foot of the tower is at the same level as the middle point of a vertical flag pole. From the top of the tower the angle of depression of the top and the bottom of the pole are $$15^{ o }$$ and $$45^{ o }$$ respectively. Find the length of the pole.
Let $$AB=2h$$
The angles of depression of $$A$$ and $$B$$ as seen from $$C$$, the top of the tower, are $${15}^{o}$$ and $${45}^{o}$$ respectively.
$$OC$$ be the height of the tower standing on a sloping ground $$OB.$$
$$\Rightarrow OC=50$$
And $$BD=OM=AE=x$$
In $$\triangle CAE,$$
$$\tan {15^\circ}=\dfrac{50-h}{x}$$ $$...(1)$$
In $$\triangle CBD,$$
$$\tan {45^\circ}=\dfrac{50+h}{x}$$ $$...(2)$$
Divide $$(2)$$ by $$(1)$$ in order to eliminate $$x$$
$$\dfrac { 50+h }{ 50-h } =\dfrac { \tan { 45^\circ } }{ \tan { 15^\circ } }$$
Applying componendo and dividend,
we get $$\dfrac { 2h }{ 100 } =\dfrac { \sin { \left( 45-15 \right) } }{ \sin { \left( 45+15 \right) } } $$
$$=\dfrac { \sin { 30 } }{ \sin { 60 } } $$
$$=\dfrac { 1 }{ \sqrt { 3 } }$$
$$\therefore \quad 2h=\dfrac { 100 }{ \sqrt { 3 } }$$
$$ =\dfrac { 100\sqrt { 3 } }{ 3 }$$
The width of a road is $$b$$ feet., on one side of which there is a window $$h$$ feet height. A building in front of it subtends an angle $$\theta$$ at it. Prove that the height of the building is $$\dfrac{ (b^{ 2 }+h^{ 2 }) \sin \theta }{ b \cos \theta + h \sin \theta }$$
We have to find the value of $$BC=x$$ in terms of known quantities $$b,h$$ and $$\theta$$.
$$\therefore \quad h=b \tan \alpha$$
$$x-h=b \tan (\theta - \alpha)$$
$$=b\dfrac{ \tan \theta - \tan \alpha }{ 1+ \tan \theta \tan \alpha }$$
Put for $$\tan \alpha$$ from $$(1)$$
$$\therefore \quad x=h+b\dfrac{ \tan \theta h/b }{ 1+\tan \theta. h/b }$$
$$=h+b.\dfrac{ (b \sin \theta h \cos \theta) }{ b \cos \theta + h \sin \theta }$$
or $$x=\dfrac{ bh \cos \theta + h^{ 2 } \sin \theta + b^{ 2 } \sin \theta bh \cos \theta }{ b \cos \theta + h \sin \theta }$$
$$=\dfrac{ (b^{ 2 }+h^{ 2 })\sin \theta }{ b \cos \theta + h \sin \theta }$$
Note : You can do it by $$m-n$$ theorem with $$\theta=90^{ o },m=ME=h,n=EC-h$$.
$$\therefore \quad h=b \tan \alpha$$
$$x-h=b \tan (\theta - \alpha)$$
$$=b\dfrac{ \tan \theta - \tan \alpha }{ 1+ \tan \theta \tan \alpha }$$
Put for $$\tan \alpha$$ from $$(1)$$
$$\therefore \quad x=h+b\dfrac{ \tan \theta h/b }{ 1+\tan \theta. h/b }$$
$$=h+b.\dfrac{ (b \sin \theta h \cos \theta) }{ b \cos \theta + h \sin \theta }$$
or $$x=\dfrac{ bh \cos \theta + h^{ 2 } \sin \theta + b^{ 2 } \sin \theta bh \cos \theta }{ b \cos \theta + h \sin \theta }$$
$$=\dfrac{ (b^{ 2 }+h^{ 2 })\sin \theta }{ b \cos \theta + h \sin \theta }$$
Note : You can do it by $$m-n$$ theorem with $$\theta=90^{ o },m=ME=h,n=EC-h$$.
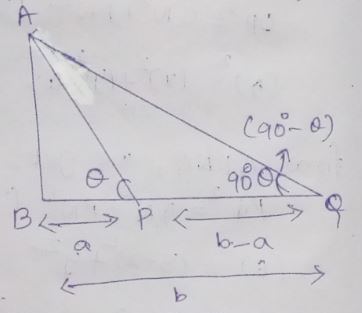
The angles of elevation of the top of a tower standing on a horizontal plane from two points on a line passing through the foot of the tower at distance $$a$$ and $$b$$ respectively are complementary angles. Prove that the height of the tower is $$\sqrt { ab }$$. If the line joining the two points subtends and angle $$\theta$$ at the top of the tower, show that $$\sin \theta =\dfrac{ (a-b) }{ (a+b) }$$.
$$h=a \tan { \alpha } ,\quad h=b\tan { \left( 90^{o} -\alpha \right) } =b\cot { \alpha }.$$
Multiply $${h}^{2}=ab\tan { \alpha }\cot { \alpha }=ab.$$
$$\therefore \quad h=\sqrt { ab }$$
Also $$\tan { \alpha } =\dfrac { h }{ \alpha } =\dfrac { \sqrt { ab } }{ a } =\sqrt { \left( \dfrac { b }{ a } \right) }$$ ...$$(1)$$
If $$AB$$ subtends an angle $$\theta$$ at $$Q$$ then
$${90}^{o}-\alpha= \theta+\alpha$$
or $$\theta={90}^{o}-2 \alpha$$
$$\therefore \quad \sin { \theta } =\cos { 2\alpha } =\dfrac { 1-\tan ^{ 2 }{ \alpha } }{ 1+\tan ^{ 2 }{ \alpha } }$$
or $$\sin { \theta } =\dfrac { 1-b/a }{ 1+b/a } =\dfrac { a-b }{ a+b }$$, by $$(1)$$
Multiply $${h}^{2}=ab\tan { \alpha }\cot { \alpha }=ab.$$
$$\therefore \quad h=\sqrt { ab }$$
Also $$\tan { \alpha } =\dfrac { h }{ \alpha } =\dfrac { \sqrt { ab } }{ a } =\sqrt { \left( \dfrac { b }{ a } \right) }$$ ...$$(1)$$
If $$AB$$ subtends an angle $$\theta$$ at $$Q$$ then
$${90}^{o}-\alpha= \theta+\alpha$$
or $$\theta={90}^{o}-2 \alpha$$
$$\therefore \quad \sin { \theta } =\cos { 2\alpha } =\dfrac { 1-\tan ^{ 2 }{ \alpha } }{ 1+\tan ^{ 2 }{ \alpha } }$$
or $$\sin { \theta } =\dfrac { 1-b/a }{ 1+b/a } =\dfrac { a-b }{ a+b }$$, by $$(1)$$
A tower subtends an angle $$\alpha$$ at a point $$A$$ in the plane of its base and the angle of depression of the foot of the tower at a point $$b\ ft$$. just above $$A$$ is $$\beta$$. Prove that the height of the tower is $$b \tan \alpha \cot \beta$$.
Let height of the tower be $$h$$.
From figure,
$$h=xtan\alpha$$ ......(1)
$$b=xtan\beta$$ .......(2)
From (1) & (2),
$$h=\dfrac{b}{tan\beta}.tan\alpha$$
Thertefore,
$$b=tan\alpha.cot\beta$$
Hence proved.
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is $${60}^{\circ}$$, when he retires $$40$$ feet from the bank he finds the angle to be $${30}^{\circ}$$. Find the height of the tree and the breadth of the river.
A balloon moving in a straight line passes vertically above two points $$A$$ and $$B$$ on a horizontal plane $$1000\ ft.$$ apart. When above $$A$$ it has an altitude of $${60}^{o}$$ as seen from $$B$$ and when above $$B$$ it has an altitude of $${45}^{o}$$ as seen from $$A$$. Find the distance from $$A$$ of the point at which it will touch the plane.
Let the balloon touch the horizontal plane through $$A$$ in $$R$$. We have to determine $$AR$$.
$$AB=1000$$ and let $$BR=x$$.
In $$\triangle PAB$$
$$PA=AB\tan{60}^{o}=1000\sqrt { 3 }$$
In $$\triangle QAB$$,
Now from similar triangles,$$\triangle APR$$ and $$\triangle BQR$$, we have
$$\tan { \theta } =\dfrac { AP }{ AR } =\dfrac { BQ }{ BR }\\ \implies \dfrac { 1000\sqrt { 3 } }{ 1000+x } =\dfrac { 1000 }{ x } $$
$$\implies \quad x\sqrt { 3 } =1000+x$$
$$AB=1000$$ and let $$BR=x$$.
In $$\triangle PAB$$
$$PA=AB\tan{60}^{o}=1000\sqrt { 3 }$$
In $$\triangle QAB$$,
$$\angle QAB =\angle BQA$$
$$\therefore AB=QB=1000$$
Now from similar triangles,$$\triangle APR$$ and $$\triangle BQR$$, we have
$$\tan { \theta } =\dfrac { AP }{ AR } =\dfrac { BQ }{ BR }\\ \implies \dfrac { 1000\sqrt { 3 } }{ 1000+x } =\dfrac { 1000 }{ x } $$
$$\implies \quad x\sqrt { 3 } =1000+x$$
$$\implies x\left( \sqrt { 3 } -1 \right) =1000$$
$$\implies \quad x=\dfrac { 1000 }{ \sqrt { \left( 3 \right) } -1 }\times \dfrac{ \sqrt { 3 } +1 }{ \sqrt { 3 } +1 }\\ \ \ \quad \ \ \ \ \\ \ \ \ \ \ \ \ \ =\dfrac { 1000\left( \sqrt { 3 } +1 \right) }{ 3-1 } =500\left( \sqrt { 3 } +1 \right) $$
$$\implies \quad x=\dfrac { 1000 }{ \sqrt { \left( 3 \right) } -1 }\times \dfrac{ \sqrt { 3 } +1 }{ \sqrt { 3 } +1 }\\ \ \ \quad \ \ \ \ \\ \ \ \ \ \ \ \ \ =\dfrac { 1000\left( \sqrt { 3 } +1 \right) }{ 3-1 } =500\left( \sqrt { 3 } +1 \right) $$
$$\therefore\quad AR=1000+x$$
$$=1000+500\left( \sqrt { 3 } +1 \right) $$
$$=500\left( 2+\sqrt { 3 } +1 \right) =500\sqrt { 3 } \left( \sqrt { 3 } +1 \right) $$ ft.
From an aeroplane vertically over a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be $$\alpha$$ and $$\beta$$. Show that the height in miles of aeroplane above the road is given by
$$\dfrac { \tan { \alpha } \tan { \beta } }{ \tan { \alpha } +\tan { \beta } } .$$
$$h=BD \tan \alpha =DC \tan \beta$$
But $$BD+DC=1 mile$$
$$h(\dfrac{ 1 }{ \tan \alpha }+\dfrac{ 1 }{ \tan \beta })=1$$
$$\therefore \quad h=\dfrac{ \tan \alpha \tan \beta }{ \tan \alpha \tan \beta }$$
But $$BD+DC=1 mile$$
$$h(\dfrac{ 1 }{ \tan \alpha }+\dfrac{ 1 }{ \tan \beta })=1$$
$$\therefore \quad h=\dfrac{ \tan \alpha \tan \beta }{ \tan \alpha \tan \beta }$$
Fill in the blanks
The angle of elevation of a tower at a place $$A$$ due south it is $$\theta$$ and at a place due west of $$A$$ and at a distance $$a$$ from it, the elevation is $$\phi$$, the height of tower is ____________.
$$\dfrac{AB sin \alpha sin \beta}{\sqrt{(sin^2 \alpha - sin^2 \beta)} }$$ or $$\dfrac{AB sin \alpha sin \beta}{\sqrt{[sin ( \alpha + \beta) sin ( \alpha - \beta)]} }$$ or $$\dfrac{AB tan \alpha tan \beta}{\sqrt{(tan^2 \alpha - tan^2 \beta)} }$$
$$AP = h cot \alpha, BP = h cot \beta$$
$$BP^2 = AB^2 + AP^2$$
$$h^2 ( cot^2 \beta - cot^2 \alpha) = a^2$$ Where AB = a
Now change to tan or sin and cosine etc.
Fill in the blanks
The angle of elevation of the top of a tower from a point $$A$$ on the ground is $$\theta$$ and that from $$B$$ is $$\phi$$. If $$AB=100$$ metres and $$AB$$ is perpendicular to the line joining $$A$$ with the foot of the tower, then the height of the tower is ________________.
Given $$\cot{ \theta }=3/10$$ and $$\cot{ \phi }=1/2$$.
From the bottom of a pole of height h, the angle of elevation of the top of the tower is $$\alpha$$. The pole subtends an angle $$\beta$$ at the top of the tower. The height of the tower is____
H = $$\dfrac{h\,sin\,\alpha\,cos\,(\alpha - \beta)}{sin\,\beta}$$
OA = H cot $$\alpha$$, BM = (H - h) tan $$(90^{0} - \alpha + \beta)$$
$$\therefore$$ H cot $$\alpha$$ = (H - h) cot $$(\alpha - \beta)$$
$$\therefore$$ H[cot ($$\alpha$$ - $$\beta$$) - cot $$\alpha$$] = h cot cot $$(\alpha - \beta)$$.
Change to sin and cos.
OA = H cot $$\alpha$$, BM = (H - h) tan $$(90^{0} - \alpha + \beta)$$
$$\therefore$$ H cot $$\alpha$$ = (H - h) cot $$(\alpha - \beta)$$
$$\therefore$$ H[cot ($$\alpha$$ - $$\beta$$) - cot $$\alpha$$] = h cot cot $$(\alpha - \beta)$$.
Change to sin and cos.
From the top of a cliff $$200\ ft$$. high, the angles of depression of the top and bottom of a tower are observed to be $$30^{\circ}$$ and $$60^{\circ}$$ respectively. The height of the tower is________
Consider the $$\triangle BAP$$
$$tan 30^{\circ}=\dfrac{AP}{AB}=\dfrac{x}{200}$$
$$\dfrac{1}{\sqrt 3}=\dfrac{x}{200}$$
$$x=\dfrac{200}{\sqrt 3}$$......(1)
Now consider the $$\triangle BRQ$$
$$tan 30^{\circ}=\dfrac{RQ}{BR}=\dfrac{200-h}{x}$$
$$\dfrac{1}{\sqrt 3}=\dfrac{200-h}{x}$$
$$\dfrac{x}{\sqrt 3}={200-h}$$
$$h={200-\dfrac{x}{\sqrt 3}}$$
substitute the value of $$x$$ from eq (1), we get
$$h={200-\dfrac{200}{(\sqrt 3)^2}}$$
$$=200-\dfrac{200}{3}$$
$$=\dfrac{600-200}{3}$$
$$=\dfrac{400}{3}$$
Hence, the height of tower is $$h=\dfrac{400}{3}\ ft$$
Hence, the height of tower is $$h=\dfrac{400}{3}\ ft$$
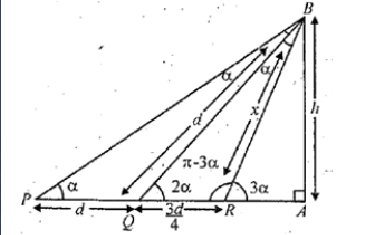
A man observes a tower $$AB$$ of height $$h$$ from a point $$P$$ on the ground. He moves a distance d towards the foot of the tower and finds that the angle of elevation is doubled. He further moves a distance $$\dfrac{3d}{4}$$ in the same direction and finds that the angle of elevation is three times that of $$P$$.
Prove that $$36h^2 = 35d^2$$.
$$RB=x$$
$$\angle BQR$$ $$\text{is an ext }$$ $$\angle$$ of $$\triangle PBQ$$
$$\therefore \angle PBQ=2\alpha-\alpha=\alpha$$
$$\text{In }$$$$\triangle PBQ$$
$$\angle PBQ=\angle QPB$$
$$\angle PBQ=\angle QPB$$
$$\Rightarrow PQ=QB=d$$
$$\text{Also}$$ $$\angle BRA$$ $$\text{is an ext }$$ $$\angle$$ of $$\triangle BQR$$
$$\therefore \angle BQR=3\alpha-2\alpha=\alpha$$
And $$\angle QBR=\pi-3\alpha$$ $$\textbf{(linear pair)}$$
$$\text{Now in}$$ $$\triangle BQR$$ $$\text{by applying Sine law, we get}$$
$$d/\sin(\pi-3\alpha)=3d/4\sin \alpha=x/\sin 2\alpha$$
$$\Rightarrow d/\sin 3\alpha=3d/4\sin \alpha=x/\sin^{2}\alpha$$
$$\Rightarrow d/3\sin\alpha-4\sin^{3}\alpha=3d/4\sin\alpha=x/2\sin\alpha\cos\alpha$$
$$\Rightarrow d/3-4\sin^{2}\alpha=3d/4=x/2\cos\alpha $$ $$....equ(1)$$
$$\Rightarrow d/3-4\sin^{2}\alpha=3d/4\Rightarrow 4=9-12\sin^{2}\alpha$$
$$\Rightarrow \sin^{2}\alpha=5/12\Rightarrow \cos^{2}\alpha=7/12$$
$$\Rightarrow 3d/4=x/2\cos\alpha$$
$$\Rightarrow 4x^{2}=9d^{2}\cos^{2}\alpha$$
$$\Rightarrow 4x^{2}=9d^{2}\cos^{2}\alpha$$
$$\Rightarrow x^{2}=9d^{2}/4=7/12=21/16 d^{2}$$ $$....equ(2)$$
$$\text{Again, from }$$ $$\triangle ABR$$ $$\text{we have }$$
$$\Rightarrow \sin 3\alpha=h/x$$
$$\Rightarrow \sin 3\alpha=h/x$$
$$\Rightarrow 3\sin\alpha-4\sin^{3}\alpha=h/x\Rightarrow \sin\alpha(3-4\sin^{2}\alpha)=h/x$$
$$\Rightarrow \sin\alpha [3-4\times 5/12]=h/x$$ $$(using, $$ $$\sin^{2}\alpha=5/12)$$
$$\Rightarrow 4/3\sin\alpha=h/x$$
$$\text{Squaring both sides we get}$$
$$16/9\sin^{2}\alpha=h^{2}/x^{2}16/9\times 2/12=h^{2}/x^{2}$$ $$\text{(again using }$$$$\sin^{2}\alpha=5/12$$)
$$\Rightarrow h^{2}=4\times 5/9\times 3x^{2}\Rightarrow h^{2}=20/27\times 21/16\ d^{2}$$
$$\text{using value of}$$ $$x^{2}$$ from eq $$(2)$$
$$\Rightarrow h^{2}=35/36\ d^{2}\Rightarrow 36 h^{2}=35\ d^{2}$$
$$\text{ Hence, proved }$$
$$\text{ Hence, proved }$$
A man on a hill observes that three towers on a horizontal plane subtend equal angles on his eye and that the angles of depression of their bases are $$\theta, \phi$$ and $$\psi$$. Prove that if a, b and c are their heights, then
$$\dfrac{sin ( \theta - \phi)}{c sin \psi} + \dfrac{sin ( \phi - \psi)}{a sin \theta} + \dfrac{sin (\psi - \theta)}{b sin \phi} = 0$$
Let $$\alpha$$ be the equal angle subtended by the towers at the man at P. The height of P be taken as x. Both x and $$\alpha$$ are unknown and they have to be eliminated. $$\alpha$$ comes in $$\Delta APB$$ and x comes in $$\Delta APO$$ and both have side AP common which is to be eliminated. By sine in $$\Delta ABP.$$
$$\dfrac{a}{sin \alpha} = \dfrac{AP}{cos (\theta - \alpha)}$$ ...(1)
Now $$\dfrac{x}{sin \theta} = \dfrac{AP}{sin 90^o}$$ $$\therefore AP = \dfrac{x}{sin \theta}, \Delta OAP$$
Putting in (1) we get
$$\dfrac{a}{sin \alpha} = \dfrac{x}{sin \theta cos (\theta - \alpha)}$$
$$\therefore \dfrac{x sin \alpha}{a sin \theta} = cos (\theta - \alpha)$$
$$\dfrac{x sin \alpha}{b sin \phi} = cos (\phi - \alpha)$$
$$\dfrac{x sin \alpha}{c sin \psi} = cos (\psi - \alpha)$$
$$T_1 = \dfrac{sin (\theta - \phi)}{c sin \psi } = \dfrac{sin [(\theta - \alpha) - (\phi - \alpha)]}{c sin \psi }$$
$$= \dfrac{sin (\theta - \alpha) cos (\phi - \alpha) - cos (\theta - \alpha) sin (\phi - \alpha)}{c sin \psi }$$
$$= \dfrac{1}{c sin \psi } \left[ sin (\theta - \alpha) \dfrac{x sin \alpha}{b sin \phi} - sin (\phi - \alpha) \dfrac{x sin \alpha}{a sin \theta} \right]$$
$$= \dfrac{x sin \alpha}{abc sin \theta sin \phi sin \psi} [ sin \theta sin ( \theta - \alpha) - sin \phi sin (\phi - \alpha)]$$
$$T_1= k [ sin \theta sin (\theta - \alpha) - sin \phi sin (\phi - \alpha)]$$
Similarly write $$T_2$$ and $$T_3$$ by symmetry and then
add. $$T_1+ T_2+T_3 = 0$$ as $$\sum (a-b) =0$$
$$\dfrac{a}{sin \alpha} = \dfrac{AP}{cos (\theta - \alpha)}$$ ...(1)
Now $$\dfrac{x}{sin \theta} = \dfrac{AP}{sin 90^o}$$ $$\therefore AP = \dfrac{x}{sin \theta}, \Delta OAP$$
Putting in (1) we get
$$\dfrac{a}{sin \alpha} = \dfrac{x}{sin \theta cos (\theta - \alpha)}$$
$$\therefore \dfrac{x sin \alpha}{a sin \theta} = cos (\theta - \alpha)$$
$$\dfrac{x sin \alpha}{b sin \phi} = cos (\phi - \alpha)$$
$$\dfrac{x sin \alpha}{c sin \psi} = cos (\psi - \alpha)$$
$$T_1 = \dfrac{sin (\theta - \phi)}{c sin \psi } = \dfrac{sin [(\theta - \alpha) - (\phi - \alpha)]}{c sin \psi }$$
$$= \dfrac{sin (\theta - \alpha) cos (\phi - \alpha) - cos (\theta - \alpha) sin (\phi - \alpha)}{c sin \psi }$$
$$= \dfrac{1}{c sin \psi } \left[ sin (\theta - \alpha) \dfrac{x sin \alpha}{b sin \phi} - sin (\phi - \alpha) \dfrac{x sin \alpha}{a sin \theta} \right]$$
$$= \dfrac{x sin \alpha}{abc sin \theta sin \phi sin \psi} [ sin \theta sin ( \theta - \alpha) - sin \phi sin (\phi - \alpha)]$$
$$T_1= k [ sin \theta sin (\theta - \alpha) - sin \phi sin (\phi - \alpha)]$$
Similarly write $$T_2$$ and $$T_3$$ by symmetry and then
add. $$T_1+ T_2+T_3 = 0$$ as $$\sum (a-b) =0$$
A man in a boat rowed away from a cliff 150 meters high takes 2 minutes to change the angle of elevation from 60 toThe speed of the boat is______
A chimney $$20$$ metres high, standing on the top of a building subtends an angle whose tangent is $$\dfrac{1}{6}$$ at a distance $$70$$ metres from the foot of the building. Find the height of the building.
As shwon in the fig. let $$CB$$ and $$AB$$ be the heights of the chimney and building respectively.
According to the given condition,
$$tan \theta = \dfrac{1}{5}$$,$$tan \beta = \dfrac{H}{70}, tan \alpha = \dfrac{H+20}{70}$$
$$\alpha = \theta + \beta$$
$$\therefore tan \alpha = \dfrac{tan \theta + tan \beta}{1 - tan \theta tan \beta}$$
or $$\dfrac{H+20}{70} = \dfrac{70 +6H}{420 -H}$$
or $$(20+H)(420 - H) = 70 (70+6H)$$
or $$8400 + 400 H - H^2 = 4900 +420H$$
or $$H^2 + 20 H - 3500 =0$$
or $$(H+70)(H-50) =0$$
$$\Rightarrow H=50$$
A wireless pole $$25$$ metres high is fixed on a top of a verandah of a house which is $$15$$ metres high. At a point $$R$$ on the ground, directly opposite, the wireless pole and verandah subtend equal angles. The distance of $$R$$ from the verandah is______
A tower $$51\ m$$, high has a mark at a height of $$25\ m$$. from the ground. Find at what distance the two parts subtend equal angles to an eye at the height of $$5\ m$$, from the ground.
$$\angle CQB = \angle AQB$$ given.
$$\therefore QB$$ is bisector of angle $$AQC$$ and as such it divides the base $$AC$$ in the ratio of the arms of the angle
$$\dfrac{AB}{BC} = \dfrac{QA}{ QC}$$
or $$\dfrac{25}{26} = \dfrac{\sqrt{QD^2 +DA^2}}{\sqrt{(QD^2 + DC^2)}}$$
or $$\dfrac{25}{26} = \dfrac{\sqrt{x^2 +5^2}}{\sqrt{(x^2 + 46^2)}}$$. Square
$$625 (x^2 + 46^2) = 676 (x^2 + 25)$$
$$51 x^2 = ( 625 \times 46^2 - 676 \times 25)$$
or $$x^2 = \dfrac{100 [13225 -169]}{51}$$
or $$x^2 = 100 \times \dfrac{13056}{51} = 100 \times 256$$
$$x = 10 \times 16 = 160\ m$$
$$\therefore QB$$ is bisector of angle $$AQC$$ and as such it divides the base $$AC$$ in the ratio of the arms of the angle
$$\dfrac{AB}{BC} = \dfrac{QA}{ QC}$$
or $$\dfrac{25}{26} = \dfrac{\sqrt{QD^2 +DA^2}}{\sqrt{(QD^2 + DC^2)}}$$
or $$\dfrac{25}{26} = \dfrac{\sqrt{x^2 +5^2}}{\sqrt{(x^2 + 46^2)}}$$. Square
$$625 (x^2 + 46^2) = 676 (x^2 + 25)$$
$$51 x^2 = ( 625 \times 46^2 - 676 \times 25)$$
or $$x^2 = \dfrac{100 [13225 -169]}{51}$$
or $$x^2 = 100 \times \dfrac{13056}{51} = 100 \times 256$$
$$x = 10 \times 16 = 160\ m$$
A vertical tower stands on a declivity which is, inclined at $$15^\circ$$ to the horizon. From the foot of the tower a man ascends the declivity for 80 feet and then finds that the tower subtends an angle of $$30^\circ$$. Prove that the height of the tower is
$$40 (\sqrt{6} - \sqrt{2})$$ feet.
Using sine formula in $$\triangle ABC$$:
$$\dfrac{BC}{\sin 75^\circ} = \dfrac{AB}{\sin 30^\circ}$$
$$\dfrac{BC}{\sin 75^\circ} = \dfrac{AB}{\sin 30^\circ}$$
GIven that: $$BC=80\ \mathrm{ft}$$
$$ = \dfrac{40 . 2 \sqrt{2} ( \sqrt{3} - 1)}{3-1}\ \mathrm{ft.} = 40 \sqrt{2} ( \sqrt{3} - 1) \ \mathrm{ft.}= 40 (\sqrt{6} - \sqrt{2})\ \mathrm{ft.}$$.
$$AB=h = 80 \dfrac{\sin 30^\circ}{\sin (45^\circ + 30^\circ)} = \dfrac{40 \times 2 \sqrt{2}}{[ \sqrt{(3)} + 1]}\ \mathrm{ft.}$$
$$ = \dfrac{40 . 2 \sqrt{2} ( \sqrt{3} - 1)}{3-1}\ \mathrm{ft.} = 40 \sqrt{2} ( \sqrt{3} - 1) \ \mathrm{ft.}= 40 (\sqrt{6} - \sqrt{2})\ \mathrm{ft.}$$.
A tower is $$b$$ ft. high having a flag staff at its top. The tower and the flag staff subtend equal angles at a point distant $$a$$ feet from the foot of the tower. Show that the length of the flagstaff is $$\dfrac{b (a^2+b^2)}{a^2-b^2}$$.
In $$\triangle PAB$$,
$$\dfrac{b}{a} = tan \theta$$In $$\triangle PAC$$,
$$\dfrac{b+x}{a} = \dfrac{ 2 tan \theta}{1 - tan^2 \theta}$$
$${b+x} = \dfrac{ 2 a^2b}{a^2 - b^2}$$
$$x = \dfrac{a^2 b + b^3}{a^2 - b^2}\\ \ \\ = \dfrac{b(a^2 + b^2)}{a^2 - b^2}$$
$$ \dfrac{b+x}{a} = tan 2 \theta$$
$$\dfrac{b+x}{a} = \dfrac{ 2 tan \theta}{1 - tan^2 \theta}$$
$$\dfrac{b+x}{a} = \dfrac{2. \dfrac{b}{a}}{1 - \dfrac{b^2}{a^2}}$$
$${b+x} = \dfrac{ 2 a^2b}{a^2 - b^2}$$
$$ x = \dfrac{2 a^2 b}{a^2 - b^2} - b$$
$$x = \dfrac{a^2 b + b^3}{a^2 - b^2}\\ \ \\ = \dfrac{b(a^2 + b^2)}{a^2 - b^2}$$
A tower has flag staff at its top which subtends equal angles $$\alpha$$ at a points distance 9 yds and 11 yds from the foot of the tower. If $$tan \alpha = \dfrac{1}{10}$$, find the height of the tower and the flag staff.
AB = y, tower, BC = x, flagstaff, AP = 9, AQ = 11. BC subtends equal angles $$\alpha$$ at P and Q s.t. $$tan \alpha = \dfrac{ 1}{10}$$. Hence the circle through C and B must also pass through P and Q as angles in the same segment are equal. From the figure it is clear that segment BP subtends equal angles say $$\beta$$ at C and Q.
$$y+ 11 tan \beta$$ ...(1)
and $$x+y = 11 tan (\alpha+ \beta)$$ ...(2)
$$AP = 9 = (x+y) tan \beta$$ ...(3)
$$\therefore 9 = 11 tan (\alpha+ \beta) tan \beta$$,
from (2) and (3),
or $$9 = 11 tan \beta \left( \dfrac{tan \alpha + tan \beta}{1 - tan \alpha tan \beta} \right)$$
Put $$tan \alpha = \dfrac{1}{10}$$.
$$\therefore 9 \left[ 1 - \left( - \dfrac{1}{10} \right) tan \beta \right] = 11 tan \beta \left( \dfrac{1}{10} + tan \beta \right)$$
$$9 (10 - tan \beta) = 11 tan \beta (1+ 10 tan \beta )$$.
$$110 tan^2 \beta + 20 tan \beta - 90 = 0$$
or $$11 tan^2 \beta = 2 tan \beta - 9 = 0$$
$$(11 tan \beta - 9 )(tan \beta + 1) = 0$$
$$\therefore tan \beta = \dfrac{9}{11} ( \beta acute)$$
Hence from (1),
$$y = 11 tan \beta = 11. \dfrac{9}{11} = 9$$
From (3),
$$9 = (x+y) tan \beta = (x+9) . \dfrac{9}{11}$$.
$$\therefore x + 9 = 11$$ or $$x=2$$.
$$y+ 11 tan \beta$$ ...(1)
and $$x+y = 11 tan (\alpha+ \beta)$$ ...(2)
$$AP = 9 = (x+y) tan \beta$$ ...(3)
$$\therefore 9 = 11 tan (\alpha+ \beta) tan \beta$$,
from (2) and (3),
or $$9 = 11 tan \beta \left( \dfrac{tan \alpha + tan \beta}{1 - tan \alpha tan \beta} \right)$$
Put $$tan \alpha = \dfrac{1}{10}$$.
$$\therefore 9 \left[ 1 - \left( - \dfrac{1}{10} \right) tan \beta \right] = 11 tan \beta \left( \dfrac{1}{10} + tan \beta \right)$$
$$9 (10 - tan \beta) = 11 tan \beta (1+ 10 tan \beta )$$.
$$110 tan^2 \beta + 20 tan \beta - 90 = 0$$
or $$11 tan^2 \beta = 2 tan \beta - 9 = 0$$
$$(11 tan \beta - 9 )(tan \beta + 1) = 0$$
$$\therefore tan \beta = \dfrac{9}{11} ( \beta acute)$$
Hence from (1),
$$y = 11 tan \beta = 11. \dfrac{9}{11} = 9$$
From (3),
$$9 = (x+y) tan \beta = (x+9) . \dfrac{9}{11}$$.
$$\therefore x + 9 = 11$$ or $$x=2$$.
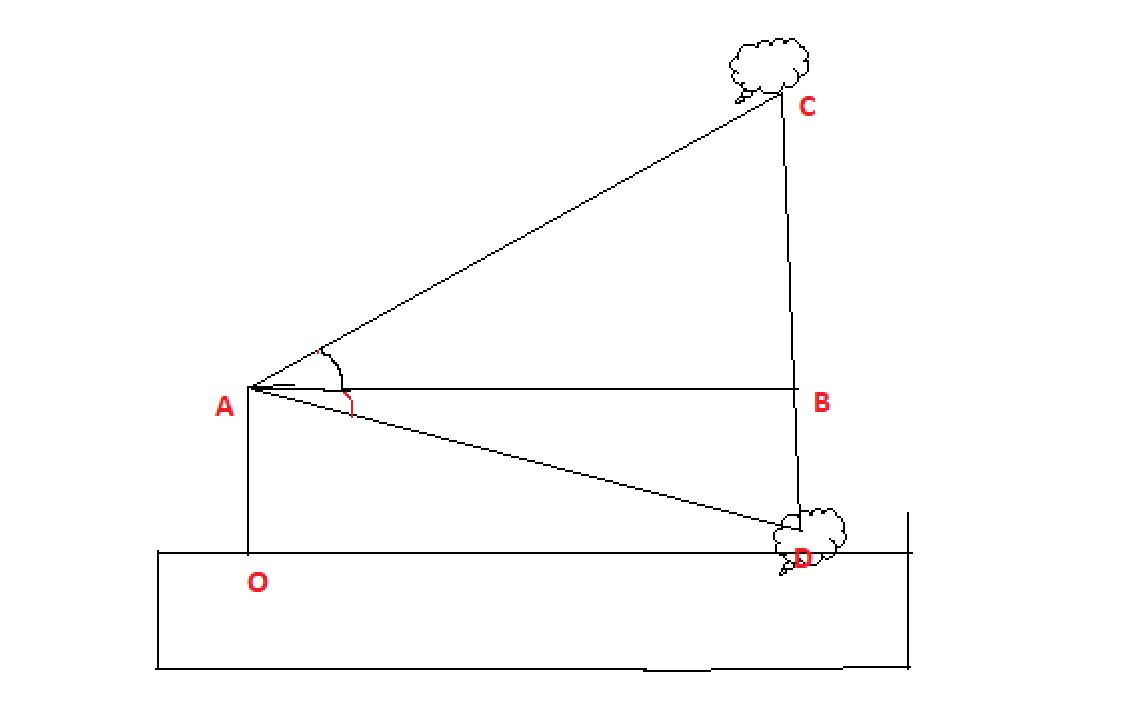
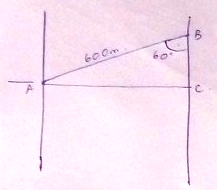
An observer at an anti-aircraft post A identifies an enemy aircraft due East of his post at an angle of elevation of $$60^o$$. At the same instant a detection post D situated 4 kms South of A reports the aircraft at an elevation of $$30^o$$. Calculate the altitude at which the plane is flying.
PQ is $$\perp$$ to AP and DP where
$$AP = h cot 60^o, DP = h cot 30^o$$
$$\therefore AP = \dfrac{h}{\sqrt{3}} , DP = h \sqrt{3}$$
Now from right-angled triangle DAP we have
$$DP^2 = AD^2 + AP^2$$
$$\therefore (h \sqrt{3})^2 = 4^2 + \left( \dfrac{h}{\sqrt{3}} \right)^2$$
$$h^2 \left( 3 - \dfrac{1}{3} \right) = 16$$
$$h^2 = 6$$ or $$h = \sqrt{6} km$$.
$$AP = h cot 60^o, DP = h cot 30^o$$
$$\therefore AP = \dfrac{h}{\sqrt{3}} , DP = h \sqrt{3}$$
Now from right-angled triangle DAP we have
$$DP^2 = AD^2 + AP^2$$
$$\therefore (h \sqrt{3})^2 = 4^2 + \left( \dfrac{h}{\sqrt{3}} \right)^2$$
$$h^2 \left( 3 - \dfrac{1}{3} \right) = 16$$
$$h^2 = 6$$ or $$h = \sqrt{6} km$$.
A statue standing on a column subtends equal angles $$\alpha$$ at two points which are at a distance of 18 m. and 22 m. from the column. If $$tan \alpha = \dfrac{1}{10}$$, find the height of the column and the statue.
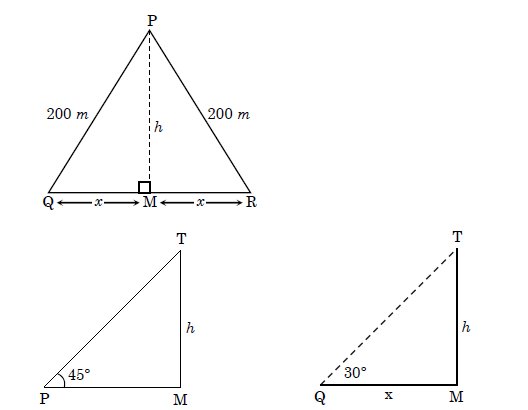
PQR is a triangular park with PQ = PR = $$200 \text{ m}$$. A television tower stands at the midpoint of QR. The angles of elevation of the top of the tower at P, Q, and R are $$45^{\circ}, 30^{\circ} , 30^{\circ}$$ respectively. Find the height of the tower.
From $$\triangle PMT,$$
$$\tan 45^{\circ}=\dfrac{MT}{PM}$$
$$\implies 1=\dfrac{MT}{PM}$$
$$\implies MT=PM=h$$ -------(1)
From $$\triangle QMT$$
$$\tan 30^{\circ}=\dfrac{MT}{QM}$$
$$\implies \dfrac{1}{\sqrt 3}=\dfrac{MT}{QM}=\dfrac{h}{x}$$
$$\implies x=\sqrt{3}h$$ --------(2)
From $$\triangle QPM$$
$$QP^2=QM^2+PM^2$$ (as per Pythagoras theorem)
$$\implies 200^2=x^2+h^2$$
$$\implies 200^2=3h^2+h^2$$ (on using (2))
$$\implies 4 \times 100^2=4h^2$$
$$\implies h^2=100^2$$
$$\implies h= \pm 100$$
$$\implies h=100 \text{ m}$$ (since, height can not bee negative)
$$\therefore$$ Height of the tower is $$100\text{ m}$$
A person observes the top P of a vertical tower OP of height h from a station $$S_1$$ and finds that $$\beta_1$$ is the angle of elevation. He moves in a horizontal plane to second station $$S_2$$ and finds that $$\angle PS_2S_1$$ is $$\gamma_1$$ and the angle subtended by $$S_2S_1$$ at P is $$\delta_1$$ and the angle of elevation is $$\beta_2$$. He moves again to a third station $$S_3$$ such that $$S_3S_2 =S_2S_1$$, $$\angle PS_3S_2 = \gamma_2$$ and the angle subtended by $$S_3S_2$$ at P is $$\delta_2$$. Show that
$$\dfrac{\sin \gamma_1 \sin \beta_1}{\sin \delta_1} = \dfrac{\sin \gamma_2 \sin \beta_2}{\sin \delta_2} = \dfrac{h}{S_1 S_2}$$
$$h = PS_1 sin \beta_1 $$ or $$PS_1 = h cosec \beta_1 $$.
From $$\Delta PS_1S_2$$ by sine formula
$$\dfrac{PS_1}{sin \gamma_1} = \dfrac{S_1S_2}{sin \delta_1}$$
or $$\dfrac{h}{sin \beta_1 sin \gamma_1} = \dfrac{S_1 S_2}{sin \delta_1}$$ by (1)
or $$\dfrac{h}{S_1 S_2} = \dfrac{sin \beta_1 sin \gamma_2}{sin \delta_1}$$
Similarly, $$\dfrac{h}{S_2 S_3} = \dfrac{sin \beta_2 sin \gamma_2}{sin \delta_2}$$
But $$S_2 S_3 = S_1 S_2$$ given
$$\therefore \dfrac{sin \beta_1 sin \gamma_1}{sin \delta_1} = \dfrac{sin \beta_2 sin \gamma_2}{sin \delta_2} = \dfrac{h}{S_1 S_2}$$
From $$\Delta PS_1S_2$$ by sine formula
$$\dfrac{PS_1}{sin \gamma_1} = \dfrac{S_1S_2}{sin \delta_1}$$
or $$\dfrac{h}{sin \beta_1 sin \gamma_1} = \dfrac{S_1 S_2}{sin \delta_1}$$ by (1)
or $$\dfrac{h}{S_1 S_2} = \dfrac{sin \beta_1 sin \gamma_2}{sin \delta_1}$$
Similarly, $$\dfrac{h}{S_2 S_3} = \dfrac{sin \beta_2 sin \gamma_2}{sin \delta_2}$$
But $$S_2 S_3 = S_1 S_2$$ given
$$\therefore \dfrac{sin \beta_1 sin \gamma_1}{sin \delta_1} = \dfrac{sin \beta_2 sin \gamma_2}{sin \delta_2} = \dfrac{h}{S_1 S_2}$$
A pole stands at the bank of a circular pond. A man walking along the bank finds that the angle of elevation of the top of the pole from the two points A and B is $$30^o$$ each and from the third point C, it is $$45^o$$. If the distances from A to B and from B to C measured along the bank are 40 m and 20 m respectively; find the radius of the pond and the height of the pole.
A semicircular arch AB of length 2L and a vertical tower PQ are situated in the same vertical plane. The feet A and B of the arch and the base Q of the tower are at the same horizontal level, with B between A and Q. A man at A finds the tower hidden from his view due to the arch. He starts crawling up the arch and just sees the topmost point P of the tower after covering a distance $$\dfrac{L}{2}$$ along the arch. He crawls further to the topmost point of the arch and notes the angle of elevation of P to be $$\theta$$. Compute the height of the tower in terms of L and $$\theta$$.
$$2L = \pi r$$ (semi circumference)
$$\therefore \dfrac{L}{2} = \dfrac{\pi r}{4}$$
Since $$ \dfrac{l}{r} = \theta$$ $$\therefore \dfrac{L/2}{r} = \dfrac{\pi r}{4}$$
i.e., when the man is at M then arc AM subtend and angle of $$\dfrac{\pi}{4}$$ at O. From M we can just see the top of tower so that MP is a tangent to arc at M
$$\therefore$$ OM is normal.
$$\therefore \angle PMO = 90^o$$ or $$\angle PMN = 45^o = \angle CMO$$
We have to find the height PQ of tower in term of $$\theta$$ and L, were
$$2L = \pi r$$ or $$ r = \dfrac{2L}{\pi}$$ ...(1)
Let $$PD = x$$ so that $$PQ = x+r$$ ...(2)
No $$CD = x \cot \theta$$ in $$\Delta FCD$$.
$$MN = PN \cot 45^o = PN$$
$$MK + KN = PD +DN$$
$$\dfrac{r}{\sqrt{2}} + CD = x + (DQ - NQ)$$
$$\dfrac{r}{\sqrt{2}} + x \cot \theta = x + \left( r - \dfrac{r}{\sqrt{2}} \right)$$
$$\therefore r ( \sqrt{2} - 1) = x (1- \cot \theta)$$
$$\therefore x = \dfrac{r ( \sqrt{2} - 1)}{1 - \cot \theta}$$
$$\therefore PQ = x + r = \dfrac{r ( \sqrt{2} - 1)}{1 - \cot \theta} + r$$
or $$ PQ = \dfrac{\sqrt{2} - \cot \theta}{1 - \cot \theta} = \dfrac{2L}{\pi} \left( \dfrac{\sqrt{2} - \cot \theta}{1 - \cot \theta} \right)$$ by (1)
$$\therefore \dfrac{L}{2} = \dfrac{\pi r}{4}$$
Since $$ \dfrac{l}{r} = \theta$$ $$\therefore \dfrac{L/2}{r} = \dfrac{\pi r}{4}$$
i.e., when the man is at M then arc AM subtend and angle of $$\dfrac{\pi}{4}$$ at O. From M we can just see the top of tower so that MP is a tangent to arc at M
$$\therefore$$ OM is normal.
$$\therefore \angle PMO = 90^o$$ or $$\angle PMN = 45^o = \angle CMO$$
We have to find the height PQ of tower in term of $$\theta$$ and L, were
$$2L = \pi r$$ or $$ r = \dfrac{2L}{\pi}$$ ...(1)
Let $$PD = x$$ so that $$PQ = x+r$$ ...(2)
No $$CD = x \cot \theta$$ in $$\Delta FCD$$.
$$MN = PN \cot 45^o = PN$$
$$MK + KN = PD +DN$$
$$\dfrac{r}{\sqrt{2}} + CD = x + (DQ - NQ)$$
$$\dfrac{r}{\sqrt{2}} + x \cot \theta = x + \left( r - \dfrac{r}{\sqrt{2}} \right)$$
$$\therefore r ( \sqrt{2} - 1) = x (1- \cot \theta)$$
$$\therefore x = \dfrac{r ( \sqrt{2} - 1)}{1 - \cot \theta}$$
$$\therefore PQ = x + r = \dfrac{r ( \sqrt{2} - 1)}{1 - \cot \theta} + r$$
or $$ PQ = \dfrac{\sqrt{2} - \cot \theta}{1 - \cot \theta} = \dfrac{2L}{\pi} \left( \dfrac{\sqrt{2} - \cot \theta}{1 - \cot \theta} \right)$$ by (1)
The angle of elevation of the top of a tower from a point A due South of the tower is $$\alpha$$ and from B due East of the tower is $$\beta$$. If AB = d, show that the height of the tower is
$$\dfrac{d}{\sqrt{(cot^2 \alpha + cot^2 \beta)}}$$
PQ is $$\perp$$ to PA and PB both
$$h=PA tan \alpha$$ and $$h = PB tan \beta$$
$$\therefore PA = h cot \alpha, PB = h cot \beta$$.
Also, $$AB^2 = PA^2 + PB^2$$
or $$d^2 = h^2 (cot^2 \alpha + cot^2 \beta)$$.
$$\therefore h = \dfrac{d}{\sqrt{cot^2 \alpha + cot^2 \beta}}$$
$$h=PA tan \alpha$$ and $$h = PB tan \beta$$
$$\therefore PA = h cot \alpha, PB = h cot \beta$$.
Also, $$AB^2 = PA^2 + PB^2$$
or $$d^2 = h^2 (cot^2 \alpha + cot^2 \beta)$$.
$$\therefore h = \dfrac{d}{\sqrt{cot^2 \alpha + cot^2 \beta}}$$
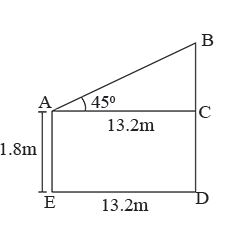
An observer of height $$1.8 \text{ m}$$ is $$13.2 \text{ m}$$ away from a palm tree. The angle of elevation of the top of the tree from his eyes is $$45^\circ$$. What is the height of the palm tree?
$$\text{Height of observer}=AE$$
$$=1.8\text{ m}$$
$$ ED=AC$$
$$=13.2\text{ m}$$
In $$\triangle ABC,$$
$$\begin{aligned}{}\tan {45^\circ } &= \frac{{BC}}{{AC}}\\1 &= \frac{{BC}}{{13.2}}\\BC &= 13.2\text{ m}\end{aligned}$$
The height of the palm tree will be equal to $$BD$$. So,
$$\begin{aligned}{}BD &= BC + CD\\ &= 13.2 + AE\\ &= 13.2 + 1.8\\& = 15\text{ m}\end{aligned}$$
So, the height of the palm tree is equal to $$15\text{ m}.$$
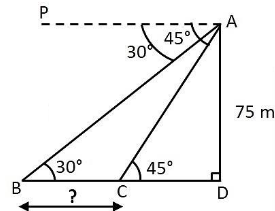
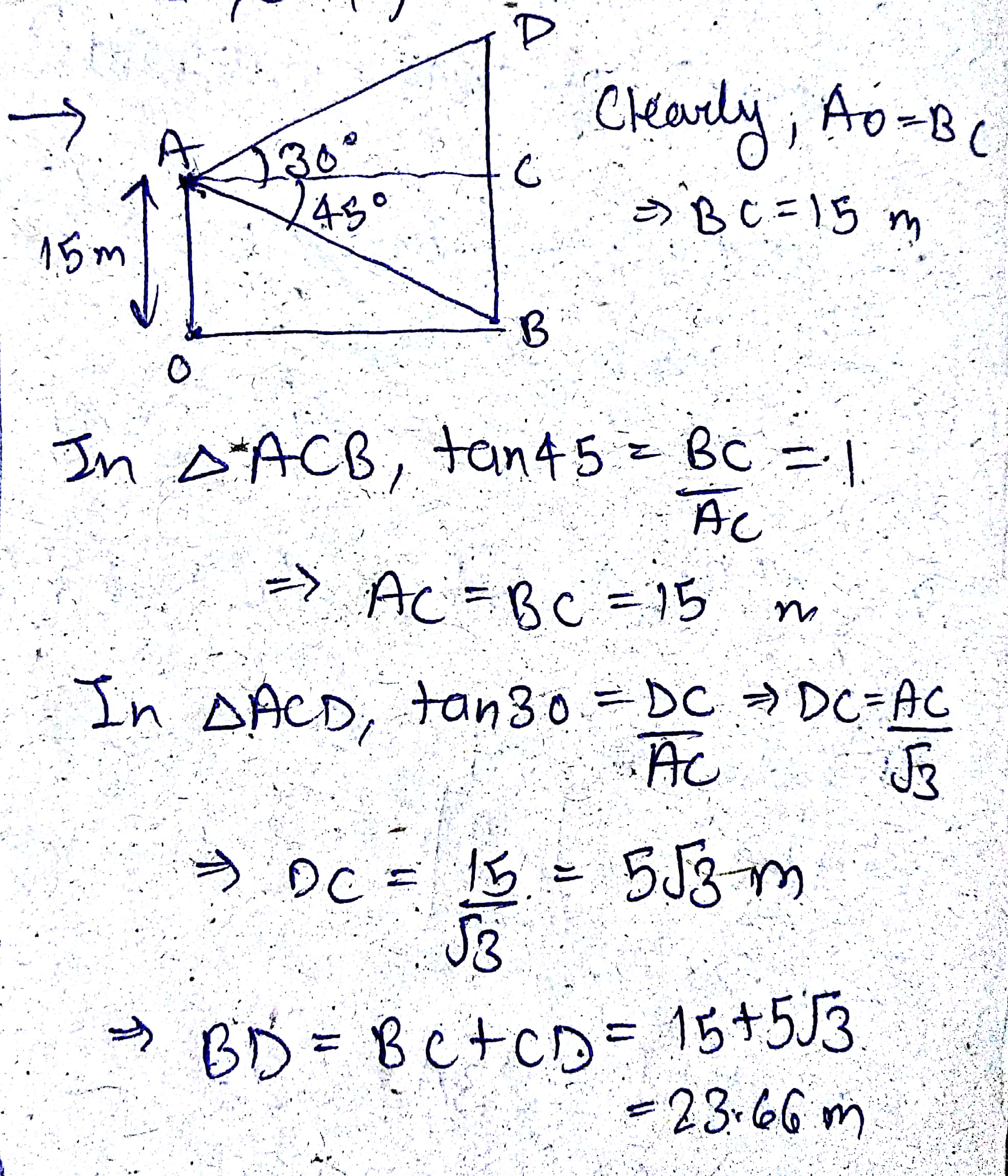
From a window 15 meters heigh above the ground in a street , the angles of elevation and depression of the top and the foot of another house on the opposite side of the street are $$30^{\circ} \, and \, 45^{\circ}$$ respectively show that the height of the opposite house is 23.66 meters. (Take $$\sqrt{3}$$ = 1.732)
As observed from the top of a light house, 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from $$30^{\circ} \, to \, 40^{\circ}$$. Determine the distance travelled by the ship during the period of observation.
Let A and B be the two positions of the ship. Let d be the distance travelled by the ship during the period of observation i.e. AB = d metres.
Let the observer be at O, the top of the lighthouse PO.
It is given that PO = 100 m and the angle of depression from O of A and B are $$30^{\circ}$$ and $$45^{\circ}$$ respectively.
$$\therefore \, \angle OAP \, = \, 30^{\circ} \, and \, \angle OBP \, = \, 45^{\circ}$$
In $$\Delta$$ OPB, we have
$$tan \, 45^{\circ} \, = \, \dfrac{OP}{BP}$$
$$\Rightarrow \, 1 \, = \, \dfrac{100}{BP}$$
$$\Rightarrow$$ BP = 100 m
In $$\Delta$$ OPA, we have
$$\Rightarrow \, tan \, 30^{\circ} \, = \, \dfrac{OP}{AP}$$
$$\Rightarrow \, \dfrac{1}{\sqrt{3}} \, = \, \dfrac{100}{d \, + \, BP}$$
$$\Rightarrow$$ d + BP = 100$$\sqrt{3}$$
$$\Rightarrow$$ d + BP = 100$$\sqrt{3}$$
$$\Rightarrow$$ d = 100$$\sqrt{3}$$ - 100
$$\Rightarrow$$ d = 100($$\sqrt{3}$$ - 1) = 100(1.732 - 1) = 73.2 m.
Hence, the distance travelled by the ship from A to B is 73.2 m.
Let the observer be at O, the top of the lighthouse PO.
It is given that PO = 100 m and the angle of depression from O of A and B are $$30^{\circ}$$ and $$45^{\circ}$$ respectively.
$$\therefore \, \angle OAP \, = \, 30^{\circ} \, and \, \angle OBP \, = \, 45^{\circ}$$
In $$\Delta$$ OPB, we have
$$tan \, 45^{\circ} \, = \, \dfrac{OP}{BP}$$
$$\Rightarrow \, 1 \, = \, \dfrac{100}{BP}$$
$$\Rightarrow$$ BP = 100 m
In $$\Delta$$ OPA, we have
$$\Rightarrow \, tan \, 30^{\circ} \, = \, \dfrac{OP}{AP}$$
$$\Rightarrow \, \dfrac{1}{\sqrt{3}} \, = \, \dfrac{100}{d \, + \, BP}$$
$$\Rightarrow$$ d + BP = 100$$\sqrt{3}$$
$$\Rightarrow$$ d + BP = 100$$\sqrt{3}$$
$$\Rightarrow$$ d = 100$$\sqrt{3}$$ - 100
$$\Rightarrow$$ d = 100($$\sqrt{3}$$ - 1) = 100(1.732 - 1) = 73.2 m.
Hence, the distance travelled by the ship from A to B is 73.2 m.
An aeroplane at an altitude of 1200 meters finds that two ships are sailing towards it in the same direction . The angle of depression of the ships as observed from the planner are $$ 60^{\circ }$$ and $$ 30^{\circ} $$ respectively. Find the distance between the two ships.
Let the aeroplane be at B and let the two ships be at C and D such that their angles of depression from B are $$ 60^{\circ }$$ and $$ 30^{\circ} $$ respectively.
We have AB = 1200 metres. Let AC = x and CD = y.
In $$\Delta CAB$$ , we have.
$$tan \, \, 60^{\circ} \, = \, \dfrac{AB}{CA}$$
$$\Rightarrow \, \sqrt{3} \, = \, \dfrac{1200}{x}$$
$$\Rightarrow \, x \, = \, \dfrac{1200}{\sqrt{3}} \, = \, 400\sqrt{3}$$
In $$\Delta BAD$$ , we have
$$tan \, \, 30^{\circ} \, = \, \dfrac{AB}{AD}$$
$$\Rightarrow \, \dfrac{1}{\sqrt{3}}\, = \, \dfrac{1200}{x \, + \, y}$$
$$\Rightarrow \,x \, + \, y \, = \, 1200\sqrt{3}$$
$$\Rightarrow \, y \, = \, 1200\sqrt{3} \, - \, x$$
$$\Rightarrow \, y \, = \, 1200\sqrt{3} \, - \, 400\sqrt{3} \, = \, 800\sqrt{3} \, = \, 800 \, \times \, 1.732 \, = \, 1385.6$$
Hence, the distance between the two ships is 1385.6 metres.
We have AB = 1200 metres. Let AC = x and CD = y.
In $$\Delta CAB$$ , we have.
$$tan \, \, 60^{\circ} \, = \, \dfrac{AB}{CA}$$
$$\Rightarrow \, \sqrt{3} \, = \, \dfrac{1200}{x}$$
$$\Rightarrow \, x \, = \, \dfrac{1200}{\sqrt{3}} \, = \, 400\sqrt{3}$$
In $$\Delta BAD$$ , we have
$$tan \, \, 30^{\circ} \, = \, \dfrac{AB}{AD}$$
$$\Rightarrow \, \dfrac{1}{\sqrt{3}}\, = \, \dfrac{1200}{x \, + \, y}$$
$$\Rightarrow \,x \, + \, y \, = \, 1200\sqrt{3}$$
$$\Rightarrow \, y \, = \, 1200\sqrt{3} \, - \, x$$
$$\Rightarrow \, y \, = \, 1200\sqrt{3} \, - \, 400\sqrt{3} \, = \, 800\sqrt{3} \, = \, 800 \, \times \, 1.732 \, = \, 1385.6$$
Hence, the distance between the two ships is 1385.6 metres.
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island . P and Q are points directly opposite to each other an two banks and in the line with the tree . If the angle of elevation of the top of the tree from P and Q are respectively $$30^ {\circ}$$ and $$ 45^{\circ} $$ find the height of the tree
Let OA be the tree of height h metre.
In triangle POA and QOA, we have
tan $$30^\circ \, = \, \dfrac{OA}{OP}$$ and tan $$45^\circ \, = \, \dfrac{OA}{OQ}$$
$$\Rightarrow \, \, \, \, \dfrac{1}{\sqrt{3}} \, = \, \dfrac{h}{OP} \, and \, 1 \, = \, \dfrac{h}{OQ}$$
$$\Rightarrow \, \, \, \, OP \, = \, \sqrt{3} \, h \, and \, OQ \, = \, h$$
$$\Rightarrow \, \, \, \, OP \, + \, OQ \, = \, \sqrt{3} \, h \, + \, h$$
$$\Rightarrow \, \, \, \, PQ \, = \, (\sqrt{3} \, + \, 1) \, h$$
$$\Rightarrow \, \, \, \, 100 \, = \, (\sqrt{3} \, + \, 1) \, h \, \, [\because \, PQ \, = \, 100 \, m]$$
$$\Rightarrow \, \, \, \, h \, = \, \dfrac{100}{\sqrt{3} \, + \, 1} m$$
$$\Rightarrow \, \, \, \, h \, = \, \dfrac{100 \, (\sqrt{3} \, + \, 1)}{2} m$$
$$\Rightarrow \, \, \, \, h \, = \, 50 (1.732 \, - \, 1) \, m \, = \, 36.6 \, m$$
Hence, the height of the tree is 36.6 m.
In triangle POA and QOA, we have
tan $$30^\circ \, = \, \dfrac{OA}{OP}$$ and tan $$45^\circ \, = \, \dfrac{OA}{OQ}$$
$$\Rightarrow \, \, \, \, \dfrac{1}{\sqrt{3}} \, = \, \dfrac{h}{OP} \, and \, 1 \, = \, \dfrac{h}{OQ}$$
$$\Rightarrow \, \, \, \, OP \, = \, \sqrt{3} \, h \, and \, OQ \, = \, h$$
$$\Rightarrow \, \, \, \, OP \, + \, OQ \, = \, \sqrt{3} \, h \, + \, h$$
$$\Rightarrow \, \, \, \, PQ \, = \, (\sqrt{3} \, + \, 1) \, h$$
$$\Rightarrow \, \, \, \, 100 \, = \, (\sqrt{3} \, + \, 1) \, h \, \, [\because \, PQ \, = \, 100 \, m]$$
$$\Rightarrow \, \, \, \, h \, = \, \dfrac{100}{\sqrt{3} \, + \, 1} m$$
$$\Rightarrow \, \, \, \, h \, = \, \dfrac{100 \, (\sqrt{3} \, + \, 1)}{2} m$$
$$\Rightarrow \, \, \, \, h \, = \, 50 (1.732 \, - \, 1) \, m \, = \, 36.6 \, m$$
Hence, the height of the tree is 36.6 m.
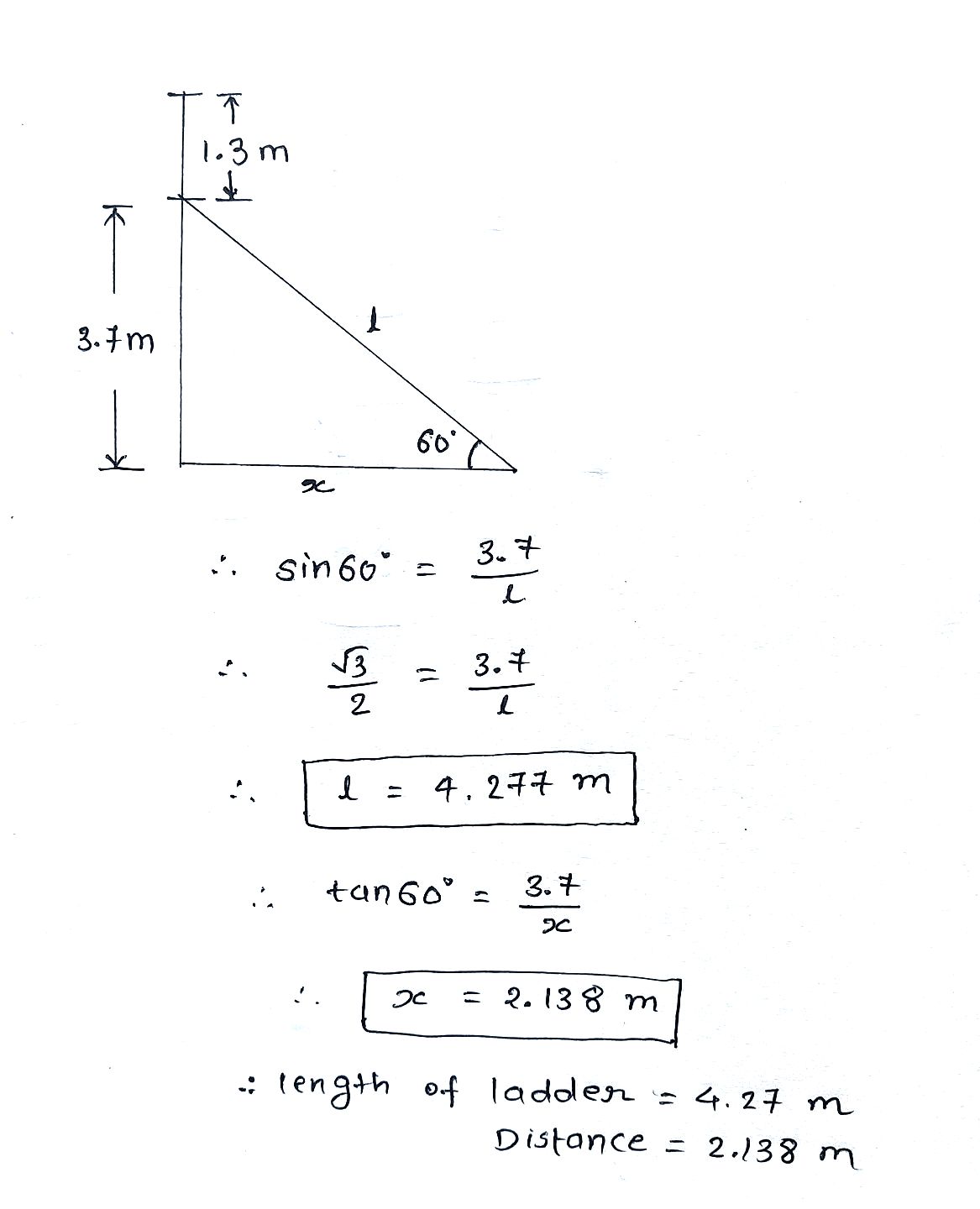
An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60$$^{\circ}$$ to the horizontal would enable him to reach the required position?
Let AC be the electricpole of height 4 m. Let B be a point 1.3 m below the top A of the pole AC.
Then, BC = AC - AB = (4 - 1.3)m = 2.7 m
Let BD be the inclined at an angle of $$60^{\circ}$$ to the horizontal.
In $$\Delta$$BCD, we have
$$sin \, 60^{\circ} \, = \, \dfrac{BC}{BD}$$
$$\Rightarrow \, \dfrac{\sqrt{3}}{2} \,= \, \dfrac{2.7}{BD}$$ $$[\because \, BC \, = \, 2.7 \, m]$$
$$\Rightarrow \, BD \, = \, \dfrac{2 \, \times \, 2.7}{\sqrt{3}}m \, = \, \dfrac{5.4}{\sqrt3}m \, = \, \dfrac{5.4 \, \times \, \sqrt{3}}{3}m$$
$$\Rightarrow \, BD \, = \, (1.8)\sqrt{3} \, m \, = \, \dfrac{9}{5}\sqrt{3}m$$
Hence, the length of the ladder should be $$\dfrac{9\sqrt{3}}{5}m.$$
Then, BC = AC - AB = (4 - 1.3)m = 2.7 m
Let BD be the inclined at an angle of $$60^{\circ}$$ to the horizontal.
In $$\Delta$$BCD, we have
$$sin \, 60^{\circ} \, = \, \dfrac{BC}{BD}$$
$$\Rightarrow \, \dfrac{\sqrt{3}}{2} \,= \, \dfrac{2.7}{BD}$$ $$[\because \, BC \, = \, 2.7 \, m]$$
$$\Rightarrow \, BD \, = \, \dfrac{2 \, \times \, 2.7}{\sqrt{3}}m \, = \, \dfrac{5.4}{\sqrt3}m \, = \, \dfrac{5.4 \, \times \, \sqrt{3}}{3}m$$
$$\Rightarrow \, BD \, = \, (1.8)\sqrt{3} \, m \, = \, \dfrac{9}{5}\sqrt{3}m$$
Hence, the length of the ladder should be $$\dfrac{9\sqrt{3}}{5}m.$$
A person walks along a straight road and observes that the greatest angle subtended by two objects is $$\alpha$$; from the point where this greatest angle is subtended he walks distance c along the road, and finds that the two objects are now in a straight line which makes an angle $$\beta$$ with the road; prove that the distance between the objects is
$$c \sin \alpha \sin \beta \sec \dfrac{\alpha + \beta}{2} \sec \dfrac{\alpha - \beta}{2}$$ or $$\dfrac{2c \sin \alpha \sin \beta}{\cos \alpha + \cos \beta}$$
Four ships A, B, C and D are at sea in the following relative positions : B is on the straight line segment AC, B is due north of D, and D is due west of C. The distance between B and D is 2 km, $$\angle BDA = 40^o, \angle BCD = 25^o$$. What is the distance between A and D? (Take $$sin 25^o = 0.423$$).
The figure is self explanatory. In $$\Delta ADC$$, we have $$\angle ADC= 40^o +90^o =130^o$$
and $$\angle DCA = 25^o$$
$$\therefore \angle DAC = 180^o - (130^o + 25^o) = 25^o$$
Hence $$AD = DC = 2 \cot 25^o = 2 . \dfrac{\sqrt{1 - \sin^2 25^o}}{\sin 25^o}$$
$$= \dfrac{2 \times .906}{0.423} = 4.283 km$$.
and $$\angle DCA = 25^o$$
$$\therefore \angle DAC = 180^o - (130^o + 25^o) = 25^o$$
Hence $$AD = DC = 2 \cot 25^o = 2 . \dfrac{\sqrt{1 - \sin^2 25^o}}{\sin 25^o}$$
$$= \dfrac{2 \times .906}{0.423} = 4.283 km$$.
A ten meter high tower is standing at the centre of an equilateral triangle and each side of the triangle subtends an angle of $$60^o$$ at the top of the tower. Prove that the length of each side of the triangle is $$5 \sqrt{6}$$ metres.
Let $$ABC$$ be the equilateral triangle and $$PQ$$, the tower standing at the centre $$P$$ of the triangle, as shown in the figure above.
Here, $$PQ = 10 \ m$$.
Since each side of the triangle subtends an angle of $$60^o$$ at Q, the top of the tower, we have:
$$\angle BQC = \angle CQA= \angle AQB = 60^o$$
$$\angle BQC = \angle CQA= \angle AQB = 60^o$$
Hence, $$AQ = QB$$
Since, $$\angle AQB = 60^o,\ \Delta AQB$$ is equilateral.
Hence, $$QA = QB = AB = 2a\ (let)$$
Similarly, $$\Delta BQC$$ is equilateral.
Hence, $$QB = QC = 2 a$$
$$\therefore \ QA = QB = QC = 2 a$$
We know that, a centroid is a point on the median, which is at $$\left(\dfrac23\right)^{rd}$$ distance from the vertex.
Hence, $$AP = \dfrac{2}{3} AD$$
We also know that, the median of an equilateral triangle is a perpendicular bisector.
Hence, $$\Delta ABD$$ is a right-angled triangle.
Also, since $$\Delta ABC$$ is equilateral, $$\angle ABD=60^o$$
We know that, $$\sin \theta=\dfrac{\text{Opposite Side}}{\text{Hypotenuse}}$$
Hence, $$\sin 60^o=\dfrac{AD}{2a}$$
$$\Rightarrow AD=2a\sin 60^o$$
So, $$AP= \dfrac{2}{3} \times 2 a \sin 60^o $$
$$= \dfrac{4 a}{3} \times \dfrac{\sqrt{3}}{2}\quad \quad \left[\because \ \sin { 60^o } =\dfrac{\sqrt3}{2}\right]$$
$$\therefore \ AP= \dfrac{2 a}{\sqrt{3}}$$
$$\Delta APQ$$ is also a right-angled triangle.
Hence, by Pythagoras theorem, we have,
Hence, by Pythagoras theorem, we have,
$$AQ^2 = AP^2 + PQ^2$$
$$\Rightarrow AQ^2 - AP^2 = PQ^2$$
$$\Rightarrow 4 a^2 - \dfrac{4 a^2}{3} = 10^2$$
$$\Rightarrow \dfrac{8 a^2}{3} = 100$$
$$\Rightarrow a^2 = \dfrac{75}{2}$$
$$\Rightarrow a = 5 \sqrt{\dfrac{3}{2}}$$
Now, the length of the side $$AB = 2 a $$
$$= 2 \times 5 \sqrt{\dfrac{3}{2}} $$
$$= 5 \sqrt{6} \ m$$
Hence, it is proved that the length of each side of the triangle is $$5\sqrt 6 \ m$$.
A helicopter is flying at an altitude of $$250m$$ between two banks of a river. From the helicopter it is observed that the angles of a river. From the helicopter its is observed that the angle of depression of two boats on the opposite banks are $$45^o$$ and $$60^o$$ respectively. Find the width of the river. Given your answer correct to nearest metre.
Now,
$$\tan { { 30 }^{ \circ } } =\cfrac { HC }{ AC } =\cfrac { 250 }{ AC } \quad ;\quad \quad \tan { { 45 }^{ \circ } } =\cfrac { HC }{ BC } \\ \therefore AC=250\sqrt { 3 } m\quad \quad ;HC=BC=250m$$
$$\therefore$$ Width of the river is $$=\left| AB \right| =250\sqrt { 3 } +250$$
$$ =250(\sqrt { 3 } +1)\\ \cong 683m$$
A $$150$$ cm tallboy stands at a distance of $$8$$ m from a lamp post and casts a shadow of $$2$$ m. Find the height of the lamp post.
Therefore, from the above figure,
$$\tan\theta =\dfrac { 1.5 }{ 2 } $$ {$$150cm=1m$$}
$$\tan\theta =\dfrac { h }{ 8+2 } $$
Equating both we get,
$$\Rightarrow \dfrac { 1.5 }{ 2 } =\dfrac { h }{ 10 }$$
$$ \Rightarrow h=\dfrac { 1.5\times 10 }{ 2 } =7.5m$$
$$h=7.5m$$
A vertically straight tree, $$15$$m high is broken by the wind in such a way that it top just touches the ground and makes an angle of $$30^0$$ with the ground, at what height from the ground did the tree break?
Height of tree $$=OB+AB=15 m$$
At point B tree has broken.
$$\sin 30=\cfrac{OB}{AB}$$
$$AB=2OB$$
$$\therefore 30B=15$$
$$OB=5m$$
$$\therefore$$, At $$5m$$ from ground, tree was token.
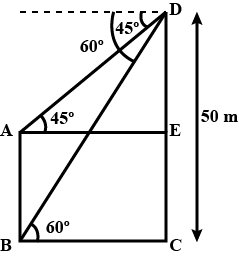
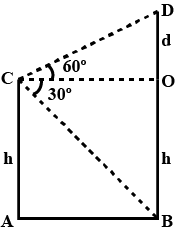
Two man standing outside his house,the angles of elevation of top and both am of window are $$60^o$$ and $$45^o$$. Height of the man is AB=180 cmAB=180 cm, the distance between the man and the wall is BE=5 m.Find length of the window.
Let $$AB$$ be the man and $$CD$$ be the window
Given that the height of the man, $$AB = 180\ cm$$, the distance between the man and the wall, $$BE = 5\ m$$,
$$\angle DAF=45^\circ$$ , $$\angle CAF = 60^\circ$$
From the diagram, $$AF = BE = 5 m$$
From the right triangle $$AFD$$,
$$\tan 45^\circ=\dfrac{DF}{AF}$$
$$1=\dfrac{DF}{5}$$
$$DF = 5$$ ⋯(1)
From the right triangle $$AFC$$,
$$\tan 60^\circ=\dfrac{CF}{AF}$$
$$\sqrt{3}=\dfrac{CF}{5}$$
$$CF=\dfrac{5}{\sqrt 3}$$ ⋯(2)
Length of the window
$$= CD = (CF - DF)$$
$$=5\sqrt3−5$$ [ Substituted the value of $$CF$$ and $$DF$$ from (1) and (2) ]
$$=5(\sqrt3−1)$$
$$=5(1.73−1)$$
$$=5(0.73)$$
$$=3.65\ m$$
The angle of elevation of the top of a tower from a point on the ground which is 30 m away from the foot of the tower is 30$$^0$$. Find the height of the tower.
Given that, the angle of elevation of the top of a tower from a point on the ground which is $$30 \ m$$ away from the foot of the tower is $$30^\circ$$.
To find out: The height of the tower.
Consider, the right angled $$\triangle ABC$$, as shown in the above figure.
We know that, $$\tan B=\dfrac{Opposite \ \ Side}{Adjacent\ \ side}=\dfrac{AC}{BC}$$
$$\therefore \ \tan 30^\circ=\dfrac{h}{30}$$
We know that, $$\tan 30^\circ=\dfrac{1}{\sqrt3}$$
$$\therefore \ \dfrac{1}{\sqrt{3}}=\dfrac{h}{30}$$
$$\Rightarrow h=\dfrac{30}{\sqrt{3}}$$
$$\Rightarrow h=\dfrac{30}{\sqrt{3}} \times \dfrac{\sqrt3}{\sqrt3}=\dfrac{30\sqrt3}{3}$$
$$\therefore\ h=10\sqrt3\ m$$
Hence, the height of the tower is $$10\sqrt{3}\ m$$.
From the top of a house,$$'h'$$ meters high from the ground, the elevation and depression of the top and bottom of a tower on the other side of the street are $$\theta$$ and $$\phi$$ respectively. Prove that the height of the tower is $$h(1+\tan\theta \cot\phi)$$
$$\\tan\theta=(\frac{l-h}{d}) \to (1)\\and tan\phi =(\frac{h}{d}) \to (2)\\divide (1)by (2)\\tan\theta\>cot\phi=(\frac{l-h}{h})\\or\>htan\theta\>cot\phi=l-h\\h(1+tan\theta\>cot\phi)=l$$
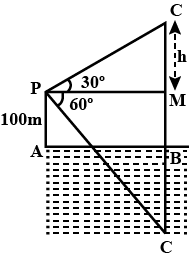
The angle of elevation of a cloud from a point $$60\ m/s$$ above the surface of the water a lake is $$30^{o}$$ and the angle of depression of its shadow from the same point in water of lake is $$60^{o}$$. Find the height of the cloud from the surface of water.
$$ \displaystyle DC =H. $$
$$ \displaystyle DB = D'B = (60 + H) $$
In $$ \displaystyle \triangle ECD \tan 30^0 = \frac{DC}{EC} = \frac{H}{EC} $$
$$ \displaystyle EC =\sqrt{3} \, H $$
In $$ \displaystyle \triangle ECD \tan 60^0 = \frac{D'C}{EC} = \frac{D'B+BC}{EC} = \frac{60+H+60}{\sqrt{3} \, H} $$
$$ \displaystyle 3H =120 + H $$
$$ \displaystyle H = 60 m $$
Height of cloud $$ = 60 + 60 = 120 m. $$
A tree break due to storm and the broken part bends so that the top of the tree touches the ground making an angle $$30^o$$ with it. The distance between the foot of the tree to the point where the top touches the ground is $$8$$m . find the height of the tree.
An observed standing $$40\ m$$ away from a building observed that the angle of elevation of the top and bottom of a flagstaff, which is surmounted on the building are $$60^{o}$$ and $$45^{o}$$ respectively. Find the height of the building and the length of the flagstaff $$(\sqrt {3}=1.732)$$
An Aapache helicopter of enemy is flying along the curve given by $$y={x}^{2}+7$$. A soldier, placed at $$(3, 7)$$, wants to shoot down the helicopter when it is nearest to him. Find the nearest distance.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the top and bottom of the flagstaff are $$\theta $$ and $$\phi $$ respectively. Find the height of the tower.
Let distance between the foot of tower and point of observation
$$CD=x$$
$$y =$$ height of tower
In $$\Delta ACD$$
$$\cot \theta =\displaystyle {x \over {h + y}}$$
$$\left( {h + y} \right)\cot \theta = x$$...............(1)
IN $$\Delta BCD$$
$$\cot \phi = {x \over y}$$
$$x = y\cot \phi $$......................... (2)
From (1) & (2) $$\left( {h + y} \right)\cot \theta = y\cot \phi $$
$$h\cot \theta =y(\cot \theta - \cot \phi) $$
$$y = \dfrac{{h\;\cot \theta }}{{\cot \phi - \cot \theta }} = \dfrac{h}{{\tan \theta }}\left( {\dfrac{{\tan \theta \tan \phi }}{{\tan \theta - \tan \phi }}} \right)$$
(height of tower ) $$y =\displaystyle {{h\cos \phi } \over {\tan \theta - \tan \phi }}$$
The angles of elevation of the top of a tower from the bottom and top of a building of height d are $$\beta $$ and $$\alpha $$ respectively. Find the height of the tower.
Given $$\angle ABD=\beta,\angle ECD=\alpha,BC=d, AB=EC$$
$$AB=\dfrac{AD}{\tan \beta}$$
$$AB=\dfrac{AD}{\tan \beta}$$
$$EC=\dfrac{ED}{\tan \alpha}=\dfrac{AD-d}{\tan \alpha}$$
We know that $$AB=EC$$
$$\dfrac{AD}{\tan \beta}=\dfrac{AD-d}{\tan \alpha}$$
Height of the tower $$AD=\dfrac{d\tan \beta}{\tan\beta-\tan \alpha}$$
The angles of elevation of the top of a tower measured from the points A and B on a horizontal line, on the either side of the foot of the tower are $$\alpha $$ and $$\beta $$. If AB = d, then find the height of the tower.
A contractor wants to set up a slide for the children to play in the park. He wants to set it up the height of $$2\ m$$ and by making an angle of $$30^{o}$$ with the ground. What should be the length of the slide?
The height of the slide is $$2\;{\rm{m}}$$. Then, in $$\Delta ABC$$,
$$\sin 30^\circ = \dfrac{{AB}}{{AC}}$$
$$AC = \dfrac{{AB}}{{\sin 30^\circ }}$$
$$AC = \dfrac{2}{{\dfrac{1}{2}}}$$
$$AC = 4\;{\rm{m}}$$
Therefore, the length of the slide is $$4\;{\rm{m}}$$.
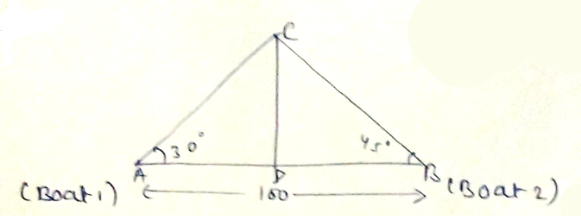
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are $$30^o$$ and $$45^o$$ respectively. If the lighthouse is $$100\ \text{m}$$ high, find the distance between the two ships.
Let $$AC=x$$ and $$AD=y$$
In $$\triangle ABC$$
$$\begin{matrix} \\ \tan { 30^{ \circ } } =\dfrac { { AB } }{ { AC } } \\ \Rightarrow \dfrac { 1 }{ { \sqrt { 3 } } } =\dfrac { { 100 } }{ x } \\ \Rightarrow x=100\sqrt { 3 } \\ \end{matrix}$$
similarly,
In $$\triangle ABD$$
$$\begin{matrix} \\ \tan { 45^{ \circ } } =\dfrac { { AB } }{ { AD } } \\ \Rightarrow 1=\dfrac { { 100 } }{ y } \\ \Rightarrow y=100 \\ \end{matrix}$$
Hence,
Distance between two ships $$ = \left( {x + y} \right)$$
$$\begin{matrix} =100\sqrt { 3 } +100 \\ =100\left( { \sqrt { 3 } +1 } \right) \text{ m} \\ \end{matrix}$$
Find the height of ladder if the height of the wall is $$50\ cm$$ and angle of elevation is $$60^{o}$$.
Given that
height of wall $$l=50cm$$
angle of elevation$$=60^0$$
Let height of ladder be $$h$$
From the image we can see that,
$$\Rightarrow tan(60^0)=\dfrac{50}{h}$$
$$\Rightarrow \sqrt 3=\dfrac{50}{h}$$
$$\Rightarrow h=\dfrac{50}{\sqrt 3}cm$$
$$\Rightarrow h=28.87cm$$
Therefore, the height of ladder is $$28.87cm$$
A ladder of length $$4 m$$ makes an angle $${30^ \circ }$$ with the floor while leaning against one wall of a room. If the foot of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of $${60^ \circ }$$ with the floor. Find the distance between the two walls of the room.
Length of walls of room will same $$AB=ED$$
$$30^o=\dfrac{BC}{AC}\Rightarrow \dfrac{\sqrt3}{2}=\dfrac{BC}{4}\Rightarrow BC=2\sqrt 3m$$
$$\cos 60^o=\dfrac{CD}{EC}\Rightarrow \dfrac{1}{2}=\dfrac{CD}{4}\Rightarrow CD=2m$$
$$\therefore $$ Length of from $$l$$ distance between walls
$$=BD=BC+CD$$
$$2\sqrt 3+2=2(\sqrt3+1)m$$
The angle of elevation of the top of building from the foot of the tower is $$30^{o}$$ and the angle of top of the tower from the foot of the building is $$60^{o}$$. If the tower is $$50m$$ high. Find the height of the building.
$$\Rightarrow$$ Height of tower $$(CD)=50\,m$$
In right angled $$\triangle DBC$$,
$$\tan\,60^o=\dfrac{DC}{BC}$$
$$\Rightarrow$$ $$\sqrt{3}=\dfrac{50}{BC}$$
$$\therefore$$ $$BC=\dfrac{50}{\sqrt{3}}$$
$$\Rightarrow$$ Similarly, in right angled $$\triangle ABC,$$
$$\Rightarrow$$ $$\tan\,30=\dfrac{AB}{BC}$$
$$\Rightarrow$$ $$\dfrac{1}{\sqrt{3}}=\dfrac{AB}{\dfrac{50}{\sqrt{3}}}$$
$$\Rightarrow$$ $$\dfrac{1}{\sqrt{3}}=AB\times \dfrac{\sqrt{3}}{50}$$
$$\Rightarrow$$ $$AB=\dfrac{1}{\sqrt{3}}\times \dfrac{50}{\sqrt{3}}$$
$$\Rightarrow$$ $$AB=\dfrac{50}{3}\,m$$
Hence, height of building is $$\dfrac{50}{3}m$$
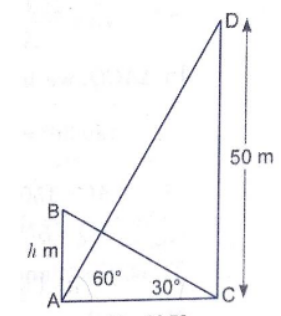
One side of a road, there is a tower and on other side, a house is situated. The angle of depression from the top of a tower to top and bottom of house are $$45^{0}$$ and $$60^{o}$$ respectively. Find the height of tower.
Let $$AB=H$$
$$CD=h$$
$$AC=b$$
$$\therefore \tan{{60}^{0}}=\dfrac{H}{b}$$
$$\Rightarrow H=b\sqrt{3}$$
And $$\tan{{45}^{0}}=\dfrac{H-h}{b}$$
$$\Rightarrow b=H-h$$
$$\Rightarrow \dfrac{H}{\sqrt{3}}=H-h$$
$$\Rightarrow h=H\left(1-\dfrac{1}{\sqrt{3}}\right)$$
$$\Rightarrow H=\dfrac{\sqrt{3}h}{\sqrt{3}-1}$$ where $$h$$ is the height of the house.
In the given figure, $$CD=40\ m$$, $$\angle ADB=45^{o}$$ and $$\angle ADB=60^{o}$$. Calculate the length of $$AB$$ and $$BC$$.
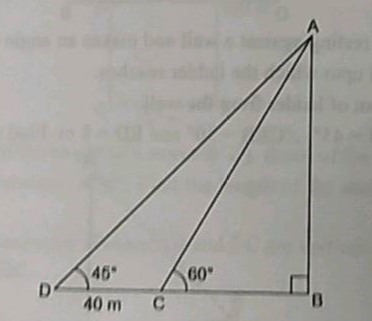
In the given figure, $$ \angle ACE = 30^o , \angle ADB = 45^o , CE = 12 m $$ and $$ CD = 10 m. $$ Find $$AD$$ .
$$CE=12\ m=DB \left(since\ BDCE\ is\ rectangle\right)$$
$$CD=10\ m=BE$$
In triangle $$ABD$$
$$\tan{45^{o}}=\left(\dfrac{AB}{BD}\right)$$
$$1=\dfrac{AB}{BD} \Rightarrow \boxed {AB=BD=12\ m}$$
$${AD}^{2}={AB}^{2}+{BD}^{2} \left(ABD\ is\ a\ right\ triangle \right)$$
$${AD}^{2}={12}^{2}+{12}^{2}=288$$
$$\Rightarrow AD=12\sqrt{2}m$$
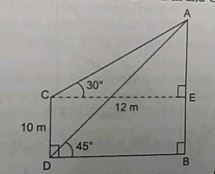
From the top of a building, the angle of elevation of the top of a cell tower is $${45}^{o}$$ and the angle of depression to foot is $${60}^{o}$$. If height of cell tower is $$46\ meters$$ then find the distance between building and tower, and height of the building?
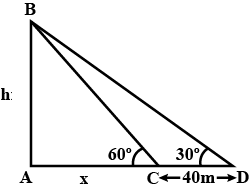
The angle of elevation of the top of a tower as observed from a point in a horizontal plane through the foot of the tower isWhen the observer moves towards the tower a distance of 100 in, he finds the angle of elevation of the top lobeFind the height of the tower and the distance of the first position from the tower. (Take tan 32 = 0,624S and tan 63 = 1.9626)
From a point on the ground the angles of elevation of the bottom and top of a transmission tower fixed at the top of 20 m high building are $$45^o$$ and $$60^o$$, respectively. Find the height of the transmission tower.
Let DC be the tower and BC be the building. Then,
$$\angle CAB=45^o, \angle DAB=60^o, BC=20 \ m$$
Let height of the tower, $$DC= h \ m$$.
In right $$\triangle ABC$$,
$$\tan 45^o=\dfrac{BC}{AB}$$
$$1=\dfrac{20}{AB}$$
$$AB=20 \ m$$
In right $$\triangle ABD$$,
$$\tan 60^o=\dfrac{BD}{AB}$$
$$\sqrt{3}=\dfrac{h+20}{20}$$
$$h=20(\sqrt{3}-1) \ m$$
Find the angle of evelation of the sun when the shadow of a pole $$h$$ meter high is $$\sqrt 3 h$$ meters long
From the top of a $$38m$$ high tower, the angle of depression of the top of a building is $$30^o$$. If the height of the building is $$18m$$, find the distance between the tower and the building.
Let, $$AB$$ = Height of the tower=$$38\ m$$
$$CD$$ = Height of the building=$$18\ m$$
From diagram, $$BE=CD=18\ m$$
$$AE=AB-BE=(38-18)\ m=20\ m$$
Let, the distance between tower and building be,$$BD=CE=x\ m$$
From $$\Delta AEC$$
$$\tan 30^o = \dfrac{AE}{EC}$$
$$\Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{20}{x}$$
$$\Rightarrow x=20\sqrt{3}$$
$$\Rightarrow x=20\times 1.732$$
$$\Rightarrow x=20\sqrt{3}$$
$$\Rightarrow x=20\times 1.732$$
$$\Rightarrow x=34.64$$
Hence, the distance between tower and building is $$34.64\ m$$
The length of the shadow of a tower standing on level plane is found to be $$2y$$ metres longer when the sun's altitude is $$30^o$$ that when it was $$45^o$$. Prove that the height of the tower is $$y(\sqrt{3} + 1)$$ metres.
An aeroplane flying horizontally $$1\text{ km}$$ above the ground and going away from the observer is observed at an elevation of $$60^\circ $$. After $$10$$ seconds, its elevation is observed to be $$30^\circ $$. find the uniform speed of the aeroplane in km per hour.
Let $$P_1$$ and $$P_2$$ be the before and after positions of aeroplane
Given:
$$ P_1G_1=h = 1 \text{ km} $$
$$\angle P_1OG_1=60^{\circ}$$
$$\angle P_2OG_2=30^{\circ}$$
From $$\triangle OP_1G_1$$
$$ \tan 60^{\circ} = \dfrac{P_{1}G_{1}}{OG_{1}}\Rightarrow \sqrt{3} = \dfrac{1}{OG_{1}} $$
$$ \Rightarrow OG_{1} = \dfrac{1}{\sqrt{3}} \text{ km} $$
From $$\triangle P_2OG_2$$
$$ \tan 30^{\circ} = \dfrac{P_{2}G_{2}}{OG_{2}} \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{1}{OG_{2}} $$
$$ \Rightarrow OG_{2} = \sqrt{3}\text{ km} $$
$$ G_{1}G_{2} = OG_{2}-OG_{1} = \sqrt{3}-\dfrac{1}{\sqrt{3}} = \dfrac{2}{\sqrt{3}}\text{ km} $$
$$\text{Speed} = \dfrac{\text{Distance}}{\text{Time}} = \dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{10}{3600}} = 240\sqrt{3} \text{ km/hr} $$
From a point P on the ground the angle of elevation of a 10 m tall building Is 30, A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P isFind the length of the flag-staff and the distance of the building, iron\ the point P. (Take $$\sqrt{3}$$ = 1.732 ).
In $$\Delta BAP$$
$$\tan 30^o=\dfrac{AB}{AP}$$
$$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{10}{x}$$
$$x=10\sqrt{3}m$$
Distance of building
Now,
In $$\Delta PAD$$
$$\tan 45^o=\dfrac{AD}{AP}$$
$$1=\dfrac{AD}{AP}$$
$$\Rightarrow x=AD=DB+BA$$
$$\Rightarrow 10\sqrt{3}=h+10$$
$$h=10\sqrt{3}-10$$
$$=10(\sqrt{3}-1)$$
$$h=10(1.732-1)$$
$$h=7.32$$m
Length of flag.
A 1.2m tall girls spot a ballon mowing with the wind in a horizontal line a at a height of 88.2m from the ground. The angle of elevation of the ballon from the eyes of the girl at any point instant is $${60^0}$$. After some time, the angle of elevation reduces to $${30^0}$$. Find the distance travelled by the ballon during the interval.
$$\tan 60^o=\dfrac{87}{a}$$ or $$\sqrt{3}=\dfrac{87}{a}$$ or $$a=\dfrac{87}{\sqrt{3}}$$
and $$\tan 30^o=\dfrac{87}{a+b}$$ or $$a+b=87\sqrt{3}$$
$$\therefore b=87\sqrt{3}-a$$
$$=87\sqrt{3}-\dfrac{87}{\sqrt{3}}$$
$$=87\left[\dfrac{3-1}{\sqrt{3}}\right]$$
$$=\dfrac{174}{\sqrt{3}}\times \dfrac{\sqrt{3}}{\sqrt{3}}=58\sqrt{3}$$metre.
From the top a tower of height $$50\ m$$, angle of depression of the top and bottom of a pole are $${30}^{o}$$ and $${45}^{o}$$. Find height of pole.
REF.Image
In $$\triangle ADE$$
$$tan45^{\circ}= \dfrac{AE}{DE}= \dfrac{50}{x}$$
$$1=\dfrac{50}{x}$$
$$x= 50 m$$
$$\Rightarrow $$ In $$\triangle ABC\Rightarrow tan 30^{\circ}= \dfrac{AC}{BC}= \dfrac{50-H}{x}$$
$$\dfrac{1}{\sqrt{3}}=\dfrac{50-H}{50}$$
$$H= 50(\dfrac{\sqrt{3}-1}{\sqrt{3}})= 21.13m$$
$$\therefore $$ Height of pole $$\Rightarrow 21.13m$$
The angle of elevation of the top of a vertical tower from a point on the ground is $${60}^{o}$$. From another point $$10 m$$ vertically above the first, its angle of elevation is $${45}^{o}$$. Find the height of the tower.
Let, $$AB$$ be the height of the tower $$=h$$
From $$\Delta ABD$$
$$ tan 60^o = \dfrac{AB}{BD}$$
$$\Rightarrow \sqrt{3} = \dfrac{h}{BD} $$
$$\Rightarrow h = BD\sqrt{3} $$
$$\Rightarrow BD = \dfrac{h}{\sqrt{3}} ..........(1)$$
From $$\Delta AEC$$
$$ tan45 = \dfrac{AE}{EC} $$
$$\Rightarrow 1=\dfrac{AE}{EC}$$
$$\Rightarrow AE = EC $$
$$\Rightarrow AE = BD $$
$$\Rightarrow AE = \dfrac{h}{\sqrt{3}} ..........(2)$$
We can write, $$ AE=AB-BE = h-10 .........(3)$$
From $$(2)$$ and $$(3)$$
$$ h-10 = \dfrac{h}{\sqrt{3}} $$
$$\Rightarrow h\sqrt{3}-10\sqrt{3} = h $$
$$\Rightarrow h(\sqrt{3}-1) = 10\sqrt{3} $$
$$\Rightarrow h = \dfrac{10\sqrt{3}}{\sqrt{3}-1}$$
$$\Rightarrow h = \dfrac{10\sqrt{3}}{\sqrt{3}-1}\times \dfrac{\sqrt{3}+1}{\sqrt{3}+1}$$
$$\Rightarrow h=\dfrac{10\sqrt{3}(\sqrt{3}+1)}{2}$$
$$\Rightarrow h = 5\sqrt{3}(\sqrt{3}+1) $$
$$\Rightarrow h = 15+5\sqrt{3} $$
$$\Rightarrow h = 15+5\times1.732$$
$$\Rightarrow h = 23.66 $$
Hence, the height of the tower is $$23.66\ m$$
A balloon is connected to a meteorological ground station by a cable of length $$500$$m and is inclined at $$60^o$$ to the ground. Find the height of the balloon from the ground assuming no slackness in it.
A guard observes an enemy boat, from an observation tower a height of 180 m above sea-level, to be at an angle of depression of $$30^{\circ}$$. Find the distance from between enemy's boat and foot of tower.
Let the distance between the enemy's boat and foot of the tower be $$x$$.
$$\tan 30^{\circ}=\dfrac{x}{180}$$$$\dfrac{1}{\sqrt 3}=\dfrac{x}{180}$$
$$\quad x=60\sqrt 3\ \text{m}$$
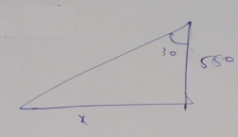
Calculate the distance of the boat from the foot of the observation tower. When observed from a tower of height $$ 550 m$$ at an angle of depression $$30^{\circ}$$
$$\tan 30=\dfrac{x}{550}\Rightarrow \dfrac{1}{550}\Rightarrow x=\dfrac{550}{\sqrt{3}}$$
A pole $$5\ m$$ high is fixed on the top of a tower. The angle of elevation of the top of the poles observed from a point $$A$$ on the ground is $${60^ \circ }$$ and the angle of depression of point $$A$$ from the tower is $${45^ \circ }$$. Find the height of the tower $$\sqrt 3 = 1.732$$.
ref image
$$AC = 100 - h$$
$$tan 45^{\circ}= \dfrac{100-h}{x}$$
$$\Rightarrow1= \dfrac{100-h}{x}$$
$$\Rightarrow x=100-h$$
$$\Rightarrow h=100-x$$.......(1)
Now $$ tan 60^{\circ}=\dfrac{100}{x}=\sqrt{3}$$
$$\Rightarrow \sqrt{3}=\dfrac{100}{x}$$
$$\Rightarrow x=\dfrac{100 \sqrt{3}}{3}$$
Substitute the value of x in equation$$(1)$$, we get
$$Now \, h = 100 -\dfrac{100\sqrt{3}}{3}$$
$$=100(1-\dfrac{\sqrt{3}}{3})$$
$$=\dfrac{100}{3}(3-\sqrt{3})$$
A tree breaks due to wind and the broken part bends so that the top of the tree touches the ground making an angle of $$60^{o}$$ with it. The distance between the foot of the tree to the point where the top touches the ground is $$9m$$. Find the total height of the tree before it was broken.
From figure,
Let say the height of the broken part is $$y$$ and it touches the ground at $$9m$$ from the foot.
Height of the tree $$=x+y$$
Therefore, from the figure:
$$tan60^o=\dfrac{x}{9}$$
$$\implies \sqrt3=\dfrac{x}{9}$$
Hence, $$x=9\sqrt3m$$
And, $$cos60^o=\dfrac{9}{y}$$
$$\implies \dfrac{1}{2}=\dfrac{9}{y}$$
Hence, $$y=18m$$
So, the height of the tree $$=x+y=9(2+\sqrt3)m$$
Two points $$A\ and B$$ are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are $${60}^{o}\ and\ \, {45}^{o}$$ respectively. If the height of the tower is $$15\ m$$, then find the distance between these points.
REF.Image.
let the distance between C & D is x m
In $$ \triangle ABC,$$
$$ tan60^{\circ} = \dfrac{AB}{BC}$$
$$ \sqrt{3} = \dfrac{15}{BC} \Rightarrow BC = 5\sqrt{3}m ...(1)$$
Now, in $$\triangle ABD $$
$$ tan 45^{\circ} = \dfrac{AB}{BD}$$
$$ 1 = \dfrac{15}{BD} = BD = 15 m ...(2)$$
From (1) & (2),
$$ x= CD = BD - BC$$
$$ = 15-5\sqrt{3}$$
$$ = 5\sqrt {3}(\sqrt{3}-1) m$$
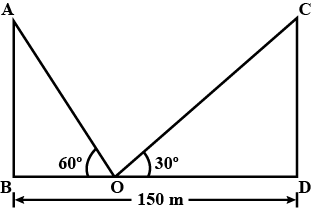
Two pillars of equal height and stand on either side of a roadway which is $$150$$ m wide. At a point in the roadway between the pillars, the angle of elevation of the top of pillars are $$60^{0}$$and $$30^{0}$$. then find height of pillars-
Let us consider the $$CD$$ and $$AB$$ are the poles and $$O$$ is the point where elevation angle is made.
In $$\Delta ABO$$
$$\quad \begin{array}{l} \dfrac { { AB } }{ { BO } } =\tan { 60^{ \circ } } \\ \dfrac { { AB } }{ { BO } } =\sqrt { 3 } \\ BO=\dfrac { { AB } }{ { \sqrt { 3 } } } \end{array}$$
In $$\Delta CDO$$
$$\begin{array}{l} \dfrac { { CD } }{ { DO } } =\tan { 30^{ \circ } } \\ \dfrac { { CD } }{ { 150-BO } } =\dfrac { 1 }{ { \sqrt { 3 } } } \\ CD\sqrt { 3 } =150-\dfrac { { AB } }{ { \sqrt { 3 } } } \\ CD\sqrt { 3 } +\dfrac { { AB } }{ { \sqrt { 3 } } } =150 \end{array}$$
Since the poles are of equal heights
therefore $$AB = CD$$
So,
$$\begin{array}{l} CD\left( { \sqrt { 3 } +\dfrac { 1 }{ { \sqrt { 3 } } } } \right) =150 \\ CD\left( { \dfrac { { 3+1 } }{ { \sqrt { 3 } } } } \right) =150 \\ CD\left( { \dfrac { 4 }{ { \sqrt { 3 } } } } \right) =150 \\ CD=37.5\sqrt { 3 } \end{array}$$
$$\begin{array}{l} BO=\dfrac { { AB } }{ { \sqrt { 3 } } } \\=\dfrac { { CD } }{ { \sqrt { 3 } } } \\ =\dfrac { { 37.5\sqrt { 3 } } }{ { \sqrt { 3 } } } \\=37.5 \\ DO=BD-BO \\ =150-37.5 \\ =112.5 \end{array}$$
Hence the height of poles are $$37.5\sqrt 3$$ and the distance of point $$O$$ from either of the poles is $$37.5 \,m$$ and $$112.5 \,m$$
A player sitting on the top of tower of height 20 m observes the angle of a depression of a ball lying on the ground as $${60}^{ \circ}$$. Find the distance between the foot of the tower and the ball. $$(take\sqrt{3}=1.732)$$
Let $$AB$$ be the tower and $$BC$$ be the distance between the foot of the tower and the ball.
As we know that $$\tan{\theta} = \cfrac{\text{Perpendicular}}{\text{Base}}$$
Now from fig.,
$$\tan{60°} = \cfrac{AB}{BC}$$
$$\Rightarrow \sqrt{3} = \cfrac{20}{BC}$$
$$\Rightarrow BC = \cfrac{20}{1.732} \; \left( \because \sqrt{3} = 1.732 \right)$$
$$\Rightarrow BC = 11.547 \; m$$
Hence the distance between the foot of the tower and the ball is $$11.547 \; m$$.
Hence the correct answer is $$11.547 \; m$$.
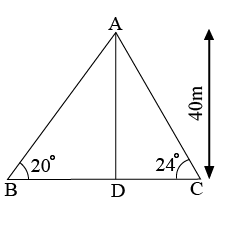
Two men are on diametrically opposite side of a tower. They measure the angle of elevation of the top of the tower as$$20^{0}$$ and $$24^{0}$$ respectively. If the height of the tower is $$40 m$$, find the distance between them.
[Hint.use tables to find tan $$20^{0}$$ and tan$$24^{0}$$]
As we know that,
$$\tan{\theta} = \cfrac{\text{Perpendicular}}{\text{Base}}$$
Therefore,
In $$\triangle{ABD}$$,$$\tan{20°} = \cfrac{AD}{BD}$$
$$\Rightarrow 0.364 = \cfrac{40}{BD}$$ $$\left( \because \tan{20°} = 0.364 \right)$$
$$\Rightarrow BD = \cfrac{40}{0.364}$$
$$\Rightarrow BD = 109.89$$
In $$\triangle{ACD}$$
$$\tan{24°} = \cfrac{AD}{CD}$$
$$\Rightarrow 0.445 = \cfrac{40}{CD}$$ $$\left( \because \tan{24°} = 0.445 \right)$$
$$\Rightarrow CD = \cfrac{40}{0.445} $$
$$\Rightarrow CD = 89.89$$
Therefore,
Required distance between the two men $$= BD + CD = (109.89 + 89.89)\ m = 199.78 \; m$$
Hence the distance between the two men is $$199.78 \; m$$.
The angle of elevation of point $$A$$ with the top of the hill is $$80^{o}$$. $$B$$ is the point at a distance of $$200\ m$$ vertically above $$A$$. If the angle of elevation of the point $$B$$ with the top of the hill is $$60^{o}$$. Find the height of the hill and the distance of point $$A$$ from the bottom of the hill.
$$(\tan 80^{o}=5.67, \tan 60^{o}=1.73)$$
Let $$AO= BE =x$$
$$\therefore \tan 80^{o} = \dfrac{h}{x} = 2.75$$
$$\therefore h= 2.75x$$
$$\therefore \tan 60^{o}= \dfrac{h-200}{x} ; (1.73)x = h-200$$
$$\therefore 1.73 x = 2.75x - 200$$
$$\therefore 200= 1.02 x$$
$$\therefore x =\dfrac{200}{1.02}= 196.07 m = $$ distance between bottom
$$\therefore h =(2.75) (196.07)= 539.1925$$
Height of hill $$=539.1925\ m$$
The horizontal distance between two poles is $$15\ m.$$ The angle of depression of the top of the first pole as seen from the top of the second pole is $${30^ \circ }$$. If the height of the second pole is $$24\ m.$$ Find the height of the first pole.
Let the length of the side $$BE$$ be $$x.$$
Now, in $$\triangle BED,$$
$$\begin{aligned}{}\tan 30^\circ &= \frac{{BE}}{{ED}}\\\frac{1}{{\sqrt 3 }} &= \frac{x}{{15}}\\x& = 5\sqrt 3\ m\end{aligned}$$
So, height of first pole will be,
$$AB=AE+BE$$
$$=24m+5\sqrt{3}m$$
$$=(24+5\sqrt{3})m$$
A status 1.45m tall stand on the top of a pedestal. From a point on the grotund, the angle of elevation the top of the statue is $${60^ \circ }$$. and from the same point,the angle of elevation of the top the statue is and from the same point,the angle of elevation of the top of the pedestal is $${45^ \circ }$$ .Find the height of the pedestal.$$\left( {\sqrt {3} = 1.73} \right)$$
Solution :-
REF.Image.
Given ; Height of statute $$= BC = 1.6m$$
Height of pedestal $$= AB = x$$
In $$ \triangle AOC , tan60^{\circ} = \dfrac{1.6+x}{OA} = \sqrt{3}...(1)$$
In $$ \triangle AOB , tan45^{\circ} = \dfrac{AB}{OA} = \dfrac{x}{OA} = 1 \Rightarrow x = OA$$
$$ \Rightarrow $$ From (1) $$ OA = \dfrac{1.6+x}{\sqrt{3}}$$
$$ \therefore x = \dfrac{1.6+x}{\sqrt{3}} \Rightarrow \sqrt{3}x = 1.6+x$$
$$ \Rightarrow (\sqrt{3}-1) x = 1.6$$
$$ \Rightarrow x = \dfrac{1.6}{\sqrt{3}-1}\times \dfrac{\sqrt{3}+1}{\sqrt{3}+1} = \dfrac{1.6(\sqrt{3}+1)}{2}$$
$$ = 0.8(\sqrt{3}+1)$$
The top of a tower, the angle of an object are on the same side of the tower end to be $$x$$ and $$b (x>b)$$. If the distance objects is 'h' meters, show that the height of 'h' is given by:
Let $$AB$$ be the tower of height $$h$$ meters and C and D are two objects which are$$y$$ meter apart
Then,
$$ AB=h\,meter $$
$$ BC=x\,meter $$
$$ CD=y\,meter $$
Then,
$$ In\,\Delta ABC, $$
$$ \tan \alpha =\dfrac{AB}{BC} $$
$$ \tan \alpha =\dfrac{h}{x} $$
$$ x=\dfrac{h}{\tan \alpha }\,\,\,\,.......\,\,\left( 1 \right) $$
Now, $$In\,\Delta ABD$$$$ \tan \beta =\dfrac{h}{x+y} $$
$$ h=\left( x+y \right)\tan \beta $$
$$ h=x\tan \beta +y\tan \beta \,\,.......\,\,\left( 2 \right) $$
By equation (1) and we get,
$$ h=y\tan \beta +\dfrac{h\tan \beta }{\tan \alpha } $$
$$ h-\dfrac{h\tan \beta }{\tan \alpha }=y\tan \beta $$
$$ h\left( 1-\dfrac{\tan \beta }{\tan \alpha } \right)=y\tan \beta $$
$$ h\left( \dfrac{\tan \alpha -\tan \beta }{\tan \alpha } \right)=y\tan \beta $$
$$ h=\dfrac{y\tan \alpha \tan \beta }{\tan \alpha -\tan \beta } $$
$$ h=\dfrac{CD\tan \alpha \tan \beta }{\tan \alpha -\tan \beta } $$
Hence, this is the answer.
From the top of a building, 60 metres high, the angle of a depression of the top and bottom of a tower are observed to be $$30^{0}$$ and $$60^{0}$$, find the height of the tower.
Consider $$AC$$ be the tower and $$BE$$ be the building
Let height of the tower be $$h\;m$$
And, it is given that the angle of depression of the top $$C$$ and bottom $$A$$ of the tower observed from top of the building be $${30^ \circ }\,and\,{60^ \circ }$$
In right triangle $$CDE$$
$$\tan {30^ \circ } = \dfrac{{DE}}{{CD}}$$
$$\begin{array}{l} \Rightarrow \dfrac { 1 }{ { \sqrt { 3 } } } =\dfrac { { 60-h } }{ { CD } } \, \, \, \, \, \, \, \, \, \, \left[ { DE=BE-BD=BE-AC } \right] \\ \Rightarrow CD=\sqrt { 3 } \left( { 60-h } \right) \, \, \, ........\left( 1 \right) \end{array}$$
And,
In right triangle $$ABE$$
$$\begin{array}{l} \tan { 60^{ \circ } } =\dfrac { { BE } }{ { AB } } \\ \Rightarrow \sqrt { 3 } =\dfrac { { 60 } }{ { CD } } \, \, \, \, \left( { AB=CD } \right) \\ \Rightarrow CD=\dfrac { { 60 } }{ { \sqrt { 3 } } } \, \, \, ........\left( 2 \right) \end{array}$$
Now,Comparing $$(1)$$ and $$(2)$$
$$\begin{array}{l} \sqrt { 3 } \left( { 60-h } \right) =\dfrac { { 60 } }{ { \sqrt { 3 } } } \\ \Rightarrow 3\left( { 60-h } \right) =60 \\ \Rightarrow 180-3h=60 \\ \Rightarrow 3h=120 \\ \Rightarrow h=40 \end{array}$$
Hence, the height of the tower is $$40\;m$$
At a point A, $$20$$ meters above the level of water in a lake, the angle of elevation of a cube is $${30^ \circ }$$. The angle of depression of the reflection of the cloud in the lake, at A is $${60^ \circ }$$. Find the distance of the cloud from A
Given that $${ AO }={ 20 }m { \angle BAC }={ 30 }^{ ° }{ \angle BAD }={ { 60 }^{ ° } }$$
So $${ AO }={ BD }={ 20 }m$$
In $$\triangle { BAD }$$
$$\tan { { 60 }^{ ° } } =\dfrac { BD }{ AB } $$
$$ \dfrac { \sqrt { 3 } }{ 1 } =\dfrac { 20 }{ AB } \\ \Rightarrow { AB }={ \dfrac { 20 }{ \sqrt { 3 } } }$$
In $$\triangle { BAC },$$
$$\cos { { 30 }^{ ° } } =\dfrac { AB }{ AC } $$
$$ \dfrac { \sqrt { 3 } }{ 2 } =\dfrac { \dfrac { 20 }{ \sqrt { 3 } } }{ AC } $$
$$ \Rightarrow { AC }=\dfrac { \dfrac { 20 }{ \sqrt { 3 } } }{ \dfrac { \sqrt { 3 } }{ 2 } } =\dfrac { 40 }{ 3 } ={ 13.333 }m$$
Distance of cloud from point A is 13.333m
A ship of height $$24\,m$$ is sighted from a lighthouse. From the top of the lighthouse, the angle of depression to the top of the mast and base of the ship is $$30^\circ$$ and $$45^\circ$$ respectively. How far is the ship from the lighthouse? ($$\sqrt{3}=1.73$$)
Let $$AB=24\ m$$ be the height of the ship and $$OC$$ be the height of the lighthouse
Let the height of the lighthouse, from above the ship be $$y$$ and the distance between the bases of the lighthouse and the ship be $$x$$
$$\Rightarrow \tan 30^\circ=\dfrac{y}{x}$$
$$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{y}{x}$$
$$\Rightarrow y=\dfrac{x}{\sqrt{3}}$$
In $$\triangle OBC$$
$$\Rightarrow \tan 45^o=\dfrac{y+24}{x}$$
$$\Rightarrow x=y+24$$
$$\Rightarrow x=\dfrac{x}{\sqrt{3}}+24$$
$$\Rightarrow x(1-\dfrac{1}{\sqrt 3})=24$$
$$\Rightarrow x=\dfrac{24\sqrt 3}{\sqrt 3-1}$$
$$\Rightarrow x=\dfrac{24\times 1.73}{0.73}$$
$$\Rightarrow x=56.88\ m$$
The horizontal distance between the two tower is $$60\ feet$$ and the angular depression of the top of the first, as seen from the top of the second, which is $$150\ feet$$ high, is $$30^{\circ}$$; Find the height of the first.
As we know that,
$$\tan{\theta} = \cfrac{\text{Perpendicular}}{\text{Base}}$$
Therefore, in $$\triangle{ADE}$$,
$$\tan{30°} = \cfrac{DP}{AP}$$
$$\Rightarrow \cfrac{1}{\sqrt{3}} = \cfrac{x}{60}$$
$$\Rightarrow x = 20 \sqrt{3} \; m = 34.64 \; m$$
Now from fig.,
$$CD = 150 \; m \; \left( \text{Given} \right)$$
Let $$h$$ be the height of the first tower.
Therefore,
$$h = 150 - 34.64 = 115.36 \; m$$
Hence the height of the first tower is $$115.36 \; m$$.
Hence the correct answer is $$115.36 \; m$$.
The pilot of an aircraft flying horizontally at a speed 1200km/hr.Observes that the angle of depression of a point on the ground c hanges from $${30^ \circ }$$ to $${45^ \circ }$$ in 15 sec.Find the height at which the aircraft is flying.
REF.Image.
Solution:-
Speed of an aircraft $$= 1200 km/hr$$
After 15 secs, angle of depression changes from $$ 30^{\circ}$$ to $$ 45^{\circ}$$
Distance covered in 15 seconds $$ = 1200 \times 15 \times 3600 = 5 km=5000m $$
Let height from ground be $$h$$
Horizontal distance $$= x$$
In $$ \triangle BDP, \angle P = 45^{\circ}, \therefore tan45^{\circ} = \dfrac{BD}{DP} = \dfrac{h}{DP}$$
$$ \therefore DP = h $$
In $$ \triangle ACP, \angle APC = 30^{\circ}$$
$$ \therefore tan30^{\circ} = \frac{AC}{CP}$$
$$ \therefore \dfrac{1}{\sqrt{3}} = \dfrac{h}{5000+h}, 5000+h = h\sqrt{3}$$
$$ \Rightarrow 5000 = h (\sqrt{3}-1)$$
$$ \Rightarrow h = 6830m = 6.830 km$$ (height of an aircrft from ground)
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of $${30}^{o}$$, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be $${60}^{o}$$. Find the time taken by the car to reach the foot of the tower from this point.
Let $$DC = x, BC = y, AC = d$$
$$\tan 30 = \dfrac{CO}{AC} = \dfrac{x}{d} = \sqrt{3}$$ ....(1)
$$\tan 60 = \sqrt{3} = \dfrac{DC}{BC} = \dfrac{x}{y}$$ ...(2)
from (1) and (2)
$$d=\sqrt{3}x = \sqrt{3}(\sqrt{3}y) = 3y$$
$$\therefore speed = \dfrac{distance}{time}$$
from A to B
speed $$= \dfrac{d-y}{6}$$
required
time $$= \dfrac{\text{distance (from B to c)}}{\text{speed}}$$
$$=\dfrac{y}{\dfrac{d-y}{6}}$$
$$=\dfrac{6y}{d-y}$$ $$(\because d-3y)$$
$$=\dfrac{6y}{3y-y}$$
$$=\dfrac{6y}{2y}$$
$$=3$$ sec
The top of a tower is observed from two points in the same horizontal line through a point on the base of the4 tower. If the angles of elevation at the two points which are on the same side of the tower are $$30^{o}$$ and$$45^{o}$$ and the distance between them is $$60\ m$$, find the height of the tower.
REF.Image
Let $$OB=x$$
$$\therefore tan 45^{\circ}= \dfrac{h}{x}=1$$ ; $$h=x$$
$$\therefore CO= h+60$$
$$\therefore tan 30^{\circ}= \dfrac{h}{h+60^{\circ}}$$
$$\therefore \dfrac{1}{\sqrt{3}}=\dfrac{h}{h+60^{\circ}}$$
$$\therefore \sqrt{3}h= h+60^{\circ}$$
$$\therefore h= (\dfrac{60}{\sqrt{3}-1})m$$
$$\therefore h= 30(\sqrt{3}+1)m$$
From a point $$P$$ on the ground the angle of elevation of the top of a $$10m$$ tall building is $${30}^{o}$$. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from $$P$$ is $${45}^{o}$$. Find the length of the flagstaff and the distance of the building from the point $$P$$. (you may tale $$\sqrt{3}=1.732$$)
In $$\triangle PBC$$
$$\tan 30^o=\dfrac {10}{y}$$
$$\dfrac {1}{\sqrt 3}=\dfrac {10}{y}$$
$$y=10\sqrt 3$$
$$y=10\times 1.732$$
$$y=17.32m$$
In $$\triangle APC$$
$$\tan 45^o=\dfrac {x+10}{y}$$
$$y=x+10$$
$$x=y-10$$
$$=17.92-10$$
$$x=7.32$$
The angle of elevation of the top of a vertical tower from a point on the ground is $${60^ \circ }$$.From another point $$10$$ m vertically above the first, its angle of elevation is $${30^ \circ }$$. Find the height of the tower.
Two boats approach a light house in mid-sea from opposite direction. The angle of elevation of the top of the lighthouse from two boats is $${30^ \circ }$$ and $${45^ \circ }$$respectively. If the distance between two boats is 100m, find the height of the light house.
Let $$AP=x$$ then $$BP=100-x$$
In $$\triangle ADC, \tan 30^o=\dfrac {1}{\sqrt {3}}=\dfrac {DC}{AD}$$
$$\dfrac {1}{\sqrt 3}=\dfrac {DC}{x}$$
$$\Rightarrow \ \dfrac {x}{\sqrt 3}=DC---(1)$$
In $$\triangle BDC, \tan 45^o=1\dfrac {DC}{BD}$$
$$1=\dfrac {DC}{100-x}$$
$$\Rightarrow \ 100-xDC----(2)$$
Equation $$(1)$$ & $$(2)$$
$$100-x=\dfrac {x}{\sqrt 3}$$
$$100\sqrt 3=x\sqrt 3=x$$
$$100\sqrt {3}=x(\sqrt 3+1)$$
$$\dfrac {100\sqrt 3}{\sqrt 3+1}=x$$
Then Height of house $$=DC=100-\dfrac {100\sqrt 3}{\sqrt 3+1}=36.60m$$
The height of a tower is $$100m$$ find the distance from ground if the angle of elevation is $$30^{\circ}$$
From $$\triangle{ABC},\,$$
$$\sin{{30}^{\circ}}=\dfrac{100}{x}$$
$$\Rightarrow\,\dfrac{1}{2}=\dfrac{100}{x}$$
$$\Rightarrow\,x=200\,m$$
Hence distance from ground is $$200\,m$$
A wire of length 18 m had been tied with electric pole at an angle of elevation $$30^0$$ with the ground.Because it was covering a long distance, it was cut and tied at an angle of elevation $$60^0$$ with the ground. How much length of the wire was cut ?
$$AD=18m$$
In $$\Delta ABD,$$
$$ \angle ABD=30°$$
$$ \therefore \sin 30°=\cfrac{AB}{AD}\Rightarrow AB=AD\sin 30°=9m$$
In $$\Delta ABC,$$
$$ \angle ABC=90°\&\angle ACB=60°$$
$$ \sin60°=\cfrac{AB}{AC}=\cfrac{9}{AC}$$
$$ \cfrac{\sqrt 3}{2}=\cfrac{9}{AC}\Rightarrow AC=\cfrac{9\times 2}{\sqrt3}=6\sqrt3m$$
$$\therefore$$ wire length cut down $$=AD-AC=(18-6\sqrt3)m=7.6m$$
The angle of elevation of the top of a building from the foot of the tower is $$30^\circ$$ and the angle of elevation of the top of the tower from the foot of the building is $$60^\circ$$. If the tower is $$60\ m$$ high, find the height of the building.
In the above figure, $$AB$$ is the building and $$CD$$ is the tower.
Let the height of the building be $$x.$$
In $$\triangle DBC,$$$$\tan 60=\dfrac{DC}{BC}$$
$$\Rightarrow \sqrt3=\dfrac{60}{BC}$$
$$\Rightarrow BC=20\sqrt3\ m$$
Similarly, in $$\triangle ABC,$$
$$\tan 30=\dfrac{AB}{BC}$$
$$\Rightarrow \dfrac{1}{\sqrt3}=\dfrac{AB}{20\sqrt3}$$
$$\Rightarrow AB=20\ m$$
Hence, the height of the building is $$20\ m.$$
The persons on the same side of a tall building notice the angle of elevation of the top of the building to be $$30^{o}$$ and $$60^{o}$$ respectively. If the height of the building is $$72 m$$, find the distance between the two persons. $$(\sqrt{3}=1.73).$$
A observe 15 m tall is 28.5 m away from a chimney. The angle of elevation of the top of chimey from his eyes is $$45^{\circ}$$ . Find the height of the chimney.
Given height observer $$'AB' = 15 cm$$
Ref. image
Let $$CE$$ be the height of chimney
$$CE = h$$
Then $$DE = h - 15$$
Given distance between observer and the chimney $$= 28.5 m$$
i.e, $$BC = 28.5 = AD$$
Also given angle of elevation of the top of chimney from his eyes (from point 'A') is $$45^{\circ}$$ from $$\Delta ADE$$
$$\tan 45^{\circ} = \dfrac{opposite \, side}{adjacent \, side} = \dfrac{DE}{BC}$$
$$1 = \dfrac{h - 15}{28.5}$$
$$h = 15 = 28.5$$
$$h = 28.5 + 15 = 43.5$$
$$h = 43.5 m$$
$$\therefore$$ Height of the chimney is $$43.5 m$$
From a point 100 m above a lake the angle of elevation of a stationary helicopter is $${ 30 }^{ \circ }$$ and the angle of depression of reflection of the helicopter in the lake is $${ 60 }^{ \circ }$$. Find the height of the helicopter above the lake.
Let AB be the surface of the lake and P be the point of observation such that $$AP=BM=100\ m$$.
Let C be the position of the helicopter and C' be its reflection in the lake
Then, $$CB=C'B$$
Let PM be perpendicular from P on CB
Then, $$\angle{CPM}=30^{o}$$ and $$\angle{CPM}=60^{o}$$
Let $$CM=h$$
Then, $$CB=h+100$$ and $$C'B=h+100$$
In right $$\triangle{CMP}$$
$$\Rightarrow\tan30=\dfrac{CM}{PM}$$
$$\Rightarrow\dfrac{1}{\sqrt3}=\dfrac{h}{PM}$$
$$\Rightarrow PM=\sqrt{3}h......(i)$$
In right $$\triangle{PMC'}$$
$$\Rightarrow\tan60=\dfrac{C'M}{PM}$$
$$\Rightarrow\sqrt{3}=\dfrac{C'B+BM}{PM}$$
$$\Rightarrow\sqrt{3}=\dfrac{h+100+100}{PM}$$
$$\Rightarrow PM=\dfrac{h+200}{\sqrt3}.....(ii)$$
From (i) and (ii), we get
$$\sqrt{3}h=\dfrac{h+200}{\sqrt3}$$
$$\Rightarrow 3h=h+200$$
$$\Rightarrow 2h=100$$
$$\Rightarrow h=100$$
Now,
$$CB=CM+MB=h+100=100+100=200$$
Hence, the height of the helicopter from the surface of the lake is 200 m.
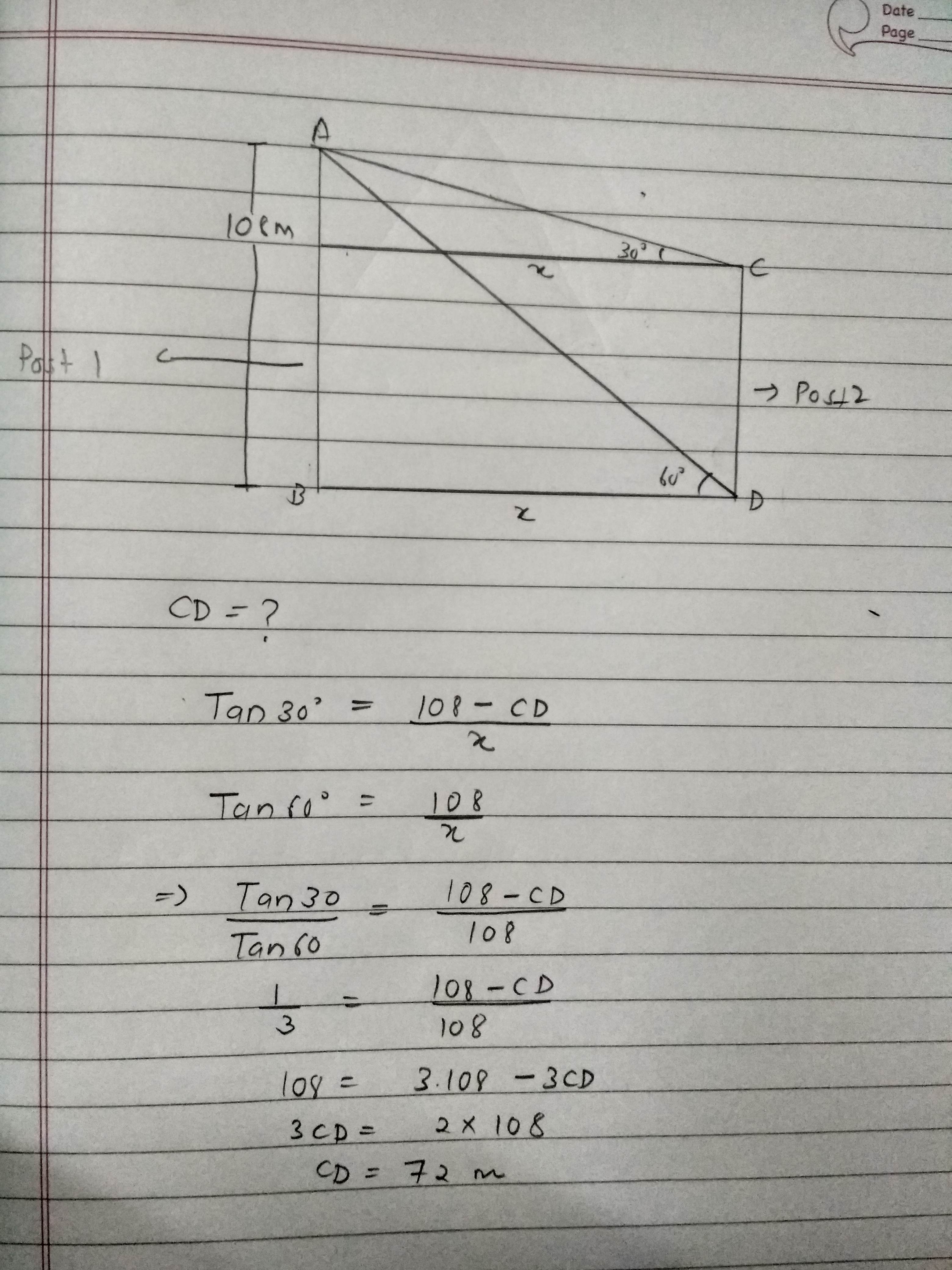
There are two verticals posts, one on each side of a road, just opposite to each other.One post is $$108$$ metre high. From the top of this post, the angles of depression of the top and foot of the other post are $$30^0$$ and $$60^0$$ respectively. The height of the other post, in metre is:
From a point on the ground, the angle of elevation of the top of a tower is observed to be $$60 ^ { \circ }$$. From a point 40$$\mathrm { m }$$ vertically above the first point of observation, the angle of elevation of the top of the tower is $$30 ^ { \circ }$$. Find the height of the tower and its horizontal distance from the point of observation.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at $${60^ \circ }$$ to the horizontal. Determine the height to the balloon from the ground. There is no slack in cable.
Here A is the position of balloon
Now, in $$\Delta$$ABC, $$\sin 60^o=\dfrac{AB}{AC}$$
$$AB=AC\sin 60^o$$
$$=215\times \dfrac{\sqrt{3}}{2}$$
$$=186$$m
$$\Rightarrow$$ Height of the balloon from the ground is $$186$$m.
As observed from the top of a $$75m$$ high lighthouse from the sea-level, the angles of depression of two ships are $${30}^{o}$$ and $${45}^{o}$$. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Lines PA and BD are parallel and AB is the transversal
$$\therefore\angle{ABD}=\angle{PAB}$$ [Alternate angles]
So,$$\angle{ABD}=30^{o}$$
Similarly,
Lines PA and BD are parallel and AC is the transversal
$$\therefore\angle{ACD}=\angle{PAC}$$ [Alternate angles]
So,$$\angle{ABD}=45^{o}$$
Since lighthouse is perpendicular to ground
$$\angle{ADB}=90^{o}$$
In right angled triangle ACD
$$\tan 45=\dfrac{AD}{CD}$$
$$1=\dfrac{75}{CD}$$
$$CD=75\ m$$
Similarly,
In a right angled triangle ABD
$$\tan 30=\dfrac{AD}{BD}$$
$$\dfrac{1}{\sqrt3}=\dfrac{75}{BD}$$
$$BD=75\sqrt{3}\ m$$
$$BC+CD=75\sqrt{3}$$
$$BC+75=75\sqrt{3}$$
$$BC=75(\sqrt{3}-1)\ m$$
Hence the distance between two ships id $$75(\sqrt{3}-1)\ m$$
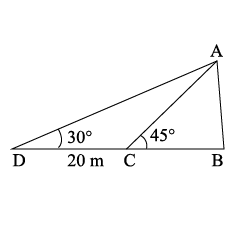
On a straight line passing through the foot of a tower, two points C and D are at distance of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
Based on the given information, we can draw the diagram shown above.
Given, $$\angle{C}$$ and $$\angle{D}$$ are complementary.Hence, if $$\angle{C}=\theta$$ then,
$$\angle{D}=90^{o}-\theta$$
We know that, $$\tan \theta=\dfrac{\text{Opposite Side}}{\text{Adjacent Side}}$$
Hence, in $$\Delta ABC$$ and $$\Delta ABD$$,
$$\tan\theta=\dfrac{h}{4}...(1)$$
$$\tan(90-\theta)=\dfrac{h}{16}$$
$$\Rightarrow \cot\theta=\dfrac{h}{16}\quad \quad [\because \ \tan(90-\theta)=\cot \theta]$$
$$\Rightarrow \dfrac{1}{\cot\theta}=\dfrac{16}{h}$$
$$\Rightarrow \tan\theta=\dfrac{16}{h}....(2)$$
Solving $$(1)$$ and $$(2)$$, we get,
$$\dfrac{h}{4}=\dfrac{16}{h}$$
$$h^2=64$$
$$h=\pm 8$$
But, $$h$$ cannot be negative.
Hence, $$h=8\ m$$
Hence, the height of the tower is $$8\ m$$.
The angle of elevation of the top of the tower from two points $$P$$ and $$Q$$ at distance $$a$$ and $$b$$ respectively form the base and in the same straight line with it are complementary. Prove that the height of the tower is $$\sqrt{ab}$$
Given,
the angle of elevation of the top of the tower from two points P & Q is at a distance of a & b.
Also given, to prove that the tower
height$$=\sqrt{ab}$$
($$\because$$ complementary angle $$=(90^o-\theta)$$)
From $$\Delta$$ABP
$$\tan\theta =\dfrac{AB}{BP}=\dfrac{AB}{a}$$ ……..$$(1)$$
From $$\Delta$$ABQ
$$\tan(90-\theta)=\dfrac{AB}{BQ}$$
$$(\because\tan(90-\theta)=\cot\theta)$$
$$(\cot\theta =\dfrac{1}{\tan\theta})$$
We get,
$$\cot\theta =\dfrac{BQ}{AB}=\dfrac{b}{AB}$$ ……..$$(2)$$
by equation $$(1)$$ & $$(2)$$ we get,
$$\dfrac{AB}{a}=\dfrac{b}{AB}$$
$$\Rightarrow AB^2=ab\Leftrightarrow AB=\sqrt{ab}$$
$$\therefore AB=$$height$$=\sqrt{ab}$$
Hence proved.
A vertical stick $$20cm$$ long costs a shadow $$6cm$$ long on the ground . At the some time , a tower costs a shadow $$15m$$ long on the ground. find the height of the tower.
In $$\triangle ABE$$,
$$\tan\theta=\cfrac{EB}{AB}=\cfrac{20}{6}$$
In $$\triangle ACD$$,
$$\tan \theta=\cfrac{CD}{AC}=\cfrac{h}{15}$$
Equating, we get
$$ \cfrac{20}{6}=\cfrac{h}{15}$$
$$\Rightarrow h=50m$$
A pole $$6\ m$$ hight casts a shadow $$2\sqrt {3}\ m$$ long on the ground, then find the angle of elevation of the sun.
$$\tan \theta =\cfrac{6}{2\sqrt{3}}$$
$$\theta =\tan ^{-1}(\sqrt{3})=\cfrac{\pi}{3}=60°$$
The length of the shadow of a tower standing on level plane is found to be $$2x$$ meters longer when the sun's altitude is $${\text{3}}{{\text{0}}^{\text{o}}}$$ than when it was $${\text{4}}{{\text{5}}^{\text{o}}}$$. Prove that height of tower is $$x\left( {\sqrt 3 + 1} \right)$$ meters.
In $$\triangle BCD$$
$$\tan45^{\circ}=\dfrac{h}{y}=1$$
$$\Rightarrow h=y$$
In $$\triangle ABC$$
$$\tan 30^{\circ}=\dfrac{h}{2x+y}=\dfrac{1}{\sqrt{3}}$$
$$\dfrac{y}{2x+y}=\dfrac{1}{\sqrt{3}}$$
$$\sqrt{3}y= 2x+y$$
$$y(\sqrt{3}-1)=2x$$
$$y=\dfrac{2x}{\sqrt{3}-1}$$
$$y=x(\sqrt{3}+1)$$
But $$y=b=x(\sqrt{3}+1)$$ meters
From a window $$15\ m$$ high above the ground in a street, the angles of elevation and depression of the top and foot of another house on the opposite side of the street are $$30^{o}$$ and $$45^{o}$$, respectively. Show that the height of the opposite house is $$23.66\ m$$. [take $$\sqrt{3}=1.732$$]
As observer from the top of a lighthouse $$100$$ $$\text{m}$$ high observe sea level, the angle of depression of a ship sailing directly towards it, changes from $$30 ^ { \circ }$$ to $$60 ^ { \circ }$$ . Determine the distance travelled by the ship during the period of observation.
In $$\triangle ABD$$,
$$\therefore \tan 30^{\circ}=\cfrac{AB}{BD}$$
$$\Rightarrow \cfrac{1}{\sqrt 3}=\cfrac{100}{BD}$$
$$\Rightarrow BD=100\sqrt{3} \text{ m}$$
In $$\triangle ABC$$,
$$\tan 60^{\circ}=\cfrac{AB}{BC}$$
$$\Rightarrow \sqrt 3=\cfrac{100}{BC}$$
$$\Rightarrow BC=\dfrac{100}{\sqrt 3}$$
$$\therefore$$ Distance travelled by the ship$$=CD=BD-BC$$
$$=(100\sqrt 3-\cfrac{100}{\sqrt 3})$$
$$=100\left(\cfrac{2}{\sqrt 3}\right)\,$$
$$=\cfrac{200}{\sqrt 3}\, \text{ m}$$
At some time of the day, the length of the shadow of a tower is equal to its height. Find the sun's altitude at that times.
The angle of elevation of a cloud from a point $$60$$ metres above a lake is $${30^ \circ }$$ and the angle of depression of the reflection of the cloud in the lake is $${60^ \circ }$$. find the height of cloud from the surface of the lake
In the given figure, the top of a tower is observed from two points on the same horizontal line through a point on the base of the tower . If the angles of elevation at the two points be $${30^ \circ }$$ and $${45^ \circ }$$ , and the distance between them is $$20$$ m, find the height of the tower.
Let $$AB$$ be the height of the tower
$$\tan 45^o=\dfrac{AB}{BC}$$
$$AB=BC---(1)$$
$$\tan 30^o=\dfrac{AB}{BD}$$
$$\dfrac{1}{\sqrt3}=\dfrac{AB}{BC+20}$$
$$BC+20=AB\sqrt3$$
from equation $$(1)$$ $$AB=BC$$
$$\therefore AB+20=AB\sqrt3$$
$$AB=\dfrac{20}{\sqrt3-1}\dfrac{\sqrt3+1}{\sqrt3+1}=10(\sqrt3+1)$$
$$AB=10(\sqrt3+1) \ m$$
$$\therefore$$ height of the tower is $$10(\sqrt3+1) \ m$$
A man 2m high walk at uniform speed of 5m /min away from a lamppost 5m high. Find rate at which length of its shadow increases.
An aeroplane is flying at a height of $$300\ m$$ above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are $${ 45 }^{ o }$$ and $${ 60 }^{ o }$$ respectively. Find width of the river. $$\left[ \mathrm{Use}\ \sqrt { 3 } =1.732 \right]$$
Let $$A$$ be the aeroplane $$BD$$ is the length of the river
$$\tan{45}^{o}=\cfrac{AC}{BC}$$
$$1=\cfrac{300}{BC}$$
$$BC=300\;m$$
$$\tan {60}^{o}=\cfrac{AC}{CD}$$
$$\sqrt{3}=\cfrac{300}{CD}$$
$$CD=\cfrac{300}{\sqrt{3}}\times \cfrac{\sqrt{3}}{\sqrt{3}}$$
$$=\cfrac{300\sqrt{3}}{3}=100\sqrt{3}=1.732\times 100=173.2$$
width of river $$=BC+CD=300+173.2=473.2\;m$$
A building 15 m high casts a shadow 1.8 m long. What will be height of that pole whose shadow at that time in 60 cm?
From an airplane vertically above a straight horizontal road, the angles of depression of two consecutive kilometers stones on opposite sides of the airplane are observed to be $$60^{o}$$ and $$30^{o}$$. Show that the height of airplane above the road is $$\dfrac{\sqrt{3}}{4}$$ km.
The angle of depression towards the roads on opposite side are $${ 30 }^{ \circ}$$ and $$ { 60 }^{ \circ }.$$
Let x and y be the distance on the opposite side of an aeroplane. Let 'h' be the height of aeroplane from the road.
$$ x+y=1$$ (given consecutive mile markers) -----(1)
$$ \tan { 30 }^{ \circ }=\dfrac { h }{ x } =\dfrac { 1 }{ \sqrt { 3 } } $$
$$ \Longrightarrow x=\sqrt { 3 } h$$
$$ \tan { 60 }^{ \circ }=\dfrac { h }{ y } =\sqrt { 3 } $$
$$ y=\dfrac { h }{ \sqrt { 3 } } $$
putting these values in (1), we get
$$ \Longrightarrow \sqrt { 3 } h+\dfrac { h }{ \sqrt { 3 } } =1$$
$$ \Longrightarrow \dfrac { 3h+h }{ \sqrt { 3 } } =1$$
$$ \Longrightarrow \dfrac { 4h }{ \sqrt { 3 } } =1$$
$$ \Longrightarrow h=\dfrac { \sqrt { 3 } }{ 4 } km$$
Two points $$A$$ and $$B$$ are on opposite sides of a tower. The top of the towers makes angles of $$30^{o}$$ and $$45^{o}$$ at $$A$$ and $$B$$ respectively. If the height of the tower is $$40\ m$$, find the distance $$AB$$. $$[\sqrt {3}=1.32].$$
Rajender observes a person standing on the ground from a helicopter at an angle of depression $$45^{o}$$, If the helicopter flies at a height of $$500\ meters$$ from the ground, what is the distance of the person from Rajender?
Based on the given information, we can draw the figure shown above.
$$1=\cfrac{BC}{AC}\quad \quad \left[\because \ \tan 45^o=1\right]$$
$$AC=500\ m$$
Since, triangle ABC is right angled triangle,
$$AB^2=AC^2+BC^2\\$$
$$\Rightarrow AB^2=500^2+500^2\\$$
$$\therefore \ AB=500\sqrt2 \ m\\$$
Distance between them is $$500\sqrt2 \ m$$
From the top of a 7 m high building, the angle of elevation of the top of a cable tower measures $$60^0$$ and the angle of depression of its foot measures $$45^0.$$ Determine the height of the tower. $$(\sqrt { 3 } =1.732)$$
The diagram will be as shown
$$AB$$ =building
$$CD=$$ Cable tower
$$CE=AB$$
In $$\triangle ABC$$
$$\cfrac{AB}{BC}=\tan{45}^{o}$$
$$\Rightarrow$$ $$AB=BC=7m$$
$$AE=BC=7m$$
In $$\triangle AED$$
$$\cfrac{DE}{AE}=\tan{60}^{o}$$
$$\Rightarrow$$ $$DE=AE(\sqrt 3)=7\sqrt 3$$
Heignt of cable tower $$=CD$$
$$=CE+DE$$
$$=7+7\sqrt{3}$$
$$=7(1+\sqrt{3})$$
$$=7(2.732)$$
$$=19.124m$$
A man goes $$10m$$ due east and then $$24m$$ due north. Find the distance from the starting point
We have,
Towards North$$=24$$m
Towards East$$=10$$m
Using Pythagoras Theorem,
$$(Hypotenuse)^2=(base)^2+(height)^2$$
$$=(10)^2+(24)^2$$
$$=100+576$$
$$=676$$
$$=(26)^2$$
Starting point $$=\sqrt{(Hypotenuse)^2}$$
$$=\sqrt{(26)^2}$$
$$=26$$m
Hence, this is answer.
There is a flag on a tower of height $$20$$ m. At a point on the ground the angles of elevation of the foot and the top of the flag are $${ 45 }^{ 0 }$$ and $${ 60 }^{ 0 }$$ respectively. Find the height of the flag staff.
$${ \tan45 }^{ 0 }=\dfrac { 20 }{ x } $$
$$\Rightarrow x=20m$$
$$\tan{ 60 }^{ 0 }=\dfrac { h+20 }{ x } $$
$$\Rightarrow \sqrt { 3 } =\dfrac { h+20 }{ 20 } \Rightarrow h=20\left( \sqrt { 3 } -1 \right) =14.28m$$
A tree $$ 12 m $$ high is broken by the wind in such a way that its top touches the ground and makes an angle $$ {60}^{0} $$ with the ground. At what height from the bottom the tree is broken the wind ? $$ ( \sqrt {3}= 1.73 ) $$
$$\begin{array}{l} \sin 60^{ \circ }=\dfrac { h }{ { 12-h } } =\dfrac { { \sqrt { 3 } } }{ 2 } \\ \Rightarrow \left( { 2+1.73 } \right) h=12\times 1.73 \\ 3.73h=20.76 \\ h=5.56\, m \end{array}$$
A pole $$20 m$$ high cast a shadow $$10 m$$ long on the ground. Calculate the angle of elevation of the sun.
Kishor observes a person standing on the ground from a helicopter at an angle of depression $$30^{\circ}$$ if the helicopter flies at a height of 100 m from the ground what is the distance of the person from Kishor.
In $$\Delta PKH$$,
$$\tan 30^o = \dfrac{PK}{HK} \,\, \therefore \dfrac{1}{\sqrt{3}} = \dfrac{x}{100}$$
$$\therefore x = \dfrac{100}{\sqrt{3}} m$$
The angle of elevation of a cloud from a point $$60$$ $$m$$ above the surface of the water of a late is $$30^{o}$$ and the angle of depression of its shadow from the same point in water of lake is $$60^{o}$$. Find the height of the cloud from the surface of water.
In the above figure, $$C$$ is the cloud and $$F$$ is its reflection on the surface of the lake $$AB.$$ And $$E$$ is the point of observation.
In $$\triangle CDE,$$
$$\begin{aligned}{}\tan 30^\circ& = \frac{{CD}}{{DE}}\\\frac{1}{{\sqrt 3 }}& = \frac{x}{y}\\y &= \sqrt 3 x\quad\quad\quad\quad\dots(i)\end{aligned}$$
According to laws of reflection, $$BC$$ will be equal to $$BF.$$
So,
$$BF=BC$$
$$=BD+DC$$
$$=60+x$$
In $$\triangle EDF,$$
$$FD=BF+BD$$
$$=60+x+AE$$
$$=60+x+60$$
$$=120+x$$
So,
$$\begin{aligned}{}\tan 60^\circ& = \frac{{FD}}{{DE}}\\\sqrt 3 & = \frac{{120 + x}}{y}\\\sqrt 3 \times \sqrt 3 x &= 120 + x\quad\quad\quad\quad\dots[\text{By using }(i)]\\3x - x &= 120\\2x &= 120\\x& = 60\ m\end{aligned}$$
So, the height of the cloud from the surface of the lake will be,
$$BC=60+x$$
$$=60+60$$
$$=120\ m$$
The angles of elevation of the top of a lower from two points at a distance of 4 m and 9 m, find the height of the tower from the base of the tower and in the same straight line with it are complementary.
From the above information we can getIt is given that $$ \alpha $$ and $$ \beta $$ are supplementary so, $$ \alpha+\beta=90^{\circ} $$
$$ \operatorname{In} \Delta A B P $$
$$\text{ tan} \ \alpha=\dfrac{A B}{B P} \ldots \ldots \ldots \ldots \ldots \ldots \ldots .(1) $$
In $$ \triangle A B Q $$
$$ \operatorname{tan} \beta=\dfrac{A B}{B Q} $$
$$ \operatorname{tan}(90-\alpha)=\dfrac{A B}{B Q} $$
$$ \text {cot} \alpha=\dfrac{A B}{B Q} $$
$$ \operatorname{tan} \alpha=\dfrac{B Q}{A B} \ldots \ldots \ldots \ldots \ldots \ldots \ldots .(2) $$
From(1) and (2)
$$ \dfrac{B Q}{A B}=\dfrac{A B}{B P} $$
$$ B Q \times B P=(A B)^{2} $$
$$ 9 \times 4=(A B)^{2} $$
$$ (A B)^{2}=36 $$
$$ A B=6 m $$
Therefore, height of the tower is $$ 6 \mathrm{m} $$.
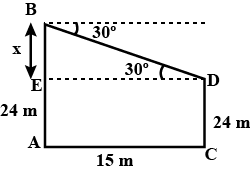
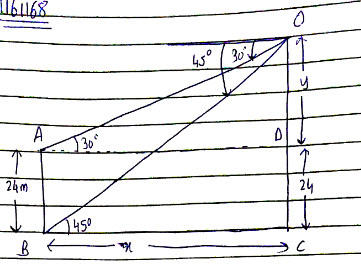
A ladder $$15\ m$$ long reaches a window which is $$9\ m$$ above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window $$12\ m$$ high. Find the width of the street.
In $$\triangle CDA$$
$$CD=15$$ m
$$DA=9$$ m
Using Pythagoras theorem,
$$CA=\sqrt{CD^{2}-DA^{2}}=\sqrt{225-81}=\sqrt{144}$$
$$\implies CA=12$$ m
In $$\triangle EBC$$
$$EB=12$$ m
$$CE=15$$ m
$$BC=\sqrt{EC^{2}-EB^{2}}=\sqrt{225-144}=\sqrt{81}=9$$ m
$$\therefore AB=AC+BC = 12 + 9 = 21 $$ m
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of $${ 30 }^{ \circ }$$, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be $${ 60 }^{ \circ }$$. Find the time taken by the car to reach the foot of the tower from this point.
$$\angle PAB=30^o$$
after $$6$$ sec
$$\angle PAC=60^o, \angle ADB=90^o$$
$$\angle ABD=\angle PAB$$ so $$\angle ABD=30^o$$
$$\angle ACD=\angle PAC$$ so $$\angle ACD=60^o$$
$$\tan 60^o=\dfrac{AD}{CD}$$
$$AD=\sqrt{3}CD$$ ……….$$(1)$$
$$\tan 30^o=\dfrac{AD}{BD}$$
$$AD=\dfrac{BD}{\sqrt{3}}$$
$$\sqrt{3}CD=\dfrac{BD}{\sqrt{3}}$$
$$3CD=BD$$
$$CD=BC+CD$$
$$CD=\dfrac{BC}{2}$$
Time taken to cover $$BC=6$$ sec
Time taken to cover $$\dfrac{BC}{2}=\dfrac{6}{2}$$
Time taken to cover $$CD=3$$sec
Hence it takes $$3$$ sec to reach to the foot of the tower.
A man in a boat rowing away from a lighthouse $$150\mathrm { m }$$ high, takes $$2$$ minutes to change the angle of elevation of the top of the lighthouse from $$60 ^ { \circ }$$ to $$45 ^ { \circ }.$$ Find the speed of the boat.
A peacock is sitting on the top of a tree. It observes a serpent on the ground making an angle of depression of $$30^ {o}$$. The peacock with the speed of $$300\ m/min$$ catches the serpent in $$12$$ seconds. What height of the tree?
Given,
$$\text{Speed }= 300 \text{ m/min}$$
We know that $$\cfrac{\text{distance}}{\text{time}} = \text{speed}$$
$$\therefore AB = 300 \text{ m/min} \times 12 \text{ seconds}$$
$$= \cfrac{300}{60}\times 12$$
$$AB = 60 \text{ m}$$
Now,
$$\tan 30^{\circ} = \cfrac{h}{AB}$$
$$\therefore h = \tan \left(30^{\circ}\right)\times AB$$
$$= \cfrac{1}{\sqrt{3}}\times 60$$
$$= \cfrac{60}{\sqrt{3}} \text{ m}$$
$$= 34.64 \text{ m}$$
Find the length of the shadow on the ground of a pole of height $$6m$$ when the angle of elevation $$\theta$$ of the Sun is such that $$\tan \theta = \dfrac { 3 } { 4 }.$$
$$\tan\theta =\dfrac{P}{B}$$
$$\dfrac{3}{4}=\dfrac{6}{d}$$
$$d=\dfrac{6\times 4}{3}$$
$$d=8m$$.
A kite is flying at a height of $$30m$$ from the ground. The length of string from the kite to the ground is $$60m.$$ Assuming that there is no slack in the string. find the angle of elevation of the kite at the ground.
Perpendicular$$=30$$m
Hypotenuse$$=60$$m
$$\theta =?$$
$$\sin\theta =\dfrac{P}{H}$$
$$=\dfrac{30}{60}$$
$$\sin\theta =\dfrac{1}{2}$$
So $$\sin\dfrac{1}{2}=30^o$$
So $$\theta =30^o$$.
If two towers of height $${h_1}$$ and $${h_2}$$ substends angles of $${60^ \circ }$$ and $${30^ \circ }$$ mid point of the line joining their feet. Then what is $${h_1}:{h_2}$$
REF.Image
$$tan 30^{\circ}=\frac{h_{2}}{x}$$ $$tan 60^{\circ}=\frac{h_{1}}{x}$$
$$\frac{tan 60^{\circ}}{tan 30^{\circ}}=\frac{h_{1}/x}{h_{2}/x}=\frac{h_{1}}{h_{2}}$$
$$\frac{h_{1}}{h_{2}}=\frac{\sqrt{3}}{\frac{1}{\sqrt{3}}}=\frac{3}{1}$$
The angle of elevation of an airplane from a point on the ground is $${60^ \circ }$$. After a flight of 30 seconds, the angle of elevation become $${30^ \circ }$$. If the airplane is flying at a constant height of $$3000\sqrt 3 \,m$$, find the speed of the airplane.
REF.Image
$$tan 60^{\circ}=\frac{3000\sqrt{3}}{x}$$
$$x=\frac{3000\sqrt{3}}{\sqrt{3}}= 3000 m$$
$$tan 30^{\circ}=\frac{3000\sqrt{3}}{1/\sqrt{3}}=9000 m$$
distance covered = 9000- 3000
= 6000 m.
speed = $$\frac{6000}{30}= 200 m/s$$
A solid metallic right circular cone $$20cm$$ height whose vertical angle is $$60^{o}$$, is cut into two parts at the middle of its height by a plane parallel to its base. if the frustum so obtained to be drawn in to a wire of diameter $$\dfrac{1}{12}\ cm$$, find the length of the wire?
Let, $$OCD$$ be the metallic cone and $$ABDC$$ be the required frustum.
Since, frustum is drawn into wire of volume of frustum $$ABCD = $$ Volume of cylindrical wire.
$$\begin{array}{l} OQ=QP=10\, \, cm \\ \angle QOB=30^{ \circ } \end{array}$$
Height of frustum $$ = h = QP = 10\,\,cm$$
Let $$PD=r_1$$ and $$QB=r_2$$
$$\begin{array}{l} \tan 30^o=\dfrac { { PD } }{ { OP } } \ \,{and}\ \ tan 30^o=\dfrac { { QB } }{ { OQ } } \\ \tan 30^{ \circ }=\dfrac { 1 }{ { \sqrt { 3 } } } =\dfrac { { { r_{ 1 } } } }{ { 20 } }\ and\ tan 30^{ \circ }=\dfrac { 1 }{ { \sqrt { 3 } } } =\dfrac { { { r_{ 2 } } } }{ { 10 } } \\ { r_{ 1 } }=\dfrac { { 20 } }{ { \sqrt { 3 } } } \, \, cm\, \, \, \, { r_{ 2 } }=\dfrac { 10 }{ { \sqrt { 3 } } } \, \, cm \\ \therefore Volume\, \, of\, \, frustum=\dfrac { { \pi h } }{ 3 } \left( { r_{ 1 }^{ 2 }+r_{ 2 }^{ 2 }+{ r_{ 1 } }{ r_{ 2 } } } \right) \\ =\dfrac { { \pi \times 10 } }{ 3 } \left( { { { \left( { \dfrac { { 20 } }{ { \sqrt { 3 } } } } \right) }^{ 2 } }+{ { \left( { \dfrac { { 10 } }{ { \sqrt { 3 } } } } \right) }^{ 2 } }+\dfrac { { 20 } }{ { \sqrt { 3 } } } \times \dfrac { { 10 } }{ { \sqrt { 3 } } } } \right) \\ =\dfrac { { 10\pi } }{ 3 } \left( { \dfrac { { 400 } }{ 3 } +\dfrac { { 100 } }{ 3 } +\dfrac { { 200 } }{ 3 } } \right) \\ =\dfrac { { 10\pi } }{ 3 } \left( { \dfrac { { 700 } }{ 3 } } \right) \\=\dfrac { { 7000\pi } }{ 9 } \, \, c{ m^{ 3 } } \end{array}$$
Given diameter $$ = \dfrac{1}{{12}}\,\,cm$$
Volume of wire $$=$$ volume of frustum
Let $$h$$ be the length of the wire
$$\begin{array}{l} \pi { r^{ 2 } }h=\dfrac { { 7000\pi } }{ 9 } \\ h=\dfrac { { 7000 } }{ 9 } \times { \left( { \dfrac { 1 }{ { \dfrac { 1 }{ { 24 } } } } } \right) ^{ 2 } }=4480\, \, m \\ \therefore h=4480\, \, m \end{array}$$
A pit $$7\ m$$ long and $$3.5\ m$$ wide is dug to a certain depth. If the volume of earth taken out of it is $$98\ m^{3}$$, what is the depth of the pit?
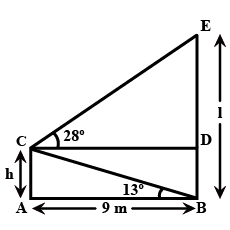
A man stands $$9\mathrm { m }$$ away from a flag-pole, He observes that angle of elevation of the top of the pole is $$28 ^ { \circ }$$ and the angle of depression of the bottom of the pole is $$13 ^ { \circ } .$$ Calculate the height of the pole.
Let the height of pole and man be $$l\ meter$$ and $$h\ meter$$ respectively.
In $$\Delta ABC$$
$$tan 13^o=\cfrac{h}{9}\\\Rightarrow h=9 tan\ 13^o$$
In $$\Delta CDE$$
$$tan 28^o=\cfrac{l-h}{9}\\ \Rightarrow l=9 tan28^o+9 tan 13^o\\=9\times 0.531+9\times 0.230\\=6.86m$$
The height of a light house is $$85\ m$$. An observer on it found the angle of depression to a boat to be $$30^{o}$$, which was sailing towards the light house. After $$2$$ minutes, the angle of depression for the same boat was $$60^{o}$$. What was the speed of the boat in $$km/hr$$?
Let $$AB$$ be the lighthouse, $$C$$ be the initial point and $$D$$ be the final point of the boat.
It can be observed that $$\triangle ABC$$ and $$\triangle ABD$$ are right angled triangles.
In $$\triangle ABC$$,
$$\tan {60^0} = \dfrac{{85}}{y}$$
$$\sqrt 3 = \dfrac{{85}}{y}$$
$$y = \dfrac{{85}}{{\sqrt 3 }}m$$
In $$\triangle ABD$$
$$\tan {30^0} = \dfrac{{85}}{{x + y}}$$
$$\dfrac{1}{{\sqrt 3 }} = \dfrac{{85}}{{x + y}}$$
$$x + y = 85\sqrt 3 $$
$$x = 85\sqrt 3 - \dfrac{{85}}{{\sqrt 3 }}$$
$$ = \left( {\dfrac{{255 - 85}}{{\sqrt 3 }}} \right)$$
$$x = \dfrac{{170}}{{\sqrt 3 }}\,m$$
Distance travelled in $$2$$ minutes $$x = \dfrac{{170}}{{\sqrt 3 }}\,m$$
distance travelled in $$1$$ minutes $$x = \dfrac{{170}}{{2\sqrt 3 }}\,m/\min $$
$$ = \dfrac{{170 \times 60}}{{1000\sqrt 3 \times 2}}km/hr$$
$$ = 1.24\,km/hr$$
Hence,Speed of boat is $$1.24 \ km/hr$$
From the top of a tower $$20\ m$$ high, the angle of elevation of the top of the building is $$45^{o}$$ and the angle of depression of its foot is $$15^{o}$$. Find the height of the building. (given $$\tan{75^{o}}=3.7321$$)
$$\begin{array}{l} BC=DE=20m \\ \tan 75=\dfrac { { BD } }{ { BC } } =\dfrac { { BD } }{ { 20 } } =3.7321 \\ \Rightarrow BD=74.642 \\ \tan \left( { \angle ADB } \right) =\dfrac { { AB } }{ { BD } } \\ \Rightarrow 1=\dfrac { { AB } }{ { 74.642 } } \end{array}$$
Height of tower $$=AB+BC$$
$$=94.642\ m$$
Hence, this is the answer.
Find the angle of depression of a point on the ground, at a 10m distance from base of the tower, from the top of the tower whose height is $$10$$ m.
REF.Image
$$ tan \theta =\frac{L}{1}\Rightarrow \theta = 45^{\circ}$$
From a point P on the ground, the angles of elevation of the top of 20m tall building and of a helicopter, hovering at some height above the top of the building are $$30^0$$ and $$60^0$$ respectively. Find the height at which the helicopter is hovering. (above the ground)
Let the height of plane be $$h$$m
$$\tan { { 30 }^{ \circ } } =\cfrac { DB }{ PB } \quad \Rightarrow \cfrac { 1 }{ \sqrt { 3 } } =\cfrac { 20 }{ PB } \quad \Rightarrow PB=20\sqrt { 3 } m\\ \tan { { 60 }^{ \circ } } =\cfrac { BC }{ PB } \quad \Rightarrow \sqrt { 3 } =\cfrac { h }{ 20\sqrt { 3 } } \\ \Rightarrow h=\sqrt { 3 } \times 20\sqrt { 3 } =20\times 3=60m$$
$$\therefore$$ height of plane$$=60$$m
A person observed the angle of elevation of the top of a tower as $$30^o$$. He walked $$50m$$ towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as $$60^o$$. Find the height of the tower.
In $$\Delta$$ ABD, $$\tan 30^{\circ} = \dfrac{h}{x + 50}$$ --- (i)
In $$\Delta$$ ABC, $$\tan 60^{\circ} = \dfrac{h}{x}$$ --- (ii)
(ii)/(i) $$\implies \dfrac{h/x}{h/x + 50} = \dfrac{\tan 60^{\circ}}{\tan 30^{\circ}}$$
$$\implies \dfrac{x + 50}{x} = \dfrac{\sqrt{3}}{1/\sqrt{3}}$$
$$\implies$$ $$x + 50 = 3x$$
$$\implies$$ $$x = 25 \text{ m}$$
$$h = x\tan 60^{\circ} = 25\sqrt{3} \text{ m}$$ [from (ii)]
Two posts are $$K$$ meter apart and the height of one double that of the other. If from the mid point of the line segment joining their feet, an observer finds the angles of elevation of their tops to be complementary, then find the height of the shortest post.
From the top of a $$70m$$ tall tower, the angle of depression of the top and the base of a pole are found to be $$30$$ and $$45$$ respectively. Find the distance of the pole from the tower and the height of the pole.
$$\begin{array}{l} Pole=CD\, \, \\ Tower=AB \\ \sin ce,\, \, in\, \, \Delta ABC,\, \, \angle AVB={ 45^{ 0 } } \\ \therefore \Delta ABC\, \, is\, { 45^{ 0 } }-{ 45^{ 0 } }-{ 90^{ 0 } }\, \, \, triangle \\ \therefore AB=BC=70\, \, m \\ in\, \, right\, \, triangle\, \, AED \\ \Delta AED\, \, is\, { 30^{ 0 } }-{ 60^{ 0 } }-{ 90^{ 0 } }\, \, triangle \\ \dfrac { { AE } }{ { ED } } =\dfrac { 1 }{ { \sqrt { 3 } } } \\ \therefore AE=\dfrac { { 70 } }{ { \sqrt { 3 } } } \\ \therefore BE=AB-AE=70-\dfrac { { 70 } }{ { \sqrt { 3 } } } =29.5854\, \, m. \end{array}$$
Two poles of height 7 m and 12 m stand in a plane ground . If the distance between their feet is 12 m , then find the distance between their tops ?
Let pole $$BD=7m$$
$$AD=12m\\DE=12m$$
Distance between the pole tops $$=AC$$
$$AD-BD=5cm$$
$$AC^2=AB^2+CB^2\\ \Rightarrow AC^2=12^2+5^2\\ \Rightarrow AC^2=169\\ AC=\sqrt{169}m$$
Hence, $$AC=13m$$
If the length of the shadow cast by a pole is $$3$$ times the length of the pole, then find the angle of elevation of sun.
A person in flying a kite at an angle of elevation $$\alpha$$ and the length of thread from his hand to kite is $$l$$ draw diagram for the following situation
REF.Image
l= length of the thread
$$ \alpha $$ = angle of elevation
A man of height $$5\ meter$$ is moving away from a lamppost at the rate $$2\ meter\ per\ sec$$. If the height of the lamppost is $$4.5\ meter$$. Find the rate at which
i) his shadow is lengthening.
ii) the tip of his shadow is moving.
Consider the following figure.
Given ,
$$\dfrac{{dx}}{{dt}} = 1.2\,m/s$$
From similarly of both triangle $$\left( {\Delta AOB\& \Delta DOC} \right)$$
$$\begin{array}{l} \dfrac { { 1.5 } }{ { L-k } } =\dfrac { { 4.5 } }{ L } \\ LSL=4.5L-4.5x \\ 4.5x=3L \\ Hence,\, \frac { { dL } }{ { dt } } =1.5\times 1.2=1.8\, m/s \end{array}$$
Hence, $$tip(0)$$ is moving with $$1.8 m/s$$
Shadow is Lenghtening with $$(1-x)=0.6 m/s$$
In a right angled $$\triangle ABC.$$ $$m\angle ABC =90^o$$, $$m\angle=30^o$$. If $$BC=9$$ cm then $$AC$$?
Given $$\angle ABC=90^o$$
$$\angle A=30^o$$
$$BC=9$$cm
To find AC
In rt $$\Delta ABC$$,
$$\tan 30^o=\dfrac{BC}{AB}$$
$$\dfrac{1}{\sqrt{3}}=\dfrac{BC}{AB}$$
$$\Rightarrow AB=\sqrt{3}BC$$
$$=\sqrt{3}(9)$$
$$=9\sqrt{3}$$cm.
By Pythagoras theorem,
$$(AC)^2=(AB)^2+(BC)^2$$
$$=(9\sqrt{3})^2+9^2$$
$$=9^2(3)+9^2$$
$$=9^2(3+1)$$
$$=9^2(4)=324$$
$$AC=\sqrt{324}=18$$cm.
An electric pole, $$14$$ meter high casts a shadow of $$10$$ meters. Find the height of a tree that casts a shadow of $$15$$ meters under similar conditions.
A vertical tower of height $$150m$$ if the angle of elevation from a point on ground is $$30^{\circ}$$ Find the distance from the tower to the point
The angles of depression of the top of an 8 m tall building from the top of a multi-storeyed building is $${ 45 }^{ \circ }$$. Find the height of the multi-storeyed building if the distance between the two buildings is $$10m$$
the angle of election of the top of a tower ,from a point on the ground and at a distance of 150 m from its foot ,is $${ 30 }^{ \circ }$$. find the height of the tower correct to the place of decimal
The angle of depression from a tower of height $$200m$$ changes from $$60^{\circ}$$ to $$45^{\circ}$$ find the distance covered during the change.
Due to strong wind, a part of tree $$18\ m$$ high broke at a distance of $$5\ m$$ from the ground, without separating from the main stem, top of the tree touched the ground. At what distance from the foot of the step did the top of the tree fall on the ground?
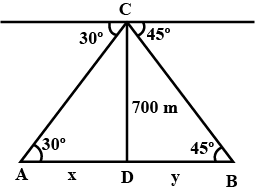
The angles of elevation of top of a building of an organisation working for conservation of wild life, from two points at a distance of 4 m and 9 m from the base of the builiding and in the same straight line with it are complementary. Prove that the height of the building is 6 m Why do we need conserve wild life?
Let AB be the building .
Let C and D be the two points at the distances of A and B respectively from the base of the tower.
Then AC=a=9 m , AD=b=4 m .
Let $$\angle ACB=\theta$$ and $$\angle ADB=90^o-\theta$$.
Let h be the height of the building .
In triangle CAB, we have
$$tan\theta=\dfrac{AB}{AC}=\dfrac{h}{9}$$ ..........................1
In triangle DAB we have,
$$tan(90^o-\theta)=\dfrac{AB}{AD}=\dfrac{h}{4}$$
$$cot\theta=\dfrac{h}{4}$$ ......................2
From eq. `1 and 2 we have,
$$tan\theta\times{cot\theta}=\dfrac{h^2}{36}$$
$$1=\dfrac{h^2}{36}$$
$$h^2=36$$
$$h=6 m $$
We need to conserve wildlife because they are the beauty of our nature.
A vertical pole of length $$12m$$ casts a shadow $$4m$$ long on the ground and at the same time a tower casts a shadow $$21m$$ long. Find the height of the tower.
If the height of a pole is $$2\sqrt{3}$$ metres and the length of its shadow is $$2$$ metres, find the angle of elevation of the sun.
$$\textbf{The angle of elevation of sun is given by}$$
$$\text{From the figure we get,}$$
$$\text{Let AB be the pole and AC be its shadow, then,}$$
$$\text{Let angle of elevation,}$$ $$\angle{ACB}=\theta$$
$$\text{We have given,}$$ $$AB=2\sqrt{3}\ m$$ $$\text{&}$$ $$AC = 2\ m$$
$$\tan{\theta}=\dfrac{AB}{AC}=\dfrac{2\sqrt{3}}{2}=\sqrt{3}=\tan 60^0$$
$$\Rightarrow\theta={60}^{\circ}$$
$$\textbf{Hence the angle of elevation of sun is}$$ $$\boldsymbol{{60}^{\circ}}$$.
A vertical pillar stands on the plain and is surmounted by a flagstaff of height $$5$$ m. From a point on a ground, the angles of elevation of the bottom of the flagstaff is $${45^ \circ }$$ and that of the top of the flagstaff is $${60^ \circ }$$. Find height of the pillar. (use $$\sqrt 3 = 1.732$$)
A vertical pole is $$15$$m high and the length of its shadow is $$20$$m.What is the angle of elevation of the sun?
Let $$AB$$ be the pole and $$AC$$ be the shadow.
Here $$AB=15$$m and $$AC=20$$m
In right angled triangle $$\triangle{BAC}$$, let $$\angle{ACB}=\theta$$
$$\therefore \tan{\theta}=\dfrac{AB}{AC}\\=\dfrac{15}{20}\\=0.75$$
$$\Rightarrow \theta={\tan}^{-1}{0.75}\\={36}^{\circ}{53}^{\prime}$$
(from the trigonometric table)
The height of a tower is $$100m$$ and angle of elevation from a point on the ground to top of tower is $$30^{\circ}$$ find the distance of the point from the tower .
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increase from $${ 30 }^{ \circ } $$ to $${ 60 }^{ \circ }$$ as he walks towards the building. Find the distance he walked towards the building.
REF.Image
AB= 30-1.5=28.5 cm
In $$\Delta ABD:- tan 30^{\circ}=\frac{AB}{BD}$$
$$\Rightarrow BD=(28.5)\sqrt{3}$$
In $$\Delta ABC :- tan 60^{\circ}=\frac{AB}{BC}$$
$$\Rightarrow BC=\frac{(28.5)}{\sqrt{3}}$$
CD= BD-BC
$$= 28.5 (\sqrt{3}-\frac{1}{\sqrt{3}})$$
$$= 28.5(\frac{2}{\sqrt{3}})= 32.91 m$$
Two poles of heights $$6\ m$$ and $$11\ m$$ stand on a plane ground. If the distance between their feet is $$12\ m$$, find the distance between their tops.
A tree breaks due to a storm and the broken part bends such that the top of the tree touches the ground making an angle measuring $$30^o$$ with the ground. The distance from the foot of the tree to the point where the top touches the ground is $$30\ m$$ . Find the height of the tree.
The angle of elevation of the top of a building from the food of the tower is $${\text{3}}{{\text{0}}^{\text{o}}}$$ and the angle of elevation of the top of the tower from the food of the building is $${\text{6}}{{\text{0}}^{\text{o}}}$$. if the tower is $${\text{50}}$$ m high, find the height of the building.
CD=50 cm, $$\angle ACB=30^{\circ},\angle DBC=60^{\circ}$$
$$tan B=\frac{DC}{BC}$$
$$60^{\circ}=\frac{50}{BC}\Rightarrow BC=\frac{50}{\sqrt{3}}$$
$$tan30^{\circ}=\frac{AB}{BC}$$
$$AB=\frac{1}{\sqrt{3}}\times \frac{50}{\sqrt{3}}=\frac{50}{3}m$$
height of building = $$AB=\frac{50}{3}m$$
The height of tower is $$100m$$ find the distance from tower to a point where the angle of depression from top of tower is $$30^{\circ}$$
The length of a string between a kite and a point on the ground is $$90$$m if the string makes an angle $$\theta$$ with the ground level such that $$\tan{\theta}=\dfrac{15}{8}$$, how high is the kite?Assume that there is no slack in the string.
$$tan\theta = \dfrac{15}{8}= \dfrac{BC}{AB}=\dfrac{h}{AB}$$
$$\Rightarrow h= AB tan \theta $$ ______ (1)
By Pythagoras Theorem,
$$90^{2}=h^{2}+AB^{2}$$
$$= AB^{2}tan^{2}\theta +AB^{2}$$
$$\Rightarrow AB^{2}(1+ tan^{2}\theta )=90^{2}$$
$$\displaystyle \Rightarrow AB^{2}=\frac{90^{2}}{1+ tan^{2}\theta }=\frac{90^{2}}{1+\frac{15^{2}}{8^{2}}}=\frac{90^{2}\times 64}{289}$$
$$\Rightarrow \displaystyle AB=\sqrt{\frac{90^{2}\times 64}{289}}=\frac{90\times 8}{17}= 42.35m$$
$$\therefore AB= 42.35 m$$
$$h=AB tan \displaystyle \theta = 42.35\times \frac{15}{8}= \frac{90\times 8}{17}\times \frac{15}{8}$$
$$=\dfrac{90\times 15}{17}= 79.42 m$$
Hence height of the kite $$=79.42 m$$
A $$10\ \text{m}$$ long flagstaff is fixed on the top of a tower on the horizontal plane. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are $$60^\circ$$ and $$45^\circ$$ respectively. Find the height of the tower.
The angle of elevation of a ladder leaning against a wall is $${ 60 }^{ 0 }$$ and the foot of the ladder is $$7.5$$ m away from the wall. Find the length of the ladder.
A 1.3 m tall girl spots a balloon moving with the wind in horizontal line at a constant height of 91.3 m from the ground. The angle of elevation of the balloon from the eyes of the girl at an instant has measure $$60^\circ$$. After some time, the angle of elevation is reduced in measure to $$30^\circ$$. Find the distance travelled by the balloon during the interval.
In $$\Delta ABC$$:
$$\tan 60^\circ=\dfrac{BC}{AC}$$
$$AC=\dfrac{90}{\sqrt{3}}=30\sqrt{3}$$
In $$\Delta ADE$$ :
$$\tan 30^\circ=\dfrac{ED}{AD}$$
$$AD=90\sqrt{3}$$
$$CD=AD-AC$$
$$=90\sqrt{3}-30\sqrt{3}$$
$$=60\sqrt{3}$$ m $$=$$ Distance travelled by the balloon.
From the top of a cliff $$92\ m$$ high, the angle of depression of a buoy is $$20^{o}$$. Calculate, to the nearest, a distance of the buoy from the foot of the cliff.
Let $$AB$$ be the cliff and $$C$$ be the buoy.
$$AB = 92 \; m \quad \left( \text{Given} \right)$$
Also,
$$\angle{ACB} = 20°$$
Therefore,
In $$\triangle{ABC}$$,
$$\tan{20°} = \cfrac{AB}{Bc}$$
$$\Rightarrow BC = \cfrac{92}{0.364} \approx 253 \; m$$
Hence the buoy is at a distance of $$253 \; m$$ from the foot of the cliff.
From a point on the ground $$20\ \mathrm{m}$$ away from the foot of a vertical tower the angle of elevation of the top of the tower is $$60^{\circ}$$. Find the height of the tower. (Use $$\sqrt{3} = 1.732)$$
Given the tower is $$20\ \mathrm{m}$$ away from the point A.
Let the height of tower be $$x$$.
$$\tan 60^{\circ}=\dfrac{BC}{AB}$$
$$BC=AB\tan 60^{\circ}$$
$$=20\sqrt{3} \ \mathrm{m}$$
$$=20\times 1.732\ \mathrm{m}$$
$$=2\times 17.32\ \mathrm{m}$$
Height of tower $$=34.64\ \mathrm{m}$$.
Two ships are sailing in the sea on either side of the lighthouse; the anglession of two ships as observed from the top of the lighthouse are $$ 60 ^ { \circ } $$ and $$ 45 ^ { \circ } $$ respectively. If the distance between the ships is 200$$ \left( \frac { \sqrt { 3 } + 1 } { \sqrt { 3 } } \right) $$ meters, find the height of the lighthouse.
From the top of the light house, an observer looking at a ship and makes angle of depression of$$ { 60 }^{ \circ }$$.If the height o the light house is 90 metres, then find how far the ship is from the light house$$.\left( \sqrt { 3 } =1.73 \right) $$
From a point $$30$$ m away from the foot of a tower, the angle of elevation of the top of the tower is $$30^o$$. find the height of tower. $$(Use \sqrt{3} = 1.732)$$
Given the tower is $$30$$m away from point A.
Given angle of elevation of top of tower is $$30$$.
Let the height of tower be x
$$\tan 30=\dfrac{BC}{AB}$$
$$=\dfrac{1}{\sqrt{3}}=\dfrac{x}{30}$$
$$x=\dfrac{30}{\sqrt{3}}\cdot \dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{30\times \sqrt{3}}{3}$$
$$=10\sqrt{3}$$
$$\therefore$$ Height of tower $$=10\sqrt{3}=10\times 1.732$$
$$=17.32$$m.
If a pole $$6\ m$$ high casts a shadow $$2\sqrt{3}\ m$$ long on the ground, find the sun's elevation.
Refer the figure,
$$\tan\theta=\dfrac{6}{2\sqrt{3}}\\=\dfrac{3}{\sqrt{3}}\\=\sqrt{3}$$
$$\Rightarrow \theta=60^{o}$$
Find the angle of elevation of the sun when the shadow of a pole $$h\ m$$ high is $$\sqrt 3\ h\ m$$ long.
Given that the shadow of a pole that is $$h\ m$$ high is $$\sqrt3 h\ m$$ long.
To find out: The angle of elevation of the sun.
Based on the given information, we can draw the figure shown above.
In $$\triangle ABC$$,
$$\tan \theta =\dfrac{AB}{BC} = \dfrac{h}{ \sqrt 3 h}$$
$$\Rightarrow \tan \theta =\dfrac{1}{ \sqrt 3 } = \tan 30^o$$
$$\therefore \ \theta =30^o$$
Hence, the angle of elevation of the sun is $$30^o$$.
The height of a tower is $$100m$$.The angle of depression of a point on the ground from the top of the tower is $$30^{\circ}$$ .The distance of the point from the tower is
Given,
The height of the tower is $$AB=100m$$
The angle of depression $$=30^{\circ}$$
Let the distance of the point be $$x$$
Now, from $$\Delta ABC,$$
$$\tan 30^o=\dfrac {AB}{BC}\\\Rightarrow \dfrac 1{\sqrt 3}=\dfrac {100 }{x}\\\Rightarrow x=100\sqrt{3}$$
$$\Rightarrow x=100\times1.732$$
$$\Rightarrow x=173.2$$
Hence, the distance of the point is $$173.2\ m$$
At the foot of a mountain, the elevation of its summit is $$45 ^ { \circ }.$$ After ascending $$1000 \text{ m}$$ towards the mountain up a slope of $$30 ^ { \circ }$$ inclination, the elevation is found to be $$60 ^ { \circ } .$$ Find the height of the mountain.
In $$\triangle ADE$$
By $$\sin 30^{\circ} = \dfrac {DE}{AD}$$
$$\dfrac {1}{2} = \dfrac {DE}{1000}$$
$$DE = 500\ m$$
By $$\cos 30^{\circ} = \dfrac {AE}{AD}$$
$$\dfrac {\sqrt {3}}{2} = \dfrac {AE}{1000}$$
$$AE = 500\sqrt {3} m$$
Let $$EB = x\ m$$
then $$EB = DF = x\ m$$
In $$\triangle DLF, \tan 60^{\circ} = \dfrac {CF}{DF}$$
$$\Rightarrow \sqrt {3} = \dfrac {CF}{DF}$$
$$\Rightarrow CF = x \sqrt {3}$$
In $$\triangle ABC$$
$$\tan 45^{\circ} = \dfrac {BC}{AB}$$
$$1 = \dfrac {BC}{AB}$$
$$\Rightarrow AB = BC$$
$$x + 500\sqrt {3} = 500 + \sqrt {3} x$$
$$x(\sqrt {3} - 1) = 500(\sqrt {3} - 1)$$
$$x = 500\ m$$
$$Height = x\sqrt {3} + 500$$
$$= 500\sqrt {3} + 500$$
$$= 500 (\sqrt {3} + 1) m$$
$$\therefore$$ Height of the mountain is $$500(\sqrt{3}+1)\text{ m}$$
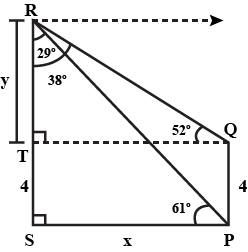
Roshani saw an eagle on the top of a tree at an angle of elevation of $${ 61 }^{ \circ }$$, while she was standing at the door of her house. She went on the terrace of the hose so that she could see it clearly. The terrace was at a height of $$4$$ m. While observing the eagle from there the angle of elevation was $${ 52 }^{ \circ }$$. At what height from the ground was the eagle?
A pole $$5{ m }$$ high is fixed on the top of a tower. The angle of elevation of the top the pole observed from a point $$A$$ on the ground is $$60 ^ { \circ }$$ and the angle of depression of the point $$A$$ from the top of the tower is $$45 ^ { \circ } .$$ Find the height of the tower.
REF.Image
$$tan 60^{\circ}= \frac{BD}{AB}$$ $$tan 45^{\circ}=\frac{BC}{AB}$$
$$\sqrt{3}=\frac{BD}{AB}$$ $$1=\frac{BC}{AB}$$
$$AB=\frac{BD}{\sqrt{3}}$$ _____ (1) $$AB=BC$$ _____ (2)
From (1) & (2)
$$\frac{BD}{\sqrt{3}}= BC$$
$$(BC+5)=\sqrt{3}BC$$
$$5=1.732 BC-BC$$
$$5=0.732 BC$$
$$BC=\frac{5}{0.732}$$
$$BC= 6.83 m$$
Two poles of equal height are standing opposite each other on either side of the road which is $$80m$$ wide.From a point between then on the road the angles of elevation of top of the poles are $$60^o$$ and $$30^o$$. Find the height of the poles and distance of the point from the poles.
Let AB and CD be two poles.
Therefore,
$$AB = CD$$
Length of road $$= 80 \; m \quad \left( \text{Given} \right)$$
$$\therefore BC = 80 \; m$$
Let point $$P$$ be the point on the road between poles.
Since poles are perpendicular to the ground.
$$\angle{ABP} = \angle{DCP} = 90°$$
As we know that,
$$\tan{\theta} = \cfrac{\text{Perpendicular}}{\text{Base}}$$
Now, in right angled triangle $$DPC$$,
$$\tan{30°} = \cfrac{CD}{CP}$$
$$\Rightarrow CD = \cfrac{CP}{\sqrt{3}} ..... \left( 1 \right)$$
Similarly in right angled triangle $$APB$$,
$$\tan{60°} = \cfrac{AB}{BP}$$
$$\Rightarrow AB = \sqrt{3} BP$$
$$\Rightarrow CD = \sqrt{3} BP ..... \left( 2 \right) \quad \left( \because AB = CD \right)$$
From equation $$\left( 1 \right) \& \left( 2 \right)$$, we have
$$\cfrac{CP}{\sqrt{3}} = \sqrt{3} BP$$
$$\Rightarrow CP = 3 BP ..... \left( 3 \right)$$
Now,
$$BC = BP + CP$$
$$\Rightarrow 80 = BP + 3 BP \quad \left( \text{From } \left( 3 \right) \right)$$
$$\Rightarrow BP = \cfrac{80}{4} = 20 \; m$$
Now from equation $$\left( 3 \right)$$, we have
$$CP = 3 \times 20 = 60 \; m$$
Again from equation $$\left( 1 \right)$$, we have
$$CD = \cfrac{60}{\sqrt{3}} = 20 \sqrt{3} \; m$$
Therefore,
Height of the pole is $$20 \sqrt{3} \; m$$.
Distance of point $$P$$ from pole $$CD$$ is $$60 \; m$$.
Distance of point from pole $$AB$$ is $$20 \; m$$.
A round balloon of radius r subtends an angle $$\alpha $$ at the eye of the observer while the angle of elevation of its center is $$\beta $$. Prove that the height of the center of the balloon is r sin $$\beta $$ cosec $$\alpha $$/2.
REF.Image
Let P be age of observer. PA & PB are tangents to round balloon,
$$\angle APB = \alpha $$
$$\therefore \angle CPA= \angle CPB =\frac{\alpha }{2}$$
$$CA=CB=r$$ and CQ= height = h
In $$\Delta CBP$$
$$sin (\frac{\alpha }{2})=\frac{BC}{CP}=\frac{r}{CP}$$
$$\therefore CP=\frac{r}{sin (\frac{\alpha }{2})}=r cosec (\frac{\alpha }{2})$$
In $$\Delta CPQ$$,
$$sin\beta =\frac{CQ}{CP}$$ $$\therefore CQ= CP sin \beta $$
$$CQ= r coesc (\frac{\alpha }{2}), sin\beta $$ [from (1)]
Hence,
height = h= CQ = $$r sin \beta , cosec (\frac{\alpha }{2})$$
An electric pole is $$10$$ metres high. If its shadow is $$10\sqrt{3}$$ metres in length, find the elevation of the sun.
Consider
$$AB$$ as the pole and $$OB$$ as its shadow,
It is given that,
$$AB=10m\ ,\ OB=10\sqrt{3}m$$ and $$\theta$$ is the angle of elevation of the sun.
In right $$\triangle OBA$$,
$$\tan \theta =\dfrac{AB}{OB}$$
Substituting the values,
$$\Rightarrow \tan \theta =\dfrac{10}{10\sqrt{3}}=\dfrac1{\sqrt{3}}$$
We know that
$$ \tan 30^{o}=\dfrac1{\sqrt{3}}$$
$$\therefore\tan\theta =\tan30^{o}$$
$$\Rightarrow \theta =30^{o}$$.
Hence, the elevation of the sun is $$30^o$$.
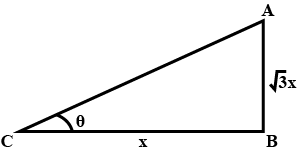
In the figure, ABC is a right triangle in which $$AB = 8 \,m, \angle BCA = 30^\circ,$$ then find the angle of elevation of A at C.
From the diagram, it is clear that the angle of elevation of A with
respect to C is $$30^\circ$$ where BC becomes the horizontal.
In the figure, ABC is a right triangle in which $$AB = 8 \,m, \angle BCA = 30^\circ,$$ then find
the angle of depression of C at A.
DC is a vertical line drawn from A so that we get a reference line from which we can measure the depression angle.
As AD and BC are both vertical lines therefore they are parallel.
Now $$\angle ACB = \angle CAD$$ as they are alternate angles along two parallel lines
therefore, $$\angle CAD = 60^\circ$$
Now, from the diagram drawn before we can easily say that
The angle of depression of C at A is $$60^\circ$$
As AD and BC are both vertical lines therefore they are parallel.
Now $$\angle ACB = \angle CAD$$ as they are alternate angles along two parallel lines
therefore, $$\angle CAD = 60^\circ$$
Now, from the diagram drawn before we can easily say that
The angle of depression of C at A is $$60^\circ$$
The height of a telephone pole is $$\dfrac{1}{\sqrt 3}$$ times the length of its shadow. Find the angle of elevation of the source of light.
It is given that, the height of a telephone pole is $$\dfrac{1}{\sqrt 3}$$ times the length of its shadow.
$$\Rightarrow\tan \theta = \dfrac{1}{\sqrt 3}$$
$$\Rightarrow \theta = 30^\circ$$
Hence, the angle of elevation of the source of light is $$30^\circ.$$
Let, length of the shadow$$(BC)=x\ unit$$
$$\therefore$$ Height of the pole $$( AB)=\dfrac{x}{\sqrt{3}}\ unit$$
From $$\triangle ABC,$$
$$\tan\theta = \dfrac{AB}{BC}$$
$$\Rightarrow\tan\theta = \dfrac{\dfrac{x}{\sqrt 3}}{x}$$
From $$\triangle ABC,$$
$$\tan\theta = \dfrac{AB}{BC}$$
$$\Rightarrow\tan\theta = \dfrac{\dfrac{x}{\sqrt 3}}{x}$$
$$\Rightarrow\tan \theta = \dfrac{1}{\sqrt 3}$$
$$\Rightarrow \theta = 30^\circ$$
Hence, the angle of elevation of the source of light is $$30^\circ.$$
What is the angle of elevation of the sun when the length of the shadow of a vertical pole is equal to its height.
Consider
$$AB$$ as the pole and $$CB$$ as its shadow.
$$\theta$$ is the angle of elevation of the sun,
Let us take $$AB=x$$ m and $$BC=x$$ m
In right $$\triangle ABC$$
$$\tan \theta =\dfrac{AB}{CB}=\dfrac xx$$
$$\Rightarrow \tan \theta=1=\tan 45^o\qquad[\because \tan45^o=1]$$
$$\theta =45^{o}$$
Hence, the angle of elevation of the sun is $$45^{o}$$.
The height of a tree is $$\sqrt{3}$$ times the length of its shadow. Find the angle of elevation of the sun.
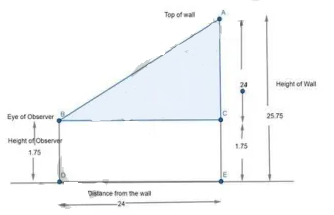
An observer $$1.75 \,m$$ tall is at a distance of $$24 \,m$$ from a wall $$25.75 \,m$$ high. Find the angle of elevation of the top of the wall at the observer's eye.
Drawing a diagram for a better perspective of the problem,
We know that from trigonometric ratios that,
$$tan\theta = \dfrac{perpendicular}{base} = \dfrac{AC}{BC}$$
The angle of elevation of top of the wall will be $$\angle ABC.$$
Now let $$\angle ABC = \theta$$
Therefore,
$$\tan\theta = \dfrac{AC}{BC}$$
From the figure we can see that,
$$AC = BC = 24 \,m.$$
Therefore,
$$tan\theta = \dfrac{1}{1}$$
We know that from trigonometric ratios that,
$$tan\theta = \dfrac{perpendicular}{base} = \dfrac{AC}{BC}$$
The angle of elevation of top of the wall will be $$\angle ABC.$$
Now let $$\angle ABC = \theta$$
Therefore,
$$\tan\theta = \dfrac{AC}{BC}$$
From the figure we can see that,
$$AC = BC = 24 \,m.$$
Therefore,
$$tan\theta = \dfrac{1}{1}$$
$$tan\theta = tan 45^0$$
$$\theta = 45^\circ$$
Therefore, the angle of elevation of top of the wall from the eyes of the observer is $$45^\circ.$$
Therefore, the angle of elevation of top of the wall from the eyes of the observer is $$45^\circ.$$
An observer $$1.5 \ m$$ tall is $$20.5\ m$$ away from a tower $$22\ m$$ high. Determine the angle of elevation of the top of the tower from the eye of the observer.
Consider
$$AB$$ as the tower and $$CD$$ as the observer,
$$\theta$$ as the angle of elevation,
Given
$$AB=22\ m$$ , $$CD=1.5\ m$$ and $$BD=2.5m$$
From the point $$C$$ construct $$CE$$ parallel to $$DB$$,
Thus, $$AE=22-1.5=20.5m$$
and $$CE=DB=20.5m$$
In right triangle $$AEC$$,
$$\tan \theta=\dfrac{AE}{CE}$$
Substituting the values,
$$\Rightarrow \tan \theta =\dfrac{20.5}{20.5}=1$$
We know that, $$\tan 45^{o}=1$$
$$\therefore \theta =45^{o}$$.
Hence, the angle of elevation of the top of the tower is $$45^o$$
A ladder of length $$30 \,m$$ is placed against a wall such that it just reaches the top of the $$15 \,m$$ high wall. At what angle is the ladder inclined to the ground ?
Drawing the given problem so that we get a better understanding,
In the given diagram $$\theta$$ is the required angle as asked in the problem
We know that,
$$sin \,\theta = \dfrac{perpendicular}{hypotenuse}$$
$$= \dfrac{AC}{BC}$$
$$= \dfrac{15}{30} = \dfrac{1}{2}$$
$$\theta = \sin^{-1} \left ( \dfrac{1}{2} \right )$$
$$= 30^\circ$$
therefore the required angle the ladder makes with the wall is $$30^\circ.$$
In the given diagram $$\theta$$ is the required angle as asked in the problem
We know that,
$$sin \,\theta = \dfrac{perpendicular}{hypotenuse}$$
$$= \dfrac{AC}{BC}$$
$$= \dfrac{15}{30} = \dfrac{1}{2}$$
$$\theta = \sin^{-1} \left ( \dfrac{1}{2} \right )$$
$$= 30^\circ$$
therefore the required angle the ladder makes with the wall is $$30^\circ.$$
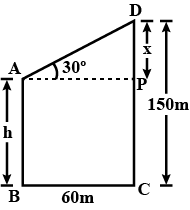
Angle of elevation of top of a tower from a $$7 m$$ high building is $$60^{0}$$ and angle of depression of its foot is $$45^{0}$$. Find the height of the tower.
Let $$AB$$ is a tower and $$CD$$ is a building of height $$7 m$$.
The angle of elevation and angle of depression are $$60^{0}$$ and $$45^{0}$$ respectively.
i.e., $$\angle ACE = 60^{0}$$
and $$\angle ECB = 45^{0}$$
$$BD || CE, CD || BE$$
$$CD = BE = 7 m$$
From right angled $$\Delta CBD$$
$$\tan 45^{0} =\frac{CD}{DB}$$
$$1 =\frac{7}{DB}$$
$$DB = 7 m$$
$$CE = DB = 7 m$$
Again from right angled $$\Delta AEC$$
$$\tan 60^{0} =\frac{AE}{CE}$$
$$\sqrt{3}=\frac{AE}{7}$$
$$AE = 7\sqrt{3} m$$
Hence, height of tower $$AB = AE + EB$$
$$= 7\sqrt{3} + 7$$
$$= 7(\sqrt{3} + 1) m$$
Hence, height of tower $$AB = 7(\sqrt{3} + 1) m$$.
The angle of elevation and angle of depression are $$60^{0}$$ and $$45^{0}$$ respectively.
i.e., $$\angle ACE = 60^{0}$$
and $$\angle ECB = 45^{0}$$
$$BD || CE, CD || BE$$
$$CD = BE = 7 m$$
From right angled $$\Delta CBD$$
$$\tan 45^{0} =\frac{CD}{DB}$$
$$1 =\frac{7}{DB}$$
$$DB = 7 m$$
$$CE = DB = 7 m$$
Again from right angled $$\Delta AEC$$
$$\tan 60^{0} =\frac{AE}{CE}$$
$$\sqrt{3}=\frac{AE}{7}$$
$$AE = 7\sqrt{3} m$$
Hence, height of tower $$AB = AE + EB$$
$$= 7\sqrt{3} + 7$$
$$= 7(\sqrt{3} + 1) m$$
Hence, height of tower $$AB = 7(\sqrt{3} + 1) m$$.
Two buildings are in front of each other on a road of width 15 metres. Form the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is $$30^\circ$$. What is the height of the second building?
Here, $$AB = 12 \text{ m}, BD = 15 \text{ m}, \angle \; CAE = 30º$$ and $$AE ⊥ CD$$
So,
$$CE = CD − ED = (h − 12) \text{ m}$$ $$(ED = AB)$$
$$AE = BD = 15 \text{ m}$$
In right $$\triangle AEC$$,
$$\tan 30^\circ= \dfrac{CE}{AE}$$
$$\implies= \dfrac{1}{\sqrt{3}}= \dfrac{h-12}{15}$$
$$\implies h= (12 +5\sqrt{3}) \text{ m}$$
Thus, the height of the second building is $$(12+5\sqrt 3) \text{ m}$$
The shadow of a vertical tower on level ground is increased by $$40\ m$$, when the altitude of the sun changes from $$60^{\circ}$$ to $$30^{\circ}$$. Find the height of the tower.
Let $$CD$$ is a tower of height $$h$$. Let from its base $$C$$, a point $$B$$ with distance $$x$$, the angle of elevation of top of tower is $$60^{\circ}$$.
When the shadow of the tower becomes $$40$$ meter more from $$B$$ than the angle of elevation from $$A$$ becomes $$30^{\circ}$$.
Let $$BC = x$$ m and $$\angle CBD = 60^{\circ}$$, $$\angle CAD = 30^{\circ}$$
From right angled $$\Delta BCD$$,
$$\tan 60^{\circ} =\dfrac{h}{x}$$
$$\sqrt{3} =\dfrac{h}{x}$$
$$x =\dfrac{h}{\sqrt{3}}$$
From right angled $$\Delta ACD$$
$$\tan30^{\circ}=\dfrac{CD}{AC}$$
$$\dfrac{1}{\sqrt{3}}=\dfrac{h}{AB+BC}$$
$$\dfrac{1}{\sqrt{3}}=\dfrac{h}{40+x}$$
$$(40+x)=\sqrt{3}h$$
Put the value of $$x$$ from equation,
$$40+\dfrac{h}{\sqrt{3}}=\sqrt{3}h$$
$$\sqrt{3}h-\dfrac{h}{\sqrt{3}}=40$$
$$h\left [ \sqrt{3}-\dfrac{1}{\sqrt{3}} \right ]=40$$
$$h\left [ \dfrac{3-1}{\sqrt{3}} \right ]=40$$
$$h=\dfrac{40\sqrt{3}}{2}$$
$$=20\sqrt{3}\ m$$
$$=20\times1.732\ m$$
$$=34.64\ m$$
Hence, height of tower is $$34.64\ m$$.
A $$1.5 m$$ tall boy is standing at some distance away from a $$30 m$$ high building when he moves towards the building then angle of elevation from his eye became $$60^{0}$$ from $$30^{0}$$. Find how much distance he covered towards the building?
If the angle of elevation top of point $$D$$ of leaning tower at the point $$A$$ and $$B$$ is $$\alpha$$ and $$\beta$$. If slope of tower is $$\theta$$, then prove that
$$\cot\theta=\frac{b\cot\alpha-\alpha\cot\beta}{b-a}$$
Where $$a$$ and $$b$$ are the distances of $$A$$ and $$B$$ from tower $$(b > a)$$.
Let $$CD$$ is a leaning tower and angles of elevations of top of point $$D$$ at the place $$A$$ and $$B$$ are $$\alpha$$ and $$\beta$$.
So, $$\angle DBM = \beta, \angle DAM = \alpha$$
Let $$\angle DCM = \theta$$ and $$DM = h$$ m, $$CM = x$$ m and $$AC = a, BC = b$$.
From right angled $$\Delta DMC$$,
$$\tan \theta =\dfrac{DM}{CM}$$
$$\tan \theta =\dfrac{h}{x}$$
$$x =\dfrac{h}{\tan\theta} = h \cot \theta$$ ….(i)
From right angled $$\Delta DMA$$,
$$\tan \alpha =\dfrac{DM}{AM}$$
$$\tan \alpha =\dfrac{h}{a+x}$$
$$a + x = = h \cot \alpha$$
$$a = h \cot \alpha – x$$
$$= h \cot \alpha – h \cot \theta$$
$$= h[\cot \alpha – \cot \theta]$$ ……(ii)
For right angled $$\Delta DMB$$,
$$\tan \beta =\dfrac{DM}{BM}$$
$$\cot \beta =\dfrac{BM}{DM}$$
$$\cot \beta =\dfrac{b+x}{h}$$
$$b + x = h \cot \beta$$
$$b = h \cot \beta – x$$
$$b = h \cot \beta – h \cot \theta$$
$$= h [\cot \beta – \cot \theta]$$ ……(iii)
Divide equation (iii) in equation (ii),
$$\dfrac{a}{b}=\dfrac{h(\cot\alpha-\cot\theta)}{h(\cot\beta-\cot\theta)}$$
$$a(\cot \beta – \cot \theta) = b(\cot \alpha – \cot \theta)$$
$$(b – a)\cot \theta = b \cot \alpha – a \cot \beta$$
$$\cot\theta=\dfrac{b\cot\alpha-\alpha\cot\beta}{b-a}$$
An aeroplane when flying at a height of $$3000 m$$ from the ground passes vertically above another aeroplane at an instant when the angles of elevation of the two planes from the same point on the ground are $$60^{0}$$ and $$45^{0}$$ respectively. Find first aeroplane is how much high with second aeroplane.
Let height of first aeroplane is $$BD$$ which is flying at $$3000 \ m$$ height and height of second aeroplane $$BC = h\ m$$. Let angles of elevation from point $$A$$ are $$60^{0}$$ and $$45^{0}$$ respectively.
So, $$\angle BAD = 60^{0}$$ and $$\angle CAB = 45^{0}$$ and Let $$AB = x\ m$$
From right angled $$\Delta ABD$$,
$$\tan 60^{0}=\frac{BD}{AB}$$
$$\sqrt{3}=\dfrac{3000}{x}$$
From right angled $$\Delta ABC$$,
$$\tan45^{0}=\dfrac{BC}{AB}$$
$$1=\dfrac{h}{x}$$
$$1=\dfrac{h}{1000\sqrt{3}}$$
$$h=1000\sqrt{3}=1000*1.732$$
$$=1732m$$
Hence, height of second plane from first plane
$$CD = BD – BC = 3000 – 1732 = 1268\ m$$
The shadow of a vertical pillar of length $$6m$$. On earth is $$4m$$ where as at the same time shadow of a tower is $$28m$$. Find the height of the tower.
The shadow $$DE=4$$ of $$6m$$. long pillar $$CD$$ is obtained. At the same time shadow $$BE$$ $$28m$$ of a tower of height (say $$h$$) is obtained.
To find: height ($$h$$) of tower $$AB$$
Calculation: $$\triangle ABE$$ and $$\triangle CDE$$ are similar
$$\cfrac{AB}{CD}=\cfrac{BE}{DE}$$
$$\Rightarrow$$ $$\cfrac{h}{6}=\cfrac{28}{4}$$
$$\Rightarrow$$ $$h=\cfrac{28}{4}\times 6$$
$$h=42m$$
Height of tower $$=42m$$
To find: height ($$h$$) of tower $$AB$$
Calculation: $$\triangle ABE$$ and $$\triangle CDE$$ are similar
$$\cfrac{AB}{CD}=\cfrac{BE}{DE}$$
$$\Rightarrow$$ $$\cfrac{h}{6}=\cfrac{28}{4}$$
$$\Rightarrow$$ $$h=\cfrac{28}{4}\times 6$$
$$h=42m$$
Height of tower $$=42m$$
One skyscraper is $$100 dm$$. At some time the shadow of a $$1 dm$$ high pole is $$3\sqrt{3} dm$$ long from the light of the sun. What will be the angle of elevation of sun and the length of the shadow and the shadow of the skyscraper at the same time.
Let $$BC$$ is a skyscraper of height $$100 dm$$. and $$DE$$ is a pole of height $$9 dm$$.
Let elevation angle of sun is $$\theta$$.
According to question, $$\angle DAE = \angle CAB = \theta$$ and $$AE = 3\sqrt{3} dm$$
From right angled $$\Delta DEA$$
$$\tan \theta =\frac{DE}{AE}$$
$$=\frac{9}{3\sqrt{3}}$$
$$= \sqrt{3}$$
$$= \tan 60^{0} = \theta = 60^{0}$$
Hence, angle of elevation of sun $$= 60^{0}$$
Again from right angled $$\Delta ABC$$,
$$\tan \theta =\frac{BC}{AB}$$
$$\tan 60^{0} =\frac{100}{AB}$$
$$\sqrt{3} =\frac{100}{AB}$$
$$AB =\frac{100}{\sqrt{3}}$$
Hence, angle of elevation of sun is $$60^{0}$$ and length of shadow of skyscraper $$\frac{100}{\sqrt{3}}$$ decimeter.
Let elevation angle of sun is $$\theta$$.
According to question, $$\angle DAE = \angle CAB = \theta$$ and $$AE = 3\sqrt{3} dm$$
From right angled $$\Delta DEA$$
$$\tan \theta =\frac{DE}{AE}$$
$$=\frac{9}{3\sqrt{3}}$$
$$= \sqrt{3}$$
$$= \tan 60^{0} = \theta = 60^{0}$$
Hence, angle of elevation of sun $$= 60^{0}$$
Again from right angled $$\Delta ABC$$,
$$\tan \theta =\frac{BC}{AB}$$
$$\tan 60^{0} =\frac{100}{AB}$$
$$\sqrt{3} =\frac{100}{AB}$$
$$AB =\frac{100}{\sqrt{3}}$$
Hence, angle of elevation of sun is $$60^{0}$$ and length of shadow of skyscraper $$\frac{100}{\sqrt{3}}$$ decimeter.
A $$2$$ meter long observer is at $$28$$ meter distance from a tower. The angle of elevation of top of tower from his eyes is $$60^{0}$$. Find the height of tower.
Let $$AB$$ a tower and $$CD$$ is a observer. The distance between tower and observer = $$28 m$$ and angle of elevation is $$60^{0}$$ i.e.,
$$BC = DE = 28 m$$
$$CD = BE =2 m$$ and $$\angle ADE = 60^{0}$$
Form right angled $$\Delta AED$$
$$\tan 60^{0} =\dfrac{AE}{ED}$$
$$\sqrt{3}=\dfrac{AE}{28}$$
$$AB = 28\sqrt{3} m$$
$$= 28 \times 1.732 = 48.496 m$$
Height of tower $$AB = BE + AE = 2 + 48.496$$
$$= 50.5$$ meter (approx)
Hence, height of tower is $$50.5 m$$ (approx)
A light house which faces the north, throws light beam in the shape of a fan from north-cart to north-west in the sky. On a ship a man that is going to west looks the light for the first time. When he is at $$8 km$$ distance from the light house and continuously looks it for $$15\sqrt{2}$$ minutes then find out the speed of the ship in km/h.
$$O$$ is a light house which faces north. when ship reaches pint $$A$$ then it looks light, where $$OA = 8 km$$. When the ship reaches at point $$B$$ after $$15\sqrt{2}$$ minutes, then it happens to see the light.
So, $$OB = OA = 8 km$$
From right angled $$\Delta BCO$$.
$$\sin45^{0} =\frac{BC}{BO}=\frac{1}{\sqrt{2}}$$
$$\frac{BC}{8}=\frac{1}{\sqrt{2}}$$
$$BC=\frac{8}{\sqrt{2}}=4\sqrt{2}$$
$$=8\sqrt{2}km$$
Speed = Distance / Speed $$=\frac{8\sqrt{2}}{15\sqrt{2}}km/min$$
$$=\frac{8}{15}*60km/h$$
$$=32km/h$$
Hence, speed of aeroplane $$= 30 km/h$$
So, $$OB = OA = 8 km$$
From right angled $$\Delta BCO$$.
$$\sin45^{0} =\frac{BC}{BO}=\frac{1}{\sqrt{2}}$$
$$\frac{BC}{8}=\frac{1}{\sqrt{2}}$$
$$BC=\frac{8}{\sqrt{2}}=4\sqrt{2}$$
$$=8\sqrt{2}km$$
Speed = Distance / Speed $$=\frac{8\sqrt{2}}{15\sqrt{2}}km/min$$
$$=\frac{8}{15}*60km/h$$
$$=32km/h$$
Hence, speed of aeroplane $$= 30 km/h$$
The distance of a point from the top of a tower is $$40\ m$$ which is horizontally at the same level with the foot of the tower at a distance of $$20\ m$$. Find out the angle of elevation of the top of the tower from that point. Find out the height of the tower.
Let height of tower $$AB = h\ m$$.
Form right angled $$\Delta ABC$$,
$$\cos \theta =\dfrac{BC}{AC}$$
$$\Rightarrow \cos\theta=\dfrac{20}{40}$$
Let angle of elevation is $$\theta$$
$$AC=40\ m$$ and $$BC=20\ m$$
Form right angled $$\Delta ABC$$,
$$\cos \theta =\dfrac{BC}{AC}$$
$$\Rightarrow \cos\theta=\dfrac{20}{40}$$
$$\Rightarrow \cos\theta=\dfrac{1}{2}$$
$$\Rightarrow \cos\theta=\cos60^{\circ}$$
$$\Rightarrow \theta=60^{\circ}$$
Again from right angled $$\Delta ABC$$,
$$\tan \theta =\dfrac{AB}{BC}$$
$$\Rightarrow \tan 60^{0} =\dfrac{h}{20}$$
$$\Rightarrow \sqrt{3} =\dfrac{h}{20}$$
$$\Rightarrow h = 20\sqrt{3} $$
Hence, the angle of elevation of the top of tower is $$60^{\circ}$$ and height of the tower is $$ 20\sqrt{3} \ m$$.
Again from right angled $$\Delta ABC$$,
$$\tan \theta =\dfrac{AB}{BC}$$
$$\Rightarrow \tan 60^{0} =\dfrac{h}{20}$$
$$\Rightarrow \sqrt{3} =\dfrac{h}{20}$$
$$\Rightarrow h = 20\sqrt{3} $$
Hence, the angle of elevation of the top of tower is $$60^{\circ}$$ and height of the tower is $$ 20\sqrt{3} \ m$$.
The angle of depression of two consecutive stones from a aeroplane are $$\alpha$$ and $$\beta$$. Prove that height of aeroplane is
$$\frac{1}{\cot\alpha+\cot\beta}$$
Let two km stones are $$B$$ and $$C$$ for which distance between them $$1 km$$ i.e. $$BC = 1 km$$.
The angle of depression of $$B$$ and $$C$$ from $$A$$ are $$\alpha$$ and $$\beta$$ and plane is at h height from ground. So $$AD = h$$.
Let $$BD=x$$, then $$DC=(1-x)$$
$$\because \angle ABD=\alpha.\angle ACD=\beta$$
From right angled $$\Delta ADB$$,
$$\tan\alpha=\frac{AD}{BD}=\frac{h}{x}$$
$$x=\frac{h}{\tan\alpha}$$.............(i)
from right angled $$\Delta ADC$$,
$$\tan \beta=\frac{AD}{CD}$$
$$\tan \beta=\frac{h}{1-x}$$
$$1-x=\frac{h}{\tan\beta}$$............(ii)
Adding equation (i) and (ii)
$$x+(1-x)=\frac{h}{\tan\alpha}+\frac{h}{\tan\beta}$$
$$1=h[\frac{1}{\tan\alpha}+\frac{1}{\tan\beta}]$$
$$1=h[\cot\alpha\cot\beta]$$
$$h=\frac{1}{\cot\alpha+\cot\beta}$$
The angle of depression of $$B$$ and $$C$$ from $$A$$ are $$\alpha$$ and $$\beta$$ and plane is at h height from ground. So $$AD = h$$.
Let $$BD=x$$, then $$DC=(1-x)$$
$$\because \angle ABD=\alpha.\angle ACD=\beta$$
From right angled $$\Delta ADB$$,
$$\tan\alpha=\frac{AD}{BD}=\frac{h}{x}$$
$$x=\frac{h}{\tan\alpha}$$.............(i)
from right angled $$\Delta ADC$$,
$$\tan \beta=\frac{AD}{CD}$$
$$\tan \beta=\frac{h}{1-x}$$
$$1-x=\frac{h}{\tan\beta}$$............(ii)
Adding equation (i) and (ii)
$$x+(1-x)=\frac{h}{\tan\alpha}+\frac{h}{\tan\beta}$$
$$1=h[\frac{1}{\tan\alpha}+\frac{1}{\tan\beta}]$$
$$1=h[\cot\alpha\cot\beta]$$
$$h=\frac{1}{\cot\alpha+\cot\beta}$$
An aeroplane flying at $$1500 \text{ m}$$ height from the earth has an angle of elevation $$60^{\circ}$$ from the airport. Find out the horizontal distance of the aeroplane from the airport.
Let horizontal distance of aeroplane from airport be $$OQ = x$$.
Height of aeroplane $$QP = 1500 \text{ m}$$ and angle of elevation of aeroplane from airport = $$60^{\circ}$$
$$\implies \angle POQ=60^{0}$$
From right angled $$\Delta OQP$$
$$\tan60^{\circ}=\dfrac{PQ}{OQ}$$
$$\implies \sqrt{3}=\dfrac{1500}{x}$$
$$\implies x=\dfrac{1500}{\sqrt{3}}$$
From right angled $$\Delta OQP$$
$$\tan60^{\circ}=\dfrac{PQ}{OQ}$$
$$\implies \sqrt{3}=\dfrac{1500}{x}$$
$$\implies x=\dfrac{1500}{\sqrt{3}}$$
$$\implies x=\dfrac{1500}{\sqrt 3} \times \dfrac{\sqrt 3}{\sqrt 3}$$ ( on rationalisation )
$$x=500 \sqrt 3 \text{ m}$$
Hence, the horizontal distance of the plane from the airport $$=500 \sqrt 3 \text{ m}$$.
$$x=500 \sqrt 3 \text{ m}$$
Hence, the horizontal distance of the plane from the airport $$=500 \sqrt 3 \text{ m}$$.
A man looks from the top of tower that the angle of depression of a point of the earth is $$60^{0}$$. If the distance of the point is $$25 m$$ from the base of the tower, them find out the height of the tower.
$$AB$$ is a tower. The angle of depression of top of tower from point $$A$$ to point $$C$$ is $$60^{0}$$.
So $$\angle XAC = 60^{0}$$
$$\angle ACB = 60^{0}$$
From right angled $$\Delta ABC$$,
$$\tan 60^{0} =\frac{AB}{BC}$$
$$\sqrt{3}=\frac{AB}{25}$$
Hence, height of tower $$= 25\sqrt{3} m$$
So $$\angle XAC = 60^{0}$$
$$\angle ACB = 60^{0}$$
From right angled $$\Delta ABC$$,
$$\tan 60^{0} =\frac{AB}{BC}$$
$$\sqrt{3}=\frac{AB}{25}$$
Hence, height of tower $$= 25\sqrt{3} m$$
Anderi stands on level horizontal ground, $$294\ m $$ from the foot of a vertical tower which is $$55\ m $$ high.
Anderi walks a distance $$x$$ meters directly towards the tower.
The angle of elevation of the top of the tower is now $$24.8^{\circ}$$.
Calculate the value of $$x$$.
A round balloon of radius r subtends an angle $$\theta$$ at the eye of the observer, while angle of elevation of its center is $$\phi$$. Find the height of the center of the balloon.
Let center of balloon of radius $$r$$ of $$O$$ and $$A$$ is the position of observer. let $$AP$$ and $$AQ$$ are too tangents to the balloon.
$$OB = h$$ m
Balloon of radius $$r$$, subtends an angle $$\theta$$ and angle of elevation of its center is $$\phi$$.
Then
$$\angle PAQ = \theta$$
and $$\angle PAO = \angle QAO = \theta/2$$
$$OP = r$$ and $$\angle PAB = \phi$$
$$\angle APO = \angle AQO = 90^{0}$$
[$$because$$ Radius and tangents are perpendicular to each other]
From right angled $$\Delta OAB$$,
$$\sin \phi =\frac{OB}{AO}$$
$$\sin \phi =\frac{h}{AO}$$
$$h = AO \sin \phi$$ ….(i)
From right angled $$\Delta AOP$$,
$$\sin\frac{\theta}{2} =\frac{OP}{AO}$$
$$\sin\frac{\theta}{2} =\frac{r}{AO}$$
$$AO = r.cosec\frac{\theta}{2}$$ ……(ii)
Put the value of $$AO$$ in equation (i),
$$h = r.cosec\frac{\theta}{2} \sin \phi$$
Hence, height of the center of the balloon (h) = $$r. cosec\frac{\theta}{2} \sin \phi$$
$$OB = h$$ m
Balloon of radius $$r$$, subtends an angle $$\theta$$ and angle of elevation of its center is $$\phi$$.
Then
$$\angle PAQ = \theta$$
and $$\angle PAO = \angle QAO = \theta/2$$
$$OP = r$$ and $$\angle PAB = \phi$$
$$\angle APO = \angle AQO = 90^{0}$$
[$$because$$ Radius and tangents are perpendicular to each other]
From right angled $$\Delta OAB$$,
$$\sin \phi =\frac{OB}{AO}$$
$$\sin \phi =\frac{h}{AO}$$
$$h = AO \sin \phi$$ ….(i)
From right angled $$\Delta AOP$$,
$$\sin\frac{\theta}{2} =\frac{OP}{AO}$$
$$\sin\frac{\theta}{2} =\frac{r}{AO}$$
$$AO = r.cosec\frac{\theta}{2}$$ ……(ii)
Put the value of $$AO$$ in equation (i),
$$h = r.cosec\frac{\theta}{2} \sin \phi$$
Hence, height of the center of the balloon (h) = $$r. cosec\frac{\theta}{2} \sin \phi$$
A man observes the angle of elevation of the top of the tower to be $$45^0$$. He walks towards it in a horizontal line through its base. On covering $$20 $$m the angle of elevation changes to $$60^0$$. Find the height of the tower correct to $$2$$ significant figures.
Let $$AB$$ be the tower of height $$h\,m$$. $$P$$ and $$Q$$ are the two observing points, such that $$\angle APB=45^0,\angle AQB=60^0,PQ=20m$$
In right-angled $$\Delta QBA$$ (Refer image)
$$\dfrac{AB}{QB}=\tan 60^0$$
$$\dfrac{h}{QB}=\sqrt{3}\Rightarrow QB=\dfrac{h}{\sqrt{3}}$$
In right-angled $$\Delta QBA$$
$$\dfrac{AB}{PB}=\tan 45^0$$
$$\dfrac{h}{PQ+QB}=1$$
$$\Rightarrow h=20+\dfrac{h}{\sqrt{3}}=h(\dfrac{\sqrt{3}-1}{\sqrt{3}})=20$$
$$\Rightarrow h=\dfrac{20\sqrt{3}}{\sqrt{3-1}}\times \dfrac{\sqrt{3+1}}{\sqrt{3+1}}=\dfrac{20(3+\sqrt{3})}{2}=10(3+1.73)=47.3$$
In right-angled $$\Delta QBA$$ (Refer image)
$$\dfrac{AB}{QB}=\tan 60^0$$
$$\dfrac{h}{QB}=\sqrt{3}\Rightarrow QB=\dfrac{h}{\sqrt{3}}$$
In right-angled $$\Delta QBA$$
$$\dfrac{AB}{PB}=\tan 45^0$$
$$\dfrac{h}{PQ+QB}=1$$
$$\Rightarrow h=20+\dfrac{h}{\sqrt{3}}=h(\dfrac{\sqrt{3}-1}{\sqrt{3}})=20$$
$$\Rightarrow h=\dfrac{20\sqrt{3}}{\sqrt{3-1}}\times \dfrac{\sqrt{3+1}}{\sqrt{3+1}}=\dfrac{20(3+\sqrt{3})}{2}=10(3+1.73)=47.3$$
Hence, the height of the tower is $$47.3m$$
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60$$^{\circ}$$. What is the height of the tree?
Given that, an observer at a distance of $$12\ m$$ from a tree looks at the top of the tree, the angle of elevation is $$60^o$$.
To find out: The height of the tree.
Based on the given information, we can draw the figure shown above.
Let the height of the tree be $$h\ m$$.
We know that, $$\tan \theta=\dfrac{\text{Opposite Side}}{\text{Adjacent Side}}$$
$$\therefore \ In\ \Delta ABC$$,
$$\tan 60^o=\dfrac{h}{12}\\$$
We know that, $$\tan 60^o=\sqrt3$$
$$\therefore \ \sqrt3=\dfrac{h}{12}\\$$
$$\Rightarrow \ h=12\sqrt3$$
Hence, the height of the tree is $$12\sqrt3\ m$$.
Anderi stands on level horizontal ground, $$294\ m $$ from the foot of a vertical tower which is $$55\ m $$ high.
Calculate the angle of elevation of the top of the tower.
A ladder is placed in such a way that its foot is at a distance of $$7 \ m$$ from the wall. If its other end reaches a window, a height of $$24 \ m$$, then find the length of the ladder.
In $$\triangle ABC$$,
$$AC^2 = AB^2 + BC^2$$
(Using Baudhayan theorem)
$$AC^2 = (24)^2 + (7)^2$$
$$= 576 + 49 = 625$$
$$\implies AC= 25 \ m$$
$$AC^2 = AB^2 + BC^2$$
(Using Baudhayan theorem)
$$AC^2 = (24)^2 + (7)^2$$
$$= 576 + 49 = 625$$
$$\implies AC= 25 \ m$$
An aeroplane flying horizontally at height of $$2500\sqrt{3} $$ mts above that ground; is observed to be at angle of elevation $$60^{\circ}$$ from the ground. After a flight of $$25$$ seconds the angle of elevation is $$30^{\circ} $$. Find the speed of the plane in m/sec.
Let $$P$$ and $$Q$$ be the two positions of the aeroplane.
$$QB = 2500 \sqrt{3} $$ mts
Let the speed of the aeroplane be s m/sec.
$$ \tan 60^{\circ} = \dfrac{2500 \sqrt{3}}{x} $$
$$ \Rightarrow \dfrac{2500 \sqrt{3}}{x} = \sqrt{3} $$ $$ \therefore x = \dfrac{2500 \sqrt{3}}{\sqrt{3}} = 2500\ m $$
$$ \tan 30^{\circ} = \dfrac{2500 \sqrt{3}}{x + y} \Rightarrow \dfrac{2500 \sqrt{3}}{x + y} = \dfrac{1}{\sqrt{3}} \Rightarrow x + y = 2500 \sqrt{3} \times \sqrt{3} $$
$$ = 2500 \times 3 $$
$$ = 7500 \therefore\ y = 7500 - 2500 $$
$$ = 5000\ m $$
To travel $$5000\ m $$ the aeroplane takes $$25$$ seconds.
$$ \therefore $$ The speed of the plane $$ = \dfrac{5000}{25} = 200\ m/sec $$.
$$QB = 2500 \sqrt{3} $$ mts
Let the speed of the aeroplane be s m/sec.
$$ \tan 60^{\circ} = \dfrac{2500 \sqrt{3}}{x} $$
$$ \Rightarrow \dfrac{2500 \sqrt{3}}{x} = \sqrt{3} $$ $$ \therefore x = \dfrac{2500 \sqrt{3}}{\sqrt{3}} = 2500\ m $$
$$ \tan 30^{\circ} = \dfrac{2500 \sqrt{3}}{x + y} \Rightarrow \dfrac{2500 \sqrt{3}}{x + y} = \dfrac{1}{\sqrt{3}} \Rightarrow x + y = 2500 \sqrt{3} \times \sqrt{3} $$
$$ = 2500 \times 3 $$
$$ = 7500 \therefore\ y = 7500 - 2500 $$
$$ = 5000\ m $$
To travel $$5000\ m $$ the aeroplane takes $$25$$ seconds.
$$ \therefore $$ The speed of the plane $$ = \dfrac{5000}{25} = 200\ m/sec $$.
The angle of elevation of the top of a tower from two points distant $$s$$ and $$t$$ from its front are complementary. Prove that the height of the tower is $$ \sqrt{st} $$.
Let $$BC = s ; PC = t $$
Let the height of the tower be $$AB = h $$.
$$ \angle ABC = \theta $$ and $$ \angle APC = 90^{\circ} - \theta $$
($$ \because $$ the angle of elevation of the top of the tower from two points $$P$$ and $$B$$ are complementary)
In triangle $$ABC$$,
$$ \tan \theta = \dfrac{AC}{BC} = \dfrac{h}{s} $$ ............(i)
In triangle $$APC$$,
$$ \tan (90^{\circ} - \theta) = \dfrac{AC}{PC} = \dfrac{h}{t} $$
$$ \cot \theta = \dfrac{h}{t}$$ .........(ii)
Multiplying (i) and (ii)
$$ \tan \theta \times \cot \theta = \left (\dfrac{h}{s} \right ) \times \left (\dfrac{h}{t} \right ) $$
$$1 = \dfrac{h^2}{st} $$
$$h^{2} = st $$
$$h = \sqrt{st} $$
Hence, the height of the tower is $$ \sqrt{st} $$.
Let the height of the tower be $$AB = h $$.
$$ \angle ABC = \theta $$ and $$ \angle APC = 90^{\circ} - \theta $$
($$ \because $$ the angle of elevation of the top of the tower from two points $$P$$ and $$B$$ are complementary)
In triangle $$ABC$$,
$$ \tan \theta = \dfrac{AC}{BC} = \dfrac{h}{s} $$ ............(i)
In triangle $$APC$$,
$$ \tan (90^{\circ} - \theta) = \dfrac{AC}{PC} = \dfrac{h}{t} $$
$$ \cot \theta = \dfrac{h}{t}$$ .........(ii)
Multiplying (i) and (ii)
$$ \tan \theta \times \cot \theta = \left (\dfrac{h}{s} \right ) \times \left (\dfrac{h}{t} \right ) $$
$$1 = \dfrac{h^2}{st} $$
$$h^{2} = st $$
$$h = \sqrt{st} $$
Hence, the height of the tower is $$ \sqrt{st} $$.
The diagram shows the positions of three small islands G , H and J
The bearing of H from G is $$045^{\circ} $$
The bearing of J from G is $$126^{\circ} $$.
The bearing of J from H is $$164^{\circ} $$.
The distance HJ is $$63\ km$$.
Calculate the distance GJ.
A tower $$AB$$ stands on a horizontal plane. $$BC,\ BD$$ are its shadows at noon and $$6\ PM.$$ When the altitude of the sun is $$\tan^{-1}\left (\dfrac{45}{28}\right)$$ and $$45^o$$ respectively. It is given that $$BD$$ is $$17\ m$$ longer than $$BC,$$ then
It is given that $$BD$$ is $$17\ m$$ longer than $$BC$$ so,
$$BC=BD-17$$
$$\cfrac { AB }{ BD } =\tan { 45^o }$$
$$ \Rightarrow AB=BD\quad\quad\quad\dots (i)$$
Similarly in $$\triangle ABC,$$
$$\angle ABC =\tan ^{ -1 }{ \cfrac { 45 }{ 28 } } $$
$$\Rightarrow \tan { \angle ABC} =\cfrac { 45 }{ 28 } $$
Now,
$$\cfrac { AB }{ BC } =\tan { \angle ABC} $$
$$\Rightarrow \cfrac { AB }{ BD-17 } =\cfrac { 45 }{ 28 } $$
$$\Rightarrow \cfrac { AB }{ AB-17 } =\cfrac { 45 }{ 28 } $$ $$[$$From $$(i)]$$
$$\Rightarrow 28AB = 45AB-45\times17 $$
$$\Rightarrow -17AB=-45\times 17$$
$$\Rightarrow AB=45\ m$$
Therefore
$$BC=BD-17$$
$$BC=BD-17$$
$$=45-17$$
$$=28\ m$$
By using Pythagoras theorem in $$\triangle ABC$$ we get,
$$ AC=\sqrt { { AB }^{ 2 }+{ BC }^{ 2 } }$$
$$ =\sqrt { { 45 }^{ 2 }+{ 28 }^{ 2 } }$$
$$ =\sqrt { 2025+784 }$$
$$ =\sqrt { 2809 }$$
$$ =53\ m$$
By using Pythagoras theorem in $$\triangle ABD$$ we get,
$$ AD=\sqrt { { AB }^{ 2 }+{ BD }^{ 2 } }$$
$$ =\sqrt { 2{ AB }^{ 2 } } $$ $$[$$From $$(i)]$$
$$=45\sqrt { 2 } \ m$$
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is $$\displaystyle { 60 }^{ \circ }$$. From a point Y, $$40$$ m vertically above X, the angle of elevation of the top Q of tower is $$\displaystyle { 45 }^{ \circ }$$. Find the height of the tower PQ and the distance PX. (Use $$\displaystyle \sqrt { 3 } =1.73$$)
In $$\Delta YRQ$$, we have
$$tan 45^o =\dfrac{QR}{YR}$$
$$1=\dfrac{x}{YR}$$
$$YR = x$$ or $$XP = x$$ [because $$YR = XP$$] ---- (1)
Now In $$\Delta XPQ$$ we have
$$tan 60^o = \dfrac{PQ}{PX}$$
$$\sqrt{3}=\dfrac{x+40}{x}$$ (from equation 1)
$$x(\sqrt{3}-1)=40$$
$$x=\dfrac{40}{\sqrt{3}-1}$$
$$x = \dfrac{40}{1.73-1}=54.79$$ m
So, height of the tower, $$PQ = x + 40 = 54.79 + 40 = 94.79$$ m.
Distance $$PX = 54.79$$ m.
Find the value of '$$x$$'
The angles of elevation of the top of a cliff as seen from the top and bottom of a building are $${45}^{\circ}$$ and $${60}^{\circ}$$ respectively. If the height of the building is $$24 \text{ m}$$, find the height of the cliff.
Let $$x$$ be the total height of the cliff. Therefore, the height of the cliff above the building is $$(x-24)$$ and let $$y$$ be the distance from the base of the building to the base of the cliff.
From the above adjoining figure, $$DE=BC=y$$.
We know that $$\tan { \theta } =\dfrac { \text{Opposite side} }{ \text{Adjacent side }} =\dfrac { AB }{ BC }$$
In $$\triangle ABC,$$ $$\angle B={ 90 }^{ 0 }$$ and $$\angle BCA={ 60 }^{ 0 }$$.
Here, $$\theta ={ 60 }^{ 0 }$$, $$BC=y \text{ m}$$ and $$AB=x\text{ m}$$, therefore,
$$\tan { \theta } =\dfrac { AB }{ BC } \\ \Rightarrow \tan { 60^{ 0 } } =\dfrac { x }{ y } \\ \Rightarrow \sqrt { 3 } =\dfrac { x }{ y } \quad \quad \quad \quad \quad \quad \left( \because \quad \tan { 60^{ 0 } } =\sqrt { 3 } \right) \quad \quad \quad \quad \quad \quad \\ \Rightarrow x=\sqrt { 3 } y\quad ...........(1)$$
Also, in $$\triangle AED,$$ $$\angle E={ 90 }^{ 0 }$$ and $$\angle D={ 45 }^{ 0 }$$.
Here, $$\theta ={ 45 }^{ 0 }$$, $$AE=(x-24)\text{ m}$$ and $$EC=y\text{ m}$$, therefore,
$$\tan { \theta } =\dfrac { AE }{ EC } \\ \Rightarrow \tan { 45^{ 0 } } =\dfrac { x }{ y } \\ \Rightarrow 1=\dfrac { x-24 }{ y } \quad \quad \quad \quad \quad \quad \left( \because \quad \tan { 45^{ 0 } } =1 \right) \quad \quad \quad \quad \quad \quad \\ \Rightarrow y=x-24\quad ...........(2)$$
Substitute the value of equation $$(1)$$ in equation $$(2)$$, we get
$$y=\sqrt { 3 } y-24\\ \Rightarrow y-\sqrt { 3 } y=24\\ \Rightarrow y(\sqrt { 3 } -1)=24\\ \Rightarrow y=\dfrac { 24 }{ \sqrt { 3 } -1 }$$
Now, substitute the value of $$y$$ in equation $$(1)$$:
$$x=\sqrt { 3 } \left( \dfrac { 24 }{ \sqrt { 3 } -1 } \right) \\ \Rightarrow x=\dfrac { 24\sqrt { 3 } }{ \sqrt { 3 } -1 }$$
Hence, the height of the cliff is $$\dfrac { 24\sqrt { 3 } }{ \sqrt { 3 } -1 }\text{ m}$$
A tall building casts a shadow of $$300 m$$ long when the sun's altitude (elevation) is $${30}^{o}$$. Find the height of the tower.
Let $$\triangle ABC$$ be a right angled triangle where $$\angle B={ 90 }^{ 0 }$$ and $$\angle C={ 30 }^{ 0 }$$ as shown in the above figure.
Let $$x$$ be the height of the tower.
We know that $$\tan { \theta } =\dfrac { Opposite\quad side }{ Adjacent\quad side } =\dfrac { AB }{ BC }$$
Here, $$\theta ={ 30 }^{ 0 }$$, $$BC=300$$ m and $$AB=x$$ m, therefore,
$$\tan { \theta } =\dfrac { AB }{ BC } \\ \Rightarrow \tan { 30^{ 0 } } =\dfrac { x }{ 300 } \\ \Rightarrow \dfrac { 1 }{ \sqrt { 3 } } =\dfrac { x }{ 300 } \quad \quad \quad \quad \quad \quad \left( \because \quad \tan { 30^{ 0 } } =\dfrac { 1 }{ \sqrt { 3 } } \right) \quad \quad \quad \quad \quad \quad \\ \Rightarrow \sqrt { 3 } x=300\\ \Rightarrow x=\dfrac { 300 }{ \sqrt { 3 } } \\ \Rightarrow x=\dfrac { 300\times \sqrt { 3 } }{ \sqrt { 3 } \times \sqrt { 3 } } =\dfrac { 300\times \sqrt { 3 } }{ 3 } =100\sqrt { 3 }$$
Hence, the height of the tower is $$100\sqrt { 3 }$$ m.
From the top of the lighthouse of height $$200$$ m, the lighthouse keeper observes a Yacht and a Barge along the same line of sight. The angles of depression for the Yacht and the Barge are $$45^{\circ}$$ and $$30^{\circ}$$ respectively. For safety purposes, the two sea vessels should be at least $$300$$ m apart. If they are less than $$300$$ m, the keeper has to sound the alarm. Does the keeper have to sound the alarm?
Let $$AB$$ be light house, $$C, D$$ represent Yacht and Barge.
$$AB = 200$$ m
$$AB = 200$$ m
Let $$BC = x$$
In $$\triangle ABC$$,
In $$\triangle ABC$$,
$$\tan 45^{\circ} = \dfrac {AB}{BC}$$
$$\Rightarrow 1 = \dfrac {200}{x}$$
$$\Rightarrow x = 200\ m$$
$$\Rightarrow 1 = \dfrac {200}{x}$$
$$\Rightarrow x = 200\ m$$
Let $$CD = y$$
In $$\triangle ABD$$,
$$\Rightarrow \tan 30^{\circ} = \dfrac {AB}{BD}$$
$$\Rightarrow \dfrac {1}{\sqrt {3}} = \dfrac {200}{x + y}$$
$$\Rightarrow \dfrac {1}{\sqrt {3}} = \dfrac {200}{200 +y}$$
$$\Rightarrow 200 + y = 200\sqrt {3}$$
$$\Rightarrow y = 200 \sqrt {3} - 200 = 200 (\sqrt {3} - 1)$$
$$= 200(1.732 - 1) = 200(0.732)$$
$$= 146.400$$ m $$
$$\Rightarrow \tan 30^{\circ} = \dfrac {AB}{BD}$$
$$\Rightarrow \dfrac {1}{\sqrt {3}} = \dfrac {200}{x + y}$$
$$\Rightarrow \dfrac {1}{\sqrt {3}} = \dfrac {200}{200 +y}$$
$$\Rightarrow 200 + y = 200\sqrt {3}$$
$$\Rightarrow y = 200 \sqrt {3} - 200 = 200 (\sqrt {3} - 1)$$
$$= 200(1.732 - 1) = 200(0.732)$$
$$= 146.400$$ m $$
Since $$146.4m < 300$$ m
Therefore, Yes, the keeper has to sound the alarm.
Therefore, Yes, the keeper has to sound the alarm.
From the top of a building $$16 m$$ high, the angular elevation of the top of a hill is $${60}^{o}$$ and the angular depression of the foot of the hill is $${30}^{o}$$. Find the height of the hill.
Let $$x$$ be the total height of the hill. Therefore, the height of the hill above the building is $$(x-16)$$ and let $$y$$ be the perpendicular distance from the top of the building to the hill.
We know that $$\tan { \theta } =\dfrac { Opposite\quad side }{ Adjacent\quad side } =\dfrac { BC }{ AB }$$
In $$\triangle ABC,$$ $$\angle B={ 90 }^{ 0 }$$ and $$\angle A={ 30 }^{ 0 }$$.
Here, $$\theta ={ 30 }^{ 0 }$$, $$BC=16$$ m and $$AB=y$$ m, therefore,
$$\tan { \theta } =\dfrac { BC }{ AB } \\ \Rightarrow \tan { 30^{ 0 } } =\dfrac { 16 }{ y } \\ \Rightarrow \dfrac { 1 }{ \sqrt { 3 } } =\dfrac { 16 }{ y } \quad \quad \quad \quad \quad \quad \left( \because \quad \tan { 30^{ 0 } } =\frac { 1 }{ \sqrt { 3 } } \right) \quad \quad \quad \quad \quad \quad \\ \Rightarrow y=16\sqrt { 3 } \quad ...........(1)$$
Also, in $$\triangle ABD,$$ $$\angle B={ 90 }^{ 0 }$$ and $$\angle A={ 60 }^{ 0 }$$.
Here, $$\theta ={ 60 }^{ 0 }$$, $$BD=(x-16)$$ m and $$AB=y$$ m, therefore,
$$\tan { \theta } =\dfrac { BD }{ AB } \\ \Rightarrow \tan { 60^{ 0 } } =\dfrac { x-16 }{ y } \\ \Rightarrow \sqrt { 3 } =\dfrac { x-16 }{ y } \quad \quad \quad \quad \quad \quad \left( \because \quad \tan { 60^{ 0 } } =\sqrt { 3 } \right) \quad \quad \quad \quad \quad \quad \\ \Rightarrow \sqrt { 3 } y=x-16\quad ...........(2)$$
Substitute the value of equation 1 in equation 2, we get
$$\sqrt { 3 } \times 16\sqrt { 3 } =x-16\\ \Rightarrow 3\times 16=x-16\\ \Rightarrow 48=x-16\\ \Rightarrow x=48+16=64$$
Hence, the height of the hill is $$64$$ m.
A tree is broken over by the wind forms a right angled triangle with the ground. If the broken part makes an angle of $${60}^{o}$$ with the ground and the top of the tree is now $$20 m$$ from its base, how tall was the tree?
Let $$\triangle ABC$$ be a right angled triangle where $$\angle B={ 90 }^{ 0 }$$ and $$\angle C={ 60 }^{ 0 }$$ as shown in the above figure.
Let $$x$$ be the length of remaining part of the tree and $$y$$ be the length of part of tree which is broken.
We know that $$\tan { \theta } =\dfrac { Opposite\quad side }{ Adjacent\quad side } =\dfrac { AB }{ BC }$$
Here, $$\theta ={ 60 }^{ 0 }$$, $$BC=20$$ m and $$AB=x$$ m, therefore,
$$\tan { \theta } =\dfrac { AB }{ BC } \\ \Rightarrow \tan { 60^{ 0 } } =\dfrac { x }{ 20 } \\ \Rightarrow \sqrt { 3 } =\dfrac { x }{ 20 } \quad \quad \quad \quad \quad \quad \left( \because \quad \tan { 60^{ 0 } } =\sqrt { 3 } \right) \quad \quad \quad \quad \quad \quad \\ \Rightarrow x=20\sqrt { 3 } \quad ...........(1)$$
We also know that $$\cos { \theta } =\dfrac { Adjacent\quad side }{ Hypotenuse } =\dfrac { BC }{ AC }$$
Here, $$\theta ={ 60 }^{ 0 }$$, $$BC=20$$ m and $$AC=y$$ m, therefore,
$$\cos { \theta } =\dfrac { BC }{ AC } \\ \Rightarrow \cos { 60^{ 0 } } =\dfrac { 20 }{ y } \\ \Rightarrow \dfrac { 1 }{ 2 } =\dfrac { 20 }{ y } \quad \quad \quad \quad \quad \quad \left( \because \quad \cos { 60^{ 0 } } =\dfrac { 1 }{ 2 } \right) \quad \quad \quad \quad \quad \quad \\ \Rightarrow y=20\times 2\\ \Rightarrow y=40\quad ...........(2)$$
Now, total length of the tree is $$x+y=20\sqrt {3}+40=20(\sqrt {3}+2)$$ m.
Hence, the length of the tree is $$20(\sqrt { 3 }+2)$$ m.
The angle of elevation of the top of a flag post from a point on a horizontal ground is found to be $${30}^{o}$$. On walking $$6 m$$ towards the post, the elevation increased by $${15}^{o}$$. Find the height of the flag post.
Let $$y$$ be the height of the flag post and $$x$$ be the initial distance from flag post.
Now, after travelling $$6$$ m towards the post the distance from the base of pole is $$(x-6)$$ m.
We know that $$\tan { \theta } =\dfrac { Opposite\quad side }{ Adjacent\quad side } =\dfrac { AB }{ BC }$$
In $$\triangle ABC,$$ $$\angle B={ 90 }^{ 0 }$$ and $$\angle C={ 30 }^{ 0 }$$.
Here, $$\theta ={ 30 }^{ 0 }$$, $$BC=x$$ m and $$AB=y$$ m, therefore,
$$\tan { \theta } =\dfrac { AB }{ BC } \\ \Rightarrow \tan { 30^{ 0 } } =\dfrac { y }{ x } \\ \Rightarrow \dfrac { 1 }{ \sqrt { 3 } } =\dfrac { y }{ x } \quad \quad \quad \quad \quad \quad \left( \because \quad \tan { 30^{ 0 } } =\dfrac { 1 }{ \sqrt { 3 } } \right) \quad \quad \quad \quad \quad \quad \\ \Rightarrow x=\sqrt { 3 } y\quad ...........(1)$$
Also, in $$\triangle ABD,$$ $$\angle B={ 90 }^{ 0 }$$ and $$\angle D={ 45 }^{ 0 }$$.
Here, $$\theta ={ 45 }^{ 0 }$$, $$BD=(x-6)$$ m and $$AB=y$$ m, therefore,
$$\tan { \theta } =\dfrac { AB }{ BD } \\ \Rightarrow \tan { 45^{ 0 } } =\dfrac { y }{ x-6 } \\ \Rightarrow 1=\dfrac { y }{ x-6 } \quad \quad \quad \quad \quad \quad \left( \because \quad \tan { 45^{ 0 } } =1 \right) \quad \quad \quad \quad \quad \quad \\ \Rightarrow x-6=y\quad \\ \Rightarrow x=y+6\quad ...........(2)$$
Comparing equations 1 and 2, we get
$$\sqrt { 3 } y=y+6\\ \Rightarrow \sqrt { 3 } y-y=6\\ \Rightarrow y(\sqrt { 3 } -1)=6\\ \Rightarrow y=\dfrac { 6 }{ \sqrt { 3 } -1 }$$
Hence, the height of the flag post is $$\dfrac { 6 }{ \sqrt { 3 } -1 }$$ m.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground by making $${30}^{\circ}$$ angle with the ground. The distance between the foot of the tree and the top of the tree on the ground is $$6\ m$$. Find the height of the tree before falling down.
$$\textbf{Step -1 : Try to draw the diagram for the following problem}$$
$$\text{Height of tree before falling down = AB + AC}$$
$$\textbf{Step -2 : Finding the actual height of the tree.}$$
$$\mathrm{In\ \triangle ABC,}$$
$$\Rightarrow \tan30^\circ=\dfrac{AB}{BC}$$
$$\Rightarrow \dfrac{1}{\sqrt3}=\dfrac{AB}{6}$$
$$\Rightarrow AB=\dfrac{6}{\sqrt3}$$
$$\Rightarrow AB=2\sqrt3$$
$$\mathrm{Again\ in\ \triangle ABC,}$$
$$\Rightarrow \cos30^\circ=\dfrac{BC}{AC}$$
$$\Rightarrow \dfrac{\sqrt3}{2}=\dfrac{6}{AC}$$
$$\Rightarrow AC=\dfrac{12}{\sqrt3}$$
$$\Rightarrow AC=4\sqrt3$$
$$\text{Now, AB+AC}=(2\sqrt3+4\sqrt3)\ m$$
$$=6\sqrt3\ m$$
$$=10.39\ m$$
$$\textbf{Hence, the height of the tree before falling down was 10.39 m.}$$
A person in a helicopter flying at a height of $$700$$ m, observes two objects lying opposite to each other on either bank of a river. The angles of depression of the objects are $$30^o$$ and $$45^o$$; find the width of the river. $$($$ $$\sqrt 3$$ $$= 1.732$$ $$)$$
Let $$C$$ be the position of a person in a helicopter. $$A, B$$ be two objects lying opposite to each other on either bank of a river.
Let $$AD = x, BD = y$$
In $$\Delta ACD$$,
$$\Rightarrow \tan 30^o = \dfrac{CD}{AD}$$
$$\Rightarrow \dfrac{1}{\sqrt 3} = \dfrac{700}{x}$$
$$\Rightarrow x = 700 \sqrt 3$$
In $$\Delta BCD$$,
Let $$AD = x, BD = y$$
In $$\Delta ACD$$,
$$\Rightarrow \tan 30^o = \dfrac{CD}{AD}$$
$$\Rightarrow \dfrac{1}{\sqrt 3} = \dfrac{700}{x}$$
$$\Rightarrow x = 700 \sqrt 3$$
In $$\Delta BCD$$,
$$\tan 45^{\circ}=\dfrac{CD}{BD}$$
$$\implies BD=CD$$
$$\implies BD=y=700$$
$$\therefore$$ the width of the river $$= x + y$$
$$\implies 700\sqrt 3+ 700 \text{ m}$$
$$\therefore$$ the width of the river $$= x + y$$
$$\implies 700\sqrt 3+ 700 \text{ m}$$
Hari, standing on the top of a building, sees the top of a tower at an angle of elevation of $$50^{\circ}$$ and the foot of the tower at an angle of depression of $$20^{\circ}$$. Height of Hari is $$1.6$$ metre and height of the building on which he is standing is $$9.2$$ metre.
(a) Draw a rough sketch according to the given information.
(b) How far is the tower from the building?
(c) Calculate the height of the tower.
$$\sin 20^{\circ} = 0.34, \cos 20^{\circ} = 0.94, \tan 20^{\circ} = 0.36$$,
$$\sin 50^{\circ} = 0.77, \cos 50^{\circ} = 0.64, \tan 50^{\circ} = 1.19$$.
(a)
(b)
The distance between the tower and the building is $$BC = DE = FG$$
Consider $$\triangle BCG$$:
$$\tan 20^{\circ} = \dfrac {CG}{BC}\Rightarrow BC = \dfrac {CG}{\tan 20^{\circ}}$$
$$\Rightarrow BC = \dfrac {CE + EG}{0.36} = \dfrac {1.6 + 9.2}{0.36} = 30\ \text{m}$$
(c) The height of the tower is $$AG = AC + CE + EG = AC + 1.6 + 9.2 = AC + 10.8$$
Consider $$\triangle ABC$$, let $$AC = h$$
$$\tan 50^{\circ} = \dfrac {AC}{BC}$$
$$\Rightarrow 1.19 = \dfrac {h}{30}$$
$$\Rightarrow h = 35.7\ \text{m}$$
Thus, total height of the tower $$= 35.7 + 10.8 = 46.5\ \text{m}$$
The rough sketch is as follows:
Hari is standing at $$D$$ and his height is $$1.6\ \text{m}$$.
Height of the building is $$DF = 9.2\ \text{m}$$.
The angle of elevation of the top of the tower is $$50^{\circ}$$ and the angle of depression of the foot of the tower is $$20^{\circ}$$.
Hari is standing at $$D$$ and his height is $$1.6\ \text{m}$$.
Height of the building is $$DF = 9.2\ \text{m}$$.
The angle of elevation of the top of the tower is $$50^{\circ}$$ and the angle of depression of the foot of the tower is $$20^{\circ}$$.
(b)
The distance between the tower and the building is $$BC = DE = FG$$
Consider $$\triangle BCG$$:
$$\tan 20^{\circ} = \dfrac {CG}{BC}\Rightarrow BC = \dfrac {CG}{\tan 20^{\circ}}$$
$$\Rightarrow BC = \dfrac {CE + EG}{0.36} = \dfrac {1.6 + 9.2}{0.36} = 30\ \text{m}$$
(c) The height of the tower is $$AG = AC + CE + EG = AC + 1.6 + 9.2 = AC + 10.8$$
Consider $$\triangle ABC$$, let $$AC = h$$
$$\tan 50^{\circ} = \dfrac {AC}{BC}$$
$$\Rightarrow 1.19 = \dfrac {h}{30}$$
$$\Rightarrow h = 35.7\ \text{m}$$
Thus, total height of the tower $$= 35.7 + 10.8 = 46.5\ \text{m}$$
A boy, 1.4 metres tall standing at the edge of a river bank sees the top of a tree on the edge of the other bank at an elevation of 55$$^o$$. Standing back by 3 metres, he sees it at an elevation of 45$$^o$$.
(a) Draw a rough figure showing these facts.
(b) How wide is the river and how tall is the tree?
$$[\sin 55^o = 0.8192, \cos 55^o = 0.5736, \tan 55^o = 1.4281]$$
The rough sketch is as follows
BF represents the tree, DG is the first position of the boy and AE is the new position.
CD represents the river.
We have : AE = DG
Let DC = x, then EC = (x + 3) m.
$$tan 45^o = \dfrac{CF}{EC}$$
$$\Rightarrow 1 = \dfrac{CF}{x + 3}$$
$$\Rightarrow CF = x + 3$$ ...... (i)
$$tan 55^o = \dfrac{CF}{DC}$$
$$\Rightarrow 1.4281 = \dfrac{CF}{x}$$
$$\Rightarrow CF = 1.4281 \times x$$ ..... (ii)
From (i) and (ii), we have
$$1.4281 x = x + 3$$
$$0.4281 x = 3 \Rightarrow x = \dfrac{3}{0.4281} \sim 7 m$$
Width of the river = CD = 7 m
Height of the tree = BF = BC = CF = (1.4 + 7 + 3)m = 11.4 m
BF represents the tree, DG is the first position of the boy and AE is the new position.
CD represents the river.
We have : AE = DG
Let DC = x, then EC = (x + 3) m.
$$tan 45^o = \dfrac{CF}{EC}$$
$$\Rightarrow 1 = \dfrac{CF}{x + 3}$$
$$\Rightarrow CF = x + 3$$ ...... (i)
$$tan 55^o = \dfrac{CF}{DC}$$
$$\Rightarrow 1.4281 = \dfrac{CF}{x}$$
$$\Rightarrow CF = 1.4281 \times x$$ ..... (ii)
From (i) and (ii), we have
$$1.4281 x = x + 3$$
$$0.4281 x = 3 \Rightarrow x = \dfrac{3}{0.4281} \sim 7 m$$
Width of the river = CD = 7 m
Height of the tree = BF = BC = CF = (1.4 + 7 + 3)m = 11.4 m
Gopi and Gautham stand on opposite sides of a tower. The children and the tower are on a straight line also. Gopi sees the top of the tower at an angle of elevation of $$36^o$$ and Gautham sees it at an angle of elevation of $$52^o$$. The distance between thechildren is 60 metres.
a) Draw a rough figure according to the given information.
b) Find the height of the tower. (Height of children can be neglected. Necessary values can be taken from the following table).
| Angle | sin | cos | tan |
| $$36^o$$ | 0.59 | 0.81 | 0.72 |
| $$52^o$$ | 0.79 | 0.62 | 1.28 |
(b) Let AB be the height of the tower.
Let C and D be the point at which Gopi and Gautam are standing respectively.
Let BD = x m
CB = 60-x m
$$\tan 36^o=\dfrac{AB}{CB}$$
$$0.72=\dfrac{AB}{60-x}$$
$$AB=43.2-0.72x$$ ....... (1)
$$\tan 52^o=\dfrac{AB}{BD}$$
$$1.28=\dfrac{AB}{x}$$
$$AB=1.28x$$ ....... (2)
From (1) and (2) we get
$$1.28x = 43.2 - 0.72x$$
$$2x = 43.2$$
$$x = 21.6 m$$
$$AB = 1.28x =1.28\times 21.6 = 27.648 cm$$
Therefore height of the tower is $$27.648 cm$$
Let C and D be the point at which Gopi and Gautam are standing respectively.
Let BD = x m
CB = 60-x m
$$\tan 36^o=\dfrac{AB}{CB}$$
$$0.72=\dfrac{AB}{60-x}$$
$$AB=43.2-0.72x$$ ....... (1)
$$\tan 52^o=\dfrac{AB}{BD}$$
$$1.28=\dfrac{AB}{x}$$
$$AB=1.28x$$ ....... (2)
From (1) and (2) we get
$$1.28x = 43.2 - 0.72x$$
$$2x = 43.2$$
$$x = 21.6 m$$
$$AB = 1.28x =1.28\times 21.6 = 27.648 cm$$
Therefore height of the tower is $$27.648 cm$$
A person standing by the side of a road observes a row of equidistant telephone poles of equal height. Neglecting the height of the person's eye, the tenth and seventeenth poles subtend the same angles that they would do if they were in the position of the first pole and were respectively 1/2 and 1/3 of their height. Find, correct to one place of decimal, the secant of the angle between the base line of the poles and the line drawn from the person's eye to the base of the first pole.
Subject to correction if any.
This is a difficult question as it is not simple to understand its language. A
is a person on one side of road and Q, R, S are respectively the 1st, 10th, and
17th poles of height h standing on other side of the road each pole being at
equal distances of d so that QR = 9d and QS = 16d. Let $$\alpha,
\beta$$ be the angles subtended by the 10th and 17th pole at A.
$$\theta$$ is the angle between the base line PQRS of the poles and the
line AQ drawn from the person's eye to the base of the first pole. Now from
ground right angled triangles APQ, APR and APS, we have
$$AQ^2 = (x^2 + y^2) ,
AR^2 = (x^2 +(y + 9d)^2)$$,
$$AS^2 = x^2 + (y +
16d)^2$$
...(1)
10th Pole $$AR = h \cot
\alpha$$ ...(2)
Now consider 10th pole placed
at 1st pole's position but of height $$\dfrac{h}{2}$$.
$$\therefore AQ = \dfrac{h}{2}
\cot \alpha$$
$$\therefore 2AQ = h \cot
\alpha = Ar$$, by (2)
Similarly consider 17th pole
$$AS= h \cot \beta$$
...(3)
Now consider 17th pole placed
at 1st position but of height $$\dfrac{h}{3}$$.
$$AQ = \dfrac{h}{3} \cot
\beta$$
$$\therefore 3AQ = h \cot
\beta = AS$$, by (3)
...(4)
From (2) and (3), on squaring
$$4AQ^2 = AR^2$$ and $$9AQ^2
= AS^2$$
Putting the values from (1),
we have the equations
$$4(x^2 +y^2) = x^2 + y^2 +
18yd + 81d^2$$
$$9(x^2 +y^2) = x^2 + y^2 +
32yd + 256d^2$$
These two equations on
simplification reduce to
$$x^2 + y^2 = 6yd + 27d^2$$
and $$x^2 + y^2 = 4yd +
32d^2$$
Subtracting these, we get
$$5d^2 - 2yd =0$$ or $$d(5d
-2y)=0$$
$$\therefore d = \dfrac{2y}{5}$$
...(1)
Putting $$d = \dfrac{2y}{5}$$
in any, we get
$$x^2 = \dfrac{143}{25}
y^2$$ ...(2)
Hence from ground triangle
APQ.
$$\sec \theta = \dfrac{AQ}{PQ}
= \dfrac{\sqrt{x^2 + y^2}}{y}$$
$$= \sqrt{ \dfrac{x^2 +
y^2}{y^2}} = \sqrt{ \dfrac{x^2}{y^2} + 1} = \sqrt{\left( \dfrac{168}{25}
\right)}$$
$$= \dfrac{13}{5} = 2.6$$
approximately.
PQ is a vertical tower. P is the foot, Q the top of the tower. A, B, C are three points in the horizontal plane through P. The angles of elevation of Q from A, B, C are equal and each is equal to $$\theta$$. The sides of the triangle ABC are a, b, c and the area of the triangle ABC is $$\Delta$$. Find m if the height of the tower is $$\dfrac{(abc tan \theta)}{m\Delta}$$
There are two towers one on each bank of a river, just opposite to each other one tower is $$50m$$ high. From the top of this tower, the angles of depression of the top and foot of the other tower are $${30}^{o}$$ and $${60}^{o}$$ respectively. Find the width of the river and the height of the other tower.
Let $$AB$$ and $$CD$$ be the two tower and $$BC$$ be the width of the river. Then $$\angle ADE=30^\circ$$ and $$\angle ACB=60^\circ$$
Given: $$AB=50\ m$$
In $$\Delta ABC, tan\:60^\circ=\dfrac{AB}{BC}$$
$$\Rightarrow \sqrt{3}=\dfrac{50}{BC}$$
$$\Rightarrow BC=\dfrac{50}{\sqrt{3}}=28.867\:m$$
In $$\Delta AED, \tan\:30^\circ=\dfrac{AE}{ED}=\dfrac{AB-BE}{BC}=\dfrac{AB-DC}{BC}$$
$$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{50-DC}{\dfrac{50}{\sqrt{3}}}$$
$$\Rightarrow \dfrac{50}{3}=50-DC$$
$$\Rightarrow DC=50-\dfrac{50}{3}=\dfrac{100}{3}=33.33\ m$$
Hence the width of the river is $$28.867\:m$$ and height of the other tower is $$33.33\ m$$
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is $$60^o$$. When he moves 40 m away from the bank, he finds the angle of elevation to be $$30^o$$. Find the height of the tree and the width of the river. ($$\sqrt{3} = 1.73$$)
Let the height of the tree be $$'h'$$ meters and width of the river be $$ 'x' $$ meters.
In $$\triangle ABC,$$
$$\Rightarrow \tan { 60° } =\dfrac { AB }{ AC } =\dfrac { h }{ x } $$
$$\Rightarrow \sqrt { 3 } =\dfrac { h }{ x } $$
$$\Rightarrow h=\sqrt { 3 } x\rightarrow \left( 1 \right) $$
In $$\triangle ABD,$$
$$\Rightarrow \tan { 30° } =\dfrac { AB }{ AD } =\dfrac { h }{ x+40 } $$
$$\Rightarrow \dfrac { 1 }{ \sqrt { 3 } } =\dfrac { h }{ x+40 } $$
$$\Rightarrow \sqrt { 3 } h=\left( x+40 \right) \rightarrow \left( 2 \right) $$
From $$\left( 1 \right)\; \&\;\left( 2 \right),$$ we get
$$\Rightarrow \sqrt { 3 } \left( \sqrt { 3 } x \right) =x+40$$
$$\Rightarrow 3x-x=40$$
$$\Rightarrow 2x=40$$
$$\Rightarrow x=20m$$
$$\therefore h=\sqrt{3}x$$
$$=20 \times 1.73$$
$$=34.60m$$
Hence, the answer is $$34.60m, 20m$$
If the angle of elevation of a cloud from a point $$h$$ metres above a lake is $$\alpha$$ and the angle of depression of its reflection in the lake be $$\beta$$, prove that the distance of the cloud from the point of observation is $$\dfrac { 2h\sec { \alpha } }{ \tan { \beta -\tan { \alpha } } }$$
Let $$A$$ be a point $$h\,m$$ above the lake $$AF$$ and $$B$$ be the position of the cloud.
Draw a line parallel to $$EF$$ from $$A$$ on $$BD$$ at $$C$$.
But, $$BF = DF$$
Let, $$BC = m$$
so, $$BF = (m + h)$$
$$\Rightarrow$$ $$BF = DF = (m + h)\,m$$
Consider $$\triangle BAC$$, $$\sin\alpha=\dfrac{BC}{AB}$$
$$\Rightarrow$$ $$\sin\alpha=\dfrac{m}{AB}$$
$$\therefore$$ $$AB = m\,cosec\,\alpha$$ ---------- (1)
and, $$AC = m\,\cot\,\alpha$$
Consider $$\triangle ACD,$$ $$\tan\,\beta=\dfrac{CD}{AC}$$
$$\Rightarrow$$ $$\tan\,\beta=\dfrac{2h+m}{AC}$$
$$AC = (2h + m) \cot\beta$$
Therefore, $$m\,\cot\,\alpha = (2h + m)\cot\,\beta$$
Substituting the value of m in (1) we get,
$$\Rightarrow$$ $$AB = cosec\alpha [2h \cot \beta/ (\cot \alpha - \cot \beta)]$$
$$\Rightarrow$$ $$AB=\dfrac{2h\sec\alpha}{\tan\beta-\tan\alpha}$$
A man standing South of a lamp post observes his shadow on the horizontal plane to be 24 feel long. On walking Eastwards 300 feet, he finds his shadow as 30 feet. If his height is 6 ft., obtain the height of the lamp above the plane.
PQ = h is the lamp post; AL the man due South of it and of height 6 ft. and AC = 24 ft. is the length of the shadow. After walking 300 ft. Eastwards he comes to B and now the length of shadow is BD =30 ft.
Now let AP = x and BP = y, AC = 24, BD = 30.
From $$\Delta 's$$ QPC and LAC
We have $$\dfrac{h}{6} = \dfrac{24 + x}{24} \,\,\, \therefore x = 4(h - 6)$$ ...(1)
Similarly from $$\Delta^s$$ QPD and MBD
$$\dfrac{h}{6} = \dfrac{y+30}{30} \,\,\,\,\, \therefore y = 5(h - 6)$$ ...(2)
From (1) and (2), we get
$$h = \dfrac{24+x}{4} = \dfrac{y+30}{5}$$ $$\therefore y = \dfrac{5}{4} x$$.
Again from rt. angled triangle PAB in which
$$\angle PAB =90^o$$
$$PB^2 = PA^2 + AB^2$$ or $$y^2 - x^2 =(300)^2$$
Putting for y and x from (1) and (2) in (3), we get
$$(h - 6)^2 [25-16]=300^2 =9.100^2$$
$$\therefore h - 6 = 100$$ or $$h=6+100=106 ft.$$
Now let AP = x and BP = y, AC = 24, BD = 30.
From $$\Delta 's$$ QPC and LAC
We have $$\dfrac{h}{6} = \dfrac{24 + x}{24} \,\,\, \therefore x = 4(h - 6)$$ ...(1)
Similarly from $$\Delta^s$$ QPD and MBD
$$\dfrac{h}{6} = \dfrac{y+30}{30} \,\,\,\,\, \therefore y = 5(h - 6)$$ ...(2)
From (1) and (2), we get
$$h = \dfrac{24+x}{4} = \dfrac{y+30}{5}$$ $$\therefore y = \dfrac{5}{4} x$$.
Again from rt. angled triangle PAB in which
$$\angle PAB =90^o$$
$$PB^2 = PA^2 + AB^2$$ or $$y^2 - x^2 =(300)^2$$
Putting for y and x from (1) and (2) in (3), we get
$$(h - 6)^2 [25-16]=300^2 =9.100^2$$
$$\therefore h - 6 = 100$$ or $$h=6+100=106 ft.$$
The angle of elevation of a cliff from fixed point is $$\theta$$. After going up a distance of $$k$$ meters towards the top of the cliff at are angle of $$\phi$$, it is found that the angle of elevations is $$\alpha$$. Show that height of a cliff is $$\cfrac { k\left( \cos { \phi } -\sin { \phi }\cot { \alpha } \right) }{ \cot { \theta } -\cot { \alpha } } $$
The pictorial representation of the given data is represented by the figure
In $$\Delta DEF, \dfrac{DE}{DF}=\sin\: \phi, \dfrac{EF}{DF}=\cos\:\phi$$
$$\Rightarrow DE=k\:\sin\:\phi, EF=k\:\cos\:\phi$$ $$[DF=k\:km]$$
Let $$AB=x$$
$$\therefore AC=AB-BC=AB-DE=x-k\:\sin\:\phi$$
In $$\Delta ACD, \dfrac{AC}{CD}=\tan\: \alpha$$
$$\Rightarrow \dfrac{x-k\:\sin\: \phi}{CD}=\tan \:\alpha$$
$$\Rightarrow CD=(x-k\:\sin\:\phi)\cot\:\alpha$$
$$BF=EF+BE=EF+CD=k\:\cos\:\phi+(x-k\:\sin\:\phi)\cot\:\alpha$$
In $$\Delta ABF, \dfrac{AB}{BF}=\tan\:\theta$$
$$\Rightarrow \dfrac{x}{k\:\cos\:\phi+(x-k\sin\:\phi)\cot\:\alpha}=\tan\:\theta$$
$$\Rightarrow x\cot\:\theta=k\cos\:\phi+x\cot\:\alpha-k\sin\:\phi \cot\:\alpha$$
$$\Rightarrow (\cot\:\theta-\cot\:\alpha)x=k(\cos\:\phi-\sin\:\phi\:\cot\:\alpha)$$
$$\Rightarrow x=\dfrac{k(\cos\:\phi-\sin\:\phi\:\cot\:\alpha)}{\cot\:\theta-\cot\:\alpha}$$
Thus the height of the cliff is $$\dfrac{k(\cos\:\phi-\sin\:\phi\:\cot\:\alpha)}{\cot\:\theta-\cot\:\alpha}$$
A wheel with diameter AB touches the horizontal ground at the point A. There is a rod BC fixed at B such that ABC is vertical. A man from a point P on the ground, in the same plane as that of wheel and at a distanced from A is watching C and finds that its angle of elevation is $$\alpha$$. The wheel is then rotated about its fixed centre O such that C moves away from the man. The angle of elevation of C when it is just about to disappear is $$\beta$$. Find the radius of the wheel and the length of the rod. Also find distance PC when C is just to disappear.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is $${60^ \circ }$$ and the angle of depression of the bottom of the tower is $${30^ \circ }$$. Find the height of the pole, if the height of the tower is 75 m.
$$AC$$ is pole.
$$BD$$ is tower.
Height of pole$$=h$$.
Height of tower$$=h+d=75$$
$$\tan 60^o=\cfrac{d}{OC}$$
$$ \Rightarrow d=OC\sqrt 3$$
$$\tan 30^o=\cfrac{h}{OC}$$
$$ \Rightarrow h=\cfrac{OC}{\sqrt 3}$$
$$h+d=\cfrac{4OC}{\sqrt 3}=75$$
$$ \Rightarrow OC=\cfrac{75\sqrt 3}{4}$$
$$\therefore$$ Height of pole$$=h=\cfrac{75}{4}=18.75 m$$
A vertical tower is $$20\ m$$ high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is $$0.53$$. How far is he standing from the foot of the tower?
$$\textbf{To find the distance between the man and tower we have,}$$
$$\text{The given data is,}$$
$$\text{Height of tower, AB=20m}$$
$$\cos\theta=0.53$$
$$\text{To find the value of BC i.e., distance between man and tower , 1st we have to find the value of AC.}$$
$$\text{We know that }$$ $$\cos\theta=\dfrac{b}{h}=\dfrac{BC}{AC} $$ $$\text{and}$$ $$\sin\theta=\dfrac{p}{h}=\dfrac{AB}{AC}$$
$$\Rightarrow\sin^2\theta + \cos^2\theta=1$$
$$\Rightarrow\sin\theta=\sqrt{1-\cos^2\theta}$$ [$$\because$$ $$\textbf{using trigonometric identity}$$]
$$\Rightarrow\sin\theta=\sqrt{1-(0.53)^2}=0.848$$
$$\textbf{Now, we have }$$
$$\tan\theta=\dfrac{p}{b}=\dfrac{\sin\theta}{\cos\theta}=\dfrac{0.848}{0.53}$$;
$$\Rightarrow b=\dfrac{0.53*p}{0.848}=\dfrac{0.53*20}{0.848}=12.5$$
$$\textbf{Hence the distance between Tower and the man is 12.5}$$
A $$20\ m$$ high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole, is $${60^ \circ }$$ and the angle of elevation of the top of the pole as seen from the foot of the tower is $${30^ \circ }$$.
Find the height of the tower
Let, $$AC$$ be the pole and $$BD$$ be the tower.
Height of pole $$ =h=20m$$
Height of tower$$=H$$
Both triangles $$\triangle DBA$$ and $$\triangle CAB$$ are right angled.
Both triangles $$\triangle DBA$$ and $$\triangle CAB$$ are right angled.
$$\tan 30^o=\cfrac{AC}{AB}=\cfrac{h}{AB}\\ \Rightarrow AB=20\sqrt 3\ m$$
$$\tan 60^o=\cfrac{BD}{AB}=\cfrac{H}{AB}\\ \Rightarrow H=AB\sqrt 3$$
$$\Rightarrow H=60\ m$$
$$\therefore$$ Height of tower$$=60\ m$$
A curve in the shape of a quadrant of a circle, has n posts, at its ends and at equal distances along the curve. A man stationed at a point on one of the extreme radii produced sees the pth and qth post from the end nearest to him in a straight line. Show that the radius of the curve is $$\dfrac{b}{2} \cos (p + q)\phi \ \text{cosec} p \phi \ \text{cosec} q \phi$$ where $$\phi= \dfrac{\pi}{4 (n-1)}$$ and b is the distance of the man from the nearest end of the curve.
OAB is a quadrant of a circle, $$\angle AOB = \dfrac{\pi}{2}$$ and radius r. There are n posts, one at A, the other at B and remaining (n - 2) posts along the arc at equal distances. There is a man M standing whose distance from the nearest post is b = AM. This man sees the pth and qth posts in a straight line. In between any two consecutive posts there will be equal angle each equal to $$\dfrac{1}{n-1} . \dfrac{\pi}{2} = 2 \phi$$ by given condition. Hence the angle at the centre subtended by pth and qth posts are $$2p \phi$$ and $$2 q \phi$$ as shown in the figure. Front P and Q draw perpendiculars PR and QS on OM. Hence from similar $$\Delta^s$$ MQS and MPR, we have
$$\dfrac{QS}{SM} = \dfrac{PR}{RM} = \tan \alpha$$
$$\dfrac{QS}{PR} = \dfrac{SM}{RM}$$ or $$\dfrac{r \sin 2 q \phi}{r \sin 2 p \phi} = \dfrac{SA + b}{RA + b}$$
or $$\dfrac{ \sin 2 q \phi}{ \sin 2 p \phi} = \dfrac{OA -OS + b}{OA - OR + b}$$
or $$\dfrac{ \sin 2 q \phi}{ \sin 2 p \phi} = \dfrac{r - r \cos 2 q \phi + b}{r - r \cos 2 p \phi + b}$$
or $$\dfrac{ \sin 2 q \phi}{ \sin 2 p \phi} = \dfrac{r . 2 \sin^2 q \phi + b}{r . 2 \sin^2 p \phi + b}$$
$$\therefore 2 r (\sin^2 p \phi (2 \sin q \phi \cos q \phi) - \sin^2 q \phi ( 2 \sin p \phi \cos p \phi ))$$
$$ = b ( \sin 2 p \phi - \sin 2q \phi)$$
or $$4r \sin p \phi \sin q \phi (\sin p \phi \cos q \phi - \cos p \phi \sin q \phi)$$
$$= b. 2 \sin (p-q) \phi . \cos (p+q) \phi$$
or $$4r \sin p \phi \sin q \phi \sin (p - q) \phi$$
$$= b. 2 \sin (p-q) \phi . \cos (p+q) \phi$$
$$\therefore r = \dfrac{1}{2} b \cos (p+q) \phi cosec p \phi cosec q \phi$$
$$\dfrac{QS}{SM} = \dfrac{PR}{RM} = \tan \alpha$$
$$\dfrac{QS}{PR} = \dfrac{SM}{RM}$$ or $$\dfrac{r \sin 2 q \phi}{r \sin 2 p \phi} = \dfrac{SA + b}{RA + b}$$
or $$\dfrac{ \sin 2 q \phi}{ \sin 2 p \phi} = \dfrac{OA -OS + b}{OA - OR + b}$$
or $$\dfrac{ \sin 2 q \phi}{ \sin 2 p \phi} = \dfrac{r - r \cos 2 q \phi + b}{r - r \cos 2 p \phi + b}$$
or $$\dfrac{ \sin 2 q \phi}{ \sin 2 p \phi} = \dfrac{r . 2 \sin^2 q \phi + b}{r . 2 \sin^2 p \phi + b}$$
$$\therefore 2 r (\sin^2 p \phi (2 \sin q \phi \cos q \phi) - \sin^2 q \phi ( 2 \sin p \phi \cos p \phi ))$$
$$ = b ( \sin 2 p \phi - \sin 2q \phi)$$
or $$4r \sin p \phi \sin q \phi (\sin p \phi \cos q \phi - \cos p \phi \sin q \phi)$$
$$= b. 2 \sin (p-q) \phi . \cos (p+q) \phi$$
or $$4r \sin p \phi \sin q \phi \sin (p - q) \phi$$
$$= b. 2 \sin (p-q) \phi . \cos (p+q) \phi$$
$$\therefore r = \dfrac{1}{2} b \cos (p+q) \phi cosec p \phi cosec q \phi$$
A person walking on a straight road towards a tower observes that the angle of elevation of the top of a flag staff on the tower is $$\alpha$$; after going a distance $$a$$ towards the tower he finds that the flag staff subtends the greatest angle $$\beta$$. Prove that the length of the flag staff is $$\dfrac{2a \sin \alpha \sin \beta}{ \cos \alpha - \sin (\alpha - \beta)}$$.
Let OP and PQ represent the tower and flag staff respectively and let the circle through P, Q touch the road AO at B where A is the initial position of the person where the elevation of Q is $$\alpha$$. Then B is the point at which the flag staff subtends the greatest angle $$\beta$$, Now if $$\angle PBO= \theta$$, then by geometry, $$\angle PQB = \theta$$ also.
Hence from $$\Delta OBQ, \beta + \theta + \theta = 90^o$$ ...(1)
so that $$2 \theta =90^o -\beta$$. Also $$\angle AQB = \beta + \theta - \alpha$$.
As in part (a) we shall apply sine rule on $$\Delta BQP$$ and $$\Delta BQA$$ and eliminate the common side BQ to get PQ in terms of $$\alpha$$.
Note from $$\Delta ABQ$$,
$$\dfrac{BQ}{ \sin \alpha} = \dfrac{1}{\sin ( \beta + \theta - \alpha)}$$ ...(2)
and from $$\angle BPQ$$,
$$ \dfrac{BQ}{\sin ( \pi (\beta + \theta) )} = \dfrac{PQ}{\sin \beta}$$
Hence from (2) and (3), on equating the value of BQ, we get
$$BQ = \dfrac{a \sin \alpha}{\sin (\beta + \theta - \alpha)} = \dfrac{\sin (\beta + \theta)}{\sin \beta} PQ$$
or $$PQ = \dfrac{a \sin \alpha \sin \beta}{\sin (\beta + \theta - \alpha) \sin (\beta + \theta)}$$
$$ = \dfrac{2a \sin \alpha \sin \beta}{2 \sin (\beta + \theta - \alpha) \sin (\beta + \theta)}$$
$$ = \dfrac{2a \sin \alpha \sin \beta}{\cos \alpha - \cos (2 \beta +2 \theta - \alpha) }$$
$$ = \dfrac{2a \sin \alpha \sin \beta}{\cos \alpha - \cos (\alpha - \beta) }$$ by (1)
Hence from $$\Delta OBQ, \beta + \theta + \theta = 90^o$$ ...(1)
so that $$2 \theta =90^o -\beta$$. Also $$\angle AQB = \beta + \theta - \alpha$$.
As in part (a) we shall apply sine rule on $$\Delta BQP$$ and $$\Delta BQA$$ and eliminate the common side BQ to get PQ in terms of $$\alpha$$.
Note from $$\Delta ABQ$$,
$$\dfrac{BQ}{ \sin \alpha} = \dfrac{1}{\sin ( \beta + \theta - \alpha)}$$ ...(2)
and from $$\angle BPQ$$,
$$ \dfrac{BQ}{\sin ( \pi (\beta + \theta) )} = \dfrac{PQ}{\sin \beta}$$
Hence from (2) and (3), on equating the value of BQ, we get
$$BQ = \dfrac{a \sin \alpha}{\sin (\beta + \theta - \alpha)} = \dfrac{\sin (\beta + \theta)}{\sin \beta} PQ$$
or $$PQ = \dfrac{a \sin \alpha \sin \beta}{\sin (\beta + \theta - \alpha) \sin (\beta + \theta)}$$
$$ = \dfrac{2a \sin \alpha \sin \beta}{2 \sin (\beta + \theta - \alpha) \sin (\beta + \theta)}$$
$$ = \dfrac{2a \sin \alpha \sin \beta}{\cos \alpha - \cos (2 \beta +2 \theta - \alpha) }$$
$$ = \dfrac{2a \sin \alpha \sin \beta}{\cos \alpha - \cos (\alpha - \beta) }$$ by (1)
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is $${60^ \circ }$$ and the angle of depression of the bottom of the tower is $${30^ \circ }$$. Find the height of the tower, if the height of the pole is 20 m.
Let $$AC$$ be the pole and $$BD$$ be the tower.
Height of pole$$=h=20\ m$$
Height of tower$$=h+d$$
In $$\triangle OCB, $$
$$ \tan 30^o=\cfrac{h}{OC}$$
$$\dfrac{1}{\sqrt{3}} = \cfrac{h}{OC}$$
$$ \therefore OC= h\sqrt 3=20\sqrt 3m$$
In $$\triangle OCD ,$$
$$ \tan 60^o=\cfrac{d}{OC} $$
$$ \sqrt 3=\cfrac{d}{OC} $$
$$ \sqrt 3=\cfrac{d}{OC} $$
$$\Rightarrow d=OC\sqrt 3=60 m$$
Height of tower$$=h+d=(20\sqrt 3+60)m$$
A, B, C are three consecutive milestones on a straight road from each of which a distant spire is visible. The spire is observed to bear North-East at A, East at B and $$60^o$$ East of South at C. Prove that the shortest distance of the spire from the road is $$\dfrac{7+ 5\sqrt{3}}{13}$$ miles.
A tower on a hill subtends the same angle at two points A and B on the level ground and the angles of elevation of the top of the tower from these points are respectively $$\alpha$$ and $$\beta$$. If the tower and the two points of observation are in the same vertical plane, prove that the height of the tower is
$$AB \dfrac{| cos ( \alpha + \beta) |}{sin ( \alpha - \beta) }$$
Let PQ represent the tower in a hill OP and A, B the points of observation on the ground. Since PQ subtends the same angle at A and B, the four point Q, P, A and B are concyclic. Since angle of elevation of Q at A and B arc respectively $$\alpha$$ and $$\beta$$, we have
$$\angle QAO =\alpha$$ and $$\angle QBO = \beta$$ so that
$$\angle BQA = (\alpha - \beta)$$
Let C be the centre of circle.
Now draw CM and CR perpendiculars to the chords AN and PQ so that $$AM = BM = \dfrac{1}{2} AB$$
and $$PR = QR = \dfrac{1}{2} PQ$$. Join CA, CB, CP and CQ.
Now $$\angle ACB = 2 \angle AQB = 2(\alpha - \beta).$$
Hence $$\angle ACM = \angle BCM = \alpha - \beta .$$
If $$\angle PBQ = \theta$$; then $$\angle PCQ = 2\theta$$
so that $$\angle PCR = \angle QCR = \theta$$
We have $$\beta = 90^o - \alpha + \theta$$
so that $$\theta = \alpha + \beta - 90^o$$
Now $$BC = CQ = \left( \dfrac{x}{2} \right) cosec \theta$$ where PQ = x.
Then $$BC \sin (\alpha - \beta) = BM = \dfrac{1}{2} AB$$.
or $$x = \dfrac{\sin \theta}{\sin (\alpha - \beta)}, AB = \dfrac{\sin (\alpha + \beta - 90^o)}{\sin (\alpha - \beta)}$$
Hence, $$PQ = x =\dfrac{| \cos (\alpha - \beta) |}{\sin (\alpha - \beta) } AB$$.
$$\angle QAO =\alpha$$ and $$\angle QBO = \beta$$ so that
$$\angle BQA = (\alpha - \beta)$$
Let C be the centre of circle.
Now draw CM and CR perpendiculars to the chords AN and PQ so that $$AM = BM = \dfrac{1}{2} AB$$
and $$PR = QR = \dfrac{1}{2} PQ$$. Join CA, CB, CP and CQ.
Now $$\angle ACB = 2 \angle AQB = 2(\alpha - \beta).$$
Hence $$\angle ACM = \angle BCM = \alpha - \beta .$$
If $$\angle PBQ = \theta$$; then $$\angle PCQ = 2\theta$$
so that $$\angle PCR = \angle QCR = \theta$$
We have $$\beta = 90^o - \alpha + \theta$$
so that $$\theta = \alpha + \beta - 90^o$$
Now $$BC = CQ = \left( \dfrac{x}{2} \right) cosec \theta$$ where PQ = x.
Then $$BC \sin (\alpha - \beta) = BM = \dfrac{1}{2} AB$$.
or $$x = \dfrac{\sin \theta}{\sin (\alpha - \beta)}, AB = \dfrac{\sin (\alpha + \beta - 90^o)}{\sin (\alpha - \beta)}$$
Hence, $$PQ = x =\dfrac{| \cos (\alpha - \beta) |}{\sin (\alpha - \beta) } AB$$.
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60∘.
Calculate : the width of the river and the height of the tree.
$$OB$$ is the width of river.
$$OB=d$$
$$OC$$ is the height of tree.
$$OC=h$$
$$\tan 30^{\circ}=\cfrac{h}{d+50} \Rightarrow h\sqrt 3=d+50$$
$$\tan 60^{\circ}=\cfrac{h}{d} \Rightarrow h=\cfrac{d}{\sqrt 3}$$
$$\therefore h\sqrt 3=3d=d+50$$
$$d=25$$
$$\therefore h=25\sqrt 3$$
Width of river$$=25m$$
Height of tree$$=25\sqrt 3 m$$
An electrician has to repair an electric fault on a pole of height 5m.She needs to reach a point 1.3 m below the top of the pole to undertake the repair work.What should be the length of the ladder that she should use which,when inclined at an angle of $$ {60} ^{0} $$ to the horizontal,would enable her to reach the required position?Also,how far from the foot of the pole should she place the foot of the ladder?( you may take $$ \sqrt {3} =1.73 $$ )
Two boats approach the light house in mid-sea from opposite directions. The angles of elevation of the top of the light house from two boats are $$30^ \circ$$ and $$45^ \circ$$. If the distance between the two boats is 100 m find the height of the light house.
Let $$AB=x, \,then \,AC=100-x, OA=h$$
In $$\triangle OAB$$,
$$\tan 45^{\circ}=\cfrac{OA}{AB}=\cfrac{h}{x}$$
$$\Rightarrow 1=\cfrac{h}{x}$$
$$\Rightarrow h=x$$-----------------(1)
In $$\triangle OAC$$,
$$\tan 30^{\circ}=\cfrac{1}{\sqrt 3}=\cfrac{OA}{AC}$$
$$\Rightarrow \cfrac{1}{\sqrt 3}=\cfrac{h}{100-x}$$
$$\Rightarrow 100-x=\sqrt 3h$$--------------(2)
Eliminating 'x' from Equation(2) using (1), we get
$$100-h=\sqrt 3h$$
$$\Rightarrow h=\cfrac{100}{(\sqrt 3+1)}=50(\sqrt 3-1)m$$
The angles of elevation of the top of a tower from two points at a distance of $$4m$$ and $$9m$$ from the base of the tower and in the same direction and they are complimentary. Prove that the height of the tower is $$6m$$.
Given,
$$\theta+\phi=\cfrac{\pi}{2}=90^{\circ}$$
In $$\triangle ABC$$,
$$\tan\theta=\cfrac{AB}{BC}=\cfrac{h}{4}$$-------(1)
In $$\triangle ABD$$
$$\tan\phi=\cfrac{AB}{BD}=\cfrac{h}{9}$$
$$\tan(\cfrac{\phi}{2}-\theta)=\cfrac{h}{9}$$
$$\Rightarrow \cot\theta=\cfrac{h}{9}$$------------(2)
Multiplying (1) & (2), we get
$$\tan\theta\cdot\cot\theta=\cfrac{h^{2}}{4\times 9}=\cfrac{h^{2}}{36}$$
$$\therefore \Rightarrow \tan\theta\cdot\cfrac{1}{\tan\theta}=\cfrac{h^{2}}{36}$$
$$\Rightarrow h^{2}=36$$
$$\Rightarrow h=6\,meter$$
The angle of elevation of jet fighter from a point $$A$$ on the ground is $$60^0$$. After a flight of $$10$$ seconds, the angle of elevation changes to $$30^0$$. If the jet is flying at a speed of $$448 \ \text{k/h}$$. Find the constant height at which the jet is flying.
Given that, the angle of elevation of jet fighter from a point $$A$$ on the ground is $$60^o$$. After a flight of $$10 \ seconds$$, the angle of elevation changes to $$30^o$$. The jet is flying at a speed of $$448 \ kmph$$.
To find out: The constant height at which the jet is flying.
Based on the given information, we can draw the figure shown above.
Let $$h$$ be the constant height of the jet, distance $$AL$$ be $$x\ m$$ and $$LM$$ be $$y\ m$$
We have, time taken $$=10\ sec$$
and speed $$=448\ kmph$$
We know that $$1 \ km=1000\ m$$ and $$1 \ hour=60\times 60=3600 \ sec$$
$$\therefore \ Speed=\dfrac { 448\times 1000 }{ 3600 } m/s=\dfrac { 1120 }{ 9 } m/s\\$$
We also know that, $$Distance=Speed\times time$$
$$\therefore \ $$ Distance $$=\dfrac { 1120 }{ 9 } \times 10$$
$$=\dfrac { 11200 }{ 9 } \ m$$
Hence, $$LM=y=\dfrac { 11200 }{ 9 } \ m$$
We know that, $$\tan \theta=\dfrac{\text{Opposite Side}}{\text{Adjacent Side}}$$
$$\therefore \ In\ \Delta ALB, \ \tan60^o=\dfrac { h }{ x } $$
Also, $$\tan 60^o=\sqrt3$$
$$\therefore \ \dfrac { h }{ \sqrt { 3 } } =x$$
$$In\ \Delta AMC,\ \tan30^o=\dfrac { h }{ x+y } \\$$
$$\because \ \tan 30^o=\dfrac{1}{\sqrt3}\ and\ x=\dfrac { h }{ \sqrt { 3 } }\\$$
$$\therefore \ \dfrac { h }{ \sqrt { 3 } } =\dfrac { h }{ \dfrac { h }{ \sqrt { 3 } } +y } \\$$
$$\Rightarrow \dfrac { h }{ 3 } +\dfrac { y }{ \sqrt { 3 } } =h\\$$
$$\Rightarrow \dfrac { y }{ \sqrt { 3 } } =\dfrac { 2h }{ 3 } \\$$
$$\Rightarrow h=\dfrac{3y}{2\sqrt3}\\$$
$$\Rightarrow h=\dfrac{\sqrt3 y}{2}\\$$
We have, $$y=\dfrac { 11200 }{ 9 } \ m$$
$$\therefore \ h=\dfrac{\sqrt3}{2}\times \dfrac{11200}{9}\ m\\$$
$$\Rightarrow h=\dfrac{5600\sqrt3}{9}\ m\approx 1077.72\ m$$
Hence, the constant height at which the jet is flying is approximately $$1077.72\ m$$.
The angle of elevation of the top of a tower from two-point at a distance $$4\ m$$ and $$9\ m$$ from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is $$6\ m.$$
In the above figure, let $$AB$$ is the tower of height $$h$$ and point $$C$$ and $$D$$ are $$4\ m$$ and $$9\ m$$ respectively.
In $$\triangle ABC,$$
$$\tan\theta=\dfrac{AB}{AC}$$
$$\Rightarrow \tan\theta=\dfrac h4\quad\quad\quad\dots(1)$$
Now, in $$\triangle ABD,$$
$$\tan (90-\theta) =\dfrac{AB}{BD}$$
$$\Rightarrow\cot\theta = \dfrac h9\quad\quad\quad\dots(2)$$
Multiply equation $$(1)$$ and $$(2),$$
$$\tan \theta \times \cot \theta = \dfrac{h}{4} \times \dfrac{h}{9}$$
$$\Rightarrow 1 = \dfrac{{{h^2}}}{{36}}$$
$$\Rightarrow {h^2} = 36$$
$$\Rightarrow {h} = 6\ m$$
Hence, proved height of the tower is equal to $$6\ m.$$
The angle of elevation of the top of a tower from a point on the ground,which is $$30\ m$$ away from the of the tower,is $${30^ \circ }$$,find the height of the tower.
$$\tan 30°=\dfrac{h}{30}$$
$$\Rightarrow h=10\sqrt{3}=17.320m$$
Hence, the answer is $$17.320m.$$
A boat has to cross a river. It crosses the river by making an angle of $$60^0$$ with the bank of the river due to the stream of the river and travels a distance of 600 m to reach the another side of the river. What is the width of the river?
$$AB=$$ Distance traveled by the boat $$=600m$$
$$AC=$$ Width of the river
$$\sin 60=\dfrac{AC}{AB}$$
$$\dfrac{\sqrt3}{2}=\dfrac{AC}{600}$$
$$AC=\dfrac{600\sqrt3}{2}$$
$$AC=300\sqrt3\ m$$
Hence width of the river is $$300\sqrt3\ m$$
A tower is $$50$$ m high and angle of elevation of the sun from a point on its shadow is $$30^o$$. Find the length of shadow of tower?
A vertical tower stands on horizontal plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, The angle of elevation of the bottom of the flagstaff is $$\alpha $$ and that of the top o flagstaff is $$\beta $$ . Prove that the height of the tower is $$\dfrac{h tan \alpha }{tan \beta -tan \alpha }$$
Let height be y $$\Delta OAC$$
$$\tan\theta =\dfrac{P}{B}$$
$$\tan\beta =\dfrac{CA}{OA}$$
$$\tan\beta =\dfrac{y+h}{x}$$ $$(y+h)\rightarrow$$ Let AB, AB$$+$$BC
Let OA$$\rightarrow$$ x
$$x=\left[\dfrac{y+x}{\tan\beta}\right]$$
Consider $$\Delta OAB$$
$$\tan\alpha =\dfrac{y}{x}=\dfrac{perpendicular}{Base}$$
$$x=\dfrac{y}{\tan\alpha}$$
$$\dfrac{y}{\tan\alpha}=\dfrac{y+h}{\tan\beta}$$
$$y\tan\beta =\tan\alpha y+\tan\alpha h$$
$$y\tan\beta -\tan y=\tan \alpha h$$
$$y(\tan\beta -\tan\alpha)=\tan\alpha h$$
$$y=\dfrac{h\tan\alpha}{\tan\beta -\tan\alpha}$$
This proved.
In an equilateral triangle of side $$12$$ cm , a circle is inscribed touching its sides . Find the area of the portion of the triangle not included in the circle . Take $$\sqrt{3} = 1.73$$ and $$\pi = 3.14$$ .
REF.Image
side of equilateral triangle is 12 cm
height = $$\dfrac{\sqrt{3}}{2}a$$ $$=\dfrac{\sqrt{3}}{2}\times 12$$ $$=6\sqrt{3}cm$$
$$tan30^{\circ}=\dfrac{r}{6}$$
$$\dfrac{1}{\sqrt{3}}=\dfrac{r}{6}$$
$$\dfrac{6}{\sqrt{3}}=r$$
$$\therefore r=\dfrac{6}{\sqrt{3}}cm$$
area not included = $$\dfrac{\sqrt{3}}{4}a^{2}-\pi r^{2}$$
$$=\dfrac{\sqrt{3}}{4}\times (12)^{2}-\pi \times (\frac{6}{\sqrt{3}})^{2}$$
$$=\dfrac{\sqrt{3}}{4}\times 144-\pi \times \dfrac{36}{3}$$
$$=36\sqrt{3}-3.14\times 12$$
$$=62.35-37.68$$
$$=24.67 cm^{2}$$
A ladder $$15$$m long just reaches the top of a vertical wall. If the ladder makes an angle of $${60}^{\circ}$$ with the wall. Find the height of the wall.
Let the length of the ladder be $$=15$$m(hypotenuse)
The angle between the ladder and the wall $$\angle{BCA}={60}^{\circ}$$
Angle between ladder and the ground $$\angle{CAB} ={90}^{\circ}-{60}^{\circ}={30}^{\circ}$$
Height of the wall $$= BC$$
$$\sin{{30}^{\circ}}=\dfrac{BC}{15}$$
$$\Rightarrow \dfrac{1}{2}=\dfrac{BC}{15}$$
$$\Rightarrow BC=\dfrac{15}{2}=7.5$$m
An electrician has to repair an electric fault on an electric pole of height $$4\ m.$$ He needs to reach a point $$1.3\ m$$ below the top of the pole in order to undertake the repair work. What should be the length of the ladder that he should use which, when inclined at an angle of $$ 60 ^ { \circ } $$ to the horizontal, would enable him to reach the required position? Also how far from the foot of the pole should he place the foot of the ladder? (Use $$\sqrt{3}=1.732$$)
In the above figure, let $$AB$$ is the ladder of length $$x$$ and $$DC$$ is the pole of height $$4\ m.$$ Let $$A $$ be the point at a distance $$y$$ from the base of the pole.
$$CD=BC+BD$$
$$\Rightarrow 4=BC+1.3$$
$$\Rightarrow BC=2.7\ m$$
Now, in $$\triangle ABC,$$
$$\sin 60^{\circ}=\dfrac{BC}{AB}$$
$$\Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{2.7}{x}$$
$$\Rightarrow x=2.7\times\dfrac{2}{\sqrt{3}}$$
$$\Rightarrow x\approx3.1176\ m$$
Also,
$$\tan 60^{\circ}=\dfrac{BC}{AC}$$
$$\Rightarrow {\sqrt{3}}=\dfrac{2.7}{y}$$
$$\Rightarrow y=2.7\times\dfrac{1}{\sqrt{3}}$$
$$\Rightarrow y\approx 1.559\ m$$
A person standing on the bank of a river, observes that the angle subtended by a tree on the opposite bank has measure $$60^0$$. When he retreats $$20$$ m from the bank, then find the angle to have measure $$30^0$$. Find height of the tree and breadth of the river.
Class 10 Maths Extra Questions
- Areas Related To Cricles Extra Questions
- Arithmetic Progressions Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Introduction To Trigonometry Extra Questions
- Pair Of Linear Equations In Two Variables Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadratic Equations Extra Questions
- Real Numbers Extra Questions
- Some Applications Of Trigonometry Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions