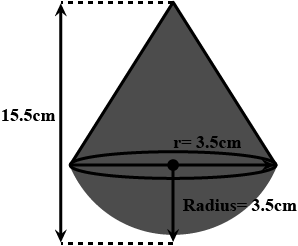
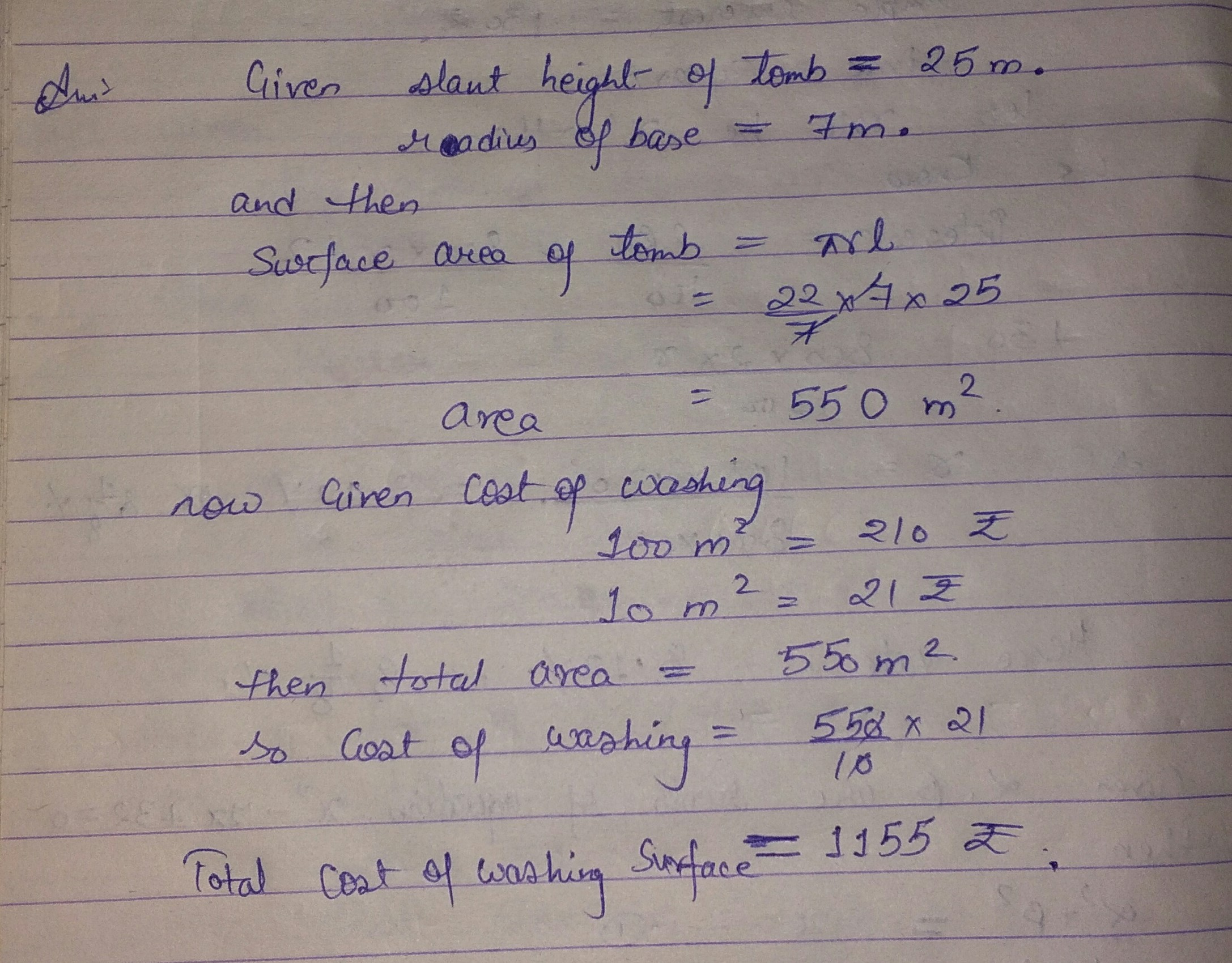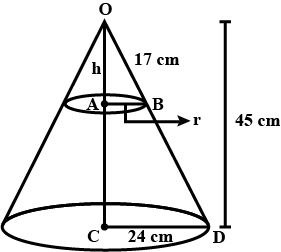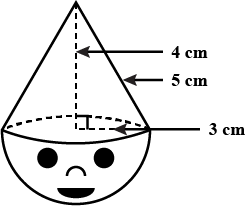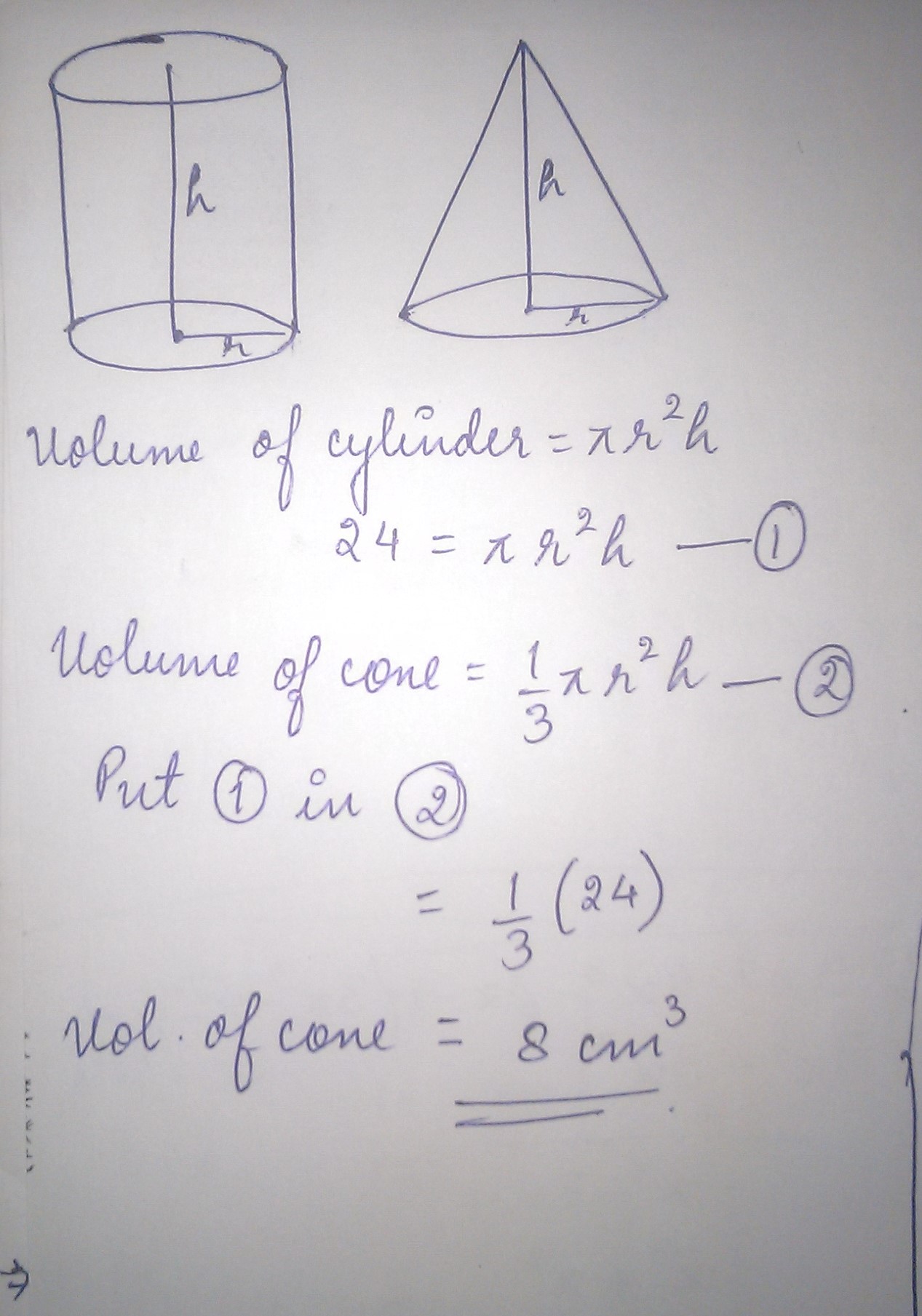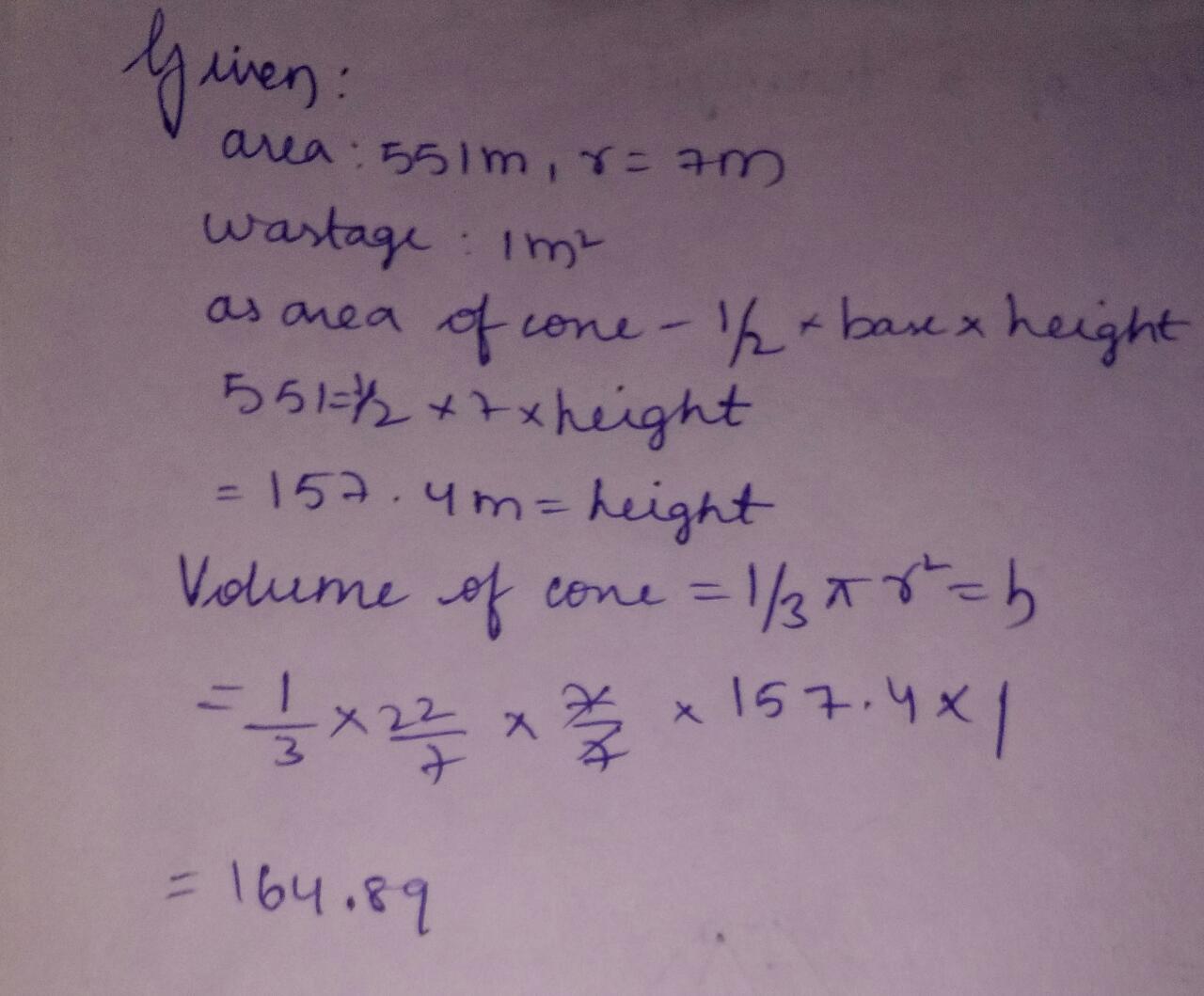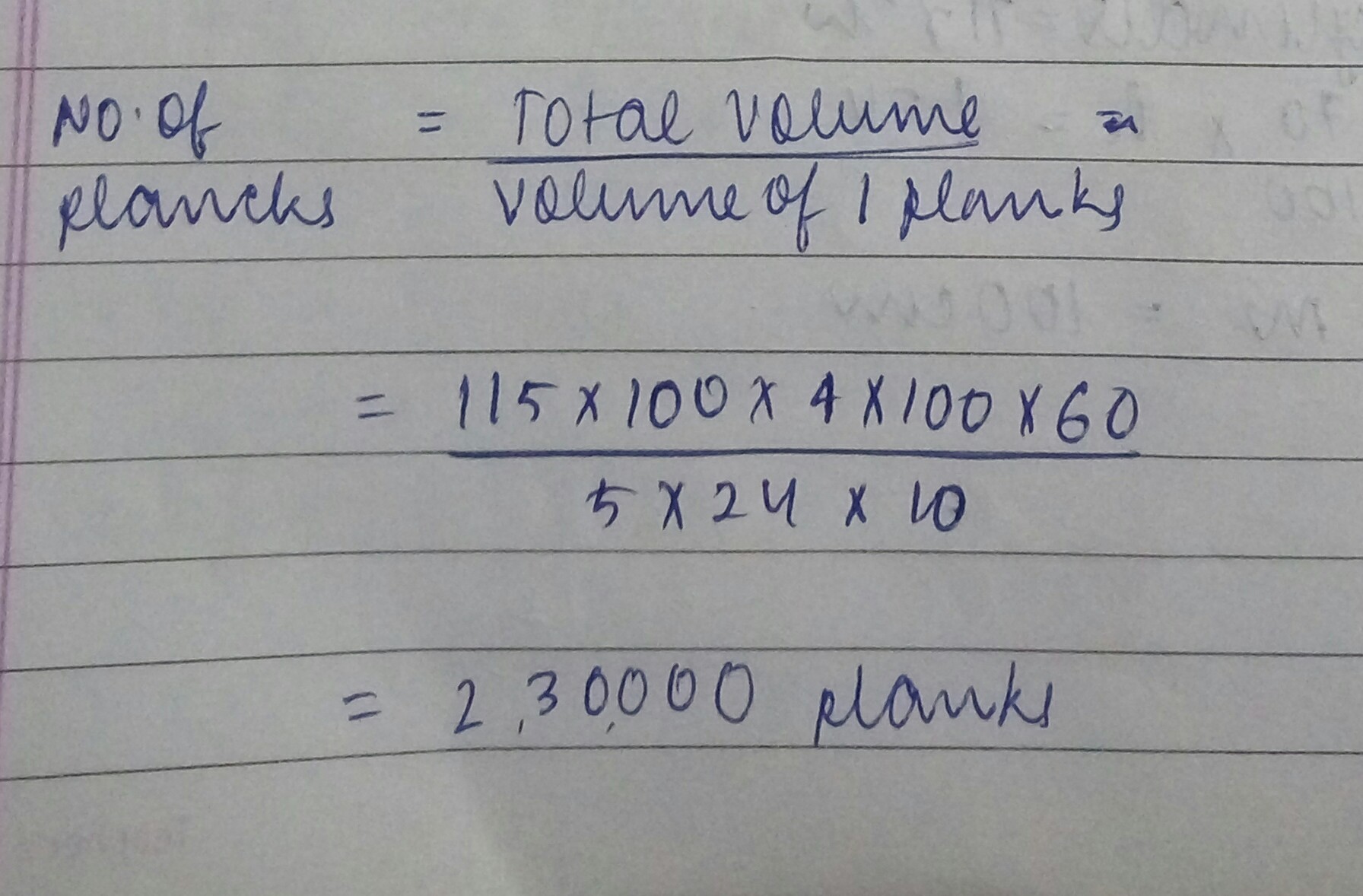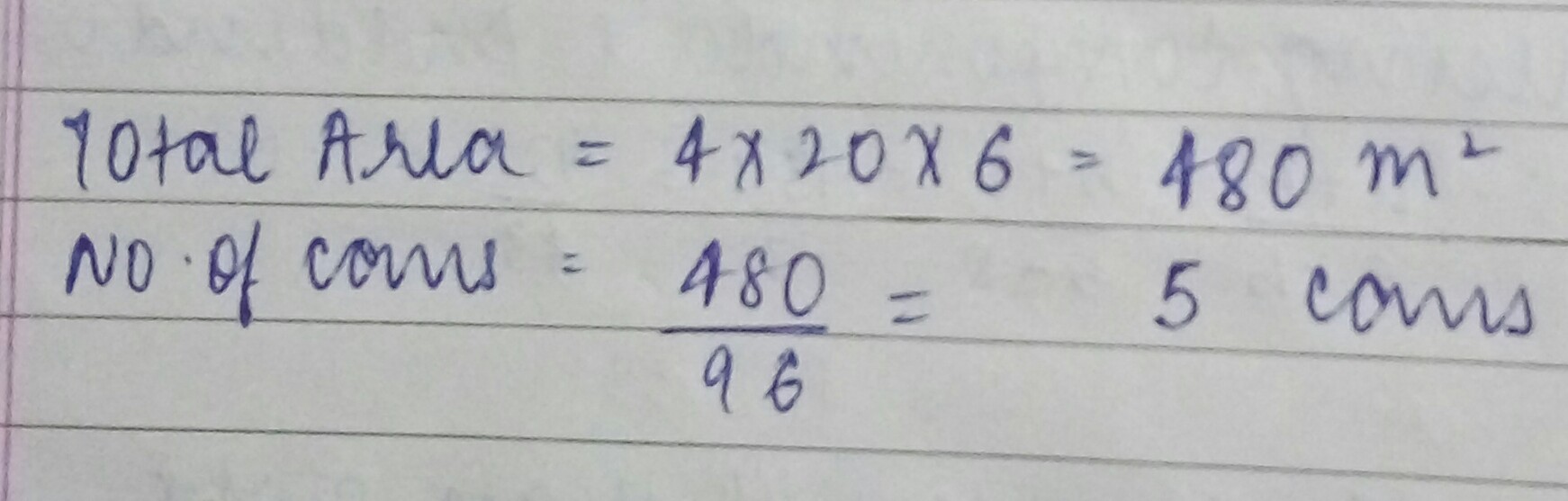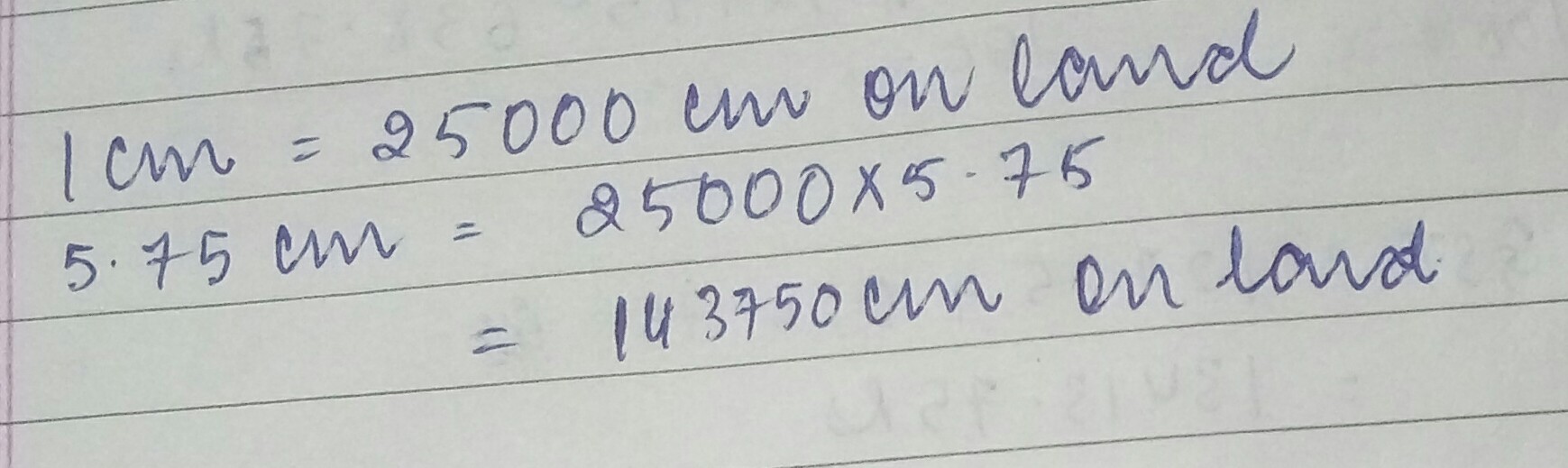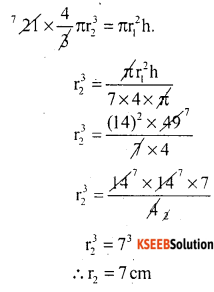Surface Areas And Volumes - Class 10 Maths - Extra Questions
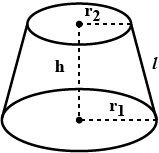
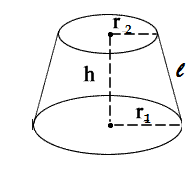
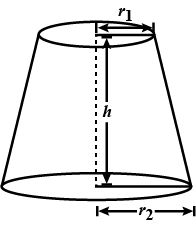
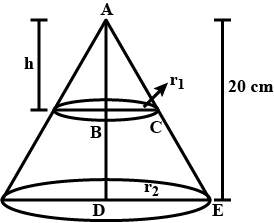
Consider a frustum of cone with larger and smaller radius equal to $$r_1 \ and\ r_2$$, respectively. Then, the total surface area of frustum of a cone is $$\pi l(r_1+r_2)+\pi (r_{1}^{2}+r_{2}^{2})$$. if correct enter 1 else enter 0
State True(1) or False(0).
The volume of the frustum of a cone is $$\frac{1}{3}\pi h\left [ r_{1}^{2}r_{2}^{2}-r_{1}r_{2} \right ],$$ where h is vertical
height of the frustum and $$r_1, r_2$$ are the radii of the ends.
height of the frustum and $$r_1, r_2$$ are the radii of the ends.
State True(1) or False(0).
An open metallic bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The surface area of the metallic sheet used is equal to curved surface area of frustum of a cone + area of circular base + curved surface area of cylinder
Consider a frustum of the cone with larger and smaller radius equal to $$r_1 \ and\ r_2$$, respectively. Then, the curved surface area of a frustum of a cone is $$\pi l (r_1+r_2)$$. If true enter 1 else 0.
A spherical ball of radius $$3\ cm$$ is melted and recast into three spherical balls. The radii of the two of the balls are $$1.5\ cm$$ and $$2\ cm$$ respectively. Find the radius of the third ball.
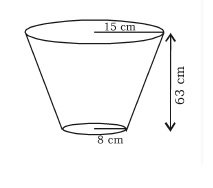
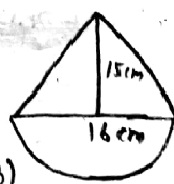
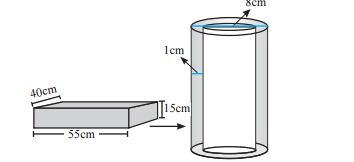
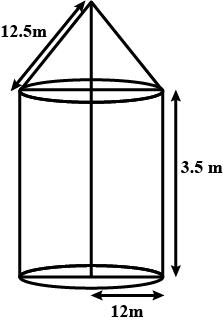
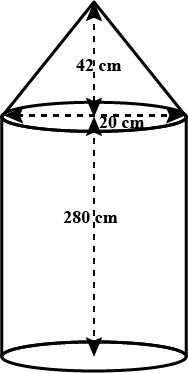
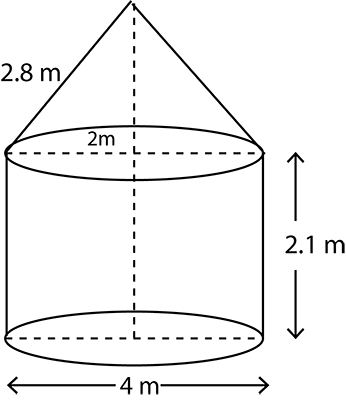
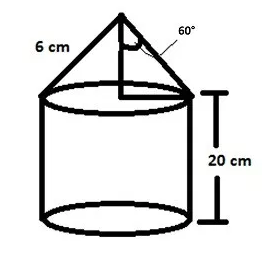
A fraction clutch is in the form of a frustum of a cone, the diameter of the ends being $$32\ cm$$ and $$20\ cm$$ and length $$8\ cm$$. Find its bearing surface and volume.[Take $$\pi=3.14$$]
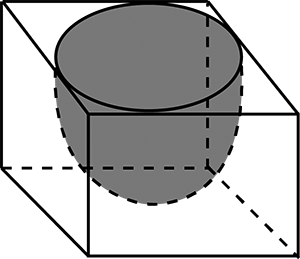
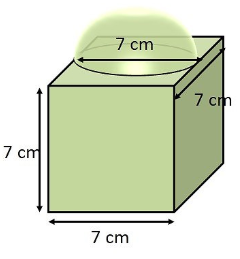
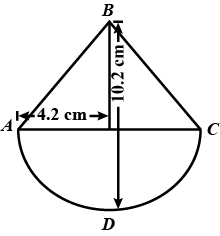
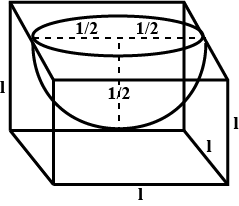
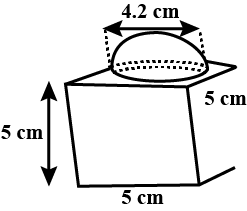
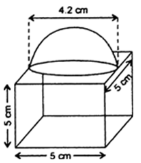
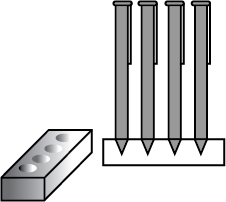
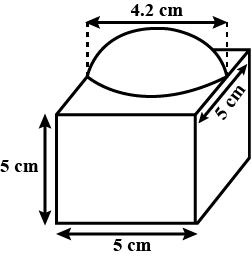
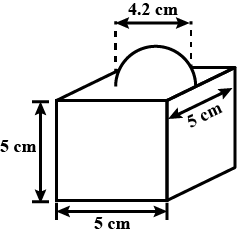
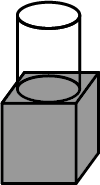
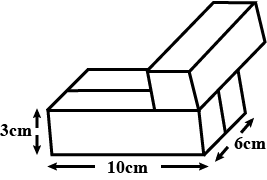
The decorative block shown in Fig. 13.7 is made of two solids - a cube and a hemisphere. The base of the block is a cube with edge 5 cm. and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block. $$\left(Take \pi =\dfrac { 22 }{ 7 } \right) $$
How many spherical bullets each of $$5cm$$ in diameter can be cast from a rectangular block of metal $$11dm\times 1m\times 5dm$$?
A $$16\text{ m}$$ deep well with diameter $$3.5\text{ m}$$ is dug up and the earth from it is spread evenly to form a platform $$27.5\text{ m}$$ by $$7\text{ m}$$. Find the height of the platform.
A well of diameter $$2\ m$$ is dug $$14\ m$$ deep. The earth taken out of it is spread evenly all around it to form an embankment of height $$40\ cm$$. Find the width of the embankment.
Rain water, which falls on a flat rectangular surface of length $$6m$$ and breadth $$4m$$ is transferred into a cylindrical vessel of internal radius $$20cm$$. What will be the height of water in the cylindrical vessel if a rainfall of $$1cm$$ has fallen? (Use $$\pi =\cfrac { 22 }{ 7 } $$)
Find the volume of the largest right circular cone that can be cut out of a cube whose edge is $$9cm$$.
$$50$$ circular plates each of diameter $$14cm$$ and thickness $$0.5cm$$ are placed one above the other to form a right circular cylinder. Find its total surface area.
A cylindrical tub of radius $$12cm$$ contains water to a depth of $$20cm$$. A spherical form ball of radius $$9cm$$ is dropped into the tub and thus the level of water is raised by $$hcm$$. What is the value of $$h$$?
A conical flask is full of water. The flask has base-radius $$r$$ and height $$h$$. The water is poured into a cylindrical flask of base-radius $$mr$$. Find the height of water in the cylindrical flask.
A hollow sphere of internal and external radii $$2\ cm$$ and $$4\ cm$$ respectively is melted into a cone of base radius $$4\ cm$$. Find the height and slant height of the cone.
A hollow sphere of internal and external diameters $$4cm$$ and $$8cm$$ respectively is melted into a cone of base diameter $$8cm$$. Calculate the height of the cone.
$$25$$ circular plates, each of radius $$10.5cm$$ and thickness $$1.6cm$$, are placed one above the other to form a solid circular cylinder. Find the curved surface area and the volume of the cylinder so formed.
If $$h$$, $$s$$, $$V$$ be the height, curved surface area and volume of a cone respectively, then $$\left( {3\pi V{h^3} + 9{V^2} - {s^2}{h^2}} \right) = ?$$
The largest sphere is to be carved out of a right circular cylinder of radius $$7cm$$ and height $$14cm$$. Find the volume of the sphere.
A vessel in the shape of a cuboid contains some water. If three identical spheres are immersed in the water, the level of water is increased by $$2cm$$. If the area of the base of the cuboid is $$160{cm}^{2}$$ and its height $$12cm$$, determine the radius of any of the spheres.
The diameter of a metallic sphere is equal to $$9cm$$. It is melted and drawn into a long wire of diameter $$2mm$$ having a uniform cross-section. Find the length of the wire.
A copper sphere of radius $$3\ cm$$ is melted and recast into a right circular cone of height $$3\ cm$$. Find the radius of the base of the cone.
A self help group wants to manufacture jokes caps (conical shapes) of $$3 \text cm$$ radius and $$4cm$$ height. If the available colour paper sheets is $$1000 \text cm^{2}$$, then how many caps can be manufactured from that paper sheet?
$$\Rightarrow$$ We have given, $$Height(h)=4\,cm$$ and
$$radius(r)=3\,cm$$
.$$\Rightarrow$$ Let slant height be $$l$$.
We know that,
$$l^2=h^2+r^2$$
$$l^2=(4)^2+(3)^2$$
$$l^2=16+9$$
$$l^2=25$$
$$\therefore$$ $$l=5\,cm$$
$$\Rightarrow$$ Curve surface area of $$1$$ joker cap $$=\pi r l$$
$$=\dfrac{22}{7}\times 3\times 5$$
$$=47.14\,cm^2$$
$$\Rightarrow$$ Available color paper sheet $$=1000\,cm^2$$
$$\Rightarrow$$ Number of caps manufacture from $$1000\,cm^2$$ paper sheet $$=\dfrac{1000}{47.14}=21.21$$
A spherical ball of radius $$3\ cm$$ is melted and recast into three spherical balls. The radii of two of the balls are $$1.5\ cm$$ and $$2\ cm$$. Find the diameter of the third ball.
Metal spheres, each of radius $$2cm$$, are packed into a rectangular box of internal dimension $$16cm\times 8cm\times 8cm$$ when $$16$$ spheres are packed the box is filled with preservative liquid. Find the volume of this liquid. (Use $$\pi =\dfrac{669}{213}$$)
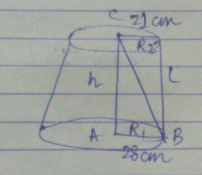
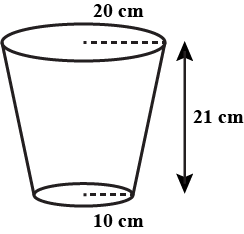
A washing tub in the shape of a frustum of a cone has height $$21\ cm$$. The radii of the circular top and bottom are $$20\ cm$$ and $$15\ cm$$ respectively. What is the capacity of the tub ? $$(\pi=\dfrac{22}{7})$$
The radius of a solid sphere is $$7$$ cm. If the solid sphere is melt to form small spheres of radius $$3.5$$ cm. Then how many small spheres can be formed?
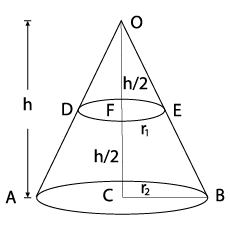
Given : $$ED = 14 cm $$
R.E.F image
Area of shaded region$$ED=14cm$$ (Given)
$$ar(\triangle EBD)=ar(\triangle ACDE)-ar(\triangle ABE)-ar(\triangle BED)$$...(1)
$$ED=AC=14cm=2AB$$ (Since $$AB=BC$$)
$$\Rightarrow AB=BC=7cm=AE=CD$$
$$\therefore ar(ACDE)=AC\times CD=14\times 7\Rightarrow 98cm^2$$
$$ar(\triangle ABE )=\dfrac{1}{2}\times AB\times BC=\dfrac{1}{2}\times 7\times 7=\dfrac{49}{2}cm^2$$
$$ar(\triangle BCD)=\dfrac{1}{2}\times BC\times CD=\dfrac{1}{2}\times 7\times 7=\dfrac{49}{2}cm^2$$
$$\therefore \boxed{ae(\triangle EBD)=98-\dfrac{49}{2}-\dfrac{49}{2}=49cm^2}$$
$$ar(semi \,circle )\dfrac{\pi r^2}{2}=\dfrac{\pi}{2}(\dfrac{7}{2})^2=\dfrac{\pi}{2}\times (\dfrac{14}{2})^2$$
$$=\dfrac{22}{7}\times \dfrac{1}{2}\times 7\times 7$$
$$\boxed{area(semicircle)=77cm^2)}$$
$$\therefore$$ area of shaded region $$=(1)+(2)$$
$$\therefore 77+49$$
$$\therefore 126cm^2$$
The slant height of a cone with hemispherical base is $$5$$ cm. If the total surface area of the article is $$103.62 cm^2$$, find its height.
A rectangular reservoir is 120 m long and 75 m wide. At what speed per hour must water flow into it through a square pipe of 20 cm wide so that the water rises by 2.4 m in 18 hours ?
Threee cubes of the same metals, whose edges are 6,8,10 cm are melted and formed into a single cube. find the diagonal of these single cube.
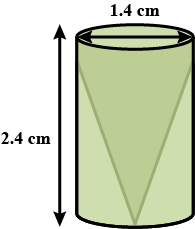
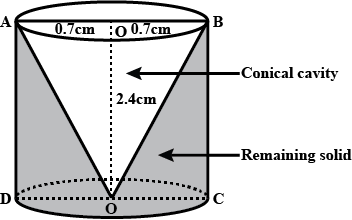
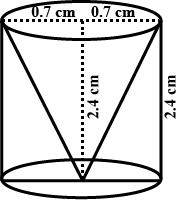
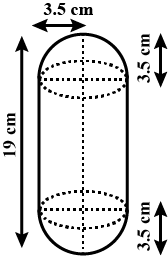
From a solid cylinder whose height is $$2.4cm$$ and diameter $$1.4cm$$ a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest $${cm}^{2}$$
We have
Height of solid cylinder $$=2.4$$ cm
diameter of solid cylinder $$= 1.4$$ cm
$$l=\sqrt{r^{2}+h^{2}}=\sqrt{(0.7)^{2}+(2.4)^{2}}$$
$$=2.5$$
clearly,
Total surface area of the remaining solid = Curved surface area of the cylinder + Area of the base of the cylinder + Curved surface area of the cone.
Surface Area
$$=(\pi r^{2})+(2\pi rh)+(\pi rl)$$
$$=\pi ((0.7)^{2}+(2)(0.7)(2.4)+(0.7)(2.5))$$
$$=\pi (5.6)$$
$$=\dfrac{22}{7}(5.6)$$
$$=17.6 cm^{2}$$
Find the volume of the largest circular cone that can be cut out of a cube whose edge is $$9\ cm. \left (\pi = \dfrac {22}{7}\right )$$.
Since the edge of cube is 9 cm this will be the altitude of the cone.
The radius of circular cone will be 9:2=4.5 cm.
The volume of cone is given by formula:
, where R is the radius and H the altitude of cone. Since we are asked for the largest cone, its volume must be equal or less than the volume of cube. We write:
=
=
V=
The radius of circular cone will be 9:2=4.5 cm.
The volume of cone is given by formula:
V=
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped small bottles, each of diameter 3 cm and height 4 cm. How many bottles are needed to empty the bowl ?
A cylindrical container with diameter of base $$42\ cm$$ contains sufficient water to submerge a rectangular solid of iron with dimensions $$22\ cm\times 14\ cm \times 10.5\ cm$$. Find the rise in level of the water when the solid is sub-merged.
The height of a cone is $$40\ cm$$ A Small cone is cut off at the top by a plane parallel to its base. If its volume be $$\dfrac {1}{64}$$ of the volume of the given cone at what height above the base is the section cut?
How many silver coins, $$1.75cm$$ in diameter and of thickness $$2mm$$, must be melted to form a cuboid of dimensions $$5.5cm\times 10cm\times 3.5cm$$?
In figure, the object is made of two solids a cube and a hemisphere. The base of the figure is a cube with edges of 5 cm and the hemisphere fixed on the top has a diameter of 4.2 cm . Find the total surface area of the object (take pi = 22/7 ) .
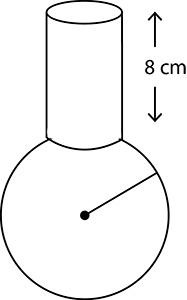
A spherical glass vessel has a cylindrical neck $$8\;cm$$ long $$2\;cm$$ in diameter, the diameter of a spherical part is $$8.5\;cm$$. By measuring the amount of water it holds, a child finds its volume to be $$345\;cm^3$$. Check whether she is correct, taking the above as the inside measurements, and $$\pi=3.14$$
Diameter of spherical glass vessel = 8.5 cm
$$\therefore r = 4.25$$ cm
Length of cylindrical neck = 8 cm
Diameter = 2 cm
$$\therefore$$ Radius, r = 1 cm
Volume of water she found = 345 cm$$^3$$
(i) Volume of cylinder neck, V
$$= \pi r^2 h$$
$$= \pi \times (1)^2 \times 8$$
$$= 8 \pi cm^3$$
(ii) Volume of cylindrical vessel $$= \frac{4}{3} \pi r^3$$
$$= \frac{4}{3} \times \pi \times (4.25)^3$$
$$\therefore$$ Total volume of water, V
$$= 8 \pi + \frac{4}{3} \pi \times (4.25)^3$$
$$= 8 \times 3.14 + \frac{4}{3} \times 3.14 \times (4.25)^3$$
$$= 25.12 + 321.38$$
$$= 346.5 cm^3$$
$$\therefore$$ Her answer is not correct.
$$\therefore r = 4.25$$ cm
Length of cylindrical neck = 8 cm
Diameter = 2 cm
$$\therefore$$ Radius, r = 1 cm
Volume of water she found = 345 cm$$^3$$
(i) Volume of cylinder neck, V
$$= \pi r^2 h$$
$$= \pi \times (1)^2 \times 8$$
$$= 8 \pi cm^3$$
(ii) Volume of cylindrical vessel $$= \frac{4}{3} \pi r^3$$
$$= \frac{4}{3} \times \pi \times (4.25)^3$$
$$\therefore$$ Total volume of water, V
$$= 8 \pi + \frac{4}{3} \pi \times (4.25)^3$$
$$= 8 \times 3.14 + \frac{4}{3} \times 3.14 \times (4.25)^3$$
$$= 25.12 + 321.38$$
$$= 346.5 cm^3$$
$$\therefore$$ Her answer is not correct.
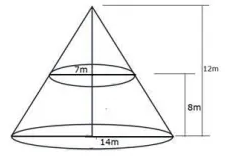
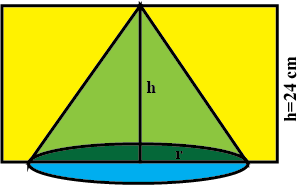
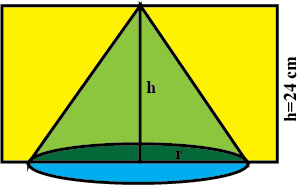
The radii of circular ends of a bucket of height 24 cm24 cm. Find the area of its curved surface.
REF. Image.
Since it is a bucket. Therefore, it can act as a frustum of $$h =24 cm$$
$$ r = 5 cm $$
$$ R = 15 cm $$
Slant height = $$ l = \sqrt{h^{2} + (R - r)^{2}}$$
$$ l = \sqrt{(24)^{2}+(15-5)^{2}} = \sqrt{(24)^{2}+(10)^{2}}$$
$$ l = \sqrt{576+100}$$ $$ = \sqrt{676}$$ $$= 26cm$$
C.S.A$$ = \pi (R+r)l.$$
$$= \frac{22}{7} (15 + 5) 26$$
$$ = \frac{22}{7}\times 20\times 26$$ $$ = \frac{11440}{7}$$ $$cm^{2}$$
$$ = 1634.28571 cm^2$$
The slant height of the frustum of a cone is $$5\ cm$$. If the difference between the radii of its two circular ends is $$4cm$$. Calculate the height of the frustum.
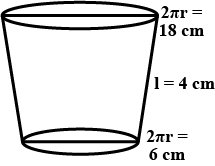
The slant height of the frustum of a cone is $$4cm$$. If the perimeters of its circular bases be $$18cm$$ and $$6cm$$, find the curved surface area of the frustum and also find the cost of painting its total surface at the rate of Rs. $$12.50$$ per $$100{cm}^{2}$$
R.E.F image
$$2\pi R=18$$ $$2\pi r=4$$$$\pi R=9$$ $$\pi r=2$$
$$R=\dfrac{9}{\pi}$$ $$r=\dfrac{2}{\pi}$$
Curved surface area $$=\pi (R+2)l$$
$$=\left(\dfrac{9}{\pi}+\dfrac{2}{\pi}\right)4$$
$$=44cm^2$$
Total cost $$=\dfrac{12.50}{100}\times 44$$
$$=5.5 Rs$$
Fill in the blanks:
A rectangular pyramid has____ faces.
If the total surface area of a solid hemisphere is $$46c{m^2}$$, find its volume
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m ? Assume that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm.
A sphere is inscribed in a cylinder than find the ratio of volume of sphere to volume of cylinder.
A sphere is inscribed in a cylinder
here height of cylinder $$h = 2r$$
Volume of sphere $$ = \dfrac{4}{3}\pi {r^3}$$
and Volume of cylinder $$ = \pi {r^2}h$$
$$\begin{array}{l} =\pi { r^{ 2 } }\left( { 2r } \right) \\ =2\pi { r^{ 3 } } \end{array}$$
Ratio of volume of sphere to volume of cylinder $$ = \dfrac{{4\pi {r^3}}}{{3 \times 2\pi {r^3}}} = 2:3$$
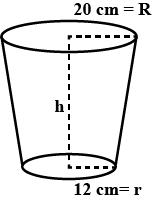
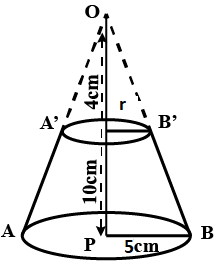
A bucket is in the form of a frustum of a cone of height is $$30\ cm$$ with radii of its lower and upper ends as $$10\ cm$$ and $$20\ cm$$ respectively. Find the capacity of the bucket.
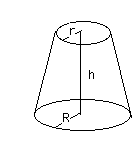
Write the formula for finding volume of a frustum of a cone.
Let $$h$$ be the height, $$R$$ the radius of the lower base, and $$r$$ the radius of the upper base.
Volume of a frustum of a cone $$= \cfrac{\pi}{3} h \left( {R}^{2} + {r}^{2} + Rr \right)$$
The silant height and base diametors of a conical to mb we 25m and 14 m qupertiuity. Find the cost of washisg its surface surface at the rate of RS 210 per 100$$m^{ 2 }$$
A metallic bucket, open at the top, of height $$24cm$$ is in the form of the frustum of a cone, the radii of whose lower and upper circular ends are $$7cm$$ and $$14cm$$ respectively. Find
the volume of water which can completely fill the bucket;
the area of the metal sheet used to make the bucket.
A sphere of diameter $$18\text{ cm}$$ is dropped into a cylindrical vessel of diameter $$36\text{ cm},$$ partly filled with water. If the sphere is completely submerged, then the increase in water level ($$\text{in cm}$$) will be
In the above figure, area of a square $$ABCD$$ is $$S$$ and area of each shaded portion is $$P$$ and area of inner circle is $$Q$$. Then the area of remaining part of a square is
Find the ratio of the volumes of a cone and of a cylinder whose base diameter and heights are equal.
How many planks of size $$2\ cm\times 25\ cm\times 8\ cm$$ can be prepared from a wooden block $$5\ m$$ long. $$70\ cm$$ broad and $$32\ cm$$ thick, assuming that there is no wastage?
Fill in the blanks to make the correct statements true.
A cube of side 4 cm is painted on all its sides. If it is sliced in 1 cubic cm cubes, then number of such cubes that will have exactly two of their faces painted is ____________.
Fill in the blanks the statements are true.
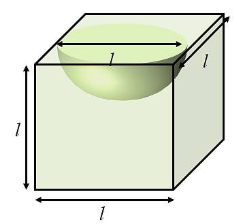
The surface area of a cylinder which exactly fits in a cube of side b is ________.
Mr. Ahuja has to square plots of land which he utilises for two different purposes one for providing free education to the children below the age of $$14$$ years and the other to provide free medical services for the needy villagers. The sum of the areas of two square plots is $$15425{m}^{2}$$. If the difference of their perimeter is $$60m$$, find the sides of the two squares.
Which qualities of Mr. Ahuja are being depicted in the question?
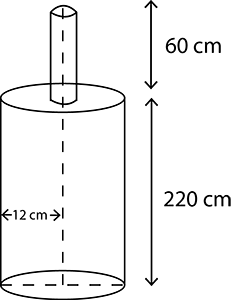
A wooden cylindrical pole is $$7\ m$$ high and its base radius is $$10\ cm$$. Find its weight if the wood weights $$225\ kg$$ per cubic meter.
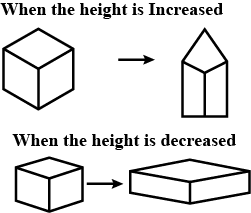
What figure is formed if only the height of a cube is increased or decreased?
If we only increase on decrease the height of a cube, the obtained figure is cuboid.
Fill in the blanks to make the statement true.
The volume of a cylinder which exactly first in a cube of side a is ________.
How many envelopes of size 25 cm $$\times$$ 15 cm can be made from a rectangular sheet of size 4 m $$\times$$ 1.2 m?
A solid sphere of radius $$6cm$$ is melted into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is $$5$$ cm and its height is $$32$$ cm, then find the thickness of the cylinder.
A solid right circular cone of radius 4cm and height 7cm is melted to a sphere. Find the radius of sphere.
State True(1) or False(0).
The curved surface area of a frustum of a cone is $$\pi l (r_1+r_2)$$ and $$l=\sqrt{h^{2}+\left ( r_{1} -r_{2} \right )^{2}}$$ where, $$r_{1}\ and\ r_{2}$$ are the radii of the two ends of the frustum and $$h$$ is the vertical height.
Curved Surface area of a frustum of a cone $$=\pi l({ r }_{ 1 }+{ r }_{ 2 })$$ where $$l$$ is the slant height $$ = \sqrt { { h }^{ 2 }+{ ({ r }_{ 1 }-{ r }_{ 2 }) }^{ 2 } } $$, $$h$$ is the height, $$ { r }_{ 1 } $$ and $${ r }_{ 2 }$$ are the radii of the lower and upper ends of a frustum of a cone.
A bucket is in the form of a frustum of a cone and holds $$28.490$$ litres of water. The radii of the top
and bottom are $$28\ cm$$ and $$21\ cm$$ respectively. Find the height of the bucket.
State True(1) or False(0).
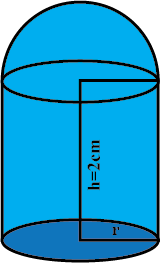
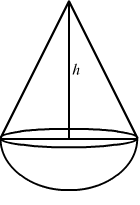
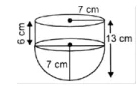
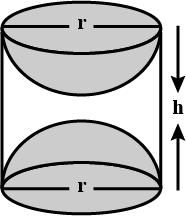
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the Fig. 12.7 is
$$\pi \cfrac{r^{2}}{3}(3h-2r)$$
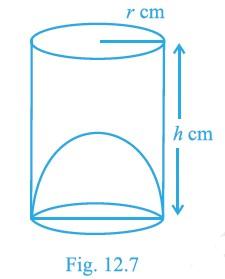
$$\pi \cfrac{r^{2}}{3}(3h-2r)$$
Two identical solid hemispheres of equal base radius $$r$$ cm are stuck together along their bases. The total surface area of the combination is $$k \pi r^2.$$ Find $$k$$.
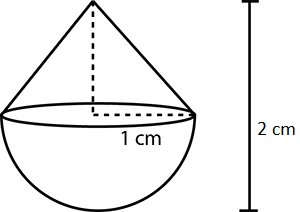
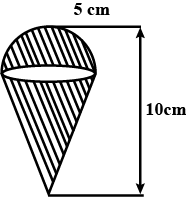
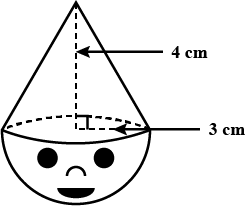
An ice cream cone full of ice cream having radius $$5$$ cm and height $$10$$ cm as shown. Calculate the volume of ice cream (to the nearest integer, in cm$$^3$$), provided that its $$\dfrac{1}{6}$$th part is left unfilled with ice cream. Insert answer in nearest integer.
A milk container of height $$16\ cm$$ is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as $$8\ cm$$ and $$20\ cm$$ respectively. If the approximate cost of milk at the rate of $$Rs.\ 22$$ per litre which the container can hold is Rs___________.
The curved surface area of the frustum of a cone is $$180$$ sq. cm and the circumference of its circular bases are $$18$$ cm and $$6$$ cm respectively. Find the slant height of the frustum of a cone (in cm).
Curved Surface area of a frustum of a cone $$=\pi l({ r }_{ 1 }+{ r }_{ 2})$$ where $$l$$ is the slant height,
$$ { r }_{ 1 } $$ and $${ r }_{ 1 }$$ are the radii of the lower and upper ends of a frustum of a cone.
Circumference of the lower circular base $$ = 2 \pi\ {r}_{1} = 18 $$
$$ \Rightarrow {r}_{1} = \dfrac {9}{\pi} $$ cm
Circumference of the upper circular base $$ = 2 \pi\ {r}_{2} = 6 $$
$$ \Rightarrow {r}_{2} = \dfrac {6}{\pi} $$ cm
Given, curved Surface area of the frustum of a cone $$= \pi \times l \times \left(\dfrac {9}{\pi} + \dfrac {6}{\pi}\right) = 180 $$
$$ l = 12 $$ cm
Circumference of the lower circular base $$ = 2 \pi\ {r}_{1} = 18 $$
$$ \Rightarrow {r}_{1} = \dfrac {9}{\pi} $$ cm
Circumference of the upper circular base $$ = 2 \pi\ {r}_{2} = 6 $$
$$ \Rightarrow {r}_{2} = \dfrac {6}{\pi} $$ cm
Given, curved Surface area of the frustum of a cone $$= \pi \times l \times \left(\dfrac {9}{\pi} + \dfrac {6}{\pi}\right) = 180 $$
$$ l = 12 $$ cm
A container open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm respectively. Find the cost of milk (correct upto two decimal places) which can completely fill the container at the rate of rs. 21 per litre. $$[ Take \; \pi=\frac {22}{7}]$$
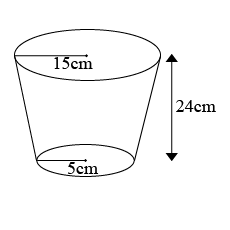
A bucket is $$40cm$$ in diameter at the top and $$28cm$$ in diameter at the bottom. Find the capacity of the bucket in litres, if it is $$21cm$$ deep. Also find the cost of tin sheet used in making the bucket, if the cost of tin is $$Rs.\space 1.50$$ per sq dm.
$$\Rightarrow r_1 = 20\space cm, r_2 = 14\space cm$$ and $$h = 21\space cm$$
Now, the required capacity (i.e. volume) of the bucket
$$= \displaystyle\frac{\pi h}{3}(r_1^2 + r_1r_2 + r_2^2) $$
$$= \displaystyle\frac{22\times21}{7\times3}(20^2 + 20\times14 + 14^2) $$
$$= 22\times576\space cm^3 $$
$$= 19272\space cm^3 $$
$$= \displaystyle\frac{19272}{1000} litres = 19.272\space litres$$
Now,
$$l = \sqrt{(r_1 - r_2)^2 + h^2}$$
$$l= \sqrt{(20 - 14)^2 + 21^2}$$
$$l= \sqrt{6^2 + 21^2}$$
$$l= \sqrt{36+441} = \sqrt{477} = 21.84\space cm$$
$$\therefore$$ Total surface area of the bucket (which is open at the top)
$$= \pi l (r_1 + r_2) + \pi r_2^2$$
$$= \pi[(r_1 + r_2)l + r_2^2]$$
$$= \displaystyle\frac{22}{7}[(20+14)21.84 + 14^2] = 2949.76\space cm^2$$
$$\therefore$$ Required cost of the tin sheet at the rate of $$Rs. 1.50$$ per $$dm^2$$ i.e. $$100\space cm^2$$
$$= \displaystyle\frac{1.50\times2949.76}{100} \approx Rs. 44.25$$
From a cylinder whose height is 8 cm and radius is 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid. $$\displaystyle \left ( \pi =\frac{22}{7} \right )$$.
Three cubes whose edges are $$3$$ cm, $$4$$ cm and $$5$$ cm, respectively are melted to from a single cube. Find the surface area of the new cube.
Three solid spheres of gold whose radii are $$1$$ cm, $$6$$ cm and $$8$$ cm, respectively are melted into a single solid sphere. Find the radius of the sphere.
A spherical ball of radius $$3\ cm$$ is melted and recast into three spherical balls. The radii of two of the balls are $$1.5\ cm$$ and $$2\ cm.$$ Find the radius of the third ball.
If a sphere of radius $$6 \ cm$$ is melted and drawn into a wire of radius $$0.02\ cm$$ then what is the length of the wire ?
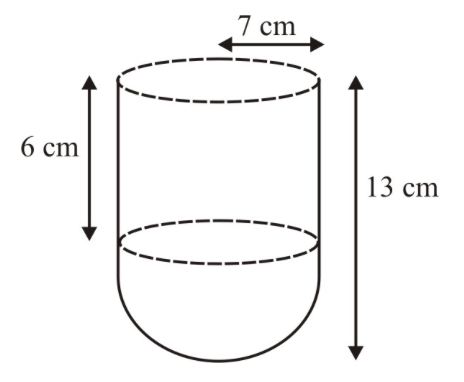
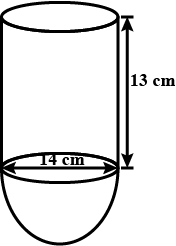
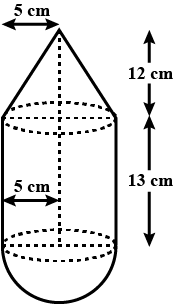
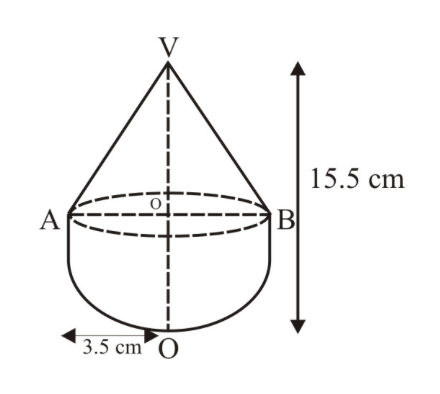
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is $$14\ cm$$ and the total height of the vessel is $$13\ cm$$. Find the inner surface area of the vessel.
The radius(r) of the cylindrical part and the hemispherical part is the same (i.e., 7 cm)
Height of hemispherical part = Radius $$= 7$$ cm
Height of cylindrical part (h) $$= 13 - 7 = 6$$ cm
Inner surface area of vessel = $$2\times \dfrac{22}{7}\times 7 \times 6+ 2\times \dfrac{22}{7}\times 7\times 7$$
= $$44(6 + 7)$$
= $$44 \times 13$$
= $$572 cm^2$$
Height of hemispherical part = Radius $$= 7$$ cm
Height of cylindrical part (h) $$= 13 - 7 = 6$$ cm
Inner surface are of the vessel = CSA of cylindrical part + CSA of hemispherical part
= $$2\pi rh + 2\pi r^2$$
= $$2\pi rh + 2\pi r^2$$
Inner surface area of vessel = $$2\times \dfrac{22}{7}\times 7 \times 6+ 2\times \dfrac{22}{7}\times 7\times 7$$
= $$44(6 + 7)$$
= $$44 \times 13$$
= $$572 cm^2$$
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to $$1\ cm$$ and the height of the cone is equal to its radius. Find the volume of the solid in terms of $$\pi$$.
Given:
Height ($$h$$) of conical part = radius ($$r$$) of conical part $$= 1\ cm$$
Radius ($$r$$) of hemispherical part = radius of conical part $$= 1\ cm$$
Volume of solid = Volume of conical part + Volume of hemispherical part
Height ($$h$$) of conical part = radius ($$r$$) of conical part $$= 1\ cm$$
Radius ($$r$$) of hemispherical part = radius of conical part $$= 1\ cm$$
Volume of solid = Volume of conical part + Volume of hemispherical part
$$=\dfrac{1}{3}\pi r^2h+\dfrac{2}{3} \pi r^3$$
$$=\dfrac{1}{3}\pi \times 1^2\times 1+\dfrac{2}{3}\pi\times 1^3$$
$$=\dfrac{1}{3}\pi \times 1 + \dfrac{2}{3}\pi \times 1$$
$$=\dfrac{\pi}{3}+\dfrac{2\pi}{3}=\pi $$ $$cm^3$$
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is $$10\ cm$$, and its base is of radius $$3.5\ cm$$, find the total surface of the article.
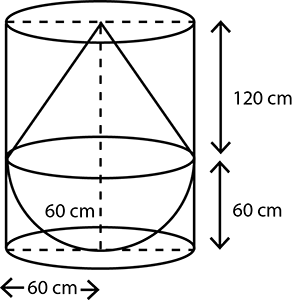
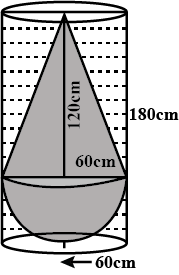
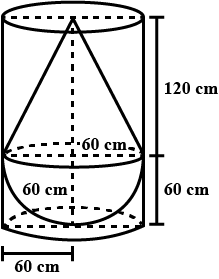
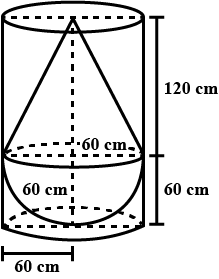
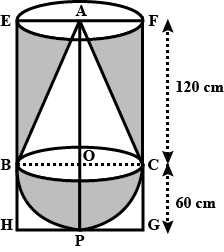
A solid consisting of a right circular cone of height $$120$$ cm and radius $$60$$ cm standing on a hemisphere of radius $$60$$ cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is $$60$$ cm and its height is $$180$$ cm.
Given:
Radius ($$r$$) of hemispherical part = Radius ($$r$$) of conical part $$= 60 $$cm
Height ($$h_1$$) of conical part of solid $$= 120$$ cm
Height ($$h_1$$) of cylinder $$= 180$$ cm
Radius ($$r$$) of cylinder $$= 60$$ cm
Volume of water left = Volume of cylinder - Volume of solid
= Volume of cylinder - (Volume of cone + Volume of hemisphere)
$$=\pi r^2 h_1 -[\dfrac{1}{3}\pi r^2 h_2+\dfrac{2}{3}\pi r^3]$$
$$=\pi\times 60^2 \times (180)-[\dfrac{1}{3}\pi \times 60^2 \times 120 + \dfrac{2}{3}\pi \times 60^3]$$
$$= \pi (60)^2[180 - (40 + 40)]$$
$$= \pi (3600)[100]$$
$$ = 3,60,000\times \dfrac{22}{7}=1131428.57 \space\ $$ cm$$^3 $$
Radius ($$r$$) of hemispherical part = Radius ($$r$$) of conical part $$= 60 $$cm
Height ($$h_1$$) of conical part of solid $$= 120$$ cm
Height ($$h_1$$) of cylinder $$= 180$$ cm
Radius ($$r$$) of cylinder $$= 60$$ cm
Volume of water left = Volume of cylinder - Volume of solid
= Volume of cylinder - (Volume of cone + Volume of hemisphere)
$$=\pi r^2 h_1 -[\dfrac{1}{3}\pi r^2 h_2+\dfrac{2}{3}\pi r^3]$$
$$=\pi\times 60^2 \times (180)-[\dfrac{1}{3}\pi \times 60^2 \times 120 + \dfrac{2}{3}\pi \times 60^3]$$
$$= \pi (60)^2[180 - (40 + 40)]$$
$$= \pi (3600)[100]$$
$$ = 3,60,000\times \dfrac{22}{7}=1131428.57 \space\ $$ cm$$^3 $$
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Diameter of hemisphere = Edge of the cube $$= l$$
Radius of hemisphere $$r=\dfrac{l}{2}$$
Total surface area of solid = Surface area of cubical part + Closed Surface of hemisphere part - Area of base of hemispherical part
$$= 6(Edge)^2 + 2\pi r^2 - \pi r^2= 6(Edge)^2+\pi r^2$$
Total surface are of solid = $$6l^2 + \pi \times \left(\dfrac{l}{2}\right)^2$$
= $$6l^2 +\dfrac{\pi l^2}{4}$$
= $$6l^2 +\dfrac{\pi l^2}{4}$$
$$ = \dfrac{1}{4}[24+\pi] l^2$$ sq. units
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are $$15$$ cm by $$10$$ cm by $$3.5$$ cm. The radius of each of the depressions is $$0.5$$ cm and the depth is $$1.4$$ cm. Find the volume of wood in the entire stand .
Depth (h) of each conical depression $$= 1.4$$ cm
Radius (r) of each conical depression $$= 0.5$$ cm
Radius (r) of each conical depression $$= 0.5$$ cm
$$\mbox{Volume of wood = Volume of cuboid - 4 (Volume of a conical depression)}$$
$$= l \times b\times h-4\times \dfrac{1}{3}\pi r^2 h$$
$$= l \times b\times h-4\times \dfrac{1}{3}\pi r^2 h$$
$$= 15 \times 10 \times 3.5 - 4 \times \dfrac{1}{3}\times \dfrac{22}{7}\times \left(\dfrac{1}{2}\right)^2\times 1.4$$
$$=525 - 1.47$$
$$=523.53 \space\ \text{cm}^3$$
A spherical glass vessel has a cylindrical neck $$8\ cm$$ long, $$2\ cm$$ in diameter; the diameter of the spherical part is $$8.5\ cm$$. By measuring the amount of water it holds, a child finds its volume to be $$345$$ $$cm^3$$. Check whether she is correct, taking the above as the inside measurements, and $$\pi$$ $$= 3.14$$.
Given:
Height (h) of cylindrial part $$= 8$$ cm
Height (h) of cylindrial part $$= 8$$ cm
Radius ($$r_2$$) of cylindrical part = $$\dfrac{2}{2} = 1$$ cm
$$=\dfrac{4}{3}\pi r_{1}^3 + \pi r_{2}^2 h$$
Radius ($$r_1$$) of spherical part = $$\dfrac{8.5}{2}=4.25$$ cm
$$\mbox{Volume of vessel = Volume of sphere + Volume of cylinder}$$
$$=\dfrac{4}{3}\pi r_{1}^3 + \pi r_{2}^2 h$$
$$=\dfrac{4}{3}\pi \left(\dfrac{8.5}{2}\right)^3 +\pi (1)^2 (8)$$
$$= \dfrac{4}{3}\times 3.14 \times 76.765625 + 8 \times 3.14$$
$$= 321.392 + 25.12$$
$$= 346.51 $$ cm $$^3$$
So, the child measurement is wrong.
A cubical block of side $$7\ cm$$ is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
The diagram shows that the greatest diameter possible for such hemisphere is equal to the length of cube edge, i.e., $$7$$cm.
Radius $$(r)$$ of hemispherical part $$=\dfrac{7}{2}$$ $$= 3.5$$cm
Total surface area of solid $$=$$ Surface area of remaining cubical part $$+$$ CSA of hemispherical part $$+$$ Area of base of hemispherical part
$$=6(Edge)^2 + 2\pi r^2- \pi r^2 \\= 6(Edge)^2+ \pi r^2$$
$$=6(7)^2+\dfrac{22}{7}\times \dfrac{7}{2}\times \dfrac{7}{2}$$
$$=294 + 38.5 $$
$$=332.5$$ $$cm^2$$
The frustum cone curved surface area is $$210 m^2$$. The upper and lower circle area of a cone is $$24$$ and $$15 m^2$$. Find the total surface area.
Find the volume of a frustum cone, whose base and upper area of a circle is $$40cm^2$$ and $$90cm^2$$. (Insert answer in nearest integer).
The total surface area of frustum cone is $$1200 ft^2$$. The radius of a top cone is $$3$$ and the bottom cone is $$6$$ ft. What is the curved surface area of a frustum of cone?
The radii of the circular ends of a frustum of height 4 cm are 7 cm and 4 cm respectively. Find the total surface area. (Use $$\pi = 3$$).
Find the volume of the frustum cone whose base and top radius is $$8$$ cm and $$4$$ cm respectively. The height of the cone is $$5$$ cm. (Use $$\pi = \dfrac{22}{7}$$).
(Insert answer in nearest integer).
The base and top radius of a cone is $$2.1$$ m and $$0.8$$ m respectively. The height of the cone is $$24$$ m. What is the volume of frustum of a cone? (Use $$\pi = 3.14$$). Insert answer in nearest integer,
A cone has base radius 55 cm is cut from the top. Calculate the volume of the frustum. Insert answer in terms of $$\pi$$.
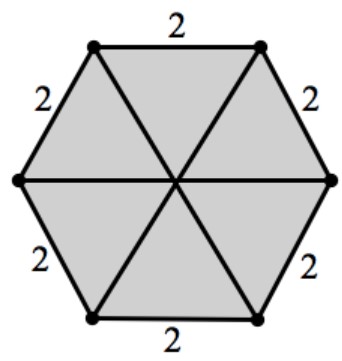
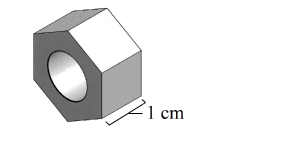
The figure shows a 3-D view of a metal nut. The metal nut has two regular hexagonal faces. The side of a hexagonal face is $$2\ cm$$ and has a thickness of $$1\ cm.$$ A hole of a diameter of $$2\ cm$$ is present in the metal nut. Given the density of the metal is $$7.9$$ grams per cubic cm., calculate the mass of this nut.
The area of an equilateral triangle $$=\dfrac { 1 }{ 2 } (b)\left( \dfrac { b\sqrt { 3 } }{ 2 } \right)$$
$$=\dfrac { 1 }{ 2 } (2)\left( \dfrac { 2\sqrt { 3 } }{ 2 } \right) $$
$$=\sqrt { 3 }$$
There are $$6$$ of those, so the area of the hexagon is $$6\sqrt { 3 }$$ square cms.
The diameter of the hole is $$2\ cm$$, so it has a radius of $$1\ cm$$
Therefore the area of the hole $$=π$$ square cms.
$$\therefore$$ Area of the hexagonal face of the nut $$=6\sqrt { 3 } -π$$ square cms.
Hence volume of the nut $$=(6\sqrt { 3 } -π)\times 1$$
$$=6\sqrt { 3 } -π$$ cubic cms.
We know that $$\mathrm{Density=\dfrac{Mass}{Volume}}$$
Given, the density of nut $$=7.9$$ grams per cubic cm
$$\Rightarrow 7.9=\dfrac { m }{ 6\sqrt { 3 } -π } $$
$$ \Rightarrow 7.9(6\sqrt { 3 } -π)=m$$
$$ \Rightarrow 57.2706=m$$
$$\Rightarrow m=57$$
Hence, the mass of the nut is $$57$$ grams (approx).
A container open at the top, is in the form of a frustum of a cone of height $$24$$ cm with radii of its lower and upper circular ends, as $$8$$ cm and $$20$$ cm respectively. Find the cost of milk which can completely fill the container at the rate of $$21 $$ per litre. [Use $$\displaystyle \pi =\frac { 22 }{ 7 } $$].
The slant height of the frustum of a cone is $$4$$cm, and the perimeter of its circular bases are $$18$$cm and $$6$$cm respectively. Find the curved surface area and total surface area of the frustum.
The radii of two circular ends of a frustum shaped dust bin are $$15$$cm and $$8$$cm. If its depth is $$63$$cm, find volume of the dust bin.
Given $$r_1=15$$cm, $$r_2=8$$cm, $$h=63$$cm
Volume of the dustbin (frustum)$$=\displaystyle\frac{1}{3}\pi h(r^2_1+r^2_2+r_1r_2)$$
$$=\displaystyle\frac{1}{3}\times \frac{22}{7}\times 63(15^2+8^2+15\times 8)$$
$$=\displaystyle\frac{1}{3}\times \frac{22}{7}\times 63(225+64+120)$$
$$=66\times 409=26, 994$$
$$\therefore$$ Volume of the dustbin$$=26, 994cm^3$$.
Volume of the dustbin (frustum)$$=\displaystyle\frac{1}{3}\pi h(r^2_1+r^2_2+r_1r_2)$$
$$=\displaystyle\frac{1}{3}\times \frac{22}{7}\times 63(15^2+8^2+15\times 8)$$
$$=\displaystyle\frac{1}{3}\times \frac{22}{7}\times 63(225+64+120)$$
$$=66\times 409=26, 994$$
$$\therefore$$ Volume of the dustbin$$=26, 994cm^3$$.
From the top of a cone of base radius $$12$$cm and height $$20$$cm, a small cone of base radius $$3$$cm is to be cut off. How far down the vertex is the cut to be made? Find the volume of the frustum so obtained.
Given, $$r_1=12cm, h_1=20cm, r_2=3cm, h_2=?$$
We know, $$\displaystyle\frac{r_1}{r_2}=\frac{h_1}{h_2}$$
$$\therefore \displaystyle\frac{12}{3}=\frac{20}{h_2}$$
$$\therefore h_2=\displaystyle\frac{3\times 20}{12}=5cm$$
$$\therefore$$ The cut to be made at $$5$$cm from the vertex.
Volume of the frustum$$=\displaystyle\frac{1}{3}\pi h(r^2_1+r^2_2+r_1r_2)$$
$$=\displaystyle\frac{1}{3}\times \frac{22}{7}\times 15(12^2+3^2+12\times 3)=\frac{110}{7}\times (144+9+36)$$
$$=\displaystyle\frac{110}{7}\times 189=2,970$$
$$\therefore$$Volume of the frustum$$=2,970cm^3$$.
We know, $$\displaystyle\frac{r_1}{r_2}=\frac{h_1}{h_2}$$
$$\therefore \displaystyle\frac{12}{3}=\frac{20}{h_2}$$
$$\therefore h_2=\displaystyle\frac{3\times 20}{12}=5cm$$
$$\therefore$$ The cut to be made at $$5$$cm from the vertex.
Volume of the frustum$$=\displaystyle\frac{1}{3}\pi h(r^2_1+r^2_2+r_1r_2)$$
$$=\displaystyle\frac{1}{3}\times \frac{22}{7}\times 15(12^2+3^2+12\times 3)=\frac{110}{7}\times (144+9+36)$$
$$=\displaystyle\frac{110}{7}\times 189=2,970$$
$$\therefore$$Volume of the frustum$$=2,970cm^3$$.
A flower vase is in the form of a frustum of a cone. The perimeter of the ends are $$44$$cm and $$8.4\pi$$cm. If the depth is $$14$$cm, find how much water it can hold?
A vessel is in the form of a frustum of a cone. Its radius at one end is $$8\ cm$$ and the height is $$14\ cm$$. If its volume is $$\displaystyle\dfrac{5676}{3}\ cm^3$$, find the radius of the other end.
A petrol tank is in the shape of a cylinder with hemispheres of same radius attached to both ends. If the total length of the tank is $$6$$m and the radius is $$1$$m, what is the capacity of the tank in litres.
Tank is in the shape of a cylinder with hemispheres of same radius attached to both ends.
Given : Length of the tank $$=6\ m$$
Radius $$r=1\ m$$ is same for all shapes
Height of hemispheres $$=$$ Radius $$(r)=1\ m$$
$$\therefore$$ Height of the cylinder $$(h)=6-2=4\ m$$
And radius of hemisphere $$=1\ m$$
Now, volume of the tank $$=$$ volume of two hemipheres $$+$$ volume of a cylinder
Volume of a cylinder $$=\pi r^2 h$$
$$=\pi (1)^2\times 4$$
$$=4 \pi$$
Volume of a hemisphere $$=\dfrac{2}{3}\pi r^3$$
$$=\dfrac{2}{3}\pi (1)^3$$
$$=\dfrac{2 \pi}{3}$$
$$\therefore$$ Volume of the tank $$=2\times \dfrac{2\pi}{3}+4\pi$$
$$=\dfrac{16\pi}{3}$$
$$=16.75516\ m^3$$
$$=16577.16$$ litres
A storage tank consists of a circular cylinder with a hemisphere adjoined on either ends. The external diameter of the cylinder is $$1.4$$m and length is $$8$$m, find the cost of painting it on the outside at the rate of Rs.$$10$$per $$m^2$$.
External diameter of cylinder $$= 1.4m$$
$$\therefore $$ External radius = $$\dfrac { 1.4 }{ 2 } =0.7m$$
or Radius of hemisphere = 0.7 m
Height of cylinder, h = 8 m
Total outer area to be painted = $$2\pi rh+\pi { r }^{ 2 }+2\pi { r }^{ 2 }$$
= $$\pi r\left( 2h+3r \right) $$
= $$\dfrac { 22 }{ 7 } \times 0.7\left( 2\times 8+3\times 0.7 \right) $$
= $$2.2\times 18.1=38.82{ m }^{ 2 }$$
Cost of painting = Rs. $$\left( 38.82\times 10 \right) =Rs.388.2$$
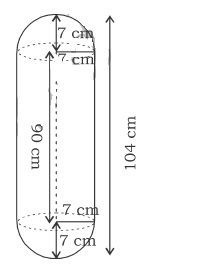
A solid is composed of a cylinder with hemispherical ends. If the whole lengthe of the solid is $$104$$cm and the radius of each hemispherical end is $$7$$cm, find the cost of polishing its surface at the rate of Rs. $$4$$ per $$100cm^2$$.
Hemispherical part: $$r=7cm$$
Cylindrical part: $$r=7cm, h=104-(7+7)=90cm$$
Total surface area of the solid$$=$$ CSA of cylindricall part$$+2\times $$CSA of hemispherical part
$$=2\pi rh+2\times 2\pi r^2=2\pi r(h+2r)$$
$$=2\times \displaystyle\frac{22}{7}\times 7[90+2(7)]cm^2$$
$$=44\times 104cm^2=4576cm^2$$
$$\therefore$$ TSA of the solid$$=4.576cm^2$$
Cost of polishing at the rate of Rs.$$4$$ per $$100cm^2$$
$$=4576\times\displaystyle\frac{Rs.4}{100}=Rs.183.04$$
$$\therefore$$ Cost of polishing the solid$$=Rs. 183.04$$.
Cylindrical part: $$r=7cm, h=104-(7+7)=90cm$$
Total surface area of the solid$$=$$ CSA of cylindricall part$$+2\times $$CSA of hemispherical part
$$=2\pi rh+2\times 2\pi r^2=2\pi r(h+2r)$$
$$=2\times \displaystyle\frac{22}{7}\times 7[90+2(7)]cm^2$$
$$=44\times 104cm^2=4576cm^2$$
$$\therefore$$ TSA of the solid$$=4.576cm^2$$
Cost of polishing at the rate of Rs.$$4$$ per $$100cm^2$$
$$=4576\times\displaystyle\frac{Rs.4}{100}=Rs.183.04$$
$$\therefore$$ Cost of polishing the solid$$=Rs. 183.04$$.
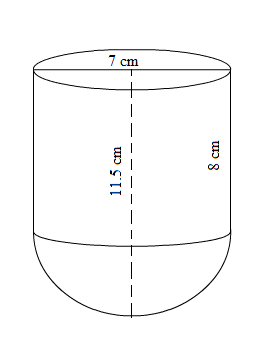
A cup is in the form of a hemisphere surmounted by a cylinder. The height of the cylindrical portion is $$8\ cm$$ and the total height of teh cup is $$11.5\ cm.$$ Find the total surface area of the cup.
Given:
Height of the cylinder $$=8\ cm$$
Total height of the cup $$=11.5\ cm$$
Height of hemisphere $$=11.5-8$$
$$=3.5\ cm$$
The radius of the hemisphere will be equal to the height of the hemisphere that is $$3.5\ cm.$$
Radius, $$r=3.5\ cm$$
Now, total surface area of the cup $$=$$ Curved surface area of cylinder $$+$$ Curved surface area of hemisphere
$$=2\pi rh+2\pi r^2$$
$$=2\pi r(h+r)$$
$$=2\pi\times 3.5(8 + 3.5)$$
$$=7\pi(11.5)$$
$$=253\ cm^2$$
Hence, the total surface area of the cup is $$253\ cm^2.$$
From the top of a cone of base radius $$24$$cm and height $$45$$cm, a cone of slant height $$17$$cm is cut off. What is the volume of the remaining frustum of the cone?
$${ L }^{ 2 }={ R }^{ 2 }+{ H }^{ 2 }\Rightarrow L=\sqrt { { 24 }^{ 2 }+{ 45 }^{ 2 } } =\sqrt { 2601 } =51cm$$
we know that, $$\triangle OAB\sim \triangle OCD$$, therefore
$$\dfrac { r }{ 24 } =\dfrac { h }{ 45 } =\dfrac { 17 }{ 51 } $$
$$\Rightarrow \quad \dfrac { r }{ 24 } =\dfrac { 17 }{ 51 } \Rightarrow r=\dfrac { 24 }{ 3 } =8cm$$
$$\Rightarrow \quad \dfrac { h }{ 45 } =\dfrac { 17 }{ 51 } \Rightarrow h=\dfrac { 45 }{ 3 } =15cm$$
$$\therefore $$ Height of frustum $$= 45 - 15 = 30cm$$
$$\therefore $$ Volume of frustum = $$\dfrac { 1 }{ 3 } \pi \left( { R }^{ 2 }+{ r }^{ 2 }+Rr \right) h=\dfrac { 1 }{ 3 } \times \dfrac { 22 }{ 7 } \times 30\left( { 24 }^{ 2 }+{ 8 }^{ 2 }+24\times 8 \right) $$
= $$\dfrac { 220 }{ 7 } \times 832=26148.57{ cm }^{ 3 }$$
A toy is in the form of a cone mounted on a hemisphere with the same radius. The diameter of the conical portion is $$6$$cm and its height is $$4$$cm. Determine the surface area and volume of the solid.
Conical portion
$$r=3cm, h=4cm$$
$$l^2=r^2+h^2=3^2+4^2=9+16$$
$$l^2=25$$
$$l=\sqrt{25}=5$$cm
Spherical portion $$r=3cm$$
Surface area of the toy$$=$$ CSA of hemisphere$$+$$ CSA of cone
$$=2\pi r^2+\pi rl=2\times\displaystyle\frac{22}{7}\times 3\times 3cm^2+\frac{22}{7}\times 3\times 5cm^2$$
$$=\displaystyle\frac{396}{7}cm^2+\frac{330}{7}cm^2=\frac{726}{7}cm^2=103.71cm^2$$
Surface area of the toy$$=103.71cm^2$$
Volume of the toy$$=$$ Volume of hemisphere$$+$$ Volume of cone
$$=\displaystyle\frac{2}{3}\pi r^3+\frac{1}{3}\pi r^2h=\displaystyle\frac{2}{3}\times \frac{22}{7}\times 3\times 3\times 3cm^3+\frac{1}{3}\times \frac{22}{7}\times 3\times 3\times 4cm^3$$
$$=\displaystyle\frac{396}{7}cm^3+\frac{264}{7}cm^3=\frac{660}{7}cm^3$$
$$\therefore$$ Volume of the toy$$=94.28cm^3$$.
$$r=3cm, h=4cm$$
$$l^2=r^2+h^2=3^2+4^2=9+16$$
$$l^2=25$$
$$l=\sqrt{25}=5$$cm
Spherical portion $$r=3cm$$
Surface area of the toy$$=$$ CSA of hemisphere$$+$$ CSA of cone
$$=2\pi r^2+\pi rl=2\times\displaystyle\frac{22}{7}\times 3\times 3cm^2+\frac{22}{7}\times 3\times 5cm^2$$
$$=\displaystyle\frac{396}{7}cm^2+\frac{330}{7}cm^2=\frac{726}{7}cm^2=103.71cm^2$$
Surface area of the toy$$=103.71cm^2$$
Volume of the toy$$=$$ Volume of hemisphere$$+$$ Volume of cone
$$=\displaystyle\frac{2}{3}\pi r^3+\frac{1}{3}\pi r^2h=\displaystyle\frac{2}{3}\times \frac{22}{7}\times 3\times 3\times 3cm^3+\frac{1}{3}\times \frac{22}{7}\times 3\times 3\times 4cm^3$$
$$=\displaystyle\frac{396}{7}cm^3+\frac{264}{7}cm^3=\frac{660}{7}cm^3$$
$$\therefore$$ Volume of the toy$$=94.28cm^3$$.
A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is $$16$$cm and its height is $$15$$cm. Find the cost of painting the toy at $$7$$per Rs.$$100cm^2$$.
Total area to be painted = $$\pi rl+2\pi { r }^{ 2 }$$
= $$\pi r\left( l+2r \right) $$
= $$\dfrac { 22 }{ 7 } \times 8\left( \sqrt { { r }^{ 2 }+{ h }^{ 2 } } +2\times 8 \right) $$
= $$\dfrac { 176 }{ 7 } \left( \sqrt { { 8 }^{ 2 }+{ 15 }^{ 2 } } +16 \right) $$
= $$\dfrac { 176 }{ 7 } \times \left( 17+16 \right) =\dfrac { 176\times 33 }{ 7 } =829.71{ cm }^{ 2 }$$
Cost of painting = Rs. $$\left( \dfrac { 7 }{ 100 } \times 829.71 \right) =Rs.58.08$$
A rocket is in the shape of a cylinder with a cone attached to one end and a hemisphere attached to the other. All of them are of the same radius of $$1.5$$m. The total length of the rocket is $$7$$m and height of the cone is $$2$$m. Calculate the volume of the rocket.
Given :
Radius $$r=1.5\ m$$, Total length =$$7\ m$$
Height of the cone $$(h_1)=2\ m$$
Height of hemisphere $$=$$ Radius of hemisphere $$=1.5\ m$$
Height of cylinder $$(h_2)=$$ Total length $$-h_1-r=7-2-1.5=3.5\ m$$
Now, volume of the rocket $$=$$ Volume of the cylinder $$+$$ volume of a cone $$+$$ volume of a hemisphere ........ $$(i)$$
We know that, Volume of the cylinder $$=\pi r^2 h_2$$
$$=\pi(1.5)^2\times 3.5$$
$$=7.875\pi\ m^3$$
Volume of a cone $$=\pi r^2 \dfrac{h_1}{3}$$
$$=\pi(1.5)^2\times \dfrac{2}{3}$$
$$=1.5\pi\ m^3$$
Volume of a hemisphere $$=\dfrac{2}{3}\pi r^3$$
$$=\dfrac{2}{3}\pi\times (1.5)^3$$
$$=2.25\pi\ m^3$$
From $$(i)$$
Volume of the rocket $$=7.875\pi+1.5\pi+2.25\pi$$
$$=11.625\pi\ m^3$$
$$=36.521\ m^3$$
A bucket is in the shape of a frustum with the top and bottom circles of radii $$15$$cm and $$10$$cm. Its depth is $$12$$cm. Find its curved surface area and total surface area. (Express the answer in terms of $$\pi$$).
Two similiar cones have volumes 12$$\pi$$ cu. units and 96 $$\pi$$ cu. units. If the curved surface area of the smaller cone is 15 $$\pi$$ sq. units, what is the curved surface area of the larger one
A bucket is in the form of frustum of cone and holds $$28.490$$ litres of water. The radii of the top and bottom are $$28$$ cm and $$21$$ cm respectively. Find the height of the bucket.
A test tube has diameter $$20\ mm$$ and height is $$15\ cm$$. The lower portion is a hemisphere. Find the capacity of the test tube. $$(\pi = 3.14)$$
The volume of a cone is the same as that of volume of a cylinder whose height is 9 cm and diameter 40 cm. Find the radius of the base of the cone if its height is 108 cm.
Two cubes each of volume $$27\ cm^{3}$$ are joined end to end to form a solid. Find the surface area (cm$$^2$$) of the resulting cuboid.
The perimeter of the ends of a frustum of a cone are $$44$$ cm and $$8.4$$ $$\pi$$ cm. If the depth is $$14$$ cm, then find its volume.
The radii of two circular ends of a frustum of a cone shaped dust bin are $$15\ cm$$ and $$8\ cm$$. If its depth is $$63\ cm$$, find the volume of the dust bin.
The radii of two circular ends of a frustum shaped bucket are $$15$$ cm and $$8$$ cm. If its depth is $$63$$ cm, find the capacity of the bucket in litres. (Take $$\pi = \dfrac{22}{7}$$)
The curved surface area of a cone is $$1159\dfrac{5}{7}\ cm^2$$.Area of its base is $$254\dfrac{4}{7}\ cm^2$$.Find its volume.
A solid is in the form of one mounted on a right circular cylinder both having same radii of their bases. The base of the cone is placed on the top base of the cylinder. If the radius of the base and height of the cone be $$7\ cm$$ and $$10\ cm$$ respectively and the total height of the solid be $$30\ cm$$, find the volume of the solid.
A solid wooden toy is in the form of a cone surmounted on a hemisphere. If the radii of the hemisphere and the base of the cone are $$3.5\text{ cm}$$ each and the total height of the toy is $$17.5\text{ cm}$$, then find the volume of wood used in the toy. Use $$\pi =\cfrac { 22 }{ 7 } $$
Hemispherical portion:
Radius $$r=3.5\text{ cm}$$
Conical portion:
Radius $$r=3.5\text{ cm}$$
Heignt, $$h=17.5-3.5=14\text{ cm}$$
Volume of the wood $$=$$ Volume of the hemisphere $$+$$ Volume of the cone
$$=\cfrac { 2 }{ 3 } \pi { r }^{ 3 }+\cfrac { 1 }{ 3 } \pi { r }^{ 2 }h$$
$$=\cfrac { \pi { r }^{ 3 } }{ 3 } (2r+h)$$
$$=\cfrac { 22 }{ 7 } \times \cfrac { 3.5\times 3.5 }{ 3 } \times (2\times 3.5+14)$$
$$=269.5\text{ cm}^3$$
Hence, the volume of the wood used in the toy is equal to $$269.5\text{ cm}^3$$
On a Hemisphere, frustrum of a cone shaped shuttle-cock is used for playing Badminton. The outer radius of the frustrum of cone is $$5cm$$ and its inner radius is $$2cm$$. The height of the entire shuttle-cock is $$7cm$$. Find the outer surface area of the shuttle-cock.
Radius of hemisphere $$r=$$ smaller radius of frustrum of cone $$=2cm$$
For the frustrum of cone
$${r}_{1}=$$ bigger radius $$=5cm$$
$${r}_{2}=$$ smaller radius $$=2cm$$
Height$$(h)=$$ total height $$-$$ radius of hemisphere
$$=7-2=5\ cm$$
Now, $$l=\sqrt { { h }^{ 2 }+{ \left( { r }_{ 1 }-{ r }_{ 2 } \right) }^{ 2 } } =\sqrt { { 5 }^{ 2 }+{ (5-2) }^{ 2 } } =\sqrt { 25+9 } =\sqrt { 34 } $$
$$l=5.83\ cm=$$ slant height of the frustrum of a cone.
External surface area of the shuttle cock
$$=$$ Curved Surface Area of frustum of a cone $$+$$ Curved Surface Area of hemisphere
$$=\pi l\left( { r }_{ 1 }+{ r }_{ 2 } \right) +2\pi { r }^{ 2 }$$
$$=\pi \left[ l\left( { r }_{ 1 }+{ r }_{ 2 } \right) +2{ r }^{ 2 } \right] $$
$$=\cfrac { 22 }{ 7 } \left[ 5.83(5+2)+2(4) \right] $$
$$=\cfrac { 22 }{ 7 } \left[ 5.83\times 7+8 \right] $$
$$=\cfrac { 22 }{ 7 } \times 48.81=153.40\ { cm }^{ 2 }$$
For the frustrum of cone
$${r}_{1}=$$ bigger radius $$=5cm$$
$${r}_{2}=$$ smaller radius $$=2cm$$
Height$$(h)=$$ total height $$-$$ radius of hemisphere
$$=7-2=5\ cm$$
Now, $$l=\sqrt { { h }^{ 2 }+{ \left( { r }_{ 1 }-{ r }_{ 2 } \right) }^{ 2 } } =\sqrt { { 5 }^{ 2 }+{ (5-2) }^{ 2 } } =\sqrt { 25+9 } =\sqrt { 34 } $$
$$l=5.83\ cm=$$ slant height of the frustrum of a cone.
External surface area of the shuttle cock
$$=$$ Curved Surface Area of frustum of a cone $$+$$ Curved Surface Area of hemisphere
$$=\pi l\left( { r }_{ 1 }+{ r }_{ 2 } \right) +2\pi { r }^{ 2 }$$
$$=\pi \left[ l\left( { r }_{ 1 }+{ r }_{ 2 } \right) +2{ r }^{ 2 } \right] $$
$$=\cfrac { 22 }{ 7 } \left[ 5.83(5+2)+2(4) \right] $$
$$=\cfrac { 22 }{ 7 } \left[ 5.83\times 7+8 \right] $$
$$=\cfrac { 22 }{ 7 } \times 48.81=153.40\ { cm }^{ 2 }$$
Hence, outer surface area is $$153.40\ cm^2$$
A cuboid shaped slab of iron whose dimensions are $$55cm\times 40cm\times 15cm$$ is melted and reacast into a pipe. The outer diameter and thickness of the pipe are $$8cm$$ and $$1cm$$ respectively. Find the length of the pipe. (Take $$\pi =\cfrac { 22 }{ 7 } $$)
Let $${h}_{1}$$ be the length of the pipe.
Let $$R$$ and $$r$$ be the outer and inner radii of the pipe respectively.
Iron slab:
Length $$=55cm$$
Breadth $$=40cm$$
Height $$=15cm$$
Volume $$=lbh=55\times 40\times 15\ cm^3$$
Iron pipe:
Outer diameter, $$2R=8cm$$
$$\therefore$$ Outer radius, $$R=4cm$$
Thichness, $$w=1cm$$
$$\therefore$$ Inner radius $$r=R-w=(4-1)cm=3cm$$
Now,
The volume of the iron pipe $$=$$ Volume of iron slab
$$\Rightarrow \pi { h }_{ 1 }(R^2-r^2)=lbh$$
$$\Rightarrow \cfrac { 22 }{ 7 } \times { h }_{ 1 }(4^2-3^2)=55\times 40\times 15$$
$$\Rightarrow \cfrac { 22 }{ 7 } \times { h }_{ 1 }\times 7=55\times 40\times 15$$
$$\Rightarrow 22 \times { h }_{ 1 }=55\times 40\times 15$$
$$\Rightarrow { h }_{ 1 }=\dfrac{55\times 40\times 15}{22}$$
$$\Rightarrow { h }_{ 1 }=1500$$
Thus, the length of the pipe, $${ h }_{ 1 }=1500cm=15m$$
A vessel is in the form of a frustum of a cone. Its radius at one end and the height are $$8cm$$ and $$14cm$$ respectively. If its volume is $$\cfrac{5676}{3}{cm}^{3}$$, then find the radius(in cm) at the other end.
The radii of two circular ends of a frustum shaped bucket are $$15\text{ cm}$$ and $$8\text{ cm}$$. If its depth is $$63\text{ cm}$$, find the capacity of the bucket in litres. (Take $$\pi =\cfrac { 22 }{ 7 } $$)
Let $$R$$ and $$r$$ are radii of the circular ends at the top and bottom and $$h$$ be the depth of the bucket respectively.
Given that $$R=15\text{ cm},r=8\text{ cm}$$ and $$h=63\text{ cm}$$
The volume of the bucket (frustum)
$$=\cfrac { 1 }{ 3 } \pi ({ R }^{ 2 }+{ r }^{ 2 }+Rr)\times h$$
$$=\cfrac { 1 }{ 3 } \times \cfrac { 22 }{ 7 } \times 63\times \left( { 15 }^{ 2 }+{ 8 }^{ 2 }+15\times 8 \right) =29664\text{ cm}^3$$
$$=\cfrac { 26994 }{ 1000 } $$ litres $$[\because 1000\text{ cm}^3=1$$ litre$$]$$
Thus, the capacity of the bucket $$=26.994$$ litres.
Given that $$R=15\text{ cm},r=8\text{ cm}$$ and $$h=63\text{ cm}$$
The volume of the bucket (frustum)
$$=\cfrac { 1 }{ 3 } \pi ({ R }^{ 2 }+{ r }^{ 2 }+Rr)\times h$$
$$=\cfrac { 1 }{ 3 } \times \cfrac { 22 }{ 7 } \times 63\times \left( { 15 }^{ 2 }+{ 8 }^{ 2 }+15\times 8 \right) =29664\text{ cm}^3$$
$$=\cfrac { 26994 }{ 1000 } $$ litres $$[\because 1000\text{ cm}^3=1$$ litre$$]$$
Thus, the capacity of the bucket $$=26.994$$ litres.
A hollow sphere of external and internal diameters of $$8cm$$ and $$4cm$$ respectively is melted and made into another solid in the shape of a right circular cone of base diameter $$8cm$$. Find the height of the cone.
Let $$R$$ and $$r$$ be the external and internal radii of the hollow sphere.
Let $$h$$ and $${r}_{1}$$ be the height and the radius of the cone to be made.
Hollow sphere
External:
$$2R=8cm$$
$$\Rightarrow$$ $$R=4cm$$
Internal
$$2r=4cm$$
$$\Rightarrow$$ $$r=2cm$$
Cone
$$2{r}_{1}=8$$
$$\Rightarrow$$ $${r}_{1}=4$$
When the hollow sphere is melted and made into a solid cone, we have
Volume of the cone $$=$$ Volume of the hollow sphere
$$ \cfrac { 1 }{ 3 } \pi { r }_{ 1 }^{ 2 }h=\cfrac { 4 }{ 3 } \pi \left[ { R }^{ 3 }-{ r }^{ 3 } \right] $$
$$ \cfrac { 1 }{ 3 } \times \pi \times { 4 }^{ 2 }\times h=\cfrac { 4 }{ 3 } \times \pi \times \left( { 4 }^{ 3 }-{ 2 }^{ 3 } \right) $$
$$ h=\cfrac { 64-18 }{ 4 } =14$$
Hence, the height of the cone $$h=14cm$$
Let $$h$$ and $${r}_{1}$$ be the height and the radius of the cone to be made.
Hollow sphere
External:
$$2R=8cm$$
$$\Rightarrow$$ $$R=4cm$$
Internal
$$2r=4cm$$
$$\Rightarrow$$ $$r=2cm$$
Cone
$$2{r}_{1}=8$$
$$\Rightarrow$$ $${r}_{1}=4$$
When the hollow sphere is melted and made into a solid cone, we have
Volume of the cone $$=$$ Volume of the hollow sphere
$$ \cfrac { 1 }{ 3 } \pi { r }_{ 1 }^{ 2 }h=\cfrac { 4 }{ 3 } \pi \left[ { R }^{ 3 }-{ r }^{ 3 } \right] $$
$$ \cfrac { 1 }{ 3 } \times \pi \times { 4 }^{ 2 }\times h=\cfrac { 4 }{ 3 } \times \pi \times \left( { 4 }^{ 3 }-{ 2 }^{ 3 } \right) $$
$$ h=\cfrac { 64-18 }{ 4 } =14$$
Hence, the height of the cone $$h=14cm$$
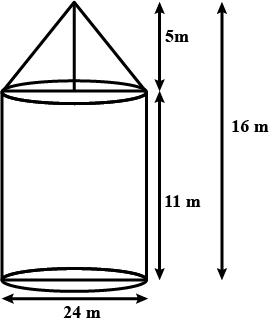
A circus tent is to be erected in the form of a cone surmounted on a cylinder. The total height of the tent is $$49m$$. Diameter of the base is $$42m$$ and height of the cylinder is $$21m$$. Find the cost of canvas needed to make the tent, if the cost of canvas is Rs.$$12.50/{m}^{2}$$. (Take $$\pi =\cfrac { 22 }{ 7 } $$)
Cylindrical Part
Diameter $$2r=42m$$
Radius, $$r=21m$$
Height $$h=21m$$
Conical Plant
Radius, $$r=21m$$
Height $${h}_{1}=49-21=28m$$
Slant height, $$l=\sqrt { { h }_{ 1 }^{ 2 }+{ r }^{ 2 } } $$
$$=\sqrt { { 28 }^{ 2 }+{ 21 }^{ 2 } } =7\sqrt { { 4 }^{ 2 }+{ 3 }^{ 2 } } =35m$$
Total area of the canvas needed $$=$$CSA of the cylindrical part $$+$$ CSA of the conical part
$$=2\pi rl+\pi rl=\pi r(2h+l)$$
$$=\cfrac { 22 }{ 7 } \times 21(2\times 21+35)=5082$$
Therefore, area of the canvas $$=5082{ m }^{ 2 }$$
Now, the cost of the canvas per sq.m $$=$$ Rs.$$12.50$$
Thus, the total cost of the canvas $$=5082\times 12.5=$$Rs. $$63525$$
Diameter $$2r=42m$$
Radius, $$r=21m$$
Height $$h=21m$$
Conical Plant
Radius, $$r=21m$$
Height $${h}_{1}=49-21=28m$$
Slant height, $$l=\sqrt { { h }_{ 1 }^{ 2 }+{ r }^{ 2 } } $$
$$=\sqrt { { 28 }^{ 2 }+{ 21 }^{ 2 } } =7\sqrt { { 4 }^{ 2 }+{ 3 }^{ 2 } } =35m$$
Total area of the canvas needed $$=$$CSA of the cylindrical part $$+$$ CSA of the conical part
$$=2\pi rl+\pi rl=\pi r(2h+l)$$
$$=\cfrac { 22 }{ 7 } \times 21(2\times 21+35)=5082$$
Therefore, area of the canvas $$=5082{ m }^{ 2 }$$
Now, the cost of the canvas per sq.m $$=$$ Rs.$$12.50$$
Thus, the total cost of the canvas $$=5082\times 12.5=$$Rs. $$63525$$
The radius of a cone is $$7cm$$ and its height is $$9cm$$. The volume of this cone is equal to lateral surface area of another cone which has same radius. Find the slant height of the cone.
A cylinder has hemispherical ends having radius 7 cm and total height of solid is 104 cm. If its outer surface is to polished & cost of polish is Rs. 100 per sq. mtr. find the total cost of polish.
Radius of each hemisphere = r = 7 cm
Height of total solid = 104 c
Height of cylinder, $$h = 104 - 2 \times 7 = 90 cm$$
Then,
T.S.A. of the solid = C.S.A. of the cylinder + 2 $$\times$$ C.S.A. of the hemisphere
$$= 2 \pi r h + 2 \times 2 \pi r^2$$
$$= 2 \pi r (h + 2r)$$
$$= 2 \times \dfrac{22}{7} \times 7 (90 + 2 \times 7)$$
$$= 44 \times 104$$
$$= 4576 cm^2$$
$$= 0.4576 m^2$$
$$\therefore $$ Total surface of the given solid is 0.4576 m$$^2$$.
Cost of polish is Rs. 100 per sq. mtr.
$$\therefore$$ Cost of polishing the solid of area $$0.4576 m^2 = 0.4576 \times 100 = 45.76$$
Total cost of polish is Rs. 45.76.
Height of total solid = 104 c
Height of cylinder, $$h = 104 - 2 \times 7 = 90 cm$$
Then,
T.S.A. of the solid = C.S.A. of the cylinder + 2 $$\times$$ C.S.A. of the hemisphere
$$= 2 \pi r h + 2 \times 2 \pi r^2$$
$$= 2 \pi r (h + 2r)$$
$$= 2 \times \dfrac{22}{7} \times 7 (90 + 2 \times 7)$$
$$= 44 \times 104$$
$$= 4576 cm^2$$
$$= 0.4576 m^2$$
$$\therefore $$ Total surface of the given solid is 0.4576 m$$^2$$.
Cost of polish is Rs. 100 per sq. mtr.
$$\therefore$$ Cost of polishing the solid of area $$0.4576 m^2 = 0.4576 \times 100 = 45.76$$
Total cost of polish is Rs. 45.76.
A tank is in the shape of a cylinder with two hemispheres attached to both ends as shown in the figure. Its common diameter is $$2\text{ m}$$ and total length is $$8\text{ m}$$. Find the total cost of painting the outer surface of this tank at the rate of $$\text{Rs. }60$$ per square metre. (use $$\pi = 3.14$$ as an approximation)
Given, Common diameter $$= 2\text{ m}$$
Radius $$= 1\text{ m}$$
Total length of tank $$= 8\text{ m}$$
Length of cylinder $$= h = 8 - 2(1) = 6 \text{ m}$$
Surface area of the tank
= Surface area of two hemispheres + lateral surface area of the cylinder
$$=2\times 2\pi r^2+2\pi rh$$
$$=2\pi r(2r+h)$$
$$=2\times 3.14\times 1(2\times 1+6)$$
$$=50.26 \text{ m}^2$$
Cost of painting $$=50.26\times 60 = \text{Rs. } 3015.92$$
$$\therefore$$ Cost of painting the tank is $$\text{Rs. }$$ $$3015.92$$
Radius $$= 1\text{ m}$$
Total length of tank $$= 8\text{ m}$$
Length of cylinder $$= h = 8 - 2(1) = 6 \text{ m}$$
Surface area of the tank
= Surface area of two hemispheres + lateral surface area of the cylinder
$$=2\times 2\pi r^2+2\pi rh$$
$$=2\pi r(2r+h)$$
$$=2\times 3.14\times 1(2\times 1+6)$$
$$=50.26 \text{ m}^2$$
Cost of painting $$=50.26\times 60 = \text{Rs. } 3015.92$$
$$\therefore$$ Cost of painting the tank is $$\text{Rs. }$$ $$3015.92$$
A cylindrical container having a diameter of $$16$$ cm and a height of $$40$$ cm is full of ice cream. The ice cream is to be filled into cones of height $$12$$ cm and diameter $$4$$ cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
A wooden toy is in the shape of a cone mounted on a cylinder as shown in the figure. If the height of the cone is $$24\ \mathrm{cm}$$, the total height of the toy is $$60\ \mathrm{cm}$$ and the radius of the base of the cone is equal to $$10\ \mathrm{cm}$$ and is twice the radius of the base of the cylinder. Find the total surface area of the toy. [Take $$\pi=3.14$$]
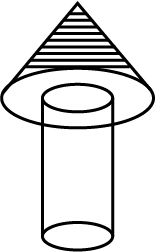
In an experiment of Maths, frustum of cone is made up of seven rings.The radius of uppermost ring is 4 cm and the radius of each ring is increased by 1 cm, so that the radius of the last ring is 10 cm. If the width of each ring is 3 cm. Then find the volume of entire frustum. (avoid the spaces between rings).
The radius of lower ring is $$r_1 = 10 cm$$
The radius of upper ring is $$r_2 = 4 cm$$
Width of each ring is $$3\ cm$$.
So, width of $$7$$ rings $$= 21 cm$$.
$$\therefore$$ Height of frustum $$= 21\ cm$$.
Volume of frustum $$= \dfrac{1}{3} \pi h [r_1^2 + r_2^2 + r_1 r_2]$$
$$= \dfrac{1}{3} \times \dfrac{22}{7} \times (21) [(10)^2 + (4)^2 + 40]$$
$$= 22[156]$$
$$= 3432 cm^3$$
The radius of upper ring is $$r_2 = 4 cm$$
Width of each ring is $$3\ cm$$.
So, width of $$7$$ rings $$= 21 cm$$.
$$\therefore$$ Height of frustum $$= 21\ cm$$.
Volume of frustum $$= \dfrac{1}{3} \pi h [r_1^2 + r_2^2 + r_1 r_2]$$
$$= \dfrac{1}{3} \times \dfrac{22}{7} \times (21) [(10)^2 + (4)^2 + 40]$$
$$= 22[156]$$
$$= 3432 cm^3$$
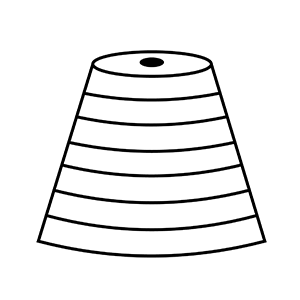
From a solid right circular cylinder of a height $$2.4$$ cm and radius $$0.7$$ cm, a right circular cone of same height and same radius is cut. Find the total surface area of the remaining solid.
For both Cylinder and Cone : $${ h } = 2.4 $$ cm, $$r = 0.7 $$ cm
Total surface area of remaining solid $$= $$Total surface area of cylinder $$-$$ Total surface area of cone .... $$(a)$$
Total surface area of cylinder $$= 2\pi r (r+h)$$
$$= 2\pi\times \dfrac {7}{10} \times \left(\dfrac {7} {10}+\dfrac {24}{10}\right)$$
$$=\dfrac {14 \pi \times 31}{100}$$ ....(1)
Total surface area of cone $$= \pi r ( r +l )$$
$$= \pi \times \dfrac{7}{10} \left(\dfrac{7}{10} + \sqrt{h^2 + r^2}\right)$$
$$= \pi \times \dfrac{7}{10} \left[\dfrac{7}{10} +\sqrt{\left(\dfrac{24}{10}\right)^2+\left(\dfrac{7}{10}\right)^2}\right]$$
$$=\dfrac{7\pi}{10}\left(\dfrac{7}{10}+\sqrt{\dfrac{576+46}{100}}\right)$$
$$=\dfrac{7\pi}{10} \left(\dfrac{7}{10}+\dfrac{25}{10}\right)$$
$$=\dfrac{7\pi}{10}\times \dfrac{32}{10} \ \ \ \ \ ...(2)$$
Substituting $$(1)$$ and $$(2)$$ in $$(a)$$,
We get,
Total surface area of remaining solid $$=\pi \left(\dfrac{434}{100}-\dfrac{224}{100}\right)$$
Total surface area of remaining solid $$= 6.6 cm^2$$.
A solid consisting of a right circular cone of height $$120\ cm$$ and radius $$60\ cm$$ standing on a hemisphere of radius $$60\ cm$$ is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, (in $$m^{3}$$) if the radius of the cylinder is $$60\ cm$$ and its height is $$180\ cm$$?
In the given question,
Volume of water in the cylinder $$=$$ Volume of cylinder $$-$$ Volume of Solid
Given:
Radius of the base of the cone $$r_1=60\ cm$$
Height of the cone $$h_1=120\ cm=2r1$$
Radius of the hemisphere $$r_2=60\ cm=r_1$$
Height of the cylinder $$h_2=180\ cm=3r_1$$
Radius of the base of the cylinder $$r_3=60\ cm=r_1$$
Now,
Volume of the solid $$=\dfrac{2}{3}\pi (r_1)^3+\dfrac{1}{3}\pi (r_1)^2(2r_1)$$
$$=\dfrac{2}{3}\pi (60)^3+\dfrac{1}{3}\pi (60)^2(2\times 60)\\$$
$$=\dfrac{1}{3}\pi (60)^3[2+2]\\$$
$$=\dfrac{4}{3}\pi (60)^3$$
Again,
Volume of the cylinder $$=\pi (r_1)^2(3r_1)$$
$$=3\pi (60)^3$$
Therefore,
Required volume of water $$=\pi (60)^3\left [3-\dfrac{4}{3}\right]$$
$$=\dfrac{5}{3}\pi (60)^3$$
$$=1130973.35\ cm^3$$
$$=1.131m^3$$ (approx.)
A gulab jamun, contains sugar syrup up to about $$30\%$$ of its volume. Find approximately how much syrup would be found in $$45$$ gulab jamuns, each shaped like a cylinder with two, hemispherical ends with length $$5\ cm$$ and diameter $$2.8\ cm$$.
A solid is composed of a cylinder with a hemisphere at one end and a cone at other end as shown in the figure. If the radius of each of these solids is 7 cm and height of the cylinder is equal to slant height of the cone, find the total surface area of the solid if slant height is 4 cm.
Two dairy owners $$A$$ and $$B$$ sell flavoured milk filled to capacity in mugs of negligible thickness, which are cylindrical in shape with a raised hemispherical bottom. The mugs are $$14\ cm$$ high and have diameter of $$7\ cm$$ as shown in given figure. Both $$A$$ and $$B$$ sell flavoured milk at the rate of $$Rs. 80$$ per litre. The dairy owner $$A$$ uses the formula $$\pi {r}^{2}h$$ to find the volume of milk in the mug and charges $$Rs. 43.12$$ for it. The dairy owner $$B$$ is of the view that the price of actual quantity of milk, should be charged. What according to him should be the price of one mug of milk? Which value is exhibited by the diary owner $$B$$? (Use $$\pi =\dfrac { 22 }{ 7 } $$)
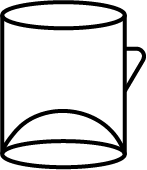
A toy is in the form of a cone mounted on a hemisphere as shown in the figure. If the radius of each of these solids is $$\displaystyle \frac{7}{2}$$ cm and height of the cone is 5 cm, find the volume of the toy.
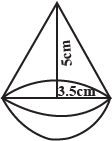
A bucket is in the form of a frustum of a cone and it can hold $$28.49$$ litres of water. If radii of its circular ends are $$28cm\ and\ 21cm$$, find the height of the bucket. Hence find its slant height.
$$r_1=28cm,r_1=21cm$$
Volume of frustum$$=28.49cm^3\times1000$$
$$\cfrac{1}{3}\pi(R_2^2-R_1^2)h=28490$$
$$\implies \cfrac{1}{3}\pi(28^2-21^2)h=28490$$
$$\implies h=\cfrac{4.07}{22\times 7}\times 300cm=872.14cm$$
In $$\triangle ABC$$
$$l=\sqrt {h^2+r^2}=\sqrt{28^2+872.14^2}=872.59cm$$
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water.The radii of the top and bottom are 28 cm and 21 cm respectively.Find the height of the buckrt.
The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is $$7$$cm. The height of the cylinder and cone are each of $$4$$cm. Find the volume of the solid.
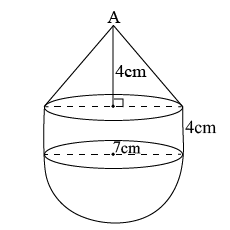
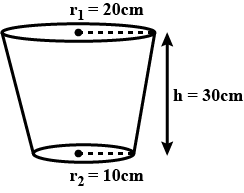
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are $$10\ cm$$ and $$30\ cm$$ respectively. If its height is $$24\ cm$$, find
(i) The area of the metal sheet used to make the bucket ?
(ii) Why we should avoid the bucket made by ordinary plastic (Use $$\pi=3.14$$)
A cylindrical bucket, $$32cm$$ high and $$18cm$$ of radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is $$24cm$$, find the radius and slant height of the heap.
The length of a road roller is $$2.1$$m and its diameter is $$1.4$$m. For levelling a ground $$500$$ rotations of the road roller were required. How much area of ground was levelled by the road roller? Find the cost of levelling at the rate of Rs$$7$$ per sq.m
A cylinder with the greatest lateral surface is inscribed in a cone. Find the ratio of the altitude of the cone to that of the cylinder.
Let radius and height of cone be R and H respectively and r and h be the radius and height of cylinder
Then, $$S=2\pi rh$$
Now, $$h=-\cfrac { H }{ R } r+H$$
$$\Rightarrow S=2\pi r\left[ -\cfrac { H }{ R } r+H \right] =2\pi rH-\cfrac { 2\pi H }{ R } { r }^{ 2 }$$
$$\cfrac { dS }{ dr } =0\Rightarrow 2\pi H-\cfrac { 4\pi H }{ R } r=0\Rightarrow R-2r=0\Rightarrow r=\cfrac { R }{ 2 } $$
$$\therefore h=\cfrac { -H }{ R } \times \cfrac { R }{ 2 } +H\Rightarrow h=\cfrac { H }{ 2 } \Rightarrow \cfrac { H }{ h } =2$$
Set up an equation of a tangent to the graph of the following function.
Find the altitude of the cylinder with the greatest lateral area which can be inscribed in a sphere of radius B.
Radius of sphere$$=B$$, let radius of base of cylinder be 'r' and height be 'h'. Then,
$$S=2\pi rh$$
Now, $$r=B\sin { \alpha } ,h=2B\cos { \alpha } $$ where $$\alpha $$ be the angle between radius and axis of the cylinder. Then,
$$S=2\pi { r }^{ 2 }\sin { \alpha } \cos { \alpha } $$
For maximum, differentiate S w.r.t. $$\alpha $$ and put equals to $$0$$
$$\cfrac { dS }{ d\alpha } =2\pi { B }^{ 2 }\left[ \cos ^{ 2 }{ \alpha } -\sin ^{ 2 }{ \alpha } \right] $$
Now, $$\cfrac { dS }{ d\alpha } =0\Rightarrow 2\pi { B }^{ 2 }\left[ \cos ^{ 2 }{ \alpha } -\sin ^{ 2 }{ \alpha } \right] =0$$
$$2\pi { B }^{ 2 }\neq 0\quad \therefore \cos ^{ 2 }{ \alpha } -\sin ^{ 2 }{ \alpha } =0\Rightarrow \tan ^{ 2 }{ \alpha } =1\Rightarrow \alpha =45°$$
Now, $$h=2B\cos { 45° } =\sqrt { 2 } B$$
A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is $$2\ cm$$ and the diameter of the base is $$4\ cm$$. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volume of the cylinder and toy. (Take $$\pi = 3.14)$$.
Volume of the toy
$$=\cfrac{1}{3}\pi r^2h+\cfrac{2}{3}\pi r^3$$
$$=\cfrac{1}{3}\pi\times 2^2\times 2+\cfrac{2}{3}\pi\times 2^3$$
$$=25.12cm^3$$
Volume of the cylinder circumscribing
$$h=4cm$$
$$r=2cm$$
$$v=\pi r^2h=\pi\times 4\times 4=50.24cm^3$$
Difference in volume$$=(50.24-25.12)cm^3=25.12cm^3$$
Three solid cubes of sides 1cm,6cm and 8 cm are melted to form a new cube.Find the surface area of the cube so formed.
A tent of height $$77dm$$ is in the form of a right circular cylinder of diameter $$36m$$ and height $$44dm$$ surmounted by a right circular cone. Find the cost of the canvas at Rs. $$3.50$$ per $${m}^{2}$$ (Use $$\pi =22/7$$)
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are $$5cm$$ and $$13cm$$ respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Find the surface area of the toy if the total height of the toy is $$30cm$$.
A toy is in the form of a cone surmounted on a hemisphere. The diameter of the base and the height of the cone are $$6\ \text{cm}$$ and $$4\ \text{cm}$$ respectively. Determine the surface area of the toy. (Use $$\pi=3.14$$)
A cylindrical tub of radius $$5cm$$ and length $$9.8cm$$ is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the hemisphere is immersed in the tub. If the radius of the hemisphere is $$3.5cm$$ and height of the cone outside the hemisphere is $$5cm$$, find the volume of the water left in the tub (Take $$\pi=22/7$$)
A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius $$2.5m$$ and height $$21m$$ and the cone has the slant height $$8m$$. Calculate the total surface area and the volume of the rocket.
A solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is $$8\ cm$$ and the heights of the cylindrical and conical portions are $$10cm$$ and $$6cm$$ respectively. Find the total surface area of the solid. (Use $$\pi=22/7$$)
A petrol tank is a cylinder of base diameter $$21cm$$ and length $$18cm$$ fitted with conical ends each of axis length $$9cm$$. Determine the capacity of the tank.
A tent of height $$77\ dm$$ is in the form of a right circular cylinder of diameter $$36\ m$$ and height $$44\ dm$$ surmounted by a right circular cone. Find the cost of the canvas at $$Rs.\ 3.50$$ per square meter.
Sushant has a vessel, of the form of an inverted cone, open at the top, of height $$11cm$$ and radius of top as $$2.5cm$$ and is full of water. Metallic spherical balls each of diameter $$0.5cm$$ are put in the vessel due to which $$(\cfrac{2}{5})$$th of the water in the vessel flows out. Find how many balls were put in the vessel. Sushant made the arrangement so that the water that flows out irrigates the flower beds. What value has been shown by Sushant?
A circus tent has cylindrical shape surmounted by a conical rood. The radius of the cylindrical base is $$20m$$. The heights of the cylindrical and conical portions are $$4.2m$$ and $$2.1m$$ respectively. Find the volume of the tent.
A conical hole is drilled in a circular cylinder of height $$12cm$$ and base radius $$5cm$$. The height and the base radius of the cone are the same as the Cylinder. Find the Curved Surface Area and volume of the remaining solid.
An wooden toy is made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is $$10cm$$, and its base is of radius $$3.5cm$$, find the volume of wood in the toy. (Use $$\pi=22/7$$)
A boiler is in the form of a cylinder $$2m$$ long with hemispherical ends each of $$2$$ metre diameter. Find the volume of the boiler.
A toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is $$21cm$$ and its volume is $$\dfrac{2}{3}$$ of the volume of the hemisphere, calculate the height of the cone and the surface area of the toy. (Use $$\pi=22/7$$)
A solid is composed of a cylinder with hemispherical ends. If the length of the cylindrical part is $$104cm$$ and the radius of each of the hemispherical ends is $$7cm$$, find the cost of polishing its surface at the rate of Rs. $$10$$ per $${dm}^{2}$$.
A solid toy is in the form of a hemisphere surmounted by a right circular cone. Height of the cone is $$2cm$$ and the diameter of the base is $$4cm$$. If a right circular cylinder circumscribes the toy, find how much more space it will cover.
Volume of toy $$=$$ Vol. of cone + Vol.of hemisphere
$$=\dfrac { 1 }{ 3 } \pi { r }^{ 2 }H+\dfrac { 2 }{ 3 } \pi { r }^{ 3 }=\dfrac { 1 }{ 3 } \pi { r }^{ 2 }\left[ H+2r \right] h$$
$$=\dfrac { 1 }{ 3 } \times \dfrac { 22 }{ 7 } \times 2\times 2\left[ 2+2\times 2 \right] $$
$$=\dfrac { 1 }{ 3 } \times \dfrac { 22 }{ 7 } \times 4\times { 6 }^{ 2 }=25.12{ cm }^{ 3 }$$
Volume of cylinder $$=\pi { r }^{ 2 }h=\dfrac { 22 }{ 7 } \times 2\times 2\left[ 2+2 \right] =\dfrac { 22 }{ 7 } \times 16=50.24{ cm }^{ 3 }$$
Difference in volume $$=50.24-25.12=25.12{ cm }^{ 3 }$$
Hence, cylinder cover $$25.12{ cm }^{ 3 }$$ more space.
A vessel in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is $$14cm$$ and the height of cylindrical part is $$13cm$$. Find the inner surface area of the vessel.
Inner surface area of vessel $$=$$ CSA of hemisphere + CSA of cylinder
$$=2\pi { r }^{ 2 }+2\pi rh=2\pi r\left( r+h \right) $$
$$=2\times \dfrac { 22 }{ 7 } \times 7\left( 7+13 \right) =44\times 20=880{ cm }^{ 2 }$$
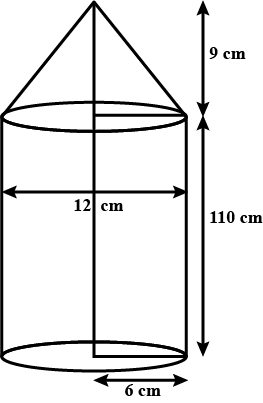
A solid iron pole having a cylindrical portion $$110\text{ cm}$$ high and of base diameter $$12\text{ cm}$$ is surmounted by a cone $$9\text{ cm}$$ high. Find the mass of the pole, given that the mass of $$1\text{ cm}^{3}$$ of iron is $$8\text{ gm}$$.
Given: Diameter of cone $$=12\text{ cm}$$
So, Radius of cone $$=6\text{ cm}$$
and height of cone $$=9\text{ cm}$$
Volume of cone $$=\dfrac 13 \pi r^2h$$
$$=\dfrac{1}{3}\times \dfrac{22}{7}\times 6\times 6\times 9$$
$$=339.428\text{ cm}^3$$
Radius of the cylinder, $$R=$$ Radius of cone $$=6\text{ cm}$$
Height of the cylinder, $$H=110\text{ cm}$$
Volume of cylinder $$=\pi R^2H$$
$$=\dfrac {22}{7}\times 6\times 6\times 110$$
$$=12445.714\text{ cm}^3$$
Hence,
Volume of pole $$=$$ Volume of the conical part $$+$$ Volume of the cylindrical part
$$=339.43+12445.714$$
$$=12785.142\text{ cm}^3$$
Required mass of pole $$=8\times 12785.142$$
$$=102281.13\text{ gm}$$
$$=102.281\text{ kg}$$
A tent is in the form of a cylinder of diameter $$20m$$ and height $$2.5m$$, surmounted by a cone of equal base and height $$7.5m$$. Find the capacity of the tent and the cost of the canvas at RS. $$100$$ per square metre.
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them being $$3.5cm$$ and the total height of solid is $$9.5cm$$. Find the volume of the solid. (Use $$\pi=22/7$$)
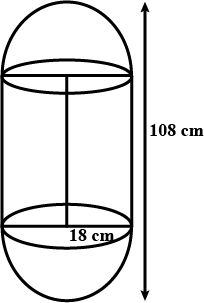
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is $$108cm$$, and the diameter of the cylinder is $$36cm$$, find the cost of polishing the surface at the rate of $$7$$ paise per $${cm}^{2}$$.
CSA of solid=CSA of cylinder$$+2\times $$CSA of hemisphere
$$=2\pi rh+2\times 2\pi { r }^{ 2 }$$
$$=2\pi r\left( h+2r \right) $$
$$=2\times \cfrac { 22 }{ 7 } \times 18\left( \left( 108-36 \right) +2\times 18 \right) $$
$$=12219.43㎠$$
Cost of polishing=Rs.$$\left( 12219.43\times 0.07 \right) $$=Rs.$$855$$
The interior of a building is in the form of a cylinder of base radius $$12m$$ and height $$3.5m$$ surmounted by a cone of equal base and slant height $$12.5m$$. Find the internal curved surface are and the capacity of the building.
Internal CSA$$=2\pi rH+\pi rl$$
$$=\pi r\left[ 2h+l \right] $$
$$=\cfrac { 22 }{ 7 } \times 12\left[ 2\times 3.5+12.5 \right] $$
$$=\cfrac { 22 }{ 7 } \times 12\times 19.5=735.43m^{3}$$
Capacity of building$$=\cfrac { 1 }{ 3 } \pi { r }^{ 2 }h+\pi { r }^{ 2 }H$$
$$=\pi { r }^{ 2 }\left[ \cfrac { 1 }{ 3 } \sqrt { { l }^{ 2 }-{ r }^{ 2 } } +H \right] =\cfrac { 22 }{ 7 } \times { 12 }^{ 2 }\left[ \cfrac { 1 }{ 3 } \sqrt { { 12.5 }^{ 2 }-{ 12 }^{ 2 } } +3.5 \right] $$
$$=\cfrac { 22 }{ 7 } \times 144\left[ \cfrac { 3.5 }{ 3 } +3.5 \right] =2112m^{3}$$
A toy is in the form of a cone mounted on a hemisphere with the same radius. The diameter of the base of the conical portion is $$6\ cm$$ and its height is $$4\ cm$$. Determine the surface area of the toy. (Use $$\pi=3.14$$)
Surface area of the toy$$=\pi rl+2\pi { r }^{ 2 }$$
$$=\pi r\left( l+2r \right) =3.14\times 3\left[ \sqrt { { r }^{ 2 }+{ h }^{ 2 } } +2\times 3 \right] $$
$$=9.42\left( \sqrt { { 3 }^{ 2 }+{ 4 }^{ 2 } } +6 \right) =9.42\left( 5+6 \right) $$
$$=103.62\ {cm}^2$$
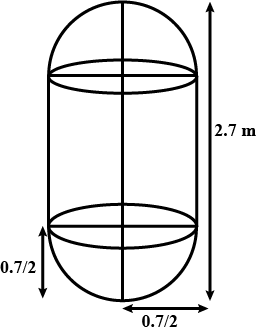
Find the volume of a solid in the form of a right circular cylinder with hemispherical ends whose length is $$2.7\ m$$ and the diameter of each hemispherical end is $$0.7\ m$$
Volume of solid$$=\pi { r }^{ 2 }h+2\times \cfrac { 2 }{ 3 } \pi { r }^{ 3 }$$
$$\Rightarrow \pi { r }^{ 2 }\left[ h+\cfrac { 4 }{ 3 } r \right] =\cfrac { 22 }{ 7 } \times { \left( \cfrac { 0.7 }{ 2 } \right) }^{ 2 }\left[ \left( 2.7-2\times \cfrac { 0.7 }{ 2 } \right) +\cfrac { 4 }{ 3 } \times \cfrac { 0.7 }{ 2 } \right] $$
$$=\cfrac { 22 }{ 7 } \times \cfrac { 0.7 }{ 2 } \times \cfrac { 0.7 }{ 2 } \times 2.47=0.95\ m^{3}$$
An iron pillar consists of a cylindrical portion $$2.8m$$ high and $$20cm$$ in diameter and a cone $$42cm$$ high is surrounding it. Find the weight of the pillar, given that $$1$$cubic $$cm$$ of iron weights $$7.5gm$$.
Given,
An iron pillar consists of a cylindrical portion and a cone mounted on it.
The height of the cylindrical portion of the pillar, $$H=2.8\ m=280\ cm$$
The height of the conical portion of the pillar, $$h=42\ cm$$
The diameter of the cylindrical portion of the pillar = diameter of the circular base of cone =$$D=20\ cm$$
The radius of the circular base of cylinder/ cone $$r=\dfrac{D}{2}=10\ cm$$
Now,
Volume of the pillar, $$(V)$$= Volume of the cylindrical portion of pillar + volume of the conical portion of the pillar.
$$\rightarrow V=\pi r^{2}H + \dfrac{1}{3}\pi r^{2}h$$
$$\rightarrow V=\bigg(\dfrac{22}{7} \times 10^{2}\times280 + \dfrac{1}{3}\times\dfrac{22}{7} \times10^{2}\times42\bigg)\ cm^{3}$$
$$\rightarrow V=\bigg(22 \times 100\times40 + 22 \times100\times2\bigg)\ cm^{3}$$
$$\rightarrow V=\bigg(88000 + 4400\bigg)\ cm^{3}$$
$$\rightarrow V=92400\ cm^{3}$$
Hence, volume of iron pillar is $$92400\ cm^{3}$$Given,
Weight of $$1\ cm^{3}$$ iron $$=7.5\ gm.$$
Hence, weight of $$92400\ cm^{3}$$ iron $$=7.5\times92400\ gm.$$
$$=693000\ gm.$$
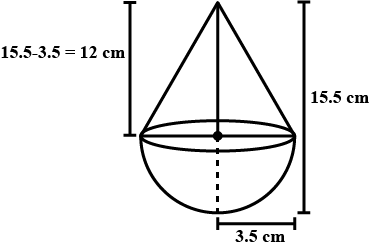
A toy is in the form of a cone mounted on a hemisphere of radius $$3.5cm$$. The total height of the toy is $$15.5cm$$, find the total surface area and volume of the toy.
We know radius of cone $$=$$ radius of hemisphere $$=r=3.5$$ cm
Slant height of the cone $$l=\sqrt {r^2+h^2}$$
$$=\sqrt {(3.5)^2+(12)^2}$$
$$=12.5$$ $$cm^2$$
TSA of toy $$=\pi rl+2\pi { r }^{ 2 }$$
$$=\pi r\left( l+2r \right) $$
$$=\cfrac { 22 }{ 7 } \times 3.5\left( 12.5 +2\times 3.5 \right) $$
$$=214.5\ cm^{2}$$
Volume of toy $$=\cfrac { 1 }{ 3 } \pi { r }^{ 2 }h+\cfrac { 2 }{ 3 } \pi { r }^{ 3 }$$
$$=\cfrac { 1 }{ 3 } \pi { r }^{ 2 }\left[ h+2r \right] $$
$$=\cfrac { 1 }{ 3 } \times \cfrac { 22 }{ 7 } \times 3.5\times 3.5\left( 12+2\times 3.5 \right)$$
$$ =243.83\ cm^{3}$$
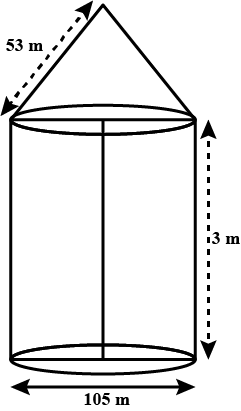
A circus tent is cylindrical to a height of $$3$$ metres and conical above it. If its diameter is $$105m$$ and the slant height of the conical portion is $$53m$$, calculate the length of the canvas $$5m$$ wide to make the required tent.
Canvas required$$=\pi rl+2\pi rh=\pi r\left( l+2h \right) $$
$$=\cfrac { 22 }{ 7 } \times \cfrac { 105 }{ 2 } \left( 53+3\times 2 \right) $$
$$=165\times 59$$
$$=9735㎡$$
Let length of canvas be l then
$$l\times 5=9735㎡\Rightarrow l=\cfrac { 9735 }{ 5 } =1947m$$
Therefore, length of canvas$$=1947m$$
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of the base of the cylinder or the cone is $$24m$$. The height of the cylinder is $$11m$$. If the vertex of the cone is $$16m$$ above the ground, find the area of the canvas required for making the tent. (Use $$\pi=22/7$$)
Area of canvas required$$=\pi rl+2\pi rH$$
$$\Rightarrow \pi r\sqrt { { r }^{ 2 }+{ h }^{ 2 } } +2\pi rH=\pi r\left( \sqrt { { r }^{ 2 }+{ h }^{ 2 } } +2H \right) $$
$$=\cfrac { 22 }{ 7 } \times 12\left( \sqrt { { 12 }^{ 2 }+{ 5 }^{ 2 } } +2\times 11 \right) =1320m^{2}$$
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is $$108\ cm$$ and the diameter of the cylinder is $$36\ cm$$, find the cost of polishing the surface at the rate of $$7$$ paise per $${cm}^{2}$$. (Use $$\pi=3.1416$$)
In the figure, from the top of a solid cone of height $$12cm$$ and base radius $$6cm$$, a cone of height $$4cm$$ is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use $$\pi=22/7$$ and $$\sqrt{5}=2.236$$)
$$\triangle OAB\sim \triangle OCD$$ [By AA similarity]
$$ \dfrac { OA }{ OC } =\dfrac { AB }{ CD }$$
$$ AB=\dfrac { 4\times 6 }{ 12 }$$
$$ =2cm$$
TSA of frustum $$=\pi \left( { R }_{ 1 }+{ R }_{ 2 } \right) l+\pi \left( { R }_{ 1 }^{ 2 }+{ R }_{ 2 }^{ 2 } \right) $$
$$=\pi \left[ \left( { R }_{ 1 }+{ R }_{ 2 } \right) \sqrt { { \left( { R }_{ 1 }-{ R }_{ 2 } \right) }^{ 2 }+{ h }^{ 2 } } +{ R }_{ 1 }^{ 2 }+{ R }_{ 2 }^{ 2 } \right] $$
$$=\dfrac { 22 }{ 7 } \left[ \left( 6+2 \right) \sqrt { { \left( 6-2 \right) }^{ 2 }+{ 8 }^{ 2 } } +{ 6 }^{ 2 }+{ 2 }^{ 2 } \right]$$
$$ =\dfrac { 22 }{ 7 } \left[ 8\times 4\sqrt { 5 } +36+4 \right] $$
$$=\dfrac { 22 }{ 7 } \left[ 32\times 2.236+40 \right]$$
$$=350.59{ cm }^{ 2 }$$
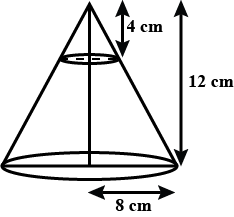
The radii of the ends of a frustum of a right circular cone are $$5$$ metres and $$8$$ metres and its lateral height is $$5$$ metres. Find the lateral surface area and volume of the frustum.
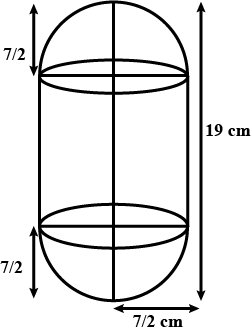
A solid is in the form of a cylinder with hemispherical ends. Total height of the solid is $$19cm$$ and the diameter of the cylinder is $$7cm$$. Find the volume and total surface area of the solid.
Volume of solid$$=\pi { r }^{ 2 }h+2\times \cfrac { 2 }{ 3 } \pi { r }^{ 3 }$$
$$=\pi { r }^{ 2 }\left[ h+\cfrac { 4r }{ 3 } \right] =\cfrac { 22 }{ 7 } \times \cfrac { 7 }{ 2 } \times \cfrac { 7 }{ 2 } \left[ \left( 19-7 \right) +\cfrac { 4\times 7 }{ 3\times 2 } \right] $$
$$=38.5\left( 12+\cfrac { 14 }{ 3 } \right) =38.5\times \cfrac { 50 }{ 3 } $$
$$=641.67cm^3$$
TSA of solid$$=2\pi rh+2\times 2\pi { r }^{ 2 }=2\pi r\left( h+2r \right) $$
$$=2\times \cfrac { 22 }{ 7 } \times \cfrac { 7 }{ 2 } \left[ \left( 19-7 \right) +2\times \cfrac { 7 }{ 2 } \right] $$
$$=22\left( 12+7 \right) =22\times 19$$
$$=418cm^2$$
The radii of the ends of a bucket of height $$24cm$$ are $$15cm$$ and $$5cm$$. Find its capacity. (Take $$\pi=22/7$$)
A golf ball has a diameter equal to $$4.2\;cm$$. Its surface has $$200$$ dimples each of radius $$2\;mm$$. Calculate the total surface area which is exposed to the surroundings assuming that the dimples are hemispherical.
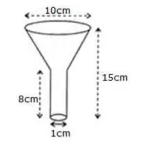
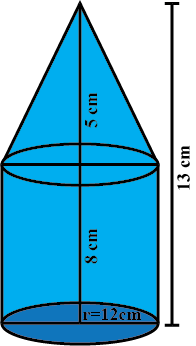
An oil funnel of tin sheet consists of a cylindrical portion $$10cm$$ long attached to a frustum of a cone. If the total height be $$22cm$$, the diameter of the cylindrical portion $$8cm$$ and the diameter of the top of the funnel $$18cm$$, find the area of the tin required.
Area of tin required$$=\pi \left( R+r \right) l+2\pi r{ h }_{ 1 }$$
$$=\pi \left[ \left( R+r \right) \sqrt { { \left( R-r \right) }^{ 2 }+{ h }_{ 2 }^{ 2 } } \right] +2\pi \times 4\times 10$$
$$=\cfrac { 22 }{ 7 } \left[ \left( 9+4 \right) \sqrt { { \left( 9-4 \right) }^{ 2 }+{ 12 }^{ 2 } } +2\times 4\times 10 \right] $$
$$=\cfrac { 22 }{ 7 } \left[ 13\times \sqrt { 169 } +80 \right] =\cfrac { 22 }{ 7 } \times \left( \left( 13\times 13 \right) +80 \right) $$
$$=\cfrac { 22 }{ 7 } \times 249=249\pi cm^{2}$$
The largest sphere is carved out of a cube of side $$10.5cm$$. Find the volume of the sphere.
Let $$r$$ be the radius of sphere.
Diameter of sphere$$=$$side of cube =$$2r=10.5 \ cm$$
Diameter of sphere$$=$$side of cube =$$2r=10.5 \ cm$$
$$\therefore $$Radius $$=\cfrac { 10.5 }{ 2 } =5.25 \ cm$$
Volume$$=\cfrac { 4 }{ 3 } \pi { r }^{ 3 }=\cfrac { 4 }{ 3 } \times \cfrac { 22 }{ 7 } \times { \left( 5.25 \right) }^{ 3 }$$
$$=606.375cm^{3}$$
If a cone of radius $$10cm$$ is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts.
Volume of cone$$=\cfrac { 1 }{ 3 } \pi { r }_{ 1 }^{ 2 }{ h }_{ 1 }=\cfrac { 1 }{ 3 } \pi { \left( \cfrac { r }{ 2 } \right) }^{ 2 }\times \cfrac { h }{ 2 } $$
$$=\cfrac { 1 }{ 3 } \pi { \left( \cfrac { 10 }{ 2 } \right) }^{ 2 }\times \cfrac { h }{ 2 } $$
$$=\cfrac { 25\pi h }{ 6 } cm^3$$
Volume of frustum ABCD$$=\cfrac { 1 }{ 3 } \pi { h }_{ 2 }\left( { R }^{ 2 }+{ r }^{ 2 }+Rr \right) $$
$$=\cfrac { 1 }{ 3 } \pi \times \cfrac { h }{ 2 } \left( { 10 }^{ 2 }+{ 5 }^{ 2 }+10\times 5 \right) $$
$$=\cfrac { 175\pi h }{ 6 } $$
Required ratio$$=\cfrac { \cfrac { 25\pi h }{ 6 } }{ \cfrac { 175\pi h }{ 6 } } =\cfrac { 25 }{ 175 } =\cfrac { 1 }{ 7 } =1:7$$
A frustum of a cone is $$9cm$$ thick and the diameters of its circular ends are $$28cm$$ and $$4cm$$. Find the volume and lateral surface area of the frustum. (Take $$\pi=22/7$$)
A container open at the top, is in the form of a frustum of a cone of height $$24cm$$ with radii of its lower and upper circular ends as $$8cm$$ and $$20cm$$ respectively. Find the cost of milk which can completely fill the container at the rate of Rs. $$21$$ per litre. (Use $$\pi=22/7$$)
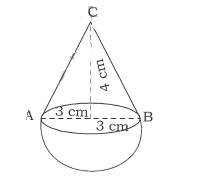
A conical vessel of radius $$6cm$$ and height $$8cm$$ is completely filled with water. A sphere is lowered into water and its size is such that when it touches the sides, it is just immersed as shown in figure. What fraction of water over flows
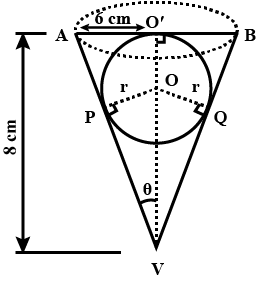
A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is $$19cm$$ and the diameter of the cylinder is $$7cm$$. find the volume and total surface area of the solid (Use $$\pi =22/7$$)
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are $$13cm$$ and $$5cm$$ respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if the height of the conical part is $$12cm$$.
Let $$r$$ cm be the radius and $$h$$ cm the height of the cylindrical part. Then, $$r=5cm,h=13cm$$
Clearly radii of the spherical part and base of the conical part are also $$r$$ cm. Let $${h}_{1}$$ cm be the height, $$l$$ cm be the slant height of the conical part.
Now
surface area of the toy$$=$$
curved surface area of the cylindrical part + curved surface area of hemispherical part + curved surface area of conical part
$$=\left( 2\pi rh+2\pi { r }^{ 2 }+\pi rl \right) { cm }^{ 2 }$$
Clearly radii of the spherical part and base of the conical part are also $$r$$ cm. Let $${h}_{1}$$ cm be the height, $$l$$ cm be the slant height of the conical part.
Then
$${ l }^{ 2 }={ r }^{ 2 }+{ h }_{ 1 }^{ 2 }\Rightarrow l=\sqrt { { r }^{ 2 }+{ h }_{ 1 }^{ 2 } } \Rightarrow l=\sqrt { { 5 }^{ 2 }+{ 12 }^{ 2 } } =13cm\quad $$
$${ l }^{ 2 }={ r }^{ 2 }+{ h }_{ 1 }^{ 2 }\Rightarrow l=\sqrt { { r }^{ 2 }+{ h }_{ 1 }^{ 2 } } \Rightarrow l=\sqrt { { 5 }^{ 2 }+{ 12 }^{ 2 } } =13cm\quad $$
Now
surface area of the toy$$=$$
curved surface area of the cylindrical part + curved surface area of hemispherical part + curved surface area of conical part
$$=\left( 2\pi rh+2\pi { r }^{ 2 }+\pi rl \right) { cm }^{ 2 }$$
$$=\pi r\left( 2h+2r+l \right) { cm }^{ 2 }$$
$$=\left\{ \cfrac { 22 }{ 7 } \times 5\times \left( 2\times 13+2\times 5+13 \right) \right\} { cm }^{ 2 }$$
$$=770{ cm }^{ 2 }\quad $$
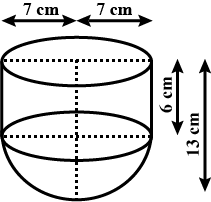
A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the sphere is $$14cm$$ and the total height of the vessel is $$13cm$$. Find its capacity. (Take $$\pi =22/7$$)
Let $$r$$ be the radius of the hemispherical bowl and $$h$$ be the height of the cylinder.
Total capacity of the bowl
$$=$$ volume of the cylinder + volume of the hemisphere
$$=\left( \pi { r }^{ 2 }h+\cfrac { 2 }{ 3 } \pi { r }^{ 3 } \right) { cm }^{ 3 }$$
$$=1642.66{ cm }^{ 3 }$$
Then, $$r=7cm$$ and $$h=6cm$$
Total capacity of the bowl
$$=$$ volume of the cylinder + volume of the hemisphere
$$=\left( \pi { r }^{ 2 }h+\cfrac { 2 }{ 3 } \pi { r }^{ 3 } \right) { cm }^{ 3 }$$
$$=\pi { r }^{ 2 }\left( h+\cfrac { 2 }{ 3 } r \right) { cm }^{ 3 }$$
$$=\cfrac { 22 }{ 7 } \times { 7 }^{ 2 }\times \left( 6+\cfrac { 2 }{ 3 } \times 7 \right) { cm }^{ 3 }$$
$$=1642.66{ cm }^{ 3 }$$
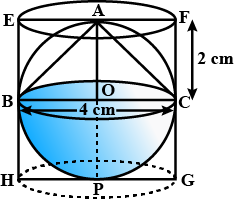
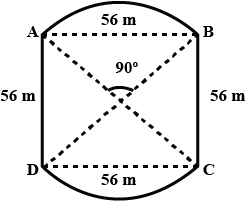
In figure two circular flower beads have been shown on two sides of a square lawn ABCD of side 56 m. If the center of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawns and the flower beds.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their respective volume is
The radius of a solid iron sphere is $$8cm$$. Eight rings of iron plate of external radius $$6\cfrac { 2 }{ 3 } cm$$ and thickness $$3cm$$ are made by melting this sphere. Find the internal diameter of each ring.
The interior of a building is in the form of cylinder of diameter $$4.3m$$ and height $$3.8m$$ surrounded by a cone whose vertical angle is a right angle. Find the area of the surface and the volume of the building (Take $$\pi =3.14$$)
A solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is $$3.5cm$$ and the height of the cone is $$4cm$$. The solid is placed in a cylindrical tub, full of water, in such a way that the whole solid is submerged in water. If the radius of the cylinder is $$5cm$$ and its height is $$10.5cm$$, find the volume of water left in the cylindrical tub $$\left (Use \ \pi=\dfrac{22}7 \right )$$
A circus tent is cylindrical up to a height of $$3m$$ and conical above. If the diameter of the base is $$105m$$ and the slant height of the conical part is $$53m$$, find the total canvas used in making the tent.
We have
Total canvas used = curved surface area of cylinder + curved surface area of cone
Total canvas used $$=\left( 2\times \cfrac { 22 }{ 7 } \times 52.3\times 3+\cfrac { 22 }{ 7 } \times 52.5\times 53 \right) { m }^{ 3 }\left[ \because S=2\pi rh+\pi rl \right] $$
$$=\cfrac { 22 }{ 7 } \times 52.5\left( 6+53 \right) { m }^{ 2 }=9735{ m }^{ 2 }$$
Total canvas used = curved surface area of cylinder + curved surface area of cone
Total canvas used $$=\left( 2\times \cfrac { 22 }{ 7 } \times 52.3\times 3+\cfrac { 22 }{ 7 } \times 52.5\times 53 \right) { m }^{ 3 }\left[ \because S=2\pi rh+\pi rl \right] $$
$$=\cfrac { 22 }{ 7 } \times 52.5\left( 6+53 \right) { m }^{ 2 }=9735{ m }^{ 2 }$$
Mayank made a bird-bath for his garden in the shape of cylinder with a hemispherical depression at one end as shown in figure. The height of the hollow cylinder is $$1.45\ m$$ and its radius is $$30\ cm$$. Find the total surface area of the bird-bath. (Take $$\pi=22/7$$)
A solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is $$4.2cm$$ and the height of the cylindrical and conical portions are $$12cm$$ and $$7cm$$ respectively. Find the volume of the solid toy. (Use $$\pi =22/7$$)
We have
volume of the solid toy $$=$$ volume of the conical portion $$+$$ volume of the cylindrical portion $$+$$volume of the hemispherical portion
volume of the solid toy $$=$$ volume of the conical portion $$+$$ volume of the cylindrical portion $$+$$volume of the hemispherical portion
Let $$V$$ be the volume of toy
$$=\cfrac { 1 }{ 3 } \pi \times { (2.1) }^{ 2 }\times 7+\pi \times { (2.1) }^{ 2 }\times 12+\cfrac { 2 }{ 3 } \times \pi \times { (2.1) }^{ 3 }$$
$$V=\dfrac13 \pi r^2 h+\pi r^2h+\dfrac23 \pi r^3$$
$$=\cfrac { 1 }{ 3 } \pi \times { (2.1) }^{ 2 }\times 7+\pi \times { (2.1) }^{ 2 }\times 12+\cfrac { 2 }{ 3 } \times \pi \times { (2.1) }^{ 3 }$$
$$=(32.31+166.16+19.38) cm^3$$
$$=217.85cm^3$$
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to $$1\ cm$$ and the height of the cone is equal to its radius. Find the volume of the solid in terms of $$\pi$$.
A Gulab Jamun when completely ready for eating contains sugar syrup up to about $$30\%$$ of its volume. Find approximately how much syrup would be found in $$45$$ Gulab Jamun shaped like a cylinder with two hemispherical ends, if the complete length of each of the Gulab Jamun is $$5 \ cm$$ and its diameter is $$2.8 \ cm$$.
A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is $$2cm$$ and the diameter of the base is $$4cm$$. If a right circular cylinder circumscribes the solid. Find how much more space it will cover.
Let $$BPC$$ be the hemisphere and $$ABC$$ be the cone mounted on the base of the hemisphere.
Radius of the hemisphere $$=BO=\cfrac { 1 }{ 2 } BC=\cfrac { 4 }{ 2 } cm=2cm$$
$$OP=2cm$$
$$AP=OP+OA=2+2=4cm$$
Volume of the right circular cylinder
$$\Rightarrow\pi r^2h=\pi \times { 2 }^{ 2 }\times 4{ cm }^{ 3 }=16\pi { cm }^{ 3 }$$
volume of the solid toy $$=\left\{ \cfrac { 2 }{ 3 } \pi \times { 2 }^{ 3 }+\cfrac { 1 }{ 3 } \pi \times { 2 }^{ 2 }\times 2 \right\} { cm }^{ 3 }=8\pi { cm }^{ 3 }$$
Required space $$=$$ volume of the right circular cylinder - volume of the toy
$$=16\pi { cm }^{ 3 }-8\pi { cm }^{ 3 }$$
Let $$EFGH$$ be the right circular cylinder circumscribing.
We have
Height of the cone$$=OA+2cm$$
Diameter of the base of the cone$$=BC=4cm$$
We have
Height of the cone$$=OA+2cm$$
Diameter of the base of the cone$$=BC=4cm$$
Radius of the hemisphere $$=BO=\cfrac { 1 }{ 2 } BC=\cfrac { 4 }{ 2 } cm=2cm$$
$$OP=2cm$$
$$AP=OP+OA=2+2=4cm$$
Volume of the right circular cylinder
$$\Rightarrow\pi r^2h=\pi \times { 2 }^{ 2 }\times 4{ cm }^{ 3 }=16\pi { cm }^{ 3 }$$
volume of the solid toy $$=\left\{ \cfrac { 2 }{ 3 } \pi \times { 2 }^{ 3 }+\cfrac { 1 }{ 3 } \pi \times { 2 }^{ 2 }\times 2 \right\} { cm }^{ 3 }=8\pi { cm }^{ 3 }$$
Required space $$=$$ volume of the right circular cylinder - volume of the toy
$$=16\pi { cm }^{ 3 }-8\pi { cm }^{ 3 }$$
$$=8\pi \ { cm }^{ 3 }$$
A wooden toy rocket is in the shape of a cone mounted on a cylinder as shown in figure. The height of the entire rocket is $$26cm$$, while the height of the conical part is $$6cm$$. The base of the conical portion has a diameter of $$5cm$$, while the base diameter of the cylindrical portion is $$3cm$$. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these coloures . (Take $$\pi=22/7$$)
Let $$r$$ be the radius of the base of the cone and its slant height be $$l$$. Further, let $${r}_{1}$$ be the radius of the cylinder and $${h}_{1}$$ be its height
We have
$$r=2.5cm,h=6cm$$
$${ r }_{ 1 }=1.5cm;{ h }_{ 1 }=20cm$$
Now $$\quad l=\sqrt { { r }^{ 2 }+{ h }^{ 2 } } \Rightarrow l=\sqrt { { (2.5) }^{ 2 }+{ 6 }^{ 2 } } =6.5cm=\sqrt { 4.25+36 } =\sqrt { 40.25 } $$
Now
area to be painted orange = curved surface area of the cone + base area of the cone - base area of the cylinder
$$\Rightarrow \pi rl+\pi { r }^{ 2 }-\pi { r }_{ 1 }^{ 2 }$$
Area to be painted yellow
$$=$$ curved surface area of the cylinder + area of the base of the cylinder
$$=2\pi { r }_{ 1 }{ h }_{ 1 }+\pi { r }_{ 1 }^{ 2 }$$
We have
$$r=2.5cm,h=6cm$$
$${ r }_{ 1 }=1.5cm;{ h }_{ 1 }=20cm$$
Now $$\quad l=\sqrt { { r }^{ 2 }+{ h }^{ 2 } } \Rightarrow l=\sqrt { { (2.5) }^{ 2 }+{ 6 }^{ 2 } } =6.5cm=\sqrt { 4.25+36 } =\sqrt { 40.25 } $$
Now
area to be painted orange = curved surface area of the cone + base area of the cone - base area of the cylinder
$$\Rightarrow \pi rl+\pi { r }^{ 2 }-\pi { r }_{ 1 }^{ 2 }$$
$$=\pi \left\{ rl+{ r }^{ 2 }-{ r }_{ 1 }^{ 2 } \right\}$$
$$=\pi \left\{ 2.5\times 6.6+{ (2.5) }^{ 2 }-{ (1.5) }^{ 2 } \right\} { cm }^{ 2 }$$
$$=3.14\left( 16.25+6.25-2.25 \right) { cm }^{ 2 }=63.585{ cm }^{ 2 }$$
Area to be painted yellow
$$=$$ curved surface area of the cylinder + area of the base of the cylinder
$$=2\pi { r }_{ 1 }{ h }_{ 1 }+\pi { r }_{ 1 }^{ 2 }$$
$$=\pi { r }_{ 1 }\left( 2{ h }_{ 1 }+{ r }_{ 1 } \right) $$
$$=3.14\times 1.5(2\times 20+1.5){ cm }^{ 2 }$$
$$=195.465{ cm }^{ 2 }\quad $$
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figures. If the height of the cylinder is $$10cm$$ and its base is of radius $$3.5cm$$, find the total surface area of the article.
From a solid cylinder whose height is $$2.4cm$$ and diameter $$1.4cm$$, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest $${cm}^{2}$$.
We have,
Height of solid cylinder $$=$$ 2.4cm
diameter of solid cylinder $$=$$ 1.4cm
clearly,
Total surface area of the remaining solid $$=$$ Curved surface area of the cylinder + Area of the base of the cylinder + Curved surface area of the cone.
$$=2 \pi rh+\pi r^2+\pi r \sqrt{{r^2} +{h^2}}$$
$$=2\times \cfrac { 22 }{ 7 } \times 0.7\times 2.4+\cfrac { 22 }{ 7 } \times { (0.7) }^{ 2 }+\cfrac { 22 }{ 7 } \times 0.7\times \sqrt { { (2.4) }^{ 2 }+{ (0.7) }^{ 2 } } \left[ \because l=\sqrt { { r }^{ 2 }+{ h }^{ 2 } } \right]$$
Total surface area of the remaining solid $$=$$ Curved surface area of the cylinder + Area of the base of the cylinder + Curved surface area of the cone.
$$=2 \pi rh+\pi r^2+\pi r \sqrt{{r^2} +{h^2}}$$
$$=2\times \cfrac { 22 }{ 7 } \times 0.7\times 2.4+\cfrac { 22 }{ 7 } \times { (0.7) }^{ 2 }+\cfrac { 22 }{ 7 } \times 0.7\times \sqrt { { (2.4) }^{ 2 }+{ (0.7) }^{ 2 } } \left[ \because l=\sqrt { { r }^{ 2 }+{ h }^{ 2 } } \right]$$
$$ =10.56+1.54+5.5c{ m }^{ 2 }$$
$$=17.6c{ m }^{ 2 }\quad \quad $$
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are $$15\ cm \times$$$$10\ cm \times$$$$3.5\ cm.$$ The diameter of each of the depressions $$1\ cm$$ and the depth is $$1.4\ cm.$$ Find the volume of the wood in the entire stand.
volume of the cuboid $$=(15\times 10\times 3.5){cm}^{3}=525{cm}^{3}$$
It is given that there are four conical depressions such that the radius of each depression is $$0.5\ cm$$ and the depth is $$1.4\ cm$$
Volume of wood taken out to make four cavities $$=4\times$$ volume of a cone of base radius $$0.5\ cm$$ and height $$1.4\ cm$$
$$=4 \times \dfrac13 \pi r^2 h$$
$$=4\times \cfrac { 1 }{ 3 } \times \cfrac { 22 }{ 7 } \times 0.5\times 0.5\times 1.4{ cm }^{ 3 }$$
$$=\cfrac { 22 }{ 15 } { cm }^{ 3 }=1.47{ cm }^{ 3 }$$ (approximately)
Hence volume of the wood in the entire stand $$=\left( 525-1.47 \right) { cm }^{ 3 }=523.53\ { cm }^{ 3 }$$
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are $$2.1\ \text{m}$$ and $$4\ \text{m}$$, and slant height of the top is $$2.8\ \text{m}$$, find the area of the canvas used for making the tent. Also, find the cost of canvas of the tent at the rate of $$\text{Rs.}\ 500/\text {m}^{2}$$
For conical portion we have
$$r=2\text{ m} ~; l=2.8\text{ m}$$
$${S}_{1}=$$ curved surface area of conical portion
$$\Rightarrow { S }_{ 1 }=\pi rl\quad \quad$$
for the cylindrical portion, we have
$$r=2\text{ m}~ ; l=2.1\text{ m}$$
$${S}_{2}=$$ curved surface area of the cylindrical portion
$$\Rightarrow { S }_{ 2 }=2\pi rh=2\pi \times 2\times 2\times 2.1\text{ m}=8.4\pi \text{ m }^{ 2 }\quad \quad $$
Area of the canvas used for makine the tent $$={ S }_{ 1 }+{ S }_{ 2 }=\left( 5.6\pi +8.4\pi \right)\text { m }^{ 2 }=14\times \cfrac { 22 }{ 7 } \text{ m }^{ 2 }=44\text{ m }^{ 2 }\quad $$
Total cost of the canvas at the rate of $$\text{Rs. }500/\text{m }^{ 2 }=\text{Rs. }(500\times 44)=\text{ Rs. } 22000$$
$$r=2\text{ m} ~; l=2.8\text{ m}$$
$${S}_{1}=$$ curved surface area of conical portion
$$\Rightarrow { S }_{ 1 }=\pi rl\quad \quad$$
$$\Rightarrow { S }_{ 1 }=\pi \times 2\times 2.8\text{ m }^{ 2 }\quad \quad $$
$$\Rightarrow { S }_{ 1 }=5.6\pi \text{ m }^{ 2 }$$
for the cylindrical portion, we have
$$r=2\text{ m}~ ; l=2.1\text{ m}$$
$${S}_{2}=$$ curved surface area of the cylindrical portion
$$\Rightarrow { S }_{ 2 }=2\pi rh=2\pi \times 2\times 2\times 2.1\text{ m}=8.4\pi \text{ m }^{ 2 }\quad \quad $$
Area of the canvas used for makine the tent $$={ S }_{ 1 }+{ S }_{ 2 }=\left( 5.6\pi +8.4\pi \right)\text { m }^{ 2 }=14\times \cfrac { 22 }{ 7 } \text{ m }^{ 2 }=44\text{ m }^{ 2 }\quad $$
Total cost of the canvas at the rate of $$\text{Rs. }500/\text{m }^{ 2 }=\text{Rs. }(500\times 44)=\text{ Rs. } 22000$$
A bucket is in the form of a frustum of a cone and holds $$28.490$$ litres of water. The radii of the top and bottom are $$28cm$$ and $$21cm$$ respectively. Find the height of the bucket.
If the radii of the circular ends of a conical bucket which is $$45cm$$ high are $$28cm$$ and $$7cm$$, find the capacity of the bucket (Use $$\pi =22/7$$)
A decorative block shown in figure, is made of two solids- a cube and a hemisphere. The base of the block is a cube with edge $$5cm$$, and the hemisphere fixed on the top has a diameter $$4.2cm$$. Find the total surface area of the block (Take $$\pi =22/7$$)
The slant height of the frustum of a cone is $$4cm$$, and the perimeter of its circular bases are $$18cm$$ and $$6cm$$. Find the curved surface area of the frustum of a cone
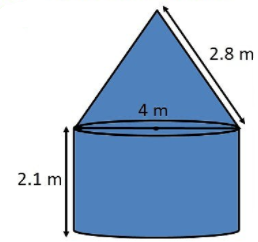
A container, open from the top, made up of a metal sheet is in the form of a frustum of a cone of height $$8\ cm$$ with radii of its lower and upper ends as $$4\ cm$$ and $$10\ cm$$ respectively. Find the cost of milk which can completely fill the container at the rate of Rs. $$50$$ per litre and the cost of metal sheet used, if the costs Rs. $$50$$ per $$100\ cm^{2}$$. (Use $$\pi =3.14$$)
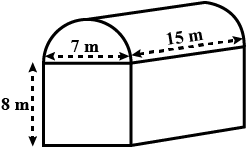
Shanta runs an industry in a shed that was in the shape of a cuboid surmounted by half-cylinder. If the base of the shed is $$7\ m \times 15\ m$$ and height of the cuboidal portion is $$8\ m$$, find the volume of the air that the shed can hold. If the industry requires machinery which would occupy a total space of $$300\ {m}^{3}$$, and there are $$20$$ workers each of whom would occupy $$0.08\ {m}^{3}$$ space on an average, how much air would be in the shed when it is working. $$\left (Take \ \pi=\dfrac{22}{7} \right )$$
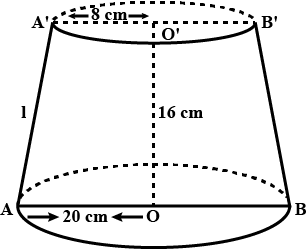
A friction clutch is in the form of a frustum of a cone, the diameter of the ends being $$32cm$$ and $$20cm$$ and length $$8cm$$. Find its bearing surface and volume.
Let ABB'A be the friction clutch of slant height $$l$$ cm
We have
$${r}_{1}=16cm,{r}_{2}=10cm$$ and $$h=8cm$$
$${ l }^{ 2 }={ h }^{ 2 }+{ \left( { r }_{ 1 }-{ r }_{ 2 } \right) }^{ 2 }\quad \Rightarrow { l }^{ 2 }=64+36\Rightarrow l=10cm$$
Now Bearing surface of the clutch $$=$$ lateral surface of the furstum
$$=\pi \left( { r }_{ 1 }+{ r }_{ 2 } \right) l$$
Volume $$=\cfrac { 1 }{ 3 } \pi \left( { r }_{ 1 }^{ 2 }+{ r }_{ 2 }^{ 2 }+{ r }_{ 1 }{ r }_{ 2 } \right) h\quad$$
We have
$${r}_{1}=16cm,{r}_{2}=10cm$$ and $$h=8cm$$
$${ l }^{ 2 }={ h }^{ 2 }+{ \left( { r }_{ 1 }-{ r }_{ 2 } \right) }^{ 2 }\quad \Rightarrow { l }^{ 2 }=64+36\Rightarrow l=10cm$$
Now Bearing surface of the clutch $$=$$ lateral surface of the furstum
$$=\pi \left( { r }_{ 1 }+{ r }_{ 2 } \right) l$$
$$=\cfrac { 22 }{ 7 } \times \left( 16+10 \right) \times 10{ cm }^{ 2 }$$$
$$=817.14{ cm }^{ 2 }\quad $$
Volume $$=\cfrac { 1 }{ 3 } \pi \left( { r }_{ 1 }^{ 2 }+{ r }_{ 2 }^{ 2 }+{ r }_{ 1 }{ r }_{ 2 } \right) h\quad$$
$$ =\cfrac { 1 }{ 3 } \times \cfrac { 22 }{ 7 } \times 8\times \left( { 16 }^{ 2 }+16\times 10+{ 10 }^{ 2 } \right) { cm }^{ 3 }\quad$$
$$ =\cfrac { 176 }{ 21 } \times 516{ cm }^{ 3 }$$
$$=4324.57{ cm }^{ 3 }\quad $$
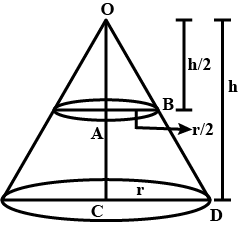
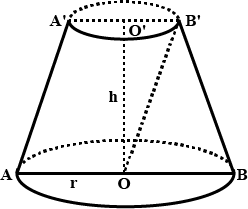
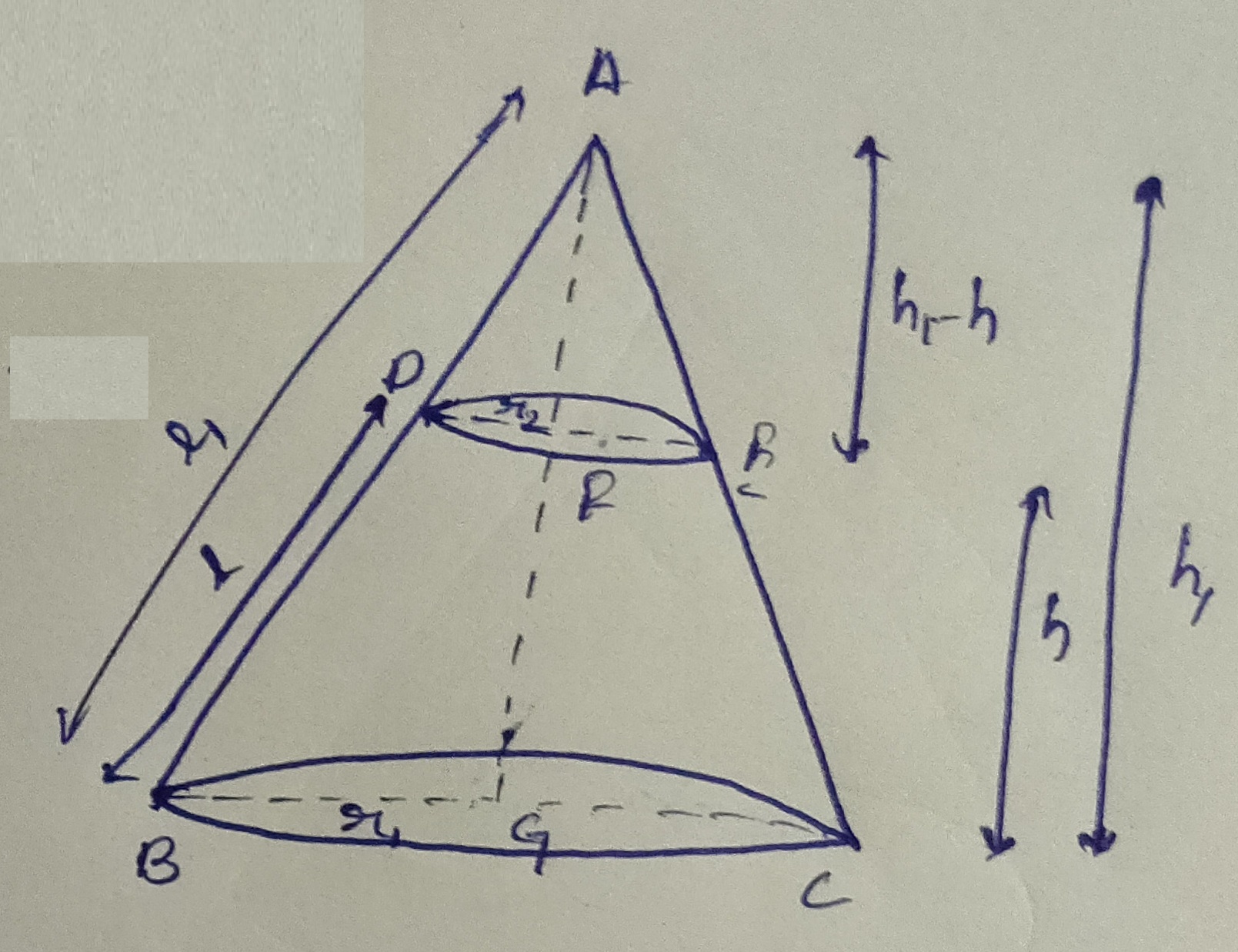
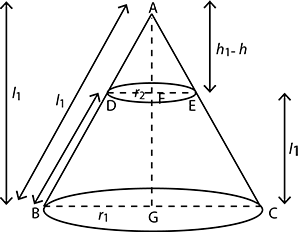
The radius of the base of a right circular cone is $$r$$. It is cut by a plane parallel to the base at a height $$h$$ from the base. The distance of the boundary of the upper surface from the centre of the base of the frustum is $$\sqrt { { h }^{ 2 }+\cfrac { { r }^{ 2 } }{ 9 } } $$. Show that the volume of the frustum is $$\cfrac{13}{27}\pi { r }^{ 2 }h$$
We have
$$OA=r,OO'=h,OB'\sqrt { { h }^{ 2 }+\cfrac { { r }^{ 2 } }{ 9 } } $$
In $$\triangle {OO'B}$$ we have
$${ OB' }^{ 2 }={ OO' }^{ 2 }+{ O'B }^{ 2 }$$
$$OA=r,OO'=h,OB'\sqrt { { h }^{ 2 }+\cfrac { { r }^{ 2 } }{ 9 } } $$
In $$\triangle {OO'B}$$ we have
$${ OB' }^{ 2 }={ OO' }^{ 2 }+{ O'B }^{ 2 }$$
$$\Rightarrow { h }^{ 2 }+\cfrac { { r }^{ 2 } }{ 9 } ={ h }^{ 2 }+{ O'B' }^{ 2 }$$
$$\Rightarrow O'B'=\cfrac { r }{ 3 } $$
Volume of the frustum $$=\cfrac { 1 }{ 3 } \pi \left( { r }_{ 1 }^{ 2 }+{ r }_{ 2 }^{ 2 }+{ r }_{ 1 }{ r }_{ 2 } \right) h$$
volume of the frustum $$=\cfrac { 1 }{ 3 } \pi \left\{ { r }^{ 2 }+{ \left( \cfrac { r }{ 3 } \right) }^{ 2 }+r\times \cfrac { r }{ 3 } \right\} h\quad \quad $$
$$=\cfrac { 1 }{ 3 } \pi \left\{ { r }^{ 2 }+\cfrac { { r }^{ 2 } }{ 9 } +\cfrac { { r }^{ 2 } }{ 3 } \right\} h$$
$$=\cfrac { 13 }{ 27 } \pi { r }^{ 2 }h$$ $$[Hence \ proved]$$
A solid consisting of a right cone standing on a hemisphere is placed upright in a right circular cylinder full of water and touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is $$60cm$$ and its height is $$180cm$$, the radius of the hemisphere is $$60cm$$ and height of the cone is $$120cm$$, assuming that the hemisphere and the cone have common base.
For the cylinder we have
Radius of the base$$=r=60cm$$
Height $$=h=180cm$$
Volume of water that the cylinder contains $$=V=\pi { r }^{ 2 }h=\left\{ \pi \times { 60 }^{ 2 }\times 180 \right\} {cm}^{3}$$
For conical part, we have
Radius of the base $$=r=60cm$$
Height $$={h}_{1}=120cm$$
Volume of conical part $${V}_{1}=\cfrac { 1 }{ 3 } \pi { r }^{ 2 }{ h }_{ 1 }=\cfrac { 1 }{ 3 } \pi \times { 60 }^{ 2 }\times 120{ cm }^{ 3 }=\left\{\pi \times { 60 }^{ 2 }\times 40 \right\} { cm }^{ 3 }$$
For hemispherical part, we have
Radius $$=r=60cm$$
Volume of the hemisphere $${ V }_{ 2 }=\left\{ \cfrac { 2 }{ 3 } \pi \times { 60 }^{ 3 } \right\} { cm }^{ 3 }\quad $$
$$\Rightarrow { V }_{ 2 }=\left\{ 2\pi \times { 60 }^{ 2 }\times 20 \right\} { cm }^{ 3 }=\left( 40\pi \times { 60 }^{ 2 } \right) { cm }^{ 3 }\quad \quad $$
Hence volume of the water left out in the cylinder
$$\Rightarrow V={ V }_{ 1 }-{ V }_{ 2 }\quad =\left\{ \pi \times { 60 }^{ 2 }\times 180-\pi \times { 60 }^{ 2 }\times 40-40\pi \times { 60 }^{ 2 } \right\} { cm }^{ 3 }=\pi \times { 60 }^{ 2 }\times \left\{ 180-40-40 \right\} { cm }^{ 3 }$$
$$=\cfrac { 22 }{ 7 } \times 3600\times 100{ cm }^{ 3 }$$
Radius of the base$$=r=60cm$$
Height $$=h=180cm$$
Volume of water that the cylinder contains $$=V=\pi { r }^{ 2 }h=\left\{ \pi \times { 60 }^{ 2 }\times 180 \right\} {cm}^{3}$$
For conical part, we have
Radius of the base $$=r=60cm$$
Height $$={h}_{1}=120cm$$
Volume of conical part $${V}_{1}=\cfrac { 1 }{ 3 } \pi { r }^{ 2 }{ h }_{ 1 }=\cfrac { 1 }{ 3 } \pi \times { 60 }^{ 2 }\times 120{ cm }^{ 3 }=\left\{\pi \times { 60 }^{ 2 }\times 40 \right\} { cm }^{ 3 }$$
For hemispherical part, we have
Radius $$=r=60cm$$
Volume of the hemisphere $${ V }_{ 2 }=\left\{ \cfrac { 2 }{ 3 } \pi \times { 60 }^{ 3 } \right\} { cm }^{ 3 }\quad $$
$$\Rightarrow { V }_{ 2 }=\left\{ 2\pi \times { 60 }^{ 2 }\times 20 \right\} { cm }^{ 3 }=\left( 40\pi \times { 60 }^{ 2 } \right) { cm }^{ 3 }\quad \quad $$
Hence volume of the water left out in the cylinder
$$\Rightarrow V={ V }_{ 1 }-{ V }_{ 2 }\quad =\left\{ \pi \times { 60 }^{ 2 }\times 180-\pi \times { 60 }^{ 2 }\times 40-40\pi \times { 60 }^{ 2 } \right\} { cm }^{ 3 }=\pi \times { 60 }^{ 2 }\times \left\{ 180-40-40 \right\} { cm }^{ 3 }$$
$$=\cfrac { 22 }{ 7 } \times 3600\times 100{ cm }^{ 3 }$$
$$=\cfrac { 22\times 36 }{ 700 } { m }^{ 3 }$$
$$=1.1314{ m }^{ 3 }$$
The radii of the circular ends of a frustum of height $$6\ cm$$ are $$14\ cm$$ and $$6\ cm$$ respectively. Find the lateral surface area and total surface area of the frustum.
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see figure). The length of the entire capsule is $$14mm$$ and the diameter of the capsule is $$5mm$$. Find its surface area.
From the figure, it can be seen that, the capsule is a combination of cylinder and two hemispheres.
Total surface area of capsule will be sum of surface area of cylinders and twice the surface area of hemisphere.
From the figure, length of cylinder $$=9\ cm$$
radius of cylinder $$=$$ radius of hemisphere $$= \dfrac{5}{2}$$
Surface area of cylinder :
$$=2\pi r \ell $$
$$=2\pi (\dfrac{5}{2})(9)$$
$$=45\pi$$
Surface area of two hemispheres :
$$=2 \times 2\pi r^2$$
$$=2(2\pi (\dfrac{5}{2})^{2})$$
$$=4\pi \dfrac{25}{4}$$
$$ = 25\pi$$
Total surface area :
$$=25\pi +45\pi $$
$$=70\pi cm^{2}$$
$$=\dfrac{22}{7}\times 70$$
$$=220 cm^{2}$$
A toy is in the form of a cone of radius $$3.5cm$$ mounted on a hemisphere of same radius. The total height of the toy is $$15.5cm$$. Find the total surface area of the toy.
A cylinder and $$a$$ cone have equal bases. The height of the cylinder is $$3\ cm$$ and the area of its base is $$100\ cm^{2}$$. The cone is placed upon the cylinder. Volume of the solid figure so formed is $$500\ cm^{3}$$. Find the total height (in $$cm$$) of the figure.
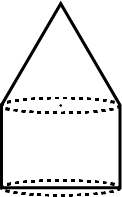
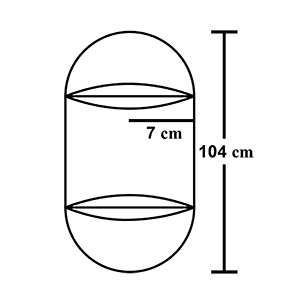
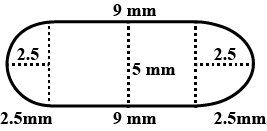
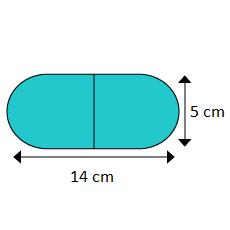
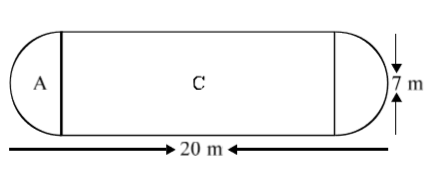
The shape of a garden is rectangular in the middle and semi-circular at the ends as shown in the diagram. Find the area and the perimeter of this garden. (Length of a rectangle is $$20-(3.5+3.5)$$ metres)
A vessel is in the form of a hollow hemisphere mounted on a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
A cubical block of side $$7cm$$ is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
The hemisphere is mounted on the cubical block
The diameter of the hemisphere $$ =$$ the side of the cube $$ = 7cm$$
$$\Rightarrow TSA$$ of the solid $$= TSA$$ of cube$$ -$$ Area of base of hemisphere $$+ CSA $$ of hemisphere
$$\Rightarrow TSA = (6\times 7^2) –(\pi \times (3.5)^2) +( 2\times \pi \times (3.5)^2)$$
$$\Rightarrow TSA=(6\times 7^2) + (\pi \times (3.5)^2)$$
$$\Rightarrow TSA = 332. 465\ cm^2$$
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are $$3.5\ m$$ and $$2\ m$$ respectively, and the slant height of the top is $$3.5\ m$$, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs. $$1000$$ per $${m}^{2}$$. (Note that the base of the tent will not be covered with canvas)
$$Area \ of\ Canvas=Curved \ Area \ of \ Cone+Curved \ Surface \ Area \ of \ the \ Cylinder$$
$$Lets\ calculate\ the\ Curved\ Surface\ area\ of\ Cone:$$
$$Diameter \ of \ cone=Diameter \ of \ Cylinder=4 \ m$$
$$\implies radius=\dfrac{4}{2}=2 \ m$$
$$Slant \ height=l=2.8\ m$$
$$ Curved \ Surface \ area \ of \ Cone=\pi rl$$
$$=\dfrac{22}{7} \times2\times2.8=17.6 \ m^2$$
$$Curved \ Surface \ area \ of \ Cylinder=2\pi rh$$
$$=2\times\dfrac{22}{7}\times2\times2.1=26.4 \ m^2$$
$$\therefore The \ Area \ of \ Canvas=17.6 + 26.4 = 44 m^2$$
Now,
$$Cost\ of\ the\ canvas\ of\ the\ tent\ for\ 1 \ m^2 = Rs \ 500$$
$$Cost\ of\ the\ canvas\ of\ the\ tent\ for\ 44 \ m^2 = 500\times44=Rs \ 22000$$
$$\therefore Total \ Cost=22000\ rupees$$
A hemispherical depression is cut out from one face of a cuboidal block such that the diameter $$l (\text{cm})$$ of the hemisphere is equal to the edge of the cube. Find the surface area of the remaining solid.
Surface area of solid=area of cube + curved surface area of hemisphere -base area of hemisphere
$$=6(side)^2+2 \pi r^2-\pi r^2$$
$$=6l^2+2 \pi\left ( \dfrac{l}{2} \right )^2- \pi \left ( \dfrac{l}{2} \right )^2$$
$$=6l^2+\pi\dfrac{l^2}{2}-\pi\dfrac{l^2}{4}$$
$$=6l^2+\pi\dfrac{l^2}{4}$$
$$=l^2\left ( 6+\dfrac{\pi}{4} \right )$$
$$=\dfrac{1}{4}l^2(\pi+24)$$
A toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm . The total height of the toy is $$15.5 cm$$ . Find the total surface area and volume of the toy .
Given: toy in form of a cone mounted on a hemisphere
radius of hemisphere $$= 3.5$$ cm
Total height of toy $$= 15.5$$ cm
To find: Total surface area TSA = ? Volume, V = ?
Solution :
$$h = 12$$ cm
$$r = 3.5$$ cm
Assuming that the cone is completed mounted on hemisphere
TSA of toy = CSA of cone + CSA of hemisphere
$$=\pi rl+2\pi r^{2}$$ [$$r\rightarrow $$ radius of both cone and hemisphere as it is here]
$$= \pi r[l+2r]\\$$
$$=\dfrac{22}{7}\times \dfrac{35}{10}\left [ \sqrt{(12)^{2}+(3.5)^{2}}+2\times \dfrac{35}{10} \right ]\\$$
$$= 11\left [ \sqrt{144+12.25}+7 \right ]= 11\left [ \sqrt{156.25}+7 \right ]$$
$$=11(12.5+7)$$
$$= 11\times 19.5$$
$$= 214.5\, cm^{2}$$
Volume of toy = $$\dfrac{1}{3}\pi r^{2}h+\dfrac{2}{3}\pi r^{3}$$
$$=\dfrac{1}{3}\pi r^{2}[h+2r]\\$$
$$= \dfrac{1}{3}\times \dfrac{22}{7}\times \dfrac{35}{10}\times \dfrac{25}{10}\left[12+2\times \dfrac{35}{10}\right]\\$$
$$=\dfrac{77}{6}[ 12+7]=\dfrac{77\times 19}{6}=\dfrac{1463}{6}$$
$$= 243. 83\, cm^{3}$$
Water flows at the rate of $$10$$m per minute through a cylindrical pipe $$5$$ mm in diameter. How long would it take to fill a conical vessel whose diameter at the base is $$40$$cm and depth $$24$$cm?
Two cylinders are 12 cm and 18 cm in height. Their diameters are 12 cm and 16 cm respectively. Both the cylinders are melted and the material is moulded into a solid right circular cone of height 33 cm. Find its diameter.
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand .
$$3$$ cubes of edge $$4 cm$$ are joined end to end. Find surface area of resulting cuboid.
Pragya wrapped a cord around a circular pipe of radius $$4\ cm$$ (adjoining figure) and cut off the length required of the cord. Then she wrapped it around a square box of side $$4\ cm$$ (also shown). Did she have any cord left? $$(\pi=3.14)$$
A metal cube of side $$11\;cm$$ is completely submerged in water contained in a cylindrical vessel with the diameter $$28\;cm$$. Find the rise in the level of water.
How many shots each having diameter $$4.2cm$$ can be made from cuboidal lead solid of dimensions $$66cm\times 42cm\times 21cm$$.
A tent is in the form of a cylinder whose height is $$5\ m$$ surmounted by a cone of equal base. The diameter of base is $$105\ m$$. The slant height of cone is $$50\ m$$. Find the cost of cloth at $$Rs.\ 15$$ per square meter to make the tent.
Tent cylinder height$$=5$$m
Diameter of base$$=105$$m
Slant height of cone$$=50m=l$$
Cost of cloth let Rs. $$15$$ per $$m^2$$.
Area of cylinder
$$=2\pi rh$$
$$=2\times \dfrac{22}{7}\times \left(\dfrac{105}{2}\right)\times5$$
$$=1650m^2$$
Area of cone
$$=\pi r h$$
$$=\dfrac{22}{7}\times \left(\dfrac{105}{2}\right)\times 50$$
$$=8250m^2$$
Total area$$=1650+8250=9900m^2$$
Total cost$$=9900\times 15$$
$$=Rs\, 1,48,500$$
A metal cylinder with height 10 cm and diameter of base 70 cm is melted to make a number of small discs with radius 1 cm and thickness 0.5 cm. How many such discs could be made from the cylinder?
The diameter of base of a chimney of kiln is 80 cm and height is 12.5 m. What will be the cost of painting this chimney from outside at the rate of Rs. 140 per sq m?
The decorative block shown in the figure is made of two solids, a cube, and a hemisphere. The base of the block is a cube with edge $$5\;{ cm }$$ and the hemisphere fixed on the top has a diameter of $$4.2\;{ cm }$$. Find the total surface area of the block. (Take $$\pi = \dfrac { 22 } { 7 } )$$
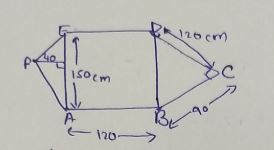
Find the area of the field ABCDEF, as shown below:
Area of field ABCDEF$$=$$Area of rectangle ABDE$$+$$Area of $$\Delta$$BCD$$+$$Area of $$\Delta$$AEF
$$=(120\times 150)cm^2+\left(\dfrac{1}{2}\times 90\times 120\right)cm^2+\dfrac{1}{2}\times40\times 150$$
$$=18,000+5400+3,000$$
$$=26,400cm^2$$.
A farmer connects a pipe of internal diameter $$20\ cm$$ form a canal into a cylindrical tank in her field, which is $$10\ m$$ in diameter and $$2\ m$$ deep. If water flows through the pipe at the rate of $$3\ km\ h^{-1}$$, in how much time will the tank be filled ?
The radii of ends of a frustum are $$14\text{ cm}$$ and $$6\text{ cm}$$ respectively and its height is $$6\text{ cm}$$. Find its volume.
Shankar made the pictures shown above.
What shapes can they be broken into so that we can find their areas easily?
We can break down the given shapes as shown above.
That way, we can easily find out their areas.
The volume of a right circular cone is $$4710\ cu.cm$$. if the radius and height of the cone are in the ratio $$3:4$$, find its slant height, when $$\pi=3 \cdot 14$$.
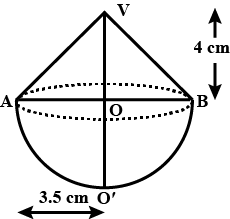
A semicircular sheet of metal of diameter $$28cm$$ is bent into an open conical cup. Find the depth and capacity of cup.$$(\sqrt{3}=1.73)$$
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is $$\dfrac{4r}{3}$$. Also show that the maximum volume of the cone is $$\dfrac{8}{27}$$ of the volume of the sphere.
Radius of sphere=r
Radius of cone=R
Height of cone=h
$$BC=\sqrt { { r }^{ 2 }-{ R }^{ 2 } } $$
$$\therefore h=r+\sqrt { { r }^{ 2 }-{ R }^{ 2 } } $$
$$\therefore $$Volume of cone$$=\cfrac { 1 }{ 3 } \pi { R }^{ 2 }\left( r+\sqrt { { r }^{ 2 }-{ R }^{ 2 } } \right) $$
$$\cfrac { dV }{ dR } =\cfrac { 2 }{ 3 } \pi Rr+\cfrac { 2\pi }{ 3 } R\sqrt { { r }^{ 2 }-{ R }^{ 2 } } +\cfrac { \pi { R }^{ 2 } }{ 3 } .\cfrac { \left( -2R \right) }{ 2\sqrt { { r }^{ 2 }-{ R }^{ 2 } } } $$
$$=\cfrac { 2\pi Rr }{ 3 } +\cfrac { 2\pi R\left( { r }^{ 2 }-{ R }^{ 2 } \right) -\pi { R }^{ 3 } }{ 3\sqrt { { r }^{ 2 }-{ R }^{ 2 } } } $$
$$=\cfrac { 2\pi Rr }{ 3 } +\cfrac { 2\pi R{ r }^{ 2 }-3\pi { R }^{ 3 } }{ 3\sqrt { { r }^{ 2 }-{ R }^{ 2 } } } $$
For max. volume
$$\cfrac { dV }{ dR } =0$$
$$\Rightarrow \cfrac { 2\pi Rr }{ 3 } =\cfrac { 3\pi { R }^{ 2 }-2\pi { r }^{ 2 } }{ 3\sqrt { { r }^{ 2 }-{ R }^{ 2 } } } $$
$$\Rightarrow 2Rr=\cfrac { 3{ R }^{ 3 }-2{ r }^{ 2 }R }{ \sqrt { { r }^{ 2 }-{ R }^{ 2 } } } \Rightarrow 2r\sqrt { { r }^{ 2 }-{ R }^{ 2 } } =3{ R }^{ 2 }-2{ r }^{ 2 }$$
$$\Rightarrow 9{ R }^{ 4 }-8{ r }^{ 2 }{ R }^{ 2 }=0$$
$$\therefore { R }^{ 2 }=0$$
$$\cfrac { 8{ r }^{ 2 } }{ 9 } $$
$$\cfrac { { d }^{ 2 }V }{ d{ R }^{ 2 } } <0$$
$${ R }^{ 2 }=\cfrac { 8{ r }^{ 2 } }{ 9 } $$
$$\therefore $$For $${ V }_{ max },{ R }^{ 2 }=\cfrac { 8{ r }^{ 2 } }{ 9 } $$
$$\therefore h=r+\cfrac { r }{ 3 } =\cfrac { 4r }{ 3 } $$
$$V=\cfrac { 1 }{ 3 } \times \cfrac { 8{ r }^{ 2 } }{ 9 } \times \cfrac { 4r }{ 3 } =\cfrac { 8 }{ 27 } \cfrac { 4\pi { r }^{ 3 } }{ 3 } $$
Derive the formula for the volume of the frustum of a cone, given to you in Section $$13.5$$ using the symbols as explained.
let $$ABC$$ be a cone. A frustum $$DECB$$ is cut by a plane parallel to its base.
let $$r_1 \ and \ r_2$$ be the radil of the ends of the frustum of the cone
and $$h$$ be the height of the frustum of the cone
In $$\triangle ABG$$ and $$\triangle ADR, DR \parallel BG$$
$$\therefore \triangle ABG\sim \triangle ADF$$
$$\dfrac{DF}{BG}=\dfrac{AF}{AG}=\dfrac{AD}{AB}$$
$$\dfrac{r_2}{r_1}=\dfrac{h_1-h}{h_1}=\dfrac{l_1-l}{l_1}$$
$$\dfrac{l-l}{l_1}=\dfrac{r_2}{r_1}$$
$$\dfrac{l}{l_1}=\dfrac{r_1-r_2}{r_1}$$
$$\dfrac{l_1}{l}=\dfrac{r_1}{r_1-r_2}$$
$$l_1=\dfrac{r_1 l}{r_1-r_2}$$
$$CSA$$ of frustum $$DECB=CSA$$ of cone $$ABC- CSA$$ of cone $$ADE$$
$$=\pi r_1 l_1-\pi r_2(l_1-l)$$
$$=\pi r_1\left(\dfrac{lr_1}{r_1-r_2}\right)-\pi r_2\left[\dfrac{r_1l}{r_1-r_2-l}-l\right]$$
$$=\dfrac { { \pi { r_{ 1 } }^{ 2 }l } }{ { r_{ 1 }-r_{ 2 } } } -\pi r_{ 2 }\left[ \dfrac { r_{ 1 }l-r_{ 1 }l+r_{ 2 }l }{ r_{ 1 }-r_{ 2 } } \right] $$
$$\dfrac{\pi{r_1}^2l}{r_1-r_2}-\dfrac{\pi{r_2}^2l}{r_1-r_2}$$
$$=\dfrac{\pi r(({r_1})^2-{r_2}^2)}{r_1-r_2}$$
CSA frustum $$=\pi l(r_1+r_2)$$
Total surface area $$=CSA$$ of frustum $$+$$ Area of upper conedar end $$+$$ Area of lower conedar end
$$=\pi(r_1+r_2)l+\pi{r_2}^2+\pi {r_1}^2$$
$$=\pi\left((r_1+r_2)l+{r_2}^2+ {r_1}^2\right)$$
The given figure shows a solid formed of a solid cube of side
$$40$$$$\mathrm { cm }$$ and a solid cylinder of radius 20$$\mathrm { cm }$$ and height $$50$$$$\mathrm { cm }$$
attached to the cube as shown.Find the volume and the total
surface area of the whole solid
ITake $$\pi = 3 \cdot 14 ]$$
A field is $$60\ m$$ long and $$20\ m$$ wide. A tank $$12\ m$$ long, $$10\ m$$ broad and $$3\ m$$ deep is dug in the field. The earth taken out of it is spread evenly over field. How mach is the level of the field raised supporting the earth taken out increases by $$\dfrac {1}{8}$$ of the volume?
What length of canvas $$3\ m$$ wide will be required to make a conical tent of height $$8\ m$$ and radius of base $$6\ m$$. (use $$\pi=3.14$$)
3 m wide canvas, height 8 m & radius 6 m
$$ \rightarrow $$ curved surface Area of tent = $$ \pi .rl.$$
$$ r = 6 \,m, h = 8 \,m $$
slant height $$ l = \sqrt{h^{2}+r^{2}}= \sqrt{8^{2}+6^{2}}=\sqrt{64+36}= \sqrt{100}= 10 m$$
curved surface Area $$ = \pi .r l = 3.14\times 6\times 10 = 188.4 \,m^{2}$$
Now,
Area of canvas = Area of tend
$$ L\times breadth = 188.4\,m^{2}$$
$$ L\times 3\,m = 188.4\,m^{2}$$
$$ L = \frac{188.4}{3}$$
$$ L = 62.8 \,meter$$
A toy is in the form of a cone of radius $$3.5\text{ cm}$$ mounted on a hemisphere of the same radius. The total height of the toy is $$15.5\text{ cm}$$. Find the total surface area of the toy.
Radius of cone $$= 3.5\text{ cm},$$ height of cone $$= 15.5 – 3.5 = 12\text{ cm}.$$
Slant height of cone can be calculated as follows:
$$l=\sqrt{{h}^{2}+{r}^{2}}$$
$$=\sqrt{{12}^{2}+{3.5}^{2}}$$
$$=\sqrt{144+12.25}$$
$$=\sqrt{156.25}$$
$$=12.5\text{ cm}$$
Curved surface area of cone $$=\pi rl$$
$$=\dfrac{22}{7}\times3.5\times 12.5$$
$$=137.5\text{ cm}^{2}$$
Curved surface area of hemispherical portion $$=2\pi{r}^{2}$$
$$=2\times\dfrac{22}{7}\times3.5\times 3.5$$
$$=77\text{ cm}^{2}$$
Hence, total surface area of the toy is equal to $$137.5+77=214.5\text{ cm}^{2}$$
- A cylinder, a cone and a hemisphere are of same base and of same height. Find the ratio of their volumes ?
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold Pens. The dimensions of the cuboid are 15$$\mathrm { cm }$$ by 10$$\mathrm { cm }$$ by 3.5$$\mathrm { cm }$$ . The radius of each of the depression is 0.5$$\mathrm { cm }$$ and the depth is 1$$\cdot 4 \mathrm { cm }$$ .Find the volume of the wood in the entire stand,correct to 2 decimal places.
Figure 7.13 shows a toy. Its lower part is a hemisphere and the upper part is a cone. Find the volume and the surface area the toy from the measures shows in the figure.$$(\pi =3.14)$$
REF.image
Volume of the toy
= Volume of cone + Volume of hemisphere
$$ = \frac{1}{3} \pi\, r^{2} h + \frac{2}{3} \pi \, r^{3}$$
$$ = \frac{\pi r^{2}}{3}\left [ h + 2r \right ] = \frac{3.14 \times3^{2}}{3} \left [ 4 + 2 \times 3 \right]$$
$$ = 9.42 \times 10 = 94.2 cm^{3}$$
Total surface area of the toy
= CSA of cone + CSA of hemisphere
$$ = \pi r l + 2 \pi r^{2} $$
$$ = \pi r (l+2r)$$
$$ = 3.14 \times 3 \left [ 5 + 2 \times 3 \right ]$$
$$= 103.62 \,cm^{2}$$
A cylinder and a cone have the same height and the same radius. The volume of the cylinder is $$24\ \text{cm}^{3}$$. What will be the volume of the cone.
An ice-cream cone consisting of the cone is surmounted by a hemisphere.The common radius of a hemisphere & cone is $$3.5\ cm$$ & the total height of ice cream is $$12.5\ cm$$. Calculate the volume of ice-cream in the solid shape .
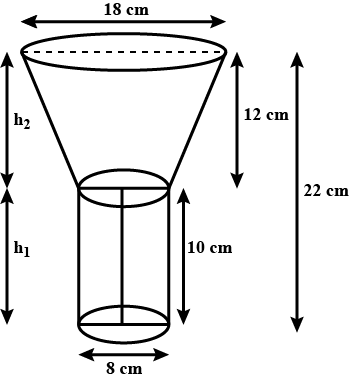
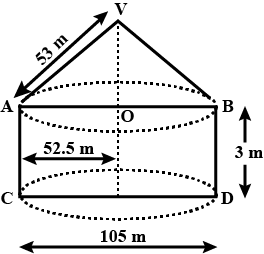
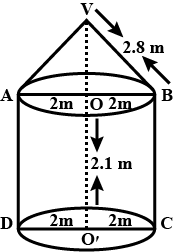
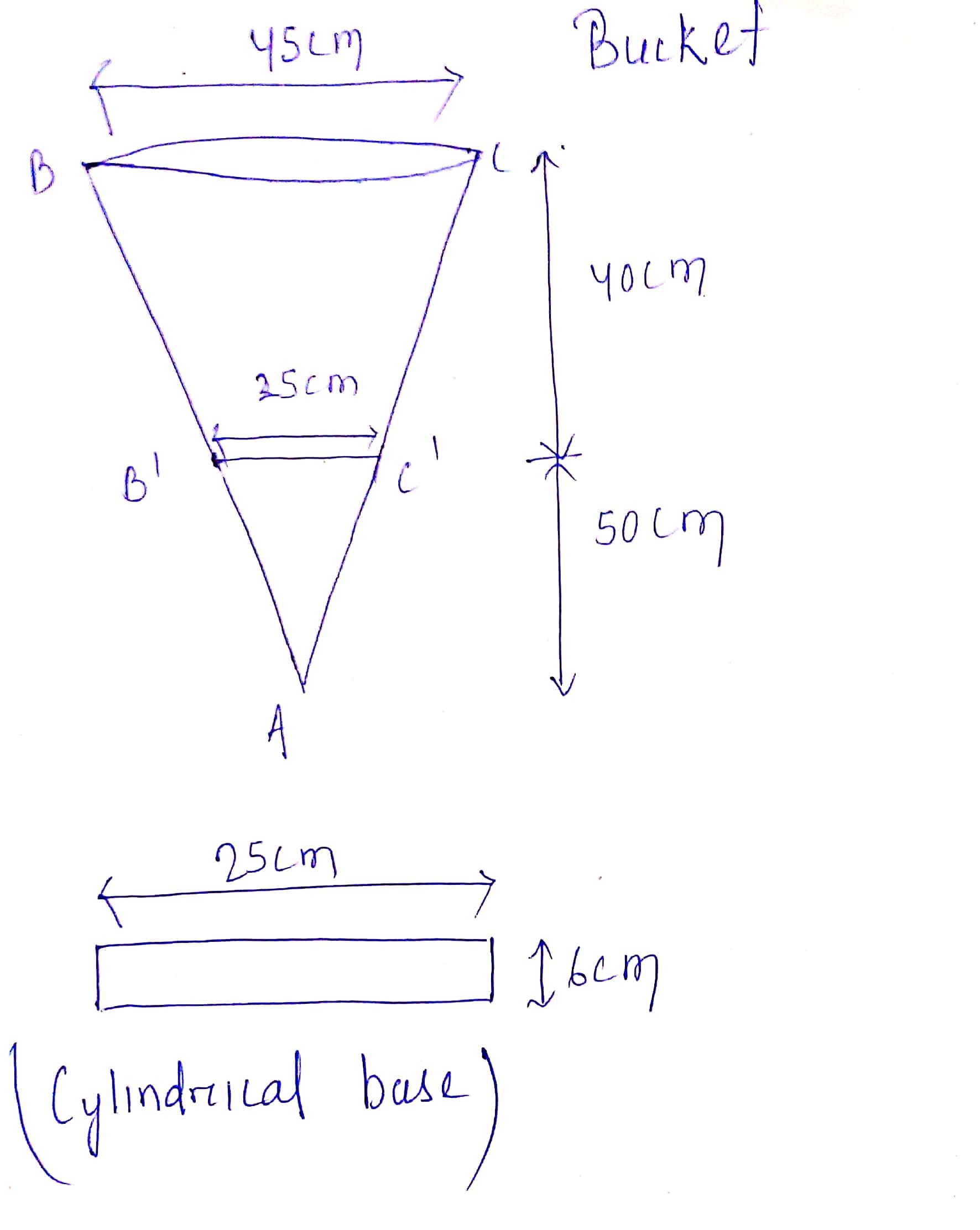
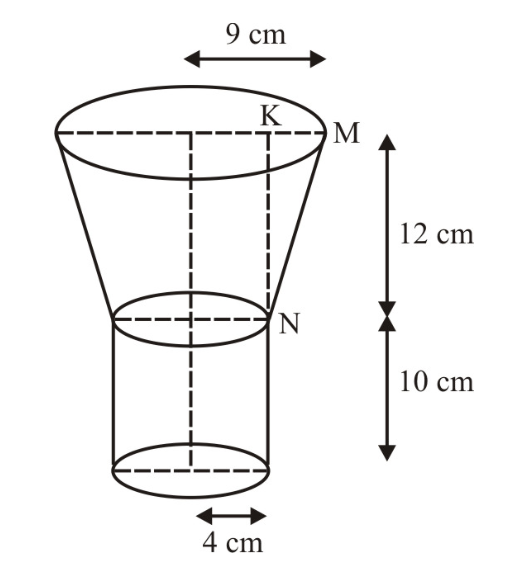
An open metal bucket is in the shape of frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The diameter of the two circular end of buckets are $$45$$cm and $$25$$ cm, the total vertical height of the bucket is $$40$$ cm and that of cylindrical base is$$6$$ cm. Find the area of the metalic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also find the volume of water the bucket can hold. [Take $$\pi=\dfrac{22}{7}$$]
Curved bucket surface area $$BB'C'C$$ $$=$$curved surface area of cone $$ABC$$$$-$$curved surface area of$$AB'C'$$
slant height of cone $$ABC$$$$=$$$$\sqrt { { 90 }^{ 2 }+{ 22.5 }^{ 2 } } $$$$=$$$$92.77cm$$
slant height of cone $$AB'C'=$$$$\sqrt { { 50 }^{ 2 }+{ 12.5 }^{ 2 } } $$$$=$$$$50.12$$$$cm$$
so curved surface area of bucket $$BB'C'C=$$$$\pi \times 22.5\times 92.77-\pi \times 12.5\times 50.12$$
$$=4587{ cm }^{ 2 }$$
surface area of cylindrical base$$=2\times 3.14\times { 12.5 }^{ 2 }+2\times 3.14\times 12.5\times 6\\ =1452.25{ cm }^{ 2 }$$
total surface area$$=1452.25+4587=6039.25{ cm }^{ 2 }$$
volume of water$$=\frac { \pi { \times 22.5 }^{ 2 }\times 90 }{ 3 } -\frac { \pi \times { 12.5 }^{ 2 }\times 50 }{ 3 } \\ =39511.67{ cm }^{ 3 }\\ =\frac { 39511.67 }{ 1000 } ℓ\\ =39.5ℓ$$
The radii of the ends of frustum of a cone 45 cm high are 28 cm and 7 cm. Find its volume, the curved surface area and the total surface area
A cistern, internally measuring $$150$$cm $$\times 120$$cm $$\times 110$$cm, has $$129600cm^3$$ of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being $$22.5$$cm$$\times 7.5$$cm$$\times 6.5$$cm?
Find the surface area of biggest sphere that can fit inside a cube of side $$4a\ cm$$.
A container shaped like a right circular cylinder having diameter $$12cm$$ and height $$15cm$$ is full of ice cream. The ice cream is to be filled into cones of height $$12cm$$ and diameter $$6cm$$, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a come on the other. The radius and height of the cylindrical pan are $$5\ cm$$ and $$13\ cm$$ respectively. The radii of the hemispherical and the conical parts are the same as that of the cylindrical part. Find the surface area of the toy, if the total height of the toy is $$30\ cm$$.
Perimeter is the sum of the length of boundary of any shape
$$H = 30\ cm \,\, h = 13\ cm$$
$$r = 5\ cm$$
$$ h_c = H - h - r$$
$$= 30 - 13 - 5 = 12\ cm$$
SA of toy $$= CSA$$ of cone $$+ CSA$$ of cylinder $$+ CSA$$ of hemisphere
$$= \pi rl + 2 \pi r h + 2 \pi r^2$$
$$= \pi r \sqrt{r^2 + h^2} + 2 \pi r (h + r)$$
$$= \pi [5(13) + 2 (5) (18)]$$
$$= 245 \pi$$
$$ = 769.69\ cm^2$$
Monica has a piece of canvas whose area is $$551$$ $$m^2$$. She uses it to have a conical tent made, with a base radius of $$7$$m. Assuming that all the stitching margins and the wastage incurred while cutting, amounts to approximately $$1 m^2$$, find the volume of the tent that can be made with it.
Given :
area : 551 m, r = 7 m
wastage :$$ 1m^{2}$$
as area of cone $$ - \frac{1}{2}\times base\times height$$
$$ 551 = \frac{1}{2}\times 7\times height$$
$$ = 157.4m$$ = height
Volume of cone = $$ \frac{1}{3}\pi r^{2} = h$$
$$ = \frac{1}{3}\times \frac{22}{7}\times \frac{7}{7}\times 157.4\times 1$$
$$ = 164.89$$
A toy is in the form of a cone mounted on a hemisphere with same radius. The diameter of the conical base is 7 cm and the height of the toy is 14.5 cm. Find the volume of the toy
Diameter of hemisphere$$=7$$cm
Radius of hemisphere$$r=d/2$$
$$=\dfrac{7}{2}=3.5$$cm
Height of hemisphere$$=$$Radius of hemisphere
$$=3.5$$cm
Height of Toy$$=14.5$$cm
Height of cone$$=14.5-3.5=11$$cm
Radius of cone$$=3.5$$cm
$$\therefore$$ Volume of cone$$=$$Volume of cone$$+$$Volume of hemisphere
$$=\dfrac{1}{3}\cdot \pi r^2h+\dfrac{4}{3}\cdot \pi r^3$$
$$=\dfrac{1}{3}\cdot \dfrac{22}{7}\cdot (3.5)^2\cdot 11+\dfrac{4}{3}\cdot \dfrac{22}{7}(3.5)^3$$
Volume of toy$$=320.83cm^3$$.
A field is 700 m long and 40 m broad, A trench which is 10 m long, 30 m broad and 14 m deep is dug in the field .The earth taken out of it is evenly spread over the remaining part of the filed. Find the rise in the level of the field.
If the triangle ABC is revolved about the side $$5$$cm, then find the volume of the solid so obtained.
Cone is formed when $$ \Delta ABC $$ is revolved about $$ 5 cm $$
$$ r =12 cm $$
$$ h = 5 cm $$
$$\therefore V = \frac {1}{3} \times \frac {22}{7} \times (12)^2 \times 5 $$
$$\therefore V=\frac { 1 }{ 3 } \times \frac { 22 }{ 7 } \times 144\times 5$$
$$\therefore V=754.285\ cm^{ 3 }$$
$$ r =12 cm $$
$$ h = 5 cm $$
Volume of cone is given by,
$$V = \frac {1}{3} \pi r^2 h$$
$$V = \frac {1}{3} \pi r^2 h$$
$$\therefore V = \frac {1}{3} \times \frac {22}{7} \times (12)^2 \times 5 $$
$$\therefore V=\frac { 1 }{ 3 } \times \frac { 22 }{ 7 } \times 144\times 5$$
$$\therefore V=\frac { 22\times 144\times 5 }{ 21 }$$
$$\therefore V=754.285\ cm^{ 3 }$$
Find the total volume of these three identical toy blocks.
An umbrella has $$8$$ ribs which are equally spaced. Assuming umbrella to be flat circle of radius $$45\ cm$$, find the area between the two consecutive ribs of the umbrella.
If a sphere is inscribed in a cube, then find the ratio of the volume of sphere to the volume of the cube.
$$\textbf{Step -1: Finding the required volume of the cube and the volume of the sphere.}$$
$$\text{Let the side of the cube be }a \text{ units.}$$
$$\because \mathbf{\text{Diameter of the sphere inscribed in the cube }=\text{ Side of the cube.}}$$
$$\therefore \text{Radius of the sphere inscribed in the cube of side }a\text{ would be }\dfrac{a}{2}\text{ units.}$$
$$\text{As, }\mathbf{\text{Volume of cube}=\text{(Side)}^3}$$
$$\text{Here, Volume of the required cube}=a^3\text { cubic units.}$$
$$\text{and }\mathbf{\text{Volume of sphere}=\dfrac{4}{3}\pi\text{(Radius)}^3}$$
$$\therefore \text{The volume of the required sphere}=\dfrac{4}{3}\pi \left(\dfrac{a}{2}\right)^3=\dfrac{1}{6}\pi a^3\text{ cubic units.}$$
$$\textbf{Step -2: Finding the required ratio.}$$
$$\dfrac{\text{Volume of sphere}}{\text{Volume of cube}}=\dfrac{\dfrac{1}{6}\pi a^3}{a^3}=\dfrac{\pi}{6}$$
$$\textbf{Hence, the ratio of the volumes of the Sphere to the Cube is }\mathbf{\dfrac{\pi}{6}}$$
Find the volume of largest sphere covered out of a cube of side $$7\ cm$$.
A wooden pole is $$7\ m$$ high and $$20\ cm$$ in diameter. Find its weight if the wood weight $$225\ kg$$ per $$m^3$$.
Radius $$= 10$$ cm $$= 0.1$$ m
height $$= 7$$ m
volume $$=
$$
$$=\dfrac{22}{ 7} × 0.1 × 0.1 × 7$$
$$=0.22$$ meter cube
height $$= 7$$ m
volume $$=
$$=\dfrac{22}{ 7} × 0.1 × 0.1 × 7$$
$$=0.22$$ meter cube
Density $$=225$$ kg/meter cube
$$225 =\dfrac{ mass }{ 0.22}$$
mass $$= 225 × 0.22 = 49.5 $$ kg.
$$225 =\dfrac{ mass }{ 0.22}$$
mass $$= 225 × 0.22 = 49.5 $$ kg.
A cylindrical tube of radius $$12\ cm$$ contains water to a depth of $$20\ cm$$. A spherical form ball is dropped into the tube and thus the level of water is raised by $$6.75\ cm$$. What is the radius of the ball?
A solid consisting of a right circular cone of height $$120$$ cm and radius $$60$$ cm standing on a hemisphere of radius $$60$$ cm is placed upright in a right circular cylinder full of water such that it touches the bottom. How many litres of water is left in the cylinder, If the radius of the cylinder is $$60$$ cm and its height is $$180$$ cm.
$$=\dfrac{22}{7}\times (60)^2\times 180 $$
$$=\dfrac{22\times 3600\times 180}{7}=\dfrac{14256000}{7}\text{ cm}^3$$
The volume of solid $$=$$ Volume of cone $$+$$ volume of the hemisphere
$$=\dfrac{1}{3}\pi r^2h+\dfrac{2}{3}\pi r^3$$
$$=\dfrac{1}{3}\times \dfrac{22}{7}\times 60^2\times 120 +\dfrac{2}{3}\times \dfrac{22}{7}\times 60^3$$
$$=\dfrac{3168000}{7}+\dfrac{3168000}{7}=\dfrac{6336000}{7}\text{ cm}^3$$
Volume of water left in the cylinder $$=$$ Volume of the cylinder $$-$$ Volume of the solid
$$=\dfrac{14256000}{7}-\dfrac{6336000}{7}=\dfrac{7920000}{7}$$
$$=1131428.57142\text{ cm}^3$$
$$=1.131\text{ m}^3$$ $$(\because 1 \text{ m}^3=1000000\text{ cm}^3)$$
If a sphere in inscribed a cube, then find the ratio of the volume of the cube to the volume of the sphere.
$$\textbf{Step -1: Finding the required volume of the cube and the volume of the sphere.}$$
$$\text{Let the side of the cube be }a \text{ units.}$$
$$\because \mathbf{\text{Diameter of the sphere inscribed in the cube }=\text{ Side of the cube.}}$$
$$\therefore \text{Radius of the sphere inscribed in the cube of side }a\text{ would be }\dfrac{a}{2}\text{ units.}$$
$$\text{As, }\mathbf{\text{Volume of
cube}=\text{(Side)}^3}$$
$$\text{Here, Volume of the required cube}=a^3\text { cubic units.}$$
$$\text{and }\mathbf{\text{Volume of sphere}=\dfrac{4}{3}\pi\text{(Radius)}^3}$$
$$\therefore \text{The volume of the required sphere}=\dfrac{4}{3}\pi \left(\dfrac{a}{2}\right)^3=\dfrac{1}{6}\pi a^3\text{ cubic units.}$$
$$\textbf{Step -2: Finding the required ratio.}$$
$$\dfrac{\text{Volume of cube}}{\text{Volume of sphere}}=\dfrac{a^3}{\dfrac{1}{6}\pi a^3}=\dfrac{6}{\pi}$$
$$\textbf{Hence, the ratio of the volumes of the cube to the sphere is }\mathbf{\dfrac{6}{\pi}}$$
A solid sphere of radius $$15$$cm is melted and recast into solid right circular cones of radius $$2.5$$cm and height $$8$$cm. Calculate the number of cones recast.
A hollow sphere of external and internal diameters of $$8\ cm$$ and $$4\ cm $$ respectively is melted and made into another solid in the shape of a right circular cone of base diameter of $$8\ cm$$. Find the height of the cone.
How many planks each measuring $$5\ m$$ by $$24\ cm$$ by $$10\ cm$$ can be stored in a plank $$115\ m$$ long. $$4\ m$$ wide and $$60\ cm$$ deep?
No. of planks $$=\dfrac{Total\quad volume}{volume\quad of\quad planks}$$
$$=\dfrac{115\times 100\times 4\times 100\times 60}{5\times 24\times 10}$$
$$= 2,30000$$ planks.
The dimensions of a cuboid are $$44\ cm, 21\ cm, 12\ cm$$. it is melted and a cone of height $$24\ cm$$ is made. Find the radius of its base.
A hollow sphere of internal and external radii $$6$$cm and $$8$$cm respectively is melted and recast into small cones of base radius $$2$$cm and height $$8$$cm. Find the number of cones.
What is the area of the glass?
A solid wooden toy is in the shape of right circular cone mounted on a hemisphere of radius $$4.2\ cm$$. The total height of the toy is $$10.2\ cm$$ find the volume of the toys.
Radius of hemisphere $$= 4.2 \; cm$$
Height of toy $$= 10.2 \; cm$$
$$\Rightarrow$$ Height of the cone $$= 10.2 - 4.2 = 6 \; cm$$
And the radius of the cone $$= 4.2 \; cm$$
The volume of the toy $$=$$ Volume of the hemisphere $$+$$ Volume of the cone
Volume of the toy $$= \cfrac{2}{3} \pi {r}^{3} + \cfrac{1}{3} \pi {r}^{2} h$$
$$ = \cfrac{1}{3} \pi {r}^{2} \left( 2r + h \right)$$
$$= \cfrac{1}{3} \times \cfrac{22}{7} \times {\left( 4.2 \right)}^{2} \times \left( 2 \times 4.2 + 6 \right)$$
$$= 266.112 \; {cm}^{3}$$
Total volume of three identical cones is the same as that of a bigger cone whose height is $$9$$cm and diameter $$40$$cm. Find the radius of the base of each smaller cone, if height of each is $$108$$cm.
Find the rate of change of volume of a cone w.r.t. its radius, when the height is kept constant.
A godown measures $$40$$m $$\times 25$$ m $$\times 10$$m. Find the maximum number of wooden crates each measuring $$1.5$$m $$\times 1.25$$m $$\times 0.5$$m that can be stored in the godown.
Suhail wants to paint the flour walls of a room having dimensions $$20\ m\times 6\ m$$. From each can of paint, $$96$$ sq. m of the area is painted. How many cans of paint will he need to paint the room?
Total Area $$ = 4\times 20\times \times 6 =480m^{2}$$
No. of rooms $$ = \frac{480}{96} = 5 $$ rooms
On a map, a length of $$1 cm$$ represents $$25,000 cm$$ on land. If a road measure $$5.75 cm$$ on a map, what is its actual length in metres?
1 cm = 25000 cm on land
5.75 cm $$ = 25000\times 5.75$$
= 143750 cm on land
A soft drink is available in two packs (i) a tin can with a rectangular base 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
Height of a cylindrical barrel is $$50$$ cm and radius of its base is $$20$$ cm. When it was empty, Anurag started to fill the barrel with water, by a cylindrical mug. The diameter and height of the mug was $$10$$ cm and $$15$$ cm respectively. How many minimum number of mugs will be required for the barrel to overflow?
A bucket, in the shape of a frustum of a cone, has a height of $$6\ cm$$. Its top and its bottom have radii of $$24\ cm$$ and $$16\ cm$$ respectively. Find its curved surface area.
A laboratory is $$9\ m$$ long, $$8\ m$$ broad and $$6\ m$$ high. It has $$2$$ doors each of size $$3 \ m\times 1.5\ m$$ and four windows each of size $$1.5\ m\times 1\ m$$. find the cost of whitewashing the walls of the laboratory at the rate of $$Rs. 1.75$$ per $$sq. m$$.
Area of walls $$ = 2h (l+b) = 2\times 6(17) = 204 m^{2}$$
Area of doors $$ = 2\times 3\times 1.5 = 9m^{2} $$
Area of window $$ = 4\times 1.5\times 1 = 6 m^{2}$$
Area to be whitewashed $$ = 204-9-6 =189 m^{2}$$
Total cost $$ = 1.75\times 189 $$
= 330.75 RS
The radii of the circular ends of a solid frustum of a cone are $$33\ cm$$ and $$27\ cm$$ and its slant height is $$10\ cm$$. Find its total surface area.(take $$\pi =3.14$$)
A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in fig. The height of the entire rocket is $$26\ cm,$$ while the height of the conical part is $$6\ cm.$$ The base of the conical portion has a diameter of $$5\ { cm } ,$$ while the base diameter of the cylindrical portion is $$3\ { cm } .$$ If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take $$\pi = 3.14$$ )
Kanika had a piece of cloth 1 m long and 60 cm broad. She cut it into square shaped handkerchiefs, each side measuring 20 cm, and put a lace on the boundary. How much lace is needed for the handkerchiefs?
A cone, a hemisphere and a cylinder stand on the same base and have equal height. Find the ratio of their volumes.
The shape of a garden is rectangular in the middle and semicircular at the ends.Find the area of the garden?
A bucket is in the form of a frustum of a cone and holds $$28.490$$ litres of water. The radii of the top and bottom are $$28$$ cm and $$21$$ cm respectively. Find the height of the bucket.
from the given information in the figure find slant height of cone.
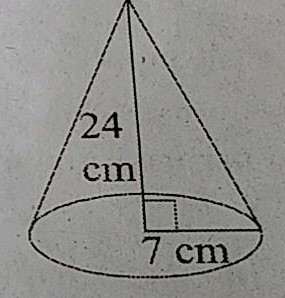
The height of a cone is $$20\text{ cm}$$. A small cone is cut off from the top by a plane parallel to the base. If its volume is $$\dfrac{1}{125}$$ of the volume of the original cone, determine at what height above the base the section is made.
Volume of a cone of radius $$r$$ and height $$h$$ is $$=\cfrac { \pi { r }^{ 2 }h }{ 3 } $$
$$\Rightarrow \cfrac { 1 }{ 3 } \pi { r }^{ 2 }h=\cfrac { 1 }{ 125 } \cfrac { 1 }{ 3 } \pi { R }^{ 2 }(20)\\ \Rightarrow { r }^{ 2 }h={ R }^{ 2 }\cfrac { (20) }{ 125 } \quad \quad -(1)$$
Also $$BE||CD$$ (given)
In $$\triangle ABE$$ & $$\triangle ACD$$
$$\angle BAE= \angle CAD $$ (common )
$$\angle ABE = \angle ACD$$ (corresponding angles)
$$\triangle ABE\sim \triangle ACD$$ by $$AA$$ criterion
thereby the sides will be in proportion
$$\Rightarrow \cfrac { BE }{ CD } =\cfrac { AB }{ AC } \\ \Rightarrow \cfrac { r }{ R } =\cfrac { h }{ 20 } \quad \quad -(3)$$
Substituting $$(2)$$ in $$(1)$$ we get
$$(\cfrac { { r }^{ 2 } }{ { R }^{ 2 } } )h=20\\ \Rightarrow { (\cfrac { h }{ 20 } ) }^{ 2 }h=\cfrac { 20 }{ 125 } \\ \Rightarrow { h }^{ 3 }=\cfrac { 20\times 20\times 20 }{ 5\times 5\times 5 } $$
$$ \Rightarrow h=\cfrac { 20 }{ 5 } =4\text{ cm}$$
Therefore, the section is made $$(20-4)\text{ cm}=16\text{ cm}$$ above the base of original cone.
Curved Surface area of a cone is $$ 308 cm^{2}$$ and its slant height is $$ 14 cm$$. Find
(i) radius of the base
(ii) Total surface area of the cone.
The radii of the bases of two right circular solid cones of same height are $$r_{1}$$ and $$r_{2}$$ respectively. The cones are melted and recast into a solid sphere of radius R. Show that the height of each cone is given by $$h=\dfrac{4R^3}{r_{1}^2+r_{2}^2}$$.
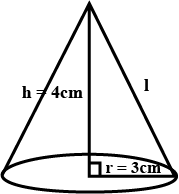
The radius of a cone is $$3$$ cm and vertical height is $$4$$ cm. Find the area of the curved surface.
A cube is made by arranging $$64$$ cubes having side of $$1\ cm$$, find total surface area of cube so formed.
Write the formula for volume of frustum of right circular cone .
Water in a canal, 30 dm wide and 12 dm deep, is flowing with a velocity of 20 km per hour. How much area will it irrigate in 30 min, if 9 cm of standing water is desired ?
If $$r, h, c, v$$ are radius curved surface area and volume of a cone respectively, then prove that $$3\pi vh^{3}-c^{2}h^{2}+9v^{2}=0$$
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Slant height of a i frustum of a cone, I = 4 cm
Circumference of its circular ends = 18 cm. and 6 cm
$$2 \pi r = 18 cm$$
$$\therefore R = \frac{9}{\pi}$$
$$2 \pi r = 6$$
$$r = \frac{3}{\pi}$$ cm
$$\therefore$$ Lateral surface area of a frustum of a cone
$$= \pi (R + r)l$$
$$= \pi \left ( \frac{9}{\pi} + \frac{4}{\pi} \right ) \times 4$$
$$= \pi \left ( \frac{12}{\pi} \right ) \times 4$$
$$= 48 cm^3$$
Circumference of its circular ends = 18 cm. and 6 cm
$$2 \pi r = 18 cm$$
$$\therefore R = \frac{9}{\pi}$$
$$2 \pi r = 6$$
$$r = \frac{3}{\pi}$$ cm
$$\therefore$$ Lateral surface area of a frustum of a cone
$$= \pi (R + r)l$$
$$= \pi \left ( \frac{9}{\pi} + \frac{4}{\pi} \right ) \times 4$$
$$= \pi \left ( \frac{12}{\pi} \right ) \times 4$$
$$= 48 cm^3$$
A metal cuboid of dimension $$22 \ \text{cm} \times 15\ \text{cm} \times 7.5 \ \text{cm}$$ was melted and cast into a cylinder of height $$14$$ cm. What is its radius?
A cylindrical glass of radius 7 cm is filled with mango juice up to a height of 17 cm when carefully, observed, the bottom of glass is covered by a transparent cone of height 6 cm and radius 7 cm. What is the actual volume of juice ?
Volume $$=$$ volume $$-$$ volume of juice of cylinder of cone.
$$=\pi (7)^2(17)-\dfrac{1}{3}\pi (7)^2(6)$$
$$=\pi (49)(17)-\pi (49)(2)$$
$$=\pi (49)(17-2)$$
$$=\pi (49)(15)=2309.07 cm^3$$.
The base radius and height of a right circular cone are $$2$$ cm and $$8$$ cm respectively. It is melted to change into sphere of diameter $$2$$ cm each. Find the number of sphere formed.
A cube of metal of $$6$$ cm edge is melted and cast into a cuboid whose base is $$9$$ cm $$\times$$ $$8$$ cm. Find the height.
A right circular cylinder having radius $$6$$ cm and height $$15$$cm is full or ice-cream. the ice-cream. the ice-cream is to be filled in cones of height $$12$$cm and radius $$3$$cm having a hemispherical top.Find the number of such cones that are required to empty the cylinder.
(Take,$$\pi = \frac{{22}}{7}$$)
A fight circular cone is $$3.6\ cm$$ high and radius is $$1.6\ cm$$ it is melted and recast into a cylinder with radius $$1.2\ cm$$. This is height.
Volume of cone $$=$$ Volume of cylinder
$$\Rightarrow \dfrac{1}{3}\pi R^2H= \pi r^2h$$
$$\Rightarrow \dfrac{1}{3}\times 1.6\times 1.6\times 3.6=1.2\times 1.2\times h$$
$$h=\dfrac{1.6\times 1.6\times 3.6}{3\times 1.2\times 1.2}$$
$$h=2.13$$cm.
A pen stand is made of wood in the shape of cuboid with three concial depressions to hold the pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depression is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand.
A rocket is in the shape of a cone mounted on a right circular cylinder, their common base diameter is $$8 \text{ cm}.$$ The height of cylindrical and conical shapes are $$6 \text{ cm}$$ and $$3 \text{ cm}$$ respectively. Find the volume of the rocket.
A solid metallic spherical ball of radius 28 cm is melted down and recast into small cones. If the diameter of the base of the cone is 28 cm and the height is 4 cm, find the number of such cones can be made?
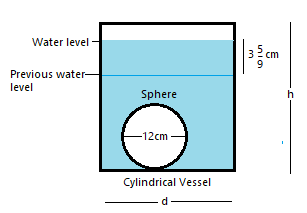
A sphere of diameter $$12$$ cm is dropped in a right circular cylinder vessel partly filled with water . If the sphere is completely submerged in water,the water level of cylindrical vessel rises by $$3\dfrac{5}{9}$$ cm . Find the diameter of the cylindrical vessel .
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. 0.5 cm are dropped into the vessel one- fourth a the water flows out. Find the number of lead shots dropped in the vessel
Let the number of lead shots dropped $$=n$$
The total number of number of lead shots $$=1/4$$ volume of the conical vessel
Lead shots
Radius, $$r=0.5\ cm$$
Volume, $$V=\dfrac{4}{3}\ \pi r^3$$
$$\dfrac{4}{3}.\dfrac{22}{7}.0.5 \times 0.5 \times 0.5 =\dfrac{4}{3} \times \dfrac{22}{7} \times 0.125$$
Cone
Radius, $$r=5\ cm$$
Height, $$h=8\ cm$$
Volume, $$V=\dfrac{1}{3} \pi r^2 h$$
$$=\dfrac{1}{3}.\dfrac{22}{7} \times 5 \times 5 \times 8=\dfrac{1}{3} \times \dfrac{22}{7} \times 200$$
$$ \dfrac{1}{4}th \ volume=\dfrac{1}{4} \times \dfrac{1}{3} \times \dfrac{22}{7} \times 200$$
Total volume of number of shots
$$=n \times \dfrac{4}{3} \times \dfrac{22}{7} \times 0.125$$
$$n \times \dfrac{4}{3} \times \dfrac{22}{7} \times 0.125=\dfrac{1}{4} \times \dfrac{1}{3} \times \dfrac{22}{7} \times 200$$
$$n=\dfrac{1}{4} \times \dfrac{1}{3} \times \dfrac{22}{7} \times 200 \times \dfrac{3}{4} \times \dfrac{7}{22} \times \dfrac{1}{0.125}$$
$$=\dfrac{200}{4 \times 4 \times 0.125}=\dfrac{200}{2}=100$$
$$\therefore $$ The number of lead shots $$=100$$
The total number of number of lead shots $$=1/4$$ volume of the conical vessel
Lead shots
Radius, $$r=0.5\ cm$$
Volume, $$V=\dfrac{4}{3}\ \pi r^3$$
$$\dfrac{4}{3}.\dfrac{22}{7}.0.5 \times 0.5 \times 0.5 =\dfrac{4}{3} \times \dfrac{22}{7} \times 0.125$$
Cone
Radius, $$r=5\ cm$$
Height, $$h=8\ cm$$
Volume, $$V=\dfrac{1}{3} \pi r^2 h$$
$$=\dfrac{1}{3}.\dfrac{22}{7} \times 5 \times 5 \times 8=\dfrac{1}{3} \times \dfrac{22}{7} \times 200$$
$$ \dfrac{1}{4}th \ volume=\dfrac{1}{4} \times \dfrac{1}{3} \times \dfrac{22}{7} \times 200$$
Total volume of number of shots
$$=n \times \dfrac{4}{3} \times \dfrac{22}{7} \times 0.125$$
$$n \times \dfrac{4}{3} \times \dfrac{22}{7} \times 0.125=\dfrac{1}{4} \times \dfrac{1}{3} \times \dfrac{22}{7} \times 200$$
$$n=\dfrac{1}{4} \times \dfrac{1}{3} \times \dfrac{22}{7} \times 200 \times \dfrac{3}{4} \times \dfrac{7}{22} \times \dfrac{1}{0.125}$$
$$=\dfrac{200}{4 \times 4 \times 0.125}=\dfrac{200}{2}=100$$
$$\therefore $$ The number of lead shots $$=100$$
A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the hemispherical is 14 cm and the total height of the vessel is 13 cm. Find
Water flows through a cylindrical pipe of internal diameter $$7 cm$$ at $$5 m$$ per sec. Calculate
(i) the volume in litres of water discharged by the pipe in one minute.
(ii) the time in minutes, the pipe would take to fill an empty rectangular tank of size $$4m \times 3 m \times 2.31 m$$ .
Two cylindrical vessels are filled with milk. The radius of one vessel is $$15\,cm$$ and height is $$40\,cm$$, and the radius of other vessel is $$20\,cm$$ and height is $$45\,cm$$, Find the radius of another cylindrical vessel of height $$30\,cm$$ which may just contain the milk which is in the two given vessels.
A cylinder whose height is two-third of its diameter has the same volume as a sphere of radius $$4$$cm. Calculate the radius of the base of the cylinder.
The diagram shows a section of a rocket firework. If this section can be completely filled with gunpowder what is the volume of gunpowder required?
A vessel is in the form of hemispherical bowl surmounted by a hollow cylinder of same diameter.The diameter of the hemispherical bowl is $$14$$cm and the total height of the vessel is $$13$$cm.Find the total surface area of the vessel. (Use $$\pi=\dfrac{22}{7}$$)
REF.Image
Let the radius and height of cylinder be r cm and h cm respectively.
Diameter of the hemispherical bowl = 14 cm
$$\therefore $$ Radius of the hemispherical bowl =
Radius of cylinder = $$r=\frac{14}{2} cm = 7 cm$$
Total height of the vessel = 13 cm.
$$\therefore $$ Height of the cylinder, h=13 cm - 7 cm = 6 cm
Total surface area of the vessel=
2(CSA of cylinder + CSA of hemisphere)
Since, the vessel is hollow
$$=2(2\pi rh+2\pi r^{2})$$
$$=4\pi r (h+r)$$
$$=4\times \dfrac{22}{7}\times 7\times (6+7)cm^{2}=1144 cm^2$$
Assume that a drop of water is spherical and its diameter is one tenth of a cm. A conical glass has height equal to its diameter of the rim. If 2048000 drops of water fill the glass completely then find the height of the glass.
A swimming pool is 40 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 3 m deep respectively. If the bottom of the pool slopes uniformly. find the amount of water in litres required to fill the pool.
A metal cuboid of dimension $$ 22 \,cm \times 15 \,cm \times 7.5 \,cm$$ was melted and casted into a cylinder of height $$14\, cm$$. Find the radius of cylinder.
A cuboid measuring $$15cm \times 12cm \times 6cm$$ is melted. How many new cubes of side $$3cm$$ can be made?
The picture shows the shape of a boiler. The total height of the boiler is $$12m$$ and the diameter is $$6 m$$, also the height of the cylindrical shape is $$6 m$$.
a. What is the height of the cone?
b. How many litres can the boiler hold? $$(1m^3 = 1000 litre)$$
There are $$25$$ persons in a tent which is conical in shape. Every person needs an area of $$4$$ sq. m. of the ground inside the tent. If height of the tent is $$18$$m, find the volume of the tent.
The radii of the circular ends of a solid frustum of a cone are $$33$$ cm and $$27$$ cm and its slant height is $$10$$ cm. Find the volume. [Take $$\pi =\dfrac{22}{7}$$]
A bucket open at the top is in the form of a frustum of a cone with a capacity of $$12308.8 \mathrm { cm } ^ { 3 }$$. The radii of the top and bottom circular ends are $$20 \,cm$$ and $$12 \,cm$$ respectively. Find the height of the bucket and the area of metal sheet used in making it. (Use $$\pi = 3.14$$)
Given,
Volume of bucket $$(V) = 12408.8 cm^3$$
$$R = 20 cm$$ (top radii)
$$r = 12 cm$$ (bottom radii)
Now, volume of frustum
$$= \dfrac{\pi}{3} h (R^2 + r^2 + Rr)$$
$$\Rightarrow 12408.8 = \dfrac{\pi}{3} \times h (20^2 + 12^2 + 20 \times 12)$$
$$\Rightarrow h = \dfrac{12408.8 \times 3}{\pi \times 784} = \dfrac{37226.4}{2485.28} cm$$
$$\Rightarrow h = 14.98 cm \approx 15 cm$$
$$\therefore$$ Area of metal sheet used
$$ = TSA$$ of the frustum
$$= CSA + $$ area of bottom
$$= \pi (R + r) \sqrt{(R - r)^2 + h^2} + \pi r^2$$
$$= \pi (20 + 12) \sqrt{(20 + 2)^2 + 15^2} + \pi \times 12^2$$
$$= \pi \times 32 \times \sqrt{289} + 144 \pi$$
$$= (544 + 144) \pi cm^2$$
$$= 688 \times 3.14 = 2160.32 cm^2$$
So, Height of the bucket is $$15 cm$$ and area of metal sheet used in making it is $$2160.32 cm^2$$.
A rectangle is $$16\mathrm { m }$$ by $$9\mathrm { m } .$$ Find the side of a square whose area equals the area of the rectangle. By how much does the perimeter of the rectangle exceed the perimeter of the square?
A metalic containers in the shape of a frustum of a cone.if the diameter of the cicrular ends are 20cm and 16cm, respectively and the vertical height is 42cm,find the volume of the container.also find the cost milk it can hold,if the rate of milk is Rs.40 per litre.
Three cubes, whose edge are x cm, 8 cm and 10 cm respectively, are melted and recasted into a single cube of edge 12 cm. Find 'x',
A rectangle field is $$48\ m$$ long and $$20\ m$$ wise. How many right triangular flower beds, whose sides containing the right angle measure $$12\ m$$ and $$5\ m$$ can be laid in this field?
A cylindrical tube of radius $$12\ cm$$ contains water to a depth of $$20\ cm.$$ A spherical ball is dropped into the tub and thus the level of water is raised by $$6.75\ cm$$. What is the radius of the ball?
If the volumes of two cones are in the ratio of 1:4 and their diameters are in the ratio of 4:5, them find the ratio of their heights.
A bucket in the form of a frustum of a cone height $$30\text{ cm}$$ with radii of its lower and upper ends as $$10\text{ cm}$$ and $$20\text{ cm}$$, respectively. Find the capacity of the bucket. Also, find the cost of milk which can completely fill the bucket at the rate of $$\text{Rs. }40$$ per litre. $$\left(\text{Use} \,\,\pi=\dfrac{22}{7}\right)$$
We know that volume/capacity of frustum of a cone is given by $$= \dfrac{1}{3} \pi h (R^2 + r^2 + R\times r)$$.
Here, $$h$$ is the height of the frustum and $$R,r$$ is the radius of both the ends.
By using above formula,
$$\text{Capacity} = \dfrac{1}{3} \times \pi \times 30 (20^2 + 10^2 + 20 \times 10)$$
$$= 10 \times (400 + 100 + 200)$$
$$= 7000 \pi \text{ cm}^3$$
$$= 7000 \times \dfrac{22}{7}$$
$$= 22000\text{ cm}^3$$
Cost of milk will be equal to cost of per litre milk times volume of the bucket in litres.
$$\text{Cost}= 40 \times 22000 \times 10^{-3}$$ $$\{ \because 1\text{ cm}^3 = 10^{-3}\text{litre}\}$$
$$= \text{Rs. }880$$
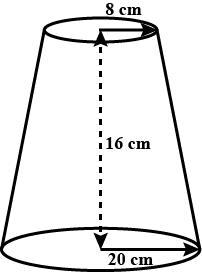
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 16 cm and 12 cm. Find the capacity of the glass.
The radii of the circular ends of a solid frustum of a cone are 18 cm and 12 cm and its height is 8 cm. Find its total surface area.
A metallic bucket,open at the top, of height 24 cm is in the from of the frustum of a cone, the radii of whose lower and upper circular ends are 7 cm and,respectively.Find (i) the volume of water which can completely fill the bucket;
(ii) the care of the metal sheet used to make the bucket.
A container,open at the top,is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm, respectively.Find the cost of milk which can completely fill the container at the rate of Rs.21 litre.
A cylindrical tub of radius 16 cm contains water to a depth of 30 cm. A spherical iron ball is dropped into the tub and thus level of water is raised by 9 cm. what is the radius of the ball (in cm) ?
An open metal bucket is in the shape of a frustum of cone of height $$21 cm$$ with radii of its lower and upper ends are $$10 cm$$ and $$20 cm$$ respectively. Find the cost of milk which can completely fill the bucket at the rate of $$Rs. 40$$ per litre.
We know,
Volume of frustum
$$= \dfrac{1}{3} \pi h (R^2 + r^2 + R \times r)$$
Hence, $$R = 20, r = 10$$
$$= \dfrac{1}{3} \times \dfrac{22}{7} \times 21 (400 + 100 + 20 \times 10)$$
$$\dfrac{1}{3} \times \dfrac{22}{7} \times 21 \times 700$$
$$= 22 \times 7 \times 100$$
$$= 15400 cm^3$$
$$= 15400 \times 10^{-3}ltr$$
$$= 15.4ltr$$
$$\therefore$$ cost of milk $$= 15.4 \times 40$$
$$ = 616 Rs.$$
A night camp was organized for class X students for two days and their accommodation was planned in tents. Each tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are $$2.1\ \text{m}$$ and $$4\ \text{m}$$ respectively and the slant height of the top is $$2.8\ \text{m}$$, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of $$\text{Rs. } 500$$ per $$\text{m}^2$$. ( Note that the base of the tent will be covered with canvas.) Is camping helpful to students in their development? Justify your answer.
Due to a heavy flood in a state, thousands were rendered homeless. 50 schools collectively offered to the state to provide place and the canvas for 1500 tents to be fixed by the government and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 m and height 3.5 m, with conical upper part of the same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per square metre, find the amount shared by each school to set up the tents.
What value is generated by the above problem $$\left( \text{use}\ \pi=\dfrac{22}{7}\right)$$
A manufacturer involved ten children in colouring playing top (lattu) which is shaped like a cone surmounted by a hemisphere. The entire top is $$5\ cm$$ in height and the diameter of the top is $$3.5\ cm$$. Find the area they had to paint if $$50$$ playing tops were given to them. $$\left( \text{Take}\ \pi =\dfrac{22}{7}\right)$$
How is child labour an abuse for society?
A circus tent is cylindrical to a height of $$3$$ metres and conical above it. If its diameter is $$15\ m$$ and the slant height of the conical portion is $$53\ m$$, calculate the length of the canvas $$5\ m$$ wide to make the required tent.
How many bricks each of size $$25\ cm\times 13.5\ cm\times 6\ cm$$, will be required to build a wall $$8\ m$$ long, $$5.4\ m$$ high and $$33\ cm$$ thick?
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. What is the total surface area of the combined solid?
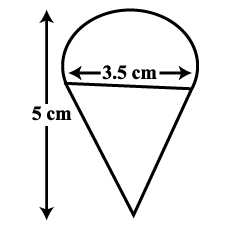
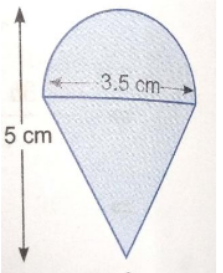
A manufacturer involved ten children in colouring playing top ( lattu) which is shaped like a cone surmounted by a hemisphere. The entire top is $$5\ cm$$ in height and the diameter of the top is $$3.5\ cm$$.
What steps can be taken to abolish child labour?
The radii of two circles are $$8\ cm$$ and $$6\ cm$$ respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
The size of matchbox is $$4\ cm\times 2.5\ cm\times 1.5\ cm$$. What is the volume of a packet containing $$144$$ matchboxes? How many such packets can be placed in a carton of size $$1.5\ m\times 84\ cm\times 60\ cm$$?
Two identical solid hemispheres of equal base radius $$r$$ cm are struck together along their bases. What will be the total surface area of the combination?
The radii of the ends of a frustum of a cone $$40$$ cm high are $$20$$ cm and $$11$$ cm. Find its slant height.
A rectangular water tank of base $$11 m \times 6 m$$ contains water upto a height of $$5 m$$. If the water in tank is transferred to a cylindrical tank of radius $$3.5cm$$, find the height of the water level in the tank.
Rectangular water tank, below figure 1
$$l = 11 m$$,
$$b = 6 m$$,
$$H = 5 m$$
Cylindrical tank, below figure 2
$$r = 3.5 m$$
$$h$$ = ?
Water is transferred from cuboid to cylinder, so, the volume of water in both vessels will be same.
$$\therefore \pi r^{2}h=1\times b\times H$$
$$\Rightarrow \dfrac{22}{7}\times3.5\times3.5\times h=11\times6\times5$$
$$\Rightarrow h=\dfrac{11\times6\times5\times7\times100}{22\times35\times35}=\dfrac{60}{7}$$
$$\Rightarrow h=8.6m$$(approx.)
Hence, the height of water level in cylindrical tank is $$8.6 m.$$
Priyanka took a wire and bent it to form a circle of radius $$14 \,cm$$. Then she bent it into a rectangle with one side $$24\, cm$$ long. What is the length of the wire? Which shape encloses more area, the circle or the rectangle?
How many cubic centimetres of iron is required to construct an open box whose external dimensions are $$36 cm, 25 cm$$ and $$16.5 cm$$ provided the thickness of the iron is $$1.5 cm$$. If one cubic centimetre of iron weighs $$7.5 g$$, find the weight of the box.
The barrel of a fountain pen, cylindrical in shape, is $$7cm$$ long and $$5mm$$ in diameter. A full barrel of ink in the pen is used up on writing $$3300$$ words on an average. How many words can be written in a bottle of ink containing onefifth of a litre?
A square sheet of paper is converted into a cylinder by rolling it along its side. What is the ratio of the base radius to the side of the square?
A cube of side 5 cm is cut into as many 1 cm cubes as possible. what is the ration of the surface area of the original cube to that of the sum of the surface areas of the Smaller cubes?
If the slant height of the frustum of a cone is $$10$$ cm and the perimeters of its circular base are $$18$$ cm and $$28$$ cm respectively. What is the curved surface area of the frustum?
Use the Fig showing the layout of a farmhouse:
(a) What is the area of land used to grow hay?
(b) It costs $$Rs. 91/m^2$$ to fertilize the vegetable garden. What is the total cost ?
(c) A fence is to be enclosed around the house. The dimensions of the house are $$18.7\, m \times 12.6\, m$$. At least how many meters of fencing are needed ?
(d) Each banana tree required $$1.25\, m^2$$ of ground space. How many banana trees can there be in the orchard ?
Find the area of flower bed (with semi-circular ends) shown in figure.
The figure has two semi-circles and one rectangle.
the radius of the semi-circles $$= \dfrac{10}{2} \,cm$$
$$\Rightarrow r = 5 \,cm$$
The length of the rectangle
$$= l = 38 \,cm$$
Breadth $$= b = 10 \,cm$$
Area of the flower bed = Area of rectangle + Area of two semi-circles
$$= l \times b + 2 \times \dfrac{\pi r^2}{2} = l \times b + \pi r^2$$
$$= 38 \times 10 + \dfrac{22}{7} \times 5 \times 5 = (380 + 25 \pi)cm^2$$
Hence, the area of flower bed is $$(380 + 25 \pi) \,cm^2.$$
the radius of the semi-circles $$= \dfrac{10}{2} \,cm$$
$$\Rightarrow r = 5 \,cm$$
The length of the rectangle
$$= l = 38 \,cm$$
Breadth $$= b = 10 \,cm$$
Area of the flower bed = Area of rectangle + Area of two semi-circles
$$= l \times b + 2 \times \dfrac{\pi r^2}{2} = l \times b + \pi r^2$$
$$= 38 \times 10 + \dfrac{22}{7} \times 5 \times 5 = (380 + 25 \pi)cm^2$$
Hence, the area of flower bed is $$(380 + 25 \pi) \,cm^2.$$
A solid right circular cone of height $$120cm$$ and radius $$60cm$$ is placed in a right circular cylinder full of water of height $$180cm$$ such that it touches the bottom. Find the volume of water left in cylinder, if the radius of the cylinder is equal to the radius to the cone.
Cone
$$r=60cm$$
$$h=120cm$$
Cylinder
$$R=r=60cm$$
$$H=180cm$$
Cone is placed inside the cylindrical vessel full of water. So, the volume of water from cylinder will over flow equal to the volume of cone.
Hence, the water left in cylinder = Vol. of cylinder – Vol. of cone (i)
Volume of water left after immersing the cone into cylinder full of water
= Volume of cylinder – Volume of cone,
$$=\pi R^{2}H-\dfrac{1}{3}\pi r^{2}h$$
$$\therefore$$ Required volume of water in cylinder,
$$=\pi r^{2}H-\dfrac{1}{3}\pi r^{2}h$$ [$$\because R=r$$]
$$=\pi r^{2}\left [ H-\dfrac{1}{3}h \right ]=\dfrac{22}{7}\times60\times60\left [ 180-\dfrac{120}{3} \right ]$$
$$=\dfrac{22}{7}\times60\times60\times140cm^{3}$$
$$=\dfrac{22\times60\times60\times140}{7\times100\times100\times100}=\dfrac{22\times72}{1000}=\dfrac{1584}{1000}m^{3}$$
$$\therefore$$ Volume of water in cylinder = $$1.584 m^{3}$$.
Hence, required volume of water left = $$1.584 m^{3}$$.
Find the area of the shaded field shown in the given figure.
Redraw the figure and divide it into well known shapes. It is clear from the figure that there is one semicircle and one rectangle.
Rectangle Circle
$$l = 8 \,m$$ $$r = 6 - 4 = 2$$
$$b = 4 \,m$$
Area of shaded region = Area of rectangle + Area of semicircle
$$= l \times b + \dfrac{\pi r^2}{2} = 8 \times 4 + \pi \times \dfrac{2 \times 2}{2} = (32 + 2 \pi) \,m^2$$
Hence, the required area of shaded region $$= 38.28 \,m^2.$$
Rectangle Circle
$$l = 8 \,m$$ $$r = 6 - 4 = 2$$
$$b = 4 \,m$$
Area of shaded region = Area of rectangle + Area of semicircle
$$= l \times b + \dfrac{\pi r^2}{2} = 8 \times 4 + \pi \times \dfrac{2 \times 2}{2} = (32 + 2 \pi) \,m^2$$
Hence, the required area of shaded region $$= 38.28 \,m^2.$$
A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contain $$41\frac{19}{21}m^{3}$$ of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building.
Water flows at the rate of $$10m$$ per minute through a cylindrical pipe $$5mm$$ in diameter. How long would it take to fill a conical vessel whose diameter at the base is $$40cm$$ and depth $$24cm$$?
$$16$$ glass sphere each of radius $$2cm$$ are packed into cuboidal box of internal dimensions $$16cm*8cm*8cm$$ and then the box is filled with water. Find the volume of water. filled in the box.
A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of cylinder. The diameter and height of cylinder are $$6cm$$ and $$12cm$$, respectively. If the slant height of the conical portion is $$5cm$$, then find the total surface area and volume of rocket. (Use $$\pi = 3.14$$)
Cylinder
$$r=\dfrac{6}{2}=3cm$$
$$H=12cm$$
Cone
$$l=5cm$$
$$\therefore l^{2}=r^{2}+h^{2}$$ or $$h^{2}=l^{2}-r^{2}$$
$$=5^{2}-3^{2}=25-9=16$$
$$\Rightarrow h=\sqrt{16}=4cm$$
Now, volume of rocket
= Volume of cylinder + Volume of cone
$$=\pi r^{2}H+\dfrac{1}{3}\pi r^{2}h=\pi r^{2}\left [ H+\dfrac{1}{3}h \right ]$$
$$=3.15\times3\times3\left [ 12+\dfrac{1}{3}\times4 \right ]$$
$$=3.14\times9\left [ \dfrac{40}{3} \right ]=3.14\times3\times40=376.8cm^{3}$$.
$$\therefore$$ Volume of Rocket = $$376.8cm^{3}$$
Total surface area of rocket = Curved surface area of cylinder + Curved surface area of cone + Area of base of cylinder [As it is closed (Given)]
$$=2\pi rH+\pi rl+\pi r^{2}=\pi r[2H+l+r]$$
$$=3.14\times3[2\times12+5+3]$$
$$=3.14\times3\times32$$
$$301.44cm^{2}$$
Hence, the surface area of the rocket is $$301.44cm^{2}$$.
A milk container of height $$16cm$$ is made of metal sheet in the form of a frustrum of a cone with radii of its lower and upper ends as $$8cm$$ and $$20cm$$ respectively. Find the cost of milk at the rate of $$22$$ per L, which the container can hold.
Here, $$r_{1} = 8cm$$
$$r_{2} = 20cm$$
$$h = 16cm$$
$$\therefore$$ Volume of milk = Volume of frustrum as it is filled completely
$$= \dfrac{1}{3}\pi h(r_{1}^{2}+r_{2}^{2}+r_{1}r_{2})$$
$$=\dfrac{1}{3}\times\dfrac{22}{7}\times16[8^{2}+20^{2}+8\times20]$$
$$=\dfrac{22\times16}{21}[64+400+160]$$
$$=\dfrac{352}{21}\times624=\dfrac{352\times208}{7}=\dfrac{73216}{7}$$
$$=10459.428cm^{3}=10.459$$liter
Volume of milk = $$10.459$$litre
$$\therefore$$ Cost of milk = ₹$$22\times10.459$$ = ₹$$230.098$$
Hence, the cost of milk = ₹$$230.098$$
A hemispherical bowl of internal radius $$9cm$$ is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius $$1.5cm$$ and height $$4cm$$. How many bottles are needed to empty the bowl?
$$n$$ cylinder bottle
$$r=1.5cm$$
$$h=4cm$$
Hemisphere$$R=9cm$$
As the volume of liquid does not change
So, Volume of n bottles = Volume of hemisphere
$$\Rightarrow n\pi r^{2}h=\dfrac{2}{3}\pi R^{3}$$
$$\Rightarrow nr^{2}h=\dfrac{2}{3}R^{3}$$
$$\Rightarrow n\times1.5\times1.5\times4=\dfrac{2}{3}\times9\times9\times9$$
$$\Rightarrow n=\dfrac{2\times9\times9\times9\times100}{3\times15\times15\times4}=54$$
Hence, $$54$$ bottles are needed.
How many spherical lead shots each of diameter $$4.2cm$$ can be obtained from a solid rectangular lead piece with dimensions $$66 cm, 42 cm$$ and $$21 cm$$?
Let $$n$$ spherical shots (as shown in below figure 1) can be obtained,
$$r=\dfrac{4.2}{2}=2.1cm$$
$$\Rightarrow r=2.1cm$$
Cuboid (as shown in below figure 2)
$$l = 66 cm$$
$$b = 42 cm$$
$$h = 21 cm$$
Spherical lead shots are recasted from cuboid of lead. So, volume of $$n$$ spherical lead shots is equal to the volume of cuboid.
$$\therefore$$ Volume of $$n$$ spherical lead shots = Volume of lead cuboid
$$\Rightarrow n\times\dfrac{4}{3}\pi r^{3}=l\times b\times h$$
$$\Rightarrow n\times\dfrac{4}{3}\times\dfrac{22}{7}\times2.1\times2.1\times2.1=66\times42\times21$$
$$\Rightarrow n=\dfrac{66\times42\times21\times3\times7\times1000}{4\times22\times21\times21\times21}$$
$$\Rightarrow n=3\times500=1500$$
Hence, the number of lead shots are $$= 1500$$.
Two cones with same base radius $$8cm$$ and height $$15cm$$ are joined together along their bases. Find the surface area of the shape so formed.
How many spherical lead shots of diameter $$4 cm$$ can be made out of a solid cube of lead whose edge measures $$44cm$$?
A wall $$24m$$ long, $$0.4m$$ thick and $$6m$$ high is constructed with the bricks each of dimensions $$25 cm * 16 cm * 10 cm$$. If the mortar occupies $$\frac{1}{10}$$th of the volume of the wall, then find the number of bricks used in constructing the wall.
A cone of radius $$8cm$$ and height $$12cm$$ is divided into two parts by a plane through the midpoint of its axis parallel to its base. Find the ratio of the volumes of two parts.
| $$Cone$$ $$I$$ | $$Cone$$ $$II$$ | $$Frustrum$$ |
| $$(ABO)$$ | $$(ODE)$$ | $$(DEBA)$$ |
| $$r_{2}=8cm$$ | $$r_{1}=\dfrac{r_2}{2}=4cm$$ | $$r_{1}=4cm$$ |
| $$h=12cm$$ | $$h_{1}=\dfrac{h}{2}=\dfrac{12}{2}\ cm$$ | $$r_{2}=8cm$$ |
| $$\Rightarrow h_{1}=6cm$$ | $$h_{2}=6cm$$ |
Let, $$OF=h_1$$ and $$FC=h_2$$
$$\Rightarrow h_{1}=$$$$h_{2}=\dfrac{12}{2}cm =6cm$$
$$\Delta OEF\sim \Delta OBC$$ [By AA criterion of similarity]
$$\therefore \dfrac{r_{1}}{r_{2}}=\dfrac{h_{1}}{h}\Rightarrow \dfrac{r_{1}}{8}=\dfrac{h/2}{h}=\dfrac{1}{2}$$
$$\Rightarrow r_{1}=4cm$$
Required ratio$$=\dfrac {Volume\ of frustrum (DEBA)}{Volume \ of \ cone (ODE)}$$
$$=\dfrac{\dfrac{1}{3}\pi h_{2}[r_{1}^{2}+r_{2}^{2}+r_{1}r_{2}]}{\dfrac{1}{3}\pi r_{1}^{2}h_{1}}$$
$$=\dfrac{6[4^{2}+8^{2}+4\times8]}{4\times4\times6}=\dfrac{[16+64+32]}{4\times4}=\dfrac{112}{16}=7$$
$$\therefore$$ Volume of frustrum : Volume of smaller cone = $$7 : 1$$.
The slant height of the frustum of a cone is 4 cm, and perpendicular of its circular bases are 18 cm and 6 cm respectively. Find the curved surface area of the frustum.
From a solid cube of side $$7cm$$, a conical cavity of height $$7cm$$ and radius $$3cm$$ is hollowed out. Find the volume of remaining solid.
In the given figure, find the area of the path (shown shaded) which is 2 m wide all around.
The perimeters of the ends of the frustum of a cone are $$96\ cm$$ and $$68\ cm$$. If the height of the frustum be $$20 cm$$, find itd radii, slant height , volume and total surface. [Take $$\pi=\dfrac{22}{7}$$]
Let radii of the circular ends of the frustum are $$R$$ and $$r$$ respectively.
Given that perimeter of one end $$=96\ cm$$
$$\Rightarrow 2\pi R=96$$
$$\Rightarrow R=\dfrac{96}{2\pi}$$
$$\Rightarrow R=\dfrac{96\times 7}{2\times 22}$$
$$\Rightarrow R=15.27\ cm$$
Perimeter of other end $$=68\ cm$$
$$\Rightarrow 2\pi r=68$$
$$\Rightarrow r=\dfrac{68}{2\pi}$$
$$\Rightarrow r=\dfrac{68\times 7}{2\times 22}$$
$$r=10.82\ cm$$
It is given that height of the frustum $$=20\ cm$$
So, Slant height, $$l=\surd {h^{2}+(R-r)^{2}}$$
$$=\surd {(20)^{2}+(15.27-10.82)^{2}}$$
$$=\surd 400+(4.45)^{2}$$
$$=\surd 400+19.80$$
$$=\surd 419.80$$
$$=20.49\ cm$$
Now,
Volume of the frustum $$=\dfrac{1}{3}\pi h(R^{2}+r^{2}+Rr)$$
$$=\dfrac{1}{3}\times \dfrac{22}{7}\times 20[(15.27)^{2}+(10.82)^{2}+15.27\times 10.82]$$
$$\dfrac{22\times 20}{21}[233.1729+117.0724+165.2214]$$
$$\dfrac{22\times 20\times 515.4667}{21}$$
$$10800.25\ cm^{3}$$
Total Surface area of the frustum $$\pi R^{2}+\pi r^{2}+\pi l(R+r)$$
$$=\pi[(15.27)^{2}+(10.82)^{2}+20.49\times (15.27+10.82)]$$
$$=\pi[233.1729+117.0724+534.5841]$$
$$=\dfrac{22}{7}\times 884.83$$
$$=2780.89\ cm^{2}$$
Given that perimeter of one end $$=96\ cm$$
$$\Rightarrow 2\pi R=96$$
$$\Rightarrow R=\dfrac{96}{2\pi}$$
$$\Rightarrow R=\dfrac{96\times 7}{2\times 22}$$
$$\Rightarrow R=15.27\ cm$$
Perimeter of other end $$=68\ cm$$
$$\Rightarrow 2\pi r=68$$
$$\Rightarrow r=\dfrac{68}{2\pi}$$
$$\Rightarrow r=\dfrac{68\times 7}{2\times 22}$$
$$r=10.82\ cm$$
It is given that height of the frustum $$=20\ cm$$
So, Slant height, $$l=\surd {h^{2}+(R-r)^{2}}$$
$$=\surd {(20)^{2}+(15.27-10.82)^{2}}$$
$$=\surd 400+(4.45)^{2}$$
$$=\surd 400+19.80$$
$$=\surd 419.80$$
$$=20.49\ cm$$
Now,
Volume of the frustum $$=\dfrac{1}{3}\pi h(R^{2}+r^{2}+Rr)$$
$$=\dfrac{1}{3}\times \dfrac{22}{7}\times 20[(15.27)^{2}+(10.82)^{2}+15.27\times 10.82]$$
$$\dfrac{22\times 20}{21}[233.1729+117.0724+165.2214]$$
$$\dfrac{22\times 20\times 515.4667}{21}$$
$$10800.25\ cm^{3}$$
Total Surface area of the frustum $$\pi R^{2}+\pi r^{2}+\pi l(R+r)$$
$$=\pi[(15.27)^{2}+(10.82)^{2}+20.49\times (15.27+10.82)]$$
$$=\pi[233.1729+117.0724+534.5841]$$
$$=\dfrac{22}{7}\times 884.83$$
$$=2780.89\ cm^{2}$$
What length of solid cylinder $$2$$ cm in diameter must be taken to recast into a hollow cylinder of external diameter $$20$$ cm, $$0.25$$ cm thick and $$15$$ cm long?
A tent is made in the form of a conic frustum, surmounted by a cone. The diameters of the base and top of the frustum are $$14\ $$ and $$7\ m$$ and its height is $$8\ m$$. The height of the tent is $$12\ m$$. Find the quantily of canvas required. [Take $$\pi=\dfrac{22}{7}$$]
For the lower portion of the tent:
Diameter of the base $$=14\ m$$
Radius, $$R$$, of the base $$=7\ m$$
Diameter of the top end of the frustum $$=7\ m$$
Radius of the top end of the frustum $$=r=\dfrac{7}{2}m =3.5\ m$$
height of the frustum $$=h=8\ m$$
slant height,$$l=\surd{h^{2}-(R-r)^{2}}$$
$$=\surd {(8)^{2}+(7-3.5)^{2}}$$
$$=\surd 64+(3.5)^{2}$$
$$=\surd 64+12.25$$
$$=\surd 76.25\ m$$
$$=8.73\ m$$
For the conical part
Radius of the cone base $$=r=3.5\ m$$
Height of the cone $$=$$ height of the tent - height of frustum
$$12-8=4\ m$$
Slant height of cone $$=L=\surd {(4)^{2}+(3.5)^{2}}$$
$$=\surd 16+12.25$$
$$\surd 28.25=5.3\ m$$
Total quantity of canvas $$=CSA$$ of frustum $$+CSA$$ of conical top
$$=\pi l(R+r)+\pi rL$$
$$=\pi[8.73(7+3.5)+3.5\times 5.3]$$
$$=\dfrac{22}{7}[91.66+18.6]$$
$$=\dfrac{22}{7}[110.26]$$
$$346.5\ m^{2}$$
Diameter of the base $$=14\ m$$
Radius, $$R$$, of the base $$=7\ m$$
Diameter of the top end of the frustum $$=7\ m$$
Radius of the top end of the frustum $$=r=\dfrac{7}{2}m =3.5\ m$$
height of the frustum $$=h=8\ m$$
slant height,$$l=\surd{h^{2}-(R-r)^{2}}$$
$$=\surd {(8)^{2}+(7-3.5)^{2}}$$
$$=\surd 64+(3.5)^{2}$$
$$=\surd 64+12.25$$
$$=\surd 76.25\ m$$
$$=8.73\ m$$
For the conical part
Radius of the cone base $$=r=3.5\ m$$
Height of the cone $$=$$ height of the tent - height of frustum
$$12-8=4\ m$$
Slant height of cone $$=L=\surd {(4)^{2}+(3.5)^{2}}$$
$$=\surd 16+12.25$$
$$\surd 28.25=5.3\ m$$
Total quantity of canvas $$=CSA$$ of frustum $$+CSA$$ of conical top
$$=\pi l(R+r)+\pi rL$$
$$=\pi[8.73(7+3.5)+3.5\times 5.3]$$
$$=\dfrac{22}{7}[91.66+18.6]$$
$$=\dfrac{22}{7}[110.26]$$
$$346.5\ m^{2}$$
A godown building is in the form as shown in the adjoining figure. The vertical cross-section parallel to the width side of the building is a rectangle of size $$7\ m\times 3\ m$$ mounted by a semicircle of radius $$3.5\ m$$. The inner measurement of the cuboidal portion are $$10\ m \times 7\ m\times 3\ m$$. The inner measurement of the cuboidal portion are $$10\ m\times 7\ m\times 3\ m$$ Find the
volume of the godown.
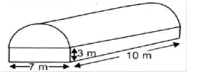
From a rectangular solid of metal $$42$$ cm by $$30$$ cm by $$20$$ cm, a conical cavity of diameter $$14$$ cm and depth $$24$$ cm is drilled out. Find the surface area of the remaining solid.
Given,
Dimensions of rectangular solid $$l = 42$$ cm,$$b = 30$$ cm and $$h = 20$$ cm
Conical cavity’s diameter$$= 14$$ cm
So, its radius$$= 7$$ cm
Depth (height)$$= 24$$ cm
Total surface area of cuboid$$= 2 (lb + bh + lh)$$
$$= 2 (42 \times 30 + 30 \times 20 + 20 \times 42)$$
$$= 2 (1260 + 600 + 840)$$
$$= 2 (2700)$$
$$= 5400\,cm^2$$
Diameter of the cone$$= 14\,cm$$
So, its radius$$= 14/2 = 7\,cm$$
Area of circular base$$= \pi r^2 = \dfrac{22}7 \times 7 \times 7 = 154\,cm^2$$
We know that,
$$l = (7^2 + {24}^2)^{1/2} = (49 + 576)^{1/2} = (625)^{1/2} = 25$$
Area of curved surface area of cone$$= \pi rl = \dfrac{22}7 \times 7 \times 25 = 22 \times 25 = 550\,cm^2$$
Surface area of remaining part$$= 5400 + 550 – 154 = 5796\, cm^2$$
A student was asked to make a model in his workshop, which shaped like a cylinder with two cones attached at its two ends, using a thin aluminium sheet. The diameter of the model is $$3\ cm$$ and its length is $$10\ cm$$. If each cone has a height of $$2\ cm$$ find the volume of air contained in the model. ( Consider the outer and inner dimensions of the model to be nearly the same).
Given that diameter of cylinder $$=3\ cm$$
So,
Radius $$=\dfrac 32=1.5\ cm$$
Given: Height of cone $$=2\ cm$$ and
Height of the cylinder +height of cone +height of cone =$$10\ cm$$
Height of the cylinder $$+2+2=10$$
Height of the cylinder $$=6\ cm$$
So, Volume of the cylinder $$=\pi r^2h$$
$$=\dfrac{22}{7}\times \dfrac{3}{2}\times \dfrac{3}{2}\times 6$$
$$=42.428\ cm^3$$
$$=42.43\ cm^3$$ ( approx).
Volume of $$1st$$ cone $$=\dfrac 13 \pi r^2h$$
$$=\dfrac 13 \times \dfrac{22}{7}\times \dfrac{3}{2}\times \dfrac{3}{2}\times 2$$
$$=4.71\ cm^3$$
Volume of $$1^{st}$$ cone = Volume of $$2^{nd}$$ cone =$$4.71\ cm^3$$
So, Total volume of the model
= Volume of cylinder + Volume of $$1^{st}$$ cone +volume of $$2^{nd}$$ cone
$$=42.43+4.71+4.71$$
$$=51.85\ cm^3$$
So,
Radius $$=\dfrac 32=1.5\ cm$$
Given: Height of cone $$=2\ cm$$ and
Height of the cylinder +height of cone +height of cone =$$10\ cm$$
Height of the cylinder $$+2+2=10$$
Height of the cylinder $$=6\ cm$$
So, Volume of the cylinder $$=\pi r^2h$$
$$=\dfrac{22}{7}\times \dfrac{3}{2}\times \dfrac{3}{2}\times 6$$
$$=42.428\ cm^3$$
$$=42.43\ cm^3$$ ( approx).
Volume of $$1st$$ cone $$=\dfrac 13 \pi r^2h$$
$$=\dfrac 13 \times \dfrac{22}{7}\times \dfrac{3}{2}\times \dfrac{3}{2}\times 2$$
$$=4.71\ cm^3$$
Volume of $$1^{st}$$ cone = Volume of $$2^{nd}$$ cone =$$4.71\ cm^3$$
So, Total volume of the model
= Volume of cylinder + Volume of $$1^{st}$$ cone +volume of $$2^{nd}$$ cone
$$=42.43+4.71+4.71$$
$$=51.85\ cm^3$$
An oil funnel of tin sheet consists of a cylindrical portion $$8\ cm$$ along attached to a frustum of a cone. It the total height be $$15\ cm$$, the diameter of the cylindrical portion $$1\ cm$$ and diameter of the top of the funnel $$10\ cm$$, find the area of the tin required. [Take $$\pi=22/7$$]
Diameter of top of funnel $$=10\ cm$$
So, Radius $$(R)=5\ cm$$
Diameter of cylindrical portion $$1\ cm$$
So,
radius $$(r)=\dfrac{1}{2}=0.5\ cm$$
Height of frustum = Total height - Height of cylindrical part
$$=15-8=7\ cm$$
and Slant height, $$l=\surd{h^{2}-(R-r)^{2}}$$
$$=\surd {(7)^{2}+(5-0.5)^{2}}$$
$$=\surd 49+(4.5)^{2}$$
$$=\surd 49+20.25$$
$$=\surd 69.25$$
$$=8.32\ cm$$
Now, $$CSA$$ of frustum $$=\pi l(R+r)$$
$$=\dfrac{22}{7}\times 8.32\times (5+0.5)$$
$$=\dfrac{22}{7}\times 8.32\times (5.5)$$
$$=143.81\ cm^{2}$$
Height of cylinder, $$H=8\ cm$$
Now, $$CSA$$ of cylinder $$2\pi r H$$
$$=2\times \dfrac{22}{7}\times 0.5\times 8$$
$$=25.14\ cm^{2}$$
Area of tin required $$=CSA $$ of Frustum $$+CSA$$ of cylinder
$$=143.81+25.14$$
$$=168.95\ cm^{2}$$
So, Radius $$(R)=5\ cm$$
Diameter of cylindrical portion $$1\ cm$$
So,
radius $$(r)=\dfrac{1}{2}=0.5\ cm$$
Height of frustum = Total height - Height of cylindrical part
$$=15-8=7\ cm$$
and Slant height, $$l=\surd{h^{2}-(R-r)^{2}}$$
$$=\surd {(7)^{2}+(5-0.5)^{2}}$$
$$=\surd 49+(4.5)^{2}$$
$$=\surd 49+20.25$$
$$=\surd 69.25$$
$$=8.32\ cm$$
Now, $$CSA$$ of frustum $$=\pi l(R+r)$$
$$=\dfrac{22}{7}\times 8.32\times (5+0.5)$$
$$=\dfrac{22}{7}\times 8.32\times (5.5)$$
$$=143.81\ cm^{2}$$
Height of cylinder, $$H=8\ cm$$
Now, $$CSA$$ of cylinder $$2\pi r H$$
$$=2\times \dfrac{22}{7}\times 0.5\times 8$$
$$=25.14\ cm^{2}$$
Area of tin required $$=CSA $$ of Frustum $$+CSA$$ of cylinder
$$=143.81+25.14$$
$$=168.95\ cm^{2}$$
A hollow sphere of internal and external diameters $$4$$ cm and $$8$$ cm respectively is melted into a cone of base diameter $$8$$ cm. Find the height of the cone.
A godown building is in the form as shown in the adjoining figure. The vertical cross-section parallel to the width side of the building is a rectangle of size $$7\ m\times 3\ m$$ mounted by a semicircle of radius $$3.5\ m$$. The inner measurement of the cuboidal portion are $$10\ m \times 7\ m\times 3\ m$$. The inner measurement of the cuboidal portion are $$10\ m\times 7\ m\times 3\ m$$ Find the
total internal surface area excluding the floor.
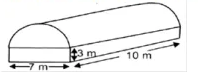
A cone of height 15 cm and diameter 7 cm is mounted on a hemisphere of same diameter. Determine the volume of the solid thus formed.
Given,
Height of the cone$$= 15\,cm$$
Diameter of the cone$$= 7\,cm$$
So, its radius$$= 3.5\,cm$$
Radius of the hemisphere$$= 3.5\,cm$$
Now,
Volume of the solid $$=$$ Volume of the cone $$+$$ Volume of the hemisphere
We know that, volume of a cone $$=\dfrac13 \pi r^2h$$
And, volume of a hemisphere $$=\dfrac23 \pi r^3$$
$$\therefore \ $$ Volume of the solid $$= \dfrac13 \times \dfrac{22}7 \times (3.5)^2 \times 15 + \dfrac23 \times \dfrac{22}7 \times (3.5)^3\quad \quad \left[\because \ \pi=\dfrac{22}{7}\right]$$
$$= \dfrac13 \times\dfrac {22}7 \times (3.5)^2 (15 + 2\times3.5)$$
$$= \dfrac{847}3$$
$$= 282.33\,cm^3$$
Hence, the volume of the solid is $$282.33\ cm^3$$
A sphere, a cylinder and a cone have the same radius and same height. Find the ratio of their volumes.
[Diameter of the sphere is equal to the height of the cylinder and the cone]
Volume of the sphere $$=V_{1}=\dfrac{4}{3}\pi r^{3}$$
Volume of the cylinder $$=V_{2}=\pi r^{2}h$$
Volume of the cone $$=V_{3}=\dfrac{1}{3}\pi r^{2}h$$
Ratio of their volumes $$=V_{1} : V_{2} : V_{3}$$
$$\Rightarrow \dfrac{4}{3}\pi r^{3} : \pi r^{2} h:\dfrac{1}{3}\pi r^{2}h$$ $$(\because h=2r)$$
$$\Rightarrow \dfrac{4}{3}\pi r^{3} : \pi r^{2}2r: \dfrac{1}{3}\pi r^{2}2r$$
$$\Rightarrow 4\pi r^{3} : 3\times 2\pi r^{3} : 2\pi r^{3}$$ (Multiply by $$3$$)
$$\Rightarrow 4r^{3} : 6r^{3} : 2r^{3}$$
$$\Rightarrow 4 : 6 : 2$$
Volume of the cylinder $$=V_{2}=\pi r^{2}h$$
Volume of the cone $$=V_{3}=\dfrac{1}{3}\pi r^{2}h$$
Ratio of their volumes $$=V_{1} : V_{2} : V_{3}$$
$$\Rightarrow \dfrac{4}{3}\pi r^{3} : \pi r^{2} h:\dfrac{1}{3}\pi r^{2}h$$ $$(\because h=2r)$$
$$\Rightarrow \dfrac{4}{3}\pi r^{3} : \pi r^{2}2r: \dfrac{1}{3}\pi r^{2}2r$$
$$\Rightarrow 4\pi r^{3} : 3\times 2\pi r^{3} : 2\pi r^{3}$$ (Multiply by $$3$$)
$$\Rightarrow 4r^{3} : 6r^{3} : 2r^{3}$$
$$\Rightarrow 4 : 6 : 2$$
$$\Rightarrow 2 : 3 : 1$$
From a rectangular solid of metal $$42$$ cm by $$30$$ cm by $$20$$ cm, a conical cavity of diameter $$14$$ cm and depth $$24$$ cm is drilled out. Find the volume of remaining solid.
Volume of the rectangular solid$$= (42 \times 30 \times 20)\,cm^3 = 25200\, cm^3$$
Radius of conical cavity (r)$$= 7\,cm$$
Height (h)$$= 24\,cm$$
Volume of cone$$= \dfrac13 \pi r^2 h$$
$$= \dfrac13 \times \dfrac{22}7 \times 7 \times 7 \times 24$$
$$= 1232\,cm^3$$
A circus tent is cylindrical to a height of $$8$$ m surmounted by a conical part. If total height of the tent is $$13$$ m and the diameter of its base is $$24$$ m; calculate area of canvas, required to make this tent allowing $$10\%$$ of the canvas used for folds and stitching.
Area of canvas used in stitching = total area of canvas
Total area of canvas $$= 7656/7$$ + total area of canvas/10
Total area of canvas – Total area of canvas/10$$= 7656/10$$
Total area of canvas$$(1 – \dfrac1{10}) = \dfrac{7656}7$$
Total area of canvas$$\times \dfrac9{10} = \dfrac{7656}7$$
Total area of canvas$$= \dfrac{7656}7 \times \dfrac{10}9 = \dfrac{76560}{63}$$
Therefore, the total area of canvas$$= 1215.23\,m^2$$
From a rectangular solid of metal $$42$$ cm by $$30$$ cm by $$20$$ cm, a conical cavity of diameter $$14$$ cm and depth $$24$$ cm is drilled out. Find the weight of the material drilled out if it weighs $$7$$ gm per $$cm^3$$.
Volume of the rectangular solid$$= (42 \times 30 \times 20)\,cm^3 = 25200\, cm^3$$
Radius of conical cavity (r)$$= 7\,cm$$
Height (h)$$= 24\,cm$$
Volume of cone$$= \dfrac13 \pi r^2 h$$
$$= \dfrac13 \times \dfrac{22}7 \times 7 \times 7 \times 24$$
$$= 1232\,cm^3$$
Weight of material drilled out$$= 1232 \times 7g = 8624g = 8.624\,kg$$
A cylindrical boiler, $$2\text{ m}$$ high, has $$3.5\text{ m}$$ diameter. It has a hemispherical lid. Find the volume of its interior, including the part covered by the lid.
Given,
Diameter of cylindrical boiler $$= 3.5\text{ m}$$
So, the radius (r)$$= \dfrac{3.5}{2} = \dfrac{35}{20} = \dfrac{7}{4}\text{ m}$$
Height (h)$$= 2\text{ m}$$
Radius of hemisphere (R)$$= \dfrac{7}{4}\,\text{m}$$
Total volume of the boiler $$=$$ Volume of cylinder $$+$$ volume of hemisphere $$= \pi r^2h + \dfrac23 \pi r^3$$
$$= \pi r^2(h + \dfrac23r)$$
$$= \dfrac{22}7 \times \dfrac74 \times \dfrac74 \left(2 + \dfrac23 \times \dfrac74\right)$$
$$= \dfrac{77}{8} \left(2 + \dfrac76\right)$$
$$= \dfrac{77}8 \times \dfrac{19}6 = \dfrac{1463}{48}$$
$$= 30.48\,\text{m}^3$$
The lateral surface area of the cylinder is equal to the curved surface area of a cone. If their bases are the same, find the ratio of the height of the cylinder to the slant height of the cone.
A cylinder and cone have bases of equal radii and are of equal heights. Show that their volumes are in the ratio $$3:1$$.
A toy made in the form of hemisphere surmounting by a right cone whose circular base is joined with the plane surface of the hemisphere. The radius of the base of the cone is $$6cm$$ and its volume is $$\dfrac{3}{2}$$ of the hemisphere.
Calculate the height of the cone and the surface area of the toy correct to $$2$$ places of decimal.$$\left(\pi=3\dfrac{1}{7}\right)$$
Radius of cone,$$r=7cm$$
Volume of cone $$=\dfrac{3}{2}$$ volume of the hemisphere
$$\dfrac{1}{3}\pi r^2h=\dfrac{3}{2}\times \dfrac{2}{3}\pi r^3$$
$$\Rightarrow h=3r=3\times 7=21cm$$
Surface area of the toy $$=$$ curved
Surface area of the cone $$+$$ curved
Surface area of the hemisphere.
Radius of cone,$$r=7cm$$
Height of cone,$$h=21cm$$
Slant height $$=l=\sqrt{r^2+h^2}$$
$$=\sqrt{7^2+21^2}=\sqrt{49+441}=\sqrt{490}=22.135cm$$
Curved surface area $$=\pi rl$$
$$=\dfrac{22}{7}\times 7\times 22.135=486.99cm^2$$
Radius of hemisphere $$=7cm$$
Curved surface area $$=2\pi r^2$$
$$=2\times \dfrac{22}{7}\times 7\times 7=308cm^2$$
Curved surface area of the toy $$=486.99+308=794.99cm^2$$
What is the least number of solid metallic spheres, each of $$6$$ cm diameter, that should be melted and recast to form a solid metal cone whose height is $$45$$ cm and diameter is $$12$$ cm?
In the following diagram a rectangular platform with a semicircular end on one side is $$22\ m$$ long from one end to the other end. If the length of the half circumference is $$11\ m$$ , find the cost of constructing the $$1.5\ m$$ high platform at the rate of $$Rs.4$$ per cubic meters.
A solid cube of edge 14 cm is melted down and recasted into smaller and equal cubes each of edge 2 cm; find the number of smaller cubes obtained
Four cubes , each of edge 9 cm , are joined as shown below.
Write the dimension of the resulting cuboid obtained . Also fine the total surface area and the volume of the resulting cuboid.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure If the height of the cylinder is $$10\ cm$$. and its radius of the base us $$3.5\ cm$$, find the total surface area of the article.
The external diameter of a closed wooden box are $$27\ cm, 19\ cm$$ and $$11\ cm$$. If the thickness of the wood in the box is $$1.5\ cm$$, find:
Volume of the wood in the box;
The dimensions of a classroom are: length = 15 m, breadth = 12 m and height = 7.5 m. Find, how many children can be accommodated in this classroom, assuming 3.6 m$$^{3}$$ of air is needed for each child.
Spherical marbles of diameter $$1.4cm$$ are dropped into a cylindrical beaker of diameter $$7cm$$, which contains some water. Find the number of marbles that should be dropped into the beaker, so that water levek rises by $$5.6cm$$.
Radius of beaker $$=\dfrac {d}{2}=\dfrac {7}{2}=3.5\ cm$$
Height of the rise, $$h=5.6\ cm$$
Volume of teh water rise $$=V=\pi r^2 h$$
$$=\dfrac {22}{7}\times 3.5\times 3.5\times 5.6=215.6\ cm^3$$
Volume of each spherical marble dropped $$=\dfrac 43 \pi r^3$$
Radius of marble $$=r=\dfrac {d}{2}=\dfrac {1.4}{2}=0.7\ cm$$
Volume $$=\dfrac {4}{3}\times \dfrac {22}{7}\times 0.7\times 0.7\times 0.7=1.4373\ cm^3$$
Volume of the water level rise = Total volume of the marbles
If the number of marble$$'n'$$
$$n\times $$ volume of each marble = volume of the water level rise
$$n\times 1.4373=215.6$$
$$\Rightarrow n=\dfrac {215.6}{1.4373}=150$$
$$\therefore $$ Number of marbles $$=150$$
Height of the rise, $$h=5.6\ cm$$
Volume of teh water rise $$=V=\pi r^2 h$$
$$=\dfrac {22}{7}\times 3.5\times 3.5\times 5.6=215.6\ cm^3$$
Volume of each spherical marble dropped $$=\dfrac 43 \pi r^3$$
Radius of marble $$=r=\dfrac {d}{2}=\dfrac {1.4}{2}=0.7\ cm$$
Volume $$=\dfrac {4}{3}\times \dfrac {22}{7}\times 0.7\times 0.7\times 0.7=1.4373\ cm^3$$
Volume of the water level rise = Total volume of the marbles
If the number of marble$$'n'$$
$$n\times $$ volume of each marble = volume of the water level rise
$$n\times 1.4373=215.6$$
$$\Rightarrow n=\dfrac {215.6}{1.4373}=150$$
$$\therefore $$ Number of marbles $$=150$$
The external diameter of a closed wooden box are $$27\ cm, 19\ cm$$ and $$11\ cm$$. If the thickness of the wood in the box is $$1.5\ cm$$, find:
The cost of the box, if wood costs $$Rs. 1.20\ cm^3$$.
In the figure, the height of a solid cylinder is 10 cm and diameter is 7 cm. Two equal conical holes of radius 3 cm and height 4 cm are cut off as shown in the figure. Find the volume of the remaining solid.
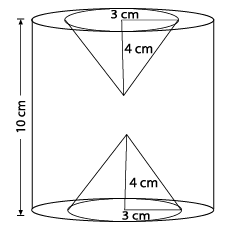
A cylindrical tube of radius $$5\text{ cm}$$ and height $$9.8\text{ cm}$$ is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed into the mug. The radius of the hemisphere is $$3.5\text{ cm}$$ and the height of the conical part $$5\text{ cm}$$. Find the volume of water left in the cylindrical tube.
A pen stand is made of wood in the shape of cuboid with three conical depressions to hold the pens. The dimensions of the cuboid are $$15cm$$ by $$3.5cm$$. The radius of each of the depression is $$0.5cm$$ and the depth is $$1.4cm$$. Find the volume of the wood in the entire stand.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below. Find the area of the remaining card-board.
The radii of ends of a frustum are $$14$$ cm and $$6$$ cm respectively and its height is $$6$$ cm. Find its total surface area.
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter I of the hemisphere is equal to the edge of the cube. Determine the surface area of the cube. Determine the surface area of the remaining solid.
Let, Length of each edge of cubical block = Diameter of hemisphere = I
$$\therefore$$ Radius of hemisphere, $$r = \frac{1}{2}$$ unit.
Total surface area of newly formed cube = Curved surface area of cube - upper part of cube + area of hemisphere which is depressed
$$= 6l^2 - \pi \left ( \frac{1}{2} \right )^2 + 2 \pi \left ( \frac{1}{2} \right )^2$$
$$= 6l^2 + \pi \left ( \frac{1}{2} \right )^2$$
$$= \frac{1}{4} (24l^2 + \pi l^2)$$
$$= \frac{1}{4} l^2 (24 + \pi)$$
$$\therefore$$ Radius of hemisphere, $$r = \frac{1}{2}$$ unit.
Total surface area of newly formed cube = Curved surface area of cube - upper part of cube + area of hemisphere which is depressed
$$= 6l^2 - \pi \left ( \frac{1}{2} \right )^2 + 2 \pi \left ( \frac{1}{2} \right )^2$$
$$= 6l^2 + \pi \left ( \frac{1}{2} \right )^2$$
$$= \frac{1}{4} (24l^2 + \pi l^2)$$
$$= \frac{1}{4} l^2 (24 + \pi)$$
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.
(i) Surface area of cylindrical capsule, $$= 2 \pi rh$$
$$= 2 \pi \times (\frac{5}{2}) \times 9$$
$$= 45 \pi mm^2$$
(ii) Surface area of both hemispheres,
$$= 2 \{ 2 \pi \times (\frac{5}{2})^2 \} mm^2$$
$$= 25 \pi mm^2$$
$$\therefore$$ Total surface area of capsule $$= 45 \pi + 25 \pi mm^2$$
$$= 70 \pi mm^2$$
$$= 70 \times \frac{22}{7}$$
$$= 220 mm^2$$
$$= 2 \pi \times (\frac{5}{2}) \times 9$$
$$= 45 \pi mm^2$$
(ii) Surface area of both hemispheres,
$$= 2 \{ 2 \pi \times (\frac{5}{2})^2 \} mm^2$$
$$= 25 \pi mm^2$$
$$\therefore$$ Total surface area of capsule $$= 45 \pi + 25 \pi mm^2$$
$$= 70 \pi mm^2$$
$$= 70 \times \frac{22}{7}$$
$$= 220 mm^2$$
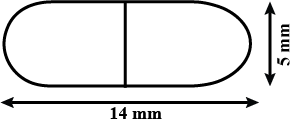
The circumferences of circular faces of a frustum are $$132$$ cm and $$88$$ cm and its height is $$24$$ cm. To find the curved surface area of the frustum complete the following activity.$$([\pi = \frac{22}{7}])$$
The radii of ends of a frustum are $$14$$ cm and $$6$$ cm respectively and its height is $$6$$ cm. Find its curved surface area.
A circle of largest area is cut from a rectangular piece of cardboard with dimensions $$ 55 \mathrm{cm} $$ and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
The given figures shows a rectangle ABCD inscribed in a circle as shown alongside. If $$ A B=28 \mathrm{cm} $$ and $$ \mathrm{BC}=21 \mathrm{cm}, $$ find the area of the shaded portion of the given figure.
In the given figure, a cylindrical wrapper of flat tablets is shown. The radius of a tablet is $$7$$ mm and its thickness is $$5$$ mm. How many such tablets are wrapped in the wrapper?
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure. If the height of the cylinder is 10 cm. and its base is of radius 3.5 cm. find the total surface area of the article.
Radius of base of cylinder, r = 3.5 cm
Height, h = 10 cm.
Total area of article = Curved surface of cylinder + 2 x Area of Hemisphere
$$= 2 \pi rh + 2 \times 2 \pi r^2$$
$$= 2 \times \frac{22}{7} \times 3.5 \times 10 + 2 \times 2 \times \frac{22}{7} \times (3.5)^2$$
$$= 3.5 \times 34 \times \frac{22}{7}$$
$$= 374$$ sq.cm.
Height, h = 10 cm.
Total area of article = Curved surface of cylinder + 2 x Area of Hemisphere
$$= 2 \pi rh + 2 \times 2 \pi r^2$$
$$= 2 \times \frac{22}{7} \times 3.5 \times 10 + 2 \times 2 \times \frac{22}{7} \times (3.5)^2$$
$$= 3.5 \times 34 \times \frac{22}{7}$$
$$= 374$$ sq.cm.
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
(i) Radius of cylinder GHEF, r = 60 cm.
Height, h = 120 + 60 = 180 cm
Volume of cylinderical vessel $$= \pi r^2 h = \pi \times (60)^2 \times 180$$
(ii) Volume of hemisphere + volume of cone
$$= \frac{2}{3} \pi r^3 + \frac{1}{3} \pi r^2 h$$
$$= \frac{2}{3} \pi \times (60)^3 + \frac{1}{3} \times \pi \times (60)^2 \times 120$$
$$= \frac{4}{3} \pi \times (60)^3 cm^3$$
(iii) Quality of water remained in cylinder.
$$= \pi \times (60)^2 \times 180 - \frac{4}{3} \pi \times (60)^3 cm^3$$
$$= (60)^3 \times \{ \frac{3}{4}\pi - \frac{4}{3} \pi \}$$
$$= 216000 \times \frac{5}{3} \pi$$
$$= 360000 \pi cm^3$$
$$= 360000 \times \frac{22}{7} cm^3$$
$$= \frac{360000 \times 22}{(100)^3 \times 7} m^3$$
$$= 1.131 m^3$$
Height, h = 120 + 60 = 180 cm
Volume of cylinderical vessel $$= \pi r^2 h = \pi \times (60)^2 \times 180$$
(ii) Volume of hemisphere + volume of cone
$$= \frac{2}{3} \pi r^3 + \frac{1}{3} \pi r^2 h$$
$$= \frac{2}{3} \pi \times (60)^3 + \frac{1}{3} \times \pi \times (60)^2 \times 120$$
$$= \frac{4}{3} \pi \times (60)^3 cm^3$$
(iii) Quality of water remained in cylinder.
$$= \pi \times (60)^2 \times 180 - \frac{4}{3} \pi \times (60)^3 cm^3$$
$$= (60)^3 \times \{ \frac{3}{4}\pi - \frac{4}{3} \pi \}$$
$$= 216000 \times \frac{5}{3} \pi$$
$$= 360000 \pi cm^3$$
$$= 360000 \times \frac{22}{7} cm^3$$
$$= \frac{360000 \times 22}{(100)^3 \times 7} m^3$$
$$= 1.131 m^3$$
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollow out. Find the total surface area of the remaining solid to the nearest cm$$^2$$?.
Height of the cylinder, h = 2.4 m.
Diameter of the cylinder, d = 1.4 m.
$$\therefore$$ Radius, r = 0.7 m.
(i) Outer Curved surface area of cylinder $$= 2 \pi rh$$
$$= 2 \times \frac{22}{7} \times (0.7) \times 2.4$$
$$= 44 \times 0.24$$
$$= 10.56 cm^2$$
(ii) Area of base of $$= \pi r^2$$
$$= \frac{22}{7} \times (0.7)^2$$
$$= \frac{22}{7} \times 0.49$$
$$= 1.54 cm^2$$
(iii) Inner surface area of cylinder, $$= \pi rl$$
$$= \frac{22}{7} \times 0.7 \times \sqrt{(0.7)^2 + (2.4)^2}$$
$$= \frac{22}{7} \times 0.7 \times 2.5$$
$$= 5.5 cm^2$$
$$\therefore$$ Total surface area of newly formed cube = 10.56 + 1.54 + 5.5 = 17.6 cm$$^2$$
$$\therefore$$ Nearest value is 18 sq.cm
Diameter of the cylinder, d = 1.4 m.
$$\therefore$$ Radius, r = 0.7 m.
(i) Outer Curved surface area of cylinder $$= 2 \pi rh$$
$$= 2 \times \frac{22}{7} \times (0.7) \times 2.4$$
$$= 44 \times 0.24$$
$$= 10.56 cm^2$$
(ii) Area of base of $$= \pi r^2$$
$$= \frac{22}{7} \times (0.7)^2$$
$$= \frac{22}{7} \times 0.49$$
$$= 1.54 cm^2$$
(iii) Inner surface area of cylinder, $$= \pi rl$$
$$= \frac{22}{7} \times 0.7 \times \sqrt{(0.7)^2 + (2.4)^2}$$
$$= \frac{22}{7} \times 0.7 \times 2.5$$
$$= 5.5 cm^2$$
$$\therefore$$ Total surface area of newly formed cube = 10.56 + 1.54 + 5.5 = 17.6 cm$$^2$$
$$\therefore$$ Nearest value is 18 sq.cm
Write the formula to find slant height of an frustum cone.
Write the formula to find the lateral surface area of frustum of cone.
A solid hemisphere of wax of radius 12 cm is melted and made into a cone of base radius 6 cm. Calculate the height of the cone.
Radius of the hemisphere, $$r_1 = 12$$ cm
Radius of the base of the cone, $$r_2 = 6$$ cm
Height of the cone = h = ?
volume of wax cone = volume of wax hemisphere.
Radius of the base of the cone, $$r_2 = 6$$ cm
Height of the cone = h = ?
volume of wax cone = volume of wax hemisphere.
21 spheres of equal radii are melted to form a cylinder of radius 14 cm and height 49 cm. Find the radius of sphere.
radius of cylinder $$= r_1 = 14 cm$$
height h = 49 cm and radius of sphere $$= r_2$$
Total volume of 21 spheres = volume of cylinder.
height h = 49 cm and radius of sphere $$= r_2$$
Total volume of 21 spheres = volume of cylinder.
A Gulab Jamun contains sugar syrup upto about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm.
The cores of three cubes are $$ 8 \mathrm{cm}, 6 \mathrm{cm} $$ and $$ 1 \mathrm{cm} $$ respectively. Having melted these cubes a new cube is recastesd. Find the total surface area of the new cube recanted.
A conical vessel with base radius $$ 10 \mathrm{cm} $$. contains some water in it. The water level in the vessel is $$ 18 \mathrm{cm} $$ high. It is pored into another cylindrical vessel with a radius $$ 5 \mathrm{cm} $$. Find the water level in the cylindrical vessel.
How many silver coins, 1.75 cm. in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm x 10 cm x 3.5 cm?
A cylinder is made of glass, whose radius and height are $$ 4 \mathrm{cm} $$ and $$ 10 \mathrm{cm} $$ respectively. By melting it, how many sphere with radii $$ 2 \mathrm{cm} $$ each can be recasted?
How many cones with radius $$ 3 \mathrm{cm} $$ and height $$ 6 \mathrm{cm} $$ can be formed by melting a metallic sphere with radius $$ 9 \mathrm{cm} $$.
Twenty seven solid iron spheres, each of radius $$ r $$ and surface area $$ S $$ are melted to from a sphere with surface area $$ S_1 $$. Find the
(i) radius $$ r $$ of the new sphere,
(ii) ratio of $$ S $$ and $$ S_1 $$
Three metal cubes whose edges measure $$3\ cm, 4\ cm$$ and $$5\ cm$$ respectively are melted to form a single cube find side-length
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top pf the funnel is 18 cm, find the area of the tin sheet required to make the funnel.
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of glass.
Height of drinking glass, h = 14 cm
Diameter of circular ends
D = 4 cm $$\therefore$$ r = 2 cm
d = 2 cm $$\therefore$$ r = 1 cm
Capacity of glass = ?
Volume of glass = Radius with 2 cm + Volume of frustum with radius 1 cm.
$$= \frac{1}{3} \pi h (R^2 + r^2 + Rr)$$
$$= \frac{1}{3} \times \frac{22}{7} \times 14 (2^2 + 1^2 + 2 \times 1)$$
$$= \frac{1}{3} \times \frac{22}{7} \times 14 (4 + 1 + 2)$$
$$= \frac{1}{3} \times \frac{22}{7} \times 14 \times 7$$
$$= \frac{308}{3}$$
$$= 102 \frac{2}{3} cm^3$$
Diameter of circular ends
D = 4 cm $$\therefore$$ r = 2 cm
d = 2 cm $$\therefore$$ r = 1 cm
Capacity of glass = ?
Volume of glass = Radius with 2 cm + Volume of frustum with radius 1 cm.
$$= \frac{1}{3} \pi h (R^2 + r^2 + Rr)$$
$$= \frac{1}{3} \times \frac{22}{7} \times 14 (2^2 + 1^2 + 2 \times 1)$$
$$= \frac{1}{3} \times \frac{22}{7} \times 14 (4 + 1 + 2)$$
$$= \frac{1}{3} \times \frac{22}{7} \times 14 \times 7$$
$$= \frac{308}{3}$$
$$= 102 \frac{2}{3} cm^3$$
Three metal cubes whose edges measure $$3\ cm, 4\ cm$$ and $$5\ cm$$ respectively are melted to form a single cube find total surface are of a new cube. What is the difference between total surface area of the new cube and the sum of total surface areas of the original cubes?
The radius of a solid metallic sphere is $$r$$. A solid metallic cone of height $$h$$ has base radius $$r$$. The two are melted together and recast into a solid right circular cone with base radius $$r$$. Prove that the height of the resulting cone is $$4 r + h.$$
A solid iron pole consists of a cylinder of height $$220$$ cm and base diameter $$24$$ cm, which is surmounted by another cylinder of height $$60$$ cm and radius $$8$$ cm. Find the mass of the pole, given that 1 $$cm^3$$ of iron has approximately $$8$$ g mass. (Use $$\pi$$ = 3.14)
Height ($$h_1$$) of larger cylinder $$= 220$$ cm
Radius ($$r_1$$) of larger cylinder = $$\dfrac{24}{2} = 12$$ cm
Height ($$h_2$$) of smaller cylinder = $$60$$ cm
Radius ($$r_2$$) of smaller cylinder =$$ 8$$ cm
Total volume of pole = Volume of larger cylinder + Volume of smaller cylinder
$$=\pi r_{1}^2 h_1 +\pi r_{2}^2 h_2$$
$$=(\pi (12)^2\times 220) + (\pi (8)^2 \times 60)$$
$$=\pi[144 \times 220 + 64 \times 60]$$
$$=3.14[31,680 + 3,840]$$
$$=3.14 \times 35520 = 111,532.8 $$ cm $$^3$$
Mass of 1 $$cm^3$$ iron = $$8$$ g
Mass of $$111532.8 $$ cm $$^3$$ iron = $$11532.8 \times 8 = 892262.4$$ g
Radius ($$r_1$$) of larger cylinder = $$\dfrac{24}{2} = 12$$ cm
Height ($$h_2$$) of smaller cylinder = $$60$$ cm
Radius ($$r_2$$) of smaller cylinder =$$ 8$$ cm
Total volume of pole = Volume of larger cylinder + Volume of smaller cylinder
$$=\pi r_{1}^2 h_1 +\pi r_{2}^2 h_2$$
$$=(\pi (12)^2\times 220) + (\pi (8)^2 \times 60)$$
$$=\pi[144 \times 220 + 64 \times 60]$$
$$=3.14[31,680 + 3,840]$$
$$=3.14 \times 35520 = 111,532.8 $$ cm $$^3$$
Mass of 1 $$cm^3$$ iron = $$8$$ g
Mass of $$111532.8 $$ cm $$^3$$ iron = $$11532.8 \times 8 = 892262.4$$ g
A farmer connects a pipe of internal diameter 20 cm form a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 kilometer per hour, in how much time will the tank be filled?
The front compound wall of a house is decorated by wooden spheres of a diameter $$21\ cm$$, placed on small supports as shown in the figure. Eight such spheres are used for this purpose and are to be painted silver. Each support is a cylinder of radius $$1.5\ cm$$ and height $$7\ cm$$ and is to be painted black. Find the cost of paint required if silver paint costs $$25\ paise\ per\ cm^{2}$$.
A vessel is in the form of an inverted cone. Its height is $$8\ cm $$ and the radius of its top, which is open, is $$5\ cm$$. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius $$0.5\ cm $$ are dropped into the vessel, $$\dfrac {1}{4}$$ of the water flows out. Find the number of lead shots dropped in the vessel.
Given:
Height ($$h$$) of conical vessel $$= 8$$ cm
Radius ($$r_1$$) of conical vessel $$ = 5$$ cm
Radius ($$r_2$$) of lead shots $$= 0.5$$ cm
Let $$x$$ number of lead shots were dropped in the vessel.
Volume of water spilled = Volume of dropped lead shots
$$\dfrac{1}{4}\times \dfrac{1}{3}\pi r_{1}^{2}h=x\times \dfrac{4}{3} \times \pi r_{2}^{3}$$
$$\Longrightarrow 5^2 \times 8 =x \times 16 \times (0.5)^3$$
$$\Longrightarrow 200 = x \times 2$$
$$\Longrightarrow x = \dfrac{200}{2}$$
Therefore, the number of lead shots dropped in the vessel is $$100$$.
Height ($$h$$) of conical vessel $$= 8$$ cm
Radius ($$r_1$$) of conical vessel $$ = 5$$ cm
Radius ($$r_2$$) of lead shots $$= 0.5$$ cm
Let $$x$$ number of lead shots were dropped in the vessel.
Volume of the cone $$ =\dfrac{1}{3} \pi (r_1)^3$$
Volume of water spilled = Volume of dropped lead shots
According to the question
$$\dfrac{1}{4}\times \dfrac{1}{3}\pi r_{1}^{2}h=x\times \dfrac{4}{3} \times \pi r_{2}^{3}$$
$$\Longrightarrow r_{1}^{2}h= x\times 16 r_{2}^{3}$$
$$\Longrightarrow 5^2 \times 8 =x \times 16 \times (0.5)^3$$
$$\Longrightarrow 200 = x \times 2$$
$$\Longrightarrow x = \dfrac{200}{2}$$
$$\Rightarrow$$$$x = 100.$$
Therefore, the number of lead shots dropped in the vessel is $$100$$.
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is $$3\ cm$$ and its length is $$12\ cm$$. If each cone has a height of $$2\ cm$$, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
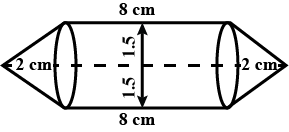
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are $$2.1 $$ m and $$4$$ m respectively, and the slant height of the top is $$2.8$$ m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs $$500$$ per $$m^2$$. (Note that the base of the tent will not be covered with canvas.) (Use $$\pi = \dfrac{22}{7}$$).
Given:
Height (h) of the cylindrical part = $$2.1$$ m
Diameter of the cylindrical part = $$4$$ m
Radius of the cylindrical part = $$2$$ m
Slant height (l) of conical part = $$2.8$$ m
Area of canvas used = CSA of conical part + CSA of cylindrical part
Height (h) of the cylindrical part = $$2.1$$ m
Diameter of the cylindrical part = $$4$$ m
Radius of the cylindrical part = $$2$$ m
Slant height (l) of conical part = $$2.8$$ m
Area of canvas used = CSA of conical part + CSA of cylindrical part
$$=\pi rl + 2\pi r h$$
$$=\pi\times 2 \times 2.8 + 2\pi \times 2 \times 2.1$$
$$=2\pi[2.8 + 4.2]$$
$$=2\pi[2.8 + 4.2]$$
$$= 2\times \dfrac{22}{7}\times 7$$
$$ = 44 m^2$$
Cost of $$1 $$ m $$^2$$ canvas $$= 500$$ rupees
Cost of $$44$$ m $$^2$$ canvas $$= 44 \times 500 = 22000$$ rupees.
Cost of $$44$$ m $$^2$$ canvas $$= 44 \times 500 = 22000$$ rupees.
Therefore, it will cost $$22000$$ rupees for making such a tent.
A gulab jamun contains sugar syrup up to about 30$$\%$$ of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm.
A toy is in the form of a cone of radius $$3.5$$ cm mounted on a hemisphere of same radius. The total height of the toy is $$15.5$$ cm. Find the total surface area of the toy rounded off to the nearest integer.
As per the question we can draw the diagram.
Given:
The radius of the conical part and the hemispherical part is same (i.e., $$ 3.5\text{ cm}$$)
Height of the hemispherical part, $$r= 3.5 = \dfrac{7}{2}$$
Height of conical part, $$h = 15.5 - 3.5 = 12\text{ cm}$$
Slant height ($$l$$) of conical part $$l=\sqrt{r^2 + h^2}$$
= $$\sqrt{\left( \dfrac{7}{2}\right)^2 + 12^2}= \sqrt{\dfrac{49}{4} + 144}=\sqrt{\dfrac{49+576}{4}}$$
$$=\sqrt{\dfrac{625}{4}}=\dfrac{25}{2}$$
Total surface area of toy = CSA of conical part + CSA of hemispherical part
$$=\pi rl +2\pi r^2$$
$$=\dfrac{22}{7}\times\dfrac{7}{2}\times \dfrac{25}{2} + 2 \times \dfrac{22}{7}\times \dfrac{7}{2}\times \dfrac{7}{2}$$
$$=214.7$$
Given:
The radius of the conical part and the hemispherical part is same (i.e., $$ 3.5\text{ cm}$$)
Height of the hemispherical part, $$r= 3.5 = \dfrac{7}{2}$$
Height of conical part, $$h = 15.5 - 3.5 = 12\text{ cm}$$
Slant height ($$l$$) of conical part $$l=\sqrt{r^2 + h^2}$$
= $$\sqrt{\left( \dfrac{7}{2}\right)^2 + 12^2}= \sqrt{\dfrac{49}{4} + 144}=\sqrt{\dfrac{49+576}{4}}$$
$$=\sqrt{\dfrac{625}{4}}=\dfrac{25}{2}$$
Total surface area of toy = CSA of conical part + CSA of hemispherical part
$$=\pi rl +2\pi r^2$$
$$=\dfrac{22}{7}\times\dfrac{7}{2}\times \dfrac{25}{2} + 2 \times \dfrac{22}{7}\times \dfrac{7}{2}\times \dfrac{7}{2}$$
$$=214.7$$
Water in canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Derive the formula for the volume of the frustum of a cone.
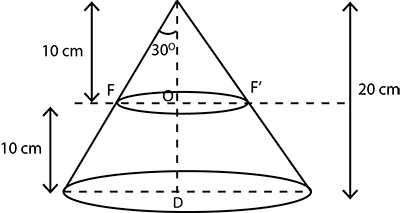
A solid is in the form of a hemisphere surmounted by a right circular cone. If height of the cone is $$12\text{ cm}$$ and diameter of the base is $$10\text{ cm}$$. Calculate the surface area of the toy.
Given, Radius, $$r$$ of cone $$= 5\text{ cm}$$
Height, $$h$$ of cone $$= 12\text{ cm}$$
slant height, $$l = \sqrt{h^2+r^2}$$
$$l = \sqrt{12^2+5^2}$$
$$l=\sqrt{144+25}$$
$$l=\sqrt{169}$$
$$l = 13\text{ cm}$$
Surface area of the toy = Curve surface area of cone + curved surface area of hemisphere
$$=\pi r l + 2\pi r^2$$
$$=\pi r(l+2r)$$
$$=3.14 \times 5(13+2\times 5)$$
$$= 361.1 \text{ cm}^{2}$$
Height, $$h$$ of cone $$= 12\text{ cm}$$
slant height, $$l = \sqrt{h^2+r^2}$$
$$l = \sqrt{12^2+5^2}$$
$$l=\sqrt{144+25}$$
$$l=\sqrt{169}$$
$$l = 13\text{ cm}$$
Surface area of the toy = Curve surface area of cone + curved surface area of hemisphere
$$=\pi r l + 2\pi r^2$$
$$=\pi r(l+2r)$$
$$=3.14 \times 5(13+2\times 5)$$
$$= 361.1 \text{ cm}^{2}$$
A right-angled triangle whose sides are $$3\ cm$$ and $$4\ cm$$ (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose a value of $$\pi$$ as found appropriate.)
The double cone so formed by revolving this right-angled triangle ABC about its hypotenuse is shown in the figure.
$$\Rightarrow \dfrac{1}{2}\times AC\times DB = \dfrac{1}{2}\times 4\times 3$$
$$\Rightarrow\dfrac{1}{2}\times 5\times DB = 6$$
So, DB = $$\dfrac{12}{5}=2.4$$ cm
$$=\dfrac{1}{3}\pi r^2 h_1 +\dfrac{1}{3}\pi r^2 h_2$$
$$=\frac{1}{3}\pi r^2[h_1 + h_2]=\dfrac{1}{3}\pi r^2[DA+DC]$$
$$=\dfrac{1}{3}\times 3.14\times 2.4^2\times 5$$
$$= 30.14\space\ cm^3$$
$$= \pi r l_1 + \pi r l_2$$
$$=\pi r[4+3]=3.14\times2.4\times 7$$
$$= 52.75$$ cm$$^2$$
Hypotenuse, AC = $$\sqrt{3^2+4^2}$$
$$=\sqrt{9+16}=\sqrt{25}=5$$ cm
$$=\sqrt{9+16}=\sqrt{25}=5$$ cm
Area of $$\Delta ABC = \dfrac{1}{2}\times AB \times AC$$
$$\Rightarrow \dfrac{1}{2}\times AC\times DB = \dfrac{1}{2}\times 4\times 3$$
$$\Rightarrow\dfrac{1}{2}\times 5\times DB = 6$$
So, DB = $$\dfrac{12}{5}=2.4$$ cm
The volume of double cone = Volume of cone 1 + Volume of cone 2
$$=\dfrac{1}{3}\pi r^2 h_1 +\dfrac{1}{3}\pi r^2 h_2$$
$$=\frac{1}{3}\pi r^2[h_1 + h_2]=\dfrac{1}{3}\pi r^2[DA+DC]$$
$$=\dfrac{1}{3}\times 3.14\times 2.4^2\times 5$$
$$= 30.14\space\ cm^3$$
The surface area of double cone = Surface area of cone 1 + Surface area of cone 2
$$= \pi r l_1 + \pi r l_2$$
$$=\pi r[4+3]=3.14\times2.4\times 7$$
$$= 52.75$$ cm$$^2$$
An oil funnel made of tin sheet consists of a $$10\ cm$$ long cylindrical portion attached to a frustum of a cone. If the total height is $$22\ cm$$, diameter of the cylindrical portion is $$8\ cm$$ and the diameter of the top of the funnel is $$18\ cm$$, find the area of the tin sheet required to make the funnel .
Given:
Radius $$(R)$$ of upper circular end of frustum part = $$\dfrac{18}{2}=9$$ cm
Radius $$(r)$$ of lower circular end of frustum part = Radius of circular end of cylindrical part =$$\dfrac{8}{2}=4$$ cm
Radius $$(R)$$ of upper circular end of frustum part = $$\dfrac{18}{2}=9$$ cm
Radius $$(r)$$ of lower circular end of frustum part = Radius of circular end of cylindrical part =$$\dfrac{8}{2}=4$$ cm
Height $$(h_1)$$ of frustum part $$= 22 - 10 = 12$$ cm
Height $$(h_2)$$ of cylindrical part $$= 10$$ cm
Height $$(h_2)$$ of cylindrical part $$= 10$$ cm
Slant height (l) of frustum part = $$\sqrt{(R-r)^2+h_{1}^2}=\sqrt{(9-4)^2+ 12^2}=\sqrt{25+144}$$
$$=\sqrt{169}=13$$ cm
$$=\sqrt{169}=13$$ cm
Area of tin sheet required = CSA of frustum part + CSA of cylindrical part
$$=\pi(R+r)l+2\pi r h_2$$
$$=\pi(R+r)l+2\pi r h_2$$
$$=\dfrac{22}{7}\times (9+4)\times 13+2\times \dfrac{22}{7}\times 4\times 10$$
$$=\dfrac{22}{7}[169 +80]=\dfrac{22\times249}{7}$$
$$=782\dfrac{4}{7}\space\ $$ cm$$^2$$
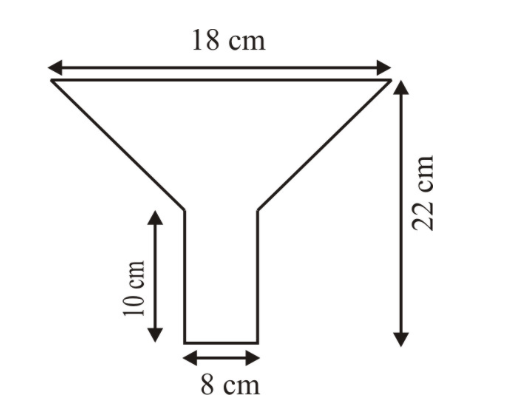
From a solid cylinder of height $$7$$ cm and base diameter $$12$$ cm, a conical cavity of same height and same base diameter is hollowed out. Find the total surface area of the remaining solid. $$\left [ Use \ \pi = \dfrac{22}{7} \right ].$$
Given:
Height $$(h)$$ of cylindrical part $$=$$ height $$(h)$$ of the conical part $$= 7$$ cm
Diameter of the cylindrical part $$= 12$$ cm
Therefore, Radius $$(r)$$ of the cylindrical part $$=\dfrac{12}{2}=6$$ cm
So, Radius of the conical part $$= 6$$ cm
Slant height $$(l)$$ of conical part =$$\sqrt{r^2+h^2}$$ cm
$$=\sqrt{6^2+7^2}$$
$$=\sqrt{36+49}$$
$$=\sqrt{85}$$
$$\approx 9.22$$ cm.
The total surface area of the remaining solid $$=$$ CSA of the cylindrical part $$+$$ CSA of the conical part $$+$$ Base area of the circular part
$$=2\pi r h + \pi r l+\pi r^2$$
$$=2\times \dfrac{22}{7}\times 6\times 7+\dfrac{22}{7}\times 6\times 9.22+\dfrac{22}{7}\times 6\times 6$$
$$=264+173.86+113.14$$
$$=551$$ $$cm^2$$
Height $$(h)$$ of cylindrical part $$=$$ height $$(h)$$ of the conical part $$= 7$$ cm
Diameter of the cylindrical part $$= 12$$ cm
Therefore, Radius $$(r)$$ of the cylindrical part $$=\dfrac{12}{2}=6$$ cm
So, Radius of the conical part $$= 6$$ cm
Slant height $$(l)$$ of conical part =$$\sqrt{r^2+h^2}$$ cm
$$=\sqrt{6^2+7^2}$$
$$=\sqrt{36+49}$$
$$=\sqrt{85}$$
$$\approx 9.22$$ cm.
The total surface area of the remaining solid $$=$$ CSA of the cylindrical part $$+$$ CSA of the conical part $$+$$ Base area of the circular part
$$=2\pi r h + \pi r l+\pi r^2$$
$$=2\times \dfrac{22}{7}\times 6\times 7+\dfrac{22}{7}\times 6\times 9.22+\dfrac{22}{7}\times 6\times 6$$
$$=264+173.86+113.14$$
$$=551$$ $$cm^2$$
A bucket is in the form of a frustum of a cone and it can hold $$28.49\ liters $$ of water. If the radii of its circular ends are $$28\ cm$$ and $$21\ cm$$, find the height of the bucket. $$\left [ Use \ \pi = \dfrac{22}{7} \right ].$$
Derive the formula for the curved surface area and total surface area of the frustum of a cone.
Let $$ABC$$ be a cone. A frustum $$DECB$$ is cut by a plane parallel to its base.
Let $$r_1$$ and $$r_2$$ be the radii of the ends of the frustum of the cone and $$h$$ be the height of the frustum of the cone.
Therefore, $$\angle ABG \sim \angle ADF$$
$$\dfrac{DF}{BG}=\dfrac{AF}{AG}=\dfrac{AD}{AB}$$
$$\dfrac{DF}{BG}=\dfrac{AF}{AG}=\dfrac{AD}{AB}$$
$$\dfrac{r_2}{r_1}=\dfrac{h_1 - h}{h_1}=\dfrac{l_1 - l}{1_1}$$
$$\dfrac{r_2}{r_1}= 1-\dfrac{h}{h_1}=1-\dfrac{l}{l_1}$$
$$1-\dfrac{l}{l_1}=\dfrac{r_2}{r_1}$$
$$1-\dfrac{l}{l_1}=1-\dfrac{r_2}{r_1}=\dfrac{r_1 - r_2}{r_1}$$
$$\dfrac{l_1}{l}=\dfrac{r_1}{r_1 - r_2}$$
$$l_1 = \dfrac{r_1 l}{r_1 - r_2}$$
CSA of frustum $$DECB =$$ CSA of cone $$ABC -$$ CSA cone $$ADE$$
$$=\pi r_{1}l_{1}-\pi r_{2}(l_{1}-l)$$
$$=\pi r_{1}l_{1}-\pi r_{2}(l_{1}-l)$$
$$=\pi r_{1}\left(\dfrac{r_1}{r_1 - r_2} \right)-\pi r_{2}\left(\dfrac{r_1}{r_1 - r_2} - l\right)$$
$$\dfrac{\pi r_{1}^2l}{r_{1}-r_{2}}-\pi r_{2}\left (\dfrac{r_1 l- r_1 l+r_2 l}{r_1 - r_2}\right)$$
$$=\dfrac{\pi r_1^2 l}{r_1 - r_2}-\dfrac{\pi r_2^2 l}{r_1 - r_2}$$
$$=\pi l[\dfrac{r_{1}^2 - r_{2}^2}{r_1 - r_2}]$$
CSA of frustum = $$\pi (r_1 + r_2)l$$.
Total surface area of frustum = CSA of frustum + Area of upper circular end + Area of lower circular end.
$$=\pi (r_1 + r_2)l+\pi r_{2}^2+\pi r_{1}^2$$
$$=\pi[(r_1 + r_2)l+r_{1}^2+r_{2}^2]$$
$$=\pi (r_1 + r_2)l+\pi r_{2}^2+\pi r_{1}^2$$
$$=\pi[(r_1 + r_2)l+r_{1}^2+r_{2}^2]$$
A bucket opens at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is $$24\ cm$$ and the diameters of its upper and lower circular ends are $$30\ cm$$ and $$10\ cm$$ respectively. Find the cost of metal sheet used in it at the rate of $$Rs\ 10$$ per $$100\ cm^2$$. $$\displaystyle \left[ Use\ \pi = 3.14 \right]$$.Insert answer in nearest integer.
Diameter of upper end of bucket = $$30 cm$$
Diameter of lower end of bucket = $$10 cm$$
Then, radius of upper end of bucket $$r_{1}=\cfrac{30}{2}=15$$ cm
And, radius of lower end of bucket $$r_{2}=\cfrac{10}{2}=5$$ cm
Height of bucket = $$24\ cm$$
Slant height of bucket = $$\sqrt{(r_{2}-r_{1})^{2}+h^{2}}$$
$$=\sqrt{(15-5)^{2}+(24)^{2}}=\sqrt{(10)^{2}+(24)^{2}}$$
$$=\sqrt{100+256}=\sqrt{676}=26\ cm$$
Area of metal sheet used to make bucket
$$=\pi (r_{1}+r_{2})l+\pi( r_{2})^{2}=\pi (15+5)26+\pi (5)^{2}$$
$$=520\pi +25\pi =545\pi\ cm^{2}$$
Given cost of $$100$$ sq cm metal sheet =Rs.$$10$$
Cost of $$545\pi\ cm^{2}$$ metal sheet $$=\dfrac{545\times 3.14\times 10}{100}=171.13\ Rs.$$
Cost of metal sheet used for making bucket $$= \ Rs. 171.13$$
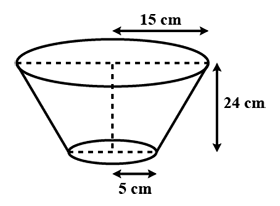
A cistern, internally measuring $$150$$ cm x $$120$$ cm x $$110$$ cm, has $$129600$$ cm $$^3$$ of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being $$22.5$$ cm x $$7.5 $$cm x $$6.5$$ cm
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to $$7$$ cm and the height of the cone is equal to its diameter. Find the volume of the solid. $$\left [ Use \ \pi = \dfrac{22}{7} \right ].$$
A funnel of tin sheet consists of a cylindrical portion, $$10\ cm$$ long, attached to a frustum of a cone. If a diameter of the top and bottom of the frustum is $$18\ cm$$ and $$8\ cm$$ respectively and the slant height of the frustum of cone is $$13\ cm$$, find the surface area of the tin required to make the funnel.
We know $$\dfrac { EC }{ EB } =\dfrac { OD }{ KA } $$ (Similar triangle)
$$\dfrac { x }{ x+13 } =\dfrac { 4 }{ 9 } $$
$$\Rightarrow 9x=4x+52$$
$$\Rightarrow 5x=52$$
$$\Rightarrow x=10.4$$
Surface area of cone $$=\pi r\left( r+l \right) $$
where $$r$$ is radius and $$l$$ is slant height
So, surface area of conical part $$=$$ Surface area of bigger cone $$-$$ Surface area of small imaginary cone
$$=\pi \times 9\times \left( 9+(13+10.4) \right) -\pi \times 9\times (4+10.4)$$
$$=\pi \times 234$$
Surface area of cylindrical part $$=2\pi rh$$
$$=2\times \pi \times 4\times 10$$
$$=80\pi $$
So, total surface area $$=234\pi +80\pi $$
$$=314\pi $$ sq. units
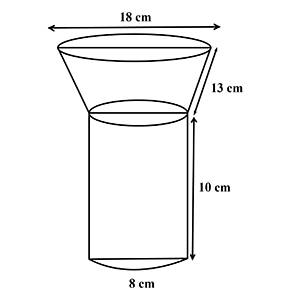
From the top a conical shaped jaggery of base diameter $$10$$cm and height $$10$$cm, a small cone is cut off by slicing parallel to the base, $$4$$cm from the vertex. Find the surface area and volume of the frustum so obtained.
Diameter of the cone ABO$$=10$$cm
$$\therefore$$ radius $$r_1=\displaystyle\frac{10}{2}=5$$cm
Height of the cone ABO$$=h_1=10$$cm
Height of the cone $$A^|B^|O=h_2=4$$cm
First, let us find the other required data.
Radius of cone $$A^|B^|O=r_2$$
Let the Slant height of cones $$ABO$$ and $$A^|B^|O,$$ be $$\ l_1$$ and $$l_2$$ respectively.
$$\therefore$$ radius $$r_1=\displaystyle\frac{10}{2}=5$$cm
Height of the cone ABO$$=h_1=10$$cm
Height of the cone $$A^|B^|O=h_2=4$$cm
First, let us find the other required data.
Radius of cone $$A^|B^|O=r_2$$
Let the Slant height of cones $$ABO$$ and $$A^|B^|O,$$ be $$\ l_1$$ and $$l_2$$ respectively.
$$\therefore \displaystyle\frac{r_1}{r_2}=\frac{h_1}{h_2}, \frac{5}{r_2}=\frac{10}{4}$$
$$\therefore r_2=\displaystyle\frac{5\times 4}{10}=2$$cm
$$l^2_1=h^2_1+r^2_1=10^2+5^2=100+25=125$$
$$\therefore l_1=\sqrt{125}=5\sqrt{5}$$cm
$$l^2_2=h^2_2+r^2_2=4^2+2^2=16+4=20$$
$$\therefore l_2=\sqrt{20}=2\sqrt{5}$$cm
(i) Lateral surface area of cone ABO$$=\pi r_1l_1=\pi \times 5\times 5\sqrt{5}=25\sqrt{5}\pi$$
$$\therefore$$ LSA of cone ABO$$=25\sqrt{5}\pi cm^2$$
Lateral surface area of cone $$A^|B^|O=\pi r_2l_2=\pi\times 2\times 2\sqrt 5=4\sqrt 5\pi$$
$$\therefore$$ LSA of cone $$A^|B^|O=4\sqrt 5\pi cm^2$$
$$\therefore$$ Lateral surface area of frustum$$=$$ LSA of cone ABO$$-$$ LSA of come $$A^|B^|O$$
$$=25\sqrt{5}\pi -4\sqrt{5}\pi =21\sqrt{5}\pi=21\times \sqrt{5}\times \displaystyle\frac{22}{7}=66\sqrt{5}cm^2$$
$$\therefore$$ LSA of frustum$$=66\sqrt{5}$$sq. cm. or $$147.84cm^2$$
(ii) Total surface area of cone ABO$$=\pi r_1(r_1+l_1)$$
$$=\pi\times 5\times (5+5\sqrt{5})=\pi\times 5\times 5(1+\sqrt{5})$$
$$\therefore$$ TSA of cone ABO$$=25(1+\sqrt{5})\pi \ cm^2$$
Lateral surface area of cone $$A^|B^|O=\pi r_2l_2=\pi \times 2\times 2\sqrt{5}=4\sqrt{5}\pi$$
$$\therefore$$ LSA of cone $$A^|B^|O=4\sqrt{5}\pi cm^2$$
The total surface area of frustum$$=$$ TSA of cone ABO$$-$$ LSA of cone $$A^|B^|O+\pi r^2_2$$
$$=25(1+\sqrt{5})\pi - 4\sqrt{5}\pi +4\pi$$
$$=\pi (25+25\sqrt{5}-4\sqrt{5}+4)$$
$$=\pi(29+21\sqrt{5})$$
$$=\displaystyle\frac{22}{7}\times 75.95$$
$$\therefore$$ TSA of frustum$$=238.70cm^2$$
(iii)Volume of cone ABO$$=\displaystyle\frac{1}{3}\pi r^2_1h_1=\frac{1}{3}\times \pi\times 5\times 5\times 10$$
$$\therefore$$ Volume of cone ABO$$=\displaystyle\frac{250}{3}\pi cm^3$$
Volume of cone $$A^|B^|O=\displaystyle\frac{1}{3}\pi r^2_2h_2=\frac{1}{3}\times \pi\times 2\times 2\times 4$$
$$\therefore$$ Volume of cone $$A^|B^|O=\displaystyle\frac{16}{3}\pi cm^3$$
$$\therefore$$ Volume of the frustum$$=$$ Volume of cone ABO$$-$$ Volume of cone $$A^|B^|O$$
$$=\displaystyle\frac{250}{3}\pi -\frac{16}{3}\pi =\frac{234}{3}\pi$$
$$\therefore$$ Volume of the frustum$$=78\pi cm^3$$ or $$245.14cm^3$$
We can also directly find the lateral surface area, total surface area, and volume of the frustum by using the formulae.
A circus tent is made if canvas and is in the form of a right circular cylinder and a right circular cone above it. The diameter and height of the cylindrical part of the tent are $$126$$m and $$5$$m respectively. The total height of the tent is $$21$$m. Find the total cost of the canvas used to make the tent when the cost per $$m^2$$ of the canvas is Rs. $$15$$.
Cylindrical part: $$r=\displaystyle\frac{126}{2}=63m, h=21-5=16m$$
$$l=\sqrt{r^2+h^2}=\sqrt{63^2+16^2}$$
$$=\sqrt{3969+256}=\sqrt{4225}$$
$$\therefore l=65m$$
Total canvas used$$=$$CSA of cylindrical part$$+$$ CSA of conical part
$$=2\pi rh+\pi rl=2\times \displaystyle\frac{22}{7}\times 63\times 5m^2+\frac{22}{7}\times 63\times 65m^2$$
$$=1980m^2+12870m^2=14850m^2$$
$$\therefore$$ Total canvas used$$=14, 850m^2$$
Cost of canvas at the rate of Rs. $$16$$per $$m^2=14, 850\times Rs.15=Rs. 2,22,750$$
$$\therefore$$ Cost of canvas$$=Rs. 2,22,750$$.
$$l=\sqrt{r^2+h^2}=\sqrt{63^2+16^2}$$
$$=\sqrt{3969+256}=\sqrt{4225}$$
$$\therefore l=65m$$
Total canvas used$$=$$CSA of cylindrical part$$+$$ CSA of conical part
$$=2\pi rh+\pi rl=2\times \displaystyle\frac{22}{7}\times 63\times 5m^2+\frac{22}{7}\times 63\times 65m^2$$
$$=1980m^2+12870m^2=14850m^2$$
$$\therefore$$ Total canvas used$$=14, 850m^2$$
Cost of canvas at the rate of Rs. $$16$$per $$m^2=14, 850\times Rs.15=Rs. 2,22,750$$
$$\therefore$$ Cost of canvas$$=Rs. 2,22,750$$.
A solid is in the form of a cone mounted on a right circular cylinder, both having same radii of their bases. Base of the cone is placed on the top base of the cylinder. If the radius of the base and height of the cone be $$7$$cm and $$10$$cm respectively, and the total height of the solid be $$30$$cm, find the volume of the solid.
Cylindrical part: $$r=7cm, h=30-10=20cm$$
Conical part: $$r=7cm, h=10cm$$
Volume of the solid$$=$$ Volume of cylinder$$+$$ Volume of cone
$$=\displaystyle\pi r^2h+\frac{1}{3}\pi r^2h$$
$$=\displaystyle\frac{22}{7}\times 7\times 7\times 20cm^2+\frac{1}{3}\times \frac{22}{7}\times 7\times 7\times 10$$
$$=3080cm^3+\displaystyle\frac{1540}{3}cm^3$$
$$=3080+513.33cm^3$$
Volume of the solid$$=3593.33cm^3$$.
Conical part: $$r=7cm, h=10cm$$
Volume of the solid$$=$$ Volume of cylinder$$+$$ Volume of cone
$$=\displaystyle\pi r^2h+\frac{1}{3}\pi r^2h$$
$$=\displaystyle\frac{22}{7}\times 7\times 7\times 20cm^2+\frac{1}{3}\times \frac{22}{7}\times 7\times 7\times 10$$
$$=3080cm^3+\displaystyle\frac{1540}{3}cm^3$$
$$=3080+513.33cm^3$$
Volume of the solid$$=3593.33cm^3$$.
A metallic right circular cone $$20\ cm$$ hight and whose vertical angle is $$60^{\circ}$$ is cut into two puts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter $$\dfrac {1}{16}\ cm$$, find the length of the wire.
A bucket made up of a metal sheet is in the form of a frustum of a cone of height $$16cm$$ with diameters of its lower and upper ends as $$16cm$$ and $$40cm$$ respectively. Find the volume of the bucket. Also, find the cost of the bucket if the cost of metal sheet used is Rs. $$20$$ per $$100{cm}^{2}$$. (Use $$\pi=3.14$$)
Given,
Hight of frustum of cone $$h=16\ cm$$
Diameter of lower circular end $$d=16\ cm$$
Diameter of upper circular end $$D=40\ cm$$
Hence,
Radius of lower circular end $$r=\dfrac{d}{2}=8\ cm$$
Radius of upper circular end $$R=\dfrac{D}{2}=20\ cm$$
Now,
Volume of frustum of cone $$V=\dfrac{\pi}{3}h(R^{2}+r^{2}+R\times r)$$
$$=\dfrac{\pi}{3}\times 16\times(20^{2}+8^2+20\times 8)\ cm^3$$
$$=\dfrac{\pi}{3}\times 16\times(400+64+160)\ cm^3$$
$$=\dfrac{3.14}{3}\times 16\times624\ cm^3$$
$$=\dfrac{31349.76}{3}\ cm^3$$
Volume of frustum of cone $$V=10449.92\ cm^3$$
$$\text{Surface area of bucket (S) = curved surface area of a frustum of cone + area of lower circular end}$$
$$S= \pi (R+r)\sqrt{(R-r)^{2}+h^{2}}+\pi r^{2}$$
$$= \bigg((R+r)\sqrt{(R-r)^{2}+h^{2}}+r^{2}\bigg)\pi$$
$$= \bigg((20+8)\sqrt{(20-8)^{2}+16^{2}}+8^{2}\bigg)\pi \ cm^{2}$$
$$= \bigg((28)\sqrt{(12)^{2}+256}+64\bigg)\pi\ cm^{2}$$
$$= \bigg((28)\sqrt{(144+256)}+64\bigg)\pi\ cm^{2}$$
$$= \bigg((28)\sqrt{(400}+64\bigg)\pi\ cm^{2}$$
$$= \bigg(28\times 20+64\bigg)\pi\ cm^{2}$$
$$= \bigg(560+64\bigg)\times 3.14\ cm^{2}$$
$$= 624\times 3.14\ cm^{2}$$
$$= 1959.36\ cm^{2}$$
$$\text{Total surface area of meatal sheet used}=1959.36 \ cm^{2}$$
Cost of $$100\ cm^2$$ metal sheet$$=20\ Rs.$$
Cost of $$1\ cm^2$$ metal sheet$$=\dfrac{20}{100}\ Rs=0.2\ Rs..$$
Cost of $$1959.36\ cm^2$$ metal sheet$$=0.2\times 1959.36\ Rs.=391.872\ Rs.$$
A frustrum of a right circular cone has a diameter of base $$20\text cm$$, of top $$12cm$$, and height $$3cm$$. Find the area of its whole surface and volume.
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylinder is $$\cfrac{14}{3}m$$ and the diameter of hemisphere is $$3.5m$$. Calculate the volume and the internal surface of the solid.
The perimeters of the ends of a frustum of a right circular cone are $$44\ cm$$ and $$33\ cm.$$ If the height of the frustum is $$16\ cm,$$ find its volume, the slant surface, and the total surface.
A reservoir in the form of the frustum of a right circular cone contains $$44\times {10}^{7}$$ litres of water which fills it completely. The radii of the bottom and top of the reservoir are $$50$$ metres and $$100$$ metres respectively. Find the depths of water and the lateral surface area of the reservoir. (Take $$\pi=22/7$$)
A cylindrical vessel of diameter $$14\text{ cm}$$ and height $$42 \text{ cm}$$ is fixed symmetrically inside a similar vessel of diameter $$16\text{ cm}$$ and height $$42\text{ cm}$$. The total space between the two vessels is filled with cork dust for heat insulation purposes. How many cubic centimeters of cork dust will be required?
The height of a cone is $$20\ cm$$. A small cone is cut off from the top by a plane parallel to the base. If its volume be $$\dfrac{1}{125}$$ of the volume of the original cone, determine at what height above the base the section is made.
$$\triangle ABC\sim \triangle ADE$$ [ By AA similarity]
$$\therefore \dfrac { AB }{ AD } =\dfrac { BC }{ DE }$$
$$ \Rightarrow \dfrac { h }{ 20 } =\dfrac { { r }_{ 1 } }{ { r }_{ 2 } } $$
$${ V }_{ ABC }=\dfrac { 1 }{ 125 } { V }_{ ADE }$$
$$\Rightarrow \dfrac { 1 }{ 3 } \pi { r }_{ 1 }^{ 2 }h=\dfrac { 1 }{ 3 } \pi { r }_{ 2 }^{ 2 }\times 20\times \dfrac { 1 }{ 125 } $$
$$\Rightarrow { \left( \dfrac { { r }_{ 1 } }{ { r }_{ 2 } } \right) }^{ 2 }=\dfrac { 20 }{ 125h }$$
$$ \Rightarrow { \left( \dfrac { h }{ 20 } \right) }^{ 2 }=\dfrac { 20 }{ 125h }$$
$$ \Rightarrow { h }^{ 3 }=\dfrac { 20\times 20\times 20 }{ 125 } =64$$
$$\Rightarrow \quad h=\sqrt [ 3 ]{ 64 } =4cm$$
Therefore section is made $$(20-4=16cm)$$ above the base.
A metallic right circular cone $$20\text{ cm}$$ high and whose vertical angle is $${90}^{\circ}$$ is cut into two parts at the middle point of its axis by a plane parallel to the base. If the frustum so obtained be drawn into a wire of diameter $$\dfrac {1}{16}\text{ cm}$$, find the length of the wire.
Volume of frustum ABDC
$$V=\dfrac { \pi h }{ 3 } \left[ { R }_{ 1 }^{ 2 }+{ R }_{ 2 }^{ 2 }+{ R }_{ 1 }{ R }_{ 2 } \right] $$
$$h=20cm$$, cone is cut at the middle $$\therefore \quad OQ=QP=10cm$$
$$\angle QOB={ 45 }^{ 0 }$$, In $$\triangle QOB,\quad { R }_{ 1 }=PD\quad \& \quad { R }_{ 2 }=QB$$
$$\tan{ 45 }^{ 0 }=\dfrac { QB }{ OQ } \Rightarrow OQ=QB\Rightarrow { R }_{ 2 }=10cm$$
In $$\triangle OPD,\quad tan{ 45 }^{ 0 }=\dfrac { OP }{ PD } \Rightarrow PD=OP\Rightarrow { R }_{ 1 }=20cm$$
$$\therefore \quad V=\dfrac { \pi \times 10 }{ 3 } \left[ { \left( 20 \right) }^{ 2 }+{ \left( 10 \right) }^{ 2 }+20\times 10 \right] =\dfrac { 10\pi }{ 3 } \left[ 400+100+200 \right] $$
$$V=\dfrac { 7000\pi }{ 3 } $$
Volume of cylindrical wire $$=\pi { r }^{ 2 }h=\pi { \left( \dfrac { 1 }{ 32 } \right) }^{ 2 }\times h$$
$$\Rightarrow \pi \times { \left( \dfrac { 1 }{ 32 } \right) }^{ 2 }\times h=\dfrac { 7000\pi }{ 3 } \Rightarrow h=\dfrac { 7000\times 32\times 32 }{ 3 } =2389333.33cm$$
$$\Rightarrow h=23893.33m$$
$$\therefore $$ Length of wire $$=23893.33m$$
A milk container is made of metal sheet in the shape of frustum of a cone whose volume is $$10459\cfrac{3}{7}\ {cm}^{3}$$. The radii of its lower and upper circular ends are 8 cm and 20 cm respectively. Find the cost of metal sheet used in making the container at the rate of Rs. 1.40 per $${cm}^{3}$$. (Use $$\pi=\frac{22}{7}$$)
The above figure can be constructed using the given information.
Given that, the volume of the bucket $$V=10459\dfrac{3}{7} \ cm^{3}$$
$$\Rightarrow V=\dfrac{73216}{7}$$
The radii of bottom circular end, $$R=20 \ cm$$
The radii of top end, $$r=8 \ cm$$
We know that, the volume of frustum of cone $$V=\dfrac{\pi}{3}h(R^{2}+r^{2}+R\times r)$$
Hence, height of frustum of cone will be:
$$ h=\dfrac{3V}{\pi(R^{2}+r^{2}+R\times r)}\ cm$$
$$\therefore \ h=\dfrac{3\times\dfrac{73216}{7}}{\dfrac{22}{7}\times (20^{2}+8^{2}+20\times 8)}\ cm$$
$$\Rightarrow h=\dfrac{3\times 73216}{22\times (400+64+160)} \ cm$$
$$\Rightarrow h=\dfrac{219648}{22\times 624}\ cm$$
$$\Rightarrow h=\dfrac{219648}{13728}\ cm$$
Now, for calculating the area of metal sheet used, we have to calculate total surface area of frustum of the cone.
$$\text{Total surface area of = curved surface area + area of bottom circular end}$$
$$= \pi (R+r)\sqrt{(R-r)^{2}+h^{2}}+\pi R^{2}$$
$$= \bigg((R+r)\sqrt{(R-r)^{2}+h^{2}}+R^{2}\bigg)\pi$$
$$= \bigg((20+8)\sqrt{(20-8)^{2}+16^{2}}+20^{2}\bigg)\pi \ cm^{2}$$
$$= \bigg((28)\sqrt{(12)^{2}+256}+400\bigg)\pi\ cm^{2}$$
$$= \bigg((28)\sqrt{(144+256)}+400\bigg)\pi\ cm^{2}$$
$$= \bigg((28)\sqrt{(400}+400\bigg)\pi\ cm^{2}$$
$$= \bigg(28\times 20+400\bigg)\pi\ cm^{2}$$
$$= \bigg(560+400\bigg)\times \dfrac{22}{7}\ cm^{2}$$
$$= 960\times \dfrac{22}{7}\ cm^{2}$$
$$= \dfrac{21120}{7}\ cm^{2}$$
$$\text{Total surface area of meatal sheet used}=\dfrac{21120}{7} \ cm^{2}$$
Now, cost of $$1 \ cm^2 $$ metal sheet $$=Rs.\ 1.40$$
$$\therefore \ $$cost of $$\dfrac{21120}{7} \ cm^2 $$ metal sheet$$=Rs.\ 1.40\times \dfrac{21120}{7}=Rs.\ 4224$$
Hence, the cost of making the container is $$Rs.\ 4224$$.
A solid consisting of a right circular cone of height $$120cm$$ and radius $$60cm$$ standing on a hemisphere of radius $$60cm$$ is placed upright in a right circular cylinder full of water such that it touches the bottoms. Find the volume of water left in the cylinder, if the radius of the cylinder is $$60cm$$ and its height is $$180cm$$.
If the volumes of two cones are in the ratio of 1:4 and their diameters are in the ratio of 4:5, then find the ratio of their heights.
A hemispherical bowl of internal diameter 30 cm contains some liquid.This liquid is to be poured into cylindrical bottles of diameter 5 cm and height 6 cm each. Find the number of bottles necessary to empty the bowl.
Write whether the following statements are true or false. Justify your answer:
(i) The volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere.
(ii) The volume of the largest right circular cone that can be fitted in a cube whose edge is $$2 r$$ equals the volume of a hemisphere of radius $$r$$.
(iii) A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is $$1:2:3$$.
The given figure shows a solid trophy made of shining glass. If one cubic centimetre of glass costs $$Rs \ 0.75$$, find the cost of the glass for making the trophy.
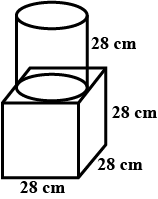
A conical tent is $$10$$ m high and the radius of its base is $$24$$ m. Find the slant height of the tent. If the cost of $$1$$ $$m^2$$ canvas is Rs. $$70$$, find the cost of the canvas required to make the tent.
In a figure (i) given below , Calculate the area of the shaded region correct to two decimal places .Take $$ \pi =3.142 $$
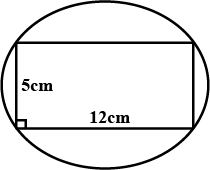
The diagram shows a toy.
The shape of the toy is a cone, with radius $$4\ cm $$ and height $$9\ cm $$, on top of a hemisphere with radius $$4\ cm$$.
Calculate the volume of the toy.
Give your answer correct to the nearest cubic centimeter.
[The volume, V of a cone with radius $$r$$ and height $$h$$ is $$ V = \dfrac{1}{3} \pi r^{2} h $$]
[The volume, V of a sphere with radius $$r$$ is $$V = \dfrac{4}{3} \pi r^{3}$$].
A cone of radius 10 cm is divided two parts by a plane parallel to its base at the middle of its height. Find the ratio of volumes of two parts.
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
Class 10 Maths Extra Questions
- Areas Related To Cricles Extra Questions
- Arithmetic Progressions Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Introduction To Trigonometry Extra Questions
- Pair Of Linear Equations In Two Variables Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadratic Equations Extra Questions
- Real Numbers Extra Questions
- Some Applications Of Trigonometry Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions