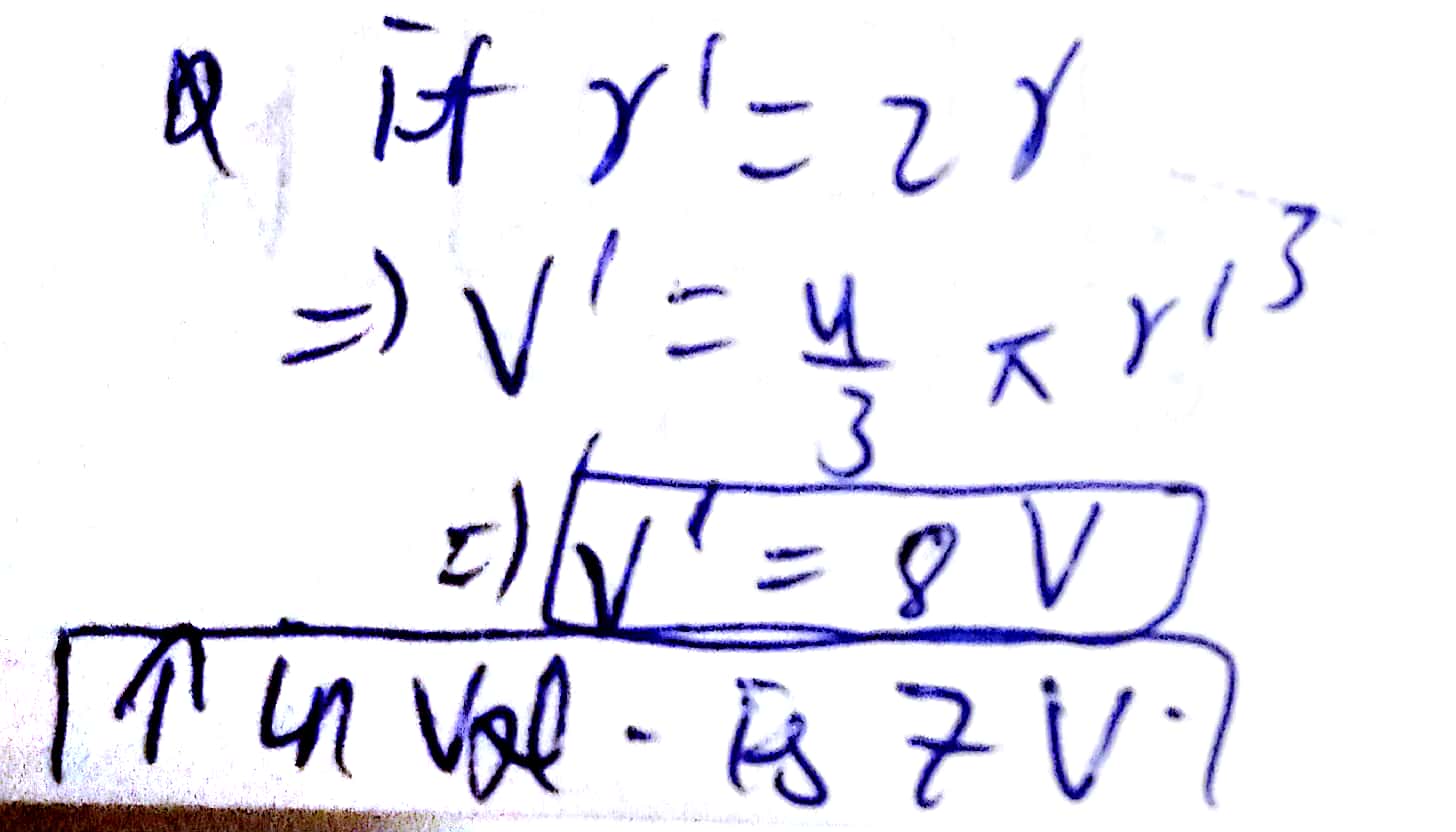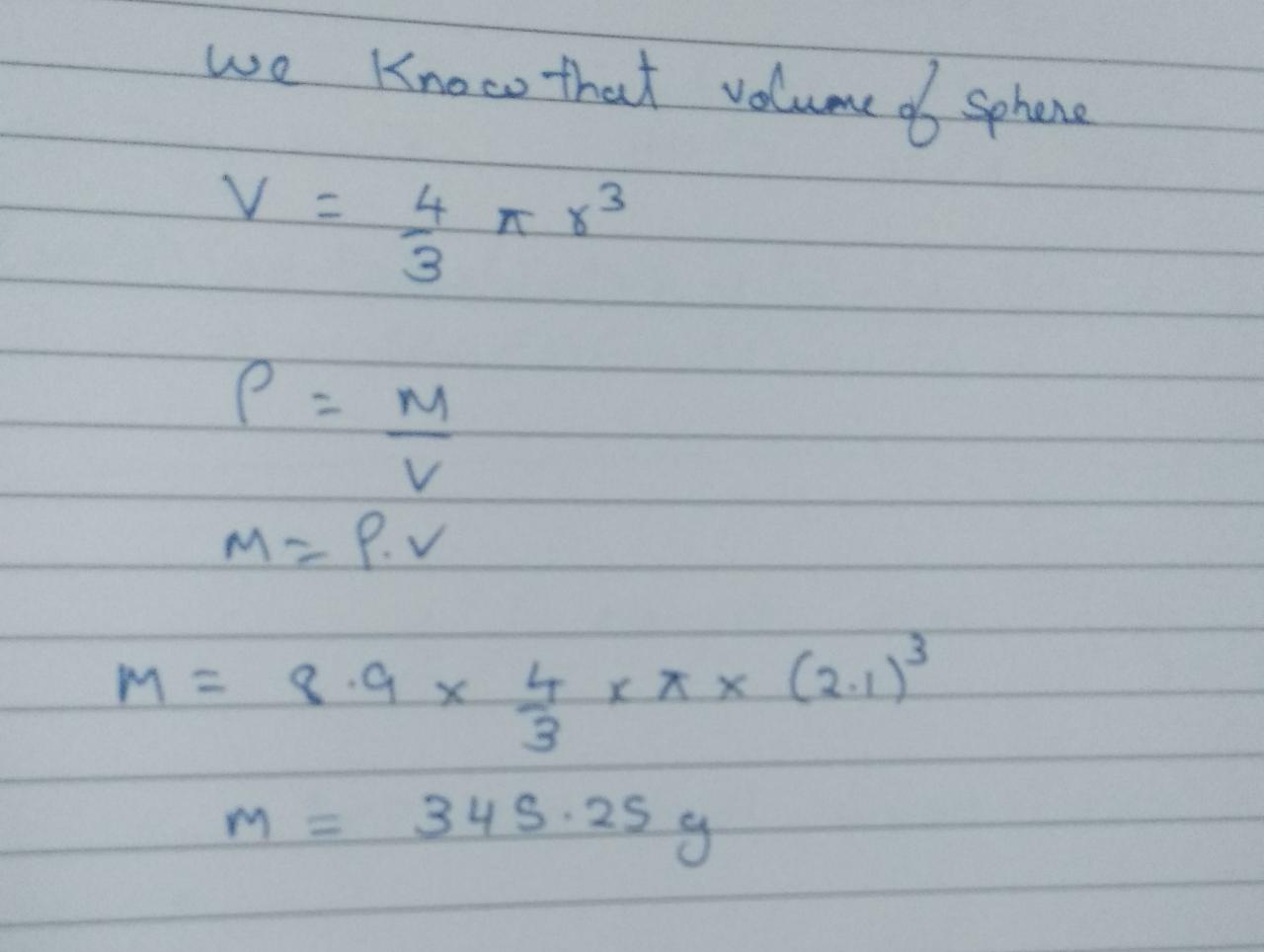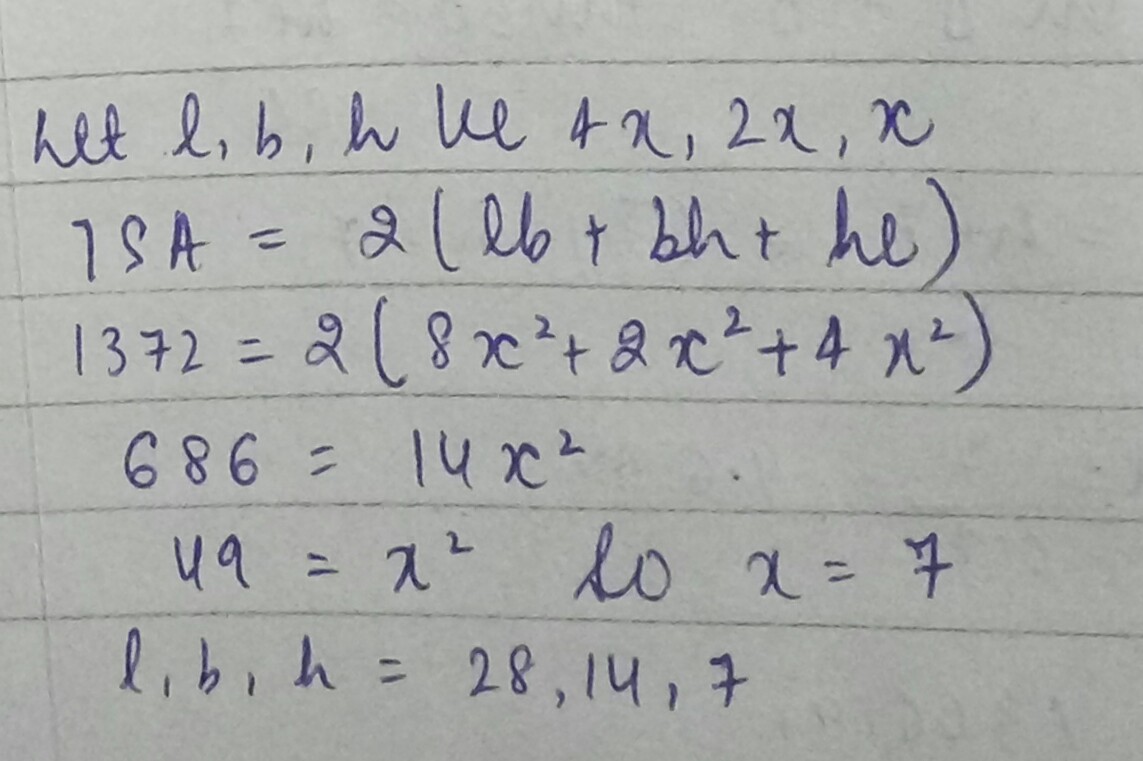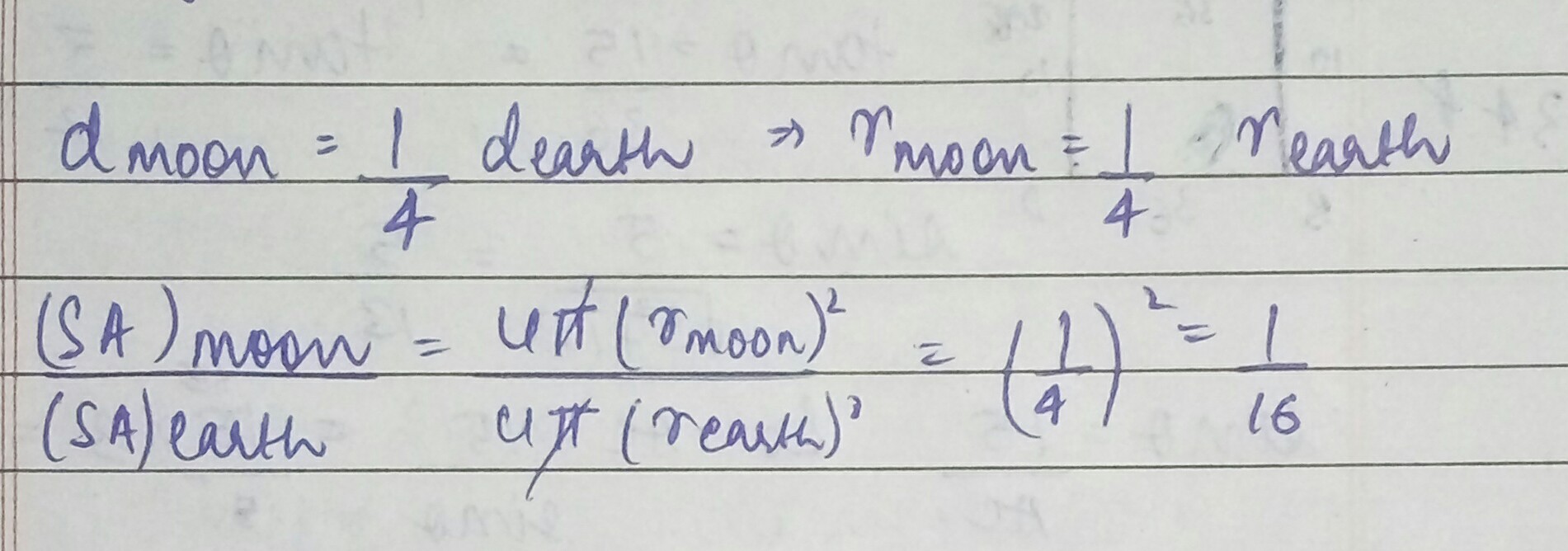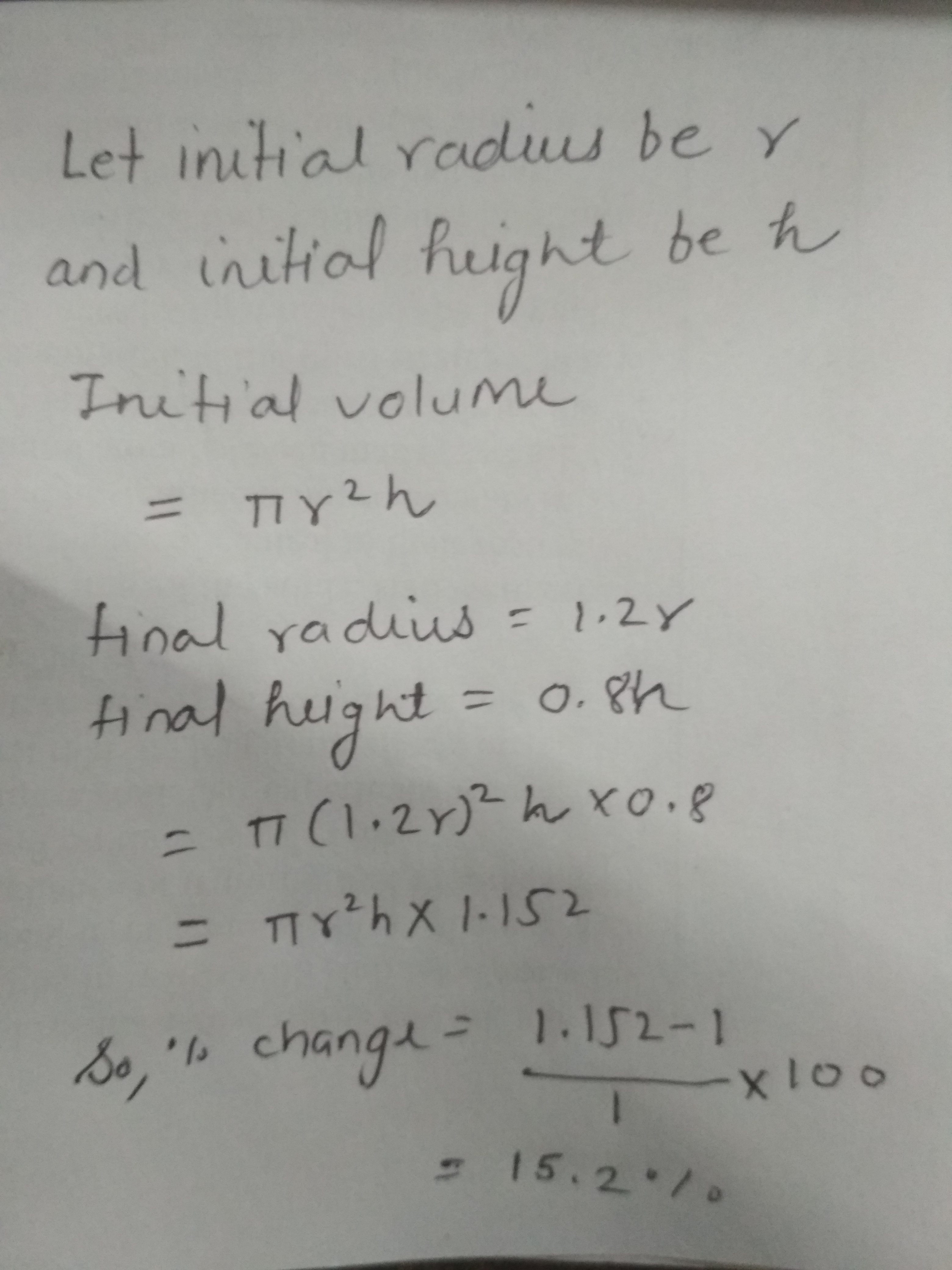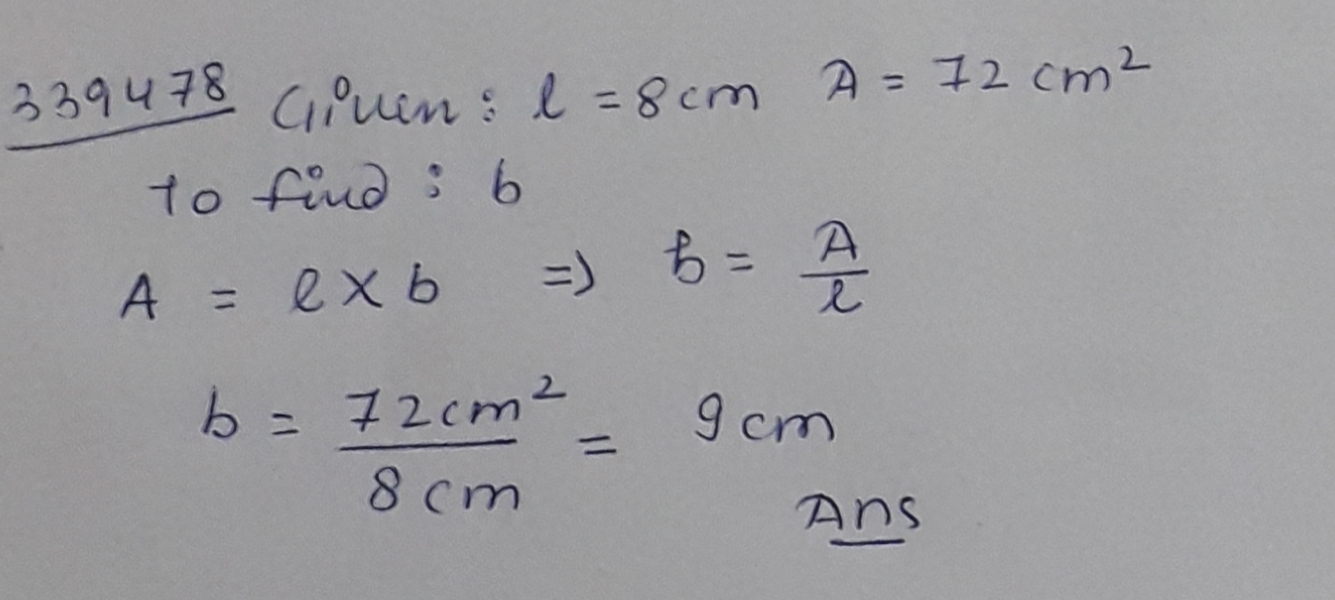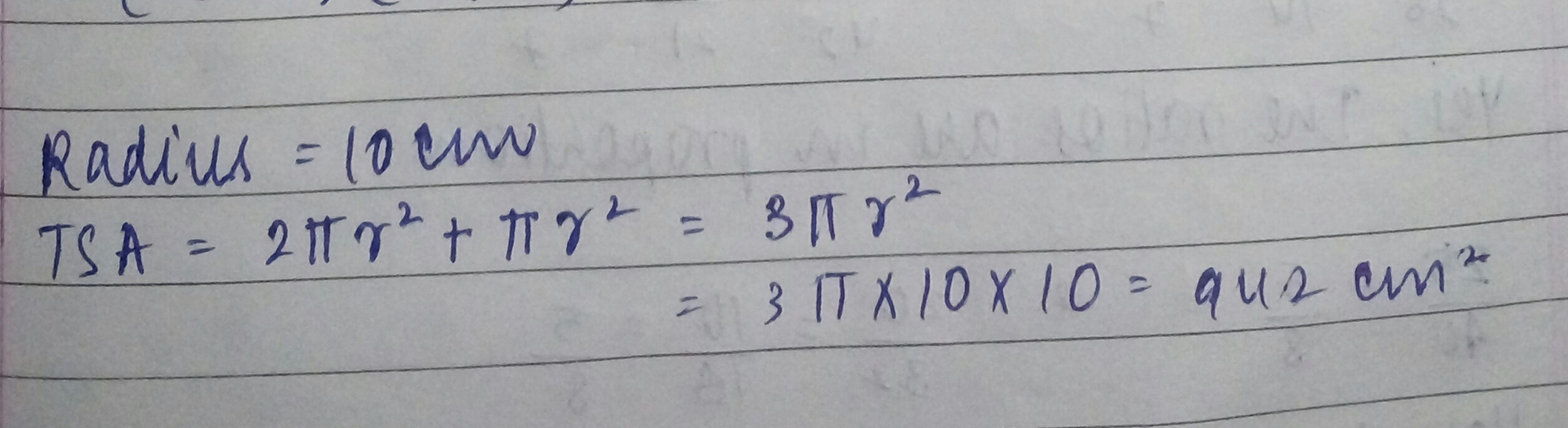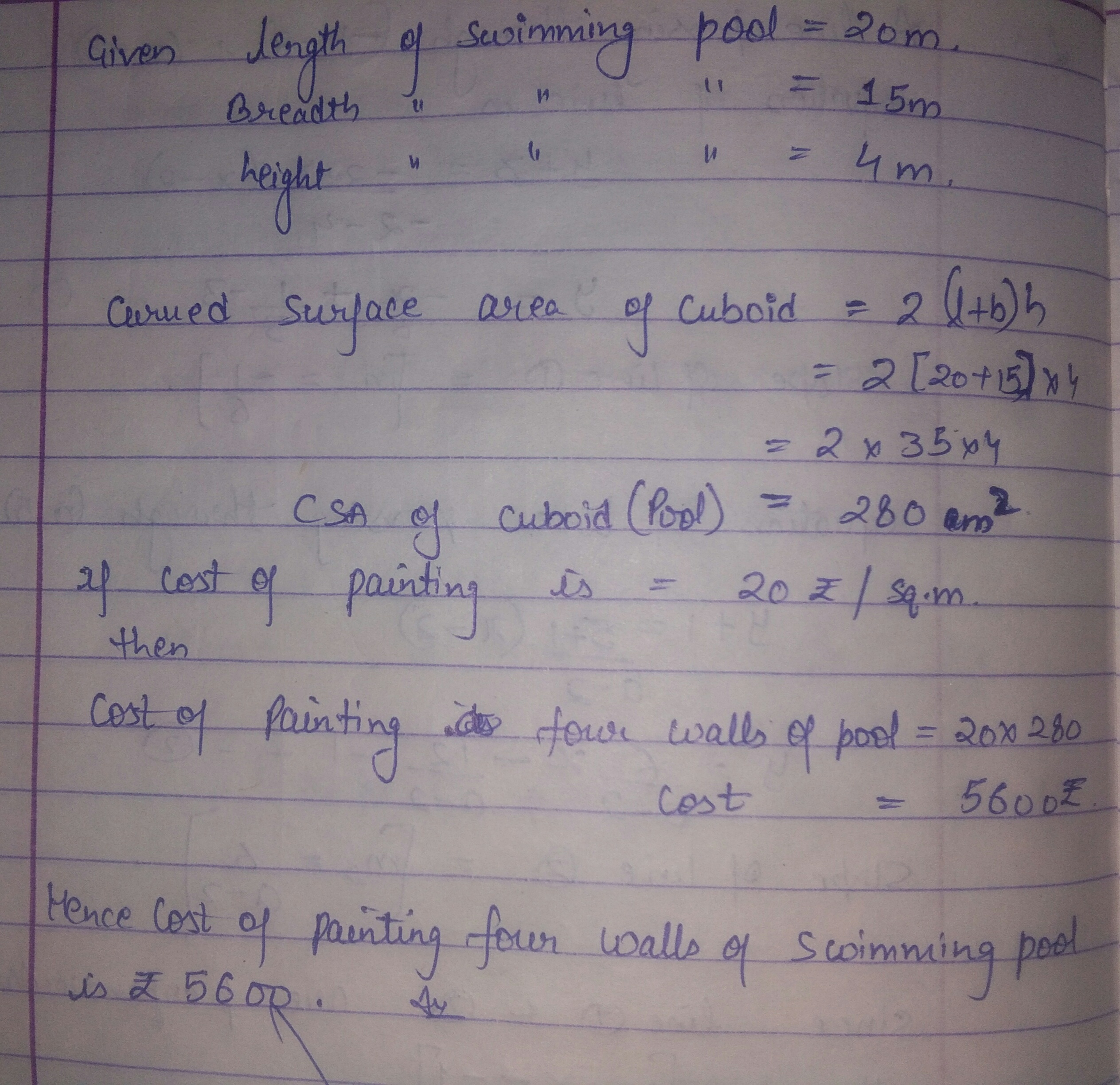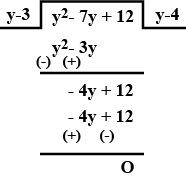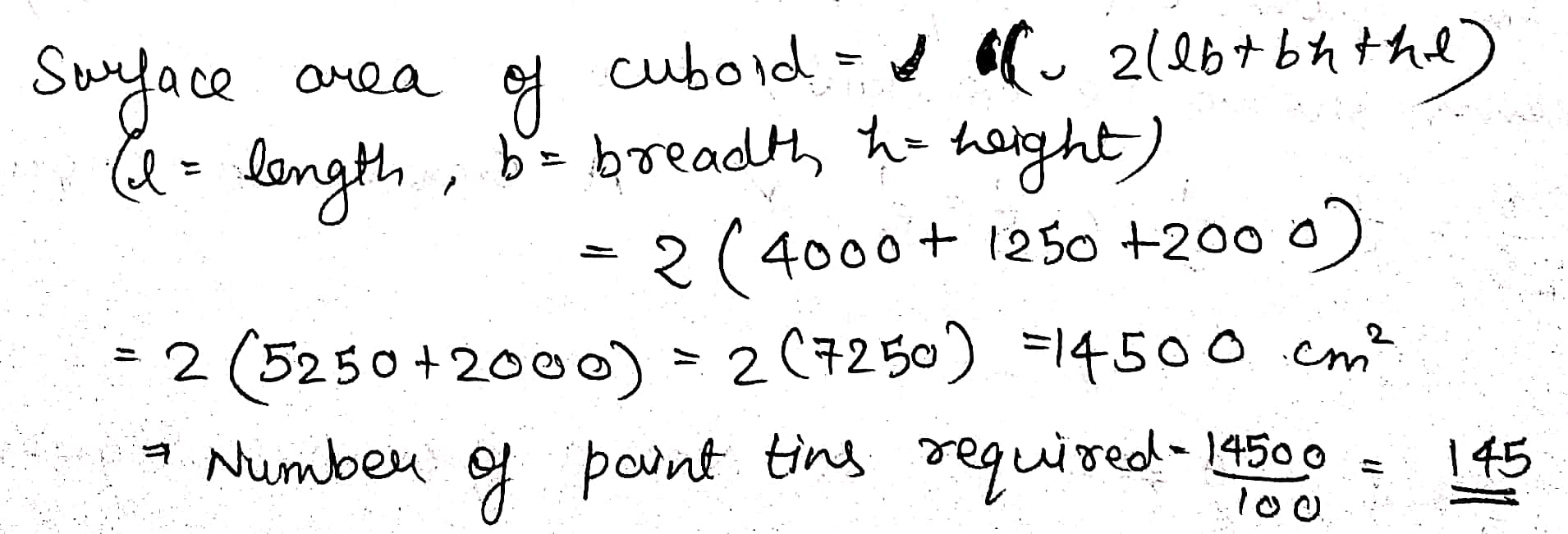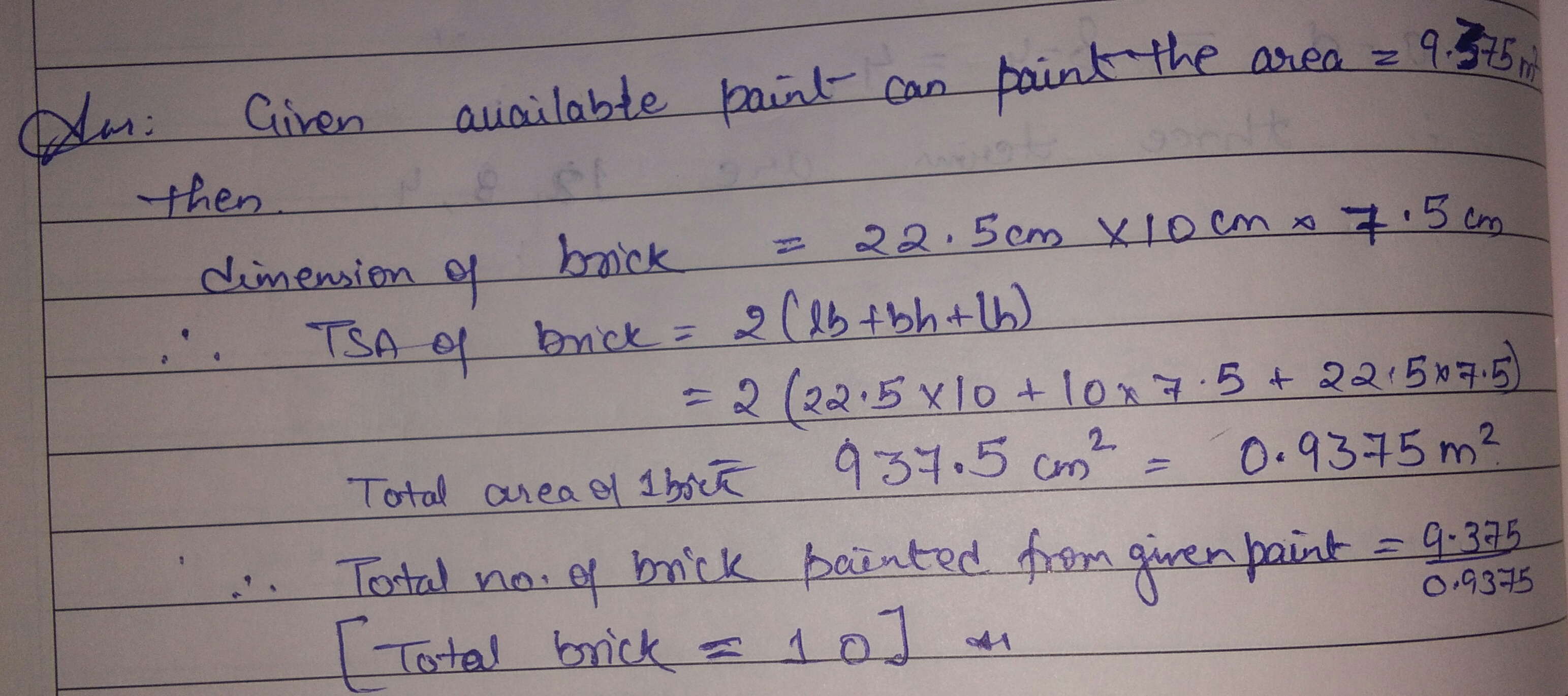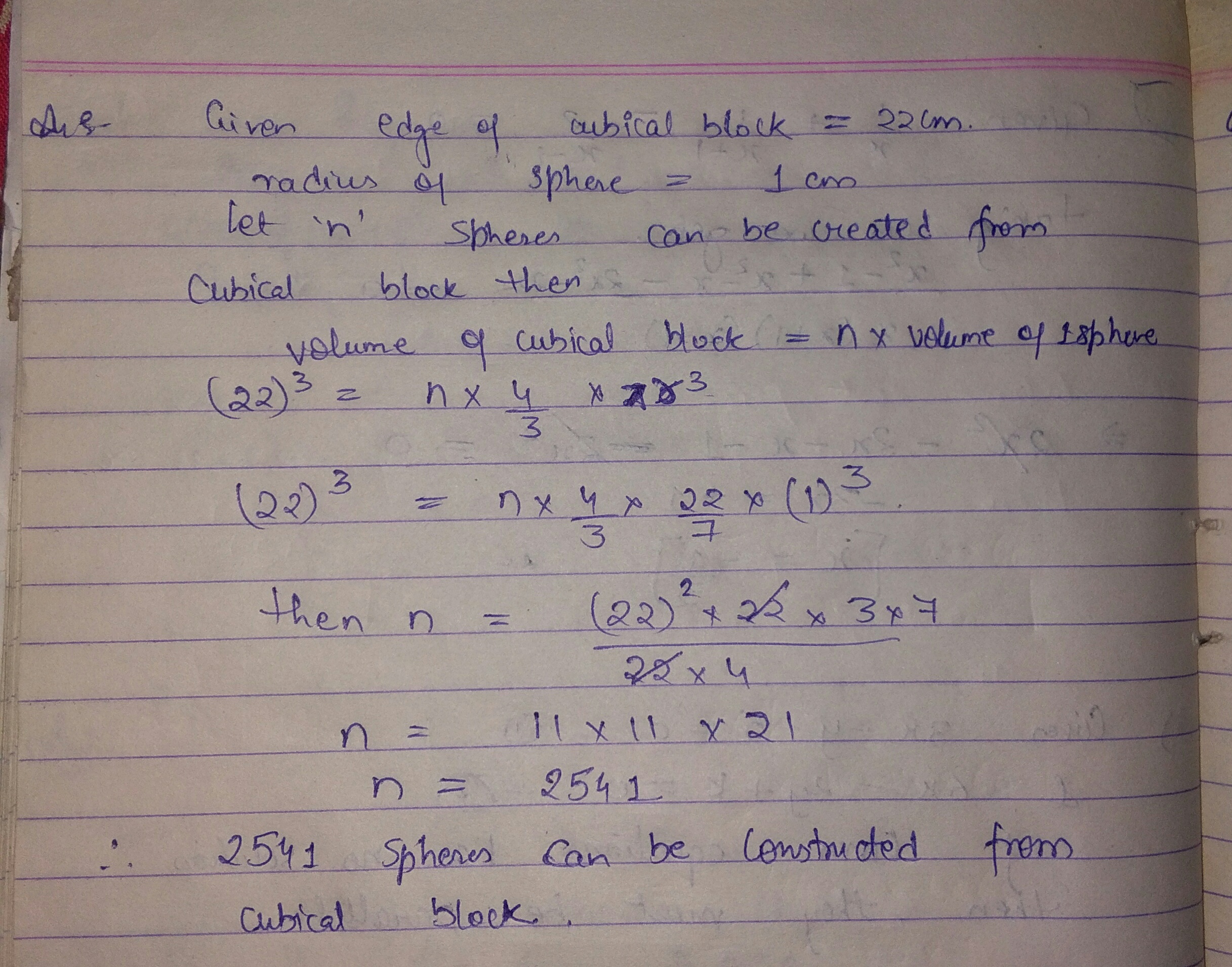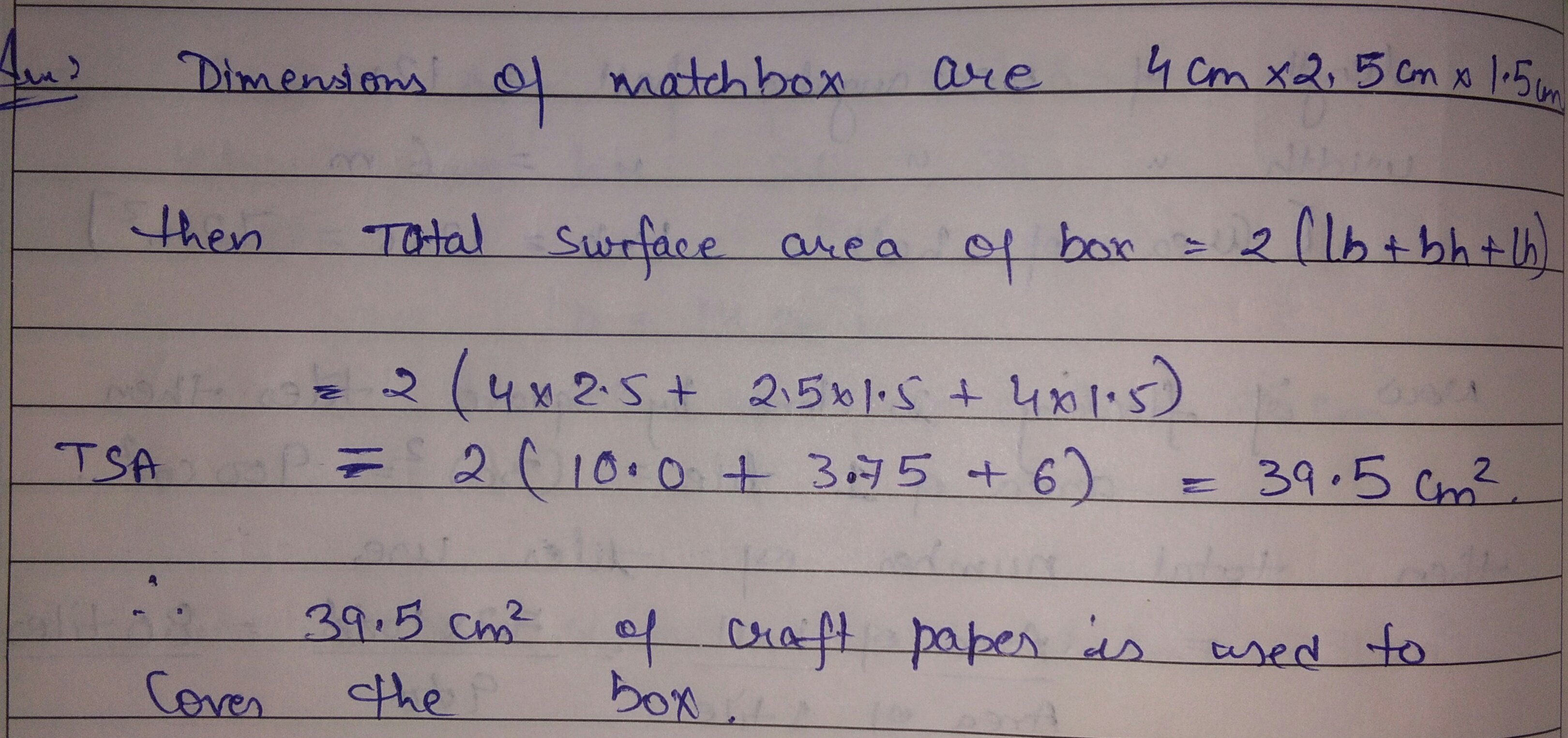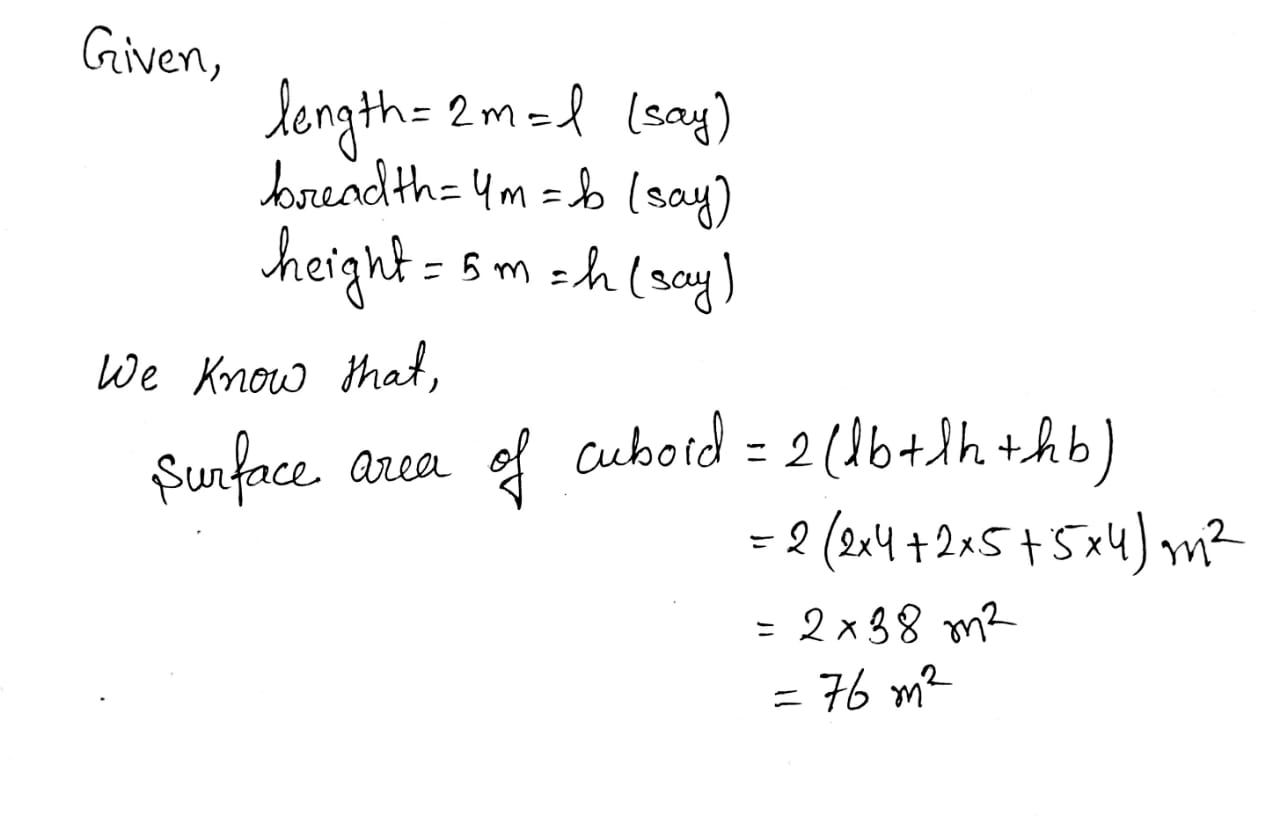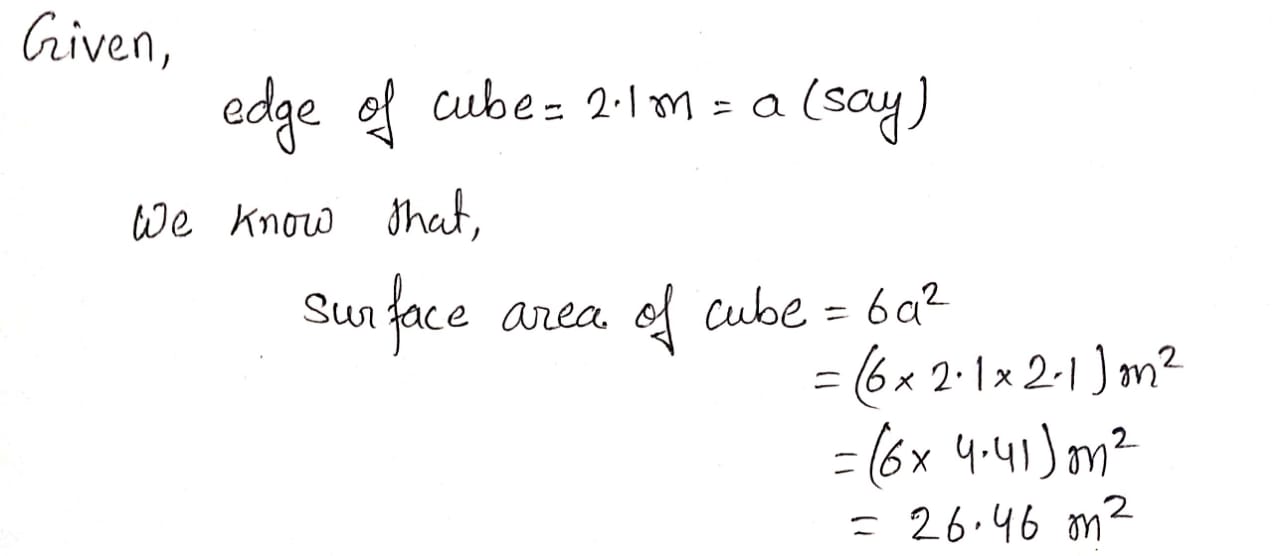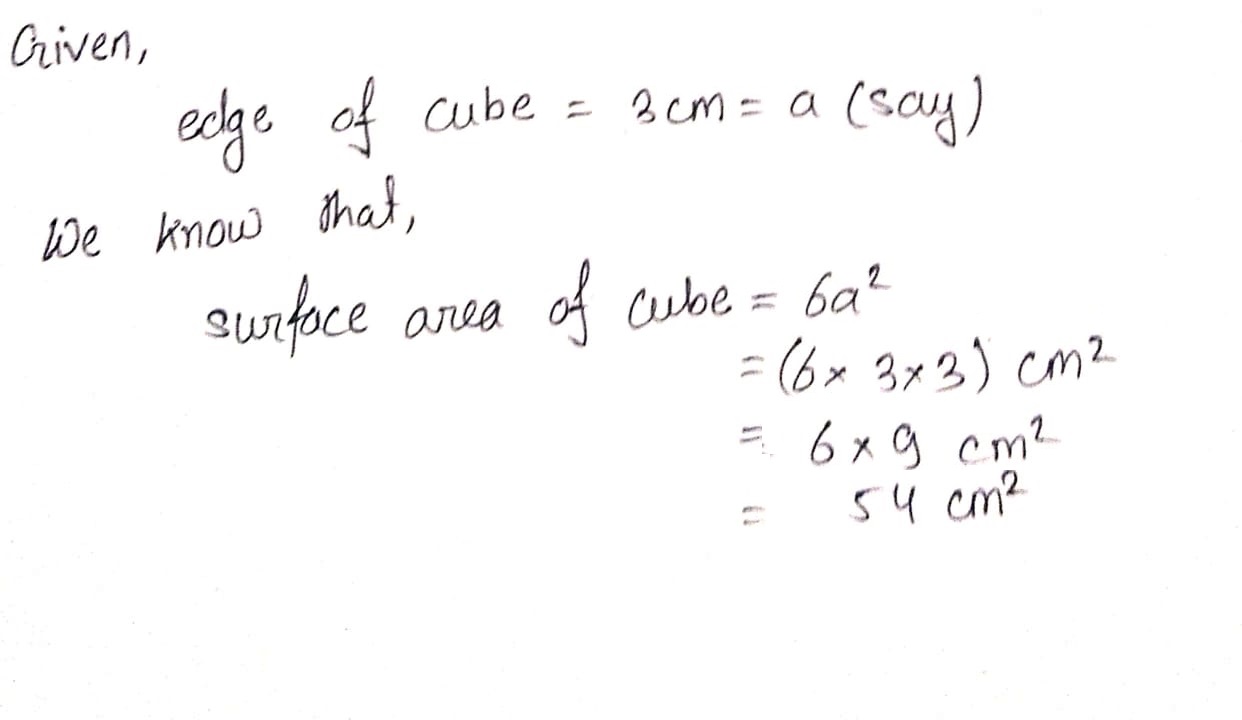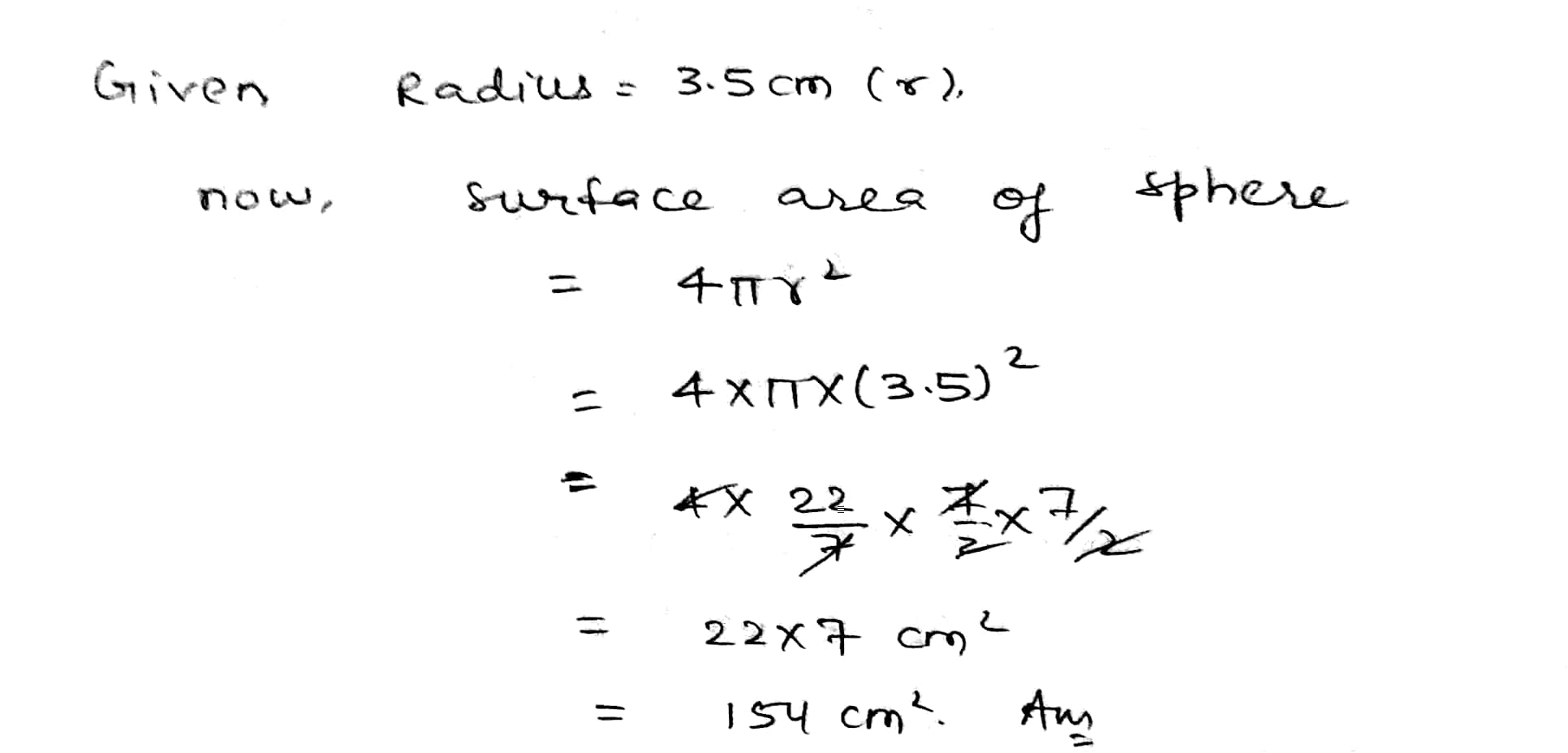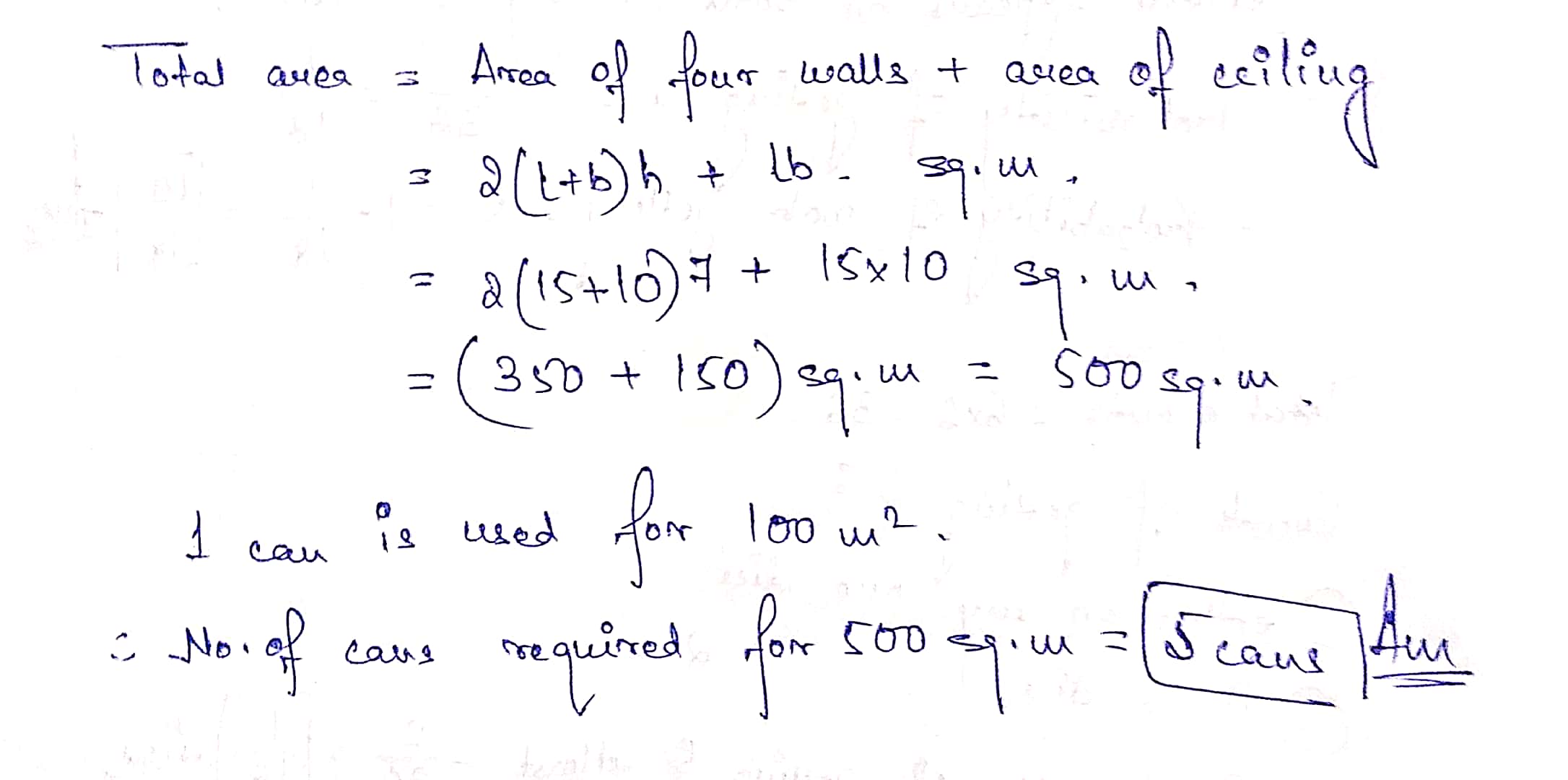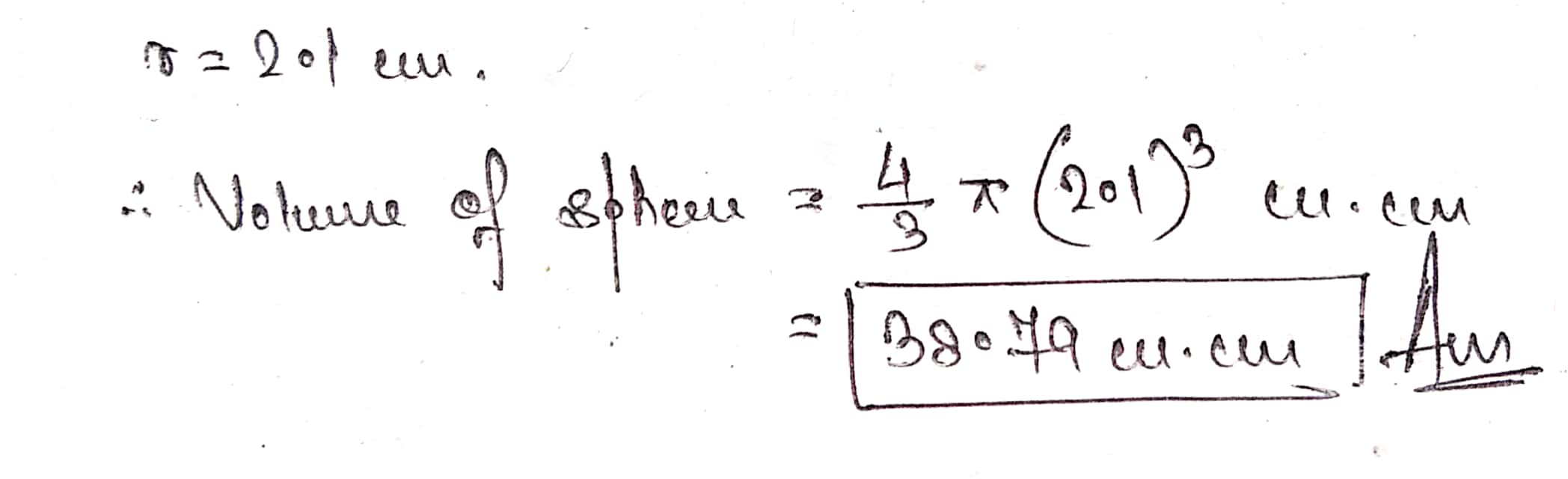Surface Areas And Volumes - Class 9 Maths - Extra Questions
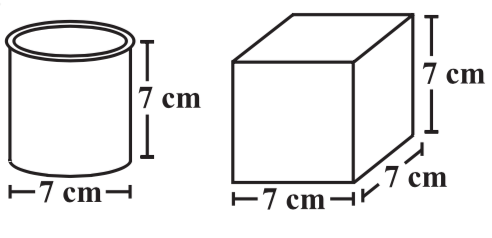
Find the volume(in cm$$^3$$) of a cuboid, whose length = 15 cm, breadth = 10 cm and height = 8 cm
The dimensions of a cuboid in cm are $$16\times 14\times 20$$. Find its total surface area.
The cuboid water tank has length 2 m, breadth 1.6m and height 1.8m. Find the capacity of the tank in litres.
What is the length of the sheet, $$2$$ meter wide, required for making an open tank $$15 $$ m long, $$10$$ m wide and $$5$$ m deep?
Diameter of a sphere is $$28$$ cm. Find its surface area(in $$cm^2$$).
The volume of a cuboid is 1200 cm$$^3$$. The length is 15 cm and breadth is 10 cm. Find its height.
If the radius of a sphere is doubles, by how much its volume is increased?
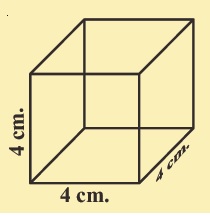
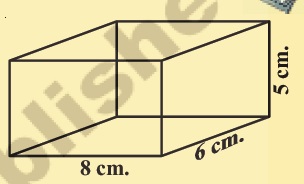
Find the lateral surface area and total surface area of the following right prisms.
Find the area of four walls of a room (Assume that there are no doors or windows) if its length 12 m, breadth 10 m, and height 7.5 m.
Find the later surface area and total surface area of the following right prisms.
How does the total surface area of a box change if
Each dimension is tripled?
Express in words. Can you find the area if each dimension is multiplied n times?
Write the formula to find the total surface area of a cylinder.
Find the volume of a sphere of radius $$2.1\ cm$$ $$\left(\text{use}\, \pi = \dfrac{22}{7}\right)$$.
A metallic cylinder of diameter 5 cm and height $$3 \dfrac{1}{3}$$ is melted and cast into a sphere. What is its diameter.
Find the total surface area of a cube with side length $$1\text{ m}$$.
If the surface area of a hemisphere is '$$S$$', then express '$$r$$' in terms of '$$S$$'.
Write the number of faces of a cube and cuboid
Curved surface area of a hemisphere with radius '$$r$$' is ________.
If radius of a cylinder is $$14$$ $$cm$$ and height is $$10$$ $$cm$$, find the area of its curved surface. $$\left (\pi =\cfrac { 22 }{ 7 } \right)$$
Find the height of the cuboid whose length, breadth and volume are 35 cm, 15 cm and 14175 $$cm^3$$ respectively
The formula to find the volume of sphere is _______
The surface area of a sphere is $$616\ { cm }^{ 2 }$$. Find the diameter of the sphere (in $$cm$$).
A cement block is 30 cm long, 23 cm wide and 1 cm height. Find the volume of this block in $$cm^3$$
If the radius of a sphere $$3r$$, then What is its volume?
A cubical box has each edge $$10cm$$ and another cuboidal box is $$12.5cm$$ long, $$10cm$$ wide and $$8cm$$ high.
(i) Which box has the greater lateral surface area and by how much?
(ii) Which box has the smaller total surface area and by how much?
A plastic box $$1.5\ m$$ long, $$1.25\ m$$ wide and $$65 \ cm$$ deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet, determine:
(i) Area of the sheet required for making box.
(ii) The cost of sheet for it, if a sheet measuring $$1\ {m}^{2}$$ $$Rs.\ 20$$.
A vessel has $$7\ litres$$ of ice-cream. How many scoops of $$40ml$$ each can be made from it? What quantity of ice cream will be left behind?
Fill in the blank
$$1\ dl=\_\_\_\_\_hl$$
A cuboidal vessel is $$10\ m$$ long and $$8\ m$$ wide. How high must it be made to hold $$192\ m^{3}$$ of liquid
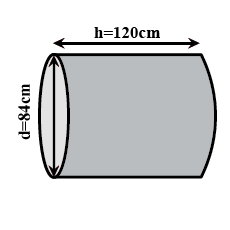
The diameter of a roller is $$84\ cm$$ and its length is $$120\ cm$$. It takes $$500$$ complete revolution to move once over to level a playground. Find the area of the playground in $${m}^{2}$$? [Assume $$\pi=\dfrac{22}{7}$$]
The radius of Jupiter is $$7.1 \times 10^3 m$$ and that of the Earth is $$6.3 \times 10^6 m$$. Compare the volume of the two.
Find approximately the volume of the sphere of radius $$1.001$$.
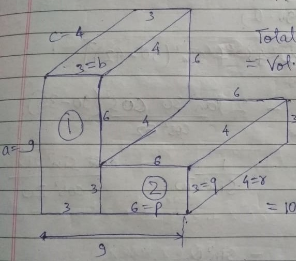
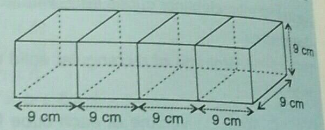
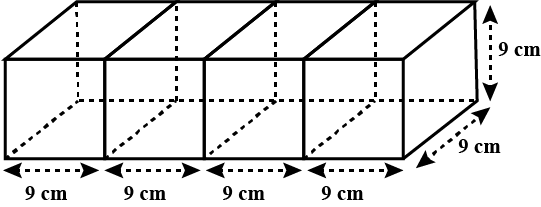
Four cubes, each of edge $$9 cm$$, are joined as shown below:
Write the dimensions of the resulting cuboid obtained.
Total surface area of a cube $$=6a^{2}$$
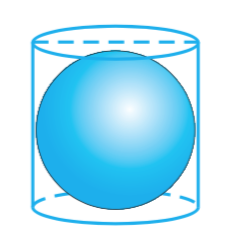
A right circular cylinder just encloses a sphere (see figure). If the height of the cylinder is $$21cm$$, then find the surface area of cylinder (Take of $$\pi =\cfrac { 22 }{ 7 } $$)
The circumference of the base of the cylinder is $$25.45$$ cm and its height is $$15$$ cm. Find the curved surface area.
The circumference of the base of the cylinder is $$132cm$$ and its height is $$72cm$$. Find its lateral surface area.
A cylinder has radius $$7$$cm and height $$10$$cm.Find the total surface area of the cylinder.
If a largest sphere is inscribed in a cube of side $$7\ cm$$ then find the volume of the sphere.
What is total surface area of sphere?
An ice cream cone consists of a right circular cone of height $$14cm$$ and diameter of the circular top is $$5cm$$ It has hemisphere on the top with the same diameter as of circular top. Find the volume of ice cream in the cone?
The radius of a sphere shrinks from 10 cm to 9.8 cm. Find approximately the decrease in its volume.
Find the volume of a sphere whose radius is:
(i) 7 cm
(ii) 0.63 m
A capsule of medicine is in the shape of a sphere of diameter $$3.5mm$$. How much medicine (in $${mm}^{3}$$) is needed to fill this capsule?
Find the volume of the following:
(i) A cuboid whose dimensions are $$1.6\ m\times 0.8m\times0.4m$$
(ii) A cube whose each edge in $$9\ cm$$.
(iii) A cylinder whose radius is $$6.3\ cm$$ and height is $$12\ cm$$.
Circumference of the edge of a hemispherical bowl is $$132\ cm$$. Find the capacity of the bowl.
The radius of a spherical balloon increases from $$7cm$$ to $$14cm$$ as air is being pumped into it. Find the ratio of surface area of the balloon in the two cases.
An empty cubical carton is of side $$9$$cm. Can you fit in $$1000$$ cubes of side $$1$$cm in it?
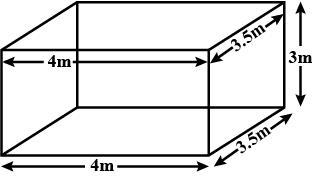
A bathroom is $$4m$$ long, $$3.5m$$ broad and $$3m$$ high. Find the cost of laying tiles in its floor and four walls at the rate of Rs. $$100$$ per $${m}^{2}$$
Find the volume ($$m^3$$) of the container of measurement $$5.5\ m,4\ m,3\ m$$
Find the height of a cuboid whose base area is $$180{cm}^{2}$$ and volume is $$900{cm}^{3}$$?
The dimensions of a solid cuboidal slab of lead is $$66 \mathrm { cm } , 42 \mathrm { cm }$$ and 21$$\mathrm { cm }$$ respectively. Find by melting this, how many sphere of diameter $$4.2\mathrm { cm }$$ can be formed?
How many liters of milk can a hemispherical bowl of diameter $$10.5\;cm$$ hold ?
A hollow hemispherical vessel has internal and external radius are $$42 \mathrm { cm }$$ and $$43 \mathrm { cm }$$ respectively. If cost of polishing the surface it, is $$7$$ paise per square cm, then find the cost of polishing the surface.
Find the volume of sphere if its surface area is $$5544$$ $$\mathrm { cm } ^ { 2 }$$
The radius of a sphere is $$2$$r, then find its volume.
The radius of a sphere is $$3.5$$cm. Find the surface area and volume.
Find the volume of a cube, one face of which has an area of $$64 \,m^2$$.
Two cubes of edge $$6\ cm$$ are joined to form a cuboid. Find the total surface area of the cuboid.
Find the curved surface of a right-circular cylinder whose height is $$13\ dm$$ and diameter of the base is $$5\ dm$$.
What is the formula for the total surface area of a cube?
Find the volume of a sphere radius is 2 cm.
The Height of cylinder is $$10cm$$ and radius is $$7cm$$ Find the Curved surface area of Cylinder
Find the volume of a sphere of radius $$11.2$$cm.
Fill in the blanks:
A point where three surface of a solid meet is called a___
Find the surface area of the wooden box which is in the shape of a cube, if the edge of the box is $$27$$ cm.
Write the formula of T.S.A of cylinder.
A cube has_________faces, egdes and _______vertices.
A verandah 1.25 m is constructed all along outside of a room 7.5 m long and 5 m wide. Find
(i) the area of the verandah.
(ii) the cost of cementing the floor of the verandah at the rate of Rs.15 per $$m^{2}$$.
Fill in the blanks
If each edge of a cube is doubled,then the surface area of the new cube will become _____ times.
Find the lateral or curved surface area of a closed cylindrical petrol storage tank that is $$4.2$$ m in diameter and $$4.5$$ m high.
The diameter of a metallica ball is $$4.2\ cm$$. What is the mass of the ball, if the density of the metal is $$8.9\ g$$ per $$cm^{3}$$?
What is the formula for volume of sphere ?
The radius of a sphere is 2.1cm. Find its surface area.
The area of a rectangular stage is 750 sq.m. If its height is 1.5 m, find its volume.
The volume of a cuboid is $$1200\,{\rm{c}}{{\rm{m}}^3}.$$ The length is $$15\,{\rm{cm}}$$. and breadth is $$10\,{\rm{cm}}$$. Find its height.
A cylindrical vessel, open at the top,has a radius 10 cm height 14 cm . Find the total surface of the vessel
Find the volume of sphere of radius 42 cm?
The length, breadth and height of a cuboid are in the ratio $$4:2:1$$ and its total surface area is $$1372\ m^{2}$$. Find the dimensions of the cuboid.
Find the total surface area of cubes having the following sides.
$$5.5\ m$$
Find the total surface area of a hemisphere of radius $$10 \text{ cm}$$.
Find the total surface area of cubes having the following sides.
$$3\ cm$$
The length, breadth and height of a notebook are 10 cm, 6 cm and 5 cm respectively. What is the volume of a pack of 12 such notebooks?
Find the surface area of a sphere of radius :
$$14\ cm$$
Find the surface area of a sphere of radius :
$$5.6\ cm$$
Find the $$T.S.A.$$ of a cube, whose volume is $$3\sqrt {3}\ a^{3}$$ cubic units.
Find the curved surface area of cylinder of radius 14 cm and height 21 cm.
Find the total surface area of cubes having the following sides.
$$6.8\ m$$
The ratio of the volume of the sphere to the surface area of the sphere is 7 :Find the surface area of the sphere ?
Find the cost of painting $$20$$ cylindrical pillars of an institution at the rate of Rs. $$3 $$ per $$\mathrm{m}^{2}$$, if the radius and the height of each pillar are $$36 \ \mathrm{cm} $$ and $$ 3.5\ \mathrm{ m} $$ respectively.
Find the amount of water displaced by a solid spherical ball of diameter $$4.2$$ cm, when it is completely immersed in water.
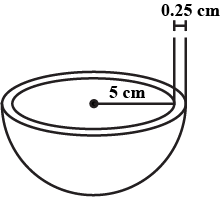
A hemispherical bowl is made of steel, $$0.25$$ cm thick. The inner radius of the bowl is $$5$$ cm. Find the outer curved surface area of the bowl.
Find the volume of a cuboid whose dimensions are: (a) length = 15 cm, width = 12 cm and height = 8 cm (b) length = 4 m, width = 2.6 m and height = 80 cm
The volume of a cuboid is $$440$$ $$cm^{3}$$ and the area of its base is $$88$$ $$cm^{2}$$. Find its height.
Find the surface area of a sphere of radius $$7$$ cm.
A balloon which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the radius is 10 cm.
Assume $$\pi =\dfrac{22}{7}$$ , unless stated otherwise.
Find the volume of a sphere whose radius is
(i) $$7$$ cm
(ii) $$0.63$$ m
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
How many boxes,each of size $$12\ cm\times 8\ cm\times 6\ cm$$ can be packed in a carbon of size $$60\ cm\times 48\ cm\times 36\ cm$$
Find the volume of cuboid with $$6\text{ cm},8\text{ cm}, 10\text{ cm}$$ as its dimensions
If the volume of a cuboid is $$880\ cm^{3}$$ and area of base is $$88\ cm^{2}$$. Find the height.
A hollow hemispherical bowl of thickness $$1\ cm$$ has an inner radius of $$6\ cm$$. Find the volume of metal required to make the bowl.
The surface area of cube is $$150cm^2$$ find its volume.
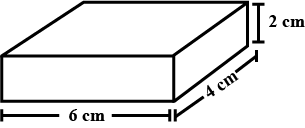
Find the total surface area of the following cuboid.
If volume of cube is $$64\ cm^{3}$$, find its surface area.
Find the volume of a cuboid if its surface area is 208 sq cm and the ratio of length, breadth and height is 2:3:4
Find the amount of water displaced by a solid spherical balls of diameter $$3\ cm$$, when it is completely immersed in water.
For the given figure find the surface area?
Radius and height of a cylinder are $$10 \ \text{ cm }$$ and $$12\ \text{ cm }$$ respectively. Find total surface area of the cylinder. $$( \pi = 3.14 )$$
Find volume of Cuboid of $$l = 3\ m, b = 2\ m, h = 4\ m$$.
Find the volume of sphere whose radius is $$3$$ cm.
A capsule of medicine is in the shape of a sphere of diameter $$3.5$$ mm. How much medicine ( in $$mm^3$$ ) is needed to fill this capsule?
Calculate total surface area of cube whose one side is 6cm.
Find the volume of a sphere whose radius is
$$0.63\ m$$
A wooden toy in the form of cone surmounted on a hemisphere. The diameter of the base of the cone is $$6\ cm$$ and height is $$4\ cm$$. Find the cost of painting the toy at the rate of $$Rs. 5$$ per $$1000\ cm^{2}$$.
Find the volume of a sphere whose radius is
$$7\ cm$$
Find the volume and the surface area of the cuboid having the following measures:Length $$= 6 \ \text{m}$$ ,breadth $$ =4\ \text {m} $$ and height $$ =3 \ \text{m} $$
Find the curved surface area of a solid sphere whose radius is $$7\ cm$$.
Find the volume, curved surface area and total surface area of a cylinder whose dimensions are radius of the base $$=5.6\ m$$ and height $$=1.25\ m$$
Find the volume of a cuboid (in $$cm^3$$)whose
length $$=1.2\ cm$$, breadth $$=30\ cm$$, height $$=15\ cm$$
What shape is a sweet laddu?
The dimensions of cuboid are $$5\times 4\times 2$$ find the volume of cuboid
The dimensions of a cuboid is $$22.5\ cm\times 10\ cm\times 7.5\ cm$$ . Find the surface area of the cuboid .
A river $$2\ m$$ deep and $$45\ m$$ wide is flowing at the rate of $$3\ km/h$$. Find the quantity of water that runs into the sea per minute.
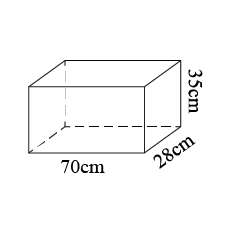
What shape is a brick?
If the radius of a sphere is doubled, then what is the ratio of their volumes?
Find the volume of a box if its length , breadth and height are $$20$$ cm , $$10.5$$ cm and $$8$$ cm respectively .
The rainfall recorded on a certain day was $$5\ cm$$. Find the volume of water that fell on a $$2$$ hectare field.
Fill in the blanks the statements are true.
Total surface area of a cylinder of radius h and height r is ______
Fill in the blanks the statements are true.
Curved surface area of a cylinder of radius h and height r is ________.
The volume of a cylinder of height $$8\ cm$$ is $$1232\ cm^{3}$$. Find its curved surface area and total surface area.
Fill in the blanks to make the statements true.
The surface area of a cuboid formed by joining two cubes of side a face to face is ________.
A cylindrical roller $$2.5\ m$$ in length, $$1.75\ m$$ in radius when rolled on a road was found to cover the area of $$5500\ m^2$$. How many revolutions did it make?
$$30$$ circular plates, each of radius $$14$$ cm and thickness $$3$$ cm are placed one above the another to form a cylindrical solid. Find the total surface area.
A closed cylindrical tank of radius $$7 m$$ and height $$3\ m$$ is made from a sheet of metal. How much sheet of metal is required?
A factory manufactures $$120000$$ pencils daily. The pencils are cylindrical in shape each of length $$25$$ cm and circumference of base as $$1.5$$ cm. Determine the cost of coloring the curved surfaces of the pencils manufactured in one day at Rs $$0.05$$ per $$dm^2.$$
A road roller takes $$750$$ complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is $$84\ cm$$ and lenght is $$1\ m$$.

A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
Find the height of a cuboid whose base area is $$180\ cm^2$$ and volume is $$900$$ $$cm^3$$?
The dimensions of a Cinema Hall are $$100$$ m, $$60$$ m and $$15$$ m. How many person can sit in the hall, if each requires $$150$$ $$m^{3}$$ of air ?
The radius of the base of a right circular cylinder is $$3\ cm$$ and height is $$7\ cm$$. Find the curved surface area (in sq. cm.)
Four cubes, each of edge 9 cm, are joined as shown below, then the volume of the resulting cuboid is in $$cm^3$$
A cylinder has a diameter of $$20$$ cm. The area of the curved surface is $$100$$ $$\displaystyle \text{cm}^{2}$$ (sq. cm). The height of the cylinder correct to one decimal place is $$1.6$$ cm
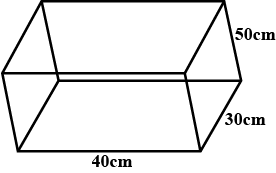
A fish tank is in the form of a cuboid, external measures of that cuboid are $$80 $$ cm $$\times 40$$ cm $$\times 30$$ cm. The base, side faces and back face are to be covered with a coloured paper. Find the area of the paper needed in cm$$^2$$
The side of a cube is $$25$$ cm. Find the total surface area of the cube. (in $$cm^3$$)
If the total surface area of a solid hemisphere is 462 $$cm^2$$, find its volume.
[Take $$\pi=\dfrac {22}{7}]$$
How many balls each of radius $$1$$ cm, can be made from a copper sphere whose radius is $$8$$ cm?
The curved surface of a cylindrical pillar is $$264$$ $$\displaystyle \text{cm}^{2}$$ and its volume is $$924$$ $$\displaystyle \text{cm}^{3}$$. Find the diameter.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height What is the ratio of their respective volumes ?
Two cubes each of edge $$12$$ cm are joined end to end. Find the surface area of the resulting cuboid.
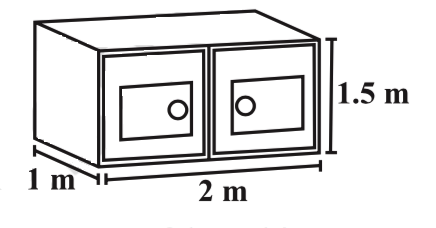
Rukhsar painted the outside of the cabinet of measure $$1\ m\ \times\ 2m\ \times\ 1.5\ m$$ . How much surface area did she cover if she painted all except the bottom of the cabinet?
A road roller takes $$750$$ complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is $$84$$ cm and length is $$1$$ m.

Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area ?
A plastic box $$1.5$$ m long, $$1.25$$ m wide and $$65 $$ cm deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet,
(i) determine the area of the sheet
(ii) the cost of sheet for it, if a sheet measuring $$1$$ m$$^{2}$$ costs Rs.$$20$$.
Find the side of a cube whose surface area is $$600$$ sq. cm
A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required?
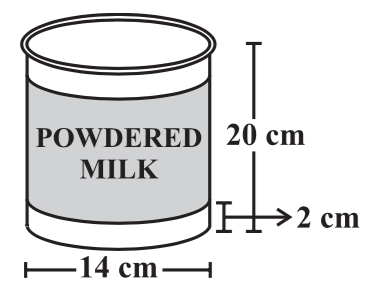
A company packages its milk powder in cylindrical container whose base has a diameter of $$14$$ cm and height $$20$$ cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed $$2$$ cm from top and bottom, what is the area of the label.
A metal pipe is $$77$$ cm long. The inner diameter of a cross section is $$4$$ cm, the outer diameter being $$4.4$$ cm (see figure). Find its
(i) inner curved surface area.
(ii) outer curved surface area
(iii) Total surface area

The diameter of a roller is $$84$$ cm and its length is $$120$$ cm. It takes $$500$$ complete revolutions to move once over to level a playground. Find the area of the playground in m$$^{2}$$
The length, breadth and height of a room are $$5\ m$$, $$4\ m$$ and $$3\ m$$ respectively. Find the cost white washing the walls of the room and ceiling at the rate of $$Rs.\ 7.50$$ per $$m ^ { 2 }$$.
The floor of a rectangular hall has a perimeter $$250\ m$$. If the cost of painting the four walls at the rate of $$10$$ per $$m^{2}$$ is $$15000$$, find the height of the hall (in meters).
A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is $$30\ cm$$ long, $$25\ cm$$ wide and $$25\ cm$$ high.
(i) What is the area of the glass?
(ii) How much of tape is needed for all the $$12$$ edges?
Curved surface area of a right circular cylinder is $$4.4$$ m$$^{2}$$. If the radius of the base of the cylinder is $$0.7$$m, find its height.
The curved surface area of a right circular cylinder of height $$14 \,cm$$ is $$88\,cm^{2}$$. Find the diameter of the base of the cylinder.
The paint in a certain container is sufficient to paint an area equal to $$9.375\ m^{2}$$. How many bricks of dimensions $$22.5\ cm \times 10\ cm \times 7.5\ cm$$ can be painted out of this container?
It is required to make a closed circular cylindrical tank of height $$1\ m$$ and base diameter $$140\ cm$$ from a metal sheet. How many square meters of the sheet are required for the same?
A cylindrical pillar is $$50$$ cm in diameter and $$3.5$$ m in height. Find the cost of painting the curved surface of the pillar at the rate of $$12.50$$ per m$$^{2}$$.
In the figure, you see the frame of a lampside. It is to be covered with a decorative cloth. The frame has a base diameter of $$20\ cm$$ and height of $$30\ cm$$. A margin of $$2.5\ cm$$ is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.
Find the surface area of a sphere of radius
(i) $$10.5$$cm (ii) $$5.6$$cm (iii) $$14$$cm
Find
(i) The lateral or curved surface area of a closed cylindrical petrol storage tank that is $$4.2\ m$$ in diameter and $$4.5\ m$$ high.
(ii) How much steel was actually used, if $$\cfrac{1}{12}$$ of the steel actually used was wasted in making the tank?
The inner diameter of a circular well is $$3.5\ m$$. It is $$10\ m$$ deep. Find
$$(i)$$ its inner curved surface area
$$(ii)$$ the cost of plastering the curved surface at the rate of $$Rs.\ 40$$ per $$m^{2}$$
Find the total surface area of a hemisphere of radius $$10$$ cm.
The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius $$3\ cm$$ and height $$10.5\ cm$$. The Vidyalaya was to supply the competitors with cardboard. If there were $$35$$ competitors, how much cardboard was required to be bought for the competition?
In a hot water heating system, there is a cylindrical pipe of length $$28\ m$$ and diameter $$5\ cm$$. Find the total radiating surface in the system.
A hemispherical bowl made of brass has inner diameter $$10.5\ cm$$. Find the cost of tin-planting it on the inside at the rate of $$16$$ per $$100\ cm^{2}$$.
The radius of a spherical balloon increases from $$7\ cm$$ to $$14\ cm$$ as air is being pumped into it. Find ratio of surface areas of the balloon in the two cases.
Find the surface area of a sphere of diameter:
(i) $$14$$ cm (ii) $$21$$ cm (iii) $$3.5$$ m.
Find the cost of digging a cuboidal pit $$8$$ m long, $$6$$ m broad and $$3$$ m deep at the rate of $$30$$ per m$$^{3}$$.
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
A right circular cylinder just encloses a sphere of radius $$r$$ (see figure). Find the
(i) surface area of the sphere,
(ii) curved surface area of the cylinder and (iii) ratio of the surfaces obtained in (i) and (ii).
A village, having a population of $$4000$$, requires $$150$$ litres of water per head per day. It has a tank measuring $$20$$ m $$\times 15$$ m $$\times 6$$ m. For how many days will the water of this tank last?
Find the radius of a sphere whose surface area is $$154$$ cm$$^{2}$$.
A hemispherical bowl is made of steel, $$0.25\ cm$$ thick. The inner radius of the bowl is $$5\ cm$$. Find the outer curved surface area of the bowl.
A cuboidal vessel in $$10$$ m long and $$8$$ m wide. How high must it be made to hold $$380$$ cubic metres of a liquid?
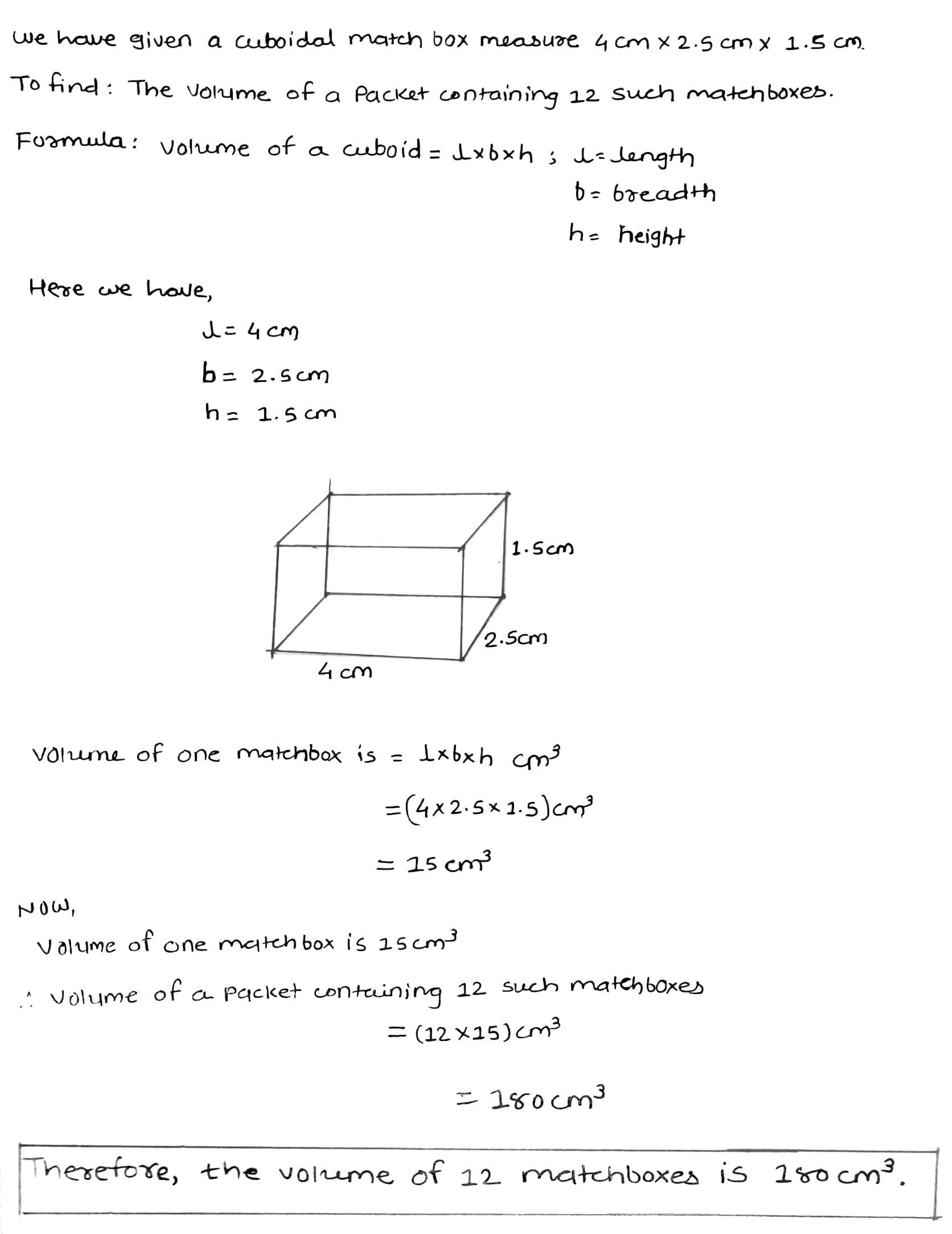
A match box measures $$4$$ $$cm$$ $$\times 2.5$$ $$cm$$ $$\times 1.5$$ $$cm$$. What will be the volume of a packet containing $$12$$ such boxes?
The capacity of a cuboidal tank is $$50000$$ litres of water. Find the breadth of the tank, if its length and depth are respecrively $$2.5$$ m and $$10$$ m
A cuboidal water tank is $$6$$ m long, $$5$$ m wide and $$4.5$$ m deep. How many litres of water can it hold?
How many litres of milk can a hemispherical bowl of diameter $$10.5$$ cm hold?
The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
A hemispherical tank is made up of an iron sheet $$1$$ cm thick. If the inner radius is $$1$$ m, then find the volume of the iron used to make the tank.
The capacity of a closed cylindrical vessel of height $$1$$ m is $$15.4$$ litres. How many square metres of metal sheet would be needed to make it?
Find the volume of a sphere whose radius is
$$(i)$$ $$7$$ cm
$$(ii)$$ $$0.63$$ m
A godown measures $$40\ m$$ $$\times 25\ m$$ $$\times 15\ m$$. Find the maximum of wooden crates each measuring $$1.5\ m$$ $$\times 1.25\ m$$ $$\times 0.5\ m$$ that can be stored in the godown.
Find the volume of a sphere whose surface area is $$154$$ cm$$^{2}$$.
Find the amount of water displaced by a solid spherical ball of diameter
(i) $$28\ cm$$
(ii) $$0.21\ m$$
The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm$$^3$$?
A solid cube of side $$12$$ cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas.
Twenty seven solid iron spheres, each of radius $$r$$ and surface area $$S$$ are melted to form a sphere with surface area $$S'$$. Find the
(i) radius $$r'$$ of the new sphere and
(ii) ratio of $$S$$ and $$S'$$
A capsule of medicine is in the shape of a sphere of a diameter $$3.5\ mm^{3}$$ is needed to fill this capsule?
Find the surface area of the hemisphere whose radius is $$7$$ cm.
What is the surface area of the hemisphere whose diameter is $$28\text{ cm}$$?
Find the total surface area of the hemisphere whose radius is $$35$$ m.
$$150$$ spherical marbles, each of diameter $$1.4\ cm$$, are dropped in a cylindrical vessel of diameter $$7\ cm$$ containing some water, which are completely immersed in water. Find the rise in the level of water in the vessel.
A cubical block of side $$10$$cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs. $$5$$ per sq. cm. $$\displaystyle \left[ Use \,\,\, \pi = 22/7 \right]$$
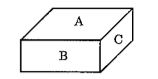
The figure shows a cuboid. The area of the 3 faces A, B and C are $$48$$ $$\displaystyle { cm }^{ 2 }$$, $$40$$ $$\displaystyle { cm }^{ 2 }$$ and $$30$$ $$\displaystyle { cm }^{ 2 }$$ respectively. Find the volume of the cuboid.
The given figure shows the net of a cuboid with a square base. Find the volume of the cuboid.

A room is 6 m long, 4 m broad and 3 m high. Find the cost of laying tiles on its floor and four walls at the cost of Rs. 80/m$$^2$$.
Find the total surface area of the cuboid with $$l = 4\ m, b = 3\ m$$ and $$h = 1.5 \ m$$.
A closed box is $$40$$ cm long, $$50$$ cm wide and $$60$$ cm deep. Find the area of the foil needed for covering it.
Two cubes, each of volume $$512$$ cm$$^3$$ are joined end to end. Find the lateral and total surface areas of the resulting cuboid.
The length, breadth and height of a cuboid are in the ratio $$6:5:3$$. If the total surface area is $$504$$ $$cm^2$$,find its dimension. Also find the volume of the cuboid.
Find the total surface area and volume of a cube whose length is $$12$$ cm.
The circumference of the base of a cylinder is $$132$$cm and its height is $$25$$cm. Find the volume of the cylinder.
A wooden box has inner dimensions $$l = 6 m, b = 8$$ and $$ h = 9m$$ and it has uniform thickness of 10 cm. The lateral surface of the outer side has to be painted at the rate of Rs. 50/m$$^2$$. What is the cost of painting?
A match box measure $$4$$ cm, $$2.5$$ cm and $$1.5$$ cm. What will be the volume of the packet containing 12 such boxes
An iron pipe $$20$$cm long has external radius equal to $$12.5$$cm and internal radius equal to $$11.5$$cm. Find the total surface area of the pipe.
The height of a right circular cylinder is $$14\ cm$$ and the radius of its base is $$2\ cm.$$ Find its total surface area.
The CSA of a right circular cylinder of height $$14$$cm is $$88cm^2$$. Find the radius of the base of the cylinder.
A solid cylinder has a TSA of $$462cm^2$$. Its CSA is one-third of its TSA. Find the volume of the cylinder.
The height of a right circular cylinder is $$14$$cm and the radius of its base is $$2$$cm. Find its CSA.
Find the lateral surface area and total surface area of a cuboid which is $$8$$m long, $$5$$ m broad and $$3.5$$ m high.
The radii of two right circular cylinders are in the ratio $$2:3$$ and their heights are in the ratio $$5:4$$. Calculate the ratio of their curved surface areas.
Find the volume of a sphere of radius $$3$$cm.
A cylindrical piller has a diameter of $$56 cm$$ and is of $$35 m$$ high. There are $$16$$ pillars around the building. Find the cost of painting the curved surface area of all the pillars at the rate of $$Rs. 5.50$$ per $$1m^2$$
A hemispherical bowl of internal radius $$18\text{ cm}$$ is full of fruit juice. The juice is to be filled into cylindrical shaped bottles each of radius $$3\text{ cm}$$ and height $$9\text{ cm}$$. How many bottles are required to empty the bowl?
A closed cylindrical tank of height 1.4 m and radius of the base is 56 cm is made up of a thick metal sheet. How much metal sheet is required (Express in square meters)
Find the surface area of a sphere of radius $$21$$cm.
A hemispherical bowl has inner diameter $$9$$cm. Find the volume of milk it can hold.
The diameter of a garden roller is $$1.4$$m and $$2$$m long. How much area will it cover in $$5$$ revolutions?
How does the total surface area of a box change if
Each dimension is doubled?
Express in words. Can you find the area if each dimension is multiplied n times?
The radii of two right circular cylinders are in the ratio $$2:3$$ and the ratio of their curved surface areas is $$5:6$$. Find the ratio of their heights.
A hemispherical bowl has diameter 9 cm. The liquid is poured into cylindrical bottles of diameter 3 cm and height 3 cm. If a full bowl of liquid is filled in the bottles, find how many bottles are required.
If the surface area of a sphere is $$154 cm^2$$, find its radius.
How much steel sheet was actually used, if $$\dfrac{1}{12}$$ of the steel was wasted in making the tank. Area of the tank is $$87.12 m^2$$
A shotput is a metallic sphere of radius 4.9 cm. If the density of the metal is 7.8 g. per cm$$^3$$, find the mass of the shotput.
The surface area of a solid metallic sphere is $$2464\ cm^2$$. Calculate the radius of the sphere (in $$cm$$).
The hollow sphere, in which the circus motor cyclist performs his stunts, has a diameter of $$7$$ m. Find the area available to the motor cyclist for riding.
A hemispherical bowl has a radius of $$3.5\; cm.$$ What would be the volume of water it would contain?
The surface area of a sphere is $$1018 \dfrac{2}{7}$$ sq. cm. Find its volume
The length of equator of the globe is $$44$$ cm. Find its surface area.
The diameter of a roller is $$84$$ cm and its length is $$120$$ cm. It takes $$500$$ complete revolutions to roll once over the playground in m$$^2$$. Find the area of the playground
A circus tent is to be erected in the form of a cone surmounted on a cylinder. The total height of the tent is $$49\ m$$. Diameter of the base is $$42\ m$$ and height of the cylinder is $$21\ m$$. Find the cost of canvas needed to make the tent, if the cost of canvas is Rs. $$12.50\ m^2$$. (Take $$= \dfrac{22}{7}$$)
Find the volume and surface area of a sphere of radius $$6.3\ cm$$
Find the total surface area of a cube with side $$9 cm$$. (in $$cm^2$$)
The length, breadth and height of a cuboid are $$6\, cm$$, $$4 \,cm$$ and $$5 \,cm$$ respectively. Find the total surface area of the cuboid.
Find the surface area of a sphere whose radius is $$3 cm$$. $$\left(\pi = 3.14\right)$$.
The radius of a sphere is $$28$$ cm. Find its curved surface area. $$\left ( \pi = \dfrac{22}{7} \right )$$
Find the surface area of a sphere of radius $$1.4\ \text{cm}$$. $$\left ( \pi =\dfrac{22}{7} \right )$$
The radius of the base of a right circular cylinder is $$3 cm$$ and its height is $$7 cm$$, find the curved surface area.
A solid right circular cylinder has radius of $$14 $$ cm and height of $$8$$ cm. Find its total surface area.
How many litres of water will a hemispherical tank hold whose diameter is $$4.2$$ m?
Find the volume of a sphere-shaped metallic shotput having a diameter of $$8.4$$ cm (Take $$\pi =\cfrac { 22 }{ 7 } $$)
The angular elevation is $$60^{\circ}$$. The internal and external radii of a hollow cylinder are $$12\ cm$$ and $$18\ cm$$ respectively. If its height is $$14\ cm$$, then find its curved surface area. (Take $$\pi = \dfrac {22}{7})$$
If the circumference of the base of a solid right circular cylinder is $$154$$ cm and its height is $$16$$ cm, then find its curved surface area.
The radius of a spherical balloon increases from $$7cm$$ to $$14cm$$ as air is pumped into it. Find the ratio of the volumes of the balloon before and after pumping the air.
A tent is in the shape of a right circular cylinder surmounted by a cone. The total height and the diameter of the base are $$13.5$$ m and $$28$$ m. If the height of the cylindrical portion is $$3$$ m, find the total surface area of the tent
A cubical container of side $$3.5$$m is to be painted both inside and outside. Find the area to be painted and the total cost of painting it at the rate of Rs $$75$$ per square meter.
Find the L.S.A of a cuboid whose dimensions are given by $$3m\times 5m\times 4m$$.
Three metallic cubes of side $$3\ cm, 4\ cm$$ and $$5\ cm$$ respectively are melted and are recast into a single cube. Find the total surface area of the new cube.
Find the total surface area of a cuboid whose length, breadth and height are 20 cm, 12 cm and 9 cm respectively.
Find the total surface area of a hemisphere of radius $$3.5\ cm$$.
A cubical tank can hold 27,000 litres of water. Find the dimension of its side.
A cubical tank can hold $$64,000$$ litres of water. Find the length of the side of the tank.
If $$V$$ is the volume of cuboid whose length is $$'a'$$, breadth is $$b$$ and height is $$c$$ and $$S$$ is its surface area then prove that-
$$\dfrac {1}{V} = \dfrac {2}{S}\left (\dfrac {1}{a} + \dfrac {1}{b} + \dfrac {1}{c}\right )$$
Find the volume of a box having measure $$2 \,metre \times 3 \,metre \times 1 \,metre$$ in $$m^3$$
The measurement of a brick is $$24 cm \times 10 cm \times 8 cm$$ , find the volume of a brick in $$cm^3$$
The length , breadth and height of a cuboid are $$10 cm , 8 m ,$$ and $$6 m$$ respectively, find the volume.
The length of one side of a stone in the shape of cube is 40 cm, what is the volume of this stone ?
The length of a cuboidal room is $$6$$ metres , breadth is $$4$$ metres and height is $$3$$ metres.In this room how many cubic boxes of $$1$$ metre length can be arranged ?
A cuboidal shaped milk -tank measures $$2 m \times 50 cm \times 40 cm$$. This tank is completely filled with milk. How many 200 ml milk packets can be filled with this milk ?
The measurement of a compass-box is $$16 cm \times 4 cm \times 2 cm$$, find the volume of a compass-box in $$cm^3$$
In a cuboidal box $$30 \text{ cm } \times 20 \text{ cm } \times 10 \text{ cm }$$, how many cubes of $$5 \text{ cm}$$ length each can be arranged ?
A vessel is in the form of a hollow hemisphere. The diameter of the hemisphere is $$14cm$$. Find the inner surface area of the vessel.
A tank measuring $$3 m \times 2 m \times 2 m$$ was made to store water in Gattu's bunglow.In this tank, how many litres of water can be stored?
In a cuboid having the measurement m of 60 cm X 54 cm X 30 cm, how many cubes of 6 cm length can be arranged ?
A box for putting medicines is 48 cm long, 30 cm wide and 20 cm high. In this box, how many boxes of 15 cm length, 6 cm breadth and 4 cm height can be arranged ?
A copper wire of diameter $$6$$ mm is evenly wrapped on a cylinder of length $$15$$ cm and diameter $$49$$ cm to cover its whole surface. Find the length and volume of the wire. If the specific gravity of copper is $$9 \ \dfrac{g}{{cm}^3}$$, then find the weight of the wire.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio $$1 : 2 : 3$$.
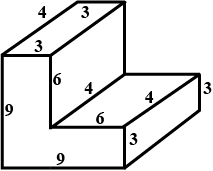
The figure shows a solid of uniform cross section. Find the volume of the solid. It is being given that all the measurements are in $$cm$$ and each angle in the figure is a right angle
(Hint: This consists of two cuboids of dimensions
[$$(4\times 6\times 3){cm}^{3}$$ and $$(4\times 3\times 9){cm}^{3}$$]
Praveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height $$2.5\ m$$, with base dimensions $$4\ m\times 3\ m$$?
The area of the base of a right circular cylinder is $$81\pi$$ $${cm}^{2}$$ and height of the cylinder is $$14cm$$. Find its curved surface.
If a sphere of $$21$$ cm radius melted and formed as a solid cuboid of length $$77$$ cm and breadth $$36$$ cm, then find the height of cuboid.
A metal pipe is $$77$$cm long. The inner diameter of a cross section is $$4$$ cm, the outer diameter being $$4.4$$ cm. Find its outer curved surface area.

If 'V' is the volume of a cuboid of dimensions a $$\times$$ b $$\times$$ c and 'S' is its surface area, then prove that:
$$\displaystyle\frac{1}{V}=\frac{2}{S}\left[\displaystyle\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right]$$.
A metal pipe is $$77$$cm long. The inner diameter of a cross section is $$4$$ cm, the outer diameter being $$4.4$$ cm. Find its inner curved surface area.

A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Figure. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, find the total surface area of the article.
Three solid spheres of radii $$3\text{ cm},4\text{ cm}$$ and $$5\text{ cm}$$ respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
If the total surface area of a solid hemisphere is $$462{cm}^{2}$$, find its volume. (Take $$\pi=22/7$$)
The diameter and height of a cylindrical chimney are $$2\ m$$ and $$14\ m $$ respectively. Find the cost of painting its exterior curved surface at the rate of Rs. $$150$$ per $$m^2$$.
A sphere of diameter $$6cm$$ is dropped in a right circular cylindrical vessel partly filled with water. The diameter of the cylindrical vessel is $$13cm$$. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel
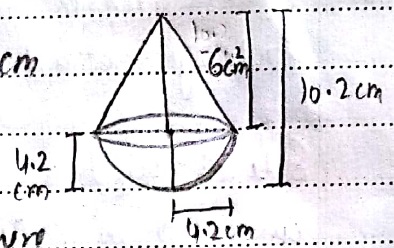
A solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of the wooden toy (nearly).
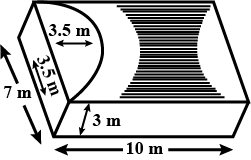
A godown building is in the form as shown in figure. The vertical cross-section parallel to the width side of the building is a rectangle $$7m\times 3m$$, mounted by a semi-circle of radius $$3.5m$$. The inner measurements of the cuboidal portion of the building are $$10m\times 7m\times 3m$$. Find the volume of the godown and the total interior surface area excluding the floor (Base). (Take $$\pi =22/7$$)
A hemispherical tank full of water is emptied by a pipe at the rate of $$3\cfrac { 4 }{ 7 } $$ litres per second. How much time will it take to make the tank half-empty, if the tank is $$4\ m$$ in diameter
Three cubes each of side $$5cm$$ are joined end to end. Find the surface area of the resulting cuboid.
Two cubes, each of side $$4$$cm are joined end to end. Find the surface area of the resulting cuboid.
The dimensions of a tin box are $$ 12\,cm\, \times \,10.5\,cm\, \times \,8\,cm$$. If $$20$$ such boxes are to be made, find the area of the tin sheet required in $${m^2}$$.
Raj made a cuboid plasticine. Length, breadth and height of the cuboid are $$15$$cm, $$30$$cm, $$15$$cm respectively. Find the volume of cuboid plasticine.
The radius of a spherical balloon is inflated from $$1.5\ cm$$ to $$2.5\ cm$$ by pumping more air in it. Find the ratio of surface area of resulting balloon to the original balloon.
What is the total volume of the smallest number of cubes that must be added to make the given figure a cuboid?

The area of three adjacent faces of a cuboidal box are $$120c{m^2}$$, $$72c{m^2}$$ and $$60c{m^2}$$, respectively. Its volume is
The sum of the length, breadth and depth of a cuboid is $$19\ cm$$ and the length of its diagonal is $$11\ cm$$. Find the surface area of the cuboid.
The diameter of a solid hemisphere is 42 cm. Find its volume, curved surface area and total surface area.
Circumference of the edge of hemispherical bowl is $$132\;cm$$. Find the capacity of the bowl.
The surface area of a solid cylinder of radius 2.0 cm and height 10.0 cm is equal to____$$(mm)^2$$
What are the possible expressions for the dimensions of the cuboids whose volume are given?
Volume: $$3x^2-12x$$.
An Olympic swimming pool is in the shape of a cuboid of dimensions $$50\ m$$. Long and $$25\ m$$. wide. If it is $$3\ m$$ deep throughout, how many liters of water does it hold?
$$(1\ cu.m=1000 liters)$$
A solid consisting of a right circular cone standing on a hemisphere, is placed upright in a right circular cylinder full of water and touches the bottom. Find the volume of water left in the cylinder, given that the radius of the cylinder is 3 cm, and its height is 6 cm. The radius of the hemisphere and cone is 2 cm, and the height of the cone is 4 cm. $$\left(Take \,\pi = \dfrac{22}{7}\right)$$.
The curved surface area of the cylinder is $$1760\ c{m^2}$$ and its volume is $$24640\ c{m^2}$$. Find its height.
A door of length $$2\ m$$ and breadth $$1\ m$$ is fitted in a wall. The length of the wall is $$4.5$$ and the breadth is $$3.6\ m$$. Find the cost of the wall washing the wall, if the rate white washing the wall is $$Rs. 20$$ per $${m^2}$$
If the surface area of a sphere is $$616c{m^2}$$ , then find its radius.
Find the total surface area of cuboid whose length , breadth and height and height are $$8\,cm\,\, 7\, cm$$ and $$4\, cm$$ respectively.
External dimensions of a wooden cuboid are $$30\ cm\times 25\ cm \times 20\ cm$$. If the thickness of wood is $$2\ cm$$ all round find the volume of the wood contained in cuboid formed.
The area of the base of a right circular cylinder is $$81\pi$$. If its height is $$14\ cm$$, find the curved surface of the cylinder.
If radius$$=2$$ and height $$=7\ cm$$ then find carved surface area of cylinder?
The T.S.A. of right circular cylinder is $$3432$$ $${ cm }^{ 2 }$$ . Its C.S.A. is $$\frac { 5 }{ 26 } $$ of its T.S.A. Determine the radius of the base and height.
Diameter of the beach ball is $$42\ cm$$. Find the surface area and volume.
Determine the ratio of the volume of a cube to that of a sphere which will exactly fit inside the cube.
Find the volume of wood used to make a closed box of outer dimensions $$60\ cm\times 45\ cm\times 32\ cm$$, the thickness of wood being $$2.5\ cm$$ all around.
Bricks measuring $$40cm\, \times \,5cm\, \times 7cm$$ are to be painted. If there are $$60$$ bricks, find the total area to b painted.
The dimensions of a cuboid are in the ratio 1:2:3 and its total surface area is $$88 \ m^2$$. Find the dimensions.
A rectangular hall is $$25\,m$$ long and $$10\,m$$ wide and its height is $$6\,m$$. Find the cost of painting the walls of the hall at the rate of $$RS\,2$$ per sq.m.
A rectangular room of the dimension $$8m\times 6m\times 3m$$ is to be painted. If it costs Rs.60 per square metre, find the cost of painting the walls of the room.
If the volume of a cuboid is $$448{cm}^{3}$$ and its height is $$7$$ cm and the base is a square.find (i)the side of the square base (ii) surface area of the cuboid.
Find the cost of painting the outside surface of a solid cylinder of diameter $$7m$$ and height $$20m$$ at Rs 5 per $$m ^ { 2 }$$.
The diameter of a metallic ball is 4.2 cm . What is the mass of the ball, if the density of the metal is 8.9 g per cm$$^3$$ ?
The dimensions of a cuboid are in the ratio $$1:2:3$$ and its volume is $$384\,cu.m$$. Find the dimensions and surface area.
From a closed cardboard cylinder of height 30 cm and diameter of base 21 cm, 15 rectangles of size 2 cm $$\times$$ 1.5 cm are cut out. Find the total surface area of the remaining cylinder.
Find the volume of a sphere whose surface area is 154 cm$$^2$$.
The dimension of Mr Narula's bedroom is 8 m x 7 m x 5 m. It has two windows, each measuring 2 m x 1 m and one door measuring 3 m x 1 m. Find the cost of white washing the room at Rs. 50 per square metre.
A toy is in the shape of cone mounted on hemisphere of same base radius. If the volume of the toy is $$231\ {cm}^{3}$$ and its diameter is $$7\ cm$$, find the height of the toy.
A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Two cubes each with 12 cm are joined end to end . Find the surface area of the resulting cuboid.
Find the total surface area of a closed box of wood whose dimensions are 2 m, 1.5 m and 80 cm, cost of wood used to make it at the rate of Rs.120.55 per $$m^{2}$$.
Find the total surface area of the following cuboids.
Length$$=7\ cm$$, breadth$$=4\ cm$$, height$$=3\ cm$$
In a shower, $$5\ cm$$ of rain falls. Find the volume of water that falls on $$2$$ hectares of ground.
Find the $$z-$$score that corresponds to the $$65^{th}$$ percentille of the standard Normal curve.
The radius of a sphere is increased by $$p\%$$. By what percent its surface area increases?
A rectangular field is $$70m$$ long and $$60m$$ broad. A well of dimensions $$14m\times 5m\times 6m$$ is dug outside the field and the earth dugout from this well is spread evenly in the field. How much will the earth level rise?
A spherical glass vessel has a cylindrical neck which is $$4 $$ cm long and $$2 $$ cm in diameter. The diameter of the spherical part is $$6 $$ cm. Find the amount of water it can hold?
How many balls of $$1\ cm$$ radius can be made from a solid sphere of lead of radius $$8\ cm$$.
A hemispherical bowl has a radius $$3.5$$ cm. Its volume _______ cm$$^3$$.
Obtain the volume of rectangle boxes with the following length, breath and height respectively,
$$\left( i \right)\,5a,\,3{a^2},\,7{a^4}$$ $$\left( {ii} \right)\,2p,\,4q,\,8r$$ $$\left( {iii} \right)\,xy,\,2{x^2}y,\,2x{y^2}$$ $$\left( {iv} \right)\,a,\,2b\ ,c$$
Find the surface area and volume of a bouch ball shown in figure.

Find the total surface area of the given figure.
The area of three adjacent faces of a cuboid are $$x, y$$ abd $$z$$. If the volume is $$V$$, prove that $$V^{2}=xyz$$.
A hemispherical tank is made up of an iron sheet 1$$\mathrm { cm }$$ thick. If the inner radius is $$1$$m then find the volume of the iron used to make the tank.
Three cubes whose edges of radii $$3\ cm,\ 4\ cm$$ and $$5\ cm$$ are melted together from a single cube. Find the surface area of the new cube.
Shanti Sweets stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The Bigad was of dimension 25 CM 20 CM 5 cm and the smaller dimension 15 CM 12 CM 5 cm. For all the overlaps, 5% of total surface area is required extra. If the cost of the cardboard is rupees 4000 CM square find the cost of cardboard required for supplying 250 boxes of each kind.
If areas of three adjacent faces of cuboid be $$x,y$$ and $$z$$ respectively, then find the volume of the cuboid.
Find the volume of a cuboid having surface areas of three adjacent faces as $$x, y$$ and $$z$$.
A sphere, cylinder & a cone gave the same radius & same height, find the ratio of their curved surface areas.
If the areas of three adajacent faces of a cuboid are $${ 8\ \text{cm} }^{ 2 },{ 18\ \text{cm} }^{ 2 } $$ and $$ { 25\ \text{cm} }^{ 2 }$$, then determine volume of cuboid.
Find the surface area of a cuboid whose dimension are $$7\ cm \times 0.57\ dm\times 0.14\ m$$
The surface areas of a sphere and cube are equal. Prove that their volumes are in the ratio $$1:\sqrt { \pi /6 }. $$
The total surface area of a cube is $$486cm^2$$. Calculate its edge
The diameter of a hemisphere is decreased by $$20\%$$. What will be the percentage change in itscurved surface area?
The radius of a sphere is 10 cm. If the radius is increased by 1 cm, then prove that volume of the sphere increases by 33.1$$\%$$.
The volume of a sphere is $$4851\ cm^{3}$$. How much should its radius be reduced so that its volume become $$\dfrac{4312}{3}\ cm^{3}$$?
The diameter of a sphere is decreased by $$25 \%$$ . By what per cent does its curved surface area decrease?
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is $$14$$$$\mathrm { cm }$$ and the total height of the vessel is $$13$$$$\mathrm { cm } .$$ Find the inner surface area of the vessel.
How much steel sheet was actually used, if $$\dfrac{1}{12}$$ of the steel was wasted in making the tank with diameter of 4.2 m and 4.5 m in height.
How many cubic centimeters of iron is required to construct an open box , whose external dimensions are 36 cm, 25 cm and 16.5 cm , provided the thickness of the iron is 1.5 cm . If one cubic cm of iron weight 7.5 g. Find weight of the box.
The radius of sphere is 5 cm. If the radius is increased by 20$$\%$$, then find the percentage increase in the volume?
The radius of a solid right circular cylinder increases by $$20\% $$ and its height decrease by $$20\% $$. Find the percentage change in its volume.
A village has a population of $$6000; \ 50$$ litres of water is required per person per day. The village has a water tank measuring $$60\ m\ \times \ 30\ m\ \times \ 8\ m$$ completely filled with water. For how many days the water of this tank is sufficient.
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients ?
Find the volume of the recycled material used in making the solid as shown in figure. It is given that diameter of cylinder is 20 cm and diameter of each of two equal conical cavity is 10 cm. What values are reflected by using recycled material ?
A wooden articles was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure. If the height of the cylinder is $$10\ cm$$, and its base is of radius $$3.5\ cm$$, find the total surface area of the article.
The largest sphere is curved out of cube of side $$14cm$$. Find surface area of sphere.
If surface areas of two spheres are in the ratio of $$4:9$$ ,then find the ratio of their volumes.
$$2$$ cubes of volumes $$664\ cm^{3}$$ are joined end to end. Fin the surface area of the reacting cuboid.
The inner diameter of a glass is $$7\ cm$$ and it has raised portion in the bottom in the shape of a hemisphere as shown in the figure. If the height of the glass is $$16\ cm$$, find the apparent capacity and the actual capacity of the glass, $$\left( Take\ \pi =\dfrac { 22 }{ 7 } \quad \right)$$

Find the volume of a cuboid measuring $$4$$m,$$2.5$$m and $$35$$cm
There are two cuboid boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
Find the surface area and lateral surface area of a cuboid measuring $$4\ cm$$ by $$3\ cm$$ by $$2\ cm$$.
Find the total surface area of a cuboid of its length, breadth and height are $$7$$ cm ,$$5$$cm, and $$10$$ cm respectively.
Find the volume of a cuboid measuring $$6\ m\times 4\ m\times 3\ m$$.
The surface area of a sphere is $$448 \, \text{cm}^2$$. then find its radius?
Find surface area of sphere if its radius is $$4\ cm$$.
A dome of a building is in the form of a hemisphere. From inside, it was whitewashed at the cost of Rs 498.if the cost of whitewashing is Rs 2.00 per square meter, find the inside surface area of the dome
Find the radius of a cylinder if its curved surface area is 352 $$cm^2$$ and its height is 16 cm.
Find the volume of cuboid whose dimensions are $$\left( x ^ { 2 } - 2 \right) , ( 2 x + 4 )$$ and $$( x - 3 ).$$
The dimensions of a cuboid are in the ratio of 1 : 2 : 3 and its total surface area is 88 $$m^{2}$$. Find the dimensions of the cuboid.
The area of three adjacent faces of a cuboid are $$x, y$$ and $$z$$. If $$V$$ is the volume of the cuboid, then prove that $$V^{2}=xyz$$.
Find the volume of a sphere of diameter $$6 \text{ cm}$$.
Find the volume of a sphere whose radius is
(i) 7cm (ii) 0.63m
A river $$3\ m$$ deep and $$40\ m$$ wide is flowing at the rate of $$2\ km$$ per hour. How much water wall fall into the sea in a minute?
A hall is $$15$$ m long and $$12$$ m broad. If the sum of the areas of the floor and the ceilling is equal to the sum of the areas of the four walls, the volume of the hall ( in $$m^3$$ ) is
The surface area of a cuboid is 4150 cm$$^{2}$$. If its length and breadth are 35 cm and 25 cm respectively, find its height.
A wooden box with lid is made of $$2.5\ cm$$ thick. Inner length, breadth and height of box are $$1\ m. 65\ cm$$ and $$55\ cm$$. Find the total expenditure of colouring its out surface area at the rate of $$Rs.15$$ per square meter.
Three cubes of metal whose edges are in the ratio $$3:4:5$$ are melted and formed into a single cube where diagonal is $$12\sqrt { 3 } cm$$ Find the edges of three cubes.
Find the area of cardboard required to prepare a closed box of dimensions $$12\ cm\times 10\ cm \times 8\ cm$$.
Find the surface area of a sphere of diameter:
$$21\ cm$$
Find the surface area of a sphere of diameter $$3.5\ cm$$.
Find the surface area of a sphere of diameter:
$$14\ cm$$
A box is $$1\ m$$ long, $$60\ cm$$ wide and $$40\ cm$$ high. Find the expenditure of colouring its all outer side without its bottom at the rate of $$Rs.20$$ per square meter.
The total surface area of a circular cylinder is $$1540$$sq.cm.If the height is four times the radius of the base , find the height of the cylinder.
Assuming pool is $$15\ m$$ in length, $$12\ m$$ in breadth and $$2\ m$$ in depth. Find the cost of cementing the floor and wall at the rate of $$Rs.15$$ per $$sq.m$$.
The radius and height of a cylinder are in the ratio $$7 : 2$$. If the volume of the cylinder is $$8316\ cm^{3}$$. Find the total surface area of the cylinder.
Find the missing measurement in each of the following:-
$$l=8cm$$
$$A=72sq cm$$ $$b=?$$
The volumes of the two spheres are in the ratio $$64:27$$. Find the ratio of their surface areas.
Four cubes of volume $$125\ cm^{3}$$ each are joined end to end in a row. Find the surface area of the resulting cuboid.
A cube of side $$4\ cm$$ contains a sphere touching its sides. Find the volume of the gap in between.
A cubical box has each edge 10$$\mathrm { cm }$$ and another cuboidal box is $$12.5 \mathrm { cm }$$ long, 10$$\mathrm { cm }$$ wide and $$8 \mathrm { cm }$$ high.
i) Which box has the greater lateral surface area and by how much?
ii) Which box has the smaller total surface area and by how much?
A vessel is in the form of an inverted cone. Its height is $$8$$cm and the radius of its top, which is open, is $$5$$cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius $$0.5$$cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
What is the surface area of a cube of side $$15\ cm$$?
The internal dimensions of a closed box, made up of iron $$1$$ cm thick, are $$24$$ cm by $$18$$ cm by $$12$$ cm. Find the volume of iron in the box.
A solid cubical block of wood costs Rs. $$256$$ at Rs. $$5.00 $$ per $${ m }^{ 3 }$$. Find its volume and the length each side.
$$1.1cm^{3}$$ of gold is drawn into a wire of $$0.1mm$$ in diameter.Find the length of the wire in metre.
Find the total surface area of a hemisphere of radius $$10\ cm$$.
The radius of a cylinder is $$7\ cm$$. The curved surface area is $$660\ cm^{2}$$. Find its height.
Two identical cubes are placed adjointly in a row. Find the ratio of total surface area of the new cuboid to that of the sum of the surface areas of two cubes.
Measure the volume of the following shape.
A hemisphere bowl is made of steel, $$0.25\ cm$$ thick. the inner radius of the bowl is $$5\ cm$$. Find the outer curved surface area of the bowl.
A swimming pool is 20m in length, 15m in breadth and 4m in depth. Find the cost of Painting its four walls at the rate of Rs. 20 per spuare metre.
An open box is made of 3cm thick. Its external length, breadth, and hights are 1.48 m, 1.16m, 8.3dm. Find the cost of painting the inner surface at 50 p per 100 $$cm^{2}$$
The curved surface area of a cylinder is $$ 2\pi (y^{2}-7y+12)$$ and its radius is (y-3). Find the height of the cylinder.
Find the surface area of a cuboid of length $$5$$m,breadth$$\,2$$m and height$$\,3$$m
A closed cylindrical tank of diameter $$21\ m$$ and height $$4\ m$$ is made of steel. How much area of steel sheet is required?
A rectangular room is $$6\ m$$ long, $$5\ m$$ wide and $$4\ m$$ high. Find the total surface area of the four walls.
Find the surface area of a sphere of radius $$6.5$$ cm.
A hemispherical tank full of water is emptied by a pipe at the rate of $$3\dfrac{4}{7}$$ litres per second. How much time will it take to make the tank half-empty, if the tank is $$3\ m$$ in diameter ?
A hemispherical bowl has inner diameter $$11.2$$ cm. Find the volume of milk it can hold.
The perimeter of a godown is 240 m . Length of the godown is double its breadth . Find the storage capacity of the godown if its walls are 8 m high .
Find the total surface area of the cuboids of length, breadth and height as given below
(i) 12 cm, 10 cm, 5 cm,
(ii) 5 cm, 3.5 cm, 1.4 cm.
(iii) 2.5 cm, 2m, 2.4 m
(iv) 8 m, 5m, 3.5 m
Find the surface area of a sphere of radius:
$$10.5$$cm
Find the total surface area of a hemisphere of radius $$10$$ cm. (Use $$\pi=3.14$$)
How many paint tins having speed capacity of $$100\ cm^{2}$$ will be required to paint external surface of box having dimensions $$80\ cm \times 50\ cm \times 25\ cm$$.
A cuboidal tin measures $$30\ cm\times 20\ cm\times 15\ cm$$. Fiind its volume.
The internal dimensions of a box are $$1.2$$m ,$$80$$cm and $$50$$cm. How many cubes each of edge $$7$$cm can be packed in the box with faces parallel to the side of the box. Also find the space left empty in the box.
Find the volume of sphere with radius $$12$$ cm.
A metallic sphere of radius $$15\ cm$$ is melted and recast into the shape of a cylinder of radius $$15\ cm$$. Find the height of the cylinder.
The dimensions of a room are given as $$l=12\text{ cm},\ b=10\text{ cm},\ h=8\text{ cm}$$. Find the total area of $$4$$ walls.
500 men took dip in a tank which is 80 m long, 50 m broad. What is the rise in water level if the average displacement of water by a man is 4 $$m^{3}$$
The diameter of a roller 1 m long is 70 cm. .If it takes 200 revolutions to level a playground, find the cost of levelling at the rate of 75 paisa per sq.m.
The floor of a cuboidal hall has perimeter equal to 250 m and height 6 m. Find the cost of painting its four walls (including doors etc) at the rate of Rs.8 per square metre.
Find the volume of metal used to construct a hollow metallic sphere of internal and external diameters as $$10$$ cm and $$13$$ cm respectively.
An aquarium is in the form of a cuboid whose external measures are $$70\text{ cm}\times 28\text{ cm}\times 35\text{ cm}$$. The base, side faces, and back faces are to be covered with colored paper. Find the area of the paper needed.
The curved surface area of a cylinder is $$1980\ { cm }^{ 2 }$$ and the radius of its base is $$15\ cm$$. Find the height of the cylinder.$$\left( { \pi } = \dfrac { 22 }{ 7 }\right)$$
A lateral surface area of cube is $$256 { m }^{ 2 }$$. find its volume
Find the total surface area of a hemisphere of radius $$10\ cm$$. $$(use\,\,\pi = 3.14)$$
The water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank contains 50 kilolitres of water. Water is pumped into the tank to fill to its capacity. Find the volume of water pumped into the tank.
The height of cylinder is $$7cm$$ its radius is $$5cm$$ find its Total surface area and Curved surface area
How many planks each of which is 2 m long, 2.5 cm broad and 4 cm thick can be cut-off from a wooden block 6 m long, 15 cm broad and 40 cm thick?
If the edge of a cube is doubled. Find the ratio of the original volume to new volume.
If the volume of a cylinder is $$3080 \ \text{cm}^3$$ and the base radius is $$7$$ cm, find the total surface area of the cylinder.
An ice cream cone is the union of a right circular cone and a hemisphere that has the same circular base as the cone. Find the volume of the ice cream, if the height of the cone is $$9\ cm$$ and the radius of its base is $$2.5\ cm$$.
A solid in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is $$2.1\ cm$$ and the height of the cone is $$4\ cm$$.The solid is placed in a cylindrical vessel ,full of water ,in such a way that the whole solid is submerged in water.If the radius of the cylindrical vessel is $$5\ cm$$ and its height is $$9.8\ cm$$ ,find the volume of water left in the tub to the nearest $$cm^3$$.
The paint in a certain container is sufficient to paint an area equal to $$9.375\,\,{m^2}.$$ How many bricks of dimensions $$22.5\,\,cm \times 10\,\,cm \times 7.5\,\,cm$$ can be painted out of this container ?
The lateral or curved surface area of a closed cylindrical petrol storage tank that is $$4.2$$ m in diameter and $$4.5$$ m high.
The length, breadth and height of a cuboid are $$10$$ cm, $$5$$ cm and $$3$$ cm. Find its volume.
Find the volume of a sphere whose surface area is $$154\ \text{cm}^2.$$
The $$TSA$$ of cube $$=726\ cm^ {2}$$ find the edge. (in cm)
Find the total surface area of a solid cylinder of radius $$5\,cm$$ and height $$10\,cm$$. Leave your answer in term of $$\pi$$.
A shot-put is a metallic sphere of radius $$4.9\ cm$$. If the density of the metal is $$7.8\ g\ per\ cm^{3}$$, find the mass of the shot-put. (Take $$\pi=22/7$$)
If the total surface area of a cuboid whose length is equal to $$12 \text{ cm}$$ and breadth is equal to $$9 \text{ cm}$$ is equal to $$468 \text{ cm}^2$$ then find the height of the cuboid.
A cylindrical tub of radius 12 $${cm}$$ contains water to a depth of 20$${cm}$$. A spherical ball is dropped into the tub and the height of the water is raised by 6.75$$cm$$. Find the radius of the ball
The volume of a metallic cylindrical pipe is 748 $${ cm }^{ 3 }$$ . Its length is 14 cm and its external radius is 9 cm .Find its thickness .
The length, breadth and height of a cuboid are in the ratio $$6 : 4 : 7$$. If total surface area of the cuboid is given as $$1692\ \text{ cm }^{ 2 }$$, find its volume.
A cubical block of edge 22 cm is melted into small sphases of radius 1 cm. calculate the number of sphases that can be made from it.
A cubical box has each edge $$10$$cm and another cuboidal box is $$12.5$$cm long,$$10$$cm wide and $$8$$ cm high. Which box has the smaller total surface area and by how much?
A matchbox is 4 cm long, 2.5 am broad and 1.5 cm in height. Its outer sides are to be covered exactly with craft paper. How much paper will be required to do so ?
In a building there are 4 cylindrical pillars. The radius of each pillar is 21 cm and height is 5 m. Find the curved surface area of four pillars.
Find the volume of the hemisphere of diameter $$6r$$ units.
How many cubic cm, of wood are there in a box, which measures 24 cm by 22 cm by 17 cm
The radius of the base of a cylinder is $$20$$ cm and in height $$13$$ cm. Find its curved surface area.
The side of a cubical chalk box is $$4\,cm$$. Find the total surface area of the chalk box a length of its diagonal.
Find the radius of a sphere whose surface area is $$154 { cm }^{ 2 }$$.
A hemispherical tank is made up of an iron sheet 1 cm thick, If the inner radius is 7 cm then find the volume of the iron used to make the tank.
Radius of a cylinder is $$r$$ and height is $$h$$. find the change in the volume, if the height is doubled and radius half.
Find the volume of the cuboidal object : length $$= 80 \mathrm { cm },$$ width $$= 45 \mathrm { cm },$$ height $$= 40 \mathrm { cm }$$ and volume $$=?$$
A solid spherical ball of radius $$r$$ is converted into a solid circular cylinder of radius $$R$$. If the height of the cylinder is twice the radius of the sphere ,then find the relation between these two with respect to radius.
The internal measures of a cuboidal room are $$12m\times 8m\times 4m.$$ Find the total cost of whitewashing all four walls of a room, if the cost of white washing is 5 per $${ m }^{ 2 }.$$ What will be the cost of white washing if the ceiling of the room is also whitewashed.
The total surface area of a cuboid of length 6 m and breadth 5 m is 126 sq. m. Find its height.
Find the area of four walls of a room whose length is 3.5, breadth 2.5 m and height 3m.
Find the surface area of a cuboid whose length is 0.5 m, breadth 25 cm and height 15 cm ?
Write the number of surfaces of a right circular cylinder.
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand .

Length, breadth and height of a cuboid shape box of medicine is $$20\ { cm },12\ { cm }$$ and$$10\ { cm } .$$ respectively. Find the surface area of vertical faces and total surface area of this box.
Each edge of a cube is increased by $$20\%$$ .What is the percentage increase in surface area of the cube?
The surface area of a sphere is $$5544 cm^{2}$$, find its diameter in $$cm$$.
Find the volume of a sphere (in $$cm^3$$) whose radius is : 10.5 cm
Find the surface area of a sphere in $$(cm^{2}$$) if its diameter is $$3.5 cm$$.
Find the volume of a sphere (in $$cm^3$$) whose diameter is : 14 cm
Find the volume of a sphere(in $$dm^3$$) whose diameter is : 3.5 dm
Find the volume of a sphere (in $$cm^3$$) whose radius is : 2 cm
Find the surface area of a sphere, if its diameter is $$21 cm$$.
Find the volume of a sphere whose radius is 3.5 cm.
How many bullets can be made out of a cube of lead, whose edge measures $$22\ cm,$$ each bullet being $$2\ cm$$ in diameter?
A cylinder whose height is two-thirds of its diameter has the same volume as a sphere of radius $$4$$ cm. Calculate the radius of the base of the cylinder(in cm).
A hemi-spherical dome of a building needs to be painted. If the circumference of the base of the dome is 17.6 m, find the cost of painting it, given the cost of painting is Rs. 5 per $$100\, cm^{2}$$.
Find the volume in cubic metre $$(cu.m)$$
length $$=10\ m$$, breadth $$=25\ dm$$, height $$=25\ cm$$
Find the volume (in $$cm^3$$) of a cuboid whose length is $$15\ cm$$, breadth is $$2.5\ cm$$ and height is $$8\ cm$$.
The area of the base of a right circular cylinder is $$ 616 cm^2 $$ and its height is $$2.5$$ cm. find the curved surface area of the cylinder.
Find the volume of a sphere (in $$m^3$$) whose diameter is : $$2.1$$ m
Fill in the blanks in each of the following so as to make the statement true:
The volume of a cube of side $$8\ cm$$ is .........
Find the surface area(in $$dm^2$$) of a cuboid whose
length $$=3.2\ m$$, breadth $$=30\ dm$$, height $$=250\ cm$$.
Find the surface area of a cuboid whose
length $$=6\ dm$$, breadth $$=8\ dm$$, height $$=10\ dm$$
Find the value of $$a$$
$$1\ cu.km= 10^a \,\,cu.m$$
Fill in the blanks in each of the following so as to make the statement true:
The volume of a wooden cuboid of length $$10\ cm$$ and breadth $$8\ cm$$ is $$4000\ cm^{3}$$.
The height of the cuboid is ......... $$cm$$.
Fill in the blanks in each of the following so as to make the statement true:
$$1\ ml=......cu.cm$$
Find the surface area of a cuboid whose length $$=2\ m$$, breadth $$=4\ m$$, height $$=5\ m$$.
Find the surface area (in m$$^2$$) of a cube whose edge is 1.2 m.
Fill in the blanks in each of the following so as to make the statement true:
$$1\ cu.dm= ........ cu.mm$$
Find the surface area of a cuboid whose
length = 10 cm, breadth = 12 cm, height = 14 cm.
The square on the diagonal of a cube has an area of $$1875\ sq. cm$$. Calculate the total surface area of the cube.
The surface area of a sphere is $$2464 cm^2$$. If its radius be doubled,then what will be the surface area of the new sphere?
Find the surface area (up to two decimal places) of a cube whose edge length is $$2.1\ m$$
Two cubes each of volume $$27 cm^3$$ are joined end to form a solid. Find the surface area of the resulting cuboid.
What is the shape of:
a brick
Find the surface area of a cube whose edge is
$$3\ cm$$
If the total surface area of a solid hemisphere is $$462 \ cm^2$$, them find its volume.
Find the surface area (in $$cm^2$$)of a cube whose edge is
$$27\ cm$$
The square on the diagonal of a cube has an area of $$1875\ sq. cm.$$ Calculate the side of the cube.
A cuboidal box is $$5\ cm$$ by $$5\ cm$$ by $$4\ cm$$. Find its surface area.
A box made of sheet metal costs $$Rs. 6480$$ at $$Rs. 120$$ per square metre. If the box is $$5m$$ long and $$3m$$ wide, find its height.
The lateral surface area of a cylinder is $$94.2\ cm^{2}$$ and its height is $$5\ cm$$. Find the radius of its base
The capacity of a closed cylindrical vessel of height $$1\ m$$ is $$15.4$$ litres. Find the area of the metal sheet needed to make it.
A matchbox measure $$4cm \times 2.5cm\times 1.5\ cm$$. What is the volume of a packet containing $$12$$ such matchboxes?
The volume of a cube is $$729 cm^3.$$Find its surface area
Find the volume, the lateral surface area and the total surface area of the cuboid whose dimensions are :
length $$=24m$$, breadth $$=25cm$$ and height $$=6m$$.
The curved surface area of a right circular cylinder is $$4.4\ m^{2}$$. If the radius of its base is $$0.7\ m$$, find its height
The surface area of a cuboid is $$758cm^2$$. Its length and breadth are $$14cm$$ and $$11cm$$ respectively. Find its height.
Find the volume, the lateral surface area and the total surface area of the cuboid whose dimensions are :
length $$=15\ m$$, breadth $$=6\ m$$ and height $$=5\ cm$$
Find the volume, the lateral surface area and the total surface area of the cuboid whose dimensions are :
length $$=12\;cm$$, breadth $$=8\;cm$$ and height $$=4.5\;cm$$
Find the volume of a sphere whose surface area is $$154\ cm^2$$.
$$1\ cm^{3}$$ of gold is drawn into a wire $$0.1\ mm$$ in diameter. Find the length of the wire.
The surface area of sphere is $$(576 \pi)cm^2$$. Find its volume.
A cylindrical tub of radius $$12cm$$ contains water into a depth of $$20cm$$. A spherical ball is dropped into the tub and thus the level of water is raised by $$6.75cm$$. What is the radii of the ball?
The radius of the base and the height of a cylinder are in the ratio $$2:3$$. If its volume is $$1617\ cm^{3}$$, find the total surface area of the cylinder.
Find the volume and surface area of a sphere whose radius is:
$$3.5\ cm$$
A cylindrical bucket with base radius $$15cm$$ is filled with water up to a height of $$20cm$$. A heavy iron spherical ball of radius $$9cm $$ is dropped into the bucket to submerge completely in the water. find the increase in the level of water .
The volume of a cube is $$512 cm^3$$. Find its surface area.
A hemispherical bowl made of brass has an inner diameter $$10.5cm$$. Find the cost of tin-plating it on the inside at the rate of $$Rs. 32$$ per $$100cm^2$$?
In a water heating system there is a cylindrical pipe of length $$28\ cm$$ and diameter $$5\ cm$$. Find the total radiating surface in the system.
Find the volume, lateral surface area and the total surface area of the cuboid whose dimension are:
Length $$=15\ m$$, breadth $$=6\ m$$ and height $$=9\ m$$
Find the volume of a sphere of radius:
(i) $$0.63 \ m$$
(ii) $$11.2 \ cm$$
Count the number of cubes in the given shape
A pen stand made of wood is in the shape of cuboid with four conical depressions and a cubical depression to hold the pens and pins respectively. The dimensions of cuboid are $$10cm,5cm,4cm$$. The radius of each of the conical depression is $$0.5 cm$$ and depth is $$2.1cm$$. The edge of the cubical depression is $$3cm$$. Find the volume of the wood in the entire stand.
Find the diameter of a sphere whose surface area is $$154 \ cm^2$$.
Find the volume, lateral surface area and the total surface area of the cuboid whose dimension are:
Length $$=24\ m$$, breadth $$=25\ cm$$ and height $$=6\ m$$
The radius and height of a cylinder area in the ratio $$7:2$$. If the volume of the cylinder is $$8316\ cm^{3}$$, find the surface area of cylinder.
The figure
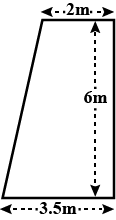
Given below shows the cross of a concrete wall to be constructed. It is 2 m wide at the top, 3.5 m wide at the bottom and its height is 6 m and its length is 400 m . Calculate
Volume of concrete in the wall.
The given figure shows a metal pipe $$77cm$$ long. The inner diameter of cross section is $$4cm$$ and the outer one is $$4.4cm$$.
Find its
(i) inner curved surface area
(ii) outer curved surface are
(iii) total surface area
A cuboidal fish tank has a length of $$30cm$$, a breadth of $$20cm$$ and a height of $$20cm$$. The tank is placed on a horizontal table and it is three-quarters full of water. Find the area of the tank which is in contact with water.
The lateral surface area of a cuboid is $$224{cm}^{2}$$. Its height is $$7cm$$ and the base is a square. Find
(i) side of the square base
(ii) the volume of the cuboid
The volume of a cuboid is $$448{cm}^{3}$$. Its height is $$7cm$$ and the base is a square. Find
(i) a side of the square base
(ii) surface area of the cuboid
Two identical cubes each of volume $$64cm^{3}$$ are joined together end to end. What is the surface area of the resulting cuboid?
Find the volume of rectangular boxes with the following length, breadth and height respectively:
$$2pq, 4q^2, 8rp$$
Cardboard boxes of two different sizes are made. The bigger has dimensions $$20\text{ cm}, 15\text{ cm}$$ and $$5\text{ cm}$$ and the smaller dimensions $$16\text{ cm}, 12\text{ cm}$$ and $$4\text{ cm}$$. $$5\%$$ of the total surface area is required extra for all overlaps. If the cost of the cardboard is $$\text{Rs. }20$$ for one square meter, find the cost of the cardboard for supplying $$200$$ boxes of each kind.
The volume of one sphere is $$27$$ times that of another sphere. Calculate the ratio of their radii.
The length, breadth and height of a cuboid are in the ratio 5:3:2. If its volume is $$240cm^3$$ find its dimensions. (Dimensions means: its length, breadth and height). Also find the total surface area of the cuboid
The diameter of a Cinema Hall are $$100\ m, 60\ m$$ and $$15\ m$$. How many person can sit in the hall, if each requires $$150\ cm^3$$ of air?
The volume of a cube is $$729\ cm^3$$. Find its total surface area.
A largest sphere is to be carved out of a right circular cylinder of radius $$7$$ cm and height $$14$$ cm. Find the volume of the sphere. (Answer correct to the nearest integer)
A closed box is cuboid in shape with length $$40\text{ cm}$$, breadth $$30\text{ cm}$$ and height $$50\text{ cm}.$$ It is made of a thin metal sheet. Find the cost of metal sheet required to make $$20$$ such boxes, if $$ 1 \text{m}^{2}$$ of metal sheet costs $$\text{Rs. } 45$$
Find the volume and the total surface area of a cuboid, whose:
Length = 15cm, breadth = 10cm and height = 8cm
The surface area of a sphere is $$2464\,cm^2$$, find its volume.
The length, breadth and height of a room are $$6 m$$, $$5.4 m$$ and $$4 m$$ respectively. Find the area of its four walls.
Find the volume of a sphere, if its surface area is $$154\ sq.cm$$
The square on the diameter of a cube has an area of $$1875\ sq. cm$$. Calculate:
The side of the cube
The square on the diameter of a cube has an area of $$1875\ sq. cm$$. Calculate:
The total surface area of the cube
Find the total surface area of a cylinder if the radius of its base is $$5$$ cm and height is $$40$$ cm.
If the radius of a solid hemisphere is $$5\ cm$$, then find its curved surface area and total surface area $$(\pi=3.14)$$
If the surface area of a sphere is $$2856\ cm^{2}$$ then find its volume. $$(\pi=3.14)$$
Volume of a hemisphere is $$18000\pi$$ cubic $$cm$$. Find its diameter.
Side of a cube is $$4.5\ cm$$. Find the surface area of all vertical faces and total surface area of the cube.
A cubical box has edge $$10m$$ and another cubical box is $$12.5cm$$ long, $$10cm$$ wide and $$8cm$$ high
If each edge of the cube is doubled, how many times will its $$T.S.A$$ increase?
A cubical box has edge $$10m$$ and another cubical box is $$12.5cm$$ long, $$10cm$$ wide and $$8cm$$ high
Which has a smaller total surface area?
Each of the faces of the cube is 100 sq. $$ \mathrm{cm} $$. If the cube Is cut of parallel to its base and divided into two equal parts. Find the total surface area of each part separately.
A closed box is $$40m$$ long, $$50cm$$ wide and $$60$$ deep. Find the area of the foil needed for coverage it.
A box with out upper lid is made of wood of width 3 cm. Its external length, breadthand height are $$ 146 \mathrm{cm}, 116 \mathrm{cm} $$ and $$ 83 \mathrm{cm} $$ respectively.Find cost of painting inside if the rate of painting $$ = 2 $$ per 1000 sq.cm.
The height, breadth and length of a cuboid are $$ 5 \mathrm{cm}, 9 \mathrm{cm} $$ and $$ 12 \mathrm{cm} $$ respectively. Find the total surface area and the volume of cuboid.
The measures of a box are $$ 50 \mathrm{cm} \times 36 \mathrm{cm} \times 25 \mathrm{cm} $$. To make the cover of the box.How much cloth is needed?
The length, breadth and height of a cuboid are in the ratio $$5:3:2$$ If its volume is $$1078.110 mm^3$$ find its dimension. Also find the total surface area of the cuboid
If the width of a hollow cylinder is $$ 2 \mathrm{cm} $$. Its internal diameter is $$ 14 \mathrm{cm} $$ and height $$ 26 \mathrm{cm} $$. The two ends ofcylinder are opened. Find the total surface area of the hollow cylinder.
The height and the radius of a cylinder are $$ 7.5 \mathrm{cm} $$ and $$ 3.5 \mathrm{cm} $$ respectively. Find the ratio of its total surface area and curved surface area.
The ratio of radii of two right circular cylinders is $$2:3$$ and the ratio of their heights is $$5:4$$. Find the ratios of their curved surface areas and volumes.
The ratio of the length, breadth, and height of a cuboid is 5: 3:If the total surface area of the cuboid in 558 cm$$^2$$. Find the length of its sides.
A room contains $$ 180 \mathrm{m}^{3} $$ air in it. Find the height of the room if its floor is a square with side 6 meters.
The surface area of a sphere is $$ 616 \mathrm{cm}^{2} $$. Find the volume of the sphere.
In a cylindrical vessel $$ 30800 \mathrm{cm}^{3} $$ water can be filled. If the internal radius of vessel is $$ 14 \mathrm{cm} $$. Find it curved surface area.
The height of a right circular cylinder is $$ 7 \mathrm{cm} $$ and radius is $$ 3 \mathrm{cm} $$. Find its curvedsurface area, total surface area and volume.
The sum of the length, breadth and height of a cuboid is $$ 19 \mathrm{cm} $$ and the length of its diagonal is $$ 11 \mathrm{cm} $$. Find the total surface area of the cuboid.
The area of one end of a cylinder is $$ 154\ {cm}^{2} $$ and its height is $$ 21\ {cm} $$. Find the volume and curved surface area of cylinder.
A cuboid has volume $$288\ cm^{3} $$.
$$1\ cm^{3}$$ of the cuboid has a mass of $$4\ g $$.
Work out the mass of the cuboid.
A cuboid has volume $$288\ cm^{3} $$.
The cuboid has length $$12\ cm $$ and width $$5\ cm $$.
Calculate the height of the cuboid.
If surface area of a sphere in $$ 5544 \mathrm{cm}^{2} $$, then find its volume.
A right circular cylinder is $$3m$$ high and the circumference of its base is $$22 m$$. Find its curved surface area.
The diameter of a sphere is $$ 0.7 \mathrm{cm} $$. From a water tank, 3000 spheres completely filled with water is thrown out. Find the volume of the water thrown out.
Find the surface area of a sphere of radius $$3.5 cm$$.
How many square centimeters will be required to cover the box whose dimensions are $$40\,cm$$, $$30\,cm$$, and $$20\,cm$$ respectively?
Radius of a hemisphere is $$ 4.5 \mathrm{cm} $$. Find its total surface area and volume.
A cubical vessel contains $$8$$ litres of water. Find the total surface area of the vessel.
A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of $$498.96$$. If the cost of white-washing is $$2.00$$ per square metre, find
(i) the inside surface area of the dome and
(ii) volume of the air inside the dome.
Shanti sweets stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions $$25\ cm$$ $$\times 20\ cm$$ $$\times 5\ cm$$ and the smaller of dimensions $$15\ cm$$ $$\times 12\ cm$$ $$\times 5\ cm$$. For all the overlaps, $$5\% $$of the total surface area is required extra. If the cost of the cardboard is $$4$$ for $$1000\ {cm}^{2}$$, find the cost of cardboard required for supplying $$250$$ boxes of each kind.
A wooden bookshelf has external dimensions as follows:
Height $$=110\text{ cm}$$ , Depth $$=25\text{ cm}$$ , and Breadth $$=85\text{ cm}$$ (see figure). The thickness of the plank is $$5\text{ cm}$$ everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is $$20$$ paise per $$\text{cm}^{2}$$ and the rate of painting is $$10$$ paise per $$\text{cm}^{2}$$, find the total expenses required for polishing and painting the surface of the bookshelf.
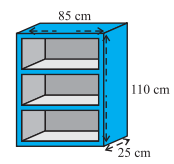
The diameter of a sphere is decreased by $$25\%$$. By what percent does its curved surface area decrease?
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius $$r$$ is $$\dfrac {4r}{3}$$. Also find maximum volume in terms of volume of the sphere
OR
Find the intervals in which $$f(x) = \sin 3x - \cos 3x, 0 < x < \pi$$, is strictly increasing or strictly decreasing
Find the volume of a sphere whose radius is $$7$$ cm.
The diameter of a roller 120 cm long is 84 cm. If it takes 500 completed revolutions to level a play ground, determine the cost of levelling it at the rate of Rs. 2.50 per square metre.
Find the area of four walls of a room having length, breadth and height as $$8$$ m, $$5$$ m and $$3$$ m respectively. Find the cost of white-washing the walls at the rate of Rs. $$15 / m^2$$.
Using clay, a student made a right circular cone of height $$48$$ cm and base radius $$12$$ cm. Another student reshapes it in the form of a sphere. Find the radius of the sphere.
The length, breadth and height of a cuboid are in the ratio $$5 : 3 : 2$$. If its volume is $$35.937 \ m^3$$, find its dimension. Also find the total surface area of the cuboid.
A hemispherical bowl made of wood has inner diameter of $$10.5$$cm. Find the cost of painting it on the inside at the rate of Rs.$$12$$ per $$100cm^2$$.
Prove that the volume of largest cone that can be inscribed in a sphere of radius R is $$\displaystyle\frac { 8 }{ 27 } $$ of the volume of the sphere.
The diameter of the moon is approximately one-fouth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
If $$V$$ is the volume of cuboid whose length is '$$a$$', breadth is '$$b$$' and height is '$$c$$' and '$$s$$' is the surface area, then prove that
$$\cfrac { 1 }{ v } =\cfrac { 2 }{ s } \left( \cfrac { 1 }{ a } +\cfrac { 1 }{ b } +\cfrac { 1 }{ c } \right) $$
A metal pipe is 77 cm77 cm long. The inner diameter of a cross-section is 4 cm4 cm, the outer diameter being 4.4 cm4.4 cm, then find its total surface area.

Evaluate $$\displaystyle \int { \frac { dx }{ \sqrt { \left( x-\alpha \right) \left( \beta -x \right) } } ,\beta >\alpha }$$
The sum of length, breadth and depth of a cuboid is 19cm and the length of its diagonal is 11cm. Find the area of cuboid.
The surface area of solid metallic sphere is $$1256$$ sq. m. Calculate radius.
Find the total surface area of a solid hemisphere of radius 10 cm. [Use $$\pi =3.14$$]
From a solid wooden cube of sides $$14\ cm$$ a biggest hemispherical depression is carved out. What is the total surface area of the remain solid?
An open box of length $$1.5 m$$, breadth $$1m$$, and height $$1m$$ is to be made for use on a trolley for carrying garden waste. How much sheet metal will be required to make this box? The inside and outside surface of the box is to be painted with rust proof paint. At a rate of $$150$$ rupees per sqm, how much will it cost to paint the box?
In each example given below, radius of base of a cylinder and its height are given. Then find the curved surface area and total surface area.
(1) r=7 cm, h= 10 cm
(2) r=1.4 cm, h= 2.1 cm
(3) r= 2.5 cm, h=7 cm
(4) r =70 cm, h= 1.4 cm
(5) r=4.2 cm, h=14 cm
Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of $$15$$m, $$10$$m and $$7$$m respectively. From each can of paint $$100m^2$$ of area is painted.
A godown measures $$40m\times 25m\times 10m$$. Find the maximum number of wooden crates each measuring $$1.5m\times 1.25m\times 0.5m$$ that can be stored in the godown.
Radius of a spherical ballon is increasing with respect to time at the rate of $$2/\pi$$ m/s. Find the rate of change in volume (in $$m^3/s$$) of the ballon when radius is 0.5 m ?
if $$V$$ is the volume of a cuboid of dimensions $$a,b,c$$ and $$S$$ is its surface area, then prove that
$$\cfrac{1}{V}=\cfrac{2}{S}(\cfrac{1}{a}+\cfrac{1}{b}+\cfrac{1}{c})$$
Find the volume of a sphere of radius 2.1 cm.
Mary wants to decorate her Christmas tree. She wants to place the tree on a wooden block covered with colored paper with a picture of Santa Claus on it. She must know the exact quantity of paper to buy for this purpose. If the box has length, breadth and height as $$80cm,40cm$$ and $$20cm$$ respectively. How many square sheets of paper of side $$40cm$$ would she require?
If the length of a cuboid is doubled, breadth is halved and height remains the same, find the ratio of the volume of the original cuboid to the volume of the new cuboid.
A cuboid has total surface area of $$372 \text{ cm}^{2}$$ and its lateral surface area is $$180 \text{ cm}^{2}$$, find the area of its base.
If the perimeter of each face of a cube is $$32cm$$, find its lateral surface area. Note that four faces which meet the base of a cube are called its lateral faces.
The radius of a sphere is $$9 \ cm$$. It is melted and drawn into a wire of diameter $$2 \ mm$$. Find the length of the wire in metres.
Water in a canal $$30dm$$ wide and $$12dm$$ deep, is flowing with a velocity of $$100km$$ per hour. How much area will it irrigate in $$30$$ minutes, if $$8cm$$ of standing water is desired?
Find the edge of a cube whose surface area is $$432{m}^{2}$$.
The radius and height of a cylinder are in the ration 3 : 2 and its volume is 19404 cmFind its radius and height.
The surface area of a cuboid is $$1300\ {cm}^{2}$$. If its breadth is $$10\ cm$$ and height is $$20\ {cm}^{2}$$, find its length.
Find the volume, the lateral surface area and the total surface area of the cuboid whose dimensions are :
length $$=26m$$, breadth $$=14m$$ and height $$=6.5m$$
The areas of three adjacent faces of a cuboid are $$x,y,z$$. If the volume is $$V$$, prove that $${V}^{2}=xyz$$
Three cubes of each side $$4cm$$ are joined end to end. Find the surface area of the resulting cuboid.
A swimming pool is 50 metres long and 15 metes wide and 15 meters wide. Its shallow and deep ends are $$1\dfrac { 1 }{ 2 } $$ meters and $$4\dfrac { 1 }{ 2 } $$ meters deep respectively.If the bottom of the pool slopes uniformly, find the amount of water required to fill the pool.
The thickness of a hollow metallic cylinder is 2 cm. It is 70 cm long with outer radius of 14 cm. Find the volume of the metel used in making the cylinder assuming that it is open at both the ends Also find its weight if the metal weighdds 8 g per cm3.
Class 9 Maths Extra Questions
- Areas Of Parallelograms And Triangles Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Heron'S Formula Extra Questions
- Introduction To Euclid'S Geometry Extra Questions
- Linear Equations In Two Variable Extra Questions
- Lines And Angles Extra Questions
- Number Systems Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadrilaterals Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions