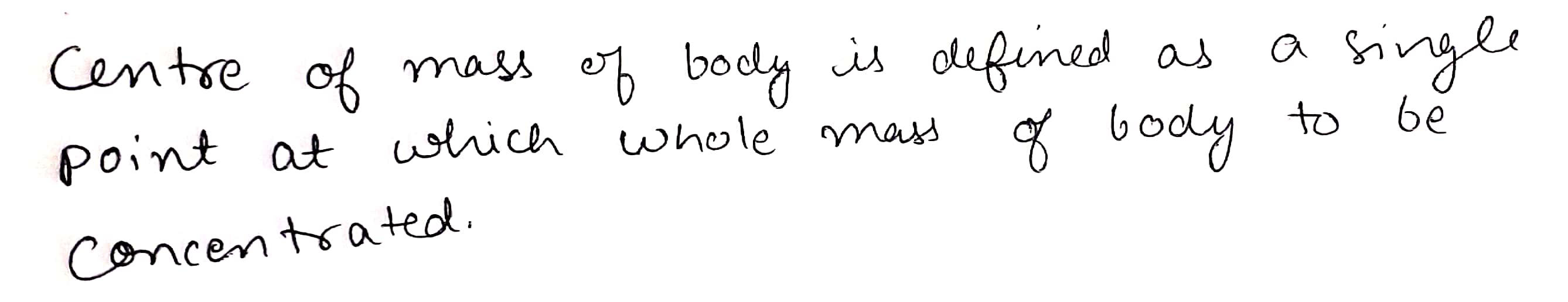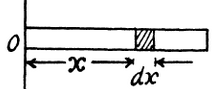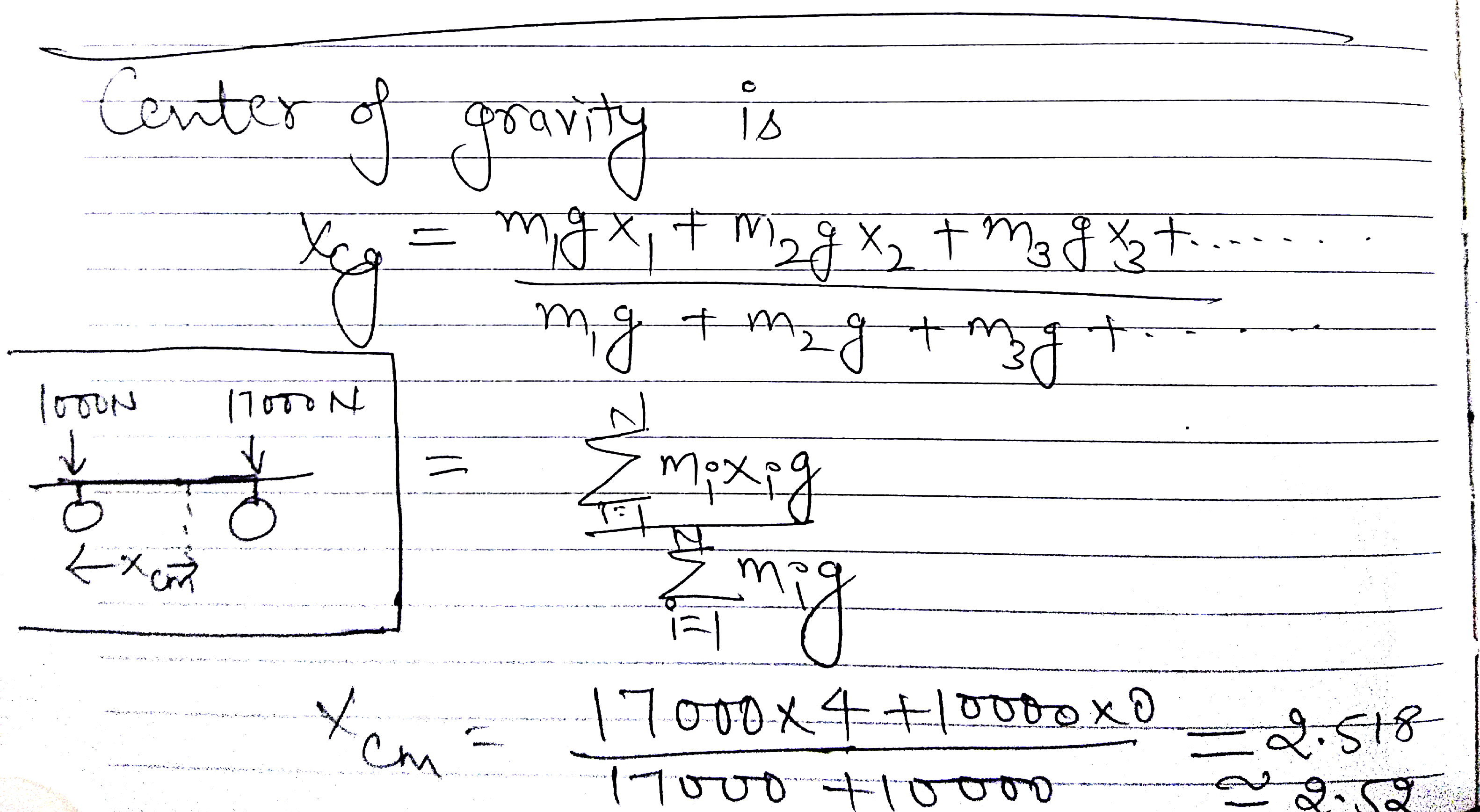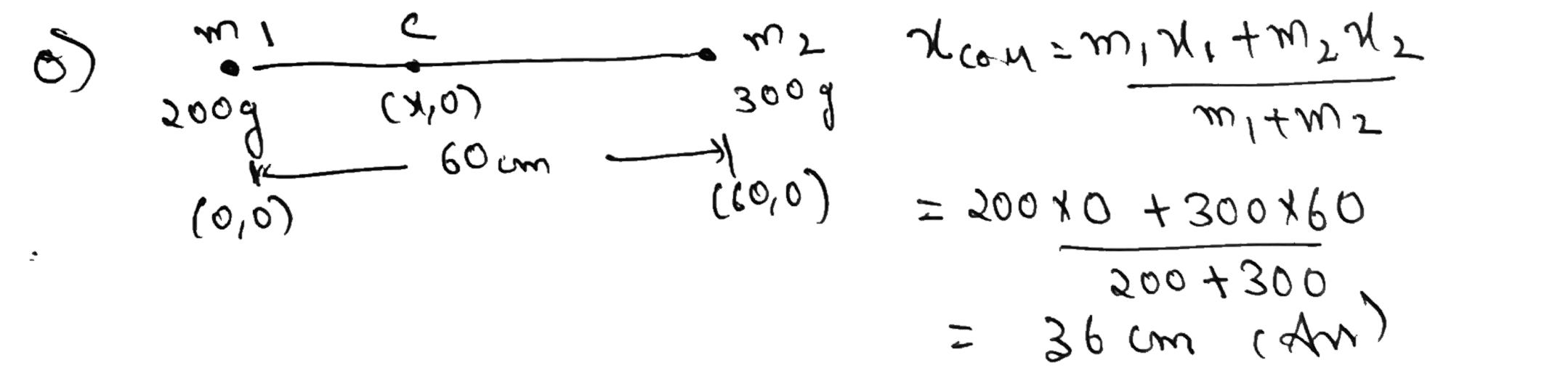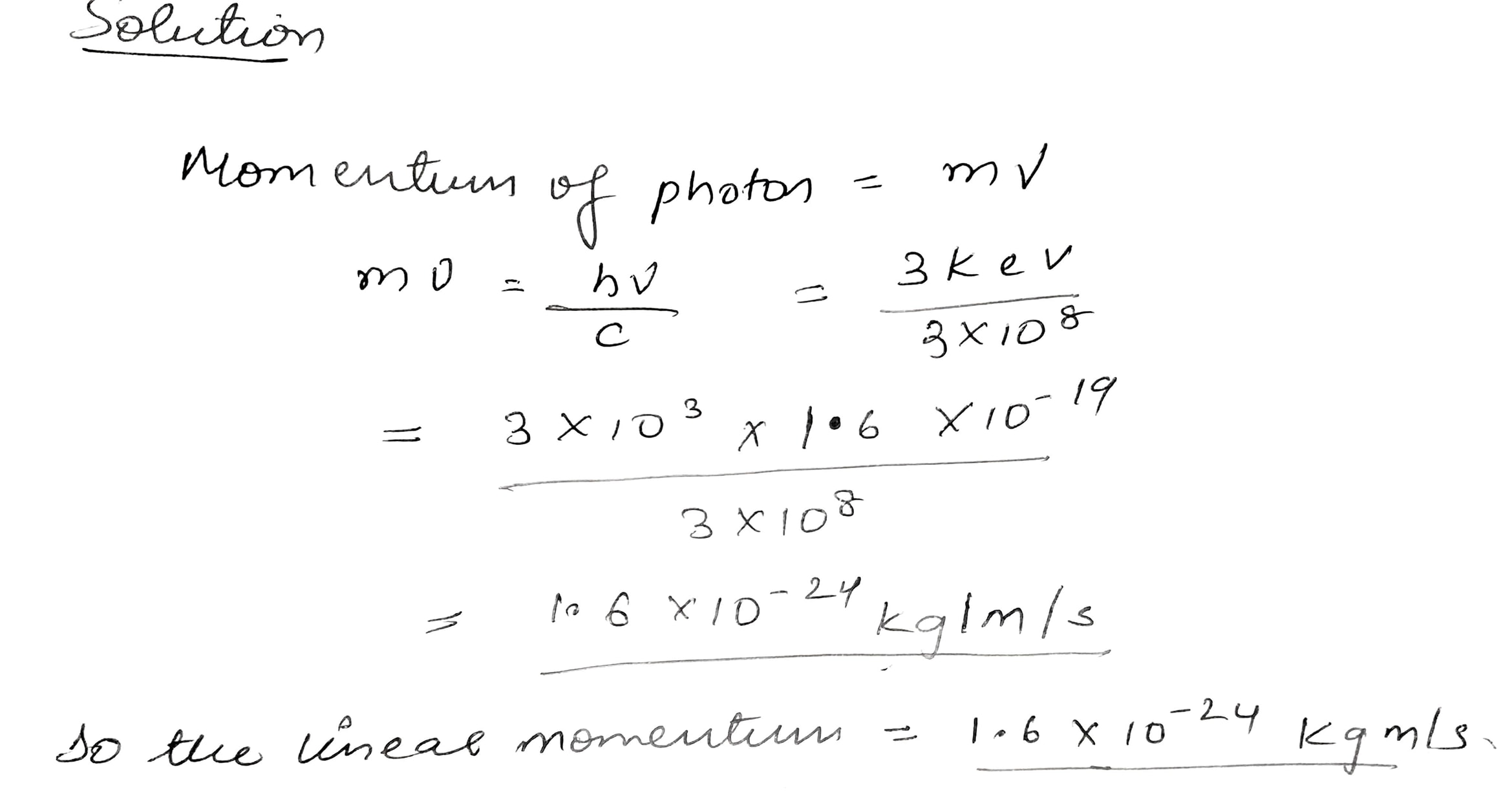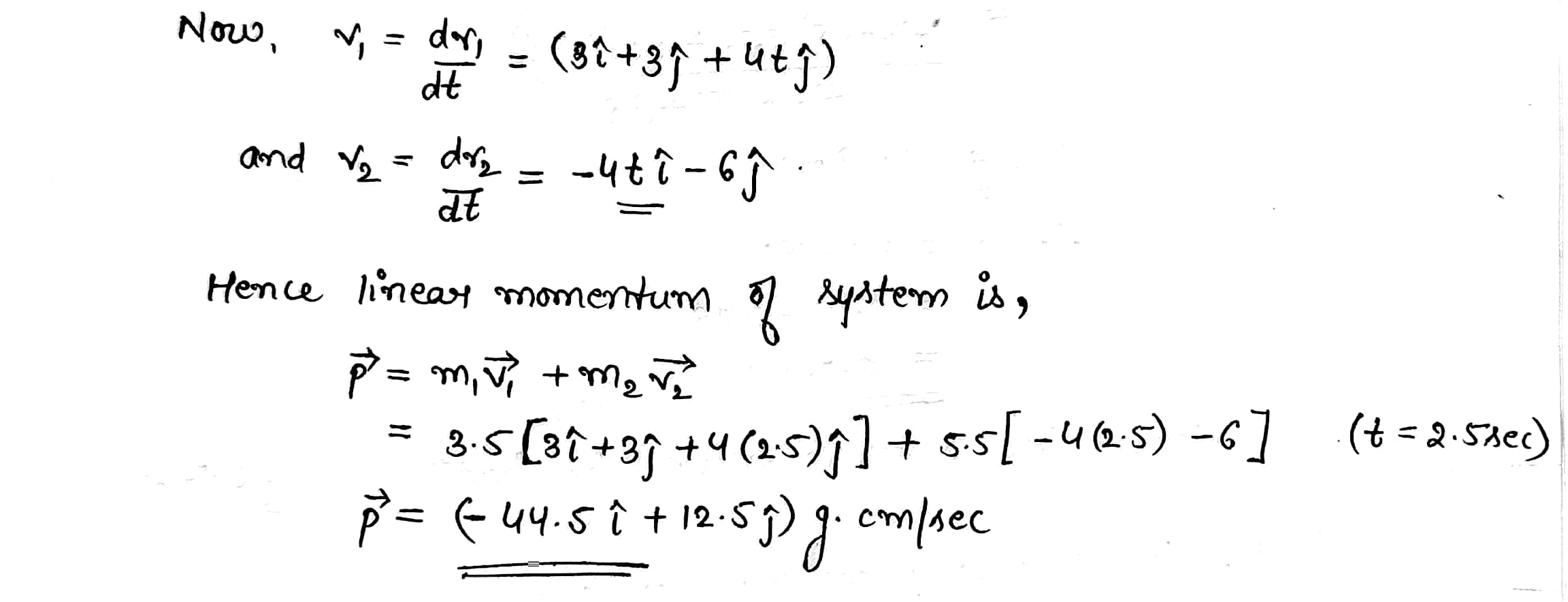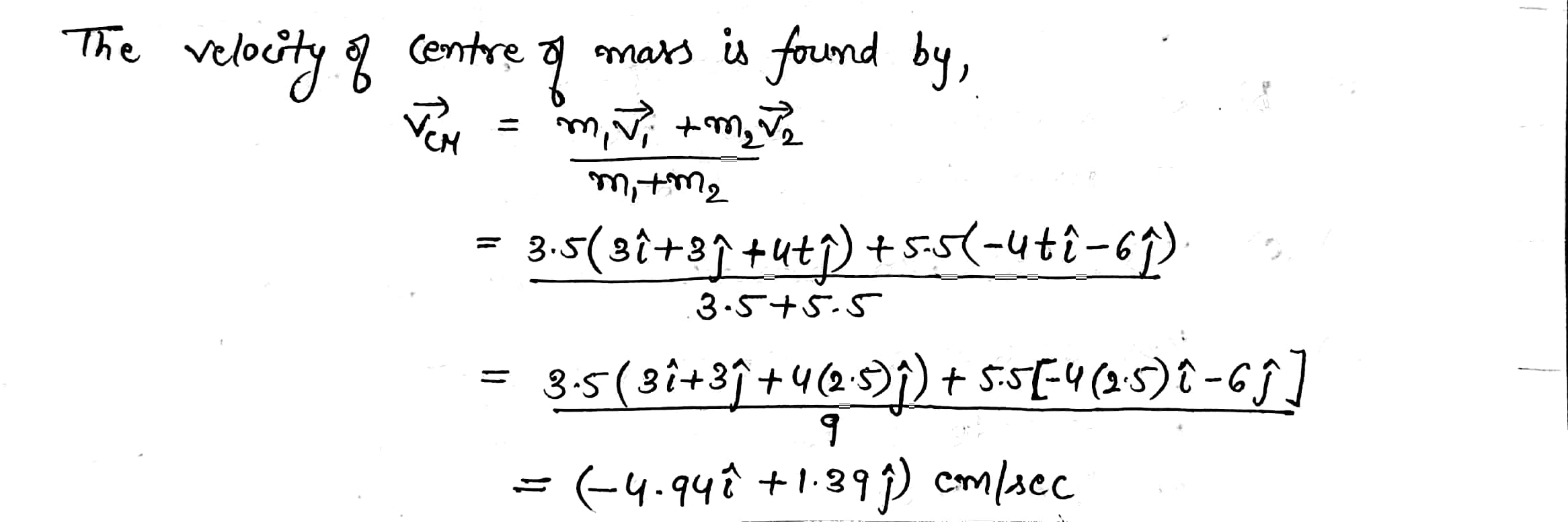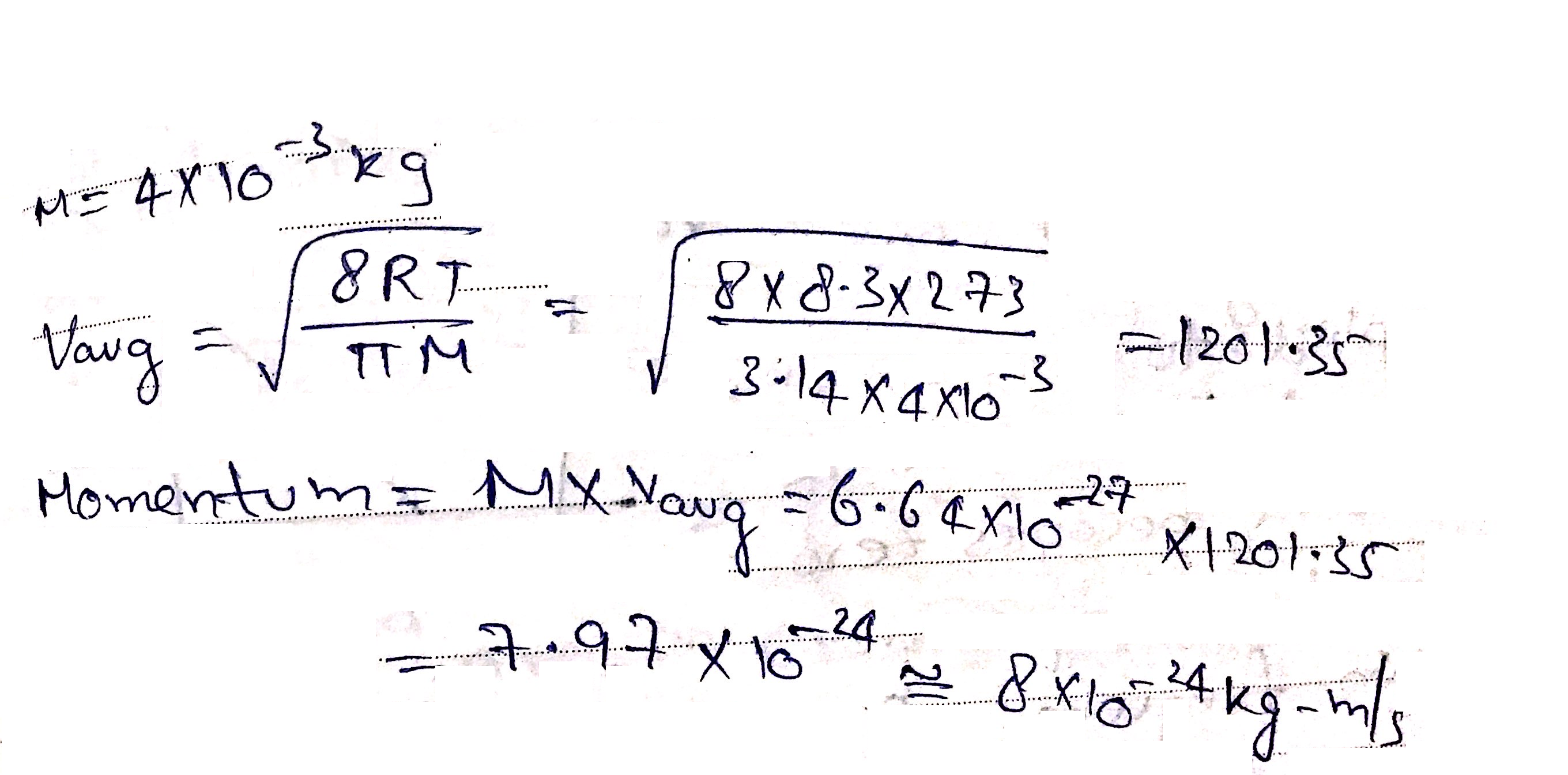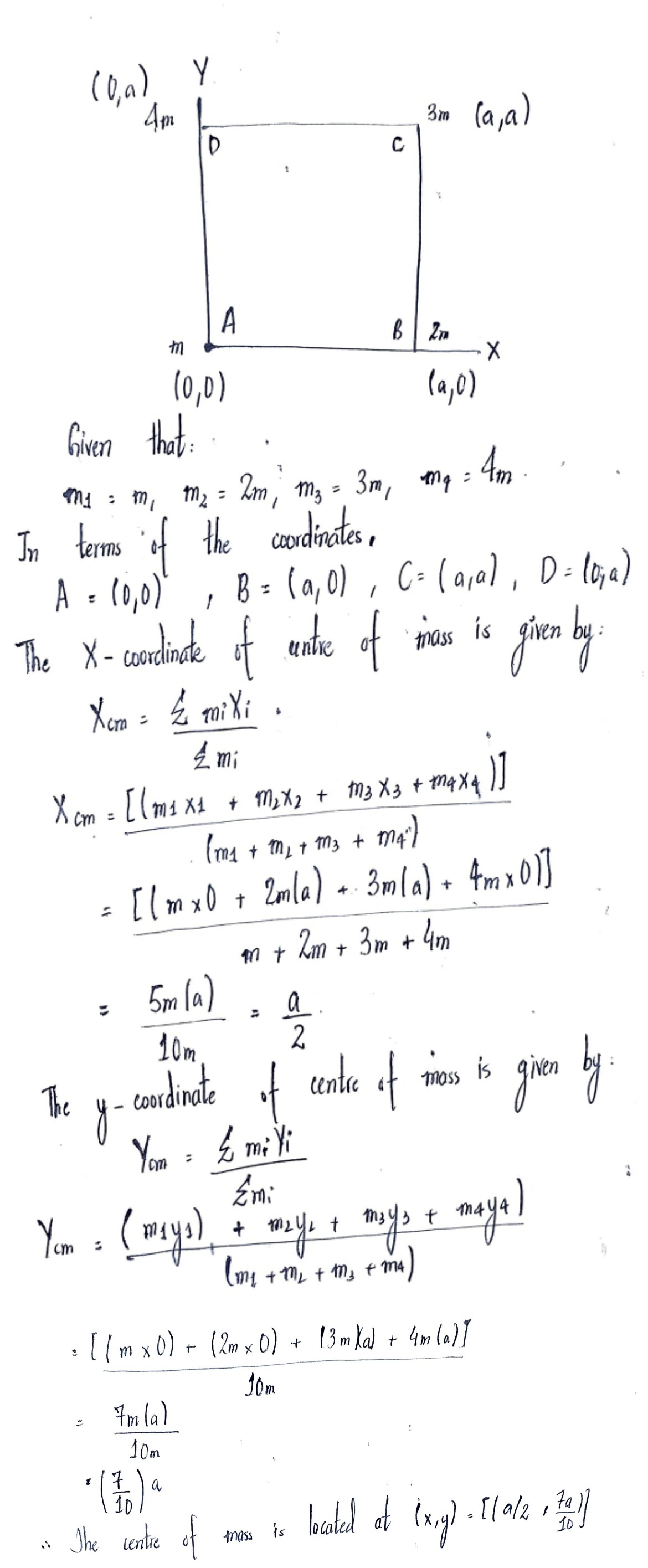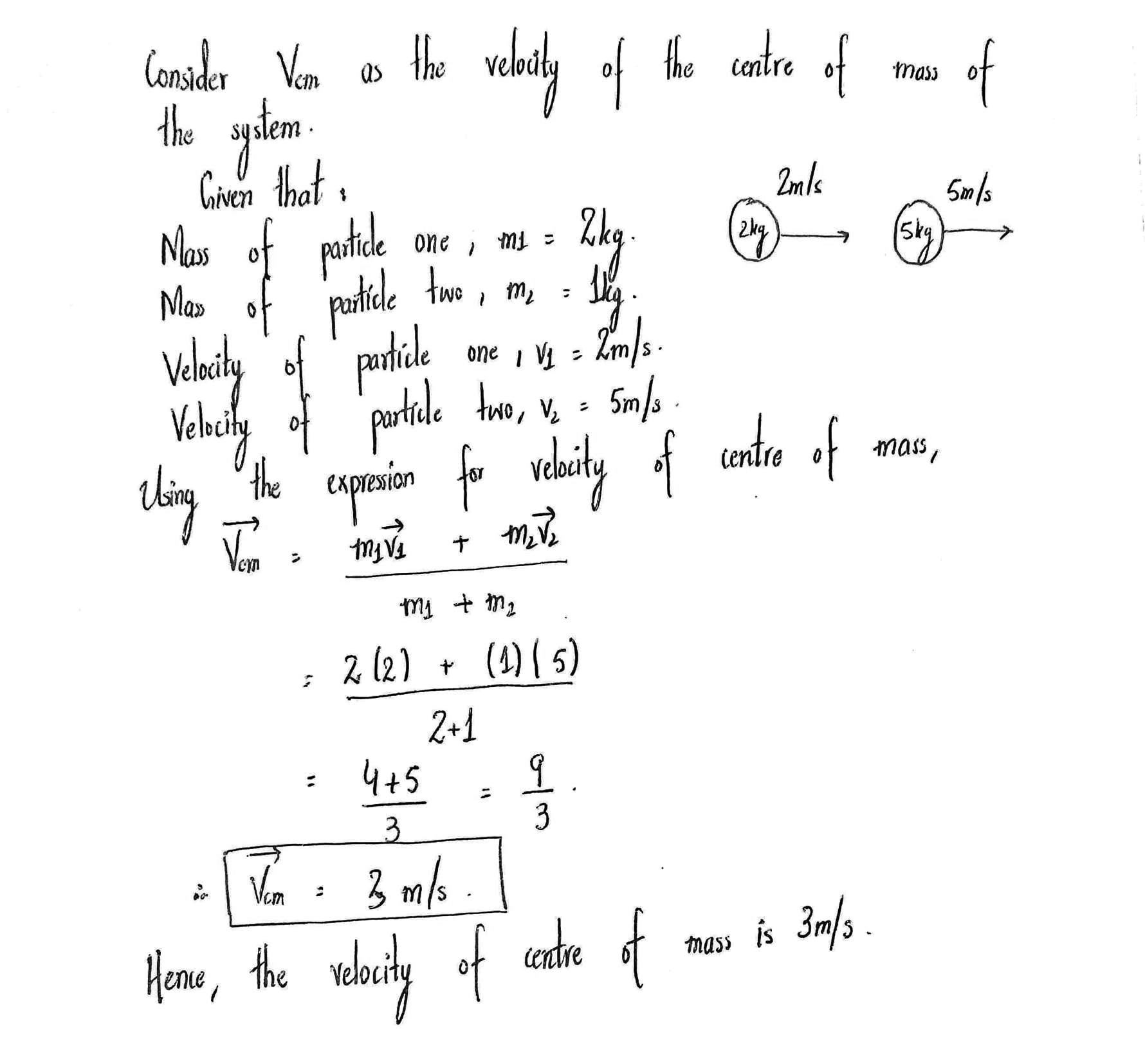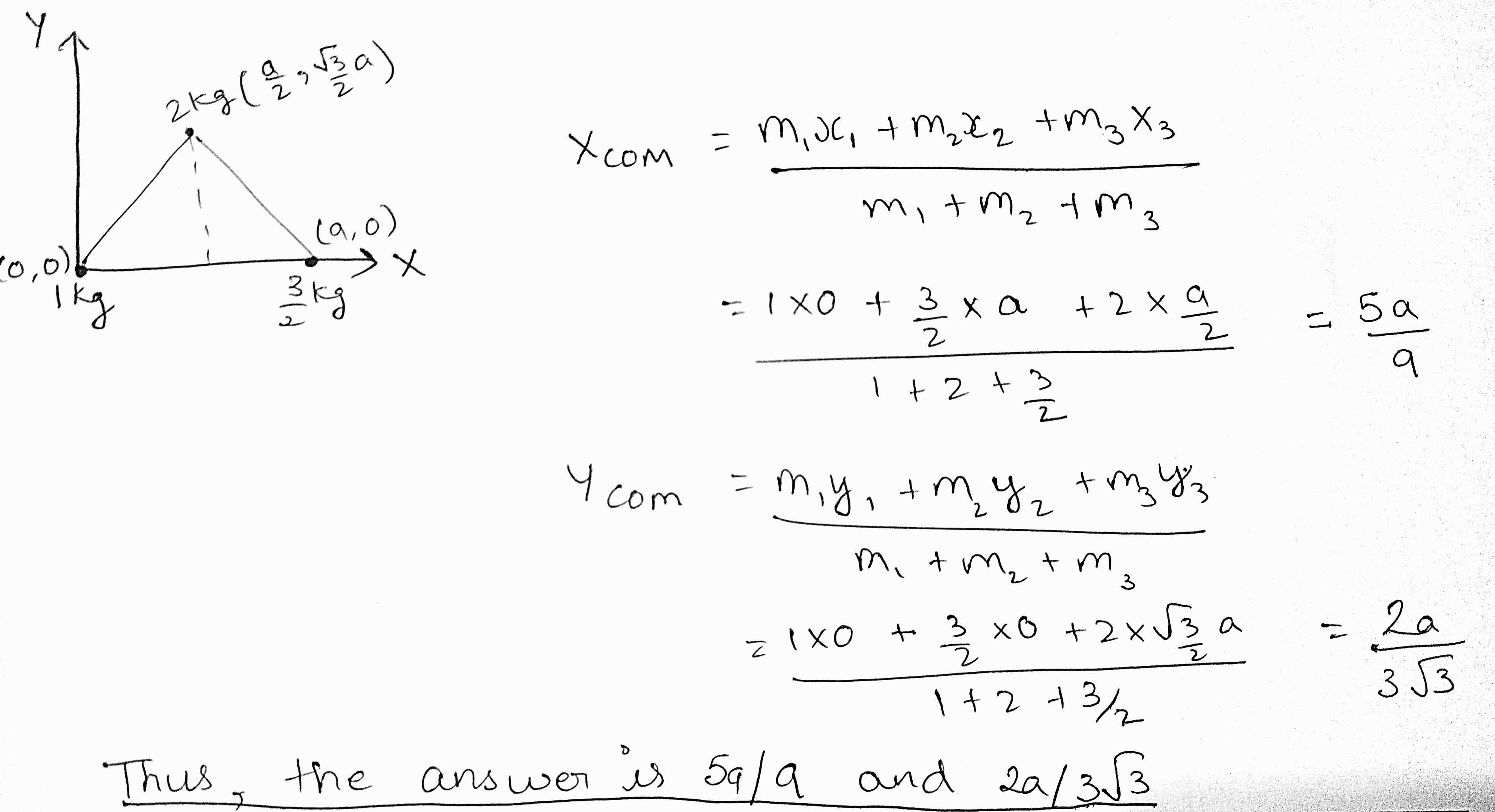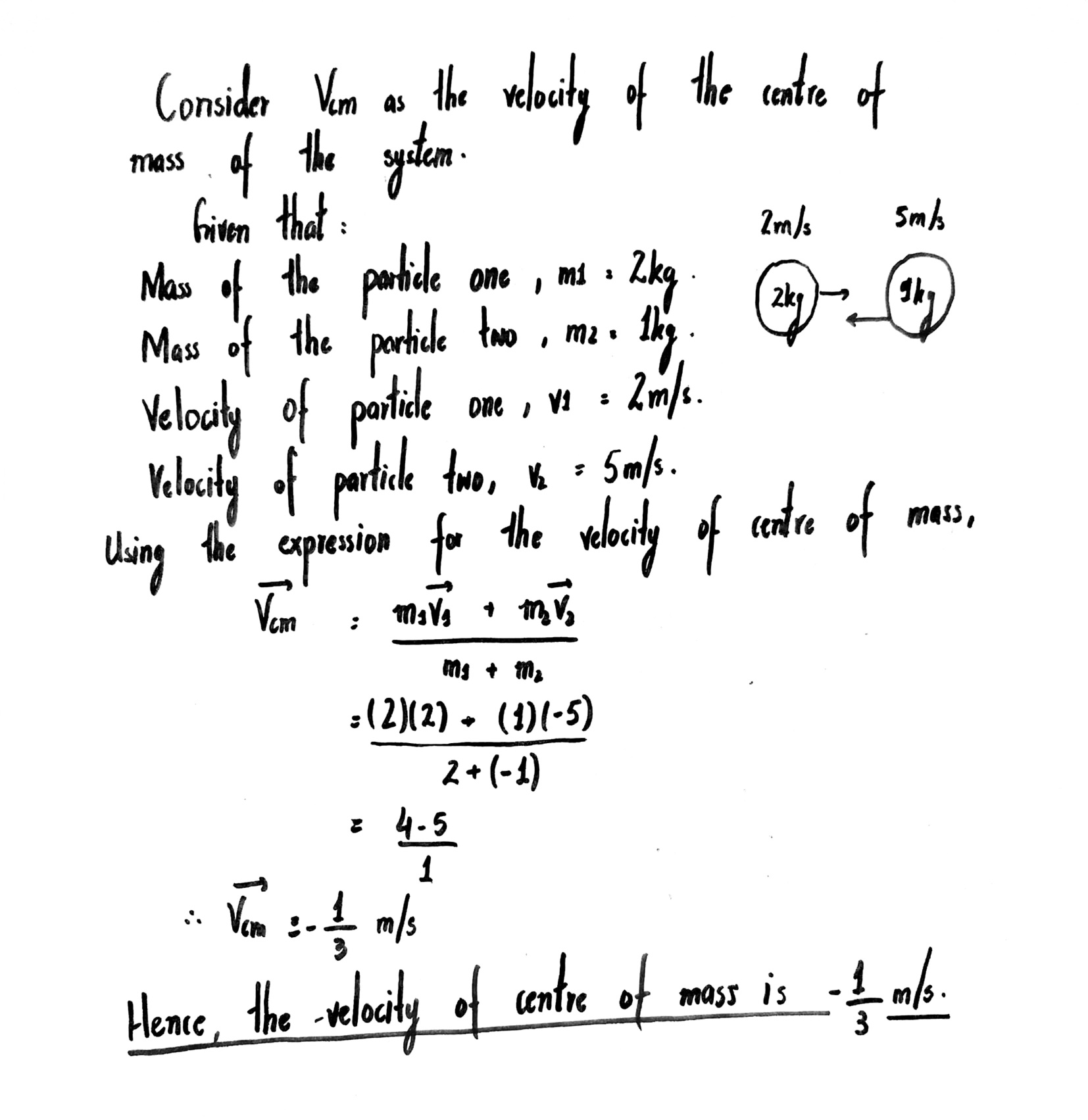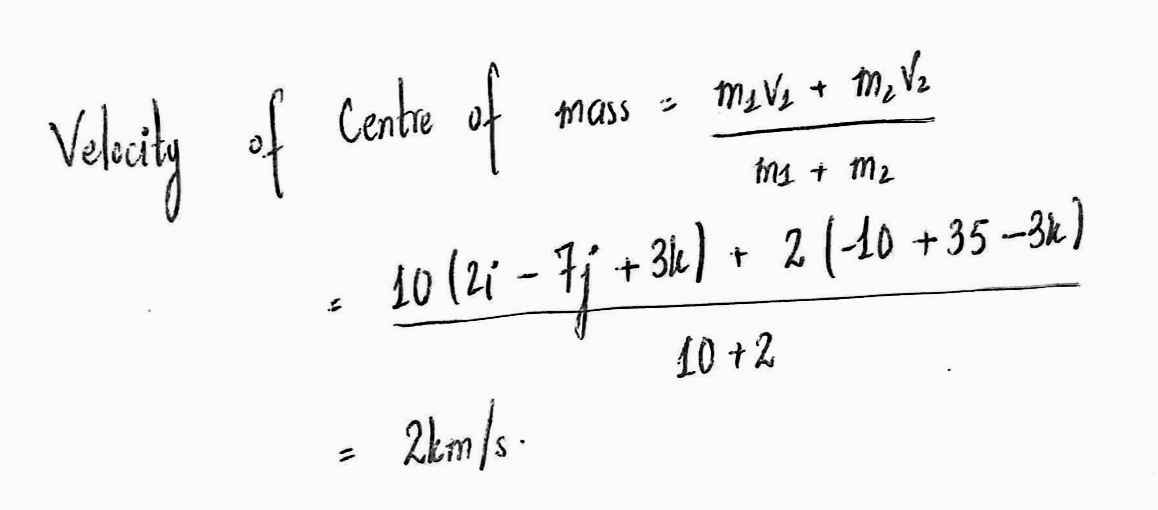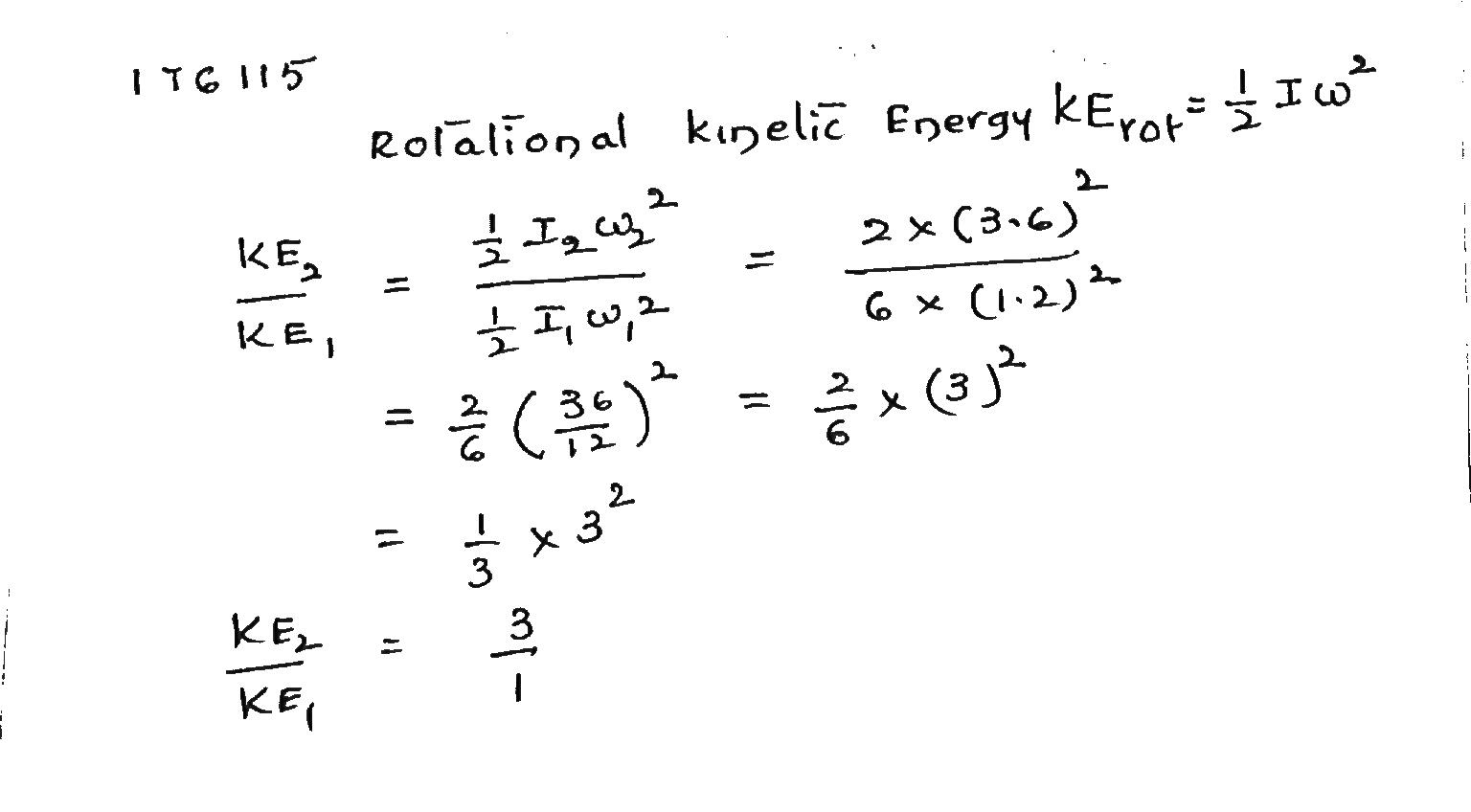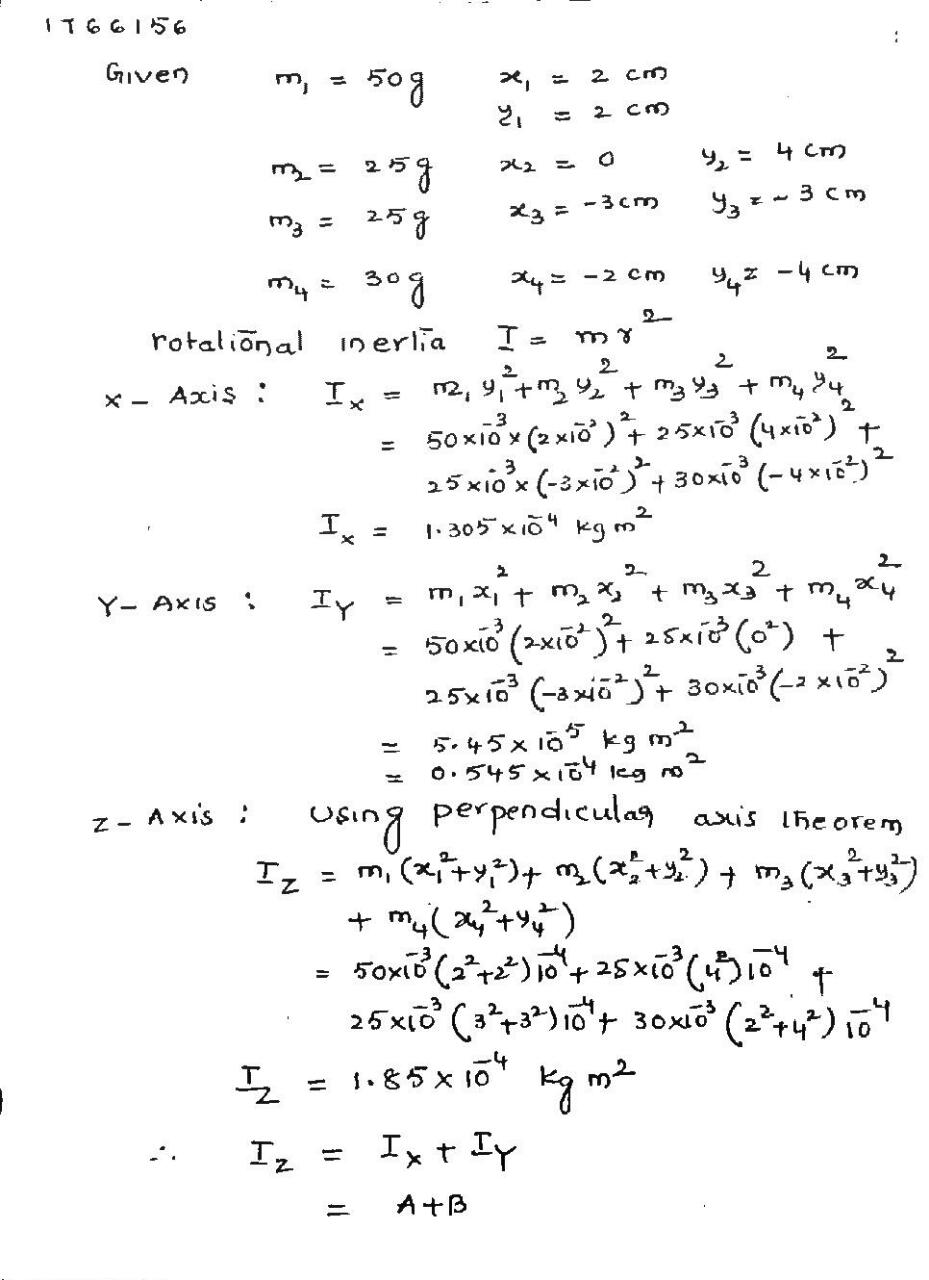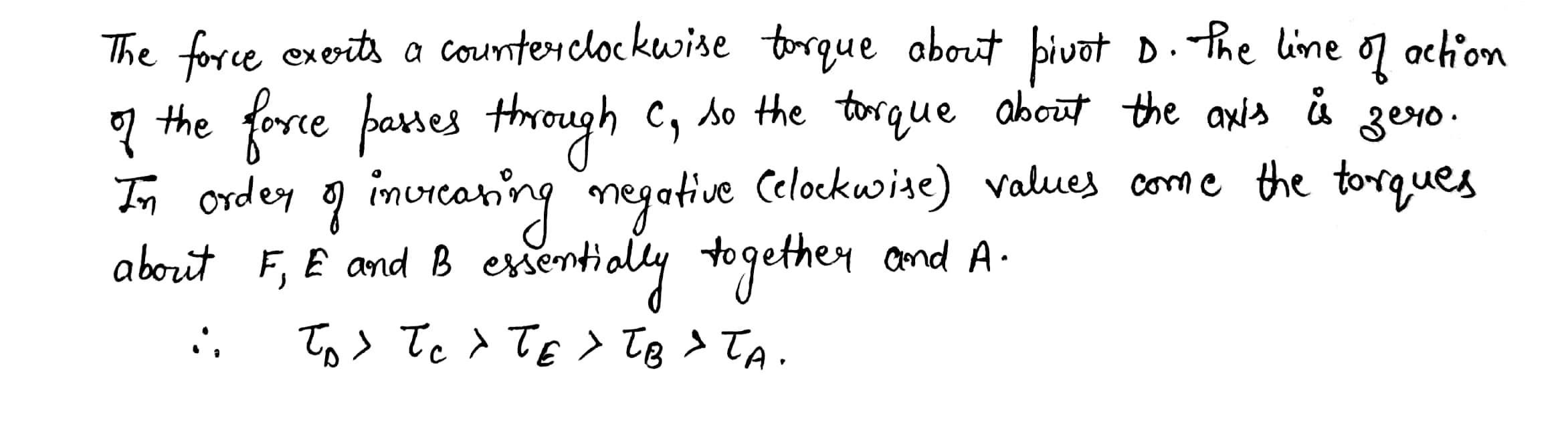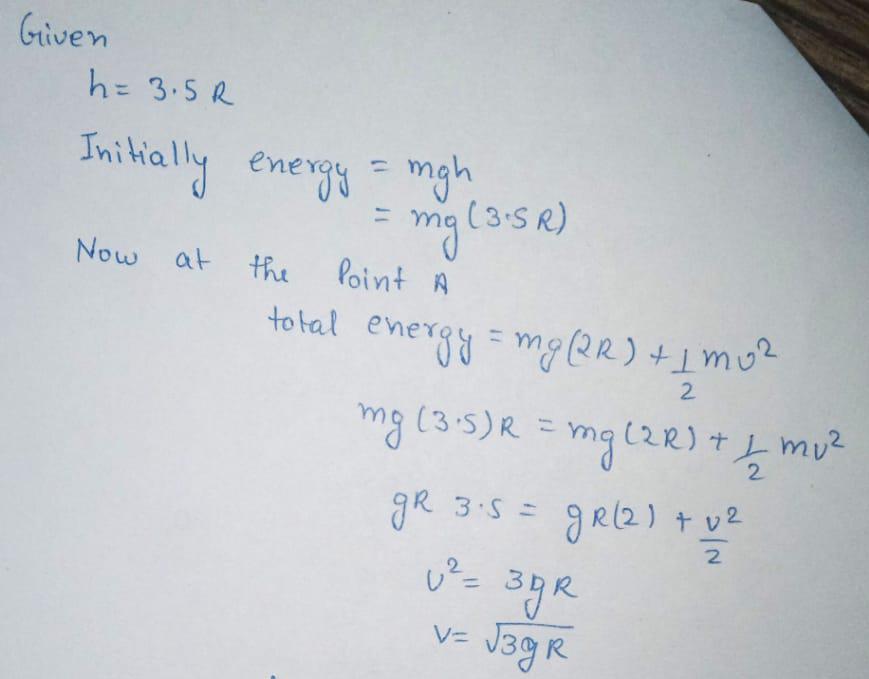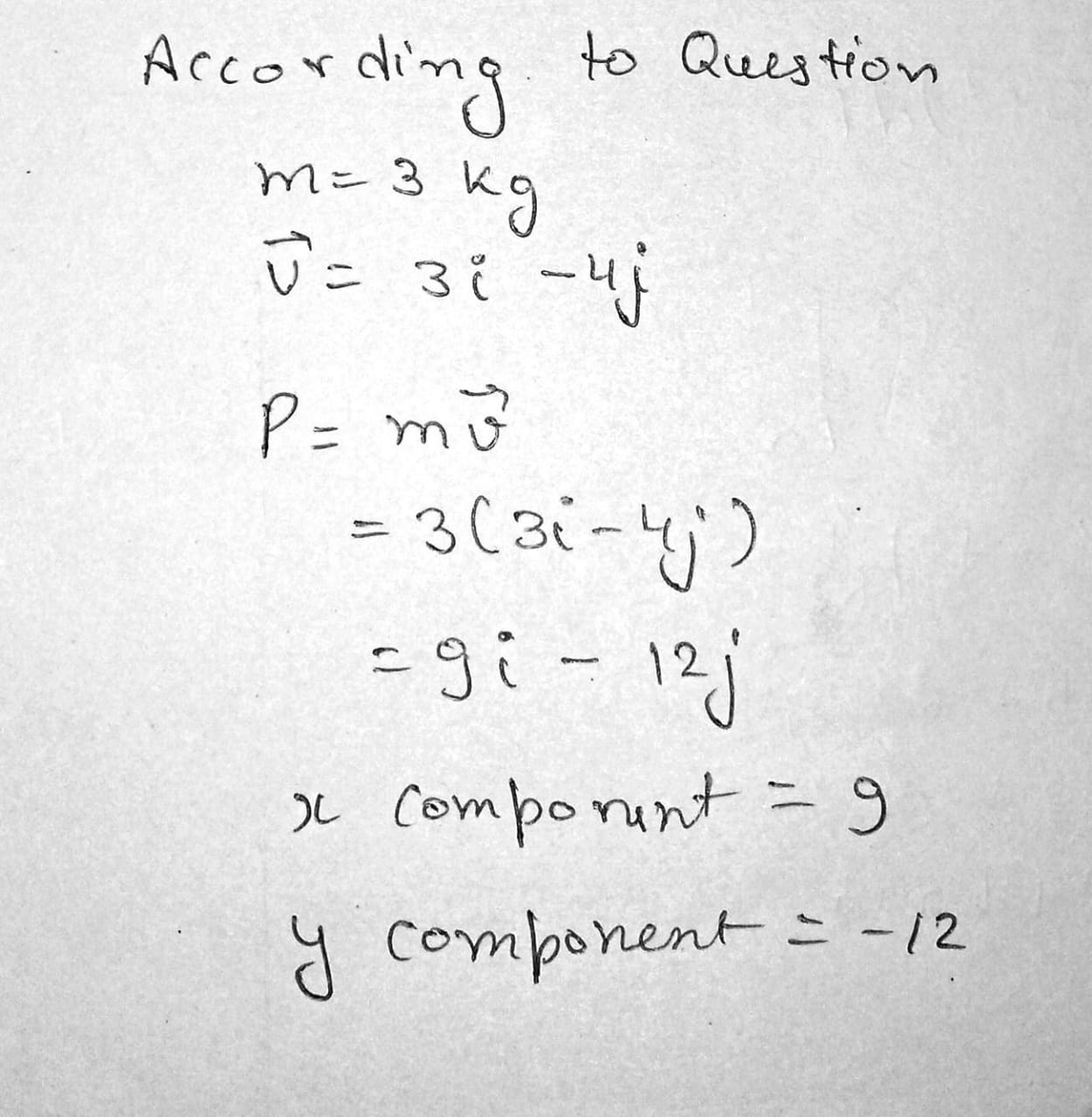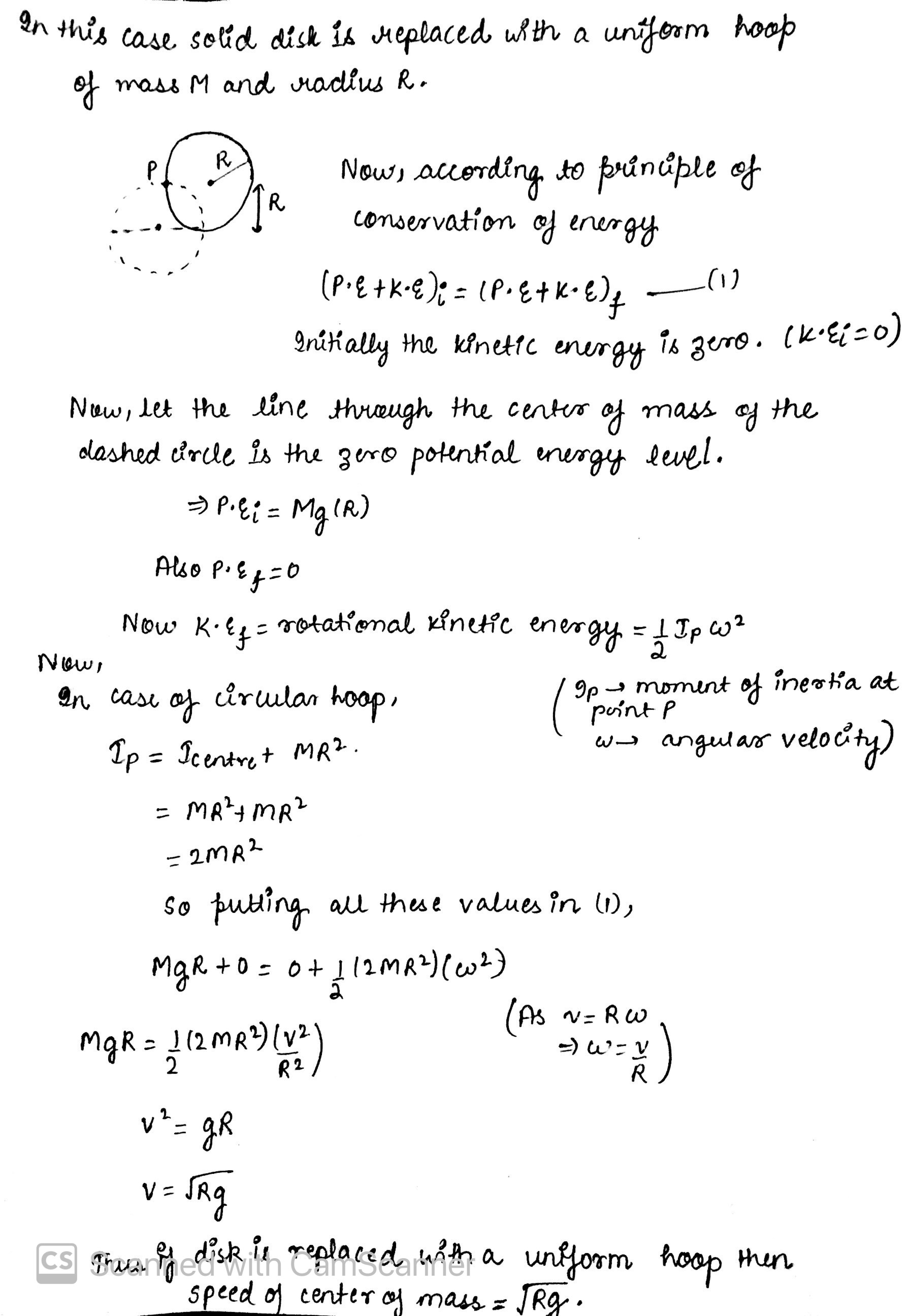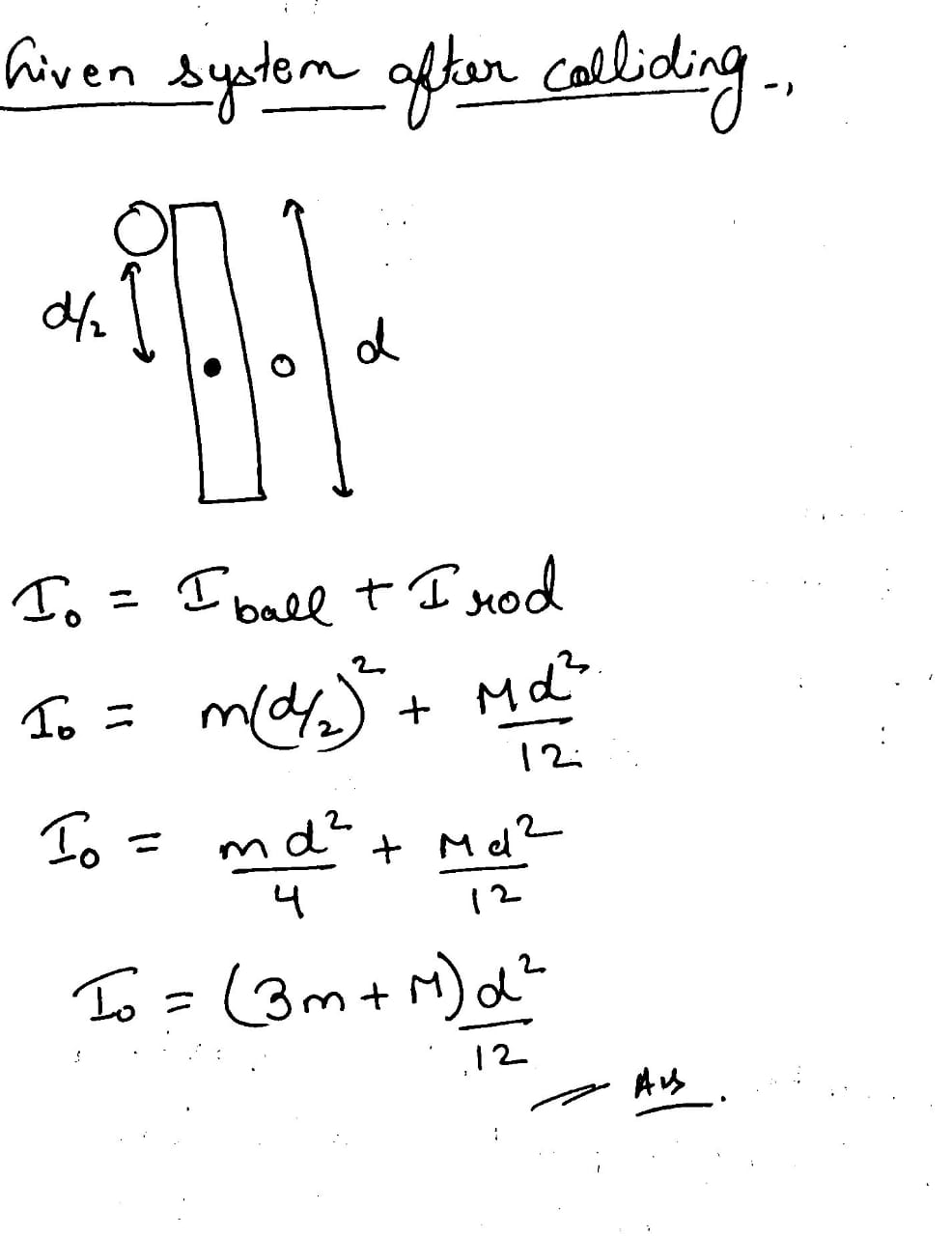Systems Of Particles And Rotational Motion - Class 11 Engineering Physics - Extra Questions
CG of a triangular lamina is at its _____.
The centre of gravity of regular shaped objects is at their _____.
Why are the number of passengers allowed to stand on the top deck of a double decker bus limited
When do you say an object is in rotatory motion?
A ball moving with a momentum of $$5\ kg\ {ms}^{-1}$$ strikes against a wall at an angle of $${45}^{o}$$ and is reflected at the same angle. Calculate the change in momentum.
If a heavier and a lighter body have the same kinetic energy and they are stopped by applying the same force, which one will stop first?
Can a body have energy without having momentum ? Explain?
Two bodies having different masses have the same linear momentum. Which one of them will move faster?
If weight of a body is 1000 dyne, then the mass of the body will be (take g= $$loms^{-2}$$)
What is the order of magnitude of the seconds present in a day?
Centre of mass of a ring will be at a position.
Express $$42$$ seconds as a percent of $$6$$ minutes.
Define centre of mass .
Write down the equation for calculating momentum.
Momentum of a car moving with velocity of $$72km/h$$ is $$20,000kg$$ $$m/s$$. How much is its mass?
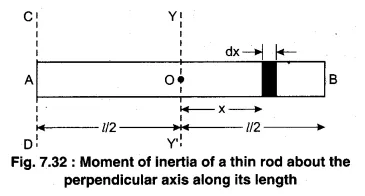
The moment of inertia of a thin uniform rod (of mass $$m$$ and length $$l$$) relative to the axis which is perpendicular to the rod and passes through its end is $$\displaystyle I=\frac{ml^2}{a}$$. Find the value of $$a$$.
Consider a strip of length $$dx$$ at a perpendicular distance $$x$$ from the axis about which we have to find the moment of inertia of the rod.
The elemental mass of the rod equals
$$\displaystyle dm=\frac{m}{l}dx$$
Moment of inertia of this element about the axis
$$\displaystyle dI=dmx^2=\frac{m}{l}dx.x^2$$
Thus, moment of inertia of the rod, as a whole about the given axis
$$\displaystyle I=\int_0^l{\frac{m}{l}x^2dx}=\frac{ml^2}{3}$$
The elemental mass of the rod equals
$$\displaystyle dm=\frac{m}{l}dx$$
Moment of inertia of this element about the axis
$$\displaystyle dI=dmx^2=\frac{m}{l}dx.x^2$$
Thus, moment of inertia of the rod, as a whole about the given axis
$$\displaystyle I=\int_0^l{\frac{m}{l}x^2dx}=\frac{ml^2}{3}$$
Radius of gyration of a body about an axis at a distance $$6 cm$$ from its centre of mass is $$10 cm.$$ Find its
radius of gyration (in cm) about a parallel axis through its centre of mass.
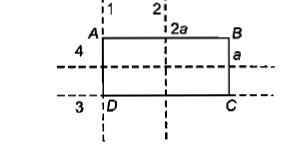
A rectangular slab $$ABCD$$ have dimensions $$a \times 2a $$ as shown in figure. Match the following two columns
The radius of gyration of a uniform disc about a line perpendicular to the disc equals its radius $$R$$. The distance of the line from the centre is $$\dfrac{R}{\sqrt x}$$. Find $$x$$.
The radius of gyration of a rod of mass $$m $$ and length $$2l$$ about an axis passing through one of its ends and perpendicular to its length is $$ \dfrac{2}{\sqrt{x}}l$$. Find $$x$$.
Four thin rods each of mass $$m$$ and length $$l$$ are joined to make a square. If the moment of inertia of all the four rods about any side of the square is $$\dfrac{x}{3}ml^2$$, find the value of $$x$$.
$$I=I_{1}+I_{2}+I_{3}+I_{4}$$
$$\displaystyle=0+\frac{ml^{2}}{3}+ml^{2}+\frac {ml^{2}}{3}$$
$$\displaystyle =\frac{5}{3} ml^{2}$$
$$\displaystyle=0+\frac{ml^{2}}{3}+ml^{2}+\frac {ml^{2}}{3}$$
$$\displaystyle =\frac{5}{3} ml^{2}$$
Show that if a rod held at angle $$\theta $$ to the horizontal and released, its lower end will not slip if the friction coefficient between rod and ground is greater than $$\displaystyle \frac{3\sin \theta \cos \theta}{1+3\sin^{2} \theta}$$
Point $$A$$ is momentarily at rest
$$ \displaystyle \alpha =\frac{mg\frac{l}{2} \cos \theta}{\frac{ml^{2}}{3}} =\frac{3}{2} \frac{g\cos \theta}{l}$$
$$\displaystyle \therefore a_{C}=\frac{l}{2}\alpha =\frac{3}{4} g\cos \theta$$
Now $$\mu N=ma_{x}$$
or $$ \mu N =ma_{C}\sin \theta $$ or $$\displaystyle \mu N =\frac{3}{4} mg \sin \theta \cos \theta ...(i)$$
Further, $$mg -N =ma_{y}$$
or $$ N=mg-ma_{C}\cos \theta$$
or $$\displaystyle N=mg-\frac{3}{4} mg\cos^{2} \theta ...(ii)$$
Dividing Eq. (i ) by Eqs. (ii). we have
$$\displaystyle
\mu=\frac{\frac{3}{4} \sin \theta \cos \theta}{1-\frac{3}{4} \cos^{2}
\theta}=\frac{3 \sin \theta \cos \theta}{4-3 \cos^{2} \theta}$$
$$\displaystyle =\frac{3 \sin \theta \cos \theta}{1+3\sin ^{2} \theta}$$
Hence proved.
$$ \displaystyle \alpha =\frac{mg\frac{l}{2} \cos \theta}{\frac{ml^{2}}{3}} =\frac{3}{2} \frac{g\cos \theta}{l}$$
$$\displaystyle \therefore a_{C}=\frac{l}{2}\alpha =\frac{3}{4} g\cos \theta$$
Now $$\mu N=ma_{x}$$
or $$ \mu N =ma_{C}\sin \theta $$ or $$\displaystyle \mu N =\frac{3}{4} mg \sin \theta \cos \theta ...(i)$$
Further, $$mg -N =ma_{y}$$
or $$ N=mg-ma_{C}\cos \theta$$
or $$\displaystyle N=mg-\frac{3}{4} mg\cos^{2} \theta ...(ii)$$
Dividing Eq. (i ) by Eqs. (ii). we have
$$\displaystyle
\mu=\frac{\frac{3}{4} \sin \theta \cos \theta}{1-\frac{3}{4} \cos^{2}
\theta}=\frac{3 \sin \theta \cos \theta}{4-3 \cos^{2} \theta}$$
$$\displaystyle =\frac{3 \sin \theta \cos \theta}{1+3\sin ^{2} \theta}$$
Hence proved.
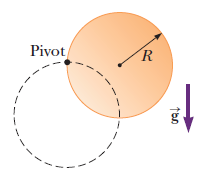
A thin plank of mass $$M$$ and length $$l$$ is pivoted at one end. The plank is released at $$ 60^{\circ}$$ from the vertical.What is the magnitude and direction of the force on the pivot when the plank is horizontal?
Let $$\omega$$ be the angular velocity and $$\alpha $$ the angular acceleration of rod in horizontal position. Then
$$\displaystyle \alpha =\frac{(Mg)\frac{l}{2}}{\frac{Ml^{2}}{3}}=\frac{3}{2} \frac{g}{l} ....(i) $$
$$\displaystyle \frac{1}{2} \left( \frac{Ml^{2}}{3}\right) \omega^{2} =Mg\frac{l}{4} $$
$$\displaystyle \therefore \omega =\frac{3}{2} \cdot \frac{g}{l} ....(ii) $$
$$\displaystyle
F_{x} =M\left( \frac{l}{2} \right) \omega^{2} =M \left(
\frac{l}{2}\right) \left( \frac{3g}{2l} \right) =\frac{3}{4} Mg $$
$$\displaystyle Mg-F_{y} =M(\alpha) \left( \frac{l}{2} \right) $$
$$\displaystyle F_{y} =Mg -\frac{3}{4} Mg =\frac{Mg}{4}$$
$$ \therefore F=\sqrt{ F_{x}^{2}+F_{y}^{2}}$$
$$\displaystyle =\frac{\sqrt{10}}{4} Mg $$
$$\displaystyle \tan \alpha=\frac{F_{y}}{F_{x}}=\frac{(Mg/4)}{(3 Mg/4)}$$
$$\displaystyle =\frac{1}{3} $$
$$\displaystyle \therefore \alpha =\tan _{-1} \left(\frac{1}{3}\right) $$
$$\displaystyle \alpha =\frac{(Mg)\frac{l}{2}}{\frac{Ml^{2}}{3}}=\frac{3}{2} \frac{g}{l} ....(i) $$
$$\displaystyle \frac{1}{2} \left( \frac{Ml^{2}}{3}\right) \omega^{2} =Mg\frac{l}{4} $$
$$\displaystyle \therefore \omega =\frac{3}{2} \cdot \frac{g}{l} ....(ii) $$
$$\displaystyle
F_{x} =M\left( \frac{l}{2} \right) \omega^{2} =M \left(
\frac{l}{2}\right) \left( \frac{3g}{2l} \right) =\frac{3}{4} Mg $$
$$\displaystyle Mg-F_{y} =M(\alpha) \left( \frac{l}{2} \right) $$
$$\displaystyle F_{y} =Mg -\frac{3}{4} Mg =\frac{Mg}{4}$$
$$ \therefore F=\sqrt{ F_{x}^{2}+F_{y}^{2}}$$
$$\displaystyle =\frac{\sqrt{10}}{4} Mg $$
$$\displaystyle \tan \alpha=\frac{F_{y}}{F_{x}}=\frac{(Mg/4)}{(3 Mg/4)}$$
$$\displaystyle =\frac{1}{3} $$
$$\displaystyle \therefore \alpha =\tan _{-1} \left(\frac{1}{3}\right) $$
A body is projected with velocity $$v$$ at an angle ofprojection $$\theta$$. Then :
Two uniform identical rods each of mass M and length l are joined to form a cross as shown in the figure. Find the moment of inertia of the cross about anyone of the bisector as shown in the figure with dotted.
A solid cylinder of mass 20 kg rotates about its axis with angular speed $$100\ rad\ s^{-1}$$. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?
What is the moment of inertia of a rod of mass M, length l about an axis perpendicular to it through one end?
Match the description in List 1 with the images in List 2 :
State S.I. unit of angular momentum. Obtain its dimensions.
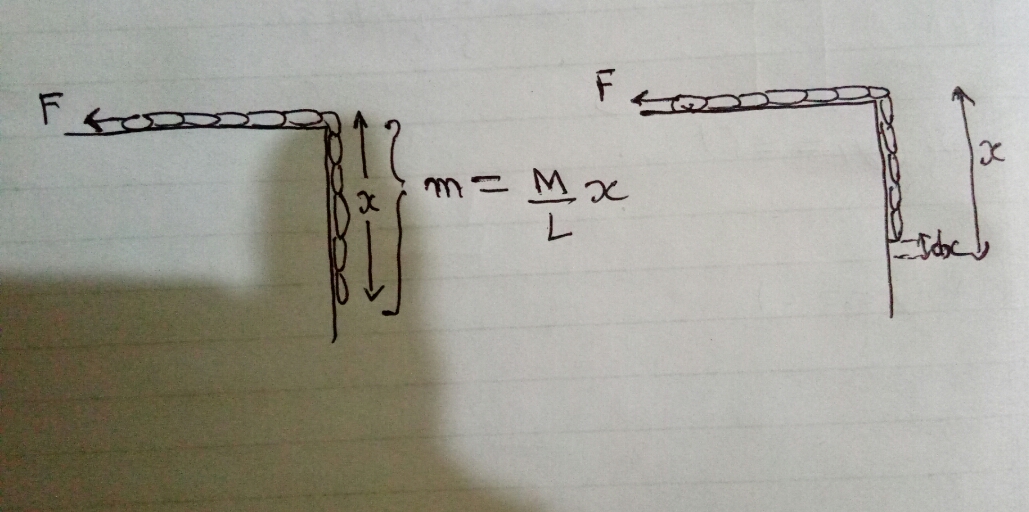
A flexible chain of length l and mass m is slowly pulled at constant speed up over the edge of a table by a force F parallel to the surface of the table. Assuming that there is no friction between the table and chain, calculate the work done by force F till the chain reaches to the horizontal surface of the table.
Its total weight is M and total length is L
Let the x length of a chain is not lying on the table its weight is
$$mg = \dfrac{Mgx}{L}$$
work done required to move a dx part of a chain to upward is=
$$dW=Fdx$$
$$F=mg = \dfrac{Mgx}{L}$$
$$\int_{0}^{W}dW= \int_{l}^{0}\dfrac{Mgx}{L}dx$$
$$W= \left ( \dfrac{Mgx^2}{2L} \right )_l^0$$
$$W= -\dfrac{MgL}{2}$$N/m
A ball of mass $$5kg$$ is suspended from a chord of length $$l=0.5m$$ is attached to a cart $$A$$ of mass $$2.5kg$$, which slides freely on a frictionless horizontal track as shown in figure. The ball given an initial horizontal velocity $$1m/s$$ relative to the $$ground$$ while the cart is at rest.
Find
(a) The velocity of the ball when string makes $$minimum$$ angle with vertical
(b) The maximum vertical distance through which the ball will rise.
(a) At time of horizontal velocity of ball is same of cart velocity .
By linear momentum conservation
$$5x_{ 1 }=5xv+2.5v\\ \cfrac { 5 }{ 7.5 } =v\\ v=\cfrac { 2 }{ 3 } m/s$$
(b) By energy conservation theorem
$$\cfrac { 1 }{ 2 } 5(1)^{ 2 }=\cfrac { 1 }{ 2 } 5\times { v }^{ 2 }+\cfrac { 1 }{ 2 } 2.5\times { v }^{ 2 }+5g(h)\\ 5=\cfrac { 20 }{ 9 } +\cfrac { 10 }{ 9 } +10gh\\ 5-\cfrac { 30 }{ 9 } =10\times 10h\\ \cfrac { 15 }{ 9 } =100h\\ h=\cfrac { 5 }{ 300 } m\\ =\cfrac { 5 }{ 3 } cm$$
A stone of mass $$m$$, tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity.) The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by $$T = Ar^{n}$$ where $$A$$ is constant, $$r$$ is the instantaneous radius of the circle, and $$n =$$ _________.
The radius of gyration of a uniform disc about a line perpendicular to the disc equals its radius. Find the distance of the line from the centre.
A rod of length 'L' has the linear density given by the equation $$\lambda = Kx +\lambda_0$$ where K is the constant. Where does the centre of the mass lie?
( Origine is at the left end of the rod)
The radius of gyration of a uniform disc about a line perpendicular to the disc equals its radius. Find the distance of the line from the center.
A uniform thin rod of length L is hinged about one of its end and is free to rotate about the hinge without friction. Neglect the effect of gravity. A force F is applied at a distance x from the hinge on the rod such that force is always perpendicular to the rod. Find the normal reaction at the hinge as function of 'x' , at the initial instant when the angular velocity of rod is zero.
At horizontal position the reaction 'N'.
Let the mass of rod is m.
The moment of inertia of rod about the axis passig through the end and perpendicular to its plane is
$$I=\cfrac{1}{3}ml^2$$
For rotation of rod,
Moment of force = Applied torque
$$\implies x\times F = I\alpha$$
$$\implies \alpha = \cfrac{xF}{\cfrac{1}{3} ml^2} = \cfrac{3xF}{ml^2}$$
Here $$ \alpha $$ is angular acceleration about hinge .
The position of centre of mass is aat the middle.
So the linear acceleration of centre of mass,$$a=\alpha \cfrac{l}{2}$$
$$a=\cfrac{3xF}{2ml}$$
So, the net force in vertical on centre of mass is
$$=ma$$
$$=\cfrac{3xF}{2l}$$
This should be equal to N.
So, N=$$\cfrac{3xF}{2l}$$
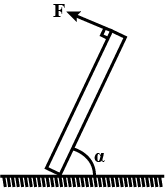
A uniform rod of mass m and length L is held at rest by a force F applied at it's end as shown in the vertical plane. The ground is sufficiently rough.
Find
(a) Force F
(b) Normal reaction exerted by the ground
(c) Frictional force exerted by the ground (magnitude and dirtection)
N is the reactional force on rod by the ground C is the centre of mass of the rod .
f is the friction force $$=\mu N$$
Length of Rod $$=AB=L$$
The equation for translation of rod are
$$Fcos\alpha =mg-N---------(1)$$
$$Fsin\alpha=\mu N-----------(2)$$
Now for rotational equilibrium torque about point Q should be balance
$$Fcos\alpha . BD+Fsin\alpha .AD=mg\times BE$$
So,$$Fcos\alpha . Lcos\alpha+Fsin\alpha .sin\alpha=mg(\cfrac{L}{2}cos\alpha)$$
$$\implies FL(cos^2\alpha +sin^2\alpha)=\cfrac{mgL}{2}cos\alpha$$
$$F=\cfrac{mg}{2}cos\alpha$$
Putting this value in one we get
$$\cfrac{mg}{2}cos^2\alpha=mg-N$$
$$\implies N=\cfrac{mg}{2} (2-cos^2\alpha)$$
$$\implies N=\cfrac{mg}{2}(1+sin^2\alpha)$$
Frictional force
$$f=\mu N$$
$$f=\cfrac{\mu mg}{2}(1+sin^2 \alpha)$$
The direction of this force towards right to stop the sliding.
The moment of inertia of a uniform rod of mass $$0.50kg$$ and length $$1m$$ is $$0.10kg-{m}^{2}$$ about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
Find the radius of gyration of a circular ring of radius $$r$$ about a line perpendicular to the plane of the ring and passing through one of its particles.
Moment of inertia at the center and perpendicular to the plane of ring
So, about a point on the rim of the ring and the axis $$\bot $$ to the plane of the ring
$$MOI=m{ R }^{ 2 }+m{ R }^{ 2 }=2m{ R }^{ 2 }$$ (parallel axis theorem)
$$m{ K }^{ 2 }=2m{ R }^{ 2 }$$ ($$k=$$radius of gyration)
$$\therefore \quad K=\sqrt { 2{ R }^{ 2 } } =R\sqrt { 2 } $$
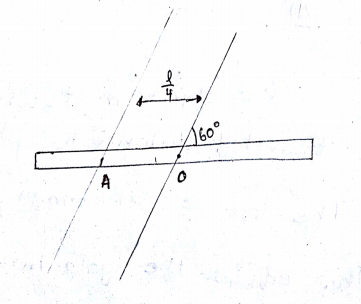
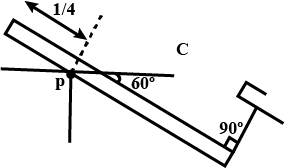
The moment of inertia of a thin uniform rod of length $$l$$ and mass $$m$$ about an axis passing through about an axis passing through a point at distance $$l/4$$ from the centre $$O$$ and at an angle $$60$$ degrees to the rod is?
$$MI$$ about an axis passing through $$0$$ and inclined at $$60°$$
$$=\cfrac{ m{ l }^{ 2 }{ sin }^{ 2 }60° }{ 12 } \\ =\cfrac{ m{ l }^{ 2 } }{ 16 } $$
$$MI$$ about an axis passing through $$A$$and inclined at $$60°$$
$$=\cfrac{ m{ l }^{ 2 } }{ 16 } +m{ \left( \cfrac{ l }{ 4 } \right) }^{ 2 }\\ =\cfrac{ m{ l }^{ 2 } }{ 8 } $$
A uniform thin rod of mass $$m$$ and length $$l$$ is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes and angle $$\theta$$ with horizontal.
A uniform rod of mass $$m$$ and length $$l$$ is in equilibrium under the action of constraint forces, gravity and tension in the string. Find the
(a) frictional force acting on the rod
(b) tension in the string
(c) normal reaction on the rod
Now the string is cut. Find the
(d) angular acceleration of the rod just after the string is cut
(e) normal reaction on the rod just after the string is cut
Resolving the forces parallel and perpendicular to rod.
Along the length of rod.
$$f=mg\sin { { 60 }^{ o } } =\cfrac { \sqrt { 3mg } }{ 2 } $$
Hence friction force action on rod at support $$P$$ will be $$mg/2$$
(b) for finding tension we can take torque about support $$P$$
$$T\left( \cfrac { 3 }{ 4 } l \right) =mg\left( \cfrac { l }{ 4 } \right) \quad or\quad T=\cfrac { mg }{ 3 } $$
(c) Just before cutting the string the rod is at equilibrium. Considering the forces perpendicular to rod length
$$N+T=mg\cos { { 60 }^{ o } } \Rightarrow N=\cfrac { mg }{ 2 } -\cfrac { mg }{ 3 } =\cfrac { mg }{ 6 } $$
(d) Just after cutting the string the equilibrium of the rod will disturbed. The rod will have angular acceleration.
As the rod does not slip point $$P$$ will be at rest at the time just after cutting the string
We can apply torque equation about $${ \tau }_{ P }={ I }_{ P }\alpha $$
$$\left( mg\cos { { 60 }^{ o } } \right) \cfrac { l }{ 4 } =\left( \cfrac { m{ l }^{ 2 } }{ 12 } +m{ \left( \cfrac { l }{ 4 } \right) }^{ 2 } \right) \alpha \Rightarrow \alpha =\cfrac { 6g }{ 7l } $$
(e) If we apply torque equation about centre of mass
$$N.\cfrac { l }{ 4 } =\left( \cfrac { m{ l }^{ 2 } }{ 12 } \right) \alpha $$
$$N.\cfrac { l }{ 4 } =\left( \cfrac { m{ l }^{ 2 } }{ 12 } \right) \left( \cfrac { 6g }{ 7l } \right) \Rightarrow N=\cfrac { 2 }{ 7 } mg\quad $$
Find the dimensions of
(a) angular speed $$\omega$$
(b) angular acceleration $$\alpha$$,
(c) torque $$\Gamma$$ and
(d) moment of inertia $$I$$
Three identical thin rods, each of mass $$m$$ and length $$l$$, are joined to form an equilateral triangular frame. Find the moment of inertia of the frame about an axis parallel to its one side and passing through the opposite vertex. Also, find its radius of gyration about the given axis.
Moment of inertia of each of rod $$AC$$ and $$BC$$ about the given axis $$OO'$$ is
$${ I }_{ AC }={ I }_{ BC }=\cfrac { m{ l }^{ 2 } }{ 3 } \sin ^{ 2 }{ { 60 }^{ o } } =\cfrac { m{ l }^{ 2 } }{ 4 } $$
and $$MI$$ of rod $$AB$$ about the given axis $$OO'$$ is
$${ I }_{ AB }=m{ \left( \cfrac { l\sqrt { 3 } }{ 2 } \right) }^{ 2 }=\cfrac { 3 }{ 4 } m{ l }^{ 2 }\quad $$
Hence, $$I-{ I }_{ AC }+{ I }_{ BC }+{ I }_{ AB }=\cfrac { m{ l }^{ 2 } }{ 4 } +\cfrac { m{ l }^{ 2 } }{ 4 } +\cfrac { 3 }{ 4 } m{ l }^{ 2 }=\cfrac { 5 }{ 4 } m{ l }^{ 2 }$$
Now, $${ I }_{ AC }={ I }_{ BC }=\cfrac { m{ l }^{ 2 } }{ 3 } \sin ^{ 2 }{ { 60 }^{ o } } =\cfrac { m{ l }^{ 2 } }{ 4 } $$
and $$MI$$ of rod $$AB$$ about the given axis $${ I }_{ AB }=m{ \left( \cfrac { l\sqrt { 3 } }{ 2 } \right) }^{ 2 }=\cfrac { 3 }{ 4 } m{ l }^{ 2 }$$$
Hence, $$I-{ I }_{ AC }+{ I }_{ BC }+{ I }_{ AB }=\cfrac { m{ l }^{ 2 } }{ 4 } +\cfrac { m{ l }^{ 2 } }{ 4 } +\cfrac { 3 }{ 4 } m{ l }^{ 2 }=\cfrac { 5 }{ 4 } m{ l }^{ 2 }\quad $$
Now, $$I=M{ K }^{ 2 }\Rightarrow K=\sqrt { \cfrac { I }{ M } } =\sqrt { \cfrac { \cfrac { 5 }{ 4 } m{ l }^{ 2 } }{ 3m } } =l\sqrt { \cfrac { 5 }{ 12 } } $$
A uniform bar of length $$6a$$ and mass $$8m$$ lies on a smooth horizontal table. Two point masses $$m$$ and $$2m$$ moving in opposite direction in the same horizontal plane with speed $$2v$$ and $$v$$, respectively. strike the bar and stick to the bar after collision. Calculate.
The velocity of the centre of mass after collision.
R.E.F image
conserving momentum of system
Initial momentum = final momentum
$$ 2m(-V)+m(2V)+8m(0) = (2m+m+8m)V_{e} $$
$$ V_{e} = 0 $$
after coliseum new com $$ = \dfrac{8m(0)+2m(-a)+m(2a)}{8m+2m+m} $$
$$ = 0 $$
distance between new com and com of rod $$ = 0 $$
$$ \bar{V}$$ com of rod $$= \bar{V}$$ com of rod about system $$+\bar{V}$$com
$$ = \bar{r}\times\bar{w}+0 $$
(dist b/w com of rod 0 and syst com)
$$ \bar{V} $$ com of rod $$ = 0 $$
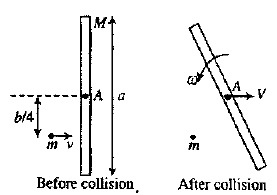
A uniform rod of mass $$M$$ and length $$a$$ lies on a smooth horizontal plane. A particle of mass $$m$$ moving at a speed $$v$$ perpendicular to the length of the rod strikes it at a distance $$a/ 4$$ from the centre and stops after the collision. Find
a. The velocity of the centre of the rod and
b. the angular velocity of the rod about its centre just after the collision.
R.F.F image
First we converse linear momentum
initial linear momentum = final linear momentum
mv = MV
$$\boxed{v = \dfrac{mv}{M}} $$
$$ y_{com} = \dfrac{-ma}{4(m+M)} $$
Now we converse angles momentum about com of system,
Initial angles momentum = final angular momentum
$$ mv\left(\dfrac{a}{4}-|y_{com}|\right) = \dfrac{Ml^{2}}{12}w-MV $$
$$ MV (\dfrac{Ma}{4(m+M)}) = \dfrac{Ml^{2}}{12}w-MV(-y_{com}) $$
$$ \dfrac{ml^{2}}{12}w = \dfrac{mv^{a}}{4}\left(\dfrac{M-m}{M+m}\right) $$
$$\boxed{w = \dfrac{3aV}{l^{2}}(\dfrac{M-m}{M+m})\dfrac{m}{M}} $$
Two particles of mass $$1kg$$ and $$0.5kg$$ are moving in the same direction with speed of $$2m/sec$$ and $$6m/sec$$ respectively on a smooth horizontal surface. Find the speed of centre of mass of the system.
A man throws a ball weighing $$500g$$ vertically upwards with a speed of $$10m/s$$
(i) what will be its initial momentum?
(ii) What would be its momentum at the highest point of its flight?
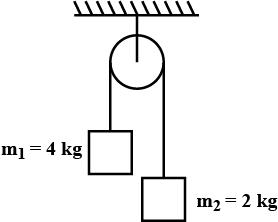
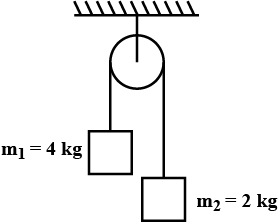
Two masses $$m_1=4kg$$ and $$m_2=2kg$$ are released from rest as shown in figure. Find
(i) The distance travelled b centre of mass in $$9s$$
(ii) The speed of centre of mass after $$9S$$
Given, Two masses $$M_1=4kg,m_2=2kg$$
So the net force at the point is:
$$F=m_1g-m_2g=4g-2g=2\times10=20N$$
Acceleration on the center of mass is:
$$a=\dfrac{F}{m_1+m_2}=\dfrac{20}{2+4}=\dfrac{10}{3}m/s^2$$
a) Distance traveled in $$9s$$
$$S=\dfrac{1}{2}at^2=\dfrac{1}{2}\times\dfrac{10}{3}\times9^2=135m$$
b) The Speed of the CoM in $$9s$$
$$V=at=\dfrac{10}{3}\times9=30m/s$$
The radius of the sun is $$7\times 10^8$$m and its mass is $$2\times 10^{30}kg$$. What is the order of magnitude of density of the sun?
Assuming the earth to be a homogeneous sphere, determine the density of the earth from the following data :
g=9.8 m/s$$^2$$ , G=6.673 x 10$$^{-11}$$ Nm$$^2/kg^2$$, R=6400 km.
A ball of mass $$50g$$ moving at a speed of $$2.0 m/s$$ strikes a plane surface at an angle of incidence $$45^o$$ The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate (a) the magnitude of the change in momentum of the ball (b) the change in the magnitude of the momentum of the ball
Given,
Mass of ball $$= 50 g = 0.05 kg$$
$$v = 2 \cos 45^0 \hat i - 2 \sin 45^0 \hat j$$
$$v_1 = -2 \cos 45^0 \hat i - 2 \sin 45^0 \hat j$$
(a) Change in momentum $$⇒ m v - m v_1$$
$$\implies0.05( 2 \cos 45^0 \hat i - 2 \sin 45^0 \hat j ) - 0.05 (-2 \cos 45^0 \hat i - 2 \sin 45^0 \hat j)$$
$$\implies0.1 \cos 45^0 \hat i - 0.1 \sin 45^0 \hat j + 0.1 \cos 45^0 \hat i + 0.1 \sin 45^0 \hat j$$
$$\implies 0.2 \cos 45^0 \hat i$$
Therefore , Magnitude $$= \sqrt{[\dfrac{0.2}{\sqrt2}]^2} = \dfrac{0.2}{\sqrt2} = \dfrac{0.2}{1.4} = 0.14 kg m/s$$
(b) Change in magnitude of momentum of the ball $$= P(initial) - P(final)$$
$$ = (2 \times 0.5) - (2 \times 0.5)=0$$
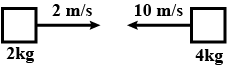
Two blocks of masses 10 kg and 4 kg and are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is
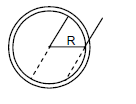
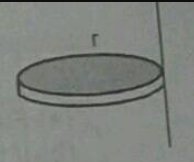
Calculate the radius of gyration of a uniform circular disk of radius $$r$$ and thickness t about a line perpendicular tothe plane of this disk and tangent to the disk as shown in figure.
The radius of gyration of a uniform solid sphere of radius R is $$\sqrt\frac{2}{5}$$ R for rotation about its diameter. Show that its radius of gyration for rotation about a tangential axis of rotation is $$\sqrt\frac{7}{5}$$ R.
Two identical parties move towards each other with velocity $$2V$$ & $$V$$ respectively. What is the velocity of centre of mass?
Three badies $$A,B$$ and $$C$$ having masses $$10\ kg,5\ kg$$ and $$15\ kg$$ representively are projected from top of a tower with $$A$$ vertically upwards with $$10\ m/s,B$$ with $$20\ m/s\ 53^{o}$$ above east horizontal and $$C$$ horizontally southward with $$15\ m/s$$. Find
(a) Velocity of centre of mass of the systrem.
Which of the following is a rotating motion.
(i) Bullet shot from a gun
(ii) Hands of a clock
(iii) Strings of guitar.
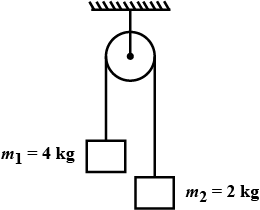
Two masses $$m_{1}=4\ kg$$ and $$m_{2}=2\ kg$$ are released from as shown in figure. Find
(i) The distance travelled by centre of mass in $$9\ s$$.
(ii) The speed of centre of mass after $$9\ s$$
Establish the relation between moment of inertia and angular momentum. Define moment of inertia on the basis of this relation.
A ball of mass $$100$$ g is moving with a velocity of $$10$$. The ball is stopped by the boy in $$0.2ms$$. Find the force of the ball?
A disc of mass M and radius R is reshaped in the form of ring of same mass but radius $$2$$ R. The radius of gyration increased by a factor:
Four rod each of mass m from a square length of diagonal b rotates about its diagonal. Its moment of inertia is:-
The moment of inertia of a uniform rod of mass $$0.50\ kg$$ and length $$1\ m$$ is $$0.10\ kg-m^{2}$$ about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.?
Length of the rod $$=1\ m$$
Mass of the rod $$=0.5\ kg$$
Let at a distance $$d$$ from the centre the rod is moving
Applying parallel axis theorem :
The moment of inertia about the point
$$\Rightarrow (mL^2/12)+md^2=0.10$$
$$\Rightarrow (0.5\times 1^2)/12+0.5\times d^2=0.10$$
$$\Rightarrow d^2=0.2-0.082=0.118$$
$$\Rightarrow d=0.342\ m$$ from the centre.
How will you weight the sun that estimates its mass? The mean orbital radius of the earth around the sun is
Three men A, B, C of mass 40kg,50kg and 60 kg are standing on a plank of mass 90kg which is kept on a smooth horizontal plane B sits in the middle of the plane B sits in the middle of the plane A and C sit 2 meters away from opposite sides. If A and C exchange there positions then mass B will shift
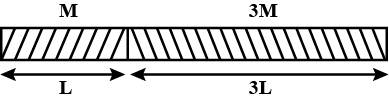
Two thin uniform rods $$A (M,\ L)$$ and $$B (3M,\ 3L)$$ are joined as shown. Find the $$MI$$ about an axis passing through the centre of mass of system of rods and perpendicular to the length.
COM of the system
$$x=\dfrac{ML\dfrac{1}{2}+3M\left(L+\dfrac{3L}{2}\right)}{M+3M}=2L$$
So,
$$\therefore I=I_{M-1}I_{3M}=\left[\dfrac{ML^{2}}{12}+M\left(L-\dfrac{L}{2}\right)^2+3M\dfrac{(3L)^{2}}{12}+3M\left(\dfrac{5L}{2}-2L\right)^{2}\right]$$
$$\Rightarrow ML^{2}\left(\dfrac{1}{12}+\dfrac{9}{4}+\dfrac{9}{4}+\dfrac{3}{4}\right)$$
$$I=\dfrac{16}{3}ML^{2}$$
Calculate the change in momentum of a car of mass 1000 Kg when it's speed increases from 36 Km/h to 108 Km/h uniformly?
Two bodies of different masses $$2\ kg$$ and $$4\ kg$$ are moving with velocities $$2\ m/s$$ and $$10\ m/s$$ towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
Taking direction of $$4kg\,Qs+Ve$$,
$$V_{CM}=\dfrac{(m_1\times v_1)+(m_2\times v_2)}{m_1+m_2}$$
$$=\dfrac{2\times (-2)+4\times 10}{2+4}$$
$$\Rightarrow \dfrac{-4+40}{6}=\dfrac{36}{6}=6m/s$$
$$6m/s$$ in direction of $$4kg$$ block.
Find the ratio of radius of gyration of a solid sphere about its diameter to radius of gyration of hollow sphere about its tangent.(Given Radius of both the spheres is same)
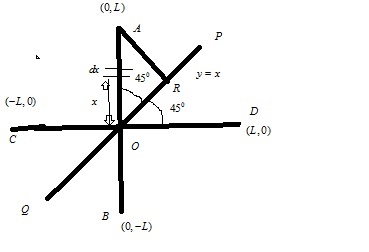
A circular arc $$(AB)$$ of thin wire frame of radius $$R=\sqrt{2}\pi $$cm and mass $$M$$ makes an angle of $$90^o$$ at the origin.Find the y co-ordinate of the CM. Taking O as the origin in cm:
$$x \sin45= \dfrac{2R}{\pi}$$
$$\dfrac{2\sqrt{2}\pi}{\pi}$$
$$\dfrac{y}{\sqrt{2}}=2\sqrt{2}$$
$$y=4cm$$
$$\dfrac{2\sqrt{2}\pi}{\pi}$$
$$\dfrac{y}{\sqrt{2}}=2\sqrt{2}$$
$$y=4cm$$
Show that radius of gyration of disc about transverse axis through centre of mass is equal to radius of gyration of a ring about an axis coinciding with its diameter,if disc and ring have same radius.
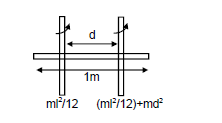
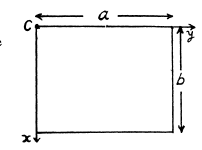
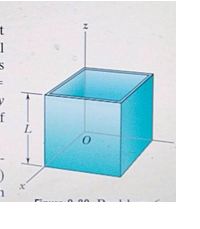
Shows a cubical box that has been constructed from a uniform metal plate of negligible thickness. The box is open at the top and has edge length L= 40cm. find (a) the x coordinate, (b) the y coordinate, and (c) the z, coordinate of the center of mass of the box.
A uniform rod mass m and length l is attached to smooth hinge at end A and to a string at end B as shown in figure. It is at rest . The angular acceleration of the rod just after the string is cut is:
When the string is cut, let angular acceleration of rod be $$\alpha$$.
The Torque due to in own weight $$(mg)$$ provides the needed angular acceleration $$(\alpha)$$, given by :-
$$\tau = I_A \alpha \rightarrow $$ $$(1)$$
Where,
$$\tau = $$ Torque on rod
$$= mg \dfrac{L}{2} cos \theta$$ [ As Torque = $$\vec{r} \times \vec{F}$$ $$= r \bot .F ]$$
and, $$I_A$$ = moment of Inertia about axis through A (end of rod)
$$I_A = \dfrac{ML^2}{3}$$
Thus, from $$(1)$$,
$$\Rightarrow mg \dfrac{L}{2} cos \theta = \dfrac{L}{3} \alpha$$
$$\Rightarrow \alpha = \dfrac{3}{2} g \, cos \theta$$
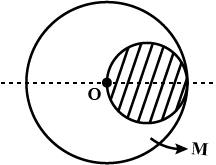
From a uniform disc of radius R, a disc of radius $$\dfrac{R}{2}$$ is scooped out such that they have the common tangent. Find the centre of mass of the length remaining part
If the initial disc had a mass $$M$$, The cutout part would have a man $$m_2=M/4$$ (assuming man is uniforming distributed)
The center of mass of initial disc,
$$\vec{r_1}=O\hat{i}+O\hat{j}$$ and that of cutout disc
$$\vec{r_2}=\left(\dfrac{R}{2}\hat{i}+O\hat{j}\right)$$ [from fig.]
Thus, $$COM$$ of remaining part,
$$\vec{r}=\dfrac{m_1\vec{r_1}-m_2\vec{r_2}}{m_1-m_2}= \dfrac{M(O\hat{i}+O\hat{j})-\dfrac{M}{4}\left(\dfrac{R}{2}\hat{i}+O\hat{j}\right)}{M-\dfrac{M}{4}}$$
$$=\dfrac{-\dfrac{MR}{8}\hat{i}+O\hat{j}}{\dfrac{3m}{4}}=\left(-\dfrac{R}{6}\hat{i}+O\hat{j}\right)$$
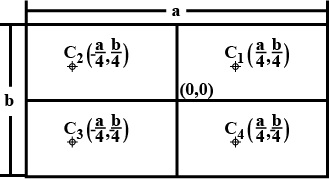
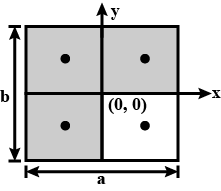
Consider a rectangular plate of dimensions $$a \times b$$. If the plate is considered to be made up of four rectangles of dimensions $$ \dfrac { a } { 2 } \times \dfrac { b } { 2 } $$ and we now remove one out of the four rectangles, find the position where the centre of mass of the remaining system will be:
Given,
Mass of each plate is $$m$$
$${{m}_{a}}={{m}_{b}}={{m}_{c}}={{m}_{d}}=m$$
The center of mass of each square in X, Y coordinate $${{C}_{1}}\left( \dfrac{a}{4},\dfrac{b}{4} \right),\,{{C}_{2}}\left( \dfrac{-a}{4},\dfrac{b}{4} \right),\,{{C}_{3}}\left( \dfrac{-a}{4},\dfrac{-b}{4} \right)\,\,and\,\,{{C}_{4}}\left( \dfrac{a}{4},\dfrac{-b}{4} \right)$$ of the square are by,
Formula for center of mass.
$$X=\dfrac{{{m}_{a}}{{x}_{a}}+{{m}_{b}}{{x}_{b}}+{{m}_{c}}{{x}_{c}}-{{m}_{d}}{{x}_{d}}}{{{m}_{a}}+{{m}_{b}}+{{m}_{c}}-{{m}_{d}}}$$
$$Y=\dfrac{{{m}_{a}}{{y}_{a}}+{{m}_{b}}{{y}_{b}}+{{m}_{c}}{{y}_{c}}-{{m}_{d}}{{y}_{d}}}{{{m}_{a}}+{{m}_{b}}+{{m}_{c}}-{{m}_{d}}}$$
$$\text{ }~\text{ }X=\dfrac{\left[ \dfrac{ma}{4}+\dfrac{m(-a)}{4}+\dfrac{m(-a)}{4}-\dfrac{ma}{4}~\text{ } \right]}{m+m+m-m}=\dfrac{-a}{4}$$
$$\text{ }~\text{ }X=\dfrac{\left[ \dfrac{mb}{4}+\dfrac{mb}{4}+\dfrac{m(-b)}{4}-\dfrac{m(-b)}{4}\text{ }~\text{ } \right]}{m+m+m-m}=\dfrac{-b}{4}$$
Hence, position of center of mass $$\left( \dfrac{-a}{4},\dfrac{-b}{4} \right)$$
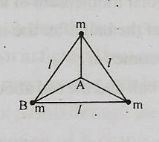
Three equal masses $$m$$ are rigidly connected to each other by massless rods of length $$l$$ forming an equilateral triangle, as shown in the figure. What is the ratio of the moment of inertia of the assembly for an axis through $$B$$ compared with that for an axis through $$A$$ (centroid). Both the axis are perpendicular to the plane of triangle.
REF.Image.
Solution
$$\displaystyle I_{A} = 3\times m(\frac{l}{\sqrt{3}})^{2}$$
$$\displaystyle I_{A} = 3 \times \frac{ml^{2}}{3} = ml^{2}$$
As point p is also the cone of
the system.
By Parallel Axis Theorem,
$$ \displaystyle I_{B} = I_{A}+(3m)(\dfrac{l}{\sqrt{3}})^{2}$$
$$ \displaystyle I_{B} = ml^{2}+ml^{2} = 2ml^{2}$$
So, $$ I_{B} = 2I_{A}$$
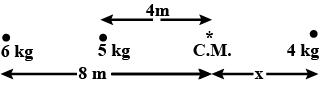
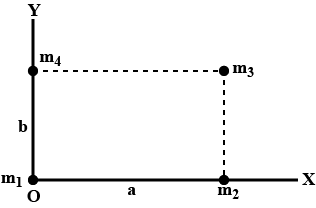
The front wheels of a trick together support 10000 N and its rear wheels together support 17000 N. If the distance between the axles is 4m, find the position of the centre of gravity of the truck.
What should be the $$L/R$$ ratio for a cylinder having radius R and length L so that Moment of Inertia about an axis passing through the middle of the rod is minimum?
R.E.F image
Moment of inertia of a cylinder about in perpendicular
bisector is given by :
$$ I = \frac{1}{4}MR^{2}+\frac{1}{12}ML^{2} $$
$$ = \frac{M}{4}(R^{2}+\frac{L^{2}}{3}) $$
To minimise $$ I, f = R^{2}+\frac{L^{2}}{3} $$ should be minimum
$$ \Rightarrow \frac{df}{dl} = 2R\frac{dR}{dL}+\frac{2L}{3} = 0 $$ (to obtain minima)
$$ \Rightarrow \frac{dr}{dL} = \frac{-L}{3R} \rightarrow (1) $$
also values of cylinder,
$$ v = \pi R^{2}L = $$ constant
$$ \Rightarrow dv = 2\pi RLdR+\pi R^{2}dL = 0 $$
$$ \Rightarrow \frac{dR}{dL} = \frac{-R}{2L}$$ ___(2)
From (1) & (2)
$$ \frac{L}{3R} = \frac{R}{2L} \Rightarrow 2L^{2} = 3R^{2} $$
$$ \Rightarrow \frac{L}{R} = \sqrt{\frac{3}{2}} $$
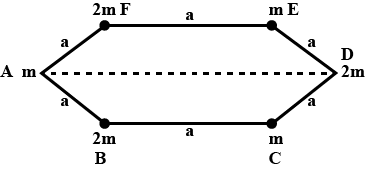
Calculate the moment of inertia of a rectangular frame formed by uniform rods having mass $$m$$ each as shown in figure about an axis passing through its centre and perpendicular to the plane of frame? Also find moment of inertia about an axis passing through $$PQ$$?
State the factors on which radius of gyration depends.
The moment of a force of $$10\ N$$ about a fixed point O is $$5\ N\ m$$. Calculate the distance of the point $$O$$ from the line of action of the force.
Find the center of mass of a uniform L shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 Kg.
(i) A particle of mass m is moving in a circular orbit of radius r with a uniform speed v: Find:
(1) The acceleration of the particle towards the center of the circular path,
Two point masses are connected by a light rigid as shown in figure. The minimum value of moment of inertia of the system about a lin perpendicular to the length of road , is
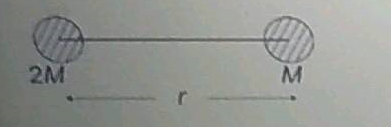
Define radius of gravitation. And state its physical significance.
When does a body rotate? State one way to change the direction of rotation of the body .Give a suitable example
The velocity of centre of mass of the system remains constant, if the total external force acting on the system is
A uniform rod of mass $$300g$$ and length $$50cm$$ rotates at a uniform angular speed of $$2rad/s$$ about an axis perpendicular to the rod through an end. Calculate $$(a)$$ the angular momentum of the rod about the axis of rotation, $$(b)$$ the speed of the centre of the rod and $$(c)$$ its kinetic energy.
A block at rest explodes into three equal parts. Two parts starts moving of along x and y axis respectively with equal speed of $$10 m/s$$. Find the initial velocity of the third part.
Difference between mass and weight.
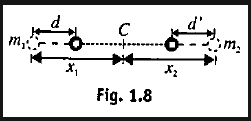
NoLi $$m_1$$ is displaced by $$x_1$$ while $$m_2$$ is displaced by $$x_2$$ along line joing them. then centre of mass remains at P. Find $$\dfrac{x_1}{x_2}$$
$$\begin{array}{l} { m_{ 1 } }{ x_{ 1 } }={ m_{ 2 } }{ x_{ 2 } } \\ \Rightarrow \dfrac { { { x_{ 1 } } } }{ { { x_{ 2 } } } } =\dfrac { { { m_{ 2 } } } }{ { { m_{ 1 } } } } \\ \therefore \dfrac { { { x_{ 1 } } } }{ { { x_{ 2 } } } } =\dfrac { { { m_{ 2 } } } }{ { { m_{ 1 } } } } ----\left( 1 \right) \end{array}$$
State the condition when a force produces translational motion.
The rate of change of linear momentum of a body falling freely under gravity is equal to it's ____
From a rifle of mass $$4\ kg$$, a bullet of mass $$50\ g$$ is fired with an initial velocity of $$35\ m\ s^{1}$$. Calculate the intial recoil velocity of the rigile.
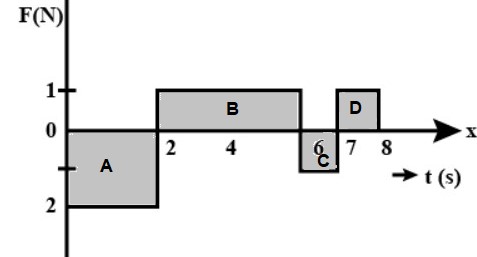
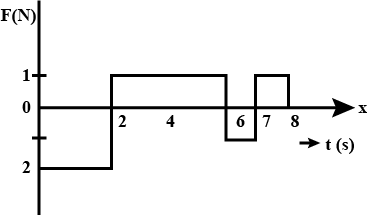
A force time graph for the motion of a body is shown in figure. Change in linear momentum between 0 and 8 s is
$$\textbf{Hint:}$$
$$\rightarrow$$ $$\textbf{Area under Force-time graph gives change in linear momentum.}$$
$$\rightarrow$$ $$\textbf{Linear momentum change = Force}$$ $$\mathbf{\times}$$ $$\textbf{ time.}$$
Linear momentum in part A, $$A=-2\times 2$$
Linear momentum in part B, $$B=4\times 1$$
Linear momentum in part C, $$C=-1\times 1$$
Linear momentum in part D, $$D=1\times 1$$
From figure, Change in momentum $$=A+B+C+D$$
$$=(-2\times 2)+(4\times 1)+(-1\times 1)+(1\times 1)$$
$$=-4+4-1+1$$
$$=0$$
$$\therefore$$ $$\textbf{Change in linear momentum of the body between}$$ $$\mathbf{0}$$ $$\textbf{and}$$ $$\mathbf{8}$$ $$\textbf{is}$$ $$\mathbf{0.}$$
A bomb of mass 4 m at rest explodes into three pieces of masses in the ratio $$1:1:2$$ Two identical pieces fly in mutually perpendicular directions each with a velocity $$V$$. The magnitude of velocity of third piece is
A hollow hemisphere and a solid hemisphere of equal radius and mass are placed as shown, the coordinates of their mutual centre of mass are
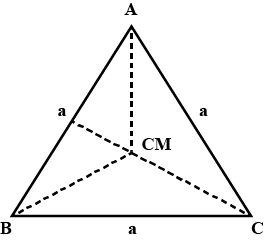
Find the center of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are $$100\ g$$, $$150\ g$$ and $$200\ g$$ respectively. Each side of the equilateral triangle is $$0.5\ m$$ long.
Let
$$\begin{array}{l} { m_{ 1 } }=100g,{ m_{ 2 } }=150g,{ m_{ 3 } }=200g \\ a=0.5m=50cm \end{array}$$
Center of mass coordinates:-
$$\begin{array}{l} x=\dfrac { { \left[ { \dfrac { { -a } }{ 2 } \times { m_{ 1 } }+0\times { m_{ 2 } }+\dfrac { a }{ 2 } \times { m_{ 3 } } } \right] } }{ { { m_{ 1 } }+{ m_{ 2 } }+{ m_{ 3 } } } } \\ =\dfrac { { \left( { { m_{ 3 } }-{ m_{ 1 } } } \right) a } }{ { 2\left( { { m_{ 1 } }+{ m_{ 2 } }+{ m_{ 3 } } } \right) } } =\dfrac { { \left( { 200-100 } \right) 50 } }{ { 2\times 450 } } =\dfrac { { 50 } }{ 9 } cm \\ y=\dfrac { { \left( { 0\times { m_{ 1 } }+\dfrac { { \sqrt { 3 } } }{ 2 } \times a\times { m_{ 2 } }+0\times { m_{ 3 } } } \right) } }{ { { m_{ 1 } }+{ m_{ 2 } }+{ m_{ 3 } } } } \\ =\dfrac { { \dfrac { { \sqrt { 3 } } }{ 2 } \times a\times { m_{ 2 } } } }{ { { m_{ 1 } }+{ m_{ 2 } }+{ m_{ 3 } } } } \\ =\dfrac { { \dfrac { { \sqrt { 3 } } }{ 2 } \times 50\times 150 } }{ { 450 } } \\ =\dfrac { { 25 } }{ { \sqrt { 3 } } } cm \end{array}$$
$$y$$ coordinates of the centroid of the triangle
$$=\dfrac { 1 }{ { \sqrt { 3 } } } \times \dfrac { { \sqrt { 3 } } }{ 2 } \times a=\dfrac { { 25 } }{ { \sqrt { 3 } } } cm$$
$$\therefore$$ the center mass is $$\dfrac{{50}}{9}cm$$.
what is radius of gyration?
The masses of two particles are 300 g and 200 g . They are separated by 60 cm.Determine the distance of centre of mass from 200 g particle.
The energy of a photon is equal to 3 kilo eV.Calculate its liner momentum?
Centre of mass is shown, find
' x '
Define radius of gyration. Write its physical significance.
Can the centre of mass of a body be at a point outside the body?.
A rod of length L is placed along the X-axis between $$x=0$$ and $$x=L$$. The linear density(mass/length) $$\rho$$ of the rod varies with the distance x from the origin as $$\rho =a+bx$$. Find the mass of the rod in terms of a, b and L.
The weight Mg of an extended body is generally shown in a diagram to act through the centre of mass. Does it mean that the earth does not attract other particles ?
If the total mechanical energy of a particle is zero, is its linear momentum necessarily zero ? Is it necessarily nonzero ?
A $$ 2.00\, kg $$ particle has the $$ xy $$ coordinates $$ (-1.20\, m, 0.500\, m) $$,and a $$ 4.00\, kg $$ particle has the $$ xy $$ coordinates $$ (0.600\, m, -0.750\, m) $$.Both lie on a horizontal plane. At what (a) $$ x $$ and (b) $$ y $$ coordinates must you place a $$ 3.00\, kg $$ particle such that the center of mass of the three-particle system has the coordinates $$ (-0.500 \,m , -0.700\, m)$$ ?
Match the column
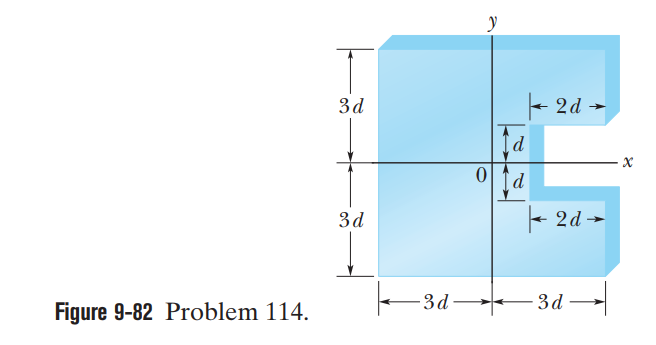
Figure $$9-82$$ shows a uniform square plate of edge length $$ 6d = 6.0\, m $$ from which a square piece of edge length $$2d$$ has been removed .What are (a) the x coordinate and (b) the y coordinate of the center of mass of the remaining piece?
If a 32.0 N torque on a wheel causes angular acceleration 25,0 rad/$$ S^{2} $$ What is the wheel's rotational inertia
A big olive $$ (m = 0.50\, kg) $$ lies at the origin of an xy coordinate system, and a big Brazil nut $$ (M = 1.5 \,kg) $$ lies at the point $$ (1.0, 2.0) \,m $$. At $$ t = 0,$$ a force $$ \vec{F}_{0} = (2.0 \hat{i} + 3.0\hat{j})\,N $$ begins to act on the olive, and a force $$ \vec{F}_n = (-3.0\hat{i} - 2.0\hat{j} )\,N $$ begins to act on the nut. In unit-vector notation, what is the displacement of the center of mass of the olivenut system at $$t = 4.0 s,$$ with respect to its position at $$ t = 0 $$ ?
A solid sphere of weight $$36.0\ N$$ rolls up an incline an angle of $$30.0^{o}$$. At the bottom of the incline, the center of mass of the sphere has a transnational speed of $$4.90\ m/s$$.Find the distance traveled?
A yo-yo has rotational inertia of $$950\ g.cm^{2}$$ and a mass of $$20\ g$$. Its axle radius is $$3.2\ mm$$, and its string is $$120\ cm$$ long. The yo-yo rolls from rest down to the end of the string.
How long does it take to reach the end of the string?
(i)What is momentum? (ii)Write its $$SI$$ unit. Interpret force in terms of momentum. (iii)Represent the following graphically.
Momentum versus velocity when mass is fixed.
Momentum versus velocity when mass is fixed.
$$\large\textbf{Part i: Definition of momentum}$$
$$\bullet$$Momentum is defined as the product of mass (m) and the velocity (v). If an object is
steady so its velocity is zero resulting in zero momentum.
Momentum $$(p)=$$ mass $$(m)\times $$ velocity $$(v)$$
$$\large\textbf{Part ii: SI unit and force in terms of momentum}$$
$$SI$$ unit of momentum is $$\large{kg\ ms^{-1}}$$
We can Interpret force by newton's second law which states that force is equal to rate of change of linear momentum.
i.e.,
Force $$F=$$ Rate of change in linear momentum $$=$$ $$\dfrac{\triangle P}{\triangle t}$$
$$\large\textbf{Part iii: Graph Momentum vs Velocity}$$
we know,
$$P = mV$$
or $$P \propto V$$ when mass is constant
A body of radius $$R$$ and mass $$m$$ is rolling smoothly with speed $$v$$ on a horizontal surface. It then rills up a hill to a maximum height $$h$$.What might the body be?
What are (a) the x coordinate and (b) the y coordinate of the center of mass for the uniform plate shown in Fig. 9-38 if $$ L = 5.0\,cm $$ ?
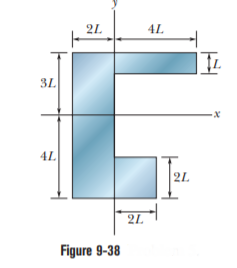
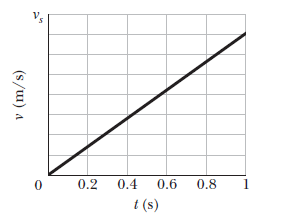
Figure shows the speed $$v$$ versus time $$t$$ for a $$0.500\ kg$$ object of radius $$6.00\ cm$$ that rools smoothly down a $$30^o$$ ramp. The scale on the velocity axis is set by $$v_s =4.0\ m/s$$. What is the rotational inertia of the object?
On what factor does the position of the centre of gravity of a body depend? Explain your answer with an example.
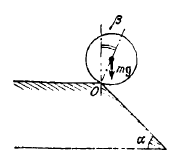
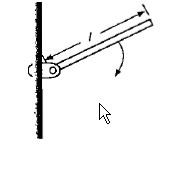
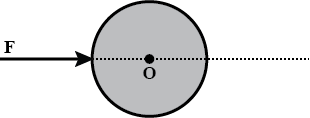
In fig. a force $$ F $$ is applied in a direction passing through the pivoted point $$ O $$ of the body. Will the body rotate? Give reason to support your answer.
Find out the increase in moment of inertia I of a uniform rod (coefficient of linear expansion $$\alpha$$) about its perpendicular bisector when its temperature is slightly increased by $$\triangle T.$$
Find the centre of mass of a uniform (a) half-disc, (b) quarter-disc.
Velocity of a body of mass $$m_{1}$$ is $$10m/s$$ and velocity of a body of mass $$m_{2}$$ is $$108km/h$$. If their momenta are equal find ratio of their masses.
Write the formula for the momentum of a body.
A body's angular velocity is changed from $$1$$ cycle / second to $$16$$ cycles / second without applying any torque on it. In both the cases what would be the ratio of radii of gyration ?
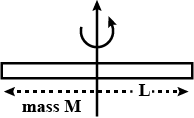
What do you understand by the term couple? State its effect. Give two examples of a couple of action in our daily life.
Define the term center of gravity of a body.
When is a body said to have rotational motion? Give an example.
Define the following.
A dancer standing on a rotating table raises her hands suddenly what happens?
A car of $$1000\ kg$$ moves with a velocity of $$10\ m/s$$. On applying brake sit comes to rest in $$5s$$. Then what are its initial momentum and final momentum?
Consider a rigid body capable to rotate about an axis
Derive an equation for the angle covered by a rotating rigid body (subject to uniform angular acceleration) in the $$ n^{th} $$ second.
Why is it useful to define the radius of gyration ?
The moment of inertia $$(MI)$$ of a body about a given rotation axis depends upon (i) the mass of the body and (ii) the distribution of mass about the axis of rotation. These two factors can be separated by expressing the $$MI$$ as the product of the mass $$(M)$$ and the square of a particular distance $$(k) $$ from the axis of rotation. This distance is called the radius of gyration and is defined as given above. Thus,
$$I = \sum m_{i} r^{2}_{i} = Mk^2$$
$$ \therefore \,k = \sqrt{\dfrac{1}{M}} $$
Physical significance: The radius of gyration is less if $$I$$ is less i.e., if the mass is distributed close to the axis ; and it is more if $$I$$ is more , i.e., if the mass is distributed away from the axis. Thus, it gives an idea about the distribution of mass about the axis of rotation.
$$I = \sum m_{i} r^{2}_{i} = Mk^2$$
$$ \therefore \,k = \sqrt{\dfrac{1}{M}} $$
Physical significance: The radius of gyration is less if $$I$$ is less i.e., if the mass is distributed close to the axis ; and it is more if $$I$$ is more , i.e., if the mass is distributed away from the axis. Thus, it gives an idea about the distribution of mass about the axis of rotation.
Discuss the necessity of radius of gyration. Define it. On what factors does it depend and it does not depend ? Can you locate come similarity between the center of mass and radius of gyration ? What can you infer if a uniform ring and a uniform disc have the same radius of gyration ?
Definition: The radius of gyration of a body rotating about an axis is defined as the distance between the axis of rotation and the point at which the entire mass of the body can be supposed to be concentrated so as to give the same moment of inertia as that of the body about the given axis.
The moment of inertia $$(MI)$$ of a body about a given rotation axis depends upon (i) the mass of the body and (ii) the distribution of mass about the axis of rotation. These two factors can be separated by expressing the $$MI$$ as the product of the mass $$(M)$$ and the square of a particular distance $$(k) $$ from the axis of rotation. This distance is called the radius of gyration and is defined as given above. Thus,
$$I = \sum m_{i} r^{2}_{i} = Mk^2$$
$$ \therefore \,k = \sqrt{\dfrac{1}{M}} $$
Physical significance: The radius of gyration is less if $$I$$ is less i.e., if the mass is distributed close to the axis ; and it is more if $$I$$ is more , i.e., if the mass is distributed away from the axis. Thus, it gives an idea about the distribution of mass about the axis of rotation.
The center of mass (CM) coordinates locates a point where if the entire mass M of a system of particles or that of a rigid body can be thought to be concentrated such that the acceleration of this point mass obeys Newton's second law of motion, viz.,
$$ \vec{F}_{net} = M \vec{a}_{CM} $$ , where $$ \vec{F}_{net} $$ is the sum of all the external forces acting on the body or on the individual particles of the system of a particles.
Similarly, radius of gyration locates a point from the axis of rotation where the entire mass M can be thought to be concentrated such that the angular acceleration of that point mass about the axis of rotation obeys the relation, $$ \vec{\tau}_{net} = M \vec{\alpha} $$ , where $$ \vec{\tau}_{net} $$ is the sum of all the external torques acting on the body or on the individual particles of the system of particles.
The radius of gyration of a thin ring of radius $$R_{r} $$ about its transverse symmetry axis is
$$ k_{r} = \sqrt{I_{CM} / M_{r}} = \sqrt{R_{r}^{2}} = R_{r} $$
The radius of gyration of a thin disc of radius $$R_{d}$$ about it transverse symmetry axis is
$$k_{d} = \sqrt{I_{CM} / M_{d}} = \dfrac{\sqrt{M_{d}R^{2}_{d} / 2}}{M_{d}} = \dfrac{1}{\sqrt{2}} R_{d} $$
Given $$ k_{r} = k_{d} $$
$$ R_{r} = \dfrac{1}{R_{d}}$$ or, equivalently , $$R_{d} = \sqrt{2}R_{r} $$.
The moment of inertia $$(MI)$$ of a body about a given rotation axis depends upon (i) the mass of the body and (ii) the distribution of mass about the axis of rotation. These two factors can be separated by expressing the $$MI$$ as the product of the mass $$(M)$$ and the square of a particular distance $$(k) $$ from the axis of rotation. This distance is called the radius of gyration and is defined as given above. Thus,
$$I = \sum m_{i} r^{2}_{i} = Mk^2$$
$$ \therefore \,k = \sqrt{\dfrac{1}{M}} $$
Physical significance: The radius of gyration is less if $$I$$ is less i.e., if the mass is distributed close to the axis ; and it is more if $$I$$ is more , i.e., if the mass is distributed away from the axis. Thus, it gives an idea about the distribution of mass about the axis of rotation.
The center of mass (CM) coordinates locates a point where if the entire mass M of a system of particles or that of a rigid body can be thought to be concentrated such that the acceleration of this point mass obeys Newton's second law of motion, viz.,
$$ \vec{F}_{net} = M \vec{a}_{CM} $$ , where $$ \vec{F}_{net} $$ is the sum of all the external forces acting on the body or on the individual particles of the system of a particles.
Similarly, radius of gyration locates a point from the axis of rotation where the entire mass M can be thought to be concentrated such that the angular acceleration of that point mass about the axis of rotation obeys the relation, $$ \vec{\tau}_{net} = M \vec{\alpha} $$ , where $$ \vec{\tau}_{net} $$ is the sum of all the external torques acting on the body or on the individual particles of the system of particles.
The radius of gyration of a thin ring of radius $$R_{r} $$ about its transverse symmetry axis is
$$ k_{r} = \sqrt{I_{CM} / M_{r}} = \sqrt{R_{r}^{2}} = R_{r} $$
The radius of gyration of a thin disc of radius $$R_{d}$$ about it transverse symmetry axis is
$$k_{d} = \sqrt{I_{CM} / M_{d}} = \dfrac{\sqrt{M_{d}R^{2}_{d} / 2}}{M_{d}} = \dfrac{1}{\sqrt{2}} R_{d} $$
Given $$ k_{r} = k_{d} $$
$$ R_{r} = \dfrac{1}{R_{d}}$$ or, equivalently , $$R_{d} = \sqrt{2}R_{r} $$.
Three particles are arranged as shown in the figure.
Find the position of their centre of mass.
Co-ordinates of $$ B ( 0 , 0) $$ co-ordinates of $$ C (a, 0) $$
Co-ordinates of $$ A ( \dfrac{a }{2 }, \sqrt { \dfrac {a}{2} }) $$
$$ \therefore X_{cm} = \dfrac { \sum m_iX_i} {\sum m_i} = \dfrac { m (0) + m(a) + m( \dfrac {a}{2} ) }{3m} $$
$$ =\dfrac { 3am}{ 2(3m) } = \dfrac {a}{2} $$
$$ Y_{CM} = \dfrac { \sum m_iY_i}{ \sum m_i} = \dfrac { m(0) + m(0) + m( \sqrt {3} \dfrac {a}{2} ) }{3m} $$.
$$ = \dfrac { \sqrt { 3} ma }{ 2 (3m) } = \dfrac { \sqrt {3} a}{6} $$
here CM is the centroid of the triangle as shown
The coordinates of $$ CM $$ is $$ (\dfrac{a}{2} , \dfrac { \sqrt {3} a }{6} ) $$
the distance of $$ CM $$ from $$ A, B $$ or $$ C $$ is same and d is
$$ = \sqrt { \dfrac {a^2}{4} + \dfrac { 3a^2}{36} } $$
$$ = \dfrac {a}{2} \times \dfrac {2}{ \sqrt {3}} = \dfrac {a}{ \sqrt {3} } $$
Co-ordinates of $$ A ( \dfrac{a }{2 }, \sqrt { \dfrac {a}{2} }) $$
$$ \therefore X_{cm} = \dfrac { \sum m_iX_i} {\sum m_i} = \dfrac { m (0) + m(a) + m( \dfrac {a}{2} ) }{3m} $$
$$ =\dfrac { 3am}{ 2(3m) } = \dfrac {a}{2} $$
$$ Y_{CM} = \dfrac { \sum m_iY_i}{ \sum m_i} = \dfrac { m(0) + m(0) + m( \sqrt {3} \dfrac {a}{2} ) }{3m} $$.
$$ = \dfrac { \sqrt { 3} ma }{ 2 (3m) } = \dfrac { \sqrt {3} a}{6} $$
here CM is the centroid of the triangle as shown
The coordinates of $$ CM $$ is $$ (\dfrac{a}{2} , \dfrac { \sqrt {3} a }{6} ) $$
the distance of $$ CM $$ from $$ A, B $$ or $$ C $$ is same and d is
$$ = \sqrt { \dfrac {a^2}{4} + \dfrac { 3a^2}{36} } $$
$$ = \dfrac {a}{2} \times \dfrac {2}{ \sqrt {3}} = \dfrac {a}{ \sqrt {3} } $$
What is a couple?
Acar and a bus are travelling with the same velocity. What has greater momentum? Why?
A car ofmass $$1000\ kg$$ runs with a velocity of $$10\ m/s$$. What is the momentum of this car?
Initial momentum of $$B=$$...
Find the total momentum of electrons in a straight wire of length $$l = 1000\ m$$ carrying a current $$I = 70\ A$$.
Final momentum of B $$=$$...
of a copper uniform rod relative to the axis which is perpendicular to the rod and passes through its end, if the mass of the rod is $$m$$ and its length $$l$$;
Consider an elementry disc of thickness $$dx$$. Moment of inertia of this element about the $$z-$$ axis, passing through it $$C.M.$$
$$dt_{z}=\dfrac{(dm)R^{2}}{2}=\rho S\ dx\dfrac{R^{2}}{2}$$
where $$\rho=$$ density of the material of the plate and $$S=$$ area of cross section of the plate.
Thus the sought moment of inertia
$$I_{z}=\dfrac{\rho SR^{2}}{2}\displaystyle\int_{0}^{b}dx=\dfrac{R^{2}}{2}\rho Sb$$
$$=\dfrac{\pi}{2}\rho b R^{4}(as\ S=\pi R^{2})$$
putting all the values we get, $$I_{x}=2. gm.m^{2}$$
The mass of a copper atom is $$1.06 \times 10^{-25} \ kg$$, and the density of copper is $$8.920\ kg/m^3$$
Determine the numbers of atoms in $$1\ cm^3$$ of copper
The vector position of a $$3.50-g$$ particle moving in the $$xy$$ plane varies in time according to $$\vec{r}_{1}=(3\hat{i}+3\hat{j})t+2\hat{j}t^{2}$$, where $$t$$ is in seconds and $$\vec{r}$$ is in centimeters. At the same time, the vector position of a $$5.50\ g$$ particle varies as $$\vec{r}_{2}=3\hat{i}-2\hat{i}t^{2}-6\hat{j}t$$. At the $$t=2.50\ s$$, determine
the linear momentum of the system,
A car-travels with a velocity of $$15\ m/s$$. The total of the car and the passengers in it is $$1000\ kg$$. find the momentum of the car.
A scientist arriving at a hotel asks a bellhop to carry a heavy suitcase. When the bellhop rounds a corner, the suitcase suddenly swings away from him for some unknown reasons. The alarmed bellhop drops the suitcase and runs away. What might be in the suitcase?
Define couple.
A ball of mass m is thrown straight up into the air with an initial speed $$v_i$$. Find the momentum of the ball
at its maximum height
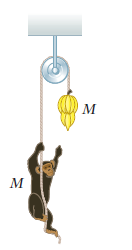
A light rope passes over a light, frictionless pulley. One end is fastened to a bunch of bananas of mass $$M$$, and a monkey of mass $$M$$ clings to the other end. The monkey climbs the rope in an attempt to reach the bananas.
Will the monkey reach the bananas?
Why does a long pole help a tightrope walker stay balanced?
The vector position of a $$3.50-g$$ particle moving in the $$xy$$ plane varies in time according to $$\vec{r}_{1}=(3\hat{i}+3\hat{j})t+2\hat{j}t^{2}$$, where $$t$$ is in seconds and $$\vec{r}$$ is in centimeters. At the same time, the vector position of a $$5.50\ g$$ particle varies as $$\vec{r}_{2}=3\hat{i}-2\hat{i}t^{2}-6\hat{j}t$$. At the $$t=2.50\ s$$, determine
the velocity of the center of mass,
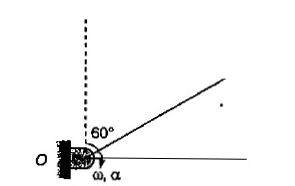
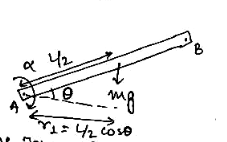
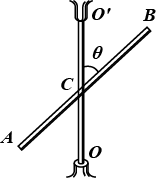
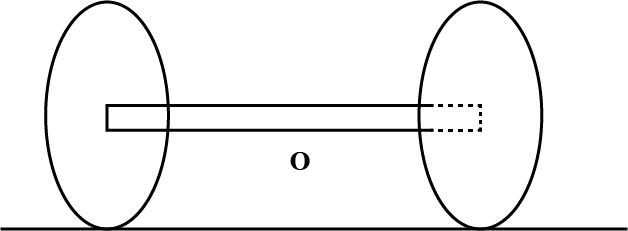
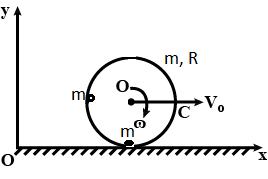
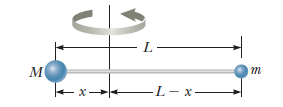
A midpoint of a thin uniform rod $$AB$$ of mass $$m$$ and length $$l$$ is rigidly fixed to a rotation axle $$OO^\prime$$ as shown in figure above. The rod is set into rotation with a constant angular velocity $$\omega$$. If the resultant moment of the centrifugal forces of inertia relative to the point $$C$$ in the reference frame fixed to the axle $$OO^\prime$$ and to the rod is given by $$\displaystyle N=\frac{1}{x}m\omega^2l^2\sin{2\theta}$$, then the value of $$x/4$$ is :
Consider a small element of length $$dx$$ at a distance $$x$$ from the point $$C$$, which is rotating in a circle of radius $$r=x\sin{\theta}$$
Now, mass of the element $$\displaystyle=\left(\frac{m}{l}\right)dx$$
So, centrifugal force acting on this element
$$\displaystyle=\left(\frac{m}{l}\right)dx\omega^2x\sin{\theta}$$ and
moment of this force about $$C$$,
$$\displaystyle|dN|=\left(\frac{m}{l}\right)dx\omega^2x\sin{\theta}\cdot x\cos{\theta}$$
$$\displaystyle=\frac{m\omega^2}{2l}\sin{2\theta}x^2dx$$
and hence, total moment
$$\displaystyle N=2\int_0^{\displaystyle\frac{l}{2}}{\frac{m\omega^2}{2l}\sin{2\theta}x^2dx}=\frac{1}{24}m\omega^2l^2\sin{2\theta}$$
Now, mass of the element $$\displaystyle=\left(\frac{m}{l}\right)dx$$
So, centrifugal force acting on this element
$$\displaystyle=\left(\frac{m}{l}\right)dx\omega^2x\sin{\theta}$$ and
moment of this force about $$C$$,
$$\displaystyle|dN|=\left(\frac{m}{l}\right)dx\omega^2x\sin{\theta}\cdot x\cos{\theta}$$
$$\displaystyle=\frac{m\omega^2}{2l}\sin{2\theta}x^2dx$$
and hence, total moment
$$\displaystyle N=2\int_0^{\displaystyle\frac{l}{2}}{\frac{m\omega^2}{2l}\sin{2\theta}x^2dx}=\frac{1}{24}m\omega^2l^2\sin{2\theta}$$
A horizontal circular platform of radius $$0.5 m$$ and mass $$0.45 kg$$ is free to rotate about its axis. Two massless spring toy-guns, each carrying a steel ball of mass $$0.05 kg$$ are attached to the platform at a distance $$0.25 m$$ from the centre on its either sides along its diameter (see figure). Each gun simultaneously fires the ball horizontally and perpendicular to the diameter in opposite directions. After leaving the platform, the ball have horizontal speed of $$9 ms$$$$^{-1}$$ with respect to the ground. The rotational speed of the platform in $$rad s$$$$^{-1}$$ after the balls leave the platform is :
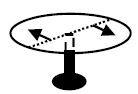
Two rods of equal mass $$m$$ and length $$l$$ lie along the x axis and y axis with their centres origin. If the moment of inertia of both about the line x=y is given as $$ \dfrac{ml^2}{x} $$. Find $$x$$.
Line PQ represents $$y=x$$
MI of AB about PQ which makes an angle $$45^{\circ}$$ with x-axis is two times the MI of AO about PQ.
MI of CD about PQ is same as that of MI of AB about PQ.
Hence, MI of two rods is 4 times the MI of AO about PQ.
$$AR \perp PQ$$Consider a small length dx of rod AO at a distance x from O.
MI of dx about PQ is $$\displaystyle dI = \frac{m}{l}dx (x \sin 45^{\circ})^2= \frac{m}{2l} \frac{x^3}{3}$$
$$\displaystyle \therefore I = \int_{0}^{\frac{l}{2}} \frac{m}{2l} \frac{x^3}{3}=\frac{m}{2l} \frac{(\frac{l}{2})^3}{3}=\frac{ml^2}{48}$$
$$ \therefore$$ MI of the two rods is $$\displaystyle 4 \times \frac{ml^2}{48}=\frac{ml^2}{12}=\frac{ml^2}{x}$$
$$ \Rightarrow x =12$$
MI of AB about PQ which makes an angle $$45^{\circ}$$ with x-axis is two times the MI of AO about PQ.
MI of CD about PQ is same as that of MI of AB about PQ.
Hence, MI of two rods is 4 times the MI of AO about PQ.
$$AR \perp PQ$$Consider a small length dx of rod AO at a distance x from O.
MI of dx about PQ is $$\displaystyle dI = \frac{m}{l}dx (x \sin 45^{\circ})^2= \frac{m}{2l} \frac{x^3}{3}$$
$$\displaystyle \therefore I = \int_{0}^{\frac{l}{2}} \frac{m}{2l} \frac{x^3}{3}=\frac{m}{2l} \frac{(\frac{l}{2})^3}{3}=\frac{ml^2}{48}$$
$$ \therefore$$ MI of the two rods is $$\displaystyle 4 \times \frac{ml^2}{48}=\frac{ml^2}{12}=\frac{ml^2}{x}$$
$$ \Rightarrow x =12$$
calculate the force of friction on each disc.
LET $$a' \rightarrow$$ acceleration of C.M of $$2$$ disk.
$$\Rightarrow 2F_{psendo}-2f=2Ma'$$
or, $$F_{psendo}-f=Ma'$$
or, ,$$Ma-f=Ma' \longrightarrow \left(1\right)$$
For pure rolling to take place
$$\Rightarrow fr=\dfrac{Ia'}{r}$$ or $$a'=\dfrac{fr^2}{I}$$
$$=\dfrac{2fr^2}{Mr^2}=\dfrac{2f}{M}\longrightarrow \left(2\right)$$
From $$\left(1\right)$$ and $$\left(2\right)$$ we get,
$$\Rightarrow Ma-f=\dfrac{M\left(2f\right)}{M}$$
or $$Ma=3f,$$ or $$f=\dfrac{Ma}{3}$$
$$=\dfrac{2\times 9}{3}$$
$$=6N.$$
Hence, the answer is $$6N.$$
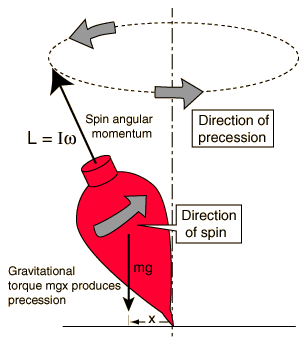
A top of mass $$m=1.0\:kg$$ and moment of inertia relative to its own axis $$I=4.0\:g m^2$$ spins with an angular velocity $$\omega=310\:rad/s$$. Its point of rest is located on a block which is shifted in a horizontal direction with a constant acceleration $$w=1.0\:m/s^2$$. The distance between the point of rest and the centre of inertia of the top equals $$l=10\:cm$$. If the angular velocity of precession $${\omega}^\prime$$ is $$x$$ find the value of $$10x$$.
Consider a top precessing about vertical axis as shown above.
Let the angle between the axis along top and the vertical axis be $$\phi$$.
The torque on the top due to gravitational force is balanced by the angular momentum's effect of its precession.
$$\implies \tau=\omega_{p}Lsin\phi$$
$$\implies mgl\sin \phi=\omega_{p}(I\omega)\sin \phi$$
$$\implies \omega_{p}=\dfrac{mgl}{I\omega}=0.8/s$$
The vector $$\vec{w_p}$$ forms an angle $$\displaystyle\theta=\tan^{-1}{\frac{w_p}{g}}=6^\circ$$ with the normal vertical.
A man standing on a trolley pushes another identical trolley (both trolleys are at rest on a rough surface), so that they are set in motion and stop after some time. If the ratio of mass of first trolley with man to mass of second trolley is 3, then find the ratio of the stopping distances of the second trolley to that of the first trolley. (Assume coefficient of friction to be the same for both the trolleys)
A solid disc and a ring, both of radius 10 cm are placed on a horizontal table simultaneously, with initial angular speed equal to $$10\pi$$ rad $$s^{-1}$$. Which of the two will start to roll earlier ? The co-efficient of kinetic friction is $$\mu_k = 0.2$$.
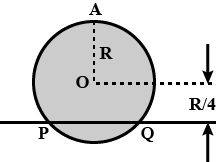
A uniform circular disc has radius $$R$$ and mass $$m$$. A particle also of mass $$m$$ is fixed at a point $$A$$ on the edge of the disc as shown in the figure. The disc can rotate freely about a fixed horizontal chord $$PQ$$ that is at a distance $$R/4$$ from the centre $$C$$ of the disc. The line $$AC$$ is perpendicular to $$PQ$$. Initially the disc is held vertical with the point $$A$$ at its highest position. If is then allowed to fall so that it starts rotating about $$PQ$$. The linear speed of the particle as it reaches its lowest position is $$\sqrt { ngR } $$, where $$n$$ is an integer. Find the value of $$n$$ $$ $$:
Co-ordinates of center of mass w.r.t. $$A$$.
Co-ordinates of centre of mass with respect to A
$$X_{cm}=\cfrac{m_1X_1+m_2X_2+m_3X_3+...}{m_1+m_2+m_3+....}\\ \quad=\cfrac{2\times a+m\times a+2\times a+m\times a+\cfrac{2}{3}a}{2+m+2+m+\cfrac{2}{3}}$$
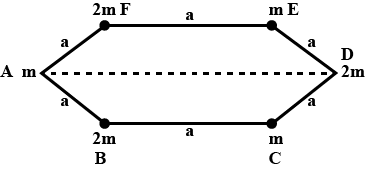
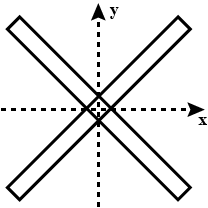
Two uniform identical rods each of mass $$M$$ and length $$l$$ are joined to form a cross as shown in figure. Find the moment of inertia of the cross about a bisector shown by dotted lines in the figure.
Consider a two-particle system with the particles having masses $$m_1$$ and $$m_2$$. If the first particle is pushed towards the centre of mass through a distance $$d$$, by what distance should be the second particle be moved so as to keep the centre of mass at the same position?
Consider Fig. Suppose the distance of $$m_1$$ from the centre of mass $$C$$ is $$x_1$$ and that of $$m_2$$. Suppose mass $$m_2$$ is moved through a distance $$d'$$ towards $$C$$ so as to keep the centre of mass at $$C$$.
Then, $$m_1x_1 = m_2x_2$$ ...........(i)
and $$m_1(x_1 - d_) = m_2(x_2 - d')$$ ............(ii)
Subtracting Eq. (ii) from Eq. (i), we get
$$m_1d = m_2d'$$ or $$d' = (m_1/m_2)d$$
Then, $$m_1x_1 = m_2x_2$$ ...........(i)
and $$m_1(x_1 - d_) = m_2(x_2 - d')$$ ............(ii)
Subtracting Eq. (ii) from Eq. (i), we get
$$m_1d = m_2d'$$ or $$d' = (m_1/m_2)d$$
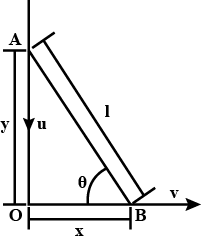
The velocity of end A of a rigid rod placed between two smooth vertical walls is $$u$$ along vertical direction. Find out the velocity of end $$B$$ of that rod, rod always remains in contact with the vertical wall and also find the velocity of centre of rod. Also find equation of path of centre of rod.
Mark the intersection of the horizontal and vertical wall as origin, O.
Now,
$$OA=y$$
$$OB=x$$
In triangle $$AOB$$
$$y=lsin\theta$$
$$x=l cos \theta$$
Velocity of end A $$u$$ will be given by the rate of change of $$y$$ with respect to time $$t$$.
Thus,
$$u=y'=lcos\theta\ \theta'$$
$$v=x'=-lsin\theta\ \theta'$$
As
$$l\ \theta'=\dfrac{u}{cos\theta}$$
Thus,
$$v=-\dfrac{u}{cos\theta}\times sin\theta$$
$$v=-u\ tan\theta$$
Thus the velocity of the point B will be given by $$-u\ tan\theta$$
Let the Position of Centre of Mass of the rod be $$(x_g,\ y_g)$$
The CM of the rod will lie at a distance $$\dfrac l2$$ of the rod.
Thus,
$$x_g=\dfrac l2 cos\theta = \dfrac x2$$
$$y_g=\dfrac l2 sin\theta = \dfrac y2$$
Trajectory of Center of rod will be given by:
$$x_g \hat i+y_g \hat j=\dfrac 12(x \hat i+y\hat j)$$
Therefore, Velocity of centre of rod is given by:
$$ \dfrac{d(x_g \hat i+y_g \hat j)}{dt}=\dfrac 12\dfrac{d (x\hat i+y \hat j)}{dt}$$
$$\overrightarrow v_g=\dfrac 12 (\overrightarrow v + \overrightarrow u)$$
$$v_g=\dfrac12\sqrt{(lcos\theta \ \theta')^2+(-lsin\theta\ \theta')^2}$$
$$v_g=\dfrac{l}{2}\dfrac{d\theta}{dt}$$
or
$$v_g=\dfrac{u}{2cos\theta}$$
Therefore, the velocity of centre of rod will be given by; $$v_g=\dfrac{u}{2cos\theta}$$
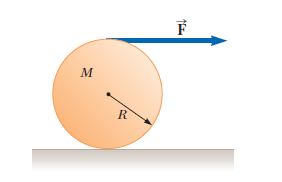
A disc of mass $$m$$, radius $$r$$ wrapped over by a light and inextensible string is pulled by force $$F$$ at the free end of the string. If it moves on a smooth horizontal surface, find linear and angular acceleration of the disc.
$$a$$ given as
$$F=ma \Rightarrow a= \dfrac { F }{ m } $$
$$\because \quad \tau=FR \quad \quad$$ & $$I_{0}=\dfrac {1}{2}mR^{2}$$
$$\Rightarrow \quad \alpha=\dfrac {\tau}{I_{0}}=\dfrac {FR}{(1/2)mR^{2}}=\dfrac {2F}{mR}$$
If the radius of a solid sphere is 35 cm, calculate the radius of gyration when the axis is along, a tangent :
Three identical uniform rods each of length $$1\ m$$ and $$2\ kg$$ are arranged to from an equilateral triangle. What is the moment of inertia of the system about an axis passing through one corner and perpendicular to the plane of the triangle?
Two identical balls each of radius $$10 cm $$ are placed touching each other. The distance of their centre of mass from the point of contact is :
The moment of inertia of a straight thin rod of mass $$M$$ , length $$L$$ about an axis perpendicular to its length and passing through its one end is :
A flywheel of mass $$25\ kg$$ has a radius of $$0.2\ m$$. If is making $$240\ rpm$$. What is the torque necessary to bring it to rest in $$20\ s$$? If the torque is due to a force applied tangentially on the rim of the flywheel, what is the force?
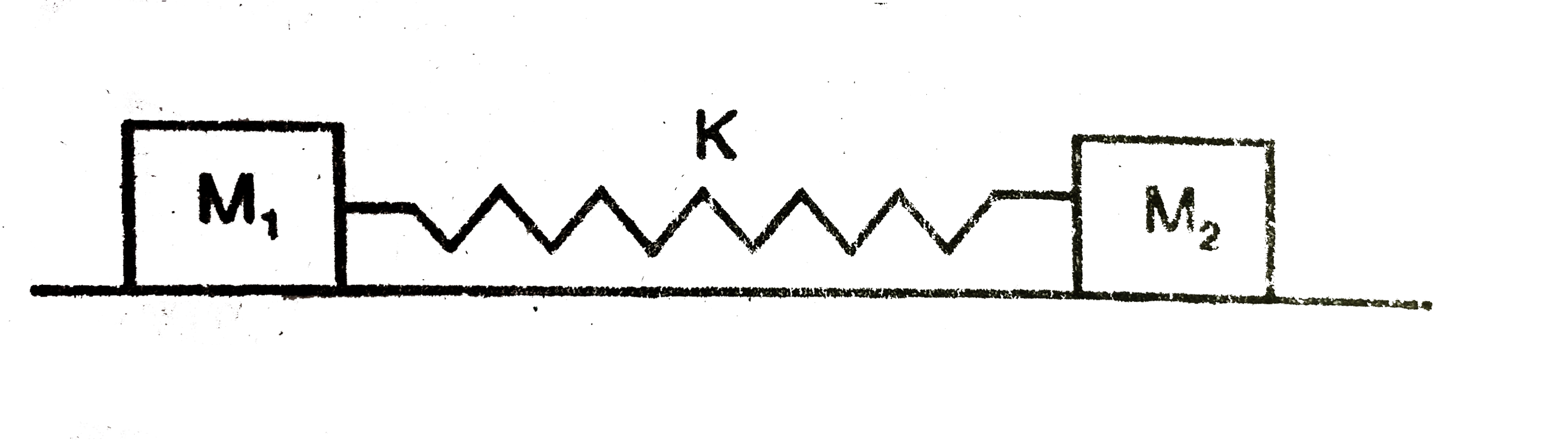
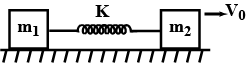
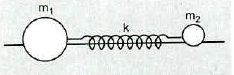
Two block of mass $$m_{1}$$ and $$m_{2}$$ are connected with the help of a spring constant $$k$$ initially the spring in its natural length as shown. A sharp impulse is given to mass $$m_{2}$$ so that it acquires a velocity $$v_{0}$$ towards right. If the system is kept on smooth floor then find (a) the velocity of the centre of mass, (b) the maximum elongation that the spring will suffer?
Two uniforms, thin identical rods each of mass M and length L are joined at the middle so as to form a cross.Then:-
The angular velocity of a body changes from one revolution per $$9$$ seconds to $$1$$ revolution per second without applying any yorque the ratio of its radius of gyration in the two cases is.
The Sun is a hot plasma (ionized matter) with its inner core at a temperature exceeding $$10^7 K$$, and its outer surface at a temperature of about $$6000 K$$. At these high temperatures, no substances remain in a solid or liquid phase. In what range do you expect the mass density of the Sun to be, in the range of densities of solids and liquids or gases? Check if your is correct from the following data: mass of the Sun $$= 2.0 \times 10^{30} kg$$, radius of the Sun $$7.0 \times 10^8m$$.
The velocity of the end 'A' of a rigid rod placed between two smooth vertical walls is $$'u'$$ along the vertical direction. Find out the velocity of end 'B' of the rod if rod always remains in contact with the vertical wall and also find the velocity of the centre of the rod. Also, find the equation of path of the centre of the rod.
$$\textbf {Hint :}$$ The point to be noted is that the ladder remains in contact with the floor and the wall during its entire motion. Also there is nothing mentioned about the composition of the weight so we assume that the composition is uniform throughout.
At any instant,
$$x^2 + y^2 = l^2$$
$$\Rightarrow \dfrac{2xdx}{dt} + \dfrac{2ydy}{dt} = 0$$
$$\Rightarrow x.\dfrac{dx}{dt} = -y \dfrac{dy}{dt}$$
$$\Rightarrow l\cos \theta . \dfrac{dx}{dt} = l\sin \theta. u$$
$$\Rightarrow \dfrac{dx}{dt} = u \tan \theta$$,
So, velocity of end $$B$$ is $$ u \tan \theta$$
$$\textbf{Step 2: }$$ Similarly for centre,
$$V_x = \dfrac{d\left(\dfrac{x}{2}\right)}{dt}$$; $$V_y = \dfrac{d\left(\dfrac{y}{2}\right)}{dt}$$
$$\Rightarrow V_x = \dfrac{1}{2} \dfrac{dx}{dt} = \dfrac{u \tan \theta}{2}$$; $$V_y = \dfrac{1}{2} \dfrac{dy}{dt} = \dfrac{-u}{2}$$
so, velocity of $$C$$ is $$\left(\dfrac{u\tan \theta}{2} \hat{i}, -\dfrac{u}{2}\hat{i}\right)$$.
$$x$$ coordinate of $$C$$ is always $$\dfrac{1}{2} \cos \theta$$; when $$\theta$$ is parameter.
$$y$$ coordinate of $$C$$ is always $$\dfrac{1}{2}\sin \theta$$.
$$\textbf{Step 3: }$$ Eliminating $$\theta$$ from both we get.
$$x^2 + y^2 = \left(\dfrac{l}{2}\right)^2 (\sin^2\theta + \cos^2\theta)$$
$$\Rightarrow x^2 + y^2 = \left(\dfrac{l}{2}\right)^2$$
A uniform meter rule balances horizontally on a knife edge placed at the $$58$$ cm mark when a weight of $$20$$ gf is suspended from one end.
The angular velocity of a body changes from one revolution per $$9$$ seconds to $$1$$ revolution per second without applying any torque the ratio of its radius of gyration in the two cases is.
A bead lies on a frictionless hoop of radius R that rotates around a vertical diameter with constant angular frequency W. what should W be so that the bead maintains the same position on the hoop at angle $$\theta$$ with respect to the verticle? what is the special value W and why is it special?
$$\omega =\sqrt { \dfrac { g }{ Rcos\theta } } $$
The horizontal component of the normal force provided by the ring on the bead keeps it moving in its circular path. It is directed perpendicular to the tangential velocity of the bead. The vertical component of the normal force has to equal the weight of the bead.
N is normal surface
m is mass
g is acceleration due to gravity
$${ N }_{ v }=mg$$
$${ N }_{ cos\theta }=mg$$
$$N=\dfrac { mg }{ cos\theta } $$
$${ N }_{ H }=Nsin\theta $$
$${ N }_{ H }=\dfrac { mg }{ cos\theta } sin\theta $$
Now we can begin working with the centripetal force equation
$$F_{ c }\quad is\quad centripital\quad force$$
$$\omega \quad is\quad rotational\quad velocity$$
$$R\quad is\quad radius\quad ofcircular\quad path\quad Rsin\theta $$
$$\sum { F }_{ c }=m{ \omega }^{ 2 }R$$
$$\dfrac { mg }{ cos\theta } sin=m{ \omega }^{ 2 }Rsin\theta $$
$$\omega =\sqrt { \dfrac { g }{ cos\theta } } $$
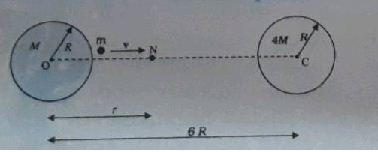
Two uniform solid spheres of equal radii $$R$$, but mass $$M$$ and $$4$$ $$M$$ have a centre to centre separation $$6$$ $$R$$, as shown in Figure. The two spheres are held fixed. A projectile of mass $$m$$ is projected from the surface of the sphere of mass $$M$$ directly towards the centre of the second sphere. Obtain an expression for the minimum speed $$v$$ of the projectile so that it reaches the surface of the second sphere.
A circular loop of mass m and R rests flat on a horizontal frictionless surface.A bullet also of mass m, and moving with a velocity v, strikes the loop and gets embedded in it. The thickness of the hoop is much smaller than R. The anguler velocity with system rotates after the bullet strikes the hoop is
Two block masses $$m_1$$ and $$m_2$$ are connected with the help of a spring of spring constant $$k$$ initially the spring in its natural length as shown. A sharp impulse is given to mass $$m_2$$ so that it acquires a velocity $$v_0$$ towards right. If the system is kept on smooth floor then find :
(a) the velocity of the centre of mass
(b) the maximum elongation that the spring will suffer?
A rotating disc moves in the positive direction of x-axis as shown. Find the equation y(x) describing the position of the instantaneous axis of rotation if at the initial moment the centre C of the disc was located at origin after which
a. it moved with constant acceleration 'a' (initial velocity zero) while the disc rotating anticlockwise with constant angular velocity $$\omega$$.
b. it moved with constant velocity v while the disc started rotating anticlockwise with a constant angular acceleration $$\alpha$$ (with initial angular velocity zero).
Here,
Motion of solid can be imagined to be in pure rotation about a point (say I) at a certain Instant. The instantaneous axis whose positive sense is directer ding $$w$$ of the solid and which passes through the point $$I$$ is Instantaneous axis of Rotation.
velocity vector of an point (P) of the solid
is $$\vec {V_p } =\vec { W } \times \vec { r_{PL} } $$...........(1)
on the basis of eq (1) for the (M.Cc)
of the disc:-
$$\vec { V_c } =\vec { W } \times \vec { r_d } $$............(2)
According to the given problem : $$\vec {V_c } \uparrow i$$
and $$\vec { w } \uparrow \uparrow\hat{x}$$ i,e $$\vec{w}\bot x-y$$ plane, so to satisfy the Eqn (2), $$\vec { r_C } $$ is directed along $$(\vec {-j } )$$. Hence point I is at distance $$\vec {r_{cy} } =y$$
Using above : equation (2) becomes:-
$$V_c=wy$$ or $$y=\dfrac{v_C}{w}$$..........(3)
(b) From the angular kinematics Equation:-
$$W_2=W_{O_2}+\beta_2 t(\beta_2$$ is acc along axis)
$$w=|3t\,bx|$$
on other hande, $$x=vt$$ (where 'x' is the ordinate of the O.M)
$$\therefore t=\dfrac{x}{v}$$...........(5)
From (4) and (5) $$cv=\dfrac{\beta x}{v}$$
From (3)
and $$y=\dfrac{v_c}{w}=\dfrac{v}{\beta x/v}=\dfrac{v^2}{\beta x}$$ (Hyper bola)
Given
$$\beta=\alpha$$
$$\therefore y=\dfrac{v^2}{\alpha x}$$
(a) and As centre $$'C'$$ moves with constant acceleration (a), with
zero initial velocity:-
$$x=\dfrac{}{}at^2$$ and $$v_c=at$$
$$\therefore V_c=a\sqrt{\dfrac{2x}{a}}=\sqrt{2xa}$$
Hence $$y=\dfrac{v_c}{w}=\dfrac{2x}{w}$$
Is linear momentum of a system always conserved?
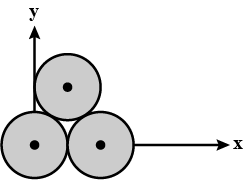
Three identical sphere each of radius $$R$$ are placed touching each other on a horizontal table as shown in figure. The coordinates of centre of mass are:
A uniform solid
The distance of centre of mass from pt . B
Find the average of magnitude of linear momentum of helium molecules in a sample of helium gat at temperature of $$273 \ K$$. Mass of a helium molecules $$4 \times 10^{-3} $$ kg and R = 8.3 $$ J-m o l^{-1} k^{-1} $$
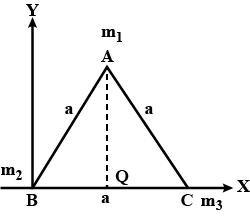
Four particles $$A, B, C,$$ and $$D$$ of masses $$m, 2 m, 3 m$$ and $$4 m$$ respectively are placed at corners of a square of side $$a$$. Locate the centre of mass.
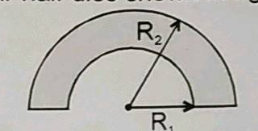
ABC is a part of ring having $${ R }_{ 2 }$$ and ADC is part of disc having inner radius $${ R }_{ 1\quad }$$ and outer $${ R }_{ 2 }$$ part ABC and ADC have same mass. then centre of mss will be located from the centre O
Two particles of mass m each are rightly attached to a disc of the same mass and radius R at its periphery as shown. Disc at this moment is rolling without slipping on the fixed horizontal surface of the center of the disc is $$V_0$$, the total kinetic energy of the system at this instant will be
Two particles of mass 2 kg and 1 kg are moving along the same straight line with speed 2 m/s and 5 m/s respectively. what is the speed of the center of mass of the system if both the particle s are moving (a) in the same direction
Three particles of masses 1 kg, $$\dfrac { 3 }{ 2 } kg,$$ and 2 kg are located at the vertices of an equilateral triangle of side a. The x, y coordinates of the center of mass are
Two particles of mass 2 kg and 1 kg are moving along the same straight line with speed 2 m/s and 5 m/s respectively. What is the speed of the center of mass of the system if both the particles are moving
In opposite direction?
I can imagine 2 similar objects rotating around a sphere at the same velocity but at different orbits. One object would rotate around the sphere faster than the other, right? What is puzzling to me is that if I think of both objects going now in a straight line one could not say that one object was going faster than the other. Can someone help me through this? Is there a subtlety here?
Two bodies of masses 10 kg and 2 kg are moving with velocities $$\left( 2\hat { i } -7\hat { j } +3\hat { k } \right) $$ and $$\left( -10\hat { i } +35\hat { j } -3\hat { k } \right) $$ m/s respectively. Calculate the velocity of their centre of mass.
Four particles of masses $${ m }_{ 1 }=1 kg$$, $${ m }_{ 2 }= 2 kg$$, $${ m }_{ 3 }= 3 kg $$ and $${ m }_{ 4 }= 4 kg $$ are located at the corners of a rectangle as shown in fig. 5(a)56 Locate the position of center of mass.
Find the centre of mass of an annular half disc shown in figure.
A particle of mass 1 kg has velocity $$ \bar v_1 = (2t)\hat i $$ and another particle of mass $$2\ kg$$ has velocity $$ \bar v_2 = (t^2)\hat j $$
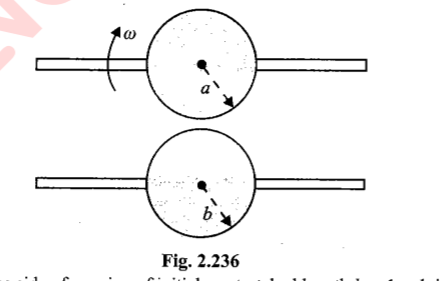
Two uniform spheres shown if fig rotate separately on two parallel horizontal axis passing through their centers.the upper sphere ha an angular speed $$ \omega_0 $$ and the lower sphere is at rest. Now the two spheres are moved together so that their now the two Sphehers, now in the contatc are rotating without slipping. find the final rate of rotation of upper sphere $$ I_1 = 4 kg m^2 $$ , moment of inertia of lower sphere $$ I_2 = 2 kg m^2 , a = 2 m , b = 1 , \omega_0 = 12 rad/s. $$
A Texas cockroach of mass $$0.17\ kg$$ runs counterclockwise around the rim of a lazy Susan (a circular disk mounted on a vertical axle) that has radius $$15\ cm$$, rotational inertia $$5.0\times 10^{-3}kg. m^{2}$$, and frictionless bearings. The cockroach's speed (relative to the angular) is $$2.0\ m/s$$, and the lazy Susan turns clockwise with angular speed $$\omega =2.8\ rad/s$$. The Cockroach finds a bread crumb on the rim and, of course, tops.Is mechanical energy conserved as it stops?
A man stands on a platform that its rotating (with out friction) with an angular speed of $$1.2\ rev/s$$; his arms are outstretches and he holds a brick in each hand. The rotational inertia of the system consisting of the man, bricks, and platform about the central vertical axis of the platform is $$6.0\ kg\ m^2$$. If by moving the bricks the man decreases the rotational inertia of the system to $$2.0\ kg. m^2$$, what are the ratio of the new kinetic energy of the system to the original kinetic energy?
A man stands on a platform that its rotating (with out friction) with an angular speed of $$1.2\ rev/s$$; his arms are outstretches and he holds a brick in each hand. The rotational inertia of the system consisting of the man, bricks, and platform about the central vertical axis of the platform is $$6.0\ kg\ m^2$$. If by moving the bricks the man decreases the rotational inertia of the system to $$2.0\ kg. m^2$$, What source provided the added kinetic energy?
Calculate the rotational inertia of a meter stick, with mass 0.56 kg, about an axis perpendicular to the stick and located at the 20 cm mark. (Treat the stick as a third rod.)
Two spheres with the masses $$m_1 $$ and $$m_2$$ can slide without friction along a thin horizontal rod as shown in the figure. The sphere are connected by a massless spring of spring constant $$k$$. The sphere are pulled in opposite directions and are then released.
What is the velocity of the centre of mass?
The masses and coordinates of four particles are as follows: 50 g,x=2.0 cm,y=2.0 cm; 25 g, x=0, y=4.0 cm; 25 g, x= -3.0 cm, y= - 3.0 cm, y= -3.0 cm, 30 g x = -2.0 cm, y= -4.0 cm. What are the rotational inertias of this collection about the (a) x, (b) y, and (c) z axes (d) Suppose that we symbolize the answers to (a) and (b) as A and B, respectively. Then what is the answer to (c) in terms of A and B
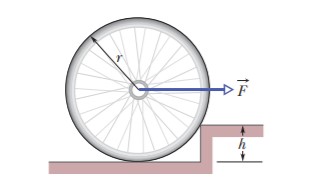
In Figure, what magnitude of (constant) force applied horizontally at the axle of the wheel is necessary to raise the wheel over a step obstacle of height $$h = 3.00$$ cm? The wheel’s radius is $$r = 6.00$$ cm, and its mass is $$m = 0.800$$ kg.
We consider the wheel as it leaves the lower floor. The floor no longer exerts a force on the wheel, and the only forces acting are the force F applied horizontally at the axle, the force of gravity mg acting vertically at the center of the wheel, and the force of the step corner, shown as the two components $$f_h$$ and $$f_v$$. If the minimum force is applied the wheel does not accelerate, so both the total force and the total torque acting on it are zero.
We calculate the torque around the step corner. The second diagram indicates that the distance from the line of F to the corner is r – h, where r is the radius of the wheel and h is the height of the step.
The distance from the line of mg to the corner is $$\sqrt{r^2+(r-h)^2}=\sqrt{2rh-h^2}$$ . Thus,
$$F(r-h)-mg\sqrt{2rh-h^2}=0$$
The solution for $$F =\dfrac{\sqrt{2rh-h^2}}{r-h}mg=\dfrac{\sqrt{2(6.00\times10^{-2} m)(3.00\times 10^{-2} m) -(3.00\times 10^{-2} m)^2}}{(6.00\times 10^{-2} m)- (3.00\times 10^{-2} m)}(0.800 kg)(9.80 m/s^2 )$$
$$=13.6$$ N
Note: The applied force here is about 1.73 times the weight of the wheel. If the height is increased, the force that must be applied also goes up. Next we plot $$F/mg$$ as a function of the ratio $$h/r$$ .The required force increases rapidly as $$h/r \rightarrow 1$$.
We calculate the torque around the step corner. The second diagram indicates that the distance from the line of F to the corner is r – h, where r is the radius of the wheel and h is the height of the step.
The distance from the line of mg to the corner is $$\sqrt{r^2+(r-h)^2}=\sqrt{2rh-h^2}$$ . Thus,
$$F(r-h)-mg\sqrt{2rh-h^2}=0$$
The solution for $$F =\dfrac{\sqrt{2rh-h^2}}{r-h}mg=\dfrac{\sqrt{2(6.00\times10^{-2} m)(3.00\times 10^{-2} m) -(3.00\times 10^{-2} m)^2}}{(6.00\times 10^{-2} m)- (3.00\times 10^{-2} m)}(0.800 kg)(9.80 m/s^2 )$$
$$=13.6$$ N
Note: The applied force here is about 1.73 times the weight of the wheel. If the height is increased, the force that must be applied also goes up. Next we plot $$F/mg$$ as a function of the ratio $$h/r$$ .The required force increases rapidly as $$h/r \rightarrow 1$$.
A meter stick balances horizontally on a knife-edge at the $$50.0$$ cm mark. With two $$5.00$$ g coins stacked over the $$12.0$$ cm mark, the stick is found to balance at the $$45.5$$ cm mark. What is the mass of the meter stick?
The x-axis is along with the meter stick, with the origin at the zero position on the scale. The forces acting on it are shown in the diagram below. The nickels are at $$x = x_1 = 0.120$$ m, and m is their total mass. The knife-edge is at $$x = x_2 = 0.455$$ m and exerts force $$\vec F$$. The mass of the meter stick is M and the force of gravity acts at the center of the stick, $$x = x_3 = 0.500$$ m. Since the meter stick is in equilibrium, the sum of the torques about $$x_2$$ must vanish:
$$Mg(x_3 – x_2) – mg(x_2 – x_1) = 0$$.
Thus,
$$M=\dfrac{x_2-x_1}{x_2-x_2}m=\Bigg(\dfrac{0.455m -0.120m}{0.500m -0.455m}\Bigg)(10.0g)=74.4$$ g
$$Mg(x_3 – x_2) – mg(x_2 – x_1) = 0$$.
Thus,
$$M=\dfrac{x_2-x_1}{x_2-x_2}m=\Bigg(\dfrac{0.455m -0.120m}{0.500m -0.455m}\Bigg)(10.0g)=74.4$$ g
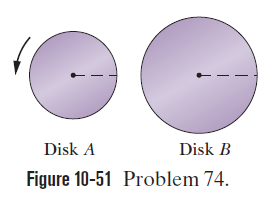
Racing disks. Figure 10-51 shows two disks that can rotate about their centers like a merry-go-round. At time t=0, the reference lines of the two disks have the same orientation. Disk A is already rotaining, with a constant angular velocity of 9.5 rad/s. Disk B has been stationery but now begins to rotate at a constant angular acceleration of 2.2 rad/ $$ S^{2} $$.(a) At what time t will the reference lines of the two disks momentarily have the same angular displacement $$ \theta $$ Will that time t be the first time since t=0 that the reference lines are momentarily aligned
A wheel is rotating freely at angular speed $$800\ rev/min$$ on a shaft whose rotational inertia is negligible. A second wheel, initially at rest and with twice the rotational inertia of the first, is suddenly couple to the same left.
What is the angular speed of the resultant combination of the shaft and two wheels?
A solid sphere of weight $$36.0\ N$$ rolls up an incline an angle of $$30.0^{o}$$. At the bottom of the incline the center of mass of the sphere has a transnational speed of $$4.90\ m/s$$. What is the kinetic energy of the sphere at the bottom of the incline?
In fig.10-49, a small disk of radius r=2.00 cm has been glued to the edge of a larger disk of radius R=4.00 cm so that the disks lie in the sme plane. The disks can be rotated around a perpendicular axis through point O at the center of the larger disk. The disks both have a uniform thickness of 5.00 mm. What is the roatational inertia of the two-disk assembly about the rotation axis through O
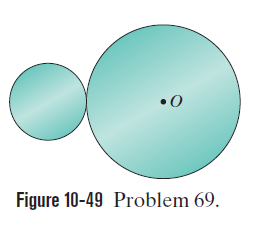
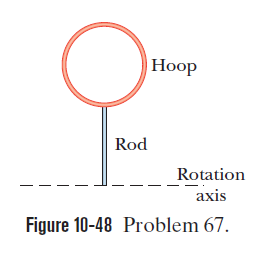
Figure 10-48 shows a rigid assembly of thin hoop (of mass m and radius R= 0.150 m) and a thin radial rod (of mass m and length L = 2.00 R ). the assembly is upright, but if we give it a slight nudge, it will rotate around a horizontal axis in the plane of the rod and hoop, through the lower end of the rod.Assuming that the energy given to the assembly in such a nudge is negligible, what would be the assembly's angular speed about the rotation axis when it passes through the upside-down (inverted) orientation
In Figure, a horizontal scaffold, of length $$2.00$$ m and uniform mass $$50.0$$ kg, is suspended from a building by two cables. The scaffold has dozens of paint cans stacked on it at various points. The total mass of the paint cans is $$75.0$$ kg. The tension in the cable at the right is $$722$$ N. How far horizontally from that cable is the center of mass of the system of paint cans?
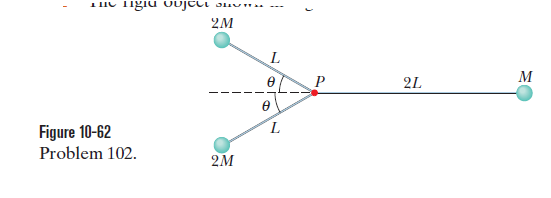
The rigid object shown in Fig. 10-62 consists of three balls and three connecting rods, with M= 1,6 kg, L= 0.60 m, and $$\theta = 30^{\circ} $$ . The balls may be treated as particles, and the connecting rods have negligible mass. Determine the rotational kinetic energy of the object if it has an angular speed of 1.2 rad/s about (a) an axis that passes through point P and is perpendicular to the plane of the figure and (b) an axis that passes througth point P, is perpendicular to the rod of length 2 L, and lies in the plane of the figure.
A ball starts from rest and accelerates at $$0.500 m/s^{2}$$ while moving down an inclined plane $$9.00 m$$ long. When it reaches the bottom, the ball rolls up another plane, where it comes to rest after moving $$15.0 m$$ on that plane. (a) What is the speed of the ball at the bottom of the first plane? (b) During what time interval does the ball roll down the first plane? (c) What is the acceleration along the second plane? (d) What is the balls speed $$8.00 m$$ along the second plane?
Calculate the moment of inertia of a symmetrical thin rod along the axis passing through its end and perpendicular to its length.
Moment of Inertia of a Thin Rod
Moment of Inertia of a Thin Rod about the Axis perpendicular to the length and Passing through the Center
Take a uniform thin rod AB whose mass is M and length is l. YY' axis passes through the center of the rod and perpendicular to the length of the rod. We have to calculate the moment of inertia about this axis YY'.
Suppose, small piece dx is at a distance x from the YY' axis. Hence, mass of length dx is $$= (\dfrac{M}{l})dx$$ The moment of inertia of small piece about the YY' axis
$$sl = \left [ (\dfrac{M}{l}) dx \right ]x^2$$
Therefore, the moment of inertia of the complete rod about the YY' axis,
$$I = \displaystyle \int dI = \displaystyle \int_{-l/2}^{l/2} \left [ \dfrac{M}{l} \right ] dx \,x^2$$
$$= \dfrac{2M}{l} \displaystyle \int_{0}^{l/2} x^2 dx = \left [ \dfrac{x^3}{3} \right ]_{0}^{l/2}$$
$$I_{YY'} = \dfrac{Ml^2}{12}$$ .........(1)
A door has a height of $$2.1$$ m along a y-axis that extends vertically upward and a width of 0.91 m along with an x-axis that extends outward from the hinged edge of the door.A hinge $$0.30$$ m from the top and a hinge $$0.30$$ m from the bottom each support half the door’s mass, which is $$27$$ kg. In unit-vector notation, what are the forces on the door at (a) the top hinge and (b) the bottom hinge?
A disc of radius $$R$$ is rotating with an angular speed $$\omega_0$$ about a horizontal axis. It is placed on a horizontal table. The coefficient of kinetic friction is $$\mu k$$.
(a) What was the velocity of its centre of mass before being brought in contact with the table?
(b) What happens to the linear velocity of a point on its rim when placed in contact with the table?
(c) What happens to the linear speed of the centre of mass when disc is placed in contact with the table?
(d) Which force is responsible for the effects in (b) and (c).
(e) What condition should be satisfied for rolling to begin?
(f) Calculate the time taken for the rolling to begin.
the value of $$r_0$$ corresponding to the equilibrium position of the particle; examine whether this position is steady;
In Figure, a uniform $$40.0$$ kg beam is centered over two rollers. Vertical lines across the beam mar off equal lengths. Two of the lines are centered over the rollers; a $$10.0$$ kg package of tamales is centered over roller B.What are the magnitudes of the forces on the beam from (a) roller A and (b) roller B? The beam is then rolled to the left until the right-hand end is centered over roller B. What now are the magnitudes of the forces on the beam from (c) roller A and (d) roller B? Next, the beam is rolled to the right. Assume that it has a length of 0.800 m. (e) What horizontal distance between the package and roller B puts the beam on the verge of losing contact with roller A?
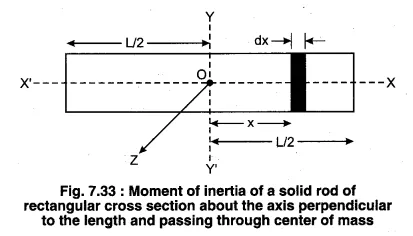
Establish the formula of moment of inertia of a rectangular rod along the axis passing through its center of mass and perpendicular to the length of the rod.
Solid Rod of Rectangular Cross Section
Moment of Inertia about the axis perpendicular to the length and passing through the Center of Mass
A rectangular solid rod is shown in the figure, whose length is L, breadth B, width d and mass is M. We can assume that this is made up of various thin rectangular cross-sections. The total moment of inertia of the rod would be equal to the sum of the moment of inertia of all these rectangular cross-sections.
Suppose every rectangular cross-section’s mass is m. According to the figure a cross-section of dx breadth is at a distance x parallel to the YY’ axis. If mass of unit area of the strip is a then the whole cross-section mass is $$B \,dx\sigma.$$ Therefore, the moment of inertia about the YY'axis is $$= B \,dx\sigma \,x^2$$
The moment of inertia of the total rectangular cross-section about the YY' axis
$$DI_{YY'} = \displaystyle \int_{-L/2}^{+L/2} \sigma Bx^2 dx$$
$$= 2\sigma B \displaystyle \int _{0}^{L/2} x^2 dx = 2\sigma B \left [ \dfrac{x^3}{3} \right ]_{0}^{L/2}$$
or $$dI_{YY'} = \sigma B \dfrac{L^3}{12} = \dfrac{mL^2}{12}$$
Here, $$m = \sigma BL$$ is the mass rectangular cross-section.
Similarly, the moment of inertia about the XX' axis is;
$$dl_{XX'} = \dfrac{mB^2}{12}$$
$$dl_{XX'} $$ and $$dI_{YY'}$$ are the moment of inertia of two perpendicular axis in the same plane. Figure (7.33) shows the axis OZ perpendicular to the intersection point of these two axis and its inertia;
$$dl_{oz} = dl_{YY'} + dl_{XX}$$
$$= \dfrac{mL^2}{12} + \dfrac{mB^2}{12} = m \left [ \dfrac{L^2 + B^2}{12} \right ]$$
The moment of inertia of such rectangular laminas will be the sum of all about the Z axis. Hence, the moment of inertia about the OZ axis, which is perpendicular to length and passing through the center is;
$$I = \Sigma dI = \Sigma mdI = \Sigma m \left [ \dfrac{L^2 + B^2}{12} \right ]$$
$$I = M \left [ \dfrac{L^2 + B^2}{12} \right ]$$
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination,
Will it reach bottom with the same speed in each case.
2.Will it take longer to roll down one plane than the other?
3.If so, which one and why?
Two particles of masses $$5 \,g$$ and $$2 \,g$$ respectively; have velocity $$(\hat{i} + \hat{j} - \hat{k})$$ and $$(3\hat{i} - 2\hat{j} + \hat{k})$$ cm/s; and form a two particles system. What will be the velocity of center of mass of the system ?
A heavy pipe rolls from the same height down two hills with different profils (Figs $$1$$ and $$2$$). In the former case, the pipe rolls down without slipping while in the latter case, it slips on a certain region.
In what case will the velocity of the pipe at the end of the path be lower?
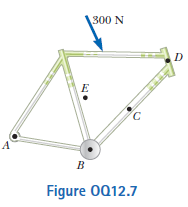
Assume a single $$300-N$$ force is exerted on a bicycle frame as shown in Figure $$OQ12.7$$. Consider the torque produced by this force about axes perpendicular to the plane of the paper through each of the points. A through $$E$$, where $$E$$ is the center of mass of the frame. Rank the torques $$T_A,T_B,T_C,T_D,$$ and $$T_E$$ from largest to smallest, nothing that zero is greater than a negative quantity. If two torques are equal, note their equality in your ranking.
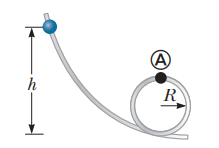
Review A bead slide without friction around a loop-the-loop (Fig) The bead is released from rest at a height $$h=3.50 R$$
What is its speed at point $$A$$?
A $$3.00-kg$$ particle has a velocity of $$(3.00\hat{i}-4.00\hat{j})m/s$$.
Find its $$x$$ and $$y$$ components of momentum.
A grinding wheel is in the form of a uniform solid disk of radius $$7.00\ cm$$ and mass $$2.00\ kg$$. It starts from rest and accelerates uniformly under the action of the constant torque of $$0.600\ N.m$$ that the motor exerts on the wheel. How long does the wheel take to reach its final operating speed of $$1200\ rev/min$$?
A $$150-kg$$ merry-go-round in the shape of a uniform, solid, horizontal disk of radius $$1.50\ m$$ is set in motion by wrapping a rope about the rim of the disk and pulling on the rope. What constant force must be exerted on the rope to bring the merry-go-round from rest to an angular speed of $$0.500\ rev/s$$ in $$2.00\ s$$?
Two coupled wheels (i.e. light wheels of radius $$r$$ fixed to a thin heavy axle) roll without slipping at a velocity $$v$$ perpendicular to the boundary over a rough horizontal plane changing into an inclined plane of slope $$\alpha$$ see in fig.
Determine the values of $$v$$ at which the coupled wheels roll from the horizontal to the inclined plane without being separated from the surface.
Since the wheels move without slipping, the axle of the coupled wheels rotates about point $$O$$ while passing through the boundary between the planes (Fig. $$172$$). At the moment of separation, the force of pressure of the coupled wheels on the plane and the force of friction are equal to zero, and hence the angle 13 at which the separation takes place can be found from the condition
$$mg\cos \beta=\dfrac{mv_{1}^{2}}{r}$$
From the energy conservation law, we obtain
$$\dfrac{mv^{2}}{2}=\dfrac{mv_{1}^{2}}{2}-mgr(1-\cos \beta)$$.
No separation occurs if the angle $$\beta$$ determined from these equations is not smaller than $$\alpha$$, and hence
$$\cos \beta\le \cos \alpha$$.
Therefore, we find that the condition
$$v\le \sqrt{gr(3\cos \alpha-2)}$$
is a condition of crossing the boundary between the planes by the wheels without separation. If $$3\cos \alpha-2 < 0$$, i.e. $$\alpha > ar\cos (2/3)$$, the separation will take place at any velocity $$v$$.
$$mg\cos \beta=\dfrac{mv_{1}^{2}}{r}$$
From the energy conservation law, we obtain
$$\dfrac{mv^{2}}{2}=\dfrac{mv_{1}^{2}}{2}-mgr(1-\cos \beta)$$.
No separation occurs if the angle $$\beta$$ determined from these equations is not smaller than $$\alpha$$, and hence
$$\cos \beta\le \cos \alpha$$.
Therefore, we find that the condition
$$v\le \sqrt{gr(3\cos \alpha-2)}$$
is a condition of crossing the boundary between the planes by the wheels without separation. If $$3\cos \alpha-2 < 0$$, i.e. $$\alpha > ar\cos (2/3)$$, the separation will take place at any velocity $$v$$.
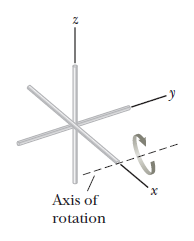
Three identical thin rods, each of length $$L$$ and mass $$m$$, are welded perpendicular to one another as shown in figure. The assembly is rotated about an axis that passes through the end of one rod and is parallel to another. Determine the moment of inertia of this structure about this axis.
A ball of mass $$0.200\ kg$$ with a velocity of $$1.50 \hat{i}\ m/s$$ meets a ball of mass $$0.300\ kg$$ with a velocity of $$-0.400 \hat{i}\ m/s$$ in a head-on, elastic collision.
Find the velocity of their center of mass before and after the collision.
Two balls with masses $$M$$ and $$m$$ are connected by a rigid rod of length $$L$$ and negligible mass as shown in Figure. For an axis perpendicular to the rod, Show that this moment of inertia is $$I=\mu L^2$$, where $$\mu=mM/(m+M)$$.
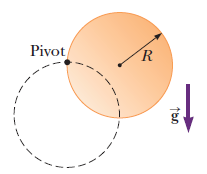
A uniform solid disk of radius $$R$$ and mass $$M$$ is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown by the coppercolored circle, What if? Repeat part (a) using a uniform hoop.
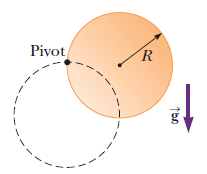
A uniform solid disk of radius $$R$$ and mass $$M$$ is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown by the coppercolored circle, What is the speed of the lowest point on the disk in the dashed position?
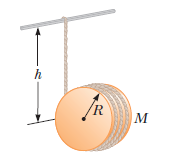
A string is wound around a uniform disk of radius $$R$$ and mass $$M$$. The disk is released from rest with the string vertical and its top end tied to a fixed bar. Verify your answer to part (c) using the energy approach.
A uniform solid disk of radius $$R$$ and mass $$M$$ is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown by the coppercolored circle, what is the speed of its center of mass when the disk reaches the position indicated by the dashed circle?
A spool of wire of mass $$M$$ and radius $$R$$ is unwound under a constant force $$\vec F$$. Assuming the spool is a uniform, solid cylinder that doesn't slip, show that If the cylinder starts from rest and rolls without slipping, what is the speed of its center of mass after it has rolled through a distance $$d$$?
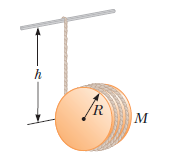
A string is wound around a uniform disk of radius $$R$$ and mass $$M$$. The disk is released from rest with the string vertical and its top end tied to a fixed bar. Show that the speed of the center of mass is $$(4gh/3)^{1/2}$$ after the disk has descended through distance $$h$$.
A uniform solid disk and a uniform hoop are placed side by side at the top of an incline of height $$h$$. Verify your answer by calculating their speeds when they reach the bottom in terms of $$h$$.
A ball of mass m is thrown straight up into the air with an initial speed $$v_i$$. Find the momentum of the ball
halfway to its maximum height.
A $$4.00-m$$ length of light nylon cord is wound around a uniform cylindrical spool of radius $$0.500\ m$$ and mass $$1.00\ kg$$. The spool is mounted on a frictionless axle and is initially at rest. The cord is pulled from the spool with a constant acceleration of magnitude $$2.50\ m/s^2$$.
How much cord is left on the spool when it reaches this angular speed?
A $$4.00-m$$ length of light nylon cord is wound around a uniform cylindrical spool of radius $$0.500\ m$$ and mass $$1.00\ kg$$. The spool is mounted on a frictionless axle and is initially at rest. The cord is pulled from the spool with a constant acceleration of magnitude $$2.50\ m/s^2$$.
How long does it takes the spool to reach this angular speed?
Two boys are sliding towards each other on a frictionless, ice-covered parking lot. Jacob, mass $$45.0\ kg$$ is gliding to the right at $$8.00\ m/s$$ and Ethan mass $$31.0\ kg$$ is gliding to the left at $$11.0\ m/s$$ along the same line. When they meet, they grab each other and hang on.
Find the velocity of their center of mass.
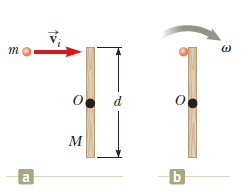
A projectile of mass $$m$$ moves to the right with a speed $$c_i$$. The projectile strikes and sticks to the end of a stationary rod of mass $$M$$, length $$d$$, pivoted about a frictionless axle perpendicular to the page through $$O$$. We wish to find the frictionless change of kinetic energy of the system due to collision.
What is the moment of inertia of the system about an axis through $$O$$ after the projectile sticks to the rod?
Class 11 Engineering Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Physical World Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work,Energy And Power Extra Questions