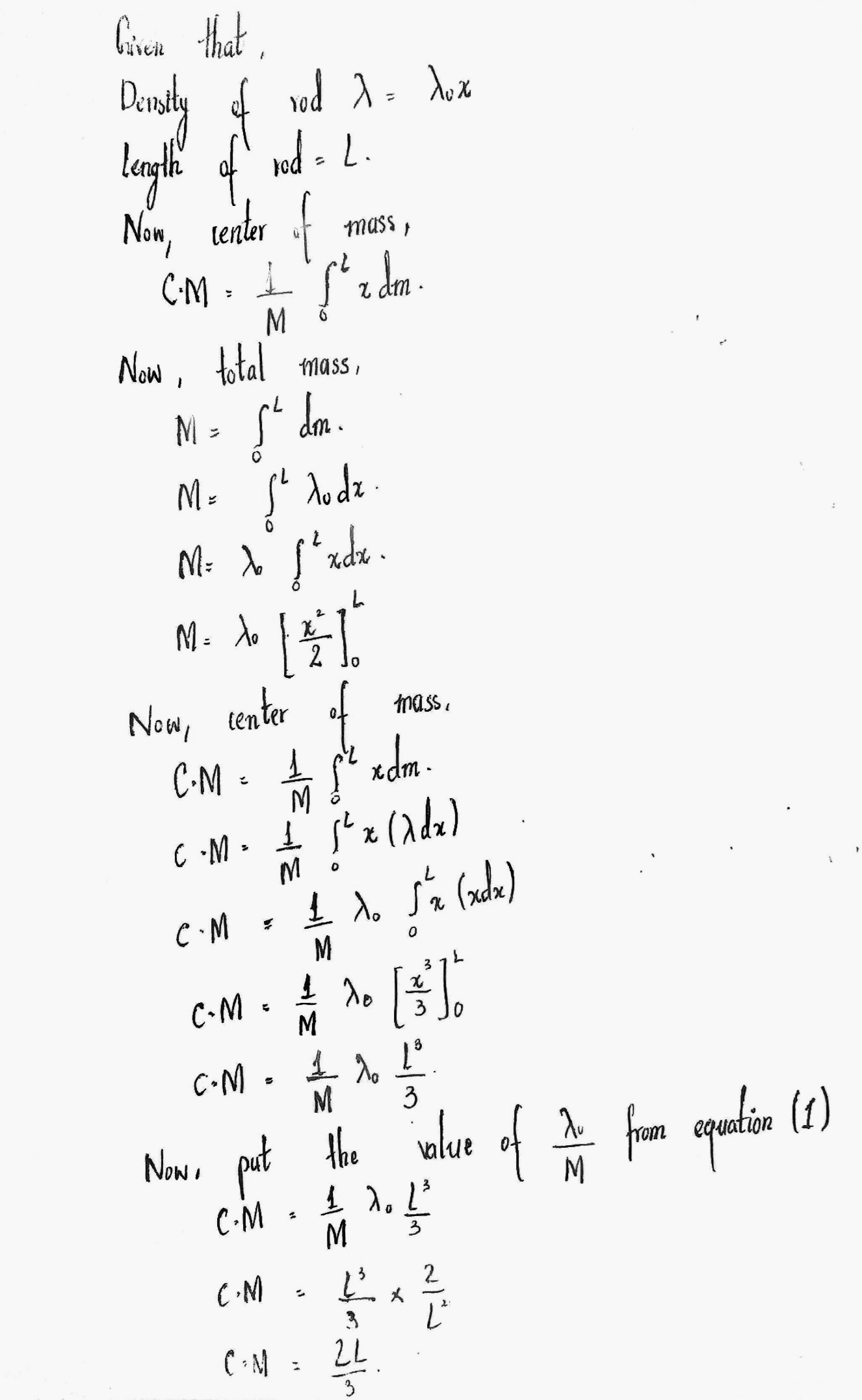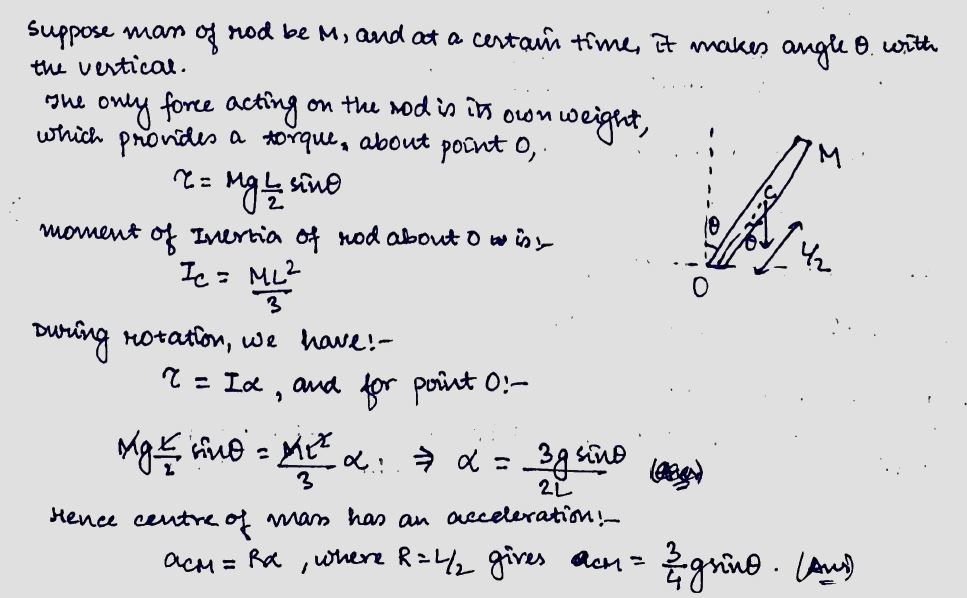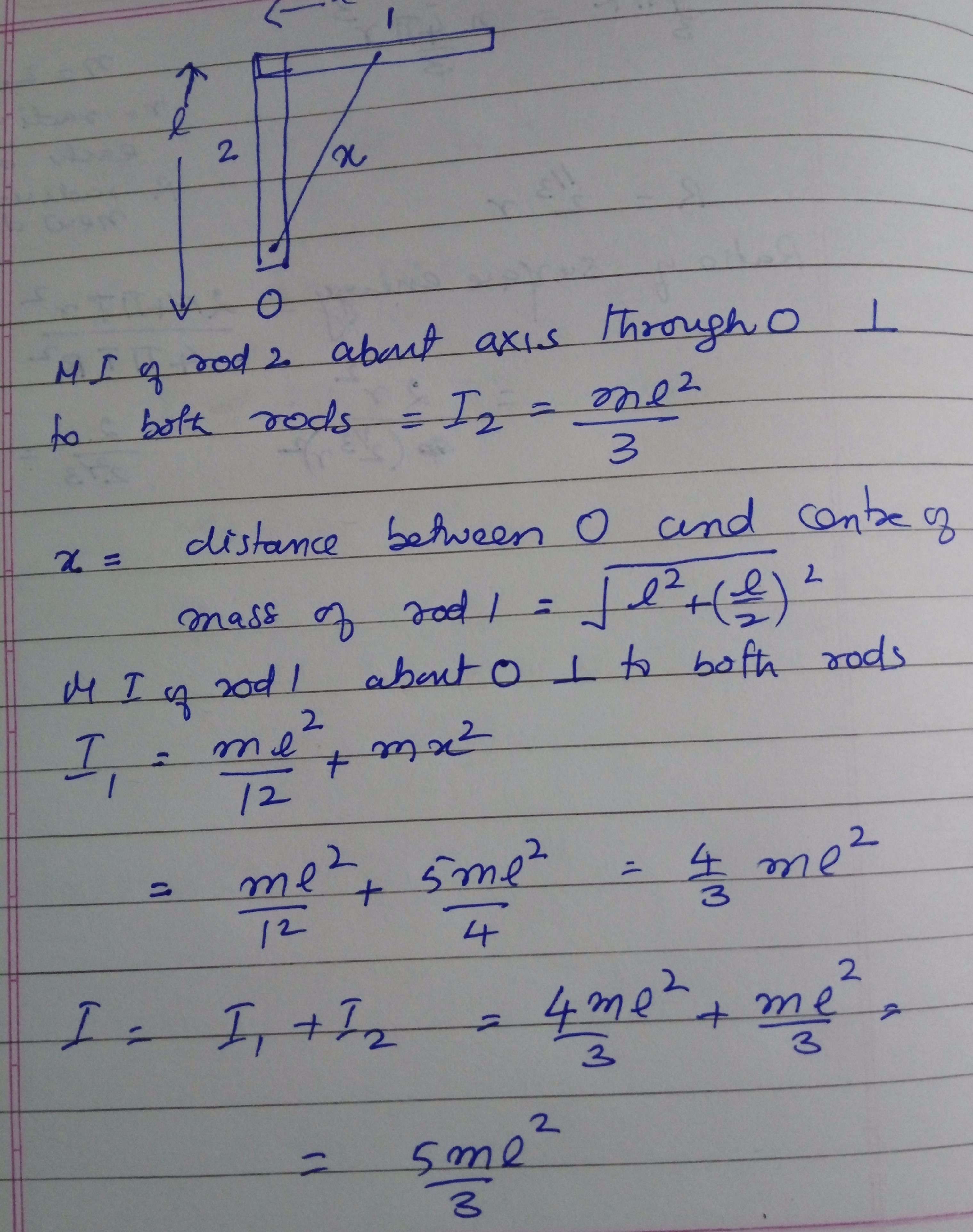Systems Of Particles And Rotational Motion - Class 11 Medical Physics - Extra Questions

what is the inertial mass?

Inertial mass is a mass parameter giving the inertial resistance to acceleration of the body when responding to all type of forces.


What is centre of mass?


2182391_1089978_ans_6d5b97dc5cb349668a9510efdfcd97b4.jpeg


Differentiate between stable and unstable equilibrium. 


1314817_1135518_ans_10c88b6e5731425485a91dea08b3fbc3.jpg


If momentum of a body increases by $$50\%$$ by what $$\%$$ its K.E. change?

Let the initial momentum be  $$P_i = P$$
Final momentum  $$P_f = 1.5 P$$
Initial kinetic energy   $$K.E_i = \dfrac{p^2}{2m}$$
Final kinetic energy  $$K.E_f = \dfrac{p_f^2}{2m} =\dfrac{(1.5P)^2}{2m} = 2.25K.E_i$$
Percentage increase in kinetic energy   $$\dfrac{K.E_f-K.E_i}{K.E_i}\times 100 = \dfrac{2.25-1}{1}\times 100 = 125 \ $$ %


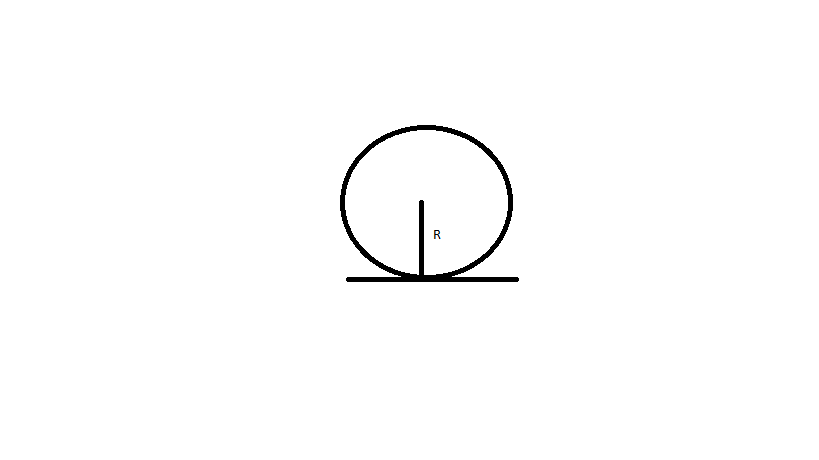
Write the value of radius of gyration of a solid sphere relative to its tangent.

Moment of inertia of a solid sphere about its tangent, if radius of gyration be K, then
$$l = MK^2$$
$$\therefore MK^2 = \dfrac{7}{5} MR^2 \Rightarrow K = R \sqrt{ \dfrac{7}{5}}$$


Define center of mass.

The specific point of the body where all the mass of the body is supposed to be contained and the body moves such that all the external force act at this point, is known as the center of mass of the body.


A locomotive is propelled by a turbine whose axle is parallel to the axes of wheels. The turbine's rotation direction coincides with that of wheels. The moment of inertia of the turbine rotor relative to its own axis is equal to $$I=240\:kg\cdot m^2$$. If the additional force exerted by the gyroscopic forces on the rails when the locomotive moves along a circle of radius $$R=250\:m$$ with velocity $$v=50\:km/h$$ is $$\displaystyle F_{add}=\frac{x}{10} \:kN.m$$, find the value of $$x$$. The gauge is equal to $$l=1.5\:m$$. The angular velocity of the turbine equals $$n=1500\:rpm$$.

A couple $$\displaystyle\frac{2\pi Inv}{R}$$ must come in play. This can be done if a force, $$\displaystyle\frac{2\pi Inv}{Rl}$$ acts on the rails in opposite directions in addition to the centrifugal and other forces. The force on the outer rail is increased and that on the inner rail decreased. The additional force in this case has the magnitude $$1.4\:kN.m$$


Find the moment of inertia of the two uniform joint rods having mass m each about point P as shown in figure. Using parallel axis theorem.
299944_bbb732e79fe74d79b61c0c7d1f9a5273.png

From the figure , A is the mid point of rod OB,
Using Pythagoras theorem $$\Rightarrow AP= \sqrt{l^2 + \dfrac{l^2}{4}}$$= $$\dfrac { \sqrt5}{2}l$$,
Moment of inertia (MOI) of rod OP about point P= $$ \dfrac{ml^2}{3}$$
Using parallel axis theorem, MOI of rod OB about point P=$$ \dfrac{ml^2}{12} + \dfrac{5}{4} ml^2 = \dfrac{4}{3} ml^2 $$
Adding MOI= $$ \dfrac{ml^2}{3}$$ + $$ \dfrac{4}{3}ml^2$$= $$ \dfrac {5}{3} ml^2$$

925049_299944_ans_4f4dfa9a473740a5acbbfee7dc50a497.png


Find the radius of gyration of a solid uniform sphere of radius R about its tangent.

Given,
 
A solid sphere having radius $$R$$

For solid sphere

$$I_{cm}=\dfrac{2}{5}MR^2$$

$$I_{tangent}=I_cm+MR^2$$

$$=\dfrac{2}{5}MR^2+MR^2$$

$$=\dfrac{7}{5}MR^2$$

Thus, the radius of gyration is $$\sqrt{\dfrac{7}{5}}R$$ Where  M is constant

956309_299951_ans_1996aa65ea724690b61e5de4c02387f4.png


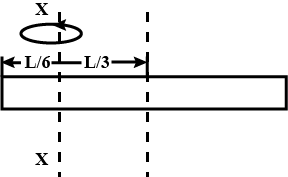
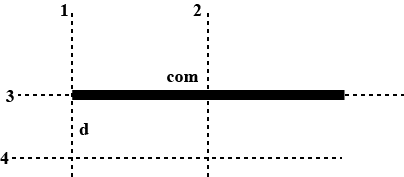
Calculate the moment of inertia of a uniform rod of mass M and length l about an axis 1,2,3 and 4.
299749_419e9c7a08854c46b660eb0a83ac1a60.png

$$(I_1)\, =\, \displaystyle {\int (dm)r^2\, =\, \int_{0}^{l} \left (\frac{M}{l}dx \right )x^2\, =\, \frac{Ml^2}{3}}$$
$$(I_2)\, =\, \displaystyle \int (dm)r^2\, =\, \int_{-l/2}^{l/2}\left ( \displaystyle \frac{M}{l}dx \right )x^2\, =\, \displaystyle \frac{Ml^2}{12}$$
$$(I_3)$$ = 0 (axis 3 passing through the axis of rod)
$$(I_4)\, =\, d^2 \int (dm)\, =\, Md^2$$
836419_299749_ans_927d9490421044b29e0a5a9cecf2616e.png


Differentiate between Rolling motion and Random motion.

The motion in which there is simultaneous occurrence of both rotational
and translational motion is called Rolling motion while the motion in
which a moving object frequency changes its direction of motion 
unpredictably is called the Random or irregular motion 


A wheel of radius r rolls (rolling without slipping) on a level road as shown in figure. Angular velocity of the wheel is $$\omega$$, as shown in figure. Find out velocity of point A and B.
302624_62c044f097264977b11142e13e01197c.png

The surface of the contact should be in rest for pure rotation.
So velocity of the point "A" is zero.
Velocity of point B is $$v_{B} = v + wr = 2wr =2v$$
Here $$v=wr$$


$$(i)$$  On what factor does the position of the centre of gravity of a body depend?
$$(ii)$$ What is the S.I.unit of the moment of force?

(i)The postion of centre of gravity of a body of a particular mass depends on the size and shape of the body. 
(ii) SI unit of the moment of force is $$Nm$$, ie, Newton $$\times$$ metre.


What are the sign conventions for anticlockwise and clockwise rotations of moment?

As a matter of convention, an anticlockwise moment is taken as positive and a clockwise moment is taken as negative. The direction of a moment depends upon the axis of rotation with respect to which you are measuring the turning effect. Clockwise and counterclockwise qualifications are dependent upon the observer's viewpoint. For example, if you place a book on a table and take an axis through the book's centre vertically, a force applied rightwards to the top edge would be considered clockwise while a force applied rightwards to the bottom edge would be considered anticlockwise if you are seeing from above.


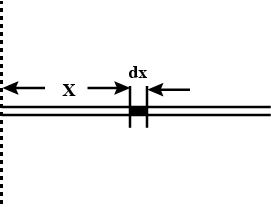
A non - uniform thin rod of length $$\ell $$ lies along the x-axis with one end at the origin. It has a linear mass density $$\lambda \quad $$ kg/m, given by $$\lambda \quad $$ =$${ \lambda  }_{ 0 }\quad $$ (1+x/$$\ell $$ ). Find the center of mass of the rod.


2048620_1395879_ans_44e18a16600842d0ac1965c8c88fed7b.jpg


A rod of length l is standing vertically frictionless surface. It is disturbed slightly from this position. Let $$\omega$$ and $$\alpha$$ be the angular speed and angular acceleration of the rod, when the rod turns through an angle $$\theta$$ with the vertical, then find the value of acceleration of centre of mass of the rod.

Suppose mass of rod be M, and at a certain time, it makes angle $$\theta$$ with the vertical.
The only force acting on the rod is its own weight, which provides a torque about point O,
$$\tau =Mg\dfrac{L}{2}\sin\theta$$
Moment of inertia of rod about I is:
$$I_C=\dfrac{ML^2}{3}$$
During rotation, we have:-
$$\tau =I\alpha$$, and for point O:
$$Mg\dfrac{L}{2}\sin\theta =\dfrac{ML^2}{3}\alpha$$
$$\Rightarrow \alpha =\dfrac{3g\sin\theta}{2L}$$
Hence centre of mass has an acceleration:
$$a_{CM}=R\alpha$$, where $$R=\dfrac{L}{2}$$ gives $$a_{CM}=\dfrac{3}{4}g\sin \theta$$.

1101253_697557_ans_a6e9a009bbcc4a7b9c2dfdaf22e43f78.JPG


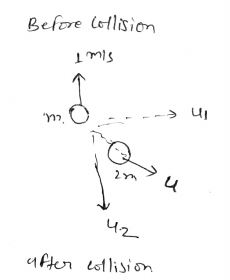
A mass $$'m'$$ moves with velocity $$v = \sqrt {3}m/s$$ and collides with another mass $$2m$$ initially at rest. After collision first mass move with velocity $$\dfrac {v}{\sqrt {3}}$$ in the direction perpendicular to initial direction of motion. Speed of second mass (in m/s) after collision is ____________.

By momentum conservation Horizontal .
$$m\sqrt { 3 } =2m{ u }_{ 1 }\\ { u }_{ 1 }=\dfrac { \sqrt { 3 }  }{ 2 } $$
vertical $$m\times 1-2m{ u }_{ 2 }=0$$
$$ { u }_{ 2 }=\dfrac { 1 }{ 2 } \\ u=\sqrt { { u }_{ 1 }^{ 2 }+{ u }_{ 2 }^{ 2 } } =\sqrt { \dfrac { 3 }{ 4 } +\dfrac { 1 }{ 4 }  } \\ =1m/s$$

951359_765778_ans_7ec9d6dab0ec4dc58089bd7a21cc0fbc.JPG


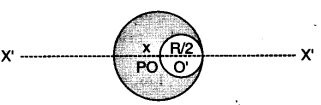
From a uniform disk of radius $$R$$, a circular hole of radius $$R/2$$ is cut out. The centre of the hole is at $$R/2$$ from the centre of the original disc.Locate the centre of gravity of the resulting flat body.

If the mass per unit area of the disc is $$m$$,
then mass of the portion remove from the disc is $$M'=\pi(R/2)^2\times m=(\pi R^2/4)m=M/4$$
In figure centre of mass of $$M$$ is at $$O$$ and for $$M'$$ is at $$O'$$
But $$OO'=R/2$$.
After mass $$M'$$ is removed the remaining portion can be taken as two masses $$M$$ at $$O$$ and $$-M'=-M/4$$  at $$O'$$ we taking $$-M'$$ because we are removing this mass.
distance of centre of gravity(P) of remaining part is :
$$X=\dfrac{M \times 0-M' \times R/2}{M+M'}$$

$$X=\dfrac{-M/4\times R/2}{M-M/4}$$
$$X=-R/6$$
Minus sign indicates that $$P$$ is to the left of $$O$$.

774923_732377_ans_0efbe7638e784ab2b784d3da1a4e4caf.png


Can a body in translatory motion have angular momentum? Explain.

Yes, a body in translatory motion can have angular momentum, unless the fixed point about which angular momentum is taken lies on the line of motion of the body.
This follows from $$L=r \times mv$$


A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.
875123_e9da9548a87240faa6036cc7ae798b7e.png

Given: a tangential force F acts at the top of a thin spherical shell of mass m and radius R. 
To find the acceleration of the shell if it rolls without slipping.
Solution:
Let the distance of point of application of force from center is equal to Radius (R)
If sphere rolls without slipping:
$$\alpha=\dfrac aR$$
where $$\alpha$$ is angular acceleration, $$a$$ is acceleration of the center of the sphere.
Newton's law of motion:
$$(F+F_{fr})R=I\alpha.......(i)$$
and $$F-F_{fr}=ma..........(ii)$$
where $$F_{fr}$$ is force of friction, $$I$$ is moment of inertia (for solid sphere, $$I=\dfrac 25mR^2$$)
$$\\\implies F-F_{fr}=\dfrac IR\times \dfrac aR$$
Substituting the values of $$a$$ and $$I$$ in eqn(i), we get
$$F+F_{fr}=\dfrac 25mR^2\times \dfrac a{R^2}\\\implies F+F_{fr}=\dfrac 25ma.......(iii)$$
Adding eqn(ii) and eqn(iii), we get
$$F+F_{fr}=\dfrac 25ma$$
$$\underline{F-F_{fr}=ma}$$
$$\\\therefore, 2F=\dfrac {2ma}5+ma\\\implies 2F=\dfrac 75ma\\\implies F=\dfrac 7{10}ma\\\implies a=\dfrac {10F}{7m}$$
is the acceleration of the shell if it rolls without slipping.


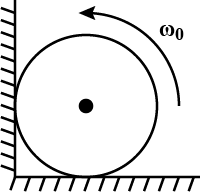
A uniform cylinder of radius $$R$$ is spinned about its axis to the angular velocity $${\omega}_{0}$$ and then placed into a corner. The coefficient of friction between the corner walls and the cylinder is $${\mu}_{k}$$. How many turns will the cylinder accomplish before it stops?
982309_45ad1adec62247328a4a49c59a4ffb59.png

As the centre of mass of the cylinder does not accelerate hence $$\sum { F } =0\quad$$
$$\sum { { F }_{ x } } =0,{ N }_{ 2 }={ \mu  }_{ k }{ N }_{ 1 }=0...(i)$$ 
$$\sum { { F }_{ x } } =0,{ N }_{ 1 }={ \mu  }_{ k }{ N }_{ 2 }-mg=0...(ii)\quad $$
solving these equations $${ N }_{ 1 }=\cfrac { mg }{ 1+{ \mu  }_{ k }^{ 2 } } ,{ N }_{ 2 }=\cfrac { { \mu  }_{ k }mg }{ 1+{ \mu  }_{ k }^{ 2 } } \quad \quad $$
The torque on the cylinder about the axis of rotation
$${ \tau  }_{ CM }=mg\times \times 0+{ N }_{ 1 }\times 0+{ N }_{ 2 }\times 0+{ \mu  }_{ k }{ N }_{ 2 }R=\cfrac { { \mu  }_{ k }\left( 1+{ \mu  }_{ k } \right)  }{ \left( 1+{ \mu  }_{ k } \right)  } mgR$$
The moment of inertia about axis of rotation $$\quad { I }_{ CM }=\cfrac { 1 }{ 2 } m{ R }^{ 2 }$$
The torque equation, $$\tau =I\alpha $$
$$\cfrac { { \mu  }_{ k }\left( 1+{ \mu  }_{ k } \right)  }{ \left( 1+{ \mu  }_{ k } \right)  } mgR=\left( \cfrac { 1 }{ 2 } m{ R }^{ 2 } \right) \alpha \Rightarrow \alpha =\cfrac { { 2\mu  }_{ k }\left( 1+{ \mu  }_{ k } \right) g }{ \left( 1+{ \mu  }_{ k }^{ 2 } \right) R } $$
Using equation $${ \omega  }^{ 2 }={ \omega  }_{ 0 }^{ 2 }-2\alpha \theta$$
calculate the angular displacement $$\theta$$
$${ 0 }^{ 2 }={ \omega  }_{ 0 }^{ 2 }-2\left[ \cfrac { { 2\mu  }_{ k }\left( 1+{ \mu  }_{ k } \right) g }{ \left( 1+{ \mu  }_{ k }^{ 2 } \right) R }  \right] \theta $$
$$\Rightarrow \theta =\cfrac { \left( 1+{ \mu  }_{ k }^{ 2 } \right) { \omega  }_{ 0 }^{ 2 }R }{ 4{ \mu  }_{ k }\left( 1+{ \mu  }_{ k } \right) g } $$
Revolution accomplished
$$n=\cfrac { \theta  }{ 2\pi  } =\cfrac { \left( 1+{ \mu  }_{ k }^{ 2 } \right) { \omega  }_{ 0 }^{ 2 }R }{ 2\pi \times 4{ \mu  }_{ k }\left( 1+{ \mu  }_{ k } \right) g } =\cfrac { \left( 1+{ \mu  }_{ k }^{ 2 } \right) { \omega  }_{ 0 }^{ 2 }R }{ 8\pi { \mu  }_{ k }\left( 1+{ \mu  }_{ k } \right) g } $$

1028934_982309_ans_ec85c2926d6d48e0b7c1f020afb6c27e.png


Why is it easier to roll a gas cylinder than to pull it along the road?

During pulling we have to oppose the kinetic friction whereas during rolling we have to oppose the rolling friction.
Rolling friction being smaller than the kinetic friction causes less force in rolling the cylinder.


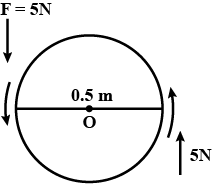
A steering wheel of diameter 0.5 m is rotated anticlockwise by applying two forces each of magnitude 5 N. Draw a diagram to show the application of forces and calculate the moment of couple applied.

Moment of the force applied about $$o=F\times R$$
$$=5N\times 0.25m$$
= 1.25Nm


1175201_1065534_ans_65d321f5bd934701947671ce3854de3d.png


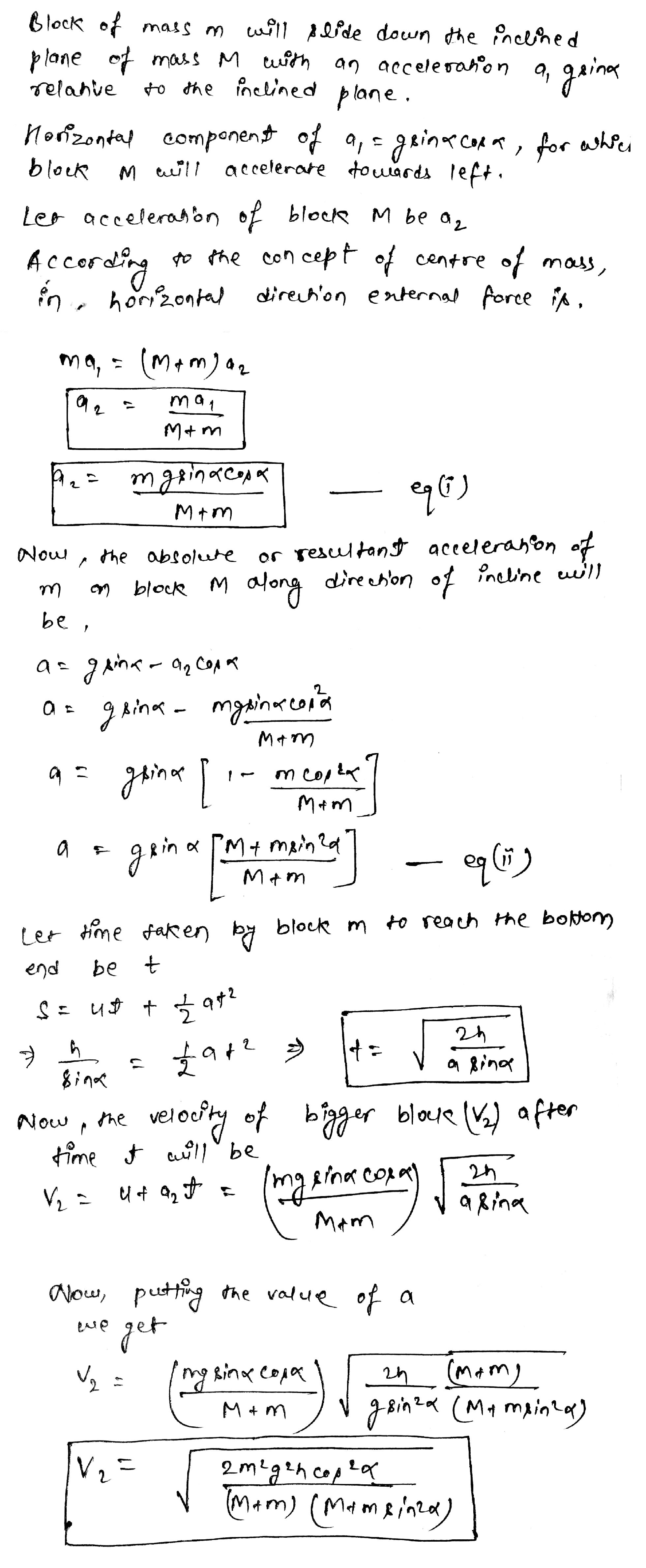
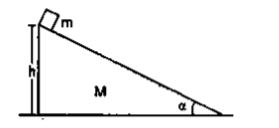
A block of mass $$m$$ is placed on a triangular block of mass $$M$$, which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
1713332_ac9122811ded463b98ae1dfe22beca4a.JPG


1671187_1713332_ans_e1030d2091ee4482a83947f8e8030e91.jpg


Find (1) radius of gyration (2) M.I of a rod of mass 100g & length 100 cm about an axis passing through its centre & to its length.

Given,

Mass of rod, $$M=0.1\ kg$$
Length of rod, $$L=0.1\ m$$

Radius of gyration at center, $${{K}_{c}}=\dfrac{{{L}^{2}}}{12}=\dfrac{{{0.1}^{2}}}{12}=8.3\times {{10}^{-4}}{{m}^{2}}$$

Radius of gyration at length's end, $${{K}_{e}}=\dfrac{{{L}^{2}}}{3}=\dfrac{{{0.1}^{2}}}{3}=3.3\times {{10}^{-3}}{{m}^{2}}$$

Moment of inertia at center, $${{I}_{c}}=\dfrac{M{{L}^{2}}}{12}=\dfrac{0.1\times {{0.1}^{2}}}{12}=8.3\times {{10}^{-5}}\ kg{{m}^{2}}$$

Moment of inertia at length's end, $${{I}_{e}}=\dfrac{M{{L}^{2}}}{3}=\dfrac{0.1\times {{0.1}^{2}}}{3}=3.3\times {{10}^{-4}}\ kg{{m}^{2}}$$ 



A thin rod of the length L is suspended from one end and rotates with n rotation per second the rotational kinetic energy of rod will be?

$$Angular \ velocity \ w=2πn$$

$$Rotational \ ke=½iw²$$

where i=moment of inertia of rod $$= ml²/3$$

now rotational $$k.e=½(ml²/3)\times(2πn)²$$

$$=2/3\times mπ²n²l²$$


Two identical uniform rod each of mass m and length t joined perpendicular to each other . An axis passes through junction and in the plane of rods. Then M of system about the axis is.


1108565_1094107_ans_fd3202c8c1b945d5af135788a2db8d31.jpg


Initially stable two particles $$x$$ and $$y$$ start moving towards other under mutual attraction. If at one time the velocities of $$X$$ and $$Y$$ are $$V$$ and $$2V$$ respectively, what will be the velocity of centre of mass of the system?

As initially both the particles are at rest momentum of both the particles will be 0.
$${p}_{1}={p}_{2}=0$$
Now as both the particle does experience any external force their will be no change in the momentum of center of mass of the particle, thus 0.
And we know momentum$$p=mv$$ as mass cannot be 0 , its velocity will be 0 



What is the MOI of the following
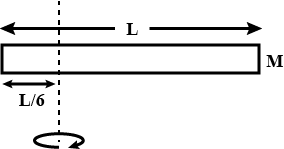
1175229_87f6f2d6c514474ebde198c73c52e498.png

Given,

Mass, $$M$$  and Length $$L$$

Inertia at center of mass, $${{I}_{cm}}=\dfrac{1}{12}M{{L}^{2}}$$

Apply parallel axis theorem,

Inertia at x-x, $${{I}_{x-x}}=\dfrac{1}{12}M{{L}^{2}}+M{{\left( \dfrac{L}{3} \right)}^{2}}=\dfrac{7M{{L}^{2}}}{36}$$

Hence, moment of inertia is $$\dfrac{7M{{L}^{2}}}{36}$$


1061968_1175229_ans_d9ee3a280e6f44cb9d30861ab138761e.png


Two rods OA and OB of equal length and mass are lying in xy plane as shown in figure. Let $$I_x, I_y$$ and $$I_z$$ be the moment of inertia of both the rods about x, y and z axis respectively. Then?
1213912_b1bfd92797b4425fbf08e8dd17d072b5.PNG

$${ I }_{ x }={ I }_{ y }=2\left[ \dfrac { { ml }^{ 2 } }{ 3 } { sin }^{ 2 }{ 45 }^{ 0 } \right] =\dfrac { { ml }^{ 2 } }{ 3 } $$

$${ I }_{ z }=2\left[ \dfrac { { ml }^{ 2 } }{ 3 }  \right] =\dfrac { 2{ ml }^{ 2 } }{ 3 } \quad { I }_{ x }={ I }_{ y }<{ I }_{ z }$$


Motion of centre of mass

The center of mass is a unique point in space where the weighted relative position of the distributed mass sums up to zero$$.$$ It is the point where a force applied causes the motion in the direction of motion without any rotation$$.$$ The mass of the body is distributed around the center of mass$$.$$


What do you understand by the clockwise and anticlockwise moment of force? When is it taken positive?

If the effect of the body is to turn in anticlockwise$$,$$ moment of force is called anticlockwise moment and it is taken positive$$.$$ If the effect of the body is to turn it clockwise the moment of force is called clockwise moment and it is taken negative$$.$$


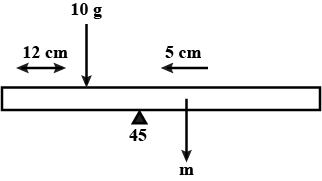
A meter stick is balanced on a knife edge at its centre. When two coins each of mass $$5g$$ are put one on top of the other at $$12.0cm$$ mark, the stick is found to be balanced at $$45.0 cm$$. What is the mass of the meter stick?

Figure shows the forces on the stick
The mass of metre stick is concentrated at $$ CM=50 cm $$
Consider the torques around $$ 0$$.Since the stick is in rotational equilibrium,
$$ \bar{\tau}_{ext}=m(5 cm)-(10g)(45-12)=0$$
$$ \therefore =10g \dfrac{(33cm)}{(5cm)}=66gm .$$
1776706_1315885_ans_8220bf6d3ddf40bf9d307cbe5b9ab7e1.png


Four identical thin rods each of mass M and length $$l$$ , form a square frame . Form of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is :

Moment of inertia for the rod $$AB$$ rotating about an axis through the midpoint of $$AB$$ perpendicular to the plane of the paper is $$\dfrac{MI^2}{12}$$

Moment of inertia about the axis through the centre of the square and parallel to this axis,

$$I=I_0+Md^2=M(\dfrac{l^2}{12}+\dfrac{l^2}{4})=\dfrac{Ml^2}{3}$$

For all the four roads, $$I=\dfrac 43MI^2$$.

1449260_1393243_ans_15ab9e362a754765a02fbd6d02ef9cf8.PNG


Define radius of gyration.

Radius of gyration of a body about an axis is defined as the distance from the axis at which the entire mass of the body must be concentrated in order to give the same moment of inertia of the body about the given axis.


Define the term moment of force .

Movement of force is the turning effect of force acting on a body about an axis is called the moment of force.
Moment of force $$ (O) $$ = $$ F \times $$ perpendicular distance of force from axis$$ O $$.
$$ i .e. $$ Moment of force =  $$ F \times r $$


What will be the moment of inertia of a thin rod of mass M and length l along the axis perpendicular to its length and passing through one point from a distance l /4 from one end.


1764612_1466945_ans_7f220324551f4d3eaa5bf12d90274537.jpg


Three particles of masses $$1.0 kg, \ 2.0 kg$$ and $$30 kg$$ are placed at the corners $$A, B$$ and $$C$$ respectively of an equilateral triangle $$ABC$$ of edge $$1 m$$. Locate the centre of mass of the system.

$$m_1= 1\, kg$$   $$m_2= 2\,kg$$,  $$m_3=3kg$$
$$x_1= 0$$  $$x_2= 1$$   $$x_3= 1/2$$
$$y_1= 0$$  $$y_2= 0$$   $$y_3= \sqrt{3}/2$$

The position of centre of mass is
$$C.M =\left ( \dfrac {m_1 x_1+m_2 x_2+m_3x_3}{m_1+m_2+m_3}, \dfrac {m_1 y_1+m_2 y_2+m_3y_3}{m_1+m_2+m_3} \right )$$

           $$=\left ( \dfrac{(1\times 0)+(2 \times 1)+(3\times 1/3)}{1+2+3}, \dfrac{(1\times 0)+(2 \times 0)+(3\times (\sqrt{3}/2))}{1+2+3} \right )$$

$$CM=\left ( \dfrac {7}{12}, \dfrac {3\sqrt{3}}{12} \right )$$ from the point $$B$$


The variation of angular position $$\theta$$, of a point on a rotating rigid body, with time $$t$$ is shown in Figure. Is the body rotating clock-wise or anti-clockwise?
1793802_f23cde319287428596fa179fea6f82c6.png

we find that slope of $$\theta-t$$  graph is positive, which by convention, respresents anticlockwise rotation.
As $$\theta $$ is positive and we know that $$\omega=\dfrac{d\theta}{dt}$$ and from $$tan\alpha=\dfrac{d\theta}{dt}>0$$ which means $$\omega>0$$ 
So the rotation must be anticlockwise .


Write the conditions for mechanical equilibrium of rigid bodies.

Conditions for mechanical equilibrium should satisfy it for rotational as well as linear motions of the bodies. These conditions are.
$$\Sigma F = 0$$ for linear motion
and $$\Sigma \tau = 0$$ for rotational motion.


Calculate the moment of inertia of a thin rod about an axis perpendicular to the length and passing through one edge.

Moment of inertia of a Thin rod
(a) Moment of Inertia of a Thin Rod about the Axis Perpendicular to the Length and Passing through the Center. Take a uniform thin rod AB whose mass is M and length is l. YY’ axis passes through the center of the rod and perpendicular to the length of the rod. We have to calculate the moment of inertia about this axis. YY’.
Suppose, small piece dx is at a distance x from the YY' axis. Hence, mass of length dx is $$= (\dfrac{M}{l})dx$$ The moment of inertia of small piece about the YY' axis
$$dl = \left [ (\dfrac{M}{l})dx \right ] x^2$$
Therefore, the moment of inertia of the complete rod about the YY' axis.
b) Moment of Inertia about the axis perpendicular to the the length and passing through the Corner If $$I_{CD}$$ is the moment of inertia about the axis CD perpendicular to the length of a thin rod and passing through the point A then, by theorem of parallel axis;
$$l_{CD} = l_{YY'} + Md^2$$
$$= \dfrac{Ml^2}{12} + M(\dfrac{l}{2})^2$$
$$l_{CD} = \dfrac{Ml^2}{3}$$ .........(2)


Write down the relation between angular momentum, moment of inertia and angular velocity.

$$J = l\omega;$$ where J is angular momentum, l is the moment of inertia and $$\omega,$$ the angular velocity.


Establish the relation between angular momentum and angular velocity.

Total kinetic energy of a body at the bottom rolling down on an inclined plane E = Translational kinetic energy + Rotational kinetic energy


1764640_1833053_ans_84905c32a9294fb2849851e22252a891.png


Answer in brief:
A big dumb-bell is prepared by using a uniform rod of mass $$60\,g$$ and length $$20\,cm$$. Two identical solid spheres of mass $$50\,g$$ and radius $$10\,cm$$ each are at the two ends of the rod. Calculate the moment of about an axis passing through its center and perpendicular to the length.

$$M_{sph} = 50\,g , R_{sph} = 10\,cm , M_{rod} = 60\,g , L_{rod} = 20\,cm $$ 
The $$MI$$ of a solid sphere about its diameter is 
$$ I_{sph, CM} = \dfrac{2}{5} M_{sph} R^{2}_{sph} $$ 
The distance of the rotation axis(transverse symmetry axis of the dumbbell) from the center of sphere , $$ h = 30\,cm $$.
The $$MI$$ of a solid sphere about the rotation axis,
$$I_{sph} = I_{sph, CM} + M_{sph}h^2 $$ 


A metallic ring of mass $$1\,kg$$ has a moment of inertia $$1 \,kg \,m^2$$ when rotating about one of its diameters. It is molten and remolded into a thin uniform disc of the same radius. How mush will its moment of inertia be , when rotated about its own axis.

Mass of ring and disc is $$M = 1 m\,kg $$ 
Moment of inertia of ring at diameter $$(Ir)d = 1\,kg \,m^2 $$ 
$$Rr = Rd $$ 
What we have to find out:-
Moment of inertia of disc about own axis $$ = Id = $$ ?
Using theorem of perpendicular axes, for a ring M.I about its any diameter, which is given by,
$$ (Ir) c = 2(Ir) d $$ 
$$ = 2 \times 1 $$ 
$$ MRr^2 = 2\,kg \,m^2 $$ 
$$Rr^2 = Rd^2 = 2 $$ meter 
Hence, 
Moment of inertia of disc about own axis is given by,
$$ Id = \dfrac{1}{2} MRd^2 $$ 

$$ = \dfrac{1}{2} \times 1 \times 2 $$ 

$$Id = 1 \, kg \,m^2 $$ 


State the law of moments.

The algebraic sum of the moments of any number of forces about any point is  to the moment of their resultant about the same point.


Write expression for moment of inertia of thin rod

Moment of inertia of a thin rod of length $$L$$ and mass $$M$$ about an axis passing through its centre and oerpendicular to its length is,
$$ l=\dfrac{ML^2}{12} $$


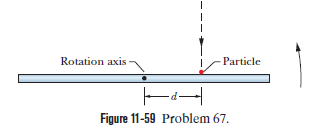
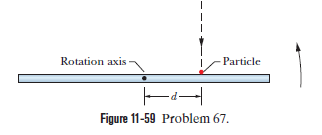
Figure is an over head view of a thin uniform rod of length $$0.600\ m$$ and mass $$M$$ rotating horizontally at $$80.0\ rad/s$$ counterclockwise about an axis through its center. A particle of mass $$M/3.00$$ and traveling horizontally at speed $$40.0\ m/s$$ hits the rod and sticks. The particle's path is perpendicular to the rod at the instant of the hit, at a distance $$d$$ from the rods center.
In which direction do rod and particle rotate if $$d$$ is greater than this value?
1766481_3388c59b5c664a889c142094c96d1de5.png


1746840_1766481_ans_073ea4a16dda4594be26e988b2be29e0.jpg


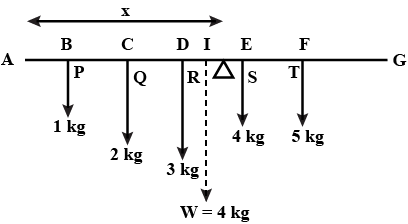
Five bodies $$ 1kg \quad wt.,2kg\quad wt., 3k\quad wt.,4kg\quad wt. $$ and $$ 5kg\quad wt$$. are suspended at a distance of $$ 1m,2m,3m,4m,$$ and $$ 5m $$ from one end of a uniform rod of mass $$ 4kg $$ and $$ 6 $$ meters length. Find the point about which the rod will balance about the knife edge placed at a distance of $$ 'X '$$ from the end $$ A. $$

Resultant force acting vertically downwards on the rod 
$$ = P  +Q +R +S +T +W $$
$$ = 1 + 2 +3 +4 +5 +4 = 19 kg wt $$
Thus force of $$ 19 $$ kgwt acting vertically upwards will balance the rod . this force acts at a distance 'x' from A.
i.e. $$ R_1 = 19 kg wt $$
Taking the moments about A 
$$ P \times AV  + Q \times AC  + R \times AD  + S \times AE  + T  \times AF  + W \times AI = R_1 x $$
$$  1 \times  1  + 2 \times 2 +3 \times 3 +4 \times  4 + 5 \times  5 + 4 \times  3 = R_1x = 19 x $$
$$ 1 + 4 + 9 + 16 + 25 + 12 = 19 x $$
$$ 67 = 19x $$ or $$ x = \dfrac {67}{19} = 3.52 m $$
$$ \therefore$$ Distance of the knife edge from the end $$ A $$ is  $$ 3.52 m $$
1779361_1845067_ans_91581b7ca18b4f9faac3037a0b1db75e.png


The figure illustrates the position and masses of $$ 3 $$ particles. Find the position of their centre of mass.
1845181_1a058ac46f0e4c40a233d46ba2a98275.png

The position $$ A $$ is $$ ( 0 , 0 , 0 ) $$
The position of $$ B $$ is $$( 3 , 2 , 0 ) $$
The position of $$ C $$ is$$ ( 5 , 4 , 0 ) $$
$$ X_{cm} = \dfrac { \sum m_iX_i}{ \sum m_i} = \dfrac { [ 1 (0 ) + 3( 3 ) + 4( 5) ]}{ [1+3+4] } $$
 $$ = \dfrac {29}{8} = 3.625 m $$
$$ Y_{cm} = \dfrac { \sum m_iY_i}{\sum m_i } = \dfrac { [ 1 (0) + 3(2) + 4 (4) ] }{ [ 1+3+4 ] } $$
$$ = \dfrac { 22}{8} = 2.75 m $$
$$ Z_{cm} = \dfrac { \sum m_iZ_i}{\sum m_i} = \dfrac { ( 0+ 0 + 0) }{ 8} = 0 m $$
the position of centre of mass os the system is $$ ( 3.625 , 2.75 , 0 ) $$


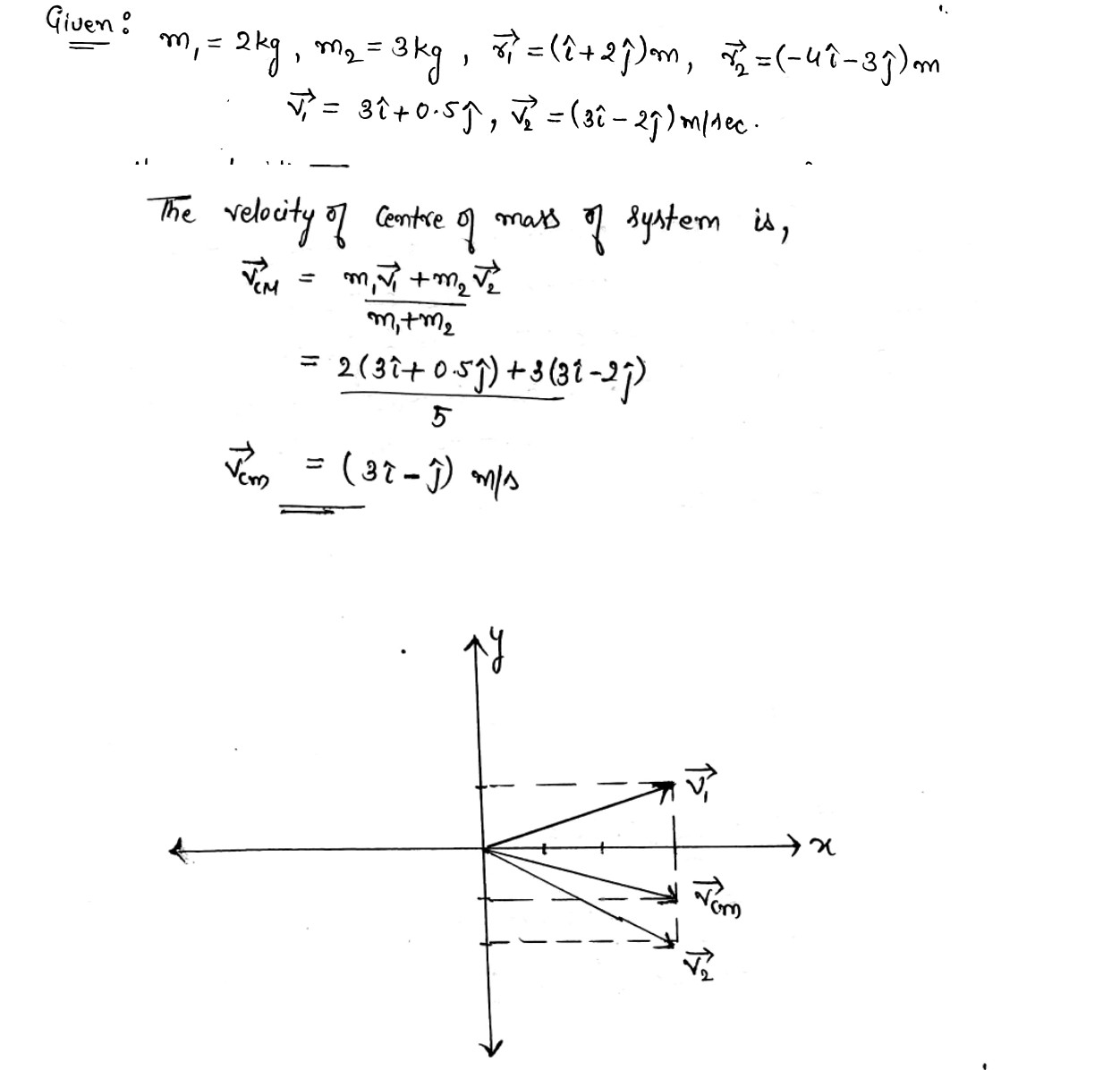
Consider a system of two particles in the $$xy$$ plane: $$m_{1}=2.00\ kg$$ is at the location $$\vec{r}_{1}=(1.00\hat{i}+2.00\hat{j})m$$ and has a velocity of $$(3.00\hat{i}+0.500\hat{j})\ m/s; m_{2}=3.00\ kg$$ is at $$\vec{r}_{2}=(-4.00\hat{i}-3.00\hat{j})\ m$$ and has velocity $$(3.00\hat{i}-2.00\hat{j})\ m/s$$.
Plot these particles on a grid or graph paper. 
What is the total linear momentum of the system?


1900219_1864923_ans_602cca4a201247c0ab2c9aac8403e320.jpg


A $$2.00-kg$$ particle has a velocity $$(2.00 \hat{i} - 3.00 \hat{j})\ m/s$$, and a $$3.00-kg$$ particle has a velocity $$(1.00 \hat{i}+ 6.00 \hat{j})\ m/s$$. Find
the velocity of the center of mass


1900207_1864912_ans_129020ff720e4c95b3835da245148d63.jpg


Four objects are situated along the $$y$$ axis as follows: a $$2.00-kg$$ object is at $$+3.00\ m$$, a $$3.00-kg$$ object is at $$+2.50\ m$$, a $$2.50-kg$$ object is at the origin, and a $$4.00-kg$$ object is at $$-0.500\ m$$. Where is the center of mass of these objects?


1898099_1864881_ans_13b87ff4343b491d9d610db54c3a1c48.jpg


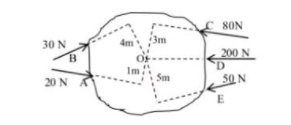
Calculate the resultant torque from the following diagram:
1980447_07321989672b4cf383bbebea1cd9c3f6.PNG



What is the minimum coefficient of friction required to maintain pure rolling motion for the disk?

f = force of friction

I = moment of inertia

a = translational acceleration (of the center of mass if the object rolls without slipping)

(alpha) = angular acceleration

(tau) = torque

R = radius

m = mass

N = Normal Force

F = force

(theta) is the angle of the incline

(meu) = coefficient of friction

fR = (tau) = I(alpha)

(alpha) = a/R

f = Ia/(R^2)

At the critical angle before the object slides (meu) N = f

(meu)N = mg cos (theta)

(meu)mg cos (theta) = Ia/(R^2)

I for a disk is (1/2) mR^2

Now we just need a

F = ma = mg sin (theta) - f

F = ma = mg sin (theta) - [Ia/R^2]

ma + [Ia/R^2] = mgsin(theta)

a = [ mgsin(theta)/(1 + (I/mR^2))]

Substitute I = 1/2 mR^2

a = 2/3 g sin (theta)

Substitute I and a into:

(meu)mg cos (theta) = Ia/(R^2)

(meu)mg cos(theta) = (1/2 mR^2)(1/2 g sin (theta))/R^2

(meu) cos(theta) = 1/4 sin (theta)

(meu) = 1/4 tan (theta)



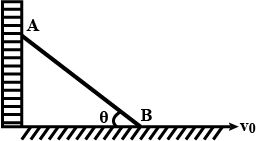
The end $$B$$ of uniform rod $$AB$$ which makes angle $$\theta$$ with the floor is being pulled with a velocity $$v_{0}$$ as shown. Taking the length of rod as $$l$$, calculate the following at the instant when $$\theta = 37^{\circ}$$.
(a) The velocity of end $$A$$
(b) The angular velocity of rod
(c) Velocity of $$CM$$ of the rod.
772057_de7c3238606b45beaf83d167b2b89b30.png

(i)$${ v }_{ A }={ v }_{ B }\tan { \theta  } \\ =v+\tan { 37° } \\ =\dfrac { 3 }{ 4 } $$
(ii) Angular speed $$\omega$$
$${ v }_{ A }=\omega \times x\\ =\omega \times \dfrac { l }{ 2 } \cos { \\ 37°\\  } \\ =\omega \times l\dfrac { 2 }{ 5 } \\ =\omega \dfrac { { v }_{ A } }{ \left( \dfrac { 2l }{ 5 }  \right)  } =\dfrac { 3 }{ 4v } \dfrac { v }{ \dfrac { 2l }{ 5 }  } =\dfrac { 15v }{ 8l } $$
(iii)Let downward velocity of com is vd
$$\dfrac{\dfrac12}{v_d \cos \theta} = \dfrac { l }{ { v }_{ A } } =\cos { \theta  } $$
$$\quad vd=\dfrac { 1 }{ 2 } vA=\dfrac { 3 }{ 8 } v$$
Horizontal velocity $$={ v }_{ h }=\dfrac { v }{ 2 } $$
$$\left( \dfrac { v }{ 2 } \hat { i } -\dfrac { 3 }{ 8 } \hat { j }  \right) $$

951944_772057_ans_efbfb4f852844d1784141e7e01c38bab.png


Write the equation corresponding to the ones given, for rotational motion about a fixed axis.
$$(i) \times (t) = x (0) + v (0) t + 1 a/2 \ t^2$$ 
(ii) $$v^2(t) = v^2 (0) + 2a [x (t) - x (0)]$$
(iii) $$\bar{v} = \frac{v(t) - v(0)}{2}$$
(iv) $$v(t)  = v(0) + at$$

(i) $$\theta(t)  = \theta(0) + \omega(0)+\frac{1}{2} at^2$$
(ii) $$\omega^2 (t) =  \omega^2(0) + 2 a \alpha [\theta (t) - \theta(0)]$$
(iii)$$\bar{\omega} = \frac{\omega(t) - \omega(0)}{2}$$
(iv) $${\omega}(t)  = {\omega}(0) + at$$


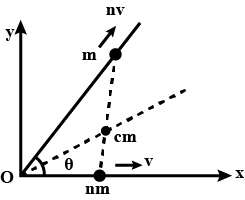
Two masses, $$nm$$ and $$m$$, start simultaneously from the intersection of two straight lines with velocities $$\nu$$ and $$n\nu$$ respectively. It is observed that the path of their bisecting the angle between the given straight lines. Find the magnitude of the velocity of centre of mass. [Here $$\theta =$$ angle between the lines].
983377_bbd5082bbd7a480dba008e19d25e3bdb.png

$$\overrightarrow{\nu}_{cm} = \dfrac{m_1 \overrightarrow{\nu}_2}{m_1 + m_2}$$

$$\overrightarrow{\nu}_{cm} = \dfrac{nm \,\,\nu \hat{i} + m \,\,n\nu \,\,cos\theta \hat{i} + nm\nu \,\,sin \theta \hat{j}}{m (1 + \pi)}$$

$$\nu_{cm} = \dfrac{\sqrt{(nm\nu + mn\nu \,\,cos \theta)^2 + ( nm\nu \,\,sin \theta)^2}}{m (1 + \pi)}$$

$$\nu_{cm} = \dfrac{nm\nu \sqrt{(1 + cos\theta)^2 + (sin \theta)^2}}{m (1 + n)}$$

$$= \dfrac{n\nu \sqrt{1 + cos^2 \theta + 2cos \theta + sin^2 \theta}}{(1 + n)}$$

$$\left(\dfrac{n\nu}{n + 1}\right) \sqrt{2 cos \dfrac{\theta}{2}}$$

$$\nu_{cm} = \dfrac{2n\nu \,\,cos \dfrac{\theta}{2}}{n +1}$$


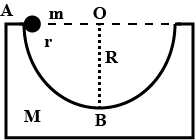
A block of mass $$M$$ with a semi-circular track of radius $$R$$, rests on a horizontal frictionless surface. A uniform cylinder of radius $$r$$ and mass $$m$$ is released from rest at the top point $$A$$ (See fig.). The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track? How fast is the block moving when the cylinder reaches the bottom of the track
831357_82914a7be32c481dba735e5332780672.png

Using the concept of center of mass.
Let block m move x left and cylinder of mass m move $$(R-r-x)$$ right.
Now let center of mass and origin therefore
$$X_{com}=\cfrac{m(R-r-x)-xM}{m+M}=0\\ \quad=m(R-r)-mx-xM=0\\ \quad x=\cfrac{m(R-r)}{(M+m)}$$


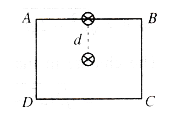
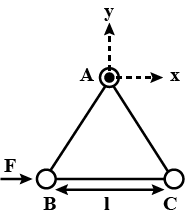
Three particles $$A,B,C$$ each of mass $$m$$ are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side $$l$$. This body is placed on a horizontal frictionless table (x-y plane) and is hinged at point $$A$$ so that it can move without friction about the vertical axis through $$A$$. The body is set into rotational motion on the table about this axis with a constant angular velocity $$\omega$$ (a) Find the magnitude of the horizontal force exerted by the hinge on the body (b) At time $$T$$, when side $$BC$$ is parallel to  x-axis, force $$F$$ is applied on $$B$$ along $$BC$$ (as in the figure). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time $$T$$.
982315_dd6cd2177b8b4df28272f14bd4dc1352.png

The centre of mass of the system is at the centroid of a triangular assembly. The CM moves along a circular path with constant angular velocity. Therefore, there must be a horizontal centripetal force directed towards the axis at the hinge
From figure we find
$$AD=l\sin { { 60 }^{ o } } =\cfrac { l\sqrt { 3 }  }{ 2 } $$
$$\quad AO=\cfrac { 2 }{ 3 } AD=\cfrac { { l }^{ 2 } }{ \sqrt { 3 }  } =r$$
the centripetal acceleration $${ a }_{ c }={ \omega  }^{ 2 }r={ \omega  }^{ 2 }\left( \cfrac { l }{ \sqrt { 3 }  }  \right) $$
Tangential acceleration $$\quad { a }_{ t }=\alpha r=\alpha \left( \cfrac { l }{ \sqrt { 3 }  }  \right) $$
(b) Let $${F}_{x}$$ and $${F}_{y}$$ be the forces applied by the hinges along x-axis and y-axis respectively. The system is in non-centroidal rotation. The three equations of motion are
$$\sum { { F }_{ x } } ={ F }_{ x }+F=(3m){ a }_{ t }=3m\left( \cfrac { l }{ \sqrt { 3 } \alpha  }  \right) ...(i)\quad \quad $$
$$\sum { { F }_{ x } } ={ F }_{ y }+3m\left( \cfrac { l }{ \sqrt { 3 }  }  \right) { \omega  }^{ 2 }....(ii)\quad $$
$$\sum { \tau  } =F\times \left( \cfrac { \sqrt { 3 }  }{ 2 } l \right) =2m{ l }^{ 2 }\alpha ....(iii)$$
From Eq (iii) $$\alpha =\cfrac { \sqrt { 3 } F }{ 4ml } $$
From Eq (i), $${ F }_{ x }+F=3m\left( \cfrac { l }{ \sqrt { 3 } \alpha  }  \right) \times \cfrac { \sqrt { 3 } F }{ 4ml } =\cfrac { 3F }{ 4 } $$
$$\Rightarrow { F }_{ x }=\cfrac { F }{ 4 } $$
from Eq. (ii) $${ F }_{ y }=\sqrt { 3 } ml{ \omega  }^{ 2 }$$

1028946_982315_ans_51d0d9df84bf4e8fa29a602f57563000.png


If the radius of solid sphere is $$35$$ cm  calculate the radius of gyration when the axis is along a tangent

I tangent = Ic + MR² = 2/5 Ma² + MR² = 7/5 MR ²

7/5 MR² = Mk²

K = √7/5 (35)²  

= 7 √35 cm



A uniform meter rule balances horizontally on a knife-edge placed at the $$60\ cm$$ mark when a weight of $$1\ g$$ is suspended from one end. What is the weight of the rule? 

make a meter scale and on the last end place the weight of $$ 20 gf$$.

At 58 cm mark the fulcrum and at $$50 cm$$ mark the weight of scale (downward direction both can be depicted by arrows.

a sum of anticlockwise force= sum of the clockwise force

hence let the weight of meter-scale be$$ x$$

$$x\times$$ distance from fulcrum( here 8 cm) $$= 20 \times 42$$

$$x = 105 gf$$

 

 



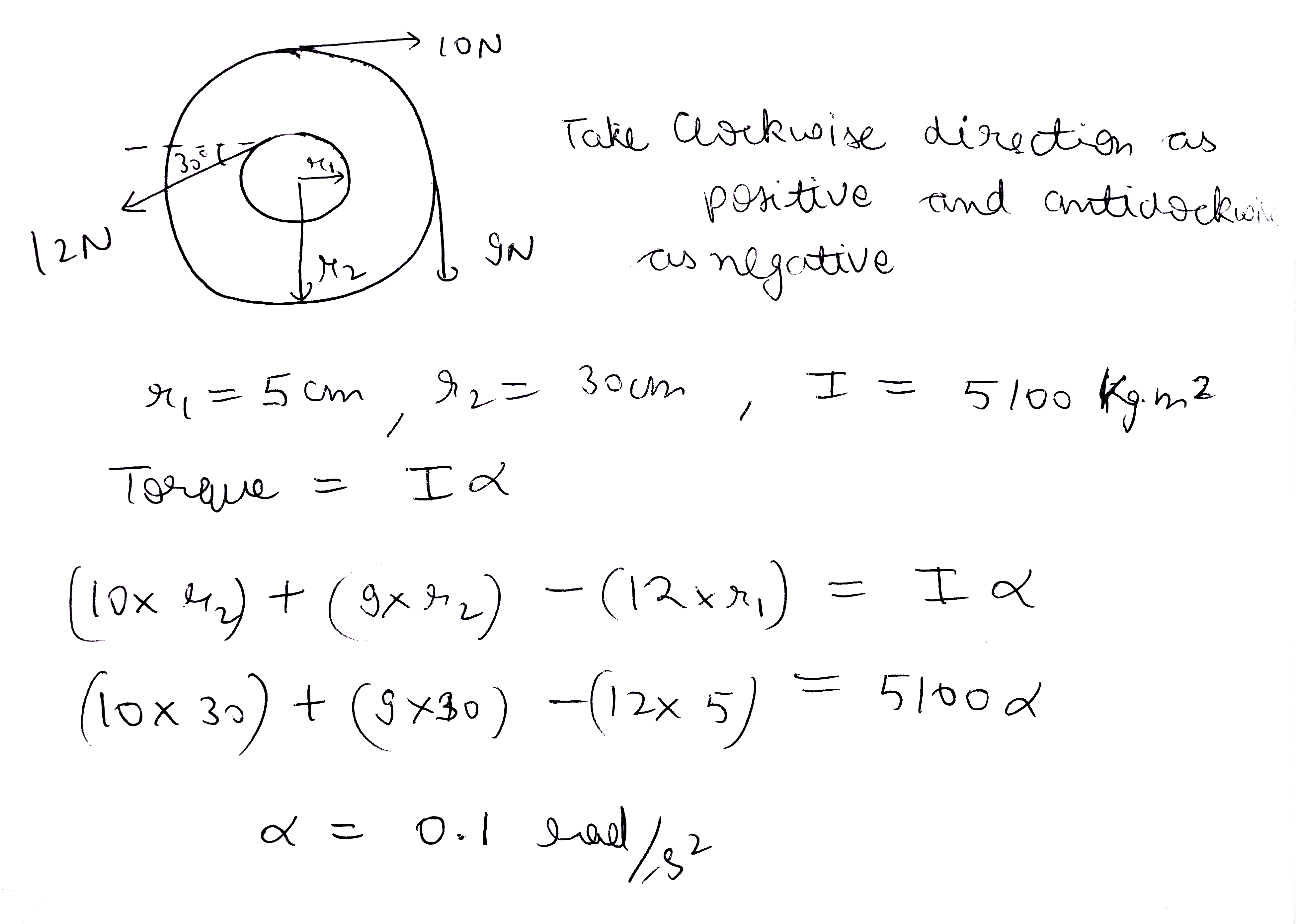
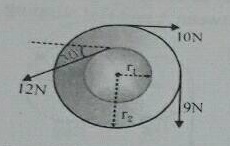
In the following figure $$r_{1}$$ and $$r_{2}$$ are $$5\ cm$$ and $$30\ cm$$ respectively. If the moment of inertia of the wheel is $$5100\ kg - m^{2}$$ about the axis passing through its centre and perpendicular to the plane of wheel, then what will be its angular acceleration?
1112448_241522150e8a4c8f86eba1bae2d83848.jpg

Total clockwise direction as positive and anticlockwise as negative.
$$r_1=5cm,r_2=30cm,I=5100Kgm^2$$
$$Torque=I \alpha$$
$$(10\times r_2)+(9\times r_2)-(12\times r_1)=I\alpha$$
$$(10\times 30)+(9\times 30)-(12\times 5)=5100\alpha$$
$$\alpha=0.1 rad/ r^2$$

1064666_1112448_ans_dd4507dc7ce94e969e8d387b800e3edf.png


A uniform steel rod of $$1 m$$ in length is bent in a $$90^\circ $$ angle at its mid point. Determine the position of its center of mass from the corner at bent.

To find:
Location of corner from origin
$$x_{com}=\dfrac{m_1x_1+m_2x_2}{m_1+m_2}$$,                           $$y_{com}=\dfrac{m_1y_1+m_2y_2}{m_1+m_2}$$

$$x_{com}=\dfrac{ \dfrac{m}{2}\left(-\dfrac{L}{4}\right)+\left(\dfrac{M}{2}\right)(0)}{M},$$     $$y_{com}=\dfrac{\left(\dfrac{M}{2}\right)(0)+\left(\dfrac{M}{2}\right)\left(\dfrac{L}{4}\right)}{M}$$

$$x_{com}=-\dfrac{ML/8}{M}$$,                                         $$y_{com}=\dfrac{ML/8}{M}$$

$$x_{com}, y_{com}=\left(-\dfrac{L}{8}, \dfrac{L}{8}\right)$$
Distance between origin & com $$=\sqrt{\left(\dfrac{L}{8}\right)^2+\left(\dfrac{L}{8}\right)^2}$$
$$=\dfrac{L}{8}\sqrt{2}$$

$$=\dfrac{L}{4\sqrt{2}}$$.

Given $$L=1$$
$$\therefore $$ Distance$$=\dfrac{1}{4 \sqrt2}$$



A body of mass  M and radius r rolling on a smooth horizontal floor with velocity v, rolls up an irregular inclined plane(sufficiently rough) up to verticle  height $$ ( 3v^2 /4g) $$ compute the moment of inertia of the body.
1735033_72429742963b487bb072bb56c11c6e94.png

Given,
           $$h=\frac{3{v}^2}{4g}$$

            $$\omega = \frac{v}{r}$$
By conservation of energy,
            $$mgh=\frac{1}{2}m{v}^2+\frac{1}{2}{I{\omega}^2}$$

            $$mg(\frac{3{v}^2}{4g})=\frac{1}{2}m{v}^2+\frac{1}{2}{I{\frac{v}{r}}^2}$$

             $$\frac{3m{v}^2}{4}=\frac{1}{2}m{v}^2(1 + \frac{I}{m{r}^2})$$

              $$\frac{1}{2} = \frac{I}{m{r}^2}$$

              $$I =\frac{m{r}^2}{2}$$




Each object shown in column I has mass $$2m$$. The ring has mass $$m$$ and radius $$R$$. The other components rod, lamina have total mass $$m$$. The shaded part in any figure represent a lamina axis $$I$$ and $$II$$ are in plane of figure, moment of inertia about their axis is represented by $$I_1, I_2$$. Moment of inertia about axis through $$O$$ and perpendicular to plane of figure is given by $$I_0$$.

by perpendicular axis theorem theorem,For a planar object, the moment of inertia about an axis perpendicular to the plane is the sum of the moments of inertia of two perpendicular axes through the same point in the plane of the object. so $$I_o=I_1+I_2$$.
x and y axis are symtrical so $$I_1=I_2$$


(B)by perpendicular axis theorem theorem,For a planar object, the moment of inertia about an axis perpendicular to the plane is the sum of the moments of inertia of two perpendicular axes through the same point in the plane of the object. so $$I_o=I_1+I_2$$.
x and y axis are symtrical so $$I_1=I_2$$


(C)by perpendicular axis theorem theorem,For a planar object, the moment of inertia about an axis perpendicular to the plane is the sum of the moments of inertia of two perpendicular axes through the same point in the plane of the object. so $$I_o=I_1+I_2$$.
x and y axis are not symmtrical so $$I_1\ne I_2$$


(D)by perpendicular axis theorem theorem,For a planar object, the moment of inertia about an axis perpendicular to the plane is the sum of the moments of inertia of two perpendicular axes through the same point in the plane of the object. so $$I_o=I_1+I_2$$.
x and y axis are  not symmtrical so $$I_1\ne I_2$$


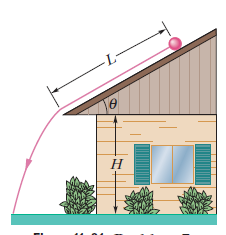
In figure a solid cylinder of radius $$10\ cm$$ and mass $$12\ kg$$ starts from rest and rolls without slipping a distance $$L=6.0\ m$$ down a roof that is inclined at angle $$\theta =30^o$$.
The roof's edge is at height $$H=5.0\ m$$. How far horizontally from the roof's edge does the cylinder hit the level ground?

1766015_a47631d5b93b4db5a2d053415732cfee.png


1687799_1766015_ans_ae4a8319104d451b812cad959671e684.jpg


A vertical container with base area measuring $$14.0\ cm$$ by $$17.0\ cm$$ is being filled, with identical pieces of candy, each with a volume of $$50.0\ mm^3$$ and a mass of $$0.0200\ g$$. Assume that the volume of empty spaces between the candies in negligible. If the height of the candies in the container increases at the rate of $$0.250\ cm/s$$, at what rate (kilograms per minute) does the mass of the candies in the container increase?

The mass density of the candy is

$$\rho =\dfrac {m}{V}=\dfrac {0.0200\ g}{50.0\ mm^3}=4.00\times 10^{-4}\ g/mm^3=4.00\times 10^{-4} kg/cm^3$$.

If we neglect the volume of the empty spaces between the candies, then the total mass of the candies in the containers when filled to height $$h$$ is $$M=\rho Ah$$, where $$A=(14.0\ cm)(17.0\ cm)=238\ cm^2$$ is the base of the container that remains unchanged. Thus, the rate of mass change is given by

$$\dfrac {dM}{dt}=\dfrac {d(\rho Ah)}{dt}=\rho A \dfrac {dh}{dt}=(4.00\times 10^{-4}kg/ cm^3)(238\ cm^2)(0.250\ cm/s)$$

$$=0.0238\ kg/s =1.43\ kg/ min$$.



In fig.10.37 two particles each with mass m=0.85 kg , are fastened to each other , and to a rotation axis at O, by two thin rods, each with length d=5.6 cm and mass M=1.2 kg. The combination rotates around the rotation axis with the angular speed $$ \omega $$=0.30 rad/s. Measured about O, what are combination's (a) rotational inertia and (b) kinetic energy
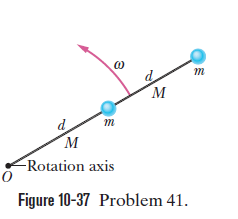
1766148_c0e94c009e424fda91e0f7afa0419d07.PNG


1742124_1766148_ans_340b1a310aed46ada6f512e779202a51.jpg


Figure is an over head view of a thin uniform rod of length $$0.600\ m$$ and mass $$M$$ rotating horizontally at $$80.0\ rad/s$$ counterclockwise about an axis through its center. A particle of mass $$M/3.00$$ and traveling horizontally at speed $$40.0\ m/s$$ hits the rod and sticks. The particle's path is perpendicular to the rod at the instant of the hit, at a distance $$d$$ from the rods center.
At what value of $$d$$ are rod and particle stationary after the hit?
1766479_828796f1b440495884f731064def7a0f.png


1746809_1766479_ans_7d159747b98846bd8b4692ff1ced8ffb.jpg


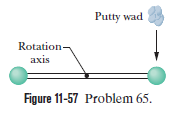
Two $$2.00\ kg$$ balls are attached to the ends of a thin rod of length $$50.0\ cm$$ and negligible mass. The rod is free to rotate in a vertical plan without friction about a horizontal axis through its center. With the rod initially horizontal, a $$50.0\ g$$ wad of wet putty drops onto one of the balls, hitting it with a speed of $$3.00\ m/s$$ and then sticking to it. 
What is the ration of the kinetic energy of the system after the collision so that of the putty wad just before?
1766467_c16adae9c3e048e8b3222d4e0f1c8a54.png


1692918_1766467_ans_b551408476304bd5bb8c31ef6e351ec4.png


A uniform sphere of mass $$m$$ and radius $$R$$ is placed on a rough horizontal surface (Figure). The sphere is struck horizontally at a height $$h$$ from the floor. Match the following:
1793804_3f1c4cb3dc94413ab381ab68b48e1f18.png

Mass of the sphere $$= m$$
Radius $$= R$$
$$h = $$ height of the floor
The sphere will roll without slipping when, $$w \dfrac{v}{R}$$

Where, $$v = $$ linear velocity of the sphere
$$w =$$ angular velocity of the sphere.

Now, angular momentum of sphere, about centre of mass (applying conservation of angular momentum just before and after struch)

$$mv (h - R) = I w = \left(\dfrac{2}{5} mR^2\right) \left(\dfrac{v}{R}\right)$$

$$\Rightarrow mv (h - R) = \dfrac{2}{5} mvR$$

$$\Rightarrow h - R = \dfrac{2}{5} R \Rightarrow h = \dfrac{7}{5} R$$

Therefore, the sphere will roll without slipping with a constant velocity and hence, no loss of energy when $$h = \dfrac{7}{5} R$$
So, (D) matches (1)

Now, Torque due to applied force about C.M.,
$$\tau = F (h - R) $$    [Clockwise]

For $$\tau = 0, h = R$$ sphere will have only translational motion. It would lose energy by friction.

Hence, (B) matches with (4).

If $$h > R, \tau \rightarrow $$ positive, sphere will spin clockwise.
So, (C) matches with (2)

If $$h <  R, \tau \rightarrow $$ negative, sphere will spin anticlockwise.

So, (A) matches with (3).

2042618_1793804_ans_0ecd29e3c8d5412b8efe05f6b91b0851.png


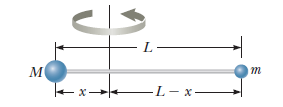
Two balls with masses $$M$$ and $$m$$ are connected by a rigid rod of length $$L$$ and negligible mass as shown in Figure. For an axis perpendicular to the rod, show that the system has the minimum moment of inertia when the axis passes through the centre of mass.
1864468_9d3a1d3e32644c41b34872972ef91892.png


1891808_1864468_ans_702588d9b3df4bde9d2cf857d7152af2.jpg


A uniform piece of sheetmetal is shaped as shown in Figure $$P9.48$$. Compute the $$x$$ and $$y$$ coordinates of the center of mass of the piece.
1864896_57f54cb815004e54a62782bc82eb2c9f.png


1898112_1864896_ans_e65270e6aefc4164be67fb2cc1d3d560.jpg


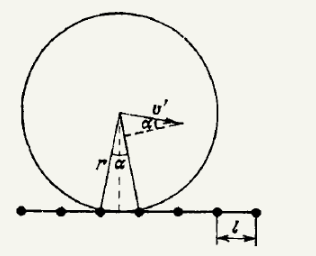
An inextensible rope tied to the axle of a wheel of mass $$m$$ and radius $$r$$ is pulled in the horizontal direction in the plane of the wheel. The wheel rolls without jumping over a grid consisting of parallel horizontal rods arranged at a distance $$l$$ from one another $$(l\ll r)$$. Determine the average tension T of the rope at which the wheel moves at a constant velocity v, assuming the mass of the wheel to be concentrated at its axle.

At the moment of the impact against the next rod, the centre of mass of the wheel has a certain velocity v' perpendicular to the line connecting it to the previous rod. This velocity can be obtained from the energy conservation law:

$$m g h+\dfrac{m v^{2}}{2}=\dfrac{m v^{\prime 2}}{2}$$

$$\text { Here } h=r-\sqrt{r^{2}-l^{2} / 4} $$

$$\quad \approx l^{2} /(8 r)$$

Therefore
$$v^{\prime}=v \sqrt{1+\dfrac{g l^{2}}{4 r v^{8}}}$$

Assuming  the impact of the wheel against the rod is perfectly inelastic. 
So, the projection of the momentum of the wheel on the straight line connecting the centre of the wheel to the rod vanishes. 

Thus, during each collision, the energy

$$\Delta W=\dfrac{m\left(v^{\prime} \sin \alpha\right)^{2}}{2}$$

where $$\sin \alpha \approx 1 / r,$$ is lost (converted into heat). 
For the velocity $$v$$ to remain constant, the work done by the tension $$\mathrm{T}$$ of the rope over the path $$\mathrm{I}$$ must compensate for this energy loss. 
Therefore,

$$T l=\dfrac{m v^{2}}{2}\left(1+\dfrac{g l^{2}}{4 r v^{2}}\right) \dfrac{l^{2}}{r^{2}}$$

where

$$T=\dfrac{m v^{2} l}{2 r^{2}}\left(1+\dfrac{g l^{2}}{4 r v^{2}}\right) \approx-\dfrac{m v^{2} l}{2 r^{2}}$$



1937285_1860582_ans_c8ef30be02a34bd196a1b714ca5f4ba1.png


A $$2.00-kg$$ particle has a velocity $$(2.00 \hat{i} - 3.00 \hat{j})\ m/s$$, and a $$3.00-kg$$ particle has a velocity $$(1.00 \hat{i}+ 6.00 \hat{j})\ m/s$$. Find
the total momentum of the system.


1900209_1864913_ans_0663a60f1575460d858e16375f3ef972.jpg


A $$6.00\ kg$$ woman stands at the western rim of a horizontal turntable having moment of inertia of $$500\ kg.\ m^2$$ and a radius of $$2.00\ m$$. The woman then starts walking around the rim clockwise at a constant speed of $$1.50\ m/s$$ relative to the Earth. Consider the woman turntable system as motion beings.
In what direction and with what angular speed does the turntable rotate?


1899237_1865562_ans_c3f00f51732c412db692b4788e08e9bf.jpg


Consider a system of two particles in the $$xy$$ plane: $$m_{1}=2.00\ kg$$ is at the location $$\vec{r}_{1}=(1.00\hat{i}+2.00\hat{j})m$$ and has a velocity of $$(3.00\hat{i}+0.500\hat{j})\ m/s; m_{2}=3.00\ kg$$ is at $$\vec{r}_{2}=(-4.00\hat{i}-3.00\hat{j})\ m$$ and has velocity $$(3.00\hat{i}-2.00\hat{j})\ m/s$$.
Plot these particles on a grid or graph paper. 
Determine the velocity of the center of mass and also show it on the diagram.


1900222_1864922_ans_ff137b185cbe4dadb4e01e33b32084ee.jpg


Class 11 Medical Physics Extra Questions