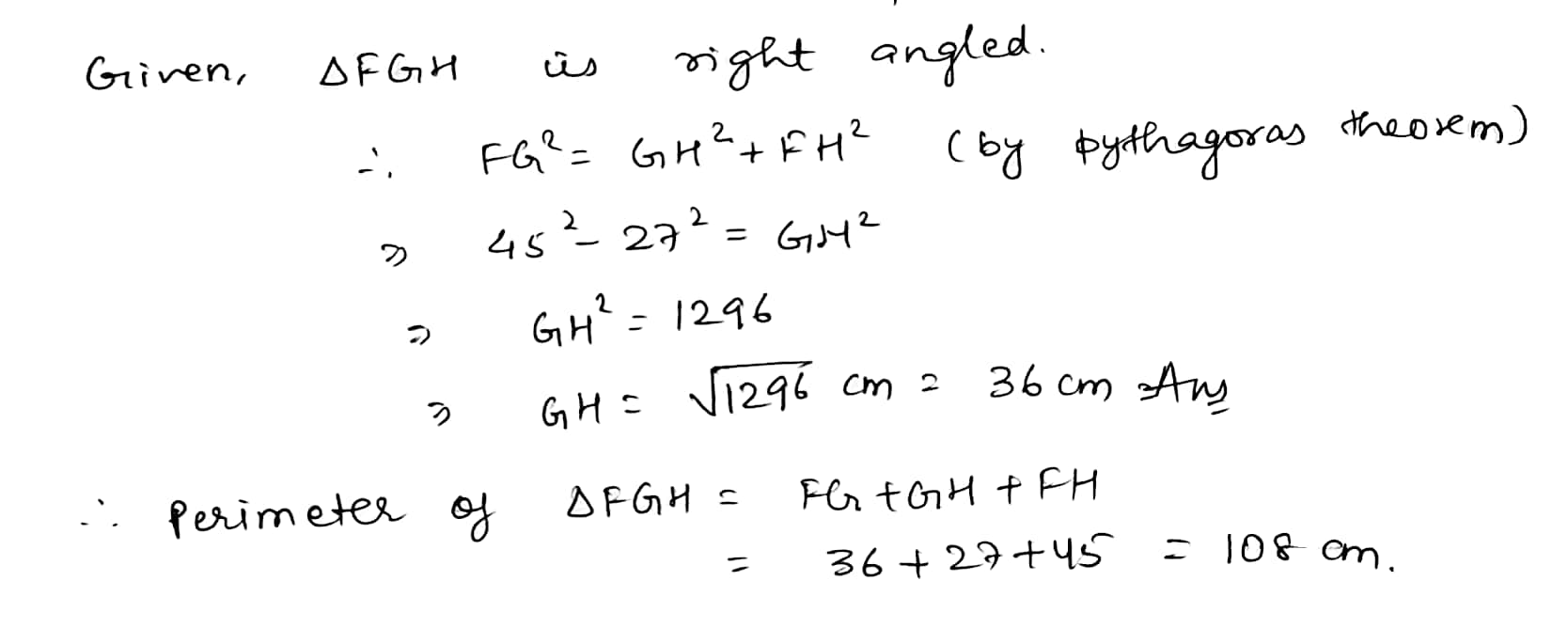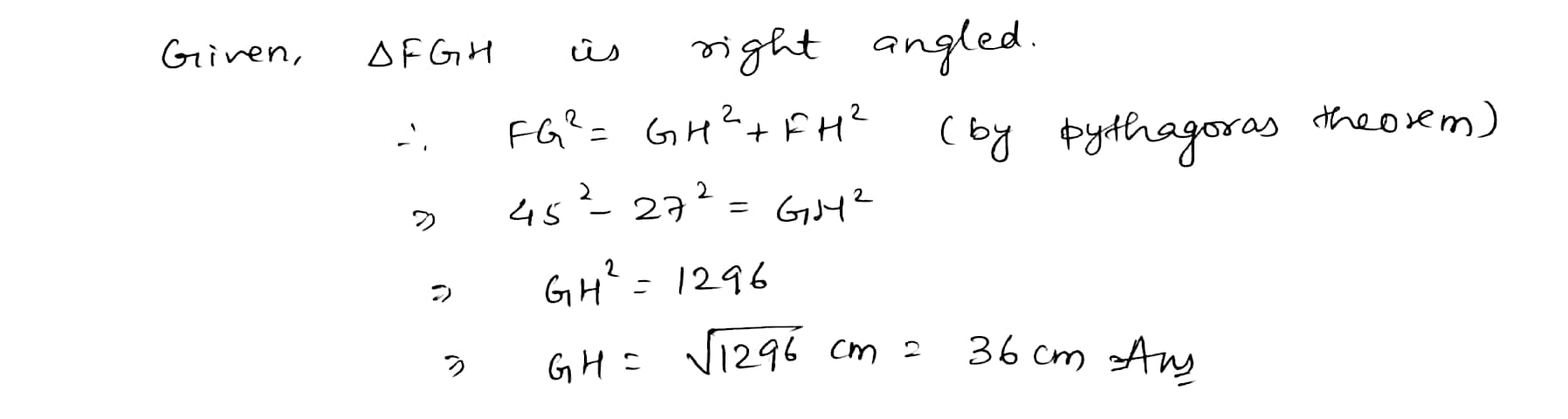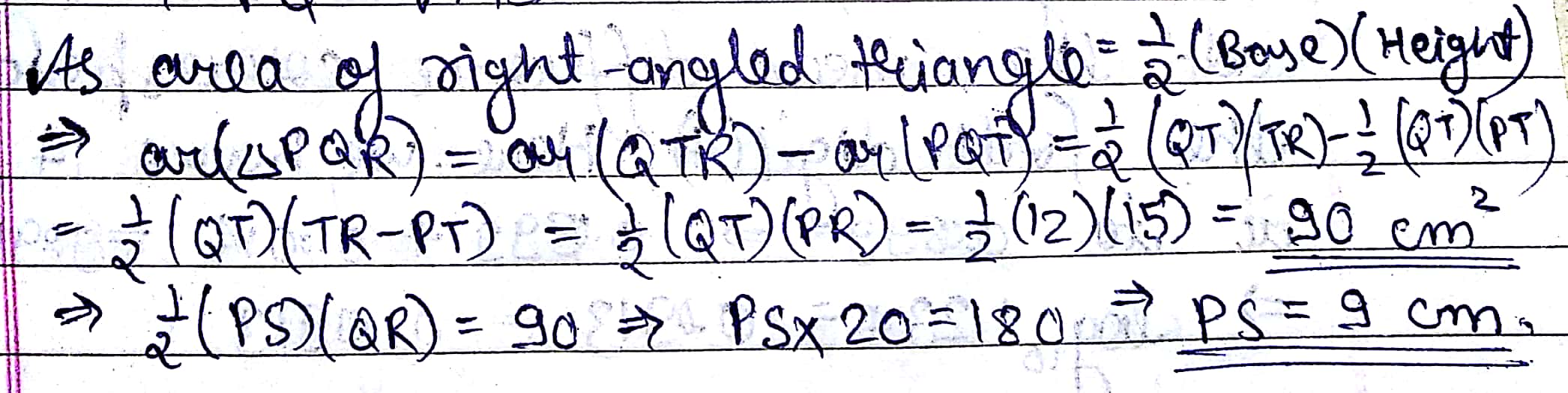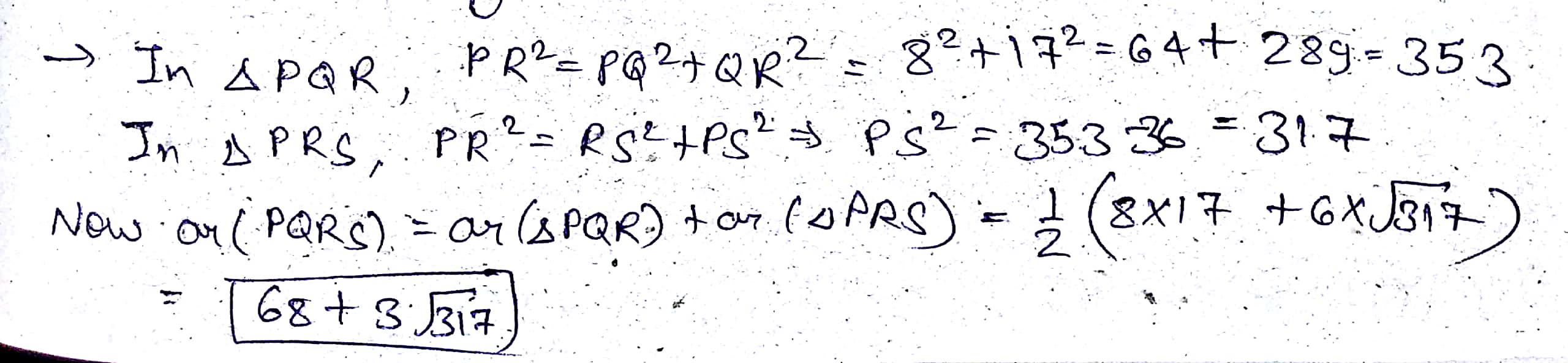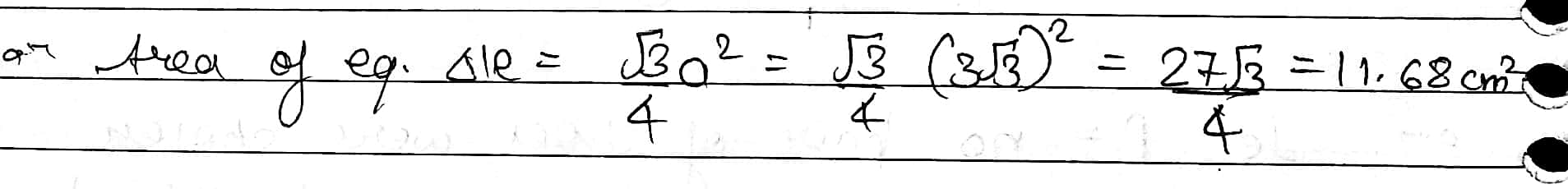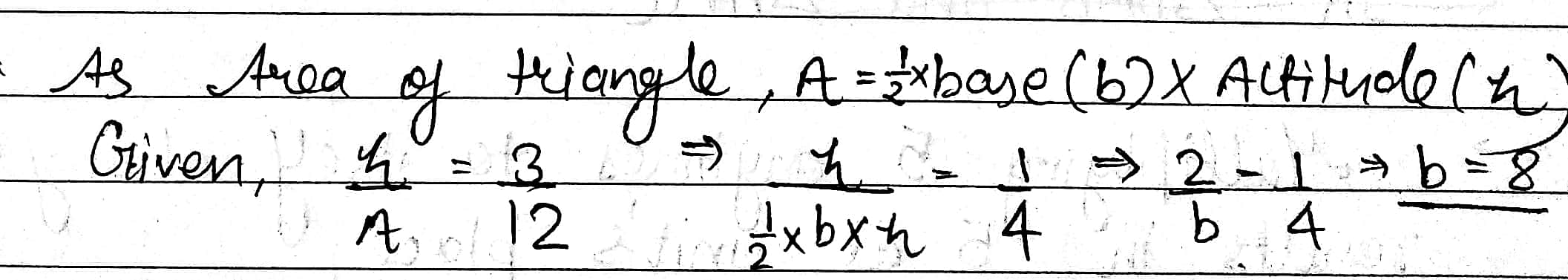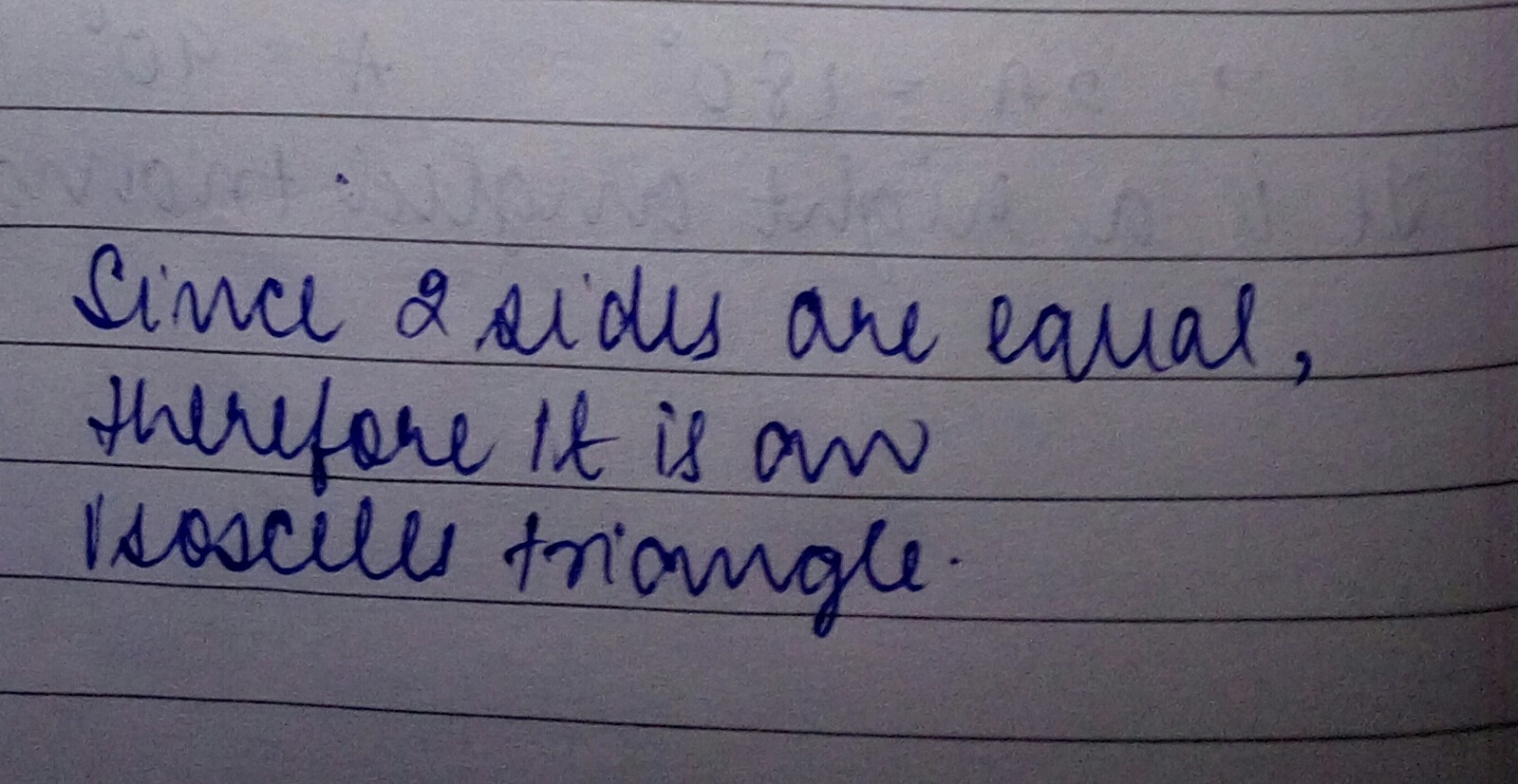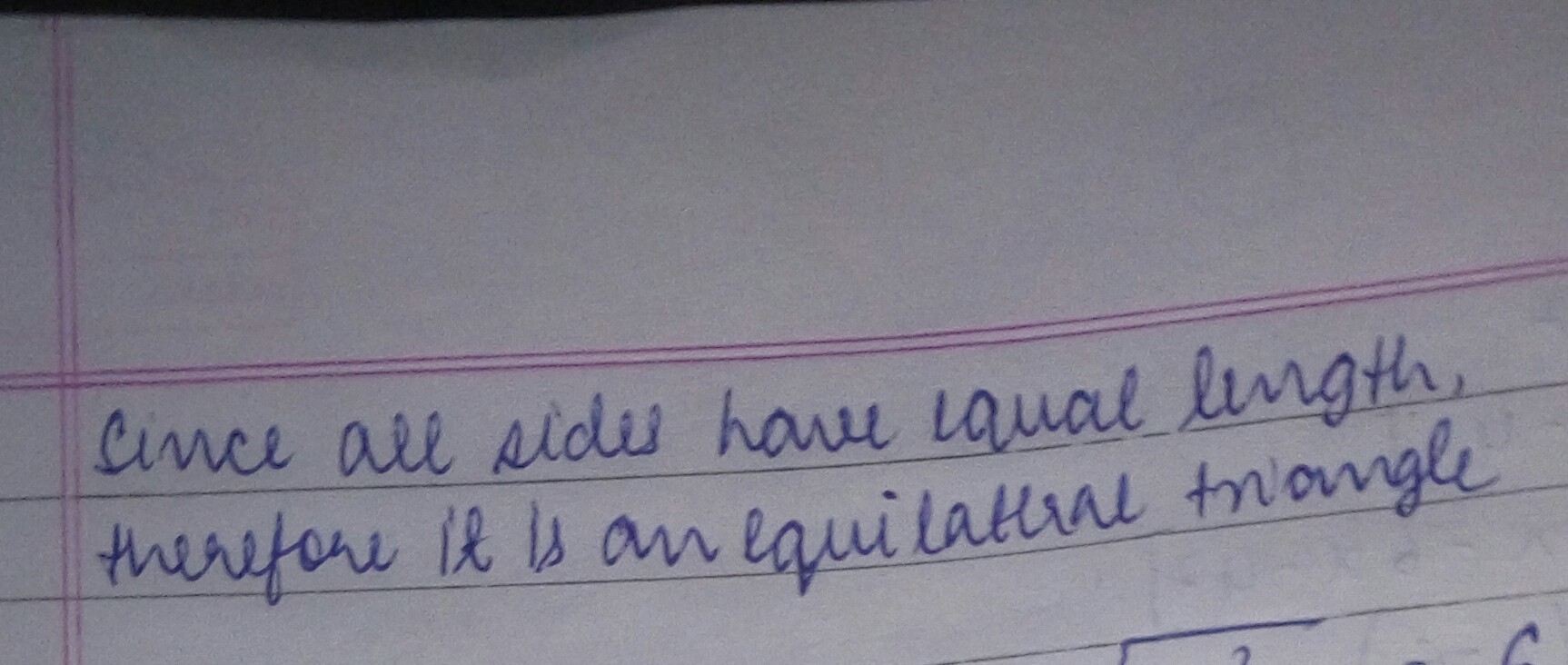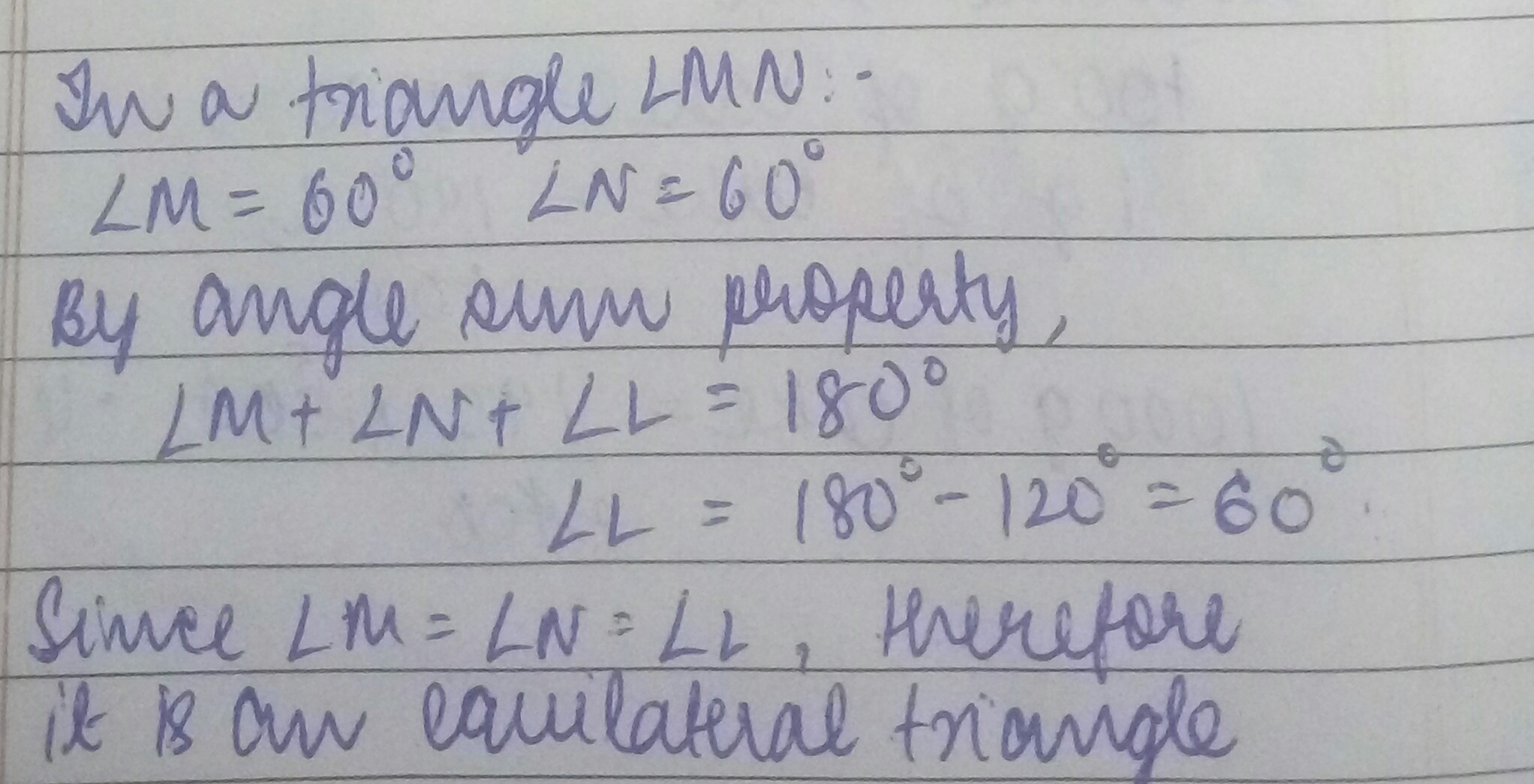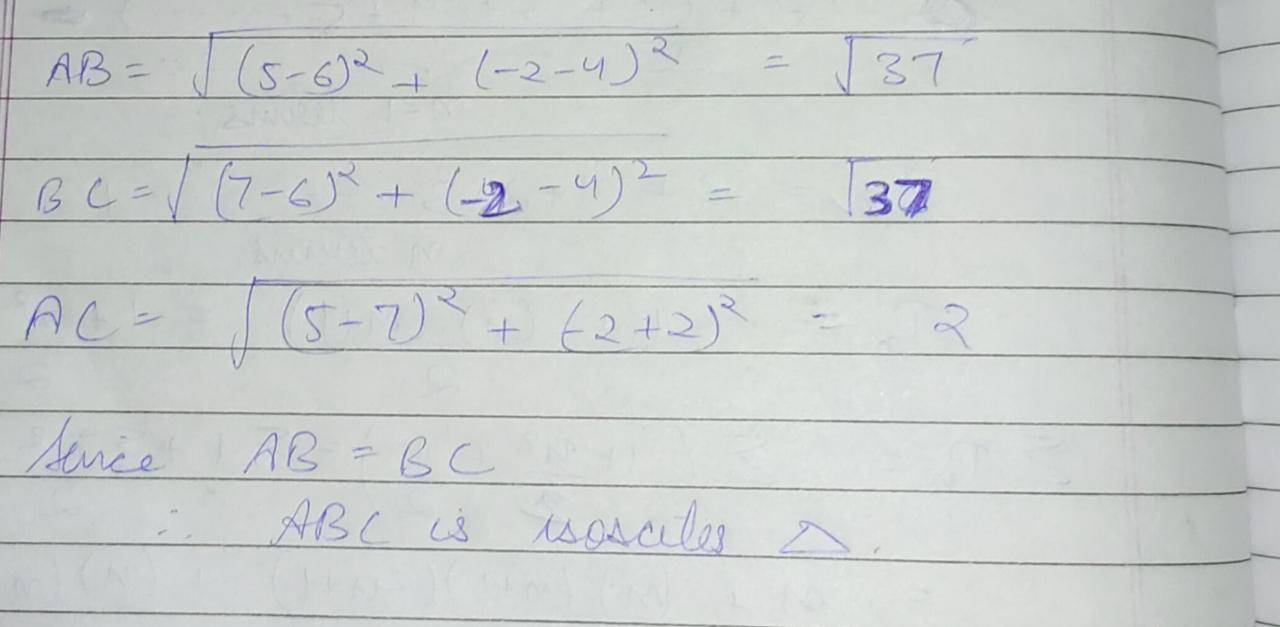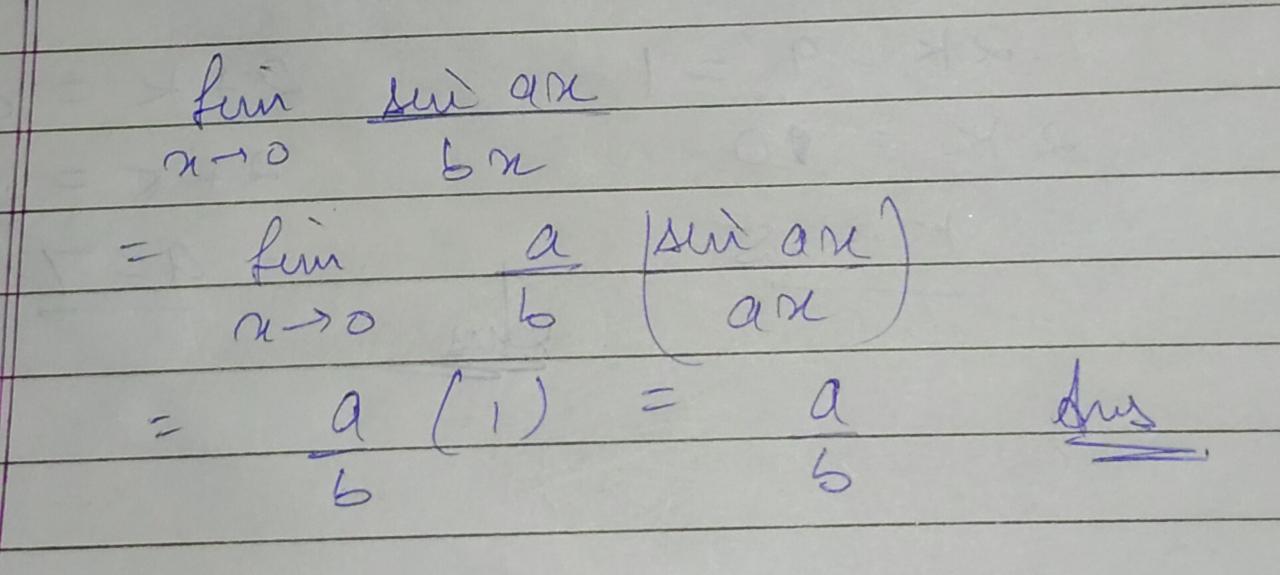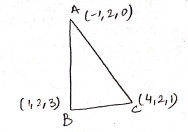The Triangle And Its Properties - Class 7 Maths - Extra Questions
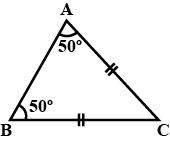
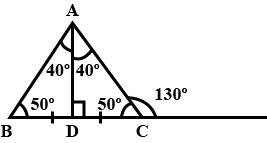
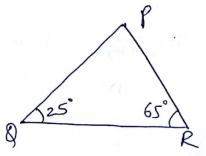
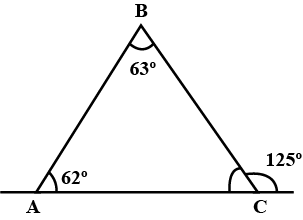
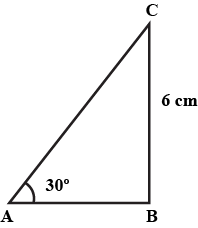
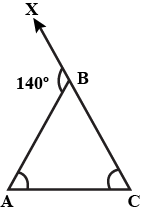
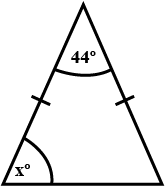
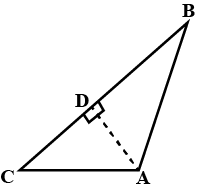
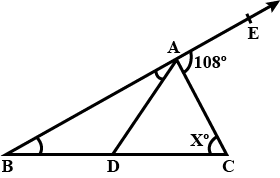
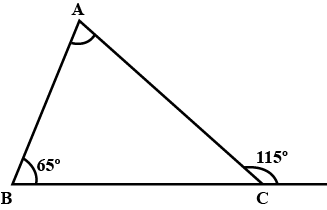
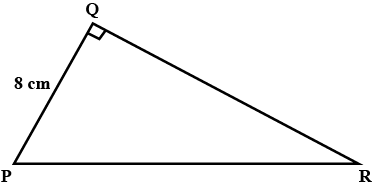
In Fig., there is a triangle. The measures of some angles have been indicated. State whether triangle is acute, right or obtuse.
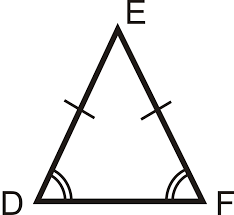
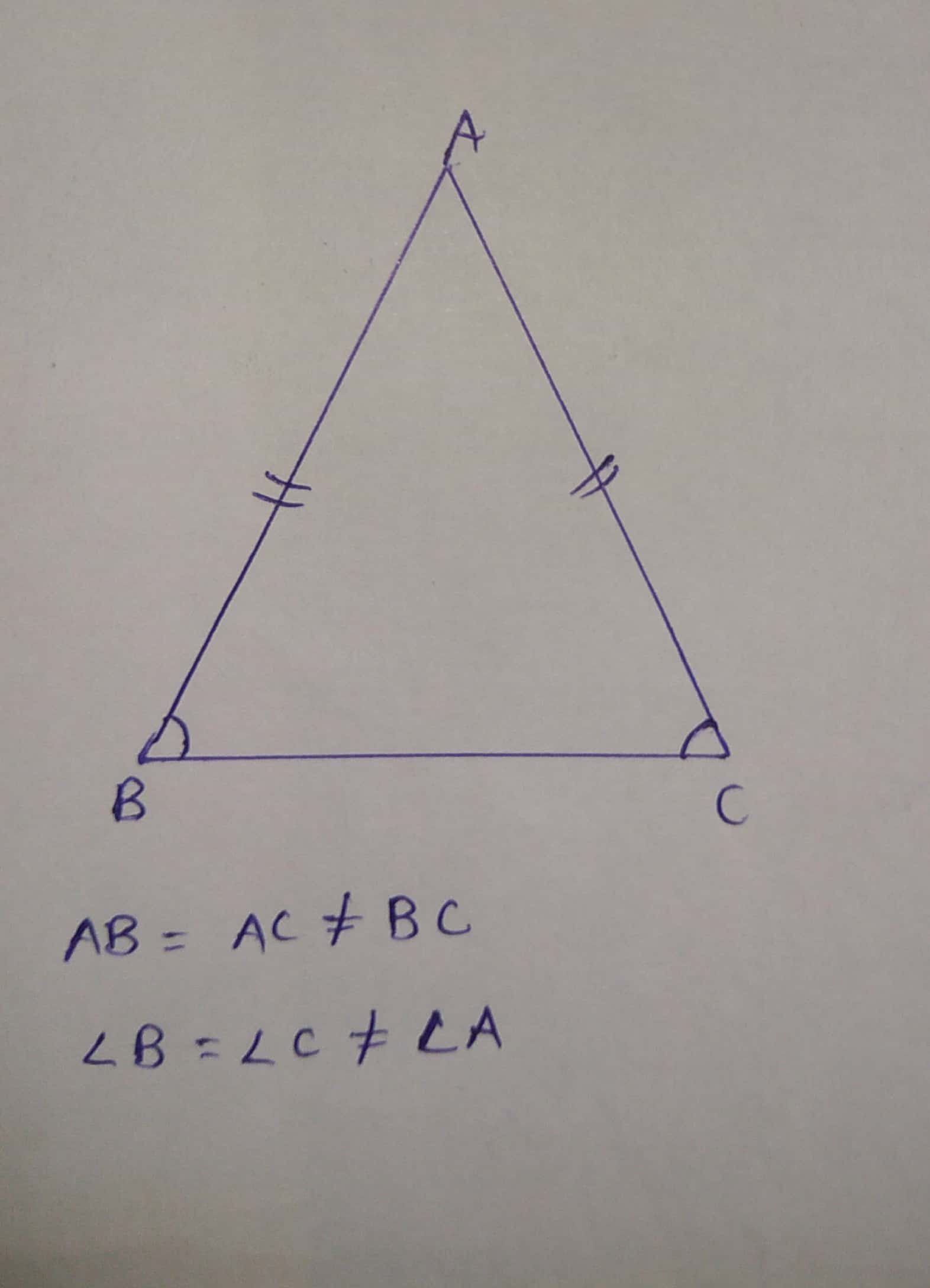
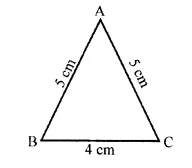
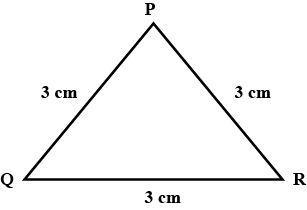
The diagram shows an isosceles triangle.
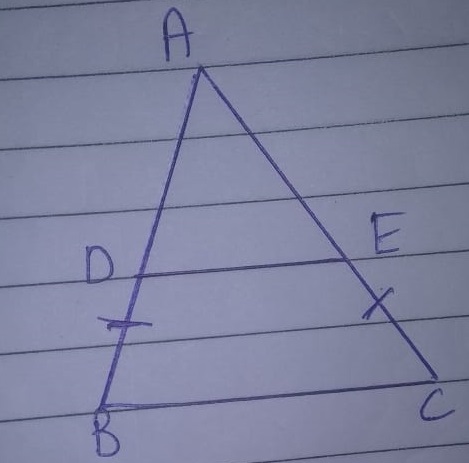
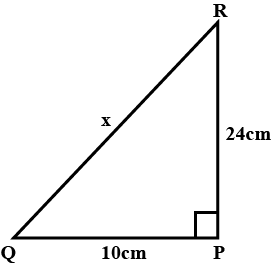
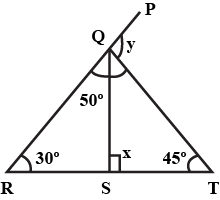
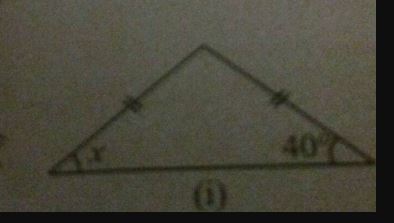
Find the value of $$x$$.
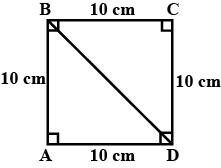
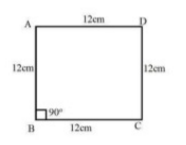
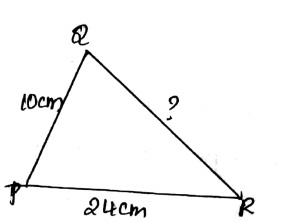
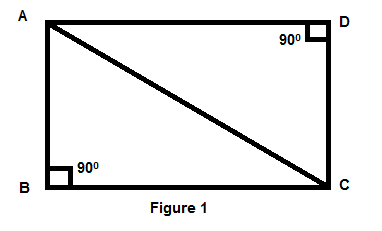
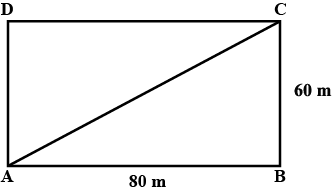
Find the length of the diagonal of a rectangle whose sides are to 10 cm and 8 cm.
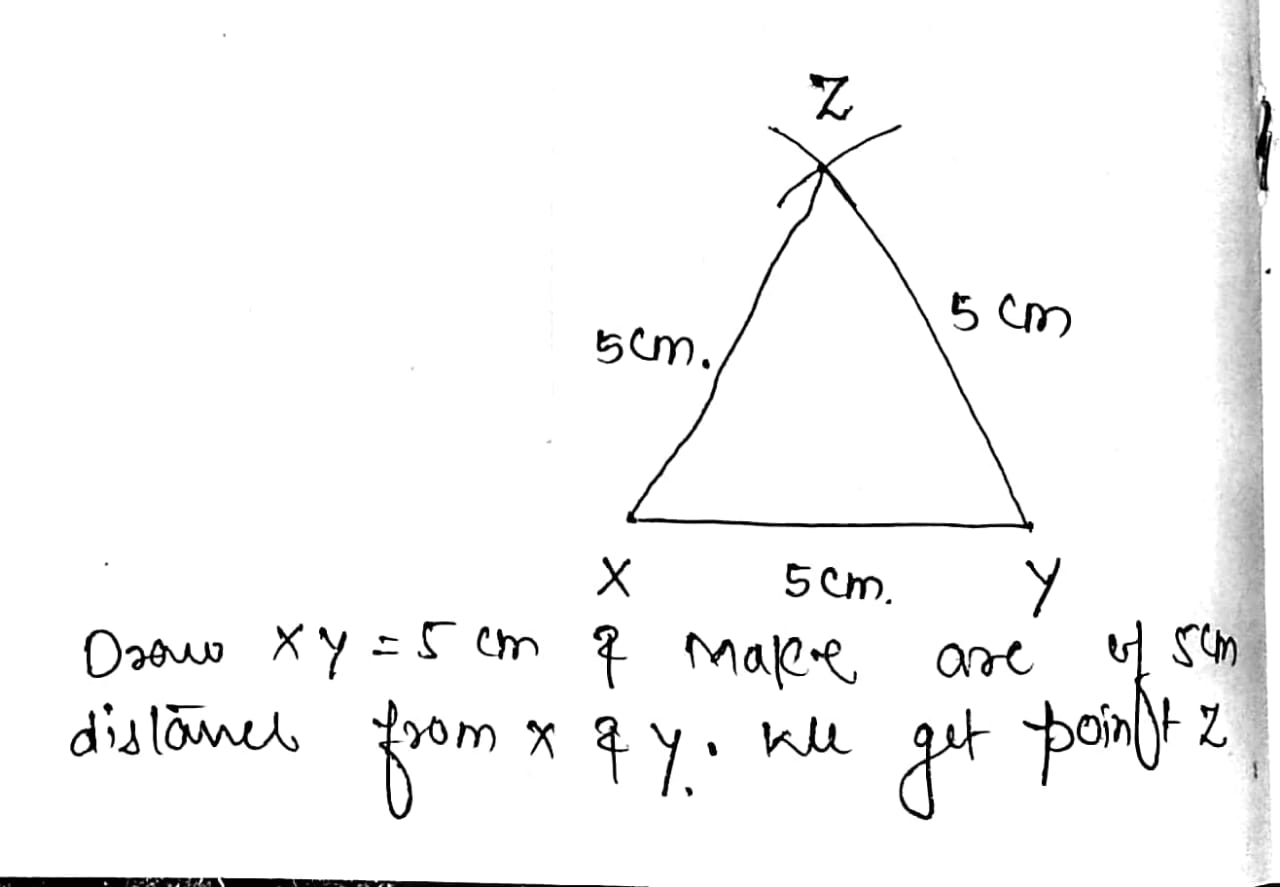
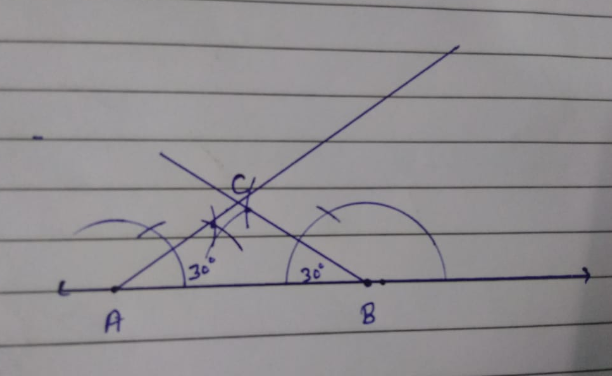
Construct the following triangle :
(i) Equilateral $$\Delta XYZ$$ with $$X Y = Y Z = X Z = 5 \mathrm { cm }.$$
Ref.Image.
Draw x y = 5 cm & make are of 5 cm
Distance from x & y we get point z
The lengths of sides of a triangle are $$3\ cm, 4\ cm$$ and $$5\ cm$$. Is the triangle a right angle? Give reason.
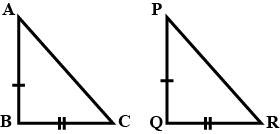
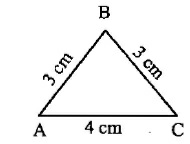
Identify the triangles as equilateral, isosceles or scalene.Answer: Isosceles
Mark answer as 1 if true else 0 if false
Mark answer as 1 if true else 0 if false
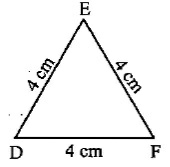
Identify the triangles as equilateral, isosceles or scalene.Answer: Equilateral
Mark answer as 1 if true else 0 if false
Mark answer as 1 if true else 0 if false
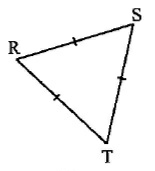
Identify the triangles as equilateral, isosceles or scalene.
Answer : Equilateral
Mark answer as 1 if true else 0 if false
Mark answer as 1 if true else 0 if false
Identify the triangles as equilateral, isosceles or scalene.
Answer: Scalene
Mark answer as 1 if true else 0 if false
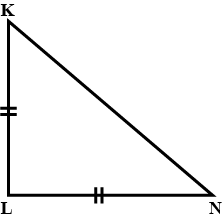
Mark answer as 1 if true else 0 if false
Identify the triangle as equiangular, acute, obtuse or right.
Answer: Equiangular
Mark answer as 1 if true else 0 if false
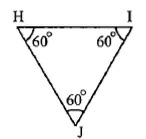
Mark answer as 1 if true else 0 if false
Identify the triangle as equiangular, acute, obtuse or right.
Triangle is obtuse angled.Mark answer as 1 if true and 0 if false.
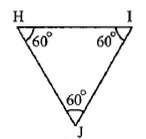
Mark answer as 1 if true and 0 if false.
One angle of an isosceles obtuse-angled triangle is $$35^{\circ}$$. Find the measure of its obtuse angle in degrees.
Each angle of equilateral triangle is $${ 60 }^{ 0 }$$. If true enter 1 else 0.
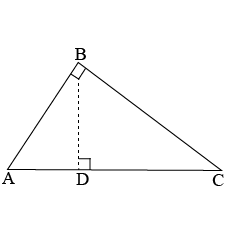
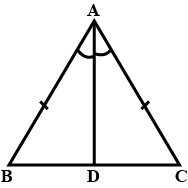
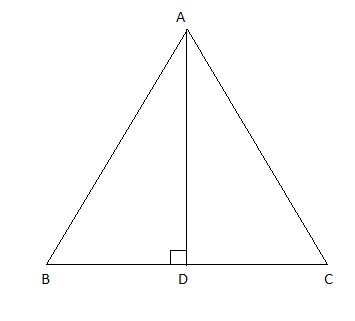
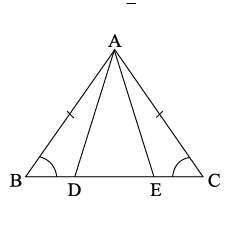
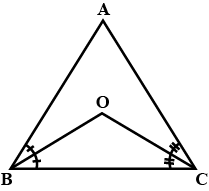
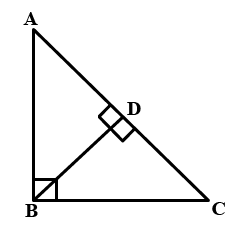
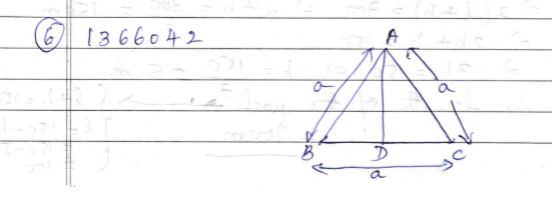
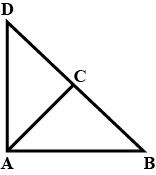
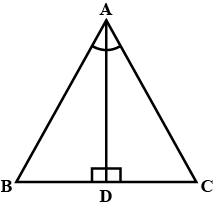
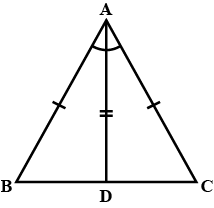
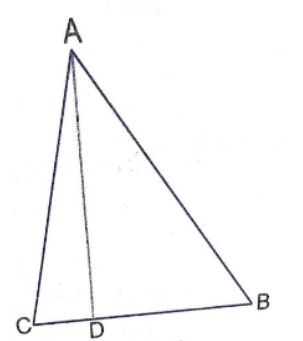
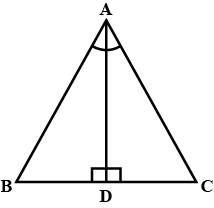
$$ \displaystyle \bigtriangleup ABC $$ is an isosceles triangle such that AB = AC Then prove that altitude AD from A on BC bisects BC
Based on the sides, classify the following triangles
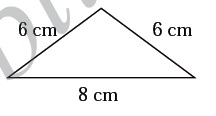
Based on the sides, classify the following triangles
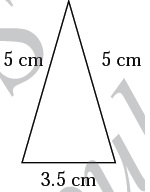
Based on the sides, classify the following triangles
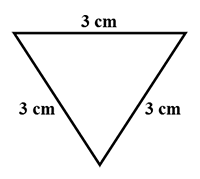
Find the diagonal of a square whose side is $$10\ cm$$
The side of square is $$10\ cm$$
In right angled $$\triangle ABD$$
$$AB^{2} + AD^{2} = BD^{2}$$ [according to Pythagoras theorem]
$$(10)^{2} + (10)^{2} = BD^{2}$$$
$$100 + 100 = BD^{2}$$
$$BD^{2} = 200$$
$$BD = 10\sqrt {2}cm$$
$$\therefore$$ Diagonal of square $$= 10 \sqrt {2}cm$$.
In right angled $$\triangle ABD$$
$$AB^{2} + AD^{2} = BD^{2}$$ [according to Pythagoras theorem]
$$(10)^{2} + (10)^{2} = BD^{2}$$$
$$100 + 100 = BD^{2}$$
$$BD^{2} = 200$$
$$BD = 10\sqrt {2}cm$$
$$\therefore$$ Diagonal of square $$= 10 \sqrt {2}cm$$.
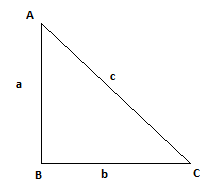
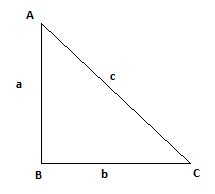
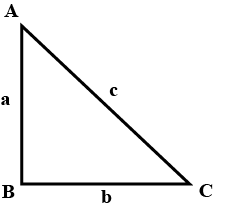
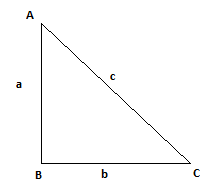
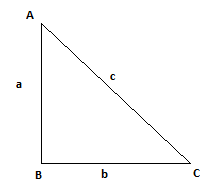
Write the length of the hypotenuse of the following right angled $$\triangle ABC$$.
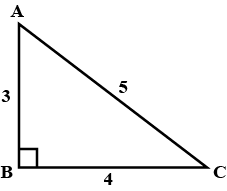
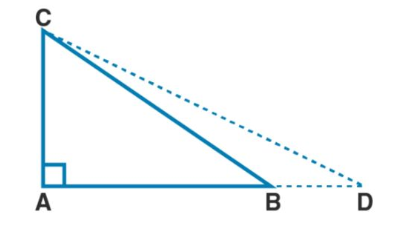
In $$\triangle ABC$$, $$C$$ is a point on $$BD$$ such that $$BC : CD = 1 : 2$$ and $$\triangle ABC$$ is an equilateral triangle. Prove that $${AD}^{2} = 7{AC}^{2}$$
Data: In $$\triangle ABD$$, $$BC : CD = 1 : 2$$
In $$\triangle ABC$$, $$AB = BC = CA$$
To Prove: $${AD}^{2} = 7{AC}^{2}$$
Construction: Draw $$AE \perp BC$$
Proof: In $$\triangle ABC$$,
$$BE = EC = \dfrac{a}{2}$$ and
$$AE = \dfrac{a\sqrt{3}}{2}$$
In $$\triangle ADE$$, $$\angle AED = {90}^{o}$$ [$$\because$$ Construction]
$$\therefore$$ $${AD}^{2} = {AE}^{2} + {ED}^{2}$$ [$$\because$$ Pythagoras theorem]
$${AD}^{2} = {\left(\dfrac{a\sqrt{3}}{2}\right)}^{2} + {\left(2a + \dfrac{a}{2}\right)}^{2}$$
$${AD}^{2} = \dfrac{3{a}^{2}}{4} + {\left(\dfrac{5a}{2}\right)}^{2}$$
$${AD}^{2} = \dfrac{3{a}^{2}}{4} + \dfrac{25{a}^{2}}{4}$$
$${AD}^{2} = \dfrac{3{a}^{2} + 25{a}^{2}}{4}$$
$${AD}^{2} = \dfrac{28{a}^{2}}{4}$$
$${AD}^{2} = 7{a}^{2}$$
$$\therefore$$ $${AD}^{2} = 7{AC}^{2}$$
In $$\triangle ABC$$, $$AB = BC = CA$$
To Prove: $${AD}^{2} = 7{AC}^{2}$$
Construction: Draw $$AE \perp BC$$
Proof: In $$\triangle ABC$$,
$$BE = EC = \dfrac{a}{2}$$ and
$$AE = \dfrac{a\sqrt{3}}{2}$$
In $$\triangle ADE$$, $$\angle AED = {90}^{o}$$ [$$\because$$ Construction]
$$\therefore$$ $${AD}^{2} = {AE}^{2} + {ED}^{2}$$ [$$\because$$ Pythagoras theorem]
$${AD}^{2} = {\left(\dfrac{a\sqrt{3}}{2}\right)}^{2} + {\left(2a + \dfrac{a}{2}\right)}^{2}$$
$${AD}^{2} = \dfrac{3{a}^{2}}{4} + {\left(\dfrac{5a}{2}\right)}^{2}$$
$${AD}^{2} = \dfrac{3{a}^{2}}{4} + \dfrac{25{a}^{2}}{4}$$
$${AD}^{2} = \dfrac{3{a}^{2} + 25{a}^{2}}{4}$$
$${AD}^{2} = \dfrac{28{a}^{2}}{4}$$
$${AD}^{2} = 7{a}^{2}$$
$$\therefore$$ $${AD}^{2} = 7{AC}^{2}$$
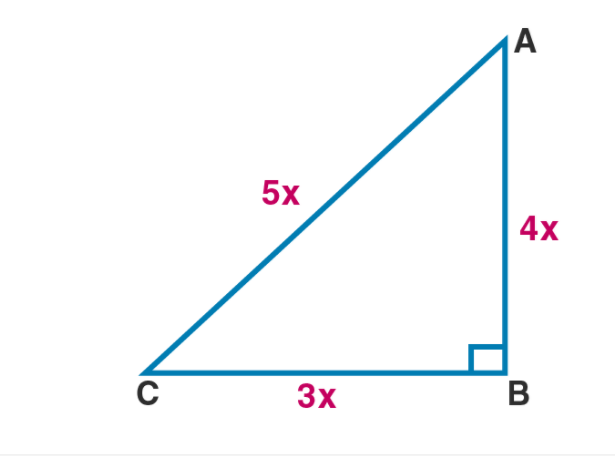
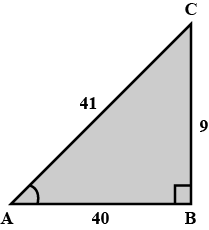
If the sides a triangle are $$6\ cm, 8\ cm$$ and $$10\ cm$$ respectively, determine whether the triangle is right angled triangle or not.
In $$\triangle ABC$$, $${AC}^{2}={AB}^{2}+{BC}^{2}$$, then right angle is at ___________.
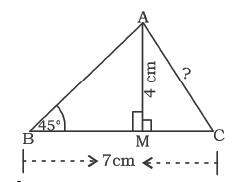
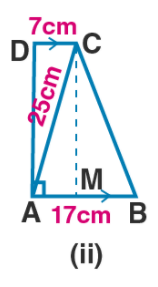
In $$\triangle ABC$$, $$ABC = {45}^{o}$$, $$AM \perp BC$$, $$AM = 4 cm$$ and $$BC = 7 cm$$. Find the length of $$AC$$.
In $$\triangle AMB$$, $$\angle AMB = {90}^{o}$$, $$\angle ABM = {45}^{o}$$ $$\therefore \angle BAM = {45}^{o}$$
$$\therefore \triangle AMB$$ is an isosceles right angled triangle
$$\therefore MA = MB = 4 cm$$
$$MC = BC - MB = 7 - 4 = 3 cm$$
$$\therefore MC = 3 cm$$
In $$\triangle AMC$$, $${AC}^{2} - {AM}^{2} + {MC}^{2}$$ [$$\because$$ Pythagoras theorem]
$${AC}^{2} = {4}^{2} + {3}^{2}$$
$${AC}^{2} = 16 + 9$$
$${AC}^{2} = 25$$
$$AC = \sqrt{25} = 5 cm$$
$$\therefore \triangle AMB$$ is an isosceles right angled triangle
$$\therefore MA = MB = 4 cm$$
$$MC = BC - MB = 7 - 4 = 3 cm$$
$$\therefore MC = 3 cm$$
In $$\triangle AMC$$, $${AC}^{2} - {AM}^{2} + {MC}^{2}$$ [$$\because$$ Pythagoras theorem]
$${AC}^{2} = {4}^{2} + {3}^{2}$$
$${AC}^{2} = 16 + 9$$
$${AC}^{2} = 25$$
$$AC = \sqrt{25} = 5 cm$$
In $$\Delta ABC$$, $$\angle A=\angle B={ 50 }^{ 0 }$$. Name the pair of sides which are equal.
In $$\triangle ABC$$,
$$\angle A = \angle B=50^o$$
Hence, $$AC=BC$$ {Converse of property of isosceles triangle having equal sides}
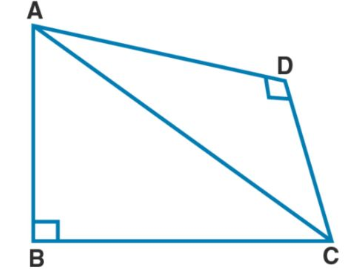
In the given figure, $$AD \perp BC$$, Prove that $${AB}^{2} + {CD}^{2} = {BD}^{2} + {AC}^{2}$$
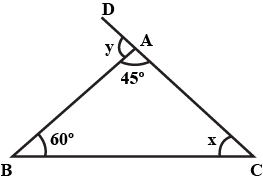
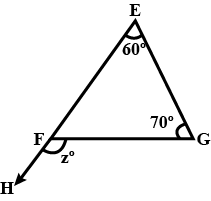
In the given triangles, find $$\angle z$$
Check whether the following can be the sides of a right angled triangle:
$$AB=25\ \text{cm}, BC=24\ \text{cm}, AC=7\ \text{cm}$$.
In $$\triangle ABC,m\angle B={ 90 }^{ o }$$. Prove that $${ AC }^{ 2 }={ AB }^{ 2 }+{ BC }^{ 2 }$$.
Given: In $$\triangle ABC,m\angle{B}={90}^{o}$$
To prove: $${AC}^{2}={AB}^{2}+{BC}^{2}$$
Construction: Draw $$BD\bot AC$$
Proof:
$$\quad \triangle ADB\sim \triangle ABC$$
If two triangles are similar, then their corresponding sides are proportional.
So, $$\cfrac { AD }{ AB } =\cfrac { AB }{ AC } $$
or $$AD.AC={AB}^{2}....(1)$$
Also, $$\triangle BDC\sim \triangle ABC$$
Similarly, $$\cfrac { CD }{ BC } =\cfrac { BC }{ AC } \quad CD.AC={ BC }^{ 2 }...(2)$$
Adding $$(1)$$ and $$(2)$$
$$AD.AC+CD.AC={AB}^{2}+{BC}^{2}$$
$$AC(AD+CD)={AB}^{2}+{BC}^{2}$$
$$AC.AC={AB}^{2}+{BC}^{2}$$
$${AC}^{2}={AB}^{2}+{BC}^{2}$$
To prove: $${AC}^{2}={AB}^{2}+{BC}^{2}$$
Construction: Draw $$BD\bot AC$$
Proof:
We know that, if a perpendicular is drawn from the vertex of the right angle of a right angled triangle to the hypotenuse, then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
$$\quad \triangle ADB\sim \triangle ABC$$
If two triangles are similar, then their corresponding sides are proportional.
So, $$\cfrac { AD }{ AB } =\cfrac { AB }{ AC } $$
or $$AD.AC={AB}^{2}....(1)$$
Also, $$\triangle BDC\sim \triangle ABC$$
Similarly, $$\cfrac { CD }{ BC } =\cfrac { BC }{ AC } \quad CD.AC={ BC }^{ 2 }...(2)$$
Adding $$(1)$$ and $$(2)$$
$$AD.AC+CD.AC={AB}^{2}+{BC}^{2}$$
$$AC(AD+CD)={AB}^{2}+{BC}^{2}$$
$$AC.AC={AB}^{2}+{BC}^{2}$$
$${AC}^{2}={AB}^{2}+{BC}^{2}$$
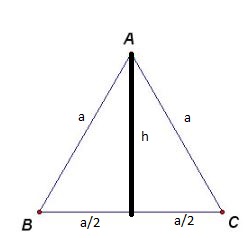
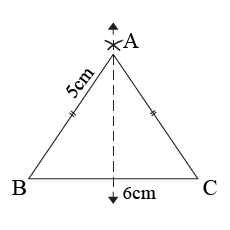
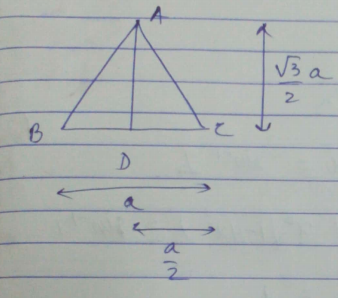
Find the height of an equilateral triangle whose side is $$6$$ units.
Prove that in an equilateral triangle, three time the square of a side is equal to four time the square of its altitude.
Write the pythogorean triplet whose one member is 16.
If $$a : b : c = 13 : 5 : 12$$, then prove that the triangle is right angled at $$A$$.
An isosceles triangle has perimeter $$30$$ cm and length of its congruent sides is $$12$$ cm. Find the area of the triangle.
Prove that the cubic equation whose roots are the radii $$r_1, \, r_2, \, r_3$$ of escribed circles of a triangle is $$t^3 \, - \, (r \, + \, 4R)t \, + \, s^2t \, - \, s^2r \, = \, 0$$
State the Pythagoras theorem.
In a right angled triangle," The sum of the squares of the length of the two sides is equal to the square of the length of the hypotenuse(or the longest side.)". This is known as the Pythagoras theorem.
Here, $$a=$$Perpendicular side, $$b=$$ base and $$c=$$ hypotenuse.
If the sides of triangle are $$3\ cm, 4\ cm$$ and $$6\ cm$$ long, determine whether the triangle is a right-angled triangle.
State Pythagoras theorem and its converse.
Look at the figure and complete the given statements.
(a) Interior opposite angles corresponding to the exterior angle $$\angle 5$$ are ______and ____.
(b) Interior adjacent angle corresponding to $$\angle 6$$ is_______
(c) The exterior angle at the vertex $$R$$ is _____
(d) The interior opposite angles corresponding to the exterior angle $$\angle 6$$ are _______ and ____
(e) Interior angle adjacent angle corresponding to the exterior angle at vertex $$P$$ is_____
An isosceles right angled triangle has area $$8cm^{2}$$. Find the length of its hypotenuse.
if the area of an equalatral $$\Delta $$ is $$36\sqrt 3 c{m^2}$$. Find its hight.
Let 'a' be the side of equilateral triangle and 'h' be the height
Now given that area of \Delta ABC $$=36\sqrt{3}cm^{2}=\dfrac{\sqrt{3}}{4}a^{2}$$
$$\Rightarrow a=12cm$$
Let 'a' be the side of equilateral triangle and 'h' be the height
Now given that area of \Delta ABC $$=36\sqrt{3}cm^{2}=\dfrac{\sqrt{3}}{4}a^{2}$$
$$\Rightarrow a=12cm$$
$$ \Rightarrow h$$
$$=\sqrt{a^{2}-(\dfrac{a}{2})^{2}}$$
$$=\dfrac{\sqrt{3}a}{2} $$
$$=6\sqrt{3}cm $$
Traingle ABC is right angled at C. If AB is 20 cm and BC is 12 cm, find AC.
Triangles in which all the three sides are of equal length are called ............triangle.
An ..............angle of a triangle is equal to the sum of its two interior opposite angle.
Find a pythagorean triplet whose smallest member is $$12$$.
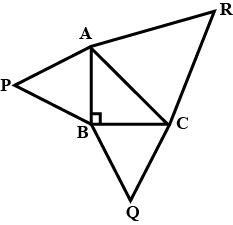
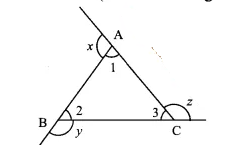
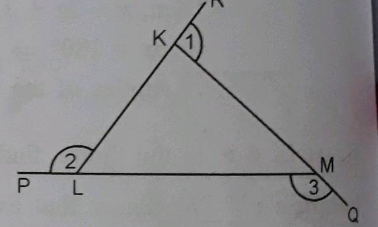
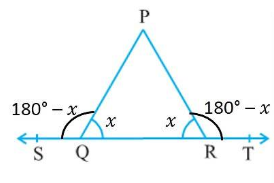
If the sides of $$\triangle KLM$$ are produced to $$P, Q$$ and $$R$$ as shown, find the sum of exterior angles $$\angle 1, \angle 2$$ and $$\angle 3$$.
Calculate the area and the height of an equilateral triangle whose perimeter is $$60$$ cm.
In an isosceles triangle, the vertex angle is $$50^{\circ}$$. What are the base angles of the triangle?
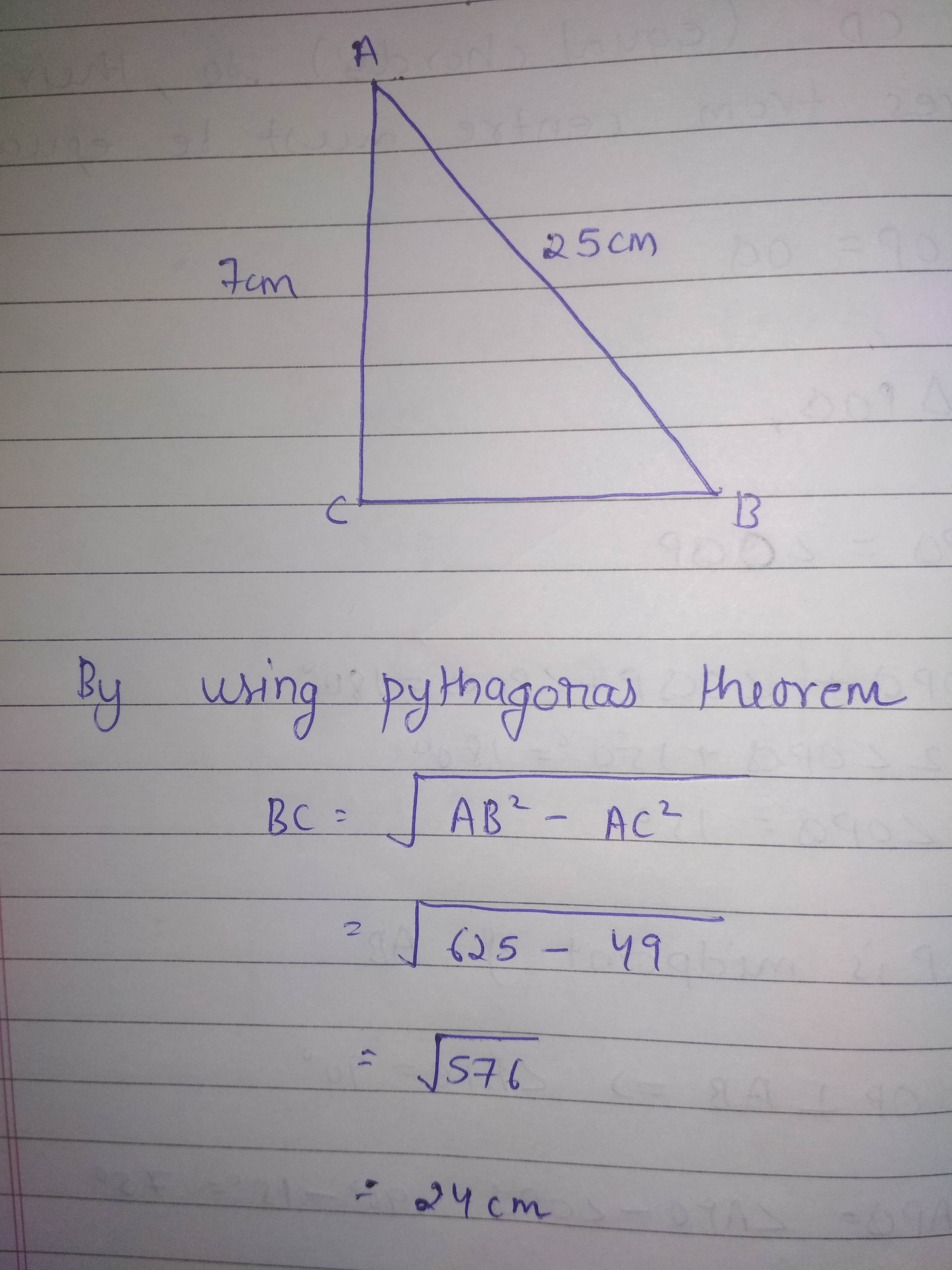
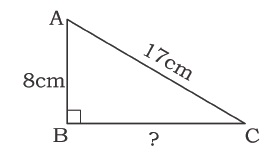
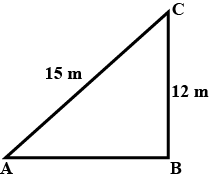
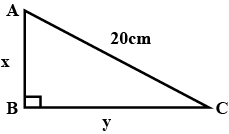
ABC is a triangle right-angled at C . If AB = 25 cm and AC = 7 cm , find BC .
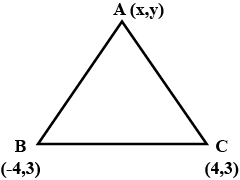
If $$(-4, 3)$$ and $$(4, 3)$$ are two vertices of an equilateral triangle, find the co-ordinates of the third vertex.
Let find out $$A (x,y)$$
$$BC=\sqrt{(-4-4)^{2}+(3-3)^{2}} = 8$$
In equilateral triangle .
$$AB=BC=\sqrt{(x+4)^{2}+(y-3)^{2}} = 8$$ .....(i)
$$AC=BC=\sqrt{(x-4)^{2}+(y-3)^{2}} = 8 $$ .....(ii)
from (i) and (ii) we get,
$$x=0 , y=4\sqrt{3}+3$$
$$A(0,4\sqrt{3}+3)$$
Show that the points $$(-1,6)$$ and $$(-4,9)$$ and $$(0,7)$$ form an isosceles triangle.
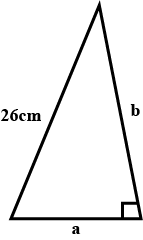
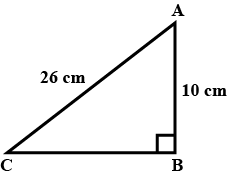
The hypotenuse of a right angled triangle is $$26\ cm$$ . If the sum of the other two sides is $$34\ cm$$, find the other two sides.
#1215097
$$a+b =34cm$$
$$as\>we \>know$$ $$26^2=a^2+b^2$$
$$or\>26^2=(34-b)^2+b^2$$
$$or\>676=34^2+b^2-2. 34. b+b^2$$
$$or\>676=1156+b^2-68b+b^2$$
$$or\>2b^2-68b-480=0$$
$$b^2-34b-240=0$$
$$b^2-24b-10b-240=0$$
$$b(b-24)-10(b-24)=0$$
$$(b-24)(b-10)=0$$
$$\therefore\>b=10\>or\>b=24$$
$$then\>a=34-b=34-10=24$$
$$then\>a=34-b=34-24=10$$
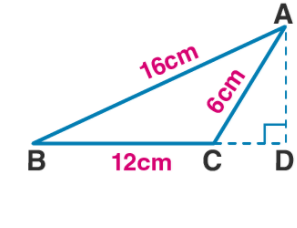
From the given figure calculate :
$$\angle ADC$$
$$\angle ACE=130^{\circ}\Rightarrow ACD=50^{\circ}[\because 180^{\circ}]-130^{\circ}=50^{\circ}$$
In$$\triangle ADC,\angle C=50^{\circ},\angle D=90^{\circ}\Rightarrow \angle A=180-(90+50)=40^{\circ}$$
As$$\angle ADB=\angle ADC\Rightarrow \angle D=90^{\circ} and \angle A=40^{\circ}$$
In$$\triangle ADB, \angle B=180-(\angle A+\angle D)=180-(40+50)=50^{\circ}$$
$$\therefore $$
i)
$$\angle ADC=90^{\circ}$$
ii)
$$\angle ABC=50^{\circ}$$
iii)
$$\angle BAC=80^{\circ}[40^{\circ}+40^{\circ}]$$
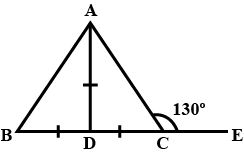
Prove that the bisector of the vertical angle of an isosceles triangle bisects the base at right angles.
Let $$\Delta ABC$$ be the isoceleus triangle with $$AB=AC$$ and $$AD$$ as vertical angle bisector
$$AB=AC\\\angle B=\angle C\\\angle BAD=\angle CAD$$
So by $$ASA$$ criteria the triangles are congruent.
$$\implies BD=DC$$
So the bisector of vertical angel bisects the base
Length of the hypotenuse of a right-angled triangle is $$61\ cm$$. Its one side is $$11\ cm$$. Find the length of the other side.
Two verities of an equilateral triangle are $$(-1,0)$$ and $$(1,0)$$ and its third vertex lies above the $$x-$$axis. The equation of its circumcircle is________
The altitude of a triangle is $$7 cm$$ less then its base. If the hypotenuse is $$13 cm$$, Find the other two sides.
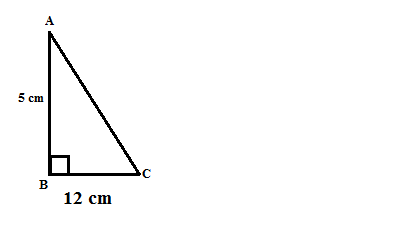
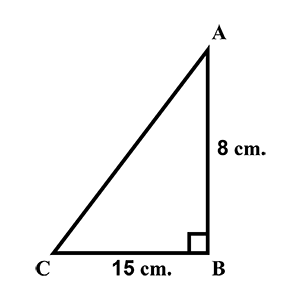
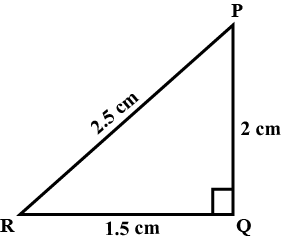
Find the length of the hypotenuse of a right triangle, the other two sides of which measure $$9\ cm$$ and $$12\ cm$$.
If $$a$$ and $$b$$ are real number between $$0$$ and $$1$$ such that the point $$(a,1),(1,b)$$ and $$(0,0)$$ from an equilateral triangle find $$a$$ and $$b$$.
A] Let $$z^{1}=a+i$$
$$x^{2}=1+bi$$
$$z^{3}=0$$
$$\therefore 12^{1}-z21^{2}=(a-1)^{2}+(1-b)^{2}$$
$$12^{2}-z31^{2}=1+b^{2}$$
$$12^{3}-z11^{2}=a^{2}+1$$
These are equal
$$\Rightarrow 1+b^{2}=a^{2}+1$$
$$\Rightarrow b^{2}=a^{2}$$
$$\Rightarrow a=b$$
$$1+a^{2}=(a-1)^{2}+(1-b)^{2}$$
$$\Rightarrow 1+a^{2}=(a-1)^{2}+(1-b^{2})$$
$$\Rightarrow 1+a^{2}=2(a-1)^{2}$$
$$\Rightarrow 1+a^{2}=2a^{2}-4a+2$$
$$\Rightarrow 0=a^{2}-4a+1$$
$$\therefore a=2\pm \sqrt{3}$$
For the desired range,
$$a=b=2-\sqrt{3}$$
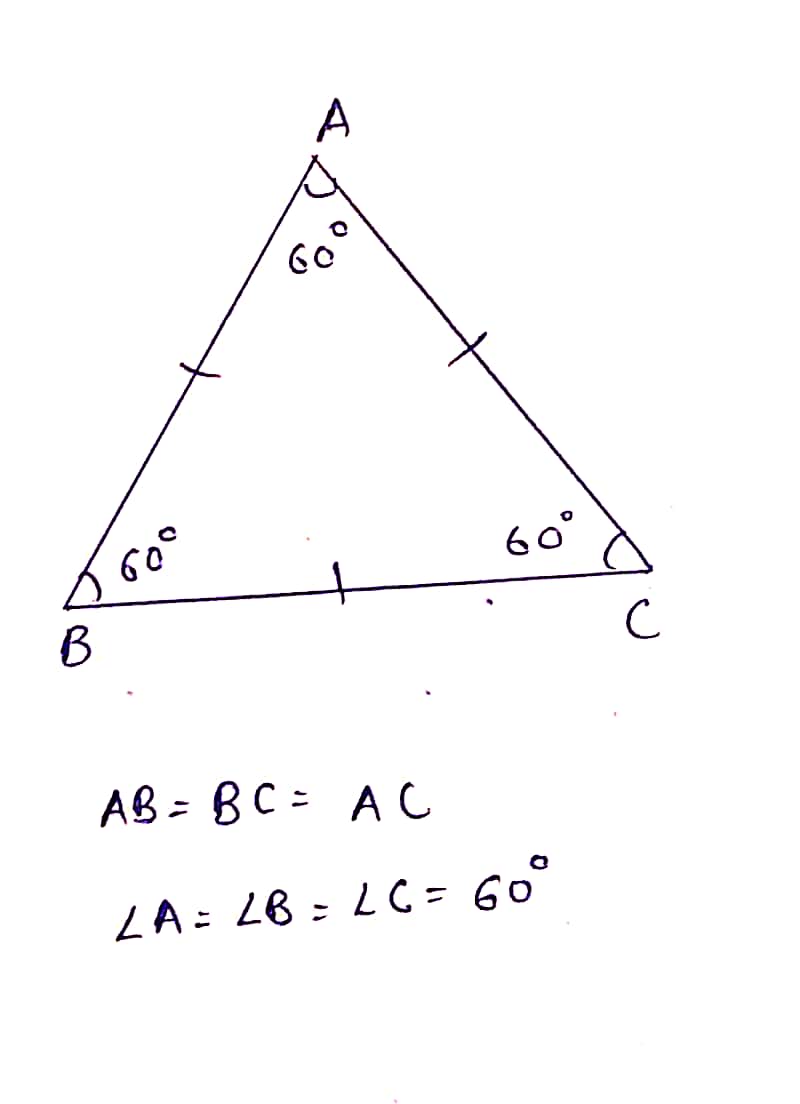
Show that the angles of an equilateral triangle are $${60^ \circ }$$ each
$$AB=AC$$, $$AC=BC$$
$$\Rightarrow \angle C=\angle B$$ $$\angle B=\angle A$$
$$\angle A=\angle B+\angle C$$
$$\angle A+\angle A+\angle A=180$$
$$3\angle A=180$$
$$\angle A=60^o$$.
Construct an isosceles $$\Delta A B C$$ such that :
(i) base $$A B = 4.2 cm ,$$ base angle $$= 30 ^ { \circ }.$$
We draw the above construct in the figure
In a right triangle, the sides are $$12cm,16cm $$ find its hypotenuse.
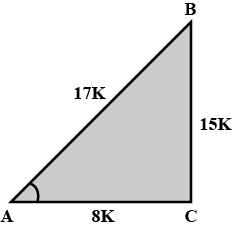
Determine whether $$50\ cm,80\ cm,100\ cm$$ can be the sides of a right triangle or not.
Define Isosceles triangle.
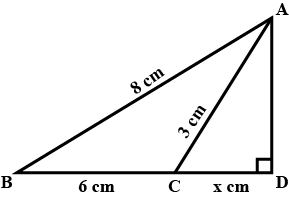
In triangle $$ABC,AD$$ is perpendicular to $$BC$$.Prove that:$$AB^2-AC^2=BD^2-CD^2$$
Since triangles $$ABD$$ and $$ACD$$ are right angled at $$D$$.
Therefore, $$AB^2=AD^2+BD^2$$ ......................1
And, $$AC^2=AD^2+CD^2$$ ........................2
Subtracting 2 from 1 we get
$$AB^2-AC^2=BD^2-CD^2$$
One of the two equal angles of an isosceles triangle measures $$55^{\circ}$$ determine the other angles.
Given two equal angle of isoscles triangle
are $$55^{\circ}$$
Let third angle be x then
$$x+55+55=180^{\circ}$$ [angle sum property]
$$x=180-110^{\circ}$$
$$(x=70^{\circ})$$
$$\therefore$$ the other angle is $$ 70^{\circ}$$
Find the area of an equilateral triangle of side $$20\ m$$.
Find the length of hypotenuse if $$12 $$ adn $$5$$ are other sides of right angles triangle
Show that the angle of an equilateral triangle are $$60^ {o}$$ each.
If the 2 sides of right angles triangle is $$7,24 $$ find the hypotenuse.
In an equilateral triangle of side $$3\sqrt 3 $$, find the length of the altitude.
REF.Image
Given
side of an equilateral triangle
$$ABC= 3\sqrt{3}cm$$
$$AB=BC-AC=3\sqrt{3}cm$$
Let AD=h (altitude)
$$BD=\frac{1}{2}B$$ (Altitude bisect the base)
$$BD=\frac{1}{2}.3\sqrt{3}=3\sqrt{3}/2$$ cm
$$AB^{2}= AD^{2}+BD^{2} $$
$$ (3\sqrt{3})^{2} = (h)^{2} + (3\sqrt{3}/2)^{2}$$
$$ \Rightarrow 27 = h^{2} + 27/4$$
$$\Rightarrow h^{2}=27-27/4$$
$$\Rightarrow h^{2}=(4.27-27)/4$$
$$\Rightarrow h^{2}=108-27/4$$
$$\Rightarrow h^{2}=81/7$$
$$\Rightarrow h=\sqrt{81/4}$$
$$\Rightarrow h=9/2$$
$$\Rightarrow h= 4.5 cm $$
Hence, the length of the altitude h is 4.5 cm
In an equilateral triangle of side $$ 3 \sqrt{3} \mathrm{cm}, $$ find the length of the altitude.
in a right triangle the hypotenuse is the .....side
Write the definition of Pythagoras theorem.
A piece of wire is $$36$$ cm long what will be the be length of each side if we form an equilateral triangle.
The sides of right angles triangle are $$63,9$$ find its hypotenuse .
State Pythagoras theorem.
$$\textbf{Statement:}$$ $$\text{The pythagoras theorem states that in any right triangle, the square of the length}$$
$$\text{ of the hypotenuse equals to the sum of the squares of the length of legs of right triangle.}$$.
Name the following triangles with regards to sides :
Height of a pole is $$8 m$$. Find the length of rope tied with its top from a point on the ground at a distance of $$6 m$$ from its bottom. Solution: Let $$ABC$$ be the right-angled triangle? Give reason
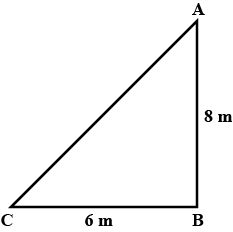
Jiya walks $$6km$$ due east and then $$8km$$ due north. How far is she from her starting place ?
Let $$B$$ be the end point while $$A$$ is the starting point of Jiya.
Triangle $$ABC$$ is a right-angled.
$$(AB)^{2} = 6^{2} + 8^{2}$$
$$\Rightarrow$$ $$AB = \sqrt {36 + 64}$$
$$\Rightarrow$$ $$AB = \sqrt{100}$$
$$\Rightarrow$$ $$AB = 10km$$
Therefore, $$10km$$ is the distance that Jiya traveled.
Triangle $$ABC$$ is a right-angled.
$$(AB)^{2} = 6^{2} + 8^{2}$$
$$\Rightarrow$$ $$AB = \sqrt {36 + 64}$$
$$\Rightarrow$$ $$AB = \sqrt{100}$$
$$\Rightarrow$$ $$AB = 10km$$
Therefore, $$10km$$ is the distance that Jiya traveled.
The height of a pole is $$8\ m$$. Find the length of rope tied with its top from a point on the ground at a distance of $$6\ m$$ from its bottom.
Let $$ABC$$ be the right-angled triangle formed by the pole and rope
By using Pythagoras theorem in right $$\triangle ABC$$
$$(AC)^{2}=8^{2}+6^{2}$$
$$\Rightarrow {AC}^2=64+36$$
$$\Rightarrow AC=\sqrt{64+36}$$
$$\Rightarrow AC=\sqrt{100}$$
$$\Rightarrow AC=10\ m$$
Therefore, the length of the rope is $$10m$$
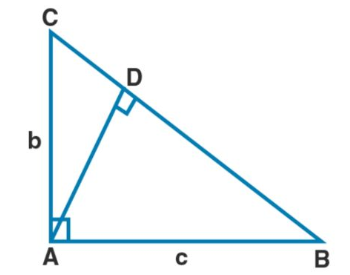
In the given figure, find the length of AD in terms of b and c.
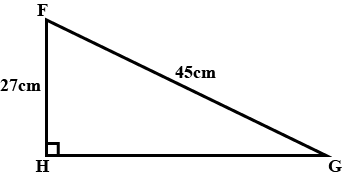
Solve the question :
FGH is a right-angled triangle
Calculate the perimeter of the triangle.
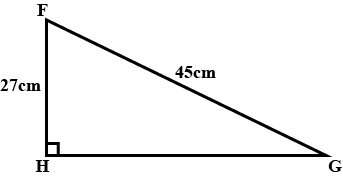
Solve the question :
FGH is a right-angled triangle
Calculate the area of the triangle
Classify the following triangles according to sides:
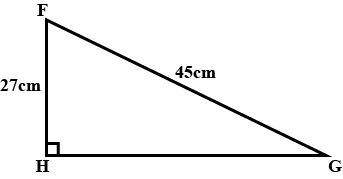
Solve the question :
FGH is a right-angled triangle.
Calculate GH
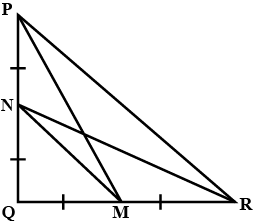
In a right angled triangle $$ABC, \angle B = { 90 }^{ \circ }$$.
If $$AC = 13\ cm, BC = 5\ cm$$, find $$AB$$
$$\triangle$$ ABC is a right-angled triangle.
By Pythagoras theorem,
$$AC^2 =BC^2+AB^2$$
$$\Rightarrow 13^2 =5^2+AB^2$$
$$\Rightarrow AB^2=-(5)^2+13^2$$
$$\Rightarrow AB^2=-25+169$$
$$\Rightarrow AB^2=144$$
$$\Rightarrow AB =\sqrt { 144 } $$
$$\Rightarrow AB =12\ cm.$$
By Pythagoras theorem,
$$AC^2 =BC^2+AB^2$$
$$\Rightarrow 13^2 =5^2+AB^2$$
$$\Rightarrow AB^2=-(5)^2+13^2$$
$$\Rightarrow AB^2=-25+169$$
$$\Rightarrow AB^2=144$$
$$\Rightarrow AB =\sqrt { 144 } $$
$$\Rightarrow AB =12\ cm.$$
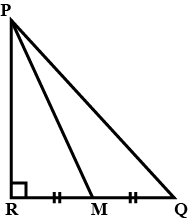
$$4 PM^{2} = 4 PQ^{2} + QR^{2}$$
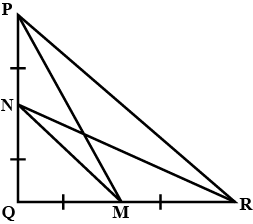
$$4 RN^{2}= PQ^{2} + 4QR^{2}$$
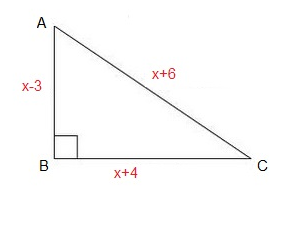
In $$\Delta ABC$$, $$\angle B=90^{\circ}$$, Find the sides of the triangle, if $$AB = \left ( x-3 \right )\ cm, BC = \left ( x+4 \right )\ cm$$ and $$AC = \left ( x+6 \right )\ cm$$.
In a right angled triangle with right angle at $$B$$,
$$AB$$ and $$BC$$ for the sides and $$AC$$ is the hypotenuse.
So, as per the pythagoras theorem, $$ {AC}^{2} = {AB}^{2} + {BC}^{2} $$
$$ \Rightarrow {(x+6)}^{2} = {(x-3)}^{2} + {(x+4)}^{2} $$
$$ \Rightarrow {x}^{2} + 12x + 36 = {x}^{2} - 6x + 9 + {x}^{2} + 8x + 16$$
$$ \Rightarrow {x}^{2} - 10x - 11 = 0 $$
$$ \Rightarrow {x}^{2} - 11x+ x - 11 = 0 $$
$$ \Rightarrow x(x-11)+ 1(x - 11) = 0 $$
$$ \Rightarrow x = -1, x = 11 $$
When $$ x = -1, $$ side $$ AB = -4 $$ which is not possible.
Hence, $$ x = 11 $$ and sides are $$ AC = x + 6 = 11 ; AB = x - 3 = 8 ; BC = x +4 = 15 $$
In triangle $$\displaystyle ABC,\angle B = 90^{\circ}$$ and $$D$$ is the mid-point of side Be. Prove that :
$$\displaystyle AC^2=AD^2+3CD^2$$
In $$\Delta ABC,$$
$${ AB }^{ 2 }+{ BC }^{ 2 }={ AC }^{ 2 }$$
as $$[BC =2CD]$$
$${ AB }^{ 2 }+{4CD }^{ 2 }={ AC }^{ 2 }$$ --(1)
In $$\Delta ABD,$$
$${ AD }^{ 2 }={ AB }^{ 2 }+{ BD }^{ 2 }= { AB }^{ 2 }+{ CD }^{ 2 }$$ --(2)
Subtracting (1) and (2)
$${ AC }^{ 2 }-{ AD }^{ 2 }= { AB }^{ 2 }+{ 4CD }^{ 2 } - ({ AB }^{ 2 }+{ CD }^{ 2 })\\ { AC }^{ 2 }-{ AD }^{ 2 }= { 3CD }^{ 2 }\\ { AC }^{ 2 } = { AD }^{ 2 }+{ 3CD }^{ 2 }$$
Hence proved.
In an isosceles triangle $$ABC$$ with $$AB=AC,$$ $$BD$$ is perpendicular from $$B$$ to side $$AC.$$ Prove that $$BD^{2}-CD^{2}=2CD.AD$$
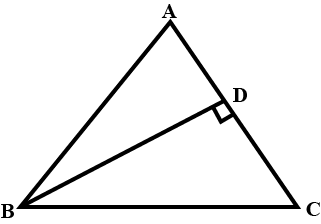
In a triangle $$ABC,$$ let $$D$$ be a point on the segment $$BC$$ such that $$AB + BD = AC + CD$$. Suppose that the points $$B,C,$$ and the centroids of $$\Delta ABD$$ & $$\Delta ACD$$ lie on a circle. Prove that $$AB = AC$$.
Using converse of Pythagoras theorem, check whether the sides form a right angled triangle $$13, 15$$ and $$16$$?
According to the Pythagoras theorem-In a right angle triangle square of the hypotenuse is equals to the sum of the square of the other two sides.
$$\Rightarrow a^2+b^2=c^2$$
$$\therefore 13^2+15^2=16^2$$
$$\Rightarrow 13^2+15^2\Rightarrow 169+225=394$$
$$\Rightarrow 16^2=256$$
$$\therefore 394\neq 256$$
Hence, the given sides does not form a right angled triangle.
Using converse of Pythagoras theorem, check whether the sides form a right angled triangle $$63, 65$$ and $$16$$?
According to the Pythagoras theorem-In a right angle triangle square of the hypotenuse is equals to the sum of the square of the other two sides.
$$\Rightarrow a^2+b^2=c^2$$
$$\therefore 63^2+16^2=65^2$$
$$\Rightarrow 63^2+16^2\Rightarrow 3969+256=4225$$
$$\Rightarrow 65^2=4225$$
$$\therefore 4225= 4225$$
Hence, the given sides form a right angled triangle.
In the figure, $$\angle PQR=\angle PRQ$$, then prove that $$\angle PQS=\angle PRT$$.
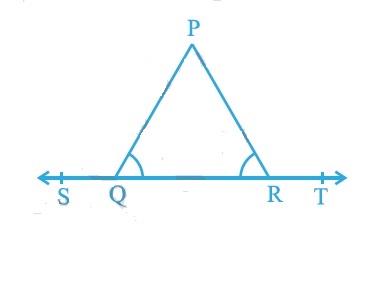
Which side is the hypotenuse for the sides, $$48, 73$$ and $$55$$ in a right angled ? (Apply Converse of Pythagoras theorem).
According to the Pythagoras theorem, In a right angle triangle square of the hypotenuse equals the sum of the square of the other two sides.
$$\Rightarrow a^2+b^2=c^2$$
$$\therefore 48^2+55^2=73^2$$
$$\Rightarrow 48^2+55^2\Rightarrow 2304+3025=5329$$
Also, $$\Rightarrow 73^2=5329$$
$$\therefore LHS=RHS=5329$$
Hence the given sides form a right-angled triangle.
As the longest side of the triangle is called the hypotenuse,
$$\therefore 73$$ is the hypotenuse.
Check whether the sides form a right angled triangle $$35, 12$$ and $$34$$? (Apply Converse of Pythagoras theorem).
According to the Pythagoras theorem,
In a right angle triangle square of the hypotenuse is equals to the sum of the square of the other two sides.
In $$\triangle ABC$$, let
$$a = 12 cm$$
$$b=34 cm$$
$$c=34 cm$$
If $$a^2+b^2=c^2$$, then the triangle is right angled triangle.
Let us first find $$a^2+b^2$$
$$\Rightarrow 12^2+34^2$$
$$\Rightarrow 12^2+34^2$$
$$\Rightarrow 144+1156=1300$$
$$\Rightarrow c^2 = 35^2=1225$$
Here $$ 1300\neq 1225$$
Hence, the given sides does not form a right angled triangle.
Check whether the sides form a right angled triangle $$65, 72$$ and $$97$$? (Apply Converse of Pythagoras theorem).
According to the Pythagoras theorem-In a right angle triangle square of the hypotenuse is equals to the sum of the square of the other two sides.
$$\Rightarrow a^2+b^2=c^2$$
$$\therefore 65^2+72^2=97^2$$
$$\Rightarrow 65^2+72^2\Rightarrow 4225+5184=9409$$
$$\Rightarrow 97^2=9409$$
$$\therefore 9409=9409$$
Hence, the given sides form a right angled triangle.
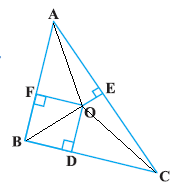
In the above figure, $$O$$ is a point in the interior of a triangle $$ABC,$$ $$OD \bot BC, \,OE \bot AC$$ and $$OF\bot AB$$. Show that:
(i) $$OA^2 + OB^2 + OC^2 -OD^2 -OE^2 -OF^2 = AF^2 + BD^2 + CE^2$$
(ii) $$AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2$$
Construction: Join $$AO$$, $$BO$$ and $$OC.$$
(i)
In $$\triangle AOE,$$
By Pythagoras Theorem,
$$AO^2=AE^2+OE^2\,.....(1)$$
In $$\triangle AOF,$$
By Pythagoras Theorem,
$$AO^2=AF^2+FO^2\,.....(2)$$
In $$\triangle FBO,$$
By Pythagoras Theorem,
$$BO^2=BF^2+FO^2\,.....(3)$$
In $$\triangle BDO,$$
By Pythagoras Theorem,
$$BO^2=BD^2+OD^2\,.....(4)$$
In $$\triangle DOC,$$
By Pythagoras Theorem,
$$OC^2=OD^2+DC^2\,.....(5)$$
In $$\triangle OCE,$$
By Pythagoras Theorem,
$$OC^2=OE^2+EC^2\,.....(6)$$
In $$\triangle ABC,$$
By Pythagoras Theorem,
$$AC^2=AB^2+BC^2\,.....(7)$$
Add equations $$(2), (4)$$ and $$(6)$$ then,
$$A{O^2} + B{O^2} + O{C^2} = A{F^2} + F{O^2} + B{D^2} + O{D^2} + O{E^2} + E{C^2}$$
Subtract equation $$(3)$$ from $$(4),$$ we get,
$$0=BD^2+OD^2-BF^2-FO^2$$
$$\Rightarrow BD^2+OD^2=BF^2+FO^2\,......(9)$$
Subtract equation $$(5)$$ from $$(6),$$ we get,
$$0=OE^2+EC^2-OD^2-DC^2$$
$$\Rightarrow OE^2+EC^2=OD^2+DC^2\,........(10)$$
Add equations $$(8), (9)$$ and $$(10)$$ we get,
$$AF^2+BD^2+CE^2=AE^2+CD^2+BF^2$$
(i)
In $$\triangle AOE,$$
By Pythagoras Theorem,
$$AO^2=AE^2+OE^2\,.....(1)$$
In $$\triangle AOF,$$
By Pythagoras Theorem,
$$AO^2=AF^2+FO^2\,.....(2)$$
In $$\triangle FBO,$$
By Pythagoras Theorem,
$$BO^2=BF^2+FO^2\,.....(3)$$
In $$\triangle BDO,$$
By Pythagoras Theorem,
$$BO^2=BD^2+OD^2\,.....(4)$$
In $$\triangle DOC,$$
By Pythagoras Theorem,
$$OC^2=OD^2+DC^2\,.....(5)$$
In $$\triangle OCE,$$
By Pythagoras Theorem,
$$OC^2=OE^2+EC^2\,.....(6)$$
In $$\triangle ABC,$$
By Pythagoras Theorem,
$$AC^2=AB^2+BC^2\,.....(7)$$
Add equations $$(2), (4)$$ and $$(6)$$ then,
$$A{O^2} + B{O^2} + O{C^2} = A{F^2} + F{O^2} + B{D^2} + O{D^2} + O{E^2} + E{C^2}$$
$$\Rightarrow A{O^2} + B{O^2} + O{C^2} - O{D^2} - O{E^2} - O{F^2} = A{F^2} + B{D^2} + E{C^2}$$
(ii)
Subtract equation $$(1)$$ from $$(2),$$ we get,
$$0=AF^2+FO^2-AE^2-OE^2$$
$$\Rightarrow AF^2+FO^2=AE^2+OE^2\,......(8)$$
$$0=AF^2+FO^2-AE^2-OE^2$$
$$\Rightarrow AF^2+FO^2=AE^2+OE^2\,......(8)$$
Subtract equation $$(3)$$ from $$(4),$$ we get,
$$0=BD^2+OD^2-BF^2-FO^2$$
$$\Rightarrow BD^2+OD^2=BF^2+FO^2\,......(9)$$
Subtract equation $$(5)$$ from $$(6),$$ we get,
$$0=OE^2+EC^2-OD^2-DC^2$$
$$\Rightarrow OE^2+EC^2=OD^2+DC^2\,........(10)$$
Add equations $$(8), (9)$$ and $$(10)$$ we get,
$$AF^2+BD^2+CE^2=AE^2+CD^2+BF^2$$
Hence, proved.
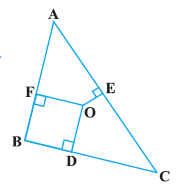
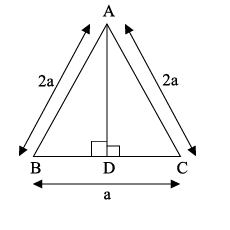
$$ABC$$ is an equilateral triangle of side $$2a.$$ Find each of its altitudes.
Since $$ABC$$ is an Equilateral Triangle,
Hence,
$$AB=BC=AC=2a$$
and
$$CD=BE=AF=$$ Altitudes
$$\therefore$$ $$CD=BE=AF=\dfrac{\sqrt3}{2}\times2a=$$$$\sqrt3 a$$ $$[\because $$ length of an altitude of an equilateral triangle of side length $$x$$ is $$\dfrac{\sqrt3}{2}\times x]$$
Hence,
$$AB=BC=AC=2a$$
and
$$CD=BE=AF=$$ Altitudes
$$\therefore$$ $$CD=BE=AF=\dfrac{\sqrt3}{2}\times2a=$$$$\sqrt3 a$$ $$[\because $$ length of an altitude of an equilateral triangle of side length $$x$$ is $$\dfrac{\sqrt3}{2}\times x]$$
In Figure, the side $$QR$$ of $$\triangle PQR$$ is produced to a point $$S$$. If the bisectors of $$\angle PQR$$ and $$\angle PRS$$ meet at point $$T$$, then prove that $$\angle QTR=\dfrac { 1 }{ 2 } \angle QPR$$.
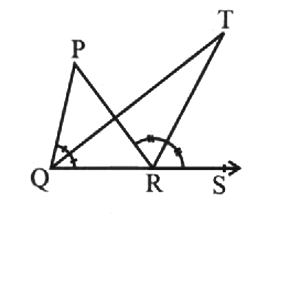
The altitudes of $$\Delta ABC$$, AD, BE and CF are equal. Prove that $$\Delta ABC$$ is an equilateral triangle.
Given that the altitudes of a triangle $$ABC$$ are equal
i.e. $$AD=BE=CF$$
Area of $$\Delta ABC=\dfrac{1}{2}(BC)\times (AD)$$
Area of $$\Delta ABC=\dfrac{1}{2}(AB)\times (CF)$$
Area of $$\Delta ABC=\dfrac{1}{2}(AC)\times (BE)$$
$$\therefore \dfrac{1}{2}(BC)\times (AD)=\dfrac{1}{2}(AB)\times (CF)=\dfrac{1}{2}(AC)\times (BE)$$
But $$AD=BE=CF$$ then
$$\Rightarrow (BC)\times (AD)=(AB)\times (AD)=(AC)\times (AD)$$
$$\Rightarrow BC=AB=AC$$
So three sides of the triangle are same.
Thus, the triangle $$ABC$$ is an equilateral triangle.
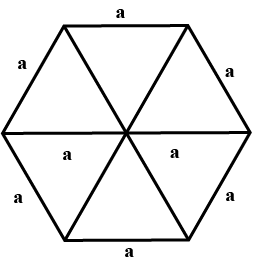
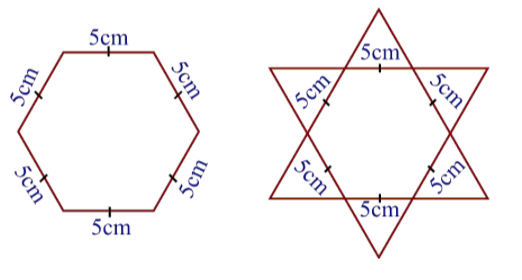
Complete the hexagonal and star shaped Rangolies [see Fig. (i) and (ii)] by filling them with as many equilateral triangles of side $$1$$ cm as you can. Count the number of triangles in each case. Which has more triangles?
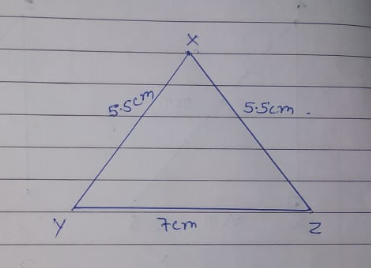
Construct $$\triangle XYZ$$ with $$YZ = 7 cm,\, XY = 5.5 cm$$ and $$XZ =5.5 cm$$.
Given that
$$YZ=7cm$$
$$XY=5.5cm$$
And,$$XZ=5.5cm$$
step of construction
(i) Draw a line segment $$YZ=7cm$$
(ii) With $$Z$$ as centre and radius $$5.5cm$$ draw an arc.
(iii) With $$Y$$ as centre and radius $$5.5cm$$ draw an arc cutting the previous arc at $$X$$
(iv) join $$XZ$$ and $$XY$$ then $$\Delta XYZ$$ is the required triangle
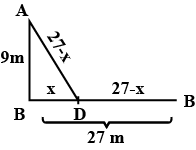
An insect $$8 m$$ away from the foot of a lamp post which is $$6 m$$ tall, crawls towards it. After moving through a distance, its distance from the top of the lamp post is equal to the distance it has moved. How far is the insect away from the foot of the lamp post? [Bhaskaracharya's Leelavathi]
Distance between the insect and the foot of the lamp post $$= BD = 8\ m$$.
The height of the lamp post $$= AB = 6\ m$$.
After moving a distance, let the insect be at $$C$$,
Let $$AC = CD = x \ m$$.
$$\therefore BC = \left(8 - x\right) m$$.
In $$\triangle ABC$$, $$\angle B = {90}^{o}$$
$$\therefore {AC}^{2} = {AB}^{2} + {BC}^{2}$$ ($$\because$$ Pythagoras theorem)
$${x}^{2} = {6}^{2} + {\left(8 - x\right)}^{2}$$
$${x}^{2} = 36 + 64 - 16x + {x}^{2}$$
$$\therefore 16x = 100$$
$$x = \dfrac{100}{16} = 6.25$$ Note: We can also consider $$BC = x$$, then $$CD = AC = \left(8 - x\right)$$
$$\therefore BC = 8 - x = \left(8 - 6.25\right) = 1.75 m$$
The insect is $$1.75 m$$ away from the foot of the lamp post.
The height of the lamp post $$= AB = 6\ m$$.
After moving a distance, let the insect be at $$C$$,
Let $$AC = CD = x \ m$$.
$$\therefore BC = \left(8 - x\right) m$$.
In $$\triangle ABC$$, $$\angle B = {90}^{o}$$
$$\therefore {AC}^{2} = {AB}^{2} + {BC}^{2}$$ ($$\because$$ Pythagoras theorem)
$${x}^{2} = {6}^{2} + {\left(8 - x\right)}^{2}$$
$${x}^{2} = 36 + 64 - 16x + {x}^{2}$$
$$\therefore 16x = 100$$
$$x = \dfrac{100}{16} = 6.25$$ Note: We can also consider $$BC = x$$, then $$CD = AC = \left(8 - x\right)$$
$$\therefore BC = 8 - x = \left(8 - 6.25\right) = 1.75 m$$
The insect is $$1.75 m$$ away from the foot of the lamp post.
In a right angled $$\triangle ABC$$, $$\angle B = {90}^{o}$$, $$AC = 17 cm$$ and $$AB = 8 cm$$, find $$BC$$.
Given, in $$\triangle ABC$$, $$\angle B = {90}^{o}$$
$$\therefore {AC}^{2} = {AB}^{2} + {BC}^{2}$$ [$$\because$$ Pythagoras theorem]
$$\Rightarrow {BC}^{2} = {AC}^{2} - {AB}^{2}$$
$${BC}^{2} = {17}^{2} - {8}^{2}$$
$${BC}^{2} = 289 - 64 = 225$$
$$\therefore BC = \sqrt{225} = 15 cm$$
$$\therefore {AC}^{2} = {AB}^{2} + {BC}^{2}$$ [$$\because$$ Pythagoras theorem]
$$\Rightarrow {BC}^{2} = {AC}^{2} - {AB}^{2}$$
$${BC}^{2} = {17}^{2} - {8}^{2}$$
$${BC}^{2} = 289 - 64 = 225$$
$$\therefore BC = \sqrt{225} = 15 cm$$
The sides of a right angled triangle containing the right angle are $$5 cm$$ and $$12 cm$$, find its hypotenuse.
Let $$AB$$ and $$BC$$ be the sides of the triangle containing right angle and $$AC$$ be the hypotenuse as shown in the above figure:
It is given that $$AB=5$$ cm $$BC=12$$ cm
According to the pythagoras theorem
$$AC^{ 2 }=AB^{ 2 }+BC^{ 2 }\quad \\ \Rightarrow AC^{ 2 }=5^{ 2 }+12^{ 2 }\quad \\ \Rightarrow AC^{ 2 }=25+144\quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \Rightarrow AC^{ 2 }=169\\ \Rightarrow AC=\sqrt { 169 } \\ \Rightarrow AC=13$$
Hence, the hypotenuse $$AC=13$$ cm.
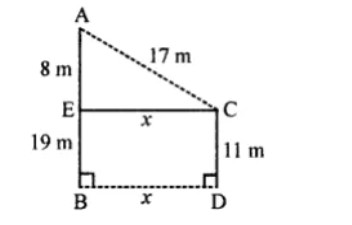
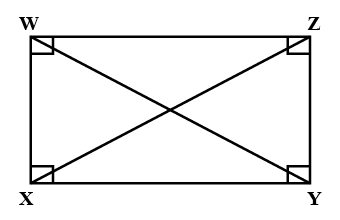
In the rectangle $$WXYZ$$, $$XY + YZ = 17 cm$$ and $$XZ + YW = 26 cm$$, calculate the length and breadth of the rectangle.
Find the length of the diagonal of a square of side $$12\ cm$$.
Let $$ABCD$$ be the square and $$AC$$ be the diagonal as shown in the above figure:
It is given that $$AB=BC=CD=DA=12$$ cm
In $$△ABC$$, $$∠B=90^{ 0 }$$
According to the pythagoras theorem
$$AC^{ 2 }=AB^{ 2 }+BC^{ 2 }\quad \\ \Rightarrow AC^{ 2 }=12^{ 2 }+12^{ 2 }\quad \\ \Rightarrow AC^{ 2 }=144+144\quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \Rightarrow AC^{ 2 }=288\\ \Rightarrow AC=\sqrt { 288 } \\ \Rightarrow AC=\sqrt { 12^{ 2 }\times 2 } \\ \Rightarrow AC=12\sqrt { 2 }$$
Hence, the length of the diagonal is $$AC=12\sqrt { 2 }$$ cm.
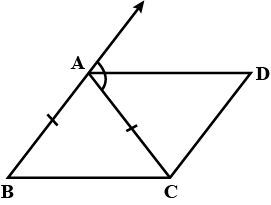
$$ABC$$ is an isosceles triangle in which $$AB = AC. AD$$ bisects exterior angle $$QAC$$ and $$CD\parallel BA$$ as shown in the figure. Show that $$\angle DAC = \angle BCA$$
In an equilateral triangle $$ABC$$, the side $$BC$$ is trisected at point $$D$$. Prove that $$9{AD}^{2}=7{AB}^{2}$$. (Hint : Draw $$AE \perp BC$$).
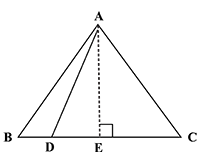
If the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
Produce AD upto E such that $$AD=DE$$
In $$\triangle ABD$$ and $$\triangle EDC$$
$$AD=DE$$ [By construction]
$$BD=CD$$ [Given]
$$\angle 1=\angle 2$$ [Vertically opposite angles]
$$\therefore \triangle ABD\cong \triangle EDC$$ [SAS}
$$\Rightarrow AB=CE...........(1)$$
and $$\angle BAD=\angle CED$$
But, $$\angle BAD=\angle CAD$$ [AD is bisector of $$\angle BAC$$]
$$\therefore \angle CED=\angle CAD$$
$$\Rightarrow AC=CE...........(2)$$
From (1) and (2)
$$AB=AC$$
Hence, ABC is an isosceles triangle.
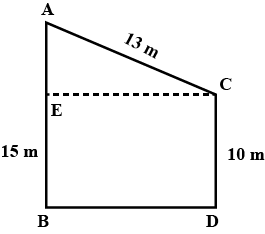
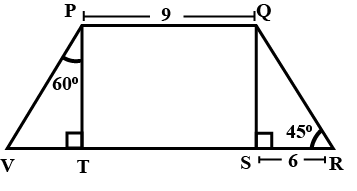
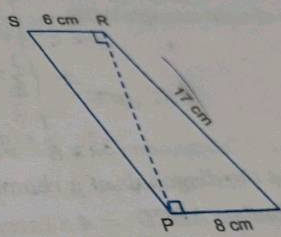
In the following figure, quadrilateral $$PQRV$$ is a trapezium in which $$PQ \parallel VR, SR = 6\text{ cm}, PQ = 9\text{ cm}$$, then find $$VR$$.
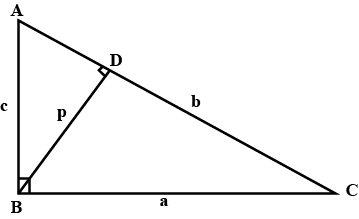
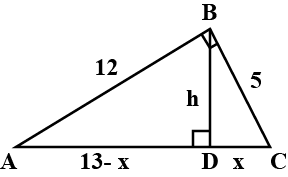
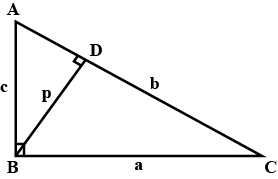
In $$\triangle ABC$$, $$\angle ABC = {90}^{o}$$, $$BD \perp AC$$. If $$AB =$$ '$$c$$' units, $$BC =$$ '$$a$$' units, $$BD =$$ '$$p$$' units, $$CA =$$ '$$b$$' units.
Prove that $$\dfrac{1}{{a}^{2}} + \dfrac{1}{{c}^{2}} = \dfrac{1}{{p}^{2}}$$.
Given $$\angle ABC=90^o$$,$$BD$$ is perpendicular to $$AC, AB=c; BC=a; BD=p; CA=b$$.
Area of $$\triangle ABC=\cfrac 12 \times AC \times BD$$
$$=\cfrac 12 \times b \times p = \cfrac 12 bp$$
Area of $$\triangle ABC=\cfrac 12 \times BC \times AB$$
$$=\cfrac 12 ca$$
$$\Rightarrow \cfrac 12 bp= \cfrac 12 ca$$
$$\therefore bp=ca$$
$$\Rightarrow b=\cfrac {ca}p$$
In right triangle $$ABC$$,
$$AC^2=AB^2+BC^2$$
$$\Rightarrow b^2=c^2+a^2$$
$$\therefore (\cfrac {ca}p)^2=c^2+a^2$$
$$\Rightarrow \cfrac {c^2a^2}{p^2}=c^2+a^2$$
$$\therefore \cfrac 1{p^2}=\cfrac {c^2+a^2}{c^2a^2}$$
$$\therefore \cfrac 1{p^2}=\cfrac 1{a^2}+\cfrac 1{c^2}$$
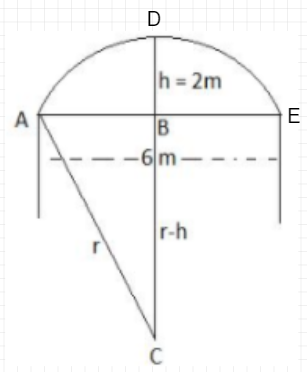
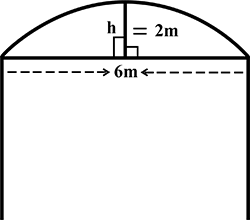
A door of width $$6$$ meter has an arch above it having a height of $$2\ m$$. Find the radius of the arch.
Given: Width of door $$=AE=6\ m$$
Let $$C$$ be the centre of the semicircle that makes the arch.
Let $$r$$ be the radius of the arch.
Then $$BC=CD-BD$$
$$=$$ radius $$-$$ height of the arch
$$=r-h$$
In right-angled triangle $$ABC,$$
$$AC^2=AB^2+BC^2$$ (By Pythagoras theorem)
$$\Rightarrow r^2=3^2+(r-2)^2$$
$$\Rightarrow r^2=9+r^2-4r+4$$
$$\Rightarrow 4r=13$$
$$\Rightarrow r=\cfrac{13}{4}=3.25\ m$$
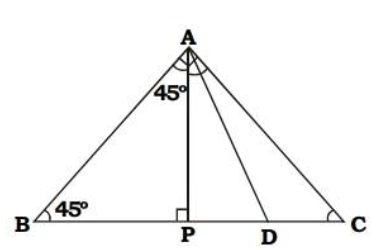
Find the angles of the triangle $$ABC$$, given in the figure.
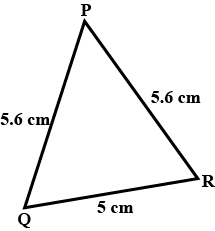
$$\angle Q$$ and $$\angle R$$ of a triangle PQR are $$25^o$$ and $$65^o$$. Is $$\triangle PQR$$ a right angled triangle?
Moreover PQ is 4 cm and PR is 3 cm. Find QR.
Given :
In $$\triangle PQR$$
$$\angle PQR=25°, PQ=4cm$$
$$\angle PRQ=65°, PR=3cm$$
$$\therefore \angle QPR=180°-90°=90°$$
$$\therefore \triangle PQR$$ is a right angle triangle.
So, By pythagoras theorem,
$${QR}^{2}={PQ}^{2}+{PR}^{2}$$
$${QR}^{2}={4}^{2}+{3}^{2}$$
$${QR}^{2}=25$$
$$QR=5cm$$
State Pythagoras theorem.
$$ {\textbf{Step 1: Statement}} $$
$$ {\text{In a right angled triangle}},{\text{the square of the hypotenuse is equal to the sum of the squares }} $$
$$ {\text{of the other two sides}}{\text{.}} $$
$$ {\text{ABC is a triangle in which}}\;\angle ABC = {90^ \circ } $$
$$ \Rightarrow {\text{A}}{{\text{B}}^{\text{2}}}{\text{ + B}}{{\text{C}}^{\text{2}}}{\text{ = A}}{{\text{C}}^{\text{2}}} $$
$$\textbf{Hence above statement is required statement}$$
In the given figure, $$\dfrac{PK}{KS} = \dfrac{PT}{TR}$$ and $$\angle PKT = \angle PRS$$. Prove that $$\Delta PSR$$ is an isosceles triangle.
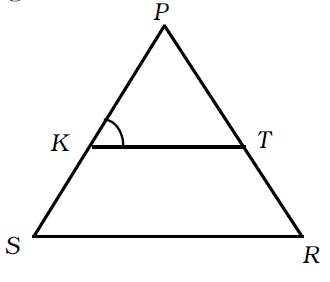
$$PQR$$ is a triangle right angled at $$P$$. If $$PQ = 10\ cm$$ and $$PR = 24\ cm$$, find $$QR$$.
It is given that $$PQR$$ is a right angled triangle.
$$PR=24cm, PQ=10cm$$
In $$\triangle PQR$$,
$$PR=$$ base, $$PQ=$$ height and $$QR=$$ hypotenuse
By using Pythagoras Theorem,
$$(PR)^2+(QP)^2=(QR)^2$$
$$(24)^2+(10)^2=(QR)^2$$
$$\Rightarrow QR= \sqrt{676}=26 cm$$
Are the numbers $$12, 5$$ and $$13$$ form a Pythagorean Triplet?
Show that the following points form an isosceles triangle.
(1, -2), (-5, 1) and (1, 4)
Show that the following points form an isosceles triangle.
(2, 3), (5, 7) and (1, 4)
Show that the following points form an isosceles triangle.
(-1, -3), (2, -1) and (-1, 1)
Show that the following points form an equilateral triangle. (a, 0), (-a, 0) and (0, a$$\sqrt 3$$)
Show that the following points form an isosceles triangle.
(1, 3), (-3, -5) and (-3, 0)
Construct $$\triangle ABC $$ with $$AB=5 cm,\, BC =5 cm$$ and $$AC= 5 cm$$.
Given that
AB $$=$$ 5cm
BC $$=$$ 5cm
AC $$=$$ 5cm
Step of construction
(i) Draw a line BC $$=$$ 6 cm
(ii) With B as centre and radius 5 cm, draw an arc.
(iii) With C as centre and radius 5 cm, draw another arc which cut the previous arc at A.(iv) Join AB and AC.
(v)Thus ABC is the required triangle.
Show that the following points form an equilateral triangle. $$(\sqrt 3, 2), (0, 1)$$ and $$(0, 3)$$
In a right angled triangle, the length of perpendicular and base are $$8\ cm$$ and $$15\ cm$$ respectively, then find its hypotenuse.
In a right triangle, by Pythagoras theorem:
$$(Hypotenuse)^{2} = (Perpendicular)^{2} + (Base)^{2}$$
$$AC^2=AB^2+BC^2$$
$$= 8^{2} + 15^{2}$$
$$= 64 + 225 = 289$$
$$(Hypotenuse)^{2} = (Perpendicular)^{2} + (Base)^{2}$$
$$AC^2=AB^2+BC^2$$
$$= 8^{2} + 15^{2}$$
$$= 64 + 225 = 289$$
Taking square roots on both sides, we get
$$\therefore Hypotenuse \; AC = \sqrt {289} = 17\ cm$$.
$$\therefore Hypotenuse \; AC = \sqrt {289} = 17\ cm$$.
If $$d$$ and $$e$$ are points on sides $$AB$$ and $$AC$$ respectively of a $$\triangle {abc}$$ such that $$DE\parallel BC$$ and $$BD=CE$$. Prove triangle $$abc$$ is isosceles.
$$\Rightarrow$$ $$\dfrac{AD}{DB}=\dfrac{AE}{EC}$$
By adding $$1$$ on both sides,
$$\Rightarrow$$ $$\dfrac{AD}{DB}+1=\dfrac{AE}{EC}+1$$
$$\Rightarrow$$ $$\dfrac{AD+DB}{DB}=\dfrac{AE+EC}{EC}$$
$$\Rightarrow$$ $$\dfrac{AB}{DB}=\dfrac{AC}{CE}$$
It is given that, $$DE\parallel BC$$ and $$BD=EC$$
$$\Rightarrow$$ $$\dfrac{AB}{BD}=\dfrac{AC}{BD}$$ [ $$CE=BD$$ ]
$$\Rightarrow$$ $$AB=AC$$
$$\therefore$$ $$\triangle ABC$$ is isosceles triangle.
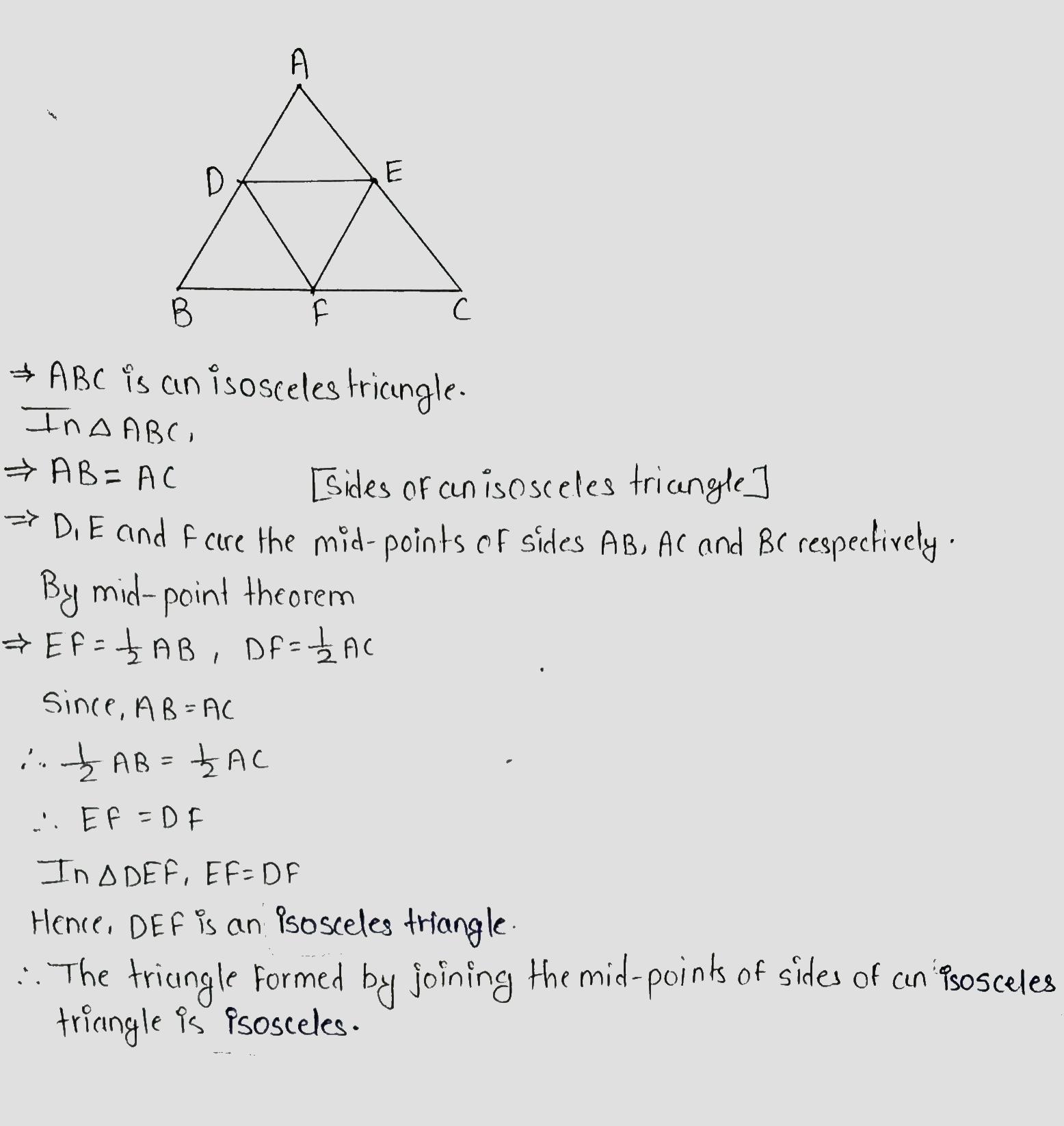
D, E, and F are, respectively the mid-points of sides BC, CA and AB of an equilateral triangle ABC. Prove that DEF is also an equilateral triangle.
Let ABC be the triangle and D, E and F be the mid-point of BC, CA and AB respectively. We have to show triangle formed DEF is an equilateral triangle. We know the line segment joining the mid-points of two sides of a triangle is half of the third side.
Therefore $$DE=\dfrac{1}{2}AB, \, EF=\dfrac{1}{2}BC$$ and $$FD=\dfrac{1}{2}AC$$
Now, $$\Delta ABC$$ is an equilateral triangle
$$\Rightarrow AB=BC=CA $$
$$\Rightarrow \dfrac{1}{2} AB = \dfrac{1}{2} BC = \dfrac{1}{2} CA $$
$$\Rightarrow DE=EF=FD $$
$$\therefore \Delta DEF$$ is an equilateral triangle.
In the given figure, $$\triangle ABC$$ is an equilateral triangle and $$\square AWXB$$ and $$\square AYZC$$ are two squares. The value of $$\dfrac{1}{10}(\angle ZXA)$$ is:
Given that $$ABC$$ is an equilateral triangle.
Therefore, $$\angle ABC = \angle CBA =\angle BAC = 60^{o}$$
GIven that $$ABXW$$ and $$AYZC$$ are two squares.
Therefore, $$AX$$ is a diagonal of square $$ABXW$$ - as shown in the figure.
All interior angles of a square are equal to $$ 90^{o}$$
Therefore, $$ \angle BAW = 90^{o}$$
The diagonal of a square bisects the angle at the vertex.
Therefore, $$ \angle BAX = \angle AXW =45^{o}$$
$$ \Rightarrow \angle OAX = 45^{o}$$ -------$$(1)$$
Join vertices $$X$$ and $$Z$$ - as shown in the figure. Join $$ZX$$, a straight line.
Line $$ZX$$ cuts the sides $$AB$$ and $$AC$$, of the Equilateral triangle $$ABC$$, at $$O$$ and $$N$$ respectively.
The smaller triangle $$AON$$ is similar to triangle $$ABC$$ are similar, thus triangle $$AON$$ is also an equilateral triangle.
Therefore, $$\angle NAO = \angle AON =\angle ANO = 60^{o}$$
Line $$A0$$ is cutting the straight line $$XZ$$, hence
$$\angle ZOA + \angle XOA =\angle ZOX = 180^{o}$$
$$ 60^{o} + \angle XOA = 180^{o}$$
$$ \angle XOA = 180^{o} - 60^{o}$$
$$ \angle XOA = 120^{o}$$ -------$$(2)$$
Consider triangle $$AOX$$ - in figure:
Here, $$\angle XOA + \angle OAX +\angle OXA = 180^{o}$$
$$ 120^{o} + 45^{o} + \angle OXA = 180^{o}$$, from equations $$(1)$$ and $$(2)$$
$$ \angle OXA = 180^{o} - 120^{o} - 45^{o} $$
$$ \angle OXA = 15^{o} $$
$$ \angle OXA = \angle ZXA = 15^{o} $$
Therefore,
$$ \dfrac {1}{10} { \angle ZXA} = \dfrac {1}{10} \times 15^{o} $$
$$ \dfrac {1}{10} { \angle ZXA} = 1.5^{o} $$
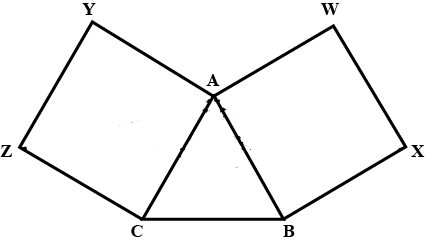
"An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are $$60^o$$ each." Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all sides and all angles are equal in a equilateral triangle
Find the length of the altitude of an equilateral triangle with side $$6$$cm.
Let the length of the altitude of an equilateral triangle be $$x\:cm$$
Given the sides of the equilateral triangle is $$6\:cm$$
From the figure,
$$x=\sqrt{6^2-3^2}$$
$$=\sqrt{36-9}$$
$$=\sqrt{27}$$
$$=3\sqrt{3}$$
$$\therefore x=3\sqrt{3}\:cm \approx 5.1961\:cm$$
Thus, the altitude of the triangle is $$3\sqrt{3}\:cm$$ or $$5.1961\:cm$$
In the fig. If AB || CD, EF $$\perp$$ CD and $$\angle GED = 126^0,$$ find $$\angle AGE , \angle GEF $$ and $$\angle FGE$$.
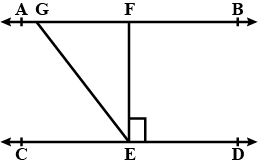
A point $$D$$ is on the side $$BC$$ of an equilateral triangle $$ABC$$, such that $$DC =\cfrac { 1 }{ 4 } BC.$$ Prove that $${ AD }^{ 2 }={ 13CD}^{ 2 }.$$
In the given figure, $$\triangle ABC$$ is an isosceles triangle in which AB-AC. If $$BD\bot AC$$ and $$CE\bot AB$$, prove that BD=CE.
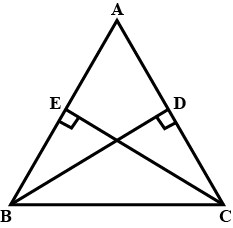
In a quadrilateral ABCD, given that $$\angle A+ \angle D = 90^{\circ}$$. Prove that $${ AC }^{ 2 }+{ BD }^{ 2 }={ AD }^{ 2 }+{ BC}^{ 2 }.$$
Extend AB and CD to intersect at O
Now $$\angle AOD =90^{°}$$ because given $$\angle A+\angle D=90^{°}$$
$$\Rightarrow AC^{2}=OA^{2}+OC^{2}$$ and $$\Rightarrow BD^{2}=OB^{2}+OD^{2}$$
Adding both equations ;
$$\Rightarrow AC^{2}+BD^{2}=\left (OA^{2}+OD^{2}\right )+\left (OB^{2}+OC^{2}\right )$$
$$\Rightarrow AC^{2}+BD^{2}=AD^{2}+BC^{2}$$
A man goes 15 metres due west and then 8 metres due north. How far is he from starting point?
First the person moves from A to B and then B to C.
His distance from the starting point is AC.
AC can be calculated using Pythagoras Theorem.
Applying Pythagoras theorem
$$(AB)^{2}+(BC)^{2}=(CA)^{2}$$
$$(15)^{2}+(8)^{2}=(x)^{2}$$
$$225+64=(x)^{2}$$
$$x^{2}=289$$
$$x=\sqrt{289}=17m$$
Hence the man is $$17m $$ from the starting point.
The sides of certain triangles are given below. Determine which of them are right angled triangles.
(i) a = 7 cm, b = 24 cm and c = 25 cm
(ii) a = 9 cm, b = 16 cm and c = 18 cm
(iii) a = 1.6 cm, b = 3.8 cm and c = 4 cm
(iv) a = 8 cm, b = 10 cm and c = 6 cm
In given figure, $$\dfrac { PS }{ SQ } =\dfrac { PT }{ TR } $$ and $$\angle PST=\angle PRQ$$. Prove that $$\triangle PQR$$ is an isosceles triangle.
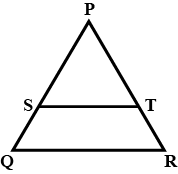
The hypotenuse of a right triangle is $$3\sqrt { 5 } cm$$. If the smaller side is tripled and the larger side is doubled, the new hypotenuse will be $$15cm$$. Find the length of each side.
In given figure equilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
Given A right angled triangle ABC with right angle at B. Equilateral triangles PAB, QBC and RAC are described on sides AB, BC and Ca respectively.
To prove $$Area(\triangle PAB)+Area(\triangle QBC)=Area(\triangle RAC)$$.
Proof Since triangles PAB, QBC and RAC are equilateral. Therefore, they are equiangular and hence similar.
$$\therefore $$ $$\dfrac { Area(\triangle PAB) }{ Area(\triangle RAc) } +\dfrac { Area(\triangle QBC) }{ Area(\triangle RAC) } =\dfrac { { AB }^{ 2 } }{ { AC }^{ 2 } } +\dfrac { { BC }^{ 2 } }{ { AC }^{ 2 } } $$
$$\Rightarrow $$ $$\dfrac { Area(\triangle PAB) }{ Area(\triangle RAC) } +\dfrac { Area(\triangle QBC) }{ Area(\triangle RAC) } =\dfrac { { AB }^{ 2 }+{ BC }^{ 2 } }{ { AC }^{ 2 } } $$
$$\Rightarrow $$ $$\dfrac { Area(\triangle PAB) }{ Area(\triangle RAC) } +\dfrac { Area(\triangle QBC) }{ Area(\triangle RAC) } =\dfrac { { AC }^{ 2 } }{ { AC }^{ 2 } } =1$$
[$$\because \triangle $$ $$ is\ a\ right\ angled\ triangle\ with $$ $$\angle B=90^0\therefore { AC }^{ 2 }={ AB }^{ 2 }+{ BC }^{ 2 }$$]
$$\Rightarrow $$ $$\dfrac { Area(\triangle PAB)+Area(\triangle QBC) }{ Area(\triangle RAC) } =1$$
$$\Rightarrow $$ $$Area(\triangle PAB)+Area(\triangle QBC)=Area(\triangle RAC)$$ $$[Hence \ proved]$$
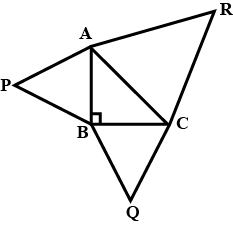
In the figure , X is any point in the interior of triangle . Point x is joined to the vertices of triangle
$$seg{\rm{ }}PQ\parallel seg{\rm{ }}DE$$
$$seg{\rm{ }}PR\parallel seg{\rm{ }}DF$$proove:$$seg{\rm{ }}QR\parallel seg{\rm{ }}EF$$
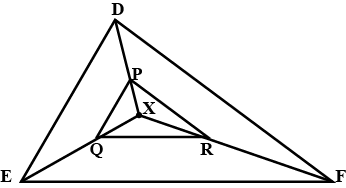
In $$\triangle ABC$$, AD is perpendicular to BC. Prove that :$${ AB }^{ 2 }+{ CD }^{ 2 }={ AC }^{ 2 }+{ BD }^{ 2 }$$
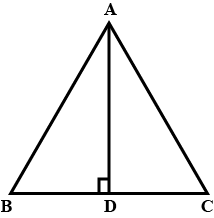
Find the altitude of an equilateral triangle if one of its sites measures $$10\sqrt 3 $$ cm
In the given figure, $$\triangle ABC$$ is an isosceles with AB = AC, D and E are points on BC such that BE = CD. show that AD=AE.
Given an isosceles triangle $$\triangle ABC$$,
$$ \therefore AB=AC$$
Also, $$BE=CD$$
We have to prove that $$AD=AE$$
Since, $$AB=AC$$
$$ \therefore \angle C=\angle B\quad $$ [Angles opposite to equal sides are equal] .... (1)
In $$\triangle ACD$$ and $$\triangle ABE$$,
$$AC=AB$$ (Given)
$$\angle C=\angle B$$ (From (1))
$$CD=BE$$ (Given)
So, $$\triangle ACD\cong \triangle ABE\quad $${ SAS congruence rule}
$$ \therefore AD=AE\quad $${ By CPCT}
Hence proved.
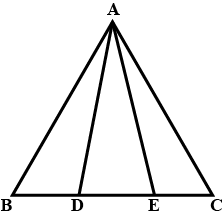
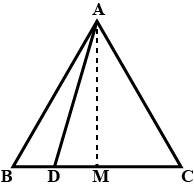
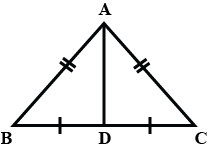
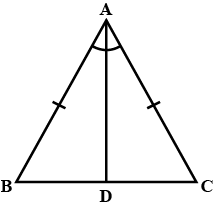
Show that the median to the base of an isosceles triangle is perpendicular to base.
Let $$ABC$$ be an isosceles triangle in which $$|\vec{AB}| =|\vec{ AC}|$$
Let $$A$$ be the point of reference (origin) and let
$$\vec{AB} = \vec{b}, \vec{AC} = \vec{c}$$
Let $$D$$ be the middle point $$BC$$.
Then, $$AD = \dfrac{\vec{b} +\vec{ c}}{2}$$
Now, $$BC =\vec{ c} -\vec{ b}$$
$$\therefore \vec{AD}\cdot \vec{BC} = \left(\dfrac{\vec{b} + \vec{c}}{2}\right) \cdot (\vec{c} - \vec{b})=\dfrac{1}{2}(|\vec{c}|^2-|\vec{b}|^2)=0$$ [ Since $$|\vec{b}|=|\vec{c}|$$
Let $$A$$ be the point of reference (origin) and let
$$\vec{AB} = \vec{b}, \vec{AC} = \vec{c}$$
Let $$D$$ be the middle point $$BC$$.
Then, $$AD = \dfrac{\vec{b} +\vec{ c}}{2}$$
Now, $$BC =\vec{ c} -\vec{ b}$$
$$\therefore \vec{AD}\cdot \vec{BC} = \left(\dfrac{\vec{b} + \vec{c}}{2}\right) \cdot (\vec{c} - \vec{b})=\dfrac{1}{2}(|\vec{c}|^2-|\vec{b}|^2)=0$$ [ Since $$|\vec{b}|=|\vec{c}|$$
So $$\vec{AD}.\vec{BC}=0 \Rightarrow $$ $$\vec{AD}$$ is perpendicular to $$\vec{BC}$$.
Hence the problem,
If $$\Delta ABC$$ is an equilateral triangle of side$$ a$$ and D is a point on $$BC$$ such that $$ BD = \dfrac{1}{3}BC$$ then the prove that $$AD = \dfrac{{\sqrt 7 a}}{3}$$
$$Let\quad AB=AC=BC=3a$$
Accordingly $$BD=a$$ and $$MC=\cfrac { 3 }{ 2 } a$$
$$ AM=AC\sin { { 60 }^{ \circ } } =3a\cfrac { \sqrt { 3 } }{ 2 } $$
$$ DM=BC-BD-MC=3a-a-\cfrac { 3 }{ 2 } a=\cfrac { a }{ 2 } $$
In$$\triangle ADM$$
$$ AD=\sqrt { { AM }^{ 2 }+{ DM }^{ 2 } } $$
$$ =\sqrt { \cfrac { 27 }{ 40 } { a }^{ 2 }+\cfrac { 1 }{ 4 } { a }^{ 2 } } $$
$$ =\cfrac { \sqrt { 28a } }{ 2 } =\sqrt { 7 } a$$
$$AD = \dfrac{{\sqrt 7 a}}{3}$$
If $$\cos A + \cos B+ \cos C = \dfrac{3}{2}$$, then show that the triangle is equilateral.
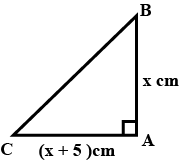
In triangle ABC ; Angle $$A =90^{0}$$ , side AB = x cm, AC = (x+5) cm and area $$ =150 cm ^{2}$$. Find the sides of triangle.
R.E.F. Image.
Area $$ = 150 \,cm^{2}$$
Area $$ = \frac{1}{2}\times base\times height =\frac{1}{2}\times AC\times AB$$
$$ 150=\frac{1}{2}\times (x+5)\times x$$
$$ \Rightarrow 300 = x^{2}+5x $$
$$ \Rightarrow x^{2}+5x-300 = 0$$
$$ \Rightarrow x^{2}+20x-15x-300=0$$
$$ \Rightarrow x^{2}(x+20)-15(x+20)=0$$
$$ \Rightarrow (x+20)(x-15)=0$$
$$ \Rightarrow x = 15$$
$$ \therefore AB = 15 \,cm , AC = x+5 = 15+5 = 20 \,cm,$$
$$ BC = \sqrt{15^{2}+20^{2}} = 25 \,cm $$
Length of diagonals of a rhombus $$ABCD$$ are $$16cm$$ and $$12cm$$. Find the side and perimeter of the rhombus.
In the figure, $$AD$$ is the internal bisector of $$\angle A$$ and $$CE\parallel DA$$. If $$CE$$ meets $$BA$$ produced at $$E$$, prove that $$\Delta CAE$$ is isosceles.
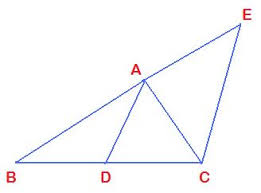
If $$AD \bot BC$$, prove that $$AB^{2}+CD^{2}=BD^{2}+AC^{2}$$
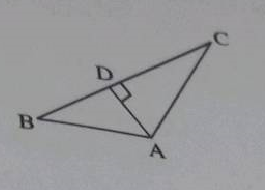
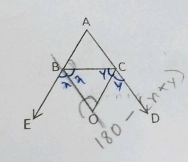
In triangle $$ABC$$, $$BC$$ is produced to $$D$$, $$A$$ & $$D$$ are joined. If $$\angle{BAC}={60}^{o}$$, $$\angle{ABC}={45}^{o}$$. Find $$\angle{ACD}$$
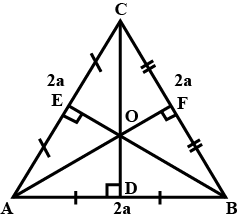
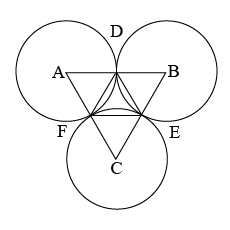
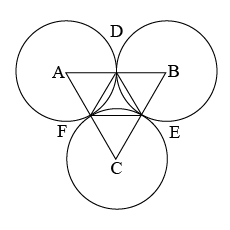
Three congruent circles with centres $$A, B$$ and $$C$$ with radius $$5\ cm$$ each, touch each other in point $$D, E, F$$ as shown in figure.
(i) What is the perimeter of $$\Delta ABC$$?
(ii) What is the length of side $$DF$$ of $$\Delta DEF$$?
Given $$A, B, C$$ are congruent circles with radius $$=5\ cm$$ each.
(i) For the perimeter of $$\Delta ABC$$
$$\Rightarrow AB=(5+5)\ cm=10\ cm$$
$$BC=(5+5)\ cm=10\ cm$$
$$CA=(5+5)\ cm=10\ cm$$
$$\therefore$$ Perimeter of $$\Delta ABC$$$$=AB+BC+CA=(10+10+10)\ cm$$$$=30\ cm$$
(ii) Consider $$\Delta ADF$$
$$\because$$ From triangle $$ABC$$, all sides are equal.
$$\therefore \angle A=60^o$$ [equilateral triangle]
$$AF=AD$$
$$\therefore \angle F=\angle D=x(let)$$ [If $$2$$ sides are equal then their opposite angles are also equal]
$$\therefore x+x+60=180$$
$$\Rightarrow 2x=120$$
$$\Rightarrow x=60^o$$
$$\therefore$$ $$ADF$$ is a equilateral triangle
$$\therefore DF=AD=5\ cm$$.
Hence the length of $$DF$$ is $$5\ cm$$
In the following triplet pythagorean ? show working
(18, 79, 82)
A girl goes on a bicycle to East for $$15 km$$, then turns back and comes to the starting point, then goes to west for $$13 km$$ and turns back again and stops after $$5 km$$. In which direction is she when she stops? How far is she from the starting point? How much total distance has she covered?
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25 . Find the ratio of their corresponding heights.
Bisectors of angles $$B$$ and $$C$$ of an isosceles triangle intersect each other at $$O$$ and $$AB=AC$$. $$BO$$ is produced to a point $$M$$ on side $$AC$$. Prove that $$\angle MOC = \angle ABC$$.
Given:
Lines $$OB$$ and $$OC$$ are the bisectors of $$\angle B$$ and $$\angle C$$ of an isosceles $$\Delta ABC$$ such that $$AB=AC$$ which intersect each other at $$O$$ and $$BO$$ is produced to $$M$$.
To prove:
$$\angle MOC=\angle ABC$$
Consider the diagram shown below.
Proof:
In $$\Delta ABC$$,
$$AB=AC$$ (given)
$$\angle ACB=\angle ABC$$ (angles opposite to equal sides are equal)
$$\dfrac{1}{2}\angle ACB=\dfrac{1}{2}\angle ABC$$ (dividing both sides by 2)
Therefore,
$$\angle OCB=\angle OBC$$ …… (1)
(Since, $$OB$$ and $$OC$$ are the bisector of $$\angle B$$ and $$\angle C$$)
Now, from equation (1), we have
$$ \angle MOC=\angle OBC+\angle OCB $$ $$\because$$ sum of interior angle = Exterior angle
$$ \angle MOC=2\angle OBC $$
$$ \Rightarrow \angle MOC=2\angle ABC \times\dfrac{1}{2} = \angle ABC$$
(Since, $$OB$$ is the bisector of $$\angle B$$)
Hence, proved.
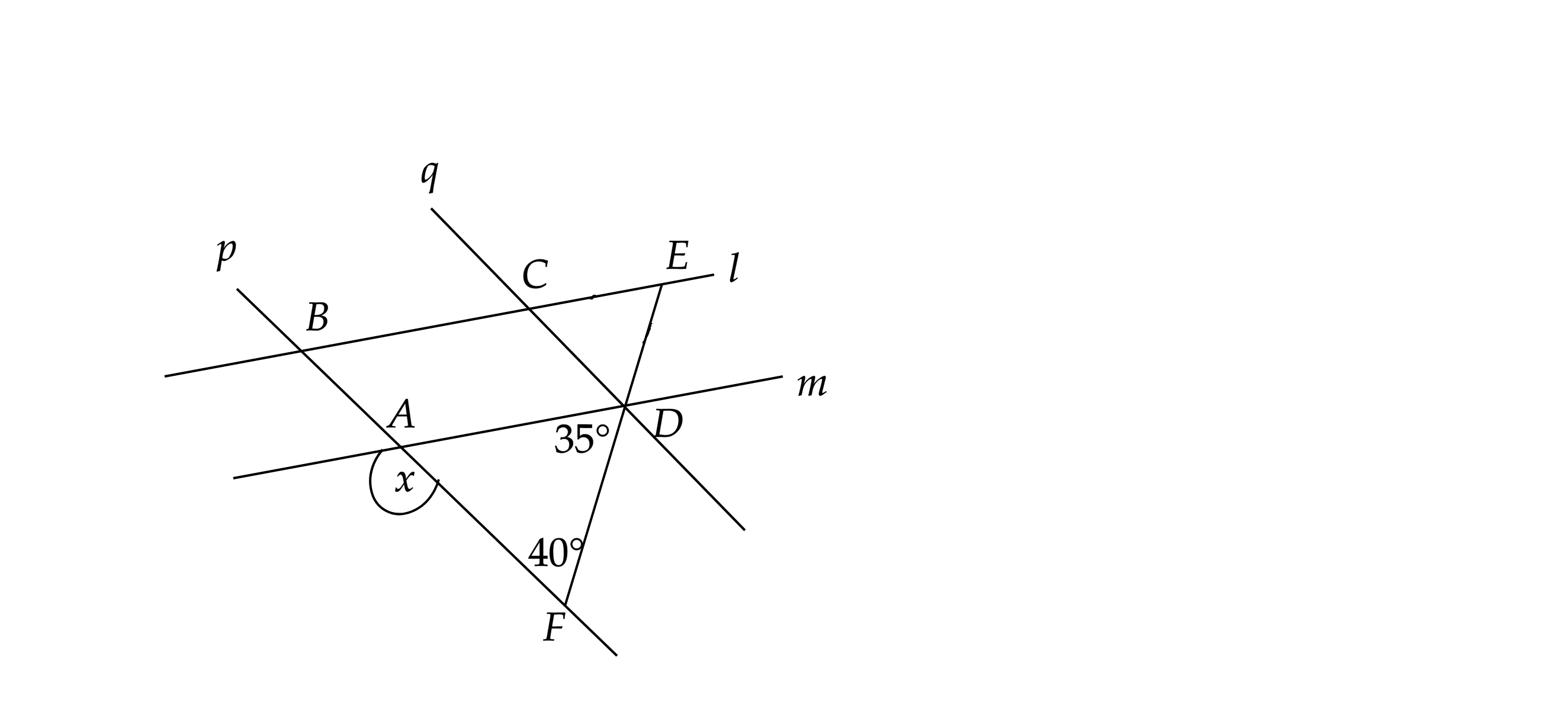
In the figure. Find x , If $$l\parallel m$$ & $$p\parallel q$$ .
Prove that the median to the base of an isosceles triangle is perpendicular to the base.
Let ABC is an isosceles triangle with AB=AC and let AD be the median to the base BC.then D is the mid-point of BC.
$$\Delta ABD\cong \Delta ADC$$ by SSS
so, $$\angle ADC=\angle ADB=x$$
$$\therefore \angle ADB+\angle ADC=180^{\circ}$$
$$x+x=180$$
$$x=\dfrac{180}{2}=90^{\circ}$$
$$\therefore \angle ADB=\angle ADC=90^{\circ}$$
If $$\Delta$$ABC is right-angled at B, then show that $$AB^2+BC^2=AC^2$$.
In the given figure, $$PQ || RT$$. Find the value of $${a} + {b}$$.
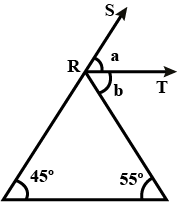
Name the type of the triangle:
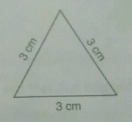
$$\triangle PQR$$ such that $$PQ = QR = PR = 5\ cm$$
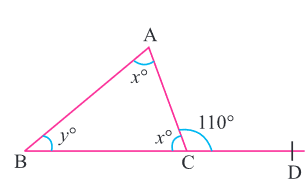
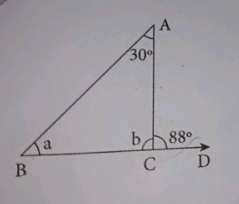
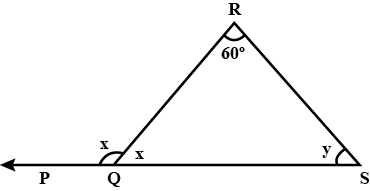
$$\angle ACD$$ is an exterior angle of $$\Delta ABC$$ the measure of $$\angle A$$ and $$\angle B$$ are equal. If $$\angle ACD = {140^ \circ }$$, find the measure of the angles $$\angle A$$ and $$\angle B$$
Name the types of following triangles :
$$\triangle XYZ$$ with $$m\angle Y = 90^{\circ}$$ and $$XY = YZ$$.
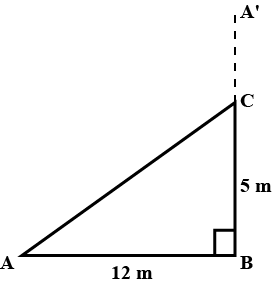
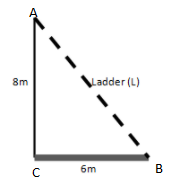
A $$15m$$ long ladder reached a window $$12m$$ high from the ground on placing it against a wall . Find the distance of the foot of the ladder from the wall .
Using Pythagoras theorem in $$\triangle ABC$$,
$$AC^2=AB^2+BC^2$$
$$15^2=AB^2+12^2$$
$$AB^2=225-144$$
$$AB^2=81$$
$$AB=9m$$
Hence, the distance of the foot of ladder from the wall is $$9m$$.
The hypotenuse of a right triangle is $$1$$ metres more than twice the shortest side. If the third side is $$7$$ metres less than the hypotenuse, find the sides of the triangle.
In a rectangle $$ABCD$$, prove that
$${AC}^{2}+{BD}^{2}={AB}^{2}+{BC}^{2}+{CD}^{2}+{DA}^{2}$$
To prove:
$$AC^2+BD^2=AB^2+BC^2+CD^2+DA^2$$
Given:
A rectangle $$ABCD$$
Consider the diagram shown above.
Applying the Pythagoras theorem in the two right angled triangles:
In $$\triangle ABC$$,
$$AC^2=AB^2+BC^2$$....(1)
In $$\triangle BAD$$,
$$BD^2=AB^2+DA^2$$-----(2)
Adding (1) and (2)
$$\ AC^2+BD^2= AB^2+BC^2+AB^2+DA^2$$
Since, the given figure is a rectangle,
$$AB=CD$$
$$AB^2=CD^2$$
Therefore,
$$ AC^2+BD^2=AB^2+BC^2+CD^2+DA^2\quad \quad [Hence\ proved]$$
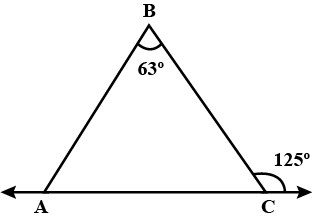
"In the given figure ,$$\angle BAC$$ is $${62^ \circ }$$ says Sita . Do you agree with her?
Consider the given figure,
$$\angle ABC={{63}^{0}}$$
Let $$\angle ABC={{x}^{0}}$$ and $$\angle ACB={{y}^{0}}$$
Now,
$$ \angle ACB+{{125}^{0}}={{180}^{0}} $$
$$ \angle ACB={{180}^{0}}-{{125}^{0}} $$
$$ \angle ACB={{55}^{0}} $$
In $$\Delta ABC$$
$$ \angle ABC+\angle ACB+\angle CAB={{180}^{0}} $$
$$ {{63}^{0}}+{{55}^{0}}+\angle CAB={{180}^{0}} $$
$$ \angle CAB={{180}^{0}}-{{118}^{0}} $$
$$ \angle CAB={{62}^{0}} $$
The length of hypotenuse of a right angled triangle is $$15$$. Find the length of the median of the hypotenuse.
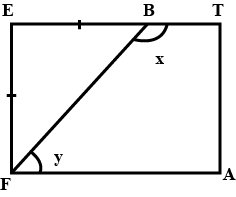
A playground is in the form of a rectangle FATE. Two players are standing at the points F and B. Where EF=EB Find the values of x and y.
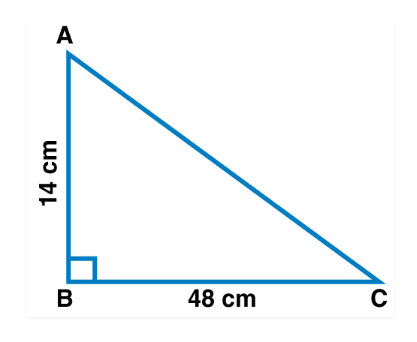
In $$\triangle ABC,\angle B$$ is a right angle. If $$AB=8$$ and $$BC=6$$. find $$AC$$.
In an isosceles triangle, the base is two third of each of other two equal sides. If the perimeter of the triangle is $$24 \ m$$, find the length of all the three sides.
A boat in a circular lakes lies at the center, about $$10m$$ away from a bridge lying in $$40$$ m distance across the circular lake. How much distance will boat have to reach to the extreme point of the left side of the bridge?
Say boat is $$AC=10m$$ away from bridge $$AB=40m$$ then
Boat have to travel distance $$BC$$.
Now,
$$BC^2=AC^2+AB^2$$
$$BC^2=10^2+40^2$$
$$BC^2=100+1600$$
$$BC=\sqrt{1700}=41.23m$$
$$\Delta A B C$$ is an isosceles triangle with $$A B = A C . AD$$ bisects $$\angle A$$ . Prove that $$\angle B = \angle C$$
Given : $$AB=AC$$ & $$AD$$ bisects $$\angle A$$
To prove : $$\angle B=\angle C$$
Proof :
In $$\Delta ABD$$ & $$\Delta ADC$$
$$AB=AC$$ (given)
$$\angle BAD=\angle DAC$$ (given)
$$AD=AD$$ (common)
Hence $$\angle ABD$$ is congruento $$\angle ADC$$ by the side-angle-side rule.
Therefore
$$\angle ABD=\angle ACD$$
$$\Rightarrow$$ $$\angle B=\angle C$$
Hence proved.
In a $$\Delta \angle ABC,\,\angle ACB$$ and the bisectors of $$\angle ABC$$ and $$\angle ACB$$ at $$O$$ such that $$\angle BOC = {120^0}$$
show that $$\angle A = \angle B = \angle C = {60^0}$$
Given
In $$\Delta ABC$$
$$\angle ABC= \angle ACB$$
Divide both sides by $$2$$
$$\displaystyle \frac{1}{2}\angle ABC = \frac{1}{2} \angle ACB$$
$$\Rightarrow \angle OBC= \angle OCB$$
$$\displaystyle \angle BOC= 90^{\circ}+\frac{1}{2}\angle A$$
$$120-90= \dfrac{1}{2}\angle A$$
$$30= \dfrac{1}{2}\angle A$$
$$\angle A = 60$$
$$\angle A+\angle ABC+\angle ACB=180^{\circ}$$
$$2\angle ABC=120$$
$$\angle ABC=60$$
$$\angle ACB=60$$
$$\angle A=\angle B=\angle C=60^{\circ}$$
Hence Proved
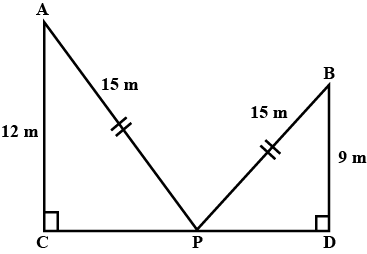
In the given figure, angle $$ACP = \angle BDP = 90^{o},\ AC=12\ m,\ BD=9\ m$$ and $$PA=PB=15\ m$$. Find
(i) $$CP$$
(ii) $$PD$$
(iii) $$CD$$
It is given that
$$ACP = ∠BDP = 90°$$
$$AC = 12 m$$
$$BD = 9 m$$
$$PA= PB = 15 m$$
(i) In the right angled triangle ACP
$$AP^2 = AC^2 + CP^2$$
Substituting the values
$$15^2 = 12^2 + CP^2$$
By further calculation
$$225 = 144 + CP^2$$
$$CP^2 = 225 – 144 = 81$$
So we get
$$CP = √81 = 9 m$$
(ii) In the right angled triangle BPD
$$PB^2 = BD^2 + PD^2$$
Substituting the values
$$152 = 92 + PD^2$$
By further calculation
$$225 = 81 + PD^2$$
$$PD^2 = 225 – 81 = 144$$
So we get
$$PD = √144 = 12 m$$
(iii) We know that
$$CP = 9 m$$
$$PD = 12 m$$
So we get
$$CD = CP + PD$$
Substituting the values
$$CD = 9 + 12 = 21 m$$
$$ACP = ∠BDP = 90°$$
$$AC = 12 m$$
$$BD = 9 m$$
$$PA= PB = 15 m$$
(i) In the right angled triangle ACP
$$AP^2 = AC^2 + CP^2$$
Substituting the values
$$15^2 = 12^2 + CP^2$$
By further calculation
$$225 = 144 + CP^2$$
$$CP^2 = 225 – 144 = 81$$
So we get
$$CP = √81 = 9 m$$
(ii) In the right angled triangle BPD
$$PB^2 = BD^2 + PD^2$$
Substituting the values
$$152 = 92 + PD^2$$
By further calculation
$$225 = 81 + PD^2$$
$$PD^2 = 225 – 81 = 144$$
So we get
$$PD = √144 = 12 m$$
(iii) We know that
$$CP = 9 m$$
$$PD = 12 m$$
So we get
$$CD = CP + PD$$
Substituting the values
$$CD = 9 + 12 = 21 m$$
Show that $$(m^{2} - 1), (2m), m^{2} + 1$$ always form a pythagoran triplet.
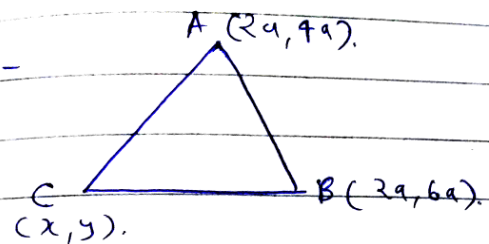
If A (2a,4a) and B (2a,6a) are two vertices of a equilateral triangle ABC then the vertex C is given by
$$AB=\sqrt{(2a-2a)^{2}+(6a-4a)^{2}}=2a$$
then $$BC=2a=\sqrt{(x-2a)^{2}+(y-6a)^{2}}$$
also
$$AC=2a=\sqrt{(x-2a)^{2}+(y-4a)^{2}}$$
on solving,
$$ x=(\sqrt{3}+2)a\ y=5a$$
$$c((\sqrt{3}+2)a,5a)$$
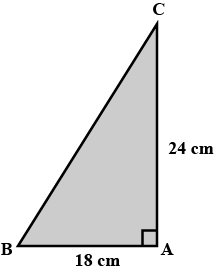
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if $$AB=18$$ and $$AC=24$$ cm.
It is given that
$$\triangle ABC$$ is right-angled at vertex $$A$$
$$AB = 18\ cm$$ and $$AC = 24\ cm$$
Using Pythagoras Theorem
$$BC^2 = AB^2 + AC^2$$
Substituting the values
$$BC^2 = 18^2 + 24^2$$
By further calculation
$$BC^2 = 324 + 576 = 900$$
$$BC = \sqrt {900} = \sqrt{(30 × 30)}$$
So we get, $$BC= 30\ cm$$
In $$\triangle {ABC}$$, if $$AD$$ is the median, then show that $${AB}^{2}+{AC}^{2}=2({AD}^{2}+{BD}^{2})$$
In $$\Delta PQR$$, if $$PR^2 = PQ^2 + QR^2$$, prove that $$\angle Q$$ is right angle.
This is converse of Pythagoras theorem
We can prove this contradiction sum $$q^2 = p^2+r^2$$ in $$\Delta P QR$$ while triangle is not a rightangle
Now consider another triangle $$\Delta ABC$$ we construct $$\Delta ABC$$ $$AB = q \quad CB = b$$ and C is a Right angle
By the Pythagorean theorem $$(AC)^2 = p^2 + r^2$$
But we know $$p^2 + r^2 = q^2$$ and $$q=PR$$
So $$(AB)^2 = p^2 + r^2 = (SR)^2$$
Since $$PQ$$ and $$AB$$ are length of sides we can take positive square roots
$$AC = PQ$$
All the these sides $$\Delta ABC$$ are congruent to $$\Delta PQR$$
So they are congruent by sss theorem
The sides of a triangle are $$4 cm, 60 cm, 61 cm$$. Verify that it is a right angle triangle or not.
Area of a regular hexagon of side $$ a$$ cm is the sum of the $$5$$ equilateral $$\Delta$$ with side $$a$$ cm. Is this statement true or false ?
It can be observed that a regular hexagon consist of six equilateral triangles.
Area of regular hexagon$$=6\times[$$ area of equilateral $$\Delta$$ with side length equal to $$a\ cm]$$.$$\therefore$$Therefore the given statement is false.
From the adjacent figure find the value of (i) $$\angle PRS$$ (ii) $$\angle PTS$$ (iii) $$\angle STR$$ (iv) $$\angle PRQ$$
From $$\triangle{PQR}, \angle{RPQ}+\angle{PQR}+\angle{PRQ}={180}^{\circ}$$ using angle sum property,
$$\Rightarrow {50}^{\circ}+{35}^{\circ}+\angle{PRQ}={180}^{\circ}$$
$$\Rightarrow \angle{PRQ}={180}^{\circ}-{85}^{\circ}={95}^{\circ}$$
As $$QS$$ is a straight line, $$\angle{QRS}={180}^{\circ}$$
$$\Rightarrow \angle{QRS}=\angle{QRT}+\angle{TRS}$$
$$\Rightarrow {180}^{\circ}={95}^{\circ}+\angle{TRS}$$
$$\Rightarrow \angle{TRS}={180}^{\circ}-{95}^{\circ}={85}^{\circ}$$
In $$\triangle{TRS}, \angle{TRS}+\angle{RST}+\angle{STR}={180}^{\circ}$$
$$\Rightarrow {85}^{\circ}+{45}^{\circ}+\angle{STR}={180}^{\circ}$$
$$\Rightarrow \angle{STR}={180}^{\circ}-{130}^{\circ}={50}^{\circ}$$
Again $$PR$$ is a straight line and $$R$$ is a point on the line $$PR$$
$$\Rightarrow \angle{PTR}={180}^{\circ}$$
$$\Rightarrow \angle{PTS}+\angle{STR}=\angle{PTR}$$
$$\Rightarrow \angle{PTS}+{50}^{\circ}={180}^{\circ}$$
$$\therefore \angle{PTS}={180}^{\circ}-{50}^{\circ}={130}^{\circ}$$
Hence
$$\left(i\right)\angle{PRS}=\angle{TRS}={85}^{\circ}$$
$$\left(ii\right)\angle{PTS}={130}^{\circ}$$
$$\left(iii\right)\angle{STR}={50}^{\circ}$$
$$\left(iv\right)\angle{PRQ}={95}^{\circ}$$
In the figure, find the area of $$\triangle {PQR}$$ and the height $$PS$$.
As area of right angled triangle$$=\dfrac{1}{2}$$(Base)(Height)
$$\Rightarrow ar(\Delta PQR)=ar(QTR)-ar(PQT)=\dfrac{1}{2}(QT)(TR)-\dfrac{1}{2}(QT)(PT)$$
$$=\dfrac{1}{2}(QT)(TR-PT)=\dfrac{1}{2}(QT)(PR)=\dfrac{1}{2}(12)(15)=90cm^2$$
$$\Rightarrow \dfrac{1}{2}(PS)(QR)=90$$
$$\Rightarrow PS\times 20=180$$
$$\Rightarrow PS=9$$cm.
In an equilateral $$\triangle ABC$$, if $$AD \bot BC$$ then prove that $$AD^{2}=3\ BD^{2}$$
Let each side be a unit
then height $$AD=\cfrac{\sqrt3}{2}a\\AD^2=(\cfrac{\sqrt3}{2}a)^2=\cfrac{3}{4}a^2$$
and $$BD^2=\cfrac{a^2}{4}$$
$$\Rightarrow \cfrac{AD^2}{BD^2}=\cfrac{3a^2}{4}\div\cfrac{a^2}{4}=3\\ \Rightarrow AD^2=3BD^2$$
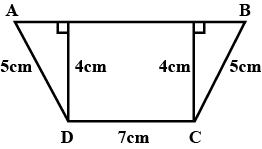
$$ABCD$$ is a trapezium in which $$AB\parallel DC$$, $$DC=7cm$$ distance between $$AB$$ and $$DC$$ is $$4cm$$. Find $$AB$$.
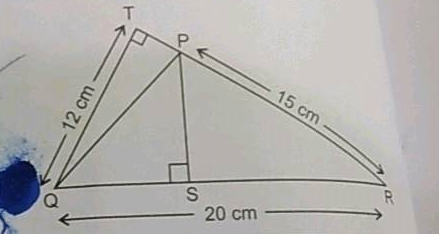
Calculate the area of the quadrilateral $$PQRS$$ shown in the adjoining figure, given that $$PQ=8\ cm, RQ=17\ cm, \angle{RPQ}={90}^{o}, RS=6\ cm$$ and $$\angle {PRS}={90}^{o}$$.
$$ \rightarrow $$ In $$\triangle PQR, PR^{2} = PQ^{2}+QR^{2} = 8^{2}+17^{2} = 64+289 = 353$$
In $$ \triangle PRS, PR^{2} = RS^{2}+PS^{2} \Rightarrow PS^{2} = 353-36 = 317 $$
Now $$ ar(PQRS) = ar(\triangle PQR)+ar(\triangle PRS) = \frac{1}{2}(8\times 17+6\times \sqrt{317})$$
$$ = 68+3\sqrt{317} $$
The equation of two equal sides of an isosceles triangle are $$7x-y+3=0$$ and $$x+y+3=0$$ and its third side is passes through the point $$(1,\ -10) $$. The equation of the third side is
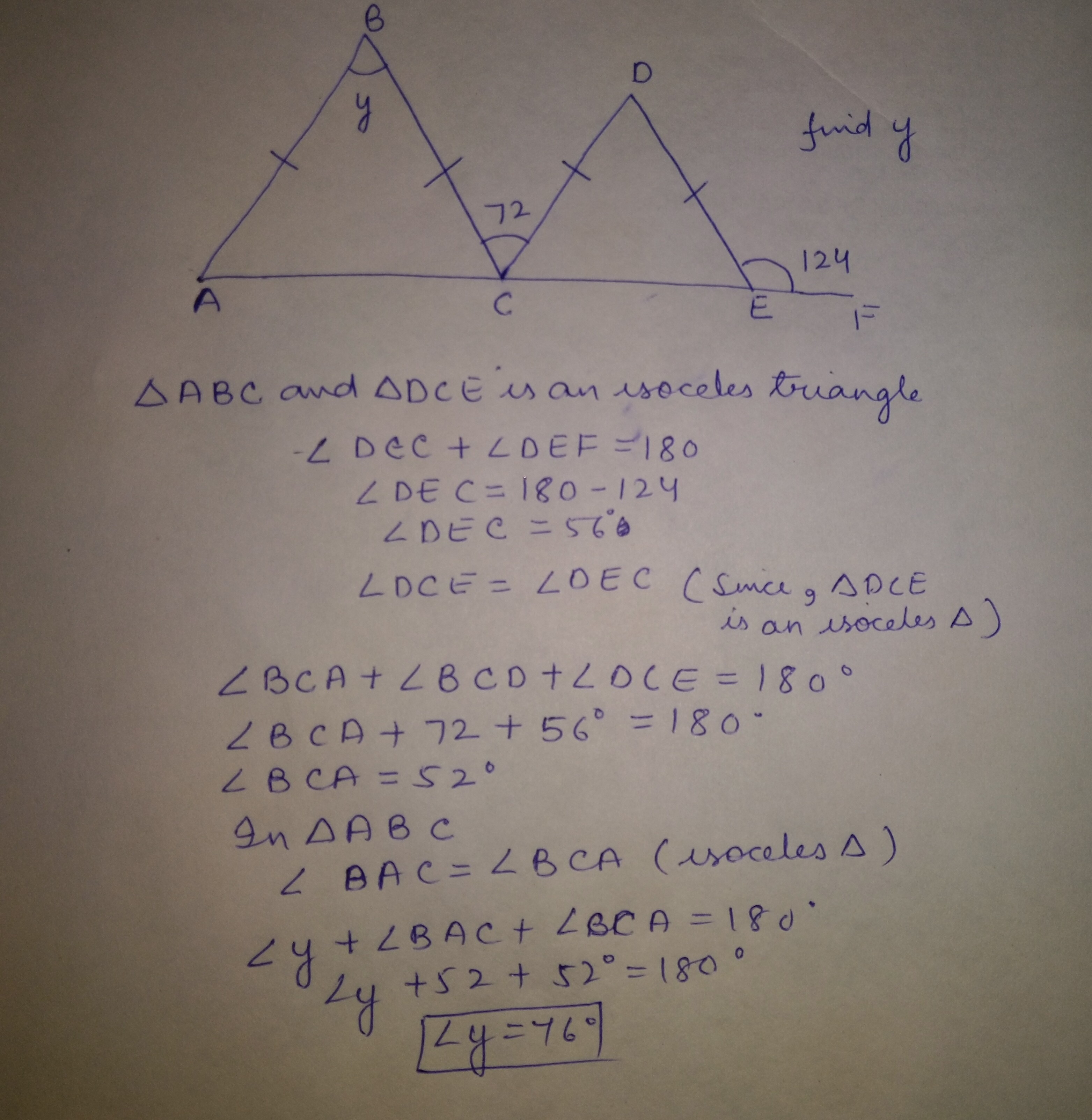
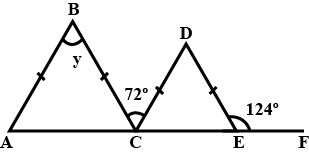
Triangles $$ABC$$ and $$CDE$$ are isosceles triangles, $$ACEF$$ is a straight line. Find the value of $$y$$.
Find the values of $$\angle a$$ $$\angle b$$ in the figure given below.
In an equilateral triangle with side '$$a$$', prove that the area of the triangle is $$\dfrac{\sqrt{3}}{4} a^2$$.
Proof- Since all the $$3$$ sides of an equilateral triangle are same $$AB=BC=CA=a$$
For altitude of $$\triangle ABC$$
Draw a $$\bot$$ from point $$C$$ on $$AB$$.
So that $$CO\bot AB$$. Let $$OC=h$$
In $$\triangle AOC$$
By using Pythagoras Theorem
$$AC^2=AO^2+OC^2$$
$$OC^2=AC^2-AO^2$$
$$h^2=a^2-\left(\dfrac{a}{2}\right)^2$$
$$h^2=a^2-\dfrac{a^2}{4}$$
$$h^2=\dfrac{3a^2}{4}\Rightarrow h=\dfrac{\sqrt{3}}{2}a$$
Now Area of $$\triangle ABC=\dfrac{1}{2}\times Base\times Height$$
$$=\dfrac{1}{2}\times a\times \dfrac{\sqrt{3}}{2}a$$
Area = $$\dfrac{\sqrt{3}}{4}a^2$$
So Area of equilateral $$\triangle$$ comes is $$\dfrac{\sqrt{3}}{4}a^2$$
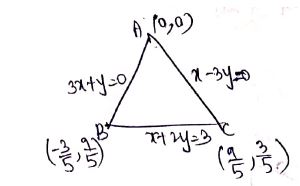
The sides of a triangle are equal and have equations 2x-y=0,3x+y=0 ,x-3y+10=0, respectively find the equation of three medians of the triangle and verify that they are concurrent
$$\Delta ABC $$ is a equilateral triangle.Radius=20. Find AB
In the given figure, the side $$QR$$ of $$\Delta PQR$$ is produced to a point $$S$$. If the bisectors of $$\angle PQR$$ and $$\angle PRS$$ meets at point $$T$$, then prove that $$\angle QTR=\dfrac{1}{2}\angle QPR$$
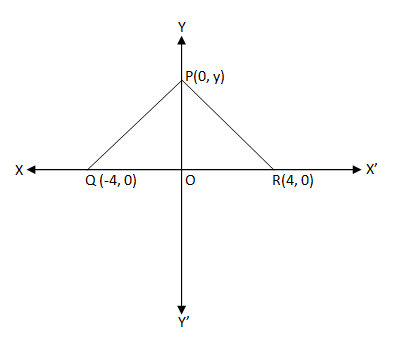
The base $$QR$$ of an equilateral triangle $$PQR$$ lies on x-axis. The coordinates of the point $$Q$$ are $$(-4,0)$$ and origin is the midpoint of the base. Find the coordinates of the points $$P$$ and $$R$$.
We have,
$$PQR$$ is an equilateral triangle such that $$QR$$ lies on $$x-axis$$.
$$O$$ is the midpoint of $$QR$$.
So,
$$OQ=QR=4\ units.$$
$$\Rightarrow $$ Coordinates of point $$R$$ are $$\left( 4,0 \right)$$.
Now,
Point $$P$$ lies on the $$y-axis$$.
Let the coordinate of point $$P$$ be $$\left( 0,y \right).$$
So,
$$PQ=QR$$
$$ \Rightarrow \sqrt{{{\left( 0+4 \right)}^{2}}+{{\left( y-0
\right)}^{2}}}=\sqrt{{{\left( 4+4 \right)}^{2}}+{{0}^{2}}} $$
$$ \Rightarrow \sqrt{16+{{y}^{2}}}=\sqrt{64} $$
$$ \text{On}\,\text{squaring}\,\text{both}\,\text{side}\,\text{and}\,\text{we}\,\text{get,} $$
$$ \Rightarrow 16+{{y}^{2}}=64 $$
$$ \Rightarrow {{y}^{2}}=64-16 $$
$$ {{\Rightarrow }y^{2}}=48 $$
$$ \Rightarrow y=\pm 4\sqrt{3} $$
Hence, the coordinate of points $$P$$ are $$\left( 0,4\sqrt{3}
\right)$$ above $$x-axis.$$
And $$\left( 0,-4\sqrt{3} \right)$$ below $$x-axis$$.
The equation of the base of an equilateral triangle with vertex at $$(2,-1)$$ is $$x+y-2=0$$. Then find its length of sides.
The base of an isosceles triangle is 18 cm and its area is 108 cm. Find its perimeter.
In isosceles $$\Delta $$ has perimeter $$30\ cm$$ and each of the equal sides is $$12\ cm$$. Find the area of the $$\Delta $$.
Find the area of the equilateral triangle which has the height is equal to $$\dfrac{\sqrt{3}}{2}$$.
The side of an equilateral triangle is $$3\sqrt{3}$$ cm. Find the area of the triangle [Take \sqrt{3} = 1.732]
Area of equation $$ \Delta le = \frac{\sqrt{30}^{2}}{4} = \frac{\sqrt{3}}{4} (3\sqrt{3})^{2}== \frac{27\sqrt{3}}{4} = 11.68 cm^{2}$$
If non-parallel sides of an isosceles trapezium are prolonged, an equilateral triangle ABC with sides of $$6 cm$$ would be formed. Knowing that the trapezium is half the height of the triangle, calculate the area of the trapezium.
Prove that the three angles of an equilateral triangle are equal.
Given:-
let ABC is an equilateral triangle
$$\therefore AB=BC=AC$$
(all sides of an equilateral triangle are equal)
To prove:
$$\angle A= \angle B= \angle C$$
Proof:
$$AB=AC$$
$$\implies \angle B= \angle C $$ .......(1) $$[\because$$ angles opposite to equal sides are equal $$]$$
$$BC=AC$$
$$\implies \angle A= \angle B$$ .........(2) $$[\because$$ angles opposite to equal sides are equal $$]$$
From (1) and (2)
$$\angle A= \angle B= \angle C$$
Hence proved.
Can you prove this that in a right-angled triangle:
$$\text{Base}^{ 2 }+{ \text{Perpendicular} }^{ 2 }={ \text{Hypotenuse} }^{ 2 }$$
Let us consider a right-angled triangle $$ABC$$ with a right angle at $$B.$$
Construction: Draw $$BD\perp AC.$$
In $$\Delta ADB$$ and $$\Delta ABC,$$
$$AB=AB$$ [Common side]
$$\angle ADB=\angle ABC$$ [Both are $$90^\circ$$]
$$\angle A=\angle A$$ [Common angle]
By $$ASA$$ condition for similarity,
$$\Delta ADB\sim \Delta ABC$$
$$\Rightarrow \dfrac{AB}{AC}=\dfrac{BD}{BC}=\dfrac{AD}{AB}$$
$$\Rightarrow \dfrac{AB}{AC}=\dfrac{AD}{AB}$$
$$\Rightarrow AB^2=AD.AC\quad\quad\quad\quad\dots(i)$$
In $$\Delta BDC$$ and $$\Delta ABC,$$
$$BC=BC$$ [Common side]
$$\angle BDC=\angle ABC$$ [Since both are $$90^o$$]
$$\angle C=\angle C$$ [Common angle]
By $$ASA$$ condition for similarity,
$$\Delta BDC \sim\Delta ABC$$
$$\Rightarrow \dfrac{BC}{AC}=\dfrac{DC}{BC}=\dfrac{BD}{AB}$$
$$\Rightarrow \dfrac{BC}{AC}=\dfrac{DC}{BC}$$
$$\Rightarrow BC^2=AC.DC\quad\quad\quad\quad\dots(ii)$$
Adding equation $$(i)$$ and $$(ii)$$,
$$AB^2+BC^2=AD.AC+AC.DC$$
$$\Rightarrow AB^2+BC^2=AC(AD+DC)$$
$$\Rightarrow AB^2+BC^2=AC.AC$$
$$\Rightarrow AB^2+BC^2=AC^2$$
$$\Rightarrow \text{Base}^2+\text{Perpendicular}^2=\text{Hypotenuse}^2$$
Find angle $$x$$ in each figure :
A lawn in a garden is in the shape of an equilateral triangle. If the length of the one side of the equilateral triangle is 75 m, find the of cost of fencing at the rate of Rs. 12 per metre?
An isosceles triangle has perimeter $$36 cm $$ and each of its equal sides is $$13 cm$$ long . The area of the triangle is
The base of an equilateral triangle with side 2$$a$$ lies along the $$y$$ -axis such that the mid-point of the base is at the origin. Find vertices of the triangle.
If the ratio of the altitude and area of a triangle is $$3:12$$, then find the length of the base of triangle.
As Area of traingle , $$ A =\frac{1}{2}\times base(b)\times Atiatude (h)$$
Given ,$$\frac{h}{A}=\frac{3}{12}\Rightarrow \frac{h}{\frac{1}{2}\times b\times h}=\frac{1}{4}\Rightarrow \frac{2}{b} - \frac{1}{4}\Rightarrow b=8$$
In an isosceles triangle $$ABC$$, one of the equal sides $$BC$$ and the base $$AC$$ are in the ratio of $$7:5$$. If the perimeter of the triangle is $$532\ cm$$, find the measures of all the three sides.
$$PQRS$$ is a square and $$\Delta TSR$$ is an isosceles triangle with $$TS=TR$$. Prove that $$PT=QT$$.
As opposite angles to equal sides of a triangle are equal, $$\Rightarrow \angle TSR = \angle TRS $$
In $$\Delta TSP $$ and $$ \Delta TRQ,$$
TS = TR (Given)
$$ \angle TSP = \angle TRQ (TSP\angle = 90^{\circ} + \angle TSR =90^{\circ} +\angle TRS = \angle TRQ)$$
SP = RQ (sides of square are equal)
$$\Rightarrow$$ By S.A.S concurrency, $$\Delta $$TSP $$\cong \Delta $$ TRQ
As in congruent triangles , corresponding sides are equal, $$ \Rightarrow $$ PT = TQ
Prove that the lines represented by $$3x^2-8xy-3y^2=0$$ and $$x+2y=3$$ form the sides of an isosceles right angled triangle.
$$\Rightarrow 3x^2-9xy+xy-3y^2=0$$
$$\Rightarrow 3x(x-3y)+y(x-3y)=0$$
$$\Rightarrow (3x+y)(x-3y)=0$$
Lines are $$3x+y=0$$ and $$x-3y=0$$
(Refer to Image)
Vertices are $$(0,0)$$
$$x+2y=3$$ $$y=-3x$$
$$x-3y=0$$ $$x+2(-3x)=3$$
$$x=3y$$ $$-5x=3$$
$$3x+2y=3$$ $$x=-3/5, y=-3(-3/5)=9/5$$
$$5y=3$$
$$y=3/5$$ $$x=3(3/5)$$
$$x=9/5$$
$$|AB|=|AC|$$
$$\triangle ABC$$ is isosceles triangle.
$$|AB|^2=\sqrt {\left(\cfrac {3}{5}\right)+\left(\cfrac {9}{5}\right)^2}=\cfrac {90}{25}$$
$$\Rightarrow |AC|^2=\cfrac {90}{25}$$
$$\Rightarrow AB^2+AC^2=\cfrac {180}{25}$$
$$\Rightarrow |BC|=\sqrt {\left(\cfrac {12}{5}\right)^2+\left(\cfrac {6}{5}\right)^2}=\sqrt {\cfrac {144+36}{25}}=\sqrt {\cfrac {180}{25}}$$
$$\Rightarrow BC^2=\cfrac {180}{25}$$
$$\Rightarrow AB^2+AC^2=BC^2$$
$$\therefore$$ $$\triangle ABC$$ is an isosceles right angles triangle.
In an equilateral $$\triangle BAC$$, point $$D$$ is the midpoint of side $$BC$$. Prove that $$4AD^{2}=3BC^{2}$$.
Let AB,BC,ACBE equal
to a
D is the midpoint of
BC.
By Pythagoras theorem
$$AB^{2}=AD^{2}+BD^{2}$$
$$a^{2}=AD^{2}+(a/2)^{2}$$
$$a^{2}-\frac{a^{2}}{4}=AD^{2}$$
$$\frac{3a^{2}}{4}=AD^{2}$$
But AB =a
$$3AB^{2}=4AD^{2}$$
$$\therefore $$ $$4AD^{2}=3AB^{2}$$
Find the perimeter of the following shape:
An equilateral triangle of side $$11\ \text{cm}$$
In the given figure AD divides $$\angle BAC$$ in the ration 1 : 3 and AD = DB betermine the value of X.
A right triangle ABC with sides $$7$$cm, $$24$$cm and $$25$$cm is revolved about the side $$24$$cm. Find the volume of the solid so obtained.
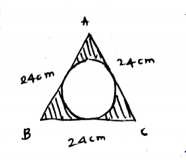
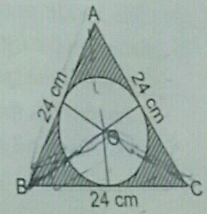
In an equilateral triangle of side $$24\ cm$$, a circle is inscribed touching its sides. Find the area of the remaining portion of the triangle.
We have $$R=\cfrac{A}{s}$$
$$A=$$Area of triangle
$$s=$$ Semi perimeter
$$R=$$ Radius of incircle
$$s=\cfrac{24\times 3}{2}=36\ cm$$
$$A=(\sqrt 3/4)24^2=144\sqrt 3\ cm^2$$
$$R=\cfrac{144\sqrt 3}{36}=4\sqrt3\ cm$$
Area of in circle$$=\pi R^2=\pi\times 4^2\times 3=48\pi\ cm^2$$
Area of remainig portion$$=(144\sqrt3-48\pi)\ cm^2$$
Name the following triangle :
$$XY=7\ cm, YZ=7\ cm, ZX=4\ cm$$
Since 2 ridus are equal, therfore it is an isoscills triangle.
Do these sides that are given below form a right angle triangle?
$$2.5$$cm, $$6.5$$cm, $$6$$cm
In the case of a right-angled triangle, identify the side opposite to the right angle.
Prove that area of an equilateral triangle is equal to $$\dfrac{\sqrt{3}}{4}{a}^{2}$$, where $$a$$ is the side of the triangle.
Draw $$AD\bot BC$$
$$\Rightarrow \triangle{ABD}\cong\triangle{ACD}$$ by R.H.S
$$\therefore BD=DC$$ by CPCT
$$\because BC=a$$
$$\therefore BD=DC=\dfrac{a}{2}$$
In right angled triangle $$\triangle{ABD},\,{AD}^{2}={AB}^{2}-{BD}^{2}$$
$${AD}^{2}={a}^{2}-{\left(\dfrac{a}{2}\right)}^{2}={a}^{2}-\dfrac{{a}^{2}}{4}=\dfrac{3{a}^{2}}{4}$$
$$AD=\dfrac{a\sqrt{3}}{2}$$
Area of $$\triangle{ABC}=\dfrac{1}{2}\times BC\times AD=\dfrac{1}{2}\times a\times \dfrac{a\sqrt{3}}{2}=\dfrac{{a}^{2}\sqrt{3}}{4}$$
Prove that in a right angled triangle, square of the hypotenuse is equal to sum of the squares of other two sides.
$${\textbf{Step - 1: Proving similarity}}$$
$${\text{The triangle ABC is right angled at B}}$$
$${\text{In }}\vartriangle {\text{ABC and }}\vartriangle {\text{ADB,}}$$
$$\angle {\text{ADB = }}\angle {\text{ABC = 90}}^\circ $$
$$\angle {\text{BAD = }}\angle {\text{BAC (common)}}$$
$${\text{AB side common}}$$
$$\therefore {\text{ }}\vartriangle {\text{ABC }} \sim {\text{ }}\vartriangle {\text{ADB}}$$
$${\text{Similarly, in }}\vartriangle {\text{ABC and }}\vartriangle {\text{BDC}}$$
$$\angle {\text{BDC = }}\angle {\text{ABC = 90}}^\circ $$
$$\angle {\text{BCD = }}\angle {\text{BCA (common)}}$$
$${\text{BC side common}}$$
$$\therefore {\text{ }}\vartriangle {\text{ABC }} \sim {\text{ }}\vartriangle {\text{BDC}}$$
$${\textbf{Step - 2: Proving pythagoras theorem}}$$
$${\text{Since, }}\vartriangle {\text{ABC }} \sim {\text{ }}\vartriangle {\text{ADB}}$$
$$\dfrac{{{\text{AD}}}}{{{\text{AB}}}}{\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{AC}}}}{\text{ (sides are proportional)}}$$
$$ \Rightarrow {\text{ AD}} \times {\text{AC = A}}{{\text{B}}^{\text{2}}}{\text{ }} \to {\text{ Equation 1}}$$
$${\text{Also, }}\vartriangle {\text{ABC }} \sim {\text{ }}\vartriangle {\text{BDC}}$$
$$\dfrac{{{\text{CD}}}}{{{\text{BC}}}}{\text{ = }}\dfrac{{{\text{BC}}}}{{{\text{AC}}}}{\text{ (sides are proportional)}}$$
$$ \Rightarrow {\text{ CD}} \times {\text{AC = B}}{{\text{C}}^{\text{2}}}{\text{ }} \to {\text{ Equation 2}}$$
$${\text{Adding Equation 1 and Equation 2,}}$$
$$\left( {{\text{AD}} \times {\text{AC}}} \right){\text{ + }}\left( {{\text{CD}} \times {\text{AC}}} \right){\text{ = A}}{{\text{B}}^{\text{2}}}{\text{ + B}}{{\text{C}}^{\text{2}}}$$
$$ \Rightarrow {\text{ AC}}\left( {{\text{AD + CD}}} \right){\text{ = A}}{{\text{B}}^{\text{2}}}{\text{ + B}}{{\text{C}}^{\text{2}}}$$
$$ \Rightarrow {\text{ AC }} \times {\text{ AC = A}}{{\text{B}}^{\text{2}}}{\text{ + B}}{{\text{C}}^{\text{2}}}$$
$$ \Rightarrow {\text{ A}}{{\text{C}}^{\text{2}}}{\text{ = A}}{{\text{B}}^{\text{2}}}{\text{ + B}}{{\text{C}}^{\text{2}}}$$
$${\textbf{Hence, Proved}}$$
In the given figure,$$\angle{PRQ}=\angle{PQR},$$ then prove that $$\angle{PQS}=\angle{PRT}$$
State the kind of triangle in the adjoining figure.
Since are sides have equal length, therefore it is an equilateral triangle.
If in a triangle $$LMN$$:
$$\angle M=60^{o}, \angle N=60^{o}$$, find $$\angle L$$
Mention the kind of triangle also.
In a triangle LMN :-
$$\angle M=60^o$$, $$\angle N= 60^o$$
By angle sum property,
$$\angle M+\angle N+\angle L=180^o$$
$$\angle L=180^o-120^o=60^o$$
Since $$\angle M=\angle N=\angle L$$, therefore it is an equilateral triangle.
In a right-angled triangle the hypotenuse is of $$13$$ cm and the difference between the other sides is $$7$$ cm, then find the two sides.
Find the value of $$x$$
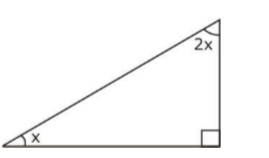
In the given figure, OO is right-angled.
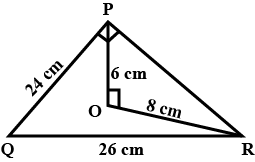
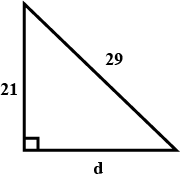
Solve
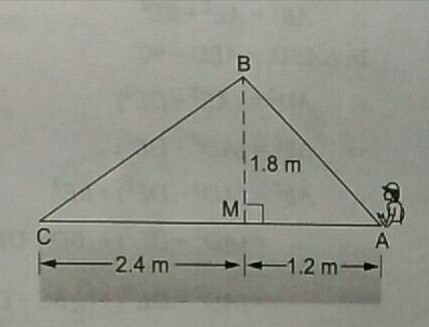
Naman is doing fly-fishing in a stream. The tip of his fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away from him and 2.4 m from the point directly under the tip of the rod. Find the length of the string.
Prove that each angle of an equilateral triangle is $$60^{\circ}$$.
The sides of a triangle is given below. Determine if it is a right angled triangle.
$$1.4 cm, 4.8 cm, 5 cm $$
The sides AB and AC of $$\Delta ABC$$ are produced to points E and D respectively. If Bisectors BO and CO of, $$\angle CBE\,\,and\,\,\angle BCD$$ respectively meet at point O, then prove that $$\angle BOC = {90^0} - \frac{1}{2}\angle BAC.$$
In $$UABC\ \hat {e}BAC=90^{o}, AB=AC seg APo$$ side $$BC, B-P-C$$. $$D$$ is any points on side $$BC$$. Prove that: $$2AD^{2}=BD^{2}+CD^{2}$$
In a triangle, if the square of one side is equal to the sum of the squares of other two sides, then the angle opposite to the first side is a right angle. Prove it
Given:- $$ABC$$ is a triangle
$${AC}^{2} = {AB}^{2} + {BC}^{2}$$
To prove:- $$\angle{B} = 90°$$
Construction:- Construct a triangle $$PQR$$ right angled at $$Q$$ such that, $$PQ = AB$$ and $$QR = BC$$
Proof:-
In $$\triangle{PQR}$$
$${PR}^{2} = {PQ}^{2} + {QR}^{2} \quad \left( \text{By pythagoras theorem} \right)$$
$$\Rightarrow {PR}^{2} = {AB}^{2} + {BC}^{2}..... \left( 1 \right) \quad \left( \because AB = PQ \text{ and } QR = BC \right)$$
$${AC}^{2} = {AB}^{2} + {BC}^{2} ..... \left( 2 \right) \quad \left( \text{Given} \right)$$
From equation $$\left( 1 \right) \& \left( 2 \right)$$, we have
$${AC}^{2} = {PR}^{2}$$
$$\Rightarrow AC = PR ..... \left( 3 \right)$$
Now, in $$\triangle{ABC}$$ and $$\triangle{PQR}$$
$$AB = PQ$$
$$BC = QR$$
$$AC = PR \quad \left( \text{From } \left( 3 \right) \right)$$
$$\therefore \triangle{ABC} \cong \triangle{PQR} \quad \left( \text{By SSS congruency} \right)$$
Therefore, by C.P.C.T.,
$$\angle{B} = \angle{Q}$$
$$\because \angle{Q} = 90°$$
$$\therefore \angle{B} = 90°$$
Hence proved.
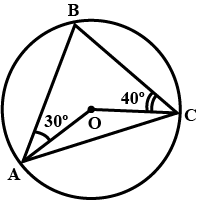
In the given figure, O is the centre of the circle . $$\angle OAB$$ and $$\angle OCB$$ are $$30^{ \circ }$$ and $$40^{ \circ }$$ respectively . Find $$\angle AOC$$. Show your steps of working
In $$ \triangle \mathrm{PQR}, \angle \mathrm{PQR}=90^{\circ} $$ if $$PR=15$$ and $$PQ=9cm$$ find $$QR$$
If the side of a triangle are in the ratio 3:4:5, prove that it is right -angled triangle.
Given the sides are in the ratio $$3:4:5.$$
Let $$ABC$$ be the given triangle.
Let the sides be $$3x, 4x$$ and hypotenuse be $$5x.$$
According to Pythagoras theorem,
$$AC^2 = BC^2+AB^2$$
$$BC^2+AB^2= (3x)^2+(4x)^2$$
$$= 9x^2+16x^2$$$$= 25x^2$$
$$AC^2 = (5x)^2 = 25x^2$$
$$AC^2 = BC^2 + AB^2$$
Hence $$ABC$$ is a right angled triangle.
Let $$ABC$$ be the given triangle.
Let the sides be $$3x, 4x$$ and hypotenuse be $$5x.$$
According to Pythagoras theorem,
$$AC^2 = BC^2+AB^2$$
$$BC^2+AB^2= (3x)^2+(4x)^2$$
$$= 9x^2+16x^2$$$$= 25x^2$$
$$AC^2 = (5x)^2 = 25x^2$$
$$AC^2 = BC^2 + AB^2$$
Hence $$ABC$$ is a right angled triangle.
In an isosceles triangle, angles opposite to equal sides are___ .
In an isosceles triangle, angles opposite to equal sides are equal.
Write the following statements:-
in $$\angle ABC,AB = 6\sqrt 3 $$ cm, $$AC = 12$$ cm, $$BC = 6$$ cm. Find measure of $$B$$.
Explain the following term.
Equilateral triangle.
Equilateral triangle is a triangle in which all sides are equal.
All angles of equilateral triangle are $$60^0$$.
In above figure $$\Delta ABC$$ is an equilateral triangle.
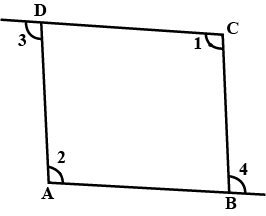
In the given figure, $$\angle 3$$ and $$\angle 4$$ are exterior angles of quadrilateral $$ABCD$$ at point $$D$$ and $$B$$ respectively, and $$\angle A = \angle 2,\angle C = \angle 1$$, prove that $$\angle 3 + \angle 4 = \angle 1 + \angle 2$$
Let us join $$A$$ and $$C$$.
We know that, exterior angle of a triangle is equal to sum of two opposite interior angles of that triangle.
Now, $$\angle 4$$ is the exterior angle of $$\triangle ABC$$
So,
$$\angle 4=\angle ACB+\angle CAB.........(1)$$
Again, $$\angle 3$$ is the exterior angle of $$\triangle ADC$$
So,
$$\angle 3=\angle ACD+\angle CAD.........(2)$$
Adding eq$$(1)$$ and eq$$(2)$$
$$\angle 4+\angle 3=\angle ACB+\angle CAB+\angle ACD+\angle CAD$$
$$\Rightarrow \angle 3+\angle 4=(\angle ACB+\angle ACD)+(\angle CAB+\angle CAD)$$
$$\Rightarrow \angle 3+\angle 4=\angle 1+\angle 2$$
$$Hence\ proved$$ .
Suppose a triangle is equilateral. prove that it is equi-angular.
In $$\triangle ABC$$, right angled at $$B,AC=20\ cm$$ and $$\tan{\angle ACB=\cfrac{3}{4}}$$, calculate the measure of $$AB$$ and $$BC$$.
Can $$(\angle ACB)=\dfrac{x}{y}=\dfrac{3}{4}$$
$$x=\dfrac{3y}{4}$$ -----(1)
Pythagoras theorem $$\Rightarrow x^2+y^2=20^2$$
$$\Rightarrow 9y^2+y^2=400$$
$$\Rightarrow 25y^2=16\times 400$$
$$\Rightarrow y^2=16\times 16$$
$$y=16cm=BC$$
$$\Rightarrow x=\dfrac{3y}{4}=12cm=AB$$
From the given figure, find $$x$$.
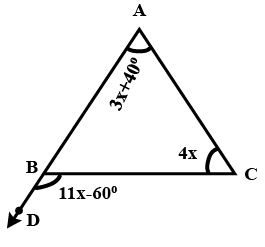
If $$AD$$ is perpendicular to $$BC$$, then find the length of $$AB$$.
In the right-angled $$\triangle PQR,\angle P={ 90 }^{ \circ }.$$ If $$l(PQ) = 24$$ cm and $$l(PR) = 10$$ cm, find the length of side $$QR?$$
Prove that in a right triangle,the square of the hypotenuse is equal to the sum of the square of the other sides.
Given:- A right triangle $$ABC$$ right angled at $$B$$.
To prove:- $${AC}^{2} = {AB}^{2} + {BC}^{2}$$
Construction:- Draw $$BD \perp AC$$
Proof:-
In $$\triangle{ABC}$$ and $$\triangle{ABD}$$
$$\angle{ABC} = \angle{ADB} \quad \left( \text{Each } 90° \right)$$
$$\angle{A} = \angle{A} \quad \left( \text{Common} \right)$$
$$\therefore \triangle{ABC} \sim \triangle{ABD} \quad \left( \text{By AA} \right)$$
$$\cfrac{AB}{AC} = \cfrac{AD}{AB} \quad \left( \because \text{Sides of similar triangles are proportional} \right)$$
$$\Rightarrow {AB}^{2} = AD \cdot AC ..... \left( 1 \right)$$
Similarly, in $$\triangle{ABC}$$ and $$\triangle{BCD}$$
$$\angle{ABC} = \angle{BDC} \quad \left( \text{Each } 90° \right)$$
$$\angle{C} = \angle{C} \quad \left( \text{Common} \right)$$
$$\therefore \triangle{ABC} \sim \triangle{BCD} \quad \left( \text{By AA} \right)$$
$$\therefore \cfrac{DC}{BC} = \cfrac{BC}{AC}$$
$$\Rightarrow {BC}^{2} = DC \cdot AC ..... \left( 2 \right)$$
Adding equation $$\left( 1 \right) \& \left( 2 \right)$$, we have
$${AB}^{2} + {BC}^{2} = AD \cdot AC + DC. AC$$
$$\Rightarrow {AB}^{2} + {BC}^{2} = AC \left( AD + DC \right)$$
$$\Rightarrow {AB}^{2} + {BC}^{2} = {AC}^{2}$$
Hence proved.
Check whether A(5,-2),B(6,4) and C(7,-2) are the vertices of an isosceles triangle.
If the area of an equilateral triangle is 21.2 sq.cm, find the length of its each side.
In the given figure, $$\angle A = 90^{\circ}$$ and $$AD \perp BC$$ If $$BD = 2 cm$$ and $$CD = 8 cm$$, find $$AD$$.
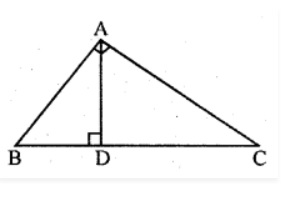
If two angles of a triangle are completely then what type of triangle will be formed.
Do these sides that are given below form a right angled triangle?
$$1.5$$cm, $$2$$cm, $$2.5$$cm
In the case of right angled triangles, identify the side opposite to right angle.
Let us consider, the larger side be the hypotenuse and also using Pythagoras theorem,
$$(Hypotenuse)^2=(Base)^2+(Perpendicular)^2$$$$1.5\ cm$$, $$2\ cm$$, $$2.5\ cm$$
In $$\Delta PQR$$, $$(PR)^2=(PQ)^2+(RQ)^2$$
L.H.S.$$=(25)^2=6.25$$cm
R.H.S.$$=(1.5)^2+(2)^2=2.25+4=6.25$$cm
Since, $$L.H.S.=R.H.S.$$
Therefore, the given sides are of the right angled triangle.
Right angle lies opposite to the greater side $$2.5\ cm$$
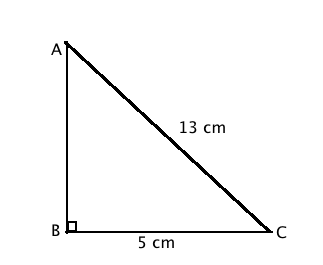
ABC is a triangle, right-angled at C. If AB $$=25$$cm and AC $$=7$$cm, find BC.
Do the sides $$2$$ cm, $$2$$ cm, $$5$$ cm form a right-angled triangle?
In the case of right-angled triangles, identify the side opposite to the right angle.
A tree is broken at a height of $$5$$m from the ground and its top touches the ground at a distance of $$12$$m from the base of the tree. Find the original height of the tree.
Let A'CB represents the tree before it broken at the point C and let the top A' touches the ground at A after it broke. Then $$\Delta$$ABC is a right angled triangle, right angled at B.
AB$$=12$$m and BC$$=5$$mUsing Pythagoras theorem, In $$\Delta$$ABC
$$(AC)^2+(AB)^2+(BC)^2$$
$$\Rightarrow (AC)^2=(12)^2+(5)^2$$
$$\Rightarrow (AC)^2=144+25$$
$$\Rightarrow (AC)^2=169$$
$$\Rightarrow AC=13$$m
Hence, the total height of the tree$$=AC+CB=13+5=18$$m.
A $$15$$ m long ladder reached a window $$12$$ m high from the ground on placing it against a wall at a distance of $$a$$ m. Find the distance of the foot of the ladder from the wall.
Let AC be the ladder and A be the window.
Given: $$AC=15$$m, $$AB=12$$m, $$CB=a$$mIn right angled triangle ACB,
$$(Hypotenuse)^2=(Base)^2+[Perpendicular)^2$$ [By Pythagoras theorem]
$$\Rightarrow (AC)^2=(CB)^2+(AB)^2$$
$$\Rightarrow (15)^2=(a)^2+(12)^2$$
$$\Rightarrow 225=a^2+144$$
$$\Rightarrow a^2=225-144=81$$
$$\Rightarrow a=\sqrt{81}=9$$cm
Thus, the distance of the foot of the ladder from the wall is $$9$$m.
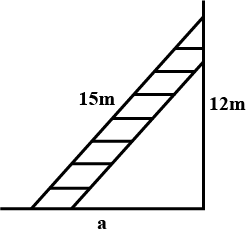
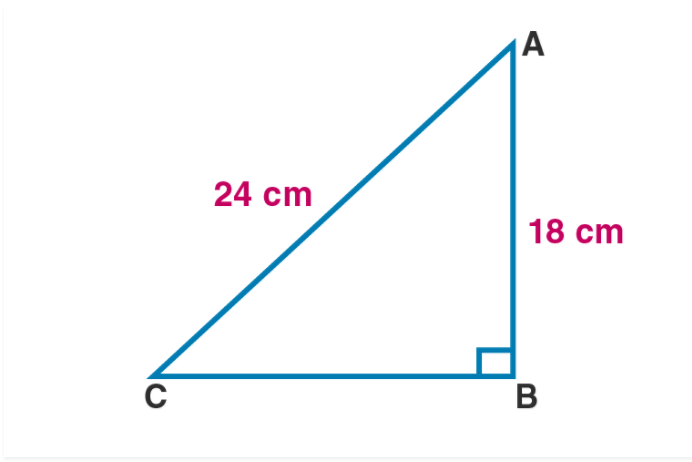
PQR is a triangle, right angled at P. If PQ $$=10$$ cm and PR $$=24$$ cm, then find QR.
Given: PQ$$=10$$cm, PR$$=24$$cm
Let QR be x cm.In right angled triangle QPR,
$$(Hypotenuse)^2=(Base)^2+(Perpendicular)^2$$ [By Pythagoras theorem]
$$\Rightarrow (QR)^2=(PQ)^2+(PR)^2$$
$$\Rightarrow x^2=(10)^2+(24)^2$$
$$\Rightarrow x^2=100+576=676$$
$$\Rightarrow x=\sqrt{676}=26$$cm
Thus, the length of QR is $$26$$cm.
In a $$ \Delta ABC, \angle ABC = \angle ACB $$ and the bisectors of $$ \angle ABC $$ and $$ \angle ACB $$ intersect at O such that $$ \angle BOC = 120^{\circ}.$$ Show that $$ \angle A = \angle B = \angle C = 60^{\circ}.$$
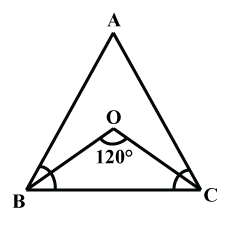
Fill in the blank:
In a $$ \Delta ABC $$ if $$ \angle A = \angle C, $$ then AB = .....
In $$\triangle ABC,$$
$$\angle A=\angle C$$ [ Given ]
We know, that, sides opposite to equal angles are also equal.
$$\therefore$$ $$AB=BC$$
$$\therefore$$ In a $$\triangle ABC$$ is $$\angle A=\angle C,$$ then $$AB=BC$$
Fill in the blanks to make the following statements then the opposite interior angles.
An exterior angle of a triangle is equal to the sum of two ______ opposite angles.
An exterior angle of a triangle is always _______ than either of the interior opposite angles.
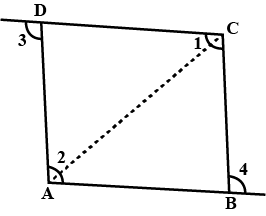
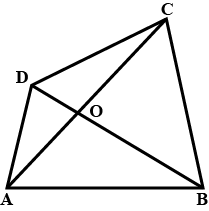
In Fig., $$A, B, C$$ and $$D$$ are four points, and no three points are collinear. $$AC$$ and $$BD$$ intersect at $$O$$. There are eight triangles that you can observe. Name all the triangles.
Explain the following terms:
Isosceles triangle
Triangle having two sides of equal length is called as isosceles triangle.(Shown in figure)
In Fig., the length (in cm) of each side has been indicated along the side. State for each triangle whether it is scalene, isosceles or equilateral:
Fill in the blanks to make the following statements correct.
The triangle formed by joining the mid-points of the sides of an isosceles triangle is ______
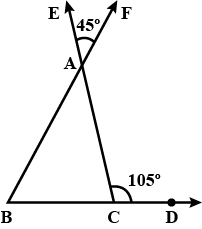
In figure, the sides BC, CA and BA of a $$\Delta ABC$$ have been produced to D, E and F respectively. If $$\angle ACD=105^o$$ and $$\angle EAF=45^o$$; find all the angles of the $$\Delta ABC$$.
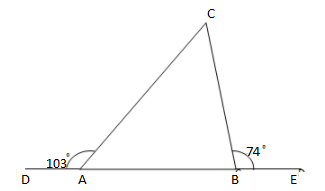
A student when asked to measure two exterior angles of $$\Delta ABC$$ observed that the exterior angles at A and B are of $$103^o$$ and $$74^o$$ respectively. Is this possible? Why or why not?
Given: $$\angle ACD=103^{\circ}$$ and $$\angle CBE=74^{\circ}$$
Solution: Clearly, $$\angle ACD+\angle BAC=180^{\circ}\quad$$[Linear pair]
$$\Rightarrow 103^{\circ}+\angle BAC=180^{\circ}$$
$$\Rightarrow \angle BAC=180^{\circ}-103^{\circ}$$
$$\Rightarrow \angle BAC=77^{\circ}$$
Similarly, $$\angle CBE+\angle ABC=180^{\circ}\quad$$[Linear pair]
$$\Rightarrow 74^{\circ}+\angle ABC=180^{\circ}$$
$$\Rightarrow \angle ABC=180^{\circ}-74^{\circ}$$
$$\Rightarrow \angle ABC=106^{\circ}$$
Now, Sum of internal angles is given by
$$\angle ABC+\angle BAC=106^{\circ}+77^{\circ}=183^{\circ}$$
It means that the sum of internal angles at $$A$$ and $$B$$ is greater than $$180^{\circ}$$ which cannot be possible.
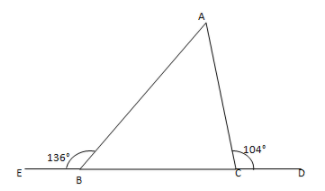
The exterior angles, obtained on producing the base of a triangle both ways are $$104^o$$ and $$136^o$$. Find all the angles of the triangle.
Givne: $$\angle ABE=136^{\circ}$$ and $$\angle ACD=104^{\circ}$$
To find: ALL angle of $$\triangle ABC$$
Solution: Clearly, $$\angle ABE+\angle ABC=180^{\circ}\quad$$[Linear pair]
$$\Rightarrow 136^{\circ}+\angle ABC=180^{\circ}$$
$$\Rightarrow \angle ABC=180^{\circ}-136^{\circ}$$
$$\Rightarrow \angle ABC=44^{\circ}$$
Similarly, $$\angle ACD+\angle ACB=180^{\circ}\quad$$[Linear pair]
$$\Rightarrow 104^{\circ}+\angle ACB=180^{\circ}$$
$$\Rightarrow \angle ACB=180^{\circ}-104^{\circ}$$
$$\Rightarrow \angle ACB=76^{\circ}$$
Now, In $$\triangle ABC$$ by angle sum property of triangle, we have
$$\angle BAC+\angle ABC+\angle ACB=180^{\circ}$$
$$\Rightarrow \angle BAC+44^{\circ}+76^{\circ}=180^{\circ}$$
$$\Rightarrow \angle BAC=180^{\circ}-44^{\circ}-76^{\circ}$$
$$\Rightarrow \angle BAC=60^{\circ}$$
The foot of a ladder is $$6$$m away from a wall and its top reaches a window $$8$$m above the ground. If the ladder is shifted in such a way that its foot is $$8$$m away from the wall, then to what height does its top reach?
Given: Let say Wall height $$= AC=8\space\mathrm{m}$$ and Distance of ladder's foot from the wall $$= BC=6\space\mathrm{m}$$
Using the Pythagoras theorem, we get
$$(AB)^2=(AC)^2+(BC)^2$$
$$\Rightarrow (AB)^2=(8)^2+(6)^2$$
$$\Rightarrow (AB)^2=64+36$$
$$\Rightarrow (AB)^2=100$$
$$\Rightarrow (AB)=\sqrt {100}$$
$$\Rightarrow AB=10$$
$$\therefore$$ Length of the ladder $$=10\space\mathrm{m}$$
When the ladder is shifted:
Let the height of the ladder after it is shifted be $$H\space\mathrm{m}$$ w.r.t. ground.
Then by using the Pythagoras theorem, we can find the height of the ladder after it is shifted.
$$8^2+H^2=10^2$$
$$\Rightarrow H^2=10^2-8^2$$
$$\Rightarrow H^2=100-64$$
$$\Rightarrow H^2=36$$
$$\Rightarrow H=\sqrt{36}$$
$$\Rightarrow H=6$$
Thus, the height of the ladder is $$6\space\mathrm{m}$$.
Explain the following term.
Isosceles triangle.
An isosceles triangle is a triangle with (at least) two equal sides.
In above image $$\Delta ABC $$ is an isosceles triangle.
If cos $$ \theta = 0.6 $$, show that $$ (5 sin \theta-3 tan \theta) =$$
The sides of certain triangles are given below. Determine which of them are right triangles.
$$1.6 cm, 3.8 cm, 4 cm $$
If $$sin A = \dfrac{9}{41}$$, find the values of $$cos A$$ and $$tan A$$.
Draw a triangle, $$ \triangle ABC, Let \angle ACB = \theta$$ and $$\angle B = 90 \ degrees $$
$$sin A = \dfrac{perpendicular}{hypotenuse} =\dfrac{ 9}{14}$$
By pythagoras theorem:
$$ AC^2 = AB^2 + BC^2$$
$$AB^2 = AC^2 - BC^2$$
$$AB^2= 41^2 - 9^2$$
$$AB^2= 1600$$
$$AB = 40$$
Find other T-rations using definitions:
$$\cos A = \dfrac{base}{hypotenuse} =\dfrac{ 40}{41}$$
$$ \tan A = \dfrac{perpendicular }{base} =\dfrac{ 9}{40}$$
If 15 cot A = 8,find the values of sin A and secA.
$$\cot A = \dfrac{(8k)}{(15k)} = \dfrac{1}{\tan A }= \dfrac{AC}{BC}$$
Where k is any positive.
By pythagoras theorem:
$$AB^2 = BC^2 + AC^2$$
$$ =(15k)^2 + (8k)^2$$
$$= 289k^2$$
$$ AB = 17 k$$
Find other T - rations using their definitions:
$$\sin A = \dfrac{perpendicular} { hypotenuse} = \dfrac{(15k)}{(17k)} = \dfrac{15}{17} $$
$$ \sec A = \dfrac{hypotenuse}{base} = \dfrac{17}{8}$$
The sides of certain triangles are given below. Determine which of them are right triangles.
$$ (a - 1) cm, 2\sqrt{a} cm, (a + 1) cm $$
The sides of certain triangles are given below. Determine which of them are right triangles.
$$9 cm, 16 cm, 18 cm$$
The sides of certain triangles are given below. Determine which of them are right triangles.
$$1 cm, 24 cm, 25 cm $$
A ladder is placed in such a way that its foot is at a distance of $$15$$ m from a wall and its top reaches a window $$20$$ m above the ground. Find the length of the ladder.
Height of window $$AC = 20 m$$
Let length of ladder $$AB = x m $$
Distance between the foot of the ladder and the building $$(BC) = 15 m$$
In the figure:
By Pythagoras Theorem:
$$AB^2 = AC^2 + BC^2 $$
$$x^2 = 20^2 + 15^2$$
$$ = 400 + 225$$
$$ = 625$$
or $$x = 25$$
Length of ladder is $$25 m $$
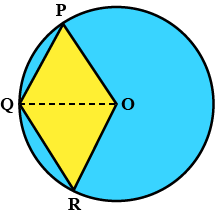
In the given figure, OPQR is a rhombus, three of whose vertices lie on a circle with centre O. If the area of the rhombus is $$\displaystyle 32\sqrt{3} \ cm^2$$, find the radius of the circle.
From figure: OP = OQ = OR = radius of circle
Let OQ and PR intersect at S.
We know, the diagonals of a rhombus bisect each other at right angle.
$$\displaystyle OS = \frac{1}{2} r$$ and $$\displaystyle \angle OSR = 90^0$$
$$\displaystyle SR = \sqrt{OR^2 - OS^2} = \sqrt{r^2 - \frac{r^2}{4}} = \frac{\sqrt{3}r}{2}$$
$$\displaystyle PR = 2 \times SR = \sqrt{3} r$$
Area of Rhombus = $$\displaystyle \frac{1}{2} \times OQ \times PR = \frac{1}{2} \times r \times \sqrt{3}r =\frac{\sqrt{3}r^2}{2}$$
$$\Rightarrow \displaystyle \frac{\sqrt{3}r^2}{2} = 32\sqrt{3}$$
$$\Rightarrow \displaystyle r^2 = \frac{32\sqrt{3}}{\sqrt{3}} \times 2 = 64 \ cm$$
$$\therefore \displaystyle r = 8 \ cm$$
Find the length of altitude AD of an isosceles $$\Delta$$ ABC in which AB = AC = 2a units and BC = a units.
In an isosceles $$\Delta ABC$$ in which $$AB = AC = 2a$$ units, $$BC = a$$ units
$$AD$$ is the altitude. Therefore, $$D$$ is the midpoint of $$BC$$
$$\Rightarrow BD = \dfrac{a}{2}$$
We have two right triangles: $$\Delta ADB$$ and $$\Delta ADC$$
By Pythagoras theorem,
$$AB^2 = BD^2 + AD^2 $$
$$(2a)^2 = \left(\dfrac a2\right)^2 + AD^2 $$
$$(2a)^2 = \dfrac{a^2}{4} + AD^2$$
$$AD^2 = \dfrac{16a^2 - a^2}{4} = \dfrac{15a^2}{4}$$
$$AD = \dfrac{a\sqrt{15}}{2}$$
Hence, the length of the altitude $$AD$$ is $$\dfrac{a\sqrt{15}}{2}\ units$$.
In the adjoining figure, $$\triangle ABC$$ is a right-angled at $$B$$ and $$\angle A = 30^{\circ}$$. If $$BC = 6\ cm$$, Find (i) $$AB$$, (ii) $$AC$$.
Here $$\sin 30 = \dfrac{BC}{ AC}$$
$$\dfrac {1}{2} = \dfrac{6}{AC}$$
Or $$AC = 12\ cm$$
By Pythagoras theorem:
$$(AB)^{2} = (AC)^{2} - (BC)^{2}$$
$$= (12)^{2} - (6)^{2}$$
$$= 108$$
$$AB = 6\sqrt {3} cm$$.
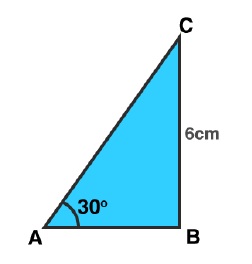
A man goes $$80 m$$ due east and then $$150 m$$ due north. How far is he from the starting point?
A man goes $$80 m$$ from $$O$$ to east side and reaches $$A$$, then he goes $$150 m$$ due north from $$A$$ and reaches $$B$$.
From right $$\Delta OAB$$,
By Pythagoras Theorem:
$$OB^2 = OA^2+ AB^2$$
$$ \Rightarrow OB^2 = (80)^2 + (150)^2 $$
$$ \Rightarrow OB^2 = 6400 + 22500$$
$$ \Rightarrow OB^2 = 6400 + 22500$$
$$ \Rightarrow OB^2 = 28900$$
$$ \Rightarrow OB = \sqrt{28900} $$
$$ \Rightarrow OB = 170 $$
Hence, the man is $$170 m$$ away from the starting point.
In the adjoining figure, $$\triangle ABC$$ is a right-angled triangle in which $$\angle B = 90^{\circ}, \angle A = 30^{\circ}$$ and $$AC = 20\ cm$$.
Find (i) $$BC$$, (ii) $$AB$$.
Here $$\sin 30 = \dfrac{BC}{AC}$$
$$\dfrac {1}{2} = \dfrac{BC}{ 20}$$
Or $$BC = 10\ cm$$
By Pythagoras theorem:
$$(AB)^{2} = (AB)^{2} - (BC)^{2}$$
$$= (20)^{2} - (10)^{2}$$
$$= 300$$
$$AB = 10\sqrt {3} cm$$.
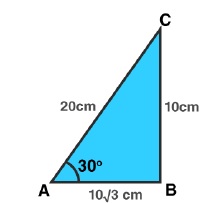
A $$13$$-m-long ladder reaches a window of a building $$12$$ m above the ground. Determine the distance of the foot of the ladder from the building.
Height of the window $$= 12 m$$
Length of a ladder $$= 13 m $$
In the figures,
Let $$AB$$ is ladder, $$A$$ is window of building $$AC$$
By Pythagoras Theorem:
$$AB^2 = AC^2 + BC^2$$
$$(13)^2 = (12)^2 + x^2$$
$$(13)^2 = (12)^2 + x^2$$
$$169 = 144 + x²$$
$$ x² = 169 - 144 = 25$$
or $$x = 5$$
Distance between foot of ladder and building $$= 5 m$$.
A 5.5m long ladder is leaned against a wall. The ladder reaches the wall to a height of 4.4m. Find the distance between the wall and the foot of the ladder.
A man goes $$10 m$$ due south and then $$24 m$$ due west. How far is he from the starting point?
A man goes $$10 m$$ due south from $$O$$ and reaches $$A$$ and then $$24 m$$ due west from $$A$$ and reaches $$B$$.
$$= (10)² + (24)² $$
Draw a figure based on given instructions:
From right $$\Delta OAB$$,
By Pythagoras Theorem:
$$OB^2 = OA^2+ AB^2 $$
$$= (10)² + (24)² $$
$$= 676 $$
or $$OB = 26 $$
Man is $$26 m$$ away from the starting point.
In the adjoining figure,$$ \,DCBA\,$$ is a trapezium where $$AL\,\,and\,\,BM $$ are perpendicular to $$DC$$ and $$DL=MC$$. It is given that $$AL=BM=4cm$$, $$BC=AD=5cm$$ and $$AB=LM=7cm$$. Also $$AL \,||\, BM$$. Then find area of trapezium $$DCBA$$ and also find the length of DC. DCBA is a and
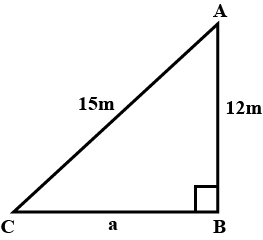
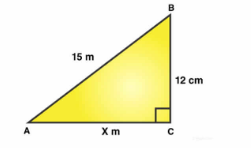
The length of one side of a right triangle is $$4.5cm$$ and the length of its hypotenuse is $$7.5cm$$. Find the length of its third side.
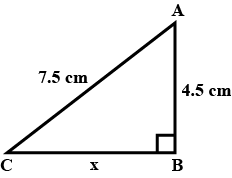
Find the length of the hypotenuse of a right triangle, the other two sides of which measures $$9\ cm$$ and $$12\ cm$$
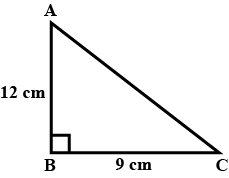
The distance between the middle point of BC and the foot of the perpendicular from A is $$\dfrac{b^2- c^2}{2a}$$
$$DE=CD-CE$$
$$DE=\dfrac{a}{2}-b\cos C$$
$$DE=\dfrac{a}{2}-b\dfrac{a^2+b^2-c^2}{2ab}$$
$$DE=\dfrac{c^2-b^2}{2a}$$
$$\therefore$$ $$DE=\dfrac{b^2-c^2}{2a}$$
The two legs of a right triangle are equal and the square of its hypotenuse is $$50$$. Find the length of its third side.
The hypotenuse of a right triangle is $$26cm$$ long. If one of the remaining two sides is $$10cm$$ long, find the length of the other side.
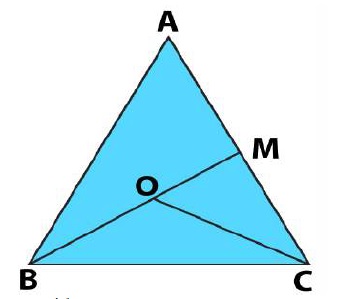
The bisectors $$\angle B$$ and $$\angle C$$ of and isosceles triangle with $$AB = AC$$ intersect each other at a point $$O$$. $$BO$$ is produced to meet $$AC$$ at a point $$M$$. Prove that $$\angle MOC = \angle ABC$$.
A $$15m$$ long ladder is placed against a wall to reach a window $$12m$$ high. Find the distance of the foot of the ladder from the wall.
The perimeter of a triangle is $$28\ cm$$. One of its sides is $$8\ cm$$. Write all the sides of the possible isosceles triangles with these measurements.
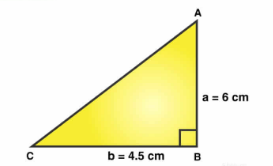
In right $$\triangle ABC$$, the lengths of its legs are given as $$a=6cm$$ and $$b=4.5cm$$. Find the length of its hypotenuse.
The perpendicular from $$A$$ on side $$B C$$ of a $$ \Delta A B C$$ intersects $$B C$$ at $$D$$ such that $$D B=3 C D$$ (see figure). Prove that $$2AB^{2}=2 AC^{2}+BC^{2}$$
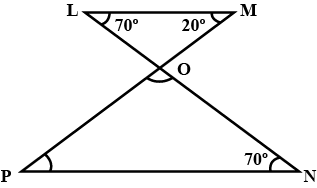
In Figure find thee measures of $$\angle PON $$ and $$\angle NPO$$
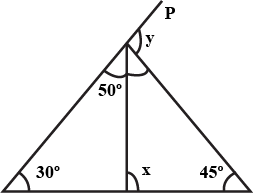
In $$\triangle $$ABC$$, if \angle A=\angle C,$$ and exterior angle $$ABX=140^{o}$$, then find the angles of the triangle.
$$\angle ABX=\angle BAC+\angle BCA$$
$$\Rightarrow 140^{o}=2 \angle BAC(\angle A=\angle C)$$
$$\Rightarrow \angle BAC=\frac{140^{o}}{2}$$
$$\Rightarrow \angle BAC=70^{o}$$
$$\Rightarrow \angle A=70^{o}$$
$$ \therefore \angle BAC=\angle BAC=70^{o}$$ .......(1)
$$\angle A+\angle B+\angle C=180^{o}$$
$$\Rightarrow \angle B=180^{o}-70^{o}-70^{o}$$
$$\Rightarrow \angle B=40^{o}$$
Therefore, the angles of triangles are
$$\angle A=70^{o}$$
$$\angle B=40^{o}$$
$$\angle C=70^{o}$$
$$\Rightarrow 140^{o}=2 \angle BAC(\angle A=\angle C)$$
$$\Rightarrow \angle BAC=\frac{140^{o}}{2}$$
$$\Rightarrow \angle BAC=70^{o}$$
$$\Rightarrow \angle A=70^{o}$$
$$ \therefore \angle BAC=\angle BAC=70^{o}$$ .......(1)
$$\angle A+\angle B+\angle C=180^{o}$$
$$\Rightarrow \angle B=180^{o}-70^{o}-70^{o}$$
$$\Rightarrow \angle B=40^{o}$$
Therefore, the angles of triangles are
$$\angle A=70^{o}$$
$$\angle B=40^{o}$$
$$\angle C=70^{o}$$
Find the values of $$x$$ and $$y$$ Figure
In triangle $$QRS$$,
$$\Rightarrow x=30^{o}+50^{o}$$
$$\Rightarrow x=80^{o}$$
Also, in triangle QRT,
$$\Rightarrow y=30^{o}+45^{o}$$
$$\Rightarrow y=75^{o}$$
Therefore,
$$\Rightarrow x=80^{o}$$
$$\Rightarrow y=75^{o}$$
$$\Rightarrow x=30^{o}+50^{o}$$
$$\Rightarrow x=80^{o}$$
Also, in triangle QRT,
$$\Rightarrow y=30^{o}+45^{o}$$
$$\Rightarrow y=75^{o}$$
Therefore,
$$\Rightarrow x=80^{o}$$
$$\Rightarrow y=75^{o}$$
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures $$60 meters\times 80 meters$$. How much shorter is the route across the park than the route around its edges?
Let $$ABCD$$ in right-angled.
Triangle $$ABC$$ is right-angled.
$$\Rightarrow (AC)^2=(80)^2+(60)^2$$
$$\Rightarrow AC=\sqrt{6400+3600}$$
$$\Rightarrow AC=\sqrt{10000}$$
$$\Rightarrow AC=100$$
Hence, length of the route across the park $$= 100m$$
Length of route around the edges $$= (80+60)=140km$$
Therefore, the shorter route is
$$\Rightarrow 140m−100m=40m$$
Triangle $$ABC$$ is right-angled.
$$\Rightarrow (AC)^2=(80)^2+(60)^2$$
$$\Rightarrow AC=\sqrt{6400+3600}$$
$$\Rightarrow AC=\sqrt{10000}$$
$$\Rightarrow AC=100$$
Hence, length of the route across the park $$= 100m$$
Length of route around the edges $$= (80+60)=140km$$
Therefore, the shorter route is
$$\Rightarrow 140m−100m=40m$$
If the sides of a triangle are produced in an order, show that the sum of the exterior angles so formed is $$360^{o}$$
Let $$ABC$$ be triangle and $$BD$$, $$CE$$ and $$AF$$ are the extended side in order.
$$\Rightarrow \angle ACD=\angle CAB+\angle CBA$$ ......(1)
$$\Rightarrow \angle BAE= \angle ABC+ \angle ACB$$ .....(2)
$$\Rightarrow \angle CBF=\angle BAC+ \angle BCA$$ ..........(3)
Addition of equation 1,2 and 3
$$\Rightarrow \angle ACD+\angle BAE+\angle CBF$$
$$ = \angle CAB+\angle CBA + \angle ABC+\angle ACB+\angle BAC+\angle BCA $$
$$\Rightarrow \angle ACD+\angle BAE+\angle CBF$$
$$=2[\angle ABC+\angle ACB+\angle BCA]$$
$$=2(180^{o})$$
$$\Rightarrow 360^{o}$$
$$\Rightarrow \angle ACD=\angle CAB+\angle CBA$$ ......(1)
$$\Rightarrow \angle BAE= \angle ABC+ \angle ACB$$ .....(2)
$$\Rightarrow \angle CBF=\angle BAC+ \angle BCA$$ ..........(3)
Addition of equation 1,2 and 3
$$\Rightarrow \angle ACD+\angle BAE+\angle CBF$$
$$ = \angle CAB+\angle CBA + \angle ABC+\angle ACB+\angle BAC+\angle BCA $$
$$\Rightarrow \angle ACD+\angle BAE+\angle CBF$$
$$=2[\angle ABC+\angle ACB+\angle BCA]$$
$$=2(180^{o})$$
$$\Rightarrow 360^{o}$$
In Figure, find the measures of $$\angle x$$ and $$\angle y$$.
In triangle $$ABC$$,
$$\Rightarrow$$ $$45^{o} + 60^{o} + x = 180^{o}$$
$$\Rightarrow$$ $$x = 180^{o} - 105^{o}$$
$$\Rightarrow$$ $$x = 75^{o}$$
Now,
$$\angle BAD = \angle ABC + \angle ACB$$
$$\Rightarrow$$ $$y = 60^{o} + x$$
$$\Rightarrow$$ $$y = 60^{o} + 75^{o}$$
$$\Rightarrow$$ $$y = 135^{o}$$
Therefore,
$$x = 75^{o}$$, and $$y = 135^{o}$$
$$\Rightarrow$$ $$45^{o} + 60^{o} + x = 180^{o}$$
$$\Rightarrow$$ $$x = 180^{o} - 105^{o}$$
$$\Rightarrow$$ $$x = 75^{o}$$
Now,
$$\angle BAD = \angle ABC + \angle ACB$$
$$\Rightarrow$$ $$y = 60^{o} + x$$
$$\Rightarrow$$ $$y = 60^{o} + 75^{o}$$
$$\Rightarrow$$ $$y = 135^{o}$$
Therefore,
$$x = 75^{o}$$, and $$y = 135^{o}$$
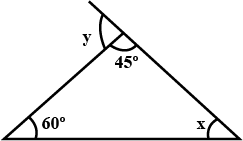
Find the measure of $$\angle A$$ in Figure
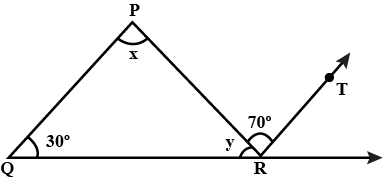
In Figure, $$QP || RT$$. Find the value of $$x$$ and $$y$$.
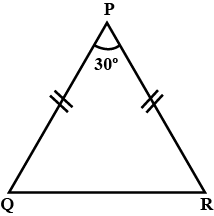
In $$\triangle PQR$$ of Figure $$PQ=PR$$. Find the measures of $$\angle Q$$ and $$\angle R$$.
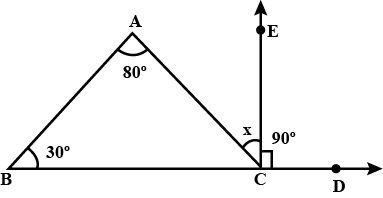
Find the value of $$x$$ in Figure
Find the length of the side of a square if the length of its diagonal is 10cm.
The sum of an exterior angle of a triangle and its adjacent angle is always ______.
Measures of each of the angles of an equilateral triangle are ______.
In an isosceles triangle, two angles are always ______.
Fill in the blanks to make the statements true.
The sides of a right triangle whose hypotenuse is 17 cm are ______ and ______.
Can a right triangle with sides 6cm, 10cm and 8cm be formed? Give reason.
The dimensions of a rectangular field are 80m and 18m. Find the length of its diagonal.
In Fig., if $$ST=SU$$, then find the values of $$x$$ and $$y$$.
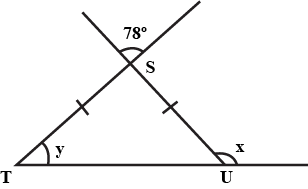
In Fig. if $$y$$ is five times $$x$$, find the value of $$z$$.
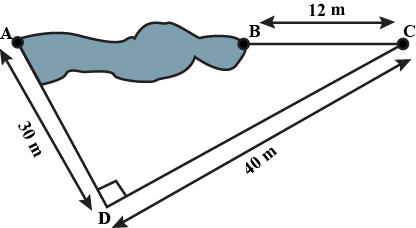
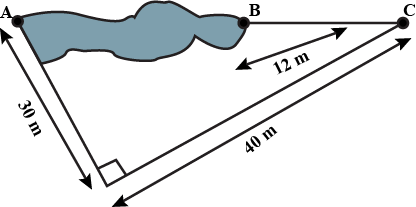
Point $$A$$ and $$B$$ are on the opposite edges of a pond as shown in Figure. To find the distance between the two points, the surveyor makes a right angled triangle as shown. FInd the distance $$AB$$
Here, $$ADC$$ is a right-angled triangle.
$$\Rightarrow (AC)^{2}=(30)^{2}+(40)^{2}$$
$$\Rightarrow (AC)^{2}=900+1600$$
$$\Rightarrow (AC)^{2}=2500$$
$$\Rightarrow AC=\sqrt{2500}$$
$$\Rightarrow AC=50\,m$$
Now,
$$\Rightarrow AB=AC-BC$$
$$\Rightarrow AB=50-12$$
$$\Rightarrow AB=38$$
Therefore, $$38m$$ is the distance of $$AB$$
The foot of a ladder is $$6 m$$ away from its wall and its top reaches a window $$8 m$$ above the ground,
(a)If the ladder is shifted in such a way that its foot is $$8 m$$ away from the wall, to what height does its top reach?
REF Image. for the second condition.
Let $$AC$$ be the ladder's length.
From the first condition using the Pythagoras theorem we get,
Ladder's length $$AC$$ $$= \sqrt{8^2+6^2} = $$ $$10m$$
Now, $$BC=8m$$
Now, in triangle $$ABC$$,
$$(AC)^{2}=(AB)^{2}+(BC)^{2}$$
$$\Rightarrow (AC)^{2}=(AB)^{2}+8^2$$
$$\Rightarrow (10)^{2}-64=(AB)^{2}$$
$$\Rightarrow AB=\sqrt{36}$$
$$\Rightarrow AB=6m$$
Therefore, the ladder is $$6m$$ above the ground.
Two poles of $$10\ m$$ and $$15 \ m$$ stand upright on a plane ground. If the distance between the tops is $$13 \ m$$ , find the distance between their feet.
Let $$AB$$ and $$CD$$ be the poles of heights $$15\ m$$ and $$10\ m$$
given $$ AC=13\ m$$.
from the diagram, we can write
$$CD=BE=10\ m$$
$$ AE=AB-BE=15-10=5\ m$$
from $$\triangle AEC$$,
$$AC^2=AE^2+EC^2$$ (using pythagoras theorem)
$$\Rightarrow (13)^{2} \ \ =\ 5^{2}+(EC)^{2}$$
$$\Rightarrow (EC)^{2}=169-25$$
$$\Rightarrow \ EC\ \ \ =\ \ \sqrt{144}$$
$$\Rightarrow \ EC\ \ \ =\ \ 12$$
$$\therefore EC=BD=12\ m$$
Therefore $$12\ m$$ is the distance between the feet of the poles.
The foot of a ladder is $$6 m$$ away from its wall and its top reaches a window $$8 m$$ above the ground, (a) Find the length of the ladder.
(a) Let $$AC$$ be the given ladder such that $$BC=6m$$ and $$AB=8m$$
Now, in triangle $$ABC$$
$$(AC)^{2}=(AB)^{2}+(BC)^{2}$$
$$\Rightarrow (AC)^{2}=8^{2}+6^{2}$$
$$\Rightarrow AC=\sqrt{64+36}$$
$$\Rightarrow AC=\sqrt{100}$$
$$\Rightarrow AC=10m$$
Therefore, $$10m$$ is the length of the ladder.
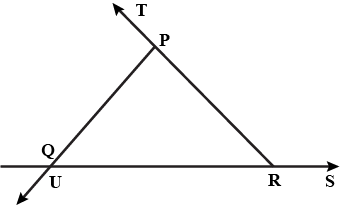
In Fig.,
(i) $$\angle TPQ = \angle$$ ______ $$+ \angle$$ ______
(ii) $$\angle UQR = \angle$$ ______ $$+ \angle$$ ______
(iii) $$\angle PRS = \angle$$ ______ $$+ \angle$$ ______
Rahul walks $$12m$$ north from his house and turns west to walk $$35m$$ to reach his friend's house. While returning, he walks diagonally from his friend's house to reach back to his house. What distance did he walk while returning?
Lengths of sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse:$$13$$ cm, $$12$$ cm, $$5$$ cm
A vertical tree is broken by the wind at height of $$6$$ meter from its foot and top touches the ground at a distance of $$8$$ meter from the foot of the tree. Calculate the distance between the top of tree before breaking and the point at which tip of the touches the ground, after it breaks.
Let $$x$$ be the length of broken part.
Total height of tree $$=x+6\ m$$
Distance between foot of tree and the point where the tree touch the ground $$=8\ m$$
In triangle $$BCD$$
$$BD^2=BC^2+CD^2$$
Using Pythagoras theorem
$$(Hypotenuse)^2=(Base)^2+(Perpendicular\,side)^2$$
$$x^2=6^2+8^2=36+64=100$$
$$x=\sqrt{100}=10\ m$$
Total height of tree $$=x+6=10+6=16\ m$$
In triangle $$ACD$$
$$AD^2=AC^2+CD^2$$
Substitute the values
$$AD^2=(16)^2+8^2$$
$$AD^2=256+64$$
$$AD^2=320$$
$$AD=\sqrt{320}=8\sqrt{5}\ m$$
Hence, the distance between the top and the point where the tree touches the ground $$=8\sqrt{5}\ m$$
Area of a triangle $$PQR$$ right-angled at $$Q$$ is $$60\, cm^2$$ (Fig). If the smallest side is $$8\, cm$$ long, find the length of the other two sides.
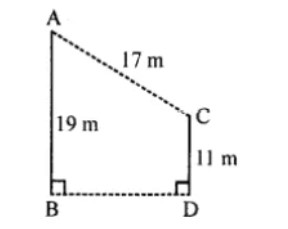
In the given figure, AB and CD are two vertical poles of height $$19 m$$ and $$11 m$$ respectively. If the shortest distance between their tops is $$17 m$$, find how far apart they are?
Pole $$AB = 19m$$, Pole $$CD=11m$$
Distance between their tops $$AC = 17 cm$$
Draw EC || BD, then
Let $$BD = CE=x$$
$$EB=CD=11m$$
$$AE = AB-EB=19-11=8m$$
Now in right $$\Delta AEC$$,
$$AC^2 = AE^2 + EC^2$$
$$\Rightarrow (17)^2 = (8)^2 + x^2$$
$$\Rightarrow 289 = 64+ x^2$$
$$\Rightarrow x^2 = 289 - 64 = 225 = (15)^2$$
$$\Rightarrow x=15$$
$$BD =EC =x=15m$$
Distance between their tops $$AC = 17 cm$$
Draw EC || BD, then
Let $$BD = CE=x$$
$$EB=CD=11m$$
$$AE = AB-EB=19-11=8m$$
Now in right $$\Delta AEC$$,
$$AC^2 = AE^2 + EC^2$$
$$\Rightarrow (17)^2 = (8)^2 + x^2$$
$$\Rightarrow 289 = 64+ x^2$$
$$\Rightarrow x^2 = 289 - 64 = 225 = (15)^2$$
$$\Rightarrow x=15$$
$$BD =EC =x=15m$$
Lengths of sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse:$$1.4$$ cm, $$4.8$$ cm, $$5$$ cm.
In a right triangle $$ABC, \angle B=90^{\circ}.$$ If $$AB=14\ cm, BC=48\ cm$$, find $$AC.$$
By using Pythagoras theorem $$\triangle ABC,$$
$$\begin{aligned}{}A{C^2}& = A{B^2} + B{C^2}\\ &= {14^2} + {48^2}\\ &= 196 + 2304\\& = 2500\\& = 50\;cm\end{aligned}$$
$$\begin{aligned}{}A{C^2}& = A{B^2} + B{C^2}\\ &= {14^2} + {48^2}\\ &= 196 + 2304\\& = 2500\\& = 50\;cm\end{aligned}$$
Hence, the length of the side $$AC$$ is equal to $$50\; cm.$$
Lengths of sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse:
(i) $$3$$ cm, $$8$$ cm, $$6$$ cm
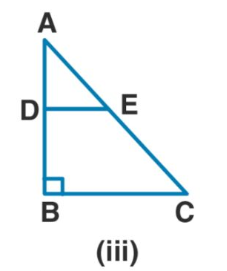
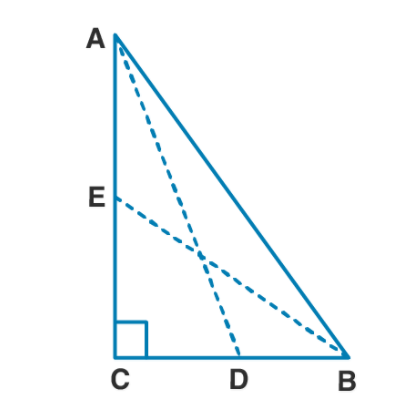
(c) In figure (iii) given below, triangle ABC is right angled at B. Given that AB = 9 cm, AC = 15 cm and D, E are mid-point of the sides AB and AC respectively, calculate
(i) the length of BC
(ii) the area of $$\Delta$$ ADE.
In a right-angled triangle, if hypotenuse is $$20 cm$$ and the ratio of the other two sides is $$4:3,$$ find the sides.
In figure (i) given below, $$BC = 5 cm,B =90, AB = 5AE, CD = 2AE$$ and $$AC = ED.$$ Calculate the lengths of $$EA, CD, AB$$ and $$AC.$$
In the figure given above, $$\angle D = 90°, AB = 16 cm, BC = 12 cm$$ and $$CA = 6 cm.$$ Find $$CD.$$
$$(b)$$ In figure (ii) given below, $$PSR = 90, PQ = 10 cm, QS = 6 cm$$ and $$RQ = 9 cm.$$ Calculate the length of $$PR.$$
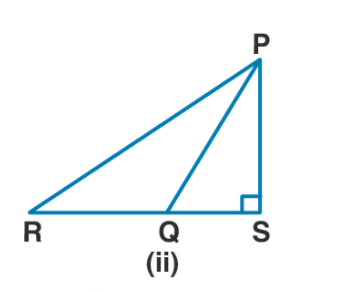
In the figure (ii) given below, $$ABC$$ is a right triangle right angled at $$C.$$ If $$D$$ is mid-point of $$BC,$$ prove that $$AB^2= 4AD^2 3AC^2.$$
A guy attached a wire $$24$$ m long to a vertical pole of height $$18$$ m and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be tight?
Let $$AC$$ be the wire and $$AB$$ be the height of the pole.
$$AC = 24 cm$$
$$AB = 18 cm$$
According to Pythagoras theorem,
$$AC^2 = AB^2+BC^2$$
$$24^2 = 18^2+BC^2$$
$$576 = 324+BC^2$$
$$BC^2 = 576-324$$
$$BC^2 = 252$$
Taking square root on both sides,
$$BC = √252$$
$$= √(4×9×7)$$
$$= 2×3√7$$
$$= 6√7 cm$$
Hence the distance is $$6√7$$ cm.
$$AC = 24 cm$$
$$AB = 18 cm$$
According to Pythagoras theorem,
$$AC^2 = AB^2+BC^2$$
$$24^2 = 18^2+BC^2$$
$$576 = 324+BC^2$$
$$BC^2 = 576-324$$
$$BC^2 = 252$$
Taking square root on both sides,
$$BC = √252$$
$$= √(4×9×7)$$
$$= 2×3√7$$
$$= 6√7 cm$$
Hence the distance is $$6√7$$ cm.
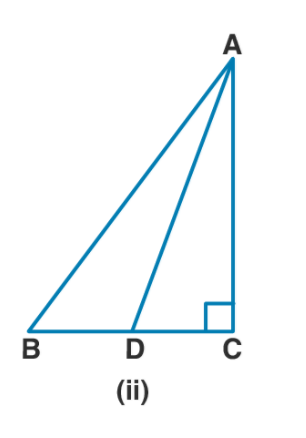
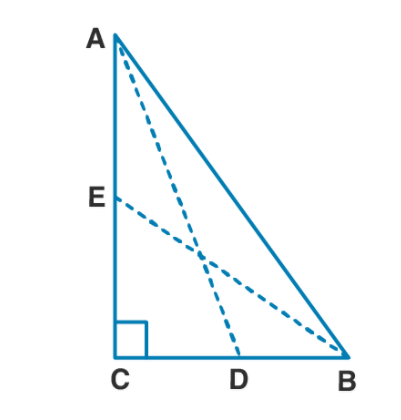
In figure (i) given below, $$D$$ and $$E$$ are mid-points of the sides $$BC$$ and $$CA$$ respectively of a $$ABC$$, right angled at $$C.$$
Prove that : (i) $$4AD^2=4AC^2 + BC^2$$
In figure (ii) given below, $$AB || DC, A = 90, DC = 7 cm, AB = 17 cm$$ and $$AC = 25 cm.$$ Calculate $$BC.$$
In figure (i) given below, $$D$$ and $$E$$ are mid-points of the sides $$BC$$ and $$CA$$ respectively of a $$ABC$$, right angled at $$C.$$
Prove that : (ii) $$4BE^2 = 4BC^2+AC^2$$
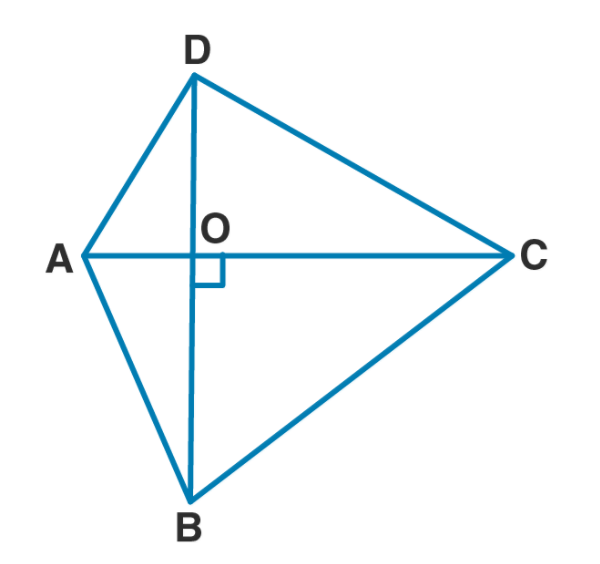
In fig. (i) given below, the diagonals $$AC$$ and $$BD$$ of a quadrilateral $$ABCD$$ intersect at $$O,$$ at right angles.
Prove that $$AB^2 + CD^2 = AD^2 + BC^2$$
In a right angled triangle ABC, right angled at C, P and Q are the points on the sides CA and CB respectively which divide these sides in the ration 2:1.
Prove that
(i) $$9 AQ^2$$ = $$9 AC^2$$ + $$4 BC^2$$
(ii) $$9 BP^2$$ = $$ 9 BC^2$$ + $$ 4 AC^2$$
(iii) 9 ($$AQ^2$$ + $$BP^2$$) = $$ 13 AB^2$$.
In a $$ ABC, A = 90, CA = AB$$ and $$D$$ is a point on $$AB$$ produced. Prove that : $$DC^2 BD^2 = 2ABAD$$.
Given $$\angle A = 90^{\circ}$$
$$ CA = AB$$
Proof:
In $$\Delta ACD$$
$$ DC^2 = CA^2 + AD^2$$ [Pythagoras theorem]
$$ DC^2 = CA^2 + (AB + BD)^2$$
$$ DC^2 = CA^2 + AB^2 + BD^2 + 2AB \times BD$$
$$ DC^2 - BD^2 = CA^2 + AB^2 + 2 AB \times BD$$
$$ DC^2 - BD^2 = AB^2 + AB^2 + 2 AB \times BD$$ [ $$\because CA = AB$$]
$$ DC^2 - BD^2 = 2 AB^2 + 2 AB \times BD$$
$$ DEC^2 - BD^2 = 2 AB ( AB + BD)$$
$$ DC^2 - BD^2 = 2 AB \times AD$$ [ $$A - B - D$$]
Hence proved.
$$ CA = AB$$
Proof:
In $$\Delta ACD$$
$$ DC^2 = CA^2 + AD^2$$ [Pythagoras theorem]
$$ DC^2 = CA^2 + (AB + BD)^2$$
$$ DC^2 = CA^2 + AB^2 + BD^2 + 2AB \times BD$$
$$ DC^2 - BD^2 = CA^2 + AB^2 + 2 AB \times BD$$
$$ DC^2 - BD^2 = AB^2 + AB^2 + 2 AB \times BD$$ [ $$\because CA = AB$$]
$$ DC^2 - BD^2 = 2 AB^2 + 2 AB \times BD$$
$$ DEC^2 - BD^2 = 2 AB ( AB + BD)$$
$$ DC^2 - BD^2 = 2 AB \times AD$$ [ $$A - B - D$$]
Hence proved.
In a quadrilateral $$ABCD,$$ $$B = 90 = D.$$ Prove that $$2 AC^2 BC^2 = AB^2 + AD^2 + DC^2.$$
Given $$ \angle B = \angle D = 90^{\circ}$$
So $$ \Delta ABC$$ and $$ \Delta ADC$$ are right triangles.
In $$ \Delta ABC$$,
$$ AC^2 = AD^2 + BC^2$$ ...(i) [Pythagoras theorem]
$$ \Delta ADC$$,
$$ AC^2 = AD^2 + DC^2$$ ...(ii) [Pythagoras theorem]
Adding (i) and (ii)
$$2 AC^2 = AB^2 + BC^2 + AD^2 + DC^2$$
$$\therefore 2 AC^2 - BC^2 = AB^2 + AD^2 + DC^2$$
Hence proved.
So $$ \Delta ABC$$ and $$ \Delta ADC$$ are right triangles.
In $$ \Delta ABC$$,
$$ AC^2 = AD^2 + BC^2$$ ...(i) [Pythagoras theorem]
$$ \Delta ADC$$,
$$ AC^2 = AD^2 + DC^2$$ ...(ii) [Pythagoras theorem]
Adding (i) and (ii)
$$2 AC^2 = AB^2 + BC^2 + AD^2 + DC^2$$
$$\therefore 2 AC^2 - BC^2 = AB^2 + AD^2 + DC^2$$
Hence proved.
A peacock on a pillar of $$9$$ feet height on seeing a snake coming towards its hole situated just below the pillar from a distance of $$27$$ feet away from the pillar will fly to catch it. If both possess the same speed, how far from the pillar they are going to meet?
Let the peacock and snake meet at $$x$$ m from the pillar as shown in the above figure:
Let $$BD=x$$. It is given that the peacock is on a pillar of $$9$$ feet height, therefore, $$AB=9$$ and the given distance is $$27$$ feet from the pillar, therefore, $$AD=(27-x)$$
In $$△ABD$$, using pythagoras theorem, we have
$$AD^{ 2 }=AB^{ 2 }+BD^{ 2 }\quad \\ \Rightarrow (27-x)^{ 2 }=9^{ 2 }+x^{ 2 }\quad \quad \\ \Rightarrow 27^{ 2 }+x^{ 2 }-(2\times 27\times x)=81+x^{ 2 }\quad \quad \quad \quad (∵(a-b)^{ 2 }=a^{ 2 }+b^{ 2 }-2ab)\quad \\ \Rightarrow 729+x^{ 2 }-54x=81+x^{ 2 }\\ \Rightarrow 729+x^{ 2 }-54x-81-x^{ 2 }=0\\ \Rightarrow 54x-648=0\\ \Rightarrow 54x=648\\ \Rightarrow x=\cfrac { 648 }{ 54 } \\ \Rightarrow x=12$$
Hence, the peacock and snake are going to meet at a distance of $$12$$ feet from the pillar.
In the given figure, $$\Delta$$ PQR is right angled at Q and point S and T trisect side QR. Prove that $$ PT^2$$ = $$ 3PR^2$$ + $$ 5PS^2$$.
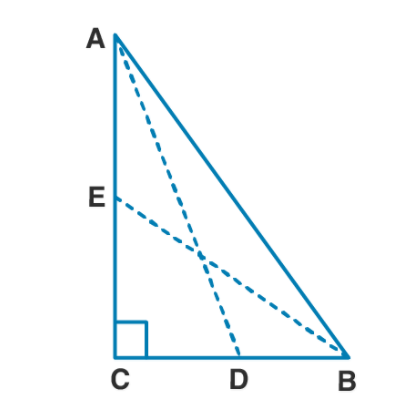
In the given figure, $$D$$ and $$E$$ are mid-points of the sides $$BC$$ and $$CA$$ respectively of a $$ΔABC$$, right angled at $$C.$$
Prove that : $$4(AD^2+BE^2) = 5AB^2$$
A ladder $$10 \ m$$ long just reaches the top of a building $$8 \ m$$ high from the ground. Find the distance of the foot of the ladder from the building.
The exterior angles of a triangle obtained by producing, the sides in order are $$ 110^{\circ} $$,$$ 130^{\circ} $$ and $$ x $$. Find $$ x . $$
The exterior angles of a triangle obtained by producing, the sides in order are $$110^o,\space 130^o$$ and x. Find x.
Prove that the sum of the exterior angles of a triangle formed by producing the sides of the triangle in order is equal to 4 right angles.
In $$ \Delta \mathrm{ABC} $$
$$ \angle y=\angle 1+\angle 3 . $$.. (i) (due to ext. angle property)
and $$ \angle z=\angle 1+\angle 2 $$... (ii) (due to ext. angle property)
also $$ \angle x=\angle 2+\angle 3 $$... (iii) (due to ext. angle property)
Adding equation (i), (ii) and (iii), we get
$$ \angle x+\angle y+\angle z=\angle 1+\angle 3+\angle 1+\angle 2+\angle 2+\angle 3 $$
$$ \Rightarrow \angle x+\angle y+\angle z=2 \angle 1+2 \angle 2+2 \angle 3 $$
$$ \Rightarrow \angle x+\angle y+\angle z=2(\angle 1+\angle 2+\angle 3)=2 \times 180^{\circ}=360^{\circ} $$
Hence, $$ \angle x+\angle y+\angle z=4 $$ right angles.
$$ \angle y=\angle 1+\angle 3 . $$.. (i) (due to ext. angle property)
and $$ \angle z=\angle 1+\angle 2 $$... (ii) (due to ext. angle property)
also $$ \angle x=\angle 2+\angle 3 $$... (iii) (due to ext. angle property)
Adding equation (i), (ii) and (iii), we get
$$ \angle x+\angle y+\angle z=\angle 1+\angle 3+\angle 1+\angle 2+\angle 2+\angle 3 $$
$$ \Rightarrow \angle x+\angle y+\angle z=2 \angle 1+2 \angle 2+2 \angle 3 $$
$$ \Rightarrow \angle x+\angle y+\angle z=2(\angle 1+\angle 2+\angle 3)=2 \times 180^{\circ}=360^{\circ} $$
Hence, $$ \angle x+\angle y+\angle z=4 $$ right angles.
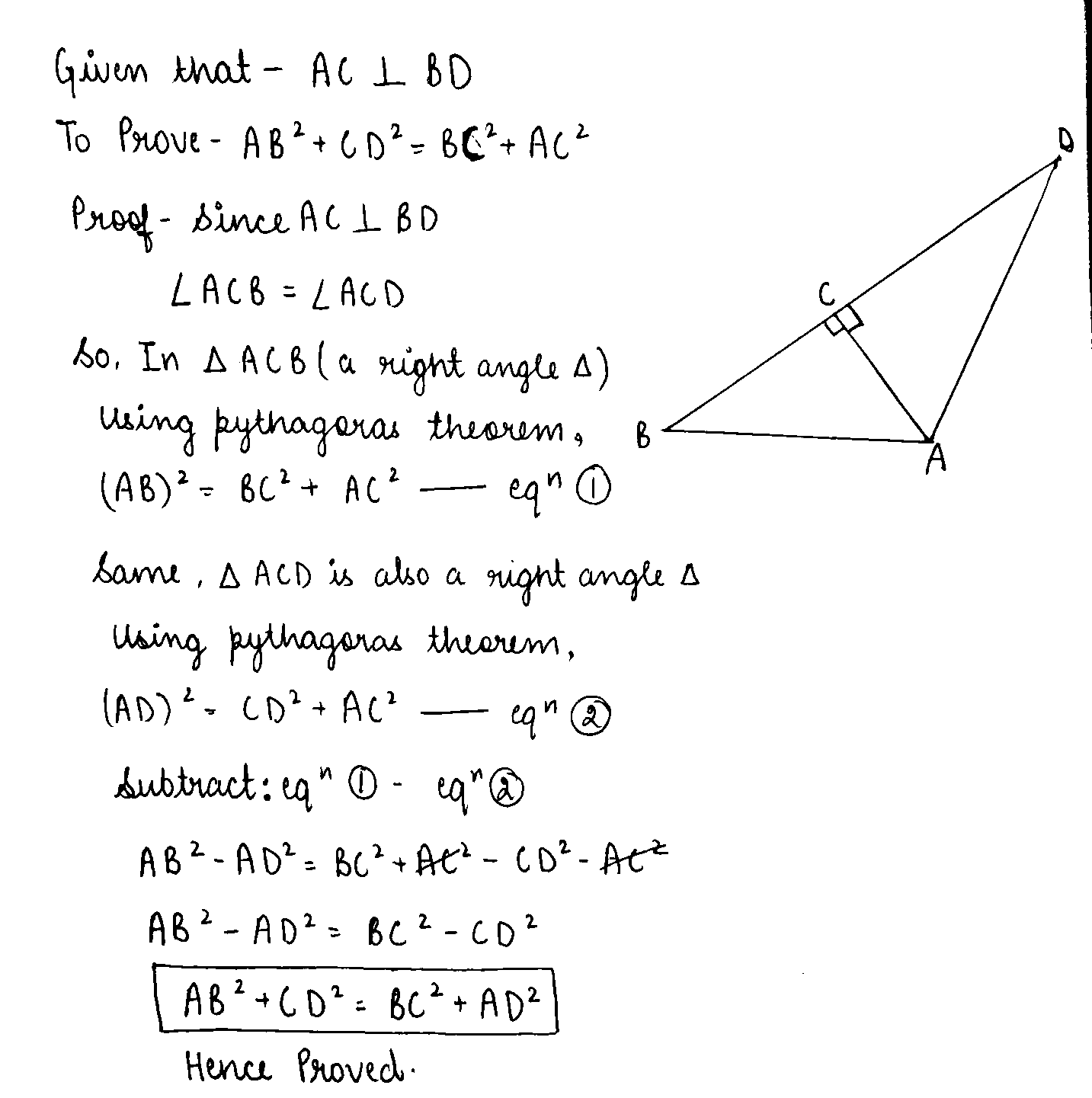
Given : AC is perpendicular to BD.
Prove : $$ AB^2 + CD^2 = BC^2 + AD^2$$
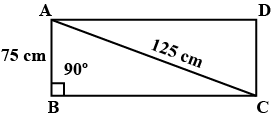
The length of the diagonal of a rectangular playground is $$125 \ m$$ and the length of one side is $$75\ m$$. Find the length of the other side.
Let $$ABCD$$ be the rectangle and $$AC$$ be the diagonal as shown in the above figure:
It is given that the diagonal $$AC=125$$ m and length of $$AB=75$$ m
In $$△ABC$$, $$∠B=90^{ 0 }$$
According to the pythagoras theorem
$$AC^{ 2 }=AB^{ 2 }+BC^{ 2 }\quad \\ \Rightarrow 125^{ 2 }=75^{ 2 }+BC^{ 2 }\quad \\ \Rightarrow 15625=5625+BC^{ 2 }\quad \quad \quad \quad \quad \quad \quad \quad \\ \Rightarrow BC^{ 2 }=15625-5625\\ \Rightarrow BC^{ 2 }=10000\\ \Rightarrow BC=\sqrt { 10000 } \\ \Rightarrow BC=\sqrt { 100^{ 2 } } \\ \Rightarrow BC=100$$
Hence, the length of the other side$$BC=100$$ m.
In $$\Delta ABC$$, $$\angle B=90^{\circ}$$, Find the sides of the triangle, if $$AB = x\ cm, BC = \left ( 4x+4 \right )\ cm$$ and $$AC = \left ( 4x+5 \right )\ cm$$
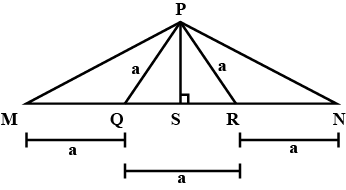
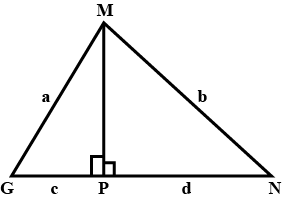
In $$\triangle MGN$$, $$MP \perp GN$$. If $$MG = a$$ units, $$MN = b$$ units, $$GP = c$$ units and $$PN = d$$ units.
Prove that $$\left(a + b\right) \left(a - b\right) = \left(c + d\right) \left(c - d\right)$$.
In a right triangle the lengths of the medians of the acute angles are $$9$$ cm and $$13$$ cm. Find the length of the hypotenuse of the triangle.
$$E$$ is the mid point. $$BC$$ so that $$AE=9$$ units. $$D$$ is the midpoint on $$AD$$ so that $$BD=13$$ units.
As $$BC=2EC$$ and $$AC=2DC$$ and $$DCE$$
1) a corner of both it follows that $$ABC$$ and $$DEC$$ are similar and $$AB=2DE$$ we therefore only need to find length of $$DE$$
Let $$CE=x$$ $$CD=y$$
Pythagoras give,
$${ BD }^{ 2 }={ CD }^{ 2 }+{ BC }^{ 2 }$$
$$\Rightarrow { \left( 13 \right) }^{ 2 }={ y }^{ 2 }+{ \left( 2x \right) }^{ 2 }$$
$${ y }^{ 2 }+{ 4x }^{ 2 }=169\quad \longrightarrow \left( 1 \right) $$
$${ \left( AE \right) }^{ 2 }={ \left( AC \right) }^{ 2 }+{ \left( CE \right) }^{ 2 }$$
$${ 9 }^{ 2 }={ \left( 2y \right) }^{ 2 }+{ x }^{ 2 }$$
$${ x }^{ 2 }+{ 4y }^{ 2 }=81\quad \longrightarrow \left( 2 \right) $$
If we add $$(1)$$ and $$(2)$$ we get
$${ 5x }^{ 2 }+{ 5y }^{ 2 }=250$$
$$\Rightarrow { x }^{ 2 }+{ y }^{ 2 }=50$$
$${ DE }^{ 2 }={ x }^{ 2 }+{ y }^{ 2 }=50=2\times 25$$
$$DE=5\sqrt { 2 } .\quad \quad AB=2DE=10\sqrt { 2 } $$ or $$Ca$$ $$14,14$$
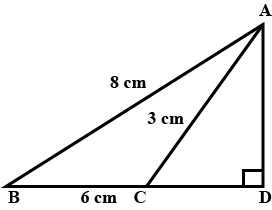
In Figure $$AB=8 cm$$, $$BC=6$$cm, $$AC=3$$cm and the $$\angle $$ADC$$=90^{\circ}$$. Calculate $$CD$$.
Let, $$CD\ =x$$ cm
Then from $$\Delta$$ ADC, using Pythagoras theorem ,
$$AD^2+CD^2=AC^2$$
$$\Rightarrow AD^2+x^2=3^2$$
$$\Rightarrow AD^2=(9-x^2)$$.........(1)
In $$\Delta$$ ABD , using Pythagoras theorem,
$$AB^2=BD^2+AD^2$$
$$\Rightarrow 8^2=(6+x)^2+(9-x^2)$$[Using equation (1)]
$$\Rightarrow 64=36+x^2+12x+9-x^2$$
$$\Rightarrow 12x=64-45$$
$$\Rightarrow x=\large{\frac{19}{12}}$$
$$\therefore CD=$$$$ \large{\frac{19}{12}}$$ cm$$=1.58\overline{3}$$ cm
Show that the following points form an equilateral triangle. (-$$\sqrt 3$$, 1), (2 $$\sqrt 3$$, -2) and (2 $$\sqrt 3$$, 4)
The straight lines 3x + 4y = 5 and 4x - 3y = 15 -intersect at the point A. On these lines, the points B and C are chosen so that AB = AC. Find possible equation of the line BC passing through the point (1, 2).
The given lines are perpendicular and as AB = AC , Therefore $$ \triangle $$ ABC is art . angled isosceles . Hence the line BC through ( 1 , 2) will make an angles of $$\pm 45^{\circ}$$ with the given lines . Its equations is y - 2 = m (x - 1) where m = 1 / 7 and -7 as in .Hence the possible equations are 7x + y - 9 = 0 and x - 7y + 13 = 0 Alt :
The two lines will be parallel to bisectors of angle between given lines and they pass through ( 1, 2)
$$ \therefore $$ y - 2 = m ( x - 1)
where m is slope of any of bisectors given by
$$ \dfrac {3x \, + \, 4y \, - \, 5 }{5} \, = \, \pm \dfrac {4x \, - \, 3y \, - \, 15 }{5}$$
or x - 7y + 13 = 0 or 7x + y - 20 = 0
$$ \therefore $$ m = 1 / 7 or - 7
putting in (1) , the required lines are 7x + y - 9 = 0
and x - 7y + 13 = 0 as found above
Two parallel lines - are at a distance 1 apart and a point P between them is at a distance p from one of them. Q and R are chosen on these two parallel, lines such that $$\Delta$$ PQR is an equilateral triangle. Prove that the length of the side of this equilateral triangle is$$\sqrt{\dfrac{p^2 \, - \, p \, + \, 1}{3}}$$
y = 0 and y = 1 are two parellel lines , distance QL = 1apart . P is point between then such that PM = p and $$\Delta$$ PQR is equilateralLet Q lie on y = 1 and R on y = 0 may be chosen as origin (0,0) if RP be inclined at $$\theta$$ , then
p = a sin $$\theta$$ ........(1)
QL = 1 = QR sin $$(\theta \, + \, 60^{\circ}) \, = \, a sin \, (\theta \, + \, 60^{\circ})$$
or 1 = a $$(sin \, \theta \, cos \, 60^{\circ} \, + \, cos \, \, \theta \, sin \, 60^{\circ})$$ .... (2)
We have to eliminate $$\theta$$ between (1) and (2) and the find the length of side a in terms of known quantity p.
$$\left ( 1 \, - \, \dfrac{a \, sin \theta}{2} \right )^2 \, = \, \dfrac{3a^2 \, cos^2 \, \theta}{4}\, = \, \dfrac{3a^2}{4}( 1 \, - \, sin^2 \, \theta )$$
Now put sin $$\theta$$ = p/a from (1)
$$\left ( 1 \, - \, \dfrac{p}{2} \right )^2 \, + \, \dfrac{3a^2}{4}\left [ 1 \, - \, \dfrac{p^2}{a^2} \right ] \, = \,\dfrac{3a^2}{4} \, - \, \dfrac{3p^2}{4}$$
or 4 - 4p = $$p^2 \, + \, 3p^2 \, = \, 3a^2$$
or a = 2$$\sqrt{\dfrac{p^2 \, - \, p \, + \, 1}{3}}$$
$$\triangle ABD $$ is a right triangle right-angled at A and $$AC\bot BD.$$ Show that (i) $${ AB }^{ 2 } = BC.BD$$(ii) $${ AC }^{ 2 } = BC.DC$$(iii) $${ AD }^{ 2 } = BD \cdot CD$$(iv) $$\dfrac { { AB }^{ 2 } }{ { AC }^{ 2 } } = \dfrac { BD }{ DC }$$
$$\angle DAB=\angle ACB$$ [ Each $$90^o$$ ]
$$\angle ADB=\angle CBA$$ [ Common angle ]
$$\therefore$$ $$\triangle ADB\sim\triangle CAB$$
$$\therefore$$ $$\dfrac{AB}{CB}=\dfrac{BD}{AB}$$
$$\therefore$$ $$AB^2=BC\times BD$$ [ Hence proved ]
$$( ii)$$ Let $$\angle CAB=x$$ --- ( 1 )
In $$\triangle CBA$$
$$\angle CBA=180^o-90^o-x$$
$$\therefore$$ $$\angle CBA=90^o-x$$ --- ( 2 )
Similarly in $$\angle CAD$$,
$$\angle CAD=90^o-\angle CAD$$
$$\therefore$$ $$\angle CAD =90^o-x$$ ---- ( 3 )
$$\angle CDA=180^o-90^o-(90^o-x)$$
$$\angle CDA=x$$ --- ( 4 )
In $$\triangle CBA$$ and $$\triangle CAD$$
$$\angle CBA=\angle CAD$$ [ From ( 2 ) and ( 3 ) ]
$$\angle CAB=\angle CDA$$ [ From ( 1 ) and ( 4 ) ]
$$\therefore$$ $$\triangle CBA\sim\triangle CAD$$ [ By AA similarity ]
$$\therefore$$ $$\dfrac{AC}{DC}=\dfrac{BC}{AC}$$
$$\therefore$$ $$AC^2=BC\times DC$$ ---- [ Hence proved ]
$$(iii)$$ In $$\triangle DCA$$ and $$\triangle DAB$$
$$\angle DCA=\angle DAB$$ [ Each $$90^o$$]
$$\angle CDA=\angle ADB$$ [ Common angle ]
$$\therefore$$ $$\triangle DCA\sim\triangle DAB$$
$$\therefore$$ $$\dfrac{DC}{DA}=\dfrac{DA}{DB}$$
$$\therefore$$ $$AD^2=BD\times CD$$ ---- [ Hence proved ]
$$( iv)$$ $$\dfrac{AB^2}{AC^2}=\dfrac{BC\times BD}{BC\times DC}$$
$$\therefore$$ $$\dfrac{AB^2}{AC^2}=\dfrac{BD}{DC}$$
If in the given $$\triangle ABC, AB=BD=BC$$, then find the ratio of $$\angle ACD$$ : $$ \angle ADC$$
In this fig. $$M$$ is the midpoint of $$Q R$$, $$\angle P R Q = 90 ^ { \circ }$$, then prove that, $$P Q ^ { 2 } = 4 P M ^ { 2 } - 3 P R ^ { 2 }$$
To prove : $${ PQ }^{ 2 }={ 4PM }^{ 2 }-3{ PR }^{ 2 }$$
Proof :-
In $$\Delta PRM$$
$${ PM }^{ 2 }={ PR }^{ 2 }+{ RM }^{ 2 }$$ (Pythagoras theorem) $$\longrightarrow \left( 1 \right) $$
Also,
In $$\Delta PQR$$
$${ PQ }^{ 2 }={ PR }^{ 2 }+{ RQ }^{ 2 }$$
$$={ PR }^{ 2 }+{ \left( RM+MQ \right) }^{ 2 }$$
$$={ PR }^{ 2 }+{ \left( RM+RM \right) }^{ 2 }$$ $$\left( \because \quad RM=MQ \right) $$
$$={ PR }^{ 2 }+{ 4RM }^{ 2 }\quad \quad \longrightarrow \left( 2 \right) $$
From $$(1)$$,
$${ RM }^{ 2 }={ PM }^{ 2 }-{ PR }^{ 2 }\quad \quad \longrightarrow \left( 3 \right) $$
Putting $$(3)$$ in $$(2)$$ we get
$${ PQ }^{ 2 }={ PR }^{ 2 }+4\left( { PM }^{ 2 }-{ PR }^{ 2 } \right) $$
$${ PQ }^{ 2 }={ PR }^{ 2 }+{ 4PM }^{ 2 }-{ 4PR }^{ 2 }$$
$${ PQ }^{ 2 }={ 4PM }^{ 2 }-3{ PR }^{ 2 }$$
Hence proved.
If 5,12,135,12,13 are the length of the side of a triangle. show that the triangle is right angled. Find the length of altitude on the hypotenuse.
Let the sides of the triangle be $$a = 5$$, $$c = 12$$ and $$b = 13$$.
$${a^2} + {c^2} = {\left( 5 \right)^2} + {\left( {12} \right)^2}$$
$$ = 25 + 144$$
$$ = 169$$
$${b^2} = {\left( {13} \right)^2}$$
$$ = 169$$
This shows that $${a^2} + {c^2} = {b^2}$$.
If the sum of square of two sides of a triangle is equal to the square of the third side, then the triangle is a right angled triangle. (Pythogoras' Theorem)
$$\therefore$$ the given triangle is a right angled triangle.
To find the altitude on the hypotenuse $$(h)$$
We have,
$$h^2 + x^2 = 5^2$$ $$ -(1)$$
$$h^2 + (13-x)^2 = 12^2$$ $$ -(2)$$
Subtracting $$(1)$$ from $$(2)$$:
$$(13-x)^2 - x^2 = 12^2-5^2$$
$$169 -2*13*x +x^2 -x^2 = 144-25$$
$$169-119 = 26x$$
$$x = \dfrac{50}{26}$$
Substituting in $$(1)$$
$$h^2 + \left(\dfrac{50}{26}\right) ^2 = 25$$
$$h^2 = 25- \dfrac{50^2}{26^2}$$
$$h^2 = \dfrac{16900-2500}{26^2}$$
$$h^2 = \dfrac{14400}{26^2}$$
$$h^2 = \left(\dfrac{120}{26}\right)^2$$
$$h = \left(\dfrac{120}{26}\right)$$
$$h$$ (height of altitude on the hypotenuse) $$=\dfrac{60}{13}$$
From the information given in the figure, prove that PM=PN= $$\sqrt { 3 } \times a$$
$$PQ=QR=PR=a$$
Now, $$\Delta PMS$$ is right angled
$$=\Delta PQR$$ is equilateral
$$QS=SR=\dfrac{1}{2}QR$$
$$QS=\dfrac{a}{2}$$
$$PS$$ is altitude of $$\Delta$$
$$=PS=\dfrac{\sqrt{3}}{2}a$$
Now ,$$MS=MQ+QS$$
$$=a+\dfrac{q}{2}$$
$$MS=\dfrac{3q}{a}$$
Now, $$\Delta PMS$$ is right angled
By Pythagoras theorm,
$$PM^2=MS^2+RS^2$$
$$=\left(\dfrac{3q}{2}\right)^2+\left(\dfrac{\sqrt{3}}{2}a\right)^2$$
$$=\dfrac{9a^2+3a^2}{4}$$
$$PM^2=\dfrac{12a^2}{4}=3a^2$$
so $$PM=\sqrt{3}a$$
Since figure is symmetrical, we can prove in the same way for PN
$$=PM=PN=\sqrt{3}a$$
Hence Proved
If $$(-5,4)$$ and $$(5,4)$$ are tow vertices of an equilateral triangle, then find coordinates of the third vertex, given that the origin lies in the interior of the triangle.
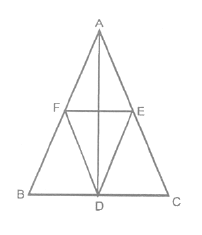
In the given figure $$\triangle{ABC}$$ is isosceles with $$AB=AC$$.$$D,E$$ and $$F$$ are respectively the mid-points of $$BC,CA$$ and $$AB$$.Show that the line segment $$AD$$ is perpendicular to the line segment $$EF$$ and is bisected by it.
R.E.F image
Given : $$\bigtriangleup $$ ABC is isosceles with AB=AC ,E and F are the mid-points of BC, CA and AB
To prove: AD$$\perp EF$$and is bisected by t
construction: Join D, F and F
Proof: $$ DE\left | \right |AC$$ and $$ DE= \frac{1}{2}AB$$
and $$ DF\left | \right |Ac$$ and$$ DE =\frac{1}{2}AC$$
The line segment joining midpoints of two sides of a triangle is parallel to the third side and is half of it
DE = DF $$(\because AB=AC)$$ Also AF=AE
$$\therefore AF =\frac{1}{2}AB,AE=\frac{1}{2}AC$$
$$\therefore DE=AE=AF=DF$$
and also DF$$\left | \right |$$ AE and $$DE\left | \right |AF$$
$$\Rightarrow $$ DEAF is a rhombus.
since diagrams of a rhombus bisect each other of right angles
$$\therefore AD\perp EF $$ and is bisected by it
If $$A$$ is $$( - 1,2,0 ) , B$$ is $$( 1,2,3 )$$ and $$C$$ is $$( 4,2,1 ) ,$$ then prove that $$\Delta A B C$$ is an isosceles right triangle.
$$A\left( -1,2,0\right) \;\;B\left( 1,2,3\right)\;\;C\left( 4,2,1\right)$$
Distance formula $$=\sqrt{\left( x_2-x_1\right)^2+\left( y_2-y_1\right)^2+\left( z_2-z_1\right)^2}$$
$$\Rightarrow AB=\sqrt{\left( 1+1\right)^2+\left( 2-2\right)^2+\left( 3-0\right)^2}=\sqrt{4+9}=\sqrt{13}$$
$$\Rightarrow BC=\sqrt{\left( 4-1\right)^2+\left( 2-2\right)^2+\left( 1-3\right)^2}=\sqrt{9+4}=\sqrt{13}$$
$$\Rightarrow AC=\sqrt{\left( 4+1\right)^2+\left( 2-2\right)^2+\left( 1-0\right)^2}=\sqrt{25+1}=\sqrt{26}$$
$$\Rightarrow AB^2+BC^2=AC^2$$
$$\left( \sqrt{13}\right)^2+\left( \sqrt{13}\right)^2=\left( \sqrt{26}\right)^2$$
$$13+13=26$$
$$26=26$$ Pythagoras theorem satisfied
and $$AB=BC$$ $$\therefore \angle B=90°$$
$$\therefore$$ The given triangle is right angled isosceles triangle
Hence, proved.
In the adjoining figure, $$A B C$$ is a triangle in which $$A D$$ is the bisector of $$\angle A$$. If $$A D \perp B C$$, show that $$\Delta A B C$$ is isosceles.
Given : $$AD$$ bisects $$\angle A$$ and is perpendicular to $$BC$$.
To prove : $$\Delta ABC$$ is isoceles
Proof :
In $$\Delta ABD$$ & $$\Delta ADC$$
$$\angle BAD=\angle DAC$$ ($$\because$$ $$D$$ bisects $$\angle A$$)
$$\angle ADB=\angle ADC$$
$$\Rightarrow \angle ABD=\angle ACD$$
($$\because$$ if two angles in a triangle are equal to two angles in another triangle, then the third angle of both the triangles must also be equal)
$$\Rightarrow \angle B=\angle C$$
$$\therefore$$ $$AB=AC$$ (if two angles are equal then the side opposite to the angles will also be equal)
Hence proved.
Show that the points $$A(1, 2), B(1, 6), C(1 + 2 \sqrt{3}, 4)$$ are vertices of an equilateral triangle.
Show that difference of any two sides of a triangle is less than to the third side.
To prove: AC-AB< BC
Construction: Mark a point 'D' on AC such that the distance AB=AD
Therefore, we have to prove that AC-AD<BC
So, we have to prove that CD < BC
Proof:
Consider triangle ABD,
since AB=AD
Since, opposite angles opposite to the equal opposite sides are always equal.
So,
So, p = p
Now, let
Now, using exterior angle property in triangle ABD,
Exterior angle property of a triangle states that the measure of an exterior angle is equal to the sum of the two interior angles.
(equation 1)
Now, using exterior angle property in triangle BCD,
(equation 2)
Now, by comparing equation 1 and 2,
So, y > x
BC > CD
CD < BC
AC - AD < BC
Since, AD = AB
Therefore, AC - AB < BC
Hence, proved.
Class 7 Maths Extra Questions
- Algebraic Expressions Extra Questions
- Comparing Quantities Extra Questions
- Data Handling Extra Questions
- Exponents And Powers Extra Questions
- Fractions And Decimals Extra Questions
- Integers Extra Questions
- Lines And Angles Extra Questions
- Perimeter And Area Extra Questions
- Practical Geometry Extra Questions
- Rational Numbers Extra Questions
- Simple Equations Extra Questions
- Symmetry Extra Questions
- The Triangle And Its Properties Extra Questions
- Visualising Solid Shapes Extra Questions