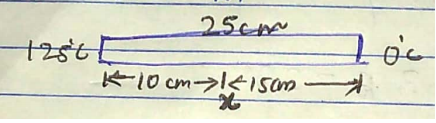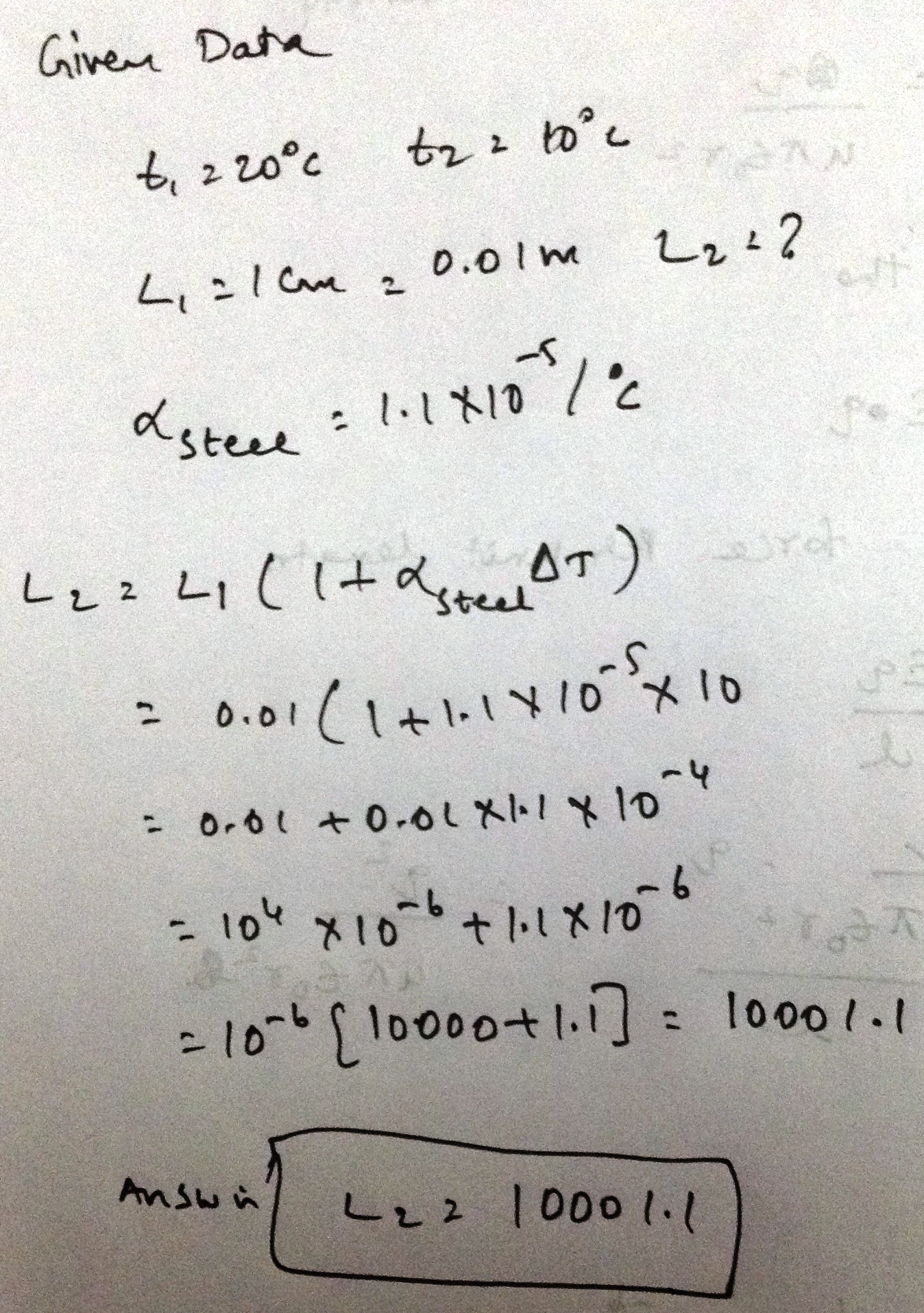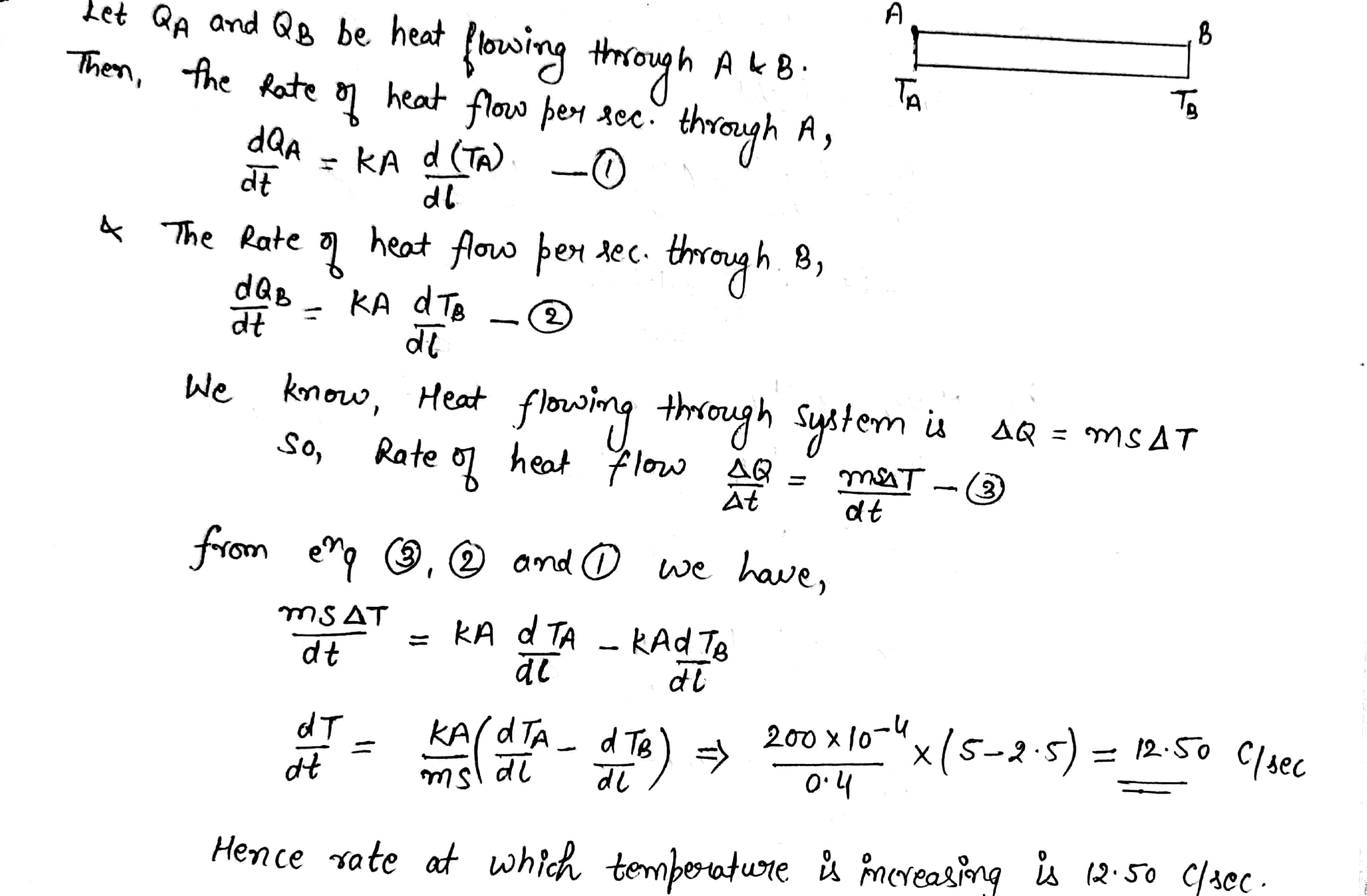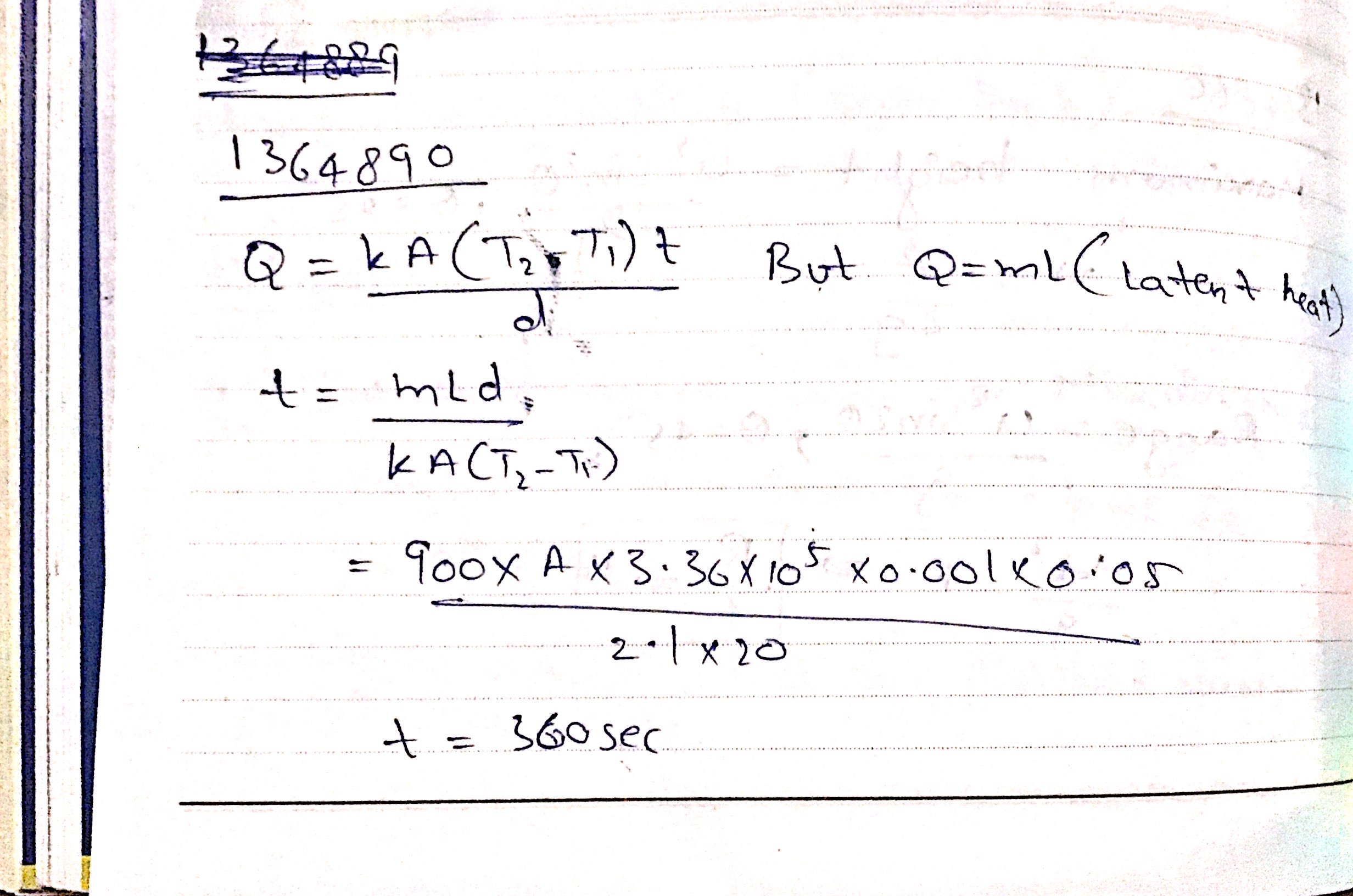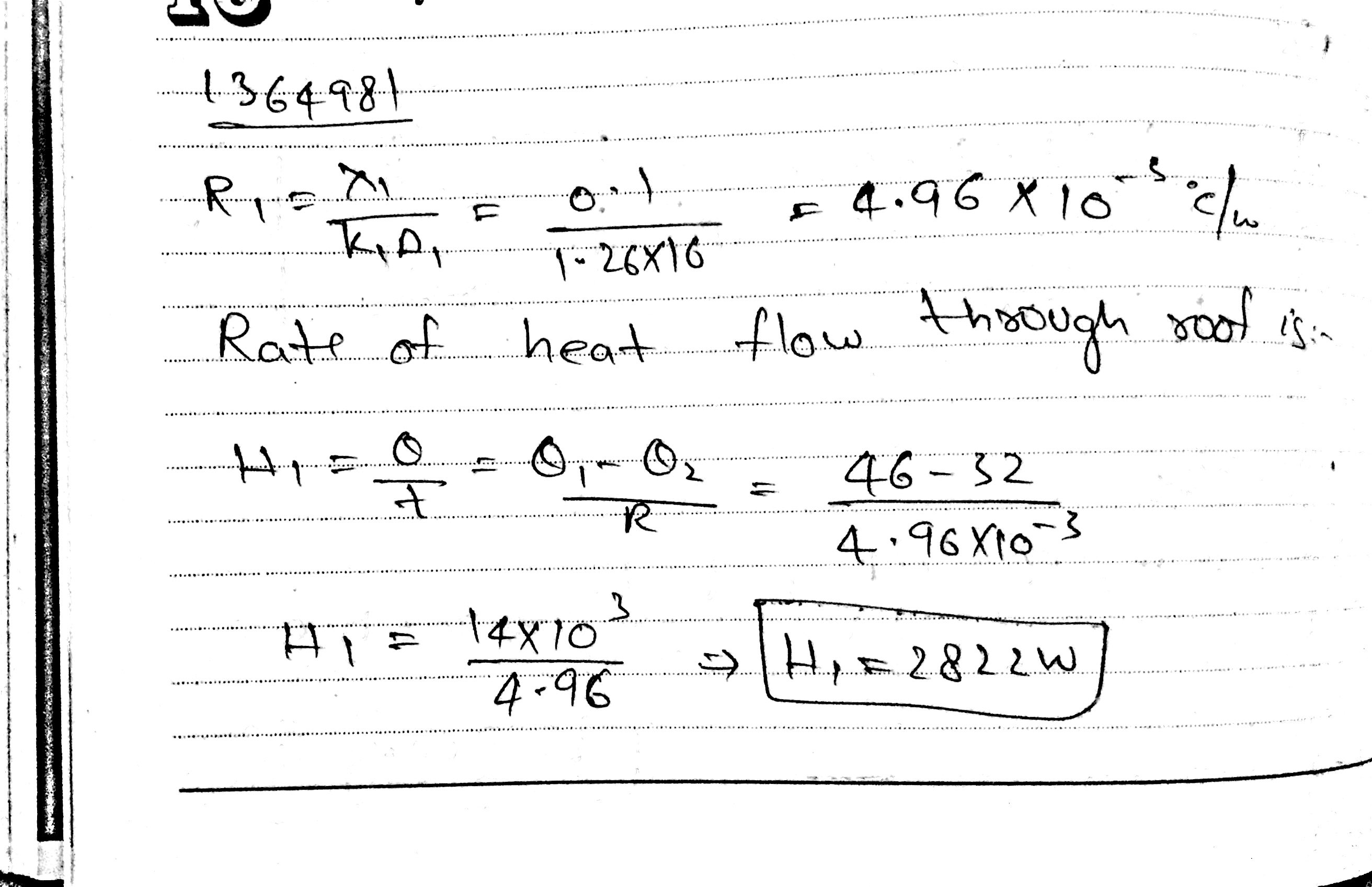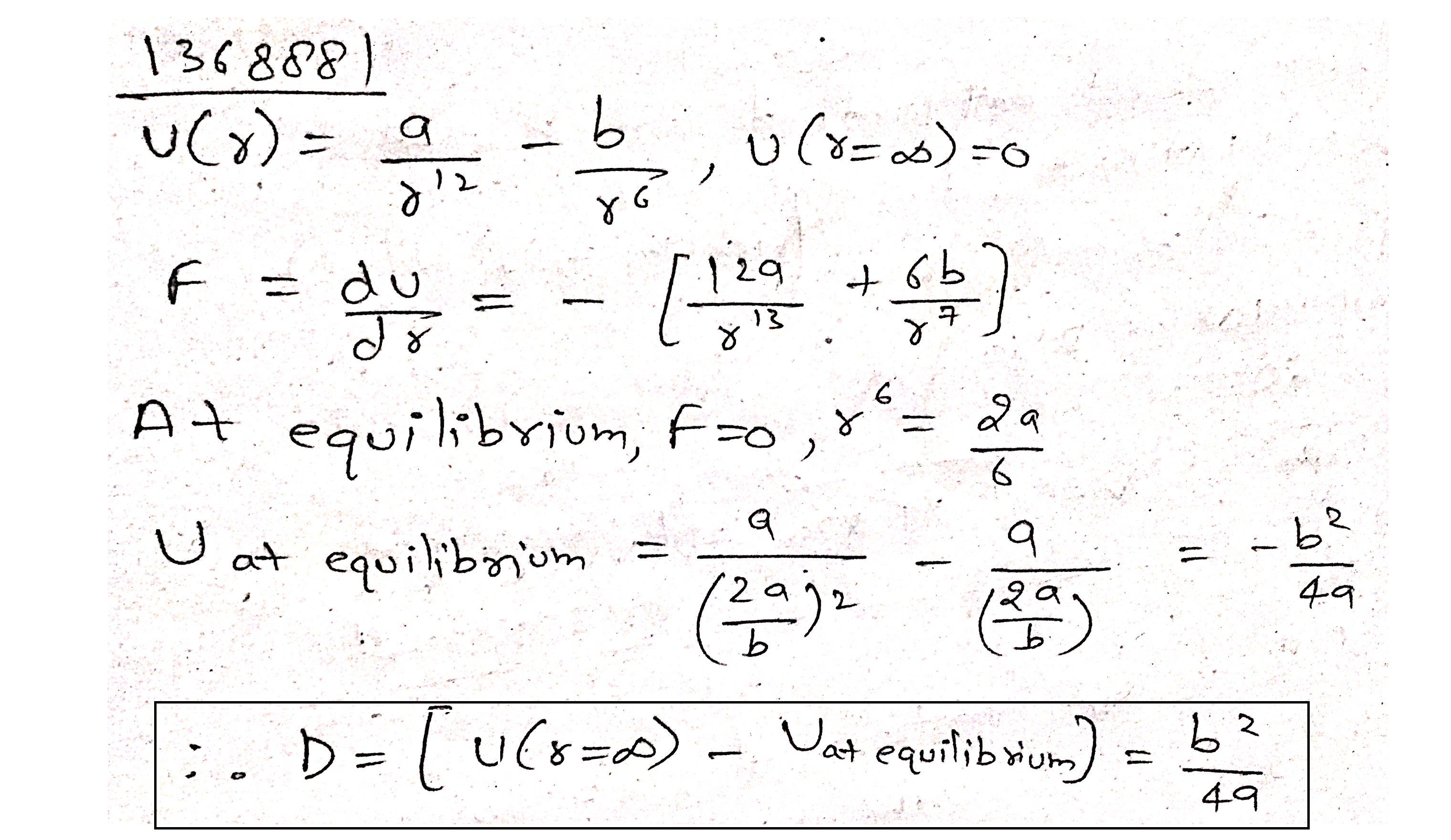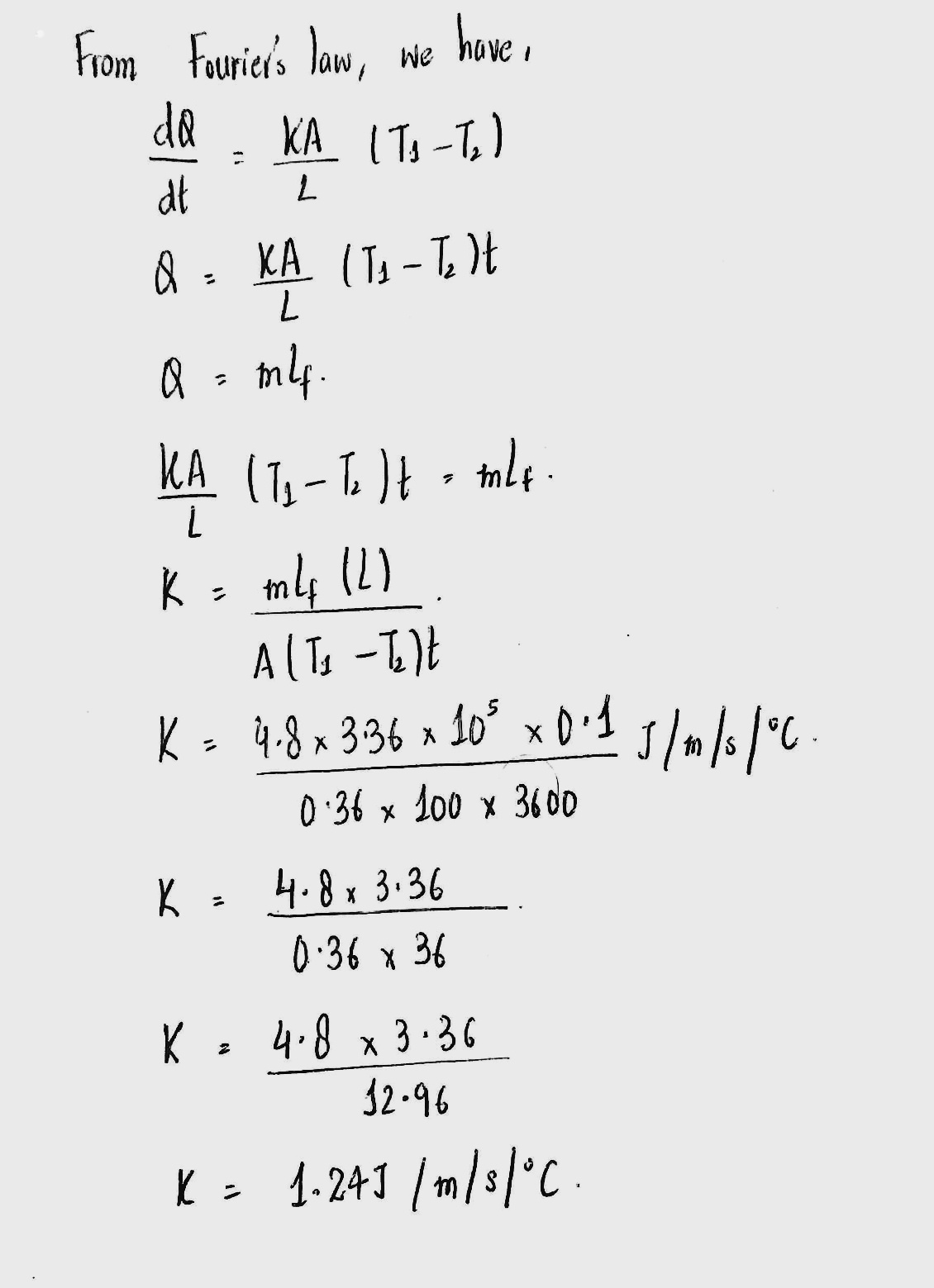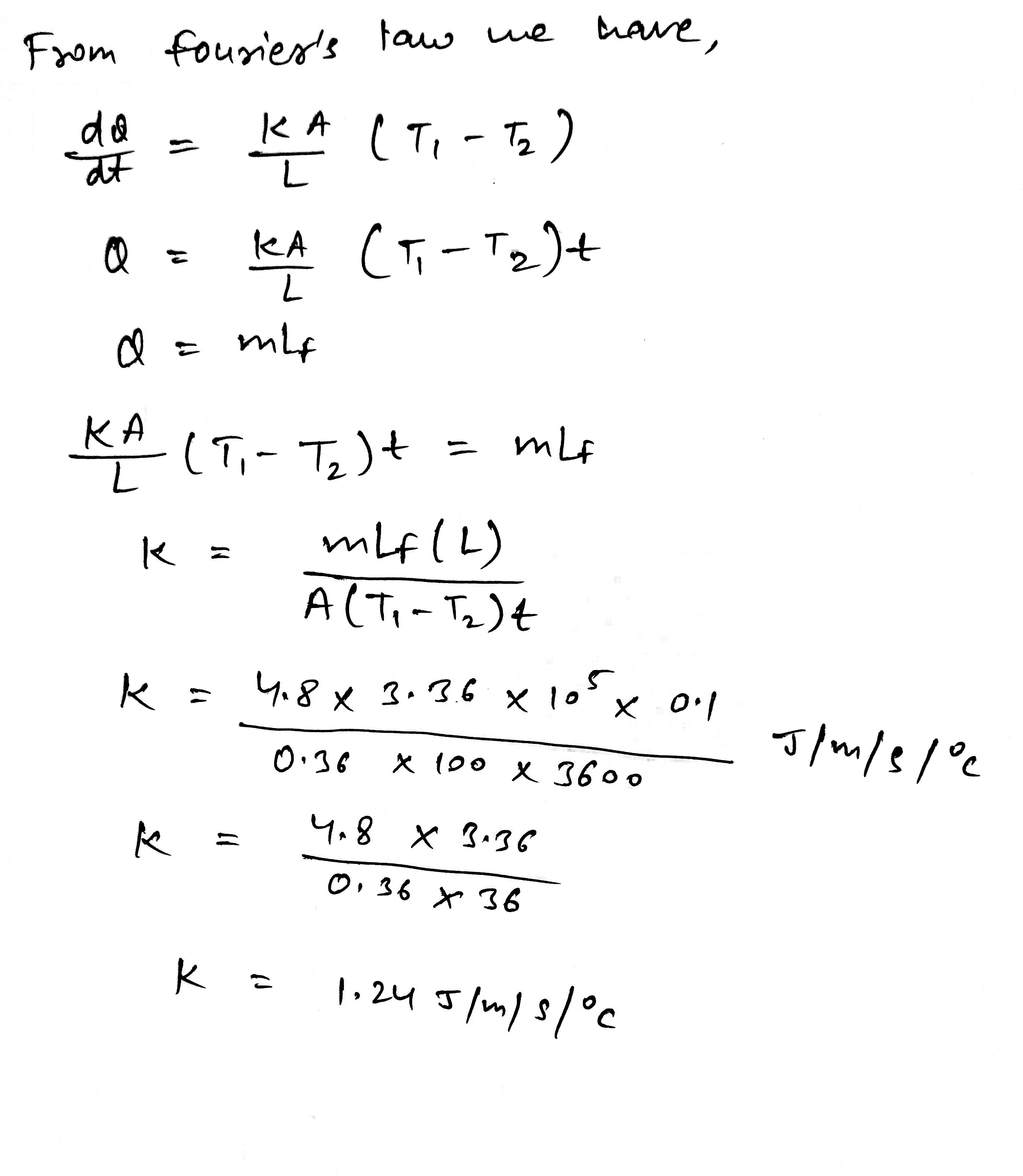Thermal Properties Of Matter - Class 11 Engineering Physics - Extra Questions
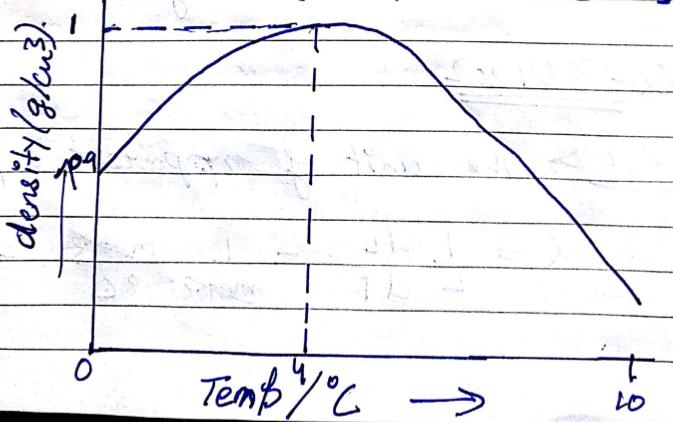
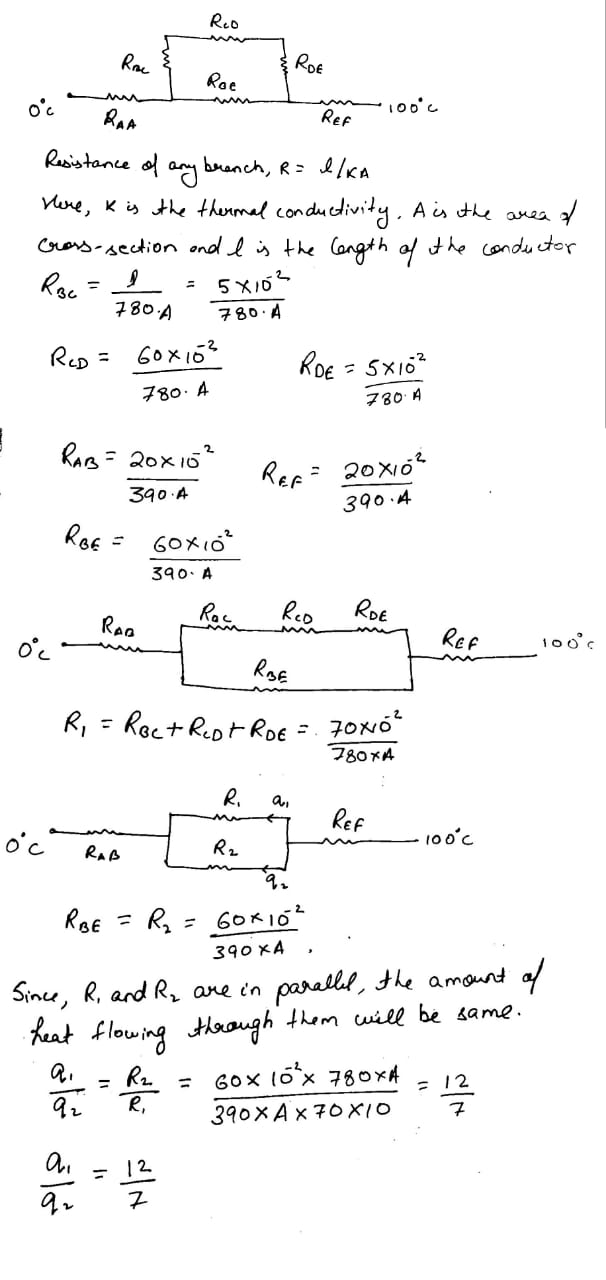
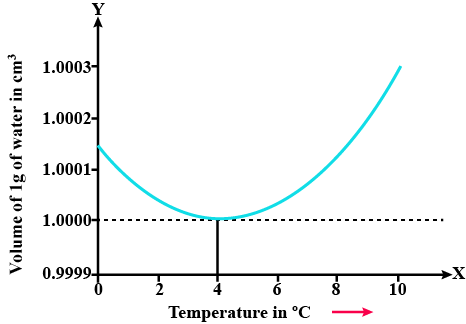
In a graph that shows the variation in density of water with the temperature in the range from $$0^oC$$ to $$10^oC$$. the maximum density attains at which temperature in $$^oC$$
The density increases till $$4^oC$$ and then decreases.
At what temperature the density of water is maximum? State its value.
A given mass of water is cooled from $$10C$$ to $$0C$$. The volume of liquid decreases in the process of condensing steam.Type 1 for true and 0 for false
When water is cooled from 10–0 degrees C,
From 10–4°C water will start contracting as all liquids do. But from 4–0°C volume of water will starting increasing this due to water’s unique property known as ‘Anamalous Expansion of Water’. From 4–0°C water will start expanding. Hence ice and water of same weight has different volumes.
On a Fahrenheit scale, the distance between the ice point and steam point is $$18 cm$$ Length of a degree on the thermometer is x then $$\frac{1}{x}$$
At what speed does heat radiation travel? What path does it follow?
If heat is received by a body from a source only by radiation, how is medium in between them, affected?
Name the process by which a slice of bread gets heat form the heated filament in a toaster. Give reason for your answer.
Convection cannot take place in________
Radiant heat can easily pass through_______
Define heat transfer due to Radiation.
Define the process of convection.
How are convection currents formed when a liquid is heated?
The faster mode of transmission of heat is _______
Why are glass tumblers made of thin glass?
Why are cold storages constructed with double walls?
If we sit near a fire,we feel warm. Explain.
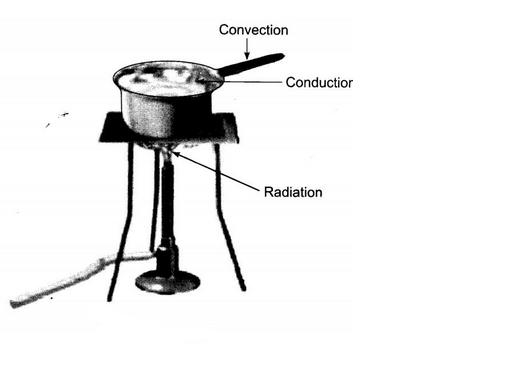
Look at figure. Mark where the heat is being transferred by conduction, by convention and by radiation.
Why is it not possible to cool the liquid at absolute 0K?
The process by which heat is transferred without the help of any material medium is called ............. .
Absolute scale of temperature is known as____ (Celsius scale, Kelvin scale)
Mr.Mehra gave one -third of his money to his son, one-fifth of his money to his daughter and the remaining amount to his wife.If his wife got Rs.$$91,000,$$how much money did Mr.Mehra have originally?
A gas at temperature of $$250K$$ is contained in a closed vessel. If the gass is heated through the percentage increase in the pressure is
The coefficient of performance of a refrigerator is 5 .If the temperarture inside freezer is - 20$$^{0}$$C, the temperature of the surroundings to which it rejects heat is
What is the value of universal gas constant
While deciding the unit for heat, which temperature interval is chosen? Why?
Given reasons for the following
(i) During summers, earthen pots help to cool water, kept inside them.
In $$1964$$, the temperature in the Siberian village of Oymyakon reached $$-71^oC$$. What temperature is this on the Fahrenheit scale?
You will find if you search.
A thermometer is used to measure _________ .
Observe the given graph and answer the following questions:
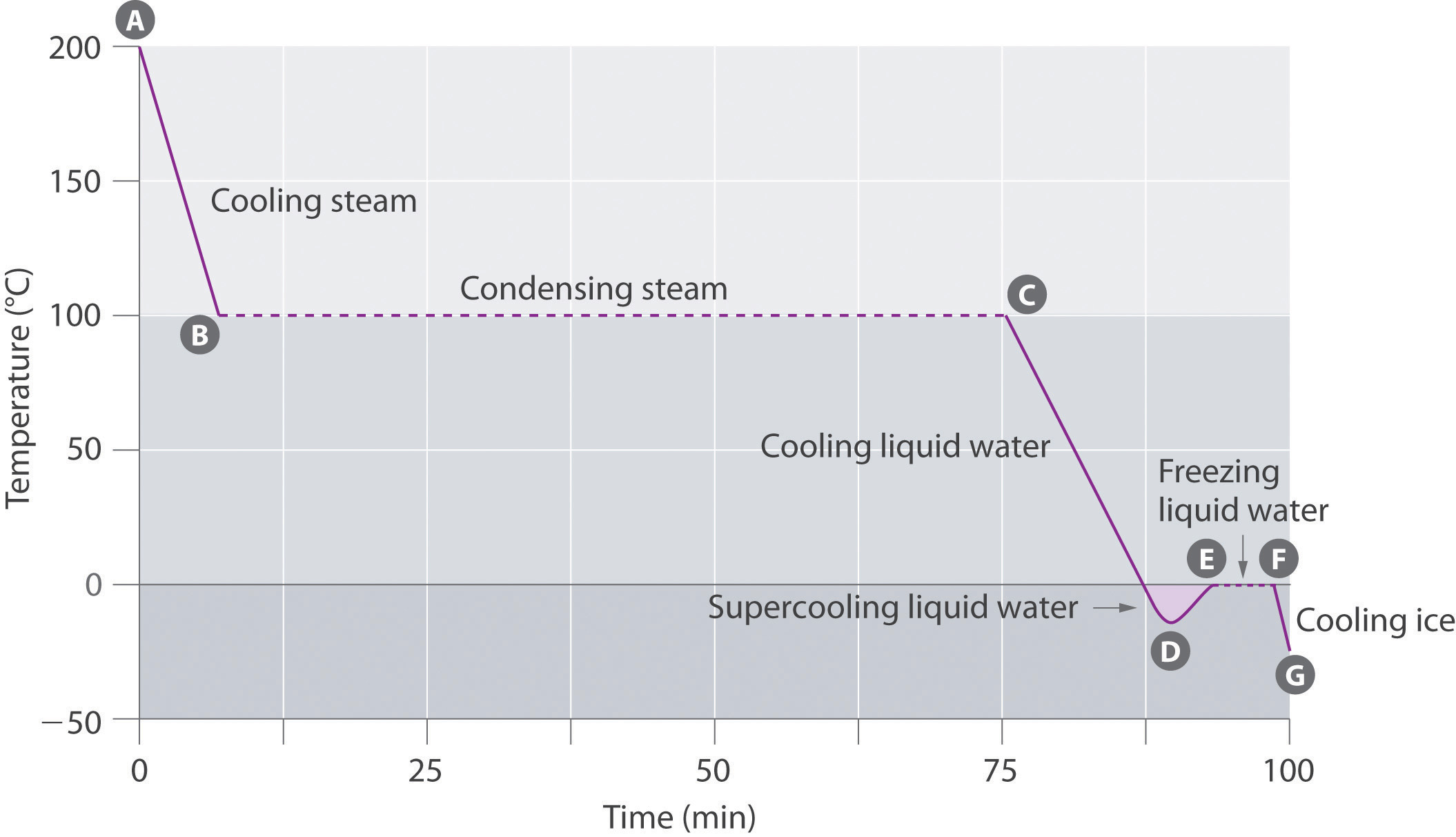
At what temperature does this process take place ?
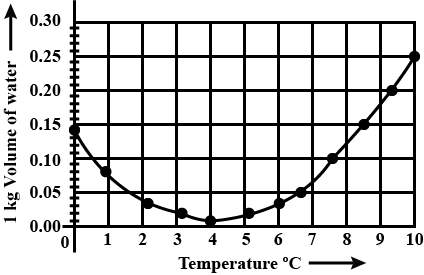
How will you demonstrate the thermal expansion in a liquid? Describe an experiment.
An ordinary mercury thermometer is first put in a beaker containing dry ice and is then transferred into another beaker containing hot water. The mercury thread rises four-fifth of the distance between the lower and upper fixed points. Find the temperature of water (i) in degree Celsius is m and (ii) in degree Fahrenheit is n then m+n =
A mercury thermometer is transferred from melting ice to a glass of milk. The mercury level rises by three-fifth of the distance between the lower and upper fixed points. Calculate the temperature of milk (i) in $$C$$ is m and (ii) in $$F$$ is n then m+n =
Describe an experiment to demonstrate the thermal expansion in a gas.
In a thermometer, distance between the upper and lower fixed points is $$80 cm$$, (a) Find the temperature on Celsius scale if the mercury level rises to a height $$10.4 cm$$ above the lower fixed point. What will be the temperature recorded in part
Explain why :
(a) A body with large reflectivity is a poor emitter
(b) A brass tumbler feels much colder than a wooden tray on a chilly day
(c) An optical pyrometer (for measuring high temperatures ) calibrated for an ideal black body radiation gives too low a value for the temperature of a red hot iron piece in the open but gives a correct value for the temperature when the same piece is in the furnace
(d) The earth without its atmosphere would be inhospitably cold
(e) Heating systems based on circulation of steam are more efficient in warming a building than those based on circulation of hot water
A brass boiler has a base area of $$0.15\,m^{2}$$ and thickness 1.0 cm. It boils water at the rate of 6.0 kg / min when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass $$= 109\,J\,s^{-1}m^{-1}K^{-1}$$; Heat of vaporisation of water $$=2256\times 10^{3}J kg^{-1}$$.
Liquids expand more than______but less than______.
What is meant by Anomalous expansion of water?
Are there any other materials subject to anomalous expansion except water?
What is the anomalous expansion?
Explain anomalous expansion of water and draw graph of density of water v/s temperature.
Liquids generally have lower density as compared to solids but ice floats on water. Why?
Describe anomalous behaviour of lanthanide?
At what temperature does the competing effects of contraction and expansion produce the smallest volume for liquid water?
A glass test tube containing some water is immersed in boiling water so that the upper end of the test is outside. It is found that water in the test tube does not boil even if it is kept there for a long time. Why?
What is the difference between Conduction and Convection?
Conduction transfers heat via direct molecular collision. An area with greater kinetic energy will transfer thermal energy to an area with lower kinetic energy. Higher-speed particles will collide with slower-speed particles. The slower-speed particles will increase in kinetic energy as a result. Conduction is the most common form of heat transfer and occurs via physical contact. Examples would be to place your hand against a window or place metal into an open flame.
Convection: When a fluid, such as air or a liquid, is heated and then travels away from the source, it carries the thermal energy along. This type of heat transfer is called convection. The fluid above a hot surface expands, becomes less dense, and rises.
3 kg of gold at a temperature of $$20^oC$$ is placed into contact with 1 kg of copper at a temperature of $$80^oC$$. The specific heat of gold is 1$$30 J/kg \cdot ^oC$$ and the specific heat of copper is $$390 J/kg \cdot ^oC$$. At what temperature do the two substances reach thermal equilibrium?
State True or False.Heat travels much faster in insulators than in conductors.
An ungraduated thermometer of uniform bore is attached to a centimeter scale and is found to read $$10\ cm$$ in melting ice, $$30\ cm$$ in boiling water and $$16\ cm$$ in a liquid. Find temperature of the liquid.
It is given that rate of heat transfer in convection is directly proportional to area of plate across which fluid flows$$A$$,density of fluid ($$\rho$$), velocity of flow ($$V$$),temperature difference ($$t$$) with proportionality constant of 2 units.Also fluid is flowing across edge to edge on a square plate of side length of 0.1 unit with density of fluid is 10 units and velocity of 2 units. Then what will be the rate of heat conducted through the plate if temperature difference between plate and fluid is unity?(assume that all $$units$$ are in international standards)
Ice at $$0$$ is a better coolant than water at $$0$$. Justify.
Calculate the heat energy required to raise the temperature of $$2\ kg$$ water from $$10^{o}C$$ to $$50^{o}C$$. (specific heat capacity of water is $$4200$$J $$kg^{-1}K^{-1}$$)
Define (i) Van't Hoff-Boyle;s law (ii) Van't Hoff Charle's law.
Why is the base of a cooking pan generally made thick?
An object floats in the water at room temperature. Explain your observation when
i) The water is heated.
ii) The water is cooled to $$4^0$$C.
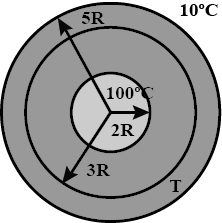
A spherical annular thermal resistor of thermal conductivity $$K$$ and inner and outer radii $$2R$$ and $$5R$$ respectively, is in steady state with its inner surface maintained at $$100^{\circ}C$$ and its outer surface maintained at $$10^{\circ}C$$ (heat flow is radially outwards). The temperature of the concentric spherical interface of radius $$3R$$ in steady state is $$T$$.
Given: A spherical annular thermal resistor of thermal conductivity $$K$$ and inner and outer radii $$2R$$ and $$5R$$ respectively, is in steady state with its inner surface maintained at $$100^∘C$$ and its outer surface maintained at $$10^∘C$$ (heat flow is radially outwards). The temperature of the concentric spherical interface of radius $$3R$$ in steady state is $$T$$.
To find the temperature of the concentric spherical interface of radius $$3R$$ in steady state
Solution:
Cut a sphere of width $$dr$$ and radius
$$\dfrac{dQ}{dt}=H=\dfrac{KAdT}{dr}$$
This can be understood,
$$H=\dfrac { KA{ \pi r }^{ 2 }dT }{ dr } $$
$$\dfrac { Hdr }{ { r }^{ 2 } } =KdT$$
$$H\left[ \dfrac { 1 }{ { R }_{ 1 } } -\dfrac { 1 }{ R } \right] =K\left( \Delta T \right) $$
$$H\left[ \dfrac { 1 }{ { R }_{ 1 } } -\dfrac { 1 }{ { R }_{ 2 } } \right] =K\left( { T }_{ 1 }-{ T }_{ 2 } \right) $$.....(1)
Now in fig(ii):
There are two layers and those layers are in series.
Heat current will be same across layers from formula (1)
For layer A heat current $$=\dfrac { K\left( 100-T \right) \left( 2R\times 3R \right) }{ R } $$......(2)
For layer B heat current $$=\dfrac { K\left( T-10 \right) \left( 3R\times 5R \right) }{ 2R } $$.....(3)
eqn(2) and eqn(3) should be equal
$$\dfrac { K\left( 100-T \right) \times { 6R }^{ 2 } }{ R } =\dfrac { K\left( T-10 \right) 15{ R }^{ 2 } }{ 2R } $$
$$(100-T)6\times 2 = 15(T-10)$$
$$1200-12T=15T-150$$
$$1350=27T$$
$$T=50°C$$
is the temperature of the concentric spherical interface of radius $$3R$$ in steady state
In the steady state of temperature at the end of a copper rod of length $$25cm$$ and area of cross-section $$1.0{cm}^{2}$$ are $${125}^{o}C$$ and $${0}^{o}C$$ respectively. Calculate the temperature gradient, rate of heat flow and the temperature at a distance $$10cm$$ from the hot end. [$$K$$ for copper $$=9.2\times {10}^{-3}kilocal/{m}^{o}C-s$$]
$$l=25cm=0.25m\\A=1cm^2=1\times 10^{-4}m^2 \\K=9.2\times 10^{-3}kcal/m^oCs$$
$$\cfrac { 125-0 }{ \cfrac { 25\times { 10 }^{ -2 } }{ 9.2\times { 10 }^{ -3 }\times 1\times { 10 }^{ -4 } } } =\cfrac { x-0 }{ \cfrac { 15\times { 10 }^{ -2 } }{ 9.2\times { 10 }^{ -3 }\times 1\times { 10 }^{ -4 } } } \\ \Rightarrow \cfrac { 125 }{ 25 } =\cfrac { x }{ 15 } \\ \Rightarrow x=75℃$$
Temperature gradient (at 10cm from hotter end)
$$=\cfrac { 75-0 }{ 0.15 } K/m\\ =500K/m$$
How is the transference of heat energy by radiation prevented in a calorimeter?
Name the radiations which are absorbed by greenhouse gases in the earth's atmosphere.
The percentage change in the pressure of a given mass of a gas filled in a container at constant temperature is $$100$$%. Calculate the percentage change in its volume.
A metal cylinder $$0.628\ m$$ long and $$0.04\ m$$ in diameter has one end in boiling water at $$100^oC$$ and other end is melting ice. The co-efficient of Thermal conductivity of the metal is $$378\ Wm^{-1}k^{-1}$$. Latest heat of Ice is $$3.36\times 10^{5} Jkg^{-1}$$. Find the mass of ice melts in one hour.
Hot milk is easier to drink from a bowl than from a glass. Mention the reason.
How does the average kinetic energy of a gas molecule depend on the absolute temperature of the gas?
A body cools from $$62^{\circ}C$$ to $$50^{\circ}C$$ in $$10$$ minutes and to $$42^{\circ}C$$ in the next $$10$$ minutes. Find the temperature of surroundings.
A gas is filed in a rigid container at pressure$${{\rm{P}}^{\rm{0}}}$$. If the mass of each molecule is halved
Keeping the total number of molecules same and their r.m.s
speed is doubled then find the new pressure.
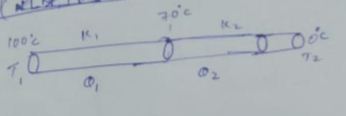
Two rods of same dimension, but made of different materials are joined end to end with their free ends being maintained at $$100^{o}C$$ and $$0^{o}C$$ respectively. The temperature of the junction is $$70^{o}C$$. Then the temperature of the junction if the rods are interchanged will be equal to $$T\ ^{o}C$$ Find $$T:$$
$$\frac{{{k_1}.A\left( {100 - 70} \right)}}{l} = \frac{{{k_2}.A\left( {70 - 0} \right)}}{l}$$
$${k_1} \times 30 = {k_2} \times 70$$ $${{k_1} = \frac{7}{2}{k_2}}$$
$$\frac{{{k_2}.A\left( {100 - T`} \right)}}{l} = \frac{{{k_1}.A\left( {T - 0} \right)}}{l}$$
$${k_2}\left( {100 - T} \right) = \frac{7}{3}{k_2}\left( T \right)$$
$$3\left( {100 - T} \right) = 7T$$
$$300 - 3T = 7T$$
$$10T = 300$$
Hence, $${T = {{30}^0}}$$
A refrigirator converts $$100g$$ of water at $${20}^{o}C$$ to ice at $$-{10}^{o}C$$ in $$35$$ min. Calculate the average rate of heat extraction in watt. The specific heat capacity of water is $$4.2J{g}^{-1}$$ $${K}^{-1}$$, specific heat of ice is $$336J{g}^{-1}$$ and the specific heat capacity of ice is $$2.1J{g}^{-1}$$ $${K}^{-1}$$.
A meter scale of steel is calibrated at to $${20^\circ}C$$ give a correct reading.F ind the distance between 50 cm mark and 51 cm mark if the scale is used at $${10^\circ}C$$. Coefficient of linear expansion of steel is $${1.1 \times 10^{ - 5}} ^{\circ}{C^{- 1}}$$
The coefficient of linear expansion, α, for a material is defined as the fractional change in length, divided by the change in temperature.
Density and Molar Mass of Gaseous Substances
A $$60\ kg$$ boy running at $$5.0\ m/s$$ while playing basketball falls down on the floor and skids along on his leg until he stops. How many calories of heat are generated between his leg and the floor?
Assume that all this heat energy is confined to a volume of $$2.0\ cm^{3}$$ of his flesh. What will be temperature change of the flesh? Assume $$c = 1.0\ cal/ g^{\circ}C$$ and $$\rho = 950\ kg/ m^{3}$$ for flesh.
The raise in the temperature of a given mass of an ideal gas at constant pressure and at temperature $$27$$ to double its volume is.
Find the number of molecules in $$1\ cm^3$$ of an ideal gas at $$0^0\ C$$ and at a pressure of $$10^{-5}mm$$ of mercury.
Why do our hands become warm when rubbed against each other? Explain.
Find the temperature at which volume and pressure of 28 gm nitrogen gas becomes $$10dm^{3}$$ & 2.46 atm respectively. (Molar mass of nitrogen gas = $$28\space g/mo1^{-1}$$)
A one litre glass flask contains some mercury. It is found that at different temperatures the volume of air inside the flask remains the same. What is the volume of mercury in this flask if coefficient of linear expansion of glass is $$9 \times {10^{ - 6}}{/^ \circ }C$$ while of volume expansion of mercury is $$1.8 \times {10^{ - 4}}{/^ \circ }C$$
One day in the morning , Ramesh filled up 1/3 bucket of hot water from geyser, to take bath. Remaining 2/3 was to be filled by cold water (at room temperature) to bring mixture to a comfortable temperature. Suddenly Ramesh had to attend to something which would take some times, say 5-10 minutes before he could take bath. Now he had two options:
(i) Fill the remaining bucket completely by cold water and then attained to the work,
(ii) First attend to the work and fill the remaining bucket just before taking bath. Which option do you think would have water warmer? Explain.
What is the difference between resistance and reactance?
In an insulated vessel, 0.05 kg steam at 373 K and 0.45 kg of ice at 253 K are mixed. Find the final temperature of the mixture (in kelvin).
Calculate the volume occupied by gram of Acetely $$(C_2H_2)$$ at $$50^o$$ and 740 mm pressure.
Use kinetic theory of gases to show that the average Kinetic energy of a molecule of an ideal gas is directly proportional to the absolute temperature of the gas.
A resistance thermometer reads $$R={ 20 }^{ \circ }0\Omega ,27.5\Omega ,$$ and $${ 50 }^{ \circ }0\Omega $$ at the ice point $$\left( { 0 }^{ \circ }C \right) ,$$ the steam point $$\left( { 100 }^{ \circ }C \right) ,$$ and the zine point $$\left( { 420 }^{ \circ }C \right) ,$$ respectively. Assuming that the resistance varies with temperature as $${ R }_{ \theta }={ R }_{ 0 }\left( { 1+\alpha \theta +\beta \theta }^{ 2 } \right) ,$$ find the values of $${ R }_{ 0 },$$ $$\alpha $$ and $$\beta$$. Here $$\theta $$ represents the temperature on Celsius scale.
Write any 2 properties of thermal radiations ?
Equal heat is gives to two objects A and B of mass 1 g. Temperature of A increases by $$3^oC$$ and B by $$5^oC$$. Which object has more specific heat? And by what factor?
A piece of iron of mass 2.0 kghas a heat capacity of $$966J{ K }^{ -1 }$$.
Find : (i) heat energy needed to warm it by $${ 15 }^{ 0 }C$$, and
(ii) its specific heat capacity in S.I unit.
Observe the given graph and answer the following questions:
Name the process represented in the figure.
A platinum resistance thermometer reads $$0^o$$ when its resistance is $$80\Omega$$ and $$100^o$$ when its resistance is $$90\Omega$$. Find the temperature at the platinum scale at which the resistance is $$86\Omega$$.
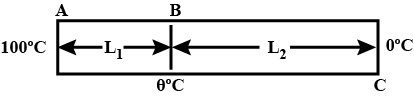
The ends of meter sticks are maintained at $$ 100^0C $$ and $$ 0^0 C $$ . one end of a rod is maintained at $$ 25^0 c $$ where should its other end be touched on the meter stick so that there is no heat current in the rod in steady state?
let the point to be touched be B
No heat will flow when, the temp at that points also $$ 25^0 C$$
i.e. $$ Q_{AB} = Q_{AB} $$
So $$ , \dfrac { KA ( 100-25)}{100- x} = \dfrac {KA(25-0) }{x} $$
$$ \Longrightarrow 75 x = 2500 - 25x \Longrightarrow 100 x = 2500 \Longrightarrow x = 25 cm $$ from the end with $$ 0^0 C $$
No heat will flow when, the temp at that points also $$ 25^0 C$$
i.e. $$ Q_{AB} = Q_{AB} $$
So $$ , \dfrac { KA ( 100-25)}{100- x} = \dfrac {KA(25-0) }{x} $$
$$ \Longrightarrow 75 x = 2500 - 25x \Longrightarrow 100 x = 2500 \Longrightarrow x = 25 cm $$ from the end with $$ 0^0 C $$
A steel frame $$ ( k = 45 \ W/m\ ^\circ C$$ of total length 60 cm and cross-sectional area $$ 0.20 cm^2 $$ forms three sides of a square . the free ends are maintained at $$20^0 C $$ and $$ 40^0 c $$ . find the rate of heat flow through a cross-section of the frame.
Given:
$$ K = 45 W/m\ ^0 C $$
$$ t= 60 cm = 60 \times 10^{-2} m $$
$$ A = 0.2 cm^2 = 0.2 \times 10^{-4}m^2 $$
$$Q_1=40^\circ C\\Q_2=20^\circ C$$
$$ t= 60 cm = 60 \times 10^{-2} m $$
$$ A = 0.2 cm^2 = 0.2 \times 10^{-4}m^2 $$
$$Q_1=40^\circ C\\Q_2=20^\circ C$$
Rate of the heat flow,
$$ = \dfrac {KA(\theta_1 - \theta_2) }{l} = \dfrac { 45 \times 0.2 \times 10^{-4} \times 20 }{ 60 \times 10^{-2} }= 30 \times 10^{-3}= 0.03 W $$
$$ = \dfrac {KA(\theta_1 - \theta_2) }{l} = \dfrac { 45 \times 0.2 \times 10^{-4} \times 20 }{ 60 \times 10^{-2} }= 30 \times 10^{-3}= 0.03 W $$
A liquid nitrogen container is made of 1-cm thick styrofoam sheet having thermal conductivity $$ 0.025 J s^{-1} m^{-1^0 }C^{-1} $$ . liquid nitrogen at 80 K is kept in it . A total area of $$ 0.80 m^2 $$ is in contact with liquid nitrogen. the atmospheric temperature is 300 K, calculate the rate of heat flow from atmosphere to the liquid nitrogeri.
Steam at $$ 120^0 C $$ is continueously passed through a 50 cm long rubber tube of inner and outer radii 1.0 cm and 1.2 cm . the room temperature is $$ 30^0 C $$ calculate the rate of heat flow though the walls of the tube. thermal conductivity of rubber $$ = 0.15 Js^{-1} m^{-1^0}C^{-1} $$
Given,
$$K_{rubber}= 0.15 J.m-s^0 C $$
$$ T_2 -T_1 = 90^0 C $$
we know for radial conduction in a cylinder
$$ \dfrac {Q}{t} = \dfrac { 2 \pi (T_2-T_1)}{In(R_2 /R_1) } $$
$$ = \dfrac { 2 \times 3.14 \times 15 \times 10^{-2} \times 50 \times 10^{-1} \times 90 }{ In ( 1.2 /1) } = 232.5 = 233 j/s $$
$$K_{rubber}= 0.15 J.m-s^0 C $$
$$ T_2 -T_1 = 90^0 C $$
we know for radial conduction in a cylinder
$$ \dfrac {Q}{t} = \dfrac { 2 \pi (T_2-T_1)}{In(R_2 /R_1) } $$
$$ = \dfrac { 2 \times 3.14 \times 15 \times 10^{-2} \times 50 \times 10^{-1} \times 90 }{ In ( 1.2 /1) } = 232.5 = 233 j/s $$
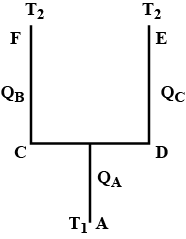
Four identical rods Ab, CD,CF and DE are joined as shown in figure . the length , cross -sectional area and thermal conductivity of each rod are. i, A and K respectively. the ends A, E and F are maintained at temperatures $$ T_1, T_2 and T_3 $$ respectively.assuming no loss of heat to the atmosphere , find the temperature at B.
Let the temp. at B be T
$$ \frac {Q_A}{t} = \frac {Q_B}{t}+ \frac {Q_C}{t} $$
$$ \Longrightarrow \frac {T-1-T}{I} = \frac {T-T_3}{3I/2} + \frac {T-T_2}{3I/2} $$
$$ -7T = 3T_1-2(T_2 +T_3) $$
$$ \Longrightarrow \frac {KA(T_1-T)}{I} = \frac { KA(T-T_3)}{I +(I/2)} + \frac {KA(T-T_2)}{ I+ (I/2) } $$
$$ \Longrightarrow 3T_1-3T = 4T -2(T_2+T_3) $$
$$ \Longrightarrow T = \frac {3T_1+ 2(T_2 +T_3)}{7} $$
$$ \frac {Q_A}{t} = \frac {Q_B}{t}+ \frac {Q_C}{t} $$
$$ \Longrightarrow \frac {T-1-T}{I} = \frac {T-T_3}{3I/2} + \frac {T-T_2}{3I/2} $$
$$ -7T = 3T_1-2(T_2 +T_3) $$
$$ \Longrightarrow \frac {KA(T_1-T)}{I} = \frac { KA(T-T_3)}{I +(I/2)} + \frac {KA(T-T_2)}{ I+ (I/2) } $$
$$ \Longrightarrow 3T_1-3T = 4T -2(T_2+T_3) $$
$$ \Longrightarrow T = \frac {3T_1+ 2(T_2 +T_3)}{7} $$
A hollow tube has length l, inner radius $$ R_1$$ and outer radius $$ R_2 $$. the material has thermal conducticity K. find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperatures $$ T_1 $$ and $$ T_2(T_2>T_1) $$ (b) the inside of the tube is maintained at temperature $$ T_1$$ and the outside is maintained at $$ T_2 $$
Figure shows a copper rod joined to steel rod. the rods have equal length and equal cross sectional area. the free end of the copper rod is kept at $$ 0^0C $$ and that of the steel rod is kept at $$ 100^0 C $$find the temperature at the junction of the rods.conductivity of copper = $$ 390W m^{-1^0}C^{-1} $$ and that of steel = $$ 46 Wm^{-1^0}C^{-1} $$
$$ K_{Cu} = 390 W/m-^0 C $$
Now since they are in series connection , so the heat passed through the crossection in the same.
So, $$ Q_1 = Q_2 $$
or $$ \dfrac {K_{cu} \times A \times ( \theta -0)}{I}= \dfrac {K_{st} \times A \times ( 100 - \theta)}{I} $$
$$ \Longrightarrow 390 ( \theta- 0)= 46 \times 100 - 46 \theta $$
$$ \Longrightarrow 436 \theta = 4600 $$
$$ \Longrightarrow \theta = \dfrac {4600}{436} = 10.55 = 10.6^0 C $$
Now since they are in series connection , so the heat passed through the crossection in the same.
So, $$ Q_1 = Q_2 $$
or $$ \dfrac {K_{cu} \times A \times ( \theta -0)}{I}= \dfrac {K_{st} \times A \times ( 100 - \theta)}{I} $$
$$ \Longrightarrow 390 ( \theta- 0)= 46 \times 100 - 46 \theta $$
$$ \Longrightarrow 436 \theta = 4600 $$
$$ \Longrightarrow \theta = \dfrac {4600}{436} = 10.55 = 10.6^0 C $$
A room has a window fitted with a single $$ 1.0 m \times 2.0 , $$ glass of thickness 2mm (a) calculate the rate of heat flow through the closed window when the temperature inside the room is $$ 32^0 C $$ and tht outside is $$ 40^0 C $$ (b). the glass is now replaced by two glasspaned , each having a thickness of 1 mm and separated by distance of 1 mm. calculate the rate of heat floe under the same conditions of temperatures . thermal conductivity of window flass = $$ 1.0 Js^{-1}m^{-1^0}C^{-1} $$ and that of air $$ = 0.025 J s^{-1} m^{-1}C^{-1} $$
(a) $$ \dfrac {Q}{t} = \dfrac { KA(\theta_1- \theta_2) }{l} = \dfrac { 1 \times 2 \times 1(40 -32)}{2 \times 10^{-3} } = 8000 J/sec $$
(b) resistance of glass =$$ \dfrac {l}{ak_g} + \dfrac {l}{ak_g} $$
Resistance of air = \dfrac {l}{ak_a} $$
net resistance = \dfrac {l}{ak_g} + \frac {l}{ak_g}+ \frac {l}{ak_a} $$
= $$ \dfrac {l}{a} ( \dfrac {2}{k_g} + \dfrac {1}{K_a} ) = \dfrac {l}{a} ( \dfrac { 2K_a+ K_g}{K_gk_a} ) $$
$$ = \dfrac { 1 \times 10^{-3}}{2} ( \dfrac { 2 \times 0.025 +1}{0.025} )$$
$$ = \dfrac { 1\times 10^{-3} \times 1.05}{0.05} $$
$$ \dfrac {Q}{t} = \dfrac { \theta_1 - \theta_2}{R} = \dfrac { 8 \times 0.05 }{1.10^{-3} \times 1.05}= 380.9 = 381 W $$
(b) resistance of glass =$$ \dfrac {l}{ak_g} + \dfrac {l}{ak_g} $$
Resistance of air = \dfrac {l}{ak_a} $$
net resistance = \dfrac {l}{ak_g} + \frac {l}{ak_g}+ \frac {l}{ak_a} $$
= $$ \dfrac {l}{a} ( \dfrac {2}{k_g} + \dfrac {1}{K_a} ) = \dfrac {l}{a} ( \dfrac { 2K_a+ K_g}{K_gk_a} ) $$
$$ = \dfrac { 1 \times 10^{-3}}{2} ( \dfrac { 2 \times 0.025 +1}{0.025} )$$
$$ = \dfrac { 1\times 10^{-3} \times 1.05}{0.05} $$
$$ \dfrac {Q}{t} = \dfrac { \theta_1 - \theta_2}{R} = \dfrac { 8 \times 0.05 }{1.10^{-3} \times 1.05}= 380.9 = 381 W $$
A metal rod of cross sectional area $$ 1.0 cm^2 $$ is being heated at one end. at one time , the temperature gradient is $$5.0 ^0 cm^{-1} $$ at cross section A and is $$ 2.5^0 cm^{-1} $$at cross section B. calculate the rate at which the temperature is increasing in the part AB =$$ 0.40 J^{\circ}C^{-1} $$ , thermal conductivity of the material of the rod = $$200 W m^{-1^0}C^{-1} $$ neglect any loss of heat to the atmosphere
Consider the situation shown in figure the frame is made of the same material and has a uniform cross-sectional area everywhere. calculate the amount of heat flowing per second through a cross-section of the bent part if the total heat taken out per second from the end at $$ 100^0 C $$ is 130 J
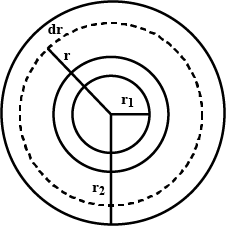
A hole of radius $$ r_1 $$ is made centrally in a uniform circular disc of thickness d and radius $$ r_2 $$ .. the inner surface ( a cylinder of length d and radius $$ r_1 $$).is maintained at a temperature $$ \theta_2 ( \theta_1 > \theta_2) $$ . the thermal conductivity of the material of the disc is K.calculate the heat flowing per unit time through the disc.
$$ \dfrac {dQ}{dt} = $$ rate of flow of heat
let us consider a strip at a distance r from the center of thickness dr.
$$ \dfrac {dQ}{dt} = \dfrac { K \times 2 \pi rd \times d \theta}{dr} $$
$$ \Longrightarrow C= \dfrac { K \times 2 \pi rd \times d \theta}{ dr} $$
$$ \Longrightarrow c \frac {dr}{r}= K2 \pi d d \theta $$interrating
$$ \Longrightarrow C \int^{f2}_{t_1} = K 2 \pi d \int^{ \theta_2}_{ \theta_1} d \theta $$
$$ \Longrightarrow C log r = K 2 \pi d( \theta_2 - \theta_1) $$
$$ \Longrightarrow C ( log r_2 - log r_1) =K 2 \pi d (\theta_2 - \theta_1) $$
$$ \Longrightarrow C log ( \dfrac {r_2}{r_1}) = K 2 \pi d ( \theta_2 - \theta_1) $$
$$ \Longrightarrow C = \dfrac {K2 \pi d( \theta_2 - \theta_1}{log(r_2/r_1)}$$
let us consider a strip at a distance r from the center of thickness dr.
$$ \dfrac {dQ}{dt} = \dfrac { K \times 2 \pi rd \times d \theta}{dr} $$
$$ \Longrightarrow C= \dfrac { K \times 2 \pi rd \times d \theta}{ dr} $$
$$ \Longrightarrow c \frac {dr}{r}= K2 \pi d d \theta $$interrating
$$ \Longrightarrow C \int^{f2}_{t_1} = K 2 \pi d \int^{ \theta_2}_{ \theta_1} d \theta $$
$$ \Longrightarrow C log r = K 2 \pi d( \theta_2 - \theta_1) $$
$$ \Longrightarrow C ( log r_2 - log r_1) =K 2 \pi d (\theta_2 - \theta_1) $$
$$ \Longrightarrow C log ( \dfrac {r_2}{r_1}) = K 2 \pi d ( \theta_2 - \theta_1) $$
$$ \Longrightarrow C = \dfrac {K2 \pi d( \theta_2 - \theta_1}{log(r_2/r_1)}$$
Suppose the bent part of the frame of the previous problem has a thermal conductivity of $$ 780 Js^{-1} m^{-1^0}C^{-1} $$ whereas it is $$ 390 J s^{-1}m^{-1^0}C^{-1} $$ for the straight part. calculate the ratio of the rate of heat flow through the bent part to the rate of heat flow through the straight part.
An aluminium rod and a copper rod of equal length 1.0 m and cross -sectional area $$ 1 cm^2 $$ are welded together as shown in figure . one end is kept at a temperature of $$ 20^0 C $$and the other at $$ 60^0 C $$ . calculate the amount of heat taken out per second from the hot end . thermal conductivity of aluminium= $$ 200 W m^{-1^0}C^{-1} $$ and of copper = $$ 390 Wm^{-1^0}{C^{-1}}$$
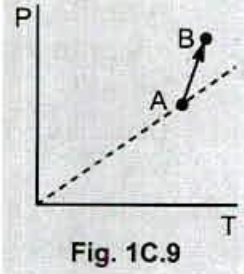
Fig . 1C.9 shows a plot of pressure versus temperature for a process that taken an ideal gas from point $$ A $$ to point $$ B $$ . What happens to the volume of the gas ?
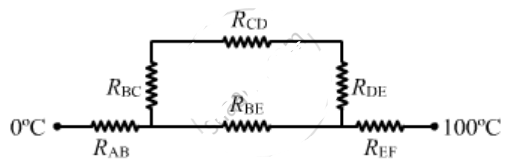
Seven rods A,B,C,D,E,F and G are joined as shown in figure .all the rods have equal cross-sectional area A and length l. the thermal conductivities of the rods are $$ K_A= K_C=K_0 ,K_B= K_D= 2K_0, K_E= 3K_0,K_p=4K_0 and K_G= 5K_0 $$. the rod E is kept at a constant temperature $$ T_1 $$ and the rod G is kept at a constant temperatures $$ T_2(T_2 >T_1 ) $$ (a) show that the rod F has a uniform temperature $$ T =(T_1 +2T_2)/3 $$.(b) find the rate of heat flowing from the source which maintains the temperatures $$ T_2$$?
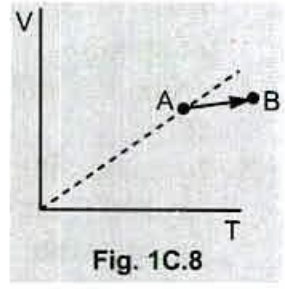
Fig . 1C.8 shows a plot of volume versus temperature for a process that taken an ideal gas from point $$ A $$ to point $$ B $$ . What happens to the pressure of the gas ?
At $$ 1 \,atm $$ pressure and $$ 100^{\circ} C $$ , a given mass of steam occupies $$ 1672 $$ times the volume occupied by an equal mass of water . What is the approximate ratio of the mean distance between the water molecules in steam to the diameter of the water molecules ?
In two experiments with a continuous flow calorimeter to determine the specific heat capacity of a liquid, an input power of 16 W produced a rise of 10 K in the liquid. When the power was doubled, the same temperature rise was achieved by making the rate of flow of liquid three times faster. Find the power lost (in W) to the surrounding in each case.
A cylindrical beer can made up of aluminium contains $$500 cm^3$$ of beer. The area of cross section of can is $$125 cm^3$$ at $$10^{o} C$$. Find the rise in level of beer if temperature of can increase to $$80^{o}C$$. Given that coefficient of linear expansion of aluminium is $$\alpha_{AI} = 2.3 \times 10^{-5}/^{o}C$$ and that for cubical expansion of beer is $$\gamma_{Beer} = 3.2 \times 10^{-4/^oC}$$.
An aluminium rod $$ 0.500\,m $$ in length and with a cross-sectional area $$ 2.50\,cm^{2} $$ is inserted into a thermally insulated vessel containing liquid helium at $$ 4.20\,K $$ . The rod is initially at $$ 300\, K $$ . (a) If one half of the rod is inserted into the helium , how many litres of helium boil off by the time the inserted half cools to $$ 4.20\,K $$ ? ( Assume that the upper half does not yet cool .) (b) If the upper end of the rod is maintained at $$ 300 \,K $$ , what is the approximate boil-off rate of liquid helium after the lower half has reached $$ 4.20\,K $$ ? (Aluminium has a thermal conductivity of $$ 31.0 \,J/s-cm-K $$ at $$ 4.2\,K $$ ; ignore its temperature variation . Aluminium has a specific heat of $$ 0.210\,cal\,g^{\circ} C $$ and density of $$ 2.70\,g/cm^{3} $$ . The density of liquid helium is $$ 0.125\,g/cm^{3} . $$ )
On a linear $$X$$ temperature scale, water freezes at $$-125.0^oX$$ and $$-70.00^oY$$ and boils at $$-30.00^oY$$. A temperature of $$50.00^oY$$ corresponds to what temperature on the $$X$$ scale?
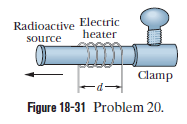
In a certain experiment a small radioactive source must move at selected, extremely slow speeds. This motion is accomplished by fastening the sources to one end of an aluminium rod and heating the central section of the rod in the controlled way. If the effective heated section of the rod in Fig $$18-31$$ has length $$d=2.00\ cm$$, at what constant rate must the temperature of the rod be changed if the source is to move at a constant speed of $$100\ nm/s$$?
An insulated Thermos contains $$130\ cm^3$$ of hot coffee at $$80.0^oC$$. You put in a $$12.0\ g$$ ice cube at its melting to cool the coffee. By how many degrees has your coffee cooled once the ice has melted and equilibrium is reached? Treat the coffee as though it were pure water and neglect energy changes with the environment.
A cylindrical copper rod of length $$1.2\ m$$ cross-sectional area $$4.8\ cm^{2}$$ is insulated along its side. The ends are held at a temperature difference of $$100\ C^{o}$$ by having one end in a water -ice mixture and the other in a mixture of boiling water and steam. At that rate
is energy conducted by the rod
Suppose that on a linear temperature scale. $$X$$, water boils at $$-53.5^oX$$ and freezes at $$-170^oX$$. What is a temperature of $$340\ K$$ on the $$X$$ scale? (Approximate water's boiling point as $$373\ K$$).
A $$150\ g$$ copper bowl contains $$220\ g$$ of water, both at $$20.0^oC$$. A very hot $$300\ g$$ copper cylinder is dropped into the water, causing the water to boil, with $$5.00\ g$$ being converted to steam. The final temperature of the system is $$100^oC$$. Neglect energy transfers with the environment. How much energy is transferred to the water as heat?
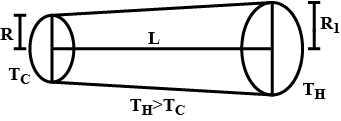
Consider the slab shown in Fig $$18-18$$. Suppose that $$L=25.0\ cm, A=90.0\ cm^{2}$$, and the material is copper. If $$T_{H}=125^{o}C, T_{C}=10.0^{o}C$$, and a steady state is reached, find the conduction rate through the slab.
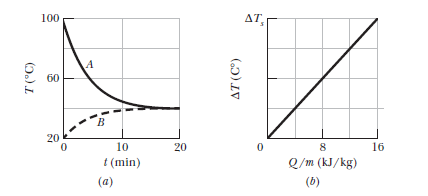
Samples $$A$$ and $$B$$ are at different initial temperatures when they are placed in a thermally insulated container and allowed to come to thermal equilibrium. Figure gives their temperatures $$T$$ versus time $$t$$. Sample $$A$$ has a mass of $$5.0\ kg$$ sample $$B$$ has a mass of $$1.5\ kg$$. Figure is a general plot for the material of sample $$B$$. It shows the temperature change $$\Delta T$$ that the material undergoes when energy is transferred to it as heat $$Q$$. The change $$\Delta T$$ is plotted versus the energy $$Q$$ per unit mass of the material, and the scale of the vertical axis is set by $$\Delta T_s=4.0\ C^0$$.
What is the specific heat of sample $$A$$?
A certain substance has a mass per mole of $$50.0\ mol$$. When $$314\ J$$ is added to a $$30.0\ g$$ sample, the sample's temperature rises from $$25.0^oC$$ to $$45.0^oC$$. What are the specific heat.
Ice has formed on a shallow pond and a steady state has been reached, with the air above the ice at $$-5.0^{o}C$$ and the bottom of the pond at $$4.0^{o}C$$. If the total depth of ice+water is $$1.4\ m$$, how thick is the ice? (Assume that the thermal conductivities of ice and water are $$0.40$$ and $$0.12\ cal/m.C^{o}$$.s, respectively.)
The temperature of a $$0.700\ kg$$ cube of ice is decreased to $$-150$oC$$. Then energy is gradually transferred to the cube as heat while it is otherwise thermally isolated from its environment. The total transfer is $$0.6993\ MJ$$/ Assume the value of $$c_{ice}$$ given in is valid for temperature from $$-150^oC$$ to $$0^oC$$. What is the final temperature of the water?
An object of mass $$6.00\ kg$$ falls through a height of $$50.0\ m$$ and, by means of a mechanical linkage, rotates a paddle wheel that stirs $$0.600\ kg$$ of water. Assume that the initial gravitational potential energy of the object is fully transferred to thermal energy of the water,which is initially at $$15.0^oC$$. What is the temperature rise of the water?
Consider the liquid in a barometer whose coefficient of volume expansion is $$6.6 \times 10^{-4}C^o$$. Find the relative changes in the liquid's height if the temperature changes by $$12\ C^o$$ while the pressure remains constant. Neglect the expansion of the glass tube.
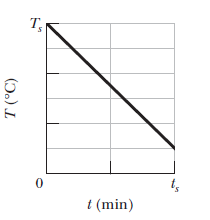
A $$0.300\ kg$$ sample is placed in a cooling apparatus that removes energy as heated at a constant rate of $$2.81\ W.$$Figure gives the temperature $$T$$ of the sample versus time $$t$$. The temperature scale is set by $$T_s=30^oC$$ and the time scale is set by $$t_s=20\ min$$. What is the specific heat of the sample?
At $$273\ K$$ and $$1.00\times 10^{-2}\ atm$$, the density of a gas is $$1.24\times 10^{-5}g/cm^{3}$$.
identify the gas.
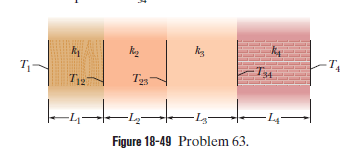
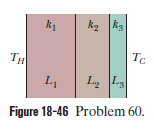
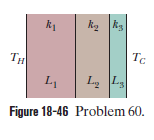
Figure $$18-49$$ shows (in cross section) a wall consisting of four layers, with thermal conductivities $$k_{1}=0.060\ W/m.K, k_{3}=0.040\ W/m.K$$, and $$L_{1}=1.5\ cm, L_{3}=2.8\ cm$$, and $$L_{4}=3.5\ cm$$ ($$L_{2}$$ is not known). The known temperatures are $$T_{1}=30^{o}C, T_{12}=25^{o}C$$, and $$T_{4}=-10^{o}C$$. Energy through the wall is steady. What is interface temperature $$T_{34}?$$
A $$150\ g$$ copper bowl contains $$220\ g$$ of water, both at $$20.0^oC$$. A very hot $$300\ g$$ copper cylinder is dropped into the water, causing the water to boil, with $$5.00\ g$$ being converted to steam. The final temperature of the system is $$100^oC$$. Neglect energy transfers with the environment. How much to the bowl?
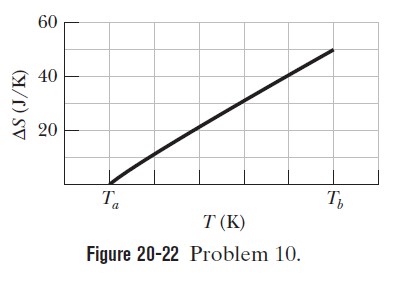
A 364 g block is put in contact with a thermal reservoir. The block is initially at a lower temperature than the reservoir. Assume that the consequent transfer of energy as heat from the reservoir to the block is reversible. Figure 20-22.
gives the change in entropy $$\Delta S$$ of the block until thermal equilibrium is reached. The scale of the horizontal axis is set by $$T_{a}=280 \mathrm{K}$$ and $$T_{b}=380 \mathrm{K} .$$ What is the specific heat of the block?
A $$150\ g$$ copper bowl contains $$220\ g$$ of water, both at $$20.0^oC$$. A very hot $$300\ g$$ copper cylinder is dropped into the water, causing the water to boil, with $$5.00\ g$$ being converted to steam. The final temperature of the system is $$100^oC$$. Neglect energy transfers with the environment. What is the original temperature of the cylinder?
Though a hot iron emits radiations, yet it is not visible in the dark, why?
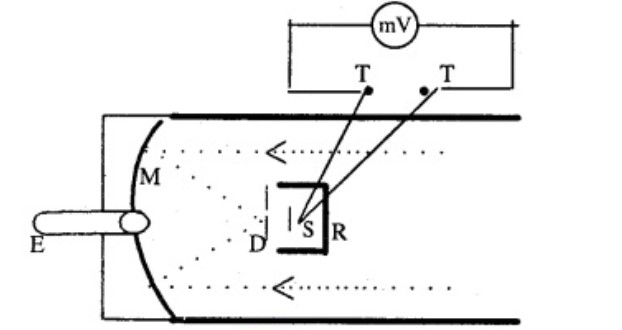
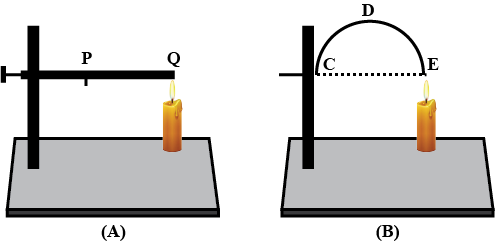
Look at Figure.
The length of wire $$PQ$$ in case of $$A$$ is equal to the diameter of the semicircle formed by the wire $$CDE$$, in case $$B$$. One pin is attached to each wire with the help of wax as shown in above Figure. Which pin will fall first? Explain.
Calculate the temperature which has the same numeral value on celsius and Fahrenheit scale.
These days people use steel utensils with copper bottom. This is supposed to be good for uniform heating of food. Explain this effect using the fact that copper is the better conductor.
Fill in the blanks: On heating a body, its temperature ____________.
Fill in the blanks:_________ determines the degree of hotness or coldness of a body.
For setting curd, a small amount of curd is added to warm milk. The microbes present in the curd help in setting if the temperature of the mixture remains approximately between $$35^{o}C$$ to $$40^{o}C$$. At places, where room temperature remains much below the range, setting of curd becomes difficult. Suggest a way to set curd in such a Situation.
Write the expression for the heat energy $$Q$$ received by the substance when $$m \ kg$$ of substance of specific heat capacity $$c$$ $$J \ kg^{-1} K^{ -1}$$ is heated through $$\triangle t^\circ C$$.
Why is the base of a cooking pan made thick and heavy?
An empty glass bottle is filled with a narrow tube at its mouth. The open end of the tube is kept in a beaker containing water. When the bottle is heated, bubbles of air are seen escaping into water. Explain the reason.
Convert $$40^{0}C$$ to the
(a) Fahrenheit scale.
(b) Kelvin Scale.
A molten metal of mass $$150\, g$$ is kept at its melting point $$80^o C$$. When it is allowed to freeze at the same temperature, it gives out $$75,000\, J$$ of heat energy.
(a) What is the specific latent heat of the metal?
(b) If the specific heat capacity of metal is $$200 J kg^{-1} K^{-1}$$, how much additional heat energy will the metal give out in cooling to $$-50^o C$$?
Calculate the amount of heat energy required to raise the temperature of 100 g of copper from $$20^oC$$ to $$70^oC$$. specific heat capacity of copper = $$390 J kg^{-1}K^{-1}$$.
By imparting heat to a body its temperature rises by $$15^oC$$. what is the corresponding rise in temperature on kelvin scale?
Define the term heat.
The temperature of a body rises by $$1^{0}C$$. What is the corresponding rise on the
(a) Fahrenheit scale.
(b) Kelvin scale.
State the volume charges observe when a given mass of water is heated from $$0^oC$$ to $$10^oC$$. Sketch a temperature volume graph to shoe the behavior.
The volume charge, it decreases when a given mass of water is heated from $$0^oC$$ to $$4^oC$$ i.e., it contracts. The increases when it is heated from $$4^oC$$ to $$10^oC$$ i.e., it expands.
The following temperature volume graph shows the behavior:
The following temperature volume graph shows the behavior:
Two bodies at different temperatures are placed in contact. State the direction in which heat will flow.
Define temperature and write its $$S.I$$ unit.
A refrigerator converts $$100 \,g$$ of water at $$20^o $$ to ice at $$-10^o C$$ in $$73.5$$ min. Calculate the average the rate of heat extraction in watt. The specific heat capacity of water is $$4.2 J g^{-1} K^{-1}$$, Specific latent heat of ice is $$336 J g^{-1}$$ and the specific heat capacity of ice if $$2.1 J g^{-1} K^{-1}$$.
What do you mean by anomalous expansion of water?
A given mas of water is cooled from $$10^oC$$ to $$0^oC$$. State the volume charge observed. Represent these on a temperature volume graph.
When water is cooled from $$10^oC$$, the density of water first increases up to and the decreases on cooling, further $$4^oC$$ to $$0^oC$$. Hence, the density of water is maximum at $$4^oC$$ which is equal to $$1\ g\ cm^{-3}$$.
Name the radiations for which the green house gases are (A) transparent (b) opaque.
$$250\, g$$ of water at $$30^o C$$ is contained in a copper vessel of mass $$50\, g$$. Calculate the mass of ice required to bring down the temperature of the vessel and its contents to $$5^o C$$. Given: specific latent heat of fusion of ice = $$336 103J kg^{-1}$$, specific heat capacity of copper = $$400 J kg^{-1} K^{-1}$$, specific heat capacity of water = $$ 4200 J kg^{-1} K^{-1}$$ .
0.5 kg of lemon squash at 30 C is placed in a refrigerator which can remove heat at an average
rate of $$30 J s^{-1
}$$. How long will it take to cool the lemon squash to 5C? Specific heat capacity of squash = $$4200 J kg^{-1} K^{
-1}$$
$$2\, kg$$ of ice melts when water at $$100^o C$$ is poured in a hole drilled in a block of ice. What mass of water was used? Given: Specific heat capacity of water $$= 4200\, J \, kg^{-1} K^{-1}, L_{ice}= 336 \times 10^3 \, J\,kg^{-1}$$.
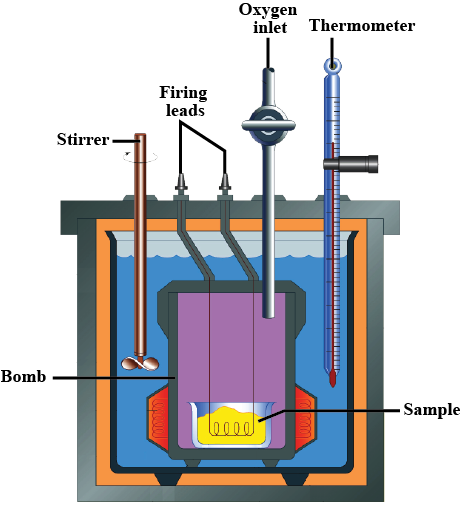
Write brief answers : Explain the construction of a calorimeter. Draw the necessary figure.
1. A device used for heat measurement is called a calorimeter.
2. $$Construction\ of\ a\ Calorimeter$$ :
It consists of a metallic vessel and stirrers. They are made of copper or aluminum.
The vessel is then kept inside a wooden jacket which contains heat-insulating materials.
The outer wooden jacket acts as a heat shield and reduces the heat loss from the inner vessel.
The outer jacket has an opening through which a mercury thermometer is inserted into the calorimeter .
Can heat be supplied without increasing the temperature of gas?
One end of a 0.35 m long metal bar is in system and the other is in contact with ice . If 10 ice melts per minute , what is the thermal conductivity of the metal ? Given cross - section of the bar $$ = 7 times 10 ^{-4} m ^{2} $$ and latent heat of ice is $$ 3.4 \times 10 ^{5} J /kg $$ ,
Solve the following example. At $$15 ^\circ C$$ the height of Eifel tower is $$324$$ m. If it is made of iron, what will be the increase in length in cm, at $$30 ^\circ C$$?
Why is coal tar heated before use?
What is thermal radiation?
Mention the different effect produced by heat.
Write the ideal gas equation for a mass of $$7$$ g of nitrogen gas.
Define athermanous substances and diathermanous substances.
What is an ideal gas ? Mention the ideal gas equation.
Mention the properties of thermal radiation.
Give an example of some familiar process in which no heat is added to or removed from a system, but the temperature of the system changes.
What is meant by heat?
What are the basic requirements of a cooking utensil in respect of:
- Specific heat and
- thermal conductivity
Define Convection with an experiment.
Describe a total radiation pyrometer.
It consists of a concave mirror M made of copper and plated with nickel. The mirror has a small hole at the center at which an eyepiece E is fitted. A diaphragm D is placed at the focus of M; which has a hole to allow radiation to pass through it. A blackened metal strip S is placed behind D. To the other surface of S, one junction of a thermocouple TT is connected. The thermocouple is connected to a millivoltmeter. A screen R is used to protect the strip from direct radiation. The mirror can be adjusted for focus.
The two faces of the metal plate of thickness $$40mm$$ and area $$10^2m^2$$ maintained at $$273K$$ and $$373K$$. The coefficient of thermal conductivity of the metal is $$ 380W\,m^{-1}k^{-1} $$ Find the quantity of heat flows, through the plate in one hour.
At what temperature do the Celsius and Fahrenheit thermometers show the same measurement? Prove it by calculation.
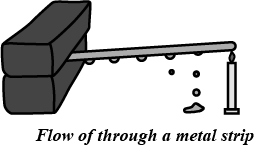
Draw a neat diagram and explain the flow of heat through a metal strip.
Flow Sheaf throe* a metal strip Take a rod or flat strip of a metal. Fix a few small wax pieces on the rod. These pieces should be at nearly equal distances. Clam the rod to a stand or place one end of the rod in between two bricks. Heat the other end of the rod by a candle. Observe. The heat from the candle side passes towards the other end by dissolving wax pieces on the rod. This experiment shows that heat is transferred from the hotter end to the colder end.
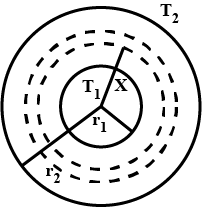
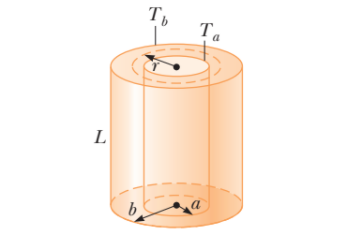
Two thin metallic spherical shells of radii $$r_1$$ and $$r_2$$ ($$r_1 < r_2$$) are placed with their centers coinciding. A material of thermal conductivity k is filled in the space between the shells. The inner shell is maintained at temperature $$T_1$$ and the outer shell at temperature $$T_2 (T_1 < T_2)$$. Calculate the rate at which heat flows radially through the material.
Consider two spherical shells of radii x and $$x + dx$$ concentric with the given system. Let the temperatures at these shells be T and $$T + dt$$ respectively. The amount of heat flowing radially inward through the material between x and $$x + dx$$ is
$$\therefore$$Rate of heat flow$$=\dfrac{4\pi Kr_1r_2(T_2-T_1)}{r_2-r_1}$$
A metal rod $$0.3m$$ long & $$0.02m$$ in diameter has one end at $$100^\circ C$$ & another end at $$0^\circ C$$. Calculate the total amount of heat conducted in $$2$$ minutes. Given $$k = 385 JS^{-1}m^{-1}K^{-1}$$.
Fill in the blanks :
No medium is required for transfer of heat by the process of _____.
Define radiation with an example.
A thermally insulated vessel containing a gas whose molar mass is equal to $$M$$ and the ratio of specific heats $$C_p/C_v = \gamma$$ moves with a velocity $$v$$. Find the gas temperature increment resulting from the sudden stoppage of the vessel.
For the case of an ideal gas find the equation of the process (in the variables T, V) in which the molar heat capacity varies as: (a) $$C = C_v + \alpha T$$; (b) $$C = C_v + \beta V$$; (c) $$C = C_v + ap$$, where $$\alpha, \beta$$, and a are constants.
The normal temperature of human body is_________
Find the specific heat capacities $$c_v$$ and $$c_p$$ for a gaseous mixture consisting of $$7.0 \ g$$ of nitrogen and $$20 \ g$$ of argon. The gases are assumed to be ideal.
One end of a rod, enclosed in a thermally insulating sheath, is kept at a temperature $$T_1$$ while the other, at $$T_2$$. The rod is composed of two sections whose lengths are $$l_1$$, and $$l_2$$ and heat conductivity coefficients $$x_1$$ and $$x_2$$. Find the temperature of the interface.
Liquid nitrogen has a boiling point of $$-195.81^0C$$ at atmospheric pressure. Express this temperature (a) in degrees Fahrenheit and (b) in kelvins.
Calculate the zero-point energy per one gram of copper whose Debye temperature is $$ \Theta = 330\,K $$
Why is the following situation impossible? An ideal gas undergoes a process with the following parameters: $$Q=10.J,W=12.0 J$$ and , $$\Delta T=-2.00^0C$$
Name the material used for making a Calorimeter.
In a constant-volume process, 209 J of energy is transferred by heat to 1.00 mol of an ideal monatomic gas initially at 300 K. Find (a) the work done on the gas,(b) the increase in internal energy of the gas, and(c) its final temperature.
A concrete slab is 12.0 cm thick and has an area of $$5.00 m^2$$. Electric heating coils are installed under the slab to melt the ice on the surface in the winter months.What minimum power must be supplied to the coils to maintain a temperature difference of $$20.^0C$$ between the bottom of the slab and its surface? Assume all the energy transferred is through the slab.
The tungsten filament of a certain 100-W lightbulb radiates 2.00 W of light. (The other 98 W is carried away by convection and conduction.) The filament has a surface area of $$0.250 mm^2$$ and an emissivity of 0.950.Find the filaments temperature. (The melting point of tungsten is 3 683 K.)
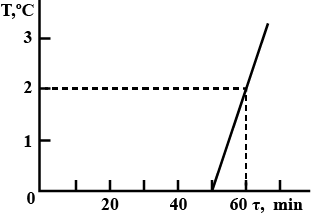
A bucket contains a mixture of water and ice of mass $$m = 10\, kg$$. The bucket is brought into a room, after which the temperature of the mixture is immediately measured. The obtained $$T(\tau)$$ dependence is plotted in Fig. The specific heat of water is $$c_w = 4.2\,J/(kg.K)$$, and the latent heat of fusion of ice is $$\lambda = 340\,kJ/kg.$$ Determine the mass $$m_{ice}$$ of ice in the bucket at the moment it is brought in the
room, neglecting the heat capacity of the bucket.
Answer the question:
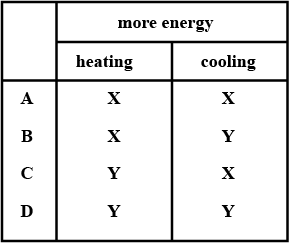
Two metal blocks X and Y are at room temperature. Each block is heated so that its temperature rises by $$10^\circ C.$$
The blocks are now allowed to cool back to room temperature.
Block Y has a greater thermal capacity than block X.
Which block need more thermal (heat) energy to heat it up by $$10^\circ C$$ and which block loses more thermal (heat) energy as it cools back to room temperature ?
A sample of a diatomic ideal gas has pressure P and volume V. When the gas is warmed, its pressure triples and its volume doubles. This warming process includes two steps, the first at constant pressure and the second at constant volume. Determine the amount of energy transferred to the gas by heat.
Why is a Calorimeter made-up of thin sheets of copper ?
A thermally insulated vessel contains two liquid at temperature $$T_1$$ and $$T_2$$ respectively and specific heats $$C_1$$ and $$C_2$$ separated by a non-conducting partition. The partition is removed and the difference between the initial temperature of one of the liquids and the temperature T established in the vessel turns out to be equal to half the difference between the initial temperature of the liquids. Determine the ratio $$\displaystyle \dfrac{m_1}{m_2}$$ (masses of the liquids).
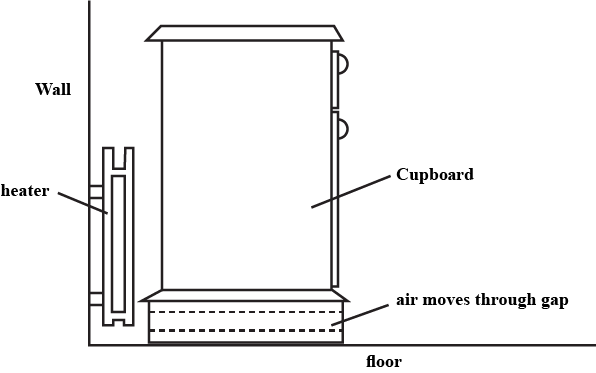
Answer the question:
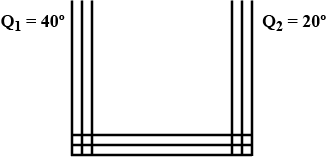
A cupboard is placed in front of a heater. Air can move through a gap under the cupboard.
Which row described the temperature, and the direction of movement, of the air in the gap ?
| air temperature | air direction | |
| A | cool | away from the heater |
| B | cool | towards the heater |
| C | warm | away from the heater |
| D | warm | towards the heater |
If $$4200 J$$ is needed to raise the temperature of $$1 kg$$ of water through $$1^oC$$, then ... $$J$$ is needed to raise the temperature of $$2 kg$$ of water through $$1^oC$$ and ........ $$J$$ is needed to raise the temperature of $$2 kg$$ of water through $$10^o C$$ respectively:
$$C_P\, \, 29\, J\, mol^{-1}\, K^{-1}$$ in the process PT = constant.
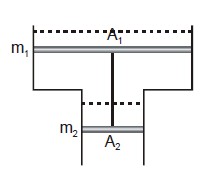
Consider a vertical tube open at both ends. The tube consists of two parts, each of different cross-sections and each part having a piston which can move smoothly in respective tubes. The two pistons are joined together by an in-extensible wire. The combined mass of the two pistons is 5 kg and area of the cross-section of the upper piston is 10 $$cm^{2}$$ greater than that of the lower piston. Amount of gas enclosed by the pistons is one mole. When the gas is heated slowly, pistons move by 50 cm. Find rise in temperature of the gas, in the form $$\frac{15x}{R} K$$, where R is universal gas constant. Use $$g = 10m/s^{2}$$ and outside pressure $$=10^{5} N/m^{2}).$$ Fill value of '$$x$$'.
Here the pressure $$(P)$$ inside tube is not changed due to heating because piston will move. For equilibrium,
The upward force $$=$$ the downward force.
$$PA_1+P_0A_2+T=P_0A_1+m_1g+m_2g+PA_2+T$$
or $$P(A_1-A_2)=P_0(A_1-A_2)+(m_1+m_2)g$$
or $$P \frac{\Delta V}{l}=P_0\Delta A+mg ...(1)$$ where $$\Delta V=(A_1-A_2)l, l=$$ displacement of pistons and $$m=m_1+m_2$$, combined mass.
now, $$P\Delta V=nR\Delta T $$ using $$PV=nRT$$
using (1), $$(P_0\Delta A+mg)l=nR\Delta T$$
$$\displaystyle \Delta T=\frac{(P_0\Delta A+mg)l}{nR}=\frac{[10^5(10\times 10^{-4})+5(10)](50\times 10^{-2})}{1(R)}=\frac{75}{R}$$
thus, $$x=5$$
The upward force $$=$$ the downward force.
$$PA_1+P_0A_2+T=P_0A_1+m_1g+m_2g+PA_2+T$$
or $$P(A_1-A_2)=P_0(A_1-A_2)+(m_1+m_2)g$$
or $$P \frac{\Delta V}{l}=P_0\Delta A+mg ...(1)$$ where $$\Delta V=(A_1-A_2)l, l=$$ displacement of pistons and $$m=m_1+m_2$$, combined mass.
now, $$P\Delta V=nR\Delta T $$ using $$PV=nRT$$
using (1), $$(P_0\Delta A+mg)l=nR\Delta T$$
$$\displaystyle \Delta T=\frac{(P_0\Delta A+mg)l}{nR}=\frac{[10^5(10\times 10^{-4})+5(10)](50\times 10^{-2})}{1(R)}=\frac{75}{R}$$
thus, $$x=5$$
Transfer of thermal energy ends when two objects that are in contact, are at the.... temperature
A gas is enclosed in a vessel of volume $$V$$ at a pressure $$P$$. It is being pumped out of the vessel by means of a piston pump with a stroke volume $$\dfrac {V}{100}$$. What is the final pressure in the vessel after $$n$$ strokes of the pump? Assume no change in temperature during pumping out of gas.
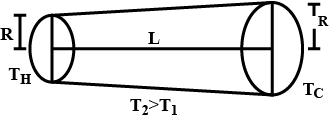
Find the rate of heat flow through a cross-section of the rod shown in figure $$(T_H > T_C)$$. Thermal conductivity of the material of the rod is K.
Conductivity of the material of the rod is $$=K$$
$$\cfrac{dQ}{dt}=\cfrac{KA(T_H-T_e)}{x}$$
The heat produced per unit time by the source is P. This heat is distributed over inner surface of the spherical shell having area $$A=4\pi R^2$$
Let $$x$$ be thickness of the shell.
The rate of heat transfer due to conduction is
$$\cfrac{dQ}{dt}=\cfrac{KAT}{r}$$
One face of the sheet of cork, $$3mm$$ thick is placed in contact with one face of a sheet of glass $$5mm$$ thick, both sheets being $$20cm$$ square. The outer face of this square composite sheet are maintained at $${100}^{o}C$$ and $${20}^{o}C$$, the glass being at the higher mean temperature. Find: (i) The temperature of glass-cork interface and (ii) The rate at which heat is conducted across the sheet neglecting edge effects.
Thermal conductivity of cork$$=6.3\times {10}^{-2}W{m}^{-1}{K}^{-1}$$
Thermal conductivity of glass $$=7.2\times {10}^{-1}W{m}^{-1}{K}^{-1}$$
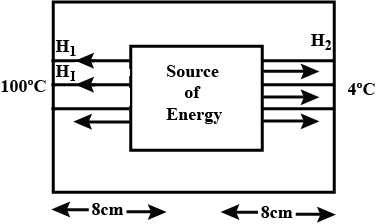
A closed cubical box is made of a thickness $$8cm$$ and the only way for heat to enter or leave the box is through two solid metallic cylindrical plugs, each of cross-sectional area $$12{cm}^{2}$$ and length $$8cm$$, fixed in the opposite walls of the box. The outer surface $$A$$ on one plug is maintained at $${100}^{o}C$$ while the outer surface $$B$$ of the other plug is maintained at $${4}^{o}C$$. The thermal conductivity of the material of each plug is $$0.5cal/_{ }^{ o }{ C }/cm$$. A source of energy generating $$36cal/s$$ is enclosed inside the box. Assuming the temperature to be the same at all points on the inner surface, find the equilibrium temperature of the inner surface of the box.
Temperature at inner points are same and be T,
Total heat current =$$H_1+H_2$$ (1)
We know that heat current =$$\dfrac { KA\Delta T }{ l } $$
Where, K=Thermal conductivity
A=Area
$$\Delta$$T=Temperature difference
l=Length along heat traveled
We are given total heat current=36cal/second
$$36=H-1+H_2$$
$$36=\dfrac { KA\left( T-100 \right) }{ 8 } +\dfrac { KA\left( T-4 \right) }{ 8 } $$
$$36=\dfrac { 0.5\times 12\left( T-100 \right) }{ 8 } +\dfrac { 0.5\times 12\left( T-4 \right) }{ 8 } $$
$$36=\dfrac { 6 }{ 8 } \left( T-100 \right) +\dfrac { 6 }{ 8 } \left( T-4 \right) $$
$$48=2T-104$$
$$2T=152$$
$$T=76°C$$
One end of a copper rod of uniform cross-section and length $$1.5$$ meters is in contact with melting ice and the other end with boiling water. At what point along its length should a temperature of $${200}^{o}C$$ be maintained, so that in steady state, the mass of ice melting is equal to that of steam produced in the same interval of time? Assume that the whole system is insulated from the surroundings.
Melting ice at 0°
Boiling water at 100°C
Let the distance be x from point A
Where the temperature is 200°C
We know that,
$$\dfrac { d\theta }{ dt } =\dfrac { KA\Delta T }{ l } $$ (1)
Where,
$$\dfrac { d\theta }{ dt }$$= Rate of flow of heat.
K=Thermal conductivity
A=Area
$$\Delta$$T=Temperature difference
l= Length of material
We know,
$$\theta$$=mL [heat=$$\theta$$,m=mass,L=latent heat]
Differentiating on both sides
$$\dfrac { d\theta }{ dt } =\dfrac { dm }{ dt } L$$ (2)
From 1 and 2
$$\dfrac { dm }{ dt } =\dfrac { KA\Delta T }{ Ll }$$ (3)
At steady state
Rate at which ice is melting= Rate at which steam is produced
$${ \left( \dfrac { dm }{ dt } \right) }_{ ice }={ \left( \dfrac { dm }{ dt } \right) }_{ steam }$$
Using 3
$$\dfrac { KA\left( 200-0 \right) }{ { L }_{ ice }x } =\dfrac { KA\left( 200-100 \right) }{ \left( 1.5-x \right) { L }_{ steam } } $$
$$\dfrac { 2 }{ x\times 80 } =\left( \dfrac { 1 }{( 1.5-x)540 } \right) $$
$$\dfrac { 1 }{ 4x } =\left( \dfrac { 1 }{ 54(1.5-x) } \right) $$
$$54\times1.5-54x=4x$$
$$54\times1.5=58x$$
$$x=\dfrac { 54\times 1.5 }{ 58 } $$
=$$1.4$$ meters
The temperature of equal masses of three different liquids $$A, B$$ and $$C$$ are $$12^{\circ}C, 19^{\circ}C$$ and $$28^{\circ}C$$ respectively. The temperature when $$A$$ and $$B$$ are mixed is $$16^{\circ}C$$ and when $$B$$ and $$C$$ are mixed it is $$23^{\circ}C$$. What should be the temperature when $$A$$ and $$C$$ are mixed?
A cylindrical block of length $$0.4\ m$$ and area of cross-section $$0.04\ m^{2}$$ is placed coaxially on a thin metal disc of mass $$0.4 kg$$ and of the same cross-section. The upper face of the cylinder is maintained at a constant temperature of $$400\ K$$ and the initial temperature of disc is $$300\ K$$. If the thermal conductivity of the material of disc is $$600\ J/kg-K$$. How long will it take for the temperature of the disc of increase to $$350\ K$$? Assume, for purpose of calculation, the thermal conductivity of the disc to be very high and the system to be thermally insulated, except for the upper face of the cylinder.
A container holds $$600$$ litres of air at a pressure of $$2$$ atmospheres. If the pressure on the gas is increased to $$5$$ atmospheres, what will its volume become?
(Assume that the temperature remains constant)
A pitcher with 1-mm thick porous walls contains 10 kg of water. Water comes to its outer surface and evaporates at the rate of 0.1 g $$s^{-1}$$. The surface area of the pitcher (one side)= 200$$cm^2$$. The room temperature =$$42^0$$C, latent heat of vaporization = $$2.27 \times 10^6 J kg^{-1}$$ and the thermal conductivity of the porous walls = 0.08$$ J s^{-1}m^{-1_0}C^{-1}$$. Calculate the temperature of water in the pitcher when it attains a constant value.
Find the time for which a layer of ice 5 cm thick on the surface of a pond will increase its thickness temperature of the surrounding air is $$-20^oC$$.
Thermal conductivity of ice$$=2.1 Wm{-1}K^{-1}$$
density of ice$$=900 kg
m^{-3}$$
Latent heat of ice$$=3.36 \times 10^{5}J kg^{-1}$$
Find the time for which a layer of ice 5 cm thick on the surface of a pond will increase its thickness by 0.1 cm when temperature of the surrounding air is $$-20^oC$$
Thermal conductivily of ice$$=2.1 Wm^{-1}K^{-1}$$
density of ice$$=900 Kgm^{-3}$$
Latent heat of ice $$=3.36 \times 10^5J Kg^{-1}$$
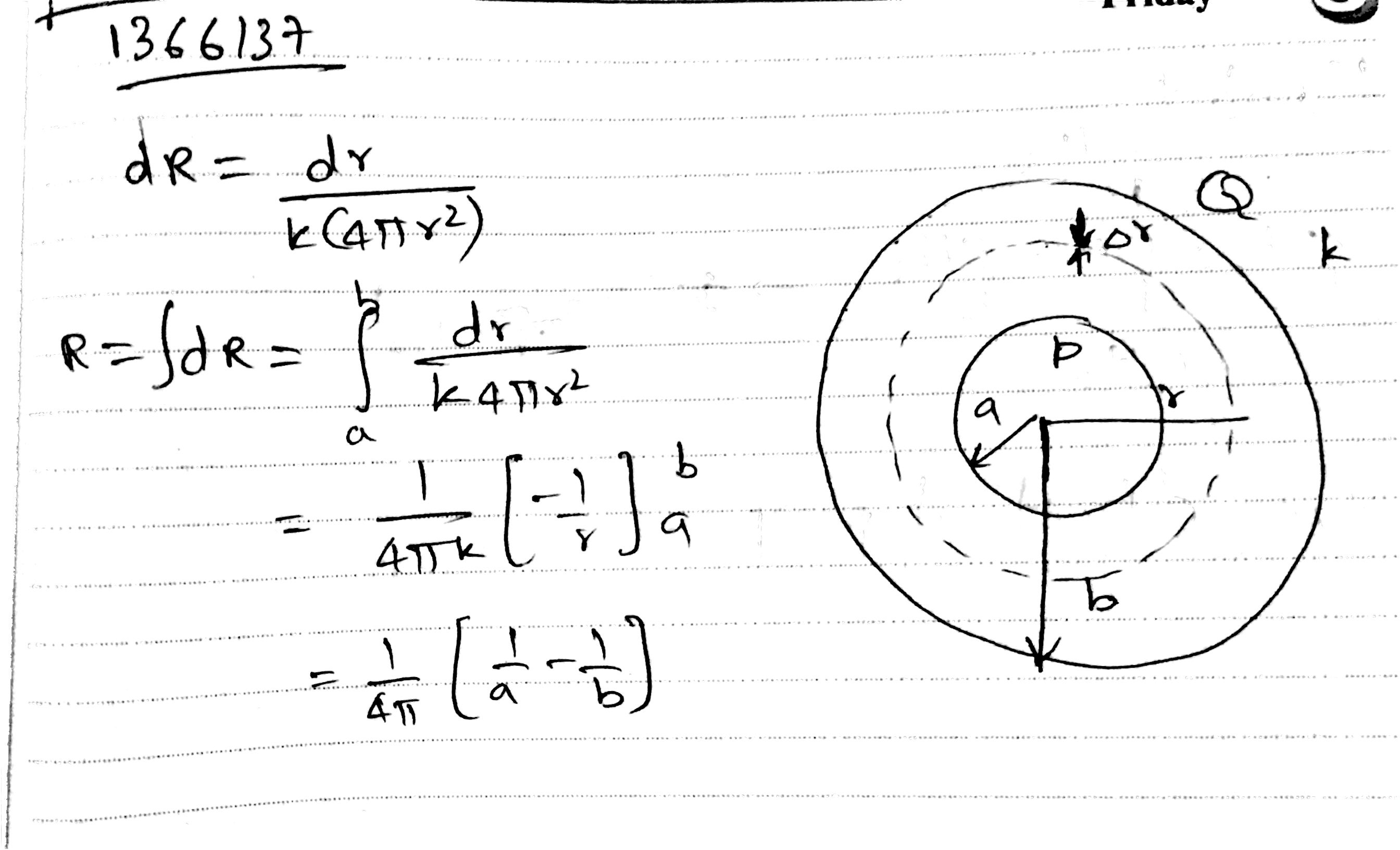
A spherical body of radius 'b' has a concentric cavity of radius 'a' as shown. Thermal conductivity of the material is K. Find thermal resistance between inner surface P and outer surface Q.
The dimension of the ceiling of a room are 4m x 4m x 10 cm .Thermal conductivity of the concrete in the ceiling is 1 . 26 W m$$^{-1}$$ $$^{0} C^{-1}$$ At one moment the temperature of outside and inside the room are 46$$^{0}$$C and 32$$^{0}$$C.
(i) Find the amount of heat flowing through the ceiling in 1 second?
The potential energy for the force between two atoms in a diatomic molecule is approximately given by
$$U(x)=\frac { a }{ { x }^{ 12 } } -\frac { b }{ { x }^{ 6 } } $$,
where a and b are constants and x is the distance between the atoms. If the dissociation energy of the molecule is $$D=\left[ U(x-\infty )-{ U }_{ at\quad equilibrium } \right] $$, D is
A slab of stone of area $$0.36{ m }^{ 2 }$$ and thinkness 0.1 m is exposed on the lower surface to steam at $${ 100 }^{ \circ }C$$ A block of ice at $${ 0 }^{ \circ }C$$ rest on the upper surface of he slab. In one hour, 4.8 Kg of its melted. Calculated the thermal conductivity of stone
A stand of stone of area 0.36 m and thickness 0.1 as exposed on lower surface to steam of $${ 100 }^{ \circ }C$$ A block of ice of $${ O }^{ \circ }C$$ rest on the upper surface of the stand.In one hour. 4.8 kg of is method. Calculated the conduction of stone
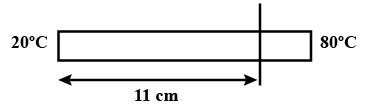
The left end of a copper rod (length = 20 cm, area of cross-section = $$0.20 cm^2$$) is maintained at $$20^o C$$ and the right end is maintained at $$80^oC$$. Neglecting any loss of heat through radiation, find (a) the temperature at a point 11 cm from the left end and (b) the heat current through the rod. Thermal conductivity of copper $$=385 $$ W $$m^{-1} \ ^o C^{-1}$$.
$$ t= 20 cm = 20 \times 10^{-2} m $$
$$ A = 0.2 m^2 = 0. 2 \times 10^{-4} m^2 $$
$$ \theta _1 = 80^0 C $$
$$ \theta _2 = 20^0 C $$ $$K = 385$$
(a) Constant heat current follow through the wire, temperature gradient
$$ A = 0.2 m^2 = 0. 2 \times 10^{-4} m^2 $$
$$ \theta _1 = 80^0 C $$
$$ \theta _2 = 20^0 C $$ $$K = 385$$
(a) Constant heat current follow through the wire, temperature gradient
$$C=\dfrac{dt}{L}=\dfrac{80-20}{20}=3\ ^\circ C/cm$$
For 11 cm fro left end,
$$T=20+C\times 11\\T=20+3\times 11=53\ ^\circ C$$
(b) $$ \dfrac {Q}{t}= \dfrac {KA (\theta_1 - \theta_2)}{l} = \dfrac { 385 \times 0.2 \times 10^{-4} (80-20) }{20 \times 10^{-2} } = 2.31 $$
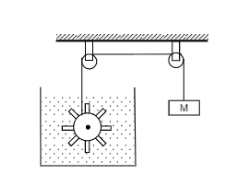
Figure shows water in container having 2.0 mm thick walls made of a material of thermal conductivity $$ 0.50 W m^{-1^0}C^{-1} $$ . the container is kept in a melting ice bath at $$ 0^0 C $$ . the total surface area in contract with water is $$ 0.05 m^2 $$ . A wheel is clamped inside the water and is coupled to a block of mass M as shown in the figure as the block goes down, the wheel rotates. it is found that after some time a steady state is reached in which the block goes down with constant speed of $$ 10 cm s^{-1} $$and the temperature of the water remains constant at $$ 1.0^0C $$ find the mass M of the block. assume that the heat flows out of the water only through the walls in contact. take $$ g= 10 ms^{-2} $$
Given $$ \theta_1 =1^0 C $$
$$ \theta_2 = 0^0 C $$
K = 0.50 W/m C
$$ d= 2mm = 2 \times 10^{-3} m $$
$$A = 5 \times 106{-2}m^2 v = 10 cm/s = 0.1 m/s $$
$$ power = force \times velcoity = Mg \times v $$
Again Power =$$ \frac {dQ}{dt}= \frac {KA(\theta_1 - \theta_2)}{d} $$
So , Mgv = $$ \frac { KA( \theta_1 - \theta_2)}{d} $$
$$ \Longrightarrow M = \frac { KA(\theta_1 - \theta_2)}{dvg}= \frac { 5 \times 10^{-1} \times 56{-2} \times 1}{ 2 \times 10^{-3} \times 106{-1} \times {10} } = 12.5 kg $$
$$ \theta_2 = 0^0 C $$
K = 0.50 W/m C
$$ d= 2mm = 2 \times 10^{-3} m $$
$$A = 5 \times 106{-2}m^2 v = 10 cm/s = 0.1 m/s $$
$$ power = force \times velcoity = Mg \times v $$
Again Power =$$ \frac {dQ}{dt}= \frac {KA(\theta_1 - \theta_2)}{d} $$
So , Mgv = $$ \frac { KA( \theta_1 - \theta_2)}{d} $$
$$ \Longrightarrow M = \frac { KA(\theta_1 - \theta_2)}{dvg}= \frac { 5 \times 10^{-1} \times 56{-2} \times 1}{ 2 \times 10^{-3} \times 106{-1} \times {10} } = 12.5 kg $$
A semicircular rod is joined at its end to a straight rod of the same material and the same cross-sectional area. the straight rod forms a diameter of the other rod. the junctions are maintained at different temperatures . find the ratio of the heat transferred through a cross section of the semcircular rod to the heat transferred through a cross section of the straight rod in a given time.
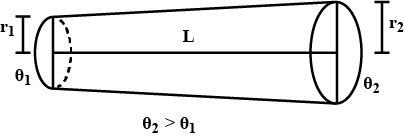
Find the rate of heat flow through a cross section of the rod shown in figure $$ ( \theta_2 > \theta_1 ) $$ . thermal conductivity of the material of the rod is K
A rod of negligible heat capacity has length 20 cm , area of cross section $$ 1.0 cm^2 $$ and thermal conductivity $$ 200Wm^{1^0}C^{-1} $$ .the temperature of one the end is maintained at $$ 0^0 C $$ and that of the other end is maintained at $$ 0^0 C $$and that of the other end is slowly and linearly varied from $$ 0^0 c $$ to $$ 60^0 C $$in 10 minutes. assuming no loss of heat through the rod in these 10 minutes.
An amount n (in moles )of monayomic gas at an initial temperature $$ T_0 $$ is enclosed in cylindrical vessel fitted with a light piston. the surrounding air has a temperature $$ T_s(>T_0 ) $$ and the atmospheric pressure is $$ P_a$$. Heat may be conducted between the surrounding and the gas through the bottom of the cylinder . the bottom has a surface area A, thickness x and thermal conductivity K. assuming all changes to be slow , find the distance moved by piston in time t.
A constant - volume gas thermometer with a triple -point pressure $$ P_3 = 500 $$ torr is used to measure the boiling point of some substance . When the thermometer is placed in thermal contact with the boiling substance , its pressure is $$ 734 $$ torr . Some of the gas in the thermometer is then allowed to escape so that its triple - point pressure is $$ 200 $$ torr . When it is again placed in thermal contact with the boiling substance , its pressure is $$ 293.4 $$ torr . Again , some of the gas is removed from the thermometer so that its triple - point pressure is $$ 100 $$ torr . When the thermometer is placed in thermal contact with the boiling substance once again , its pressure is $$ 146.55 $$ torr . Find the ideal - gas temperature of the boiling substance.
Three rod of lengths 20 cm each and area of cross section $$ 1 cm^2 $$ are joined to form a triangle ABC . the conductivites of the rods are $$KP_{AB} = 50 J s^{-1} m^{-1^0}C^{-1} $$,$$ K_{BC}= 200 J s^{-1} m^{-1^0}C^{-1} $$ and $$ K_{AC} = 400 J s^{-1} m^{-1^0}C^{-1} $$ the juctions A, B and C are maintained at $$ 40^0 C , 80^0 C \,and\, 80^0 C $$ respectively . find the rate of heat flowing through the rods AB, AC and BC.
Two bodies of masses $$ m_1 \ and\ m_2 $$ and specific heat capacities $$ s_1\ and\ s_2 $$ are connected by a rod of length $$l$$, cross-sectional area $$A$$, thermal conductivity $$K$$ and negligible heat capacity, the whole system is thermally insulated. at time t =0 , the temperature of the first body is $$ T_1$$ and the temperature of the second body is $$ T_2(T_2 > T_1) $$ find the temperature difference between the two bodies at time t.
Figure shows two adiabatic vessels , each containing a mass m of water at different temperatures . the ends of a metal rod of length L,area of cross section A and Thermal conductivity K, are inserted in the water as shown in the figure, find the time taken for the difference between the temperatures in the vessels to become half of the original value. the specific heat capacity of water is s, neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.
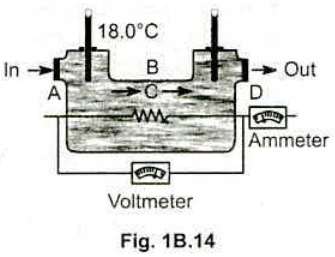
An engineer is developing an electric water heater to provide a continuous supply of hot water . One trial design is shown in Fig. 1B.14 . Water is flowing at the rate of $$ 0.500 \,kg / min $$ , the inlet thermometer registers $$ 18.0^{\circ} C $$ , the voltmeter reads $$ 120 V $$ , and the ammeter reads $$ 15.0 A $$ ( corresponding to a power input of $$ ( 120 V ) (15.0 A ) = 1800 W $$ ) . (a) When a steady state is finally reached , what is the reading of the outlet thermometer ? (b) Why is it unnecessary to take into account the heat capacity $$ mc $$ of the apparatus itself ?
B] It is unnecessary to take into account the heat capacity of apparatus because water takes heat from it also and in this way its temperature remains constant.
Two identical conducting rods are first, connected independently to two vessels, one containing water at $$100^{0}C$$ and the other containing ice at $$0^{0}C$$. In the second case, rods are joined end to end and are connected to the same vessels. If $$q_1$$ and $$ q_2$$ (in g/s) are the rates of melting of ice in two cases, then find the ratio of $$q_1$$ / $$q_2$$.
2 kg of ice at $$-15^{0}C$$ is mixed with 2.5 kg of water at $$25^{0}C$$ in an insulating container. If the specific heat capacities of ice and water are $$0.5 \space cal/g^{0}C$$ and $$1 \space cal/g^{0}C$$, find the amount of water present in the container? (in kg nearest integer)
A leaf of area $$ 40 cm^{2} $$ and mass $$ 4.5 \times 10^{-4}\,kg $$ directly faces the sun on a clear day. The leaf has an emissivity of $$ 0.85 $$ and a specific heat of $$ 0.80 \,kcal / kg K.$$ (a) Estimate the rate of rise of the leaf's temperature. (b) Calculate the temperature the leaf would reach if it lost all its heat by radiation ( the surrounding are at $$ 20^{\circ} C $$ ). (c) In what other ways can the heat be dissipated by the leaf?
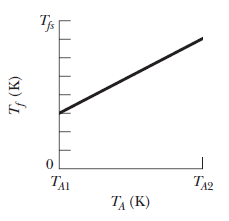
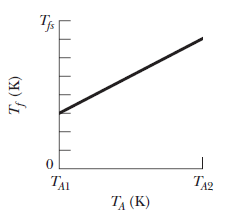
In a series of experiments, block $$B$$ is to be placed in a thermally insulated container with block $$A$$, which has the same mass as block $$B$$. In each experiment, block $$B$$ is initially at a certain temperature $$T_B$$ but temperature $$T_A$$ of block $$A$$ is changed from experiment to experiment. Let $$T_f$$ represent the final temperature of the two blocks when they reach thermal equilibrium in any of the experiments. Figure gives temperature $$T_f$$ versus the initial temperature $$T_A$$ for a range of possible values of $$T_A$$, from $$T_{A1}=0\ K$$ to $$T_{A2}=500\ K$$. The vertical axis scale is set by $$T_{fx}=400\ K.$$ What are temperate $$T_B$$.
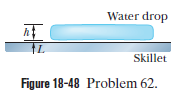
Leidenfrost effect. A water drop wall last about $$1\ s$$ on a hot skillet wiht a temperature between $$100^{o}C$$ and about $$200^{o}C$$. However, if the skillet is several minutes, an effect named after an early investigator. The longer lifetime is due to the support of a thin layer of air and water vapor that separates the drop from the metal (by distance $$L$$ in Fig $$18-48$$). Let $$L=0.100\ mm$$, and assume that the drop is flat with height $$h=1.50\ mm$$ and bottom face area $$A=4.00\times 10^{-6}m^{2}$$. Also assume that the skillet has a constant temperature $$T_{s}=300^{o}C$$ and the drop has a temperature of $$100^{o}C$$. Water has density $$\rho =1000\ kg/m^{3}$$, and the supporting layer has thermal conductivity $$k=0.026\ W/m.K$$
At what rate is energy conducted from the skillet to the drop through the drop's bottom surface?
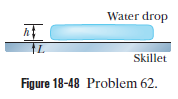
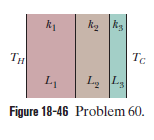
Figure $$18-46$$ shows the cross section of a wall made of three layers. The layer thicknesses are $$L_{1}, L_{2}=0.700\ L_{1}$$, and $$L_{3}=0.350\ L_{1}$$. The thermal conductivities are $$k_{1}, k_{2}=0.900\ k_{1}$$, and $$k_{3}=0.800\ k_{1}$$. The temperature at the left side and right side of the wall are $$T_{H}=30.0^{o}C$$ and $$T_{C}=-15.0^{o}C$$, respectively. Thermal conduction is steady.
what would be the value of $$\Delta T_{2}$$?
The average rate at which energy is conducted outward through the ground surface in North America is $$54.0\ m\ W/m^2$$, and the average thermal conductivity of the near-surface rocks is $$2.50\ W/m \ K$$. Assuming a surface temperature of $$10.0^oC$$, find the temperature at a depth of $$35.0\ km$$ (near the base of the crust). Ignore the heat generated by the presence of radioactive elements.
In a series of experiments, block $$B$$ is to be placed in a thermally insulated container with block $$A$$, which has the same mass as block $$B$$. In each experiment, block $$B$$ is initially at a certain temperature $$T_B$$ but temperature $$T_A$$ of block $$A$$ is changed from experiment to experiment. Let $$T_f$$ represent the final temperature of the two blocks when they reach thermal equilibrium in any of the experiments. Figure gives temperature $$T_f$$ versus the initial temperature $$T_A$$ for a range of possible values of $$T_A$$, from $$T_{A1}=0\ K$$ to $$T_{A2}=500\ K$$. The vertical axis scale is set by $$T_{fx}=400\ K.$$ What are the ratio $$c_B/c_A$$ of the specific heats of the blocks?
On the average, the temperature of the earth' s crust increases $$1^{o} C$$ for every 30 m of depth. The average thermal conductivity of the earth's crust is 0.75 J/m s K. Solar constant is $$1.35 kW/m^{2}$$. Match the items in Column I with that in Column II:
Figure $$18-46$$ shows the cross section of a wall made of three layers. The layer thicknesses are $$L_{1}, L_{2}=0.700\ L_{1}$$, and $$L_{3}=0.350\ L_{1}$$. The thermal conductivities are $$k_{1}, k_{2}=0.900\ k_{1}$$, and $$k_{3}=0.800\ k_{1}$$. The temperature at the left side and right side of the wall are $$T_{H}=30.0^{o}C$$ and $$T_{C}=-15.0^{o}C$$, respectively. Thermal conduction is steady.
would the rate at which energy is conducted through the wall be greater than, less than, or the same as previously
A $$5.0\ cm$$ slab has formed on an outdoor tank of water. The air is at $$-10^{o}C$$. Find the rate of ice formation (centimeters per hour). The ice has thermal conductivity $$0.0040\ cal/s.cm.C^{o}$$ and density $$0.92\ g/cm^{3}$$. Assume there is no energy transfer through the walls or bottom.
Figure $$18-46$$ shows the cross section of a wall made of three layers. The layer thicknesses are $$L_{1}, L_{2}=0.700\ L_{1}$$, and $$L_{3}=0.350\ L_{1}$$. The thermal conductivities are $$k_{1}, k_{2}=0.900\ k_{1}$$, and $$k_{3}=0.800\ k_{1}$$. The temperature at the left side and right side of the wall are $$T_{H}=30.0^{o}C$$ and $$T_{C}=-15.0^{o}C$$, respectively. Thermal conduction is steady.
What is the temperature difference $$\Delta T_{2}$$ across layer $$2$$ (between the left and right slides of the layer)? If $$k_{2}$$ were, instead, equal to $$1.1 k_{1}$$
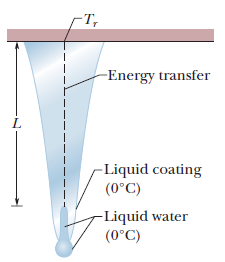
Icicles. Liquid water coats an active (growing) icicle and extends up a short, narrow tube along the central axis. Because the water-ice interface must have a temperature of $$0^oC$$, the water in the tube cannot lose energy through the sides of the icicle or down through the tip because there is no temperature changes in those direction. It can lose energy and freeze only by sending energy up ()through distance L to the top of the icicle, where the temperature $$T_r$$ can be below $$0^oC$$. Take $$L=0.12\ m$$ and $$T_r=-5^oC$$. Assume that the central tube and the upward conduction path both have cross-sectional area A. In terms of A, what rate is At waht rate does the top of the tube move downward because of water freezing there? The thermal conductivity of ice is $$0.400\ W/m.K,$$ and the density of liquid water is $$1000\ kg/m^3$$.
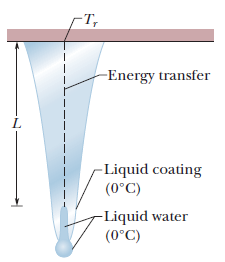
Icicles. Liquid water coats an active (growing) icicle and extends up a short, narrow tube along the central axis. Because the water-ice interface must have a temperature of $$0^oC$$, the water in the tube cannot lose energy through the sides of the icicle or down through the tip because there is no temperature changes in those direction. It can lose energy and freeze only by sending energy up ()through distance L to the top of the icicle, where the temperature $$T_r$$ can be below $$0^oC$$. Take $$L=0.12\ m$$ and $$T_r=-5^oC$$. Assume that the central tube and the upward conduction path both have cross-sectional area A. In terms of A, what rate is mass converted from liquid to ice at the top of the central tube?
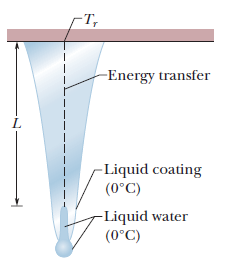
Icicles. Liquid water coats an active (growing) icicle and extends up a short, narrow tube along the central axis. Because the water-ice interface must have a temperature of $$0^oC$$, the water in the tube cannot lose energy through the sides of the icicle or down through the tip because there is no temperature changes in those direction. It can lose energy and freeze only by sending energy up ()through distance L to the top of the icicle, where the temperature $$T_r$$ can be below $$0^oC$$. Take $$L=0.12\ m$$ and $$T_r=-5^oC$$. Assume that the central tube and the upward conduction path both have cross-sectional area A. In terms of A, what rate is energy conducted upward.
Explain briefly the process of heat transfer by radiation.
(a) Same amount of heat is supplied to two liquid A and B. The liquid A and B. The liquid A shows a greater rise in temperature. What can you say about the heat capacity of A as compared to that of B?
(b) Two metallic blocks P and Q of masses in ratio 2 : 1 are given same amount of heat. If their temperature rise by same amount, compare their specific heat capacities.
Leidenfrost effect. A water drop wall last about $$1\ s$$ on a hot skillet wiht a temperature between $$100^{o}C$$ and about $$200^{o}C$$. However, if the skillet is several minutes, an effect named after an early investigator. The longer lifetime is due to the support of a thin layer of air and water vapor that separates the drop from the metal (by distance $$L$$ in Fig $$18-48$$). Let $$L=0.100\ mm$$, and assume that the drop is flat with height $$h=1.50\ mm$$ and bottom face area $$A=4.00\times 10^{-6}m^{2}$$. Also assume that the skillet has a constant temperature $$T_{s}=300^{o}C$$ and the drop has a temperature of $$100^{o}C$$. Water has density $$\rho =1000\ kg/m^{3}$$, and the supporting layer has thermal conductivity $$k=0.026\ W/m.K$$
If conduction is the primary way energy moves from the skillet to the drop, how long will the drop last?
Describe an experiment to show that air expands on heating.
Aim: To show that air expands on heating.
Equipments required:
An empty bottle, a rubber balloon, a water bath and some water
Labelled diagram of experiment arrangement:
Procedure:
First of all, take an empty bottle. Actually the empty bottle contains air.
After that attach a rubber balloon to its neck as shown in Figure above. Initially, the balloon is deflated.
Then place the bottle in a water bath containing boiling water.
After some time has passed, we will notice that the balloon has inflated as depicted in Figure.
The reason for this is that when the air inside the bottle heats up, it expands and fills the balloon.
Now, take the bottle out of the water bath and allow it to cool by itself.
The balloon will deflate and eventually collapse, as we will see.
This is due to the fact that the air inside the balloon and bottle has contracted as it has cooled. The balloon deflates as the air from the balloon passes through the bottle.
Conclusion:
The above observation shows that air expands on heating
Give one example of heat transfer by radiation.
Heat One mole of an ideal gas with heat capacity at constant pressure $$C_p$$ undergoes the process $$T = T_0 + \alpha V$$, where $$T_0$$ and $$\alpha$$ are constants. Find:
(a) heat capacity of the gas as a function of its volume;
(b) the amount of heat transferred to the gas, if its volume in-creased from $$V_1$$ to $$V_2$$.
Find the temperature distribution in the space between two coaxial cylinders of radii $$R_1$$ and $$R_2$$ filled with a uniform heat conducting substance if the temperatures of the cylinders are constant and are equal to $$T_1$$ and $$T_2$$ respectively.
Two metal rods of the same area of cross-section and with their lengths in the ratio $$1:3$$ are joined together to form a compound rod. One end of this compound rod is kept at $$100^\circ C$$ and the other at $$0^\circ C$$. Calculate the temperature at the Junction if the thermal conductivity is in the ratio $$1:3$$.
Let AB and BC be the two rods of length $$L_1$$ and $$L_2$$ and having the same area of cross-section A, joined together to form a compound rod as shown in the figure.
If ‘ $$\theta$$ ’ is the steady temperature at the junction B during the steady-state, then, rate of flow of heat through AB = rate of flow through BC
$$\therefore \dfrac{100-\theta}{\theta}=\dfrac{K_2}{K_1}\,\dfrac{L_1}{L_2}$$
But, $$\dfrac{K_2}{K_1}\,\dfrac{3}{1}$$ and $$\dfrac{L_1}{L_2}\,\dfrac{1}{3}$$
$$\therefore \dfrac{100-\theta}{\theta}=1$$ or $$\theta=50^\circ C$$
The thermal power of density $$\omega$$ is generated uniformly inside a uniform sphere of radius $$R$$ and heat conductivity coefficient $$x$$. Find the temperature distribution in the sphere provided the steady-state temperature at its surface is equal to $$T_0$$.
A rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as $$x = \alpha /T$$, where $$\alpha$$ is a constant. The ends of the rod are kept at temperatures $$T_1$$ and $$T_2$$. Find the function $$T (x)$$, where $$x$$ is the distance from the end whose temperature is $$T_1$$, and the heat flow density.
A metallic rod $$1.5m$$ long and $$2\times10^4\,m^2$$ in the area is heated at one end. The coefficient of thermal conductivity of the material of the metallic rod is $$210 Js^{-1}m^{-1}K^{-1}$$. In the steady-state, the temperature of the ends of the rod is $$373K$$ and $$263\, K$$. Calculate.
- Temperature gradient In the rod.
- Temperature at a point $$0.8$$ m from the hot end.
- Rate of heat transmission.
An ideal gas goes through a polytropic process. Find the polytropic exponent $$n$$ if in this process the coefficient
(a) of diffusion; (b) of viscosity; (c) of heat conductivity remains constant.
Two chunks of metal with heat capacities $$C_1$$ and $$C_2$$ are interconnected by a rod of length $$l$$ and cross-sectional area $$S$$ and fairly low heat conductivity $$x$$. The whole system is thermally insulated from the environment. At a moment $$t = 0$$ the temperature difference between the two chunks of metal equals $$(\Delta T)_0$$. Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chunks as a function of time.
A box with a total surface area of $$1.20 m^2$$ and a wall thickness of 4.00 cm is made of an insulating material.A 10.0-W electric heater inside the box maintains the inside temperature at $$15.0^0C$$ above the outside temperature. Find the thermal conductivity k of the insulating material.
A glass windowpane in a home is 0.620 cm thick and has dimensions of 1.00 m x 2.00 m. On a certain day,the temperature of the interior surface of the glass is $$25.0^0C$$ and the exterior surface temperature is $$0^C$$.(a) What is the rate at which energy is transferred by heat through the glass? (b) How much energy is transferred through the window in one day, assuming the temperatures on the surfaces remain constant?
Assuming the propagation velocities of longitudinal and transverse vibrations to be the same and equal to v, find the Debye temperature
(a) for a unidimensional crystal, i.e. a chain of identical atoms, incorporating $$n_{0}$$ atoms per unit length;
(b) for a two-dimensional crystal, i.e. a plane square grid consisting of identical atoms, containing $$n_{0}$$ atoms per unit area;
(c) for a simple cubic lattice consisting of identical atoms, containing $$n_{0}$$ atoms per unit volume.
Above figure, shows students studying the thermal conduction of energy into cylindrical blocks of ice. This process is described by the equation
$$\frac{Q}{\Delta t}=\frac{k\pi d^{2}(T_{h}-T_{c})}{4L}$$
For experimental control, in one set of trials all quantities except $$d$$ and $$\Delta t$$ are constant. (a) If $$d$$ is made three times larger, does the equation predict that $$\Delta t$$ will get larger or get smaller? By what factor? (b) What pattern of proportionality of $$\Delta t$$ to $$d$$ does the equation predict? (c) To display this proportionality as a straight line on a graph, what quantities should you plot on the horizontal and vertical axes? (d) What expression represents the theoretical slope of this graph?
The density of gasoline is $$730 kg/m^3$$ at $$0^0C$$. Its average coefficient of volume expansion is $$9.60 \times 10^{-4}(^0C)^{-1}$$.Assume 1.00 gal of gasoline occupies $$0.003 80 m^3$$. How many extra kilograms of gasoline would you receive if you bought 10.0 gal of gasoline at $$0^0C$$ rather than at $$20.0^0C$$ from a pump that is not temperature compensated?
Review. A 670-kg meteoroid happens to be composed of aluminum. When it is far from the Earth, its temperature is $$215.0^0C$$ and it moves at 14.0 km/s relative to the planet. As it crashes into the Earth, assume the internal energy transformed from the mechanical energy of the meteoroidEarth system is shared equally between the meteoroid and the Earth and all the material of the meteoroid rises momentarily to the same final temperature. Find this temperature. Assume the specific heat of liquid and of gaseous aluminum is $$1 170 J/kg . ^0C$$.
Death Valley holds the record for the highest recorded temperature in the United States. On July 10, 1913, at a place called Furnace Creek Ranch, the temperature rose to $$134^0F$$. The lowest U.S. temperature ever recorded occurred at Prospect Creek Camp in Alaska on January 23, 1971, when the temperature plummeted to $$-79.8^0 F$$. (a) Convert these temperatures to the Celsius scale. (b) Convert the Celsius temperatures to Kelvin.
An underground gasoline tank can hold $$1.00 \times 10^3$$ galIons of gasoline at $$52.0^0F$$. Suppose the tank is being filled on a day when the outdoor temperature (and the temperature of the gasoline in a tanker truck) is $$95.0^0F$$. When the underground tank registers that it is full, how many gallons have been transferred from the truck, according to a non-temperature-compensated gauge on the truck? Assume the temperature of the gasoline quickly cools from $$95.0^0F$$ to $$52.0^0F$$ upon entering the tank.
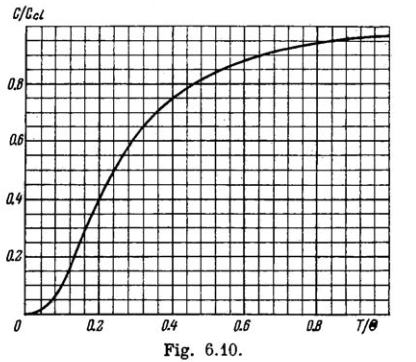
Fig. 6.10 shows heat capacity of a crystal vs temperature in terms of the Debye theory. Here $$ Cd $$ is classical heat capacity, $$ \Theta $$ is the Debye temperature. Using this plot, find:
(a) the Debye temperature for silver if at a temperature $$T = 65\,K$$ its molar heat capacity is equal to $$15 J/(mol \cdot K)$$;
(b) the molar heat capacity of aluminium at $$T = 8\, K$$ if at $$T = 250\,K$$ it is equal to $$22.4 J/(mol \cdot K)$$;
(c) the maximum vibration frequency for copper whose heat capacity at $$T = 125\,K$$ differs from the classical value by $$25\%$$
For bacteriological testing of water supplies and in medical clinics, samples must routinely be incubated for 24 h at $$37^0C$$. Peace Corps volunteer and MIT engineer Amy Smith invented a low-cost, low-maintenance incubator. The incubator consists of a foam-insulated box containing a waxy material that melts at $$37.0^0C$$ interspersed among tubes, dishes, or bottles containing the test samples and growth medium (bacteria food).Outside the box, the waxy material is first melted by a stove or solar energy collector. Then the waxy material is put into the box to keep the test samples warm as the material solidifies. The heat of fusion of the phase-change material is 205 kJ/kg. Model the insulation as a panel with surface area $$0.490 m^2$$, thickness 4.50 cm,and conductivity $$0.012 0 W/m .^0C$$. Assume the exterior temperature is $$23.0^0C$$ for 12.0 h and $$16.0^0C$$ for 12.0 h. (a) What mass of the waxy material is required to conduct the bacteriological test? (b) Explain why your calculation can be done without knowing the mass of the test samples or of the insulation.
(a) The inside of a hollow cylinder is maintained at a temperature Ta, and the outside is at a lower temperature, $$T_a$$ . The wall of the cylinder has a thermal conductivity k. Ignoring end effects, show that the rate of energy conduction from the inner surface to the outer surface in the radial direction is
$$\dfrac{dQ}{dt}=2 \pi Lk[\dfrac{T_a-T_b}{ln(b/a)}]$$
Suggestions: The temperature gradient is dT/dr. A radial energy current passes through a concentric cylinder of area $$2\pi rL$$. (b) The passenger section of a jet airliner is in the shape of a cylindrical tube with a length of 35.0 m and an inner radius of 2.50 m. Its walls are lined with an insulating material 6.00 cm in thickness and having a thermal conductivity of $$4 .00 \times 10^{5} cal/s.cm.^0C$$. A heater must maintain the interior temperature at $$25.0^0C$$ while the outside temperature is $$235.0^0C$$. What power must be supplied to the heater?
A 1.00-L insulated bottle is full of tea at $$90.0^0C$$. You pour out one cup of tea and immediately screw the stopper back on the bottle. Make an order-of-magnitude estimate of the change in temperature of the tea remaining in the bottle that results from the admission of air at room temperature. State the quantities you take as data and the values you measure or estimate for them.
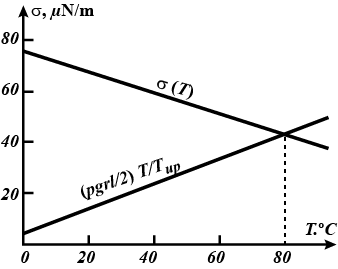
The lower end of a capillary of radius $$r =0.2\,mm$$ and length $$\ell=8\,cm$$ is immersed in water whose temperature is constant and equal to $$T_{low} = 0 ^\circ C$$. The temperature of the upper end of the capillary is $$T_{up} = 100 ^\circ C$$. Determine the height h to which the water in the capillary rises, assuming that the thermal conductivity of the capillary is much higher than the thermal conductivity of water in it. The heat exchange with the ambient should be neglected.
Hint. Use the following temperature dependence of the surface tension of water:
Water is kept in the capillary by surface tension. If $$\sigma_h$$ is the surface tension at the temperature $$T_h$$,
we can write
$$h=\dfrac{\sigma_h}{\rho_wgr}$$
where $$\rho_w$$ is the density of water. Hence we obtain
$$\sigma_h=\dfrac{\rho grh}{2}=\Bigg(\dfrac{\rho grl}{2}\Bigg)\Bigg(\dfrac{T_h}{T_{up}}\Bigg)$$
Using the hint in the conditions of the problem, we plot the graph of the function $$\sigma (T)$$. The temperature $$T_h$$ on the level of the maximum ascent of water is determined by the point of intersection of the curves describing the $$(\rho grl{2})\, T_h/T_{up}$$ and $$\sigma(T)$$ dependences. Figure shows that $$T_h=80^\circ C$$. Consequently,
$$h=\dfrac{lT_h}{T_{up}}=6.4\,cm$$
The problem can also be solved analytically if we note that the (T) dependence is practically linear.
we can write
$$h=\dfrac{\sigma_h}{\rho_wgr}$$
where $$\rho_w$$ is the density of water. Hence we obtain
$$\sigma_h=\dfrac{\rho grh}{2}=\Bigg(\dfrac{\rho grl}{2}\Bigg)\Bigg(\dfrac{T_h}{T_{up}}\Bigg)$$
Using the hint in the conditions of the problem, we plot the graph of the function $$\sigma (T)$$. The temperature $$T_h$$ on the level of the maximum ascent of water is determined by the point of intersection of the curves describing the $$(\rho grl{2})\, T_h/T_{up}$$ and $$\sigma(T)$$ dependences. Figure shows that $$T_h=80^\circ C$$. Consequently,
$$h=\dfrac{lT_h}{T_{up}}=6.4\,cm$$
The problem can also be solved analytically if we note that the (T) dependence is practically linear.
The shell of a space station is a blackened sphere in which a temperature $$T = 500\, K$$ is maintained due to the operation of appliances of the station. The amount of heat given away from a unit surface, the area is proportional to the fourth power of thermodynamic temperature.
Determine the temperature $$T_x$$ of the shell if the station is enveloped by a thin spherical black screen of nearly the same radius as the radius of the shell.
A space object has the shape of a sphere of radius R. Heat sources ensuring the heat evolution at a constant rate are distributed uniformly over its volume. The amount of heat liberated by a unit surface the area is proportional to the fourth power of thermodynamic temperature. In what proportion would the temperature of the object change if its radius decreased by half?
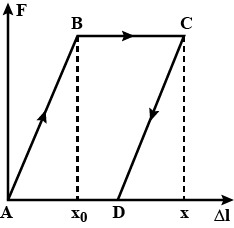
The residual deformation of an elastic rod can be roughly described by using the following model. If the elongation of the rod $$\Delta l < x_0$$ (where $$x_0$$ is the quantity present for the given rod), the force required to cause the elongation $$\Delta l$$ is determined by Hooke's law: $$F = k \Delta l$$, where k is the rigidity of the rod. If $$\Delta l > x_0$$, the force does not depend on elongation any longer (the material of the rod starts "flowing"). If the load is then removed, the elongation of the rod will decrease along CD which for the sake of simplicity will be taken straight and parallel to the segment AB (Fig.). Therefore, after the load has been removed completely, the rod remains deformed (point D in the figure). Let us suppose that the rod is initially stretched by $$\Delta l = x > x_0$$ and then the load is removed. Determine the maximum change of $$\Delta T$$ in the rod temperature if its heat capacity is C and the rod are thermally insulated.
A long tungsten heater wire is rated at 4 kW $$m^{-1}$$ and is $$5 \times 10^{-4}m$$ in diameter. It is embedded along the axis of a ceramic cylinder of diameter 0.12 m. When operating at the rated power, the wire is at $$1500^\circ C;$$ the outside of the cylinder is at $$20^\circ C.$$ Find the thermal conductivity of the ceramic.
The cylindrical ceramic portion can be considered to be a series combination of thin cylindrical shells.
The elemental shell will be having a thickness dx and are $$2\pi LX$$, where L is the length of the cylinder.
The thermal resistance $$dR=\dfrac{dx}{KA}-\dfrac{dx}{K2\pi LX}$$
Resistance $$\displaystyle =\int dR=\dfrac{1}{2\pi K L}\int^{R_2}_{R_1}\dfrac{dx}{X}$$
$$=\dfrac{1}{2\pi KL}\log_e(\dfrac{R_2}{R_1})$$
Thermal current $$=\dfrac{\Delta T}{R}=\dfrac{2\pi Kl\Delta T}{\log_e(\dfrac{R_2}{R_1})}=\dfrac{dQ}{dt}$$
Given $$\dfrac{dQ}{dt}=power =3kw/mn$$ (per meter)
$$\Delta T=1500-20=1480$$ $$R_2=0.06m=600\times 10^{-4}m$$
When $$L=1,\dfrac{dQ}{dt}=3\times 10^3$$ $$R_1=2.5\times 10^{-4}m$$
$$\therefore 3\times 10^3=\dfrac{2\pi K\times 1480}{\log_e\left(\dfrac{600}{2.5}\right)}\Rightarrow \dfrac{3\times 10^3\times \log_e\left(\dfrac{600}{2.5}\right)}{2\pi\times 1480}$$
$$=1.768W/mK$$
The thermal conductivity of the ceramic is $$1.786W/nk$$
"The amount of heat present in hot water is greater than that in cold water"- explain whether the statement is correct or not.
Why is the following situation impossible? A group of campers arises at 8:30 a.m. and uses a solar cooker, which consists of a curved, reflecting surface that concentrates sunlight onto the object to be warmed . During the day, the maximum solar intensity reaching the Earths surface at the cookers location is $$I = 600 W/m^2$$. The cooker faces the Sun and has a face diameter of d 5 0.600 m. Assume a fraction f of 40.0% of the incident energy is transferred to 1.50 L of water in an open container, initially at $$20.0^0C$$. The water comes to a boil, and the campers enjoy hot coffee for breakfast before hiking ten miles and returning by noon for lunch.
Class 11 Engineering Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Physical World Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work,Energy And Power Extra Questions