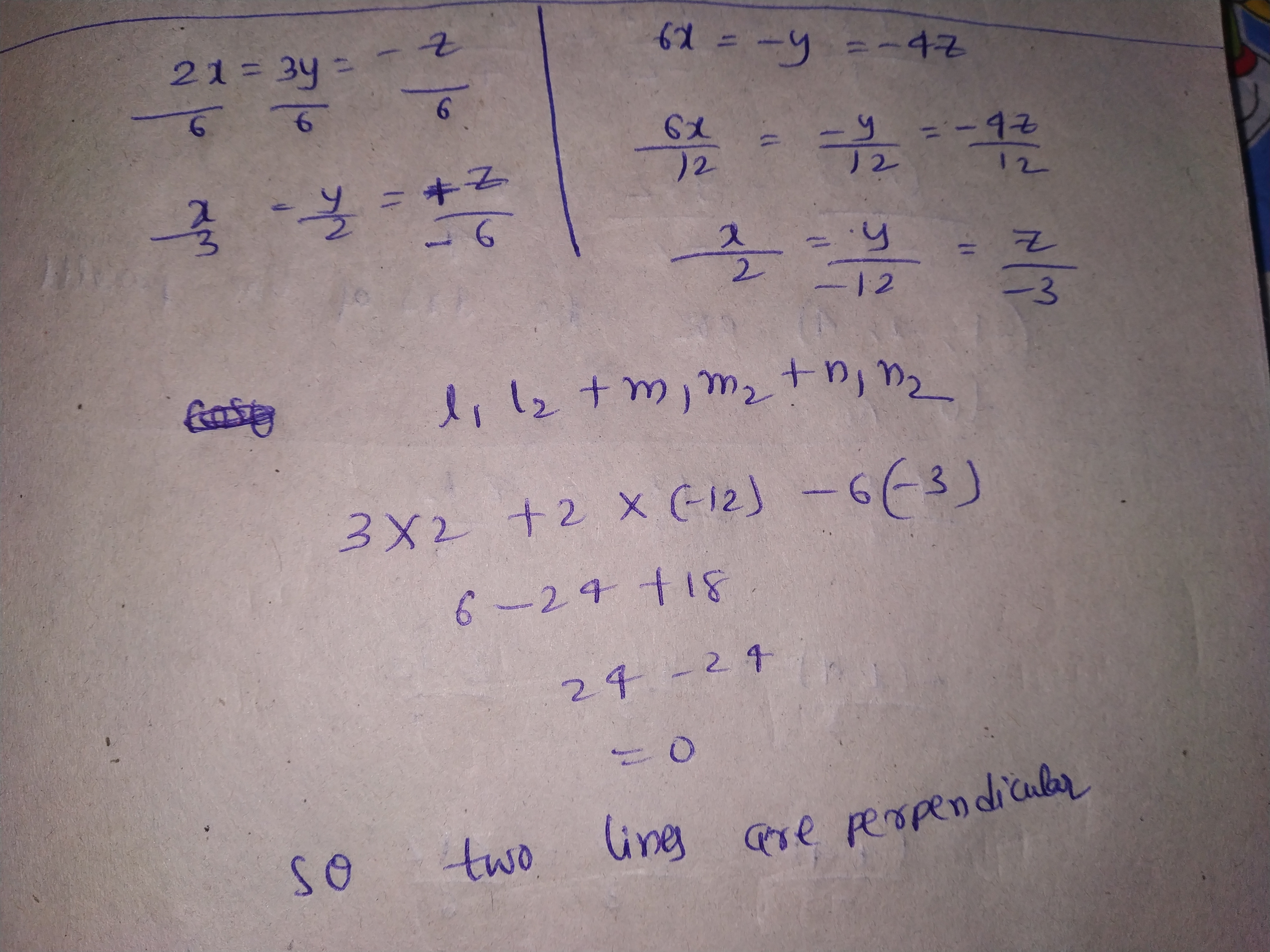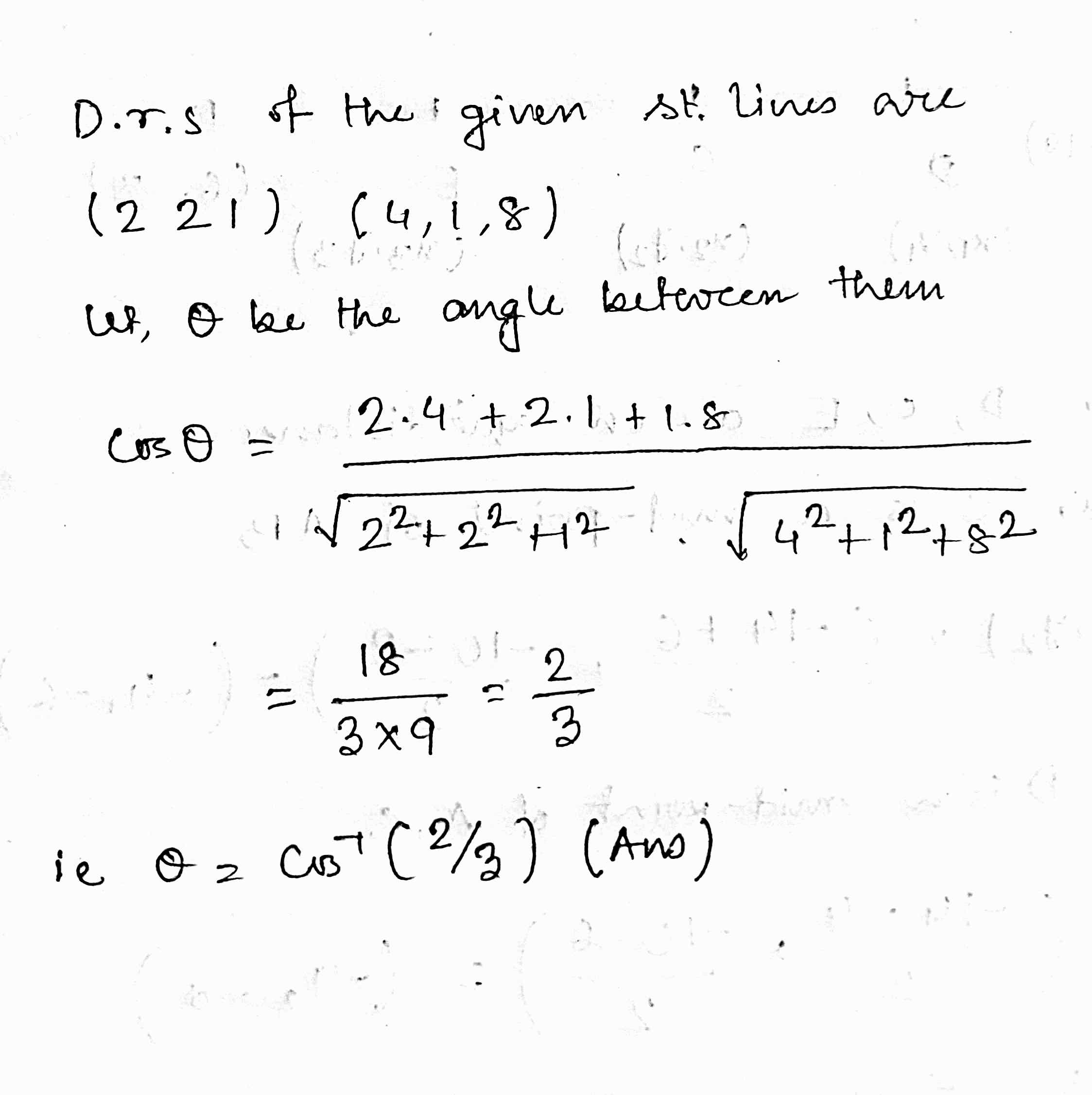Three Dimensional Geometry - Class 12 Engineering Maths - Extra Questions

If the coordinates of the points $$A,B,C,D$$ be $$(1,2,3), (4,5,7), (-4,3,-6)$$ and $$(2,9,2)$$ respectively, then find the angle between the lines $$AB$$ and $$CD$$

The coordinates of $$A,B,C$$ and $$D$$ are $$(1,2,3), (4,5,7), (-4,3,-6)$$ and $$(2,9,2)$$ respectively.
The direction ratios of $$AB$$ are $$(4-1)=3, (5-2)=3$$ and $$(7-3)=4$$
The direction ratios of $$CD$$ are $$(2-(-4))=6, (9-3)=6$$ and $$(2-(-6))=8$$
It can be seen that $$\cfrac { { a }_{ 1 } }{ { a }_{ 2 } } =\cfrac { { b

}_{ 1 } }{ { b }_{ 2 } } =\cfrac { { c }_{ 1 } }{ { c }_{ 2 } } =\cfrac {

1 }{ 2 } $$
Therefore, $$AB$$ is parallel to $$CD$$.
Thus, the angle between $$AB$$ and $$CD$$ is either $${0}^{o}$$ or $${180}^{o}$$.


Angle between lines whose direction cosine satisfy $$l+m+n=0, {l}^{2}+{m}^{2}-{n}^{2}=0$$.

$$l+m+n=0\quad -(i)\\ { l }^{ 2 }+{ m }^{ 2 }+{ n }^{ 2 }=1\quad -(ii)\\ { l }^{ 2 }+{ m }^{ 2 }-{ n }^{ 2 }=0\quad -(iii)\\ (ii)+(iii)\\ 2({ l }^{ 2 }+{ m }^{ 2 })=1\\ 2{ n }^{ 2 }=1\Rightarrow n=\pm \cfrac { 1 }{ \sqrt { 2 }  } \\ { l }^{ 2 }+{ m }^{ 2 }=\cfrac { 1 }{ 2 } \\ l+m=\cfrac { 1 }{ \sqrt { 2 }  } \\ { l }^{ 2 }+{ (\cfrac { 1 }{ \sqrt { 2 }  } -l) }^{ 2 }=\cfrac { 1 }{ 2 } \\ { l }^{ 2 }+{ l }^{ 2 }+\cfrac { 1 }{ 2 } -\sqrt { 2 } l=\cfrac { 1 }{ 2 } \\ 2{ l }^{ 2 }-\sqrt { 2 } l=0\\ l=0,\cfrac { 1 }{ \sqrt { 2 }  } \\ \Rightarrow m=\cfrac { 1 }{ \sqrt { 2 }  } ,0\\ { l }^{ 2 }+{ m }^{ 2 }=\cfrac { 1 }{ 2 } \\ l+m=\cfrac { -1 }{ \sqrt { 2 }  } \\ { l }^{ 2 }+{ (\cfrac { -1 }{ \sqrt { 2 }  } -l) }^{ 2 }=\cfrac { 1 }{ 2 } \\ { l }^{ 2 }+\cfrac { 1 }{ 2 } +{ l }^{ 2 }+\sqrt { 2 } l=\cfrac { 1 }{ 2 } \\ 2{ l }^{ 2 }+\sqrt { 2 } l=0\\ l=0,\cfrac { -1 }{ \sqrt { 2 }  } \\ \Rightarrow \cfrac { -1 }{ \sqrt { 2 }  } ,0$$
Possible values of $$(l,m,n)$$ are:
$$(0,\cfrac { 1 }{ \sqrt { 2 }  } ,\cfrac { -1 }{ \sqrt { 2 }  } ),(\cfrac { 1 }{ \sqrt { 2 }  } ,0,\cfrac { -1 }{ \sqrt { 2 }  } ),(0,\cfrac { -1 }{ \sqrt { 2 }  } ,\cfrac { 1 }{ \sqrt { 2 }  } ),(\cfrac { -1 }{ \sqrt { 2 }  } ,0,\cfrac { 1 }{ \sqrt { 2 }  } )$$


Find the vector equation of the plane passing through the points $$4\overline{i} - 3\overline{j} - \overline{k}, 3\overline{i} +7 \overline{j}-10\overline{k}$$ and $$2\overline{i} + 5\overline{5} - 7\overline{k}$$ and find if the point $$\overline{i} + 2\overline{j} - 3\overline{k}$$ lies on the plane.

The vector equation of plane through point with position vector 

$$\overline a  = 4\widehat i - 3\widehat j - \widehat k$$
$$\overline b  = 3\widehat i + 7\widehat j - 10\widehat k$$
$$\overline c  = 2\widehat i + 5\widehat j - 7\widehat k$$

$$ = \left( {1 - s - t} \right)\overline a  + s\overline b  + t\overline c $$  s and t is scalar

$$\overline r  = \left( {1 - s - t} \right)\left( {4\widehat i - 3\widehat j - \widehat k} \right) + s\left( {3\widehat i + t\widehat j - 10\widehat k} \right) + t\left( {2i + 5j - tk} \right)$$

$$\overline r  = 4\widehat i - 3\widehat j - \widehat k + s\left( { - \widehat i + 10\widehat j - 9\widehat k} \right) + t\left( { - 2\widehat i + 58 - \widehat {6k}} \right)$$
 
to find if point $$\widehat i + 2\widehat j - 3\widehat k$$ lies on the above plane 

$$\widehat i + 2\widehat j - 3\widehat k = s\left( { - \widehat i + 10\widehat j - 9\widehat k} \right) + t\left( { - 2\widehat i + 58 - \widehat {6k}} \right)$$

$$ - 3\widehat i + 5\widehat j - 2\widehat k = s\left( { - \widehat i + 10\widehat j - 9\widehat k} \right) + t\left( { - 2\widehat i + 58 - \widehat {6k}} \right)$$
 
i , j ,k coefficient 

-3 = -5 -2t is equation  (1)
5 = 10s+8t  is equation  (2)
-2 = -9s -6t is equation  (3) 

solve equation  (1) and (2)

$$s=\frac { { -7 } }{ 6 } \, \, \, t=\frac { { 14 } }{ 6 } $$

RHS of  equation  $$(3) -9s - 6t$$

$$\begin{array}{l} =-9\left( { \frac { { -7 } }{ 6 }  } \right) \, -6\left( { \frac { { 14 } }{ 6 }  } \right)  \\ \frac { { 63-84 } }{ 6 } =-\frac { { -21 } }{ 6 } =\frac { { -7 } }{ 2 }  \\ \frac { { -7 } }{ 2 } \ne -2 \end{array}$$

$$\left( {\widehat i + 2\widehat j - 3\widehat k} \right)$$  does not lie on above plane. 



Find the angle between two lines, one of which has direction ratios $$2, 2, 1$$ while the other one is obtained by joining the points $$(3, 1, 4)$$ and $$(7, 2, 12)$$.

Given  that,
Direction ratios of first line are $$2,2,1$$
Direction ratios of second line joining the points $$(3,1,4)(7,2,12)$$ and $$(7-3),(2-1),(12-4)$$
i.e   $$4,1,8$$
Let $$ \theta$$ be the angle between the two lines.
$$\begin{array}{l} \therefore \cos  \theta =\frac { { 2\left( 4 \right) +2\left( 1 \right) +1\left( 8 \right)  } }{ { \sqrt { { { \left( 2 \right)  }^{ 2 } }+{ { \left( 2 \right)  }^{ 2 } }+{ { \left( 1 \right)  }^{ 2 } } } \sqrt { { { \left( 4 \right)  }^{ 2 } }+{ { \left( 1 \right)  }^{ 2 } }+{ 8^{ 2 } } }  } }  \\ \left[ { \cos  \theta =\frac { { { a_{ 1 } }{ a_{ 2 } }+{ b_{ 1 } }{ b_{ 2 } }+{ c_{ 1 } }{ c_{ 2 } } } }{ { \sqrt { a_{ 1 }^{ 2 }+b_{ 1 }^{ 2 }+c_{ 1 }^{ 2 } } \sqrt { a_{ 2 }^{ 2 }+b_{ 2 }^{ 2 }+c_{ 2 }^{ 2 } }  } }  } \right]  \\ =\frac { { 8+2+8 } }{ { 3\times 9 } } =\frac { { 18 } }{ { 3\times 9 } } =\frac { 2 }{ 3 }  \\ \therefore \theta ={ \cos ^{ 1 }  }\left( { \frac { 2 }{ 3 }  } \right)  \end{array}$$


Find the angle between the lines $$y-\sqrt{3}x-5=0$$ and $$\sqrt{3}y-x+6=0$$.

We have,
$$\begin{array}{l} y=\sqrt { 3x } -5=0\, \, \, \, \, \, \, \, \, \, { m_{ 1 } }=\sqrt { 3 }  \\ \sqrt { 3y } =x-6\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, { m_{ 2 } }=\frac { 1 }{ { \sqrt { 3 }  } }  \\ \tan  \theta =\left| { \dfrac { { { m_{ 1 } }-{ m_{ 2 } } } }{ { 1+{ m_{ 1 } }{ m_{ 2 } } } }  } \right| =\dfrac { 1 }{ { \sqrt { 3 }  } }  \\ \therefore \, \, \theta ={ 30^{ 0 } } \end{array}$$
$$\therefore$$ Angle b/w llines is $$30^0$$.


Find the angle between the following pairs of lines:
$$\dfrac {x - 5}{1} = \dfrac {2y + 6}{-2} = \dfrac {z - 3}{1}$$ and $$\dfrac {x - 2}{3} = \dfrac {y + 1}{4} = \dfrac {z - 6}{5}$$

Parallel vector of first line = $$\hat{i}-\hat{j}+\hat{k}$$

Parallel vector of second line = $$3\hat{i}+4\hat{j}+5\hat{k}$$

Let the angle between two lines be $$\theta$$

Then, Cos$$\theta = \dfrac{(\hat{i}-\hat{j}+\hat{k}).(3\hat{i}+4\hat{j}+5\hat{k})}{|\hat{i}-\hat{j}+\hat{k}||3\hat{i}+4\hat{j}+5\hat{k}|} = \dfrac{4}{\sqrt{50}\sqrt{3}} = \dfrac{4}{5\sqrt{6}}$$

Thus, $$\theta = cos^{-1}\dfrac{4}{5\sqrt{6}}$$


Find the angle between the following pairs of lines:
$$\dfrac {5 - x}{-2} = \dfrac {y + 3}{1} = \dfrac {1 - z}{3}$$ and $$\dfrac {x}{3} = \dfrac {1 - y}{-2} = \dfrac {z + 5}{-1}$$

Parallel vector of first line = $$-2\hat{i}+\hat{j}+3\hat{k}$$
Parallel vector of second line = $$3\hat{i}-2\hat{j}-\hat{k}$$

Let the angle between two lines be $$\theta$$
Then, Cos$$\theta = \dfrac{(-2\hat{i}+\hat{j}+3\hat{k}).(3\hat{i}-2\hat{j}-\hat{k})}{|-2\hat{i}+\hat{j}+3\hat{k}||3\hat{i}-2\hat{j}-\hat{k}|} = \dfrac{-11}{\sqrt{14}\sqrt{14}} = \dfrac{-11}{14}$$
Thus, $$\theta = cos^{-1}\dfrac{-11}{14}$$


Find the angle between the following pairs of lines:
$$\dfrac {x - 1}{2} = \dfrac {y - 2}{3} = \dfrac {z - 3}{-3}$$ and $$\dfrac {x + 3}{-1} = \dfrac {y - 5}{8} = \dfrac {z - 1}{4}$$

Parallel vector of first line = $$2\hat{i}+3\hat{j}-3\hat{k}$$
Parallel vector of second line = $$-\hat{i}+8\hat{j}+4\hat{k}$$

Let the angle between two lines be $$\theta$$
Then, Cos$$\theta = \dfrac{(2\hat{i}+3\hat{j}-3\hat{k}).(-\hat{i}+8\hat{j}+4\hat{k})}{|2\hat{i}+3\hat{j}-3\hat{k}||-\hat{i}+8\hat{j}+4\hat{k}|} = \dfrac{10}{\sqrt{22}\sqrt{81}} = \dfrac{10}{9\sqrt{22}}$$
Thus, $$\theta = cos^{-1}\dfrac{10}{9\sqrt{22}}$$


Find the angle between the following pairs of lines:
$$\vec {r} = 3\hat {i} + \hat {j} - 2\hat {k} + \lambda (\hat {i} + \hat {j} - 2\hat {k})$$ and $$\vec {r} = 2\hat {i} - \hat {j} - 56\hat {k} + \mu (3\hat {i} - 5\hat {j} - 4\hat {k})$$.

The given lines are parallel to the vectors, $$\vec { { b }_{ 1 } }

=\left( \hat { i } -\hat { j } -2\hat { k }  \right) $$ and $$\vec { { b

}_{ 2 } } =\left( 3\hat { i } -5\hat { j } -4\hat { k }  \right) $$ respectively.
Therefore, $$\left| \vec { { b }_{ 1 } }  \right|

=\sqrt { { \left( 1 \right)  }^{ 2 }+{ \left( -1 \right)  }^{ 2 }+{

\left( -2 \right)  }^{ 2 } } =\sqrt { 6 } $$
and $$\left| \vec { { b }_{ 2

} }  \right| =\sqrt { { \left( 3 \right)  }^{ 2 }+{ \left( -5 \right)

 }^{ 2 }+{ \left( -4 \right)  }^{ 2 } } =5\sqrt { 2 } $$
Thus $$\vec { { b

}_{ 1 } } .\vec { { b }_{ 2 } } =\left( \hat { i } -\hat { j } -2\hat {

k }  \right) .\left( 3\hat { i } -5\hat { j } -4\hat { k }  \right) $$
$$= 1.3-1(-5)-2(-4)$$
$$=3+5+8=16$$
If $$\theta$$ is the angle between the given lines then,
$$\cos

{ \theta } =\left| \cfrac { \vec { { b }_{ 1 } } .\vec { { b }_{ 2 } }  }{

\left| \vec { { b }_{ 1 } }  \right| \left| \vec { { b }_{ 2 } }

 \right|  }  \right| $$
$$\Rightarrow$$ $$\cos { \theta } =\cfrac { 16 }{

\sqrt { 6 } .5\sqrt { 2 }  } =\cfrac { 16 }{ \sqrt { 2 } .\sqrt { 3 }

.5\sqrt { 2 }  } =\cfrac { 16 }{ 10\sqrt { 3 }  } $$
$$\Rightarrow$$ $$\cos { \theta } =\cfrac { 8 }{ 5\sqrt { 3 }  } $$
$$\Rightarrow$$ $$\theta=\cos ^{ -1 }{ \left( \cfrac { 8 }{ 5\sqrt { 3 }  }  \right)  } $$

This the required angle between the given pair of lines.


Find the angle between the following pair of lines:
(i) $$\vec { r } =2\hat { i } -5\hat { j } +\hat { k } +\lambda \left( 3\hat { i } -2\hat { j } +6\hat { k }  \right) $$ and $$\vec { r } =7\hat { i } -6\hat { k } +\mu \left( \hat { i } +2\hat { j } +2\hat { k }  \right) $$
(ii) $$\vec { r } =3\hat { i } +\hat { j } -2\hat { k } +\lambda \left( \hat { i } -\hat { j } -2\hat { k }  \right) $$ and $$\vec { r } =2\hat { i } -\hat { j } -56\hat { k } +\mu \left( \hat { 3i } -5\hat { j } -4\hat { k }  \right) $$

(i)
If $$\theta$$ be the angle between the given lines.
Then  $$\cos { \theta } =\left| \cfrac { \vec { {

b }_{ 1 } } .\vec { { b }_{ 2 } }  }{ \left| \vec { { b }_{ 1 } }

 \right| \left| \vec { { b }_{ 2 } }  \right|  }  \right| $$
where $$ \vec { { b }_{ 1 } } =\left(

3\hat { i } +2\hat { j } +6\hat { k }  \right) $$ and $$\vec { { b }_{ 2

} } =\left( \hat { i } +2\hat { j } +2\hat { k }  \right) $$
$$\therefore$$ $$\left| \vec { { b }_{ 1 } }  \right| =\sqrt { { 3 }^{ 2 }+{ 2 }^{ 2 }+{ 6 }^{ 2 } } =7$$
$$\left| \vec { { b }_{ 2 } }  \right| =\sqrt { { 1 }^{ 2 }+{ 2 }^{ 2 }+{ 2 }^{ 2 } } =3$$
$$\vec

{ { b }_{ 1 } } .\vec { { b }_{ 2 } } =\left( 3\hat { i } +2\hat { j }

+6\hat { k }  \right) .\left( \hat { i } +2\hat { j } +2\hat { k }

 \right) $$
$$=3\times 1+2\times 2+6\times 2=3+4+12=19$$
$$\Rightarrow$$ $$\cos { \theta } =\cfrac { 19 }{ 7\times 3 } $$
$$\Rightarrow$$ $$\theta=\cos ^{ -1 }{ \left( \cfrac { 19 }{ 21 }  \right)  } $$

(ii)
The given lines are parallel to the vectors, 
$$\vec { { b }_{ 1 } } =\left( \hat { i } -\hat { j } -2\hat { k }  \right) $$ and $$\vec { { b }_{ 2 } } =\left( 3\hat { i } -5\hat { j } -4\hat { k }  \right) $$ respectively.
$$\therefore$$ $$\left| \vec { { b }_{ 1 } }  \right|=\sqrt { { \left( 1 \right)  }^{ 2 }+{ \left( -1 \right)  }^{ 2 }+{ \left( -2 \right)  }^{ 2 } } =\sqrt { 6 } $$
$$\left| \vec { { b }_{ 2} }  \right| =\sqrt { { \left( 3 \right)  }^{ 2 }+{ \left( -5 \right)  }^{ 2 }+{ \left( -4 \right)  }^{ 2 } } =5\sqrt { 2 } $$
$$\vec { { b}_{ 1 } } .\vec { { b }_{ 2 } } =\left( \hat { i } -\hat { j } -2\hat {k }  \right) .\left( 3\hat { i } -5\hat { j } -4\hat { k }  \right) $$
$$1.3-1(-5)-2(-4)=3+5+8=16$$
If $$\theta$$ is the angle between the given lines then,
$$\cos{ \theta } =\left| \cfrac { \vec { { b }_{ 1 } } .\vec { { b }_{ 2 } }  }{ \left| \vec { { b }_{ 1 } }  \right| \left| \vec { { b }_{ 2 } }  \right|  }  \right| $$
$$\Rightarrow$$ $$\cos { \theta } =\cfrac { 16 }{ \sqrt { 6 } .5\sqrt { 2 }  } =\cfrac { 16 }{ \sqrt { 2 } .\sqrt { 3 } .5\sqrt { 2 }  } =\cfrac { 16 }{ 10\sqrt { 3 }  } $$
$$\Rightarrow$$ $$\cos { \theta } =\cfrac { 8 }{ 5\sqrt { 3 }  } $$
$$\Rightarrow$$ $$\theta=\cos ^{ -1 }{ \left( \cfrac { 8 }{ 5\sqrt { 3 }  }  \right)  } $$


Find the angle between the following pair of lines:
(i) $$\cfrac{x-2}{2}=\cfrac{y-1}{5}=\cfrac{z+3}{-3}$$ and $$\cfrac{x+2}{-1}=\cfrac{y-4}{8}=\cfrac{z-5}{4}$$
(ii) $$\cfrac{x}{2}=\cfrac{y}{2}=\cfrac{z}{1}$$ and $$\cfrac{x-5}{4}=\cfrac{y-2}{1}=\cfrac{z-3}{8}$$

(i)
Let $$\vec { { b }_{ 1 } } $$ and $$\vec { { b }_{ 2 } } $$ be the  vectors parallel to the pair of lines,
$$\cfrac{x-2}{2}=\cfrac{y-1}{5}=\cfrac{z+3}{-3}$$ and
$$\cfrac{x+2}{-1}=\cfrac{y-4}{8}=\cfrac{z-5}{4}$$ respectively,
then $$\vec { { b }_{ 1 } } =\left( \hat { 2i } +5\hat { j } -3\hat { k }

 \right) $$ and $$\vec { { b }_{ 2 } } =\left( -\hat { i } +8\hat { j }

+4\hat { k }  \right) $$
$$\left| \vec { { b }_{ 1 } }  \right|= \sqrt

{ { \left( 2 \right)  }^{ 2 }+{ \left( 5 \right)  }^{ 2 }+{ \left( -3

\right)  }^{ 2 } } =\sqrt { 38 } $$
$$\left| \vec { { b }_{ 2 } }

 \right| =\sqrt { { \left( -1 \right)  }^{ 2 }+{ \left( 8 \right)  }^{ 2

}+{ \left( 4 \right)  }^{ 2 } } =\sqrt { 81 } =9$$
$$\vec { { b }_{ 1

} } .\vec { { b }_{ 2 } } =\left( \hat { 2i } +5\hat { j } -3\hat { k }

 \right) .\left( -\hat { i } +8\hat { j } +4\hat { k }  \right) $$
$$=2(-1)+5\times 8+(-3).4=-2+40-12=26$$
The angle $$\theta$$ between the given pair of lines is given by the relation,
$$\Rightarrow \cos

{ \theta } =\left| \cfrac { \vec { { b }_{ 1 } } .\vec { { b }_{ 2 } }  }{

\left| \vec { { b }_{ 1 } }  \right| \left| \vec { { b }_{ 2 } }

 \right|  }  \right| $$
$$\Rightarrow$$ $$\cos { \theta } =\cfrac { 26 }{ 9\sqrt { 38 }  } $$
$$\Rightarrow$$ $$\theta=\cos ^{ -1 }{ \left( \cfrac { 26 }{ 9\sqrt { 38 }  }  \right)  } $$

(ii)
We have,
$$\vec { { b }_{ 1 } } =\left( \hat { 2i } +2\hat { j } +\hat { k }  \right) $$
$$\vec { { b }_{ 2 } } =\left( 4\hat { i } +\hat { j } +8\hat { k }  \right) $$
$$\therefore$$ $$\left| \vec { { b }_{ 1 } }  \right| =\sqrt { { \left( 2 \right)  }^{

2 }+{ \left( 2 \right)  }^{ 2 }+{ \left( 1 \right)  }^{ 2 } } =\sqrt { 9

} =3$$
$$\left| \vec { { b }_{ 2 } }  \right| =\sqrt { { \left( 4 

\right)  }^{ 2 }+{ \left( 1 \right)  }^{ 2 }+{ \left( 8 \right)  }^{ 2 }

} =\sqrt { 81 } =9$$
$$\vec { { b }_{ 1 } } .\vec { { b }_{ 2 } } 

=\left( \hat { 2i } +2\hat { j } +\hat { k }  \right) .\left( 4\hat { i }

+\hat { j } +8\hat { k }  \right) $$
$$=2\times 4+2\times 1+1\times 8=8+2+8=18$$
If $$\theta$$ is the angle between the given pair of lines, then $$\cos { \theta } 

=\left| \cfrac { \vec { { b }_{ 1 } } .\vec { { b }_{ 2 } }  }{ \left| 

\vec { { b }_{ 1 } }  \right| \left| \vec { { b }_{ 2 } }  \right|  } 

 \right| $$
$$\Rightarrow$$ $$\cos { \theta } =\cfrac { 18 }{ 3\times 9 } =\cfrac { 2 }{ 3 } $$
$$\Rightarrow$$ $$\theta =\cos ^{ -1 }{ \left( \cfrac { 2 }{ 3 }  \right)  } $$


Find the angle between the two straight lines whose direction cosines are given by $$2l+2m-n=0$$ and $$mn+nl+lm=0$$.

Let the angle between the lines be $$\alpha$$

Given Direction cosines of two lines are $$<l,m,n>$$ 
 
Also given that    $$2 l+2 m-n=0\implies n=2 l+2 m\cdots(1)$$

$$m n+n l+l m=0\cdots(2)$$

$$\implies m(2 l+2 m)+l(2 l+2 m)+l m=0$$                     $$(\because \text{from}(1)\ )$$

$$\implies 2 m^2+5 l m+2 l^2=0$$

$$\implies 2 m^2+4 l m+l m+2 l^2=0$$

$$\implies 2 m(m+2 l)+l(m+2 l)=0$$

$$\implies (2 m+l)(m+2 l)=0$$

$$\implies m=-\dfrac{l}{2},-2 l$$

$$n=2 l+2 m=2 l+2\bigg(-\dfrac{l}{2}\bigg),2 l+2(-2 l)=2 l-l,2 l-4 l=l,-2 l$$

So the direction cosines of two lines are $$<l,-\dfrac{l}{2},l>$$ and $$<l,-2 l,-2 l>$$

So the direction ratios will be $$<2,-1,2>$$ and $$<1,-2,-2>$$

As we know that

If $$\theta$$ is the angle between the two lines having direction ratios as $$<a,b,c>$$ and $$<d,e,f>$$ 
                                                        then $$\cos \theta=\dfrac{a d+be +c f}{\sqrt{a^2+b^2+c^2}\sqrt{d^2+e^2+f^2}}$$

Hence $$\cos \alpha=\dfrac{(2)(1)+(-1)(-2)+2(-2)}{\sqrt{2^2+(-1)^2+2^2}\sqrt{1^2+(-2)^2+(-2)^2}}=\dfrac{2+2-4}{3\times 3}=0$$

$$\implies \alpha=\dfrac{\pi}{2}$$

So the angle between the two lines is $$\dfrac{\pi}{2}$$


Measure of angle between $$\dfrac{x}{2}=\dfrac{y}{2}=\dfrac{z}{1}$$ and $$\dfrac{x}{2}=\dfrac{y}{-1}=\dfrac{z}{-2}$$ is


1372831_1126752_ans_7655ba4f89864ac496baa0b7e05bf47a.jpg


The angle between the lines $$\dfrac{x-2}{3} = \dfrac{y+1}{-2} = z-2$$ and $$\dfrac{x-1}{1}= \dfrac{2y+3}{3} = \dfrac{z+5}{2}$$ is equal to:

The given lines are
$$\dfrac{x-2}{3} = \dfrac{y+1}{-2} = \dfrac{z-2}{0}$$

$$\dfrac{x-1}{1}=\dfrac{y+\dfrac{3}{2}}{\dfrac{3}{2}}=\dfrac{z+5}{2}$$

Now, angle b/w the lines
$$cos\theta = |\dfrac{3+(-3)+0}{\sqrt{9+4} \sqrt{1+\dfrac{9}{4}+4}}|$$

$$cos\theta=0$$
$$\theta=90^{o}$$


Find the angle between the following pairs of lines:
$$\dfrac {x + 4}{3} = \dfrac {y - 1}{5} = \dfrac {z + 3}{4}$$ and $$\dfrac {x + 1}{1} = \dfrac {y - 4}{1} = \dfrac {z - 5}{2}$$

Parallel vector of first line = $$3\hat{i}+5\hat{j}+4\hat{k}$$
Parallel vector of second line = $$\hat{i}+\hat{j}+2\hat{k}$$

Let the angle between two lines be $$\theta$$
Then, Cos$$\theta = \dfrac{(3\hat{i}+5\hat{j}+4\hat{k}).(\hat{i}+\hat{j}+2\hat{k})}{|3\hat{i}+5\hat{j}+4\hat{k}||\hat{i}+\hat{j}+2\hat{k}|} = \dfrac{16}{\sqrt{50}\sqrt{6}} = \dfrac{16}{5\sqrt{12}}$$
Thus, $$\theta = cos^{-1}\dfrac{16}{5\sqrt{12}}$$


Find the angle between the lines $$\vec {r} = (2\hat{i} - 5\hat {j} + \hat {k}) + \lambda (3\hat {i} + 2\hat {j} + 6\hat {k})$$ and $$\vec {r} = 7\hat {i} - 6\hat {j} + \mu (\hat {i} + 2\hat {j} + 2\hat {k})$$.

$$\cos\theta\dfrac{l_1.l_2+m_1m_2+n_1.n_2}{\sqrt{1^2_1+m^2_1+n^2_1}\sqrt{1^2_2+m^2_2+n^2_2}}$$

$$=\dfrac{3\times 1+2\times 2+6\times 2}{\sqrt{3^2+2^2+6^2}.\sqrt{1^2+2^2+2^2}}$$

$$=\dfrac{3+4+12}{7.3}$$

$$\cos\theta=\dfrac{19}{21}\Rightarrow\theta=\cos^{-1}\left(\dfrac{19}{21}\right)$$


Find the angle between the lines $$2x = 3y = -z$$ and $$6x = -y = -4z$$.


1503599_1663308_ans_93a8f0b6d53344f7bf4f98ead551ec10.jpg


Find the angle between the following pair of lines:
$$\dfrac {x - 2}{2} = \dfrac {y - 1}{5} = \dfrac {z + 3}{-3}$$ and $$\dfrac {x + 2}{-1} = \dfrac {y - 4}{8} = \dfrac {z - 5}{4}$$.


1959463_1860025_ans_bb9ac53b8e1b401b9fcd8d406ae66653.png


Find the angle between the following pair of lines:
$$\dfrac {x}{2} = \dfrac {y}{2} = \dfrac {z}{1}$$ and $$\dfrac {x - 5}{4} = \dfrac {y - 2}{1} = \dfrac {z - 3}{8}$$.


1959466_1860028_ans_485edf43c1424200853042debaa48111.jpg


Find the angle between the lines 
$$\dfrac{x}{2}=\dfrac{y}{2}=\dfrac{z}{1}$$ and $$\dfrac{x-5}{4}=\dfrac{y-2}{1}=\dfrac{z-3}{8}$$

Dc's of line $$\dfrac{x}{2}=\dfrac{y}{2}=\dfrac{z}{1}$$ are $$2,2,1$$ and 
dc's of line $$\dfrac{x-5}{4}=\dfrac{y-2}{1}\dfrac{z-3}{8}$$ are $$4,1,8$$.
$$\therefore a_1=2,b_1=2,c_1=1$$
$$a_2=4,b_2=1,c_2=8$$
Angle between both lines.
$$\cos \theta =\dfrac{a_1a_2+b_1b_2+c_1c_2}{\sqrt{a_1^2+b_1^2+c_2^2}.\sqrt{a_2^2+b_2^2+c_2^2}}$$
$$=\dfrac{2\times 4+2\times 1+1\times 8}{\sqrt{(2)^2+(2)^2+(1)^2}.\sqrt{(4)^2+(1)^2+(8)^2}}$$
$$=\dfrac{8+2+8}{\sqrt{4+4+1}.\sqrt{16+1+64}}$$
$$=\dfrac{81}{\sqrt{9}.\sqrt{81}}=\dfrac{81}{3\times 9}=\dfrac{2}{3}$$
$$\therefore \theta =\cos^{-1}\left(\dfrac{2}{3}\right)$$


Class 12 Engineering Maths Extra Questions