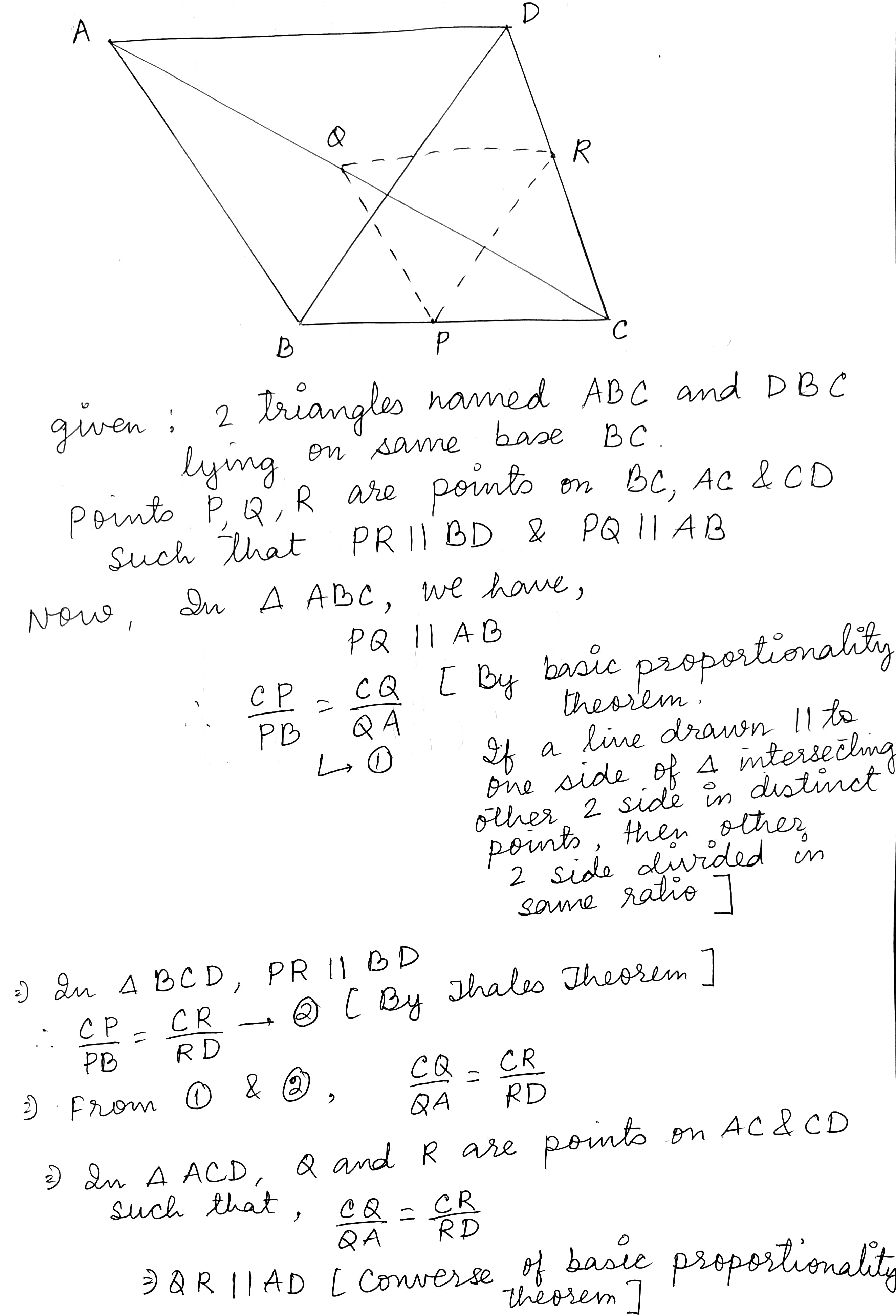
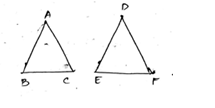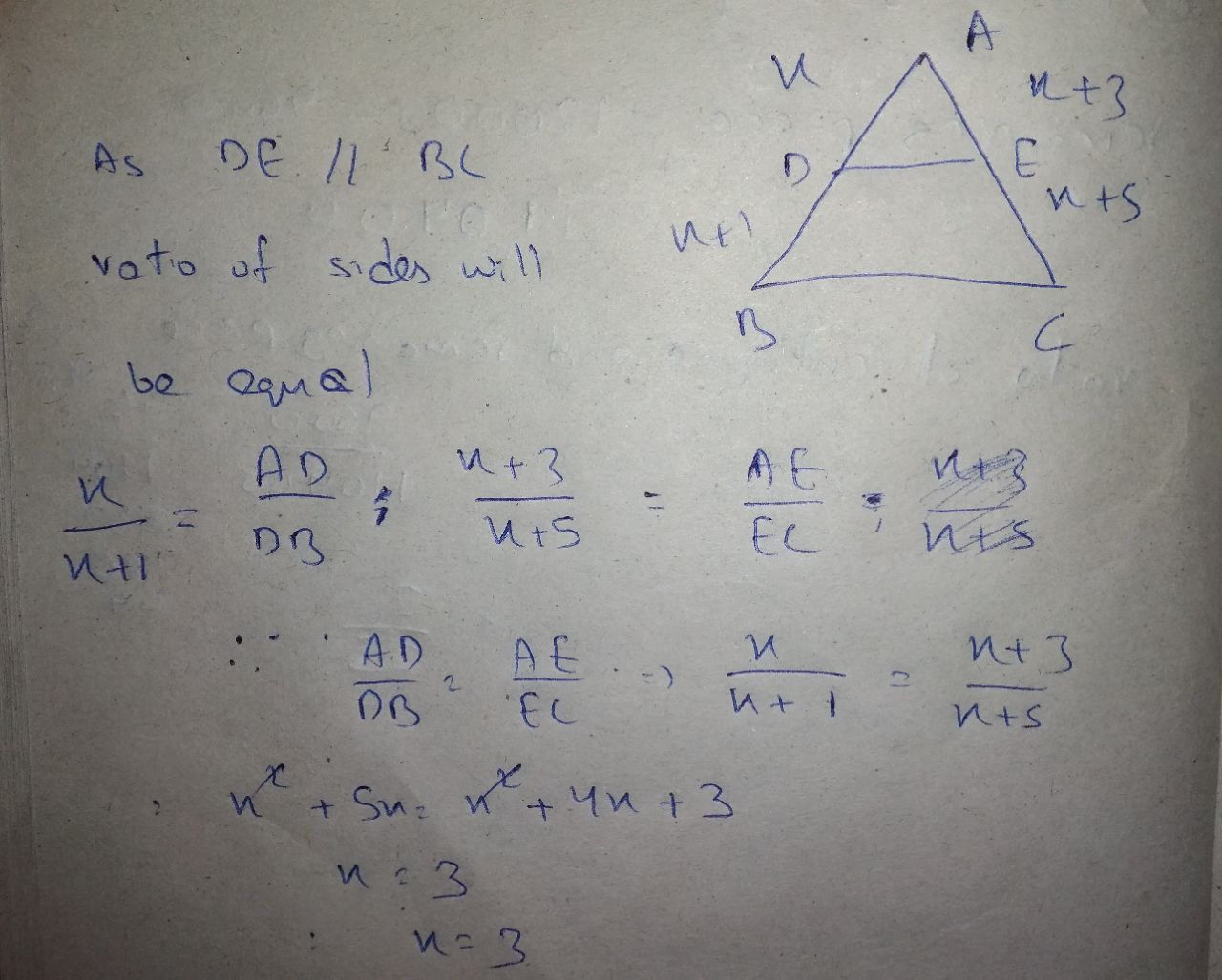Triangles - Class 10 Maths - Extra Questions
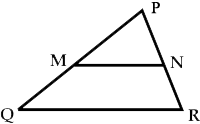
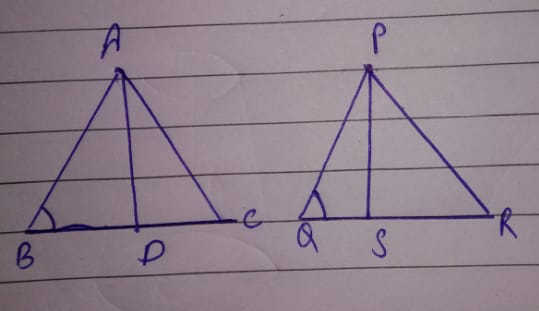
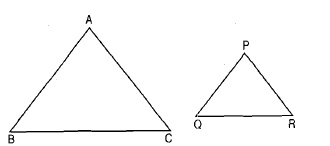
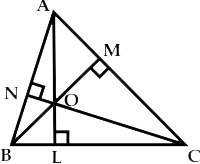
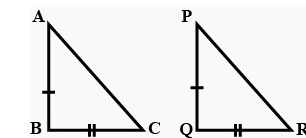
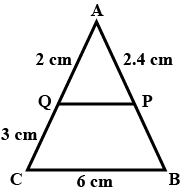
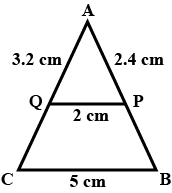
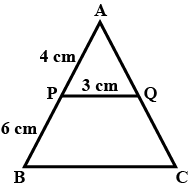
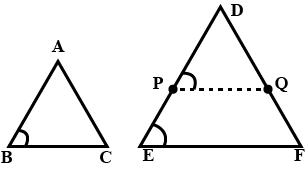
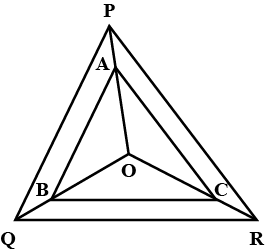
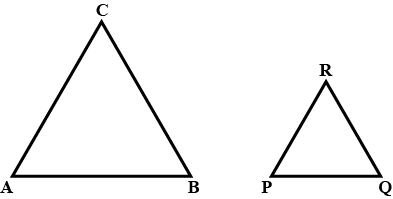
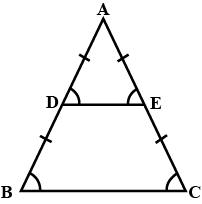
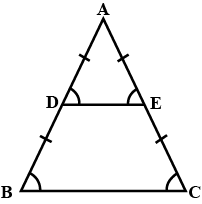
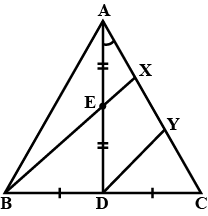
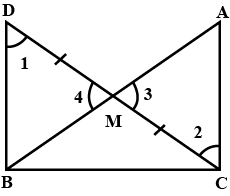
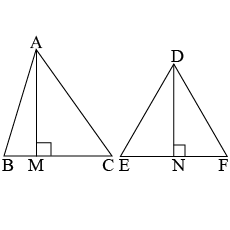
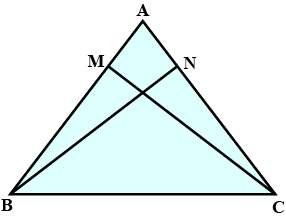
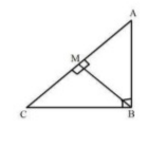
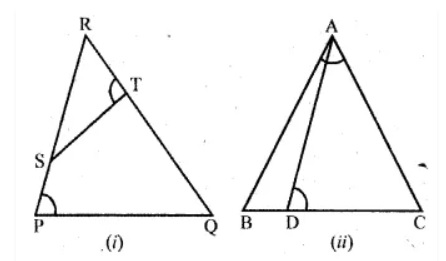
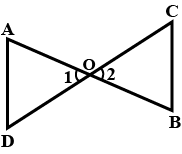
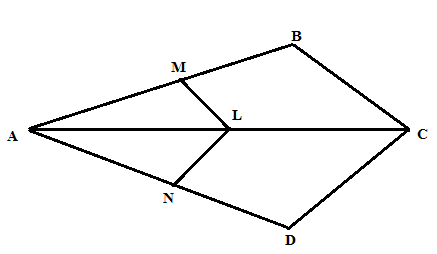
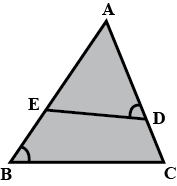
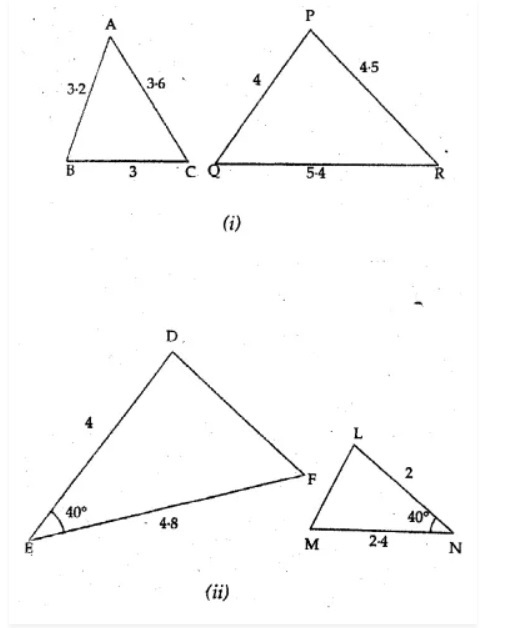
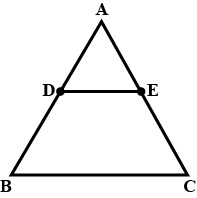
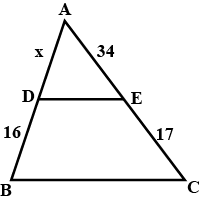
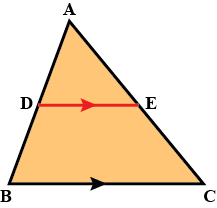
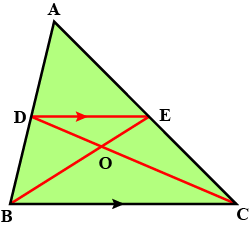
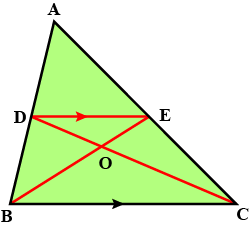
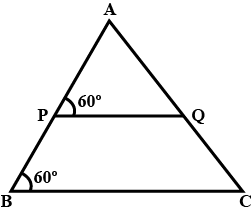
In the given figure you find two triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
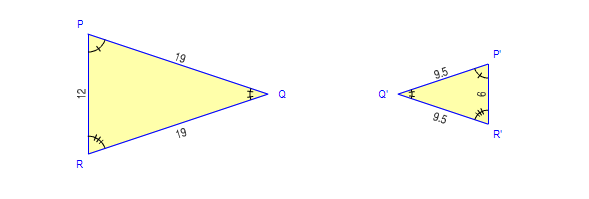
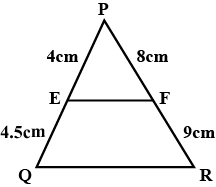
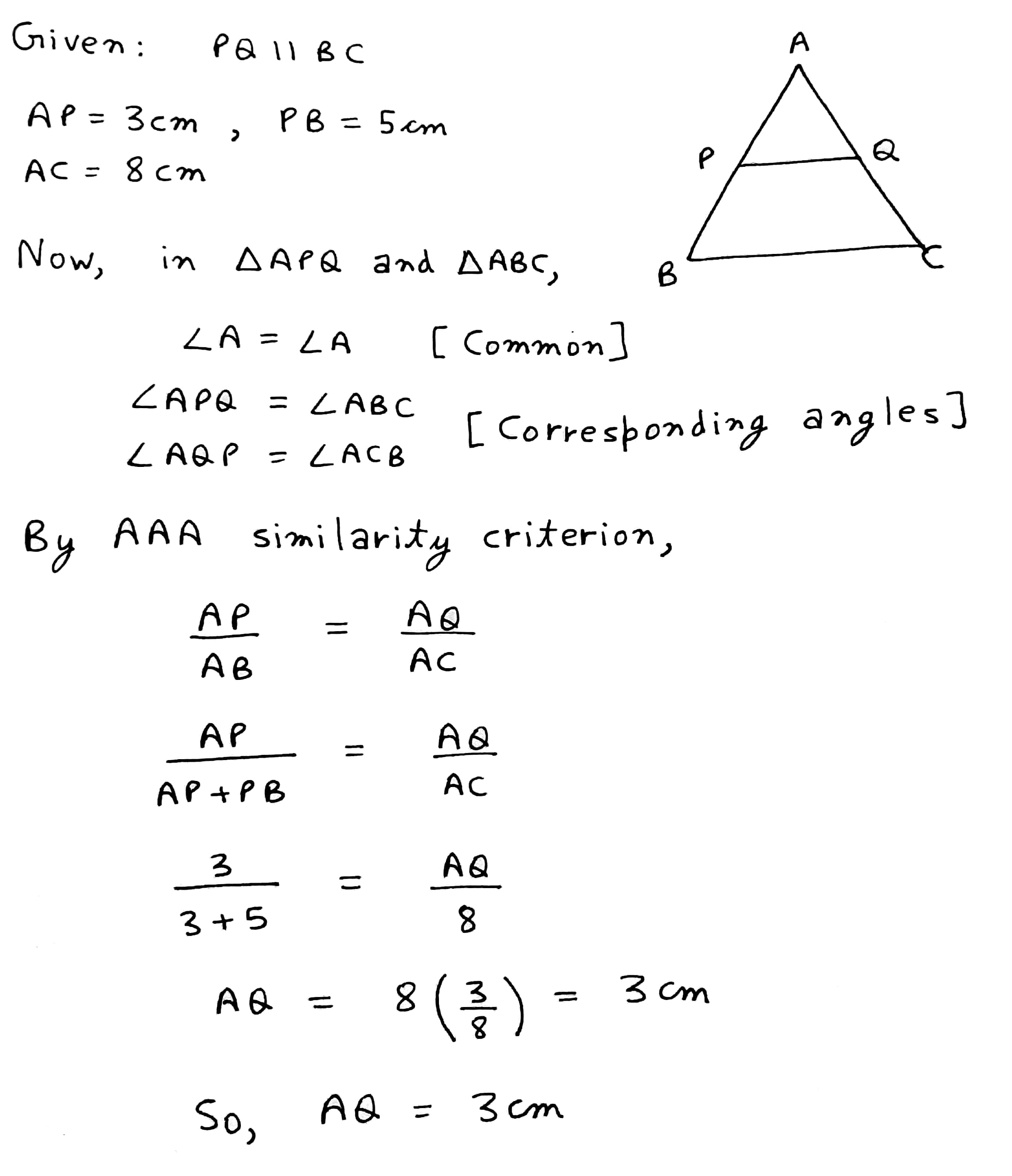
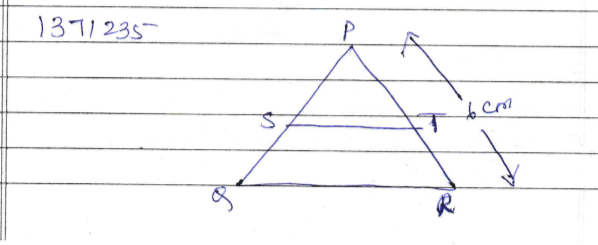
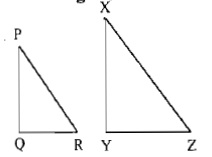
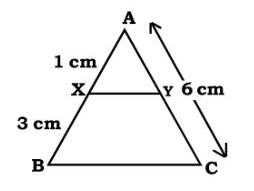
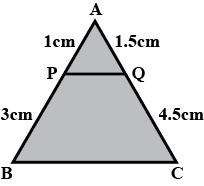
In fig $$PQ = 5, XY = 7.5, QR = 4,YZ =PR = 6, XZ = 9.$$ Are $$\Delta PQR$$ and $$\Delta XYZ$$ similar? If yes, state the test and the correspondence of similarity.
Without drawing exact triangles, state, giving reasons, whether the given pairs of triangle are congruent or not :
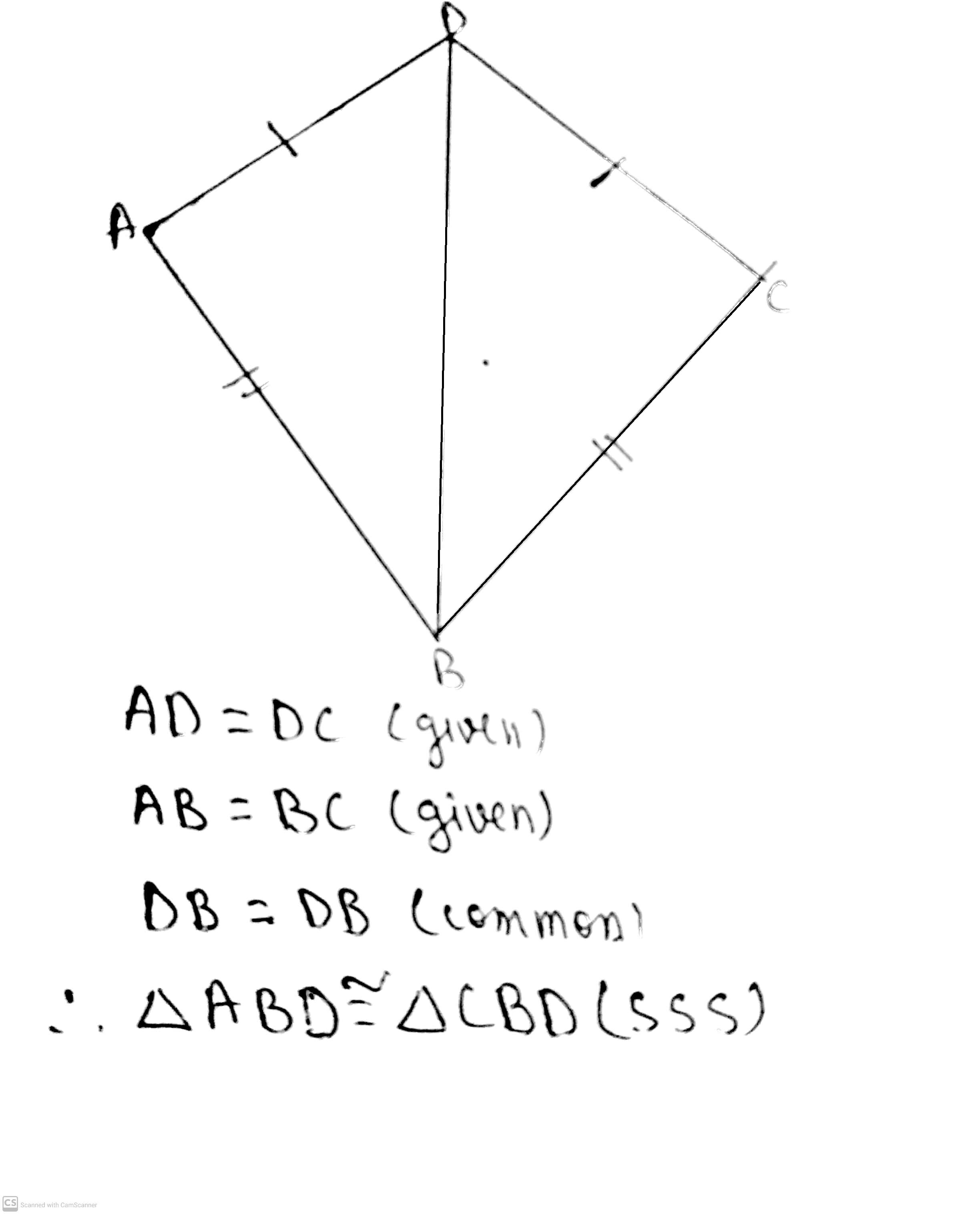
In $$ \Delta ABC \,\,\, and \,\,\, \Delta PBC; AB=BP, AC=PC$$
BP = 2AC
If the above statement is true then mention answer as 1, else mention 0 if false
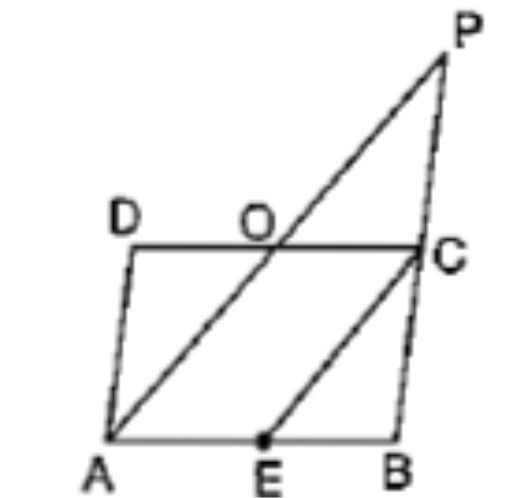
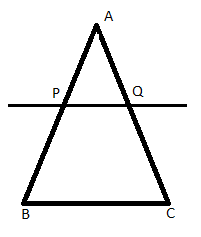
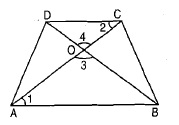
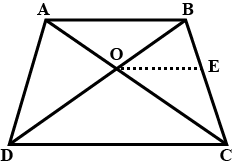
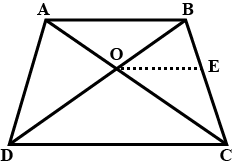
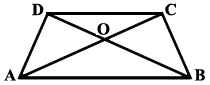
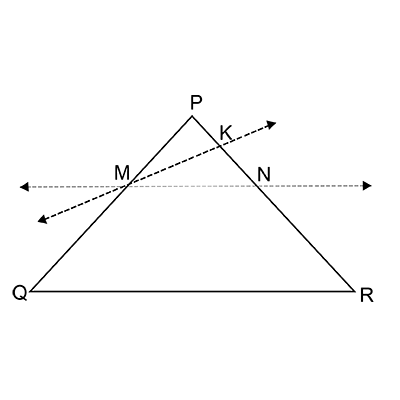
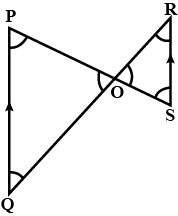
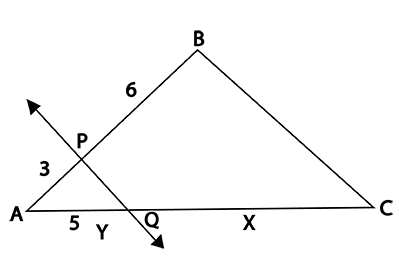
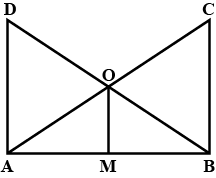
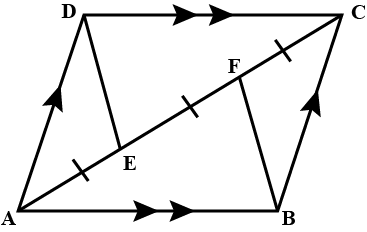
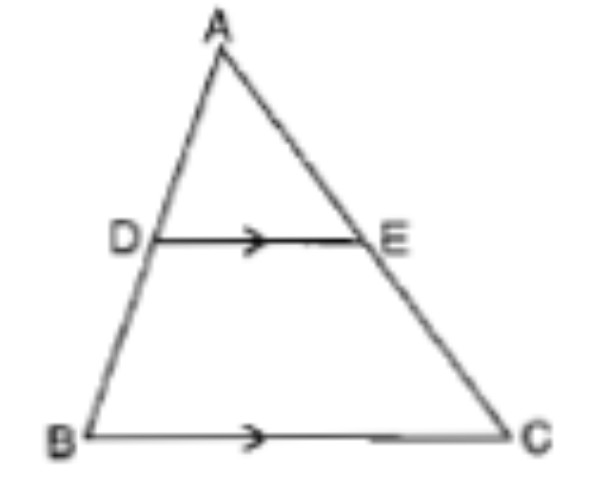
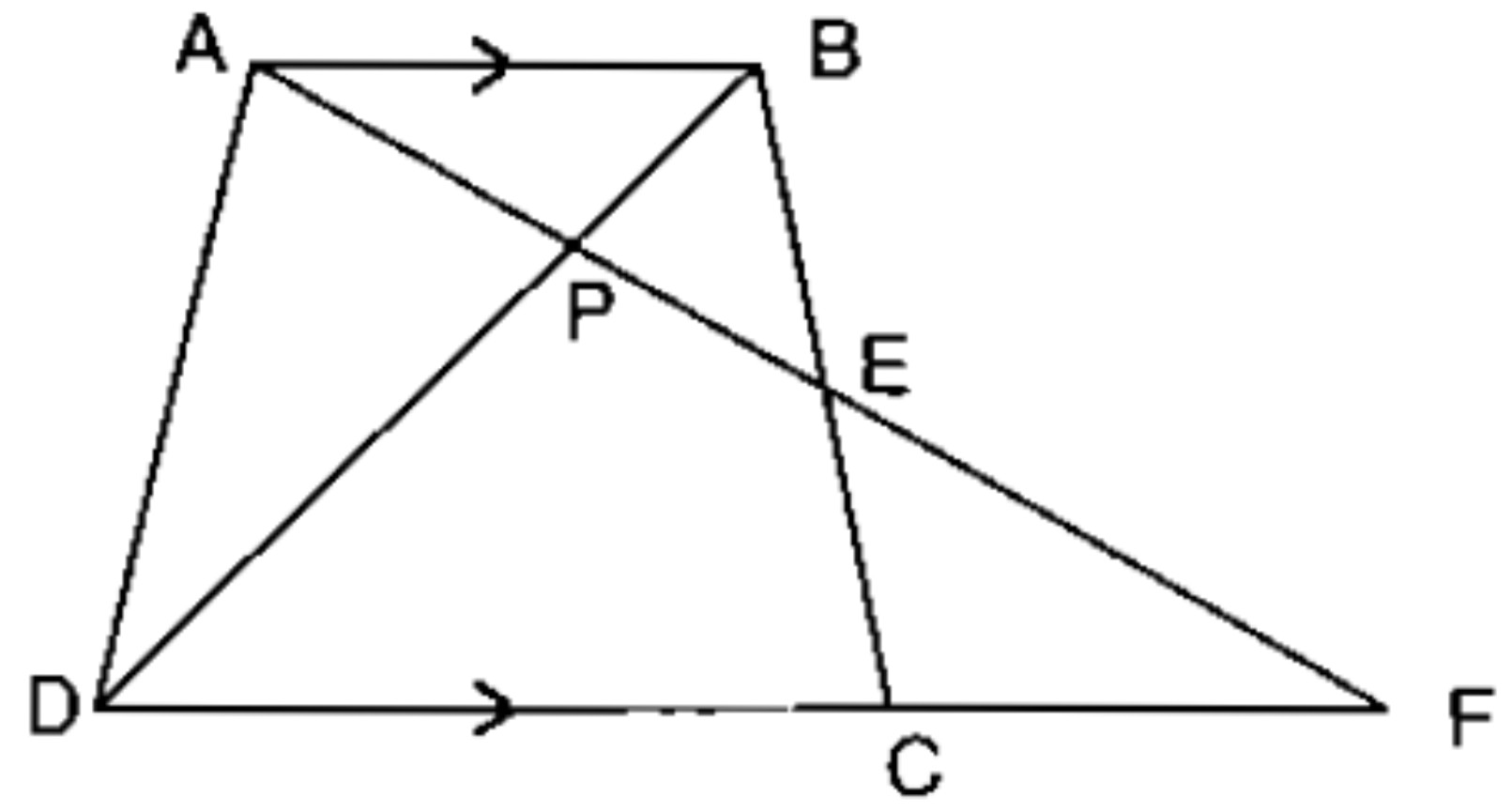
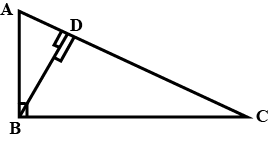
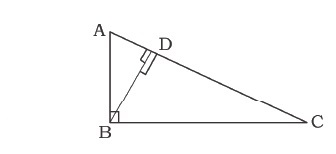
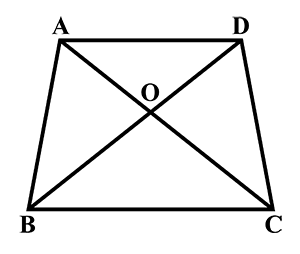
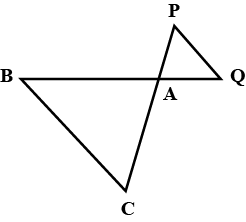
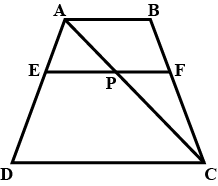
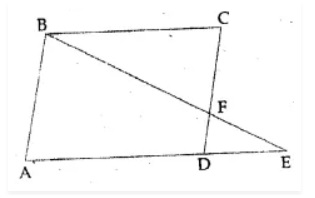
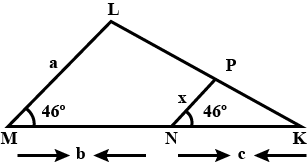
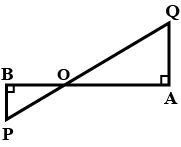
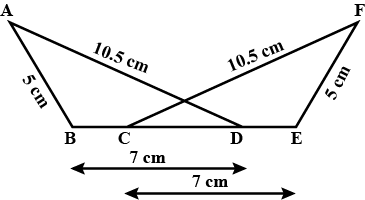
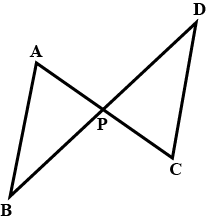
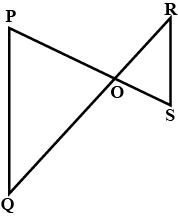
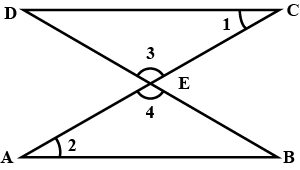
In the figure above, straight lines $$AB$$ and $$CD$$ intersect at $$P$$, and $$AC \ || \ BD$$. Then $$\Delta\,APC$$ and $$\Delta\,BPD$$ are similar.If true enter 1 else 0.
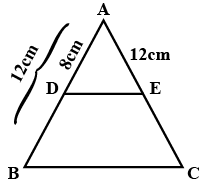
A vertical stick $$12$$m long casts a shadow $$8$$m long on the ground. At the same time a tower casts the shadow of length $$40$$m on the ground. Determine the height of the tower.
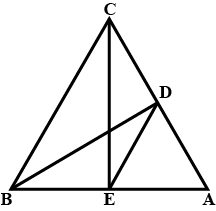
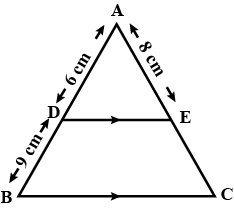
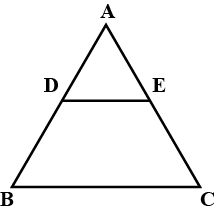
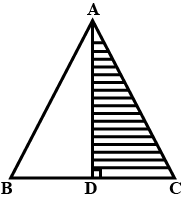
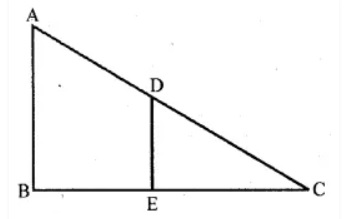
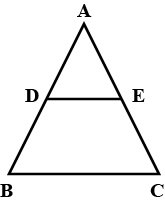
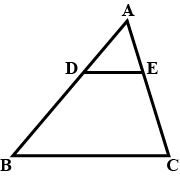
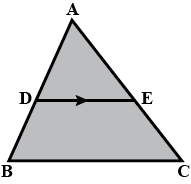
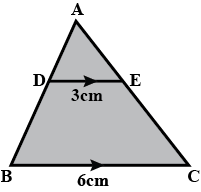
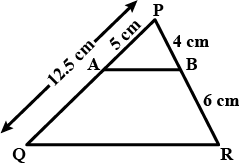
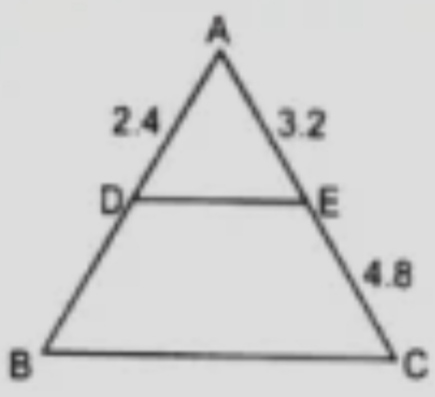
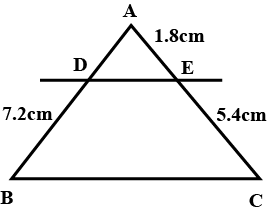
In the figure $$DE\parallel BC$$ , $$DE=4\,cm$$, $$BC=8\,cm$$, $$A\displaystyle(\triangle ADE)=25\,{ cm }^{ 2 }$$, find $$A\displaystyle(\triangle ABC)$$
If $$\triangle ABC\sim \triangle DEF$$ and if $$A\,\triangle ABC=\,9\,{ cm }^{ 2 }$$, $$A\,\triangle DEF=\,64\,{ cm }^{ 2 }$$, $$DE=5.6\,cm$$, then find $$AB$$.
In $$\Delta ABC$$, the bisector of $$\angle A$$ intersects the base $$BC$$ at the point $$D$$. Prove that $$AB\times AC=BD\times DC+AD^2$$.
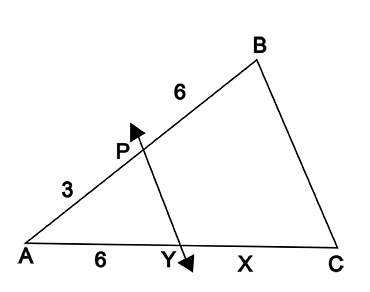
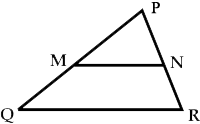
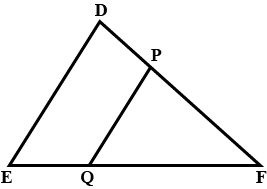
In the given figure if, line $$PY$$ $$\parallel$$ side $$BC$$, $$AP=3$$, $$PB=6$$, $$AY=6$$ and $$YC=x$$, then find $$x$$.
Write the conditions that are required for "Two polygons to be similar to each other".
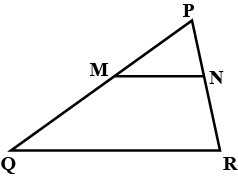
In $$\triangle PQR \ 2PM = 3PN$$ and $$2PQ = 3PR$$. Prove that MQRN is a trapezium
Given : $$2PM=3PN$$ and $$2PQ=3PR$$
Proof:
(i) $$\dfrac{2 PM}{2 PQ} = \dfrac{3PN}{3 PR}$$ .......... [Given]
$$\implies \dfrac{PM}{PQ} = \dfrac{PN}{PR}$$
$$\therefore MN \parallel QR$$ .......... [Using Converse of Basic Proportionality theorem]
(ii) Since $$QP$$ and $$RP$$ intersects at $$P$$, $$QP$$ cannot be parallel to $$RP$$
$$\implies $$ $$MQRN$$ is a trapezium
[$$\because$$ If only one pair of opposite sides of a quadrilateral is parallel then it is a trapezium]
$$\implies \dfrac{PM}{PQ} = \dfrac{PN}{PR}$$
$$\therefore MN \parallel QR$$ .......... [Using Converse of Basic Proportionality theorem]
(ii) Since $$QP$$ and $$RP$$ intersects at $$P$$, $$QP$$ cannot be parallel to $$RP$$
$$\implies $$ $$MQRN$$ is a trapezium
[$$\because$$ If only one pair of opposite sides of a quadrilateral is parallel then it is a trapezium]
In the following figure drawn, line $$PY$$ $$\parallel$$ side $$BC$$, $$AP=5, PB=10, AY=8, YC=x$$, then find $$x$$.
In $$\triangle ABC, \angle ABC = \angle DAC, AB = 8\ cm, AC = 4\ cm, AD = 5\ cm$$.Find $$\dfrac{\text{area of}\, \triangle ABC}{\text{area of}\, \triangle ACD}$$
What is similar triangles?
Two triangles are similar if and only if corresponding angles have the same measure: this implies they are similar if and only if the length of corresponding sides are proportional.
Note: Triangles are similar if they have the same shape, but not necessarily the same size.
Example of similar triangles : From above, $$\triangle PQR \sim \triangle{P}{'}{Q}{'}{R}{'}$$
Prove that "In a trapezium, the line joining the mid points of non-parallel sides is (i) parallel to the parallel sides and (ii) Half of the sum of the parallel sides"
Data: In the trapezium ABCD,
AD || BC, AX = XB and DY = YC
To Prove: (i) XY || AD or XY || BC
(ii) XY = $$\dfrac{1}{2}$$(AD + BC)
Construction: Extend BA and CD to meet at Z.
Join A and C. Let it cut XY at P
Proof: (i) In $$\triangle ZBC, AD || BC $$ [$$\because$$ Data]
$$\therefore \dfrac{ZA}{AB} = \dfrac{ZD}{DC}$$ [$$\because$$ BPT]
$$\therefore \dfrac{ZA}{2AX} = \dfrac{ZD}{2DY}$$ [$$\because$$ X & Y are mid points of AB and DC]
$$\therefore \dfrac{ZA}{AX} = \dfrac{ZD}{DY}$$
$$\Rightarrow XY || AD$$ [$$\because$$ Converse of B.P.T.]
(ii) In $$\triangle ABC, AX = XB$$ [$$\because$$ Data]
$$XP || BC$$ [$$\because$$ Proved]
$$\therefore AP = PC$$ [$$\because$$ Converse of mid point theorem]
$$\therefore XP = \dfrac{1}{2} BC$$ [$$\because$$ Midpoint Theorem]
In $$\triangle ADC, PY = \dfrac{1}{2} AD$$
By adding, we get $$XP + PY = \dfrac{1}{2} BC + \dfrac{1}{2} AD$$
$$\therefore XY = \dfrac{1}{2} (BC + AD)$$
AD || BC, AX = XB and DY = YC
To Prove: (i) XY || AD or XY || BC
(ii) XY = $$\dfrac{1}{2}$$(AD + BC)
Construction: Extend BA and CD to meet at Z.
Join A and C. Let it cut XY at P
Proof: (i) In $$\triangle ZBC, AD || BC $$ [$$\because$$ Data]
$$\therefore \dfrac{ZA}{AB} = \dfrac{ZD}{DC}$$ [$$\because$$ BPT]
$$\therefore \dfrac{ZA}{2AX} = \dfrac{ZD}{2DY}$$ [$$\because$$ X & Y are mid points of AB and DC]
$$\therefore \dfrac{ZA}{AX} = \dfrac{ZD}{DY}$$
$$\Rightarrow XY || AD$$ [$$\because$$ Converse of B.P.T.]
(ii) In $$\triangle ABC, AX = XB$$ [$$\because$$ Data]
$$XP || BC$$ [$$\because$$ Proved]
$$\therefore AP = PC$$ [$$\because$$ Converse of mid point theorem]
$$\therefore XP = \dfrac{1}{2} BC$$ [$$\because$$ Midpoint Theorem]
In $$\triangle ADC, PY = \dfrac{1}{2} AD$$
By adding, we get $$XP + PY = \dfrac{1}{2} BC + \dfrac{1}{2} AD$$
$$\therefore XY = \dfrac{1}{2} (BC + AD)$$
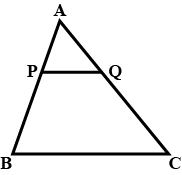
In the figure, line $$PQ$$ is parallel to side $$BC$$. Find the value of '$$x$$'. If $$AP=3$$, $$PB=6$$, $$AQ=5$$, $$QC=x$$.
In $$\triangle ABC$$, line $$PQ \parallel$$ side $$BC$$. Find the value of $$x$$ from the information given in the following figure.
In the figure, it is given that $$BR = PC$$ and $$\angle ACB = \angle QPR$$ and $$AB \parallel PQ$$. Prove that $$
AC= QR$$.
State the converse of Pythagorean Theorem.
Prove that
"If two triangles are equiangular then their corresponding sides are in proportion"
Data : In $$\triangle ABC$$ and $$\triangle DEF$$
$$\angle BAC = \angle EDF$$
$$\angle ABC = \angle DEF$$
To prove : $$\dfrac {AB}{DE} = \dfrac {BC}{EF} = \dfrac {CA}{FD}$$
Construction : Mark points $$G$$ and $$H$$ on $$AB$$ and $$AC$$ such that $$AG = DE$$ and $$AH = DF$$. Join $$G$$ and $$H$$.
Proof : In $$\triangle AGH$$ and $$\triangle DEF$$
$$AG = DE\because Construction$$
$$\angle GAH = \angle EDF \because Data$$
$$AH = DF \therefore Construction$$
$$\therefore \triangle AGH \cong \triangle DEF \because SAS$$
$$\angle AGH = \angle DEF$$
But, $$\angle ABC = \angle DEF$$
$$\Rightarrow \angle AGH = \angle ABC$$
$$\therefore GH\parallel BC$$.
In $$\triangle ABC = \dfrac {AB}{AG} = \dfrac {BC}{GH} = \dfrac {CA}{HA}$$
Hence $$\dfrac {AB}{DE} = \dfrac {BC}{EF} = \dfrac {CA}{FD}$$.
$$\angle BAC = \angle EDF$$
$$\angle ABC = \angle DEF$$
To prove : $$\dfrac {AB}{DE} = \dfrac {BC}{EF} = \dfrac {CA}{FD}$$
Construction : Mark points $$G$$ and $$H$$ on $$AB$$ and $$AC$$ such that $$AG = DE$$ and $$AH = DF$$. Join $$G$$ and $$H$$.
Proof : In $$\triangle AGH$$ and $$\triangle DEF$$
$$AG = DE\because Construction$$
$$\angle GAH = \angle EDF \because Data$$
$$AH = DF \therefore Construction$$
$$\therefore \triangle AGH \cong \triangle DEF \because SAS$$
$$\angle AGH = \angle DEF$$
But, $$\angle ABC = \angle DEF$$
$$\Rightarrow \angle AGH = \angle ABC$$
$$\therefore GH\parallel BC$$.
In $$\triangle ABC = \dfrac {AB}{AG} = \dfrac {BC}{GH} = \dfrac {CA}{HA}$$
Hence $$\dfrac {AB}{DE} = \dfrac {BC}{EF} = \dfrac {CA}{FD}$$.
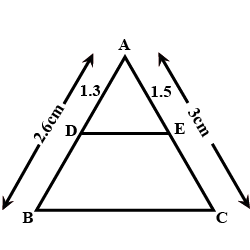
In the following figure, $$DE \parallel AB$$. If $$AD = 7\ cm, CD = 5\ cm$$ and $$BC = 18\ cm$$, find $$CE$$.
$$\triangle {ABC}\sim \triangle{DEF}$$. Their areas are $$64\ {cm}^{2}$$ and $$121\ {cm}^{2}$$.
Then ratio of corresponding sides $$=$$
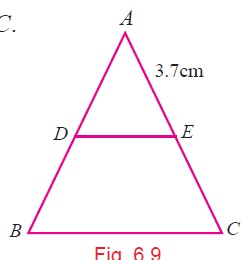
In $$\triangle ABC, DE\parallel BC$$ and $$\dfrac {AD}{DB} = \dfrac {2}{3}$$. If $$AE = 3.7\ cm$$, find $$EC$$
In $$\triangle ABC, DE\parallel BC$$
$$\therefore \dfrac {AD}{DB} = \dfrac {AE}{EC}$$
$$\Rightarrow EC = \dfrac {AE\times DB}{AD}$$
Thus, $$EC = \dfrac {3.7\times 3}{2} = 5.55\ cm$$
$$\therefore \dfrac {AD}{DB} = \dfrac {AE}{EC}$$
$$\Rightarrow EC = \dfrac {AE\times DB}{AD}$$
Thus, $$EC = \dfrac {3.7\times 3}{2} = 5.55\ cm$$
State Thale's theorem.
If the ratio of corresponding medians of two similar triangles are $$9:16$$, then find the ratio of their areas.
Fill in the blanks using the correct word given in brackets:
All .......... triangles are similar (isosceles, equilateral).
The corresponding sides of two similar triangles are in the ratio 1 :If the area of the smaller triangle in 40 $$\text{ cm }^{ 2 }$$, find the area of the larger triangle.
Prove that, in a right-angled triangle, the square of hypotenuse is equal to the sum of the square of remaining two sides.
Consider a right angled triangle with length of hypotenuse as $$c$$ and the remaining two sides as $$a$$ and $$b$$ respectively.
We arrange 4 such triangles in such a fashion that they form a square of side $$a+b$$ (as shown in the figure).
Area of the figure $$A=$$ $$(a+b)(a+b)$$ $$.......(1)$$
Also area of the figure can be written as, $$A = 4 \times ar(Blue\, right\, triangle) + ar(central\, yellow\, square)$$
$$A = 4 \times \frac{1}{2}ab + c^2$$ $$.......(2)$$
Equating (1) and (2) we get,
$$c^2 + 2ab = a^2 + b^2 + 2ab$$
Consequently, $$c^2 = a^2 + b^2$$. Hence, Pythagoras theorem is proved.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively find the ratio of their areas.
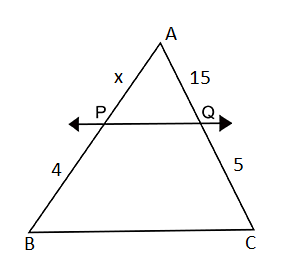
What values of x will make DE $$\parallel$$ AB in the given figure?
The area of two similar triangles $$ABC$$ and $$PQR$$ are in the ratio $$9 : 16$$. If $$BC = 4.5 cm$$, find the length of $$QR$$.
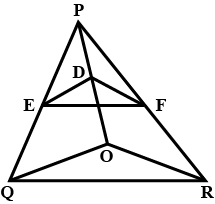
In $$\Delta$$PQR, MN is parallel to QR and $$\displaystyle\frac{PM}{MQ}=\frac{2}{3}$$. Find, Area of $$\Delta$$OMN:Area of $$\Delta$$ORQ.
Given $$\Delta$$ ABC $$\sim$$ $$\Delta$$ PQR, if $$\displaystyle\frac{AB}{PQ}=\frac{1}{3}$$, then find $$\displaystyle\frac{ar \Delta ABC}{ar \Delta PQR}$$.
Let $$AD$$ be the perpendicular dropped from $$A$$ to the side $$BC$$ and $$PS$$ be the perpendicular dropped from $$P$$ to the side $$QR$$ respectively.
Since, $$\Delta ABC \sim \Delta PQR$$, we have $$\Delta ABD \sim \Delta PQS$$.
Therefore, $$\dfrac{AB}{PQ} = \dfrac{AD}{PS} = \dfrac{BC}{QR}$$
$$\Rightarrow \dfrac{ar \Delta ABC}{ar \Delta PQR} = \dfrac{AD\times BC}{PS \times QR} = \dfrac{AB}{PQ}\times \dfrac{AB}{PQ} = \dfrac{AB^2}{PQ^2} = \dfrac{1}{9}$$
$$ABC$$ is a triangle in which $$\angle A= 90^{o}$$, $$AN \bot BC$$, $$BC=12\ cm$$ and $$AC=5\ cm$$. Find the ratio of the areas of $$\triangle ANC$$ and $$\triangle ABC$$.
$$\angle ANC=\angle BAC=90^{\circ}$$
$$\angle ACN=\angle BCA$$
So by AA similarity, $$\triangle ANC \sim \triangle BAC$$
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$$\dfrac{area(\triangle ANC)}{area(\triangle BAC)}=\dfrac{AC^{2}}{BC^{2}}$$
$$\dfrac{area(\triangle ANC)}{area(\triangle BAC)}=\dfrac{5^{2}}{12^{2}}$$
$$\dfrac{area(\triangle ANC)}{area(\triangle BAC)}=\dfrac{25}{144}$$
Hence the ratio of areas of $$\triangle ANC $$ and $$\triangle BAC$$ is $$25:144$$
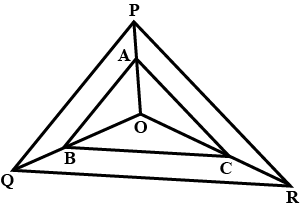
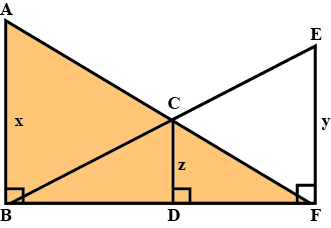
In the given Figure, $$\triangle ABC \sim\triangle$$ $$PQR$$ and quad $$ABCD$$ $$\sim$$ quad $$PQRS$$. Determine the values of $$x, y, z$$ in each case.
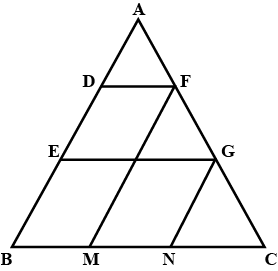
Give two different examples of pair of
(ii) non-similar figures.
(1) Circle and rectangle
(2) Triangle and Hexagon
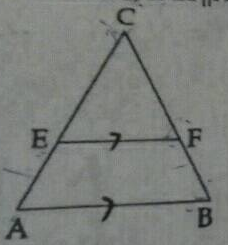
Give two different examples of pair of (i) similar figures
(1) Any two rectangles.
(2) Any two squares.
Hence, this is the answer.
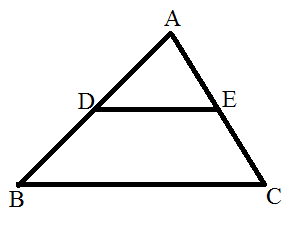
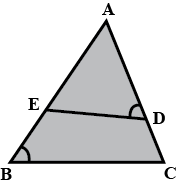
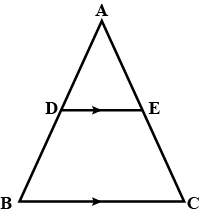
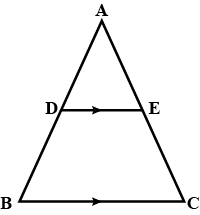
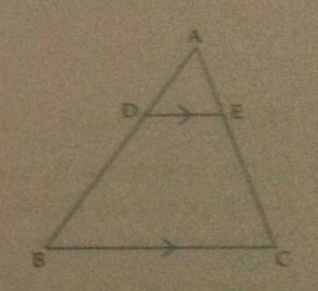
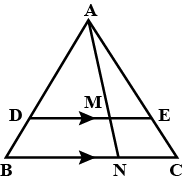
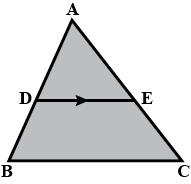
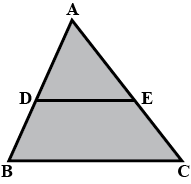
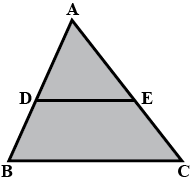
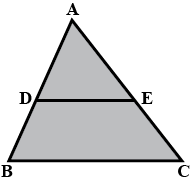
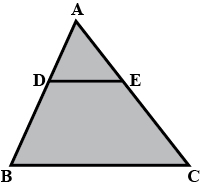
In the figure, $$DE \parallel BC$$
(i) Prove that $$\triangle ADE$$ and $$\triangle ABC$$ are similar
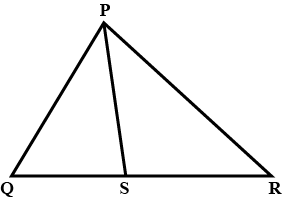
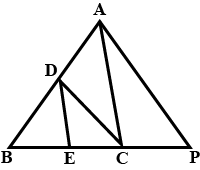
In the figure $$PS=3,SQ=6.QR=5,PT=x$$ and $$TR=y$$.Give any two pairs of value of $$x$$ and $$y$$ such that line $$ST||QR$$
Area of similar triangles are in the ratio $$25:36$$ then ratio of their similar sides is _________?
Write the properties of similar triangles.
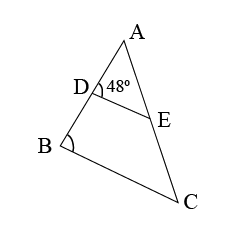
In figure if $$AD=6\ cm, DB=9\ cm, AE=8\ cm$$ and $$EC=12\ cm$$ and $$\angle ADE=48^{o}$$. Find $$\angle ABC$$.
Given that $$\Delta ABC \sim \Delta DEF,BC = 3\,cm,EF = 4\,cm$$ ans the area of $$\Delta ABC$$ is $$54\,sq.cm.$$Then find the area of $$\Delta DEF.$$
Solution -
REF. Image
$$\dfrac{Area\, \triangle ABC}{Area\, \triangle DEF}= \left ( \dfrac{BC}{EF} \right )^{2}$$
Area $$\triangle DEF = 54\times \dfrac{4^{2}}{3^{2}}$$
Area $$(\triangle DEF)= 6\times 4^{2}$$
$$= 96\, cm^{2}$$
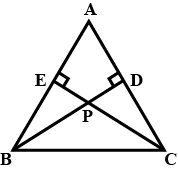
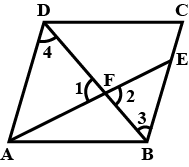
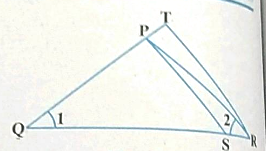
In figure $$\angle 1=\angle 2$$ and $$\Delta NSQ\cong \Delta MTR$$, then prove that $$\Delta PTS\sim \Delta PRQ$$.
$$DA,CB,OM$$ are each perpendicular to line segment $$AB$$ where $$O$$ is the point of intersection of $$AC$$ and $$DB$$.If $$OA=2.4$$cm,$$OC=3.6$$cm then find the ratio of $$AM:BM$$
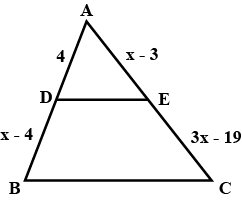
In $$\Delta ABC, \bar{PQ} || \bar{BC}$$ and $$AP = 3x - 19, PB = x - 5, AQ = x - 3, QC = 3 \,cm$$. Find $$x$$.
Ler $$\Delta A B C \sim \Delta D E F$$ and their areas be respectively, 64$$\mathrm { cm } ^ { 2 }$$ and 121$$\mathrm { cm } ^ { 2 } .$$ If EF $$=15.4 $$ find BC
In figure, $$AC\parallel BD$$ and $$CE\parallel DF$$ Find CD,where OD=7,OA=10.5,AB=4.5
Prove that the ratio of the area of two similar triangle is equal to the square of the ratio of their corresponding sides.
Given:- Let $$\triangle{ABC} \sim \triangle{PQR}$$
$$AD$$ and $$PS$$ are corresponding medians.
To prove:- $$\cfrac{ar{\left( \triangle{ABC} \right)}}{ar{\left( \triangle{PQR} \right)}} = {\left( \cfrac{AD}{PS} \right)}^{2}$$
Proof:- In $$\triangle{ABC}$$
$$\because AD$$ is median.
$$\therefore BD = CD = \cfrac{1}{2} BC$$
Similarly, in $$\triangle{PQR}$$
$$PS$$ is median.
$$\therefore QS = RS = \cfrac{1}{2} QR$$
Now,
$$\triangle{ABC} \sim \triangle{PQR} \left( \text{Given} \right)$$
$$\angle{B} = \angle{Q} ..... \left( 1 \right) \quad \left( \text{Corresponding angles of similar triangles are equal} \right)$$
$$\cfrac{AB}{PQ} = \cfrac{BC}{QR} \quad \left( \text{Corresponding sides of similar triangles are proportional} \right)$$
$$\Rightarrow \cfrac{AB}{PQ} = \cfrac{2 BD}{2 QS} \quad \left( \because \text{AD and PS are medians} \right)$$
$$\cfrac{AB}{PQ} = \cfrac{BD}{QS} ..... \left( 2 \right)$$
Now, in $$\triangle{ABD}$$ and $$\triangle{PQS}$$,
$$\angle{B} = \angle{Q} \quad \left( \text{From } \left( 1 \right) \right)$$
$$\cfrac{AB}{PQ} = \cfrac{BD}{QS} \quad \left( \text{From } \left( 2 \right) \right)$$
$$\therefore \triangle{ABD} \sim \triangle{PQS} \quad \left( \text{By SAS Property} \right)$$
Therefore,
$$\cfrac{AB}{PQ} = \cfrac{AD}{PS} ..... \left( 3 \right) \quad \left( \because \text{Corresponding sides of similar triangles are proportonal} \right)$$
Now,
$$\because \triangle{ABC} \sim \triangle{PQR}$$
As we know that ratio of area of similar triangles is always equal to the square of ratio of their corresponding side.
Therefore,
$$\cfrac{ar{\left( \triangle{ABC} \right)}}{ar{\left( \triangle{PQR} \right)}} = {\left( \cfrac{AB}{PQ} \right)}^{2}$$
$$\cfrac{ar{\left( \triangle{ABC} \right)}}{ar{\left( \triangle{PQR} \right)}} = {\left( \cfrac{AD}{PS} \right)}^{2} \quad \left( \text{From } \left( 3 \right) \right)$$
Hence proved.
If D and E are points on sides AB and AC respectively of ABC and AB- 12 cm, AD= 8 cm,AE = 12 cm, AC =18 cm, then prove that $$DE \parallel BC$$.
State whether the following pair of triangle is similar or not.
In the adjoining figure,$$DE \parallel BC$$,find x.
State whether the following pair of triangle is similar or not. Write the similarity criterion used and write it in symbolic form.
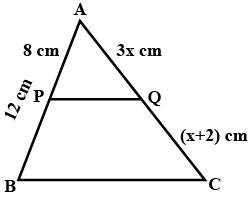
In the adjoining figure, $$P$$ and $$Q$$ are points on sides $$AB$$ and $$AC$$ respectively of mix such that $$PQ \parallel BC$$ and $$AP = 8\ cm, AB =12\ cm,AQ = 3x\ cm, QC = (x+2)\ cm.$$
Find x.
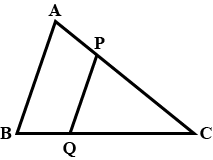
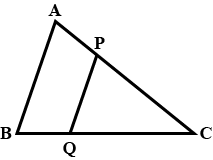
P and Q are points on sides AB and AC respectivelyof $$\triangle $$ ABC. For each of the following cases, statewhether PQ$$\parallel $$BC.AB = 5 cm, AC =10 cm, AP: 4 cm, AQ = 8 cm.
State whether the following pair of triangle is similar or not. Write the similarity criterion used and write it in symbolic form.
If DE has been drawn parallel to side BC of ABC cutting AB and AC at points D and E respectively , such that $$\frac{AD}{DB} = \frac {3}{4}$$ then and the value of $$\frac {AE}{EC}$$
P and Q are points on sides AB and AC respectivelyof $$\triangle $$ ABC. For each of the following cases, statewhether PQ$$\parallel $$BC.
AP: 8 cm, PB = 3 cm, AC = 22 cm and AQ =16 cm.
State whether the following pair of triangle is similar or not. Write the similarity criterion used and write it in symbolic form.
Give two different examples of pair of similar figures.
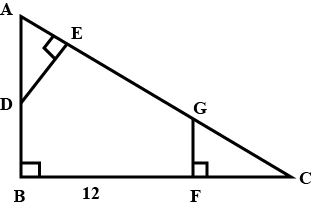
In the following figure , $$ABCD$$ is a trapezium with AB || DC. If $$AB = 9 $$$$cm$$, $$DC = 18$$ $$cm$$, $$CF = 13.5$$ $$cm$$, $$AP = 6$$ $$cm$$ and $$BE = 15$$ $$cm$$. Find the value of $$AF$$
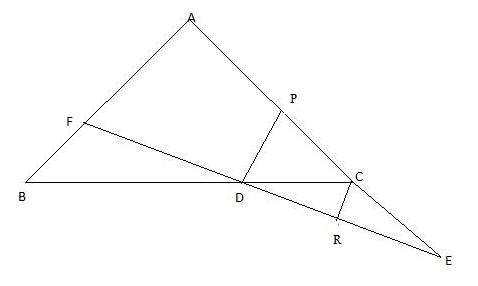
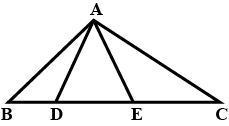
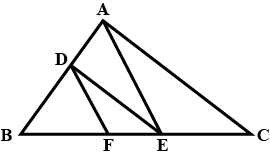
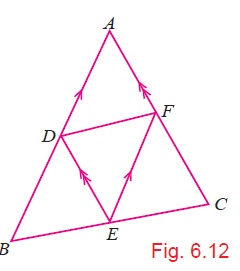
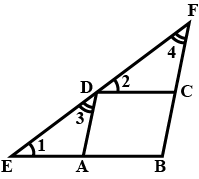
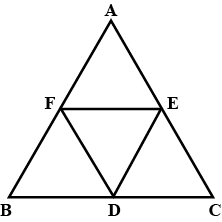
In triangle $$ABC, D$$ and $$E$$ are points on side $$AB$$ such that $$AD=DE=EB$$. Through $$D$$ and $$E$$ lines are drawn parallel to $$BC$$ which meet side $$AC$$ at points $$F$$ and $$G$$ respectively.
Through $$F$$ and $$G$$, lines are drawn parallel to $$AB$$ which meet side $$BC$$ at points $$M$$ and $$N$$ respectively. Prove that : $$BM=MN=NC$$.
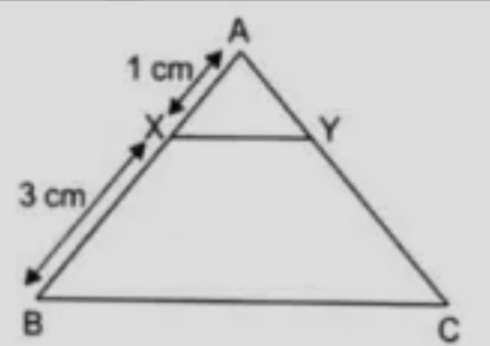
In the given figure, $$XY \parallel BC$$. Find the length of XY, given BC = 6 cm
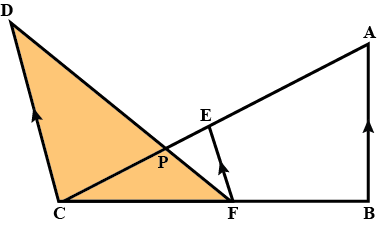
In the figure given below, AB EF CD. If $$AB = 22.5\,cm$$, $$EP = 7.5\,cm$$,$$PC = 15\,cm$$ and $$DC = 27\,cm$$. Calculate EF.
In a $$ \Delta ABC , BD $$ is the median to the side AC , BD is produce to E such that BD = DE
Prove that AE is parallel to BC.
Given : A $$ \Delta ABC $$ in which BD is the median to AC
BD is produce to E such that BD = DE
We need to prove that AE || BC
Construction: join AE
$$\angle EAD = \angle BCD $$ [cpct]
But these are alternate angles and $$AC$$ is the transversal
Thus, $$AE || BC$$
BD is produce to E such that BD = DE
We need to prove that AE || BC
Construction: join AE
Proof:
In $$ \Delta BDC$$ and $$ \Delta ADE $$$$AD = DC$$ [$$BD$$ is median]
$$BD = DE$$ [Given]$$ \angle BDC = \angle ADE = 90^{o}$$ [Vertically opposite angles]
So, $$ \Delta BDC \cong \Delta ADE $$
The corresponding parts of the congruent triangles are congruent$$\angle EAD = \angle BCD $$ [cpct]
But these are alternate angles and $$AC$$ is the transversal
Thus, $$AE || BC$$
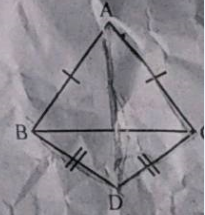
The following figure shows a triangle ABC in which AB = AC . M is a point on AB and N is a point AC such that BM = CN
Prove that
BN = CM
Statements in the List I have to be matched with statements in the List II.
In trapezium $$ ABCD $$, sides $$ AB $$ and $$ DC $$ are parallel to each other. $$ F $$ is mid-point of $$ AD $$ and $$ E $$ is mid-point of $$ BC $$. Can it be concluded that $$ AB + DC= 2EF $$ ?
If the above statement is true then mention answer as 1, else mention 0 if false
In $$\triangle FDP$$ and $$\triangle ADB$$,
$$\angle ADB = \angle FDP$$ (Common angle)
$$\angle DAB = \angle DFP$$ (Corresponding angles)
$$\angle DBA = \angle DPF$$ (Corresponding angles)
Thus, $$\triangle FDP \sim \triangle ADB$$ (AAA rule)
hence, $$\frac{FP}{AB} = \frac{FD}{AD}$$
$$\frac{FP}{AB} = \frac{1}{2}$$ (Since, AF = FD)
or $$FP = \frac{1}{2} AB$$...(I)
Since, $$AB \parallel FB \parallel CD$$
By equal Intercept theorem, $$BE = EC$$
Hence, $$PE = \frac{1}{2} CD$$ ...(II)
Thus, adding I and II
$$PF + PE = \frac{1}{2} (AB + CD)$$
$$2 EF = AB + CD$$
$$\angle ADB = \angle FDP$$ (Common angle)
$$\angle DAB = \angle DFP$$ (Corresponding angles)
$$\angle DBA = \angle DPF$$ (Corresponding angles)
Thus, $$\triangle FDP \sim \triangle ADB$$ (AAA rule)
hence, $$\frac{FP}{AB} = \frac{FD}{AD}$$
$$\frac{FP}{AB} = \frac{1}{2}$$ (Since, AF = FD)
or $$FP = \frac{1}{2} AB$$...(I)
Since, $$AB \parallel FB \parallel CD$$
By equal Intercept theorem, $$BE = EC$$
Hence, $$PE = \frac{1}{2} CD$$ ...(II)
Thus, adding I and II
$$PF + PE = \frac{1}{2} (AB + CD)$$
$$2 EF = AB + CD$$
In figure, $$\Delta$$UVW is right angled triangle and $$\angle$$UVW $$=$$ 90$$^o$$, UV $$=$$ 6cm, and UW $$=$$ 8 cm, $$\sin$$ W = $$p:m$$, then $$p+m$$ =
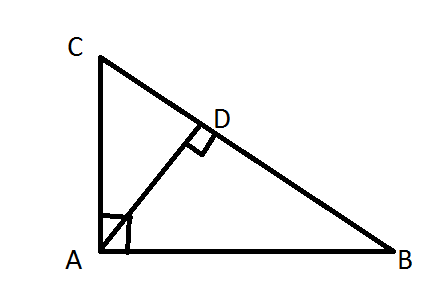
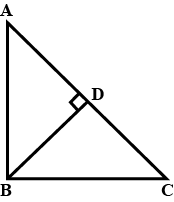
In the given figure; $$\displaystyle \angle BAC= 90^{\circ}$$ and $$\displaystyle AD\perp BC.$$ Show that $$\displaystyle \Delta ADC$$ and $$\displaystyle \Delta BAC$$ are similar.
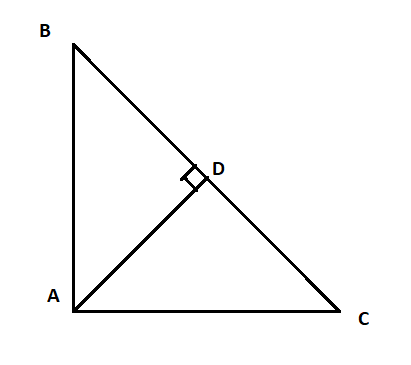
In a triangle,$$\displaystyle \angle BAC= 90^{\circ}$$ and $$\displaystyle AD\perp BC.$$
If AC=13.5 cm and CD =4.5cm; calculate the length of 2BC
In $$\triangle ADC$$ and $$\triangle BAC$$,
$$\angle ADC = \angle BAC$$ (Each $$90^{\circ}$$)
$$\angle DCA = \angle BCA$$ (Common)
$$\angle DAC = \angle ABC$$ (Third angle)
Thus, $$\triangle ADC \sim \triangle BAC$$ (AAA rule)
$$\dfrac{AC}{BC} = \dfrac{CD}{AC} $$ (Corresponding sides)
$$AC^2 = CD \times BC$$
$$(13.5)^2 = 4.5 \times BC$$
$$BC = 40.5 cm $$
$$\angle ADC = \angle BAC$$ (Each $$90^{\circ}$$)
$$\angle DCA = \angle BCA$$ (Common)
$$\angle DAC = \angle ABC$$ (Third angle)
Thus, $$\triangle ADC \sim \triangle BAC$$ (AAA rule)
$$\dfrac{AC}{BC} = \dfrac{CD}{AC} $$ (Corresponding sides)
$$AC^2 = CD \times BC$$
$$(13.5)^2 = 4.5 \times BC$$
$$BC = 40.5 cm $$
$$2BC=81 cm$$
Find whether the sides of the triangle as given below form a right-triangled or not: $$9$$ cm, $$12$$ cm and $$15$$ cm
If a line parallel to $$BC$$ intersects side $$AB$$ and $$AC$$ of triangle $$ABC$$ at $$P$$ and $$Q,$$ then prove that $$\dfrac {AP}{AB}=\dfrac {AQ}{AC}.$$
In $$\triangle APQ$$ and $$\triangle ABC$$,
$$\angle A$$ is common.
$$\\ \angle APQ = \angle ABC$$ ...[corresponding angles]
$$\\ \angle AQP = \angle ACB$$ ...[corresponding angles]
$$\\ \therefore \triangle APQ \sim \triangle ABC$$ ...(By $$AAA$$)
So, once the triangles are similar, their corresponding sides would be proportional.
$$\dfrac { AP }{ AB } =\dfrac { AQ }{ AC } $$
Hence proved.
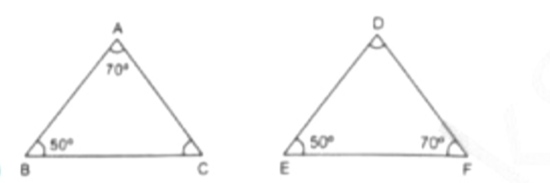
In the given figure you find two triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
In the following figure, $$\displaystyle \angle ABC=90^{\circ},AB =\left ( x+8 \right )\ cm, BC=\left ( x+1 \right )\ cm$$ and $$\displaystyle AC=(x + 15)\ cm$$.
Find the value of $$x$$.
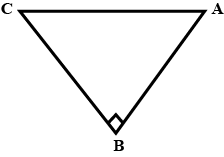
$$\displaystyle \Delta ABD\equiv \Delta ADC$$
If the above statement is true then mention answer as 1, else mention 0 if false
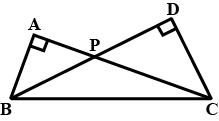
O is mid-point of AP
If the above statement is true then mention answer as 1, else mention 0 if false
In the given figure, $$DE//BC$$, $$AE$$ = $$15$$ cm, $$EC$$ = $$9$$ cm, $$NC$$ = $$6$$ cm and $$BN$$ = $$24$$ cm.Find lengths of $$ME(in\ cm)$$.
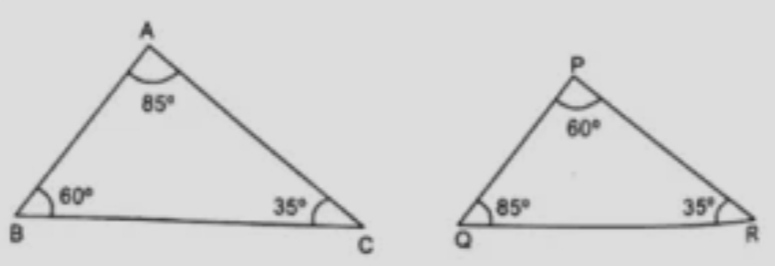
Two angles of one triangle are $$85^{\circ}$$ and $$65^{\circ}$$ is equal to angles of the other. Are they similar? Prove it.
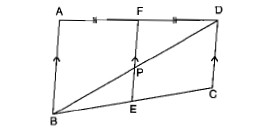
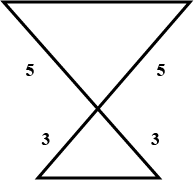
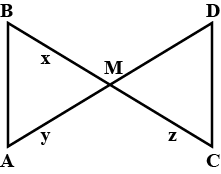
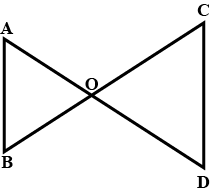
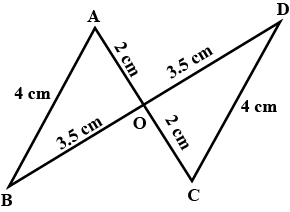
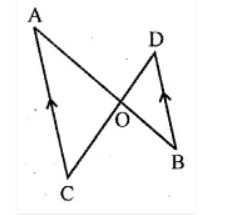
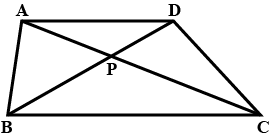
$$\Delta\,APB$$ is similar to $$\Delta\,CPD$$.
Enter 1 if true , else 0
Prove: 3DF = EF
Given: In $$\triangle ABC$$, D is mid point of BC and $$DP \parallel BA \parallel CR$$
To Prove: 3 DF = EF
In $$\triangle ABC$$, D is the midpoint of BC and DP are drawn parallel to BA.
Therefore, P is the midpoint of AC.
$$AP = PC$$
Now, $$FA \parallel DP \parallel RC$$ and APC is transversal such that AP = PC and FDR is the another transversal
Hence, $$FD = DR$$ .........(I) (by intercept theorem)
$$EC = \dfrac{1}{2} AC = PC$$
In $$\triangle EPD$$,
C is the midpoint of EP and $$CR \parallel DP$$ .
R must be the midpoint of DE.
Thus, $$DR = RE$$ .....(II)
Hence, $$FD = DR = RE$$ (from (I) and (II))
$$FE = 3 DF$$
To Prove: 3 DF = EF
In $$\triangle ABC$$, D is the midpoint of BC and DP are drawn parallel to BA.
Therefore, P is the midpoint of AC.
$$AP = PC$$
Now, $$FA \parallel DP \parallel RC$$ and APC is transversal such that AP = PC and FDR is the another transversal
Hence, $$FD = DR$$ .........(I) (by intercept theorem)
$$EC = \dfrac{1}{2} AC = PC$$
In $$\triangle EPD$$,
C is the midpoint of EP and $$CR \parallel DP$$ .
R must be the midpoint of DE.
Thus, $$DR = RE$$ .....(II)
Hence, $$FD = DR = RE$$ (from (I) and (II))
$$FE = 3 DF$$
Write all possible pairs of similar triangles.
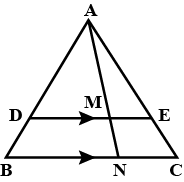
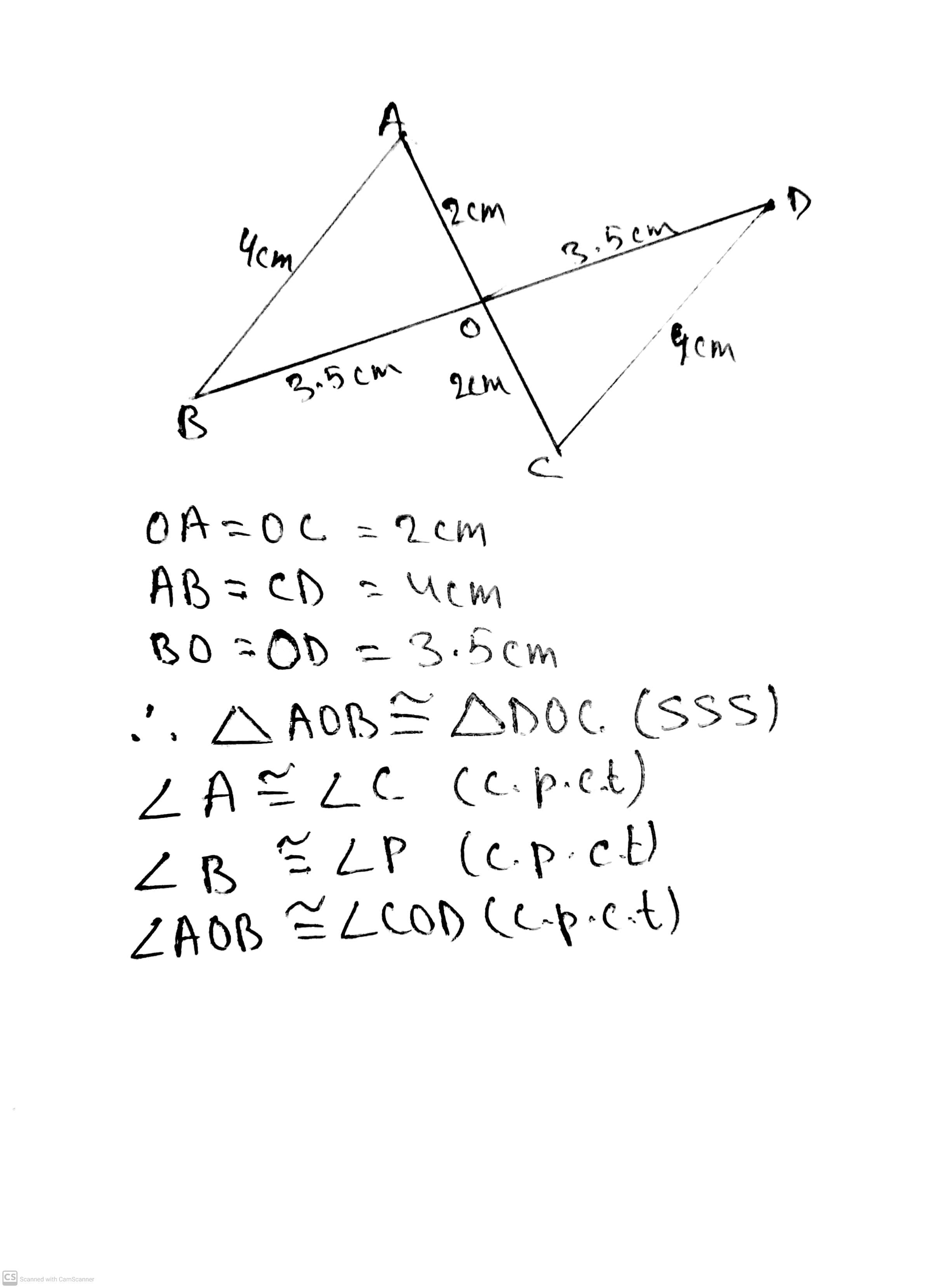
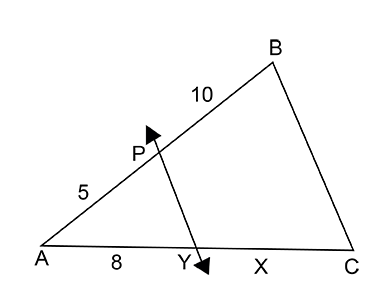
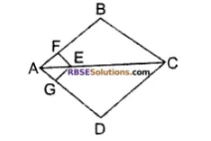
In the figure given below, straight lines $$AB$$ and $$CD$$ intersect at $$P$$, and $$AC || BD$$. If $$BD = 2.4\ cm$$, $$AC=4.8\ cm$$; find the value of $$\cfrac { AP }{ PB } $$.
In parallelogram ABCD, the bisector of angle A meets DC in P and $$AB = 2AD.$$ Find $$\angle APB $$.
DE = FB
$$\displaystyle\,\dfrac{CP}{PA}=\dfrac m{3}$$.Find $$m$$
PQ
$$DE$$ is parallel to $$FB$$
$$DEBF$$ is a parallelogram.
$$\displaystyle\,\frac{AE}{EC}$$
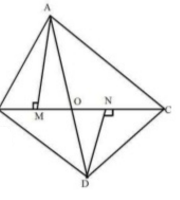
In the given figure, AD = AE and $$AD^{2}\,=\,BD\,\times\,EC$$.
Hence , $$\triangle ABD$$ $$\sim$$ $$\triangle CAE $$.
If the above statement is true then mention answer as 1, else mention 0 if false
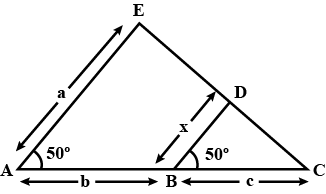
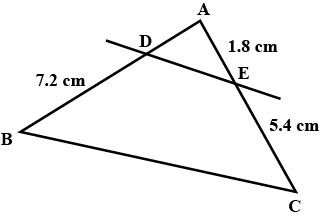
DE = 2.4 cm, find the length of BC.
BC = 4.8 cm, the length of DE = 1.8cm (Enter 1 f true otherwise 0)
PQR is a right-angle triangle right angled at Q. XY is parallel to QR. PQ = 6 cm and PX : XQ = 1:Calculate the lengths of PR and QR.
In the following figure, $$XY$$ is parallel to $$BC$$, $$AX = 9\ cm$$. $$XB = 4.5 cm $$ and $$BC = 18\ cm$$.
What is the value of $$\displaystyle\,\dfrac{AY}{YC}$$?
$$\triangle ABC \sim \triangle PQR$$. If AD and PM are corresponding medians of the two triangles , then $$\frac{AB}{PQ}\,=\,\frac{AD}{PM}$$.
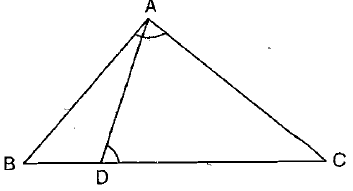
In triangle $$ABC$$, the bisector of angle $$BAC$$ meets opposite side $$BC$$ at point $$D$$. If $$BD = CD$$, prove that $$\Delta ABC$$ is isosceles.
Given $$AD$$ is angle bisector and $$BD=CD.$$
Construction:
Draw a line from $$C$$ parallel to $$AB$$ with length $$AC.$$
Now, in $$\triangle ABD$$ and $$\triangle FCD,$$
$$\angle ABD=\angle FCD$$ [Corresponding Angles]
$$\angle BAD=\angle CFD$$ [Corresponding Angles]
So, by AAA criteria of similarity,
$$\triangle ABD\sim \triangle FCD$$
$$\Rightarrow \cfrac { AB }{ BD } =\cfrac { CF }{ CD } $$
But given $$BD=CD$$ and we took $$CF=AC$$
$$\Rightarrow AB=AC$$
$$\therefore \triangle ABC$$ is isosceles.
In the given figure , $$ABCD$$ is a trapezium with AB || DC. If $$AB = 9 $$$$cm$$, $$DC = 18$$ $$cm$$, $$CF = 13.5$$ $$cm$$, $$AP = 6$$ $$cm$$ and $$BE = 15$$ $$cm$$. .What is the value of $$EC$$ in mm?
In the following figure, $$XY$$ is parallel to $$BC$$, $$AX = 9\ cm$$. $$XB = 4.5 cm $$ and $$BC = 18\ cm$$. Find $$XY$$ in cm.
In the following figure , $$ABCD$$ is a trapezium with $$AB \parallel DC.$$ If $$AB = 9 $$ $$cm$$, $$DC = 18$$ $$cm$$, $$CF = 13.5$$ $$cm$$, $$AP = 6$$ $$cm$$ and $$BE = 15$$ $$cm$$. Find the value of $$PE.$$
In the given figure, $$\Delta \,ABC\,\sim\,\Delta\,ADE$$. If
$$AE : EC = 4 : 7$$ and $$DE = 6.6\ cm,$$ find $$BC$$. If x be the length of the perpendicular from $$A$$ to $$DE$$, find the length of perpendicular from $$A$$ and $$BC$$ in terms of $$x.$$
ABCD a parallelogram. $$E$$ is a point on $$AD$$ and $$CE$$ is produced to meet $$BA$$ at $$F$$. If $$AE = 4 $$ $$cm$$, $$AF = 8$$ $$cm$$ and $$AB = 12$$ $$cm$$. Find the perimeter (in $$cm$$) of parallelogram $$ABCD$$.
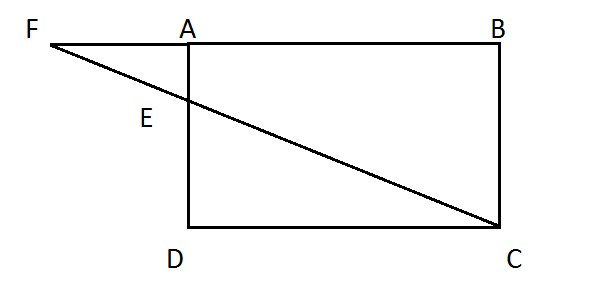
Calculate $$AF$$.
ABCD is a trapezium. Further if CD = 4.5 cm; find the length of 2AB in cm.
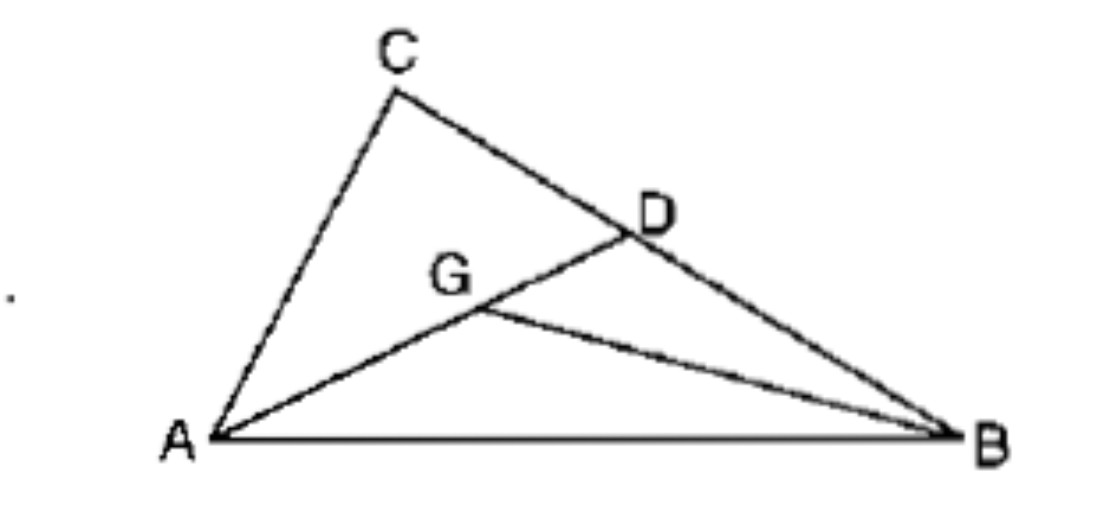
Area $$(\Delta AGB) = \frac{2}{3} \times\, Area (\Delta ADB)$$
Given $$AD$$ and $$BC$$ are the medians
In $$\triangle AGB,AG$$ will be the median
In $$\triangle AGC ,AG$$ will be the median
$$\therefore Ar(\triangle AGB)=Ar(\triangle AGC)$$
Similarly $$BG$$ is the median
$$Ar(\triangle AGB)=Ar(\triangle BGD)$$
$$\implies Ar(\triangle AGB)=Ar( \triangle AGC)=Ar(\triangle BGD)$$
$$Ar(\triangle ABC)=2\times Ar(\triangle ADB)$$
$$Ar(\triangle ABC)=Ar(\triangle AGB)+Ar(\triangle AGC)+Ar(\triangle BGD)$$
$$Ar(\triangle AGB)=\dfrac{1}{3}\times Ar(\triangle ABC)=\dfrac{2}{3}\times Ar(\triangle ABC)$$
Show that a diagonal divides a parallelogram into two triangles of equal area.
Let $$ABCD$$ be a parallelogram and $$BD$$ is one of its diagonal. As we know that the opposite sides of a parallelogram are equal.
$$\therefore AB=CD$$ and $$AD=BC$$
In $$\triangle ABD$$ and $$\triangle CDB$$,
$$AB=CD, AD=BC$$ [given]
$$BD=BD$$ [common]
$$\therefore \triangle ABD \cong \triangle ADC$$
$$\Rightarrow ar(\triangle ABD)=ar(\triangle CBD)$$
$$\Rightarrow ar(\triangle ABC)=ar(\triangle CDA)$$
i.e congruent triangles have equal area
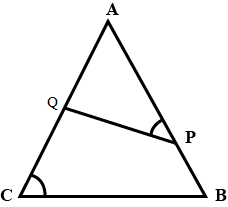
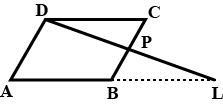
In the figure, given alongside, $$\angle \,APQ\,=\,\angle\,C$$. Hence, If AQ = 9 cm, BP = 3 cm and AP = 15 cm; find AC in cm
$$\Delta\,OAB\,\sim\,\Delta\,OAD$$
If the above statement is true then mention answer as 1, else mention 0 if false
$$D$$ is a point on the side $$BC$$ of $$\triangle ABC$$ such that $$\angle ADC=\angle BAC.$$ Prove that $$\displaystyle \frac{CA}{CD}=\frac{CB}{CA}$$ or $$CA^{2}=CB\times CD$$
In $$\Delta ABC,\;AN\;\bot\;BC\;and\;BM\;\bot\;AC$$ if $$AC=8\;cm\;and\;BC=7.5\;cm$$, If $$AN=8.0\;cm$$, and length of $$BM$$ is given by $$\dfrac pq$$, where p and q are co-primes, then find the value of $$p - 7q$$.
PQ = 1.28 cm; PR = 2.56 cm,
PM =0.16 cm; PN =0.32 cm.
In the following figure, LM $$\parallel$$ AB. If AL = x - 3, AC = 2x, BM = x - 2, BC = 2x + 3, then find the value of x.
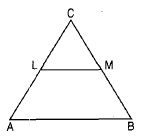
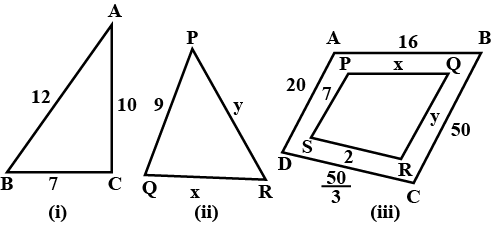
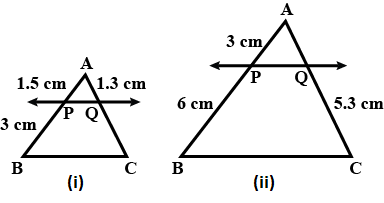
If in fig. (i) and (ii), PQ $$\parallel$$ BC, find QC in (i) and AQ in (ii).
In $$\Delta ABC , PQ \parallel BC$$
$$\therefore$$ By basic Proportionality Theorem, we get
$$\displaystyle \frac{AP}{PB} = \frac{AQ}{QC}$$
$$\displaystyle \Rightarrow \frac{1.5}{3} = \frac{1.3}{QC}$$
$$\displaystyle \Rightarrow QC = \frac{1.3 \times 3}{15} = \frac{13}{5} = 2.6 cm$$
Hence, $$QC = 2.6 cm$$
$$\therefore$$ By basic Proportionality Theorem, we get
$$\displaystyle \frac{AP}{PB} = \frac{AQ}{QC}$$
$$\displaystyle \Rightarrow \frac{1.5}{3} = \frac{1.3}{QC}$$
$$\displaystyle \Rightarrow QC = \frac{1.3 \times 3}{15} = \frac{13}{5} = 2.6 cm$$
Hence, $$QC = 2.6 cm$$
In fig. (ii) given above
In $$\Delta ABC, PQ \parallel BC$$
$$\therefore$$ By Basic Proportionality Theorem, we get
$$\displaystyle \frac{AP}{PB} = \frac{AQ}{QC} \Rightarrow \frac{3}{6} = \frac{AQ}{5.3}$$
$$\displaystyle \Rightarrow AQ = \frac{3 \times 5.3}{6} = \frac{5.3}{2} = 2.65 cm$$
In $$\Delta ABC, PQ \parallel BC$$
$$\therefore$$ By Basic Proportionality Theorem, we get
$$\displaystyle \frac{AP}{PB} = \frac{AQ}{QC} \Rightarrow \frac{3}{6} = \frac{AQ}{5.3}$$
$$\displaystyle \Rightarrow AQ = \frac{3 \times 5.3}{6} = \frac{5.3}{2} = 2.65 cm$$
PM =4 cm; QM =4.5 cm;
PN = 4 cm; NR = 4.5 cm
$$\displaystyle \dfrac{PM}{QM}
= \dfrac{4}{4.5}$$ and $$\displaystyle \dfrac{PN}{NR} = \dfrac{4}{4.5}$$
$$\displaystyle \therefore \dfrac{PM}{QM} = \dfrac{PN}{NR}$$
$$\displaystyle \left[ Each\, ratio = \dfrac{4}{4.5} \right]$$
$$\Rightarrow$$ By the converse of Basic Proportinality
theorem, we get, MN $$\parallel$$ QR.
In triangle $$ABC,\;\angle BAC=90^{\circ},$$ and $$AD$$ is its bisector. If $$DE$$ is drawn $$\bot\;AC$$, prove that $$DE\times (AB+AC)=AB\times AC$$.
It is given that $$AD$$ is the bisector of $$\angle A$$ of $$\Delta ABC$$.
$$\therefore\;\displaystyle\frac{AB}{AC}=\displaystyle\frac{BD}{DC}$$
$$\Rightarrow\;\displaystyle\frac{AB}{AC}+1=\displaystyle\frac{BD}{DC}+1\;\;\;\;\;\;\;[Adding\;1\;on\;both\;sides]$$
$$\Rightarrow\;\displaystyle\frac{AB+AC}{AC}=\displaystyle\frac{BD+DC}{DC}$$
$$\Rightarrow\;\displaystyle\frac{AB+AC}{AC}=\displaystyle\frac{BC}{DC}\;\;\;\;\;\;\;\;\;\;\;\;\;......(i)$$
In $$\Delta's CDE\;and\;CBA$$, we have
$$\angle DCE=\angle BCA\;\;\;\;\;\;\;\;\;\;\;[Common]$$
$$\angle DEC=\angle BAC\;\;\;\;\;\;\;\;\;\;\;[Each\;equal\;to\;90^{\circ}$$
So, by $$AA$$-criterion of similarity
$$\Delta CDE\;\sim\;\Delta CBA$$
$$\Rightarrow\;\displaystyle\frac{CD}{CB}=\displaystyle\frac{DE}{BA}$$
$$\Rightarrow\;\displaystyle\frac{AB}{DE}=\displaystyle\frac{BC}{DC}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;.....(ii)$$
From (i) and (ii) we have
$$\Rightarrow\;\displaystyle\frac{AB+AC}{AC}=\displaystyle\frac{AB}{DE}$$
$$\Rightarrow\;DE\times (AB+AC)=AB\times AC$$.
$$\therefore\;\displaystyle\frac{AB}{AC}=\displaystyle\frac{BD}{DC}$$
$$\Rightarrow\;\displaystyle\frac{AB}{AC}+1=\displaystyle\frac{BD}{DC}+1\;\;\;\;\;\;\;[Adding\;1\;on\;both\;sides]$$
$$\Rightarrow\;\displaystyle\frac{AB+AC}{AC}=\displaystyle\frac{BD+DC}{DC}$$
$$\Rightarrow\;\displaystyle\frac{AB+AC}{AC}=\displaystyle\frac{BC}{DC}\;\;\;\;\;\;\;\;\;\;\;\;\;......(i)$$
In $$\Delta's CDE\;and\;CBA$$, we have
$$\angle DCE=\angle BCA\;\;\;\;\;\;\;\;\;\;\;[Common]$$
$$\angle DEC=\angle BAC\;\;\;\;\;\;\;\;\;\;\;[Each\;equal\;to\;90^{\circ}$$
So, by $$AA$$-criterion of similarity
$$\Delta CDE\;\sim\;\Delta CBA$$
$$\Rightarrow\;\displaystyle\frac{CD}{CB}=\displaystyle\frac{DE}{BA}$$
$$\Rightarrow\;\displaystyle\frac{AB}{DE}=\displaystyle\frac{BC}{DC}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;.....(ii)$$
From (i) and (ii) we have
$$\Rightarrow\;\displaystyle\frac{AB+AC}{AC}=\displaystyle\frac{AB}{DE}$$
$$\Rightarrow\;DE\times (AB+AC)=AB\times AC$$.
In the given fig. DE $$\parallel$$ BC. If AD = x, DB = x - 2, AE = x + 2 and EC = x - 1, find the value of x.
The ratio of the corresponding sides of similar triangles $$ABC$$ and $$A'B'C'$$ is $$2 : 1$$. Also, the altitudes $$CD$$ and $$C'D',$$ that we have drawn in these triangles are also in the same ratio $$2: 1$$. Then, prove that the ratio of their areas is equal to the square of the ratio of their corresponding sides.
According to the given condition let the length of $$CD$$ and $$C'D'$$ be $$2x$$ and $$x$$ respectievly.
Area of a triangle$$ = \dfrac{1}{2} \times base \times altitude$$
$$\displaystyle \therefore \frac{Area of \Delta ABC}{Area of \Delta A'B'C'} = \frac{\displaystyle \frac{1}{2} \times 42 \times 2x}{\displaystyle \frac{1}{2} \times 21 \times x}$$
$$=\displaystyle \frac{42 \times 2}{21 \times 1} \\= \dfrac{84}{21} \\= \dfrac{4}{1} \\= \left(\dfrac{2}{1} \right)^2$$
$$\therefore$$ The ratio of the areas of these similar triangles is the square of the ratio of the measures of the corresponding sides.
In a trapezium ABCD, O is the point of intersection of AC and BD, AB $$\parallel$$ CD and $$AB = 2 CD$$. If the area of $$\Delta AOB = 84 cm^2$$, find the area of $$\Delta COD$$.
ABCD is a trapezium in which, AB $$\parallel$$ CD and diagonals AC and BD intersect each other at O.
In $$\Delta AOB$$ and $$\Delta COD$$ we have
$$\angle 1 = \angle 2$$ [Alt $$\angle s]$$
$$\angle 3 = \angle 4$$ [vert opp. \angle s$$
$$\therefor \Delta AOB \sim \Delta COD$$
[By AA criterion of similarity]
$$\displaystyle \Rightarrow \frac{ar(\Delta AOB)}{ar(\Delta COD)} = \frac{(2CD)^2}{(CD)^2}$$
[AB = 2CD (Given)]
$$\displaystyle = \frac{4CD^2}{CD^2} = 4$$
$$\displaystyle = \frac{84}{ar(\Delta COD)} = 4$$;
$$\therefore ar(\Delta COD) = 84 + 4 = 21 cm^2$$
In $$\Delta AOB$$ and $$\Delta COD$$ we have
$$\angle 1 = \angle 2$$ [Alt $$\angle s]$$
$$\angle 3 = \angle 4$$ [vert opp. \angle s$$
$$\therefor \Delta AOB \sim \Delta COD$$
[By AA criterion of similarity]
$$\displaystyle \Rightarrow \frac{ar(\Delta AOB)}{ar(\Delta COD)} = \frac{(2CD)^2}{(CD)^2}$$
[AB = 2CD (Given)]
$$\displaystyle = \frac{4CD^2}{CD^2} = 4$$
$$\displaystyle = \frac{84}{ar(\Delta COD)} = 4$$;
$$\therefore ar(\Delta COD) = 84 + 4 = 21 cm^2$$
$$\Delta ABC \sim \Delta PQR$$. Also, $$ar(\Delta ABC) = 4 ar(\Delta PQR)$$. If $$BC = 12\ cm,$$ then find $$QR$$.
Given: $$ar(\Delta ABC) = 4 ar(\Delta PQR)$$
$$\displaystyle \Rightarrow \frac{ar(\Delta ABC)}{ar(\Delta PQR)} = \frac{4}{1}$$
$$\displaystyle \Rightarrow \frac{BC^2}{QR^2} = \frac{4}{1}$$
[$$\therefore$$ The ratio of the areas of two similar $$\Delta s$$ is equal to the ratio of the squares of any two corresponding sides]
$$\displaystyle \Rightarrow \frac{(12)^2}{QR^2} = \frac{4}{1}$$ [$$\therefore$$ QR= 12 cm]
$$\displaystyle \Rightarrow QR^2 = \frac{12 \times 12}{4} = 36$$
$$\therefore QR = \sqrt{36} = 6cm$$
$$\displaystyle \Rightarrow \frac{ar(\Delta ABC)}{ar(\Delta PQR)} = \frac{4}{1}$$
$$\displaystyle \Rightarrow \frac{BC^2}{QR^2} = \frac{4}{1}$$
[$$\therefore$$ The ratio of the areas of two similar $$\Delta s$$ is equal to the ratio of the squares of any two corresponding sides]
$$\displaystyle \Rightarrow \frac{(12)^2}{QR^2} = \frac{4}{1}$$ [$$\therefore$$ QR= 12 cm]
$$\displaystyle \Rightarrow QR^2 = \frac{12 \times 12}{4} = 36$$
$$\therefore QR = \sqrt{36} = 6cm$$
$$\Delta ABC$$ is similar to $$\Delta PQR$$, ar($$\Delta ABC$$) = 36 sq. cm. and ar($$\Delta PQR$$) =49 sq.cm. If BC = 12 cm, find QR.
$$\because \Delta ABC
\sim \Delta PQR$$
$$\displaystyle \therefore \dfrac{ar(\Delta ABC)}{ar(\Delta
PQR)} = \dfrac{BC^2}{QR^2}$$
$$\displaystyle \Rightarrow \dfrac{36}{49} = \dfrac{12^2}{QR^2}$$
$$\displaystyle \Rightarrow (QR)^2 = \dfrac{12 \times 12
\times 49}{36} = 4 \times 49$$
$$\Rightarrow QR = + \sqrt{4 \times 49}$$
$$= 2 \times 7 = 14 cm$$
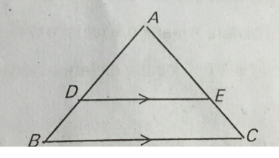
Prove that the line segments joining the midpoints of the sides of a triangle from four triangles each of which is similar to the original triangle.
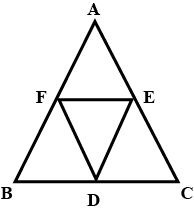
If three or more parallel lines are intersected by two transversals prove that the intercepts made by them on the transversals are proportional
In Fig., $$DE\,||\,OQ$$ and $$DF\,||\,OR$$. Show that $$EF\,||\,QR$$.
In given figure, $$A, B$$ and $$C$$ are points on $$OP, OQ$$ and $$OR$$ respectively such that $$AB\,||\,PQ$$ and $$AC\,||\,PR$$. Show that $$BC\,||\,QR$$.
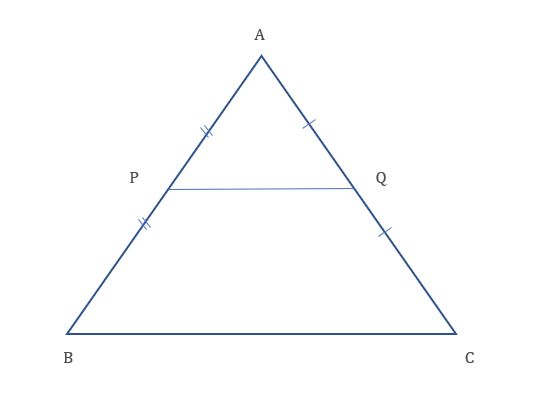
Using Theorem $$6.1,$$ prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
Theorem 6.1: If a line is drawn parallel to one side of a triangle to intersect the
other two sides in distinct points, the other two sides are divided in the same
ratio.
Given:
In $$\triangle\, ABC, D$$ is midpoint of $$AB$$ and $$DE$$ is parallel to $$BC.$$
$$\therefore$$ $$AD=DB$$
$$\therefore$$ $$AD=DB$$
To prove:
$$AE = EC$$
Proof:
Since, $$DE \parallel BC$$
$$\therefore$$ By Basic Proportionality Theorem,
$$\dfrac{AD}{DB}=\dfrac{AE}{EC}$$
$$\therefore$$ By Basic Proportionality Theorem,
$$\dfrac{AD}{DB}=\dfrac{AE}{EC}$$
Since, $$AD = DB$$
$$\therefore$$ $$\dfrac{AE}{EC}=1$$
$$\therefore$$ $$AE=EC$$
$$\therefore$$ $$\dfrac{AE}{EC}=1$$
$$\therefore$$ $$AE=EC$$
In Fig., (i) and (ii), $$DE \,||\, BC$$. Find $$EC$$ in (i) and $$AD$$ in (ii).
In Fig., $$DE\, ||\, AC$$ and $$DF\, ||\, AE$$. Prove that $$\dfrac{BF}{FE}=\dfrac{BE}{EC}$$.
In Fig., if $$LM \,||\, CB$$ and $$LN\, ||\, CD$$, prove that $$\dfrac{AM}{AB}=\dfrac{AN}{AD}$$.
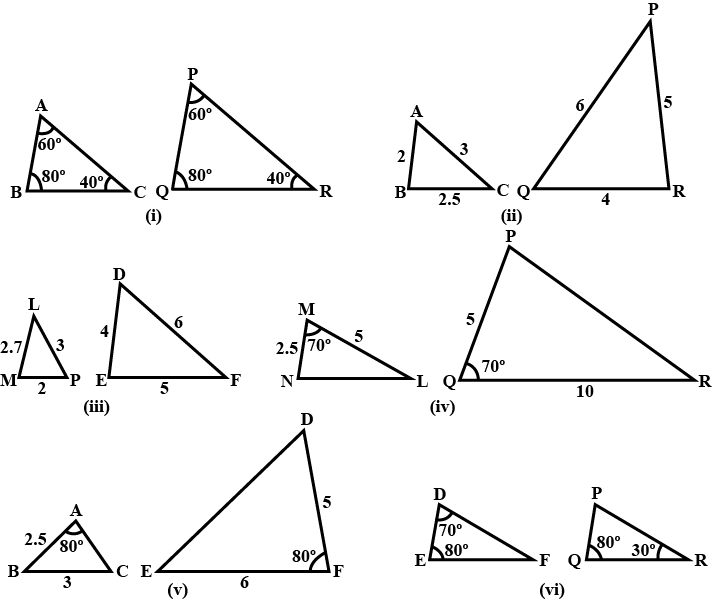
State which pairs of triangles in Fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :
$$E$$ and $$F$$ are points on the sides $$PQ$$ and $$PR$$ respectively of a $$\triangle PQR$$. For each of the following cases, state whether $$EF \,|| \,QR$$ :
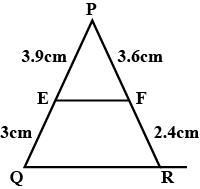
(i) $$PE = 3.9$$ cm, $$EQ = 3$$ cm, $$PF = 3.6$$ cm and $$FR = 2.4$$ cm
(ii) $$PE = 4$$ cm, $$QE = 4.5$$ cm, $$PF = 8$$ cm and $$RF = 9$$ cm
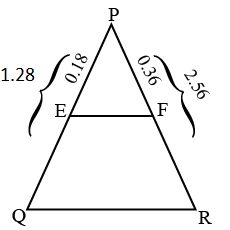
(iii) $$PQ = 1.28$$ cm, $$PR = 2.56$$ cm, $$PE = 0.18$$ cm and $$PF = 0.36$$ cm
$$E$$ and $$F$$ are two points on side $$PQ$$ and $$PR$$ in $$\triangle PQR.$$
(i) $$PE = 3.9$$ cm, $$EQ = 3$$ cm and $$PF = 3.6$$ cm, $$FR = 2.4$$ cm
Using Basic proportionality theorem,
$$\therefore \dfrac{PE}{EQ} = \dfrac{3.9}{3 }= \dfrac{39}{30} =\dfrac{13}{10} = 1.3$$
$$\dfrac{PF}{FR} = \dfrac{3.6}{2.4} =\dfrac{ 36}{24} =\dfrac{ 3}{2} = 1.5$$
$$\dfrac{PE}{EQ} \neq \dfrac{ PF}{FR}$$
So, $$EF$$ is not parallel to $$QR.$$
(ii) $$PE = 4$$ cm, $$QE = 4.5$$ cm, $$PF = 8$$ cm, $$RF = 9$$ cm
Using Basic proportionality theorem,
$$\therefore \dfrac{PE}{QE} = \dfrac{4}{4.5} =\dfrac{ 40}{45} =\dfrac{ 8}{9}$$
$$\dfrac{PF}{RF} = \dfrac{8}{9}$$
$$\dfrac{PE}{QE} = \dfrac{PF}{RF}$$
So, $$EF$$ is parallel to $$QR.$$
(iii) $$PQ = 1.28$$ cm, $$PR = 2.56$$ cm, $$PE = 0.18$$ cm, $$PF = 0.36$$ cm
Using Basic proportionality theorem,
$$EQ = PQ - PE = 1.28 - 0.18 = 1.10$$ cm
$$ FR = PR - PF = 2.56 - 0.36 = 2.20$$ cm
$$\dfrac{PE}{EQ} = \dfrac{0.18}{1.10} = \dfrac{18}{110} = \dfrac{9}{55 }$$... (i)
$$\dfrac{PE}{FR} = \dfrac{0.36}{2.20} = \dfrac{36}{220} =\dfrac{ 9}{55}$$ ... (ii)
$$\therefore \dfrac{PE}{EQ} =\dfrac{ PF}{FR.}$$
So, $$EF$$ is parallel to $$QR.$$
Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
Theorem 6.2: If a line divides any two sides of a
triangle in the same ratio, then the line is parallel
to the third side.
Given: In $$\triangle ABC, D$$ and $$E$$ are midpoints of $$AB$$ and $$AC$$ respectively,
i.e., $$AD=DB$$ and $$AE=EC$$
To Prove: $$DE \parallel BC$$
Proof:
Since, $$AD=DB$$
$$\therefore$$$$\dfrac{AD}{DB}=1............(1)$$
Also,
$$AE=EC$$
$$\therefore$$$$\dfrac{AE}{EC}=1............(2)$$
From $$(1)$$ and $$(2)$$,
$$\dfrac{AD}{DB}$$ $$=$$ $$\dfrac{AE}{EC}$$ $$=\,1$$
i.e.,$$\dfrac{AD}{DB}$$ $$=$$ $$\dfrac{AE}{EC}$$
$$\therefore$$ By converse of Basic Proportionality theorem,
$$DE \parallel BC$$
i.e., $$AD=DB$$ and $$AE=EC$$
To Prove: $$DE \parallel BC$$
Proof:
Since, $$AD=DB$$
$$\therefore$$$$\dfrac{AD}{DB}=1............(1)$$
Also,
$$AE=EC$$
$$\therefore$$$$\dfrac{AE}{EC}=1............(2)$$
From $$(1)$$ and $$(2)$$,
$$\dfrac{AD}{DB}$$ $$=$$ $$\dfrac{AE}{EC}$$ $$=\,1$$
i.e.,$$\dfrac{AD}{DB}$$ $$=$$ $$\dfrac{AE}{EC}$$
$$\therefore$$ By converse of Basic Proportionality theorem,
$$DE \parallel BC$$
The diagonals of a quadrilateral $$ABCD$$ intersect each other at the point $$O$$ such that $$\dfrac{AO}{BO}=\dfrac{CO}{DO}$$. Show that $$ABCD$$ is a trapezium.
Given:
The diagonals of a quadrilateral ABCD intersect each other at the point O such that $$\dfrac{AO}{BO}=\dfrac{CO}{DO}$$
i.e., $$\dfrac{AO}{CO}=\dfrac{BO}{DO}$$
To Prove: $$ABCD$$ is a trapezium
Construction:
Draw $$OE\parallel DC$$ such that $$E$$ lies on $$BC.$$
Proof:
In $$\triangle BDC$$,
By Basic Proportionality Theorem,
$$\dfrac{BO}{OD}=\dfrac{BE}{EC}\,............(1)$$
But, $$\dfrac{AO}{CO}=\dfrac{BO}{DO}$$ (Given) $$.........(2)$$
$$\therefore$$ From $$(1)$$ and $$(2)$$
$$\dfrac{AO}{CO}=\dfrac{BE}{EC}$$
Hence, By Converse of Basic Proportionality Theorem,
$$OE\parallel AB$$
Now Since, $$AB\parallel OE\parallel DC$$
$$\therefore$$ $$AB\parallel DC$$
Hence, $$ABCD$$ is a trapezium.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that $$\dfrac{AO}{BO}=\dfrac{CO}{DO}$$
i.e., $$\dfrac{AO}{CO}=\dfrac{BO}{DO}$$
To Prove: $$ABCD$$ is a trapezium
Construction:
Draw $$OE\parallel DC$$ such that $$E$$ lies on $$BC.$$
Proof:
In $$\triangle BDC$$,
By Basic Proportionality Theorem,
$$\dfrac{BO}{OD}=\dfrac{BE}{EC}\,............(1)$$
But, $$\dfrac{AO}{CO}=\dfrac{BO}{DO}$$ (Given) $$.........(2)$$
$$\therefore$$ From $$(1)$$ and $$(2)$$
$$\dfrac{AO}{CO}=\dfrac{BE}{EC}$$
Hence, By Converse of Basic Proportionality Theorem,
$$OE\parallel AB$$
Now Since, $$AB\parallel OE\parallel DC$$
$$\therefore$$ $$AB\parallel DC$$
Hence, $$ABCD$$ is a trapezium.
Diagonals $$AC$$ and $$BD$$ of a trapezium $$ABCD$$ with $$AB\,||\,DC$$ intersect each other at the point $$O.$$ Using a similarity criterion for two triangles, show that $$\dfrac{OA}{OC}=\dfrac{OB}{OD}$$.
Given:
ABCD is a trapezium with $$AB\parallel DC$$.
O is the point of intersection of two diagonals
To Prove:
$$\dfrac{OA}{OC}=\dfrac{OB}{OD}$$
Proof:
In $$\triangle\,AOB$$ and $$\triangle\,DOC$$
$$\angle BAO=\angle OCD$$ (Alternate Angles)
$$\angle ABO=\angle ODC$$ (Alternate Angles)
$$\angle AOB=\angle DOC$$ (Vertically opposite angles)
$$\therefore$$ By AAA criterion of similarity, $$\triangle\,AOB \sim \triangle\,DOC$$
$$\therefore$$ $$\dfrac{OA}{OC}=\dfrac{OB}{OD}$$ (Corresponding Sides of Similar Triangles)
ABCD is a trapezium with $$AB\parallel DC$$.
O is the point of intersection of two diagonals
To Prove:
$$\dfrac{OA}{OC}=\dfrac{OB}{OD}$$
Proof:
In $$\triangle\,AOB$$ and $$\triangle\,DOC$$
$$\angle BAO=\angle OCD$$ (Alternate Angles)
$$\angle ABO=\angle ODC$$ (Alternate Angles)
$$\angle AOB=\angle DOC$$ (Vertically opposite angles)
$$\therefore$$ By AAA criterion of similarity, $$\triangle\,AOB \sim \triangle\,DOC$$
$$\therefore$$ $$\dfrac{OA}{OC}=\dfrac{OB}{OD}$$ (Corresponding Sides of Similar Triangles)
In Fig, altitudes $$AD$$ and $$CE$$ of $$\triangle ABC$$ intersect each other at the point $$P. $$ Show that:
(i) $$\triangle AEP \sim \triangle CDP$$
(ii) $$\triangle ABD \sim \triangle CBE$$
(iii) $$\triangle AEP \sim \triangle ADB$$
(iv) $$\triangle PDC \sim \triangle BEC$$
$$E$$ is a point on the side $$AD$$ produced of a parallelogram ABCD and $$BE$$ intersects $$CD$$ at $$F.$$ Show that $$\triangle ABE \sim \triangle CFB$$.
In $$\triangle ABE$$ and $$\triangle CFB,$$
$$\angle ABE=\angle CFB$$ (Alternate angles)
$$\angle BAE=\angle BCF$$ (opposite angles of a parallelogram)
$$\therefore$$ By AA criterion of similarity, $$\triangle ABE$$ $$\sim$$ $$\triangle CFB$$
$$\angle ABE=\angle CFB$$ (Alternate angles)
$$\angle BAE=\angle BCF$$ (opposite angles of a parallelogram)
$$\therefore$$ By AA criterion of similarity, $$\triangle ABE$$ $$\sim$$ $$\triangle CFB$$
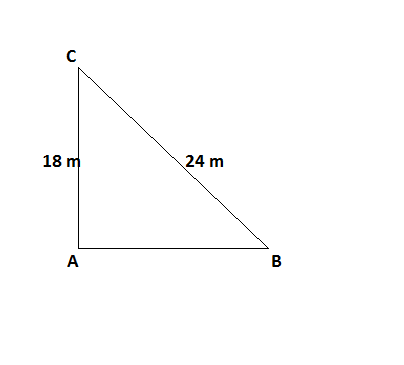
A guy wire attached to a vertical pole of height $$18\ m$$ is $$24\ m$$ long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Let $$AC=18\ m$$ be the pole.
$$BC=24\ m$$ is the length of a guy wire and is attached to stake $$B.$$
$$BC=24\ m$$ is the length of a guy wire and is attached to stake $$B.$$
$$\therefore$$ In $$\triangle ABC$$
By pythagoras theorem,
$$BC^2=AB^2+AC^2$$
$$\therefore$$ $$24^2=AB^2+18^2$$
$$\Rightarrow AB^2=576-324=252$$
$$\therefore$$ $$AB=6\sqrt7\,m$$
Hence, the stake has to be $$6\sqrt7\,m$$ from base $$A.$$
In Fig., $$ABC$$ and $$AMP$$ are two right triangles, right angled at $$B$$ and $$M$$ respectively. Prove that:
(i) $$\triangle ABC \sim \triangle AMP$$
(ii) $$\dfrac{CA}{PA} = \dfrac{BC}{MP}$$
In the given figure., if $$\triangle ABE \cong \triangle ACD$$, show that $$\triangle ADE \sim \triangle ABC.$$
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Given:
$$ABCD$$ is a rhombus.
Hence, $$AB=BC=CD=AD$$
And, AC perpendicular to BD
$$DO=\dfrac{1}{2}DB$$ and $$AO=\dfrac{1}{2}AC$$
To Prove:
$$AB^2+BC^2+CD^2+AD^2=AC^2+BD^2$$
Proof:
In $$\triangle AOD$$, By Pythagoras Theorem,
$$AD^2=AO^2+OD^2\,.....(1)$$
Similarly,
$$DC^2=DO^2+OC^2\,.....(2)$$
$$BC^2=OB^2+OC^2\,.....(3)$$
$$AB^2=AO^2+OB^2\,.....(4)$$
Adding 1, 2, 3, 4 we get,
$$AB^2+BC^2+CD^2+AD^2=2AO^2+2BO^2+2CO^2+2DO^2\,....(5)$$
Since, $$DO=OB=\dfrac{1}{2}DB$$ and $$AO=OC=\dfrac{1}{2}AC\,....(6)$$
From 5 and 6,
$$AB^2+BC^2+CD^2+AD^2=\dfrac{AC^2}{2}+\dfrac{BD^2}{2}+\dfrac{AC^2}{2}+\dfrac{BD^2}{2}$$
$$\therefore$$ $$AB^2+BC^2+CD^2+AD^2=AC^2+BD^2$$
$$ABCD$$ is a rhombus.
Hence, $$AB=BC=CD=AD$$
And, AC perpendicular to BD
$$DO=\dfrac{1}{2}DB$$ and $$AO=\dfrac{1}{2}AC$$
To Prove:
$$AB^2+BC^2+CD^2+AD^2=AC^2+BD^2$$
Proof:
In $$\triangle AOD$$, By Pythagoras Theorem,
$$AD^2=AO^2+OD^2\,.....(1)$$
Similarly,
$$DC^2=DO^2+OC^2\,.....(2)$$
$$BC^2=OB^2+OC^2\,.....(3)$$
$$AB^2=AO^2+OB^2\,.....(4)$$
Adding 1, 2, 3, 4 we get,
$$AB^2+BC^2+CD^2+AD^2=2AO^2+2BO^2+2CO^2+2DO^2\,....(5)$$
Since, $$DO=OB=\dfrac{1}{2}DB$$ and $$AO=OC=\dfrac{1}{2}AC\,....(6)$$
From 5 and 6,
$$AB^2+BC^2+CD^2+AD^2=\dfrac{AC^2}{2}+\dfrac{BD^2}{2}+\dfrac{AC^2}{2}+\dfrac{BD^2}{2}$$
$$\therefore$$ $$AB^2+BC^2+CD^2+AD^2=AC^2+BD^2$$
Hence Proved
An aeroplane leaves an airport and flies due north at a speed of $$1000\ km$$ per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of $$1200\ km$$ per hour. How far apart will be the two planes after $$1\dfrac{1}{2}$$ hours?
The first aeroplane leaves an airport and flies due north at a speed of $$1000$$ km per hr.
$$\therefore$$ Distance travelled in $$1.5$$ hrs.
$$=1000\times1.5=1500$$ km
Similarly, Distance traveled by second aeroplane,
$$=1200\times1.5=1800$$ km
In $$\triangle ABC$$,
$$BC$$ is distance travelled by first aeroplane and $$BA$$ is the distance traveled by second aeroplane.
Hence, applying Pythagoras Theorem,
$$AC^2=AB^2+BC^2$$
$$\therefore$$ $$AC^2=1500^2+1800^2$$
$$\therefore$$ $$ AC=300\sqrt{61}$$ km
Hence, two planes are $$300\sqrt{61}$$ km apart.
$$\therefore$$ Distance travelled in $$1.5$$ hrs.
$$=1000\times1.5=1500$$ km
Similarly, Distance traveled by second aeroplane,
$$=1200\times1.5=1800$$ km
In $$\triangle ABC$$,
$$BC$$ is distance travelled by first aeroplane and $$BA$$ is the distance traveled by second aeroplane.
Hence, applying Pythagoras Theorem,
$$AC^2=AB^2+BC^2$$
$$\therefore$$ $$AC^2=1500^2+1800^2$$
$$\therefore$$ $$ AC=300\sqrt{61}$$ km
Hence, two planes are $$300\sqrt{61}$$ km apart.
In Fig.,$$\dfrac{QR}{QS}=\dfrac{QT}{PR}$$ and $$\angle 1 = \angle 2$$. Show that $$\triangle PQS \sim \triangle TQR$$.
In given figure $$E$$ is a point on side $$CB$$ produced of an isosceles triangle $$ABC$$ with $$AB = AC.$$ If $$AD \bot BC$$ and $$EF \bot AC,$$ prove that $$\triangle ABD \sim \triangle ECF$$.
State and prove Pythagoras theorem.
Given triangle ABC is a right angle triangle at B
Draw BD perpendicular to AC
In $$\Delta ABC $$ and $$\Delta ADB$$
$$\angle ABC=\angle ADB $$
$$\angle A=\angle A$$
$$\therefore \Delta ABC\sim \Delta ADB$$
$$\therefore \dfrac{AB}{A D}=\dfrac{BC}{DB}=\dfrac{AC}{AB}$$
$$\Rightarrow AB^{2}=AC\times AD$$.............................................(1)
In$$\Delta ABC$$ and $$\Delta BDC$$
$$\angle ABC=\angle BDC $$
$$\angle C=\angle C$$
$$\therefore \Delta ABC\sim \Delta BDC$$
$$\therefore \dfrac{AB}{BD}=\dfrac{BC}{DC}=\dfrac{AC}{BC}$$
$$\Rightarrow BC^{2}=AC\times DC$$
Add (1) and (2) we get
$$AB^{2}+BC^{2}=AC\times AD+AC\times DC$$
$$=AC(AD+DC)=AC\times AC$$
$$=AC^{2}$$
Hence proved.
$$D$$ and $$E$$ are points on the sides $$CA$$ and $$CB$$ respectively of a triangle $$ABC$$ right angled at $$C.$$ Prove that $$AE^2 + BD^2 = AB^2 + DE^2$$.
Given:
$$\triangle\,ACB$$ is a right angles triangle at C.
Construction:
Join $$AE\,,BD$$ and $$ED$$.
To Prove:
$$AE^2+BD^2=AB^2+DE^2$$
Proof:
In $$\triangle \,ACE$$
By pythagoras theorem,
$$AE^2=EC^2+AC^2\,.....(1)$$
In $$\triangle \,BCD$$
By pythagoras theorem,
$$BD^2=BC^2+CD^2\,.....(2)$$
In $$\triangle \,ECD$$
By pythagoras theorem,
$$ED^2=EC^2+DC^2\,.....(3)$$
In $$\triangle \,ABC$$
By pythagoras theorem,
$$AB^2=BC^2+AC^2\,.....(4)$$
Adding 1) and 2) we get,
$$AE^2+BD^2=EC^2+AC^2+BC^2+CD^2\,......(5)$$
From 3), 4) and 5) we get,
$$AE^2+BD^2=AB^2+DE^2$$ $$[hence \, proved]$$
$$\triangle\,ACB$$ is a right angles triangle at C.
Construction:
Join $$AE\,,BD$$ and $$ED$$.
To Prove:
$$AE^2+BD^2=AB^2+DE^2$$
Proof:
In $$\triangle \,ACE$$
By pythagoras theorem,
$$AE^2=EC^2+AC^2\,.....(1)$$
In $$\triangle \,BCD$$
By pythagoras theorem,
$$BD^2=BC^2+CD^2\,.....(2)$$
In $$\triangle \,ECD$$
By pythagoras theorem,
$$ED^2=EC^2+DC^2\,.....(3)$$
In $$\triangle \,ABC$$
By pythagoras theorem,
$$AB^2=BC^2+AC^2\,.....(4)$$
Adding 1) and 2) we get,
$$AE^2+BD^2=EC^2+AC^2+BC^2+CD^2\,......(5)$$
From 3), 4) and 5) we get,
$$AE^2+BD^2=AB^2+DE^2$$ $$[hence \, proved]$$
In Fig., two chords AB and CD intersect each other at the point P. Prove that :
(i) $$\triangle APC \sim \triangle DPB$$
(ii) $$AP . PB = CP . DP$$
Nazima is fly fishing in a stream. The tip of her fishing rod is $$1.8$$ m above the surface of the water and the fly at the end of the string rests on the water $$3.6$$ m away and $$2.4$$ m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Fig.)? If she pulls in the string at the rate of $$5$$ cm per second, what will be the horizontal distance of the fly from her after $$12$$ seconds?
Let AB is the height of the tip of the fishing rod from the water surface .Let BC is the horizontal distance of the fly from the tip of the fishing rod.
Then AC is the length of the string.
Then according to the Pythagorean theorem-
$$\Rightarrow AC^2=AB^2+BC^2$$
$$\Rightarrow AC^2=(1.8)^2+(2.4)^2$$
$$\Rightarrow AC^2=3.24+5.76$$
$$\Rightarrow AC^2=9.00$$
$$\Rightarrow AC=\sqrt{9 }m=3m$$
$$\therefore$$The length of the string out is $$3$$ m.
She pulls the string at the rate of 5 cm per second .
$$\therefore $$She pulls in 12 seconds=$$12\times 5=60 cm=0.6 m$$
Let the fly be at a point of D after 12 seconds
Length of the string out of 12 second is AD.
AD=AC-string pull by Nazima after 12 sec.
$$AD=3-.6=2.4 m$$
In $$\triangle ADB $$
$$AD^2=AB^2+BD^2$$
$$\Rightarrow BD^2=AD^2-AB^2$$
$$\Rightarrow BD^2=(2.4)^2-(1.8)^2$$
$$\Rightarrow BD^2=5.76-3.24$$
$$\Rightarrow BD^2=2.52$$
$$\Rightarrow BD=\sqrt{2.52}=1.587 m$$
Horizontal distance to fly$$=BD+1.2$$
$$\Rightarrow 1.587+1.2\Rightarrow 2.787 $$ m
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Given:
$$\triangle ABC$$ is an Equilateral Triangle.
$$AB=BC=AC$$
$$CD$$ Perpendicular to $$AB$$
To Prove:
$$3AC^2=4CD^2$$
Proof:
In $$\triangle ADC$$
$$\triangle ABC$$ is an Equilateral Triangle.
$$AB=BC=AC$$
$$CD$$ Perpendicular to $$AB$$
To Prove:
$$3AC^2=4CD^2$$
Proof:
In $$\triangle ADC$$
By Pythagoras Theorem,
$$AC^2=AD^2+DC^2\,.....(1)$$
In $$\triangle BDC$$
By Pythagoras Theorem,
$$BC^2=DC^2+BD^2\,.....(2)$$
Adding 1) and 2) We get,
$$2AC^2=2DC^2+AD^2+BD^2$$ $$(Since\,\, AC=BC)$$
Since, $$AD=BD=\dfrac{1}{2}AC$$ $$(Since\,\,AC=AB)$$
$$\therefore$$ $$2AC^2=2DC^2+\dfrac{1}{2}AC^2$$
$$\therefore$$ $$2AC^2-\dfrac{1}{2}AC^2=2DC^2$$
$$\therefore$$ $$3AC^2=4CD^2$$
In fig., $$PS$$ is the bisector of $$\angle QPR$$ of $$\triangle PQR$$. Prove that $$\dfrac{QS}{SR}=\dfrac{PQ}{PR}$$.
Given:
$$\angle QPS=\angle RPS$$
To Prove:
$$\dfrac{QS}{SR}=\dfrac{PQ}{PR}$$
Construction:
Extend $$RP$$ to $$T$$ and
Join $$QT$$ such that $$TQ\parallel PS$$
Proof:
Since, $$QT\parallel PS$$
$$\therefore$$ $$\angle TQP=\angle QPS$$ (Alternate Angles)
Also,
$$\angle QTP=\angle RPS=\angle QPS$$ (Corresponding Angles and $$PS$$ is the bisector of $$\angle QPR$$ of $$\triangle PQR$$)
$$\therefore$$ $$\angle TQP=\angle QTP$$
$$\therefore\,TP=QP\,.......(1)$$
Since, $$QT\parallel PS,$$ by basic proportionality theorem,
$$\therefore$$ $$\dfrac{QS}{SR}=\dfrac{TP}{PR}$$
$$\therefore$$ $$\dfrac{QS}{SR}=\dfrac{PQ}{PR}$$ (From 1)
$$\angle QPS=\angle RPS$$
To Prove:
$$\dfrac{QS}{SR}=\dfrac{PQ}{PR}$$
Construction:
Extend $$RP$$ to $$T$$ and
Join $$QT$$ such that $$TQ\parallel PS$$
Proof:
Since, $$QT\parallel PS$$
$$\therefore$$ $$\angle TQP=\angle QPS$$ (Alternate Angles)
Also,
$$\angle QTP=\angle RPS=\angle QPS$$ (Corresponding Angles and $$PS$$ is the bisector of $$\angle QPR$$ of $$\triangle PQR$$)
$$\therefore$$ $$\angle TQP=\angle QTP$$
$$\therefore\,TP=QP\,.......(1)$$
Since, $$QT\parallel PS,$$ by basic proportionality theorem,
$$\therefore$$ $$\dfrac{QS}{SR}=\dfrac{TP}{PR}$$
$$\therefore$$ $$\dfrac{QS}{SR}=\dfrac{PQ}{PR}$$ (From 1)
Hence proved
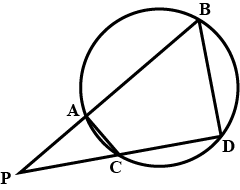
In Fig., two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that:
(i) $$\triangle PAC \sim \triangle PDB$$
(ii) $$PA . PB = PC . PD$$
In fig., $$ABC$$ is a triangle in which $$\angle ABC > 90^o$$ and $$AD \bot CB$$ produced. Prove that $$AC^2 = AB^2 + BC^2 + 2 BC . BD$$.
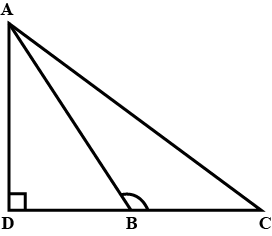
In Fig., $$D$$ is a point on side $$BC$$ of $$\triangle ABC$$ such that $$\dfrac{BD}{CD}=\dfrac{AB}{AC}.$$ Prove that $$AD$$ is the bisector of $$\angle BAC$$.
$$D$$ is a point on $$BC$$ of $$ABC.$$
and $$\dfrac{BD}{CD}=\dfrac{AB}{AC}$$
Let us construct $$BA$$ to $$E$$ such that $$AE = AC.$$ Join $$CE.$$
Now, as $$AE = AC$$,
$$\dfrac{BD}{CD}=\dfrac{AB}{AC}$$
$$\Rightarrow \dfrac{BD}{CD}=\dfrac{AB}{AE}$$
Also, $$\angle AEC=\angle ACE$$ (angles opp. to equal sides of a triangle are equal) ....... (i)
By converse of Basic Proportionality Theorem,
$$DA\parallel CE$$
$$\angle DAC=\angle ACE$$ ...... (ii) ...[Alternate angles]
$$\angle BAD=\angle AEC$$ ......... (iii) ...[Corresponding ∠s]
Also, $$\angle AEC=\angle ACE$$ ...[From (i)]
and $$\angle BAD=\angle DAC$$ ...[From (ii) and (iii)]
So, $$AD$$ is the bisector $$\angle BAC$$.
Two triangles are similar but not congruent and the lengths of the sides of the first are $$6$$ cm, $$11$$ cm and $$12$$ cm. The sides of the second also have integral lengths, and one of them is congruent to a side of the first. What is the perimeter of the second triangle?
In $$\triangle$$ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 8 cm, AB = 12 cm, AE = 12 cm, find CE.
The basic proportionality theorem states that if a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points then it divides the two sides in the same ratio.
Using the basic proportionality theorem, we have
$$\frac { AD }{ AB } =\frac { AE }{ AC } =\frac { DE }{ BC } \\ \Rightarrow \frac { AD }{ AB } =\frac { AE }{ AC } \\ \Rightarrow \frac { 8 }{ 12 } =\frac { 12 }{ AC } \\ \Rightarrow 8AC=12\times 12\\ \Rightarrow 8AC=144\\ \Rightarrow AC=\frac { 144 }{ 8 } =18$$
Now, $$CE=AC-AE=18-12=6$$ cm
Hence, $$CE=6$$ cm.
In $$\triangle$$PQR 2PM = 3 PN and 2PQ = 3PR. Prove that MQRN is a trapezium
(i) $$\dfrac{2PM}{2PQ} = \dfrac{3 PN}{3 PR}$$ [$$\because$$ Data]
$$\dfrac{PM}{PQ} = \dfrac{PN}{PR}$$
$$\therefore MN || QR$$ [$$\because$$ Converse of corollary 2 of B.P.T.]
(ii) Since $$QP$$ and $$RP$$ intersects at '$$P$$',
$$MQ$$ cannot be parallel to $$RN$$
$$\Rightarrow MQRN$$ is a trapezium
[$$\because$$ If only one pair of opposite sides of a quadrilateral is parallel then it is a trapezium]
$$\dfrac{PM}{PQ} = \dfrac{PN}{PR}$$
$$\therefore MN || QR$$ [$$\because$$ Converse of corollary 2 of B.P.T.]
(ii) Since $$QP$$ and $$RP$$ intersects at '$$P$$',
$$MQ$$ cannot be parallel to $$RN$$
$$\Rightarrow MQRN$$ is a trapezium
[$$\because$$ If only one pair of opposite sides of a quadrilateral is parallel then it is a trapezium]
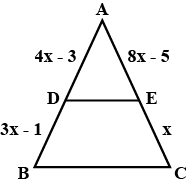
In $$\triangle$$ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = $$4x-3$$, BD = $$3x-1$$, AE = $$8x-7$$ and CE = $$5x-3$$ find the value $$x$$.
The basic proportionality theorem states that if a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points then it divides the two sides in the same ratio.
Using the basic proportionality theorem, we have
$$\frac { AD }{ BD } =\frac { AE }{ AC } \\ \Rightarrow \frac { 4x-3 }{ 3x-1 } =\frac { 8x-5 }{ x } \\ \Rightarrow x(4x-3)=(3x-1)(8x-5)\\ \Rightarrow 4x^{ 2 }-3x=3x(8x-5)-1(8x-5)\\ \Rightarrow 4x^{ 2 }-3x=24x^{ 2 }-15x-8x+5\\ \Rightarrow 4x^{ 2 }-3x=24x^{ 2 }-23x+5\\ \Rightarrow 24x^{ 2 }-23x+5-4x^{ 2 }+3x=0\\ \Rightarrow 20x^{ 2 }-20x+5=0\\ \Rightarrow 5(4x^{ 2 }-4x+1)=0\\ \Rightarrow 4x^{ 2 }-4x+1=0\\ \Rightarrow (2x)^{ 2 }-(2\times 2x\times 1)x+1^{ 2 }=0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (∵(a-b)^{ 2 }=a^{ 2 }+b^{ 2 }-2ab)\\ \Rightarrow (2x-1)^{ 2 }=0\\ \Rightarrow (2x-1)=0\\ \Rightarrow 2x=1\\ \Rightarrow x=\frac { 1 }{ 2 }$$
Hence, $$x=\frac { 1 }{ 2 }$$.
Prove that: In a trapezium, the line joining the midpoints of non-parallel sides is
(i) Parallel to the parallel sides and
(ii) Half of the sum of the parallel sides.
In $$\triangle$$PQR, E and F are points on the sides PQ and PR respectively. verify EF || QR. PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm, FR = 2.4 cm.
The basic proportionality theorem states that if a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points then it divides the two sides in the same ratio.
Using the basic proportionality theorem, we have
$$\frac { PE }{ EQ } =\frac { 3.9 }{ 3 } =1.3\\ \frac { PF }{ FR } =\frac { 3.6 }{ 2.4 } =1.5$$
Since $$\frac { PE }{ EQ } ≠\frac { PF }{ FR }$$
Hence, $$EF$$ is not parallel to $$QR$$.
In $$\triangle$$PQR, E and F are points on the sides PQ and PR respectively. Then verify that EF || QR if PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm, PF = 0.36 cm.
The basic proportionality theorem states that if a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points then it divides the two sides in the same ratio.
We find the following:
$$EQ=PQ-PE=1.28-0.18=1.10$$ cm
$$FR=PR-PF=2.56-0.36=2.20$$ cm
Using the basic proportionality theorem, we have
$$\frac { PE }{ EQ } =\frac { 0.18 }{ 1.10 } =0.1636\\ \frac { PF }{ FR } =\frac { 0.36 }{ 2.20 } =0.1636$$
Since $$\frac { PE }{ EQ } =\frac { PF }{ FR }$$
Hence, $$EF$$ is parallel to $$QR$$.
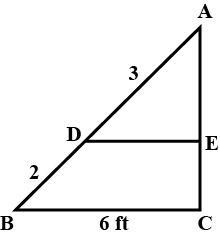
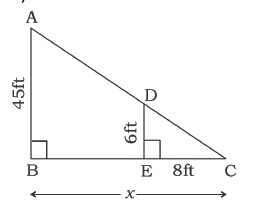
At a certain time of the day, a man 6 feet tall, casts his shadow 8 feet long. Find the length of the shadow cast by a building 45 feet high, at the same time which is next to the man.
Let the length of the shadow of the building $$= x$$.
In $$\triangle $$ABC, AB || DE (both are standing vertically on the ground)
$$\dfrac{AB}{DE} = \dfrac{BC}{EC}$$
$$\dfrac{45}{6} = \dfrac{x}{8} \Rightarrow x = \dfrac{45 \times 8}{6} = 60\ ft$$
$$\therefore $$ Length of shadow cast by the building is $$60\ ft$$.
In $$\triangle $$ABC, AB || DE (both are standing vertically on the ground)
$$\dfrac{AB}{DE} = \dfrac{BC}{EC}$$
$$\dfrac{45}{6} = \dfrac{x}{8} \Rightarrow x = \dfrac{45 \times 8}{6} = 60\ ft$$
$$\therefore $$ Length of shadow cast by the building is $$60\ ft$$.
In $$\triangle$$PQR, E and F are points on the sides PQ and PR respectively. Verify EF || QR. Given that PE = 4 cm, QE = 4.5 cm, PF = 8 cm and FR = 9 cm.
The basic proportionality theorem states that if a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points then it divides the two sides in the same ratio.
Using the basic proportionality theorem, we have
$$\dfrac { PE }{ EQ } =\dfrac { 4 }{ 4.5 } =0.88\\ \dfrac { PF }{ FR } =\dfrac { 8 }{ 9 } =0.88$$
Since $$\dfrac { PE }{ EQ } =\dfrac { PF }{ FR }$$
Hence, $$EF$$ is parallel to $$QR$$.
In $$\triangle$$ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 6 cm, DB = 9 cm and AE = 8 cm, find AC.
The basic proportionality theorem states that if a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points then it divides the two sides in the same ratio.
Using the basic proportionality theorem, we have
$$\frac { AD }{ AB } =\frac { AE }{ AC } =\frac { DE }{ BC } \\ \Rightarrow \frac { AD }{ AB } =\frac { AE }{ AC } \\ \Rightarrow \frac { 6 }{ 15 } =\frac { 8 }{ AC } \\ \Rightarrow 6AC=15\times 8\\ \Rightarrow 6AC=120\\ \Rightarrow AC=\frac { 120 }{ 6 } =20$$
Hence, $$AC=20$$ cm.
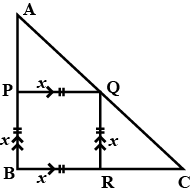
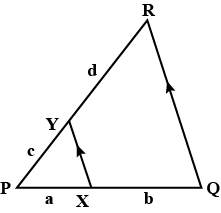
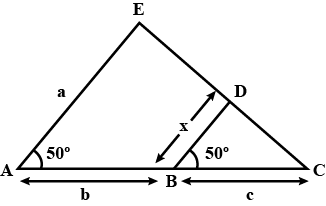
Study the adjoining figure. Write the ratios in relation to basic proportionality theorem, in terms of $$a, b, c$$ and $$d$$.
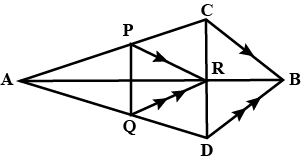
In the figure, $$PR \parallel BC$$ and $$QR \parallel BD$$. Prove that $$PQ || CD$$.
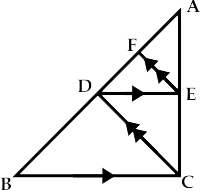
In $$\triangle ABC, DE \parallel BC$$ and $$CD \parallel EF$$. Prove that $$AD^2 = AF \times AB$$.
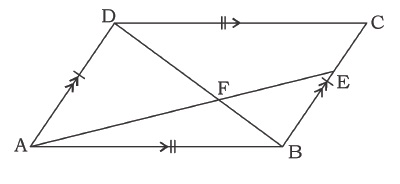
The diagonal BD of parallelogram ABCD intersects AE at 'F'. 'E' is any point on BC.
Prove that DE.EF = FB. FA
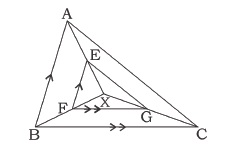
X is any point inside $$\triangle$$ABC. XA, XB and XC are joined. 'E' is any point on AX. If EF || AB, FG || BC. Prove that EG || AC.
A girl of height 90 cm is walking away from the base of a lamp - post at a speed of 1.2 m/s. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
Let the girl of height be at point $$D$$ on the ground from the lamp post after $$4$$ seconds. Therefore,
$$AD = 1.2$$ m/sec $$× 4$$ sec $$= 4.8$$ m $$= 480$$ cm
Suppose the length of the shadow of the girl be $$x$$ cm when she at position $$D$$. Therefore,
$$BD = x$$ cm
In $$∆BDE$$ and $$∆BAC$$,
$$∠BDE = ∠BAC$$ $$(90°)$$
$$∠DBE = ∠ABC$$ (Common)
Thus, $$∆BDE ∼ ∆BAC$$ (AA similarity)
$$\dfrac { BE }{ BC } =\dfrac { DE }{ AC } =\dfrac { BD }{ AB }$$
( Corresponding sides are proportional )
$$\dfrac { 90 }{ 360 } =\dfrac { x }{ 480+x } \\ \Rightarrow \dfrac { 1 }{ 4 } =\dfrac { x }{ 480+x } \\ \Rightarrow 4x=480+x\\ \Rightarrow 4x-x=480\\ \Rightarrow 3x=480\\ \Rightarrow x=\dfrac { 480 }{ 3 } =160$$
Hence length of her shadow after $$4$$ seconds is $$160$$ cm.
In the figure
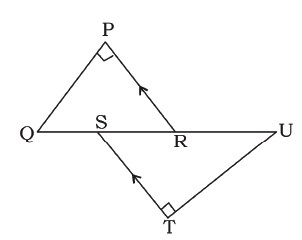
$$\angle QPR = \angle UTS = 90^o$$ and PR || TS
Prove that $$\triangle PQR \sim \triangle TUS$$
In $$\triangle$$ABC, $$\angle B = \angle C$$, D and E are the points on AB and AC such that BD = CE, prove that DE || BC.
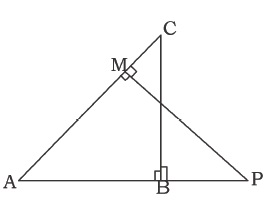
In the adjoining figure $$\angle ABC = 90^o$$ and $$\angle AMP = 90^o$$
Prove that
(i) $$\triangle ABC \sim \triangle AMP$$
(ii) $$\dfrac{CA}{PA} = \dfrac{BC}{MP}$$
If the diagonals of a quadrilateral divide each other proportionally, then prove that the quadrilateral is a trapezium.
Let $$ABCD$$ be a quadrilateral as shown in the above figure:
Diagonal $$AC$$ and $$BD$$ divide each other proportionately that is,
$$\dfrac { AO }{ OC } =\dfrac { BO }{ OD }$$
Therefore, the triangles containing these sides are equiangular that is $$△AOB$$ and $$△COD$$ and thus,
$$∠OAB = ∠OCD$$
$$∠OBA = ∠ODC$$ (Alternate angles)
Therefore, $$DC||AB$$
Hence, $$ABCD$$ is a trapezium.
A ladder resting against a vertical wall has its foot on the ground at a distance of 6ft. from the wall. A man on the ground climbs two - thirds of the ladder. What will be his distance from the wall now?
Man climb $$\cfrac{2}{3}$$ of the ladder.
So, in $$\triangle ADE$$ & $$\triangle ABC$$
$$\angle A=\angle A$$ (common)
$$\angle ADE=\angle ABC $$ (corresponding Angle)
$$\angle AED=\angle ACB$$ (corresponding Angle)
$$\triangle ADE\sim\triangle ABC$$
$$\Longrightarrow \cfrac{AD}{AB}=\cfrac{DE}{BC}$$
$$\Longrightarrow \cfrac{3}{5}=\cfrac{DE}{6}\Longrightarrow DE=\cfrac{18}{5}=3.6ft$$
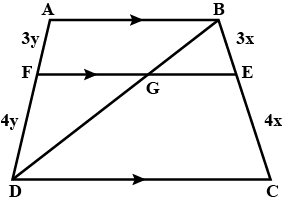
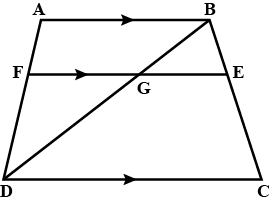
In the trapezium $$ABCD$$
$$AB \parallel DC, EF \parallel AB, DC = 2AB$$ and $$\dfrac{BE}{EC} = \dfrac{3}{4}$$. Prove that $$7EF = 10AB$$.
Let us consider that
$$\cfrac {BE}{EC}=\cfrac {AF}{FD}=\cfrac 34$$
From $$\triangle BDC$$,
$$\cfrac {GE}{CD}=\cfrac 37$$
$$\Rightarrow \cfrac {GE}{2AB}=\cfrac 37$$
$$\therefore GE=\cfrac {6AB}7$$[Since $$CD=2AB$$]....(i)
From $$\triangle DAB$$
$$\Rightarrow \cfrac {DF}{AF}=\cfrac 43$$
$$\therefore \cfrac {FG}{AB}=\cfrac 47$$
$$\therefore GF=\cfrac {4AB}7$$....(ii)
Adding (i) and (ii),
$$GE+FG=\cfrac {6AB}7+\cfrac {4AB}7$$
$$\Rightarrow FE=\cfrac {10AB}7$$
$$\Rightarrow 7FE=10AB$$
$$AM = 8x^2, MC = 2x^2$$, then find BM and AB.
In $$\triangle ABC, \angle ABC = 90^o, BD \perp AC$$ If $$BD = 8$$ cm, $$AD = 4$$ cm, find $$CD$$
In $$\triangle ABC, \angle ABC = 90^o, BD \perp AC$$ If $$AB = 5.7$$ cm, $$BD = 3.8$$ cm, $$CD = 5.4$$ cm, find $$BC$$
In given figure $$\triangle $$ABC and $$\triangle$$BDC are on the same base BC
Prove that $$\dfrac{area(\triangle ABC)}{area(\triangle DBC)} = \dfrac{AO}{DO}$$
Prove that $$\dfrac{area(\triangle ABC)}{area(\triangle DBC)} = \dfrac{AO}{DO}$$
In the given figure, construct $$AM$$ and $$DN$$ such that $$△ABC$$ and $$△BDC$$ are on the same base $$BC$$ with $$AM⊥BC$$ and $$DN⊥BC$$ as shown in the above figure:
We know that the area of a triangle is $$A=\dfrac {1}{2}\times b\times h$$ where $$b$$ is the base and $$h$$ is the height of the triangle.
Here, area of $$△ABC$$ is $$A_1=\dfrac {1}{2}\times BC\times AM$$ and area of $$△BDC$$ is $$A_2=\dfrac {1}{2}\times BC\times DN$$
Dividing both the areas, we get
$$\dfrac { { A }_{ 1 } }{ { A }_{ 2 } } =\dfrac { \dfrac { 1 }{ 2 } \times BC\times AM }{ \dfrac { 1 }{ 2 } \times BC\times DN } =\dfrac { AM }{ DN } \quad .......(1)$$
Now, consider $$△AOM$$ and $$△DON$$,
$$∠AMO=∠DNO=90^{ 0 }$$ (Construction)
$$∠AOM=∠DON$$ (Vertically opposite angles)
Therefore, $$△AOM∼△DON$$ (A similarity criterion)
Thus,
$$\dfrac { AM }{ DN } =\dfrac { AO }{ DO } \quad .......(2)$$
Substitute equation $$(2)$$ in equation $$(1)$$ as follows:
$$\dfrac { { A }_{ 1 } }{ { A }_{ 2 } } =\dfrac { AM }{ DN } =\dfrac { AO }{ DO } $$
$$\Rightarrow \dfrac { { A }rea(△ABC) }{ { A }rea(△BDC) } =\dfrac { AO }{ DO }$$ $$[hence \quad proved]$$
Rhombus $$PQRB$$ is inscribed in $$\triangle ABC$$ such that $$\angle B$$ is one of the its angle, $$P$$, $$Q$$ and $$R$$ lie on $$AB$$, $$AC$$ and $$BC$$ respectively. If $$AB = 12 \text{ cm}$$ and $$BC = 6 \text{ cm}$$ find the sides of rhombus $$PQRB$$.
In $$\triangle ABC, PQ || BC$$ ......... ($$\because$$ In a rhombus, opposite sides are parallel)
$$\therefore \dfrac{AP}{AB} = \dfrac{PQ}{BC}$$ ......... (Using Corollary of Thales theorem)
$$\implies \dfrac{12 - x}{12} = \dfrac{x}{6}$$
$$\implies 12 x = 72 - 6x$$
$$\implies 18 x = 72$$
$$\therefore x = 4\ cm$$
The sides of the rhombus is $$4$$ cm each.
$$\therefore \dfrac{AP}{AB} = \dfrac{PQ}{BC}$$ ......... (Using Corollary of Thales theorem)
$$\implies \dfrac{12 - x}{12} = \dfrac{x}{6}$$
$$\implies 12 x = 72 - 6x$$
$$\implies 18 x = 72$$
$$\therefore x = 4\ cm$$
The sides of the rhombus is $$4$$ cm each.
In △ABC,∠ABC=90o,BD⊥AC△ABC,∠ABC=90o,BD⊥AC△ABC,∠ABC=90o,BD⊥AC. If $$AB=75AB=75$$
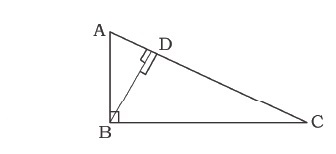
In $$\triangle PQR, \angle PQR = 90^o, QD \perp PR$$.
If $$PD = 4DR$$. Prove that $$PQ = 2QR$$.
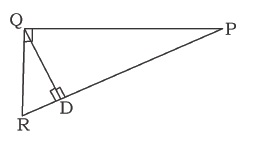
In the adjacent figure $$\triangle ABC \sim \triangle PQR$$, and $$\angle C = 53^{\circ}$$. Find the side $$PR$$ and $$\angle P$$
$$\triangle ABC \sim \triangle PQR$$
When two triangles are similar their corresponding angles are equal and corresponding angles are equal and corresponding sides are in proportion.
$$\dfrac {PR}{AC} = \dfrac {PQ}{AB}\Rightarrow \dfrac {PR}{5} = \dfrac {2}{4}$$
$$PR = \dfrac {2}{4} \times 5 = 2.5$$
Again
$$\angle R = \angle C = 53^{\circ}$$
Sum of all three angles in a triangle as $$180^{\circ}$$
i.e. $$\angle P + \angle Q + \angle R = 180^{\circ}$$
$$\angle P = 90^{\circ} + 53^{\circ} = 180^{\circ}$$
$$\angle P = 180^{\circ} - 143^{\circ} = 37^{\circ}$$
When two triangles are similar their corresponding angles are equal and corresponding angles are equal and corresponding sides are in proportion.
$$\dfrac {PR}{AC} = \dfrac {PQ}{AB}\Rightarrow \dfrac {PR}{5} = \dfrac {2}{4}$$
$$PR = \dfrac {2}{4} \times 5 = 2.5$$
Again
$$\angle R = \angle C = 53^{\circ}$$
Sum of all three angles in a triangle as $$180^{\circ}$$
i.e. $$\angle P + \angle Q + \angle R = 180^{\circ}$$
$$\angle P = 90^{\circ} + 53^{\circ} = 180^{\circ}$$
$$\angle P = 180^{\circ} - 143^{\circ} = 37^{\circ}$$
In the above figure find the ratio between the $$\triangle$$AOB and $$\triangle$$COD, if $$AB = 3CD$$.
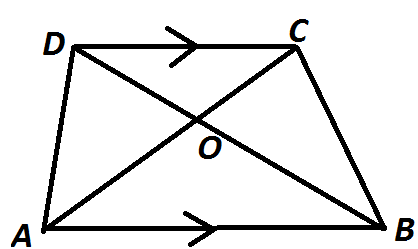
$$ABC$$ is a right angled triangle with $$\angle ABC={ 90 }^{ o }$$. $$D$$ is any point on $$AB$$ and $$DE$$ is perpendicular to $$AC$$. Prove that :
(i) $$\triangle ADE\sim \triangle ACB$$.
(ii) If $$AC=13 cm$$, $$BC=5 cm$$ and $$AE=4 cm$$. Find $$DE$$ and $$AD$$.
(iii) Find, area of $$\triangle ADE : $$ area of quadrilateral $$BCED$$.
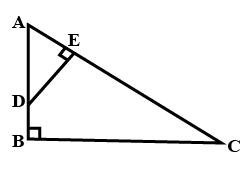
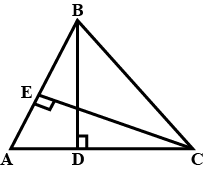
In the given figure, $$AB$$ and $$DE$$ are perpendicular to $$BC$$.
(i) Prove that $$\triangle ABC \sim \triangle DEC$$
(ii) If $$AB = 6\ cm: DE = 4\ cm$$ and $$AC = 15\ cm$$, calculate $$CD$$.
(iii) Find the ratio of the area of $$\triangle ABC$$ : area of $$\triangle DEC$$.
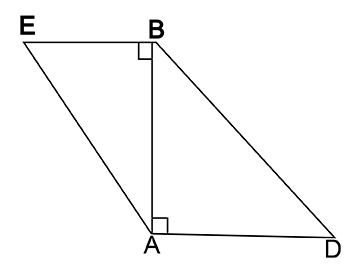
In the given figure drawn, seg $$BE \perp$$ set $$AB$$ and seg $$BA \perp$$ seg $$AD$$.
If $$BE=6$$ and $$AD=9$$, find $$\dfrac { A\left( \Delta ABE \right) }{ A\left( \Delta BAD \right) } $$
Draw two congruent figures. Are they similar? Explain
The congruent figures are similar as they are same in shape when compared.
Congruent figures are identical in size, shape and measure. The corresponding sizes between two triangles are sides in the same relative position. Two figures are similar if they have the same shape, but not necessarily the same size.
In the trapezium $$ABCD,\; AB \parallel DC$$ and $$\triangle AED \sim \triangle BEC$$. Prove that $$AD = BC.$$
To Prove: $$AD = BC$$
Proof: Compare $$\triangle EDC$$ and $$\triangle EBA$$
$$\angle EDC = \angle EBA$$ [Alternate Angles]
$$\angle ECD = \angle EAB$$ [Alternate Angles]
By $$AA$$ criterion of similarity,
$$\triangle EDC \sim \triangle EBA$$
$$\triangle EDC \sim \triangle EBA$$
$$\Rightarrow \dfrac{ED}{EB} = \dfrac{EC}{EA}$$ [By CPST]
$$\Rightarrow \dfrac{ED}{EC} = \dfrac{EB}{EA}\quad\quad\quad\dots(i)$$
But, $$\triangle AED \sim \triangle BEC$$ [Given]
$$\Rightarrow \dfrac{ED}{EC} = \dfrac{EA}{EB} = \dfrac{AD}{BC}$$ $$\dots(ii)$$ [By CPST]
$$\dfrac{EB}{EA} = \dfrac{EA}{EB} $$ [From $$(i)$$ and $$(ii)$$]
$$\Rightarrow EA^2 = EB^2$$
$$\Rightarrow EA = EB$$
Hence, from equation $$(ii),$$
$$\dfrac{AD}{BC} = 1$$
$$\dfrac{AD}{BC} = 1$$
$$\Rightarrow AD = BC$$
Hence proved.
In $$\triangle ABC, \angle ABC = \angle DAC, AB = 8\ cm, AC = 4\ cm, AD = 5\ cm$$. Prove that $$\triangle ACD$$ is similar to $$\triangle BCA$$
$$\Delta DEF \sim \Delta MNK$$. If $$DE=2, MN=5$$, then find the value of $$\cfrac{Area(\Delta DEF)}{Area(MNK)}$$
In $$\triangle ABC$$, $$AL, BM$$ and $$CN$$ are the altitudes which intersect at 'O'.
Prove that (i) $$\triangle AMB \sim \triangle ANC$$ (ii) $$\dfrac{AN}{BN}. \dfrac{BL}{CL}. \dfrac{CM}{AM} = 1$$
In $$\triangle AMB$$ and $$\triangle ANC$$
$$\angle AMB = \angle ANC = 90^o$$ .......... ($$\because$$ Data)
$$\angle BAM = \angle NAC $$
$$\angle AMB = \angle ANC = 90^o$$ .......... ($$\because$$ Data)
$$\angle BAM = \angle NAC $$
$$\angle ABM = \angle ACN$$
$$\therefore \triangle AMB \sim \triangle ANC$$ ......... [By AAA rule]
Also, $$\triangle BLA \sim \triangle BNC$$
and $$\triangle BMC \sim \triangle ALC$$
Now, $$\triangle AMB \sim \triangle ANC$$
and $$\triangle BMC \sim \triangle ALC$$
Now, $$\triangle AMB \sim \triangle ANC$$
$$\therefore \dfrac{AN}{AM} = \dfrac{AC}{AB}$$
$$\triangle BLA \sim \triangle BNC$$
$$\therefore \dfrac{BL}{BN} = \dfrac{AB}{BC}$$
$$\triangle BMC \sim \triangle ALC$$
$$\therefore \dfrac{CM}{CL} = \dfrac{BC}{AC}$$
$$\dfrac{AN}{AM} \times \dfrac{BL}{BN} \times \dfrac{CM}{CL} = \dfrac{AC}{AB} \times \dfrac{AB}{BC} \times \dfrac{BC}{AC}$$
$$\therefore \dfrac{AN}{BN} \times \dfrac{BL}{LC} \times \dfrac{CM}{AM} = 1$$
or $$AN \times BL \times CM = BN \times LC \times AM$$
Take two similar shapes. If you slide rotate or flip one of them, does the similarity remain.
In the figure D, E are points on the sides AB and AC respectively of $$\triangle$$ABC such that $$area(\triangle DBC) = area (\triangle EBC)$$. Prove that DE || BC.
Given D and E are point on sides AB and AC respectively of triangle ABC such that $$Area(\Delta DBC)$$ $$=$$ $$Area(\Delta EBC)$$.
Given that $$Area(\Delta DBC)$$ $$=$$ $$Area(\Delta EBC)$$.
Then the height of triangle DBC and Triangle EBC are the same because both triangles are the same
Then it possible that both triangle on the same base and between parallel line BC and DE
Therefore, they will lie between the same parallel lines.
$$\therefore BC \parallel DE$$ $$[hence \, proved]$$
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then prove that the two sides are divided in the same ratio.
Given:
$$DE || BC$$
To prove that:
$$\cfrac{EC}{AE} = \cfrac{BD}{AD}$$
Proof:
$$\angle AED = \angle ACB$$ Corresponding angles
$$\angle ADE = \angle ABC$$ Corresponding angles
$$\angle EAD$$ is common to both the triangles
$$\Rightarrow \Delta AED \sim \Delta ACB$$ by $$AAA$$ similarity
$$\Rightarrow \cfrac{AC}{AE} = \cfrac{AB}{AD}$$
$$\Rightarrow \cfrac{AE+EC}{AE} = \cfrac{AD + BD}{AD}$$
$$\Rightarrow \cfrac{EC}{AE} = \cfrac{BD}{AD}$$
Hence proved
Prove that, if a line parallel to a side of a triangle intersect the other sides in two distinct points, then the line divides those sides in proportion.
Given: In a $$\triangle PQR$$, line $$l\parallel $$ side $$QR$$, line $$l$$ intersect the sides $$PQ$$ and $$PR$$ in two distinct points $$M$$ and $$N$$ respectively.
To prove: $$\dfrac {PM}{MQ} = \dfrac {PN}{NR}$$ ... (i)
Construction: $$seg QN$$ and $$seg RM$$ are drawn.
Proof: $$\dfrac {A(\triangle PMN)}{A(\triangle QMN)} = \dfrac {PM}{MQ}$$
(Both triangles have equal height with common vertex $$M$$)
$$\therefore \dfrac {A(\triangle PMN)}{A(\triangle RMN)} = \dfrac {PN}{NR} $$ ... (ii)
But $$A(\triangle QMN) = A(\triangle RMN)$$, because they are between parallel lines $$MN$$ and $$QR$$ and have equal height corresponding to their common base $$MN$$ ..... (iii)
From (i), (ii) and (iii), we get
$$\dfrac {A(\triangle PMN)}{A(\triangle QMN)} = \dfrac {A(\triangle PMN)}{A(\triangle RMN)}$$
$$\therefore \dfrac {PM}{MQ} = \dfrac {PN}{NR}$$ $$[hence \, proved]$$
To prove: $$\dfrac {PM}{MQ} = \dfrac {PN}{NR}$$ ... (i)
Construction: $$seg QN$$ and $$seg RM$$ are drawn.
Proof: $$\dfrac {A(\triangle PMN)}{A(\triangle QMN)} = \dfrac {PM}{MQ}$$
(Both triangles have equal height with common vertex $$M$$)
$$\therefore \dfrac {A(\triangle PMN)}{A(\triangle RMN)} = \dfrac {PN}{NR} $$ ... (ii)
But $$A(\triangle QMN) = A(\triangle RMN)$$, because they are between parallel lines $$MN$$ and $$QR$$ and have equal height corresponding to their common base $$MN$$ ..... (iii)
From (i), (ii) and (iii), we get
$$\dfrac {A(\triangle PMN)}{A(\triangle QMN)} = \dfrac {A(\triangle PMN)}{A(\triangle RMN)}$$
$$\therefore \dfrac {PM}{MQ} = \dfrac {PN}{NR}$$ $$[hence \, proved]$$
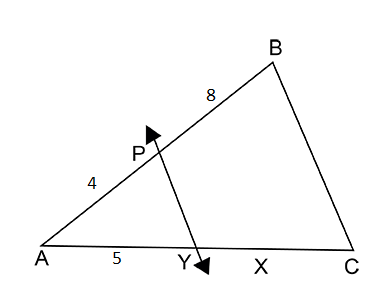
In the given figure, line $$PY \parallel $$ side $$BC$$, $$AP=4$$, $$PB=8$$, $$AY=5$$ and $$YC=x$$. Find $$x$$.
$$\Delta ABC \sim \Delta PQR$$ and $$A(\Delta ABC) = 144 cm^2$$ and $$A(\Delta PQR) = 100 cm^2$$. If BC = 12 cm, then find the value of QR.
Prove that "If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side".
Given : The line $$l$$ intersects the sides $$PQ$$ and side $$PR$$ of $$\Delta PQR$$ in the points $$M$$ and $$N$$ respectively such that $$\dfrac{PM}{MQ} = \dfrac{PN}{NR}$$ and $$P-M-Q$$, $$P-N-R$$.
To Prove : Line $$l$$ $$\parallel$$ Side $$QR$$
Proof : Let us consider that line $$l$$ is not parallel to the side $$QR$$. Then there must be another line passing through $$M$$ which is parallel to the side $$QR$$.
Let line $$MK$$ be that line.
Line $$MK$$ intersects the side $$PR$$ at $$K$$, $$\left(P-K-R\right)$$
In $$\Delta PQR$$, line $$MK \parallel $$ side $$QR$$
$$\therefore$$ $$\dfrac{PM}{MQ} = \dfrac{PK}{KR}$$ ....(1) (B.P.T.)
But $$\dfrac{PM}{MQ}=\dfrac{PN}{NR}$$ ....(2) (Given)
$$\therefore$$ $$\dfrac{PK}{KR}=\dfrac{PN}{NR}$$ [From (1) and (2)]
$$\therefore$$ $$\dfrac{PK+KR}{KR} = \dfrac{PN+NR}{NR}$$ ($$P-K-R$$ and $$P-N-R$$)
$$\therefore$$ the points $$K$$ and $$N$$ are not different.
$$\therefore$$ line $$MK$$ and line $$MN$$ coincide
$$\therefore$$ line $$MN \parallel$$ Side $$QR$$
Hence, the converse of B.P.T. is proved.
To Prove : Line $$l$$ $$\parallel$$ Side $$QR$$
Proof : Let us consider that line $$l$$ is not parallel to the side $$QR$$. Then there must be another line passing through $$M$$ which is parallel to the side $$QR$$.
Let line $$MK$$ be that line.
Line $$MK$$ intersects the side $$PR$$ at $$K$$, $$\left(P-K-R\right)$$
In $$\Delta PQR$$, line $$MK \parallel $$ side $$QR$$
$$\therefore$$ $$\dfrac{PM}{MQ} = \dfrac{PK}{KR}$$ ....(1) (B.P.T.)
But $$\dfrac{PM}{MQ}=\dfrac{PN}{NR}$$ ....(2) (Given)
$$\therefore$$ $$\dfrac{PK}{KR}=\dfrac{PN}{NR}$$ [From (1) and (2)]
$$\therefore$$ $$\dfrac{PK+KR}{KR} = \dfrac{PN+NR}{NR}$$ ($$P-K-R$$ and $$P-N-R$$)
$$\therefore$$ the points $$K$$ and $$N$$ are not different.
$$\therefore$$ line $$MK$$ and line $$MN$$ coincide
$$\therefore$$ line $$MN \parallel$$ Side $$QR$$
Hence, the converse of B.P.T. is proved.
In $$\triangle RST$$, line $$PQ\parallel seg ST$$, $$R-P-S$$ and $$R-Q-T$$. If $$RP=4,PS=8,RQ=3$$, then find $$QT$$.
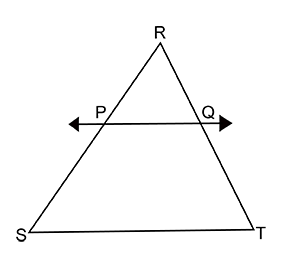
In the following figure drawn, line $$PY$$ $$\parallel$$ side $$BC$$, $$AP=6$$, $$PB=12$$, $$AY=5$$, $$YC=x$$, then find $$x$$.
If $$\triangle LMN\sim \triangle RST$$ and $$Ar\left( \triangle LMN \right) =100\ sq.cm,\ Ar\left( \triangle RST \right) =144\ sq.cm$$ and $$LM=5\ cm,$$ then find $$RS.$$
In the given figure ABC is a triangle. If $$\dfrac{AD}{AB} = \dfrac{AE}{AC}$$, then prove that DE || BC.
Prove that in a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle.
$$ {\textbf{Step - 1: Apply pythagoras theorem}} $$
$$ {\text{Given: - ABC is a triangle}} $$
$$ {\text{A}}{{\text{C}}^2} = {\text{A}}{{\text{B}}^2} + {\text{B}}{{\text{C}}^2} $$
$$ {\text{In }}\Delta{\text{PQR}} $$
$$ {\text{P}}{{\text{R}}^2} = {\text{P}}{{\text{Q}}^2} + {\text{Q}}{{\text{R}}^2}\;\;{\text{(by pythagoras theorem)}} $$
$$ \Rightarrow {\text{P}}{{\text{R}}^2} = {\text{A}}{{\text{B}}^2} + {\text{B}}{{\text{C}}^2}\;......(1)\;(\because AB = PQ\;{\text{and QR = BC}}) $$
$$ {\text{given}} $$
$$ {\text{A}}{{\text{C}}^{\text{2}}}{\text{ = A}}{{\text{B}}^{\text{2}}}{\text{ + B}}{{\text{C}}^2}\;\;.....(2) $$
$$ {\text{From equation 1 and 2 we have}} $$
$$ {\text{A}}{{\text{C}}^2} = P{R^2} $$
$$ \Rightarrow {\text{AC = PR}}\;\;....{\text{(3)}} $$
$$ {\textbf{Step - 2: Find congruency }} $$
$$ {\text{Now}} {\text{in }}{{\Delta }}{\text{ABC and } \Delta PQR} $$
$$ {\text{i)AB = PQ}} $$
$$ {\text{ii)BC = QR}} $$
$$ {\text{iii)AC = PR}}\;{\text{(from}}\;{\text{3)}} $$
$$ \therefore {\Delta \text{ ABC}} \cong \Delta{\text{PQR(by sss congruency)}} $$
$$ {\text{Therefore, by CPCT}} $$
$$ \angle {\text{B = }}\angle {\text{Q}} $$
$$ \because \angle {\text{Q}} = {90^ \circ } $$
$$ \therefore \angle {\text{B}} = {90^ \circ } $$
$$ {\textbf{Hence,Proved}} $$
The points $$D$$ and $$E$$ are on the sides $$AB$$ and $$AC$$ of $$\triangle ABC$$ respectively, such that $$DE\parallel BC$$. If $$AB = 3\ AD$$ and the area of $$\triangle ABC$$ is $$72\ \text{cm}^{2}$$, then find the area of the quadrilateral $$DBCE$$
State and prove the Pythagoras theorem.
Statement: In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Given: ABC is a triangle in which $$\angle ABC={90}^{\circ}$$
Construction: Draw $$BD\bot AC$$.
Proof:
In $$\triangle ADB$$ and $$\triangle ABC$$
$$\angle A=\angle A$$ [Common angle]
$$\angle ADB=\angle ABC$$ [Each $${90}^{\circ}$$]
$$\triangle ADB \sim \triangle ABC$$ [$$A-A$$ Criteria]
So, $$\dfrac {AD}{AB}=\dfrac{AB}{AC}$$
Now, $${AB}^{2}=AD\times AC$$ ..........(1)
Similarly,
$${BC}^{2}=CD\times AC$$ ..........(2)
Adding equations (1) and (2) we get,
$${AB}^{2}+{BC}^{2}=AD\times AC+CD\times AC$$
$$=AC(AD+CD)$$
$$=AC\times AC$$
$$\therefore{AB}^{2}+{BC}^{2}={AC}^{2}$$ $$[hence \, proved]$$
State and prove Basic Proportionality theorem.
Basic Proportionality Theorem states that, if a line is parallel to a side of a triangle which intersects the other sides into two distinct points,then the line divides those sides of the triangle in proportion.
Let $$ABC$$ be the triangle.
The line $$l$$ parallel to $$BC$$ intersect $$AB$$ at $$D$$ and $$AC$$ at $$E$$.
To prove $$\dfrac{AD}{DB}=\dfrac{AE}{EC}$$
Join $$BE,CD$$
Draw $$EF \perp AB$$, $$DG \perp CA$$
Since $$EF \perp AB$$,
$$EF$$ is the height of triangles $$ADE$$ and $$DBE$$
Area of $$\triangle ADE = \dfrac{1}{2} \times$$ base $$\times$$ height$$=\dfrac{1}{2}AD \times EF$$
Area of $$\triangle DBE = \dfrac{1}{2} \times DB \times EF$$
$$\dfrac { area\quad of\quad \Delta ADE }{ area\quad of\quad \Delta DBE } =\dfrac { \dfrac { 1 }{ 2 } \times AD\times EF }{ \dfrac { 1 }{ 2 } \times DB\times EF } =\dfrac { AD }{ DB } $$ ........(1)
Similarly,
$$\dfrac { area\quad of\quad \Delta ADE }{ area\quad of\quad \Delta DCE } =\dfrac { \dfrac { 1 }{ 2 } \times AE\times DG }{ \dfrac { 1 }{ 2 } \times EC\times DG } =\dfrac { AE }{ EC } $$ ......(2)
$$\dfrac { area\quad of\quad \Delta ADE }{ area\quad of\quad \Delta DBE } =\dfrac { \dfrac { 1 }{ 2 } \times AD\times EF }{ \dfrac { 1 }{ 2 } \times DB\times EF } =\dfrac { AD }{ DB } $$ ........(1)
Similarly,
$$\dfrac { area\quad of\quad \Delta ADE }{ area\quad of\quad \Delta DCE } =\dfrac { \dfrac { 1 }{ 2 } \times AE\times DG }{ \dfrac { 1 }{ 2 } \times EC\times DG } =\dfrac { AE }{ EC } $$ ......(2)
But $$\Delta DBE$$ and $$\Delta DCE$$ are the same base $$DE$$ and between the same parallel straight line $$BC$$ and $$DE$$.
Area of $$\Delta DBE=$$ area of $$\Delta DCE$$ ....(3)
From (1), (2) and (3), we have
$$\dfrac{AD}{DB}=\dfrac{AE}{EC}$$
Hence proved.
The points $$D, E$$ and $$F$$ are taken on the sides $$AB, BC$$ and $$CA$$ of a $$\triangle ABC$$ respectively, such that $$DE\parallel AC$$ and $$FE \parallel AB$$.
Prove that $$\dfrac {AB}{AD} = \dfrac {AC}{FC}$$
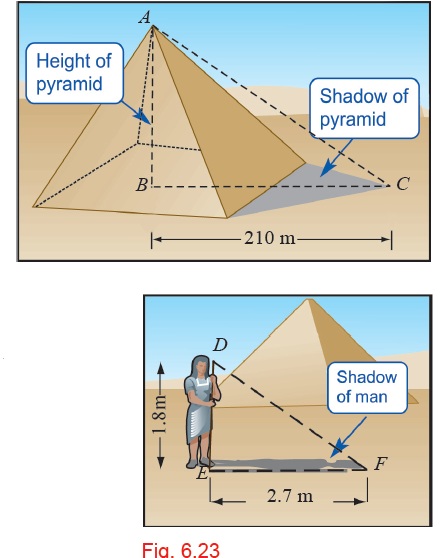
A man of height $$1.8\ m$$ is standing near a Pyramid. If the shadow of the man is of length $$2.7\ m$$ and the shadow of the Pyramid is $$210\ m$$ long at that instant, find the height of the Pyramid
Let $$AB$$ and $$DE$$ be the heights of the Pyramid and the man respectively.
Let $$BC$$ and $$EF$$ be the lengths of the shadows of the Pyramid and the man respectively.
In $$\triangle ABC$$ and $$\triangle DEF$$, we have
$$\angle ABC = \angle DEF = 90^{\circ}$$
$$\angle BCA = \angle EFD$$ (angular elevation is same at the same instant)
$$\therefore \triangle ABC\sim \triangle DEF$$ ($$AA$$ similarity criterion)
Thus, $$\dfrac {AB}{DE} = \dfrac {BC}{EF}$$
$$\Rightarrow \dfrac {AB}{1.8} = \dfrac {210}{2.7} \Rightarrow = \dfrac {210}{2.7}\times 1.8 = 140$$.
Hence, the height of the Pyramid is $$140\ m$$.
Let $$BC$$ and $$EF$$ be the lengths of the shadows of the Pyramid and the man respectively.
In $$\triangle ABC$$ and $$\triangle DEF$$, we have
$$\angle ABC = \angle DEF = 90^{\circ}$$
$$\angle BCA = \angle EFD$$ (angular elevation is same at the same instant)
$$\therefore \triangle ABC\sim \triangle DEF$$ ($$AA$$ similarity criterion)
Thus, $$\dfrac {AB}{DE} = \dfrac {BC}{EF}$$
$$\Rightarrow \dfrac {AB}{1.8} = \dfrac {210}{2.7} \Rightarrow = \dfrac {210}{2.7}\times 1.8 = 140$$.
Hence, the height of the Pyramid is $$140\ m$$.
Prove that the areas of two similar acute triangles are proportional to the squares of the corresponding sides.
Statement: Ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Given: Two triangles $$ABC$$ and $$PQR$$ such that $$\triangle ABC\sim \triangle PQR$$
To prove: $$\cfrac { area\quad (ABC) }{ area\quad (PQR) } ={ \left( \cfrac { { AB }^{ 2 } }{ PQ } \right) }^{ }={ \left( \cfrac { { BC }^{ } }{ PQ } \right) }^{ 2 }={ \left( \cfrac { { CA }^{ } }{ RP } \right) }^{ 2 }\quad $$
Proof: For finding the areas of the two triangles,we draw altitudes $$AM$$ and $$PN$$ of the triangles.
Now, $$area\quad (ABC)=\cfrac { 1 }{ 2 } BC\times AM$$
And $$area\quad (PQR)=\cfrac { 1 }{ 2 } QR\times PN$$
So, $$\cfrac { area\quad (ABC) }{ area\quad (PQR) } =\cfrac { \cfrac { 1 }{ 2 } \times BC\times AM }{ \cfrac { 1 }{ 2 } \times QR\times PN } =\cfrac { BC\times AM }{ QR\times PN } .....(1)\quad $$
Now, in $$\triangle ABC$$ and $$\triangle PQN$$
$$\angle B=\angle Q$$ (As $$\triangle ABC\sim \triangle PQR$$)
and $$\angle M=\angle N$$ (Each$$={90}^{o}$$)
so, $$\triangle ABM\sim \triangle PQN$$ (AA similarity criterion)
Therefore $$\cfrac { AM }{ PN } =\cfrac { AB }{ PQ } .....(2)$$
Also, $$\triangle ABC\sim \triangle PQR$$
$$\cfrac { AB }{ PQ } =\cfrac { BC }{ QR } =\cfrac { CA }{ RP } .......(3)$$
$$\cfrac { area\quad (ABC) }{ area\quad (PQR) } =\cfrac { AB }{ PQ } \times \cfrac { AM }{ PN } $$ (from (1) and (3))
Therefore $$=\cfrac { AB }{ PQ } \times \cfrac { AB }{ PQ } ={ \left( \cfrac { AB }{ PQ } \right) }^{ 2 }$$ (from (2))
Now using (3) we get
$$\cfrac { area\quad (ABC) }{ area\quad (PQR) } ={ \left( \cfrac { { AB }^{ 2 } }{ PQ } \right) }^{ }={ \left( \cfrac { { BC }^{ } }{ PQ } \right) }^{ 2 }={ \left( \cfrac { { CA }^{ } }{ RP } \right) }^{ 2 }$$
The perimeter of two similar triangles are $$30\ cm$$ and $$20\ cm$$ respectively. If one side of the first triangle is $$12\ cm$$, determine the corresponding side of the second triangle.
In a $$\triangle ABC, D$$ and $$E$$ are points on $$AB$$ and $$AC$$ respectively such that $$\dfrac {AD}{DB} = \dfrac {AE}{EC}$$ and $$\angle ADE = \angle DEA$$. Prove that $$\triangle ABC$$ is isosceles
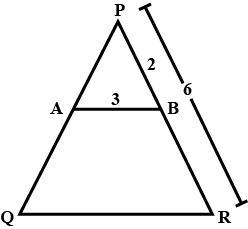
In $$\triangle PQR, AB\parallel QB$$. If $$AB$$ is $$3\ cm, PB$$ is $$2\ cm$$ and $$PR$$ is $$6\, cm$$, then find the length $$QR$$
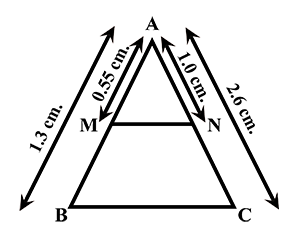
In $$\triangle ABC$$ the points $$M$$ and $$N$$ are on $$AB$$ and $$AC$$. If $$AB = 1.3\ cm, AC = 2.6\ cm, AM =0.5\ cm, AN = 1.0\ cm$$ then show that $$MN \parallel BC$$ or not?
If for acute angled $$\Delta ABC$$ and $$\Delta PQR$$ are similar by $$ ABC \leftrightarrow PQR$$ correspondance, then prove that $$\dfrac{A(ABC)}{A(PQR)} = \dfrac{AB^2}{PQ^2} = \dfrac{BC^2}{QR^2} = \dfrac{AC^2}{PR^2}$$
We are given two triangles ABC and PQR such that $$\Delta ABC \leftrightarrow \Delta PQR$$.
Draw altitudes AM and PN of the triangles.
Now, $$A(ABC) = \dfrac{1}{2} \times BC \times AM$$
and $$A(PQR) = \dfrac{1}{2} \times QR \times PN$$
So, $$\dfrac{A(ABC)}{A(PQR)} = \dfrac{\dfrac{1}{2} \times BC \times AM}{\dfrac{1}{2} \times QR \times PN} = \dfrac{BC \times AM}{QR \times PN}$$ ............. (1)
In $$\Delta ABM$$ and $$\Delta PQN$$,
$$\angle B = \angle Q$$ (As $$\Delta ABC \leftrightarrow \Delta PQR$$)
and $$\angle M = \angle N $$ (Each of $$90^o$$)
So, $$\Delta ABM \leftrightarrow \Delta PQN$$ (AA similarity criterion)
$$\therefore \dfrac{AM}{PN} = \dfrac{AB}{PQ}$$ .......... (2)
Also $$\Delta ABC \leftrightarrow \Delta PQR$$
So, $$\dfrac{AB}{PQ} = \dfrac{BC}{QR} = \dfrac{CA}{RP}$$ ......... (3)
$$\therefore \dfrac{ABC}{PQR} = \dfrac{AB}{PQ} \times \dfrac{AM}{PN}$$ [From (1) and (3)]
$$= \dfrac{AB}{PQ} \times \dfrac{AB}{PQ}$$ [From (2)]
$$= \left( \dfrac{AB}{PQ}\right )^2$$
Now using (3), we get
$$\dfrac{A(ABC)}{A(PQR)} = \left( \dfrac{AB}{PQ} \right )^2 = \left( \dfrac{BC}{QR} \right )^2 = \left( \dfrac{CA}{RP} \right )^2$$
Draw altitudes AM and PN of the triangles.
Now, $$A(ABC) = \dfrac{1}{2} \times BC \times AM$$
and $$A(PQR) = \dfrac{1}{2} \times QR \times PN$$
So, $$\dfrac{A(ABC)}{A(PQR)} = \dfrac{\dfrac{1}{2} \times BC \times AM}{\dfrac{1}{2} \times QR \times PN} = \dfrac{BC \times AM}{QR \times PN}$$ ............. (1)
In $$\Delta ABM$$ and $$\Delta PQN$$,
$$\angle B = \angle Q$$ (As $$\Delta ABC \leftrightarrow \Delta PQR$$)
and $$\angle M = \angle N $$ (Each of $$90^o$$)
So, $$\Delta ABM \leftrightarrow \Delta PQN$$ (AA similarity criterion)
$$\therefore \dfrac{AM}{PN} = \dfrac{AB}{PQ}$$ .......... (2)
Also $$\Delta ABC \leftrightarrow \Delta PQR$$
So, $$\dfrac{AB}{PQ} = \dfrac{BC}{QR} = \dfrac{CA}{RP}$$ ......... (3)
$$\therefore \dfrac{ABC}{PQR} = \dfrac{AB}{PQ} \times \dfrac{AM}{PN}$$ [From (1) and (3)]
$$= \dfrac{AB}{PQ} \times \dfrac{AB}{PQ}$$ [From (2)]
$$= \left( \dfrac{AB}{PQ}\right )^2$$
Now using (3), we get
$$\dfrac{A(ABC)}{A(PQR)} = \left( \dfrac{AB}{PQ} \right )^2 = \left( \dfrac{BC}{QR} \right )^2 = \left( \dfrac{CA}{RP} \right )^2$$
If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
$$\textbf{Step 1: Apply property of congruent triangles}$$
$$Construction- Draw$$ $$DB'$$ $$equal\ to$$ $$AB$$ $$and$$ $$DC'$$ $$equal\ to$$ $$AC$$ $$in$$ $$\triangle DEF$$ $$and\ join$$ $$B'C'$$.
$$AB = BD'$$ By construction
$$AC = DC'$$ by construction
$$\angle A = \angle D$$ Given
$$\triangle ABC \cong \triangle DB'C'$$ $$...(S.A.S\ test\ of\ Congruence)$$
$$\angle B = \angle DB'C'$$ ...C.A.C.T
$$\angle C = \angle DC'B'$$ ....C.A.C.T
$$\therefore \triangle ABC\sim \triangle DB'C'$$ $$....(A.A.A\ test\ of\ similarity)$$
$$\textbf{Step 2: Apply property of congruent triangles}$$
$$\cfrac {AB}{DB'} = \dfrac {AC}{DC'} = \dfrac {BC}{B'C'}$$ $$ ....(C.S.S.T)$$
$$But$$ $$\cfrac {AB}{DE} = \cfrac {AC}{DF}$$ ...Given
$$Or$$ $$\cfrac {DB'}{DE} = \cfrac {DC'}{DF}$$
$$\left \{AB = DB', AC = DC'\right \}$$
$$\Rightarrow B'C'\parallel EF$$. $$\text{(Side divides the two side in the same ratio then it is parallel to third side).}$$
$$\therefore \angle DB'C' = \angle E = \angle B$$
$$\angle DC'B' = \angle F = \angle C$$
$$\therefore \triangle ABC \sim \triangle DEF$$ $$\text{(S.A.S.test of similarity)}$$
$$\textbf{Hence Proved}$$
In trapezium $$ABCD$$, side $$AB\parallel CD$$ and diagonals $$AC$$ and $$BD$$ intersect each other at $$O$$. Prove that: $$\cfrac { OA }{ OC } =\cfrac { OD }{ OB } $$.
Write property of side-angle-side similarity and side-side-side similarity.
The areas of two similar triangles are $$250sq.cm$$ and $$360sq.cm$$, then determine the ratio of their corresponding sides.
Write converse of Pythagoras theorem and prove it.
Converse of Pythagoras Theorem.
Statement:
In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Proof:
We need to prove that $$\angle B = 90^o$$.
To start with, we construct a $$\Delta$$PQR right-angled at Q such that $$PQ = AB$$ and $$QR = BC.$$
Now, from $$\Delta $$ PQR, we have:
$$Pr^2 = PQ^2 + QR^2$$ (Pythagoras Theorem, as $$\angle Q = 90^o$$)
or $$PR^2 = AB^2 + BC^2$$ (By construction)........ (1)
But $$AC^2 = AB^2 + BC^2$$ (Given).......... (2)
So, $$AC = PR$$ (From (1) and (2)).............. (3)
Now, in $$\Delta ABC $$ and $$\Delta PQR$$,
$$AB = PQ$$ (By construction)
$$BC = QR$$ (By construction)
$$AC = PR$$ (Proved in (3))
So, $$\Delta ABC \simeq \Delta PQR$$ (SSS congruence)
$$\angle B = \angle Q$$ (Corresponding angles of congruent triangles)
$$\angle Q = 90^o$$ (By construction)
So $$\angle B = 90^o$$
Statement:
In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Proof:
Here, we are given a triangle ABC in which $$Ac^2 = AB^2 + BC^2$$.
We need to prove that $$\angle B = 90^o$$.
To start with, we construct a $$\Delta$$PQR right-angled at Q such that $$PQ = AB$$ and $$QR = BC.$$
Now, from $$\Delta $$ PQR, we have:
$$Pr^2 = PQ^2 + QR^2$$ (Pythagoras Theorem, as $$\angle Q = 90^o$$)
or $$PR^2 = AB^2 + BC^2$$ (By construction)........ (1)
But $$AC^2 = AB^2 + BC^2$$ (Given).......... (2)
So, $$AC = PR$$ (From (1) and (2)).............. (3)
Now, in $$\Delta ABC $$ and $$\Delta PQR$$,
$$AB = PQ$$ (By construction)
$$BC = QR$$ (By construction)
$$AC = PR$$ (Proved in (3))
So, $$\Delta ABC \simeq \Delta PQR$$ (SSS congruence)
$$\angle B = \angle Q$$ (Corresponding angles of congruent triangles)
$$\angle Q = 90^o$$ (By construction)
So $$\angle B = 90^o$$
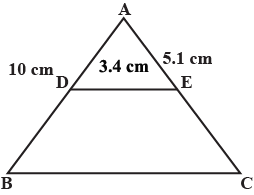
In $$\triangle ABC,DE\parallel BC$$, point $$D$$ lies $$AB$$ and $$E$$ lies on $$AC$$. If $$AD=3.4cm, AB=10cm, AE=5.1cm$$ then find the value of $$AC$$.
$$In:\triangle ABC$$ using the Thales's Theorem ("If a line is drawn parallel to one side of a triangle intersecting other two sides, then it divided the two sides in the same ratio. ")
$$In:\triangle ABC$$
$$DE||BC$$ (given)
Therefore, $$\dfrac { AD }{ AB } =\dfrac { AE }{ AC } $$
$$\dfrac { 3.4 }{ 10 } =\dfrac { 5.1 }{ AC } $$
$${ AC= }\dfrac { 10\times 5.1 }{ 3.4 } =15cm$$
The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
If two triangles are similar, then the ratio of the area of both triangles is proportional to square of the ratio of their corresponding sides.
To prove this theorem, consider two similar triangles $$ΔABC$$ and $$ΔPQR$$
According to the stated theorem
$$\dfrac { ar\triangle ABC }{ ar\triangle PQR } ={ \left( \dfrac { AB }{ PQ } \right) }^{ 2 }={ \left( \dfrac { BC }{ QR } \right) }^{ 2 }={ \left( \dfrac { CA }{ RP } \right) }^{ 2 }$$
Since area of triangle $$=\dfrac { 1 }{ 2 } \times base\times altitude$$
To find the area of $$ΔABC$$ and $$ΔPQR$$ draw the altitudes $$AD$$ and $$PE$$ from the vertex $$A$$ and $$P$$ of $$ΔABC $$ and $$ΔPQR$$
Now, area of $$ΔABC$$ $$=\dfrac { 1 }{ 2 } \times BC\times AD$$
area of $$ΔPQR$$ $$=\dfrac { 1 }{ 2 } \times QR\times PE$$
The ratio of the areas of both the triangles can now be given as:
$$\dfrac { ar\triangle ABC }{ ar\triangle PQR } =\dfrac { \dfrac { 1 }{ 2 } \times BC\times AD }{ \dfrac { 1 }{ 2 } \times QR\times PE } $$
$$\dfrac { ar\triangle ABC }{ ar\triangle PQR } =\dfrac { BC\times AD }{ QR\times PE } $$
Now in $$\triangle ABD$$ and $$\triangle PQE$$ it can be seen
$$∠ABC = ∠PQR$$ (Since $$ΔABC\sim ΔPQR$$ )
$$∠ADB = ∠PEQ$$ (Since both the angles are $$90°$$)
From $$AA$$ criterion of similarity $$ΔADB\sim ΔPEQ$$
$$\dfrac { AD }{ PE } =\dfrac { AB }{ PQ } $$
Since it is known that $$ΔABC\sim ΔPQR$$
$$\dfrac { AB }{ PQ } =\dfrac { BC }{ QR } =\dfrac { CA }{ RP } $$
Substituting this value in equation , we get
$$\dfrac { ar\triangle ABC }{ ar\triangle PQR } =\dfrac { AB }{ PQ } \times \dfrac { AD }{ PE } $$
we can write
$$\dfrac { ar\triangle ABC }{ ar\triangle PQR } ={ \left( \dfrac { AB }{ PQ } \right) }^{ 2 }$$
Similarly we can prove
$$\dfrac { ar\triangle ABC }{ ar\triangle PQR } ={ \left( \dfrac { AB }{ PQ } \right) }^{ 2 }={ \left( \dfrac { BC }{ QR } \right) }^{ 2 }={ \left( \dfrac { CA }{ RP } \right) }^{ 2 }$$
For two acute angled $$\triangle ABC$$ and $$\triangle PQR$$ if $$\triangle ABC\sim \triangle PQR$$ then prove that $$\dfrac {area(\triangle ABC)}{area(\triangle PQR)} = \dfrac {AB^{2}}{PQ^{2}} = \dfrac {BC^{2}}{QR^{2}} = \dfrac {AC^{2}}{PR^{2}}$$.
Construction: Draw $$AD$$ perpendicular to $$BC$$ and $$PS$$ perpendicular to $$QR$$
As $$\Delta ABC \sim \Delta PQR$$
So $$\dfrac{AB}{PQ}=\dfrac{BC}{QR}=\dfrac{CA}{RP}$$ (1)
Also $$\angle A=\angle P$$ , $$\angle B=\angle Q$$ , $$\angle C=\angle R$$ (2)
Now consider $$\Delta ABD$$ and $$\Delta PQS$$
$$\angle B=\angle Q$$ (from (2))
$$\angle ADB=\angle PSQ=90{^\circ}$$ (by construction)
So by AA similarity $$\Delta ABD \sim \Delta PQS$$
Therefore $$\dfrac{AB}{PQ}=\dfrac{BD}{QS}=\dfrac{DA}{SP}$$ (3)
$$area(\Delta ABC)=\dfrac{1}{2}\times AD\times BC$$ (4)
$$area(\Delta PQR)=\dfrac{1}{2}\times PS\times QR$$ (5)
Dividing (4) by (5)
$$\dfrac{area(\Delta ABC)}{area(\Delta PQR)}=\dfrac{\dfrac{1}{2}\times AD\times BC}{\dfrac{1}{2}\times PS\times QR}$$ (6)
From (1) and (3)
$$\dfrac{DA}{SP}=\dfrac{BC}{QR}$$ (7)
Substituting (7) in (6)
$$\dfrac{area(\Delta ABC)}{area(\Delta PQR)}=\dfrac{\dfrac{1}{2}\times BC\times BC}{\dfrac{1}{2}\times QR\times QR}=\dfrac{(BC)^{2}}{(QR)^{2}}$$
From (1)
$$\dfrac{area(\Delta ABC)}{area(\Delta PQR)}=\dfrac{(BC)^{2}}{(QR)^{2}}=\dfrac{(AB)^{2}}{(PQ)^{2}}=\dfrac{(AC)^{2}}{(PR)^{2}}$$
Hence proved
In the given figure, find the value of x which will make DE || AB ?
Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
Given:- A right angled triangle $$ABC$$, right angle at $$B$$
To prove:- $$AC^{2}=AB^{2}+BC^{2}$$
Proof:- Draw a perpendicular $$BD$$ from $$B$$ to $$AC$$
In $$\triangle ABC$$ and $$\triangle ABD$$
$$\angle ADB=\angle ABC=90^{o}$$
$$\angle DAB=\angle BAC$$ ..... (Common angle)
$$\therefore \triangle ABC \sim \triangle ABD$$ ...... (Using AA similarity criteria)
Now, $$\dfrac{AD}{AB}=\dfrac{AB}{AC}$$ ..... (Corresponding sides are proportional)
$$\Rightarrow AB^{2}=AD\times AC$$ ...... $$(i)$$
Similarly, $$\triangle ABC \sim \triangle BDC$$
$$\therefore BC^{2}=CD\times AC$$ ...... $$(ii)$$
Adding equations $$(i)$$ and $$(ii)$$, we get
$$AB^{2}+BC^{2}=AD\times AC+CD\times AC$$
$$\Rightarrow AB^{2}+BC^{2}=AC(AD+CD)$$
$$\Rightarrow AB^{2}+BC^{2}=AC\times AC$$
$$\Rightarrow AB^{2}+BC^{2}=AC^{2}$$ $$[hence \, proved]$$
In the given figure, $$AB\perp BC, FG\perp BC$$ and $$DE\perp AC$$. Prove that $$\triangle ADE$$ ~ $$\triangle GCF$$.
In a $$\triangle ABC, P$$ and $$Q$$ are points on sides $$AB$$ and $$AC$$ respectively, such that $$PQ \parallel BC$$. If $$AP = 2.4 cm, AQ = 2 cm,QC = 3 cm$$ and $$BC = 6 cm$$, find $$AB$$ and $$PQ.$$
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Hence $$\dfrac{AQ}{QC}=\dfrac{AP}{PB}$$
$$\dfrac{2}{3}=\dfrac{2.4}{PB}$$
$$PB=3.6cm$$
$$AB=AP+PB=2.4+3.6=6cm$$
As $$PQ\parallel BC$$
$$\angle AQP=\angle ACB$$
$$\angle APQ=\angle ABC$$
So by $$AAA$$ $$ \triangle AQP\sim \triangle ACB$$
Hence $$\dfrac{AQ}{AC}=\dfrac{QP}{CB}$$
$$\dfrac{2}{5}=\dfrac{QP}{6}$$
$$QP=2.4cm$$
So $$AB=6cm$$ and $$QP=2.4cm$$
In a $$\triangle ABC, D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively such that $$DE\parallel BC$$. If $$AD = 2.4\ cm, AE = 3.2\ cm, DE \parallel BC$$. If $$AD = 2.4\ cm, AE = 3.2\ cm, DE = 2\ cm$$ and $$BC = 5\ cm$$, find $$BD$$ and $$CE$$.
If a line is drawn parallel to one side of a triangle to intersect the
other two sides in distinct points, the other two sides are divided in the same ratio.
As $$DE\parallel BC$$
$$\angle ADE=\angle ABC$$
$$\angle AED=\angle ACB$$
So by $$AAA$$ $$ \triangle AED\sim \triangle ACB$$
Hence $$\dfrac{AE}{AC}=\dfrac{ED}{CB}$$
$$\therefore\dfrac{3.2}{AC}=\dfrac{2}{5}$$
$$\Rightarrow AC=8cm$$
$$AC=8cm=AE+EC=3.2+EC$$
$$EC=8-3.2=4.8cm$$
Also $$\dfrac{AD}{AB}=\dfrac{ED}{CB}$$
$$\therefore \dfrac{2.4}{AB}=\dfrac{2}{5}$$
$$AB=6cm=AD+DB=2.4+DB$$
$$\Rightarrow DB=3.6cm$$
So $$BD=3.6cm$$ and $$CE=4.8cm$$
$$\triangle PQR$$ is right angled at $$Q, QX\perp PR, XY\perp RQ$$ and $$XZ \perp PQ$$ are drawn. Prove that $$XZ^{2} = PZ \times ZQ$$.
In fig $$\triangle ACB \sim \triangle APQ$$. If $$BC = 10\ cm,\ PQ = 5\ cm,\ BA = 6.5\ cm$$ and $$AP= 2.8\ cm$$, find $$CA$$ and $$AQ$$. Also find the area $$(\triangle ACB)$$ : area $$(\triangle APQ)$$.
ABCD is a trapezium in which AB $$\parallel$$ CD. The diagonals AC and BD intersect at O. Prove that:
(i) $$\triangle AOB \sim \triangle COD$$ (ii) If OA = 6 cm, OC = 8cm,
Find:
(a) $$\dfrac { Area\left( \triangle AOB \right) }{ Area\left( \triangle COD \right) }$$
(b) $$\dfrac { Area\left( \triangle AOD \right) }{ Area\left( \triangle COD \right) }$$
(a) $$\dfrac { Area\left( \triangle AOB \right) }{ Area\left( \triangle COD \right) }$$
The diagonals $$AC$$ and $$BD$$ intersect at $$O$$. $$OA=6 \ cm$$ and $$OC=8\,cm$$
In $$\triangle AOB$$ and $$\triangle COD$$,
$$\angle AOB=\angle COD$$ [ Vertically opposite angles ]
$$\angle OAB=\angle OCD$$ [ Alternate angles ]
$$\therefore$$ $$\triangle AOB\sim\triangle COD$$ [ By AA similarity ]
$$(a)$$ $$\dfrac{ar(\triangle AOB)}{ar(\triangle COD)}=\dfrac{OA^2}{OC^2}$$ [ By area theorem ]
$$\Rightarrow$$ $$\dfrac{ar(\triangle AOB)}{ar(\triangle COD)}=\dfrac{(6)^2}{(8)^2}$$
$$\Rightarrow$$ $$\dfrac{ar(\triangle AOB)}{ar(\triangle COD)}=\dfrac{36}{64}=\dfrac{9}{16}$$
$$(b)$$ Draw $$DP\perp AC$$
$$\dfrac{ar(\triangle AOD)}{ar(\triangle COD)}=\dfrac{\dfrac{1}{2}\times AO\times DP}{\dfrac{1}{2}\times CO\times DP}$$ [ By area theorem ]
$$\Rightarrow$$ $$\dfrac{ar(\triangle AOD)}{ar(\triangle COD)}=\dfrac{AO}{CO}$$
$$\Rightarrow$$ $$\dfrac{ar(\triangle AOD)}{ar(\triangle COD)}=\dfrac{6}{8}=\dfrac{3}{4}$$
Triangles $$ABC$$ and $$DEF$$ are similar.
(i) If area ($$\triangle$$ ABC)= $$16$$ $$cm^{2}$$, area($$\triangle$$ DEF)= $$25$$ $$cm^{2}$$ and BC = $$2.34$$ cm, find EF.
(ii) If area ($$\triangle$$ ABC)= $$9$$ $$cm^{2}$$, area($$\triangle$$ DEF) = $$64$$ $$cm^{2}$$ and DE= $$5.1$$ cm, find AB.
(iii) If AC = $$19$$ cm and DF=$$8$$ cm, ratio of the area of two triangles.
(iv) If area ($$\triangle$$ ABC)= $$36$$ $$cm^{2}$$, area ($$\triangle$$ DEF) =$$64$$ $$cm^{2}$$ and DE= $$6.2$$ cm, find AB.
(v) If AB= $$1.2$$ cm and DE=$$1.4$$ find the ratio of the areas of triangle ABC and DEF.
Triangles ABC and DEF are similar.
(i) If area ($$\triangle ABC$$)= 16 $$\text{cm}^{2}$$, area($$\triangle$$ DEF)= 25 $$\text{cm}^{2}$$ and $$BC = 2.3\ \text{cm}$$, find $$EF$$.
(ii) If area ($$\triangle ABC$$)= 9 $$\text{cm}^{2}$$, area($$\triangle$$ DEF) = 64 $$\text{cm}^{2}$$ and $$DE= 5.1\ \text{cm}$$, find $$AB$$.
(iii) If $$AC = 19\ \text{cm}$$ and $$DF=8\ \text{cm}$$, find ratio of the area of two triangles.
(iv) If area ($$\triangle ABC$$)= 36 $$\text{cm}^{2}$$, area ($$\triangle$$ DEF) =64 $$\text{cm}^{2}$$ and $$DE= 6.2\ \text{cm}$$, find $$AB$$.
(v) If $$AB= 1.2\ \text{cm}$$ and $$DE=1.4\ \text{cm}$$, find the ratio of the areas of triangle $$ABC$$ and $$DEF$$.
(ii) If area ($$\triangle ABC$$)= 9 $$\text{cm}^{2}$$, area($$\triangle$$ DEF) = 64 $$\text{cm}^{2}$$ and $$DE= 5.1\ \text{cm}$$, find $$AB$$.
(iii) If $$AC = 19\ \text{cm}$$ and $$DF=8\ \text{cm}$$, find ratio of the area of two triangles.
(iv) If area ($$\triangle ABC$$)= 36 $$\text{cm}^{2}$$, area ($$\triangle$$ DEF) =64 $$\text{cm}^{2}$$ and $$DE= 6.2\ \text{cm}$$, find $$AB$$.
(v) If $$AB= 1.2\ \text{cm}$$ and $$DE=1.4\ \text{cm}$$, find the ratio of the areas of triangle $$ABC$$ and $$DEF$$.
The area of two similar triangle are $$81$$ $$cm^2$$cm2 and $$49\ cm^2$$ respectively. Find ratio of their corresponding heights. What is the ratio of their corresponding medians?
The area of two similar triangles are 169 $$cm^{2}$$ and 121 $$cm^{2}$$ respectively, If the longest side of the largest triangle is 26 cm, find the longest side of the smaller triangle?
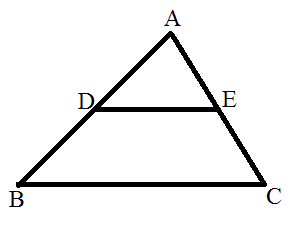
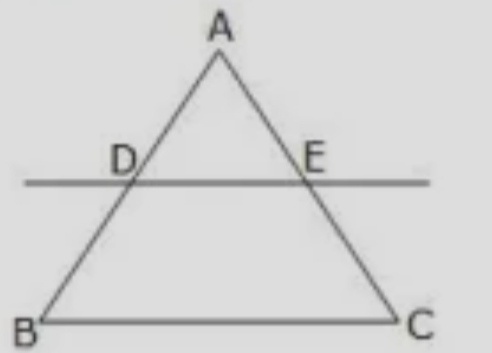
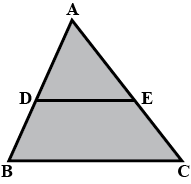
In the given figure, $$DE \parallel BC$$
(i) If DE = 4 cm, BC= 6 cm and Area ($$\triangle$$ ADE)= 16 $$cm^{2}$$, find the area of $$\triangle$$ ABC.
(ii) If DE = 4 cm BC = 8 cm and Area ($$\triangle$$ ADE)= 25 $$cm^{2}$$, find the area of $$\triangle$$ ABC.
(iii) If DE : BC = 3 :Calculate the ratio of the areas of $$\triangle$$ ADE and the area of BCED.
Two isosceles triangles have equal vertical angles and their area are in the ratio of the $$16 : 25$$. Find the ratio of their corresponding heights.
$$AB=AC\quad$$ (given)
$$ \therefore \cfrac { AB }{ AC } =1\quad -(1)$$
$$DE=DF$$ (given)
$$ \cfrac { DE }{ DF } =1\quad -(2)$$
comparing$$(1)\& (2)$$
$$ \cfrac { AB }{ AC } =\cfrac { DE }{ DF } \quad \implies\quad \cfrac { AB }{ DE } =\cfrac { AC }{ DF } $$
$$ In \ \triangle ABC \ \& \ \triangle DEF$$
$$ \cfrac { AB }{ DE } =\cfrac { AC }{ DF } \quad \implies\quad \angle A=\angle D$$
$$ \therefore$$ By using SAS similar condition
$$ \triangle ABC\sim \triangle DEF$$
$$ \cfrac { ar(\triangle ABC) }{ ar(\triangle DEF) } =\cfrac { { AD }^{ 2 } }{ { DQ }^{ 2 } } $$
$$ \therefore$$ The area of two similar $$\triangle les$$ are in the ratio of the square of the corresponding altitude.
$$\cfrac { 16 }{ 25 } =\cfrac { { AP }^{ 2 } }{ { DQ }^{ 2 } } $$
$$\implies\quad \cfrac { AP }{ DQ } =\cfrac { 4 }{ 5 } $$
The area of two similar triangles are $$36\ cm^{2}$$ and $$25\ cm^{2}$$. If an altitude of the first triangle is $$2.4\ cm$$, find the corresponding altitude of the other triangle.
The area of two similar triangle are 100 $$cm^{2}$$ and 49 $$cm^{2}$$ respectively. If the altitude of the bigger triangle is 5 cm, find the corresponding altitude of the other.
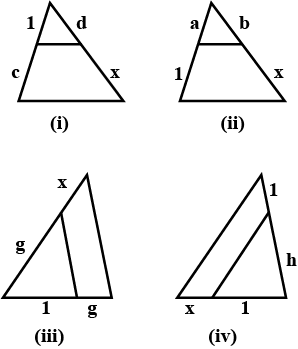
In each of the figure, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segments are marked. Find the value of $$x$$ in each of the following :
$$ABC$$ is a triangle and $$PQ$$ is a straight line meeting $$AB$$ in $$P $$ and $$AC$$ in $$Q$$. If $$AP = 1$$ cm, $$PB = 3$$ cm, $$AQ = 1.5$$ cm, $$QC = 4.5$$ m, prove that area of $$\triangle$$ $$APQ$$ is one- sixteenth of the area of $$\triangle$$ $$ABC$$.
$$AP=1\,cm,\,PB=3\,cm,\,AQ=1.5\,cm,\,QC=4.5\,cm$$ [ Given ]
Then, $$AB=AP+PB=1+3=4\,cm$$
In $$\triangle APQ$$ and $$\triangle ABC$$,
$$\angle A=\angle A$$ [ Common angle ]
$$\dfrac{AP}{AB}=\dfrac{AQ}{AC}$$ [ Each equal to $$\dfrac{1}{4}$$ ]
$$\therefore$$ $$\triangle APQ\sim \triangle ABC$$ [ By SAS similarity ]
$$\therefore$$ $$\dfrac{area(\triangle APQ)}{area(\triangle ABC)}=\dfrac{AP^2}{AB^2}$$ [ By area of similar triangle theorem ]
$$\therefore$$ $$\dfrac{area(\triangle APQ)}{area(\triangle ABC)}=\dfrac{1^2}{4^2}$$
$$\therefore$$ $$\dfrac{area(\triangle APQ)}{area(\triangle ABC)}=\dfrac{1}{16}$$
$$\therefore$$ $$area(\triangle APQ)=\dfrac{1}{16}\times area(\triangle ABC)$$
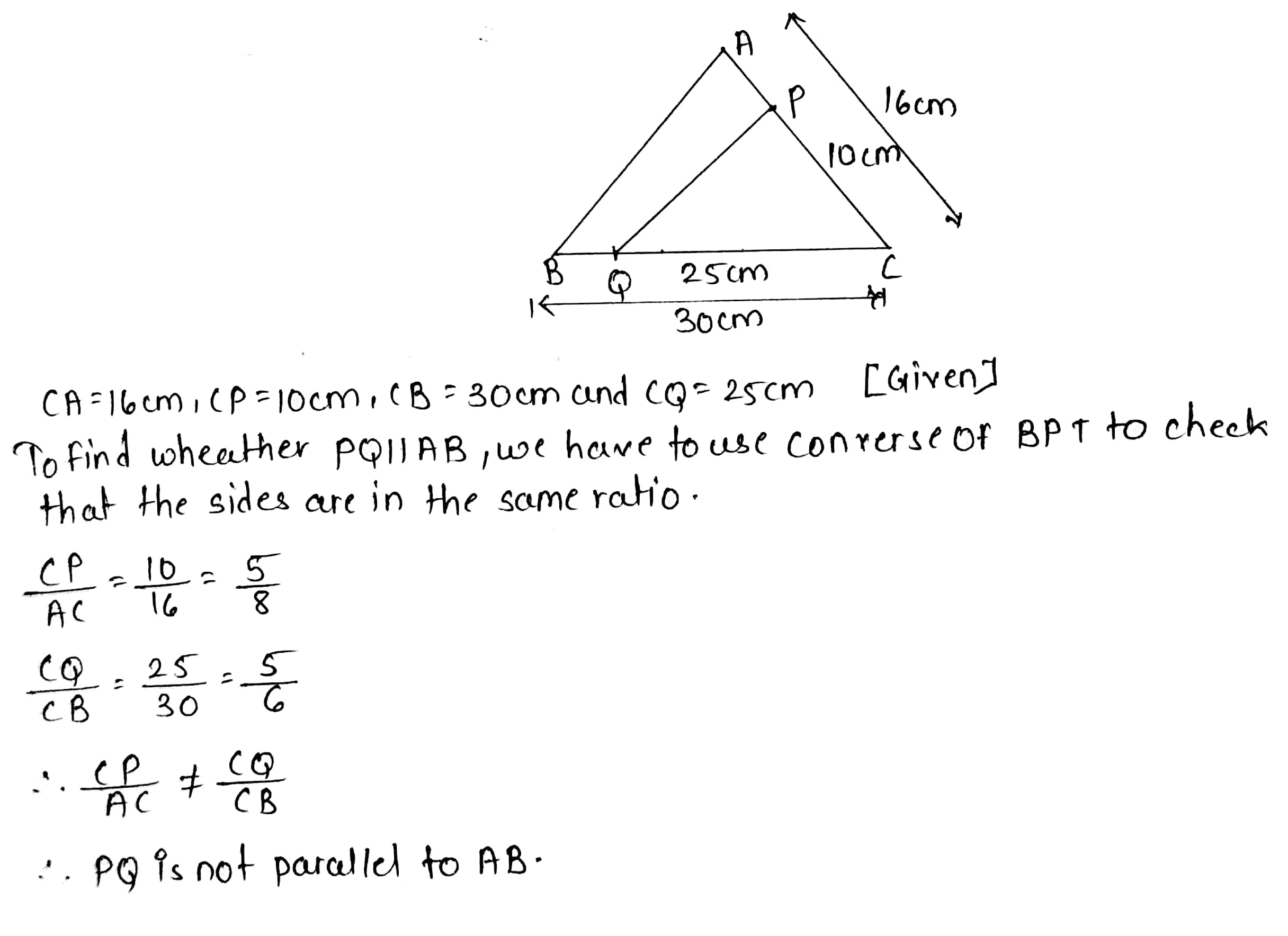
In $$\triangle$$ ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, AC = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ $$\parallel$$ AB?
In $$\triangle$$ ABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ $$\parallel$$ BC and PQ divides $$\triangle$$ ABC into two parts equal in area. Find $$\dfrac { BP }{ AB }$$.
Since the line $$PQ$$ divides $$\triangle ABC$$ into two equal parts,
$$area(\triangle APQ)=area(\triangle BPQC)$$
$$\Rightarrow$$ $$area(\triangle APQ)=area(\triangle ABC)-area(\triangle APQ)$$
$$\Rightarrow$$ $$2area(\triangle APQ)=area(\triangle ABC)$$
$$\therefore$$ $$\dfrac{area(\triangle ABC)}{area(\triangle APQ)}=\dfrac{2}{1}$$ ---- ( 1 )
Now, in $$\triangle ABC$$ and $$\triangle APQ$$,
$$\angle BAC=\angle PAQ$$ [ Common angles ]
$$\angle ABC=\angle APQ$$ [ Corresponding angles ]
$$\therefore$$ $$\triangle ABC\sim \triangle APQ$$ [ By AA similarity ]
$$\therefore$$ $$\dfrac{area(\triangle ABC)}{area(\triangle APQ)}=\dfrac{AB^2}{AP^2}$$
$$\therefore$$ $$\dfrac{2}{1}=\dfrac{AB^2}{AP^2}$$ [ From ( 1 ) ]
$$\Rightarrow$$ $$\dfrac{AB}{AP}=\dfrac{\sqrt{2}}{1}$$
$$\Rightarrow$$ $$\dfrac{AB-BP}{AB}=\dfrac{1}{\sqrt{2}}$$
$$\Rightarrow$$ $$1-\dfrac{BP}{AB}=\dfrac{1}{\sqrt{2}}$$
$$\Rightarrow$$ $$\dfrac{BP}{AB}=1-\dfrac{1}{\sqrt{2}}$$
$$\therefore$$ $$\dfrac{BP}{AB}=\dfrac{\sqrt{2}-1}{\sqrt{2}}$$
If D is a point on the side AB of $$\triangle$$ ABC such that AD : DB = 3:2 and E is a point on BC such that DE $$ \parallel$$ AC. Find the ratio of areas of $$\triangle$$ ABC and $$\triangle$$ BDE.
$$\dfrac{AD}{DB}=\dfrac{3}{2}$$ [ Given ]
$$\therefore$$ $$\dfrac{AD}{DB}+1=\dfrac{3}{2}+1$$
$$\therefore$$ $$\dfrac{AD+DB}{DB}=\dfrac{3+2}{2}$$
$$\therefore$$ $$\dfrac{AB}{DB}=\dfrac{5}{2}$$ --- ( 1 )
$$\angle B=\angle B$$ [ Common ]
$$\angle BAC=\angle BDE$$ [ $$\because DE\parallel AC$$ ]
$$\therefore$$ $$\triangle ABC\sim\triangle BDE$$ [ By AA similarity criteria ]
$$\dfrac{ar(\triangle ABC)}{ar(\triangle BDE)}=\dfrac{AB^2}{DB^2}=\dfrac{5^2}{2^2}=\dfrac{25}{4}$$ [ From ( 1 ) ]
$$\therefore$$ $$ar(\triangle ABC):ar(\triangle BDE)=25:4$$
In $$\triangle$$ ABC, P and Q are points on sides AB and AC respectively such that PQ $$\parallel$$ BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
So, by proportionality theorem
$$\dfrac{AP}{PB}=\dfrac{AQ}{QC}=\dfrac{PQ}{BC}$$
$$\dfrac{4}{6}=\dfrac{AQ}{QC}=\dfrac{3}{BC}$$
$$\Rightarrow$$ $$\dfrac{4}{6}=\dfrac{3}{BC}$$
$$\therefore$$ $$BC=4.5\,cm$$
If $$\triangle ABC \sim \triangle DEF$$ such that AB = 5 cm, area $$(\triangle ABC ) = 20\ { cm }^{ 2 }$$ and area $$(\triangle DEF ) = 45\ { cm }^{ 2 }$$, determine DE.
In $$\triangle ABC ,\ \angle A$$ is obtuse, $$PB \perp AC$$ and $$QC \perp AB.$$ Prove that:
(I) $$AB \times AQ=AC\times AP$$
(ii) $${ BC }^{ 2 } = ( AC \times CP + AB \times BQ )$$
(I) $$AB \times AQ=AC\times AP$$
(ii) $${ BC }^{ 2 } = ( AC \times CP + AB \times BQ )$$
In $$\triangle BPA$$ and $$\triangle AQC$$
$$\angle P = \angle Q = 90^o$$
$$\angle PAB = \angle QAC$$ [Vertically opposite angles]
and $$\angle A$$ is the common angle
$$\therefore$$ $$ \triangle BPA \sim \triangle AQC$$ [AAA similarity criterion]
$$\Rightarrow$$ $$\dfrac{AB}{AC}=\dfrac{AP}{AQ}$$
$$\therefore$$ $$AB\times AQ=AC\times AP$$ --- ( 1 ) [ Hence proved ]
Consider, right angled $$\triangle BCQ$$
$$\Rightarrow$$ $$BC^2 = CQ^2 + BQ^2$$ [By Pythagoras theorem]
$$\Rightarrow$$ $$BC^2 = CQ^2 + (AB + AQ)^2$$ [Since BQ = AB + AQ]
$$\Rightarrow$$ $$BC^2 = [CQ^2 + AQ^2] + AB^2 + 2AB \times AQ $$ ----- (2)
In right $$\triangle ACQ$$, $$CQ^2 + AQ^2 = AC^2$$ [By Pythagoras theorem]
Hence equation (2) becomes,
$$\Rightarrow$$ $$ BC^2 = AC^2 + AB^2 + AB \times AQ + AB \times AQ$$
$$\Rightarrow$$ $$BC^2 = AC^2 + AB^2 + AB \times AQ + AP \times AC$$ [From (1)]
$$\Rightarrow$$ $$BC^2 = AC^2 + AP \times AC + AB^2 + AB \times AQ$$
$$\Rightarrow$$ $$BC^2 = AC (AC + AP) + AB (AB + AQ)$$
$$\Rightarrow$$ $$BC^2 = AC × CP + AB × BQ$$ [From the figure]
Hence Proved.
In $$\triangle$$ PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN $$\parallel$$ QR.
We have, $$PM=15\,cm,NR=8\,cm,PQ=25\,cm$$ and $$PR=20\,cm$$
Now,
$$MQ=PQ-PM=25-15=10\,cm$$ and $$PN=PR-NR=20-8=12\,cm$$
Hence,
$$\dfrac{PM}{MQ}=\dfrac{15}{10}=\dfrac{3}{2}$$
Also,
$$\dfrac{PN}{NR}=\dfrac{12}{8}=\dfrac{3}{2}$$
$$\therefore$$ $$MN\parallel QR$$ [ By converse proportionality theorem ]
In the given figure, DE $$\parallel$$ CB. Determine AC and AE.
ABCD is a trapezium in which AB $$\parallel$$ DC. P and Q are points on sides AD and BC such that PQ $$\parallel$$ AB. If PD = 18cm, BQ = 35cm and QC = 15cm, find AD.
Construction: Join $$BD$$
In $$\triangle ABD$$, $$PO\parallel AB$$ [$$\because$$ $$PQ\parallel AB$$ ]
$$\Rightarrow$$ $$\dfrac{DP}{AP}=\dfrac{DO}{OB}$$ [ By basic proportionality theorem ] ------ ( 1 )
$$\Rightarrow$$ In $$\triangle BDC$$, $$OQ\parallel DC$$ [
$$\because$$ $$PQ\parallel DC$$ ]
$$\dfrac{BQ}{QC}=\dfrac{OB}{OD}$$ [ By basic proportionality theorem ]
$$\Rightarrow$$ $$\dfrac{QC}{BQ}=\dfrac{OD}{OB}$$ ----- ( 2 )
$$\Rightarrow$$ $$\dfrac{DP}{AP}=\dfrac{QC}{BQ}$$ [ From ( 1 ) and ( 2 ) ]
$$\Rightarrow$$ $$\dfrac{18}{AP}=\dfrac{15}{35}$$
$$\therefore$$ $$AP=\dfrac{18\times 35}{15}=42$$
$$\therefore$$ $$AD=AP+DP=42+18=60\,cm$$
Prove that if in two triangles, corresponding angles are equal then their corresponding sides are in the same ratio and hence the two triangles are similar.
$$Two\triangle les\quad \triangle ABC\& \triangle DEF\quad such\quad that$$
$$ \angle A=\angle D,\angle B=\angle E\& \angle C=\angle F$$
$$ Draw\quad P\quad and\quad Q\quad on\quad DE\& DF\quad such\quad that\quad DP=AB$$
$$\& DQ=AC\quad resp.Join\quad PQ$$
$$ In\triangle ABC\& \triangle DPQ AB=DP\quad (by\quad construction)$$
$$ \angle A=\angle D\quad (given)$$
$$ AC=DQ\quad (by\quad construction)$$
$$ \implies\quad \triangle ABC\cong \triangle DPQ\quad (by\quad SAS\quad criterion)$$
$$ \angle B=\angle P\quad \{ by\quad CPCT\} $$
$$ \angle B=\angle E\quad (given)\quad implies\quad \angle P=\angle E$$
$$ For\quad lines\quad PQ\quad and\quad EF\quad with\quad transversal\quad PE,$$
$$ \angle P\& \angle E\quad are\quad corresponding\quad angles\quad and\quad they$$
$$ are\quad equal.Hence,\quad PQ||EF.$$
In given figure, If $$EF||DC||AB$$. prove that $$\dfrac { AE }{ ED } =\dfrac { BF }{ FC } $$.
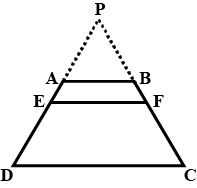
In given figure $$EF||AB||DC$$. Prove that $$\dfrac { AE }{ ED } =\dfrac { BF }{ FC } $$
In a given $$\triangle ABC, DE||BC$$ and $$\dfrac { AD }{ DB } =\dfrac { 3 }{ 5 } $$. If $$AC=5.6$$, find AE.
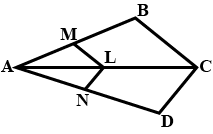
In the given figure, $$\triangle AMB \sim \triangle CMD$$; determine $$MD$$ in terms of $$x,\;y$$ and $$z$$.
$$\triangle AMB\sim \triangle CMD$$ [ Given ]
$$\therefore$$ $$\dfrac{AM}{CM}=\dfrac{MB}{MD}$$ [ By proportionality theorem ]
$$\therefore\;\dfrac{y}{z}=\dfrac{x}{MD}$$
$$\therefore\;MD=\dfrac{xz}{y}$$
In $$\triangle$$ ABC, P and Q are points on sides AB and AC respectively such that PQ $$\parallel$$ BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
ABCD is a parallelogram, P is a point on side BC such that DP produced meets AB produced at L.. Prove that
(i) $$\dfrac { DP }{ PL } =\dfrac { DC }{ BL } $$
(ii) $$\dfrac { DL }{ DP } =\dfrac { AL }{ DC } $$
(i) $$\dfrac { DP }{ PL } =\dfrac { DC }{ BL } $$
(ii) $$\dfrac { DL }{ DP } =\dfrac { AL }{ DC } $$
Let X be any point on the side BC of a triangle ABC. If XM, XN are drawn parallel to BA and CA, meeting CA, BA in M, N respectively. M and N are joined and produced to meet the line passing through BC at T as shown in the figure. Prove that $${ TX }^{ 2 }=TB\times TC$$.
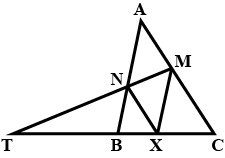
In given figure, (i) and (ii), $$PQ||BC$$. Find $$QC$$ in (i) and $$AQ$$ in (ii).
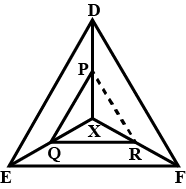
Any point X inside $$\triangle DEF$$ is joined to its vertices. From a point $$P$$ on $$DX,\ PQ$$ is drawn parallel to $$DE$$ meeting $$XE$$ at $$Q$$ and $$QR$$ is drawn parallel to $$EF$$ meeting $$XF$$ at $$R.$$ Prove that $$PR\parallel DF.$$
In the given figure, If PQ||BC and PR||CD. Prove that
(i) $$\dfrac { AR }{ AD } =\dfrac { AQ }{ AB } $$
(ii) $$\dfrac { QB }{ AQ } =\dfrac { DR }{ AR } $$
(i) $$\dfrac { AR }{ AD } =\dfrac { AQ }{ AB } $$
(ii) $$\dfrac { QB }{ AQ } =\dfrac { DR }{ AR } $$
In given figure, $$DE||AC$$ and $$DC||AP$$. Prove that $$\dfrac { BE }{ EC } =\dfrac { BC }{ CP } $$
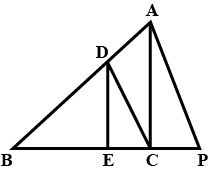
In given figure $$D$$ and $$E$$ are respectively the points on the sides $$AB$$ and $$AC$$ of a $$\triangle ABC$$ such that $$AB=5.6\ cm, AD=1.4\ cm, AC=7.2\ cm$$ and $$AE=1.8\ cm$$. Then show that $$DE||BC$$.
In given figure, $$DE||BC$$ and $$CD||EF$$. Prove that $${ AD }^{ 2 }=AB\times AF$$
In the given figure ABC is a triangle in which AB=AC. Points D and E are points on the sides AB and AC respectively such that AD=AE. Show that the points B,C,E and D are concyclic.
In given figure, $$\angle CAB=90^0$$ and $$AD \bot BC$$. If AC=75 cm. AB=1 m and BD=1.25 m, find AD
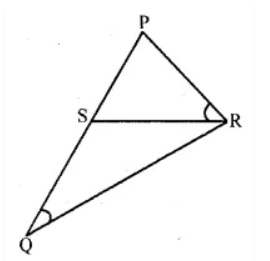
In the figure given below, $$\angle P = \angle RTS$$.
Prove that $$\triangle RPQ \sin \triangle RTS$$.
$$D$$ and $$E$$ are points on sides $$AB$$ and $$AC$$ respectively such that $$BD=CE$$. If $$\angle B=\angle C$$, show that $$DE||BC$$.
In $$\triangle ABC$$, we have
$$\angle B=\angle C$$.
$$\Rightarrow AC=AB$$ [Sides opposite to equal angles are equal]
$$\Rightarrow AE+EC=AD=+DB$$
$$\Rightarrow AE+CE=AD+BD$$
$$\Rightarrow AE+CE=AD+CE$$ [because BD=CE]
$$\Rightarrow AE=AD$$
Thus, we have
$$AD=AE$$ and $$BD=CE$$
$$\therefore \dfrac { AD }{ BD } =\dfrac { AE }{ CE } $$
$$\Rightarrow \dfrac { AD }{ DB } =\dfrac { AE }{ EC } $$
$$\Rightarrow DE||BC$$ [By the converse of Basic Proportionality Theorem] $$[hence \, proved]$$
Two triangles ABC and DBC lie on the same side of the base BC. From a point P on BC, PQ||AB and PR||BD are drawn. They meet AC in Q and DC in R respectively. Prove that QR||AD.
Let $$ABC$$ be a triangle and $$D$$ and $$E$$ be two points on side $$AB$$ such that $$AD=BE$$. If $$DP||BC$$ and $$EQ||AC$$, then prove that $$PQ||AB$$.
In given figure, If $$\angle A=\angle C$$, then prove that $$\triangle AOB\sim \triangle COD$$.
In given figure, If $$\dfrac { AD }{ DC } =\dfrac { BE }{ EC } $$ and $$\angle CDE=\angle CED$$, prove that $$\triangle CAB$$ is isosceles.
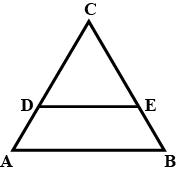
In $$\triangle ABC$$, if AD is the bisector of $$\angle A$$, prove that
$$\dfrac { Area(\triangle ABD) }{ Area(\triangle ACD) } =\dfrac { AB }{ AC } $$
$$\dfrac { Area(\triangle ABD) }{ Area(\triangle ACD) } =\dfrac { AB }{ AC } $$
The side BC of a triangle ABC is bisected at D; O is any point in AD. BO and CO produced meet AC and AB in E and F respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO:AX=AF:AB and show that FE||BC.
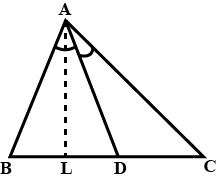
In given figure D is a point on the side BC of $$\triangle ABC$$ such that $$\angle ADC=\angle BAC$$. Prove that
$$\dfrac { CA }{ CD } =\dfrac { CB }{ CA } $$ or $${ CA }^{ 2 }=CB\times CD$$.
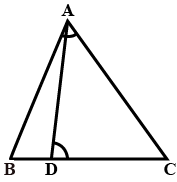
In given figure ABC is a triangle in which AB=AC and D is a point on AC such that $${ BC }^{ 2 }=AC\times CD$$. Prove that BD=BC.
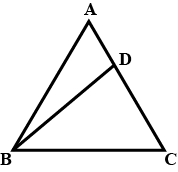
In the given figure $$P$$ and $$Q$$ are points on sides $$AB$$ and $$AC$$ respectively of $$\triangle ABC.$$ If $$AP=3 \;cm, \;PB= 6\; cm, \;AQ=5\; cm$$ and $$QC=10\; cm,$$ show that $$BC=3 PQ.$$
In given figure, considering triangles BEP and CPD, prove that
$$BP\times PD=EP\times PC$$
In given figure through the vertex D of a parallelogram ABCD, a line is drawn to intersect the sides BA and BC produced at E and F respectively. Prove that
$$\dfrac { DA }{ AE } =\dfrac { FB }{ BE } =\dfrac { FC }{ CD } $$
In the figure given below, $$E$$ is a point on the side $$AD$$ produced of a parallelogram $$ABCD$$ and $$BE$$ intersects $$CD$$ at $$F$$. Show that $$\triangle ABE \sim \triangle CFB$$.
In given figure the diagonal $$BD$$ of a parallelogram $$ABCD$$ intersects the segment $$AE$$ at the point $$F$$, where $$E$$ is any point on the side BC. Prove that $$DF\times EF=FB\times FA$$
In given figure two triangles BAC and BDC, right angled at A and D respectively, are drawn on the same base BC and on the same side of BC. If AC and DB intersect at P, prove that $$AP\times PC=DP\times PB$$
In a $$\triangle ABC$$ BD and CE are the altitudes. Prove that $$\triangle ADB$$ and $$\triangle AEC$$ are similar. Check whether $$\triangle CDB\ \ and\ \triangle BEC$$ are similar.
In given figure, express x in terms of a, b and c.
In $$\Delta ABC$$, if $$EF || AB$$ and $$ar(\Delta CEF) = ar(\Box EFBA)$$, then find ratio of $$CA$$ and $$EA$$.
Draw a perpendicular from $$C$$ onto $$AB$$ to meet $$AB$$ at $$G$$ and $$EF$$ at $$H$$
Area $$\triangle ABC=1/2\times AB\times CG$$
$$=ar(EFBA)+ar(CEF)$$
$$=2\times \triangle CEF=EF\times CH$$ $$(because\ ar(EFBA)=ar(CEF)$$ and $$ar(CEF)=1/2\times CH\times EF)$$
$$AB*CG=2\times EF\times CH ..... (i)$$
$$\triangle ABC$$ and $$\triangle CEF$$ are similar triangles. So, the ratios of their corresponding sides and altitudes are equal.
$$EF/AB=CE/CA=CF/CB=CH/CG$$
$$CH=EF*CG/AB$$
So $$(1)= > AB*CG=2\ EF^{2}*CG/AB$$
$$AB^{2}=2\ EF^{2}$$
$$AB\surd{2}EF$$
$$AB/EF=CA/CE=\surd{2}$$
The ratio of the sides in the two triangles is $$\surd{2}$$
$$CA=\surd{2}CE$$
$$CA/EA=CA/(CA-CE)=\surd{2}CE/(\surd{2}CE-CE)$$
$$CA/EA=\surd{2}/(\surd{2}-1)=\surd{2}(\surd{2}+1)$$
If the areas of two similar triangles are equal, prove that they are concurrent.
$$Let\quad \triangle les\quad be\triangle ABC\quad \& \quad \triangle DEF.$$
$$ Both\quad \triangle les\quad are\quad similar.$$
$$\implies\quad \triangle ABC\sim \triangle DEF$$
$$ areas\quad are\quad equal.So,ar\triangle ABC=ar\triangle DEF$$
$$ We\quad know\quad that\quad if\quad two\quad \triangle les\quad are\quad similar,$$
$$ Ratio\quad of\quad area\quad is\quad equal\quad to\quad square\quad of\quad ratio$$
$$ of\quad its\quad corresponding\quad sides.$$
$$ \cfrac { ar(\triangle ABC) }{ ar(\triangle DEF) } ={ (\cfrac { BC }{ EF } ) }^{ 2 }={ (\cfrac { AB }{ DE } ) }^{ 2 }={ (\cfrac { AC }{ DF } ) }^{ 2 }$$
$$ (given\quad as\quad \triangle ABC=\triangle DEF)$$
$$ 1={ (\cfrac { BC }{ EF } })^{ 2 }={ (\cfrac { AB }{ DE } ) }^{ 2 }={ (\cfrac { AC }{ DF } ) }^{ 2 }$$
$$ 1={ (\cfrac { BC }{ EF } ) }^{ 2 }$$
$$\implies\quad 1=\cfrac { BC }{ EF } $$
$$ \therefore BC=EF$$
$$ 1={ (\cfrac { AB }{ DE } ) }^{ 2 }$$
$$ 1=\cfrac { AB }{ DE } $$
$$ AB=DE$$
$$ 1={ (\cfrac { AB }{ DE } ) }^{ 2 }$$
$$ AC=DF$$
$$ In\triangle ABC\& \triangle DEF$$
$$ EF=BC,\quad AB=DE,\quad AC=DF$$
$$ Hence\quad by\quad SSS\quad congruency.$$
$$ \triangle ABC\cong \triangle DEF$$
$$ hence\quad proved$$
In given figure, DEFG is a square and $$\angle BAC=90^0$$. Prove that
(i) $$\triangle AGF\sim \triangle DBG$$
(ii) $$\triangle AGF\sim \triangle EFC$$
(iii) $$\triangle DBG\sim \triangle EFC$$
(iv) $${ DE }^{ 2 }=BD\times EC$$
(i) $$\triangle AGF\sim \triangle DBG$$
(ii) $$\triangle AGF\sim \triangle EFC$$
(iii) $$\triangle DBG\sim \triangle EFC$$
(iv) $${ DE }^{ 2 }=BD\times EC$$
In the given figure, $$AB||CD||EF$$ given $$AB=7.5\ cm$$ $$DC=ycm$$ $$EF=4.5\ cm$$, $$BC=x\ cm$$. Find the value of $$x$$ and $$y$$
Given $$\triangle ABC \sim \triangle PQR$$, if $$\dfrac{AB}{PQ}=\dfrac{1}{3}$$, then find $$\dfrac{ar (\triangle ABC)}{ar( \triangle PQR)}$$.
Prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
In $$\triangle ABC$$, $$P$$ and $$Q$$ are mid points of side $$AB$$ and $$AC$$, respectively.
$$AP = PB$$ and $$AQ = QC$$
$$\dfrac{AP}{PB} = \dfrac{AQ}{QC} = 1$$
Using converse theorem of Proportionality (If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.) we get,
$$PQ\parallel BC$$ Hence Proved.
In given figure if a perpendicular is drawn from the right angle vertex of a right triangle to the hypotenuse, then prove that the triangle on each side of the perpendicular is similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.
In given figure, PB and Qa are perpendiculars to segment AB. If PO=5 cm, QO=7 cm and Area $$\triangle POB=150 {cm}^{2}$$ find the area of $$\triangle QOA$$.
In given figure, $$\dfrac { OA }{ OC } =\dfrac { OD }{ OB } $$. then prove that $$\angle A=\angle C$$ and $$\angle B=\angle D$$.
In given figure, $$\triangle FEC\cong \triangle GBD$$ and $$\angle 1=\angle 2$$. then prove that $$\triangle ADE\sim \triangle ABC$$.
State and prove pythagorus theorum.
Pythagoras theorem
In a right-angled triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides
Given :
$$\triangle ABC$$ right angles at $$B$$
To prove : $$AC^2=AB^2+AC^2$$
Construction : Draw $$DB\bot AC$$
Proof: Since $$BD\bot AC$$
Therefore by AAS silimalrity criterion,
$$\triangle ADB\sim \triangle ABC\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad | \triangle BDC\sim \triangle ABC$$
Since sides of similar triangles are in same ratio $$|$$ since similar triangle sides are in same ratio then
$$\dfrac{AD}{AB}=\dfrac{AB}{AC}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad\quad | \dfrac{CD}{BC}=\dfrac{BC}{AC}$$
$$AD.AC=AB^2------(1)$$ $$|$$ $$AC.CD=BC^2-------(2)$$
Add $$(1)$$ and $$(2)$$ we get,
$$AD.AC+CD.AC=AB^2+BC^2$$
$$AC(AD+DC)=AB^2+BC^2$$
$$AC\times AC=AB^2+BC^2$$
$$AC^2=AB^2+BC^2$$
Hence proved
In the given figure, $$CM$$ and $$RN$$ are respectively the medians of $$\triangle ABC$$ and $$\triangle PQR$$. If $$\triangle ABC \sim \triangle PQR$$, prove that:
(i) $$\triangle AMC \sim \triangle PQR$$
(ii) $$CM/ RN = AB/ PQ$$
(iii) $$\triangle CMB \sim \triangle RNQ$$.
Given : $$\triangle ABC \sim \triangle PQR $$ 7 $$CM$$ and $$RN$$ are medians of $$\triangle ABC $$ & $$\triangle PQR$$ respectively.
To prove : $$(i) \triangle AMC \sim \triangle PNR, (ii) \dfrac{CM}{RN} =\dfrac{AB}{PQ}, (iii) \triangle CMB \sim \triangle RNQ$$
Proof : $$(i)$$ since $$\triangle ABC \sim \triangle PQR.$$
So, $$\angle A = \angle P$$
$$\angle B= \angle Q, \angle C= \angle R$$
& $$\dfrac{AB}{PQ}= \dfrac{BC}{QR} =\dfrac{CA}{RP}, \dfrac{AB}{PQ}= \dfrac{x+x}{y+y} = \dfrac{2x}{2y} =\dfrac{x}{y}$$
Let $$Am=MB= x $$ (Given)
$$PN= NQ= y $$ (Given)
In $$\triangle AMC$$ & $$ \triangle PNR$$
$$\dfrac{x}{y}=\dfrac{AM}{PN}, \dfrac{x}{y} =\dfrac{AB}{PQ}=\dfrac{CA}{RP}$$
So, $$\dfrac{AM}{PN}= \dfrac{CA}{RP}$$ & $$\angle A= \angle P$$
Therefore, $$\triangle AMC \sim \triangle PNR$$ (by side angle side similarity)
$$(ii)$$ As $$\triangle AMC \sim \triangle PNR$$
So, $$\dfrac{CM}{RN}= \dfrac{AM}{PN}$$ Proved (by similar parts of similar triangles are similar)
$$\dfrac{CM}{RN}= \dfrac{AM}{PN}=\dfrac{x}{y} =\dfrac{AB}{PQ}$$ Proved
$$(iii)$$ In $$\triangle CMB $$ & $$\triangle RNQ$$
$$\dfrac{BC}{QR}=\dfrac{AB}{PQ}= \dfrac{x}{y} = \dfrac{BM}{QN}= \dfrac{x}{y}$$
So, $$\dfrac{BC}{QR} =\dfrac{BM}{QN}, \angle B= \angle Q$$
Therefore , $$\triangle CMB \sim \triangle RNQ$$
(by $$SAS$$ similarly )
State and Prove the relation between areas of two similar triangles.
Given : $$\triangle ABC \sim \triangle PQR$$
To prove,
$$\dfrac{Area(\triangle ABC)}{Area(\triangle PQR)}=\dfrac{BC^2}{QR^2}=\dfrac{AB^2}{PQ^2}=\dfrac{AC^2}{PR^2}$$
Construction : Draw segment $$AD\bot $$ side $$BC \,\,\&\,\,PS\bot $$ side $$QR$$
Proof: $$\triangle ABC \sim \triangle PQR$$ (given)
$$\therefore \dfrac{AB}{PQ}=\dfrac{BC}{QR}=\dfrac{AC}{PR}..........(i)$$
$$\angle B=\angle Q\,\,\, \&\,\,\, \angle C=\angle R...........(ii)$$
Now in $$\angle ADB\,\,\&\,\, \triangle PSQ,$$
$$\angle ABD=\angle PQS$$ (from ii)
$$\angle ADB=\angle PSQ$$ ($$=90^0$$)
$$\therefore \triangle ADB\sim \triangle PSQ$$ (A-A similarity)
$$\therefore \dfrac{AB}{PQ}=\dfrac{BD}{QS}=\dfrac{AD}{PS}$$
$$\therefore $$ From (i) and (iii)
$$\dfrac{AB}{PQ}=\dfrac{BC}{QR}=\dfrac{AD}{PS}$$......(iv)
Area of $$\triangle =\dfrac{1}{2}\times b\times h=\dfrac{\dfrac{1}{2}\times AD \times BC}{\dfrac{1}{2}\times PS\times QR}=\dfrac{Area(\triangle ABC)}{Area(\triangle PQR)}$$
$$=\dfrac{AD\times BC}{PS\times QR}=\dfrac{AD}{PS}\times \dfrac{BC}{QR}=\dfrac{BC}{QR}\times \dfrac{BC}{QR}[\because\dfrac{AD}{PS}=\dfrac{BC}{QR}]$$
$$=\dfrac{BC^2}{QR^2}$$
$$\therefore \dfrac{A\,of\, (\triangle ABC)}{A\,of\, (\triangle PQR)}=\dfrac{BC^2}{QR^2}=\dfrac{AB^2}{PQ^2}=\dfrac{AC^2}{PR^2}$$
$$\left[\because \dfrac{AB}{PQ}=\dfrac{BC}{QR}=\dfrac{AC}{PR}(from\,\,i)\right]$$
$$AX$$ and $$DY$$ are altitiudes of two triangles $$\triangle ABC$$ and $$\triangle DEF$$. Prove that $$AX:DY=AB:DE$$.
How to prove areas of similar triangles theorem
Draw $$AM \bot BC\,\,\& \,\,PN \bot QR$$
and $$\Delta ABC \sim \Delta PQR$$
$$\begin{array}{l} \frac { { ar\left( { \Delta ABC } \right) } }{ { ar\left( { \Delta PQR } \right) } } =\frac { { \frac { 1 }{ 2 } \times BC\times AM } }{ { \frac { 1 }{ 2 } \times QR\times PN } } & \\ { { Sin } }ce,\, \, \Delta ABC\sim \Delta PQR & \\ \therefore \frac { { AB } }{ { PQ } } =\frac { { BC } }{ { QR } } =\frac { { AC } }{ { PR } } & \\ In\, \, \Delta ABM\, \, \& \, \, \Delta PQN & \\ \angle B=\angle Q & \left[ { \because \Delta ABC\sim \Delta PQR } \right] \\ \angle M=\angle N=90^{ \circ } & \\ \therefore \Delta ABM\sim \Delta PQN & \\ \therefore \frac { { AB } }{ { PQ } } =\frac { { AM } }{ { PN } } & \\ \therefore \frac { { ar\left( { \Delta ABC } \right) } }{ { ar\left( { \Delta PQR } \right) } } =\frac { { AB } }{ { PQ } } \times \frac { { AB } }{ { PQ } } ={ \left( { \frac { { AB } }{ { PQ } } } \right) ^{ 2 } }={ \left( { \frac { { BC } }{ { QR } } } \right) ^{ 2 } }={ \left( { \frac { { AC } }{ { PR } } } \right) ^{ 2 } } & \end{array}$$
In the Figure, if $$LM \parallel CB$$ and $$LN \parallel CD$$, prove that $$\dfrac{AM}{AB}=\dfrac{AN}{AD}$$.
In $$\Delta ABC$$, as $$LM\parallel BC$$, so by basic proportionality theorem,
$$\dfrac{{AL}}{{AC}} = \dfrac{{AM}}{{AB}}$$ ........... $$(1)$$
In $$\Delta ADC$$, as $$LN\parallel CD$$, so by basic proportionality theorem,
$$\dfrac{{AL}}{{AC}} = \dfrac{{AN}}{{AD}}$$ ........... $$(2)$$
From equation $$(1)$$ and $$(2),$$
$$\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AD}}$$.
In the given figure, $$\dfrac{{QR}}{{QS}} = \dfrac{{QT}}{{PR}}\,\,and\,\,\angle 1 = \angle 2.$$ Show that $$ \Delta PQS$$ $$ \sim $$ $$\Delta TQR$$
$$E$$ and $$F$$ are points on the sides $$PQ$$ and $$PR$$ respectively of a $$\Delta PQR$$. For each of the following cases state whether $$EF\parallel \,QR$$
(1) $$PE = 3.9\,cm,\,EQ = 3\,cm,\,PF = 3.6\,cm\,\,and\,\,FR = 2.4$$
(2) $$PE = 4\,cm,\,QE = 4.5\,cm,\,PF = 8\,cm\,\,\,and\,\,\,RF = 9\,cm$$
(3) $$PQ = 1.28\,cm\,{\mathop{\rm PR}\nolimits} = 2.56\,cm,\,PE = 0.18\,cm\,\,\,and\,PF = 0.36\,cm$$
In A, B and C are points on OP, OQ and OR respectively such that AB$$||$$PQ and AC$$|$$ PR. Show that BC$$||$$QR.
In $$\triangle OPQ$$, we have
$$AB\parallel PQ$$
Therefore, by using basic proportionality theorem , we have
$$\dfrac{OA}{AP}=\dfrac{OB}{BQ}.................(i)$$
IN $$\triangle OPR$$, we have
$$AC\parallel PR$$
Therefore, by using basic proportionality theorem , we have
$$\dfrac{OC}{CR}=\dfrac{OA}{AP}.................(ii)$$
Comparing (i)&(ii), we get
$$\dfrac{OB}{BQ}=\dfrac{OC}{CR}$$
Therefore, by using converse of basic proportionality theorem, we get
$$BC\parallel QR$$
Write the statement of Basic proportionality theorem.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR.
Sow that $$\Delta \,ABC\, \sim \,\Delta \,PQR$$.
(Image 1)
Given: $$\triangle ABC$$ & $$\triangle PQR$$
AD is the median of $$\triangle ABC$$
PM is the median of $$\triangle PQR$$
$$\cfrac { AB }{ PQ } =\cfrac { AC }{ PR } =\cfrac { AD }{ PM } \rightarrow 1$$
To prove: $$\triangle ABC\sim \triangle PQR$$
Proof:Let us extend AD to point D such that that $$AD=DE$$ and PM upto point L such that $$PM=ML$$
Join B to E, C to E, & Q to L and R to L
(Image 2)
We know that medians is the bisector of opposite side
Hence $$BD=DC$$ & $$AD=DE$$ *By construction)
Hence in quadrilateral ABEC, diagonals AE and BC bisect each other at point D
$$\therefore ABEC$$ is a parallelogram
$$\therefore AC=BE$$ & $$AB=EC$$ (opposite sides of a parallelogram are equal) $$\rightarrow 2$$
Similarly we can prove that
$$PQLR$$ is a parallelogram.
$$PR=QL,PQ=LR$$ (opposite sides of a parallelogram are equal) $$\rightarrow 3$$
Given that
$$\cfrac { AB }{ PQ } =\cfrac { AC }{ PR } =\cfrac { AD }{ PM } $$ (frim $$1$$)
$$\Rightarrow \cfrac { AB }{ PQ } =\cfrac { BE }{ QL } =\cfrac { AD }{ PM } $$ (from $$2$$ and $$3$$)
$$\Rightarrow \cfrac { AB }{ PQ } =\cfrac { BE }{ QL } =\cfrac { 2AD }{ 2PM } $$
$$\Rightarrow \cfrac { AB }{ PQ } =\cfrac { BE }{ QL } =\cfrac { AE }{ PL } $$ (As $$AD=DE,AE=AD+DE=AD+AD=2AD$$ & $$PM=ML,PL=PM+ML=PM+PM=2PM$$)
$$\therefore \triangle ABE\sim \triangle PQL$$ (By SSS similarity criteria)
We know that corresponding angles of similar triangles are equal
$$\therefore \angle BAE=\angle QPL\rightarrow 4$$
Similarly we can prove that
$$\triangle AEC\sim \triangle PLR$$
We know that corresponding angles of similar triangles are equal
$$\angle CAE=\angle RPL\rightarrow 5$$
Adding $$4$$ and $$5$$, we get
$$\angle BAE+\angle CAE=\angle QPL+\angle RPL$$
$$\Rightarrow \angle CAB=\angle RPQ\rightarrow 6$$
In $$\triangle ABC$$ and $$\triangle PQR$$
$$\cfrac { AB }{ PQ } =\cfrac { AC }{ PR } $$ (from $$1$$)
$$\angle CAB=\angle RPQ$$ (from $$6$$)
$$\therefore \triangle ABC\sim \triangle PQR$$ (By SAS similarity criteria)
Hence, proved
Given: $$\triangle ABC$$ & $$\triangle PQR$$
AD is the median of $$\triangle ABC$$
PM is the median of $$\triangle PQR$$
$$\cfrac { AB }{ PQ } =\cfrac { AC }{ PR } =\cfrac { AD }{ PM } \rightarrow 1$$
To prove: $$\triangle ABC\sim \triangle PQR$$
Proof:Let us extend AD to point D such that that $$AD=DE$$ and PM upto point L such that $$PM=ML$$
Join B to E, C to E, & Q to L and R to L
(Image 2)
We know that medians is the bisector of opposite side
Hence $$BD=DC$$ & $$AD=DE$$ *By construction)
Hence in quadrilateral ABEC, diagonals AE and BC bisect each other at point D
$$\therefore ABEC$$ is a parallelogram
$$\therefore AC=BE$$ & $$AB=EC$$ (opposite sides of a parallelogram are equal) $$\rightarrow 2$$
Similarly we can prove that
$$PQLR$$ is a parallelogram.
$$PR=QL,PQ=LR$$ (opposite sides of a parallelogram are equal) $$\rightarrow 3$$
Given that
$$\cfrac { AB }{ PQ } =\cfrac { AC }{ PR } =\cfrac { AD }{ PM } $$ (frim $$1$$)
$$\Rightarrow \cfrac { AB }{ PQ } =\cfrac { BE }{ QL } =\cfrac { AD }{ PM } $$ (from $$2$$ and $$3$$)
$$\Rightarrow \cfrac { AB }{ PQ } =\cfrac { BE }{ QL } =\cfrac { 2AD }{ 2PM } $$
$$\Rightarrow \cfrac { AB }{ PQ } =\cfrac { BE }{ QL } =\cfrac { AE }{ PL } $$ (As $$AD=DE,AE=AD+DE=AD+AD=2AD$$ & $$PM=ML,PL=PM+ML=PM+PM=2PM$$)
$$\therefore \triangle ABE\sim \triangle PQL$$ (By SSS similarity criteria)
We know that corresponding angles of similar triangles are equal
$$\therefore \angle BAE=\angle QPL\rightarrow 4$$
Similarly we can prove that
$$\triangle AEC\sim \triangle PLR$$
We know that corresponding angles of similar triangles are equal
$$\angle CAE=\angle RPL\rightarrow 5$$
Adding $$4$$ and $$5$$, we get
$$\angle BAE+\angle CAE=\angle QPL+\angle RPL$$
$$\Rightarrow \angle CAB=\angle RPQ\rightarrow 6$$
In $$\triangle ABC$$ and $$\triangle PQR$$
$$\cfrac { AB }{ PQ } =\cfrac { AC }{ PR } $$ (from $$1$$)
$$\angle CAB=\angle RPQ$$ (from $$6$$)
$$\therefore \triangle ABC\sim \triangle PQR$$ (By SAS similarity criteria)
Hence, proved
State converse of Pythagoras theorem.
CM and RN are respectively the medians of $$\Delta \,ABC$$ and $$\Delta \,PQR$$. If $$\Delta \,ABC \sim \Delta \,PQR$$, prove that:
(A) $$\Delta \,AMC \sim \,\Delta \,PNR$$
(B) $$\dfrac{{CM}}{{RN}} = \dfrac{{AB}}{{PQ}}$$
(B) $$\dfrac{{CM}}{{RN}} = \dfrac{{AB}}{{PQ}}$$
$$(A)$$ Given, $$\triangle ABC$$ and $$\triangle PQR$$
CM is the median of $$\triangle ABC$$
and RN is the median of $$\triangle PQR$$
$$\Rightarrow \cfrac { AM }{ PN } =\cfrac { CA }{ RP } \quad .....(3)$$
$$\cfrac { CM }{ RN } =\cfrac { 2AM }{ 2PN } $$
$$\Rightarrow \cfrac { CM }{ RN } =\cfrac { AB }{ PQ } $$ $$[Hence\ proved]$$
CM is the median of $$\triangle ABC$$
and RN is the median of $$\triangle PQR$$
Also, $$\triangle ABC \sim \triangle PQR$$
To prove:$$\triangle AMC \sim \triangle PNR$$
Proof:
CM is the median of $$\triangle ABC $$
So, $$AM=MB=\cfrac { 1 }{ 2 } AB\quad ..... (1)$$
Similarly, RN is the median of $$\triangle PQR$$
So, $$PN=QN=\cfrac { 1 }{ 2 } PQ\quad ..... (2)$$
CM is the median of $$\triangle ABC $$
So, $$AM=MB=\cfrac { 1 }{ 2 } AB\quad ..... (1)$$
Similarly, RN is the median of $$\triangle PQR$$
So, $$PN=QN=\cfrac { 1 }{ 2 } PQ\quad ..... (2)$$
Given, $$\triangle ABC\sim \triangle PQR$$
$$\therefore \ \cfrac { AB }{ PQ } =\cfrac { BC }{ QR } =\cfrac { CA }{ RP } $$ (Corresponding sides of similar triangle are proportional)
$$\therefore \ \cfrac { AB }{ PQ } =\cfrac { BC }{ QR } =\cfrac { CA }{ RP } $$ (Corresponding sides of similar triangle are proportional)
$$\Rightarrow \cfrac { AB }{ PQ } =\cfrac { CA }{ RP } \Rightarrow \cfrac { 2AM }{ 2PN } =\cfrac { CA }{ RP } $$ [From $$(1)$$ and $$(2)$$]
$$\Rightarrow \cfrac { AM }{ PN } =\cfrac { CA }{ RP } \quad .....(3)$$
Also, since $$\triangle ABC\sim \triangle PQR$$
$$\angle A=\angle P$$ (corresponding angles of similar triangles are equal) $$\ \ ......(4)$$
In $$\triangle AMC$$ & $$\triangle PNR$$,
$$\angle A=\angle P$$ [From $$(4)$$]
Also, $$\cfrac { AM }{ PN } =\cfrac { CA }{ RP } $$ [From $$(3)$$]
Hence, by SAS similarity,
$$\triangle AMC\sim \triangle PNR$$ $$[Hence\ proved]$$
$$(B)$$ $$\triangle AMC\sim \triangle PNR$$
So, $$\cfrac { CM }{ RN } =\cfrac { AC }{ PR } =\cfrac { AM }{ PN } $$ (corresponding sides of similar triangle are proportional)
Therefore,
$$\cfrac { CM }{ RN } =\cfrac { AM }{ PN } $$
$$\cfrac { CM }{ RN } =\cfrac { AM }{ PN } $$
$$\cfrac { CM }{ RN } =\cfrac { 2AM }{ 2PN } $$
$$\Rightarrow \cfrac { CM }{ RN } =\cfrac { AB }{ PQ } $$ $$[Hence\ proved]$$
In the adjoining figure $$AB \parallel CD $$, prove that $$\Delta AOB \sim \Delta DOC$$
In the figure if $$PQ \parallel RS$$, prove that $$\triangle POQ \sim \triangle SOR$$.
Solution:-
Given:-
$$PQ \parallel RS$$
To prove:- $$\triangle{POQ} \sim \triangle{SOR}$$
Proof:-
In $$\triangle{POQ}$$ and $$\triangle{SOR}$$
$$\angle{POQ} = \angle{SOR} \; \left[ \because \text{Vertically opposite angles} \right]$$
$$\angle{P} = \angle{S} \; \left[ \because \text{As } PQ \parallel RS, \text{ Alternate angles} \right]$$
$$\angle{Q} = \angle{R} \; \left[ \because \text{As } PQ \parallel RS, \text{ Alternate angles} \right]$$
Using AAA similarity function criteria,
$$\triangle{POQ} \sim \triangle{SOR}$$
Hence proved.
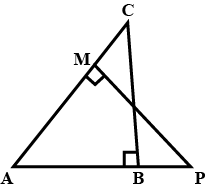
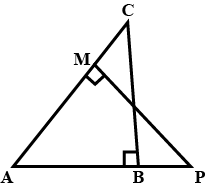
$$\triangle ABC$$ and $$\triangle AMP$$ are two right triangles right angled at B and M respectively. Prove that
i) $$\triangle ABC\sim \triangle AMP$$ ii) $$\cfrac { CA }{ PA } =\cfrac { BC }{ MP } $$
Given figure : (Image )
i) To prove
$$\triangle ABC$$ is ismilar to triangle AMP
We can prove this using angle-angle similarity postulate
In triangles AMP and ABC
$$\angle AMP=\angle ABC=90°$$
$$\angle MAP=\angle BAC=$$same angle (common angle)
Hence, two angles of the required triangles are same
$$\therefore $$By angle-angle (AA) similarity:
We can say that $$\triangle ABC\sim \triangle AMP$$
ii) To prove $$\rightarrow \cfrac { CA }{ PA } =\cfrac { BC }{ MP } $$
$$\because $$ In part i) we already proved
that $$\angle AMP=\angle ABC=90°$$
and $$\angle MAP=\angle BAC=$$ common angle
and sum of $$3$$ angles of a triangle$$=180°$$
$$\therefore \angle APM=\angle ACB$$
From side-angle-side similarity theorem,
we can that the sides including the angles which are equal must be proportional to each other
Sides including $$\angle APM=AP$$ and $$MP$$
Sides including $$\angle ACB=AC$$ & $$BC$$
Using S-A-S similarity theorem
$$\cfrac { AP }{ MP } =\cfrac { AC }{ BC } $$
$$\Rightarrow \cfrac { BC }{ MP } =\cfrac { AC }{ AP } $$
$$\cfrac { CA }{ PA } =\cfrac { BC }{ MP } $$
Hence proved.
In the given figure, $$\Delta$$ABC and $$\Delta$$AMP are right angled at B and M respectively.
Given AC$$=10$$cm, AP $$=15$$cm and PM$$=12$$ cm.
Prove that : $$\Delta$$ABC $$\sim\Delta$$ AMP.
In the given figure, $$\Delta$$ABC and $$\Delta$$AMP are right angled at B and M respectively.
Given AC$$=10$$cm, AP$$=15$$cm and PM$$=12$$cm. Find : AB and BC.
In $$\Delta ABC$$, $$DE\ II\ BC$$, $$AD=2.5\ cm$$, $$DB=5\ cm$$, $$AE=3\ cm$$ and $$EC=x\ cm$$
Find the value of $$x$$ ?
Solution:
$$\dfrac{AD}{AD+BD}=\dfrac{AE}{AE+EC}$$
$$\dfrac{2.5}{7.5}=\dfrac{3}{3+x}$$
$$3+x=9$$
$$x=6$$
In fig. $$S$$ and $$T$$ are the points on the sides $$PQ$$ and $$PR$$ respectively of $$\Delta PQR$$, such that $$PT = 4$$ cm, $$TR = 4$$ cm & $$ST \parallel QR$$. Find the ratio of areas of $$\Delta PST $$ & $$\Delta PQR$$.
If $$\triangle ABC$$ is right-angled at$$B$$. then prove that $${ AB }^{ 2 }+{ BC }^{ 2 }=AC^{ 2 }$$
We know that if a perpendicular is drawn from the vertex of a right angle of a right angled triangle to the hypotenuse, then triangle on both sides of the perpendicular are similar to the whole triangle and to each other.
We have
$$\triangle ADB\sim\triangle ABC$$
$$\therefore \dfrac{AD}{AB}=\dfrac{AB}{AC}$$ (In similar triangles corresponding sides are equal)
$$AB^2=AD\times AC.........(1)$$
Also $$\triangle BDC\sim\triangle ABC$$
$$\therefore \dfrac{CD}{BC}=\dfrac{BC}{AC}$$ (In similar triangles corresponding sides are equal)
$$BC^2=CD\times AC.........(2)$$
Adding (1) and (2) we get
$$AB^2+BC^2=AD\times AC+CD\times AC$$
$$AB^2+BC^2=AC(AD+A=CD)$$
From the figure $$AD+CD=AC$$
$$AB^2+BC^2=AC.AC$$
Therefore, $$AB^2+BC^2=AC^2$$
In figure, the line segment XY is parallel to side AC of $$ \Delta ABC $$ and it divides the triangle into two parts of equal areas. Find the ratio $$ \dfrac{AX}{AB} $$.
REF.Image
2 Area (xy) = Area (ABC)
In $$\Delta ABC$$ & $$\Delta XBY$$
$$\angle ABC=\angle XBY$$(common)
$$\angle ACB=\angle XYB$$ (since XY||AC, angles are equal)
$$\Delta ABC\sim \Delta XBY$$ (AA similarity)
$$(\dfrac{AB}{XB})^{2}=\dfrac{Area(\Delta ABC)}{Area(\Delta BXY)}=2$$
$$(AB)^{2}=2(XB)^{2}$$ $$AB=\sqrt{2}\times B$$
$$AX=AB-XB=AB-\dfrac{AB}{\sqrt{2}}=(\dfrac{\sqrt{2}-1}{\sqrt{2}})AB$$
$$\dfrac{AX}{AB}=\dfrac{\sqrt{2}-1}{\sqrt{2}}$$
Prove that the ratio of the area of two similar triangles is equal to the ratio of squares on the corresponding sides.
$$Given:\triangle ABC\sim\triangle PQR$$
To prove :$$ \dfrac{ar\left(ABC\right)}{ar\left(PQR\right)}={\left(\dfrac{AB}{PQ}\right)}^{2}={\left(\dfrac{BC}{QR}\right)}^{2}={\left(\dfrac{AC}{PR}\right)}^{2}$$
Proof:-
$$arABC=\dfrac { 1 }{ 2 } \times base\times height=\dfrac { 1 }{ 2 } \times BC\times AM---(i)$$
$$ar\left( PQR \right) =\dfrac { 1 }{ 2 } \times base\times hight=\dfrac { 1 }{ 2 } \times QP\times PN----(ii)$$
$$\dfrac{ar\left(ABC\right)}{ar\left(PQR\right)}=\dfrac {BC \times AM}{QR\times PN}----(A)$$
In $$\triangle ABM$$ and $$\triangle PQN, <B=<Q, <M=<N$$
$$\triangle ABM\sim \triangle PQN$$
$$\therefore \dfrac{AB}{PQ}=\dfrac{AM}{PN}---(B)$$
From $$\left(A\right)$$
$$\dfrac{ar\left(ABC\right)}{ar\left(PQR\right)}= \dfrac{BC\times AM}{QR\times PN}= \dfrac{BC}{QR}\times \dfrac{AB}{PQ}---(C)$$
Now, given $$\triangle ABC \sim \triangle PQR \Rightarrow \dfrac{AB}{PQ}=\dfrac{BC}{QP}= \dfrac{AC}{PR}$$
Putting in $$\left(C\right) \quad \dfrac{ar\left(ABC\right)}{ar\left(PQR\right)}= {\left(\dfrac{AB}{PQ}\right)}^{2}$$
Similarly
$$\Rightarrow\dfrac{ar\left(ABC\right)}{ar\left(PQR\right)}= {\left(\dfrac{AB}{PQ}\right)}^{2}{\left(\dfrac{BC}{QR}\right)}^{2}={\left(\dfrac{AC}{PR}\right)}^{2}$$
Hence proved
Cut out two identical right angled triangles. Name the vertices of the A, B, C on both sides .Draw the altitude on the hypotenuse of one of the foot of the perpendicular as D. cut the triangle on its altitude an triangles. state the correspondences by which the three triangle an one another.
We have,
Given that:-
$$\Delta ABC$$ right angled at point $$B$$.and perpendicular from $$B$$ intersecting $$AC$$ at point $$D$$.
To prove :-
$$ \Delta ADB\sim \Delta ABC $$
$$ \Delta BDC\sim \Delta ABC $$
$$ \Delta ADB\sim \Delta BDC $$
Proof:-
$$ In\,\Delta BDC\,\,and\,\,\Delta ABC $$
$$ \angle C=\angle C\,\,\,\left( Common \right) $$
$$ \angle BDC=\angle ABC\,\,\,\left( Each\,{{90}^{o}} \right) $$
$$ \text{Then,} $$
$$ \Delta BDC\sim \Delta ABC\,\,\,(By\,AA\,similarity) $$
$$ In\,\Delta ADB\,\,and\,\,\Delta ABC $$
$$ \angle A=\angle A\,\,\,\left( Common \right) $$
$$ \angle ADB=\angle ABC\,\,\,\left( Each\,{{90}^{o}} \right) $$
$$ \text{Then,} $$
$$ \Delta ADB\sim \Delta ABC\,\,\,(By\,AA\,similarity) $$
Hence proved.
Corresponding sides of two similar triangles are $$3cm$$ and $$4cm$$. If the area of the larger triangle is $$48cm^{2}$$, find the area of the smaller triangle.
In figure $$\angle {1}=\angle{2}$$ and $$\triangle {NSQ}\cong \triangle{MTR}$$, then prove that $$\triangle PTS \sim \triangle {PRQ}$$
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two side,then it divides the two sides in the same ratio.
Given $$DE\parallel BC\\ In\quad \triangle ADE\quad and\triangle ABC\\ \angle DAE=\angle BAC\quad (common\quad angle)\\ \angle ADE=\angle ABC\quad \left[ \because DE\parallel BC\\ \therefore corresponding\quad angles\quad are\quad equal \right] \\ \angle AED=\angle ACB\\ \therefore \triangle ADE\sim \triangle ABC\\ Hence\quad \dfrac { AD }{ AB } =\dfrac { AE }{ AC } \left( In\quad similar\quad triangle,\quad corresponding\quad sides\quad are\quad in\quad same\quad ratio \right) $$
$$\because \dfrac { AD }{ AB } =\dfrac { AE }{ AC } \\ \Rightarrow \dfrac { AB }{ AD } =\dfrac { AC }{ AE } \\ \Rightarrow \dfrac { AB }{ AD } -1=\dfrac { AC }{ AE } -1\\ \Rightarrow \dfrac { AB-AD }{ AD } =\dfrac { AC-AE }{ AE } \\ \Rightarrow \dfrac{ DB }{ AD } =\dfrac { EC }{ AE } \\ \Rightarrow \dfrac { AD }{ DB } =\dfrac { AE }{ EC } $$
It is proved that if a line is drawn parallel to one side of a triangle intersecting the other two side, then it divides the two sides in the same ratio.
In the given figure $$DE\parallel AC$$ and $$DF\parallel AE$$. Prove that.
$$\cfrac{BF}{FE}=\cfrac{BE}{EC}$$
Given: $$D$$ is any point on side $$AB$$ of $$\triangle ABC$$ and $$E$$ and $$F$$ are two points on side $$BC$$, line segment $$DF, DE$$ and $$AE$$ are drawn
To prove that: $$\cfrac{BF}{FE}=\cfrac{BE}{EC}$$
Proof: In $$\triangle BCA$$
$$DE\parallel AC$$ (given)
By basic proportionality theorem, if two triangles are similar then their corresponding sides are proportional.
By basic proportionality theorem, if two triangles are similar then their corresponding sides are proportional.
$$\cfrac{BE}{EC}=\cfrac{BD}{DA}$$...(i)
Again in $$\triangle BEA$$, $$DF\parallel AE$$ (given)
$$\cfrac{BF}{FE}=\cfrac{BD}{DA}$$....(ii) (by basic proportionality theorem)
From equation (i) and (ii), we can write
$$\cfrac{BF}{FE}=\cfrac{BE}{EC}$$
If $$\angle{A}$$ and $$\angle {P}$$ are acute angles such that $$\sin{A}=\sin{P}$$ then prove that $$\angle {A}=\angle {P}$$
$$\triangle {ABC}$$ and $$\triangle {DBC}$$ are two isosceles triangles on the same base $$BC$$ (in figure). Show that $$\angle{ABD}=\angle{ACD}$$.
$$\triangle{ABC}$$ is isosceles
So, $$AB=AC.........(1)$$
$$\triangle{DBC}$$ is isosceles
So, $$DB=DC.........(2)$$
In $$\triangle{ABD}$$ and $$\triangle{ACD}$$
$$AB=AC$$ [From (1)]
$$BD=CD$$ [From (2)]
$$AD=AD$$ [Common]
$$\therefore \triangle{ABD}\cong\triangle{ACD}$$ [SSS congruency]
$$\therefore \angle{ABD}=\angle{ACD}$$ [CPCT}
Hence proved.
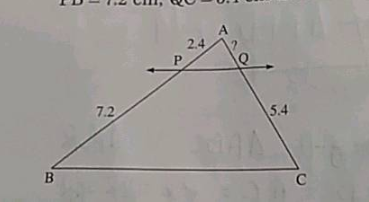
In the figure,line $$PQ|| side BC,AP=2.4cm,PB=7.2cm,QC=5.4$$cm then find $$AQ$$?
If the areas of two similar triangles are in ratio $$25 : 64 ,$$ write the ratio of their corresponding sides.
Diagonals of a trapezium $$ABCD$$ with $$AB\parallel DC$$ intersect each other at the point $$O$$. If $$AB=2CD$$, find the ratio of the areas of triangles $$AOB$$ and $$COD$$
In $$\triangle{AOB}$$ and $$\triangle{COD}$$
$$\angle{AOB}=\angle{COD}$$ [Vertically opposite angles]
$$\angle{OAB}=\angle{OCD}$$ [Since AB||CD with AC as traversal alternate angle are equal]
Hence, $$\triangle{AOB}\sim\triangle{COD}$$ [AA similarity]
We know that if two triangle re similar, then
Ration of areas is equal to square of ratio of its corresponding sides
Hence, $$\dfrac{Area\ \triangle{AOB}}{Area\ \triangle{COD}}=\left(\dfrac{AB}{CD}\right)^2$$
$$\dfrac{Area\ \triangle{AOB}}{Area\ \triangle{COD}}=\left(\dfrac{2CD}{CD}\right)^2$$
$$\dfrac{Area\ \triangle{AOB}}{Area\ \triangle{COD}}=\left(\dfrac{2}{1}\right)^2$$
$$\dfrac{Area\ \triangle{AOB}}{Area\ \triangle{COD}}=\dfrac{4}{1}$$
$$\therefore Area\ \triangle{AOB}:Area\ \triangle{COD}=4:1$$
Hence ratio of areas is 4:1.
In the figure given below, $$\angle PQR = \angle PRS$$. Prove that triangles $$PQR$$ and $$PRS$$ are similar. If $$PR = 8\ cm, PS = 4\ cm$$, calculate $$PQ$$.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Let the two triangles be:
$$\Delta \mathrm{ABC} \ and \ \Delta \mathrm{PQR}$$
Area of $$ \Delta A B C=\dfrac{1}{2} \times B C \times A M \ldots \ldots \ldots \ldots \ldots . .(1) $$
Area of $$ \Delta P Q R=\dfrac{1}{2} \times Q R \times P N \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots . .(2) $$
Dividing (1) by (2)
$$ \dfrac{\operatorname{ar}(A B C)}{\operatorname{ar}(P Q R)}=\dfrac{\dfrac{1}{2} \times B C \times A M}{\dfrac{1}{2} \times Q R \times P N} $$
$$ \dfrac{a r(A B C)}{a r(P Q R)}=\dfrac{B C \times A M}{Q R \times P N} \ldots \ldots \ldots \ldots \ldots \ldots \ldots . .(1) $$
In $$ \Delta A B M $$ and $$ \Delta P Q N $$
$$ \angle B=\angle Q $$ (Angles of similar triangles)
$$ \left.\angle M=\angle N \text { (Both } 90^{\circ}\right) $$
Therefore, $$ \Delta A B M \sim \Delta P Q N $$
So, $$ \dfrac{A B}{A M}=\dfrac{P Q}{P N} \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots .(2) $$
From 1 and 2
$$ \dfrac{a r(A B C)}{a r(P Q R)}=\dfrac{B C}{Q R} \times \dfrac{A M}{P N} $$
$$ \Rightarrow \dfrac{a r(A B C)}{a r(P Q R)}=\dfrac{B C}{Q R} \times \dfrac{A B}{P Q} \ldots \ldots \ldots \ldots \ldots \ldots \ldots . .(3) $$
$$ \dfrac{A B}{P Q}=\dfrac{B C}{Q R}=\dfrac{A C}{P R} \ldots \ldots \ldots \ldots .(\Delta A B C \sim \Delta P Q R) $$
Putting in ( 3 )$$ \dfrac{a r(A B C)}{a r(P Q R)}=\dfrac{A B}{P Q} \times \dfrac{A B}{P Q}=\left(\dfrac{A B}{P Q}\right)^{2} $$
$$ \Rightarrow \dfrac{a r(A B C)}{a r(P Q R)}=\left(\dfrac{A B}{P Q}\right)^{2}=\left(\dfrac{B C}{Q R}\right)^{2}=\left(\dfrac{A C}{P R}\right)^{2} $$
Sides $$A B$$ and $$B C$$ and median $$AD$$ of a triangle $$A B C$$ are respectively proportional to sides $$P Q$$ and $$Q R$$ and median $$P M$$ of $$\Delta P Q R .$$ Show that $$\Delta A B C$$ $$\sim \Delta P Q R$$ ?
Given $$\dfrac{AB}{PQ}=\dfrac{AD}{PM}=\dfrac{BC}{QR}$$.
$$\dfrac{BC}{QR}=\dfrac{BC/2}{QR/2}=\dfrac{BD}{QM}$$.
$$\therefore \dfrac{AB}{PQ}=\dfrac{AD}{PM}=\dfrac{BD}{QM}$$
$$\Rightarrow \triangle ABD \sim \triangle PQM$$ ( sss similarly).
Hence $$\angle B=\angle Q$$.
From $$\triangle ABC$$ and $$\triangle PQR$$, we have
$$\dfrac{AB}{PQ}=\dfrac{BC}{QR}$$ and $$\angle B=\angle Q$$.
$$\Rightarrow \triangle ABC\sim \triangle PQR$$
Hence Proved.
Given $$\Delta A B C \sim \Delta P Q R , \text { if } \dfrac { A B } { P Q } = \frac { 1 } { 3 } \text { find } \dfrac { a r \Delta A B C } { a r \Delta P Q R }$$
Area of two similar triangle are $$144\text{ cm}^2$$ and $$81\text{ cm}^2$$. If one side of the first triangle is $$6\text{ cm}$$, then find the corresponding side of the second triangle.
$$\Delta ABC \sim \Delta DEF$$, area of $$\Delta ABC=64\ cm^{2}$$ and area of $$\Delta DEF=121\ cm^{2}$$. If $$EF=15.4\ cm$$, find $$BC$$.
In the adjoining figure, DEFG is a square and $$\angle BAC = {90^0}$$.
Prove that:
$${\rm{D}}{{\rm{E}}^{\rm{2}}}{\rm{ = BD \times EC}}$$
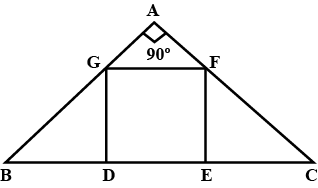
The ratio of the corresponding altitudes of two similar triangles is $$\dfrac{3}{5}$$. Is it correct to say that ratio of their areas is $$\dfrac{6}{5}$$ ?Why ?
False: If two triangles are similar, then the ratio of areas of two triangles will be equal to the square of the ratio of their corresponding sides or altitudes or angle bisectors.
If $$\Delta ABC\sim \Delta PQR$$, then
Refer image,
$$\dfrac{ar(\Delta ABC)}{ar(\Delta PQR)}=\left(\dfrac{AD}{PM}\right)^2$$ (By area theorem)
$$\Rightarrow \dfrac{ar(\Delta ABC)}{ar(\Delta PQR)}=\left(\dfrac{3}{5}\right)^2$$
$$=\dfrac{9}{25}\neq \dfrac{6}{5}$$
So, the given statement is false.
It is possible to draw i) an obtuse-angled equilateral triangle ii)a right-angled equilateral triangle iii)a triangle with two right angles.
In the given figure, $$ST\parallel RQ,PS=3$$ cm and $$SR=4$$cm. Find the ratio of the areas of $$\triangle{PST}$$ to the area of $$\triangle{PRQ}$$
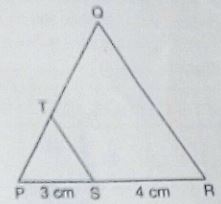
$$A$$ and $$B$$ are respectively the points on the sides $$PQ$$ and $$PR$$ of a triangle $$PQR$$ such that $$PQ = 12.5\ cm, PA = 5\ cm, BR = 6\ cm$$ and $$PB = 4\ cm$$. Is $$AB \parallel QR$$? Give reasons for your answer.
From the dimensions given in the question,
Consider the $$\triangle PQR$$
So, $$PQ/PA = 12.5/5$$
$$= 2.5/1$$
$$PR/PB = (PB + BR)/PB$$
$$= (4 + 6)/4$$
$$= 10/4$$
$$= 2.5$$
By comparing both the results,
$$2.5 = 2.5$$
Therefore, $$PQ/PA = PR/PB$$
So, $$AB$$ is parallel to $$QR$$.
Consider the $$\triangle PQR$$
So, $$PQ/PA = 12.5/5$$
$$= 2.5/1$$
$$PR/PB = (PB + BR)/PB$$
$$= (4 + 6)/4$$
$$= 10/4$$
$$= 2.5$$
By comparing both the results,
$$2.5 = 2.5$$
Therefore, $$PQ/PA = PR/PB$$
So, $$AB$$ is parallel to $$QR$$.
In the figure, it is given $$TS=TR, \angle 1=2\angle =$$ and $$\angle 4=2\angle 2\angle 3$$. Prove that $$\triangle RBT\cong \triangle SAT$$.
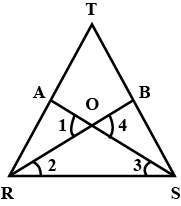
$$\triangle ABC$$ is right angled at A and $$AD\bot BC$$. If $$BC=13$$cm and $$AC=5$$cm, find the ratio of the areas of $$\triangle ABC$$ and $$\triangle ADC$$.
In figure, $$ABC$$ and $$AMP$$ are two right triangles, right angled at $$B$$ and $$M$$ respectively. Prove that
$$\dfrac{CA}{PA}=\dfrac{BC}{MP}$$
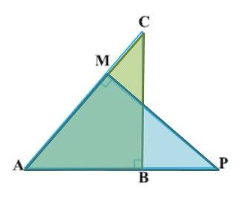
In $$\triangle {ABC}$$ and $$\triangle {AMP}$$
$$\angle CAB=\angle MAP$$ (common angle)
$$\angle {ABC}=\angle {AMP}$$ (both $${90}^{o}$$)
using AA similarity
$$\triangle {ABC}\sim \triangle {AMP}$$
We know that if two triangles are similar, the ratio of their corresponding sides are proportional
$$\cfrac{CA}{PA}=\cfrac{BC}{MP}=\cfrac{AB}{AM}$$
$$\therefore$$ $$\cfrac{CA}{PA}=\cfrac{BC}{MP}$$
In $$\triangle ABC, DE\parallel BC$$, find the value of $$x$$.
Since the $$\Delta ADE$$ and $$\Delta ABC$$ are similar.
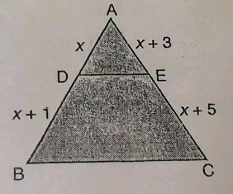
In the given figure $$AP=12$$, $$RP=4$$, $$PS=6$$. Find $$BS$$
In the diagrams of the following figure, same the triangles which is represent to the $$\triangle ABC$$ keeping the letters. In the right order. State the congruence conditions wise.
In the figure, altitudes $$AD$$ and $$CE$$ of $$\triangle{ABC}$$ intersect each other at the point $$P$$.Show that $$\triangle{AEP}\sim\triangle{CDP}$$
STATE BPT THEOREM AND PROVE IT.
Basic proportionality theorem :
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.
Given:
A $$\triangle$$ ABC in which $$DE \parallel BC$$ and DE intersects AB and AC at D and E respectively.
To prove :
$$\dfrac{AD}{DB}=\dfrac{AE}{EC}$$
Construction :
Join BE and CD.
Draw $$EL \perp AB$$ and $$DM \perp AC$$.
Proof :
We have,
$$ar(\triangle ADE)=\dfrac{1}{2} \times AD \times EL$$
$$ar(\triangle DBE) =\dfrac{1}{2} \times DB \times EL$$
Therefore,
$$\dfrac{ar(\triangle ADE)}{ar(\triangle DBE)}=\dfrac{AD}{DB}$$ ...(1)
Again,
$$ar(\triangle ADE)=ar(\triangle AED)=\dfrac{1}{2} \times AE \times DM$$
$$ar(\triangle ECD)=\dfrac{1}{2} \times EC \times DM$$
Therefore,
$$\dfrac{ar(\triangle ADE)}{ar(\triangle ECD)}=\dfrac{AE}{EC}$$ ....(2)
Now, $$\triangle DBE$$ and $$\triangle ECD$$ being on the same base DE and between the same parallels DE and BC, we have,
$$ar(\triangle DBE)=ar(\triangle ECD)$$ ....(3)
From 1, 2 & 3, we have,
$$\dfrac{AD}{DB}=\dfrac{AE}{EC}$$
In the adjacent figure $$XY\parallel BC$$ find the length of $$AY$$ and $$CY$$
Side $$AB$$ and $$BC$$ and median $$AD$$ of a triangle $$ABC$$ are respectively proportional to sides $$PQ$$ and $$QR$$ and median $$PM$$ of $$PQR$$. Show that $$ABC\sim PQR$$ .
Given :
A $$\triangle$$ ABC where AD is the median, $$\triangle$$ PQR where PM is the median.
And, $$\dfrac{AB}{PQ} = \dfrac{BC}{QR}=\dfrac{AD}{PM}$$
To prove :
$$\triangle ABC \sim \triangle PQR$$
Proof :
Since AD is the median,
$$BD=CD=\dfrac{1}{2}BC$$
Similarly, PM is the median,
$$QM=RM=\dfrac{1}{2}QR$$
Given that
$$\dfrac{AB}{PQ}=\dfrac{BC}{QR}=\dfrac{AD}{PM}$$
$$\dfrac{AB}{PQ}=\dfrac{2BD}{2QM}=\dfrac{AD}{PM}$$
$$\dfrac{AB}{PQ}=\dfrac{BD}{QM}=\dfrac{AD}{PM}$$
Since all 3 sides are proportional
$$\triangle ABD \sim \triangle PQM$$ [By SSS similarity]
Hence, $$\angle B =\angle Q$$
In $$\triangle ABC$$ and $$\triangle PQR$$
$$\angle B = \angle Q$$
$$\dfrac{AB}{PQ}=\dfrac{BC}{QR}$$
Hence, by SAS similarity,
$$\triangle ABC \sim \triangle PQR$$
$$D$$ and $$E$$ are respectively the points on the sides $$AB$$ and $$AC$$ of a $$\triangle{ABC}$$ such that $$AB=2.6\ cm,AD=1.3\ cm$$ and $$AE=1.5\ cm$$,Show that $$DE\parallel BC$$
Here $$\dfrac{AB}{AD}=\dfrac{2.6}{1.3}=2$$
$$\dfrac{AC}{AE}=\dfrac{3}{1.5}=2$$
$$\therefore \dfrac{AB}{AD}=\dfrac{AC}{AE}$$
By the converse of BPT,
$$DE\parallel BC$$
Hence proved.
In $$\triangle{PQR},\,ST\parallel QR$$ and $$\dfrac{PS}{SQ}=\dfrac{3}{5}$$ if $$PR=6$$cm find $$PT$$
In $$\triangle{PQR},$$ we have $$ST\parallel QR$$
By Basic proportionality theorem,
$$\dfrac{PS}{SQ}=\dfrac{PT}{TR}$$
$$\Rightarrow \dfrac{PS}{SQ}=\dfrac{PT}{PR-PT}$$
$$\Rightarrow \dfrac{3}{5}=\dfrac{PT}{6-PT}$$
$$\Rightarrow 18-3PT=5PT$$
$$\Rightarrow 8PT=18$$
$$\Rightarrow PT=\dfrac{18}{8}=2.25$$cm
$$ABCD$$ is a rhombus . $$AC$$ is a diagonal. Is $$\angle{BAC}\cong\angle{DAC}$$? Give reason.
If the ratio of the perimeter of two similar triangles is $$4 : 25$$, then find the ratio of the areas of the similar triangles .
In the following figure you are given two triangles answer weather two triangles are similar? Give reason also.
In figure, AD$$=$$DC and AB$$=$$BC. State the three parts of matching pairs you have used to answer.(Is $$\Delta$$ABD$$\cong\Delta$$CBD).
In the given figure, $$AD=DC$$ and $$AB=BC.$$ Is $$\Delta ABD \cong\Delta CBD?$$
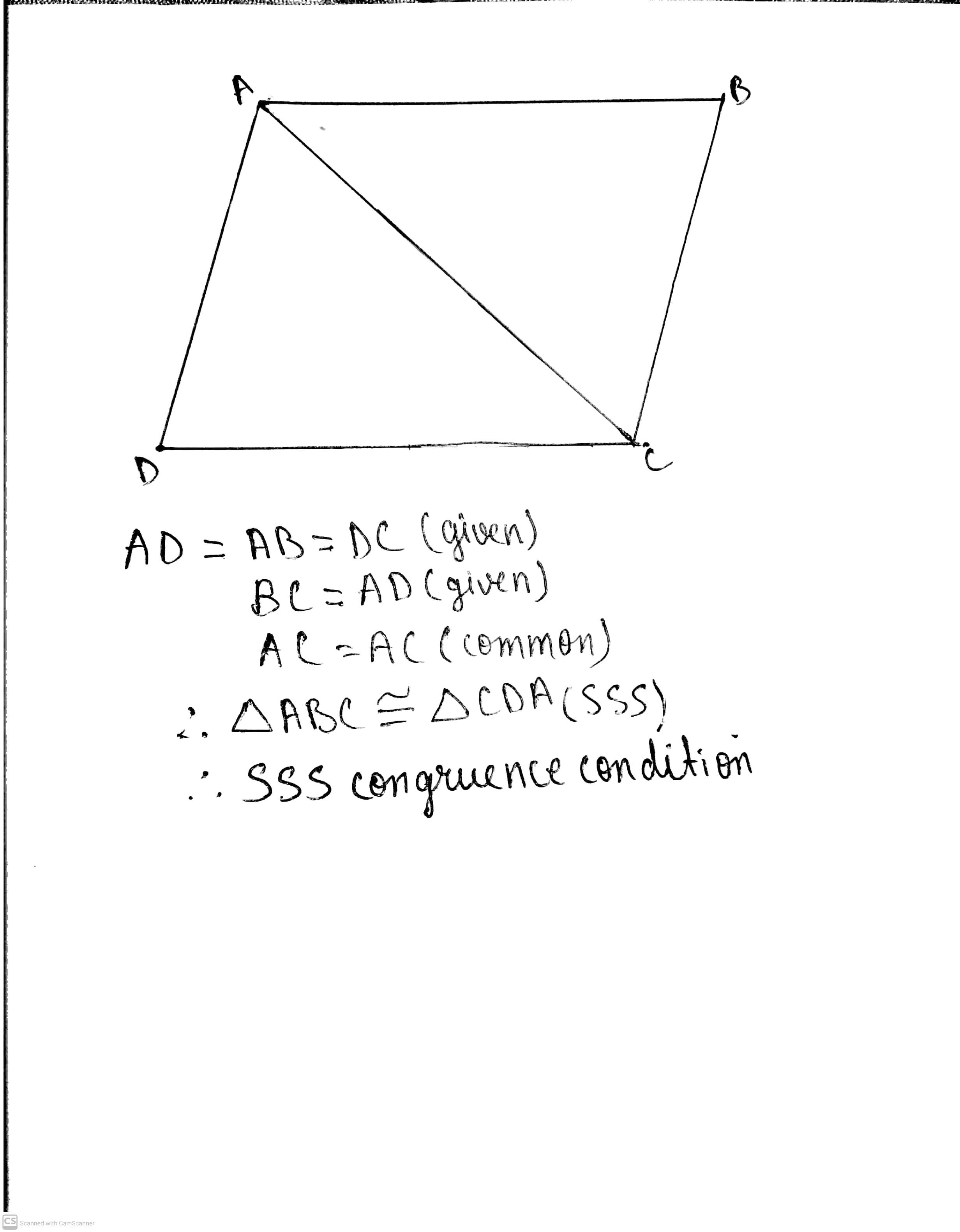
In the following triangle, the lengths of the sides are indicated along sides. By applying SSS condition, determine which are congruent. State the result in symbolic form.
If $$\Delta$$PQR$$\cong\Delta$$EFD, which angles of $$\Delta$$PQR equals $$\angle E$$?
ABC and DBC are both isosceles triangles on a common base BC such that A and D lie on the same side of BC. Are triangles ADB and ADC congruent? Which condition do you use? If $$\angle BAC=40^o$$ and $$\angle BDC=100^o$$; then find $$\angle ADB$$.
In Fig. Prove that:
$$ CD + DA + AB > BC $$
In the following triangle, the lengths of the sides are indicated along sides. By applying SSS condition, determine which are congruent. State the result in symbolic form.
In figure, $$AB||DC$$, AB$$=$$DC and BC$$=$$AD. You have used some fact to say theat $$\triangle ADC\cong\triangle CBA$$, not given in the question, what is that?
In figure, AB$$=$$DC and BC$$=$$AD. What congruence condition have you used?
In $$DE||AC$$ and $$DC||AP$$. Prove that $$\dfrac{BE}{EC}=\dfrac{BC}{CP}$$
Given $$DE || AC \, \& \, DC || AP$$
To prove :- $$\dfrac{BE}{EC} = \dfrac{BE}{CP}$$
Proof :-
In $$\Delta BPA$$, we have $$DC || AP$$
So, by Basic proportionality theorem (B . P. T.), we get
$$\dfrac{BC}{CP} = \dfrac{BD}{DA} $$ ... (i)
In $$\Delta BCA$$, we have $$DE || AC$$ (given)
$$\dfrac{BE}{EC} = \dfrac{BD}{DA} $$ ___(ii) (by B.P. T.)
Comparing (i) & (ii) , we get
$$\dfrac{BC}{CP} = \dfrac{BD}{DA} = \dfrac{BE}{EC}$$
$$\Rightarrow \dfrac{BE}{EC} = \dfrac{BC}{CP}$$
Fill in the blank.
Given $$\Delta ABC \sim \Delta PQR$$, if $$\dfrac{AB}{PQ} = \dfrac{1}{3} , $$ then $$\dfrac{ar (\Delta ABC)}{ar (\Delta PQR)} = $$______ .
$$D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively of a $$\Delta ABC$$ such that $$DE || BC$$. if $$\dfrac{AD}{AB} = \dfrac{8}{15}$$ and $$EC = 3.5 cm$$, find $$AE$$.
Solve the following :
In $$\Delta PQR , \, NM || RQ$$. If $$PM = 15, MQ = 10, NR = 8$$, then find $$PN$$.
$$D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively of a $$\Delta ABC$$ such that $$DE || BC$$. Find the value of $$x$$, when $$AD = x cm, DB = (x - 2) cm, AE = (x + 2) cm$$ and $$EC = (x - 1) cm$$.
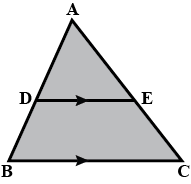
$$D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively of a $$\Delta ABC$$ such that $$DE || BC$$. If $$\dfrac{AD}{DB} = \dfrac{4}{7}$$ and $$AC = 6.6 cm$$, find $$AE$$.
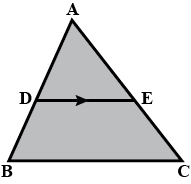
$$D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively of a $$\Delta ABC$$ such that $$DE || BC$$. If $$AD = 3.6 cm, AB = 10 cm$$ and $$AE = 4.5 cm$$, find $$EC$$ and $$AC$$.
$$BL$$ nad $$CM$$ are median of a $$\triangle ABC$$, right angled at $$A$$, Prove that $$4(BL^{2}+CM^{2})=5BC^{2}$$
$$\triangle ABC$$ is right angled at $$A.$$ Where, $$BL$$ and $$CM$$ are the medians.
$$\Rightarrow$$ $$AL=CL=\dfrac{1}{2}AC$$ ------ ( 1 )
Similarly, $$CM$$ is the median,
$$\Rightarrow$$ $$AM=MB=\dfrac{1}{2}AB$$ ----- ( 2 )
In right-angled $$\triangle BAC,$$
$$\Rightarrow$$ $$(BC)^2=(AB)^2+(AC)^2$$ [ By Pythagoras theorem ]
In $$\triangle BAL,$$
$$\Rightarrow$$ $$(BL)^2=(AB)^2+(AL)^2$$ [ By Pythagoras theorem ] ------- ( 3 )
$$\Rightarrow$$ $$(BL)^2=(AB)^2+\left(\dfrac{AC}{2}\right)^2$$
$$\Rightarrow$$ $$(BL)^2=(AB)^2+\dfrac{(AC)^2}{4}$$
$$\Rightarrow$$ $$(BL)^2=\dfrac{4(AB)^2+(AC)^2}{4}$$
$$\Rightarrow$$ $$4(BL)^2=4(AB)^2+(AC)^2$$ ------ ( 4 )
In $$\triangle MAC,$$
$$\Rightarrow$$ $$(CM)^2=(AM)^2+(AC)^2$$ [ By Pythagoras theorem ]
$$\Rightarrow$$ $$(CM)^2=\left(\dfrac{AB}{2}\right)^2+(AC)^2$$
$$\Rightarrow$$ $$(CM)^2=\dfrac{(AB)^2}{4}+(AC)^2$$
$$\Rightarrow$$ $$(CM)^2=\dfrac{(AB)^2+4(AC)^2}{4}$$
$$\Rightarrow$$ $$4CM^2=AB^2+4AC^2$$ ------- ( 5 )
Adding ( 4 ) and ( 5 ),
$$\Rightarrow$$ $$4BL^2+4CM^2=4AB^2+AC^2+AB^2+4AC^2$$
$$\Rightarrow$$ $$4(BL^2+CM^2)=5AB^2+5AC^2$$
$$\Rightarrow$$ $$4(BL^2+CM^2)=5(AB^2+AC^2)$$
From ( 3 ),
$$\Rightarrow$$ $$4(BL^2+CM^2)=5BC^2$$
$$D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively of a $$\Delta ABC$$ such that $$DE || BC$$. Find the value of $$x$$, when $$AD = 4 \text{ cm}, DB = (x - 4) \text{ cm}, AE = 8 \text{ cm}$$ and $$EC = (3x - 19) \text{ cm}$$.
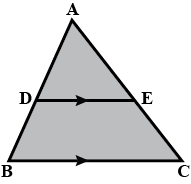
$$D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively of a $$\Delta ABC$$ such that $$DE || BC$$. If $$AB = 13.3 cm, AC = 11.9 cm$$ and $$EC = 5.1 cm$$, find $$AD$$.
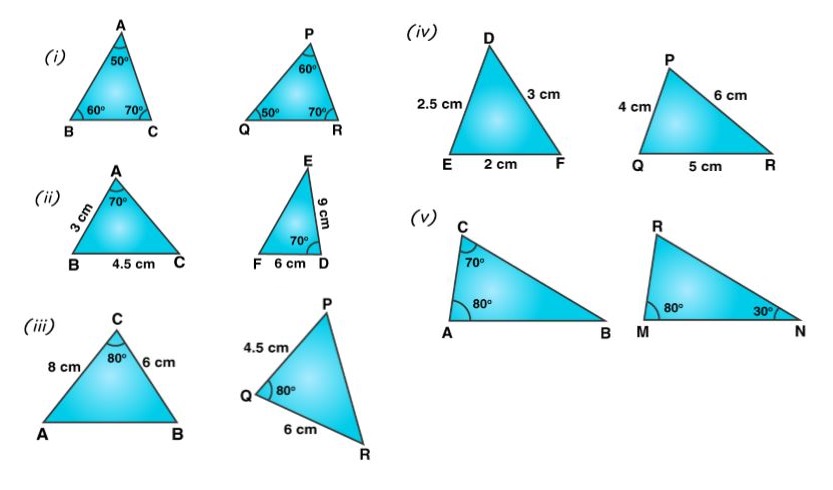
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
$$\Delta ABC \sim \Delta DEF$$ and their areas are respectively $$64 cm^2$$ and $$121 cm^2$$. If $$EF = 15.4 cm$$, find $$BC$$.
$$\Delta ABC \sim \Delta PQR$$ and $$ar (\Delta ABC) = 4ar (\Delta PQR)$$. If $$BC = 12 cm$$, find $$QR$$.
$$D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively of a $$\triangle ABC$$. In each of the following cases, determine whether $$DE || BC$$ or not. $$AD = 5.7 cm, DB = 9.5 cm, AE = 4.8 cm$$ and $$EC = 8 cm$$
$$D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively of a $$\Delta ABC$$. In each of the following cases, determine whether $$DE || BC$$ or not. $$AB = 10.8 cm, AD = 6.3 cm, AC = 9.6 cm$$ and $$EC = 4 cm$$.
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel to the parallel sides.
Here, $$AB || DC$$
$$M$$ and $$N$$ are the mid points of sides $$AD$$ and $$BC$$ respectively.
$$MN$$ is joined.
To prove : $$MN || AB$$ or $$DC$$.
Produce $$AD$$ and $$BC$$ to meet at $$P$$.
Now, In $$\triangle PAB$$
$$DC ||AB$$
$$\dfrac{PD}{DA} = \dfrac{PC}{CB}$$
$$\dfrac{PD}{2PM} = \dfrac{PC}{2CN}$$
$$M$$ and $$N$$ are midpoints of $$AD$$ and $$BC$$ respectively.
$$\dfrac{PD}{PM} = \dfrac{PC}{CN}$$
$$MN||DC$$ But $$DC ||AB$$
Therefore, $$MN || DC ||AB $$
In a $$\Delta ABC,\, M$$ and $$N$$ are points on the sides $$AB$$ and $$AC$$ respectively such that $$BM = CN$$. If $$\angle B = \angle C$$ then show that $$MN || BC$$.
In $$\Delta ABC$$, $$M$$ and $$N$$ are points on the sides $$AB$$ and $$AC$$ respectively.
If $$\angle B = \angle C$$,we know that, sides opposite to equal angles are equal $$AB = AC $$
$$BM = CN$$ ....... (1)
$$AB - BM = AC - CN $$
$$\Rightarrow AM = AN$$ ......... (2)
From $$\Delta ABC$$
Dividing (2) by (1), we get
$$\dfrac{AM}{MB} = \dfrac{AN}{NC}$$
By converse of basic proportionality theorem,
$$MN ||BN$$
In the given figure, if $$\angle ADE = \angle B$$, show that $$\Delta ADE \sim \Delta ABC$$. If $$AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm$$ and $$BC = 4.2 cm$$, find $$DE$$.
From given figure,
$$\angle ADE = \angle B$$
To prove: $$\Delta ADE \sim \Delta ABC$$ and
find $$DE$$
Given: $$AD = 3.8 cm, \ AE = 3.6 cm, \ BE = 2.1 cm$$ and $$BC = 4.2 cm$$
Now, In $$\Delta ADE$$ and $$\Delta ABC$$
$$\angle ADE = \angle B$$ (given)
$$\angle A = \angle A$$ (common)
$$\Delta ADE \sim \Delta ABC$$ (By AA)
Again,
$$\dfrac{AD}{AB} = \dfrac{DE}{BC}$$
$$\dfrac{AD}{AE + EB} = \dfrac{x}{4.2}$$
$$\dfrac{3.8}{3.6 + 2.1} = \dfrac{x}{4.2}$$
$$\dfrac{3.8}{5.4} = \dfrac{x}{4.2}$$
$$x = 2.8$$
$$DE = 2.8cm$$
$$D$$ and $$E$$ are the points on the sides $$AB$$ and $$AC$$ respectively of a $$\Delta ABC$$. If $$AB = 11.7 cm, AC = 11.2 cm, BD = 6.5 cm$$ and $$AE = 4.2 cm$$ then determine whether $$DE || BC$$ or not.
$$D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively of a $$\Delta ABC$$. In each of the following cases, determine whether $$DE || BC$$ or not. $$AD = 7.2 \text{ cm}, AE = 6.4 \text{ cm}, AB = 12 \text{ cm}$$ and $$AC = 10 \text{ cm}$$.
The areas of two similar triangles are $$81 cm^2$$ and $$49 cm^2$$ respectively. If the altitude of the first triangle is $$6.3 cm$$, find the corresponding altitude of the other.
The areas of two similar triangles are $$100 cm^2$$ and $$64 cm^2$$ respectively. If a median of the smaller triangle is $$5.6 cm$$, find the corresponding median of the other.
State the SAS-similarity criterion.
State the SSS-criterion for similarity of triangles.
State the AA-similarity criterion.
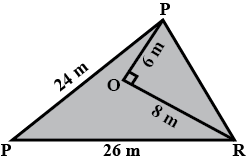
In the given figure, $$O$$ is a point inside a $$\Delta PQR$$ such that $$\angle POR = 90^o,\ OP = 6 cm$$ and $$OR = 8 cm$$. If $$PQ = 24 cm$$ and $$QR = 26 cm$$, prove that PQR is right-angled.
State the AAA-similarity criterion.
In the given figure, $$ABC$$ is a triangle and $$PQ$$ is a straight line meeting $$AB$$ in $$P$$ and $$AC$$ in $$Q$$. If $$AP = 1 cm,\ PB = 3cm, \ AQ = 1.5 cm, \ QC = 4.5 cm$$, prove that area of $$\Delta APQ$$ is $$1/16$$ of the area of $$\Delta ABC$$.
In the given figure, $$DE || BC$$. If $$DE = 3 cm, \ BC = 6 cm$$ and $$ar (\Delta ADE) = 15 cm^2$$, find the area of $$\Delta ABC$$.
State the converse of Thales theorem.
If the equal sides $$AB$$ and $$AC$$ of an isosceles triangle be produced to $$E$$ and $$F$$ so that
$$BE\cdot CF=AB^{2}$$, show that the line $$EF$$ will always pass through a fixed point.
In the given figure, $$DE || BC$$ such that $$AD = x cm,\ DB = (3x + 4) cm,\ AE = (x + 3) cm$$ and $$EC = (3x + 19) cm$$. Find the value of $$x$$.
In the above figure, $$CA \parallel BD$$, the lines $$AB$$ and $$CD$$ meet at $$O.$$
(i) Prove that $$\triangle ACO \sim \triangle BDO.$$
(ii) If $$BD = 2.4\text{ cm}, OD = 4\text{ cm}, OB = 3.2\text{ cm}$$ and $$AC = 3.6\text{ cm}$$, calculate $$OA$$ and $$OC.$$
State which pairs of triangles in the figure given below are similar. Write the similarity rule used and also write the pairs of similar triangles in symbolic form (all lengths of sides are in cm):
Two triangles $$ABC$$ and $$PQR$$ are such that $$AB = 3 cm, \ AC = 6 cm, \ \angle A = 70^o, \ PR = 9 cm, \ \angle P = 70^o$$ and $$PQ = 4.5 cm$$. Show that $$\Delta ABC \sim \Delta PQR$$ and state the similarity criterion.
In the given figure, $$DB \perp DC, DE\perp AB$$ and $$AC \perp BC$$. Prove that $$BE/ DE = AC/BC$$.
In the figure given below, $$PQRS$$ is a parallelogram; $$PQ = 16\ cm, QR = 10\ cm. L$$ is a point on $$PR$$ such that $$RL : LP = 2 : 3 : QL$$ produced meets $$RS$$ at $$M$$ and $$PS$$ produced at $$N$$.
Name a triangle similar to triangle $$RLM$$. Evaluate $$RM$$.
In triangles $$\text{PQR}$$ and $$\text{TSM}$$, $$\angle \text{P}=55^{\circ}, \angle \text{Q}=25^{\circ}, \angle \text{M}=100^{\circ}$$ and $$\angle \text{S}=25^{\circ} .$$ Is $$\Delta
\text{QPR} \sim \Delta \text{TSM}$$? Why?
In Figure, $$DE \parallel OQ$$ and $$DF \parallel O R,$$ Show that $$EF \parallel QR$$
S and T are points on sides $$\mathrm{PR}$$ and $$\mathrm{QR}$$ if $$\Delta P Q R$$
such that $$\angle P=\angle R T S$$. Show that $$\Delta \mathrm{RPQ} \sim
\Delta \mathrm{RTS}$$
$$A$$ and $$B$$ are respectively the points on the sides $$P Q$$ and $$P R$$ of a $$\Delta PQR$$ such that $$\mathrm{PQ}=12.5 \mathrm{cm}, \mathrm{PA}=5 \mathrm{cm}, \mathrm{BR}=6 \mathrm{cm}$$ and $$\mathrm{PB}=4 \mathrm{cm} .$$ Is $$AB\|\mathrm{QR} ?$$ Give reason.
$$E$$ and $$F$$ are points on the sides $$P Q$$ and $$PR$$ respectively of a $$\Delta P Q R$$. Show that $$EF || QR$$. If $$P Q=1.28 \mathrm{cm}, P R=2.56 \mathrm{cm}, P E=0.18 \mathrm{cm}$$ and $$\mathrm{PF}=0.36
\mathrm{cm}$$
If it is given that $$\Delta \mathrm{ABC} \sim \Delta P Q R$$ with $$\dfrac{BC}{QR}=\dfrac{1}{3},$$ then find $$\dfrac{ar(\Delta P Q R)}{a r(\Delta A B C)}$$
In Figure, if $$\mathrm{LM} \parallel \mathrm{CB}$$ and $$\mathrm{LN} \parallel\mathrm{CD},$$ prove that $$\dfrac{A M}{A B}=\dfrac{A N}{A D}$$
$$ \Delta DEF \sim \Delta ABC,$$ if $$DE: A B=2: 3$$ and $$ar(\Delta D E F)$$ is equal to 44 square units. Find the area of $$(\Delta ABC)$$
Using converse of Basic proportionality Theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
State which pairs of triangles in the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form.
$$\mathrm{D}$$ is a point on the side $$\mathrm{BC}$$ of a triangle $$\mathrm{ABC}$$ such that $$\angle \mathrm{ADC}=\angle \mathrm{BAC}$$. Show that $$C A^{2}=C B . C D$$
In the given figure $$, \Delta {ABC}$$ and $$\Delta{DBC}$$ are on the same base $$BC$$. If $${AD}$$ intersects $$B C$$ at $$O .$$ prove that $$\dfrac{a r(\Delta A B C)}{a r(\Delta D B C)}=\dfrac{A O}{D O}$$
In the Fig., we have
$$BX = \frac{1}{2} AB$$
$$BY= \frac{1}{2} BC$$ and $$AB = BC$$.
Show that $$BX = BY$$.
In Figure $$, P$$ is the mid-point of $$B C$$ and $$Q$$ is the mid-point of $$A P .$$ If $$B Q$$ when produced meets $$A C$$ at $$R,$$ prove that $$R A=\dfrac{1}{3} C A$$
Using Basic proportionality Theorem, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Sides $$A B$$ and $$A C$$ and median $$A D$$ of a triangle $$A B C$$ are respectively proportional to sides $$\mathrm{PQ}$$ and $$PR$$ and median $$PM$$ of another triangle $$PQR$$. Show that $$\triangle A B C \sim \triangle P Q R$$
Given:
In $$\Delta A B C$$ and $$\Delta P Q R, A D$$ and $$P M$$ are their medians respectively such that $$ \dfrac{A B}{P Q}=\dfrac{A D}{P M}=\dfrac{A C}{P R}\qquad \ldots(i)$$
To prove: $$\triangle A B C \sim \Delta P Q R$$
Construction:
Produce $$AD$$ to $$E$$ such that $$A D=D E$$ and produce $$PM$$ to $$N$$ such that, $${PM}={MN}$$
Join $$BE, CE, QN, RN.$$
Proof:
Since, $$BD=DC$$ and $$AD=DE$$
$$\Rightarrow $$ Quadrilateral $$ABEC$$ is a $$\parallel$$gm.
Similarly, $$QM=MR$$ and $$PM=MN$$
$$\Rightarrow $$ Quadrilateral $$PQNR$$ is a $$\parallel$$gm.
$$\Rightarrow B E=A C$$ and $$ Q N=P R$$
$$\Rightarrow \dfrac{B E}{Q N}=\dfrac{A C}{P R} $$
$$ \Rightarrow \dfrac{B E}{QN}=\dfrac{A B}{P Q} \quad$$ [ From $$(i)$$]
i.e., $$\dfrac{A B}{P Q}=\dfrac{B E}{Q N} \quad \quad \dots (ii)$$
From $$(i)$$,
$$\dfrac{A B}{P Q}=\dfrac{A D}{P M}=\dfrac{2 A D}{2 PM}=\dfrac{AE}{P N} $$
$$\Rightarrow \dfrac{A B}{P Q}=\dfrac{A E}{P N} \quad \quad \dots (iii)$$
From $$(ii)$$ and $$(iii)$$,
$$\dfrac{AB}{P Q}=\dfrac{B E}{Q N}=\dfrac{A E}{P N}$$
$$\Rightarrow \Delta A B E \sim \Delta P Q N $$ (SSS similarity criterion)
$$\Rightarrow \angle 1=\angle 2\qquad\dots(iv) $$
Similarly, we can prove
$$\Delta A C E \sim \Delta P R N\\ \Rightarrow \angle 3=\angle 4 \quad \dots({v})$$
Adding (iv) and (v), we get
$$\angle 1+\angle 3=\angle 2+\angle 4 $$
$$\Rightarrow \angle A=\angle P$$
And $$\dfrac{AB}{P Q}=\dfrac{A C}{P R}$$ (Given)
$$\therefore\Delta A B C \sim \Delta P Q R$$ (By SAS criterion of similarity)
In the adjoining figure, DE ll BC, $$ AD = 2.4 cm, AB =3.2 cm, CE = 4.8 cm $$ , flnd BD.
In figure, $$DE||BC$$ . Find AD
If $$\triangle ABC \sim \triangle DEF, AB= 10 \ cm$$, area $$(\triangle ABC)= 20 \ sq. cm$$, area $$(\triangle DEF)= 45 \ sq. cm$$. Determine $$DE$$
In ABC, P and Q are two points on AB and AC. respectively such that PQ || BC and $$\dfrac {AP}{PB} = \dfrac{2}{3}$$ then find $$\dfrac{AQ}{ QC}$$.
Given: PQ || BC and $$\dfrac{AP}{PB}=\frac{2}{3}$$
By Basic Proportionality theorem . which states that if a line is drawn parallel to one side of a triangle the other two sides in distinct points, then the other two sides are divided in the same ratio.
$$\because \dfrac{AP}{PB} = \dfrac{AQ}{QC}$$
$$ \implies \dfrac {AP}{PB} = \dfrac{AQ}{QC} = \dfrac{2}{3}$$
By Basic Proportionality theorem . which states that if a line is drawn parallel to one side of a triangle the other two sides in distinct points, then the other two sides are divided in the same ratio.
$$\because \dfrac{AP}{PB} = \dfrac{AQ}{QC}$$
$$ \implies \dfrac {AP}{PB} = \dfrac{AQ}{QC} = \dfrac{2}{3}$$
In a $$\triangle ABC, DE || BC$$, where D is a point on AB and E is a point on AC, then
$$\dfrac{EC}{DB}$$ =...........
we have $$\dfrac{AB}{DB} = \dfrac{AC}{EC}$$
In figure, $$DE||BC$$ . Find $$AD$$
State whether the following pair of triangle is similar or not. Write the similarity criterion used and write it in symbolic form.
In figures DE || BC. Find EC..
In the adjoining figure, $$AD = 2 cm, DB = 3 cm,AB = 5 cm$$ and $$DE || BC$$, then find $$EC$$.
In the above figure, $$DE \parallel BC.$$ Find $$x.$$
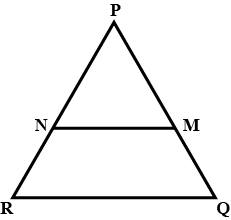
In the given $$\triangle QPR$$, $$LM$$ is parallel to $$QR$$ and $$PM: MR = 3: 4$$. Calculate the value of the ratio $$PL: PQ$$ and then $$LM : QR$$.
In the following figure, $$XY$$ is parallel to $$BC$$, $$AX = 9\ cm$$. $$XB = 4.5 cm $$ and $$BC = 18\ cm$$.
What is the value of $$\displaystyle\,\dfrac{YC}{AC}$$?
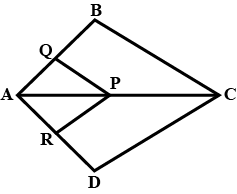
In the following figure, $$AB=AC;BC=CD$$ and $$DE$$ is parallel to $$BC$$. Calculate:
$$\angle CDE$$
In the following figure, point D divides AB in the ratio $$3: 5$$. Find:$$BC = 4.8\,cm$$, find the length of DE.
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.If AB = x and; CD = z unit and EF = y unit, prove that: 1/x + 1/y = 1/z.
A line PQ is drawn parallel to the side BC of Δ ABC which cuts side AB at P and side AC at Q. If $$AB = 9.0\,cm$$, $$CA = 6.0\,cm$$ and $$AQ = 4.2\, cm$$, find the length of AP.
In the given figure, PQ AB;$$CQ = 4.8\,cm$$ $$QB = 3.6\,cm$$ and $$AB = 6.3\,cm$$. Find:
If AP = x, then the value of AC in terms of x.
In the given figure, PQ ‖ AB;$$CQ = 4.8\,cm$$ $$QB = 3.6\,cm$$ and $$AB = 6.3\,cm$$. Find:
$$\dfrac{CP}{PA}$$
In the figure given below, AB EF CD. If $$AB = 22.5\,cm$$, $$EP = 7.5\,cm$$,$$PC = 15\,cm$$ and $$DC = 27\,cm$$. Calculate AC.
In the following figure, $$\angle{AXY} =\angle{AYX}.$$ If $$\dfrac{BX}{AX} =\dfrac{ CY}{AY},$$ show that $$\triangle ABC$$ is isosceles.
In the following figure, $$OAB$$ is a triangle and $$AB\parallel DC.$$
If the area of triangle $$CAD=140\ cm^{2}$$ and the area of triangle $$ODC=172\ cm^{2},$$ find
The area of triangle $$ODB$$
In the following figure, $$OAB$$ is a triangle and $$AB\parallel DC.$$
If the area of triangle $$CAD=140\ cm^{2}$$ and the area of triangle $$ODC=172\ cm^{2},$$ find
The area of triangle $$OAC$$
In the following figure, $$OAB$$ is a triangle and $$AB\parallel DC.$$
If the area of triangle $$CAD=140\ cm^{2}$$ and the area of triangle $$ODC=172\ cm^{2},$$ find
The area of triangle $$DBC$$
In the following figure, $$AB=AC;BC=CD$$ and $$DE$$ is parallel to $$BC$$. Calculate:
$$\angle DCE$$
In adjoining $$ AP \perp BC , AD || BC, $$ then find $$ A \left ( \Delta ABC \right ) : A \left (\Delta BCD \right )$$
Base of a is 9 and height is 5 . Base of another triangle is 10 and height is 6 . Find the ratio of areas of these triangle .
In the following figure, $$DE$$ is parallel to $$BC$$. Shows that:
Area $$(\triangle BOD)=$$ Area $$(\triangle COE)$$
In the following figure, $$DE$$ is parallel to $$BC$$. Shows that:
Area $$(\triangle ADC)=$$ Area $$(\triangle AEB)$$
In the given figure $$ BC \perp AB $$ and $$ AD \perp AB $$ , BC = 4 , AD = 8 , then find $$ \dfrac{A\left ( \Delta ABC \right )}{A\left ( \Delta ADB \right )}$$
In $$ \Delta ABC $$ , ray BD bisects $$ \angle ABC $$ and ray CE bisects $$\angle ACB $$ . If seg$$ AB\cong seg AC $$ then prove that ED || BC .
Given
ray BD bisects $$ \angle ABC $$
ray BD bisects $$ \angle ACB $$
seg$$ AB\cong seg AC $$
In$$ \Delta ABC , \angle ABD = \angle DBC $$
$$\dfrac{AD}{DC} = \dfrac{AB}{BC}$$....(I)(By angle bisector theorem)
In$$\Delta ABC , \angle BEC = \angle ACE $$
$$\dfrac{AE}{EB} = \dfrac{AC}{BC}$$ .(II)(By angle bisector theorem)
From (I)and (II)
$$\dfrac{AD}{DC} = \dfrac{AE}{EB} \left ( \therefore seg AB\cong seg AC \right ) ED || BC $$ (converse of basic proportional theorem)
In $$ \Delta PQR , $$ PM = 15 , PQ = 25 PR = 20 , NR = 8 . State whether line NM is parallel to side RQ . Give reason .
If $$ \Delta ABC \sim \Delta PQR $$ and AB : PQ = 2 :3 , then fill in the blanks $$ \dfrac{A\left ( \Delta ABC \right )}{A\left ( \Delta PQR \right )} = \dfrac{AB^{2}}{...} = \dfrac{2^{2}}{3^{2}} = \dfrac{........}{.......} $$
Measure ofsome angles in the figure are given . Prove that $$ \dfrac{AP}{PB} = \dfrac{AQ}{QC} $$
If $$ \Delta ABC \sim \Delta PQR$$ $$A (\Delta ABC) = 80 (\Delta PQR) = 125 $$ then, fill in the blanks $$ \dfrac{A\left ( \Delta ABC \right )}{A\left ( \Delta .... \right )} = \dfrac{80}{125} \therefore \dfrac{AB}{PQ} = \dfrac{.....}{......}$$
In adjoining figure $$ PQ \perp BC , AD \perp BC $$ then find following ratios.
$$ \dfrac{A\left ( \Delta ADC \right )}{A\left ( \Delta PQC \right )}$$
In adjoining figure $$ PQ \perp BC , AD \perp BC $$ then find following ratios.
$$ \dfrac{A\left ( \Delta ABC \right )}{A\left ( \Delta ADC \right )} $$
In adjoining figure $$ PQ \perp BC , AD \perp BC $$ then find following ratios.
$$ \dfrac{A\left ( \Delta PQB \right )}{A\left ( \Delta PBC \right )} $$
In the given figure , seg AC and BD intersect each other in point P and $$ \dfrac{AP}{CP} = \dfrac{BP}{DP} $$ Prove that , $$ \Delta ABP \sim \Delta CDP $$
In the given figure , X is any point in the interior of triangle . Point X is joined to vertices of triangles .Seg PQ || seg DE , sed QR || seg EF . Fill in the blanks to prove that, sef PR || seg DF .
Proof : In $$ \Delta XDE , PQ || DE $$
$$ \therefore \dfrac{XP}{[ ]} = \dfrac{[ ]}{QE} $$ ...(I)(Basic proportionality theorem)
In $$ \Delta XEE, QR || EF$$
$$ \therefore \dfrac{[ ]}{[ ]} = \dfrac{[ ]}{[ ]}$$.......(II)_______
$$ \dfrac{[ ]}{[ ]} = \dfrac{[ ]}{[ ]} $$ ...From (I)and (II)
$$\therefore seg PR || seg DE$$........(converse of basic proportionality theorem)
$$ \Delta LMN \sim \Delta PQR , 9 \times A \left ( \Delta LMN \right ) =16 \times A (\Delta LMN )$$ . IF QR = 20 then find MN.
Find the length of the side and perimeter of an equilateral triangle whose height is $$\sqrt{3}cm$$
Since , $$\Delta ABC$$ is an equilateral triangle $$, CD$$ is the perpendicular bisector of $$AB$$
Now. According to pythagoras theorem ,
$$In \bigtriangleup ACD$$
$$AC^{2} = AD ^{2} + CD ^{2} $$
$$\Rightarrow (2a)^{2} = a^{2} + (\sqrt{3})^{2} $$
$$\Rightarrow 4a^{2} - a^{2} = 3 $$
$$\Rightarrow 3a^{2} = 3 $$
$$\Rightarrow a^{2} = 1 $$
$$\Rightarrow a = \sqrt{1}= 1 cm $$
Hence , the length of the side of an equilateral triangle is 2 cm.
Now, Perimeter of the triangle $$ = (2 + 2 + 2 ) cm $$
$$=6 cm $$
Hence perimeter of an equilateral triangle is 6 cm
In $$ \square ABCD , seg AD || seg BC $$ .Diagonal AC and diagonal BD intersect each other in point P .Then show that $$\dfrac{AP}{PD} = \dfrac{PC}{BP}$$
In the given figure , A - D - C and B - E - C seg || side AB If AD = 5 , DC = 3 , BC = 6.4 then find BE.
Do sides 7 cm , 24 cm , 25 cm form a right angled triangle ? Give reason
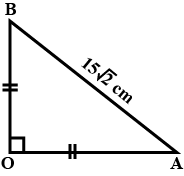
Pranali and Prasad started walking to the East and to the North respectively , from the same point and at the same speed. After 2 hours distance between them was $$15\sqrt{2}$$ km. Find their speed per hour.
It is given that , Pranali and Prasad have same speed.
Thus, they cover same distance in $$2$$ hours .
i.e. $$OA = OB$$
By pythagoras theorem ,
$$In \bigtriangleup AOB$$
$$AB^{2} = AO^{2} + OB^{2} $$
$$\Rightarrow (15\sqrt{2})^{2} = AO^{2} + OA^{2} $$
$$\Rightarrow 450 = 2AO^{2}$$
$$\Rightarrow AO^{2} = \dfrac{450}{2}$$
$$\Rightarrow AO^{2} = 225$$
$$\Rightarrow AO = 15 km$$
$$\Rightarrow BO = 15 km $$
$$\Rightarrow Speed = \dfrac{Distance}{Time}$$
$$=\dfrac{15}{2}$$
$$ = 7.5 km $$ per hour
$$ \Delta MNT \sim \Delta QRS $$ .Length of altitude drawn from point T is 5 and length of altitude drwan from point S is 9 .Find the ratio $$ \dfrac{A\left ( \Delta MNT \right )}{A\left ( \Delta QRS \right )}$$
Areas of two similar triangles are $$225 sq .cm$$ and $$81 sq. cm$$. If a side of the smaller triangle is $$12 cm$$, then find the corresponding side of the bigger triangle.
Refer image,
Given,Area of bigger triangle $$=225cm^2$$
Area of smaller triangle $$=81cm^2$$
One side of smaller triangle $$=12cm$$
Let us draw a suitable diagram,
As we know, for two similar triangles,
Ratio of their area =Square of the ratios of corresponding sides
$$\dfrac{Area\,of\,\Delta ABC}{Area\,of\,\Delta PQR}=\dfrac{AB^2}{PQ^2}$$
$$\Rightarrow \dfrac { 225 }{ 81 } =\dfrac {AB^2 }{12^2 } \Rightarrow \dfrac { 25 }{ 9 } =\dfrac {AB }{ 12 } \Rightarrow \dfrac { 25 }{ 9} \times 12=AB$$
$$\Rightarrow AB=\dfrac{25}{9}\times 12=\dfrac{25}{3}\times 4=\dfrac{100}{3}=33.33cm$$
How the corresponding side of the bigger triangle measures $$33.33cm$$ (approx)
In the given figure 1.66 , seg PQ || seg DE , $$ A\left ( \Delta PQF \right ) = 20$$ units ,$$PF = 2 DP $$then find $$ A \left ( \square DPQE \right ) $$ by completing the following activity .
In $$\bigtriangleup$$PQR, PQ = $$\sqrt{8}$$, QR = $$\sqrt{5}$$ and PR = $$\sqrt{3}$$. Is $$\bigtriangleup$$PQR a right angled triangle? If yes, which angle is of 90$$^0$$?
In a $$\triangle ABC, D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively such that $$DE \parallel BC$$.
In $$AD=4x-3,AE=8x-7,BD=3x-1$$ and $$CE=5x-3$$ then find $$x$$.
In $$\triangle ABC$$, $$DE\parallel BC$$
$$\cfrac{AD}{DB}=\cfrac{AE}{CE}$$
(By B.P theorem)
$$\cfrac{4x-3}{3x-1}=\cfrac{8x-7}{5x-3}$$
$$(4x-3)(5x-3)=(8x-7)(3x-1)$$
$$\Rightarrow$$ $$20{x}^{2}-12x-15x+9=24{x}^{2}-8x-21x+7$$
$$\Rightarrow$$ $$24{x}^{2}-20{x}^{2}-29x+27x-9+7=0$$
$$\Rightarrow$$ $$4{x}^{2}-2x-2=0$$
$$\Rightarrow$$ $$2{x}^{2}-x-1=0$$
$$\Rightarrow$$ $$2{x}^{2}-2x+x+1=0$$
$$\Rightarrow$$ $$2x(x-1)+1(x-1)=0$$
$$\Rightarrow$$ $$(x-1)(2x+1)=0$$
$$\Rightarrow$$ $$x-1=0$$
$$\Rightarrow$$ $$x=1$$
or $$2x+1=0$$
$$2x=-1$$
$$x=-\cfrac{1}{2}$$
Thus, $$x=1,-\cfrac{1}{2}$$
$$\cfrac{AD}{DB}=\cfrac{AE}{CE}$$
(By B.P theorem)
$$\cfrac{4x-3}{3x-1}=\cfrac{8x-7}{5x-3}$$
$$(4x-3)(5x-3)=(8x-7)(3x-1)$$
$$\Rightarrow$$ $$20{x}^{2}-12x-15x+9=24{x}^{2}-8x-21x+7$$
$$\Rightarrow$$ $$24{x}^{2}-20{x}^{2}-29x+27x-9+7=0$$
$$\Rightarrow$$ $$4{x}^{2}-2x-2=0$$
$$\Rightarrow$$ $$2{x}^{2}-x-1=0$$
$$\Rightarrow$$ $$2{x}^{2}-2x+x+1=0$$
$$\Rightarrow$$ $$2x(x-1)+1(x-1)=0$$
$$\Rightarrow$$ $$(x-1)(2x+1)=0$$
$$\Rightarrow$$ $$x-1=0$$
$$\Rightarrow$$ $$x=1$$
or $$2x+1=0$$
$$2x=-1$$
$$x=-\cfrac{1}{2}$$
Thus, $$x=1,-\cfrac{1}{2}$$
Points $$D$$ and $$E$$ lie on sides $$AB$$ and $$AC$$ of $$\triangle ABC$$, respectively. In the following questions check whether $$DE\parallel BC$$ or not.
$$AB=5.6cm$$, $$AD=1.4cm$$, $$AC=9.0cm$$ and $$AE=1.8cm$$
Points $$D$$ and $$E$$ lie on sides $$AB$$ and $$AC$$ of $$\triangle ABC$$, respectively. In the following questions check whether $$DE\parallel BC$$ or not.
$$AD=10.5cm$$, $$BD=4.5cm$$, $$AC=4.8cm$$ and $$AE=2.8cm$$
Points $$D$$ and $$E$$ lie on sides $$AB$$ and $$AC$$ of $$\triangle ABC$$, respectively. In the following questions check whether $$DE\parallel BC$$ or not.
$$AB=12cm$$, $$AD=8cm$$, $$AE=12cm$$ and $$AC=18cm$$
$$\cfrac{AD}{BD}=\cfrac{AD}{AB-AD}=\cfrac{8}{12-8}$$
$$\cfrac{AD}{BD}=\cfrac{8}{4}=\cfrac{2}{1}$$
$$\cfrac{AE}{CE}=\cfrac{AE}{AC-AE}=\cfrac{12}{18-12}$$
$$\cfrac{AE}{CE}=\cfrac{12}{6}=\cfrac{2}{1}$$
$$\cfrac{AD}{BD}=\cfrac{AE}{CE}=\cfrac{2}{1}$$
Thus $$DE\parallel BC$$
$$\cfrac{AD}{BD}=\cfrac{8}{4}=\cfrac{2}{1}$$
$$\cfrac{AE}{CE}=\cfrac{AE}{AC-AE}=\cfrac{12}{18-12}$$
$$\cfrac{AE}{CE}=\cfrac{12}{6}=\cfrac{2}{1}$$
$$\cfrac{AD}{BD}=\cfrac{AE}{CE}=\cfrac{2}{1}$$
Thus $$DE\parallel BC$$
In a $$\triangle ABC, D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively such that $$DE \parallel BC$$.
If $$\cfrac { AD }{ DB } =\cfrac { 4 }{ 13 } $$ and $$AC=20.4cm$$. Then find $$EC$$.
In $$\triangle ABC$$, $$DE\parallel BC$$
$$\cfrac{AD}{DB}=\cfrac{AE}{CE}$$
(By B.P theorem)
$$\cfrac{4}{13}=\cfrac{AC-CE}{CE}$$
$$(AE+CE=AC)$$
$$\cfrac{4}{13}=\cfrac{20.4-CE}{CE}$$
$$4\times CE=13(20.4-CE)$$
$$4\times CE+13CE=13\times 20.4$$
$$17CE=13\times 20.4$$
$$CE=\cfrac{13\times 20.4}{17}=13\times 1.2$$
$$CE=15.6cm$$
$$\cfrac{AD}{DB}=\cfrac{AE}{CE}$$
(By B.P theorem)
$$\cfrac{4}{13}=\cfrac{AC-CE}{CE}$$
$$(AE+CE=AC)$$
$$\cfrac{4}{13}=\cfrac{20.4-CE}{CE}$$
$$4\times CE=13(20.4-CE)$$
$$4\times CE+13CE=13\times 20.4$$
$$17CE=13\times 20.4$$
$$CE=\cfrac{13\times 20.4}{17}=13\times 1.2$$
$$CE=15.6cm$$
In a $$\triangle ABC, D$$ and $$E$$ are points on the sides $$AB$$ and $$AC$$ respectively such that $$DE \parallel BC$$.
If $$\cfrac { AD }{ DB } =\cfrac { 7 }{ 4 } $$ and $$AE=6.3cm$$ then find $$AC$$.
In $$\triangle$$, $$DE\parallel BC$$
$$\cfrac{AD}{DB}=\cfrac{AE}{CE}$$
(By B.P theorem)
$$\cfrac{7}{4}=\cfrac{6.3}{AC-AE}$$
$$\cfrac{7}{4}=\cfrac{6.3}{AC-6.3}$$
$$7(AC-6.3)=4\times 6.3$$
$$AC-6.3=\cfrac{4\times 6.3}{7}$$
$$AC=6.3+3.6=9.9cm$$
$$\cfrac{AD}{DB}=\cfrac{AE}{CE}$$
(By B.P theorem)
$$\cfrac{7}{4}=\cfrac{6.3}{AC-AE}$$
$$\cfrac{7}{4}=\cfrac{6.3}{AC-6.3}$$
$$7(AC-6.3)=4\times 6.3$$
$$AC-6.3=\cfrac{4\times 6.3}{7}$$
$$AC=6.3+3.6=9.9cm$$
In a triangle ABC , AB = AC . Suppose P is a point on AB and Q is point on AC such that AP = AQ Prove that $$\bigtriangleup APC \cong \bigtriangleup AQB $$
In $$ \bigtriangleup APC $$ and $$ \bigtriangleup AQB$$
$$ AP = AQ $$ [ data]
$$AC = AB $$ [data]
$$\angle PAC = \angle BAQ $$ [ common angle ]
$$\therefore \bigtriangleup APC \cong \bigtriangleup AQB $$ [ SAS postulate ]
$$AC = AB $$ [data]
$$\angle PAC = \angle BAQ $$ [ common angle ]
$$\therefore \bigtriangleup APC \cong \bigtriangleup AQB $$ [ SAS postulate ]
Draw the shape of any two examples of similar figures.
Two quadrilaterals are similar because their corresponding angles are equal and corresponding sides are proportional.
In given figure $$L,M$$ and $$N$$ are points on $$OA,OB$$ and $$OC$$ such that $$LM\parallel AB$$ and $$MN\parallel BC$$, then show that $$LN\parallel AC$$
Points $$D$$ and $$E$$ lie on sides $$AB$$ and $$AC$$ of $$\triangle ABC$$, respectively. In the following questions check whether $$DE\parallel BC$$ or not.
$$AD=5.7cm$$, $$BD=9.5cm$$, $$AE=3.3cm$$ and $$EC=5.5cm$$
$$\cfrac{AD}{BD}=\cfrac{5.7}{9.5}=\cfrac{3}{5}$$
$$\cfrac{AE}{CE}=\cfrac{3.3}{5.5}=\cfrac{3}{5}$$
$$\cfrac{AD}{CD}=\cfrac{AE}{CE}=\cfrac{3}{5}$$
By B.P Theorem
$$\Rightarrow$$ $$DE\parallel BC$$
$$\cfrac{AE}{CE}=\cfrac{3.3}{5.5}=\cfrac{3}{5}$$
$$\cfrac{AD}{CD}=\cfrac{AE}{CE}=\cfrac{3}{5}$$
By B.P Theorem
$$\Rightarrow$$ $$DE\parallel BC$$
Solve the following questions:
In $$\triangle ABC$$ and $$DE\parallel BC$$ and $$AD:DB=2:3$$ then find the ratio of areas of $$\triangle ADE$$ and $$\triangle ABC$$
In $$\triangle ABC$$ $$BC\parallel DE$$ and $$\cfrac{AD}{DB}=\cfrac{2}{3}$$ (given)
In $$\triangle ABC$$ and $$\triangle DEA$$
$$\angle B=\angle D$$
$$\angle C=\angle E$$
AA similarity cirterion
$$\cfrac { ar.\left( \triangle ADE \right) }{ ar.\left( \triangle ABC \right) } =\cfrac { { \left( AD \right) }^{ 2 } }{ { \left( AB \right) }^{ 2 } } =\cfrac { { \left( AD \right) }^{ 2 } }{ { \left( AD+DB \right) }^{ 2 } } $$
$$=\cfrac { { \left( \cfrac { AD }{ BD } \right) }^{ 2 } }{ { \left( \cfrac { AD }{ BD } +1 \right) }^{ 2 } } ={ \left( \cfrac { AD }{ BD } \right) }^{ 2 }\times \cfrac { 1 }{ { \left( \cfrac { AD }{ BD } +1 \right) }^{ 2 } } ={ \left( \cfrac { 2 }{ 3 } \right) }^{ 2 }\times \cfrac { 1 }{ { \left( \cfrac { 2 }{ 3 } +1 \right) }^{ 2 } } =\cfrac { 4 }{ 9 } \times \cfrac { 9 }{ 25 } =\cfrac { 4 }{ 25 } $$
In $$\triangle ABC$$ and $$\triangle DEA$$
$$\angle B=\angle D$$
$$\angle C=\angle E$$
AA similarity cirterion
$$\cfrac { ar.\left( \triangle ADE \right) }{ ar.\left( \triangle ABC \right) } =\cfrac { { \left( AD \right) }^{ 2 } }{ { \left( AB \right) }^{ 2 } } =\cfrac { { \left( AD \right) }^{ 2 } }{ { \left( AD+DB \right) }^{ 2 } } $$
$$=\cfrac { { \left( \cfrac { AD }{ BD } \right) }^{ 2 } }{ { \left( \cfrac { AD }{ BD } +1 \right) }^{ 2 } } ={ \left( \cfrac { AD }{ BD } \right) }^{ 2 }\times \cfrac { 1 }{ { \left( \cfrac { AD }{ BD } +1 \right) }^{ 2 } } ={ \left( \cfrac { 2 }{ 3 } \right) }^{ 2 }\times \cfrac { 1 }{ { \left( \cfrac { 2 }{ 3 } +1 \right) }^{ 2 } } =\cfrac { 4 }{ 9 } \times \cfrac { 9 }{ 25 } =\cfrac { 4 }{ 25 } $$
In $$\triangle ABC$$ and $$\triangle DEF$$; $$\angle A=\angle D$$, $$\angle B=\angle F$$. Is $$\triangle ABC\sim \triangle DEF$$?Given reason for your answer.
In $$\triangle ABC$$, $$D$$ and $$E$$ points lie on sides $$AB$$ and $$AC$$ such that $$BD=CE$$. If $$\angle B=\angle C$$ then show that $$DE\parallel BC$$.
In $$\triangle ABC,D$$ and $$E$$ lie on sides $$BD=CE$$ and $$\angle B=\angle C$$
To prove: $$DE\parallel BC$$
Proof: In $$\triangle ABC$$,
$$\angle B=\angle C$$
$$AB=AC$$ (opposite sides of equals angles are same)
$$\Rightarrow$$ $$AD+DB=AE+CE$$ ($$\because DB=CE$$)
$$\Rightarrow$$ $$AD=AE$$
$$\angle D=\angle E$$ (opposite angles of equal sides are same)
$$\Rightarrow$$ $$\triangle ADE$$ is an isosceles triangle
So, $$\triangle ABC$$ and $$\triangle ADE$$ are isosceles triangle in which vertex angle $$\angle A$$ is common in both triangles.
$$\angle B=\angle C=\angle D=\angle E$$
$$\angle B=\angle D$$ (corresponding angle)
$$\Rightarrow$$ $$DE\parallel BC$$
To prove: $$DE\parallel BC$$
Proof: In $$\triangle ABC$$,
$$\angle B=\angle C$$
$$AB=AC$$ (opposite sides of equals angles are same)
$$\Rightarrow$$ $$AD+DB=AE+CE$$ ($$\because DB=CE$$)
$$\Rightarrow$$ $$AD=AE$$
$$\angle D=\angle E$$ (opposite angles of equal sides are same)
$$\Rightarrow$$ $$\triangle ADE$$ is an isosceles triangle
So, $$\triangle ABC$$ and $$\triangle ADE$$ are isosceles triangle in which vertex angle $$\angle A$$ is common in both triangles.
$$\angle B=\angle C=\angle D=\angle E$$
$$\angle B=\angle D$$ (corresponding angle)
$$\Rightarrow$$ $$DE\parallel BC$$
In figure $$PQ$$ and $$RS$$ are parallel then prove that: $$\triangle POQ\sim \triangle SOR$$.
In $$\triangle POQ$$ and $$\triangle SOR$$
$$PQ\parallel RS$$ (Given)
$$\angle OPQ=\angle OSR$$ (alternative angle)
$$\angle POQ=\angle ROS$$ (Vertically opposite angles)
and $$\angle OQP=\angle ORS$$ (alternate angles)
By AAA similarity law
$$\triangle POQ\sim \triangle SOR$$
$$PQ\parallel RS$$ (Given)
$$\angle OPQ=\angle OSR$$ (alternative angle)
$$\angle POQ=\angle ROS$$ (Vertically opposite angles)
and $$\angle OQP=\angle ORS$$ (alternate angles)
By AAA similarity law
$$\triangle POQ\sim \triangle SOR$$
Solve the following questions:
In figure, find $$x$$ in terms of $$a,b$$ and $$c$$
$$\angle A=\angle B={50}^{o}$$ (corresponding angle)
$$AE\parallel BD$$
In $$\triangle BDC$$ and $$\triangle AEC$$
$$\angle A=\angle B={50}^{o}$$ (Given)
$$\angle E=\angle D$$ (corresponding angles)
By AA similarity criterion
$$\triangle BDC\sim \triangle AEC$$
$$\cfrac{BC}{AC}=\cfrac{BD}{AE}$$
$$\Rightarrow$$ $$\cfrac{c}{b+c}=\cfrac{x}{a}$$
$$\Rightarrow$$ $$x=\cfrac{ac}{b+c}$$
$$AE\parallel BD$$
In $$\triangle BDC$$ and $$\triangle AEC$$
$$\angle A=\angle B={50}^{o}$$ (Given)
$$\angle E=\angle D$$ (corresponding angles)
By AA similarity criterion
$$\triangle BDC\sim \triangle AEC$$
$$\cfrac{BC}{AC}=\cfrac{BD}{AE}$$
$$\Rightarrow$$ $$\cfrac{c}{b+c}=\cfrac{x}{a}$$
$$\Rightarrow$$ $$x=\cfrac{ac}{b+c}$$
In $$\triangle ABC,\angle B={90}^{o}$$ and $$BD$$ is perpendicular to hypotenuse $$AC$$ then prove that
$$\triangle ADB\sim \triangle BDC$$
In $$\triangle ABC$$
$$\angle A+\angle C={90}^{o}$$ ($$\because \angle B={90}^{o}$$)...(i)
In $$\triangle BDC$$
$$\angle DBC+\angle C={90}^{o}$$ ($$\because \angle BDC={90}^{o}$$)...(ii)
from equation (i) and (ii)
$$\angle A+\angle C=\angle DBC+\angle C$$
$$\angle A=\angle DBC$$...(iii)
Now In $$\triangle ADB$$ and $$\triangle BDC$$
$$\angle ADB=\angle BDC={90}^{o}$$ (given)
$$\angle DAB=\angle DBC$$ (by eq. (ii))
By AA similarity cirterion
$$\triangle ADB\sim \triangle BDC$$
$$\angle A+\angle C={90}^{o}$$ ($$\because \angle B={90}^{o}$$)...(i)
In $$\triangle BDC$$
$$\angle DBC+\angle C={90}^{o}$$ ($$\because \angle BDC={90}^{o}$$)...(ii)
from equation (i) and (ii)
$$\angle A+\angle C=\angle DBC+\angle C$$
$$\angle A=\angle DBC$$...(iii)
Now In $$\triangle ADB$$ and $$\triangle BDC$$
$$\angle ADB=\angle BDC={90}^{o}$$ (given)
$$\angle DAB=\angle DBC$$ (by eq. (ii))
By AA similarity cirterion
$$\triangle ADB\sim \triangle BDC$$
$$D$$ is a mid-point of side $$BC$$ of $$\triangle ABC$$. A line is drawn through $$B$$ and bisects $$AD$$ at point $$E$$ and $$A$$ at $$C$$, then prove that $$\cfrac{EX}{BE}=\cfrac{1}{3}$$
Given: $$D$$ is mid point of side $$BC$$ of $$\triangle ABC$$
$$BD=DC$$
and $$AE=ED$$
To prove: $$\cfrac{EX}{BE}=\cfrac{1}{3}$$
Construction: Draw $$DY\parallel BX$$ meeting $$AC$$ at $$Y$$
Proof: In $$\triangle BCX$$ and $$\triangle DCY$$
$$\angle BCX=\angle DCY$$ (common)
$$\angle BXC=\angle DYC$$ (corresponding angle)
So, $$\triangle BCX\sim \triangle DCY$$ (AA similarity)
$$\Rightarrow$$ $$\cfrac{BX}{DY}=\cfrac{BC}{DC}=\cfrac{CX}{CY}$$ (corresponding sides are proportional)
$$\Rightarrow$$ $$\cfrac{BX}{DY}=\cfrac{2CD}{CD}$$ ($$D$$ is the mid point of $$BC$$)
$$\Rightarrow$$ $$\cfrac{BX}{DY}=2$$....(i)
Similarly, $$\triangle AEX\sim \triangle ADY$$
$$\cfrac{EX}{DY}=\cfrac{AE}{ED}=\cfrac{1}{2}$$....(ii) ($$E$$ is the midpoint of $$AD$$)
from (i) and (ii) on dividing (i) by (ii) we get
$$\cfrac{BX}{EX}=4$$
$$\Rightarrow$$ $$BE+EX=4\times EX$$
$$\Rightarrow$$ $$3EX=BE$$
$$\Rightarrow$$ $$\cfrac{EX}{BE}=\cfrac{1}{3}$$
$$BD=DC$$
and $$AE=ED$$
To prove: $$\cfrac{EX}{BE}=\cfrac{1}{3}$$
Construction: Draw $$DY\parallel BX$$ meeting $$AC$$ at $$Y$$
Proof: In $$\triangle BCX$$ and $$\triangle DCY$$
$$\angle BCX=\angle DCY$$ (common)
$$\angle BXC=\angle DYC$$ (corresponding angle)
So, $$\triangle BCX\sim \triangle DCY$$ (AA similarity)
$$\Rightarrow$$ $$\cfrac{BX}{DY}=\cfrac{BC}{DC}=\cfrac{CX}{CY}$$ (corresponding sides are proportional)
$$\Rightarrow$$ $$\cfrac{BX}{DY}=\cfrac{2CD}{CD}$$ ($$D$$ is the mid point of $$BC$$)
$$\Rightarrow$$ $$\cfrac{BX}{DY}=2$$....(i)
Similarly, $$\triangle AEX\sim \triangle ADY$$
$$\cfrac{EX}{DY}=\cfrac{AE}{ED}=\cfrac{1}{2}$$....(ii) ($$E$$ is the midpoint of $$AD$$)
from (i) and (ii) on dividing (i) by (ii) we get
$$\cfrac{BX}{EX}=4$$
$$\Rightarrow$$ $$BE+EX=4\times EX$$
$$\Rightarrow$$ $$3EX=BE$$
$$\Rightarrow$$ $$\cfrac{EX}{BE}=\cfrac{1}{3}$$
In figure, $$EF\parallel DC\parallel AB$$. Then prove that: $$\cfrac{AE}{ED}=\cfrac{BF}{FC}$$.
Given: $$EF\parallel DC\parallel AB$$
To prove: $$\cfrac{AE}{ED}=\cfrac{BF}{FC}$$
Construction: Join $$AC$$
Proof: In $$\triangle ADC$$
$$GE\parallel DC$$
$$\cfrac{AE}{ED}=\cfrac{AG}{GC}$$...(i) (Basic proportionality theorem)
Now in $$\triangle ABC$$
$$AB\parallel GF$$
$$\cfrac {CF}{BF}=\cfrac{CG}{AG}$$
or $$\cfrac{BF}{CF}=\cfrac{AG}{GC}$$....(ii)
From (i) and (ii)
$$\cfrac{AE}{ED}=\cfrac{BF}{FC}$$
To prove: $$\cfrac{AE}{ED}=\cfrac{BF}{FC}$$
Construction: Join $$AC$$
Proof: In $$\triangle ADC$$
$$GE\parallel DC$$
$$\cfrac{AE}{ED}=\cfrac{AG}{GC}$$...(i) (Basic proportionality theorem)
Now in $$\triangle ABC$$
$$AB\parallel GF$$
$$\cfrac {CF}{BF}=\cfrac{CG}{AG}$$
or $$\cfrac{BF}{CF}=\cfrac{AG}{GC}$$....(ii)
From (i) and (ii)
$$\cfrac{AE}{ED}=\cfrac{BF}{FC}$$
In figure if $$EF\parallel BC$$ and $$GE\parallel DC$$ then, prove that $$\cfrac{AG}{AD}=\cfrac{AF}{AB}$$
In figure, $$DE\parallel BC$$ and $$CD\parallel EF$$ then prove that: $${AD}^{2}=AB\times AF$$
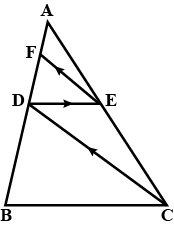
Point $$D$$ and $$E$$ lie on side $$AB$$ of $$\triangle ABC$$ such that $$AD=BE$$. If $$DP\parallel BC$$ and $$EQ\parallel AC$$ then prove that $$PQ\parallel AB$$.
Given: $$\triangle ABC$$ in which
$$AD=BE$$
$$DP\parallel BC$$ and $$EQ\parallel AC$$
To prove $$PQ\parallel AB$$
Proof: In $$\triangle ABC$$ $$DP\parallel BC$$
$$\cfrac{AD}{BD}=\cfrac{AP}{CP}$$....(i) (By B.P theorem)
and $$QE\parallel AC$$
$$\cfrac{BE}{AE}=\cfrac{BQ}{QC}$$.....(ii)
$$AD=BE$$ (given)....(iii)
$$AD+DE=BE+DE$$
$$AE=BD$$....(iv)
putting values from equation (iii) and (iv) in (ii)
$$\cfrac{BE}{AE}=\cfrac{AD}{BD}=\cfrac{BQ}{QC}$$
From equation (i) and (v)
$$\cfrac{AP}{DB}=\cfrac{AP}{CP}=\cfrac{BQ}{QC}$$
$$\cfrac{AP}{CP}=\cfrac{BQ}{QC}$$
$$\cfrac{CP}{AP}=\cfrac{QC}{BQ}$$
$$PQ\parallel AB$$
$$AD=BE$$
$$DP\parallel BC$$ and $$EQ\parallel AC$$
To prove $$PQ\parallel AB$$
Proof: In $$\triangle ABC$$ $$DP\parallel BC$$
$$\cfrac{AD}{BD}=\cfrac{AP}{CP}$$....(i) (By B.P theorem)
and $$QE\parallel AC$$
$$\cfrac{BE}{AE}=\cfrac{BQ}{QC}$$.....(ii)
$$AD=BE$$ (given)....(iii)
$$AD+DE=BE+DE$$
$$AE=BD$$....(iv)
putting values from equation (iii) and (iv) in (ii)
$$\cfrac{BE}{AE}=\cfrac{AD}{BD}=\cfrac{BQ}{QC}$$
From equation (i) and (v)
$$\cfrac{AP}{DB}=\cfrac{AP}{CP}=\cfrac{BQ}{QC}$$
$$\cfrac{AP}{CP}=\cfrac{BQ}{QC}$$
$$\cfrac{CP}{AP}=\cfrac{QC}{BQ}$$
$$PQ\parallel AB$$
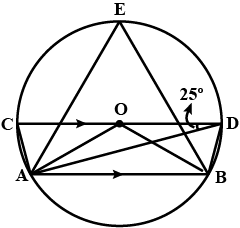
In fig, $$O$$ is center of circle and $$AB || CD$$, if $$\angle ADC = 25^{0}$$, then find $$\angle AEB$$.
In given figure, line segment $$XY$$ is parallel to side $$AC$$ of $$\triangle ABC$$ and divides the triangle in two equal parts. Find ratio $$\cfrac{AX}{AB}$$.
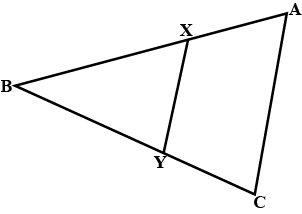
Points $$E$$ and $$F$$ lie on sides $$PQ$$ and $$PR$$ of any $$\triangle PQR$$. From the following, for each case find is $$EF\parallel QR$$
(i) $$PE=3.9cm,EQ=3cm.PF=3.6cm$$ and $$FR=2.4cm$$
(ii) $$PE=4cm,QE=4cm, PF=8cm$$ and $$RF=9cm$$
(iii) $$PQ=1.28cm,PR=2.56cm,PE=0.18cm$$ and $$PF=0.36cm$$
In $$\triangle PQR$$, two point $$E$$ and $$F$$ lie on sides $$PQ$$ and $$PR$$ respectively
(i) $$\cfrac{PE}{EQ}=\cfrac{3.9}{2}=1.3cm$$
$$\cfrac{PF}{FR}=\cfrac{3.6}{2.4}=\cfrac{36}{24}=\cfrac{3}{2}=1.5cm$$
$$\cfrac{PE}{EQ}\ne \cfrac{PF}{FR}$$
$$EF$$ is not parallel to $$QR$$
(ii) $$PE=4cm$$, $$QE=4.5cm$$, $$PF=8cm$$ and $$RF=9cm$$
$$\cfrac{PE}{QE}=\cfrac{4}{4.5}=\cfrac{40}{45}=\cfrac{8}{9}$$...(i)
and $$\cfrac{PF}{RF}=\cfrac{8}{9}$$
From equation (i) and (ii)
$$\cfrac{PE}{QE}=\cfrac{PF}{RF}$$ (by converse of basic prop. theorem)
$$EF\parallel QR$$
(iii) $$PQ=1.28cm,PR=2.56cm,PE=0.18cm$$ and $$PF=0.36cm$$
$$=1.28-0.18=1.10cm$$
$$FR=PR-PF$$
$$2.56-0.36=2.20cm$$
$$\cfrac{PE}{EQ}=\cfrac{0.18}{1.10}=\cfrac{18}{110}=\cfrac{9}{55}$$...(i)
and $$\cfrac{PF}{FR}=\cfrac{0.36}{2.20}=\cfrac{36}{220}=\cfrac{9}{55}$$...(ii)
from equation (i) and (ii)
$$\cfrac{PE}{EQ}=\cfrac{PF}{FR}$$ (by converse of basic prop. theorem)
$$EF\parallel QR$$
(i) $$\cfrac{PE}{EQ}=\cfrac{3.9}{2}=1.3cm$$
$$\cfrac{PF}{FR}=\cfrac{3.6}{2.4}=\cfrac{36}{24}=\cfrac{3}{2}=1.5cm$$
$$\cfrac{PE}{EQ}\ne \cfrac{PF}{FR}$$
$$EF$$ is not parallel to $$QR$$
(ii) $$PE=4cm$$, $$QE=4.5cm$$, $$PF=8cm$$ and $$RF=9cm$$
$$\cfrac{PE}{QE}=\cfrac{4}{4.5}=\cfrac{40}{45}=\cfrac{8}{9}$$...(i)
and $$\cfrac{PF}{RF}=\cfrac{8}{9}$$
From equation (i) and (ii)
$$\cfrac{PE}{QE}=\cfrac{PF}{RF}$$ (by converse of basic prop. theorem)
$$EF\parallel QR$$
(iii) $$PQ=1.28cm,PR=2.56cm,PE=0.18cm$$ and $$PF=0.36cm$$
$$=1.28-0.18=1.10cm$$
$$FR=PR-PF$$
$$2.56-0.36=2.20cm$$
$$\cfrac{PE}{EQ}=\cfrac{0.18}{1.10}=\cfrac{18}{110}=\cfrac{9}{55}$$...(i)
and $$\cfrac{PF}{FR}=\cfrac{0.36}{2.20}=\cfrac{36}{220}=\cfrac{9}{55}$$...(ii)
from equation (i) and (ii)
$$\cfrac{PE}{EQ}=\cfrac{PF}{FR}$$ (by converse of basic prop. theorem)
$$EF\parallel QR$$
In figure, if $$AB || CD$$ and $$E$$ is the mid-point of $$AC$$, then show that $$E$$ is the midpoint of $$BD$$.
In right triangle $$ABC$$, right angled at $$C, M$$ is the mid-point of hypotenuse $$AB$$. $$C$$ is joined to $$M$$ and produced to a point $$D$$ such that $$DM = CM$$. Point $$D$$ is joined to point $$B$$ (see figure).
Show that:
(i) $$\Delta AMC \cong \Delta BMD$$
(ii) $$\angle DBC$$ is a right angle.
(iii) $$\Delta DBC \cong \Delta ACB$$
(iv) $$CM = \frac{1}{2}AB$$
(i) In $$\Delta AMC$$ and $$\Delta BMD$$
$$DM = CM$$ (given)
$$\angle 3 = \angle 4$$ (vertically opposite angles)
$$AM = MB$$ (as $$M$$ is the mid-point of $$AB$$)
$$\Delta AMC \cong \Delta BMD$$ (by SAS congruency rule)
(ii) $$\because \Delta AMC \cong \Delta BMD$$
$$\angle 1 = \angle 2$$ (by c.p.c.t)
But they are alternate angles,
so $$AC || BD$$
$$\angle ACB + \angle DBC = 180^{0}$$
(sum of the interior angles on the same side of a transversal is equal to $$180^{0}$$)
But $$\angle ACB = 90^{0}$$ (given)
$$\angle DBC = 180^{0} = 90^{0}$$
(iii) In $$\Delta DBC$$ and $$\Delta ACB$$
$$\angle DBC = \angle ACB = 90^{0}$$
$$BC = BC$$ (common side)
$$BD = CA$$ $$(\because \Delta AMC \cong \Delta BMD)$$
$$\therefore \Delta DBC \cong \Delta ACB$$ (by SAS congruency rule)
(iv) $$\because \Delta DBC \cong \Delta ACB$$
$$DC = AB$$
But $$M$$ mid-point of $$DC$$
$$2CM = CD$$
$$2CM = AB [\because DC = AB]$$
$$CM =\frac{1}{2} AB$$.
Hence proved.
$$DM = CM$$ (given)
$$\angle 3 = \angle 4$$ (vertically opposite angles)
$$AM = MB$$ (as $$M$$ is the mid-point of $$AB$$)
$$\Delta AMC \cong \Delta BMD$$ (by SAS congruency rule)
(ii) $$\because \Delta AMC \cong \Delta BMD$$
$$\angle 1 = \angle 2$$ (by c.p.c.t)
But they are alternate angles,
so $$AC || BD$$
$$\angle ACB + \angle DBC = 180^{0}$$
(sum of the interior angles on the same side of a transversal is equal to $$180^{0}$$)
But $$\angle ACB = 90^{0}$$ (given)
$$\angle DBC = 180^{0} = 90^{0}$$
(iii) In $$\Delta DBC$$ and $$\Delta ACB$$
$$\angle DBC = \angle ACB = 90^{0}$$
$$BC = BC$$ (common side)
$$BD = CA$$ $$(\because \Delta AMC \cong \Delta BMD)$$
$$\therefore \Delta DBC \cong \Delta ACB$$ (by SAS congruency rule)
(iv) $$\because \Delta DBC \cong \Delta ACB$$
$$DC = AB$$
But $$M$$ mid-point of $$DC$$
$$2CM = CD$$
$$2CM = AB [\because DC = AB]$$
$$CM =\frac{1}{2} AB$$.
Hence proved.
Prove that ratio of areas of two similar triangles is equal to ratio of their corresponding medians.
Proof: $$\triangle ABC\sim \triangle DEF$$
$$\cfrac{AB}{DE}=\cfrac{BC}{EF}$$
$$\Rightarrow$$ $$\cfrac{AB}{DE}=\cfrac{2BX}{2EY}$$
($$\because AX$$ and $$DY$$ medians $$BC=2BX,EF=2EY$$)
$$\Rightarrow$$ $$\cfrac{AB}{DE}=\cfrac{BX}{EY}$$...(i)
In $$\triangle ABX$$ and $$\triangle DEY$$
$$\angle B=\angle E$$ ($$\because \triangle ABC\sim \triangle DEF$$)
$$\cfrac{AB}{DE}=\cfrac{BX}{EY}$$
SAS similarity criterion
$$\triangle ABX\sim \triangle DEY$$
$$\cfrac{AB}{DE}=\cfrac{AX}{DY}$$...(ii)
Ratio of areas of two similar triangles is equal to ratio of squares of their corresponding sides
$$\cfrac { ar.\quad \triangle ABC }{ ar.\quad \triangle DEF } =\cfrac { { AB }^{ 2 } }{ { DE }^{ 2 } } =\cfrac { { AX }^{ 2 } }{ { DY }^{ 2 } } $$
$$\cfrac{AB}{DE}=\cfrac{BC}{EF}$$
$$\Rightarrow$$ $$\cfrac{AB}{DE}=\cfrac{2BX}{2EY}$$
($$\because AX$$ and $$DY$$ medians $$BC=2BX,EF=2EY$$)
$$\Rightarrow$$ $$\cfrac{AB}{DE}=\cfrac{BX}{EY}$$...(i)
In $$\triangle ABX$$ and $$\triangle DEY$$
$$\angle B=\angle E$$ ($$\because \triangle ABC\sim \triangle DEF$$)
$$\cfrac{AB}{DE}=\cfrac{BX}{EY}$$
SAS similarity criterion
$$\triangle ABX\sim \triangle DEY$$
$$\cfrac{AB}{DE}=\cfrac{AX}{DY}$$...(ii)
Ratio of areas of two similar triangles is equal to ratio of squares of their corresponding sides
$$\cfrac { ar.\quad \triangle ABC }{ ar.\quad \triangle DEF } =\cfrac { { AB }^{ 2 } }{ { DE }^{ 2 } } =\cfrac { { AX }^{ 2 } }{ { DY }^{ 2 } } $$
In figure $$LM\parallel CB$$ and $$LN\parallel CD$$. Prove that $$\cfrac{AM}{MB}=\cfrac{AN}{AD}$$
Sides $$AB$$ and $$AC$$ and median $$AD$$ of a triangle and respectively proportional to sides $$PQ$$ and $$PR$$ and median $$PM$$ of another triangle. Show that $$\triangle ABC\sim \triangle PQR$$
Given: $$\cfrac{AB}{PQ}=\cfrac{AC}{PR}=\cfrac{AD}{PM}$$...(i)
Construction: Produce $$AD$$ upto $$E$$ such that $$AD=DE$$. Join $$BE$$ and $$CE$$ and produce $$PM$$ up to $$N$$ such that $$PM=MN$$. Join $$QN$$ and $$NR$$
Proof: Diagonals $$AE$$ and $$BC$$ of quadrilateral $$ABEC$$ bisect each other at point $$D$$.
Quadrilateral $$ABEC$$ is a parallelogram
$$BE=AC$$...(ii)
Similarly $$PQNR$$ is a parallelograom
$$QN=PR$$...(iii)
Dividing equation (ii) by (iii)
$$\cfrac{BE}{QN}=\cfrac{AC}{PR}$$...(iv)
Now, $$\cfrac{AD}{PM}=\cfrac{2AD}{2PM}=\cfrac{AD}{PM}=\cfrac{AE}{PN}$$....(v)
In equation (i), (iv), (v)
$$\cfrac{AB}{PQ}=\cfrac{BE}{QN}=\cfrac{AE}{PN}$$
$$\triangle ABE\sim \triangle PQN$$ (By SSS)
$$\angle BAE=\angle QPN$$...(vi)
Similarly
$$\triangle AEC\sim \triangle PNR$$
$$\angle EAC=\angle NPR$$...(vii)
Adding equation (vi) and (vii)
$$\angle BAE+\angle EAC=\angle QPN+\angle NPR$$
$$\Rightarrow$$ $$\angle BAC=\angle QPR$$
Now, in $$\triangle ABC$$ and $$\angle PQR$$
$$\cfrac{AB}{PQ}=\cfrac{AC}{PR}$$ (from equation (i))
$$\angle A=\angle P$$
By SAS similarity criterion
$$\triangle ABC\sim \triangle PQR$$
Construction: Produce $$AD$$ upto $$E$$ such that $$AD=DE$$. Join $$BE$$ and $$CE$$ and produce $$PM$$ up to $$N$$ such that $$PM=MN$$. Join $$QN$$ and $$NR$$
Proof: Diagonals $$AE$$ and $$BC$$ of quadrilateral $$ABEC$$ bisect each other at point $$D$$.
Quadrilateral $$ABEC$$ is a parallelogram
$$BE=AC$$...(ii)
Similarly $$PQNR$$ is a parallelograom
$$QN=PR$$...(iii)
Dividing equation (ii) by (iii)
$$\cfrac{BE}{QN}=\cfrac{AC}{PR}$$...(iv)
Now, $$\cfrac{AD}{PM}=\cfrac{2AD}{2PM}=\cfrac{AD}{PM}=\cfrac{AE}{PN}$$....(v)
In equation (i), (iv), (v)
$$\cfrac{AB}{PQ}=\cfrac{BE}{QN}=\cfrac{AE}{PN}$$
$$\triangle ABE\sim \triangle PQN$$ (By SSS)
$$\angle BAE=\angle QPN$$...(vi)
Similarly
$$\triangle AEC\sim \triangle PNR$$
$$\angle EAC=\angle NPR$$...(vii)
Adding equation (vi) and (vii)
$$\angle BAE+\angle EAC=\angle QPN+\angle NPR$$
$$\Rightarrow$$ $$\angle BAC=\angle QPR$$
Now, in $$\triangle ABC$$ and $$\angle PQR$$
$$\cfrac{AB}{PQ}=\cfrac{AC}{PR}$$ (from equation (i))
$$\angle A=\angle P$$
By SAS similarity criterion
$$\triangle ABC\sim \triangle PQR$$
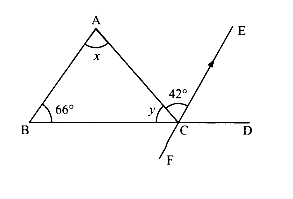
If in $$\triangle ABCD$$ is any point on $$BC$$ such that $$\cfrac{AB}{AC}=\cfrac{BD}{DC}$$ and $$\angle B={70}^{o}$$, $$\angle C={50}^{o}$$, then find $$\angle BAD$$
In $$\triangle ABC$$
$$\angle B={70}^{o}$$, $$\angle C={50}^{o}$$
$$\angle A+\angle B+\angle C={180}^{o}$$
$$\Rightarrow$$ $$\angle A={180}^{o}-(\angle B+\angle C)$$
$$\Rightarrow$$ $$\angle A={180}^{o}-({70}^{o}+{50}^{o})$$
$$\Rightarrow$$ $$\angle A={180}^{o}-{120}^{o}$$
$$\Rightarrow$$ $$\angle A={60}^{o}$$
Thus, $$\cfrac{AB}{AC}=\cfrac{BD}{DC}$$ (given)
$$\triangle ABD\sim \triangle ADC$$
$$\Rightarrow$$ $$\angle BAD$$ and $$\angle DAC$$ will be equal to each other
$$2\angle BAD={60}^{o}$$
$$\angle BAD=\cfrac{60}{2}$$
$$\angle BAD={30}^{o}$$
$$\angle B={70}^{o}$$, $$\angle C={50}^{o}$$
$$\angle A+\angle B+\angle C={180}^{o}$$
$$\Rightarrow$$ $$\angle A={180}^{o}-(\angle B+\angle C)$$
$$\Rightarrow$$ $$\angle A={180}^{o}-({70}^{o}+{50}^{o})$$
$$\Rightarrow$$ $$\angle A={180}^{o}-{120}^{o}$$
$$\Rightarrow$$ $$\angle A={60}^{o}$$
Thus, $$\cfrac{AB}{AC}=\cfrac{BD}{DC}$$ (given)
$$\triangle ABD\sim \triangle ADC$$
$$\Rightarrow$$ $$\angle BAD$$ and $$\angle DAC$$ will be equal to each other
$$2\angle BAD={60}^{o}$$
$$\angle BAD=\cfrac{60}{2}$$
$$\angle BAD={30}^{o}$$
In $$\triangle ABC$$, $$DE\parallel BC$$ and $$AD=6cm,DB=9cm$$ and $$AE=8cm$$, then find $$AC$$.
In $$\triangle ABC$$,
$$DE\parallel BC$$
$$\cfrac{AD}{DB}=\cfrac{AE}{EC}$$ (by basic proportionality theorem)
$$\Rightarrow$$ $$\cfrac{6}{9}=\cfrac{8}{CE}$$
$$\Rightarrow$$ $$6\times CE=9\times 8$$
$$\Rightarrow$$ $$CE=\cfrac{8\times 9}{6}$$
$$\Rightarrow$$ $$CE=12cm$$
$$AC=AE+CE$$
$$=(8+12)cm=20cm$$
Thus, $$AC=20cm$$
$$DE\parallel BC$$
$$\cfrac{AD}{DB}=\cfrac{AE}{EC}$$ (by basic proportionality theorem)
$$\Rightarrow$$ $$\cfrac{6}{9}=\cfrac{8}{CE}$$
$$\Rightarrow$$ $$6\times CE=9\times 8$$
$$\Rightarrow$$ $$CE=\cfrac{8\times 9}{6}$$
$$\Rightarrow$$ $$CE=12cm$$
$$AC=AE+CE$$
$$=(8+12)cm=20cm$$
Thus, $$AC=20cm$$
In figure, $$D, E$$ and $$F$$ are the mid-points of the sides $$BC, CA$$ and $$AB$$ respectively. If $$AB= 4.3 \ cm; BC= 5.6 \ cm$$ and $$AC= 3.9 \ cm$$, then find the perimeter of the following:
(i) $$ADEF$$ and
(ii) quad. $$BDEF$$
In figure, find $$ \angle x, \angle y $$ and $$ \angle A C D $$ where line $$ B A \| F E . $$
In figure, $$X$$ and $$Y$$ are the points on equal sides of $$AB$$ and $$AC$$ such that $$AX = AY$$. Show that $$XC = BY$$.
In $$\Delta ABC, D$$ is the mid-point of side $$AC$$ such that $$BD =\frac{1}{2} AC$$. Show that $$\angle ABC = 90^{0}$$.
$$D$$ is mid-point of $$AC$$
$$AD = DC =\frac{1}{2} AC$$
But $$BD = \frac{1}{2}AC$$ (given)
$$AD = DC = BD$$
In $$\Delta ABD$$
$$AD = BD$$
$$\angle 2 = \angle 1 = x$$ (angles opposite to equal sides are equal)
Also $$BD = DC$$
$$\angle 3 = \angle 4 = x$$
In $$\Delta ABC$$
$$\angle 1 + (\angle 2 + \angle 3) + \angle 4 = 180^{0}$$
$$x + (x + x) + x = 180^{0}$$
$$4x = 180^{0}$$
$$x = 45^{0}$$
$$\angle ABC = x + x = 45^{0} + 45^{0} = 90^{0}$$
Hence proved.
$$AD = DC =\frac{1}{2} AC$$
But $$BD = \frac{1}{2}AC$$ (given)
$$AD = DC = BD$$
In $$\Delta ABD$$
$$AD = BD$$
$$\angle 2 = \angle 1 = x$$ (angles opposite to equal sides are equal)
Also $$BD = DC$$
$$\angle 3 = \angle 4 = x$$
In $$\Delta ABC$$
$$\angle 1 + (\angle 2 + \angle 3) + \angle 4 = 180^{0}$$
$$x + (x + x) + x = 180^{0}$$
$$4x = 180^{0}$$
$$x = 45^{0}$$
$$\angle ABC = x + x = 45^{0} + 45^{0} = 90^{0}$$
Hence proved.
In the figure, $$ABC$$ and $$DBC$$ are two triangles on the same base $$BC$$. If $$AD$$ intersects $$BC$$ at $$O$$, show that $$\dfrac{ar(ABC)}{ar(DBC)}=\dfrac{AO}{DO}$$
Find the height of a cone of diameter $$30m$$ and slant height $$25m$$.
$$\textbf{ Step 1: Use Pythagoras theorem to find the height of the cone.}$$
$$\text{Given,}$$
$$\text{l = 25 m and d = 30 m}$$
$$\text{Now,}$$
$$r=\dfrac{30}{2}=15m$$ $$\left[\because\boldsymbol{r=\dfrac{d}{2}}\right]$$
$$\text{By using Pythagoras theorem}$$
$$h=\sqrt{l^2-r^2}$$
$$h=\sqrt{25^2-15^2}$$ $$\left[\because\boldsymbol{h=\sqrt{l^2-r^2}}\right]$$
$$\,=\sqrt{625-225}$$
$$\,=\sqrt{400}$$
$$h=20 \text{ m}$$
$$h=\sqrt{25^2-15^2}$$ $$\left[\because\boldsymbol{h=\sqrt{l^2-r^2}}\right]$$
$$\,=\sqrt{625-225}$$
$$\,=\sqrt{400}$$
$$h=20 \text{ m}$$
$$\textbf{Hence, height of cone is 20 }\boldsymbol{m.}$$
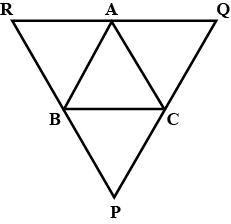
Through $$A, B$$ and $$C$$ lines $$RQ, PR$$ and $$QP$$ have been drawn respectively parallel to sides $$BC, CA$$ and $$AB$$ of a $$\triangle ABC$$ as shown in figure. Show that $$BC= \dfrac12 QR$$.
In figure, $$D$$ and $$E$$ are the mid-points of the sides $$AB$$ and $$AC$$ respectively of $$\triangle ABC$$. If $$BC= 6.4\ cm$$, find $$DE$$.
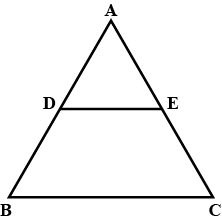
Derive the formula for height and area of an equilateral triangle.
Let $$△ABC$$ be the triangle where $$AP⊥BC,AB=AC=a,BP=PC=\cfrac {a}{2}$$ and $$AP=h$$ as shown in the above figure:
In $$△APC$$, $$∠P=90^{ 0 }$$
Using pythagoras theorem, we have
$$AC^{ 2 }=AP^{ 2 }+PC^{ 2 }\\ \Rightarrow a^{ 2 }=h^{ 2 }+\left( \cfrac { a }{ 2 } \right) ^{ 2 }\quad \\ \Rightarrow a^{ 2 }=h^{ 2 }+\cfrac { a^{ 2 } }{ 4 } \quad \quad \\ \Rightarrow h^{ 2 }=a^{ 2 }-\cfrac { a^{ 2 } }{ 4 } \\ \Rightarrow h^{ 2 }=\cfrac { 4a^{ 2 }-a^{ 2 } }{ 4 } \\ \Rightarrow h^{ 2 }=\cfrac { 3a^{ 2 } }{ 4 } \\ \Rightarrow h=\sqrt { \cfrac { 3a^{ 2 } }{ 4 } } \\ \Rightarrow h=\cfrac { \sqrt { 3 } a }{ 2 }$$
Now, the area of the triangle is $$A=\cfrac { 1 }{ 2 } bh$$ therefore,
$$A=\cfrac { 1 }{ 2 } \times b\times h=\cfrac { 1 }{ 2 } \times a\times \cfrac { \sqrt { 3 } a }{ 2 } =\cfrac { \sqrt { 3 } a^{ 2 } }{ 4 }$$
Hence, height of an equilateral triangle is $$h=\cfrac { \sqrt { 3 } a }{ 2 }$$ and area is $$A=\cfrac { \sqrt { 3 } a^{ 2 } }{ 4 }$$.
In $$\triangle ABC$$, $$a + b = 18$$ units, $$b + c = 25$$ units and $$c + a = 17$$ units. What type of triangle is $$ABC$$? Give reason.
Using basic proportionality theorem, prove that a line drawn through the midpoint of one side of a triangle and parallel to another side bisects the third side.
In $$\triangle MNS$$, line KL $$\parallel$$ side NS .....(given)
$$\therefore \dfrac {MK}{KN} = \dfrac {ML}{LS}$$ ..... (By BPT)
But $$MK = KN$$
$$\therefore \dfrac {MK}{KN}=1$$
$$\therefore \dfrac {ML}{LS} = 1$$
$$\therefore ML=LS$$
This means that line KL bisects side MS.
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the square of the other two sides.
Given triangle ABC is a right angle triangle at B
Draw BD perpendicular to AC
In $$\Delta ABC $$ and $$\Delta ADB$$
$$\angle ABC=\angle ADB $$
$$\angle A=\angle A$$
$$\therefore \Delta ABC\sim \Delta ADB$$
$$\therefore \dfrac{AB}{AD}=\dfrac{BC}{DB}=\dfrac{AC}{AB}$$
$$\Rightarrow AB^{2}=AC\times AD$$.............................................(1)
In$$\Delta ABC$$ and $$\Delta BDC$$
$$\angle ABC=\angle bDC $$
$$\angle C=\angle C$$
$$\therefore \Delta ABC\sim \Delta BDC$$
$$\therefore \dfrac{AB}{BD}=\dfrac{BC}{DC}=\dfrac{AC}{BC}$$
$$\Rightarrow BC^{2}=AC\times DC$$
Add (1) and (2) we get
$$AB^{2}+BC^{2}=AC\times AD+AC\times DC$$
$$=AC(AD+DC)=AC\times AC$$
$$=AC^{2}$$
Hence proved.
The corresponding altitudes of two similar triangles are 3 cm and 5 cm respectively. Find the ratio between their areas.
As shown in the above figure, let $$△ABC$$ and $$△DEF$$ be the similar triangles with altitudes $$AM$$ and $$DN$$ and with $$AM⊥BC$$ and $$DN⊥EF$$.
We know that the arc of similar triangles are proportional to squares of their corresponding altitude, therefore with the given altitudes $$3$$ cm and $$5$$ cm, we have,
$$\dfrac { { A }r(△ABC) }{ { A }r(△DEF) } =\dfrac { AM^{ 2 } }{ DN^{ 2 } } \\=\dfrac { 3^{ 2 } }{ 5^{ 2 } } \\=\dfrac { 9 }{ 25 }$$
Hence the ratio between the areas is $$9:25$$.
Two isosceles triangles are having equal vertical angles and their areas are in the ratio 9 :Find the ratio of their corresponding altitudes.
As shown in the above figure, let $$△ABC$$ and $$△DEF$$ are the isosceles triangles with altitudes $$AM$$ and $$DN$$ and with $$∠A=∠D$$, therefore,
$$∠B=∠C$$ and $$∠E=∠F$$ that is
$$∠B=∠C=∠E=∠F$$
Thus, $$△ABC∼△DEF$$
We know that the arc of similar triangles are proportional to squares of their corresponding altitude, therefore with the given ratio of area of triangles $$9:16$$, we have,
$$\frac { { A }r(△ABC) }{ { A }r(△DEF) } =\frac { AM^{ 2 } }{ DN^{ 2 } } \\ \Rightarrow \frac { 9 }{ 16 } =\frac { AM^{ 2 } }{ DN^{ 2 } } \\ \Rightarrow \sqrt { \frac { AM^{ 2 } }{ DN^{ 2 } } } =\sqrt { \frac { 9 }{ 16 } } \\ \Rightarrow \frac { AM }{ DN } =\frac { 3 }{ 4 } \\ \Rightarrow AM:DN=3:4$$
Hence the ratio of their altitudes is $$3:4$$.
$$\triangle BAC$$ and $$\triangle$$BDC are two right-angled triangles with common hypotenuse BC. The sides $$AC$$ and $$BD$$ intersect at $$'P'$$
Prove that $$AP. PC = DP. PB$$
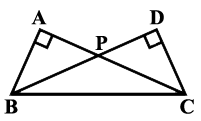
The shortest distance $$AP$$ from a point '$$A$$' to $$QR$$ is $$12 cm$$. $$Q$$ and $$R$$ are $$15 cm$$ and $$20 cm$$ respectively from '$$A$$' and on opposite sides of $$AP$$. Prove that $$\angle QAR = {90}^{o}$$.
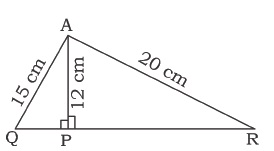
In the figure shown above, AC || BD and CE || DF. If OA = 12 cm, AB = 9 cm, OC = 8 cm and EF = 4.5 cm, find OE.
In $$\triangle ABC, \angle ABC = 90^o, BM \perp AC$$ , $$BM = x + 2, AM = x + 7, CM = x$$, find $$x$$
It is given that $$∠ABC=90^{ 0 }$$ and $$BM⊥AC$$ as shown in the above figure:
Now with $$BM=(x+2)$$, $$CM=x$$ and $$AM=(x+7)$$, consider,
$$BM^{ 2 }=CM\times AM\\ \Rightarrow (x+2)^{ 2 }=x\times (x+7)\\ \Rightarrow x^{ 2 }+4x+4=x^{ 2 }+7x\\ \Rightarrow x^{ 2 }+4x+4-x^{ 2 }-7x=0\\ \Rightarrow -3x+4=0\\ \Rightarrow -3x=-4\\ \Rightarrow x=\frac { 4 }{ 3 }$$
Hence, $$x=\frac { 4 }{ 3 }$$.
In the isosceles $$\triangle ABC$$, $$AB = AC$$, $$BC = 18 cm$$, $$AD \perp BC$$, $$AD = 12 cm$$, $$BC$$ is produced to '$$E$$' and $$AE = 20 cm$$. Prove that $$\angle BAE = {90}^{o}$$.
$$\triangle$$ABC and $$\triangle $$BDE are two equilateral triangles and BD = DC. Find the ratio between areas of $$\triangle$$ABC and $$\triangle$$BDE.
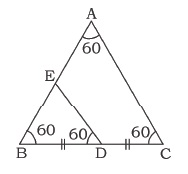
In the quadrilateral $$ABCD$$, $$\angle ADC = {90}^{o}$$, $$AB = 9 cm$$, $$BC = AD = 6 cm$$ and $$CD = 3 cm$$. Prove that $$\angle ACB = {90}^{o}$$
In the adjoining figure, DE || AB, AD = 7 cm, CD = 5 cm and BC = 18 cm. Find BE and CE.
In the given figure, $$XY||AC$$, if $$2AX=3BX$$ and $$XY=9$$ find the value of $$AC$$
In $$\triangle ABC$$ $$DE||BC$$ and $$\dfrac{AD}{DB}=\dfrac{3}{5}$$$$AC =5.6$$ find $$AE$$ ?
In a fig. a crescent is formed by two circles which touch at A. C is the center of a larger circle. The width of the crescent at BD is 9 cm and at EF it is 5 cm. Find the radii of two circles.
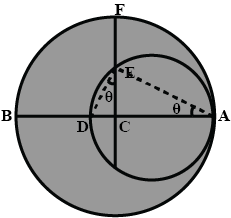
In a triangle $$ABC,AB=AC$$ and $$D$$ is a point on side $$AC$$ such that $$BC^{2}=AC \times CD$$ prove that $$BD=BC$$
In given figure, find $$\angle F$$
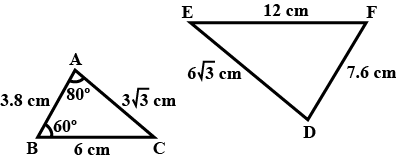
In $$\Delta ABC, \bar{PQ}\parallel \bar{AB}$$, P,Q are on BC and CA respectively if CQ: QA=1:3 are CP=4 then BC=......
Let $$ \triangle ABC\sim \triangle DEF$$ and there areas be, respectively $$64cm^{2}$$ and $$121cm^{2}$$ if $$EF=15.4cm$$ find $$BC$$ ?
In the given fig, the line segment $$xy$$ in parallel to $$AC$$ of $$\triangle ABC$$ and its dividend the triangle into two points of equal areas. Prove that $$\dfrac {Ax}{AB}=\dfrac {\sqrt {2-1}}{\sqrt {2}}$$
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR.
Show that $$\Delta ABC\, \sim \,\Delta PQR$$
In the trapezium ABCD, AB || DC, AB = 2CD and ar ($$\triangle$$AOB) = 84 cm$$^2$$, find the area of $$\triangle $$COD
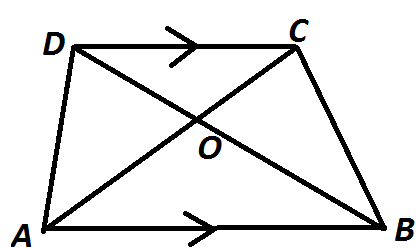
Prove that the ratio of the area of two similar triangles is equal to the square of the ratio of their corresponding medians.
State and prove that basic proportionality theorem.
In the given figure, $$3SR = 2SP,\,\,\left. {ST} \right|\left| {PM} \right.$$ and $$ar\left( {\triangle PMR} \right) = 50\,\,c{m^2}.$$
Find the -
1. $$ar\left( {\triangle RST} \right)$$2. $$ar\left( {PMTS} \right)$$
1. $$ar\left( {\triangle RST} \right)$$
In figure, two triangles ABC and DBC lie on the same side of base BC.P is a point on BC such that PQ || BA and PQ || BA and PR || BD. prove that QR || AD.
Prove that $$\triangle ABC\sim \triangle EDC$$
$$\Delta ABC\sim \Delta DEF$$ and their areas are respectively $$100{ cm }^{ 2 }$$ and $$49{ cm }^{ 2 }$$. If the altitude of $$\Delta ABC$$ is $$5 \ cm$$, find the corresponding altitude of $$\Delta DEF$$.
In the figure, $$\ ED\parallel QO$$ and $$DF\parallel OR$$. Prove that,
$$EF \parallel QR$$
Triangles ABC and DBC have side BC common, AB$$=$$BD and AC$$=$$CD. Are the two triangles congruent? State in symbolic form. which congruence condition do you use? Does $$\angle$$ABD equal $$\angle$$ACD? Why or why not?
Triangles ABC and DBC have side BC common, AB$$=$$BD and AC$$=$$CD.
So,
$$BC=BC\cdots\cdots[\text{common side}]$$
$$AB=BD\cdots\cdots[\text{given}]$$
$$AC=CD\cdots\cdots[\text{given}]$$
So, by $$SSS$$ test we can say that,
$$\Delta ABC\cong\Delta DBC$$
Congruence condition used is $$SSS$$
Then, $$\angle ABD\neq\angle ACD$$
Then they will not be equal.
Because , $$\angle ABD=\angle ABC\pm\angle DBC$$
and $$\angle ACD=\angle ACB\pm\angle DCB$$
From congruency, $$\angle ABC\cong\angle DBC$$ and $$\angle ACB\cong\angle DCB$$
So, we cannot say that $$\angle ABD$$ is equal to $$\angle ACD$$
The ratio of corresponding sides of similar triangles is 3 : 5, then find the ratio of their areas.
$$ABC$$ is a right angle triangle such that $$AB = AC$$ and bisector of angle $$C$$ intersects the side $$AB$$ at $$D$$ P.T. $$AC + AD = BC$$.
$$\textbf{Step 1: Use pythagoras theorem}$$
$$\text{Let AB = AC = a and AD = b}$$
$$\Delta$$ $$\text{ABC is right angled at A}$$
$$AB^2 + AC^2 = BC^2$$
$$a^2 + a^2 = BC^2 \Rightarrow BC = a\sqrt{2}$$
$$\textbf{Step 2: Find relation between a and b}$$
$$\dfrac{AD}{BD} = \dfrac{AC}{BC}$$ $$\text{(Angle bisector theorem)}$$
$$\dfrac{b}{a - b} = \dfrac{a}{a\sqrt{2}} = \dfrac{1}{\sqrt{2}}$$
$$b = \dfrac{a}{1 + \sqrt{2}} = a(\sqrt{2} - 1)$$
$$b = a(\sqrt{2} - 1)\Rightarrow a + b = a\sqrt{2}$$ $$....(1)$$
$$\textbf{Step 3: Compare values of AC, AD and BC}$$
$$\text{AC = a, AD = b, BC =}$$ $$a\sqrt{2}$$
$$\text{Now}$$
$$\text{AC + AD = BC}$$
$$a + b = a\sqrt{2}$$ $$\text{(from equation 1)}$$
$$\textbf{Hence, required result is proved.}$$
In the adjoining figure, the diagonals of a parallelogram intersect at $$O. OE$$ is drawn parallel to $$CB$$ to meet $$AB$$ at $$E$$. Find the following ratio:Area of $$\triangle AOE$$ : Area of parallelogram $$ABCD$$.
The sides of certain triangle are given. Determine whether it is right triangle.
$$a=9$$cm, $$b=16$$cm and $$c=18$$cm.
$$ \operatorname{In} \Delta A B C, D E \| B C $$. If $$ A D=5 \mathrm{cm}, B D=7 \mathrm{cm} $$ and $$ A C=18 \mathrm{cm}, $$ find the length of $$ A E .$$
Class 10 Maths Extra Questions
- Areas Related To Cricles Extra Questions
- Arithmetic Progressions Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Introduction To Trigonometry Extra Questions
- Pair Of Linear Equations In Two Variables Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadratic Equations Extra Questions
- Real Numbers Extra Questions
- Some Applications Of Trigonometry Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions