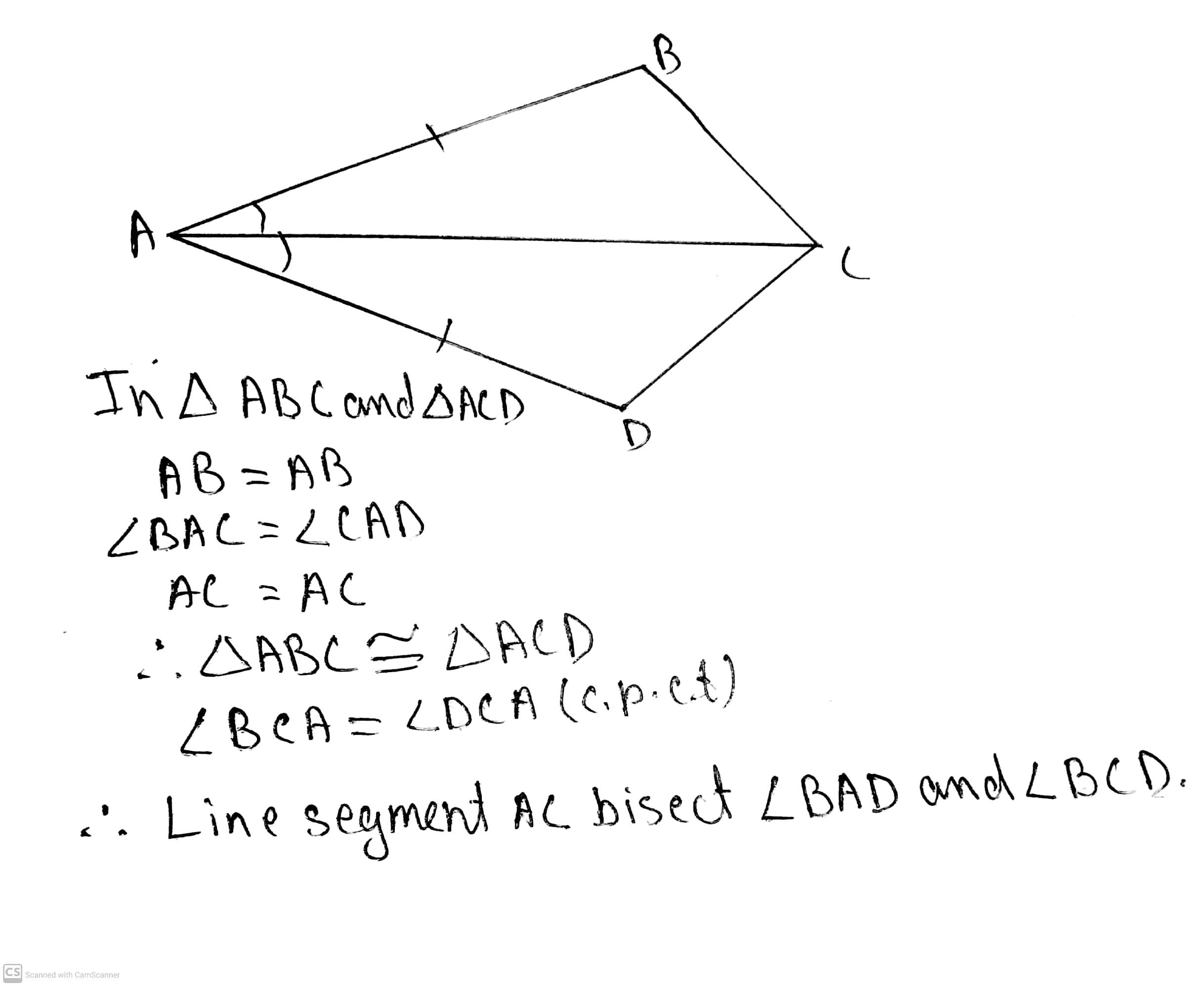
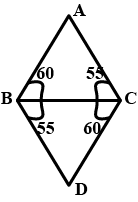
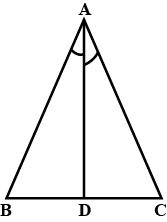
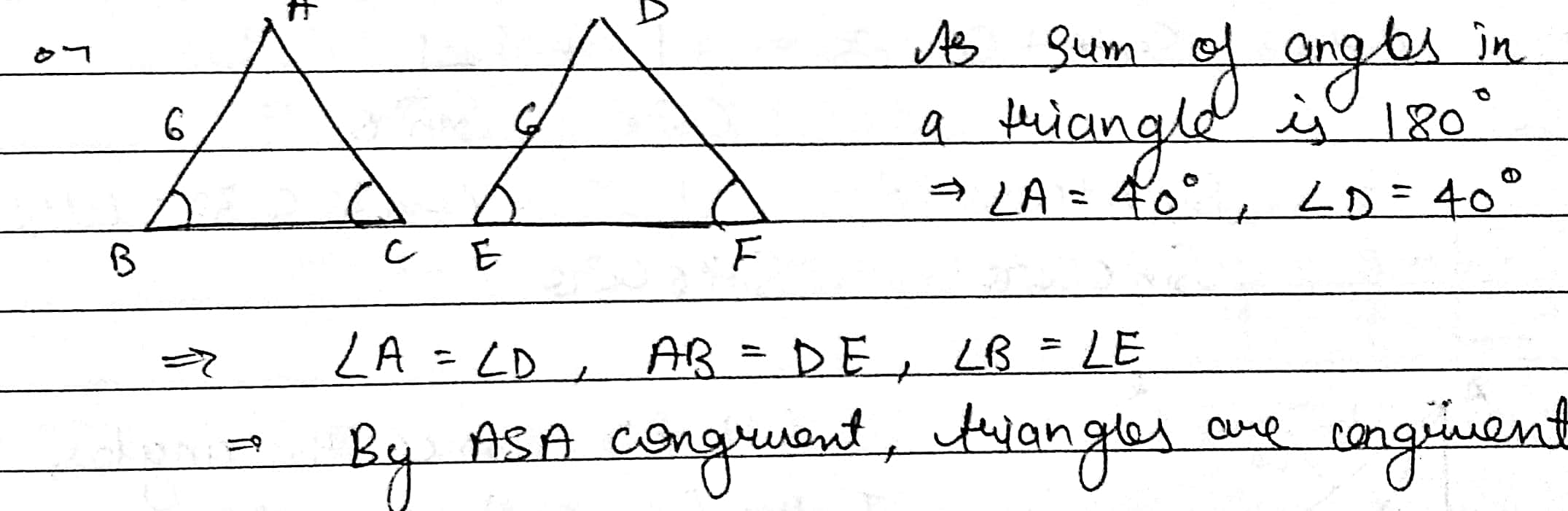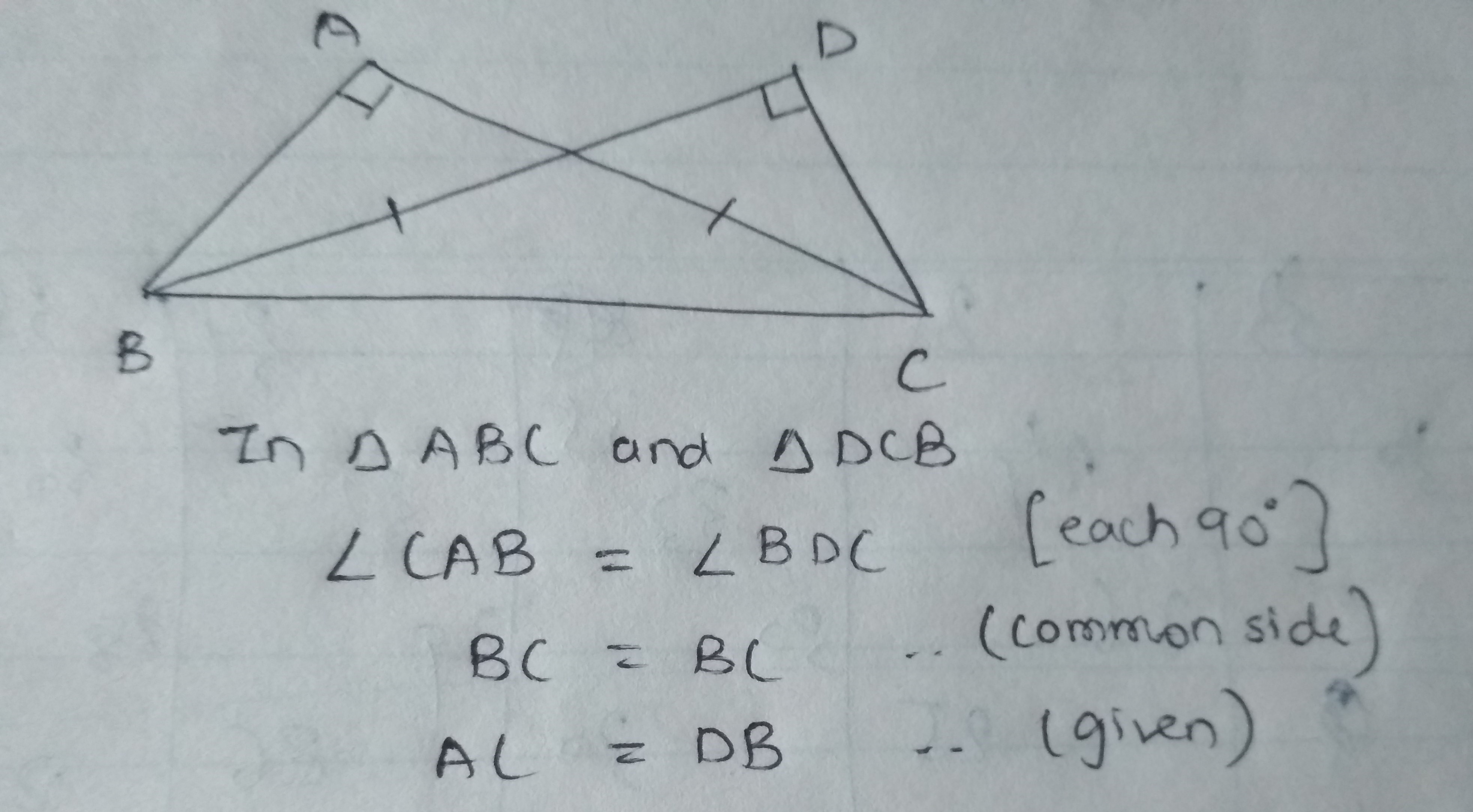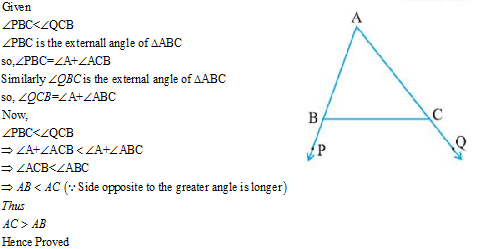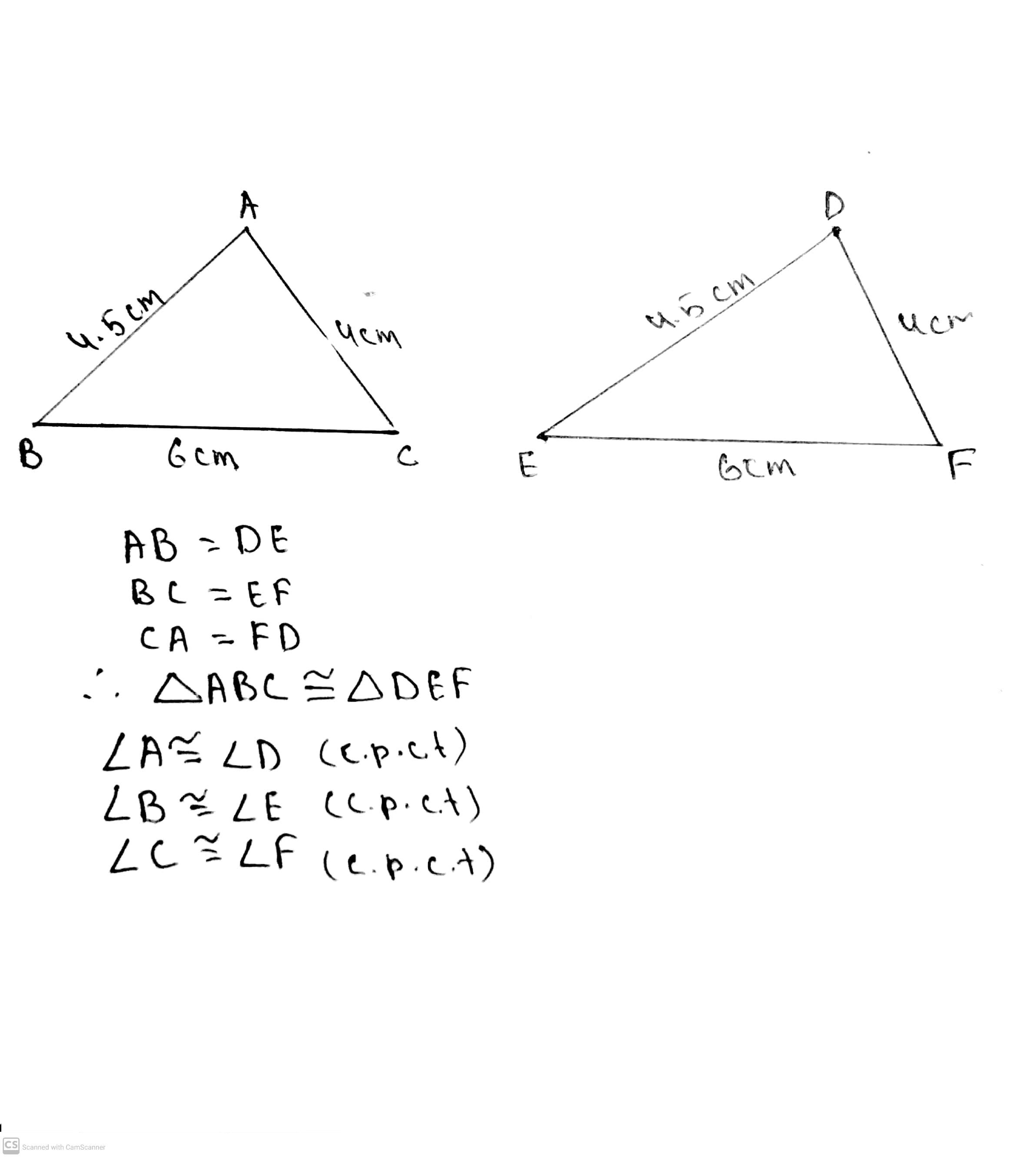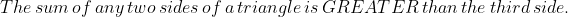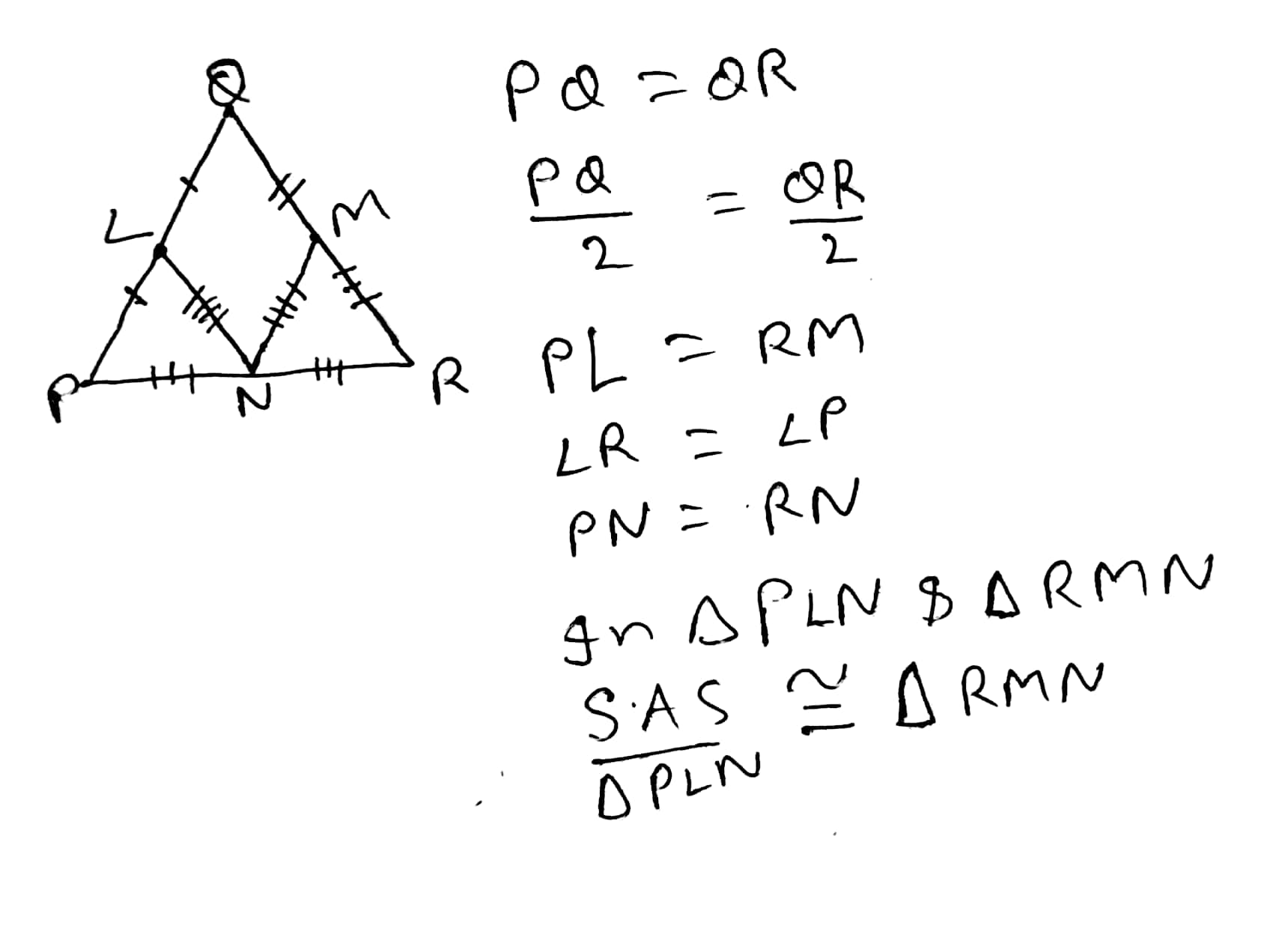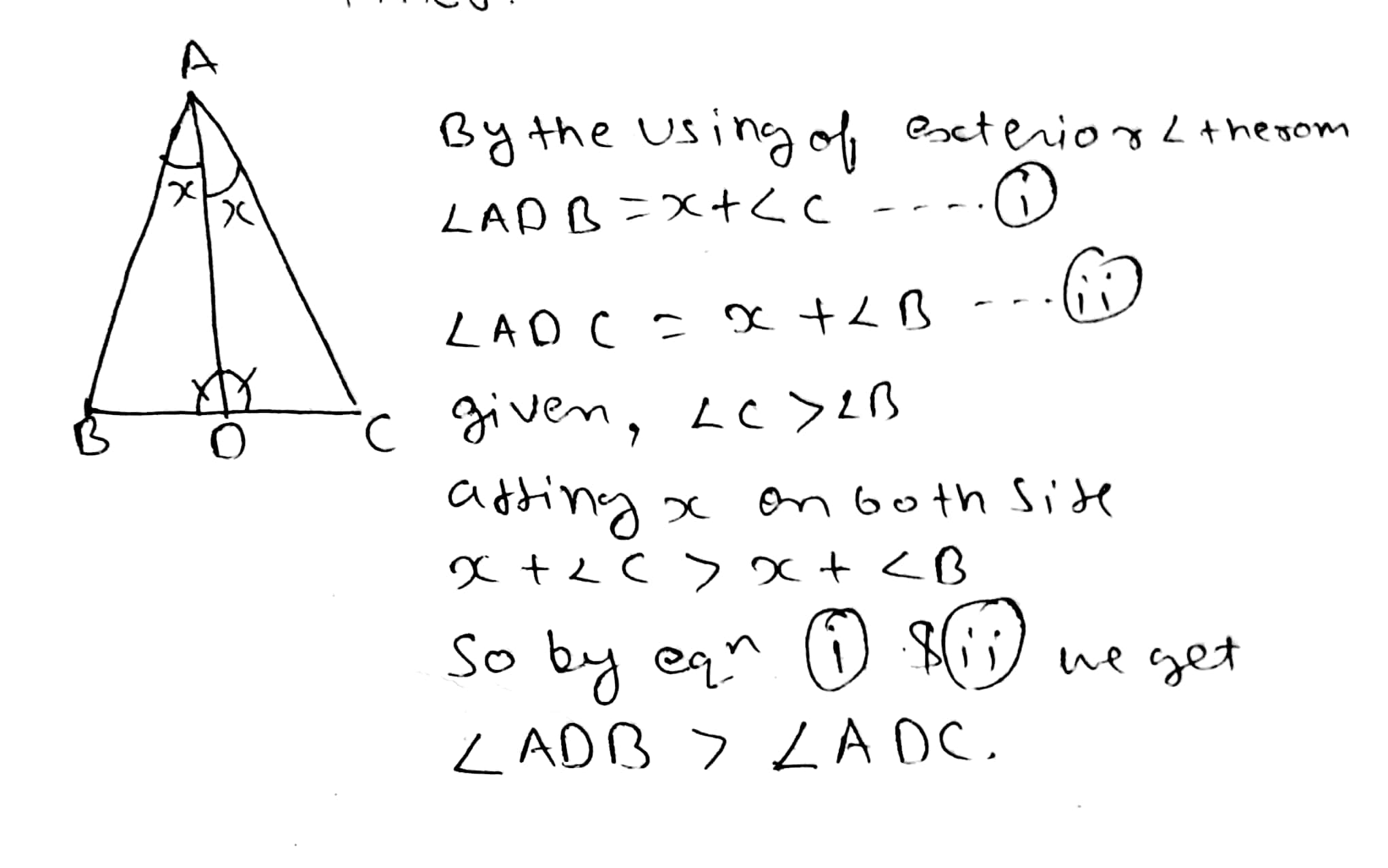Triangles - Class 9 Maths - Extra Questions
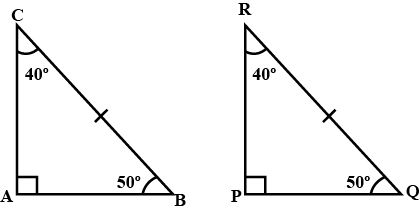
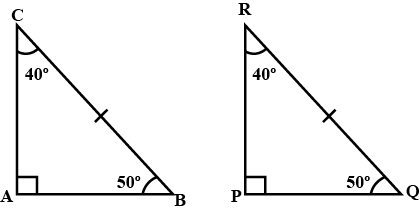
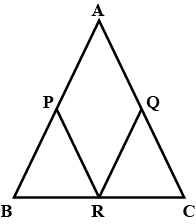
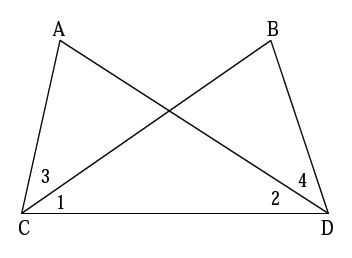
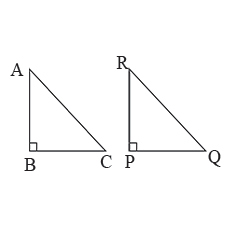
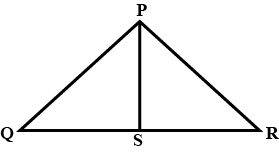
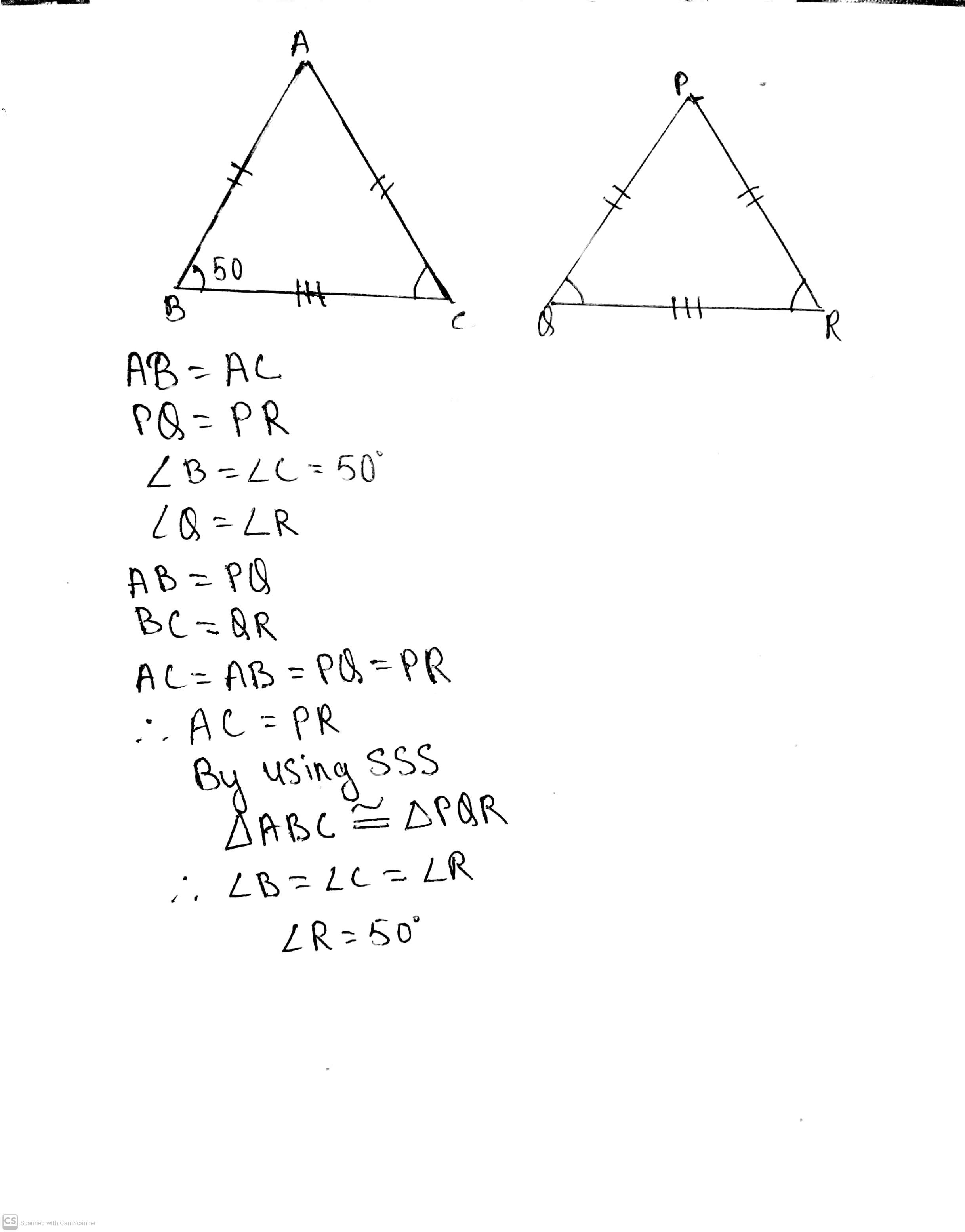
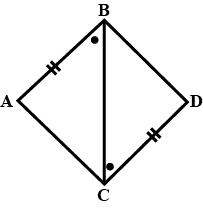
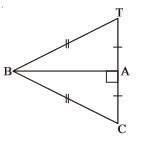
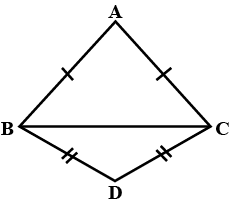
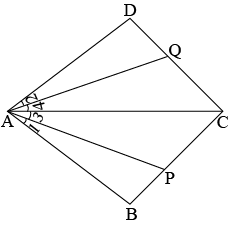
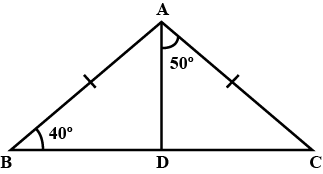
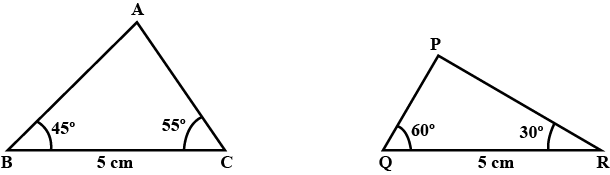
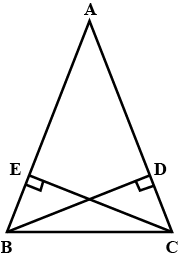
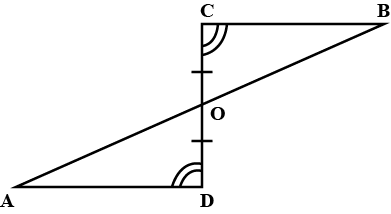
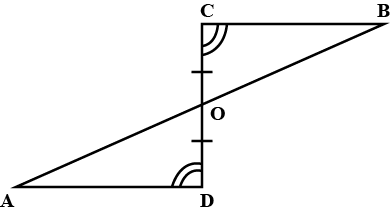
In $$\triangle ABC$$ and $$\triangle PQR$$, $$BC=QR, \angle A=90^{\circ},\angle C =\angle R=40^{\circ}\ and\ \angle Q=50^{\circ}.$$
Above two triangles are congruent by ASA test
If true then enter $$1$$ else if False enter $$0.$$
In $$\bigtriangleup ABC \ and \bigtriangleup PQR, AB=PQ,AC=PR\:and\:BC =QR$$, then the two triangles are congruent by which test?
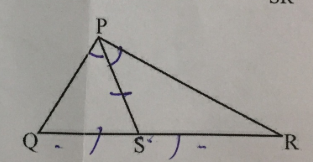
In $$\Delta$$PQR, seg $$PQ$$ $$\cong$$ seg $$QR$$ and $$\angle P = 70^o$$, then find the measures of angle $$Q$$ is:
Without drawing exact triangles, state whether the given pairs of triangle are congruent or not, if congruent use '1' else '0'.
In $$ \Delta ABC \,\,\, and \,\,\, \Delta DEF; AB=EF, BC=DF \,\, and \,\, \angle B = \angle F$$
In $$\Delta ABC,$$ if $$ AB = 76$$ cm, $$BC=69$$ cm and $$CA=61$$ cm, then the smallest angle is $$B$$.If true then enter $$1$$ and if false then enter $$0$$.
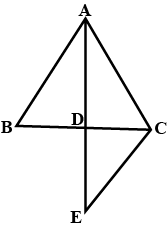
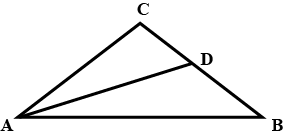
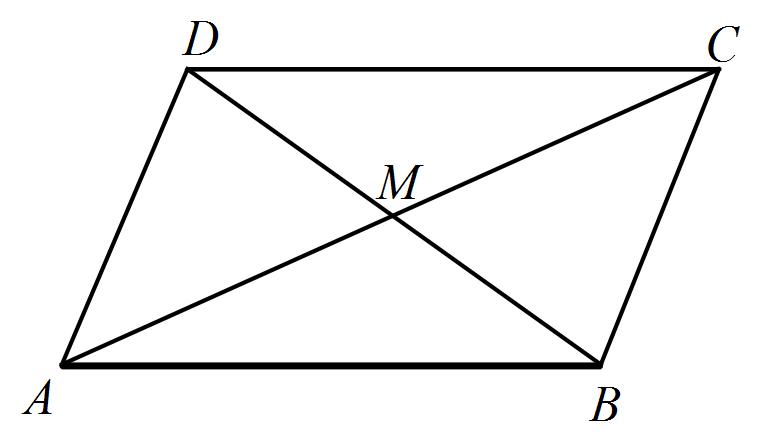
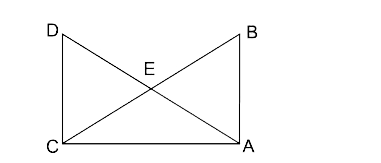
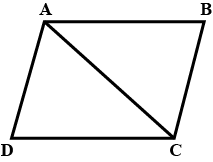
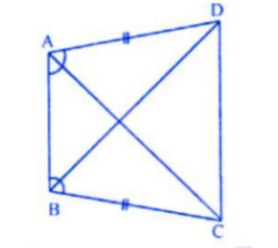
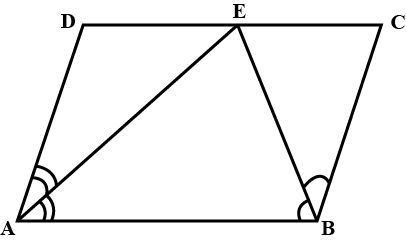
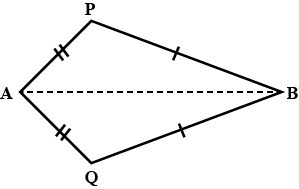
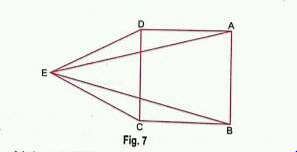
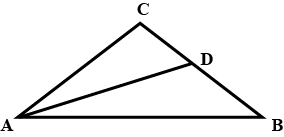
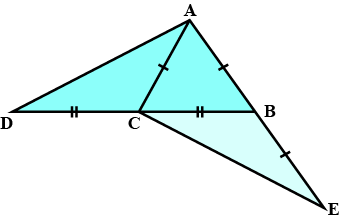
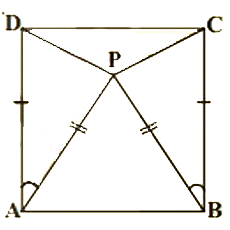
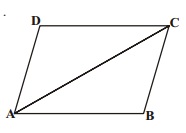
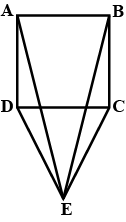
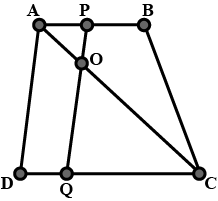
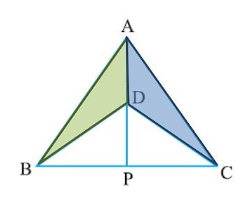
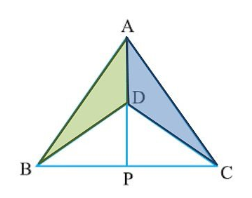
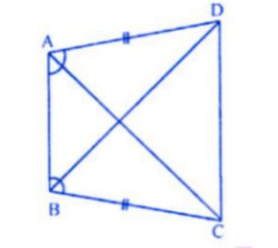
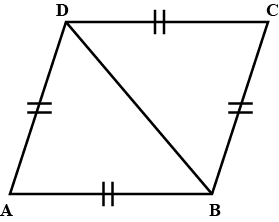
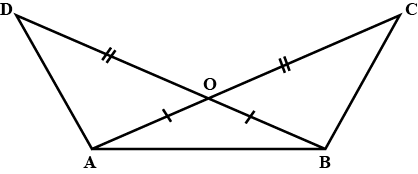
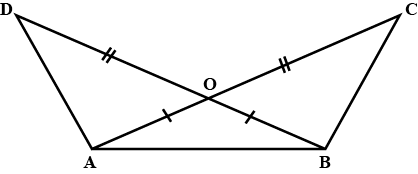
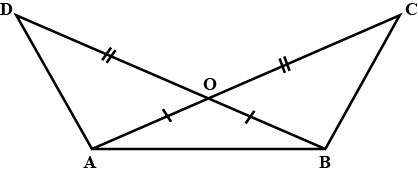
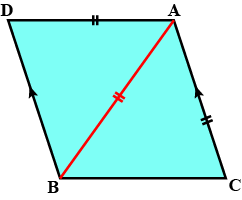
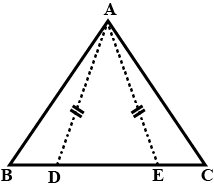
In the alongside diagram, $$ABCD$$ is parallelogram. Prove that : $$AB = 2 BC$$
Without drawing exact triangles, state, giving reasons, whether the given pairs of triangle are congruent or not :
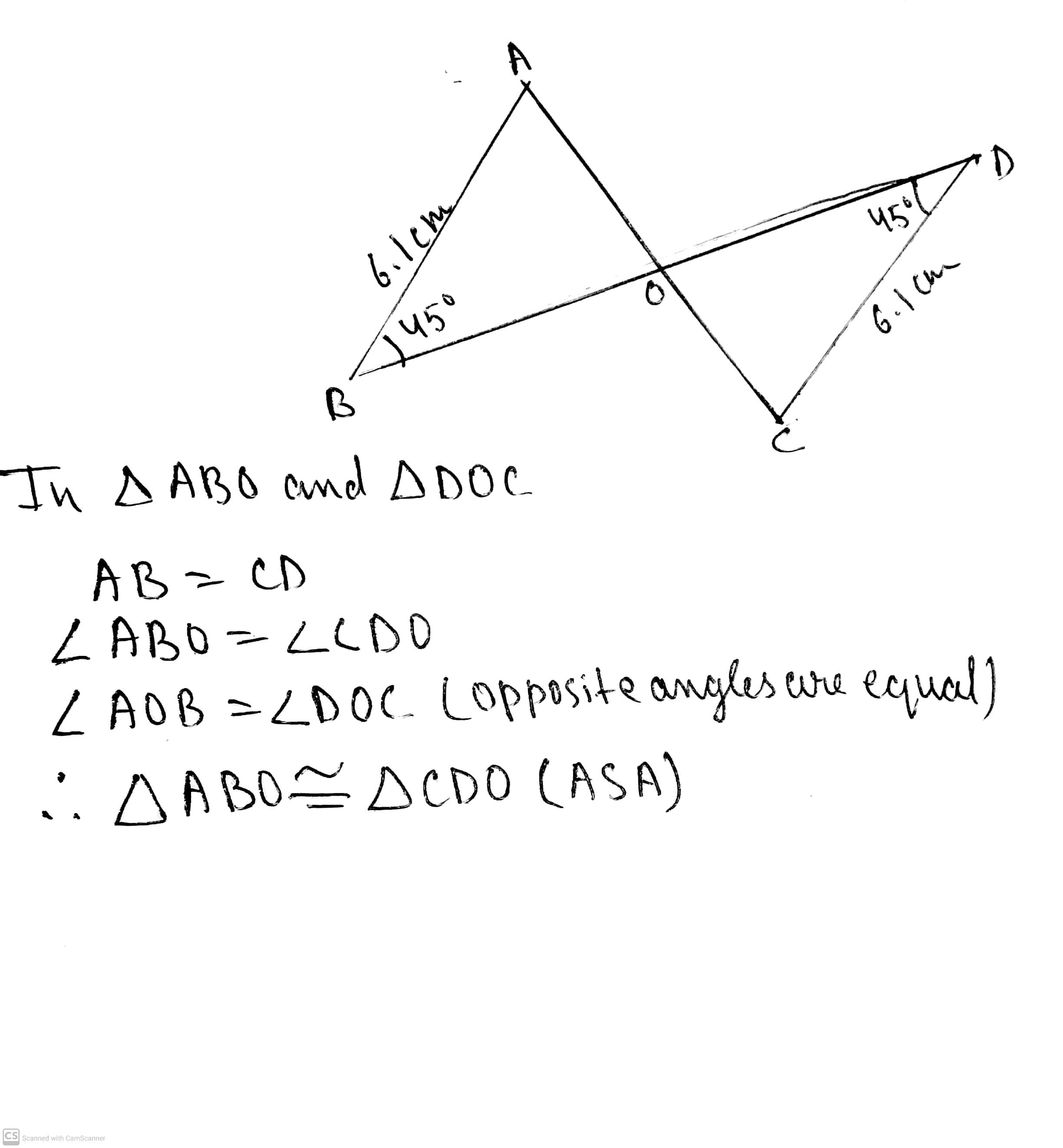
$$ \Delta PQR \,\,\, and \,\,\, \Delta SQR; PQ=SR\,\, and \,\, \angle PQR = \angle SQR$$.
Without drawing exact triangles, state, giving reasons, whether the given pairs of triangle are congruent or not :
In $$\Delta ABC \ and \ \Delta PQR; AB=QR, AC=PR \,\, and \,\, \angle B = \angle R$$.
If the two sides and the included angle of a triangle are respectively equal to two sides and the included angle of the other triangle, the two triangles are congruent. If true enter 1 else 0.
If $$\triangle DEF\cong \triangle RPQ$$, then $$\angle D=\angle Q$$.If true enter $$1$$, else $$0$$.
If $$\triangle PQR\cong \triangle CAB$$, $$PQ = CA$$.If true enter $$1$$, else $$0$$.
If $$\triangle ABC\cong \triangle PRQ$$ then $$AB = PQ$$.If true enter $$1$$, else $$0$$.
State whether the given statement is True(Press 1) or False(Press 0):If the two angles and the included sides of one triangle are respectively equal to the two angles and the included side of the other triangle, then the two triangles are congruent.
Two right triangles are congruent, if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle. If true enter 1 else 0.
State true or false:If the two sides of a triangle are unequal, then the larger side has the smaller angle opposite to it.If true enter 1, else 0.
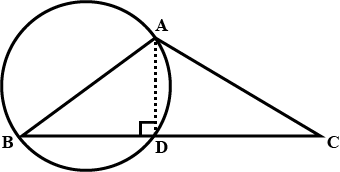
Prove that the circle drawn with any equal side of an isosceles triangle as diameter bisects the base
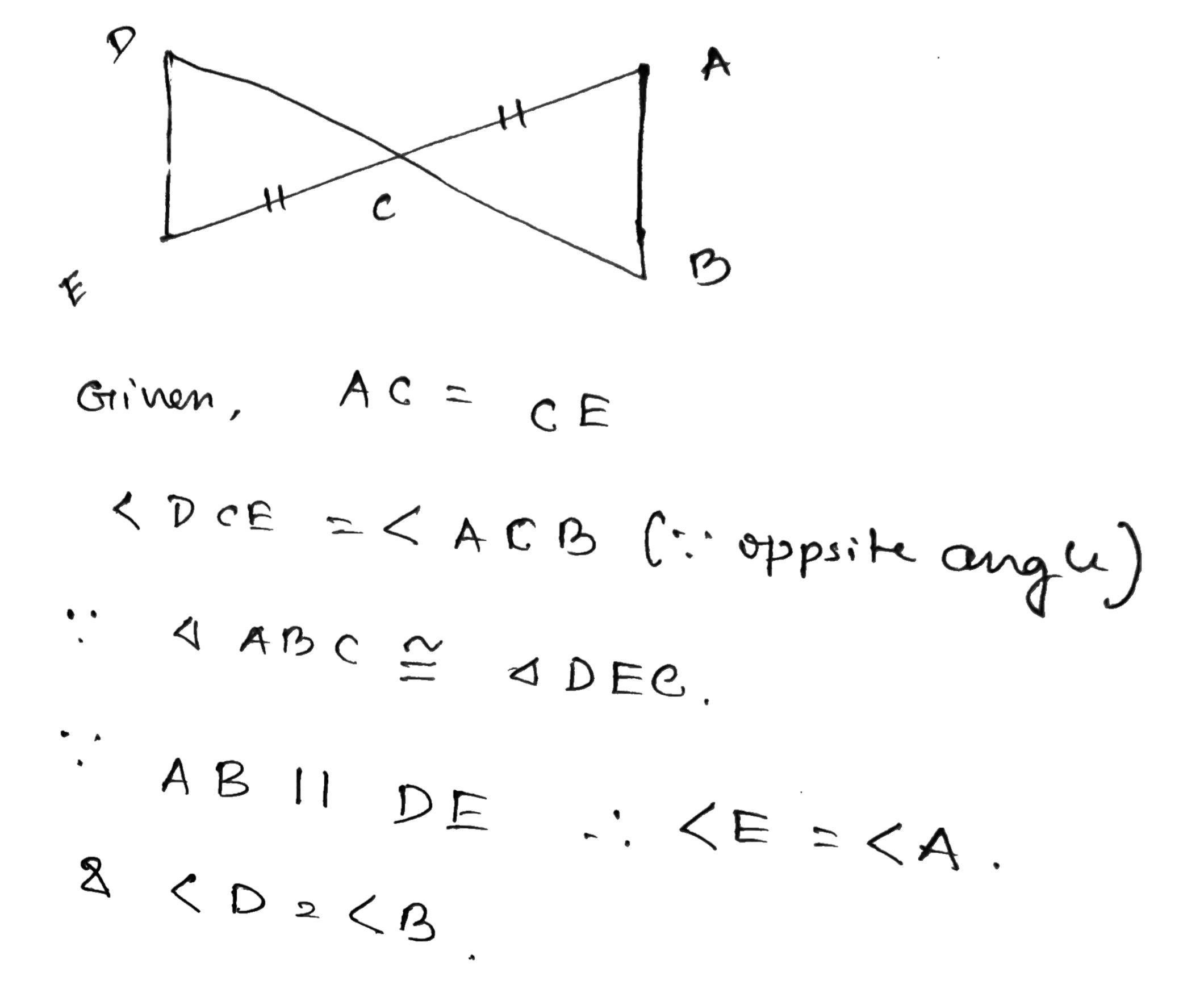
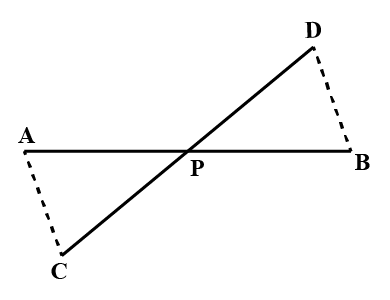
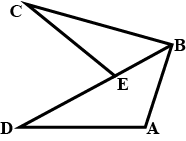
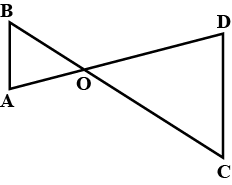
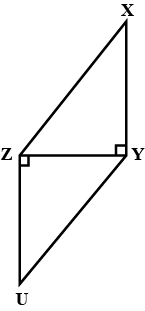
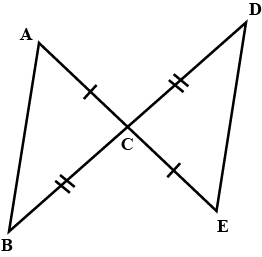
AB is a line segment AX and BY are two equal line segments drawn opposite sides of line AB such that AX ||BY.
If line segments AB and XY intersect each other at point P. Prove that
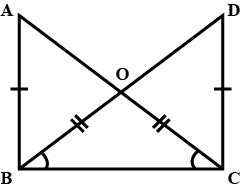
(a) $$\Delta APX \cong \Delta BPY$$ (b) line segments AB and XY bisect each other at P.
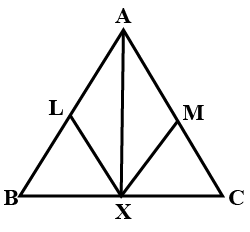
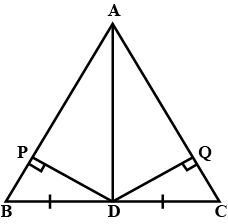
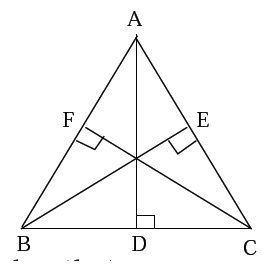
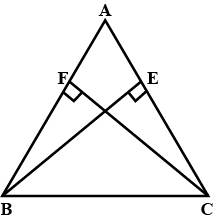
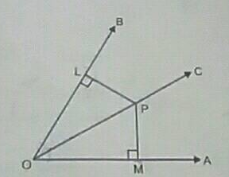
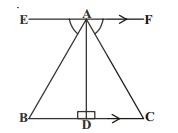
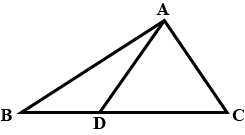
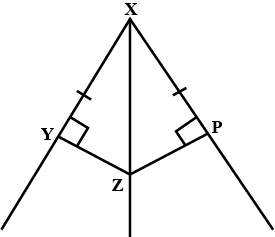
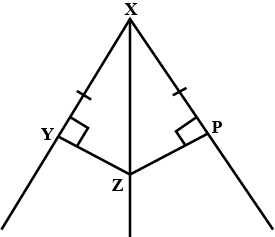
In $$\Delta ABC$$, the bisector AX of $$\angle A$$ intersects BC at X. $$XL\perp AB$$ and $$XM \perp AC$$ are drawn. Is XL = XM?
Why or why not?
Given : $$AX$$ is the bisector of $$\angle A$$ meet $$BC$$ on $$X$$
And $$XL\perp AB$$ and $$XM\perp AC$$
Then, in $$\Delta ALX$$ and $$\Delta AMX$$
$$\angle LAX=\angle XAM$$ ...... ($$AX$$ is the bisector of angle A)
$$\angle ALX=\angle AMX=90^{o}$$ ...... ($$XL\perp AB$$ and $$XM\perp AC$$)
$$AX=AX$$ ....... [Common side]
Then, $$\Delta ALX\simeq\Delta AMX$$ ...... [By ASA rule of congruence]
$$\therefore LX=MX$$
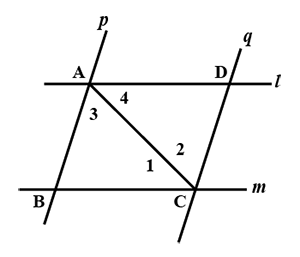
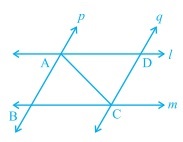
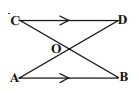
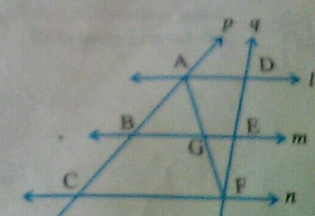
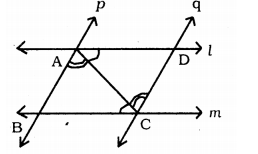
Two parallel lines $$l$$ and $$m$$ are intersected by another pair of parallel lines $$p$$ and $$q$$ as in the figure. Show that triangles $$ABC$$ and $$CDA$$ are congruent.
In the figure AD = BC and BD = CA. Prove that $$\angle ADB = \angle BCA $$ and $$\angle DAB = \angle CBA$$.
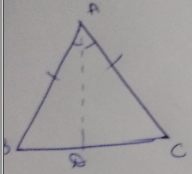
In $$\triangle ABC, AB = BC$$ and $$\angle B = 64^o$$. Find $$\angle C$$.
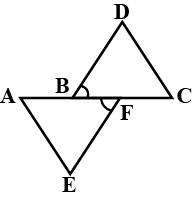
In the figure, C is the mid point of AB, $$\angle BAD = \angle CBE, \angle ECA= \angle DCB$$.
Prove that (a) $$\Delta DAC \cong \Delta EBC$$ (b) DA = EB.
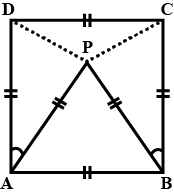
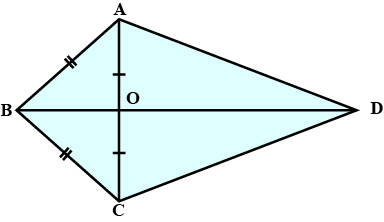
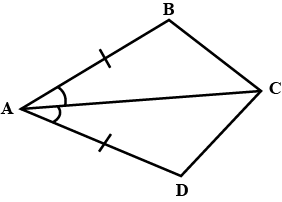
In a quadrilateral ACBC, AC = AD and AB bisect $$\angle A$$. Show that $$\triangle ABC$$ is congruent to $$\triangle ABD$$.
In the figure, it is given that AE = AD and BD = CE. Prove that $$\triangle AEB$$ is congruent $$\triangle ADC$$.
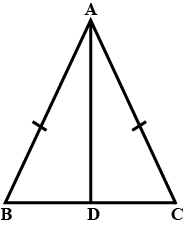
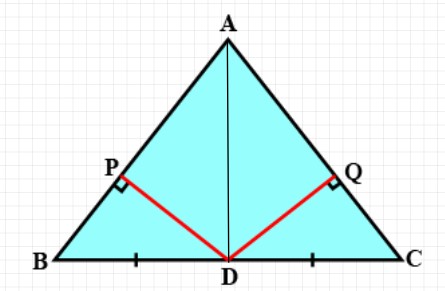
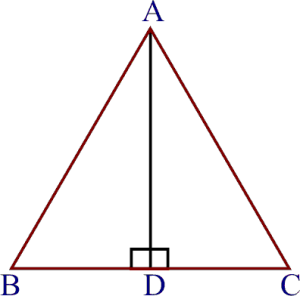
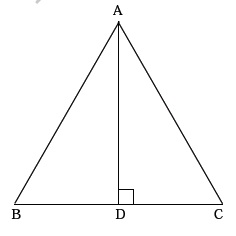
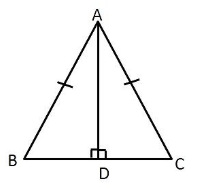
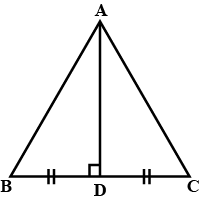
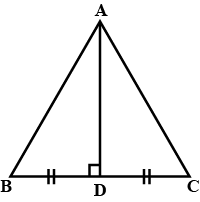
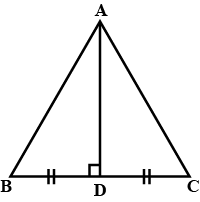
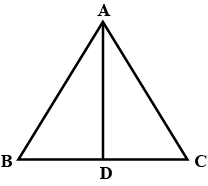
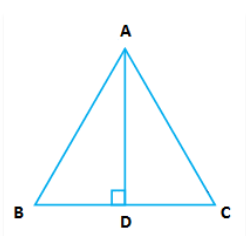
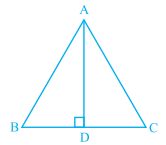
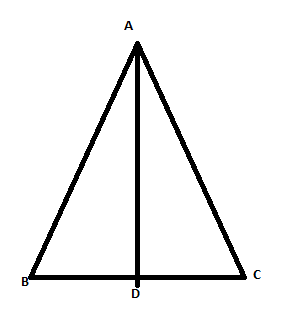
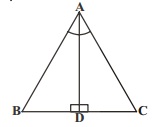
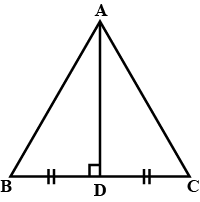
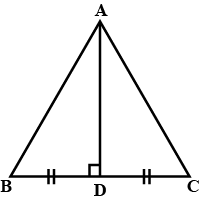
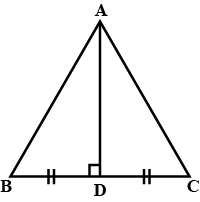
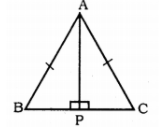
In $$\triangle ABC, AD$$ is the perpendicular bisector of $$BC$$ (see given figure). Show that $$\triangle ABC$$ is an isosceles triangle in which $$AB = AC$$
In the given figure, the point $$P$$ bisects $$AB$$ and $$DC$$. Prove that
$$\triangle APC\cong \triangle BPD$$
In given figure P bisect AB and DC
Then P is the mid point of AB and CD
Then $$AP=PB$$
And $$CP=PD$$
Then in $$\Delta APC$$ and $$\Delta BPD$$
$$AP=PB$$
$$CP=PD$$
$$\angle APC=\angle BPD$$............(vertically opposite angles)
$$\therefore \Delta APC\cong \Delta BPD$$
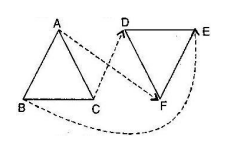
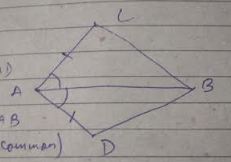
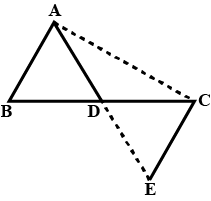
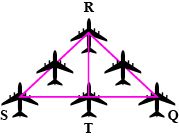
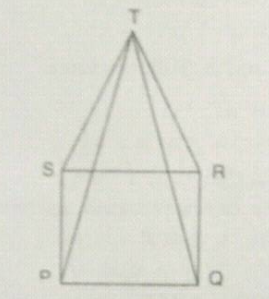
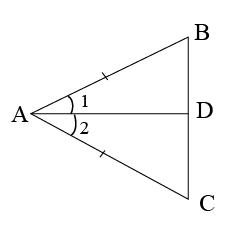
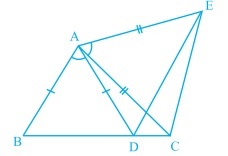
The Indian Navy flight fly in a formation that can be viewed as two triangles with common side. Prove that $$\triangle SRT \cong \triangle QRT$$, if $$T$$ is the midpoint of $$SQ$$ and $$SR = RQ$$.
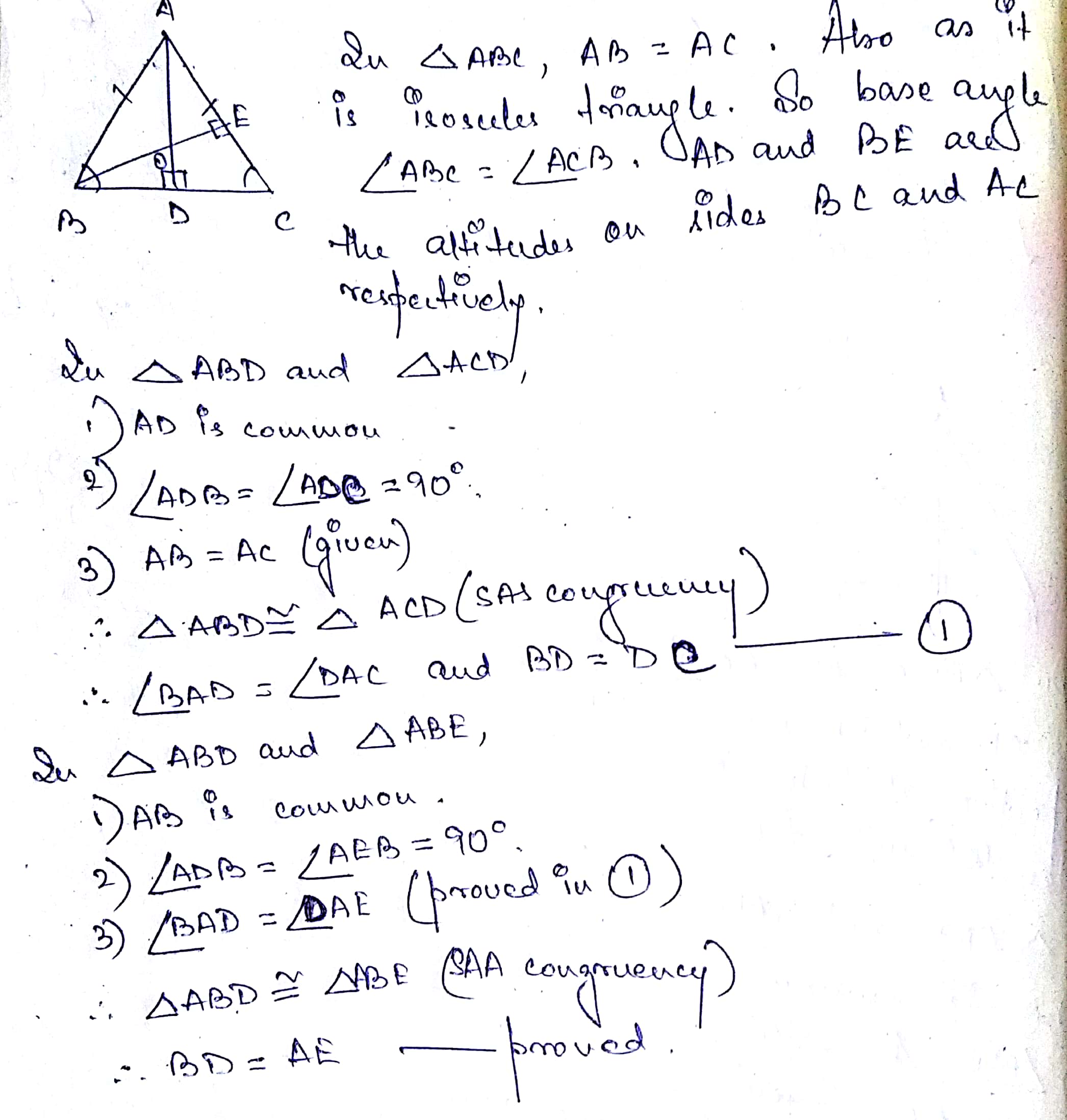
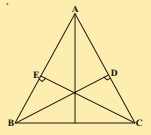
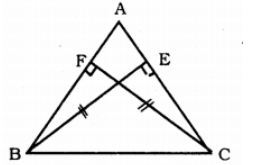
$$ABC$$ is an isosceles triangle in which altitudes $$BD$$ and $$CE$$ are drawn to equal sides $$AC$$ and $$AB$$ respectively (see figure). Show that these altitudes are equal
ABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively .
Given ABC is an isosceles triangle
Then AB=AC
$$\therefore\angle ABC=\angle ACB$$
Or $$\therefore\angle EBC=\angle DCB$$
In $$\Delta EBC,$$ $$\Delta DCB $$.....................(1)
$$\angle BEC=\angle CDB=90^{0}$$
$$BC=CB$$
$$\angle EBC =\angle DCB$$
$$\Delta BEC \cong \Delta CFB $$.......(SAA test)
$$ \therefore BD=EC$$
Then these altitudes are equal.
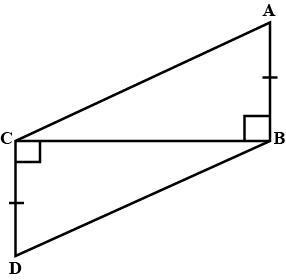
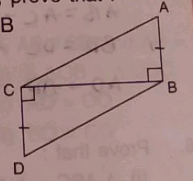
In the figure given below, $$AB = DC$$ and $$AC = DB$$. Is $$\Delta ABC \cong \Delta DCB$$.
Complete the congruence statement.
$$\Delta ABC \equiv $$ ?
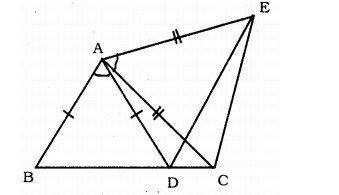
DE = EC show that AB + BC > AD.
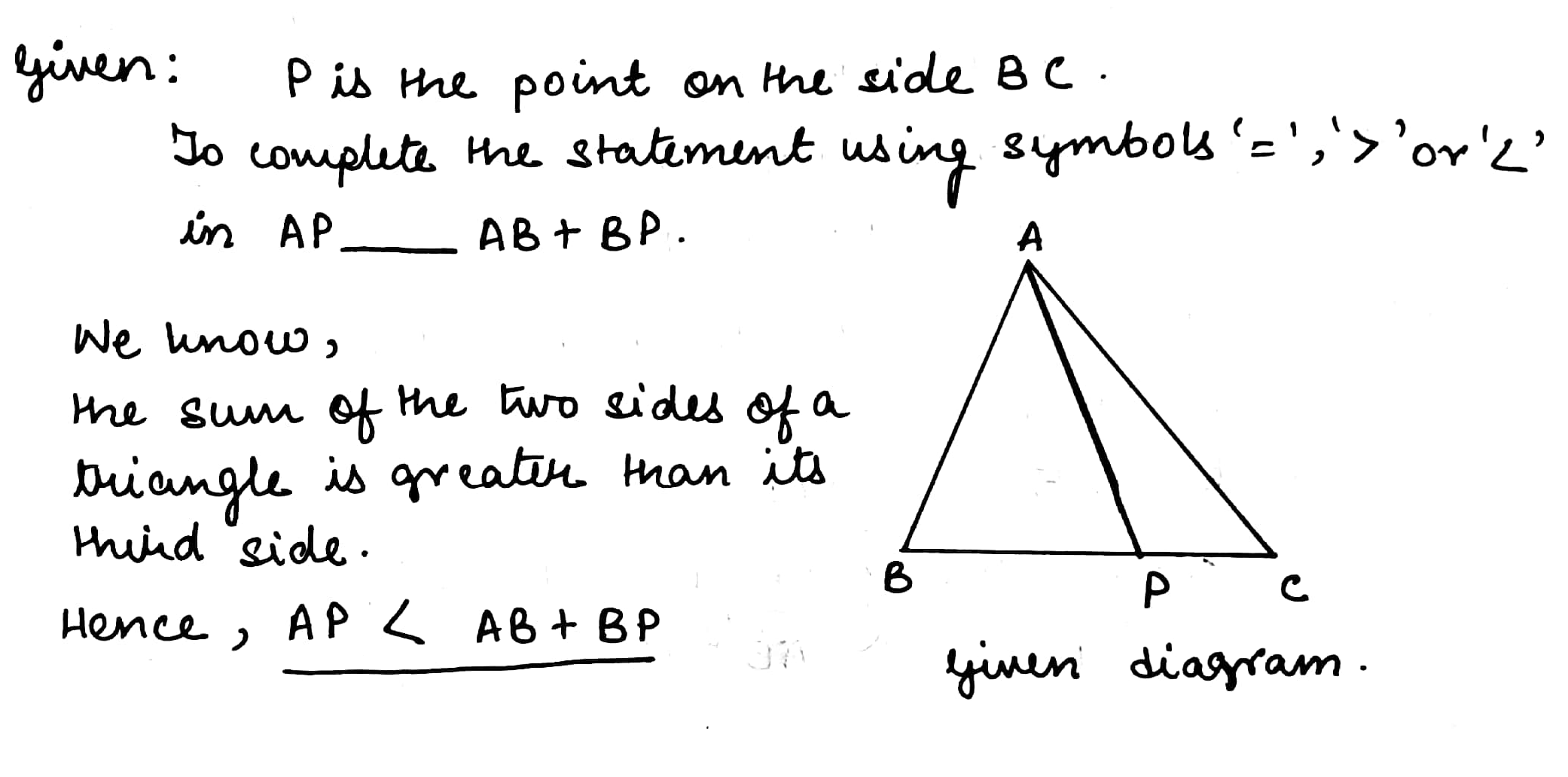
If $$S$$ is any point in the interior of $$\Delta PQR$$, prove that $$(SQ + SR) < (PQ + PR)$$.
From $$\triangle PQT$$, we have
$$PQ+PT>QT$$
$$PQ+PT>SQ+ST$$ ----------(1)
$$ST+TR > SR$$ ----------(2)
Adding equation(1) and (2),
$$PQ+PT+ST+TR>SQ+ST+SR$$
$$PQ+PT+TR>SQ+SR$$
$$PQ+PR>SQ+SR$$
$$\Rightarrow SQ+SR<PQ+PR$$
$$PQ+PT+ST+TR>SQ+ST+SR$$
$$PQ+PT+TR>SQ+SR$$
$$PQ+PR>SQ+SR$$
$$\Rightarrow SQ+SR<PQ+PR$$
Hence proved.
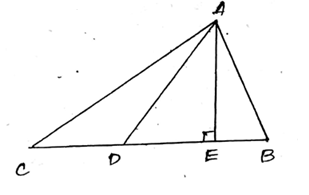
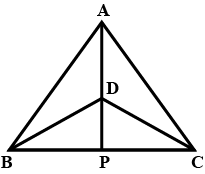
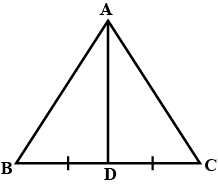
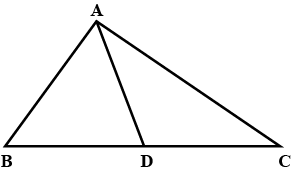
Prove that a median divides a triangle into equal parts
$$In\triangle ABC,AD$$ is median
$$ BD=DC$$
$$ draw\quad AE\bot BC$$
area of$$\triangle ABD=\cfrac { 1 }{ 2 } \times BD\times AE\quad [since\quad BD=DC]$$
=area of$$\triangle ADC$$
$$ \therefore$$ Median of a $$ \triangle gle$$ divides it into two $$\triangle gles$$ of equal area.
In the adjoining figure $$\angle{ABD}={132}^{o}$$ & $$\angle{EAC}={120}^{o}$$. Prove that $$AB>AC$$
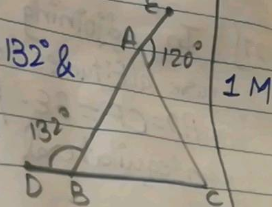
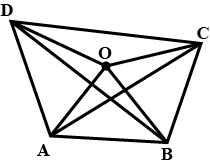
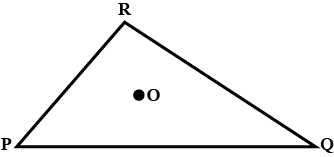
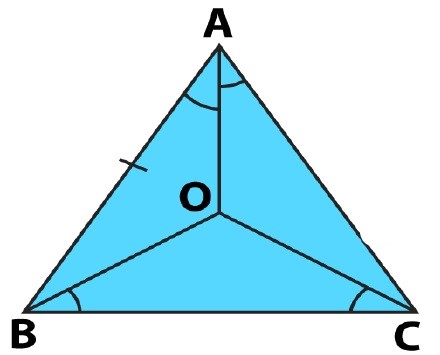
Write down the total number of True statement:Take any point O in the interior of a triangle PQR.Is
(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
"If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent". Is the statement true? Why?
In figure The sides $$BA$$ and $$CA $$ have been produced such that $$BA=AD$$ and $$CA=AE$$ prove that segment $$DE\parallel BC$$
In $$\Delta ABC$$ and $$\Delta ADE$$
$$BA=AD$$
$$CA=AE$$
$$\angle BAC=\angle EAD$$ (vertically opposite angles)
$$\Delta ADA\cong \Delta BAC$$ (SAS)
$$ED||BC$$ (cpct)
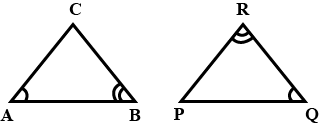
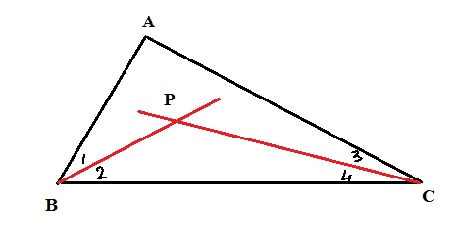
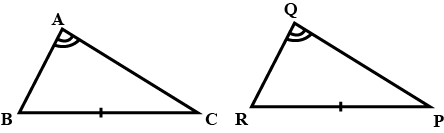
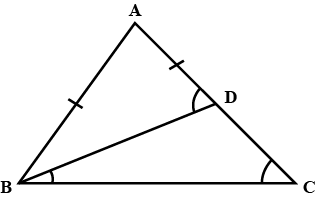
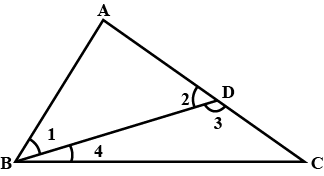
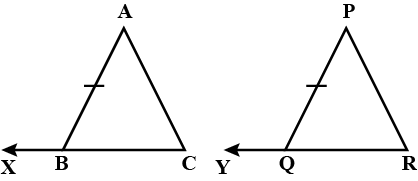
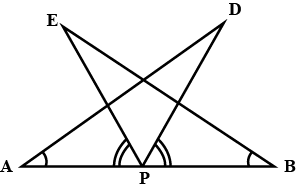
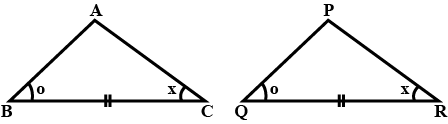
In triangles $$ABC$$ and $$PQR, \angle A = \angle Q$$ and $$\angle B = \angle R$$. Which side of $$\Delta PQR$$ should be equal to side $$AB$$ of $$\Delta ABC$$ so that the two triangle are congruent? Give reason for your answer.
In fig., PQRS is square and SRT is an equilateral triangle. Prove that
(i) $$ PT = QT $$ (ii) $$\angle TQR = {15^ \circ }$$
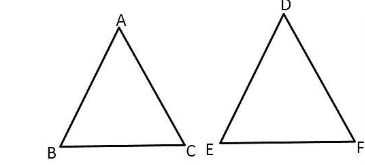
Give any two real-life examples for congruent shapes.
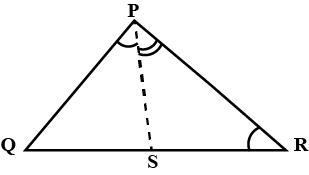
In figure, $$PR>PO$$ and $$PS$$ bisect $$OPR$$. Prove that $$\angle{PSR}>\angle{PSO}$$
If the point $$p\left( {{a^2},\,a} \right)\,$$ lies in the region. Corresponding in the acute angle between the lines $$2y = x\,\,and\,\,4y = x,$$ then find the value of $$a$$ or the range in which $$a$$ lies.
In the given fig $$\triangle PQC$$ & $$PRC$$ such that $$QC=CR$$, $$PQ=PR$$. Prove that $$\triangle PQC\cong\triangle CPR$$
If the area of two similar triangles are equal, prove that they are congruent.
Given that:
$$ar \triangle ABC =ar \triangle DEF$$
Prove that:
$$\triangle ABC\cong \triangle DEF$$
Proof:
Two triangles ABC and DEF are shown in figure.
$$ar \triangle ABC =ar \triangle DEF$$ (given)
$$\dfrac{ar\triangle ABC} {ar \triangle DEF} = 1$$
$$\dfrac{AB^2}{DE^2} = \dfrac{BC^2}{EF^2} = \dfrac{CA^2}{FD^2}= 1$$ [ USING THEOREM OF AREA OF SIMILAR TRIANGLES]
$$AB= DE , BC= EF, CA= FD$$
Thus, $$\triangle ABC\cong \triangle DEF$$ [BY SSS criterion of congruence]
Give any two real-life examples of congruent shapes.
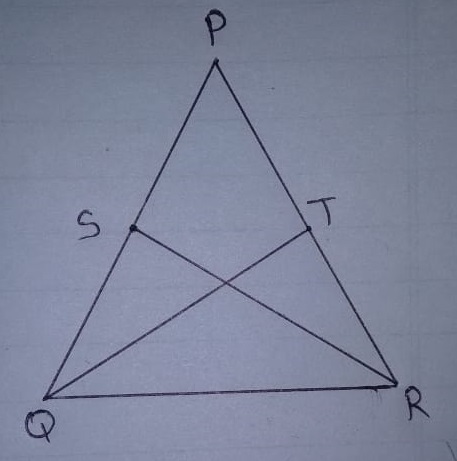
$$S$$ and $$T$$ are respectively the mid points of equal sides $$PQ$$ and $$PR$$ of $$\triangle {PQR}$$. Show that $$Qt=RS$$.
$$PQ=PR$$ ------ [ Given ]
$$\triangle PQR$$ is an isosceles triangle.
$$\therefore$$ $$\angle PQR=\angle PRQ$$ [ Angles of isosceles triangle ]
i.e $$\angle SQR=\angle TRQ$$ ------ ( 1 )
Here, $$S$$ and $$T$$ are mid-point of $$PQ$$ and $$PR$$
$$\therefore$$ $$SQ=TR$$ ----- ( 2 )
Now, in $$\triangle SQR$$ and $$\triangle TRQ$$
$$\Rightarrow$$ $$SQ=TR$$ [ From ( 2 ) ]
$$\Rightarrow$$ $$\angle SQR=\angle TRQ$$ [ From ( 1 ) ]
$$\Rightarrow$$ $$QR=RQ$$ [ Common side ]
$$\therefore$$ $$\triangle SQR\cong\triangle TRQ$$ [ By $$SAS$$ criteria ]
$$\therefore$$ $$RS=QT$$ [ By c.p.c.t ]
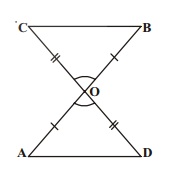
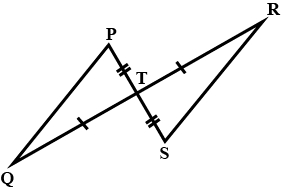
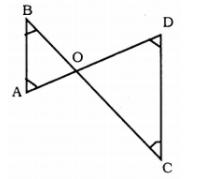
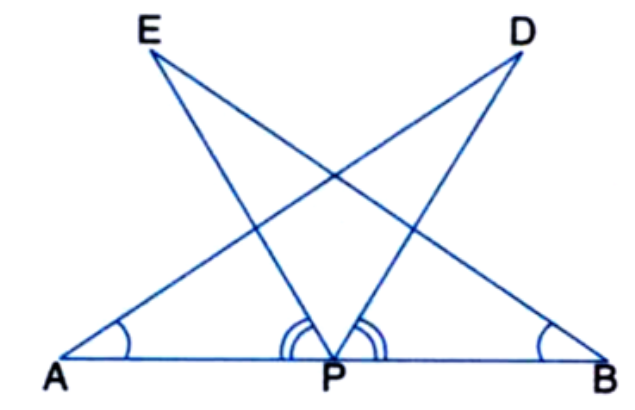
You want to show that $$\Delta ART \cong \Delta PEN$$.
If it is given that $$AT = PN$$ and you are to use ASA criterion, you need to have
i) ?
ii) ?
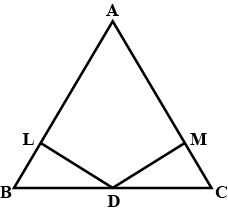
$$\Delta$$ABC and $$\Delta$$DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that $$\Delta$$ ABP$$\cong$$ $$\Delta$$ ACP.
To prove : $$\triangle ABP\cong \triangle ACP$$
Proof: In $$\triangle ABD$$ and $$\triangle ACD$$
$$AB=AC$$ [Given]
$$BD=DC$$ [Given]
$$AD$$ is common
$$\triangle ABD \cong \triangle ACD$$ [SSS postulate]
$$ \hat { BAD }= \hat { CAD }$$ [CPCT]
$$\Rightarrow \hat { BAP } = \hat {CAP } $$
In $$\triangle ABP$$ and $$\triangle ACP,$$
$$AB=AC$$ [Given]
$$AP$$ is common\]
$$ \hat { BAP } = \hat { CAP } $$ [proved]
$$\therefore \triangle BAP\cong \triangle CAP$$ [By SAS postulates]
In $$\triangle PQR, PQ=PR$$ and $$m \angle P=40^{o}$$ then $$m \angle Q=.$$
Given that $$PQ=PR$$ then $$\angle R=\angle Q=x$$
$$\angle P+\angle Q+\angle R=180^\circ$$
$$x+x+40^\circ=180^\circ$$
$$x=70^\circ.$$
$$\angle R=\angle Q=70^\circ.$$
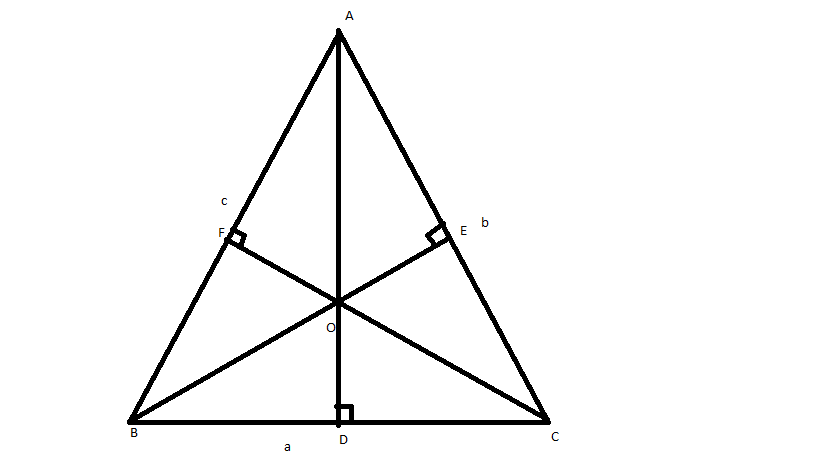
In a $$\triangle ABC,BC=a,CA=b$$ and $$\angle BCA=120^{o},CD$$ is angle bisector of $$\angle BCA$$ which meets $$AB$$ on $$D$$ find the length of $$CD$$
In the given figure $$\Delta ABC \cong \, \Delta ABT$$, write all the corresponding sides.
In the adjoining figure, PQ$$=$$PR and QL$$=$$MR. Prove that PL$$=$$PM.
In $$\triangle PQL$$ and $$\triangle PRM$$
$$PQ=PR$$ [ Given ]
$$\angle PQL=\angle PRM$$ [ angles opposite to equal sides are also equal ]
$$QL=MR$$ [ Given ]
$$\therefore$$ $$\triangle PQL\cong\triangle PRM$$ [ By SAS congruence rule ]
$$\Rightarrow$$ $$PL=PM$$ [ CPCT ]
Explain, why ?
$$\Delta A B C = \Delta F E D$$
In figure $$ABCD$$, $$ABFE$$ and $$CDEF$$ are parallelograms. Prove that $$ar(\triangle {ADE})=ar(\triangle{BCF)}$$
In $$\Delta ADE$$ & $$\Delta BCF \rightarrow $$
$$AD=BC\,(ABCD$$ is a parallelogram) (opp. sides of $$11 gm)$$
$$AE=BE\,(ABFE$$ is a parallelogram) (opp. sides of $$11 gm)$$
$$ED=FC\, (CDEF$$ is a $$11 gm)$$ (opp. sides of $$11 gm)$$
$$\therefore \Delta ADE \cong \Delta BCF$$ (by SSS)
Since $$\Delta ADE$$ & $$\Delta BCF$$ are congruent
$$arc(\Delta ADE)= arc (\Delta BCF)$$
If $$\bigtriangleup ABC\cong\bigtriangleup FED$$ $$ under\ the\ corresponding \ ABC \leftrightarrow FED.$$ Write all the corresponding congruent part of the triangle.
In the following figure, $$\angle A = \angle C$$ and $$AB = BC.$$
Prove that $$\Delta ABD \cong \Delta CBE$$
Prove that in a right angled triangle, hypotenuse is the longest side.
Given: $$\Delta A \bot AB$$, $$CB \bot AB $$ and $$AC = BD$$
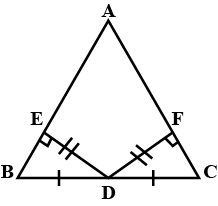
State $$3$$ points of equal pairs in $$\Delta ABC $$ & $$\Delta ABD$$ & Congruence rule.
ABC is a right isosceles triangle right angled at A. Find the value of $$\angle B$$ and $$\angle C$$.
In the given figure, equal sides $$BA$$ and $$CA$$ of $$\Delta ABC$$ are produced to $$Q$$ and $$P$$ respectively such that $$AP = AQ$$. Prove that $$PB = QC$$.
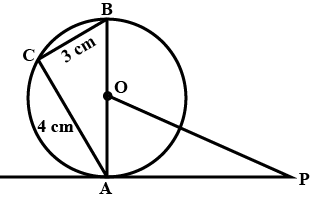
PA is tangent to the circle with centre O. If BC = 3cm, AC = 4 cm and $$\Delta ACB \sim \Delta PAO,$$ then find OA and $$\frac{OP}{AP}$$.
Is it possible to have a triangle with the following sides?2 cm, 3 cm,5 cm
In figure, equal sides have been marked by the same signs.
Can we say $$\Delta ABC\cong \Delta DBC$$?
In $$\triangle ABC$$ and $$\triangle DCB$$
$$BC=BC$$ (common)
$$AB=DC$$ (given)
$$AC=BC$$ (given)
$$\therefore \triangle ABC \cong \triangle DCB$$ [by SSS]
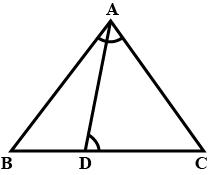
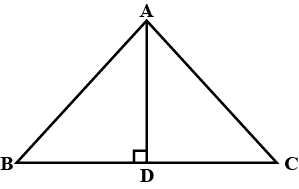
In $$\triangle ABC$$, AD is perpendicular bisector of BC (See adjacent figure). Show that $$\triangle ABC$$ is an isosceles triangle in which $$AB=AC$$
In the figure, $$AP =AQ$$ and $$BP= BQ.$$
Prove that $$AB$$ is the bisector of $$\angle PAQ$$ and $$\angle PBQ.$$
Prove that $$AB$$ is the bisector of $$\angle PAQ$$ and $$\angle PBQ.$$
In figure, $$AB=AC$$ and $$\angle 1=\angle 2$$. Is $$\Delta ABD\cong \Delta ACD$$ ?(Give reason)
If $$\Delta A B C \cong \Delta F E D$$ under the correspondence $$A B C \leftrightarrow F E D$$, write all the corresponding congruent parts of the triangles.
Given that triangle ABC is Congruent to triangle FED. The corresponding congruent parts of the triangle are:
$$\angle A\leftrightarrow \angle F$$
$$\angle B \leftrightarrow \angle E$$
$$ \angle C \leftrightarrow \angle D$$
$$AB \leftrightarrow FE$$
$$BC \leftrightarrow ED$$
$$AC \leftrightarrow FD$$
If $$\Delta A B C \cong \triangle N M O ,$$ name the congruent sides and angles.
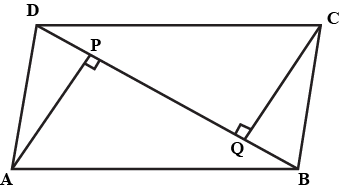
Consider the figure, $$PQRS$$ is a rectangle. $$PT$$ and $$RU$$ are perpendicular from $$P$$ and $$R$$ on $$SQ$$. Prove that $$\Delta PTS\cong \Delta QRU$$
REF.Image.
In $$ \triangle PTS $$ and $$ \triangle QUR $$
$$ \angle PTS = \angle QUR = 90^{\circ}$$ (given)
$$ \angle TSP = \angle UQR $$ [alternate angles ]
$$ \Rightarrow \angle TPS = \angle QRU$$
$$ SP = QR $$ (given)
$$ \therefore $$ By Angle side Angle (A.S.A) axiom of congruence.
$$ \triangle PTS \cong \triangle RUQ $$
In figure, equal sides have been marked by the same signs.
Is $$\Delta ABC\cong \Delta DCB$$?
In $$\triangle ABC$$ and $$\triangle DCB$$
$$BC=BC$$ (common)
$$AB=DC$$ (given)
$$AB=DC$$ (given)
$$\therefore \triangle ABC \cong \triangle DCB$$ [by SAS]
In the figure, $$\Delta CDE$$ is an equilateral triangle formed on a side $$CD$$ of a square $$ABCD$$. Show that $$\Delta ADE \cong \Delta BCE$$.
(Refer to Image)
Given $$ABCD$$ is a square. $$CDE$$ is an equilateral $$\triangle$$ .
To prove that $$\Delta ADE \cong \Delta BCE$$
Proof: $$AD=BC$$ (sides of a square)
$$DE=EC$$ (sides of equilateral $$\triangle$$)
$$\angle ADE=\angle BCE=(90^o+60^o)=150^o$$
Hence, $$\Delta ADE \cong \Delta BCE$$
By $$SAS$$ congruency.
In the given figure, prove that:
$$AC=DB$$
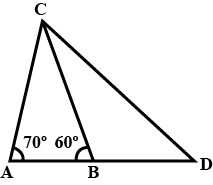
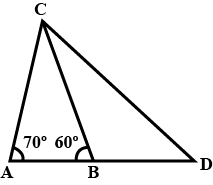
One of the angles of a $$\triangle $$ is $${ 75 }^{ }.$$ If the difference of the other two other is $${ 35 }^{ }.$$
Find the largest angle of the $$\triangle .$$
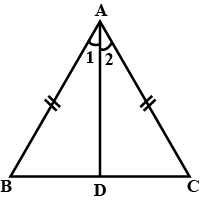
In $$\triangle{ABC}$$,$$AB=AC$$ and $$AD$$ is the perpendicular bisector of $$BC$$. Show that $$\triangle{ADB}\cong\triangle{ADC}$$
In the given figure, prove that:
$$\triangle ABC\cong \triangle DCB$$
If the area of two similar triangles are equal, prove that they are congruent.
Given:-
$$ar{\left( \triangle{ABC} \right)} = ar{\left( \triangle{DEF} \right)} \\ \triangle{ABC} \sim \triangle{DEF}$$
To prove $$\triangle{ABC} \cong \triangle{DEF}$$
Proof:-
$$\because \triangle{ABC} \sim \triangle{PQR} \quad \left( \text{Given} \right)$$
$$\therefore \cfrac{{AB}^{2}}{{DE}^{2}} = \cfrac{{BC}^{2}}{{EF}^{2}} = \cfrac{{CA}^{2}}{{DF}^{2}} = \cfrac{ar{\left( \triangle{ABC} \right)}}{ar{\left( \triangle{DEF} \right)}}$$
$$\because ar{\left( \triangle{ABC} \right)} = ar{\left( \triangle{DEF} \right)}$$
$$\therefore \cfrac{{AB}^{2}}{{DE}^{2}} = 1$$
$$\Rightarrow AB = DE$$
Similarly,
$$BC = EF$$
$$AC = DF$$
Now,
In $$\triangle{ABC}$$ and $$\triangle{DEF}$$,
$$AB = DE$$
$$BC = EF$$
$$AC = DF$$
By SSS congruency,
$$\triangle{ABC} \cong \triangle{DEF}$$
Hence proved.
I the given figure, we have $$PQ=SR$$ and $$PR=SQ$$. Prove that $$\triangle PQR \cong \triangle SRQ$$.
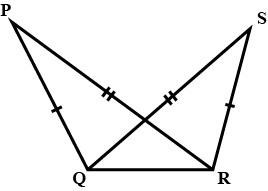
In the given$$AB$$ and $$CD$$ bisect each other at $$O$$.State the three pairs of equal parts in two triangles $$AOC$$ and $$BOD$$
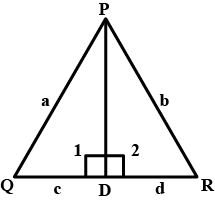
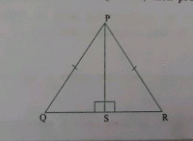
If $$\Delta PQR$$ is an isosceles triangle such that PQ=PR , then prove that the attitude PS from P on QR bisects QR
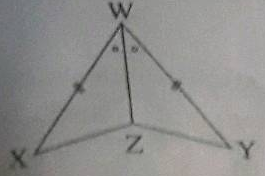
You want to establish $$\triangle DEF\cong \triangle MNP$$, using ASA congruence rule. You are given that $$\angle D=\angle M$$ and $$\angle F=\angle P$$. What information is needed to establish the congruence ?
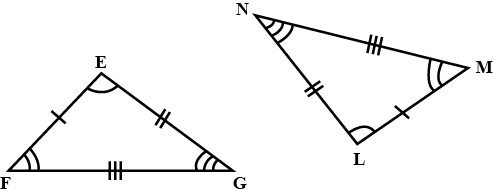
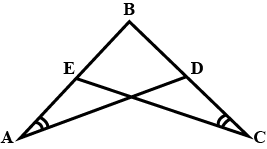
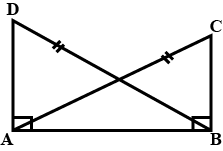
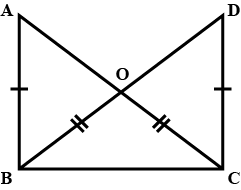
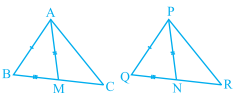
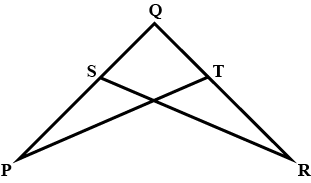
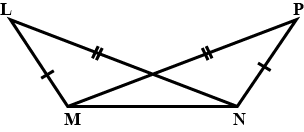
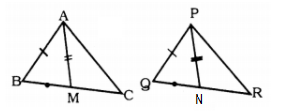
In pair of triangle in the following figure, parts bearing identical marks are congruent. State the test and correspondence if vertices by which triangle in each pair are congurent.
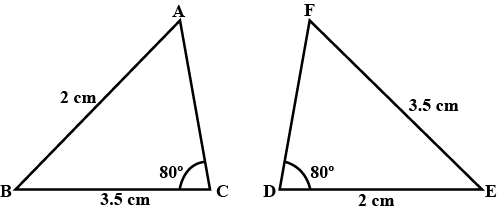
Check whether $$\triangle{ABC}\cong\triangle{DEF}$$.Give Reason
In$$\triangle ABC: AB=6\ cm,\angle B=50^{\circ}$$ and $$\angle C=90^{\circ}$$
In $$\triangle DEF: DE=6\ cm,\angle E=50^{\circ}, \angle F=90^{\circ}$$.
REF.Image
As sum of angles in a triangle is $$180^{\circ}$$
$$\Rightarrow \angle A= 40^{\circ}, \angle D= 40^{\circ}$$
$$\Rightarrow \angle A=\angle D, AB= DE, \angle B=\angle E$$
$$\Rightarrow $$ By ASA congruent, triangles are congruent
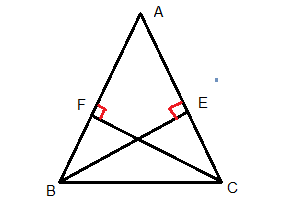
In the given figure, $$\overline{PL}\bot \overline{OB}$$ and $$\overline{PM}\bot \overline{OA}$$ such that $$\overline{PL}=\overline{PM}$$. Is $$\triangle PLO\cong \triangle PMO$$? Give reasons in support of your answer.
Write converse of the theorem "In $$\triangle ABC$$, if $$AB=AC$$ then $$\angle C=\angle B$$"
In the given figure, PS is the bisector of $$\angle QPR$$ of $$\Delta PQR$$ Prove that $$\frac{QS}{SR}=\frac{PQ}{PR}$$
Is it possible to construct a triangle with sides 9 cm, 6 cm and 17 cm ? If not, why ?
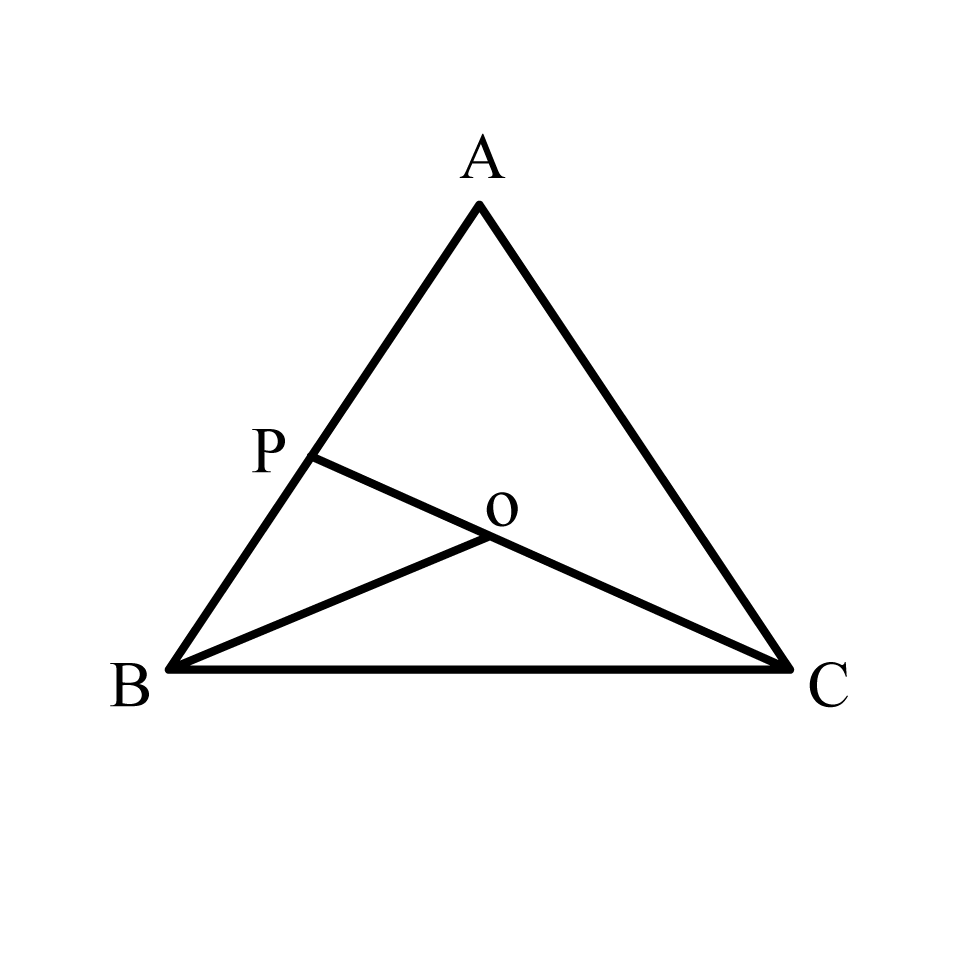
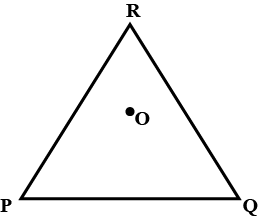
Take any point $$O$$ in the interior of a $$\triangle{PQR}$$.Is $$OR+OP>RP$$?
State SSS congruency Rule of traingles.
SSS Criterion (Side - Side -Side Criterion) :
If all three sides of one triangle are equal to the corresponding sides of another triangle, then the two triangles are said to be congruent by SSS Rule.
In the given figure, $$AB=PQ,QR=BC$$ and $$AC=PR$$
Hence, $$\triangle{ABC}\cong\triangle{PQR}$$
Take any point O in the interior of a triangle PQR. is
$$OQ+OR>QR?$$
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.
Give any two real time examples for congruent shapes.
Is $$\Delta ABC\cong \Delta DEF?$$ Give reasons in support of your answer.
REF.Image
$$\angle B=\angle E$$ ......(given)
$$\angle A=\angle D$$.......(given)
side $$BC=$$ side $$EF$$ ......(given)
$$\therefore $$ By ASA (Angle Side Angle) test of similarity
$$\Delta ABC \cong \Delta DEF$$
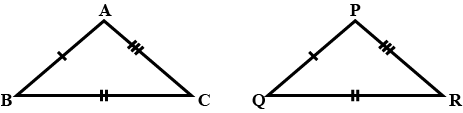
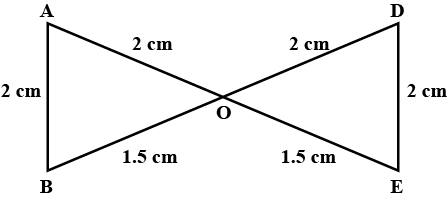
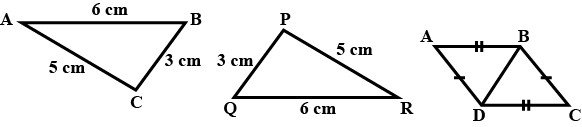
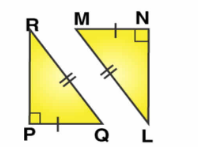
In the following, pairs of triangles of Fig., the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
Without drawing the triangles write all size pairs of equal measures in each of the following pairs of congruent triangles.
$$\triangle ABC \cong \triangle LMN$$
In the following, pairs of triangles of Fig., the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
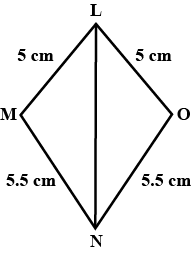
In $$\triangle PQR$$ and $$\triangle SQR$$ are both isosceles triangle on a common base $$QR$$ such that $$P$$ and $$S$$ lie on the same side of $$QR$$. Are triangles $$PSQ$$ and $$PSR$$ congruent ? Which condition do you use ?
In Fig.6.49, it is given that $$LM = ON$$ and $$NL = MO$$
(a) State the three pairs of equal parts in the triangles $$NOM$$ and $$MLN$$.
(b) Is $$\triangle NOM \cong \triangle MLN$$. Give reason ?
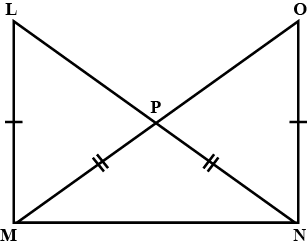
In the following, pairs of triangles of Fig., the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
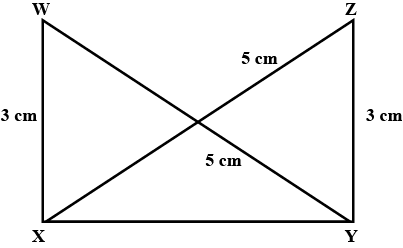
In the following, pairs of triangles of Fig. the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
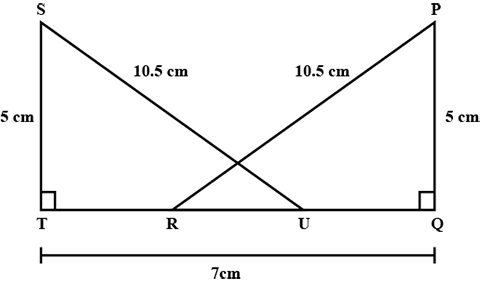
In the following, pairs of triangles of Fig. the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
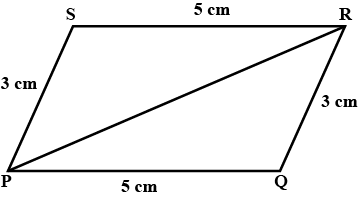
In the following, pairs of triangles of Fig. the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
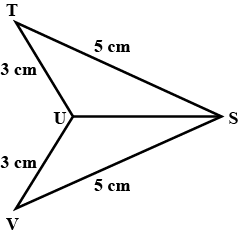
Without drawing the triangles write all size pairs of equal measures in each of the following pairs of congruent triangles.
$$\triangle STU \cong \triangle DEF$$
check if the following pair of triangles is congruent? also, state the condition of congruency :
In$$ \Delta ABC$$ and $$\Delta QRP , AB =QR ,~ \angle B = \angle R$$ and $$\angle C= \angle P .$$
In $$ \Delta ABC$$ and $$\Delta QRP $$
$$ \angle B = \angle R $$ [Given]
$$ \angle C = \angle P $$ [Given]
$$AB = QR$$ [Given]
By Angle - Angle -Side congruency , the triangles
$$ \Delta ABC $$ and $$\Delta QRP $$ are congruent to each other
$$ \Delta ABC \cong \Delta QRP $$
$$ \angle B = \angle R $$ [Given]
$$ \angle C = \angle P $$ [Given]
$$AB = QR$$ [Given]
By Angle - Angle -Side congruency , the triangles
$$ \Delta ABC $$ and $$\Delta QRP $$ are congruent to each other
$$ \Delta ABC \cong \Delta QRP $$
In $$\Delta$$DEF, DM and EN are two medians. Prove that $$3(DF + EF) > 2(DM + EN)$$.
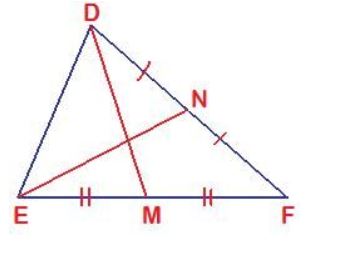
which of the following pairs of triangle are congruent ? In each case , state the condition of congruency :
In$$ \Delta ABC$$ and $$\Delta DEF, AB = DE , BE = EF$$ and $$\angle B = \angle E. $$
In $$ \Delta ABC$$ and $$\Delta DEF $$
$$AB = DE $$ [Given]
$$ \angle B = \angle E $$ [Given]
$$BC = EF $$ [Given]
By side - Angle - side criteion of congruent , the triangles $$\Delta ABC$$ and $$\Delta DEF$$ are congruent to each other ,
$$ \Delta ABC \cong \Delta DEF $$
$$AB = DE $$ [Given]
$$ \angle B = \angle E $$ [Given]
$$BC = EF $$ [Given]
By side - Angle - side criteion of congruent , the triangles $$\Delta ABC$$ and $$\Delta DEF$$ are congruent to each other ,
$$ \Delta ABC \cong \Delta DEF $$
In Fig. which paise of triangles are congruent by SAS congruence criterion (condition)? If congruent, write the congruence of the two triangles in symbolic form.
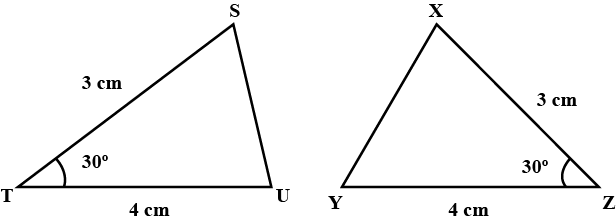
In Fig. which paise of triangles are congruent by SAS congruence criterion (condition)? If congruent, write the congruence of the two triangles in symbolic form.
In Fig. which paise of triangles are congruent by SAS congruence criterion (condition)? If congruent, write the congruence of the two triangles in symbolic form.
In Fig. which paise of triangles are congruent by $$SAS$$ congruence criterion (condition)? If congruent, write the congruence of the two triangles in symbolic form.
In $$ \Delta ABC$$ and $$\Delta DEF \angle B = \angle E= 90^{o}: AC = DF $$ and $$BC = EF $$
In $$ \Delta ABC$$ and $$\Delta DEF $$
$$ \angle B = \angle E =90^{o}$$
Hyp , $$AC =$$ Hyp $$DF$$
$$BC = EF$$
By Right Angle -Hypotenuse - Side congruent the triangle .
$$ \Delta ABC$$ and $$\Delta DEF $$ are congruent to each other .
$$ \Delta ABC \cong \Delta DEF $$
$$ \angle B = \angle E =90^{o}$$
Hyp , $$AC =$$ Hyp $$DF$$
$$BC = EF$$
By Right Angle -Hypotenuse - Side congruent the triangle .
$$ \Delta ABC$$ and $$\Delta DEF $$ are congruent to each other .
$$ \Delta ABC \cong \Delta DEF $$
In Fig. which paise of triangles are congruent by SAS congruence criterion (condition)? If congruent, write the congruence of the two triangles in symbolic form.
In Fig. which paise of triangles are congruent by SAS congruence criterion (condition)? If congruent, write the congruence of the two triangles in symbolic form.
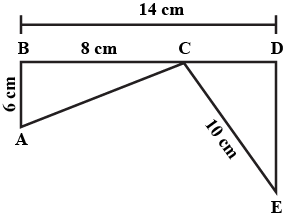
From the following figure: prove that
$$AB + AC > BC$$
$$D$$ is a point in side $$BC$$ of triangle $$ABC$$. If $$AD > AC$$ show that $$AB > AC$$.
$$AD > AC $$ (given)
$$\Rightarrow \angle C > \angle ADC ...(1)$$
Now, $$\angle ADC > \angle B +\angle BAC$$ (Exterior Angle Property)
$$\Rightarrow \angle ADC > \angle B ....(2)$$
From (1) and (2), we have
$$\angle C > \angle ADC > \angle B$$
$$\Rightarrow \angle C > \angle B$$
$$\Rightarrow AB > AC$$
$$\Rightarrow \angle C > \angle ADC ...(1)$$
Now, $$\angle ADC > \angle B +\angle BAC$$ (Exterior Angle Property)
$$\Rightarrow \angle ADC > \angle B ....(2)$$
From (1) and (2), we have
$$\angle C > \angle ADC > \angle B$$
$$\Rightarrow \angle C > \angle B$$
$$\Rightarrow AB > AC$$
From the following figure: prove that
$$AC > CD$$
In the following figure, $$ABC$$ is an equilateral triangle $$P$$ is any point in $$AC$$; prove that:
$$BP > PA$$
From the following figure: prove that
$$AB > BD$$
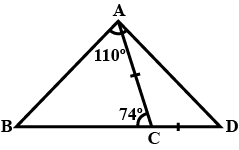
In the following figure:
$$AC=CD; \angle BAD =1100$$ and $$\angle ACB =740$$
Prove that: $$BC > CD$$
Which of the following pairs of triangle are congruent ? In each case , state the condition of congruency :
In$$ \Delta ABC$$ and $$\Delta PQR , AB =PQ ,AC = PR$$ and $$BC = QR .$$
In $$ \Delta ABC$$ and $$\Delta PQR $$
$$AB = PQ $$ [Given]
$$AC = PR $$ [Given]
$$BC = QR $$ [Given]
By Side - Side -Side criterion of congruency to each other
$$ \Delta ABC \cong \Delta PQR $$
$$AB = PQ $$ [Given]
$$AC = PR $$ [Given]
$$BC = QR $$ [Given]
By Side - Side -Side criterion of congruency to each other
$$ \Delta ABC \cong \Delta PQR $$
In the following figure, $$\angle BAC =60^o$$ and $$\angle ABC=65^o$$
Prove that:
$$CF > AF$$
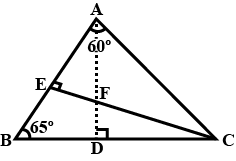
In the following figure, $$\angle BAC =60^o$$ and $$\angle ABC=65^o$$
Prove that:
$$DC > DF$$
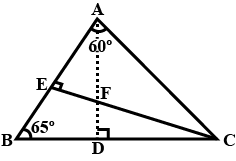
Which of the following pairs of triangle are congruent ? In each case , state the condition of congruency :
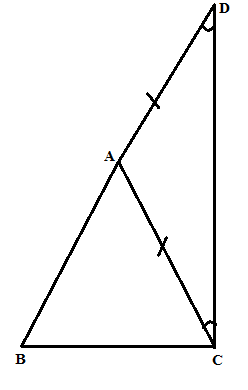
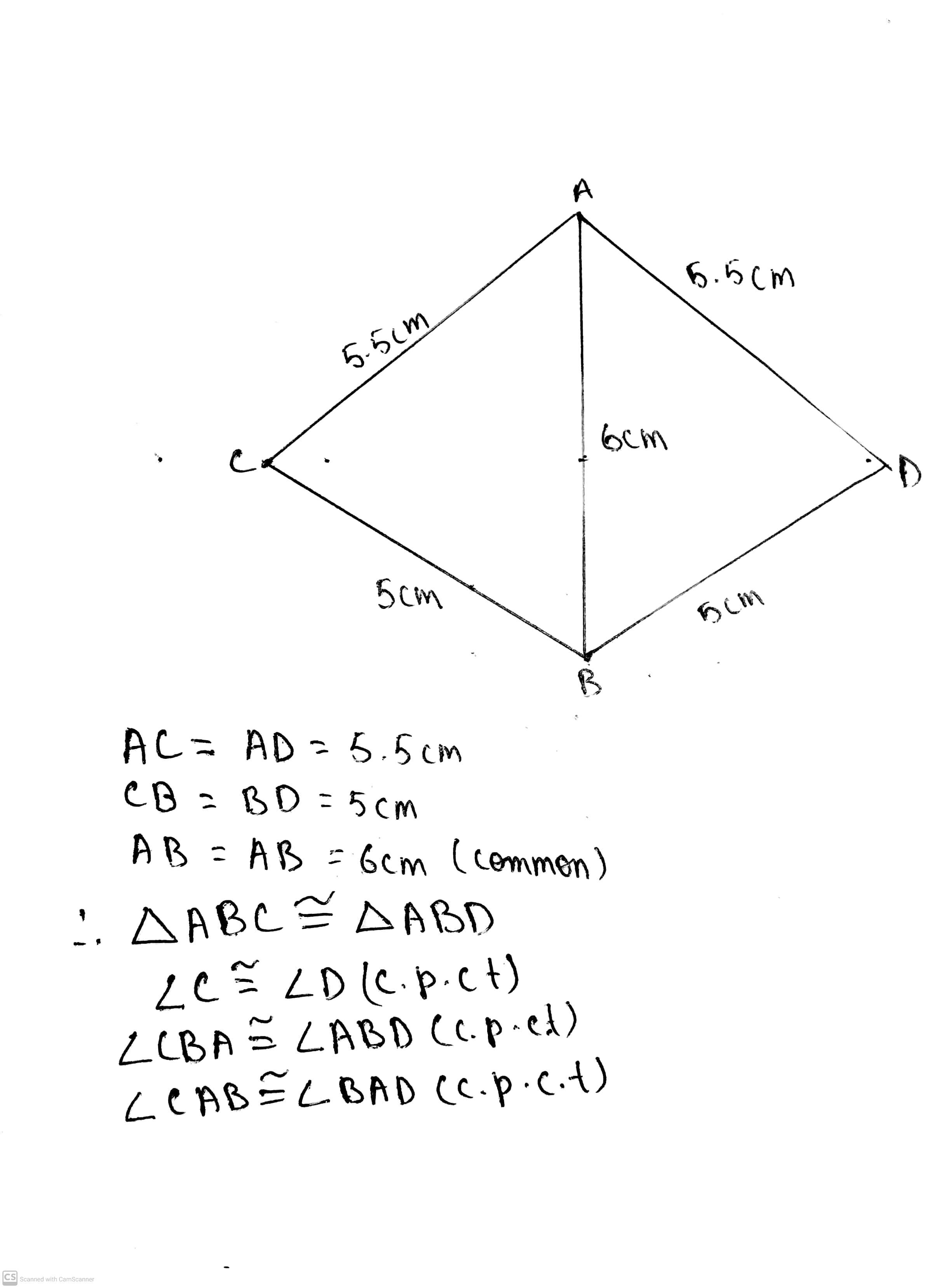
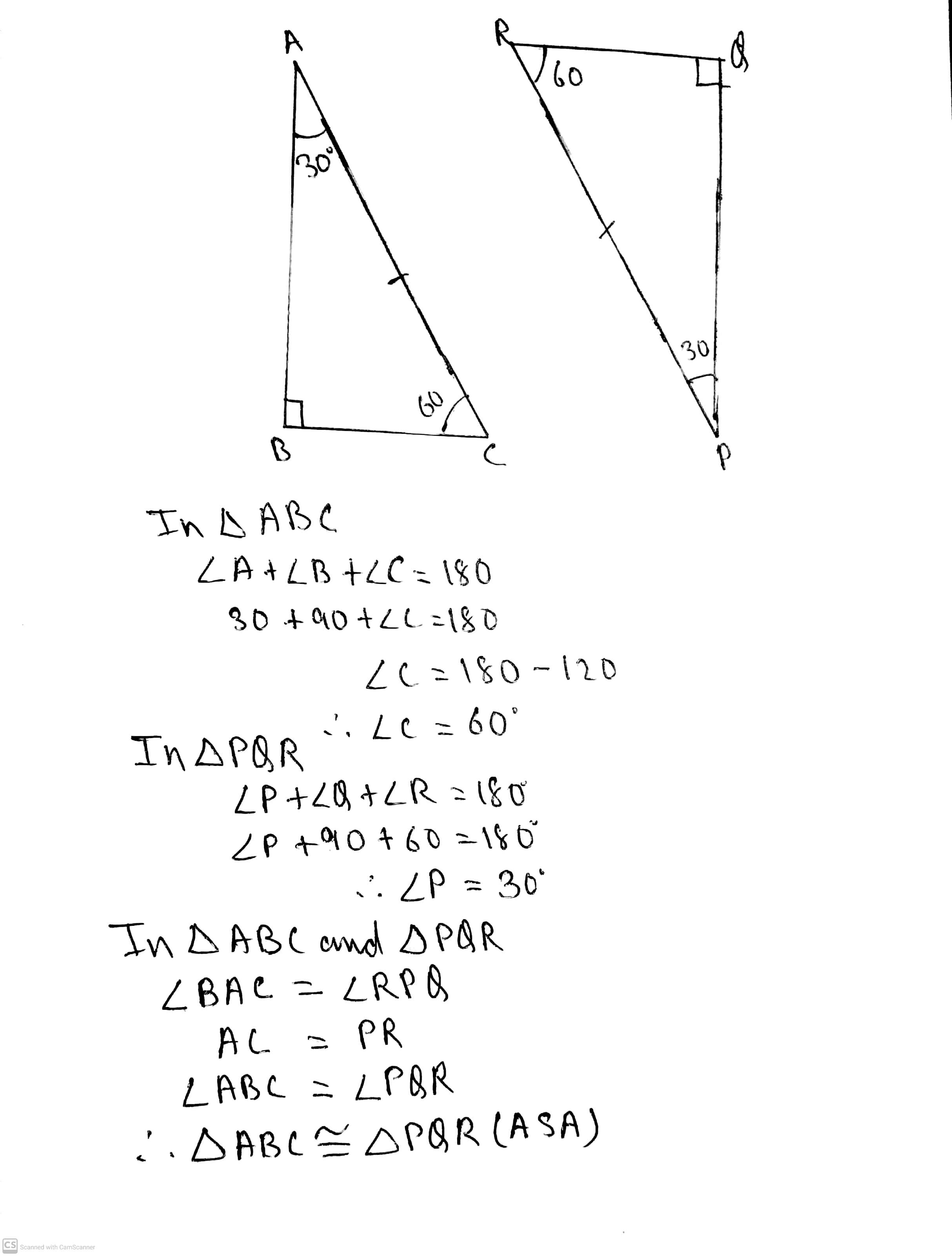
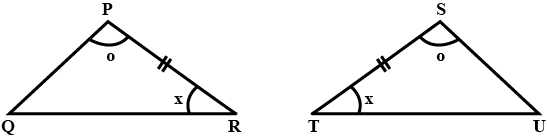
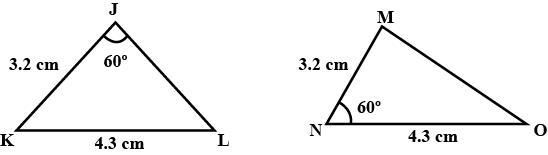
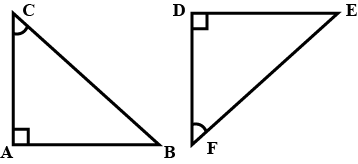
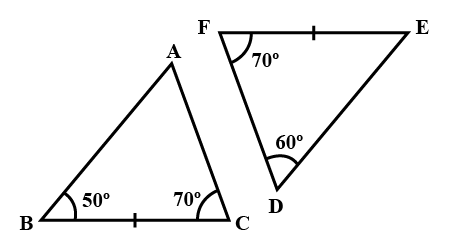
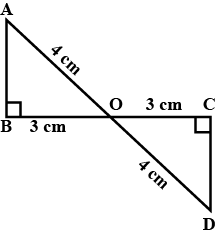
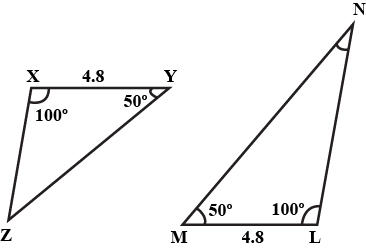
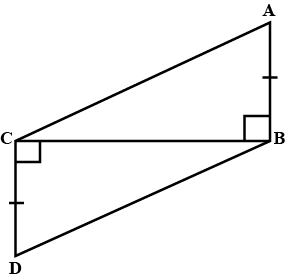
In $$ \Delta ABC$$ and $$\Delta PQR , BC = QR = \angle A = 90^{o} , \angle C= \angle R = 40 ^{o} $$ and $$\angle Q = 50^{o}$$
In $$ \Delta PQR $$
$$ \angle R = 40^{o} , \angle Q = 50^{o} $$ $$\angle \angle P +\angle Q +\angle R = 180^{o} \left [ Sum of all the angles in a triangle = 180^{0} \right ]$$
$$ \Rightarrow \angle P + 50^{o} + 40^{o} = 180^{o} $$
$$\Rightarrow \angle P + 90^{o} = 180^{o} $$
$$ \Rightarrow \angle P = 180^{o} - 90^{o} $$
$$\Rightarrow \angle P = 90^{o}$$
In $$ \Delta ABC$$ and $$\Delta PQR $$
$$ \angle A = \angle P $$
$$ \angle C = \angle R $$
$$ BC = QR $$
By Angle - Angle - Side crition of congruency , the triangle
$$ \Delta ABC$$ and $$\Delta PQR $$ are congruent to each other
$$\therefore \Delta ABC \cong \Delta PQR $$
$$ \angle R = 40^{o} , \angle Q = 50^{o} $$ $$\angle \angle P +\angle Q +\angle R = 180^{o} \left [ Sum of all the angles in a triangle = 180^{0} \right ]$$
$$ \Rightarrow \angle P + 50^{o} + 40^{o} = 180^{o} $$
$$\Rightarrow \angle P + 90^{o} = 180^{o} $$
$$ \Rightarrow \angle P = 180^{o} - 90^{o} $$
$$\Rightarrow \angle P = 90^{o}$$
In $$ \Delta ABC$$ and $$\Delta PQR $$
$$ \angle A = \angle P $$
$$ \angle C = \angle R $$
$$ BC = QR $$
By Angle - Angle - Side crition of congruency , the triangle
$$ \Delta ABC$$ and $$\Delta PQR $$ are congruent to each other
$$\therefore \Delta ABC \cong \Delta PQR $$
In the following figure, $$ABC$$ is an equilateral triangle $$P$$ is any point in $$AC$$; prove that:
$$BP > PC$$
$$P$$ is any point inside the triangle $$ABC$$. Prove that $$\angle BPC > \angle BAC$$.
Let $$\angle PBC =x$$ and $$\angle PCB=y$$
then,
$$\angle BPC =180^o - (x+y)....(i)$$
Let $$\angle ABP =a$$ and $$\angle ACP =b$$
then,
$$\angle BAC =180^o -(x+a)-(y+b)$$
$$\Rightarrow \angle BAC =180^o -(x+y)-(a+b)$$
$$\Rightarrow \angle BAC =\angle BPC -(a+b)$$
$$\Rightarrow \angle BPC =\angle BAC + (a+b)$$
$$\Rightarrow \angle BPC > \angle BAC$$
then,
$$\angle BPC =180^o - (x+y)....(i)$$
Let $$\angle ABP =a$$ and $$\angle ACP =b$$
then,
$$\angle BAC =180^o -(x+a)-(y+b)$$
$$\Rightarrow \angle BAC =180^o -(x+y)-(a+b)$$
$$\Rightarrow \angle BAC =\angle BPC -(a+b)$$
$$\Rightarrow \angle BPC =\angle BAC + (a+b)$$
$$\Rightarrow \angle BPC > \angle BAC$$
The sides $$AB$$ and $$AC$$ of a triangle $$ABC$$ are produced; and the bisects of the external angles at $$B$$ and $$C$$ meet at $$P$$. Prove that if $$AB > AC$$, then $$PC > PB$$.
In $$\triangle ABC$$,
$$AB > AC$$
$$\Rightarrow \angle ABC < \angle ACB$$
$$\therefore 180^o - \angle ABC > 180^o -\angle ACB$$
$$\Rightarrow \angle CBP > \angle BOP$$ [$$BP$$ is bisector of $$\angle CBD$$ and $$CP$$ is bisector to $$\angle BCE$$]
$$\Rightarrow PC > PB$$ [side opposite to greater angle is greater]
$$AB > AC$$
$$\Rightarrow \angle ABC < \angle ACB$$
$$\therefore 180^o - \angle ABC > 180^o -\angle ACB$$
$$\Rightarrow \dfrac {180^o -\angle ABC}{2} > \dfrac {80^o -\angle ACB}{2}$$
$$\Rightarrow 90^o -\dfrac 12 \angle ABC > 90^o -\dfrac 12 \angle ACB$$
$$\Rightarrow PC > PB$$ [side opposite to greater angle is greater]
In quadrilateral $$ABCD$$, side $$AB$$ is the longest and side $$DC$$ is the shortest. Prove that:
$$\angle C > \angle A$$
In the quad $$ABCD$$
Since $$AB$$ is the longest side and $$DC$$ is the shortest side:
(i) $$\angle 1 > \angle 2 [AB > BC]$$
$$\angle 7> \angle 4 [AD > DC]$$
$$\therefore \angle 1+\angle 7 > \angle 2+\angle 4$$
$$\Rightarrow \angle C > \angle A$$
Since $$AB$$ is the longest side and $$DC$$ is the shortest side:
(i) $$\angle 1 > \angle 2 [AB > BC]$$
$$\angle 7> \angle 4 [AD > DC]$$
$$\therefore \angle 1+\angle 7 > \angle 2+\angle 4$$
$$\Rightarrow \angle C > \angle A$$
In a triangle ABC, D is the midpoint of BC; AD is produced up to E so that DE = AD prove that:
$$ \angle DAB = \angle DEC $$
Given: $$ \Delta ABC $$ in which D is the midpoint of BC
AD is produced to E so that DE = AD
We need to prove that
Also, $$ \angle DAB = \angle DEC $$ [The corresponding parts of congruent triangles are equal]
AD is produced to E so that DE = AD
We need to prove that
(1) $$\Delta ABD \cong \Delta ECD $$
(2) AB = EC
In $$ \Delta ABD$$ and $$\Delta ECD $$,
BD = DC [D is the midpoint of BC]
$$ \angle ADB = \angle CDE $$ [Vertically opposite angles]
AD = DE [Given]
By Side - Angle - Side criterion of congruence we have
$$ \Delta ABD \cong \Delta ECD $$
BD = DC [D is the midpoint of BC]
$$ \angle ADB = \angle CDE $$ [Vertically opposite angles]
AD = DE [Given]
By Side - Angle - Side criterion of congruence we have
$$ \Delta ABD \cong \Delta ECD $$
Also, $$ \angle DAB = \angle DEC $$ [The corresponding parts of congruent triangles are equal]
In the given figure, $$AB=AC.$$ Prove that:
$$DP=DQ$$
Construction :
join $$AD.$$
In $$\triangle ABC,$$
$$AB=AC$$ [Given]
$$\therefore \angle C=\angle B$$....(i) [angles opp.to equal sides are equal]
In $$\triangle BPD$$ and $$\triangle CQD,$$
$$\angle BPD=\angle CQD$$ [Each $$=90^{o}$$]
$$\angle B=\angle C$$ [Proved]
$$BD=DC$$ [Given]
$$\therefore \triangle BPD\cong \triangle CQD$$ [$$AAS$$ criterian]
$$\therefore DP=DQ$$ [$$cp ct$$]
join $$AD.$$
In $$\triangle ABC,$$
$$AB=AC$$ [Given]
$$\therefore \angle C=\angle B$$....(i) [angles opp.to equal sides are equal]
In $$\triangle BPD$$ and $$\triangle CQD,$$
$$\angle BPD=\angle CQD$$ [Each $$=90^{o}$$]
$$\angle B=\angle C$$ [Proved]
$$BD=DC$$ [Given]
$$\therefore \triangle BPD\cong \triangle CQD$$ [$$AAS$$ criterian]
$$\therefore DP=DQ$$ [$$cp ct$$]
In isosceles triangle $$ABC$$ sides, $$AB$$ and $$AC$$ are equal. If point $$D$$ lies in base $$BC$$ and point $$E$$ lies on $$BC$$ produced ($$BC$$ being produced to vertex $$C$$). prove that:
$$AC > AD$$
We know that the bisector of the angle at the vertex of an triangle bisects the base at right angle.
Using Pythagoras theorem i $$\triangle AFB$$
$$AB^2 =AF^2+BF^2 ....(i)$$
In $$\triangle AFD$$,
$$AD^2 =AF^2 +DF^2 .....(ii)$$
We know $$ABC$$ is isosceles triangle and $$AB=AC$$
$$AC^2 =AF^2 +BF^2 .....(iii)$$
Subtracting (ii) from (iii)
$$AC^2 -AD^2 =AF^2+BF^2-AF^2-DF^2$$
$$AC^2-AD^2 =BF^2-DF^2$$
Let $$2DF =BF$$
$$AC^2 -AD^2=(2DF)^2 - DF^2$$
$$AC^2-AD^2=4DF^2-DF^2$$
$$AC^2=AD^2+3DF^2$$
$$\Rightarrow AC^2 > AD^2$$
$$\Rightarrow AC > AD$$
Similarly $$AE > AC$$ and $$AE > AD$$.
Using Pythagoras theorem i $$\triangle AFB$$
$$AB^2 =AF^2+BF^2 ....(i)$$
In $$\triangle AFD$$,
$$AD^2 =AF^2 +DF^2 .....(ii)$$
We know $$ABC$$ is isosceles triangle and $$AB=AC$$
$$AC^2 =AF^2 +BF^2 .....(iii)$$
Subtracting (ii) from (iii)
$$AC^2 -AD^2 =AF^2+BF^2-AF^2-DF^2$$
$$AC^2-AD^2 =BF^2-DF^2$$
Let $$2DF =BF$$
$$AC^2 -AD^2=(2DF)^2 - DF^2$$
$$AC^2-AD^2=4DF^2-DF^2$$
$$AC^2=AD^2+3DF^2$$
$$\Rightarrow AC^2 > AD^2$$
$$\Rightarrow AC > AD$$
Similarly $$AE > AC$$ and $$AE > AD$$.
Prove that the straight line joining the vertex of an isosceles triangle to any point in the base is smaller than either of the equal sides of the triangle.
We know that exterior angle of a triangle is always greater than each of the interior opposite angles.
$$\therefore $$ In $$\triangle ABD$$
$$\angle ADC > \angle B ....(i)$$
In $$\triangle ABC$$,
$$AB =AC$$
$$\therefore \angle B =\angle C....(ii)$$
From (i) and (ii)
$$\angle ADC > \angle C$$
(i) In $$\triangle ADC$$
$$\angle ADC > \angle C$$
$$\therefore AC > AD .....(iii)$$ [side opposite to greater angle is greater]
(ii) In $$\triangle ABC$$,
$$AB =AC$$
$$\Rightarrow AB > AD$$
$$\therefore $$ In $$\triangle ABD$$
$$\angle ADC > \angle B ....(i)$$
In $$\triangle ABC$$,
$$AB =AC$$
$$\therefore \angle B =\angle C....(ii)$$
From (i) and (ii)
$$\angle ADC > \angle C$$
(i) In $$\triangle ADC$$
$$\angle ADC > \angle C$$
$$\therefore AC > AD .....(iii)$$ [side opposite to greater angle is greater]
(ii) In $$\triangle ABC$$,
$$AB =AC$$
$$\Rightarrow AB > AD$$
In a triangle ABC , D is mid - point of BC ; AD is produced upto E so that DE = AD prove that :
$$ \Delta ABD$$ and $$\Delta ECD$$ are congruent
Given ; A $$ \Delta ABC $$ in which D is the mid - point of BC
AD is produce to E so that DE = AD
We need to prove that
$$\Delta ABD \cong \Delta ECD $$
AB = EC
AB \\ EC
In $$ \Delta ABD$$ and $$\Delta ECD $$
BD = DE [D is the midpoint of BC]
$$ \angle ADB = \angle CDE $$ [Vertically opposite angles]
AD = DE [Given]
By Side - Angle - Side criterion of congruence we have
$$ \Delta ABD \cong \Delta ECD $$
AD is produce to E so that DE = AD
We need to prove that
$$\Delta ABD \cong \Delta ECD $$
AB = EC
AB \\ EC
In $$ \Delta ABD$$ and $$\Delta ECD $$
BD = DE [D is the midpoint of BC]
$$ \angle ADB = \angle CDE $$ [Vertically opposite angles]
AD = DE [Given]
By Side - Angle - Side criterion of congruence we have
$$ \Delta ABD \cong \Delta ECD $$
In a triangle ABC , D is mid - point of BC ; AD is produced upto E so that DE = AD prove that :
AB = EC
Given ; A $$ \Delta ABC $$ in which D is the mid - point of BC
AD is produced to E so that DE = AD
We need to prove that
AD is produced to E so that DE = AD
We need to prove that
$$\Delta ABD \cong \Delta ECD $$
AB = EC
AB \\ EC
In $$ \Delta ABD$$ and $$\Delta ECD $$
BD = DE [D is the midpoint of BC]
$$ \angle ADB = \angle CDE $$ [Vertically opposite angles]
AD = DE [Given]
By Side - Angle - Side criterion of congruence we have
$$ \Delta ABD \cong \Delta ECD $$
AB = EC [The corresponding parts of congruent triangles are equal]AB \\ EC
In $$ \Delta ABD$$ and $$\Delta ECD $$
BD = DE [D is the midpoint of BC]
$$ \angle ADB = \angle CDE $$ [Vertically opposite angles]
AD = DE [Given]
By Side - Angle - Side criterion of congruence we have
$$ \Delta ABD \cong \Delta ECD $$
In isosceles triangle $$ABC$$ sides, $$AB$$ and $$AC$$ are equal. If point $$D$$ lies in base $$BC$$ and point $$E$$ lies on $$BC$$ produced ($$BC$$ being produced vertex $$C$$). prove that:
$$AE > AC$$
We know that the bisector of the angle at the vertex of an triangle bisects the base at right angle.
Using Pythagoras theorem i $$\triangle AFB$$
$$AB^2 =AF^2+BF^2 ....(i)$$
In $$\triangle AFD$$,
$$AD^2 =AF^2 +DF^2 .....(ii)$$
We know $$ABC$$ is isosceles triangle and $$AB=AC$$
$$AC^2 =AF^2 +BF^2 .....(iii)$$
Subtracting (ii) from (iii)
$$AC^2 -AD^2 =AF^2+BF^2-AF^2-DF^2$$
$$AC^2-AD^2 =BF^2-DF^2$$
Let $$2DF =BF$$
$$AC^2 -AD^2=(2DF)^2 - DF^2$$
$$AC^2-AD^2=4DF^2-DF^2$$
$$AC^2=AD^2+3DF^2$$
$$\Rightarrow AC^2 > AD^2$$
$$\Rightarrow AC > AD$$
Similarly $$AE > AC$$ and $$AE > AD$$.
Using Pythagoras theorem i $$\triangle AFB$$
$$AB^2 =AF^2+BF^2 ....(i)$$
In $$\triangle AFD$$,
$$AD^2 =AF^2 +DF^2 .....(ii)$$
We know $$ABC$$ is isosceles triangle and $$AB=AC$$
$$AC^2 =AF^2 +BF^2 .....(iii)$$
Subtracting (ii) from (iii)
$$AC^2 -AD^2 =AF^2+BF^2-AF^2-DF^2$$
$$AC^2-AD^2 =BF^2-DF^2$$
Let $$2DF =BF$$
$$AC^2 -AD^2=(2DF)^2 - DF^2$$
$$AC^2-AD^2=4DF^2-DF^2$$
$$AC^2=AD^2+3DF^2$$
$$\Rightarrow AC^2 > AD^2$$
$$\Rightarrow AC > AD$$
Similarly $$AE > AC$$ and $$AE > AD$$.
In the given figure $$AB / FD , AC/GE$$ and $$BD = CE$$ : prove that :
$$CF = EG$$
In isosceles triangle $$ABC$$ sides, $$AB$$ and $$AC$$ are equal. If point $$D$$ lies in base $$BC$$ and point $$E$$ lies on $$BC$$ produced ($$BC$$ being produced vertex $$C$$). prove that:
$$AE > AD$$
We know that the bisector of the angle at the vertex of an triangle bisects the base at right angle.
Using Pythagoras theorem i $$\triangle AFB$$
$$AB^2 =AF^2+BF^2 ....(i)$$
In $$\triangle AFD$$,
$$AD^2 =AF^2 +DF^2 .....(ii)$$
We know $$ABC$$ is isosceles triangle and $$AB=AC$$
$$AC^2 =AF^2 +BF^2 .....(iii)$$
Subtracting (ii) from (iii)
$$AC^2 -AD^2 =AF^2+BF^2-AF^2-DF^2$$
$$AC^2-AD^2 =BF^2-DF^2$$
Let $$2DF =BF$$
$$AC^2 -AD^2=(2DF)^2 - DF^2$$
$$AC^2-AD^2=4DF^2-DF^2$$
$$AC^2=AD^2+3DF^2$$
$$\Rightarrow AC^2 > AD^2$$
$$\Rightarrow AC > AD$$
Similarly $$AE > AC$$ and $$AE > AD$$.
Using Pythagoras theorem i $$\triangle AFB$$
$$AB^2 =AF^2+BF^2 ....(i)$$
In $$\triangle AFD$$,
$$AD^2 =AF^2 +DF^2 .....(ii)$$
We know $$ABC$$ is isosceles triangle and $$AB=AC$$
$$AC^2 =AF^2 +BF^2 .....(iii)$$
Subtracting (ii) from (iii)
$$AC^2 -AD^2 =AF^2+BF^2-AF^2-DF^2$$
$$AC^2-AD^2 =BF^2-DF^2$$
Let $$2DF =BF$$
$$AC^2 -AD^2=(2DF)^2 - DF^2$$
$$AC^2-AD^2=4DF^2-DF^2$$
$$AC^2=AD^2+3DF^2$$
$$\Rightarrow AC^2 > AD^2$$
$$\Rightarrow AC > AD$$
Similarly $$AE > AC$$ and $$AE > AD$$.
Given: $$ED=EC$$
Prove : $$AB + AD > BC$$
In triangle $$ABC, AB > AC$$ and $$D$$ is a point in side $$BC$$. Show that: $$AB > AD$$.
Given that, $$AB > AC$$
$$\Rightarrow \angle C > \angle B.....(i)$$
Also In $$\triangle ADC$$
$$\angle ADB=\angle DAC +\angle C$$
$$\Rightarrow \angle ADB > \angle C$$
$$\Rightarrow \angle ADB > \angle C > \angle B$$
$$\Rightarrow \angle ADB > \angle B$$
$$\Rightarrow AB > AD$$
$$\Rightarrow \angle C > \angle B.....(i)$$
Also In $$\triangle ADC$$
$$\angle ADB=\angle DAC +\angle C$$
$$\Rightarrow \angle ADB > \angle C$$
$$\Rightarrow \angle ADB > \angle C > \angle B$$
$$\Rightarrow \angle ADB > \angle B$$
$$\Rightarrow AB > AD$$
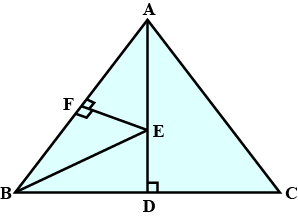
In the following figure AB = AC and AD is perpendicular to BC . BE bisects angle B and EF is perpendicular to AB
Prove that
ED = EF
In the given figure, $$AB=AC.$$ Prove that:
$$AP=AQ$$
Draw a line joining $$A$$ with the midpoint of $$BC.$$
In $$\triangle ABC,$$
$$AB=AC$$ [Given]
$$\therefore \angle C=\angle B$$ ...(I) [angles opp.to equal sides are equal]
So, $$\triangle BPD\cong \triangle CQD$$
In $$\triangle BPD$$ and $$ \triangle CQD$$, we have:
$$BD=DC$$ [Given]
$$\angle C=\angle B$$ [From (I)]
$$\angle BPD=\angle CQD$$ [Each $$=90^0$$]
Also, $$BP=CQ$$ [cpct]
Now,
$$AB=AC$$ [Given]
$$\Rightarrow AB-BP=AC-CQ$$
$$\Rightarrow AP=AQ$$
Use the information in the given figure to prove ;
AB = FE
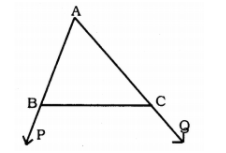
A triangles ABC has $$ \angle B = \angle C $$
Prove that
The perpendicular from the mid - point of BC to AB and AC are equal'
Given ; A $$ \Delta ABC in which \angle B = \angle C .$$
DL is the perpendicular from D to AB
DM is the perpendicular from A to AC
We need to prove that.
DL = DM
Proof ;
In $$ \Delta DLB$$ and $$\Delta DMC $$
$$ \angle DLB = \angle DMC = 90^{o} $$ $$[DL \perp AB$$ and $$DM \perp AC]$$
$$ \angle B = \angle C $$ [Given]
$$BD = DC$$ [D is the mid point of BC]
By Angle - Angle - Side criterion of congruence
$$ \Delta DLB \cong \Delta DMC $$
The corresponding parts of the congruent triangles are congruent
$$DL = DM$$ [c.p.c.t]
DL is the perpendicular from D to AB
DM is the perpendicular from A to AC
We need to prove that.
DL = DM
Proof ;
In $$ \Delta DLB$$ and $$\Delta DMC $$
$$ \angle DLB = \angle DMC = 90^{o} $$ $$[DL \perp AB$$ and $$DM \perp AC]$$
$$ \angle B = \angle C $$ [Given]
$$BD = DC$$ [D is the mid point of BC]
By Angle - Angle - Side criterion of congruence
$$ \Delta DLB \cong \Delta DMC $$
The corresponding parts of the congruent triangles are congruent
$$DL = DM$$ [c.p.c.t]
A triangles ABC has $$ \angle B = \angle C $$
Prove that
The perpendicular from B and C to the opposite sides are equal .
Given ; A $$ \Delta ABC$$ in which $$\angle B = \angle C $$
BP is the perpendicular from D to AC
CQ is the perpendicular from C to AB
We need to prove that
BP = CQ
Proof
In $$ \Delta BPC$$ and $$\Delta CQB $$
$$ \angle B = \angle C $$ [Given]
$$ \angle BPC = \angle CQB = 90^{o} [BP \perp AC and CQ \perp AB ]$$
BC = BC [common]
By Angle - Angle - Side criterion of congruence ,
$$\Delta BPC \cong \Delta CQB $$
The corresponding parts of the congruent ;triangle are congruent
BP = CQ [c . p . c. t ]
BP is the perpendicular from D to AC
CQ is the perpendicular from C to AB
We need to prove that
BP = CQ
Proof
In $$ \Delta BPC$$ and $$\Delta CQB $$
$$ \angle B = \angle C $$ [Given]
$$ \angle BPC = \angle CQB = 90^{o} [BP \perp AC and CQ \perp AB ]$$
BC = BC [common]
By Angle - Angle - Side criterion of congruence ,
$$\Delta BPC \cong \Delta CQB $$
The corresponding parts of the congruent ;triangle are congruent
BP = CQ [c . p . c. t ]
Use the information in the given figure to prove ;
BD = CF
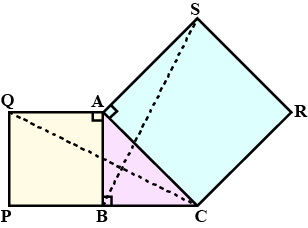
In the figure given below triangles $$ABC$$ is right-angled at $$B .\ ABPQ $$ and $$ACRS$$ are squares. Prove that :
$$ \Delta ACQ$$ and $$ \Delta ASB $$ are congruent
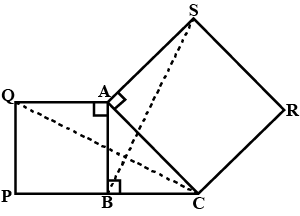
In the figure given below triangles ABC is right - angled at B . ABPQ and ACRS are square . Prove that :
CQ = BS
Use the information in the given figure to prove ;
BC = DF
In triangle $$ABC$$ ; $$AB=AC.\ P,Q$$ and $$R$$ are mid-points of sides $$AB,AC$$ and $$BC$$ respectively. Prove that:
$$PR=QR$$
In $$\triangle ABC,$$
$$AB=AC$$ [Given]
$$\Rightarrow \dfrac{1}{2}AB=\dfrac{1}{2}AC$$
$$\Rightarrow AP=AQ$$......(i) [Since $$P$$ and $$Q$$ are mid-points]
In $$\triangle BCA,$$
$$PR=\dfrac{1}{2}AC$$ [$$PR$$ is line joining the mid-points of $$AB$$ and $$BC$$]
$$\Rightarrow PR=AQ$$......(ii)
In $$\triangle CAB,$$
$$QR=\dfrac{1}{2}AB$$ [$$QR$$ is line joining the mid-points of $$AC$$ and $$BC$$]
$$\Rightarrow QR=AP$$......(iii)
From (i)(ii) and (iii)
$$PR=QR$$
$$AB=AC$$ [Given]
$$\Rightarrow \dfrac{1}{2}AB=\dfrac{1}{2}AC$$
$$\Rightarrow AP=AQ$$......(i) [Since $$P$$ and $$Q$$ are mid-points]
In $$\triangle BCA,$$
$$PR=\dfrac{1}{2}AC$$ [$$PR$$ is line joining the mid-points of $$AB$$ and $$BC$$]
$$\Rightarrow PR=AQ$$......(ii)
In $$\triangle CAB,$$
$$QR=\dfrac{1}{2}AB$$ [$$QR$$ is line joining the mid-points of $$AC$$ and $$BC$$]
$$\Rightarrow QR=AP$$......(iii)
From (i)(ii) and (iii)
$$PR=QR$$
In the given figure, $$AB=AC$$ and $$\angle DBC=\angle ECB=90^{o}.$$
$$BD=CE$$
In triangle $$ABC$$ ; $$AB=AC.\ P,Q$$ and $$R$$ are mid-points of sides $$AB,AC$$ and $$BC$$ respectively. Prove that:
$$BQ=CP$$
$$AB=AC$$ [Given]
$$\Rightarrow \angle B=\angle C$$
Also,
$$\dfrac{1}{2}AB=\dfrac{1}{2}AC$$
$$\Rightarrow BP=CQ$$ [$$P$$ and $$Q$$ are mid- points of $$AB$$ $$ AC$$]
In $$\triangle BPC$$ and $$\triangle CQB,$$
$$BP=CQq$$
$$\angle B=\angle C$$
$$BC=BC$$
Hence, $$\triangle BPC\cong\triangle CQB$$ [SAS]
$$BQ=CP$$ [C.P.C.T]
$$\Rightarrow \angle B=\angle C$$
Also,
$$\dfrac{1}{2}AB=\dfrac{1}{2}AC$$
$$\Rightarrow BP=CQ$$ [$$P$$ and $$Q$$ are mid- points of $$AB$$ $$ AC$$]
In $$\triangle BPC$$ and $$\triangle CQB,$$
$$BP=CQq$$
$$\angle B=\angle C$$
$$BC=BC$$
Hence, $$\triangle BPC\cong\triangle CQB$$ [SAS]
$$BQ=CP$$ [C.P.C.T]
In the given figure, $$AB=AC$$ and $$\angle DBC=\angle ECB=90^{o}.$$
$$AD=AE$$
From the following figure, Prove that:
$$AD=CE$$
From the following figure, Prove that:
$$\angle ACD=\angle CBE$$
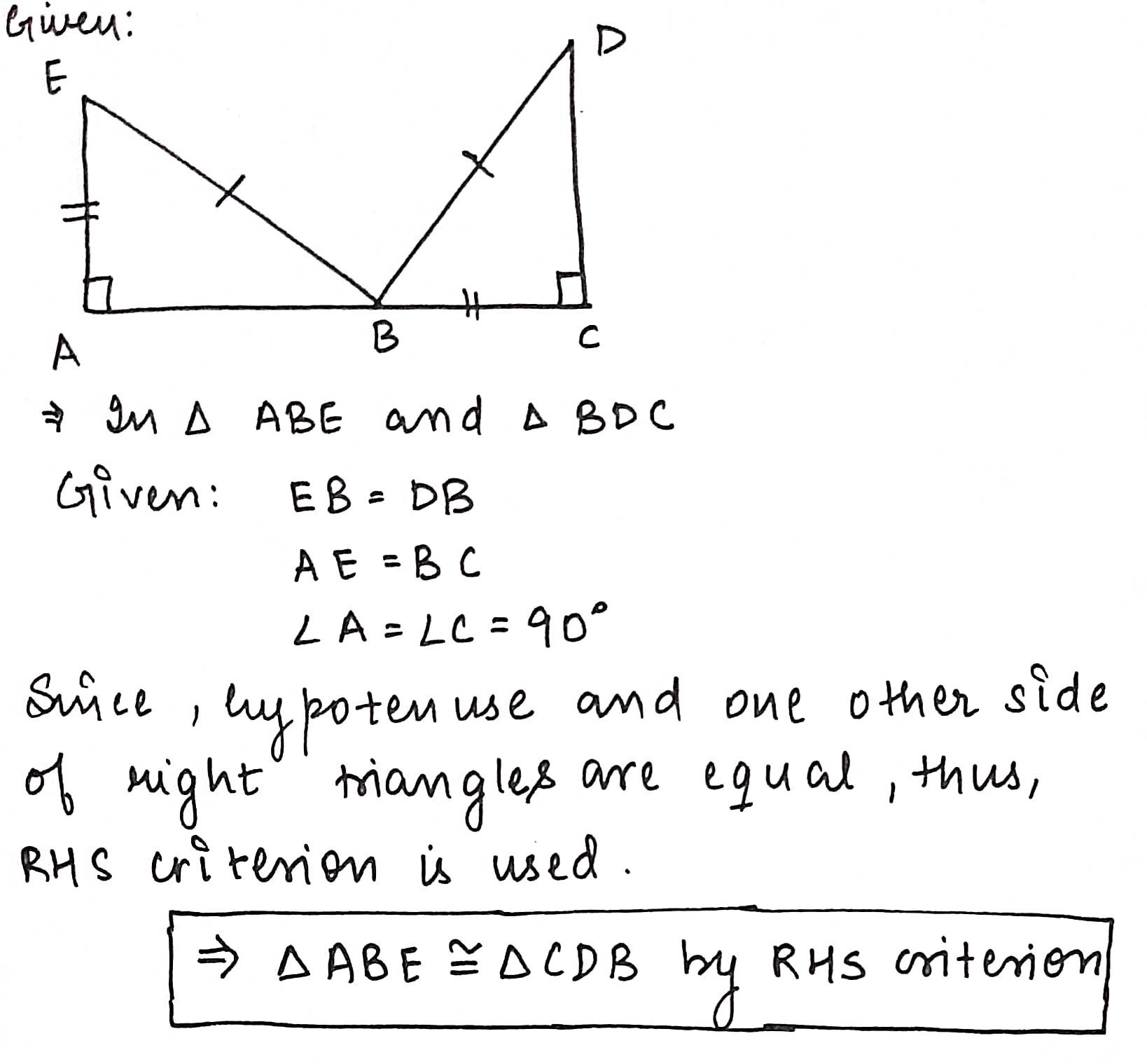
In the following figure AB = EF , BC = DE and $$ \angle B = \angle E = 90^{o}$$
Prove that AD = FC
Given that, $$BC = DE$$
$$ \Rightarrow BC + CD = DE + CD$$ (Adding $$CD$$ on both sides)
$$\Rightarrow BD = CE $$ ...(1)
Now, In$$ \Delta ABD$$ and $$\Delta EFC $$
$$ AB = EF $$ ...[Given]
$$\angle ABD = \angle FEC $$ ...[Both $$=90^0$$, perpendiculars]
$$ BD = CE $$ ...[From (1)]
$$\Rightarrow ABD \cong \Delta \Delta EFC $$ ...[SAS congruence criterion]
$$ \Rightarrow AD = FC $$ ...[cpct]
$$ \Rightarrow BC + CD = DE + CD$$ (Adding $$CD$$ on both sides)
$$\Rightarrow BD = CE $$ ...(1)
Now, In$$ \Delta ABD$$ and $$\Delta EFC $$
$$ AB = EF $$ ...[Given]
$$\angle ABD = \angle FEC $$ ...[Both $$=90^0$$, perpendiculars]
$$ BD = CE $$ ...[From (1)]
$$\Rightarrow ABD \cong \Delta \Delta EFC $$ ...[SAS congruence criterion]
$$ \Rightarrow AD = FC $$ ...[cpct]
In the following figure , OA = OC and AB = BC ,
prove that :
$$ \angle AOB = 90^{o}$$
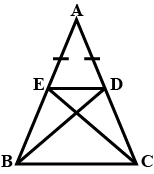
The following figure shows a triangle ABC in which AB = AC . M is a point on AB and N is a point AC such that BM = CN
Prove that
AM = AN
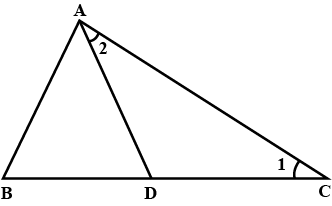
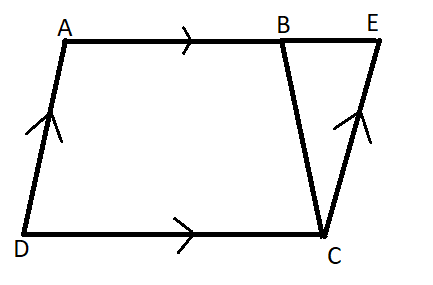
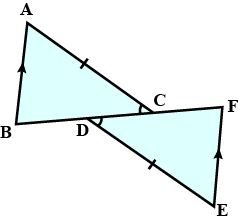
In the adjoining figure If $$\angle C = \angle F $$ , then AB = ______ and BC _______
In the following figure , OA = OC and AB = BC ,
prove that :
AD = CD
In triangle $$ABC,D$$ is a points on $$BC$$ such that $$Ab=AD=BD=DC.$$ Show that:
$$\angle ADC:\angle C=4:1$$
Since $$AB=AD=BD$$
$$\therefore \triangle ABD$$ is an equilateral triangle.
$$\therefore \angle ADB=60^{o}$$
$$\Rightarrow \angle ADC=180^{o}-\angle ADB$$
$$=180^{o}-60^{o}$$
$$=120^{o}$$
Again in $$\triangle ADC,$$
$$AD=DC$$
$$\therefore \angle 1=\angle 2$$
But ,
$$\angle 1+\angle 2+\angle ADC=180^{o}$$
$$\Rightarrow 2\angle 1+120^{o}=180^{o}$$
$$\Rightarrow 2\angle 1=60^{o}$$
$$\Rightarrow \angle 1=30^{o}$$
$$\Rightarrow \angle C=30^{o}$$
$$\therefore \angle ADC:\angle C=120^{o}:30^{o}$$
$$\Rightarrow \angle ADC:\angle C=4:1$$
$$\therefore \triangle ABD$$ is an equilateral triangle.
$$\therefore \angle ADB=60^{o}$$
$$\Rightarrow \angle ADC=180^{o}-\angle ADB$$
$$=180^{o}-60^{o}$$
$$=120^{o}$$
Again in $$\triangle ADC,$$
$$AD=DC$$
$$\therefore \angle 1=\angle 2$$
But ,
$$\angle 1+\angle 2+\angle ADC=180^{o}$$
$$\Rightarrow 2\angle 1+120^{o}=180^{o}$$
$$\Rightarrow 2\angle 1=60^{o}$$
$$\Rightarrow \angle 1=30^{o}$$
$$\Rightarrow \angle C=30^{o}$$
$$\therefore \angle ADC:\angle C=120^{o}:30^{o}$$
$$\Rightarrow \angle ADC:\angle C=4:1$$
M is a point on side BC of a triangle ABC such that AM is the bisector of $$\angle BAC.$$ Is it true to say that perimeter of the triangle is greater than 2 AM? If True enter 1, else if False enter 0.
Show that no triangle has two sides each shorter than its corresponding altitude (from the opposite vertex).
Assume that $$AD>BC$$ and $$BE>AC$$
then $$AD>BC\ge BE$$ (Because hypotenuse of a right angled triangle is greater)
According to our assumption $$BE>AC$$
So, $$AD>BC\ge BE>AC$$
But, $$AC\ge AD$$
So, we got a contradiction.
Our assumption is not possible.
Let a, b, c be the three sides of a triangle. Suppose that $$\dfrac{a}{b}=\dfrac{b}{c}=q.$$ Prove that $$\dfrac{\sqrt{5}-1}{2}<q<\dfrac{\sqrt{5}+1}{2}$$
The sides of a triangle have lengths $$11, ~15$$ and $$k,$$ where $$k$$ is an integer. For how many values of $$k$$ is the triangle obtuse?
Show that in any triangle with sides a, b and c, we have $$(a + b + c)^2 < 4 (ab + bc + ca).$$
State whether the given statement is true/false:
In the following diagram, $$AB = AC$$ then which of the following is correct?
$$AE>AF$$
$$AF>AE$$
In the given figure,$$\displaystyle BC=CE $$ and $$\displaystyle \angle 1=\angle 2$$ Then,
:$$\displaystyle \Delta GCB \equiv \Delta DCE $$
If the above statement is true then mention answer as 1, else mention 0 if false
In $$\triangle ABC$$, $$AB=AC$$ and bisector of angle $$A$$ meets $$BC$$ at $$D$$, then prove that $$AD$$ is perpendicular to $$BC$$.
In $$\triangle ABD$$ and $$\triangle ACD$$,
As we know that, corresponding angles of congruent triangles are equal so,
Now,
Thus, $$AD \perp BC$$
$$AD = AD$$ [Common]
$$\angle BAD = \angle CAD $$ [$$AD$$ is the bisector of angle $$A$$]
$$AB = AC$$ [Given]
$$\angle BAD = \angle CAD $$ [$$AD$$ is the bisector of angle $$A$$]
$$AB = AC$$ [Given]
So, by $$SAS$$ rule of congruence,
$$\triangle ABD \cong \triangle ACD$$
$$\triangle ABD \cong \triangle ACD$$
As we know that, corresponding angles of congruent triangles are equal so,
$$\angle ADC = \angle ADB = x$$
Now,
$$\angle ADC + \angle ADB = 180^{\circ} $$ [Linear Pair]
$$\Rightarrow 2x = 180^{\circ} $$
$$\Rightarrow x = 90^{\circ}$$
$$\Rightarrow \angle ADC = \angle ADB = 90^{\circ}$$
$$\Rightarrow 2x = 180^{\circ} $$
$$\Rightarrow x = 90^{\circ}$$
$$\Rightarrow \angle ADC = \angle ADB = 90^{\circ}$$
Thus, $$AD \perp BC$$
AB + BC + CD > DA
If the above statement is true, then enter 1 or else enter 0.
In $$ \triangle ABC $$, we have sum of two sides > third side
$$ => AB + BC > AC $$ -- (1)
Also, in $$ \triangle ADC $$, we have sum of two sides > third side
$$ => DC + AC > AD $$ ---- (2)
Adding equations $$ 1, 2 $$ we get
$$ => AB + BC + CD + AC > AC + AD $$
$$ => AB + BC + CD > AD $$
The given figure shows $$\displaystyle PQ=PR $$ and $$\displaystyle \angle Q=\angle R $$ Prove that $$\displaystyle \Delta PQS \equiv \Delta PRT $$
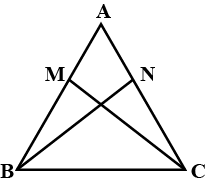
The given figure shows a triangle $$ABC$$ in which $$AB = AC$$. $$M$$ is a point on $$AB $$ and $$N$$ is a point on $$AC$$ such that $$BM = CN$$. Hence, $$BN=CM$$.
If the above statement is true, then mention answer as 1, else mention 0 if false.
In triangle ABC, AB > AC and D is a point in side BC.
then, AB > AD.
If the above statement is true then mention answer as 1, else mention 0 if false
Here AB > AC and D is a point in side BC.
here AE is altitude,
So, As per Pythagorean Theorem,
$$AD^2=AE^2+ED^2$$...........eq1
& $$AB2=AE^2+EB^2$$
$$AB^2=AE^2+(ED+DB)^2$$........Eq2
So, As per eq1 & eq2 , it is clearly seen that
$$AB>AD$$
and any line starting from A inside the triangle ABC, on the base BC will be smaller then longest side.
Answer is 1
$$AB$$ and $$PQ$$ bisect each other.
If the above statement is true then mention answer as $$1$$, else mention $$0$$ if false.
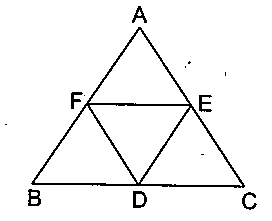
In the given triangle $$ABC$$, $$D, E$$ and $$F$$ are the mid-points of sides $$BC,CA$$ and $$AB$$ respectively. Prove that
$$\displaystyle \dfrac{AB-BC}{2}< AE< \dfrac{AB+BC}{2}.$$
$$\displaystyle \dfrac{AB-BC}{2}< AE< \dfrac{AB+BC}{2}.$$
Show that in an isosceles triangle angles opposite to equal sides are equal
Let $$ \displaystyle \bigtriangleup ABC $$ be an isosceles triangle such that AB =AC Then we have to prove that $$ \displaystyle \angle B=\angle C $$ Draw the bisector AD of $$ \displaystyle \angle A $$ meeting BC in D
Now in triangles ABD and ACD We have $$AB=AC$$ (Given)
$$ \displaystyle \angle BAD = \angle CAD $$ (because AD is bisector of $$ \displaystyle \angle A $$
$$AD = AD$$ (Common side)
Therefore by SAS congruence condition we have
$$ \displaystyle \bigtriangleup ABC\cong \bigtriangleup ACD $$
$$ \displaystyle \Rightarrow \angle B=\angle C $$
(Corresponding parts of congruent triangles are equal )
Now in triangles ABD and ACD We have $$AB=AC$$ (Given)
$$ \displaystyle \angle BAD = \angle CAD $$ (because AD is bisector of $$ \displaystyle \angle A $$
$$AD = AD$$ (Common side)
Therefore by SAS congruence condition we have
$$ \displaystyle \bigtriangleup ABC\cong \bigtriangleup ACD $$
$$ \displaystyle \Rightarrow \angle B=\angle C $$
(Corresponding parts of congruent triangles are equal )
Using triangle inequality theorem check whether the given side lengths $$a = 3, b = 5$$ and $$c = 1$$ will form a triangle or not.
Using triangle inequality theorem check whether the given side lengths $$a = 4, b = 5$$ and $$c = 8$$ will form a triangle or not.
In Fig, $$AC = AE, AB = AD$$ and $$\angle BAD = \angle EAC$$. Show that $$BC = DE$$
In right angled triangle $$ABC$$, right angled at $$C, M$$ is the mid-point of hypotenuse $$AB$$. $$C$$ is joined to $$M$$ and produced to a point $$D$$ such that $$DM = CM$$. Point $$D$$ is joined to point $$B$$. Show that:
(i) $$\triangle AMC\cong \triangle BMD$$
(ii) $$\angle DBC$$ is a right angle.
(iii) $$\triangle DBC\cong \triangle ACB$$
(iv) $$CM = \dfrac {1}{2} AB$$
$$ABCD$$ is a quadrilateral in which $$AD = BC$$ and $$\angle DAB = \angle CBA$$ . Prove that
(i) $$\triangle ABD \cong\triangle BAC$$
(ii) $$BD = AC$$
(iii) $$\angle ABD = \angle BAC$$
In $$\triangle ABC, AD$$ is the perpendicular bisector of $$BC$$. Show that $$\triangle ABC$$ is an isosceles triangle in which $$AB = AC$$.
In an isosceles triangle $$ABC$$, with $$AB = AC$$, the bisectors of $$\angle B$$ and $$\angle C$$ intersect each other at $$O$$. Join $$A$$ to $$O$$. Show that :
(i) $$OB = OC$$ (ii) $$AO$$ bisects $$\angle A$$
(i) In $$\triangle ABC$$, we have
$$AB = AC$$
$$\Rightarrow \angle C=\angle B$$ $$\mid$$ Since angles opposite to equal sides are equal
$$\Rightarrow \dfrac{1}{2}\angle B=\dfrac{1}{2}\angle C$$
$$\Rightarrow \angle OBC=\angle OCB$$
$$\Rightarrow \angle ABO=\angle ACO$$ $$\dots(1)$$
$$\Rightarrow OB = OC$$ $$\mid$$ Since sides opp. to equal ∠s are equal $$\dots(2)$$
(ii) Now, in $$\triangle ABO $$ and $$\triangle ACO $$, we have
$$AB = AC $$ $$\mid$$ Given
$$\angle ABO=\angle ACO$$ $$\mid$$ From (1)
$$OB = OC$$ $$\mid$$ From (2)
$$\therefore$$ By SAS criterion of congruence, we have
$$\triangle ABO \cong \triangle ACO$$
$$\Rightarrow \angle BAO=\angle CAO$$ $$\mid$$ Since corresponding parts of congruent triangles are equal
$$\Rightarrow $$ $$AO$$ bisects $$\angle A$$
$$l$$ and $$m$$ are two parallel lines intersected by another pair of parallel lines $$p$$ and $$q$$. Show that $$\triangle ABC \cong \triangle CDA$$
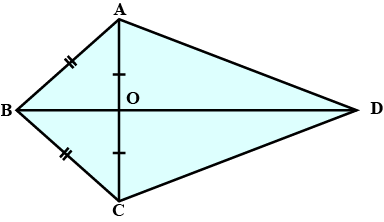
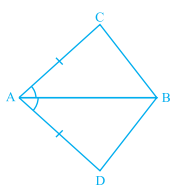
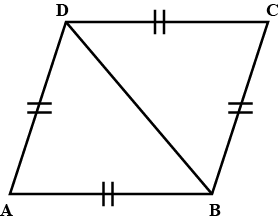
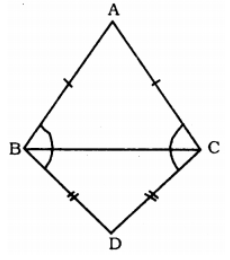
In quadrilateral $$ACBD, AC = AD$$ and $$AB$$ bisects $$\angle A$$. Show that $$\triangle ABC \equiv \triangle ABD$$. What can you say about $$BC$$ and $$BD$$
$$AB$$ is a line segment and $$P$$ is its mid-point. $$D$$ and $$E$$ are points on the same side of $$AB$$ such that $$\angle BAD = \angle ABE$$ and $$\angle EPA = \angle DPB$$. Show that
(i) $$\triangle DAP \cong \triangle EBP$$
(ii) $$AD = DE$$
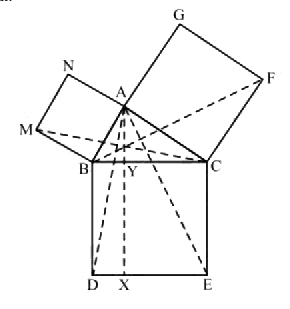
In fig, $$ABC$$ is a right triangle right angled at $$A.BCED, ACFG$$ and $$ABMN$$ are square on the sides $$BC, CA$$ and $$AB$$ respectively. Line segment $$AX\perp DE$$ meets $$BC$$ at $$Y$$. Show that:
(i) $$\triangle MBC\cong \triangle ABD$$
(ii) $$ar(BYXD) = 2ar(MBC)$$
(iii) $$ar(BYXD) = ar (ABMN)$$
(iv) $$\triangle FCB\cong \triangle ACE$$
(v) $$ar(CYXE) = 2ar (FCB)$$
(vi) $$ar(CYXE) = ar(ACFG)$$
(vii) $$ar(BCED) = ar(ABMN) + ar(ACFG)$$
Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler
proof of this theorem in Class X.
(i)
In $$\Delta \ MBC$$ and $$\Delta ABD$$, we have
$$BC = BD$$
$$BC = BD$$
[Sides of the square BCED]
$$MB = AB$$
[Sides of the square ABMN]
$$\angle MBC=\angle ABD$$
[Since Each $$ = 90º + ∠ABC$$]
Therefore by SAS criterion of congruence, we have
$$\Delta MBC\cong \Delta ABD$$
(ii)
$$\Delta MBC\cong \Delta ABD$$
(ii)
$$\Delta ABD$$ and square $$BYXD$$ have the same base $$BD$$ and lie between the same parallel lines $$BD$$ and $$AX$$.
Therefore $$ar(ABD) = \dfrac{1}{2} ar (BYXD) $$
Therefore $$ar(ABD) = \dfrac{1}{2} ar (BYXD) $$
But $$ΔMBC≅ΔABD$$ [Proved in part (i)]
$$\Rightarrow ar(MBC) = ar (ABD) $$
Therefore $$ar(MBC) = ar (ABD) = \dfrac{1}{2} ar (BYXD) $$
$$\Rightarrow ar(BYXD) = 2 ar (MBC).$$
(iii)
$$\Rightarrow ar(BYXD) = 2 ar (MBC).$$
(iii)
Square $$ABMN$$ and $$\Delta MBC$$ have the same base $$MB$$ and are between same parallel lines $$MB$$ and $$NA$$.
Therefore $$ar(MBC) = \dfrac{1}{2} ar (ABMN) $$
Therefore $$ar(MBC) = \dfrac{1}{2} ar (ABMN) $$
$$\Rightarrow ar(ABMN) = 2ar (MBC)$$
$$= ar (BYXD) $$ [Using part (ii)]
(iv)
(iv)
In $$\Delta $$ACE and $$\Delta BCF$$, we have
$$CE = BC$$ [Sides of the square BCED]
$$AC = CF$$ [Sides of the square ACFG]
and $$∠ACE=∠BCF$$ [Since Each$$ = 90º + ∠BCA$$]
Therefore by SAS criterion of congruence,
$$ΔACE≅ΔBCF$$
(v)
$$CE = BC$$ [Sides of the square BCED]
$$AC = CF$$ [Sides of the square ACFG]
and $$∠ACE=∠BCF$$ [Since Each$$ = 90º + ∠BCA$$]
Therefore by SAS criterion of congruence,
$$ΔACE≅ΔBCF$$
(v)
$$\Delta ACE$$ and square $$CYXE$$ have the same base $$CE$$ and are between same parallel lines $$CE$$ and $$AYX$$.
Therefore $$ar(ACE) = \dfrac{1}{2} ar (CYXE)$$
Therefore $$ar(ACE) = \dfrac{1}{2} ar (CYXE)$$
$$\Rightarrow ar(FCB) = \dfrac{1}{2} ar (CYXE)$$ [Since $$ΔACE≅ΔBCF$$, part (iv)]
$$\Rightarrow ar(CYXE) =2 ar (FCB)$$ .
(vi)
(vi)
Square $$ACFG$$ and $$\triangle BCF$$ have the same base $$CF$$ and are between same parallel lines $$CF$$ and $$AG$$.
Therefore $$ar(BCF) = \dfrac{1}{2} ar(ACFG) $$
Therefore $$ar(BCF) = \dfrac{1}{2} ar(ACFG) $$
$$\Rightarrow \dfrac{1}{2}ar(CYXE) = \dfrac{1}{2} ar (ACFG)$$ [Using part (v)]
$$\Rightarrow ar(CYXE) = ar (ACFG)$$
(vii)
(vii)
From part (iii) and (vi) we have
$$ar (BYXD) = ar (ABMN)$$
and
$$ar (BYXD) = ar (ABMN)$$
and
$$ar (CYXE) = ar (ACFG) $$
On adding we get
$$ar (BYXD) + ar(CYXE) = ar (ABMN) + ar(ACFG) \\
ar (BCED) = ar (ABMN) + ar(ACFG)$$
$$ar (BYXD) + ar(CYXE) = ar (ABMN) + ar(ACFG) \\
ar (BCED) = ar (ABMN) + ar(ACFG)$$
In $$\triangle ABC$$ and $$\triangle DEF, AB = DE, AB \parallel DE, BC = EF$$ and $$BC \parallel EF$$. Vertices $$A, B$$ and $$C$$ are joined to vertices $$D, E$$ and $$F$$ respectively. Show that
(i) Quadrilateral $$ABED$$ is a parallelogram
(ii) Quadrilateral $$BEFC$$ is a parallelogram
(ii) $$AD \parallel CF$$ and $$AD = CF$$
(iv) Quadrilateral $$ACFD$$ is a parallelogram
(v) $$AC = DF$$
(vi) $$\triangle ABC \cong \triangle DEF$$
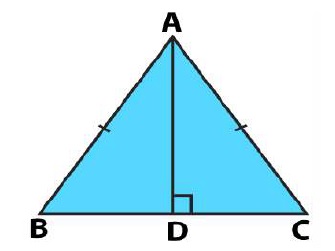
$$ABC$$ is an isosceles triangle with $$AB = AC$$. Draw $$AP \perp BC$$. Show that $$\angle B = \angle C$$
In $$\Delta ABP$$ and $$\Delta ACP,$$
$$\angle APB=\angle APC$$ (Both equal to $$90^0$$)
$$AB = AC$$ [$$\because \Delta ABC$$ is an isosceles triangle.]
$$AP = AP$$ (Common Side)
By R.H.S. criterion of congruence,
$$\triangle ABP\cong \triangle ACP $$
$$\Rightarrow \angle B=\angle C$$ (CPCT)
$$\triangle ABC$$ and $$\triangle DBC$$ are two isosceles triangles on the same base $$BC$$ and vertices $$A$$ and $$D$$ are on the same side of $$BC$$. If $$AD$$ is extended to intersect $$BC$$ at $$P$$, show that
(i) $$\triangle ABD \cong \triangle ACD$$
(ii) $$\triangle ABP \cong \triangle ACP$$
(iii) $$AP$$ bisects $$\angle A$$ as well as $$\triangle D$$.
(iv) $$AP$$ is the perpendicular bisector of $$BC$$.
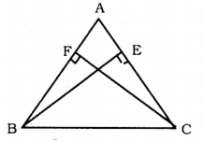
$$ABC$$ is a triangle in which altitudes $$BE$$ and $$CF$$ to sides $$AC$$ and $$AB$$ are equal (see Fig.). Show that
(i) $$\triangle ABE\cong \triangle ACF$$
(ii) $$AB = AC$$, i.e., $$ABC$$ is an isosceles triangle.
$$AD$$ is an altitude of an isosceles triangle $$ABC$$ in which $$AB = AC$$. Show that
(i) $$AD$$ bisects $$BC$$ (ii) $$AD$$ bisects $$\angle A$$
$$AD$$ is the altitude drawn from vertex $$A$$ of an isosceles $$\triangle ABC$$ to the opposite base $$BC$$ so that $$AB = AC$$,
$$\angle ADC=\angle ADB= 90^{\circ}$$
Now, in $$\triangle ADB$$ and $$\triangle ADC$$, we have
Hypotenuse $$AB =$$ Hypotenuse $$AC$$ (Given)
$$AD = AD$$ $$ (Common)
and $$\angle ADC=\angle ADB$$ (Each equal to $$90^\circ$$)
Therefore by $$RHS$$ criterion of congruence, we have
$$\triangle ADB\cong \triangle ADC $$
$$\Rightarrow BD = DC$$ and $$\angle BAD=\angle DAC$$ $$ (Since corresponding parts of the congruent triangle are equal.)
Hence, $$AD$$ bisects $$BC$$, which proves $$(i)$$ and $$AD$$ bisects $$\angle A,$$ which proves $$(ii)$$.
In given figures two sides $$AB$$ and $$BC$$ and median $$AM$$ of one triangle $$ABC$$ are respectively equal to sides $$PQ$$ and $$QR$$ and median $$PN$$ of $$\triangle PQR$$. Show that:
(i) $$\triangle ABM\cong \triangle PQN$$
(ii) $$\triangle ABC \cong \triangle PQR$$
$$BE$$ and $$CF$$ are two equal altitudes of a triangle $$ABC$$. Using RHS congruence rule, prove that the triangle $$ABC$$ is isosceles.
In $$\Delta BCF$$ and$$\Delta CBE$$,
$$\angle BFC=\angle CEB$$ (Each $$ 90º$$)
Hyp. $$BC =$$ Hyp. $$BC$$ (Common Side)
Side $$FC =$$ Side $$EB $$ (Given)
$$\therefore$$ By R.H.S. criterion of congruence, we have
$$\Delta BCF\cong \Delta CBE$$
$$\therefore \angle FBC=\angle ECB$$ (CPCT)
In $$\Delta ABC$$,
$$\angle ABC=\angle ACB $$
[$$\because \angle FBC= \angle ECB$$]
$$ \therefore AB = AC $$ (Converse of isosceles triangle theorem)
$$\therefore$$ $$\Delta ABC$$ is an isosceles triangle.
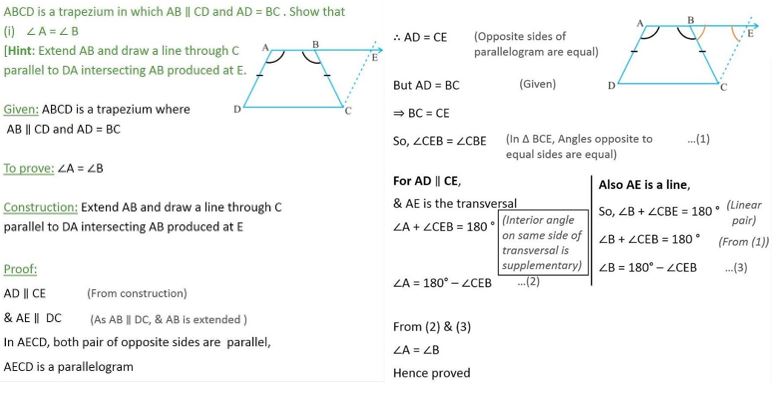
In given figure $$ABCD$$ is a trapezium in which $$AB\parallel CD$$ and $$AD = BC$$. Show that
(i) $$\angle A = \angle B$$
(ii) $$\angle C = \angle D$$
(iii) $$\triangle ABC \cong \triangle BAD$$
(iv) diagonal $$AC =$$ diagonal $$BD$$
Given that ABCD is a trapezium,
$$AB\parallel CD$$ and $$AD=BC$$
To prove: (i) $$\angle A = \angle B$$
(ii) $$\angle C= \angle D$$
(iii) $$\triangle ABC \cong \triangle BAD$$
(iv) $$AC =BD$$
Construction: Draw $$CE\parallel AD$$ and extend AB to intersect CE at E.
Poof:
$$(i)$$ As AECD is a parallelogram.
By construction, CE is parallel to AD and AE is parallel to CD,
$$\therefore \,\,AD=EC$$
But, $$AD=BC$$ (Given)
$$\therefore \,\,BC=EC$$
$$\Rightarrow \,\angle 3=\angle 4$$ (Angle opposite to equal side are equal)
Now, $$\angle 1+\angle 4={{180}^{0}}$$ (consecutive interior angle of parallelogram )
And $$\angle 2+\angle 3={{180}^{0}}$$ (linear pair )
$$\Rightarrow \angle 1+\angle 4=\angle 2+\angle 3$$ $$\Rightarrow \angle 1=\angle 2\,\,\,\,\,\,\,\,\,\,\,\,\because \angle 3=\angle 4$$ (so get cancelled with each other )
$$\Rightarrow \,\angle A=\angle B$$
$$(ii)$$ $$AB\parallel CD$$
$$\therefore \ \angle A +\angle D=\angle B+\angle C=180^o$$ [Angles on the same side of transversal]
But, $$\angle A=\angle B$$
Hence, $$\angle C=\angle D$$
$$(iii)$$ In $$\triangle ABC$$ and $$\triangle BAD$$, we have
$$BC = AD$$ (Given)
$$AB = BA$$ (Common)
$$\angle A = \angle B $$ (Proved)
Hence, by SAS congruence criterion,
$$\triangle ABC \cong \triangle BAD$$
$$(iv)$$ We have proved that, $$\triangle ABC \cong \triangle BAD$$
$$\therefore \ AC = BD$$ (CPCT)
Hence, all the four required results have been proved.
Show that the sum of the three altitudes of a triangle is less than the sum of its three sides.
Let $$ABC$$ be the triangle with sides $$BC, AC, AB$$ opposite angles $$A,B,C$$ being in length equal to $$a,b,c$$ respectively.
Draw $$AD, BE, CF$$ perpendicular from $$A,B,C$$ to opposite sides meeting sides $$BC, AC, AB$$ at $$D,E, F$$ respectively.
Now perpendicular $$AD^2=AC^2-CD^2$$
$$\Rightarrow AD^2<AC^2$$
$$\Rightarrow AD<AC$$
$$\Rightarrow AD<b$$ .... (1)
Also, $$BE^2=AB^2-AE^2$$
$$\Rightarrow BE^2<AB^2$$
$$\Rightarrow BE<AB$$
$$\Rightarrow BE<c$$ ..... (2)
Likewise $$CF^2=BC^2-BF^2$$
$$\Rightarrow CF^2<BC^2$$
$$\Rightarrow CF<BC$$
$$\Rightarrow CF<a$$ ..... (3)
Adding inequalities, (1), (2) and (3), we get
$$AD+BE+CF<a+b+c$$
Hence Proved.
In $$\Delta ABC \,and \, \Delta PQR$$, AB = PQ, BC = QR; CB and RQ are extended to X and Y respectively. $$\angle ABX= \angle PQY$$. Prove that $$\Delta ABC = \Delta PQR$$.
In the given figure, AB = CF, EF = BD $$\angle AFE = \angle DBC$$. Prove that $$\Delta AFE = \Delta CBD$$
In the figure, $$\angle BCD = \angle ADC$$ and $$\angle ACB = \angle BDA$$. Prove that AD = BC and $$\angle A = \angle B$$.
We have $$\angle 1 = \angle 2$$ and $$\angle 3 = \angle 4$$
$$\Rightarrow \angle 1 + \angle 3 = \angle 2 + \angle 4$$
$$\Rightarrow \angle ACD = \angle BDC$$.
Thus in triangles ACD and BDC, we have,
Thus in triangles ACD and BDC, we have,
$$\angle ADC = \angle BCD$$ (given);
CD = CD (common);
CD = CD (common);
$$\angle ACD = \angle BDC$$ (proved).
By ASA condition $$\triangle ACD \cong \triangle BDC$$. Therefore
$$AD = BC$$ and $$\angle A = \angle B$$.
In a $$\triangle ABC, AB = AC$$ and $$\angle A = 50^o$$. Find $$\angle B$$ and $$\angle C$$.
In a $$\triangle ABC,$$ we have $$AB = 4 \ cm$$, $$BC = 5.6 \ cm$$ and $$CA = 7.6 \ cm$$. Write the angles of the triangle in ascending order of measures.
Axiom $$1:$$ Angle opposite to the largest side is largest and vice-versa.
Axiom $$2:$$ Angle opposite to smallest side is smallest and vice-versa.
By using axiom $$1,$$
From given data $$AC = 7.6\ cm$$ is largest, the angle opposite to $$AC$$ is $$\angle B.$$
$$\therefore$$ Largest angle in $$\triangle ABC$$ is $$\angle B.$$
By using axiom $$2,$$
Also, $$AB=4\ cm$$ is smallest, the angle opposite to $$AB$$ is $$\angle C.$$
$$\therefore$$ Smallest angle in $$\triangle ABC$$ is $$\angle C.$$
Hence, the angles in ascending order will be,
$$\angle C<\angle A<\angle B$$
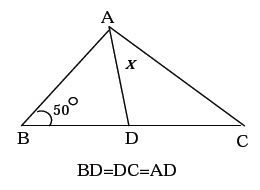
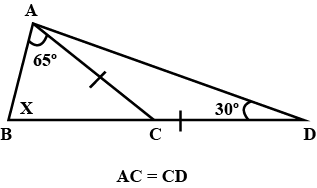
In the given figure, find the value of $$x$$
$$\textbf{Step -1: Apply the first property mentioned.}$$
$$\text{Given figure is, }$$
$$\text{We know that, BD = DC = AD}$$
$$\angle\text{ABD}=50^{\circ}$$
$$\text{In triangle ABD, BD = AD}$$
$$\therefore\angle\text{BAD}=\angle\text{ABD}=50^{\circ}$$
$$\text{Also, }\angle\text{ABD}+\angle\text{BAD}=\text{External }\angle\text{ADC}\Rightarrow\text{External }\angle\text{ADC}=50^\circ+50^\circ=100^\circ$$
$$\textbf{Step -2: Finding the value of x }$$
$$\text{In triangle ADC, AD = DC}$$
$$\angle\text{ACD}=\angle\text{DAC}=x$$
$$\text{According to angle property, the sum of the angles of a triangle is }180^\circ.$$
$$\angle\text{ACD}+\angle\text{DAC}+\angle\text{ADC}=180^\circ$$
$$\Rightarrow{x}+x+100^\circ=180^\circ$$
$$\Rightarrow2x=180^\circ-100^\circ=80^\circ$$
$$\Rightarrow{x}=\dfrac{80^\circ}{2}=40^\circ$$
$$\textbf{Hence, the value of }\mathbf{x}\textbf{ is }\mathbf{50^\circ}.$$
In given figure diagonal AC of a quadrilateral, ABCD bisects the angles $$\angle A$$ and $$\angle C$$. Prove that AB = AD and CB = CD.
Since diagonal AC bisects the angles $$\angle A$$ and $$\angle C$$,
we have $$\angle BAC = \angle DAC$$ and $$\angle BCA = \angle DCA$$.
In triangles ABC and ADC,
we have
$$\angle BAC = \angle DAC$$ (given);
$$\angle BCA = \angle DCA$$ (given);
AC = AC (common side).
So, by ASA postulate, we have
$$\triangle BAC \cong \triangle DAC$$
$$\Rightarrow$$ BA = AD and CB = CD (Corresponding parts of congruent triangle).
we have $$\angle BAC = \angle DAC$$ and $$\angle BCA = \angle DCA$$.
In triangles ABC and ADC,
we have
$$\angle BAC = \angle DAC$$ (given);
$$\angle BCA = \angle DCA$$ (given);
AC = AC (common side).
So, by ASA postulate, we have
$$\triangle BAC \cong \triangle DAC$$
$$\Rightarrow$$ BA = AD and CB = CD (Corresponding parts of congruent triangle).
In the figure O is the midpoint of AB and CD. Prove that
(i) $$\triangle AOC \cong \triangle BOD$$; (ii) $$AC = BD$$.
In triangles AOC and BOD, we have
AO = BO (O, the midpoint of AB);
$$\angle AOC = \angle BOD$$, (vertically opposite angles);
$$CO = OD$$, (O, the midpoint of CD)
So by SAS postulate we have
$$\triangle AOC \cong \triangle BOD$$.
Hence, AC = BD, as they are corresponding parts of congruent triangles.
AO = BO (O, the midpoint of AB);
$$\angle AOC = \angle BOD$$, (vertically opposite angles);
$$CO = OD$$, (O, the midpoint of CD)
So by SAS postulate we have
$$\triangle AOC \cong \triangle BOD$$.
Hence, AC = BD, as they are corresponding parts of congruent triangles.
In the figure, find the value of $$x$$.
In a triangle ABC, AB = AC and the bisectors of angles B and C intersect at O. Prove that BO = CO and AO is the bisector of angle $$\angle BAC$$.
In the figure AB = AC and DB = DC. Prove that $$\angle ABD = \angle ACD$$.
In $$\triangle ABC$$, we have
$$AB = AC \Rightarrow \angle ABC = \angle ACB$$
Again in $$\triangle DBC$$, we have
$$DB = DC$$ ......... (given)
Hence we obtain
$$\angle ABC - \angle DBC = \angle ACB - \angle DCB$$.
This gives
$$\angle ABD = \angle ACD$$. $$[hence \quad proved]$$
$$AB = AC \Rightarrow \angle ABC = \angle ACB$$
(angles opposite to equal sides.)
Again in $$\triangle DBC$$, we have
$$DB = DC$$ ......... (given)
$$\Rightarrow \angle DBC = \angle DCB$$ (angles opposite to equal sides).
Hence we obtain
$$\angle ABC - \angle DBC = \angle ACB - \angle DCB$$.
This gives
$$\angle ABD = \angle ACD$$. $$[hence \quad proved]$$
In given figure the altitudes AD, BE and CF of triangle ABC are equal. Prove that ABC is an equilateral triangle.
In right-angle triangles BCE and CBF, we have,
BC = BC (common hypotenuse);
BE = CF (given).
Hence BCF and CBF are congruent, by RHS theorem. Comparing the triangles, we get $$\angle B = \angle C$$.
This implies that
AC = AB (sides opposite to equal angles).
Similarly,
$$AD = BE \Rightarrow \angle B = \angle A$$
$$\Rightarrow AC = BC$$
Together, we get $$AB = BC = AC $$or $$\triangle ABC$$ is equilateral. $$[hence \quad proved]$$
BC = BC (common hypotenuse);
BE = CF (given).
Hence BCF and CBF are congruent, by RHS theorem. Comparing the triangles, we get $$\angle B = \angle C$$.
This implies that
AC = AB (sides opposite to equal angles).
Similarly,
$$AD = BE \Rightarrow \angle B = \angle A$$
$$\Rightarrow AC = BC$$
Together, we get $$AB = BC = AC $$or $$\triangle ABC$$ is equilateral. $$[hence \quad proved]$$
If $$\triangle ABC \cong \triangle NMO$$, name the congruent sides and angles.
Prove that the base angles of an isosceles trapezium are equal
Given: $$\overline {AB}=\overline {CD}$$
To Prove: $$\angle A=\angle D$$.
Proof:-
Let $$ABCD$$ is a trapezium with $$AB=CD.$$ Drop perpendiculars from $$B$$ and $$C$$ as shown in the above figure. So, we have $$BE$$ and $$CF$$ perpendicular to $$AD.$$
Now, in $$\triangle ABE $$ and $$\triangle CFD$$,
$$\overline {BE} = \overline {CF}\quad$$ (altitudes of trapezium)
$$\overline {AB}=\overline {CD}\quad$$ (Given)
$$\angle AEB = \angle DFC\quad$$ (right angle)
From $$R.H.S$$ congruence,
$$\triangle ABE \cong \triangle CFD$$
$$\angle A =\angle D\quad \dots \left[CPCT\right]$$
Hence proven base angles of an isosceles trapezium are equal.
Which minimum measurements do you require to check if the given figures are congruent:
Two rectangles
What are the minimum measurements required for two rhombuses to be congruent?
Suppose ABC is an isosceles triangle such that AB = AC and AD is the altitude from A on BC. Prove that (i) AD bisects $$\angle A$$, (ii) AD bisects BC.
We have to show that
$$\angle BAD = \angle CAD$$ and BD = DC.
In right triangles ADB and ADC, we have
AB = AC (given);
AD = AD (common side).
So by RHS congruency of triangles, we have $$\triangle ABD \cong \triangle ACD$$. Hence, $$\angle BAD = \angle CAD $$ and $$BD = DC$$.
$$\angle BAD = \angle CAD$$ and BD = DC.
In right triangles ADB and ADC, we have
AB = AC (given);
AD = AD (common side).
So by RHS congruency of triangles, we have $$\triangle ABD \cong \triangle ACD$$. Hence, $$\angle BAD = \angle CAD $$ and $$BD = DC$$.
State whether the following triangles are congruent or not? Give reasons for your answer
In the figure, it is given that AB = CD and AD = BC. Prove that triangles ADC and CBA are congruent.
State whether the following triangles are congruent or not? Give reasons for your answer.
In the adjoining figure, AB = CD and AD = BC. Show that $$\angle 1 = \angle 2$$
$$\triangle ABC$$ and $$\triangle DBC$$ are two isosceles triangles on the same base $$BC$$ (see figure). Show that $$\angle ABD =\angle ACD$$
Given $$\Delta ABC$$ and $$\Delta DBC$$ are two isosceles triangles on the same base BC
In isosceles $$\Delta ABC$$
$$AB=AC$$
Then $$\angle ABC=\angle ACB$$................................(1)
In isosceles $$\Delta BDC$$
$$BD=DC$$
Then $$\angle CBD=\angle BCD$$..................................(2)
Add (1) and (2) we get
$$\angle ABC+\angle CBD=\angle ACB+\angle BCD$$
But $$\Delta ABC$$ and $$\Delta DBC$$ on same base
$$\therefore \angle ABD=\angle ACD$$
$$l$$ and $$m$$ are two parallel lines intersected by another pair of parallel lines $$p$$ and $$q$$. Show that $$\triangle ABC\cong \triangle CDA$$
$$BE$$ and $$CF$$ are two equal altitudes of a triangle $$ABC$$. Using $$RHS$$ congruence rule, prove that the triangle $$ABC$$ is isosceles
$$\textbf{Step 1: Showing that the 2 angles of }\mathbf{\triangle ABC}\textbf{ are equal}$$
$$\text{In }\triangle BCF\text{ and }\triangle CBE$$
$$BC=BC\text{ (Common Side)}$$
$$BE=CF\text{ (Given)}$$
$$\therefore\triangle BCF\cong\triangle CBE\text{ (RHS criterion of congruence)}$$
$$\implies \angle FBC=\angle ECB\text{ (By CPCT)} $$
$$\textbf{Step 2: Proving triangle ABC is isosceles}$$
$$\angle FBC=\angle ECB$$
$$\implies \angle FBC=\angle ECB$$
$$\therefore AB=AC\text{ (Converse of isosceles triangle theorem)}$$
$$\therefore \triangle ABC \text{ is isosceles}$$
$$\textbf{Hence proved that triangle ABC is isosceles}$$
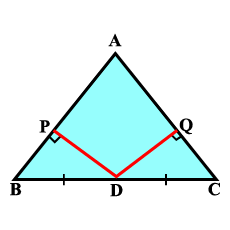
In the adjacent figure $$\triangle ABC, D$$ is the midpoint of $$BC$$. $$DE\perp AB, DF\perp AC$$ and $$DE = DF$$. Show that $$\triangle BED \cong \triangle CFD$$
From $$\triangle BED$$ and $$\triangle CFD$$
$$BD= CD$$ (D is a midpoit of BC)
$$DE =DF$$ (Given)
$$\angle DEB = \angle DFC$$ ($$DE \bot AB$$ and $$ DF \bot AC$$)
Thus,
$$\triangle BED \cong \triangle CFD$$ (By RHS)
In the adjacent figure $$\triangle ABC$$ is isosceles as $$\overline {AB} = \overline {AC}, \overline {BA}$$ and $$\overline {CA}$$ are produced to $$Q$$ and $$P$$ such that $$\overline {AQ} = \overline {AP}$$. Show that $$\overline {PB} = \overline {QC}$$
In given figure $$AD$$ is an altitude of an isosceles triangle $$ABC$$ in which $$AB = AC$$.
Show that, $$AD$$ bisects $$\angle A$$
In the adjacent figure $$ABCD$$ is a square and $$\triangle APB$$ is an equilateral triangle. Prove that $$\triangle APD\cong \triangle BPC$$
Given that $$APB$$ is an equilateral triangle, so the sides of an equilateral triangle are equal.
$$AP = BP$$ ...... (1)
and $$ABCD$$ is a square. All the sides of a square are equal.
$$AD = BC$$ .....(2)
and
$$\angle PAD=\angle DAB - \angle PAB=90^{0}-60^{0}=30^{0}$$
$$\angle PBC=\angle ABC - \angle PBA=90^{0}-60^{0}=30^{0}$$
$$\therefore \angle DAP=\angle BPC$$ ......(3)
So, from the $$S.A.S.$$ congruency,
$$\therefore \Delta APD\cong \Delta BPC$$
ABC is a right angled triangle in which $$\angle A = 90^{\circ}$$ and AB = AC. Show that $$\angle B = \angle C$$.
Given: $$ABC$$ is a right-angled triangle with $$\angle A =90^o$$ and $$AB=AC$$
Draw AD perpendicular from point A on line BC
In $$\Delta ADC$$ and $$\Delta ADB$$
$$AB=AC$$ ...Given
$$AD=AD$$ ...Common side
$$\angle ADC=\angle ADB = 90^o$$
Hence, by RHS congruence criterion,
$$\Delta ADC\cong ADB$$
$$\therefore \ \angle B=\angle C$$ ....CACT $$\quad [hence \ proved]$$
$$\triangle ABC$$ is an isosceles triangle in which $$AB = AC$$. Show that $$\angle B = \angle C$$
We have to draw $$AD$$ perpendicular to $$BC$$.
Since $$\triangle ABC$$ is isosceles, $$AB=AC.......(1)$$
Now, $$AD$$ perpendicular to $$BC$$
$$\therefore \angle ADB=\angle ADC=90^o.......(2)$$
In $$\triangle ABD$$ and $$\triangle ACD$$,
$$\angle ADB=\angle ADC=90^o$$ [From $$(2)$$]
$$AB=AC$$ [From $$(1)$$]
$$AD=AD$$ [common]
$$\triangle ABD \cong \triangle ACD$$ [$$RHS$$ Congruence Rule]
$$\therefore \angle B=\angle C$$ [by $$CPCT$$]
Line-segment $$AB$$ is parallel to another line-segment $$CD. O$$ is the mid-point of $$AD$$.
Show that $$O$$ is also the midpoint of $$BC$$.
If two sides of a triangle measure $$4cm$$ and $$6cm$$ find all possible measurement (positive Integers) of the third side. How many distinct triangles can be obtained?
In $$\triangle ABC$$, the bisector $$AD$$ of $$A$$ is perpendicular to side $$BC$$. Show that $$AB = AC$$ and $$\triangle ABC$$ is isosceles.
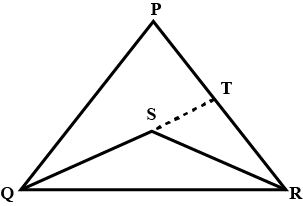
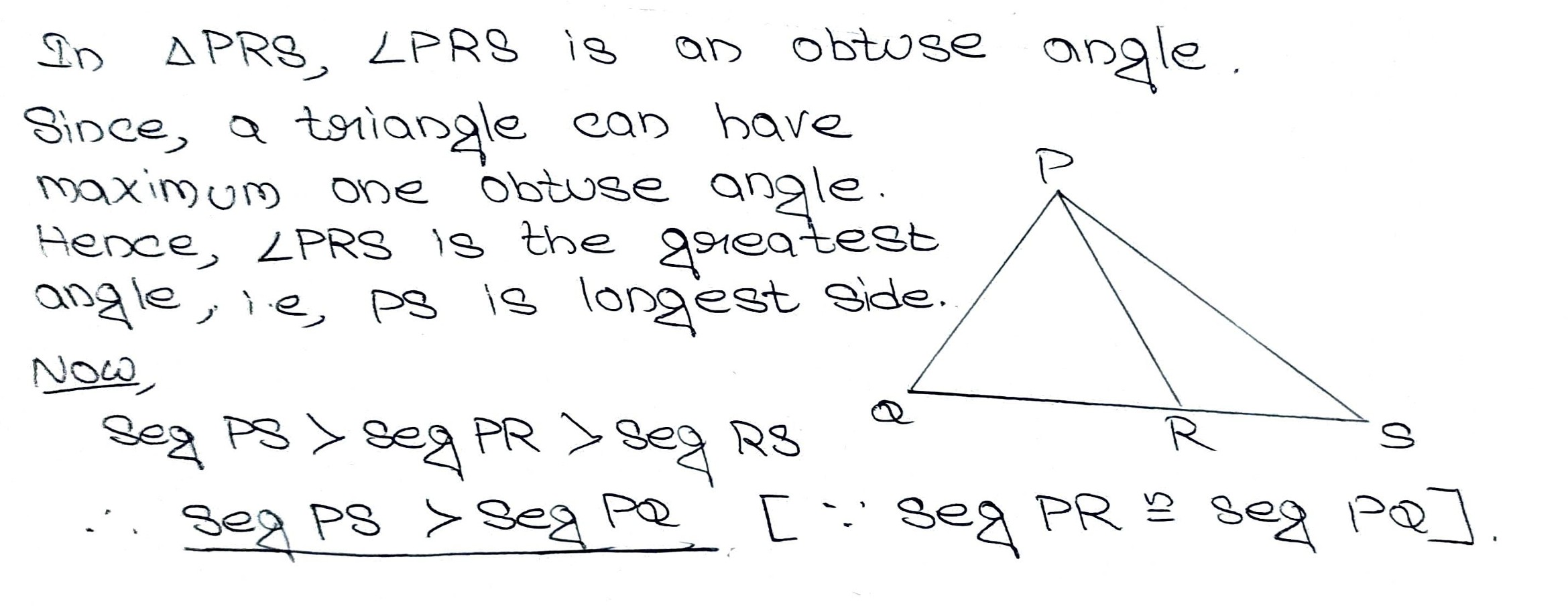
In adjacent figure, $$PR > PQ$$ and $$PS$$ bisects $$\angle QPR$$. Prove that $$\angle PSR > \angle PSQ$$
In the figure, $$AB\parallel DC$$ and $$AD\parallel BC$$ Show that $$\triangle ABC \cong \triangle CDA$$.
Show that in a right triangle, the hypotenuse is the longest side
Let $$ABC$$ be the right angled triangle in which $$\angle B=90^o$$
$$\therefore \angle A+\angle C=90^o$$
Since sum of all the angles of a triangle $$=180^o$$ [angle sum property]
$$\angle B=\angle A+\angle C$$
$$\Rightarrow \angle B > \angle A$$
and $$\angle B > \angle C$$
$$\Rightarrow AC > BC$$
$$\therefore$$ Side opposite to greater angle is longer and $$AC > AB$$
$$\therefore AC$$ is the longest side, i.e hypotenuse is the longest side.
In adjacent figure, $$\angle B < \angle A$$ and $$\angle C < \angle D$$. Show that $$AD < BC$$
In the given figure, $$AD$$ is perpendicular to $$BC$$ and $$EF \parallel BC$$, if $$\angle EAB = \angle FAC$$, show that triangles $$ABD$$ and $$ACD$$ are congruent.
Also, find the values of $$x$$ and $$y$$ if $$AB = 2x + 3, AC = 3y + 1, BD = x$$ and $$DC = y + 1$$
In the given figure, $$AL\parallel DC, E$$ is mid point of $$BC$$. Show that $$\triangle EBL\cong \triangle ECD$$
Consider $$\triangle EBL$$ and $$\triangle ECD$$
$$\angle BEL = \angle CED$$ (vertically opposite angles)
$$BE = CE$$ (since $$E$$ is mid point of $$BC$$)
$$\angle EBL = \angle ECD$$ (alternate interior angles)
$$\triangle EDL \cong \triangle ECD$$ (by ASA congruency)
$$\angle BEL = \angle CED$$ (vertically opposite angles)
$$BE = CE$$ (since $$E$$ is mid point of $$BC$$)
$$\angle EBL = \angle ECD$$ (alternate interior angles)
$$\triangle EDL \cong \triangle ECD$$ (by ASA congruency)
In the given figure, $$AB$$ and $$CD$$ intersect at $$'O', OA = OB$$ and $$OD = OC$$. Show that $$\triangle AOD \cong \triangle BOC$$.
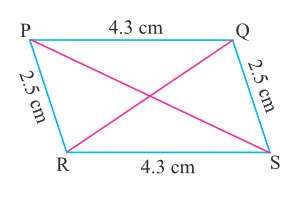
In the figure , $$PQSR$$ is a parallelogram.
$$PQ=4.3cm$$ and $$QR=2.5cm$$. Is $$\triangle PQR\equiv \triangle PSR$$?
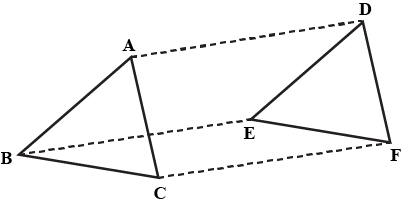
In $$\triangle^{s}ABC$$ and $$DEF, AB\parallel DE; BC = EF$$ and $$BC\parallel EF$$. Vertices, $$A, B$$ and $$C$$ are joined to vertices $$D, E$$ and $$F$$ respectively (see figure). Show that
$$\triangle ABC \cong \triangle DEF$$
In the figure, ABCD is a parallelogram is produced to E such that $$AB = BE$$. AD produced to F such that $$AD = DF$$. Show that $$\triangle FCD \cong \triangle CBE$$.
In figure, BO bisects $$\angle ABC$$ of $$\triangle ABC$$. P is any point on BO. Prove that the perpendicular drawn from P to BA and BC are equal.
In given figure $$D$$ is a point on side $$BC$$ of $$\triangle ABC$$ such that $$AD = AC$$. Show that $$AB > AD$$
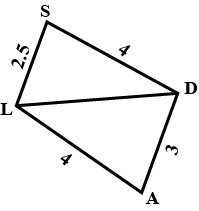
Prove that, if the areas of two similar triangles are equal, then they are congruent.
$$ABCD$$ is a parallelogram. $$AP$$ and $$CQ$$ are perpendicular lines drawn from vertices $$A$$ and $$C$$ respectively on diagonal $$BD$$ (see figure). Show that
$$\triangle APB\cong \triangle CQD$$
From the given figures, state whether the given pairs of triangles are congruent by SSS axiom
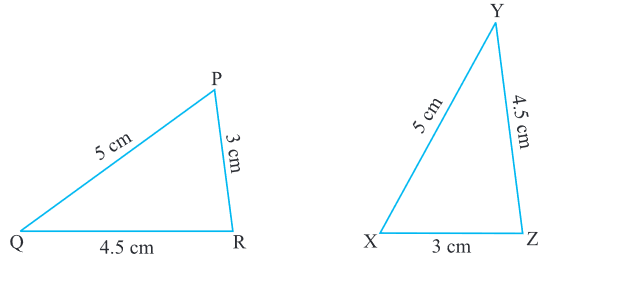
Decide whether the SSS congruence is true with the following figures. Give reasons
What additional information do you need to conclude that the two triangles given here under are congruent using SAS rule?(When$$\,\, HG = TR$$ $$ $$)
For the following congruent triangles, find the pairs of corresponding angles.
Decide whether the SSS congruence is true with the following figures. Give reasons
Complete the congruence statement.
$$\Delta QRS \cong $$
You want to show that $$\Delta ART \cong \Delta PEN$$,
If it is given that $$\angle T = \angle N$$ and you are to use SAS criterion, you need to have
(a) RT =______(b) PN =______
In Fig. $$AC = AE, AB = AD$$ and $$\angle BAD = \angle EAC$$. Show that $$BC = DE$$.
In the given figure, if $$AC=DC$$ and $$CB=CE$$, then prove that $$AB=DE$$ (State Euclid's A Used
$$O$$ is a point in the interior of a square $$ABCD$$ such that $$OAB$$ is an equilateral triangle show that $$\triangle OCD$$ is an isosceles triangle
Given, $$\Delta OAB$$ is an equilateral triangle,
$$\angle AOB=\angle OAB=\angle OBA=60^\circ$$
$$OA=AB=OB$$
Also it's given, $$ABCD$$ is a Square
$$\angle DCB=\angle BAD=\angle ABD=\angle CDA=90^\circ$$ ------ (ii)
$$DA=AB=CB=CD$$
Consider,
$$\angle OAB=\angle OBA=60^\circ$$ ------ (i)
$$\angle BAD=\angle ABD=90^\circ$$ ------ (ii)
Subtracting (i) from (ii), we get,
$$\angle BAD-\angle OAB=\angle ABD-\angle OBA=90^\circ-60^\circ=30^\circ$$
i.e., $$\angle DAO=\angle CBO=30^\circ$$ ------ (iii)
Now, in $$\triangle AOD$$ and $$\triangle BOC$$
$$AO=BO$$ [$$\Delta OAB$$ is an equilateral triangle]
$$\angle DAO=\angle CBO=30^\circ$$ [from (iii)]
$$AD=BC$$ [$$ABCD$$ is a square]
Hence, by $$SA$$ congruence criterion,
$$\triangle AOD \cong \triangle BOC$$
Hence, $$ DO=OC$$
$$\therefore \Delta OCD$$ is an isosceles triangle. $$\quad \quad [Hence\ proved]$$
Prove that the lines:
$$(a+b)x+(a-b)y-2ab=0.......(1)$$
$$(a-b)x+(a+b)y-2ab=0.......(2)$$
and $$x+y=0......(3)$$ form an isosceles triangle whose vertical angle is $$2\tan ^{ -1 }{ \left( a/b \right) } $$.
Slopes of the given lines are respectively
$$-\cfrac { a+b }{ a-b } ,-\cfrac { a-b }{ a+b } ,-1$$
The triangle will be isosceles if $$x+y=0$$ is equally inclined to other two whose slopes are written above
$$\cfrac { -1+\left( \cfrac { a+b }{ a-b } \right) }{ 1+\left( \cfrac { a+b }{ a-b } \right) } =-\cfrac { -1+\left( \cfrac { a+b }{ a-b } \right) }{ 1+\cfrac { a-b }{ a+b } } =\tan { \theta } \quad $$
$$\therefore \tan { \theta } =b/a\quad $$
$$\therefore$$ $$\triangle$$ is isosceles whose vertical angle is
$$\pi -2\theta =2\left( \cfrac { \pi }{ 2 } -\tan ^{ -1 }{ \cfrac { b }{ a } } \right) =2\left( \cot ^{ -1 }{ \cfrac { b }{ a } } \right) =2\tan ^{ -1 }{ \cfrac { a }{ b } } $$
$$-\cfrac { a+b }{ a-b } ,-\cfrac { a-b }{ a+b } ,-1$$
The triangle will be isosceles if $$x+y=0$$ is equally inclined to other two whose slopes are written above
$$\cfrac { -1+\left( \cfrac { a+b }{ a-b } \right) }{ 1+\left( \cfrac { a+b }{ a-b } \right) } =-\cfrac { -1+\left( \cfrac { a+b }{ a-b } \right) }{ 1+\cfrac { a-b }{ a+b } } =\tan { \theta } \quad $$
$$\therefore \tan { \theta } =b/a\quad $$
$$\therefore$$ $$\triangle$$ is isosceles whose vertical angle is
$$\pi -2\theta =2\left( \cfrac { \pi }{ 2 } -\tan ^{ -1 }{ \cfrac { b }{ a } } \right) =2\left( \cot ^{ -1 }{ \cfrac { b }{ a } } \right) =2\tan ^{ -1 }{ \cfrac { a }{ b } } $$
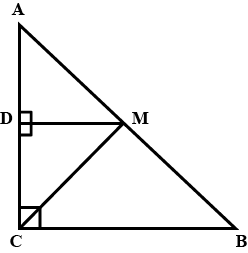
In a right angled triangle, prove that the line segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse.
Prove that in a $$\triangle PQR$$ if $$QR^{2} = PQ^{2} + PR^{2}$$ then $$\angle P$$ is a right angle.
Construction:
Draw a $$\Delta ABC$$ right angled at $$A$$ such that
$$AB=PQ$$
$$CA=RP$$
Now
In $$\Delta ABC$$, $$\angle A=90^{\circ}$$
By Pythagoras Theorem, $$(BC)^{2}=(CA)^{2}+(AB)^{2}$$
As $$AB=PQ$$ and $$CA=RP$$
$$(BC)^{2}=(RP)^{2}+(PQ)^{2}$$ (1)
Given: $$(QR)^{2}=(RP)^{2}+(PQ)^{2}$$ (2)
Hence from (1) and(2) $$BC=QR$$
In $$\Delta ABC$$ and $$\Delta PQR$$
$$AB=PQ$$ (from construction)
$$CA=RP$$ (from construction)
$$BC=QR$$
$$\Delta ABC\cong\Delta PQR$$ (By SSS congruence)
So $$\angle A=\angle P=90^{\circ}$$
Hence proved.
Prove that the inequality $$R \geqslant 2r$$ (R and r are the radii of the circumscribed and the inscribed circle) holds true in any triangle, and the equality R = 2r holds only. for a regular triangle.
I and $$m$$ are two parallel line intersected by another pair of parallel line $$p$$ and $$q$$ Fig Show taht $$\Delta ABC \cong \Delta CDA$$.
In the adjoining figure, $$D$$ and $$E$$ are points on the side $$BC$$ of $$\triangle ABC$$ such that $$BD=EC$$ and $$AD=AE$$. Show that $$\triangle ABD\cong \triangle ACE$$.
A round balloon of radius r subtends an angle $$\alpha$$ at the eye of the observer, while the angle of elevation of its centre is $$\beta$$. Prove that the height of the centre of the balloon is $$r \sin\beta\ \text{csc}\dfrac{\alpha}{2}$$.
Let $$O$$ be the centre of the balloon and $$P$$ be the eye of the observer
And $$\angle APB$$ be the angle subtended by the balloon
$$ \therefore \angle APB=\alpha $$
$$ \therefore \angle APO=\angle BPO=\cfrac { \alpha }{ 2 } $$
In $$\triangle OAP,\sin { \cfrac { \alpha }{ 2 } } =\cfrac { OA }{ OP } $$
$$\implies \sin { \cfrac { \alpha }{ 2 } } =\cfrac { r }{ OP } $$
$$\implies OP=r\text{ cosec }{ \cfrac { \alpha }{ 2 } } -(1)$$
In $$\triangle OPC$$
$$\sin { \beta } =\cfrac { OL }{ OP }$$ or $$OL=OP\sin { \beta } $$
$$ \therefore OL=r\text{ cosec }{ \cfrac { \alpha }{ 2 } } \sin { \beta } $$
Show by diagram any two real-life examples for congruent shapes.
If O is a point within a quadrilateral ABCD, prove that ; $$OA + OB + OC + OD > AC + BD$$.
In $$\Delta OAC$$
$$OA+OC > AC$$ _____ (1)
(sum of two sides of a $$\Delta $$ is greater than third side)
similarity in $$\Delta OBD$$
$$OB+OD > BD$$ _______ (2)
(1)+(2)
$$OA+OB+OC+OD > AC+BD$$
It is to be established by $$RHS$$ congruence rule that $$\triangle ABC\cong \triangle RPQ$$. What additional information is needed, if it is given that $$\angle B=\angle P=90^o$$ and $$AB=RP$$?
For two right angle triangles to be congruent, we need to show two corresponding parameters as equal, with one of them as side for sure.
$$\begin{array}{l} { { Since } },\, \, \Delta ABC\cong \Delta RPQ \\ and\; AB=RP \\ Any\ one\ of\ these\ conditions \ is\ required:\\ \;\ AC=RQ\\ \; BC=PQ \\ \angle BAC=\angle PRQ \\ and\, \, \angle ACB=\angle RQP \end{array}$$
$$\begin{array}{l} { { Since } },\, \, \Delta ABC\cong \Delta RPQ \\ and\; AB=RP \\ Any\ one\ of\ these\ conditions \ is\ required:\\ \;\ AC=RQ\\ \; BC=PQ \\ \angle BAC=\angle PRQ \\ and\, \, \angle ACB=\angle RQP \end{array}$$
In the following figure $$\angle B < \angle A$$ and $$\angle C < \angle D$$, show that $$AD < BC$$.
From figure.
$$ AO < BO $$ (side opposite to greater angle is long )
$$ OD < OC (\quad " \quad " \quad ) $$
$$ AO + OD < BO + OC $$
$$ AD < BC $$ Hence proved.
Let $$x,\ x+1,\ x+2$$, be the lengths of the three sides of a triangle.
(i) Write down the three inequations in x, each of which represents the given statement.
(ii) List the set of possible values of x which satisfy all the three inequations obtained in your answer to part (i) above, given that x is an integer.
Given that $$ABCD$$ is a quadrilateral. Is $$AB+BC+CD+DA<2(AC+BD)?$$
As we know that the sum of lengths of any two sides in a triangle should be greater than the length of third side-
Therefore,
In $$\triangle AMB, \ AB < MA + MB$$ …….(i)
In $$\triangle BMC, \ BC < MB + MC$$ …….(ii)
In $$\triangle CMD,\ CD<MD+MC$$ ..….(iii)
In $$\triangle AMD,\ DA < MD + MA$$ …….(iv)
On adding equation (i), (ii), (iii) and (iv), we get
$$ AB + BC + CD + DA < 2MA + 2MB + 2MC + 2MD $$
$$ AB + BC + CD + DA < 2[(AM + MC) + (DM + MB)] $$
Since, $$AC=AM+MC\ and\ BD=BM+MD$$
Hence,
$$ AB + BC + CD + DA < 2(AC + BD) $$
It is proved.
If $$AB>AC$$ and length of median from $$C$$ is $$4$$ units, then the length of median from $$B$$ can be-
$$CN=\cfrac { 1 }{ 2 } \sqrt { 2({ AC }^{ 2 }+{ BC }^{ 2 })-{ AB }^{ 2 } } $$
$$\implies\quad Y=\cfrac { 1 }{ 2 } \sqrt { 2({ AC }^{ 2 }+{ BC }^{ 2 })-{ AB }^{ 2 } } $$
$$\implies\quad 2({ AC }^{ 2 }+{ BC }^{ 2 })-{ AB }^{ 2 }=64\quad$$ -(1)
$$\implies\quad 2{ BC }^{ 2 }=64+{ AB }^{ 2 }-{ 2AC }^{ 2 }\quad $$-(2)
$$ BP=\cfrac { 1 }{ 2 } \sqrt { 2({ AB }^{ 2 }+{ BC }^{ 2 })-{ AC }^{ 2 } }$$
$$\implies\quad BP=\cfrac { 1 }{ 2 } \sqrt { 2({ AB }^{ 2 }+{ BC }^{ 2 })-{ AC }^{ 2 } } $$
using(2)
$$\implies\quad BP=\cfrac { 1 }{ 2 } \sqrt { 2{ AB }^{ 2 }+64+{ AB }^{ 2 }-{ 3AC }^{ 2 } } $$
$$\implies\quad BP=\cfrac { 1 }{ 2 } \sqrt { 64+3({ AB }^{ 2 }-{ AC }^{ 2 }) } $$
$$\because $$AB>AC
$$\therefore $$AB-AC>0 -(3)
$$\implies\quad BP=\cfrac { 1 }{ 2 } \sqrt { 64+3(AB-AC)(AB+AC) } $$ using(3)
$$ BP=\cfrac { 1 }{ 2 } \sqrt { 64+3(AB-AC)(AB+AC) } >\cfrac { 1 }{ 2 } \sqrt { 64+0 } $$
$$\implies BP>\cfrac { 1 }{ 2 } \times 8$$
$$\implies$$ BP>4 (BP=length of median from B)
In the given figure, $$\triangle CDE$$ is an equilateral triangle on a side $$CD$$ of a square $$ABCD$$. Show that $$\triangle ADE \cong \triangle BCE$$.
$$AB$$ is a line segment and $$P$$ is its mid-point. $$D$$ and $$E$$ are points on the same side of $$AB$$ such that $$\angle BAD=\angle ABE$$ and $$\angle EPA=\angle DPB$$. Show that
i) $$\triangle DAP\cong \triangle EBP$$
ii) $$AD=BE$$
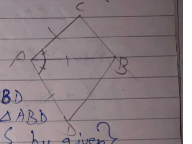
Given :- $$AC=AD$$
$$\angle CAB= \angle BAD$$
To prove :- $$\triangle ABC \cong \triangle ABD$$
Proof :- $$9n \triangle ABC$$ & $$\triangle ABD$$
$$AC=AD$$
$$\angle CAB= \angle BAD$$
$$AB=BA$$
$$\triangle ABC \cong \triangle ABD$$
$$BC=BD$$
$$\begin{array}{l} Given\, \, \angle CAB=\angle BAD \\ In\, \, \Delta CAB\, \, and\, \, DAB \\ AB=AB\, \, \left( { common } \right) \\ \angle CAB=\angle DAB\, \, \left( { given } \right) \\ AC=AD\, \, \left( { given } \right) \\ By\, \, S.A.S.\, \, congruency \\ \Delta CAB\cong DAB \\ \therefore BC=BD \end{array}$$
Prove that sum of any two sides of a triangle is greater than the third side.
Construction: In $$\Delta ABC$$, extend $$AB$$ to D in such a way that $$AD = AC$$.
In $$\Delta DBC$$, as the angles opposite to equal sides are always equal, so,
$$\angle ADC = \angle ACD$$
Therefore,
$$\angle BCD > \angle BDC$$
As the sides opposite to the greater angle is longer, so,
$$BD > BC$$
$$AB + AD > BC$$
Since $$AD = AC$$, then,
$$AB + AC > BC$$
Hence, sum of two sides of a triangle is always greater than the third side.
In the adjoining figure. AB = AC and BD = DC. Prove that $$ \Delta ADB\, \cong \,\Delta ADC$$ and hence show that
(i) $$\angle ADB\, = \,\angle ADC\,\,$$
(ii) $$\angle BAD\, = \,\angle CAD$$
The length of two sides of a triangle are $$5\ cm$$ and $$7\ cm$$. Between what two measures should the length of the third side fall?
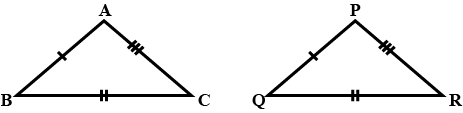
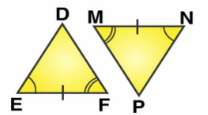
In the example given, a pair of triangles is shown. Equal parts of triangles in pairs are marked with the same signs. Observe the figures and state the test by which the triangles in pair are congruent.
$$AB = PQ$$
$$BC = QR$$
$$AC = PR$$
$$SQ$$ by SSS property
$$\Delta ABC \cong \Delta PQR$$
In triangles $$ABC$$ and $$PQR, \angle A = \angle Q$$ and $$\angle B = \angle R$$. Which side of $$\Delta PQR$$ should be equal to side $$BC$$ of $$\Delta ABC$$ so that the two triangle are congruent? Give reason for your answer.
First draw the triangles and given $$\angle A=\angle Q$$ & $$\angle B=\angle R$$
So, to prove that two triangles are congruent.
$$BC=RP$$
So, we can say that $$\Delta ABC\cong \Delta QRP$$
So, we can say that $$RP$$ of $$\Delta PQR$$ should be equal to side $$BC$$ of $$\Delta ABC$$.
"If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent". Is the statement true? Why?
Line $$l$$ is the bisector of an angle $$\angle{A}$$ and $$B$$ is any point on $$l.\,\,BP$$ and $$BQ$$ are perpendiculars from $$B$$ to the arms of $$\angle{A}$$Show that$$(i)\triangle{APB}\cong\triangle{AQB}$$$$(ii)BP=BQ$$ or $$B$$ is equidistant from the arms of $$\angle{A}$$
S is any point on side QR of a $$\Delta PQR$$. Show that : PQ + QR + RP > 2 PS
Theorem: In a triangle , sum of the length of any two sides is greater than the third side.
Draw the triangle and join the points $$P$$ and $$S$$
In the figure,
In $$ \Delta PQS$$, according to the theorem,
$$PQ+QS>PS$$ ........... (1)
In $$ \Delta PSR$$, according to the theorem,
$$PR+SR>PS$$ ........... (2)
Adding (1) and (2),
$$PQ+QS+SR+PR>PS+PS$$
$$PQ+(QS+SR)+PR>2PS$$
$$PQ+QR+PR>2PS$$
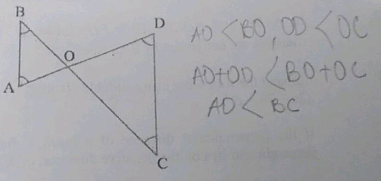
In $$\Delta$$ABC, side $$AB$$ is produced to $$D$$ such that $$BD=BC$$. If $$\angle CAB=70^o$$ and $$\angle CBA=60^o$$, prove that $$AD>AC$$.
$$AB$$ is a line segment and $$P$$ is its mid-point. $$D$$ and $$E$$ are points on the same side of $$AB$$ such that $$\angle BAD =\angle ABE$$ and $$\angle EPA =\angle DPB$$. Show that $$\Delta DAP \cong \Delta EBP$$.
$$\angle BAD=\angle ABE\Rightarrow \angle PAD=\angle PBE$$
$$\angle EPA=\angle DPB$$
$$\Rightarrow \angle DPA+\angle EPD=\angle EPD+\angle EPB$$
$$\Rightarrow \angle DPA=\angle EPB$$
$$\therefore $$ In $$\Delta DAP$$ and $$\Delta EBP$$
$$\angle PAD=\angle PBE - (i)$$
$$AP=BP - (ii)$$ (given)
$$\angle DPA=\angle EPB - (iii)$$
$$\therefore \Delta DAP \cong \Delta EBP$$ by ASA test of congruence.
In $$\Delta$$ABC, side AB is produced to D such that BD$$=$$BC. If $$\angle A=70^o$$ and $$\angle B=60^o$$, prove that AD$$>$$CD.
$$AB$$ is a line segment and $$P$$ is its mid-point. $$D$$ and $$E$$ are points on the same side of $$AB$$ such that $$\angle BAD =\angle ABE$$ and $$\angle EPA =\angle DPB$$. Show that $$AD=BE$$.
$$\angle BAD=\angle ABE\Rightarrow \angle PAD=\angle PBE$$
$$\angle EPA=\angle DPB$$
$$\Rightarrow \angle DPA+\angle EPD=\angle EPD+\angle EPB$$
$$\Rightarrow \angle DPA=\angle EPB$$
$$\therefore $$ In $$\Delta DAP$$ and $$\Delta EBP$$
$$\angle PAD=\angle PBE - (i)$$
$$AP=BP - (ii)$$
$$\angle DPA=\angle EPB - (iii)$$
$$\therefore \Delta DAP \cong \Delta EBP$$ by ASA test of congruence
$$\because$$ Two triangle are congruent
$$\therefore$$ Corresponding sides should be equal
$$AD = BE$$ (proved)
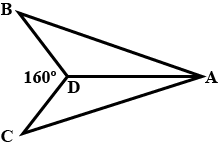
In the figure $$AB=AC,BD=DC,\angle C=40^{o}\angle BDC=160^{o}$$
Write the measure of all angles of triangle $$ABD$$.
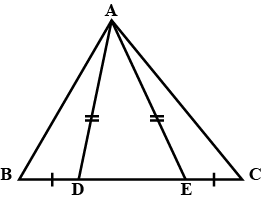
$$D$$ is any point on side $$AC$$ of a $$\Delta ABC$$ with $$AB = AC$$. Show that $$CD < BD.$$
Consider the diagram shown below.
Given:
$$AB=AC$$
To prove:
$$CD<BD$$
Proof:
$$\angle ABC=\angle ACB$$ (Isosceles Triangle) …… (1)
Here,
$$\angle ABC = \angle CBD+\angle DBA$$
$$\therefore \angle ABC>\angle CBD$$
Also, $$\Rightarrow \angle ACB = \angle DCB>\angle CBD$$ {Because $$\angle ABC = \angle DCB = \angle ACB$$}
Therefore,
$$CD<BD$$ (Converse of Angle opposite to greater side is greater in a triangle)
Hence, proved.
$$ABCD$$ is a quadrilateral in which $$AD=BC$$ and $$\angle DAB=\angle CBA.$$ Prove that $$BD =AC.$$
Let $$ABC$$ be an isosceles triangle with $$AB=AC$$ and let $$D, E, F$$ be the mid-point of $$BC, CA$$ and $$AB$$ respectively. Show that $$AD\bot EF$$ and $$AD$$ is bisected by $$EF$$.
AD is an altitude of an isosceles triangle ABC in which $$AB=AC$$. show that
(i) AD bisects BC
(ii) AD bisects $$\angle A$$
$$\Delta ABC$$
$$AD\perp BC$$
$$AB=AC........$$(Given)
$$AD=AD.......$$(Common Side)
$$\angle ADB=\angle ADC=90^{\circ}$$
$$AD\perp BC$$
$$AB=AC........$$(Given)
$$AD=AD.......$$(Common Side)
$$\angle ADB=\angle ADC=90^{\circ}$$
By $$RHS$$ criteria
$$\Delta ADB\cong \Delta ADC$$
$$\implies BD=DC\implies AD$$ bisects $$BC$$
$$\implies \angle BAD=\angle CAD\implies AD$$ bisects $$\angle A$$
AM is a median of a triangle $$ABC$$.
Is $$AB + BC + CA > 2 AM$$?
(Consider the sides of triangles $$\Delta ABM$$ and $$\Delta ABM$$.)
In the given figure, $$\angle B < \angle A$$ and $$\angle C < \angle D$$, show that $$AD < BC$$.
Let the point of intersection of $$BC$$ and $$AD$$ be $$O$$
In $$\triangle ABO$$
$$\Rightarrow \angle B<\angle A$$
Thereore, $$\Rightarrow AO<BO$$ $$(1)$$ (side opposite to greater angle is largest)
Similarly,
In $$\triangle COD$$
$$\Rightarrow \angle C<\angle D$$
Thereore, $$\Rightarrow DO<CO$$ $$(2)$$ (side opposite to greater angle is largest)
Adding $$(1)$$ and $$(2)$$ we get,
$$\Rightarrow BO+OC>AO+DO$$
$$\Rightarrow BC>AD$$
Hence proved.
In Fig., $$D$$ and $$E$$ are points on side $$BC$$ of a $$\triangle ABC$$ such that $$BD = CE$$ and $$AD = AE$$. Show that $$\triangle ABD \cong \triangle ACE$$.
Prove that any two sides of a $$\Delta$$ are together greater than twice the median drawn to the third side.
Given:Triangle ABC in which AD is the median.
To prove: $$AB+AC>2AD$$
Proof:In $$ΔADB$$ and $$ΔEDC$$
$$AD=DE$$ [By construction]
D is the midpoint BC.[$$DB=DB$$]
$$ΔADB=ΔEDC$$ [vertically opposite angles]
Therefore $$ΔADB≅ ΔEDC$$ [By SAS congruence criterion.]
$$AB=ED$$ [Corresponding parts of congruent triangles]
In$$ΔAEC$$, $$AC+ED>AE$$[sum of any two sides of a triangle is greater than the third side]
$$AC+AB>2AD$$ [$$AE=AD+DE=AD+AD=2AD $$ and $$ED=AB$$]
In quadrilateral $$ACBD$$
$$AQC=AD$$ and $$AB$$ bisects $$\angle{A}$$ (see figure). Show that $$\triangle{ABC}\cong \triangle{ABD}$$.
What can you say about $$BC$$ and $$BD$$?
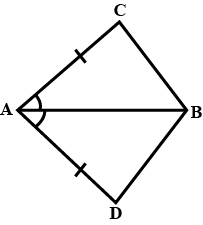
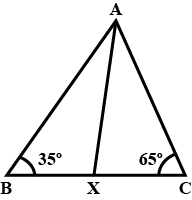
In figure, $$ABC$$ is a triangle with $$\angle B = 35^{\circ}, \angle C = 65^{\circ}$$ and bisector of $$\angle BAC$$ meets $$BC$$ in $$X$$. Arrange $$AX, BX$$ and $$CX$$ in descending order.
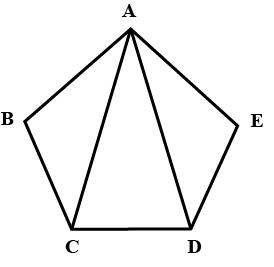
$$ABCDE$$ is a regular pentagon having all the sides and angles equal. Show that $$\triangle ABC \cong \triangle AED$$.
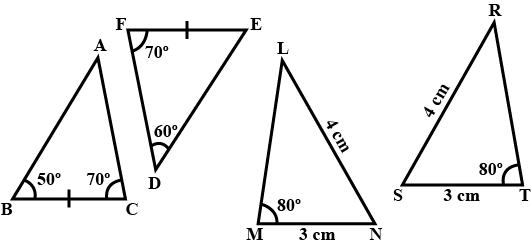
$$ABC$$ is an isosceles triangle with $$AB = AC$$ and $$BD$$ and $$CE$$ are its two medians. Show that $$BD = CE$$.
In the square $$ABCD$$ show that the two triangles $$ABC$$ and $$ADC$$ are congruent to each other
we have,
In the square $$ABCD$$
Construct:- Draw diagonal $$AC$$then makes two $$\Delta ABC\,\And \,\Delta ADC$$
Prove that:-$$\Delta ABC\cong \Delta ADC$$
Proof:- In $$\Delta ABC\,\And \,\Delta ADC$$
$$AB=DC\,\,\,\,\,\,\,\left( sides\,of\,square \right) $$
$$ AD=BC\,\,\,\,\,\,\,\left( sides\,of\,square \right) $$
$$ AC=AC\,\,\,\,\,\,\,\left( common \right) $$
Hence, $$\Delta ABC\cong \Delta ADC$$ $$\left( by\,SSS\,congruency \right)$$
Hence proved.
If two angles of a triangle are equal, then prove that sides opposite to them are also equal.
$$\angle C=\angle B$$
In $$\triangle ABD$$ & $$\triangle ACB$$
$$\angle B=\angle C$$ (Given)
$$\angle BAD=\angle CAD$$ (construction)
$$AD=AD$$
$$\triangle ABD\cong \triangle ACD$$
$$AB=AC$$
In a triangle $$ABC$$ median $$AD$$ is produced to $$X$$ such that $$AD+DX$$. Prove that $$ABXC$$ is a parallelogram.
State whether the following triangles are congruent or not? Give reasons for your answer.
In the adjoining figure, $$BA \bot AC, \, DE \bot DF$$ such that $$BA = DE$$ and $$BF = EC$$. Show that $$\Delta ABC \cong \Delta DEF$$
$$ABCD$$ is a quadrilateral
Prove that $$(AB+BC+CD+DA)>(AC+BD)$$
$$(AB+BC+CD+DA)>(AC+BD)$$
$$ABCD$$ is a quadrilateral and $$AC$$ and $$BD$$ are diagonals.
Sum of the two sides of $$\triangle$$ is greater than the third side $$\triangle ABC, BCD, CAD$$ and $$BAD$$
$$AB+BC>AC$$
$$CD+AD>AC$$
$$AB+AD>BD$$
$$BC+CD>BD$$
Adding all the above equation
$$2(AB+BC+CA+AD)>2(AC+BD)$$
$$\Rightarrow (AB+BC+CA+AD)>(AC+BD)$$
HP
In $$\Delta ABC,$$ $$AB<AC,$$ $$PB$$ and $$PC$$ are the bisectors of $$\angle B$$ and $$\angle C.$$ Prove that $$PB< PC.$$
In the figure.
The angle opposite to a larger side is larger than the angle opposite to a smaller side.
It is given
$$AB < AC$$
$$BP$$ is the bisector of $$\angle B$$
So,
$$\angle 1=\angle 2 =\dfrac12 \angle B$$
$$CP$$ is bisector of $$\angle C$$
$$\angle 3=\angle 4=\dfrac12 \angle C$$
Angle opposite to $$AB$$ is $$\angle C$$ and angle opposite to $$AC$$ is $$\angle B.$$
Now, from the property
As $$AB < AC$$
So,
$$\angle C<\angle B$$
$$\Rightarrow \dfrac12\angle C<\dfrac12 \angle B$$
$$\Rightarrow \angle 4<\angle 2$$
Side opposite to $$\angle 2$$ is $$PC$$ and side opposite to $$\angle 4$$ is $$PB.$$
Hence,
$$\angle 4<\angle 2$$
$$\Rightarrow PB < PC$$
Hence, Proved.
$$l, m$$ and $$n$$ are three parallel lines intersected by transversals $$p$$ and $$q$$ such that $$l, m$$ and $$n$$ cut off equal intercepts $$AB$$ and $$BC$$ on $$p$$. Show that $$l, m$$ and $$n$$ cut off equal intercepts $$DE$$ and $$EF$$ on $$q$$ also.
If $$\Delta$$MNO$$\cong\Delta$$QPR, write the six corresponding parts.
$$\begin{array}{l} \Delta MNO\cong \Delta QPR \\ MN=QP \\ MO=QR \\ NO=PR \\ and \\ \angle NMO=\angle PQR \\ \angle MNO=\angle QPR \\ \angle MON=\angle QRP \end{array}$$
In the quadrilateral $$ABCD,AD=CD$$ and $$\angle A ={90}^{o}=\angle C$$, prove that $$AB=BC$$.
$$D$$ is a point on the side $$BC$$ of a $$\triangle ABC$$ such that $$\angle ADC=\angle BAC$$, then prove that $$CA^2 = CB \times CD$$
Data: D is a point on the side BC of a triangle $$\triangle ABC$$ such that $$\angle ADC = \angle BAC.$$
To Prove: $$CA^{2} = CB \times CD$$
Let $$\angle ADC = \angle BAC = 100^\circ$$
In $$\triangle ABC,$$ if $$\angle B = 50^\circ,$$ then $$\angle C = 30^\circ$$
In $$\triangle ADC,$$ if $$\angle C = 30^\circ,$$ then $$\angle DAC = 50^\circ$$
In $$\triangle BCP, \angle A = 100^\circ, \angle B = 50^\circ, \angle C = 30^\circ$$
In $$\triangle ADC, \angle ADC = 100, \angle DAC = 50^\circ, \angle ACD = 30^\circ$$
Similarity criterion of $$\triangle$$ is A.A.A.
$$\therefore$$ In $$\triangle ABC$$ and $$\triangle ADC,$$
$$\dfrac{CA}{BC} = \dfrac{DC}{CA}$$
$$\therefore CA \times CA = BC \times DC$$
$$\therefore CA^{2} = BC \times DC.$$
Let $$\angle ADC = \angle BAC = 100^\circ$$
In $$\triangle ABC,$$ if $$\angle B = 50^\circ,$$ then $$\angle C = 30^\circ$$
In $$\triangle ADC,$$ if $$\angle C = 30^\circ,$$ then $$\angle DAC = 50^\circ$$
In $$\triangle BCP, \angle A = 100^\circ, \angle B = 50^\circ, \angle C = 30^\circ$$
In $$\triangle ADC, \angle ADC = 100, \angle DAC = 50^\circ, \angle ACD = 30^\circ$$
Similarity criterion of $$\triangle$$ is A.A.A.
$$\therefore$$ In $$\triangle ABC$$ and $$\triangle ADC,$$
$$\dfrac{CA}{BC} = \dfrac{DC}{CA}$$
$$\therefore CA \times CA = BC \times DC$$
$$\therefore CA^{2} = BC \times DC.$$
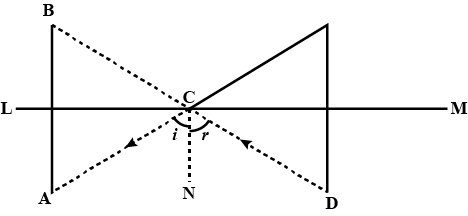
The image of an object placed at a point A before a plane mirror $$LM$$ is seen at the point $$B$$ by an observer at $$D$$ as shown in Fig. Prove that the image is as far behind the mirror as the object is in front of the mirror.
If $$P$$ is a point in the interior of $$\triangle ABC$$ then fill in the blanks with $$>$$ or $$<$$ or $$=$$.
(i) $$PA+PB.........AB$$
(ii) $$PB+PC........BC$$
(iii) $$AC.........PA+PC$$
Prove that the diagonals of a parallelogram bisect each other
$${\textbf{Step - 1: Showing congruency}}$$
$${\text{In }}\vartriangle {\text{AOB and }}\vartriangle {\text{COD,}}$$
$$\angle {\text{1 = }}\angle {\text{2 (alternate angles)}}$$
$$\angle {\text{3 = }}\angle {\text{4 (alternate angles)}}$$
$${\text{AB = CD (opposite sides of a parallelogram are equal)}}$$
$${\text{By ASA, }}\vartriangle {\text{AOB }} \cong {\text{ }}\vartriangle {\text{COD}}$$
$${\textbf{Step - 2: Proving diagonals bisect each other}}$$
$${\text{Since }}\vartriangle {\text{AOB and }}\vartriangle {\text{COD are congruent,}}$$
$$\therefore {\text{ AO = OC and BO = OD}}$$
$$ \Rightarrow {\text{ O is the midpoint of AC and BD}}$$
$$ \Rightarrow {\text{ Diagonals of parallelogram bisect each other}}$$
$${\textbf{Hence, Proved}}$$
In the figure given below , OL is perpendicular to AB and OM is perpendicular to BC such that OL = OM. Is $$\Delta OLB \cong \Delta OMB$$?
The lengths of the two sides of a triangle are $$6$$cm and $$10$$cm. Between what two wholes numbers should lie the measure of the third sides?
$$ABCD$$ is a trapzium in which $$AB||CD$$ and $$AD=BC$$. Show that
$$\angle A=\angle B$$
$$ABCD$$ is a trapzium in which $$AB||CD$$ and $$AD=BC$$. Show that $$\triangle ABC \cong \triangle BAD$$
Ref. image (I)
Given : ABCD is a trapezium where $$AB || CD $$ and $$AD = BC$$
To prove : $$\triangle ABC \cong \triangle BAD$$
Construction : Extend $$AB$$ and draw a line through $$C$$ parallel to $$DA $$ intersecting $$AB$$ produced at $$E$$
Proof :
$$AD || CE$$ (From construction) & $$AE || DC$$ (As $$AB || DC, \ \& \ AB$$ is extended)
In $$AECD$$, both pair of opposite sides are parallel, $$AECD$$ is a parallelogram
$$\therefore AD = CE$$ (Opposite sides of parallelogram are equal) ......... Ref. image (III)
But $$AD = BC$$ (Given)
$$\Rightarrow BC = CE$$
So, $$\angle CEB = \angle CBE$$ (In $$\Delta BCE$$, Angles opposite to equal sides are equal) ...(1)
For $$AD || CE$$ & $$AE$$ is the transversal
$$\angle A + \angle CEB = 180^{\circ}$$.........(Interior angle on same side of transversal is supplementary)
$$\angle A = 180^{\circ} - \angle CEB$$ ...(2)
Also $$AE$$ is a line,
So, $$\angle B + \angle CBE = 180^{\circ}$$ (Linear pair)
$$\angle B + \angle CEB = 180^{\circ} $$ (From (1))
$$\angle B = 180^{\circ} - \angle CEB$$ ...(3)
From (2) & (3)
$$\angle A = \angle B$$ ...............(4)
Now, Ref. image II
In $$\Delta ABC$$ and $$\Delta BAD$$
$$AB = BA$$ (common)
$$\angle B = \angle A$$ (Proved in part (i))
$$BC = AD$$ (Given)
$$\therefore \Delta ABC \cong \Delta BAD$$ (SAS congruence rule)
$$ABCD$$ is a trapezium in which $$AB||CD$$ and $$AD=BC$$, then show that $$\angle C=\angle D.$$
Let the line $$AB$$ is extended up to point E such that $$AD||EC$$
& $$AE||DC$$
in $$AECD$$ both pair of opposite sides parallel
$$AECD$$ is a parallelogram
$$AD=CE$$ (opposite side of parallelogram)
$$AD=BC$$
$$\Rightarrow \ BC=CE$$
$$\angle CEB=\angle CBE$$
$$AD||CE$$
$$AE$$ is the transversal
$$\angle A+\angle CEB=180^o$$
$$\angle A=180^o -\angle CEB$$
$$(2)$$ and $$(3)$$
$$\angle A=\angle B$$
Similarly $$\angle C=\angle D$$
Also $$AE$$ is a line
$$\angle B+\angle CBE=180^o$$
$$\angle B+\angle CEB=180^o$$
$$\angle B=180^o-\angle CEB$$
PR is diagonal of a parallelogram PQRS. Show that $$\Delta$$ PQR $$\cong$$ $$\Delta$$ RSP.
In the figure, ray $$AZ$$ bisects $$\angle {DAB}$$ as well as $$\angle{DCB}$$
(i) State the three pairs of equal parts in triangles $$BAC$$ and $$DAC$$.
(ii) Is $$\triangle {BAC}\cong \triangle {DAC}$$? Give reasons
(iii) Is $$AB=AD$$? Justify your answer
(iv) Is $$CD=CB$$? Give reasons.
Check whether the following pairs of triangles are congruent. If they are congruent, state the congruence criterion.
By applying $$SAS$$ congruence rule, you want to establish that $$\Delta P Q R \cong \Delta F E D.$$ It is given that $$P Q = F E \text { and } R P = D F.$$ What additional information is needed to establish the congruence ?
ABC is a triangle right angled at C. A line through the mid point M of hypotenuse AB and parallel to BC intersect AC at D .Show that :
$$CM=MA=\dfrac{1}{2}AB$$
$$In\quad \Delta ABC$$
$$M$$ is the midpoint of $$AB$$
and $$\\ MD\parallel BC$$
therefore $$D$$ is the midpoint of $$AC$$ [line drawn through midpoint of one side of a triangle parallel to another side, bisect the third side]
$$\Rightarrow AD=DC\longrightarrow (1)$$
also, $$\angle ADM=\angle CDM={ 90 }^{ o }\quad (corresponding\quad angle)\\ In\quad \Delta ADM\quad and\quad \Delta CDM\\ AD=CD\quad (from(1))\\ \angle ADM=\angle CDM={ 90 }^{ o }\\ DM=DM\quad (common)\\ \therefore \Delta ADM\cong \Delta CDM\quad (SAS)\\ \therefore AM=CM\quad (CPCT)\\ \because AM=\dfrac { 1 }{ 2 } AB\quad (M\quad is\quad the\quad midpoint\quad of\quad AB)\\ \therefore CM=MA=\dfrac { 1 }{ 2 } AB$$
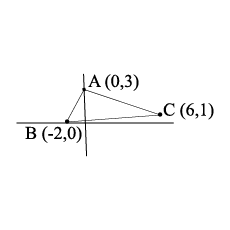
Find number of integral values of $$\lambda $$ if $$\left( {\lambda ,\lambda + 1} \right)$$ is an interior point of $$\Delta ABC$$, where $$A=(0,3), B=(-2,0)$$ and $$C=(6,1)$$.
Given, $$A=(0,3),B=(-2,0)$$ and $$C=(6,1)$$
Now, for the point to be an interior point, the basic conditions that can be applied are,
Condition $$1:$$ $$-2 < x < 6$$
Condition $$2:$$ $$0 < y < 3$$
For an interior point $$P(x,y)$$
So, if $$\lambda=-1, (\lambda,\lambda+1)=(-1,0)$$, not an interior point.$$[Using\ condition\ 2]$$
if $$\lambda=0, (\lambda,\lambda+1)=(0,1)$$, an interior point.
if $$\lambda=1, (\lambda,\lambda+1)=(1,2)$$, an interior point.
if $$\lambda=2, (\lambda,\lambda+1)=(2,3)$$, not an interior point.$$[Using\ condition\ 2]$$
Ans so on . . . .
So, we have only $$2$$ points $$(0,1)$$ and $$(1,2)$$ which will be inside the triangle $$ABC$$
And thus $$\lambda=0,1.$$
Hence $$\lambda$$ can have $$2$$ values.
In the given figure, triangles $$ABC$$ and $$DCB$$ are right-angle at $$A$$ and $$D$$ respectively and $$AC=DB$$. Prove that $$\Delta ABC \cong \Delta DCB$$
By RHS criteria both triangles are congruent
$$\Delta ABC \cong \Delta DCB$$
Express the congruence in the given triangles. Write in symbolic form.
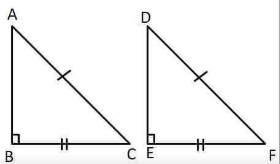
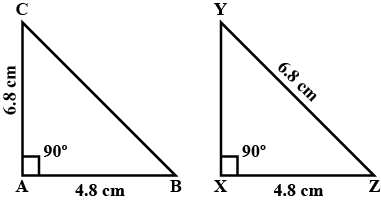
In $$\Delta XYZ,\ XY=4.2\ cm,\ XZ=6.5\ cm\ \angle Y=90^{o}$$
In $$\Delta DEF,\ FE=6.5\ cm,\ FD=4.2\ cm\ \angle D=90^{o}$$
In the figure $$AB || DC$$ and $$AC$$ and $$PQ$$ intersect each other at the point $$O$$. Prove that $$OA.CQ = OC.AP$$.
By applying $$SAS$$ congruence rule, you want to establish that $$\triangle PQR \equiv \triangle FED$$. It is given that $$PQ=FE$$ and $$RP=DE$$. What additional information is needed to establish the congruence?
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that $$DP = BQ$$ (refer to the given figure). Show that :
(i) $$\triangle APD \cong \triangle CQB$$
(ii) $$AP=CQ$$
(iii) $$\triangle AQB \cong \triangle CPD$$
(iv) $$AQ=CP$$
(v) APCQ is a parallelogram
Diagonal AC of a parallelogram ABCD bisects $$\angle A$$ (see Fig. 8.19), show that
(i) it bisects $$\angle C$$ also (ii) ABCD is a rhombus
In $$\Delta A B C$$ $$BE$$ and $$CF$$ are the two equal altitudes. Prove $$\Delta A B C$$ is isoceles by R.H.S
$$\begin{array}{l} Given \\ \angle AEB=\angle CEB={ 90^{ \circ } }\, \, \, \, \, \, \, ----\left( 1 \right) \\ Also,\, \, CF\, \, is\, \, a\, \, altitude, \\ So,\, \angle AFC=\angle BFC={ 90^{ \circ } }\, \, \, \, \, \, \, \, \, \, ---\left( 2 \right) \\ Also,\, BE=CF\, \, \, \, \, \, ---\left( 3 \right) \\ We\, have\, to\, prove\, that\, \Delta ABC\, is\, isoceles. \\ In\, \, \Delta BCF\, and\, \Delta CBE \\ \angle BFC=\angle CEB={ 90^{ \circ } }\, \, \\ FC=EB\, \, \, \left( { from3 } \right) \\ BC=CB\, \, \, \left( { common } \right) \\ \therefore \Delta BCF\, \cong \, \Delta CBE\, \, \, \, by\, RHS\, congruence\, rule \\ \therefore \angle FBC=\angle ECB \\ so,\, \angle ABC=\angle ACB \\ AB=AC \\ Hence,\, \Delta ABC\, is\, an\, isosceles\, triangle. \end{array}$$
In the given figure, $$AB=DC$$ and $$BD=CA$$. Prove that $$\Delta ABC\cong DCB$$.
Given $$AB=CD$$
$$BD=CA$$
In $$\triangle ABC$$ & $$\triangle DCB$$
$$BC=BC$$ (Common side)
$$\therefore \ $$ By $$SSS$$ congurency $$\triangle ABC\cong \triangle DCB$$
In figure, $$AB=AC$$ and $$D$$ is any point on $$BC$$ produced. Show that $$AD>AB$$.
Given : $$AB=AC$$
To prove : $$AD>AB$$
Proof :
In $$\Delta ABC$$,
$$\angle ABC=\angle ACB=\theta $$ (say) [as $$AB=AC\Rightarrow \Delta ABC$$ is isoceles]
Now, we know that, in an isoceles triangle, the base angles are acute as only one obtuse angle can exist in a triangle
Now, $$\angle ACD={ 180 }^{ 0 }-\angle ACB$$ (linear pair)
So, in $$\Delta ACD,\angle ACD$$ is the largest angle
So, from triangle inequality, side opposite to the larger angle is greater than the side opposite to the smaller angle
So, $$AD>AC$$
but, $$AC=AB$$ (given)
$$\Rightarrow AD>AB$$
Hence proved.
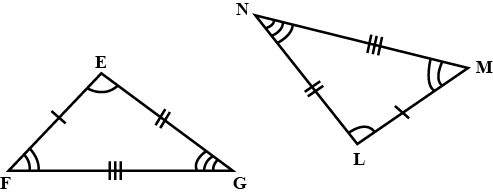
State the correspondence between the sides and angels of the following congruent triangles.
a) $$\Delta PQR \cong \Delta XYZ$$
b) $$\Delta ABC \cong \Delta TUV$$
In a $$\Delta A B C , A B = A C .$$ If the bisectors of $$\angle B$$ and $$\angle C$$ meet $$A C$$ and $$A B$$ at points $$D$$ and $$E$$ respectively, show that :
(i) $$\Delta \mathrm { DBC } \cong \Delta \mathrm { ECB }$$
(ii) $$\mathrm { BD } = \mathrm { CE }$$
$$AB=AC$$
EC is bisector of $$\angle C$$
BD is bisector of $$\angle B$$
(i) $$AB=AC \rightarrow \angle B= \angle C$$ (isosceler triangle)
in $$\Delta DBC $$ and $$ \Delta ECB$$
$$ BC \rightarrow commonside $$ ..(1)
$$\angle DBC =1/2 \angle B = 1/2 \angle C$$ $$(\because \angle B=\angle C)$$
$$\angle ECB = 1/2 \angle B$$
$$\Rightarrow \angle DBC = \angle ECB$$ ...(2)
$$\angle EBC = \angle B = \angle C = \angle DBC $$
$$\Rightarrow \angle EBC = \angle DCB$$ ...(3)
From (1), (2) & (3)
$$\Delta DBC \cong \Delta ECB $$
$$ \Rightarrow BD=CE $$ $$(\because \Delta DBC \cong ECB)$$
In figure, it is given that $$AB=CD$$ and $$AD =BC$$. Prove that $$\triangle ADC \cong \triangle CBA$$.
In $$\Delta ADC$$ and $$\Delta CBA$$
$$AB=CD$$ (Given)
$$AD=BC$$ (Given)
$$CA=CA$$ (common)
Hence $$\Delta ADC \cong \Delta CBA$$ by SSS congruence rule
$$\triangle EFG \cong \triangle LMN$$
Write the corresponding vertices, angles and sides of the two triangles.
Given : $$\triangle EFG\cong \triangle LMN$$
We are asked to find the corresponding vertices, angles sides of the two triangle.
We already know that the two triangles are congruent.
From the diagram, we can say that in $$\triangle EFG\;\&\; \triangle LMN$$:
$$\Rightarrow FG=MN$$
$$EG=LN$$
$$EF=LM$$
Hence, side corresponding to $$FG,\ EG\ and \ EF$$ is $$MN,\ LN\ and\ LM$$ respectively.
Now, again in $$\triangle EFG\;\&\; \triangle LMN$$
$$\angle FEG=\angle NLM$$
$$\angle EGF=\angle LNM$$
$$\angle EFG=\angle NML$$
Hence, angle corresponding to $$\angle FEG,\ \angle EGF\ and \ \angle EFG$$ is $$\angle NLM,\ \angle LNM\ and\ \angle NML$$ respectively.
Hence, vertex corresponding to $$E,\ F\ and \ G$$ is $$L,\ M\ and\ N$$ respectively.
In the given figure, the triangles are congruent, Find the values of x and y.
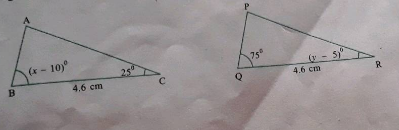
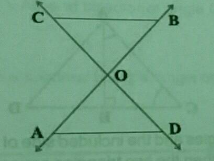
In figure, two lines $$AB$$ and $$CD$$ intersect each other at the point $$O$$ such that $$BC\parallel DA$$. Show that $$O$$ is the mid-point of both the line-segments $$AB$$ and $$CD$$.
Name pair of congruent triangle in the figure.
$$PSDA$$ is a parallelogram. Points $$Q$$ and $$R$$ are takes on $$PS$$ such that $$PQ=QR$$ and $$PA||QB||RC$$. Prove that area $$(\Delta PQE)=(\Delta CFD)$$
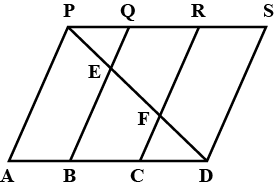
in the adjacent figure , parallelogram $$ABCD$$ , Show that $$ABC \cong CDA$$
Prove that in an isosceles triangle, the angles opposite the equal sides are equal.
R.E.F. Image.
Given ABC is an isosceles triangle.
proof :- Given :- AB = AC.
To prove :- $$\angle B=\angle C.$$
Let AD is angle bisector of angle A.
and D be point of interactions of this bisector
of $$ \angle A $$ & BC
In $$ \triangle BAD $$ & $$ \triangle CAD $$
$$ AB = AC $$ (Given)
$$ \angle BAD = \angle CAD $$ (By constriction)
$$ AD = AD $$ (common)
$$ \triangle BAD \cong \triangle CAD $$ [By SAS rule]
So $$ \angle ABD = \angle ACD$$ [CPCT]
$$ \therefore [\angle B = \angle C]$$
$$\triangle{ABC}$$ and $$\triangle{DBC}$$ are two isosceles triangles on the same base $$BC$$ and vertices $$A$$ and $$D$$ are on the same side of $$BC$$ as in figure.If $$AD$$ is extended to intersect $$BC$$ at $$P,$$Show that $$\triangle{ABP}\cong\triangle{ACP}$$
If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then prove that two triangles are congruent.
Given:Two right triangles $$\triangle{ABC}$$ and $$\triangle{DEF}$$ where $$\angle{B}={90}^{\circ}$$ and $$\angle{E}={90}^{\circ}$$, hypotenuse is equal.
i.e., $$AC=DF$$ and one side is equal i.e.,$$BC=EF$$
To prove:$$\triangle{ABC}\cong\triangle{DEF}$$
Proof:In right $$\triangle{ABC}$$
By pythagoras theorem, $${AC}^{2}={AB}^{2}+{BC}^{2}$$
$${AB}^{2}={AC}^{2}-{BC}^{2}$$ ........$$(1)$$
In right $$\triangle{DEF}$$
By pythagoras theorem, $${DF}^{2}={DE}^{2}+{EF}^{2}$$
$${DE}^{2}={DF}^{2}-{EF}^{2}$$ ........$$(2)$$
From $$(1)$$
$${AB}^{2}={AC}^{2}-{BC}^{2}$$
$$\Rightarrow {AB}^{2}={DF}^{2}-{EF}^{2}$$ since $$AC=DF$$ and $$BC=EF$$
$$\Rightarrow {AB}^{2}={DE}^{2}$$ from $$(2)$$
$$\Rightarrow AB=DE$$ ......$$(3)$$
Given:$$BC=EF$$,$$AC=DF$$
$$\Rightarrow \triangle{ABC}\cong\triangle{DEF}$$ by SSS congruence.
Hence proved.
In $$\triangle{PQR},N$$ is a point on $$PR$$ such that $$QN\bot PR$$. If $$PN\times NR={QN}^{2}$$, prove that $$\angle{PQR}={90}^{\circ}$$
$$PN\times NR=QN^2$$
Given: $$PN=QN, QN=NR$$
In $$\Delta PNQ$$ and $$\Delta QNR$$
$$\angle PNQ=\angle QNR=90^o$$
$$PN=QN, QN=NR$$
$$\Delta PNQ\sim \Delta QNR$$ by S.A.S
$$\therefore \angle PQN=\angle QRN$$
In $$\Delta QNR$$,
$$\angle QNR+\angle QRN+\angle NQR=180^o$$ by angle sum property
$$\Rightarrow 90^o+\angle PQN+\angle NQR=180^o$$
$$\Rightarrow \angle PQN+\angle NQR=180^o-90^o=90^o$$
$$\Rightarrow\angle PQR=90^o$$
Hence proved.
$$\triangle{ABC}$$ and $$\triangle{DBC}$$ are two isosceles triangles on the same base $$BC$$ and vertices $$A$$ and $$D$$ are on the same side of $$BC$$ as in figure.If $$AD$$ is extended to intersect $$BC$$ at $$P,$$Show that $$\triangle{ABD}\cong\triangle{ACD}$$
$$ABCD$$ is a square and $$BD$$ is the diagonal. Find the measure of the area of $$\triangle ABD$$.
If area of $$\triangle{ABC}=$$ area of $$\triangle{DEF}$$ then prove that $$\triangle{ABC}\cong\triangle{DEF}$$
In the given figure $$AB=CD$$ and $$AD=BC$$. Prove that $$\angle BAC= \angle ACD$$.
$$\triangle ABC$$ is a right angled in which $$LC=90^{o}$$ and $$CD\bot AB$$. If $$BC=a, CA=b, AB=c$$ and $$CD=p$$ then prove that
$$cp=ab$$
Is it possible to have a triangle with the following sides:
$$3\ cm,\ 4\ cm$$ and $$5\ cm$$
$$\triangle ABC$$ is a right angled in which $$LC=90^{o}$$ and $$CD\bot AB$$. If $$BC=a, CA=b, AB=c$$ and $$CD=p$$ then prove that
$$\dfrac{1}{p^{2}}=\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}$$
By applying ASA congruence rule, it is to be established that $$\Delta ABC \cong \Delta QRP$$ and it is given that BC$$=$$RP. What additional information is needed to establish the congruence?
Given $$BC= RP$$
And $$\Delta ABC \cong \Delta QPR$$ (By ASA congruence rule)
Since it is ASA congruence rule,
we need
Angle
Side
Angle
Here, side is $$BC=RP$$.
So, Angle on other side of it in both of those triangles should be equal
So,$$\angle A=\angle Q$$
Therefore, for another angle we need additional information on the following conditions:
$$\angle B=\angle R$$
$$\angle C=\angle P$$
AB and CD intersect each other at O and O is the midpoint of both AB and CD. Prove that AD=BC.
In the following figure, state the conditions you would use to show that $$\Delta ABC$$ and $$\Delta EDC$$ are congruent.
We have to find $$\Delta$$ABC and $$\Delta$$EDC are congruent
In $$\Delta$$ACB and $$\Delta$$EDC
$$\angle ACB=\angle ECD$$(vertically opposite angles)
$$CE=AC$$(given)
$$CB=CD$$(given)
By SAS property.
$$\Delta ACB\cong \Delta EDC$$.
$$\Delta ACB\cong \Delta EDC$$.
In the given figure, it is given that $$AB=CD$$ and $$AD=BC$$. Prove that $$\Delta ADC \cong \Delta CBA$$
In given figure explain, why $$\triangle ABC\cong \triangle FED$$
In the adjoining figure, sides $$AB$$ and $$AC$$ of $$\triangle{ABC}$$ are extended to points $$P$$ and $$Q$$ respectively.Also, $$\angle{PBC} < \angle{QCB}$$. Show that $$AC>AB.$$
REF.Image
Given
$$\angle PBC < \angle QCB$$
$$\angle PBC$$ is the external angle of $$\Delta ABC$$
so, $$\angle PBC=\angle A+\angle ACB$$
Now,
$$\angle PBC < \angle QCB$$
$$\Rightarrow \angle A+\angle ACB < \angle A+\angle ABC$$
$$\Rightarrow \angle ACB < \angle ABC$$
$$\Rightarrow AB < AC (\because $$ Side opposite to the greater angle is longer)
Thus
AC > AB
Hence Proved
Take any point $$O$$ in the interior of a triangle $$PQR$$. Is $$OQ+OR>QR?$$
Join $$O$$ with $$P, Q, R$$
Now in a $$\Delta le$$
Sum of 2 side is greater than 3rd side
$$\therefore OQ + OR > QR$$
As, $$OQR$$ is a triangle.
Is it possible to have a triangle with the following sides?
$$6$$cm, $$3$$cm, $$2$$cm.
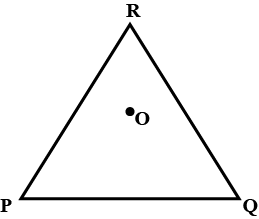
Take any point O in the interior of a $$\triangle PQR$$. Is $$OP$$$$+$$$$OQ$$$$>$$$$PQ$$$$?$$
Join $$O$$ with $$P, Q, R$$
As, $$OPQ$$ is a triangle.
Sum of two sides is always greater than the third side.
$$\therefore OP + OQ > PQ$$
Take any point $$O$$ in the interior of a triangle $$PQR$$. Is $$OR+OP>RP?$$
Join $$O$$ with $$P, Q, R$$
As, $$OPR$$ is a triangle.
Sum of 2 side is greater than 3rd side
$$\therefore OP + OR > PR$$
Is it possible to have a triangle with the following sides?
$$3$$cm, $$6$$cm, $$7$$cm.
In the given figure, $$AB=AD,\,\angle 1=\angle 2=\angle 3=\angle 4$$. Prove that $$AP=AQ$$.
Is it possible to have a triangle with the following sides?
$$1$$cm, $$3$$cm, $$5$$cm.
In the given figure, $$AB\parallel CD$$ and $$O$$ is the midpoint of $$AD$$.
Show that (i) $$\triangle AOB\cong \triangle DOC$$
(ii) $$O$$ is the midpoint of $$BC$$.
The lengths of the two sides of a triangle are $$12$$ cm and $$15$$ cm. Between what two measures should the length of the third side fall?
In Fig. $$ AD \perp CD $$ and $$ CB \perp CD. $$ If $$ AQ = BP $$ and $$ DP = CQ $$, prove that $$ \angle DAQ = \angle CBP. $$
In a rectangle $$ABCD$$, prove that $$\triangle ACB \cong \triangle CAD$$.
In $$\triangle\text{ACB}$$ and $$\triangle\text{CAD}$$
$$\text{AB}=\text{CD}$$ [Opposite sides of a rectangle are equal]
$$\text{AD}=\text{BC}$$ [Opposite sides of a rectangle are equal]
$$\text{AC}=\text{AC}$$ [Common side]
Hence, by $$\text{SSS}$$ rule of congruence,
$$\triangle\text{ACB}\cong\triangle\text{CAD}$$
Explain the following term.
Interior of a triangle.
Interior of a triangle is a set of all points lying inside of a triangle.
In above figure. shaded region inside $$\Delta ABC$$ is an interior of $$\Delta ABC$$.
In Fig., there is a triangle. The measures of some angles have been indicated. State whether triangle is acute, right or obtuse.
In Fig., there is a triangle. The measures of some angles have been indicated. State whether triangle is acute, right or obtuse.
In $$ \Delta ABC,$$ side AB is produced to D so that BD = BC. If $$ \angle B = 60^{\circ}$$ and $$ \angle A = 70^{\circ},$$ prove that:$$ AD > AC $$
The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angles is $$ 10^{\circ},$$ find the three angles.
In the given figure, it is given that $$ RT = TS, \angle 1 = 2\angle 2 $$ and $$ \angle 4 = 2\angle 3.$$ Prove that $$ \Delta RBT \cong \Delta SAT.$$
Explain the following term.
Obtuse triangle.
Obtuse triangle is a triangle in which one of the three angles is greater than $$90^0$$.
In above figure $$\Delta ABC$$ is an obtuse angle because $$\angle B>90^0$$.
Fill in the blank:
Two squares are congruent if ________.
Fill in the blank.
Two line segments are congruent if ________.
In the following triangle, the lengths of the sides are indicated along sides. By applying SSS condition, determine which are congruent. State the result in symbolic form.
Explain the concept of congruence of figures with the help of certain examples.
In the given figure, AB$$=$$DC and BC$$=$$AD. Is $$\Delta$$ABC$$\cong\Delta$$CDA?
In $$ \Delta ABC$$ and $$ \Delta CDA$$ ,
$$AB = DC$$ (given)$$BC = AD $$ (given)
$$AC = AC$$ (common)
$$\therefore \Delta ABC \cong \Delta CDA$$ {By SSS cong. rule}
Answer is Yes.
Identify the pairs of triangles are congruent by ASA condition?
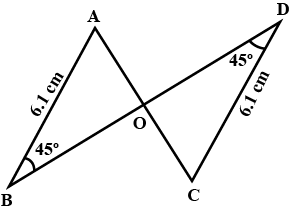
Triangles ABC and PQR are both isosceles triangles with AB$$=$$AC and PQ$$=$$PR respectively. If AB$$=$$PQ and BC$$=$$QR, then are the two triangles congruent? Which condition do you use? If $$\angle B=50^o$$, what is the measure of $$\angle R$$?
In the following pairs of triangles, the lengths of the sides are indicated along sides. By applying SSS condition, determine which are congruent. State the result in symbolic form.
In the given figure, line segments $$AB$$ and $$CD$$ bisect each other at $$O$$. Prove that, $$\Delta AOC\cong \Delta BOD$$.
In the given figure, $$AB=AD$$ and $$\angle BAC=\angle DAC$$. Complete the following, so as to make it true: Line segment $$AC$$ bisects _______ and _________.
In figure, AD bisects $$\angle$$A and AD$$\perp$$BC. Is it true to say that BD$$=$$DC?
Draw any triangle ABC. Use ASA condition to construct another triangle congruent to it.
Here, In $$ABC$$, $$\angle B=60^o$$ and $$\angle C=55^o$$
$$\Delta DCB$$ is costructed on base $$BC$$ such that
$$\angle DCB=\angle ABC=60^0$$
$$BC=CB\cdots\cdots[\text{common side}]$$
And $$\angle DBC=\angle ACB=55^o$$
So, by $$ASA$$ condition
$$\Delta ABC\cong\Delta DCB$$
Identify the pairs of triangles are congruent by ASA condition?
In figure, AO$$=$$OB and $$\angle$$A$$=\angle$$B. Is $$\Delta$$AOC$$\cong\Delta$$BOD?
State the three pairs of matching parts you have used to answer.(Is $$\Delta$$ABC$$\cong\Delta$$ACB)
In figure, AD bisects $$\angle$$A and AD$$\perp$$BC. State the three pairs of matching parts you have used after proving the triangles congruent.
In $$\Delta ABD$$ and $$\Delta ACD$$
$$\angle BAD = \angle CAD$$ ($$\therefore AD$$ bisect $$\angle A$$)
$$AD = AD$$ (common)
$$\angle ADB = \angle ADC (AD \bot BC)$$
$$\therefore \triangle ABD \cong \triangle ACD $$ (ASA)
Thus the matching pairs,
$$BD = DC$$ (c.p.c.t)
$$AB = AC$$ (c.p.c.t)
$$\angle ABC = \angle ACD$$ (c.p.c.t)
Can the pairs of triangles be congruent by ASA condition?
Is $$\Delta$$ABC$$\cong\Delta$$ACB?
Identify the pairs of triangles are congruent by ASA condition?
In figure, AX bisects $$\angle$$BAC as well as $$\angle$$BDC. State the three facts needed to ensure that $$\Delta$$ABD$$\cong\Delta$$ACD.
In figure, BD and CE are altitudes of $$\Delta$$ABC and BD$$=$$CE. Is $$\Delta$$BCD$$\cong\Delta$$CBE?
By RHS congruence condition if hypotenuse and one side of one right triangle are equal to hypotenuse and one side of other right triangle then both right triangles are congruent.
It is given that $$BD=CE$$ and $$BC$$ is the hypotenuse of small triangles $$CEB$$ and $$BDC$$
So, In right triangles $$BCD$$ and $$CBE$$
$$BC=CB=\text{common side}\cdots\cdots[\text{hypotenuse}]$$
And $$BD=CE=\text{given}\cdots\cdots[\text{sides of right triangles}]$$
So, by $$RHS$$ condition
$$\triangle BCD\cong\triangle CBE$$
In the following pairs of right triangles, the measures of some parts are indicated along side. State by the application of RHS congruence condition which are congruent. State the result in symbolic form.
In figure, $$AO=OB$$ and $$\angle A=\angle B$$. State the matching pair you have used for $$\Delta$$ $$AOC$$ $$\cong\Delta$$ $$BOD$$, which is not given in the question.
In figure, AO$$=$$OB and $$\angle A=\angle B$$. Is it true to say that $$\angle ACO=\angle BDO$$?
In the following pairs of right triangles, the measures of some parts are indicated along side. State by the application of RHS congruence condition which are congruent. State the result in symbolic form.
In figure, BD and CE are altitudes of $$\Delta$$ABC and BD$$=$$CE. State the three pairs of matching parts you have used to answer.(Is $$\Delta$$BCD$$\cong\Delta$$CBE).
In parallelogram $$ABCD$$, points $$M$$ and $$N$$ have been taken on opposite sides $$AB$$ and $$CD$$ respectively such that $$AM=CN$$. Show that $$AC$$ and $$MN$$ bisect each other.
In the figure, $$ABCD$$ is a quadrilateral and $$AC$$ is one its $$AB+BC+CD+DA> 2AC$$ diagonals. Prove that
In the given figure, $$ABCD$$ is a quadrilateral in which $$AB=AD$$ and $$BC=DC$$. Prove that
$$AC$$ bisects $$\angle A$$ and $$\angle C$$.
In the adjoining figure, $$OPQR$$ is a square. A circle drawn with centre $$O$$ cuts the square in $$X$$ and $$Y$$.
Prove that $$QX=QY$$
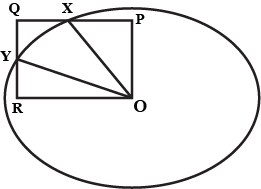
If $$O$$ is a point within a quadrilateral $$ABCD$$, show that $$OA+OB+OC+OD> AC+BD$$
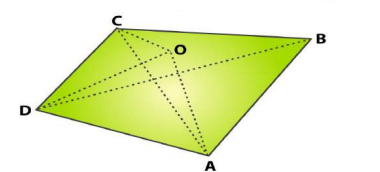
In the given figure, $$ABCD$$ is a square and $$\angle PQR={90}^{o}$$. If $$PB=QC=DR$$, prove that $$AB+BC+CD+DA> AC+BD$$
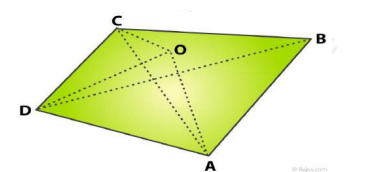
In the given figure, $$ABCD$$ is a quadrilateral in which $$AB=AD$$ and $$BC=DC$$. Prove that
$$BE=DE$$
In the given figure, $$ABCD$$ is a square and $$\angle PQR={90}^{o}$$. If $$PB=QC=DR$$, prove that $$AB+BC+CD> DA$$
$$\Delta ABC$$ is an isosceles triangle with $$AB = AC = 13 cm$$. The length of altitude from $$A$$ on $$BC$$ is $$5 cm$$. Find $$BC$$.
In the given figure, $$ABCD$$ is a quadrilateral in which $$AB=AD$$ and $$BC=DC$$. Prove that
$$\angle ABC=\angle ADC$$
Given the base $$a$$ of a triangle, the opposite angle $$A$$ and the product $$k^2$$ of the other sides, solve the triangle and show that there is no such triangle if $$a < 2k \sin \dfrac{A}{2}$$.
Let the other two sides of triangle be $$b,c$$
Given the base of the triangle is $$a$$ and its opposite angle as $$A$$
and also $$b c=k^2\implies c=\dfrac{k^2}{b}$$
Now $$\cos A=\dfrac{b^2+c^2-a^2}{2 b c}$$
$$\implies 2 b c\cos A=b^2+c^2-a^2$$
$$\implies 2 k^2\cos A+a^2=b^2+\bigg(\dfrac{k^2}{b}\bigg)^2$$
$$\implies b^4-(a^2+2 k^2\cos A)b^2+k^4=0$$
Since $$b^2$$ is real so $$\text{Discriminant}\ge 0$$
$$\implies (a^2+2 k^2 \cos A)^2-4 k^4\ge 0$$
$$\implies (a^2+2 k^2\cos A-2 k^2)(a^2+2 k^2 \cos A+2 k^2)\ge 0$$ $$(\because (a+b)(a-b)=a^2-b^2)$$
$$\implies (a^2+2 k^2(2\sin^2 A/2))(a^2+2 k^2(2 \cos^2 A/2))\ge 0$$ $$(\because \cos 2 A=2\cos^2 A-1=1-2\sin ^2 A)$$
$$\implies (a^2+4 k^2 \cos^2 A/2)(a^2-4 k^2 \sin^2 A/2)\ge 0$$
$$\implies a^2-4 k^2\sin^2 \dfrac{A}{2}\ge 0$$ $$(\because A^2+4 k^2\cos^2 \dfrac{A}{2} \text{ is always positive})$$
$$\implies \bigg(a-2 k\sin \dfrac{A}{2}\bigg)\bigg(a+2 k \sin \dfrac{A}{2}\bigg)\ge 0$$
So $$a\le -2 k \sin \dfrac{A}{2}$$ or $$a\ge 2 k \sin \dfrac{A}{2}$$
But $$a$$ must be positive which means that $$a\le -2k \sin \dfrac{A}{2}$$ is rejected
$$\implies a\ge 2 k \sin \dfrac{A}{2}$$
So $$a$$ cannot be less than $$2 k \sin \dfrac{A}{2}$$
Hence there is no triangle if $$a<2 k \sin \dfrac{A}{2}$$
The line segments joining the midpoints $$M$$ and $$N$$ are parallel sides $$AB$$ and $$DC$$ respectively of a trapezium $$ABCD$$ is perpendicular to both the sides $$AB$$ and $$DC$$. Prove that $$AD = BC$$.
In the adjoining figure, $$X$$ and $$Y$$ are respectively two points on equal sides $$AB$$ and $$AC$$ of $$\triangle ABC$$ such that $$AX = AY$$. Prove that $$CX = BY$$.
The angles of a triangle are as $$1:2:7$$; prove that the ratio of the greatest side to the least side is $$\sqrt{5}+1:\sqrt{5}-1$$.
In $$\triangle ABC, AB = AC$$ and the bisectors $$\angle B$$ and $$\angle C$$ meet at a point $$O$$. Prove that $$BO = CO$$ and the ray $$AO$$ is the bisector of $$\angle A$$.
In $$\triangle ABC, D$$ is the midpoint of $$BC$$. If $$DL \perp AB$$ and $$DM \perp AC$$ such that $$DL = DM$$, prove that $$AB = AC$$.
A square is inscribed in an isosceles right triangle so that the square and the triangle have one angle common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse.
$$\textbf{Step - 1: Applying properties}$$
$$\text{Given that }\Delta ABC \text{ is an isosceles right triangle and square }CPQR \text{ inscribed in it.}$$
$$CPQR \text{ is a square}$$
$$\therefore CP=PQ=QR=RC$$
$$\Delta ABC \text{ is an isosceles triangle }$$
$$\therefore AC=BC$$
$$\implies AR+RC=CP+BP$$
$$\implies AR=BP ......(1)(\because RC=CP)$$
$$\textbf{Step - 2: Applying properties}$$
$$AR=BP $$
$$\angle ARQ=\angle QPB =90^\text{o}$$
$$QR=PQ$$
$$\therefore \Delta ARQ \approx \Delta QPB $$
$$\implies AQ=QB$$
$$\therefore Q\text{ bisects the hypotenuse } AB$$
$$\textbf{Hence proved.}$$
If the angles of a triangle b in A.P. and the lengths of the greatest and least sides be $$24$$ and $$16$$ feet respectively, find the length of the third side and the angles, given
$$log 2=.30103$$, $$log 3=.4771213$$,
and $$L\tan 19^o6'=9.5394287$$, diff. for $$1'=4084$$.
In the given figure, $$ABCD$$ is a square and $$P$$ is a point inside it such that $$PB = PD$$. Prove that $$CPA$$ is a straight line.
In the adjoining figure, explain how one can find the breadth of the river without crossing it.
Show that for any triangle with sides a, b and c, $$3(ab + bc + ca) < (a + b +c)^2 < 4(bc + ca + ab)$$. when are the first two expressions equal?
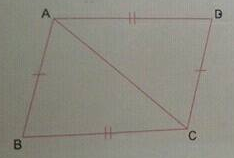
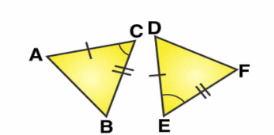
Given is a pair of congruent triangles. State the property of congruence and the name of the congruent triangles.
Given is a pair of congruent triangles. State the property of congruence and the name of the congruent triangles.
Given is a pair of congruent triangles. State the property of congruence and name of the congruent triangles.
Given is a pair of congruent triangles. State the property of congruence and the name of the congruent triangles.
State the correspondence between the vertices, sides and angles of the following pair of congruent triangles.
$$\triangle CAB\cong \triangle QRP$$
State the correspondence between the vertices, sides and angles of the following pair of congruent triangles.
$$\triangle XZY\cong \triangle QPR$$
Given is a pair of congruent triangles. State the property of congruence and the name of the congruent triangles.
State the correspondence between the vertices, sides and angles of the following pair of congruent triangles.
$$\triangle MPN\cong \triangle SQR$$
State the correspondence between the vertices, sides and angles of the following pair of congruent triangles.
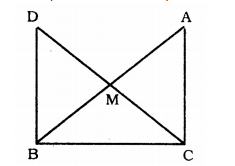
$$\triangle ABC\cong \triangle EFD$$
In the given figure, $$PA\bot AB$$, $$QB\bot AB$$ and $$PA=QB$$. Prove that $$\triangle OAP=\triangle OBQ$$. Is $$OA=OB$$?
In $$\triangle ABC, \angle A$$ is acute. $$BD$$ and $$CE$$ are perpendicular on $$AC$$ and $$AB$$ respectively. Prove that $$AB\times AE = AC \times AD$$.
Consider the $$\triangle ABC$$,
So, we have to prove that, $$AB \times AE = AC \times AD$$
Now, consider the $$\triangle ADB$$ and $$\triangle AEC$$,
$$\angle A = \angle A$$ [common angle for both triangles]
$$\angle ADB = \angle AEC$$ [both angles are equal to $$90^{\circ}$$]
$$\triangle ADB \sim \triangle AEC$$
So, $$AB/AC = AD/AE$$
By cross multiplication we get,
$$AB \times AE = AC \times AD$$.
So, we have to prove that, $$AB \times AE = AC \times AD$$
Now, consider the $$\triangle ADB$$ and $$\triangle AEC$$,
$$\angle A = \angle A$$ [common angle for both triangles]
$$\angle ADB = \angle AEC$$ [both angles are equal to $$90^{\circ}$$]
$$\triangle ADB \sim \triangle AEC$$
So, $$AB/AC = AD/AE$$
By cross multiplication we get,
$$AB \times AE = AC \times AD$$.
In figure, $$AD=BC$$ and $$AD\parallel BC$$. Is $$AB=DC$$? Give reasons in support of your answer.
In the figure, $$AB=AD$$ and $$CB=CD$$. Prove that $$\triangle ABC\cong \triangle ADC$$.
In the given figure, triangles $$ABC$$ and $$DCB$$ are right-angled at $$A$$ and $$D$$ respectively and $$AC=DB$$. Prove that $$\triangle ABC\cong \triangle DCB$$
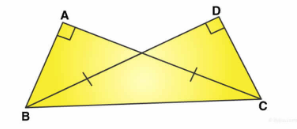
In the adjoining figure, $$AB=AC$$ and $$BD=DC$$. Prove that $$\triangle ADB\cong \triangle ADC$$ and hence show that (i) $$\angle ADB=\angle ADC={90}^{o}$$, (ii) $$\angle BAD=\angle CAD$$
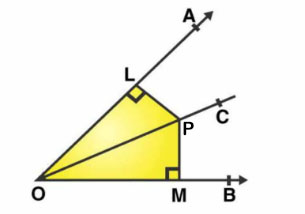
In figure, $$PL\bot OA$$ and $$PM\bot OB$$ such that $$PL=PM$$. Is $$\triangle PLO\cong \triangle PMO$$?
Give reasons in support of your answer.
In the given pairs of triangles, applying only the ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
In the given pair of triangles, applying only the ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
In given pairs of triangles in the figure, applying only the ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
In the given pairs of triangles, applying only the ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
In Fig., $$\Delta PQR \cong \Delta$$ ______
In the given pairs of triangles, applying only the ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
If $$\Delta PQR$$ and $$\Delta XYZ$$ are congruent under the correspondence $$QPR \leftrightarrow XYZ$$, then,
(i) $$\angle R =$$ ______ (ii) $$QR = $$ ______
(iii) $$\angle P =$$ ______ (iv) $$QP =$$ ______
(v) $$\angle Q =$$ ______ (vi) $$RP =$$ ______
In the given pair of triangles, using only the RHS congruence criterion, determine which pairs of triangles are congruent. In case of congruence. write the result in symbolic form
Enter 1 if it is true else enter 0.In Fig., $$\triangle PQR \cong \triangle $$$$XYZ$$
In Fig., $$\Delta$$ ______ $$\cong PQR$$
In Fig., $$AB = AD$$ and $$\angle BAC = \angle DAC$$.
Then,
(i) $$\Delta$$ ______ $$\cong \Delta ABC$$
(ii) $$BC =$$ ______
(iii) $$\angle BCA =$$ ______
(iv) Line segment $$AC$$ bisects ______ and ______.
In the given pair of triangles, using only the RHS congruence criterion, determine which pairs of triangles are congruent. In case of congruence. write the result in symbolic form:
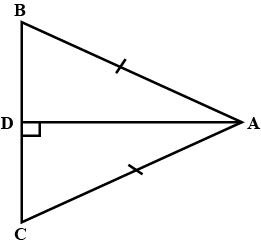
In the given pair of triangles, applying only the ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.
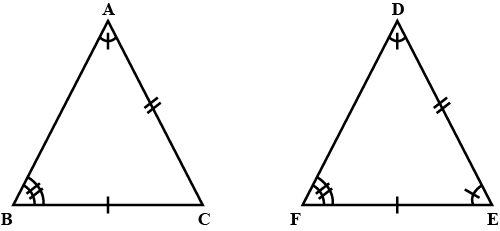
Without drawing the triangles write all size pairs of equal measures in each of the following pairs of congruent triangles.
$$\triangle XYZ \cong \triangle MLN$$
In the following, pairs of triangles of Fig. the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
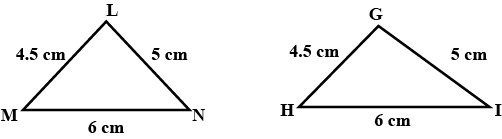
In the following, pairs of triangles of FIg. the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
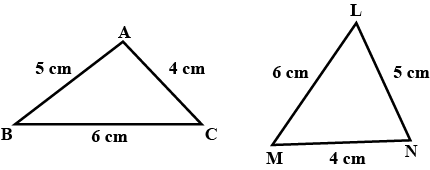
In the given pairs of triangles, using only the RHS congruence criterion, determine which pairs of triangles are congruent. In case of congruence. write the result in symbolic form:
In Fig. which phase of triangles are congruent by SAS congruence criterion (condition)? If congruent, write the congruence of the two triangles in symbolic form.
In the given pairs of triangles, using only the RHS congruence criterion, determine which pairs of triangles are congruent. In case of congruence. write the result in symbolic form:
State which of the following pairs of triangles are congruent. If yes, write them in symbolic form (you may draw a rough figure).
$$\triangle PQR : PQ = 3.5cm, QR = 4.0cm, \angle Q = 60^{o}$$
$$\triangle STU : ST = 3.5cm, TU = 4cm, \angle T = 60^{o}$$
Without drawing the triangles write all size pairs of equal measures in each of the following pairs of congruent triangles.
$$\triangle YZX \cong \triangle PQR$$
In the given pair of triangles, using only RHS congruence criterion, determine which pairs of triangles are congruent. In case of congruence. write the result in symbolic form:
In the given pairs of triangles, using only the RHS congruence criterion, determine which pairs of triangles are congruent. In case of congruence. write the result in symbolic form:
Observe, Figure and state the three pairs of equal parts in triangles ABC and DBC.
$$(i) Is \triangle ABC \cong \triangle DCB? Why?$$
$$(ii)Is AB=DC?Why?$$
$$(iii)Is AC=DB?Why?$$
In Figure, state the three pairs of equal parts in $$\triangle ABC$$ and $$\triangle EOD$$. Is $$\triangle ABC \cong \triangle EOD$$ ?Why?
In Figure $$QS \bot PR$$, $$RT \bot PQ$$ and $$QS=RT$$.
(i) Is $$\triangle QSR \cong \triangle RTQ$$? Give Reasons
(ii) Is ∠ PQR = ∠ PRQ? Give reasons.
In above figure, $$\angle 1=\angle 2$$ and $$\angle 3 =\angle 4$$.
(i) Is $$\triangle ADC \cong \triangle ABC$$? Why?
(ii)Show that $$AD=AB$$ and $$CD=CB$$.
In the figure shown above, $$DE=IH, EG=FI$$ and $$\angle E=\angle I$$. Is $$\triangle DEF \cong \triangle HIG?$$ If yes, by which congruence criterion?
$$AD$$ is a median of the triangle $$ABC$$. Is it true that $$AB+BC+CA>2AD$$? Give reason for your answer.
In $$\triangle \ ABD$$, we have
$$AB+BD>AD....(1)$$
[$$\therefore$$ Sum of the lengths of any two sides of a triangle must be greater than the third side]
Now, $$\triangle \ ADC$$, we have
$$AC+CD>AD....(2)$$
[$$\therefore$$ Sum of the lengths of any two sides of a triangle must be greater than the third side]
Adding $$(1)$$ and $$(2)$$, we get
$$AB+BD+CD+AC>2AD$$
$$\implies \ AB+BC+CA>2AD $$ [$$\therefore BD=CD$$ as $$AD$$ is median of $$\triangle \ ABC$$]
$$AB+BD>AD....(1)$$
[$$\therefore$$ Sum of the lengths of any two sides of a triangle must be greater than the third side]
Now, $$\triangle \ ADC$$, we have
$$AC+CD>AD....(2)$$
[$$\therefore$$ Sum of the lengths of any two sides of a triangle must be greater than the third side]
Adding $$(1)$$ and $$(2)$$, we get
$$AB+BD+CD+AC>2AD$$
$$\implies \ AB+BC+CA>2AD $$ [$$\therefore BD=CD$$ as $$AD$$ is median of $$\triangle \ ABC$$]
State which of the following pairs of triangles are congruent. If yes, write them in symbolic form (you may draw a rough figure).
$$\triangle ABC : AB = 4.8cm, \angle A = 90^{o}, AC = 6.8cm$$
$$\triangle XYZ : YZ = 6.8cm, \angle X = 90^{o}, ZX = 4.8cm$$
The given triangles $$ABC$$ and $$XYZ$$ are not congruent by any criterion of congruence.
In Fig. $$PQ = PS$$ and $$\angle 1 = \angle 2$$.
(i) Is $$\triangle PQR \cong \triangle PSR$$ ? Give Reasons.
(ii) Is $$QR = SR$$ ? Give reasons.
If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent. Is the statement true? Why?
In $$ \Delta $$ PQR , PD QR such that D lies on QR . If $$ PQ = a , PR = b , QD = c $$ and $$ DR = d $$ , prove that $$ (a + b) (a - b) = (c + d)(c - d) $$ .
Given : In $$\Delta PQR, PD \bot QR $$ So $$\angle 1 = \angle 2$$
$$PQ = a, PR = b, QD = c$$ and $$DR = d$$.
To prove : $$(a +b)(a-b) = (c+d)(c-d)$$
Proof: In right angled $$\angle PDQ$$,
$$PD^2 = PQ^2 - QD^2$$ [By Pythagoras theorem]
$$\Rightarrow PD^2 = a^2-c^2$$ (i)
Similarly, in right angled $$\Delta PDR$$,
PD^2 = PR^2-DR^2$$ [By Pythagoras theorem]
$$\Rightarrow PD^2= b^2 - c^2$$ (ii)
From (i) and (ii), we have
$$a^2 - c^2 = b^2 - d^2$$
$$\Rightarrow a^2 - b^2 = c^2 - d^2$$
$$\Rightarrow (a-b)(a+b) = (c-d)(c+d)$$
Hence, proved.
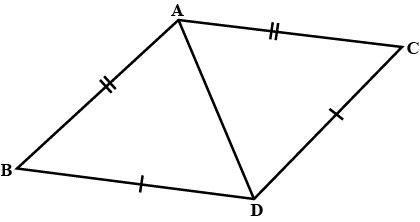
In the given figure, $$AB=AC, P$$ and $$Q$$ are points on $$BA$$ and $$CA$$ respectively such that $$AP=AQ$$. Prove that
$$\triangle APC\cong \triangle AQB$$
In the above figure, $$BA \perp AC, \ ED \perp FD$$ such that $$BA=DE$$ and $$BF=EC$$. Show that $$\triangle \ ABC \cong \triangle \ DEF$$.
The longest side of a triangle is $$3$$ times the shortest side and the third side is $$2\ cm$$ shorter than the longest side. If the perimeter of the triangle is at least $$61\ cm$$, find the minimum length of the shortest side.
We know that in a triangle, the sum of lengths of any two sides is greater than the length of the third side. Is the sum of any angles of a triangle also greater than the third angle? If no, draw a rough sketch to show such a case.
In a triangle, the sum of any two sides must be
greater than its third side but in case of its angles.
It is not necessary that the sum of any two angles be more than its third angle. Such as in this triangle sum of any two angles is less than its third angle.
Such as $$30^\circ + 20^\circ = 50^\circ < 130^\circ$$
greater than its third side but in case of its angles.
It is not necessary that the sum of any two angles be more than its third angle. Such as in this triangle sum of any two angles is less than its third angle.
Such as $$30^\circ + 20^\circ = 50^\circ < 130^\circ$$
In the given figure, $$ABCD$$ is a quadrilateral in which $$AD=BC$$ and $$\angle DAB=CBA$$. Prove that
$$\triangle ABD \cong \triangle BAC$$
The figure $$ABCD$$ is a quadrilateral
In which $$AD=BC$$
$$\angle DAB =\angle CBA$$
To prove:
(i) $$\triangle ABD =\triangle BAC$$
(ii) $$\angle ABD =\angle BAC$$
Proof: In $$\triangle ABD $$ and $$\triangle ABC$$
$$AB=AB$$ (common)
$$\angle DAB =\angle CBA$$ (Given)
$$AD=BC$$
(i) $$\triangle ABD\cong \triangle ABC$$ ($$SAS$$ axiom)
(ii) $$BD=AC$$
(iii) $$\angle ABD=\angle BAC$$
In which $$AD=BC$$
$$\angle DAB =\angle CBA$$
To prove:
(i) $$\triangle ABD =\triangle BAC$$
(ii) $$\angle ABD =\angle BAC$$
Proof: In $$\triangle ABD $$ and $$\triangle ABC$$
$$AB=AB$$ (common)
$$\angle DAB =\angle CBA$$ (Given)
$$AD=BC$$
(i) $$\triangle ABD\cong \triangle ABC$$ ($$SAS$$ axiom)
(ii) $$BD=AC$$
(iii) $$\angle ABD=\angle BAC$$
In the above figure, $$AD$$ is the bisector of $$\angle BAC$$. Prove that $$AB>BD$$.
In the adjoining figure, $$AB=CD, CE=BF$$ and $$\angle ACE =\angle DBF$$. Prove that
$$\triangle ACE\cong \triangle DBF$$
In the adjoining figure, $$ABCD$$ is a square $$P,Q$$and $$R$$ are points on the sides $$AB, BC$$ and $$CD$$ respectively such that $$AP=BQ=CR$$ and $$\angle PQR =90^o$$. Prove that
$$PQ=QR$$
State, whether the pairs of triangles given in the following figures are congruent or not:
In the figure given $$ABCD$$ is a parallelogram. $$E$$ and $$F$$ are mid-point of the sides $$AB$$ and $$CO$$ respectively. The straight lines $$AF$$ and $$BF$$ meet the straight lines $$ED$$ and $$EC$$ in points $$G$$ and $$H$$ respectively. Prove that $$\triangle HEB\cong \triangle HCF$$
In the adjoining figure, $$ABCD$$ is a square $$P,Q$$and $$R$$ are points on the sides $$AB, BC$$ and $$CD$$ respectively such that $$AP=BQ=CR$$ and $$\angle PQR =90^o$$. Prove that
$$\angle PRQ = 45^o$$
In the given figure, $$PQ || BA$$ and $$RS\ CA$$. If $$BP=RC$$, prove that :
$$RS=CQ$$
$$PQ || BA, RS || CA$$
$$BP = RC$$
To prove:
(i) $$\triangle BSR \cong \triangle PQC$$
(ii) $$RS=CQ$$
Proof: $$BP =RC$$
$$BC -RC=BC-BP$$
$$BR=PC$$
Now, in $$\triangle BSR $$ and $$\triangle PQC$$
$$\angle B =\angle P$$ (Corresponding angles)
$$\angle R =\angle C$$ (Corresponding angles)
$$BR =PC$$ (Proved)
$$\triangle BSR \cong \triangle PQC$$
$$BS=PQ$$
$$RS=CQ$$
In the adjoining figure, $$ABCD$$ is a square, $$P,Q$$and $$R$$ are points on the sides $$AB, BC$$ and $$CD$$ respectively such that $$AP=BQ=CR$$ and $$\angle PQR =90^o$$. Prove that $$\triangle PBQ \cong \triangle QCR$$.
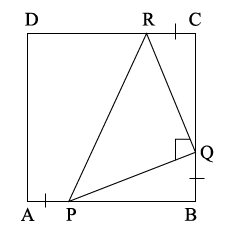
In triangle $$ABC$$ and $$DEF, \angle A= \angle D, \angle B=\angle E$$ and $$AB =EF$$. Will the two triangle be congruent? Give reasons for your answer.
State, whether the pairs of triangles given in the following figures are congruent or not:
State, whether the pairs of triangles given in the following figures are congruent or not:
$$ \Delta ABC $$ in which $$ AB = 2\,cm , BC = 3.5 \,cm $$ and $$ \angle C = 80^{\circ} $$ and $$ \Delta DEF $$ in which $$ DE = 2\,cm , DF = 3.5\,cm $$ and $$ \angle D = 80^{\circ} $$
In $$ \Delta ABC $$ ,
It is given that
$$ AB = 2\,cm , BC = 3.5 \,cm . \angle C = 80^{\circ} $$
In $$ \Delta DEF $$ ,
It is given that
$$ DE = 2\,cm , DF = 3.5\,cm $$ and $$ \angle D = 80^{\circ} $$
We get to know that two corresponding sides are equal but the included angles are not equal.
therefore , the triangles need not be congruent.
It is given that
$$ AB = 2\,cm , BC = 3.5 \,cm . \angle C = 80^{\circ} $$
In $$ \Delta DEF $$ ,
It is given that
$$ DE = 2\,cm , DF = 3.5\,cm $$ and $$ \angle D = 80^{\circ} $$
We get to know that two corresponding sides are equal but the included angles are not equal.
therefore , the triangles need not be congruent.
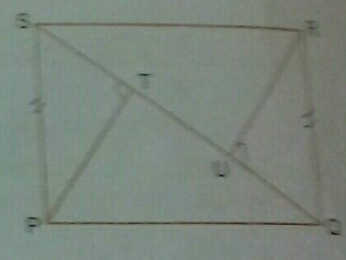
$$ \mathrm{ABCD} $$ is a rectangle and $$ \mathrm{P} $$ is mid-point of $$ \mathrm{AB} $$. DP is produced to meet $$ \mathrm{CB} $$ at $$ \mathrm{Q} $$. Prove that area of rectangle $$ \mathrm{ABCD}= $$ area of $$ \Delta \mathrm{DQC} $$.
Given:
$$ \mathrm{ABCD} $$ is a rectangle and $$ \mathrm{P} $$ is mid-point of $$ \mathrm{AB} $$.
DP is produced to meet $$ \mathrm{CB} $$ at $$ \mathrm{Q} $$.
To prove:
area of rectangle $$ \mathrm{ABCD}= $$ area of $$ \Delta \mathrm{DQC} $$
Proof :
In $$ \triangle \mathrm{APD} $$ and $$ \triangle \mathrm{BQP}, $$
$$ \mathrm{AP}=\mathrm{BP}[\text { since, } \mathrm{D} \text { is the mid-point of } \mathrm{AB}] $$
$$ \angle \mathrm{DAP}=\angle \mathrm{QBP}\left[\text { each angle is } 90^{\circ}\right] $$
$$ \angle \mathrm{APD}=\angle \mathrm{BPQ}[\text { vertically opposite angles }] $$
So, $$ \Delta \mathrm{APD} \cong \Delta \mathrm{BQP} $$ [By using ASA postulate]
ar $$ (\Delta \mathrm{APD})=\operatorname{ar}(\Delta \mathrm{BQP}) $$
Now, $$ \operatorname{ar} A B C D=\operatorname{ar}(\Delta A P D)+\operatorname{ar} P B C D $$
$$\begin{array}{l}=\operatorname{ar}(\Delta \mathrm{BQP})+\operatorname{ar} \mathrm{PBCD} \\=\operatorname{ar}(\Delta \mathrm{DQC})\end{array}$$
Hence proved.
$$ \mathrm{ABCD} $$ is a rectangle and $$ \mathrm{P} $$ is mid-point of $$ \mathrm{AB} $$.
DP is produced to meet $$ \mathrm{CB} $$ at $$ \mathrm{Q} $$.
To prove:
area of rectangle $$ \mathrm{ABCD}= $$ area of $$ \Delta \mathrm{DQC} $$
Proof :
In $$ \triangle \mathrm{APD} $$ and $$ \triangle \mathrm{BQP}, $$
$$ \mathrm{AP}=\mathrm{BP}[\text { since, } \mathrm{D} \text { is the mid-point of } \mathrm{AB}] $$
$$ \angle \mathrm{DAP}=\angle \mathrm{QBP}\left[\text { each angle is } 90^{\circ}\right] $$
$$ \angle \mathrm{APD}=\angle \mathrm{BPQ}[\text { vertically opposite angles }] $$
So, $$ \Delta \mathrm{APD} \cong \Delta \mathrm{BQP} $$ [By using ASA postulate]
ar $$ (\Delta \mathrm{APD})=\operatorname{ar}(\Delta \mathrm{BQP}) $$
Now, $$ \operatorname{ar} A B C D=\operatorname{ar}(\Delta A P D)+\operatorname{ar} P B C D $$
$$\begin{array}{l}=\operatorname{ar}(\Delta \mathrm{BQP})+\operatorname{ar} \mathrm{PBCD} \\=\operatorname{ar}(\Delta \mathrm{DQC})\end{array}$$
Hence proved.
Prove that
$$ \angle ADB = \angle ADC $$
From the figure
$$AD\perp BC$$
then,
$$\angle ADB=90^\circ\,\&\,\angle ADC=90^\circ$$
$$\therefore\,\angle ADB=\angle ADC$$
$$AD\perp BC$$
then,
$$\angle ADB=90^\circ\,\&\,\angle ADC=90^\circ$$
$$\therefore\,\angle ADB=\angle ADC$$
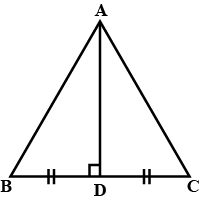
Prove that
$$ \Delta ABD \cong \Delta ACD $$
From the figure
$$ BD = CD $$
In $$ \Delta ABD $$ and $$ \Delta ACD $$
$$ BD = CD $$
$$ AD = AD $$ is common
$$\angle ADB=\angle ADC=90^o$$
$$ \Delta ABD \cong\Delta ACD $$ (SAS Axiom)
Therefore , it is proved.
$$ BD = CD $$
In $$ \Delta ABD $$ and $$ \Delta ACD $$
$$ BD = CD $$
$$ AD = AD $$ is common
$$\angle ADB=\angle ADC=90^o$$
$$ \Delta ABD \cong\Delta ACD $$ (SAS Axiom)
Therefore , it is proved.
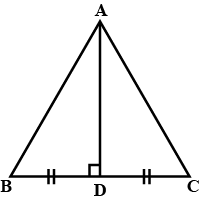
From the given figure, prove that:
$$ AB = ED $$
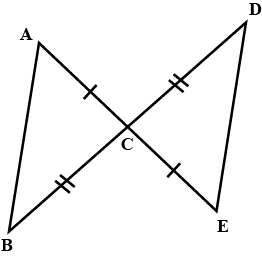
In the given figure , prove that
$$ \Delta ACB \cong \Delta ECD $$
Prove that
$$ \angle A = \angle C $$
Prove that
$$ \Delta ABD \cong \Delta BDC $$
In the given figure , prove that
$$ \Delta ABD \cong \Delta ACD $$
Prove that
$$ \angle ADB = 90^{\circ} $$
Prove that :
(i) $$ \Delta ABC \cong \Delta ADC $$
(ii) $$ \angle B = \angle D $$
(iii) $$ AC$$ bisects angle $$DCB $$.
In the given figure
$$ AB = AD $$ and $$ CB = CD $$
In $$ \Delta ABC $$ and $$ \Delta ADC $$
$$ AC = AC $$ is common
It is given that
$$ AB = AD $$ and $$ CB = CD $$
Here $$ \angle ABC \cong \Delta ADC $$ (SSS Axiom)
$$ \angle B = \angle D $$ (c.p.c.t)
So we get
$$ \angle BCA = \angle DCA $$
Therefore , $$AC $$ Bisects $$ \angle DCB $$ .
$$ AB = AD $$ and $$ CB = CD $$
In $$ \Delta ABC $$ and $$ \Delta ADC $$
$$ AC = AC $$ is common
It is given that
$$ AB = AD $$ and $$ CB = CD $$
Here $$ \angle ABC \cong \Delta ADC $$ (SSS Axiom)
$$ \angle B = \angle D $$ (c.p.c.t)
So we get
$$ \angle BCA = \angle DCA $$
Therefore , $$AC $$ Bisects $$ \angle DCB $$ .
Prove that
$$ \angle B = \angle C $$
From the figure
$$ BD = CD $$
In $$ \Delta ABD $$ and $$ \Delta ACD $$
$$ BD = CD $$
$$ AD = AD $$ is common
$$\angle ADB=\angle ADC=90^o$$
$$ \Delta ABD \equiv \Delta ACD $$ (SAS Axiom)
$$\angle B=\angle C$$ (c.p.c.t)
Therefore , it is proved.
$$ BD = CD $$
In $$ \Delta ABD $$ and $$ \Delta ACD $$
$$ BD = CD $$
$$ AD = AD $$ is common
$$\angle ADB=\angle ADC=90^o$$
$$ \Delta ABD \equiv \Delta ACD $$ (SAS Axiom)
$$\angle B=\angle C$$ (c.p.c.t)
Therefore , it is proved.
In the given figure , prove that :
$$ \Delta ADB \cong \Delta BCA $$
In the given figure , prove that :
$$ AD = BC $$
In the given figure, prove that :
$$ \Delta AOD \cong \Delta BOC $$
In the given figure , prove that :
$$ \Delta XYZ \cong \Delta XPZ $$
In the given figure , prove that :
$$ YZ = PZ $$
The given figures shows a triangle ABC in which AD is perpendicular to side BC and BD = CD. Prove that :
(i) $$ \Delta ABD \cong \Delta ACD $$
(ii) $$ AB = AC $$
(iii) $$ \angle B = \angle C $$
In the given figure , $$ \angle 1 = \angle 2 $$ and $$ AB = AC$$ .
Prove that:
(i) $$ \angle B = \angle C $$
(ii) $$ BD = DC $$
(iii) $$ AD$$ is perpendicular to $$BC $$
In the given figure , prove that :
$$ \angle YXZ = \angle PXZ $$
In the given figure , prove that :
$$ \angle ADB = \angle ACB $$
In the given figure , prove that :
$$ \Delta ABC \cong \Delta DCB $$
In the given figure $$AB , = DB$$ and $$AC = DC$$
If $$ \angle ABD = 58 ^{o}$$
$$ \angle DCB = (2x - 4) ^{o}$$
$$ \angle ACB = y + 15$$ and
$$ \angle DCB = 63 ^{o}$$ : find the values of $$x$$ and $$y $$
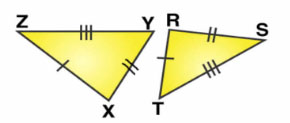
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which triangles in each pair are congruent.
By.............test
$$\Delta PQR \cong \Delta STU$$
In $$\triangle PQR$$ and $$\triangle STU$$
$$\angle P=\angle S$$
$$PR=ST$$
$$\angle R=\angle T$$
By $$ASA$$ Test
$$\Delta PQR \cong \Delta STU$$
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
By............test
$$\Delta LMN \cong \Delta PTR$$
In the given figure, $$\angle P =\angle R$$ and $$PQ =RQ.$$ Prove that, $$\Delta PQT \cong \Delta RQS$$
Observe the information shown in pair of triangle shown above. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangle.
In the given alongside figure,$$AD=AB=AC,BD$$ is parallel to $$CA$$ and $$\angle ACB=65^o$$.
Find the $$\angle DAC$$.
As shown in the following figure, in $$\Delta LMN$$ and $$\Delta PNM$$, $$LM = PN, LN = PM.$$ Write the test which assures the congruence of the two triangles. Write their remaining congruent part.
Observe the information shown in the pair of triangles given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
In the following example, a pair of triangles is shown. Equal parts of the triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
By............test
$$\Delta XYZ \cong \Delta LMN$$
In the figure, point $$ D $$ and $$ E $$ are on side $$ B C $$ of $$ \Delta A B C, $$ such that $$ B D=C E $$ and $$ A D=A E $$
show that $$\triangle ABD \cong \triangle ACE$$.
Fill in the blank using the correct word given in brackets:
All squares are _____. (similar, congruent )
Similar,
because
all squares are of same shape but
size may not be same
Hence, these are similar but not congruent.
All circles are similarAll squares are similar.
Line 1 is the bisector of an angle $$\angle A$$ and B is any point on l. BP and BQ are perpendiculars from B to the arms of $$\angle A$$. Show that :
(i) $$\triangle APB \cong \triangle AQB$$
(ii) BP = BQ or B is equidistant from the arms of $$\angle A$$.
In the given figure, bisector of $$ \angle \mathrm{BAC} $$ intersects side $$ \mathrm{BC} $$ at point $$ \mathrm{D} $$. Prove that $$ \mathrm{AB}>\mathrm{BD} $$
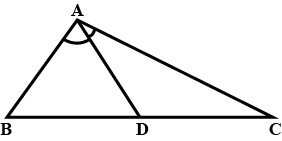
In the given figure, point $$ S $$ is any point on side $$ \mathrm{QR} $$ of $$ \Delta \mathrm{PQR} $$
Prove that $$ : \mathrm{PQ}+\mathrm{QR}+\mathrm{RP}>2 \mathrm{PS} $$
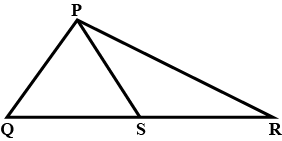
In the figure, points D and E are on side BC of $$\Delta$$ ABC, such that BD = CE and AD = AE.
Show that $$\Delta \mathrm{ABD} \cong \Delta \mathrm{ACE}$$
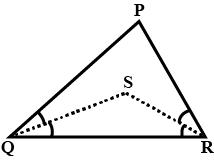
In $$ \Delta \mathrm{PQR}, $$ If $$ \mathrm{PQ}>\mathrm{PR} $$ and bisectors of $$ \angle \mathrm{Q} $$ and $$ \angle \mathrm{R} $$ intersect at $$ \mathrm{S} $$. Show that $$ \mathrm{SQ}>\mathrm{SR} $$.
Fill in the blank using the correct word given in brackets:
All circles are ______. (Congruent, similar)
Similar
because all circles are of same shape (round) but
size may not be same
Hence, these are similar but not congruent.
All circles are similar
l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that $$\triangle ABC \cong \triangle CDA$$.
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal. Show that
(i) $$\triangle ABE = \triangle ACF$$
(ii) $$AB = AC$$ i.e., $$\triangle ABC$$ is an isosceles triangle.
In fig $$\angle B < \angle A$$ and $$\angle C < \angle D$$. Show that AD < BC.
In sides AB and AC of $$\triangle ABC$$ are extended to points P and Q respectively. Also, $$\angle PBC < \angle QCB$$. Show that AC > AB.
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of $$\triangle PQR$$. Show that :
(i) $$\triangle ABM \cong \triangle PQN$$
(ii) $$\triangle ABC \cong \triangle PQR$$
ABC and DBC are two isosceles triangles on the same base BC. Show that $$\angle ABD = \angle ACD$$.
AB is a line segment and P is its midpoint. D and E are points on the same side of AB such that $$\angle BAD = \angle ABE$$ and $$ \angle EPA = \angle DPB$$. Show that
(i) $$\triangle DAP \cong \triangle EBP$$
(ii) AD = BE
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. Show that :
(i) $$\triangle AMC \cong \triangle BMD$$
(ii) $$\angle DBC $$ is a right angle.
(iii) $$\triangle DBC \cong \triangle ACB$$
(iv) $$CM = \frac{1}{2} AB$$.
Data given:
$$\angle{ACB}={90}^{0}$$
$$M$$ is the midpoint of $$AB$$
So $$AM=BM$$ .....$$\left(1\right)$$
Also, $$DM=CM$$ ......$$\left(2\right)$$
$$\left(A\right)$$Lines $$CD$$ and $$AB$$ intersect at $$M$$.
So, $$\angle{AMC}=\angle{BMD}$$ (vertically opposite angles) ......... .$$\left(3\right)$$
In $$\triangle AMC$$ and $$\triangle BMD$$
$$\triangle AMC\cong \triangle BMD$$
$$AM=BM$$ (from $$\left(1\right)$$)
$$\angle{AMC}=\angle{BMD}$$ (from $$\left(3\right)$$)
$$CM=DM$$
$$\therefore \triangle AMC\cong \triangle BMD$$ (by SAS congruence rule)
$$\therefore \angle{ACM}=\angle{BDM}$$ (by C.P.C.T)
But $$\angle{ACM}$$ and $$\angle{BDM}$$ are alternate interior angles for lines $$AC$$ and $$BD$$.
If a transversal intersects two lines such that pair of alternate interior angles is equal, then the lines are parallel.
So $$BD\parallel AC$$
Since $$BD\parallel AC$$ and considering $$BC$$ as transversal.
$$\Rightarrow \angle{DBC}+\angle{ACB}={180}^{0}$$ since interior angles on the same side of transversal are supplementary.
$$\Rightarrow \angle{DBC}+{90}^{0}={180}^{0}$$
Hence $$\angle{DBC}$$ is a right angle
From $$\left(1\right) \triangle AMC\cong\triangle BMD$$
$$\Rightarrow AC=BD$$ by C.P.C.T .....$$\left(4\right)$$
In $$\triangle DBC$$ and $$\triangle ACB$$,
$$DB=AC$$ from $$\left(4\right)$$
$$\angle{DBC}=\angle{ACB}$$ both $${90}^{0}$$
$$BC=CB$$(common)
$$\therefore \triangle DBC\cong \triangle ACB$$(SAS congruence rule)
$$\therefore DC=AB$$ by C.P.C.T
$$\Rightarrow \dfrac{1}{2}DC =\dfrac{1}{2}AB$$ as $$DM=CM$$
$$\therefore DM=CM=\dfrac{1}{2}DC$$
$$\therefore CM=\dfrac{1}{2}AB$$
In AC = AE, AB = AD and $$\angle BAD = \angle EAC$$. Show that BC = DE
$$ABC$$ is an isosceles triangle with $$AB = AC$$. Show that $$\angle B = \angle C$$.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
In ( $$ \triangle ABC , AB = BC $$ and $$ | B = 64^{\circ} $$ find | $$\angle C$$
In a triangle $$ ABC , AB = AC $$. Points G on AB and D on AC are such that $$AE = AD $$ prove that triangles BCD and CBE are congruent
Justify the following statement with reason Difference of any two side is less than the third side
In $$ \bigtriangleup ABC $$
To prove (i) $$AC - AB < BC (ii) BC - AC < AB (iii) BC - AB < AC $$
Construction Let $$ AC < AB . $$ On AC
Proof : $$AB = AD $$
$$\therefore \angle 1 = \angle 2 $$ [ Base angles of isosceles triangle]
Extr $$\angle 2 = \angle 4 + \angle 3$$
$$\angle 2 > \angle 4 $$ [ Exterior angle > each interior opp angle ]
$$\therefore $$ Extr $$ \angle 3 = \angle 1 + \angle A$$
To prove (i) $$AC - AB < BC (ii) BC - AC < AB (iii) BC - AB < AC $$
Construction Let $$ AC < AB . $$ On AC
Proof : $$AB = AD $$
$$\therefore \angle 1 = \angle 2 $$ [ Base angles of isosceles triangle]
Extr $$\angle 2 = \angle 4 + \angle 3$$
$$\angle 2 > \angle 4 $$ [ Exterior angle > each interior opp angle ]
$$\therefore $$ Extr $$ \angle 3 = \angle 1 + \angle A$$
In right triangle the make the statement true
The sum of any two sides of a triangle is ____ than the third side
In $$\bigtriangleup ABC , AC = AB $$ and the altitude AD bisects BC prove that $$ \bigtriangleup ADC = \bigtriangleup ADB $$
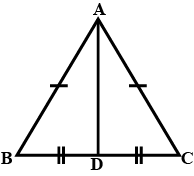
In Fg. PR > PQ and PS bisects $$\angle QPR$$. Prove that $$\angle PSR > \angle PSQ$$.
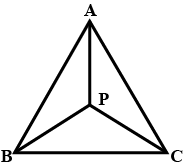
Let ABC be a triangle and P be an interior point , prove that $$AB + BC + CA < 2 ( PA + PB + PC ) $$
In the adjoining figure If $$BC = EF$$ then, $$\angle C = $$ _____ and $$\angle A = $$ _______
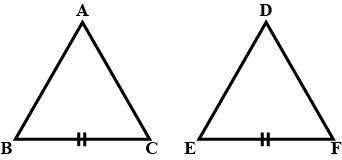
Let AABC be a triangle such that $$\angle B = 70^{\circ}$$ and $$\angle C = 40^{\circ}$$ . Suppose D is a point on BC such that $$AB = AD $$ Prove that $$Ab > CD$$
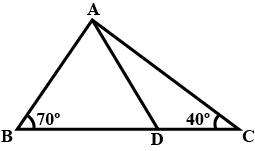
In a $$\bigtriangleup ABC , AB = AC $$ and $$ | A = 50^{\circ} $$ find $$\angle B $$ and $$ \angle C $$
Two triangles $$ABC$$ and $$DBC$$ have common base $$BC$$. Suppose $$AB= DC $$ and $$\angle ABC = \angle BCD $$, then prove that $$AC = BD$$.
In $$\bigtriangleup ABC $$ and $$\bigtriangleup DBC $$
$$AB = DC $$ (Given)
$$\angle ABC = \angle BCD $$ (Given)
$$BC = BC $$ (common side)
$$\therefore \bigtriangleup ABC \cong \bigtriangleup DBC $$ (By $$SAS$$ postulate)
$$\implies AC = BD $$ ( Corresponding sides of congruent triangles)
$$BC = BC $$ (common side)
$$\therefore \bigtriangleup ABC \cong \bigtriangleup DBC $$ (By $$SAS$$ postulate)
$$\implies AC = BD $$ ( Corresponding sides of congruent triangles)
In triangles, $$ABC$$ and $$PQR, \angle A = \angle Q$$ and $$\angle B = \angle R$$ then which side of $$\Delta PQR$$ is equal to side $$BC$$ of $$\Delta ABC$$, so that both triangles congruent? Give reasons for your answer.
If two sides and one angle of a triangle are equal to two sides and the angle of other then both the triangles must congruent to each other. Is this statement true?
Let ABC be a triangle . Drawn a triangle BDC externally on BC such that AB = BD and AC = CD Prove that $$\bigtriangleup ABC \cong \bigtriangleup DBC $$
In $$ \bigtriangleup ABC $$ and $$ \bigtriangleup DBC $$
$$AB = BD $$ [data]
$$ AC = CD $$ [ data]
$$BC = BC $$ [ common side ]
$$\therefore \bigtriangleup ABC = \triangle DBC $$ [ SSS postulate]
$$AB = BD $$ [data]
$$ AC = CD $$ [ data]
$$BC = BC $$ [ common side ]
$$\therefore \bigtriangleup ABC = \triangle DBC $$ [ SSS postulate]
In figure, $$ADBC$$ is a quadrilateral in which $$\angle ABC = \angle ABD$$ and $$BC = BD$$ then show that $$\Delta ABC \cong \Delta ABD$$.
In $$\Delta ABC$$ and $$\Delta PQR$$, $$\angle A = \angle Q$$ and $$\angle B = \angle R$$. Then which side of $$\Delta PQR$$ is equal to side $$AB$$ of $$\Delta ABC$$. So that both triangles become congruent. Give reason for your answer.
If two angles and one side of a triangle are equal to two angles and one side of other triangle then both As must congruent to each other. Is this statement true?
In the adjoining figure If $$AC = CE $$ and $$\bigtriangleup ABC \cong \bigtriangleup DEC $$ then $$\angle D = $$ _____ and $$\angle A = $$ _______
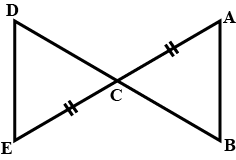
In figure, $$Q$$ is a point on side $$SR$$ of $$\Delta PSR$$ such that $$PQ = PR$$. Prove that $$PS > PQ$$.
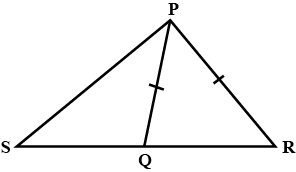
$$\Delta ABC$$ and $$\Delta DBC$$ are two isosceles $$I$$ triangles on the same base $$BC$$ and vertices $$A$$ and $$D$$ are on the same side of $$BC$$ (see figure). If $$AD$$ is extended to intersect $$BC$$ at $$P$$, show that
(i) $$\Delta ABD \cong \Delta ACD$$
(ii) $$\Delta ABP \cong \Delta ACP$$
(iii) $$AP$$ bisects $$\angle A$$ as well as $$\angle D$$
(iv) $$AP$$ is the perpendicular bisector of $$BC$$.
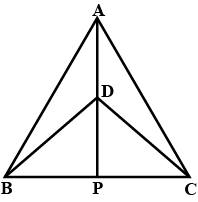
$$AD$$ is the median of any $$\Delta ABC$$. Is it true to say that $$AB + BC + CA > 2AD$$. Give reason for your answer.
Yes, if $$AD$$ is median of $$\Delta ABC$$
$$AB + BD > AD$$ …(i) (sum of any two sides of a $$A$$ is greater than third side)
and $$AC + DC > AD$$ …(iii) (reason as above)
Similarly, $$AB + (BD + DC) + AC > 2 AD$$
$$AB + BC + CA > 2AD$$
$$AB + BD > AD$$ …(i) (sum of any two sides of a $$A$$ is greater than third side)
and $$AC + DC > AD$$ …(iii) (reason as above)
Similarly, $$AB + (BD + DC) + AC > 2 AD$$
$$AB + BC + CA > 2AD$$
$$BE$$ and $$CF$$ are two equal altitudes of $$\Delta ABC$$. By using RHS congruency rule, prove that $$\Delta ABC$$ is an isosceles triangle.
In $$\Delta BFC$$ and $$\Delta CEB$$
$$\angle BFC = \angle CEB = 90^{0}$$ (given)
hyp. $$BC$$ = hyp. $$BC$$ (common)
and altitude $$CF$$ = altitude $$BE$$
$$\Delta BFC \cong \Delta CEB$$
(by RHS congruency rule)
$$\angle B = \angle C$$
$$\Delta ABC$$ is an isosceles triangle.
Hence proved.
$$\angle BFC = \angle CEB = 90^{0}$$ (given)
hyp. $$BC$$ = hyp. $$BC$$ (common)
and altitude $$CF$$ = altitude $$BE$$
$$\Delta BFC \cong \Delta CEB$$
(by RHS congruency rule)
$$\angle B = \angle C$$
$$\Delta ABC$$ is an isosceles triangle.
Hence proved.
In $$\Delta ABC$$, $$\angle A > \angle B$$ and $$\angle B > \angle C$$, then write the smallest side.
In an $$\Delta ABC$$ with $$AB = AC$$, $$D$$ is any point on the side $$AC$$. Show that $$CD < BD$$.
In $$\Delta ABC$$
$$AB = AC$$ (given)
$$\angle B = \angle C$$
$$\angle ADB = \angle DBC + \angle C$$ (exterior angle is equal to sum of opposite interior angles)
$$\angle ADB > \angle C$$
$$AB > BD$$
But $$AB = AC$$
$$AD + DC > BD$$
$$BD > CD$$
Hence proved.
$$AB = AC$$ (given)
$$\angle B = \angle C$$
$$\angle ADB = \angle DBC + \angle C$$ (exterior angle is equal to sum of opposite interior angles)
$$\angle ADB > \angle C$$
$$AB > BD$$
But $$AB = AC$$
$$AD + DC > BD$$
$$BD > CD$$
Hence proved.
In $$\Delta PQR$$, $$S$$ is any point on side $$QR$$. Show that $$PQ + QR + RP > 2PS$$.
In $$\Delta PQR$$,
$$PQ + QS > PS$$ …(i) ( $$\because$$ the sum of any two sides of a triangle is greater than the third side)
In $$\Delta PRS$$,
$$PR + RS > PS$$ ($$\because$$ The sum of any two sides of a triangle is greater than the third side)
On adding (i) and (ii), we get
$$(PQ + QS) + (PR + RS) > 2PS$$
$$PQ + (QS + RS) + PR > 2PS$$
$$PQ + QR + PR > 2PS$$
$$PQ + QR + RP > 2PS$$
Hence proved.
$$PQ + QS > PS$$ …(i) ( $$\because$$ the sum of any two sides of a triangle is greater than the third side)
In $$\Delta PRS$$,
$$PR + RS > PS$$ ($$\because$$ The sum of any two sides of a triangle is greater than the third side)
On adding (i) and (ii), we get
$$(PQ + QS) + (PR + RS) > 2PS$$
$$PQ + (QS + RS) + PR > 2PS$$
$$PQ + QR + PR > 2PS$$
$$PQ + QR + RP > 2PS$$
Hence proved.
In figure, $$AD = BD$$ and $$\angle C = \angle E$$. Prove that $$BC = AE$$.
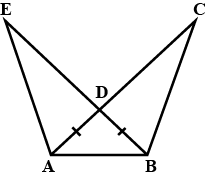
In figure, $$O$$ is an interior point of $$\Delta ABC$$. Show that: $$AB + BC + CA < 2(OA + OB +OC)$$.
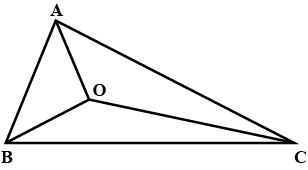
In any triangle ABC if $$AB > AC$$ and $$D$$ is any point on BC then prove that $$AB > AD$$.
In $$\Delta ABC$$
$$AB > AC$$
$$\angle ACB > \angle ABC$$ …(i) ($$\because$$ angle opposite to larger side is greater)
Now in $$\Delta ACD, CD$$ is produced to $$B$$ forming an ext. $$\angle ADB$$.
$$\angle ADB > \angle ACD$$ (exterior angle of a $$A$$ is greater than each interior opposite angle)
$$\angle ADB > \angle ACB$$ …(ii)
$$\angle ACD = \angle ACB$$
From (i) and (ii)
$$\angle ADB > \angle ABC$$
$$\angle ADB > \angle ABD [\because \angle ABC = \angle ABD]$$
$$AB > AD$$ [$$\because$$ side opposite to greater angle is larger]
Hence proved.
$$AB > AC$$
$$\angle ACB > \angle ABC$$ …(i) ($$\because$$ angle opposite to larger side is greater)
Now in $$\Delta ACD, CD$$ is produced to $$B$$ forming an ext. $$\angle ADB$$.
$$\angle ADB > \angle ACD$$ (exterior angle of a $$A$$ is greater than each interior opposite angle)
$$\angle ADB > \angle ACB$$ …(ii)
$$\angle ACD = \angle ACB$$
From (i) and (ii)
$$\angle ADB > \angle ABC$$
$$\angle ADB > \angle ABD [\because \angle ABC = \angle ABD]$$
$$AB > AD$$ [$$\because$$ side opposite to greater angle is larger]
Hence proved.
In the given figure, $$O$$ is the middle point of both $$AB$$ and $$CD$$. Prove that $$AC = BD$$ and $$AC || BD$$.
In figure, $$CB = AD$$ and $$AB = CD$$. Can we say $$\angle ABC$$ and $$\angle ADC$$ are equal? Why?
Prove that the difference of any two sides of a triangle is less than the third side.
Given: A $$\Delta ABC$$
To prove:
(i) $$AC – AB < BC$$
(ii) $$BC – AC < AB$$
(iii) $$BC – AB < AC$$
Construction: Take a point $$D$$ on $$AC$$ such that $$AB = AD$$. Join $$BD$$.
Proof: In $$\Delta ABD, AB = AD, \angle 1 = \angle 2$$ …(i)
In $$\Delta ABD$$, side $$AD$$ is produced to $$C \angle 3 > \angle 1$$ …(ii)
(ext. angle is greater than one of the opposite interior angle)
Also in $$\Delta BCD$$
$$\angle 2 > \angle 4$$ …(iii) (reason as above)
From (i) and (ii), we get
$$\angle 3 > \angle 2$$ …(iv)
From (iii) and (iv), we get
$$\angle 3 > \angle 4$$
$$BC > CD$$ (side opposite to greater angle is larger)
$$CD < BC$$
$$AC – AD < BC$$
$$AC – AB < BC$$ $$[\because AD = AB]$$
Similarly we can prove
$$BC – AC < AB$$ and $$BC – AB < AC$$
Hence proved.
To prove:
(i) $$AC – AB < BC$$
(ii) $$BC – AC < AB$$
(iii) $$BC – AB < AC$$
Construction: Take a point $$D$$ on $$AC$$ such that $$AB = AD$$. Join $$BD$$.
Proof: In $$\Delta ABD, AB = AD, \angle 1 = \angle 2$$ …(i)
In $$\Delta ABD$$, side $$AD$$ is produced to $$C \angle 3 > \angle 1$$ …(ii)
(ext. angle is greater than one of the opposite interior angle)
Also in $$\Delta BCD$$
$$\angle 2 > \angle 4$$ …(iii) (reason as above)
From (i) and (ii), we get
$$\angle 3 > \angle 2$$ …(iv)
From (iii) and (iv), we get
$$\angle 3 > \angle 4$$
$$BC > CD$$ (side opposite to greater angle is larger)
$$CD < BC$$
$$AC – AD < BC$$
$$AC – AB < BC$$ $$[\because AD = AB]$$
Similarly we can prove
$$BC – AC < AB$$ and $$BC – AB < AC$$
Hence proved.
In figure, $$\angle B > \angle A$$ and $$\angle D > \angle E$$ then show that $$AE > BD$$.
In figure, $$BA \perp AC, DE \perp EF$$, such that $$BA = DE$$ and $$BF = CD$$, prove that $$AC = EF$$.
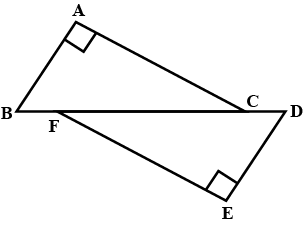
In figure, side $$AB$$ and $$AC$$ are produced to point $$D$$ and $$E$$ respectively. Bisectors $$BO$$ and $$CO$$ of $$\angle DBC$$ and $$\angle ECB$$ respectively meet at $$O$$. If $$AB > AC$$. Prove that $$OC > OB$$.
In the given figure, $$PQRS$$ is a quadrilateral. $$PQ$$ is its longest side and $$RS$$ is its shortest side. Prove that: $$\angle R > \angle P$$ and $$\angle S > \angle Q$$.
In figure, side $$QR$$ of $$\Delta PQR$$ is produced on both sides such that $$\angle PQS = \angle PRT$$. Prove that $$PQ = PR$$.
If figure, $$ABCD$$ is a quadrilateral. Prove that $$AB + BC + CD + DA > AC + BD$$.
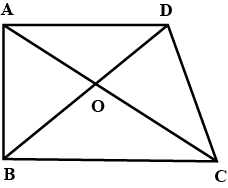
In figure, $$T$$ is a point on side $$QR$$ of $$\Delta PQR$$ and $$S$$ is a point such that $$RT = ST$$. Prove that $$PQ + PR > QS$$.
If two sides of a triangle are unequal then the longer side has greater angle opposite to it. Prove it.
Given: A $$\Delta ABC$$ in which $$AC > AB$$ (say)
To prove: $$\angle ABC > \angle ACB$$
Construction: Mark a point $$D$$ on $$AC$$ such that $$AB = AD$$. Join $$BD$$.
Proof: In $$\Delta ABD$$
$$AB = AD$$ (by construction)
$$\angle 1 = \angle 2$$ …(i) (angles opposite to equal sides are equal)
Now in $$\Delta BCD$$
$$\angle 2 > \angle DCB$$ (ext. angle is greater than one of the opposite interior angles)
$$\angle 2 > \angle ACB$$ …(ii) $$[\because \angle ACB = \angle DCB]$$
From (i) and (ii), we get
$$\angle 1 > \angle ACB$$ …(iii)
But $$\angle 1$$ is a part of $$\angle ABC$$
$$\angle ABC > \angle 1$$ …..(iv)
Now from (iii) and (iv), we get
$$\angle ABC > \angle ACB$$
Hence proved.
To prove: $$\angle ABC > \angle ACB$$
Construction: Mark a point $$D$$ on $$AC$$ such that $$AB = AD$$. Join $$BD$$.
Proof: In $$\Delta ABD$$
$$AB = AD$$ (by construction)
$$\angle 1 = \angle 2$$ …(i) (angles opposite to equal sides are equal)
Now in $$\Delta BCD$$
$$\angle 2 > \angle DCB$$ (ext. angle is greater than one of the opposite interior angles)
$$\angle 2 > \angle ACB$$ …(ii) $$[\because \angle ACB = \angle DCB]$$
From (i) and (ii), we get
$$\angle 1 > \angle ACB$$ …(iii)
But $$\angle 1$$ is a part of $$\angle ABC$$
$$\angle ABC > \angle 1$$ …..(iv)
Now from (iii) and (iv), we get
$$\angle ABC > \angle ACB$$
Hence proved.
In figure, $$PQR$$ is a triangle and $$S$$ is any point in its interior, show that $$SQ + SR < PQ + PR$$.
For the following congruent triangles, find the pairs of corresponding angles.
To find: Pair of corresponding angles
Solution: In $$\Delta POQ$$ and $$\Delta ROS$$
$$PO=RO$$ (each $$4$$ cm)
$$OQ=OS$$ (each $$4$$ cm)
$$PQ=RS$$ (each $$5$$ cm)
$$\Delta POQ\cong \Delta ROS$$(By SSS cong. rule)
$$\therefore$$ corresponding $$\angle s$$ are
$$\angle P=\angle R$$
$$\angle POQ=\angle ROS$$
$$\angle Q=\angle S$$.
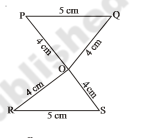
In the adjoining figure, $$AD=BD$$ $$\angle{ABD}={65}^{o}$$ & $$\angle{DAC}={22}^{o}$$.
Find $$\angle{ACD}$$
$$AD=BD$$
$$\angle BAD=\angle ABD=65$$
$$\angle BAC=\angle BAD+\angle DAC$$
$$\angle BAC=65+22$$
$$\angle BAC=87$$
$$\angle A+\angle B+\angle C=180°$$
$$87+65+\angle C=180°$$
$$\angle C=180-152$$
$$\angle C=28$$
$$\therefore \angle ACD=28$$
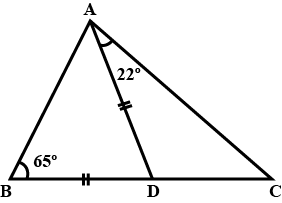
If $$a, b, c$$ are sides of a scalene triangle then prove that$$(a + b + c)^{3} > 27$$ $$(a + b - c)(b + c - a)(c + a -b)$$
In given figures sides $$AB$$ and $$BC$$ and median $$AD$$ of a $$\triangle ABC$$ are respectively proportional to sides $$PQ, QR$$ and median $$PM$$ of $$\triangle PQR$$. Show that $$\triangle ABC \sim \triangle PQR$$.
In given figure two sides $$AB, BC$$ and median $$AM$$ of one triangle $$ABC$$ are respectively equal to sides $$PQ$$ and $$QR$$ and median $$PN$$ of $$\triangle PQR$$. Show that:
$$\triangle ABM\cong \triangle PQN$$
In Fig $$7.32$$, measure of some parts of triangles are given. By applying $$RHS$$ congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form.
Given,
to find out wether the given figures are
Congruent using $$RHS$$
$$(i)\ $$ Congruence rule
so, Now let us consider figure $$(i)$$
as per $$RHS$$ congruence rule.
$$LQ=LF=90^o$$ ($$\because $$ given)
$$PR=FD$$ (given)
$$PQ\neq DE$$ ($$\because $$ given in figure $$(i)$$)
$$\therefore \ \triangle PQR$$ is not congruence to $$\triangle DEF$$
$$(ii)$$ Now let us consider figure $$(i)$$
as per $$RHS$$ congruence rule
$$LC=LD=90^o$$ ($$\because $$ given )
$$AC=BD$$ ($$\because $$ given)
$$AB=AB$$ ($$\because $$ common side)
$$\therefore \ \triangle ABC\cong \triangle ABD$$
$$(iii)$$ Now let us consider figure $$(iii)$$
as per $$RHS$$ congruence rule we get,
$$\angle B=\angle D=90^o$$ ($$\because $$ given)
$$AB=AD$$ ($$\because $$ given)
$$BC=CD$$ ($$\because $$ given)
$$\therefore \ \triangle ABC\cong \triangle ADC$$
$$(iv)$$ Let us consider figure $$(iv)$$
as per $$RHS$$ congurence rule we get,
$$\angle S=\angle S=90^o$$ (common angle )
$$PQ=PR$$ ($$\because $$ given)
$$QS=SR$$ ($$\because $$ common base)
$$\therefore \ \triangle PSQ\cong \triangle PSR$$
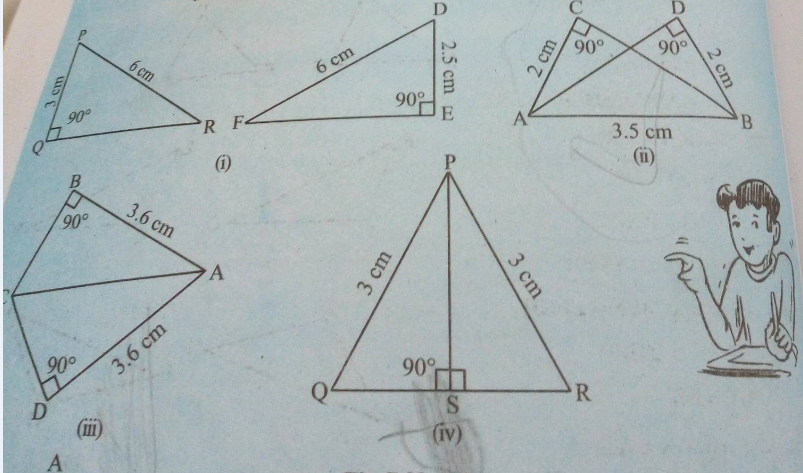
If any point $$O$$ in the interior of a triangle ABC. Prove that AB $$+$$ BC $$+$$ CA $$>$$ OA $$+$$ OB $$+$$ OC.
$$\begin{array}{l} In\, \Delta PBO \\ BP+PO>OB \\ Adding\, \, OC\, \, an\, both\, \, sides \\ we\, \, get, \\ BP+PO+OC>OB+OC\, \\ BP+PC>OB+OC \\ BP+PC>OB+OC\to (i)\, \, \, \left[ { PO+OC=PC } \right] \\ In\, \Delta APC \\ AP+AC>PC \\ Adding\, \, BP\, \, on\, \, both\, \, sides,\, we\, \, get \\ AP+AC+BP>PC+BP\to (ii)\, \, \, \left[ { AP+PB=AB } \right] \\ from\, \, \left( i \right) \, \, \& \, \, \left( { ii } \right) \\ AB+AC>BP+PC>OB+OC \\ AB+AC>OB+OC\to (iii) \\ similarly \\ BC+AC>OB+OA\to (iv) \\ AB+BC>OA+OC\to (v) \\ adding\, \, equation\, \, \left( 3 \right) \left( 4 \right) \left( 5 \right) \, \, we\, \, get \\ 2\left( { AB+BC+CA } \right) >2\left( { OA+OB+OC } \right) \\ AB+BC+CA>OA+OB+OC \end{array}$$
$$ABC$$ is an isosceles triangle right angled at $$B$$. Equilateral triangles $$ACD$$ and $$ABE$$ are constructed on sides $$AC$$ and $$AB$$. Find the ratio between the areas of $$\triangle{ABE}$$ and $$\triangle{ACD}$$.
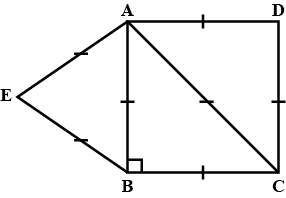
In the adjacent figure $$ABCD$$ is a square and $$\Delta A P B$$ is an equilateral triangle. Prove that $$ \Delta A P D \cong \Delta B P C$$ .
(Hint: In $$\Delta A P D$$ and $$\Delta B P C \quad \overline { A D } = \overline { B C } , \overline { A P } = \overline { B P }$$ and
$$\angle P A D = \angle P B C = 90 ^ { \circ } - 60 ^ { \circ } = 30 ^ { \circ } )$$
Given $$ABCD$$ is square
$$\therefore AB=BC=CD=AD$$
$$\angle A=\angle B=\angle C=\angle D=90^0$$
Given $$PDB$$ is equilateral
$$\therefore AB=PD=PB$$
$$\angle (PAB)=\angle (APB)=\angle (PBA)=60^0$$
$$\therefore \angle (DAP)=\angle (DAB)-\angle (PAB)$$
$$=90-60=30^0$$
$$\therefore \angle(CBP)=\angle(CBA)-\angle(PBD)$$
$$=90-60=30^0$$
In $$\Delta le$$ $$DPA$$ and $$CPB$$
$$AD=BC$$ [sides of the square]
$$PA=PB$$ [sides of the equilateral]
$$\angle(DAP)=\angle(CBP)=60^0$$
$$\therefore \Delta DPA\equiv\Delta CPB$$ [SAS axion]
$$\Rightarrow \Delta DPA\cong \Delta BPC$$
Hence proved.
O if any point in the interior of a triangle ABC. Prove that AB $$+$$ AC $$>$$ OB $$+$$ OC.
Construction=produced BO to meet AC in D
$$\begin{array}{l} oof=In\, \Delta ABD \\ =AB+AD>BD \\ =AB+AD>BO+OD\to (i) \\ In\, \, \Delta OCD \\ CD+DO>OC\to (ii) \\ Adding\, \, equation\, \, (i)\, \, \& \, \, 9ii)\, \, we\, \, get \\ AB+AC>OB+OC\, \, \, \, \, \, \, \left[ { AD+DC=AC } \right] \end{array}$$
Given : EB = DB
AE = BC
$$\angle A\, = \,\angle C\, = \,90^\circ $$
So, $$\Delta ABE\, \cong \,\Delta CDB$$
$$ABC$$ is an isosceles triangle in which $$AC=BC\ AD$$ and $$BE$$ are respectively two altitudes of side $$BC$$ and $$AC$$. Prove that $$AE=BD$$.
In the given figure, $$\angle \mathrm { BMN } = \angle \mathrm { CMN }$$ and AN bisects $$\angle B A C$$. Prove that $$\Delta A B M \equiv \Delta A C M$$.
In the adjacent figure $$ABCD$$ is a square and $$\Delta A P B$$ is an equilateral triangle. Prove that $$\Delta APD \cong \Delta PPC$$
(Hint : In $$\Delta APD$$ and $$\Delta B P C \quad \vec { A D } = \overline { B C } , \overline { A P } = \overline { B P }$$ and $$\angle P A D = \angle P B C = 90 ^ { \circ } - 60 ^ { \circ } = 30 ^ { \circ } ]$$
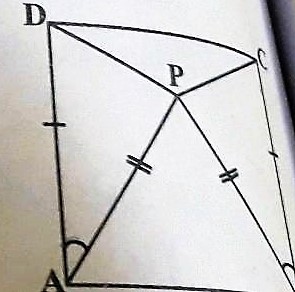
In the figure,prove that $$\triangle APM \cong \triangle APN$$ if $$PM=PN, PM\bot AB$$ and $$PN \bot AC$$
In $$\Delta PQR$$ , If PQ>PR and bisectors of $$\angle Q$$ and $$\angle R$$ interested at $$S$$. Show that SQ>SR.
Given that-
$$\Delta PQR,PQ>PR$$
$$\angle Q\,\,\& \angle R$$ have bisector intersected at $$S$$
To find-
To prove $$SQ>SR$$
$$PQ>PR$$
$$\therefore \angle PQR> \angle PRQ$$
$$\therefore \dfrac{1}{2}\angle PQR> \dfrac{1}{2}\angle PRQ$$
$$\therefore \angle SRQ> \angle SQR$$ [$$\because QS$$ and $$RS$$ bisectors of $$\angle Q$$ and $$LR$$ respectively]
$$\Rightarrow SQ>SR$$ (Since, $$\angle SRQ$$ is larger and is formed by)
Hence, proved $$SQ$$
Find
the circumcentre of the triangle with the vertices A (-3,4) , B (3,4)
and C (-4,-3). What is the circumradius of the circle?
$$ABCD$$ is a square. $$E$$ and $$F$$ are respectively the mid-point of $$BC$$ and $$CD$$. If $$R$$ is the mid point of $$EF$$ prove that
$$ar(AER)=ar(AFR) $$.
In right triangle $$ABC$$, right angled at $$C,M$$ is the mid-point of hypotenuse $$AB$$. $$C$$ is joined to $$M$$ and produced to a point $$D$$ such that $$DM = CM$$. Point $$D$$ is joined to point $$B$$. Show that $$CM = \dfrac{1}{2}AB$$
$$AM=BM=\dfrac{1}{2}AB$$
$$\Rightarrow \angle =90°$$
$$DM=CM$$
$$\triangle DBM$$ and $$\triangle BCM$$
$$\Rightarrow BM=BM$$ ( common )
$$DM=CM$$ ( given )
$$\angle DMB\cong \triangle BCM$$
$$\therefore BM=CM=\dfrac{1}{2}AB$$
Hence, solved.
In figure ,if $$seg\,PR \cong \,seg\,PQ,$$
show that $$seg\,PS > \,seg\,PQ.$$
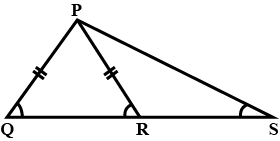
If line segments AB and CD bisect each other
at O, then using SAS congruence rule prove
that $$ \Delta AOC \equiv \Delta BOD $$.
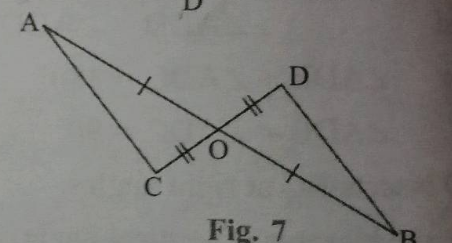
Show that the origin in with in the triangle whose angular points are (2, 1), (3, -2) and (-4, -1).
In the following diagram, AP and BQ are equal and parallel to each other.
Prove that:
(i)$$\Delta AOP \equiv \Delta BOQ$$
(ii)$$AB$$ and $$PQ$$bisect each other
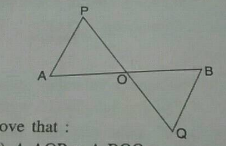
In a $$\Delta PQR$$, if $$PQ=QR$$ and L, M and N are mid-points of the sides PQ,QR and RP respectively. Prove that $$LN=MN$$.
Hence, LN=MN
In right triangle $$ABC$$, right angled at $$C$$, $$M$$ is the mid-point of hypotenuse $$AB$$. $$C$$ is joined to $$M$$ and produced to a point $$D$$ such that $$DM = CM$$. Point $$D$$ is joined to point $$B$$ (see the given figure). Show that: $$(i) \triangle{AMC}\cong \triangle{BMD} $$ $$\left(ii\right) CM = \dfrac{1}{2}AB$$
Proof (i) In $$ \Delta AMC $$ and $$ \Delta BMD $$
M is the midpoint $$ \Rightarrow AM = BM $$
$$ \Rightarrow \angle CMA = \angle DMB $$ (vertically opposite angles)
$$ CM = DM $$ (given)
Hence $$ \Delta AMC \cong \Delta BMD $$ by $$ SAS $$ congruence rule
(ii) $$ DC = AB $$ Since $$ \Delta DBC \cong \Delta ACB $$
$$ \Rightarrow DM+CM = AB $$
$$ \Rightarrow CM+CM = AB $$ Since $$ CD = CM+DM $$
$$ \Rightarrow 2CM = AB $$ and $$ CM = DM $$
Hence $$ CM = 1/2 AB $$
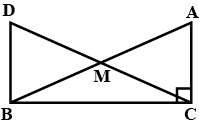
Can you construct a triangle ABC with BC$$=6$$cm, $$\angle$$B$$=60^o$$ and AB$$+$$AC$$=5$$cm? If not give reason.
$$ABC$$ and $$D B C$$ are two isosceles triangles on the same base $$B C$$ (see Fig.). Show that $$\angle ABD=\angle ACD.$$
Given :- $$\Delta ABC$$ is isosceles
$$AB = AC$$ __(1)
$$\Delta DBC$$ is isosceles
$$DB = DC$$ __(2)
To prove :- $$\angle ABD = \angle ACD$$
Proof :- let us join $$AD$$
ln $$\Delta ABD$$ and $$\Delta ACD$$,
$$AB = AC$$ [from eq. (1)]
$$BD = CD$$ [ from eq. (2)]
$$AD = AD$$ [common]
$$\Delta ABD \cong \Delta ACD$$ (sss rule)
$$\angle ABD = \angle ACD$$ (CPCT)
Hence proved
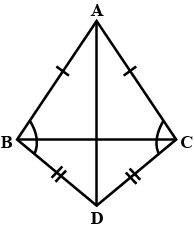
If $$\Delta ABC \sim \Delta PQR, \ ar( \Delta ABC)=16 \ cm^2 $$ and $$\ ar(\Delta PQR)=81 \ cm^2, AB=2 \ cm$$ find PQ.
In $$ \Delta ABC,BD \perp AC $$ and $$ CE \perp AB.$$ If BD and CE intersect at O, prove that $$ \angle BOC = 180^{\circ} - A. $$
In a $$ \Delta ABC, AD $$ bisects $$ \angle A $$ and $$ \angle C > \angle B. $$ Prove that $$ \angle ADB > \angle ADC. $$
In figure, P is the point on the side BC. Complete the following statement using symbol $$' = ' , ' > '$$ or $$' < '$$ so as to make it true.
$$AP.....AB+BP$$.
Class 9 Maths Extra Questions
- Areas Of Parallelograms And Triangles Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Heron'S Formula Extra Questions
- Introduction To Euclid'S Geometry Extra Questions
- Linear Equations In Two Variable Extra Questions
- Lines And Angles Extra Questions
- Number Systems Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadrilaterals Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions