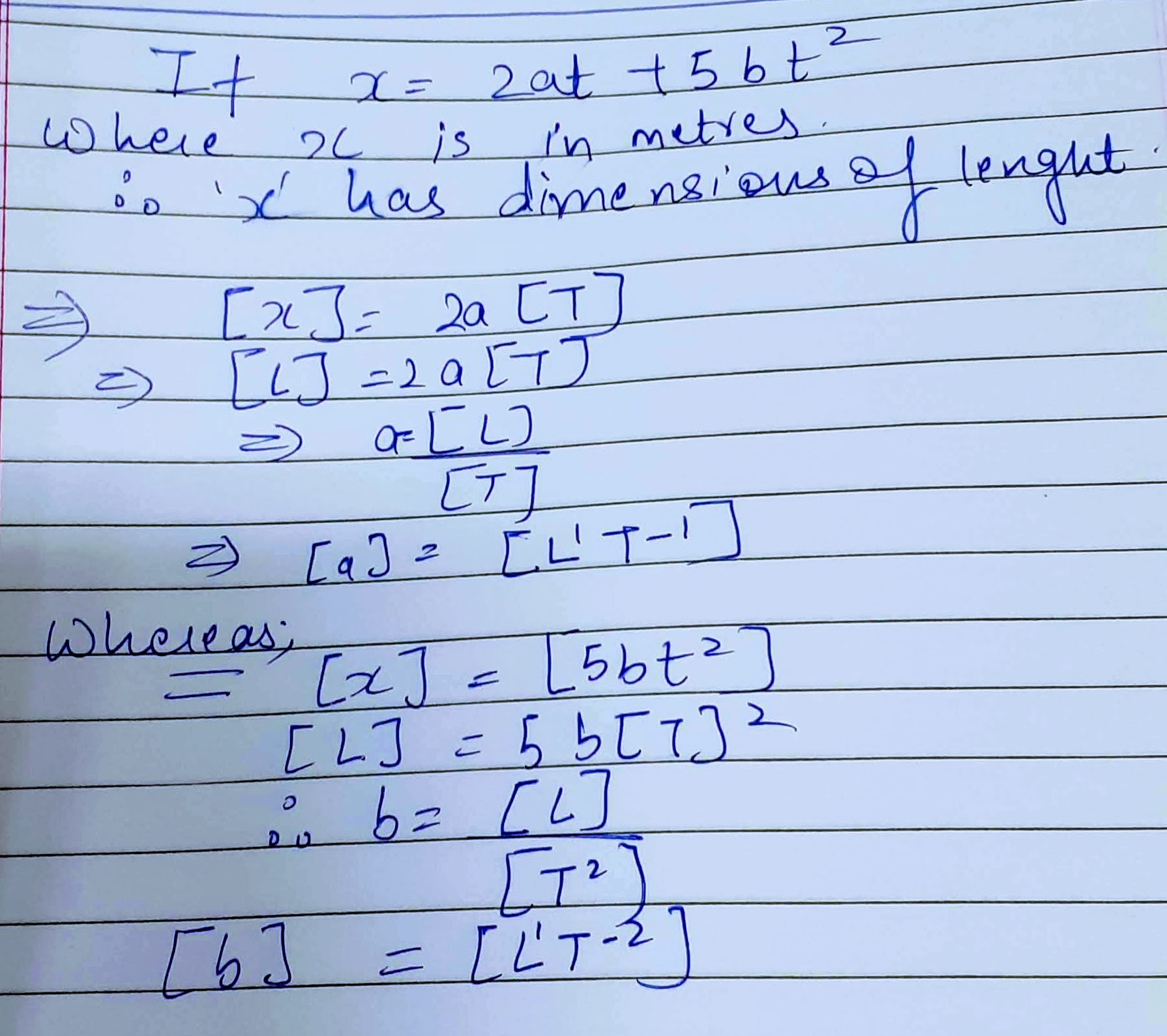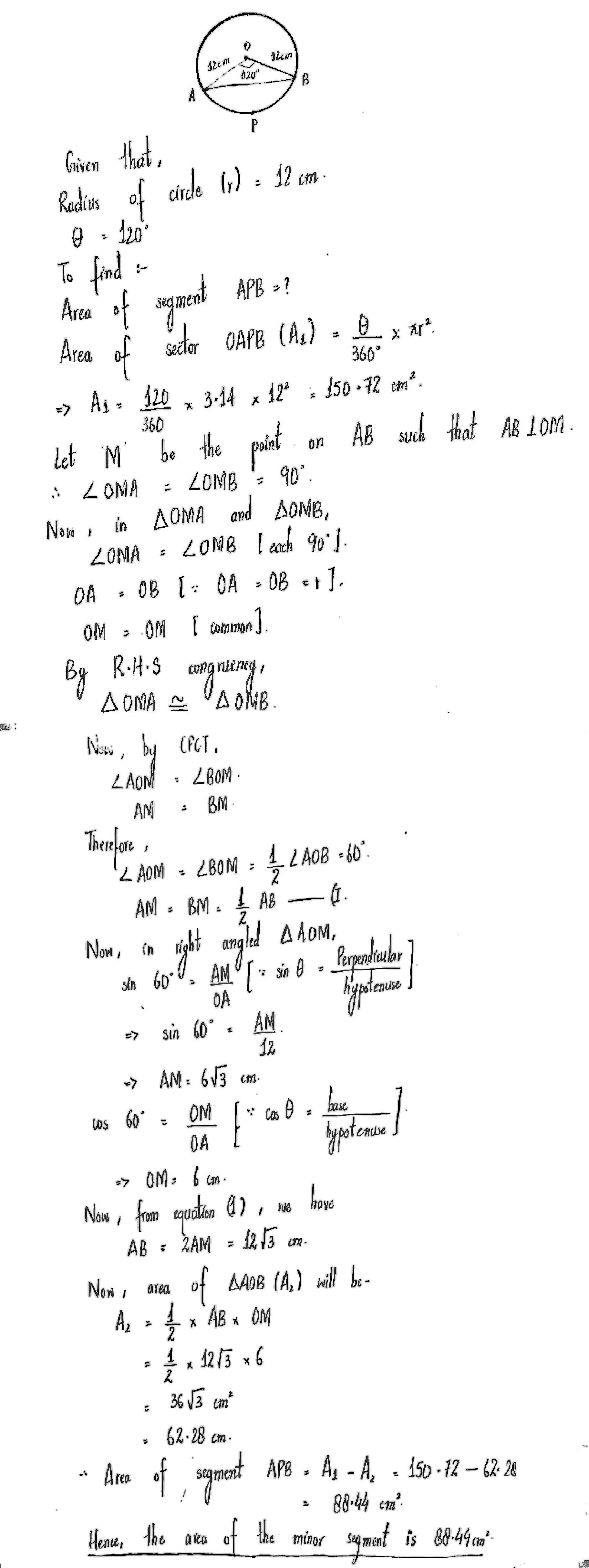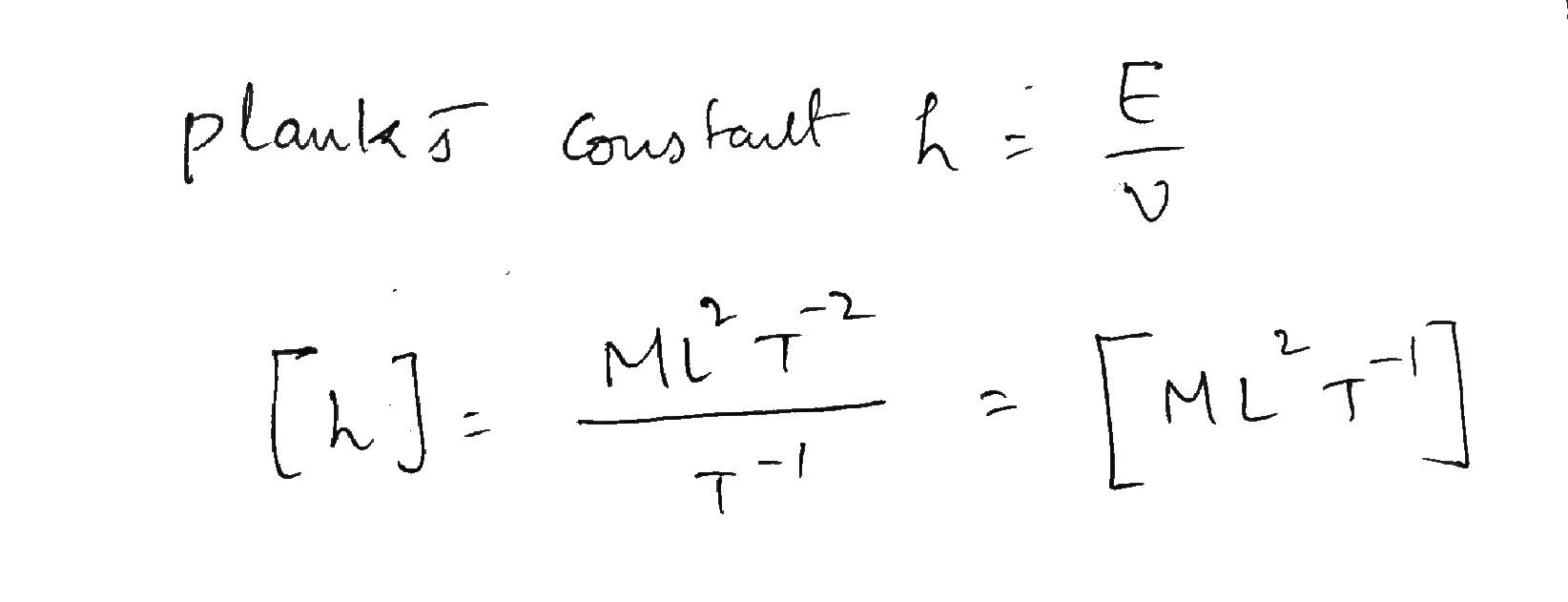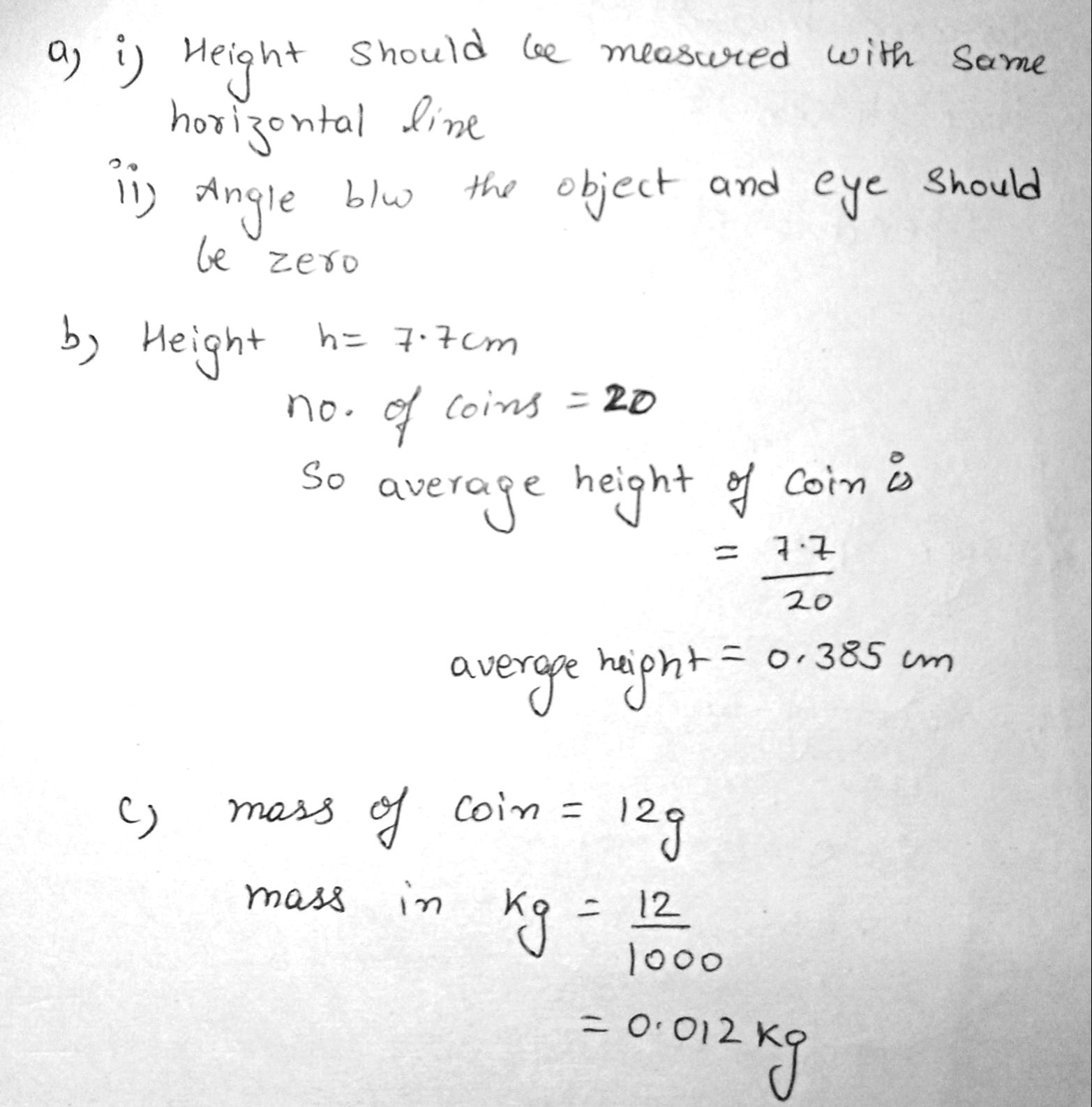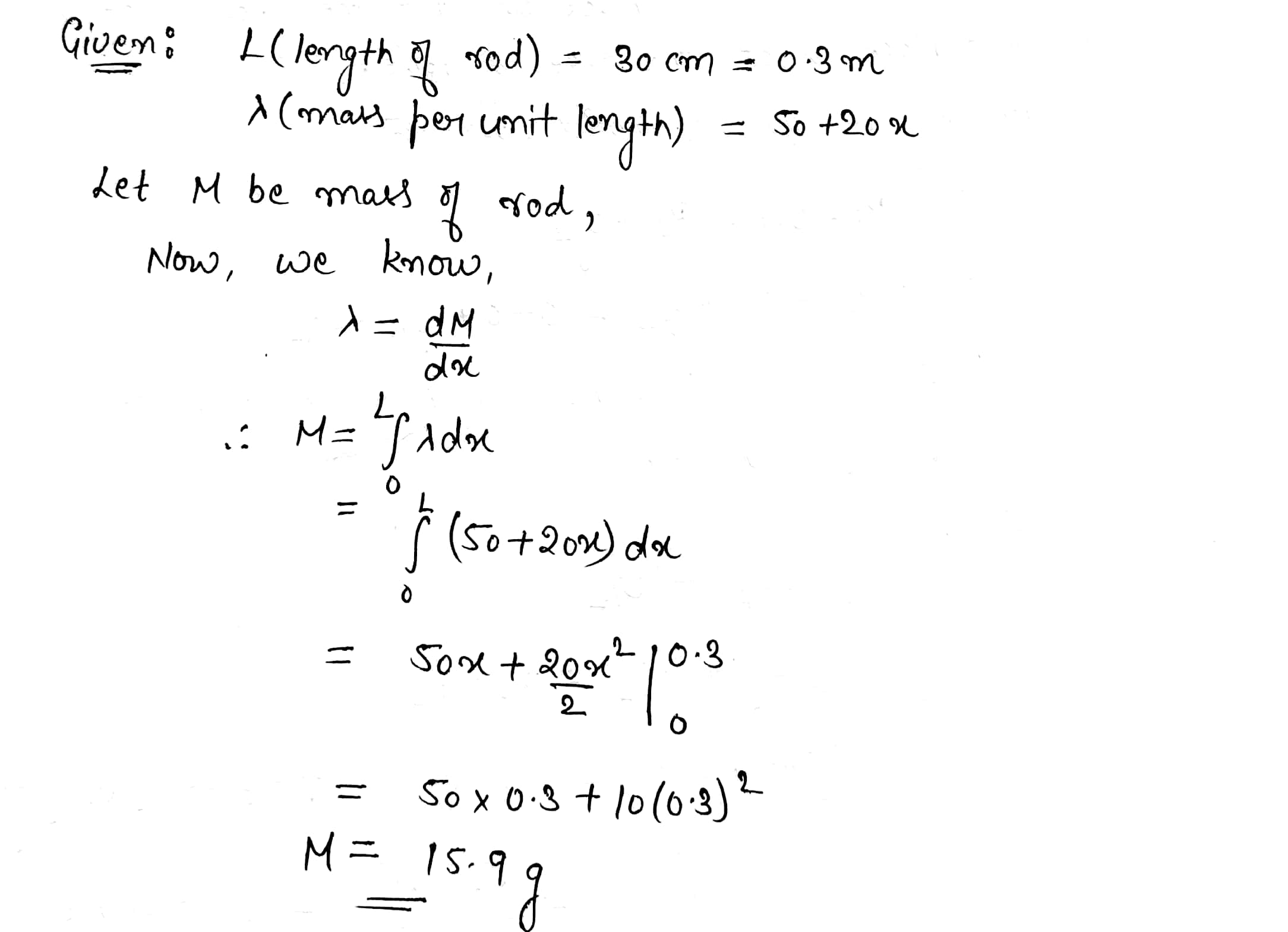Class 11 Engineering Physics - Units And Measurement

The wavelength of light of a particular colour is 5800 $$\mathring{A}$$. What is its order of magnitude in meter?

1 Angstrom, or $$1\mathring { A } $$ is $$1\times { 10 }^{ -10 }$$meter.
So, $$5800\mathring { A } $$ = $$5.8\times{ 10 }^{ 3 }\times { 10 }^{ -10 }$$meter = $$5.8\times { 10 }^{ -7 }$$meter.
Hence its magnitude in meter is $${ 10 }^{ -7 }m$$

Find the order of magnitude of 38500 kg

The order of $$38500$$ can be expressed in terms of power of $$10$$

$$\Rightarrow 3.85 \times 10^4 kg$$

0.0008 m= $$ 8 \times10 ^{-x}m$$. Find x.

Orders of magnitude are written in powers of $$10$$. For example, the order of magnitude of $$1500$$ is $$3$$, since $$1500$$ may be written as $$1.5\times { 10 }^{ 3 }$$. Similarly in the above question, $$0.0008$$ can be written as $$0.8\times { 10 }^{ -3 }$$.

Hence its order of magnitude is $${ 10 }^{ -3 }$$.

Match list - I with list - II and select the correct answer :

Spring constant : $$k =\dfrac{F}{x} = \dfrac{MLT^{-2}}{L}=M^1L^0T^{-2}$$, Hence A->3
Pascal: $$P = \dfrac{F}{A} = \dfrac{MLT^{-2}}{L^2} = M^1L^{-1}T^{-2}$$ , Hence B->4
Hertz: $$f =\dfrac{1}{T} = M^0L^0T^{-1}$$, Hence, C->2
Joule: $$W= F \times distance = M^1L^2T^{-2}$$, Hence D->1

The order of magnitude of seconds in a day is $$10^x$$. What is $$x$$.

We know that there are $$60$$ seconds in a minutes, $$60$$ minutes in an hour and $$24$$ hours in a day. Round that off to $$100$$, $$10$$ and $$100$$.
That is $${ 10 }^{ 2 }\times { 10 }^{ 2 }\times { 10 }^{ 1 } = { 10 }^{ 5 }s$$
Hence, its magnitude of seconds in a day is $${ 10 }^{ 5 }s$$

The distance of a galaxy is $$56 \times10^{25}m$$. Assume the speed of light to be $$3\times10^8 m s^{-1}$$. Express order of magnitude of time taken by light travelled to the galaxy.

We know that:

Time taken $$= \dfrac { distance \ travelled }{ speed } $$

So, time taken $$= \dfrac { 56\times { 10 }^{ 25 }m }{ 3\times { 10 }^{ 8 }m{ s }^{ -1 } } $$

So, the order is $$ {{18.6}\times { 10 }^{ 25-8 }s \ or \ 1.86\times { 10 }^{ 18 }s} $$.

The wavelength of light is 589 nm. What is its order of magnitude in metre?

1 nm is $$1\times { 10 }^{ -9 }m$$.
So, $$589nm = 5.89\times1\times { 10 }^{ 2 }\times { 10 }^{ -9 }m$$.
Hence its magnitude in m is $${ 10 }^{ -7 }m$$

The prefix 'milli' denotes the factor $$10^{-x}$$m
find x?

The prefix ' milli ' denotes the factor of $$10^{-3}$$.

For example : $$1 \ millimetre = 10^{-3} \ metre$$

Units of plane angle is _____

radian

Accuracy defines nearness of a measured value to the standard or true value. If true enter 1 else enter 0

Accuracy is defined as the extent upto which a given measurement agrees with the standard value for that measurement. If the measured value is nearer to the actual value, then the measurement is said to be accurate.
The above statement is true.

Measurement can be accurate without being precise. True=1, false = 0

You can be very precise but inaccurate. You can also be accurate but imprecise. For example, if on average, your measurements for a given substance are close to the known value, but the measurements are far from each other, then you have accuracy with precision.

What is parallax? Explain.

Parallax: When the two objects are seen on a straight line, they seem to be concident. If the objects are at different places and the eye is moved side ways then there is a relative displacement between them. The nearer object moves in the opposite direction while the further object moves in the same direction of eye.
Thus, when two objects are seen in a straight line and the eye is moved side ways when relative displacement is called parallax.

How can a measured length be expressed ?

Each measurement has :
(i) A number describing the numerical value.
(ii) The unit in which that quantity is measured.

Write the dimensional formula of pressure.

Pressure $$=\dfrac { Force }{ Area } =\dfrac { mass\times acceleration }{ Area } =\dfrac { Kg.{ ms }^{ -2 } }{ { m }^{ 2 } } ={( Kg)}{m ^{ -1 }}{ s }^{ -2 }$$

$$\therefore$$ Dimensional formula of pressure $$=\left[ { ML }^{ -1 }{ S }^{ -2 } \right] $$

Fill in the blanks type
Planck's constant has dimensions ________

$$E=h\upsilon$$

$$h\to $$ planck's constant

$$\upsilon\to T^{-1}$$

$$E\to ML^2T^{-2}$$

So, $$ML^2t^{-2}=h.T^{-1}$$

$$h\to ML^2T^{-1}$$

Three successive measurement in an experiment gave value 10.9, 11.4042 and 11.42 the correct way of reporting the average value is:

$${ V }_{ 1 }=10.9\\ { V }_{ 2 }=11.4042\\ { V }_{ 3 }=11.42$$

Average value$$= \cfrac {10.9+11.4042+11.42}{3}$$

$$=11.2414$$

$$=11.2$$

$$\therefore$$ The correct way of reporting the average value is $$11.2$$

What is meant by Precision?

Precision is refer to the amount of information that is conveyed by a number in terms of its digit it shows the closeness of two or more measurement to each other. it is independent of accuracy.

What is dimensional formula for magnetic flux densities?

The dimensional formula of magnetic flux density is $$[MT^{-2}L^0A^{-1}]$$

Simplify and round to the appropriate number of significant digits
$$(a)$$ $$16.235 \times 0.217 \times 5$$
$$(b)$$ $$0.00435 \times 4.6$$

Ans a-

$$16.235 \times 0.217 \times 5 = 17.614975$$

Since the least no.of significant digit is one, so the final answer should be rounded off upto one significant digit.

Therefore, Ans is $$ 20$$

Ans b-

$$0.00435 \times 4.6 = 0.02001$$

Since the least no.of significant digit is two, so the final answer should be rounded off upto two significant digit.

Therefore, Ans is $$ 0.02$$

Derive the dimensional formula for pressure.

$$Pressure = \dfrac{Force}{Area}$$

$$ = \,\dfrac{{M\, \times \,\frac{{velocity}}{{Time}}}}{{{{\left( {length} \right)}^2}}}$$

$$ = \,\,\dfrac{{M \times \,\frac{{length}}{{time\, \times \,time}}}}{{{{\left( {length} \right)}^2}}}$$

$$ = \,\dfrac{M}{{{{\left( {time} \right)}^2}\, \times \,length}}$$

$$ = \,\dfrac{M}{{{T^2}\, \times \,L}}$$

$$ = \,M \,{L^{ - 1}}\,{T^{ - 2}}$$

Using the dimensional method derive the relation between the units of force in the SI and CGS system.

Let $$ 1 $$ newton(SI) = $$x$$ dyne(CGS)

Dimensions of forces are $$[L^1M^1T^{-2}]$$

$$ \therefore [L_1^1M_1^1T_1^{-2}] = x[L_2^1M_2^1T_2^{-2}]$$

$$ \therefore x = (\cfrac{L_1}{L_2})^1 (\cfrac{M_1}{M_2})^1 (\cfrac{T_1}{T_2})^{-2}$$

$$ = (\cfrac{m}{cm})^1 (\cfrac{kg}{g})^1 (\cfrac{s}{s})^{-2}$$

$$ = 10^2 \times 10^3 = 10^5$$

$$ \therefore 1 \quad newton = 10^5 \quad dyne$$

If momentum $$p$$, area $$A$$ and time $$T$$ are taken to be fundamental quantities, then power has dimensional formula.

From the dimensional relations:

$$P=kp^a\ A^b\ T^c$$

Substituting the dimensions of the quantities:

$$[ML^2T^{-2}]=k\ [ML^1T^{-1}]^a[L^2]^b[T]^c$$

Comparing the dimensions:

$$a=1$$

$$a+2b=2$$

$$-a+c=-2$$

So, on solving the equations:

$$a=1,\ b=\dfrac12,\ c=-1$$

So, power can be represented as:

$$P=k\dfrac pT\sqrt{A}$$

In the equation y = A sin $$ (\omega - Kx) $$, obtain the dimensional formula of $$ \omega $$ and K.Given x is distance and t is time.

In the given equation $$y=A\sin (\omega t-kx)$$

Since, trigonometric function is a dimensionless quantity. So, $$(\omega t-kx)$$is also dimensionless quantity.

So,

$$ (\omega t-kx)=1 $$

$$ \omega t=1 $$

$$ \left[ \omega \right]=\dfrac{1}{\left[ T \right]}={{\left[ T \right]}^{-1}} $$

$$ kx=1 $$

$$ \left[ k \right]=\dfrac{1}{\left[ L \right]}={{\left[ L \right]}^{-1}} $$

Write the order of magnitude of mass of an electron $$9.1\times 10^{-31}$$ kg.

If mass of an electron is $$9.11 X 10^{-31} kg = 9.11 X10^{-28}g$$

$$1 kg = 1000 g$$

Electrons in one kg would be = $${\dfrac{1000}{9.11 X 10^{-28}}}$$

= $${\dfrac{1000} {9.11}} X 10^{-28}$$

= $$109.76 X 10^{28}$$

= $$1.0976 X 10 ^{30}$$

=$$10^{30}$$

What is the mass per unit volume of a substance called?

Mass per unit volume of substance called ‘’density’’

Find the order of magnitude of length of rod having length $$(10^6+10^3)$$m.

Length $$L= 10^6+10^3 \approx 10^6$$

So order of length is $$10^6$$.

Which of the following length measured is most accurate and why?
(a) $$500.0\ cm$$
(b) $$0.0005\ cm$$
(c) $$6.00\ cm$$

Error in $$(i) $$ is $$0.1cm=\dfrac{1}{10}cm$$

Error in$$(ii)$$ is $$0.0001=\dfrac{1}{1000}cm$$

Error in $$(iii)$$ is $$0.01cm=\dfrac{1}{100}cm$$

$$\therefore$$` Measurement $$(ii)$$ is most accurate, upto fourth

place of decimal.

Arrange the following lengths in their increasing magnitude:
$$1\ metre,$$ $$1\ centimetre,$$ $$1\ kilometre,$$ $$1\ millimetre.$$

$$1$$ centimeter $$={10}^{-2}$$ metre

$$1$$ kilometer$$={10}^{3}$$ metre

$$1$$ millimeter $$={10}^{-3}$$ metre

Hence in order of increasing magnitude

$${10}^{-3} m< {10}^{-2}m< 1m< {10}^{3}m$$

The dimensional formula of area is ?

The dimensional formula of area is $$[L^2]$$ as its $$SI$$ unit is $$m^2$$.

If an object weighs $$ 6\,kg $$ on earth . What will be its weight on moon ?

Value of g on the moon compare to earth $$g’=g/6$$

Weight of body on moon = $$ mg’=Mg/ 6 $$Th of its weight on earth,
$$ \therefore \, $$ Body will weight $$ 1 / 6 \times 6 = 1 \,kg $$ on moon

Write $$2760000$$ in scientific form.

$$2760000$$

No .of digits in $$2760000$$ is $$7$$

So it is written as $$2.76\times 10^6$$

Convert the following quantity as indicated:
$$12 \,inch \ into\ ft$$

$$12 \, inch= \,1 \,ft$$

Assuming that water has a density of exactly $$1\ g/cm^3$$, find the mass of one cubic meter of water in kilograms,

Given density of water = $$1g/cm^3$$

Mass of $$1 m^3$$ = $$density \times volume$$ = $$\dfrac{1 g}{cm^3} \times 1m^3 \times \dfrac{10^6cm^3}{m^3} \times \dfrac{10^{-3}kg}{g}$$ = $$10^3 kg$$

Fill in the blanks
Mass = $$ Density \times Volume. $$

Mass = $$ Density \times Volume. $$

What is the mass of $$5 m^3$$ of cement of density $$3000 \ kg/m^3$$

Volume $$ = 5 m^3$$
Density $$ = 3000kg/m^3$$
Density of cement $$ = \frac{mass \ of \ cement}{volume \ of \ cement}$$
mass of cement $$ = Density \ of \ cement \times volume \ of \ cement$$
$$ = 3000 \times 5 = 15000 kg$$

The mass of an oxygen atom is 16.00 u. Find its mass in kg.

Given:
Mass of oxygen atom $$=16 \mu$$
$$1 \mu$$ = $$ 1.66 \times 10^{-27} kg$$
Mass of $$ 16\mu$$

$$ =16 \times 1.66 \times 10^{-27}$$
$$ =2.656 \times 10^{-26} kg$$

A...Image cannot be obtained on a screen.

The mass is the product of the density and the volume.

Mass = density $$\times$$ Volume.

What is the dimensional formula?

A formula in which a physical quantity is expressed in terms of fundamental quantities is called the dimensional formula.

Write the dimension formula of strain.

Strain is the ratio of same physical quantities of same dimension hence it is dimensionless.

$$ \therefore $$ Dimension of strain $$ =\left[\mathrm{M}^{0} \mathrm{L}^{0} \mathrm{T}^{0}\right] $$

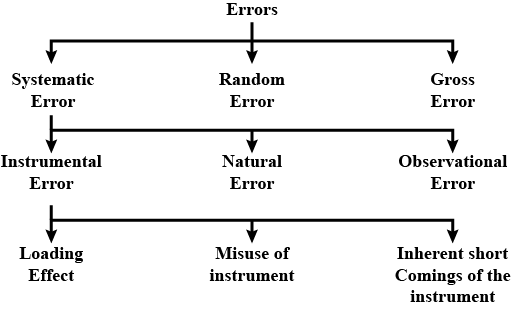
How many types of errors are there?

There are three types of error: syntax errors, logical errors and run-time errors. (Logical errors are also called semantic errors). We discussed syntax errors in our note on data type errors.

Generally errors are classified into three types: systematic errors, random errors and blunders. Gross errors are caused by mistake in using instruments or meters, calculating measurement and recording data results.

Name two dimensionless physical quantities.

Angle, Refractive index

What is meant by errors of measurement? How do errors vary with a combination of errors? Explain.

Accuracy and Errors in Measurement The measuring process is essentially a process of comparison. To measure any physical quantity, we compare it with a standard (unit) of that quantity. No measurement is perfect as the errors involved in the process cannot be removed completely. Hence, in spite of our best effort, the measured value of a quantity is always somewhat different from its actual value, or true value.
Measurement error: The measurement error is defined as the difference between the true or the actual value and the measured value
i.e., error is quantity = (True value — measurement value) of the quantity.
Absolute Error, Relative Error and Percentage Error
1. Absolute error: Absolute error in the measurement of a physical quantity is the magnitude of the difference between the true value and the measured value of the quantity.
Let a physical quantity can be measured n times. Let the measured vahie be $$a_1,a_2,a_3$$ a the arithmetic mean of these values is: $$a_m=\dfrac{a_1+a_2+a_3.....a_n}{n}$$
Usually, $$a_m$$ is taken as the true value of the quantity, if the same is unknown otherwise by definition, absolute errors in the measured value of the quantity are
$$\Delta a_1=a_m-a_1$$
$$\Delta a_2=a_m-a_2$$
$$\Delta a_n=a_m-a_n$$
Absolute errors may be positive in certain cases and negative in the other cases.
2. Mean absolute error: It is the arithmetic mean of the magnitude of absolute errors in all the measurements of the quantity it is represented by ta. Thus,
$$\Delta \overline{a}=\dfrac{|\Delta a_1|+|\Delta a_2|+....+|\Delta a_n|}{n}$$
Hence the final result of the measurement may be written as $$a=a_m \pm \Delta\overline{a}$$
This implies that any measurement of the quantity is likely to lie between $$(\alpha_m+\Delta \overline{a})$$ and $$(a_m -\Delta \overline{a})$$
3. Relative error: The relative error or fractional error of measurement is defined as the ratio of mean absolute error to the mean or value of the quantity measured. Thus,
$$Relative\, error\, =\dfrac{Mean\, absolute\,error}{Mean\, value}=\dfrac{\Delta \overline{a}}{a_m}$$
4. Percentage error: When the relative/fractional error is expressed in term of percentage, we call it a percentage error. Thus,
$$percentage\, error\,=\dfrac{\Delta \overline{a}}{a_m}\times 100%$$
1753800_1832436_ans_2efd3a3ed51040e28c748e4b44cbb911.png

1753800_1832436_ans_2efd3a3ed51040e28c748e4b44cbb911.png

Write the dimensional formula for velocity.

The dimensional formula for velocity $$LT^-1$$

Write the dimensional formula for force.

The dimensional formula for force is $$MLT^2$$

Write the dimensional formula of work.

$$ML^{2}T^{-2}$$

Write the dimensional formula of power.

the dimensional formula of power.

$$ML^{2}T^{-3}$$

If the percent difference between two measured values, $$4.6\ cm$$ and $$5.0\ cm$$ is $$n$$%. Find $$n$$ ? (Round off to the closest integer)

Sometimes it is instructed to compare the results of two measurements when there is no known or accepted value. The comparison is expressed as a percent difference, which is the ratio of the absolute difference between the experimental values $$E_{1}$$ and $$E_{2}$$ to the average or mean value of the two results, expressed as a percent.

Percent difference $$= \left ( \dfrac{\text {Absolute difference}}{\text {Average}} \right ) \times 100\%$$

$$=\dfrac{\left | E_{2}-E_{1} \right |}{\left | E_{2}+E_{1} \right |/2} \times 100\%$$

$$=\dfrac{\left | 5.0-4.6 \right |}{\left | 5.0+4.6 \right |/2} \times 100\%$$

$$=\dfrac{0.4}{4.8} \times 100\%$$

$$= 8\%$$

Match the following : (Symbols have standard meaning)

List -1	List-2
(A) $$ML^2T^{-2}A^o$$	(4) $$\cfrac {B^2}{2\mu_o}=\cfrac {Wb/m^2}{2 N/m^2}$$
(B) $$ML^{-1}T^{-2}A^o$$	(3) $$\cfrac {E_oE^2}{2}=\cfrac {NA^{-1}n^{-2}\cfrac {v}{n}}{2}$$ $$=ML^{-1}T^{-2}A^o$$
(C) $$M^{-1}L^{-3}T^{-3}A^{-2}$$	(1) Electrical conductivity
(D) $$MT^oL^{-3}A^o$$	(2) $$\cfrac {E\times B}{\mu_o}=\cfrac {\cfrac {v}{m}\times Wb/m^2}{NA^{-1}n^{-2}}$$

The number of significant figures in 500.06 is _________.

as 5 is a numerical digit after zeros at 2nd and 3rd position.

it makes all the digits before decimal significant and

after decimal as if all the digits are significant

Hence we have 5 significant digit.

A barometer is faulty. When the true barometer reading are 73 and 75 cm of Hg, the faulty barometer reads 69 cm and 70 cm respectively. What is the total length of the barometer tube?

When true barometer readings are changing for $$2 cm$$ Hg $$(75-73=2)$$, faulty barometer readings are changing for 1 cm Hg (70-69=1). The ratio between these differences is 2:1. Standard length of barometer tube is 83 cm; difference between standard tube length and maximal reading of the true barometer is 8 cm $$(83-75=8)$$, and the difference between the tube length of faulty barometer and maximal reading of the faulty barometer should be two times smaller than for the true barometer: $$\dfrac{8}{2} = 4 cm.$$

Then, tube length of faulty barometer is $$70+4 = 74 cm. $$

The dimensional formula of heat is ________.

Heat is nothing but a form of energy. And work is converted to this energy. So heat has same dimensional formula as work.

Ans: $$M{ L }^{ 2 }{ T }^{ -2 }$$

Write the number of significant figures in 0.270 cm.

According to the general rule for determining significant figures, zeros to the left of a significant figure and not bounded to the left by another significant figure are not significant. Zeroes placed after other digits but behind a decimal point are significant. So for given number 0.270 , the last three digits will represent significant figures. Thus, it has 3 significant figures.

Match the following:

A. Energy density is the product of force and displacement ($$E = FS =MLT^{2} L =ML^{2}T^{2}$$)
B. Power is the rate of doing work ($$ P = \dfrac{W}{t}=\dfrac{\left[ML^{2}T^{2}\right]}{\left[T\right]}=ML^{2}T^{3}$$
C. Electric Pressure is the measure of force exerted by charges per unit area.

Electric Pressure $$=\dfrac{F}{A}=\dfrac{\left[MLT^{2}\right]}{\left[L^{2}\right]}=ML^{-1}T^{2}$$
D. Surface tension $$ =\dfrac{force}{length}=\dfrac{\left[MLT^{2}\right]}{L}=MT^{2}$$

Explain parallax method for measuring distance of a nearly star

The distnace can be measured by measuring the parallax angle $$\theta$$. It is subtended by the distant astronomical object at the two locations on the earth separated distance b. Thus, $$ \theta=\dfrac{b}{d}$$ where d be the measuring distance.

Match the following two columns.
Column I Column II

For (A)
We know that $$F_g=GM_eM_5/r^2$$
Dimension of $$F_g$$ is $$[MLT^{-2}]$$
Dimension of $$r^2$$ is$$[L^2]$$
Therefore, putting in eq. we get
$$[MLT^{-2}]=dim(GM_eM_5)/[L^2]$$
$$dim(GM_eM_5)=[ML^3T^{-2}]$$
therefore, $$A\xrightarrow [ ]{ } 2$$

Now we know that, for a gas average kinetic energy is given by
$$KE=\dfrac{3nRT}{2}$$
$$KE=\dfrac{3wRT}{2M}$$
Therefore, $$dim(KE)=dim(\dfrac{3wRT}{2M})$$
$$dim(\dfrac{3RT}{2M})=dim(\dfrac{KE}{w})$$
$$dim(\dfrac{3RT}{2M})=\dfrac{[ML^2T^{-2}]}{[M]}$$
$$dim(\dfrac{3RT}{2M})=[L^2T^{-2}]$$
Therefore, $$B\xrightarrow [ ]{ } 3$$

We know that magnetic force is given by,
$$F=qvB\sin \theta$$
$$F=qvB$$ when $$\sin \theta =1$$
$$F^2=(qvB)^2$$
$$v^2=\dfrac{F^2}{(qB)^2}$$
$$dim(v^2)=dim(\dfrac{F^2}{(qB)^2})$$
$$dim(\dfrac{F^2}{(qB)^2})=[L^2T^{-2}]$$
therefore, $$C\xrightarrow[]{} 3$$

We know that gravitational potentialon earth's surface is given by
$$V_g=\dfrac{GM_e}{R_e}$$
$$\dfrac{U_g}{m}=\dfrac{GM_e}{R_e}$$
$$dim(\dfrac{GM_e}{R_e})=dim(\dfrac{U_g}{m})$$
$$dim(\dfrac{GM_e}{R_e})=[L^2T^{-2}]$$
therefore, $$D\xrightarrow[]{}3$$

'The order of magnitude of a physical quantity must be expressed in proper unit'. Comment on this statement

The order of magnitude of a physical quantity must be expressed in proper unit or else the power of ten in its magnitude will change. Order of magnitude: The order of magnitude tells us about the largeness or smallness of a physical quantity So to compare the physical quantities we must express them in proper units.

The mass of an oxygen atom is $$1600$$ u. Find its order of magnitude in kg.

$$1600 u = 1600 \times 1.66 \times 10^{-27} = 2.66 \times 10^{-24} Kg$$

So, the order of magnitude in kg is $$10^{-24}$$ kg.

The radius of a hydrogen atom is $$0.5\mathring{A}$$. Find the order of magnitude of volume of one hydrogen atom is $$10^{-10x}$$. The value of x is:

Given that:

Radius is 0.5$$\mathring { A } $$ $$=0.5\times { 10 }^{ -10 }m$$ $$=5\times { 10 }^{ -11 }m$$

Volume $$=\dfrac { 4 }{ 3 } \pi { r }^{ 3 } =\dfrac { 4 }{ 3 } \times 3.14\times { \left( 5\times { 10 }^{ -11 } \right) }^{ 3 }$$

$$=5.23\times { 10 }^{ -31 }{ m }^{ 3 }$$

Hence, order of magnitude is $${ 10 }^{ -31 }{ m }^{ 3 }$$.

Taking the mass of a proton to be $$1.67 \times 10^{-27}$$ kg, the order of magnitude of the number of protons in 1 g is $$5.88\times10^{(20+x)}$$. What is $$x$$.

Mass of proton is $$=1.67\times { 10 }^{ -27 }\ kg $$ $$=1.67\times { 10 }^{ -24 }\ gm$$

Number of protons in $$1\ g =$$ $$\dfrac { 1 }{ 1.67\times { 10 }^{ -24 } } $$$$=\dfrac { 1 }{ 1.67 } { 10 }^{ 24 }$$ = $$=0.588\times { 10 }^{ 24}=5.88\times 10^{23}$$

Match the following :

Angular momentum: $$L =mvr = M^1L^2T^{-1}$$, Hence A->4
Torque: $$\tau = force \times distance = ML^2T^{-2}$$, Hence B->3
Gravitational constant: $$G = \dfrac{force \times distance^2 }{mass^2}= M^{-1}L^3T^{-2}$$, Hence C->1
Tension: $$T =M^1L^1T^{-2}$$, Hence D->2

$$\displaystyle \alpha =\frac{Fv^{2}}{\beta ^{2}}\log_{e}\left ( \frac{2\pi \beta }{v^{2}} \right )$$ where F = force, v = velocity
Find the dimensions of $$\displaystyle \alpha $$ and $$\displaystyle \beta $$

Logarithm functions are dimensionless

$$\therefore \left[ \dfrac { 2\pi \beta }{ { V }^{ 2 } } \right] ={ M }^{ 0 }{ L }^{ 0 }{ T }^{ 0 }\\ \left[ \beta \right] =\left[ { V }^{ 2 } \right] \\ ={ \left( L{ T }^{ -1 } \right) }^{ 2 }\\ ={ L }^{ 2 }{ T }^{ -2 }$$

From relation,

$$\left[ \alpha \right] =\left[ \dfrac { F{ V }^{ 2 } }{ { \beta }^{ 2 } } \right] \\ =\dfrac { ML{ T }^{ -2 }.{ \left( L{ T }^{ -1 } \right) }^{ 2 } }{ { \left( { L }^{ 2 }{ T }^{ -2 } \right) }^{ 2 } } \\ =\dfrac { ML{ T }^{ -2 }.{ L }^{ 2 }{ T }^{ -2 } }{ { L }^{ 4 }{ T }^{ -4 } } \\ =M{ L }^{ -1 }{ T }^{ 0 }$$

Express the following derived units in terms of the fundamental units of length, mass and time.
1) Speed
2) Area
3) Acceleration
4) Density
5) Volume

(i) $$\displaystyle Speed=\frac { Distance }{ Time } =\frac { Length }{ Time } $$

(ii) $$\displaystyle Area=Length\times Breadth=Length\times Length={ \left( Length \right) }^{ 2 }$$

(iii) $$\displaystyle Acceleration=\frac { Velocity }{ Time } $$

$$\displaystyle =\frac { Displacement }{ Time\times Time } =\frac { Length }{ { \left( Time \right) }^{ 2 } } $$

(iv) $$\displaystyle Density=\frac { Mass }{ Volume } $$

$$\displaystyle =\frac { Mass }{ Length\times Length\times Length } =\frac { Mass }{ { Length }^{ 3 } } $$

(v) $$\displaystyle Volume=Length\times Breadth\times Height$$
$$\displaystyle =Length\times Length\times Length$$
$$\displaystyle ={ \left( Length \right) }^{ 3 }$$

When the planet Jupiter is at a distance of $$824.7$$ million kilometers from the Earth,its angular diameter is measured to be $$35.72$$ of arc. Calculate the diameter of Jupiter.

Distance of Jupiter from the Earth, $$D=824.7 \times 10^6 km$$

Angular diameter $$35.72''=35.72 \times 4.874 \times 10^{-6} rad$$

Diameter of Jupiter = d

Using the relation,

$$\theta$$ = d/ D

$$d=\theta$$ D = 824.7 x $$10^9$$ x 35.72 x 4.872 x $$10^{-6}$$ = 143520.76 x $$10^3$$ = 1.435 x $$10^5$$ Km

$$1$$ parsec = __________ metres

Diameter of Earth’s orbit $$= 3 × 10^{11} m$$

Radius of Earth’s orbit, $$r = 1.5 × 10^{11} m$$

Let the distance parallax angle be $$1" = 4.847 × 10^{–6} rad$$.

Let the distance of the star be D.

Parsec is defined as the distance at which the average radius of the Earth’s orbit subtends an angle of $$1"$$.

$$\theta=\dfrac{r}{D}$$

$$D=3.09 \times 10^{16} m$$

Hence, $$1 parsec ≈ 3.09 × 10^{16} m$$

The farthest objects in our universe discovered by modern astronomers are so distant that light emitted by them takes billions of years to reach the Earth. These objects (known as quasars) have many puzzling features, which have not yet been satisfactorily explained. What is the distance in $$km$$ of a quasar from which light takes $$3.0$$ billion years to reach us?

Time taken by quasar light to reach Earth = 3 billion years

$$= 3 \times 10^9\ years = 3 \times 109 \times 365 \times 24 \times 60 \times 60\ s $$

Speed of light $$= 3 \times 10^8\ m/s $$

Distance between the Earth and quasar $$=(3 \times 10^8) \times (3 \times 10^9 \times 365 \times 24 \times 60 \times 60) $$

$$= 283824 \times 10^{20}\ m = 2.8 \times 10^{22}\ km $$

State the number of significant figures in the following:
$$(a) 0.007 m^2$$
$$(b) 2.64 \times 10^{24} kg$$
$$(c) 0.2370 g cm^{-3}$$
$$(d) 6.320 J $$
$$(e) 6.032 Nm^{-2} $$
$$(f) 0.0006032 m^2 $$

The significant figures of a number are those digits that carry meaning contributing to its measurement resolution. This includes all digits except:
1. All leading zeros;
2. Trailing zeros when they are merely placeholders to indicate the scale of the number (exact rules are explained at identifying significant figures);
3. Spurious digits introduced, for example, by calculations carried out to greater precision than that of the original data, or measurements reported to a greater precision than the equipment supports.

(a)

$$0.007 = $$ $$ 7 \times 10^{-3}$$
Significant digit $$=7$$
Only one significant digit.

(b) Number of significant digit $$=3$$

(c)

All non-zero numbers are always significant.All zeroes before a non zero number are insignificant. All zeroes which are simultaneously to the right of the decimal point and at the end of the number are significant. The only non significant digit here is the zero before the decimal point.
Hence, number of significant digits is $$4$$.

(d)

All non-zero numbers are always significant. All zeroes which are simultaneously to the right of the decimal point and at the end of the number are significant.
Hence, number of significant digits is $$4$$.

(e)

All the digits are significant. (no leading and trailing zero)
No. of significant digits $$= 4$$

(f)

Significant digits $$= 6032$$
No. of sig. digits $$= 4$$

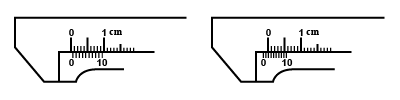
In the figures given, identify the type of zero error and also suggest the correction to be made, by reasoning it out

The zero error is positive zero error when the jaws are brought in contact, the zero of vernier scale must be right to the zero of main scale. Thus, the left image will give positive zero error.

The zero error is negative zero error when the jaws are brought in contact, the zero of vernier scale must be left to the zero of main scale. Thus, the right image will give the negative zero error.

The wavelength of monochromatic light is 6000 $$A^0$$. Write this value in nm.

$$6000\overset { \circ }{ A } =6000\times { 10 }^{ -10 }m\\ =600\times { 10 }^{ -9 }m\\ =600nm$$

Complete the table choosing the right term from the list given in brackets:($$10^9$$, micro, d, $$10^{-9}$$, milli, m, M)
Factor Prefix Symbol
$$10^{-1}$$
deci
$$10^{-6}$$ $$\mu$$
giga G
$$10^{6}$$ mega

Factor	Prefix	Symbol
$${ 10 }^{ -1 }$$	deci	$$d$$
$$ { 10 }^{ -6 }$$	micro	$$H$$
$$ { 10 }^{ 9 }$$	giga	$$G$$
$$ { 10 }^{ 6 }$$	mega	$$M$$

Name any two units of length which are bigger than the metre. Write the relation
between each of those units and the metre.

1. $$1Km=1000m$$

2. $$Light year=9.46\times { 10 }^{ 15 }m$$

If length $$'L'$$, force $$'F'$$ and time $$'T'$$ are takes as fundamental quantities. What would the dimensional equation of mass and density?

Let us apply the equation,

$$F=ma$$

Apply the fundamental units.

Thus,

$$F=mass\times L{ T }^{ -2 }\\ mass=\dfrac { F }{ L{ T }^{ -2 } } =F{ L }^{ -1 }{ T }^{ 2 }$$

Similarly,

$$density=\dfrac { mass }{ volume } =\dfrac { F{ L }^{ -1 }{ T }^{ 2 } }{ { L }^{ 3 } } =F{ L }^{ -4 }{ T }^{ 2 }$$

Let us check the dimensional correctness of the relation $$v =u + at$$.

Here u represents the initial velocity, v the final velocity, a the uniform acceleration, and t the time.
The dimensional formula of u is $$[M^0LT^{-1}]$$.
The dimensional formula of v is $$[M^0LT^{-1}]$$.
The dimensional formula of at is $$[M^0LT^{-2}][T] = [M^0LT^{-1}]$$.
Here the dimensions of every term in the given physical relation are the same, hence the given physical relation is dimensionally correct.

The position of a particle at time t is given by the relation $$x(t) = \left(\dfrac{v_0}{\alpha}\right)(1 - c^{-\alpha t})$$, where $$v_0$$ is a constant and $$\alpha > 0$$. Find the dimensions of $$v_0$$ and $$\alpha$$.

$$x\left( t \right) =\left( \dfrac { { V }_{ 0 } }{ \alpha } \right) \left( 1-{ C }^{ -\alpha t } \right) $$

$${ V }_{ 0 }$$ is constant and $$\alpha >0$$

Since, $$C$$ is constant so $$\alpha t$$ should be unitless

So unit $$\alpha ={ \sec }^{ -1 }=\left[ { T }^{ -1 } \right] $$

$$x$$ is length, $$x$$ is in metre.

$${ V }_{ 0 }=x\alpha $$

$${ V }_{ 0 }=M{ sec }^{ -1 }$$

$$\boxed { { V }_{ 0 }=\left[ { LT }^{ -1 } \right] } $$

$$\boxed { \alpha =\left[ { T }^{ -1 } \right] } $$

Find the dimensions of physical quantity X in the equation.
Force = $$\frac{X}{density}$$.

Force $$=\dfrac { X }{ density } $$

$$X=$$ force $$\times$$ density

$$=$$ Newton $$\times$$ $$\dfrac { kg }{ { m }^{ 3 } } $$ force $$=$$ mass $$\times$$ acceleration

$$=\dfrac { kg.{ ms }^{ -1 }.kg }{ { m }^{ 3 } } $$ density $$=\dfrac { mass }{ volume } $$.

$$\boxed { X={ kg }^{ 2 }{ m }^{ -2 }{ s }^{ -1 } } $$

$$\boxed { X=\left[ { M }^{ 2 }{ L }^{ -2 }{ T }^{ -1 } \right] } $$

If velocity (V), force (F), and energy (E) are taken as fundamental units, then find the dimensional formula for mass.

Let $$\left[ { ML }^{ 0 }{ T }^{ 0 } \right] ={ V }^{ a }{ F }^{ b }{ E }^{ c }$$

$$=\left[ { \left( { LT }^{ -1 } \right) }^{ a }{ \left( { MLT }^{ -2 } \right) }^{ b }{ \left( { ML }^{ 2 }{ T }^{ -2 } \right) }^{ c } \right] $$

Comparing dimensional formula

$$b+c=1$$

$$a+b+2c=0$$

$$-a-2b-2c=0$$ $$\Rightarrow$$ $$-a=2(b+c)$$ $$\Rightarrow$$ $$\boxed { a=-2 } $$

$$a+1-c+2c=0$$ $$\Rightarrow$$ $$a+1+c=0$$ $$\Rightarrow$$ $$-2+1+c=0$$ or $$\boxed { c=1 } $$

$$\boxed { b=0 } $$ $$\therefore$$ $$\left[ { ML }^{ 0 }{ T }^{ 0 } \right] =\left[ { V }^{ -2 }{ F }^{ 0 }{ E }^{ 1 } \right] $$

The mass of a box is $$2.3$$kg. Two marbles of masses $$2.15$$g and $$12.39$$ g are added to it. Find the total mass of the box to the correct number of significant figures.

$$\begin{array}{l}M a s s=m \\m_{1}=2 \cdot 3 k g\\m_{2}=2\cdot 15 \times 10^{-3} k g \\m_{3}=12 \cdot 39\times 10^{-3} k g \\\text { Required Answer =}m_1 + m_2+ m_3 \\\qquad \begin{aligned}&=2 \cdot 3+2 \cdot 15 \times 10^{-3}+12 \cdot 39 \times 10^{-3} \\&=2 \cdot 31454 \ k g\\&=2 \cdot 3 k g\end{aligned}\end{array}$$

The potential energy of a particle varies the distance $$x$$ from a fixed origin as $$U = \dfrac{A \sqrt{x}}{x^2 + B}$$, where A and B are dimensional constants, then find the dimensional formula for AB.

$$x=$$ distance from a fixed origin

$$u=\dfrac { A\sqrt { x } }{ { x }^{ 2 }+B } $$

unit of $$B$$ is same as $${ x }^{ 2 }$$. Unit of $${ x }^{ 2 }=\left[ { L }^{ 2 } \right] $$

$$B=\left[ { L }^{ 2 } \right] $$

$$u=\dfrac { \left[ { x }^{ 1/2 } \right] A }{ { x }^{ 2 }+B } $$

$$A=\dfrac { u\left( { x }^{ 2 }+B \right) }{ \sqrt { x } } =\dfrac { { kgm }^{ 2 } }{ { s }^{ 2 } } \times \dfrac { { m }^{ 2 } }{ { m }^{ 1/2 } } $$

$$A=\dfrac { kg{ m }^{ 7/2 } }{ { s }^{ 2 } } $$

$$A=\left[ { ML }^{ 7/2 }{ T }^{ -2 } \right] $$

Dimensions of $$AB=\left[ { ML }^{ 7/2 }{ T }^{ -2 } \right] \left[ { L }^{ 2 } \right] $$

Dimensions of $$AB=\left[ { ML }^{ 11/2 }{ T }^{ -2 } \right] $$

Experiments reveal that the velocity $$v$$ of water waves may depend on their wavelength $$\lambda$$, density of water $$\rho$$, and acceleration due to gravity g. Establish a possible relation between $$v$$ and $$\lambda, g, \rho^0.$$.

According to the provided information,
$$v \propto \lambda^a \rho^b g^c$$
$$\Rightarrow v = k \lambda^a \rho^b g^c$$
where k is constant of proportionality.
Using principle of homogeneity
$$[M^0L^1T^{-1}]$$

$$ = [L^a][M^1L^{-3}T^0]^b [M^0L^1T^{-2}]^c$$
Comparing powers of like quantities on both the sides, we have,
$$b = 0 (ii) a - 3b + c = 1 (iii) -2c = -1 (iv)$$
Using (ii), (iii) and (iv), we have, $$a = \frac{1}{2}, b = 0, c = 1/2$$
Using these values in (i), we have $$v = k. \lambda^{1/2}. \rho^0. g^{1/2}$$
$$\Rightarrow v = k \sqrt{\lambda g}$$
which is the required relation.

Check the accuracy of relation $$v^2 - u^2 = 2as$$, where $$v$$ and $$u$$ are final and initial velocities, $$a$$ is the acceleration, and s is the distance.

We have $$v^2 - u^2 = 2as$$.

Checking the dimensions on both sides, we get
$$LHS = [LT^{-1}]^2 - [LT^{-1}]^2$$

$$ = [L^2 T^{-2}] - [L^2 T^{-2}] = [L^2 T^{-2}]$$

$$RHS = [L^1 T^{-2}] [L] = [L^2 T^2]$$

Comparing LHS and RHS, we find LHS = RHS.
Hence, the formula is dimensionally correct.

The number of particles is given by $$n = -D \frac{n_2 - n_1}{x_2 - x_1}$$ crossing a unit area perpendicular to X-axis in unit time, where $$n_1$$ and $$n_2$$ are the number of particles per unit volume for the value of $$x$$ meant to $$x_2$$ and $$x_1$$. Find the dimensions of $$D$$ called diffusion constant.

$$N=$$ no. of particle per unit area per unit time

$${ n }_{ 1 }$$ & $${ n }_{ 2 }$$ $$=$$ no. of particle per unit volume

$${ x }_{ 1 }$$ & $${ x }_{ 2 }$$ are distance from some reference point.

Dimension of $$'N'=\left[ { L }^{ -2 }{ T }^{ -1 } \right] $$

Dimensional formula of $${ n }_{ 1 }$$ & $${ n }_{ 2 }$$ $$=\left[ { L }^{ -3 } \right] $$

Dimensional formula of $${ x }_{ 1 }$$ & $${ x }_{ 2 }$$ $$=$$ $$[L]$$

$$N=-D\dfrac { { n }_{ 2 }-{ n }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } $$

$$D=-N\left[ \dfrac { { x }_{ 2 }-{ x }_{ 1 } }{ { n }_{ 2 }-{ n }_{ 1 } } \right] $$

$$=\dfrac { \left[ { L }^{ -2 }{ T }^{ -1 } \right] \left[ L \right] }{ \left[ { L }^{ -3 } \right] } $$

$$\boxed { D=\left[ { M }^{ 0 }{ L }^{ 2 }{ T }^{ -1 } \right] } $$

The length of a rectangular sheet is $$1.5$$cm and the breadth is $$1.203$$ cm. Find the areas of the face of a rectangular sheet to the correct number of significant figures.

Length $$l=1.5$$ cm breath $$b=1.203$$ cm

Area $$l\times b=1.8045=1.8{ cm }^{ 2 }$$ } out answer cannot be more precise than least precise measurement.

If the velocity of light (c), gravitational constant (G), and Plancks' constant (h) are chosen as fundamental units, then find the dimensions of mass in new system.

Let $$m \propto [c^xG^yh^z] $$

or $$m = K[c^xG^yh^z]$$

By substituting the dimension of each quantity in both the sides,

$$[M^1L^0T^0] = K[LT^{-1}]^x[M^{-1}L^3T^{-2}]^y[ML^{2}T^{-1}]^z $$

$$M= [M^{-y+z}L^{x+3y+2z}T^{x-2y-z}]$$

By equating the power of M, L and T in both the sides :

$$ -y + z = 1,\\ x + 3y + 2z = 0,\\ -x -2y - z =0$$

By solving above three equations,

$$x= 1/2, y = -1/2, and \,\,z = 1/2.$$

$$\therefore m \propto c^{1/2} G^{-1/2} h^{1/2}$$

According to Joule's law of heating, heat produced $$H = l^2 Rt$$, where I is current, R is resistance, and t is time. If the errors in the measurement of I,R and t are $$3\%, 4\%$$ and $$6\%$$, respectively, find error in the measurement of H.

Heat produced $$H={ i }^{ 2 }RT$$

$$logH=2logi+logR+logT$$

$$\dfrac { \Delta H }{ H } =\dfrac { 2\Delta i }{ i } +\dfrac { \Delta R }{ R } +\dfrac { \Delta T }{ R } $$

$$\Rightarrow$$ Error in $$H=2\times 3+4+6=16$$%.

A physical quantity P is given by $$P = \frac{A^3 B^{1/2}}{C^{-4} D^{3/2}}$$. Which quantity among A, B, C and D brings in the maximum percentage error in P?

$$P=\dfrac { { A }^{ 3 }{ B }^{ 1/2 } }{ { C }^{ -4 }{ D }^{ 3/2 } } \Rightarrow \dfrac { \Delta P }{ P } =\dfrac { 3\Delta A }{ A } +\dfrac { 1 }{ 2 } \dfrac { \Delta B }{ B } +\dfrac { 4\Delta C }{ C } +\dfrac { 3 }{ 2 } \dfrac { \Delta D }{ D } $$.

$$\therefore$$ $$C$$ brings max % error in $$P$$.

The pressure on a square plate is measured by measuring the force on the plate and the length of the sides of the plate. If the maximum error in the measurement of force and length are, respectively, $$4\%$$ and $$2\%$$, Find the maximum error in the measurement of pressure.

Error in force $$=4$$%

error in length $$=2$$%

Pressure $$=\dfrac { Force }{ area } =\dfrac { F }{ { l }^{ 2 } } $$

$$\dfrac { \Delta P }{ P } \times 100=\left[ \dfrac { \Delta F }{ F } +\dfrac { 2\Delta l }{ l } \right] \times 100$$

$$=\left( 4+2\times 2 \right) $$%

maximum error $$=8$$%

A diamond weighs $$3.71g$$. It is put into a box weighing $$1.4 kg$$. Find the total weight of the box and diamond to the correct number of significant figures.

Weight of diamond $$=0.0371Kg$$.

Total weight $$=1.4Kg+0.0371Kg$$.

$$=1.4371Kg$$ $$\approx $$ $$1.4Kg$$.

The pressure on a square plate is measured by measuring the force on the plate and the length of the sides of the plate by using the formula $$P = F/l^2$$. If the maximum errors in the measurement of force and length are $$4\%$$ and $$2\%$$, respectively, then what is the maximum error in the measurement of pressure?

Formula $$P=\dfrac { F }{ { l }^{ 2 } } $$

$$\dfrac { \Delta P }{ P } \times 100=\left( \dfrac { \Delta F }{ F } +\dfrac { 2\Delta l }{ l } \right) \times 100$$

% error $$=\left( 4+2\times 2 \right) $$%

$$=8$$%

If $$x = 2at + 5b{t^2}$$, where x is in meters 4t in sec. Find the dimension of a and b.

1335598_1028806_ans_bf8a76b8c4fc4d5aa7777996a97fbd25.jpg

In a system of unit, unit of mass, length & time is $$100\ kg$$, $$1$$ hour, $$1\ km$$. In this system, what is $$1\ N$$ of $$F$$

The unit of the force is given as $$kg\ m/s^2$$.

$$1N=\dfrac{1kg\ m}{s^2}$$

$$1N=\dfrac{10^2 \times kg\times 10^{-2}\times 10^{-3}km}{\dfrac{1}{60^2}hr^2}$$

$$=36\times 10^{-3}\dfrac{(100kg)km}{hr^2}$$

Find the dimensions of $$a$$ & $$b$$ if
$$F=at+bt^{2}$$

According to homogeneity principle

Dimensional Formula of $$F $$ = Dimensional Formula of $$at$$ = Dimensional Formula of $$bt^2 $$

We know that Dimensional Formula of $$F = [MLT^{-2}] $$

So, Dimensional Formula of $$at$$ = $$ [MLT^{-2}] $$

$$\Rightarrow $$ Dimensional Formula of $$a$$ = $$ [MLT^{-3}] $$

Also,Dimensional Formula of $$bt^2$$ = $$ [MLT^{-2}] $$

$$\Rightarrow $$ Dimensional Formula of $$b$$ = $$ [MLT^{-4}] $$

Count total number of S.F. in $$6.020\times 10^{23}$$.

Rules for counting significant figures are as follows-

All the reported non-zero numbers in a measurement are significant. For
Zeroes sandwiched anywhere between the non-zero digits are significant.
Zeroes to the left of a first non-zero digit are not significant.
The trailing zeroes or the zeroes to the right of the last non-zero digit are significant if the number has a decimal point otherwise they are insignificant.

Based on these rules, 6.020 × 10$$^{23}$$ has 4 singnificant figures. Exponential powers are bot considered for counting significant figures.

The error in the measurement of radius of a sphere is 2%. What will be the error in the calculation of its surface area?
(surface area A=4$$\pi r^2$$) $$\dfrac{\Delta A}{A}=\dfrac{2\Delta r}{r})$$

Given, Error in a radius of the sphere is 2%

it means$$\Delta r=2%$$

Now, the surface area of the sphere is

$$A=4\pi r^2$$

$$\dfrac{\Delta A}{A}$$=$$\dfrac{2\Delta r}{r}$$

$$\dfrac{\Delta A}{A}$$=$$\dfrac{2\times 2}{1000}$$=$$0.04$$

$$\dfrac{\Delta A}{A\times 100}$$=$$0.04\times 100$$= 4%

it means % error in surface area of its measurements is 4%

Find the dimensional formula for $${\mu}_{o}$$ and $${ \varepsilon }_{ o }$$:

Since, $$k=\dfrac{1}{4\pi\epsilon_0}$$,

dimension of $$ [\epsilon_0]=[k^{-1}]=[ML^3T^{-4}A^{-2}]^{-1}=[M^{-1}L^{-3}T^4A^2]$$

Also we know that , $$c=\dfrac{1}{\sqrt(\mu_0\epsilon_0)}$$

this gives , dimension of $$ [\mu_0]=[c^2\epsilon_0]^{-1}=[MLT^{-2}A^{2}]$$

Find the dimensions of G in the equation $$F=\dfrac{Gm_{1}m_{2}}{r^{2}}$$ ; where F is the force of gravitational attraction between two bodies of point masses $$ m_{1}$$ and $$m_{2}$$ , 'r' is the distance of separation between them.

The gravitational force acting between the two bodies is given by:

$$F=G\dfrac{m_1m_2}{r^2}$$

$$G=\dfrac { F{ r }^{ 2 } }{ { m }_{ 1 }{ m }_{ 2 } } $$

The dimension of the force is $$[MLT^{-2}]$$

$$ =\dfrac { \left[ ML{ T }^{ -2 } \right] \left[ { L }^{ 2 } \right] }{ \left[ M \right] \left[ M \right] } ={ M }^{ -1 }{ L }^{ 3 }{ T }^{ -2 }$$

Find the dimensions of
(a) linear momentum,
(b) frequency and
(c) pressure.

(a) Linear momentum:

$$ =\,mass\,\times \,velocity=[{{M}^{1}}{{L}^{0}}{{T}^{0}}][{{M}^{0}}L{{T}^{-1}}] $$

$$ =\,[ML{{T}^{-1}}]$$

(b) Frequency $$=\dfrac{1}{time}=[{{M}^{0}}{{L}^{0}}{{T}^{-1}}]$$

$$ =\dfrac{Force}{Area}=\dfrac{mass\times acceleration}{Area}=\dfrac{[{{M}^{1}}{{L}^{0}}{{T}^{0}}][{{M}^{0}}L{{T}^{-2}}]}{[{{M}^{0}}{{L}^{2}}{{T}^{0}}]} $$

$$ =[{{M}^{1}}{{L}^{-1}}{{T}^{-2}}] $$

If length of a pendulum of wall clock is increased by $$0.1\%$$, then find error in time per day.

Let, length of pendulum = L

Time period $$T=\sqrt{\dfrac{L}{g}}=1\,\sec $$

Now, time in a day

$$t=1\times 60\times 60\times 24$$

Now, after increasing length o.1%

New length

$$L'=L+0.001L$$

Now, new time period

$$ T'=\sqrt{\dfrac{L'}{g}} $$

$$ T'=\sqrt{\dfrac{1.001L}{g}} $$

$$ T'=\sqrt{1.001}\times \sqrt{\dfrac{L}{g}} $$

$$ T'=\sqrt{1.001}\,s $$

Now, time in a day

$$t'=\sqrt{\left( 1.001 \right)}\times 60\times 60\times 24$$

Now, error in a day

$$ =\sqrt{\left( 1.001 \right)}\times 60\times 60\times 24-1\times 60\times 60\times 24 $$

$$ =60\times 60\times 24\left( \sqrt{\left( 1.001 \right)}-1 \right) $$

$$ =60\times 60\times 24\left( 1.0005-1 \right) $$

$$ =60\times 60\times 24\times .0005 $$

$$ =43.2\,s $$

Hence, the error in time per day is $$43.2\ s$$

Find the dimensions of work.

The dimension of work is given as

$${\rm{work = force \times distance}}$$

$${\rm{W = Mass \times acceleration \times distance}}$$

$$W = M \times L{T^{ - 2}} \times L$$

$$W = M{L^2}{T^{ - 2}}$$

The above equation shows the dimension of work done.

Find the dimensions of:
(i) Power, (ii) Forces and (iii) Permittivity of vacuum $$(\varepsilon_o)$$

(I).The formula of power is

Power $$P=\dfrac{W}{t}$$

Now, the dimension of power is

$$ P=\dfrac{M{{L}^{2}}{{T}^{-2}}}{T} $$

$$ P=M{{L}^{2}}{{T}^{-3}} $$

(II).The formula of force is

$$F=ma$$

The dimension of force is

$$F=ML{{T}^{-2}}$$

(III).The formula of permittivity is

$$ F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{d}^{2}}} $$

$$ {{\varepsilon }_{0}}=\dfrac{q}{F{{d}^{2}}} $$

$$4\pi $$ is a unit less so on neglect

So, the dimension of permittivity is

$$ {{\varepsilon }_{0}}=\dfrac{{{\left[ TA \right]}^{2}}}{\left[ ML{{T}^{-2}} \right]\left[ {{L}^{2}} \right]} $$

$$ {{\varepsilon }_{0}}={{M}^{-1}}{{L}^{-3}}{{T}^{4}}{{A}^{2}} $$

This is the answers

What is the dimensional formulae of capacitance ?

We know that,

the capacitance of a capacitor is given by:

$$C=\dfrac QV$$

the dimension of Q is $$[AT]$$

the dimension of voltage is $$[ML^2T^{-3}A^{-1}]$$

Dimensional formula of capacitance is:

$$C=\dfrac{[AT]}{[ML^2T^{-3}A^{-1}]}$$

$$=[M^{-1}L^{-2}T^4I^2]$$

Find the dimensional formula for hc/G?

Here, the given terms are:

$$H$$ is plank's constant, $$c$$ is the speed of light and $$G$$ is gravitational constant.

we know, the energy of a photon is given as:

$$E= \dfrac{hc}{wavelength}$$

the dimension of hc = dimension of energy $$\times$$ length

dimension of energy =$$ [ML^{2}T^{-2}]$$

dimension of wavelength$$ = [L]$$

so, dimension of $$hc = [ML^{2}T^{-2}] [L] = [ML^{3}T^{-2}]$$

now, dimension of G :

we know, gravitational force ,

$$F = \dfrac{GMm}{r^2}$$

so, dimension of $$G = {F \times \dfrac{r^2}{Mm}}$$

dimension of force$$ = [MLT^{-2}]$$

dimension of $$r^2 = [L^2]$$

dimension of $$M = [M]$$

dimension of $$m = [M]$$

so, dimension of G$$ = [MLT^{-2}][L^{2}]/[M][M]$$

$$= [M^{-1}L^{3}T^{-2}]$$

now, dimension of hc/G = dimension of hc/dimension of G

$$= [ML^{3}T^{-2}]/[M^{-1}L^{3}T^{-2}]$$

$$= [M^2]$$

The velocity '$$v$$' of water waves depends on the wavelength '$$\lambda$$', density of water '$$\rho$$' and the acceleration due to gravity '$$g$$'. Deduce by method of dimensions the relationship between these quantities.

1335626_1073428_ans_2b53115c609d498a86c123c4819fef11.jpg

Write dimensional formula of energy and acceleration.

1475912_1068492_ans_dd1f1f94fbc54587a89e1f6bad96bbef.jpg

Find the dimensions of
1) Force
2) power
3) density
4) momentum
5) velocity

1) 1. Force = mass x acceleration $$=\ kg\ \times \ m{{s}^{-2}}\ =kg\,m{{s}^{-2}}=[M{{L}^{1}}{{T}^{-2}}]$$

2) 2. Power = force x displacement/time $$=\ kg\ m{{s}^{-2}}\times m{{s}^{-1}}=[M{{L}^{2}}{{T}^{-3}}]$$

3) 3. Density= mass/volume $$=\ {kg/{m}^{3}}=[{{M}^{1}}{{L}^{3}}{{T}^{o}}]$$

4) 4. Momentum = mass x velocity $$=kg\times m{{s}^{-1}}=kg\,m{{s}^{-1}}=[ML{{T}^{-1}}]$$

5) 5. Velocity = Distance/meter $$=m{{s}^{-1}}=[{{M}^{o}}L{{T}^{-1}}]$$

The rate of flow of a liquid through a capillary tube of length $$L$$ and radius $$r$$ under a pressure difference $$p$$ is given by the poiseuille's formula $$V = \pi \,p\,{r^4}/8\eta L$$. Determine the dimensions of the coefficient of viscosity $$\eta $$ of the liquid.

It is given that

$$ V=\dfrac{\pi {{\Pr }^{4}}}{8\eta L} $$

$$ \eta =\dfrac{\pi {{\Pr }^{4}}}{8VL} $$

Where V is volume rate $$\left[ {{L}^{3}}{{T}^{-1}} \right]$$

P is pressure $$\left[ M{{L}^{-1}}{{T}^{-2}} \right]$$

$$\eta $$ is viscosity

L is length $$\left[ L \right]$$

So the dimensional formula of viscosity is

$$ \dfrac{\left[ M{{L}^{-1}}{{T}^{-2}} \right]\left[ {{L}^{4}} \right]}{\left[ {{L}^{3}}{{T}^{-1}} \right]\left[ L \right]} $$

$$ \left[ M{{L}^{-1}}{{T}^{-1}} \right] $$

If the velocity of the particle is given by $$v=\cfrac { a }{ t } +b{ t }^{ 2 }$$
The dimensions of a & b are given as ______

$$v=\dfrac { a }{ t } +{ bt }^{ 2 }$$

$$\left[ v \right] =\left[ \dfrac { a }{ t } \right] =\left[ { bt }^{ 2 } \right] $$ [from dimensional analysis]

$$L{ T }^{ -1 }={ a{ T }^{ -1 } }=B{ T }^{ 2 }$$

Comparing the sides we get,

$$a={L}^{1}$$

$$b=LT^{-3}$$

The Sun's angular diameter is measured to be $${1920 }$$. The distance D of the sun from the earth is $$1.496 \times {10^{"}}$$m. find the diameter of the sun?

Angular diameter of sun =
$$\theta = {1920^{"}}$$
$${1920^{''}} = {\left( {\dfrac{{1920}}{{60}}} \right)^1} = {32^1}$$
=$${\left( {\dfrac{{32}}{{60}}} \right)^{^ \circ }}$$
$$1920 = {0.533^ \circ }$$
now, $${180^ \circ } \equiv \pi $$ rad
$$\therefore {0.533^ \circ } \equiv (?)$$
$$\therefore \theta = 0.533 \times \dfrac{\pi }{{180}} \approx 9.3 \times {10^{ - 3}}$$ rad

let diameter of sun be d given that $$l = 1.496 \times {10^{11}}$$m
Now , $$\theta = \dfrac{{arc}}{{radius}} = \dfrac{d}{r}$$
$$\therefore d = \theta l$$
$$\therefore d = 9.3 \times {10^{ - 3}} \times 1.496 \times {10^{11}}$$
$$\therefore d = 13.91 \times {10^8}$$
$$\therefore d = 1.39 \times {10^9}m$$
diameter of sum is $$1.39 \times {10^9}$$

For the real gas equation $$(P + a/v^{2})(v - b)$$. Find the dimension for $$a$$ and $$b$$.

1335644_1090097_ans_225dcb20faf044cb87c962736e9f15fa.jpg

Find dimension of moment of inertia. Is moment of inertia a vector or scalar?

We know that the moment of inertia is given by:

$$I=\int { dm }{ R }^{ 2 }$$

So, the dimension of the moment of inertia is:

$$I=\left[ Mass \right] \left[ Length \right] ^{ 2 }$$

$$\left[ Mass \right]$$=$$\left[ M \right] $$ and $$\left[ Length \right] =\left[ L \right] $$

So, $$\left[ I \right]$$$$=\left[ M \right] \left[ L \right] ^{ 2 }$$

Moment of inertia in rotatory motion is equivalent to mass in translatory motion.

As mass is scalar quantity, it is also a scalar quantity.

If force (F), velocity v and time (T) are taken as fundamental units then the dimensions of mass are

2182387_1088528_ans_3599af6be71c4bb48ab64ccd870a3ad3.jpeg

What is the need for measurement of a physical quantity?

A quantity which can be measured directly or indirectly and used in explanation of physical phenomenon is called a physical quantity. For example, distance, speed, mass, pressure, force, momentum, energy. Measurements are needed in everyday life

$$\omega t=\theta $$
$$ Kx = \theta $$

What will be dimensions unit of $$K$$ in the above formula. Given $$x$$ is displacement and $$\theta$$ is angular displacement and $$\omega$$ is angular frequency.

Given that,

$$\omega t=\theta $$

$$Kx=\theta $$

distance $$=x$$

Now,

The dimension of $$\omega $$

$$ \omega t=\theta $$

$$ \omega =\dfrac{\theta }{t} $$

$$\omega=\dfrac{1}{T}$$

$$ \omega ={{T}^{-1}} $$

$$ \omega =\left[ {{M}^{0}}{{L}^{0}}{{T}^{-1}} \right] $$

Now, for $$Kx=\theta $$

The dimension of $$K$$

$$ Kx=\theta $$

$$ K=\dfrac{\theta }{x} $$

$$\omega=\dfrac{1}{l}$$

$$ K={{L}^{-1}} $$

$$ K=\left[ {{M}^{0}}{{L}^{-1}}{{T}^{0}} \right] $$

Hence, this is the required solution

The flux of magnetic field through a closed conducting loop changes with time according to the equation,$$ \Phi ={ at }^{ 2 }+bt+c$$.$$(a)$$ Write the $$SI$$ units of $$a,b$$ and $$c$$ $$(b)$$ If the magnitudes of $$a,b$$ and $$c$$ are $$0\cdot 20, 0.40$$ and $$0.60$$ respectively, find the including emf at $$t=2\ s$$.

Given:

$$ \Phi ={ at }^{ 2 }+bt+c$$
Same dimensional quantity can be added, subtracted and equated.

(a) $$a=\left[ \cfrac { \phi }{ { t }^{ 2 } } \right] =\left[ \cfrac { \phi /t }{ t } \right] =\cfrac { volt }{ sec } ; \ \ \ b=\left[ \cfrac { \phi }{ { t }^{ } } \right] =volt; \ \ \ c=\left[ \phi \right] =Weber$$

(b) $$a=0.2,b=0.4,c=0.6,t=2s$$
$$\quad E=\cfrac { d\phi }{ { dt }^{ } } =2at+b=2\times 0.2\times 2+0.4=1.2volt$$

The position of X of a particle at time t is given by $$X=\dfrac{v_0}{a}(1-e^{-at})$$, where $$v_0$$ is a constant and a >What are the dimensions of $$V_0 $$ and a

1335962_1141979_ans_36b75965295546f1b04fcb71eba2f494.jpg

Find the dimensions of
i) Force
ii) Power
iii) Electric potential
iv) Resistance
v) Refractive index
vi) Permittivity of vacuum $$(\varepsilon_0)$$
vii) Permeability

1335733_1132100_ans_c6494dbaaa8449d7808afe469e975550.jpg

If $$F$$ is given by $$F$$ = ($${\alpha / \beta}$$) ($${1 - e ^{{- \beta t^2} / m}}$$), where $$F$$ is force and $$m$$ & $$t$$ are mass and time, then dimension of $$\alpha$$ will be :

Since, $$F=\cfrac { \alpha }{ \beta } \left( 1-{ e }^{ -\cfrac { \beta { t }^{ 2 } }{ m } } \right) $$

Since exponential is an dimensionless quantity

Hence,

$$-\cfrac { \beta { t }^{ 2 } }{ m } $$ is a dimensionless quantity

$$\therefore$$ $$\left[ \cfrac { \beta { t }^{ 2 } }{ m } \right] =\left[ { M }^{ 0 }{ L }^{ 0 }{ T }^{ 0 } \right] $$

$$\Rightarrow \beta \left[ \cfrac { { T }^{ 2 } }{ M } \right] =\left[ { M }^{ 0 }{ L }^{ 0 }{ T }^{ 0 } \right] $$

Hence, $$\quad \beta =\cfrac { \left[ { M }^{ 0 }{ L }^{ 0 }{ T }^{ 0 } \right] \left[ M \right] }{ \left[ { T }^{ 2 } \right] } $$

and the two quantities cannot subtracted added until they don't have same dimension

$$\left[ F \right] =\cfrac { \alpha }{ \beta } $$

since, $$\left[ F \right] =\left[ { M }^{ 1 }{ L }^{ 1 }{ T }^{ -2 } \right] $$

$$\left[ { M }^{ 1 }{ L }^{ 1 }{ T }^{ -2 } \right] =\cfrac { \left[ \alpha \right] }{ \left[ { M }^{ 1 }{ L }^{ 0 }{ T }^{ -2 } \right] } $$

$$\therefore \left[ \alpha \right] =\left[ { M }^{ 1 }{ L }^{ 1 }{ T }^{ -2 } \right] \left[ { M }^{ 1 }{ L }^{ 0 }{ T }^{ -2 } \right] $$

$$\left[ \alpha \right] =\left[ { M }^{ 2 }{ L }^{ 1 }{ T }^{ -4 } \right] $$

A block of wood of mass $$24$$ kg floats on water. The volume of wood is $$0.032$$ $$m^3$$. Find the density of wood.(Density of water $$=1000$$ kg $$m^{-3}$$)

Density of wood= $$\dfrac {mass\ of\ wood}{volume\ of\ wood}$$

=$$\dfrac{24}{0.032}$$

=$$760 kg m^{-3}$$

Fill in the blanks with suitable units of measurements.
The distance I walk in $$10\ minutes$$ is about $$1$$_____.

$$kilometer\ (km)$$.

The distance is always measured in meters or kilometers. In $$10\ minutes$$ a person can cover approximately a distance of $$1\ km$$.

If X=a+b, the maximum percentage error in the measurement of X will be

If $$x=a+b$$

Let $$\triangle a$$ and $$\triangle b$$ be the absolute error in a & b

respectively.

Let error in x be $$\triangle x$$ $$x=a+b$$

maximum possible value of $$\triangle x=\triangle a+\triangle b$$

Relative error 1 $$\dfrac{\triangle x}{x}=\dfrac{\triangle a+\triangle b}{a+b}$$

Percentage of error $$\dfrac{\triangle x}{x}\%= \left[\left(\dfrac{\triangle a+\triangle b}{a+b}\right)100\right]\%$$

A thermometer placed under the armpit always shows a lower value than the actual body temperature. Which type of error is demonstrated in its measurement.

The goal is to determine the 'core temperature', the temperature of the interior of the body. The rectum and tongue are the most accessible areas of the body that are at core temperature. The area under the tongue, full of blood vessels, is almost as accurate as the rectal area, and a lot more pleasant place to use.Occasionally the armpit will be used for kids usually as it is difficult and inconvenient for them to hold the thermometer under the tongue. Inconvenient place for a child to keep the thermometer there long enough

When a graph between two physical quantities is straight line passing through the origin with positive slope , then the two quantities are

then those two quantities are directly proportional.

Three measurements of the time for 20 oscillations of a pendulum give $$t_1=39.6 s, t_2=39.9 s$$ and $$t_3=39.5 s$$. What is the precision in the measurements? What is the accuracy of the measurements?

precision is given by least count of the instrument { e.g., pendulum}

here, least of $$20$$ oscillation $$= 0.1 sec$$

so, least count of $$1$$ oscillation $$=\dfrac{ 0.1}{20} = 0.005sec$$

hence, precision in measurements $$= 0.005sec$$

observations are $$39.6sec, 39.9 sec , 39.5 sec$$

mean of observations $$= \dfrac{(39.6 + 39.9 + 39.5)}{3}$$

$$= \dfrac{(119)}{3 }≈ 39.6sec$$

now, maximum error in $$20$$ oscillations $$=$$ observation of highest value - mean of observations

$$= 39.9 - 39.6 = 0.3 sec$$

so, max absorbed error in $$1$$ oscillation $$= \dfrac{0.3}{20} = 0.015 sec$$

hence, accuracy of measurements is $$0.015 sec$$

In Milikan's oid drop experiment on applying a vertically upward electric field an oil drop (of mass $$m$$) moves vertically downward with certain terminal speed.On applying double the electric field in horizontal direction, the drop moves making $$45^{o}$$ with the vertical. Neglecting buoyant forc due dto the air, what is the viscous force acting on the drop in first case?

In first case the droplet of mass m and charge q moves with a constant terminal velocity (say v) under the influence downward gravitational force mg and the upward electrical force q for the upward electric field E acted on it.

If the viscous force exerted by air be Fv then due to terminal velocity v then we can write

$$mg−qE=Fv$$.....[1] [Neglecting buoyant force due to the air]

At this state of downard motion of the droplet with terminal velocity v if an electric field double in magnitude is applied in horizontal direction on the droplet it is found to move in the direction 45∘ with the vertical. This is possible only if the droplet gains same terminal velocity v in horizontal direction.

In this case horizontal electrical force should be balanced by the viscous force acting on the droplet in the horizontal direction. So we can write

$$2qE=Fv$$.....[2] [Neglecting buoyant force due to the air]

Combining [1] and [2] we get

$$mg−12Fv=Fv$$

$$\Rightarrow Fv=\dfrac{2}{3}mg$$

In a circle of radius 12 cm, a chord subtends an angle $${ 120 }^{ \circ }$$ at the center. Find the area of the corresponding minor segment of the circle (use $$\pi =3.14$$ and $$\sqrt { 3 } =1.732$$)

2047283_1393461_ans_afeaf16728e14685bac66d9d6aa20d66.jpeg

Using dimensions, show that $$1 \ newton = 10^5 \ dyne$$

Let $$1$$ $$newton$$ $$=n$$ $$dynes$$

$$n = \dfrac{{{M_1}{L_1}{t_1}^{ - 2}}}{{{M_2}{L_2}{t_2}^{ - 2}}} = \dfrac{{{M_1}}}{{{M_2}}} \times \dfrac{{{L_1}}}{{{L_2}}} \times \dfrac{{{t_1}^{ - 2}}}{{{t_2}^{ - 2}}}$$

$$ = \dfrac{{Rg}}{{gm}} \times \dfrac{m}{{cm}} \times {\left( {\dfrac{s}{s}} \right)^{ - 2}}$$

$$ = \dfrac{{{{10}^3}gm}}{{gm}} \times \dfrac{{{{10}^2}cm}}{{cm}} \times {s^0}$$

$$ = {10^3}{10^2} = {10^5}$$

$$\therefore 1\,newton = {10^5}dyne.$$

Hence,

we get,

$$1{\mkern 1mu} newton = {10^5}dyne.$$

In an experiment, refractive index of glass was observed to be 1.45, 1.56, 1.54, 1.44, 1.54, and 1.53 Calculate
Mean value of refractive index

$$\mu_{m}=\dfrac{\sum\limits_{i=1}^n \mu}{n}$$

$$ \mu_m= \dfrac{1.45 + 1.56 + 1.54+ 1.44+ 1.54+1.53}{6}=1.51 $$

Water is poured into a container that has a small leak. The mass $$m$$ of the water is given as a function of time $$t$$ by $$m=5.00\ t^{0.8}-3.00 t+20.00$$, with $$t \ge 0, m$$ in grams, and $$t$$ in seconds.
At what time is the water mass greatest.

To solve the problem, we note that the first derivative of the function with respect to times gives the rate. Setting the rate to zero gives the time at which an extreme value of the variable mass occurs; here that extreme value is a maximum.
Differentiating $$m(t)=5.00 t^{0.8}-3.00 t+20.00$$ with respect to $$t$$ gives
$$\dfrac {dm}{dt}=4.00t^{-0.2}-3.00$$.
The water mass is the greatest when $$dm/dt=0$$, or at $$t=(4.00/3.00)^{1/0.2}=4.21\ s$$.

One cubic centimeter of a typical cumulus cold contains $$50$$ to $$500$$ drops, which have a typical radius of $$10\ \mu m$$. For that range give the lower value and the higher value, respectively, for the following.
Water has a density of $$1000\ kg/m^3$$. How much mass does the water in the cloud have?

1645369_1764950_ans_e5fdb05e51774196af894e6a57bdd4f9.jpg

During heavy rain, a section of a mountainside measuring $$2.5\ km$$ horizontally, $$0.80\ km$$ up along the slope, and $$2.0\ m$$ deep slips into a valley in a mud slide. Assume that the mud ends up uniformly distributed over a surface are of the valley measuring $$0.40\ km \times 0.340\ km$$ and that mud has a density of $$1900\ kg/m^3$$. What is the mass of the mud sitting above a $$4.0\ m^2$$ area of the valley floor?

1645510_1764941_ans_5367d60b115c471daaef28a1fd76329a.jpg

Earth has a mass of $$5.88\times 10^{25}kg$$. The average mass of the atoms that make up Earth is $$40\ u$$. How ,any atoms are there in earth?

If $$M_E$$ is the mass of Earth, $$m$$ is the average mass of an atom in Earth, and $$N$$ is the number of atoms, then $$M_E=Nm$$ or $$N=M_E /m$$. We convert mass $$m$$ to kilograms using
Appendix $$D(1\ u=1.661\times 10^{-27}\ kg)$$. Thus,

$$N=\dfrac {M_E}{m}=\dfrac {5.98\times 10^{24}kg}{(40\ u)(1.661\times 10^{-27}kg/u)}=9.0\times 10^{49}$$.

A mole of atoms is $$6.02\times 10^{23}$$ atoms. To the nearest order of magnitude, how many moles of atoms are in a larger domestic cat? The masses of a hydrogen atom, an oxygen atom, and a carbon atom are $$1.0\ u, 16\ u$$, and $$12\ u$$, respectively.

as we know,

If we estimate the "typical" large domestic cat mass as $$10\ kg$$, and the "typical" atom (in the cat) as $$10\ u \sim 2\times 10^{-26}kg$$, then there are roughly $$(10\ kg)/(2\times 10^{-26}kg)\sim 5\times 10^{26}$$ atoms. This is close to being a factor of a thousand greater than Avogadro's number. Thus this is roughly a kilomole of atoms.

On a spending spree in Malaysia, you buy an ox with a weight of $$28.9$$ piculs in the local unit of weights: $$1$$ piculs =$$100$$ gains, $$1$$ gain $$=16$$ tahils, $$14$$ tahils $$=10$$ chees, and $$1$$ chee $$=10$$ hoons. The weight of $$1$$ hoon corresponds to a mass of $$0.3779\ g$$. When you arrange to ship the ox home to your astonished family, how much mass in kilograms must you declare on the shipping manifest?

The mass in kilograms is
$$28.9\ piculs=(28.9\ piculs) \left(\dfrac {100\ gin}{1\ picul}\right)\left(\dfrac {16\ tahil}{1\ gin}\right)\left(\dfrac {10\ chee}{1\ tahil}\right)\left(\dfrac {10\ hoon}{1\ chee}\right)\left(\dfrac {0.3779\ g}{1\ hoon}\right)$$

which yields $$=1.747\times 10^6g$$ or roughly $$=1.75\times 10^3 kg$$

A lecture period $$(50\ min)$$ is close to $$1$$ microcentury
Using percentage difference $$=\left(\dfrac{actual-approximation}{actual}\right)100$$, find the percentage difference from the approximation.

1645261_1764917_ans_404f1391fa1a462780b8eb411f6030eb.jpg

Water is poured into a container that has a small leak. The mass $$m$$ of the water is given as a function of time $$t$$ by $$m=5.00\ t^{0.8}-3.00 t+20.00$$, with $$t \ge 0, m$$ in grams, and $$t$$ in seconds.
In kilograms per minute, what is the rate of mass change at $$t=2.00\ s$$

Mass is given in the function of time

$$m=5.00t^{0.8}-3.00t+20.00$$
The rate of mass charge at $$t=2.00\ s$$ is
$$R=\dfrac {dm}{dt}|_{t=2.00\ s} =[4.00(2.00)^{-0.2}-3.00]g/s =0.48\ g/s=0.48\dfrac gs . \dfrac {1\ kg}{1000\ g}. \dfrac {60\ s}{1\ min}$$

$$R=2.89\times 10^{-2}kg/min$$.

A person on a diet might lose $$2.3\ kg$$ per week. Express the mass loss rate in milligrams per second, as if the dieter could sense the second by second loss.

As given,

A million miiligrams comprise a kilogram, so $$2.3\ kg$$/week is $$2.3\times 10^{6}\ mg$$$/ week. Figuring $$7$$ days a week $$24$$ hours per day $$3600$$ second per hour we find $$604800$$ second are equivalent to one week. Thus, $$(2.3\times 10^{6}\ mg/week)/(604800\ s/week)=3.8\ mg/s$$.

Using conversions and data in the chapter. determine the number of hydrogen atoms required to obtain $$1.0\ kg$$ of hydrogen. A hydrogen atom has a mass of $$1.0\ u$$.

As we know,

Equation $$1-9$$ gives (to very high precision!) the conversion fro atomic mass units to kilogram. Since this problem deals with the ratio of total mass $$(1.0\ kg)$$ divided by the mass of one atom ($$1.0\ u$$ but converted to kilogram), then the computation reduces to simply taking the reciprocal of the number given in Eq $$1-9$$ and rounding off approximately. Thus, the answer is $$6.0\times 10^{26}$$

One molecule of water $$(H_{2}O)$$ contains two atoms of hydrogen and one atom of oxygen. A hydrogen atom has a mass of $$1.0\ u$$ and an atom of oxygen has a mass of $$16\ u$$, approximately.
How many molecules of water are in the world's oceans, which have an estimated total mass of $$1.4\times 10^{21}\ kg$$?

As we know,

We divide the total mass by mass of each molecule and obtain the (approximate) number of water molecule:

$$N\approx \dfrac{1.4\times 10^{21}}{3.0\times 10^{-26}}\approx 5\times 10^{46}$$

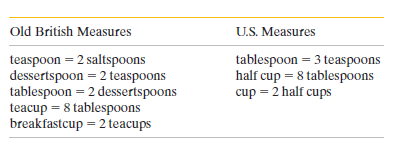
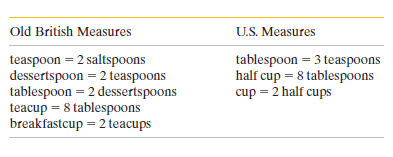
An old English cookbook carries this recipe for cream of nettle soup: Boil stock of the following amount: $$1$$ break fastcup plus $$1$$ teacup plus $$6$$ tablespoons plus $$1$$ dessertspoon. Using gloves, separate nettle tops until you have $$0.5$$ quart; add the tops to the boiling stock. Add $$1$$ tablespoon of cooked rice and $$1$$ saltspoon of salt. Simmer for $$15\ min$$. The following table gives some and among common (still premetric) U.S. measures. (These measures just scream for metrication. )For dry liquid measures, $$1$$ British teaspoon $$=2\ U.S.$$ teaspoon and $$1$$ British quart $$=1\ U.S.$$ quart. In U.S measures, how much
rice

1 breakfast cup= 2 tea cup= 16 tablespoons=32 dessert spoon= 64 teaspoon (Britain)= 128 teaspoons (US)

1 teacup= 8 table spoons= 16 dessert spoons= 32 teaspoon (Britain)= 64 teaspoon (US)

6 tablespoon= 12 dessert spoon= 24 teaspoon (British)= 48 teaspoon (US)

1 desert spoon= 2 teaspoon (British)= 4 teaspoon (USA)

1 tablespoon rice= 2 desert spoon= 4 teaspoon(British)= 8 teaspoon(US)

Hence, 8 tablespoon rice is the amount of rice in US measured.

One molecule of water $$(H_{2}O)$$ contains two atoms of hydrogen and one atom of oxygen. A hydrogen atom has a mass of $$1.0\ u$$ and an atom of oxygen has a mass of $$16\ u$$, approximately.
What is the mass in kilograms of one molecule of water?

As we know,

In atomic mass units, the mass of one molecule is $$(16+1+1)u=18\ u$$. Using Eq $$1-9$$ we find

$$18\ u=(18\ u)\left(\dfrac{1.6605402\times 10^{-27}\ kg}{lu}\right)=3.0\times 10^{-26}kg$$

What mass of water fell on the town in $$V=(26\ km^{2})(2.0\ in.)$$ ?
Water has a density of $$1.0\times 10^{3}\ kg/m^{3}$$.

The volume of the water that fell is

$$V=(26\ km^{2})(2.0\ in.)$$

$$=(26\ km^{2})\left(\dfrac{1000\ m}{1\ km}\right)^{2}(2.0\ in.)\left(\dfrac{00.0254\ m}{1\ in.}\right)$$

$$=(26\times 10^{6}m^{2})(0.0508\ m)$$
$$=1.3\times 10^{6}m^{3}$$

We write the mass per unit volume (density) of the water as
$$\rho=\dfrac{m}{V}=1\times 10^{3}\ kg/m^{3}$$

The mass of the water that fell is therefore given by $$m=\rho V$$
$$m=(1\times 10^{3} kg/m^{3})(1.3\times 10^{6}\ m^{3})=1.3\times 10^{9}\ kg$$.

Water is poured into a container that has a small leak. The mass $$m$$ of the water is given as a function of time $$t$$ by $$m=5.00\ t^{0.8}-3.00 t+20.00$$, with $$t \ge 0, m$$ in grams, and $$t$$ in seconds.
What is the greatest mass?

we note that the first derivative of the function with respect to times gives the rate. Setting the rate to zero gives the time at which an extreme value of the variable mass occurs; here that extreme value is a maximum.
Differentiating $$m(t)=5.00 t^{0.8}-3.00 t+20.00$$ with respect to $$t$$ gives
$$\dfrac {dm}{dt}=4.00t^{-0.2}-3.00$$.
The water mass is the greatest when $$dm/dt=0$$, or at $$t=(4.00/3.00)^{1/0.2}=4.21\ s$$.

for maximum mass Put $$t=4.21\ s$$,

the water mass is:

$$m(t=4.21\ s)=5.00(4.21)^{0.8}-3.00(4.21)+20.00=23.2\ g$$.

An old English children's rhymes states, Little Miss Muffet sat on a tuffet, eating her curds and whey, when along came a spider who sat down beside her...." The spider sat down not because of the curds and whey but because Miss Muffet had a stash of $$11$$ tuffet $$=2$$ pecks $$=0.50$$ Imperial bushel, where $$1$$ Imperial bushel $$=36.3687$$ litres $$(L)$$. What was Miss Muffet stash in
pecks,

As we know,

The first two conversion are easy enough that a formal conversion is not especially called for, but in the interest of practice makes perfect we go ahead and proceed formally.

$$11$$ tuffets =($$11$$ tuffets) $$\left(\dfrac{2\ peck}{1\ tuffet}\right)=22$$ pecks.

The common Eastern mole, a mammal, typically has a mass of $$75\ g$$, which corresponds to about $$7.5$$ moles of atoms. (A mole of atoms is $$6.02\times 10^{23}$$ atoms.) In atomic mass units $$(u)$$, what is the average mass of the atoms in the common Eastern mole?

$$1\ u=1.66\times 10^{-24}g$$

The mass of one mole of atoms is about $$m=(1.66\times 10^{-24}g)(6.02\times 10^{23})=1\ g$$. On the other hand the mass of one mole of atoms in the common Eastern mole is
$$m'=\dfrac{75\ g}{7.5}=10\ g$$
Therefore in atomic mass units, the average mass of one in the common Eastern mole is
$$\dfrac{m'}{N_{A}}=\dfrac{10\ g}{6.02\times 10^{23}}=1.66\times 10^{-23}g=10\ u$$

The radius of an atom is of the order of $$1 A^{\circ}$$ and radius of the nucleus is of the order of fermi. How many magnitudes higher is the volume of an atom as compared to the volume of the nucleus?

According to the question,
Radius of atom $$1 A^{\circ}=10^{-10}m$$
Radius of nucleus$$\approx fermi=10^{-15}m$$
Volume of atom $$V_{atom}=\dfrac{4}{3}\pi R^3_A$$
Volume of nucleus $$V_{nucleus}=\dfrac{4}{3}\pi R^3_N$$
$$\dfrac{V_{Atom}}{V_{Nucleus}}=\dfrac{\dfrac{4}{3}\pi R^3-A}{\dfrac{4}{3}\pi R^3_N}=(\dfrac{R_A}{R_N})^3=(\dfrac{10^{-10}}{10^{-15}})=10^{15}$$

Name the device used for measuring the mass of atoms and molecules.

The masses of atoms and molecules can be measured using an instrument called a $$mass \ spectrometer.$$ This instrument can be used to also measure their relative concentrations. The mass spectrometer functions using the magnetic force that is applied on a charged particle that is in motion.

From parallax measurement, the sun is found to be at a distance of about 400 times of earth-moon distance. Estimate the ratio of sun-earth diameters.

1823985_1793247_ans_cf8b38dfa11346d58a1f7d8b8055bcf9.png

Give an example of:
A physical quantity which has a unit but no dimension

Plane angle$$= \frac{arc}{radius}$$ is radian and solid angle - Steradian has unit but no dimensions.

Why length, mass and time are chosen as base quantities in mechanics?

The length, mass and time cannot be derived from any other physical quantities and all physical quantities of mechanics. So, length, mass and time are chosen as the base quantities in mechanics.

Fill in the blanks.
Plancks' constant has dimension_______.

1740258_1783675_ans_e199e20e8f494c2ea93a020053ace857.jpg

The displacement of a progressive wave is represented by $$y =A sin(\omega t– kx)$$, where $$x$$ is distance and $$t$$ is time. Write the dimensional formula of (i) $$\omega$$ and (ii)k.

We have to apply principle of homogeneity to solve this problem. Principle of homogeneity states that in a correct equation, the dimensions of each term added or subtracted must be same, i.e., dimensions of $$LHS$$ and $$RHS$$ should be equal.
According to the problem
$$y=A\, sin(\omega t-kx)$$
Here, $$y=[L]$$ hence
$$A\, sin (\omega t-kx)=[L]$$
Here,$$A=[L]$$,which peak value of y
So,$$\omega t-kx$$ should be dimensionless.
i) $$[\omega t]$$=constant
$$\Rightarrow [\omega]=[T^{-1}]$$
ii) $$[kx]$$=constant
$$\Rightarrow [k]=[L^{-1}]$$

Time for 20 oscillations of a pendulum is measured as $$t_1 = 39.6$$s; $$t_2 = 39.9$$s and $$t_3 = 39.5$$s. What is the precision in the measurements? What is the accuracy of measurement?

$$t_1 = 39.6$$s; $$t_2 = 39.9$$s and $$t_3 = 39.5$$s.
the least count of instrument is 0.1 s
Hence precision (LC) = 0.1 s
Mean value of time for 20 oscillations
$$= \frac{39.6 + 39.9 + 39.5}{3} = \frac{119.0}{3} = 39.7$$s
Absolute errors in measurement
$$\mid \Delta t_1 \mid = \mid \vec t - t_1\mid = \mid 39.7 - 39.6\mid = \mid 0.1 \mid = 0.1 s$$
$$\mid \Delta t_2 \mid = \mid \vec t - t_2\mid = \mid 39.7 - 39.9\mid = \mid 0.2 \mid = 0.2 s$$
$$\mid \Delta t_3 \mid = \mid \vec t - t_3\mid = \mid 39.7 - 39.5\mid = \mid 0.2 \mid = 0.2 s$$
$$\therefore$$ Mean absolute error $$= \frac{0.1 + 0.2 + 0.2}{3} = \frac{0.5}{3} \cong 0.2 s$$
$$\therefore$$ Accuracy of measurement $$= \pm 0.2$$s.

The masses of five marbles are $$50 \,g, 55 \,g, 60 \,g, 65 \,g$$ and $$70 \,g.$$ Find their average mass.

The sum of masses of all marbles
$$= 50 \,g + 55 \,g + 60 \,g + 65\,g + 70 \,g = 300 \,g$$
Number of marbles $$= 5$$
Average mass of a marble $$= \dfrac{\text{sum of mass }}{\text{no. of marbles}}$$

Average mass of a marble $$=\dfrac{ 300 } 5 \,g$$

Average mass of a marble $$= 60 \,g$$

Fill in the blanks.
In the ....... system, length is measured in centimeters.

In the CGS system, length is measured in centimeters.

How are the units$$ cm^2$$ related to the S.I. unit of area ?

hectare: One hectare is the area of a square of each side $$100$$ metre. Thus,
$$1 \,hectare = 100 \,metre \times 100 \,metre = 10000 \,metre^2$$

What do you understand by the term 'mass'? Name any one instrument used for weighing.

The amount of matter present in an object is called its mass. Instruments used to measure mass are beam balance, spring balance, physical balance, electronic weighing machines, etc.

State three differences between mass and weight.

Mass	Weight
It is the quantity of matter contained in a body.	It is the gravitational force with which the earth attracts the body.
Measured by using a beam balance	Measured by using spring balance
It is constant for a body and it does not change by changing the place of the body.	With the variation in acceleration due to gravity at different places, the weight of the body changes.
S.I. unit of mass is kilogram ( kg)	S.I. unit of weight is same as force i.e. Newton (N)

Which quantity : Mass or weight, does not change of place?

Part 1: Variation in mass and weight

The mass of a body is the quantity of matter in a body. So, it is constant and does not change by change in place.
However, Weight is the gravitational force with which the earth attracts the body. With the change in acceleration due to gravity at the place, the weight of the body changes at that place.

The weight of a girl is $$36$$ kgf. Her mass will be _______ .

36 kg

Solution:

Explanation

1 kgf force is the force that produces an acceleration equal to the acceleration due to gravity on a 1 kg body. So, 36 kgf is the force that produces an acceleration equal to the acceleration due to gravity on a 36 kg body.
Hence, the mass of the girl is 36 kg.

The weight of a body of mass $$1$$ kg on earth is $$10$$ N. If a boy of mass $$30$$ kg goes from earth to the moon surface, what will be his (a) mass (b) weight?

(a) Mass remains same it does not change
So mass of boy $$30$$ kg on earth = $$30$$ kg on moon surface
(b) Weight of boy on moon becomes $$1/6$$
$$\therefore 30$$ kg boy will weight $$30 \times 1/6 = 5$$ kg
$$1$$ kg $$ = 10 N \Rightarrow 5 \times 10 N = 50 N$$
$$\therefore $$ Weight of boy on moon surface = $$50$$ N

A block of iron has dimensions $$ 2m \times 0.5 m \times 0.25 m$$. The density of iron is $$ 7.8 g cm^{-3} $$ Find the mass of block.

Given , $$I$$ = $$2m$$
$$b$$ = $$0.5 m$$
$$h$$= $$0.25 m$$
Density of iron = $$ 7.8 g cm^{3} $$ = $$ 7.8 \times 1000 kg m^{-3} $$ = $$ 7800 kg m^{-3} $$
Volume of block = $$ l\times b\times h $$
= $$ 2\times 0.5\times 0.25 $$ = $$ 0.25 m^{3} $$
From relation d= $$ \dfrac{M}{V} $$
$$ \therefore $$ Mass of iron block $$ M= V\times d $$
= $$ 0.25 \times 7800 kg m^{3} $$
= $$1950 kg$$

On earth the weight of a body of mass $$1.0$$ kg is $$10$$ N. What will be the weight of a boy of mass $$37$$ kg in (a) kgf (b) N?

Weight of a body of mass $$1.0$$ kg body = $$10$$ N
(a) Weight of a body of mass 37kg= $$37$$ kgf
(b) Weight of a boy of $$37$$ kg in newton : $$37 \times 10 N$$ = $$370$$ N

State which of the quantities, mass or weight is always directed vertically downwards.

Explanation

The mass of a body is the quantity of matter in a body and has no direction.
Weight is the gravitational force with which the earth attracts the body. So, it is always directed towards the surface of earth i.e. vertically downwards.

Define the term weight and state its S.I. unit.

Part 1: Definition of weight

The weight of a body is the gravitational force by which earth attracts the body towards itself. It is the product of the mass of the body and acceleration due to gravity.
Weight of a body varies at different places due to variation in the gravitational force of attraction. It is represented by the symbol W.

W =mg

Part 2: S.I. unit of weight

The S.I. unit of weight is Newton (N).

1N = 1kg m/s2

How are the units of weight: kgf and newton related?

Part 1: Relation between kgf and Newton

Kgf is the unit of force according to the Gravitational metric system and Newton is the S.I. unit of force.
1 kgf is the force which produces an acceleration equal to g=10m/s2 in the body of mass 1 kg and 1 N is the force which produces an acceleration of 1 m/s2 in a body of mass 1kg.

So, 1 kgf = 10 N

The weight of a body is measured using a _________.

Answer: Spring balance

Solution:

Explanation

The weight of a body is measured using a Spring balance.
It is a type of weighing scale which measures the weight using a spring and a hook connected at one end.

Complete the following sentences:
Mass = __________ $$\times$$ density

Density is equal to mass per unit volume.

The dimension of a hail are $$ 10 m \times 7 m \times 5 m $$ . lf the density of air is 1.11 kg $$ m^{-3} $$ , find the $$ mass $$
of air in the hail .

The dimensions of hall $$ 10 m \times 7 m \times 5 m $$

i.e. $$V=350$$ $$ m^{3} $$

density of air (D) $$= 1.11$$

So, the mass is $$=1.11\times 350$$

$$= 388.5\ kg$$

Name the instrument which can measure accurately the following:
(a) The diameter of a needle
(b) The thickness of a paper
(c) The internal diameter of the neck of a water bottle
(d) The diameter of a pencil

The instrument which can measure accurately are as follows :-

(a) The diameter of a needle - screw gauge
(b) The thickness of a paper - screw gauge
(c) The internal diameter of the neck of a water bottle - vernier callipers
(d) The diameter of a pencil - screw gauge

A boy makes a ruler with graduation in cm on it (i.e., 100 divisions in 1 m). To what accuracy this ruler can measure? How can this accuracy be increased?

Given: ruler has 1000 divisions - centimetre scaling system
100 cm = 1 m
Hence the accuracy the ruler can measure up to is the centimetre division.
$$\therefore$$ the ruler cam be used to measure the length up to the accuracy of centimetre
In order to increase the accuracy, the scale must further be able to measure the next unit in-line, i.e., the millimetre divisions.

By doing so the accuracy of the ruler can increase from centimetre to millimetre.
Hence,
1 m = 100 cm = 10 mm
1 m = 1000 mm

A boy measures the length of a pencil and expresses it to be 2.6 cm. What is the accuracy of his measurement? Can he write it as 2.60 cm?

Given: The length of the pencil is 2.6 cm.
We know that

length can be expressed in different units such as metre, centimetre, millimetre etc.
Hence

we can say that the measurement may be accurate but not precise enough.
The boy can write 2.6 cm or

can express it as 2.60 cm, both are the same as the value of zero here is not significant.

What is meant by measurement?

It is the comparison of the specified physical quantity

with the known standard quality of the equivalent nature.

For example- distance is measured in meter whereas time is measured in seconds and kilogram or gram is used for measuring mass of an object.

Fill in the blanks
1 kg is the mass of ________ ml of water at $$ 4^{o}C$$ .

1 kg is the mass of 1000 ml of water at $$ 4^{o}C$$ .

Give the dimensional formula of intensity of gravitational field.

Intensity of gravitational field,

$$ E_g = \dfrac{F}{m}$$

Dimensional formula of $$E_0 = \dfrac{[M^1L^1T^{-2}]}{[M^1]}$$

$$ = [M^0L^{-2}]$$.

If the value of universal gravitational constant G is $$6.67 \times 10^{-11}Nm^{-2}/kg^2$$ in M.K.S. system, then determine its value in C.G.S. system using the dimensions.

Given : $$G= 6.67 x 10^{-11} N m^{-2}/kg^2$$
To determine the value of G s (G.S. system formula used)
$$n_2=n_1[\dfrac{M_1}{M_2}]^a[\dfrac{L_1}{L_2}]^b[\dfrac{T_1}{T_2}]^c$$
The dimensional formula of $$G = [M^{-1}L^3T^{-2}]$$
$$\therefore a=-1,b=3,c=-2$$
Suppose,
$$n_2$$ dyne $$cm^2.g^{-2} = 6.67 x 10^{-11} N. m^2 kg^{-2}$$
$$\therefore n_1=6.67 \times 10^{-11}$$
Therefore,$$n_2=6.67\times 10^{-11} [\dfrac{kg}{g}]^{-1}[\dfrac{m}{cm}]^3[\dfrac{s}{s}]^{-1}$$
$$=6.67 \times 10^{-11}[\dfrac{1000 g}{g}]^{-1}[\dfrac{100 cm}{cm}]^3.[1]^{-2}$$
$$=6.67\times 10^{-11}[1000]^{-1}\times [100]^3\times 1$$
$$=6.67 \times 10^{-11}\times \dfrac{1}{1000}\times 100 \times 100 \times 100$$
$$=6.67 \times 10^{-8}$$
$$\therefore G=6.67\times 10^{-8} dyne\, cm^2g^{-2}$$

Write the dimensional formula of G

$$M^{-1}L^{3}T^{2}$$

What is the dimensional formula of moment of force?

We have unit of mass as Kg dimensions are $$ [M^1][L^0][T^0]$$ unit of acceleration as $$m/s^ 2$$ dimensionally expressed as $$ [M^0][L^1][T^{−2}] $$ hence we have unit of force as $$ Kg\times m/s^2 $$

So dimensionally it can be written as $$ [M^1][L^0][T^0]\times[M^0][L^1][T^0][M^0][L^0][T^2] = Kg\times ms^2 $$

Hence we get dimensional formula as $$[M^1][L^1][T^{−2}]$$

Write the dimensional formula for power.

$$ML^2T^3$$

Write the dimensional formula of $$ \frac{L}{R}$$, where $$ L $$ is self inductance and $$ R $$ is resistance.

We know that $$ \dfrac{L}{R} $$ is the time constant. So. its dimension will be written as $$ [M^0L^0T^1A^0]. $$

Derive the dimensional formula for co-efficient of viscosity and hence it's unit.

$$F=-\eta A\dfrac{dv}{dn}$$

$$\therefore \eta=(-)\dfrac{F}{A\dfrac{dv}{dn}}$$

$$=\dfrac{[MLT^{-2}]}{[L^2][LT^{-1/2}]}$$

Units:
We have $$\eta=\dfrac{F}{Adv/dn}$$
in the cgs system, the unit of $$\eta$$ is called poise.
$$1$$ poise$$=\dfrac{1dyne}{1cm^2 \times (1(cm/s)/cm)}$$
$$= dyne\,cm^{-2}\,sec.$$
The S.I.unit of $$\eta$$ is Pa.s (Pascal second) or deca poise.
$$1$$ dec poise $$= \dfrac{1N}{1m^2(1ms^{−1} / m)} = 1Nsm^{-2}$$

What is the dimensional formula of moment of inertia?

The dimensional formula of moment of inertia is given by,

$$M^1 L^2 T^0$$

Where,

$$M = Mass$$

$$L = Length$$

$$T = Time$$

Derivation

Moment of Inertia $$(MOI) = Mass \times [Radius \,of\, Gyration]^2 . . . . (1)$$

Since, the dimensional formula of mass $$= M^1 L^0 T^0 . . . . . . (2)$$

And, the dimensions of the radius of gyration$$ = M^0 L^1 T^0 . . . . . (3)$$

On substituting equation (2) and (3) in equation (1) we get,

Moment of Inertia $$= Mass \times [Radius \,of \,Gyration]^2$$

Or, $$MOI = [M^1 L^0 T^0] \times [M^0 L^1 T^0]^2 = M^1 L^2 T^0.$$

Therefore, the moment of inertia is dimensionally represented as$$ M^1 L^2 T^0.$$

What is the dimensional formula of modulus of rigidity?

Dimensional formula- of modulus of rigidity is

$$ \mathrm{M}^{1} \mathrm{L}^{-1} \mathrm{T}^{-2} $$.

Write the dimensional formula and unit of magnetic field.

1880336_1834807_ans_c8af69542c804eb588a94422146294ac.jpg

What are the dimensions of efficiency of heat engine?

Efficiency of heat engine,
$$\eta =\dfrac{W}{Q_1}$$, where $$W=$$ work done
$$Q_1=$$ heat taken out from source.
$$\because W$$ and $$Q$$ have same unit,
$$\therefore$$ efficiency $$\eta$$ is dimensionless.
$$\therefore$$ Dimensional formula for $$\eta$$
$$=[M^0 L^0 T^0]$$

Give the dimensional formula for
a)Force
b) momentum

Force - $$MLT^{-2}$$
Momentum - $$MLT^{-1}$$

Estimate the mass of the air in your bedroom. State the quantities you take as data and the value you measure or estimate for each.

My bedroom is 4 m long, 4 m wide, and 2.4 m high, enclosing air at 100 k Pa and $$20^0C =293 K$$. Think of the air as $$80.0% N_2$$ and $$20.0% O_2$$.

Avogadro's number of molecules has mass

$$(0.800)(28.0 g/mol ) +(0.200)(32.0 g/mol ) =0.028 8 kg/mol $$

Then $$PV = nRT =(\dfrac{PVM}{RT} )RT=\dfrac{(1.00 \times 10^5 N/m^2)(38.4m^3)(0.028.8 kg/mol)}{(8.314 J/mol.K)(293 K)} $$

$$=45.4 kg$$

What is the dimensional formula of coefficient of thermal conductivity?

The diimensional formula of coefficient of thermal conductivity is $$MLT^{-3}\theta^{-1}$$

What mass of a material with density $$\rho$$ is required to make a hollow spherical shell having inner radius $$r_{1}$$ and outer radius $$r_{2}$$ ?

The volume of a spherical shell can be calculated from

$$V=V_{o}-V_{i}=\frac{4}{3}\pi(r_{2}^{3}-r_{1}^{3})$$

From the definition of density, $$\rho=\frac{m}{V}$$ so,

$$m=\rho V=\rho\left ( \frac{4}{3}\pi \right )(r_{1}^{3}-r_{1}^{3})=\frac{4\pi\rho(r_{2}^{3}-r_{1}^{3})}{3}$$

Calculate the mass of a solid gold rectangular bar that has dimensions of $$4.50\times 11.0\ cm \times 26.0\ cm$$.

1979659_1866920_ans_a208dd6e140d4ec08cacfc124cf79861.JPG

A pet lamb grows rapidly, with its mass proportional to the cube of its length. When the lambs length changes by $$15.8$$%, its mass increases by $$17.3$$ kg. Find the lambs mass at the end of this process.

When the length changes by $$15.8$$%, the mass changes by a much larger percentage. We will write each of the sentences in the problem as a mathematical equation.

Mass is proportional to length cubed: $$m = kl^{3}$$, where $$k$$ is a constant. This model of growth is reasonable because the lamb gets thicker as it gets longer, growing in three-dimensional space.

At the initial and final points, $$m_{i} = kl_{i}^{3}$$ and $$m_{f} = kl_{f}^{3}$$

Length changes by $$15.8$$%: $$15.8$$% of $$l$$ means $$0.158$$ times $$l$$.

Thus $$l_{i} + 0.158l_{i} = l_{f}$$ and $$l_{f} = 1.158l_{i}$$

Mass increases by $$17.3$$ kg: $$m_{i} + 17.3 kg = m_{f}$$

Now we combine the equations using algebra, eliminating the unknowns $$l_{i},l_{f},k$$ and $$m_{i}$$ by substitution:

From $$l_{f}=1.158l_{i}=l_{f}$$ we have, $$l_{f}^{3}=1.158^{3}l_{i}^{3}=1.553l_{i}^{3}$$

Then, $$m_{f}=kl_{f}^{3}=k(1.553)l_{i}^{3}=1.553kl_{i}^{3}=1.553m_{i}$$ and $$m_{i}=m_{f}/1.553$$

Next,

$$m_{i} + 17.3 kg = m_{f}$$ becomes $$m_{f} /1.553 + 17.3 kg = m_{f}$$

Solving, $$17.3 kg = m_{f} – m_{f} /1.553 = m_{f} (1 – 1/1.553) = 0.356 m_{f}$$

and $$m_{f}=\frac{17.3kg}{0.356}=48.6kg$$.

An automobile company displays a die-cast model of its first car, made from $$9.35 kg$$ of iron. To celebrate its hundredth year in business, a worker will recast the model in solid gold from the original dies. What mass of gold is needed to make the new model?

Let V represent the volume of the model, the same in $$\rho=\frac{m}{V}$$, for both

Then $$\rho_{iron}=9.35kg/V$$ and $$\rho_{gold}=\frac{m_{gold}}{V}$$

Next, $$\frac{\rho_{gold}}{\rho_{iron}}=\frac{m_{gold}}{9.35kg}$$

and $$m_{gold}=(9.35kg)\left ( \frac{19.3*10^{3}kg/m^{3}}{7.87*10^{3}kg/m^{3}} \right )=22.9kg$$

Bacteria and other prokaryotes are found deep underground, in water, and in the air. One micron $$(10^{-6} m)$$ is a typical length scale associated with these microbes. (a) Estimate the total number of bacteria and other prokaryotes on the Earth. (b) Estimate the total mass of all such microbes.

Answers may vary depending on assumptions:

typical length of bacterium: $$L = 10^{-6} m$$

typical volume of bacterium: $$L^{3} = 10^{–18} m^{3}$$

surface area of Earth: $$A = 4\pi r^{2} = 4\pi (6.38 * 10^{6}m)^{2} = 5.12 * 10^{14}m^{2}$$

(a) If we assume the bacteria are found to a depth $$d = 1000 m$$ below Earth’s surface, the volume of Earth containing bacteria is about

$$V = (4\pi r^{2})d = 5.12 * 10^{17} m^{3}$$

If we assume an average of $$1000$$ bacteria in every $$1 mm^{3}$$ of volume, then the number of bacteria is

$$\left ( \frac{1000bacteria}{1mm^{3}} \right )\left ( \frac{10^{3}mm}{1bacterium} \right )^{3}(5.12*10^{17}m^{3})\approx 5.12*10^{29}$$ bacteria.

(b) Assuming a bacterium is basically composed of water, the total mass is

$$(10^{29}bacteria)\left ( \frac{10^{-18}m^{3}}{1bacterium} \right )\left ( \frac{10^{3}kg}{1m^{3}} \right )=10^{14}kg$$

(a) Compute the order of magnitude of the mass of a bathtub half full of water. (b) Compute the order of magnitude of the mass of a bathtub half full of copper coins.

(a) We estimate the mass of the water in the bathtub. Assume the tub measures $$1.3 m$$ by $$0.5 m$$ by $$0.3 m$$. One-half of its volume is then

$$V = (0.5)(1.3)(0.5)(0.3) = 0.10 m^{3}$$

The mass of this volume of water is

$$m_{water}=\rho_{water}V=(1000kg/m^{3})(0.10m^{3})=100kg\sim 10^{2}kg$$.

(b) Pennies are now mostly zinc, but consider copper pennies filling $$50$$% of the volume of the tub. The mass of copper required is

$$m_{copper}=\rho_{copper}V=(8920kg/m^{3})(0.10m^{3})=892kg\sim 10^{3}kg$$.

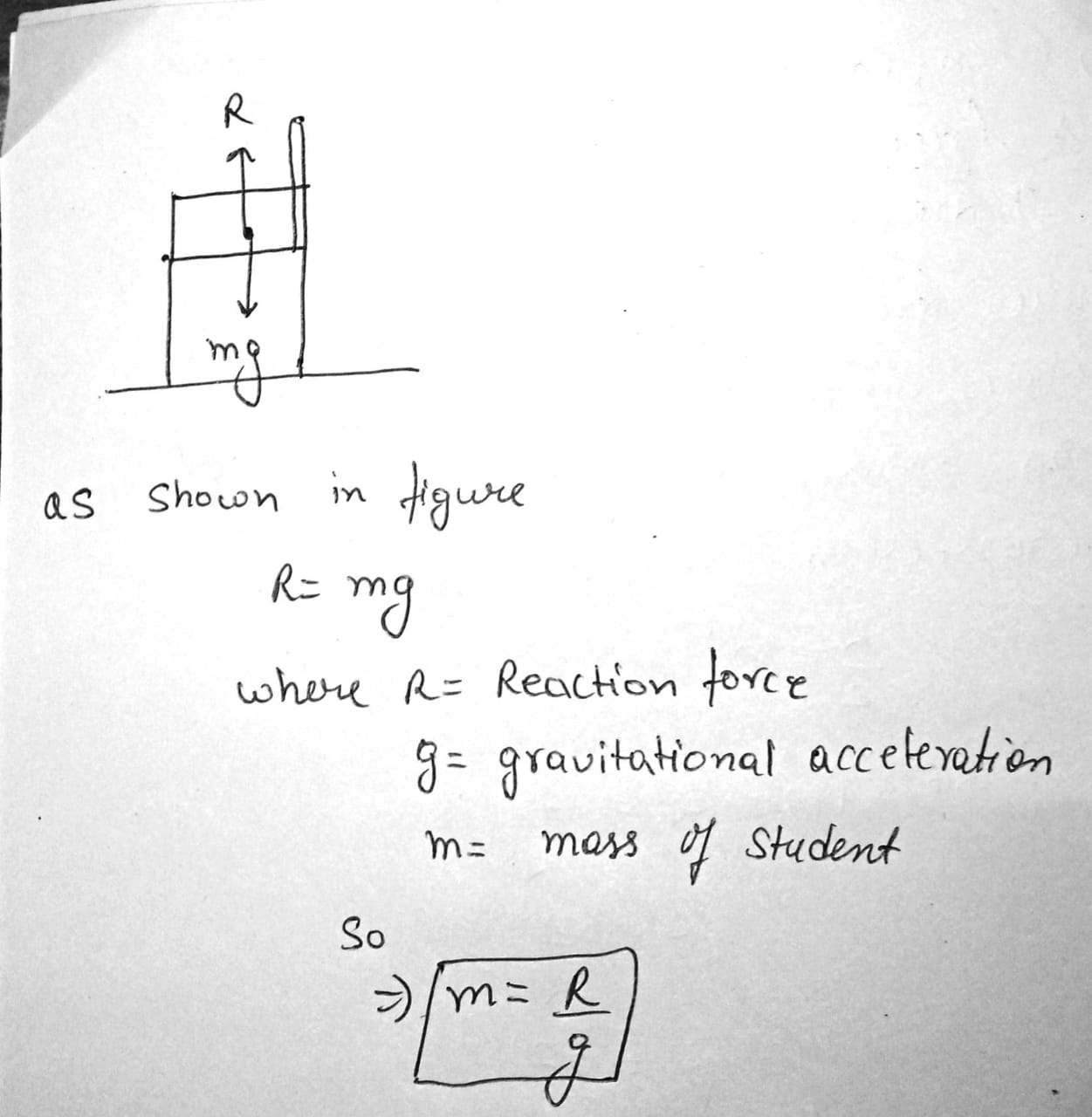
A student is sitting on a chair as shown in Figure.
Estimate the mass of the student.......

1897366_1913450_ans_4e10af0a5e0640eaa73c3d92ff17ee73.jpeg

Match the following two columns

Mass $$=[M], $$ length $$= [L], $$ time $$=T$$, current $$=[A]$$
$$F=qE$$ where $$E=$$ electric field.
$$[MLT^{-2}]=[AT][E]$$ as $$I=\dfrac{dq}{dt}$$
$$[E]=[MLA^{-1}T^{-3}]$$

Thus $$B \rightarrow 1$$.

As $$E=-\dfrac{dV}{dx}$$

So $$[V]=[E][L]=[ML^2A^{-1}T^{-3}]$$

Thus $$A \rightarrow 3$$.

Electric flux $$(\phi)= $$ electric field $$\times $$ area.
$$\therefore [\phi]=[E][L^2]=[ML^3A^{-1}T^{-3}]$$

Thus $$C \rightarrow 2$$.

As $$E=\dfrac{q}{4\pi \epsilon_0}$$

So $$[\epsilon_0]=\dfrac{[q]}{[E]}=\dfrac{[AT]}{[MLA^{-1}T^{-3}]}=[M^{-1}L^{-1}A^{2}T^{4}]$$

Thus $$D \rightarrow 4$$.

For n moles of gas Vander waal's equation is
$$\displaystyle \left ( P-\frac{a}{V^{2}} \right )(V-b)=nRT$$
Find the dimensions of a and b, where P is gas pressure, V = volume of gas T = temperature of gas

Dimension of $$P=$$ Dimension of $$\dfrac { a }{ { V }^{ 2 } } $$

$$\therefore$$Dimension of $$a=[P]\left[ { V }^{ 2 } \right] $$

$$a =M{ L }^{ -1 }{ T }^{ -2 }{ \left( { L }^{ 3 } \right) }^{ 2 }$$

$$a =M{ L }^{ 5 }{ T }^{ -2 }$$

Dimension of $$b=$$Dimension of $$V={ M }^{ 0 }{ L }^{ 3 }{ T }^{ 0 }$$

Find the dimensional formula of coefficient of viscosity $$\displaystyle \eta $$

Coefficient of viscosity is defined as tangential force required to maintain a unit velocity gradient between two parallel layers of liquid of unit area.

Mathematically,

Coefficient of viscosity (η)= Fr/Av where F = tangential force, r = distance between the layers , v = velocity.

Dimensional Formula of Force = M¹L¹T^-2

Dimensional Formula of Area= M⁰L²T⁰

Dimensional Formula of distance= M⁰L¹T⁰

Dimensional Formula of velocity= M⁰L¹T^-1

Putting these values in above equation we get,

[η]= [M¹L¹T^-2][M⁰L¹T⁰] / [M⁰L²T⁰] [M⁰L¹T^-1] = [M¹L^-1T^-1]

Dimensional Formula of Coefficient of viscosity (η)=[M¹L^-1T^-1]
SI unit of Coefficient of viscosity (η) is Pascal-second

Match List I with List II and select the correct answer using the codes given below the lists:

$$\mathrm{A}.\ \rightarrow(4)$$ ; $$\mathrm{B}.\ \rightarrow(2)$$ ;

$$\mathrm{C}.\ \rightarrow(1)$$ ; $$\mathrm{D}.\ \rightarrow(3)$$

$$\mathrm{A}.\

\displaystyle

\mathrm{K}\mathrm{E}=\frac{3}{2}\mathrm{K}\mathrm{T} \Rightarrow [\mathrm{M}\mathrm{L}^{2}\mathrm{T}^{-2}]=\mathrm{K}'[\mathrm{K}]\Rightarrow \mathrm{K}'=[\mathrm{M}\mathrm{L}^{2}\mathrm{T}^{-2}\mathrm{K}^{-1}]$$

$$\mathrm{B}.\

\mathrm{F}=6\pi\eta

\mathrm{r}\mathrm{v} \Rightarrow [\mathrm{M}\mathrm{L}\mathrm{T}^{-2}]=\eta[\mathrm{L}][\mathrm{L}\mathrm{T}^{-1}]\Rightarrow \eta

=[\mathrm{M}\mathrm{L}^{-1}\mathrm{T}^{-1}]$$

$$\mathrm{C}.\

\mathrm{E}= \mathrm{h}\mathrm{f} \Rightarrow [\displaystyle

\mathrm{M}\mathrm{L}^{2}\mathrm{T}^{-2}]=\frac{\mathrm{h}}{[\mathrm{T}]} \Rightarrow \mathrm{h}=[\mathrm{M}\mathrm{L}^{2}\mathrm{T}^{-1}]$$

$$\mathrm{D}.\

\displaystyle

\frac{\mathrm{d}\mathrm{Q}}{\mathrm{d}\mathrm{t}}=\frac{\mathrm{K}'\mathrm{A}(\Delta

\mathrm{T})}{\Delta

\mathrm{x}}\Rightarrow \frac{[\mathrm{M}\mathrm{L}^{2}\mathrm{T}^{-2}]}{[\mathrm{T}]}=\frac{\mathrm{k}[\mathrm{L}^{2}][\mathrm{K}']}{[\mathrm{L}]}$$

$$\mathrm{K}'=[\mathrm{M}\mathrm{L}\mathrm{T}^{-3}\mathrm{K}^{-1}]$$

$$\displaystyle \alpha =\frac{F}{v^{2}}\sin (\beta t)$$ (here v = velocity, F = force, t = time)
Find the dimension of $$\displaystyle \alpha$$ and $$\displaystyle \beta$$

$$\displaystyle \alpha =\frac{F}{v^{2}}\sin (\beta t)$$
dimensionless dimensionless $$\Rightarrow$$ $$\displaystyle [\beta ][t]=1=[\beta ]=[T^{-1}]$$
So $$\displaystyle [\alpha ]=\frac{[F]}{V^{2}}=\frac{[M^{1}L^{1}T^{-2}]}{[L^{1}T^{-1}]^{2}}=M^{1}L^{-1}T^{0}$$

A physical quantity P is related to four observables a, b, c and d as follows :
P $$a^3\, b^2$$ / $$\sqrt{c}$$ d
The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2%, respectively. What is the percentage error in the quantity P ? If the value of P calculated using the above relation turns out to be 3.763, to what value should you round off the result ?

$$ P = \dfrac{a^3 b^2}{\sqrt{c} d} $$

Maximum fractional error in P is given by

$$\dfrac{\Delta P}{P} = \pm \left[3\dfrac{\Delta a}{a} + 2\dfrac{\Delta b}{b}+ \dfrac{1}{2}\dfrac{\Delta c}{c}+ \dfrac{\Delta d}{d}\right]$$

On putting above value:

$$= \pm \dfrac{13}{100} = 0.13 $$

Percentage error in $$P = 13$$ %

Value of P is given as 3.763.

By rounding off the given value to the first decimal place, we get $$P = 3.8$$.

The nearest star to our solar system is 4.29 light years away. How much is this distance in terms of parsecs? How much parallax would this star (named Alpha Centauri) show when viewed from two locations of the Earth six months apart in its orbit around the Sun ?

Given:

The distance of the star is,$$ = 4.29\ ly$$

We know that one light year is the distance travelled by light in one year.

1 light year = $$3 \times 10^8\times365\times24\times60\times60$$

=$$ 94608\times 10^{11}m$$

Therefore, the distance in $$4.29\ ly$$ can be written as:

$$4.29\ ly = 405868.32 \times 10^{11}\ m$$

We know that $$1\ Parsec$$ is also the unit of distance and its value is:

$$1\ parsec = 3.08 \times 10^{16} m$$

Now, to express the distance in terms of parsec.

$$4.29 ly = \dfrac{405868.32 \times 10^{11}}{ 3.08\times10^{16}} = 1.32\ parsec$$

The diameter of the Earth's orbit is,

$$d = 3 \times 10^{11} m$$

The angle made by the star on the Earth's orbit can be given by:

$$\theta = \dfrac{3 \times 10^{11}} {405868.32 \times10^{11}} = 7.39 \times 10^{-6} rad$$

But, the angle covered in $$1 sec = 4.85\times 10^{-6} rad$$

So, the parallax in viwing the star at two different positions of the Eart's orbit:

for, $$7.39 \times 10^{-6} rad =\dfrac{ 7.39 \times 10^{-6}}{ 4.85 \times 10^{-6}} = 1.52" $$

Find the dimensions of refractive index.

The refractive index is given as

$$n = \dfrac{c}{v}$$

$$c$$ and $$v$$ Both are speed.

Hence refractive index is a dimensionless quantity having dimension $${{\rm{M}}^{\rm{0}}}{{\rm{L}}^{\rm{0}}}{{\rm{T}}^{\rm{0}}}$$

If velocity (V), force (F) and time (T) are chosen as fundamental quantities, express (a) mass and (b) energy in terms of V, F and T.

$$(a)$$

Let M = (Some number) $$(V)^a(F)^b(T)^c$$

Equating dimensions of both the sides, we get
$$M^1L^0T^0 = (1)[L^1T^{-1}]^a[M^1L^1T^{-2}]^b[T^1]^c $$

$$= M^b L^{a+b} T^{a-2b+c}$$

Get $$a = -1, b = 1, c= 1$$.

M = (Some number) $$(V^{-1} F^1 T^1)$$.
$$[M] = [V^{-1} F^1 T^1]$$

$$(b)$$

Similarly, we can also express energy in terms of V, F and T.
Let [E] = [Some number]$$ [V]^a [F]^b [T^c]$$

$$\Rightarrow [ML^2T^{-2}] = [M^0L^0T^0][LT^{-1}]^a[MLT^{-2}]^b[T^c]$$

$$\Rightarrow [M^1L^2T^{-2}] = [M^bL^{a+b+c} T^{a-2b+c}]$$

$$\Rightarrow 1 = b; 2 = a+ b +c; -2 = -a -2b +c$$
Get $$a = 1; b = 1, c = 1.$$
$$\Rightarrow E = (Some\,\, number) V^1F^1T^1 $$

or $$[E] = [V^1][F^1][T^1]$$.

In an experiment, the following observations were recorded:
$$L = 2.820 m, M = 3.00 kg, l = 0.087 cm$$, diameter $$D = 0.041 cm$$. Taking $$g = 9.81 m s^{-2}$$ and using the formula, Y =$$ \frac{4Mg}{\pi D^2 l}$$, find the maximum permissible error in Y.

$$y=\dfrac { 4Mgh }{ \Pi { D }^{ 2 }l } $$

Maximum possible error in $$y$$ is

$$\dfrac { \Delta y }{ y } \times 100=\left( \dfrac { \Delta M }{ M } +\dfrac { \Delta g }{ g } +\dfrac { 2\Delta D }{ D } +\dfrac { \Delta L }{ L } +\dfrac { \Delta l }{ l } \right) \times 100$$

$$=\left( \dfrac { 1 }{ 3.00 } +\dfrac { 1 }{ 9.81 } +\dfrac { 1 }{ 41 } \times 2+\dfrac { 1 }{ 2820 } +\dfrac { 1 }{ 87 } \right) \times 100$$

$$=0.065\times 100$$

$$=6.5$$%

Water is poured into a container that has a small leak. The mass $$m$$ of the water is given as a function of time $$t$$ by $$m=5.00\ t^{0.8}-3.00 t+20.00$$, with $$t \ge 0, m$$ in grams, and $$t$$ in seconds.
In kilograms per minute, what is the rate of mass change at $$t=5.00\ s$$

As we know,

Similarly, the rate of mass charge at $$t=5.00\ s$$ is

$$\dfrac {dm}{dt}|_{t=2.00\ s} =[4.00(5.00)^{-0.2}-3.00]g/s =0.101\ g/s=0.101\dfrac gs . \dfrac {1\ kg}{1000\ g}. \dfrac {60\ s}{1\ min}$$

$$=-6.05\times 10^{-3}kg/min$$.

A rod extending between $$x = 0$$ and $$x = 14.0 cm$$ has uniform cross-sectional area $$A = 9.00 cm^{2}$$. Its density increases steadily between its ends from $$2.70 g/cm^{3}$$ to $$19.3 g/cm^{3}$$. (a) Identify the constants $$B$$ and $$C$$ required in the expression $$\rho= B + Cx$$ to describe the variable density. (b) The mass of the rod is given by
$$m=\int_{all.material}\rho dV=\int_{all.x}\rho Adx=\int_{0}^{14.0cm}(B+Cx)(9.00cm^{2})dx$$
Carry out the integration to find the mass of the rod.

1800076_1856997_ans_07b59b7123694571adda54bec15892fc.png

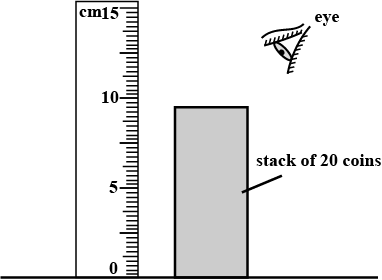
A student has a stack of $$20$$ identical coins.
Figure shows the student measuring the height of the stack using a ruler.
(a) With his eye at the position shown, the student's measurement of the height of the stack is $$6.8\,cm.$$
Suggest two reasons why the student's measurement is inaccurate.
(b) Another student correctly determines the height of the stack as $$7.7\,cm.$$
Calculate the average thickness of one coin.
(c) The mass of a single coin is $$12\,g.$$
State this mass in kg.

1897353_1913440_ans_2249a2af41dc453eabd1f60a3654b53d.jpeg

The radius of atom is of the order of $$1\space \overset{0} {A}$$ and radius of nucleus is of the order of fermi. How many magnitudes higher is the volume of atom as compared to the volume of nucleus?

Radius ($$R$$) of atom = $$1\space \overset{0} {A} = 10^{-10} \space m$$
Radius ($$r$$) of nucleus = $$1 \space fermi = 10^{-15} \space m$$
Ratio of volume of atom to nucleus : $$\frac{\frac{4} {3} \pi R^{3}} {\frac{4} {3} \pi r^{3}} = \frac{R^{3}} {r^{3}} = \left(\frac{10^{-10}} {10^{-15}} \right )^{3} = \left (10^{5} \right )^{3} = 10^{15}$$

A spherical shell has an outside radius of $$2.60 cm$$ and an inside radius of $$a$$. The shell wall has uniform thickness and is made of a material with density $$4.70 g/cm^{3}$$. The space inside the shell is filled with a liquid having a density of $$1.23 g/cm^{3}$$. (a) Find the mass $$m$$ of the sphere, including its contents, as a function of $$a$$. (b) For what value of the variable $$a$$ does $$m$$ have its maximum possible value? (c) What is this maximum mass? (d) Explain whether the value from part (c) agrees with the result of a direct calculation of the mass of a solid sphere of uniform density made of the same material as the shell. (e) What If? Would the answer to part (a) change if the inner wall were not concentric with the outer wall?

(a) The mass is equal to the mass of a sphere of radius $$2.6 cm$$ and density $$4.7 g/cm^{3}$$, minus the mass of a sphere of radius $$a$$ and density $$4.7 g/cm^{3}$$, plus the mass of a sphere of radius $$a$$ and density $$1.23 g/cm^{3}$$.

$$m=\rho_{1}\left ( \frac{4}{3}\pi r^{3} \right )-\rho_{1}\left ( \frac{4}{3}\pi a^{3} \right )+\rho_{2}\left ( \frac{4}{3}\pi a^{3} \right )$$

$$=\left ( \frac{4}{3}\pi \right )[(4.7g/cm^{3})(2.6cm)^{3}-(4.7g/cm^{3})a^{3}+(1.23g/cm^{3})a^{3}]$$

$$m-346g-(14.5g/cm^{3})a^{3}$$

(b) The mass is maximum for $$a = 0$$ .

(d) Yes. This is the mass of the uniform sphere we considered in the first term of the calculation.

(e) No change, so long as the wall of the shell is unbroken

If velocity of light c, Plancks constant h and gravitational constant G are taken as fundamental quantities, then express mass, length and time in terms of dimensions of these quantities.

We have to apply the principle of homogeneity to solve this problem. Principle of homogeneity states that in a correct equation, the dimensions of each term added or subtracted must be same, i.e., dimensions of LHS and RHS should be equal,
We know that, dimensions of
$$[h]=[ML^2 T^{-1}],[c]=[LT^{-1}]^a,[G] =[M^{-1}L^3T^{-2}]$$

i) Let, $$m\ \infty c^xh^yG^z$$

$$\Rightarrow m=lc^ah^bG^0$$...........(i)

where, $$k$$ is a dimensionless constant of proportionality.
Substituing dimensions of each term in eq.(i), we get

$$[M^0LT^0]=[LT^{-1}]^a\times [ML^2T^{-1}]^b\times [M^{-1}L^3T^{-2}]^c$$

On comparing powers of same terms on both sides , we get
$$b-c=1$$................(ii)
$$a+2b+3c=0$$.................(iii)
$$-a-b-2c=0$$.............(iv)
Adding eq (ii),(iii) and (iv) we get
$$2b=1\Rightarrow 2b=1 \Rightarrow b=\dfrac{1}{2}$$
Substituting value of b in eq.ii.
$$c=-\dfrac{1}{2}$$
From eq.iv
$$a=-b-2c$$
Substituting values of b and c,we get
$$a=-\dfrac{1}{2} -2(-\dfrac{1}{2})=\dfrac{1}{2}$$
Putting values of a ,b and c in eq.(i), we get
$$m=kc^{1/2}h^{1/2}G^{1/2}=k\sqrt{\dfrac{ch}{G}}$$

ii) Let $$L \infty c^a h^b G^c$$

$$\Rightarrow L=kc^ah^bG^0$$,............(v)

where k is a dimensionless constant.
Substituting dimensions of each term in eq.v, we get

$$[M^0LT^0]=[LT^{-1}]^a\times [ML^2T^{-1}]^b\times [M^{-1}L^3T^{-2}]^c$$

$$[M^{b-c}L^{a+2b+3c}T^{-a-b-2c}]$$

Comparing powers of same terms on both sides, we get
b-c=1........{vi}
$$a+2b+3c=1$$...............(vii)

$$-a-b-2c=0$$...............(viii)
Adding eqs $$vi,vii$$ and $$viii$$, we get

=$$2b=1 \rightarrow b \dfrac{1}{2}$$

Substituting value of $$b$$ in eq $$vi$$, we get

$$c=\dfrac{1}{2}$$

From eq.$$viii,a=-b-2c$$

Substituting values of $$a,b,c$$ in eq v,we get

$$L=kc^{-3/2}h^{1/2}G^{1/2}=k\sqrt{\dfrac{hG}{c^3}}$$

iii) Let $$T\infty c^a h^b G^c$$

$$\Rightarrow=T=c^ah^bG6c$$........(ix)

where k is a dimensionless constant.
Substituting dimensionless of each term in eq.

$$[M^0L^0T^{-1}]=[LT^{-1}]^a\times [ML^2T^{-1}]^b\times[M^{-1L*3T^{-2}}]^c$$

$$=[M^{b-c}L^{a+2b+3c}T^{a-b-2c}]$$

On comparing powers of same terms, we get
$$b-c=0................x$$
$$a+2b+3c=1.............xi$$
$$-a-b-2c=1$$

Adding eq. $$x, xi xii,$$ we get
$$2b=1 \Rightarrow b=\dfrac{1}{2}$$
Substituting the value of b in eq x, we get

$$c=b=\dfrac{1}{2}$$

From eq $$xii$$

$$a=-b-2c-1$$
substituting vales of $$b$$ and $$c$$,we get

$$a=-\dfrac{1}{2}-2(\dfrac{1}{2})=1=-\dfrac{5}{2}$$

Putting values of a,b and c in eq ix, we get

$$T=kn^{-5/2}h^{1/2}G^{1/2}=k\sqrt{\dfrac{hG}{c^5}}$$

A rod of length $$30.0\ cm$$ has linear density (mass per length) given by
$$\lambda =50.0+20.0\ x$$
where $$x$$ is the distance from one end, measured in meters, and $$\lambda$$ is in grams/ meter.
What is the mass of the rod?

1898113_1864899_ans_cf1adada3b6d4b3aba8f6ff5b26fa852.jpg

An old English cookbook carries this recipe for cream of nettle soup: Boil stock of the following amount: $$1$$ break fastcup plus $$1$$ teacup plus $$6$$ tablespoons plus $$1$$ dessertspoon. Using gloves, separate nettle tops until you have $$0.5$$ quart; add the tops to the boiling stock. Add $$1$$ tablespoon of cooked rice and $$1$$ saltspoon of salt. Simmer for $$15\ min$$. The following table gives some and among common (still premetric) U.S. measures. (These measures just scream for metrication. )For dry liquid measures, $$1$$ British teaspoon $$=2\ U.S.$$ teaspoon and $$1$$ British quart $$=1\ U.S.$$ quart. In U.S measures, how much
salt are required in the recipe?

1 breakfast cup= 2 tea cup= 16 tablespoons=32 dessert spoon= 64 teaspoon (Britain)= 128 teaspoons (US)

1 teacup= 8 table spoons= 16 dessert spoons= 32 teaspoon (Britain)= 64 teaspoon (US)

6 tablespoon= 12 dessert spoon= 24 teaspoon (British)= 48 teaspoon (US)

1 desert spoon= 2 teaspoon (British)= 4 teaspoon (USA)

1 tablespoon rice= 2 desert spoon= 4 teaspoon(British)= 8 teaspoon(US)

1 salt spoon salt= 1/2 teasoon (british)= 1 teaspoon (US)

Factor	Prefix	Symbol
$$10^{-1}$$	deci
$$10^{-6}$$		$$\mu$$
	giga	G
$$10^{6}$$	mega

Units And Measurement - Class 11 Engineering Physics - Extra Questions

The wavelength of light of a particular colour is 5800 $$\mathring{A}$$. What is its order of magnitude in meter?

Find the order of magnitude of 38500 kg

0.0008 m= $$ 8 \times10 ^{-x}m$$. Find x.

Match list - I with list - II and select the correct answer :

The order of magnitude of seconds in a day is $$10^x$$. What is $$x$$.

The distance of a galaxy is $$56 \times10^{25}m$$. Assume the speed of light to be $$3\times10^8 m s^{-1}$$. Express order of magnitude of time taken by light travelled to the galaxy.

The wavelength of light is 589 nm. What is its order of magnitude in metre?

The prefix 'milli' denotes the factor $$10^{-x}$$mfind x?

Units of plane angle is _____

Accuracy defines nearness of a measured value to the standard or true value. If true enter 1 else enter 0

Measurement can be accurate without being precise. True=1, false = 0

What is parallax? Explain.

How can a measured length be expressed ?

Write the dimensional formula of pressure.

Fill in the blanks typePlanck's constant has dimensions ________

Three successive measurement in an experiment gave value 10.9, 11.4042 and 11.42 the correct way of reporting the average value is:

What is meant by Precision?

What is dimensional formula for magnetic flux densities?

Simplify and round to the appropriate number of significant digits$$(a)$$ $$16.235 \times 0.217 \times 5$$ $$(b)$$ $$0.00435 \times 4.6$$

Derive the dimensional formula for pressure.

Using the dimensional method derive the relation between the units of force in the SI and CGS system.

If momentum $$p$$, area $$A$$ and time $$T$$ are taken to be fundamental quantities, then power has dimensional formula.

In the equation y = A sin $$ (\omega - Kx) $$, obtain the dimensional formula of $$ \omega $$ and K.Given x is distance and t is time.

Write the order of magnitude of mass of an electron $$9.1\times 10^{-31}$$ kg.

What is the mass per unit volume of a substance called?

Find the order of magnitude of length of rod having length $$(10^6+10^3)$$m.

Which of the following length measured is most accurate and why?(a) $$500.0\ cm$$(b) $$0.0005\ cm$$(c) $$6.00\ cm$$

Arrange the following lengths in their increasing magnitude:$$1\ metre,$$ $$1\ centimetre,$$ $$1\ kilometre,$$ $$1\ millimetre.$$

The dimensional formula of area is ?

If an object weighs $$ 6\,kg $$ on earth . What will be its weight on moon ?

Write $$2760000$$ in scientific form.

Convert the following quantity as indicated:$$12 \,inch \ into\ ft$$

Assuming that water has a density of exactly $$1\ g/cm^3$$, find the mass of one cubic meter of water in kilograms,

Fill in the blanksMass = $$ Density \times Volume. $$

What is the mass of $$5 m^3$$ of cement of density $$3000 \ kg/m^3$$

The mass of an oxygen atom is 16.00 u. Find its mass in kg.

A...Image cannot be obtained on a screen.

What is the dimensional formula?

Write the dimension formula of strain.

How many types of errors are there?

Name two dimensionless physical quantities.

What is meant by errors of measurement? How do errors vary with a combination of errors? Explain.

Write the dimensional formula for velocity.

Write the dimensional formula for force.

Write the dimensional formula of work.

Write the dimensional formula of power.

If the percent difference between two measured values, $$4.6\ cm$$ and $$5.0\ cm$$ is $$n$$%. Find $$n$$ ? (Round off to the closest integer)

Match the following : (Symbols have standard meaning)

The number of significant figures in 500.06 is _________.

A barometer is faulty. When the true barometer reading are 73 and 75 cm of Hg, the faulty barometer reads 69 cm and 70 cm respectively. What is the total length of the barometer tube?

The dimensional formula of heat is ________.

Write the number of significant figures in 0.270 cm.

Match the following:

Explain parallax method for measuring distance of a nearly star

Match the following two columns.Column I Column II

'The order of magnitude of a physical quantity must be expressed in proper unit'. Comment on this statement

The mass of an oxygen atom is $$1600$$ u. Find its order of magnitude in kg.

The radius of a hydrogen atom is $$0.5\mathring{A}$$. Find the order of magnitude of volume of one hydrogen atom is $$10^{-10x}$$. The value of x is:

Taking the mass of a proton to be $$1.67 \times 10^{-27}$$ kg, the order of magnitude of the number of protons in 1 g is $$5.88\times10^{(20+x)}$$. What is $$x$$.

Match the following :

$$\displaystyle \alpha =\frac{Fv^{2}}{\beta ^{2}}\log_{e}\left ( \frac{2\pi \beta }{v^{2}} \right )$$ where F = force, v = velocityFind the dimensions of $$\displaystyle \alpha $$ and $$\displaystyle \beta $$

Express the following derived units in terms of the fundamental units of length, mass and time. 1) Speed2) Area3) Acceleration4) Density5) Volume

When the planet Jupiter is at a distance of $$824.7$$ million kilometers from the Earth,its angular diameter is measured to be $$35.72$$ of arc. Calculate the diameter of Jupiter.

$$1$$ parsec = __________ metres

State the number of significant figures in the following:$$(a) 0.007 m^2$$$$(b) 2.64 \times 10^{24} kg$$$$(c) 0.2370 g cm^{-3}$$$$(d) 6.320 J $$$$(e) 6.032 Nm^{-2} $$$$(f) 0.0006032 m^2 $$

In the figures given, identify the type of zero error and also suggest the correction to be made, by reasoning it out

The wavelength of monochromatic light is 6000 $$A^0$$. Write this value in nm.

Complete the table choosing the right term from the list given in brackets:($$10^9$$, micro, d, $$10^{-9}$$, milli, m, M)FactorPrefixSymbol$$10^{-1}$$deci$$10^{-6}$$$$\mu$$gigaG$$10^{6}$$mega

Name any two units of length which are bigger than the metre. Write the relation between each of those units and the metre.

If length $$'L'$$, force $$'F'$$ and time $$'T'$$ are takes as fundamental quantities. What would the dimensional equation of mass and density?

Let us check the dimensional correctness of the relation $$v =u + at$$.

The position of a particle at time t is given by the relation $$x(t) = \left(\dfrac{v_0}{\alpha}\right)(1 - c^{-\alpha t})$$, where $$v_0$$ is a constant and $$\alpha > 0$$. Find the dimensions of $$v_0$$ and $$\alpha$$.

Find the dimensions of physical quantity X in the equation.Force = $$\frac{X}{density}$$.

If velocity (V), force (F), and energy (E) are taken as fundamental units, then find the dimensional formula for mass.

The mass of a box is $$2.3$$kg. Two marbles of masses $$2.15$$g and $$12.39$$ g are added to it. Find the total mass of the box to the correct number of significant figures.

The potential energy of a particle varies the distance $$x$$ from a fixed origin as $$U = \dfrac{A \sqrt{x}}{x^2 + B}$$, where A and B are dimensional constants, then find the dimensional formula for AB.

Experiments reveal that the velocity $$v$$ of water waves may depend on their wavelength $$\lambda$$, density of water $$\rho$$, and acceleration due to gravity g. Establish a possible relation between $$v$$ and $$\lambda, g, \rho^0.$$.

Check the accuracy of relation $$v^2 - u^2 = 2as$$, where $$v$$ and $$u$$ are final and initial velocities, $$a$$ is the acceleration, and s is the distance.

The length of a rectangular sheet is $$1.5$$cm and the breadth is $$1.203$$ cm. Find the areas of the face of a rectangular sheet to the correct number of significant figures.

The prefix 'milli' denotes the factor $$10^{-x}$$m
find x?

Fill in the blanks type
Planck's constant has dimensions ________

Simplify and round to the appropriate number of significant digits
$$(a)$$ $$16.235 \times 0.217 \times 5$$
$$(b)$$ $$0.00435 \times 4.6$$

Which of the following length measured is most accurate and why?
(a) $$500.0\ cm$$
(b) $$0.0005\ cm$$
(c) $$6.00\ cm$$

Arrange the following lengths in their increasing magnitude:
$$1\ metre,$$ $$1\ centimetre,$$ $$1\ kilometre,$$ $$1\ millimetre.$$

Convert the following quantity as indicated:
$$12 \,inch \ into\ ft$$

Fill in the blanks
Mass = $$ Density \times Volume. $$

Match the following two columns.
Column I Column II

$$\displaystyle \alpha =\frac{Fv^{2}}{\beta ^{2}}\log_{e}\left ( \frac{2\pi \beta }{v^{2}} \right )$$ where F = force, v = velocity
Find the dimensions of $$\displaystyle \alpha $$ and $$\displaystyle \beta $$

Express the following derived units in terms of the fundamental units of length, mass and time.
1) Speed
2) Area
3) Acceleration
4) Density
5) Volume

State the number of significant figures in the following:
$$(a) 0.007 m^2$$
$$(b) 2.64 \times 10^{24} kg$$
$$(c) 0.2370 g cm^{-3}$$
$$(d) 6.320 J $$
$$(e) 6.032 Nm^{-2} $$
$$(f) 0.0006032 m^2 $$

Complete the table choosing the right term from the list given in brackets:($$10^9$$, micro, d, $$10^{-9}$$, milli, m, M)
Factor Prefix Symbol
$$10^{-1}$$
deci
$$10^{-6}$$ $$\mu$$
giga G
$$10^{6}$$ mega

Name any two units of length which are bigger than the metre. Write the relation
between each of those units and the metre.

Find the dimensions of physical quantity X in the equation.
Force = $$\frac{X}{density}$$.

Find the dimensions of $$a$$ & $$b$$ if
$$F=at+bt^{2}$$

The error in the measurement of radius of a sphere is 2%. What will be the error in the calculation of its surface area?
(surface area A=4$$\pi r^2$$) $$\dfrac{\Delta A}{A}=\dfrac{2\Delta r}{r})$$

Find the dimensions of
(a) linear momentum,
(b) frequency and
(c) pressure.

Find the dimensions of:
(i) Power, (ii) Forces and (iii) Permittivity of vacuum $$(\varepsilon_o)$$

Find the dimensions of
1) Force
2) power
3) density
4) momentum
5) velocity

If the velocity of the particle is given by $$v=\cfrac { a }{ t } +b{ t }^{ 2 }$$
The dimensions of a & b are given as ______

$$\omega t=\theta $$
$$ Kx = \theta $$

What will be dimensions unit of $$K$$ in the above formula. Given $$x$$ is displacement and $$\theta$$ is angular displacement and $$\omega$$ is angular frequency.

Find the dimensions of
i) Force
ii) Power
iii) Electric potential
iv) Resistance
v) Refractive index
vi) Permittivity of vacuum $$(\varepsilon_0)$$
vii) Permeability

Fill in the blanks with suitable units of measurements.
The distance I walk in $$10\ minutes$$ is about $$1$$_____.

In an experiment, refractive index of glass was observed to be 1.45, 1.56, 1.54, 1.44, 1.54, and 1.53 Calculate
Mean value of refractive index

Water is poured into a container that has a small leak. The mass $$m$$ of the water is given as a function of time $$t$$ by $$m=5.00\ t^{0.8}-3.00 t+20.00$$, with $$t \ge 0, m$$ in grams, and $$t$$ in seconds.
At what time is the water mass greatest.

A lecture period $$(50\ min)$$ is close to $$1$$ microcentury
Using percentage difference $$=\left(\dfrac{actual-approximation}{actual}\right)100$$, find the percentage difference from the approximation.

Water is poured into a container that has a small leak. The mass $$m$$ of the water is given as a function of time $$t$$ by $$m=5.00\ t^{0.8}-3.00 t+20.00$$, with $$t \ge 0, m$$ in grams, and $$t$$ in seconds.
In kilograms per minute, what is the rate of mass change at $$t=2.00\ s$$

One molecule of water $$(H_{2}O)$$ contains two atoms of hydrogen and one atom of oxygen. A hydrogen atom has a mass of $$1.0\ u$$ and an atom of oxygen has a mass of $$16\ u$$, approximately.
What is the mass in kilograms of one molecule of water?

What mass of water fell on the town in $$V=(26\ km^{2})(2.0\ in.)$$ ?
Water has a density of $$1.0\times 10^{3}\ kg/m^{3}$$.

Water is poured into a container that has a small leak. The mass $$m$$ of the water is given as a function of time $$t$$ by $$m=5.00\ t^{0.8}-3.00 t+20.00$$, with $$t \ge 0, m$$ in grams, and $$t$$ in seconds.
What is the greatest mass?

Give an example of:
A physical quantity which has a unit but no dimension

Fill in the blanks.
Plancks' constant has dimension_______.