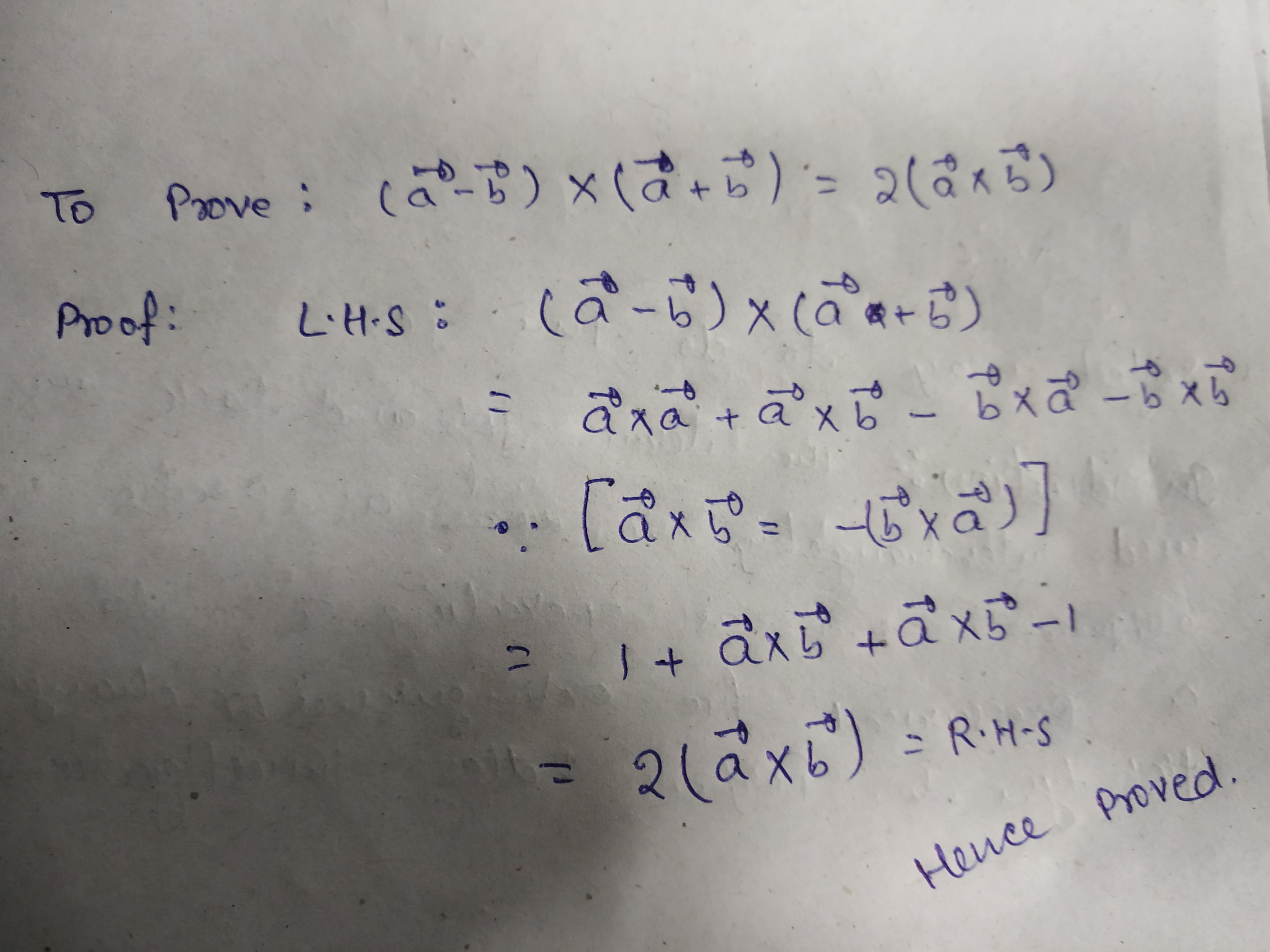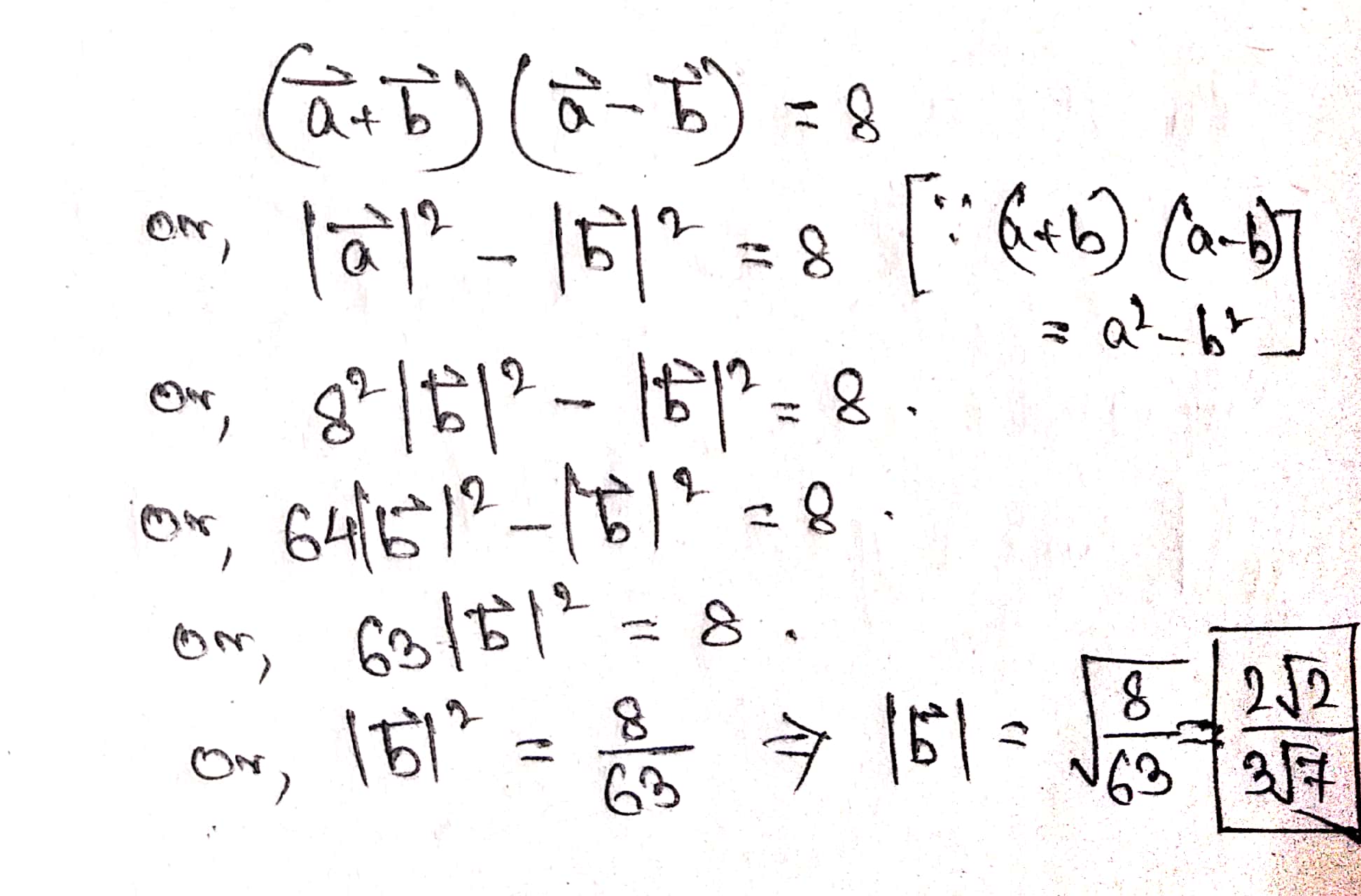Vector Algebra - Class 12 Engineering Maths - Extra Questions
Find the position vector of the mid point of the vector joining the points $$P (2, 3, 4)$$ and $$Q (4, 1, 2)$$.
Find the sum of the following vectors:
$$\vec {a} = \hat{i}-2\hat{j}, \vec{b} = 2\hat{i}-3\hat{j}, \vec{c} = 2\hat{i} + 3\hat{k}$$.
If $$\overline { a } ,\overline { b } ,\overline { c } $$ are the position vectors of the points $$A,B,C$$ respectively and $$2\overline { a } +3\overline { b } -5\overline { c } =\overline { 0 } $$, then find the ratio in which the point $$C$$ divides line segment $$AB$$.
Solve $${ (A+B) }^{ 2 }=?$$
Find the area of the parallelogram with adjacent sides formed by $$\overrightarrow { P } $$ and $$\overrightarrow { P } $$
where $$\overrightarrow { P } =2\hat { i } +3\hat { j } +4\hat { k } $$ and $$\overrightarrow { Q } =3\hat { i } +2\hat { j } -2\hat { k } $$ expressed in meter.
Let $$\bar { a } ,\bar { b } ,\bar { c } $$ be vectors of length $$3,4$$ and $$5$$ respectively. Find the length of the vector $$|\bar { a } +\bar { b } +\bar { c }| $$. if they are mutually perpendicular.
In Fig. $$ABCD$$ is a regular hexagon, which vectors are:
Coinitial

Two forces 7 and 3 N simultaneously act on a body. What is the value of their (i) maximum resultant, (ii) minimum resultant, and (iii) what will be the resultant if the forces act at right angle to each other?
Find the position vector of a point $$R$$ which divides the line joining two points $$P$$ and $$Q$$ whose position vectors are $$\hat {i}+2\hat {j}-\hat {k}$$ and $$-\hat {i}+\hat {j}+\hat {k}$$ respectively, in the ratio $$2:1$$,
(i) internally
(ii) externally
Show that $$\left(\vec{a}-\vec{b}\right)\times \left(\vec{a}+\vec{b}\right)=2\left(\vec{a}\times \vec{b}\right)$$.
If $$\left(\bar{x}+\bar{y}\right)\cdot \left(\bar{x}-\bar{y}\right)=63$$ and $$|x|=8|\bar{y}|$$ then, find $$|\bar{x}|$$.
If $$\vec R = (\vec A + \vec B),$$ Show that $$R^2 = A^2 + B^2 + 2 \ AB \ cos \theta$$
Express the vector $$\vec {a}=5 \hat {i}+5\hat {k}$$ as sum of two vector such that one is parallel to the $$\vec {b}=3\hat {i}+\hat {k}$$ and other is perpendicular to $$\vec {b}$$
Express the vector $$\vec{a}=5\hat{i}-2\hat{j}+5\hat{k}$$ as the sum of two vectors such that one is parallel to the vector $$\vec{b}=3\hat{i}+\hat{k}$$ and the other is perpendicular to $$\vec{b}$$.
The position vectors of $$A,B,C,D$$ are $$\vec a,\vec b,2\vec a + 3\vec b $$ and $$\vec a - 2\vec b$$ respectively. Show that $$\overrightarrow {DB} = 3\vec b - \vec a$$ and $$\overrightarrow {AC} = \vec a + 3\vec b$$
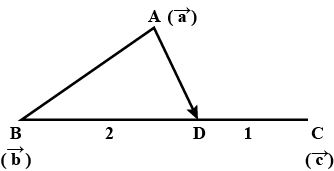
Let position vector of the points A,B and C are $$\overrightarrow a \,,\,\overrightarrow b $$ and $$\,\overrightarrow c $$ respectively. Point D divides line segment BC internally in the ratio $$2:1$$. Find vector AD
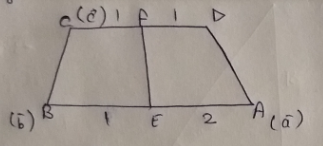
let ABCD is trapezium such that $$\overrightarrow {AB} = 3\overrightarrow {DE} \,\,$$ , E divides line segement AB internally in the ratio 2:1 and F is mid point of DC. if position vector of A,B and C are $$\overrightarrow a \,,\,\overrightarrow b \,\,\,and\,\overrightarrow c \,\,\,$$ respectively then find the vector $$\overrightarrow {FE} \,$$.
Evaluate the following:
$$[2\hat{i}\hat{j}\hat{k}]+[\hat{i}\hat{k}\hat{j}]+[\hat{k}\hat{j}2\hat{i}]$$
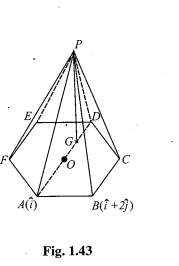
A pyramid with vertex at point P has a regular hexagonal base ABCDEF. Position vectors of points A & B are $$\hat{i}$$ and $$\hat{i} + 2 \hat{j}$$, respectively. Center of the base has position vector $$\hat{i} +\hat{j} + \sqrt{3}\hat{k}$$. Altitude drawn from P on the base meets the diagonal AD at point G. Find all the possible positions vectors of G. It is given that the volume of the pyramid is 6$$\sqrt{3}$$ cubic units and AP = 5 units.
If $$ \left| \bar { a } \right| =a $$, then find the value of the following.
$$ \left| \overrightarrow { a } \times \hat { i } \right| ^{ 2 }+\left| \overrightarrow { a } \times \hat { j } \right| ^{ 2 }+\left| \overrightarrow { a } \times \hat { k } \right| ^{ 2 } $$
Find the position vector of the mid point of the vector joining the points $$ P( 2, 3, 4) $$ and $$ Q(4 , 1, -2) $$.
Show that the points $$ A, B $$ and $$ C $$ with the position vectors.
$$ \overrightarrow {a} = 3 \hat {i} -4 \hat {j} - 4 \hat {j} -4 , \overrightarrow {b} = 2 \hat {i} - \hat {j} + \hat {k} $$ and $$ \overrightarrow {c} = \hat {i} - 3 \hat {j} - 5 \hat {k} $$
$$ABCD$$ is a parrallelogram. If $$L$$ and $$M$$ are the middle points of $$BC$$ and $$CD$$ respectively, then find (i) $$AL$$ and $$AM$$ interns of $$AB$$ and $$AD$$. (ii) $$\lambda$$, if $$AM=\lambda AD-LM$$
Find the sum of the vectors $$\vec {a} = \hat {i} - 2\hat {j} +\hat {k} = -2\hat {i} + 4\hat {j} + 5\hat {k}$$ and $$\vec {c} = \hat {i} - 6\hat {j} - 7\hat {k}.$$
Find the sum of the following vectors:
$$\vec {a} = \hat {i} - 2\hat {j}, \vec {b} = 2\hat {i} - 3\hat {j}, \vec {c} = 2\hat {i} + 3\hat {k}$$
Find the sum of the following vectors:
$$\vec {a} = \hat {i} - 3\hat {k},. \vec {b} = 2\hat {j} - \hat {k}, \vec {c} = 2\hat {i} - 3\hat {j} + 2\hat {k}$$
Let $$\vec{a}$$ and $$\vec{b}$$ are two vectors in space such that $$\vec{a}=\dfrac{3\hat{i}+5\hat{j}-\hat{k}}{\sqrt{35}}, \vec{b}=\dfrac{5i-j+10\hat{k}}{\sqrt{126}}$$, then the value of $$[\vec{a}+\vec{b} \vec{a}+2\vec{b} \vec{a}\times \vec{b}]$$ is equal to?
Find $$|\vec{b}|$$, if $$\left(\vec{a}+\vec{b}\right)\left(\vec{a}-\vec{b}\right)=8$$ and $$|\vec{a}|=8|\vec{b}|$$.
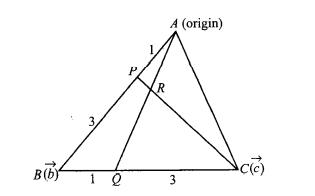
In $$\triangle ABC$$, a point P is taken on AB such that AP/BP = 1/3 and a point Q is taken BC such that CQ/BQ = 3/If R is the point of intersection of the lines AQ and CP, using vector method, find the area of $$\triangle ABC$$ if the area of $$\triangle BRC$$ is 1 unit.
Class 12 Engineering Maths Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions