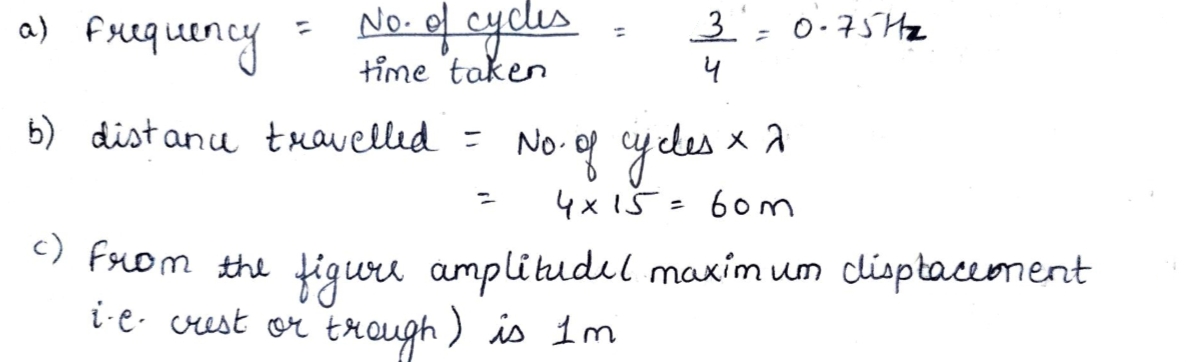Waves - Class 11 Engineering Physics - Extra Questions
Find the velocity of a wave whose frequency is 60 Hz and wavelength is 20 m.
The amplitude (in mm)
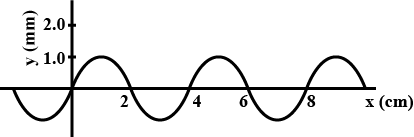
A wave $$y_i\, =\, 0.3 cos\, (2.0x\, -\, 40t)$$ is travelling along a string toward a boundary at x =Write expressions for the reflected waves if the string has a fixed end at x = 0.
A wave has a low speed but a high frequency. What can you infer about its wavelength?
When a sound is reflected from a distinct object, an echo is produced. Let the distance between the reflecting surface and the source of sound production remains the same. Do you hear echo sound on a hotter day?
List two applications of reflection of sound.
A radar sends a signal to an aircraft at a distance of $$30\ km$$ away and receives it back after $$2\times 10^{-4}$$ second. What is the speed of the signal?
Two SHM's are
$$x_{1}(mm,= sec)=1.0\sin\left[\dfrac{\pi}{4}(12t+1)\right]$$ and $$x_{2}(mm,= sec)=0.5[\sin{3\pi t}+\sqrt{3}\cos{3\pi t}]$$
Discuss the ratio of their amplitudes, frequency and find the phase difference.
A particle oscillates in a plane as per the relation $$ x = 4(cos(\pi t) + sin(\pi t))$$. Find amplitude of oscillations.
REF.Image.
Displacement of particle:-
$$ x = 4(cos(\pi t)+sin(t))$$
In superposition of oscillation in perpendicular phases,
so resultant,
$$ R^{2} = 4^{2}+4^{2}$$ (by phases addition)
$$ \Rightarrow R = 4\sqrt{2}$$ (Ans)
Calculate the amplitude of the S.H.M. represented
by $$x=5 \sqrt 2 (sin 2 \pi t +cos 2\pi t)m$$
When a wave is propagating from a rarer to a denser medium, which characteristic of the wave does not change and why ?
What is wave?
Answer the following :
Name the wave/waves produced in a long slinky.
Define amplitude.
Define the following terms.
Wave amplitude
Explain following terms
Wave
What will be the resultant amplitude when 2 waves $$ y_{1}=a \sin \omega t $$ are superposed at any point at a particular instant?
What is meant by a wave?
There is a mistake in each of the following ray diagrams given as Fig. 16.9 a, b, and c. Make the necessary correction (s).
Match the following
A travelling wave pulse is given by. $$y\, =\, \displaystyle \frac{10}{5\, +\, (x\, +\, 2t)^{2}}$$ Here, x and y are in metre and t in second. In which direction and with what velocity is the pulse propagating ? What is the amplitude of pulse?
A wave of frequency 500 Hz has a wave velocity of 350 m/s. The distance between two points which point are $$60^0 $$ out of phase is $$116 \times 10^{-x} m$$ . Find x.
A wave is represented by $$y_1\, =\, 10 cos (5x\, +\, 25 t)$$
where, x is measured in metres and t in seconds. A second wave for which $$\displaystyle y_2\, =\, 20 cos\, \left ( 5x\, +\, 25t\, +\, \frac{\pi}{3} \right )$$
interferes with the first wave. Deduce the amplitude and phase of the resultant wave.
$$x = 1.50 cm$$
$$x = 0.500 cm$$
Two sinusoidal waves combining in a medium are described by the equations
$$y_1\, =\, (3.0 cm)\, sin\, \pi (x\, +\, 0.60t)\, \quad\, and\, \quad\, y_2\, =\, (3.0 cm)\, sin\, \pi (x\, -\, 0.60t)$$
where, x is in centimetres and t is in seconds. The maximum displacement of the medium at x = 0.250 cm is $$4.24 \times 10^{-x} m$$. Find x.
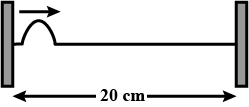
A string of length $$20\ cm$$ and linear mass density $$0.4\ g/cm$$ is fixed at both ends and is kept under a tension of $$16 \ N$$. A wave pulse is produced at $$t = 0$$ near an end as shown in the figure which travels towards the other end. Sketch the shape of the string at a time half of its time period.
Given,
Length of String $$= 20$$ cm
The linear mass density of the string $$=.4$$g/cm
Applied Tension $$= 16 N =16\times 10^5$$ dyn
velocity of the wave:
$$v =\sqrt{\dfrac{T}{\mu}} $$
$$=\sqrt{\dfrac{16\times 10^5}{.4}} $$
$$v= 2 \times 10^3$$ cm/s
$$T=\dfrac Lv=\dfrac{20}{2\times 10^3}$$
Time taken to reach other end $$ = 0.01$$ s
At $$t=0.01$$ s, there will be a trough at the right end as it is reflected.
After reflection from fixed end phase will change by $$\pi$$
Hence: Shape will be as given in the diagram.
A certain transverse wave is described by
$$\displaystyle\,y\,(x,\,t)\,=\,(6.50\,mm)\,cos\,2\,\pi\,\left ( \frac{x}{28.0\,cm}\,-\,\frac{t}{0.0360\,s} \right )$$
The wave's amplitude is $$ 6.50 \times 10^{-x} m. $$ Find the value of x.
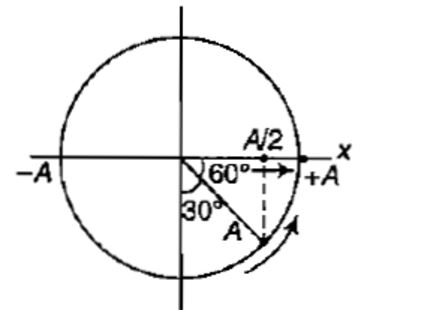
A particle executes simple harmonic motion of amplitude A along the x-axis. At $$t =0$$, the position of the particle is $$x =\dfrac{A}{2}$$ and it moves along the positive x-direction. Find the phase constant $$\delta $$, if the equation is written as $$x=A\sin \left ( \omega t+\delta \right )$$ :
At the t=0 , the amplitude is $$A/2$$
So its position from horizontal axis is
$$sin \delta=\dfrac{A/2}{A}=1/2$$
$$\delta=\dfrac{\pi}{6}$$
So $$x=Asin\bigg (\omega t+\dfrac{\pi}{6}\bigg )$$
A wave of frequency $$500 Hz$$ has a wave velocity of $$350 m/s$$. Find the phase difference in degrees between two displacements at a certain point at times $$10^{-3}$$ s apart.
Two waves of same amplitude and same intensity interfere at one point. Phase difference between them is $$\theta$$. Match the following two columns.
Name two wave interaction that can occur when a wave encounters a barrier.
Explain why you can hear two people talking even when they walk around a corner.
If the wavelength of a sound source is reduced by a factor of 2, what happens to the waves frequency? What happens to its speed?
You have learnt that a travelling wave in one dimension is represented by a function y = f (x,t) where x and t must appear in the combination x - v t or x + v t i.e. $$ \displaystyle y = f(x\pm v t)$$. Is the converse true ? Examine if the following functions for y can possibly represent a travelling wave :
(a) $$ \displaystyle (x+vt)^{2} $$
(b) $$ \displaystyle \log \left [ \left ( x+vt \right )/x_{o} \right ] $$
(c) 1/(x+vt)
A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km $$\displaystyle s^{-1} $$ ? The operating frequency of the scanner is 4.2 MHz.
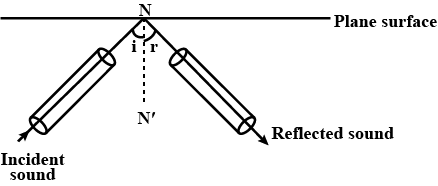
Does sound follow the same laws of reflection as light does? Explain.
Yes, sound also follows the law of reflection in the same manner as the light does.
Law of reflection for sound- The incident sound, the point of normal to the incident sound and the reflected sound all lie in same plane and also the angle of incidence with the normal & the reflected angle with the normal are equal.
$$\angle i = \angle r$$
The minimum distance between two particles in same phase is $$18 cm$$. If the velocity of the wave is $$36 m {s}^{-1}$$, then find the time interval after which the given particle undergoes a phase change of $$\pi$$.
Find the phase difference between a particle at $${1}^{st}$$ crest and a particle at $${4}^{th}$$ crest.
Ultrasonic sound of frequency $$100 kHz$$ emitted by a bat is incident on a water surface. Calculate the wavelength of reflected sound and transmitted sound? (speed of sound in air $$340 m {s}^{-1}$$)
Given that sound travels in air at $$340 {m}/{s}$$, find the wavelength of the waves in air produced by a $$20 kHz$$ sound source. If the same source is put in a water tank, what would be the wavelength of the sound waves in water? Speed of sound in water $$= 1,480 {m}/{s}$$.
A sound wave travels at a speed of $$340 {m}/{s}$$. If its wavelength is $$2 cm$$, what is the frequency of the wave? Will it be in the audible range?
Deduce the relation between wavelength, frequency and speed of sound.
A sound wave whose frequency is 220 Hz has a speed of $$440 ms^{-1}$$ in a given medium. Find the wavelength of the sound.
A transverse wave of amplitude $$0.01\ m$$ and frequency $$500\ Hz$$ is travelling along a stretched string with a speed of $$200 m/s$$. Find the displacement of a particle at a distance of $$0.7\ m$$ from the origin after $$0.01s$$. Also find the phase difference between the point where wave reaches from the origin
Find odd man out:
Give reason for your answer.
Derive the relation between the velocity of wave, wavelength and frequency.
A certain sound has a frequency of $$256$$ hertz and a wavelength of $$1.3$$m. Calculate the speed with which this sound travels.
In what time after its motion begins, will a particle oscillating according to the equation $$x = 5 cos 0.2 \pi t$$ move from the mean position to maximum displacement position?
Equations of a stationary wave and a travelling wave are $$y_{1} = a\sin kx \cos \omega t$$ and $$y_{2} = a\sin (\omega t - kx)$$. The phase difference between two points $$x_{1} = \dfrac {\pi}{3k}$$ and $$x_{2} = \dfrac {3\pi}{2k}$$ is $$\phi$$ for the first wave and $$\phi_{2}$$ for the second wave. Find the ratio $$\dfrac {\phi_{1}}{\phi_{2}}$$.
The equation of a simple harmonic wave is given by $$y=6\sin { 2\pi \left( 2t-0.1x \right) } $$, where '$$x$$' and '$$y$$' are in $$mm$$ and '$$t$$' is in seconds. Find the phase difference between two particles 2mm apart at any instant.
A certain sound has a frequency of $$256$$ hertz and a wavelength of $$1.3$$m. What difference would be felt by a listener between the above sound and another sound travelling at the same speed, but of wavelength $$2.6$$m?
An object of mass $$0.2kg$$ executes SHM along the x-axis with frequency of $$(25/ \pi)$$ Hz. At the point $$x=0.04m$$ the object has KE $$0.5J$$ and PE $$4J$$. The amplitude of oscillation is ________ .
The displacement of particle performing S.H.M. is given by
$$\displaystyle x = \left[ 5 sin \pi t + 12 sin \left( \pi t + \frac{\pi}{2} \right) \right]$$ cm. Determine the amplitude, period and initial phase of the motion.
A wave train has the equation $$y=4\sin (30\pi t+0.1x)$$ where x is in cm and t in seconds. What is the frequency of the source? How much time does a wave pulse take to reach a point $$30$$ cm from it?
Two SHMs are represented by $$y_{1}$$ = A sin ($$\omega$$t + $$\phi$$), $$y_{2}$$ = A/2 [sin $$\omega$$ t + $$\sqrt{3}$$ cos $$\omega$$t]. Find ratio of their amplitudes.
The equation of a wave propagating along a stretched string is given by $$Y=4\sin 2\pi [(t/0.02)-(x/100)]$$, where $$Y$$ and $$x$$ are in cm and $$t$$ in second. Determine the amplitude.
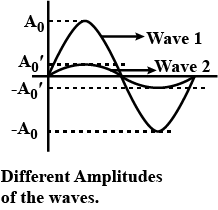
Two sinusoidal waves of the same frequency travel in the same direction along a string. If $$A_{1}=3.0\ cm, A_{2}=4.0\ cm, \phi_{1}=0,$$ and $$\phi_{2}=\pi/2\ rad$$, what is the amplitude of the resultant wave?
A string oscillates according to the equation $$y'=(0.50cm)\sin\left[\left(\dfrac{\pi}{3}cm^{-1}\right)x\right]\cos[(40\pi s^{-1})t]$$. What is the speed of the two waves(identical except for direction of travel) whose superposition gives this oscillation?
The motion of a particle executing simple harmonic motion is described by the displacement function $$x\left( t \right)= A\cos { \left( wt+\phi \right) } $$. If the initial ( t= 0) position of the particle is 1 cm and its initial velocity is w cm/s, what are its amplitude and initial phase angle? The angular frequency of the particle is $$\pi { s }^{ -1 }$$. If instead of the cosine function , we choose the sine function to describe the SHM $$ x=B\sin { (wt+\alpha ) } $$ , what are the amplitude and initial phase of particle with the above initial conditions?
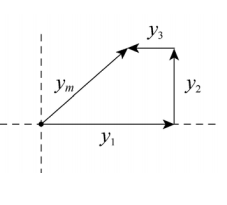
Two identical travelling waves, moving in the same direction, are out of phase by $$\pi/2\ rad.$$ What is the amplitude of the resultant wave in terms of the common amplitude $$y_{m}$$ of the two waves.
If we put a cardboard (say 20 cm x 20 cm) between a light source and our eyes, we can't see the light. But when we put the same cardboard between a sound source and our ear, we hear the sound almost clearly. Explain.
A wave has the equation $$ y = 0.1 \sin [ 100 \pi t- kx] $$ and wave velocity $$100 m/s $$ , its wave number is equal to
A particle executing simple harmonic motion completes $$1200\ oscillations\ per\ minute$$ and passes through the mean position with a velocity of $$3.14\ ms^{-1}.$$ Determine the maximum displacement of the particle from its mean position . Also obtain the displacement equation of the particle if it particle if its displacement be zero at the instant $$t = 0.$$
Draw the figures depicting low amplitude and high amplitude?
Wave one depicts high amplitude while the second wave depicts low amplitude.
What do you understand by the term wave?
A particle is executing $$S.H.M.$$ of time period $$4s$$. What is the time taken by it to move from the
a) Mean position to half of the amplitude.
b) extreme position to half of the amplitude.
Explain the reflection of sound waves from curved surface.
A car is moving towards a hill cliff. The driver sounds a horn of frequency f. The reflected sound heard by the driver has frequency 2f if v the velocity of sound, then the velocity of the car , in units will be.
A wave of amplitude 10 cm and frequency 1000 Hz is travelling with a velocity of 300 m/s. Calculate the phase difference of a particle at a distance of 3 m from the origin after 1.001 s
If the maximum speed of a particle in a traveling wave is $$v_{0}$$, then find the speed of a particle when the displacement is half of the maximum value.
The displacement at a point due to two waves are $$ y_{1}=sin(500\pi t)and y_{2} =2sin(506\pi t)$$. The result due to their superposition will be
Two wires of the same material and having the same radius have their fundamental frequencies in the ratio 1:2 and under tension in the ratio 1:8, Compare ratio of their lengths.
What is an amplitude?
How are the wave velocity $$V$$ , frequency $$f$$ and wavelength $$\lambda$$ of a wave related $$?$$ Derive therelationship.
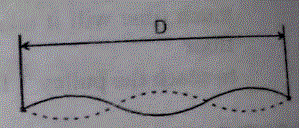
A nylon guitar string has a linear density of 7.20 g/m and is under a tension of 150 N. The fixed supports are distance D = 90.0 cm apart. The string is oscillating in the standing wave pattern shown in figure. Calculate the (a) speed. (b) wavelength, and (c) frequency of the travelling waves whose superposition gives this standing wave.
i) From differential equation of linear S.H.M., obtain an expression fro acceleration, velocity and displacement of a particle performing S.H.M.
ii) A sonometer wire $$1$$ metre long weighing $$2 \,g$$ in is resonance with a turning fork of frequency $$300 \,Hz$$. Find tension in the sonometer wire.
State any four characteristics of a simple harmonic progressive wave.
A plane harmonic wave with frequency $$\omega$$ propagation at a velocity $$v$$ in a direction forming angles $$\alpha, \beta, \gamma$$ with the $$x, y, z$$ axes. Find the phase difference between the oscillation at the points of medium with coordinates $$x_1, y_1, z_1$$ and $$x_2, y_2, z_2$$.
Equation plane wave is given by
$$\xi ( r, t)=a\cos ( \omega t - \vec k. \vec r)$$, where $$\vec k =\dfrac{\omega }{v}\hat n$$ called the wave vector and $$\hat n$$ is the unit vector normal to the wave surface in the direction of the propagation of wave.
or $$\xi (x, y, z)=a \cos ( \omega t-k_x -k_y-k_z)$$
$$=a\cos ( \omega t -kx \cos \alpha -ky \cos \beta -kz \cos \gamma )$$
Thus $$\xi (x_1, y_1, z_1, t)=a\cos ( \omega t -kx_1 \cos \alpha -ky_1 \cos \beta -kz_1 \cos \gamma )$$
and $$\xi (x_2, y_2, z_2, t)=a\cos ( \omega t-kx_2 \cos \alpha -ky_2 \cos \beta -kz_2 \cos \gamma)$$
Hence the sought wave phase difference
$$\varphi_2-\varphi_1=k [( x_1 -x_2 ) \cos \alpha +(y_1-y_2)\cos \beta +(z_1-z_2) \cos \gamma ]$$
or $$\Delta \varphi =| \varphi_2 - \varphi_1|=k | [ (x_1-x_2) \cos \alpha +( y_1 -y_2 ) \cos \beta + ( z_1 -z_2) \cos \gamma ]|$$
$$=\dfrac {\omega }{v}| [ (x_1-x_2) \cos \alpha +(y_1-y_2) \cos \beta +(z_1-z_2) \cos \gamma ]|$$
$$\xi ( r, t)=a\cos ( \omega t - \vec k. \vec r)$$, where $$\vec k =\dfrac{\omega }{v}\hat n$$ called the wave vector and $$\hat n$$ is the unit vector normal to the wave surface in the direction of the propagation of wave.
or $$\xi (x, y, z)=a \cos ( \omega t-k_x -k_y-k_z)$$
$$=a\cos ( \omega t -kx \cos \alpha -ky \cos \beta -kz \cos \gamma )$$
Thus $$\xi (x_1, y_1, z_1, t)=a\cos ( \omega t -kx_1 \cos \alpha -ky_1 \cos \beta -kz_1 \cos \gamma )$$
and $$\xi (x_2, y_2, z_2, t)=a\cos ( \omega t-kx_2 \cos \alpha -ky_2 \cos \beta -kz_2 \cos \gamma)$$
Hence the sought wave phase difference
$$\varphi_2-\varphi_1=k [( x_1 -x_2 ) \cos \alpha +(y_1-y_2)\cos \beta +(z_1-z_2) \cos \gamma ]$$
or $$\Delta \varphi =| \varphi_2 - \varphi_1|=k | [ (x_1-x_2) \cos \alpha +( y_1 -y_2 ) \cos \beta + ( z_1 -z_2) \cos \gamma ]|$$
$$=\dfrac {\omega }{v}| [ (x_1-x_2) \cos \alpha +(y_1-y_2) \cos \beta +(z_1-z_2) \cos \gamma ]|$$
By reference to two waves, state:
(i) the principle of superposition.
(ii) what is meant by coherence.
Two coherent waves $$P$$ and $$Q$$ meet at a point in phase and superpose. Wave $$P$$ has an amplitude of $$1.5\ cm$$ and intensity $$I$$. The resultant intensity at the point where the waves meet is $$3I$$.
Calculate the amplitude of wave $$Q$$.
$$amplitude =$$ _______ $$cm$$.
A wave pulse is travelling on a string with a speed v towards the positive X-axis. The shape of the string at $$t = 0$$ is given by $$g(x) = A \sin (x /a)$$ , where A and a are constants.
What are the dimensions of A and a?
A bug on the surface of a pond is observed to move up and down a total vertical distance of $$1.0\ m$$, lowest to highest point, as a wave passes.
What is the amplitude of the wave?
The equation of a wave travelling on a string stretched along the X-axis is given by
$$y = Ae^{\left(\dfrac{x}{a} + \dfrac{t}{T} \right)^2}$$
Write the dimension of A, a and T.
If loop of chain is spun at high speed, it will roll like a hoop without collapsing. Consider a chain of linear mass density $$\mu$$ that is rolling without slipping at a high speed $$v_0$$.
How far around the loop ( in degrees) will a transverse wave pulse travel in the time the hoop rolls through one complete revolution ?
Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4mm and the phase difference between the waves is $$90^{\circ}$$, what is the resultant amplitude?
Two sinusoidal sound waves with frequencies $$108\ Hz$$ and $$112\ Hz$$ at your ear simultaneously. Each wave has an amplitude of $$1.5\times 10^{-8}m$$ when it reaches your ear.
What is the maximum amplitude of the total sound wave? What is the minimum amplitude?
Two simple hormonic motion are represented by the equation $$y_{1}=10\sin\left ( 3\pi t + \pi /4 \right )$$ and $$y_{2}=\left ( 5\sin\right )3\pi t+\sqrt{3}cos3\pi t)$$ . Their amplitudes are in the ratio of ___ .
A travelling wave pulse is given by
$$y = \dfrac {10}{5 + (x + 2t)^2}$$
In which direction and with what velocity is the pulse propogating ? What is the amplitude of the pulse ?
A wave pulse is a disturbance localized only in a small part of space at a given instant (as shown in Fig. 5.62) and its shape does not change during propagation. Though a pulse can be represented by exponential or trigonometric functions also, it is usually expressed by the form
$$y = \dfrac {a}{b + (x \pm vt)^2}$$
Comparing the above with the given pulse we find that
$$f (x \pm vt) = (x + 2t)^2$$
i.e. the pulse is travelling along negative x-axis with velocity $$2 \,m/s.$$
Further amplitude is the maximum value of wave function which will be when
$$(x + 2t)^2 = 0$$
So, $$A = y_{max} = \dfrac {10}{5} = 2$$
$$y = \dfrac {a}{b + (x \pm vt)^2}$$
Comparing the above with the given pulse we find that
$$f (x \pm vt) = (x + 2t)^2$$
i.e. the pulse is travelling along negative x-axis with velocity $$2 \,m/s.$$
Further amplitude is the maximum value of wave function which will be when
$$(x + 2t)^2 = 0$$
So, $$A = y_{max} = \dfrac {10}{5} = 2$$
A plane progressive wave of frequency 25 Hz, amplitude 2.5 X $$10^{-5}$$ m and initial phase zero propagates along the negative x- direction with a velocity of 300 m/s. At any instant, the phase difference between the oscillations at two point 6 m apart along the line of propagation is _____ and the corresponding amplitude difference is ______ m.
$$\text{Wavelength}\,\lambda=\dfrac{\text{velocity (v)}}{\text{frequency(f)}}$$
$$\text{phase difference }\Delta \phi=\dfrac{2\pi}{\lambda}(\Delta x)$$
$$\therefore \Delta \phi=\dfrac{2\pi}{12}\times 6=\pi$$
What phase difference between two identical traveling waves, moving in the same direction along a stretched string, results in the combined wave having an amplitude 1.50 times that of the common amplitude of the two combining waves? Express your answer in degrees
Two identical sinusoidal waves travel in opposite direction in a wire 15 m long and produce a standing wave in the wire. If the speed of the waves is $$12 ms^{-1}$$ and there are 6 nodes in the standing wave. Find the frequency.
What phase difference between two identical traveling waves, moving in the same direction along a stretched string, results in the combined wave having an amplitude 1.50 times that of the common amplitude of the two combining waves? Express your answer in radians
Two sinusoidal waves of the same frequency are to be sent in the same direction along a taut string. One wave has an amplitude of $$ 5.0 \mathrm{mm} $$, the other $$ 8.0 \mathrm{mm} $$. What is that smallest amplitude?
We know , that amplitude is minimum when phase difference $$\phi=\pi$$.
and amplitude is given by $$A_{net}=A_1-A_2$$
In this case, the amplitude is $$ (8.0 \mathrm{mm}-5.0 \mathrm{mm})=3.0 \mathrm{mm} $$
Four waves are to be sent along the same string, in the same direction:
$$y_{1}(x, t)=(4.00 \mathrm{mm}) \sin (2 \pi x-400 \pi t)$$
$$y_{2}(x, t)=(4.00 \mathrm{mm}) \sin (2 \pi x-400 \pi t+0.7 \pi)$$
$$y_{3}(x, t)=(4.00 \mathrm{mm}) \sin (2 \pi x-400 \pi t+\pi)$$
$$y_{4}(x, t)=(4.00 \mathrm{mm}) \sin (2 \pi x-400 \pi t+1.7 \pi)$$
What is the amplitude of the resultant wave?
Two sinusoidal waves of the same frequency are to be sent in the same direction along a taut string. One wave has an amplitude of $$ 5.0 \mathrm{mm} $$, the other $$ 8.0 \mathrm{mm} $$. What phase difference $$ \phi_{2} $$ results in the largest amplitude of the resultant wave?
We know , that amplitude is maximum when phase difference $$\phi=0$$.
and amplitude is given by $$A_{net}=A_1+A_2$$
In this case, the amplitude is $$ (8.0 \mathrm{mm}+5.0 \mathrm{mm})=13.0 \mathrm{mm} $$
Two sinusoidal waves of the same frequency are to be sent in the same direction along a taut string. One wave has an amplitude of $$ 5.0 \mathrm{mm} $$, the other $$ 8.0 \mathrm{mm} $$. What is the resultant amplitude if the phase angle is $$ \left(\phi_{1}-\phi_{2}\right) / 2 ? $$
Two sinusoidal waves of the same frequency are to be sent in the same direction along a taut string. One wave has an amplitude of $$ 5.0 \mathrm{mm} $$, the other $$ 8.0 \mathrm{mm} $$. What is that largest amplitude?
We know , that amplitude is maximum when phase difference $$\phi=0$$.
and amplitude is given by $$A_{net}=A_1+A_2$$
In this case, the amplitude is $$ (8.0 \mathrm{mm}+5.0 \mathrm{mm})=13.0 \mathrm{mm} $$
These two waves travel along the same string:
$$y_{1}(x, t)=(4.60 \mathrm{mm}) \sin (2 \pi x-400 \pi t)$$
$$y_{2}(x, t)=(5.60 \mathrm{mm}) \sin (2 \pi x-400 \pi t+0.80 \pi \mathrm{rad})$$
What is the amplitude?
Two sinusoidal waves of the same frequency are to be sent in the same direction along a taut string. One wave has an amplitude of $$ 5.0 \mathrm{mm} $$, the other $$ 8.0 \mathrm{mm} $$. What phase difference $$ \phi_{1} $$ between the two waves results in the smallest amplitude of the resultant wave?
As shown in Figure, The least-amplitude resultant wave is obtained when the phase difference is $$ \pi $$ rad.
The equation of a transverse wave traveling along a very long string is $$y = 6.0 \sin \left (0.020 \pi x + 4.0 \pi t \right )$$, where $$x$$ and $$y$$ are expressed in centimeters and $$t$$ is in seconds. Determine (a) the amplitude, (b) the wavelength, (c) the frequency, (d) the speed, (e) the direction of propagation of the wave, and (f) the maximum transverse speed of a particle in the string. (g) What is the transverse displacement at $$x = 3.5 \space cm$$ when $$t = 0.26 s$$?
What phase difference between two identical traveling waves, moving in the same direction along a stretched string, results in the combined wave having an amplitude 1.50 times that of the common amplitude of the two combining waves? Express your answer in wavelengths.
A generator at one end of a very long string creates a wave given by
$$y=(6.0 \mathrm{cm}) \cos \dfrac{\pi}{2}\left[\left(2.00 \mathrm{m}^{-1}\right) x+\left(8.00 \mathrm{s}^{-1}\right) t\right]$$
and a generator at the other end creates the wave
$$y=(6.0 \mathrm{cm}) \cos \dfrac{\pi}{2}\left[\left(2.00 \mathrm{m}^{-1}\right) x-\left(8.00 \mathrm{s}^{-1}\right) t\right]$$
For $$ x \geq 0, $$ what is the location of the node having the third smallest value of x?
A sinusoidal wave of frequency 500 Hz has a speed of 350 m/s. (a How far apart are two points that differ in phase by $$pi/3$$ rad? (b) What is the phase difference between two displacements at a certain point at times 1.00 ms apart?
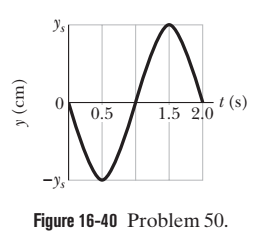
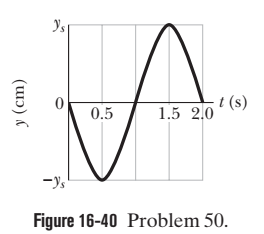
For a particular transverse standing wave on a long string, one of the antinodes is at $$ x=0 $$ and an adjacent node is at $$ x=0.10 \mathrm{m} . $$ The displacement $$ y(t) $$ of the string particle at $$ x=0 $$ is shown in Fig. $$ 16-40 $$ where the scale of the $$ y $$ axis is set by $$ y_{s}=4.0 \mathrm{cm} . $$ When $$ t=0.50 \mathrm{s}, $$ what is the displacement of the string particle at $$ x=0.20 \mathrm{m} $$
A generator at one end of a very long string creates a wave given by
$$y=(6.0 \mathrm{cm}) \cos \dfrac{\pi}{2}\left[\left(2.00 \mathrm{m}^{-1}\right) x+\left(8.00 \mathrm{s}^{-1}\right) t\right]$$
and a generator at the other end creates the wave
$$y=(6.0 \mathrm{cm}) \cos \dfrac{\pi}{2}\left[\left(2.00 \mathrm{m}^{-1}\right) x-\left(8.00 \mathrm{s}^{-1}\right) t\right]$$
For $$ x \geq 0, $$ what is the location of the node having the second smallest value of x?
The equation of a transverse wave traveling along a string is
$$y=0.15 \sin (0.79 x-13 t)$$
in which $$ x $$ and $$ y $$ are in meters and $$ t $$ is in seconds. what is $$ y_{m}$$
For a particular transverse standing wave on a long string, one of the antinodes is at $$ x=0 $$ and an adjacent node is at $$ x=0.10 \mathrm{m} . $$ The displacement $$ y(t) $$ of the string particle at $$ x=0 $$ is shown in Fig. $$ 16-40 $$ where the scale of the $$ y $$ axis is set by $$ y_{s}=4.0 \mathrm{cm} . $$ When $$ t=0.50 \mathrm{s}, $$ what is the displacement of the string particle at $$ x=0.30 \mathrm{m} ? $$
A sinusoidal transverse wave traveling in the positive direction of an $$ x $$ axis has an amplitude of $$ 2.0 \mathrm{cm}, $$ a wavelength of $$ 10 \mathrm{cm}, $$ and a frequency of $$ 400 \mathrm{Hz} $$. If the wave equation is of the form $$ y(x, t)=y_{m} \sin (k x \pm \omega t), $$ what is the correct choice of sign in front of $$ \omega ? $$
A sinusoidal transverse wave traveling in the positive direction of an $$ x $$ axis has an amplitude of $$ 2.0 \mathrm{cm}, $$ a wavelength of $$ 10 \mathrm{cm}, $$ and a frequency of $$ 400 \mathrm{Hz} $$. If the wave equation is of the form $$ y(x, t)=y_{m} \sin (k x \pm \omega t), $$ what is $$ y_{m} $$
A generator at one end of a very long string creates a wave given by
$$y=(6.0 \mathrm{cm}) \cos \dfrac{\pi}{2}\left[\left(2.00 \mathrm{m}^{-1}\right) x+\left(8.00 \mathrm{s}^{-1}\right) t\right]$$
and a generator at the other end creates the wave
$$y=(6.0 \mathrm{cm}) \cos \dfrac{\pi}{2}\left[\left(2.00 \mathrm{m}^{-1}\right) x-\left(8.00 \mathrm{s}^{-1}\right) t\right]$$
For $$ x \geq 0, $$ what is the location of the node having the smallest value of x?
Two waves are generated on a String of length $$ 3.0 \mathrm{m} $$ to produce a three-loop standing wave with an amplitude of $$ 1.0 \mathrm{cm} . $$ The wave speed is $$ 100 \mathrm{m} / \mathrm{s} $$. Let the equation for one of the waves be of the form $$ y(x, t)=y_{m} \sin (k x+\omega t) . $$ In the equation for the other wave, what is $$ y_{m} ?$$
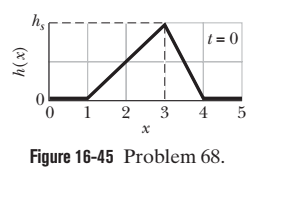
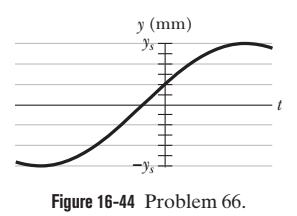
A single pulse, given by $$ h(x-5.0 t), $$ is shown in Fig. $$ 16-45 $$ for $$ t=0 . $$ The scale of the vertical axis is set by $$ h_{s}=2 . $$ Here $$ x $$ is in centimeters and $$ t $$ is in seconds.Plot $$ h(x-5 t) $$ as a function of $$ t $$ for $$ x=10 \mathrm{cm} $$
The leading edge of the pulse reaches $$ x=10 \mathrm{cm} $$ at $$ t=(10-4.0) / 5=1.2 \mathrm{s} $$.
The particle (say, of the string that carries the pulse) at that location reaches a maximum displacement $$ h=2 \mathrm{cm} $$ at $$ t=(10-3.0) / 5=1.4 \mathrm{s} $$.
Finally, the trailing edge of the pulse departs from $$ x=10 \mathrm{cm} $$ at $$ t=(10-1.0) / 5=1.8 \mathrm{s} $$.
Thus, we find for $$ h(t) $$ at $$ x=10 \mathrm{cm} $$ (with the horizontal axis, $$ t $$, in seconds):
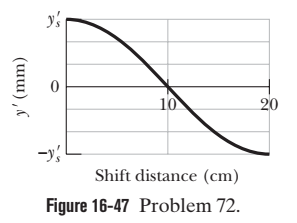
Two sinusoidal& 120Hz waves, of the same frequency and amplitude, are to be sent in the positive direction of an $$ x $$ axis that is directed along a cord under tension. The waves can be sent in phase, or they can be phase-shifted. Figure $$ 16-47 $$ shows the amplitude $$ y^{\prime} $$ of the resulting wave versus the distance of the shift (how far one wave is shifted from the other wave). The scale of the vertical axis is set by $$ y_{s}^{\prime}=6.0 \mathrm{mm} . $$ If the equations for the two waves are of the form $$ y(x, t)=y_{m} \sin (k x \pm \omega t), $$ what is $$ y_{m}$$
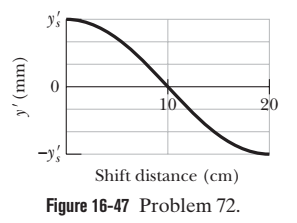
Two sinusoidal& 120Hz waves, of the same frequency and amplitude, are to be sent in the positive direction of an $$ x $$ axis that is directed along a cord under tension. The waves can be sent in phase, or they can be phase-shifted. Figure $$ 16-47 $$ shows the amplitude $$ y^{\prime} $$ of the resulting wave versus the distance of the shift (how far one wave is shifted from the other wave). The scale of the vertical axis is set by $$ y_{s}^{\prime}=6.0 \mathrm{mm} . $$ If the equations for the two waves are of the form $$ y(x, t)=y_{m} \sin (k x \pm \omega t), $$ what is the correct choice of sign in front of $$ \omega ? $$
Two sinusoidal waves, identical except for phase, travel in the same direction along a string, producing the net wave $$ y^{\prime}(x, t)=(3.0 \mathrm{mm}) \sin (20 x-4.0 t+0.820 \mathrm{rad}), $$ with $$ x $$ in meters and $$ t $$ in seconds. What are the phase difference between them?
The equation of a transverse wave traveling along a string is
$$y=(2.0 \mathrm{mm}) \sin \left[\left(20 \mathrm{m}^{-1}\right) x-\left(600 \mathrm{s}^{-1}\right) t\right]$$
Find the amplitude?
Three sinusoidal waves of the same frequency travel along a string in the positive direction of an $$ x $$ axis. Their amplitudes are $$ y_{1}, y_{1} / 2, $$ and $$ y_{1} / 3, $$ and their phase constants are $$ 0, \pi / 2, $$ and $$ \pi, $$ respectively. What is phase constant of the resultant wave?
Three sinusoidal waves of the same frequency travel along a string in the positive direction of an $$ x $$ axis. Their amplitudes are $$ y_{1}, y_{1} / 2, $$ and $$ y_{1} / 3, $$ and their phase constants are $$ 0, \pi / 2, $$ and $$ \pi, $$ respectively. What is the amplitude ?
(a) The phasor diagram is shown here: $$ y_{1}, y_{2}, $$ and $$ y_{3} $$ represent the original waves and $$ y_{m} $$ represents the resultant wave.
The horizontal component of the resultant is
$$y_{m h}=y_{1}-y_{3}=y_{1}-y_{1} / 3=2 y_{1} / 3$$
The vertical component is $$ y_{\operatorname{mv}}=y_{2}=y_{1} / 2 . $$
The amplitude of the resultant is
$$y_{m}=\sqrt{y_{m h}^{2}+y_{m v}^{2}}=\sqrt{\left(\dfrac{2 y_{1}}{3}\right)^{2}+\left(\dfrac{y_{1}}{2}\right)^{2}}=\dfrac{5}{6} y_{1}=0.83 y_{1}$$
Two sinusoidal waves, identical except for phase, travel in the same direction along a string, producing the net wave $$ y^{\prime}(x, t)=(3.0 \mathrm{mm}) \sin (20 x-4.0 t+0.820 \mathrm{rad}), $$ with $$ x $$ in meters and $$ t $$ in seconds. What is their amplitude $$ y_{m} ? $$
A single pulse, given by $$ h(x-5.0 t), $$ is shown in Fig. $$ 16-45 $$ for $$ t=0 . $$ The scale of the vertical axis is set by $$ h_{s}=2 . $$ Here $$ x $$ is in centimeters and $$ t $$ is in seconds.Plot $$ h(x-5 t) $$ as a function of $$ x $$ for $$ t=2 \mathrm{s} $$
at t=2 s:
$$h(x-5t)=h(x-10)$$
picture below shows the pulse at 2.0 s. The horizontal scale (and, presumably, the vertical one also) is in centimeters.
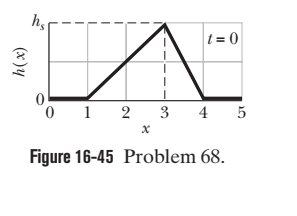
Figure $$ 16-44 $$ shows the displacement $$ y $$ versus time $$ t $$ of the point on a string at $$ x=0, $$ as a wave passes through that point. The scale of the $$ y $$ axis is set by $$ y_{s}=6.0 \mathrm{mm} . $$ The wave is given by $$ y(x, t)=y_{m} \sin (k x-\omega t+\phi) $$ What is $$ \phi ? $$ (Caution: A calculator does not always give the proper inverse trig function, so check your answer by substituting it and an assumed value of $$ \omega $$ into $$ y(x, t) $$ and then plotting the function.)
Two waves,
$$y_{1} =(2.50 \mathrm{mm}) \sin [(25.1 \mathrm{rad} / \mathrm{m}) x-(440 \mathrm{rad} / \mathrm{s}) t]$$
$$\text { and } y_{2} =(1.50 \mathrm{mm}) \sin [(25.1 \mathrm{rad} / \mathrm{m}) x+(440 \mathrm{rad} / \mathrm{s}) t]$$
travel along a stretched string. How can you change the original waves so the resultant wave is the superposition of standing and traveling waves with the same amplitudes as before but with the traveling wave moving in the opposite direction?
A sinusoidal transverse wave traveling in the negative direction of an $$ x $$ axis has an amplitude of $$ 1.00 \mathrm{cm}, $$ a frequency of $$ 550 \mathrm{Hz}, $$ and a speed of $$ 330 \mathrm{m} / \mathrm{s} $$. If the wave equation is of the form
$$y(x, t)=y_{m} \sin (k x \pm \omega t),$$ what is $$ y_{m}?$$
A sinusoidal transverse wave of amplitude $$ y_{m} $$ and wavelength $$ \lambda $$ travels on a stretched cord. Does this ratio depend on the material of which the cord is made?
A standing wave results from the sum of two transverse traveling waves given by
$$y_{1}=0.050 \cos (\pi x-4 \pi t)$$
and $$y_{2}=0.050 \cos (\pi x+4 \pi t)$$
where $$ x, y_{1}, $$ and $$ y_{2} $$ are in meters and $$ t $$ is in seconds. (a) What is the smallest positive value of $$ x $$ that corresponds to a node? Beginning at $$ t=0? $$
Two sinusoidal waves of the same wavelength travel in the same direction along a stretched string. For wave $$ 1, y_{m}=3.0 \mathrm{mm} $$ and $$ \phi= 0 ; $$ for wave $$ 2, y_{m}=5.0 \mathrm{mm} $$ and $$ \phi=70^{\circ} . $$ What is the amplitude?
At time $$ t=0 $$ and at position $$ x=0 \mathrm{m} $$ along a string, a traveling sinusoidal wave with an angular frequency of 440 rad/s has displacement $$ y=+4.5 \mathrm{mm} $$ and transverse velocity $$ u=-0.75 \mathrm{m} / \mathrm{s} $$. If the wave has the general form $$ y(x, t)=y_{m} \sin (k x-\omega t+\phi), $$ what is phase constant $$ \phi ? $$
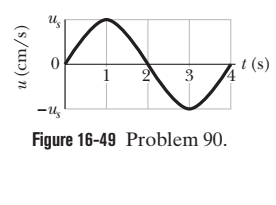
A certain transverse sinu-soidal wave of wavelength $$ 20 \mathrm{cm} $$ is moving in the positive direction of an $$ x $$ axis. The transverse velocity of the particle at $$ x=0 $$ as a function of time is shown in Fig. $$ 16-49, $$ where the scale of the vertical axis is set by $$ u_{s}=5.0 \mathrm{cm} / \mathrm{s} . $$ What is the amplitude?
A sinusoidal transverse wave traveling in the negative direction of an $$ x $$ axis has an amplitude of $$ 1.00 \mathrm{cm}, $$ a frequency of $$ 550 \mathrm{Hz}, $$ and a speed of $$ 330 \mathrm{m} / \mathrm{s} $$. If the wave equation is of the form
$$y(x, t)=y_{m} \sin (k x \pm \omega t),$$ what is the correct choice of sign in front of $$ \omega ? $$
Two sinusoidal waves of the same wavelength travel in the same direction along a stretched string. For wave $$ 1, y_{m}=3.0 \mathrm{mm} $$ and $$ \phi= 0 ; $$ for wave $$ 2, y_{m}=5.0 \mathrm{mm} $$ and $$ \phi=70^{\circ} . $$ What is the phase constant of the resultant wave?
Two waves are described by
$$y_{1}=0.30 \sin [\pi(5 x-200 t)]$$
and $$y_{2}=0.30 \sin [\pi(5 x-200 t)+\pi / 3]$$
where $$ y_{1}, y_{2}, $$ and $$ x $$ are in meters and $$ t $$ is in seconds. When these two waves are combined, a traveling wave is produced. What are the (a)amplitude, (b)wave speed?
Two waves,
$$y_{1} =(2.50 \mathrm{mm}) \sin [(25.1 \mathrm{rad} / \mathrm{m}) x-(440 \mathrm{rad} / \mathrm{s}) t]$$
$$\text { and } y_{2} =(1.50 \mathrm{mm}) \sin [(25.1 \mathrm{rad} / \mathrm{m}) x+(440 \mathrm{rad} / \mathrm{s}) t]$$
travel along a stretched string.How is the minimum amplitude related to the amplitudes of the original two waves?
The wave number for each wave is $$ k=25.1 / \mathrm{m}, $$ which means $$ \lambda=2 \pi / k=250.3 \mathrm{mm} $$ The angular frequency is $$ \omega=440 / \mathrm{s} ; $$ therefore, the period is $$ T=2 \pi / \omega=14.3 \mathrm{ms} . $$
We plot the superposition of the two waves $$ y=y_{1}+y_{2} $$ over the time interval $$ 0 \leq t \leq 15 $$ ms.
The time unit is understood to be the millisecond and vertical axis $$ (y) $$ is in millimeters.
The following three graphs show the oscillation at $$ x=\lambda / 4=62.6 \mathrm{mm} \approx 63 \mathrm{mm} $$ (graph on the left), at $$ x=3 \lambda / 8 \approx 94 \mathrm{mm} $$ (middle graph), and at $$ x=\lambda / 2 \approx 125 \mathrm{mm} $$
The smallest amplitudes is $$ y_{\min }=y_{1 m}-y_{2 m} $$ where $$ y_{1 m}=2.5 \mathrm{mm} $$ and $$ y_{2 m}=1.5 \mathrm{mm} $$ are the amplitudes of the original traveling waves.
Four sound waves are to be sent through the same tube of air, in the same direction:
$$s_{1}(x, t)=(9.00 \mathrm{nm}) \cos (2 \pi x-700 \pi t)$$
$$s_{2}(x, t)=(9.00 \mathrm{nm}) \cos (2 \pi x-700 \pi t+0.7 \pi)$$
$$s_{3}(x, t)=(9.00 \mathrm{nm}) \cos (2 \pi x-700 \pi t+\pi)$$
$$s_{4}(x, t)=(9.00 \mathrm{nm}) \cos (2 \pi x-700 \pi t+1.7 \pi)$$
What is the amplitude of the resultant wave? (Hint: Use a phasor diagram to simplify the problem.)
A sound wave of the form $$s = s_m \cos\left (kx - \omega t + \phi \right )$$ travels at 343 m/s through air in a long horizontal tube. At one instant, air molecule A at 2.000 m is at its maximum positive displacement of 6.00 nm and air molecule B at x = 2.070 m is at a positive displacement of 2.00 nm. All the molecules between A and B are at intermediate displacements. What is the frequency of the wave?
Two sound waves, from two different sources with the same frequency, 540 Hz, travel in the same direction at $$330 \space m/s^{2}$$. The sources are in phase. What is the phase difference of the wave at a point that is 4.40 m from one source and 4.00 m from the other?
Two waves,
$$y_{1} =(2.50 \mathrm{mm}) \sin [(25.1 \mathrm{rad} / \mathrm{m}) x-(440 \mathrm{rad} / \mathrm{s}) t]$$
$$\text { and } y_{2} =(1.50 \mathrm{mm}) \sin [(25.1 \mathrm{rad} / \mathrm{m}) x+(440 \mathrm{rad} / \mathrm{s}) t]$$
travel along a stretched string.How is the maximum amplitude related to the amplitudes of the original two waves?
The wave number for each wave is $$ k=25.1 / \mathrm{m}, $$ which means $$ \lambda=2 \pi / k=250.3 \mathrm{mm} $$ The angular frequency is $$ \omega=440 / \mathrm{s} ; $$ therefore, the period is $$ T=2 \pi / \omega=14.3 \mathrm{ms} . $$
We plot the superposition of the two waves $$ y=y_{1}+y_{2} $$ over the time interval $$ 0 \leq t \leq 15 $$ ms.
The time unit is understood to be the millisecond and vertical axis $$ (y) $$ is in millimeters.
The following three graphs show the oscillation at $$ x=\lambda / 4=62.6 \mathrm{mm} \approx 63 \mathrm{mm} $$ (graph on the left), at $$ x=3 \lambda / 8 \approx 94 \mathrm{mm} $$ (middle graph), and at $$ x=\lambda / 2 \approx 125 \mathrm{mm} $$
The largest amplitude can be related to the amplitudes of $$ y_{1} $$ and $$ y_{2} $$ in a simple way:
$$y_{\max }=y_{1 m}+y_{2 m}$$
where $$ y_{1 m}=2.5 \mathrm{mm} $$ and $$ y_{2 m}=1.5 \mathrm{mm} $$ are the amplitudes of the original traveling waves.
A certain loudspeaker system emits sound isotropically with a frequency of $$ 2000 \mathrm{Hz} $$ and an intensity of $$ 0.960 \mathrm{mW} / \mathrm{m}^{2} $$ at distance of $$ 6.10 \mathrm{m} $$. Assume that there are no reflections.what are the displacement amplitude ?
In which case is the speed of sound more ; the humming of a bee or the roaring of a lion ?
A sinusoidal sound wave moves at $$ 343 \mathrm{m} / \mathrm{s} $$ through air in the positive direction of an $$ x $$ axis. At one instant during the oscillations, air molecule $$ A $$ is at its maximum displacement in the negative direction of the axis while air molecule $$ B $$ is at its equilibrium position. The separation between those molecules is $$ 15.0 \mathrm{cm}, $$ and the molecules between $$ A $$ and $$ B $$ have intermediate displacements in the negative direction of the axis.
What is the frequency of the sound wave?
Two sound waves with an amplitude of $$ 12 \mathrm{nm} $$ and a wavelength of $$ 35 \mathrm{cm} $$ travel in the same direction through a long tube, with a phase difference of $$ \pi / 3 $$ rad. What is the amplitude of the net sound wave produced by their interference?
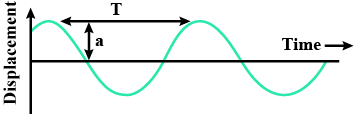
Draw displacement-time graph of a wave and show on it the amplitude and time period of wave.
The displacement-time graph is as below:
Suppose a spherical loudspeaker emits sound isotropically at $$ 10 \mathrm{W} $$ into a room with completely absorbent walls, floor, and ceiling (an anechoic chamber).
What is the ratio of the wave amplitude at $$ d=4.0 \mathrm{m} $$ to that at $$ d=3.0 \mathrm{m} ? $$
The wavelength of a wave is $$3\ m$$. If the velocity of the wave is $$330\ m/s$$ then find the frequency of that wave. Calculate the time period if the frequency of that wave is reduced to half its value.
$$Frequency = 110\ Hz$$.
Time period when frequency is half of its value
$$110/2 = 55\ Hz$$
Time Period $$= 1/n$$.
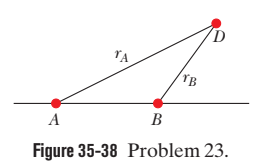
In Fig. $$ 35-38, $$ sources $$ A $$ and $$ B $$ emit long-range radio waves of wavelength $$ 400 \mathrm{m}, $$ with the phase of the emission from $$ A $$ ahead of that from source $$ B $$ by $$ 90^{\circ} . $$ The distance $$ r_{A} $$ from $$ A $$ to detector $$ D $$ is greater than the corresponding distance $$ r_{B} $$ by $$ 100 \mathrm{m} . $$ What is the phase difference of the waves at $$ D ? $$
Define following terms in relation to a wave:
(a) amplitude (b) frequency (c) wavelength and (d) wave velocity
What is the angle between the vibration of the particle of medium and the direction of propagation of the wave in a transverse wave?
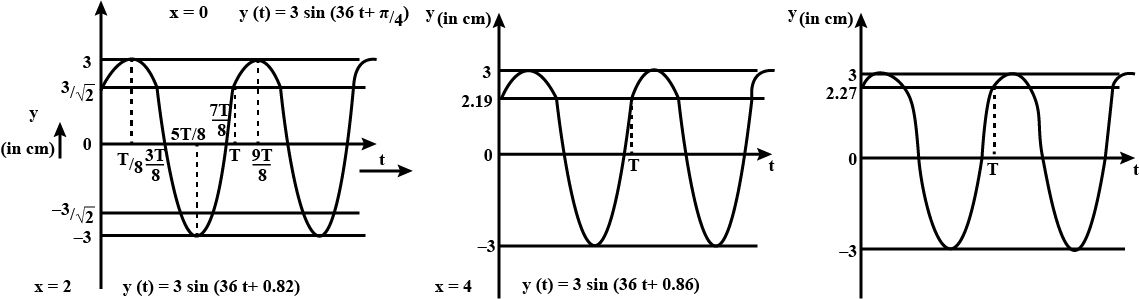
For the wave described in Exercise $$ 15.8, $$ plot the displacement (y) versus (t) graphs for $$ x=0,2 $$ and $$ 4 \mathrm{cm} . $$ What are the shapes of these graphs? In which aspects does the oscillatory motion In travelling wave differ from one point to another: amplitude, frequency or phase?
All the graph have same amplitude of frequency but a different initial phases. All graphs are sinusoidal.
Explain following terms
Amplitude of a wave
What do you understand by superposition of waves? Explain.
Superposition of Waves:
What would happen in a situation a progressive wave propagates in a medium and if we consider similarly many waves propagating in the same direction or opposite direction?
In this situation to study the displacement of the particle, we analyse two disturbances moving in the-opposite direction at the same time in a stretched string as shown in the figure. According to the situation (a); two disturbances which are in the same phase, are moving towards each other in opposite direction and at the place of their meeting the displacement of the particle is different than the initial displacement. Since the waves are in the same phase it increases and the disturbances moving ahead then take the original position. Similarly according to situation (b); if the disturbances are in opposite phase and are imposed; then the resultant displacement in the diagram is different from the initial displacement and with time as the disturbance moves ahead then displacement takes its original position.
Hence, we can see that when on a particle at the same time two or more than two waves are imposed, then they effect the displacement of the particle. Therefore; "when more than one wave is imposed on a particle at the same time, it is called superposition of waves:
As a result of superposition of waves the particle instantaneously executes motion under the total resultant effect of the imposed waves and the resultant displacement is given by the principle of superposition.
Write about the reflection of waves.
Reflection of Transverse Wave:
To understand the reflection of the transverse waves we study a stretched string as shown in the figure 9.9 whose one end is tied to a rigid base, and consider a pulse (disturbance) moving towards the stable end. This disturbance would put force on the rigid base and as a reaction the rigid base would put force on the string. Due to this the direction of the disturbance is changed which is called reflected disturbance. The direction of reflected disturbance is opposite to the direction of incident disturbance i.e., crest is reflected in the form of trough and trough is reflected in the form of crest but there is no change in their shape.
Reflection of Longitudinal Waves:
To understand the reflection of longitudinal waves we study about 4 balls of light weight (less density substance) of same mass and 4 balls of heavy weight (high density substance) and of the same mass as shown in the figure (9.13). These balls are placed on a horizontal surface which is frictionless and all balls are joined together by small and same pieces of spring. The first four balls from the left hand side are light and the remaining four are heavy.
Write the relation between angular frequency, angular wave number and wave velocity?
For the travelling harmonic wave $$ y(x, t)=2 \cos 2 \pi(10 t-0.0080 x+0.35) $$ where $$ x $$ and $$ y $$ are In centimetre and t In seconds. Calculate the phase difference between oscillatory motion of 2 points separated by a distance of
a) $$ 4 \mathrm{m} $$
b) $$ 0.5 \mathrm{m} $$
c) $$ \lambda / 2 $$
d) $$ 3 \lambda / 2 $$
What are waves?
State the principle of superposition. Name the phenomenon produced due to the superposition of waves.
What are elastic waves?
At x s 0.1 m, find the displacement at t = 0.4 sec.
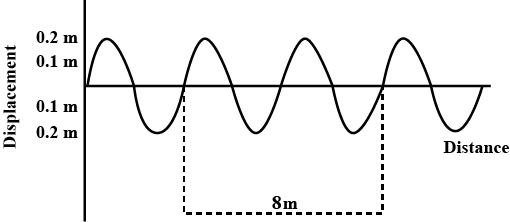
Above figure shows the distance displacement graph. The wave is formed in $$2s$$.
a) What is its amplitude?
b) What is its wavelength?
c) What is its frequency?
d) What is its velocity?
(a) If the coordinate of a particle varies as $$x= - A \ cos \ \omega t$$, what is the phase constant in Equation $$15.6$$? (b) At what position is the particle at $$t=0$$?
A sinusoidal wave propagating through air has a frequency of 150 Hz. If the wave speed is 200 ms$$^{-1}$$ how far apart are two points in the medium which have a phase difference of $$45^o$$ and $$150^o$$?
A sinusoidal wave propagating through air has frequency of 200 Hz. If the wave speed is 300 m/s, how far apart are two points in the medium with a phase difference of $$45^o$$ and $$60^o$$?
Observe the graph given above:
a) What is its amplitude?
b) What is the frequency?
c) Draw the graph of another wave with no change in the frequency and with half of its amplitude.
d) If this wave travels with velocity $$300m/s$$ in $$1s$$, calculate the wavelength?
a) amplitude of given wave, $$A=0.1m$$
b) Given, 2 cycles in $$4$$sec
$$\therefore v =$$ No of cycles in $$1$$ sec $$=\dfrac{2}{4}=\dfrac{1}{2}$$
$$\therefore v=\dfrac{1}{2}Hr$$
c) Refer image
d) $$v=300m/s$$
$$v=\dfrac{1}{2}$$
We know $$\lambda=\dfrac{v}{v}=\dfrac{300}{\dfrac{1}{2}}=600m$$
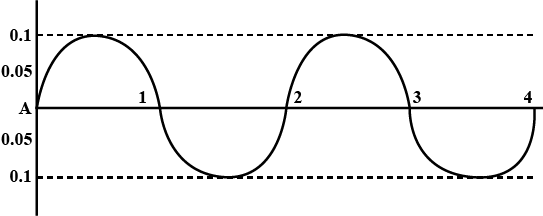
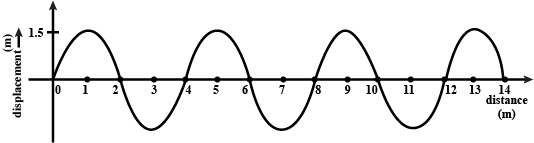
Observe the above graph:
Find out the amplitude of the wave.
What is the speed of the wave if it travels $$800 m$$ in $$2 s$$ ?
What is the frequency of the wave?
The distance between two particles on a string is 10 cm. Find the phase difference between these particles if the frequency of the wave is 400 Hz and speed is 100 m/s.
At t = 0.1 sec, find the displacement at x = 0.2m
Answer the question:
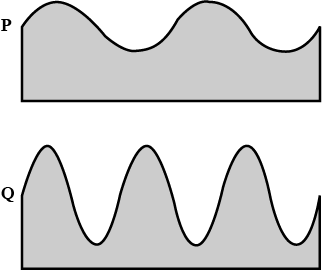
The diagram show two water waves P and Q that are travelling at the same speed on the surface of a pond. The diagrams are to the same scale.
Which wave has the greater amplitude and which wave has the greater frequency ?
| greater amplitude | greater frequency | |
| A | P | P |
| B | P | Q |
| C | Q | P |
| D | Q | Q |
A radio station serves listeners in a city to the northeast of its broadcast site. It broadcasts from three adjacent towers on a mountain ridge, along a line running east to west, in what's called a phased array. Show that by introducing time delays among the signals the individual towers radiate, the station can maximize net intensity in the direction toward the city (and in the opposite direction) and minimize the signal transmitted in other directions.
Rank the waves represented by the following functions from the largest to the smallest according to (i) their amplitudes, (ii) their wavelengths, (iii) their frequencies, (iv) their periods, and (v) their speeds. If the values of a quantity are equal for two waves, show them as having equal rank. For all functions, x and y are in meters and t is in seconds. (a) y = 4 sin (3x - 15t) (b) y = 6 cos (3x + 15t - 2) (c) y = 8 sin (2x + 15t) (d) y = 8 cos (4x + 20t) (e) y = 7 sin (6x - 24t).
Show that the two waves with wave functions given by $$ E_{1} = 6.00 sin (100 \pi t) $$ and $$ E_{2} = 8.00 sin (100 \pi t + \pi/2) $$ add to give a wave with the wave function $$ E_{R} =sin(100 \pi t + \phi).$$ Find the required values for $$ E_{R} $$ and $$ \phi $$.
When two progressive waves $$y_{1}=4\sin(2x\ - 6t)$$ and $$y_{2}=3\sin(2x-6t-\dfrac{\pi}{2})$$ are superimposed, the amplitude of the resultant wave is
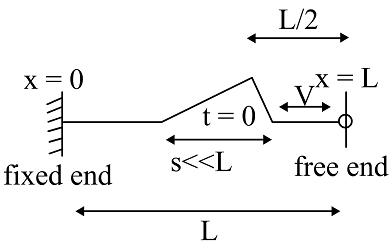
A small pulse travelling with speed $$v$$ in a string is shown at $$t = 0$$, moving towards free end. Select the shape of string from column-II at moments shown in column-I
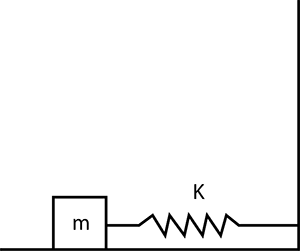
The block shown in the figure, is acted on by a spring with spring constant $$k$$ and a weak frictional force of constant magnitude $$f$$. The block is pulled a distance $$\displaystyle x_{0}$$ from equilibrium position and then released. It oscillates many times and ultimately comes to rest. Show that the decrease of amplitude is the same for each cycle of oscillation.
The initial position and velocity of a body moving in SHM with period $$T=0.25\ s$$ are $$x=5.0\ cm$$ and $$v=218\ cm/s.$$ What are the amplitude and phase difference of the motion?
The motion of a particle executing simple harmonic motion is described by the displacement function, $$x(t) = A \cos \left ( \omega t+\phi \right )$$.
If the initial $$(t = 0)$$ position of the particle is 1 cm and its initial velocity is $$\omega $$ cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is $$\pi s^{-1}$$. If instead of the cosine function we choose the sine function to describe the $$SHM : x = B\sin (\omega t + \alpha )$$, what are the amplitude and initial phase of the particle with the above initial conditions.
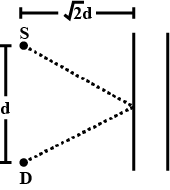
$$A$$ source $$S$$ and a detector $$D$$ are placed at a distance d apart. A big cardboard is placed at a distance $$\sqrt{2}$$d from the source and the detector as shown in figure. The source emits a wave of wavelength = $$d/2$$ which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
Two coherent transverse waves of amplitude 2A and A of same frequency propagated respectively along +ve and -ve x-axis are superimposed. The amplitude of the wave at a distance of 5 cm from the origin, $$(given \ K = \dfrac{\pi}{4}cm^{-1})$$ is:
When a transverse plane wave traverses a medium, individual particles execute periodic motion given by the equation $$ y = 0.25 cos(2\pi t-\pi x)$$. The phase difference for two position of same particle which are occupied by time intervals 0.4 second apart is
A wave of frequency 500 Hz has a velocity $${ 360ms }^{ -1 }$$ the phase difference between two displacement t a certain point at time $${ 10 }^{ -3 }$$ s apard will be
Two waves, each having a frequency of $$100 { Hz }$$ and a wavelength of $$2.0 { cm },$$ are travelling in the same direction on a string. What is the phase difference between the waves $$( a )$$ if the second wave was produced $$0.015 s$$ later than the first one at the same place, $$(b)$$ if the two waves were produced at a same instant but the first one was produced a distance $$4.0 { cm },$$ behind the second one ? $$(c)$$ If each of the waves has an amplitude of $$2.0 { mm },$$ what would be the amplitudes of the resultant waves in part $$(a)$$ and $$(b)$$ ?
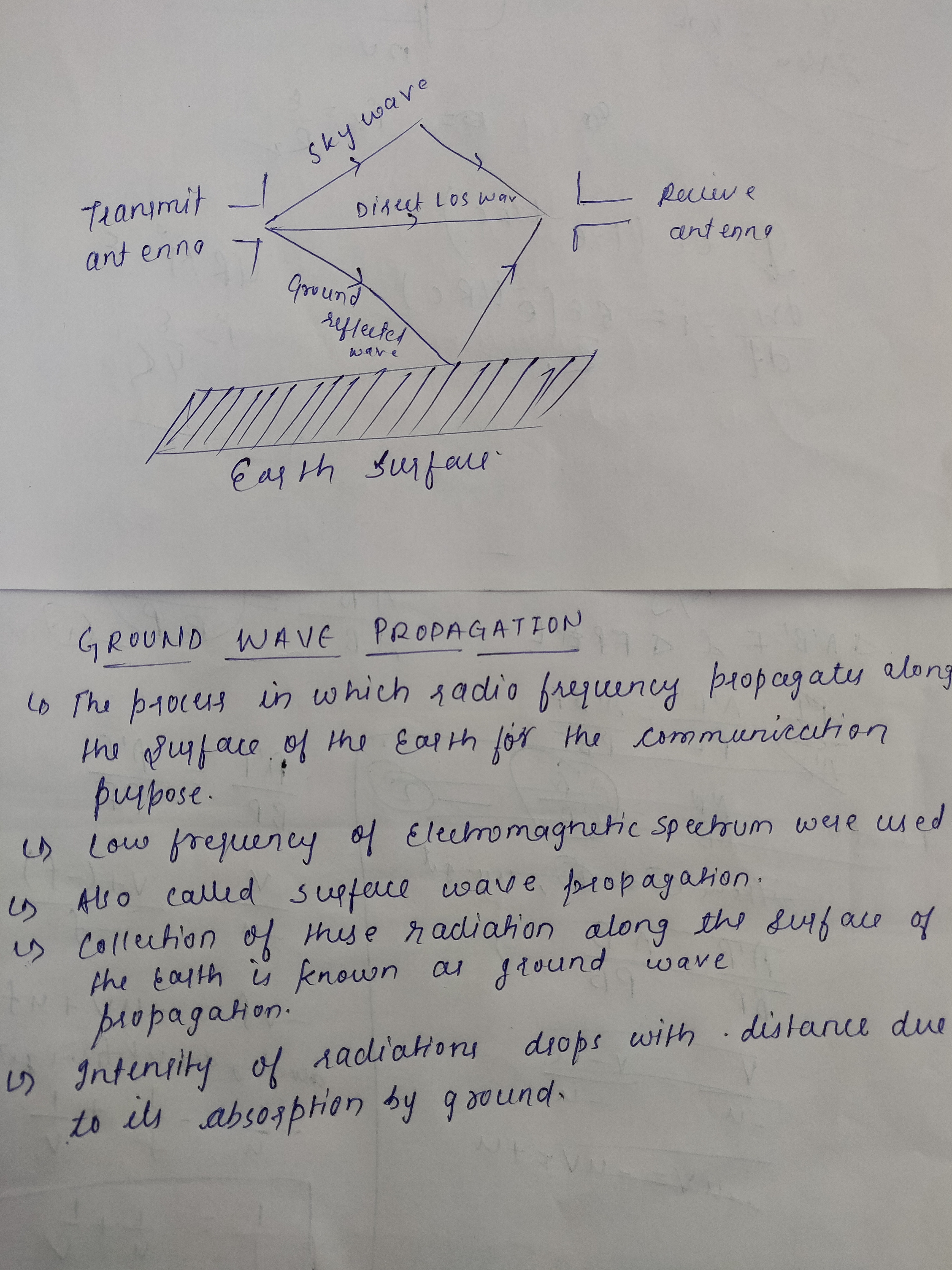
Explain ground wave propagation.
GROUND WAVE PROPAGATION
$$\rightarrow $$ The process in which radio frequency propagates along the surface of the earth for the communication purpose.
$$\rightarrow $$ Low frequency of electromagnetic spectrum were used
$$\rightarrow $$ Also called surface wave propagation.
$$\rightarrow $$ Collection of these radiation along the surface of the earth is known as ground wave propagation.
$$\rightarrow $$ Intensity of radiations drops with distance due to its absorption by ground.
Two particles describe $$S.H.M$$ of the same period and same amplitude along the same line about the same equilibrium position $$O$$. At a moment when they are at the same displacements their velocities are $$1.6\ m/s$$ in opposite directions. At another moment when their displacement are equal in magnitude but on either side of $$O$$ their velocities are $$1.2\ m/s$$ in the same direction. Find the maximum speed of the particles and the phase difference between them.
Let the phase difference is $$\phi$$
We know maximum speed is $$A\omega$$
Now, $$A\omega cos\phi = 1.2$$
$$A\omega sin\phi = 1.6$$
$$\therefore tan\phi = \dfrac{4}{3}$$
$$or, \phi = 53^{\circ}$$
So, $$cos\phi = \dfrac{3}{5}$$
$$\therefore A\omega \times \dfrac{3}{5} = 1.2$$
$$or, A\omega = 2$$
So, maximum speed is $$2 \ m/s$$ and phase difference is $$53^{\circ}$$.
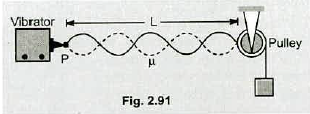
In the arrangement shown in fig. a mass can be hung from a string ( with a linear mass density of $$\mu =0.00200\ kg/m$$) that passes over a light pulley. The string is connected to a vibrator ( of constant frequency $$f$$ ), and the length of the string between point $$P$$ and the pulley is $$L=2.00\ m$$. When the mass $$m$$ is either $$16.0\ kg$$ or $$25.0\ kg$$, standing waves are observed; however, no standing waves are observed with any mass between these values.
What is the frequency of the vibrator ?
Suppose two linear waves of equal amplitude and frequency have a phase difference $$\phi$$ as they travel in the same medium. They can be represented by
$$y_1 =A \sin (kx -\omega t)$$
$$y_2 =A \sin (kx -\omega t + \phi)$$
What is the amplitude of this resultant wave? Is the wave purely sinusoidal, or not ?
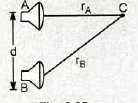
The two sources shown in figure $$2.25$$ emit sound waves, in phase, each of wavelength $$\lambda$$ and amplitude $$A$$. Consider a point such as $$C$$ in the diagram and let $$r_A$$ and $$r_B$$ be the distance of this point from source $$A$$ and source $$B$$, respectively. Show that if $$r_A$$ and $$R_B$$ are nearly equal, $$(r_A -r_B << r_A)$$, then the amplitude varies approximately with position as
$$\left(\dfrac {2A}{r_A}\right) \cos \dfrac {\pi}{\lambda}(r_A -r_B)$$
A $$100 \,Hz$$ sinusodial wave is travelling in the positive x-direction along a string with a linear mass density of $$3.5 \times 10^{-3} \,kg/m$$ and a tension of $$35 \,N.$$ At time $$t = 0,$$ the point $$x = 0$$ has maximum displacement in the positive y-direction. Next, when this point has zero displacement the slope of the string is $$\pi / 20.$$ Find (i) amplitude (ii) wave speed (iii) the expression which represents the displacement of string as a function of x (in metres) and t (in seconds).
The speed of wave in string is
$$V = \sqrt { \dfrac {T}{\mu}} = \sqrt { \dfrac {35}{3.5 \times 10^{-3}}} = 100 \,m/s$$
$$\lambda = \dfrac {v}{f} = \dfrac {100}{100} = 1 \,m$$
The shape of the string at $$t = 0 \,s$$ is as shown in Fig. 5.60
Let us assume that
$$y = A \,sin (\omega t - kx + \theta)$$
Putting $$t = 0 $$ $$x = 0$$ and $$y = + \,A$$
gives $$\theta = \dfrac {\pi}{2}$$
also $$\omega = 2\pi f = 2 \pi \times 100 = 200 \pi$$
$$k = \dfrac {2\pi}{\lambda} = \dfrac {2\pi}{1} = 2\pi$$
Hence $$y = A \,sin\left ( 200\pi t - 2\pi x + \dfrac {\pi}{2} \right )$$
It is given that
$$\dfrac {dy}{dx} = \dfrac {\pi}{20}$$ at $$t = \dfrac {T}{4} = \dfrac {1}{400} \left [ \therefore T = \dfrac {1}{f} = \dfrac {1}{100} \right ]$$
$$\left. \dfrac {dy}{dx} \right \}_{ t = \dfrac {1}{400}} = A 2 \pi \,cos \left ( 200 t - 2\pi x + \dfrac {\pi}{2} \right ) = -2 A \pi = \dfrac {\pi}{20}$$
$$A = \dfrac {1}{40} = 0.025$$
i.Amplitude $$A = 0.25 \,m$$
ii.Wave speed$$ = 100 \,m/s$$
iii. Wave equation is
$$y = A \,sin\left ( 200\pi t - 2\pi x + \dfrac {\pi}{2} \right )$$
$$V = \sqrt { \dfrac {T}{\mu}} = \sqrt { \dfrac {35}{3.5 \times 10^{-3}}} = 100 \,m/s$$
$$\lambda = \dfrac {v}{f} = \dfrac {100}{100} = 1 \,m$$
The shape of the string at $$t = 0 \,s$$ is as shown in Fig. 5.60
Let us assume that
$$y = A \,sin (\omega t - kx + \theta)$$
Putting $$t = 0 $$ $$x = 0$$ and $$y = + \,A$$
gives $$\theta = \dfrac {\pi}{2}$$
also $$\omega = 2\pi f = 2 \pi \times 100 = 200 \pi$$
$$k = \dfrac {2\pi}{\lambda} = \dfrac {2\pi}{1} = 2\pi$$
Hence $$y = A \,sin\left ( 200\pi t - 2\pi x + \dfrac {\pi}{2} \right )$$
It is given that
$$\dfrac {dy}{dx} = \dfrac {\pi}{20}$$ at $$t = \dfrac {T}{4} = \dfrac {1}{400} \left [ \therefore T = \dfrac {1}{f} = \dfrac {1}{100} \right ]$$
$$\left. \dfrac {dy}{dx} \right \}_{ t = \dfrac {1}{400}} = A 2 \pi \,cos \left ( 200 t - 2\pi x + \dfrac {\pi}{2} \right ) = -2 A \pi = \dfrac {\pi}{20}$$
$$A = \dfrac {1}{40} = 0.025$$
i.Amplitude $$A = 0.25 \,m$$
ii.Wave speed$$ = 100 \,m/s$$
iii. Wave equation is
$$y = A \,sin\left ( 200\pi t - 2\pi x + \dfrac {\pi}{2} \right )$$
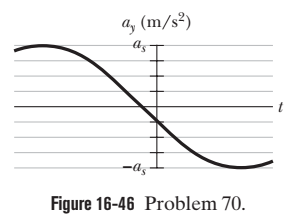
Figure $$ 16-46 $$ shows transverse acceleration $$ a_{y} $$ versus time $$ t $$ of the point on a string at $$ x=0, $$ as a wave in the form of $$ y(x, t)=y_{m} \sin (k x-\omega t+\phi) $$ passes through that point. The scale of the vertical axis is set by $$ a_{s}=400 \mathrm{m} / \mathrm{s}^{2} . $$ What is $$ \phi ? $$(Caution: A calculator does not always give the proper inverse trig function, so check your answer by substituting it and an assumed value of $$ \omega $$ into $$ y(x, t) $$ and then plotting the function.)
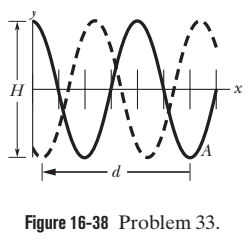
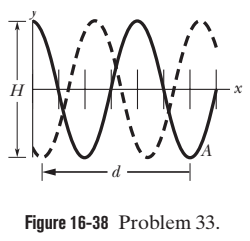
Two sinusoidal waves with the same amplitude of $$ 9.00 \mathrm{mm} $$ and the same wavelength travel together along a string that is stretched along an $$ x $$ axis. Their resultant wave is shown twice in Fig. $$ 16-38, $$ as valley $$ A $$ travels in the negative direction of the $$ x $$ axis by distance $$ d=56.0 \mathrm{cm} $$ in $$ 8.0 \mathrm{ms} . $$ The tick marks along the axis are separated by $$ 10 \mathrm{cm}, $$ and height $$ H $$ is $$ 8.0 \mathrm{mm} . $$ Let the equation for one wave be of the form $$ y(x, t)=y_{m} \sin \left(k x \pm \omega t+\phi_{1}\right), $$ where $$ \phi_{1}=0 $$ and you must choose the correct sign in front of $$ \omega . $$ For the equation for the other wave, what is $$ \phi_{2} $$
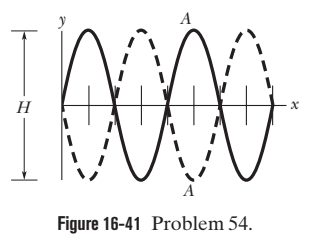
Two sinusoidal waves with the same amplitude and wavelength travel through each other along a string that is stretched along an $$ x $$ axis. Their resultant wave is shown twice in Fig. $$ 16-41 $$, as the antinode $$ A $$ travels from an extreme upward displacement to an extreme downward displacement in 6.0 ms. The tick marks along the axis are separated by $$ 10 \mathrm{cm} $$; height $$ H $$ is $$ 1.80 \mathrm{cm} $$. Let the equation for one of the two waves be of the form $$ y(x, t)=y_{m} \sin (k x+\omega t) . $$ In the equation for the other wave, what is the sign in front of $$ \omega ? $$
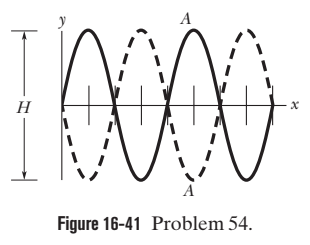
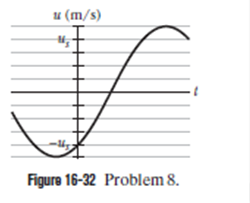
Figure 16-32 shows the transverse velocity $$u$$ versus time $$t$$ of the point on a string at $$x = 0$$, as a wave passes through it. The scale on the vertical axis is set by $$u_s = 4.0 \space m/s$$. The wave has the generic form $$y\left (x, t \right ) = y_m \sin \left (kx - \omega t + \phi \right )$$. What then is $$\phi$$? (caution : A calculator does not always give the proper inverse trig function, so check your answer by substituting it and an assumed value of $$\omega$$ into $$y\left (x, t \right )$$ and then plotting the function.)
A continuous sinusoidal longitudinal wave is sent along a very long coiled spring from an attached oscillating source. The wave travels in the negative direction of an $$ x $$ axis; the source frequency is $$ 25 \mathrm{Hz} ; $$ at any instant the distance between successive points of maximum expansion in the spring is $$ 24 \mathrm{cm} $$; the maximum longitudinal displacement of a spring particle is $$ 0.30 \mathrm{cm} ; $$ and the particle at $$ x=0 $$ has zero displacement at time $$ t=0 . $$ If the wave is written in the form $$ s(x, t)=s_{m} \cos (k x \pm \omega t), $$ what is $$s_{m}?$$
Two sinusoidal waves with the same amplitude and wavelength travel through each other along a string that is stretched along an $$ x $$ axis. Their resultant wave is shown twice in Fig. $$ 16-41 $$, as the antinode $$ A $$ travels from an extreme upward displacement to an extreme downward displacement in 6.0 ms. The tick marks along the axis are separated by $$ 10 \mathrm{cm} $$; height $$ H $$ is $$ 1.80 \mathrm{cm} $$. Let the equation for one of the two waves be of the form $$ y(x, t)=y_{m} \sin (k x+\omega t) . $$ In the equation for the other wave, what is $$ y_{m}$$
A transverse sinusoidal wave is moving along a string in the positive direction of an $$x$$ axis with a speed of 80 m/s. At $$t = 0$$, the string particle at $$x = 0$$ has a transverse displacement of 4.0 cm from its equilibrium position and is not moving. The maximum transverse speed of the string particle at $$x = 0$$ is 16 m/s. (a) What is the frequency of the wave? (b) What is the wavelength of the wave? If $$\left (x, t \right ) = y_m \sin \left (kx \pm \omega t + \phi \right )$$ is the form of the wave equation, what are (c) $$y_m$$, (d) $$k$$, (e) $$\omega$$ (f) $$\phi$$, and (g) the correct choice of sign in front of $$\omega$$ ?
Two sinusoidal waves with the same amplitude of $$ 9.00 \mathrm{mm} $$ and the same wavelength travel together along a string that is stretched along an $$ x $$ axis. Their resultant wave is shown twice in Fig. $$ 16-38, $$ as valley $$ A $$ travels in the negative direction of the $$ x $$ axis by distance $$ d=56.0 \mathrm{cm} $$ in $$ 8.0 \mathrm{ms} . $$ The tick marks along the axis are separated by $$ 10 \mathrm{cm}, $$ and height $$ H $$ is $$ 8.0 \mathrm{mm} . $$ Let the equation for one wave be of the form $$ y(x, t)=y_{m} \sin \left(k x \pm \omega t+\phi_{1}\right), $$ where $$ \phi_{1}=0 $$ and you must choose the correct sign in front of $$ \omega . $$ For the equation for the other wave, what is $$ y_{m}? $$
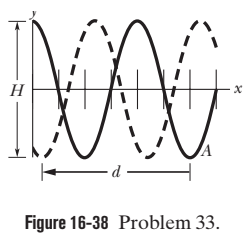
Two sinusoidal waves with the same amplitude of $$ 9.00 \mathrm{mm} $$ and the same wavelength travel together along a string that is stretched along an $$ x $$ axis. Their resultant wave is shown twice in Fig. $$ 16-38, $$ as valley $$ A $$ travels in the negative direction of the $$ x $$ axis by distance $$ d=56.0 \mathrm{cm} $$ in $$ 8.0 \mathrm{ms} . $$ The tick marks along the axis are separated by $$ 10 \mathrm{cm}, $$ and height $$ H $$ is $$ 8.0 \mathrm{mm} . $$ Let the equation for one wave be of the form $$ y(x, t)=y_{m} \sin \left(k x \pm \omega t+\phi_{1}\right), $$ where $$ \phi_{1}=0 $$ and you must choose the correct sign in front of $$ \omega . $$ For the equation for the other wave, what is the sign in front of $$ \omega ? $$
A continuous sinusoidal longitudinal wave is sent along a very long coiled spring from an attached oscillating source. The wave travels in the negative direction of an $$ x $$ axis; the source frequency is $$ 25 \mathrm{Hz} ; $$ at any instant the distance between successive points of maximum expansion in the spring is $$ 24 \mathrm{cm} $$; the maximum longitudinal displacement of a spring particle is $$ 0.30 \mathrm{cm} ; $$ and the particle at $$ x=0 $$ has zero displacement at time $$ t=0 . $$ If the wave is written in the form $$ s(x, t)=s_{m} \cos (k x \pm \omega t), $$ what is the correct choice of sign in front of $$ \omega ? $$
At a certain point, two waves produce pressure variations given by $$ \Delta p_{1}=\Delta p_{m} \sin \omega t $$ and $$ \Delta p_{2}=\Delta p_{m} \sin (\omega t-\phi) . $$ At this point, what is the ratio $$ \Delta p_{r} / \Delta p_{m}, $$ where $$ \Delta p_{r} $$ is the pressure amplitude of the resultant wave, if $$ \phi \text{ is } \pi / 2$$
A plane elastic wave $$\xi =ae^{\gamma x}\cos(\omega t-kx)$$ where $$a,\gamma,\omega,$$ and $$k$$ are constants, propagates in a homogeneous medium. Find the phase difference between the oscillation at the points where the particle' displacement amplitudes differ by $$\eta=1.0\%,$$ if $$\gamma=0.42\ m^{-1}$$ and the wavelength is $$\lambda=50\ cm.$$
The equation of a wave propagating on a string is as follows :
$$y = 10 sin \pi(0.01 x - 2.00t)$$ where y and x are in cm and t is in second. Calculate the amplitude, frequency and velocity of the wave. Calculate the phase difference between the two particles at a distance 40.0 cm at any instant.
At a certain point, two waves produce pressure variations given by $$ \Delta p_{1}=\Delta p_{m} \sin \omega t $$ and $$ \Delta p_{2}=\Delta p_{m} \sin (\omega t-\phi) . $$ At this point, what is the ratio $$ \Delta p_{r} / \Delta p_{m}, $$ where $$ \Delta p_{r} $$ is the pressure amplitude of the resultant wave, if $$ \phi \text{ is } \pi / 3$$
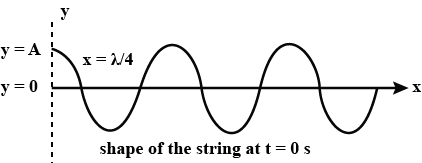
A sound wave generated in $$4$$ seconds is shown in the above graph. If wavelength of the wave is $$15m$$, calculate:
a) Frequency of the wave.
b) Distance traveled by the wave in $$4$$ seconds.
c) Find out the amplitude of the wave.
A transverse sinusoidal wave on a string has a period $$T = 25.0\ ms$$ and travels in the negative $$x$$ direction with a speed of $$30.0\ m/s$$. At $$t = 0$$, an element of the string at $$x = 0$$ has a transverse position of $$2.00\ cm$$ and is traveling downward with a speed of $$2.00\ m/s$$. (a) What is the amplitude of the wave? (b) What is the initial phase angle? (c) What is the maximum transverse speed of an element of the string? (d) Write the wave function for the wave.
Class 11 Engineering Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Physical World Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work,Energy And Power Extra Questions