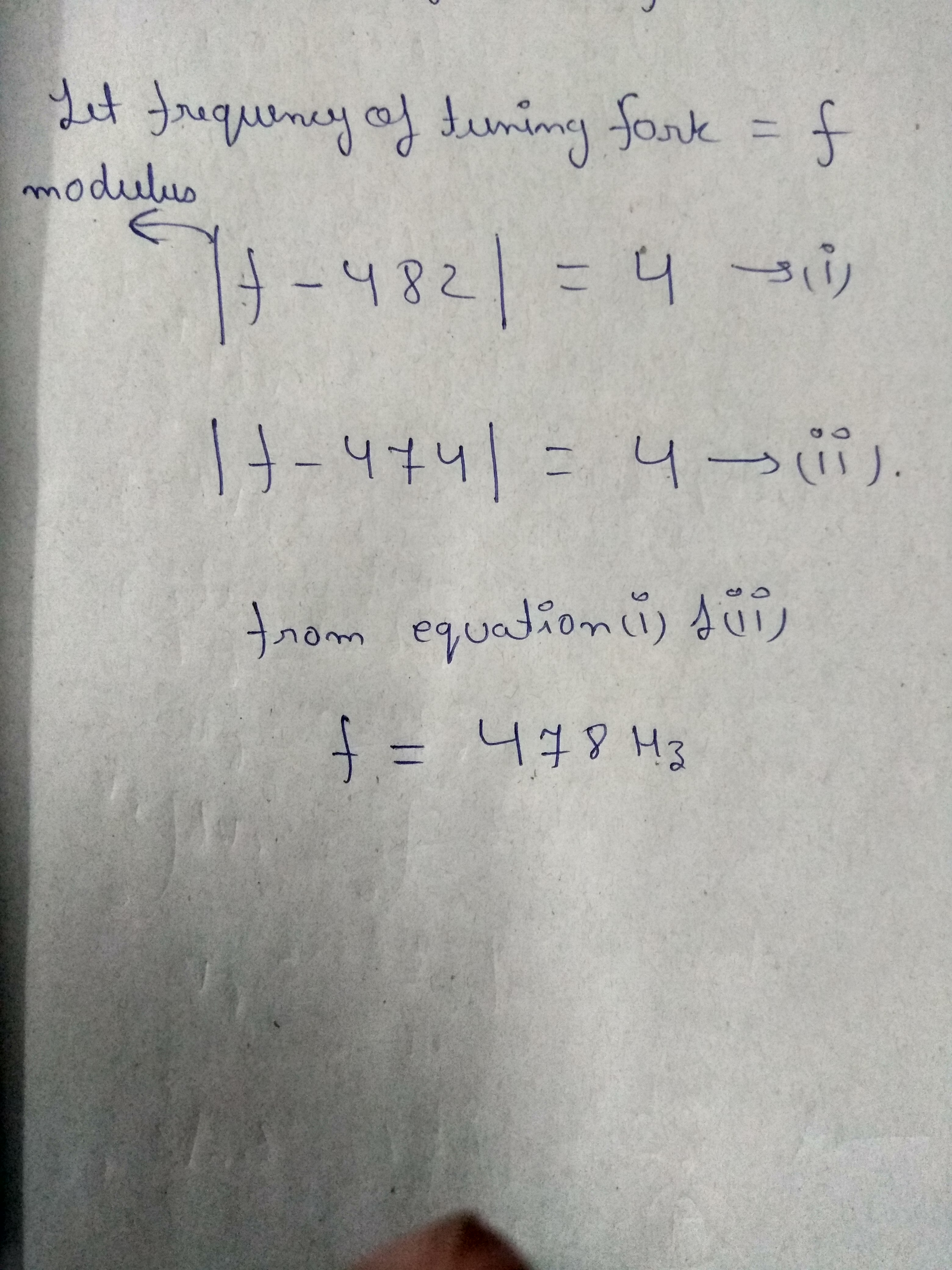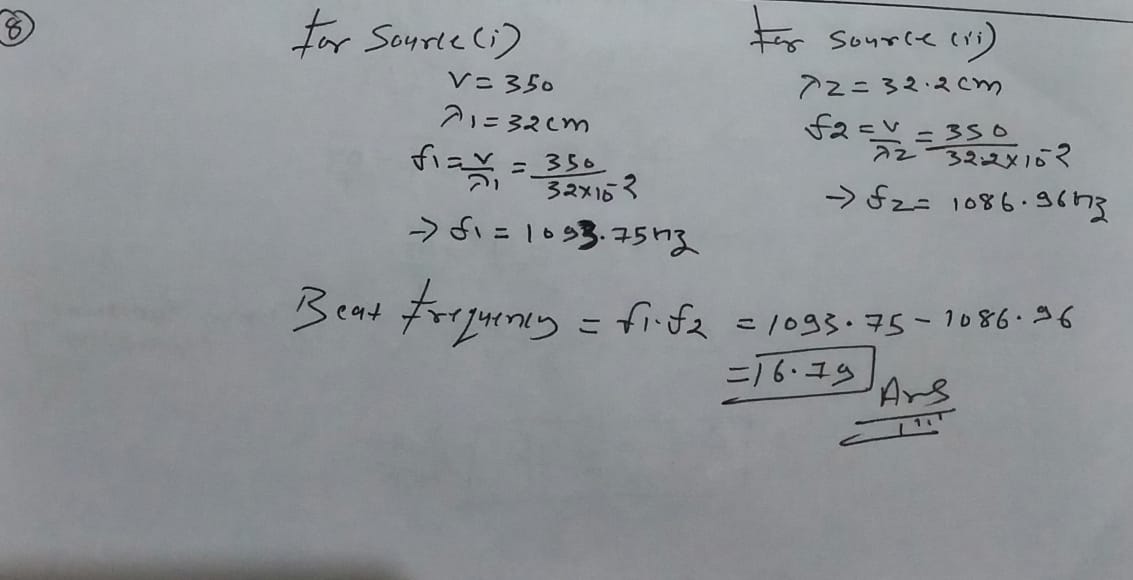Waves - Class 11 Medical Physics - Extra Questions
What are the beats?
What do you mean by tone?
Define the beat period.
One of the harmonic frequencies for a particular string under tension is $$ 325 \mathrm{Hz} $$. The next higher harmonic frequency is $$ 390 \mathrm{Hz} $$
What harmonic frequency is next higher after the harmonic frequency 195 Hz ?
| frequency / Hz | Phase lead of N |
| N over M/rad | |
| a) 0.4 | $$-\frac{\pi}{4}$$ |
| b) 2.5 | $$-\frac{\pi}{2}$$ |
| c) 2.5 | $$+\frac{\pi}{2}$$ |
| d) 2.5 | $$-\frac{\pi}{4}$$ |
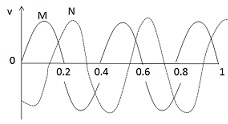
Two sinusoidal voltage of the same frequency are shown in figure.
What is the frequency and the phase relationship between the voltage?
What do you understand by Overtones?
What is Doppler Effect? Explain with an example.
A. B and C are three tuning forks. Frequency of A is 350Hz. Beats produced by A and B are 5 per second and by B and C are 4 per second. When a wax is put on A beat frequency between A and B is 2Hz and between A and C is 6Hz. Then, find the frequency of B and C respectively.
A tuning fork is placed near a vibrating stretched wire. A boy standing near the two hears a beat frequency $$f$$. It is known that frequency of tuning fork is greater than frequency of stretched wire. Match the following two columns.
A tuning fork of fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. The minimum length by which the wire be shortened so that it produces no beats with the tuning fork is $$40 \times 10^{-x} cm $$. Find $$x$$.
A tuning fork of unknown frequency makes three beats per second with a standard fork of frequency 384 Hz. The beat frequency decreases when a small piece of wax is put on a prong of the first fork. What is the frequency of this fork ? (in Hz)
What is red shift?
a hollow metallic tube closed at one end produces resonance with a tuning fork of frequency n at temperature $${T}_{0}$$. The temperature of the tube is increased by dT. If the coefficient of thermal expansion of the tube metal is $$\alpha $$, the beat frequency will be
Two tuning folks with natural frequencies $$340$$ Hz each move relative to a stationary observer. One fork moves away from the observer, while the other moves towards him at the same speed. The observer hears beats of frequency $$3$$ Hz. Find the speed of the tuning fork. (Velocity of sound in air $$=330$$ m/s).
Explain what is Doppler effect in sound and state its any four applications.
A source of sound with adjustable frequency produces $$4$$ beats per second with a tuning fork when its frequency is either $$474\ Hz$$. Or $$482\ Hz$$. What is the frequency of the tuning fork?
A stretched sonometer wire is in unison with a tuning fork. When the length is increased by 4%, the number of beats heard per second isFind the frequency of the fork.
Two tuning forks A and B are sounded together and 8 beats/s are heard. A is in resonance with a column of air 32 cm long in a pipe closed at one end and B is similarly in resonance when the length of the column is increased by one cm. Calculate the frequency of forks.
Explain Doppler effect in sound. State any two applications of Doppler effect.
Calculate the frequency of beats produced in air when two source of sound are activated, one emitting a wavelength of $$32\ cm$$ and the other of $$32.2\ cm$$. The speed of sound in air is $$350\ m/s$$.
A tuning fork of frequency 200 Hz is in unison with a sonometer wire. How many beats are heard in 30 s if the tension is increased by 1% (in terms of X 10)
A human wave. During sporting events within large, densely packed stadiums, spectators will send a wave (or pulse) around the stadium (Fig. 16-19). As the wave reaches a group of spectators, they stand with a cheer and then sit. At any instant, the width w of the wave is the distance from the leading edge (people are just about to stand) to the trailing edge (people have just sat down). Suppose a human wave travels a distance of 853 seats around a stadium in 39 s. with spectators requiring about 1.8 s to respond to the wave's passage by standing and then sitting. What are (a) the wave speed v (in seats per second) and (b) width w (in number of seats)?
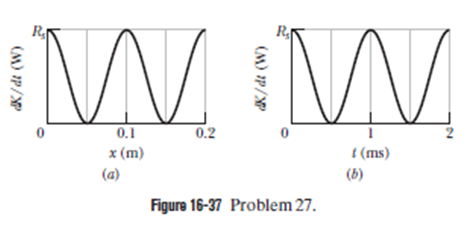
A sinusoidal wave is sent along a string with a linear density of 2.0 g/m. As it travels the kinetic energies of the mass elements along vary. Figure 16-37a gives the rate $$dK/dt$$ at which kinetic energy passes through the string elements at a particular instant, plotted as a function of distance $$x$$ along the string. Figure 16-37b is similar except that it gives the rate at which kinetic energy passes through a particular mass element (at a particular location), plotted as a function of time$$t$$. For both figures the scale on the vertical (rate) axis is set by $$R_s = 10 \space W$$.
The equation of a transverse wave traveling along a string is
$$y=0.15 \sin (0.79 x-13 t)$$
in which $$ x $$ and $$ y $$ are in meters and $$ t $$ is in seconds. what is the correct choice of sign in front of $$ \omega $$ for this second wave?
Consider a loop in the standing wave created by two waves (amplitude $$ 5.00 \mathrm{mm} $$ and frequency $$ 120 \mathrm{Hz} $$ ) traveling in opposite directions along a string with length $$ 2.25 \mathrm{m} $$ and mass $$ 125 \mathrm{g} $$ and under tension $$ 40 \mathrm{N} $$.What is the maximum kinetic energy of the string in the loop during its oscillation?
An acoustic burglar alarm consists of a source emitting waves of frequency $$ 28.0 \mathrm{kHz} $$.
What is the beat frequency between the source waves and the waves reflected from an intruder walking at an average speed of $$ 0.950 \mathrm{m} / \mathrm{s} $$ directly away from the alarm?
Given below are some functions of $$x$$ and $$t$$ to represent the displacement of an elastic wave.
(a) $$y=5 \cos (4x) \sin 20t$$
(b) $$y=4 \sin \bigg( 5x-\dfrac{t}{2} \bigg) + 3 \cos \bigg( 5x-\dfrac{t}{2} \bigg)$$
(c) $$y=10 \cos [(252-250) \ \ \pi t] \ \cos [(252+250) \ \ x$$]
(d) $$y=100 \cos (100 \pi t+0.5x)$$
State which of these represent
(a) a travelling wave along ($$-x$$) direction
(b) a stationary wave ($$c$$) beats
(c) a travelling wave along ($$+x$$) direction.
Give reasons for the answers.
What is Doppler Effect? Mention the two applications of Doppler effect.
Answer in brief:
What are harmonics and overtones?
What is Doppler's effect? Give the expression for the apparent frequency of the note at different cases.
What are the beats? define beat frequency. Explain how the frequency of tuning fork is determined using beats?
What is the Doppler effect? Give an example.
Calculate the Debye temperature for iron in which the propagation velocities of longitudinal and transverse vibrations are equal to $$5.85$$ and $$3.23\,km/s$$ respectively.
It is observed that during march-past we hear a base drum distinctly from a distance compared to the side drums.
Name the characteristic of sound associated with the above observation.
Tuning fork A when sounded with a tuning fork B of frequency 480 Hz gives 5 beats per second. When the prongs of A are loaded with wax, it gives 3 beats per second. Find the original frequency of A.
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the first tuning fork. (in Hz)
A source of the sound of frequency. $$256\ Hz$$ is moving rapidly towards a wall with a speed of $$5\ m/s$$. How many beats per second will be heard If sound travels at a speed of $$330\ m/s$$?
An organ pipe is sounded with a tuning fork of frequency $$256$$ Hz. When the air in the pipe is at a temperature of $$15^o$$C, $$23$$ beats are heard in $$10$$ sec. When the tuning fork is loaded with a small piece of wax, the beat frequency is found to decrease. What change of temperature of the air in the pipe is necessary to bring the pipe and the unloaded fork into unison?
Two identical wires are in unison when tension in one of the wires is increased by $$2$$ % $$12$$ beats are produced per two seconds the original frequency of the wires.
A bat emitting an ultrasonic wave of frequency $$4.5\times { 10 }^{ 4 }Hz$$ flies at a speed of $$6\ m/s$$ between two parallel walls.Find the two frequencies heard by the bat and the beat frequency between the two.The speed of sound is $$330\ m/s$$.
Two identical tuning forks vibrating at the same frequency $$256\ Hz$$ are kept fixed at some distance apart. A listener runs between the forks at a speed of $$3.0\ m/s$$ so that the approaches one tuning fork and recedes from the other figure. Then the beat frequency observed by the listener. Speed of sound in air $$= 332\ m/s$$.
A conveyor belt moves to the right will a speed $$v=300\ m/min$$. A very fast piemaker puts pies on the belt at a rate of $$20$$ per minute, and they are received at the other end by a pie eater.
Derive general expressions for the spacing of the pies $$\lambda$$ and the frequency $$f$$ with which they are received by the pie eater in terms of the speed of the belt $$v$$, the speed of the sender $$u_s$$, the speed of the receiver $$u_r$$ and the frequency $$f_0$$ with which the piemaker places pies on the belt.
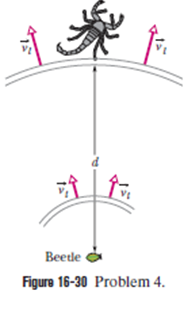
A sand scorpion can detect the motion of a nearby beetle (its prey) by the waves the motion sends along the sand surface (Fig. 16-30). The waves are of two types; transverse waves travelling at $$ v_t = 50 \space m/s$$ and longitudinal waves travelling at $$ v_t = 150 \space m/s$$. If a sudden motion sends out such waves, a scorpion can tell the distance of the arrival times of the waves at its leg nearest the beetle. If $$\Delta t = 4.0 \space ms$$, what is the beetle's distance?
What are beats? By mathematical analysis prove that the number of beats per second is equal to the difference of frequencies of the sources.
the maximum kinetic energy of the string;
the mean kinetic energy of the string averaged over one oscillation period.
Class 11 Medical Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work, Energy And Power Extra Questions