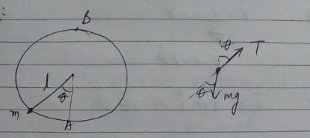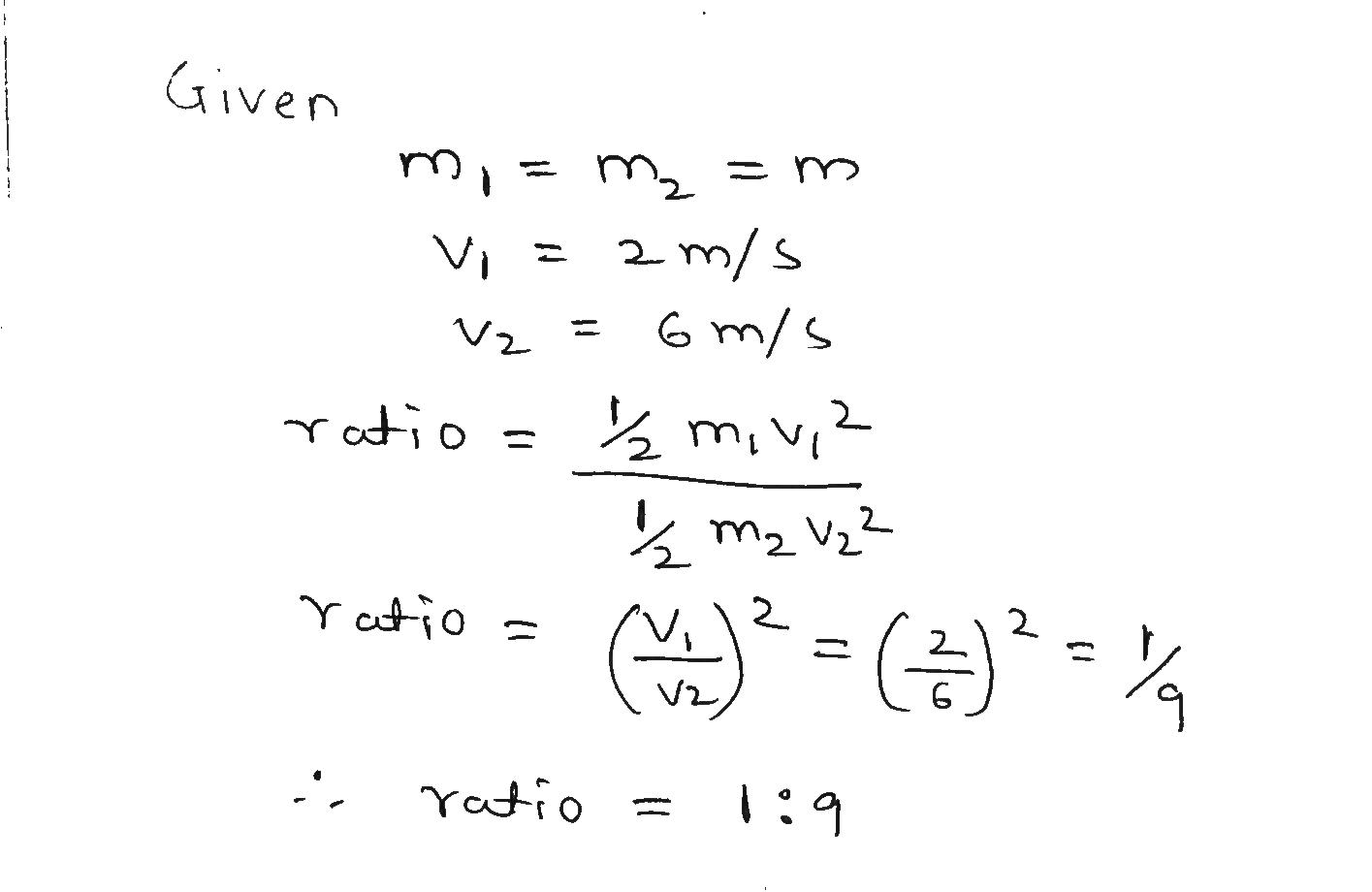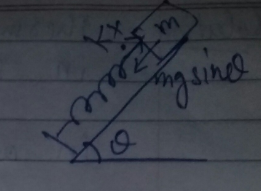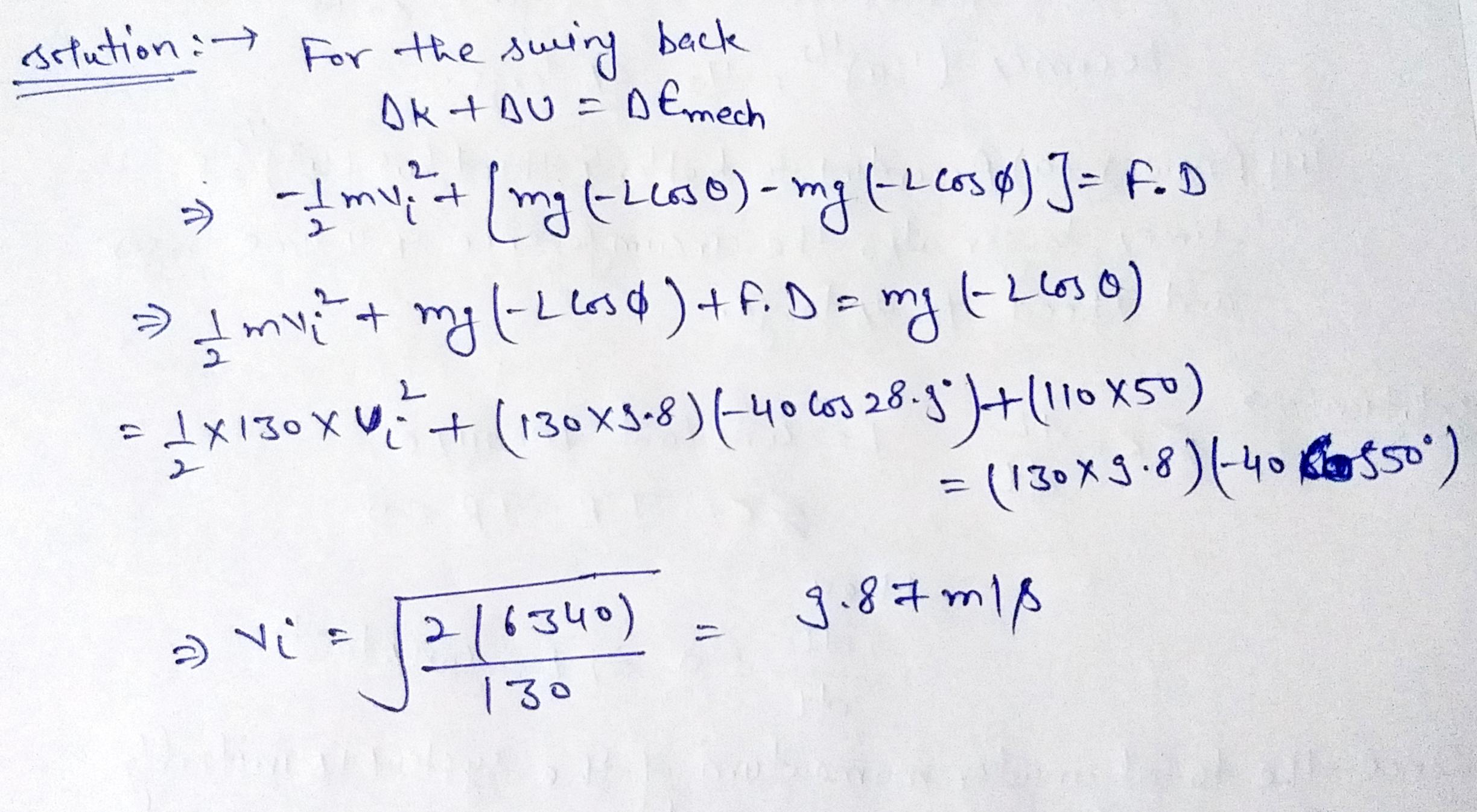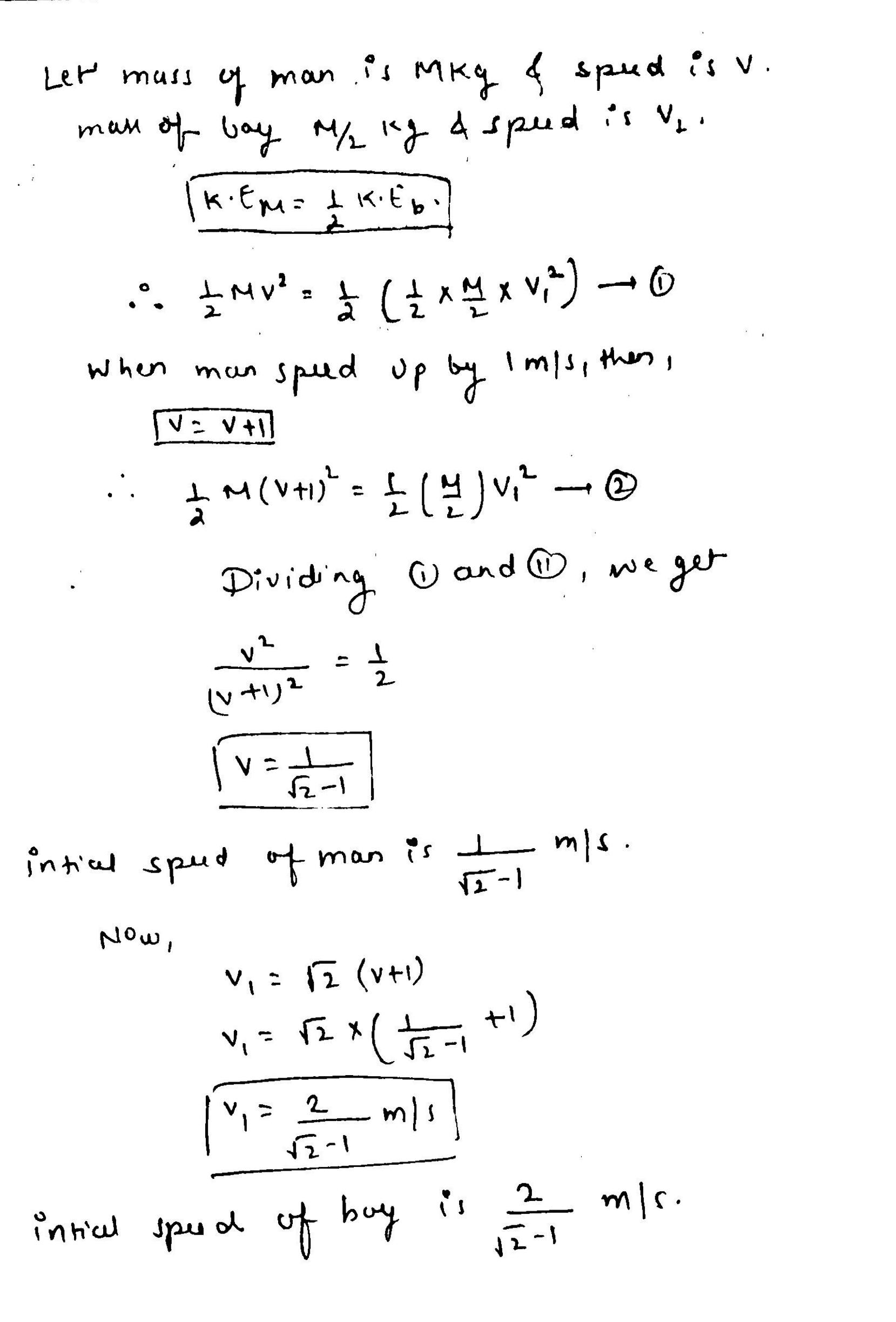Work,Energy And Power - Class 11 Engineering Physics - Extra Questions
A particle moves from a point $$\vec{r_1} = (2 \hat{i} + 3 \hat{j})$$ to another point $$\vec{r_2} = (3 \hat{i} + 2 \hat{j})$$ during which a certain force $$\vec{F} = (5 \hat{i} + 5 \hat{j})$$ acts on it. Calculate work done by the force on the particle during this displacement.
Force ,F= $$6{x^2} + 4x + 7$$. If $$x = 0$$ to $$x=2$$ ,calculate W.D.
Define the following and give one example.
Hybrid rocket propellants.
Spring of force content 100N/m is extended to 240 cm and released. Find out the work done when the extension has reduced to 10 cm.
A particle moves along X -axis from $$x=0$$ to $$x=1m$$ under the influence of a force given by $$F=3x^2+2x-10$$. Work done in the process is
A string can bear a maximum tension of $$3.16kg-wt$$. What maximum number of revolutions per second can be made by a stone of mass $$49g$$ tied to one end of a $$1m$$ long piece of this string so that the string may not break? ($$\pi =22/7$$)
A single force acts on a 3.0 kg particle-like object whose position is given by $$x = 3.0 t - 4.0 t^2 + 1.0 t^3$$, with x in meters and t in seconds. Find the work done by the force from t = 0 to t = 4.0 s.
Fill in the blanks
Work done when a body of mass 100 kg lifted up to a height of 1 mater is ..........
Show that a force that does no work must be a velocity deependent force.
An object of mass 1000 kg is traveling with a velocity 72 km/h. Calculate the work done to bring it rest.
Estimate the work done on an object of mass 80 kg to change its velocity from 5m /s to 10 m /s.
A 20 kg object is being lifted through a height of ______ m when 484 J of work is done on it.
What should be the change in velocity of a body, if its mass is increased by four times for the same K.E of the body?
Calculate the work done to raise a body of the mass $$30 kg$$ to a height of $$ 50 m$$ $$(g = 10 m s^{-2})$$
Two bodies A and B of equal masses are kept at heights of h and 2h respectively. What will be the ratio of their potential energy?
Compute the work which must be performed (in $$Kgf-m$$) to slowly pump water out of a hemispherical reservoir of radius $$R=0.6 m$$
A spring does not obey Hooke's law. Rather it follows, $$F = kx - bx^2 + cx^3$$. If the spring has natural length $$l$$ and compressed length $$l'$$ then find the work done.
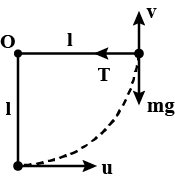
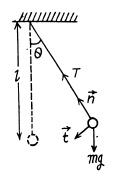
A bob of mass $$m$$ is suspended from point $$O$$ by a massless string of length $$l$$ as shown. At the bottommost point it is given a velocity $$\displaystyle u= \sqrt{12gl}$$ for $$l=1m$$ and $$m=1 kg$$, match the following two columns when string becomes horizontal $$\displaystyle \left ( g= 10ms^{-2} \right )$$
Given : $$u = \sqrt{12 gl}$$ $$m = 1 kg$$ $$l =1$$ m $$g =10 m/s^2$$
Let the velocity of the bob be $$v$$ when the string becomes horizontal.
Using work-energy theorem : $$W =\Delta K.E$$
$$\therefore$$ $$-mgl = \dfrac{1}{2}mv^2 - \dfrac{1}{2}mu^2$$
OR $$-2 gl = v^2 - (12 gl)$$ $$\implies v =\sqrt{10 gl}$$
$$\therefore$$ $$v = \sqrt{10 \times 10 \times 1} =10$$ m/s
Radial acceleration, $$a_r = \dfrac{v^2}{l} = \dfrac{10^2}{1} =100$$ $$m/s^2$$
Tension in the string, $$T = ma_r =1 \times 100 = 100$$ $$N$$
Tangential acceleration, $$a_t = mg =1 \times 10 = 10$$ $$N$$
$$\therefore$$ Total acceleration, $$a = \sqrt{a_r^2 + a_t^2} =\sqrt{(100)^2 + (10)^2} =10 \sqrt{101} = 100.5$$ $$m/s^2$$
Find work done by a force $$\vec{F} = x \hat{i} + xy \hat{j}$$ acting on a particle to displace it from point O(0, 0) to C(2, 2).
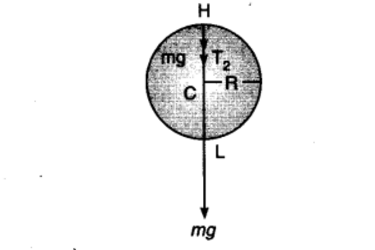
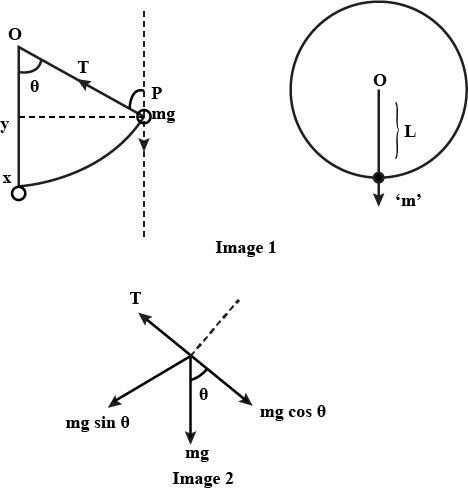
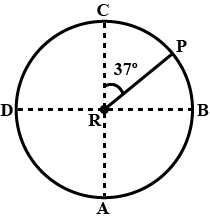
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R.The net forces at the lowest and highest points of the circle directed vertically downwards are : [Choose the correct alternative]
| Lower Point | Highest Point | |
| a. | mg - $$T_1$$ | mg + $$T_2$$ |
| b. | mg + $$T_1$$ | mg - $$T_2$$ |
| c. | mg + $$T_1 - (mv^2_1) / R$$ | mg - $$T + (mv^2_1) / R$$ |
| d. | mg - $$T_1 - (mv^2_1) / R$$ | mg + $$ T_2 + (mv^2_1) / R$$ |
In the given figure shown here $$L$$ and $$H$$ show the lowest and highest point respectively.
At point L: $$T_1$$ acts towards the centre of the circle and $$mg$$ acts vertically downwards.
Now net force on the stone at the lowest point in the downward direction $$=mg-T_1$$
At the point : Both $$T_2$$ and $$mg$$ act vertically downward towards the centre of the vertical circle.
Again the net force on the stone at the highest point in the downward direction $$=T_2+ mg$$
Hence option (a) is the correct alternative.
A molecule in a gas container hits a horizontal wall with speed 200 m $$s^{-1}$$ and angle $$30^0$$ with the normal, and rebounds with the same speed. Is momentum conserved in the collision ? Is the collision elastic or inelastic ?
An object of mass, m is moving with a constant velocity, $$v$$. How much work should be done on the object in order to bring the object to rest?
Certain force acting on a $$20\ kg$$ mass changes its velocity from $$5\ ms^{-1}$$ to $$2\ ms^{-1}$$. Calculate the work done by the force.
Calculate the work required to be done to stop a car of $$1500\ kg$$ moving at the velocity of $$60\ km/h$$?
A force is applied on a body of mass $$20 kg$$ moving with a velocity of $$40 m{s}^{-1}$$. The body attains a velocity of $$50 m{s}^{-1}$$ in $$2$$ seconds. Calculate the work done to attain this velocity.
A moving body weighing $$400N$$ possesses $$500 J$$ of kinetic energy. Calculate the velocity with which the body is moving. $$(g= 10 ms^{-1})$$
Define kinetic energy.
You did $$150 \ joules$$ of work by lifting a $$120 \ Newton$$ backpack.
a) How high did you lift the backpack?
b) How much did the backpack weigh in pounds?
b) How much did the backpack weigh in pounds?
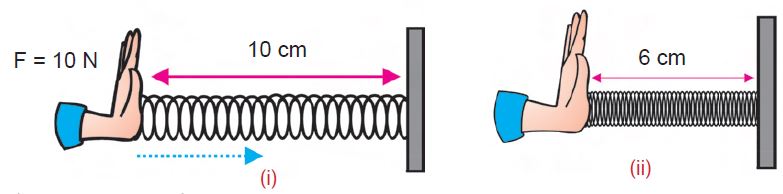
Look at the two diagrams given below. Calculate the work done in compressing each spring completely, assuming that the force applied remains constant.
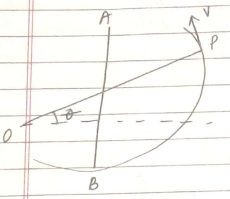
A particle is suspended vertically from a point O by an inextensible massless string of length L. A vertical line AB is at a distance $$\displaystyle{L}{8}$$ from O as shown in figure. The object is given a horizontal velocity u. At some point, its motion ceases to be circular and eventually the object passes through the line AB. At the instant of crossing AB. Its velocity is horizontal. Find u.
The particle has circular path before it passes $$AB$$ second time during its upward motion. Let the particle have circular path at $$'P'$$ and $$V$$ be its velocity at $$P$$.
Applying conservation of energy at $$P$$ and at the lowest point gives:
$$\cfrac { 1 }{ 2 } m{ u }^{ 2 }=\cfrac { 1 }{ 2 } m{ v }^{ 2 }+mgL\left( 1+\sin { \theta } \right) $$
At point $$P$$
$$T+mg\sin { \theta } =\cfrac { m{ v }^{ 2 } }{ 2 } $$
and when $$T=0$$
$$2g\sin { \theta } ={ v }^{ 2 }$$
After moving in a circular path, the particle moves along a parabolic trajectory. Since the velocity of the particle when it crosses $$AB$$ is horizontal. Therefore, it is passing through its highest point in the parabolic path. Thus, half of the range of this parabolic path $$Lcos\theta=\cfrac{L}{8}$$
Projection angle of the particle at $$P$$
$$=90°-\theta $$
$$\therefore$$ minimum range
$$=\cfrac { { v }^{ 2 }\sin { 2\left( 90-\theta \right) } }{ g } \\ \therefore \cfrac { 1 }{ 2 } \cfrac { { v }^{ 2 }\sin { 2\left( 90-\theta \right) } }{ g } =L\cos { \theta } -\cfrac { L }{ 8 } $$
$$\Rightarrow \cos { \theta =\cfrac { 1 }{ 2 } } \Rightarrow \theta =60°$$
Using the above equations:
$$u=\sqrt { \left( \cfrac { 4+3\sqrt { 3 } }{ 2 } \right) gL } $$
A particle is moving along a vertical circle of radius R. The velocity of particle at P will be (assume critical condition at C).
$$T-mg\cos\theta=\cfrac{mV^2}{R}$$
Assuming critical condition:
$$\implies T_C=0$$
$$\implies \cfrac{mV^C}{R}+mg\cos(180^o)=0$$
$$\implies V_C^2=gR$$
$$\implies V_C=\sqrt{gR}$$
From energy conservation:
$$E_A=E_C$$
$$\implies \cfrac{1}{2}mV_A^2=\cfrac{1}{2}mV_C^2+2mgR$$
$$\implies \cfrac{V_A^2}{2}=\cfrac{gR}{2}+2gR$$
$$\implies V_A=\sqrt{5gR}$$
Similarly, from energy conservation:
$$E_A=E_P$$
$$\implies \cfrac { 1 }{ 2 } mV_{ A }^{ 2 }=\cfrac { 1 }{ 2 } mV_{ P }^{ 2 }+(mgR+mgRcos 37^ o)$$
$$\implies \cfrac{5gR}{2}=\cfrac{1}{2}V_P^2+gR+0.8gR$$
$$\implies \cfrac{1}{2}V_P^2=\cfrac{5}{2}gR-gR-0.8gR$$
$$\implies \cfrac{1}{2}V_P^2=0.7gR$$
$$\implies V_P^2=1.4gR$$
$$\implies V_P=1.18\sqrt{gR}$$
A particle of mass $$m$$ moving with a speed $$v$$ hits elastically another stationary particle of mass $$2m$$ in a fixed smooth horizontal circular tube of radius $$r$$. Find the time when the next collision will take place?
By momentum conservation.
$${ v }_{ 1 }=\dfrac { 2m-m }{ 3m } v=\dfrac { v }{ 3 } \\ { v }_{ 2 }=\dfrac { 2m }{ 3m } v=\dfrac { 2 }{ 3 } v$$
after collision relatiive velocity $$={ v }_{ 1 }+{ v }_{ 2 }$$
$$=\dfrac { v }{ 3 } +\dfrac { 2v }{ 3 } =v$$
Now time taken to cover 2$$\pi$$ r distance is time of next collision.
$$t = \dfrac{2\pi r}{v}$$
Two springs have force constants $$k_{1}$$ and $$k_{2}(k_{1} > k_{2})$$. On which spring is more work done, if (i) they are stretched by the same force and (ii) they are stretched by same distance?
The bob of a simple pendulum of length $$1m$$ has mass $$100g$$ and a speed of $$1.4m/s$$ at the lowest point in its path. Find the tension in the string at this instant.
A particle of mass $$m$$ is fixed to one end of a light rigid rod of length $$l$$ and rotated in a vertical circular path about its other end. The minimum speed of the particle at its highest point must be:
Since, the string has to be taut for the mass to complete its circular motion, the tension in the string at its topmost point can be at minimum equal to zero.
$$\therefore T=\cfrac{mV_B^2}{l}+mg\cos(180^o)=0$$
$$\implies \cfrac{mV_B^2}{l}=mg$$
$$\implies V_B^2=gl$$
$$\implies V_{B_{min}}=\sqrt{gl}$$
This is the minimum speed the string of rod, must have at its highest point.
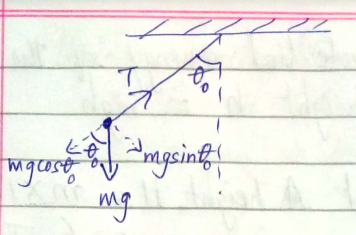
Suppose the amplitude of a simple pendulum having a bob of mass $$m$$ is $${ \theta }_{ 0 }$$. Find the tension in the string when the bob is at its extreme position.
The velocity is zero at the extreme position. The particle reaches this extreme position stays there for a very short period of time and comes back downwards due to gravitational force. In that short period of time, the force of tension is exactly balanced by the $$mg cos{ \theta }_{ 0 }$$ component.
$$\therefore T=mgcos{ \theta }_{ 0 }$$
Two capacitors $${ C }_{ 1 }$$ and $${ C }_{ 2 }$$ have equal amount of energy stored in them. What is the ratio of potential differences across their plates.
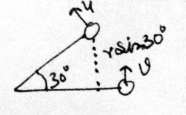
A stone tied to an inextensible string of length $$l = 1 \,m$$ is kept horizontal. If it is released, find the angular speed of the stone when the string makes an angle $$\theta =30^o$$ with horizontal.
When the stone is released, it moves down executing a circular motion. At any instant, the stone accelerates towards (w.r.t.) the center of its revolution 0, that is, centripetal acceleration a, and simultaneously accelerates down with an acceleration, that is, gravitational acceleration g; $$\vec{a}_r = \omega ^2r$$. Resolving $$\vec{a}_r$$, and along the tangent, we obtain the tangential acceleration of the stone as $$a_t =g\,\cos\,\theta$$
Angular acceleration, $$\displaystyle \alpha = \frac{a_t}{r}$$
$$\displaystyle \Rightarrow\,\,\,\alpha = \frac{g\,\cos\,\theta}{l} (since\,r=l)$$
Putting $$\displaystyle \alpha = \frac{\omega d \omega}{d \theta}$$, we obtain $$\displaystyle \frac{\omega d \omega}{d \theta} = \frac{g\,\cos\,\theta}{r}$$
$$\Rightarrow \,\,\,\omega d \omega =(g/l)cos\,\theta\,d\theta.$$
Integrating both the sides, we obtain
$$\displaystyle \int_{0}^{\omega} \omega d \theta = \frac{g}{l} \int_{0}^{\theta} \cos\,\theta \,d\theta$$
$$\displaystyle \Rightarrow \,\,\,\ \frac{\omega ^2}{2} = \frac{g}{l} \sin\,\theta \,or\,\omega =\sqrt {\frac{2g}{l} \sin\,\theta}$$
Putting $$l = 1\,m$$ and $$\theta = 30^o$$, we obtain
$$\displaystyle \omega =\sqrt{\frac{2(10)\sin\,30^o}{(1)}}= \sqrt{10} \,\,\Rightarrow \,\omega\,\cong 3.1\,rad\,s^{-1}$$
The displacement $$x$$ of a body of mass 1 kg on smooth horizontal surface as a function of time t is given by $$x=\dfrac { { t }^{ 3 } }{ 3 } $$ (where x is in metres and t is in seconds). Find the work done by the external agent for the first one second.
A bicycle chain of length 1.6 m and of mass 1 kg is lying on a horizontal floor. What is the work done in lifting it with one end touching the floor and the other end 1.6 m above the floor?
(take g=$${ 10 }ms^{ -2 }$$)
An object of mass $$0.5$$ kg attached to a rod of length $$0.5$$ m is whirled in a vertical circle at constant angular speed. If the maximum tension in the string is $$5$$ kg wt., Calculate
(i) speed of stone
(ii) maximum number of revolutions it can complete in a minute.
What is work done in lifting a body of mass $$20$$ kg at a height of $$2$$m above the ground? $$(g=10m/s^2)$$
Two springs $$A$$ and $$B$$ are identical but $$A$$ is harder than $$B\ (k_{A} > k_{B})$$. On which spring more work will be done if: (a)They are stretched through the same distance (b)They are stretched by same force?
A stone of mass $$1kg$$ is tied to a light string of length $$l=10m$$ is whirling in a circular path in the vertical plane. If the ratio of maximum to minimum tensions in the string is $$3$$, find the speeds of the stone at the lowest and highest points.
$${ T }_{ H }+mg=\dfrac { m{ v }^{ 2 } }{ r } \\ { T }_{ L }-mg=\dfrac { m{ u }^{ 2 } }{ r } \\ Energy\quad conservtion\\ \dfrac { 1 }{ 2 } m{ u }^{ 2 }=\dfrac { 1 }{ 2 } m{ v }^{ 2 }+mg(2r)\\ \dfrac { { T }_{ L } }{ { T }_{ H } } =\dfrac { 3 }{ 1 } \\ \dfrac { \dfrac { m{ v }^{ 2 } }{ r } +mg }{ \dfrac { m{ u }^{ 2 } }{ r } -mg } =3\\ as\quad { u }^{ 2 }={ v }^{ 2 }+4gr\\ \dfrac { { v }^{ 2 }+4gr+gr }{ { v }^{ 2 }-gr } =3\\ { v }^{ 2 }+5gr=3{ v }^{ 2 }-3gr\\ { 2v }^{ 2 }=8gr\\ { v }^{ 2 }=4gr\\ v=\sqrt { 4\times 10\times 10 } =20m/sec\\ u^{ 2 }={ v }^{ 2 }+4gr\\ =800\\ u=20\sqrt { 2 } m/sec$$
Position-time variation of a particle of mass $$1\ kg$$ is $$x=(2t^{3}+3)m$$. Calculate the work done by the force in first $$2\ seconds$$ .
A particle moves along the x-axis from $$x=0$$ to $$x=5m$$ under the influence of a force $$F$$ (in N) given by $$F=3{x}^{2}-2x+7$$. Calculate the work done by this force
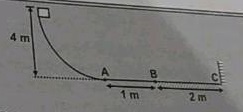
A block of mass m= 0.1 kg is released from a height of 4 m a curved smooth surface. On the horizontal surface path AB is smooth and path BC offers coefficient of friction $$\mu =0.1$$ . If the impact of block with vertical wall at C be perfectly elastic, find the total distance covered by the block on the horizontal surface before coming to rest. (Take g=10$$\frac{m}{s^{2}}$$)
Two identical copper spheres $$A$$ and $$B$$ equally charged, repel each other with a force of $$4\times {10}^{-5}N$$. A third similar copper sphere $$C$$ carrying no charge is now brought into contact with $$A$$ and placed mid-way between $$A$$ and $$B$$.what force would $$C$$ experience? $$(4\times {10}^{-5})N$$
(Comment: charge on $$A$$ and $$C$$ is $$q/2$$ each and on $$B$$ it is $$q$$. It $$r$$ is the distance between $$A$$ and $$B$$, $$q/r$$ is $$2\times {10}^{-7})$$
in the first situation $$F=\dfrac{kq^2}{r^2}=4\times10^{-5}N$$
Now in the 2nd situation when identical sphere $$C$$ touched with sphere $$A $$ then there is transfer of charge from $$A$$ to $$C$$ till both have same potential , in this situation both will acquired equal charge this gives charge on both sphere will be $$q/2$$ (since total charge should be equal to $$q $$due to conservation of charge )
so, from the figure we can see that net force on sphere $$C$$ will be effective of both by $$A$$ and $$B$$
$$F_C=\vec F_{CA}+\vec F_{CB}$$
$$=\dfrac{kq^2/4}{r^2/4}-\dfrac{k(q/2)(q)}{r^2/4}$$
$$=\dfrac{kq^2}{r^2}(1-2)$$
$$=-\dfrac{kq^2}{r^2}=-4\times10^{-5}N$$
this shows that force experienced by sphere C will be $$4\times10^{-5}N$$
Calculate the kinetic energy of an object weighing $$600 \ kg$$ moving at a velocity of $$30 \ m/s$$
A $$4\ kg$$ swing in a vertical circle at the end of the chord $$1\ m$$ long. Find out the maximum speed at which it can swing if chord can sustain maximum tension of $$140\ N$$.
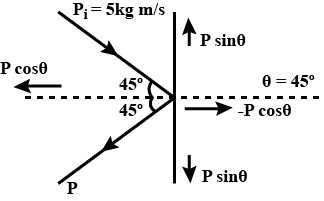
A ball moving with a momentum of $$5kgm/s$$ strikes against a wall at angle of $${45^ \circ }$$ and is deflected at the same angle. Calculate the change in momentum.
Given,
$$P=5 kg m/s$$
$$\theta=45^0$$
from the figure given above, there is no change in perpendicular component and cancel each other.
The initial momentum along the x-axis,
$$P_i=P cos\theta $$
The final momentum along the x-axis,
$$P_f=-Pcos\theta$$
So, change in momentum,
$$\Delta P=P_f-P_i$$
$$\Delta P=-2Pcos\theta$$
$$\Delta P= -2\times 5\times cos45^0$$
$$\Delta P=-7.071 kg m/s$$
A force $$F={x}^{2}+2x+1$$ acts on a particle in the x direction, where $$F$$ is in newton and $$x$$ in metre. Find the work done by this force during a displacement from $$x=-1m$$ to $$x=2.0m$$
An object is displaced from position vector $$r_{1} = (2\hat{i} + 3\hat{j})\ m$$ to $$r_{2} = (4\hat{i} + 6\hat{j})\ m$$ under a force $$F = (3x^2 \hat{i} + 2y\hat{j})\ N$$. Find the work done by this force.
A particle is moving in a circular path of radius a under the action of an attractive potential $$U=-\dfrac{K}{2r^2}$$. Its total energy is
A position-dependent force $$f=7-2x+3x^2$$ newton acts on a small body of mass $$2$$kg and displaces from $$x=0$$ to $$x=5$$. Calculate the work done by the force.
Find the ratio of the weights, as measured by a spring balance, of a $$1\,kg$$ block of iron and a $$1\,kg$$ block of wood.
Density of iron = $$7800\,kg/m^3$$, density of wood = $$800\,kg/m^3$$ and density of air= $$1.293\,kg\,m^3$$
When the bucket filled with water is resolved fast in a vertical circle, the water does not fall even when the bucket is inverted.
The relation between displacement $$x$$ and time $$t$$ for a body of mass $$2 Kg$$ moving under the action of a force is given by $$x=\dfrac{t^3}{3}$$, where $$x$$ is in meter and $$t$$ in second, calculate the work done by the body in first $$2$$ seconds.
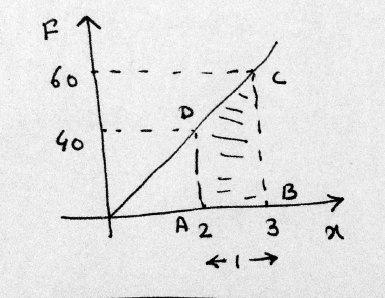
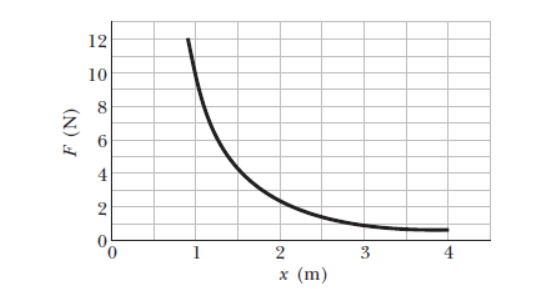
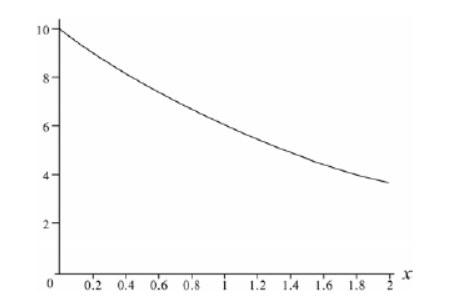
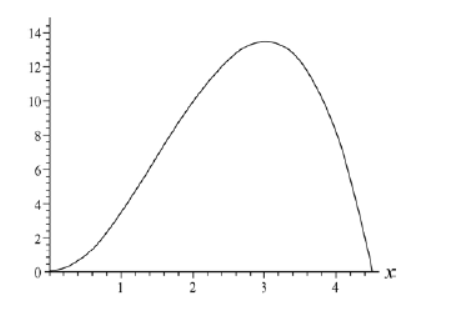
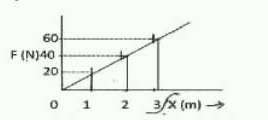
Calculate the work done in moving the object from $$x=2$$ to $$x=3$$ m from the given graph.
Work done = Area under F-x curve
Work done = Area of ABCD
$$ = \cfrac{1}{2} \times 1 \times (40+60)$$
$$ =50J$$
A 2 kg block slides on a horizontal floor with a speed of 4 m/s. It strikes an uncompressed spring, and compresses it till the block is motionless. The kinetic friction force is 15 N and spring constant is 10,000 N/m. The spring compresses by :-
The work done by an applied variable force $$F=x+x^3$$ from $$x=0m$$ to $$x=2m$$,where $$x$$ is displacement ,is
If force on a block is $$F=8/x^2$$ where $$x$$ is displacement ,then find total work done in moving block from from $$x=2m$$ to $$x=6m$$
Two ball having masses $$m$$ and $$2m$$ are fastened to two light strings of same length $$l$$ (figure 9-E18). The other ends of the strings are fixed at $$O$$. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocities of the balls just after their collision. (b) How high will the ball rise after the collision?
Explain why water stored in a dam has potential energy.
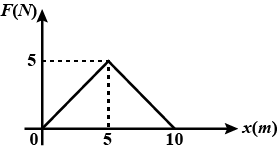
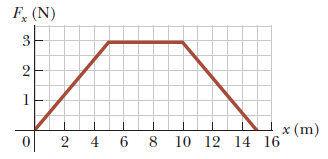
A body of mass $$2$$ kg starts with an initial velocity $$5$$ m/s. If the body is acted upon by a time dependent force (F) as shown in figure, then work done on the body in $$20$$ s is?
A car moves on a flat circular track of $$200$$ m radius with a constant speed of $$20$$ if the car weighs $$400$$ kg the centripetal force acting on the car is:
A stone of mass 1 Kg, tied to the end of a string of length 30cm, is whirled in a vertical circle such that its angular velocity when the string is horizontal is 10 rad/s. If the tension in the string at that instant is 5T, find the value of T
A stone is tied to a string of length l and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is?
You may have seen in a circus a mototcyclist driving in vertical loops inside a 'death well' (a hollow spherical chamber with holes, so the spectators can watch from outside).Explain clearlywhy the mototrcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is $$25m$$. ?
Find the velocity of a body of mass $$100g$$ having a kinetic energy of $$20J$$.
Seen the displacement X and time t for a body of mass 2 Kg moving $$ x=\dfrac { t^ 3 }{ 3 } $$, where x is in meter and t in sec. Calculate the work done by body in first 2 second.
A stone of mass 1 kg is tied up with an inextensible string of length l = 10/3 m. It is rotated in a vertical circle of l radius. If a ratio of maximum and minimum tension in the string is 4 and the value of g is 10$$ m/s^2$$ then calculate a speed of stone at the highest point of a circle.
A porter lift a luggage of $$15\ kg$$ from the ground and puts it on her head $$2\ m$$ above the ground. Calculate the work done by her on the luggage? Take $$g=10\ ms^{-2}$$
A pendulum bob has a speed of $$3ms^{-1}$$ at its lowest position. The pendulum is $$0.5m$$ long. What is the speed of the bob, when the length makes an angle of $$60^\circ$$ to the vertical? $$(g = 10ms^{-2})$$
A position dependent force $$ F = 7-2x + 3x^2 $$ newton (where x is in meter) on a small body of mass 2 Kg & displace it from $$ x = 0$$ to $$ x = 5 $$ m. Calculate the work done.
A force that object A exerts on object B is observed over a 10 second interval,as shown on the graph.How much work did object A do during that 10 s?
The car $$A$$ of mass $$1500kg$$ travelling at $$40m/s$$ collides with another car $$'B'$$ of mass $$1250kg$$ travelling at $$25m/s$$ in the same direction. After collision the velocity of car $$'A'$$ becomes $$30m/s$$. calculate the velocity of car $$'B'$$ after the collision.
A sphere is suspended by a thread of length L. What minimum horizontal velocity to has to be imparted to it so that if completes a full vertical revolution?
Two objects having equal masses are moving with uniform velocities of 2 m/s and 6m/s respectively Calculate the ratio of their kinetic energies.
The bob of a simple pendulum at rest position is given a velocity V in horizontal direction so that bob describes verticle circle of radius equal to length of pendulum L . If the tension in string is 4 times weight of of bob when the string is horizontal , the velocity of bob :
A ball of mass 100 g is suspended a string 40 cm long. Keeping the string taut , the ball describes a horizontal circle of radius 10 cm Find the angular speed.
If the velocity of the body increases 3 times how does its K.E changes?
A boy weighing $$50\, kg$$ climbs up a vertical height of $$100\,m$$. Calculate the amount of work done by him. How much potential energy does he gain ($$g=9.8\, m/{s}^{2}$$)
A block of mass $$m$$ welded with a light spring of stiffness $$k$$ is in equilibrium on an smooth inclined plane with angle of inclination $$\theta .$$ If a variable external force is applied slowly till the spring comes to its relaxed position, find the work done by spring by spring force.
ferring to the $$FBD$$ as shown in figure
At equilibrium
$$Kx=mg\sin \theta$$
$$x=\cfrac{mg\sin ]theta}{K}$$
So, $${U}_{i}=\cfrac{K{x}^{2}}{2}=\cfrac{{m}^{2}{g}^{2}\sin ^{ 2 }{ \theta } }{2K}$$
At relaxe position
$${U}_{f}=K{(0)}^{2}=0$$
As the mass is moved slowly
$$\Delta KE=0$$ so
spring $$=-\Delta U$$
$$=-{U}_{f}+{U}_{i}=\cfrac{{m}^{2}{g}^{2}\sin ^{ 2 }{ \theta } }{2K}$$
If the speed of a body is halved, what will be the change in its kinetic energy?
Certain force acting on a $$20\ kg$$ mass changes its velocity from $$5 m/{s}$$ to $$2 m/{s}$$. Calculate the work done by the force.
A man weighing 70 kg carries a weight of 10 kg to top of a tower 100 m high. Calculate the work done by the man
What is Kinetic Energy?
A car of mass $$2000\ kg$$ changes its speed from $$18\ km/h$$ to $$90\ km/hr$$. Find the work done by the engine.
What is the work done to increase the velocity of a car from $$30 \ km { h }^{ -1 }$$ to $$60 \ km { h }^{ -1 }$$, if the mass of the car is $$1500 \ kg$$?
To what height should a box of mass 150 kg be lifted, so that its potential energy may become 7350 joules?$$\left( {g = 9.8\;m/{s^2}} \right).$$
A ball of mass $$100g$$ is thrown with a speed of $$15$$ m/s. Calculate its kinetic energy.
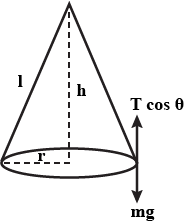
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass of 150g at its free end. If the mass is revolved in a horizontal circle of radius 0.2m around a vertical axis, calculate tension in the string $$\left ( g=9.8m/s^{2} \right )$$
$$l = 120cm = 1.2m$$
$$r = 0.2m$$
$$m = 150gm = 0.15kg$$.
tension in supporting thread (T)
By pythagoras theorem
$$l^2 = r^th^2 = Dh^2 = l^2-r^2$$
$$Dh^2 = 1.44 - 0.04 = 1.4$$
$$\therefore h = 1.183m$$.
The weight of Bob is balanced by vertical component of tension T
$$\therefore T \cos \theta = mg$$
$$\cos \theta =\dfrac{h}{l} = \dfrac{1.183}{1.2} = 0.9858$$
$$\therefore T = \dfrac{mg}{\cos \theta} = \dfrac{0.15\times 9.3}{0.9858} = 1.491N$$.
Two masses $$m$$ and $$2m$$ are dropped from height $$h$$ and $$2h$$. On reaching the ground, which will have greater kinetic energy and why?
A force 30 N is applied at the small plunger which moves down 10 m then work done by the applied force is
A bullet of mass 40 g has its kinetic energy equal to 200 J. Find the speed of the bullet.
Name the form of energy stored in a wound up spring of a watch .
What happens to potential energy of a body when its height is doubled?
In loading a trunk, a man lifts boxes of 100 N each through a height f 1.5 m,
(a) How much work does he do in lifting oe box?
(b) How much energy is transferred when one box is lifted ?
(c) if the man lifts 4 boxes per minutes, at what power is he working ? $$(g = 10 m s^{-2})$$
Find the mass of a body which has $$10\, J$$ of kinetic energy while moving at a speed of $$3\, m/s$$.
What is the kinetic energy of a body of mass $$1\,kg$$ moving with a speed of $$2\,m/s$$ ?
Write an expression for the kinetic energy of a body of mass m moving with a velocity v.
State whether the following statement is true or false :
The potential energy of a body of mass $$1\,kg$$ kept at a height of $$1\,m$$ is $$1\,J.$$
How does the kinetic energy of a moving body depends on its
a) speed
b) mass
On what factors does the kinetic energy of a body depend ?
Which would have a greater effect on the kinetic energy of an object: doubling the mass or doubling the velocity ?
A weightlifter is lifting weights of mass $$200\,kg$$ up to a height of $$2$$ meters. If $$g = 9.8\,m/s^2 ,$$ calculate :
a) potential energy acquired by the weight
b) Work done by the weightlifter
How fast should a man of $$50\,kg$$ run so that his kinetic energy will be $$625\,J$$ ?
If a car of mass $$1200 \ kg$$ is moving along a highway at $$120 \ km/h$$, what is the car’s kinetic energy as determined by someone standing alongside the highway?
What is the spring constant of a spring that stores $$25\, J$$ of elastic potential energy when compressed by $$7.5 \,cm$$ ?
The angular acceleration of a wheel is $$ \alpha =6.0t^{4}-4.0t^{2} $$, with $$ \alpha $$ in radians per second-squared and t in seconds. At time t=0, the wheel has an angular velocity of + 2.0 rad/s and an angular position of +1.0 rad. Write expressions for (a) the angular velocity (rad/s) and (b) the angular position (rad) as functions of time (s).
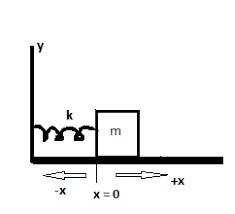
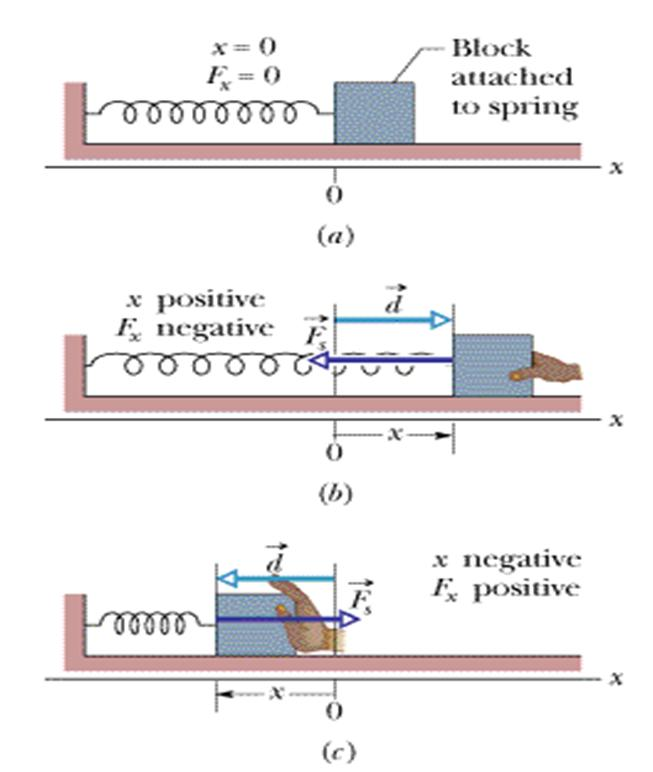
A spring and block are in the arrangement of given figure.When the block is pulled out to $$x = +4.0 \ cm$$, we must apply a force of magnitude $$360 \ N$$ to hold it there. We pull the block to $$x = 11 \ cm$$ and then release it. How much work does the spring do on the block as the block moves from $$x_i = + 5.0 \ cm$$ (a) $$x = +3.0 \ cm$$, (b) $$x = -3.0 \ cm$$, (c) $$x = -5.0 \ cm$$, and (d) $$x = -9.0 \ cm$$?
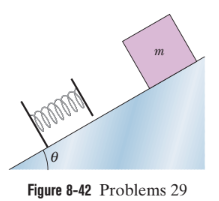
In Fig. $$8-42$$, a block of mass $$m = 3.20\,kg$$ slides from rest a distance $$d$$ down a frictionless incline at angle $$\theta = 30.0^\circ$$ where it
runs into a spring of spring constant $$431 \,N/m.$$ When the block momentarily stops, it has compressed the spring by $$21.0\, cm.$$ What are (a) distance $$d$$ and (b) the distance between the point of the first blockspring contact and the point where the blocks speed is greatest?
How much work is done by a force $$\vec{F} = (2x \ N)\hat{i} + (3 \ N)\hat{j}$$, with x in meters, that moves a particle from a position $$\vec{r_i} = (2 \ m)\hat{i} + (3 \ m) \hat{j} $$ to a position $$\vec{r_f} = -(4 \ m)\hat{i} - (3 \ m)\hat{j}$$?
A can of sardines is made to move along the x-axis from x = 0.25 m to x = 1.25 m by a force with a magnitude given by $$F = exp(-4x^2)$$, with x in meters and F in newtons. (Here exp is the exponential function.). How much work is done on the can by the force?
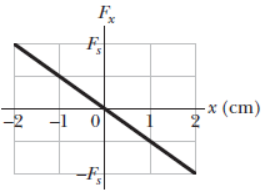
Figure gives spring force $$F_x$$ versus position $$x$$ for the spring–block arrangement. The scale is set by $$F_s = 160.0 \ N$$ We release the block at $$x = 12 \ cm$$. How much work does the spring do on the block when the block moves from $$x_i = +8.0 \ cm$$ to (a) $$x = +5.0 \ cm$$, (b) $$x = -5.0 \ cm$$, (c) $$x = -8.0 \ cm$$, and (d) $$x = -10.0 \ cm$$?
During spring semester at MIT, residents of the parallel buildings of the East Campus dorms battle one another with large catapults that are made with surgical hose mounted on a window frame. A balloon filled with dyed water is placed in a pouch attached to the hose, which is then stretched through the width of the room. Assume that the stretching of the hose obeys Hookes law with a spring constant of $$100 \ N/m$$. If the hose is stretched by $$5.00 \ m$$ and then released, how much work does the force from the hose do on the balloon in the pouch by the time the hose reaches its relaxed length?
An automobile with passengers has weight $$16 \,400 \,N$$ and is moving at $$113\, km/h$$ when the driver brakes, sliding to a stop. The frictional force on the wheels from the road has a magnitude of $$8230\,N$$. Find the stopping distance.
A $$ 91 \,kg $$ man lying on a surface of negligible friction shoves a $$ 68 \,g $$ stone away from himself, giving it a speed of $$ 4.0\, m/s.$$ What speed does the man acquire as a result?
A $$ 6100\, kg $$ rocket is set for vertical firing from the ground. If the exhaust speed is $$ 1200\, m/s,$$ how much gas must be ejected each second if the thrust (a) is to equal the magnitude of the gravitational force on the rocket and (b) is to give the rocket an initial upward acceleration of $$ 21\, m/s^2 $$ ?
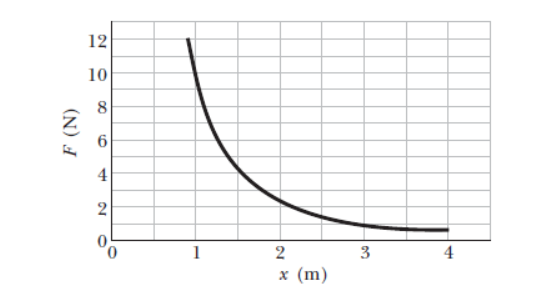
As a particle moves along an x axis, a force in the positive direction of the axis acts on it. Figure shows the magnitude F of the force versus position x of the particle.The curve is given by $$F = a/x^2$$ with $$a = 9.0 \ N.m^2$$. Find the work done on the particle by the force as the particle moves from x = 1.0 m to x = 3.0 m by (a) estimating the work from the graph (b) integrating the force function.
(a) To estimate the area under the curve between x = 1 m and x = 3 m (which should yield the value for the work done),
one can try “counting squares” (or half-squares or thirds of squares) between the curve and the axis.
Estimates between 5 J and 8 J are typical for this (crude) procedure.
(b) Since we know that,
$$\int_{1}^{3} \ \frac{a}{x^2} dx $$
$$= \frac{a}{3} - \frac{a}{1} = 6 \ J$$
where $$a = –9 \ N·m^2$$ is given in the problem statement.
A $$ 140 \,g $$ ball with speed $$ 7.8 \,m/s $$ strikes a wall perpendicularly and rebounds in the opposite direction with the same speed. The collision lasts $$ 3.80\, ms.$$ What are the magnitudes of the (a) impulse and (b) average force on the wall from the ball during the elastic collision?
Calculate the kinetic energy of a body of mass $$50 \,kg$$ moving with a velocity of $$50 \,cms^{-1}$$
A $$ 4.0 \,kg $$ mess kit sliding on a frictionless surface explodes into two $$ 2.0\, kg $$ parts: $$ 3.0\, m/s, $$ due north, and $$ 5.0\,m/s, 30^{\circ} $$ north of east .What is the original speed of the mess kit?
A force $$\vec{F}$$ in the positive direction of an x axis acts on an object moving along the axis. If the magnitude of the force is $$F = 10e^{-x/2.0} \ N$$, with x in meters, find the work done by $$\vec{F}$$ as the object moves from x = 0 to x = 2.0 m by (a) plotting F(x) and estimating the area under the curve and (b) integrating to find the work analytically.
(a) The plot of the function (with SI units understood) is shown below.
Estimating the area under the curve allows for a range of answers.
Estimates from 11 J to 14 J are typical.
(b) Evaluating the work analytically , we have
$$W = \int_{0}^{2} \ 10 e^{-x/2} dx $$
$$=-20 e^{-x/2} |_{2}^{0} $$
$$= 12.6 \ J = 13 \ J$$
Numerical integration. A breadbox is made to move along an x axis from x = 0.15 m to x = 1.20 m by a force with a magnitude given by $$F = exp(-2x^2)$$, with x in meters and F in newtons. (Here exp is the exponential function.) How much work is done on the breadbox by the force?
Does a stationary body possess kinetic energy ?
A raindrop of mass $$1.00\ g$$ falling from a height of $$1\ km$$ hits the ground with a speed of $$50\ m/s$$. Calculate the gain in $$K.E.$$ of the drop.
Find the energy possessed by an object of mass $$10 \,kg$$ when it is at a height of $$6m$$ above the ground.
Take, $$g = 9.8 \,ms^{-1}$$
To what height should a body of mass 5 kg be raised so that its potential energy is 490 J?
Take, $$g = 9.8 \,m/s^2$$
A ball is drop from a height of $$10\ m$$. If the energy of the ball reduced by $$40\%$$ after striking the ground, how much height can the ball bounce back?
Name the type of energy (kinetic or potential) possessed by the following:
A stone at rest on the top of a building.
The energy possessed by a body due to its position is called.............. energy.
Two toy-cars $$ A $$ and $$ B $$ of masses $$ 200g $$ and $$ 500g $$ respectively are moving with the same speed. Which of the two has grater kinetic energy?
Name the type of energy (kinetic or potential) possessed by the following:
A stretched rubber band.
Energy possessed by a compressed spring is ......... energy.
Kinetic energy= $$ 1/2 \times mass \times $$ ______ .
Name the type of energy (kinetic or potential) possessed by the following:
A compressed spring.
A cyclist doubles his speed. How will his kinetic energy change: increase, decrease or remain same?
What do you understand by the kinetic energy of a body?
A body of mass m is moving with a uniform velocity u. A force is applied on the body due to which its velocity changes from u to v. How much work is being done by the force.
A car is moving with a speed of $$ 15 km h^{-1} $$ and another identical car is moving with a speed of $$ 30 km h^{-1} $$ . Compare their kinetic energy.
Find the kinetic energy of a body of mass $$1\, kg$$ moving with a uniform velocity of $$10\, m\, s^{-1}$$
If the speed of a car is halved, how does its kinetic energy change?
The potential energy of a body of mass $$ 0.5\ kg $$ increases by $$ 100\ J $$ when it is taken to the top of the tower from the ground. If forces of gravity on $$ 1\ kg $$ is $$ 10\ N $$, what is the height of the tower?
A body of mass $$ 60 $$ kg is moving with a speed $$ 50 ms^{-1}$$ . find its kinetic energy .
It takes $$ 20 s $$ for a girl $$ A $$ to climb up the stairs while girl $$ B$$ takes $$ 15 s $$ for the same job. compare :
$$ (i) $$ : the work done and
$$ (ii) $$ : the power spent by then .
Two bodies of equal masses are moving with uniform velocities $$v$$ and $$2v$$. Find the ratio of their kinetic energies.
A box of weight $$150\, kgf$$ has gravitational potential energy stored in it equal to $$14700\, J$$. Find the height of the box above the ground. (Take $$g = 9.8\, N \,kg^{-1}$$)
A car is running at a speed of $$ 15\, km\, h^{-1}$$ while another similar car is moving at a speed of $$30\, km \,h^{-1}$$. Find the ratio of their kinetic energies.
Name the energy stored when a rubber band is stretched.
Name the form of energy present in the following situations:
(a) stretched bow and arrow
(b) a falling coconut
A machine moves an object of 40 kg mass to 10 m height. Find the amount of work done.
An object is moving with velocity u. Its velocity becomes v when force F is applied on it. If the object covers a distance s during this, then calculate the increase in kinetic energy of object.
Derive the formula for kinetic energy.
Which energy is stored in the spring while winding a clock? In which energy it gets converted when the clock is working?
Stressing the rubber in sling-shot, the………………… energy is stored in it.
Define kinetic energy. Give an example of a body possessing kinetic energy.
A man having a mass of 70kg is riding scooter of mass 80kg. What is the total energy if the velocity of the scooter is 10 m/s?
Three equal masses are placed on three corners of equilateral triangle. What is work done in doing this ?
Will the potential energy increase or decrease in pressing a solid or stretching a wire?
State whether the energy possed in the following is kinetic or potential.
Bird resting on the branch of a tree
What is kinetic energy ? Mention the factors that the kinetic energy of a body depends.
A car of mass $$1500\ kg$$ is moving at a velocity of $$20\ m/s$$. What is its kinetic energy?
_______ is the energy possessed by an object due to its motion.
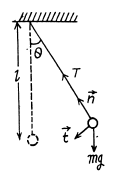
the thread tension at the moment when the vertical component of the sphere's velocity is maximum;
Vertical component of velocity $$v_{y}=v\sin \theta$$
So, $$v_{y}^{2}=v^{2}\sin^{2}\theta=2g l\cos\theta\sin^{2}\theta$$ (using $$1$$)
For maximum $$v_{y}$$ or $$v_{y}^{2}, \dfrac{d(\cos \theta\sin^{2}\theta)}{d\theta}=0$$
which yields $$\cos\theta=\dfrac{1}{\sqrt{3}}$$
Therefore from $$(2) T=3mg\dfrac{1}{\sqrt{3}}=\sqrt{3}mg$$
Calculate the kinetic energy of an athlete of mass 60 kg running with a velocity 10 m /s
$$m=60kg$$
$$v = 10 m/s$$
A bird of mass $$0.5 \ kg$$ is flying at the height of $$5 \ m$$. In this state, if its kinetic energy and potential energy are equal. What is the potential energy of the bird?
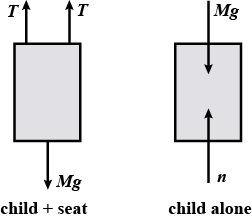
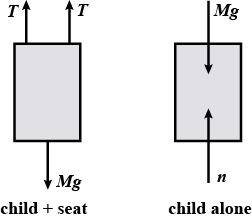
A $$40.0kg$$ child swings in a swing supported by two chains, each $$3.00 m$$ long. The tension in each chain at the lowest point is $$350 N$$. Find (a) the childs speed at the lowest point and (b) the force exerted by the seat on the child at the lowest point. (Ignore the mass of the seat.)
We first draw a force diagram that shows the forces acting on the child-seat system and apply Newton’s second law to solve the problem. The child’s path is an arc of a circle, since the top ends of the chains are fixed. Then at the lowest point the child’s motion is changing in direction: He moves with centripetal acceleration even as his speed is not changing and his tangential
acceleration is zero.
(a) Below figure shows that the only forces acting on the system of child + seat are the tensions in the two chains and the weight of the boy:
$$\sum F=F_{net}=2T-mg=ma=\dfrac{mv^{2}}{r}$$
with
$$F_{net}=2T-mg=2(350N)-(40.0kg)(9.80m/s^{2})=308N$$
solving for $$v$$ gives,
$$v=\sqrt{\dfrac{F_{net}r}{m}}=\sqrt{\dfrac{(308N)(3.00m)}{40.0kg}}=4.81m/s$$
(b) The normal force from the seat on the child accelerates the child in the same way that the total tension in the chain accelerates the child-seat system. Therefore, $$n = 2T = 700 N$$
acceleration is zero.
(a) Below figure shows that the only forces acting on the system of child + seat are the tensions in the two chains and the weight of the boy:
$$\sum F=F_{net}=2T-mg=ma=\dfrac{mv^{2}}{r}$$
with
$$F_{net}=2T-mg=2(350N)-(40.0kg)(9.80m/s^{2})=308N$$
solving for $$v$$ gives,
$$v=\sqrt{\dfrac{F_{net}r}{m}}=\sqrt{\dfrac{(308N)(3.00m)}{40.0kg}}=4.81m/s$$
(b) The normal force from the seat on the child accelerates the child in the same way that the total tension in the chain accelerates the child-seat system. Therefore, $$n = 2T = 700 N$$
Let the mass of the flower pot 15 g and the height of the sunshade 4 m. When the flower pot is on the sunshade, what is its potential energy ? $$(g = 10 m/s^2) $$
A bird of mass 0.5 kg is flying the same speed at the same height of 5 m. In this state, if its Kinetic energy and potential energy are equal. What is the velocity of the bird ?
A boy of mass 50 kg is riding a bicycle with a speed 2m /s . The bicycle has a mass of 10kg. Calculate the total kinetic energy?
Due to the external vertical force $$F_x=F_0 \cos \omega t$$ a body suspended by a spring performs forced steady-state oscillations according to the law $$x=a \cos (\omega t- \phi)$$. Find the work performing by the force $$F$$ during one oscillation period.
A body of mass $$20 \ kg$$ is moving with a velocity of $$5 \ m /s$$. Calculate its kinetic energy?
Calculate the potential energy of a body of mass 1 kg at a height of 6m from the ground ?
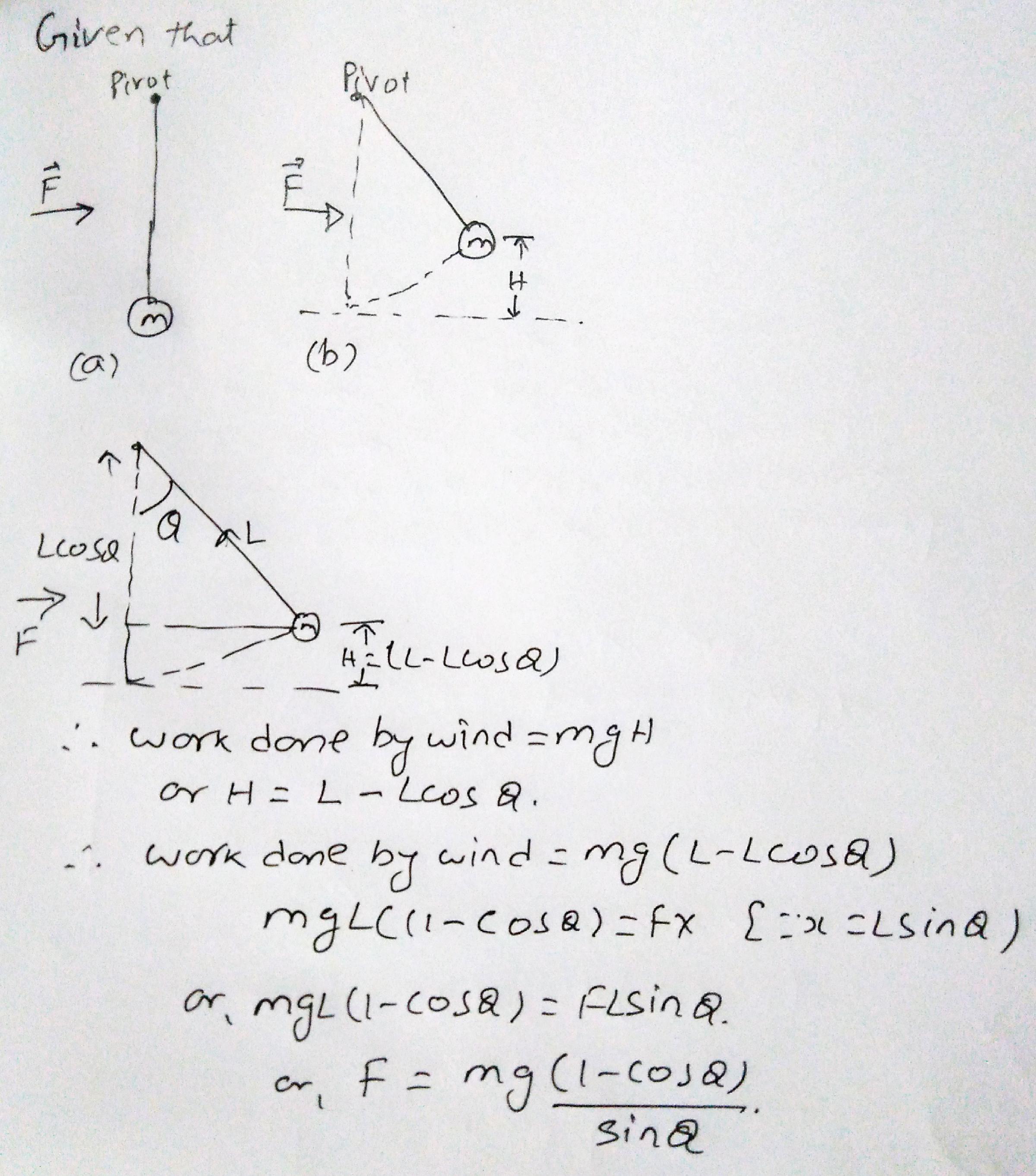
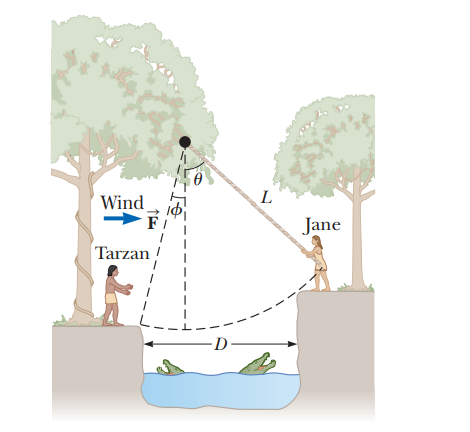
Jane, whose mass is $$50.0-kg$$ needs to swing across a river (having width $$D$$)filled with person-eating crocodiles to save Tarzan from danger. She must swing into a wind exerting constant horizontal force $$\vec F$$ on a vine having length $$L$$ and initially making an angle $$\theta$$ with the vertical Fig Take $$D=50.0\ m, F=110\ N,\ L=40.0\ m$$ and $$\theta=50.0^o$$ With what minimum speed must Jane begin her swing to just make it to the other side?
A child of mass m swings in a swing supported by two chains, each of length $$R$$. If the tension in each chain at the lowest point is $$T$$, find (a) the childs speed at the lowest point and (b) the force exerted by the seat on the child at the lowest point. (Ignore the mass of the seat.)
Follow the figure below:
(a) $$\sum F=2T-Mg=\dfrac{Mv^{2}}{R}$$
$$v^{2}=(2T-Mg)\left ( \frac{R}{M} \right )$$
$$v=\sqrt{(2T-Mg)\left ( \frac{R}{M} \right )}$$
(b) $$n-Mg=F=\frac{Mv^{2}}{R}$$
$$n=Mg+\dfrac{Mv^{2}}{R}$$
(a) $$\sum F=2T-Mg=\dfrac{Mv^{2}}{R}$$
$$v^{2}=(2T-Mg)\left ( \frac{R}{M} \right )$$
$$v=\sqrt{(2T-Mg)\left ( \frac{R}{M} \right )}$$
(b) $$n-Mg=F=\frac{Mv^{2}}{R}$$
$$n=Mg+\dfrac{Mv^{2}}{R}$$
Jane, whose mass is $$50.0-kg$$ needs to swing across a river (having width $$D$$)filled with person-eating crocodiles to save Tarzan from danger. She must swing into a wind exerting constant horizontal force $$\vec F$$ on a vine having length $$L$$ and initially making an angle $$\theta$$ with the vertical Fig Take $$D=50.0\ m, F=110\ N,\ L=40.0\ m$$ and $$\theta=50.0^o$$ Once the recure is complete, Tarzan and Jane must swing back across the river. With what minimum speed must they begin their swing? Assume tarzan has a mass of $$80.0$$kg
A flexible chain weight $$40.0N$$ hangs between two hooks located at the same height $$Fig.P12.15$$. At each hook, the tangent to the chain makes an angle $$\theta =42.0^o$$ with the horizontal. Find
The tension in the chain at its midpoint.
suggestion: make a force diagram for half of the chain.
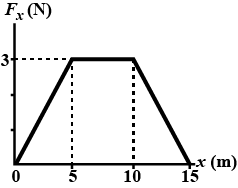
A particle is subject to a force $$F_{x}$$ that varies with position as shown in above figure. Find the work done by the force on the particle as it moves (a) from $$x = 0$$ to $$x = 5.00 m$$, (b) from $$x = 5.00 m$$ to $$x = 10.0 m$$, and (c) from $$x = 10.0 m$$ to $$x = 15.0 m$$. (d) What is the total work done by the force over the distance $$x = 0$$ to $$x = 15.0 m$$?
We use the graphical representation of the definition of work. $$W$$ equals the area under the force-displacement curve. This definition is still written $$W =\int F_{x}dx$$ but it is computed
geometrically by identifying triangles and rectangles on the graph.
(a) For the regoin $$0\leq x\leq 5.00m$$
$$W=\dfrac{(3.00N)(5.00m)}{2}=7.50J$$
(b) For the region $$5.00\leq x\leq 10.0,W=(3.00N)(5.00m)=15.0J$$
(c) For the regoin $$10.00\leq x\leq 15.0,W=\dfrac{(3.00N)(5.00m)}{2}=7.50J$$
(d) For the region $$0\leq x\leq 15.0,W=(7.50+7.50+15.0)J=30.0J$$
geometrically by identifying triangles and rectangles on the graph.
(a) For the regoin $$0\leq x\leq 5.00m$$
$$W=\dfrac{(3.00N)(5.00m)}{2}=7.50J$$
(b) For the region $$5.00\leq x\leq 10.0,W=(3.00N)(5.00m)=15.0J$$
(c) For the regoin $$10.00\leq x\leq 15.0,W=\dfrac{(3.00N)(5.00m)}{2}=7.50J$$
(d) For the region $$0\leq x\leq 15.0,W=(7.50+7.50+15.0)J=30.0J$$
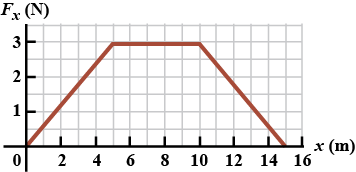
A $$4.00kg$$ particle is subject to a net force that varies with position as shown in above figure. The particle starts from rest at $$x = 0$$. What is its speed at (a) $$x = 5.00 m$$, (b) $$x = 10.0 m$$, and (c) $$x = 15.0 m$$?
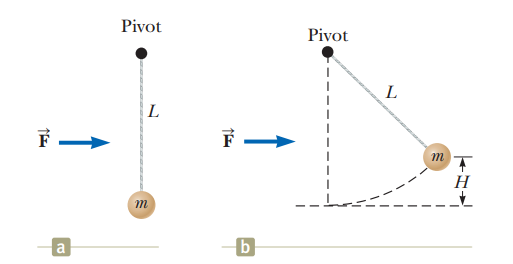
An adventurous archeologist $$(m = 85.0 kg)$$ tries to cross a river by swinging from a vine. The vine is $$10.0 m$$ long, and his speed at the bottom of the swing is $$8.00 m/s$$. The archeologist doesnt know that the vine has a breaking strength of $$1 000 N$$. Does he make it across the river without falling in?
Let the tension at the lowest point be $$T$$. From Newton’s second law $$\sum F=ma$$ and
$$T-mg=ma_{c}=\dfrac{mv^{2}}{r}$$
$$T=m\left ( g+\dfrac{v^{2}}{r} \right )$$
$$T=(85.0kg)\left [ 9.80m/s^{2}+\dfrac{(8.00m/s)^{2}}{10.0m} \right ]$$
$$=1.38kN>1000N$$
He doesn’t make it across the river because the vine breaks.
$$T-mg=ma_{c}=\dfrac{mv^{2}}{r}$$
$$T=m\left ( g+\dfrac{v^{2}}{r} \right )$$
$$T=(85.0kg)\left [ 9.80m/s^{2}+\dfrac{(8.00m/s)^{2}}{10.0m} \right ]$$
$$=1.38kN>1000N$$
He doesn’t make it across the river because the vine breaks.
A ball of mass $$m=300 g$$ is connected by a strong string of length $$L=80.0\ cm$$ to a pivot and held in p[lace with the string vertical. A wind exerts constant force $$F$$ to the night on the ball as shown Figure The ball is released from rest. The wind makes it swing up to attain maximum height $$J$$ above its starting point before it swings down again as $$F$$ approaches zero
Two bodies A and B have masses in the ratio $$5:1$$ and their kinetic energies are in the ratio $$125:9$$. Find the ratio of their velocities.
A car weighing $$1200$$ kg is uniformly accelerated from rest and covers a distance of $$40$$ m in 5 s. Calculate the work done by the engine of the car during this time. What is the final kinetic energy of the car?
A torch bulb is rated $$2.5\ V$$ and $$750\ mA$$. Calculate (i) its power, (ii) its resistance, and (iii) the energy consumed, if this bulb is lighted for four hours.
A mass $${ m }_{ 1 }$$ with initial speed $${ v }_{ 0 }$$ in the positive $$x$$-direction collides with a mass $${ m }_{ 2 }=2{ m }_{ 1 }$$ which is initially at rest at the origin, as shown in figure. After the collision $${ m }_{ 1 }$$ moves off with speed $${ v }_{ 1 }={ v }_{ 0 }/2$$ in the negative $$y$$- direction, and $${ m }_{ 2 }$$ moves off with speed $${ v }_{ 2 }$$ at angle $$\theta$$. Determine $$\tan { \theta } $$, and find $$v_{ 2 }$$ in terms of $$v_{ 0 }$$
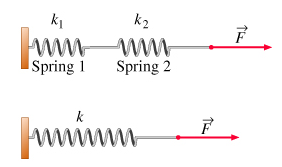
A system consists of two springs connected in series and having the stiffness coefficients $$k_1$$ and $$k_2$$. Find the minimum work to be performed in order to stretch this system by $$\Delta l$$.
Two springs are connected in series has a effective spring constant K given by,
$$K= \frac {1}{k_1}+\frac {1}{k_2}$$..............(1)
So the minimum work to be performed in order to stretch this system by an amount $$\Delta l$$ is = $$1/2\times K \times \Delta l^2$$, where K is given by equation (1).
A mass $${ m }_{ 1 }$$ with initial speed $${ v }_{ 0 }$$ in the positive $$x$$-direction collides with a mass $${ m }_{ 2 }=2{ m }_{ 1 }$$ which is initially at rest at the origin, as shown in figure. After the collision $${ m }_{ 1 }$$ moves off with speed $${ v }_{ 1 }={ v }_{ 0 }/2$$ in the negative $$y$$- direction, and $${ m }_{ 2 }$$ moves off with speed $${ v }_{ 2 }$$ at angle $$\theta$$. Write down the $$x$$ and $$y$$- components of the equation of conservation of momentum for the collision.
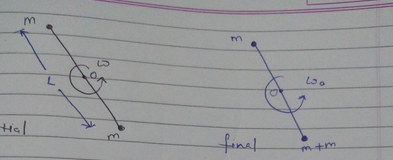
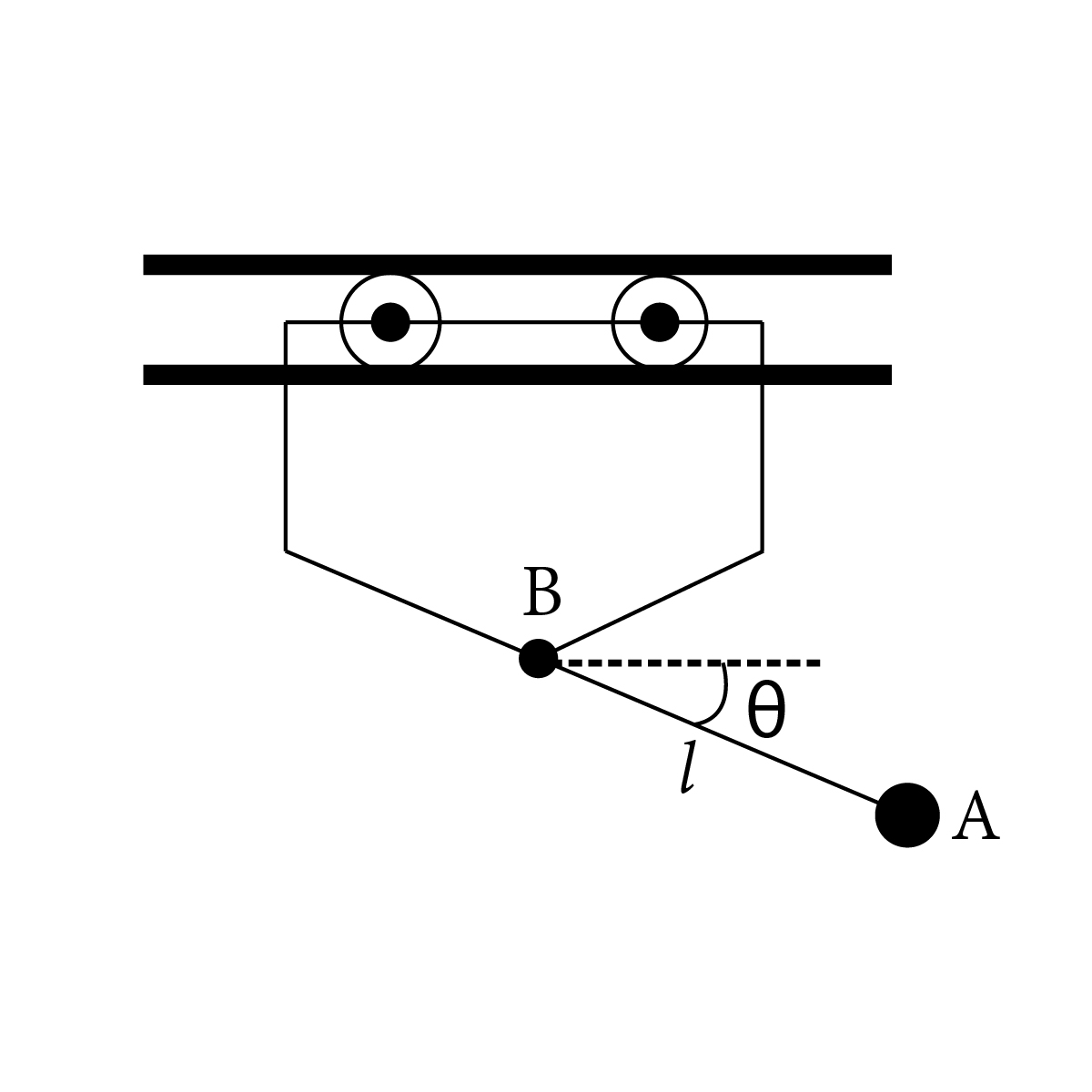
The simple pendulum $$A$$ of mass $${ m }_{ A }$$ and length $$l$$ is suspended from the trolley $$B$$ of mass $${ m }_{ B }$$. If the system is released from rest at $$\theta=0$$, determine the velocity $${ v }_{ B }$$ of the trolley and tension in the string when $$\theta={ 90 }^{ \circ }$$. Friction is negligible.
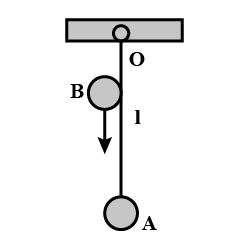
A small steel ball A is suspended by an inextensible thread of length $$l = 15 m$$ from O. Another identical ball is thrown vertically downwards such that its surface remains just in contact with thread during downward motion and collides elastically with the suspended ball. If the suspended ball just completes vertical circle after collision, calculate the velocity (in cm/s) of the falling ball just before collision : $$(g = 10 m s^{-2})$$
Since the ball just completes a vertical circle, it must have a velocity of $$\sqrt{5gl}$$
From geometry, the angle between vertical and line of collision between the balls is $$30^{\circ}$$
Thus, from conservation of momentum of both the balls and the condition of elasticity,
velocity of ball A along the horizontal direction after collision $$=0.8v_0\cos30^{\circ}=\sqrt{5gl}$$
$$\implies v_{0}=12.5m/s$$
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed $$\displaystyle \sqrt{gl}.$$ Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
Let T=mg at angle $$\displaystyle \theta $$ as shown in figure.
$$\displaystyle h= l\left ( 1-\cos \theta \right )$$ ...(i)
Applying conservation of mechanical energy between points A and B, we get
$$\displaystyle \frac{1}{2}m\left ( u^{2}-v^{2} \right )= mgh$$
Here, $$\displaystyle u^{2}= gl$$ ...(ii)
and v=speed of particle in position B
$$\displaystyle \therefore v^{2}= u^{2}-2gh$$ ...(iii)
Further, $$\displaystyle T-mg\cos \theta = \frac{mv^{2}}{l}$$
or $$\displaystyle mg-mg\cos \theta = \frac{mv^{2}}{l}$$ (T=mg)
or $$\displaystyle v^{2}= gl\left ( 1-\cos \theta \right )$$ ...(iv)
Substituting values of $$\displaystyle v^{2},u^{2}$$ and h from Eqs. (iv), (ii) and (i) in Eq. (iii), we get
$$\displaystyle gl\left ( 1-\cos \theta \right )= gl-2gl\left ( 1-\cos \theta \right )$$
or $$\displaystyle \cos \theta = \frac{2}{3}$$
or $$\displaystyle \theta = \cos ^{-1}\left ( \frac{2}{3} \right )$$
Substituting $$\displaystyle \cos \theta = \frac{2}{3}$$ in Eq. (iv), we get
$$\displaystyle v= \frac{\sqrt{gl}}{3}$$
$$\displaystyle h= l\left ( 1-\cos \theta \right )$$ ...(i)
Applying conservation of mechanical energy between points A and B, we get
$$\displaystyle \frac{1}{2}m\left ( u^{2}-v^{2} \right )= mgh$$
Here, $$\displaystyle u^{2}= gl$$ ...(ii)
and v=speed of particle in position B
$$\displaystyle \therefore v^{2}= u^{2}-2gh$$ ...(iii)
Further, $$\displaystyle T-mg\cos \theta = \frac{mv^{2}}{l}$$
or $$\displaystyle mg-mg\cos \theta = \frac{mv^{2}}{l}$$ (T=mg)
or $$\displaystyle v^{2}= gl\left ( 1-\cos \theta \right )$$ ...(iv)
Substituting values of $$\displaystyle v^{2},u^{2}$$ and h from Eqs. (iv), (ii) and (i) in Eq. (iii), we get
$$\displaystyle gl\left ( 1-\cos \theta \right )= gl-2gl\left ( 1-\cos \theta \right )$$
or $$\displaystyle \cos \theta = \frac{2}{3}$$
or $$\displaystyle \theta = \cos ^{-1}\left ( \frac{2}{3} \right )$$
Substituting $$\displaystyle \cos \theta = \frac{2}{3}$$ in Eq. (iv), we get
$$\displaystyle v= \frac{\sqrt{gl}}{3}$$
A simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle $$\displaystyle \alpha $$ with the vertical. Find the tension in the string and the magnitude of net force on the bob at that instant.
(i)The forces acting on the bob are
(a)the tension T
(b)the weight mg
AS the bob moves in a circle of radius L with centre at O. A centripetal force of magnitude $$\displaystyle \frac{mv^{2}}{L}$$ is required towards O. This force will be provided by the resultant of T and mg $$\displaystyle \cos \alpha .$$ Thus,
or $$\displaystyle T-mg\cos \alpha = \frac{mv^{2}}{L}$$
$$\displaystyle T= m\left ( g\cos \alpha +\frac{v^{2}}{L} \right )$$
(ii)$$\displaystyle \left | \vec{F}_{net} \right |= \sqrt{\left ( mg\sin \alpha \right )^{2}+\left ( \frac{mv^{2}}{L} \right )}= m\sqrt{g^{2}\sin ^{2}\alpha +\frac{v^{4}}{L^{2}}}$$
(a)the tension T
(b)the weight mg
AS the bob moves in a circle of radius L with centre at O. A centripetal force of magnitude $$\displaystyle \frac{mv^{2}}{L}$$ is required towards O. This force will be provided by the resultant of T and mg $$\displaystyle \cos \alpha .$$ Thus,
or $$\displaystyle T-mg\cos \alpha = \frac{mv^{2}}{L}$$
$$\displaystyle T= m\left ( g\cos \alpha +\frac{v^{2}}{L} \right )$$
(ii)$$\displaystyle \left | \vec{F}_{net} \right |= \sqrt{\left ( mg\sin \alpha \right )^{2}+\left ( \frac{mv^{2}}{L} \right )}= m\sqrt{g^{2}\sin ^{2}\alpha +\frac{v^{4}}{L^{2}}}$$
A ring of radius R is placed such that it lies in a vertical plane. The ring is fixed, A bead of mass m is constrained to move along the ring without any friction.One end of the spring is connected with the mass m and other end is rigidly fixed with the topmost point of the ring. Initially the spring is in un-extended position and the bead is at a vertical distance R from the lowermost point of the ring.The bead is now released from rest.
a) What should be the value of spring constant K such that the bead is just able to reach bottom of the ring.
b) The tangential and centripetal accelerations of the bead at initial and bottommost position for the same value of spring constant k.
Natural length of the spring is $$\sqrt{2}R$$. When the bead just reaches the bottom of the ring, it has zero velocity and:
$$(a)$$ $$kx=mg$$
$$\implies k(2R-\sqrt{2}R)=mg$$
$$\implies k=\cfrac{mg}{\sqrt{2}R(\sqrt{2}-1)}$$
$$\implies k=\cfrac{mg(\sqrt{2}+1)}{3\sqrt{2}R}$$
$$(b)$$ Initially, when the bead is at $$A$$, there is no spring force acting on it. Therefore, centripetal acceleration initially $$=$$ zero.
Tangentially acceleration:
$$\alpha=\cfrac{\tau}{I}$$
At $$A$$, the torque is due to gravity:
$$\therefore \alpha=\cfrac{mgR}{mR^2}$$
$$\therefore \alpha=\cfrac{g}{R}$$
At $$B$$, the bead just reaches. Therefore, its centripetal acceleration is zero, and since at this point no tangential forces are acting on it, the tangential acceleration is also zero.
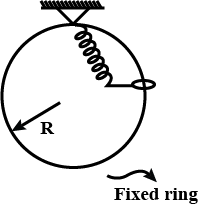
A ball of mass m is attached with a light string of length $$\ell$$ and released from positionString becomes taut at position 2 and reaches the lowest position 3, then find the velocity of the ball after the strings become taut.
The mass $$=m$$
Length$$=l$$
The acceleration of the string is $$\cfrac{v^2}{r}$$ and the force due to tension $$T$$ is $$T\cfrac{dl}{r}$$ where $$dl$$ is the length of an element of string. Both directed towards the centre of curvature
If $$T\cfrac{dl}{r}=m\cfrac{dl\times v^2}{r}$$
(m being mass/unit length)
then there is no need for the tube.
$$v^2=\cfrac{T}{m}$$
A particle of mass m is tied to one end of a string of length l. The particle is held horizontal with the string taut. It is then projected upward with a velocity u. The tension in the string is $$\frac{mg}{2}$$ when it is inclined at an angle $$30^0$$ to the horizontal. Find the value of $$u$$.
$$T=\frac { mg }{ 2 } \\ but\quad T=\frac { m{ u }^{ 2 } }{ r } \\ \therefore \quad \frac { mg }{ 2 } =\frac { m{ u }^{ 2 } }{ r } \\ ={ u }^{ 2 }=\frac { rg }{ 2 } \\ using\quad energy\quad balance,\\ \frac { 1 }{ 2 } m{ v }^{ 2 }=\frac { 1 }{ 2 } m{ u }^{ 2 }+mg(rsin{ 30 }^{ \circ })\\ \therefore \quad { v }^{ 2 }={ u }^{ 2 }+2gr\times \frac { 1 }{ 2 } \\ =\frac { rg }{ 2 } +rg=\frac { 3rg }{ 2 } \\ \therefore \quad v=\sqrt { \frac { 3rg }{ 2 } } $$
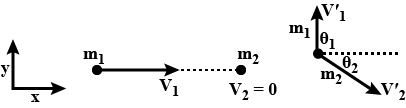
A particle of mass $$m_{1}$$ moving at a speed $$v_{1}$$ allong the positive $$x\ direction$$, collides with another particle of mass $$m_{2}$$ at rest. After the collision, the particles have velocities $$v_{1}'$$ and $$v_{2}'$$ in the $$xy$$-plane in the directions of $$\theta_{1}$$ and $$\theta_{2}$$ with the x-axis as shown in the figure. There are no external forces acting on the particles. Express your answer in terms of $$m_{1}, m_{2}, v_{1}, \theta_{1}$$ and $$\theta_{2}$$. What is the total momentum of the system before the collision (direction and magnitude)?
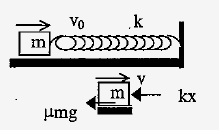
A block of mass $$m$$ initially has a velocity $${v}_{0}$$ when it just touching a spring. The block moves through a distance $$I$$ before it stops after compressing the spring. The spring constant is $$k$$ and the coefficient of kinetic friction between block and table is $$\mu$$. As the block moves the distance $$l$$
(a) what is the work done on it by the spring force? Are there other forces acting on the block, and if so, what work do they do?
(b) what is the total work done on the block?
(c) use the work energy theorem to find the value of $$l$$ in terms of $${v}_{0}, \mu, g$$ and $$k$$
(a) The net force acting on the block by the spring is equal to $${ F }_{ sprinf }=kx$$
Work done by the spring $$\int { { \overrightarrow { F } }_{ spring } } .d\overrightarrow { s } $$
$$=\int { { F }_{ sprinf } } ds\cos { { 180 }^{ o } } =-\int { { F }_{ sprinf } } .ds=-\int { kx } dx=\cfrac { -k{ l }^{ 2 } }{ 2 } $$
(b) The total work done $$W=\Delta KE=0-\left( \cfrac { 1 }{ 2 } \right) m{ v }_{ 0 }^{ 2 }=-\left( \cfrac { 1 }{ 2 } \right) m{ v }_{ 0 }^{ 2 }\quad $$
(c) The work done by friction $$=-\mu mgl\quad $$
The total work done $${ W }_{ s }+{ W }_{ f }=\Delta KE\Rightarrow -\mu mgl-\left( 1/2 \right) k{ l }^{ 2 }\Rightarrow \cfrac { 1 }{ 2 } k{ l }^{ 2 }+\mu mgl=\left( \cfrac { 1 }{ 2 } \right) m{ v }_{ 0 }^{ 2 }$$
$$\Rightarrow l=\cfrac { \mu mg }{ k } \left[ \sqrt { 1+\cfrac { k }{ m } { \left( \cfrac { { v }_{ 0 } }{ \mu g } \right) }^{ 2 } } -1 \right] $$
Work done by the spring $$\int { { \overrightarrow { F } }_{ spring } } .d\overrightarrow { s } $$
$$=\int { { F }_{ sprinf } } ds\cos { { 180 }^{ o } } =-\int { { F }_{ sprinf } } .ds=-\int { kx } dx=\cfrac { -k{ l }^{ 2 } }{ 2 } $$
(b) The total work done $$W=\Delta KE=0-\left( \cfrac { 1 }{ 2 } \right) m{ v }_{ 0 }^{ 2 }=-\left( \cfrac { 1 }{ 2 } \right) m{ v }_{ 0 }^{ 2 }\quad $$
(c) The work done by friction $$=-\mu mgl\quad $$
The total work done $${ W }_{ s }+{ W }_{ f }=\Delta KE\Rightarrow -\mu mgl-\left( 1/2 \right) k{ l }^{ 2 }\Rightarrow \cfrac { 1 }{ 2 } k{ l }^{ 2 }+\mu mgl=\left( \cfrac { 1 }{ 2 } \right) m{ v }_{ 0 }^{ 2 }$$
$$\Rightarrow l=\cfrac { \mu mg }{ k } \left[ \sqrt { 1+\cfrac { k }{ m } { \left( \cfrac { { v }_{ 0 } }{ \mu g } \right) }^{ 2 } } -1 \right] $$
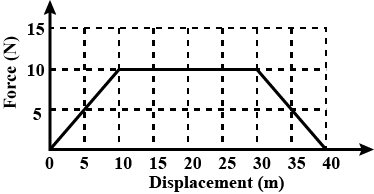
Figure shows the force-displacement graph for a moving body. What is the work done by the force in displacing body from $$x=0$$ to $$x=35m$$?
A spring of force constant k is cut in two parts at its one-third length. When both the parts are stretched by same amount. The work done in the two parts will be:
(Note - Spring constant of a spring is inversely proportional to length of spring.)
Two springs $$A$$ and $$B$$ are identical but $$A$$ is harder than $$ B (k_A > k_B ) $$. Let $$W_A$$ and $$W_B$$ represent the work done when the springs are stretched through the same of the distance and $$W'_A$$ and $$W'_B$$ are the work done when these are stretched by equal forces then which of the following is true:
Fig. shows a bead of mass $$m$$ moving with uniform speed $$v$$ through a $$U-$$shaped smooth wire the wire has a semicircular bending between $$A$$ and $$B$$. Calculate the average force exerted by the bead on the part $$AB$$ of the wire.
Discuss the motion in vertical circle. Find an expression for the minimum velocities at the lowest point and top point. Also find tension at these points?
The motion of a Particle in Vertical Circle Whenever a body is released from a height, it travels vertically downward towards the surface of the earth.
This is due to the force of gravitational attraction exerted on the body by the earth.
The acceleration produced by this force is called acceleration due to gravity and is denoted by $$‘g’$$. Value of $$‘g’$$ on the surface of the earth is taken to the 9.8 $$m/s^2$$ and it is same for all the bodies.
It means all bodies (whether an iron ball or a piece of paper), when dropped (u = 0) from same height should fall with the same rapidity and should take the same time to reach the earth, it is the minimum velocity given to the particle at the lowest point to complete the circle.
The tendency of the string to become slack is maximum when the particle is at the topmost point of the circle.
At the top, tension is given by T = $$\dfrac{mv_T^2}{R}$$ - mg,
where $$v_T$$ = speed of the particle at the top.
$$\dfrac{ mv_T^2}{R}$$ = $$T + mg$$
For $$v_T$$ to be minimum, $$T = 0$$
$$v_T = \sqrt{gR}$$
If $$V_B$$ be the critical velocity of the particle at the bottom,
then from conservation of energy:
$$Mg(2R)$$ + $$ \dfrac{1}{2} mv_T^2$$ = 0 + $$\dfrac{1}{2} mv_B^2$$
As $$v_T = \sqrt{gR} $$ > $$2 mgR$$ + $$\dfrac{1}{2} mgR $$
=$$ \dfrac{1}{2 }mv_B^2$$
so $$v_B = \sqrt{5 g R}$$
Highest point $$H ( h = 2r )$$
We have, $$v$$ = $$\sqrt{u^2 - 2gh}$$
$$v$$ = $$\sqrt{(\sqrt{5gr})^2 - 2g ( 2r )}$$
$$v$$ = $$\sqrt{5gr - 4gr} $$
= $$ \sqrt{gr}$$
Tension at the lowest point:
$$T - mg$$ = $$\dfrac{mv^2}{R}$$.........(since,v = $$\sqrt{5gr}$$)
$$T = 6mg$$
Tension at highest point:
$$T + mg$$ = $$\dfrac{mv^2}{R}$$.......(since, v = $$\sqrt{gr}$$)
$$T = 0 $$
A locomotive of mass $$m$$ starts moving so that its velocity varies according to the law $$v=\alpha \sqrt { s }$$, where $$\alpha$$ is constant and $$s$$ is the distance covered. Find the total work done by all the forces acting on the locomotive during the first $$t$$ seconds after the beginning of motion.
The mass of the cyclist together with the bike is $$90 \ kg$$. Calculate the increase in kinetic energy if the speed increases from $$6 \ km/h$$ to $$12 \ km/h$$.
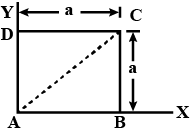
A force $$F = x^2 y ^2 i - x^2 y^2 j (N) $$ acts on a particle which moves in the $$XY$$ plane. Find the work done by $$F$$ as it moves the particle from $$A$$ to $$C$$ (fig.) along each of the paths $$ABC, ADC$$ and $$AC$$.
A particle of mass $$m$$ moves on a straight line with its velocity varying with the distance travelled according to the equation $$v = a \sqrt{x}$$, where $$a$$ is a constant. Find the total work done by all the forces during the displacement from $$x = 0$$ to $$x = d$$.
Two point mass m are connected the light rod length i and is free to roatate in vertical plane as shown. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in
Two point mass m are connected the light rod of length t and it is free to rotate in vertical plane as shown.Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in verticalfane
A stone weighing $$0.5\ kg$$ tied to a rope of length $$0.5\ m$$ revolves along a circular path in a vertical. The tension of the rope at the bottom point of the circle is $$415$$ newton. To what height will the stone if the rope breaks at the moment when the velocity is directed upwards? $$(g = 10 m/s^2)$$
A running man has half the kinetic energy as that of a boy half his mass. The man speeds up by $$1\ ms^{-1}$$. So that the kinetic energies of the boy and man are equal. Calculate the initial speeds of boy and man.
A particle of mass $$12$$ kg is acted upon by a force $$f$$ $$ = \left( {100 - 2{x^2}} \right)$$ when $$f$$ is in newton and $$x$$ is in metre. Calculate the wrok done by this force in moving the particle $$x = 0$$ to $$x = -10m$$. What will be the speed at $$x = 10m$$ if it starts from rest.
The work done by a force $$\bar{F} = (-6x^3 i) N$$ in displacing particle from $$x = a m to x = -2 m$$ is
A car and a truck are moving with the same velocity of $$60 \ km/h$$. Which one has more kinetic energy ?$$(M_T > M_C)$$.
Suppose the rod with the balls $$A$$ and $$B$$ of the previous problem is clamped at the centre in such a way that it can rotate freely about a horizontal axis through the clapm. The system is kept at rest in the horizontal position. A particle $$P$$ of the same mass $$m$$ is dropped from a height $$h$$ on the ball $$B$$. The particle collides with $$B$$ and sticks to it. (a) Find the angular momentum and and the angular speed of the system just after the collision. (b) What should be the minimum value of $$h$$ so that the system makes a full rotation after the collision.
$$(a)$$ Inertia of masses about centre $$O$$ initially$$=m{(\cfrac{L}{2})}^{2}+m{(\cfrac{L}{2})}^{2}$$
$$\cfrac{m{L}^{2}}{2}$$
So, angular momentum $$(Li)=\cfrac{m{L}^{2}}{2}\omega$$
Now
Inertia of masses about $$O$$ is finally $$=m{(\cfrac{L}{2})}^{2}+2m{(\cfrac{L}{2})}^{2}$$
$$=\cfrac{3}{4}m{L}^{2}$$
So angular momentun $$({L}_{f)})=\cfrac{3}{4}m{L}^{2}\omega$$
where, $${\omega}_{0}\rightarrow$$ final angular momentum
Applying conservation of angular momentum
i.e., $${L}_{i}={L}_{f}$$
$$\Rightarrow$$ $$\cfrac{m{L}^{2}}{2}\omega=\cfrac{3}{4}m{L}^{2}\omega$$
$$\Rightarrow$$ $${\omega}_{0}=\cfrac{2}{3}\omega$$
$$(b)$$ When the mass $$2m$$ will at the top most position and the mass $$m$$ at the at the lowest point they will automatically rotate. In this position he total gain in potential energy $$=2mg\times (\frac{l}{2})-mg(\frac{l}{2})=mg(\frac{l}{2})$$
$$\Rightarrow mg\ \frac{l}{2}=\frac{l}{2}\ l\omega^{2}$$
$$\Rightarrow mg\ \frac{l}{2}=(\frac{1}{2}\times \frac{3ml^{2}}{4}\times (\frac{8gh}{9gl^{2}})$$
$$\Rightarrow h=\frac{3l}{2}$$
$$(b)$$ When the mass $$2m$$ will at the top most position and the mass $$m$$ at the at the lowest point they will automatically rotate. In this position he total gain in potential energy $$=2mg\times (\frac{l}{2})-mg(\frac{l}{2})=mg(\frac{l}{2})$$
$$\Rightarrow mg\ \frac{l}{2}=\frac{l}{2}\ l\omega^{2}$$
$$\Rightarrow mg\ \frac{l}{2}=(\frac{1}{2}\times \frac{3ml^{2}}{4}\times (\frac{8gh}{9gl^{2}})$$
$$\Rightarrow h=\frac{3l}{2}$$
A copper wire of length $$2.2\ m$$ and a steel wire of length $$1.6\ m$$, both of diameter $$3.0\ mm$$, are connected end to end. When stretched by a load, the net elongation is found to be $$0.70\ mm$$. Obtain the load applied.
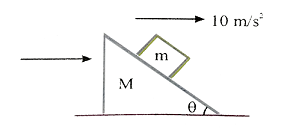
In the figure shown all the surfaces are frictionless, and mass of the block, m= $$1$$ kg. The block and wedge are held initially at rest. Now wedge is given a horizontal acceleration of $$10 m/s^2$$ by applying a force on the wedge, so that the block does not slip on the wedge. Then work done by the normal force in ground frame on the block in $$\sqrt3$$ seconds is
Calculate the change that should be affected in the velocity of a body to maintain the same K.E, if mass of the body is increased to 4 times.
A body of mass $$15$$ kg is raised to height of $$10$$ m. Calculate the potential energy at that height. What will be it's potential energy, if it is taken to double height.
A body possess potential energy of $$460\ J$$ whose mass is $$20\ kg$$ and is raised to a certain height. What is the height when $$g=10m/s^ {2}$$
The ball of mass 0.4 kg is dropped from some certain height .As it falls through 2 m. The kinetic energy acquired by it is.
A boy of mass $$50\ kg$$ climbs up a vertical height of $$100\ m$$. Calculate the amount of potential energy he gains.
A body of mass $$10 k g$$ is moving with a velocity $$20 m s ^ { - 1 }$$. If the mass of the body is doubled and its velocity is halved, find the ratio of the initial kinetic energy to the final kinetic energy.
Determine the kinetic energy possesed by a battle tank belt whose mass is m if the tank is moving with constant velocity v. Assume there is no slipping.
Show that change in potential energy is given by$$\frac { \frac { mgh }{ 1+h } }{ Re } $$
Calculate the kinetic energy of a body of mass $$20\, kg$$ moving with velocity of $$0.1\, m/s$$. How the kinetic energy will change if the velocity of the body be doubled ?
a) Define the term 'energy' of a body. What is the SI unit of energy.
b) What are the various forms of energy?
c) Two bodies having equal masses are moving with uniform speeds of $$v$$ and $$2v$$ respectively. Find the ratio their kinetic energies.
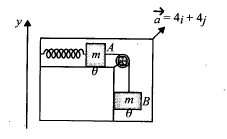
The arrangement shown in Fig is at rest. An ideal spring of natural length $$l_{0}$$ having spring constant $$k=220\ Nm^{-1}$$, is connected to block $$A$$. Blocks $$A$$ and $$B$$ are connected by an ideal string passing through a friction less pulley. The mass of each block $$A$$ and $$B$$ is equal to $$m=2\ kg$$ when the spring was in natural length, the whole system is given an acceleration $$\vec{a}$$ as shown. If coefficient of friction of both surfaces is $$\mu=0.25$$ then find the maximum extension of the spring $$(g=10\ ms^{-2})$$
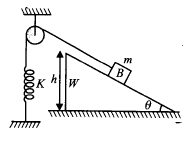
In Figure the pulley shown is smooth. The spring and the string are light. Block $$B$$ slides down from the top along the fixed rough wedge of inclination $$\theta$$. Assuming that the block reaches the end of the wedge, find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be $$\mu$$ and that the spring was relaxed when the block was released from the top of the wedge.
In Fig. $$8-46$$ , a spring with $$k = 170\,N/m$$ is at the top of a frictionless incline of angle $$\theta = 37.0^\circ.$$ The lower end of the incline is distance $$D =1.00\, m$$ from the end of the spring, which is at its relaxed length. A $$2.00 \,kg$$ canister is pushed against the spring until the spring is compressed $$0.200\, m$$ and released from rest. (a) What is the speed of the canister at the instant the spring returns to its relaxed length (which is when the canister loses contact with the spring)? (b) What is the speed of the canister when it reaches the lower end of the incline?
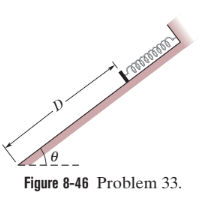
Figure 8-31 shows a ball with mass $$m = 0.341\, kg$$ attached to the end of a thin rod with length $$L = 0.452\, m$$ and negligible mass.The other end of the rod is pivoted so that the ball can move in a vertical circle. The rod is held horizontally as shown and then given enough of a downward push to cause the ball to swing down and around and just reach the vertically up position, with zero speed there. How much work is done on the ball by the gravitational force from the initial point to (a) the lowest point, (b) the highest point, and (c) the point on the right level with the initial point? If the gravitational potential energy of the ballEarth system is taken to be zero at the initial point, what is it when the ball reaches (d) the lowest point, (e) the highest point, and (f) the point on the right level with the initial point? (g) Suppose the rod were pushed harder so that the ball passed through the highest point with a nonzero speed.Would $$\Delta \,U_g$$ from the lowest point to the highest point then be greater than, less than, or the same as it was when the ball stopped at the highest point?
We move a particle along an $$x$$ axis, first outward from $$x = 1.0\, m$$ to $$x = 4.0\, m$$ and then back to $$x =1.0\, m,$$ while an external force acts on it. That force is directed along the x axis, and its x component can have different values for the outward trip and for the return trip. Here are the values (in newtons) for four situations, where x is in meters:
Find the net work done on the particle by the external force for the round trip for each of the four situations. (e) For which, if any, is the external force conservative?
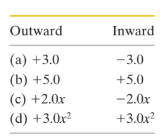
The cable of the $$1800 \,kg$$ elevator cab in Fig. $$8-56$$ snaps when the cab is at rest at the first floor, where the cab bottom is a distance $$d = 3.7\, m$$ above a spring of spring constant $$k = 0.15 \,MN/m.$$ A safety device clamps the cab against guide rails so that a constant frictional force of $$4.4\, kN$$ opposes the cabs motion. (a) Find the speed of the cab just before it hits the spring. (b) Find the maximum distance $$x$$ that the spring is compressed (the frictional force still acts during this compression). (c) Find the distance that the cab will bounce back up the shaft. (d) Using conservation of energy, find the approximate total distance that the cab will move before coming to rest. (Assume that the frictional force on the cab is negligible when the cab is stationary.)
In Fig. $$8-53,$$ a block of mass $$m = 2.5\, kg$$ slides head on into a spring of spring constant $$k = 320\, N/m.$$ When the block stops, it has compressed the spring by $$7.5\, cm.$$ The coefficient of kinetic friction between block and floor is $$0.25.$$ While the block is in contact with the spring and being brought to rest, what are (a)the work done by the spring force and (b) the increase in thermal energy of the blockfloor system? (c) What is the blocks speed just as it reaches the spring?
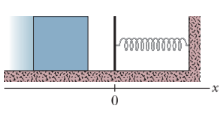
The block lies on a horizontal frictionless surface, and the spring constant is $$50 \ N/m$$. Initially, the spring is at its relaxed length and the block is stationary at position $$x = 0$$. Then an applied force with a constant magnitude of $$3.0 \ N$$ pulls the block in the positive direction of the $$x$$ axis, stretching the spring until the block stops. When that stopping point is reached, what are (a) the position of the block, (b) the work that has been done on the block by the applied force, and (c) the work that has been done on the block by the spring force? During the block’s displacement, what are (d) the block’s position when its kinetic energy is maximum and (e) the value of that maximum kinetic energy?
A certain spring is found not to conform to Hookes law. The force (in newtons) it exerts when stretched a distance x (in meters) is found to have magnitude $$52.8x + 38.4x^2$$ in the direction opposing the stretch. (a) Compute the work required to stretch the spring from $$x = 0.500\, m$$ to $$x = 1.00\, m.$$ (b) With one end of the spring fixed, a particle of mass $$2.17 \,kg$$ is attached to the other end of the spring when it is stretched by an amount $$x = 1.00\, m.$$ If the particle is then released from rest, what is its speed at the instant the stretch in the spring is $$x = 0.500\, m$$? (c) Is the force exerted by the spring conservative or nonconservative? Explain.
A force is applied of magnitude $$80 \ N$$ to hold the block stationary at $$x = -2.0 \ cm$$. From that position, we then slowly move the block so that our force does $$+4.0 \ J$$ of work on the spring - block system; the block is then again stationary.What is the block’s position? (Hint: There are two answers.)
A rope is used to pull a $$3.57\, kg$$ block at constant speed $$4.06\, m$$ along a horizontal floor. The force on the block from the rope is $$7.68\, N$$ and directed $$15.0^\circ$$ above the horizontal.What are (a) the work done by the ropes force, (b) the increase in thermal energy of the blockfloor system, and (c) the coefficient of kinetic friction between the block and floor?
(a) The work done on the block by the force in the rope is, using Eq. $$7-7,$$
$$W = Fd \,cos \,\theta = (7.68\,N)(4.06\,m) cos \,15.0^\circ = 30.1\,J.$$
(b) Using f for the magnitude of the kinetic friction force, Eq. $$8-29$$ reveals that the increase in thermal energy is
$$\Delta E_{th} = fd = (7.42\,N)(4.06\,m) = 30.1\,J.$$
(c) We can use Newton's second law of motion to obtain the frictional and normal forces, then use $$\mu_k = f/F_{N}$$ to obtain the coefficient of friction. Place the x-axis along the path of the block and the y-axis normal to the floor. The free-body diagram is shown below. The x and the y component of Newton's second law are
$$x: F \,cos\,\theta - f = 0$$
$$y: F_{N} + F \,sin \,\theta - mg = 0,$$
where m is the mass of the block, F is the force exerted by the rope, and $$\theta$$ is the angle between that force and the horizontal.
The first equation gives
The first equation gives
$$f = F \,cos\,\theta = (7.68\,N)(cos \,15.0^\circ = 7.42\,N$$
and the second gives
$$F_{N} = mg - F \,sin\,\theta = (3.57\,kg)(9.8\,m/s^2) - (7.68\,N)sin \,15.0^\circ = 33.0\,N.$$
Thus, the coefficient of kinetic friction is
$$\mu_k = \dfrac{f}{F_{N}} = \dfrac{7.42\,N}{33.0\,N} = 0.225.$$
A CD case slides along a floor in the positive direction of an x axis while an applied force $$\vec{F_a}$$ acts on the case. The force is directed along the x axis and has the x component $$F_{ax} = 9x - 3x^2$$, with x in meters and $$F_{ax}$$ in newtons. The case starts at rest at the position x = 0, and it moves until it is again at rest. (a) Plot the work $$\vec{F_a}$$ does on the case as a function of x. (b) At what position is the work maximum, and (c) what is that maximum value? (d) At what position has the work decreased to zero? (e) At what position is the case again at rest?
(a) Since we know that, the work becomes
$$W = \frac{9}{2} x^2 – x^3$$ . The plot is shown in the figure
(b) We see from the graph that its peak value occurs at $$x = 3.00 \ m$$.
This can be verified by taking the derivative of W and
setting equal to zero, or simply by noting that this is
where the force vanishes.
(c) The maximum value is $$ W = \dfrac{9}{2} (3.00)^2 - (3.00)^3 = 13.50 J$$.
(d) We see from the graph (or from our analytic expression) that W = 0 at x = 4.50 m.
(e) The case is at rest when $$v = 0$$ .
Since $$W = ΔK = mv^2 / 2$$ , the condition implies $$W = 0$$ .
This happens at $$x = 4.50 \ m$$.
A spring with a spring constant of $$3200 \,N/m$$ is initially stretched until the elastic potential energy of the spring is $$1.44\, J.$$($$U = 0$$ for the relaxed spring.) What is $$\Delta U$$ if the initial stretch is changed to (a) a stretch of $$2.0 \,cm,$$ (b) a compression of $$2.0 \,cm,$$ and(c) a compression of $$4.0 \,cm$$ ?
A rocket moving up with a velocity $$v$$. If the velocity of this rocket is suddenly tripled, what will be the ratio of two kinetic energies?
The spring in the muzzle of a childs spring gun has a spring constant of $$700 \,N/m.$$ To shoot a ball from the gun, first the spring is compressed and then the ball is placed on it. The guns trigger then releases the spring, which pushes the ball through the muzzle. The ball leaves the spring just as it leaves the outer end of the muzzle.When the gun is inclined upward by $$30^\circ$$ to the horizontal, a $$57\, g$$ ball is shot to a maximum height of $$1.83\, m$$ above the guns muzzle.Assume air drag on the ball is negligible. (a) At what speed does the spring launch the ball? (b) Assuming that friction on the ball within the gun can be neglected, find the springs initial compression distance.
An adult weighing $$600\ N$$ ralses the center of gravity of his body by $$0.25\ m$$ while taking each step of $$1\ m$$ length in jogging. If he jogs for $$6\ km$$, calculate the energy utilized by him in jogging assuming that there is no energy loss due to friction of ground and air. Assuming that the body of the adult is capable of converting $$10\%$$ of energy intake in the from of food, calculate the energy equivalent of food that would be required to compensate energy utilized for jogging.
A $$20\, kg$$ object is acted on by a conservative force given by $$F = -3.0\,x \,- 5.0 \,x^2,$$ with $$F$$ in newtons and $$x$$ in meters. Take the potential energy associated with the force to be zero when the object is at $$x = 0.$$ (a) What is the potential energy of the system associated with the force when the object is at $$x = 2.0 \,m$$ ? (b) If the object has a velocity of $$4.0\, m/s$$ in the negative direction of the x axis when it is at $$x = 5.0\, m,$$ what is its speed when it passes through the origin? (c) What are the answers to (a) and (b) if the potential energy of the system is taken to be $$-8.0\, J$$ when the object is at $$x = 0$$ ?
A spring with spring constant $$k = 200 \,N/m$$ is suspended vertically with its upper end fixed to the ceiling and its lower end at position $$y = 0.$$ A block of weight $$20\, N$$ is attached to the lower end, held still for a moment, and then released. What are (a) the kinetic energy $$K,$$ (b) the change (from the initial value)in the gravitational potential energy $$\Delta U_g,$$ and (c) the change in the elastic potential energy $$\Delta U_e$$ of the spring - block system when the block is at $$y = -5.0\,cm $$ ? What are (d) $$K$$, (e) $$\Delta U_g,$$ and (f) $$\Delta U_e$$ when $$y = -10\,cm$$, (g) $$K$$ , (h) $$\Delta U_g,$$ and (i) $$\Delta U_e$$ when $$y = -15\,cm,$$ and (j) $$K$$, (k) $$\Delta U_g,$$ and (l) $$\Delta U_e$$ when $$y = -20\,cm$$ ?
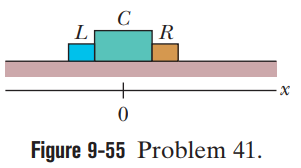
Figure 9-55 shows a two-ended rocket that is initially stationary on a frictionless floor, with its center at the origin of an x axis.The rocket consists of a central block C (of mass $$ M = 6.00 \,kg $$ )and blocks L and R (each of mass $$ m = 2.00 \,kg $$) on the left and right sides. Small explosions can shoot either of the side blocks away from block C and along the x axis. Here is the sequence: (1) At time $$ t = 0 $$, block L is shot to the left with a speed of $$ 3.00 \,m/s $$ relative to the velocity that the explosion gives the rest of the rocket. (2) Next, at time $$ t = 0.80 \,s, $$ block R is shot to the right with a speed of $$ 3.00 \,m/s$$ relative to the velocity that block C then has. At $$ t = 2.80 \, s $$, what are (a) the velocity of block C and (b) the position of its center?
Fasten one end of a vertical spring to a ceiling, attach a cabbage to the other end, and then slowly lower the cabbage until the upward force on it from the spring balances the gravitational force on it. Show that the loss of gravitational potential energy of the cabbageEarth system equals twice the gain in the springs potential energy.
A raindrop of mass $$1.00\ g$$ falling from a height of $$1\ km$$ on the ground with a speed of $$50\ m/s$$. Calculate:
The loss of $$P.E.$$ of the drop.
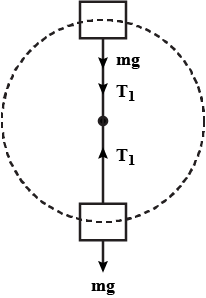
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are : [Choose the correct alternative]
| Lowest Point | Highest Point |
| $$mg - T_1$$ | $$mg + T_2$$ |
| $$mg + T_1$$ | $$mg - T_2$$ |
| $$mg + T_1 -(mv_1^2)/R$$ | $$mg - T_2 + (mv_1^2)/R$$ |
| $$mg - T_1 -(mv_1^2)/R$$ | $$mg + T_2 + (mv_1^2)/R$$ |
The net force acting on stone at the lowest point directed vertically downward = $$mg - T_1$$ & and the highest point = $$mg + T_2$$. Hence option (a) is correct answer
Consider a body of mass 'm' attached to a string of length 'L'. If the ring is forming a vertical circle, derive an expression for velocity and tension at any point. Also, find the velocity that is required for mass to just reach the peak point of the circle.
Ref. image 1
Let $$'theta'$$ be the angle the string makes with the vertical at any instant of time. Let $$v_x$$ be the velocity of body at the lowermost point x. The distance traveled by the body from the given point 'p' to 'X' in 'y' direction is given by.
$$XY = L - L \cos \theta = L(1 - \cos \theta)$$
Ref. image 2
Using the equation $$v^2 = u^2 + 2as$$, we can write
$$vx^2 = v^2 + 2g (XY)$$
i.e. $$c^2 = vx^2 - 2 g L (1 - \cos \theta)$$ .........(1)
Tension, $$T = mg \cos \theta + \frac{mv^2}{L}$$ using (1)
$$T = mg \cos \theta + \frac{m}{L}(Vx^2 - 2gL)(1 - \cos \theta)$$
$$ = mg \cos \theta + \frac{mv_x^2 }{L} - 2 mg ( 1 - \cos \theta)$$
$$T = \frac{mv_x^2}{L} + mg (3 \cos \theta - 2)$$
For the vertical circle to be reached v = 0, & $$v_x = ? $$ & $$\theta = 180^0$$
$$\Rightarrow v_x^2 = v^2 + 2gL (1 - \cos\theta)$$
$$v_x^2 = 0 + 2g L(1 - (-1))$$
$$v_x = \sqrt{4gL}$$
$$v_x = 2\sqrt{gL}$$
Let the mass of the flower pot 15 kg and hight of the sunshade 4m. What is the kinetic energy of the flower pot just before it touches the ground ?
A ball is placed on a compressed spring. What form of energy does the spring possess? On releasing the spring, the ball flies away. Give a reason.
The compressed spring has elastic potential energy due to its compressed state. Which it is released, the potential energy of the spring changes into kinetic energy which does work on the ball if placed on it and changes into kinetic energy of the ball due to which it flies away.
A body of mass $$10\, kg$$ is moving with a velocity $$20\, m \,s^{-1}$$. If the mass of the body is doubled and velocity is halved. Find the ratio of the initial kinetic energy to the final kinetic energy.
Give one example of a body that has potential energy. In each of the following:
(a) due to its position at a height,
(b) due to its elongated stretched state.
(a) $$ P.E. $$ due to its position at a height :
Water at a height has $$ P.E. $$ stored in it. Falling water from a height can be used to do work like turning a wheel,
(b) $$ P.E. $$ Due to its elongated stretched state :
A stretched rubber band (elongated state) has potential energy. it does work in restoring itself to its original state. A pebble placed on the stretched rubber catapujt , is thrown away when it is released to restore its originals state.
Give the two names which store kinetic energy and potential energy in it on the basis of daily life observation.
A ball of mass $$0.5\, kg$$ slows down from a speed of $$5 \,m \,s^{-1}$$ to that of $$3 \,m\, s^{-1}$$. Calculate the change in kinetic energy of the ball.
Why is following situation impossible? A new high-speed roller coaster is claimed to be a safe that the passengers fo not need to wear seat belts or any other restraining device. The coster is design with a vertical circular section over which the coaster travels on the inside of the circle so that the passenger are upside down section i s$$12.0m$$ and the coster enters the bottom of the circular section at a speed of $$22.0 m/s$$. Assume the coster moves without friction on the track and model teh coaster as a particle.
A box of mass 5kg was raised from the ground to the second floor of height 7m. Calculate the potential energy of the box with respect to the ground floor?
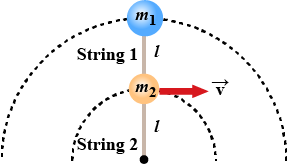
An object of mass $$m_{1} = 4.00 kg$$ is tied to an object of mass $$m_{2} = 3.00 kg$$ with String $$1$$ of length $$l= 0.500 m$$. The combination is swung in a vertical circular path on a second string, String $$2$$, of length $$l= 0.500 m$$. During the motion, the two strings are collinear at all times as shown in below figure. At the top of its motion, $$m_{2}$$ is traveling at $$v = 4.00 m/s$$. (a) What is the tension in String $$1$$ at this instant? (b) What is the tension in String $$2$$ at this instant? (c) Which string will break first if the combination is rotated faster and faster?
The radius of the path of object $$1$$ is twice that of object $$2$$. Because the strings are always “collinear,” both objects take the same time interval to travel around their respective circles; therefore, the speed of object $$1$$ is twice that of object $$2$$.
The free-body diagrams are shown below. We are given $$m_{1}= 4.00 kg, m_{2} = 3.00 kg, v = 4.00 m/s$$, and $$l = 0.500m$$
Taking down as the positive direction, we have
Object $$1$$: $$T_{1}+m_{1}g=\dfrac{m_{1}v_{1}^{2}}{r_{1}}$$, where $$v_{1}=2v,r_{1}=2l$$
Object $$2$$: $$T_{2}-T_{1}+m_{2}g=\dfrac{m_{2}V_{2}^{2}}{r_{2}}$$, where $$v_{2}=v,r_{2}=2l$$
(a) From above:
$$T_{1}=\dfrac{m_{1}v_{1}^{2}}{r_{1}}-m_{1}g=m_{1}\left ( \dfrac{v_{1}^{2}}{r_{1}}-g \right )$$
$$T_{1}=(4.00kg)\left [ \dfrac{[2(4.00m/s)]^{2}}{2(0.500m)}-9.80m/s^{2} \right ]$$
$$T_{1}=216.8N=217N$$
(b) From above:
$$T_{2}=T_{1}+\dfrac{m_{2}v_{2}^{2}}{r_{2}}-m_{2}g$$
$$T_{2}=T_{1}+m_{2}\left ( \dfrac{v_{2}^{2}}{r_{2}}-g \right )$$
$$T_{2}=T_{1}+(3.00kg)\left [ \dfrac{(4.00m/s)^{2}}{0.500m}-9.80m/s^{2} \right ]$$
$$T_{2}=216.8N+66.6N=283.4N=283N$$
(c) From above, $$T_{2} > T_{1}$$ always, so string $$2$$ will break first.
The free-body diagrams are shown below. We are given $$m_{1}= 4.00 kg, m_{2} = 3.00 kg, v = 4.00 m/s$$, and $$l = 0.500m$$
Taking down as the positive direction, we have
Object $$1$$: $$T_{1}+m_{1}g=\dfrac{m_{1}v_{1}^{2}}{r_{1}}$$, where $$v_{1}=2v,r_{1}=2l$$
Object $$2$$: $$T_{2}-T_{1}+m_{2}g=\dfrac{m_{2}V_{2}^{2}}{r_{2}}$$, where $$v_{2}=v,r_{2}=2l$$
(a) From above:
$$T_{1}=\dfrac{m_{1}v_{1}^{2}}{r_{1}}-m_{1}g=m_{1}\left ( \dfrac{v_{1}^{2}}{r_{1}}-g \right )$$
$$T_{1}=(4.00kg)\left [ \dfrac{[2(4.00m/s)]^{2}}{2(0.500m)}-9.80m/s^{2} \right ]$$
$$T_{1}=216.8N=217N$$
(b) From above:
$$T_{2}=T_{1}+\dfrac{m_{2}v_{2}^{2}}{r_{2}}-m_{2}g$$
$$T_{2}=T_{1}+m_{2}\left ( \dfrac{v_{2}^{2}}{r_{2}}-g \right )$$
$$T_{2}=T_{1}+(3.00kg)\left [ \dfrac{(4.00m/s)^{2}}{0.500m}-9.80m/s^{2} \right ]$$
$$T_{2}=216.8N+66.6N=283.4N=283N$$
(c) From above, $$T_{2} > T_{1}$$ always, so string $$2$$ will break first.
A ball of mass $$m = 0.275 kg$$ swings in a vertical circular path on a string $$L = 0.850 m$$ long as in above figure. (a) What are the forces acting on the ball at any point on the path? (b) Draw force diagrams for the ball when it is at the bottom of the circle and when it is at the top. (c) If its speed is $$5.20 m/s$$ at the top of the circle, what is the tension in the string there? (d) If the string breaks when its tension exceeds $$22.5 N$$, what is the maximum speed the ball can have at the bottom before that happens?
(a) At each point on the vertical circular path, two forces are acting on the ball (refer to below figure):
(1) The downward gravitational force with constant magnitude $$F_{g} = mg$$.
(2) The tension force in the string, always directed toward the center of the path.
(b) Below figure shows the forces acting on the ball when it is at the highest point on the path (left-hand diagram) and when it is at the bottom of the circular path (right-hand diagram). Note that the gravitational force has the same magnitude and direction at each point on the circular path. The tension force varies in magnitude at different points and is always directed toward the
center of the path.
(c) At the top of the circle, $$F_{c}=mv^{2}/r=T+F_{g}$$or,
$$T=\dfrac{mv^{2}}{r}-F_{g}=\dfrac{mv^{2}}{r}-mg=m\left ( \dfrac{v^{2}}{r}-g \right )$$
$$=(0.275kg)\left [ \dfrac{(5.20m/s)^{2}}{0.850m}-9.80m/s^{2} \right ]=6.05N$$
(d) At the bottom of the circle, $$F_{c}=mv^{2}/r=T-F_{g}=T-mg$$ and solving for the speed gives
$$v^{2}=\dfrac{r}{m}(T-mg)=r\left ( \dfrac{T}{m}-g \right )$$ and $$v=\sqrt{r\left ( \dfrac{T}{m}-g \right )}$$
If the string is at the breaking point at the bottom of the circle, then $$T = 22.5 N$$, and the speed of the object at this point must be
$$v=\sqrt{(0.850m)\left ( \dfrac{22.5N}{0.275kg}-9.80m/s^{2} \right )}=7.82m/s$$
(1) The downward gravitational force with constant magnitude $$F_{g} = mg$$.
(2) The tension force in the string, always directed toward the center of the path.
(b) Below figure shows the forces acting on the ball when it is at the highest point on the path (left-hand diagram) and when it is at the bottom of the circular path (right-hand diagram). Note that the gravitational force has the same magnitude and direction at each point on the circular path. The tension force varies in magnitude at different points and is always directed toward the
center of the path.
(c) At the top of the circle, $$F_{c}=mv^{2}/r=T+F_{g}$$or,
$$T=\dfrac{mv^{2}}{r}-F_{g}=\dfrac{mv^{2}}{r}-mg=m\left ( \dfrac{v^{2}}{r}-g \right )$$
$$=(0.275kg)\left [ \dfrac{(5.20m/s)^{2}}{0.850m}-9.80m/s^{2} \right ]=6.05N$$
(d) At the bottom of the circle, $$F_{c}=mv^{2}/r=T-F_{g}=T-mg$$ and solving for the speed gives
$$v^{2}=\dfrac{r}{m}(T-mg)=r\left ( \dfrac{T}{m}-g \right )$$ and $$v=\sqrt{r\left ( \dfrac{T}{m}-g \right )}$$
If the string is at the breaking point at the bottom of the circle, then $$T = 22.5 N$$, and the speed of the object at this point must be
$$v=\sqrt{(0.850m)\left ( \dfrac{22.5N}{0.275kg}-9.80m/s^{2} \right )}=7.82m/s$$
the angle $$\theta$$ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally.
We have $$\vec{w}=w_{i}\hat{u_{i}}+w_{n}\hat{u_{n}}$$ thus $$w_{y}=w_{t(y)}+w_{n(y)}$$
But in accordance with the problem $$w_{y}=0$$
So, $$w_{t(y)}+w_{n(y)}=0$$
or, $$g\sin \theta\sin \theta+2g\cos^{2}\theta(-\cos \theta)=0$$
or, $$\cos\theta=\dfrac{1}{\sqrt{3}}$$ or, $$\theta=54.7^{o}$$
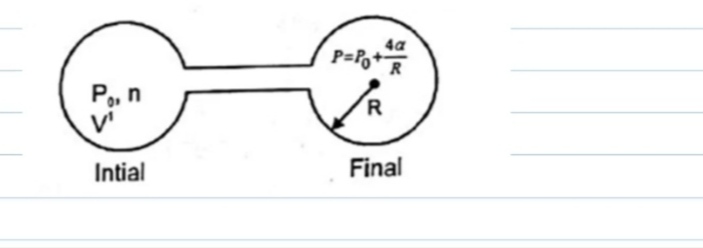
Find the work to be performed in order to blow a soap bubble of radius $$R$$ if the outside air pressure is equal to $$p_0$$ and the surface tension of the soap water solution is equal to $$\alpha$$.
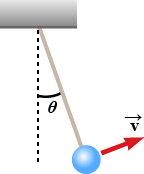
One end of a cord is fixed and a small $$0.500kg$$ object is attached to the other end, where it swings in a section of a vertical circle of radius $$2.00 m$$ as shown in above figure. When $$\theta = 20.0^{0}$$, the speed of the object is $$8.00 m/s$$. At this instant, find (a) the tension in the string, (b) the tangential and radial components of acceleration, and (c) the total acceleration. (d) Is your answer changed if the object is swinging down toward its lowest point instead of swinging up? (e) Explain your answer to part (d).
A stone of mass 2kg its thrown upward from the ground with a velocity of 3m/s. When it reaches maximum height, calculate its potential energy.
A ball whirls around in a vertical circle art the end of a string The other end of the string is fixed at the center of the circle. Assuming the total energy of the ball-Rath system remain constant, show that the tension in the string at the bottom is greater than the tension at the top by six times the ball's weight.
A ball of mass $$m=300 g$$ is connected by a strong string of length $$L=80.0\ cm$$ to a pivot and held in place with the string vertical. A wind exerts constant force $$F$$ to the right on the ball as shown Figure The ball is released from rest. The wind makes it swing up to attain maximum height $$J$$ above its starting point before it swings down again as $$F$$ approaches infinity?
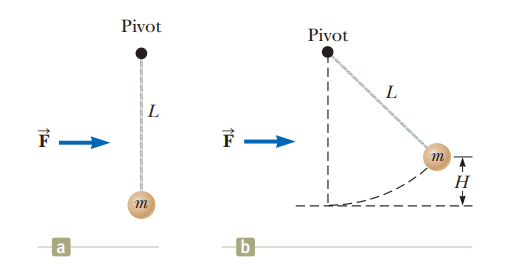
While Lost-a-Lot ponders his next move in the situation described in problem $$19$$ and illustrated in figure $$P12.19$$, the enemy attacks! An incoming projectile breaks off the stone ledge so that the end of the drawbridge can be lowered past the wall where it usually rests. In addition, a fragment of the projectile bounces up and cuts the drawbridge cable! The hinge between the castle wall and the bridge is frictionless, and the bridge swings down freely until it is vertical and smacks into the vertical castle wall below the castle entrance.
Immediately before it strikes the castle wall.
Data according to problem mentioned in ques which is missing:
$$\theta_o=20^o$$
$$l=8.00\,m$$
$$m=2000\,kg$$
Force exerted by the hinge on the bridge before the cable breaks:
According to FBD as shown in the figure we can write:
$$R_{x}=0$$ there is no force in horizontal direction before the cable breaks.
and we know that:
$$a=\omega^{2}\left(\dfrac{1}{2} \ell\right)=(1.56 \mathrm{rad} / \mathrm{s})^{2}(4.0 \mathrm{m})=9.67 \mathrm{m} / \mathrm{s}^{2} $$
$$R_{y}-m g=m a$$
solving and putting values according to the question:
$$\therefore R_{y}=(2000 \mathrm{kg})\left(9.8 \mathrm{m} / \mathrm{s}^{2}+9.67 \mathrm{m} / \mathrm{s}^{2}\right)=38.9 \mathrm{kN}$$
Thus: $$\quad R_{y}=38.9 \hat{\mathbf{j}} \mathrm{kN}$$
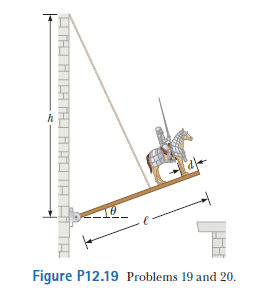
Why is the following situation impossible? An athlete test her hand strength by having an assistance hang weight from her belt as she hangs onto a horizontal bar with her hands. When the weights hanging on her belt have increased to $$80\%$$ on her body weight, her hands can no longer supports her and she drops to the floor. Frustrated at not meeting her hand-strength goal, she decides to swing on a trapeze. The trapeze consists of a bar suspended by two parallel ropes, each of length $$l$$, allowing performers to swing in a vertical circular arc Fig The athlete hold the bar and steps off an elevated platform, starting from rest with the ropes at an angle $$\theta_i=60.0^o$$ with respect to the vertical. As she swings several times back and forth in a circular arc, she forgets her frustrations related to the hand-strength test. Assume the size of the performer's body is small compared to the length $$l$$ and air resistance is negligible.
Two hypothetical planets of masses $$m_1$$ and $$m_2$$ and radii $$r_1$$ and $$r_2$$ respectively, are nearly at rest when they are an infinite distance apart. Because of their gravitational attraction, they head towards each other on a collision course.
When their center to center separation is $$d$$, find expressions for the speed to each planet and for their relative speed.
Note : Both the energy and momentum of the isolated two planet system are constant.
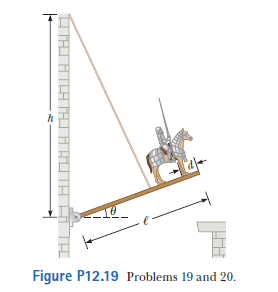
While Lost-a-Lot ponders his next move in the situation described in problem $$19$$ and illustrated in figure $$P12.19$$, the enemy attacks! An incoming projectile breaks off the stone ledge so that the end of the drawbridge can be lowered past the wall where it usually rests. In addition, a fragment of the projectile bounces up and cuts the drawbridge cable! The hinge between the castle wall and the bridge is frictionless, and the bridge swings down freely until it is vertical and smacks into the vertical castle wall below the castle entrance.
Immediately after the cable breaks
Data according to problem mentioned in ques which is missing:
$$\theta_o=20^o$$
$$l=8.00\,m$$
$$m=2000\,kg$$
Force exerted by the hinge on the bridge immediately after the cable breaks:
The linear acceleration of the bridge is:
$$ a=\dfrac{1}{2} \ell \alpha=\dfrac{1}{2}(8.0 \mathrm{m})\left(1.73 \mathrm{rad} / \mathrm{s}^{2}\right)=6.907 \mathrm{m} / \mathrm{s}^{2}$$
According to FBD s shown in diagram:
The force at the hinge + the force of gravity produce the acceleration:
$$a=6.907 \mathrm{m} / \mathrm{s}^{2}$$ at right angles to the bridge.
$$R_{x}=m a_{x}=(2000 \mathrm{kg})\left(6.907 \mathrm{m} / \mathrm{s}^{2}\right) \cos 250^{\circ}=-4.72 \mathrm{kN}$$
$$R_{y}-m g=m a_{y}$$
Solving and putting values according to the question:
$$\therefore R_{y}=m\left(g+a_{y}\right)=(2000 \mathrm{kg})\left[9.80 \mathrm{m} / \mathrm{s}^{2}+\left(6.907 \mathrm{m} / \mathrm{s}^{2}\right) \sin 250^{\circ}\right]=6.62 \mathrm{kN}$$
Thus:
$$\mathrm{R}=(-4.72 \hat{\mathbf{i}}+6.62 \hat{\mathbf{j}}) \mathrm{kN}$$
Class 11 Engineering Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Physical World Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work,Energy And Power Extra Questions