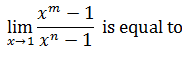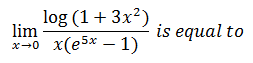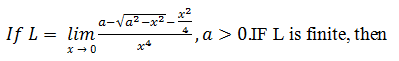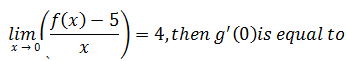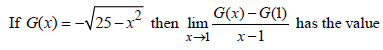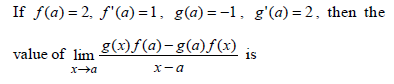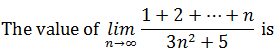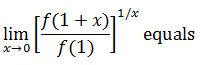- Applications Of Derivatives MCQ Quiz
- Applications Of Integrals MCQ Quiz
- Binomial Theorem And Mathematical Lnduction MCQ Quiz
- Circle And System Of Circles MCQ Quiz
- Complex Numbers MCQ Quiz
- Conic Section MCQ Quiz
- Definite Integrals MCQ Quiz
- Differential Equations MCQ Quiz
- Differentiation MCQ Quiz
- Equations And Inequalities MCQ Quiz
- Heights And Distances MCQ Quiz
- Indefinite Integrals MCQ Quiz
- Inverse Trigonometric Functions MCQ Quiz
- Limits Continuity And Differentiability MCQ Quiz
- Linear Programming MCQ Quiz
- Mathematical Logic And Boolean Algebra MCQ Quiz
- Matrices And Determinants MCQ Quiz
- Miscellaneous MCQ Quiz
- Permutations And Combinations MCQ Quiz
- Probability MCQ Quiz
- Properties Of Triangle MCQ Quiz
- Rectangular Cartesian Coordinates MCQ Quiz
- Sequences And Series MCQ Quiz
- Sets Relations And Functions MCQ Quiz
- Statics And Dynamics MCQ Quiz
- Statistics MCQ Quiz
- Straight Line And Pair Of Straight Lines MCQ Quiz
- Three Dimensional Geometry MCQ Quiz
- Trigonometric Ldentities And Equations MCQ Quiz
- Vector Algebra MCQ Quiz
Applications Of Derivatives MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16



Applications Of Derivatives Questions and Answers
| Applications Of Derivatives Quiz Question | Answer |
|---|---|
| For the function f(x) = xex the point | x = -1 is a minimum |
| The equation ex – 8 + 2x − 17 = 0 has : | one real root |
| The minimum value of sin x + cos x is | 2)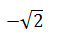 |
| If there is an error of k% in measuring the edge of a cube, then the percent error in estimating its volume is | 3k |
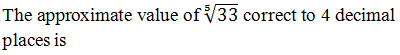 |
2.0125 |
| If the diagonal of a square is changing at the rate of 0.5 cms-1 . Then, the rate of change of area, when the area is 400 cm2, is | 2)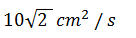 |
| A spherical iron ball of radius 10 cm, coated with a layer of ice of uniform thickness, melts at a rate of 100 it cm3/min. The rate at which the thickness layer decreases, when the thickness of ice is 5 cm, is | 1 cm/min |
| A man of 2 m height walks at a uniform speed of 6 km/h, away from a lamp post of 6 m height. The rate at which the length of his shadow increase is | 3 km/h |
| The radius of a cylinder is increasing at the rate of 3 m/s and its altitude is decreasing at the rate of 4 m/s. The rate of change of volume, when radius is 4 m and altitude is 6 m, is | 80 π cu m/s |
| A point on the parabola y2 = 18x at which the ordinate increases at twice the rate of the abscissa is | (9/8, 9/2) |
Applications Of Integrals MCQ Questions



Applications Of Integrals Questions and Answers
| Applications Of Integrals Quiz Question | Answer |
|---|---|
| The area enclosed by the curves |y + x| ≤ 1, |y - x|≤ 1 and 2x2 + 2y2 = 1 is | 2)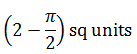 |
| The area of the region bounded by 1 - y2 = |x| and |x| + |y|= 1 is | 2/3 sq units  |
| The area of the region bounded by the lines y = mx, x = 1, x = 2 and X - axis is 6 sq units, then m is equal to | 4 |
| Area of the region bounded by two parabolas y = x2 and x = y2 is | 1/3 |
| The area bounded by the curves y = x and y = x3 is equal to | 1/2 |
| The area of the region enclosed by the curves y = x, x = e, y = 1/x and the positive X - axis is | 3/2 sq units  |
| If the area between y = mx2 and x = my2 (m >is 1/4 sq units, then the value of m is | ± 2/√3 |
| The area enclosed between y2 = x and y = x is | 1/6 sq units  |
| The area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and x = 3π/2 is | (4√2 - 2)sq units  |
| The area (in sq units) of the plane region bounded by the curve x = y2 and the line y = -x is | 9/2 |
Binomial Theorem And Mathematical Lnduction MCQ Questions



Binomial Theorem And Mathematical Lnduction Questions and Answers
| Binomial Theorem And Mathematical Lnduction Quiz Question | Answer |
|---|---|
| The coefficient of χ5 in the expansion of (1 + χ2)5 (1 + χ)4 is | 60 |
| In the expansion of (2 – 3χ3)20 , if the ratio of 10th term to 11th term is 45/22, then χ is equal to | – (2/3) |
| Given positive integers r > 1, n >2 and that the coefficient of (3r)th and (r + 2)th terms in the binomial expansion of (1+ x)2n are equal . Then | n = 2r |
| If 21st and 22nd terms in the expansion of (1 + χ)44 are equal, then χ is equal to | 7/8 |
| If the coefficient of χ8 in (aχ2 + 1/bχ )13 is equal to the coefficient of χ–8 in(aχ – 1/bχ2 )13, then a and b will satisfy the relation | ab + 1 = 0 |
| The coefficient of χ3 in the infinite series expansion of 2/(1– χ) (2 – χ), for |χ| < 1 is | 15/8 |
| If (a + bχ)–3 = 1/27 + (1/3)χ + ..., the the ordered pair (a, b) equals | (3, – 9) |
| The coefficient of three consecutive of (1 + χ)n+5 are in the ratio 5 : 10 : 14. Then, n is equal to (answer lies between 0 to 9 ) | 6 |
 |
0 |
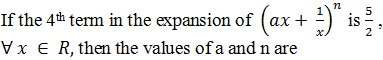 |
1/2 , 6 |
Circle And System Of Circles MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14



Circle And System Of Circles Questions and Answers
| Circle And System Of Circles Quiz Question | Answer |
|---|---|
| The angle between a pair of tangents drawn from a point P to the circle x2 + y2 + 4x – 6y + 9 sin2 α + 13 cos2 α = 0 is 2α. The equation of the locus of the point P is | x2 + y2 + 4x – 6y + 9 = 0 |
| Two circles x2 + y2 = 6 and x2 + y2 – 6x + 8 = 0 are given. Then the equation of the circle through their points of intersection and the point (1,is | x2 + y2 – 3x + 1 = 0 |
| The locus of the mid-point of a chord of the circle x2 + y2 = 4 which subtends a right angle at the origin is | x2 + y2 = 2 |
| If a circle passes through the point (a, b) and cuts the circle x2 + y2 = k2 orthogonally, then the equation of the locus of its centre is | 2ax + 2by - (a2 + b2 + k2 ) = 0 |
| If the two circles (x – 1)2 + (y – 3)2 = r2 and x2 + y2 – 8x + 2y + 8 = 0 intersect in two distinct points, then | 2 < r < 8 |
| The lines 2x – 3y = 5 and 3x – 4y = 7 are diameters of a circle of area 154 sq. units. Then the equation of this circle is | x2 + y2 – 2x + 2y = 47 |
| The centre of a circle passing through the points (0, 0), (1,and touching the circle x2 + y2 = 9 is | 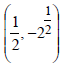 |
| The locus of the centre of a circle, which touches externally the circle x2 + y2 – 6x – 6y + 14 = 0 and also touches the y-axis, is given by the equation: | y2 – 10x – 6y + 14 = 0 |
| The circles x2 + y2 – 10x + 16 = 0 and x2 + y2 = r2 intersect each other in two distinct points if | 2 < r < 8 |
| If the line y = 7x - 25 meets the circle x2 + y2 = 25 in the points A, B, then the distance between A and B is | 5√2 |
Complex Numbers MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15



Complex Numbers Questions and Answers
| Complex Numbers Quiz Question | Answer |
|---|---|
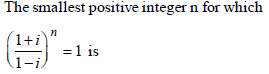 |
none of these |
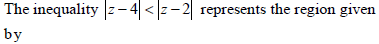 |
none of these |
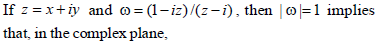 |
z lies on the real axis |
| The points z1, z2, z3 z4 in the complex plane are the vertices of a parallelogram taken in order if and only if | z1 + z3 = z2 + z4 |
| The smallest positive integer n for which (1+ i)2n = (1 - i)2n is | 2 |
The values of x and y satisfying the equation 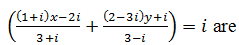 |
x = 3 y = -1 |
Let z1 ≠ z2 and |z1| = |z2|.If z1 has positive real part and z2 has negative imaginary part. Then,
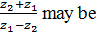 |
real and positive |
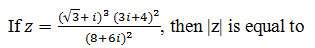 |
2 |
| If z(2- i2√3)2 = i(√3 + i)4, then amplitude of z is | 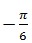 |
| If a, b, c and u, v, w are complex numbers representing the vertices of two triangles such that c = (1 – r) a + rb and w = (1 – r)u + rv, where r is a complex number, then the two triangles | are similar |
Conic Section MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16



Conic Section Questions and Answers
| Conic Section Quiz Question | Answer |
|---|---|
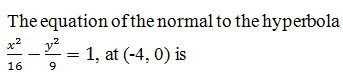 |
y = 0 |
| Eccentricity of rectangular hyperbola is | 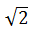 |
| The parameters from of the ellipse 4(x + 1)2 + (y - 1)2 = 4 is | x = cos θ - 1, y = 2 sin θ + 1 |
| The length of the transverse axis of a hyperbola is 2cos α. The foci of the hyperbola are the same as that of the ellipse 9x2 + 16y2 = 144. The equation of the hyperbola is | 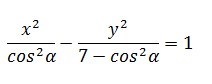 |
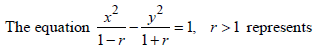 |
none of these |
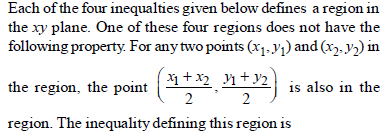 |
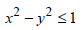 |
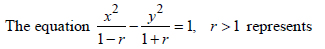 |
none of these |
| If the distance directrices of a rectangular hyperbola is 10, then distance between its foci will be | 20 |
 |
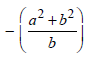 |
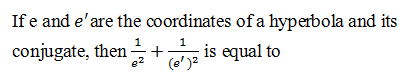 |
1 |
Definite Integrals MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16
Quiz 17
Quiz 18
Quiz 19



Definite Integrals Questions and Answers
| Definite Integrals Quiz Question | Answer |
|---|---|
| The area enclosed by the parabola y2 = 4ax and the straight line y = 2ax , is | 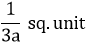 |
| Area bounded by the curve x2 = 4y and the straight line x = 4y – 2 is | 2)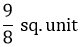 |
| If the area bounded by y = ax2 and x = ay2, a > 0, is 1,then a = | 2)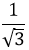 |
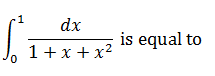 |
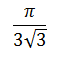 |
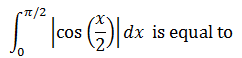 |
√2 |
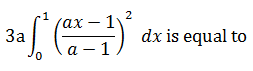 |
a - 1 + (a - 1)-2 |
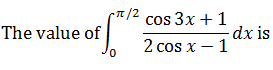 |
1 |
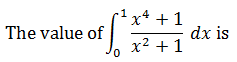 |
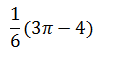 |
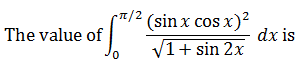 |
2 |
| If f is continuous function, then | 2)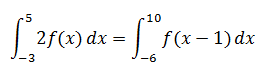 |
Differential Equations MCQ Questions



Differential Equations Questions and Answers
| Differential Equations Quiz Question | Answer |
|---|---|
| The solution of the differential equation dy/dx = sin (x + y) tan (x + y) - 1 is | x + cosec (x + y) = C |
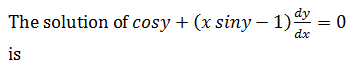 |
xsec y = tan y + C |
| The form of the differential equation of the central conics ax2 + by2 = 1 is | 2)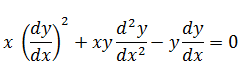 |
| The differential equation of the rectangular hyperbola, where axes are the asymptotes of the hyperbola, is | 2)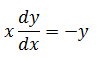 |
The order and degree of the differential equation 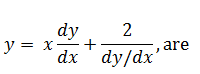 |
1, 2 |
The order and degree of differential equation 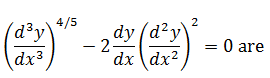 |
3, 4 |
| The differential equation of system of circles touching the Y - axis at origin is | 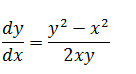 |
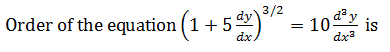 |
3 |
The degree of the differential equation satisfying 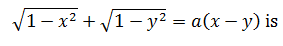 |
1 |
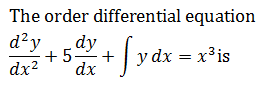 |
3 |
Differentiation MCQ Questions



Differentiation Questions and Answers
| Differentiation Quiz Question | Answer |
|---|---|
| If y = (1 + x) (1 + x2) (1 + x4), then dy/dx at x = 1 is | 28 |
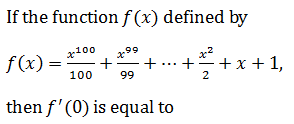 |
1 |
| If y = f(x2 +and f '(= 5, then dy/dx at x = 1 is | 10 |
| Find the deviate of √2x + 2√x – 1/√x. | 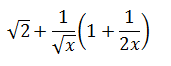 |
| The derivative of y = (1 – x) (2 – x) ...(n – x) at x = 1 is | (–1)(n – 1)! |
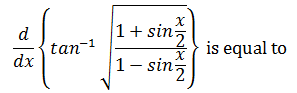 |
1/4 |
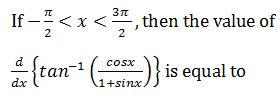 |
- (1/2) |
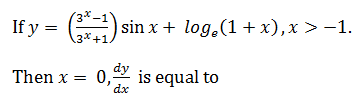 |
1 |
| If f(x) = logx {ln(x)}, then f '(e) is equal to | 1/e |
| If ex + ey = ex + y, then dy/dx at (2,is | –1 |
Equations And Inequalities MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15



Equations And Inequalities Questions and Answers
| Equations And Inequalities Quiz Question | Answer |
|---|---|
| log4 2 - log16 2 + log 2 - ... is equal to | 1 - loge 2 |
| x, y, z are +ve real numbers and x + y + z = 1/2 then | 2)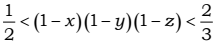 |
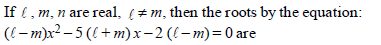 |
x = y |
| The equation x + 2y + 2z = 1 and 2x + 4y + 4z = 9 have | None of these. |
Given that, a, b ϵ {0,1,2...9} with a + b ≠ 0
and 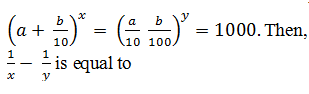 |
1/3 |
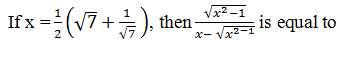 |
3 |
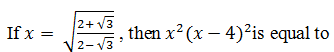 |
1 |
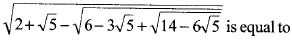 |
2 |
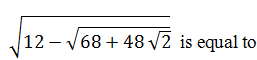 |
2 - √2 |
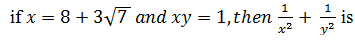 |
254 |
Heights And Distances MCQ Questions


Heights And Distances Questions and Answers
| Heights And Distances Quiz Question | Answer |
|---|---|
| A house of height 100 m subtends a right angle at the window of an opposite house. If the height of the window is 64 m, then the distance between the two houses is | 48 m |
| ABCD is a square plot. The angle of elevation of the top of a pole standing at D from A or C is 30° and that from B is θ, then tan θ is equal to | 1/√6 |
| A vertical pole PO is standing at the centre 0 of a square ABCD. If AC subtends an ∠ 90° at the top P of the pole, then the angle subtended by a side of the square at P is | 60° |
| The angles of elevation of the top of a tower at two points, which are at distances a and b from the foot in the same horizontal line and on the same side of the tower, are complementary. The height of the tower is | √ab |
| Angles of elevation of the top of a tower from three points (collinear) A ,B and C on a road leading to the foot of the tower are 30°, 45° and 60°, respectively. The ratio of AB to BC is | √3 : 1 |
| From the top of a cliff 50 m high, the angles of depression of the top and bottom of a tower are observed to be 30° and 45°. The height of tower is | 50 (1 - √3/3 ) m  |
| ABC is a triangular park with ,AB = AC = 100 m. A clock tower is situated at the mid-point of BC. The angle of elevation, if the top of the tower at A and B are cot-1 3 2 and cosec-12.6, respectively. The height of the tower is | 25 m  |
| P is a point on the segment joining the feet of two vertical poles of heights a and b. The angles of elevation of the tops of the poles from P are 45° each. Then, the square of the distance between the tops of the poles is | 2(a2 + b2) |
| The base of a cliff is circular. From the extremities of a diameter of the base angles of elevation of the top of the cliff are 30° and 60°. If the height of the cliff is 500 m, then the diameter of the base of the cliff is | 2000/√3 m |
| A round balloon of radius r subtends an angle a at the eye of the observer, while the angle of elevation of its center is β. The height of the centre of balloon is | 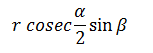 |
Indefinite Integrals MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16

Indefinite Integrals Questions and Answers
| Indefinite Integrals Quiz Question | Answer |
|---|---|
| Let f be a function such that f(= 4 and f '(x) ≥ 2 for 1 ≤ x ≤ 4. How small can f(possible be ? | 10 |
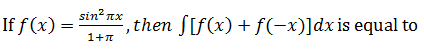 |
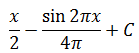 |
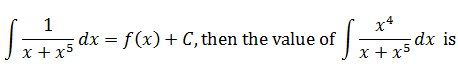 |
log x - f(x) + C |
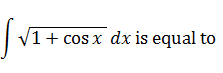 |
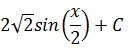 |
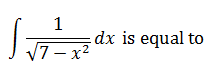 |
2)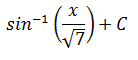 |
| If f(x) and g(x) are twice differentiable function on (0,satisfying f ''(x) = g''(x), f '(=4, g'(= 6, f(= 3, g(= 9, then f(- g(is equal to | -4 |
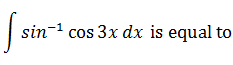 |
2)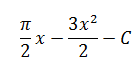 |
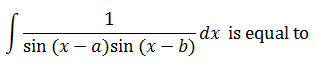 |
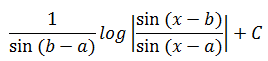 |
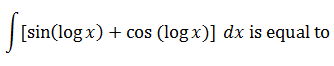 |
x sin (log x) + C |
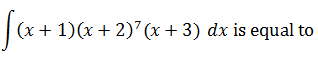 |
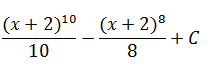 |
Inverse Trigonometric Functions MCQ Questions



Inverse Trigonometric Functions Questions and Answers
| Inverse Trigonometric Functions Quiz Question | Answer |
|---|---|
| The greatest and least values of (sin-1χ )2 + (cos-1χ)2 are respectively | 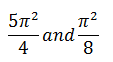 |
| The value of sin (2 sin-1 0.is | 0.96 |
| If χ > 0, y > 0, z > 0, χy + yz + zχ < 1 and tan-1 χ + tan-1 y + tan-1 z = π, then χ + y + z is equal to | χyz |
If we consider only the principle values of the inverse trigonometric functions then the value of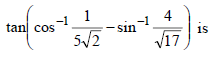 |
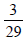 |
| tan-1 (√- cot-1 (-√is equal to | -(π/2) |
| The number of value(s) of χ, in which tan-1 (1/χ) = π tan-1 χ, 0 < χ < 1 | 0 |
| The value of sin (2 tan-1 χ), |χ| ≤ 1 is | 2χ/ (1 + χ2) |
The number of real solutions of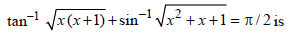 |
two |
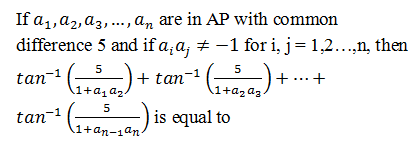 |
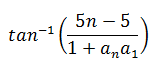 |
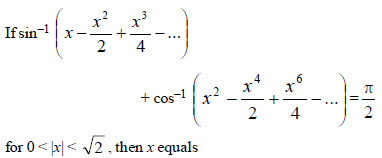 |
1 |
Limits Continuity And Differentiability MCQ Questions
Linear Programming MCQ Questions


Linear Programming Questions and Answers
| Linear Programming Quiz Question | Answer |
|---|---|
| The maximum value of z = 9x + 13y, subject to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0 and y ≥ 0 is | 79 |
| Variables of the objective function of the linear programming problem are | zero or positive |
| The area of the feasible region for the following constraints 3y + x ≥ 3 , x ≥ 0 and y ≥ 0 will be | unbounded |
| Maximum value of z =12x + 3y, subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is | 36 |
| The region represented by the inequation system x , y ≥ 0, y ≤ 6 , x + y ≤ 3 is | bounded in first quadrant |
| Which of the term is not used in a linear programming problem? | Concave region |
| The maximum value of z = 4x + 2y subject to constraints 2x + 3y ≤ 18 , x + y ≥ 10 and x , y ≥ 0 is | None of these |
| The maximum value of z is where, z = 4x + 2y subject to constraints 4x + 2y ≥ 46 , x + 3y ≤ 24 and x, y ≥ 0, is | 96 |
| Maximum value of z = 3x + 4y subject to constraints x - y ≥ -1, -x + y ≤ 0 and x , y ≥ 0, is given by | no feasible region |
| A furniture dealer deals in only two items namely tables and chairs. He has Rs 5000 to invest and space to store atmost 60 pieces. A table cost him Rs 250 and a chair Rs 60. He can sell a table at a profit of Rs 15. Assume that, he can sell all the items that he produced. The number of constraints in the problem are | 4 |
Mathematical Logic And Boolean Algebra MCQ Questions



Mathematical Logic And Boolean Algebra Questions and Answers
| Mathematical Logic And Boolean Algebra Quiz Question | Answer |
|---|---|
| If p is the statement 'Ravi races' and q is the statement `Ravi wins'. Then, the verbal translation of ~ [p ⋁ (~ q)] is | Ravi does not race and Ravi wins |
| The negation of the proposition `If 2 is prime, then 3 is odd' is | 2 is prime and 3 is not odd |
| If p ⇒(q ˅ r) is false, then the truth values of p, q, r arerespectively | T, F, F |
| The logically equivalent proposition of p ⇔ q is | (p⇒ q) ˄ (q⇒ p) |
| The false statement in the following is | (p ⇒ q) ⇔ (~q⇒~p) is a contradiction |
| ~(p ⋁ q ) ⋁ (~ p ⋀ q) is logically equivalent to | ~ p |
| The contrapositive of (p ⋁ q) → r is | ~ r → (~ p ⋀ ~ q) |
| Negation of the conditional, 'If it rains, I shall go to school' is | It rains and I shall not go to school |
| Dual of (x' ⋁ y')' = x ⋀ y is | (x' ⋀ y')' = x ⋁ y |
| The converse of the contrapositive of the conditional p → ~q is | ~ p → q |
Matrices And Determinants MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16
Quiz 17
Quiz 18



Matrices And Determinants Questions and Answers
| Matrices And Determinants Quiz Question | Answer |
|---|---|
| Consider the set A of all determinants of order 3 with entries 0 or 1 only. Let B be the subset of A consisting of all determinants with value 1. Let C be the subset of A consisting of all determinants with value –1. Then | B has as many elements as C |
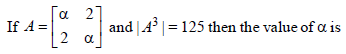 |
± 3 |
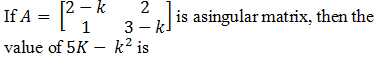 |
4 |
If n ≥ 2 is an integer 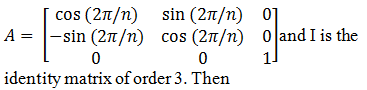 |
An = I and An-1 ≠ 1 |
| If AB = A and BA = B, then B2 is equal to | B |
Let a, b, c be the real numbers. Then following system of equations in x, y and z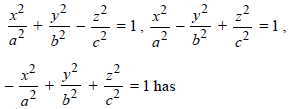 |
finitely many solutions |
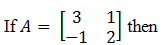 |
A2 – 5A + 7I = 0 |
| If A and B are square matrices of equal degree, then which one is correct among the followings? | A + B = B + A |
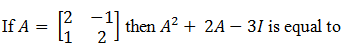 |
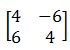 |
If P is a 3 × 3 matrix such that PT = 2P + I, where PT is the transpose of P and I is the 3 × 3 identity matrix, then there exists a column matrix, 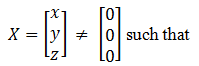 |
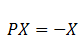 |
Miscellaneous MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16



Miscellaneous Questions and Answers
| Miscellaneous Quiz Question | Answer |
|---|---|
 |
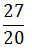 |
| In the group G = {0,1, 2, 3, 4, 5} under addition modulo 6, (2 +6 3-1 +6 4)-1 is equal to | 3 |
| Which one of the following is not correct? | Fourth roots of unity form an additive abelian group |
| The remainder obtained when 1! + 2! + 3 ! + ..... + 11 ! is divided by 12 is | 9 |
| The last three digit in 332 is | 841 |
| The sum of all proper divisors of 9900 is | 23951 |
| The least positive remainder, when 123 × 125 × 127 is divided by 124 is | 121 |
| The last digit of number 7886 is | 9 |
| The sum of 1 × 1! + 2 × 2! + ...... + 50 × 50! equals | 51! - 1 |
| The digit in the unit's place of 7171 + ( 177 ) ! is | 3 |
Permutations And Combinations MCQ Questions



Permutations And Combinations Questions and Answers
| Permutations And Combinations Quiz Question | Answer |
|---|---|
| How many different signals can be made by 5 flags from 8 flags of different colours | None of these |
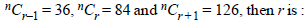 |
3 |
| Ten different letters of an alphabet are given. Words with five letters are formed from these given letters. Then the number of words which have at least one letter repeated are | 69760 |
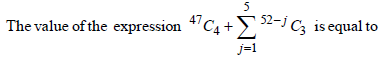 |
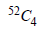 |
| Eight chairs are numbered 1 to 8. Two women and three men wish to occupy one chair each. First the women choose the chairs from amongst the chairs marked 1 to 4 ; and then the men select the chairs from amongst the remaining. The number of possible arrangements is | none of these |
| A five-digit numbers divisible by 3 is to be formed using the numerals 0, 1, 2, 3, 4 and 5, without repetition. The total number of ways this can be done is | 216 |
| How many different nine digit numbers can be formed from the number 223355888 by rearranging its digits so that the odd digits occupy even positions ? | 60 |
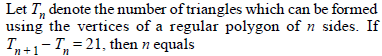 |
7 |
| If 56pr+6 : 54pr+3 = 30800 : 1, then the value of r is | 41 |
| The number of permutations by taking all letters and keeping the vowels of the word 'COMBINE' in the odd places is | 576 |
Probability MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15



Probability Questions and Answers
| Probability Quiz Question | Answer |
|---|---|
| If A and B are two independent events, then P(A/B) = | P(A) |
| A fair die is thrown twenty times. The probability that on the tenth throw the fourth six appears is | 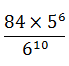 |
| A four - digit number is formed by the digits 1, 2, 3, 4 with no repetition. The probability that the number is odd, is | None of these  |
| If the integers m and n are chosen at random from 1 to 100, then the probability that a number of the from 7n + 7m is divisible by 5 equals | 1/4 |
| One mapping (function) is selected at random from all the mappings of set A = {1, 2, 3,.., n} into itself. The probability that the mapping selected is one - one, is | 2)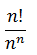 |
| The probability that a leap year selected at random contains 53 Sunday is | 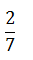 |
| Three of six vertices of a regular hexagon are chosen at random. The probability that the triangle with three vertices is equilateral equals | 1/10 |
| Ram is visiting a friend. Ram knows that his friend has 2 children and 1 of them is a boy. Assuming that a child is equally likely to be boy or a girl, then the probability that the other child is a girl is | 2/3 |
| A single letter is selected at random from the word 'PROBABILITY'.The probability that is a vowel, is | 4/11 |
| If three squares are chosen on a chess board, the chance that they should be in a diagonal line is | 7/744 |
Properties Of Triangle MCQ Questions



Properties Of Triangle Questions and Answers
| Properties Of Triangle Quiz Question | Answer |
|---|---|
| In any ∆ABC, c2 sin 2B + b2 sin 2C is equal to | 4∆ |
| In a triangle, the lengths of two larger sides are 10 cm and 9 cm. If the angles of the triangle are in AP, then the length of the third side is | 5 ± √6 |
| If the bisector of the angle P of a triangle PQR meets QR in S, then | QS : SR = PQ : PR |
| In a ∆ABC, a,b, c are the sides of the triangle opposite to the angles A, B, C, respectively. Then, the value of a3 sin (B - C) + b3 (C - A) + c3 (A - B) is | 0 |
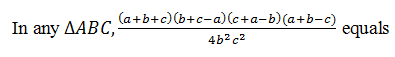 |
sin2 A |
| If the angles of a triangle are in the ratio 1 : 1 : 4, then the ratio of the perimeter of the triangle to its largest side is | √3 + 2 : √3 |
| Angles A, B, C of a ∆ABC are in AP and b : c = √3 : √2, then ∠A is given by | 75o |
| If in a ∆ABC, a tan A + b tan B = (a + b) tan (A + B)/2 , then | A = B |
| a3 cos (B - C) + b3 cos (C - A) + c3 cos (A - B) is equal to | 3abc |
| If in a ∆ABC , a/ cos A = b/ cos B, then | 2 sin A cos B = sin C |
Rectangular Cartesian Coordinates MCQ Questions



Rectangular Cartesian Coordinates Questions and Answers
| Rectangular Cartesian Coordinates Quiz Question | Answer |
|---|---|
| Area (in sq units) enclosed by y = 1, 2x + y = 2 and x + y = 2 | 1/4 |
| If algebraic sum of distances of a variable line from points (2, 0), (0,and (-2, -is zero, then the line passes through the fixed point | (0, 0) |
| If C is the reflection of A(2,in X - axis and B is the reflection of C is Y - axis, then |AB| is equal to | 4√5 |
 |
- 2 |
| Point Q is symmetric to P(4, -with respect to the bisector of the first quadrant. The length of PQ is | 5√2 |
| One possible condition for the three points (a, b), (b, a) and (a2, - b2) to be collinear, is | a = 1 + b |
| If points (5,, (10,k) and (-5,are collinear , then k = | 7 |
| The mid point of the line joining the points (-10,and (-6,divides the line joining the points (4, -and (-2,in the ratio | 2 : 1 externally  |
| The image of the center of the circles x2 + y2 = a2 with respect to the mirror image x + y = 1 is | None of these  |
| If P(1, 2), Q (4, 6), R(5,and S (a, b) are the vertices of a parallelogram PQRS, then | a = 2, b = 3 |
Sequences And Series MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16



Sequences And Series Questions and Answers
| Sequences And Series Quiz Question | Answer |
|---|---|
| The mean of the series a,a + nd, a + 2nd is | a + nd |
| If A.M and G.M of x and y are in the ratio p : q the x : y is | 2)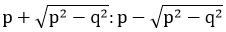 |
| The third term of a geometric progression is 4. The product of the first five terms is | 45 |
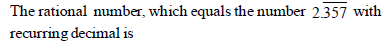 |
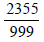 |
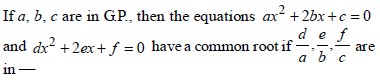 |
A.P. |
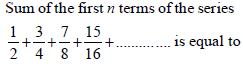 |
n + 2-n – 1 |
| The arithmetic mean of first n odd natural number is | n |
| If sum of n terms of an AP is 2n + 3n2, then rth term is | 6r - 1 |
| If the sum to 2n terms of an AP 2,5,8,11,...is equal to the sum of n terms of an AP 57,59,61,63,...,then n is equal to | 11 |
| If the sum of 12th and 22nd terms of an AP is 100, then the sum of the first 33 terms of an AP is | 1650 |
Sets Relations And Functions MCQ Questions



Sets Relations And Functions Questions and Answers
| Sets Relations And Functions Quiz Question | Answer |
|---|---|
| If n(A) = 4 and n(B )= 6. Then, the number of one-one function from A to B is | 360 |
| Let R = {(a, a)} be a relation on set A. Then r is | Symmetric and antisymmetric  |
| Let R be the relation on the set R of all real numbers defined by a R iff |a – b| ≤ 1. Then R is | Reflexive and symmetric  |
| If A = { 4n - 3n -1: n ∈ N } and B = { 9(n -:n ∈ N }, then | A ⊂ B |
| In a class of 60 students, if 25 students play cricket, 20 students play tennis and 10 students play both the games, then the number of students who play neither is | 25 |
| The set A = { x : x ∈ R, x2 = 16 and 2x = 6 } is equal to | ϕ |
| If A and B are two sets, then (A ∪ B)\' ∩ (A\' ∩ B) is equal to | None of these |
| If A = {1, 2}, B = { {1}, {2} }, C = { {1, 2} }. Then, which of the following relation is correct? | A ∈ C |
| If S = {1, 2, 3, 4}, then the total number of unordered pairs of disjoint subsets of S is | 41 |
The shaded region in the figure represents 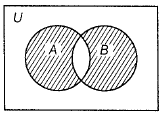 |
( A - B )∪( B - A ) |
Statics And Dynamics MCQ Questions



Statics And Dynamics Questions and Answers
| Statics And Dynamics Quiz Question | Answer |
|---|---|
| A particle is moving in a straight line with uniform velocity. Its acceleration is | zero |
| Resultant velocity of two velocities 30 km/h and 60 km/h making an angle 60° with each other is | 30 √7 km/h |
| A particle has two velocities of equal magnitude inclined to each other at an angle θ . If one of them is halved, the angle between the other and the original resultant velocity is bisected by the new resultant. Then , θ is | 120° |
| A particle having simultaneous velocities 3 m/s, 5 m/s and 7 m/s is at rest. The angle between the first two velocities is | 60° |
| A particle is thrown vertically upwards with velocity 24.5 cm/min. It will return to the original position after | None of these  |
| A particle is dropped from a height 12 g m and 4 s after another particle is projected from the ground towards it with a velocity 4g ms-1 . The time after which the second particle meets first is | 1/ 2 s |
| A ball falls from rest from top of a tower. If the ball reaches the foot of the tower in 3 s, then height of tower is (take g = 10 m/s2) | 45 m |
| A particle is thrown vertically upwards with a velocity of 490 cm/s. It will return to this position after | 1 s |
| The amount of force that is needed to accelerate a truck of mass 36000 kg from rest to a velocity of 60 km/h in 20 s is | 30 kN  |
| Two bodies of masses m and 4m are moving with equal momentum. The ratio of their KE is | 4: 1 |
Statistics MCQ Questions



Statistics Questions and Answers
| Statistics Quiz Question | Answer |
|---|---|
| The mean deviation from the mean of the set of observations -1, 0, 4 is | 2 |
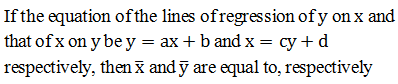 |
2)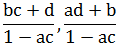 |
| The mean of the numbers a, b, 8, 5, 10, is 6 and the variance is 6.80. Then, which one of the following gives possible values of a and b ? | a = 3, b = 4 |
| The AM of 9 terms is 15. If one more term is added to this series, then AM becomes 16. The value of the added term is | 25 |
| In a moderately asymmetrical distribution, if the mean and median are 36 and 34 respectively, then find out the value of empirical mode. | 30 |
| The mean age of a combined group of men and women is 25 yr. If the mean age of the group of mean is 26 and that of the group of women is 21, then the percentage of men and women in the group is | 80, 20 |
| The values of mean, median and mode coincide, then the distribution is | symmetric distribution  |
| In a class of 100 students, there are 70 boys, whose average marks in a subject are 75. If the average marks of the complete class is 72, then what is the average marks of the girls ? | 65 |
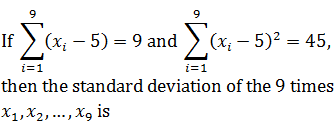 |
2 |
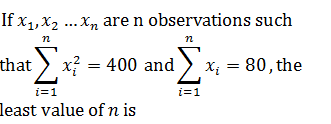 |
16 |
Straight Line And Pair Of Straight Lines MCQ Questions



Straight Line And Pair Of Straight Lines Questions and Answers
| Straight Line And Pair Of Straight Lines Quiz Question | Answer |
|---|---|
| The equation of line perpendicular to x = c is | y = d |
| The lines represented by the equation x2 - y2 - x + 3y - 2 = 0 | x - y + 1 = 0, x + y - 2 = 0  |
| The lines 15x – 18y + 1 = 0, 12x + 10y – 3 = 0 and 6x + 66y – 11 = 0 are | Concurrent  |
| If the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is | square |
| If the lines ax + 2y + 1 = 0, bx + 3y + 1 = 0 and cx + 4y + 1 = 0 are concurrent, then a,b,c are in | A.P |
| The lines 2x + y – 1 = 0, ax + 3y – 3 = 0 and 3x + 2y – 2 = 0 are concurrent for | All a |
| If lines 4x + 3y = 1 ,y = x + 5 and 5y + bx = 3 are concurrent, then b equals | 6 |
| The bisector of the acute angle formed between the lines 4x - 3y + 7 = 0 and 3x - 4y +14 = 0 has the equation | x - y + 3 = 0 |
| The points (–a, – b), (0, 0), (a, b) and (a2, ab) are : | Collinear |
| The point (4,undergoes the following three transformations successively
(i) Reflection about the line y = x. (ii) Translation through a distance 2 units along the positive direction of x-axis. (iii) Rotation through an angle p/4 about the origin in the counter clockwise direction. Then the final position of the point is given by the coordinates. |
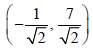 |
Three Dimensional Geometry MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16
Quiz 17



Three Dimensional Geometry Questions and Answers
| Three Dimensional Geometry Quiz Question | Answer |
|---|---|
| The distance of a point P(a, b, c) from the X - axis is | 2)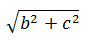 |
| The angle between two diagonals of a cube is | cos-1 (1/3) |
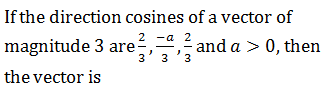 |
2)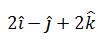 |
| The angle between a normal to the plane 2x - y + 2z - 1 = 0 and the Z - axis is | cos-1 (2/3) |
| The angle between the lines, whose direction ratios are (1, 1,, (√3, -1, -√3 - 1, 4), is | π/3 |
| The projection of any line on coordinate to the respectively 3, 4 and 5, then its length is | 5√2 |
| A line makes the same angle θ with each of the X and Z - axes. If it makes the angle β with Y - axis such that sin2 β = 3 sin2θ, then cos2 θ equals | 3/5 |
| The shortest distance of the point (1, 2,from X, Y and Z - axes respectively are | 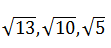 |
| The projection of a directed line segment on the coordinate axes are 12, 4,3. The direction cosines of the line are | 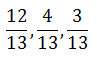 |
| If (1, -2, -and (0, 2,are direction ratios of two lines, then the direction cosines of a perpendicular to both the lines are | 2)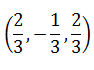 |
Trigonometric Ldentities And Equations MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16
Quiz 17
Quiz 18
Quiz 19
Quiz 20
Quiz 21
Quiz 22
Quiz 23



Trigonometric Ldentities And Equations Questions and Answers
| Trigonometric Ldentities And Equations Quiz Question | Answer |
|---|---|
| If cos (A - B) = 3/5 and tan A tan B = 2, then which one of the following is correct ? | cos (A + B) = -1/5 |
| cos 2 χ + 7 = a (2 - sinχ) can have a real solution for | a ϵ [2, 6] |
| Number of solutions of |χ - 1| = cos χ is | 2 |
| The value of sin 36o sin 72o sin 108o sin 144o is | 5/16 |
| The value of 2cot2 (π/+ 4tan2 (π/- 3cosec π/6 is | 4/3 |
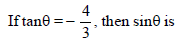 |
2)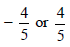 |
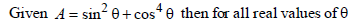 |
2)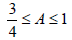 |
| If sin A + sin B + sin C = 3, then cos A + cos B + cos c is equal to | 0 |
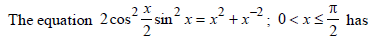 |
no real solution |
| The general solution of the trigonometric equation sin x+cos x = 1 is given by : | 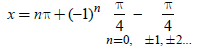 |
Vector Algebra MCQ Questions
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16



Vector Algebra Questions and Answers
| Vector Algebra Quiz Question | Answer |
|---|---|
| Out of the following which one is not true | 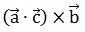 |
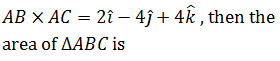 |
3 sq units  |
| Given that, |a|= 3, |b|= 4, |a ×b| = 10, then |a . b|2 is equal to | 44 |
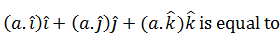 |
a |
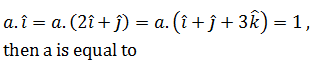 |
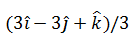 |
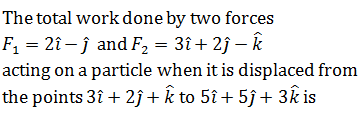 |
11 units  |
 |
{a, b1, c2} |
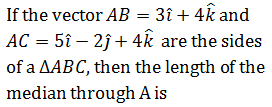 |
√33 |
If the position vectors of the vertices of ∆ABC are 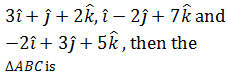 |
equilateral  |
| If the vectors a + λb + 3c, – 2a + 3b – 4c and a – 3b + 5c are coplanar, then the value of λ is | –2 |