Alternating Current - Class 12 Engineering Physics - Extra Questions
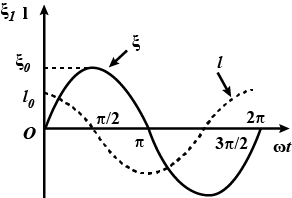
An $$AC$$ source generating a voltage $$e = e_{0}\sin \omega t$$ is connected to a capacitor of capacitance $$C$$. Find the expression for the current $$i$$ flowing through it. Plot a graph of $$e$$ and $$i$$ versus $$\omega t$$.
In the double-slit experiment of Fig. $$ 35-10 $$, the electric fields of the waves arriving at point $$ P $$ are given by
$$E_{1}=(2.00 \mu \mathrm{V} / \mathrm{m}) \sin \left[\left(1.26 \times 10^{15}\right) t\right]$$
$$E_{2}=(2.00 \mu \mathrm{V} / \mathrm{m}) \sin \left[\left(1.26 \times 10^{15}\right) t+39.6 \ \mathrm{rad}\right]$$
where time $$ t $$ is in seconds.
In a phasor diagram of the electric fields, what is the angle between the phasors?
What transformation of energy takes place when current is drawn from a cell ?
Write phase difference between current and voltage for an ac circuit, when (I) $$f={f}_{r}$$ (ii) $$f< {f}_{r}$$ (iii) $$f> {f}_{r}$$ here $${f}_{r}$$ is the resonant frequency.
Add the quantities $$ y_{1}=10 \sin \omega t, y_{2}=15 \sin \left(\omega t+30^{\circ}\right) $$ and $$ y_{3}=5.0 \sin \left(\omega t-45^{\circ}\right) $$ using the phasor method.
In the double-slit experiment of Fig. $$ 35-10 $$, the electric fields of the waves arriving at point $$ P $$ are given by
$$E_{1}=(2.00 \mu \mathrm{V} / \mathrm{m}) \sin \left[\left(1.26 \times 10^{15}\right) t\right]$$
$$E_{2}=(2.00 \mu \mathrm{V} / \mathrm{m}) \sin \left[\left(1.26 \times 10^{15}\right) t+39.6 \mathrm{rad}\right]$$
where time $$ t $$ is in seconds.
In a phasor diagram of the electric fields, at what rate would the phasors rotate around the origin?
Find the sum $$ y $$ of the following quantities:
$$y_{1}=10 \sin \omega t \quad \text { and } \quad y_{2}=8.0 \sin \left(\omega t+30^{\circ}\right)$$
Compare resistance and reactance.
An $$AC$$ circuit consists of only an inductor of inductance $$2 H$$. If the current is represented by a sine wave of amplitude $$0.25 A$$ and frequency $$60 Hz$$, calculate the effective potential difference across the inductor $$(\pi = 3.142)$$
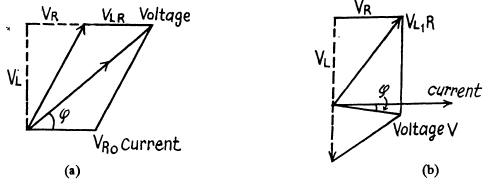
Draw the approximate voltage vector diagrams in the electric circuits shown in Fig.$$4.33$$ $$a,b.$$ The external voltage $$V$$ is assumed to e alternating harmonically with frequency $$\omega$$.
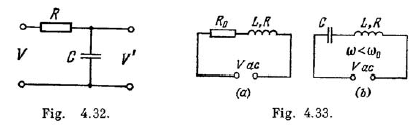
A capacitor with capacitance $$C$$ and coil with active resistance $$R$$ and inductance $$L$$ are connected in parallel to a source of sinusoidal voltage voltage of frequency $$\omega$$. Find the phase difference between the current fed to the circuit and the source voltage.
The power factor of an a.c. circuit is $$0.5$$ what is phase difference between voltage and current.
If a direct current of $$ \alpha $$ unit is superimposed with an alternating current $$ I = \beta sin \omega t $$ , then effective value of resulting current is
Match the following column
An electrical device draws $$2kW$$ power from $$AC$$ mains $$[Voltage\ 223\ V (rms) = \sqrt {50,000}V]$$. The current differs (lags) in phase by $$\phi \left (\tan \phi = \dfrac {-3}{4}\right )$$ as compared to voltage. Find (i) $$R$$, (ii) $$X_{C} - X_{L}$$, and (iii) $$I_{M}$$. Another device has twice the values for $$R, X_{C}$$ and $$X_{L}$$. How are the answers affected?
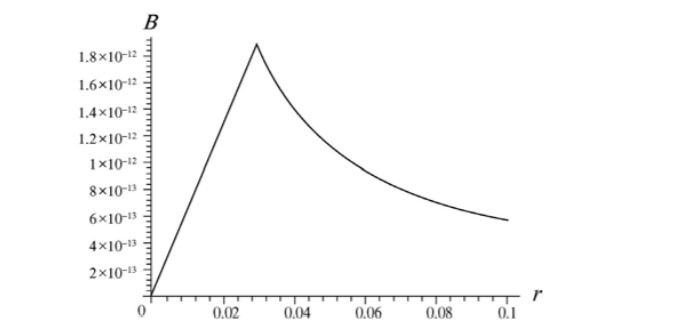
Suppose that a parallel-plate capacitor has circular plates
with radius $$R = 30$$ mm and plate separation of $$5.0$$ mm.
Suppose also that a sinusoidal potential difference with a maximum value of $$150$$ V and a frequency of $$60$$ Hz is applied across
the plates; that is,
$$V = (150 V) sin[2\pi_(60 Hz)t]$$
(a) Find $$B_{max}(R)$$, the maximum value of the induced magnetic field
that occurs at $$r = R$$. (b) Plot $$B_{max}(r)$$ for $$0 < r < 10\, cm$$.
The inductive current in the ring varies with time as $$I=I_m \sin\ (\omega t-\phi)$$, where $$I_m=\omega \phi _0\sqrt{R^2+\omega ^2L^2}$$ with $$tan\ \phi =\omega L/R$$.
Additional Problems(81)
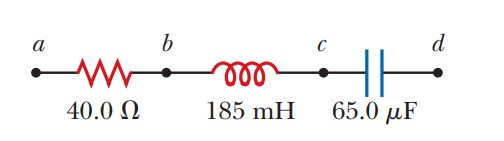
An AC source with $$\Delta = V_{rms} = 120 \,V$$ is connected between points a and $$d$$ in Figure. At what frequency will it deliver a power of $$250 \,W$$? Explain your answer.
Class 12 Engineering Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials,Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions