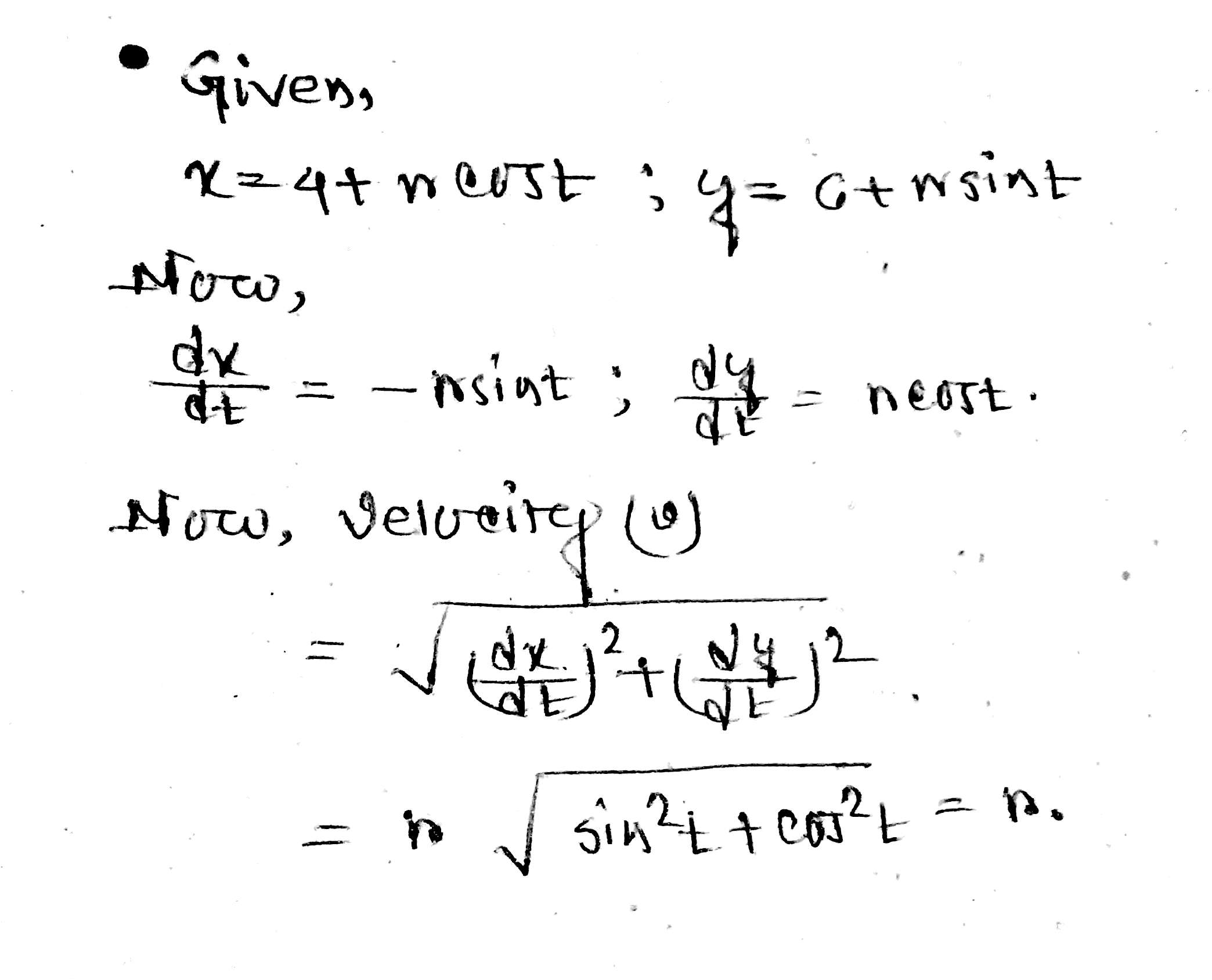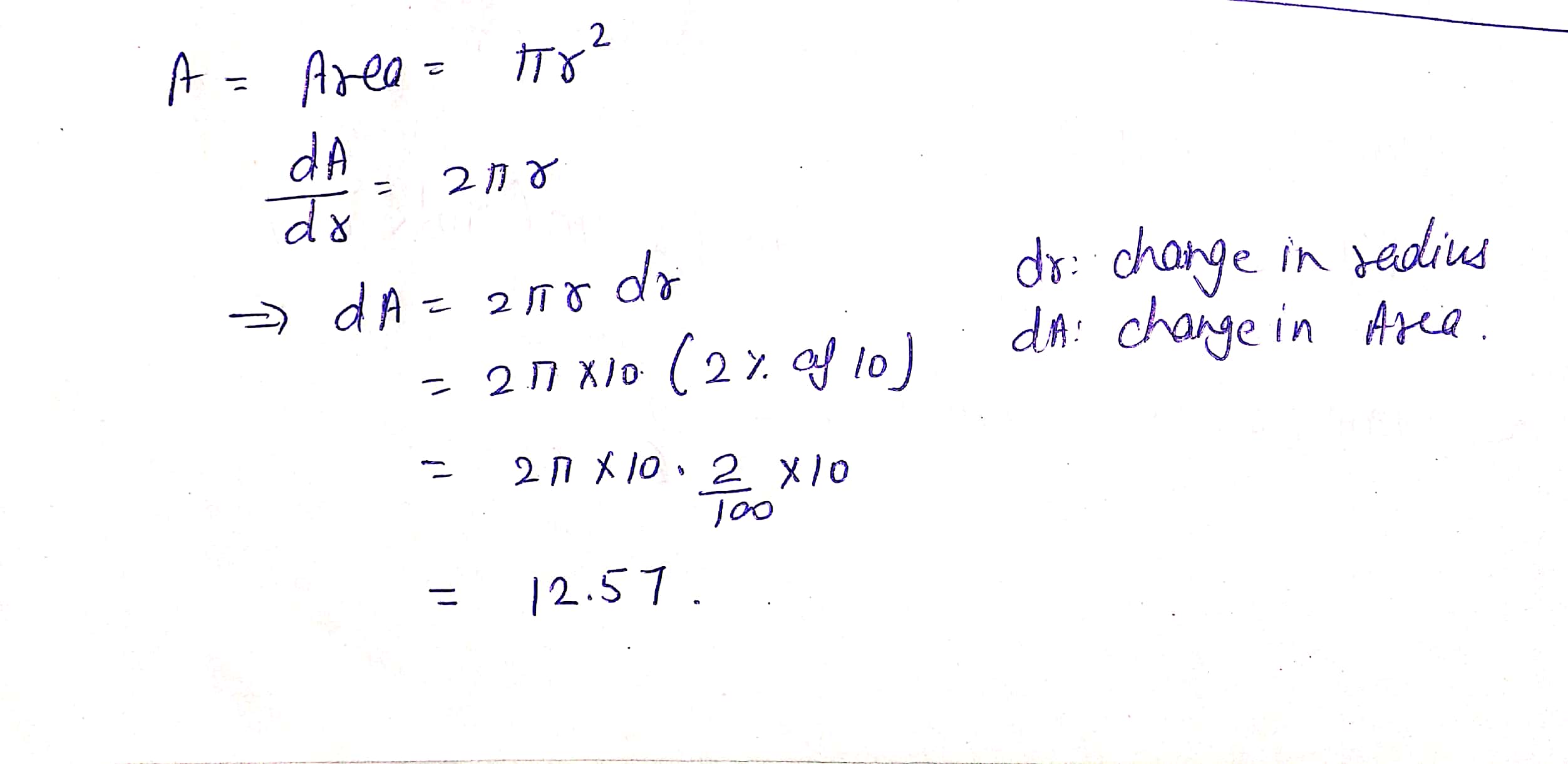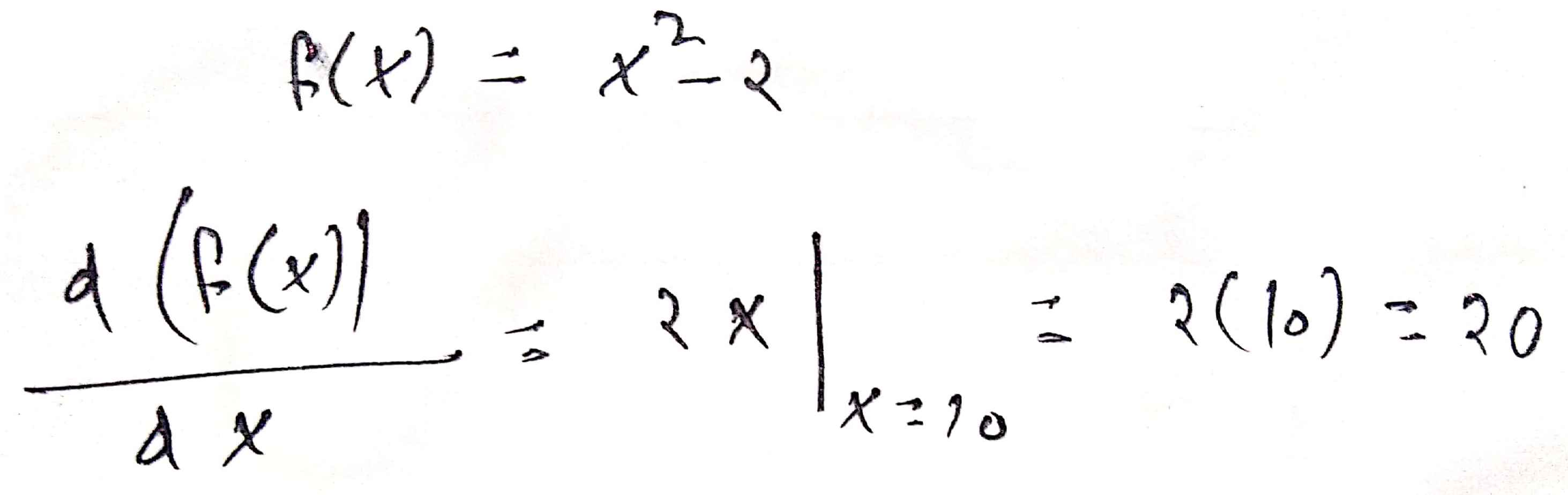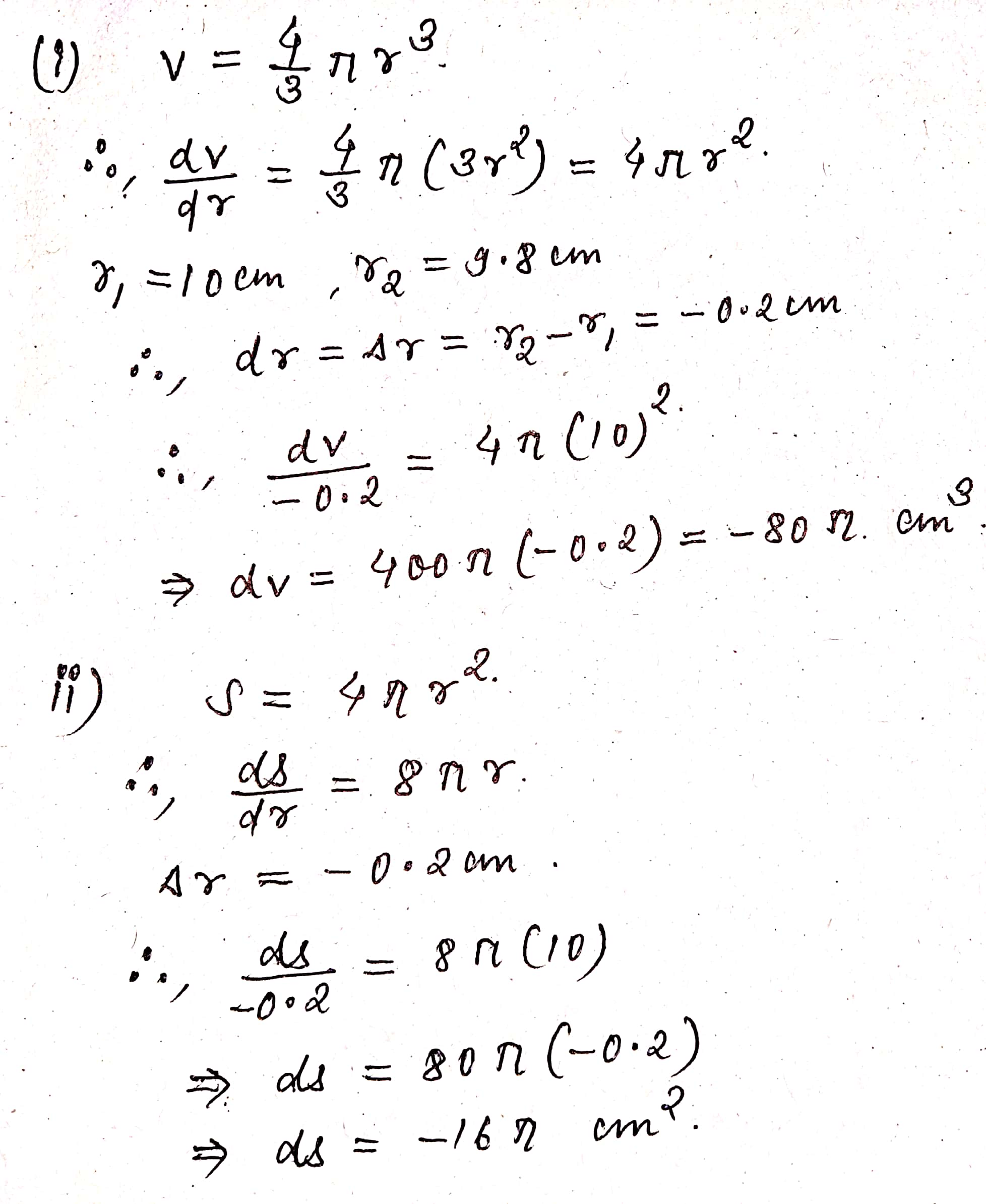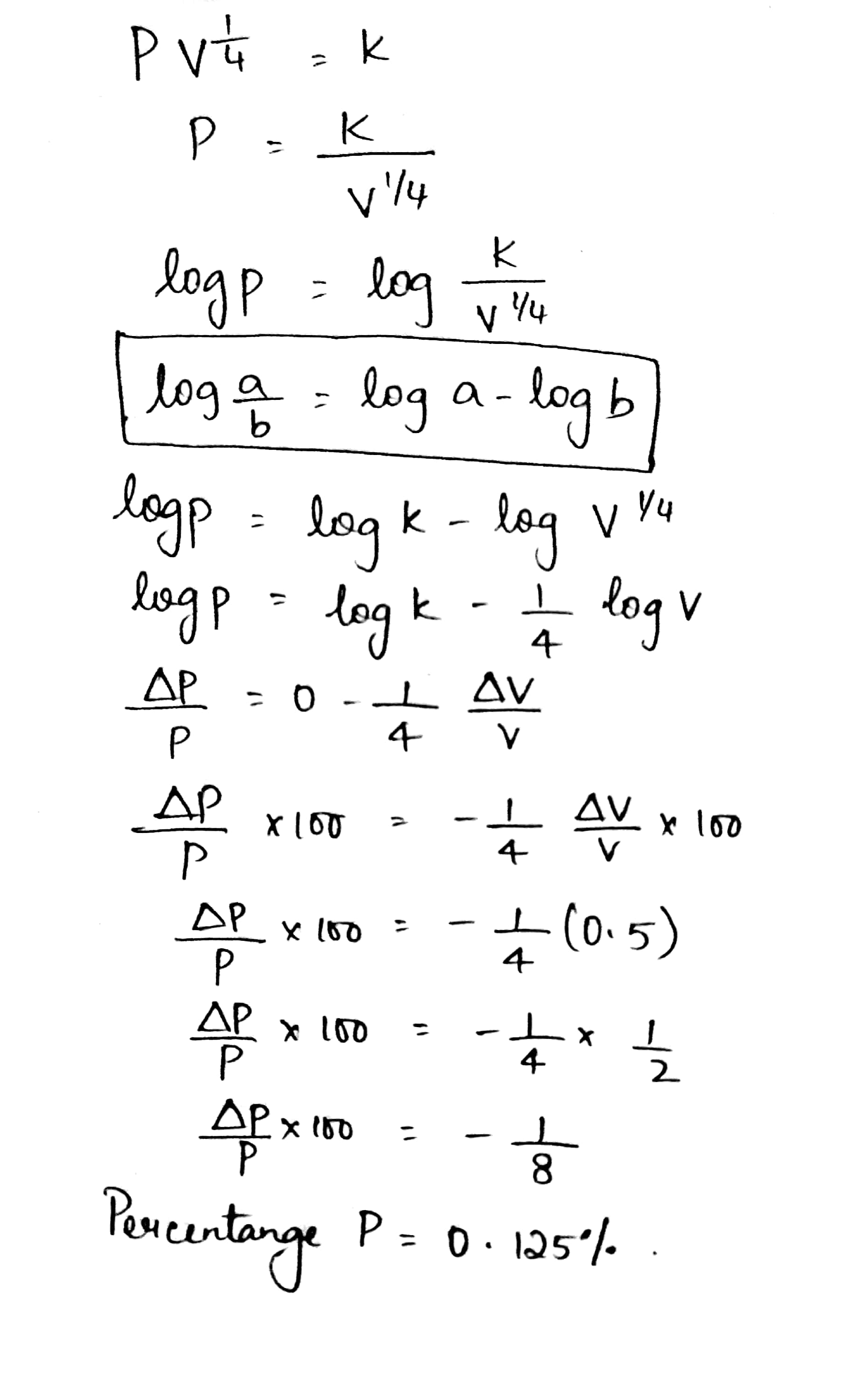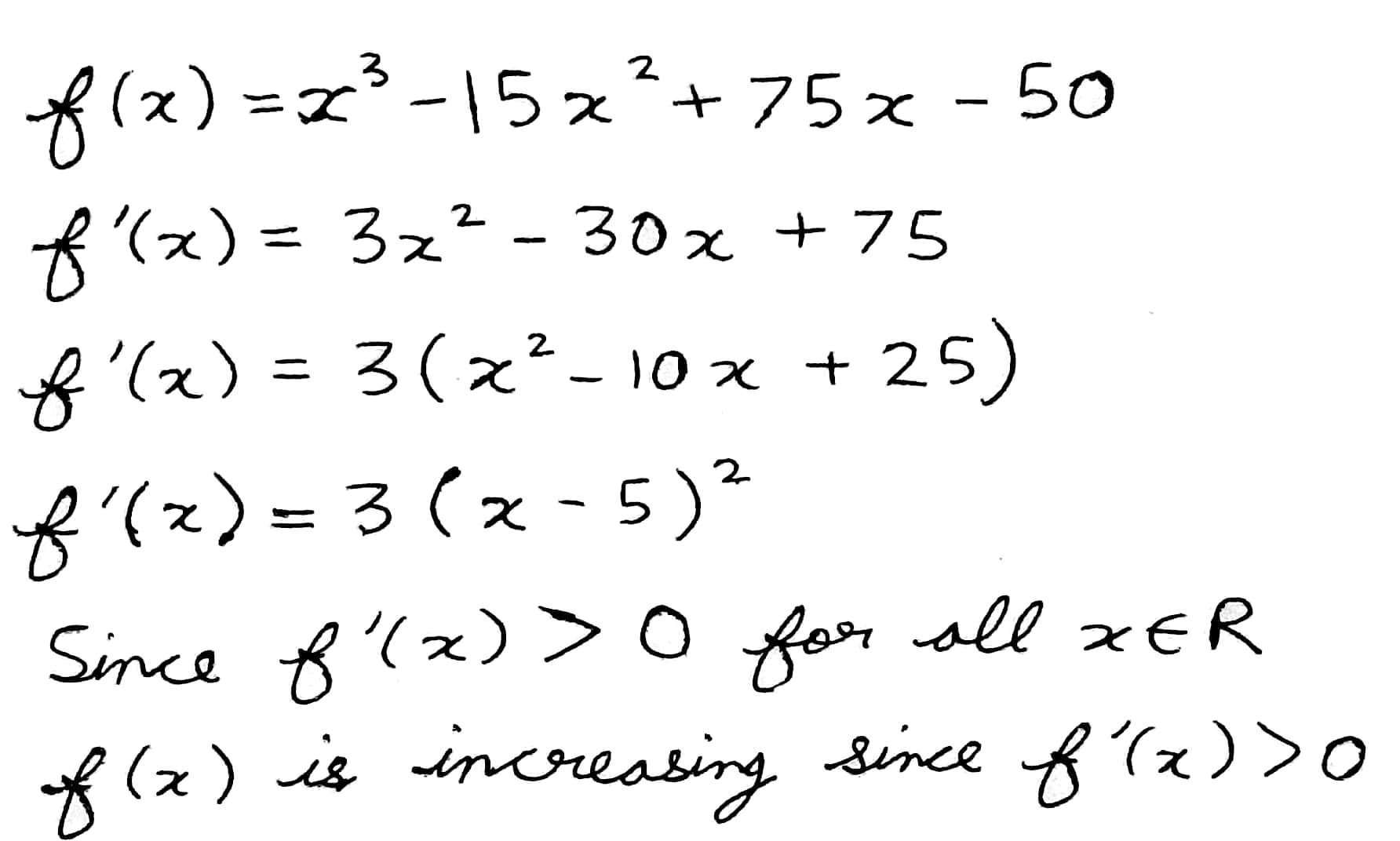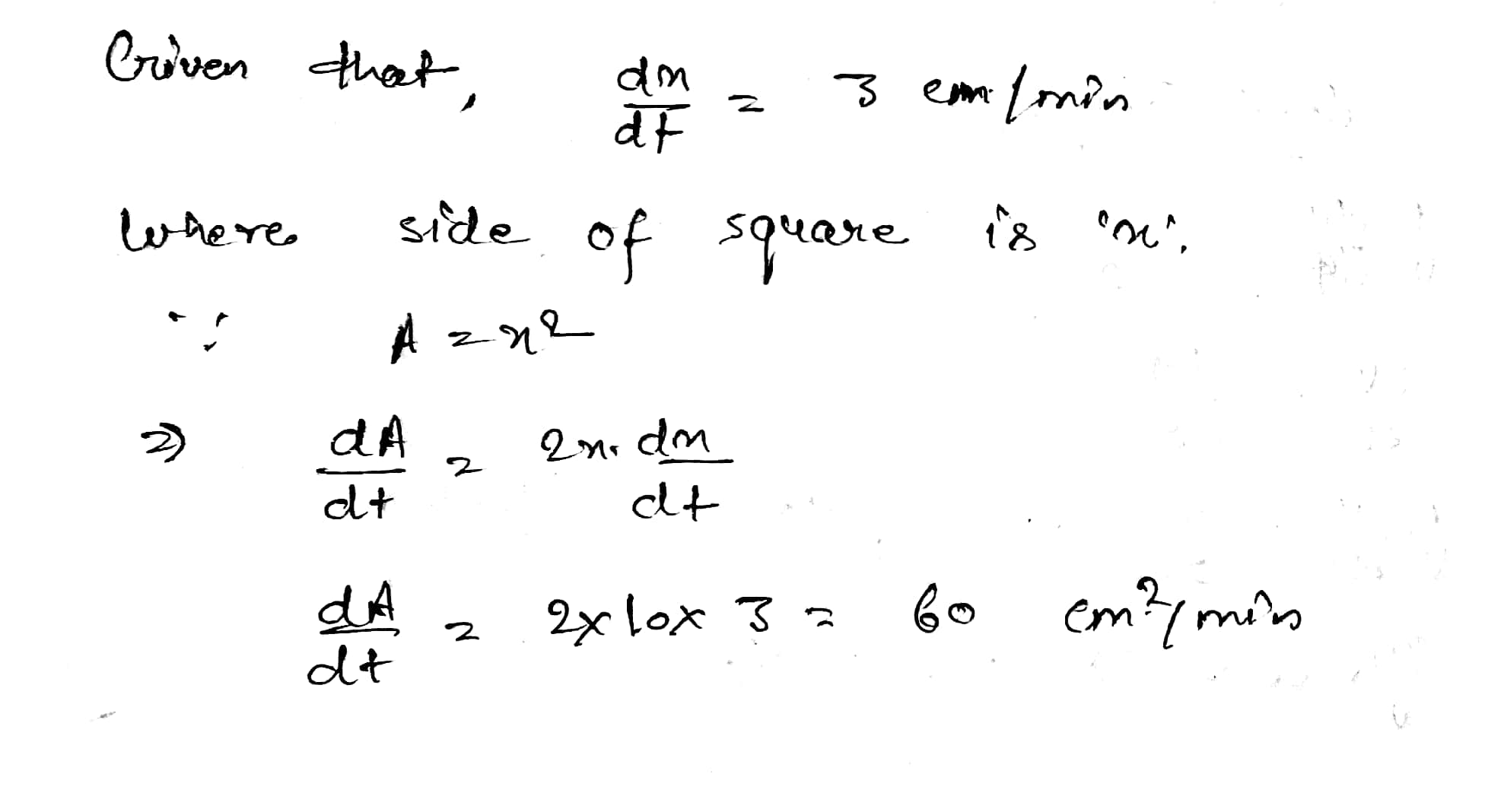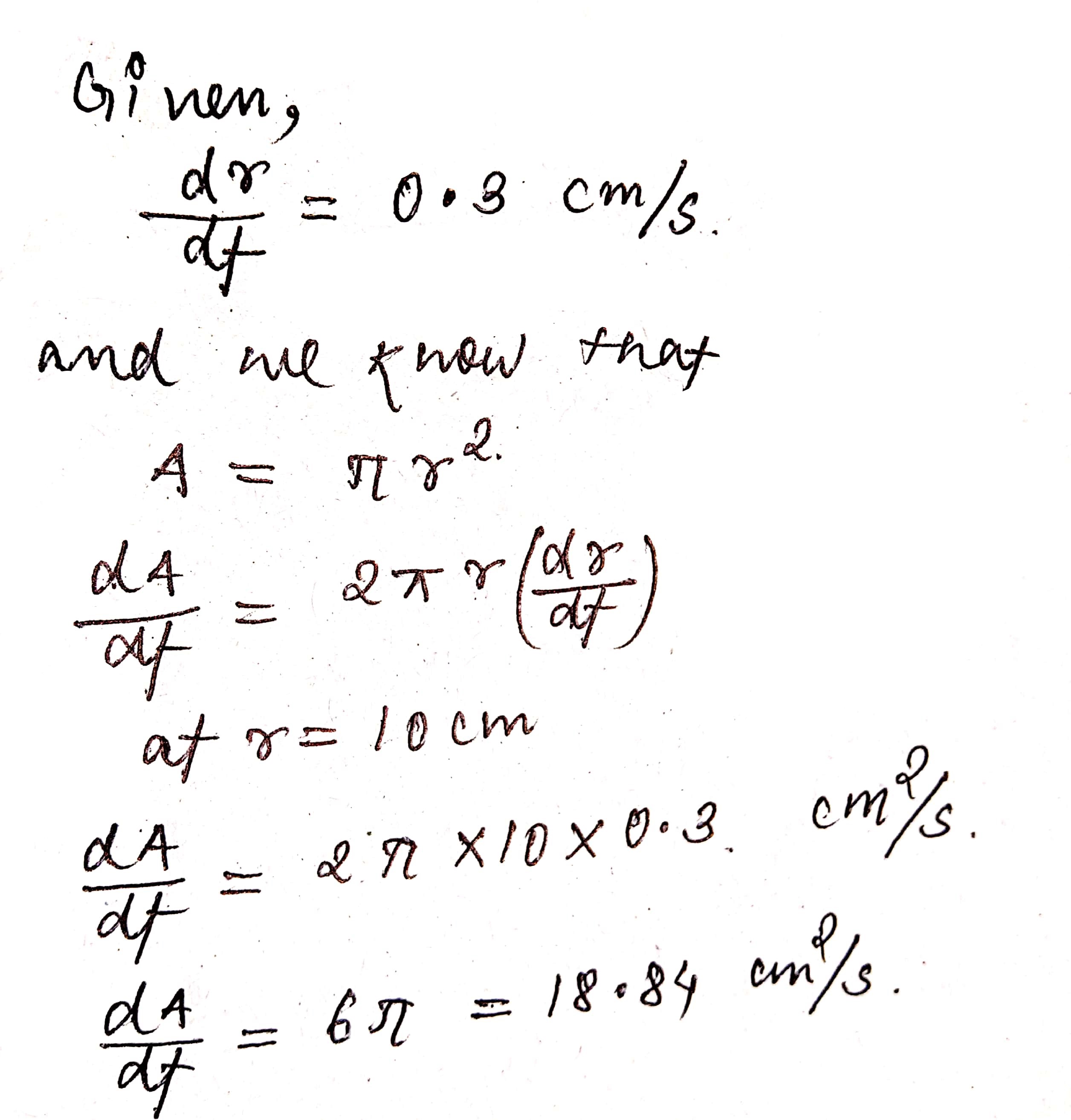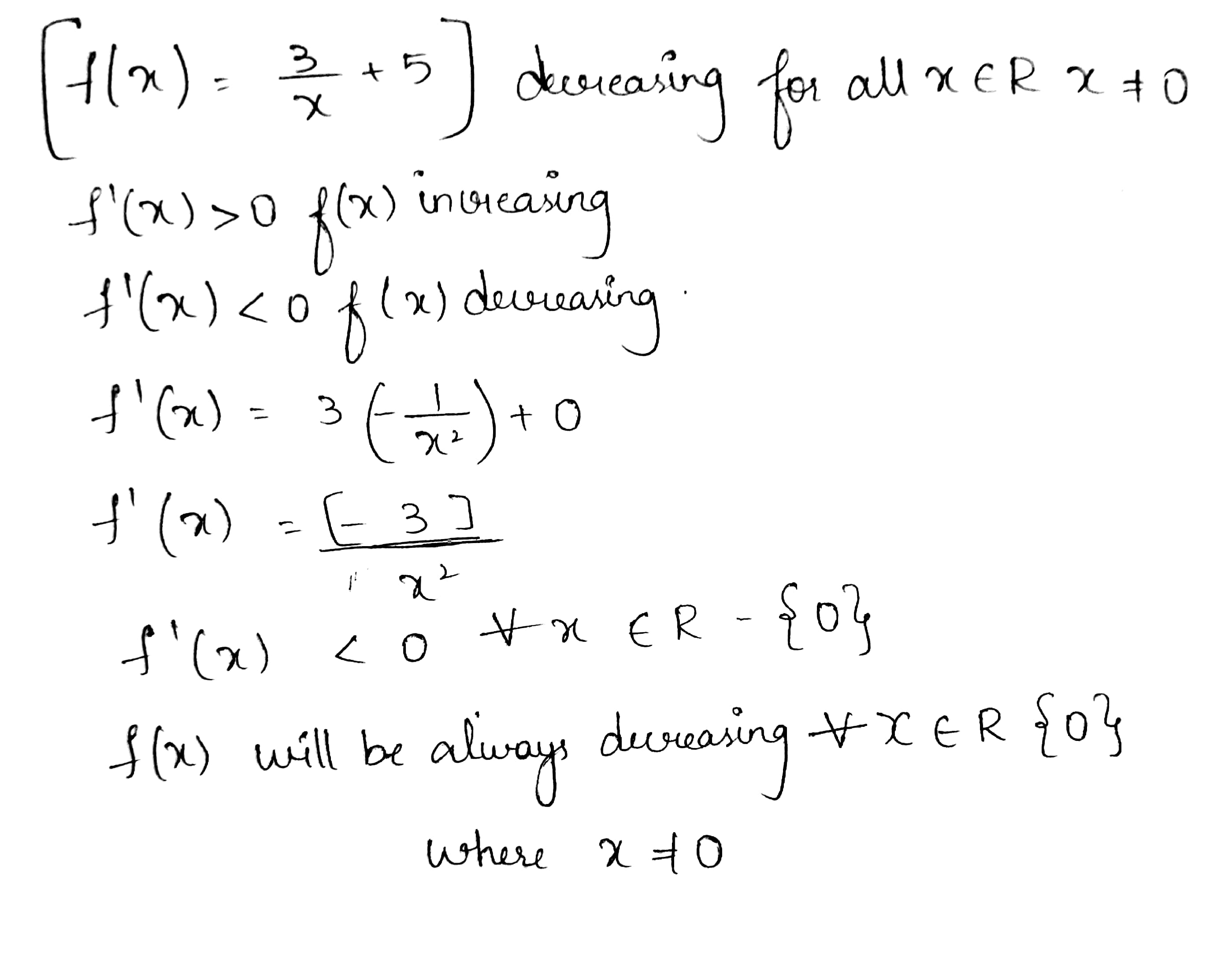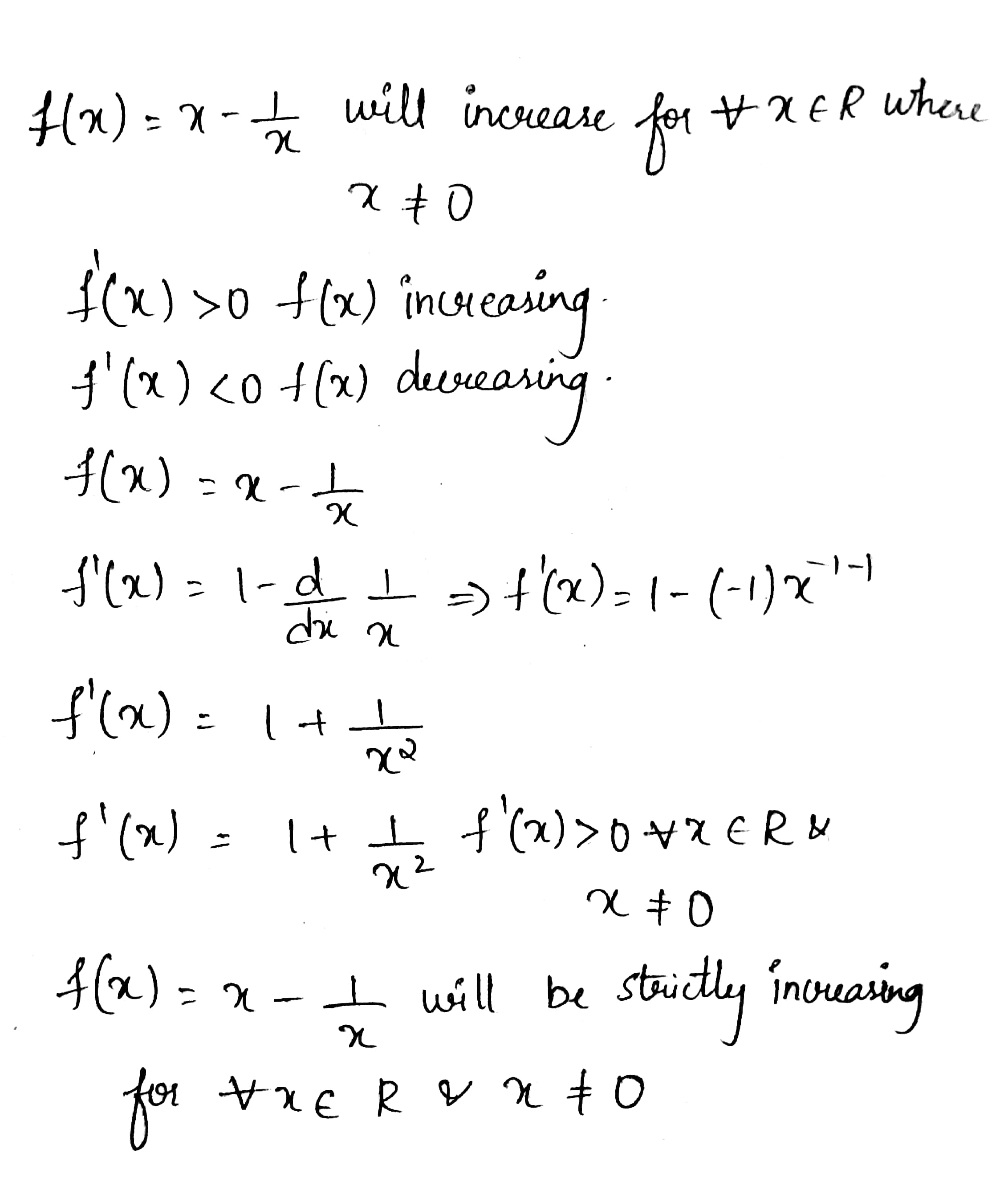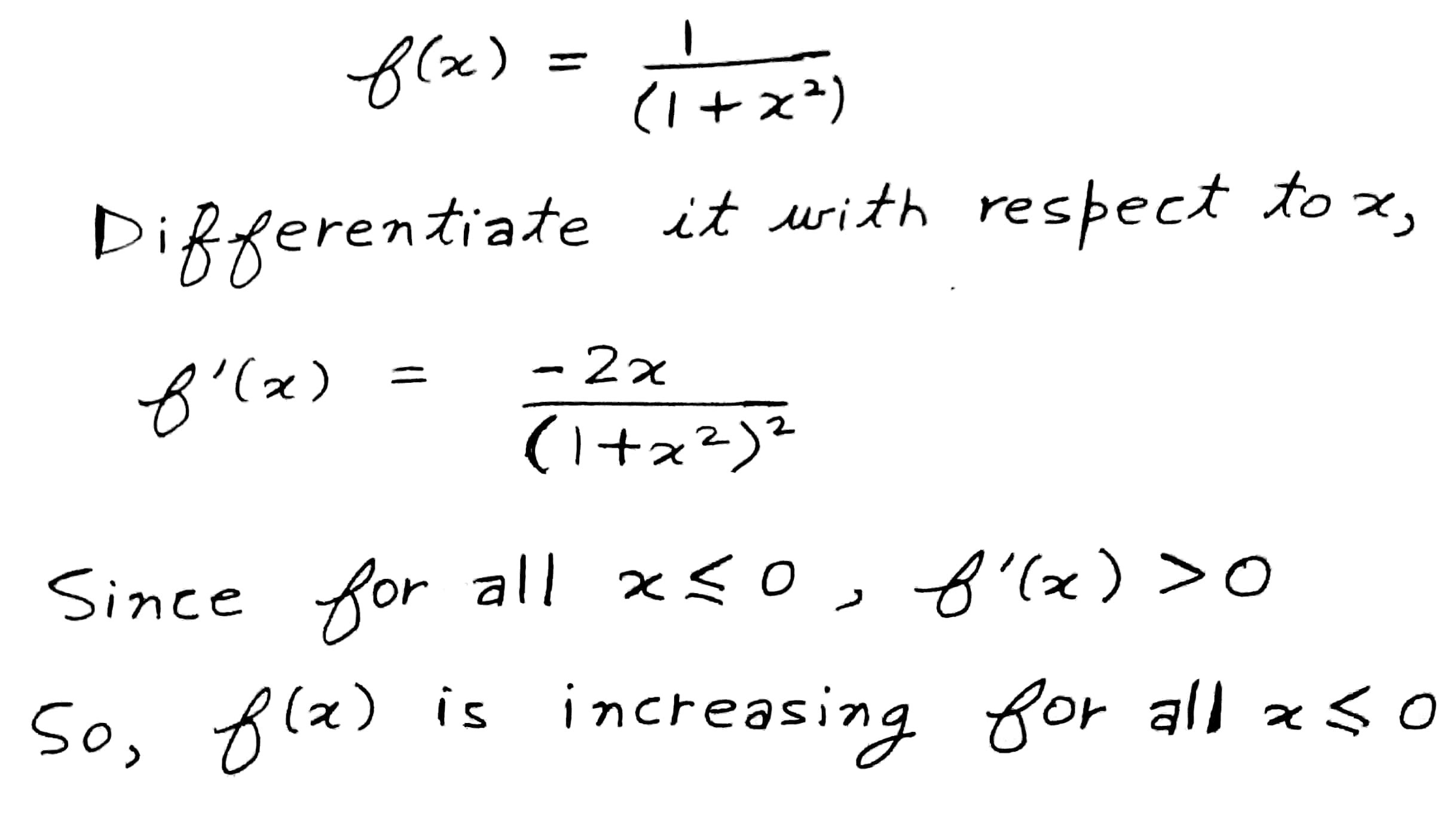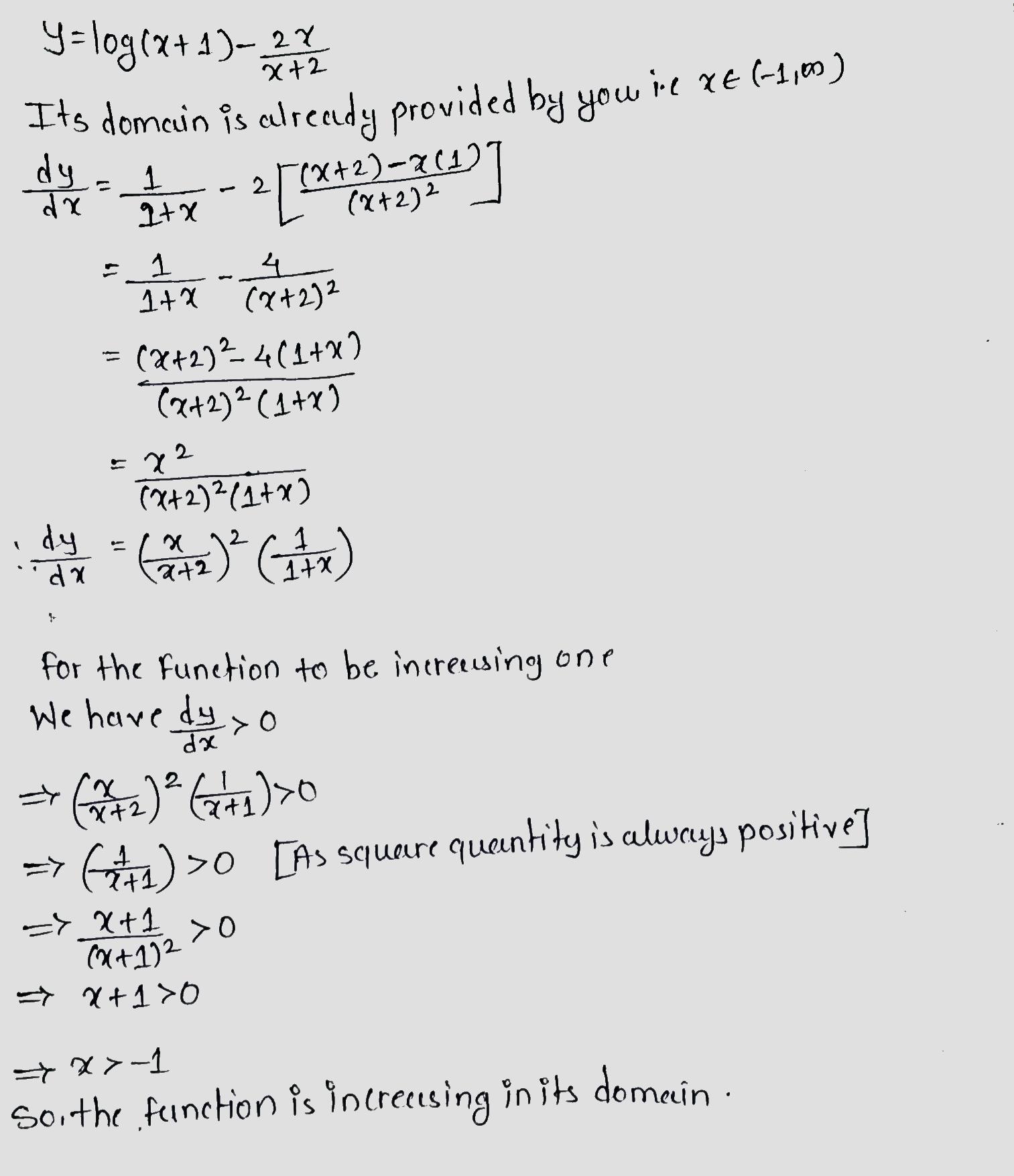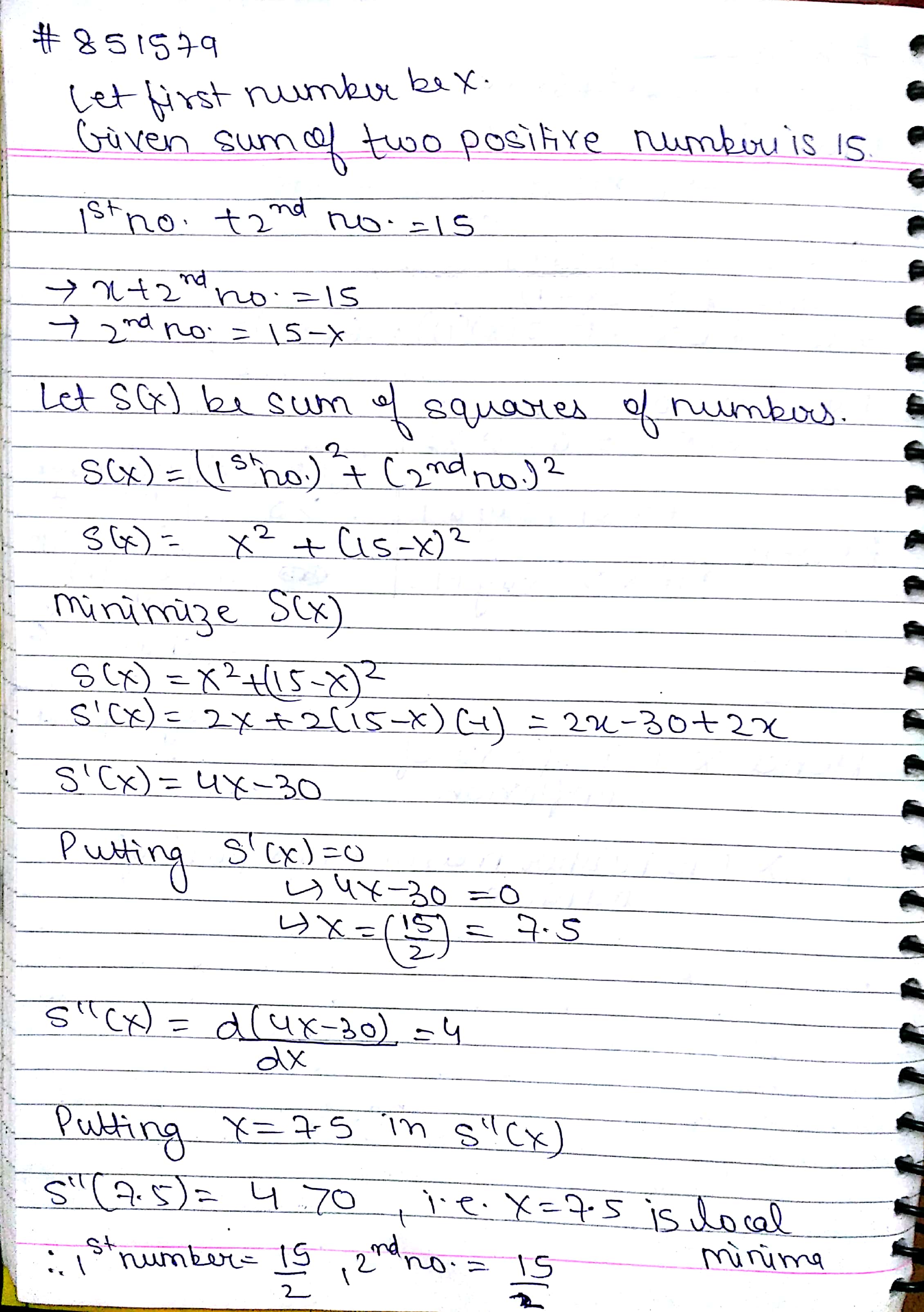Application Of Derivatives - Class 12 Commerce Applied Mathematics - Extra Questions
The total revenue in Rupees received from the sale of $$x$$ units of a product is given by $$R(x) = 13x^2 + 26x + 15$$.
Find the marginal revenue when $$x = 7$$.
The total cost $$C (x)$$ in Rupees associated with the production of $$x$$ units of an item is given by $$C(x) = 0.007x^3- 0.003x^2 + 15x + 4000$$.
Find the marginal revenue when $$x = 17.$$
Solve: $${ x }^{ 4 }-{ x }^{ 3 }+{ x }^{ 2 }-x+1=0$$
Find real values of $$x$$ for which, $$27^{\cos 2x}\cdot 81^{\sin 2x}$$ is minimum. Also find this minimum value.
Find the two positive numbers whose sum is $$15$$ and sum of whose squares is minimum.
Find the values of k for which $$f(x)=kx^3 -9kx^2 +9x+3$$ is increasing on R.
An open can of oil is accidentally dropped into a lake; assume the oil spreads over the surface as a circular disc of uniform thickness whose radius increases steadily at the rate of $$10$$ cm$$/$$sec. At the moment when the radius is $$1$$ meter, the thickness of the oil slick is decreasing at the rate of $$4$$mm$$/$$sec, how fast it is decreasing when the radius is $$2$$ meters.
The displacement $$s$$ of a moving particle at time $$t$$ is given by $$s = 5 + 20t - 2t^{2}$$. Find its acceleration when the velocity is zero.
The total cost C(x) associated with the production of x units of an item is given by $$C(x)=0.05x^3-0.02x^2+30x+5000$$. Find the marginal cost when $$3$$ units are produced, where by marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Rate of decay of a radioactive body is proportional to its mass pressure that time. After a decay of $$1$$ hour the mass of body is $$90$$ grams $$2$$ hours it is $$60$$ grams find the initial mass of the body.
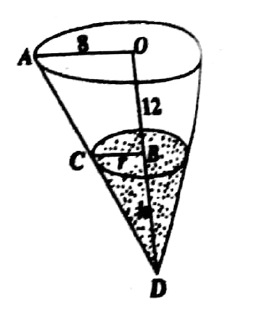
A water tank is in the shape of an inverted cone. The radius of the base is $$8$$ meters and the height is $$12$$ meters. The tank is being emptied for cleaning at the rate of $$4{met}^{3}/minute$$. Find the rate at which the water level will be decreasing, when the water is $$6$$ meters deep.
Let at any moment height and radius of a cone made by water is $$h$$ and $$r$$ respectively.
From similartiy principle of a triangle we have
$$\cfrac { OA }{ BC } =\cfrac { OD }{ BD } $$
$$\therefore \cfrac { 8 }{ r } =\cfrac { 12 }{ h } $$
$$\therefore \cfrac { 8h }{ 12 } =r$$
$$\therefore r=\cfrac { 2h }{ 3 } $$
At time $$t$$, volume of water in a tank is,
$$V=\cfrac { 1 }{ 3 } \pi { r }^{ 2 }h=\cfrac { 1 }{ 3 } \pi \left( \cfrac { 4 }{ 9 } { h }^{ 2 } \right) h\quad \quad $$
$$\therefore V=\cfrac { 4\pi }{ 27 } { h }^{ 3 }$$
$$\quad \therefore \cfrac { dV }{ dt } =\cfrac { 4\pi }{ 27 } \left( 3{ h }^{ 2 }.\cfrac { dh }{ dt } \right) $$
$$\cfrac { dh }{ dt } =\cfrac { 27 }{ 4\pi \left( 3{ h }^{ 2 } \right) } \cfrac { dV }{ dt } =\cfrac { 9 }{ 4\pi { h }^{ 2 } } \cfrac { dV }{ dt } \quad \quad $$
But $$\cfrac { dV }{ dt } =-4\cfrac { { m }^{ 3 } }{ minute } \quad $$
$$\therefore \cfrac { dh }{ dt } =\cfrac { 9 }{ 4\pi { h }^{ 2 } } (-4)$$
But we have $$h=6m$$
$$\cfrac { dh }{ dt } =-\cfrac { 9 }{ \pi (36) } =-\cfrac { 1 }{ 4\pi } m/minute$$
$$\therefore { \left( \cfrac { dh }{ dt } \right) }_{ h=3 }=\cfrac { 9 }{ \pi (36) } =-\cfrac { 1 }{ 4\pi } m/minute$$
$$\therefore$$ Rate of decrease of the height of water tank is $$\cfrac { 1 }{ 4\pi } \cfrac { m }{ minute } $$
From similartiy principle of a triangle we have
$$\cfrac { OA }{ BC } =\cfrac { OD }{ BD } $$
$$\therefore \cfrac { 8 }{ r } =\cfrac { 12 }{ h } $$
$$\therefore \cfrac { 8h }{ 12 } =r$$
$$\therefore r=\cfrac { 2h }{ 3 } $$
At time $$t$$, volume of water in a tank is,
$$V=\cfrac { 1 }{ 3 } \pi { r }^{ 2 }h=\cfrac { 1 }{ 3 } \pi \left( \cfrac { 4 }{ 9 } { h }^{ 2 } \right) h\quad \quad $$
$$\therefore V=\cfrac { 4\pi }{ 27 } { h }^{ 3 }$$
$$\quad \therefore \cfrac { dV }{ dt } =\cfrac { 4\pi }{ 27 } \left( 3{ h }^{ 2 }.\cfrac { dh }{ dt } \right) $$
$$\cfrac { dh }{ dt } =\cfrac { 27 }{ 4\pi \left( 3{ h }^{ 2 } \right) } \cfrac { dV }{ dt } =\cfrac { 9 }{ 4\pi { h }^{ 2 } } \cfrac { dV }{ dt } \quad \quad $$
But $$\cfrac { dV }{ dt } =-4\cfrac { { m }^{ 3 } }{ minute } \quad $$
$$\therefore \cfrac { dh }{ dt } =\cfrac { 9 }{ 4\pi { h }^{ 2 } } (-4)$$
But we have $$h=6m$$
$$\cfrac { dh }{ dt } =-\cfrac { 9 }{ \pi (36) } =-\cfrac { 1 }{ 4\pi } m/minute$$
$$\therefore { \left( \cfrac { dh }{ dt } \right) }_{ h=3 }=\cfrac { 9 }{ \pi (36) } =-\cfrac { 1 }{ 4\pi } m/minute$$
$$\therefore$$ Rate of decrease of the height of water tank is $$\cfrac { 1 }{ 4\pi } \cfrac { m }{ minute } $$
Find the interval of increase and decrease of the following functions.
$$f(x) \, = \, \dfrac{x}{\ln \, x}$$
The temperature of a body in a room is $${100}^{o}F$$. After five minutes, the temperature of the body becomes $${50}^{o}F$$. After another $$5$$ minutes, the temperature becomes $${40}^{o}F$$. What is the temperature of surroundings?
Find the interval of increase and decrease of the following functions.
$$f(x) \, = \, x^2 \, e^{-x}$$
Find the rate of change of the volume of a sphere with respect to its diameter.
Show that $$f(x)=x^2-x \sin \ $$ ,x is an increasing function on $$(0,\pi/2)$$.
A particle moves along the x-axis obeying the equation $$x = t(t - 1)(t - 2)$$, where $$x$$ is in meter and $$t$$ is in second
Find the time when the displacement of the particle is zero.
The radius of a circular plate is increasing at the ratio of $$0.20$$ cm/sec.At what rate is the area increasing when the radius of the plate is $$25$$ cm.
The displacement $$x$$ of a particle moving in one dimension under the action of a constant force is related to time $$t$$ by the equation $$t = \sqrt {x} + 3$$, where $$x$$ is in meter and $$t$$ is in second. Find the displacement of the particle when its velocity is zero.
Water absorbs light. As depth increases, intensity of light decreases linearly. At $$13.5$$ feet, water absorbs $$50$$ percent of light which strikes the surface. At what depth would the light at noon be reduced by $$\frac{1}{{3,00,000}}$$ of the noon light.
Prove that the following function do not have maxima or minima :$$f(x)=e^x$$
The total cost $${C_{\left( x \right)}}$$ and the total revenue $${R_{\left( x \right)}}$$ associated with production and sale of $$x$$ units of an item are given by $$C\left( x \right) = 0.1\,{x^2} + 30x + 1000$$ and $$R\left( x \right) = 0.2\,{x^2} + 36\,x - 100$$ . Find the marginal cost and the marginal revenue when $$x=20$$
Find the value of $$a$$ if $$f(x) = 2{e^x} - a{e^{ - x}} + (2a + 1)x - 3$$ is increasing for all values of $$x$$.
Find the absolute maximum value and the absolute minimum value of the following function in the given interval :$$f(x)=(x-1)^2+3, x\in [-3,1]$$
A circular disc of radius $$3$$ cm is being heated. Due to expansion, its radius increases at the rate of $$0.05\ cm/s$$. Find the rate at which its area is increasing when radius is $$3.2$$ cms.
Find the length of the perpendicular drawn from the origin on the tangent to the curve $$x=a(\theta -\sin\theta), y=a(1-\cos \theta)$$ at $$\theta =\dfrac{\pi}{2}$$.
The side of an equilateral triangle is increasing at the rate of $$5cm/\sec $$. At what rate its area increasing when the side of the triangle is $$10$$ cm?
A helicopter is flying along the curve $$y={x}^{2}+2$$. A soldier is placed at the point $$(3,2)$$, find the nearest distance between the soldier and helicopter.
Given $$f\left( x \right) = {\cos ^2}x$$ , find whether $$f(x)$$ is increasing or decreasing in the range $$\left[ {0,\dfrac{\pi }{2}} \right]$$.
find maximum and minimum value of sinxsin ($${60^ \circ }$$-x) sin($${60^ \circ }$$+x).
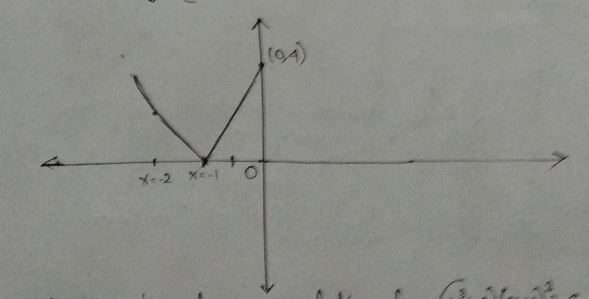
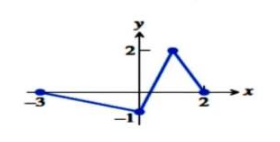
With the help of graph,find the extreme value and where they occur.
Prove that the function given by $$f(x)=\cos x$$ is strictly increasing in $$(\pi, 2\pi)$$.
Find $$\frac{{dy}}{{dx}}$$ , if $${x^{\frac{2}{3}}} + {y^{\frac{2}{3}}} = {a^{\frac{2}{3}}}$$
Prove that the function given by $$f(x)=x^3-3x^2+3x-100$$ is inreasing in R.
Find the point on the curve $$y^2=8x$$ for which the abscissa and ordinate change at the same rate.
If $$x$$ varies directly as $$y$$ and when $$x$$ is $$3$$, $$y$$ is $$8$$, find $$y$$ when $$x = 21$$.
Find the absolute maximum and absolute minimum values of a function f given by $$f(x)=2x^{3}-15x^{2}+36x+1$$ on the interval [1, 5]
A particle moving in plane has the position $$(x,y)$$ given by $$x=4+r\cos t$$ and $$y=6+4\sin t$$ where $$r$$ is constant. Then find the velocity of the particle.
Given,
$$x=4+n\cos t$$; $$y=6+n\sin t$$
Now,
$$\dfrac{dx}{dt}=-n\sin t$$; $$\dfrac{dy}{dt}=n\cos t$$
Now, velocity(v)
$$=\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}$$
$$=n\sqrt{\sin^2t+\cos^2t}=n$$.
The radius of circular plate is 2 cm. If it is being heated the expansion in its radius happens at the rate of 0.02 cm/sec. Find the rate of expansion of the area when the radius is 2.1 cm.
Show that $$f(x)=\cfrac{1}{1+{x}^{2}}$$ decreases in the interval $$[0,\infty)$$ and increases in the interval $$(-\infty, 0]$$.
Determine whether $$f(x)=-\dfrac {x}{2}+\sin x$$ is increasing or decreasing on $$\left (-\dfrac {\pi }{3},\dfrac {\pi }{3}\right)$$.
$$f(x) = \dfrac{-x}{2} + \sin x $$
$$f'(x) = \dfrac{-1}{2} + \cos x$$
$$\dfrac{-\pi}{3} < x < \dfrac{\pi}{3}$$
$$\dfrac{\sqrt{3}}{2} < \cos x < \dfrac{\sqrt{3}}{2}$$
$$\dfrac{\sqrt{3}}{2} < \cos x < 1$$
$$\dfrac{\sqrt{3} - 1}{2} < \cos x - \dfrac{1}{2} < \dfrac{1}{2}$$
$$f'(x) > 0 $$ & $$x \in \left(\dfrac{-\pi}{3} , \dfrac{\pi}{3} \right)$$
$$\therefore f(x)$$ is increasing on $$\left(\dfrac{-\pi}{3} , \dfrac{\pi}{3} \right)$$
Find an angle $$\theta, 0<\theta < \dfrac{\pi}{2}$$, which increases twice as fast as its sine.
Show that $$f(x)=x+\cos x-a$$ is an increasing function on $$R$$ for all values of $$a$$.
Show that $$\displaystyle \sin ^{p}\theta \cos ^{q}\theta $$ is maximum when $$\displaystyle \theta = \tan ^{-1}\sqrt{p/q}.$$
Show that the function $$\displaystyle f\left ( x \right )=2x+\cot^{-1}x-\log \left \{ x+\sqrt{\left ( 1+x^{2} \right )} \right \}$$ is increasing $$\forall$$ R
$$\displaystyle y= \sin x-a\sin 2x-\frac{1}{3}\sin 3x+2ax,$$ then y increases for all values of x if $$\displaystyle a> k.$$, what is k?
If $$a$$ and $$b$$ are two parts of $$8$$ such that sum of their cubes is the least possible then $$ab$$ is equal to
Let $$x$$ and $$y$$ be two real variables such that $$x > 0$$ and $$xy= 1.$$ Find the minimum value of $$x + y$$
The sum of two real numbers $$x$$ and $$y$$ is $$20$$ If $$\displaystyle xy^{3}$$ is greatest then the ratio $$\displaystyle x^{2}:y^{2}\: is\: 1:\lambda $$ Find the value of $$\displaystyle \lambda $$
The position vector of a particle at time 't' is given by $$ \overrightarrow r = t^2 \hat t + t^3 \hat j $$ . The velocity makes an angle $$\theta$$ with positive x-axis. Find the of $$\displaystyle \frac {d\,\theta} {dt} $$ at $$\displaystyle t = \frac {\sqrt {2}} {3} $$
Prove that the function $$f$$ given by $$f(x) = \log \sin x$$ is strictly increasing on $$\left ( 0, \dfrac{\pi}{2} \right )$$ and strictly decreasing on $$\left ( \dfrac{\pi}{2}, \pi \right )$$
Find the least value of $$a$$ such that the function $$f$$ given by $$f(x) = x^{2} + ax + 1$$ is strictly increasing on $$[1, 2]$$.
Let $$I$$ be any interval disjoint from $$[-1, 1]$$. Prove that the function $$f$$ given by$$f(x) =x +\dfrac{1}{x}$$ is strictly increasing in interval disjoint from $$I$$.
For what value of $$x$$, $$\displaystyle 8x^{2}-7x+2 $$ has the minimum value?
Prove that the function given by $$f(x) = x^3 - 3x^2 + 3x -100$$ is increasing in $$R$$.
Prove that the function $$f$$ given by $$f (x) = \log \cos x$$ is strictly decreasing on $$\left ( 0, \dfrac{\pi}{2} \right )$$and strictly increasing on $$\left ( \dfrac{\pi}{2}, \pi \right )$$.
Find two positive numbers $$x$$ and $$y$$ such that their sum is $$35$$ and the product $${x}^{2}{y}^{5}$$ is a maximum.
Find two positive numbers whose sum is $$16$$ and the sum of whose cubes is minimum.
In a bank, principal increases continuously at the rate of $$5\%$$ per year. An amount of $$Rs. 1000$$ is deposited with this bank, how much will it worth after $$10\ years (e^{0.5} = 1.648)$$.
The volume of spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds.
A particle moves along the curve $$6y=x^3+2$$. Find the points on the curve at which the $$y$$-coordinate is changing $$8$$ times as fast as the $$x$$-coordinate.
Find the numbers whose product is 100 and whose sum is minimum.
Find two positive numbers whose product is $$64$$ and the sum is minimum.
A telephone company in a town has $$5000$$ subscribers on its list and collects fixed rent charges of $$Rs. 3,000$$ per year from each subscriber. The company proposes to increase annual rent and it is believed that for every increase of one rupee in the rent one subscriber will be discontinued. Find what increased annual rent will bring the maximum annual income to the company
If $$y = cos^2(45^o + x) (sin x- cos x)^2$$ then the maximum value of y is:
Find the approximate changes in the volume 'V' of a cube of side x metres caused by decreasing the side by $$1\%$$.
Prove that if x + y = 2 then maximum value of the functionary $$xy^{2}$$ is $$\dfrac{32}{27}$$.
Show that $$f(x) = \dfrac{-x^{3}}{3} - x^{2} - x + 7$$ is always increasing in R.
When x is real, the greatest possible value of $$10^{x} - 100^{x}$$ is
Water is dripping out from a conical funnel of semi-vertical angle $$\displaystyle\frac{\pi}{4}$$ at the uniform rate of $$2$$ $$cm^2$$/sec in the surface, through a tiny hole at the vertex of the bottom. When the slant height of the water level is $$4$$ cm, find the rate of decrease of the slant height of the water.
Let the radius, height and the slant height of the funnel are $$r,h$$ and $$l$$ respectively.
We know the volume of funnel is $$V=\dfrac{1}{3}\pi r^2 h$$
And it's given that semi verticle angle is $$\pi/4$$
From the figure, $$\sin \dfrac{\pi}{4}=\dfrac{r}{l}=\dfrac{1}{\sqrt 2}\implies r=\dfrac{l}{\sqrt2}$$
And $$\cos \dfrac{\pi}{4}=\dfrac{h}{l}=\dfrac{1}{\sqrt 2}\implies h=\dfrac{l}{\sqrt2}$$
Let $$S$$ be the curved surface area of the water cone, then we have
$$S=\pi rl=\pi \dfrac{l}{\sqrt{2}}.l=\dfrac{\pi l^{2}}{\sqrt{2}}$$
Differentiating w.r.t $$t$$, we get
$$\dfrac{dS}{dt}=\dfrac{\pi}{\sqrt{2}}.2l\dfrac{dl}{dt}$$
Now, $$\dfrac{dS}{dt}=-2cm^{2}/sec$$ ..... $$(S$$ is negative, because it is decreasing$$)$$
$$\therefore \dfrac{dS}{dt}=\dfrac{2l \pi}{\sqrt2}\dfrac{dl}{dt}=-2\,cm^2/sec$$
$$\dfrac{dl}{dt}=-\dfrac{\sqrt{2}}{\pi l}$$
Given $$l=4 cm$$, then
$$\dfrac{dl}{dt}=-\dfrac{\sqrt2}{4\pi}$$ cm/sec
Hence, the slant height is decreasing at the rate of $$\dfrac{\sqrt{2}}{4\pi}\ cm/sec$$
Find the intervals of increase and decrease of the, following functions.
$$\displaystyle\, f\, (x)\, = (2^x \, -\, 1)(2^x \, -\, 2)^2$$
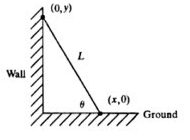
A ladder $$5$$ m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of $$2$$ cm/s. How fast is its height on the wall decreasing when the foot of the ladder is $$4$$ m away from the wall?
The height is decreasing at the rate of $$2.67$$cms$$^{-1}$$
For this we have to use Pythagoras theorem:$$x^{2}+y^{2}=h^{2}$$ ...............(1)
differentiate equition 1 with respect to 't'.
$$2x\dfrac{dx}{dt}+2y\dfrac{dy}{dt}=0$$
Since we have
$$\dfrac{dx}{dt}=2$$cms$$^{-1}$$
$$x=4m$$
so,
The length of wall is when the foot of the ladder is $$400$$cm away is:
$$y=\sqrt{5^{2}-4^{2}}=\sqrt{25-16}=\sqrt{9}=3m=300cm$$
Thus,
The decreasing of the wall is:
Erom equation (1) we get
$$\dfrac{dy}{dt}=-\dfrac{x}{y}\dfrac{dx}{dt} $$
$$=-\dfrac{400cm}{300cm}\times2$$cms$$^{-1}$$
$$=2.67$$cms$$^{-1}$$
This is the required answer.
Find the intervals in which the function $$f(x)=\displaystyle\frac{x^4}{4}-x^3-5x^2+24x+12$$ is
(a) strictly increasing, (b) strictly decreasing.
Find the greatest and the least values of the following functions.
$$\displaystyle y \, = \, x^3 \, + \, 4x^2 \, + \, 4x \, + \, 3$$ on the interval [-1, 3].
Find the least value of the function $$\displaystyle y \, = \, 7 \, + \, 3^x \, + \, 2.3^{3 \, - \, x} \, - \,x \, \ln \, 27 \, - \, 9.$$
Find all values of $$x$$ for which the function $$\displaystyle\, y \,=\, \sin x \, \, \cos^2x\, -\, 1$$ assumes the least value. What is that value?
Find the greatest value of the function $$\displaystyle y \, = \, 7 \, + \, 2x \, \ln \, 25 \, - \, 5^{x \, - \, 1} \, - \, 5^{2 \, - \, x}.$$
For what value of $$x$$ does the expression $$\displaystyle 2^{x^3} \, - \, 1 \, + \, \frac{1}{2^{x^3} \, + \, 2}$$ assume the least value.
Find the greatest and the least values of the following functions.
$$\displaystyle f \, (x) \, = \, 2x^3 \, - \, 3x^2 \, - \, 12x \, + \, 1$$ on the interval [-1, 5].
Find the interval of increase and decrease of the following functions.
$$f(x) \, = \, x \, + \, \ln \, (1 \, - \, 4x)$$
Find the absolute maximum and minimum of function $$y=2\cos 2x-\cos 4x$$.
A particle starts from rest and its angular displacement (in rad) is given by $$\theta = \dfrac {t^{2}}{20} + \dfrac {t}{5}$$. If the angular velocity at the end of $$t = 4\ s$$ is $$'k'$$.Then, what will be the value $$'5k'$$ ?
The total revenue $$R=720x-3{ x }^{ 2 }$$ where $$x$$ is the number of items sold. Find $$x$$ for which total revenue $$R$$ is increasing.
Sita is driving along a straight highway in her car. At time $$t = 0$$, when Sita is moving at $$10\ ms^{-1}$$ in the positive x-direction, she passes a signpost at $$x = 50\ m$$. Here acceleration is a function of time:
$$a = 2.0\ ms^{-2} - \left (\dfrac {1}{10} ms^{-3}\right )t$$
At what time is her velocity greatest?
Attempt the following:
The price P for demand D is given as $$P = 183 + 120D - 3D^2$$. Find D for which the price is increasing.
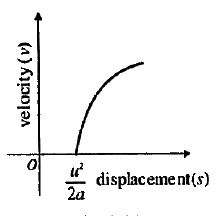
A particle starts with some initial velocity with an acceleration along the direction of motion. Draw a graph depicting the variation of velocity $$(v)$$ along y-axis with the variation of displacement $$(s)$$ along x-axis.
For uniformly accelerated motion, the relation between velocity $$(v)$$ and displacement (s) is given by $$v^{2} = u^{2} = 2as$$.
Now, the above equation should be transformed to a suitable form, before the exact shape can be known.
$$\therefore (v - 0)^{2} = 2a \left (s - \dfrac {u^{2}}{2a}\right )$$
which is of the form
$$(y - k)^{2} = 4a(x - h)$$
The vertex is at $$(h, k)$$, i.e., $$\left (\dfrac {u^{2}}{2a}, 0\right )$$
and axis coincides with $$x(i.e., s)$$ -axis.
Now, the above equation should be transformed to a suitable form, before the exact shape can be known.
$$\therefore (v - 0)^{2} = 2a \left (s - \dfrac {u^{2}}{2a}\right )$$
which is of the form
$$(y - k)^{2} = 4a(x - h)$$
The vertex is at $$(h, k)$$, i.e., $$\left (\dfrac {u^{2}}{2a}, 0\right )$$
and axis coincides with $$x(i.e., s)$$ -axis.
Find the values of x if $$f\left( x \right) =\cfrac { x }{ { x }^{ 2 }+1 } $$ is
i) an increasing functionii) a decreasing function
A swimming pool is to be drained for cleaning. If L represents the number of liters of water in the pool t seconds after the pool has been plugged off to drain and $$L = 200 (10 - t)^2$$. What is the average rate at which the water flows out during the first $$5$$ seconds $$\left(\dfrac{litres}{sec}\right)$$?
Find two number, such that their product is $$64$$ and their sum is minimum.
$$\left[ {3\sin \theta + 4\cos \theta } \right]$$ is maximum $$\left[ {given0 \le \theta \le {\pi \over 2}} \right]$$ When $$\theta = ?$$
Determine the minimum value of the function:
$$f(x) = x^{2} +\frac{16}{x^{2}}$$
Let $$\left( x \right) = {{1 + \cos 2x + 8{{\sin }^2}x} \over {\sin 2x}},x \in \left( {0,{\pi \over 2}} \right).$$ find minimum value of $$f\left( x \right)$$
A boat goes $$60km$$ upstream and downs stream in $$6hr$$ and $$2\ hr$$ respectively. Determine the product of speed of the stream and that of the boat in still water.
x = speed of bolt in upstream $$ = \dfrac{60}{6} = 10km/hr$$
y = speed of bolt in downstream $$ = \dfrac{60}{2} = 30km/hr$$
Product of speed of boat in still water of the stream
$$ = \dfrac{x+y}{2} \times \dfrac{x-y}{2} = \dfrac{x^{2}-y^{2}}{4} = \dfrac{900-100}{4} =200$$
So, Ans is 200
The minimum value of $$\dfrac{1}{3} (3\tan x + 27 \cot x)$$ is.......
Find the intervals in which the function given by $$\ f(x)=\sin{x}-\cos{x}$$, $$-\pi \le x\le \pi$$ is strictly increasing or decreasing ?
Prove that the function $$f$$ defined by $$f(x)={x}^{2}-x+1$$ is neither increasing nor decreasing in $$(-1, 1)$$. Hence find the intervals in which $$f(x)$$ is strictly increasing and strictly decreasing.
Find the intervals in which the function $$f$$ given by$$f\left( x \right) =\dfrac { 4\sin { x } -2x-x\cos { x } }{ 2+\cos { x } }$$ is
(i) strictly increasing
(ii) strictly decreasing
Points $$A$$ and $$B$$ are $$100\ km$$ apart. a car starts from $$A$$ and another from $$B$$ at the same time. If they go in the same direction they meet in $$5\ hr$$ and if they go in opposites directions they meet in $$1\ hr$$, find the product of their speeds.
Let the speed of the law which sates from place $$A=x$$km/h
the speed of the car which starts from place $$B =y$$km/h
Case-I- when the car haves in same direction.
Distance = time x speed
$$=5x$$km
The distance covered by the car which starts from place $$ A = 5x$$
The distance covered by the car which starts from place $$B=5y$$
$$AC-BC=AB$$
$$5X-5Y=100$$
$$x-y=20$$ .......(1)
Case - ii When the car moves in opposite direction
The distance covered by the car which starts from place $$A=1x$$km
The distance covered by the car which
starts from place $$B=1y$$km
$$AC+BC=AB$$
$$x+y=100$$ ........(2)
Adding equation (1) and (2)
$$2x=120$$
$$\boxed{x=60}$$
putting $$x=60$$ in equation (2)
$$60+y=100 \Rightarrow \boxed{y=40}$$
The speed of the car which starts from place $$A=60$$km/h
The speed of the car which starts from place $$B=40$$km/h
So, product of their speed is $$\boxed{2400km/h}$$
The minimum value of $$\dfrac{1}{8}(16\csc^{2}x + 9\sin^{2}x)$$ is...........
What is maximum value of $$3-7\cos\ 5x$$?
If $$0\lt \theta\lt \dfrac{\pi}{2}$$ then prove that $$\dfrac{\sin \theta}{\theta}$$ is decreasing.
Find the maximum and minimum value of $$ \sin x\sin \left( {{{60}^0} - x} \right)\sin \left( {{{60}^0} + x} \right).$$
The length x of an rectangle is decreasing at the rate $$2cm/sec$$ and width y is increasing at the rate of $$2 cm/sec$$. When $$x = 12 cm$$ and $$y = 12 cm$$, the rate of change of the area of the rectangle is $$k {cm^2} /sec$$, then $$k - 9$$ is _________
A particle moves along the curve by $$6y=x^{3}+2$$. Find the point on the curve at which the $$y-$$coordinates is changing $$8$$ times as fast as the $$x-$$ coordinate.
Determine two positive numbers whose sum is 24 and whose product is maximum.
A ladder $$5 m$$ long is leaning against a wall. The bottom of ladder is pulled along the ground, away from the wall, at the rate of $$2 cm/s$$. How fast is its height on the wall decreasing when the foot of the ladder is $$4 m$$ away from the wall?
Find the absolute maximum and minimum values of the function $$f(x) = \dfrac{-1}{x^2} $$ on $$ [0.5, 2]$$
A stone is dropped into a pond. Waves in the form of circles are generated and the radius of the outermost ripple increases at the rate of 2 inch/sec when radius is 5 inch. Find the rate of increasing area.
A circular metal plate expands under heating so that its radius increases by $$2\%$$. Using differentials find the approximate increase in the area of the plate if the radius of the plate before heating is $$10\ cm$$.
A spherical raindrop evaporates at a rate proportional to its surface area. If originally its radius be $$3\ mm$$ and $$1 hour$$ later it reduces to $$2\ mm$$, find an expression for the radius of the rain drop at any time $$t$$.
A street light is $$6\ m$$ high. A man $$180\ cm$$ tall goes away from the street light at the speed of $$120\ cm/sec$$. Find the rate of increase of length of his shadow when he is $$9\ m$$ away from the light. Also find the rate at which the tip of the shadow moves on the road.
Street light Height $$=6\ m=600\ cm$$
Man Height $$=180\ cm$$
Man speed $$=120\ cm/sec$$
Let the Distance of men from height $$=x$$
Distance of length of shadow from men $$=y$$
as $$\triangle ABC \sim \triangle PQC$$
$$\therefore \dfrac{AB}{BC}=\dfrac{PQ}{QC}$$
$$\dfrac{600}{x+y}=\dfrac{180}{y}$$
$$600y=180x+180y$$
$$180x=420y,\quad y=\dfrac{3}{7}x$$
$$\dfrac{dy'}{dt}=\dfrac{3}{7}\dfrac{dx}{dt}$$
$$\left(\dfrac{dx}{dt}=120\right)$$
$$=\dfrac{3}{7}\propto 120=\dfrac{360}{7}=51.4\ cm/sec$$
Rate of increase of shadow $$=57.4\ cm/sec$$
Show that $$f(x)=\dfrac{x}{1+x\tan{x}}, \ x\ \epsilon \ (0,\dfrac{\pi}{2})$$ is maximum when $$x=\cos{x}$$
If a point moves along the curve $$y^{2}=x$$, At what point on the curve does the $$y$$ coordinate change at the same rate as the $$x$$ coordinate.
Water is running into a conical vessel $$15\ cm$$ deep and $$5\ cm$$ in radius, at the rate of $$0.1\ cm^{3}/s$$, when the water is $$6\ cm$$ deep, find at what rate is
i) the water level is rising
ii) the water surface area increasing
iii) the welted surface of the vessel increasing.
A stone dropped into a pond of still water sends out concentric circular waves from the point of disturbance of water at the rate of $$4\ cm/sec.$$ Find the rate of change of disturbed area at the instant when the radius of wave ring is $$15\ cm$$.
Resistance to motion, $$F$$, of a moving vehicle is given by, $$F=\dfrac{5}{x}+100x$$. Determine the minimum value of resistance.
Show that $$f(x)=x^{3}-6x^{2}+18x+5$$ is an increasing function for all $$x\epsilon R$$.
Let $$A = R - \left\{ 3 \right\},\,B = R - \left\{ 1 \right\}$$, and let $$f:A \to B$$ be defined by $$f\left( x \right) = \dfrac{{x - 2}}{{x - 3}}$$. Check the nature of function.
If the function $$f(x)=2x^{3}-9mx^{2}+12m^{2}x+1$$, where $$m>0$$ attains its maximum and minimum at $$p$$ and $$q$$ respectively such that $$p^{2}=q$$, then find the value of $$m$$.
Find about maxima & minima $$f(x)=2x^{3}-15x^{2}+36x+1$$
$$f(x)=2x^3-15x^2+36x+1$$
Differentiate wrt to x,
$$f'(x)=6x^2-30x+36$$
$$\therefore f'(x)=0$$
$$\therefore 6x^2-30x+36=0$$
$$\therefore x^2-5x+6=0$$
$$\therefore (x-2)(x+3)=0$$
$$\therefore x=2, 3$$
$$\therefore f(2)=2(2)^3-15(2)^2+36(2)+1$$
$$\therefore f(2)=16-60+72+1$$
$$\therefore f(2)=29$$
$$\therefore f(3)=2(3)^3-15(3)^2+36(3)+1$$
$$\therefore f(3)=54-135+108+1$$
$$\therefore f(x)=28$$
$$\therefore$$ Maxima is not defined it tends to $$\infty$$
Minima is $$28$$.
The radius of a sphere shrinks from $$10$$cm to $$9.8$$cm. Find approximate error in its volume.
A rectangular tank is $$80m$$ long and $$25m$$ broad. Water flows into it through a pipe whose cross-section is $$25{cm}^{2}$$, at the rate of $$16km$$ per hour. How much the level of the water rises in the tank in $$45$$ minutes?
The wheel of a motor cycle is of radius $$ 35 cm$$. How many revolutions per minute must the wheel make so as to keep a speed of $$66 km/hr$$?
If $$x=a(cos2t+2t\sin2t)$$ and $$y=a(\sin 2t-2t\cos 2t)$$ then find $$\dfrac {d^{2}y}{dx^{2}}$$
Find intervals in which the function given by $$f\left( x \right) =\dfrac { 3 }{ 10 } { x }^{ 4 }-\dfrac { 4 }{ 5 } { x }^{ 3 }-{ 3x }^{ 2 }+\dfrac { 36 }{ 5 } x+11$$ is (a) strictly increasing (b) strictly decreasing.
The volume of a cubic is increasing at a rate of $$9$$ cubic centimetres per second. How fast is the surface area increasing when the length of an edge is $$10\ cm$$.
The rate of growth of bacteria is proportional to the number present. If initially, there were 1000 bacteria and the number doubles in 1 hour, find the number of bacteria after $$2 \dfrac{1}{2}$$ hours. [Take $$\sqrt{2} = 1.414$$]
Find the absolute maximum/minimum value of following function.
$$f(x)=\sin x+\cos x; x$$ in $$[0, \pi]$$.
Find the intervals in which the function $$f(x)$$ is (i) increasing, (ii) decreasing
$$f(x) = 2x^3 - 9x^2 + 12x + 15$$
Determine the intervals in which the function f (x)=$${ x }^{ 4 }-{ 8x }^{ 3 }+{ 22x }^{ 2 }-24x+ 21$$ is strictly increasing or strictly decreasing.
Suppose that a moth- ball loses volumes by evaporation at a rate proportional to its instantaneous surface area . If radius of the ball decreases from 2cm to 1 cm in 3 months, how long will it take until the ball has practically gone?
The min value of $$x^2-7x+10=0$$
Find the minimum value of $$(ax+by)$$, where $$xy=c^{2}$$.
The side of a square sheet is increasing at the rate of $$4$$ cm per minute. At what rate is the area increasing when the side is $$8$$ cm long?
Show that $$f(x)={e}^{1/x}$$, $$x\ne 0$$ is a decreasing function for all $$x\ne 0$$.
The radius of a spherical soap bubble is increasing at the rate of $$0.2$$ cm/sec. Find the rate of increase of its surface area, when the radius is $$7$$ cm.
The volume of a spherical balloon is increasing at the rate of $$ 25$$ cubic centimetre per second. Find the rate of change of its surface area at the instant when radius is $$5\ cm$$.
Show that the function $$f(x)={\cot}^{-1}(\sin x+\cos x)$$ is decreasing on $$\left (0,\dfrac {\pi }{4}\right)$$ and increasing on $$\left (\dfrac {\pi }{4},\dfrac {\pi }{2}\right)$$.
Show that $$f(x)={\tan}^{-1}(\sin x+\cos x)$$ is a decreasing function on the interval $$\left (\dfrac {\pi }{4},\dfrac {\pi }{2}\right)$$.
Show that $$f(x)=\sin x$$ is an increasing function on $$\left (-\dfrac {\pi }{2},\dfrac {\pi }{2}\right)$$
Show that $$f(x)=\log \sin x$$ is increasing on $$\left (0,\dfrac {\pi }{2}\right)$$ and decreasing on $$\left (\dfrac {\pi }{2},\pi\right)$$.
Show that $$f(x)={x}^{3}-15{x}^{2}+75x-50$$ is an increasing function for all $$x\in R$$.
Prove that the function $$f$$ given by $$f(x)=x-\left[ x \right] $$ is increasing in $$(0,1)$$.
Prove that the following functions are increasing on $$R$$:
(i) $$f(x)=3{x}^{5}+40{x}^{3}+240x$$
(ii) $$f(x)=4{x}^{3}-18{x}^{2}+27x-27$$
Show that $$f(x)=\log _{ a }{ { x }_{ } } $$, $$0< a< 1$$ is a decreasing function for all $$x> 0$$.
A balloon in the from of a right circular cone surmounted by a hemisphere, having a diameter equal to the height of the cone, is being inflated. How fast is its volume changing with respect to its total height $$h$$, when $$h = 9$$ cm?
Show that $$f(x)={\tan}^{-1}x-x$$ is a decreasing function on $$R$$.
Find the intervals in which $$f(x)$$ is increasing or decreasing:
(i) $$f(x)=x\left| x \right| ,x\in R$$
(ii) $$f(x)=\sin x+\left| \sin x \right| $$, $$0< x\le 2\pi$$
(iii) $$f(x)=\sin x(1+\cos x)$$, $$0< x< \cfrac{\pi}{2}$$
Find the values of $$a$$ for which the function $$f(x)=\sin x-ax+4$$ is increasing function on $$R$$.
Divide $$64$$ into two parts such that the sum of the cubes of two parts is minimum.
Find the point on the curve $$y^2=2x$$ which is at a minimum distance from the point $$(1, 4)$$.
Find the derivative of $$f(x)=x^2-2$$ at $$x=10$$.
The surface area of a spherical balloon is increasing at the rate of $$2cm^2/sec$$. At what rate the volume of the balloon is increasing when the radius of the balloon is $$6$$ cm ?
The least vlue of the function $$f(x) = ax + \dfrac{b}{x} (a > 0, \,b> 0, \,x > 0)$$ is _____
The radius of a circle is increasing at the rate of $$0.7\ cm/s$$. What is the rate of increases of its circumference ?
The radius of a sphere shrinks from $$10\ cm$$ to $$9.8\ cm$$. Find approximately the decrease in (i) volume, and (ii) surface area.
The pressure $$p$$ and volume $$V$$ of gas are connected by the relation, $$pV^{1/4}=k$$, where $$k$$ is a constant. Find the percentage increase in the pressure, corresponding to a diminution of $$0.5\%$$ in the volume.
If the length of a simple pendulum is decreased by $$2\%$$, find the percentage decrease in its period $$T$$, where $$T=2\pi \sqrt{\dfrac{l}{g}}$$.
The bottom of a rectangular swimming tank is $$25\ m$$ by $$40\ m$$. Water is pumped into the tank at the rate of $$500$$ cubic metres per minute. Find the rate at which the level nof water in tank is rising.
Show that $$f(x)=x^3-15x^2+75x-50$$ is increasing on $$R$$.
Oil is leaking at the rate of $$16\ ml/s$$. from a vertically kept cylindrical drum containing oil. If the radius of the drum is $$7\ cm$$ and its height is $$60\ cm$$, find the rate at which the level of the oil is changing when the oil level is $$18\ cm$$.
The side of a square sheet of metal is increasing at $$3$$ centimetre per minute. At what rate is the area increasing when the side is $$10\ cm$$ long?
The radius of a circle is increasing uniformly at the rate of $$0.3$$ centimetre per second. At what rate is the area increasing when the radius is $$10\ cm$$? (Taken $$\pi = 3.14$$.)
Show that $$f(x)=\left(\dfrac{3}{x}+5\right)$$ is decreasing for all $$x\in R$$, wherer $$x\neq 0$$.
Show that $$f(x)=\left(x-\dfrac{1}{x}\right)$$ is increasing for all $$x\in R$$, where $$x\neq 0$$.
Show that $$f(x)=\dfrac{1}{(1+x^2)}$$ is increasing for all $$x\le 0$$.
On a straight coast there are three objects $$A, B$$, and $$C$$ such that $$AB = BC = 2\ miles$$. A vessel approaches $$B$$ in a line perpendicular to the coast and at a certain point $$AC$$ is found to subtend an angle of $$60^{\circ}$$; after sailing in the same direction for ten minutes $$AC$$ is found to subtend $$120^{\circ}$$, find the rate at which the ship is going.
Find the required for a cylindrical tank of radius $$r$$ and height $$H$$ to empty through a round hole of area $$'a'$$ at the bottom. The flow through a hole is according to the law $$U(t)=u \sqrt {2gh (t)}$$ where $$v(t)$$ and $$h(t)$$ are respectively the velocity of flow through the hole and the height of the water level above the hole at time $$t$$ and $$g$$ is the acceleration due to gravity.
Determine for which values of $$ x $$ the function $$ y = x^4 - \dfrac {4x^3}{3} $$ is increasing and for which values it is decresing.
Water is dripping out at a steady rate of $$ 1 cu \quad cm/sec $$ through a tiny hole at the vertex of the conical vessel, whose axis is vertical. When the slant height of water in the vessel is $$ 4 cm $$, find the rate of decrease of slant height, where the vertical angle of the conical vessel is $$ \frac{\pi}{6}. $$
Given that $$ \dfrac {dv}{dt} = 1 c^3 / s $$ where $$ v $$ is the volume of water in the conical vessel.
From the fig $$ l = 4cm , h = l cos \dfrac { \pi}{6} = \dfrac { \sqrt {3} }{2} l $$ and $$ r = l sin \tfrac { \pi}{6} = \frac {l}{2} .$$
Therefore, $$ v = \dfrac {1}{3}\pi r^2 h = \dfrac { \pi }{3} \dfrac {l^2}{2} \dfrac { \sqrt {3}}{2} l = \dfrac { \sqrt {3}}{24} l^3 $$
$$ \dfrac {dv}{dt} = \dfrac { \sqrt {3} \pi}{8} l^2 \dfrac {dl}{dt} $$
therefore rate of decreases of slant height is $$ 4 $$ units. $$ 1 = \dfrac { \sqrt {3} \pi }{8} 16 . \dfrac {dl}{dt} $$
$$ \Rightarrow \dfrac {dl}{dt} =\dfrac {1}{ 2 \sqrt {3} \pi } cm/ s$$
Therefore, the rate of decrease of slant height $$ = \dfrac {1}{ 2 \sqrt {3} \pi} cm/s.$$
Show that $$y= log(1+x)- \dfrac{2x}{2+x}, x>$$ is an increasing function of x throughout its domain.
The values of a for which the function $$ f\left( x \right) =sin x-ax+b $$ increases on $$ R $$ are_____.
A ladder $$10$$ metres long is leaning against a vertical wall. If the bottom of the ladder is pulled horizontally away from the wall at the rate of $$1.2$$ ,meters per second, find how fast the top of the ladder is sliding down the wall, when the bottom is $$6$$ metres away from the wall.
Let $$AB$$ be the ladder, where $$AB=10$$ metres,. Let at time $$t$$ seconds, the end $$A$$ of the ladder be $$x$$ metres from the wall and the end $$B$$ be $$y$$ metres from the ground.
Since, $$OAB$$ is a right angled triangle, by Pythagoras theorem.
$$x^2+y^2=10^2$$
i.e.. $$y^2=100-x^2$$
Differentiating w.r.t $$t$$ we get
$$2y \dfrac{dy}{dt}=0-2x \dfrac{dx}{dt}$$
$$\therefore \dfrac{dy}{dt}=\dfrac{x}{y}.\dfrac{dx}{dt}...(1)$$
Now, $$\dfrac{dx}{dt}=\dfrac{12\ metres}{sec}$$ is the rate at wh the bottom of the ladder $$s$$ pulled horizontally and $$\dfrac{dy}{dt}$$ is the rate which the top of ladder $$B$$ is sliding. which the top of ladder $$B$$ is sliding.
When $$x=6, y^2=100-36=64$$
$$\therefore y=8$$
$$\therefore (1)$$ gives, $$\dfrac{dy}{dt}=-\dfrac{6}{8}(1.2)$$
$$=\dfrac{6}{8} \times \dfrac{12}{10}$$
$$-\dfrac{9}{10}$$
$$=-0.9$$
Hence, the top of the ladder is sliding down the wall, at the rate of $$\dfrac{0.9\ metre}{sec}$$
Since, $$OAB$$ is a right angled triangle, by Pythagoras theorem.
$$x^2+y^2=10^2$$
i.e.. $$y^2=100-x^2$$
Differentiating w.r.t $$t$$ we get
$$2y \dfrac{dy}{dt}=0-2x \dfrac{dx}{dt}$$
$$\therefore \dfrac{dy}{dt}=\dfrac{x}{y}.\dfrac{dx}{dt}...(1)$$
Now, $$\dfrac{dx}{dt}=\dfrac{12\ metres}{sec}$$ is the rate at wh the bottom of the ladder $$s$$ pulled horizontally and $$\dfrac{dy}{dt}$$ is the rate which the top of ladder $$B$$ is sliding. which the top of ladder $$B$$ is sliding.
When $$x=6, y^2=100-36=64$$
$$\therefore y=8$$
$$\therefore (1)$$ gives, $$\dfrac{dy}{dt}=-\dfrac{6}{8}(1.2)$$
$$=\dfrac{6}{8} \times \dfrac{12}{10}$$
$$-\dfrac{9}{10}$$
$$=-0.9$$
Hence, the top of the ladder is sliding down the wall, at the rate of $$\dfrac{0.9\ metre}{sec}$$
Solve the following: A water tank in the farm of an inverted cone is being emptied at the rate of $$2$$ cubic feet per second. The height of the cone is $$8$$ feet and the radius is $$4$$ feet. Find the rate of change of water level when the depth is $$6$$ feet.
Let $$r$$ be the radius of base, $$h$$ be the height and $$V$$ be the volume of the water level at any time $$t$$.
Since, the height of the cone is $$8$$ feet and the radius $$4$$ feet, $$\dfrac{r}{h}=\dfrac{4}{8}=\dfrac{1}{2}$$
$$\therefore r=\dfrac{h}{2}$$
Given: $$\dfrac{dV}{dt}=\dfrac{2\ cufeet}{sec}.$$
Now, $$V=\dfrac{1}{3}r^{2}h$$
$$=\dfrac{1}{3}\pi \left(\dfrac{h}{2}\right)^{2}h$$ ....[By $$(1)$$]
$$\therefore V=\dfrac{\pi}{2}h^{3}$$
Differentiating w.r.t. $$t$$, we get
$$\dfrac{dV}{dt}=\dfrac{\pi}{12}\times 3h^{2}\dfrac{dh}{dt}$$
$$=\dfrac{\pi h^{2}}{4}.\dfrac{dh}{dt}$$
$$\therefore \dfrac{dh}{dt}=\dfrac{4}{\pi h^{2}}.\dfrac{dv}{dt}$$
When $$h=6$$, then
$$\dfrac{dh}{dt}=\dfrac{4}{\pi(6)^{2}}\times 2$$
$$=\left(\dfrac{2}{9\pi}\right)\dfrac{ft}{sec}$$
Hence, the rate of change of water level is $$\left(\dfrac{2}{9\pi}\right)\dfrac{ft}{sec}$$.
Since, the height of the cone is $$8$$ feet and the radius $$4$$ feet, $$\dfrac{r}{h}=\dfrac{4}{8}=\dfrac{1}{2}$$
$$\therefore r=\dfrac{h}{2}$$
Given: $$\dfrac{dV}{dt}=\dfrac{2\ cufeet}{sec}.$$
Now, $$V=\dfrac{1}{3}r^{2}h$$
$$=\dfrac{1}{3}\pi \left(\dfrac{h}{2}\right)^{2}h$$ ....[By $$(1)$$]
$$\therefore V=\dfrac{\pi}{2}h^{3}$$
Differentiating w.r.t. $$t$$, we get
$$\dfrac{dV}{dt}=\dfrac{\pi}{12}\times 3h^{2}\dfrac{dh}{dt}$$
$$=\dfrac{\pi h^{2}}{4}.\dfrac{dh}{dt}$$
$$\therefore \dfrac{dh}{dt}=\dfrac{4}{\pi h^{2}}.\dfrac{dv}{dt}$$
When $$h=6$$, then
$$\dfrac{dh}{dt}=\dfrac{4}{\pi(6)^{2}}\times 2$$
$$=\left(\dfrac{2}{9\pi}\right)\dfrac{ft}{sec}$$
Hence, the rate of change of water level is $$\left(\dfrac{2}{9\pi}\right)\dfrac{ft}{sec}$$.
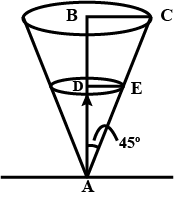
If watverted hollow cone whose semi-vertical angle is $$30^o$$, so that its dept (measured along the axis) increases at the rate of $$\dfrac{1\ cm}{sec}$$. Find therate at which the volume of water increasing when the depth is $$2\ cm$$
let $$r$$ be radius, $$h$$ be the height, $$\theta$$ be the semi-vertical angle and $$V$$ be the volume of the water at any time $$t$$
Give: $$\dfrac{dh}{dt}=\dfrac{1 cm}{sec}, \theta=30^oC$$
Now, $$V=\dfrac{1}{3} \pi r^2h$$
But, $$\tan30^o=\dfrac{r}{h}$$
$$\therefore \dfrac{1}{\sqrt 3}=\dfrac{r}{h}$$
$$\therefore r=\dfrac{h}{\sqrt 3}$$
$$\therefore V=\dfrac{1}{3} \pi \left(\dfrac{h}{\sqrt 3}\right)^2h=\dfrac{\pi}{9}h^3$$
Differentiating w.r.t $$t$$ we get
$$\dfrac{dV}{dt}=\dfrac{\pi}{9} \times 3h^2 \dfrac{dh}{dt}=\dfrac{\pi}{3}h^2\dfrac{dh}{dt}$$
When $$h=2cm, $$ then
$$\dfrac{dV}{dt}=\dfrac{\pi}{3} \times (2)^2 \times 1=\dfrac{4 \pi}{3}$$
Hence, the volume of water is increasing at the rate of $$\left(\dfrac{4 \pi}{3} \right)\dfrac{cm^3}{sec}$$
Give: $$\dfrac{dh}{dt}=\dfrac{1 cm}{sec}, \theta=30^oC$$
Now, $$V=\dfrac{1}{3} \pi r^2h$$
But, $$\tan30^o=\dfrac{r}{h}$$
$$\therefore \dfrac{1}{\sqrt 3}=\dfrac{r}{h}$$
$$\therefore r=\dfrac{h}{\sqrt 3}$$
$$\therefore V=\dfrac{1}{3} \pi \left(\dfrac{h}{\sqrt 3}\right)^2h=\dfrac{\pi}{9}h^3$$
Differentiating w.r.t $$t$$ we get
$$\dfrac{dV}{dt}=\dfrac{\pi}{9} \times 3h^2 \dfrac{dh}{dt}=\dfrac{\pi}{3}h^2\dfrac{dh}{dt}$$
When $$h=2cm, $$ then
$$\dfrac{dV}{dt}=\dfrac{\pi}{3} \times (2)^2 \times 1=\dfrac{4 \pi}{3}$$
Hence, the volume of water is increasing at the rate of $$\left(\dfrac{4 \pi}{3} \right)\dfrac{cm^3}{sec}$$
The volume of a sphere increases at the rate of $$\dfrac{20cm^3}{sec}$$. Find the rate of change of its surface area, when its radius is $$5\ cm$$.
The edge of a cube is decreasing at the rate of $$\dfrac{0.6 cm}{sec}$$. Find the rate at which its volume is decreasing, when the edge of the cube is $$2\ cm$$.
A spherical soap bubble is expanding so that its radius is inreasing at the rate of $$0.02\ cm/sec$$. At what rate is the surface area increasing, when its radius is $$5\ cm?$$
The length x of a rectangle is decreasing at the rate of5cm/minute and the width y is increasing at the of 4 cm / minute . When x = $$ 8cm $$ and $$y = 6 cm $$, find the rates of change of the area of the rectangle .
Show that $$y = log (1 + x ) - \dfrac{2x}{2 + x} , x > -1 $$ an increasing function of x throughout its domain .
A stone is dropped into a quiet lake and waves move in circles at the speed of $$5 cm / s.$$. At the instant when the radius of the circular wave is 8 cm , how fast is the enclosed area increasing ?
A ladder 5 in long is leaning against a wall. The bottom of the ladder is pulled along the ground , away from wall, at the rate of $$2 cm / s$$ . How fast is its height on the wall decreasing when the foot the ladder is $$ 4 m $$ away from the wall?
A balloon, which always remains spherical on inflation , is being inflated by pumping in $$900 $$ cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is $$15 cm $$.
Find the values of x for which $$ y = [ x (x - 2 ) ] ^{2}$$ is an increasing function
A balloon , which always remains spherical , has a variable diameter $$ \dfrac{3(2x+1)}{2} $$. Find the rate of changes of its volume with respect to $$x$$ .
A Balloon which is always spherical, is being inflated by pumping in $$900 cm^3$$ of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is $$15 cm$$.
A balloon which is always spherical, has diameter $$\frac{3}{2} (2x + 1)$$ Find rate of change of its volume w.r.t.x.
If radius and height of a cylinder is $$r$$ and $$A$$, then find the rate of change of surface area with respect to its radius.
Find the value of $$x$$ and $$y$$ for function, $$y = x^3 + 21$$ where, the rate of change ofy is three times as the rate of change of $$x$$.
If $$\displaystyle f\left ( x \right )= \cos \left ( 2x+\frac{\pi }{4} \right )$$ then show that f(x) is increasing in the interval $$\displaystyle \frac{3\pi }{8}< x< \frac{7\pi }{8}$$
If $$u(x)$$ is larger of $$\displaystyle x-\left ( x^{3}/6 \right )$$ and $$\displaystyle \tan^{-1}x$$ for $$\displaystyle 0 < x \leq 1$$ then $$48u(1/2)$$ is equal to
Investigate the behaviour of the function $$y\, =\, (x^3\, +\, 4)(x\, +\, 1)^3$$ and construct its graph. How many solutions does the equation $$(x^3\, +\, 4)(x\, +\, 1)^3\, =\, c$$ possess ?
$$y=\left( { x }^{ 3 }+4 \right) { (x+1) }^{ 3 }$$ ...... $$(1)$$
$$\Rightarrow $$point of intersection on axis
At $$x=0,y=4\times { (1) }^{ 2 }=4$$
At $$y=0,\left( { x }^{ 3 }+4 \right) { (x+1) }^{ 3 }=0$$
$$x=-1$$
$$x={ (-4) }^{ { 1 }/{ 3 } }$$
Increasing and decreasing nature
$$\cfrac { dy }{ dx } =\left( { x }^{ 3 }+4 \right) \times 3{ (x+1) }^{ 2 }+{ (x+1) }^{ 3 }\left( 3{ x }^{ 2 } \right) $$
$$\cfrac { dy }{ dx } ={ (x+1) }^{ 2 }\left[ 3{ x }^{ 3 }+12+3{ x }^{ 2 } \right] $$
$$\cfrac { dy }{ dx } =3{ (x+1) }^{ 2 }\left[ { x }^{ 3 }+{ x }^{ 2 }+4 \right]$$ ..... $$(2)$$
At $$x=-1,-2$$ from above turning point exist
For maxima and minima
$$y=\left[ { (-1) }^{ 3 }+4 \right] { (-1+1) }^{ 3 },\quad y=0$$
$$y=\left[ { (-2) }^{ 3 }+4 \right] { (-2+1) }^{ 3 },\quad y=4$$
(Image)
$$\left( { x }^{ 3 }+4 \right) { (x+1) }^{ 3 }=C$$
So, $$2$$ solutions exist.
In a bank, principal increase continuously at the rate of r% per year. Find the value of r if Rs. 100 double itself in 10 years (log_e 2=0.6931)
In a culture, the bacteria count is 1,00,The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if the rate of growth of bacteria is proportional to the number present?
Prove that $$\displaystyle y=\dfrac { 4\sin { \theta } }{ 2+\cos { \theta } } $$ is an increasing function of $$\displaystyle \theta $$ on $$\displaystyle \left[ 0,\dfrac { \pi }{ 2 } \right] $$.
The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was $$20,000$$ in $$1999$$ and $$25000$$ in the year $$2004,$$ what will be the population of the village in $$2009$$?
It is given that the graph of $$y = x^4+ax^3+bx^2+cx+d$$ (where $$a, b, c, d$$ are real) has at least 3 points of intersection with the x-axis. Prove that either there are exactly 4 distinct points of intersection, or one of those 3 points of intersection is a local minimum or maximum.
A cylindrical water tank of diameter $$1.4\ m$$ and height $$2.1\ m$$ is being fed by a pipe of diameter $$3.5\ cm$$ through which water flows at the rate of $$2\ m/s$$. Calculate the time, it takes to fill the tank.
Find 2 +ve nos. whose sum is 15 and the sum of whose squares is min.
Let first number be x
Given sum of two positive number is 15
$$1^{st} no + 2^{nd}no=15$$
$$\rightarrow x+2^{nd}no=15$$
$$\rightarrow2^{nd}=15-x$$
let $$S(x)$$ be sum of squares of numbers
$$S(x) =(1st\, no)^2+(2^{nd}\,no)^2$$
$$S(x)= x^2+(15-x)^2$$
mininize $$S(x)$$
$$S(x)=x^2+(15-x)^2$$
$$S'(x)=2x+2(15-x)(-1)=2x-30+2x$$
$$ S'(x)=4x-30$$
Putting $$S'(x) =0$$
$$\rightarrow 4x-30=0$$
$$\rightarrow x=\left(\dfrac{15}{2}\right)=7.5$$
$$S"(x)=d(\dfrac{(4x-30)}{dx}=4$$
putting $$x=7.5$$ in $$S"(x)$$
$$S"(7.5)=4>0,i.e x=7.5$$ is local minima
$$\therefore 1^{st} number =\dfrac{15}{2},2^{nd}no=\dfrac{15}{2}$$
Find two positive numbers $$x$$ and $$y$$ such that $$x+y=60$$ and $$xy^3$$ is maximum.
The sum of two positive numbers is 12 and sum of one and product of one and sqaure of the other is maximum.Find the numbers.
The radius of the soap bubble is increasing at the rate of $$0.2$$ cm/sec. If its radius is $$5$$ cm, find the rate of increasing of its volume.
If water is poured into an inverted hollow cone whose semi-vertical angle is $${30^ \circ }$$ , and its depth (measured along axis) increase at the rate of 1 cm per sec, find the rate at which the volume of water is increasing when the depth is 24 cm.
Radius $$=r$$
$${ \theta }^{ ° }=30°$$
According to question, $$\dfrac { dh }{ dt } =1cm/sec$$
$$tan\theta =\dfrac { r }{ h } \Rightarrow \dfrac { 1 }{ \sqrt { 3 } } =\dfrac { r }{ h } \Rightarrow r=\dfrac { h }{ \sqrt { 3 } } -----(1)\\ Now,\dfrac { dv }{ dt } =\dfrac { d }{ dt } \left( \dfrac { 1 }{ 3 } \pi { r }^{ 2 }h \right) =\dfrac { 1 }{ 3 } \pi \dfrac { d }{ dt } ({ r }^{ 2 }h)$$
Using $$(1)$$
$$\dfrac { dv }{ dt } =\dfrac { 1 }{ 3 } \pi \dfrac { d }{ dt } \left( { \dfrac { h^{ 2 } }{ 3 } }h \right) =\dfrac { 1 }{ 3 } \pi \cdot \dfrac { 1 }{ 3 } \dfrac { d }{ dt } \left( { h }^{ 3 } \right) \\ \dfrac { dv }{ dt } =\dfrac { 1 }{ 9 } \pi \cdot 3h^{ 2 }\dfrac { dh }{ dt } =\dfrac { \pi }{ 3 } h^{ 2 }\dfrac { dh }{ dt } \\ When\ h=24cm\\ \dfrac { dv }{ dt } =\dfrac { \pi }{ 3 } \cdot 24\cdot 24\cdot (1)=\boxed { 192\pi { cm }^{ 2 }/sec } $$
Find the points of absolute maximum and minimum of $$f (x) = (x - 1)^{1/3} \,\, (x - 2); \,\, 1 \le x \le 9$$.
If $$\theta \in \left[ {\dfrac{{5\pi }}{{12}},\, - \dfrac{\pi }{3}} \right]$$ and mamimum value of $$\dfrac{{\tan \left( {\theta + \frac{{2\pi }}{3}} \right) - \tan \left( {\theta + \dfrac{\pi }{6}} \right) + \cos \left( {\theta + \frac{\pi }{6}} \right)}}{{\sqrt 3 }}$$ is $$\frac{a}{b}$$ (where a and b are co-primes),then $$a-b$$ is equal to _________________
Find all the points of local maxima and local minima of the function
$$f(x) =-\dfrac{3}{4}x^4-8x^3-\dfrac{45}{2}x^2+105.$$
If real number x and y satisfy $${\left( {x + 5} \right)^2} + {\left( {y - 12} \right)^2} = {\left( {14} \right)^2}$$ then the minimum value of $$\sqrt {\left( {{x^2} + {y^2}} \right)} $$ is
At noon, ship $$A$$ is $$170\ km$$ west of ship $$B$$. Ship $$A$$ is sailing east at $$40\ km/h$$ and ship $$B$$ is sailing north at $$25\ km/h$$. How fast is the distance between the ships changing at $$4:00\ PM$$?
The rate of increase of bacteria is proportional to the number of bacteria present at the time . If intial number of bacteria is 100 and in first in half an hour, the number of bacteria gets doubled then at the end of 2 hours, find the number of bacteria.
Find the minimum value of a, such that function $$f(x)=x^2+ax+5$$, is increasing in interval $$[1, 2]$$.
The radius of a soap bubble is increasing at the rate of 0.2 cm/sec. At what rate the surface area of a bubble increasing when the radius is 7 cm and at what rate the volume of a bubble increasing when the radius is 5 cm ?
The population of town decrease by $$12$$ % during $$1998$$ and then increased by $$8$$ % during $$1999$$. find the population of the town ,at the beginning of $$1998$$, if at the end of $$1999$$ its population was $$285120$$.
Find intervals in which $$f(x)=\dfrac {4x^{2}+1}{x}$$ is increasing and decreasing.
Let $$f$$ defined on $$[0,1]$$ be twice differentiable such that $$|f''(x)|\le1$$ for $$x∈[0,1].$$ if $$f(0)=f(1)$$ then show that $$∣f'(x)<1$$ for all $$x∈[0,1].$$
Class 12 Commerce Applied Mathematics Extra Questions
- Application Of Derivatives Extra Questions
- Applications Of Integrals Extra Questions
- Definite Integrals Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Indefinite Integrals Extra Questions
- Linear Equations Extra Questions
- Matrices Extra Questions
- Probability Distribution And Its Mean And Variance Extra Questions
- Quantification And Numerical Applications Extra Questions
- Standard Probability Distributions Extra Questions