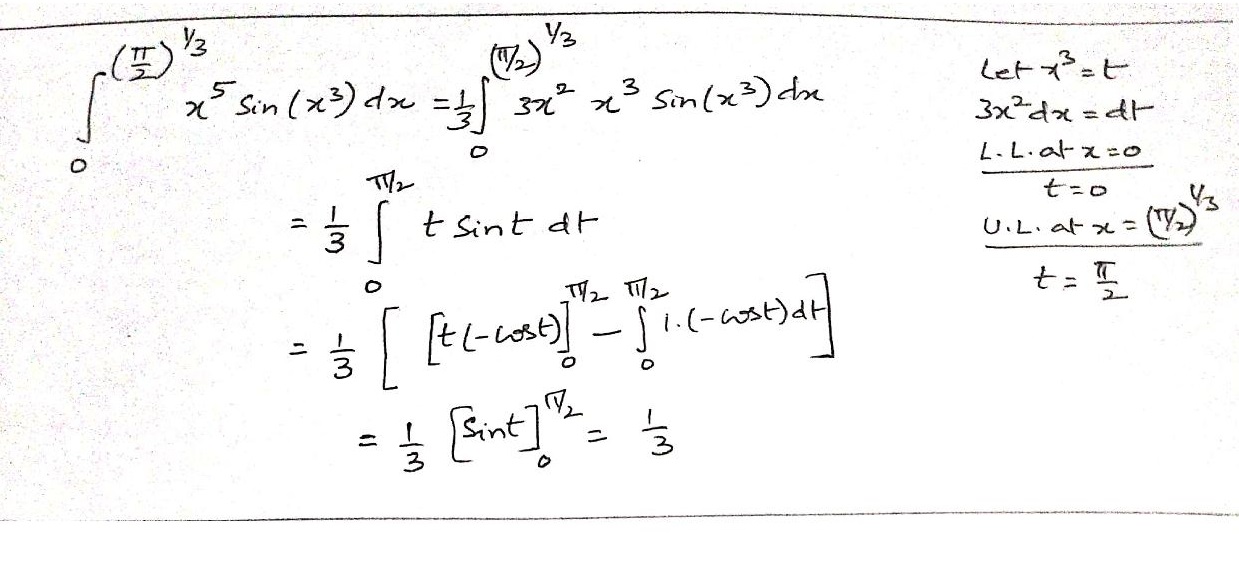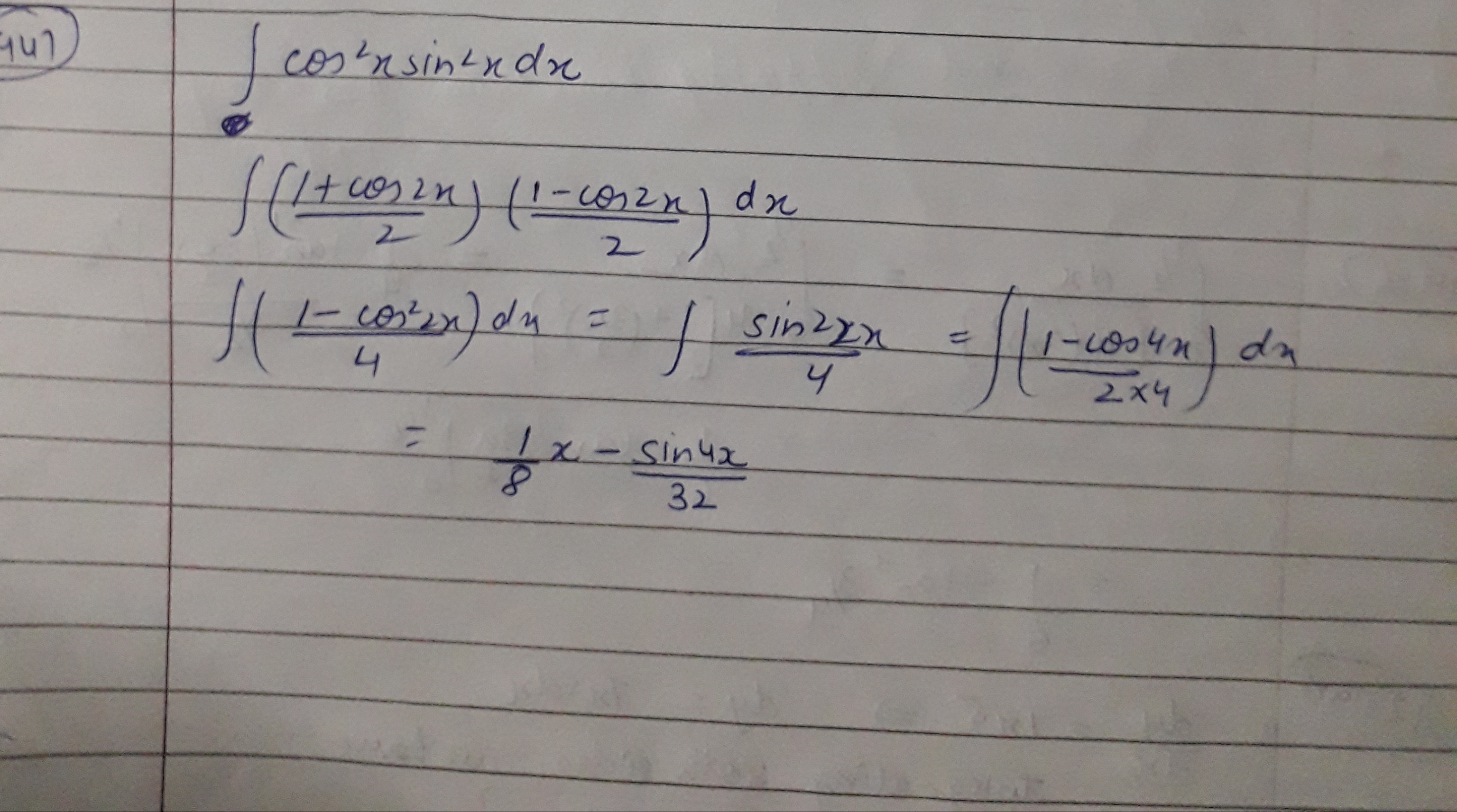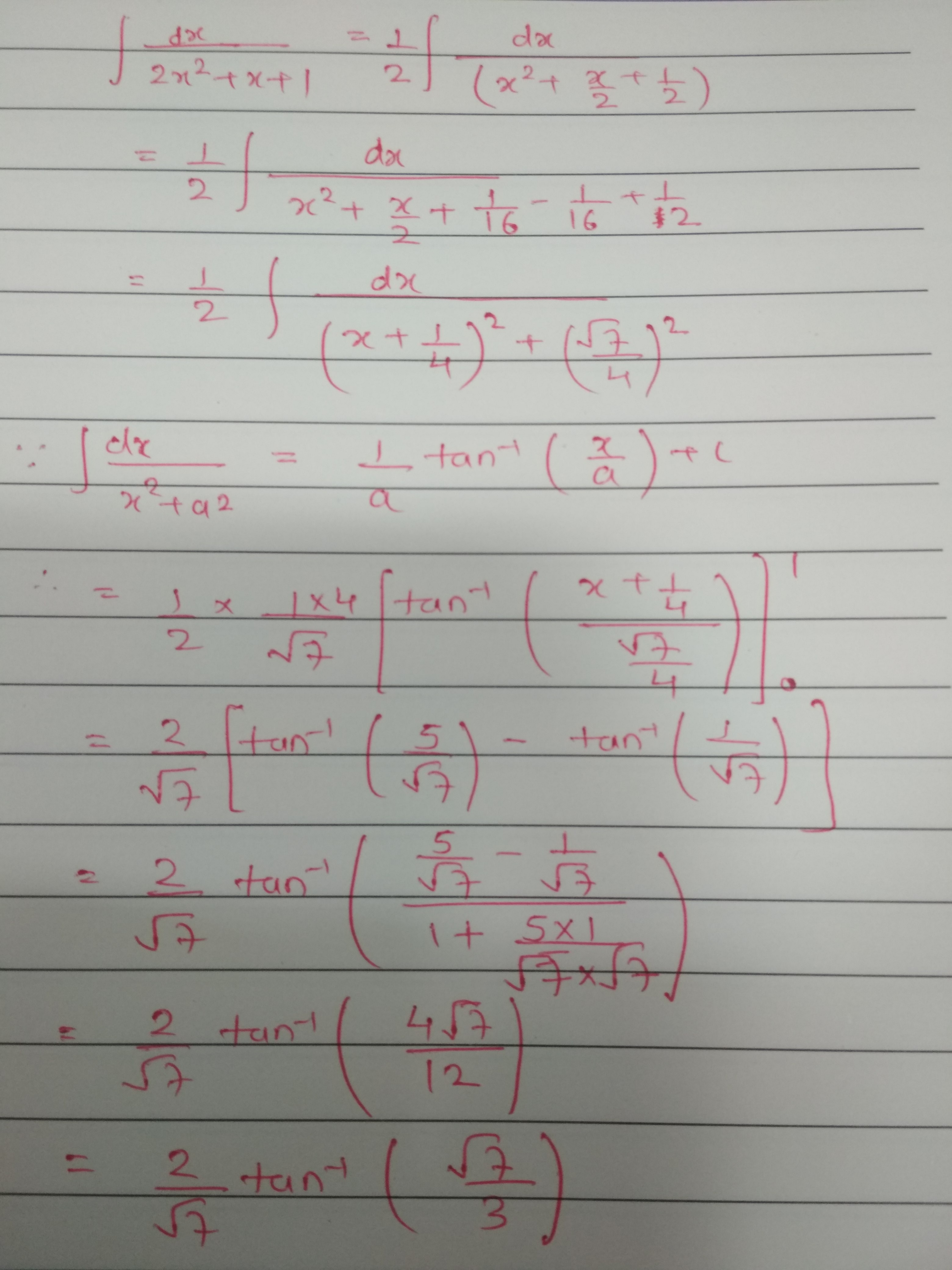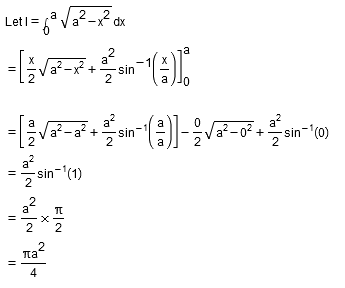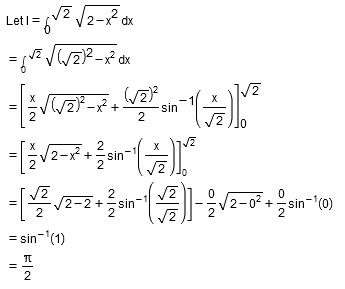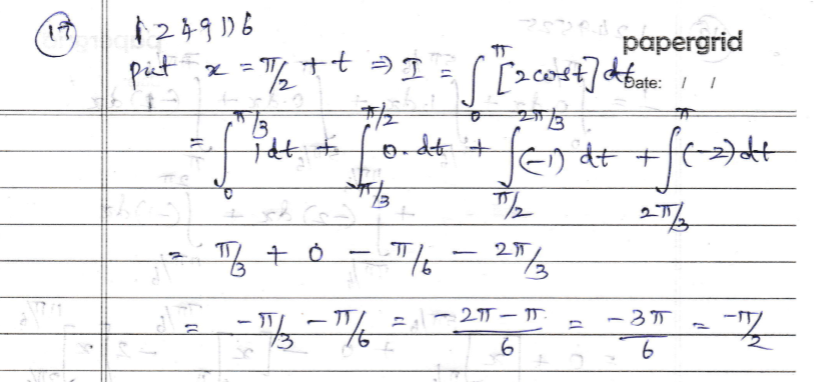Definite Integrals - Class 12 Commerce Applied Mathematics - Extra Questions
If α=∫10(e(9x+3tan−1x))(12+9x21+x2)dx , where tan−1x takes only principal values, then the value of (loge|1+α|−3π4) is
Evaluate :∫cos√x√xdx
Evaluate the integral
∫54(x2−12x+8)dx
The value of (∫π/60sec2xdx)2 is:
If y=2232x5−57−5 then dydx=
Find ∫π/20sinx.sin2x dx
Solve: π2∫0sin2xcos3xdx
Find the value π2∫−π2sin2017xcos2018x dx.
∫1+x√1−x2dx
Evaluate ∫π0x2sin2x.sin(π2cosx)dx(2x−π)
The value of integral ∫3−1(tan−1(x1+x2)+tan−1(x2+1x))dx
∫π40sinxcosxcos4x+sin4xdx
∫2−1√5x+6dx
solve 11/2∫0sin2xsin2x+cos2xdx
Solve: π3∫π6cosxdx
Evaluate :2π∫0cos5x dx
Evaluate:1∫0xx2+1dx
Evaluate :π/2∫0cos2x dx
Evaluate the following
∫31cos(logx)xdx.
Find the value of ∫(π/2)1/30x5.sinx3 dx
∫∞0logx1+x2dx
Solve : π/4∫02sinxsin2xdx
∫10√x(1−x)dx
Solve:∫π/40tan3x sec x dx
Evaluate;
∫230dx4+9x2
Evaluate the following definite integral:
∫101−x1+xdx
∫40x+exdx
Solve
∫20cosxdx
∫20x√x+2 (Put x+2=t2)
Solve:∫π/2−π/2sin2xdx
Evaluate the following definite integral:∫102x+35x2+1dx
Evaluate the following definite integral:
∫102x+35x2+1dx
Evaluate : ∫π/40tan3x.sec2xdx
I=∫π/201+2cosx(2+cosx)2dx
Solve
∫π0x dx1+sinx
Evaluate ∫10(x3+1) dx
∫10(x2+2x)dx
Evaluate:∫π/201+sinxdx
Evaluate ∫π/20sinxcosx1+sin4xdx
Evaluate the definite integrals :
∫π/20(1+cosx)dx
∫10x2+2xdx
Evaluate the following definite integrals :
\displaystyle \int_{0}^{3}x^2 \ dx
\displaystyle\int_{0}^{1}(1-x^{2}) \ dx
Evaluate the following integral:\displaystyle\int_{0}^{1}\sqrt x \ dx
\displaystyle\int_{0}^{\pi/2} \sin x \cos x\ dx
Evaluate the definite integral :
\displaystyle \int _{0}^{\pi /2} \cos^2 x\ dx
Evaluate the definite integral :\displaystyle \int _{0}^1 \dfrac {1-x}{1+x}dx
Evaluate\displaystyle\int_{0}^{1}\dfrac{1-x^{2}}{(1+x^{2})^{2}}dx
Evaluate the following definite integral:
\displaystyle \int _2^3 x^2+2x+5 \ \ dx
Evaluate the following integral:\displaystyle\int_{0}^{\pi} x\ dx
Evaluate the following definite integral:
\displaystyle\int_{0}^{1}\dfrac{1-x^{2}}{(1+x^{2})^{2}}dx
Evaluate \displaystyle \int _2^3 x^2+2x+5 \, dx
Evaluate the following definite integral:
\displaystyle \int_0^{1}(3x^2+2x)dx
Solve \displaystyle \int_{1}^{2}{(x+3)}\ dx
Evaluate \displaystyle \int_{0}^{2}(x^2+2x +1)dx
Evaluate the given integral.
\displaystyle \int_{0}^{5} x^2dx
The value of \displaystyle \int _{0}^{1}x^2+2 dx is equal to ?
The value of \displaystyle \int _{0}^{1}x^2+2 \ dx is equal to ____ .
The value of \displaystyle \int _{0}^{1}x^2+2 \ dx is equal to ____ .
Show that \displaystyle \int_{0}^{1}\frac{1}{\left ( 1+x^{2} \right )^{3/2}}dx=\frac{3}{\sqrt{\left ( 2 \right )}}
\displaystyle \int_{0}^{\infty }\frac{dx}{\left ( x+\sqrt{1+x^{2}} \right )^{n}} = f(n)
Find the value if n=6, can be expressed as a/b in simplest form, then b-a = ?
\displaystyle \int_{0}^{\pi }x\log \sin x= \frac{\pi ^{k}}{m}\log \frac{1}{n}..Find k+m+n ?
\displaystyle \int_{0}^{\pi /2}\frac{\cos x dx}{1-\sin ^{2}x+\sin ^{4}x}=\frac{\pi }{k}+\frac{1}{4\sqrt{(3)}}log(\dfrac{(2+\sqrt{3})}{(2-\sqrt{3})}). Find the value of k.
Evaluate the integral \displaystyle \int_0^1\frac {x}{x^2+1}dx using substitution.
Evaluate \displaystyle\int _{ 1 }^{ 5 }{ \frac { dx }{ \sqrt { 2x-1 } } } .
Find \begin{pmatrix}\int ^{\pi /4}_0 \dfrac{dx}{\cos^3 x\sqrt{2\sin2x}}\end{pmatrix}.
Evaluate \int \int_{R} e^{-(x^{2} + y^{2})}dx dy, where R is the region bounded by the circle x^{2} + y^{2} = a^{2}.
\int_{0}^{5}x^{3} (25 - x^{2})^{7/2} dx.
Use the substitution u={ e }^{ x } to evaluate
\displaystyle \int _{ 0 }^{ 1 }{ \sec { hx } } dx
\displaystyle\int^{\pi}_{-\pi}\frac{\cos^2x}{1+a^x}dx=?
\int _{ 0 }^{ \cfrac { \pi }{ 2 } }{ \sqrt { 1-\sin { 2x } } } dx is equal to
Find all numbers \alpha for which \displaystyle\, \int_{1}^{2}[\alpha^2 \, + \, (4 \, - \, 4\alpha)x \, + \, 4x^3]dx \leqslant 12
Find the area of the figure bounded by the following curves
Find all values of a for which the inequality \displaystyle \int_{0}^{a} \, x \, dx \, \leqslant \, a \, + \, 4 is satisfied.
Evaluate \displaystyle \int _{ 0 }^{ 2/3 }{ \cfrac { dx }{ \left( 4+9{ x }^{ 2 } \right) } }
Evaluate: \displaystyle \int_{\frac{\pi}{2}}^{\pi}\frac{1-sinx}{1-cosx}dx
Let T= \int_0^{\ln2} \frac{3e^{3x} + 2e^{2x} }{e^{3x}+e^{2x} +1} dx , then e^T=\frac{p}{q} where p and q are coprime to each other, then find the value of p+q is
Integrate \int\limits_0^1 {{x \over {1 + {x^2}}}dx}
Evaluate \displaystyle\int_0^{\tfrac{\pi }{2}} {\sqrt {\sin \phi } \, {{\cos }^5}\phi d\phi }
Prove that \int\limits_0^{\tfrac {32\pi} 3} {\sqrt {1 + \cos 2x} \,dx = \sqrt {\frac{3}{2}} }
Evaluate: \displaystyle \int\limits_0^{\frac{\pi }{4}} {{{\cos }^{\frac{3}{2}}}\left( {2x} \right)\cos \left( x \right)dx}
Prove that: \int_0^{\pi /4} {\dfrac{{dx}}{{{{\cos }^3}x\sqrt {2\sin 2x} }}} = \dfrac{6}{5}
x_{CM} = \frac{\int x dm}{\int dm} = \frac{\int\limits_0^1 x (1 + 2x) dx}{\int\limits_0^1(1 + 2x) dx}
Find
\displaystyle \int_0^{1/4 \pi} ln(1 + \tan x )dx.
Evaluate:\displaystyle\int^2_1\dfrac{dx}{x(x^4+1)}.
Solve \int\limits_2^6 {\sqrt {\left( {6 - x} \right)\left( {x - 2} \right)} dx}
\displaystyle\int^{1}_0\sin^{-1}\left(\dfrac{2x}{1+x^2}\right)dx.
Evaluate:
\displaystyle \int _{ 0 }^{ 1 } x^3+ 3x^2 dx
The value of \displaystyle\int_{0}^{\dfrac{\pi}{2}}{\dfrac{dx}{1+{\tan}^{3}{x}}} is
Evaluate the integrals using substitution.
\displaystyle\int^2_0x\sqrt{x+2} (Put x+2=t^2).
\displaystyle\int^{\dfrac{\pi}{2}}_0\dfrac{\sin x}{1+\cos^2x}dx.
Solve :
\int_2^4 {\frac{{dx}}{x}}
\displaystyle \int_2^4 (6x^3 + 5x) dx =
\displaystyle\int^{\dfrac{\pi}{4}}_0\dfrac{x\sin x}{\cos^3x}dx.
Evaluate \displaystyle \int_0^{\frac{\pi }{4}} {\frac{{dx}}{{{a^2}{{\cos }^2}x - {b^2}{{\sin }^2}x}}}
Solve :- \displaystyle \int_0^1 \ 3^x dx
Solve:\displaystyle \int_0^{\pi/2}sinx \cos^3 xdx
\int _{ 0 }^{ \dfrac { \pi }{ 2 } }{ \dfrac { \sin { ^{ 2 }x } }{ \sin { x } +\cos { x } } dx } =-\dfrac { 1 }{ 2\sqrt { 2 } } \log { \left(-2 \sqrt { 2 } +3\right) }
Solve it :-
\int\limits_{\pi /4}^{\pi /2} {\sqrt {1 - \sin 2x\,} \,\,dx}
Find m if :\displaystyle \int_{0}^{\pi}\left ( \dfrac{\sqrt{1+\cos\ 2x}}{2} \right )dx=\sqrt m
Prove that \displaystyle\int _ { 0 } ^ { \dfrac { \pi } { 4 } } \dfrac { \sin x \cos x } { \cos ^ { 4 } x + \sin ^ { 4 } x } d x
Integrate the following:\displaystyle \int\limits_{\pi /3}^{\pi /2} {{{(\tan x + \cot x)}^2}dx}
\int\limits_0^{\pi /2} {\dfrac{{\sin x\cos x}}{{1 + {{\sin }^4}x}}dx = }
Evaluate \int\limits_0^1 {\dfrac{{2x}}{{5{x^2} + 1}}dx}
Solve : \displaystyle \int_{0}^{2}{x\sqrt{x+2}dx}
\displaystyle \int _{ 2 }^{ 3 }{ \left( 1+2x \right) } dx
Solve:\displaystyle \int_{-\pi/2}^{\pi/2} \log \left(\dfrac{2-\sin x}{2+\sin x}\right)dx
Solve:\int cos^{2}xsin^{2}xdx.
Evaluate: \int\limits_0^{\dfrac{\pi }{2}} {\cos x\;{e^{\sin x}}\;{\text{dx}}}
\displaystyle \int_0^{\pi} {\dfrac{xdx}{{a^2}{{\cos }^2}x + {b^2}{{\sin }^2}x}} = {{{\pi ^2}} \over {2ab}}
Solve:
\displaystyle\int_0^{\frac{\pi }{2}} {{\left( {\sin 2x} \right)} \sin xdx}
Evaluate:
\int\limits_{\pi /4}^{\pi /2} {\sqrt {1 - \sin 2x} } dx
Solve :
\displaystyle \int_{0}^{\pi}{\sin^{3}x dx}
Solve
\displaystyle \int_{0}^{\pi} \dfrac{dx}{5+4 \cos 2x}
Solve: \displaystyle\int _{ 0 }^{ 1 }{ \dfrac { 1 }{ { 2x }^{ 2 }+x+1 } dx }
\int _{ 2 }^{ 4 }{ \frac { x }{ { x }^{ 2 }+1 } } dx
Solve:\int _{ 0 }^{ \log { 2 } }{ \cos { 2x } dx } =
Evaluate: \displaystyle\int _{ { 1 }/{ \sqrt { 2 } } }^{ { \sqrt { 3 } }/{ 2 } }{ \frac { 1 }{ \sqrt { 1-{ x }^{ 2 } } } } dx
Evaluate \displaystyle \int_{0}^{\pi} \dfrac{x}{(a^{2} \cos^{2} x+b^{2} \sin^{2} x)^{2}}dx
Find : \displaystyle \int_0^1 \dfrac{ x}{1+x^{2}} d x
Evaluate \overset { 3 }{ \underset { 0 }{\int } } \dfrac{x}{\sqrt{x^2+16}}dx.
\displaystyle\int_{0}^{\pi /2}\frac{\sin x}{1+\cos^{2}x}dx
Solve: I=2\displaystyle\int _{ 0 }^{ \pi /2 }{ \frac { \sec ^{ 2 }{ x } }{ 1+3\tan ^{ 2 }{ x } } dx }
Integrate \displaystyle \overset { 7 }{ \underset { 4 }{ \int } } \dfrac{(11 - x)^2}{x^2 + ( 11 - x)^2} dx
Evaluate \int\limits_0^{\pi /2} {\dfrac{{\sin x}}{{\sin x + \cos x}}\;d} x.
Evaluate \displaystyle\int_{1}^{2}\dfrac{1}{x(1+\log x)^{2}}dx
I = \dfrac {2}{\pi}\int_{-\pi/4}^{\pi/4} \dfrac {dx}{(1 + e^{\sin x})(2 - \cos 2x)} then find 27I^{2} equals ________.
Evaluate:\displaystyle\int_{0}^{\pi/4}\dfrac{\tan^{3}x}{1+\cos 2x}dx
Evaluate the definite integral :
\displaystyle \int_{e}^{e^2} \left\{\dfrac {1}{\log x} -\dfrac {1}{(\log x)^2}\right\} dx
Evaluate \displaystyle\int_{0}^{\pi/4}\dfrac{\tan^{3}x}{1+\cos 2x}dx
Evaluate \displaystyle\int_{-1}^{1}5x^{4}\sqrt{x^{5}+1}\ dx
\displaystyle\int_{0}^{\pi/4}\dfrac{\tan^{3}x}{1+\cos 2x}dx
Evaluate the following integrals :\displaystyle\int_{0}^{\pi/2}\dfrac{x\sin x\cos x}{\sin^{4}x+\cos^{4}x}\ dx
Evaluate the following definite integral:
\displaystyle \int_{1}^{2} e^{2x} \left (\dfrac {1}{x}-\dfrac {1}{2x^2}\right)dx.
Integrate \displaystyle \int_{2}^{3}(2x^2+1)dx
Evaluate \displaystyle \int_{1}^{3}(x^2+3x+e^{x})dx
Evaluate the following integrals
\int { \cfrac { 1 }{ 5-4\cos { x } } } dx
Evaluate the following integrals
\int { \cfrac { 1 }{ \sin { x } +\sqrt { 3 } \cos { x } } } dx
Evaluate the following definite integral:
\displaystyle \int _0^{\pi/2} \sin x \cos x dx is equal to
Evaluate \displaystyle \int_{1}^{3}(3x^2+1)dx
Evaluate the following integrals
\int { \cfrac { 1 }{ 2+\sin { x } +\cos { x } } } dx
Evaluate the following integrals
\int { \cfrac { 1 }{ \sqrt { 3 } \sin { x } +\cos { x } } } dx
Evaluate the following integral
\int { \sin ^{ -1 }{ \sqrt { \cfrac { x }{ a+x } } } } dx
Evaluate the following integrals:
\displaystyle \int { \cfrac { 1 }{ { x }^{ 3 } } } \sin { \left( \log { x } \right) } dx\quad
Evaluate the following integral
\int { x\cos ^{ 3 }{ x } } dx\quad
Evaluate the following integrals:
\int { \sqrt { 4{ x }^{ 2 }-5 } } dx\quad
Evaluate the following integral:
\displaystyle\int^a_0\sqrt{a^2-x^2}dx.
Evaluate the following integral:
\displaystyle\int^{\sqrt{2}}_0\sqrt{2-x^2}dx.
If the value of the definite integral \int_{0}^{1} \frac{\sin ^{-1} \sqrt{x}}{x^{2}-x+1} d x=\frac{\pi^{2}}{\sqrt{n}}(where n \in N ), then the value of n / 27 is
If \int\left(x^{2010}+x^{\text {804 }}+x^{402}\right)\left(2 x^{160 8}+5 x^{402}+10\right)^{1 / 402} d x
=\dfrac{1}{10 a}\left(2 x^{2010}+5 x^{804}+10 x^{402}\right)^{a / 402} . Then (a-400) is equal to
Let f(x)=\displaystyle \int_{-2}^{x} e^{(1+t)^2}dt and g(x)=f(h(x)), where h(x) is defined for all x \in R. If g'(2)=e^4 and h'(2)=1. Then, absolute value of sum for all possible value of h(2), is ...
Find the value of the following integrals:
\displaystyle \int^{\beta}_{\alpha} \frac{dx}{(x - \alpha)(\beta - x)}, \beta > \alpha
Find the value of the following integrals:
\displaystyle \int^{\beta}_{\alpha} \frac{dx}{\sqrt{(x - \alpha)(\beta - x)}}, \beta > \alpha
Find the value of the following integrals:
\displaystyle \int^{1}_{0} \frac{x^3}{\sqrt{1 - x^2}} dx
\int_{1}^{2} \dfrac {x+3}{x(x+2)} dx
Find the value of the following integrals :
\displaystyle \int _{-2}^{2} | 2x + 3 | dx
\int_{1/3}^{1} \dfrac {(x-x^3)^{1/3}}{x^4} dx
\int_{1}^{2} \dfrac {xe^x}{(1+x)^2} dx
Find the value of the following integrals:
\displaystyle \int^{\infty}_{0} \frac{x^2}{(x^2 + a^2)(x^2 + b^2)} dx
Find the value of following integrals :
\displaystyle \int_{-2}^{2} |1 - x^{2}| dx
Find the value of the following integrals :
\displaystyle \int_{1}^{4} f(x) dx, where f(x) = \left [ \begin{matrix} 7x + 3, &1 \leq x \leq 3 \\ 8x,& 3\leq x \leq 4 \end{matrix} \right ]
\int_{-2}^{2} \left | 1- x^2 \right | dx
Evaluate \displaystyle\int _{ 0 }^{ \pi }{ \dfrac { x\sin ^{ 3 }{ x } }{ 1+\cos ^{ 2 }{ x } } dx } .
Find \displaystyle \int^{1}_{0}x(\tan^{-1}x)^2dx.
\int_{0}^{\pi/2} \sin\phi \cos \phi \sqrt{(a^2\sin^2\phi +b^2\cos^2\phi )}d\phi \,\,a\neq b \,\, (a>0, b> 0)
Solve : \displaystyle \int ^{\cfrac{\pi}{2}}_{0} \frac{\sin^2 x}{\sin x+\cos x}
\displaystyle \int _{ 0 }^{ \frac{\pi}{2n}}{ \frac{dx}{1 + \cot^n nx} } =.
Evaluate \int _{ -3 }^{ 1 }{ \sqrt { \left( { x }^{ 2 }+6x+13 \right) } } dx leaving your answer in terms of natural logarithms.
The value of the integral
\displaystyle \int_{0}^{\frac {1}{2}}\frac {1 + \sqrt {3}}{(x + 1)^{2} (1 - x)^{6})^{\frac {1}{4}}}dx is _______.
Evaluate \int _{ 1 }^{ 4 }{ { 4 }^{ x }dx }
Evalute : \displaystyle \int_0^{\pi /2} \dfrac{dx}{(a^2\cos^2x+b^2\sin^2x)^2}
Integrate:
\int _{ 0 }^{ \pi }{ \dfrac { dx }{ 5+3cosx } }
Solve
\displaystyle \int_0 ^{\infty} ln \left(x + \dfrac{1}{x}\right). \dfrac{dx}{1 + x^2}
Solve:\displaystyle \int_0^{\pi/2}\dfrac{\sin \,x\,dx}{(\sin\,x +\cos \,x)^3}
Solve:
\displaystyle \int_{0}^{\pi/2}{\sin 2x.\tan^{-1}(\sin x)dx}
If {I}_{1}=\displaystyle\int_{0}^{1}{\dfrac{{\tan}^{-1}{x}}{x}dx} and {I}_{2}=\displaystyle\int_{0}^{1}{\dfrac{x}{\sin{x}}dx} then \dfrac{{I}_{1}}{{I}_{2}}
Evaluate:\displaystyle\int_{-2}^{0}{\left({x}^{3}+3{x}^{2}+3x+3+\left(x+1\right)\cos{\left(x+1\right)}\right)dx}
Evaluate:\displaystyle\int_{\tfrac{\pi}{2}}^{\tfrac{3\pi}{2}}{\left[2\sin{x}\right]dx}
Evaluate \displaystyle\int _{ 0 }^{ 1 }{ \frac { \log { \left( 1+x \right) } }{ 1+{ x }^{ 2 } } dx }
Evaluate:\int\limits_0^{\pi /4} {{{\tan }^4}xdx}
Evaluate \displaystyle \int_{0}^{1}{\cot^{-1}(1-x+x^{2})dx}
Evaluate the following integral:
\int { x\tan ^{ 2 }{ x } } dx\quad
Prove that \displaystyle \int_{0}^{x}[x]dx=x[x]-\dfrac{1}{2}[x]([x]+1), where [.] denotes the greatest integer function.
The value of the definite integral \int_{\sqrt{2}-1}^{\sqrt{2}+1} \frac{x^{4}+x^{2}+2}{\left(x^{2}+1\right)^{2}} d x\\ equals
If f(n)=\dfrac{\displaystyle \int_{0}^{n}[x]dx}{\displaystyle \int_{0}^{n}{x}dx} (where,[.] and {.} denotes greatest integer and fractional part of x and n \in N). Then, the value of f(4) is ...
If \displaystyle \int_{0}^{x}[x]dx=\displaystyle \int_{0}^{[x]}xdx,x \notin integer (where,[.] and {.} denotes the greatest integer and fractional parts respectively.then the value of 4{x} is equal to ...
\begin{array}{l}\text { Let } J=\int_{-5}^{-4}\left(3-x^{2}\right) \tan \left(3-x^{2}\right) d x \text { and } K=\int_{-2}^{-1}\left(6-6 x+x^{2}\right) \\\tan \left(6 x-x^{2}-6\right) d x, \text { then }(J+K) \text { equals }\end{array}
Let f:RR be a function defined by f(x) = \left\{\begin{array}{ll} [x], \space x \leq 2 \\ 0, \space x > 0 \end{array} \right. where [x] denotes the greatest integer less than or equal to x. If I=\displaystyle \int_{-1}^{2} \dfrac{xf(x^2)}{2+f(x+1)}dx, then the value of (4I-1) is
\text { Evaluate: } \int_{0}^{\pi / 2} 2 \sin x \cos x \tan ^{-1}(\sin x) d x
Class 12 Commerce Applied Mathematics Extra Questions
- Application Of Derivatives Extra Questions
- Applications Of Integrals Extra Questions
- Definite Integrals Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Indefinite Integrals Extra Questions
- Linear Equations Extra Questions
- Matrices Extra Questions
- Probability Distribution And Its Mean And Variance Extra Questions
- Quantification And Numerical Applications Extra Questions
- Standard Probability Distributions Extra Questions