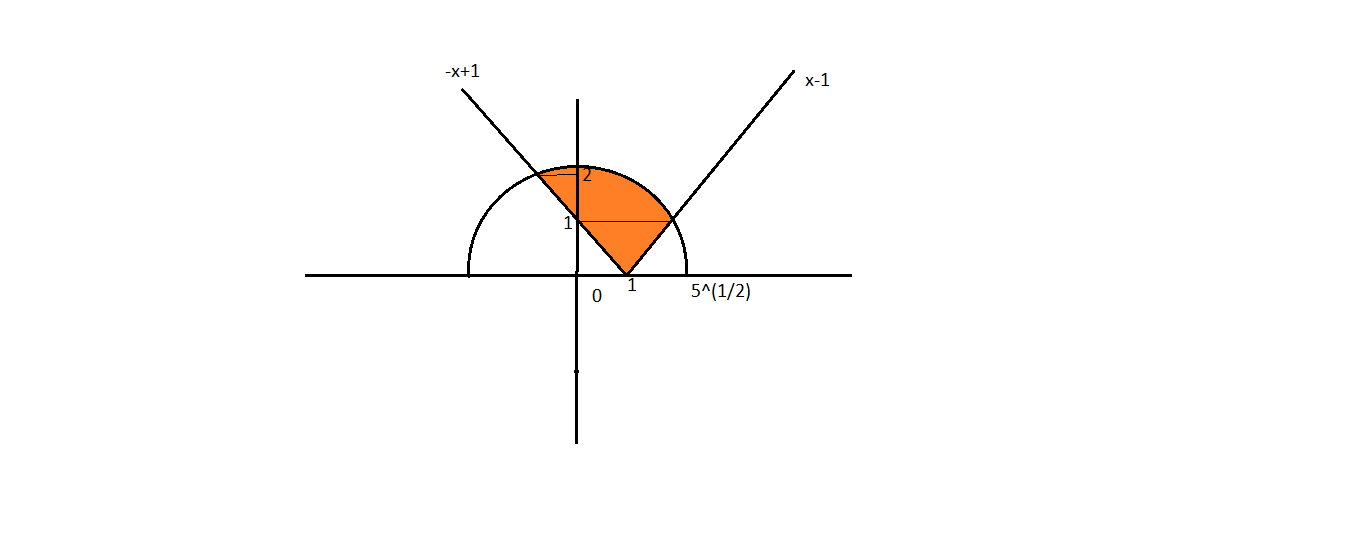Applications Of Integrals - Class 12 Commerce Applied Mathematics - Extra Questions
If $$ y = mx $$ bisects the area enclosed by the lines $$ x = 0,\: y = 0,\:x = \dfrac{3}{2} $$ and the curve $$ y =1 + 4x -x^{2} $$ then $$ 6m $$ is equal to
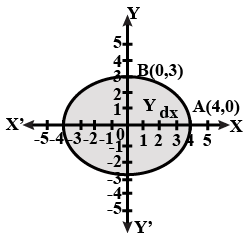
Find the area of the region bounded by the ellipse $$\displaystyle \frac {x^2}{4}+\frac {y^2}{9}=1$$.
Find the area of the region bounded by the ellipse $$\displaystyle \frac {x^2}{16}+\frac {y^2}{9}=1$$.
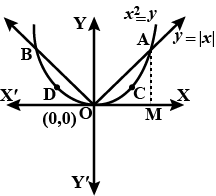
Find the area of the region bounded by the parabola $$y = x^2$$ and $$y = |x|$$.
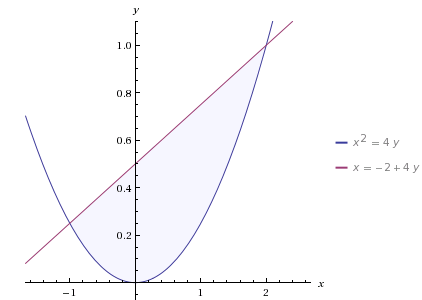
Find the area bounded by the curve $$x^2 = 4y$$ and the line $$x = 4y - 2$$.
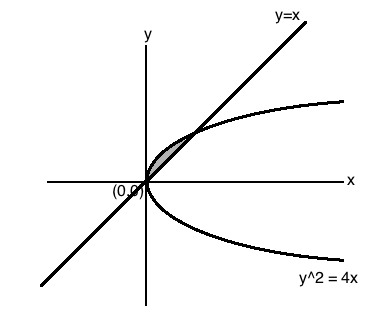
Find the area enclosed between the parabola $$y^2 = 4ax$$ and the line $$y = mx$$.
Find the area of the region bounded by the curves $$y = x^2 + 2, y = x, x = 0$$ and $$x = 3$$.
Find the area of the smaller region bounded by the ellipse $$\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1$$ and the line $$\dfrac {x}{a}+\dfrac {y}{b}=1$$
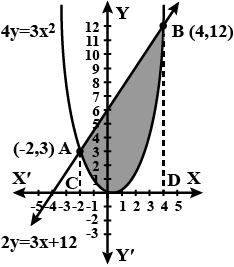
Find the area enclosed by the parabola $$4y = 3x^2$$ and the line $$2y = 3x + 12$$
Find the area of the region enclosed by the parabola $$x^{2} = y$$ and the line $$y = x + 2$$.
Find the area bounded by curves $$\left \{(x, y): y\geq x^2 \ and \ y=|x|\right \}$$
Find the area of the smaller region bounded by the ellipse $$\dfrac {x^2}{9}+\dfrac {y^2}{4}=1$$ and the line $$\dfrac {x}{3}+\dfrac {y}{2}=1$$
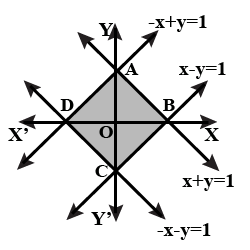
Using the method of integration find the area bounded by the curve $$|x|+|y|=1$$
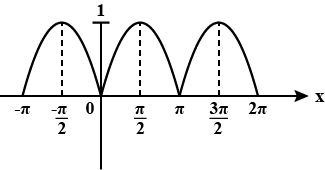
Draw the curve $$y=\sin^4x$$ between $$x=0$$ and $$x=2\pi$$.
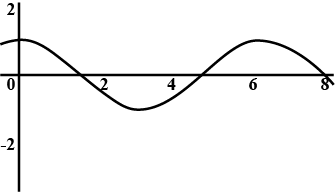
Draw the curve of $$y=\cos x$$ between $$x=0$$ and $$x=2\pi$$ .
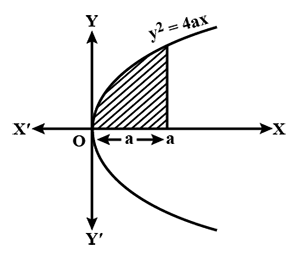
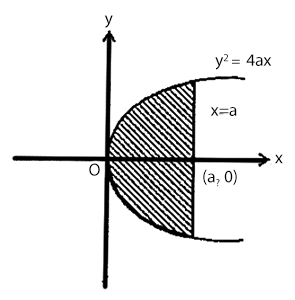
Find the area bounded by the curve $$y^{2} = 4ax$$, $$X$$-axis and the lines $$x = 0$$ and $$x = a$$.
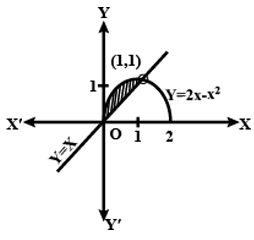
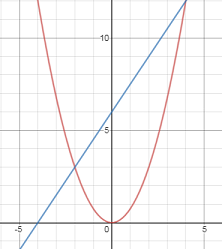
Find the area bounded by the curve $$y = 2x - x^2$$, and the line $$y = x.$$
Find the area of the region bounded by the curve $$y = x^{2}$$ and the line $$y = 4$$.
Find the area of the region bounded by the parabola $$y^{2} = 16x$$ and the line $$x = 3$$.
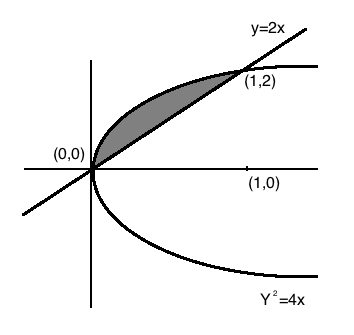
Find the area bounded by the parabola $$y^2 = 4x$$ and the straight line y = x. (Draw the figure in answer book)
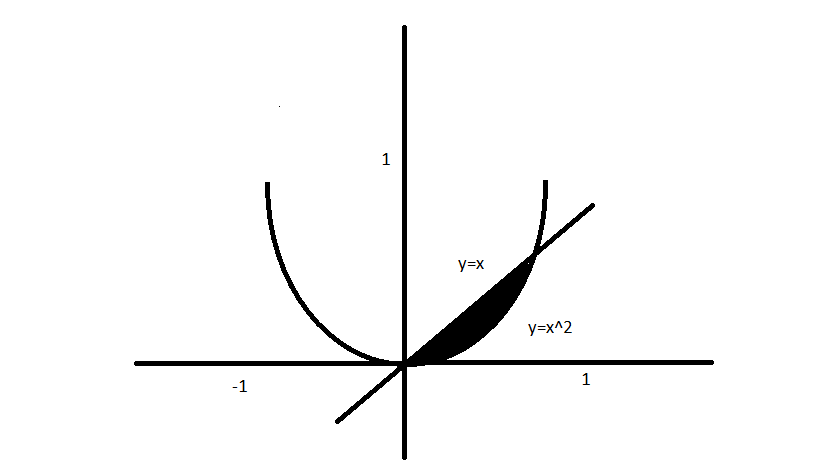
Find the area enclosed between the curves $$y=x$$ and $$y=x^2$$ from $$x=0$$ and $$x=1$$
Find the area lying between the curve $$y^2=4x$$ and the line $$y=2x$$.
Find the area of the region bounded by the curve $$y=x^2$$ and the line $$y=4$$.
Find the area of the region bounded by the curve $$y^2=4x$$ and the line $$x=3$$.
Find the area enclosed between the parabola $$4y = 3x^2$$ and the straight line $$3x - 2y + 12 = 0$$
Find the area between curve $${ x }^{ 2 }=4y$$ and the line $$x=4y-2$$.
The area above x-axis, bounded by the line $$x=4$$ and the curve $$y=f(x)$$, where $$f\left( x \right)={ x }^{ 2 },0\le x\le 1$$ and $$f\left( x \right)=\sqrt { x } ,x\ge 1$$, is
Find the area of the region $$\left \{(x, y): x^{2} + y^{2} \leq 4, x + y\geq 2\right \}.$$
Sketch the region bounded by the curves $$y=\sqrt{ 5 -x^2}$$ and $$y=| x-1|$$ and find its area using intergration.
Using integration, find the area bounded by the curve $$x^2=4y$$ and the line $$x=4y-2$$.
Find the area of the region bounded by the parabola $$y^2 = 4x$$ and the line $$2x - y = 4$$.
The area of smaller part bounded by circle $${ x }^{ 2 }+{ y }^{ 2 }={ a }^{ 2 }$$ and the line $$x=\cfrac { a }{ \sqrt { 2 } } $$ is $$\dfrac{a^2}{2}(\dfrac{\pi}{P}-1)$$. Find the value of $$P$$.
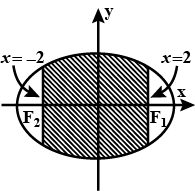
Find the area of the region bounded by the ellipse $$\dfrac {x^2}{9} + \dfrac {y^2}{5} = 1$$ between the two latus rectum.
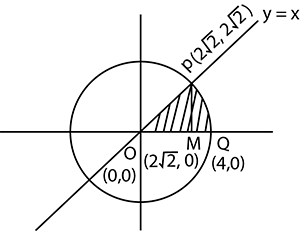
Find the area of the sector of a circle bounded by the circle $${x}^{2}+{y}^{2}=16$$ and the line $$y=x$$ in the first quadrant.
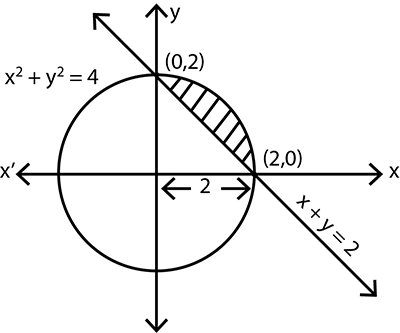
Find the smaller area enclosed by the circle $$x^2+y^2=4$$ and the line $$x+y = 2$$.
Find the area of the region bounded by the ellipse $$\dfrac{x^2}{9} + \dfrac{y^2}{5} = 1$$ between the two latus rectums.
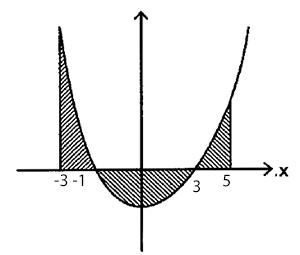
Find the area between the curves $$y={ x }^{ 2 }-2x-3$$, $$x$$-axis and the lines $$x=-3$$ and $$x=5$$.
Class 12 Commerce Applied Mathematics Extra Questions
- Application Of Derivatives Extra Questions
- Applications Of Integrals Extra Questions
- Definite Integrals Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Indefinite Integrals Extra Questions
- Linear Equations Extra Questions
- Matrices Extra Questions
- Probability Distribution And Its Mean And Variance Extra Questions
- Quantification And Numerical Applications Extra Questions
- Standard Probability Distributions Extra Questions