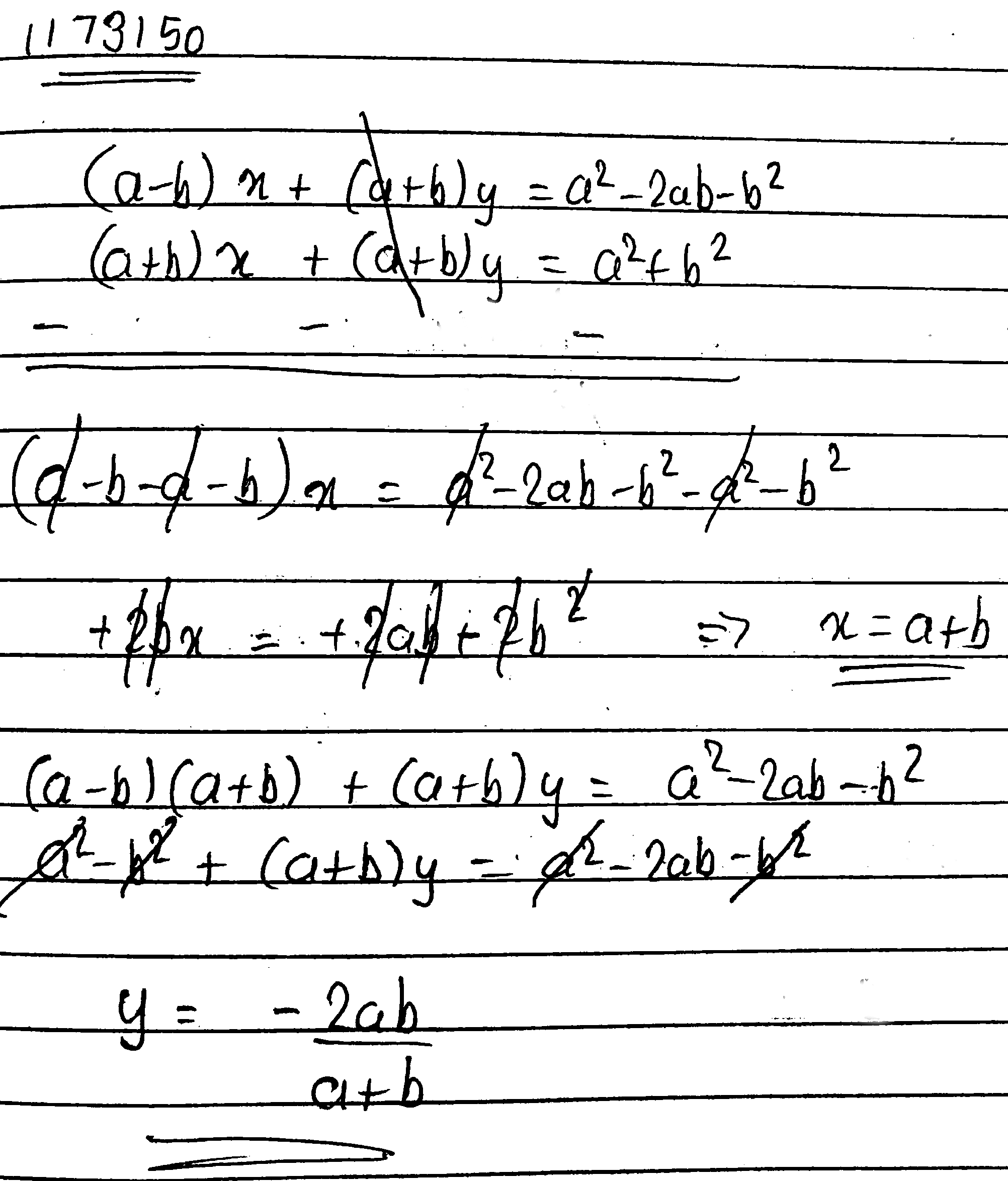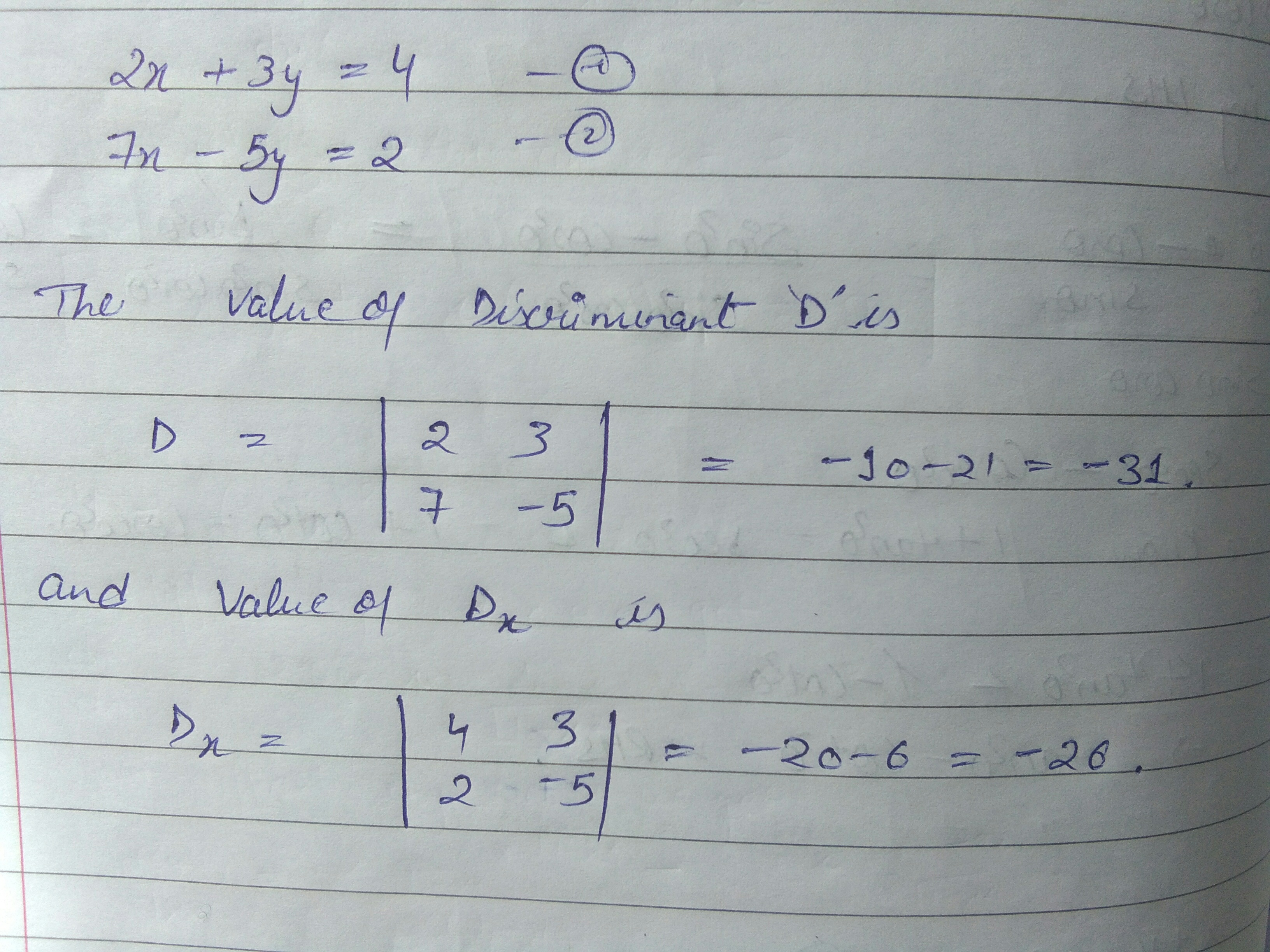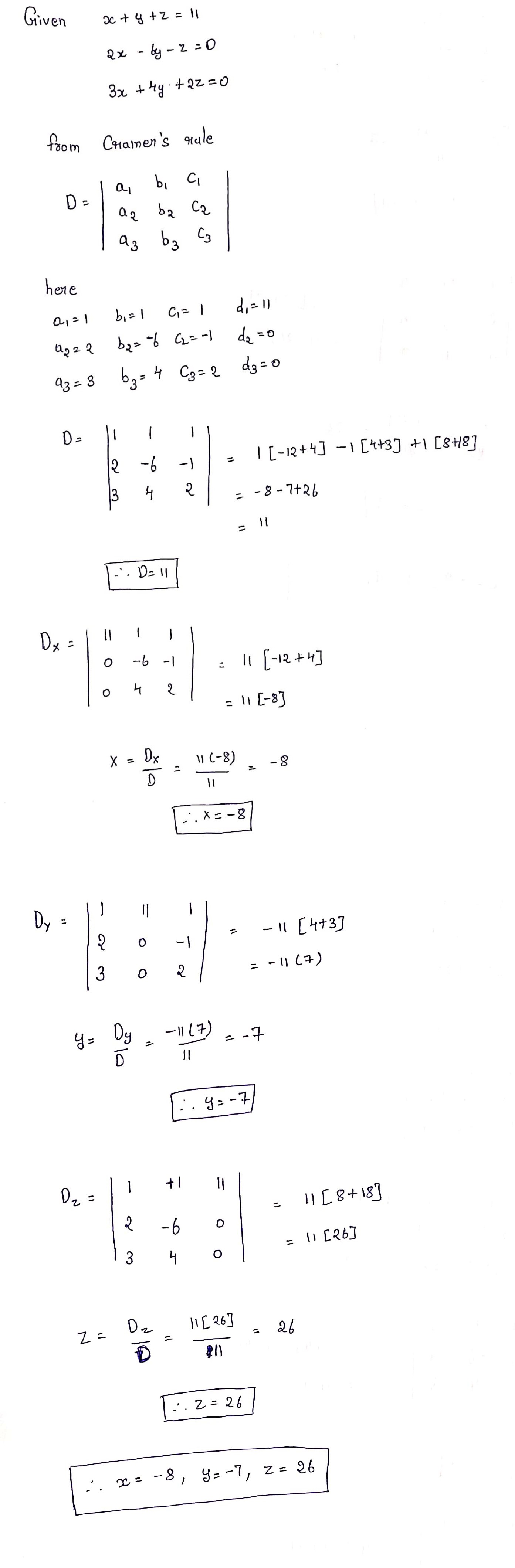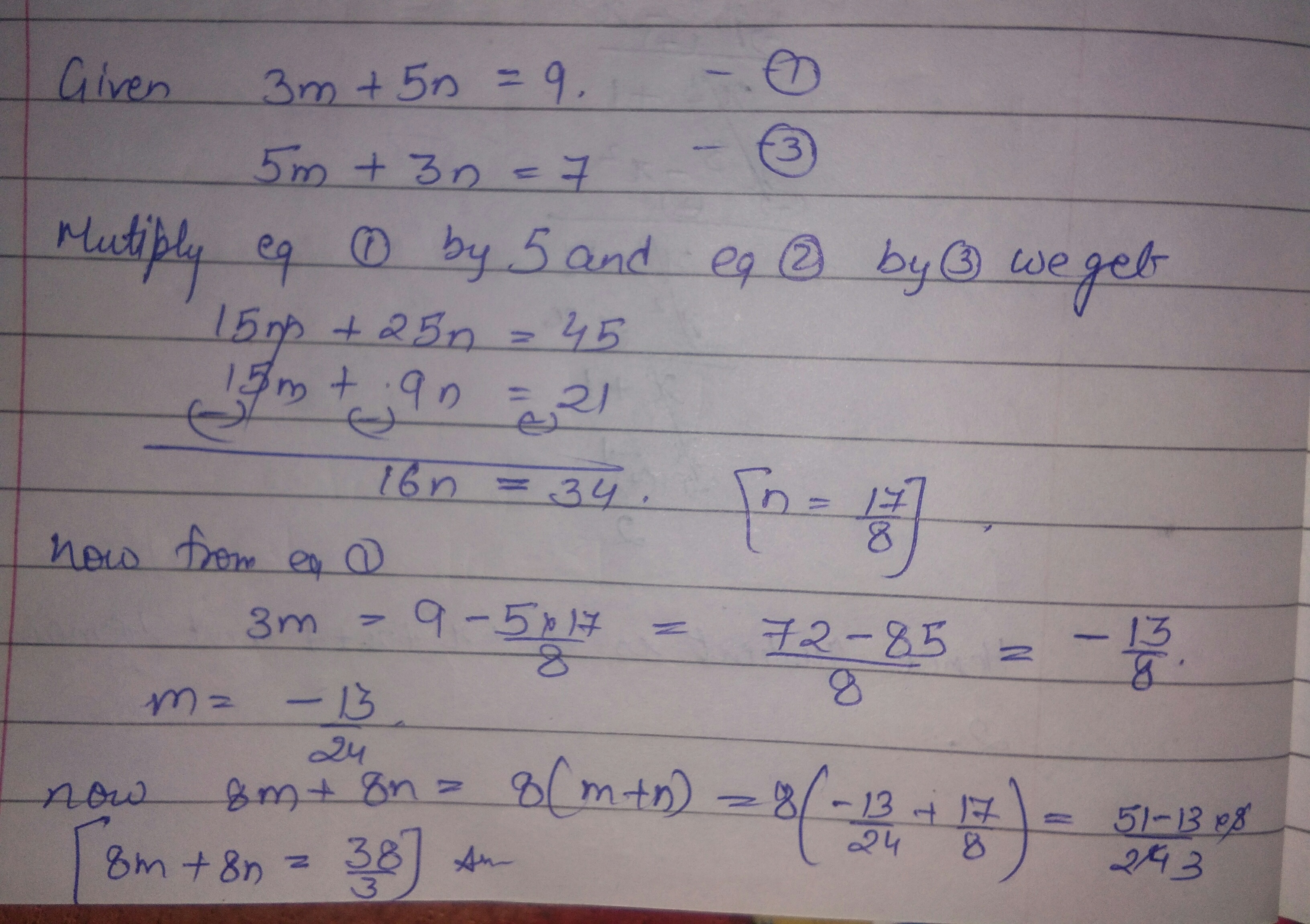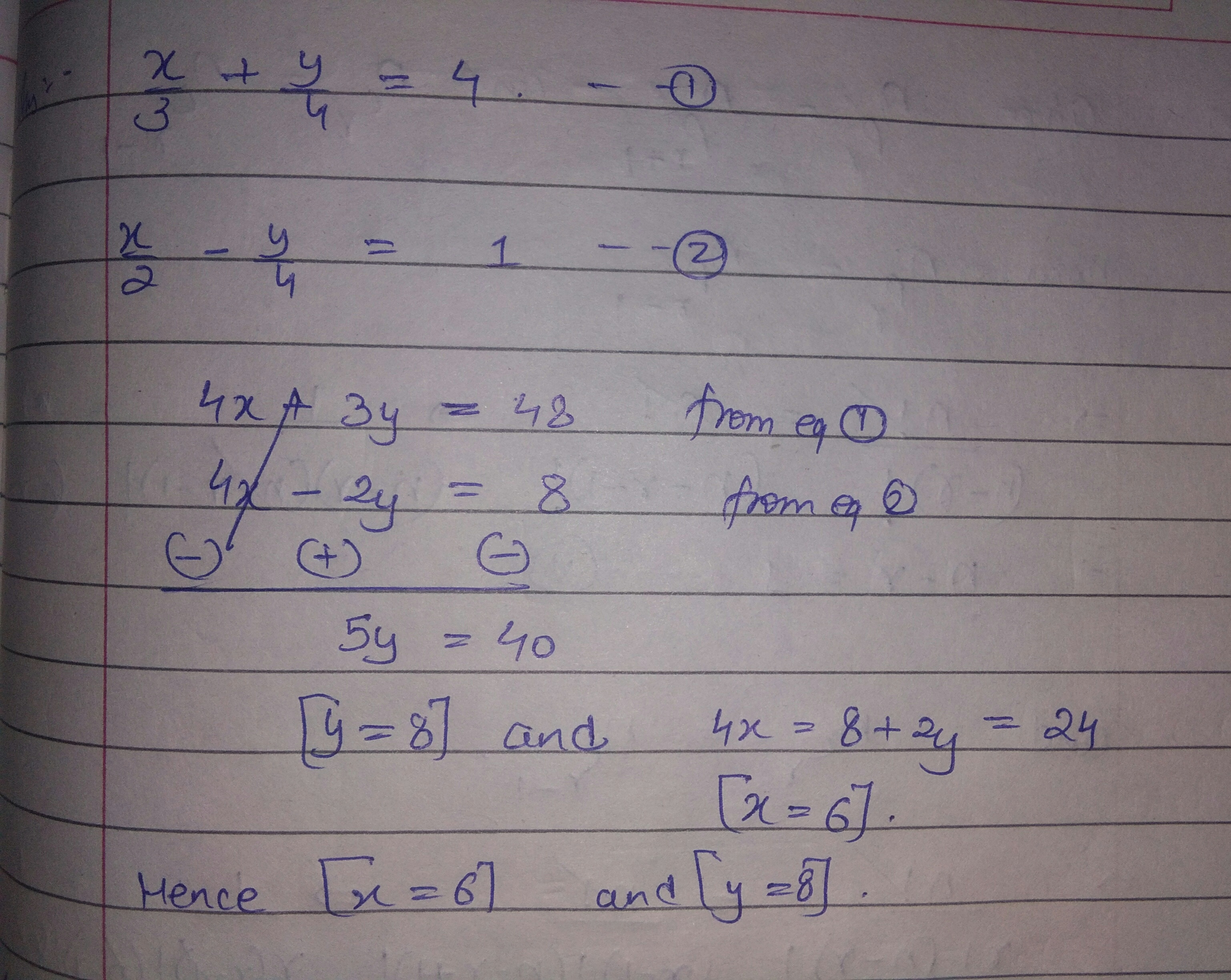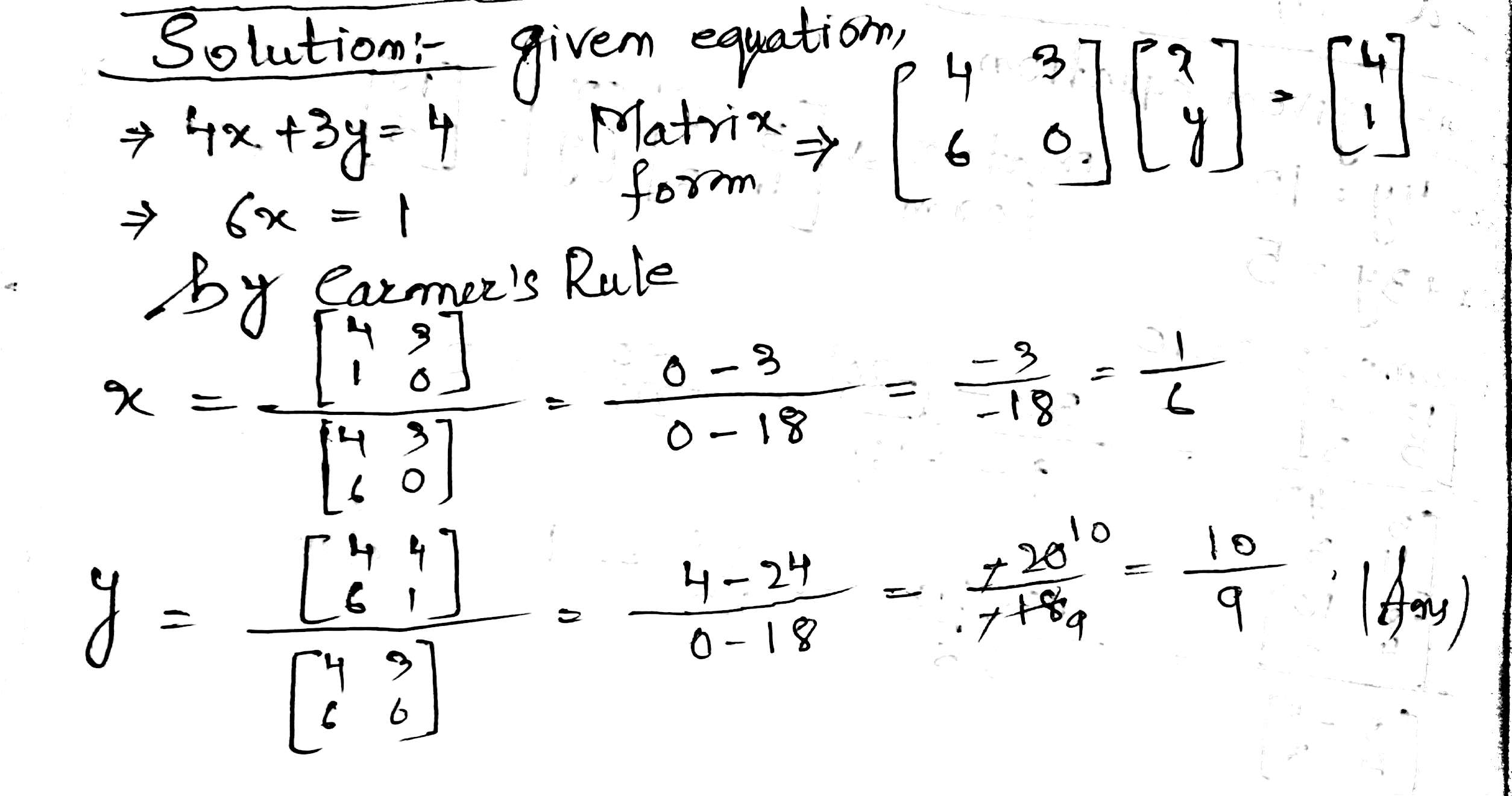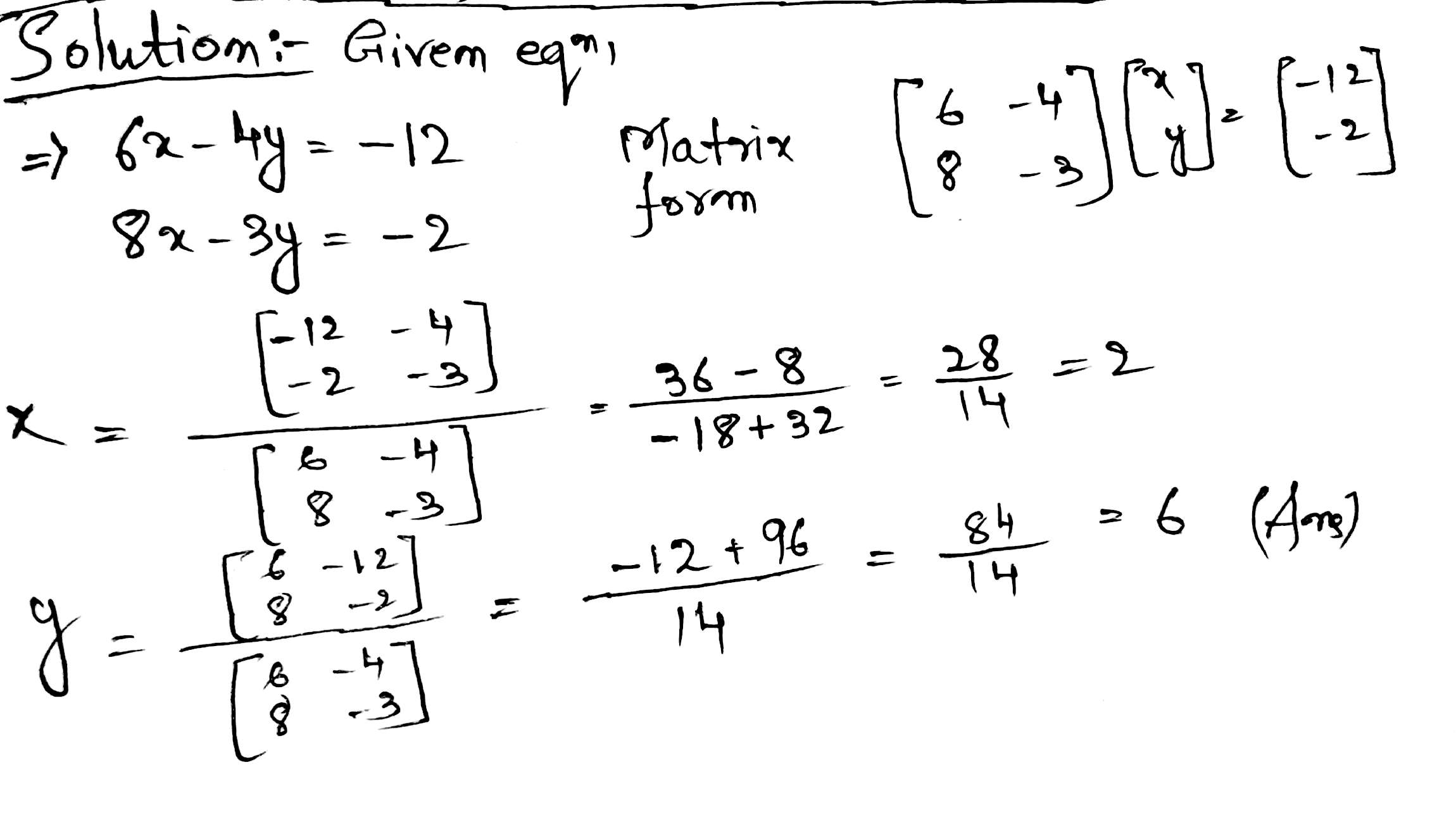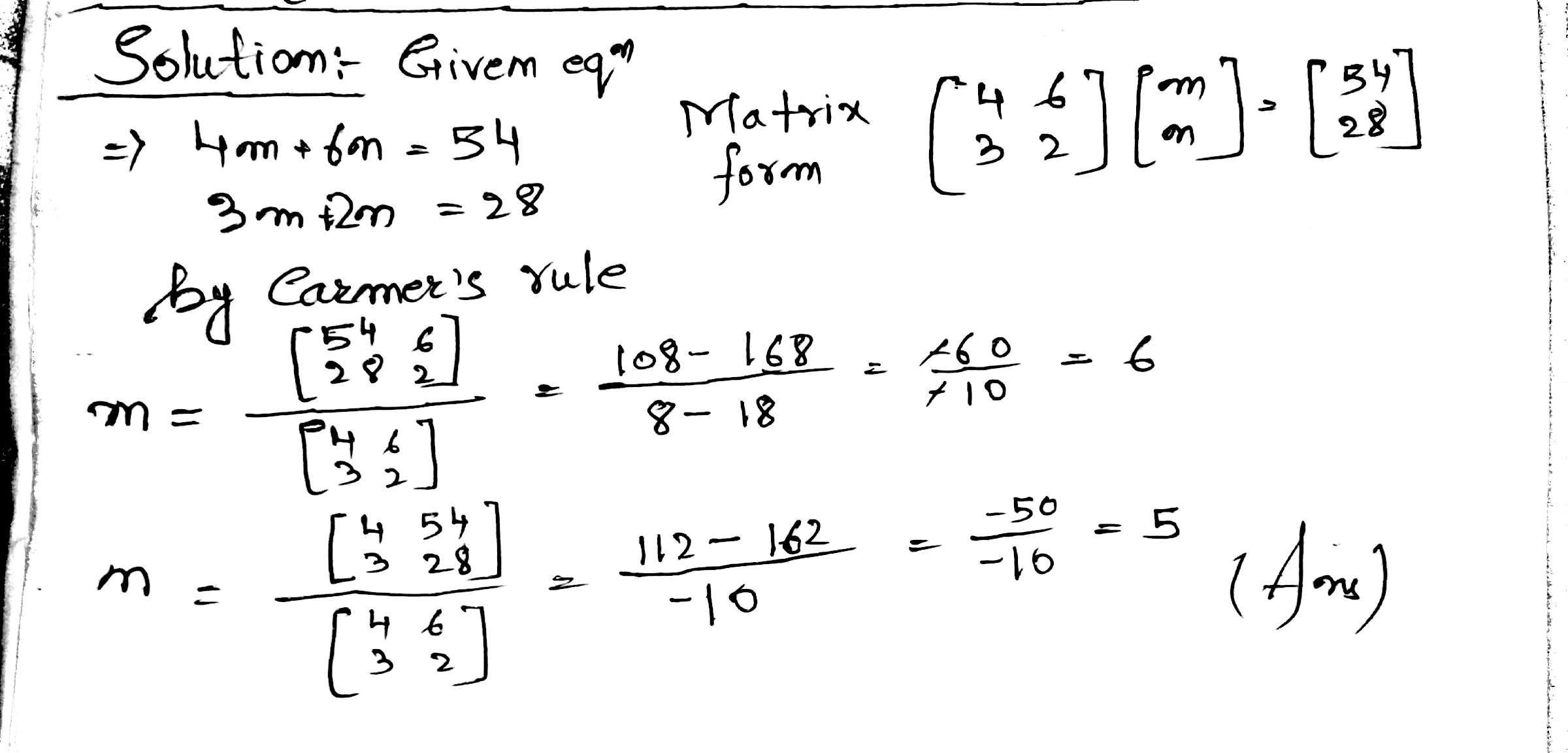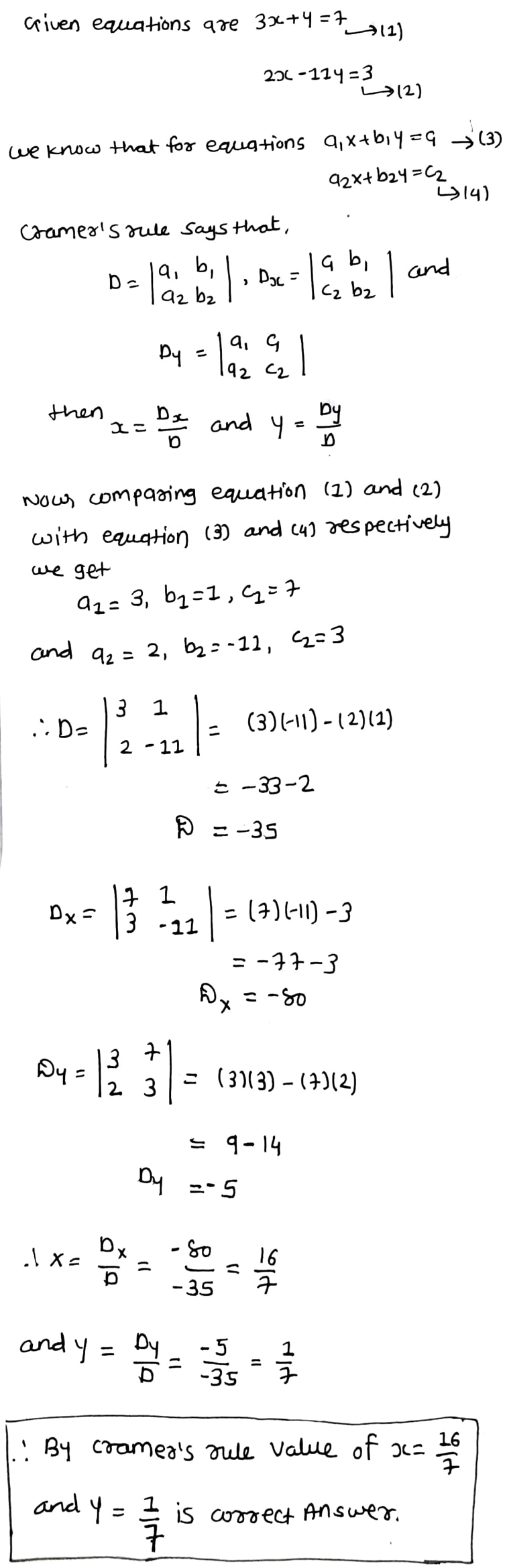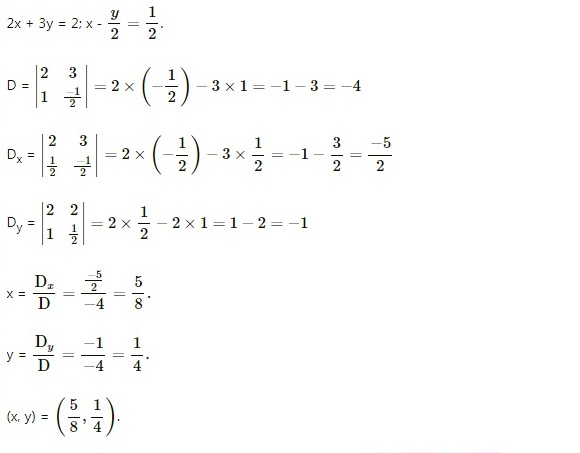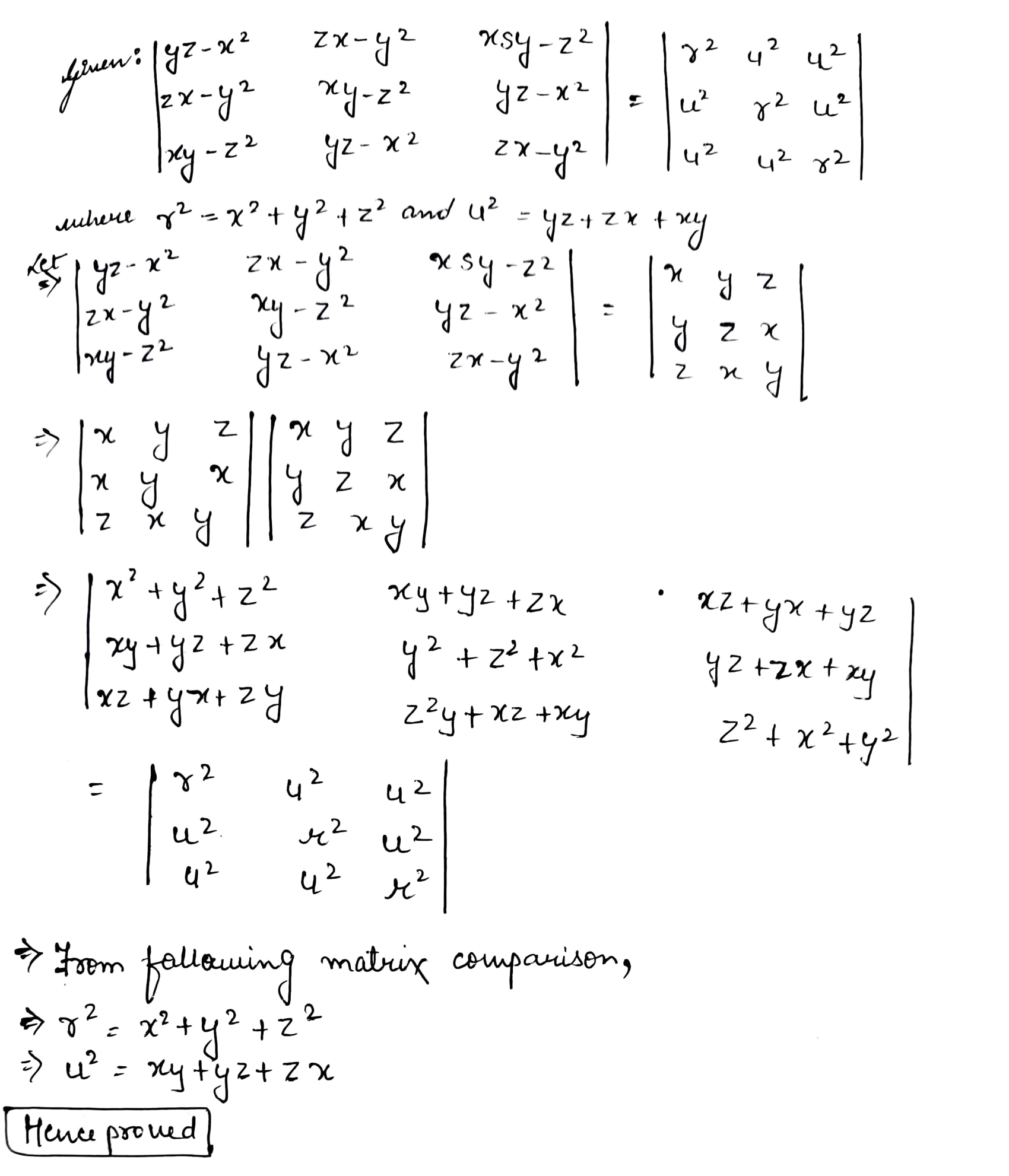Determinants - Class 12 Commerce Applied Mathematics - Extra Questions

If $$D_x\, =\, -18$$ and $$ D =\, 3$$ are the values of the determinants for certain simultaneous equations in $$x$$ and $$y$$, Find $$-x$$.

Given: $$D_x = -18$$ and $$D = 3$$
Thus we know $$x = \dfrac{D_x}{D}$$
$$\Rightarrow x =$$ $$\dfrac{-18}{3}$$ $$= -6$$
Therefore, $$-x$$ will be equal to $$6$$.


If the value of determinants $$\begin{vmatrix} x& -5\\ 3 & 4\end{vmatrix}$$ is $$31$$, then find the value of $$x$$

We have, $$\begin{vmatrix} x& -5\\ 3 & 4\end{vmatrix} = 31$$
On solving, $$4x - (-5) (3) = 31$$
$$\Rightarrow 4x + 15 = 31$$
$$\Rightarrow 4x = 31 - 15$$
$$\Rightarrow x = \dfrac {16}{4} = 4$$
$$\therefore x = 4$$


Find the value of the determinant: $$\begin{vmatrix} 4& -2\\ 3 & 1\end{vmatrix}$$

Given, $$\begin{vmatrix} 4& -2\\ 3 & 1\end{vmatrix}$$
$$= (4) (1) - (-2)(3)$$
$$= 4 + 6 = 10$$


If $$D=7,{D}_{x}=35$$ and $${D}_{y}=42$$ are the values of the determinants for certain simultaneous equations in $$x$$ and $$y$$, then find the values of $$x$$ and $$y$$.

Given, $$D=7,{D}_{x}=35$$ and $${D}_{y}=42$$
Now $$x=\cfrac { { D }_{ x } }{ D } =\cfrac { 35 }{ 7 } =5 $$
and $$y=\cfrac { { D }_{ y } }{ D } =\cfrac { 42 }{ 7 } =6$$
$$\therefore$$ The value of $$x$$ and $$y$$ is $$5$$ and $$6$$ respectively.


Find the value of the following determinant
$$\begin{vmatrix}7 & 2\\ 5 &4 \end{vmatrix}$$

$$\begin{vmatrix} 7& 2\\ 5 &4 \end{vmatrix} = (7 \times 4) - (2 \times 5)$$
$$= 28 - 10 = 18$$


solve the following simultaneous equations by using Cramer's rule:
$$x+y=7,x-y=5$$

The given equations are
$$x+y=7$$
$$x-y=5$$
$$D=\begin{vmatrix} 1 & 1 \\ 1 & -1 \end{vmatrix}=(1\times -1)-(1\times 1)=-1-1=-2$$
$${D}_{x}=\begin{vmatrix} 7 & 1 \\ 5 & -1 \end{vmatrix}=(7\times -1)-(1\times 5)=-7-5=-12$$
$${D}_{y}=\begin{vmatrix} 1 & 7 \\ 1 & 5 \end{vmatrix}=(1\times 5)-(7\times 1)=5-7=-2$$
$$\therefore$$ By cramer's rule we get
$$\therefore$$ $$x=\cfrac { { D }_{ x } }{ D } =\cfrac { -12 }{ 2 } =6$$ and $$y=\cfrac { { D }_{ y } }{ D } =\cfrac { -2 }{ 2 } =1$$


If $${ D }_{ x }=18,{ D }_{ y }=15$$ and $$D=3$$ are the values of the determinants for certain simultaneous equations in $$x$$ and $$y$$, then find the values of $$x$$ and $$y$$.

Given $${ D }_{ x }=18,{ D }_{ y }=15$$ and $$D=3$$
Now, $$x=\cfrac { { D }_{ x } }{ D } =\cfrac { 18 }{ 3 } =6$$
$$y=\cfrac { { D }_{ y } }{ D } =\cfrac { 15 }{ 3 } =5$$
$$\therefore$$ The value of $$x$$ and $$y$$ is $$6$$ and $$5$$ respectively.


Find the value of the following determinant $$\begin{vmatrix} 4 & 3\\2 & 7\end{vmatrix}$$.

$$\begin{vmatrix}4&3\\2&7\end{vmatrix}=4\times7-2\times3=28-6=22$$


Find the value of following determinant
$$\begin{vmatrix} 5& 2\\ 7 & 4 \end{vmatrix}$$

$$\begin{vmatrix}5&2\\7&4\end{vmatrix}=5\times4-7\times2=20-14=6$$


If $${D}_{x}=30,{D}_{y}=42$$ and $$D=6$$ are the values of the determinants for certain simultaneous equations in $$x$$ and $$y$$, then find the values of $$x$$ and $$y$$.

Given $${ D }_{ x }=30,{ D }_{ y }=42$$ and $$D=6$$
now $$x=\cfrac { { D }_{ x } }{ D } =\cfrac { 30 }{ 6 } =5\quad y=\cfrac { { D }_{ y } }{ D } =\cfrac { 42 }{ 6 } =7$$
$$\therefore$$ The value of $$x$$ and $$y$$ is $$5$$ and $$7$$ respectively.


Solve the following simultaneous equations by using Cramer's rule:
$$x - 2y = -18$$
$$2x - y = 9$$

Equations are
$$x - 2y = -18 ...(i)$$
$$2x - y = 9 ...(ii)$$
$$D = \begin{vmatrix}1 &-2 \\ 2 & -1\end{vmatrix}$$
$$= (18 + 18) = 36$$
$$D_{y} = \begin{vmatrix} 1& -18\\ 2 & 9\end{vmatrix}$$
$$= 9 + 36 = 45$$
By Cramer's rule, we get
$$\therefore x = \dfrac {D_{x}}{D}$$
$$= \dfrac {36}{3} = 12$$
and
$$y = \dfrac {D_{y}}{D}$$
$$= \dfrac {45}{3} = 15$$
$$\therefore x = 12$$ and $$y = 15$$ is the solution of the given simultaneous equations.


Find $$D_{x}$$ for the following simultaneous equations: $$3x + 4y = 8, x - 2y = 5$$

In cramer's rule of $${ a }_{ 1 }x+{ b }_{ 1 }y={ c }_{ 1 },{ a }_{ 2 }x+{ b }_{ 2 }y={ c }_{ 2 }$$
$$x=\dfrac { { D }_{ x } }{ D } =\dfrac { \begin{vmatrix} { c }_{ 1 } & { b }_{ 1 } \\ { c }_{ 2 } & { b }_{ 2 } \end{vmatrix} }{ \begin{vmatrix} { a }_{ 1 } & { b }_{ 1 } \\ { a }_{ 2 } & { b }_{ 2 } \end{vmatrix} } $$
$$y=\dfrac { { D }_{ y } }{ D } =\dfrac { \begin{vmatrix} { a }_{ 1 } & { c }_{ 1 } \\ { a }_{ 2 } & { c }_{ 2 } \end{vmatrix} }{ \begin{vmatrix} { a }_{ 1 } & { b }_{ 1 } \\ { a }_{ 2 } & { b }_{ 2 } \end{vmatrix} } $$
$${ D }_{ x }=\begin{vmatrix} { c }_{ 1 } & { b }_{ 1 } \\ c_{ 2 } & { b }_{ 2 } \end{vmatrix}$$
So here $${ D }_{ x }=\begin{vmatrix} 8 & 4 \\ 5 & -2 \end{vmatrix}=-36$$


If $${ D }_{ x }=24,{ D }_{ y }=32$$ are the values of the determinants for certain simultaneous equations in $$x$$ and $$y$$, then find the values of $$x$$ and $$y$$

Given $${ D }_{ x }=24,{ D }_{ y }=32$$ and $$D=8$$
Now $$x=\cfrac { { D }_{ x } }{ D } =\cfrac { 24 }{ 8 } =3$$
$$ y=\cfrac { { D }_{ y } }{ D } =\cfrac { 32 }{ 8 } =4$$
$$\therefore$$ The value of $$x$$ and $$y$$ is $$3$$ and $$4$$ respectively.


Solve the following equations by Cramer's rule:
$$3x+y+z=2,2x-4y+3z=-1,4x+y-3z=-11\quad $$

To solve the system by Cramer's rule, we do the following steps:
1. Write the system as a matrix equation $$AX=b$$ where:
$$A = \begin{bmatrix}3 & 1 & 1\\ 2 & -4 & 3\\ 4 & 1 & -3 \end{bmatrix}$$
$$X = \begin{bmatrix}x\\y\\z \end{bmatrix}$$
$$b = \begin{bmatrix}2\\-1\\-11 \end{bmatrix}$$
2. Next, we find the following determinants:
$$\Delta = \begin{vmatrix}3 & 1 & 1\\ 2 & -4 & 3\\ 4 & 1 & -3 \end{vmatrix} = |A| = 63$$
$$\Delta_1 = \begin{vmatrix}2 & 1 & 1\\ -1 & -4 & 3\\ -11 & 1 & -3 \end{vmatrix} = -63$$
$$\Delta_2 = \begin{vmatrix}3 & 2 & 1\\ 2 & -1 & 3\\ 4 & -11 & -3 \end{vmatrix} = 126$$
$$\Delta_3 = \begin{vmatrix}3 & 1 & 2\\ 2 & -4 & -1\\ 4 & 1 & -11 \end{vmatrix} = 189$$
3. The solution is now given by:
$$x = \dfrac{\Delta_1}{\Delta} = -1$$
$$y = \dfrac{\Delta_2}{\Delta} = 2$$
$$z = \dfrac{\Delta_3}{\Delta} = 3$$


Find the ratios of $$x : y : z$$ from the equations
$$7x = 4y + 8z,  3z = 12x + 11y$$.

By transposition we have $$7x - 4y - 8z = 0, 12x + 11y - 3z = 0$$.
Write down the coefficients, thus
$$x=\begin{vmatrix} -4 & -8 \\ 11 & -3\end{vmatrix}$$
$$y=\begin{vmatrix} -8 & 7 \\ -3 & 12\end{vmatrix}$$
$$z=\begin{vmatrix} 7 & -4 \\ 12 & 11\end{vmatrix}$$
whence we obtain the products
$$ (-4) \times (-3) - 11 \times (-8) , (-8) \times 12 - (-3) \times 7, 7 \times 11 \times -12 \times (-4) , $$
or $$100, -75, 125$$;
$$ \therefore \dfrac {x}{100} = \dfrac {y}{-75} = \dfrac {z}{125} , $$
that is , $$ \dfrac {x}{4} = \dfrac {y}{-3} = \dfrac {z}{5} . $$


If $$A=\left[ \begin{matrix} 1 & -1 & 2 \\ 3 & 0 & -2 \\ 1 & 0 & 3 \end{matrix} \right] $$ verify that $$A(adj\ A)=\left| A \right| I$$.

$$\left| A \right| =+1(9+2)=11$$
$$adj(A)$$=Transfer co factor matrix
$${ c }_{ 11 }=\begin{vmatrix} 0 & -2 \\ 0 & 3 \end{vmatrix}=0, { c }_{ 23 }=\begin{vmatrix} 1 & -1 \\ 1 & 0 \end{vmatrix}=-1\\ { c }_{ 12 }=\begin{vmatrix} 3 & -2 \\ 1 & 3 \end{vmatrix}=11,\ { c }_{ 31 }=\begin{vmatrix} -1 & 2 \\ 0 & -2 \end{vmatrix}=2\\ { c }_{ 13 }=\begin{vmatrix} 3 & 0 \\ 1 & 0 \end{vmatrix}=0, { c }_{ 32 }=-\begin{vmatrix} 1 & 2 \\ 3 & -2 \end{vmatrix}=8\\ { c }_{ 21 }=\begin{vmatrix} -1 & 2 \\ 0 & 3 \end{vmatrix}=3, { c }_{ 33 }=\begin{vmatrix} 1 & -1 \\ 3 & 0 \end{vmatrix}=3\\ { c }_{ 22 }=\begin{vmatrix} 1 & 2 \\ 1 & 2 \end{vmatrix}=1$$
Co factor matrix $$\begin{vmatrix} 0 & -11 & 0 \\ 3 & 1 & -1 \\ 2 & 8 & 3 \end{vmatrix}$$
$$adj(A)$$=$$\begin{vmatrix} 0 & 3 & 2 \\ -11 & 1 & 8 \\ 0 & -1 & 3 \end{vmatrix}$$
$$A(adj(A))$$=$$\begin{vmatrix} 1 & -1 & 2 \\ 3 & 0 & -2 \\ 1 & 0 & 3 \end{vmatrix}\begin{vmatrix} 0 & 3 & 2 \\ -11 & 1 & 8 \\ 0 & -1 & 3 \end{vmatrix}$$
$$\begin{vmatrix} 11 & 0 & 0 \\ 0 & 11 & 0 \\ 0 & 0 & 11 \end{vmatrix}=\left| 11 \right| I=AI$$


If
$$x + y + z = 1$$
$$3x + 5y + 6z = 4$$
$$9x + 2y - 36z = 17$$
Then find $$y$$


1926340_1003861_ans_3da0afd5480c4cc598a132c9681aa544.jpg


Solve the equation $$\dfrac{x}{a}\, + \,\dfrac{y}{b}\, = \,2\,,\,ax\, - \,by\, = \,{a^2} - \,{b^2}$$

Consider the given equation.
$$ax-by=a^2-b^2$$ 
                 
Multiplying by $$a$$ in both sides,
$$a^2x-yab=a^3-ab^2$$                    ......(1)

Since,
$$\dfrac{x}{a}+\dfrac{y}{b}=2$$
$$xb+ya=2ab$$
                  
Multiplying by $$b$$ in both sides,
$$xb^2+yab=2ab^2$$                         ......(2)

On adding equation(1) and (2),
$$x(a^2+b^2)=a^3+ab^2$$
$$x(a^2+b^2)=a(a^2+b^2)$$
$$x=a$$

Substituting this value in equation (1),
$$a\times a^2-yab=a^3-ab^2$$
$$-yab=ab^2$$
 $$y=b.$$

So, for given equation $$x=a, y=b.$$


Solve the system of linear equation $$ 3x-2y=13$$ and $$ 4x+y=21$$ 

$$a_1 =3 ,a_2 = 4,b_1 = -2,b_2 = 1,c_1 =13,c_2 =21$$

$$x = \cfrac{c_1 b_2 - c_2 b_1}{a_1 b_2 - a_2 b_1} = \cfrac{13*1 +21*2}{3*1 +8}=\cfrac{55}{11} = 5$$

$$y = \cfrac{c_2 a_1 - c_1 a_2}{a_1 b_2 - a_2 b_1} = \cfrac{21*3 -13*4}{3*1 +8}=\cfrac{11}{11} = 1$$


Solve the following simu1taneous equations. 
(1) $$5x-3y=8;$$ $$3x+y=2$$

Consider the equation $$3x+y=2$$
Multiply the quation by 3 so that we can eliminate y
$$3(3x+y=2)=3\times 2$$
$$9x+3y=6$$
Adding it with $$5x-3y=8$$
$$9x+3y+5x-3y=6+8$$
$$14x=14$$
$$x=1$$

Putting the value of x in equation $$3x+y=2$$
$$3\times 1+y=2$$
$$3+y=2$$
$$y=2-3$$
$$y=-1$$

So, we have $$ x=1\, and\, y=-1$$



Solve: (i)$$4x+5y-62=0$$
           (ii)$$3x+2y-36=0$$

$$4x+5y-62=0\\ \Rightarrow 4x+5y=62\longrightarrow (1)\\ 3x+2y-36=0\\ \Rightarrow 3x+2y=36\longrightarrow (2)\\ \because { a }_{ 1 }=4;\quad b_{ 1 }=5;\quad { c }_{ 1 }=62\\ { a }_{ 2 }=3;\quad { b }_{ 2 }=2;\quad { c }_{ 2 }=36\\ \therefore \quad x=\dfrac { \begin{vmatrix} { c }_{ 1 } & b_{ 1 } \\ { c }_{ 2 } & { b }_{ 2 } \end{vmatrix} }{ \begin{vmatrix} { a }_{ 1 } & b_{ 1 } \\ { a }_{ 2 } & { b }_{ 2 } \end{vmatrix} } =\dfrac { \begin{vmatrix} 62 & 5 \\ 36 & 2 \end{vmatrix} }{ \begin{vmatrix} 4 & 5 \\ 3 & 2 \end{vmatrix} } =8\\ y=\dfrac { \begin{vmatrix} { a }_{ 1 } & \quad { c }_{ 1 } \\ { a }_{ 2 } & { c }_{ 2 } \end{vmatrix} }{ \begin{vmatrix} { a }_{ 1 } & b_{ 1 } \\ { a }_{ 2 } & { b }_{ 2 } \end{vmatrix} } =\dfrac { \begin{vmatrix} 4 & 62 \\ 3 & 36 \end{vmatrix} }{ \begin{vmatrix} 4 & 5 \\ 3 & 2 \end{vmatrix} } =6$$


Solve.
$$3x-2y=1$$ and $$2x+y=3$$.

Given,
$$3x-2y=1$$  ..........(1)

$$2x+y=3$$  

$$y=3-2x$$  

Put in (1), we get

$$3x-2(3-2x)=1$$  

$$3x-6+4x=1$$  

$$7x=7$$  

$$x=1$$  

Put in (1)
$$3(1)-2y=1$$  

$$1-2y=1$$  

$$2y=2$$  

$$y=1$$


Solve the given pair of linear equations:
$$(a-b)x+(a+b)y={a}^{2}-2ab-{b}^{2}$$
$$(a+b)(x+y)={a}^{2}+{b}^{2}$$

$$(a-b)x+(a+b)y=a^2-2ab-b^2$$
$$(a+b)x+(a+b)y=a^2+b^2$$
$$- $$           $$  -  $$               $$ -$$
____________________________
$$(a-b-a-b)x=a^2-2ab-b^2a^2-b^2$$
$$+2bx=+2ab+2b^2$$
$$ \Rightarrow  x=a+b$$
$$(a-b)(a+b)+(a+b)y=a^2-2ab-b^2$$
$$a^2-b^2+(a+b)y=a^2-2ab-b^2$$
$$y=\dfrac{-2ab}{a+b}$$

1084256_1173150_ans_4459fc5188e84bf280aa1f3eaf60605e.png


Find co-factors of elements of the matrices $$\begin {bmatrix} -1 & 2 \\ -3 & 4\end {bmatrix}$$

$$\begin {bmatrix} -1 & 2 \\ -3 & 4\end {bmatrix}$$
co-factor of $$-1$$ and $$4$$ is $$4$$ and $$ -1$$
minor of 2 is -3 and co factor is $$ 3$$
minor of -3 is 2 and co factor is $$ -2$$
$$\therefore $$ co factor matrix $$\Rightarrow $$ $$\begin {bmatrix} 4 & 3 \\ -2 & -1\end {bmatrix}$$


Solve the following equation by cramer's method:
$$7x+3y=15 , 12y-5x=39$$

$$7x + 3y = 15; 12y - 5x = 39$$

$$D = \begin{vmatrix} 7 & {3} \\ {-5} & 12 \end{vmatrix} = 7 \times 12 - (-5) \times 3 = 84 + 15 = 99$$

$$D_x = \begin{vmatrix} {15} & {3} \\ 39 & 12 \end{vmatrix} = 15 \times 12 - 39 \times 3 = 180 - 117 = 63$$

$$D_y = \begin{vmatrix} 7 & {15} \\ -5 & 39 \end{vmatrix} = 7 \times 39 - (-5) \times 15 = 273 + 75 = 348$$

$$x = \dfrac{D_x}{D} = \dfrac{63}{99} = \dfrac{7}{11}$$

$$y = \dfrac{D_y}{D} = \dfrac{348}{99} = \dfrac{116}{33}$$

$$(x, y) = (\dfrac{7}{11}, \dfrac{116}{33})$$


Find the value of: $$\begin{vmatrix} -3 & -5 \\ -2 & -1 \end{vmatrix}$$

$$\begin{vmatrix} -3 & -5 \\ -2 & -1 \end{vmatrix}$$
$$= \left( -3 \right) \times \left( -1 \right) - \left( -5 \right) \times \left( -2 \right)$$
$$= 3 - 10 = -7$$


Find $${D}_{x}$$ and $$D$$ for the equation $$2x+3y=4;7x-5y=2$$


1212525_1363769_ans_08d330d893204690ae31a7af99586b22.JPG


Solve the following simultaneous equations. 2x - y = 5 ; 3x + 2y = 11 

2x - y = 5  .....(I) 
3x + 2y = 11 ....(II) 
Multiplying (I) with 2 we get 
4x - 2y = 10 ....(III) 
Adding (II) with (III) 
7x = 21 
⇒⇒ y = 1 


Solve the following simultaneous equations. x + y = 11 ; 2x - 3 y =7 

x + y = 11  .....(I)
2x - 3y = 7 ..... (II)
Multiply (I) with 3
3x + 3y = 33 ..... (III)
Adding (II) and (III)
5x = 40
$$\Rightarrow4$ x = 8
Putting the value of x in (I)
8 + y = 11
y = 3 


Solve by Cramer's rule
$$x+y+z=6$$
$$x-y+z=2$$
$$3x+2y-4z=-5$$. The value of x is

$$ \Delta = \begin{vmatrix} 1&1&1\\1&-1&1\\3&2&-4 \end{vmatrix} = 1(4-2)-1(-4-3)+1(3+2)=14$$

$$ \Delta_x = \begin{vmatrix} 6&1&1\\2&-1&1\\-5&2&-4 \end{vmatrix} = 6(4-2)-1(-8+5)+1(4-5)=14$$

Hence by cramer rule,
$$x=\cfrac { { \Delta  }_{ x } }{ \Delta  } =1$$


If $$D_y\, =\, -15$$ and $$D\, =\, -5$$ are the values of the determinants for certain simultaneous equations in $$x$$ and $$y$$, find $$y$$.

Given: $$D_y = -15$$ and $$D = -5$$
Thus, we know $$y = \frac{D_y}{D}$$
$$y =$$ $$\dfrac{-15}{-5}$$ $$= 3$$
Therefore, the value of $$y$$ is $$3$$.


If $$ \displaystyle a_{1}f_{1}\left ( x \right )+a_{2}f_{2}\left ( x \right )+a_{3}f_{3}\left ( x \right )=0 $$ where $$a_1,a_2,a_3$$ are constants (not all zero) and $$ \displaystyle f_{1},f_{2},f_{3} $$ are twice differentiable functions.Then $$ \displaystyle D=\begin{vmatrix}f_{1}\left ( x \right ) &f_{2}\left ( x \right )  & f_{3}\left ( x \right )\\ Df_{1}\left ( x \right ) & Df_{2}\left ( x \right ) & Df_{3}\left ( x \right )\\ D^{2}f_{1} \left ( x \right )& D^{2}f_{2}\left ( x \right ) & D^{2}f_{3}\left ( x \right )\end{vmatrix} $$ is equal to $$ \displaystyle Df_{1}\left ( x \right )=\frac{d}{dx}f_{1} $$

$${ f }_{ 1 }(x)$$ are differentiable i.e.$${ { D }^{ 3 }f }_{ 1 }(x)$$=0
$$D\triangle =\begin{vmatrix} { Df }_{ 1 }(x) & { Df }_{ 2 }(x) & { Df }_{ 3 }(x) \\ { Df }_{ 1 }(x) & { Df }_{ 2 }(x) & { Df }_{ 3 }(x) \\ { { D }^{ 2 }f }_{ 1 }(x) & { { D }^{ 2 }f }_{ 2 }(x) & { { D }^{ 3 }f }_{ 3 }(x) \end{vmatrix}+\begin{vmatrix} { f }_{ 1 }(x) & { f }_{ 2 }(x) & { f }_{ 3 }(x) \\ { { D }^{ 2 }{ f }_{ 1 }(x) } & { { D }^{ 2 }f }_{ 2 }(x) & { { D }^{ 2 }f }_{ 3 }(x) \\ { { D }^{ 2 }{ f }_{ 1 }(x) } & { { D }^{ 2 }f }_{ 2 }(x) & { { D }^{ 2 }f }_{ 3 }(x) \end{vmatrix}\\ \\ \begin{vmatrix} { f }_{ 1 }(x) & { f }_{ 2 }(x) & { f }_{ 3 }(x) \\ { Df }_{ 1 }(x) & { Df }_{ 2 }(x) & { Df }_{ 3 }(x) \\ { { D }^{ 3 }f }_{ 1 }(x) & { { D }^{ 3 }f }_{ 2 }(x) & { { D }^{ 3 }f }_{ 3 }(x) \end{vmatrix}\\ \\ D\triangle =0+0+\begin{vmatrix} { f }_{ 1 }(x) & { f }_{ 2 }(x) & { f }_{ 3 }(x) \\ { Df }_{ 1 }(x) & { Df }_{ 2 }(x) & { Df }_{ 3 }(x) \\ 0 & 0 & 0 \end{vmatrix}=0\\ \\  $$


If the polynomial $$\displaystyle f\left ( x \right )=2x^{3}+mx^{2}+nx-14$$ has $$\displaystyle \left ( x-1 \right )$$ and $$\displaystyle \left ( x+2 \right )$$ as its factors find the value of $$\displaystyle m\times n$$

Since (x-1) and (x+2) are the factors of f(x) so f(1)=0 and f(-2)=0 Hence m+n-12=0 and 2 m-n-15=0
$$\displaystyle \Rightarrow m=9, n=3 $$ Thus $$\displaystyle m\times n=27$$


For what value of $$k$$  will the following pair of linear equations have no solution?
$$2x + 3y = 1 $$ and $$(3k - 1)x +(1 - 2k) y = 2k + 3$$

Given equations are,
$$  2x + 3y = 1   $$   ....(1)
and $$(3k - 1)x + (1 - 2k)y = 2k + 3 $$   .....(2)
The pairs of linear equations have no solution, if
$$\displaystyle \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \dfrac {c_1}{c_2}$$
$$\Rightarrow \dfrac{2}{3k-1}=\dfrac{3}{1-2k}$$
$$\Rightarrow 2(1-2k)=3(3k-1)$$
$$\Rightarrow 2-4k=9k-3$$
$$\displaystyle \Rightarrow 13k=5$$
$$ \Rightarrow k=\dfrac {5}{13} $$
Therefore, for $$k=\dfrac {5}{13}$$, the equations have no solution.


If $$A=\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}$$, show that $${ A }^{ 2 }-5A+7I=O$$. Hence find $${ A }^{ -1 }$$

$$A=\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}$$

To Prove : $$A^2-5A+7I=O$$
Now, $$A^{ 2 }=\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}$$

$$\Rightarrow A^{ 2 }=\begin{bmatrix} 9-1 & 3+2 \\ -3-2 & -1+4 \end{bmatrix}$$
$$\Rightarrow A^2 =\begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix}$$

Consider , $$A^2-5A+7I$$
$$=\begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix}-5\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}+7\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$

$$=\begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix}+\begin{bmatrix} -15 & -5 \\ 5 & -10 \end{bmatrix}+\begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix}$$

$$=\begin{bmatrix} 8-15+7 & 5-5+0 \\ -5+5+0 & 3-10+7 \end{bmatrix}$$
$$=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$$
$$\Rightarrow A^2-5A+7I=O$$      ....(1)

$$A^{-1}$$ :
Multiplying eqn (1) by $$A^{-1}$$
$$A^2 A^{-1} -5AA^{-1}+7IA^{-1} =O.A^{-1}$$
$$\Rightarrow A-5I+7A^{-1}=O$$         ($$\because AA^{-1}=I , O.A=O$$)
$$\Rightarrow 7A^{-1}=5I-A$$
$$=5\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}-\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}$$
$$=\begin{bmatrix} 5 & 0 \\ 0 & 5 \end{bmatrix}-\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}$$
$$=\begin{bmatrix} 5-3 & 0-1 \\ 0-(-1) & 5-2 \end{bmatrix}$$
$$\Rightarrow 7A^{-1}=\begin{bmatrix} 2 & -1 \\ 1 & 3 \end{bmatrix}$$
$$\Rightarrow A^{-1}=\cfrac{1}{7}\begin{bmatrix} 2 & -1 \\ 1 & 3 \end{bmatrix}$$




If $$A=\begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix}$$, verify that $${ A }^{ 3 }-{ 6A }^{ 2 }+9A-4I=0$$. Hence find $$ { A }^{ -1 }$$

$$A=\begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix}$$

To Prove : $$A^3-6A^2+9A-4I=O$$

Consider, $${ A }^{ 2 }=\begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix}\begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix}$$

$$=\begin{bmatrix} 4+1+1 & -2-2-1 & 2+1+2 \\ -2-2-1 & 1+4+1 & -1-2-2 \\ 2+1+2 & -1-2-2 & 1+1+4 \end{bmatrix}$$ 

$$\Rightarrow A^{ 2 }=\begin{bmatrix} 6 & -5 & 5 \\ -5 & 6 & -5 \\ 5 & -5 & 6 \end{bmatrix}$$

Now, $${ A }^{ 3 }=A^{ 2 }A$$
$$=\begin{bmatrix} 6 & -5 & 5 \\ -5 & 6 & -5 \\ 5 & -5 & 6 \end{bmatrix}\begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix}$$

$$=\begin{bmatrix} 12+5+5 & -6-10-5 & 6+5+10 \\ -10-6-5 &5+12+5 & -5-6-10 \\ 10+5+6 & -5-10-6 & 5+5+12 \end{bmatrix}$$

$$A^3=\begin{bmatrix} 22 & -21 & 21 \\ -21 & 22 & -21 \\ 21 & -21 & 22\end{bmatrix}$$

Consider, $$A^{ 3 }-6A^{ 2 }+9A-4I$$

$$=\begin{bmatrix} 22 & -21 & 21 \\ -21 & 22 & -21 \\ 21 & -21 & 22 \end{bmatrix}-6\begin{bmatrix} 6 & -5 & 5 \\ -5 & 6 & -5 \\ 5 & -5 & 6 \end{bmatrix}+9\begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix}-4\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

$$=\begin{bmatrix} 22 & -21 & 21 \\ -21 & 22 & -21 \\ 21 & -21 & 22 \end{bmatrix}-\begin{bmatrix} 36 & -30 & 30 \\ -30 & 36 & -30 \\ 30 & -30 & 36 \end{bmatrix}+\begin{bmatrix} 18 & -9 & 9 \\ -9 & 18 & -9 \\ 9 & -9 & 18 \end{bmatrix}-\begin{bmatrix} 4 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 4 \end{bmatrix}$$

$$=\begin{bmatrix} 22-36+18-4 & -21+30-9 & 21-30+9 \\ -21+30-9 & 22-36+18-4 & -21+30-9 \\ 21-30+9 & -21+30-9 & 22-36+18-4 \end{bmatrix}$$

$$=\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}$$
$$\Rightarrow A^{ 3 }-6A^{ 2 }+9A-4I=O$$      .....(1)

$$A^{-1}$$ :
Multiplying eqn (1) by $$A^{-1}$$, we get
$$A^{ 3 }{ A }^{ -1 }-6A^{ 2 }{ A }^{ -1 }+9A{ A }^{ -1 }-4I{ A }^{ -1 }=O{ A }^{ -1 }$$
$$\Rightarrow A^{ 2 }-6A+9I-4{ A }^{ -1 }=O$$
$$\Rightarrow  4{ A }^{ -1 }=A^{ 2 }-6A+9I$$
Substituting the values in above eqn
$$\Rightarrow 4{ A }^{ -1 }=\begin{bmatrix} 6 & -5 & 5 \\ -5 & 6 & -5 \\ 5 & -5 & 6 \end{bmatrix}-6\begin{bmatrix} 2 & -1 & 1 \\ -1 & 2 & -1 \\ 1 & -1 & 2 \end{bmatrix}+9\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

$$\Rightarrow 4{ A }^{ -1 }=\begin{bmatrix} 6 & -5 & 5 \\ -5 & 6 & -5 \\ 5 & -5 & 6 \end{bmatrix}-\begin{bmatrix} 12 & -6 & 6 \\ -6 & 12 & -6 \\ 6 & -6 & 12 \end{bmatrix}+\begin{bmatrix} 9 & 0 & 0 \\ 0 & 9 & 0 \\ 0 & 0 & 9 \end{bmatrix}$$

$$\Rightarrow 4{ A }^{ -1 }=\begin{bmatrix} 6-12+9 & -5+6 & 5-6 \\ -5+6 & 6-12+9 & -5+6 \\ 5-6 & -5+6 & 6-12+9 \end{bmatrix}$$

$$\Rightarrow { A }^{ -1 }=\cfrac { 1 }{ 4 } \begin{bmatrix} 3 & 1 & -1 \\ 1 & 3 & 1 \\ -1 & 1 & 3 \end{bmatrix}$$


For the matrix $$A=\begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix}$$, show that $${ A }^{ 3 }-{ 6A }^{ 2 }+5A+11I=0$$. Hence find $${ A }^{ -1 }$$

$$A=\begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix}$$

To Prove : $$A^3-6A^2+5A+11I=O$$

Consider, $${ A }^{ 2 }=\begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix}\begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix}$$

$$=\begin{bmatrix} 1+1+2 & 1+2-1 & 1-3+3 \\ 1+2-6 & 1+4+3 & 1-6-9 \\ 2-1+6 & 2-2-3 & 2+3+9 \end{bmatrix}$$ 

$$\Rightarrow A^{ 2 }=\begin{bmatrix} 4 & 2 & 1 \\ -3 & 8 & -14 \\ 7 & -3 & 14 \end{bmatrix}$$

Now, $${ A }^{ 3 }=A^{ 2 }A$$
$$=\begin{bmatrix} 4 & 2 & 1 \\ -3 & 8 & -14 \\ 7 & -3 & 14 \end{bmatrix}\begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix}$$

$$=\begin{bmatrix} 4+2+2 & 4+4-1 & 4-6+3 \\ -3+8-28 & -3+16+14 & -3-24-42 \\ 7-3+28 & 7-6-14 & 7+9+42 \end{bmatrix}$$

$$A^3=\begin{bmatrix} 8 & 7 & 1 \\ -23 & 27 & -69 \\ 32 & -13 & 58 \end{bmatrix}$$

Consider, $$A^{ 3 }-6A^{ 2 }+5A+11I$$

$$=\begin{bmatrix} 8 & 7 & 1 \\ -23 & 27 & -69 \\ 32 & -13 & 58 \end{bmatrix}-6\begin{bmatrix} 4 & 2 & 1 \\ -3 & 8 & -14 \\ 7 & -3 & 14 \end{bmatrix}+5\begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix}+11\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

$$=\begin{bmatrix} 8 & 7 & 1 \\ -23 & 27 & -69 \\ 32 & -13 & 58 \end{bmatrix}-\begin{bmatrix} 24 & 12 & 6 \\ -18 & 48 & -84 \\ 42 & -18 & 84 \end{bmatrix}+\begin{bmatrix} 5 & 5 & 5 \\ 5 & 10 & -15 \\ 10 & -5 & 15 \end{bmatrix}+\begin{bmatrix} 11 & 0 & 0 \\ 0 & 11 & 0 \\ 0 & 0 & 11 \end{bmatrix}$$

$$=\begin{bmatrix} 8-24+5+11 & 7-12+5 & 1-6+5 \\ -23+18+5 & 27-48+10+11 & -69+84-15 \\ 32-42+10 & -13+18-5 & 58-84+15+11 \end{bmatrix}$$

$$=\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}$$
$$\Rightarrow A^{ 3 }-6A^{ 2 }+5A+11I=O$$      .....(1)

$$A^{-1}$$ :
Multiplying eqn (1) by $$A^{-1}$$, we get
$$A^{ 3 }{ A }^{ -1 }-6A^{ 2 }{ A }^{ -1 }+5A{ A }^{ -1 }+11I{ A }^{ -1 }=O{ A }^{ -1 }$$
$$\Rightarrow A^{ 2 }-6A+5I+11{ A }^{ -1 }=O$$
$$\Rightarrow  11{ A }^{ -1 }=-A^{ 2 }+6A-5I$$
Substituting the values in above eqn
$$11A^{-1}=-\begin{bmatrix} 4 & 2 & 1 \\ -3 & 8 & -14 \\ 7 & -3 & 14 \end{bmatrix}+6\begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & -3 \\ 2 & -1 & 3 \end{bmatrix}-5\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

$$=\begin{bmatrix} -4 & -2 & -1 \\ 3 & -8 & 14 \\ -7 & 3 & -14 \end{bmatrix}+\begin{bmatrix} 6 & 6 & 6 \\ 6 & 12 & -18 \\ 12 & -6 & 18 \end{bmatrix}-\begin{bmatrix} 5 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 5 \end{bmatrix}$$

$$11{ A }^{ -1 }=\begin{bmatrix} -4+6-5 & -2+6 & -1+6 \\ 3+6 & -8+12-5 & 14-18 \\ -7+12 & 3-6 & -14+18-5 \end{bmatrix}$$

$$\Rightarrow { A }^{ -1 }=\displaystyle \frac { 1 }{ 11 } \begin{bmatrix} -3 & 4 & 5 \\ 9 & -1 & -4 \\ 5 & -3 & -1 \end{bmatrix}$$


Given, $$-3x + 4y = 20$$ and $$6x +3y =15$$
If $$(x, y)$$ is the solution to the system of equations above, what is the value of $$x$$ ?

Let $$ -3x + 4y = 20 $$ ....(1)
$$ 6x + 3y = 15 $$ ....(2)
Multiplying equation (1) with $$ 2 $$, we get
$$ -6x + 8y = 40 $$....(3)
Adding equations $$ 1 $$ and $$ 3 $$, we get $$ 11y = 55 $$
$$ \Rightarrow  y = 5 $$
Substituting in equation (1), we get
$$ -3x + 4(5) = 20 $$
$$ \Rightarrow  -3x + 20 = 20 $$
$$ \Rightarrow  -3x = 0 $$
$$ \Rightarrow  x = 0 $$


Find '$$m+n$$' for the following simultaneous equations:
$$3m+4n=7$$
and $$4m+3n=14$$

$$3m+4n=7..........(1)$$
$$4m+3n=14........(2)$$
Adding equations $$(1)$$ and $$(2)$$
$$3m+4n=7$$
$$4m+3n=14$$
-------------------
$$7m+7n=21$$
$$\therefore$$ $$7(m+n)=21$$
$$\therefore$$ $$m+n=\cfrac{21}{7}$$
$$\therefore$$ $$m+n=3$$


Solve the following simultaneous equations by using Cramer's Rule
$$3x + y = 1$$,
$$2x - 11 y = 3$$

The given simultaneous equations are
$$3x + y = 1$$           ....... (1)
$$2x- 11 y = 3$$        ........ (2)
$$D = \begin{vmatrix}3 & 1\\ 2 & -11\end{vmatrix}$$
$$= 3 \times (-11) - 1 \times 2$$
$$= -33 -2 = -35$$
$$D_x = \begin{vmatrix}1 & 1\\ 3 & -11\end{vmatrix}$$
$$= 1 \times (-11) - 1 \times 3$$
$$= -11 - 3 = - 14$$
$$D_y = \begin{vmatrix} 3& 1\\ 2 & 3\end{vmatrix}$$
$$= 3 \times 3 - 1 \times 2 = 9 - 2 = 7$$
$$\therefore$$ By Cramer's rule, we get
$$x = \dfrac{D_x}{D}=\dfrac{-14}{35} = -\dfrac25$$ and $$y = \dfrac{D_y}{D}=\dfrac{7}{35} = \dfrac15$$


If $$A=\begin{bmatrix} \cos^2\theta & \cos\theta \sin\theta\\ \cos\theta\sin\theta & \sin^2\theta\end{bmatrix}$$ and $$B=\begin{bmatrix}\cos^2\Phi & \cos\Phi \sin\Phi\\ \cos\Phi \sin\Phi & \sin^2\Phi\end{bmatrix}$$, show that AB is a zero matrix if $$\theta$$ and $$\Phi$$ differ by an odd multiple of $$\displaystyle\frac{\pi}{2}$$.

$$AB=\begin{bmatrix} \cos^2\theta&\cos\theta\sin\theta\\\cos\theta\sin\theta&\sin^2\theta\end{bmatrix}\begin{bmatrix} \cos^2\phi&\cos\phi\sin\phi\\\cos\phi\sin\phi&\sin^2\phi\end{bmatrix}$$

$$\therefore AB=\begin{bmatrix} \cos^2\theta\cos^2\phi+\cos\theta\sin\theta\cos\phi\sin\phi & \cos^2\theta\cos\phi\sin\phi+\cos\theta\sin\theta\sin^2\phi \\ \cos\theta\sin\theta\cos^2\phi+\sin^2\theta\cos\phi\sin\phi & \cos\theta\sin\theta\cos\phi\sin\phi+\sin^2\theta\sin^2\phi \end{bmatrix}$$

For $$AB$$ to be a zero matrix, each element of matrix should be 0.
$$\therefore$$ from 1st term and 4th term, we have
$$ \cos^2\theta\cos^2\phi+\cos\theta\sin\theta\cos\phi\sin\phi+\cos\theta\sin\theta\cos\phi\sin\phi+\sin^2\theta\sin^2\phi=0$$
$$\therefore \cos^2\theta\cos^2\phi+2\cos\theta\sin\theta\cos\phi\sin\phi+\sin^2\theta\sin^2\phi=0$$
$$\therefore (\cos\theta\cos\phi+\sin\theta\sin\phi)^2=0$$
$$\therefore \cos\theta\cos\phi+\sin\theta\sin\phi=0$$
$$\therefore \cos(\theta-\phi)=0$$
$$\therefore \theta-\phi=n\pi+\dfrac{\pi}{2}$$
Hence, proved.


Solve the following simultaneous equations using Cramer's rule.
$$3x-2y=3$$;
$$2x+y=16$$.

Writing the system of equations in matrix form $$AX = B$$ 
where $$A$$ is the $$2 \times 2$$ coefficient matrix, $$X = \begin{pmatrix} x\\y\end{pmatrix}$$ and $$B$$ is the $$2\times 1$$ matrix of constants.

Here, $$A = \begin{pmatrix} 3 & -2\\ 2 & 1 \end{pmatrix}$$ and $$B = \begin{pmatrix} 3\\16\end{pmatrix}$$ 

We can write, $$X = A^{-1}B$$, where

$$A^{-1} = \dfrac{1}{|A|} adj(A)$$

$$A^{-1} = \dfrac{1}{7} \times \begin{pmatrix} 1 & 2\\ -2 & 3\end{pmatrix}$$ 

Substituting the values we get,

$$\begin{pmatrix} x\\y \end{pmatrix} = $$ $$\dfrac{1}{7} \times \begin{pmatrix} 1 & 2\\ -2 & 3\end{pmatrix}$$ $$\times \begin{pmatrix} 3\\16\end{pmatrix}$$ 

$$\begin{pmatrix} x\\y \end{pmatrix} = $$ $$\dfrac{1}{7} \times \begin{pmatrix} 3\times1 + 2\times16\\ (-2)\times 3 + 3 \times 16\end{pmatrix}$$

$$\begin{pmatrix} x\\y \end{pmatrix} = $$ $$\begin{pmatrix} 5\\ 6\end{pmatrix}$$.

Hence, $$x = 5$$ and $$y = 6$$.


Solve $$x + y + z = 11\\
2x - 6y - z = 0\\
3x + 4y + 2z = 0$$.


1311867_1003858_ans_a6e42ddd8e1d4f72a0c889c0c155e290.jpg


Solve the equations
$$x + 2y + 3z = 14$$
$$2x - y + 5z = 15$$
$$3x - 2y - 4z = -13$$

$$x = 1, y = 2, z = 3$$


Find x and y using Cramer's Rule if :$$\dfrac{1}{2^x}+\dfrac{2}{3^y}=10,\dfrac{3}{2^x}-\dfrac{5}{3^y}=-3$$ ?

$$\dfrac { 1 }{ { 2 }^{ x } } +\dfrac { 2 }{ { 3 }^{ y } } =10\longrightarrow (1)\\ \dfrac { 3 }{ { 2 }^{ x } } -\dfrac { 5 }{ { 3 }^{ y } } =-3\longrightarrow (2)\\ $$
Let $${ 2 }^{ x }=p\quad $$ and $${ 3 }^{ y }=q$$
Equation becomes;
$$\dfrac { 1 }{ p } +\dfrac { 2 }{ q } =10\longrightarrow (3)\\ \dfrac { 3 }{ p } -\dfrac { 5 }{ q } =-3\longrightarrow (4)\\ $$
again let, $$\dfrac { 1 }{ p } =u$$ and $$\dfrac { 1 }{ q } =v$$
Equation (3) and (4) becomes
$$u+2v=10\longrightarrow \left( 5 \right) \\ 3u-5v=-3\longrightarrow \left( 6 \right) $$
By Cramer's rule;
$$u=\dfrac { \begin{vmatrix} { c }_{ 1 } & { b }_{ 1 } \\ { c }_{ 2 } & { b }_{ 2 } \end{vmatrix} }{ \begin{vmatrix} { a }_{ 1 } & { b }_{ 1 } \\ { a }_{ 2 } & { b }_{ 2 } \end{vmatrix} } =\dfrac { \begin{vmatrix} 10 & 2 \\ -3 & -5 \end{vmatrix} }{ \begin{vmatrix} 1 & 2 \\ 3 & -5 \end{vmatrix} } =4$$
and,
$$v=\dfrac { \begin{vmatrix} { a }_{ 1 } & { c }_{ 1 } \\ { a }_{ 2 } & { c }_{ 2 } \end{vmatrix} }{ \begin{vmatrix} { a }_{ 1 } & { b }_{ 1 } \\ { a }_{ 2 } & { b }_{ 2 } \end{vmatrix} } =\dfrac { \begin{vmatrix} 1 & 10 \\ 3 & -3 \end{vmatrix} }{ \begin{vmatrix} 1 & 2 \\ 3 & -5 \end{vmatrix} } =3$$
$$\because \quad \dfrac { 1 }{ p } =u;\quad \dfrac { 1 }{ q } =v\\ \Rightarrow p=\dfrac { 1 }{ 4 } ;\quad q=\dfrac { 1 }{ 3 } \\ $$
again,
$${ 2 }^{ x }=p;\quad { 3 }^{ y }=q\\ \Rightarrow { 2 }^{ x }=\dfrac { 1 }{ 4 } ;\quad { 3 }^{ y }=\dfrac { 1 }{ 3 } \\ \Rightarrow x\log 2=\log\dfrac { 1 }{ 4 } ;\quad y\log 3=\log\dfrac { 1 }{ 3 } \\ \Rightarrow x=\log\dfrac { 1 }{ 8 } ;\quad y=\log\dfrac { 1 }{ 9 } \quad $$



Find x and y using Cramer's Rule,if $$\dfrac{1}{x}-\dfrac{2}{y}=6,\dfrac{3}{x}+\dfrac{1}{y}=8$$ ?

Given the two equations, $$\dfrac { 1 }{ x } -\dfrac { 2 }{ y } =6\quad \quad \longrightarrow (1)$$
                                           $$\dfrac { 3 }{ x } +\dfrac { 1 }{ y } =8\quad \quad \longrightarrow (2)$$
Let,  $$p=\dfrac { 1 }{ x } ,q=\dfrac { 1 }{ y } $$.
Then, equation $$(1)$$ becomes$$\Rightarrow p-2q=6\quad \quad \longrightarrow (3)$$
   and equation $$(2)$$ becomes$$\Rightarrow 3p+q=8\quad \quad \longrightarrow (4)$$.
Now, solving equation $$(3)$$ and $$(4)$$ by Cramer's rule,
    Let, $$A=\begin{pmatrix} 1 & -2 \\ 3 & 1 \end{pmatrix}$$
Finding the determinant of the matrix $$A$$,
         $$\left| A \right| =\begin{vmatrix} 1 & -2 \\ 3 & 1 \end{vmatrix}$$
                $$=1+6=7$$
 Now,for matrix $${ A }_{ p }$$, we have to replace the first column of the matrix $$A$$ with the right hand side values of equation $$(3)$$ and $$(4)$$, $${ A }_{ p }=\begin{pmatrix} 6 & -2 \\ 8 & 1 \end{pmatrix}$$
    $$\therefore \left| { A }_{ p } \right| =\begin{vmatrix} 6 & -2 \\ 8 & 1 \end{vmatrix}$$
                 $$=6+16=22$$
    $$\therefore \quad p=\dfrac { \left| { A }_{ p } \right|  }{ \left| A \right|  } =\dfrac { 22 }{ 7 } $$
Again, for matrix $${ A }_{ q }$$, we have to replace the second column of the matrix $$A$$ with the right hand side values of equation $$(3)$$ and $$(4)$$,$$\quad { A }_{ q }=\begin{pmatrix} 1 & 6 \\ 3 & 8 \end{pmatrix}$$
   $$\therefore \left| { A }_{ q } \right| =\begin{vmatrix} 1 & 6 \\ 3 & 8 \end{vmatrix}=8-18=-10$$
   $$\therefore q=\dfrac { \left| { A }_{ q } \right|  }{ \left| A \right|  } =\dfrac { -10 }{ 7 } $$
Thus, $$\dfrac { 1 }{ x } =\dfrac { 22 }{ 7 } ,\dfrac { 1 }{ y } =\dfrac { -10 }{ 7 } $$
      $$\Rightarrow x=\dfrac { 7 }{ 22 } ,y=-\dfrac { 7 }{ 10 } $$
Hence, the solutions are $$x=\dfrac { 7 }{ 22 } \quad and\quad y=-\dfrac { 7 }{ 10 } $$.


If $$A = \left[ \begin{array} { c c c } { 5 } & { 8 } & { 1 } \\ { 0 } & { 2 } & { 1 } \\ { 4 } & { 3 } & { - 1 } \end{array} \right] , B = \left[ \begin{array} { c } { 2 } \\ { - 1 } \\ { 3 } \end{array} \right]$$ and $$A X = B$$ then find $$X$$

$$A = \begin{bmatrix} 5 & 8 &  1 \\ 0 & 2 & 1 \\ 4 & 3 & -1 \end{bmatrix} \, B = \begin{bmatrix} 2 \\ -1 \\ 3 \end{bmatrix}$$

$$AX = B$$

$$\begin{bmatrix} 5 & 8 & 1 \\ 0 & 2 & 1 \\ 4 & 3 & -1 \end{bmatrix} \, \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 2 \\ -1 \\ 3 \end{bmatrix}$$

$$5x + 8y + z = 2$$.................(i)

$$2y + z = -1 \Rightarrow z = -(1 + 2y)$$

$$4x + 3y - z = 3$$...................(ii)

$$5x + 8y - 1 - 2y = 2$$...............replacing value of $$z$$ in eq. (i)

$$4x + 3y + 1 + 2y = 3$$...............replacing value of $$z$$ in eq. (ii)

$$5x + 6y = 3 $$ .... (iii)

$$4x + 5y = 2$$ ....(iv)

Now,  (iii)$$\times $$5-(iv)$$\times$$6

we get, $$x=3$$

Replacing value of $$x$$ in eq. i

we get,$$y = -2$$

$$z = -(1 + 2(-2))$$

$$z = 3$$

$$x = 3; \, y = -2$$ and $$z = 3$$

$$\begin{bmatrix} 3 \\ -2 \\ 3 \end{bmatrix} = x$$.


Find $$ A^2$$ where A is given $$A= \begin {bmatrix}1 & 2 & 3 \\ 1 & 2 & 3\\ -1 & 2 & -3 \end{bmatrix}$$

$$A= \begin {bmatrix}1 & 2 & 3 \\ 1 & 2 & 3\\ -1 & 2 & -3 \end{bmatrix}$$
$$ A^{2} = A\times A$$
$$ = \begin {bmatrix}1 & 2 & 3 \\ 1 & 2 & 3\\ -1 & 2 & -3 \end{bmatrix} \times  \begin {bmatrix}1 & 2 & 3 \\ 1 & 2 & 3\\ -1 & 2 & -3 \end{bmatrix} =  \begin {bmatrix}0 & 12 & 0 \\ 0 & 12 & 0 \\ 4 & -4 & 0 \end{bmatrix}$$


Solve $$\left| {\begin{array}{*{20}{c}}1 & 1 & 1\\a & b & c\\{{a^3}} & {{b^3}} & {{c^3}}\end{array}} \right| = \left( {a - b} \right)\left( {b - c} \right)\left( {c - a} \right)\left( {a + b + c} \right)$$

$$\begin{vmatrix}  1 & 1 & 1 \\ a & b & c \\ a^3 & b^3 & c^3 \end{vmatrix}$$
$$c_1 \rightarrow c_1 - c_2, \, c_2 \rightarrow c_2 - c_3$$
$$= \begin{vmatrix} 0 & 0 & 1 \\ a - b  & b - c & c \\ a^3 - b^3 & b^3 - c^3 & c^3 \end{vmatrix}$$
$$= \begin{vmatrix} 0 & 0 & 1 \\ a - b & b - c & c \\ (a-b)(a^2 + b^2 + ab) & (b - c)(b^2 + c^2 + bc) & c^3 \end{vmatrix}$$
$$\{(A^3 - B^3) = (A - B) (A^2 + B^2 + AB) \}$$
taking $$(a - b)$$ from $$c_1$$ and $$(b - c)$$ from $$c_2$$
$$\Rightarrow (a - b)(b - c) \begin{vmatrix} 0 & 0 & 1 \\ 1 & 1 & c \\ a^2 + b^2 +ab & b^2+ c^2 + bc & c^3 \end{vmatrix}$$
$$\Rightarrow (a - b) (b - c) [0 - 0 + (b^2 + c^2 + bc - a^2 - b^2 - an)]$$
$$\Rightarrow (a - b) (b - c) [c^2 - a^2 + b(c - a)]$$
$$\Rightarrow (a - b)(b - c) [(c - a) (c + a) + b (c - a)]$$
$$\Rightarrow (a - b)(b - c)(c - a) ( a+ b + c)$$


For what value of k , the following pair of linear equations has infinite number of solutions :
$$5x + 2y = k ;  10x + 4y = 3$$

The given equations are :

$$5x+2y-k=0$$

$$10x+4y-3=0$$

For infinitely many solutions,

$$\dfrac{a_{1}}{a_{2}} = \dfrac{b_{1}}{b_{2}} = \dfrac{c_{1}}{c_{2}}$$

Therefore,

$$\dfrac{5}{10}=\dfrac{2}{4}=\dfrac{-k}{-3}$$

$$\dfrac{k}{3}=\dfrac{1}{2}$$

$$k=\dfrac{3}{2}$$


If  3m +5n =9 and 5m +3n =7 then find the value of 8m +8n.

Given     3m+5n=9   -----(1)
5m+3n=7   -----(3)
multiply eq (1) by 5 and eq (2)by (3) we get
 15m+25n=45
 15m+9n=21
___________
16n=34.  $$[n= \frac{17}{8}]$$
 now form eq (1)
$$3m= 9-\frac{5\times 17}{8}=\frac{72-85}{8}=\frac{-13}{8}.$$
$$m=\frac{-13}{24}$$
Now $$ 8m+8n=8(m+n)=8(\frac{-13}{24}+\frac{17}{8})=\frac{51-13}{24}$$
$$[8m+8n=\frac{38}{3}]$$


1192823_1376959_ans_7a4533746cd44aa9ae3d4fa86e174760.JPG


Solve the following 
$$\frac{x}{3}+\frac{y}{4}=4, \frac{x}{2}-\frac{y}{4}=1$$ 

$$\frac{x}{3}+\frac{y}{4}=4$$----(1)
$$\frac{x}{2}-\frac{y}{4}=1$$----(2)
4x+3y=48    form eq (1) 
4x-2y=8       form eq (2)
(-) (+)  (-)
_______
5y=40
[y = 8] and 4x = 8 +  2y = 24
 [x=6]
Hence [x = 6] and  [y = 8]  


1192824_1376966_ans_24a9453b84ba4d80bd6227e1c241a50f.JPG


Solve the following simultaneous equation using cramer's rule
$$4x+3y-4=0: 6x=1$$


1208402_1543116_ans_d8a80c102d8a4ce78dbad981b006a631.jpg


Solve the following simultaneous equation using cramer's rule
$$6x-4y=-12: 8x-3y=-2$$


1208414_1543135_ans_ac4a4ad01d6e42d0b596a9c9dfbb064b.jpg


Solve the following simultaneous equation using cramer's rule 
$$4m+6n=54 : 3m +2n =28$$


1208422_1543195_ans_4a1a8b4bc8d44789a3e95f0a5cdc85bc.jpg


Solve the  simultaneous equations.
$$\dfrac { x } { 3 } + \dfrac { y } { 4 } = 4 ; \quad \dfrac { x } { 2 } - \dfrac { y } { 4 } = 1$$

$$\dfrac{x}{3}+\dfrac{y}{4}=4$$......(I) 
$$\dfrac{x}{2}-\dfrac{y}{4}=1$$ ......(II) 
Multiplying (I) with LCM of 3 and 4 which is 12 we get 
4x+3y=48  .....(Ill) 
Multiplying (I) with LCM of 3 and 4 which is 12 we get 
2x - y = 4 .....(IV) 
Multiplying (IV) with 2 
4x - 2y = 8  .....(V) 
Subtracting (V) from (III) 
5y = 40 
$$\Rightarrow$$ y = 8 
Putting this value of y in (IV) we get 
2x - 8 = 4 
$$\Rightarrow$$ 2x = 12 
$$\Rightarrow$$ x = 6 


Solve the following simultaneous equations using Cramer's rule :
 $$3x+y=7; \ 2x-11y=3.$$


2042802_1534569_ans_49dbafce071e44608c3a5a60e47b286b.jpg


Solve the following simultaneous equation using cramer's rule.
$$3x-4y=10:4x+3y=5$$

$$x=2$$ but $$y=\dfrac{15-40}{25}=\dfrac{-25}{25}=-1$$.
1208397_1543108_ans_e0cf2280af9345e6a6e646cd299ff248.jpg


Solve the following simultaneous equation using cramer's rule
$$x+2y=-1: 2x-3y=12$$


1208405_1543126_ans_f3a03f92c5b84395a6a53e5dcde2321e.jpg


Solve the following simultaneous equation using cramer's rule 
2x + 3y = 2: x-$$\frac { y }{ 2 } =\frac{1}{2}$$


2011591_1543203_ans_7e155efce1cf49d3b2d4db01e4f1b9f0.jpg


If $$A = \begin{bmatrix} 3& 2\\ 2 & 1\end{bmatrix}$$, verify that $$A^{2} - 4A - I = O$$, and hence find $$A^{-1}$$.


1537914_1705458_ans_9313de82f8fc476c99a815153cdedb2e.jpg


Show that the matrix $$A =\begin{bmatrix} -8& 5\\ 2 & 4\end{bmatrix}$$ satisifies the equation $$A^{2} + 4A - 42I = 0$$ and hence find $$A^{-1}$$.


1538687_1705460_ans_02587ff7638645e8b0153083323eaf7b.jpg


If $$A = \begin{bmatrix} -1& -1\\ 2 & -2\end{bmatrix}$$, show that $$A^{2} + 3A + 4I_{2} = O$$ and hence find $$A^{-1}$$.


1537966_1705463_ans_c6a93042f4cf4552a52e74581d981b56.jpg


If $$A = \begin{bmatrix} 3& -2\\ 4 & -2\end{bmatrix}$$, find the value of $$\lambda$$ so that $$A^{2} = \lambda A - 2I$$. Hence, find $$A^{-1}$$.


1538104_1705469_ans_48e8bcdc12044091b1bf3d8a20792e82.jpg


Show that the $$A = \begin{bmatrix}1 & 0 & -2\\ -2 & -1 & 2\\ 3 & 4 & 1\end{bmatrix}$$ satisfied the equation $$A^{3} - A^{2} - 3A - I = O$$, and hence find $$A^{-1}$$.


1538285_1705471_ans_1df07f4387774df7b3b10444949ea752.jpg


Solve the following equation:
$$\begin{vmatrix} x & 3 & 7 \\ 2 & x & 2 \\ 7 & 6 & x \end{vmatrix}=0$$


1552570_1705735_ans_53cf178037b14441a7090ea699375286.jpg


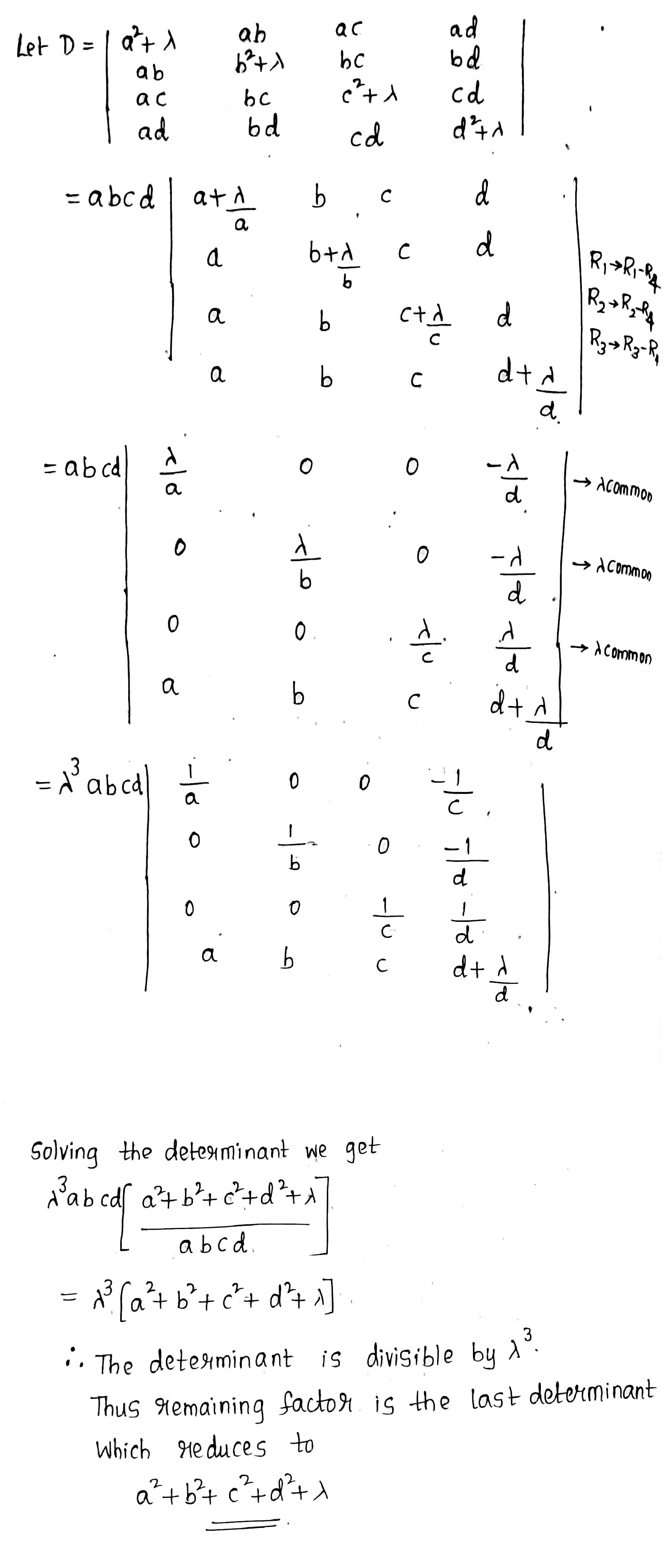
Show that $$\begin{vmatrix} a^2+\lambda  & ab & ac & ad \\ ab & b^2+\lambda  & bc & bd \\ ac & bc & c^2+\lambda  & cd \\ ad & bd & cd & d^2+\lambda  \end{vmatrix}$$
is divisible by $$\lambda^{3}$$ and find the other factor.


1578860_1747407_ans_b129007cbbaa4a44980ac2565eb95409.JPG


Absolute value of the sum of roots of the equation
$$\begin{vmatrix} x+2 & 2x+3 & 3x+4 \\ 2x+3 & 3x+4 & 4x+5 \\ 3x+5 & 5x+8 & 10x+17 \end{vmatrix}=0$$ is

$$\Delta =\begin{vmatrix} x+2 & 2x+3 & 3x+4 \\ 2x+3 & 3x+4 & 4x+5 \\ 3x+5 & 5x+8 & 10x+17 \end{vmatrix}=0$$
applying $$({ R }_{ 3 }\rightarrow { R }_{ 3 }-{ R }_{ 2 };{ R }_{ 2 }\rightarrow { R }_{ 2 }-{ R }_{ 1 })$$
$$\Delta =\begin{vmatrix} x+2 & 2x+3 & 3x+4 \\ x+1 & 3x+4 & 4x+5 \\ 3x+5 & 5x+8 & 10x+17 \end{vmatrix}=0\quad $$
$$\therefore \Delta =(x+1)(x+2)\begin{vmatrix} x+2 & 2x+3 & 3x+4 \\ 1 & 1 & 1 \\ 1 & 2 & 6 \end{vmatrix}=0$$
$$\therefore \Delta =\left( x+1 \right) \left( x+2 \right) \left( x+2 \right) .4-\left( 2x+3 \right) .5+\left( 3x+4 \right) .1=0\Rightarrow { \left( x+1 \right)  }^{ 2 }\left( x+2 \right) =0\Rightarrow x=-1,-1,-2$$


$$\begin{vmatrix} { x }^{ n } & { x }^{ n+2 } & { x }^{ n+4 } \\ { y }^{ n } & { y }^{ n+2 } & { y }^{ n+4 } \\ { z }^{ n } & { z }^{ n+2 } & { z }^{ n+4 } \end{vmatrix}=\left( \cfrac { 1 }{ { y }^{ 2 } } -\cfrac { 1 }{ { x }^{ 2 } }  \right) \left( \cfrac { 1 }{ { z }^{ 2 } } -\cfrac { 1 }{ { y }^{ 2 } }  \right) \left( \cfrac { 1 }{ { x }^{ 2 } } -\cfrac { 1 }{ { z }^{ 2 } }  \right) $$ then $$n$$ is _____.

Let $$\Delta = \begin{vmatrix} { x }^{ n } & { x }^{ n+2 } & { x }^{ n+4 } \\ { y }^{ n } & { y }^{ n+2 } & { y }^{ n+4 } \\ { z }^{ n } & { z }^{ n+2 } & { z }^{ n+4 } \end{vmatrix}$$

$$\Delta ={(xyz)}^{n}\begin{vmatrix} 1 & { x }^{ 2 } & { x }^{ 4 } \\ 1 & { y }^{ 2 } & { y }^{ 4 } \\ 1 & { z }^{ 2 } & { z }^{ 4 } \end{vmatrix}$$

$$={(xyz)}^{n}({x}^{2}-{y}^{2})({y}^{2}-{z}^{2})({z}^{2}-{x}^{2})$$

Clearly when

$$n=-4$$

$$\Delta =\left( \cfrac { 1 }{ { y }^{ 2 } } -\cfrac { 1 }{ { x }^{ 2 } }  \right) \left( \cfrac { 1 }{ { z }^{ 2 } } -\cfrac { 1 }{ { y }^{ 2 } }  \right) \left( \cfrac { 1 }{ { x }^{ 2 } } -\cfrac { 1 }{ { z }^{ 2 } }  \right) $$


If $$ x=-4 $$ is a root of $$ \Delta =  \left| \begin{matrix} x & 2 & 3 \\ 1 & x & 1 \\ 3 & 2 & x \end{matrix} \right|   = 0 $$ then find the other two roots.

Applying $$ R_1 \rightarrow (R_1+R_2+R_3), $$ we get 
$$ \left| \begin{matrix} x+4 & x+4 & x+4 \\ 1 & x & 1 \\ 3 & 2 & x \end{matrix} \right|  $$
 Taking $$ (x+4) $$ common from $$ R_1 $$ , we get
$$ \Delta=(x+4 ) \left| \begin{matrix} 1 & 1 & 1 \\ 1 & x & 1 \\ 3 & 2 & x \end{matrix} \right| $$
Applying $$ C_2 \rightarrow C_2-C_1, C_3 \rightarrow C_3-C_1 $$ we get
$$ \Delta= (x+4) \left| \begin{matrix} 1 & 0 & 0 \\ 1 & x-1 & 0 \\ 3 & -1 & x-3 \end{matrix} \right|  $$
Expanding along $$ R_1 $$,
$$ \Delta= (x+4)[(x-3)-0]. $$ Thus, $$ \Delta =0 $$ implies
$$ x=-4,1,3 $$


If $$ x = - 9 $$ is root of $$  \left| \begin{matrix} x & 3 & 7 \\ 2 & x & 2 \\ 7 & 6 & x \end{matrix} \right| =0 $$ then other two roots are _________

Since , $$  \left| \begin{matrix} x & 3 & 7 \\ 2 & x & 2 \\ 7 & 6 & x \end{matrix} \right| =0 $$
expanding along $$ R_1 $$
$$ x(x^2 - 12) - 3 (2x -14) +7 ( 12 -7x) = 0 $$
$$ \Rightarrow x^3 - 12x -6x +42 +84 - 49x = 0 $$
$$ \Rightarrow x^3 -67x +126 = 0 $$,.....(i)
Here $$ 126 \times  1 = 9 \times 2 \times 7 $$
For $$ x = 2, 2^3 - 67 \times 2 +126 = 134 - 134 = 0 $$
Hence $$ x = 2 $$ is root.
For $$ x = 7 , 7^3 - 67 \times 7 + 126 = 469 -469 = 0 $$
hence $$ x =  7 $$ is also a root.


If $$ f(x)  = \left| \begin{matrix}  (1+x)^{17}& (1+x)^{19} &(1+x)^{23}  \\ (1+x)^{23} & (1+x)^{29} & (1+x)^{34} \\ (1+x)^{41} & (1+x)^{43} & (1+x)^{47}  \end{matrix} \right|   = A +Bx +Cx^2 + ........then A $$ = ___________ 

Since $$ f(x)  =  ( 1 +x)^{17} + (1+x)^{23} (1+x) 41 \left| \begin{matrix} 1 & (1+x)^{ 2 } & (1+x)^{ 6 } \\ 1 & (1+x)^{ 6 } & (1+x)^{ 11 } \\ 1 & (1+x)^{ 2 } & (1+x)^{ 6 } \end{matrix} \right| =0 $$
[ since $$ R_1 $$ and $$ R_3 $$ are identical ]
$$ \therefore A = 0$$


Solve the following simultaneous equation.
$$3a + 5b = 26; a +  5b = 22$$

$$3a + 5b = 26$$              -------(I)
$$a + 5b = 22$$           ------------(II)
Subtracting (II) from (I)
$$2a = 4$$
$$\Rightarrow a = 2$$
Putting the value of $$a = 2$$ in (II)
$$5b = 22 - 2 = 20$$
$$\Rightarrow b = \dfrac{20}{5} = 4$$
Thus,$$a = 2$$ and $$b = 4$$.


Solve the following simultaneous equation.
$$x + 7y = 10; 3x - 2y = 7$$

$$x + 7y = 10;$$       ------------(I)
$$3x - 2y = 7$$             -----------(II)
multiplying (I) with 3
$$3x + 21y = 30;$$            ---------(III)
$$3x - 2y = 7$$       ---------------(IV)
Subtracting (IV) from (III) we get
$$3x+21y-3x+2y=30-7$$
$$23y = 23 $$
$$\Rightarrow  1$$
Putting the value of y in (IV) we get
$$3x - 2(1) = 7$$
$$\Rightarrow 3x = 7 + 2 = 9$$
$$\Rightarrow 3x = 9$$
$$\Rightarrow x = 3$$
Thus, $$(x, y) = (3, 1)$$


Solve the following simultaneous equation:
$$5m - 3n = 19; m - 6n = -7$$

$$5m - 3n = 19$$   ...........(I)
$$m - 6n = - 7$$   .............(II)
Multiplying (I) with 2 we get
$$10m - 6n =  38$$   ..........(III)
Subtracting (II) from (III) wqe get
$$10m - m - 6n - (-6n) = 38 - (-7)$$
$$\Rightarrow 9m = 45$$
$$\Rightarrow m = \dfrac{45}{9} = 5$$
Putting the value of $$m = 5$$ in (II) we get
$$5 - 6n = -7$$
$$\Rightarrow - 6n = -7 - 5$$
$$\Rightarrow - 6n = - 12$$
$$\Rightarrow n = \dfrac{-12}{-6} = 2$$
Thus, $$(m, n) = (5, 2)$$.


Solve the following simultaneous equation:
$$5x + 2y = -3; x + 5y = 4$$

$$5x + 2y = -3$$   ........(I)
$$x + 5y = 4$$   ..........(II)
Multiply (II) with 5 we get
$$5x + 25y = 20$$  ............(III)
Subtracting (III) from (I) we get
$$5x - 5x + 2y - 25y = -3 - 20$$
$$\Rightarrow - 23y = -23$$
$$\Rightarrow y = \dfrac{-23}{-23} = 1$$
Putting the value of $$y =1$$ in (II) we get
$$x + 5(1) = 4$$
$$\Rightarrow x + 5 = 4$$
$$\Rightarrow x = 4 - 5 = -1$$
Thus $$(x,y) = (-1,1)$$


Solve the following simultaneous equations.
$$\frac{7x - 2y}{xy} = 5 ;\frac{8x + 7y}{xy} = 15$$

$$\dfrac{7x - 2y}{xy} = 5 ;\dfrac{8x + 7y}{xy} = 15$$
$$\Rightarrow \dfrac{7}{y} - \dfrac{2}{x} = 5$$ and $$\dfrac{8}{y} - \dfrac{7}{x} = 15$$
Let $$\dfrac{1}{x} = u, \dfrac{1}{y} = v$$
$$7v - 2u = 5......(I)$$
$$8v + 7u = 15......(II)$$
Multiply (I) with 7 and (II) with 2
$$49v - 14u = 35....(III)$$
$$16v + 14u = 30.....(IV)$$
Adding (III) and (IV)
$$65v = 65$$
$$\Rightarrow$$ $$v = 1$$
And $$\dfrac{1}{y} = v = 1$$
$$\Rightarrow y = 1$$
Putting the value of v in (I)
$$7(1) - 2u = 5$$
$$\Rightarrow$$ $$u = 1$$
$$\dfrac{1}{x} = u = 1$$
$$\Rightarrow x = 1$$
$$(x,y) = (1,1)$$


Solve the following simultaneous equation.
$$49x - 57y = 172; 57x - 49y = 252$$

$$49x - 57y = 172$$...........(I)
$$57x - 49y = 252$$...........(II)
Adding (I) and (II)
$$49x + 57x - 57y - 49y = 172 + 252$$
$$\Rightarrow 106x - 106y = 424$$
$$\Rightarrow x - y = 4$$...............(III)
Subtracting (II) from (I) we have
$$49x + 57x - 57y - (- 49y) = 252 - 172$$
$$\Rightarrow - 8x - 8y = -80$$
$$\Rightarrow - x - y = -10$$
$$\Rightarrow x + y = 10$$...............(IV)
Adding (III) and (IV)
$$x - y = 4$$
$$x + y = 10$$
$$\Rightarrow 2x = 14$$
$$ \Rightarrow x = 7$$
Putting the value of x = 7 in (IV) we get
$$7 + y = 10$$
$$\Rightarrow y = 10 -7$$
$$\Rightarrow y = 3$$
Thus, $$(x,y) = (7,3)$$


Solve the following simultaneous equation.
$$\dfrac{1}{3}x + y = \dfrac{10}{3}; 2x + \dfrac{1}{4}y = \dfrac{11}{4}$$

$$\dfrac{1}{3}x + y = \dfrac{10}{3}.$$.........(I)
$$2x + \dfrac{1}{4}y = \dfrac{11}{4}$$......(II)
Multiply (I) with 3 and (II) with 4
$$x + 3y = 10$$.............(III)
$$8x + y = 11$$...........(IV)
Multiply (IV) with 3
$$24x + 3y = 33$$ ..............(V)
Subtracting (V) from (III)
$$x  - 24x + 3y - 3y = 10 - 33$$
$$\Rightarrow- 23x = -23$$
$$\Rightarrow x = 1$$
Putting the value of $$x = 1$$ 
$$1 + 3y = 10$$
$$\Rightarrow 3y = 10 - 1 = 9$$
$$\Rightarrow y = \dfrac{9}{3} = 3$$
Thus, $$(x,y) = (11,3)$$


Solve the following equation by Cramer's method.
$$3x - 2y = \frac{5}{2}; \frac{1}{3}x + 3y = - \frac{4}{3}$$

$$3x - 2y = \dfrac{5}{2}; \dfrac{1}{3}x + 3y = - \dfrac{4}{3}$$

$$D = \begin{vmatrix} 3 & {-2} \\ {\dfrac{1}{3}} & 3 \end{vmatrix} = 9 + \dfrac{2}{3} = \dfrac{20}{3}$$

$$D_x = \begin{vmatrix} \dfrac{5}{2} & {-2} \\ \dfrac{-4}{3} & 3 \end{vmatrix} = \dfrac{5}{2} - \dfrac{8}{3} = \dfrac{29}{6}$$

$$D_y = \begin{vmatrix} 3 & \dfrac{5}{2} \\ \dfrac{1}{3} & \dfrac{-4}{3} \end{vmatrix}$$ $$= -4 - \dfrac{5}{6} = \dfrac{-29}{6}$$

$$x = \dfrac{D_x}{D} = \dfrac{\dfrac{29}{6}}{\dfrac{29}{3}} = \dfrac{1}{2}$$

$$y = \dfrac{D_y}{D} = \dfrac{\dfrac{-29}{6}}{\dfrac{29}{3}} = \dfrac{-1}{2}$$

$$(x,y) = (\dfrac{1}{2}, \dfrac{-1}{2})$$


Solve the following simultaneous equations
$$\frac{148}{x} + \frac{231}{y} = \frac{527}{xy}; \frac{231}{x} + \frac{148}{y} = \frac {610}{xy}$$

$$\dfrac{148}{x} + \dfrac{231}{y} = \dfrac{527}{xy}; \dfrac{231}{x} + \dfrac{148}{y} = \dfrac {610}{xy}$$
Multiply by $$xy$$
$$148y + 231x = 527.....(I)$$
$$231y + 148x = 610....(II)$$
Adding (I) and (II)
$$379y + 179x = 1137$$
$$\Rightarrow x + y = 3 ......(III)$$
$$(II) - (I)$$
$$83y - 83x = 83$$
$$\Rightarrow y - x = 1 .....(IV)$$
(III) + (IV)
$$2y = 4$$
$$\Rightarrow y = 2$$
Putting the value of y in (IV)
$$2 - x = 1$$
$$\Rightarrow$$ $$x = 1$$
$$(x, y) = (1,2)$$


Solve the following equations by Cramer's method.
4m - 2n = -4; 4m + 3n = 16

$$4m - 2n = -4; 4m + 3n = 16$$ 

$$D = \begin{vmatrix} 4 & {-2} \\ 4 & 3 \end{vmatrix} = 4 \times 4 - (-2) \times 4 = 12 + 8 = 20$$

$$D_x = \begin{vmatrix} {-4} & {-2} \\ 16 & 3 \end{vmatrix} = -4 \times 3 - (-2) \times 16 = - 12 + 32 = 20$$

$$D_y = \begin{vmatrix} 4 & {-4} \\ 4 & 16 \end{vmatrix} = 4 \times 16 - (-4) \times 4 = 64 + 16 = 80$$

$$x = \dfrac{D_x}{D} = \dfrac{20}{20} = 1$$

$$y = \dfrac{D_y}{D} = \dfrac{80}{20} = 4$$

$$(x, y) = (1, 4)$$


Solve the following simultaneous equations.
$$\frac{1}{2(3x + 4y)} + \frac{1}{5(2x - 3y)} = \frac{1}{4}; \frac{5}{(3x + 4y)} - \frac{2}{(2x - 3y)} = -\frac{3}{2}$$

$$\dfrac{1}{2(3x + 4y)} + \dfrac{1}{5(2x - 3y)} = \dfrac{1}{4}; \dfrac{5}{(3x + 4y)} - \dfrac{2}{(2x - 3y)} = -\dfrac{3}{2}$$
$$\dfrac{1}{3x + 4y} = u, \dfrac{1}{2x - 3y} = v$$
$$\dfrac{1}{2}u + \dfrac{1}{5}v = \dfrac{1}{4}$$
$$\Rightarrow$$ $$10u + 4v = 5.$$....(I)
$$5u - 2v = \dfrac{-3}{2}$$
$$\Rightarrow$$ $$10u - 4v = -3$$. ......(II)
(I) + (II)
$$20u = 2$$
$$\Rightarrow u = \dfrac{1}{10}$$
Putting the value of u in (II)
$$10 \times \dfrac{1}{10} -4v = -3$$
$$\Rightarrow 1 + 3 = 4v$$
$$\Rightarrow v = 1$$
$$\dfrac{1}{3x + 4y} = u = \dfrac{1}{10}$$
$$\Rightarrow 3x + 4y = 10$$....(III)
$$\dfrac{1}{2x - 3y} = v = 1$$
$$\Rightarrow 2x - 3y = 1$$...........(VI)
Multiply (III) with 2 and (VI) with 3
$$6x + 8y = 20 ....(V)$$
$$6x - 9y = 3 .......(VI)$$
$$(V) - (VI)$$
$$17y = 17$$
$$\Rightarrow y = 1$$
Putting the value of y in (VI)
$$6x - 9 = 3$$
$$\Rightarrow 6x = 12$$
$$\Rightarrow x = 2$$
$$(x,y) = (2,1)$$


Solve the following equations by Cramer's methd.
$$6x - 3y = -10; 3x + 5y - 8 = 0$$

$$6x - 3y = -10; 3x + 5y - 8 = 0$$

$$D = \begin{vmatrix} 6 & {-3} \\ 3 & 5 \end{vmatrix} = 6 \times 5 - (-3) \times 3 = 30 + 9 = 39$$

$$D_x = \begin{vmatrix} {10} & {-3} \\ 8 & 5 \end{vmatrix} = -10 \times 5 - (-3) \times 8 = - 50 + 24 = -26$$

$$D_y = \begin{vmatrix} 6 & {-10} \\ 3 & 8 \end{vmatrix} = 6 \times 8 - (-10) \times 3 = 48 + 30 = 78$$

$$x = \dfrac{D_x}{D} = \dfrac{-26}{39} = \dfrac{-2}{3}$$

$$y = \dfrac{D_y}{D} = \dfrac{78}{39} = 2$$

$$(x, y) = (\dfrac{-2}{3}, 2)$$


Solve the following
simultaneous equation using Cramer's rule.
$$6x - 4y = -12$$
$$8x - 3y = -2$$

$$6x - 4y = -12$$
$$8x - 3y = -2$$

$$D = \begin{vmatrix} 6&-4 \\ 8&-3 \end{vmatrix} = 6 \times (-3) - (-4) \times 8 = (-18) + 32 = 14 $$

$${D}_{x} = \begin{vmatrix} -12&-4 \\ -2&-3
\end{vmatrix} = (-12) \times (-3) - (-4) \times (-2) = 36 - 8 = 28$$

$${D}_{y} = \begin{vmatrix} 6&-12 \\ 8&-2 \end{vmatrix} = 6 \times (-2) - (-12) \times 8 = -12 + 96 = 84$$

$$x = \dfrac {{D}_{x}}{D} = \dfrac {28}{14} = 2$$

$$y = \dfrac {{D}_{y}}{D} = \dfrac {84}{14} = 6$$

$$(x,y) = (2,6)$$



Solve the following simultaneous equations.
2x + y = - 2; 3x - y =7 

2x + y = -2  .....(I)
3x - y = 7  .....(II)
Adding (I) and (II)
5x = 5
⇒4⇒4 x= 1
Putting the value of x in (I)
 2 x 1 + y = -2
⇒⇒ 2 + y = -2
⇒⇒ y = - 4 


Solve the following sets of simultaneous equations.
2y -x =0; 10x + 15y = 105

Let the length be x and the breadth be y.
Perimeter of the rectangle = 2(1 + b) = 26
2(1 + b) = 26
⇒⇒2[( x - 5) + (y - 5)] = 26
⇒⇒ 2 [ x + y - 10] = 26
⇒⇒ x + y = 23
Hence, the correct answer is option (C). 


Solve the following simultaneous equations. x -2 y = -1 ; 2x - y =7 

x + y = 11  .....(I)
2x - 3y = 7 ..... (II)
Multiply (I) with 3
3x + 3y = 33 ..... (III)
Adding (II) and (III)
5x = 40
$$\Rightarrow4$ x = 8
Putting the value of x in (I)
8 + y = 11
y = 3 


Solve the following simultaneous equations. x - 2y = - 2 ; x +2y =10 

x - 2y = - 2 .....(I) 
x + 2y = 10 .......(II) 
Adding I and II 
2x = 8 
$$\Rightarrow$$ x = 4 
Putting the value of x in (I) we get 
4 - 2y = -2 
$$\Rightarrow$$ - 2y = -6 
$$\Rightarrow$$ y = 3 


If $$a,b,c$$ are real, find the factors of the determination.
$$\Delta =\begin{vmatrix} b+c & c+a & a+b \\ c+a & a+b & b+c \\ a+b & b+c & c+a \end{vmatrix}$$

$${R}_{1}\Rightarrow {R}_{1}+{R}_{2}+{R}_{3}$$
$$\Delta =\begin{vmatrix} 2\left( a+b+c \right)  & 2\left( a+b+c \right)  & 2\left( a+b+c \right)  \\ c+a & a+b & b+c \\ a+b & b+c & c+a \end{vmatrix}$$
$$=2\left( a+b+c \right) \begin{vmatrix} 1 & 1 & 1 \\ c+a & a+b & b+c \\ a+b & b+c & c+a \end{vmatrix}$$
$${c}_{2}\Rightarrow {c}_{2}-{c}_{1}$$; $${c}_{3}\Rightarrow {c}_{3}-{c}_{1}$$
$$=2\left( a+b+c \right) \begin{vmatrix} 1 & 0 & 0 \\ c+a & b-c & b-a \\ a+b & c-a & c-b \end{vmatrix}=2\left( a+b+c \right) \left[ (b-c)(c-b)-(b-a)(c-a) \right] $$
$$=2\left( a+b+c \right) [bc-{b}^{2}-{c}^{2}_bc-bc+ba+ac-{a}^{2}]$$
$$=2\left( a+b+c \right) [ab+bc+ca-{a}^{2}-{b}^{2}-{c}^{2}]$$
$$=-2\times \cfrac{1}{2}(a+b+c)[{(a-b)}^{2}+{(b-c)}^{2}+{(c-a)}^{2}$$
The factors are $$a+b+c$$ and $${a}^{2}+{b}^{2}+{c}^{2}-ab-bc-ca$$
$$=1(a+b+c)[{(a-b)}^{2}+{(b-c)}^{2}+{(c-a)}^{2}$$
If $$\Delta =0$$ then $$(a+b+c)[{(a-b)}^{2}+{(b-c)}^{2}+{(c-a)}^{2}]=0$$
then $$a+b+c=0$$ or $$a=b=c$$


Solve the following system of equation by Cramer's rule:
$$2x-7y-13=0, 5x+6y-9=0$$

Given equations
$$2x-7y-13=0, 5x+6y-9=0$$
here,
$$\Delta = \begin{vmatrix} 2 & -7 \\ 5 & 6 \end{vmatrix}=12+35=47$$
$$\Delta_1=\begin{vmatrix} 13 & -7 \\ 9 & 6 \end{vmatrix}=78+63=141$$
$$\Delta _2=\begin{vmatrix} 2 & 13 \\ 5 & 9 \end{vmatrix}=18-65=-47$$
$$\because \Delta \ne 0, \Delta_1 \ne 0$$ and $$\Delta_2 \ne 0$$
$$\therefore$$ Solution will be unique.
Using Cramer's rule
$$x=\dfrac{\Delta_1}{\Delta}=\dfrac{141}{47}=3$$
and $$y=\dfrac{\Delta_2}{\Delta}=\dfrac{-47}{47}=-1$$
Solution of equation be $$x=3, y=-1$$


Use Cramer's rule to solve the following system of equations:
$$2x-y=17$$
$$3x+5y=6$$

Given,
$$2x-y=17$$
$$3x+5y=6$$
Here, $$\Delta =\begin{vmatrix} 2 & -1 \\ 3 & 5 \end{vmatrix}=10+3=13\\ $$
 $$\Delta_a =\begin{vmatrix} 17 & -1 \\ 6 & 5 \end{vmatrix}=85+6=91\\ $$
 $$\Delta_2 =\begin{vmatrix} 2 & 17 \\ 3 & 6 \end{vmatrix}=12-51=-39\\ $$
$$\because \Delta \ne 0, \Delta_1 \ne 0$$ and $$\Delta_2 \ne 0$$
$$\therefore$$ Solution will be unique 
By using Cramer's rule
$$x=\dfrac{\Delta_1}{\Delta}=\dfrac{91}{13}=7, y=\dfrac{\Delta_2}{\Delta}=\dfrac{-39}{13}=-3$$
Hence, solution is $$x=7, y=-3$$


Solve the following system of equation by Cramer's rule:
$$2x+3y=9, 3x-2y=7$$

Given equations
$$2x+3y=9, 3x-2y=7$$
here,
$$x=\dfrac{\Delta_1}{\Delta}=\dfrac{-39}{-13}=3$$
and $$y=\dfrac{\Delta_2}{\Delta}=\dfrac{-13}{-13}=1$$
solution of equation $$x=3, y=1$$


Use Cramer's rule to solve the following system of equations:
$$3x+ay=4$$
$$2x+ay=2, a \ne 0$$

Given,
$$3x+ay=4$$
$$2x+ay=2, a \ne 0$$
$$a \ne 0$$
where, $$\Delta =\begin{vmatrix} 3 & a \\ 2 & a \end{vmatrix}=3a-2a=a\\ $$
 $$\Delta_1 =\begin{vmatrix} 4 & a \\ 2 & a \end{vmatrix}=4a-2a=2a\\ $$
 $$\Delta_2 =\begin{vmatrix} 3 & 4\\ 2 & 2 \end{vmatrix}=6-8=-2\\ $$
$$\because \Delta \ne 0, \Delta_1 \ne 0$$ and $$\Delta_2 \ne 0$$
$$\therefore$$ Solution will be unique 
By using Cramer's rule
$$x=\dfrac{\Delta_1}{\Delta}=\dfrac{2a}{a}=2, y=\dfrac{\Delta_2}{\Delta}=\dfrac{-2}{a}=\dfrac{-2}{a}$$
Hence, solution is $$x=1, y=\dfrac{-2}{a}$$


A determinant of second order is made with the elements 0 andFind the number of determinants with non-negative values.


$$\textbf{Step -1: Finding the number of possible second order determinants with elements 0 an 1.}$$

                $$\text{A determinant of second order has four elements and the choice for one element is 2, }$$

                $$\text{i.e. either 0 or 1.}$$

                $$\therefore \text{Number of possible second order determinants with elements 0 and 1}=2^4=16.$$

$$\textbf{Step -2: Finding the number of second order determinants with negative values.}$$

                $$\begin{vmatrix}0&1\\1&0\end{vmatrix},\begin{vmatrix}0&1\\1&1\end{vmatrix}\text{ and }\begin{vmatrix}1&1\\1&0\end{vmatrix}\text{ are the only determinants of second order with negative values.}$$

                $$\therefore\text{Number of second order determinants with negative values}=3.$$

$$\textbf{Step -3: Finding the number of second order determinants with non-negative values.}$$

                $$\text{Number of second order determinants with non-negative values}=16-3$$

                $$=13$$

$$\textbf{ Hence, the number of determinants with non-negative values are 13.}$$



Let $$A =\begin{bmatrix} 2&3 \\-1 &5 \end{bmatrix}$$. If $$A^{-1}=xA+yI$$, find $$x + 2y$$.

$$A\quad =\quad \begin{bmatrix} 2 & 3 \\ -1 & 5 \end{bmatrix}\\ $$

$$A^{ -1 }\quad =\quad xA\quad +\quad yI\\$$

$$ \Rightarrow \quad A^{ -1 }A\quad =\quad xAA\quad +\quad yIA\\ $$

$$\Rightarrow \quad I\quad =\quad xA^{ 2 }\quad +\quad yA\\ $$

$$\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\quad =\quad x\begin{bmatrix} 2 & 3 \\ -1 & 5 \end{bmatrix}\begin{bmatrix} 2 & 3 \\ -1 & 5 \end{bmatrix}\quad +\quad y\begin{bmatrix} 2 & 3 \\ -1 & 5 \end{bmatrix}\\$$

$$ \quad \quad \quad \quad \quad =\quad x\begin{bmatrix} 1 & 21 \\ -7 & \quad 22\quad  \end{bmatrix}\quad +\quad y\begin{bmatrix} 2 & 3 \\ -1 & 5 \end{bmatrix}\\ $$

$$comparing\quad elements\quad on\quad both\quad sides\\$$

$$ x+2y\quad =\quad 1\quad and\quad -7x-y\quad =\quad 0\\$$

$$ solving\quad above\quad equations\quad gives\\$$

$$ x\quad =\quad \displaystyle\frac { -1 }{ 13 } \quad and\quad y\quad =\quad \displaystyle\frac { 7 }{ 13 } $$

$$\Rightarrow x+2y=1$$


If $$A =\begin{bmatrix} 1&0  &0 \\0 &1  &1 \\0 &-2  &4 \end{bmatrix}$$, $$I=\begin{bmatrix} 1&0  &0 \\0 &1  &0 \\0 &0 &1 \end{bmatrix}$$ and
$$\displaystyle A^{-1}=\frac{1}{6}(A^2+\alpha A+\beta I)$$, find $$\beta/11 $$

$$If\quad A=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & -2 & 4 \end{bmatrix},\quad I=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\quad and\quad A^{ -1 }=\dfrac { 1 }{ 6 } (A^{ 2 }+\alpha A+\beta I)\\ \Rightarrow \quad A^{ -1 }A\quad =\quad \frac { 1 }{ 6 } \left( A^{ 2 }A+\alpha AA+\beta IA \right) \\ \Rightarrow \quad 6I\quad =\quad A^{ 3 }+\alpha A^{ 2 }+\beta A\quad -------\boxed { 1 } \\ A^{ 2 }\quad =\quad \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & -2 & 4 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & -2 & 4 \end{bmatrix}\quad =\quad \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 5 \\ 0 & -10 & 14 \end{bmatrix}\\ A^{ 3 }\quad =\quad \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 5 \\ 0 & -10 & 14 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & -2 & 4 \end{bmatrix}\quad =\quad \begin{bmatrix} 1 & 0 & 0 \\ 0 & -11 & 19 \\ 0 & -38 & 46 \end{bmatrix}\\ from\quad equation\quad ----\boxed { 1 } \\ \begin{bmatrix} 6 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{bmatrix}\quad =\quad \begin{bmatrix} 1 & 0 & 0 \\ 0 & -11 & 19 \\ 0 & -38 & 46 \end{bmatrix}+\alpha \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 5 \\ 0 & -10 & 14 \end{bmatrix}+\beta \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & -2 & 4 \end{bmatrix}\\ comparing\quad elements\quad on\quad both\quad sides\quad gives\\ \alpha +\beta \quad =\quad 5\quad and\quad -\alpha +\beta \quad =\quad 17\\ Hence,\quad \beta \quad =\quad 11\\ $$



The digit in the tens place of a two-digit number is three times that in the units place. If the digits are reversed, the new number will be $$36$$ less than the original number. Find the original number. Check your solution.

There are two possibility such as-
$$\Rightarrow \ 3\ 1$$
$$\Rightarrow \ 6\ 2$$
$$\Rightarrow \ 9\ 3$$
if we reversed the digit, only $$62$$ will given the resent as per question
$$62-26 \Rightarrow \  36$$
Hence original No is $$62$$



Find $$x$$ and $$y$$ using Cramer's Rule if :
$$\dfrac{1}{2x}+\dfrac{2}{3y}=10,\dfrac{3}{2x}-\dfrac{5}{3y}=-3$$

$$\dfrac { 1 }{ 2x } +\dfrac { 2 }{ 3y } =10\longrightarrow (1)\\ \dfrac { 3 }{ 2x } -\dfrac { 5 }{ 3y } =-3\longrightarrow (2)\\ Let,\quad \dfrac { 1 }{ 2x } =p\quad and\quad \dfrac { 1 }{ 3y } =q\\ \therefore \quad equation\quad becomes\quad \\ p+2q=10\longrightarrow (3)\\ 3p-5q=-3\longrightarrow (4)\\ By\quad Cramer's\quad rule\\ \begin{bmatrix} 1 & 2 \\ 3 & -5 \end{bmatrix}\left[ \begin{matrix} p \\ q \end{matrix} \right] =\left[ \begin{matrix} 10 \\ -3 \end{matrix} \right] \\ \therefore p=\dfrac { \begin{vmatrix} 10 & 2 \\ -3 & -5 \end{vmatrix} }{ \begin{vmatrix} 1 & 2 \\ 3 & -5 \end{vmatrix} } \quad and\quad q=\dfrac { \begin{vmatrix} 1 & 10 \\ 3 & -3 \end{vmatrix} }{ \begin{vmatrix} 1 & 2 \\ 3 & -5 \end{vmatrix} } \\ \Rightarrow p=4\quad and\quad q=3\\ \because p=\dfrac { 1 }{ 2x } =4\\ \Rightarrow x=\dfrac { 1 }{ 8 } \\ and\quad q=\dfrac { 1 }{ 3y } =3\\ \Rightarrow y=\dfrac { 1 }{ 9 } $$


Prove that one root of the equation is x=2 and hence find the remaining roots
  $$\left| \begin{matrix} x \\ 2 \\ -3 \end{matrix}\begin{matrix} -6 \\ -3x \\ 2x \end{matrix}\begin{matrix} -1 \\ x-3 \\ x+2 \end{matrix} \right| =0$$


$$\begin{vmatrix} x & -6 & -1\\  2 & -3x & x-3 \\ -3 & 2x & x+2 \end{vmatrix}=0$$

$$\Rightarrow x[-3x(x+2)-2x(x-3)]+6[2(x+2)+3(x-3)]-1[2(2x)-9x]=0$$

$$\Rightarrow x[-3x^2 - 6 - 2x^2+ 6]+6[2x+4+3x-9]-[4x-9x]=0$$

$$\Rightarrow x(-5x^2)+6(5x-5) + 5x = 0$$

$$\Rightarrow -5x^3 + 30(x-1)+5x=0$$

$$\Rightarrow -x^3 + 6x-6+x = 0$$

$$\Rightarrow -x^3 + 7x - 6 = 0$$

$$\Rightarrow x^3-7x+6=0$$

Let $$f(x) = x^3 - 7x + 6$$

$$f(2) = 2^3 - 7.2 + 6$$

$$= 8-14 + 6$$

$$= 14 - 14$$

$$=0$$

Hence $$x=2$$ is a root of the equation $$x^3 - 7x + 6 = 0$$  

[see image]

$$(x-2) [x(x+3) - 1(x+3) ] =0$$
$$(x-2)[x^2 + 3x - x - 3]=0$$

$$(x-2)[x(x+3) - 1(x+3)]=0$$
$$(x-2)(x-1)(x+3)=0$$

$$\therefore x = 2, 1, -3$$

Answer: Roots of the equation are $$x=2, 1, -3$$

2047422_1161645_ans_c596b71418ce4cff8d7d058a008753c4.png


If S the set of distinct values of 'b' for which the following system of linear equations
         x + y + z = 1 
         x + ay + z = 1 
         ax + by + z = 1


2039531_1296476_ans_5edf15181a33443697582dad58ff68ee.jpg


Use cramer's rule and solve 
$$3x+4y+5z=18$$
$$2x-y+8z=13$$
$$5x-2y+7z=20$$

Consider the system of equations 
$$3x+4y+5z=18$$
$$2x-y+8z=13$$
$$5x-2y+7z=20$$
Cramer's rule is applicable when determinant$$\neq 0$$
$$D=\left|\begin{matrix}3  & 4  & 5 \\ 2 &-1 & 8 \\ 5 & -2 & 7 \end{matrix}\right|$$
$$=3\left(-7+16\right)-4\left(14-40\right)+5\left(-4+5\right)$$
$$=27+104+5=136\neq 0$$
$$\therefore$$ Cramer's rule is aplicable.
$${D}_{x}=\left|\begin{matrix}18  & 4  & 5 \\ 13 &-1 & 8 \\ 20 & -2 & 7 \end{matrix}\right|$$ by replacing the coefficents of $${C}_{1}$$ by the Constants.
$$=18\left(-7+16\right)-4\left(91-160\right)+5\left(-26+20\right)$$
$$=81+276-30=321$$
$${D}_{y}=\left|\begin{matrix}3  & 18  & 5 \\ 2 &13 & 8 \\ 5 & 20 & 7 \end{matrix}\right|$$by replacing the coefficents of $${C}_{2}$$ by the Constants.
$$=3\left(91-160\right)-18\left(35-40\right)+5\left(40-65\right)$$
$$=-207+90-125=-242$$
$${D}_{z}=\left|\begin{matrix}3  & 4  & 18 \\ 2 &-1 & 13 \\ 5 & -2 & 20 \end{matrix}\right|$$by replacing the coefficents of $${C}_{3}$$ by the Constants.
$$=3\left(-20+26\right)-4\left(40-65\right)+8\left(-10+5\right)$$
$$=18+100-40=78$$
The values of $$x,y,z$$ are calculated as
$$x=\dfrac{{D}_{x}}{D}=\dfrac{321}{136}$$
$$y=\dfrac{{D}_{y}}{D}=\dfrac{-242}{136}=\dfrac{-121}{68}$$
$$z=\dfrac{{D}_{z}}{D}=\dfrac{78}{136}=\dfrac{39}{68}$$


Solve the following simultaneous equations using corner's rule.
(3) $$x+2y=-1;2x-3y=12$$


1961049_1491772_ans_1703b5c0cd7a4d1d8012ebea9c1c2247.jpg


The value of $$\begin{vmatrix} 2{ x }_{ 1 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 1 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 1 } & 2{ x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } & 2{ x }_{ 3 }{ y }_{ 3 } \end{vmatrix}$$ is

Given $$D=\left| \begin{matrix} 2{ x }_{ 1 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 1 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 1 } & 2{ x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } & 2{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| $$

$$\therefore D=\left| \begin{matrix} { x }_{ 1 }{ y }_{ 1 }+{ x }_{ 1 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 1 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 1 } & { x }_{ 2 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| $$

$$\therefore D=\left| \begin{matrix} { x }_{ 1 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 1 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 1 }{ y }_{ 3 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +\left| \begin{matrix} { x }_{ 1 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 2 }{ y }_{ 1 } & { x }_{ 2 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 3 }{ y }_{ 1 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| $$

$$\therefore D={ x }_{ 1 }\left| \begin{matrix} { y }_{ 1 } & { x }_{ 1 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { y }_{ 2 } & { x }_{ 2 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { y }_{ 3 } & { x }_{ 3 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 3 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ y }_{ 1 }\left| \begin{matrix} { x }_{ 1 } & { x }_{ 1 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 2 } & { x }_{ 2 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 3 } & { x }_{ 3 }{ y }_{ 2 }+{ x }_{ 2 }{ y }_{ 3 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| $$

$$\therefore D={ x }_{ 1 }\left| \begin{matrix} { y }_{ 1 } & { x }_{ 1 }{ y }_{ 2 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { y }_{ 2 } & { x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { y }_{ 3 } & { x }_{ 3 }{ y }_{ 2 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ x }_{ 1 }\left| \begin{matrix} { y }_{ 1 } & { x }_{ 2 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { y }_{ 2 } & { x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { y }_{ 3 } & { x }_{ 2 }{ y }_{ 3 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ y }_{ 1 }\left| \begin{matrix} { x }_{ 1 } & { x }_{ 1 }{ y }_{ 2 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 2 } & { x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 3 } & { x }_{ 3 }{ y }_{ 2 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ y }_{ 1 }\left| \begin{matrix} { x }_{ 1 } & { x }_{ 2 }{ y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 2 } & { x }_{ 2 }{ y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 3 } & { x }_{ 2 }{ y }_{ 3 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| $$

$$\therefore D={ x }_{ 1 }{ y }_{ 2 }\left| \begin{matrix} { y }_{ 1 } & { x }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { y }_{ 2 } & { x }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { y }_{ 3 } & { x }_{ 3 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ x }_{ 1 }{ x }_{ 2 }\left| \begin{matrix} { y }_{ 1 } & { y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { y }_{ 2 } & { y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { y }_{ 3 } & { y }_{ 3 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ y }_{ 1 }{ y }_{ 2 }\left| \begin{matrix} { x }_{ 1 } & { x }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 2 } & { x }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 3 } & { x }_{ 3 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ y }_{ 1 }{ x }_{ 2 }\left| \begin{matrix} { x }_{ 1 } & { y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 2 } & { y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 3 } & { y }_{ 3 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| $$

$$\therefore D={ x }_{ 1 }{ y }_{ 2 }\left| \begin{matrix} { y }_{ 1 } & { x }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { y }_{ 2 } & { x }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { y }_{ 3 } & { x }_{ 3 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ x }_{ 1 }{ x }_{ 2 }\left( 0 \right) +{ y }_{ 1 }{ y }_{ 2 }\left( 0 \right) +{ y }_{ 1 }{ x }_{ 2 }\left| \begin{matrix} { x }_{ 1 } & { y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 2 } & { y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 3 } & { y }_{ 3 } & { x }_{ 3 }{ y }_{ 3 }+{ x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| $$

$$\therefore D={ x }_{ 1 }{ y }_{ 2 }\left| \begin{matrix} { y }_{ 1 } & { x }_{ 1 } & { x }_{ 1 }{ y }_{ 3 } \\ { y }_{ 2 } & { x }_{ 2 } & { x }_{ 2 }{ y }_{ 3 } \\ { y }_{ 3 } & { x }_{ 3 } & { x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ x }_{ 1 }{ y }_{ 2 }\left| \begin{matrix} { y }_{ 1 } & { x }_{ 1 } & { x }_{ 3 }{ y }_{ 1 } \\ { y }_{ 2 } & { x }_{ 2 } & { x }_{ 3 }{ y }_{ 2 } \\ { y }_{ 3 } & { x }_{ 3 } & { x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ y }_{ 1 }{ x }_{ 2 }\left| \begin{matrix} { x }_{ 1 } & { y }_{ 1 } & { x }_{ 1 }{ y }_{ 3 } \\ { x }_{ 2 } & { y }_{ 2 } & { x }_{ 2 }{ y }_{ 3 } \\ { x }_{ 3 } & { y }_{ 3 } & { x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| +{ y }_{ 1 }{ x }_{ 2 }\left| \begin{matrix} { x }_{ 1 } & { y }_{ 1 } & { x }_{ 3 }{ y }_{ 1 } \\ { x }_{ 2 } & { y }_{ 2 } & { x }_{ 3 }{ y }_{ 2 } \\ { x }_{ 3 } & { y }_{ 3 } & { x }_{ 3 }{ y }_{ 3 } \end{matrix} \right| $$

$$\therefore D={ x }_{ 1 }{ y }_{ 2 }{ y }_{ 3 }\left| \begin{matrix} { y }_{ 1 } & { x }_{ 1 } & { x }_{ 1 } \\ { y }_{ 2 } & { x }_{ 2 } & { x }_{ 2 } \\ { y }_{ 3 } & { x }_{ 3 } & { x }_{ 3 } \end{matrix} \right| +{ x }_{ 1 }{ y }_{ 2 }{ x }_{ 3 }\left| \begin{matrix} { y }_{ 1 } & { x }_{ 1 } & { y }_{ 1 } \\ { y }_{ 2 } & { x }_{ 2 } & { y }_{ 2 } \\ { y }_{ 3 } & { x }_{ 3 } & { y }_{ 3 } \end{matrix} \right| +{ y }_{ 1 }{ x }_{ 2 }{ y }_{ 3 }\left| \begin{matrix} { x }_{ 1 } & { y }_{ 1 } & { x }_{ 1 } \\ { x }_{ 2 } & { y }_{ 2 } & { x }_{ 2 } \\ { x }_{ 3 } & { y }_{ 3 } & { x }_{ 3 } \end{matrix} \right| +{ y }_{ 1 }{ x }_{ 2 }{ x }_{ 3 }\left| \begin{matrix} { x }_{ 1 } & { y }_{ 1 } & { y }_{ 1 } \\ { x }_{ 2 } & { y }_{ 2 } & { y }_{ 2 } \\ { x }_{ 3 } & { y }_{ 3 } & { y }_{ 3 } \end{matrix} \right| $$

$$\therefore D={ x }_{ 1 }{ y }_{ 2 }{ y }_{ 3 }\left( 0 \right) +{ x }_{ 1 }{ y }_{ 2 }{ x }_{ 3 }\left( 0 \right) +{ y }_{ 1 }{ x }_{ 2 }{ y }_{ 3 }\left( 0 \right) +{ y }_{ 1 }{ x }_{ 2 }{ x }_{ 3 }\left( 0 \right) $$

$$\therefore D=0$$


Shew that $$\begin{vmatrix} yz-x^2 & zx-y^2 & xsy-z^2 \\ zx-y^2 & xy-z^2 & yz-x^2 \\ xy-z^2 & yz-x^2 & zx-y^2 \end{vmatrix}=\begin{vmatrix} r^2 & u^2 & u^2 \\ u^2 & r^2 & u^2 \\ u^2 & u^2 & r^2 \end{vmatrix}$$
where $$r^{2}=x^{2}+y^{2}+z^{2}$$ and $$u^{2}=yz+zx+xy$$


1986609_1747426_ans_096cfa2e7c4a47409e84fcf105f4df5d.jpg


Prove that $$ \left| \begin{matrix} bc-a^2 & ca-b^2 & ab-c^2 \\ ca-b^2 & ab-c^2 & bc-a^2 \\ ab-c^2 & bc-a^2 & ca-b^2 \end{matrix} \right|   $$ i divisible by $$ ( a+b+ c) $$ and find the quotient.

Let $$D=\left| \begin{matrix} bc-{ a }^{ 2 } & ca-{ b }^{ 2 } & ab-{ c }^{ 2 } \\ ca-{ b }^{ 2 } & ab-{ c }^{ 2 } & bc-{ a }^{ 2 } \\ ab-{ c }^{ 2 } & bc-{ a }^{ 2 } & ca-{ b }^{ 2 } \end{matrix} \right| $$

This matrix is cofactor matrix of $$\left| \begin{matrix} a & b & c \\ b & c & a \\ c & a & b \end{matrix} \right| $$

Thus, by property of cofactor matrix,
$$\left| \begin{matrix} bc-{ a }^{ 2 } & ca-{ b }^{ 2 } & ab-{ c }^{ 2 } \\ ca-{ b }^{ 2 } & ab-{ c }^{ 2 } & bc-{ a }^{ 2 } \\ ab-{ c }^{ 2 } & bc-{ a }^{ 2 } & ca-{ b }^{ 2 } \end{matrix} \right| ={ \left| \begin{matrix} a & b & c \\ b & c & a \\ c & a & b \end{matrix} \right|  }^{ 2 }$$

$$\therefore \left| \begin{matrix} bc-{ a }^{ 2 } & ca-{ b }^{ 2 } & ab-{ c }^{ 2 } \\ ca-{ b }^{ 2 } & ab-{ c }^{ 2 } & bc-{ a }^{ 2 } \\ ab-{ c }^{ 2 } & bc-{ a }^{ 2 } & ca-{ b }^{ 2 } \end{matrix} \right| ={ \left| \begin{matrix} a & b & c \\ b & c & a \\ c & a & b \end{matrix} \right|  }{ \left| \begin{matrix} a & b & c \\ b & c & a \\ c & a & b \end{matrix} \right|  }$$

$$\therefore \left| \begin{matrix} bc-{ a }^{ 2 } & ca-{ b }^{ 2 } & ab-{ c }^{ 2 } \\ ca-{ b }^{ 2 } & ab-{ c }^{ 2 } & bc-{ a }^{ 2 } \\ ab-{ c }^{ 2 } & bc-{ a }^{ 2 } & ca-{ b }^{ 2 } \end{matrix} \right| =-{ \left| \begin{matrix} a & b & c \\ b & c & a \\ c & a & b \end{matrix} \right|  }{ \left| \begin{matrix} a & c & b \\ b & a & c \\ c & b & a \end{matrix} \right|  }$$

$$\therefore \left| \begin{matrix} bc-{ a }^{ 2 } & ca-{ b }^{ 2 } & ab-{ c }^{ 2 } \\ ca-{ b }^{ 2 } & ab-{ c }^{ 2 } & bc-{ a }^{ 2 } \\ ab-{ c }^{ 2 } & bc-{ a }^{ 2 } & ca-{ b }^{ 2 } \end{matrix} \right| ={ \left| \begin{matrix} a & b & c \\ b & c & a \\ c & a & b \end{matrix} \right|  }{ \left| \begin{matrix} a & -c & b \\ b & -a & c \\ c & -b & a \end{matrix} \right|  }$$

$$=\left| \begin{matrix} { a }^{ 2 }-bc+bc & ab-ab+{ c }^{ 2 } & ac-{ b }^{ 2 }+ac \\ ab-{ c }^{ 2 }+ab & { b }^{ 2 }-ac+ac & bc-bc+{ a }^{ 2 } \\ ac-ac+{ b }^{ 2 } & bc-{ a }^{ 2 }+bc & { c }^{ 2 }-ab+ab \end{matrix} \right| $$

$$=\left| \begin{matrix} { a }^{ 2 } & { c }^{ 2 } & 2ac-{ b }^{ 2 } \\ 2ab-{ c }^{ 2 } & { b }^{ 2 } & { a }^{ 2 } \\ { b }^{ 2 } & 2bc-{ a }^{ 2 } & { c }^{ 2 } \end{matrix} \right| $$




Class 12 Commerce Applied Mathematics Extra Questions