Differential Equations - Class 12 Commerce Applied Mathematics - Extra Questions

If $$y=Ae^{mx}+Be^{nx}$$, show that $$\dfrac{d^2y}{dx^2}-(m+n)\dfrac{dy}{dx}+mny=0$$.

Given $$\dfrac { { d }^{ 2 }y }{ d{ x }^{ 2 } } -(m+n)\dfrac { dy }{ dx } +mny=0$$
$$Solution:y=A{ e }^{ mx }+B{ e }^{ nx }$$
$$\dfrac { dy }{ dx } =Am{ e }^{ mx }+Bn{ e }^{ nx }$$
$$\dfrac { { d }^{ 2 }y }{ d{ x }^{ 2 } } =A{ m }^{ 2 }{ e }^{ mx }+B{ n }^{ 2 }{ e }^{ nx }$$
Substituting the values in above equation we get
$$A{ m }^{ 2 }{ e }^{ mx }+B{ n }^{ 2 }{ e }^{ nx }-(m+n)(Am{ e }^{ mx }+Bn{ e }^{ nx })+mn(A{ e }^{ mx }+B{ e }^{ nx })$$
$$=0$$


Solve: $$\left( {1 + {y^2}} \right)dx + \left( {x - {e^{ - {{\tan }^{ - 1}}y}}} \right)dy = 0,y\left( 0 \right) = 0$$

$$(1+y^2)dx+(x-e^{-\tan^{-1}y})dy=0$$

$$\Rightarrow \dfrac{dx}{dy}+\dfrac{x}{1+y^2}=\dfrac{e^{-\tan^{-1}y}}{1+y^2}$$
Integrating factor $$\displaystyle e^{\displaystyle \int\dfrac{1}{1+y^2}dy}=e^{\tan^{-1}y}$$

So, $$\displaystyle xe^{\tan^{-1}y}=\int e^{\tan^{-1}y}.\dfrac{e^{-\tan^{-1}y}}{1+y^2}dy=\int \dfrac{1}{1+y^2}dy=\tan^{-1}y+c$$
$$\therefore x e^{\tan^{-1}y}=\tan^{-1}y+c$$

$$\Rightarrow x=\tan^{-1}y.e^{-\tan^{-1}y}+ c e^{-\tan^{-1}y}$$

Again $$y(0)=0$$

$$\Rightarrow 0=0.e^0+c.e^0$$
$$\Rightarrow \boxed{c=0}$$
$$\therefore \boxed{x=\tan^{-1}y e^{-\tan^{-1}y}}$$


Integrating factor of $$\cfrac{xdy}{dx}-y={x}^{4}-3x$$ is:

$$\dfrac{dy}{dx}+\left ( \dfrac{-1}{x} \right )y=x^{3}-3$$
intergrating factor $$=  e^{\int \left ( \dfrac{-1}{x} \right )dx}$$
                               $$=e^{-lnx}$$
                               $$=e^{ln \, 1/x} $$ 
                               $$=\dfrac{1}{x}$$


The volume of a sphere is increasing at the rate of 3 cubic centimetre per second. Find the rate of its surface area, when the radius is 2cm.

$$V=\dfrac{4}{3}\pi r^3$$

differentiating on both sides, we get,

$$\dfrac{dV}{dt}=4\pi r^2 \dfrac{dr}{dt}$$

$$\Rightarrow \dfrac{dr}{dt}=\dfrac{1}{4\pi r^2}\dfrac{dV}{dt}$$

$$r=2cm,\dfrac{dV}{dt}=3cm^2/sec$$

$$\therefore \dfrac{dr}{dt}=\dfrac{1}{4\pi 2^2}(3)=\dfrac{3}{16\pi}cm/sec$$

$$S=4\pi r^2$$

$$\dfrac {dS}{dt}=8 \pi r \dfrac{dr}{dt}$$

$$=8 \pi (2)\times \dfrac{3}{16\pi}cm/sec$$

$$\therefore \dfrac {dS}{dt}=3cm^2/sec$$


The differential equation of parabola with axis parallel to y-axis and length of latus rectum as 4a is of order:

Let $$\left( u,v \right) $$ be the vertex of the parabola.
The equation of required parabolas are of the form
$${ \left( x-u \right)  }^{ 2 }=4a\left( y-v \right) $$
So there are two unknown constant.


Find the integrating factor of the differential equation $$\left(\dfrac{e^{-2\sqrt{x}}}{\sqrt{x}}-\dfrac{y}{\sqrt{x}}\right)\dfrac{dx}{dy}=1$$.

On rearranging the equation, we get:
$$(\dfrac { { e }^{ -2\sqrt { x }  } }{ \sqrt { x }  } -\dfrac { y }{ \sqrt { x }  } )\dfrac { dx }{ dy } =1\\ \Rightarrow \dfrac { dy }{ dx } +\dfrac { y }{ \sqrt { x }  } =\dfrac { { e }^{ -2\sqrt { x }  } }{ \sqrt { x }  }$$
which is a first order linear non homogeneous differential equation of the form 
$$\dfrac { dy }{ dx } +P(x).y=Q(x)$$
thus the integrating factor is:
$$I.F.={ e }^{ \int { P(x)dx }  }={ e }^{ \int { \dfrac { dx }{ \sqrt { x }  }  }  }={ e }^{ 2\sqrt { x }  }$$


The rate at which the population of a city increases at any time is proportional to the population at that time. If there are $$1,30,000$$ people in the city in $$1960$$ and $$1,60,000$$ in $$1990$$, what approximate population may be anticipated in $$2020$$?
$$\left[ \log _{ e }{ \cfrac { 16 }{ 13 }  } =0.2070,{ e }^{ 0.42 }=1.52 \right] $$

Given, $$\cfrac { dx }{ dt } \propto x\Rightarrow \cfrac { dx }{ dt } =kx$$
$$\therefore \displaystyle  \int { \cfrac { dx }{ x }  } =\int { k } dt\quad $$
$$\log { x } =kt+C\Rightarrow x=C{ e }^{ kt }\quad $$
At $$t=1960,x=1,30,000$$
$$\Rightarrow 1,30,000=C{ e }^{ 1960k }$$
$$\therefore C=\cfrac { 1,30,000 }{ { e }^{ 1960k } } $$ ....$$(1)$$
At $$t=1990,x=1,60,000$$
$$\Rightarrow 1,60,000=C{ e }^{ 1960k }$$
$$=\cfrac { 1,30,000 }{ { e }^{ 1960k } } { e }^{ 1990k }$$ From $$(1)$$
$$=1,30,000{ e }^{ 30k }$$
$$\therefore { e }^{ 30k }=\cfrac { 1,60,000 }{ 1,30,000 } =\cfrac { 16 }{ 13 }$$ ...$$(2)$$
$$\therefore 30k=\log _{ e }{ \left( \cfrac { 16 }{ 13 }  \right)  } =0.2070;k=0.007$$
$$\therefore$$ $$p=1,30,000$$; $${e}^{0.007}$$ is the population at any time $$t$$
In the year $$2020$$, (i.e.,) when $$t=60$$
$$x=1,30,000\times { e }^{ 0.42 }=1,30,000\times 1.52=1,97,600\quad $$
So, the anticipated population is $$2020$$ will be $$1,97,600$$.


If the population of a country doubles in $$60$$ years, in how many years will it be triple under the assumption that the rate of increase is proportional to the number of inhabitants?
[Given: $$\log 2 = 0.6912$$ and $$\log 3 = 1.0986$$.]

Let $$P$$ be the number of population
$$\cfrac{dP}{dt} = kP$$
$$\displaystyle\int\cfrac{dP}P = \int kdt$$
$$\Rightarrow \ln P = kt + C$$……….. (Genral Solution)

When $$t=0, P = P_0$$
$$\ln P_0 = k(0) + C$$
$$\Rightarrow C = \ln P_0$$

When $$t = 60$$ years, $$P = 2P_0$$
$$\ln 2P_0 = k(60) + \ln P_0$$
$$\Rightarrow k = 0.01152$$

When $$t = ?, P = 3P_0$$
$$\ln 3P_0 = 0.01152(t) + \ln P_0$$
$$\Rightarrow t = 95$$ Years.


The solution of $$\dfrac{{dy}}{{dx}} = \dfrac{{x\log {x^2} + x}}{{\sin y + y\cos y}}$$ is 

We have,

$$\dfrac{dy}{dx}=\dfrac{x\log {{x}^{2}}+x}{\sin y+y\cos y}$$

$$\left( \sin y+y\cos y \right)dy=\left( x\log {{x}^{2}}+x \right)dx$$

 

On taking integral both sides, we get

$$ \int{\left( \sin y+y\cos y \right)dy}=\int{\left( x\log {{x}^{2}}+x \right)dx} $$

$$ -\cos y+\left[ y\left( \sin y \right)-\int{1.\sin ydy} \right]=\log {{x}^{2}}\left( \dfrac{{{x}^{2}}}{2} \right)-\int{\dfrac{1}{{{x}^{2}}}\times \left( 2x \right)\times \left( \dfrac{{{x}^{2}}}{2} \right)dx}+\dfrac{{{x}^{2}}}{2}+C $$

$$ -\cos y+\left[ y\left( \sin y \right)-\left( -\cos y \right) \right]=\log {{x}^{2}}\left( \dfrac{{{x}^{2}}}{2} \right)-\int{xdx}+\dfrac{{{x}^{2}}}{2}+C $$

$$ -\cos y+\left[ y\left( \sin y \right)+\cos y \right]=\log {{x}^{2}}\left( \dfrac{{{x}^{2}}}{2} \right)-\dfrac{{{x}^{2}}}{2}+\dfrac{{{x}^{2}}}{2}+C $$

$$ y\sin y=\dfrac{{{x}^{2}}}{2}\log {{x}^{2}}+C $$

 

Hence, this is the answer.



Solve $$2y\,\,{e^{\dfrac{x}{y}}}\,\,dx\, + \,\left( {y - 2x\,{e^{\dfrac{x}{y}}}} \right)\,\,dy = 0$$

We have,

$$2y{{e}^{\dfrac{x}{y}}}dx+\left( y-2x{{e}^{\dfrac{x}{y}}} \right)dy=0$$

$$\dfrac{dx}{dy}=-\dfrac{\left( y-2x{{e}^{\dfrac{x}{y}}} \right)}{2y{{e}^{\dfrac{x}{y}}}}$$             ……. (1)

 

Put $$x=vy$$

 

On differentiating w.r.t $$y$$, we get

$$\dfrac{dx}{dy}=v+y\dfrac{dv}{dy}$$

 

From equation (1), we get

$$ v+y\dfrac{dv}{dy}=-\dfrac{\left( y-2vy{{e}^{v}} \right)}{2y{{e}^{v}}} $$

$$ y\dfrac{dv}{dy}=-\dfrac{\left( y-2vy{{e}^{v}} \right)}{2y{{e}^{v}}}-v $$

$$ y\dfrac{dv}{dy}=-\dfrac{\left( 1-2v{{e}^{v}} \right)}{2{{e}^{v}}}-v $$

$$ y\dfrac{dv}{dy}=\dfrac{-1+2v{{e}^{v}}-2{{e}^{v}}v}{2{{e}^{v}}} $$

$$ y\dfrac{dv}{dy}=\dfrac{-1}{2{{e}^{v}}} $$

$$ 2{{e}^{v}}dv=-\dfrac{dy}{y} $$

 

On integration both sides, we get

$$ \int{2{{e}^{v}}dv}=\int{-\dfrac{dy}{y}} $$

$$ 2{{e}^{v}}=-\ln y+C $$

$$ 2{{e}^{\dfrac{x}{y}}}+\ln y=C $$

 

Hence, this is the answer.



Solve $$\dfrac{dy}{dx}=xcosx$$

We have,

$$\dfrac{dy}{dx}=x\cos x$$

$$dy=x\cos xdx$$                  …….. (1)

 

On taking integral both sides, we get

$$ \int{dy}=\int{x\cos xdx} $$

$$ y=x\sin x-\int{1\sin x}dx $$

$$ y=x\sin x-\int{\sin x}dx $$

$$ y=x\sin x-\left( -\cos x \right)+C $$

$$ y=x\sin x+\cos x+C $$

 

Hence, this is the answer.



The population of a city increases at a rate proportional to the number of inhabitants present at any time t. If the population of the city was $$200000$$ in $$1990$$ and $$250000$$ in $$2000$$, what will be the population in $$2010$$?

Let P be the population at any time t. It is given that $$\dfrac{dP}{dt}\infty P$$

$$\Rightarrow \dfrac{dP}{dt}=\lambda P$$, where $$\lambda$$ is a constant of proportionally

$$\Rightarrow \dfrac{dP}{P}=\lambda dt$$

$$\Rightarrow log P=\lambda t+log C$$ ……(i)

Initially i.e., at $$t=1990$$, $$P=200000$$ and at $$t=2000$$, $$P=250000$$

$$\therefore \log 200000=1990\lambda + \log C$$ ……..(i) and, $$log 250000=2000\lambda +\log C$$ ……..(ii)

$$\Rightarrow \log 200000-\log 250000=10\lambda$$ [On subtracting (ii) from (i)]

$$\Rightarrow \lambda =\dfrac{1}{10}log\left(\dfrac{4}{5}\right)$$

Putting $$\lambda =\dfrac{1}{10}\log\left(\dfrac{4}{5}\right)$$ in (i), we get

$$\log \  200000=1990\times \dfrac{1}{10}log\left(\dfrac{4}{5}\right)+\log C$$

$$\Rightarrow \log \  200000=199 \log \dfrac{4}{5}+\log C$$

$$\Rightarrow log C=\log 200000-199 \log\dfrac{4}{5}$$
 

Putting $$\lambda =\dfrac{1}{10}log \dfrac{4}{5}, log C=\log 200000-199 \  \log\dfrac{4}{5}$$ and $$t=2010$$ in (i), we get

$$log P=\left(\dfrac{1}{10}  \log\dfrac{4}{5}\right)2010+\log 200000-199 \log \dfrac{4}{5}$$

$$\Rightarrow \log P=\log\left(\dfrac{4}{5}\right)^{201}+\log \left(200000\times \left(\dfrac{5}{4}\right)^{199}\right)$$

$$\Rightarrow P=\left(\dfrac{4}{5}\right)^{201}\times 200000\times \left(\dfrac{5}{4}\right)^{199}=\left(\dfrac{5}{4}\right)^2\times 200000=\dfrac{25 }{16}\times 200000=312500$$.



Represent the following families of curves by forming the corresponding differential equation.(a, b being parameters).
$$y^2=4ax$$.

Consider, 
$$y^2=4ax$$

By differentiating we get,
$$2y\dfrac {dy}{dx}=4a$$

$$\dfrac {dy}{dx}=\dfrac {2a}y\\$$

$$y-2x\dfrac{dy}{dx}=0$$.



The population of a city increases at a rate proportional to the number of inhabitants present at any time t. If the population of the city was $$200000$$ in $$1990$$ and $$250000$$ in $$2000$$, what will be the population in $$2010$$?

Let P be the population at any time t. It is given that $$\dfrac{dP}{dt}\infty P$$

$$\Rightarrow \dfrac{dP}{dt}=\lambda P$$, where $$\lambda$$ is a constant of proportionally

$$\Rightarrow \dfrac{dP}{P}=\lambda dt$$

$$\Rightarrow log P=\lambda t+log C$$ ……(i)

Initially i.e., at $$t=1990$$, $$P=200000$$ and at $$t=2000$$, $$P=250000$$

$$\therefore log 200000=1990\lambda +log C$$ ……..(i) and, $$log 250000=2000\lambda +log C$$ ……..(ii)

$$\Rightarrow log 200000-log 250000=10\lambda$$ [On subtracting (ii) from (i)]

$$\Rightarrow \lambda =\dfrac{1}{10}log\left(\dfrac{4}{5}\right)$$

Putting $$\lambda =\dfrac{1}{10}log\left(\dfrac{4}{5}\right)$$ in (i), we get

$$log 200000=1990\times \dfrac{1}{10}log\left(\dfrac{4}{5}\right)+log C$$

$$\Rightarrow log 200000=199 log \dfrac{4}{5}+log C$$

$$\Rightarrow log C=log 200000-199 log\dfrac{4}{5}$$

Putting $$\lambda =\dfrac{1}{10}log \dfrac{4}{5}, log C=log 200000-199 \ log\dfrac{4}{5}$$ 

and $$t=2010$$ in (i), we get

$$log P=\left(\dfrac{1}{10} log\dfrac{4}{5}\right)2010+log 200000-199\  log \dfrac{4}{5}$$

$$\Rightarrow log P=log\left(\dfrac{4}{5}\right)^{201}+log\left(200000\times \left(\dfrac{5}{4}\right)^{199}\right)$$

$$\Rightarrow P=\left(\dfrac{4}{5}\right)^{201}\times 200000\times \left(\dfrac{5}{4}\right)^{199}=\left(\dfrac{5}{4}\right)^2\times 200000=\dfrac{25}{16}\times 200000=312500$$.

$$\therefore$$ The population in 20102010 will be 312500.


Let $$\mathrm{f}:\mathrm{R}\rightarrow \mathrm{R}$$ be a continuous function which satisfies $$\displaystyle \mathrm{f}(\mathrm{x})=\int_{0}^{\mathrm{x}}\mathrm{f}(t)dt$$ Then the value of $$\mathrm {f(ln5)}$$ is

$$f(x)=\int _{0}^{x}{f(t) }dt $$
Substitute $$x=0$$, then integral of $$f(t)$$ from $$0$$ to $$0$$ will become $$0$$.
$$\Rightarrow  f(0)=0$$
Now, differentiate both side of given integral
$${ f }^{ ' }(x)=f(x) , x>0$$
$$\Rightarrow f(x)=k{ e }^{ x } , x>0$$
$$\because f(0)=0$$ and $$f(x)$$ is continuous
 $$\Rightarrow f(x)=0$$ $$x>0$$
$$\therefore f(ln5)=0$$


A function $$y = f(x)  $$  satisfying  $$    f"(x) = x^{-3/2}, f'(4) = 2  $$  and $$ f(0) = 0 $$ is $$ -\lambda \sqrt{x}+3x$$,  then find the value of  $$\lambda$$

$$ \dfrac{d^{2}y}{dx^{2}} = x^{-3/2}$$
$$ \dfrac{dy}{dx} = \dfrac{x^{-1/2}}{-1/2} + c$$

$$\because  \dfrac{dy}{dx} \  at\     x= 4 = -1+c  \Rightarrow    2 = c-1    \Rightarrow    c= 3$$

$$ \dfrac{dy}{dx} = -\dfrac{2}{\sqrt{x}} + 3$$

$$ y = -2  \dfrac{x^{1/2}}{\dfrac{1}{2}} + 3x+d$$
$$ \because  y  \ at\  x=  0  =d   \Rightarrow    0 = d$$
$$ y = -4 \sqrt{x} + 3x$$


The largest value of $$\dfrac{2}{\pi}c$$ such that there exists a differentiable function $$h(x)$$ for $$-c <x <c$$ that is a solution of $$y'=1+y^{2}$$ with $$h(0) = 0$$ is:

$${ y }^{' }=1+{ y }^{ 2 }\Rightarrow \cfrac { dy }{ 1+{ y }^{ 2 } } =dx\Rightarrow \tan ^{ -1 }{ y } =x+c\\ y\left( 0 \right) =0\Rightarrow c=0\Rightarrow \tan ^{ -1 }{ y } =x$$
Since the range of $$\tan ^{ -1 }{ y } $$ is $$\left( -\cfrac { \pi  }{ 2 } ,\cfrac { \pi  }{ 2 }  \right) $$
The largest value of $$c$$ such that $$y=h\left( x \right) $$ is differentiable is $$\cfrac { \pi  }{ 2 } $$


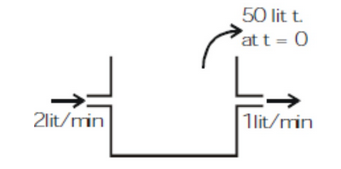
A tank consists of 50 liters of fresh water. Two liters of brine each litre containing 5 gms of dissolved salt are running into tank per minute ; the mixture is kept uniform by stirring , and runs out at the rate of one litre per minute.If $$m$$ grams of salt are present in the tank after t minute. expression of $$m$$ in terms of $$t$$ be$$\quad m\, =\, kt \left ( r+\displaystyle \frac {2p+t}{p+t} \right ) gm$$. Find $$(p/k)+r$$ ?

Input rate = 10 gm/min
After time t volume of tank = 50 + (2-1)t
Concentration of salt in time $$t\, =\, \displaystyle \frac {m}{50+t}\, gm/lit$$
Output rate $$=\, \displaystyle \frac {m}{50+t}.1\, gm/min$$
$$\Rightarrow\displaystyle \frac {dm}{dt}\, =\, \displaystyle \frac {-m}{50+t}\, +\, 10$$

$$\Rightarrow m(50+t)\, =\, \int 10(50+t)\, dt$$

$$\Rightarrow m(50+t)\, =\, 500\, t\, +\, 5t^2\, +\, c$$
$$\Rightarrow (\because \, at\, t\, =\, 0,\, m\, =\, 0\, \Rightarrow\, c\, =\, 0)$$
$$\Rightarrow m(50+t)\, =\, 5\, (100\, t+t^2)$$
$$\Rightarrow m\, =\, 5t \left ( \displaystyle \frac {100+t}{50+t} \right ) gm$$

320460_262630_ans.PNG


Let $$(x^2 + 1) \displaystyle \frac{d^2 y}{dx^2} = 2x \frac{dy}{dx},$$ where $$y'(0) = 3$$ & $$y(0) = 1$$, then $$y(1)$$ is equal to:

$$\displaystyle \frac{y''}{y'} = \frac{2x}{x^2 + 1}$$
On integrating, we get $$\ln y' = \ln (x^2 + 1) + \ln c$$
$$\Rightarrow y' = c(x^2 + 1)$$
$$y' (0) = 3 $$
$$\Rightarrow c = 3$$
$$y' = 3(x^2 + 1)$$
$$\Rightarrow y = x^3 + 3x + 1   $$
$$  \Rightarrow y (1) = 5$$


Find the particular solution of the following differential equation;
$$(x + 1)\dfrac {dy}{x} = 2e^{-y} - 1; y = 0$$ when $$x = 0$$

Given $$(x+1)\dfrac{dy}{dx}=2e^{-y}-1$$
$$\Rightarrow \dfrac{dy}{2e^{-y}-1}=\dfrac{dx}{x+1}$$\dfrac

Integrating both the sides, we get
$$\displaystyle\int \dfrac{dy}{2e^{-y}-1}=\displaystyle\int \frac{dx}{x+1}$$\dfrac

$$\Rightarrow \dfrac{e^y dy}{2-e^y}=\log \left | x+1 \right |+c$$

$$\Rightarrow -\displaystyle\int\dfrac{dz}{z}=\log \left | x+1 \right |+c$$

$$\Rightarrow -\log z=\log \left | x+1 \right |+c$$

$$\Rightarrow -\log \left | 2-e^y \right |=\log \left | x+1 \right |+c$$

$$\Rightarrow \log \left | x+1 \right |+\log \left | 2-e^y \right |=\log  k$$

$$(x+1)(2-e^y)=k$$

Putting x = 0, y = 0, we get
$$1.(2-e^0)=k\Rightarrow k = 1$$

Therefore, required particular solution is,
$$(x+1)(2-e^y)=1$$


Find the particular solution of the following differential equation:
$$(x+1)\dfrac{dy}{dx} = 2e^{-y} - 1$$, given that $$y = 0$$ when $$ x = 0$$.

$$(x+1)\dfrac { dy }{ dx } =2{ e }^{ -y }-1\longrightarrow eqn.1\\ \dfrac { dy }{ dx } +\dfrac { 1 }{ 1+x } =\dfrac { 2{ e }^{ -y } }{ 1+x } $$

Eqn.1 can be written as:

$$\dfrac { 1 }{ 2{ e }^{ -y }-1 } dy=\dfrac { 1 }{ 1+x } dx\\ \Rightarrow \dfrac { 1 }{ \dfrac { 2 }{ { e }^{ y } } -1 } dy=\dfrac { 1 }{ 1+x } dx\\ \Rightarrow \dfrac { -({ -e }^{ y }) }{ 2-{ e }^{ y } } dy=\dfrac { 1 }{ 1+x } dx\\ \Rightarrow (-\log \left| 2-{ e }^{ y } \right| )=\log \left| x+1 \right| +C\\ y=0,\quad x=0\\ \Rightarrow -\log 2=\log 1+C\\ \Rightarrow C=-\log 2$$

Answer: $$\log (x+1)-\log 2=-\log (2-{ e }^{ -y })\\ \Rightarrow \log (\dfrac { (x+1)(2-{ e }^{ -y }) }{ 2 } )=0$$



The temperature $$T$$ of a cooling object drops at a rate proportional to the difference $$(T - S)$$, where $$S$$ is constant temperature of surrounding medium. If initially $$T = 150^{\circ}C$$, find the temperature of the cooling object at any time $$'t'$$.

Let $$T$$ be the temperature of the cooling object at any time $$t$$.
Given, $$\dfrac {dT}{dt}\propto (T - S) \Rightarrow \dfrac {dT}{dt} = -K(T - S)$$ where $$k$$ is negative
$$\Rightarrow \dfrac {dT}{T - S} =-k. dt$$
$$\Rightarrow \log (T - S) = -kt + \log c$$
$$\Rightarrow \log (T - S) = -\log c = kt$$
$$\Rightarrow \log \dfrac {T - S}{c} = -kt \Rightarrow \log \dfrac {T - S}{c} = e^{-kt}$$
$$\Rightarrow T - S = c.e^{-kt} \Rightarrow T = S + ce^{-kt}$$
When $$t = 0$$ and $$T = 150$$,
$$\Rightarrow 150 = S + c \Rightarrow c = 150 - S$$
$$\therefore$$ The temperature of the cooling object at any time $$'t'$$ is $$T$$.
$$= S + (150 - S) e^{-kt}$$


The sum of Rs. $$1000$$ is compounded continuously, the nominal rate of interest being four percent per annum. In how many years will the amount be twice the original principal? $$(\log_e2 = 0.6931)$$.

Let Rs. $$x$$ be the principal.
The required differential equation is
$$\dfrac{dx}{dt} = \dfrac{4}{100}x $$ (or) $$\dfrac{dx}{x} = 0.04 dt$$
Integrating both sides, we get
$$\displaystyle \int \dfrac{dx}{x} = 0.04 \int dt$$ 
$$\Rightarrow \log  x$$ $$= 0.04 t + \log  c \Rightarrow x = ce^{0.04t}$$              ....... (1)
Given, $$x = 1000$$, when $$t = 0$$
Hence (1) becomes $$c = 1000$$
when $$x = 2000$$
$$ \Rightarrow 2000$$ $$= 1000 e^{-0.04t} $$
$$\Rightarrow 2 = e^{-0.04t}$$
$$\Rightarrow \log_e 2 = 0.04 t$$
$$\Rightarrow t = \dfrac{\log_{e}2}{0.04} = \dfrac{0.6931}{0.04} = 17.32 = 17$$ years
Thus the number of years required for the amount to be twice the principal is approximately $$17$$ years.


A radioactive substance disintegrates at a rate proportional to its mass. When its mass is $$10 $$ mg, the rate of disintegration is $$0.051 $$ mg per day. How long will it take for the mass to be reduced from $$10$$ mg to $$5$$ mg? $$\left( \log _{ 2 }{ 2 } =0.6931 \right) $$.

Let $$A$$ be amount of mass at the time $$t$$
$$\dfrac { dA }{ dt } \propto A$$
$$\dfrac { dA }{ dt } =KA$$         ........(*)
$$\dfrac { dA }{ A } =Kdt$$
$$\displaystyle\int { \dfrac { dA }{ A }  } =\displaystyle\int { Kdt }$$
$$\Rightarrow \log { A } =Kt+\log { c }$$
$$\Rightarrow \log { \dfrac { A }{ c }  } =Kt$$
$$\Rightarrow \dfrac { A }{ c } ={ e }^{ Kt }$$
$$\Rightarrow A=c{ e }^{ Kt }$$         ......(1)
when $$t=0$$, $$A=10$$
(1) $$\Rightarrow 10=c{ e }^{ 0 }$$
$$c=10$$
$$\therefore $$ the solution is $$A=10{ e }^{ Kt }$$.
Given when $$A=10$$, $$\dfrac { dA }{ dt } =-0.051$$ ($$\therefore$$ disintegration)
$$\Rightarrow  -0.051=10k$$ (by*)
$$\Rightarrow K=-0.0051$$
$$\therefore A=10{ e }^{ -0.0051t }$$
To find $$t$$ when $$A=5$$
$$\therefore A=10{ e }^{ -0.0051t }$$
To find $$t$$ when $$A=5$$
$$\Rightarrow 5=10{ e }^{ -0.0051t }$$
$$\Rightarrow \dfrac { 1 }{ 2 } ={ e }^{ -0.0051t }$$
$$\Rightarrow 2={ e }^{ -0.0051t }$$
$$\Rightarrow \log { 2 } =\log { { e }^{ -0.0051t } }$$
$$\Rightarrow  0.0051t=\log { 2 }$$
$$\Rightarrow t=\dfrac { \log { 2 }  }{ 0.0051 } =\dfrac { 0.6931 }{ 0.0051 } =136$$ days.


A body is heated at $$110^{\circ}C$$ and placed in air at $$10^{\circ}C$$. After $$1$$ hour its temperature is $$60^{\circ}C$$. How much additional time is required for it to cool to $$35^{\circ}C$$?

Let $$\theta$$ be the temperature of body at time $$t$$. Temperature of air is given to be $$10^{\circ}C$$.
Then, according to Newton's law of cooling, we have
$$\dfrac {d\theta}{dt}\propto (\theta - 10^{\circ})$$
$$\Rightarrow \dfrac {d\theta}{dt} = -k (\theta - 10^{\circ}), k > 0$$
$$\Rightarrow \dfrac {d\theta}{\theta - 10^{\circ}} = -k dt$$
On integrating both sides, we get
$$\displaystyle \int \dfrac {d\theta}{\theta - 10^{\circ}} = -k \int dt$$
$$\ln (\theta - 10^{\circ}) = -kt + c$$
$$\theta = 10^{\circ} + e^{kt + c} $$ .... (i)
when $$t = 0, \theta = 110^{\circ}$$
Substituting in the equation, we get
$$110^{\circ} = 10^{\circ} + e^{-k(0) + c}$$
$$e^{c} = 110^{\circ}$$
Substituting the above equation in (i), we get
$$\theta = 10^{\circ} + 100^{\circ} e^{-kt}$$ .... (ii)
Given that $$\theta = 60^{\circ}C$$, when $$t = 1$$, we get
$$60^{\circ} = 10^{\circ} + 100^{\circ}e^{-k}$$
$$\Rightarrow 50^{\circ} = 100^{\circ} e^{-k}$$
$$\Rightarrow e^{-k} = \dfrac {1}{2}\Rightarrow e^{k} = 2$$
$$\Rightarrow k = \log 2$$
Now, we have to find $$t$$, when $$\theta = 35^{\circ}$$
From equation (ii), we have
$$\theta = 10^{\circ} + 100^{\circ}e^{-kt}$$
$$\Rightarrow 35^{\circ} = 10^{\circ} + 100^{\circ} e^{-kt}$$
$$\Rightarrow e^{-kt} = \dfrac {1}{4}\Rightarrow e^{kt} = 4$$
$$\Rightarrow kt = \log 4$$
$$\Rightarrow t = \dfrac {\log 4}{\log 2}$$
$$\therefore$$ Additional time $$= \dfrac {\log 4}{\log 2} - 1 = 1$$ hour.


The population of a town grows at the rate of $$10\%$$ per year. Using differential equation, find how long will it take for the population to grow $$4$$ times.

Since increase in population speeds up with increase in population and let $$x$$ be the population at any time $$t$$

$$\therefore \dfrac{dx}{dt} \ \alpha\ x$$


$$\dfrac{dx}{dt}=r x$$

where $$r$$ is proportionality constant.

Rewriting,

$$\dfrac{dx}{x}=rdt$$

Integrating,

$$ln x=rt +c $$

 where $$c$$ is the a constant

Exponentiating on both sides with $$e$$

$$x=e^{rt+c}=Ae^{rt}$$, where $$A=e^c$$ 

Let  the initial population $$x_0$$, then 

$$x_0=A\dots (1)$$

If the population is increased $$4$$ times in time $$t$$, then

$$4x_0=Ae^{rt}\dots (2)$$

From (1), $$x=A$$

$$4x_0=x_0e^{rt}$$

Taking log on both sides

$$\ln 4=rt$$

 $$r=0.1$$...(as rate of increase is given as $$10 \%$$)

$$t=\dfrac{\ln4}{0.1}=\dfrac{1.38}{0.1}=13.8$$ years that is $$13$$ years and around $$10$$ months 



The rate of growth of population is proportional to the number present. If the population doubled in the last $$25$$ years and the present population is $$1$$ lac, when will the city have population $$4,00,000$$ ?

$$\cfrac{dp}{dt}\propto p$$
$$\implies \cfrac{dp}{dt}=k p$$   (where $$k$$ is constant)
$$\implies \int { \cfrac { dp }{ dt }  } =\int { k } dt$$
$$\implies \ln p=kt+c$$   (on integrating both sides)
At $$t=0,p=(1/2)lac=50,000.$$
At $$t=25,p=(1/2)lac=1,00,000.$$
$$\therefore$$ we get, $$c=\ln(50,000)$$ and $$k=\ln(2)/25$$
$$\therefore$$  For $$P=4,00,000$$
$$\ln p=\cfrac{\ln (2)}{25}t+\ln(50,000)$$
$$\ln (4,00,000)=\cfrac{\ln (2)}{25}t+\ln(50,000)$$
Solving for $$t$$, we get $$t=75$$.
Now as we have assumed $$t=0$$ after 25 years. So, city have population of $$4,00,000$$ before $$25$$ years.
Hence time $$=75-25=50$$years




$$(x^{2} + y^{2}) dy = xy dx$$. If $$y(1)$$ and $$y(x_{0})= e$$ then find the value of $$x_{0}$$.

$$(x^{2} + y^{2}) dy = xy dx\Rightarrow \int \dfrac xy dy+\int \dfrac yxdy=\int dx\Rightarrow x\log y+\dfrac{y^2}{2x}=x+c$$

Now, at $$x=1 ;y=e$$
$$x\log y+\dfrac{y^2}{2x}=x+c\Rightarrow x+\dfrac{e^2}{2}=x+c\Rightarrow c=\dfrac{e^2}{2}$$

Now at $$x=x_0;y=e$$
$$x_0\log e+\dfrac{e^2}{2x_0}=x_0+\dfrac{e^2}{2}\Rightarrow \dfrac{e^2}{2x_0}=\dfrac{e^2}{2}\Rightarrow x_0=1$$



Class 12 Commerce Applied Mathematics Extra Questions