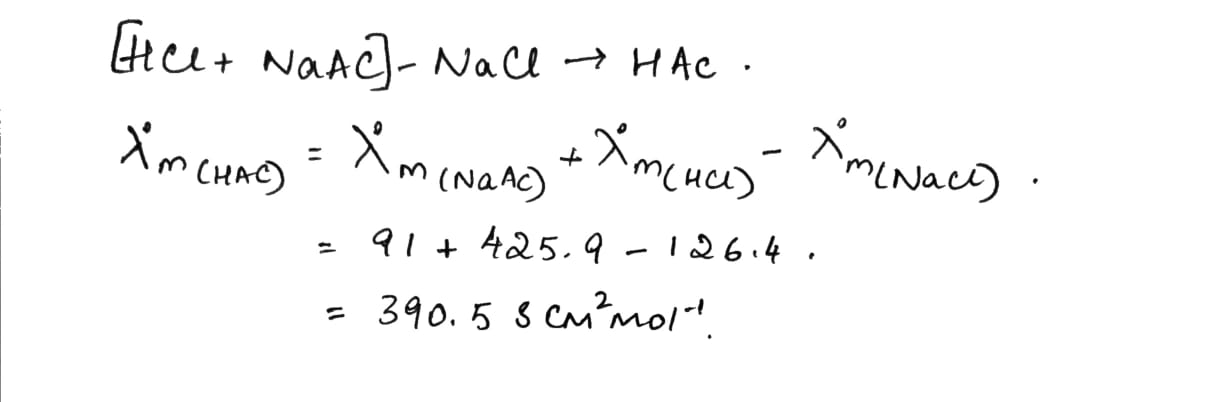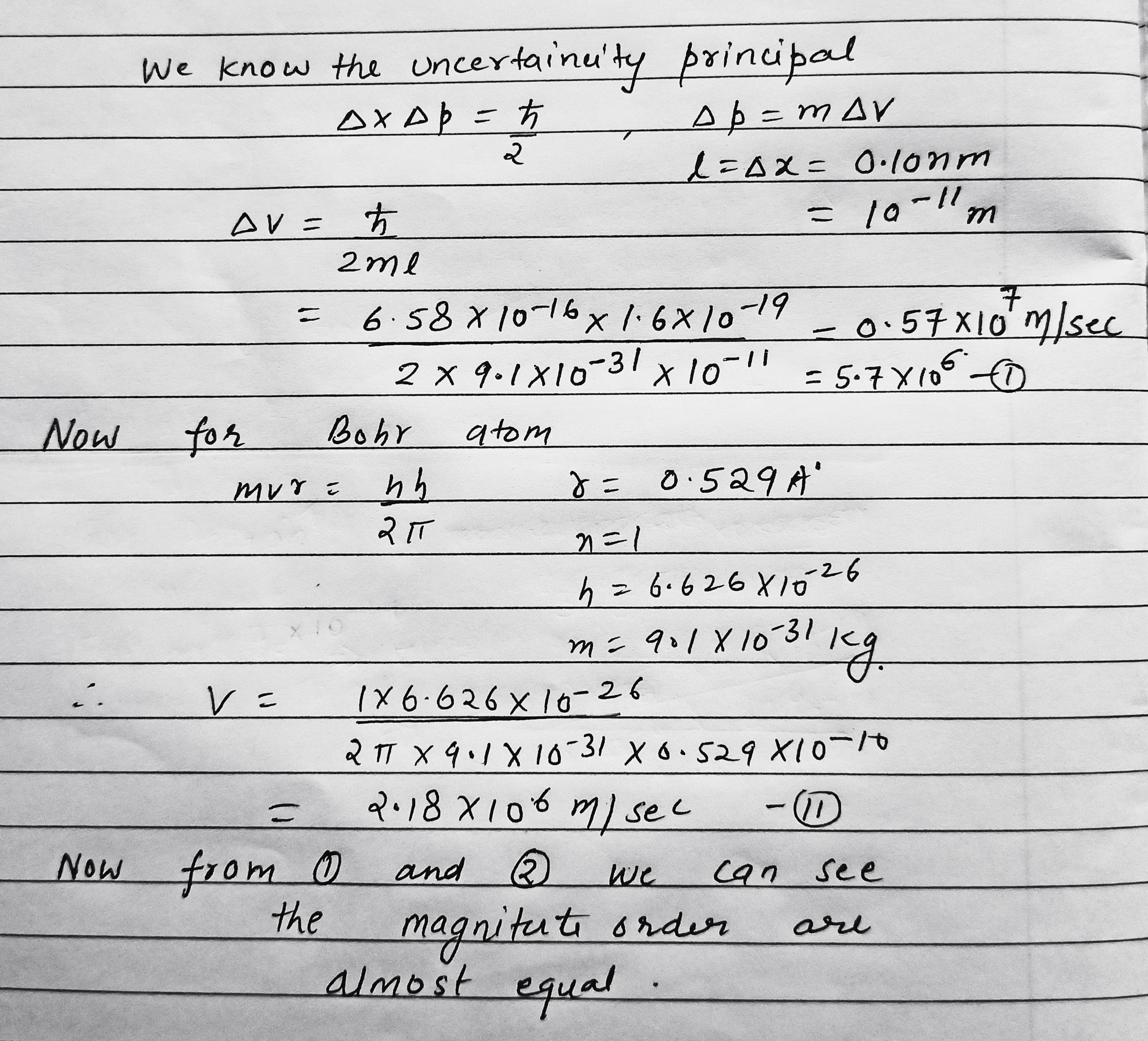Dual Nature Of Radiation And Matter - Class 12 Engineering Physics - Extra Questions
Electrons are emitted from a photosensitive surface when it is illuminated by green light but electron emission does not take place by yellow light. Will the electrons be emitted when the surface is illuminated by (i) red light, and (ii) blue light?
A photosensitive surface emits photoelectrons when red light falls on it. Will the surface emit photoelectrons when blue light is incident on it? Give reason.
Electrons are emitted from the suface when green light is incident on it, but no electrons are ejected when yellow light is incident on it. Do you expect electrons to be ejected when surface is exposed to
(i) Red light and
(ii) Blue light?
Imagine playing baseball in a universe (not ours!) where the Planck constant is $$0.60 \mathrm{J}$$. s and thus quantum physics affects macroscopic objects. What would be the uncertainty in the position of a $$0.50 \mathrm{kg}$$ baseball that is moving at $$20 \mathrm{m} / \mathrm{s}$$ along an axis if the uncertainty in the speed is $$1.0 \mathrm{m} / \mathrm{s} ?$$
Calculate the de Broglie wavelength of an electron of mass $$9.11 \times 10^{-31}kg$$ and moving with a velocity of $$1.0 \times 10^6 \,ms^{-1}$$.
Define work function for a given metallic surface.
How does the maximum kinetic energy of electrons emitted vary with the work function of the metal?
How does de Broglie wavelength depend on the momentum of a particle?
State Heisenberg's uncertainty principle.
Calculate the de-Broglie wavelength of the electron orbiting in the $$n=2$$ states of hydrogen atom.
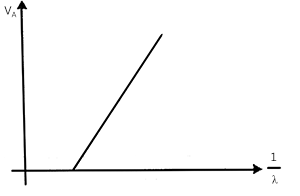
Plot the graph between Anode potential and $$\displaystyle\frac{1}{\lambda_{min}}$$. Also find its slope.
Define the term work function of a metal.
Some laws/processes are given in Column I. Match these with the physical phenomena given in Column II and
indicate your answer by darkening appropriate bubbles in the 4 4 matrix given in the ORS.
Write three characteristic features in photoelectric effect which cannot be explained on the basis of wave theory of light, but can be explained using Einstein's equation.
How can photoelectric effect be used to produce electricity.
Give reasons for the following
A 40 watt bulb and 60 watt bulb though have different intensities cannot change the kinetic energy of photoelectrons produced by them.
$$(i)$$ What is thermionic emission?
$$(ii)$$ Name the unit in which the work function of a metal is expressed.
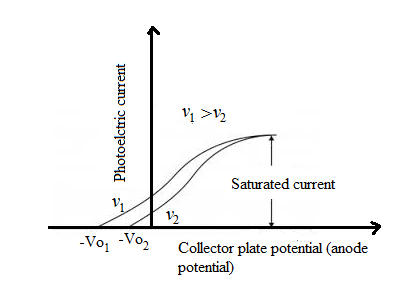
Draw a plot showing the variation of photoelectric current with collector plate potential foe two different frequencies, $$v_1 > v_2$$, of incident radiation having the same intensity. In which case will the stopping potential be higher ? Justify your answer.
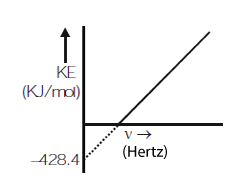
The following plot is given between $$KE$$ on y-axis and frequency of radiation $$\left(\nu\right)$$ on x-axis. If slope of this plot is $$'m'$$ find ratio $$\left(\displaystyle\frac{m}{h}\right)$$ where $$h = $$ planck's constant.
There are a large number of free electrons moving randomly in a metal. At room temperature, why do they not come out of the surface of metal?
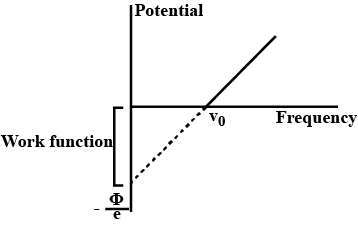
Define the terms (i) 'cut-off voltage' and (ii) 'threshold frequency' in relation to the phenomenon of photoelectric effect.
Using Einstein's photoelectric equations show how the cut-off voltage and threshold frequency for a given photosensitive material can be determined with the help of a suitable plot/graph.
(a) Describe briefly three experimentally observed features in the phenomenon of photoelectric effect.
(b) Discuss briefly how wave theory of light cannot explain these features
OR
(a) Write the important properties of photons which are used to establish Einstein's photoelectric equation.
(b) Use this equation to explain the concept of (i) threshold frequency of (ii) stopping potential
State two important properties of photon which are used to write Einsteins photoelectric equation. Define (i) stopping potential and (ii) threshold frequency, using Einsteins equation and drawing necessary plot between relevant quantities.
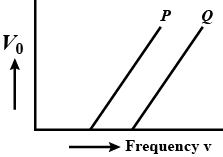
The graph shows variation of stopping potential $$V_0$$ versus frequency of incident radiation $$v$$ for two photosensitive metals A and B. Which of the two metals has higher threshold frequency and why?

A monochromatic light source of frequency $$6 \times 10^{14} Hz$$ is emitting energy at the rate $$2 \times 10^{-3} J/s$$. Calculate the number of photons emitted per second by the source.
Write Einstein's photoelectric equation and mention which important features in photoelectric effect can be explained with the help of this equation.
The maximum kinetic energy of the photoelectrons gets doubled when the wavelength of light incident on the surface changes from $$'\lambda_{1}'$$ to $$'\lambda_{2}'$$. Derive the expressions for the threshold wavelength $$'\lambda_{0}'$$ and work function for the metal surface
Write Einstein's photoelectric equations and point out any two characteristic properties of photons on which this equations is based.
Briefly explain the three observed features which can be explained by this caution.
Write Einstein's photoelectric equation. State clearly how this equation is obtained using the photon picture of electromagnetic radiation.
Write the three salient features observed in photoelectric effect which can be explained using this equation.
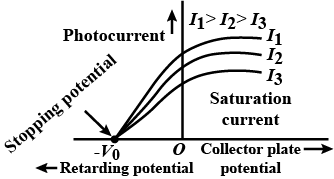
What is stopping voltage (or cut voltage)? Plot a graph of variation of photoelectric current with collector plate potential for two incident radiations of same frequency and different intensities.
Derive Einstein's photoelectric equation.
The graph between the stopping potential $$V_0$$ and frequency $$v$$ for two different metal plates P and Q are shown in the figure. Which of the metals has greater threshold wavelength and work function?
State Einstein's photoelectric equation. Explain 'two' characteristics on the basis of this equation.
Write any two types of electron emission.
Write Einstein's equation of photoelectric effect. Give Einsteins explanation of photoelectric effect.
Write down Einstein's photoelectric equation.
What is "work function"?
State Moseley's law. What is its importance?
What are de-Broglie waves? Establish the de-Broglie wavelength equation.
The planck's constant is $$h$$ and frequency of a photon is $$\nu$$ then write the formula for Einstein photo electric equation.
The mass of a moving particle is m and velocity is v, then write the formula for de-Broglie wavelength $$\lambda$$.
Write Einstein's Photo-Electric Equation and explain the terms in it.
Albert Einstein, the great physicist proposed a clear picture to explain photoelectric effect.
a) Explain Einstein's photo electric equation.
b) Name the quanta of light.
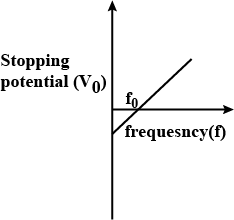
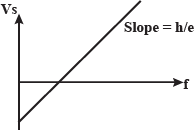
Plot a labelled graph of $$|V_s|$$ where $$V_s$$ is stopping potential versus frequency f of the incident radiation.
State how will you use this graph to determine the value of Planck's constant.
Show that de Broglie wavelength of electrons accelerated $$V$$ volts is very nearly given by:
$$\lambda \left(in \mathring{A} \right) = {\dfrac{150}{V}}^{{1}/{2}}$$.
Why do electron not leave the metal surface on their own?
How can electron be made to leave the metal surface?(State any two ways).
Write Heisenberg's uncertainty principle.
Explain photoelectric effect on the basis of quantum model and derive the photoelectric equation $$hv=\displaystyle\frac{1}{2}mv^2+hv_0$$, where symbols have their usual meanings.
Explain photoelectric emission on the basis of quantum model of light and derive the equation $$hv=\cfrac{1}{2}m{v}^{2}+h{v}_{0}$$, where symbols used have their usual meanings.
Radiations of frequency $$10 ^ { 15 } \mathrm { Hz }$$ are incident on two photosensitive surfaces A and B. Following observations are recorded: Surface A: No photo-emission takes place. Surface $$B :$$ Photo-emission takes place but photo-electrons have zero energy.Explain the above observations on the basis of Einstein's photoelectric equation. How will the observation with a surface $$B$$ change when the wavelength of incitations is decreased?
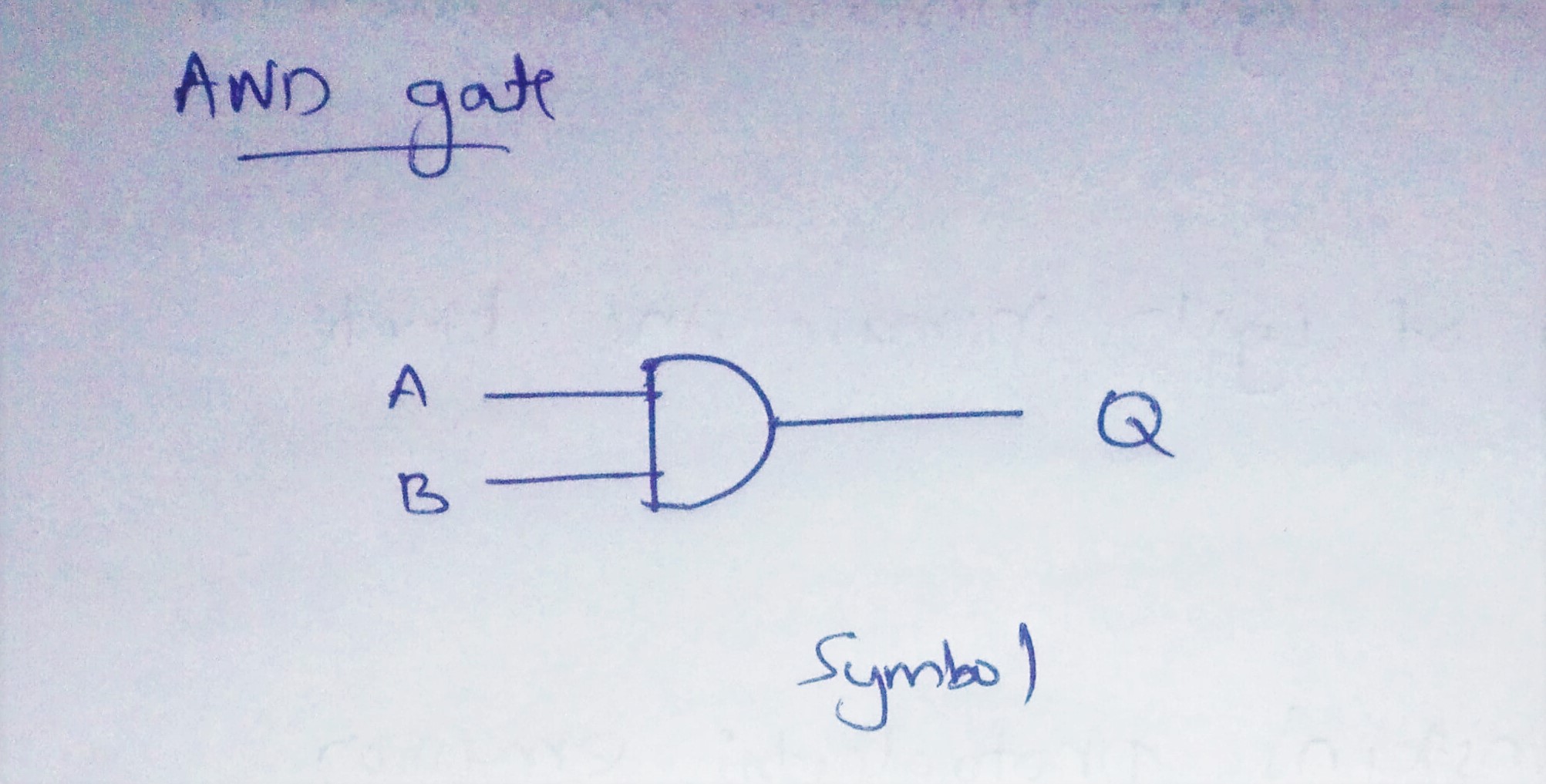
Explain photoelectric emission on the basis of quantum model of light and derive Einstein's photoelectric emission. Construct logic symbol, Boolean expression and truth table for AND gate.
Write Einstein's photoelectric effect and explain lens of photoelectric effect with the help of it.
The de-Broglie wave length of a particle moving with a velocity $$2.25 \times 10^8 ms^{-1}$$ is equal to the wavelength of a photon. The ratio of kinetic energy of the particle to the energy of the photon is [velocity of light= $$3\times 10^8 ms^{-1}$$]
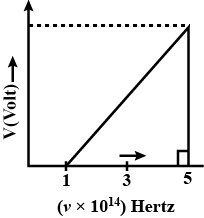
Stopping potential [V volts] is plotted against frequency of light used $$[\nu]$$. Find work function(eV). $$(h= 6.62\times 10^{-34} J\times s)$$.
The momentum of an object is doubled. How does its kinetic energy change?
Work function of sodium is $$2.3 eV$$. Does sodium show photo-electric emission for light wavelength $$6800 \mathring {A}$$?
The equation for a wave travelling in x-direction on a string is : y = 3(sin3.14x-314t),thenFind the maximum velocity of particle of the string .
What should be the ratio of velocities of $$CH_4$$ and $$O_2$$ molecules so that they are associated with de Brogile waves of equal wave lenghs ?
According to be Broglie equation = $$\lambda = \dfrac{h}{mv}$$
Mention any two types of electron emission.
A particle of mass M at rest decays into two particles of masses $$m_1$$ and $$m_2$$ having non zero velocities. The ratio of the de Broglie wavelengths of the particles, $$\lambda_1/\lambda_2$$ is?
Which colored light bulb - red, orange, yellow, green, or blue- emits photons with (a) the least energy and (b) the greatest energy? Account for your answers.
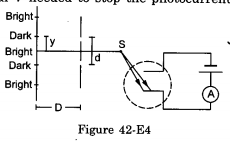
In the arrangement shown in figure , y=1.0mm, d=0.24mm and D= 1.2m. The work function of the material of the emitter is 2.2 eV. Find the stopping potential V needed to stop the photocurrent.
Show that de-Broglie wavelength of electron accelerated through V volt is nearly given by:
$$\lambda=[\frac{1550}{V}]^{1/2}$$ in $$A^{\circ}$$
An electron in hydrogen like atom, is in an excited state. It has a total energy of -3.4 eV. Calculate.
(a)The kinetic energy of electron
(b) The de broglie wavelength of electron
$$(h=6.6 \times 10^{-34}, m_e= 9.108 \times 10^{-31}kg)$$
You wish to pick an element for a photocell that will operate via the photoelectric effect with visible light. Which of the following are suitable (work functions are in parentheses): tantalumeV $$),$$ tungsten $$(4.5 \mathrm{eV}),$$ aluminum $$(4.2 \mathrm{eV}),$$ barium $$(2.5 \mathrm{eV})$$ lithium $$(2.3 \mathrm{eV}) ?$$
A nonrelativistic particle is moving three times as fast as an electron. The ratio of the de Broglie wavelength of the particle to that of the electron is $$1.813 \times 10^{-4}$$. By calculating its mass, identify the particle.
Write the wave function $$\psi(x)$$ displayed in Eq. $$38-27$$ in the form $$\psi(x)=a+i b,$$ where $$a$$ and $$b$$ are real quantities. (Assume(b) Write the time-dependent wave function $$\Psi(x, t)$$ that $$\psi_{0}$$ is real. that corresponds to $$\psi(x)$$ written in this form.
The uncertainty in the position of an electron along an $$x$$ axis is given as $$50 \mathrm{pm},$$ which is about equal to the radius of a hydrogen atom. What is the least uncertainty in any simultaneous measurement of the momentum component $$p_{x}$$ of this electron?
The frequency v of incident radiation is greater that threshold frequency $$v_0$$ in a photocell. How will the stopping potential vary if frequency (v) is increased, keeping other factors constant?
Two metals A and B have work functions 4eV and 10eV respectively. Which metal has the higher threshold wavelength?
Write the basic features of photon picture of electromagnetic radiation on which Einstein's photoelectric equation is based.
If the intensity of radiation in a photocell is increased how does the stopping potential vary?
Sketch the graphs showing variation of stopping potential with frequency of incident radiations for two photosensitive materials A and B having threshold frequencies $$V_A>V_B$$
(i) In which case is the stopping potential more and why?
(ii) Does the slope of the graph depend on the nature of the material used? Explain
Two lines A and B shown in the graph represent the de Broglie wavelength$$(\lambda)$$ as a function of $$\dfrac{1}{\sqrt{V}}$$(V is the accelerating potential) for two particles having the same charge. Which of the two represents the particle of smaller mass?

Chlorophyll present in green leaves of plants absorbs light at $$4.620\times 10^{14}Hz$$. Calculate the wavelength of radiation in nanometer, Which part of the electromagneitc spectrum does it belong to?
According to de Broglie, matter should exhibit dual behaviour, that is both particle and wave like properties. How ever, a cricket ball of mass $$100\ g$$ does not move like a wave when it is thrown by a bowler at a speed of $$100\ km/h$$. Calculate the wavelength of the ball and explain why it does not show wave nature.
In the stydy of a photoelectric effect the graph between the stopping potential V and frequency v of the incident radiation on two different metals P and Q is shown below:
(i) Which one of the two metals has higher threshold frequency?
(ii) Determine the work function of the metal which has greater value.
(iii) Find the maximum kinetic energy of electron emitted by light of frequency $$8\times10^{14}Hz$$ for this metal.

Wavelength of different radiations are given below:
$$\lambda=(A)300\ nm$$
$$\lambda (B)=300\mu\ m$$
$$\lambda (C)=3\ nm$$
$$\lambda (D)=30\overset { o }{ A } $$
Arrange these radiations in the increasing order of their energies.
Assuming an electron is confined to a 1nm wide region, find the uncertainty in momentum using Heisenberg Uncertainty principle $$(\Delta x \times \Delta p \cong h)$$. You can assume the uncertainty in position $$\Delta x$$ as 1nm. Assuming $$p \cong \Delta p$$, find the energy of the electron in electron volts.
Explain the working of photo emissive cell. Write any two applications of photoelectric cells.
A hypothetical electromagnetic wave is shown in Fig $$2.2$$. Find out the wavelength of the radiation.
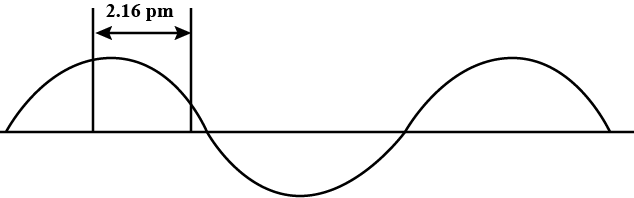
Write Heisenberg Uncertainty principle in relation to position and momentum of particle.
The uncertainty in the X-component of momentum of a moving electrons is $$ 13.18 \times 10^{-30}$$ kg-m/s. Find out the uncertaintities in the X-component of position and velocity.
What explanation was given by Einstein to explain photoelectric effect ? What do you understand by threshold frequency ?
The time period of electromagnetic pulse is $$0.30\,ms$$. Find out the uncertaintity in the energy of photon.
A proton with KE $$6MeV$$ is travelling in a particle accelerator of circular orbit $$0.75m$$. What fraction of energy does it radiate per sec?
The electron energy in hydrogen atom is given by $$E_n$$ = $$\dfrac{-21.7*10^{-19}}{n^2}$$ergs. Calculate the energy required to remove an $$e^-$$ completely from n = 2 orbit. What is the largest wavelength in cm of light that can be used to cause this transition?
An electron moves in an electric field with a kinetic energy of $$2.5 eV$$. What is the associated de Broglie wavelength?
Find the de-Broglie wave length of neutron at $$ {127^\circ }C$$.
A bulb emits light of wavelength $$4500\mathring{A}$$, the bulb is rated as $$150$$ Watt and $$8$$% of the energy is emitted as light. How many photons are emitted by the bulb per second?
$${{\lambda }}_{\text{m}}^{\text{o}}\,$$ for $${\text{NaCl,}}\,\,{\text{HCl}}\,{\text{and}}\,{\text{NaAc}}$$ are 126.4, 425.9 and 91.0 S $${\text{c}}{{\text{m}}^2}\,{\text{mo}}{{\text{l}}^{ - 1}}$$ respectively. Calculate $${{{\lambda }}^{\text{o}}}$$ for HAc.
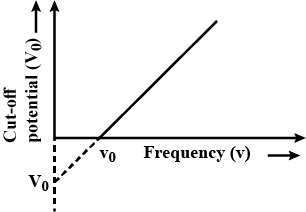
Draw a graph showing the variation of stopping potential $$(V_{0})$$ with the $$3$$ frequency of incident radiation $$(v)$$ in relation to the electric effect.
How can the value of Plancks constant be determined from this graph?
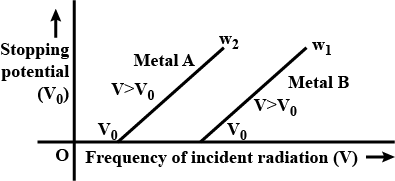
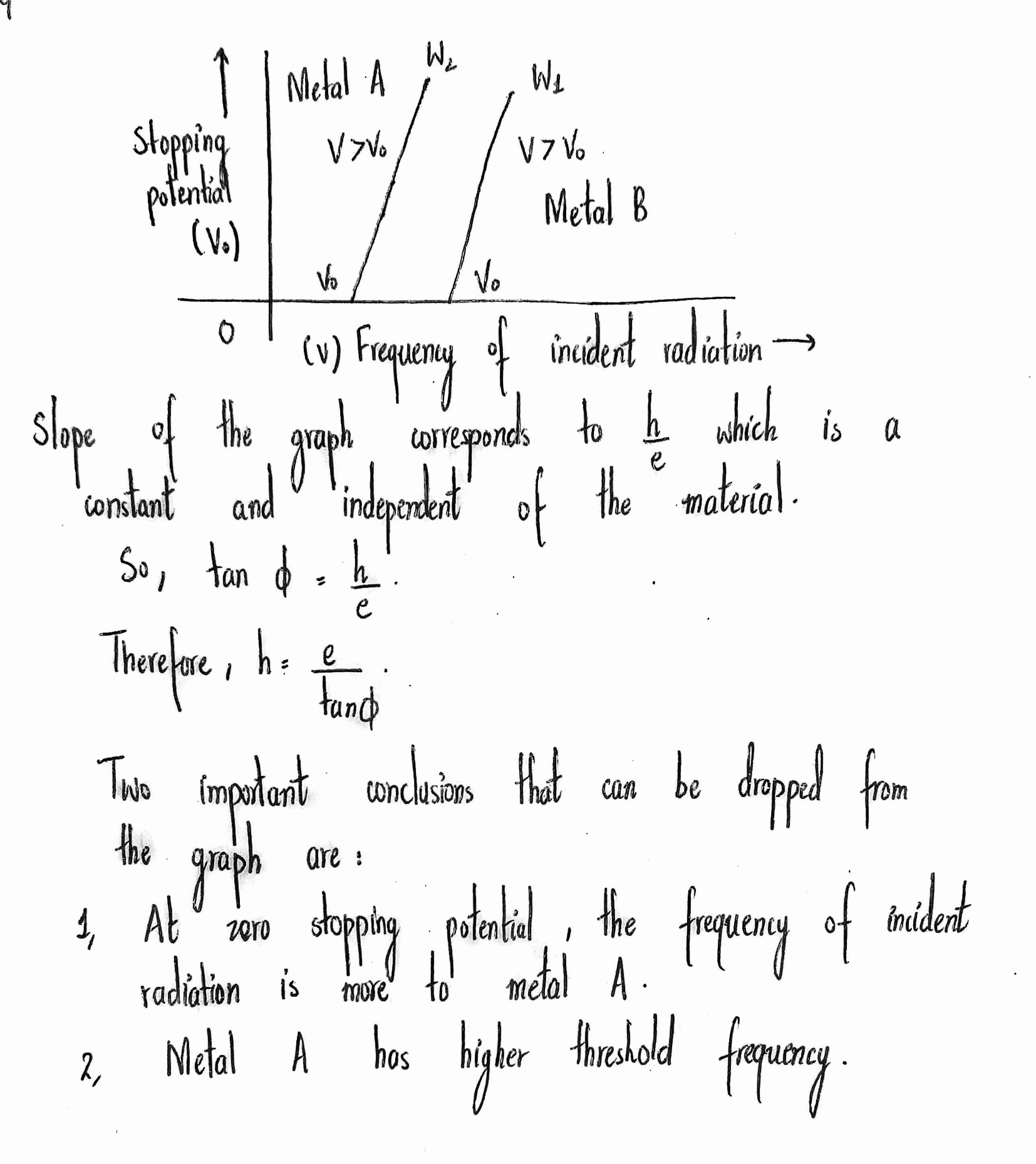
Draw a graph showing the variation of stopping potential with frequency of incident radiation for two photosensitive materials, having work function $${ W }_{ 1 } $$ and $${ W }_{ 2}$$ $$({ W }_{ 1 }>{ W }_{ 2 })$$. Write the two important conclusion that can be drawn from the study of these plots.
Consider a thin target ($$10^{-2}\ m$$ square, $$10^{-3}\ m$$ thickness ) of sodium, which produces a photo-current of $$100\ \mu A$$ when a light of intensity $$100\ W/m^{2}(\lambda=660\ nm$$) falls on it. Find the probability that a photo-electron is produced when a photon strikes a sodium atom.
[ Take density of $$Na=0.97\ kg/m^{3}$$ ]
Plot a graph showing the variation of stopping potential with the frequency of incident radiation for two different photosensitive materials having work functions $$W _ { 1 }$$ and $$W _ { 2 } \left( W _ { 1 } > W _ { 2 } \right) .$$ On what factors does the (i) slope and (ii) intercept of the line depend?
Using photon picture of light, show how Einstein's photoelectric equation can be established. Write two features of photoelectric effect which cannot be explained by wave theory.
Calculate the wavelength of moving electron having $$ 4.55 \times 10^{-25}$$ J of kinetic energy.
A 1.0 g particle is shot from a gun with velocity of 100 m/sec. Calculate its de Broglie wavelength.
Calculate the mass of a photon of sodium light having wavelength 5894 $$A^{\circ}$$ and velocity $$=3\times 10^8 ms^{-1} $$, $$h= 6.6 \times 10^{-34}\ kg m^2 s^{-1}$$
The mass of an electron is $$9.1 \times 10^{-31}$$ kg. If its K.E is $$3.0 \times 10^{-25}$$ J, calculate its wavelength in angstrom.
Two particle A and B are in motion. If the wavelength associated with particle A is $$ 5\times 10^{-8}$$ m, calculate the wavelength associated with particle B if its momentum if half of A.
Derive Einstein's photoelectric equation $$\dfrac{1}{2}mv^2=hv-hv_0.$$
Calculate the wavelength of the electron if it moving with a velocity of $$2.05\times 10^7\ ms^{-1}$$.
A bulb of $$25\ W$$ emits yellow color monochromatic light of wavelength $$0.57\ \mu m$$. Calculate the number of photons emitted per second
When radiation of $$6800\ \mathring A$$ wavelength strikes in the metal surface, the electron with zero velocity emitted. Calculate work function $$(\phi)$$ of the metal.
Calculate the energy of a photon of light having (I) frequency $$3\times 10^{15}Hz$$ (ii) the wavelength of the light as $$(0.50\mathring{A})$$
What is the wavelength associated with an electron moving with a velocity of $$\mathrm{4 \times 10^7 \ ms^{-1}}$$?
The work function of the metal is $$2.13\ eV$$. A photon having a wavelength of $$4\times 10^{-7}\ m$$ strikes the metal. Calculate the kinetic energy of the emission of the photon.
Making use of the uncertainty principle, evaluate the minimum permitted energy of an electron in a hydrogen atom and its corresponding apparent distance from the nucleus.
Employing the uncertainty principle, evaluate the indeterminancy of the velocity of an electron in a hydrogen atom if the size of the atom is assumed to be $$l = 0.10\ nm$$. Compare the obtained magnitude with the velocity of an electron in the first Bohr orbit of the given atom.
An excited electron gets relieved of its excess energy by emitting one or more photons of characteristic frequency. Find the uncertainty in the frequency of the radiation if the average period that elapses between the excitation of the atom and the time of radiation is $$10^{-8}$$ second.
A proton is confined to a nucleus of radius, $$5 \times 10^{-5} m$$. Calculate the minimum uncertainty in its momentum. Also calculate the minimum kinetic energy the proton should have. The proton mass is $$1.6 \times 10^{-27} kg$$.
Class 12 Engineering Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials,Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions