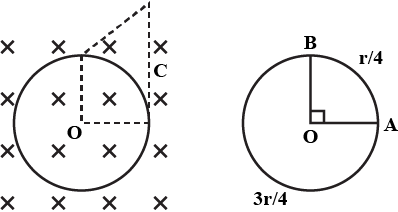Electromagnetic Induction - Class 12 Engineering Physics - Extra Questions
The SI unit of inductance is ____________.
State Faraday's law of electromagnetic induction.
When the magnetic flux associated with a coil changes an emf is induced in the circuit. State Faraday's law of electromagnetic induction.
Define the unit of self inductance .
State Faraday's law of electromagnetic induction.
describe briefly any one way of inducing e.m.f.
While travelling back to his residence in the car, Dr. Pathak was caught up in a thunderstorm. It became very dark. He stopped driving the car and waited for thunderstorm to stop. Suddenly he noticed a child walking alone on the road. He asked the boy to come inside the car till the thunderstorm stopped. Dr. Pathak dropped the boy at his residence. The boy insisted that Dr. Pathak should meet his parents. The parents expressed their gratitude to Dr. Pathak for his concern for safety of the child.
Answer the following questions based on the above information:
(a) Why is it safer to sit inside a car during a thunderstorm?
(b) Which two values are displayed by Dr. Pathak in his action?
(c) Which values are reflected in parents' response to Dr. Pathak?
(d) Give an example of similar action on your part from your everyday life?
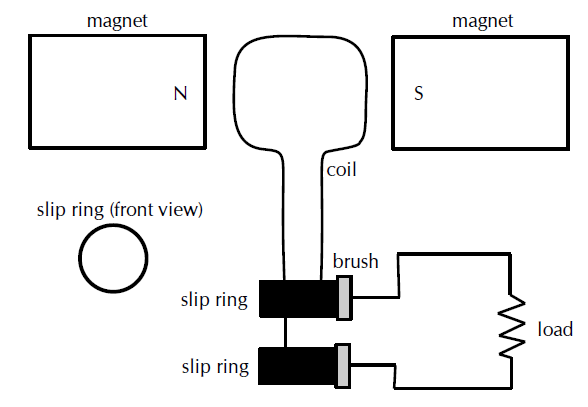
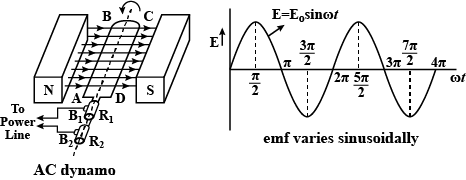
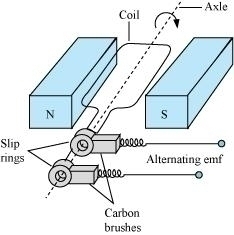
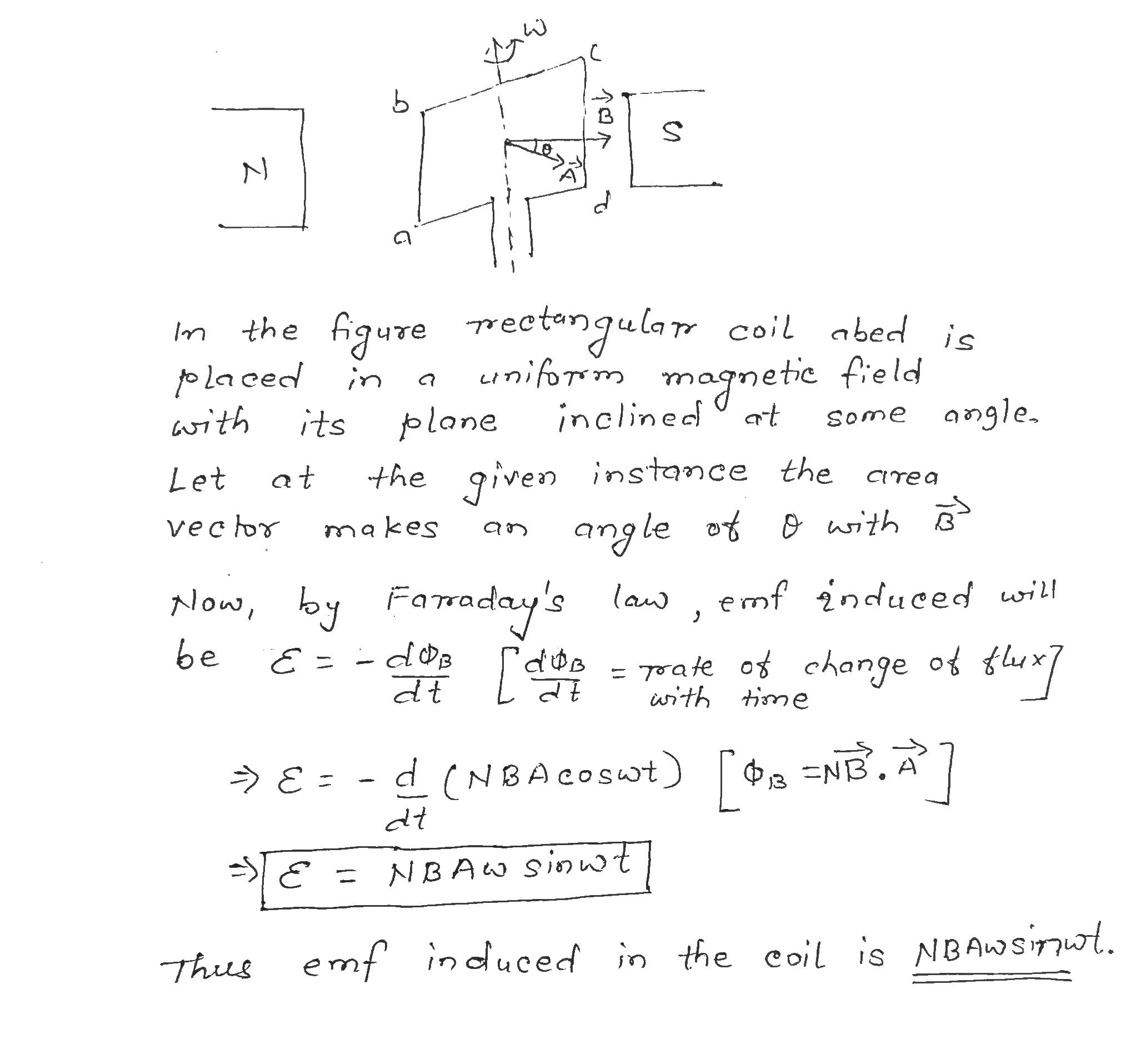
Draw a labelled diagram of an alternating current Generator. Determine the induced electromotive force by the rotation of coil in it.
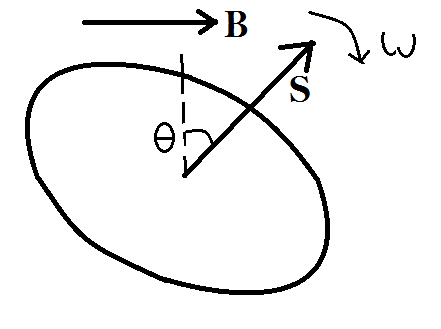
Obtain an expression for the e.m.f. induced in a coil rotating in uniform magnetic field.
Describe the principal, construction and working of a single-phase AC generator
Derive the expression for motional EMF induced in a conductor moving in a uniform magnetic field.
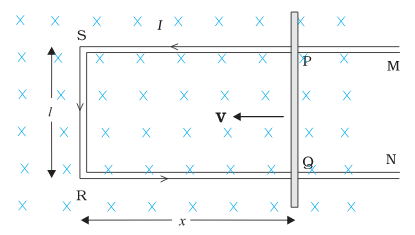
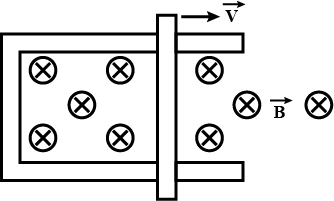
A rod lies across frictionless rails in a uniform magnetic field $$\vec {B}$$ as shown in Fig. The rod moves to the right with speed $$V$$. In order to make the induced emf in the circuit to be zero, the magnitude of the magnetic field should.
Write Faraday's laws of electro magnetic induction.
An a.c. generator consists of a coil of $$10,000$$ turns and of area $$100cm^2$$. The coil rotates at an angular speed of $$140$$ rpm in a uniform magnetic field of $$3.6\times 10^{-2}$$ T. Find the maximum value of the emf induced.
Prakash peddles a stationary bicycle, the pedals of which are attached to a $$100$$ turn coil of area $$0.1{m}^{2}$$. The coil rotates at half a revolution per second and it is placed in a uniform magnetic field of $$0.01T$$ perpendicular to the axis of rotation of the coil. Determine the maximum voltage generated in the coil.
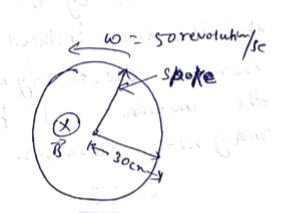
A bicycle is resting on its stand in the east-west direction and the rear wheel is rotated at an angular speed of $$50$$ revolutions per minute. If the length of each spoke is $$30.0\ cm$$ and the horizontal component of the earth's magnetic field is $$4\times 10^{-5}T$$, find the emf induced between the axis and the outer end of a spoke. Neglect centripetal force acting on the free electrons of the spoke.
State Faraday's law of electromagnetic induction. Apply the law to obtain an expression for the induced emf in a conducting rod of length $$a$$ rotating about its one end with angular velocity $$\omega$$ in uniform magnetic field B.
A jet plane is travelling towards west at a speed of 1800 km/h.What is the voltage difference developed between the ends of the wing having a span of 25 m, if the Earth's magnetic filed at the location has a magnitude of $$ 5 \times 10^{-4} T$$ and the dip angle is $$30^0$$?
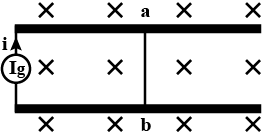
The current generator $${I}_{g}$$ shown in figure, sends a constant current $$i$$ through the circuit. The wire $$cd$$ is fixed and $$ab$$ is made to slide on the smooth thick rails with a constant velocity $$v$$ towards right. Each of these wires has resistance $$r$$. Find the current through the wire $$cd$$

The current generator $${I}_{g}$$ shown in figure, sends a constant current $$i$$ through the circuit. The wire $$ab$$ has a length $$l$$ and mass $$m$$ and can slide on the smooth, horizontal rails connected to $${I}_{g}$$. The entire system lies in a vertical magnetic field $$B$$. Find the velocity of the wire as a function of time.
A bicycle is resting on its stand in the east-west direction and the rear wheel is rotated at an angular speed of $$100$$ revolutions per minute. If the length of each spoke is $$30.0cm$$ and the horizontal component of the earth's magnetic field is $$2.0\times { 10 }^{ -5 }T$$, find the emf induced between the axis and the outer end of a spoke. Neglect centripetal force acting on the free electrons of the spoke.
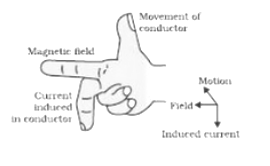
Name and state the rule to find the direction of:
current induced in a coil due to its rotation in a magnetic field.
force experienced by a current-carrying straight conductor placed in a magnetic field which is perpendicular to it.
An ac generator has emf $$\xi=\xi _{m}\sin \omega_{d}t$$, with $$\xi _{m}=25.0V$$ and $$\omega _{d}=377rad/s$$. It is connected to a $$12.7 H$$ inductor. (a) What is the maximum value of the current? (b) When the current is a maximum, what is the emf of the generator? (c) When the emf of the generator is $$-12.5 V$$ and increasing in magnitude, what is the current?
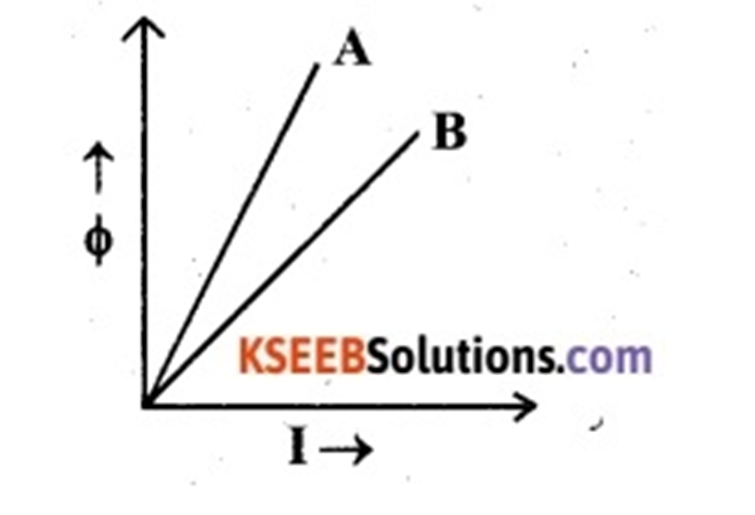
A plot of magnetic flux $$(\varphi )$$ versus current $$(I)$$, is shown in the figure for two inductors $$A$$ and $$B$$. Which of two has large value of self-inductance?

Answer the following questions
A pair of adjacent coils has a mutual inductance of $$1.5\ H$$. If the current in one coil changes from $$0$$ to $$20\ A$$ in $$0.5\ s$$, what is the change of flux linkage with the other coil?
State the law that gives the polarity of the induced emf.
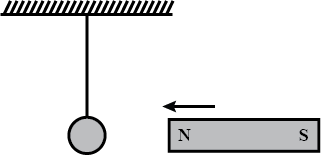
A metallic wire loop is suspended freely and a bar magnet is brought near it as shown in the diagram.
What will be the direction of induced current in the wire loop when the magnet is moved towards it.
Complete the following sentence:
The current induced in a closed circuit only if there is ..............
What do you understand by electromagnetic induction? Write the laws of Faraday related with the electromagnetic induction and wire the value of induced emf.
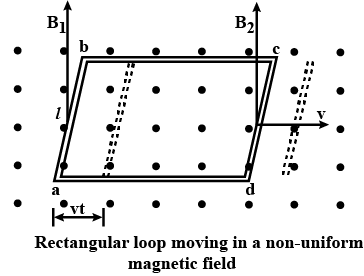
A rectangular loop moves with constant velocity perpendicular to non-uniform magnetic field. Calculate the formula for induced emf and current for it. Prove that it obeys the law of conservation on energy.
$$ A-3 \hat{k} m $$ long conductor moves with a velocity of $$ (\hat{i} + 2 \hat{j} + 3 \hat{k}) m/s $$ in a magnetic field of $$ (\hat{i} +3 \hat{j}+\hat{k})T$$. Calculate the potential difference between the ends of the conductor.
A coil of $$ 50 $$ turns is normally placed in a magnetic field of $$ 0.6 T. $$The area of this coil is $$ 0.2 m^2 $$ and the resistance in the circuit is $$ 10 \Omega $$. Calculate induced charge when:
(a) Coil is rotated by $$ 180^o. $$
(b) Coil is removed from the magnetic field.
Current in a circuit falls $$5.0A$$ to $$0.0A$$ is $$0.1s$$. Is an average emf of $$200V$$ induced, give an estimate of the self inductance of the circuit.
A pair of adjacent coils has a mutual inductance of $$1.5H$$. If the current in one coil changes from $$0$$ to $$20A$$ in $$0.5s$$, what is the change of flux linkage with the other coil?
A plot of magnetic flux $$(\phi)$$ versus current $$(I)$$ is shown in above figure, for two conductors $$A$$ and $$B$$. Which of the two has a larger value of self-inductance?
A ring of radius $$a = 50\ mm$$ made of thin wire of radius $$b = 1.0\ mm$$ was located in a uniform magnetic field with induction $$B = 0.50\ mT$$ so that the ring plane was perpendicular to the vector $$B$$. Then the ring was cooled down to a superconducting state, and the magnetic field was switched off. Find the ring current after that. Note that the inductance of a thin ring along which the surface current flows is equal to $$L = \mu a\left (ln \dfrac {8a}{b} - 2\right )$$.
(i) Define mutual inductance.
(ii) A pair of adjacent coils has a mutual inductance of $$1.5\ H$$. If the current in one coil changes from $$0$$ to $$20\ A$$ in $$0.5\ s$$, what is the change of flux linkage with the other coil?
Draw a diagram of AC generator and describe it. Derive an expression for instantaneous value of induced emf.
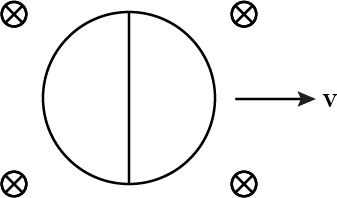
A circular copper-ring of radius $$r$$ translates in its plane with a constant velocity $$v$$. A uniform magnetic field $$B$$ exists in the space in a direction perpendicular to the plane of the ring. Consider different pairs of diametrically opposite points on the ring (a) Between which pair of points is the emf maximum? What is the value of this maximum emf? (b) Between which pair points is the emf minimum? What is the value of this minimum emf?
A metallic rod of $$'L'$$ length is rotated with angular frequency of $$'\omega'$$ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius $$L$$ about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field $$B$$ parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
A square loop of side 20 cm is initially kept 30 cm away from a region of uniform magnetic filed of 0.1 T as shown in the figure. It is then moved towards the right with a velocity of $$10\ cm\ { s }^{ -1 }$$ till it goes out of the field. plot a graph showing the variation of
(i) magnetic flux $$(\phi )$$ through the loop with time(t).
(ii) induced emf $$(\varepsilon)$$ in the loop with time t.
(iii) induced current in the loop, if it has resistance of 0.1 $$\Omega$$.

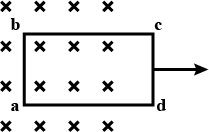
A rectangular frame of wire $$abcd$$ has dimensions $$32\ cm\times 8.0\ cm$$ and a total resistance of $$2.0\ \Omega$$. It is pulled out of a magnetic field $$B = 0.02\ T$$ by applying a force of $$3.2\times 10^{-5}N$$ (figure). It is found that the frame moves with constant speed.
Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points $$a$$ and $$b$$ and (d) the potential difference between the points $$c$$ and $$d$$.
A conducting loop is pulled outward with a constant speed.
The induced emf between the point A and B, just after the motion start is

A rectangular current loop is in an arbitrary orientation in an external uniform magnetic field. Any work required to rotate the loop about an axis perpendicular to its plane ?
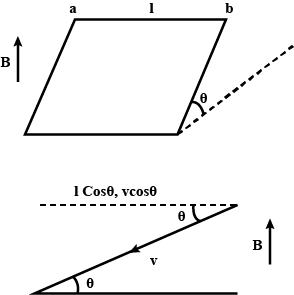
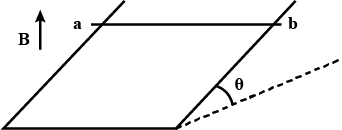
A wire ab of length l, mass m and resistance R slides on a smooth, thick pair of metallic rails joined at the bottom as shown in figure. The plane of the rails makes an angle $$\theta$$ with the horizontal. A vertical magnetic field B exists in the region. If the wire slides on the rails at a constant speed v, show that
$$B = \sqrt{\dfrac{mg \, R \, sin \theta}{vl^2 cos^2 \theta}}$$
A $$20cm$$ long conducting rod is set into pure translation with a uniform velocity of $$10cm\quad { s }^{ -1 }$$ perpendicular to its length. A uniform magnetic field of magnitude $$0.10T$$ exists in a direction perpendicular to the plane motion. (a) Find the average magnetic force on the free electrons of the rod. (b) For what electric field inside the rod, the electric force on a free electron will balance the magnetic force? How is this electric field created? (c) Find the motional emf between the ends of the rod.
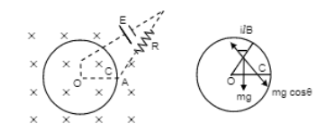
Figure shows all parameters are the same except that the battery of emf $$\varepsilon$$ and a variable resistance $$R$$ are connected between $$O$$ and $$C$$. Neglects the resistance of the connecting wires. Let $$\theta$$ be the angle made by the rod from the horizontal position (shown in the figure), measured in the clockwise direction. DUring the part of the motion $$0< \theta< \pi /4$$ the only forces acting on the rod are gravity and the forces exerted by the magnetic field and the pivot. However during the part of the motion, the resistance $$R$$ is varied in such a way that the rod continues to rotate with a constant angular velocity $$\omega$$. Find the value of $$R$$ in terms of the given quantities.
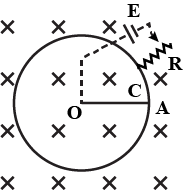
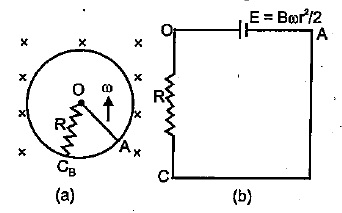
Figure shows a conducting circular loop of radius $$a$$ placed in a uniform, perpendicular magnetic field $$B$$. A thick metal rod $$OA$$ is pivoted at the centre $$O$$. The other end fo the rod touches the loop at $$A$$. The centre $$O$$ and a fixed point $$C$$ on the loop are connected by a wire $$OC$$ of resistance $$R$$. A force is applied at the middle point of the rod $$OA$$ perpendicularly so that the rod rotates clockwise at a uniform angular-velocity $$\omega$$. Suppose the wire connecting $$O$$ and $$C$$ has zero resistance but the circular loop has a resistance $$R$$ uniformly distributed along its length. The rod $$OA$$ is made to rotate with a uniform angular speed $$\omega$$ as shown in the figure. Find the current in the rod when $$\angle AOC={90}^{o}$$
The rectangular wire-frame shown in figure has a width $$d$$, mass $$m$$, resistance $$R$$ and a large length. A uniform magnetic field $$B$$ exists to the left of the frame. A constant force $$F$$ starts pushing the frame into the magnetic field at $$t=0$$ (a) Find the acceleration of the frame when its speed has increased to $$v$$, (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. Find this velocity $${v}_{0}$$ (c) Show that the velocity at time $$t$$ is given by
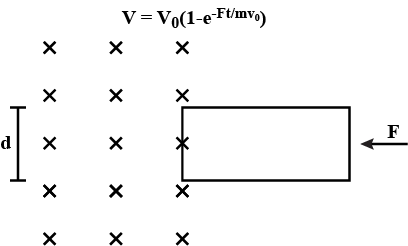
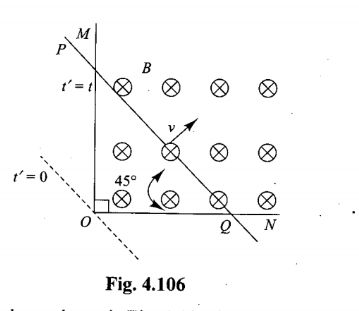
An electric circuit is composed of three conducting rods MO, ON, PQ as shown in Fig. 4.The resistance of the rods per unit length is $$\lambda$$. The rod PQ slides, as shown in the figure, at a constant velocity v, keeping its tilt angle relative to ON and MO fixed at $$45^{\circ}$$. At each instance, the circuit is closed. The whole system is embedded in a uniform magnetic field B, which is directed perpendicularly into the page. Compute the time-dependent induced electric current.
A uniform magnetic field $$B$$ exists in a cylindrical region, shown dotted in figure. The magnetic field increases at a constant rate $$\cfrac{dB}{dt}$$. Consider a circle of radius $$r$$ coaxial with the cylindrical region. (a) Find the magnitude of the electric field $$E$$ at a point on the circumference of the circle. (b) Consider a point $$P$$ on the side of the square circumscribing the circle. Show that the component of the induced electric field at $$P$$ along $$ba$$ is the same as the magnitude found in part (a).

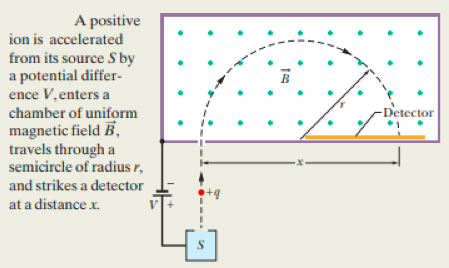
A mass spectrometer (see figure) is used to separate uranium ions of mass $$3.92 \times10^{-25}kg$$ and charge $$3.20 \times10^{-19}C$$ from related species. The ions are accelerated through a potential difference of $$100 kV$$ and then pass into a uniform magnetic field, where they are bent in a path of radius $$1.00 m$$. After traveling through $$180^{0}$$ and passing through a slit of width $$1.00 mm$$ and height $$1.00 cm$$, they are collected in a cup. If the machine is used to separate out $$100 mg$$ of material per hour, calculate
(a) the current of the desired ions in the machine and
(b) the thermal energy produced in the cup in $$1.00 h$$.
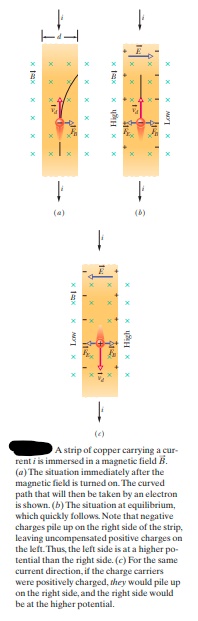
A strip of copper $$150 mm$$ thick and $$4.5 mm$$ wide is placed in a uniform magnetic field $$\vec{B}$$ of magnitude $$0.65 T$$, with $$\vec{B}$$ perpendicular to the strip. A current $$i = 23 A$$ is then sent through the strip such that a Hall potential difference $$V$$ appears across the width of the strip. Calculate $$V$$. (The number of charge carriers per unit volume for copper is $$8.47 \times10^{28} electrons/m^{3}$$.)
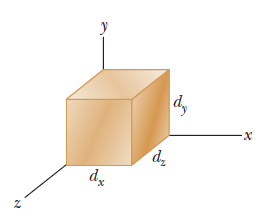
A conducting rectangular solid of dimensions $$d_{x} = 5.00 m, d_{y}=3.00 m, and/ d_{z} = 2.00 m$$ moves with a constant velocity $$\vec{v} = (20.0 m/s)\hat{i}$$ through a uniform magnetic field
$$\vec{B} = (30.0mT)\hat{j}$$ (see figure). What are the resulting
(a) electric field within the solid, in unit-vector notation, and
(b) potential difference across the solid?
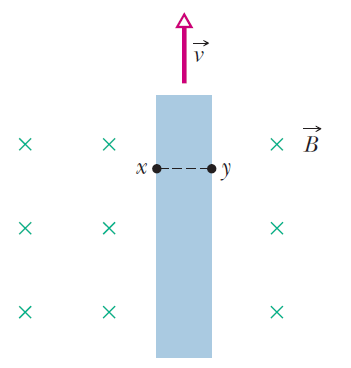
A metal strip $$6.50$$ cm long, $$0.850 cm$$ wide, and $$0.760 mm$$ thick moves with constant velocity $$\vec{v}$$ through a uniform magnetic field $$\vec{B} =1.20 mT$$ directed perpendicular to the strip, as shown in the figure. A potential difference of $$3.90 \mu V$$ is measured between points $$x$$ and $$y$$ across the strip. Calculate the speed $$v$$.
An ion source is producing $$^{6}Li$$ ions, which have charge +e and mass $$9.99\times10^{-27}kg$$. The ions are accelerated by a potential difference of $$10kV$$ and pass horizontally into a region in which there is a uniform vertical magnetic field of magnitude $$B=1.2 T$$. Calculate the strength of the smallest electric field, to be set up over the same region, that will allow the $$^{6}Li$$ ions to pass through undeflected.
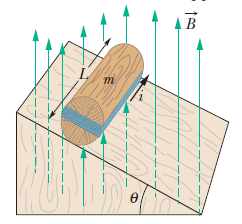
The figure shows a wood cylinder of mass $$m = 0.250 kg$$ and length $$L = 0.100 m$$, with $$N = 10.0$$ turns of wire wrapped around it longitudinally, so that the plane of the wire coil contains the long central axis of the cylinder. The cylinder is released on a plane inclined at an angle $$\theta$$ to the horizontal, with the plane of the coil parallel to the incline plane. If there is a vertical uniform magnetic field of magnitude $$0.500 T$$, what is the least current $$i$$ through the coil that keeps the cylinder from rolling down the plane?
A source injects an electron of speed $$v = 1.5 \times 10^{7} m/s$$ into a uniform magnetic field of magnitude $$B = 1.0 \times 10^{-3} T$$. The velocity of the electron makes an angle $$\theta = 10^{0}$$ with the direction of the magnetic field. Find the distance $$d$$ from the point of injection at which the electron next crosses the field line that passes through the injection point.
A rectangular wire frame, shown below, is placed in uniform magnetic field directed upward and normal to the pplane of the paper. The part $$AB$$ is connected to a spring. The spring is streched and released when the wire $$AB$$ has come to the position $$A'B' (t=0)$$. How would the induced emf vary with time? Neglect damping.

A rectangular coil of turns $$ N $$ and area $$ A $$ rotates with a uniform velocity to in a uniform magnetic field. Prove that induced emf in the coil is $$ NBA \omega $$ sin $$ \omega t. $$
The current obtained from the cell is unidirectional and is of the same magnitude. But what are the peculiarities of the current obtained by electromagnetic induction ?
A closed circuit consists of a source of constant emf $$E$$ and a choke coil of inductance $$L$$ connected in series. The active resistance of the whole circuit is equal to $$R$$. At the moment $$t = 0$$ the choke coil inductance was decreased abruptly $$\eta$$ times. Find the current in the circuit as a function of time $$t$$.
Instruction. During a stepwise change of inductance the total magnetic flux (flux linkage) remains constant.
Class 12 Engineering Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials,Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions