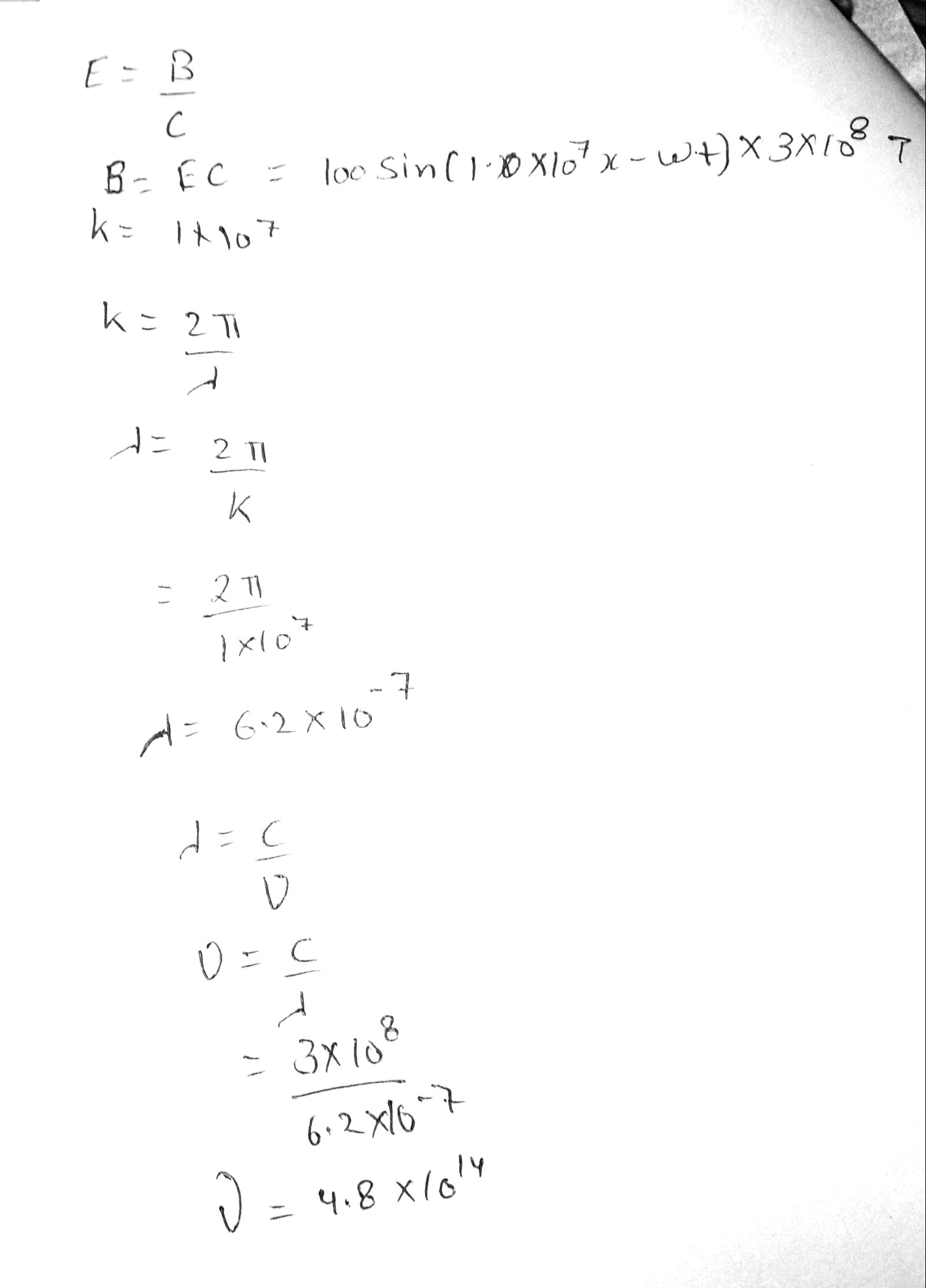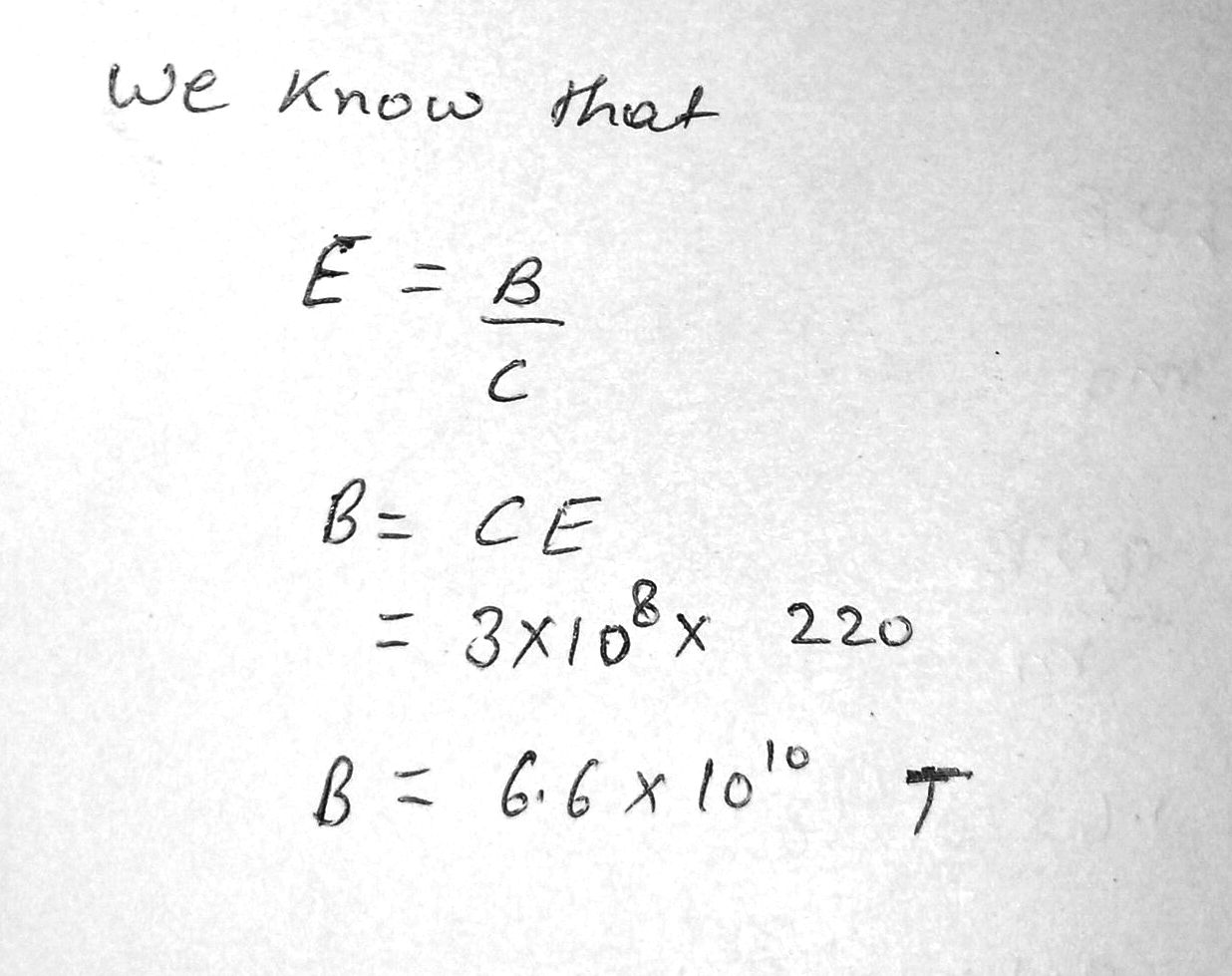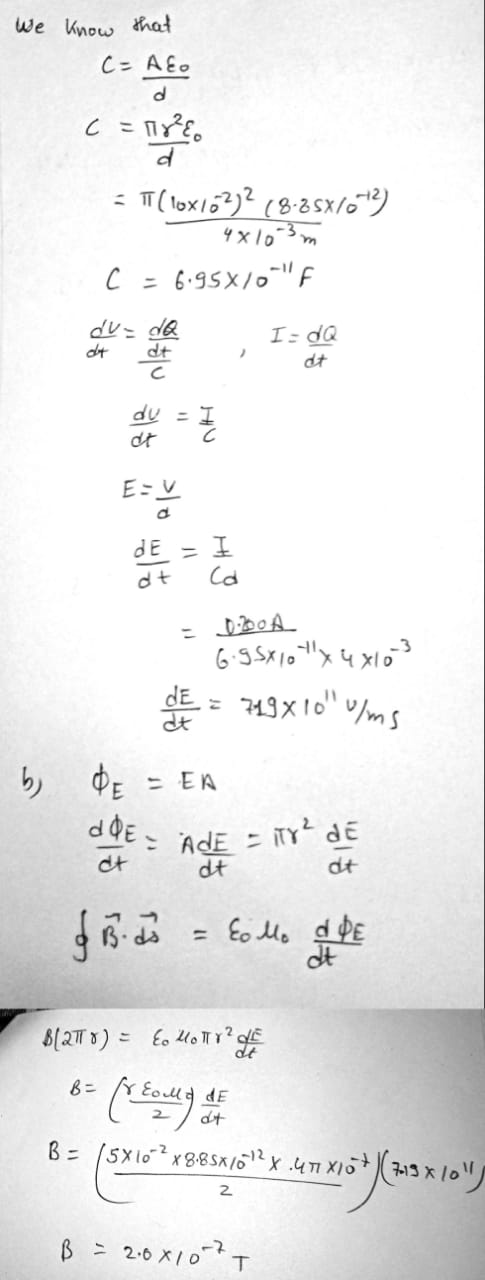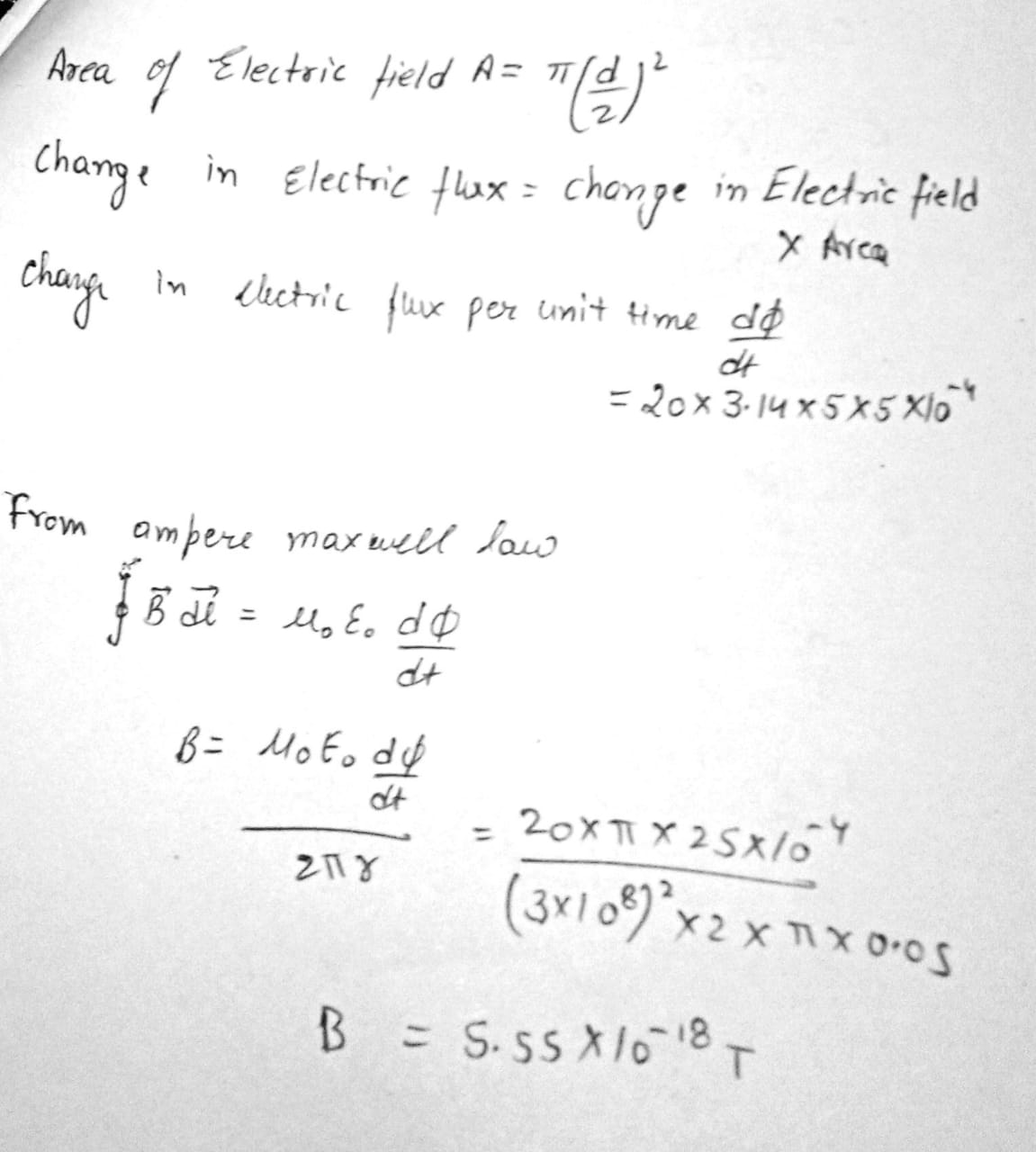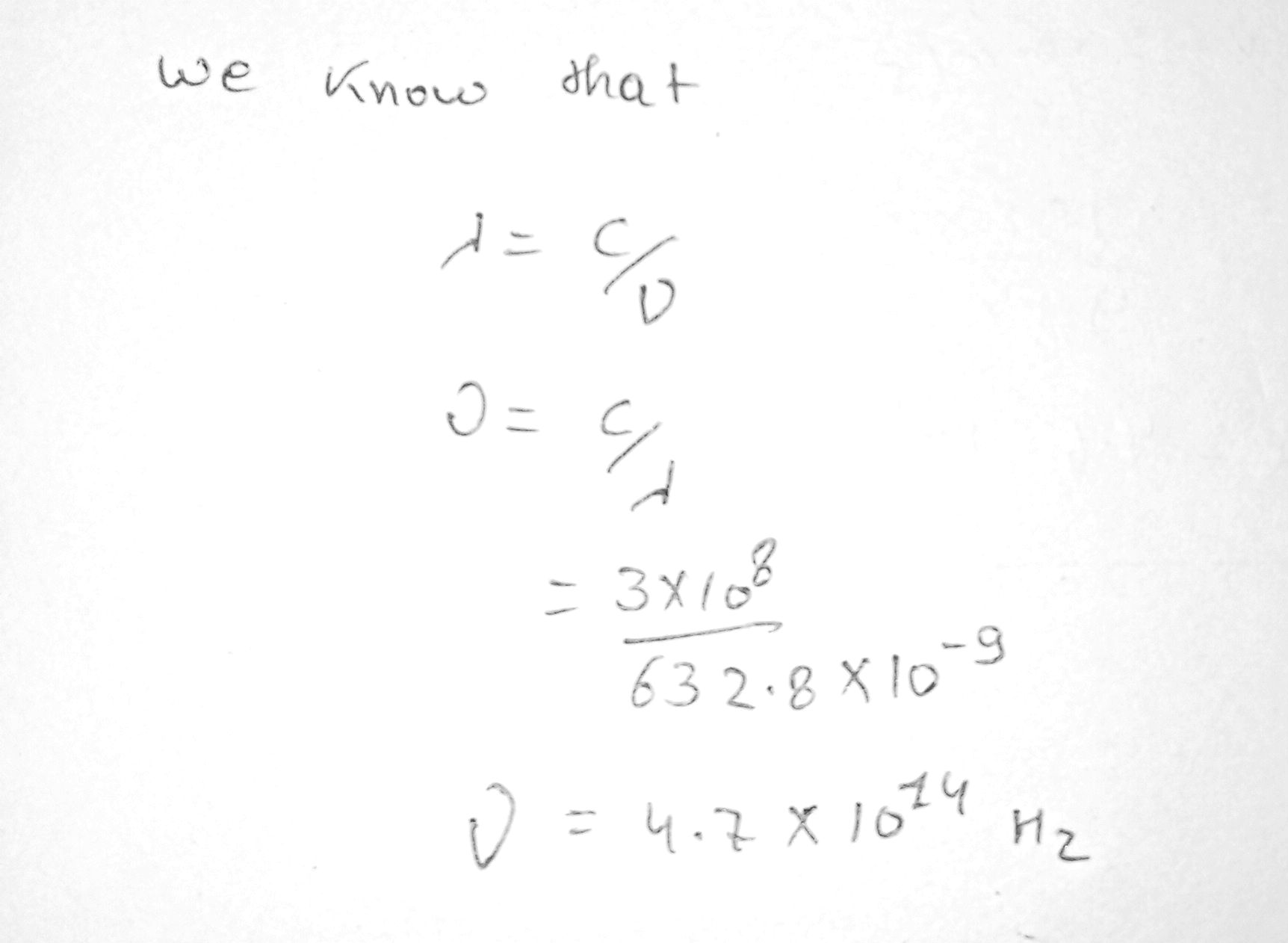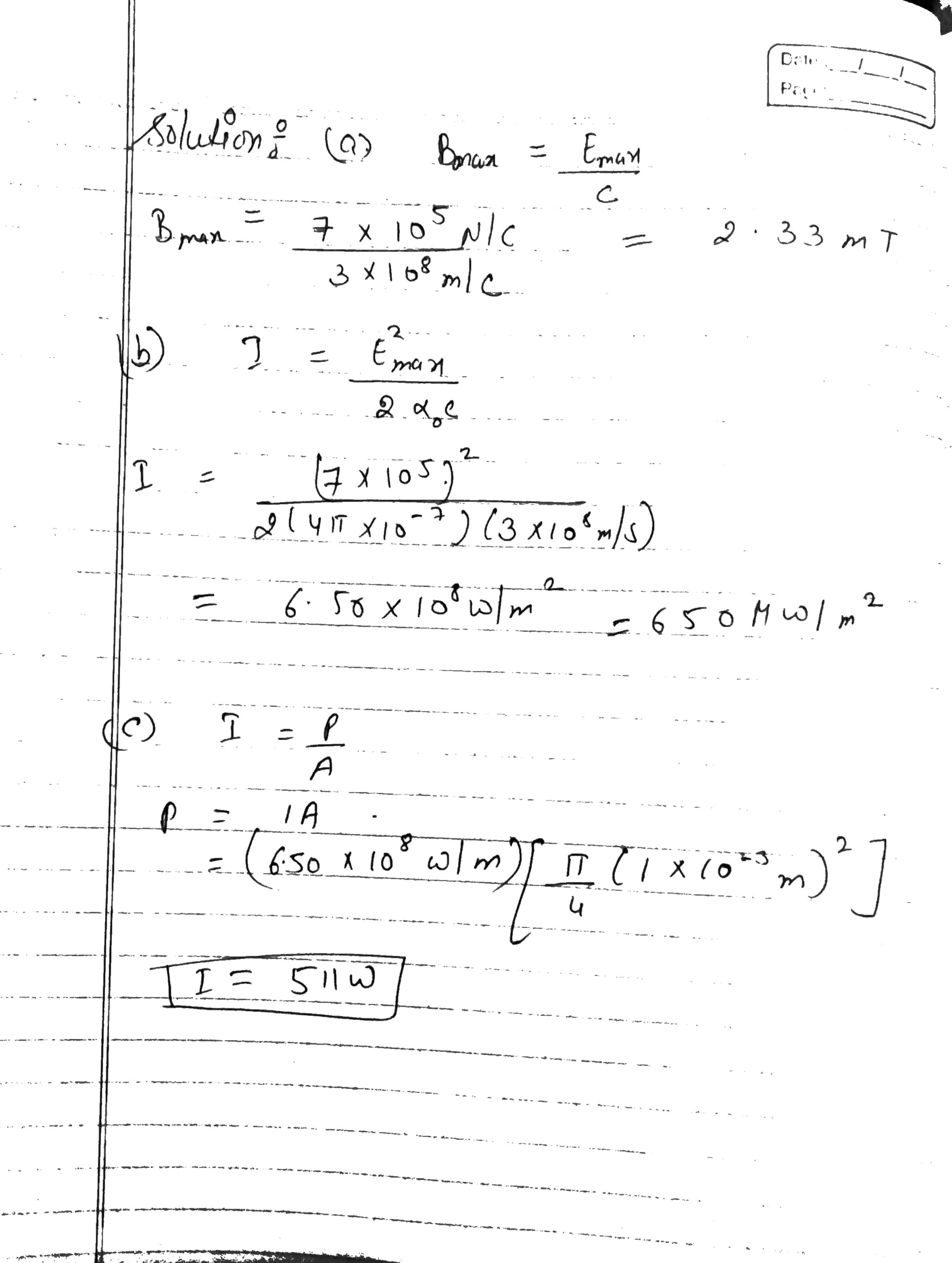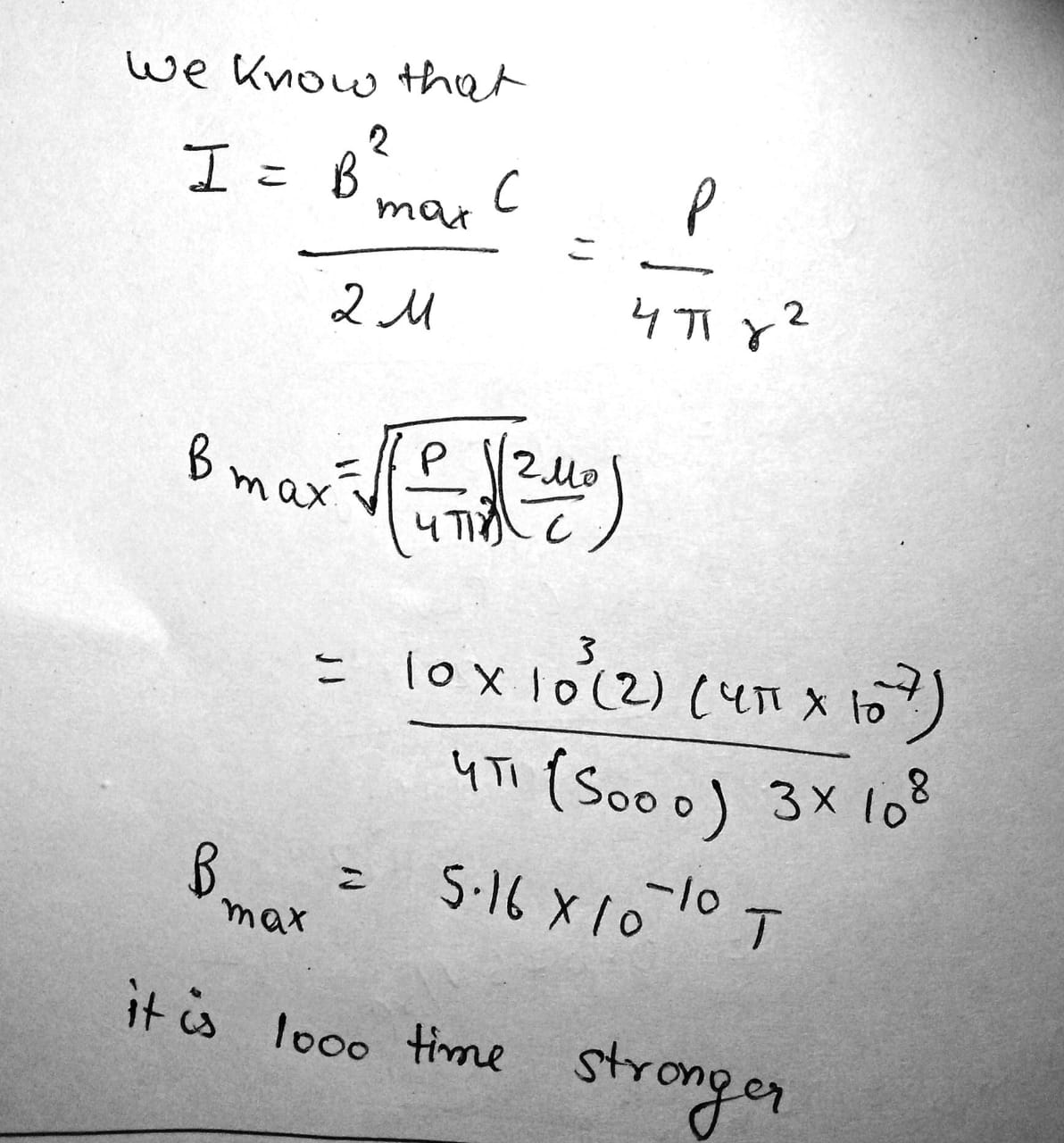Class 12 Engineering Physics - Electromagnetic Waves

Using Wien's formula, demonstrate that
(a) the most probable radiation frequency $$ \omega_{p r} \backsim T $$;

(a)The most probable radiation frequency $$\omega_{pr}$$ is the frequency for which
$$\dfrac{d}{d_{\omega}} u_{\omega} = 3 \omega ^2 F(\omega / T) + \dfrac{\omega^3}{T} F' (\omega / T) = 0$$
The maximum frequency is the root other than $$\omega = 0$$ of the equation. It is
$$\omega = \dfrac{3 TF (\omega/T)}{F'(\omega / T)}$$
Or $$\omega_{pr} = x_0 T$$ where $$x_0$$ is the solution of the transcendental equation $$3 F(x_0) + x_0 F' (x_0) = 0$$

Find the conditions under which a charged particle moving uniformaly through a medium with refractive index n emits light. Find also the direction of that radiation.

We obtain $$cos\theta = \frac{v}{V} $$ where $$v = \frac{c}{n} $$ is the phase velocity of light.

It is evident that the radiation is possible only if V>v that is when the velocity of the particle exceeds the phase velocity of light in the medium.

In a plane radio wave the maximum value of the electric field component is $$5.00 V/m$$. Calculate (a) the maximum value of the magnetic field component and (b) the wave intensity.

(a) The amplitude of the magnetic field in the wave is,
$$B_{m}=\frac{E_{m}}{c}=\frac{5.00V/m}{2.998\times10^{8}m/s}=1.67\times10^{-8}T$$.

(b) The intensity is the average of the Poynting vector:
$$I-S_{avg}=\frac{E_{m}^{2}}{2\mu _{0}c}=\frac{\left ( 5.00V/m \right )^{2}}{2\left ( 4\pi \times10^{-7}T.m/A \right )\left ( 2.998\times10^{8}m/s \right )}=3.31\times10^{-2}W/m^{2}$$.

A plane electromagnetic wave travels in vacuum along Z - direction . What can you say about the directions of its electric and magnetic field vectors ? If the frequency of the wave is 30 MH z, what is the wavelength ?

The electric and magnetic field vectors are in X Y - plane
$$ \upsilon = 30 MH z = 30 \times 10^{6} Hz $$
$$\lambda = \frac{C}{\upsilon } = \dfrac{3 \times 10^{8}}{30 \times 10^{6}} = 10 m $$

A charged particle oscillates about its mean equilibrium position with a frequency of $$10^{9} $$ What is the frequency of the electromagnetic waves produced by the oscillator.

The frequency of the electromagnetic waves produced is same as that of the oscillating charged particles . Hence the frequency of the electromagnetic waves produced is $$ U = 10^{9} Hz $$.

The speed of an electromagnetic wave in a material medium is given by $$c = \dfrac {1}{\sqrt {\mu \epsilon}}$$ being the permeability of the medium and $$\epsilon$$ its permittivity. How does it frequency change?

The frequency of electromagnetic waves does not change while travelling through a medium.

Which constituent radiation of the electromagnetic spectrum is used
(i) In RADAR,
(ii) To photograph internal parts of a human body, and
(iii) For taking photographs of the sky during night and foggy conditions?
Give one reason for your answer in each case.

a) Radio waves $$(3 \times 10^9)$$

b) X-rays $$(3 \times 10^{16} - 3 \times 10^{17})$$

c) I R Radiations $$(3 \times 10^{12} - 4 \times 10^{11})$$

The magnetic field in a plane electromagnetic wave is given by $$ B = (200\,\mu T)sin[(4.0\times 10^{15}s^{-1})(t-x/c)]$$.

$$ B = (200\,\mu T)sin [4\times 10^{15}5^{-1}](t-x/C)$$
$$a) B_{0} = 200\,\mu T $$
$$E_{0} = C\times B_{0} = 200\times 10^{-6}\times 3\times 10^{8} = 6\times 10^{4} $$
b) Average energy density $$ = \dfrac{1}{2\mu _{0}}B_{0}^{2} = \dfrac{(200\times 10^{-6})^{2}}{2\times 4\pi \times 10^{-7}} = \dfrac{4\times 10^{-8}}{8\pi \times 10^{-7}} = \dfrac{1}{20\pi } = 0.0159 = 0.016.$$

What is the wavelength of the electromagnetic wave emitted by the oscillatorantenna system of above figure, if $$L=0.253\mu H$$ and $$C=25.0 pF$$?

As we know,

The emitted wavelength is,

$$\lambda =\dfrac{c}{f}=2\pi c\sqrt{LC}$$

$$=2\pi \left ( 2.998*10^{8}m/s \right )\sqrt{\left ( 0.253*10^{-6}H \right )\left ( 25.0*10^{-12}F \right )}=4.74m$$.

Project Seafarer was an ambitious program to construct an enormous antenna, buried underground on a site about $$10000km^{2}$$ in area. Its purpose was to transmit signals to submarines while they were deeply submerged. If the effective wavelength were $$1.0*10^{4}$$ Earth radii, what would be the (a) frequency and (b) period of the radiations emitted? Ordinarily, electromagnetic radiations do not penetrate very far into conductors such as seawater and so normal signals cannot reach the submarines.

(a) The frequency of the radiation is,
$$f=\dfrac{c}{\lambda}=\dfrac{3.0*10^{8}m/s}{\left ( 1.0*10^{5} \right )\left ( 6.4*10^{6}m \right )}=4.7*10^{-3}Hz$$.

(b) The period of the radiation is,
$$T=\dfrac{1}{f}=\dfrac{1}{4.7*10^{-3}Hz}=212s=3min32s$$.

The sunlight reaching the earth has maximum electric field of $$810\,V\,m^{-1}$$. What is the maximum magnetic filed in this light?

$$E_{0} = 810\,v/m, B_{0} = ? $$
We know, $$B_{0} = \mu _{0}\,\epsilon _{0}C\,E_{0}$$
Putting the values,
$$B_{0} = 4\pi\times 10^{-7}\times 8.85\times 10^{-12}\times 3\times 10^{8}\times 810$$
$$ = 27010.9\times 10^{-10} = 2.7\times 10^{-6}T = 2.7\,\mu T.$$

Fill in the blanks with suitable words
Electric and magnetic field in Electromagnetic wave are mutually ___________ to each other.

Electric and Magnetic fiels in Electromagnectic waves are mutually perpendicular to each other.
1156864_560617_ans_39ab08d7b2f64c518f08b847f6f39c91.jpg

1156864_560617_ans_39ab08d7b2f64c518f08b847f6f39c91.jpg

Which of the wavelengths $$4000\overset{o}{A}$$ and $$8000\overset{o}{A}$$ has a higher frequency?

Speed of electromagnetic wave $$v = 3\times 10^8 \ m/s$$ in vacuum.
Frequency of wave $$\nu = \dfrac{v}{\lambda}$$
$$\implies \ \nu\propto \dfrac{1}{\lambda}$$ $$(\because v =same)$$
This means higher the wavelength of light, lower is the frequency.
Thus $$4000 \ A^o$$ light has higher frequency than $$8000 \ A^o$$ light.

Find the range of frequency of light that is visible to an average human being $$(400\ nm < \lambda < 700\ nm)$$

We know that speed of light is $$3 \times 10^8 m/s$$ and $$ v =f\lambda$$

Lower limit of frequency range of visible light will be corresponding to $$\lambda = 700 nm=7 \times 10^{-7}$$

$$f_L = \dfrac{3\times 10^8}{7\times 10^{-7}} = (4.285 \times 10^{14}) Hz$$

And, upper limit of frequency range of visible light will be corresponding to $$\lambda = 400 nm=4\times 10^{-7}$$

$$f_U = \dfrac{3\times 10^8}{4\times 10^{-7}} = (7.5 \times 10^{14}) Hz$$

So,range of frequency of light that is visible to an average human being is $$(4.285 \times 10^{14}) Hz$$ to $$ (7.5 \times 10^{14}) Hz$$

A charge particle oscillates about its mean (equilibrium) position with a frequency of $$10^{9}$$ Hz. what is the frequency of electromagnetic waves produced by the osillator?

Frequency of oscillation $$= 10^{9} H_{z}$$

the oscillation will emit electromagnetic waves of same frequency due to resonance of oscillation.

$$\therefore $$ frequency of waves emitted$$= 10^{9} H_{z}$$

A plane electromagnetic wave,with wavelength $$3.0 m$$, travels in vacuum in the positive direction of an $$x$$ axis. The electric field,of amplitude $$300V/m$$, oscillates parallel to the $$y$$ axis. What are the (a) frequency, (b) angular frequency and (c) angular wave number of the wave? (d) What is the amplitude of the magnetic field component? (e) Parallel to which axis does the magnetic field oscillate? (f) What is the time-averaged rate of energy flow in watts per square meter associated with this wave? The wave uniformly illuminates a surface of area $$2.0m^{2}$$. If the surface totally absorbs the wave, what are (g) the rate at which momentum is transferred to the surface and (h) the radiation pressure on the surface?

(a) Since $$c=\lambda f$$, where $$λ$$ is the wavelength and $$f$$ is the frequency of the wave,
$$f=\dfrac{c}{\lambda}=\dfrac{2.998*10^{8}m/s}{3.0m}=1.0*10^{8}Hz$$.

(b) The angular frequency is,
$$\omega =2\pi f=2\pi \left ( 1.0*10^{8}Hz \right )=6.3*10^{8}rad/s$$.

(c) The angular wave number is,
$$k=\dfrac{2\pi}{\lambda}=\dfrac{2\pi}{3.0m}=2.1rad/m$$.

(d) The magnetic field amplitude is,
$$B_{m}=\dfrac{E_{m}}{c}=\dfrac{300V/m}{2.998*10^{8}m/s}=1.0*10^{-6}T$$.

(e) $$\underset{B}{\rightarrow}$$ must be in the positive $$z$$ direction when $$\underset{E}{\rightarrow}$$ is in the positive $$y$$ direction in order for $$\underset{E}{\rightarrow}*\underset{B}{\rightarrow}$$ to be in the positive $$x$$ direction (the direction of propagation).

(f) The intensity of the wave is,
$$I=\dfrac{E_{m}^{2}}{2\mu _{0}c}=\dfrac{\left ( 300V/m \right )^{2}}{2\left ( 4\pi *10^{-7}H/m \right )\left ( 2.998*10^{8}m/s \right )}=119W/m^{2}\approx 1.2*10^{2}W/m^{2}$$.

(g) Since the sheet is perfectly absorbing, the rate per unit area with which momentum is delivered to it is $$I/c$$, so
$$\dfrac{dp}{dt}=\dfrac{IA}{c}=\dfrac{\left ( 119W/m^{2} \right )\left ( 2.0m^{2} \right )}{2.998*10^{8}m/s}=8.0*10^{-7}N$$.

(h) The radiation pressure is,
$$p_{r}=\dfrac{dp/dt}{A}=\dfrac{8.0*10^{-7}N}{2.0m^{2}}=4.0*10^{-7}Pa$$.

The magnetic component of a polarized wave of light is $$B_{x}=\left ( 4.010^{-6}T \right )\sin \left [ \left ( 1.5710^{7}m^{-1} \right )y+\omega t \right ]$$. (a) Parallel to which axis is the light polarized? What are the (b) frequency and (c) intensity of the light?

(a) The polarization direction is defined by the electric field (which is perpendicular to the magnetic field in the wave, and also perpendicular to the direction of wave travel). The given function indicates the magnetic field is along the $$x$$ axis (by the subscript on $$B$$) and the wave motion is along $$–y$$ axis (see the argument of the sine function). Thus, the electric field direction must be parallel to the $$z$$ axis.

(b) Since $$k$$ is given as $$1.57*10^{7}/m$$, then $$\lambda=2\pi/k=4.0*10^{-7}m$$, which means $$f=c/\lambda =7.5*10^{14}Hz$$.

(c) The magnetic field amplitude is given as $$B_{m}=4.0*10^{-6}T$$. The electric field amplitude $$E_{m}$$ is equal to $$B_{m}$$ divided by the speed of light $$c$$. The rms value of the electric field is then $$E_{m}$$ divided by $$\sqrt{2}$$ . Equation then gives $$I=1.9kW/m^{2}$$.

A plane electromagnetic wave travels in vacuum along z-direction. What can you say about the direction of electric and magnetic field vectors?

Electric field vector along X-axis.

Magnetic field vector along Y-axis.

The magnetic component of an electromagnetic wave in vacuum has an amplitude of $$85.8 nT$$ and an angular wave number of $$4.00m^{-1}$$. What are (a) the frequency of the wave, (b) the rms value of the electric component and (c) the intensity of the light?

a) Setting $$v = c$$ in the wave relation $$kv=\omega =2\pi f$$, we find $$f=1.91*10^{8}Hz$$.

(b) $$E_{rms}=E_{m}/\sqrt{2}=B_{m}/c\sqrt{2}=18.2V/m$$.

(c) $$I=\left ( E_{rms} \right )^{2}/c\mu _{0}=0.878W/m^{2}$$.

The electric component of a beam of polarized light is $$E_{y}=\left ( 5.00V/m \right )\sin \left [ \left ( 1.00*10^{6}m^{-1} \right )z+\omega t \right ]$$.
(a) Write an expression for the magnetic field component of the wave, including a value for $$\omega$$. What are the (b) wavelength, (c) period and (d) intensity of this light? (e) Parallel to which axis does the magnetic field oscillate? (f) In which region of the electromagnetic spectrum is this wave?

(a) From $$kc=\omega$$ where $$k=1.00*10^{6}m^{-1}$$, we obtain $$\omega=3.00*10^{14}rad/s$$. The magnetic field amplitude is,
$$B=E/c=\left ( 5.00V/m \right )/c=1.67*10^{-8}T$$.
From the fact that $$-\hat{k}$$ (the direction of propagation), $$\underset{E}{\rightarrow}=E_{y}\hat{j}$$ and $$\underset{B}{\rightarrow}$$ are mutually perpendicular, we conclude that the only nonzero component of $$\underset{B}{\rightarrow}$$ is $$B_{x}$$, so that we have
$$B_{x}=\left ( 1.67*10^{-8}T \right )\sin \left [ \left ( 1.00*10^{6}/m \right )z+\left ( 3.00*10^{14}/s \right )t \right ]$$.

(b) The wavelength is $$\lambda=2\pi /k=6.28*10^{-6}m$$.

(c) The period is $$T=2\pi/\omega =2.09*10^{-14}s$$.

(d) The intensity is, $$I=\frac{1}{c\mu _{0}}\left ( \frac{5.00V/m}{\sqrt{2}} \right )^{2}=0.0332W/m^{2}$$.

(e) As noted in part (a), the only nonzero component of $$\underset{B}{\rightarrow}$$ is $$B_{x}$$. The magnetic field oscillates along the $$x$$ axis.

(f) The wavelength found in part (b) places this in the infrared portion of the spectrum.

Find the wavelength of electromagnetic waves of frequency $$4\times 10^{9} Hz$$ in free space. Give its two applications.

Wavelength, $$\lambda = \dfrac {c}{v} = \dfrac {3\times 10^{8}}{4\times 10^{9}} = \dfrac {3}{40} m = \dfrac {300}{40} cm = 7.5\ cm$$.

This wavelength corresponds to microwave region (or short radio waves).

These are used in (i) RADAR (ii) Microwave ovens.

Find the wavelength of electromagnetic waves of frequency $$5\times 10^{19} Hz$$ in free space. Give its two applications.

Wavelength, $$\lambda = \dfrac {c}{v} = \dfrac {3\times 10^{8}}{5\times 10^{19}} = 6\times 10^{-12} m$$

These are gamma rays.

These are used for : (i) Nuclear reactions (ii) Radiotherapy.

The magnetic field of a beam emerging from a filter facing a floodlight is given by
$$B=12\times {10}^{-8}\sin { \left( 1.20\times { 10 }^{ 7 }z-3.6\times { 10 }^{ 15 }t \right) T } $$
What is the average intensity of the beam?

$$B=12\times {10}^{-8}\sin { \left( 1.20\times { 10 }^{ 7 }z-3.6\times { 10 }^{ 15 }t \right) T } $$...(I)
Standard equation $$B={B}_{0}\sin{(kx-\omega t)}$$....(II)
Comparing the different terms in above two (I,II) equations
$${B}_{0}=12\times {10}^{-8}$$ Tesla
$${I}_{av}=\cfrac { { B }_{ 0 }^{ 2 } }{ 2{ \mu }_{ 0 } } C=\cfrac { 12\times { 10 }^{ -8 }\times 12\times { 10 }^{ -8 }\times 3\times { 10 }^{ 8 } }{ 2\times 4\pi \times { 10 }^{ -7 } } =\cfrac { 12\times 12\times 3\times \times { 10 }^{ -8-8+8+7 } }{ 8\times 3.14 } =\cfrac { 54 }{ 3.14\times 10 } =1.72W/{ m }^{ 2 }$$

Suppose that the electric field amplitude of an electromagnetic wave is $$ E_{0} = 120 N /C $$ and that its frequency is v = 50 . 0 MH z.
Determine $$ B_{0} ,\omega , K and\lambda $$

$$ E_{0} = 120 NC^{-1}$$
$$ v = 50 MH z = 50 \times 10^{6}Hz $$
$$ B_{0} = \dfrac{E_{0}}{C} = \dfrac{120}{3 \times 10^{8}} = 4 \times 10^{-7} T $$
$$\omega = 2\pi v = 2\pi \times 50 \times 10^{6} = 3.14 \times 10^{8} rad S^{-1}$$
$$ k = \dfrac{\omega }{C} = \dfrac{3.14 \times 10^{8}}{3 \times 10^{8}} = 1.05 rad m^{-1}$$
$$and \lambda = \dfrac{C}{V} = \dfrac{3 \times 10^{8}}{3 \times 10^{6}} = 6 m $$

Name two sources for each of infrared radiations and ultraviolet radiations .

$${\Large \underline {\textbf{Explanation:}}}$$

$${\large {\textbf{Sources of infrared radiations:}}}$$

$$\bullet$$ All $$red \ hot \ bodies$$ such as heated iron ball, flame, fire etc. are the sources of infrared radiations.

$$\bullet$$ $$Sun$$ is the natural source of infrared radiations.

$${\large {\textbf{Sources of ultraviolet radiations:}}}$$

$$\bullet$$ $$Electric \ arc$$ and $$sparks$$ give ultraviolet radiations.

$$\bullet$$ $$Sun$$ is also a source of ultraviolet radiations, but ozone layer in the earth's atmosphere absorbs most of it.

Suppose that the electric field part of an electromagnetic wave in vacuum is
$$ \left \{ \left ( 3.1 N/C \right ) \cos \left [ \left ( 1.8 rad /m \right ) y + \left ( 5.4 \times 10^{6} rad / s \right ) \right ] t \right \} i $$
What is the amplitude of the magnetic field part of the wave ?

The amplitude of the magnetic field part of the wave,
$$ B_{0} = \dfrac{E_{0}}{C} = \dfrac{3.1}{3\times \times 10^{-9}} T $$
$$ = 10. 33 nT $$

In the plane electromagnetic wave the electric field oscillates sinusoidally at a frequency of 2.0 x $$10^{10} $$ Hz and amplitude $$ 48 V m^{-1} $$
What is the wavelength of the wave ?

$$ u = 2 \times 10^{10} H z $$
$$ E_{0}= 48Vm^{4}C $$
$$ = 3 \times 10^{8}ms^{-1}$$
The wavelength of the wave,
$$ A = \dfrac{C}{v} = \dfrac{3 \times 10^{8}}{2 \times 10^{10}} = 0.015 m $$

Suppose that the electric field part of an electromagnetic wave in vacuum is
$$ \left \{ \left ( 3.1 N/C \right ) \cos \left [ \left ( 1.8 rad /m \right ) y + \left ( 5.4 \times 10^{6} rad / s \right ) \right ] t \right \} i $$
What is the wavelength $$\lambda $$

The wavelength of the wave,
$$ \lambda = \dfrac{2\pi }{k} = \dfrac{2\pi }{1.8} = 3.49m $$

Suppose that the electric field part of an electromagnetic wave in vacuum is
$$ \left \{ \left ( 3.1 N/C \right ) \cos \left [ \left ( 1.8 rad /m \right ) y + \left ( 5.4 \times 10^{6} rad / s \right ) \right ] t \right \} i $$
What is the expression for the magnetic field part of the wave .

The electric field and the direction of propagation of the e.m wave are along negative X - axis and negative Y -axis respectively . Therefore , the magnetic field is along negative Z - axis and expression for it is given by
$$ B = \left ( 10.33nT \right ) \cos\left [ \left ( 1.8 rad m^{-1} \right ) y + \left ( 5.4 \times 10^{6} rads^{-1} \right ) t\right ] \hat{k}$$

Can an electromagnetic wave be deflected by magnetic or electric field ? Explain

No, an electromagnetic wave can be deflected by magnetic or electric field. It is because , they do not consist of charged particles. They propagate in the form of electric and magnetic fields varying both in space and time

Suppose that the electric field part of an electromagnetic wave in vacuum is
$$ \left \{ \left ( 3.1 N/C \right ) \cos \left [ \left ( 1.8 rad /m \right ) y + \left ( 5.4 \times 10^{6} rad / s \right ) \right ] t \right \} i $$
What is the direction of propagation ?

The electric field part of the electromagnetic wave is given by ,
$$ \underset{E}{\rightarrow} = (3.1 NC^{-1}) \cos \left \{ \left ( 3.1 N/C \right ) \cos \left [ \left ( 1.8 rad /m \right ) y + \left ( 5.4 \times 10^{6} rad / s \right ) \right ] t \right \} i $$ it follows that
$$ E_{0} = 3.1 NC^{-1} $$
$$ k = 1.8 rad m^{-1}$$
$$\omega = 5.4 \times 10^{6} rad s^{-1}$$
Since the argument of since in the expression for electric field is of type (ky + cot) , the direction of propagation of electro magnetic wave is along negative Y - axis .

Suppose that the electric field amplitude of an electromagnetic wave is $$ E_{0} = 120 N /C $$ and that its frequency is v = 50 . 0 MH z.
Find expression for E and B .

$$ E = E_{0}\sin \left ( kx - cot \right ) $$
$$ = 120 \sin \left ( 1 .05 x - 3 .14 \times 10^{8}t \right ) \left ( in V m^{-1} \right )$$
and$$ B = B_{0}\sin \left ( kn - wt \right )$$
$$ = 4 \times 10^{-7}\sin \left ( 1 . 05 x - 3.14 \times 10^{8} t\right ) (in 7)$$

Suppose that the electric field part of an electromagnetic wave in vacuum is
$$ \left \{ \left ( 3.1 N/C \right ) \cos \left [ \left ( 1.8 rad /m \right ) y + \left ( 5.4 \times 10^{6} rad / s \right ) \right ] t \right \} i $$
What is the Frequency V ?

The frequency of the wave ,
$$ V = \dfrac{C}{\lambda } = \dfrac{3 \times 10^{8}}{3. 49} = 85.96 \times 10^{6}Hz $$
$$= 85 . 96 MHz$$

The oscillating magnetic field in a plane electromagnetic wave is given by $$B_{y}=8\times 10^{6}sin[2\times 10^{-6}t+300\pi x]$$ (in t) calculate the wavelength of the wave

$$B_{y}=8\times 10^{6}sin[2\times 10^{-6}t+300\pi x]$$
The , y component of the magnetic field is given by , $$B_{y}=B_{o}sin2\pi sin2\pi \left ( \dfrac{x}{\lambda } \dfrac{t}{T}\right )$$
Comparing the given equation with above equation
$$\dfrac{2\pi }{\lambda }=300\pi $$

An electromagnetic wave of frequency $$v=3.0\ MHz$$ passes from vaccum into a non-magnetic medium with permittivity $$\varepsilon =4.0$$. Find the increment of its wavelength.

The velocity of light in a medium of relative permittivity $$\varepsilon$$ is $$\dfrac{c}{\sqrt{\varepsilon}}$$. Thus the wavelength of light ( from its value in vaccum to its value in the medium ) is
$$\Delta \lambda =\dfrac{c/\sqrt{\varepsilon}}{v}-\dfrac cv =\dfrac cv \left( \dfrac {1}{\sqrt{\varepsilon}}-1\right)=-50\ m$$.

An electromagnetic wave of frequency $$5\ \text{GHz}$$, is travelling in a medium whose relative electric permittivity and relative magnetic permeability both are $$2$$. Its velocity in this medium is _________ $$\times 10^{7}\ m/s $$.

Given: Frequency of wave $$f = 5\ \text{GHz} $$

$$ = 5 \times 10^{9}\ \text{Hz} $$

relative permittivity, $$\in_{r} = 2 $$

and Relative permeability, $$\mu_{r} = 2 $$
Since speed of light in a medium is given by,

$$v = \dfrac{1}{\sqrt{\mu \in}} = \dfrac{1}{\sqrt{\mu_{r} \mu_{0} \in_{r} \in_{0}}} $$

$$v = \dfrac{1}{\sqrt{\mu_{r} \in_{r}}} \dfrac{1}{\sqrt{\mu_{0} \in_{0}}} = \dfrac{c}{\sqrt{\mu_{r} \in_{r}}} $$

Where $$c$$ is the speed of light in vacuum.

$$\therefore v = \dfrac{3 \times 10^{8}}{\sqrt{4}} = \dfrac{30 \times 10^{7}}{2}\ m/s $$

$$ = 15 \times 10^{7}\ m/s $$

$$\therefore $$ Ans. is $$15$$

The magnetic field in a plane electromagnetic wave is given by
$$B=(200 \mu T)\sin [(4.0\times 10^15 s^{-1})(t-{x/c})]$$.
Find the maximum electric field and the average energy density corresponding to the electric field.

Given: The magnetic field in a plane electromagnetic wave is given by

$$B=(200\mu T)\sin[(4.0×10^15s^{−1})(t−x/c)].$$

To find the maximum electric field and the average energy density corresponding to the electric field.

Solution:

Maximum value of a magnetic field, $$B_0=200\mu T=200\times10^{-6}$$

The speed of an electromagnetic wave is c

So, maximum value of electric field,

$$E_0=cB_0\\\implies E_0=200\times10^{-6}\times3\times10^8\\\implies E_0=6\times10^4N/C$$

Average energy density of a magnetic field,

$$U_{av}=\dfrac 1{2\mu_0}B_0^2=\dfrac {(200\times10^{-6})^2}{2\times4\pi\times10^{-7}}\\\implies U_{av}=\dfrac {4\times10^{-8}}{8\pi\times10^{-7}}\\\implies U_{av}=0.016J/m^3$$

For an electromagnetic wave, energy is shared equally between the electric and magnetic fields.

Hence, energy density of the electric field will be equal to the energy density of the magnetic field.

In a medium ware broadcast radio can be tuned in frequency range $$300 kHz$$ to $$1200kHz$$ in circuit of this radio effective inductance is $$300cH$$, what range of variable capacitor?

Given, $${ \alpha }_{ 1 }=300\times { 10 }^{ 3 }Hz$$

$${ \alpha }_{ 2 }=1200\times { 10 }^{ 3 }Hz$$

$$L=300\mu H=300\times { 10 }^{ -6 }H$$

$${ \alpha }_{ 1 }=\dfrac { 1 }{ 2\pi \sqrt { L{ C }_{ 1 } } } $$

$${ C }_{ 1 }=\dfrac { 1 }{ 4\pi L{ \alpha }_{ 1 }^{ 2 } } $$

or, $${ C }_{ 1 }=\dfrac { 1 }{ 4{ \pi }^{ 2 }\times L\times { \left( 360\times { 10 }^{ 3 } \right) }^{ 2 } } $$

$$=\dfrac { 1 }{ 4{ \left( 3.14 \right) }^{ 2 }\times 3.06\times { 10 }^{ -6 }{ \left( 300\times { 10 }^{ 3 } \right) }^{ 2 } } $$

$$=9.39\times { 10 }^{ -8 }$$

$$=93pF$$

In the same way,

$${ C }_{ 2 }=\dfrac { 1 }{ { 4\pi }^{ 2 }L{ \alpha }_{ 2 }^{ 2 } } $$

$$=\dfrac { 1 }{ { 4\pi }^{ 2 }\times 300\times { 10 }^{ -6 }\times { \left( 1200\times { 10 }^{ +3 } \right) }^{ 2 } } $$

$$=\dfrac { 1 }{ { 4\pi }^{ 2 }\left( 300\times { 10 }^{ -6 } \right) { \left( 1200\times { 10 }^{ +3 } \right) }^{ 2 } } $$

$$=\dfrac { 1 }{ 4{ \left( 3.14 \right) }^{ 2 }\times \left( 300\times { 10 }^{ -6 } \right) \times { \left( 1200\times { 10 }^{ 3 } \right) }^{ 2 } } $$

$$=58pF$$.

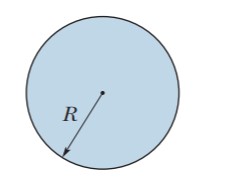
Uniform electric flux. The figure shows a circular region of radius $$R=3.00$$ cm in which a uniform
electric flux is directed out of the plane of the page. The total electric flux through the region is given by $$\phi_E (3.00 mV.(m/s)t$$, where t is in seconds.
What is the magnitude of the magnetic field
that is induced at radial distances (a) $$2.00$$ cm
and (b) $$5.00$$ cm?

(a) Inside we have $$\mu_0i_dr_1/2\pi R^2$$ , where $$r_1 = 0.0200$$ m, $$R = 0.0300$$ m, and the displacement current is given by (in SI units):

$$i_d=\epsilon_0\dfrac{d\phi_E}{dt}=(8.85 \times 10^{-12} C^2/N.m^2 )(3.00 \times 10^{-3}\, V/m.s)=2.66 \times 10^{-14} \,A$$

Thus we find
$$B=\dfrac{\mu_0i_dr_1}{2\pi R^2}=\dfrac{(4\pi \times 10^{-7}\, T.m/A)(2.66 \times 10^{-14}\, A)(0.0200\, m)}{2 \pi(0.0300\, m)^2}=1.18\times10^{-19}\,T$$

(b) Outside we have $$B=\mu_0i_d/2\pi r_2$$ where $$r_2 = 0.0500$$ cm. Here we
obtain

$$B=\dfrac{\mu_0i_d}{2\pi r_2}=\dfrac{(4\pi \times 10^{-7}\, T.m/A)(2.66 \times 10^{-14}\, A)}{2 \pi(0.0500\, m)^2}=1.06\times10^{-19}\,T$$

Nonuniform electric flux. The figure shows a circular region of radius $$R =3.00$$ cm
in which an electric flux is directed out of the
plane of the page. The flux encircled by a
concentric circle of radius r is given by $$\phi_{E,enc} = (0.600\, V.m/s)(r/R)t$$, where $$r \leq R$$ and t is in seconds. What is
the magnitude of the induced magnetic field at radial distances
(a) $$2.00$$ cm and (b) $$5.00$$ cm?

(a) Application of Eq. along the circle referred to in the second sentence of the
problem statement (and taking the derivative of the flux expression given in that sentence)
leads to

$$B(2\pi r)=\epsilon_0\mu_0(0.600\, V.m/s)\dfrac{r}{R}$$

Using $$r = 0.0200$$ m (which, in any case, cancels out) and $$R = 0.0300$$ m, we obtain

$$B=\dfrac{\epsilon_0\mu_0(0.600\, V.m/s)}{2\pi R}=\dfrac{(8.85 \times 10^{-12} C^2/N.m^2 )(4\pi \times 10^{-7} T.m/A)(0.60\, V.m/s)}{2\pi(0.0300\, m)}=3.54\times10^{-17}\,T$$

(b) For a value of r larger than R, we must note that the flux enclosed has already reached
its full amount (when r = R in the given flux expression). Referring to the equation we
wrote in our solution of part (a), this means that the final fraction (r R/ ) should be
replaced with unity. On the left-hand side of that equation, we set $$r = 0.0500$$ m and solve.
We now find

$$B=\dfrac{\epsilon_0\mu_0(0.600\, V.m/s)}{2\pi R}=\dfrac{(8.85 \times 10^{-12} C^2/N.m^2 )(4\pi \times 10^{-7} T.m/A)(0.60\, V.m/s)}{2\pi(0.0500\, m)}=2.13\times10^{-17}\,T$$

Uniform electric field. In Figure, a uniform electric field is directed out of the page within a circular region of radius $$R = 3.00$$ cm. The field magnitude is given by $$E = (4.50 \times 10^{-3}\, V/m.s)t$$,
where t is in seconds. What is the magnitude of the induced magnetic
field at radial distances (a) $$2.00$$ cm and (b) $$5.00$$ cm?

(a) Application of Eq. with $$A = πr^2$$ (and taking the derivative of the field the expression is given in the problem) leads to

$$B(2\pi r)=\mu_0\epsilon_0\pi r^2(0.00450\,V/m.s)$$

For $$r = 0.0200$$ m, this gives
$$B=\dfrac{1}{2}\epsilon_0\mu_0r(0.00450\,V/m.s)$$

$$=\dfrac{1}{2}(8.85 \times 10^{-12} C^2/N.m^2)(4\pi \times 10^{-7} \,T.m/A)(0.0200 \,m)(0.00450\,V/m.s)$$

$$=5.01\times 10^{-22}\,T$$

(b) With $$r > R$$, the expression above must be replaced by

$$B(2\pi r)=\mu_0\epsilon_0\pi R^2(0.00450\,V/m.s)$$

Substituting $$r = 0.050$$ m and $$R = 0.030$$ m, we obtain $$B = 4.51 \times 10^{−22} \,T$$.

Nonuniform electric field. In Figure, an electric field is
directed out of the page within a circular region of radius $$R= 3.00$$ cm. The field magnitude is $$E = (0.500 \,V/m.s)(1 - r/R)t$$, where t is
in seconds and r is the radial distance ($$r \leq R$$). What is the magnitude of the induced magnetic field at radial distances (a) $$2.00$$ cm
and (b) $$5.00$$ cm?

(a) Here, the enclosed electric flux is found by integrating

$$\phi_E=\int^r_0E\,2\pi rdr=t(0.500\,V/m.s)(2\pi)\int^r_0\Bigg(1-\dfrac{r}{R}\Bigg)rdr=t\pi\Bigg(\dfrac{1}{2}r^2-\dfrac{r^3}{3R}\Bigg)$$

with SI units understood. Then (after taking the derivative with respect to time) Eq. leads to

$$B(2\pi r)=\mu_0\epsilon_0\pi\Bigg(\dfrac{1}{2}r^2-\dfrac{r^3}{3R}\Bigg)$$

For $$r = 0.0200$$ m and $$R = 0.0300$$ m, this gives $$B = 3.09 \times 10^{−20} \,T$$

(b) The integral shown above will no longer (since now r > R) have r as the upper limit;
the upper limit is now R. Thus,

$$\phi_E=t\pi\Bigg(\dfrac{1}{2}R^2-\dfrac{R^3}{3R}\Bigg)=\dfrac{1}{6}t\pi R^2$$

Consequently, Eq. becomes

$$B(2\pi r)=\dfrac{1}{6}\mu_0\epsilon_0\pi R^2$$

which for $$r = 0.0500$$ m, yields

$$B=\dfrac{\mu_0\epsilon_0R^2}{12r}=\dfrac{(8.85 \times 10^{-12} )(4\pi \times 10^{-7} )(0.030)^2}{12(0.0500)}=1.67\times10^{-20}\,T$$

An isotropic point source emits light at wavelength $$500 nm$$, at the rate of $$200 W$$. A light detector is positioned $$400m$$ from the source. What is the maximum rate $$\partial B/\partial t$$ at which the magnetic component of the light changes with time at the detectors location?

From the equation immediately preceding equation $$kE_{m}\cos \left ( k_{x}-\omega t \right )=\omega B_{m}\cos \left ( k_{x}-\omega t \right )$$, we see that the maximum value of $$∂B/∂t$$ is $$\omega B_{m}$$. We can relate $$B_{m}$$ to the intensity:

$$\omega B_{m}=\frac{E_{m}}{c}=\frac{\sqrt{2c\mu _{0}I}}{c}$$.

and relate the intensity to the power $$P$$ (and distance $$r$$) using equation $$I=\frac{power}{area}=\frac{P_{s}}{4\pi r^{2}}$$. Finally, we relate $$ω$$ to wavelength $$λ$$ using $$\omega =kc=2\pi c/\lambda$$. Putting all this together, we obtain:
$$\left ( \frac{\partial B}{\partial t} \right )_{max}=\sqrt{\frac{2\mu _{0}P}{4\pi c}}\frac{2\pi c}{\lambda r}=3.44\times10^{6}T/s$$.

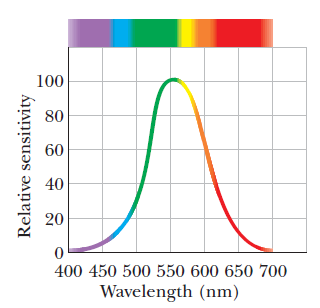
From above figure, approximate the (a) smaller and (b) larger wavelength at which the eye of a standard observer has half the eyes maximum sensitivity. What are the (c) wavelength, (d) frequency and (e) period of the light at which the eye is the most sensitive?

(a) From figure, we find the smaller wavelength in question to be about $$515 nm$$.

(b) Similarly, the larger wavelength is approximately $$610 nm$$.

(d) Using the result in (c), we have$$f=\dfrac{c}{\lambda}=\dfrac{3.00*10^{8}m/s}{555nm}=5.41*10^{14}Hz$$.

(e) The period is $$T=1/f=\left ( 5.41*10^{14}Hz \right )^{-1}=1.85*10^{-15}s$$.

A thin, totally absorbing sheet of mass $$m$$, face area $$A$$, and specific heat $$c_{s}$$ is fully illuminated by a perpendicular beam of a plane electromagnetic wave. The magnitude of the maximum electric field of the wave is $$E_{m}$$. What is the rate $$dT/dt$$ at which the sheets temperature increases due to the absorption of the wave?

Start from equations $$\frac{\partial E}{\partial x}=-\frac{\partial B}{\partial t}$$ and $$-\frac{\partial B}{\partial x}=\mu _{0}\varepsilon _{0}\frac{\partial E}{\partial t}$$ and show that $$E(x, t)$$ and $$B(x,t)$$ the electric and magnetic field components of a plane traveling electromagnetic wave, must satisfy the wave equations
$$\frac{\partial ^{2}E}{\partial t^{2}}=c^{2}\frac{\partial ^{2}E}{\partial x^{2}}$$ and $$\frac{\partial ^{2}B}{\partial t^{2}}=c^{2}\frac{\partial ^{2}B}{\partial x^{2}}$$.

1792486_1781777_ans_aeb3a73e44e049b28bdee1cb6b0fdbb9.jpg

Maxwells Equations and Hertzs Discoveries(19)
In $$SI$$ units, the electric field in an electromagnetic wave is described by
$$E_y=100 \sin(1.00 \times 10^7 \,x-\omega t)$$
Find (a) the amplitude of the corresponding magnetic field oscillations, (b) the wavelength $$\lambda$$, and (c) the frequency $$f$$.

1915395_1881069_ans_5f6055485fea406684a8e0e809e6da18.jpeg

A plane electromagnetic wave traveling in the positive direction of an $$x$$ axis in vacuum has components $$E_{x}=E_{y}=0$$ and $$E_{z}=\left (2.0V/m \right )\cos \left [ \left ( \pi \times10^{15}s^{-1} \right )\left ( t-x/c \right ) \right ]$$. (a) What is the amplitude of the magnetic field component? (b) Parallel to which axis does the magnetic field oscillate? (c) When the electric field component is in the positive direction of the $$z$$ axis at a certain point $$P$$, what is the direction of the magnetic field component there?

(a) The amplitude of the magnetic field is,
$$B_{m}=\frac{E_{m}}{c}=\frac{2.0V/m}{2.998\times10^{8}m/s}=6.67\times10^{-9}T\approx 6.7\times10^{-9}T$$.

(b) Since the $$\underset{E}{\rightarrow}$$ -wave oscillates in the $$z$$ direction and travels in the $$x$$ direction, we have $$B_{x}=B_{z}=0$$. So, the oscillation of the magnetic field is parallel to the $$y$$ axis.

(c) The direction ($$+x$$) of the electromagnetic wave propagation is determined by $$\underset{E}{\rightarrow}\times\underset{B}{\rightarrow}$$. If the electric field points in $$+z$$, then the magnetic field must point in the $$–y$$ direction.
With SI units understood, we may write:
$$B_{y}=B_{m}\cos \left [ \pi \times10^{15}\left ( t-\frac{x}{c} \right ) \right ]=\frac{2.0\cos \left [ 10^{15}\pi \left ( t-x/c \right ) \right ]}{3.0\times10^{8}}$$

$$=\left ( 6.7\times10^{-9} \right )\cos \left [ 10^{15}\pi\left ( t-\frac{x}{c} \right ) \right ]$$.

An airplane flying at a distance of $$10 km$$ from a radio transmitter receives a signal of intensity $$10\mu W/m^{2}$$. What is the amplitude of the (a) electric and (b) magnetic component of the signal at the airplane? (c) If the transmitter radiates uniformly over a hemisphere, what is the transmission power?

(a) The average rate of energy flow per unit area, or intensity, is related to the electric field amplitude, $$E_{m}$$ by $$I=E_{m}^{2}/2\mu _{0}c$$, so
$$E_{m}=\sqrt{2\mu _{0}cI}=\sqrt{2\left ( 4\pi \times10^{-7}H/m \right )\left ( 2.998\times10^{8}m/s \right )\left ( 10\times10^{-6}W/m^{2} \right )}=8.7\times10^{-2}V/m$$.

(b) The amplitude of the magnetic field is given by $$B_{m}=\frac{E_{m}}{c}=\frac{8.7\times10^{-2}V/m}{2.998\times10^{8}m/s}=2.9\times10^{-10}T$$.

(c) At a distance $$r$$ from the transmitter, the intensity is $$I=P/2\pi r^{2}$$, where $$P$$ is the power of the transmitter over the hemisphere having a surface area $$\pi r^{2}$$. Thus,
$$P=2\pi r^{2}I=2\pi \left ( 10\times10^{3}m \right )^{2}\left ( 10\times10^{-6}W/m^{2} \right )=6.3\times10^{3}W$$.

A standing electromagnetic wave with electric component $$E=E_{m}\cos kx.\cos \omega t$$ is sustained along the $$x$$ axis in vaccum. Find the magnetic component of the wave $$B(x, t)$$. Draw the approximate distribution pattern of the wave's electric and magnetic components ($$E$$ and $$B$$) at the moments $$t=0$$ and $$t=T/4$$, where $$T$$ is the oscillation period.

Here $$\vec E=\vec E_m\cos kx \cos \omega t$$
From div $$\vec E=0$$ we get $$E_{mx}=0$$ so $$\vec E_m$$ is in the $$y-z$$ plane.
Also
$$\dfrac{\partial \vec B}{\partial t}=-\vec \nabla \times \vec E =-\nabla \cos kx \times \vec E_m \cos \omega t$$
$$=\vec k \times \vec E_m \sin kx \cos \omega t$$
so $$\vec B =\dfrac{\vec k \times \vec E_m}{\omega}\sin kx \sin \omega t =\vec B_m \sin kx \sin \omega t$$
where $$| \vec B_m| =\dfrac{E_m}{c}$$ and $$\vec B_m \bot \vec E_m$$ in the $$y-z$$ plane.
At $$t=0, \vec B =0, E=E_m \cos kx $$
At $$t=T/4 \vec E=0, B=B_m \sin kx$$

The radiosity of a black body is $$ M_{e}=3.0 \mathrm{W} / \mathrm{cm}^{2} . $$ Find the wavelength corresponding to the maximum emissive capacity of that body.

T = 852.9 K

The wavelength corresponding to the maximum emissive capacity of the body is

$$\frac{b}{T} = \frac{0.29}{852.9}cm = 3.4*10^-4 = 3.4 \mu m$$

the velocity direction of the particles of the medium at the points where $$\xi=0,$$ for the case of longitudinal and transverse waves;

At the points, where $$\xi =0$$, the velocity direction in positive, i.e. along $$+ve$$ $$x$$ axis in case of longitudinal and $$+ve$$ $$y$$-axis in the case of transverse waves, where $$\dfrac{d\xi}{dt}$$ is positive and vice versa.

Assuming the spectral distribution of thermal radiation energy to obey Wien's formula $$ u(\omega, T)=A \omega^{3} \exp (-a \omega / T), $$ where $$ a=7.64 \ \mathrm{ps} \cdot \mathrm{K} $$ find for a temperature $$ T=2000 \mathrm{K} $$ the most probable
(b) Radiation wavelength.

1971313_1854895_ans_42af15899f76428ca434364b0d972419.jpg

Maxwells Equations and Hertzs Discoveries(12)
An electromagnetic wave in vacuum has an electric field amplitude of $$220 \,V/m$$. Calculate the amplitude of the corresponding magnetic field.

1915390_1881062_ans_ba8a14d360b8420db56606ac773741dd.jpeg

Displacement Current and the General Form of Ampre's Law(2)
A $$0.200-A$$ current is charging a capacitor that has circular plates $$10.0 \,cm$$ in radius. If the plate separation is $$4.00 \,mm$$, (a) what is the time rate of increase of electric field between the plates? (b) What is the magnetic field between the plates $$5.00 \,cm$$ from the center?

1915245_1881052_ans_819ed1b895ab48e69d648b74bf619781.jpeg

Displacement Current and the General Form of Ampre's Law(1)
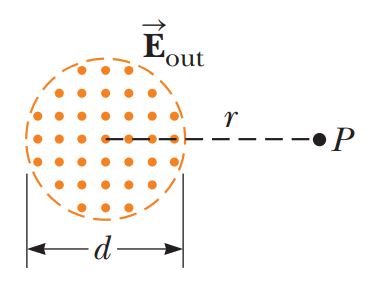
Consider the situation shown in Figure. An electric field of $$300 \,V/m$$ is confined to a circular area $$d = 10.0 \,cm$$ in diameter and directed outward perpendicular to the plane of the figure. If the field is increasing at a rate of $$20.0 \,V/m \cdot s$$, what are (a) the direction and (b) the magnitude of the magnetic field at the point $$P, \,r = 15.0 \,cm$$ from the center of the circle?

1915243_1881051_ans_96e9f440b36a4104b02e1daf4b03f7ee.jpeg

Maxwells Equations and Hertzs Discoveries(10)
The red light emitted by a helium-neon laser has a wavelength of $$632.8 \,nm$$. What is the frequency of the light waves?

1915392_1881060_ans_4a5d0d304dca4fb8a5e47e53c5e7a5a6.jpeg

Energy Carried by Electromagnetic Waves(27)
High-power lasers in factories are used to cut through cloth and metal (Figure). One such laser has abeam diameter of $$1.00 \,mm$$ and generates an electric field having an amplitude of $$0.700 \,MV/m$$ at the target. Find (a) the amplitude of the magnetic field produced, (b) the intensity of the laser, and (c) the power delivered by the laser.

undefined

1993981_1881077_ans_dc31f15256634a5792306f1add85f296.jpg

Energy Carried by Electromagnetic Waves(30)
Assuming the antenna of a $$10.0-kW$$ radio station radiates spherical electromagnetic waves, (a) compute the maximum value of the magnetic field $$5.00 \,km$$ from the antenna and (b) state how this value compares with the surface magnetic field of the Earth.

1915629_1881685_ans_169c621afeed4ec4950e7e280137478a.jpeg

Electromagnetic Waves - Class 12 Engineering Physics - Extra Questions

Using Wien's formula, demonstrate that(a) the most probable radiation frequency $$ \omega_{p r} \backsim T $$;