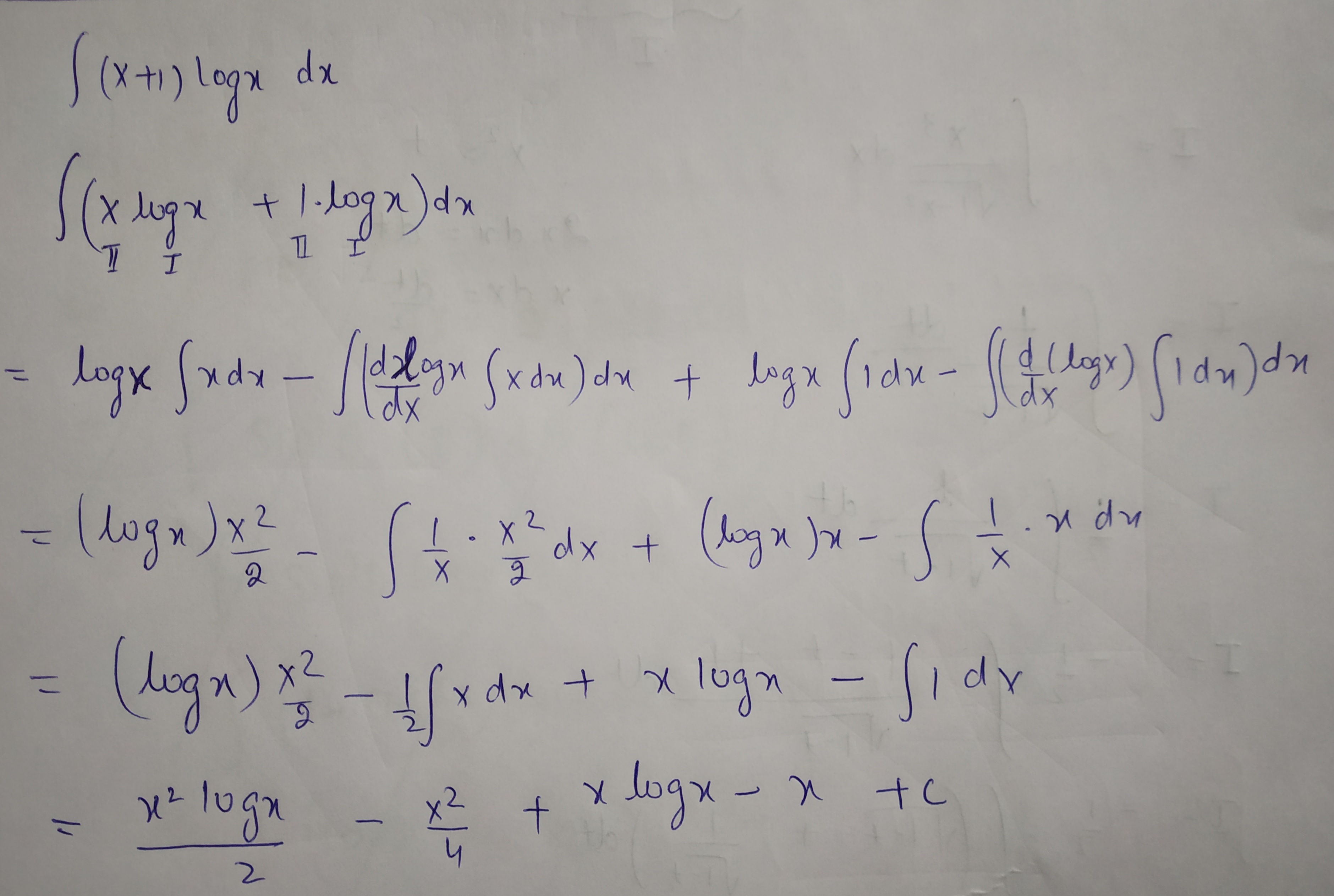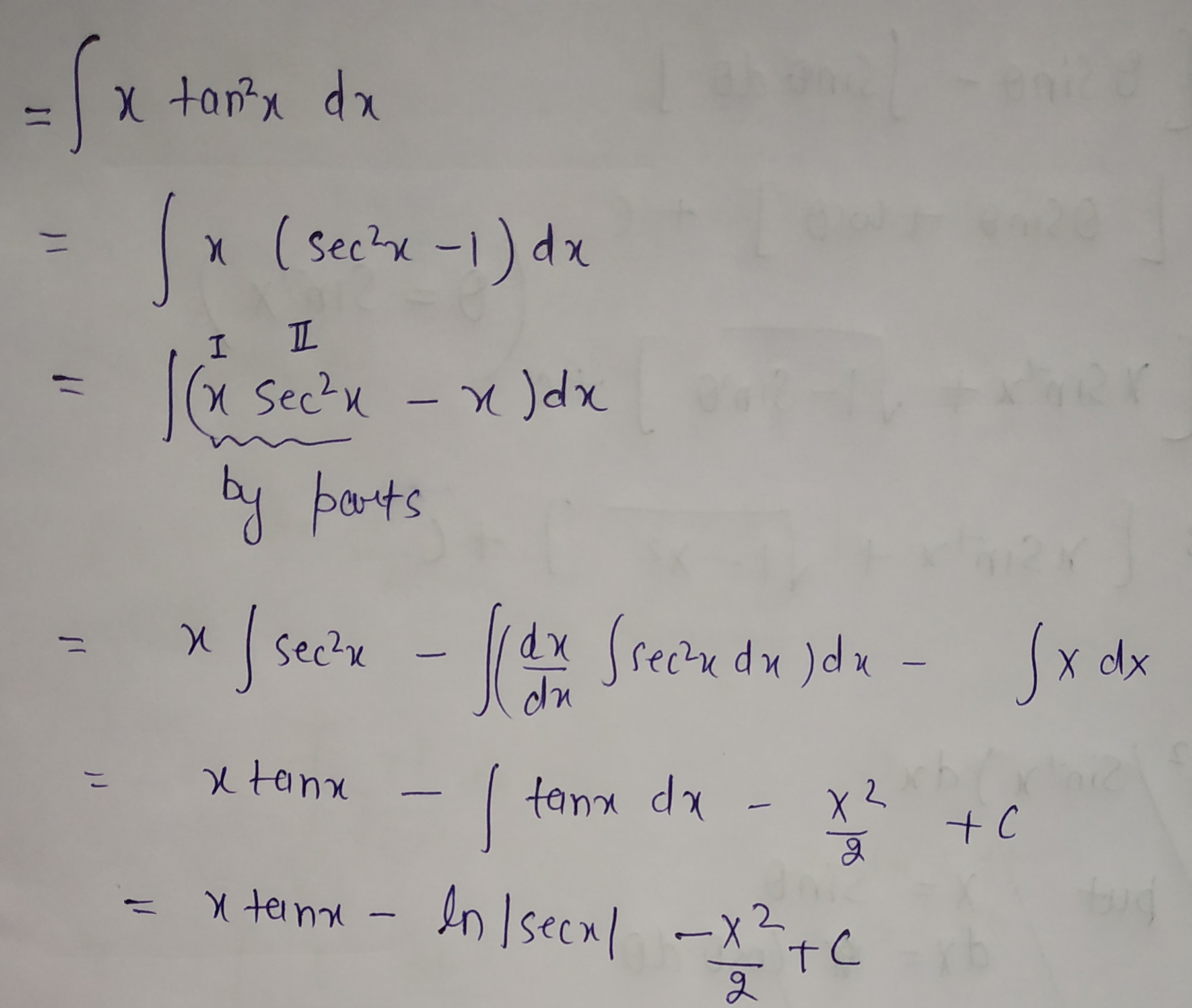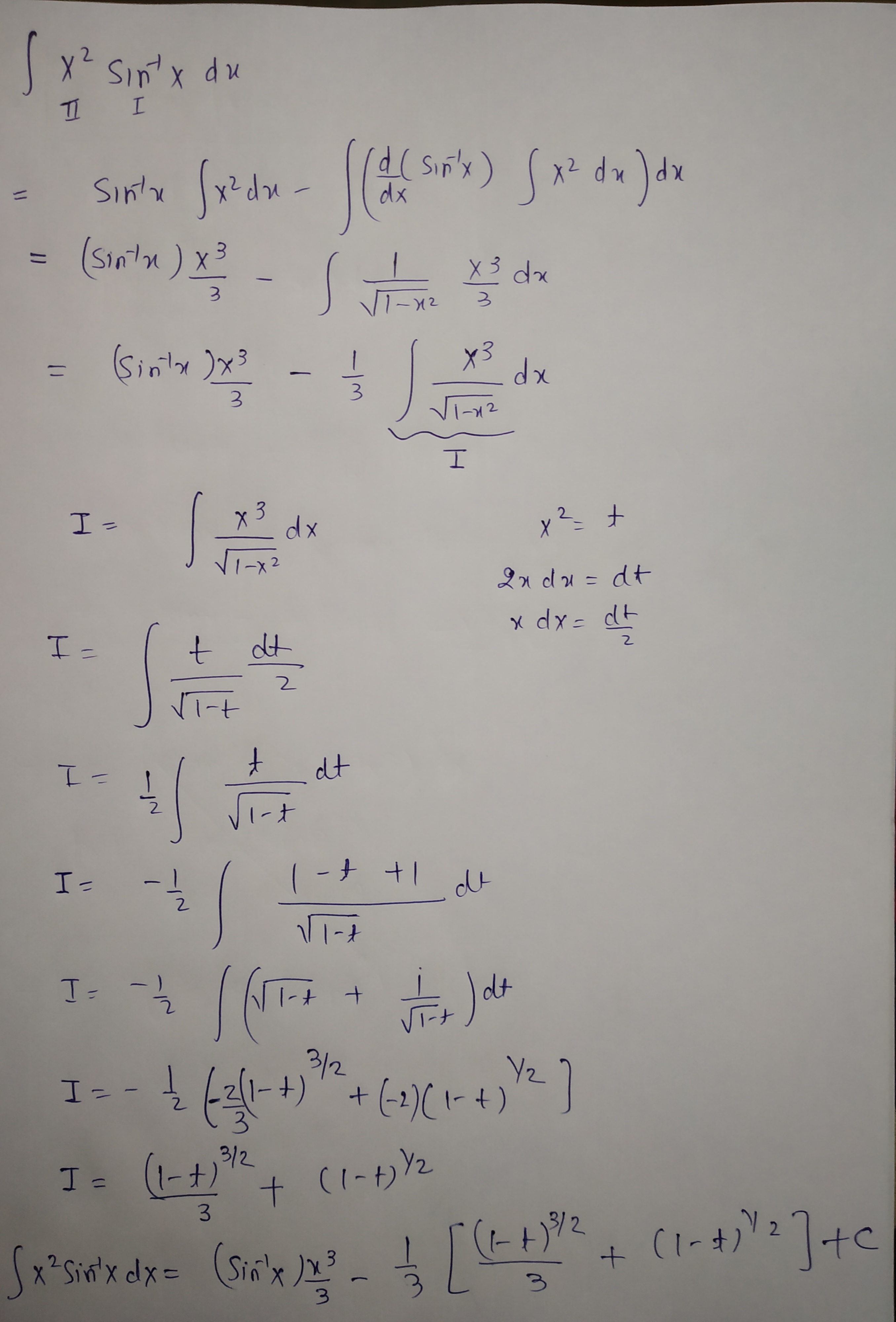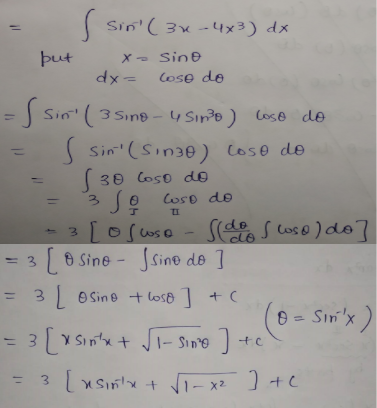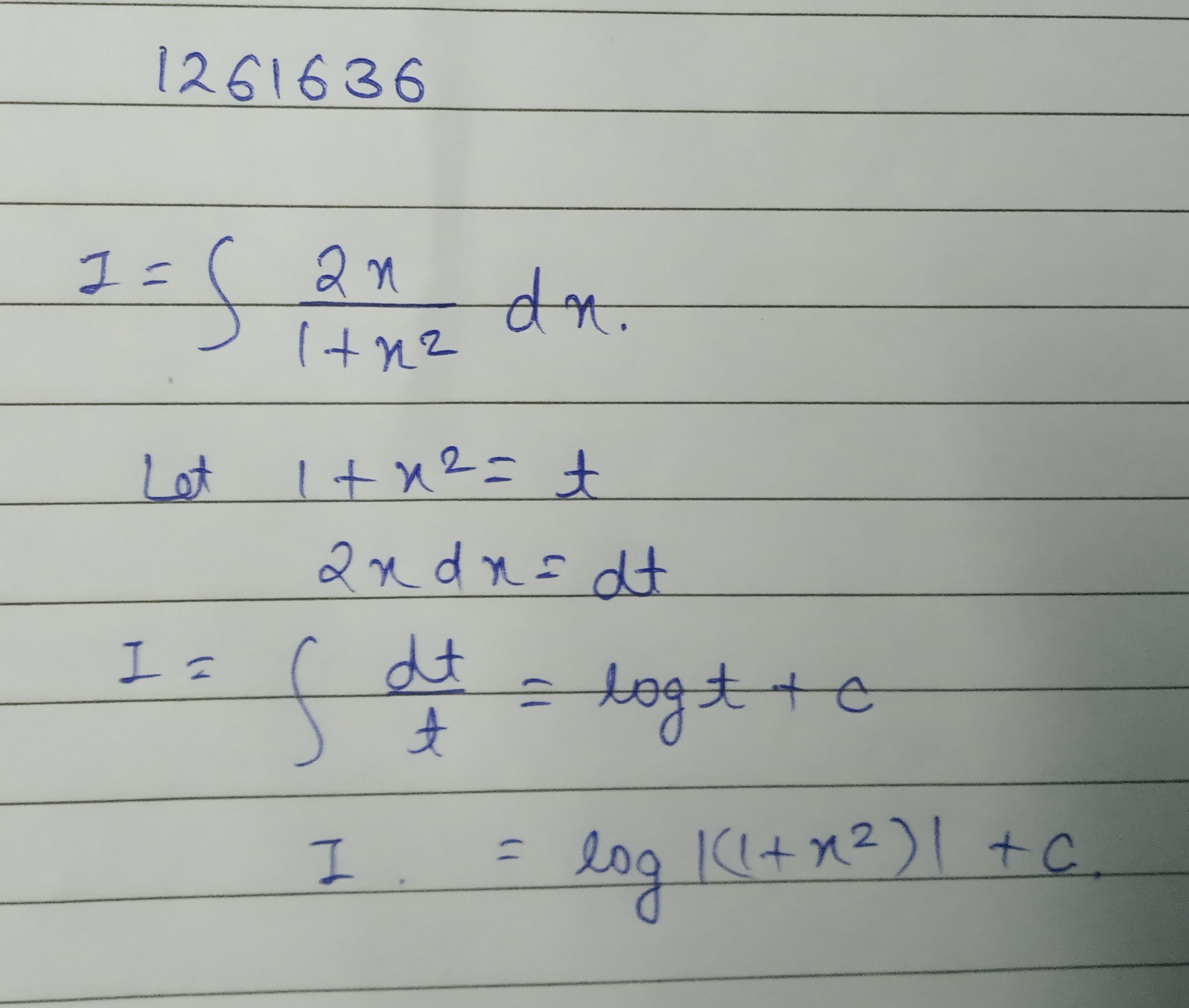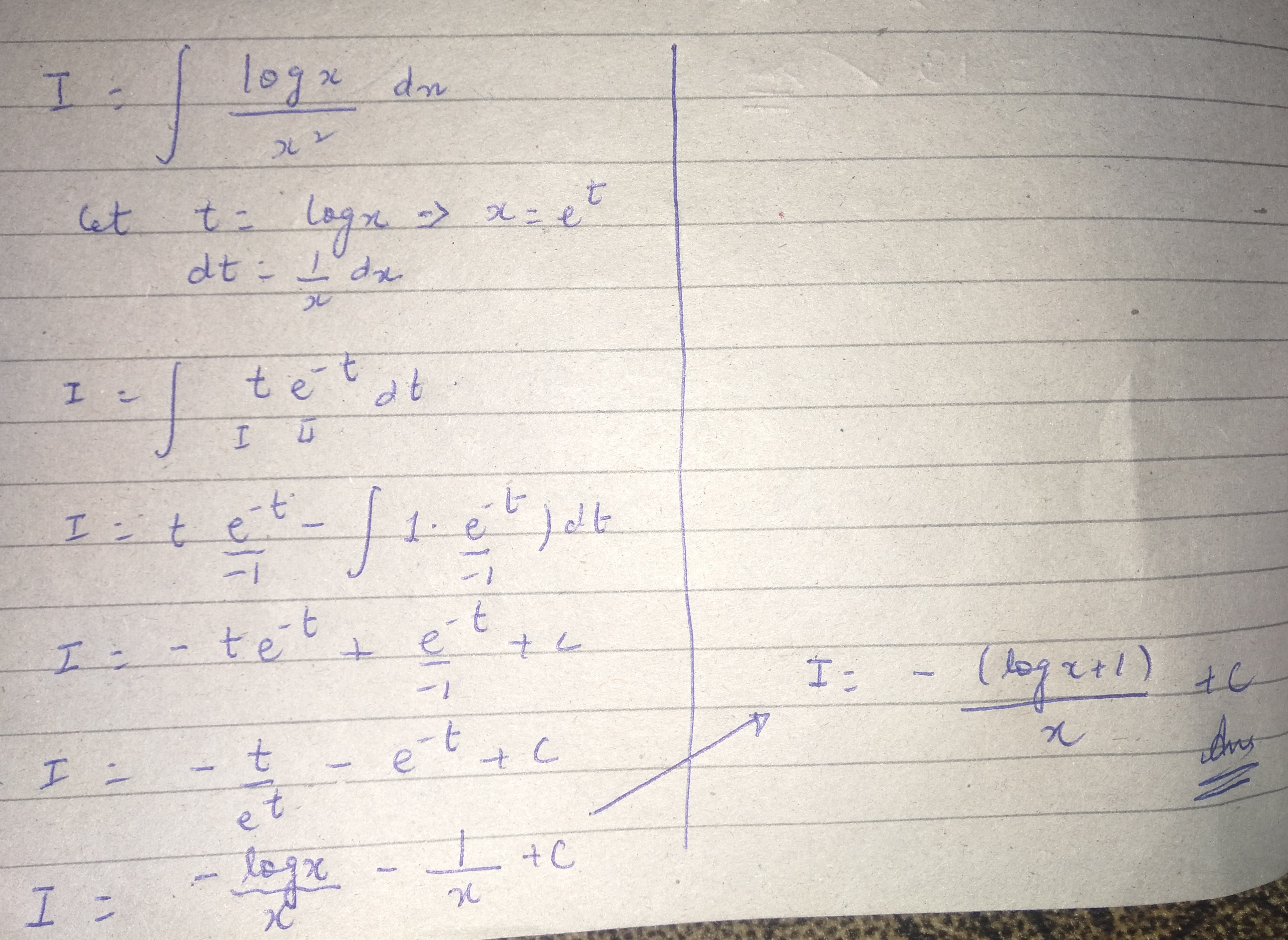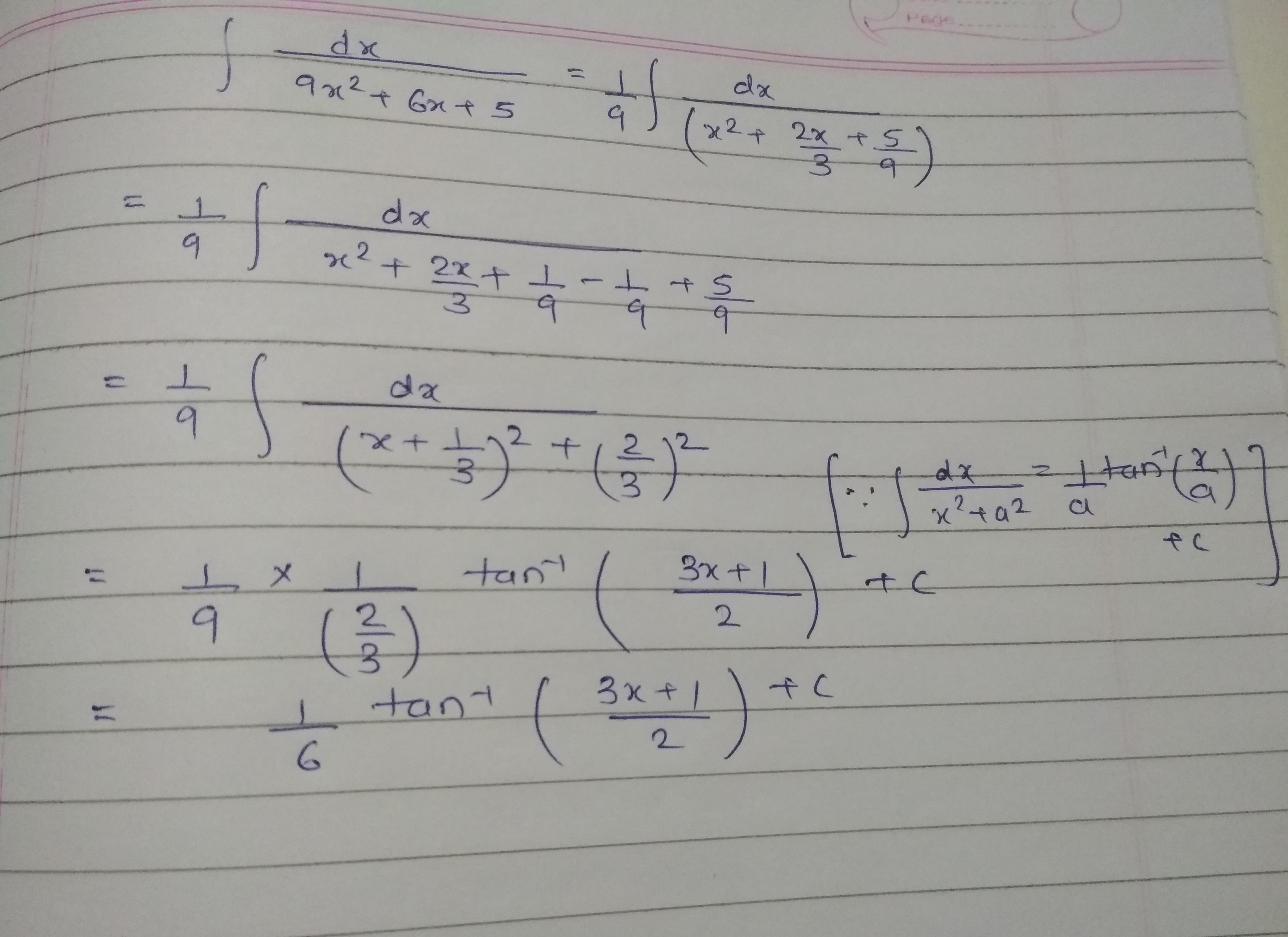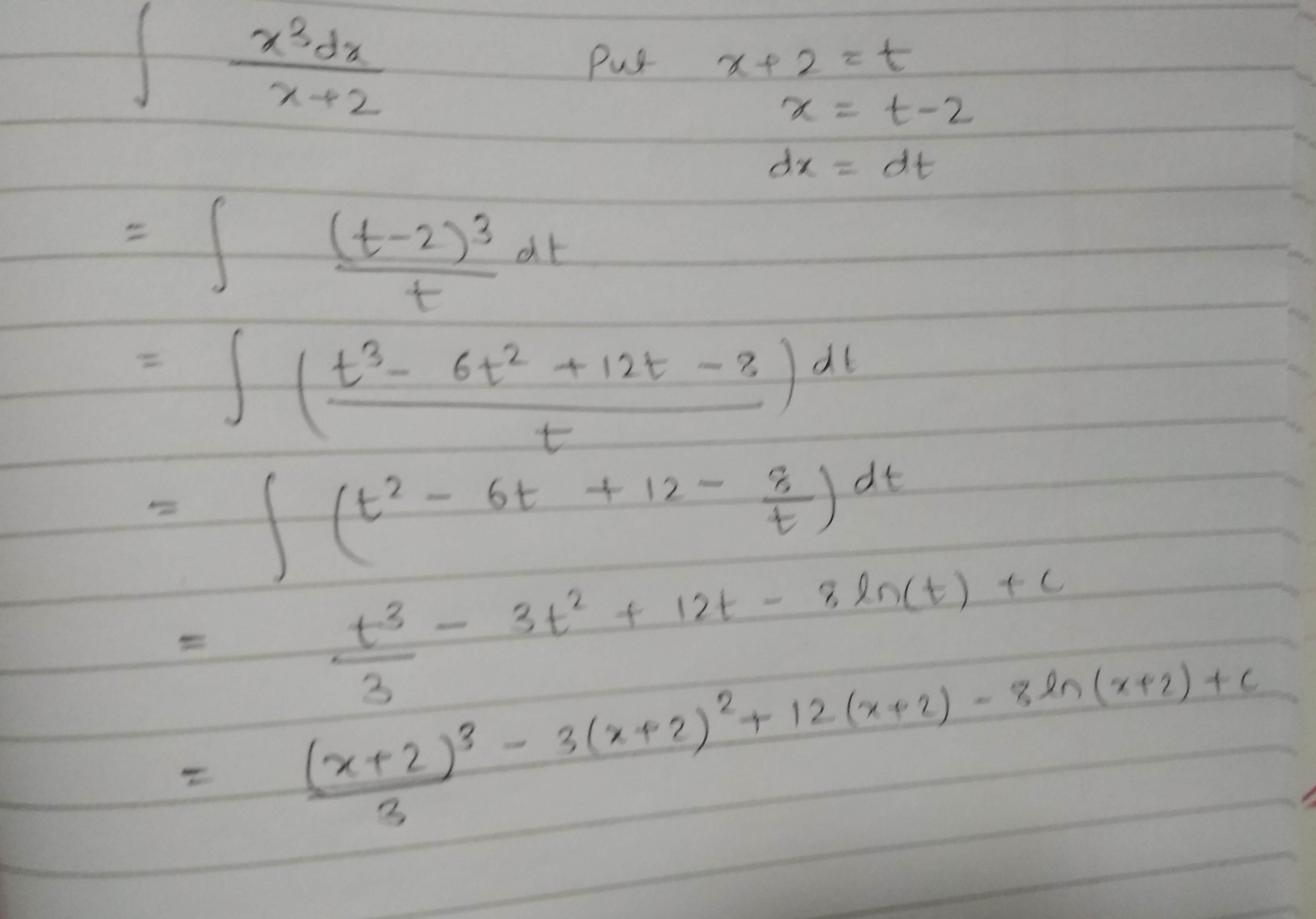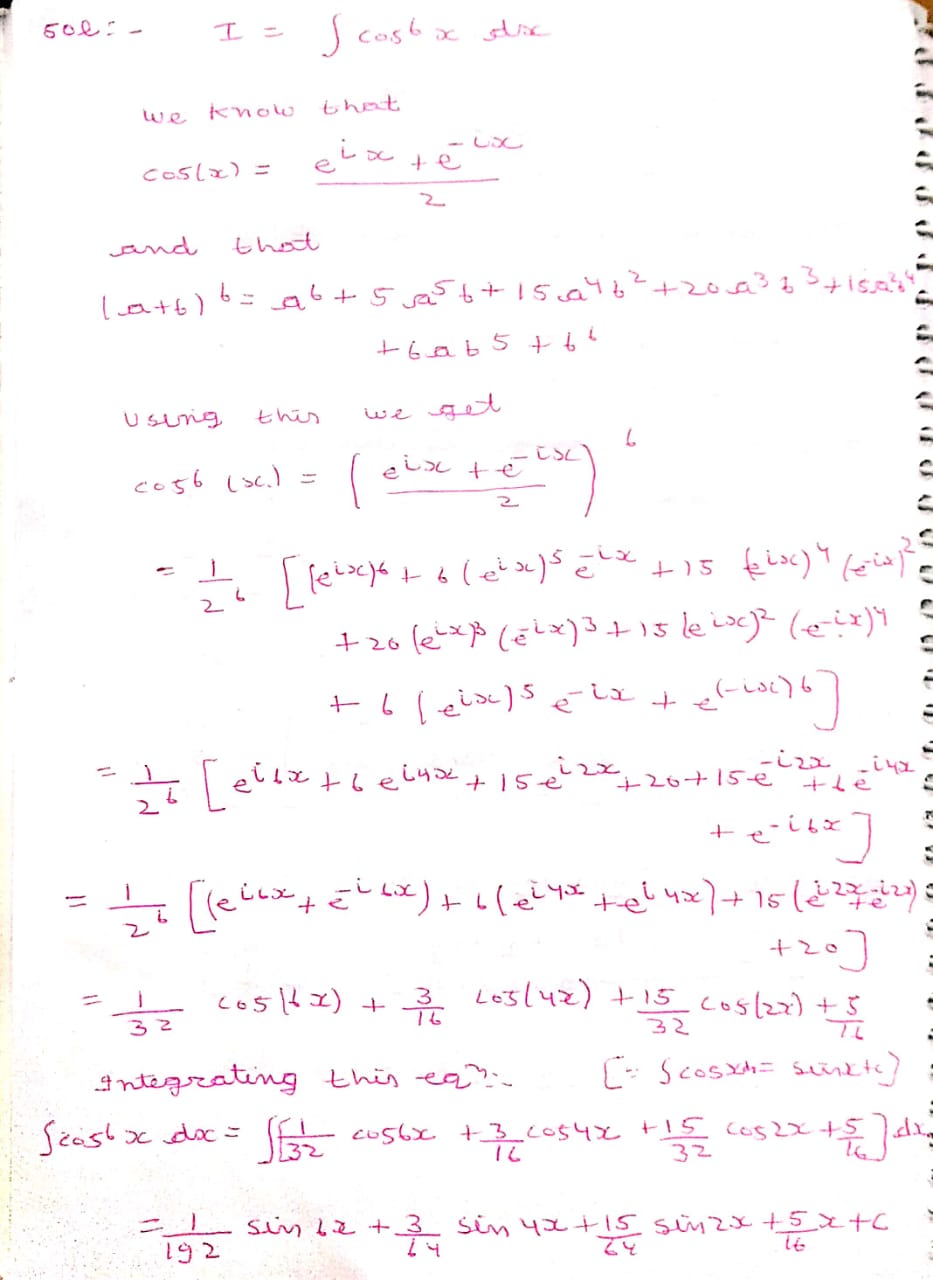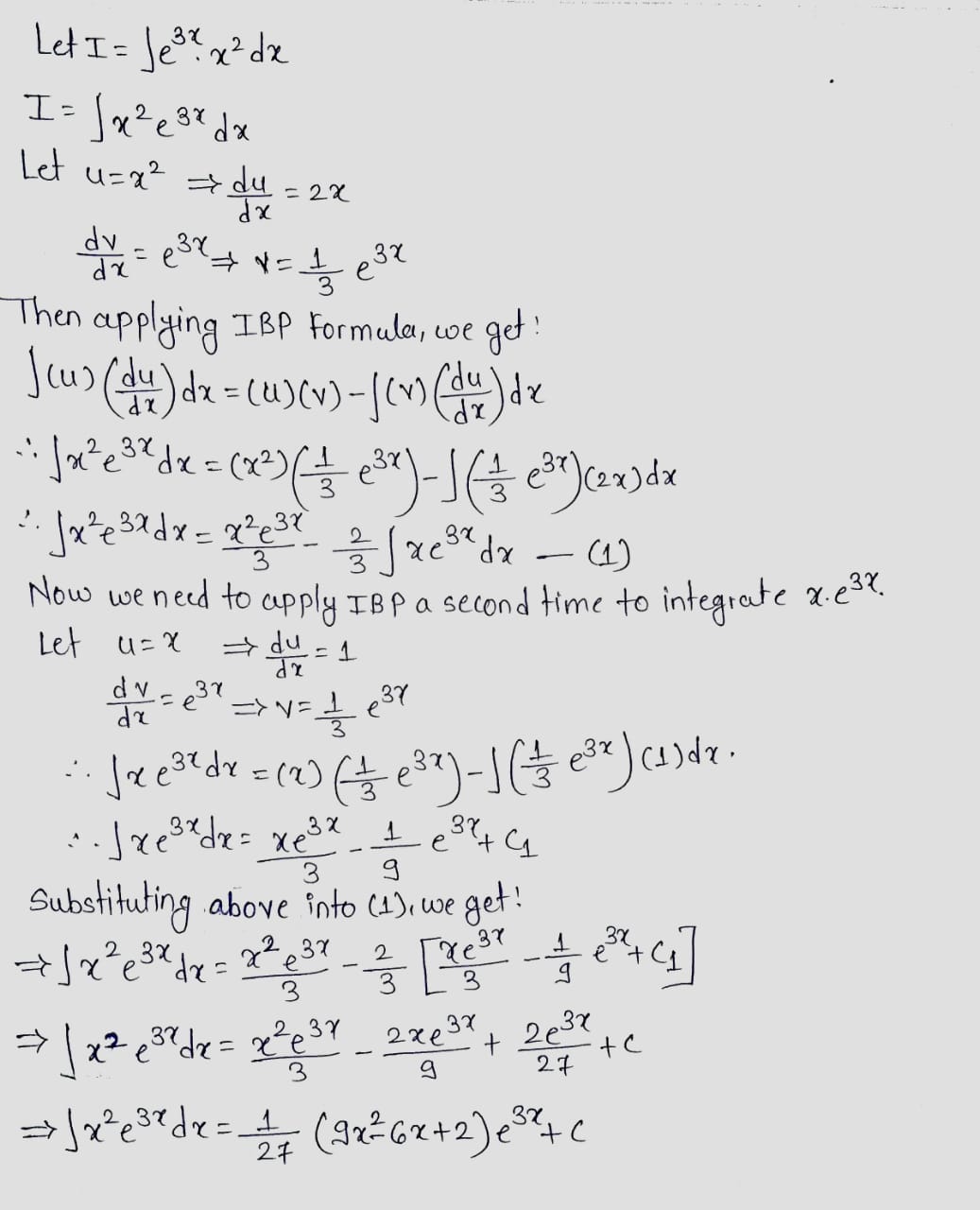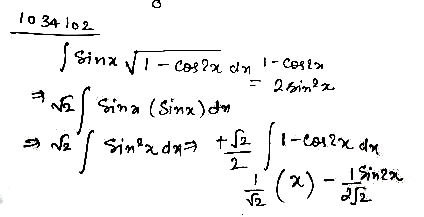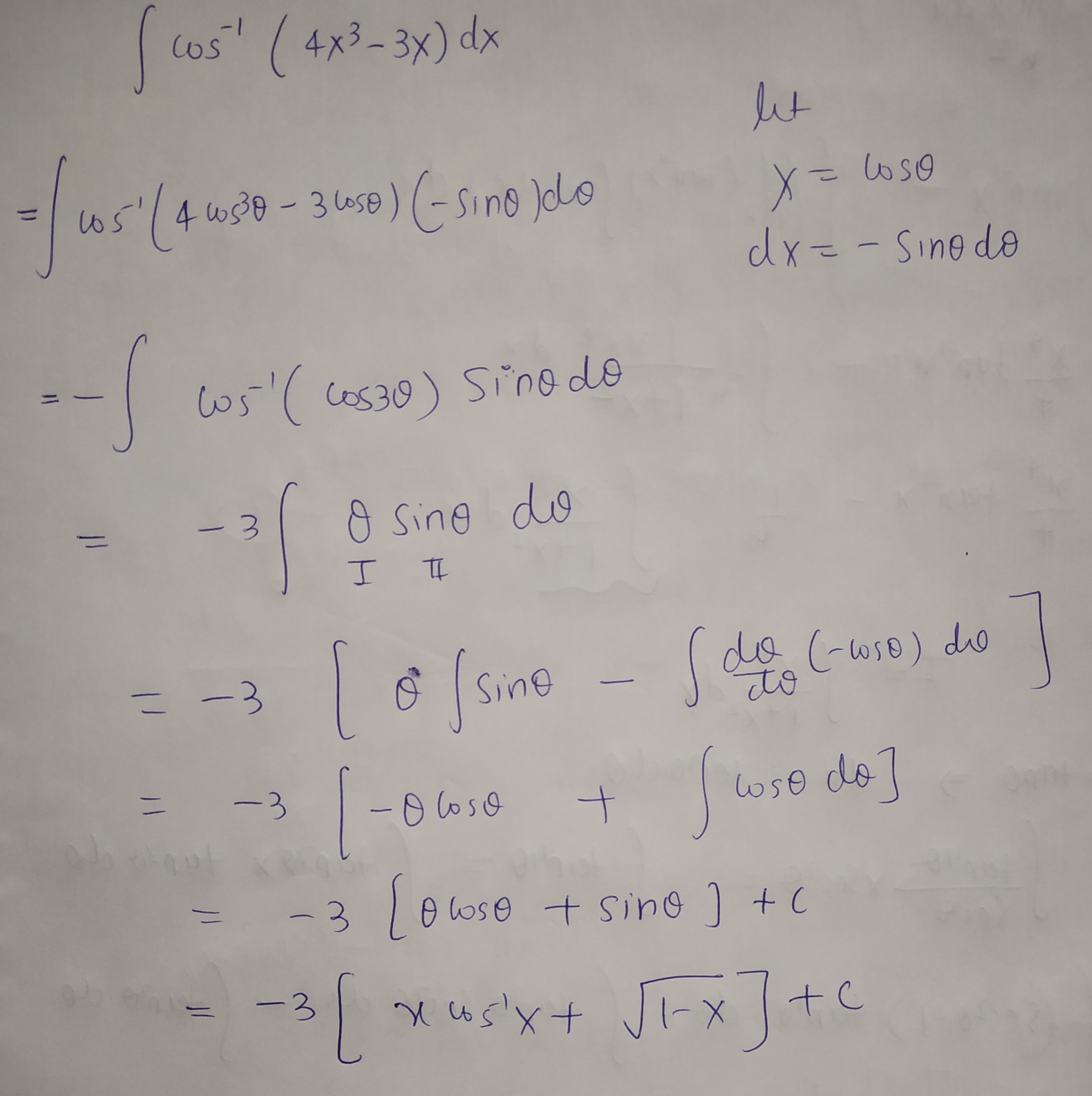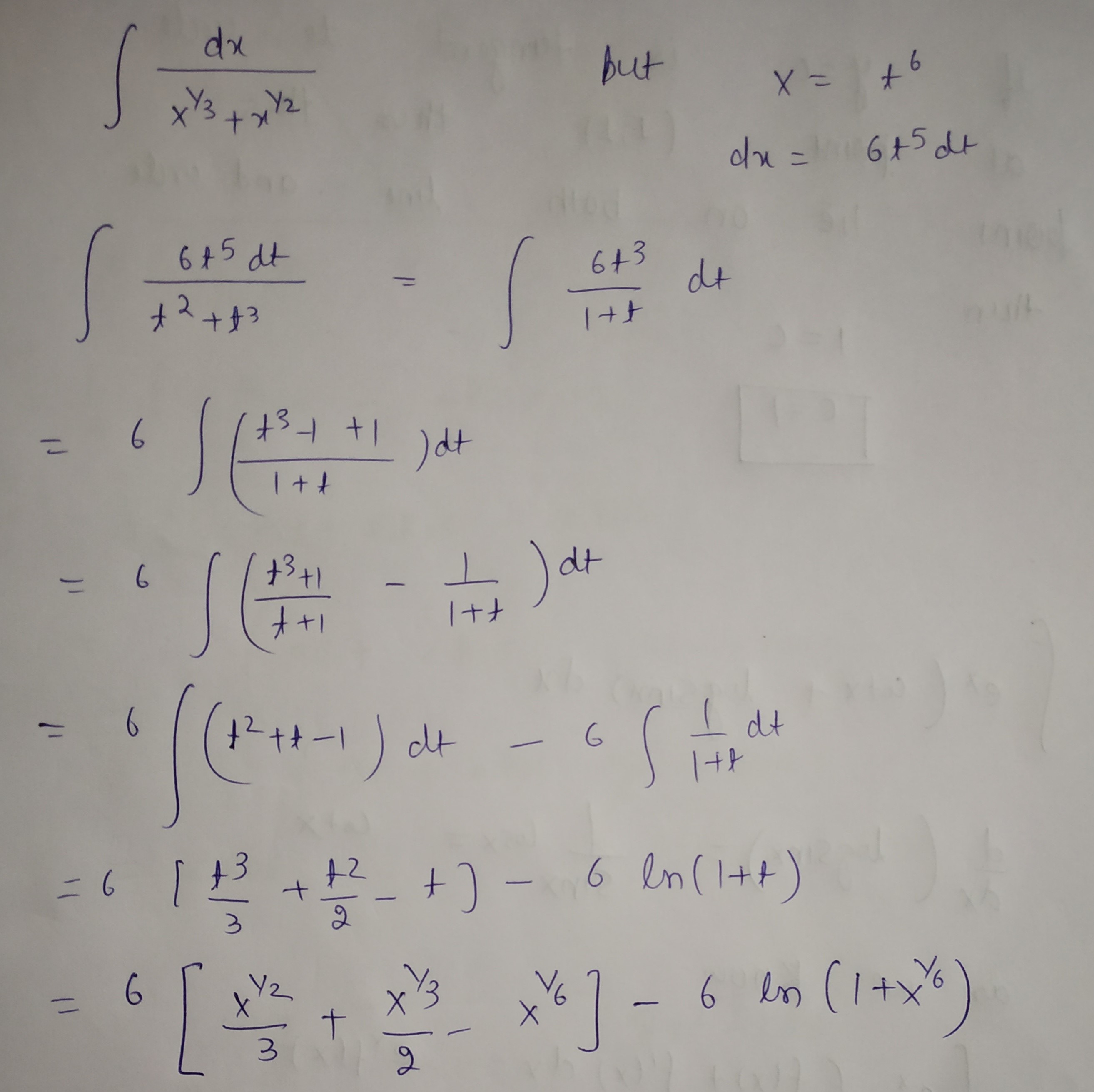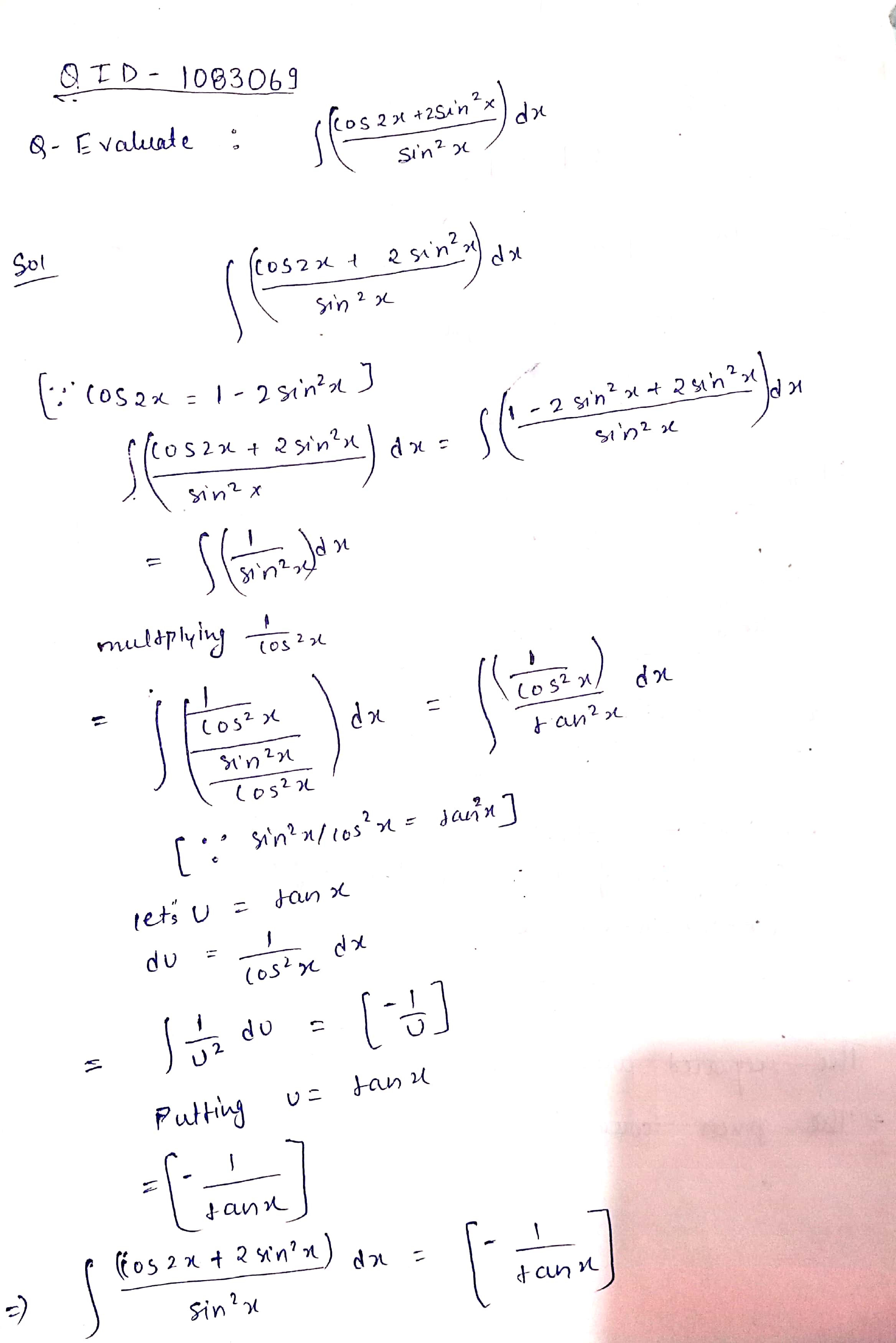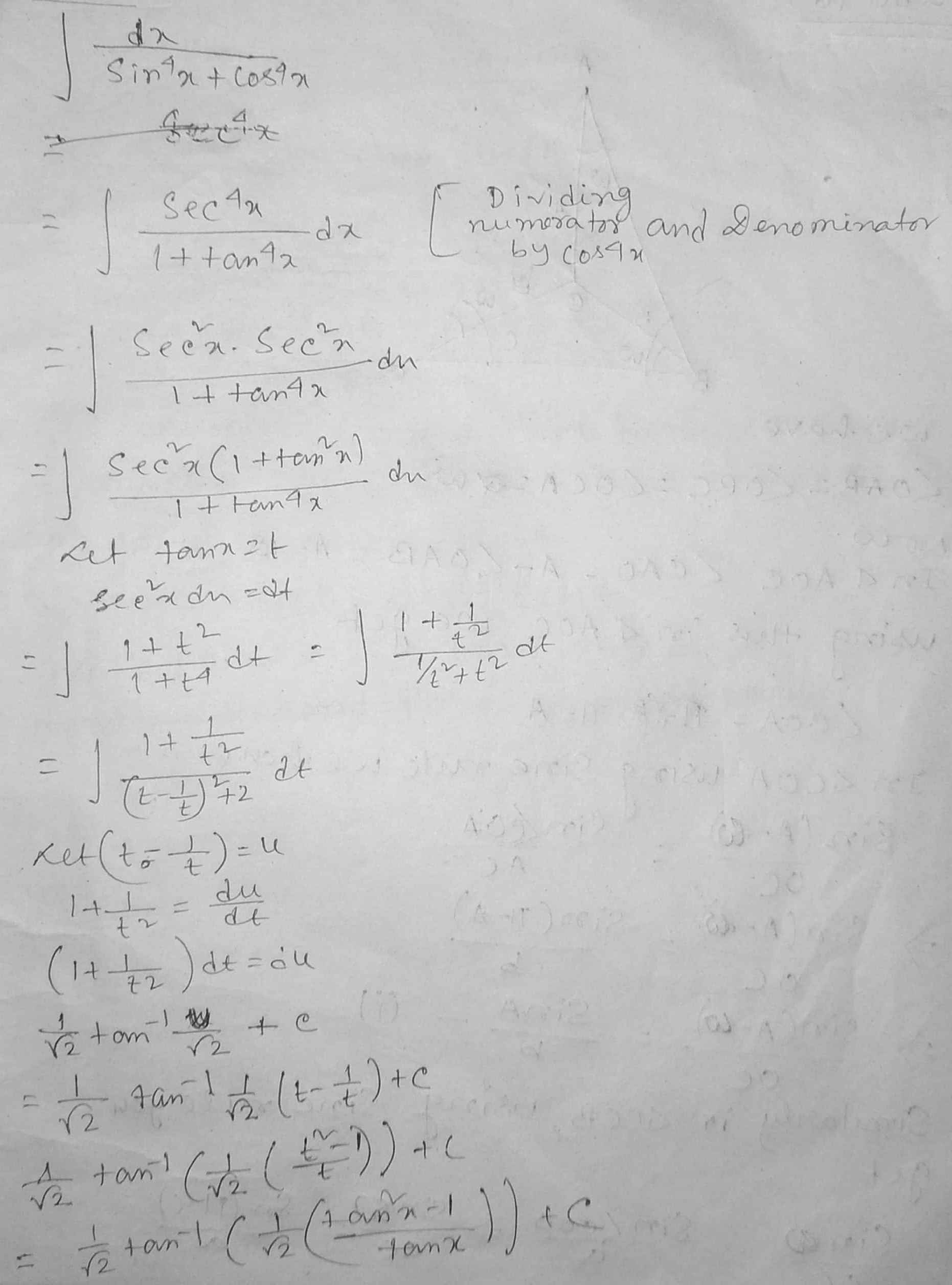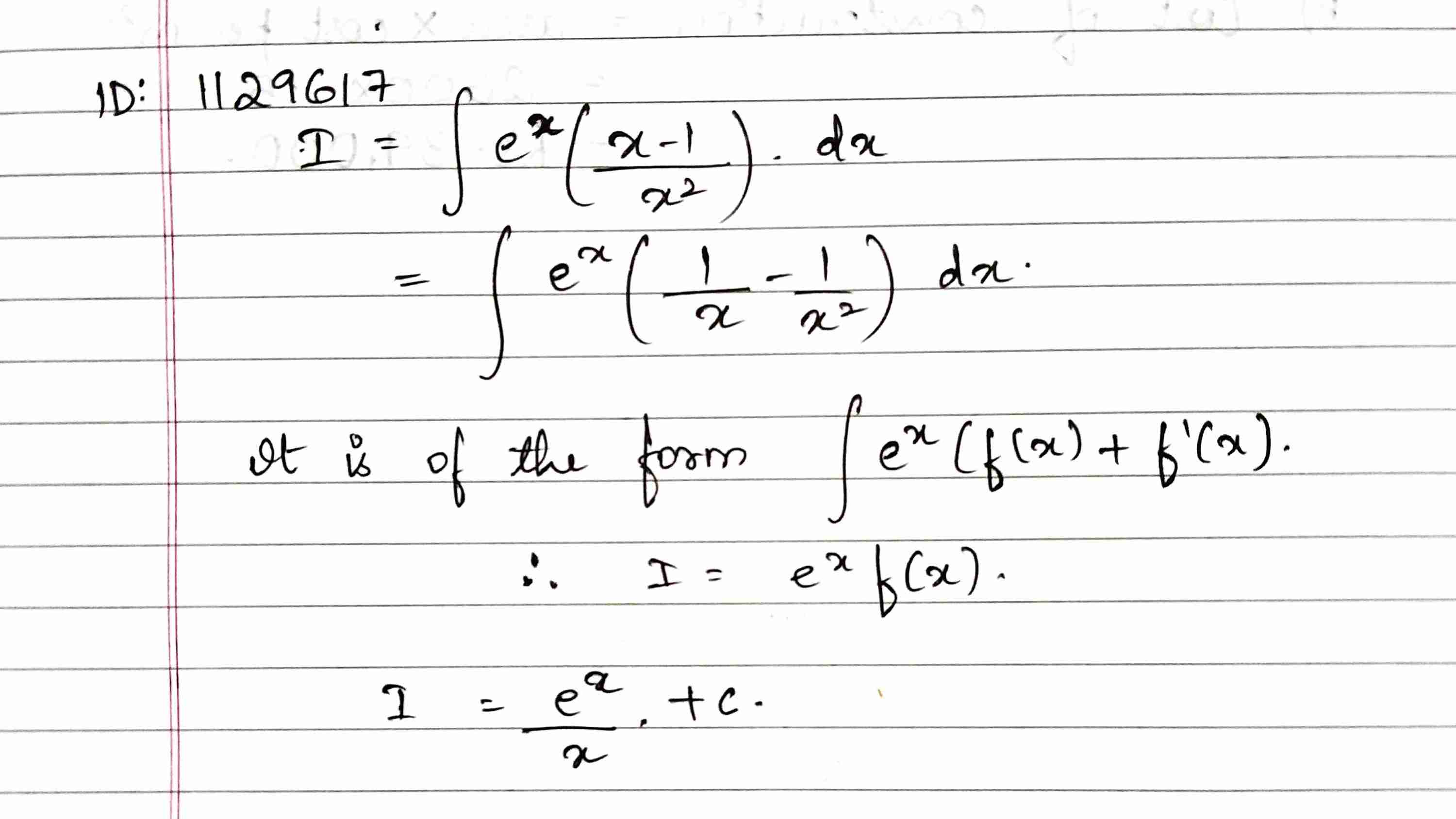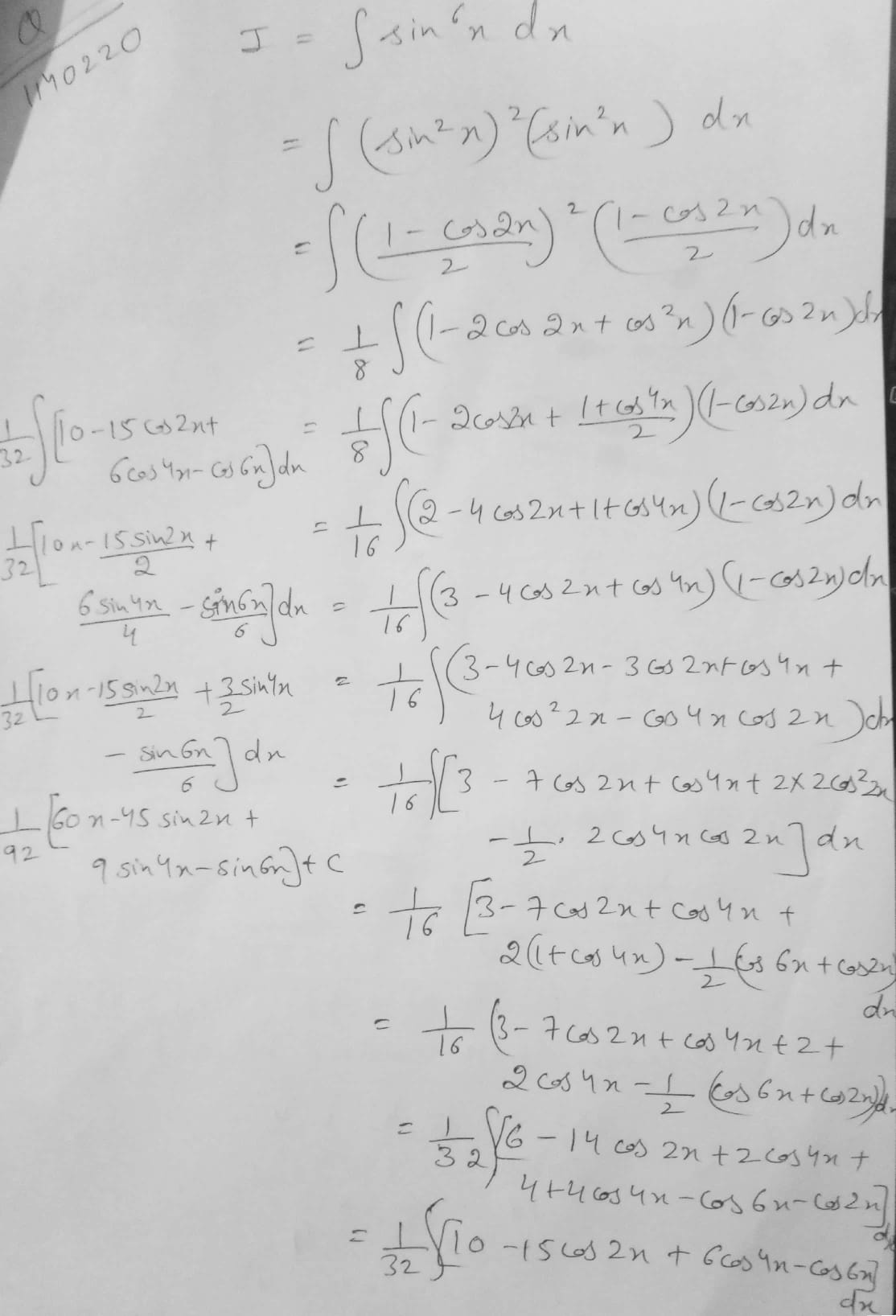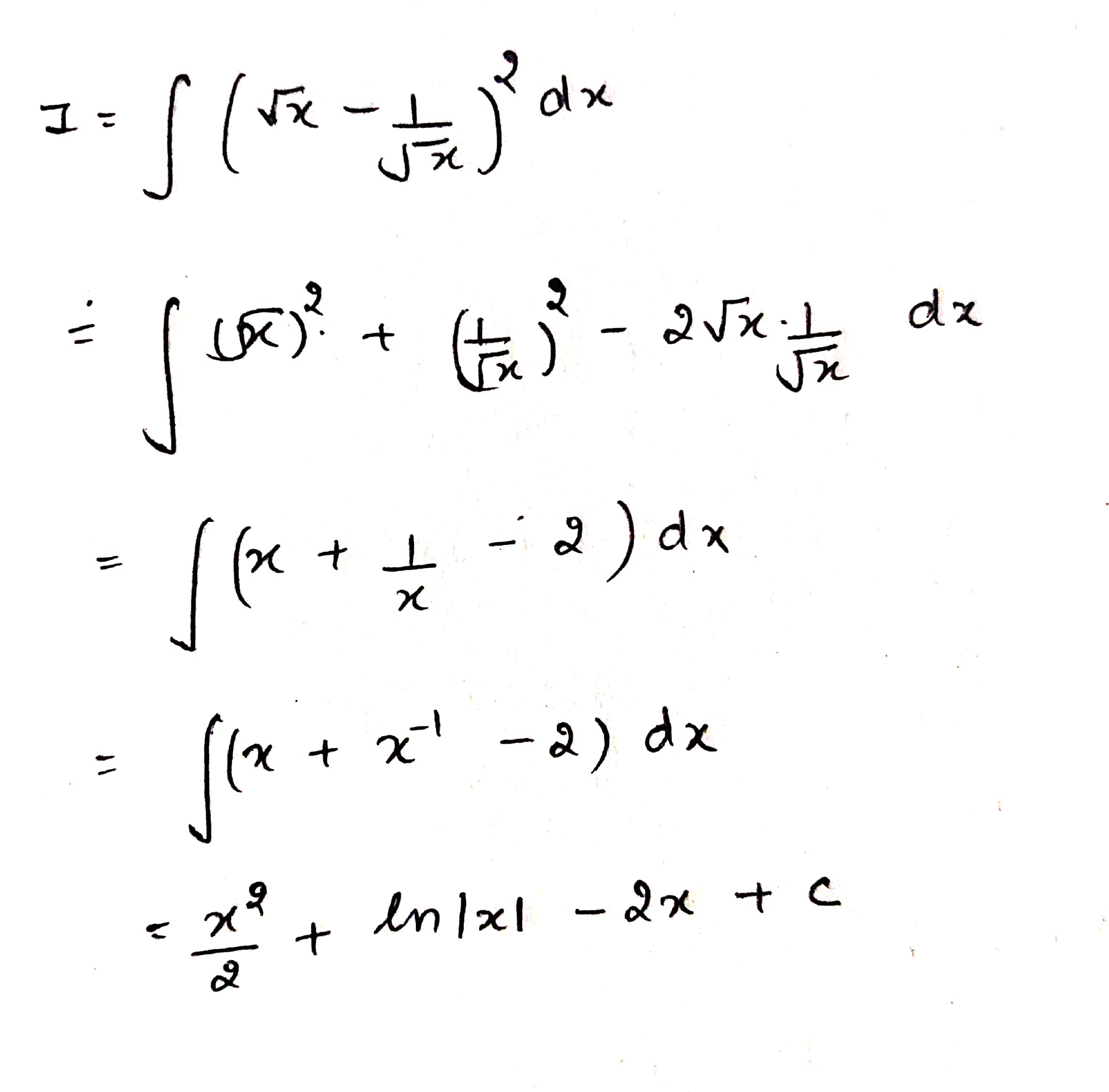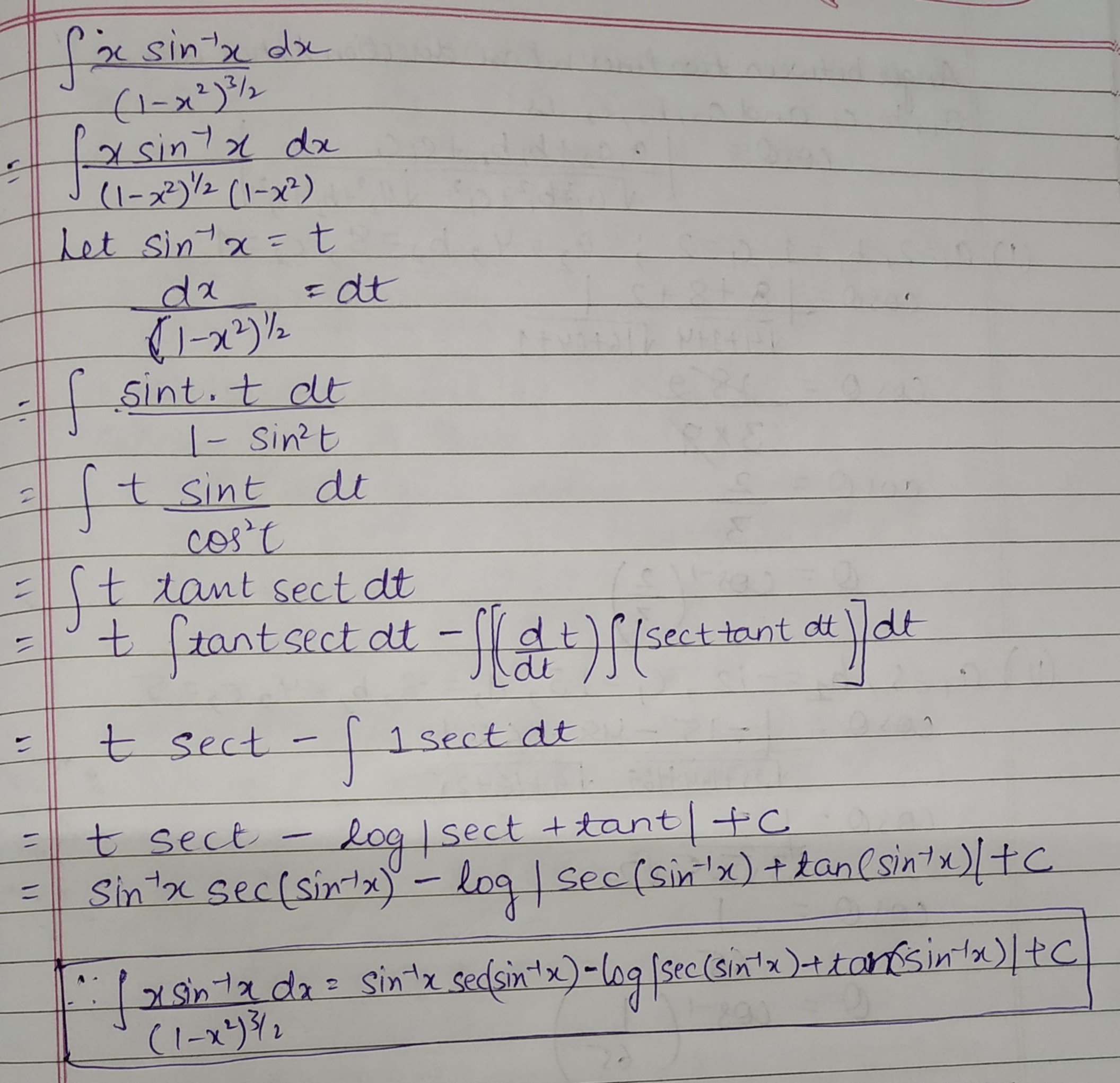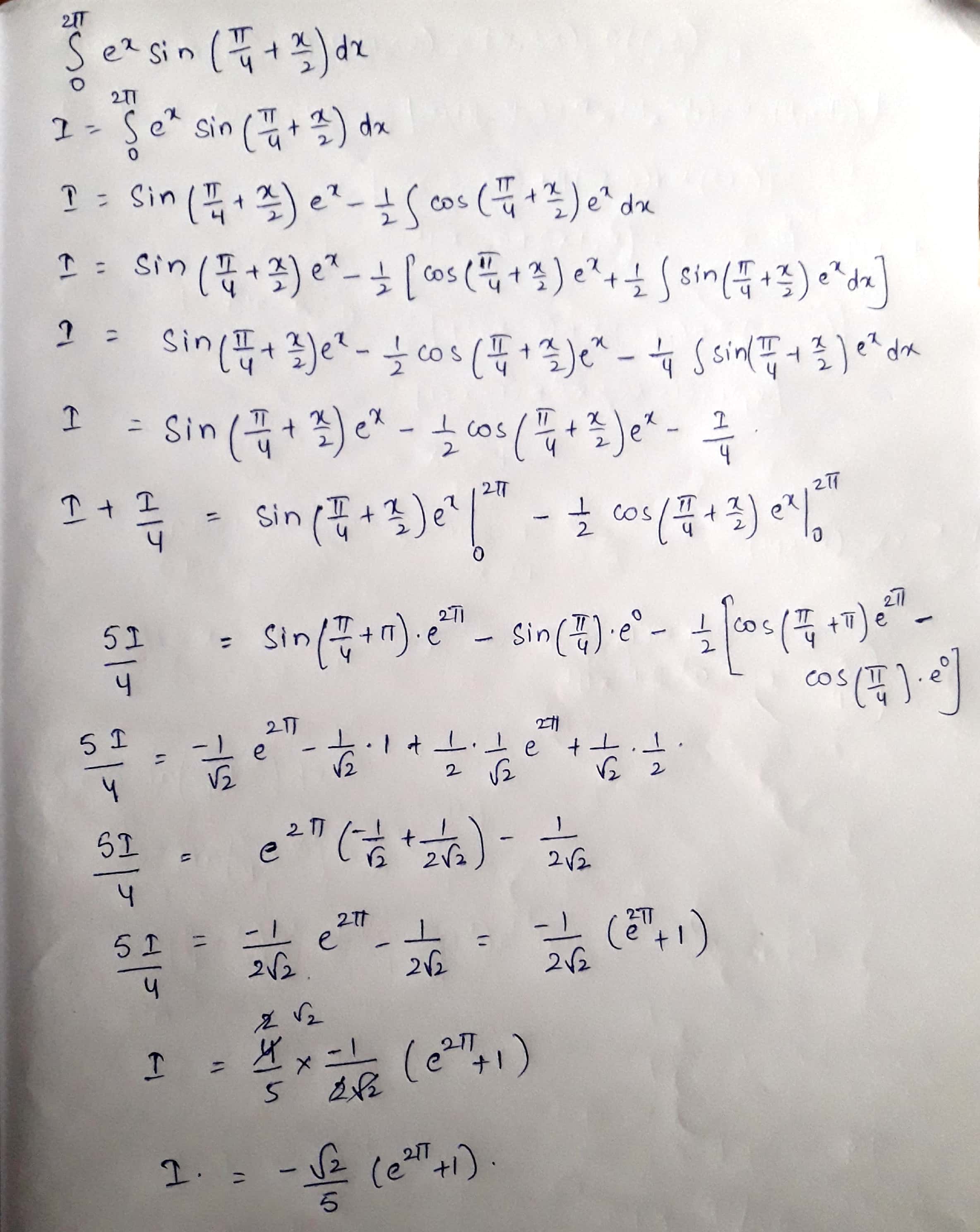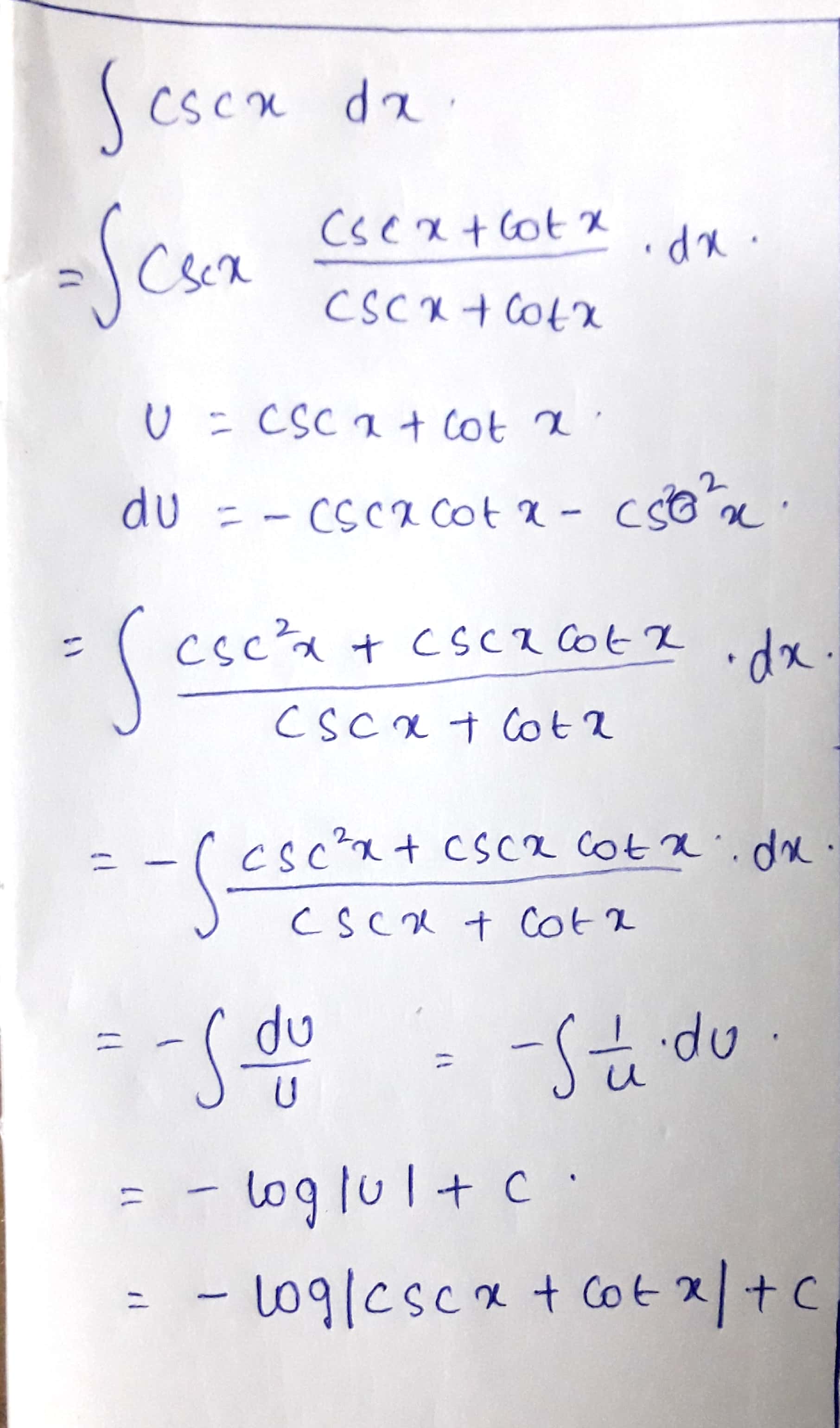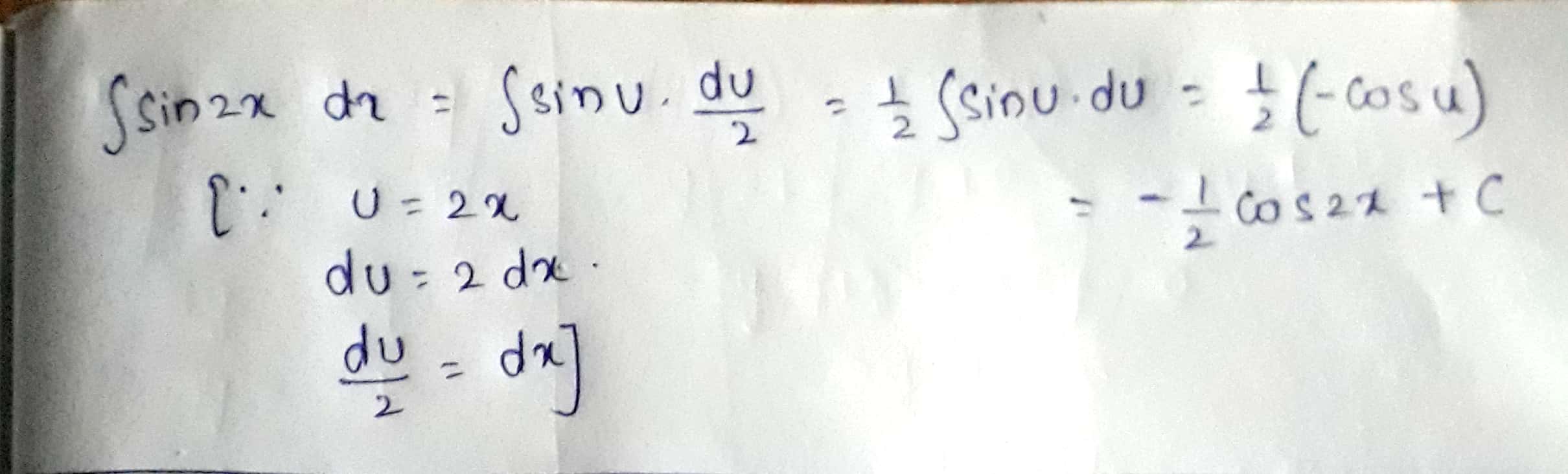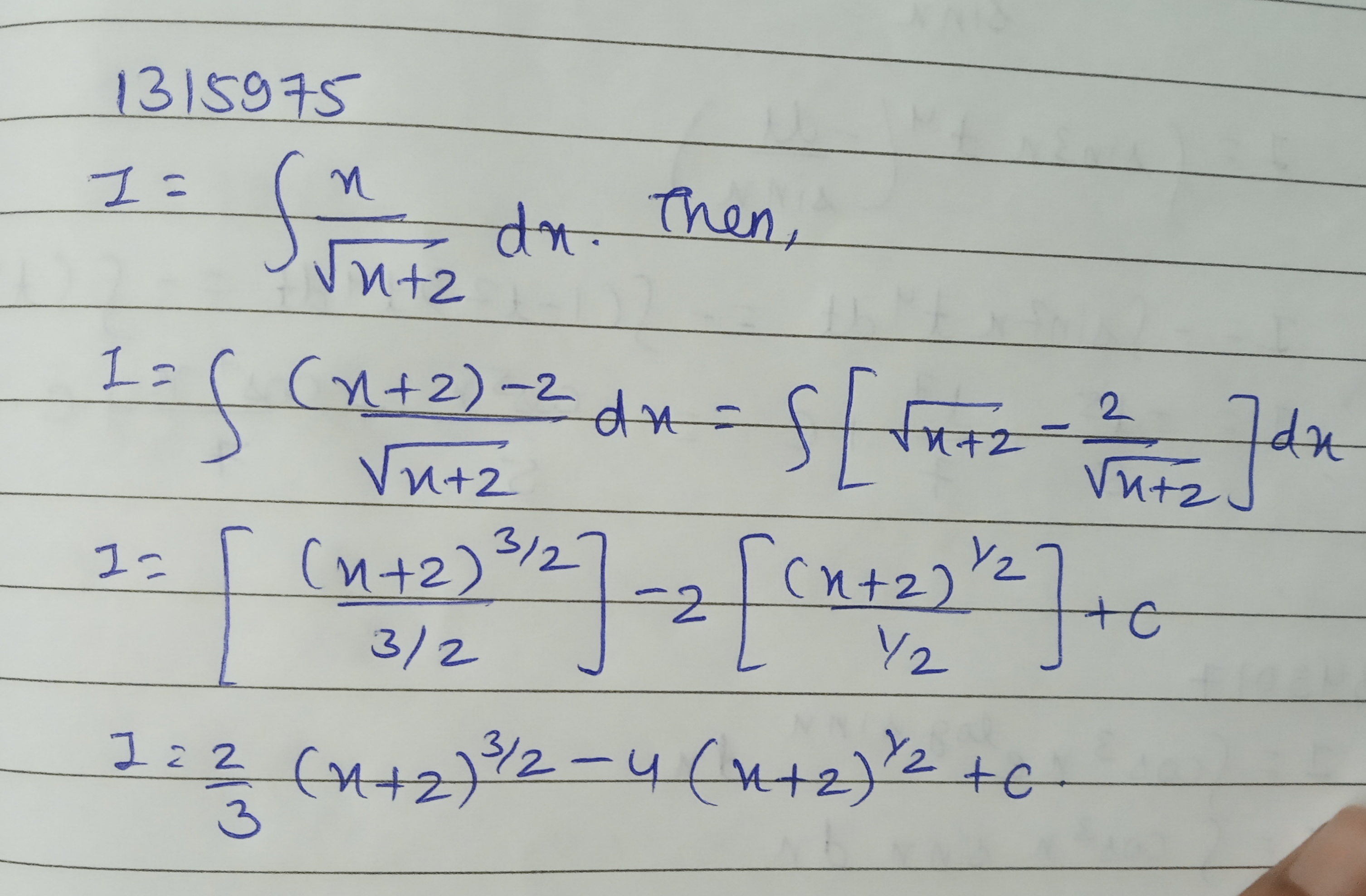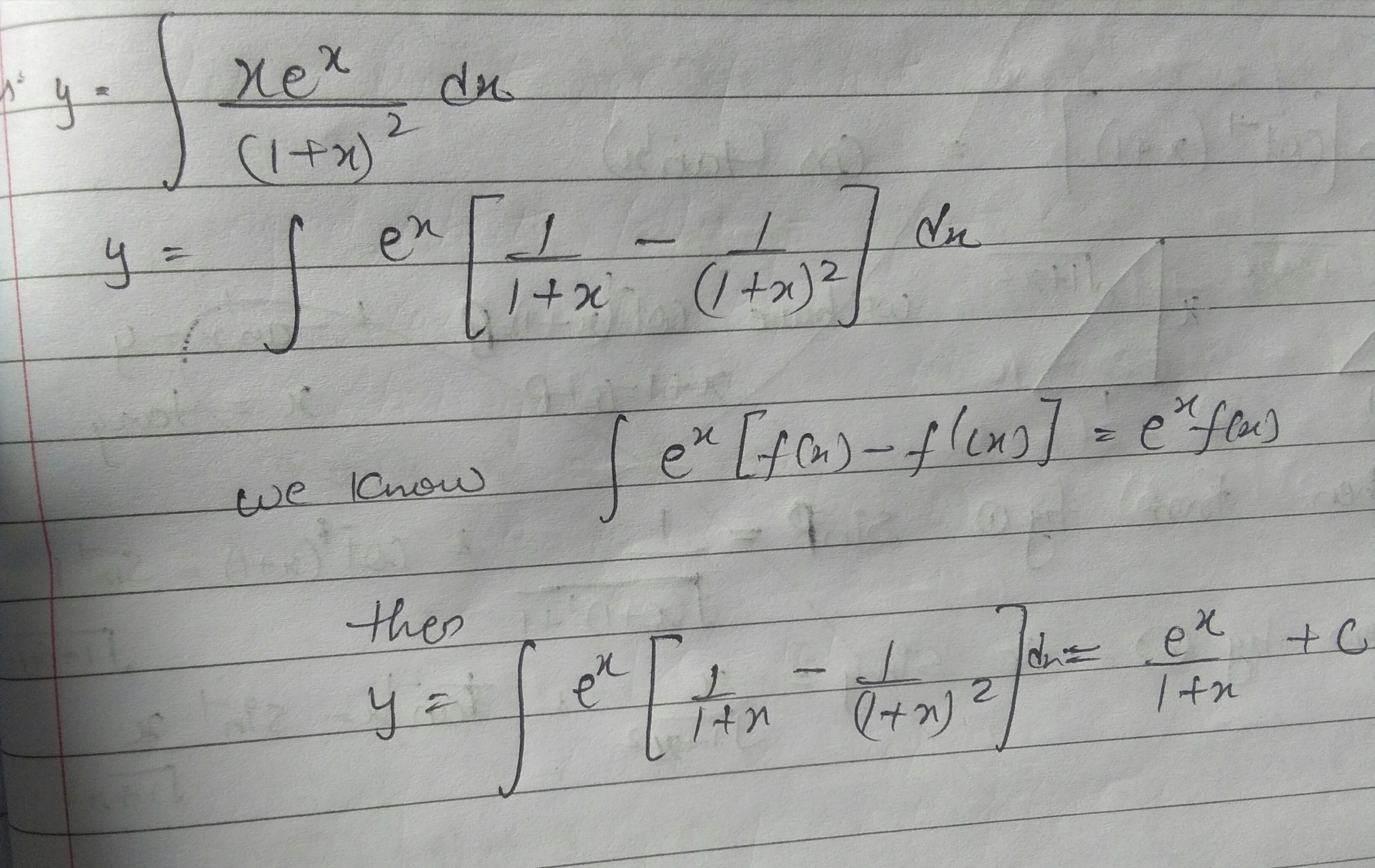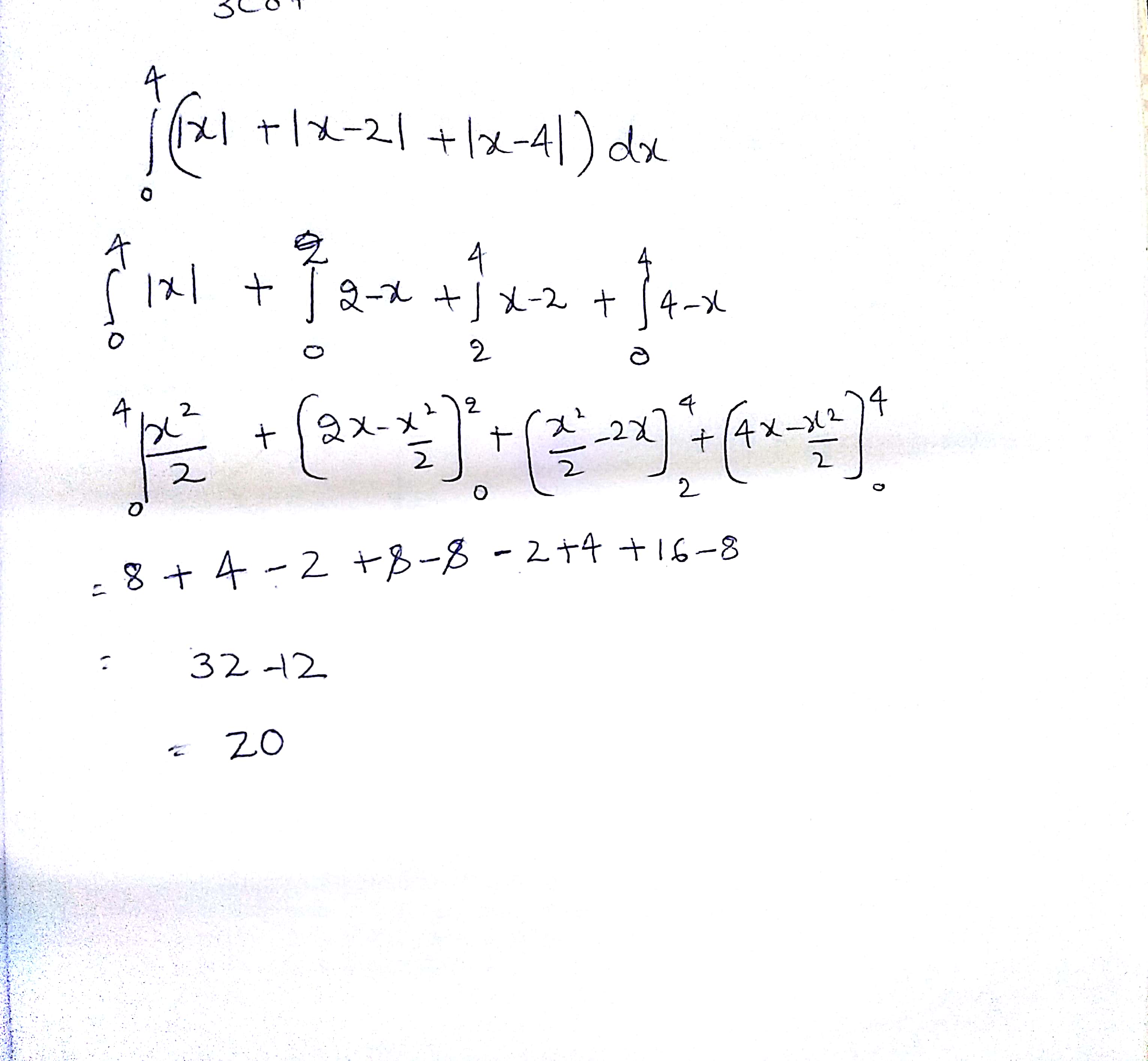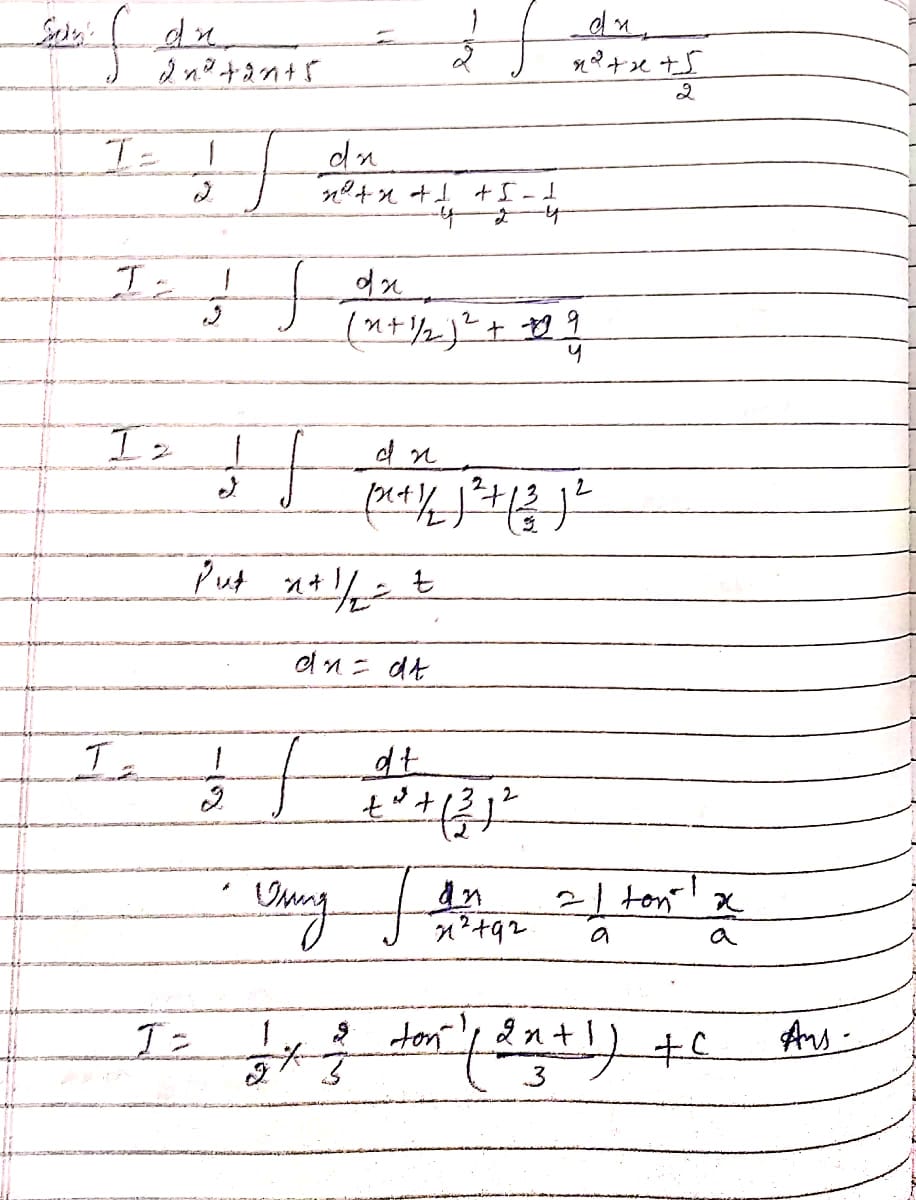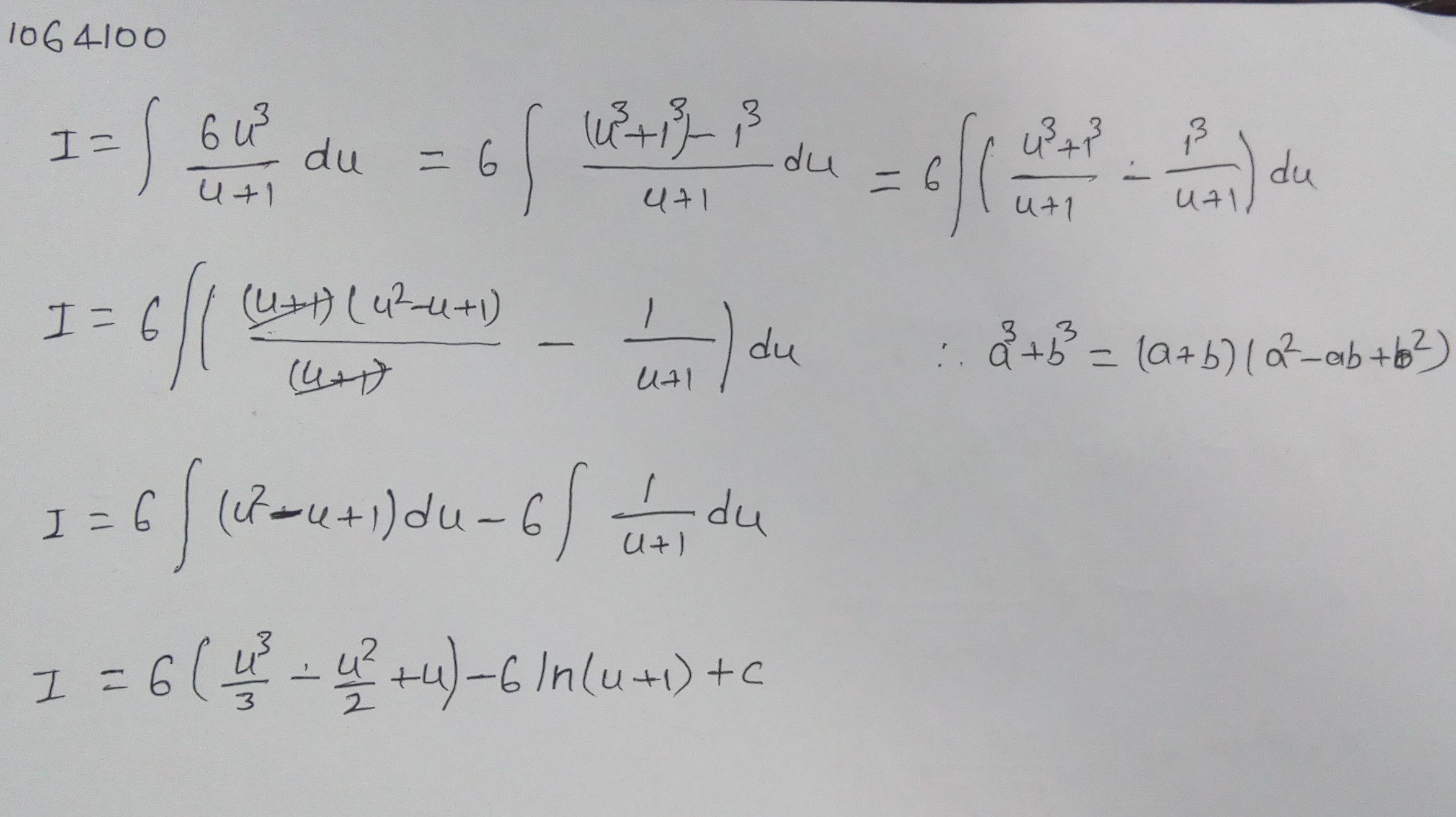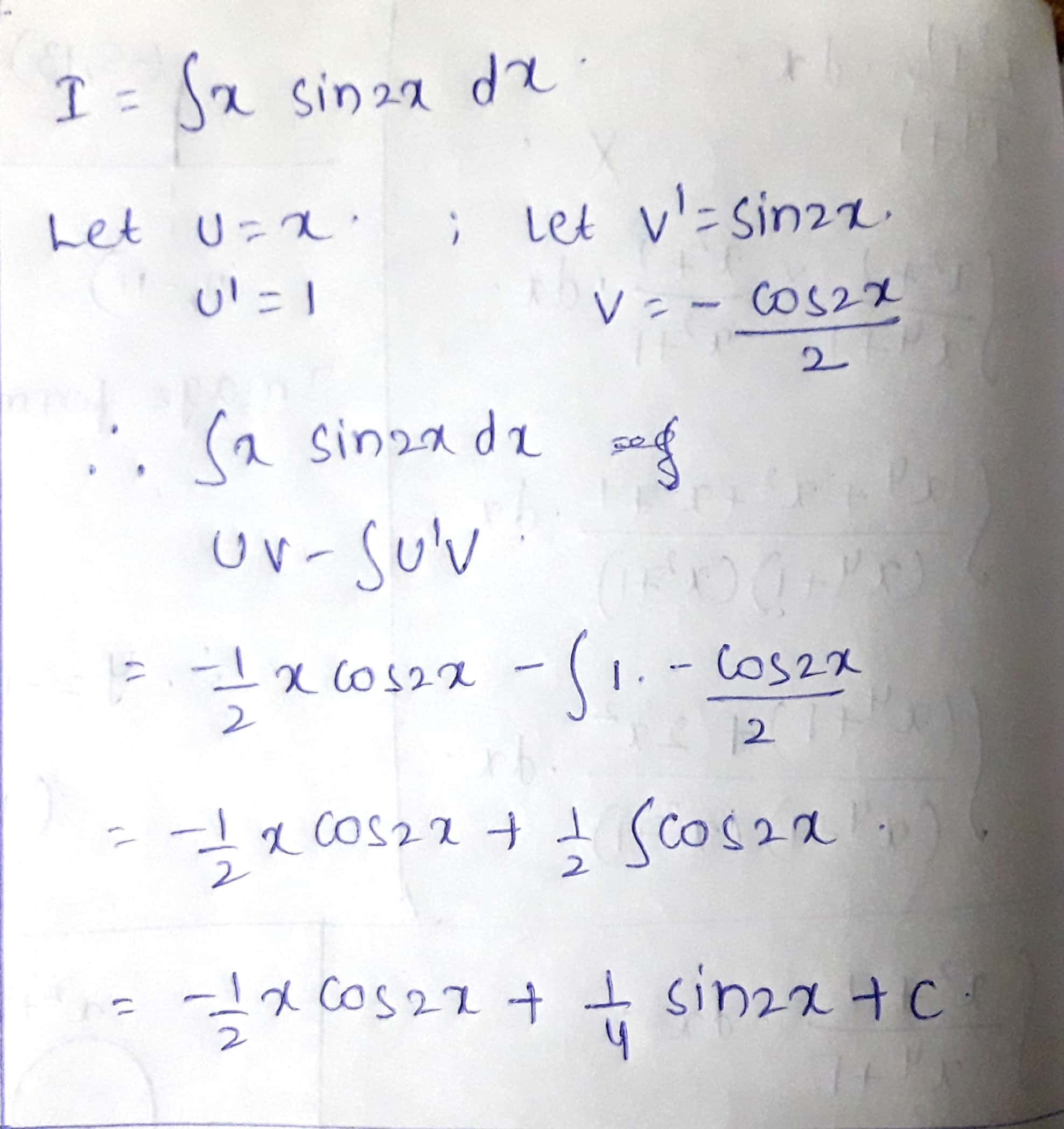Indefinite Integrals - Class 12 Commerce Applied Mathematics - Extra Questions
Integrate the following function with respect to $$x$$.
$$x\sin { hx } $$
Solve :
$$\int\limits_0^a {\dfrac{{\sqrt x }}{{\sqrt x + \sqrt {a - x} }}dx} $$
The value of $$ \left ( \int x. e ^{-x} dx \right)$$ is,
The integration of $$y=\dfrac{x^2}{2}+c$$ . What does $$c$$ represent?
$$I= \displaystyle\int{e^x}\left(\frac{2}{\cos^2x}+\frac{2\sin x\cos x}{\cos^2x}\right)dx$$
Integrate the function $$x \sin x$$
Evaluate $$\displaystyle \int x^{2}e^{x}dx$$.
Object: $$\displaystyle\int cosec^{-1}x, dx, x > 1$$.
The acceleration of a particle varies with time $$t$$ seconds according to the relation $$a = 6t + 6\ ms^{-2}$$. Find velocity and position as functions of time. It is given that the particle starts from origin at $$t = 0$$ with velocity $$2\ ms^{-1}$$.
Object: $$\displaystyle\int (ex)^x(2+log x)dx$$.
Evaluate:$$\displaystyle\int e^x\left(\dfrac{1}{x}-\dfrac{1}{x^2}\right)\ dx$$.
Evaluate:$$\displaystyle\int x^n\log_ex\ dx$$
Integrate with respect to $$x$$:
$$x \sin^{2}x$$
$$\int {{e^x}.\,{a^x}} dx =$$
Integrate the following
i) $$\log{x}$$
ii) $${\cos}^{-1}(\sqrt{x})$$
Evaluate $$\int {\dfrac{1}{{\sqrt 3 \sin x + \cos x}}dx} $$
Evaluate:
$$\int \dfrac{e^x}{\sqrt{5-4e^x-e^{2x}}}dx$$
Solve: $$\displaystyle \int {e^x}{x^2} - {e^{2x}}dx$$
Integrate: $$\displaystyle \int {e^x}\left[ {\tan x + \log \,\sec x} \right] dx$$
Solve $$\int {x{{\sin }^2}xdx} $$
Evaluate $$\int {\dfrac{{dx}}{{\sqrt {x + 1} \, - \sqrt x }}} $$
$$\int {\dfrac{{x\,{{\sin }^{ - 1}}x}}{{\sqrt {1 - {x^2}} }}dx} $$
$$y=\displaystyle\int \dfrac{\cos x}{1+\sin x}dx$$.
Using integration, find the area of the triangle $$PQR$$, whose vertices are at $$P (2 , 5), Q (4 , 7)$$ and $$R (6 , 2)$$.
Evaluate: $$\displaystyle\int \log \left( {\log x} \right) + {\left( {\log x} \right)^{ - 2}}= ?$$
Evaluate: $$\displaystyle\int e^x(x^2+2x) \ dx$$
$$\int { \left( x+1 \right) \log { x } } dx$$
$$\int {{e^{2x}}\left( {\sin \left( {ax + b} \right)} \right)} \,dx$$
$$\int { x\tan ^{ 2 }{ x } } dx$$
$$\int {\left( {\frac{1}{{\left( {\ell nx} \right)}} - \frac{1}{{{{(\ell nx)}^2}}}} \right)\,dx} $$
$$\int { { x }^{ 2 } } \sin ^{ -1 }{ x } dx$$
Solve $$\displaystyle\int {x{{\tan }^{ - 1}}x\,dx} $$
$$\int { \sin ^{ -1 }{ \left( 3x-4{ x }^{ 3 } \right) } } dx$$
Evaluate:$$\int_{} {x{e^{2x}}dx} $$
Find $$\int \left(1-\frac{1}{x^2}\right)e^{(x+\frac{1}{x}) }dx$$ on I where $$I= (0, \infty ).$$
Evaluate $$\displaystyle \int \frac{{x{e^x}}}{{{{\left( {1 + x} \right)}^2}}} dx$$
Solve $$\int { \sin ^{ -1 }{ \left( \dfrac { 2x }{ 1+{ x }^{ 2 } } \right) } dx } $$
If $$\quad \int { \cfrac { \sqrt { 4+{ x }^{ 2 } } }{ { x }^{ 6 } } } dx=\cfrac { { { \left( a+{ x }^{ 2 } \right) }^{ 3/2 } }.\left( { x }^{ 2 }-b \right) }{ 120{ x }^{ 5 } } +C$$ then $$a+b$$ equals to
$$\int {{x^3}\log xdx = } $$
Integrate with respect to $$x$$:
$$x\ ln\ x$$
$$\displaystyle \int \dfrac{(t^{2}+1)^{2}}{t^6+1} dt$$
Integrate the function w.r.t x : $$x{\left( {\log x} \right)^2}$$
Solve: $$\int\limits_0^{\pi /4} {\left( {x\cos x - \cos 3x} \right)dx} $$
Integrate with respect to $$x$$:
$$\ell n\ x$$
Simplify:-
$$\int {x\ell n\sqrt x dx} $$
Integrate with respect to $$x$$:
$$x\sin^{2}x$$
Integrate with respect to x:
(i) $$\dfrac{x}{nx}$$
(ii) $$x\sin^2x$$
Solve : $$\int \, 4 \, x^3 \sqrt{5 - x^2 } \, dx$$
Solve : $$\displaystyle \int \, \dfrac{dx}{x - \sqrt{x}}$$
Solve : $$\displaystyle \int \dfrac{2x}{x^2+5}dx$$
Solve: $$\int 3^x.e^x dx =$$?
$$ \displaystyle I = \int 3^{x}e^{x}dx$$
$$ \displaystyle I = 3^x \int e^{x}dx -\int \left ( \dfrac{d}{dx}3^{x} \right )\int e^{x}dx $$
$$ \displaystyle I = 3^{x} e^{x} -\int 3^{x}log 3 e^{x}dx$$
$$ \displaystyle I = 3^{x}e^{x}- log 3 \int 3^{x}e^{x}dx$$
$$ \displaystyle I = 3^{x} e^{x} - log 3 I$$
$$ (1+log 3) I = 3^{x}e^{x}$$
$$ I = \dfrac{1}{(1+log3)} 3^{x}e^{x}$$
$$ \boxed{\therefore 3^x e^x dx = \frac{1}{(1+log3)}3^x e^x}$$
Solve $$\int e^{ax}\sin bxdx$$.
$$\displaystyle\int cosec^3x dx$$.
Evaluate:$$\displaystyle\int \dfrac{1}{24+1}dx=?$$
Solve: $$\int tan (x)dx=?$$
$$\displaystyle \int \dfrac {3ax}{ b^{2}+c^{2}x^{2}} dx$$
Solve:$$\displaystyle\int\dfrac{(\ln x )^n}{x}dx$$
$$\int e^{\ 10x} dx$$
Evaluate: $$- 2 \int \cos 2 \theta \sin 2\theta d \theta$$
Solve:$$\sqrt{\sin x}dx$$
Prove that
$$\int e ^ { x } \left( \tan ^ { - 1 } x + \frac { 1 } { 1 + x ^ { 2 } } \right) d x$$
I= $$\int { \left( { 1-x } \right) \left( { 2+3x } \right) \left( { 5-4x } \right) dx } $$
$$\int {\tan x}dx$$
$$I = \int {\left( {3\sin x - 4\cos x + 5{{\sec }^2}x - 2\cos e{c^2}x} \right)dx} $$
Evaluate: $$\displaystyle \int{\dfrac{dx}{32-2x^{2}}}$$
$$\int {\cot xdx}$$
$$\int {cosec\;x dx}$$
$$\int {\sec xdx}$$
$$I = \int {{x^9}dx} $$
Evaluate: $$\int {\frac{{\tan x}}{{{{\left( {\cos x} \right)}^2}}}dx} $$
Evaluate :$$\displaystyle \int \dfrac{2x}{1+x^2}dx$$
Find the value of -
$$\int xdx$$
$$I = \int {\sqrt[3]{x}dx} $$
Solve:$$\displaystyle \int \dfrac{\log{x}}{x^{2}}\ dx$$
$$I=\displaystyle\int \dfrac{log x}{x^2}dx$$
Let $$t=log x$$
$$\Rightarrow x=e^t$$
$$dt=\dfrac{1}{x}dx$$
$$I=\displaystyle\int t e^{-t}dt$$
$$I=t \dfrac{e^{-t}}{-1}-\displaystyle\int 1.\dfrac{e^{-t}}{-1}dt$$
$$I=-t e^{-t}+\dfrac{e^{-t}}{-1}+c$$
$$I=-\dfrac{t}{e^t}-e^{-t}+c$$
$$I=\dfrac{-log x}{x}-\dfrac{1}{x}+c$$
$$I=-\dfrac{(log x+1)}{x}+c$$.
Solve
$$\int \dfrac{\cos (x+a)}{\cos (x-a)} dx$$
Solve:$$\displaystyle \int \dfrac{x\tan^{-1}{x^{2}}}{(1+x^{4})}\ dx$$
Write the formula for integration by parts.
Find $$\displaystyle \int \dfrac {1}{9x^{2}+6x+5}dx$$
$$ \int \frac{dx}{ax^{2}+ 6x + 5 } = \frac{1}{9} \int \frac{dx}{x^{2} + \frac{2x}{3} + \frac{5}{9}}$$
$$ = \frac{1}{9} \int \frac{dx}{x^{2} + \frac{2x}{3} + \frac{1}{9} - \frac{1}{9} + \frac{5}{9}}$$
$$ = \frac{1}{9} \int \frac{dx}{(x+\frac{1}{3})^{2} + (\frac{2}{3})^{2}}$$ $$ [\because \int \frac{dx}{x^{2}+a^{2}} $$ = $$ \frac{1}{a} tan^{-1} (\frac{x}{a}) + c ]$$
$$ = \frac{1}{9} \times \frac{1}{(\frac{2}{3})} tan^{-1} (\frac{3x+1}{2}) + c $$
$$ \frac{1}{6} tan^{-1} (\frac{3x+1}{2}) + c $$
$$\int {{x^9}dx} $$
Evaluate $$\displaystyle \int{\cos^{2}x\, dx}$$.
Evaluate $$\displaystyle \int \dfrac{\cos^{-1} x}{\sqrt {1-x^2}}dx$$
Evaluate:
$$\displaystyle\int{\dfrac{1}{4+9x^{2}}}dx$$
$$ \int \frac{dx}{4+9x^{2}} = \frac{1}{9}\int \frac{dx}{(\frac{2}{3})^{2}+x^{2}}$$
$$ \because \int \frac{dx}{a^{2}+x^{2}} = \frac{1}{a} tan^{-1}(\frac{x}{a})+c$$
$$ = \frac{1}{a}\times \frac{1}{(\frac{2}{3})} tan^{-}(\frac{3x}{2})+c$$
$$ = \frac{1}{6}tan^{-1}(\frac{3x}{2})+c$$
Evaluate $$\displaystyle \int \dfrac {x^{3}}{x+2}dx$$
$$\int \frac{x^{3}dx}{x+2}$$ put x+2=t x
x=t-2
dx=dt
=$$\int \frac{(t-2)^{3}}{t}dt$$
=$$\int (\frac{t^{3}-6t^{2}+12t-8}{t})dt$$
=$$\int (t^{2}-6t+12-\frac{8}{t})dt$$
$$=\frac{t^{3}}{3}-3t^{2}+12t-8ln(t)+c$$
$$=\frac{(x+2)^{3}}{3}-3(x+2)^{2}+12(x+2)-8ln(x+2)+c$$
Integrate $$\displaystyle \int \dfrac{\sqrt{a-x}}{x}\ dx$$
Let $$x=a\sin^2\theta$$
$$\Rightarrow dx=2a\sin\theta \cos\theta d\theta$$
$$\Rightarrow \displaystyle\int \dfrac{\sqrt{a(1-\sin^2\theta)}\cdot 2a\sin\theta \cos\theta}{a\sin^2\theta}d\theta=\displaystyle\int \dfrac{\sqrt{a}(\cos\theta)\cdot 2\cos\theta}{\sin\theta}d\theta$$
$$=2\sqrt{a}\displaystyle\int \dfrac{1-\sin^2\theta}{\sin\theta}d\theta=2\sqrt{a}\left[\displaystyle\dfrac{1}{\sin \theta}d\theta -\displaystyle\int\sin \theta d\theta\right]$$
$$=2\sqrt{a}\left[\displaystyle\int cosec \theta d\theta -\displaystyle\int \sin\theta d\theta\right]$$
$$=2\sqrt{a}\left[ln|cosec \theta -\cot\theta|+\cos\theta\right]+c$$
$$\sin^2\theta =\dfrac{x}{a}$$
$$\Rightarrow \sin\theta =\sqrt{\dfrac{x}{a}}, \cos \theta =\sqrt{1-\dfrac{x}{a}}$$
$$\Rightarrow I=2\sqrt{a}\left[ln \left|\sqrt{\dfrac{a}{x}}-\dfrac{\sqrt{a-x}}{\sqrt{x}}\right|+\sqrt{1-\dfrac{x}{a}}\right]+c$$.
Evaluate $$\int \dfrac{sec^2x}{3+tan^2x}dx$$
Evaluate $$\int \dfrac{log(\sin x)}{\tan x}dx$$
Integrate :$$\int \dfrac{2\cos x}{sin^2x}dx$$
$$ \int \sqrt{\frac{x}{a-x}} d x= $$
Evaluate :$$\int 2^x dx$$
Evaluate :$$\int (\dfrac{2}{1+2x}-\dfrac{1}{1-x})dx$$
$$I=\int ({1+x+x^{2}})dx$$
Prove that $$\displaystyle \int x^{2}a^{x}dx=\frac{a^{x}}{\left ( \log a \right )^{3}}\left [ x^{2}\left ( \log a \right )^{2}-2x\left ( \log a \right )+2 \right ].$$
$$\displaystyle\int x^{3}\left ( \log x \right )^{2}dx=\frac{x^{4}}{4}\left ( \log x \right )^{2}-\frac{1}{8}x^{4}\log x+\frac{1}{4k}x^{4}.$$ Find the value of $$k$$
$$\displaystyle\int \frac{1}{x^{2}}\log \left ( x^{2}+a^{2} \right )dx=\frac{-1}{x}\log \left ( x^{2}+a^{2} \right )+k.\frac{1}{a}\tan^{-1}\frac{x}{a}.$$ Find $$k$$.
Solve $$\displaystyle \int \frac{x}{1+\sin x}dx$$
Show that $$\displaystyle \int \left ( e^{\log x}+\sin x \right )\cos dx=x\sin x+\cos x+\frac{1}{2}\sin^{2}x.$$
$$\displaystyle \int \left [ \frac{1}{\log x}-\frac{1}{\left ( \log x \right )^{2}} \right ]dx=x \left ( \log x \right )^{-1}.$$ If this is true enter 1, else enter 0.
Show that $$\int \displaystyle x\sin x\cos x = f(x)$$, taking const. of integration as zero. Find $$f(\pi /4)$$
$$\displaystyle \int \sec ^{2}x\log \left ( 1+\sin^{2}x \right )dx=\tan x\log \left ( 1+\sin ^{2}x \right )-2x+\sqrt{k}\tan^{-1}\sqrt{k}\tan x$$. Find the value of $$k$$.
Find the value of $$\int { x\sin { x } dx } $$.
Evaluate: $$\displaystyle\int \log_ex dx$$.
Integration of $$\dfrac{\cos x}{\cos 3x}$$
Evaluate: $$\displaystyle\int\displaystyle\frac{x^3+5x^2+4x+1}{x^2}dx$$.
The value of $$\int { \cos ^{ 6 }{ x } } dx$$ is
Evaluate:
$$\displaystyle\int\dfrac{2^{x+1}-5^{x-1}}{10^x}dx$$
Find $$\displaystyle \int e^{x}\sin x\ dx$$.
$$\int { { e }^{ 3x } } \cdot { x }^{ 2 }dx$$
Integrate the following function: $$e^x\left(\dfrac{1+ sinx}{1+ cosx}\right)$$
Evaluate:$$\displaystyle\int\log x\ dx$$
Solve $$\displaystyle \int_0^{\pi/4} ln (1+tan\,\,x)dx$$
$$\displaystyle \int {\sin x\sqrt {1 - \cos 2x} } \;dx$$
$$\displaystyle \int sin\,x\sqrt{1-cos\,2x}\,\,dx\,\, 1-cos\,x = 2\,sin^{2}x $$
$$\displaystyle \Rightarrow \sqrt{2}\int sin\,x(sin\,x)dx $$
$$\displaystyle \Rightarrow \sqrt{2}\int sin^{2}x\,dx \Rightarrow \frac{+\sqrt{2}}{2}\int 1-cos\,2x\,dx $$
$$\displaystyle \frac{1}{\sqrt{2}}(x)-\frac{1}{2\sqrt{2}}sin\,2x $$
Integrate $$\displaystyle \int {\sqrt {1 + {x^2}} } dx$$ is equal to:
Find $$\displaystyle \int_{}^{} {x{e^x}dx.} $$
$$\int \frac{x^{-2/3}}{\sqrt(x^{1/3})^{2} - 4} dx$$ =
Number of real solution of the given equation for $$x$$, $$\int x^{2}\ e^{x}dx=0$$
$$\displaystyle \int \dfrac {1-x}{1+x}$$
If $$\int \dfrac{1}{1+ \sin x} dx=\tan x-m\sec x$$.Find $$m$$
Solve:$$\int { \tan { x } \tan { 2x } \tan { 3xdx } }$$
Solve :
$$\displaystyle \int \left (\log(\log x)+\dfrac{1}{(\log x)^2}\right)dx$$
Solve $$\displaystyle\int^{\pi/2}_0e^x\cdot\sin \left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)dx$$.
Solve $$\displaystyle\int {\frac{{{e^x}\left( {{x^2} + 5x + 7} \right)}}{{{{\left( {x + 3} \right)}^2}}}} dx$$
Integrate:$$\displaystyle \int e^x\sin x\ dx$$
Solve $$\displaystyle\int \dfrac{\sqrt{1+x^2}}{x^2}dx$$
Solve $$\dfrac{1}{4}\displaystyle\int \left(\dfrac{1+\cos 2x}{2}\right)^2dx$$.
Integrate $$\int x.\cos^{-1}x$$
Evaluate $$\displaystyle\int a^{x} e^{x}\ dx$$.
$$\displaystyle \int {\dfrac{7^{2x+3}\sin^2 2x+ \cos^22x}{\sin^22x}}=\dfrac{7^{2x+3}}{2\log 7}-\dfrac{(\cot x+x)}{b}$$.Find $$b$$
$$\displaystyle\int x^3\tan^{-1}xdx$$.
Integrate with respect to $$x$$.:
$$e^{x}\sin x$$
Evaluate $$\int {{e^x}\left( {\tan x - \log \,\cos \,x} \right)\,dx} $$
Evaluate $$\int {x{\mathop{\rm sintx}\nolimits} \,dx} $$
$$\int {x^2}\,{e^x}\, dx =?$$
$$\int { \cos ^{ -1 }{ \left( 4{ x }^{ 3 }-3x \right) dx } } $$
$$\int \sin x \log (\cos x)dx$$
$$\int x^{3}\cos x^{2}dx$$
Find the following integral.
$$\displaystyle\int e^x (\sec^2 x + \tan x).dx$$
Evaluate:$$\displaystyle\int{{x}^{2}{(3-x)}^{5}dx}$$
$$\int { { x }^{ 3 }\tan ^{ -1 }{ x } dx } $$
$$\int { \cos ^{ -1 }{ \left( \dfrac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } } \right) } dx } $$
$$\int { \tan ^{ -1 }{ \left( \sqrt { x } \right) } } dx$$
Evaluate $$\int\tan^{-1}x dx$$
$$\int{\dfrac{dx}{{x}^{1/3}+{x}^{1/2}}}$$
$$\int {{e^x}\left( {\cos x - \sin x} \right)dx} $$
$$\int {\ell n\left( {{x^2} + 1} \right)dx} $$
$$\int {{e^x}\left( {{{\sec }^2}x + \tan x} \right)} dx$$
Solve $$\int { \cfrac { 1 }{ 9{ x }^{ 2 }+6x+10 } dx } $$
Evaluate $$\int{\sin ^{ - 1}}xdx$$
Evaluate: $$\displaystyle \int { \dfrac { \left( x-1 \right) \left( x-2 \right) \left( x-3 \right) }{ \left( x-4 \right) \left( x-5 \right) \left( x-6 \right) } dx }$$
Evaluate $$\displaystyle \int {\frac{{{x^2}\,{e^x}}}{{{{\left( {x + \,2} \right)}^2}}}\,dx} $$
Evaluate:
$$\displaystyle \int \dfrac{\sin (x)}{\sqrt{1+ \sin (x)}} dx$$
Evaluate: $$\displaystyle\int \dfrac{\cos 2x+2\sin^2x}{\sin^2x}dx$$.
$$\displaystyle\int \dfrac{1}{\cos^4x+\sin^4x}dx$$.
$$I = \displaystyle \int{\dfrac{x\cos x+\sin x}{x\sin x}}dx$$ Then $$I = ?$$
Evaluate:$$\displaystyle\int \dfrac{\sin^3xdx}{(\cos^4x+3\cos^2x+1)\tan^{-1}(\sec x+\cos x)}$$.
Evaluate the following :
$$\displaystyle \int{\left(\dfrac{\tfrac{x}{x+1}-ln(x+1) }{x(ln(x+1)) }\right)}dx$$
Integrate:$$\displaystyle\int{\left( x+1 \right)\sqrt{3-2x-{{x}^{2}}}}dx = $$
Solve
$$\displaystyle \int{\dfrac{x}{(x^{2}+1)(x+1)}}$$
$$\int {\dfrac{1}{\sin x\ \cos^{2}x}}dx = $$
$$\int \frac{1}{x(x^n+1)}dx$$.
Simplify: $$\int {\dfrac{{{e^x}\left( {x - 1} \right)}}{{{{\left( {x + 1} \right)}^3}}}dx} $$
$$\int\frac{dx}{x^2-16}$$
Integrate with respect to $$x$$:
$$\dfrac { { x }^{ 2 }\tan ^{ -1 }{ x } }{ 1+{ x }^{ 2 } } $$
Integrate with respect to $$x$$:
$$e^{x}\sin x$$
$$\int { \dfrac { x\sin ^{ -1 }{ x } }{ \sqrt { 1-{ x }^{ 2 } } } } dx = $$
Integrate with respect to $$x$$:
$$2x^{2}e^{x^{2}}$$
$$\displaystyle \int a^{x}e^{x}dx$$
Find :
$$\int {\log xdx} $$
Solve:-
$$\int {\dfrac{{{e^x}}}{x}} \left( {1 + x.\ln x} \right)dx$$
Simplify:
$$\int {x{{\tan }^{ - 1}}xdx} $$
$$\displaystyle \int\dfrac {\cos 2x+2\sin^{2}x}{\cos^{2}x}dx$$
Solve : $$ \int (1 - x) \sqrt{x} \, dx$$
Integrate:$$\int 2x^3 \,e^{x^2}.dx$$
Integrate:$$\int e^x\sin x.dx$$
Integrate : $$\int x\sin^2x$$
Evaluate:$$\displaystyle \int x+5 dx$$
Evaluate
$$ \int { { e }^{ x }(\tan { x } +1)secx\quad dx}$$
Find $$\int {{e^x}\left( {\frac{{x - 1}}{{{x^2}}}} \right)} dx$$
Solve:
$$\int {\sin ^4}x.{\cos ^2}xdx$$
Integrate $$\displaystyle \int e^{\log (\sec x+\tan x)}\sqrt{1+\tan^2 x}\ dx$$.
The value of $$\displaystyle\int{{e}^{\ln{\sqrt{x}}}dx}$$ is
Find the integrals of the functions.
i) $$sin^2 (2x + 5)$$
ii) $$sin \, 3x \, cos \, 4x$$
iii) $$cos \, 2x \, cos \, 4x \, cos \, 6x$$
iv) $$sin^3 (2x + 1)$$
Find the integrals of the functions.
i) $$sin^3 \, x \, cos^3 \, x$$
ii) $$sin \, x \, sin \, 2x \, sin \, 3x$$
iii) $$sin \, 4x \, sin \, 8x$$
iv) $$\dfrac{1 - cos \, x}{1 + cos \, x}$$
v) $$\dfrac{cos \, x}{1 + cos \, x}$$
Evaluate:$$\displaystyle\int x \cos^3x dx$$.
Find :
$$\int {\frac{e^x(x-1)}{(x+1)^3}dx}$$
$$\displaystyle\int e^{\tan x}\cdot \tan x\cdot \sec^2x \ dx$$.
$$\displaystyle\int \sqrt{1-x^2}dx$$.
Solve:
$$\int x^2e^x\sin xdx$$
Evaluate: $$\displaystyle \int { { x }^{ 2 }{ sin }^{ -1 } } x\ dx$$
Solve :
$$ \int e^x \left( log x + \dfrac {1}{x^2} \right) dx$$
Solve $$ \int { x\sqrt { x+2 } } dx$$
$$\int e^{2} \left(\dfrac{x-1}{x^{2}}\right)$$
Solve:
$$I = \int {\dfrac{{dx}}{{18 - 4x - {x^2}}}} $$
Evaluate: $$\displaystyle\int{\dfrac{1+\cos x} { x+\sin x}dx } $$.
$$I= \int \dfrac{1}{x(1+\log x)}. dx$$
$$\displaystyle I= \int \dfrac{1}{x(1+\log x)}. dx$$
Let $$ (1+log x) = m $$
$$ \dfrac{1}{x}dx = dm $$
$$\displaystyle \int \frac{dm}{m} $$
$$ \Rightarrow ln|m|+c $$
$$ \Rightarrow ln|1+;n(x)|+c $$
Solve :
$$I=\int \sin^{6}{x}dx$$
$$\displaystyle I = \int sin^{6}x\,dx $$
$$\displaystyle = \int (sin^{2}x)^{2}(sin^{2}x)dx $$
$$\displaystyle = \int (\frac{1-cos2x}{2})^{2}(\frac{1-cos2x}{2})dx $$
$$\displaystyle = \frac{1}{8}\int (1-2cos2x+cos^{2}x)(1-cos2x)dx $$
$$\displaystyle = \frac{1}{8}\int (1-2cos2x+\frac{1+cos4x}{2})(1-cos2x)dx $$
$$\displaystyle = \frac{1}{16}\int (2-4cos2x+cos4x)(1-cos2x)dx $$
$$\displaystyle = \frac{1}{16}\int (3-4cos2x+cos4x)(1-cos2x)dx $$
$$\displaystyle = \frac{1}{16}\int (3-4cos2x-3cos2x+cos4x+4cos^{2}2x-cos4xcos2x)dx $$
$$\displaystyle = \frac{1}{16}\int [3-7cos2x+cos4x+2\times 2cos^{2}2x-\frac{1}{2}.2cos^{4}xcos2x]dx $$
$$\displaystyle = \frac{1}{16}[3-7cos2x+cos^{4}x+2(1+cos^{4}x)-\frac{1}{2}(cos6x+cos2x)]dx $$
$$\displaystyle = \frac{1}{16}(3-7cos2x+cos^{4}x+2+2cos^{4}x-\frac{1}{2}(cos6x+cos2x))dx $$
$$\displaystyle = \frac{1}{32}\int [6-14cos2x+2cos4x+4+4cos4x-cos6x-cos2x]dx $$
$$\displaystyle = \frac{1}{32}[10-15cos2x+6cos4x-cos6x]dx $$
$$\displaystyle \frac{1}{32}[10-15cos2x+6cos4x-cos6x]dx $$
$$\displaystyle \frac{1}{32}[10x-\frac{15sin2x}{2}+\frac{6sin4x}{4}-\frac{sin6x}{6}]dx $$
$$\displaystyle \frac{1}{32}[10x-\frac{15sin2x}{2}+\frac{3}{2}sin4x] $$
$$\displaystyle \frac{1}{92}[60x-45sin2x+9sin4x-sin6x]+c $$
Solve :
$$\int x^{ \sin x} \left( \dfrac {sinx}{x} + \cos x . logx \right) dx $$
Evaluate:$$\int { \sin ^{ 3 }{ x } .\cos ^{ 3 }{ x } } dx$$
$$\int \sin^{3}x\cos^{2}x dx$$ is equal to
Integrate the function:
$$\dfrac{\sin(\tan^{-1}x)}{1+x^2}$$
Evaluate:$$\int x \cdot \sin^{2}x dx$$
Solve: $$\displaystyle \int { \dfrac {dx }{ e^x+e^{-x} } } $$
$$\int \frac{ln(\frac{x-1}{x+1})}{x^{2}-1}dx$$ is equal to
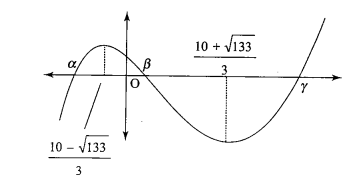
Find the integral part of the greatest root of equation $$x^{3}-10x^{2}-11x-100=0$$.
Given equation is
$$x^{3}-10 x^{2}-11 x-100=0$$
Let $$f(x)=x^{3}-10 x^{2}-11 x-100 $$
$$\Rightarrow f^{\prime}(x)=3 x^{2}-20 x-11$$
For $$ 3 x^{2}-20 x-11=0, $$
we have$$x=\dfrac{20\pm\sqrt{400+132}}{6}=\dfrac{10\pm\sqrt{133}}{3}$$
Hence, graph of $$ y=f(x) $$ is plotted
Now, $$ (10+\sqrt{133}) / 3 \cong 7.16 $$
$$ f(8)=8^{3}-10(8)^{2}-11(8)-100<0 $$
$$ f(9)=9^{3}-10(9)^{2}-11(9)-100<0 $$
$$ f(10)=10^{3}-10(10)^{2}-11(10)-100<0 $$
$$ f(11)=11^{3}-10(11)^{2}-11(11)-100<0 $$
$$ f(12)=12^{3}-10(12)^{2}-11(12)-100>0 $$
$$ \Rightarrow \quad y \in(11,12) $$
$$ \Rightarrow \quad[y] \quad=11 $$
Solve :
$$ \int 2^x . e^x dx $$
Find the following integrals:
$$\int \left (\sqrt {x} - \dfrac {1}{\sqrt {x}}\right )^{2}dx$$.
$$I=\displaystyle\int \left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2dx$$
$$=\displaystyle\int (\sqrt{x})^2+\left(\dfrac{1}{\sqrt{x}}\right)^2-2\sqrt{x}\cdot \dfrac{1}{\sqrt{x}}dx$$
$$=\displaystyle\int \left(x+\dfrac{1}{x}-2\right)dx$$
$$=\displaystyle\int (x+x^{-1}-2)dx$$
$$=\dfrac{x^2}{2}+ln |x|-2x+c$$.
Solve : $$\int e^x. \sin \,3xdx$$
Solve:-
$$\int \dfrac{{\cos \,x}}{{1 + \cos \,x}}d x$$
Solve $$\dfrac {1}{\sqrt {3}}\int \dfrac {dx}{\sin \left (x + \dfrac {\pi}{4}\right ) + 1}$$.
Solve :$$\int{x}{e^x}\sin x dx$$
$$\displaystyle\int { \sin { x\sin { \left( \cos { x } \right) } } } dx$$
Solve: $$\displaystyle \int \dfrac{x \cdot \sin^{-1}x}{(1 - x^2)^{\frac{3}{2}}} dx$$.
$$\displaystyle\int \dfrac{x\sin^{-1}x}{(1-x^2)^{3/2}}dx$$
$$=\displaystyle\int \dfrac{x\sin^{-1}x}{(1-x^2)^{1/2}(1-x^2)}dx$$
Let $$\sin^{-1}x=t$$
$$\dfrac{dx}{(1-x^2)^{1/2}}=dt$$
$$=\displaystyle\int \dfrac{\sin t.t dt}{1-\sin^2 t}$$
$$=\displaystyle\int t\dfrac{\sin t}{\cos^2t}dt$$
$$=\displaystyle\int t \tan t \sec tdt$$
$$=t\displaystyle\int \tan t\sec t dt-\displaystyle\int \left[\left(\dfrac{dt}{dt}\right)\displaystyle\int \left(\sec t\tan t dt\right)\right]dt$$.
$$=t\sec t-\displaystyle\int 1\sec t dt$$
$$=t\sec t-log |\sec t+\tan t|+c$$
$$=\sin^{-1}x\sec (\sin^{-1}x)-log|\sec(\sin^{-1}x)+\tan(\sin^{-1}x)|+c$$
$$\therefore \displaystyle\int \dfrac{x\sin^{-1}xdx}{(1-x^2)^{3/2}}=\sin^{-1}x\sec(\sin^{-1}x)-log|\sec(\sin^{-1}x)+\tan(\sin^{-1}x)|+c$$.
Solve:$$\displaystyle \int\dfrac{1}{\sqrt{1+4x^2}}dx$$
solve it.
$$I = \int {{x^2}\cos x} dx$$
Interget that :-
$$\int {x\sqrt {x + 2} } $$ $$dx$$
Evaluate
$$\displaystyle \int {x.\,\,\,{{\sin }^2}x\,\,dx} $$
solution :
$$ \rightarrow \int x sin^{2}x dx$$
$$ \int sin^{2}x\,dx = \int \frac{1}{2}(1-cos2x)dx = \frac{1}{2}(x-\frac{sin 2x}{2})+c$$
we take $$ u = x_{1}$$ $$ v = sin^{2}x$$
$$ {u}' = 1 $$ $$ {v}' =\frac{1}{2}(x-\frac{sin2x}{2})$$
w.r.t $$ \int uv = uv - \int {u}'v$$
so $$ \int x sin^{2}x dx = \frac{x}{2}(x-\frac{sin(2x)}{2})-\int \frac{1}{2}(x-\frac{sin 2x}{2})$$
$$ = \frac{x}{2}(x-\frac{sin2x}{2})-\frac{1}{2}(x^{2}+\frac{cos^{2}x}{2})$$
on simpiflying we get
Ans $$ = \frac{x^{2}}{4}-x\frac{sin(2x)}{4} - \frac{cos(2x)}{8}$$
Evaluate $$ \int {x.\,\,\,\log x\,\,dx} $$
Solve:
$$\int {{{\cos }^3}x{e^{\log \left( {\sin x} \right)}}dx} $$
Integrate:$$\int \frac{1-V}{1+V^{2}}dv.$$
$$ \int \frac{1-v}{1+v^{2}}dv $$
let $$ v = tan\theta $$ ___(1)
$$ dv = sec^{2}\theta d\theta $$
$$ \int \frac{1-tan\theta }{1+tan^{2}\theta }\times sec^{2}\theta d\theta $$
$$ \int \frac{1-tan\theta }{sec^{2}\theta }\times sec^{2}\theta d\theta $$
$$ \int d\theta -\int tan\theta d\theta $$
$$ \theta -(-ln(cos\theta ))+c $$ $$[\because \int tan\theta d\theta = ln\, tan\theta ] $$
$$ \theta +ln(cos\theta )+c$$___(2)
from (1)
$$ \theta = tan^{-1}v $$
putting in (1)
$$ tan^{-1}v+ln(tan^{-1}v)+c $$ Ans
$$\displaystyle\int \:e^x\left(x^2-x+1\right)dx$$
integrate :
$$\int {{{\tan }^{ - 1}}xdx} .$$
$$\int cos^{2}\theta d\theta $$ = ?
$$\int \dfrac {\sec^{8}x}{cosec x}dx$$.
$$\int x \sin ^ { - 1 } x \cdot d x$$
Evaluate: $$\int (3x^2 - 5)^2 dx$$
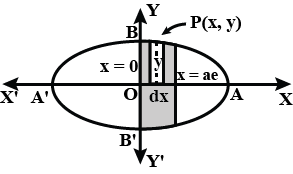
Find the area bounded by the ellipse $$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$$ and the ordinates $$x=0$$ and $$x=ae$$, where $$b^{2}=a^{2}(1-e^{2})$$ and $$e<1$$
Required area $$A$$ is given by
$$A=2$$ (Area of shaded region in first quadrant)
$$\Rightarrow A=2 \displaystyle\int_{0}^{ae}|y|\ dx=2\displaystyle\int_{0}^{ae}y\ dx$$ $$[\because y\ge 0\therefore |y|=y]$$
$$\Rightarrow A=2\dfrac{b}{a}\left[\displaystyle\int_{0}^{ae}\sqrt{a^{2}-x^{2}}dx\right]$$
$$\Rightarrow A=\dfrac{2b}{a}\left[\dfrac{1}{2}\times \sqrt{a^{2}-x^{2}}+\dfrac{1}{2}a^{2}\sin^{-1}\dfrac{x}{a}\right]_{ae}^{0}$$
$$\Rightarrow A=\dfrac{2b}{a}\left[\dfrac{ae}{2}\sqrt{a^{2}-a^{2}e^{2}}+\dfrac{1}{2}a^{2}\sin^{-1}e\right]$$
$$\Rightarrow A=\dfrac{b}{a}\left(a^{2}e\sqrt{1-e^{2}}+a^{2}\sin^{-1}e\right)=ab\left(e\sqrt{1-e^{2}}+\sin^{-1}e\right)$$
$$A=2$$ (Area of shaded region in first quadrant)
$$\Rightarrow A=2 \displaystyle\int_{0}^{ae}|y|\ dx=2\displaystyle\int_{0}^{ae}y\ dx$$ $$[\because y\ge 0\therefore |y|=y]$$
$$\Rightarrow A=2\dfrac{b}{a}\left[\displaystyle\int_{0}^{ae}\sqrt{a^{2}-x^{2}}dx\right]$$
$$\Rightarrow A=\dfrac{2b}{a}\left[\dfrac{1}{2}\times \sqrt{a^{2}-x^{2}}+\dfrac{1}{2}a^{2}\sin^{-1}\dfrac{x}{a}\right]_{ae}^{0}$$
$$\Rightarrow A=\dfrac{2b}{a}\left[\dfrac{ae}{2}\sqrt{a^{2}-a^{2}e^{2}}+\dfrac{1}{2}a^{2}\sin^{-1}e\right]$$
$$\Rightarrow A=\dfrac{b}{a}\left(a^{2}e\sqrt{1-e^{2}}+a^{2}\sin^{-1}e\right)=ab\left(e\sqrt{1-e^{2}}+\sin^{-1}e\right)$$
$$\dfrac { d y } { d x } = ( 4 x + y + 1 ) ^ { 2 }$$
Evaluate: $$\displaystyle\int {{x \over {\sqrt {x + 4} }}dx} $$
Evaluate:
$$\int {\frac{1}{{\sqrt {1 - x - {x^2}} dx}}} $$
$$\int \dfrac { \sin 2 x } { 1 + \sin ^ { 2 } x }$$
$$\displaystyle\int \dfrac{(x^2+\sin^2x)\sec^2x}{1+x^2}\cdot dx$$.
Solve:
$$\displaystyle \int_{0}^{2\pi}{e^{x}.\sin\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)dx}$$
Evaluate:$$\displaystyle\int e^x(x^2+2x)\ dx$$.
Evaluate: $$\displaystyle \int \frac { 1 } { \sqrt { x ^ { 2 } + 8 x + 25 } } d x$$
$$I = \int \frac { 1 } { \sqrt { 2 x ^ { 2 } + 3 x + 8 } } d x$$
Evaluate : $$\displaystyle \int \dfrac{x}{(x+1)^2}e^x dx$$
$$\displaystyle \int x \sin \dfrac {x}{2}=?$$
Evaluate:$$\displaystyle \int \tan ^ { 3 } 2 x \sec 2 x d x$$
Solve:$$\int \frac{dx}{\sqrt{4-x^{2}}}$$
Solve
$$I= \displaystyle\int \dfrac{x+2}{x^{2}+5x+6}dx$$
$$\int {\frac{{1 - \sin x}}{{\cos x}}} dx$$=?
Evaluate: $$\int x \sec ^ { 2 } x d x$$
Integrate: $$\sin ^ { 3 } ( 2 x + 1 )$$
Evaluate: $$\int x \sin 2 x d x$$
Solve
$$\int (4x^{3}-\dfrac{3}{x^{4}}) dx$$
Evaluate : $$\int { \sqrt { \dfrac { x }{ { x }^{ 3 }{ a }^{ 3 } } } dx } $$
Evaluate: $$\displaystyle\int \dfrac { \cos x + x \sin x } { x ( x + \cos x ) } d x $$
Evaluate
$$\int \dfrac {x+2}{2X^{2}+6x+5}dx$$
Solve: $$\displaystyle \int{\dfrac{dx}{x(a+bx^{n})^{2}}}$$
Solve
$$\int \csc x dx$$
$$\displaystyle\int csc xdx$$
$$=\displaystyle\int csc x\dfrac{cscx+\cot x}{csc x+\cot x}\cdot dx$$
$$u=cscx+\cot x$$
$$du=-cscx\cot x-\csc^2x$$
$$=\displaystyle\int \dfrac{csc^2x+cscx\cot x}{csc x+\cot x}\cdot dx$$
$$=-\displaystyle\int\dfrac{csc^2x+cscx\cot x}{csc x+\cot x}\cdot dx$$
$$=-\displaystyle\int \dfrac{du}{u}=-\displaystyle\int \dfrac{1}{u}du$$
$$=-log|u|+c$$
$$=-log|csc +\cot x|+c$$.
Prove that:
$$\displaystyle \int {\sin 2x}\ dx$$
$$ \int sin\,2x \,dx = \int sinU.\frac{dU}{2} = \frac{1}{2} \int sinU.dU = \frac{1}{2}(-cos\: u) = -\frac{1}{2} cos\,2x + c $$
$$ [\because U = 2x $$
$$dU = 2 \,dx$$
$$ \frac{dU}{2} = dx $$]
Evaluate : $$\displaystyle\int \left(\dfrac{1}{\log x} - \dfrac{1}{(\log x)^2} \right) . dx$$
Find: $$\int { \frac { cos\theta }{ (4+sin^{ 2 }\theta )(5-4{ cos }^{ 2 }\theta ) } d\theta } $$
$$\displaystyle\int { \dfrac { dx }{ { e }^{ x }+{ e }^{ -x } } } $$ equals
Evaluate $$\int \dfrac{dx}{sin^2 X cos^2 X}$$
$$\displaystyle\int \dfrac{dx}{\sin^2x\cos^2x}=\displaystyle\int cosec^2x\sec^2xdx=\displaystyle\int (1+\cot^2x)\sec^2xdx$$
$$=\displaystyle\int \sec^2xdx+\displaystyle\int cosec^2xdx=\tan x-\cot x+c$$.
$$\int { \dfrac { { x }^{ 2 }+x+1 }{ \sqrt { { x }^{ 2 } } +x-1 } } dx$$
$$\int { \left( x+2 \right) } \sqrt { { x }^{ 2 }+1 } dx$$
Find $$\displaystyle \int \dfrac{x^{3}+x+1}{x^{2}-1}\ dx$$
$$\int \frac{x^{3}x+1}{x^{2}-1}dx = \int (\frac{x^{3}}{x^{2}-1}+ \frac{x+1}{x^{2}-1})dx$$
$$ =\int \frac{x^{3}dx}{x^{2}-1} + \int \frac{(x+1)dx}{(x+1)(x-1)}$$
$$ = \int \frac{x^{3}dx}{x^{2}-1} + \int \frac{1 dx}{x-1}$$
Now $$\int \frac{x^{3}dx}{x^{2}-1}$$
Put $$ x^{2}-1$$
differentiating wrt.x
2x .dx = dt $$\therefore xdx = \frac{dt}{2}$$
$$ = \int \frac{x^{2}.xdx}{x^{2}-1} = \int \frac{t.dt}{2(t-1)}= \frac{1}{2}\int \frac{t}{t-1}$$
$$ = \frac{1}{2}[\int \frac{t-1}{t-1}dt + \int \frac{1}{t-1}dt]$$
$$ = \frac{1}{2}[\int dt + log(t-1)]$$
$$ = \frac{t}{2} + \frac{1}{2}log(t-1)$$
$$ = \frac{x^{2}}{2} + \frac{1}{2}log (x^{2}-1)+c$$
$$\therefore \int \frac{x^{3}+x+1}{x^{2}-1} = \int \frac{x^{3}dx}{x^{2}-1}+\int \frac{dx}{x-1}$$
$$ = \frac{x^{2}}{2} + \frac{1}{2}log (x^{2}-1) + log(x-1) + c$$
$$ = \frac{x^{2}}{2} + log\sqrt{x^{2}-1} + log (x-1) + c$$
$$ = \frac{x^{2}}{2} + log (\sqrt{x^{2}-1}(x-1)) +c$$
Solve : $$\displaystyle \int \dfrac{dx}{\sqrt{x^{2}-3x+2}}$$
$$\int \frac{dx}{\sqrt{x^{2}-3x+2}}=\int \frac{dx}{\sqrt{x^{2}-3x+\frac{9}{4}-\frac{9}{4}+2}}$$
$$=\int \frac{dx}{\sqrt{(x-\frac{3}{2})^{2}-(\frac{1}{2}^{2}))}}$$
$$=log (x-\frac{3}{2}+\sqrt{(x-\frac{3}{2})^{2}-\frac{1}{4}})+c$$
$$\int \because \frac{dx}{\sqrt{x^{2}-a^{2}}}= log (x+\sqrt{x^{2}-a^{2}})+c$$
$$=log (x-\frac{3}{2}+\sqrt{x^{2}-3x+2})+c$$
Solve
$$f(x)=\displaystyle\int _{ 0 }^{ 2 }{ t\left( \sin { x } -\sin { t } \right) dt } $$
Integration
$$\displaystyle\int \dfrac{x^{2}+3}{x^{6}(x^{2}+1)}dx$$
$$ = \int \frac{(x^{2}+3)}{x^{b}(x^{2}+1)}dx$$
Adding and subtrating $$ 2x^{2}$$ in numerator
$$ I = \int [\frac{3(x^{2}+1)}{x^{6}(x^{2}+1)}-\frac{2x^{2}}{x^{6}(x^{2}+1)}]dx$$
$$ =\int \frac{3}{x^{6}}dx - \int \frac{2}{x^{4}(x^{2}+1)}dx$$
Again adding a subtracting $$ 2x^{2}$$ in numerator
$$ I = \int \frac{3}{x^{6}}dx -[\int \frac{2(x^{2}+1)}{x^{4}(x^{2}+1)}dx - \frac{2x^{2}dx}{x^{4}(x^{2}+1)}]$$
$$ =\int \frac{3}{x^{6}}dx -\int \frac{2}{x^{4}} + \int \frac{2dx}{x^{2}(x^{2}+1)}$$
$$ = \int \frac{3}{x^{6}}dx-\int \frac{2}{x^{4}} +\int \frac{2dx}{x^{2}}-\int \frac{2dx}{x^{2}+1}$$
$$ = \frac{-3}{5x^{5}} + \frac{2}{3x^{2}} - \frac{2}{x} - 2tan^{-1} (x)+c$$
Solve:
$$\displaystyle \int{\dfrac{1}{x}\sqrt{\dfrac{x-1}{x+1}}dx}$$
Find $$\displaystyle \int \dfrac{1}{x\sqrt{x^{2}-1}}\ dx$$
Evaluate
$$\int{e^{x} \left(\dfrac{1+\sin x}{1+\cos x}\right)}$$
Evaluate :$$\displaystyle \int \dfrac{x}{\sqrt{x+2}}dx$$
Evaluate
$$\int \dfrac{\log (1+x)}{(1+x)}dx$$
Integrate:
$$\displaystyle \int{\dfrac{\sqrt{1-x^{2}}+\sqrt{1+x^{2}}}{\sqrt{1-x^{4}}}}dx=$$
Find:
$$\displaystyle \int \dfrac {xe^{x}}{(1+x)^{2}}dx$$
$$y = \int \frac{xe^{x}}{(1+x)^{2}}dx$$
$$y=\int [\frac{1}{1+x}-\frac{1}{(1+x)^{2}}]dx$$
We know $$\int e^{x}[f(x)-f(x)]=e^{x}f(x)$$
then
$$y=\int e^{x}[\frac{1}{1+x}-\frac{1}{(1+x)^{2}}]dx=\frac{e^{x}}{1+x}+c$$
Evaluate$$\displaystyle\int { \dfrac { { x }^{ 3 }+{ 4x }^{ 2 }-7x+5 }{ x+2 } } dx$$
$$\int \dfrac{x^2dx}{(x sin x+ cosx)^2}$$
Write the value of $$\int \dfrac{dx}{x^2+16}$$.
Evaluate:$$\displaystyle\int e^x\left[\tan^{-1} x+\dfrac{1}{1+x^2}\right] dx$$.
$$\displaystyle\int { \sqrt { 4-{ x }^{ 2 } } } dx$$ is equals to
Solve
$$\int { \cfrac { { x }^{ 2 }-1 }{ ({ x }+1) } } dx$$.
Evaluate:$$\displaystyle\int\dfrac{a^x}{a^x+1} dx,a>0$$
Find the value of $$\displaystyle\int { { x }^{ 2 }\left( 1-\dfrac { 1 }{ { x }^{ 2 } } \right) dx } $$.
Find the value of $$\displaystyle\int\dfrac{1-\cos 2x}{1+\cos 2x}dx$$
Evaluate $$\int \dfrac{(\log x)^2}{x}dx$$
Solve
$$I=\displaystyle \int (\sin 3x+ \cos 4\ x\ )dx$$
$$\displaystyle \int 2x^3+9x^2-8x+5 dx$$
$$\displaystyle \int \dfrac {x^2}{x^3+64} dx$$
$$\displaystyle \int \dfrac{8x+5}{4x^2+5x+6} dx$$
$$ \displaystyle \int \dfrac 2x+\dfrac 3x dx$$
If $$\displaystyle \int {\left (\dfrac { x-1 }{ { x }^{ 2 } } \right ){ e }^{ x }dx=f\left( x \right) { e }^{ x }+c } $$, then write the value of f(x).
Integrate:$$\int { x } \sin { 2x } dx$$
$$\displaystyle \int 4x^3+2x^3-3x+6 dx$$
$$\displaystyle \int \dfrac{ dx}{\sqrt{1 + x}}$$
Evaluate $$\displaystyle \int { \dfrac { 1-4x }{ \sqrt { 6+x-{ 2x }^{ 2 } } } } dx$$
$$\displaystyle \int \dfrac {\sin x\cos x}{\tan x \cot x}dx $$
$$\int { \frac { dx }{ \sqrt { x } -\sqrt { x-1 } } } $$
Solve
$$\int { { x }^{ 3 } } \log xdx$$
Simplify : $$\displaystyle\int{\dfrac{2dx}{\sqrt{x}}}$$
Find: $$\int { { x }^{ 2 }.\log { x } dx }$$.
Match the correct pair.
$$\int x log x dx =?$$
Evaluate : $$\displaystyle \;\int {{x^4}\left( {1 + \log x} \right)dx} $$
Find :-
$$\int {\left[ {\log (\log x) + \frac{1}{{(\log {x^2})}}} \right]dx} $$
Find : $$\displaystyle\int (log \, x)^2 dx$$
Evaluate the given integral
$$\int { x.cosec ^{ 2 }{ x } } dx$$
Evaluate the given integral.
$$\int { x\sin { x } \cos { x } } dx$$
Evaluate the given integral.
$$\int { { x }^{ n }\log { x } } dx$$
Evaluate the given integral.
$$\int { \sin { x } \log { \left( \cos { x } \right) } } dx\quad $$
Evaluate the given integral.
$$\int { { x }^{ 2 }\cos { x } } dx$$
Evaluate the given integral.
$$\int { x\cos { x } } dx\quad $$
Evaluate the given integral.
$$\int { x\sin { 2x } } dx\quad $$
Evaluate the given integral.
$$\int { { e }^{ x } } \left( \tan { x } -\log { \cos { x } } \right) dx$$
Evaluate the given integral.
$$\displaystyle \int { \cos ^{ -1 }{ \left( \cfrac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } } \right) } } dx$$
Evaluate the given integral.
$$\int { \log _{ 10 }{ x } } dx$$
Evaluate the given integral.
$$\int { { e }^{ x } } \left( \sec { x } (1+\tan { x } ) \right) dx$$
Evaluate $$\int x\cdot log (x+1) dx$$
$$\text { Evaluate: } \displaystyle \int \dfrac{e^{x}}{\sqrt{5-4 e^{x}-e^{2 x}}} \mathrm{d} \mathrm{x}$$
Find $$\displaystyle \int x^2 \,tan^{-1} \,xdx.$$
Solve:
$$\int x\sin x \ dx$$
Find $$\displaystyle \int_{0}^{1} x(tan^{-1} x)^2 dx$$
$$\displaystyle \int xe^{x}\cos x dx=\frac{e^{x}}{2}\left [ \left ( x-1 \right )\sin x+x\cos x \right ]$$. If this is true enter 1, else enter 0.
$$f$$ the graph of the antiderivative $$F(x)$$ of $$\displaystyle f\left ( x \right )=\log \left ( \log x \right )+\left ( \log x \right )^{-2}$$
passes through $$(e, 1998-e)$$ then the term independent of $$x$$ in $$F(x)$$ is
$$\displaystyle \int \sqrt{x^{6}+1}.\frac{\log \left ( x^{6}+1 \right )-6\log x}{x^{10}}dx=\frac{1}{6}\left [ \frac{2}{3}t^{3/2}\log t -\frac{2}{3}\int t^{3/2}\frac{1}{t} \right ]$$ where $$t=1+\frac{1}{x^{6}}$$. If this is true enter 1, else enter 0.
Evaluate $$\displaystyle \int { \frac { { x }^{ 2 } }{ x\left( 1+{ x }^{ 2 } \right) } } dx$$
Evaluate: $$\int \cos^{-1} (\sin x)dx.$$
Evaluate : $$\displaystyle\int \dfrac{\sin(x-a)}{\sin(x+a)}dx$$.
Find: $$\displaystyle \int x \tan^{-1} x dx$$
Prove that: $$\displaystyle \int \sqrt {a^{2} - x^{2}}dx = \dfrac {x}{2}\sqrt {a^{2} - x^{2}} + \dfrac {a^{2}}{2}\sin^{-1} \left (\dfrac {x}{a}\right ) + c$$
Prove that $$\displaystyle \int \sqrt{x^2 - a^2} dx = \dfrac{x}{2} \sqrt{x^2 - a^2} - \dfrac{a^2}{2} \log |x + \sqrt{x^2 - a^2}| + c$$.
Solve $$\int { \sqrt { \cfrac { \sin { (x-a) } }{ \sin { (x+a) } } } } dx$$
Evaluate $$\displaystyle\int\displaystyle\frac{\cos 2x}{\sqrt{1+\sin 2x}}dx$$.
Evaluate: $$\displaystyle\int \tan^{-1}\sqrt{x}dx$$.
$$ \int x^{x^2 +1} (2 \ln x + 1) dx $$
Prove that $$\int \sin^{17}x dx = -\dfrac {\sin^{16}x \cos x}{17} + \dfrac {16}{17}\int \sin^{15}x dx + c$$.
$$\int { \cfrac { { e }^{ x }\left( { x }^{ 3 }-x+2 \right) }{ { \left( 1+{ x }^{ 2 } \right) }^{ 2 } } } dx=$$
Integrate $$\int_{0}^{2[x]} \left \{\dfrac {x}{2}\right \} dx $$
Integrate $$\displaystyle \int{ \frac{1}{x^{1/2} + x^{1/3}} dx}$$
Evaluate $$\int_{0}^{4}(|x| + |x - 2| + |x - 4|)$$dx.
$$ \displaystyle \int_{0}^{4} (\left | x \right |+ \left | x-2 \right |+ \left | x-4 \right |)dx$$
$$ \displaystyle \int_{0}^{4} \left | x \right |+ \int_{0}^{2} 2-x + \int_{0}^{4}x-2+\int_{0}^{4} 4-x $$
$$ \displaystyle _{0}^{4}| \dfrac{x^2}{2}+ \left [ 2x- \dfrac{x^2}{2} \right ]_{0}^{2} + \left [ \dfrac{x^{2}}{2}-2x \right ]_{2}^{4} + \left [ 4x-\dfrac{x^2}{2} \right ]_{0}^{4}$$
$$ = 8+4-2+8-8-2+4+16-8$$
$$ = 32-12 $$
$$ = 20 $$
Evaluate : $$\int^1_0$$$$\frac{log (1 +x)}{1 + x^2}dx$$
Evaluate $$\displaystyle\int\dfrac{e^{-x}}{1+e^x}dx$$
Solve $$\left[-\displaystyle \int^{\pi/2}_0\cos \left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)e^x\right]dx$$
$$\int { { x }^{ n }\log { x } dx } $$
$$\int { \sin { 4x } .{ e }^{ \tan ^{ 2 }{ x } } } dx$$
Integrate the following functions:
$$x^{2}\cdot e^{3x}$$
$$\int {{{dx} \over {2{x^2} + 2x + 5}}} $$
Integrate $$\int { { e }^{ x }{ a }^{ x }dx } $$
Solve $$\displaystyle \int_0^{\pi/2} \dfrac{x\,\,\sin\,x \,cos\,x}{cos^4x+\sin^4x}dx$$
$$\int \sqrt {2x}.\cos 2x dx$$
$$\int _{ 0 }^{ \pi /2 }{ \underbrace { { x }^{ 2 } }_{ I } \underbrace { \csc ^{ 2 }{ xd } }_{ II } } =I$$
Solve $$\displaystyle\int \dfrac{\sin x\cos x}{5\sin^2 x+3\cos^2 x}dx$$.
Evaluate $$\int {\dfrac{{dx}}{{\left( {2x\, - \,7} \right)\,\sqrt {\left( {x\, - \,3} \right)\left( {x\, - \,4} \right)} }}} $$
Solve $$\displaystyle\int \left(\dfrac {x\sqrt {1+x}}{\sqrt {1-x}}\right)dx$$
Solve $$\displaystyle\int{\dfrac{6{u}^{3}du}{1+u}}$$
$$\int \frac{dx}{5+4Cosx}$$
$$\displaystyle\int\sqrt{a^2-x^2}dx$$.
Solve $$\int { \dfrac { \sin ^{ -1 }{ \sqrt { x } } -\cos ^{ -1 }{ \sqrt { x } } }{ \sin ^{ -1 }{ \sqrt { x } } +\cos ^{ -1 }{ \sqrt { x } } } } dx$$
Evaluate:$$\displaystyle\int { \left( { e }^{ a\ln { x } }+{ e }^{ x\ln { a } }+\sin { \alpha } \right) dx }$$
Solve the problem:-
$$\int {x{{\sin }^{ - 1}}x\,dx} $$
Integrate the following expression with respect to $$x$$. $$\dfrac{1}{x^{4}+x^{2}+1}$$
Integrate with respect to $$x$$:
$$e^{x}(\sec^{2}x+\tan x)$$
Find the integral of $$\frac{1}{{\sqrt {{a^2} - {x^2}} }}$$ with respect to x and hence evaluate $$\int {\frac{{dx}}{{\sqrt {7 - 6x - {x^2}} }}} $$
$$\displaystyle \int(\cot x+x)\cot^{2}x.dx$$
Evaluate:$$\displaystyle\int \dfrac{dx}{\sqrt{1+4x^2}}$$.
Solve : $$I = \int \dfrac{dx}{\sqrt{3x + 4} - \sqrt{3x + 1}}$$
$$\int { x{ cos }^{ 2 }2x } dx$$
Evaluate the following:
$$\int x \sin ^{2} x.dx$$ ?
$$\displaystyle\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}}{\dfrac{x\,dx}{1+\sin{x}}dx}$$
Integrate:
$$\displaystyle \int \cos x \log \cos x\ dx$$
solve: $$\int \dfrac{dx}{1+x+x^{2}}$$
Solve $$\int {\dfrac { 1-{ x }^{ 7 } }{ x\left( 1+{ x }^{ 7 } \right) } } dx$$
Evaluate: $$\int \frac { t ^ { 4 } d t } { \sqrt { 1 - t ^ { 2 } } }$$
Evaluate $$\int e ^ { 2 x } \sin x d x$$.
Evaluate :
$$\displaystyle \int \dfrac{x^{1/2}}{1+x^{3/4}}dx$$
Evaluate: $$\displaystyle \int x \sin 3 x d x$$
$$\int { x } e ^ { 2 x } d x$$
Evaluate $$\int \dfrac {\sin \theta}{\sin 3\theta} d\theta$$.
Solve: $$\displaystyle \int {\dfrac{{{x^2} - 1}}{{x\sqrt {1 + {x^4}} }}\;{\text{dx}}} $$
Evaluate: $$I=\displaystyle \int x\sin{2x}\ dx$$
$$I=\displaystyle\int x\sin 2xdx$$
Let $$U=x$$; Let $$V'=\sin 2x$$
$$U'=1$$; $$V=\dfrac{-\cos 2x}{2}$$
$$\therefore \displaystyle\int x\sin 2xdx$$
$$UV-\displaystyle\int U'V$$
$$=\dfrac{-1}{2}x\cos 2x-\displaystyle 1\cdot \dfrac{-\cos 2x}{2}$$
$$=\dfrac{-1}{2}x\cos 2x+\dfrac{1}{2}\displaystyle\int \cos 2x$$
$$=\dfrac{-1}{2}x\cos 2x+\dfrac{1}{4}\sin 2x+c$$.
Evaluate
$$\int x^{2} \tan^{-1} xdx$$
Evaluate:
$$\displaystyle \int{\sqrt{\dfrac{a+x}{a-x}}}dx$$.
$$\dfrac {1}{\left(x+1\right)\left(x^ {2}-1\right)}$$
Evaluate the given integral.
$$\int { \sec ^{ -1 }{ \sqrt { x } } } dx$$
Integrate:
$$\displaystyle \int{\dfrac{dx}{3x^{2}+13x-10}}$$
Evaluate the given integral.
$$\int { { x }^{ 2 }\cos ^{ 2 }{ x } } dx$$
Evaluate the given integral.
$$\int { \left( x+1 \right) { e }^{ x }\log { \left( x{ e }^{ x } \right) } } dx$$
Evaluate: $$\displaystyle \int \frac { \log x } { ( 1 + \log x ) ^ { 2 } } d x $$
$$\int \frac{logx}{(1+logx)^{2}}dx$$
adding and subtracting 1 from numerator
$$\int \frac{1-1+log x}{(1+log x)^{2}}dx$$
$$\int \frac{1+log x}{(1+log x)^{2}}dx-\int \frac{1}{(1+ log x)^{2}}dx$$
$$\int \frac{1}{1+log x}dx-\int \frac{1}{(1+ log x)}^{2}dx$$
For the integral
$$\int \frac{1}{1+log x}dx$$
integrate by parts within the sum : $$\int fg'=fg-\int f'g$$
$$f=\frac{1}{1+log x}dx, g'=1$$
$$f'=-\frac{1}{(1+ log x)^{2}}g=x$$
$$=-\int \frac{1}{(1+ log x)^{2}}dx-\int -\frac{1}{(1+ log x)^{2}}dx+\frac{x}{log(x)+1}$$
$$=\frac{x}{log (x)+1}$$
Prove that:
$$\displaystyle \int \dfrac {x^{2}dx}{(x\sin x+\cos x)^{2}}$$
Evaluate the given integral.
$$\displaystyle \int { \sin ^{ -1 }{ \left( \cfrac { 2x }{ 1+{ x }^{ 2 } } \right) } } dx\quad \quad $$
Evaluate the given integral.
$$\int { \cos ^{ -1 }{ \left( 4{ x }^{ 3 }-3x \right) } } dx$$
Evaluate the given integral.
$$\int {x.{\sin}^{-1}{x}} $$
Evaluate the given integral.
$$\displaystyle \int { \tan ^{ -1 }{ \left( \cfrac { 2x }{ 1-{ x }^{ 2 } } \right) } } dx\quad $$
Evaluate the given integral.
$$\int { \sin ^{ -1 }{ \left( 3x-4{ x }^{ 3 } \right) } } dx$$
Evaluate the given integral.
$$\displaystyle \int { \tan ^{ -1 }{ \left( \cfrac { 3x-{ x }^{ 3 } }{ 1-3{ x }^{ 2 } } \right) } } dx$$
Class 12 Commerce Applied Mathematics Extra Questions
- Application Of Derivatives Extra Questions
- Applications Of Integrals Extra Questions
- Definite Integrals Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Indefinite Integrals Extra Questions
- Linear Equations Extra Questions
- Matrices Extra Questions
- Probability Distribution And Its Mean And Variance Extra Questions
- Quantification And Numerical Applications Extra Questions
- Standard Probability Distributions Extra Questions