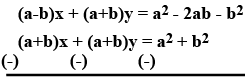Linear Equations - Class 12 Commerce Applied Mathematics - Extra Questions

Find the solution of given pair of linear equation by elimination method.
$$3x+4y=-17 \rightarrow (1)$$
$$5x+2y=-19 \rightarrow (2)$$

$$3x+4y=-17$$   (1)
$$5x+2y=-19$$   (2)
Multiplying (2) by 2
$$10x+4y=-38$$   (3)
Subtracting (1) from (3)
$$7x=-21$$
$$x=-3$$ (4)
Substituting (4) in (1)
$$3(-3)+4y=-17$$
$$4y=-8$$
$$y=-2$$
Hence the solution is $$x=-3$$ and $$y=-2$$.


A man starts his job with a certain monthly salary and earns a fixed increment every year. If his salary was Rs $$1500$$ after $$4$$ year of service and Rs $$1800$$ after $$10$$ years of service, what was his starting salary and what is the annual increment?

Let the starting salary of the man be Rs. $$x$$ and the fixed annual increment be Rs. $$y$$. Then,

Salary after $$4$$ years of service $$=$$Rs. $$(x+4y)$$
Salary after $$10$$ years of service $$=$$Rs. $$(x+10y)$$

$$\therefore x+4y=1500$$ (i)
$$x+10y=1800$$ (ii)

Substracting equation (i) from equation (ii), we get
$$6y=300\Rightarrow y=50$$

Putting $$y=50$$ in equation (i), we get $$x=1300$$.

Hence the starting salary was Rs. $$1300$$ and annual increment is Rs. $$50$$.


The value of $$x$$ and $$y$$, if $$\dfrac{1}{x-2y}=\dfrac{1}{3} $$ and $$\dfrac{1}{x+2y}=\dfrac{1}{7}$$ is 5,1 respectively.Is it true ?If true enter 1 else 0.

$$\dfrac{1}{x-2y}=\dfrac{1}{3}$$ --- (1)
$$\dfrac{1}{x+2y}=\dfrac{1}{7}$$ ---(2)
$$ \implies$$
$$x-2y=3$$ --- (1)
$$x+2y=7$$ ---(2)
_____________
$$2x=10$$
$$\therefore x=5$$
On substituting the value of $$x$$ in equ $$1$$.
$$5-2y=3$$
$$5-3=2y$$
$$\therefore y=1$$
so given statement is true.






If $$2x+y=9$$ and $$3x-y=6$$ then find the value of $$x$$.

Given,
$$2x+y=9$$--------------------------$$(1)$$
$$3x-y=6$$--------------------------$$(2)$$
Adding $$e{q^n}\left( 1 \right)$$ and $$e{q^n}\left( 2 \right)$$
$$2x+y=9$$ $$+$$ $$(3x-y=6)$$ $$=9+6$$
$$x=\dfrac { { 15 } }{ 5 } =3$$
We get, $$x=3$$



Solve: $$3x+4y=10,2x-2y=2$$ by the method of elimination.

$$3x+4y=10$$ …………..$$(1)$$
$$2x-2y=2$$ (or) $$x-y=1$$ …………$$(2)$$
$$(1)$$ $$\Rightarrow (3x+4y=10)1$$
$$(2)$$ $$\Rightarrow (x-y=1)3$$
                     _____________________
                                $$3x+4y=10$$
                                $$3x-3y=3$$
                      _____________________
                                    $$7y=7$$
$$\therefore y=1$$
Put $$y=1$$ in $$(1)$$ we get $$3x+4\times 1=10$$
$$3x=10-4=6$$
$$\therefore x=\dfrac{6}{3}=2$$
Hence $$x=2, y=1$$.

1257517_1328052_ans_af5eae8fa2eb4f97a3206f6ec031bb26.PNG


Solve the following 
$$3 a + 5 b = 26 ; a + 5 b = 27$$

$$3a+5b=26$$
$$-a-5b=-27$$
__________
$$2a=-1 $$        (on subtracting)

$$a=\dfrac{-1}{2}$$

$$5b=27-a$$

$$ 5b=27+\dfrac{1}{2}=\dfrac{55}{2}$$

$$ b=\dfrac{11}{2}$$

$$\therefore  a=\dfrac{-1}{2}, \ b=\dfrac{11}{2}$$


Solve the following simultaneous equations
$$3 a + 5 b = 20 ; a + 5 b = 22$$

$$ 3a+5b =20$$
$$ a+5b=22$$

subtracting both the equations, we get 
$$3a-a=20-22$$
$$2a=-2$$
$$a=-1$$

$$ a + 5b = 22 $$
$$ 5b = 22 - a = 22 + 1 = 23$$ 
$$ b= \dfrac {23}{5}$$

Hence $$a  = - 1$$ and $$b= \dfrac{23}{5}$$


Solve the following simultaneous equations
2x+y=5;  3x-y=5

We have 

$$2x+y=5$$         $$...(1)$$

$$3x-y=5$$          $$...(2)$$

Adding equations $$(1)$$ and $$(2),$$

$$\Rightarrow 2x+y+3x-y=5+5$$

$$\Rightarrow 5x=10$$

$$\Rightarrow x=2$$

Substitute the value of $$x$$ in equation $$(1)$$

$$\Rightarrow y=5-2\times 2$$

$$\Rightarrow y=5-4$$

$$\Rightarrow y=1$$

$$\therefore $$ The value of $$x=2$$ and $$y=1$$


Solve the following 
$$2 x - 3 y = 9 ; 2 x + y = 13$$

$$2x - 3y = 9$$
$$2x + y = 13$$

subtracting , we get 
$$y + 3y = 10 - 9$$
$$4y=4$$  
$$\Rightarrow y=1$$

$$2x - 3y = 9$$
$$2x = 9 + 3 = 12$$
$$x = 6$$

$$\therefore x=6, \ y=1$$ 


Solve the following pair of equations:
$$\cfrac{x}{3}+\cfrac{y}{4}=4;\ x+y=14 $$

Given equation,
$$\dfrac { x }{ 3 } +\dfrac { y }{ 4 } =4,\quad x+y=14$$
$$\Rightarrow 4x+3y=48\quad \longrightarrow \left( 1 \right) ,\quad 4x+4y=56\longrightarrow \left( 2 \right) $$
Subtracting equation $$(1)$$ and $$(2)$$
$$4x+3y-48=0\\ 4x+4y-56=0\\ --------\\ 0-y+8=0$$
$$y=8$$
For $$y=8, x=6$$
$$(x, y)=(6, 8)$$


Solve the following simultaneous equations by elimination method and find the value of $$x$$ $$5y-3x=14; \, \, 3y-2x=1$$

Given equations are,
$$5y-3x=14$$ .........(1)
$$3y-2x=1$$ ..........(2)

Multiply (1) by $$2$$ and (2) by $$3$$ we get,
$$10y-6x=28$$ .........(3)
$$9y-6x=3$$ ..........(4)

Subtracting (4) from (3) we get,
$$(10y-6x)-(9y-6x)=28-3$$
$$\Rightarrow y=25$$

Substituting $$y=25$$ in (1) we get,
$$5\times 25-3x=14$$
$$\Rightarrow 125-3x=14$$
$$\Rightarrow -3x=14-125$$
$$\Rightarrow -3x=-111$$
$$\Rightarrow x=37$$

Hence, the value of $$x$$ is $$37$$


Solve the following pair of linear equations by the elimination method and find the value of $$p+q$$ rounded off to the nearest integer.
$$4p=3q+5; \, \, p-q = \dfrac{7}{6}$$

$$4p=3q+5\quad\quad\quad\dots(i)$$
$$p-q = \dfrac{7}{6}\quad\quad\quad\dots(ii)$$

Rewriting $$(i)$$ we get,
$$4p-3q=5\quad\quad\quad\dots(iii)$$

Multiplying $$(ii)$$ by $$4$$ we get,
$$4p-4q = \dfrac{14}{3}\quad\quad\quad\dots(iv)$$

Subtracting $$(iv)$$ from $$(iii)$$ we get,
$$\begin{array}{l}\underline {\begin{array}{ccccccccccccccc}{4p}& - &{3q}& = &5\\{4p}& - &{4q}& = &{\dfrac{{14}}{3}}\\ - & + &{}&{}& - \end{array}} \\\;\;\;\;\;\quad\begin{array}{ccccccccccccccc}{}&{}&q& = &{\dfrac{1}{3}}\end{array}\end{array}$$

Re substituting $$q=\dfrac{1}{3}$$ in $$(i)$$ we get,
$$\begin{aligned}{}4p &= 3\left( {\frac{1}{3}} \right) + 5\\4p &= 1 + 5\\4p &= 6\\p &= \frac{3}{2}\end{aligned}$$

So,
$$\begin{aligned}{}p + q &= \frac{3}{2} + \frac{1}{3}\\ &= \frac{{9 + 2}}{6}\\ &= \frac{{11}}{6}\\ &\approx 2\end{aligned}$$


Solve the following simultaneous equations by elimination method and find the value of $$x+y$$ $$2x-y-3=0; \, \, 4x-y-5=0$$

$$2x-y=3$$ ......(1)
$$4x-y=5$$ ......(2)
Subtracting (1) and (2) we get,
$$x=1$$
Re substituting $$x=1$$ in (1) we get,
$$y=-1$$



Solve the following simultaneous equations. and find $$x+y$$ for $$\displaystyle \frac{3}{2}x + \frac{2}{3}y = 13 \frac{1}{3}; \, \, \frac{2}{3}x + \frac{3}{2}y = 8 \frac{1}{3}$$

Given,
$$\displaystyle \frac{3}{2}x + \frac{2}{3}y = 13 \frac{1}{3}$$ .....(1)

$$\displaystyle \frac{2}{3}x + \frac{3}{2}y = 8 \frac{1}{3}$$ .......(2)

Rewriting above equations we get,
 $$9x+4y=80$$ .......(3)
$$4x+9y=50$$ ........(4)

Multiplying (3) by 4 and (4) by 9 we get,
 $$36x+16y=320$$ .......(5)
$$36x+81y=450$$ ........(6)

Subtracting (5) and (6) we get,
$$y=2$$
Re substituting $$y=2$$ in (5) we get,
$$x=8$$

$$\therefore$$ $$x+y=8+2=10$$


Solve the following simultaneous equations by elimination method and find the value of $$x$$ $$3x-2y = 4; \, \, 6x+7y=19$$

$$3x-2y = 4$$ ..........(1)
$$6x+7y=19$$ .........(2)
Multiply (1) by 2 we get,
$$6x-4y = 8$$ ..........(3)
Subtracting (2) and (3) we get,
$$y=1$$
Re substituting $$y=1$$ in (1) we get,
$$x=2$$


Solve for $$x$$ & $$y$$

$$ax+by=a-b$$
$$bx-ay=a+b$$

The given set of equations is,

$$ax + by = a - b$$                           ....(1)

$$bx - ay = a + b$$                           ....(2)

Multiplying (1) by $$b$$ and (2) by $$a$$ and subtracting (2) from (1), we get:

$$\left( {{a^2} + {b^2}} \right)y =  - \left( {{a^2} + {b^2}} \right)$$

$$y =  - 1$$

Substituting $$y =  - 1$$ in (1), we get:

$$ax + b\left( { - 1} \right) = a - b$$

$$ax - b = a - b$$

$$ax = a$$

$$x = 1$$

Therefore, the solution of the given system of equations is $$x = 1,\ y =  - 1$$.



Find the fraction which becomes to $$\dfrac23$$ when the numerator is increasing by $$2$$ and equal to $$\dfrac47$$ when the denominator is increased by $$4$$ 

Consider that the fraction is $$\dfrac{x}{y}$$.

According to the question,

$$\dfrac{{x + 2}}{y} = \dfrac{2}{3}$$

$$3(x+2)=2y$$

$$3x - 2y =  - 6$$    .............. (1)

And,

$$\dfrac{x}{{y + 4}} = \dfrac{4}{7}$$

$$7x=4(y+4)$$

$$7x - 4y = 16$$    ............. (2)

From equation (1) and (2),
$$2 \times (1) - (2) \implies $$

$$6x - 4y =  - 12$$

$$7x - 4y = 16$$

$$..............$$

$$-x =-28$$

$$\implies x = 28$$

On substituting $$x = 28$$ in $$(1)$$, we get 
$$3(28)-2y =-6$$

$$2y =90$$

$$y = 45$$

Therefore, the fraction becomes $$\dfrac{{28}}{{45}}$$.



Solve the following pair of linear equations in two variables:
$$3=2x+y$$ and $$9 = 4x - y$$

Given:-
$$3 = 2x + y ..... \left( 1 \right)$$
$$9 = 4x - y ..... \left( 2 \right)$$

Adding equation $$\left( 1 \right) \& \left( 2 \right)$$, we have
$$3 + 9 = \left( 2x + y \right) + \left( 4x - y \right)$$
$$12 = 6x$$
$$\Rightarrow x = \cfrac{12}{6} = 2$$

Substituting the value of $$x$$ in equation $$\left( 1 \right)$$, we have
$$3 = 2 \times 2 + y$$
$$\Rightarrow y = 3 - 4 = -1$$

Hence the value of $$x$$ and $$y$$ are $$2$$ and $$-1$$ respectively.


Solve for $$x$$ and $$y:x-4y-14=0$$, $$5x-y-13=0$$

Given: Equation of lines $$x-4y-14=0$$ and  $$5x-y-13=0$$
or 
$$x-4y=14$$    .....$$(1)$$

$$5x-y=13$$    .....$$(2)$$

Multiplying eq 1 by 5 then subtracting eq 2 from the resultant multiplication i.e, $$5\times (1)-1\times (2)$$ we get;

$$5x-20y-5x+y=70-13$$

$$\Rightarrow -19y=57$$

$$\Rightarrow y=\dfrac{57}{-19}=-3$$

Putting  $$y=-3$$ in $$(1)$$ we get;

$$x-4\times -3=14$$

$$\Rightarrow x+12=14$$

$$\Rightarrow x=14-12=2$$

$$\therefore x=2,\,\,y=-3$$


Solve using elimination method :
$$7x + 2y = 19$$
$$x - y = 4$$

Given equations are
$$7x + 2y = 19......(1)$$
$$x - y = 4......(2)$$

Multiplying equation $$(2)$$ by $$2$$
$$2x - 2y = 8......(3)$$

Now, adding equation $$1$$ and equation $$2$$ ,
$$(7x+2y)+(2x-2y)=19+8$$

$$\Rightarrow 7x+2y+2x-2y=27$$ 

$$\Rightarrow 9x=27$$

$$\Rightarrow x=3$$

Putting $$x=3$$ in $$(2)$$ we get, 
$$3-y=4$$
$$\Rightarrow y=3-4$$
$$\Rightarrow y=-1$$

Hence, the solution is $$x=3$$ and $$y=-1$$ .


Solve the following system of equation for x and y.
$$\displaystyle \frac{5}{x-1}+\frac{1}{y-2}=2,\frac{6}{x-1}-\frac{3}{y-2}=1$$

Let $$\dfrac{1}{x-1}=a$$ and $$\dfrac{1}{y-2}=b$$
$$5a+b=2 ..... (1) .... \times 3$$
$$6a-3b=1 ..... (2) ...... \times 1$$
$$15a+3b=6$$
$$6a-3b$$
$$\_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_$$
$$21a=7$$
$$\therefore \boxed{a=\dfrac{1}{3}}$$
Putting $$a=\dfrac{1}{3}$$ in $$(1)$$
$$\dfrac{5}{3}+b=2$$
or, $$b=2-\dfrac{5}{3}=\dfrac{1}{3}$$
Substituting value of $$a$$ and $$b$$
$$\dfrac{1}{x-1}=\dfrac{1}{3}\Rightarrow x-1=3 ..... (3)$$
$$\dfrac{1}{y-2}=\dfrac{1}{3}\Rightarrow y-2=3 ...... (4)$$
From $$(3), x=4$$
From $$(4), y=5$$


Solve : $$\dfrac{x}{a}+\dfrac{y}{b}=2$$
$$ax-by=a^{2}-b^{2}$$

$$\dfrac{x}{a}+\dfrac{y}{b}=2$$
or, $$ba+ay=2ab .... (1) .....\times a$$
$$ax-by=a^{2}-b^{2} ..... (2).... \times b$$
$$abx+a^{2}y=2a^{2}b$$
$$aba-b^{2}y=a^{2}b-b^{3}$$
$$\_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_$$
$$(a^{2}+b^{2})y=(a^{2}+b^{2})b$$
$$\therefore y=b$$
Putting $$y=b$$ in $$(1)$$
$$bx+ab=2ab$$
or, $$bx=ab$$
$$\therefore x=a$$


Solve the following systems of linear equations

$$i)2x - y = 17$$

$$ii)3x + 5y = 6$$


Given equations are 
$$2x-y=17$$............(i)

$$3x+5y=6$$...........(ii)

$$10x-5y=85$$............multiplying eq. (i) with $$5$$.........(iii)

(ii)+(iii)

$$13x=91$$
$$x=7$$

Putting value of $$x$$ in (ii)

     $$14-y=17$$
$$\Rightarrow y=-3$$



Solve for $$x$$ and $$y$$:
$$2x-y+3=0$$,
$$3x-7y+10=0$$.

$$2x-y+3=0 ...(1)$$
$$3x-7y+10=0 ....(2)$$

Let us use elimination method to solve the given system of equations.
Find the value of $$y$$ from equation $$(1)$$ and substitute the value in $$(2)$$.

From $$(1)$$
$$-y=-3-2x\Rightarrow y=2x+3$$
And 

$$3x-7(2x+3)=-10\Rightarrow 3x-14x-21=-10$$
$$-11x=-10+21=11\Rightarrow x=\dfrac {11}{-11}=-1$$
and $$y=2x+3$$

$$y=2(-1)+3=-2+3=1$$
$$y=1$$

Answer : $$x=-1$$ and $$y=1$$


Solve for $$x$$ and $$y$$:
$$3x-5y-19=0$$,
$$-7x+3y+1=0$$.

$$3x-5y-19=0 ...(1)$$
$$-7x+3y+1=0 ....(2)$$

Let us use elimination method to solve the given system of equations.

Multiply $$(1)$$ by $$3$$ and $$(2)$$ by $$5$$. And add both the equations.

$$\dfrac { 9x-15y=57\\ -35x+15y=-5 }{ -26x=52 } $$

$$x=\dfrac {52}{-26}= -2$$

Substitute the value of $$x$$ in equation $$(1)$$, we have
$$3\times (-2)-5y=19\Rightarrow -6-5y=19$$
$$y=-5$$

Hence $$x=-2$$ and $$y=-5$$
$$\Rightarrow x=-2, y=-5$$


Solve for $$x$$ and $$y$$:
$$x/3+y/4=11$$,
$$5x/6-y/3=-7$$

$$x/3+y/4=11$$,
$$5x/6-y/3=-7$$

Simplify the both equations:
$$\dfrac {x}{3}+\dfrac {y}{4}=11\Rightarrow {4x+3y=132}$$ and $$\dfrac {5x}{6}-\dfrac {y}{3}=-7 \Rightarrow  {5x-2y=-42}$$

We have,
$$4x+3y=132 ...(1)$$
$$5x-2y=-42 ...(2)$$

Let us use elimination method to solve the given system of equation.
Multiply $$(1)$$ by $$2$$ and $$(2)$$ by $$3$$. And add both the equations.

$$\dfrac { 8x+6y=264\\ 15x-6y=-126 }{ 23x\quad =138 } $$

$$x=\dfrac {138}{23}=6$$

From $$(1): 4(6)+3y=132$$

$$y=108/3 =36$$

Answer $$x=6$$ and $$y=36$$


Solve for $$x$$ and $$y$$:
$$2x+3y=0$$,
$$3x+4y=5$$.

$$2x+3y=0 ....(1)$$
$$3x+4y=5 ...(2)$$

Let us the use elimination method to solve the given system of equations.
Multiply $$(1)$$by $$4$$ and $$(2)$$ by $$3$$. And subtract both the equations.
$$\dfrac { 8x+12y=0\\ 9x+12y=15\\ -\quad -\quad - }{ -x\quad =-15\Rightarrow x=15 } $$

From $$(1), y=-10$$

Hence $$x=15$$ and $$y=-10$$


The linear equation that converts Fahrenheit $$(F)$$ to Celsius $$(C)$$ is given by the relation:
$$C=\dfrac{5F - 160}{9}$$
(i) If the temperature is $$86 F$$, what is the temperature in Celsius?
(ii) If the temperature in $$35$$ C, what is the temperature in Fahrenheit?
(iii) If the temperature is $$0$$ C, what is the temperature in Fahrenheit and if the temperature is 0 F, what is the temperature in Celsius?
(iv) What is the numerical value of the temperature which is same in both the scales?

$$C=\dfrac{5F - 160}{9}$$
(i) Putting $$F = 86^{\circ }$$, we get $$C = \dfrac{5(86)-160}{9}=\dfrac{430-160}{9}=\dfrac{270}{9}=30^{\circ }$$
Hence, the temperature in Celsius in $$30^{\circ } C.$$

(ii) Putting C = $$ 35^{ \circ }$$, we get $$35^{\circ  } = \dfrac{5(F)-160}{9}$$ $$\Rightarrow 315^{\circ } = 5F - 160$$
$$\Rightarrow 5F = 315+160=475$$
$$\therefore F=\dfrac{475}{5} = 95^{\circ }$$
Hence, the temperature in Fahrenheit is $$95^{\circ }$$ F.

(iii) Putting C = $$0^{\circ }$$, we get
$$0 = \dfrac{5F-160}{9} \Rightarrow 0 = 5F - 160$$
$$\Rightarrow 5F = 160$$
$$\therefore F = \dfrac{160}{5} = 32^{\circ }$$
Now, putting F = $$0^{\circ }$$, we get
$$C = \dfrac{5F-160}{9} \Rightarrow C = \dfrac{5(0)-160}{9} =\left ( -\dfrac{160}{9} \right )^{\circ }$$
If the temperature is $$0^{\circ }$$ C, the temperature in Fahrenheit is $$32^{\circ }$$ and if the temperature is $$0^{\circ }$$ F, then the temperature in Celsius is $$\left ( -\dfrac{160}{9} \right )^{\circ }$$ C.

(iv) Putting $$C = F,$$ in the given relation, we get
$$ F = \dfrac{5F-160}{9} \Rightarrow 9F = 5F - 160$$
$$\Rightarrow 4F = - 160$$
$$\therefore F = \dfrac{-160}{4} = -40^{\circ }$$
Hence, the numerical value of the temperature which is same in both the sacales is $$-40.$$


Solve the following pair of linear equations by the elimination method  :
  3x  - 5y - 4 = 0  and 9x  = 2y  + 7


$$ 3x  - 5y = 4.........(i)$$
$$ 9x  - 2y  = 7 ........(ii)$$
Multiplying eqn (i) by 3
$$9x - 15 y = 12........(iii)$$
subtract eqn (iii) from (ii
$$13y=-5$$
$$y=-\dfrac{5}{13}$$
Put in  eqn (i)
 $$3x - 5\times\dfrac{-5}{13}  = 4$$
Multiplying by $$13$$ on both side
$$39x+25=52$$
$$39x=27$$
$$x=\dfrac{9}{13}$$


From the pair of linear equations in the following  problems , and find their solutions ( if they exist ) by the elimination method :
The sum of the digits of a two - digit number is 9 . Also , nine times this number is twice the number obtained by reversing  the order of the digits . Find the number :

Let the two digit number be  $$10x+y$$
Given, $$x+y=9         .....(1)$$
And,revers number is $$10y+x$$
 $$9(10x+y)=2(10y+x)$$

$$90x+9y=20y+2x$$

$$88x−11y=0$$           .....(2)

Multiplying (1) by 11, we get

$$11x+11y=99       ....(3)$$

Adding (1) and (3)

$$99x=99$$

$$x=1$$

Substituting this value of $$x$$ in $$(1),$$

$$1+y=9$$

$$y=8$$

Then the number is 

$$10x+y=10(1)+8=10+8=18$$

Hence, the number is 18.



From the pair of linear equations in the following  problems , and find their solutions ( if they exist ) by the elimination method :
A leading library has a fixed charge for the first three days and additional charge for each day thereafter  . Saritha paid Rs . 27 for a book kept for seven days , while Susy paid Rs 21 for the book she kept for five days . Find the fixed charge and the charge for each extra day .

Let the fixed charge be $$Rs. x$$
and the extra charge be $$Rs. y$$
$$x+4y=27⟶(i)$$
$$x+2y=21⟶(ii)$$
On substracting (ii) from (i),
$$2y=6$$
$$y=3$$
putting y in (i),
$$x+4(3)=27$$
$$x=15$$
$$x=Rs.15$$ and $$y=Rs. 3$$
 Fixed charge $$=Rs. 15$$
 Charge for each extra day $$=Rs. 3$$ .


From the pair of linear equations in the following  problems , and find their solutions ( if they exist ) by the elimination method :
Meena  went to a bank to withdraw Rs . 2000 . She asked the cashier to give her Rs . 50 and Rs 100 notes only . Meena got 25 notes in all . Find how many  notes of Rs 50 and Rs 100 she received .

Let the Rs  . 50 notes be 'x'
Rs 100 notes be 'y'
$$x+ y = 25.....(i)$$

$$50x+100y=2000$$
$$x +  2y  = 40.....(ii)$$

 Subtracting eqn (i) from  (ii)
 $$y = 15$$
Put in eqn(i)
$$x +  y = 15$$
$$x + 15 = 25$$
$$x = 25  - 15$$
$$x = 10$$

Let the $$Rs  . 50$$ notes be $$'10'$$
Rs $$100$$ notes be $$'15'$$


Solve the following pair of linear equations by the elimination method the substitution method :
  3x + 4 y =  10 and 2x  - 2y =  2

  $$3x + 4 y =  10$$ and $$2x  - 2y =  2$$
$$3x  + 4 y = 10.............(i)$$
$$2x -  2y = 2 ............(ii)$$
Multiplying eqn (ii) by 2,
$$4x  -  4y   = 4 ...........(iii)$$
Adding eqn (i) to eqn (iii),
 $$7x   =  14$$
$$x=2$$
Put in eqn (i)
 $$3x + 4 y =  10$$
$$3(2) + 4y = 10$$
$$4y = 10 - 6$$
$$4y = 4$$
$$y=1$$
$$x=2,y=1$$


Solve the following pair of linear equations by the elimination method the substitution method :
$$ \dfrac{x}{2} + \dfrac{2y}{3} = -1   and x - \dfrac{y}{3} = 3 $$

$$ \dfrac{x}{2} + \dfrac{2y}{3} = -1   and x - \dfrac{y}{3} = 3 $$

$$ \dfrac{x}{2} + \dfrac{2y}{3} = -1  \,\,\,\,\,\,\,\  \dfrac{x}{1} - \dfrac{y}{3} =  3 $$

$$ \dfrac{3x + 4y}{6} = -1\,\,\,\,\,\, \dfrac{ 3x  - y}{3} =  3 $$ 

$$ 3x  + 4y  = - 6 ...(i) $$

$$ 3x - y = 9 ............(ii)$$

Subtract eqn (ii)from (i)

$$5y=-15$$

$$  y = \dfrac{-15}{5} = - 3 $$

$$   y = -3 $$

$$  3x  + 4y = -6 $$

$$ 3x  + 4 (-3) = - 6 $$

$$ 3x  - 12  = - 6 $$

$$ 3x  = - 6  + 12 $$ 

$$3x =  6 $$

$$\therefore x  = 2 , y = 3 $$


Solve the following pair of linear equations by suitable method 
x +  y = 5 and 2x  -  3y =  4

$$x + y   = 5$$ and $$2x -  3y  = 4$$
$$x +  y   =  5 .....(i)$$
$$2x  - 3y =  4 .............(ii)$$
Multiplying eqn (i) by 3
$$3x  + 3y =  15 ..........(iii)$$
By adding  $$(ii)$$ to $$(iii)$$ , '$$y$$' is eliminated .
$$5x=19$$
$$x=\dfrac{19}{5}$$
since $$x + y = 5$$
$$ \dfrac{19}{5} + y =  5 $$
$$ y = \dfrac{5}{1} - \dfrac{19}{5} $$
$$ = \dfrac{25 - 19}{5}$$
$$y=\dfrac{6}{5}$$


Solve the following pair of linear equations 
$$ ( a -  b)  x + ( a + b) y =  a^{2} -  2ab  -  b^{2} \rightarrow  (1) $$
$$ ( a + b)  (x + y)   =  a^{2} + b^{2} $$ 

$$ ( a -  b)  x + ( a + b) y =  a^{2} -  2ab  -  b^{2} \rightarrow  (1) $$
$$ ( a + b)  (x + y)   =  a^{2} + b^{2} $$
$$ (a  +  b) x + ( a + b)y= a^{2} + b^{2} \rightarrow  (2) $$
using image
$$-2bx=-2ab-2b^2$$
$$x=a+b$$
putting in (2)
$$(a+b)^2 +(a+b)y=a^2+b^2$$
$$  y = \dfrac{-2ab}{(a + b)}$$ 
Hence Required answer

1959858_1867786_ans_6c22e5cc56c046cb951cb7d65fce73f0.png


Solve the following pair of the equations by reducing them to a pair of linear equations:
$$6x + 3y = 6xy  $$
$$2x + 4y = 5xy $$

$$6x + 3y = 6xy $$ ...............(A)
$$2x + 4y = 5xy $$         .............(B)

Dividing by $$xy$$ in LHS and RHS of both the equations we get,

$$\dfrac{6}{y}+\dfrac{3}{x}=6$$

$$\dfrac{2}{y}+\dfrac{4}{x}=5$$

Let $$u=\dfrac{1}{x},v=\dfrac{1}{y} $$ we get,

$$6v + 3u = 6$$

$$2v + 4u = 5$$

$$6v + 3u = 6\rightarrow (1)$$

$$2v + 4u = 5\rightarrow (2)$$

Multiplying eq. (2) by $$3$$ and Subtracting from (1) we get,

$$6v-6v + 3u-12u=6-15$$

$$-9u=-9$$

$$u=1$$

$$\therefore v=\dfrac{6-3}{6}=\dfrac{1}{2}$$           {Using eq. (1)}

$$\therefore x=1,y=2$$


From the pair of linear equation in the following problems  and find their solutions (if they exist ) by any algebraic method :
The area of a rectangular  gets reduced by 9 square  units , its length  is reduced by 5 nits and breadth in increased by 3 units . If we increase the length by 3 units and the breadth by 2 units , the area increases by 67 square units . Find the dimensions  of the rectangle .

$$Length\space of\space rectangular\space is\space "x"\space unit$$
$$Breadth\space of\space rectangular\space is\space "y" unit$$
$$Original \space area=xy$$
$$According \space to \space the \space first \space condition$$
$$( x- 5 ) ( y + 3 ) = xy -  9$$
$$xy +  3x  -  5y  -  15  =  xy  - 9$$
$$3x  - 5y  = -9  +  15$$
$$3x  -  5y  = 6.........(1)$$
$$According \space second \space condition$$
$$(x+3)(y+2)= xy+67$$
$$xy+2x+3y+6=xy+67$$
$$2x+3y=61........(2)$$
$$Multiply \space eq(1) \space by\space 2 \space and \space eq(2) \space by \space 3\space and \space subtracting \space we \space get$$
$$Solving \space we \space get$$
$$x=17 \space and \space y=9$$


Solve the following pair of linear equations 
$$ px  + qy  = p - q $$
$$ qx  - py   = p +  q $$

$$px  + qy  =  p -  q.......(1)$$
$$qx  - p y   =  p +  q..........(2)$$
$$Multiplying \space eqn(1 )\space p\space and\space eqn(2)\space by\space q$$
$$ p^{2}x + pqy =  p^{2} - pq ........(3)$$
$$ q^{2}x - pqy   = pq  + q^{2}........(4) $$
$$Adding\space (3)\space and\space (4)$$
$$  p ^{2}x +q^{2}x =  p^{2}+q^2$$
$$x(p^2+q^2)=p^2+q^2$$
$$\implies x=1$$
$$Multiplying \space eqn(1 )\space q\space and\space eqn(2)\space by\space p$$
$$pqx+q^2y=pq-q^2$$
$$pqx-p^2y=pq+q^2$$
$$Subtracting \space we \space get$$
$$(q^2+p^2)y=-(p^2+q^2)$$
$$\implies y=-1$$
$$x=1\space y=-1$$


Solve the simultaneous equation and find the value of y 
$$\displaystyle \frac{x+y-8}{2} = \frac{x+2y-14}{3} = \frac{3x+y-12}{11}$$

Consider two equations,

$$\displaystyle \frac{x+y-8}{2} = \frac{3x+y-12}{11}$$     ............(1)

$$\displaystyle \frac{x+y-8}{2}= \frac{x+2y-14}{3}$$     .............(2)

After solving (1) we get,
$$5x+9y=64$$                           ..............(3)
After solving (2) we get,
$$x-y=-4$$
or
$$9x-9y=-36$$                        ...............(4)
Adding (3) and (4) we get,
$$14x=28$$
$$\therefore x=2$$
Re substituting $$x=2$$ in (3) we get,
$$y=6$$


Class 12 Commerce Applied Mathematics Extra Questions