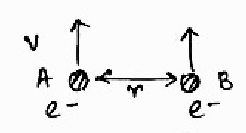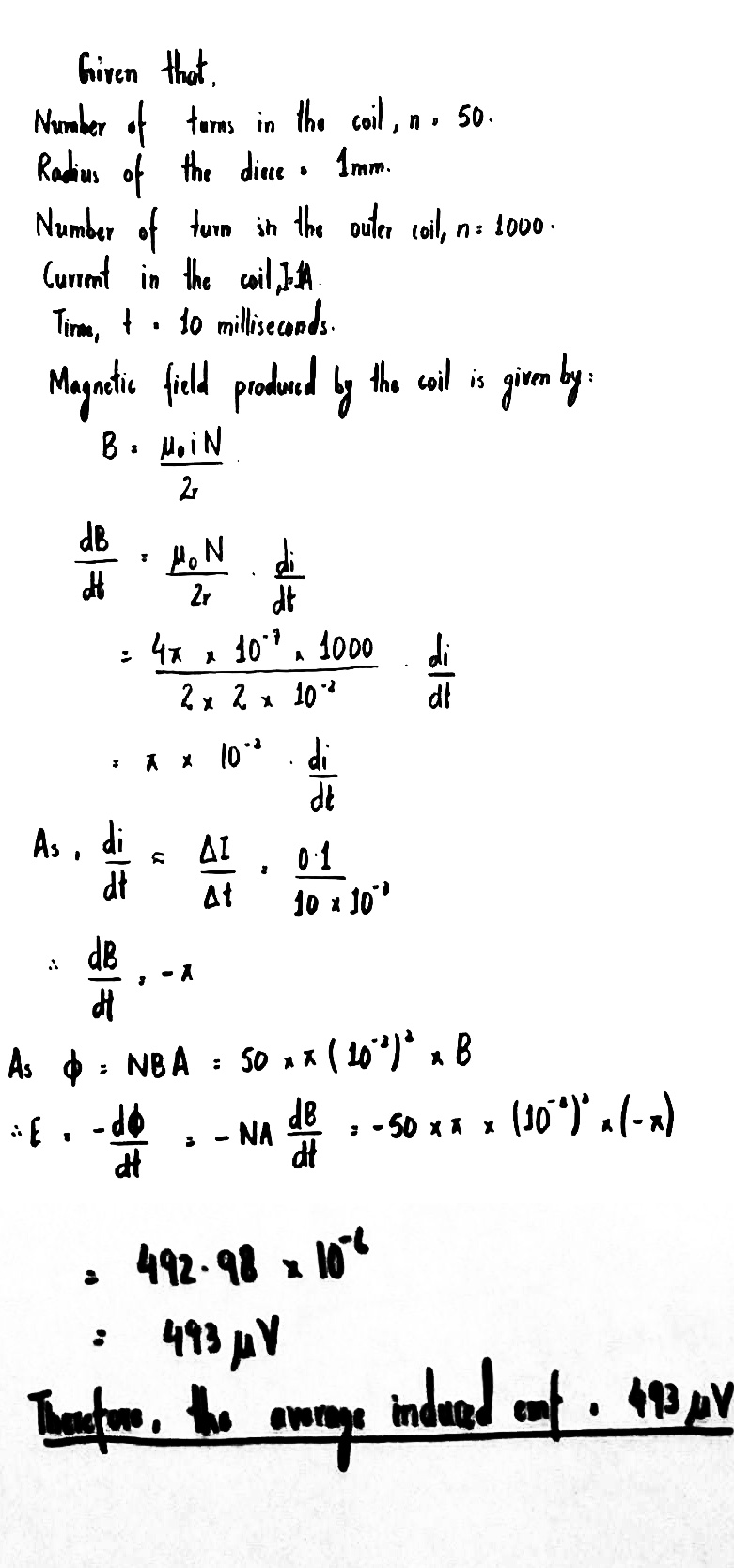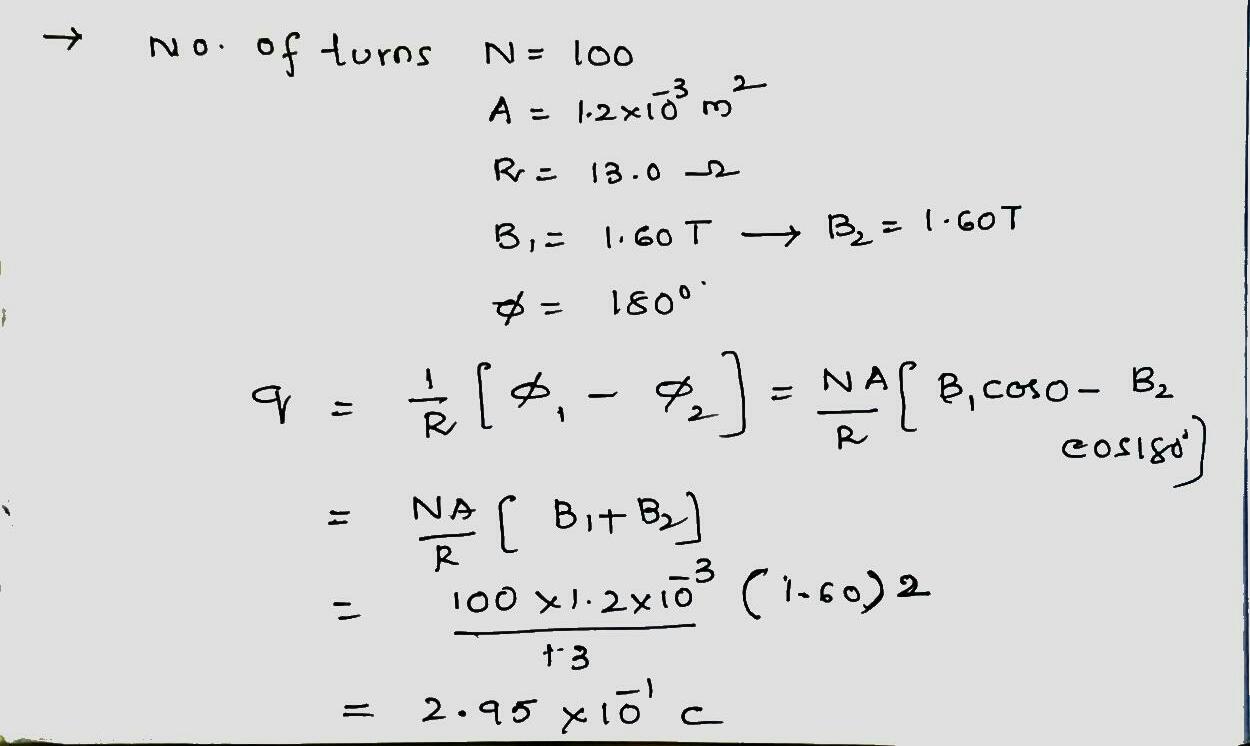Magnetism And Matter - Class 12 Engineering Physics - Extra Questions
the magnetic potential energy of the loop.
In the arrangement shown in the figure, there are two coils wound on a non-conducting cylindrical rod. Initially the key is not inserted. Then the key is inserted and later removed. Then, which of the following statement is correct?
a. The deflection in the galvanometer remains zero throughout.
b. There is a momentary deflection in the galvanometer but it dies out shortly.
What is Lenz's law ?
Explain the significance of Lenz's law to show the conservation of energy.
If the orientation of the current loop in a magnetic field is changed then potential energy of loop is also changed.Enter 1 if True and 0 if False.
Potential energy of a current loop placed inside some magnetic field does not depend upon magnetic moment of the loop.Enter 1 if True and 0 if False.
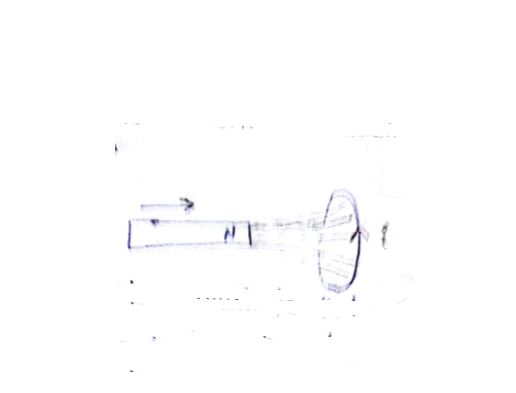
Why is it more difficult to move a magnet towards a coil which has a large number of turns ?
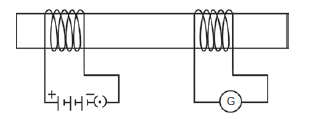
A triangular loop is placed in a dot $$\bigodot $$ magnetic field as shown in figure. The direction of induced current is clockwise in the loop if magnetic field is
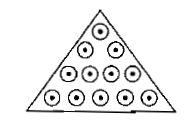
Two circular loops lie side by side in the same plane. One is connected to a source that supplies an increasing current, the other is a simple closed ring. Is the induced current in the ring is in the same direction as that in the loop connected to the source or opposite? What if the current in the first loop is decreasing?
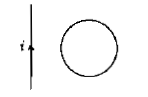
Figure shows a conducting loop placed near a long straight wire carrying a current $$i$$ as shown. If the current increases continuously, then the direction of the induced current in the loop is clockwise.
True or false?
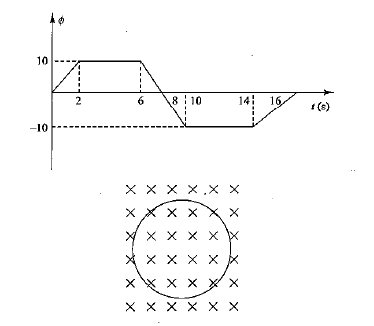
Magnetic flux in a circular coil of resistance $$10\Omega$$ changes with time as shown in figure. Cross indicates a direction perpendicular to paper inward. Match the following.
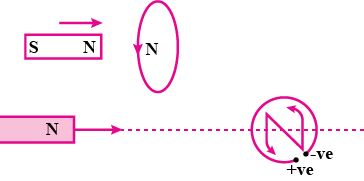
Predict the direction of induced current in the situations described by the following Figs. (a) to (f ).

Use Lenz's law to determine the direction of induced current in the situations described by Fig.(a) A wire of irregular shape turning into a circular shape;(b) A circular loop being deformed into a narrow straight wire.
If the direction of the current changes in the current carrying loop placed in some magnetic field perpendicular to loop, then Potential energy of loop is not effected because current is a scalar quantity.Enter 1 if true and 0 if False.
State Lenz's law in electromagnetic induction.
State Lenz's law.
State and explain Lenz's law for induced e.m.f.
Write the Lenz's law.
An induced current has no direction of its own. Explain. why?
State Lenz's law of electromagnetic induction.
What is the significance of Lenz's law?
(a) What are different losses in transformer, suggest steps to minimise the losses in transformer.
(b) State principle and explain the working of transformer
State Lenzs Law.
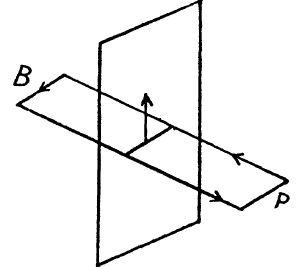
Find the magnitude and direction of the magnetic induction vector $$B$$.
(a) of an infinite plane carrying a current of linear density $$i$$; the vector $$i$$ is the same at all points of the plane;
(b) of two parallel infinite planes carrying currents of linear densities $$i$$ and $$-i$$; the vectors $$i$$ and $$-i$$ are constant at all points of the corresponding planes.
An electron moving in a electric moving potential field V enters a higher electric potential field V then the change in kinetic energy of the electron is proportional to.
An electron in an atom revolves around the nucleus in an orbit of radius $$0.53\,\mathop A\limits^0 $$. Calculate the equivalent magnetic moment, if the frequency of revolution of electron is $$6.8 \times {10^9}$$ $$MHz$$(Given :$$e = 1.6 \times {10^{ - 19}}$$ ).
Two electrons, r metres apart, move in parallel direction. What is the ratio of electric force to magnetic force experienced by an electron due to the other?
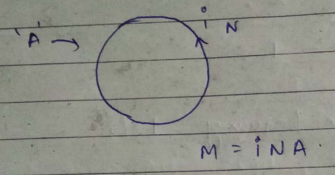
Write the expression for the equivalent magnetic moment of a planer current loop of area $$A$$. having $$N$$ turns and carrying a current $$i$$. Use the expression to find the magnetic dipole moment of a revolving electron.
A current $$I$$ flows along a lengthy thin-walled tube of radius $$R$$ with longitudinal slit of width $$h$$. Find the induction of the magnetic field inside the tube under the condition $$h < < R$$.
An electron is placed in a magnetic field $$\vec B$$ that is directed
along the z-axis. The energy difference between parallel and antiparallel alignments of the z component of the electrons spin magnetic
moment with $$\vec B$$ is $$6.00 \times 10^{-25}\, J$$. What is the magnitude of $$\vec B$$?
In the lowest energy state of the hydrogen atom, the most
probable distance of the single electron from the central proton
(the nucleus) is $$5.2 \times 10^{-11}$$ m. (a) Compute the magnitude of the
protons electric field at that distance. The component $$\mu_{s,z}$$ of the
protons spin magnetic dipole moment measured on the z-axis is $$1.4 \times 10^{-26}\, J/T$$. (b) Compute the magnitude of the protons magnetic field at the distance $$5.2 \times 10^{-11}$$ m on the z-axis. (c) What is the ratio of the spin magnetic dipole
moment of the electron to that of the proton?
What is the measured component of the orbital magnetic dipole moment of an electron with (a)$$m_l=1$$ and (b)$$m_l=-2$$?
What is the measured component of the orbital magnetic the dipole moment of an electron with the values (a)$$m_l=3$$ and
(b)$$m_l=-4$$ ?
State Lenz's law.
A metallic rod held horizontally along east-west direction, is allowed to fall under gravity. Will there be an emf induced at its ends ? Justify your answer.
Consider a metal ring kept on top of a fixed solenoid (say on a cardboard) (Fig.). The centre of the ring coincides with the axis of the solenoid. If the current is suddenly switched on, the metal ring jumps up. Explain.

Explain the Lenz's law related to electromagnetic induction. How does Lenz's law follow the law of conservation of energy?
Two coils are wrapped around iron corn whose coefficient of mutual inductance is $$ 0.5 H . $$ if in $$ 10^{-2} s$$, the value of current changes from $$ 2A $$ to $$ 3 A$$, then determine the induced emf in second coil.
A superconducting round ring of radius $$a$$ and inductance $$L$$ was located in a uniform magnetic field of induction $$B$$. The ring plane was parallel to the vector $$B$$, and the current in the ring was equal to zero. Then the ring was turned through $$90^{\circ}$$ so that its plane became perpendicular to the field. Find:
(a) the current induced in the ring after the turn;
(b) the work performed during the turn.
An electron in the ground state of hydrogen atom in revolving in anticlockwise direction in a circular orbit of radius R (see fig)
If the expression for the orbital magnetic moment of the electron is $$M=\dfrac {eh}{X\pi m}$$. Find X?
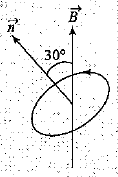
A circular coil of 100 turns has an effective radius of 0.05 m and carries a current of 0.1 A. How much work is required to turn it in an external magnetic field of $$1.5 Wb m^{-2}$$ through $$180^o$$ about an axis perpendicular to the magnetic field?
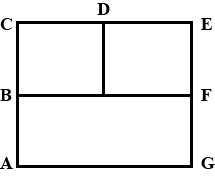
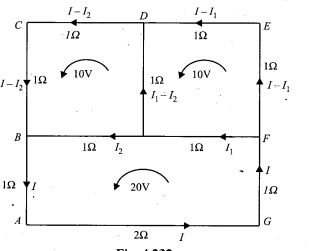
In figure, $$ABCEFGA$$ is a square conducting frame of side $$2m$$ and resistance $$1\Omega$$ $${m}^{-1}$$. A uniform magnetic field $$B$$ is applied perpendicular to the plane and pointing inward. It increases with time at a constant rate of $$10T$$ $${s}^{-1}$$. Find the rate at which heat is produced in the circuit, $$AB=BC=CD=BH$$
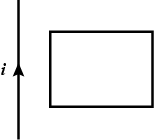
A square loop is placed near a long straight current carrying wire as shown. Match the following two columns
Show that the ratio of the magnetic dipole moment to the angular momentum ($$l = mvr$$) is a universal constant for hydrogen-like atoms and ions. Find its value.
A closed circular loop of 200 turns of mean diameter 50 cm & having a total resistance of 10$$\Omega $$ is placed with its plane at right angle to a magnetic field of strength $${ 10 }^{ -2 }$$ tesla. calculated the quantity of electric charge passed through it when the coil is turned through $$180^{ o }$$ about an axis in its plane.
A heat pacing deice consists of a coil of 50 turns and radius 1 mm just inside the body with a coil of 1000 turns and 2 cm placed concentrically and colonially just outside the body. Calculate the average induced EMF in the internal coil, if a current of 1 A in the external coil collapses in 10 milliseconds.
In Fig. ABCEFGA is a square conducting frame of side 2m and resistance $$1 \Omega /m$$. A uniform magnetic field B is applied perpendicular to the plane and pointing inwards. It increases with time at a constant rate of 10 T/s. Find the rate at which heat is produced in the circuit, AB=BC=CD=BH
A circular loop of wire having a radius of $$8.0 cm$$ carries a current of $$0.20 A$$. A vector of unit length and parallel to the dipole moment $$\vec{\mu}$$ of the loop is given by $$0.60\hat{i}-0.80\hat{j}$$. (This unit vector gives the orientation of the magnetic dipole moment vector.) If the loop is located in a uniform magnetic field given by $$\vec{B} = (0.25T)\hat{i} + (0.30T)\hat{k}$$, find the orientation energy of the loop.
One hundred turns of (insulated) copper wire are wrapped around a wooden cylindrical core of cross-sectional area $$1.20 \times 10^{-3} m^2$$. The two ends of the wire are connected to a resistor. The total resistance in the circuit is $$13.0\Omega $$. If an externally applied uniform longitudinal magnetic field in the core changes from 1.60 T in one direction to 1.60 T in the opposite direction, how much charge flows through a point in the circuit during the change?
At a certain place, Earth’s magnetic field has magnitude B = 0.590 gauss and is inclined downward at an angle of 70.0° to the horizontal. A flat horizontal circular coil of wire with a radius of 10.0 cm has 1000 turns and a total resistance of $$85.0\Omega $$.It is connected in series to a meter with $$140\Omega $$ resistance.The coil is flipped through a half-revolution about a diameter, so that it is again horizontal. How much charge flows through the meter during the flip?
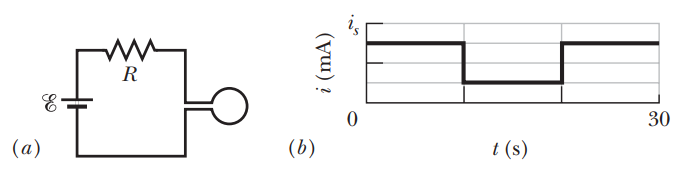
Figure a shows a circuit consisting of an ideal battery with emf $$\mathscr{E}=6.00\muV$$, a resistance R, and a small wire loop of area $$5.0cm^2$$. For the time interval t = 10 s to t = 20 s, an external magnetic field is set up throughout the loop.The field is uniform, its direction is into the page in Figure a, and the field magnitude is given by $$B=at$$, where B is in teslas, a is a constant, and t is in seconds. Figure b gives the current $$i$$ in the circuit before, during, and after the external field is set up. The vertical axis scale is set by $$i_s=2.0mA$$. Find the constant a in the equation for the field magnitude.
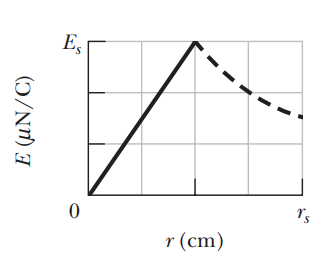
A circular region in an xy plane is penetrated by a uniform magnetic field in the positive direction of the z axis.The field’s magnitude B (in teslas) increases with time t (in seconds) according to $$B=at$$, where a is a constant. The magnitude E of the electric field set up by that increase in the magnetic field is given by Figure versus radial distance
r; the vertical axis scale is set by $$E_s=300\mu N/C$$, and the horizontal axis scale is set by $$r_s=4.00cm$$. Find a.
A long solenoid has a diameter of 12.0cm.When a current $$i$$ exists in its windings, a uniform magnetic field of magnitude B = 30.0 mT is produced in its interior. By decreasing $$i$$, the field is caused to decrease at the rate of 6.50 mT/s. Calculate the magnitude of the induced electric field (a) 2.20 cm and (b) 8.20 cm from the axis of the solenoid.
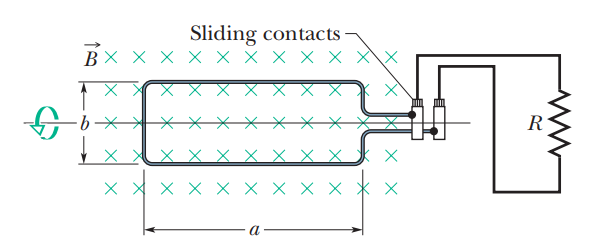
A rectangular coil of N turns and of length a and width b is rotated at frequency $$f$$ in a uniform magnetic field $$\overrightarrow {B}$$, as indicated in Figure . The coil is connected to co-rotating cylinders, against which metal brushes slide to make contact. (a) Show that the
emf induced in the coil is given (as a function of time t) by
$$\mathscr{E}=2\pi fNab\text{ }\sin{2\pi
ft}=\mathscr{E_0}\text{}\sin{2\pi ft}.$$
This is the principle of the commercial alternating-current generator. (b) What value of Nab gives an emf with $$\mathscr{E_0}=150V$$ when the loop is rotated at 60.0 rev/s in a uniform magnetic field of 0.500 T?
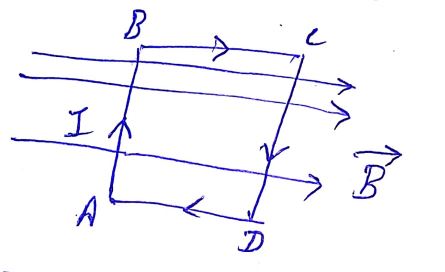
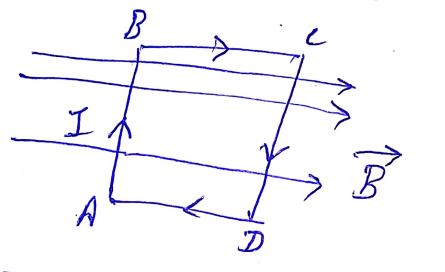
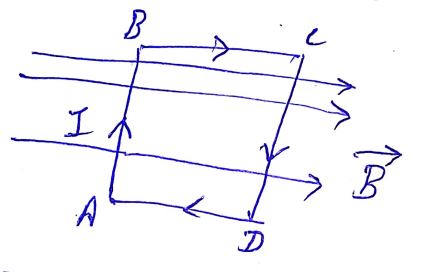
Find the current in the sliding rod $$AB (resistance = R)$$ for the arrangement shown in Fig. $$\vec {R}$$ is constant and is out of the paper. Parallel wires have no resistance. $$\vec {v}$$ is constant. Switch $$S$$ is closed at time $$t = 0$$.
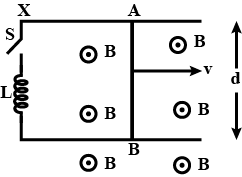
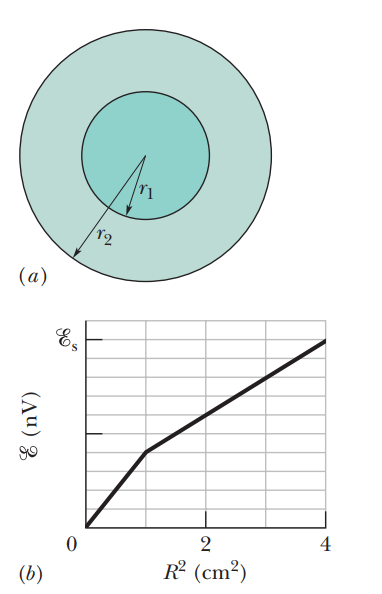
Figure a shows two concentric circular regions in which uniform magnetic fields can change. Region 1, with radius $$r_1=1.0cm$$, has an outward magnetic field $$\overrightarrow {B_1}$$ that is increasing in magnitude. Region 2, with radius $$r_2=2.0cm$$, has an outward magnetic field $$\overrightarrow {B_2}$$ that may also be changing.
Imagine that a conducting ring of radius R is centered on the two regions and then the emf $$\mathscr{E}$$ around the ring is determined. Figure b gives emf $$\mathscr{E}$$ as a function of the square $$R^2$$ of the rings radius, to the outer edge of regionThe vertical axis scale is set by $$\mathscr{E}_s=20.0nV$$. What are the rates (a) $$dB_1/dt$$ and (b) $$dB_2/dt$$? (c) Is the magnitude of $$\overrightarrow {B}_2$$increasing, decreasing, or remaining constant?
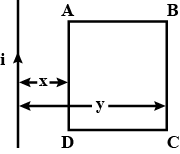
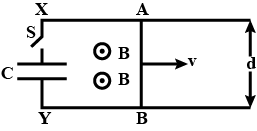
A rectangular loop of wire $$ABCD$$ is kept close to an infinitely long wire carrying a current $$I(t) = I_{0}\left (1 - \dfrac {t}{T}\right )$$ for $$0\leq t\leq T$$ and $$I(0) = 0$$ for $$t > T$$ (Fig.). Find the total charge passing through a given point in the loop, in time $$T$$. The resistance of the loop is $$R$$.
Find the current in the sliding rod $$AB (resistance = R)$$ for the arrangement shown in Fig. $$\vec {B}$$ is constant and is out of the paper. Parallel wires have no resistance. $$\vec {V}$$ is constant. Switch $$S$$ is closed at time $$t = 0$$.
The magnetic moment vectors $$ \mu_s $$ and $$ \mu $$ associated with the intrinsic spin angular momentum S and orbital angular momentum $$ 1$$ respectively of an electron are predicted by quantum theory ( and verified experimentally to a high accuracy) to be given by :
$$ \mu_s = -(e/m)S $$
$$ \mu_1 = - (e/2m) 1 $$
Which of these relations is in accordance with the result expected classically ? Outline the derivation of the classical result.
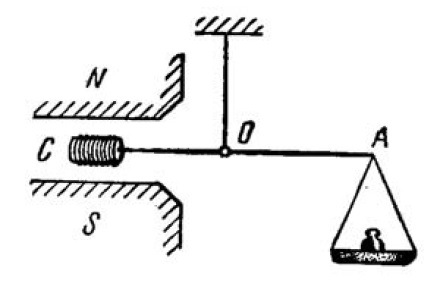
A small coil $$C$$ with $$N = 200$$ turns is mounted on one end of a balance beam an introduced between the poles of an electro-magnet as shown in Fig. The cross-sectional area of the coil is $$S = 1.0\ cm^{2}$$, the length of the arm $$OA$$ of the balance beam is $$l = 30\ cm$$. When there is no current in the coil the balance is in equilibrium. On passing a current $$I = 22\ mA$$ through the coil the equilibrium is restored by putting the additional counterweight of mass $$\triangle m = 60\ mg$$ on the balance pan. Find the magnetic induction at the spot where the coil is located.
An excited atom has the electronic configuration $$1s^2 2s^2 2p 3d $$ being in the state with the greatest possible total angular momentum. Find the magnetic moment of the atom in that state.
In an inertial reference frame $$K$$ there is only electric field of strength $$E = a(xi + yi)/ (x^{2} + y^{2})$$, where $$a$$ is a constant, $$i$$ and $$j$$ are the unit vectors of the $$x$$ and $$y$$ axes. Find the magnetic induction $$B'$$ in the frame $$K'$$ moving relative to the frame $$K$$ with a constant non-relativistic velocity $$v = uk; k$$ is the unit vector of the $$z$$ axis. The $$z'$$ axis is assumed to coincide with the $$z-axis$$. What is the shape of the magnetic induction $$B'$$?
Lenz's Law (37)
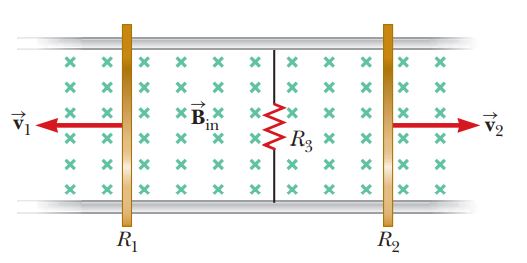
Two parallel rails with negligible resistance are $$10.0 \,cm$$ apart and are connected by a resistor of resistance $$R_3= 5.00 \Omega$$. The circuit also contains two metal rods having resistances of $$R_1 = 10.0 \Omega$$ and $$R_2 = 15.0 \,\Omega$$ sliding along the rails (Figure). The rods are pulled away from the resistor at constant speeds of $$v_1 = 4.00 \,m/s$$ and $$v_2 = 2.00 \,m/s$$, respectively. A uniform magnetic field of magnitude $$B = 0.010 0 \,T$$ is applied perpendicular to the plane of the rails. Determine the current in $$R_3$$.
Lenz's Law (23)
A truck is carrying a steel beam of length $$15.0 \,m$$ on a freeway. An accident causes the beam to be dumped off the truck and slide horizontally along the ground at a speed of $$25.0 \,m/s$$. The velocity of the center of mass of the beam is northward while the length of the beam maintains an eastwest orientation. The vertical component of the Earths magnetic field at this location has a magnitude of $$35.0 \mu T$$. What is the magnitude oft he induced emf between the ends of the beam?
Class 12 Engineering Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials,Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions