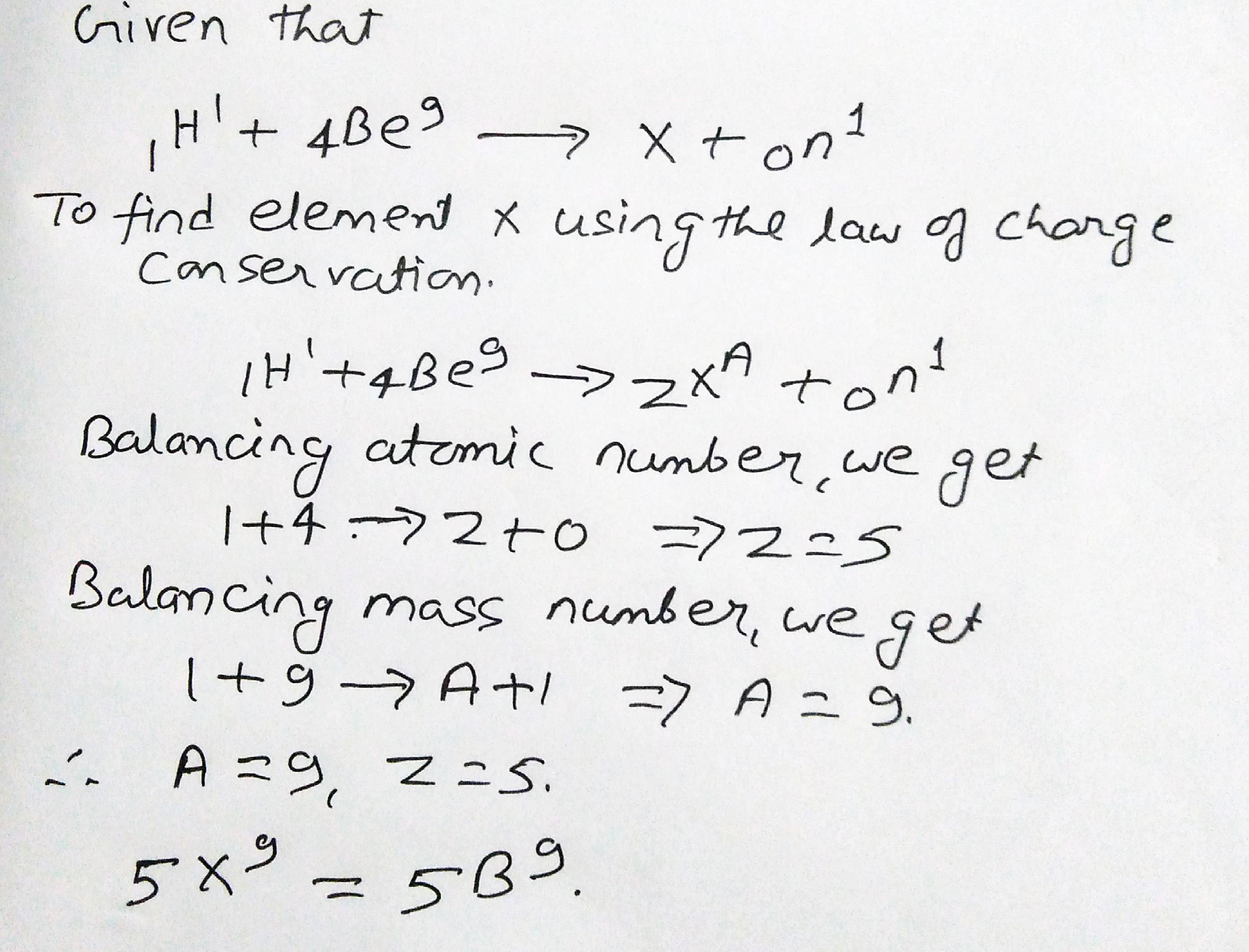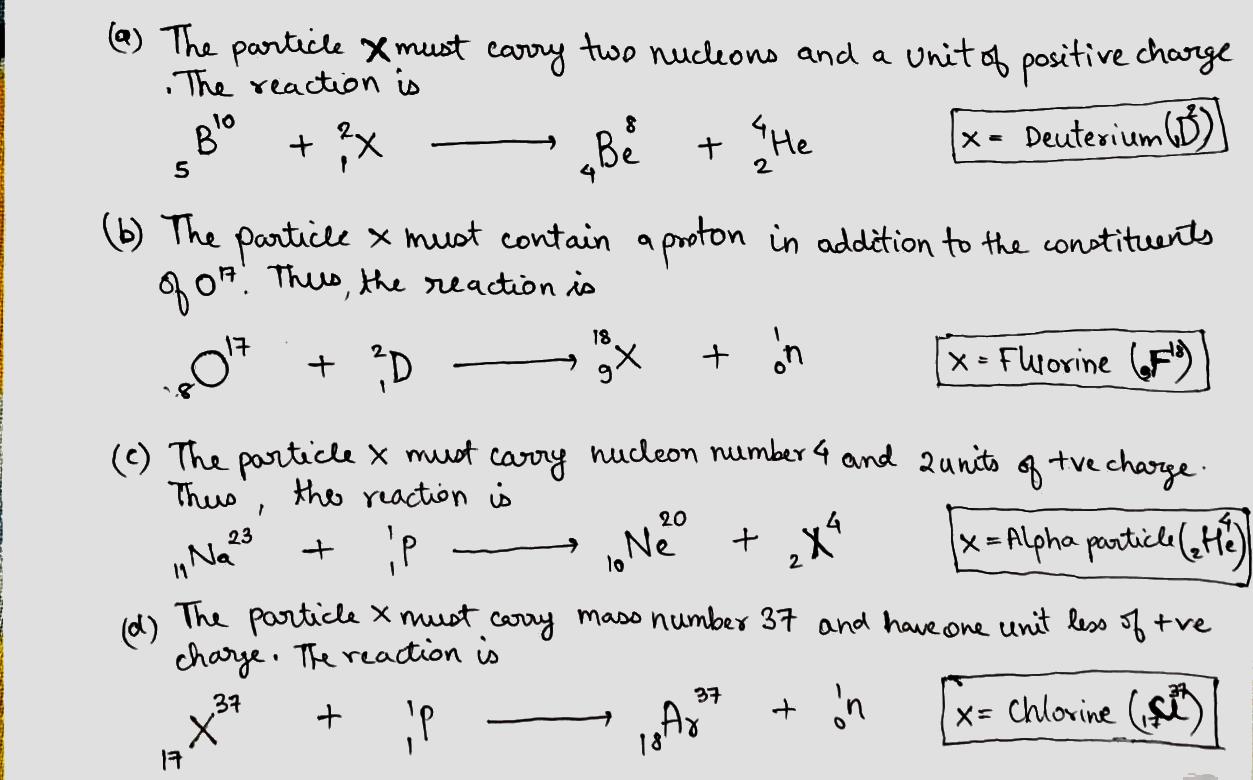Class 12 Engineering Physics - Nuclei

Give a reason for your answer.

Out of two isotopes of Uranium $$_{92}U^{235}$$ and $$_{92}U^{238}$$ given, $$_{92}U^{235}$$ is easily fissionable.
Since the nucleus having even atomic number-even mass number is the most stable isotope and rest are less stable isotopes. $$_{92}U^{235}$$ has even atomic number-odd mass number, so it is less stable and thus is easily fissionalbe.

Write down the Einsteins mass-energy equivalence relation, explaining the meaning of
each symbol used in it.

$$\Large\underline{\textbf{Answer/Explanation:}}$$

As per the Special Theory of Relativity given by Einstein, $$energy$$ and $$mass$$ are not conserved separately in a physical process but are $$interchangeable$$.

If The energy equivalent of a mass $$m$$ is $$E$$, mass-energy equivalence states that,

$$E=mc^2$$

where $$c$$ is the speed of light approximately equal to $$3\times10^8m/s$$ and is considered to constant

What would be the element X in the following nuclear reactions using the law of charge conservation
$$H^1+Be^{9}=X+n^1$$

1879911_1834558_ans_ec5e8bf848f745d1bc566d3bb94b64f4.jpg

What would be the element X in the following nuclear reactions using the law of charge conservation
$$_8N^{15} + _1H^1 \rightarrow X + _2He^4$$

1879974_1834560_ans_6d1b5e3d26f24a929acd3c07302ece9d.jpg

What would be the element X in the following nuclear reactions using the law of charge conservation
$$_6C^{12} + _1H^1 \rightarrow X,$$

1879910_1834559_ans_1029215771f54510ae077317df36ee75.jpg

What is the number of photons and neutrons in $$^{22}_{15}X$$?

Comparing with $$_ZX^A$$

so the total no of protons is
$$Z=15$$ (number of protons)
$$A=22$$

The total no of neutrons is
$$A-Z=22-15=7$$ (number of neutrons)

$$A-$$radioactive element whose mass number is $$218$$ and atomic number is $$84$$ emits $$\beta -$ particle. What would be the mass number and atomic number of element after decay?

$$_{85}X^{218}\to _{85}Y^{218}+_{-1}\beta^0+v$$
Atomic number of produces nucleus $$=85$$
Mass number $$=218$$

By which process energy is produced in stars?

In stars, energy is produced by the process of nuclear fusion.
In this process, lighter nuclei like hydrogen, deuteron, etc. combine with each other at high temperatures and form a helium nucleus. In this reaction, a large quantity of nuclear energy is released.

Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
$$A \rightarrow B \rightarrow C$$
Here B is an intermediate nuclei which is also radioactive. Considering that there are $$N_{0}$$ atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.

At $$t = 0, N_{A} = N_{0}.$$

As time increases, $$N_{A}$$ falls off exponentially,

the number of atoms of B increases, becomes maximum and finally decays to

zero at $$\infty$$ (following exponential decay law).

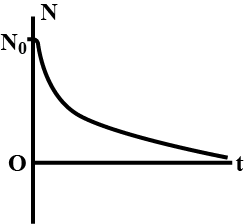
State the law of Radioactive disintegration.

Law of Radioactive disintegration: The radioactive decays per unit time are directly proportional to the total number of nuclei of radioactive compounds in the sample.

If the number of nuclei in a sample is $$N$$ and the number of radioactive decays per unit time $$\triangle t$$ is $$\triangle N$$ then,
$$\frac{\triangle N}{\triangle t} \propto N$$
$$\frac{\triangle N}{\triangle t} = \lambda N$$
where $$\lambda$$ is the constant of proportionality called the radioactive decay constant or disintegration constant.

Einstein's equation is given as-

According to Einstein's famous equation, the energy $$E$$ of a physical system is numerically equal to the product of its mass '$$m$$' and the speed of light '$$c$$' squared, i.e.,

$$E = m {c}^{2}$$

Energy released in a nuclear reaction is given by ________.

The energy absorbed or released during nuclear reaction is known as Q-value of nuclear reaction

Q-value$$=$$(Mass of reactants-mass of products)

$${ C }^{ 2 }$$joules

$$=$$(Mass of reactants-mass of products)amu

$$\triangle E=\triangle m{ c }^{ 2 }$$

Where $$\triangle E$$ is change in energy for a reaction and

$$\triangle m$$ is the difference in mass between the reactants and products

$$c=3\times { 10 }^{ 8 }㎧ is the speed of the light

State radioactive decay law. Prove that radioactive decay is exponential in nature.

Radioactive decay law states that the number of nuclei undergoing the decay per unit time is proportional to the total number of nuclei in the sample.

$$Radioactive$$ $$decay$$ $$law:$$ $$N=N_{0}e^{-\lambda t}$$

$$PROVE :$$

$$\dfrac{dN}{dt}=-\lambda N$$

$$\int \dfrac{dN}{N}=-\lambda\int dt$$

$$log_{e}N=-\lambda t+C$$

initial number of nuclei$$=N_{0}$$

$$C=log_{e}N_{0}$$

$$log_{e}(\dfrac{N}{N_{0}})=-\lambda t$$

$$N=N_{0}e^{-\lambda t}$$

Obtain the exponential law of radioactive disintegration. Explain the decay curve.

According to the Law of radioactive disintegration-

Rate of nuclei disintegrating in small time $$dt$$ is directly proportional to the number of non-disintegrated nuclei present in the sample.

$$-\dfrac{dN}{dT}\propto N$$ negative sign since $$N$$ is decreasing

$$\dfrac{dN}{dT}=-\lambda N$$. where $$\lambda=$$ disintegration constant

$$\implies \dfrac{dN}{N}=-\lambda dt$$

$$[\ln{N}]_{N_o}^{N}=-\lambda t$$

$$\implies N=N_oe^{-\lambda t}$$

At $$t=0, N=N_o$$

Theoretically, it will take infinite time for all particles to disintegrate however small is $$N_o$$.

But in about $$\dfrac{5}{\lambda}$$ time, more than $$99\% $$ of the nuclei get disintegrated.

Atoms having the same ____ but different _ are called isotopes.

Atomic number, mass number.

When four hydrogen nuclei combine to form a helium nucleus in the interior of sun, the loss in mass in $$0.0625$$ amu. How much energy is released?

Energy equivalent of 1 atomic mass unit $$= 931.5 MeV= 1.492\times 10^{-10} J$$

Energy released $$=0.0625\times 931.5=58.22 MeV$$

$$=0.0625\times 1.492\times 10^{-10}=9.325\times 10^{-12} J$$

what is the physical significance of negative energy of electron in atom?

The energy of an electron in the orbit of an atom is negative. It shows that the electron is bound to the nucleus. Greater the value of negative energy, more tightly the electron is bound to the nucleus.Binding energy of a electron is $$E= - (13.6/n^2)$$.

Write any one equation representing nuclear fusion reaction.

Fission is the splitting of an atomic nucleus into two or more lighter nuclei accompanied by energy release. The original heavy atom is termed the parent nucleus, and the lighter nuclei are daughter nuclei. Fission is a type of nuclear reaction that may occur spontaneously or as a result of a particle striking an atomic nucleus.

Ex:-Nuclear Fission of U-235

$$U^{235}_{92} + n^{1}_0 \rightarrow U^{236}_{92} \rightarrow Ba^{141}_{56} +Kr^{92}_{36}+ 3n^{1}_0 +8$$

Give two examples of nuclear fusion.

Examples of furon reaction

$$_{1}^{1}H+_{1}^{3}H\rightarrow _{2}^{4}He+Energy$$

$$_{1}^{1}H+_{1}^{1}H\rightarrow _{1}^{2}H+_{1}^{0}e^{-}+Energy$$

If both the number of protons and the number of neutrons are conserved in each nuclear reaction in what way is mass converted into energy (or vice-versa) in a nuclear reaction?

The sum of masses of nuclei of product element is less than sum of masses of reactants and hence, loss of mass takes place during the reaction. This difference of mass of product element and reactant converts into energy and liberated in the form of heat.

$$H^2_1$$ +$$H^2_1$$→ $$H^3_2 $$+ $$n^2_1$$ + $$energy$$

$$Z^{X^A}\underrightarrow { B^{+ve}decay } $$ ?

In $$\beta^+$$ decay, the atomic number of the daughter nucleus decrease by $$1$$ but mass number remains the same. Along with daughter nucleus and beta particle, a particle known as neutrino $$(\nu)$$ is also emitted.

$$Z^{X^A}\underrightarrow { B^{+ve}decay } \ \ \ _{Z-1}X^A \ + \ \beta^+ \ + \ \nu$$

In a nuclear fusion reaction hydrogen atoms combine to create a helium atom. But in a hydrogen atom there are no neutrons, then where does the neutrons in helium nucleus come from ?

There is more than one answer to this question. We can look
first about how hydrogen (with no neutrons, just one proton)
becomes helium (two protons, two neutrons) in a star like our
sun. As shown by the figure, it begins with pairs of protons
which interact and fuse in a reaction which results in
one deuteron (heavy hydrogen, one proton, and one neutron
), one positron (a positively charged electron), and
one neutrino. The deuterons thus created now fuse with
another proton to create a light isotope of helium, 3He
(one neutron, two protons), and also a
gamma ray. Two of these 3He now fuse, throwing
off two protons in the process and one alpha particle (4He,
two protons, and two neutrons). The two thrown-off protons are
now free to continue the process, so this chain, called the
proton-proton cycle is self-sustaining until the star runs
out of hydrogen which ends the life of the star. For more earth-bound hydrogen fusion, like fusion reactors or

hydrogen bombs, single-step reactions are sought. The

most frequently used is the deuterium-tritium reaction,

involving the fusion of one deuteron and one triton

Complete the following decay schemes.
(a) $$_{88}^{226}Ra \rightarrow \alpha +$$
(b) $$_{8}^{19}O \rightarrow _{9}^{19}F +$$
(c) $$_{13}^{25}Al \rightarrow _{12}^{25}Mg +$$

$$ ^{228}_{58}Ra \rightarrow ^4_2 \alpha + ^{228}_{28}Rn $$

$$ ^{19}_8O \rightarrow ^{19}_9F +^0_n \beta + ^0_0 \bar{v} $$

$$ ^{13}_{25}Cu \rightarrow ^{25}{12}MG +^0_{-1}e +v $$

Write two distinguishing feature of nuclear forces.

Two Distinguishing features of Nucleas forces :-

(i) Nuclear focus are short Range focus. They are appreciable at a distance of $$10^{-15}m$$ is less . At greater distance than this; they are negligiable

(ii) Nuclear forces are independent of electric charges. Hence; the Nuclear Interaction between two protons , two neutrons and one one proton, one neutron is all same.

In a typical nuclear reaction, e.g.

$$_{ 1 }^{ 2 }{ H }+_{ 1 }^{ 2 }{ H }\longrightarrow _{ 2 }^{ 3 }{ He }+n+3.27MeV$$,

although number of nucleons is conserved, yet energy is released.How?Explain.

In the nuclear reaction the sum of the mass of the reactant side may be greater or lesser than the product side. But, in this case although nucleons is conserved, but energy is released i.e, 3.27MeV may be due to the cause of

i) Binding energy per nucleons becomes more than $$\dfrac{BE}{A} of H^2_1$$.

ii) Mass between reactant and product Nuclei.

Initial mass of a radioactive substance is 3.2 mg. It has a half-life of 4 h. Find the mass of the substance left undecayed after 8 h.

Given data :-

Initial Mass $$= M_0 = 3.2 mg$$

$$t_{1/2} = 4 m$$

To calculate , mass of the substance left undecayed after $$8h \, [M_z = 8]$$

we know,

$$M_{(z)} = M_0 e^{-\lambda t}$$

$$\dfrac{M_0}{2} = M_0 e^{-\lambda (4)}$$

$$\Rightarrow \lambda = \dfrac{1}{4} \ln (2)$$

$$M_{(8)} = M_0 . e^{-\lambda . 8}$$

$$\Rightarrow M_{(8)} = M_0 . e^{-\dfrac{1}{4} . \ln (2) . 8}$$

$$M_{(8)} = M_0 e^{-2 \ln (2)}$$

$$M = \left(\dfrac{M_0}{4} \right)$$

$$= \dfrac{3.2 mg}{4}$$

$$M_{(8)} = 0.8 mg $$

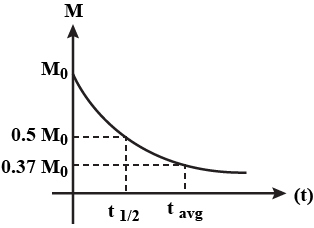
For a radioactive substance, show the variation of the total mass disintegrated as a function of time t graphically.

For a radioactive substance total mass disintegrated as a function of time (t) is given as

$$M = M_0 e^{-\lambda \ t}$$

Where, $$M_0 = $$ mass of radioactive substance at $$t= 0 \sec$$

$$M = $$ Mass of radioactive substance present at any time $$'t''$$

1497097_1700242_ans_c31a181158dd4760adcb99ba7a0b42a1.png

Nuclei of a radioactive element $$A$$ are being produced at a constant rate $$\alpha$$. The element has a decay constant $$\lambda$$. At time $$t=0$$, there are $${N}_{0}$$ nuclei of the element
(a) Calculate the number $$N$$ of nuclei of $$A$$ at time $$t$$
(b) If $$\alpha =2{N}_{0}\lambda$$, calculate the number of nuclei of $$A$$ after one half-life of $$A$$, and also the limiting value of $$N$$ as $$t\rightarrow \infty$$.

(a) At $$t=0,N={ N }_{ 0 }$$
Rate of decay $$=-\lambda N$$ and rate of formation $$=\alpha$$. thus accumulation rate of element is
$$\cfrac { dN }{ dt } =\alpha -\lambda N\Rightarrow \cfrac { dN }{ \alpha -\lambda N } =dt$$
Integrating this expression we get
$$\log _{ e }{ \left[ \cfrac { \alpha -\lambda N }{ \alpha -\lambda { N }_{ 0 } } \right] } =-\lambda t\Rightarrow \cfrac { \alpha -\lambda N }{ \alpha -\lambda { N }_{ 0 } } ={ e }^{ -\lambda t }\Rightarrow \alpha -\lambda N=\left( \alpha -\lambda { N }_{ 0 } \right) { e }^{ -\lambda t }\Rightarrow N=\cfrac { 1 }{ \lambda } \left[ \alpha -\left( \alpha -\lambda { N }_{ 0 } \right) { e }^{ -\lambda t } \right] $$

(b) If $$\alpha =2\lambda { N }_{ 0 }\Rightarrow N=\cfrac { 1 }{ \lambda } \left[ 2\lambda { N }_{ 0 }-\left( 2\lambda { N }_{ 0 }-\lambda { N }_{ 0 } \right) { e }^{ -\lambda t } \right] \Rightarrow N={ N }_{ 0 }\left( 2-{ e }^{ -\lambda t } \right) $$
At the time of half-life, $$T=0.693/\lambda$$. So,
$$N={ N }_{ 0 }\left( 2-{ e }^{ 0.693 } \right) -\cfrac { 3{ N }_{ 0 } }{ 2 } $$
Limiting value of $$N$$ (as $$t\rightarrow \infty$$) is
$$N={ N }_{ 0 }\left( 2-{ e }^{ -\infty } \right) =2{ N }_{ 0 }$$

Show that $$_{ 92 }^{ 230 }{ U }$$ does not decay by emitting a neutron or proton.
Given: $$M(_{ 92 }^{ 230 }{ U })=230.033927a.m.u$$; $$M(_{ 92 }^{ 229 }{ U })=229.033496a.m.u$$; $$M(_{ 92 }^{ 229 }{ Pa })=229.032089a.m.u$$;
$$m(n)=1.008665a.m.u$$; $$m(p)=1.007825a.m.u$$

The corresponding decay equations would be

$$_{92}^{230}U\longrightarrow _{92}^{229}U+n$$

$$_{92}^{230}U\longrightarrow _{91}^{229}Pa+p$$

In the first equation, the energy released can be given as

$$Q=\left[ 230.033927-229.033496-1.008665 \right] \times 931.2=-7.7MeV$$
because $$Q< 0$$ neutron decay is not possible spontaneously

Similarly in the second equation, the energy released can be given as $$Q=\left[ 230.033927-229.032089-1.007825 \right] \times 931.2=-5.6MeV$$

because $$Q< 0$$ proton decay is not possible spontaneously

Identify $$X$$ in the following nuclear reactions:
$$\ ^{15}N+\ ^{1}H\rightarrow \ ^{4}He+X$$. Appendix $$F$$ will help.

None of the reaction given include a beta decay so the number of protons, the number of neutrons, and the number of electrons are each conserved. Atomic numbers (numbers of protons and numbers of electrons) and molar masses (combined number of protons and neutrons) can be founded in Appendix $$F$$ of the text.
$$\ ^{15}N$$ gas $$7$$ protons, $$7$$ electrons and $$15-7=8$$ neutrons and $$\ ^{1}H$$ has $$1$$ proton, $$1$$ electron, and $$0$$ neutrons; and $$\ ^{4}He$$ has $$2$$ protons, $$2$$ electrons, and $$4-2=2$$ neutrons; so $$X$$ has $$7+1-2=6$$ protons $$6$$ electrons and $$8+0-2=6$$ neutrons. It must be nitrogen with a molar mass of $$6+6=12\ g/mol:\ ^{12}C$$

Identify $$X$$ in the following nuclear reactions:
$$\ ^{12}C+\ ^{1}H\rightarrow X$$;

None of the reactions given includes a beta decay so the number of protons, the number of neutrons, and the number of electrons are each conserved. Atomic numbers (numbers of protons and numbers of electrons) and molar masses (combined number of protons and neutrons) can be founded in Appendix $$F$$ of the text.
$$\ ^{12}C$$ gas $$6$$ protons, $$6$$ electrons and $$12-6=6$$ neutrons and $$\ ^{1}H$$ has $$1$$ proton, $$1$$ electron, and $$0$$ neutrons, so $$X$$ has $$6+1=7$$ protons $$6+1=7$$ electrons and $$6+0=6$$ neutrons. It must be nitrogen with a molar mass of $$7+6=13\ g/mol:\ ^{13}N$$

At what temperature does the thermal energy equal the
energy separation?

Thermal energy refers to several distinct physical concepts,

such as the internal energy of a system; heat or sensible heat,

which are defined as types of energy transfer

(as , heat, the phenomena are produced

by the separation of particle from particle,

so as to cause them to attract one another through a greater space.

The separation between two consecutive divisions

on the Fahrenheit scale is scale, because each degree

Fahrenheit is equal to 1.8 degrees Celsius.

What minimum energy is needed to remove this electron from the atom?

As the electron is removed from the hydrogen atom

the final energy of the proton electron system is zero.

Therefore one needs to supply at least

$$3.4\ eV$$ of energy to the system

in order to bring its energy up from $$E_{2}=-3.4\ eV$$ to zero.

(If more energy is supplied, then the electron will retain some kinetic energy after it is removed from the atom.)

State the law of radioactive decay. Plot s graph showing the number (N) of undebased nuclei as a function of time (t) for a given radioactive sample having half-life $$T_{1/2}$$. Depict in the plot the number of undecayed nuclei at
(i) $$t = 3T1/2$$ and
(ii) $$t = 5T1/2.$$

Law of radioactive decay : At any instant, the rate of radioactive disintegration is directly proportional to the number of nuclei of the radioactive element present at that instant. where λ is the constant of proportionality called radioactive decay constant.

Number of undecayed nuclei at
$$t = 3T_{1/2}$$ is $$\dfrac{N_0}{8}$$ and at $$t = 5T_{1/2},$$ it is $$\dfrac{N_0}{32}.$$

Answer the following question:
A radioactive nucleus 'A' undergoes a series of decays as given below:
$$A \overset{\alpha}{\longrightarrow} A_1 \overset{\beta}{\longrightarrow} A_2 \overset{\alpha}{\longrightarrow} A_3 \overset{\gamma}{\longrightarrow} A_4$$
Write the basic nuclear processes underlying $$\beta^{+}$$ and $$\beta^{-}$$ decays.

Basic nuclear process for $$\beta +$$ decay, $$p \rightarrow n + ^{0}_{1}e + v$$
For $$\beta^{-}$$ decay, $$n \rightarrow p + ^{0} _{-1}e + \overset{-}{v}$$

Answer the following question:
(i)State the law of radioactive decay. Write the SI unit of 'activity'.
(ii) There are $$4\sqrt{2} \times 10^6$$ radioactive nuclei in a given radioactive sample. If half-life of the sample is $$20\,s,$$ how many nuclei will decay in $$10\,s ?$$

(i)The radioactive decay law states that the probability per unit time that a nucleus will decay is a constant, independent of time. This constant is called the decay constant and is denoted by λ, “lambda”. This constant probability may vary greatly between different types of nuclei, leading to the many different observed decay rates. The radioactive decay of certain number of atoms (mass) is exponential in time.

The SI unit of activity is the becquerel (Bq)

(ii) Given $$t_{1/2} = 20\,s$$
Also, $$t_{1/2} = \dfrac{lm \,2}{\lambda} \Rightarrow \lambda = \dfrac{ln \,2}{t_{1/2}} \Rightarrow \lambda = \dfrac{ln \,2}{20}$$
Also, according to equation of radioactivity
$$N = N_{0}e^{-\lambda t}$$
$$N = 4\sqrt{2} \times 10^6 \times e^{-=\dfrac{ln \,2}{20} \times 10}$$
$$ = 4\sqrt{2} \times 10^6 \times \dfrac{1}{\sqrt{2}} = 4 \times 10^6 \,Nuclei$$

$${ _{ 1 }^{ }{ He } }^{ 3 }$$ and $${ _{ 2 }^{ }{ He } }^{ 3 }$$ nuclei have the same mass number. Do they have the same binding energy?

In $${ _{ 2 }^{ }{ He } }^{ 3 }$$ there are two protons which give electrostatic force of repulsion by in $${ _{ 1 }^{ }{ He } }^{ 3 }$$ between nucleons there is only nuclea attractive force. So binding energy of $${ _{ 1 }^{ }{ He } }^{ 3 }$$ is larger than $${ _{ 2 }^{ }{ He } }^{ 3 }$$

State Soddy-Fajan's displacement laws for radioactive transformations.

The atoms of radioactive element are unstable. When an atom of a radioactive element disintegrates, an entirely new element is formed. The new element possesses entirely new chemical and radioactive properties. The disintegrating element is called the parent element and the resulting product after disintegration is called the daughter element. Soddy and Fajan studied the successive product elements of disintegration of radioactive elements and gave the following conclusions:
(i) Alpha-Emission: a-particle is nucleus of helium atom having atomic number 2 and atomic weight 4. It is denoted by $$^{2}He_{4}.$$ Therefore when an $$\alpha$$-particle is emitted from a radioactive parent atom (X), its atomic number is reduced by 2 and atomic weight is reduced by 4. Thus the daughter element has its place two groups lower in the periodic table. Thus the process of a-emission may be expressed as
$$_{Z}X^{A} \rightarrow _{Z-2}Y^{A-4} + \underset{(\alpha-particle)}{_{2}He^{4}}$$
Examples:
(i) $$_{92}U^{238 } \rightarrow _{90}Th^{234} + _2He^4$$
(ii) $$_{80}Ra^{226} \rightarrow _{86}Rn^{222} + _2He^4$$
2. Beta-Emission: $$\beta$$-particle is an electron (e) and is denoted by $$_{-1}\beta^{0}.$$ When a $$\beta$$-particle is emitted from a parent atom (X), it is atomic number increases by $$1,$$ while atomic weight remains unchanged. As a result the daughter element (Y) has a place one group higher in the periodic table. Thus the process of $$\beta$$-emission may be expressed as
$$_{Z}X^{A} \rightarrow _{Z+1}Y^{A} + _{-1}\beta^{0} + \overset{-}{v}$$
where $$\overset{-}{v}$$ is a fundamental particle called antineutrino which is massless and chargeless.
Example $$_{90}Th^{228} \rightarrow _{89}Ac^{228} + _{-1}b^{0} + \overset{-}{v}$$
3. Gamma-Emission: The emission of $$\gamma$$-ray from a radioactive atom neither changes its atomic number nor its atomic weight. Therefore its place in periodic table remains undisplaced. In natural radioactivity $$\gamma$$-radiation is accompanied with either $$\alpha$$ or $$\beta$$-emission.

What happens to the position of an element in the periodic table when its nucleus emits a $$\beta$$ particle? Give reason for your answer.

When $$\beta$$ particle is emitted, the daughter element occupies one place to the right of the parent element in the periodic table.

Reason: As a result of $$\beta$$ decay, if a parent nucleus $$X$$ becomes a new daughter nucleus $$Y$$ then the $$\beta$$ decay can be represented as follows:

$$\overset{^{A}_{Z}X}{\text{Parent nucleus }} \rightarrow \overset{^{\ A\ }_{Z+1}Y}{\text{ Daughter nucleus }} + \overset{^{\ 0 }_{-1}He}{\text{ beta-particle }}$$

Thus it shifts one place to the right of the parent element in the periodic table as the resulting nucleus has an atomic number equal to ($$Z+1$$).

What happens to the atomic number of the nucleus when an $$\beta$$ particle is emitted?

$$\overset{^{A}_{Z}X}{\text{Parent nucleus }} \rightarrow \overset{^{\ A\ }_{Z+1}Y}{\text{ Daughter nucleus }} + \overset{^{\ 0 }_{-1}He}{\text{ beta-particle }}$$

When a $$\beta$$ particle is emitted atomic number increases by $$1$$

What changes occur in a nucleus of a radioactive element when it emits a beta particle? Give one example in support of your answer.

The following are the changes which occur when an atom emits

When beta particle emits, the atomic number increases by $$1$$ and the mass number remains unchanged
Example:
$$^{1}_{0}n\ \rightarrow\ ^{1}_{1}P\ +\ ^{\ \ \ 0 }_{-1}e$$

What happens to the mass number of the nucleus when an $$\beta$$ particle is emitted?

When a $$\beta$$ particle is emitted mass number remains unchanged.

$$\overset{^{A}_{Z}X}{\text{Parent nucleus }} \rightarrow \overset{^{\ A\ }_{Z+1}Y}{\text{ Daughter nucleus }} + \overset{^{\ 0 }_{-1}He}{\text{ beta-particle }}$$

Thus it shifts one place to the right of the parent element in the periodic table as the resulting nucleus has an atomic number equal to ($$Z+1$$).

The ratio of recoil of residual nucleus of $$Th^{232}$$ to the velocity of a particle x emitted out is 1 :Find the mass of particle x emitted.

$$\text{Conserving momentum:}$$

$$\left(M_{\text {Th }}-M_{\text {particle }}\right) v_{\text {Th }}=M_{\text {particle }}\times v_{\text {partide }}$$

$$\begin{aligned}\Rightarrow & \frac{M_{\text {particle }}}{M_{\text {Th }}-M_{\text {particle }}}={V_{\text {particle }}} \\\Rightarrow & \frac{M_{\text {particle }}}{M_{\text {Th }}-M_{\text {particle }}}=\frac{1}{57} \\\Rightarrow \quad M_{\text {particle }} &=\frac{1}{58} M_{T h} =\frac{232}{58}=4\end{aligned}$$

Calculate the separation between the particles of a system in the ground state, the corresponding binding energy and wavelength of first line in Lyman series of such a system is positronium consisting of an electron and a positron revolving round their common center.

The reduced mass of the system (electron and positron) is given by

$$ \mu = \dfrac{mm}{m+m} = \dfrac{m}{2} $$
where m = mass of electron or positron.

The radius of first Bohr's orbit is given by
$$ r_1 = \dfrac{h^2}{4 \pi^2 Ke^2(m/2)} = 2 \times$$ radius of first Bohr's orbit of hydrogen
$$ =2 \times 0.529 = 1.058 A^{\circ} $$

Energy of first Bohr's orbit is given as
$$ E_1 = \dfrac{2 \pi^2 K^2 z^2 e^4(m/2)}{h^2} $$
$$ =-\dfrac{1}{2} \times$$ ground state energy of hydrogen
$$ = -\dfrac{1}{2} \times 13.6 \ eV $$
$$ =-6.8 \ eV $$ (Binding energy)

The wavelength of Lyman series is given by
$$ \dfrac{1}{\lambda} = R_\mu \bigg[ \dfrac{1}{1^2} - \dfrac{1}{n^2} \bigg] = R_\mu \bigg ( \dfrac{1}{1^2} - \dfrac{1}{2^2} \bigg)$$
$$ \lambda = \dfrac{4}{3R_\mu} $$
$$ R_\mu = \dfrac{2 \pi^2 K^2 e^4 \mu}{3} = \dfrac{R}{m_e}\mu = \dfrac{1}{2} R $$
$$ = 10967800 \times \dfrac{1}{2} = 5483900 \ m^{-1} $$

$$\lambda = \dfrac{4}{3 \times 5483900} m $$
$$ = 2430 \ A^{\circ} $$

Centain theories predict that the proton is unstable, with a half life of about $$10^{23}$$ years. Assuming that this is true, calculate the number of proton decays you would expect to occur in one year in the water of Olympic-sized swimming pool holding $$4.32 \times 10^5$$ L water.

1771096_1785385_ans_843ac0d018dd4bc692314cfd2ea635e4.jpg

Answer the following question:
Write the process of $$\beta^-$$ decay. How can radioactive nuclei emit $$\beta-$$particles even though they do not contain them ? Why do all electrons emitted during $$\beta-$$decay not have the same energy ?

In $$\beta^{-}$$decay, the mass number A remains unchanged but the atomic number Z of the nucleus goes up by $$1.$$ A common example of $$\beta^{-}$$decay is
$$^{32}_{15}P \rightarrow ^{32}{16}S + e^{-} + \overset{-}{v}$$
A neutron of nucleus decays into a proton, an electron and an antineutrino. It is this electron which is emitted as $$\beta^{-}$$ particles.
$$^{1}_{0}n \rightarrow ^{1}_{1}p + ^{0}_{-1}e + \overset{-}{v}$$
In $$\beta$$-decay, particles like antineutrinos are also emitted along with electrons. The available energy is shared by electrons and antineutrinos in all proportions. That is why all electrons emitted during $$\beta^-$$decay not have the same energy.

The radionuclide $$_{ }^{ 11 }{ C }$$ decays according to $$_{ 6 }^{ 11 }{ C }\rightarrow _{ 5 }^{ 11 }{ B }+{ e }^{ + }+v;{ T }_{ 1/2 }=20.3min\quad $$

Maximum energy of the emitted positio$$=0.960MeV$$
$$m\left( _{ 6 }^{ 11 }{ C } \right) =11.011434amu;\quad m\left( _{ 5 }^{ 11 }{ B } \right) =11.009305amu$$
Q- value of the reacion (in terms of nuclear masses)
$$Q=\left[ { m }_{ N }\left( _{ 6 }^{ 11 }{ C } \right) -{ m }_{ N }\left( _{ 5 }^{ 11 }{ B } \right) -{ m }_{ e } \right] \times 931.5MeV$$
$${ m }_{ N }\left( _{ 6 }^{ 11 }{ C } \right) ={ m }_{ }\left( _{ 6 }^{ 11 }{ C } \right) -6{ m }_{ e };\quad { m }_{ N }\left( _{ 5 }^{ 11 }{ B } \right) ={ m }_{ }\left( _{ 5 }^{ 11 }{ B } \right) -5{ m }_{ e }$$
$$\therefore Q=\left[ \left\{ { m }_{ }\left( _{ 6 }^{ 11 }{ C } \right) -6{ m }_{ e } \right\} -\left\{ { m }_{ }\left( _{ 5 }^{ 11 }{ B } \right) -5{ m }_{ e } \right\} -{ m }_{ e } \right] \times 931.5MeV$$
$$=Q=\left[ \left\{ { m }_{ }\left( _{ 6 }^{ 11 }{ C } \right) -{ m }_{ }\left( _{ 5 }^{ 11 }{ B } \right) \right\} -2{ m }_{ e } \right] \times 931.5MeV$$
$$=\left[ 11.011434-11.009305-2\times 0.000548 \right] \times 931.5MeV=0.001033\times 931.5MeV=0.962MeV$$
The maximum energy of the emitted positron is practically equl to the Q-value of the reaction. It is because mass of the neutrino is negligibly small as compared to the mass of positron. Therefore, when they share the energy, whole of the energy is carried by the positron

A $$P^{32}$$ radionuclide with half-life $$ T = 14.3 $$ days is produced in a reactor at a constant rate $$q = 2.7 \cdot 10^{9}$$ nuclei per second. How soon after the beginning of production of that radionuclide will its activity be equal to $$ A = 1.0 \cdot 10^{9} $$ dis/s ?

1971252_1855780_ans_11305aac2f734b2eafe72d9c9a785994.jpeg

The specific activity of a preparation consisting of radioactive $$Co^{58}$$ and nonradioactive $$Co^{59}$$ is equal to $$2.2 \cdot 10^{12} $$ dis/(s $$\cdot$$ g). The half life of $$Co^{58}$$ is $$71/3$$ days. Find the ratio of the mass of radioactive cobalt in that preparation to the total mass of the preparation (in per cent).

We see that
Specific activity of the sample
$$ = \dfrac{1}{M + M'} $$ [ Activity of $$M\,gm$$ of $$Co^{58} $$ in the sample]

Here $$M$$ and $$M'$$ are the masses of $$Co^{58} $$ and $$Co^{59}$$ in the sample. Now activity of $$M\,gm$$ of $$Co^{58} $$

$$ = \dfrac{M}{58} \times 6.023 \times 10^{23} \times \dfrac{ln\ 2}{71.3 \times 86400} $$ dis/sec

$$ = 1.168 \times 10^{15} M $$

Thus from the problem
$$ 1.168 \times 10^{15} \dfrac{M}{M + M'} = 2.2 \times 10^{12} $$

or $$ \dfrac{M}{M + M'} = 1.88 \times 10^{-3} $$ i.e., $$ 0.188\%$$

Write missing symbols , denoted by $$x$$, in the following nuclear reactions:
(a) $$B^{10} (x , \alpha) Be^{8}$$;
(b) $$O^{17} (d , n ) x$$
(c) $$Na^{23} (p , x )Ne^{20} $$;
(d) $$ x (p , n) Ar^{37} $$.

1971257_1855834_ans_496f5891eadc44edb6baf3ed24f72499.jpg

Find the kinetic energy of the recoil nucleus in the positronic decay of $$Na^{13} $$ nucleus for the case when the energy of positrons is maximum.

The K.E. of the positron is maximum when the energy of neutrino is zero. Since the recoil energy of the nucleus is quite small, it can be calculated by successive approximation.
The reaction is
$$N^{13} \rightarrow C^{13} + e^{+} +\nu_{e} $$.
The maximum energy available to the positron (including its rest energy) is
$$ c^{2} $$ (Mass of $$N^{13} $$ nucleus - Mass of $$C^{13} $$ nucleus)
$$ = c^{2} $$ (Mass of $$N^{13} $$ atom - Mass of $$C^{13} $$ atom - $$m_{e} $$)
$$ = 0.00239 c^{2} - m_{e}c^{2} $$
$$ = (0.00239 \times 931 - 0.511) MeV $$
$$ = 1.71 \, MeV $$
The momentum corresponding to this energy is $$1.636\,MeV/c$$.
The recoil energy of the nucleus is then
$$ E = \dfrac{p^{2}}{2M} = \dfrac{(1.636)^{2}}{2 \times 13 \times 931} = 111\, eV = 0.111\,keV $$
on using $$Mc^{2} = 13 \times 931 \, MeV $$.

Taking the values of atomic masses from the tables, calculate the kinetic energies of a positron and a neutrino emitted by $$C^{11}$$ nucleus for the case when the daughter nucleus does not recoil.

We assume that the parent nucleus is at rest. Then since the daughter nucleus does not recoil, we have
$$\vec{p} = - \vec{p}_{\nu} $$
i.e., positron & $$\nu$$ momentum are equal and opposite. On the other hand
$$ \sqrt{c^{2} p^{2} + m^{2}_{e} c^{4}} + cp = Q = $$ total energy released. (Here we have used the fact that energy of the neutrino is $$ c|\vec{p_{\nu}}| = cp$$ )

Now Q = [(Mass of $$C^{||}$$ nucleus) - (Mass of $$B^{||} $$ nucleus)] $$c^{2} $$
= [Mass of $$C^{||}$$ atom - Mass of $$B^{||}$$ atom - $$m_{e}$$] $$c^{2} $$
$$= 0.00213 \, amu \times c^{2} - m_{e} c^{2} $$
$$ = (0.00213 \times 931 - 0.511)MeV = 1.47\,MeV $$
Then $$c^{2}p^{2} + (0.511)^{2} = (1.47 - cp)^{2} = (1.47)^{2} - 2.94 \, cp + c^{2} p^{2} $$
Thus $$cp = 0.646\, MeV $$ = energy of neutrino
Also K.E. of electron $$ = 1.47 - 0.646 - 0.511 = 0.313 \, MeV $$

Nuclei - Class 12 Engineering Physics - Extra Questions