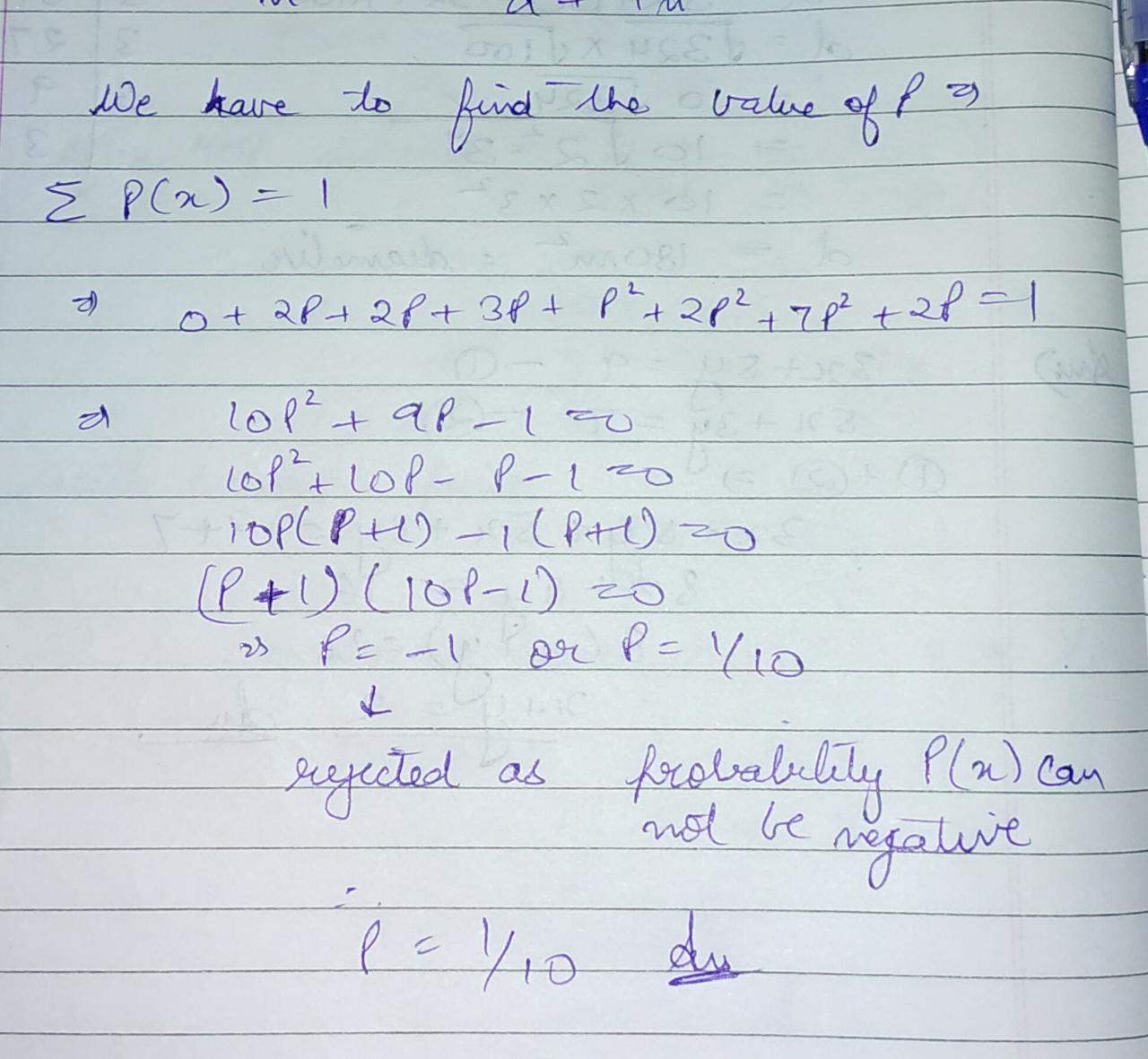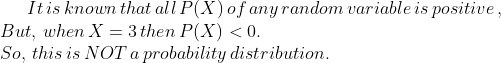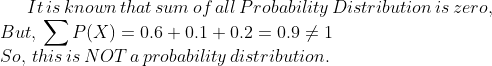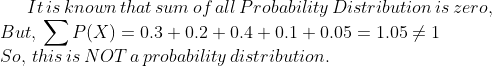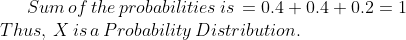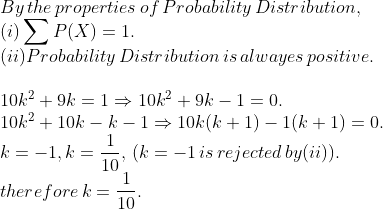Probability Distribution And Its Mean And Variance - Class 12 Commerce Applied Mathematics - Extra Questions
The probability mass function (p.m.f) of $$X$$ is given below:
| $$X=x$$ | $$1$$ | $$2$$ | $$3$$ |
| $$P(X=x)$$ | $$\cfrac{1}{5}$$ | $$\cfrac{2}{5}$$ | $$\cfrac{2}{5}$$ |
The mean and variance of a Binomial distribution is $$4$$ and $$3$$ respectively. Find its parameters.
The random variable x has a probability distribution $$P(x)$$ of the following form where $$k$$ is some number:
$$P(x)=\begin{cases}k & if\, x=0\\2k&if\, x=1 \\3k&if\, x=2\\0&otherwise \end{cases}$$
Determine the value of $$k$$ and $$P(X \le 2).$$
Find the variance and standard deviation of the random variable $$X$$ whose probability distribution is given below:
| $$x$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ |
| $$P(X = x)$$ | $$\dfrac {1}{8}$$ | $$\dfrac {3}{8}$$ | $$\dfrac {3}{8}$$ | $$\dfrac {1}{8}$$ |
The probability that a doctor successfully performs an operation is $$80\%$$. What is the value of $$625$$ times the probability that at least $$3$$ operations out of $$4$$ conducted by him will be successful?
Two cards are drawn simultaneously (or successively without replacement) from a well shuffled pack of $$52$$ cards. Find the Probability that both are king.
Three balls are drawn simultaneously from a bag containing 5 white and 4 red balls. Find the probability distribution of number of red balls drawn.
Find $$k$$ such that the function
$$P(x)=\quad \begin{cases} k\begin{pmatrix} 4 \\ x \end{pmatrix};\quad x=0,1,2,3,4,k>0 \\ 0;\quad otherwise \end{cases}$$ is a probability mass function.
Given $$X \sim B(n, p)$$, If $$E(X)=6, \text{ Var. }(X)=4.2$$, find $$n$$ and $$p$$.
In a dice game , a player pays a stake of Re $$1$$ for each throw of a die. She receives Rs. $$5$$if the die shows a $$3$$, Rs $$2$$ if the die shows a $$1$$ or $$6$$ , and nothing otherwise . What is the player’s expected profit per throw over a long series of throws ?
A random variable X has the following probability distribution
| X | 0 | 1 | 2 | 3 | 4 |
| P(X) | 0 | k | 2k | 3k | 1/2 |
A random variable has the following probability distribution :Find P

Given below is the probability distribution of $$X$$:
| $$x$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ |
| $$P[X=x]$$ | $$k$$ | $$2k$$ | $$4k$$ | $$2k$$ | $$k$$ |
$$P(X\ge 2), P(X < 3), P(X\le 1)$$.
A purse contains four coins each of which is either a rupee or two rupees coin. Find the expected value of a coin in that purse.
A pair of dice is thrown $$5$$ times. If getting a doublet is considered as a success, then find the mean and variance of successes.
There are $$100$$ tickets in a raffle (Lottery). There is $$1$$ prize each of Rs. $$1000/-,$$ Rs. $$500/-$$ and Rs. $$200/-.$$ Remaining tickets are blank. Find the expected price of one such ticket.
A pair of dice is thrown $$4$$ times. If getting a total of $$9$$ in a single throw is considered as a success then find the mean and variance of successes.
A fair die is tossed. If $$2, 3$$ or $$5$$ occurs, the player wins that number of rupees, but if $$1, 4$$ or $$6$$ occurs, the player loses that number of rupees. Then find the possible payoffs for the player.
Find the mean number of heads in three tosses of a fair coin.
Find the mean and variance for the first $$10$$ multiples of $$3$$
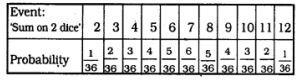
Let $$X$$ denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of $$X$$.
If $$F\left( x \right) =\dfrac { 1 }{ \pi } \left( \dfrac { \pi }{ 2 } +\tan ^{ -1 }{ x } \right)$$, $$-\infty < x < \infty $$ is a distribution function of a continuous variable $$X$$, then find $$P\left( 0\le x\le 1 \right) $$
Given the p.d.f. (probability density function) of a continuous random variable $$x$$ as
$$f(x) =\begin{cases} \dfrac{x^2}{3}\,\,\, -1 < x < 2\\\\ 0 \,\,\, \text{otherwise}\end{cases}$$
Determine the c.d.f. (cumulative distribution function) of $$x$$ and hence find $$P(x < 1), P(x \leq -2), P(x > 0), P(1 < x < 2)$$.
Find the mean and variance of distribution$$f(x) = \left\{\begin{matrix}3e^{-x} & 0<x<\infty \\ 0 & \text{elsewhere} \end{matrix}\right.$$
The following is the p.d.f. (Probability Density Function) of a continuous random variable $$X$$:
$$F(x) = \dfrac {x}{32}, 0 < x < 8; = 0$$, otherwise
Also find its value at $$x = 0.5$$ and $$9$$.
A random variable $$X$$ has the following probability distribution:
| $$X=x$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ |
| $$P(X=x)$$ | $$k$$ | $$3k$$ | $$5k$$ | $$7k$$ | $$9k$$ | $$11k$$ | $$13k$$ |
(b) Find $$P(0< X< 4)$$
(c) Obtain cumulative distribution function (c.d.f) of $$X$$.
The table gives the probability distribution of a random variable $$X$$.
| $$x$$ | 1 | 2 | 3 | 4 | 5 |
| $$P(X=x)$$ | $$0.2$$ | $$0.1$$ | $$0.3$$ | $$0.3$$ | $$p$$ |
(ii) Find the mean of $$X$$
(iii) Find the variance of $$X$$.
The range of a random variable $$X$$ is $$\{0, 1, 2\}$$.
Given that $$P(X = 0) = 3C^3, P(X = 1) = 4C - 10C^2, P(X = 2) = 5C - 1$$. Find the value of:(i) $$C$$
(ii) $$P(X < 1)$$
(iii) $$P(1 < X \leq 2)$$ and $$P(0< X \leq 3)$$.
(i) $$C$$
(ii) $$P(X < 1)$$
(iii) $$P(1 < X \leq 2)$$ and $$P(0< X \leq 3)$$.
(ii) $$P(X < 1)$$
(iii) $$P(1 < X \leq 2)$$ and $$P(0< X \leq 3)$$.
| X = | 1 | 2 | 3 | 4 | 5 |
| P(X =) | $$\dfrac{1}{2}$$ | $$\dfrac{1}{4}$$ | $$\dfrac{1}{8}$$ | $$\dfrac{1}{16}$$ | P |
(a) Find the value of P.
(b) Find the mean of X.
(c) Find the variance of X.
The mean and variance of a binomial distribution are $$4$$ and $$3$$ respectively. Fix the distribution and find $$P(X \geq 1)$$.
Verify $$f(x)=\begin{cases} 30{ x }^{ 4 }{ e }^{ -6{ x }^{ 5 } };\quad \quad x>0 \\ 0;\quad otherwise \end{cases}$$ for p.d.f if $$f(x)$$ is a p.d.f then find $$P(1)$$.
From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is draw at random with replacement.Find the probability distribution of the number defective bulbs.
From a lot of $$6$$ items containing $$2$$ defective items, a sample of $$4$$ items are drawn at random. Let the random variable X denote the number of defective items in the sample. If the sample is drawn without replacement, find Variance of X.
From a lot of $$6$$ items containing $$2$$ defective items, a sample of $$4$$ items are drawn at random. Let the random variable X denote the number of defective items in the sample. If the sample is drawn without replacement, find Mean of X.
A random variable $$x$$ has the following probability distribution:
| $$x$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ |
| $$P(X = x)$$ | $$k$$ | $$3k$$ | $$5k$$ | $$7k$$ | $$9k$$ | $$11k$$ | $$13k$$ |
The mean and standard deviation of a random variable X are $$10$$ and $$5$$ respectively. Find.$$E\left(\left(\dfrac{x-10}{5}\right)^2\right)$$.
The P.M.F of a r.v. $$X$$ is $$P\left( x \right) = \frac{1}{5}$$ for $$x = 1,2,3, \ldots 14,15;$$ $$P(x)=0$$ otherwise.
Find (i) $$E(X)$$ (ii) $$Var(X)$$
The mean and standard deviation of a random variable X are $$10$$ and $$5$$ respectively. Find.$$E\left(\left(\dfrac{x-10}{5}\right)\right)$$.
The mean and standard deviation of a random variable X are $$10$$ and $$5$$ respectively. Find $$E(X^2)$$
Find the mean of the probability distribution.
Find k, the probability distribution of X is as follows?
| X | 1 | 2 | 3 | 4 |
| P(X) | 2k | 3k | 3k | 2k |
Calculate the expected value and variance of $$x$$, if $$x$$ denotes the number obtained on the uppermost face when a fair die is thrown.
Events A and B are such that $$P\left( A \right) = \frac{1}{2},P\left( B \right) = \frac{1}{{12}}$$ and $$P\left( {notA\, \text{OR} \, not\,B} \right) = \frac{1}{4}$$ state whether A and B are independent?
A r.v. $$X$$ has the following probability distribution:
| $$X=x$$ | $$-2$$ | $$-1$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ |
| $$P(x)$$ | $$0.1$$ | $$k$$ | $$0.2$$ | $$2k$$ | $$0.3$$ | $$k$$ |
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| P(X=x) | k | 2k | 3k | 4k | 5k | 6k |
Then $$P(X\le 4)$$ =
Two number are selected at random (without replacement ) from the first six positive integers. Let X denote the larger of the numbers obtained. Find E (X).
The random variable $$X$$ has probability distribution $$P(X)$$ of the following form.
$$P(X)=\begin{cases} k\quad if\quad X=0 \\ 2k\quad if\quad X=1 \\ 3k\quad if\quad X=2 \\ 0\quad otherwise \end{cases}$$
(a) determine value of $$K$$
(b) Find $$P(X< 2), P(X\le 2), P(X\ge 2)$$
The p. m. f. X- number of major defects randomly selected appliance of a certain type is :
| X-x | 0 | 1 | 2 | 3 | 4 |
| P(a) | 0.08 | 0.15 | 0.45 | 0.27 | 0.05 |
Let a pair of dice be thrown and the random variable $$ X $$ be the sum of the numbers that appear on the two dice. Find the mean of $$ X $$ .
12 different objecs are to be distributed among 9 persons. Find the number of ways in which objects can be distributed . (All objects must be distributed and each person should get atleast 1 object)
Four red balls are numbered from $$1$$ to $$4$$ and three blue balls are numbered from $$3$$ to $$5$$. If these balls are placed in a bag and a ball is drawn from a bag, what is the probability of choosing a red ball and a blue ball numbered $$5$$?
The probability distribution of a random variable X is given below
| $$X=x_i$$ | $$P(X=x_i)$$ |
| $$1$$ | k |
| $$2$$ | $$2k$$ |
| $$3$$ | $$3k$$ |
| $$4$$ | $$4k$$ |
| $$5$$ | $$5k$$ |
Two unbiased dice are thrown together at random. Find the expected value of the total number of points shown up.
Two cards are drawn (without replacement) from a well shuffled deck of $$52$$ cards. Find probability distribution and mean of number of cards numbered $$4$$
Find the probability distribution of the number of doublets in three throws of a pair of dice
Find expected value of the random variable $$X$$ whose probability mass function is :
| $$X=x$$ | 1 | 2 | 3 |
| $$P(X=x)$$ | $$\dfrac{1}{5}$$ | $$\dfrac{2}{5}$$ | $$\dfrac{2}{5}$$ |
If $$f(x)=kx,0 < x < 2$$ $$=0$$, otherwise,
is a probability density function of a random variable $$X$$, then find:
(i) Value of $$k$$,
(ii) $$P(1 < X< 2)$$
is a probability density function of a random variable $$X$$, then find:
(i) Value of $$k$$,
(ii) $$P(1 < X< 2)$$
There are 5 cards , numbered 1 to 5, one number of each card . two cards are drawn at random without replacement . Let X denote the sum of the numbers on the two cards drawn.find the mean and variance of X.
The probability distribution of $$X$$ is :
| $$ X$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ |
| $$P(X)$$ | $$0.2$$ | $$ K$$ | $$ K $$ | $$2K$$ |
Write the value of $$ K $$ .
Consider the probability distribution of a random variable $$ x $$ :
$$\begin{array}{|l|l|l|l|l|l|}\hline \mathrm{X} & 0 & 1 & 2 & 3 & 4 \\\hline \mathrm{P}(\mathrm{X}) & 0.1 & 0.25 & 0.3 & 0.2 & 0.15 \\\hline\end{array}$$
Calculate
(ii) Variance of $$ \mathrm{X} $$
A biased die is such that $$ \mathrm{P}(4)=\dfrac{1}{10} $$ and other scores being equally likely. The die is tossed twice. If $$ X $$ is the 'number of four seen', find the variance of the random variable $$ \mathbf{X} $$
The probability distribution of a random variable X is given below:
$$\begin{array}{|l|l|l|l|l|}\hline \mathrm{X} & 0 & 1 & 2 & 3 \\\hline \mathrm{P}(\mathrm{X}) & k & \dfrac{k}{2} & \dfrac{k}{4} & \dfrac{k}{8} \\\hline\end{array}$$
(i) Determine the value of $$ \mathbf{k} $$
If $$ \mathrm{X} $$ is the number of tails in three tosses of a coin, determine the standard deviation of $$ x $$
Consider the probability distribution of a random variable $$ x $$ :
$$\begin{array}{|l|l|l|l|l|l|}\hline \mathrm{X} & 0 & 1 & 2 & 3 & 4 \\\hline \mathrm{P}(\mathrm{X}) & 0.1 & 0.25 & 0.3 & 0.2 & 0.15 \\\hline\end{array}$$
Calculate:
(i) $$ \mathrm{V}\left(\dfrac{\mathrm{X}}{2}\right) $$
A discrete random variable X has the probability distribution given as below:
$$\begin{array}{|l|ll|l|l|}\hline \mathrm{X} &0.5 & 1 & 1.5 & 2 \\\hline \mathrm{P(X)}& k & k^2 & 2k^2 & k \\\hline\end{array}$$
(ii) Determine the mean of distribution.
A die is thrown three times. Let $$ x $$ be 'the number of two seen'. Find the expectation of $$ x $$
Two cards are drawn successively without replacement from a well shuffled deck of cards. Find the mean and standard variation of the random variable X where X is the number of aces.
Find the variance of the distribution:Vedantu
$$\begin{array}{|l|l|l|l|l|l|l|}\hline \mathrm{x} & 0 & 1 & 2 & 3 & 4 & 5 \\\hline \mathrm{P}(\mathrm{x}) & \dfrac{1}{6} & \dfrac{5}{18} & \dfrac{2}{9} & \dfrac{1}{6} & \dfrac{1}{9} & \dfrac{1}{18} \\\hline\end{array}$$
Two probability distributions of the discrete random variable $$ X $$ and $$ Y $$ are given below.
$$\begin{array}{|l|l|l|l|l|}\hline \mathrm{X} & 0 & 1 & 2 & 3 \\\hline \mathrm{P}(\mathrm{X}) & \dfrac{1}{5} & \dfrac{2}{5} & \dfrac{1}{5} & \dfrac{1}{5} \\\hline\end{array}$$
$$ \begin{array}{|l|l|l|l|l|}\hline \mathrm{Y} & 0 & 1 & 2 & 3 \\\hline \mathrm{P}(\mathrm{Y}) & \dfrac{1}{5} & \dfrac{3}{10} & \dfrac{2}{5} & \dfrac{1}{5} \\\hline\end{array}$$
Prove that $$ E\left(Y^{2}\right)=2 E(X) $$
The probability distribution of a discrete random variable X is given as under:
Calculate :
(i) The value of A if E(X) = 2.94
(ii) Variance of X.
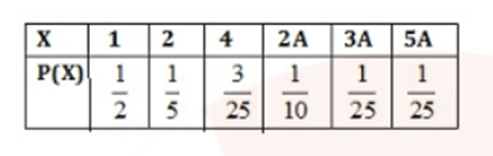
Find the probability distribution of the maximum of the two scores obtained when die is thrown twice. Determine also the mean of the distribution
Let X be a discrete random variable whose probability distribution is defined as follows:
$$P(X = x)$$ =$$ \begin{matrix} k(x + 1) & for \space x = 1, 2, 3, 4 \\ 2kx & for \space x = 5, 6, 7 \\ 0 & otherwise \end{matrix}$$
where k is a constant. Calculate
(i) the value of k
(ii) E(x)
(iii) Standard deviation of X.
State which of the following are not the probability distributions of a random variable. Give reasons for your answer.
| $$X$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ |
| $$P(X)$$ | $$0.1$$ | $$0.5$$ | $$0.2$$ | $$-0.1$$ | $$0.3$$ |
State which of the following are not the probability distributions of a random variable. Give reasons for your answer.
| $$Y$$ | $$-1$$ | $$0$$ | $$1$$ |
| $$P(Y)$$ | $$0.6$$ | $$0.1$$ | $$0.2$$ |
Let X be a random variable taking values $$x_1, x_2,....... x_n$$ with probabilities
$$p_1, p_2,......p_n$$ respectively. Then var(X) = __________.
State which of the following are not the probability distributions of a random variable. Give reasons for your answer.
| $$Z$$ | $$3$$ | $$3$$ | $$1$$ | $$0$$ | $$-1$$ |
| $$P(Z)$$ | $$0.3$$ | $$0.2$$ | $$0.4$$ | $$0.1$$ | $$0.05$$ |
State which of the following are not the probability distributions of a random variable. Give reasons for your answer.
| $$X$$ | $$0$$ | $$1$$ | $$2$$ |
| $$P(X)$$ | $$0.4$$ | $$0.4$$ | $$0.2$$ |
Find the probability distribution of $$X$$, the number of heads in a simultaneous toss of two coins.
Complete the following table:
The random variable X has a probability distribution $$P(X)$$ of the following form, where $$k$$ is some number.
$$P(X = x) = \begin{cases}k,& \text{if} \ x = 0 \\ 2k, & \text{if} \ x=1 \\ 3k, & \text{if} \ x=2 \\ 0, & \text{otherwise} \end{cases}$$
Determine the value of $$k$$.
A random variable $$X$$ has the following probability distribution:
| $$X$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ | $$7$$ |
| $$P(X)$$ | $$0$$ | $$k$$ | $$2k$$ | $$2k$$ | $$3k$$ | $$k^2$$ | $$2k^2$$ | $$7k^2+k$$ |
$$P(X>6)$$
A random variable $$X$$ has the following probability distribution:
| $$X$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ | $$7$$ |
| $$P(X)$$ | $$0$$ | $$k$$ | $$2k$$ | $$2k$$ | $$3k$$ | $$k^2$$ | $$2k^2$$ | $$7k^2+k$$ |
$$P(X<3)$$
A random variable $$X$$ has the following probability distribution:
| $$X$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ | $$7$$ |
| $$P(X)$$ | $$0$$ | $$k$$ | $$2k$$ | $$2k$$ | $$3k$$ | $$k^2$$ | $$2k^2$$ | $$7k^2+k$$ |
$$K$$
The random variable $$X$$ has a probability distribution $$P(X)$$ of the following from, where $$k$$ is some number:
$$P(X)=\left\{ \begin{matrix} k,\quad if\quad x=0 \\ 2k,\quad if\quad x=1 \\ 3k,\quad if\quad x=2 \\ 0,\quad otherwise \end{matrix} \right .$$
Find $$P(X<2),P(X\le 2),P(X\ge 2)$$
A random variable $$X$$ has the following probability distribution:
| $$X$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ | $$7$$ |
| $$P(X)$$ | $$0$$ | $$k$$ | $$2k$$ | $$2k$$ | $$3k$$ | $$k^2$$ | $$2k^2$$ | $$7k^2+k$$ |
$$P(0<X<3)$$
A fair coin is tossed until a head or five tails occur. If $$X$$ denotes the number of tosses of the coin, find the mean of $$X$$.
A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years. One student is selected in such a manner that each has the same chance of being chosen and the age $$X$$ of the selected student is recorded. What is the probability distribution of the random variable $$X$$ ? Find mean, variance and standard deviation of $$X$$.
In a meeting, 70% of the members favour and 30% oppose a certain proposal. A member is selected at random and we take $$X = 0$$ if he opposed, and $$X = 1$$ if he is in favour. Find $$E\left(X\right)$$ and $$Var\left(X\right)$$.
A die is thrown, a man $$C$$ gets a prize of Rs. $$5$$ if the die turns up $$1$$ and gets a prize of Rs. $$3$$ if the die turns up $$2,$$ else he gets nothing, A man $$A$$ whose probability of speaking the truth is $$\displaystyle \frac{1}{2}$$ tells $$C$$ that the die has turned up $$1$$ and another man $$B$$ whose probability of speaking the truth is $$\displaystyle \frac{2}{3}$$ tells $$C$$ that the die has turned up $$2.$$ Find the expectation value of $$C.$$
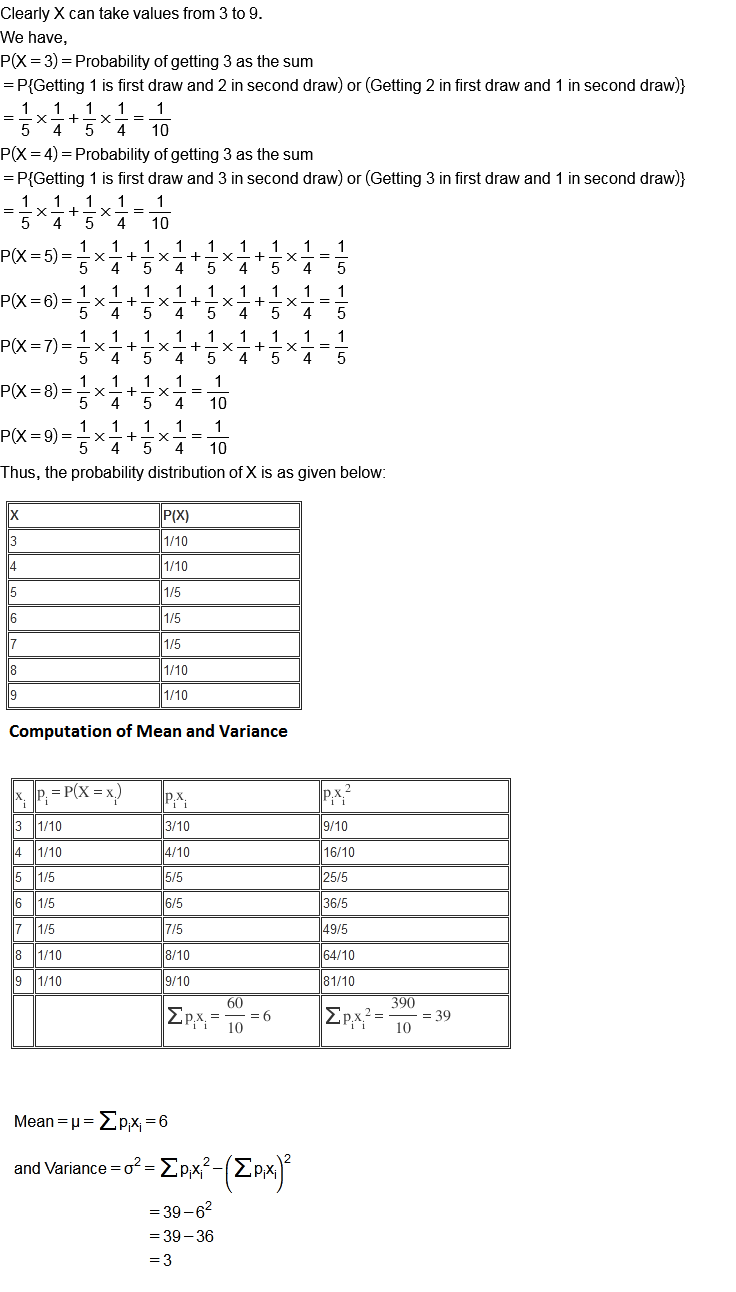
The numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers obtained. Find the probability distribution of the random variable X and hence find the means of the distribution.
Two the numbers are selected at random (without replacement) from first six positive integers. Let X denote the larger of the two numbers obtained. Find the probability distribution of X. Find the mean and variance of this distribution.
From a lot of $$15$$ bulbs which include $$5$$ defectives, a sample of $$4$$ bulbs is drawn one by one with replacement. Find the probability distribution of number of defective bulbs. Hence find the mean of the distribution.
Three numbers are selected at random (without replacement) from first six positive integers. Let $$X$$ denote the largest of the three numbers obtained. Find the probability distribution of $$X$$. Also, find the mean and variance of the distribution.
Let the p.m.f. (probability mass function) of random variable $$x$$ be
$$P(x) = \begin{cases} \left( \dfrac{4}{x} \right ) \left( \dfrac{5}{9}\right)^x \left(\dfrac{4}{x} \right )^{4 - x},\ x = 0, 1, 2, 3, 4\\ 0,\,\,\, \text{otherwise} \end{cases}$$
Find $$E(x)$$ and Var$$(x)$$.
The time (in minute) for a lab assistant to prepare the equipment for a certain experiment is a random variable $$X$$ taking values between $$25$$ and $$35$$ minutes with p.d.f.$$f(x) = \begin{cases} \dfrac {1}{10}, 25\leq x \leq 35\\ \\ 0,\,\,\, \text{otherwise} \end{cases}$$.
What is the probability that preparation time exeeds $$33$$ minutes? Also find the c.d.f. of $$X$$.
What is the probability that preparation time exeeds $$33$$ minutes? Also find the c.d.f. of $$X$$.
The range of a random variable $$X$$ is $$\left \{0, 1, 2\right \}$$. Given that $$P(X = 0) = 3C^{3}, P(X = 1) = 4C - 10C^{2}, P(X = 2) = 5C - 1$$
i) Find the value of $$C$$.
ii) $$P(X < 1), P(1 < X \leq 2)$$ and $$P(0 < X \leq 3)$$
A random variable '$$X$$' has the following probability distribution:
| X=x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(X=x) | $$0$$ | $$k$$ | $$2k$$ | $$2k$$ | $$3k$$ | $${k}^{2}$$ | $$2{k}^{2}$$ | $$7{k}^{2}+k$$ |
(i) $$k$$
(ii) The Mean and
(iii) $$P(0< X< 5)$$
Find the mean and variance for the probability density function : $$f(x)=\begin{cases} \alpha { e }^{ -\alpha x }\,\,\, \text{if}\, x>0 \\ 0\,\,\, \text{otherwise} \end{cases}$$
A random variable $$X$$ has the following probability distribution.
| $$X = x$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ | $$7$$ |
| $$P(X = x)$$ | $$0$$ | $$k$$ | $$2k$$ | $$2k$$ | $$3k$$ | $$k^{2}$$ | $$2k^{2}$$ | $$7k^{2} + k$$ |
Two cards are drawn with replacement from a well shuffled deck of $$52$$ cards. Find the mean and variance for the number of aces.
If the probability density function of a random variable is given by,
$$f(x) = \left\{\begin{matrix} k(1 - x^2),& 0 < x < 1\\ 0, & \text{elsewhere}\end{matrix} \right.$$ find $$k$$ and the distribution function of the random variable.
A random variable $$X$$ has the following probability mass function.
| $$x$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ |
| $$P(X = x)$$ | $$k$$ | $$3k$$ | $$5k$$ | $$7k$$ | $$9k$$ | $$11k$$ | $$13k$$ |
(b) Evaluate $$P(X < 4), P (X$$ $$\geq$$ $$5)$$ and $$P(3< X$$ $$\leq$$ $$6)$$.
(c) What is the smallest value of $$x$$ for which $$P(X$$ $$\leq$$ $$x) >$$ $$\dfrac{1}{2}$$?
Given the probability density function (p.d.f) of a continuous random variable $$X$$ as,
$$f(x) = \dfrac {x^{2}}{3}, -1 < x < 2 = 1$$, otherwise
Determine the cumulative distribution function (c.d.f.) of $$X$$ and hence find $$P(X < 1), P(X > 0), P(1 < X < 2)$$
A die is tossed twice. A success is getting an odd number on a toss. Find the mean and the variance of the probability distribution of the number of successes.
A player tosses $$2$$ fair coins. He wins Rs$$5$$ if $$2$$ heads appear, Rs$$2$$ if head appears and Rs$$1$$ if no head appears. Find his expected winning amount and variance of winning amount.
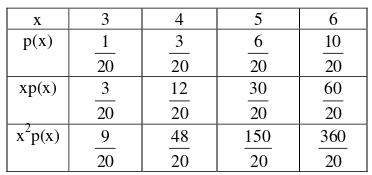
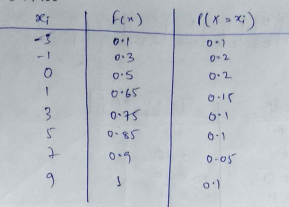
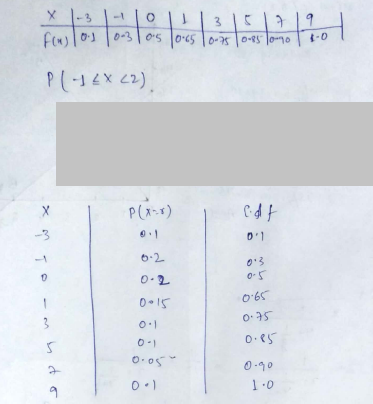
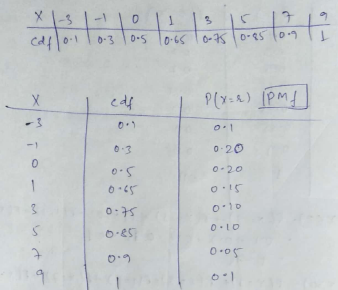
The following is the c.d.f. of a discrete r.v. X:
| X | $$-3$$ | $$-1$$ | $$0$$ | $$1$$ | $$3$$ | $$5$$ | $$7$$ | $$9$$ |
| $$F(x)$$ | $$0.1$$ | $$0.3$$ | $$0.5$$ | $$0.65$$ | $$0.75$$ | $$0.85$$ | $$0.90$$ | $$1$$ |
The following is the c.d.f. of a discrete r.v. X:
| X | $$-3$$ | $$-1$$ | $$0$$ | $$1$$ | $$3$$ | $$5$$ | $$7$$ | $$9$$ |
| $$F(x)$$ | $$0.1$$ | $$0.3$$ | $$0.5$$ | $$0.65$$ | $$0.75$$ | $$0.85$$ | $$0.90$$ | $$1$$ |
The following is the c.d.f. of a discrete r.v. X:
| X | $$-3$$ | $$-1$$ | $$0$$ | $$1$$ | $$3$$ | $$5$$ | $$7$$ | $$9$$ |
| $$F(x)$$ | $$0.1$$ | $$0.3$$ | $$0.5$$ | $$0.65$$ | $$0.75$$ | $$0.85$$ | $$0.90$$ | $$1$$ |
The following is the c.d.f. of a discrete r.v. X:
| X | $$-3$$ | $$-1$$ | $$0$$ | $$1$$ | $$3$$ | $$5$$ | $$7$$ | $$9$$ |
| $$F(x)$$ | $$0.1$$ | $$0.3$$ | $$0.5$$ | $$0.65$$ | $$0.75$$ | $$0.85$$ | $$0.90$$ | $$1$$ |
A die is thrown $$120$$ times and getting $$1$$ or $$5$$ is considered a success. Find the mean and variance of the number of sucess.
Class 12 Commerce Applied Mathematics Extra Questions
- Application Of Derivatives Extra Questions
- Applications Of Integrals Extra Questions
- Definite Integrals Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Indefinite Integrals Extra Questions
- Linear Equations Extra Questions
- Matrices Extra Questions
- Probability Distribution And Its Mean And Variance Extra Questions
- Quantification And Numerical Applications Extra Questions
- Standard Probability Distributions Extra Questions