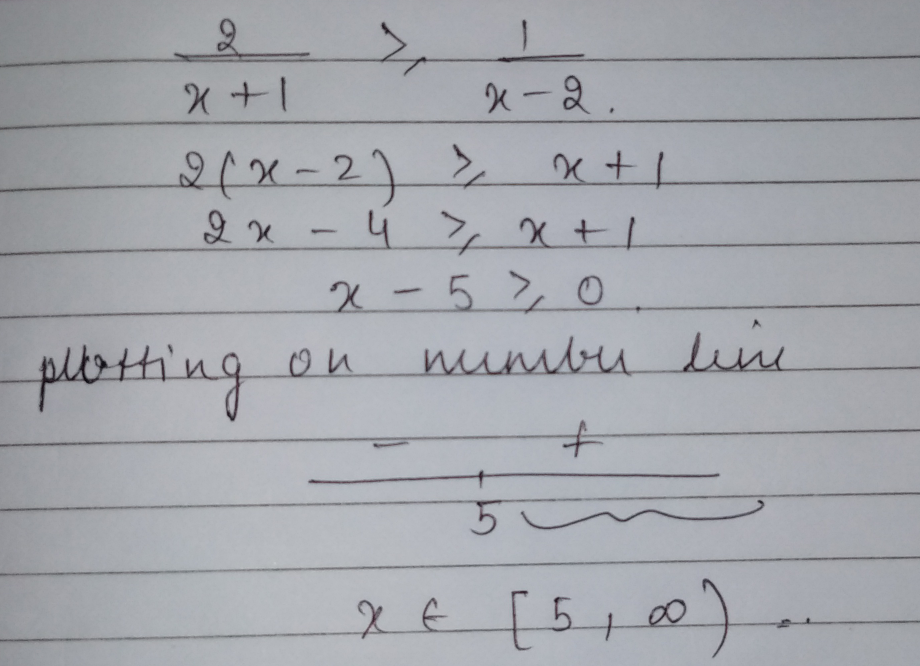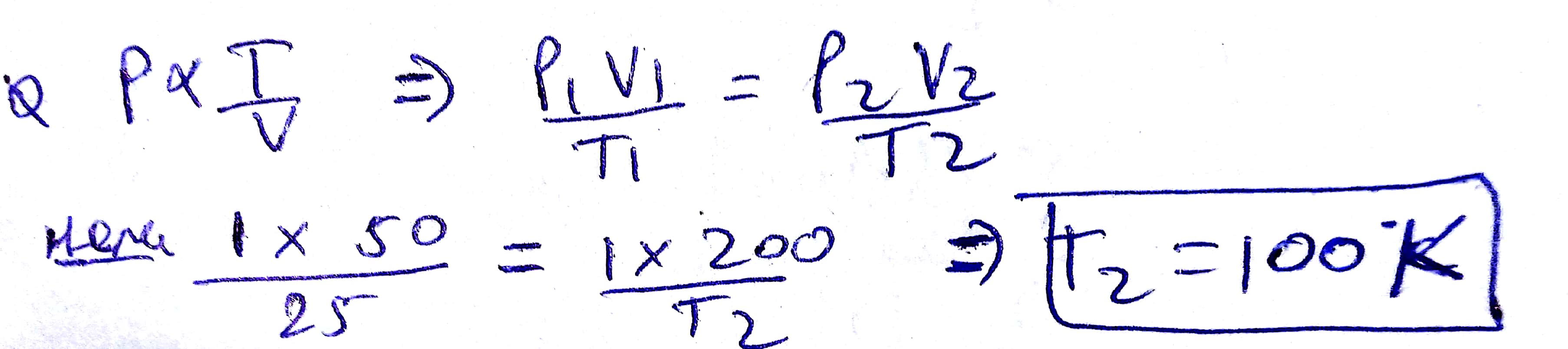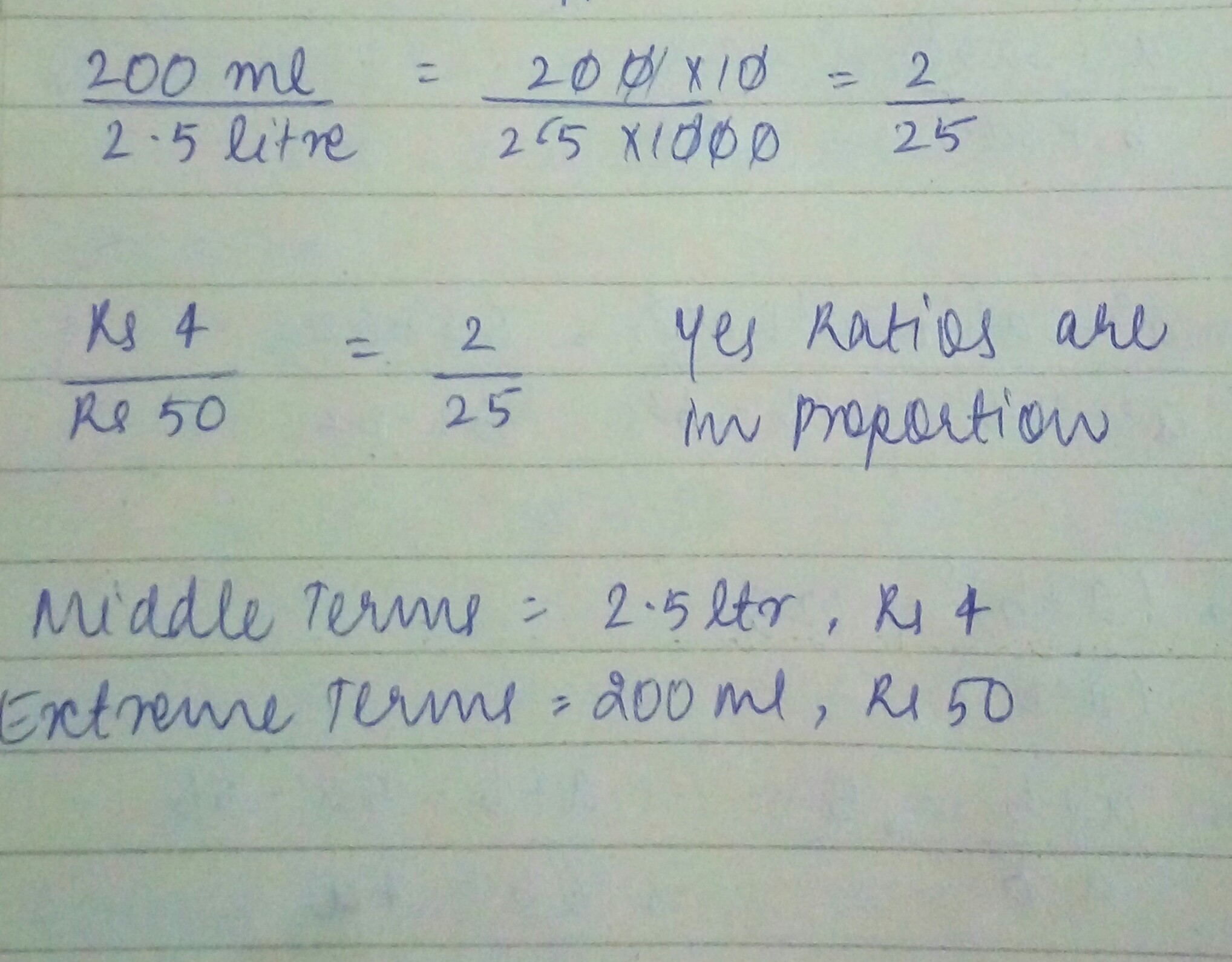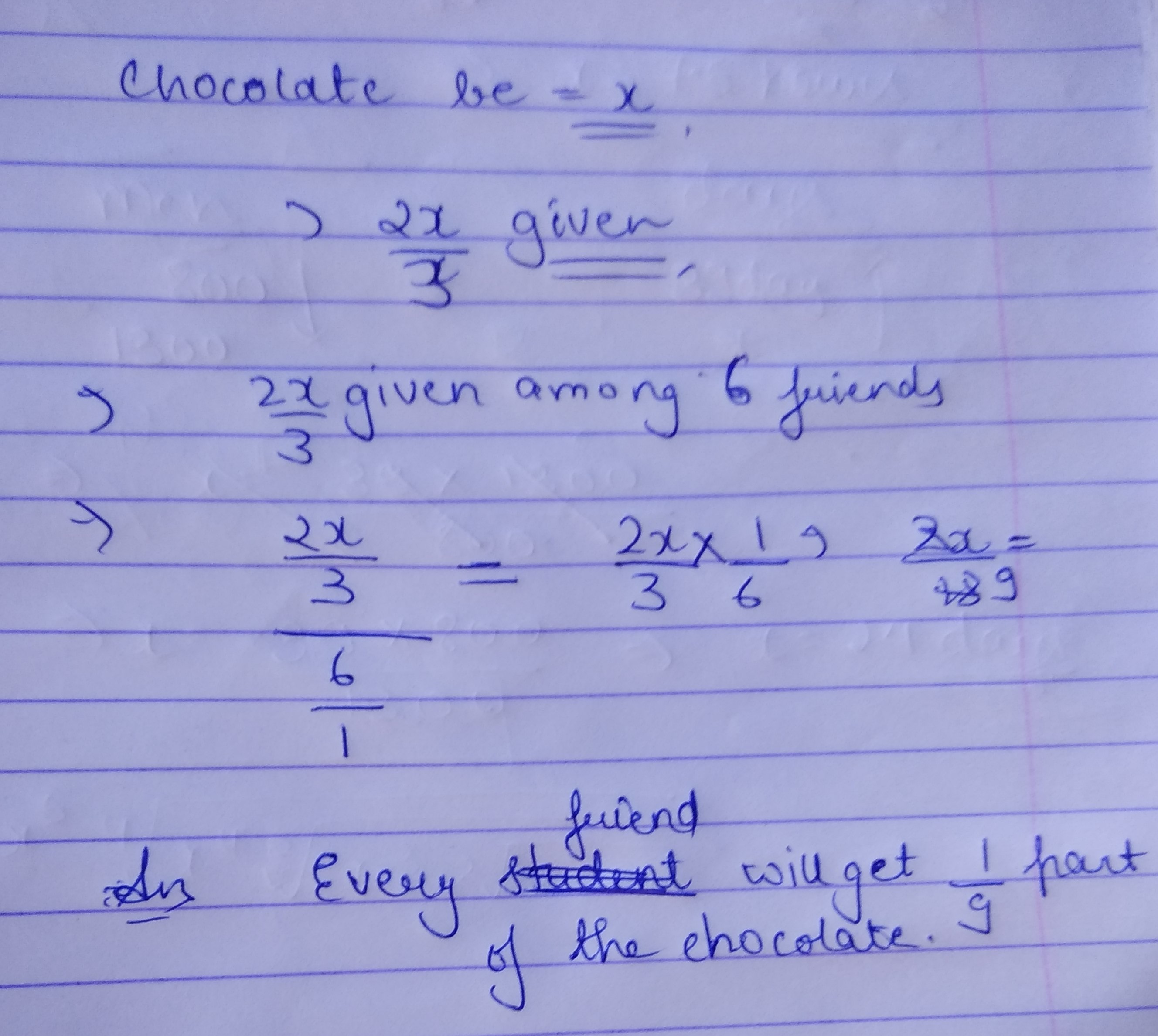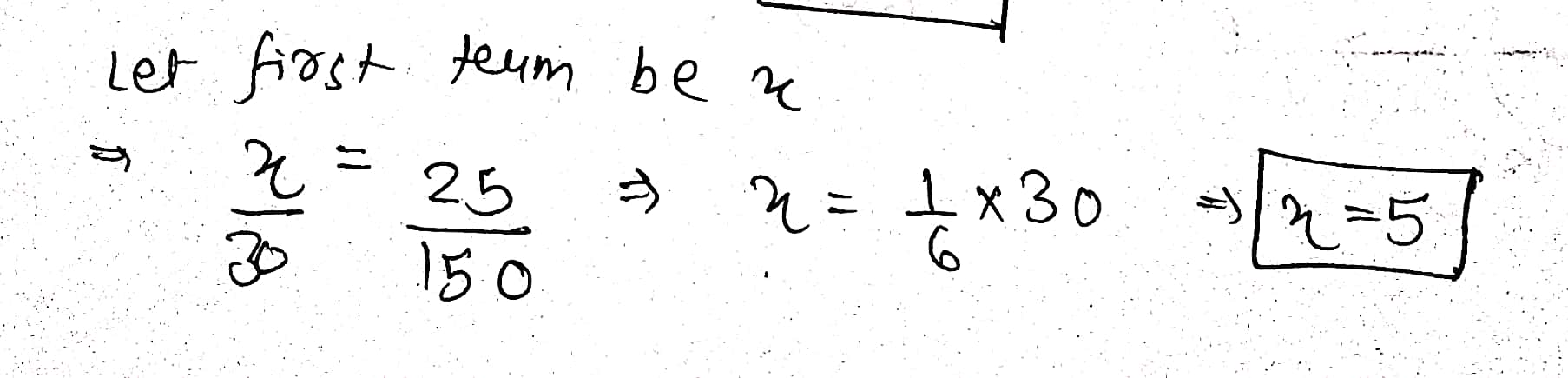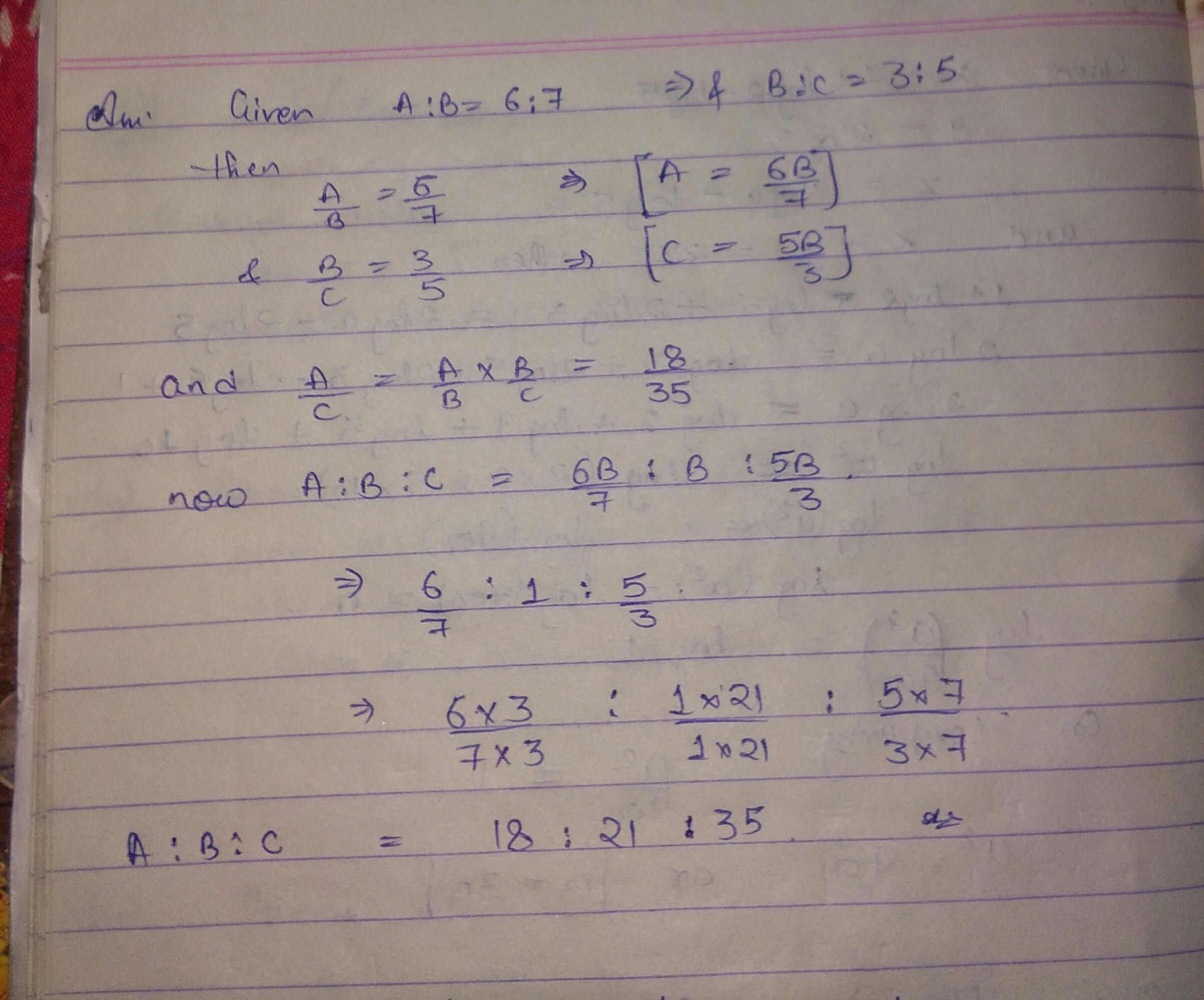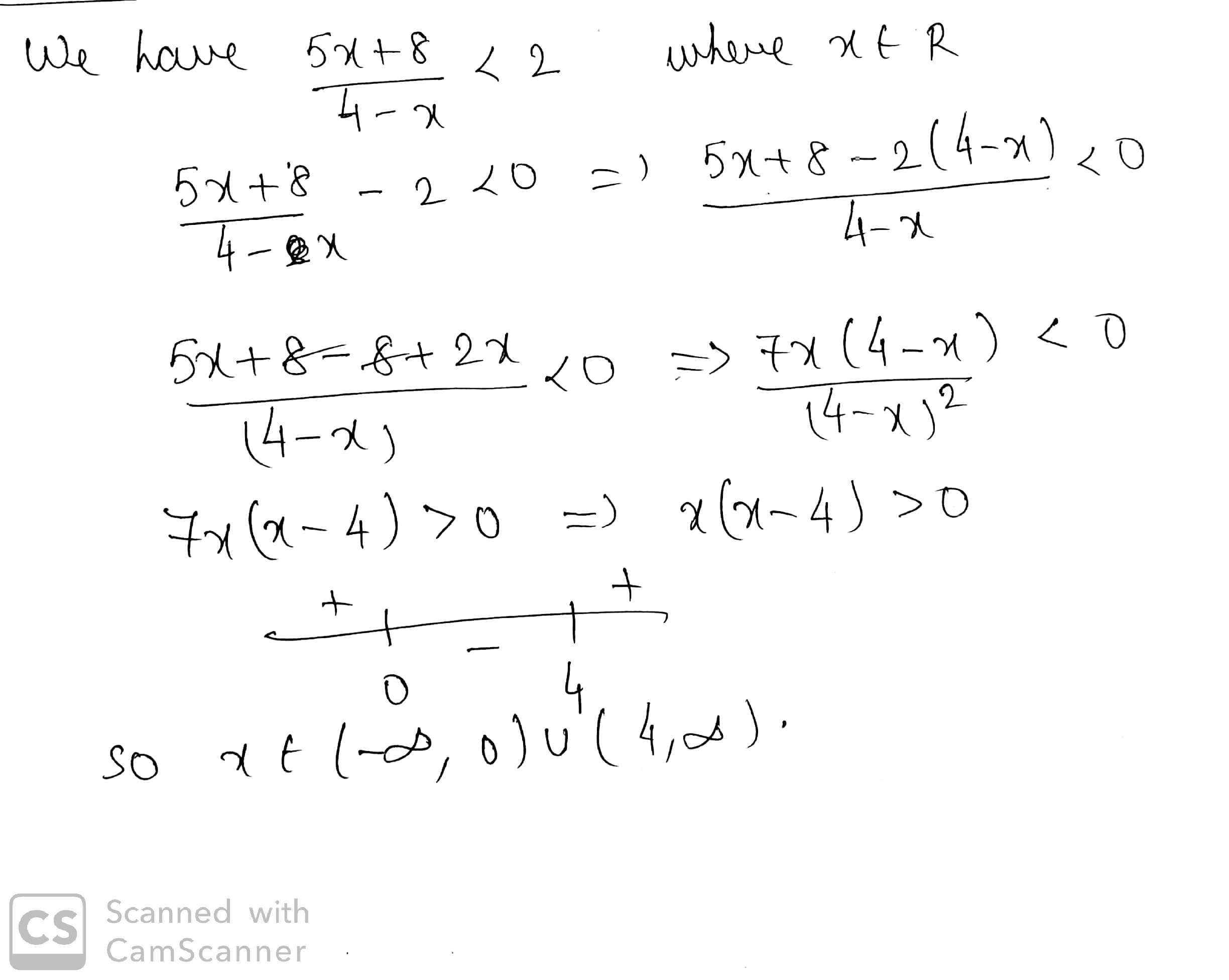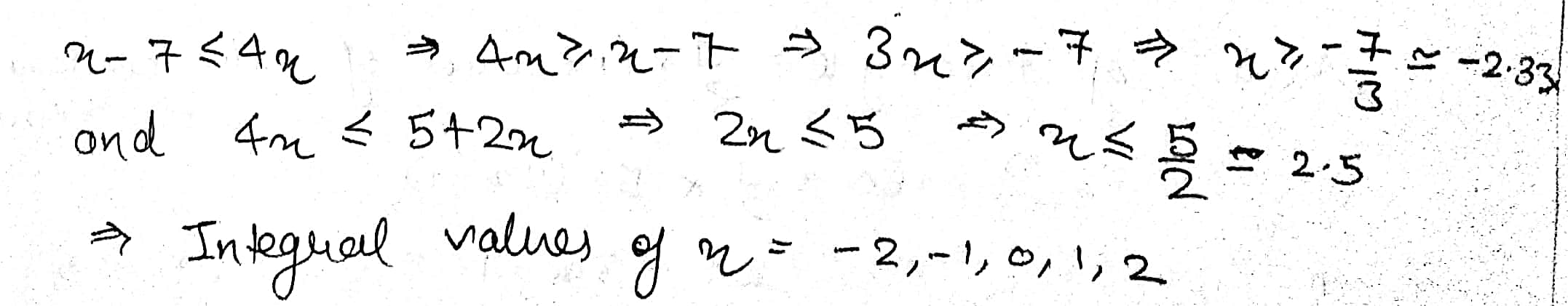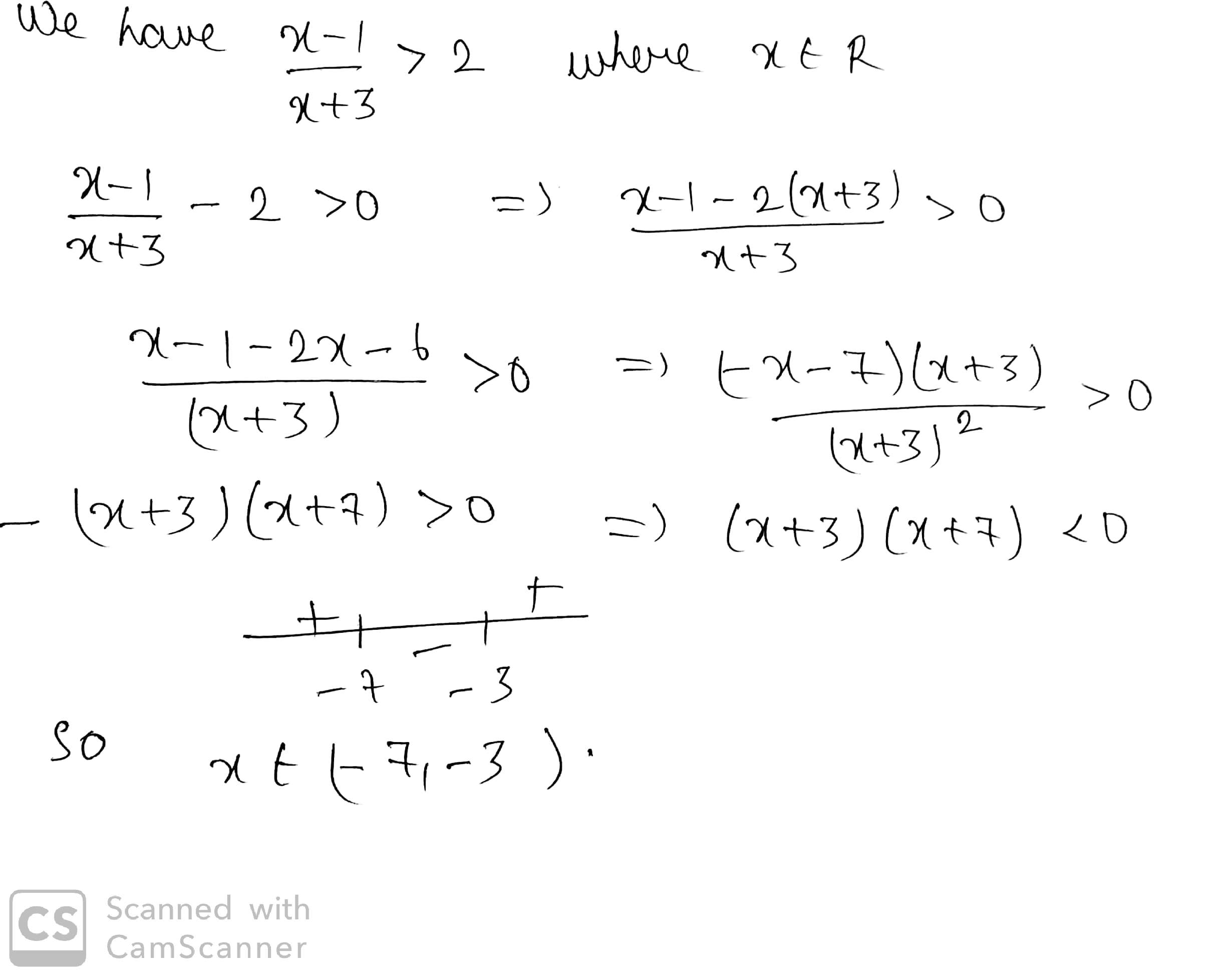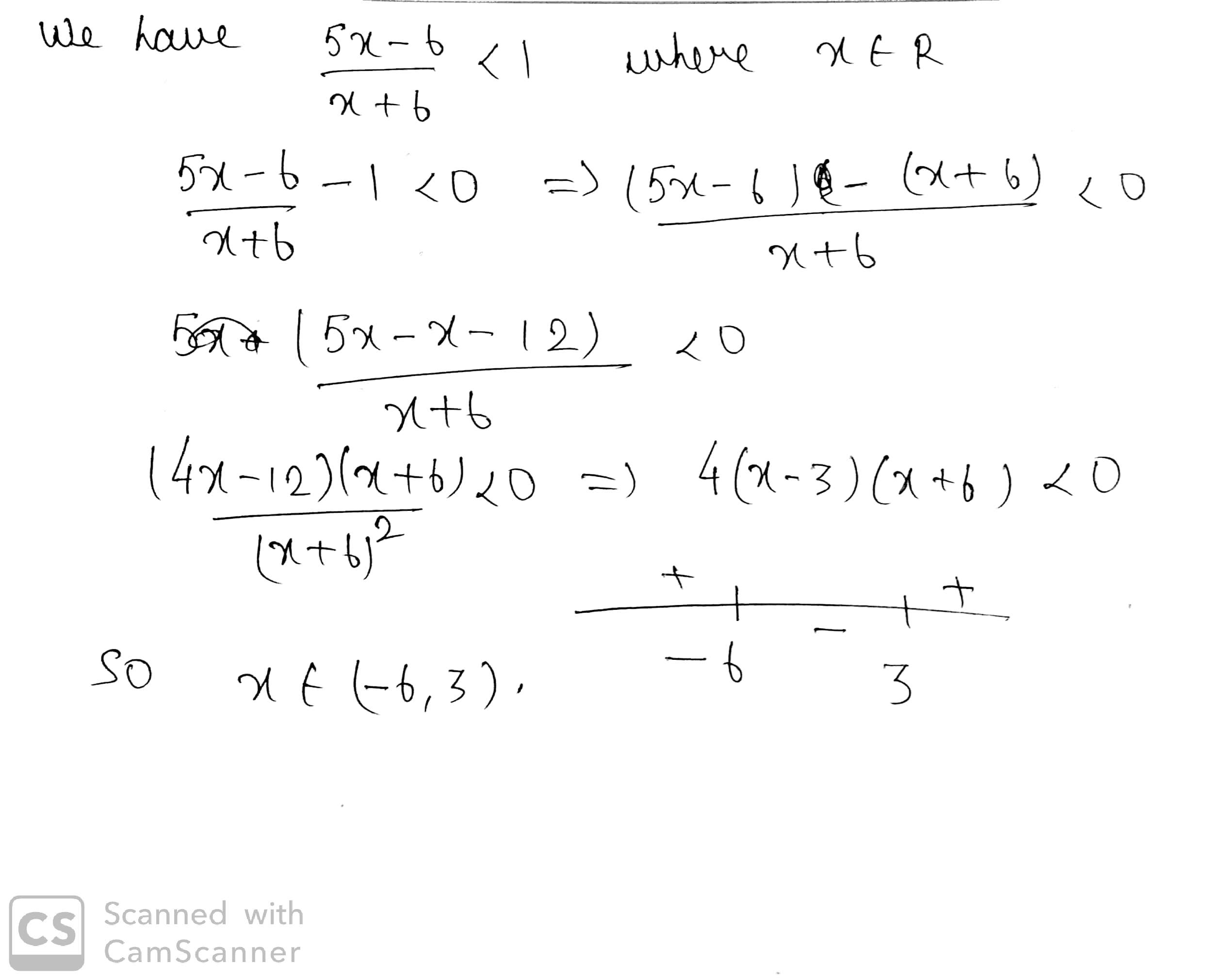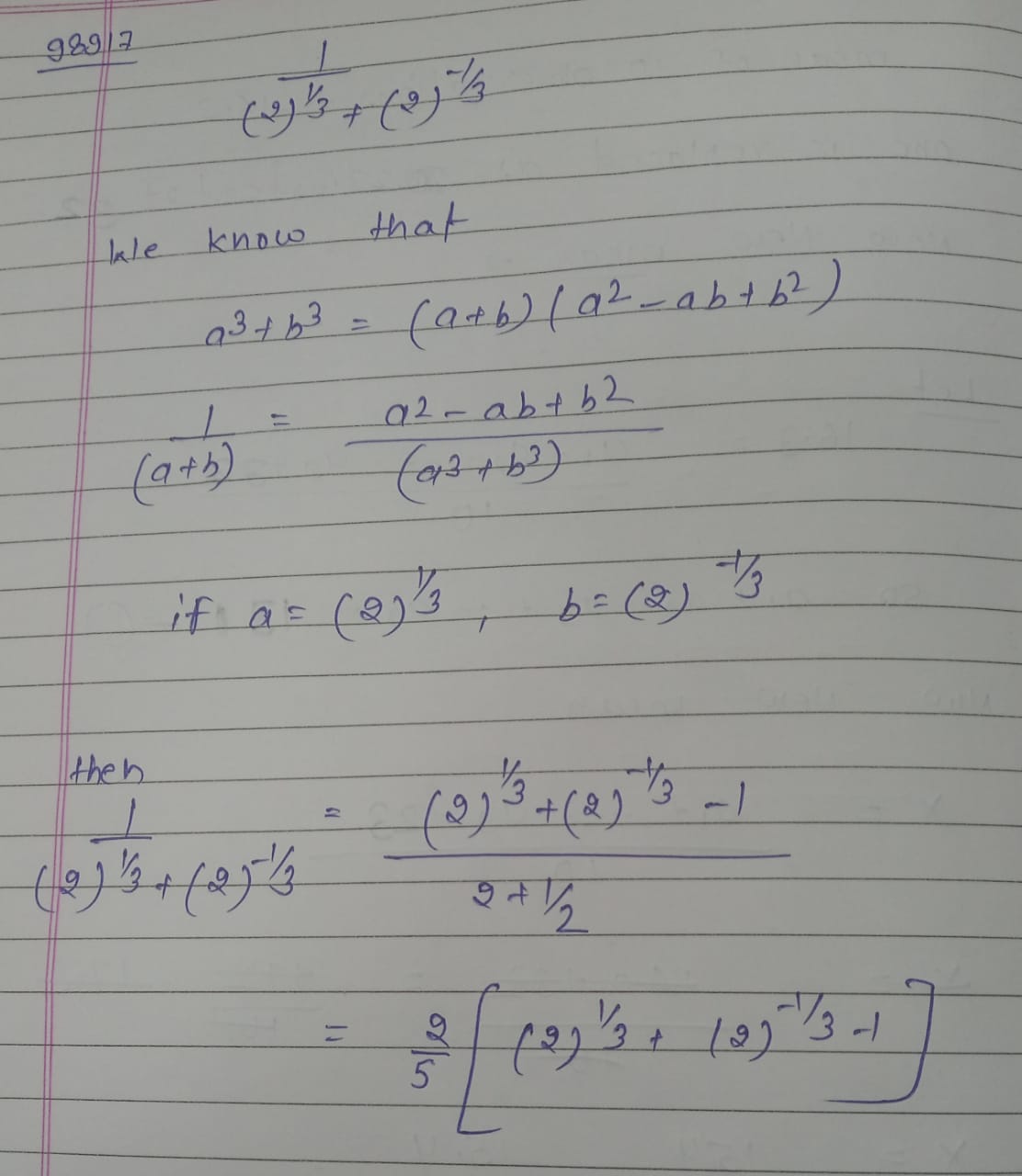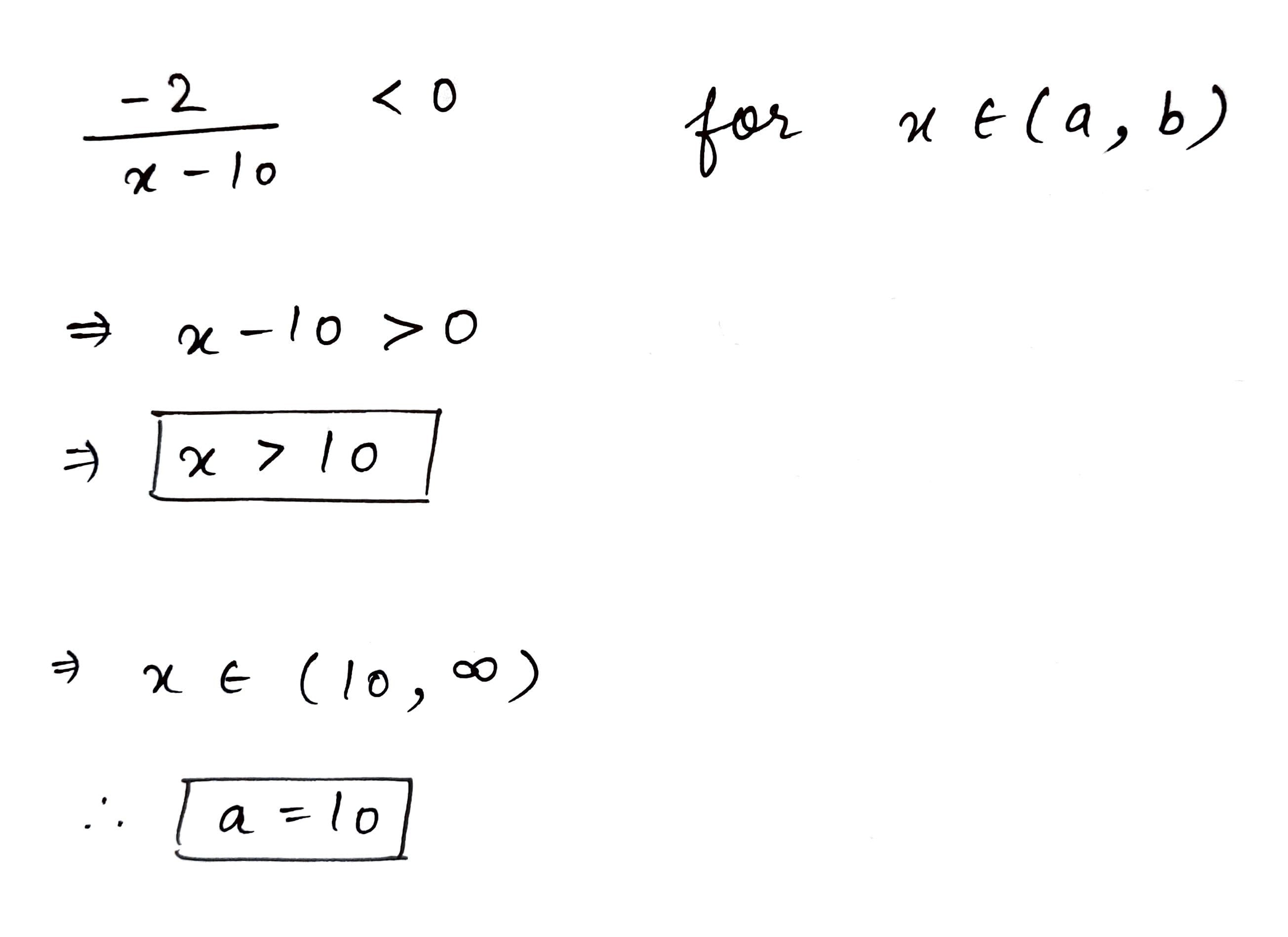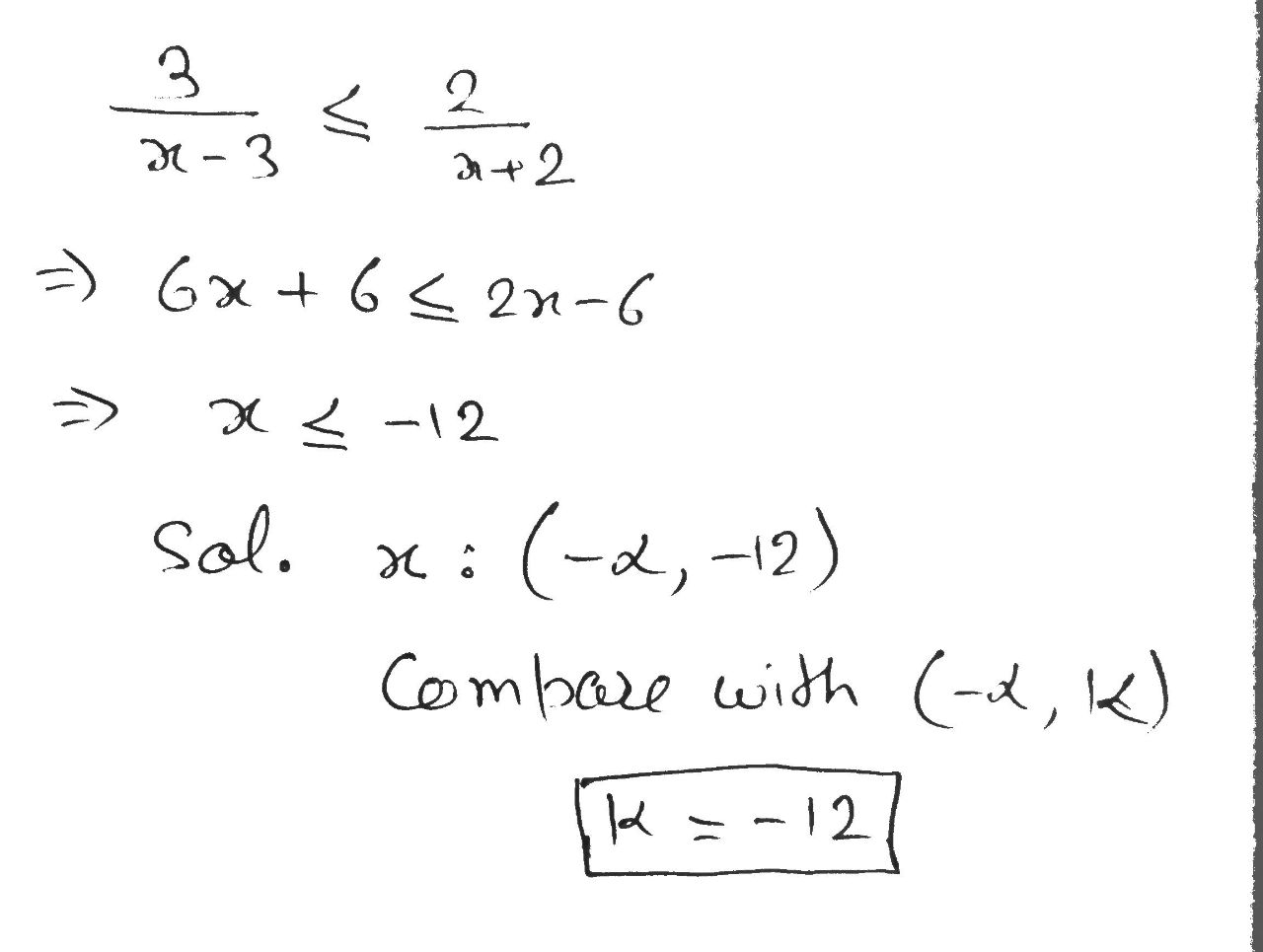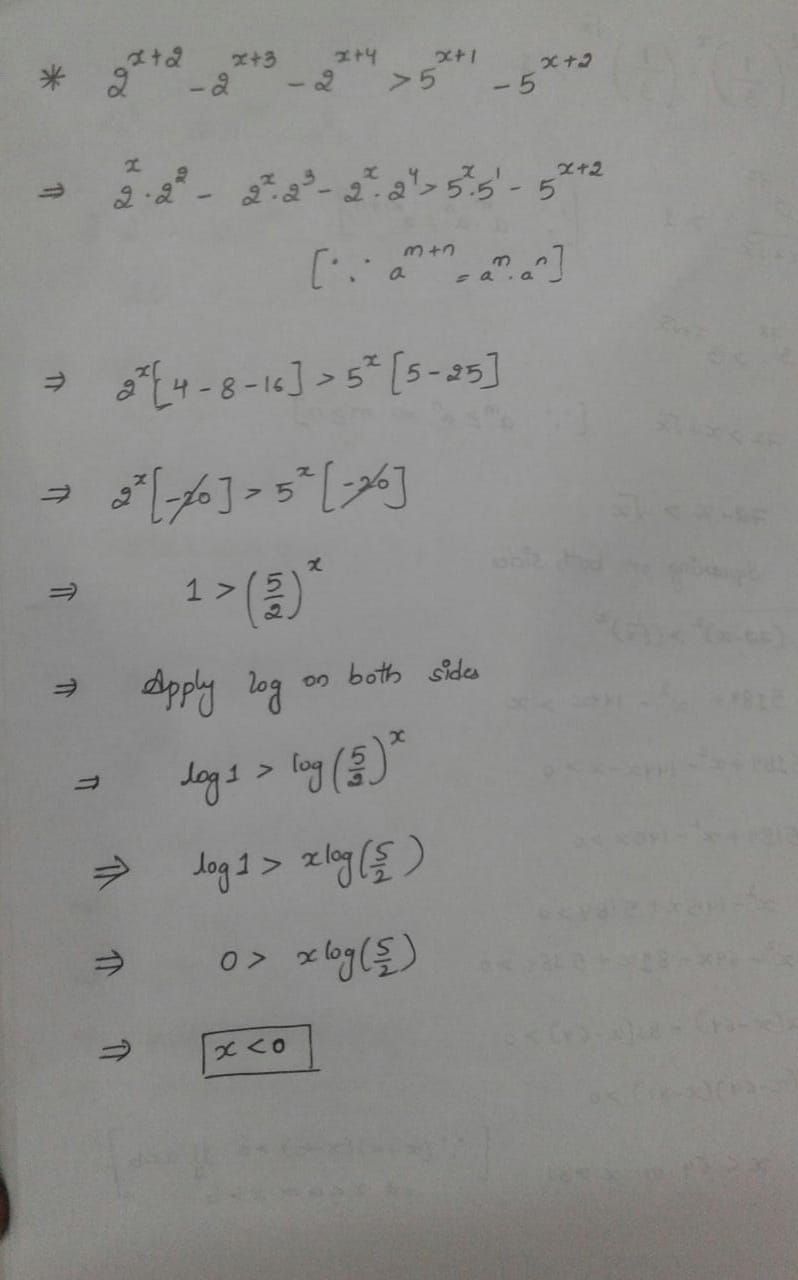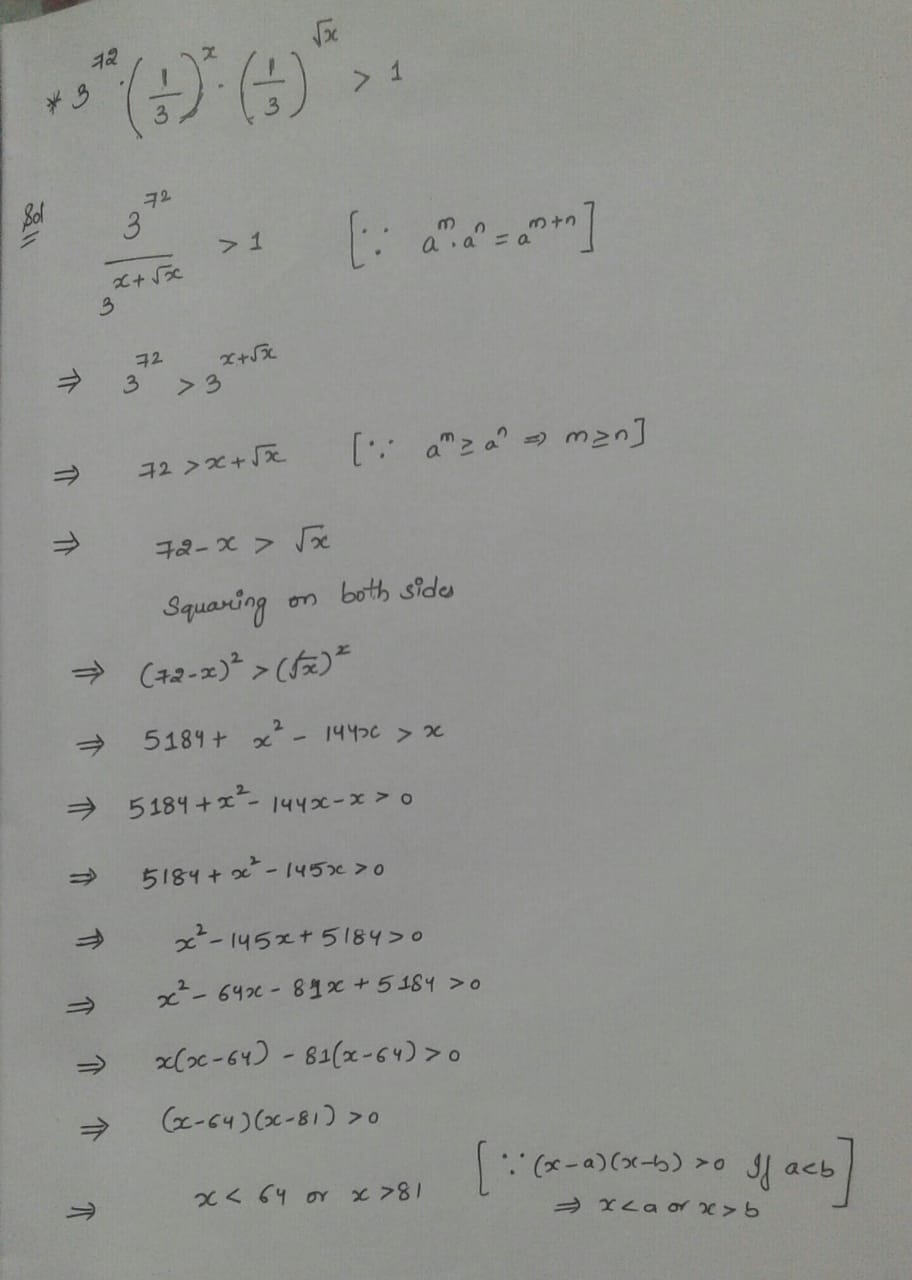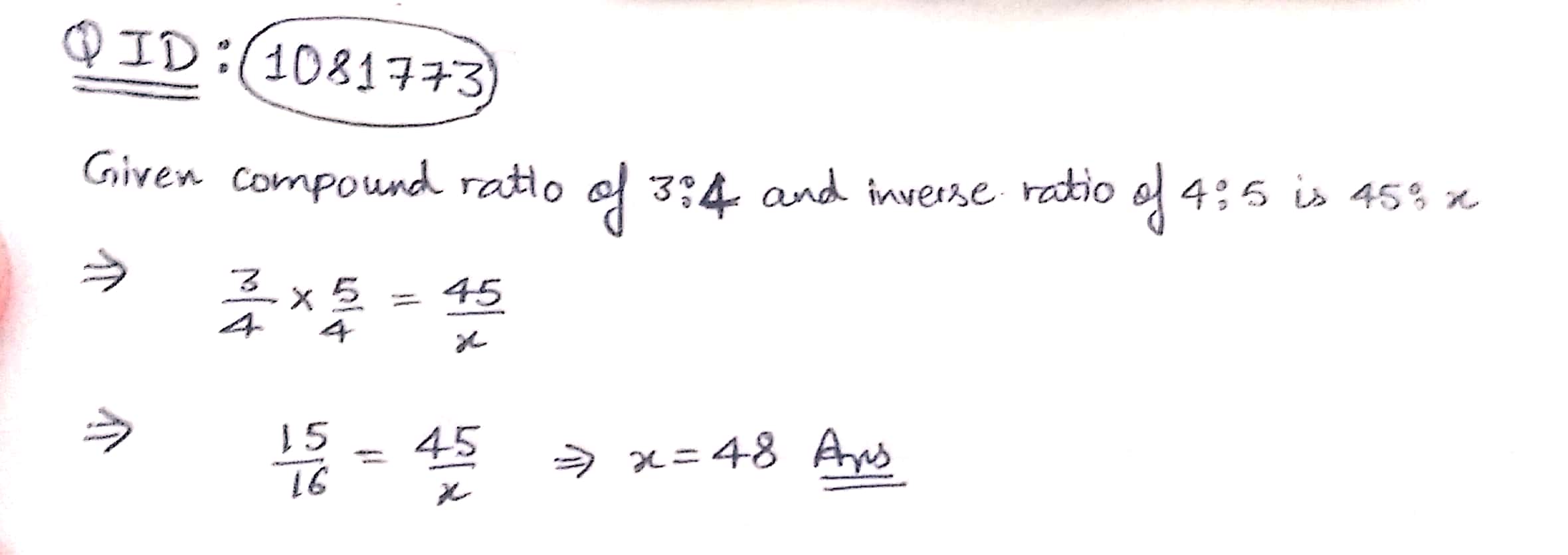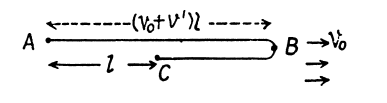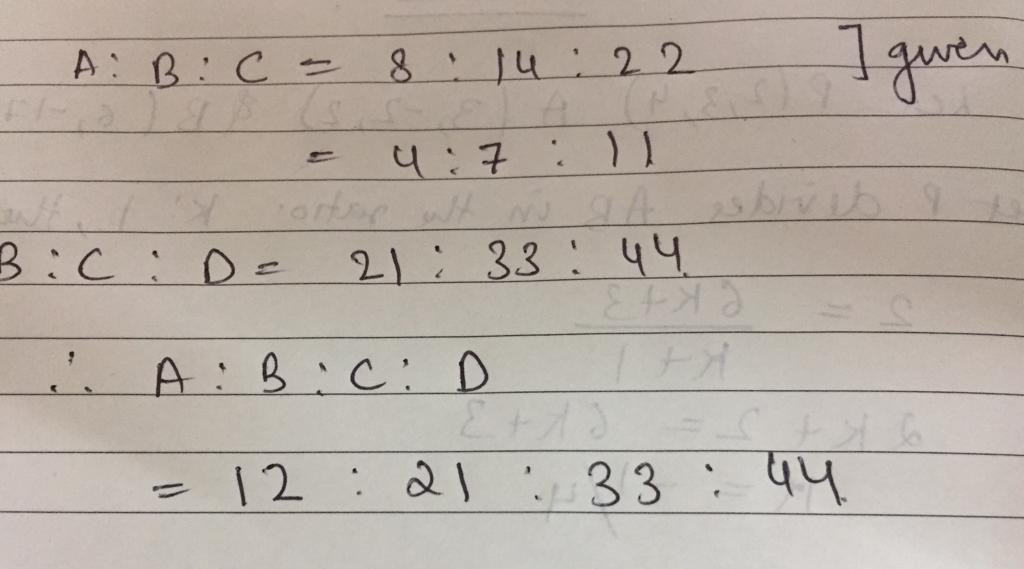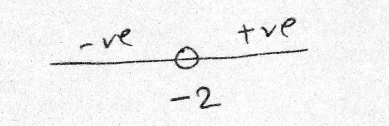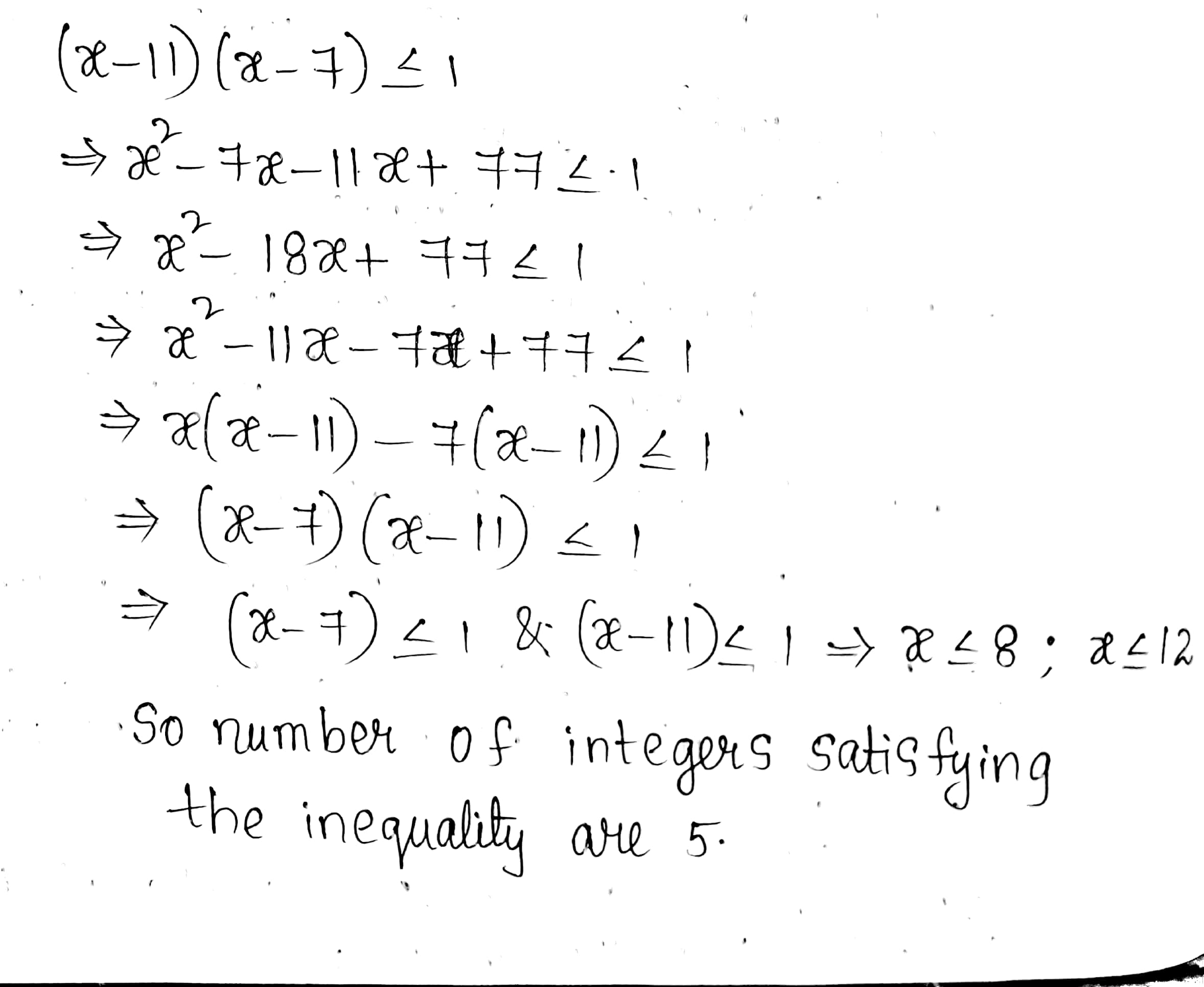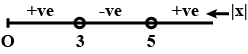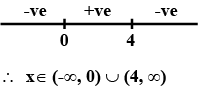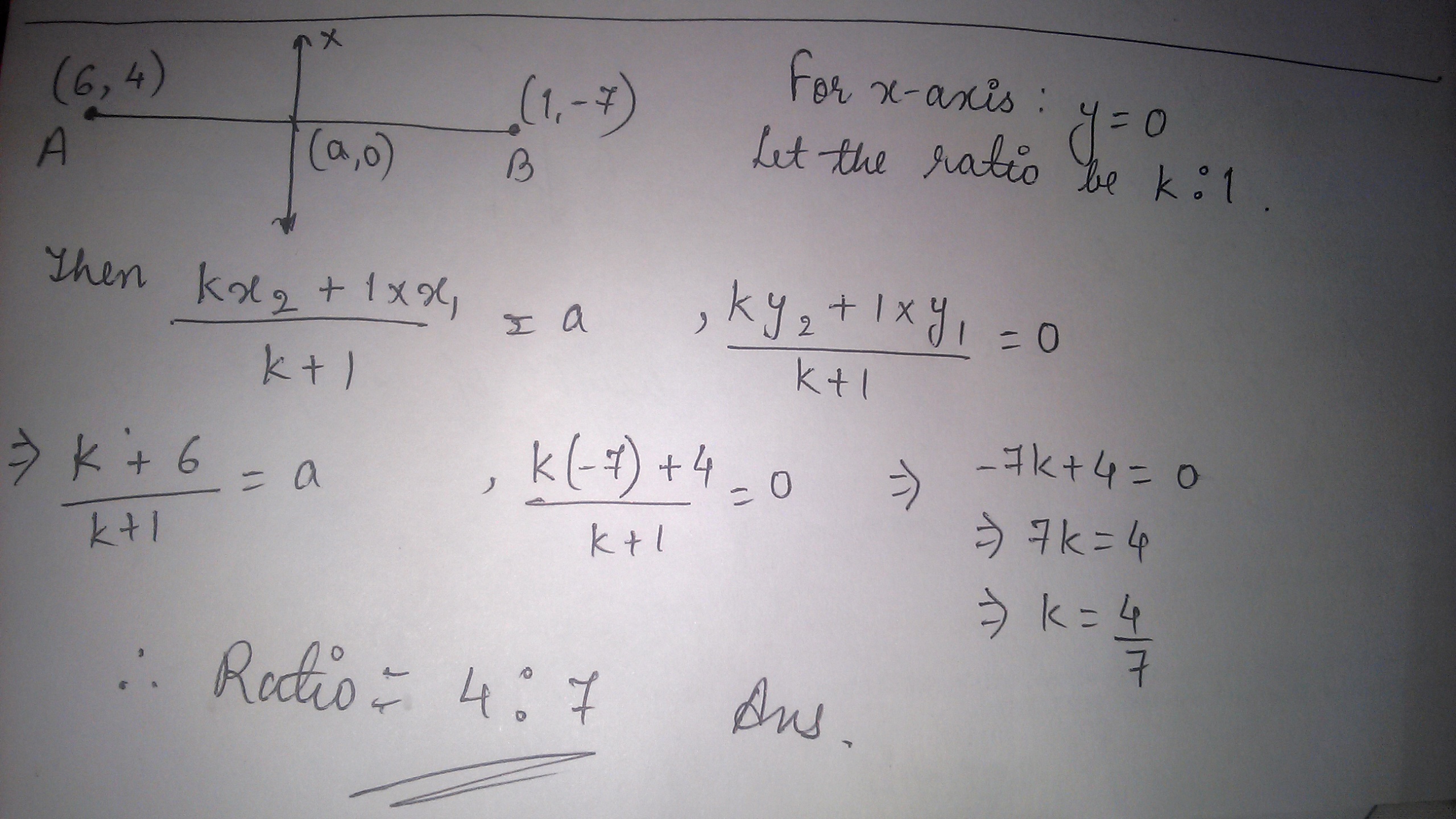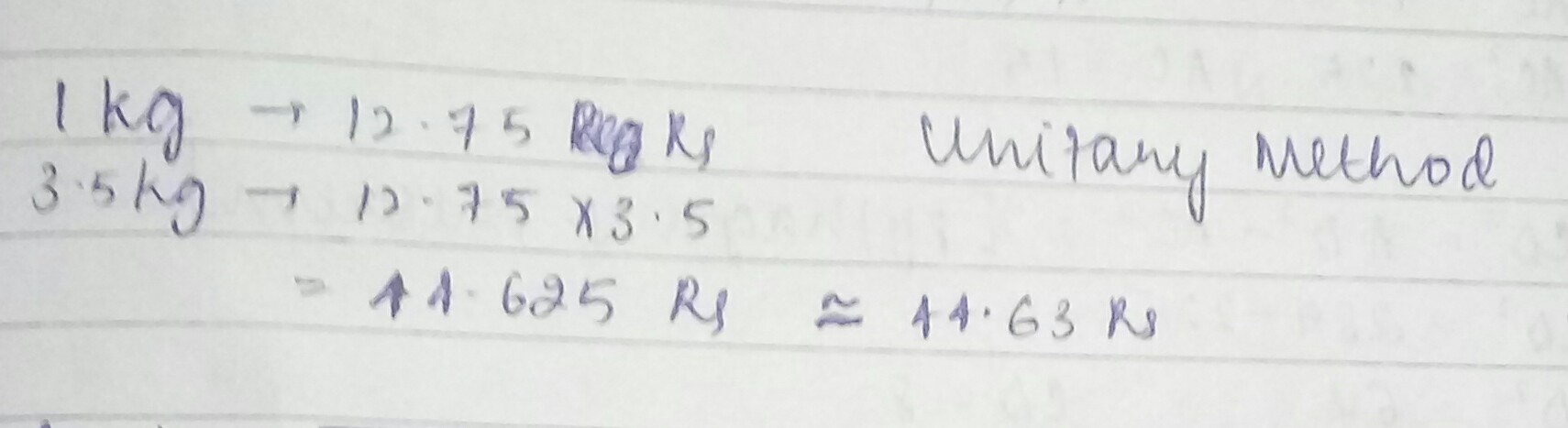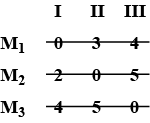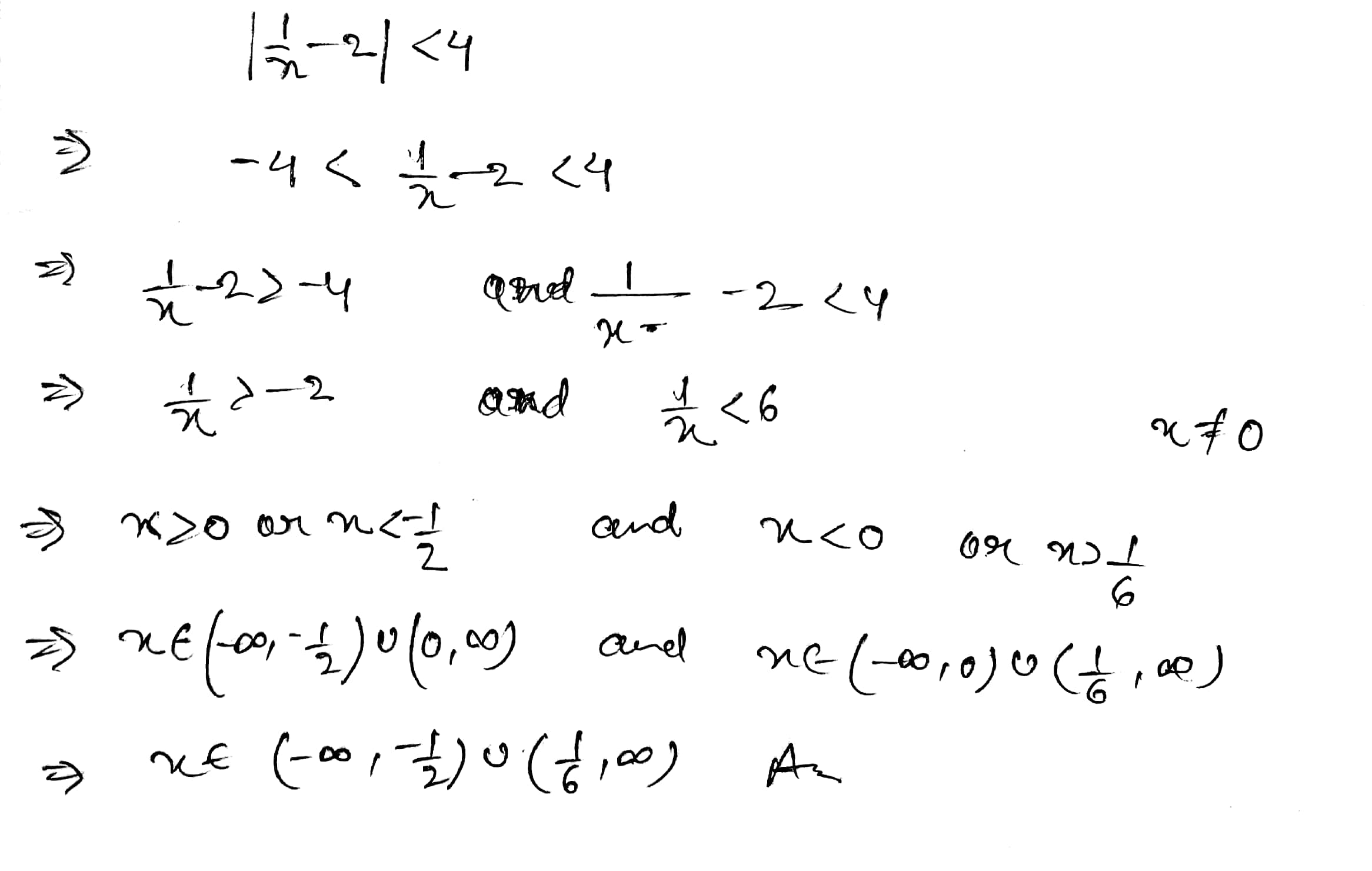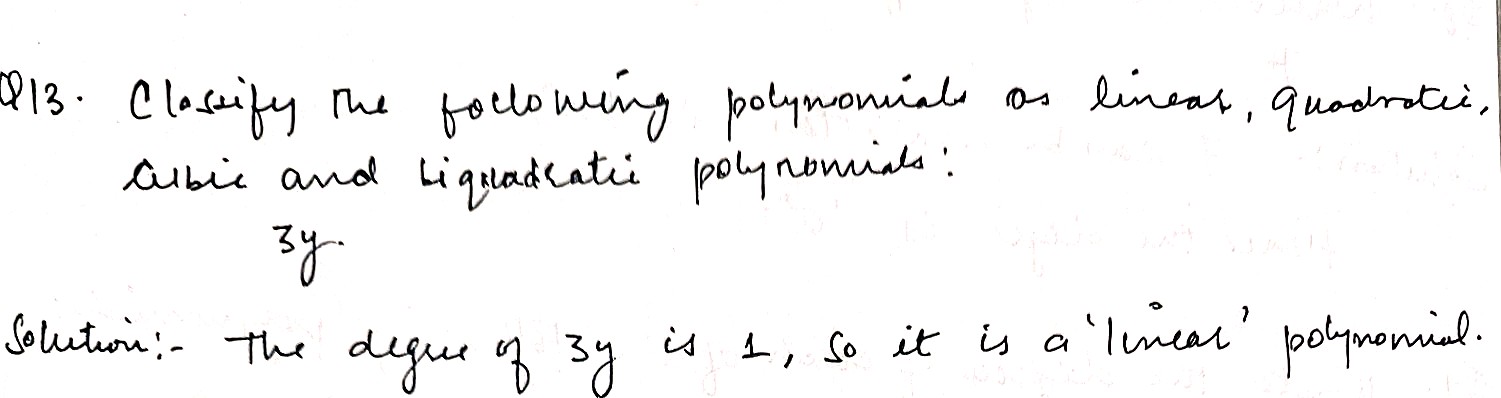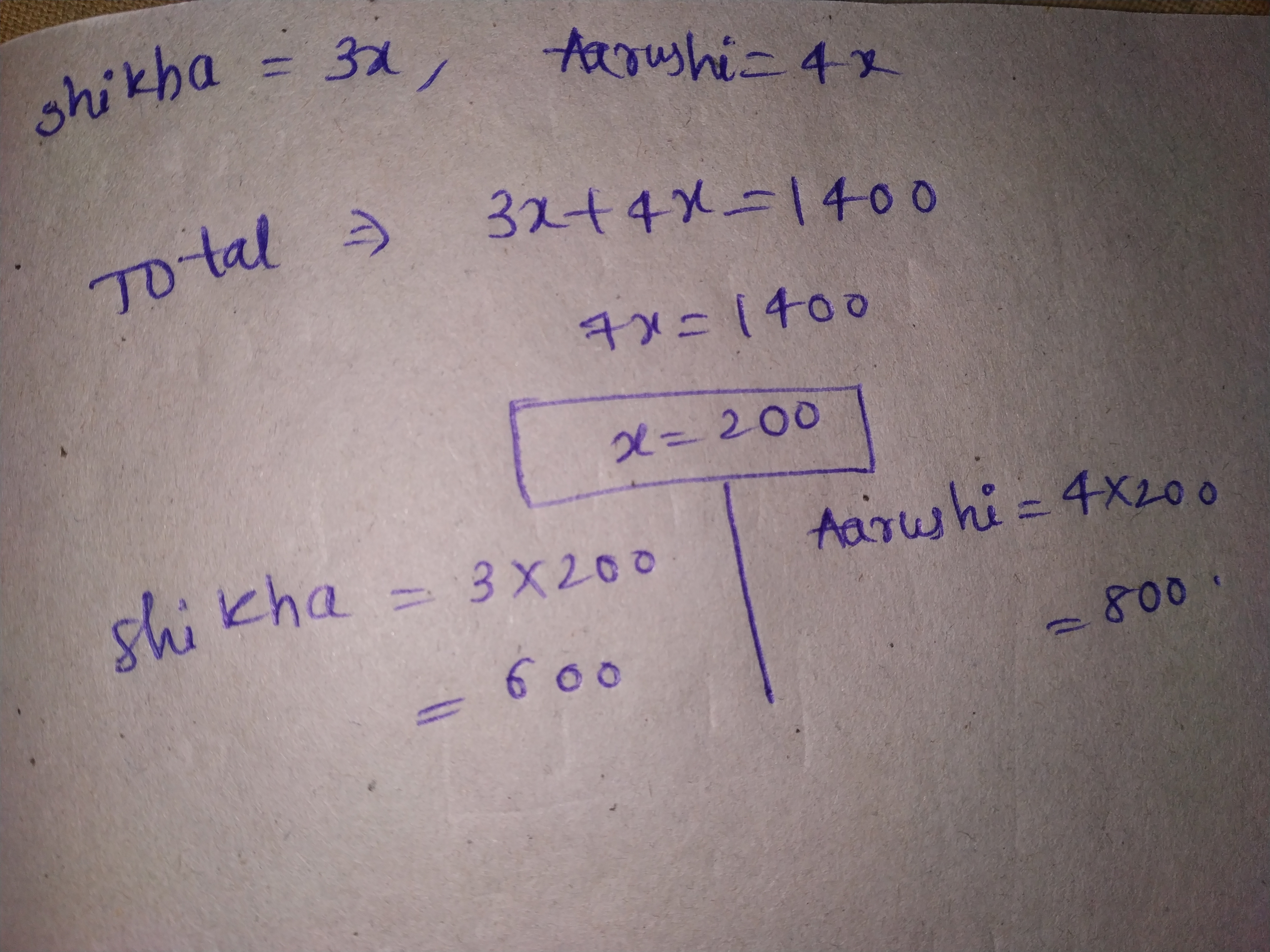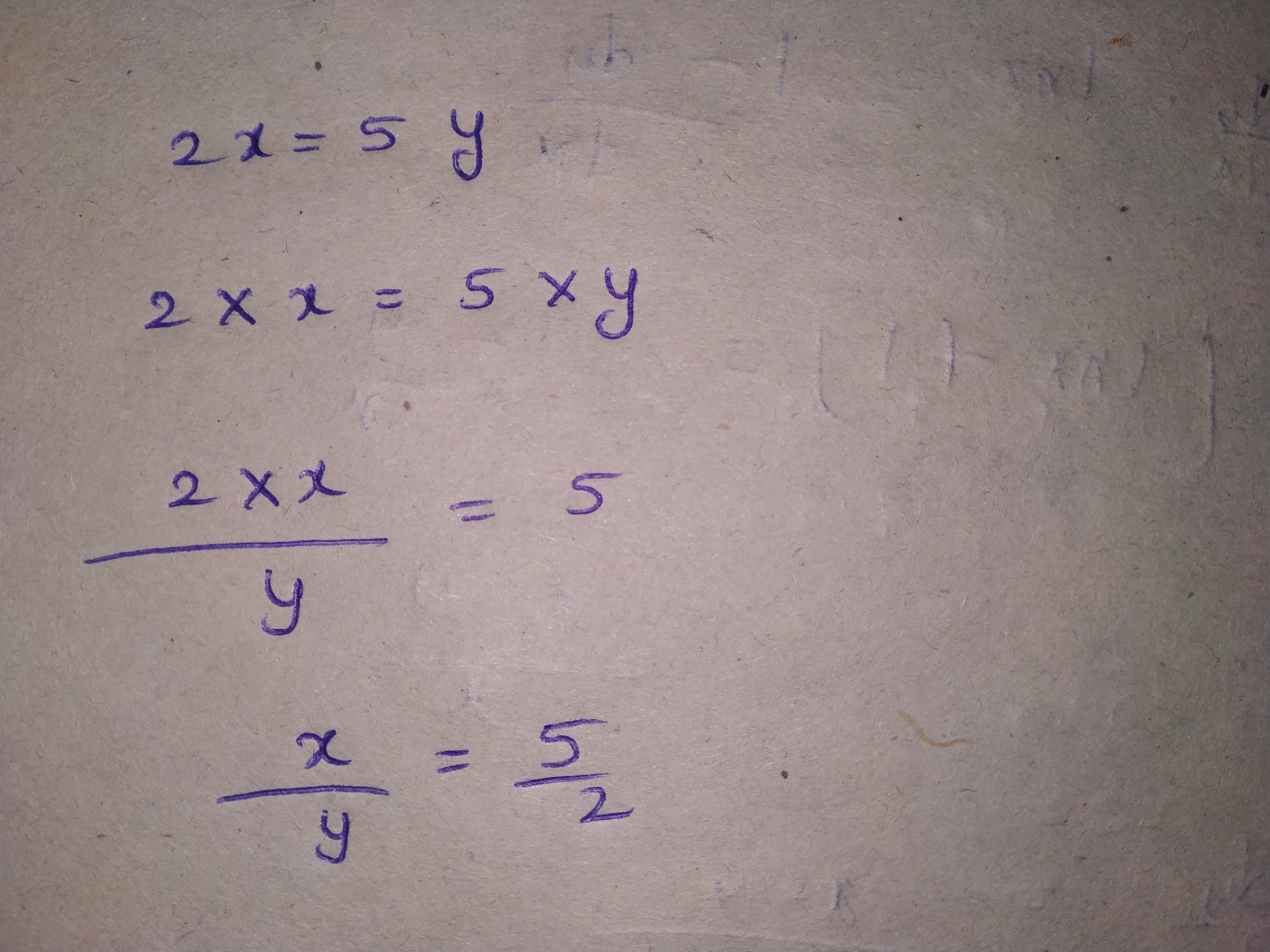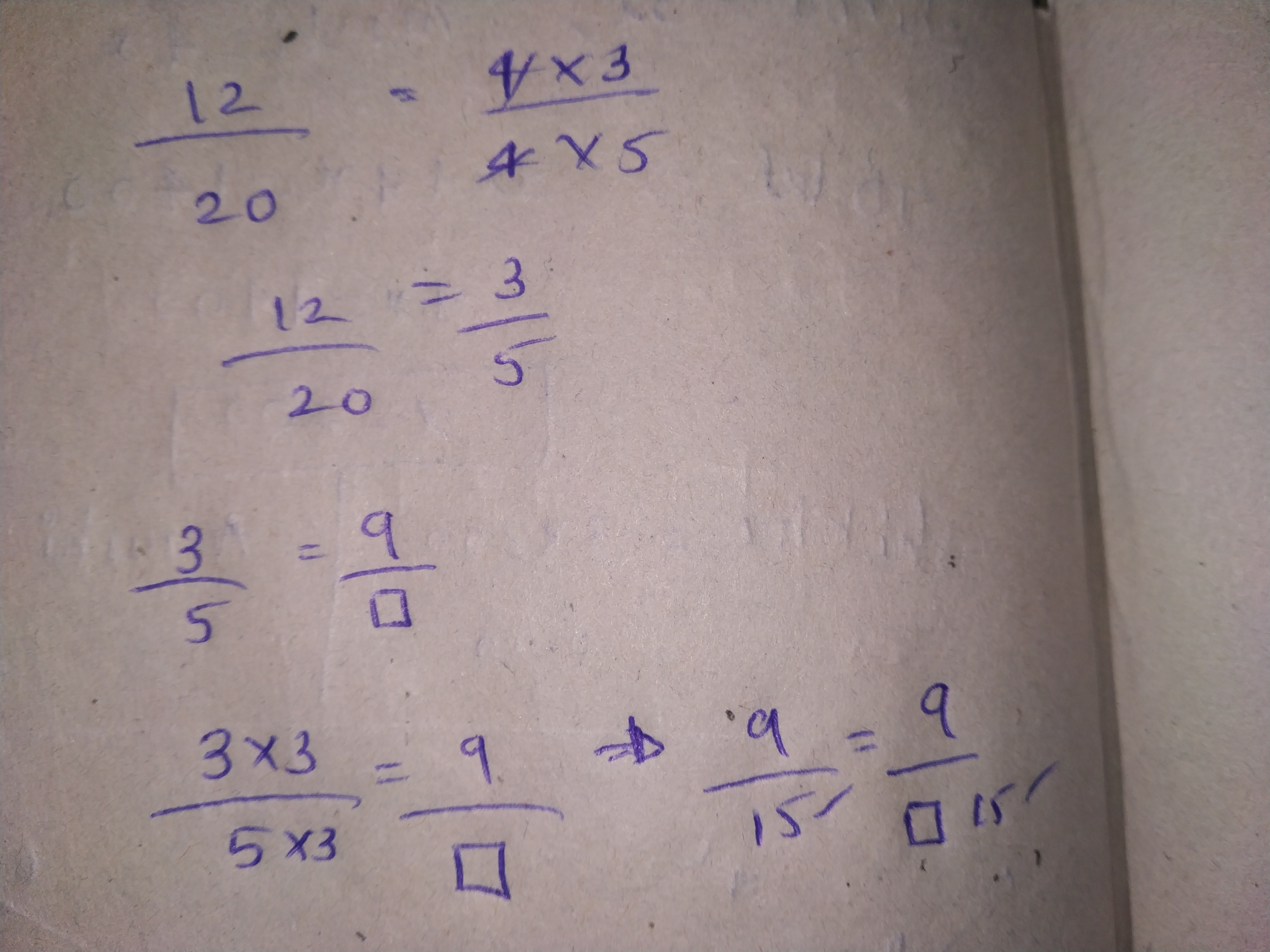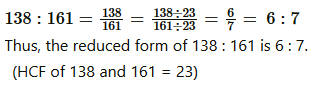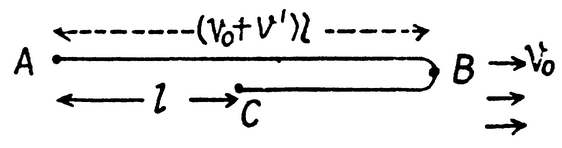Class 12 Commerce Applied Mathematics - Quantification And Numerical Applications

One side of a triangle measures 8 cm. Of the remaining two sides, one measures 2 cm more than the other. Then, the length of each side of the triangle is greater than $x$ cm. Find $x$ ?

Let the sides of the triangle in cm be

$x, x +2, 8$

Since in a triangle, the sum of two sides will be greater than the third side, we have

$x + x + 2 > 8$

$=> 2x + 2 > 8$

$=> 2x > 6$

$=> x > 3$

Hence the two unknown sides will be greater than

$3$ as they are

$x, x + 2$
Also

$8 > 3$
Hence, all the three sides of the triangle

$> 3 cm$

Solve 30x < 160 when x is an integer.

We are given

$30x < 160$

$\displaystyle \frac{30x}{30}< \frac{160}{30}$ i. e.

$x$ <

$\displaystyle \frac{16}{3}$

When x is an integer the solutions of the given inequality are ......,

$-3, -2, -1, 0, 1, 2, 3, 4, 5$
The solution set of the inequality is

${........, -3, -2, -1, 0, 1, 2, 3, 4, 5}$

Solve $\displaystyle \frac{3x-10}{2}\geq \frac{x+1}{6}-1$ , where $x$ is a ntaural no. less than 10.

We have

$\displaystyle \frac{3x-10}{2}\geq \frac{x+1}{6}-1$
or

$\displaystyle \frac{3x-10}{3}\geq \frac{x-5}{6}$
or

$\displaystyle 6x-20\geq x-5$
or

$\displaystyle 5x\geq 15$
or

$\displaystyle x\geq 3$
so the natural no. les than 10 are

$3,4,5,6,7,8,9$ .

Solve 30x < 160 when x is a natural number.

Given:

$30x < 160$

$\displaystyle \frac{30x}{30}< \frac{160}{30}$ i.e.

$\displaystyle x< \frac{16}{3}$

When x is a natural number, in this case, the following values of x make the statement true

$1, 2, 3, 4, 5$

The solution set of the inequality is

${1, 2, 3, 4, 5}$

Solve $5x - 7 < 2x + 2$ , when x is a natural number

We have

$5x - 7 < 2x + 2$
or

$5x - 7 + 7 < 2x + 2 + 7$ ..Rule 1

$5x < 2x + 9$

$3x < 9$
or

$x < 3$ .....Rule 2
When x is a natural number the solutions of the inequality are given by

$x < 3$
i. e. all natural numbers x which are less than 3.

Therefore the solution set of the inequality is

$1$ and

$2$

Solve the inequalities for real $x$ .
$4x + 3 < 5x + 7$

Given,

$4x +3 < 5x +7$

$\Rightarrow 3 -7 < 5x-4x$

$\Rightarrow x>-4$

$\Rightarrow x\in (-4, \infty)$

Solve the inequality for real $x$ .
${x +\dfrac{x}{2} + \dfrac{x}{3} < 11}$

Given,

$\displaystyle {x+\frac{x}{2}+\frac{x}{3}<11}$

$\displaystyle{\Rightarrow x\left ( 1+\frac{1}{2}+\frac{1}{3} \right )<11}$

${\Rightarrow \displaystyle x\left ( \frac{6+3+2}{6} \right )<11}$

$\displaystyle{\Rightarrow \frac{11x}{6}<11}$

$\displaystyle{\Rightarrow x<6}$

$\Rightarrow x\in (-\infty, 6)$

Solve $-12x > 30$ , when (i) $x$ is a natural number. (ii) $x$ is an integer

The given inequality is

$-12 x> 30$ .

$\displaystyle {\Rightarrow \frac{-12x}{-12}<\frac{30}{-12}}$ [ Dividing both sides by same negative number]

${\Rightarrow x<-\cfrac{5}{2}}$
(i) There is no natural number less than

${\left ( -\cfrac{5}{2} \right )}$
(ii) The integers less than

${\left ( -\cfrac{5}{2} \right )}$ are

$-\infty,......,-5,-4,-3.$

Solve $5x - 3 < 3x + 1$ when
(i) $x$ is an integer (ii) $x$ is a real number

We have

$5x - 3 < 3x + 1$

$\displaystyle \Rightarrow 5x-3+3<3x+1+3$

$\displaystyle \Rightarrow 5x<3x+4$

$\displaystyle \Rightarrow 5x-3\times <3x+4-3x$

$\displaystyle \Rightarrow 2x<4\Rightarrow x<2$
(i) When x is an integer the solutions of the given inequality are

$\{............., -4, -3, -2, -1, 0, 1\}$
(ii) When x is a real number the solutions of the inequality are given by x < 2 i.e. all real number x which are less than 2 Therefore the solution set of the inequality is

$\displaystyle x\in (-\infty ,2)$

Solve $24x < 100$ , when (i) $x$ is a natural number. (ii) $x$ is an integer

$24x < 100$

${\Rightarrow x<\cfrac{100}{24}}$

${\Rightarrow x <\dfrac{25}{6}}$
(i) It is evident that

$1,2,3$ and

$4$ are the only natural numbers less than

${\cfrac {25}{6}}$ ,
Thus when

$x$ is a natural number ,the solutions of the given inequality are

$1,2,3$ and

$4$ .
Hence, in this case, the solution set is

$\{1,2,3,4\}$ .
(ii) The integers less than

${\dfrac{25}{6}}$ are

$.......-3, -2,-1,0,1,2,3,4$ .
Hence,in this case ,the solution set is

$\{............ -3,-2,-1,0,1,2,3,4\}.$

Solve the inequality for real $x$ .
$\displaystyle {\frac{x}{3}>\frac{x}{2} +1}$

Given,

$\displaystyle {\frac{x}{3}>\frac{x}{2}+1}$

$\displaystyle{\Rightarrow \frac{x}{3}- \frac{x}{2} > 1}$

${\Rightarrow \displaystyle\frac{2x-3x}{6} > 1}$

${\Rightarrow\displaystyle \frac{-x}{6}>1}$

${\Rightarrow x< - 6}$

$\Rightarrow x\in (-\infty, -6)$

Solve the inequality for real $x$ .
$3 (2 -x) \geq 2 (1- x)$

Given,

${3(2-x) \geq 2(1-x)}$

${\Rightarrow 6-3x \geq 2-2x}$

${\Rightarrow 6-2 \geq 3x-2x}$

${\Rightarrow x \leq 4}$

$\Rightarrow x\in (-\infty, 4]$

Solve the inequalities for real $x$ .
$3x - 7 > 5x -1$

Given,

$3x -7 > 5x -1$

$\Rightarrow -7 +1> 5x -3x$

$\Rightarrow 2x <-6$

$\Rightarrow x<-3$

$\Rightarrow x\in (-\infty, -3)$

Solve the inequalities for real $x$ .
$3(x - 1) {\leq} 2 (x- 3)$

Given,

$3(x-1)\leq 2 (x-3)$

$\Rightarrow 3x -3 \leq 2x -6$

$\Rightarrow 3x -2x \leq -6 +3$

$\Rightarrow x \leq -3$

$\Rightarrow x\in (-\infty, -3]$

Solve, and express the answer graphically.
$\displaystyle\frac{3x-2}{x+4} < 2$

Solve with an

$=$

$\displaystyle\frac{3x-2}{x+4} = 2$

$3x-2=2\left(x+4\right)$

$3x-2x=10$

$x=10$
Critical values are

$x = 10$ and

$x = -4$ (denominator

$=0$ )

$ck\left( -6 \right) :\displaystyle\frac { 3\left( -6 \right) -2 }{ \left( -6 \right) +4 } =\displaystyle\frac { -20 }{ -2 } =+10$ : Not < 2

$ck\left( 0 \right) :\displaystyle\frac { 3\left( 0 \right) -2 }{ \left( 0 \right) +4 } =\displaystyle\frac { -2 }{ +4 } =-\displaystyle\frac { 1 }{ 2 }$ : yes < 2

$ck\left( 12 \right) :\displaystyle\frac { 3\left( 12 \right) -2 }{ \left( 12 \right) +4 } =\displaystyle\frac { 34 }{ 16 } =2\displaystyle\frac { 1 }{ 8 }$ : Not < 2
Solution :

$-4 < x < 10$
1027805_427022_ans_c22dfbb971114b68b67abcbc53bc154f.png

Solve the inequality for real $x$ .
$2 (2x + 3) -10 < 6 (x -2)$

Given,

${2(2x+3)-10 < 6 (x-2)}$

${\Rightarrow 4x + 6-10 <6 x -12}$

${\Rightarrow 4x -4 < 6x -12}$

${\Rightarrow -4 +12 < 6 x -4x}$

${\Rightarrow 8 < 2 x}$

${\Rightarrow x>4} \ \text{or} \ x\in (4,\infty)$

Solve the inequality for real $x$ .
$37- (3x + 5) \geq 9x -8 (x -3)$

Given,

${37 -(3x +5) \geq 9x-8 (x-3)}$

${\Rightarrow 37-3x -5 \geq 9x -8x +24}$

${\Rightarrow 32-3x \geq x+24}$

${\Rightarrow 32-24 \geq x+3x}$

${\Rightarrow 8\geq 4 x}{\Rightarrow x \leq 2} \ \text{or} \ x\in (-\infty, 2]$

Solve the inequality for real $x$ .
$\displaystyle {\frac{3(x-2)}{5}\leq \frac{5(2-x)}{3}}$

Given,

$\displaystyle {\frac{3(x-2)}{5}\leq\frac{5(2-x)}{3}}$

$\displaystyle{\Rightarrow 9(x-2)\leq 25(2-x)}$

$\displaystyle{\Rightarrow 9x-18 \leq 25 (2-x)}$

${\Rightarrow \displaystyle 9x -18 +25 x\leq 50}$

${\Rightarrow\displaystyle 34x -18 \leq 50 }$

${\Rightarrow\displaystyle 34x \leq 50 +18}$

${\Rightarrow 34 x \leq 68}{\Rightarrow x\leq 2} \ \text{or}\ x\in (-\infty, 2]$

$\displaystyle\frac { 2 }{ x+1 } \ge \displaystyle\frac { 1 }{ x-2 }$ is k, $\infty$ what is the value of the k?

R.E.F image

$\dfrac{2}{x+1}\geq \dfrac{1}{x-2}$

$2(x-2)\geq x+1$

$2x-4\geq x+1$

$x-5\geq 0$

Putting on number line

$x\epsilon [5,\infty )$

1140129_426598_ans_126ab889fbc34a7583fe5452162524f6.png

Solve, and express the answer in interval form.
$\displaystyle\frac{2x-8}{x-2} \ge 0$

Solve with an

$=$

$\displaystyle\frac{2x-8}{x-2} = 0$

$2x-8 = 0$

$x = 4$
Critical values are

$x = 4$ and

$x = 2$ (denominator

$= 0$ )

$ck\left( 0 \right) :\displaystyle\frac { 2\left( 0 \right) -8 }{ \left( 0 \right) -2 } =\displaystyle\frac { -8 }{ -2 } =4$ : yes

$\ge 0$

$ck\left( 3 \right) :\displaystyle\frac { 2\left( 3 \right) -8 }{ \left( 3 \right) -2 } =\displaystyle\frac { -2 }{ 1 } =-2$ : not

$\ge 0$

$ck\left( 5 \right) :\displaystyle\frac { 2\left( 5 \right) -8 }{ \left( 5 \right) -2 } =\displaystyle\frac { 2 }{ 3 }$ : yes

$\ge 0$
Solution:

$-\infty < x < 2$ or

$4 \le x < +\infty$
Interval form:

$\left(-\infty, 2\right) \cup$ [4,

$\infty$ )

Pressure varies inversely with volume while temperatures varies directly with volume. At a time, Volume $=50m^3$ , Temperature $=25^o$ K and Pressure $=1$ atmosphere. If the volume is increased to $200m^3$ , then find the temperature in $^o$ K

$P\,\alpha \dfrac{T}{V}\Rightarrow \dfrac{P_{1}V_{1}}{T_{1}} = \dfrac{P_{2}V_{2}}{T_{2}}$

Hence

$\dfrac{1\times 50}{25} = \dfrac{1\times 200}{T_{2}} \Rightarrow \boxed {T_{2} = 100\,k}$

1103275_515475_ans_638eec1dcb3e44a180a4ff5382e41ea1.jpg

Solve the given inequality for real x:
$\dfrac{x}{3} > \dfrac{x}{2}+1$

Given,

$\dfrac{x}{3}>\dfrac{x}{2}+1$

$\dfrac{x}{3}-\dfrac{x}{2}>1$

$-\dfrac{x}{6}>1$

$-x>6\\$

$x<-6$

Thus, all real numbers

$x,$ which are less than

$-6,$ are the solutions of the given inequality.

Hence, the solution set of the given inequality is

$(-\infty, -6)$ .

Solve the given inequality for real x :
$3(x-1) \leq 2(x-3)$

Given,

$3(x-1) \leq 2(x-3)$

$3x-3 \leq 2x-6\\$

$3x \leq 2x-3$

$x \leq -3$

Thus, all real numbers

$x$ , which are less than or equal to

$-3$ , are the solutions of the given inequality.

Hence, the solution set of the given inequality is

$(-\infty, -3]$ .

Solve $3 - 5x \leq 9$

We have,

$3 - 5x \leq 9$

$\Rightarrow -5x \leq 9 - 3 \Rightarrow - 5x \leq 6$

$\Rightarrow 5x \geq - 6 \Rightarrow x \geq - \dfrac{6}{5} \Rightarrow x \geq - 1.2$
The real numbers greater than or equal to -1.2 are solutions of given inequation.
1066198_620333_ans_d6a4190afcf44fc6bf4d1736be4bde88.jpg

1066198_620333_ans_d6a4190afcf44fc6bf4d1736be4bde88.jpg

Solve $3(5 - x) > 6$

We have,

$3(5 - x) > 6$
Dividing by 3 on both sides,

$5 - x > 2$

$\Rightarrow -x > 2 - 5 \Rightarrow -x > - 3$

$\therefore x < 3$
The real numbers less than 3 are solutions of given inequation
1066191_620332_ans_f1a14678c47848edab1eee81df825550.jpg

Solve the following inequality:
$\displaystyle\, \frac{3}{x - 2} < 1$

$\dfrac{3}{x-2}<1$

$3<x-2$

$x>5$

Solve the following inequality:
$\displaystyle\, \dfrac{6x - 5}{4x + 1} < 0$

$\cfrac { 6x-5 }{ 4x+1 } <0$

$\cfrac { x-\cfrac { 5 }{ 6 } }{ x+\cfrac { 1 }{ 4 } } <0\quad \quad$

$\quad \quad \quad \quad \quad \quad \quad (x=0\quad \cfrac { -5 }{ 6 } \times \cfrac { 4 }{ 1 } <0)$

$x \varepsilon (\cfrac { -1 }{ 4 } ,\cfrac { 5 }{ 6 } )$

Simplify the following expression:
$\displaystyle\left ( \frac{a + 3b}{(a - b)^2} + \frac{a - 3b}{a^2 - b^2} \right ) : \frac{a^2 + 3b^2}{(a - b)^2}$

$\dfrac{a+3{b}}{(a-b)^{2}}+\dfrac{a-3{b}}{a^{2}-b^{2}}$

$=\dfrac{1}{a-b}\bigg(\dfrac{a+3{b}}{a-b}+\dfrac{a-3{b}}{a+b}\bigg)$

$=\dfrac{(a+3{b})(a+b)+(a-3{b})(a-b)}{(a-b)^{2}(a+b)}$

$=\dfrac{2(a^{2}+3{b^{2}})}{(a-b)^{2}(a+b)}$

$\bigg(\dfrac{a+3{b}}{(a-b)^{2}}+\dfrac{a-3{b}}{a^{2}-b^{2}}\bigg):\dfrac{a^{2}+3{b^{2}}}{(a-b)^{2}}=\dfrac{2(a^{2}+3{b^{2}})}{(a-b)^{2}(a+b)}\times \dfrac{(a-b)^{2}}{a^{2}+3{b^{2}}}=\dfrac{2}{a+b}$

Solve the following inequation, write down the solution set and represent it on the real number line:
$-2+10x \leq 13x+10 < 24+10x$ , x $\epsilon$ Z.

$-2+10x\leq13x+10 \Rightarrow -3x \leq 12 \Rightarrow -x\leq 4\Rightarrow x\geq -4$

$13x+10<24+10x \Rightarrow 3x<14 \Rightarrow x< \cfrac{14}{3}$

Thus the range of x values satisfying the above inequalities is

$-4\leq x<\dfrac{14}{3}$

The number line depicting the range is shown above.

Solve the following inequality:
$\displaystyle\, \frac{2x - 3}{3x - 7} > 0$

$x\ne7/3$

$x<4\implies x\in (-\infty,4)-7/3$

Find all values of $a$ for which the inequality $\displaystyle\, \frac{x - 2a - 3}{x - a + 2} < 0$ is satisfied for all $x$ belonging to the interval $\displaystyle\, 1\leqslant x\leqslant 2$ .

$\cfrac { x-2a-3 }{ x-a+2 } <0$

$\cfrac { x-(2a+3) }{ x-(a-2) } <0$

$2a+3>a-2$

$2a+3\ge 2$

$2a\ge -1$

$a\ge \cfrac { -1 }{ 2 }$

$a-2\le 1$

$a\le -3$

$a\varepsilon (-5,-3]\bigcup [\cfrac { -1 }{ 2 } ,\infty )$

when

$2a+3<a-2$

$a<-5$

$a-2\ge 2$

$a\ge 4$ (not possible)

$2a+3\le 1$

$a\le -1$

$a\varepsilon (-5,3]\bigcup [\cfrac { -1 }{ 2 } ,\infty )$

Solve the following inequality:
$\displaystyle\, \frac{5x + 8}{4 - x} < 2$

$\cfrac { 5x+8 }{ 4-x } <2$

$\cfrac { 5x+8 }{ 4-x } -2<0$

$\cfrac { 5x+8-2(4-x) }{ 4-x } <0$

$\cfrac { 5x+8-8+2x }{ -(x-4) } <0$

$\cfrac { 7x }{ x-4 } >0$

$\cfrac { x }{ x-4 } >0$

$\cfrac { (x-0) }{ (x-4) } >0\quad \quad \quad \quad (x=1,\quad \cfrac { 1 }{ -3 } <0)$

$x\quad \varepsilon (-\infty ,0)\bigcup (4,\infty )$

Solve the following inequality:
$\displaystyle\, 2 + \frac{3}{x + 1} > \frac{2}{x}$

$2+\cfrac { 3 }{ x+1 } >\cfrac { 2 }{ x }$

$2+\cfrac { 3 }{ x+1 } -\cfrac { 2 }{ x } >0$

$\cfrac { 2(x(x+1))+3x-2(x+1) }{ x(x+1) } >0$

$\cfrac { 2{ (x }^{ 2 }+x)+3x-2x-2) }{ x(x+1) } >0$

$\cfrac { 2{ x }^{ 2 }+2x+3x-2x-2 }{ x(x+1) } >0$

$\cfrac { 2{ x }^{ 2 }+3x-2 }{ x(x+1) } >0$

$\cfrac { 2{ x }^{ 2 }+4x-x-2 }{ x(x+1) } >0\quad$

$\cfrac { 2x(x+2)-1(x+2) }{ x(x+1) } >0$

$\cfrac { (2x-1)(x+2) }{ (x-0)(x+1) } >0\quad \quad \quad (x=1,\quad \quad \frac { (2-1)(3) }{ 1\times 2 } >0)$

$x\quad \varepsilon \quad (-\infty ,-2)\bigcup (-1,0)\bigcup (\cfrac { 1 }{ 2 } ,\infty )$

Solve the following inequality:
$\displaystyle\, \frac{|x + 3| + x}{x + 2} > 1$

$\cfrac { \left| x+3 \right| +x }{ x+2 } >1$

$(i)when\quad (x+3)>0$

$\quad \quad \quad \quad x>-3$

$\quad \quad \cfrac { x+3+x }{ x+2 } -1>0$

$\quad \quad \cfrac { x+3+x-x-2 }{ x+2 } >0$

$\quad \quad \cfrac { (x+1) }{ (x+2) } >0$

$\quad \quad x\quad \varepsilon \quad (-\infty ,-1)\bigcup (-2,\infty )$

$\quad \quad but\quad since\quad x>-3$

$\quad x\quad \varepsilon \quad (-3,\infty )$

$(ii)when\quad (x+3)<0$

$\quad \quad x<-3$

$\quad \left| x+3 \right| =-(x+3)$

$\quad \cfrac { -x-3+x }{ x+2 } -1>0$

$\quad \cfrac { -x-3+x-x-2 }{ x+1 } >0$

$\quad \cfrac { x+5 }{ x+2 } >0$

$\quad x\quad \varepsilon \quad (-5,-2)$

$but\quad x<-3$

$x\quad \varepsilon \quad (-5,-3)$

$\\ x\quad \varepsilon \quad (-5,-3)\bigcup(-3,\infty )$

Solve the following inequality:
$\displaystyle\, \left | \frac{2x - 1}{x - 1} \right | > 2$

$\left| \cfrac { 2x-1 }{ x-1 } \right| >2$

$-2< \cfrac { 2x-1 }{ x-1 } <2$

$(i)\quad \cfrac { 2x-1 }{ x-1 } >2$

$\quad \quad \quad \cfrac { 2x-1 }{ x-1 } -2>0$

$\quad \quad \quad \cfrac { 2x-1-2x+2 }{ x-1 } >0$

$\quad \quad \quad \cfrac { 1 }{ x-1 } >0$

$\quad \quad \quad x\quad \varepsilon \quad (1,\infty )$

$(ii)\cfrac { 2x-1 }{ x-1 } +2<0$

$\quad \quad \cfrac { 2x-1+2x-2 }{ x-1 } <0$

$\quad \quad \cfrac { 4x-3 }{ x-1 } <0$

$\quad \quad \cfrac { x-\cfrac { 3 }{ 4 } }{ x-1 } <0$

$\quad x\quad \varepsilon \quad (1,\cfrac { 3 }{ 4 } )$

$\\ x\quad \varepsilon \quad (1,\infty )\quad \quad from(i)\& (ii)$

Solve the following inequality:
$\displaystyle\, \frac{|x - 1|}{x + 2} < 1$

$\cfrac { \left| x-1 \right| }{ x+2 } <1$

$(i)when\quad (x-1)>0,x>1$

$\quad \quad \cfrac { x-1 }{ x+2 } <1$

$\quad \quad \cfrac { x-1-x-2 }{ x+2 } <0$

$\quad \quad \cfrac { -3 }{ x+2 } <0$

$\quad \quad \cfrac { 1 }{ x+2 } >0$

$\quad x\quad \varepsilon \quad (2,\infty )$

$(ii)when\quad (x-1)<0,x<1$

$\quad \quad \cfrac { -x+1 }{ x+2 } <0$

$\quad \quad \cfrac { 1-x-x-2 }{ x+2 } <0$

$\quad \quad \cfrac { -2x-1 }{ x+2 } <0$

$\quad \quad \cfrac { x+\cfrac { 1 }{ 2 } }{ x+2 } >0\quad ,\quad x\quad \varepsilon (-\infty ,-2)\bigcup (\cfrac { -1 }{ 2 } ,\infty )$

$when\quad<1,\quad x\quad \varepsilon (-\infty ,-2)\bigcup(\cfrac { -1 }{ 2 } ,1)$

$x\quad \varepsilon (-\infty ,-2)\bigcup (\cfrac { -1 }{ 2 } ,1)\bigcup(2,\infty )$

Solve the following inequality:
$\displaystyle\, \left | \frac{2}{x - 4} \right | > 1$

$\left| \cfrac { 2 }{ x-4 } \right| >1$

$-1>\left| \cfrac { 2 }{ x-4 } \right| >1$

$(i)\cfrac { 2 }{ x-4 } >1$

$\quad \quad \cfrac { 2 }{ x-4 } -1>0$

$\quad \quad \cfrac { 2-x+4 }{ x-4 } >0$

$\quad \quad \cfrac { 6-x }{ x-4 } >0$

$\quad \quad \cfrac { x-6 }{ x-4 } <0$

$\quad \quad x\quad \varepsilon \quad (4,6)$

$(ii)\cfrac { 2 }{ x-4 } +1<0$

$\quad \quad \cfrac { 2+x-4 }{ x-4 } <0$

$\quad \quad \cfrac { x-2 }{ x-4 } <0$

$\quad \quad x\quad \varepsilon \quad (2,4)$

$\\ \\ \\ x\quad \varepsilon \quad (2,6)$

Solve the following inequality:
$\displaystyle\, \frac{14x}{x +1} - \frac{9x - 30}{x - 4} < 0$

$\cfrac { 14x }{ x+1 } -\cfrac { 9x-30 }{ x-4 } <0$

$\cfrac { 14x(x-4)-(9x-30)(x-1) }{ (x+1)(x-4) } <0$

$\cfrac { 14{ x }^{ 2 }-56x-(9{ x }^{ 2 }+9x-30x-30) }{ { x }^{ 2 }-4x+x-4 } <0$

$\cfrac { 14{ x }^{ 2 }-56x-9{ x }^{ 2 }-9x+30x+30 }{ (x+1)(x-4) } <0$

$\cfrac { 5{ x }^{ 2 }-35x+30 }{ (x+1)(x-4) } <0$

$\cfrac { { x }^{ 2 }-7x+6 }{ (x+1)(x-4) } <0$

$\cfrac { { x }^{ 2 }-6x-x+6 }{ (x+1)(x-4) } <0$

$\cfrac { (x-6)(x-1) }{ (x+1)(x-4) } <0\quad \quad \quad \quad \quad (x=7\quad \cfrac { 1\times 6 }{ 8\times 3 } >0)$

$x\quad \varepsilon (-1,1)\quad (4,6)$

Solve the following inequality:
$\displaystyle\, \frac{x + 7}{x - 5} + \frac{3x + 1}{2} \geqslant 0$

$\cfrac { x+7 }{ x-5 } +\cfrac { 3x+1 }{ 2 } \ge 0$

$\cfrac { 2x+14+(x-5)(3x+1) }{ 2(x-5) } \ge 0$

$\cfrac { 2x+14+3{ x }^{ 2 }+x-15x-5 }{ (x-5) } \ge 0$

$\frac { 3{ x }^{ 2 }-12x+9 }{ (x-5) } \ge 0$

$\cfrac { { x }^{ 2 }-4x+3 }{ (x-5) } \ge 0$

$\cfrac { { x }^{ 2 }-3x-x+3 }{ (x-5) } \ge 0$

$\cfrac { (x-3)(x-1) }{ (x-5) } \ge 0\quad \quad \quad \quad (x=4,\quad \cfrac { 1\times 3 }{ -1 } <0)$

$x\quad \varepsilon [1,3]\bigcup [5,\infty )$

Solve the following inequality:
$\displaystyle\, 1 + \frac{2}{x - 1} > \frac{6}{x}$

$1+\cfrac { 2 }{ x-1 } >\cfrac { 6 }{ x }$

$1+\cfrac { 2 }{ x-1 } -\cfrac { 6 }{ x } >0$

$\cfrac { x(x-1)+2x-6(x-1) }{ x(x-1) } >0$

$\cfrac { { x }^{ 2 }-x+2x-6x+6 }{ x(x-1) } >0$

$\cfrac { { x }^{ 2 }-5x+6 }{ x(x-1) } >0$

$\cfrac { { x }^{ 2 }-3x-2x+6 }{ x(x-1) } >0$

$\cfrac { (x-3)(x-2) }{ (x-0)(x-1) } >0\quad \quad \quad (x=4,\quad \cfrac { 1\times 2 }{ 4\times 3 } >0)$

$x\quad \varepsilon \quad (-\infty ,0)\bigcup (1,2)\bigcup(3,\infty )$

Solve the following inequality:
$\displaystyle\, \frac{|x - 2|}{x - 2} > 0$

$\cfrac { \left| x-2 \right| }{ x-2 } >0$

$\left| x-2 \right| \quad is\quad always>0$

$\cfrac { \left| x-2 \right| }{ x-2 } >0$

$x-2>0$

$x>2$

$x\quad \varepsilon \quad (2,\infty )$

Solve the following inequalities.
$\displaystyle x \, - \, 3 \, \sqrt{x \, - \, 3} \, - \, 1 \, > \, 0.$

$x-3\sqrt { x-3 } -1>0$

$\cfrac { x-1 }{ 3 } >\sqrt { x-3 }$

$\sqrt { x-3 } <\cfrac { x-1 }{ 3 }$

$(x-3)>0$

$x>3\quad \quad x\quad \varepsilon (3,\infty )\quad -(i)$

$x-3<{ (\cfrac { x-1 }{ 3 } ) }^{ 2 }$

$x-3<\cfrac { { x }^{ 2 }+1-2x }{ 9 }$

$9x-27<{ x }^{ 2 }-2x+1$

${ x }^{ 2 }-11x+28>0$

${ x }^{ 2 }-7x-4x+28>0$

$(x-7)(x-4)>0$

$x\quad \varepsilon (-\infty ,4)\bigcup (7,\infty )\quad -(ii)$

$from\quad (i)\& (ii)$

$x\quad \varepsilon (3,4)\bigcup (7,\infty )$

Solve the following inequality:
$\displaystyle \sqrt{\frac{x \, - \, 3}{x \, - \, 2}} \,> \, 0$

$\sqrt { \dfrac { x-3 }{ x-2 } } >0$

$\quad \dfrac { x-3 }{ x-2 } >0$

$x\quad \varepsilon (-\infty ,2)\bigcup(3,0)$

Solve the following inequality:
$\displaystyle \frac{\sqrt{a \, + \, 4}}{1 \, - \, a} \, \, < \, 0.$

$\cfrac { \sqrt { a+4 } }{ 1-a } <0$

$(\sqrt { a+4 } )\quad is\quad always\quad >0$

$so\quad \cfrac { \sqrt { a+4 } }{ 1-a } <0$

$\quad \quad \quad 1-a<0$

$\quad \quad \quad a>1$

$a\quad \varepsilon (1,\infty )$

Solve the following equation:
$\displaystyle\, \frac{3}{\sqrt{x + 1} + 1} + 2\sqrt{x + 1} = 5$

$\cfrac { 3 }{ \sqrt { x+1 } +1 } +2\sqrt { x+1 } =5$

$3+2\sqrt { x+1 } (\sqrt { x+1 } +1)=5(\sqrt { x+1 } +1)$

$3+2(x+1)+2\sqrt { x+1 } =5\sqrt { x+1 } +5$

$2x+5-5=3\sqrt { x+1 }$

$2x=3\sqrt { x+1 }$

${ (2x) }^{ 2 }={ (3\sqrt { x+1 } ) }^{ 2 }$

$4{ x }^{ 2 }=9x+9$

$4{ x }^{ 2 }-9x-9=0$

$4{ x }^{ 2 }-12x+3x-9=0$

$4x(x-3)+3(x-3)=0$

$(x-3)(4x+3)=0$

$x=3\quad and\quad \cfrac { -4 }{ 3 }$

$but\quad \sqrt { x+1 } \quad can\quad not\quad be\quad <0$

$hence\quad x=3$

Solve the following inequality:
$\displaystyle\, \frac{|x + 2| - x}{x} < 2$

$(i)when\quad (x+2)>0$

$\quad \quad x>-2$

$\cfrac { x+2-x }{ x } -2<0$

$\quad \cfrac { 2-2x }{ x } <0$

$\quad \cfrac { x-1 }{ x } >0$

$x\quad \varepsilon (-\infty ,0)\bigcup(1,\infty )$

$since\quad x>-2$

$x\quad \varepsilon (-2,0)\bigcup (1,\infty )$

$(i)when\quad (x+2)<0$

$\quad \quad x<-2$

$\cfrac { -x-2-x }{ x } -2<0$

$\cfrac { -2-2x-2x }{ x } <0$

$\cfrac { -2(2x+1) }{ x } <0$

$\cfrac { x+\cfrac { 1 }{ 2 } }{ x } <0$

$x\quad \varepsilon (-\infty ,\cfrac { -1 }{ 2 } )\bigcup (0,\infty )$

$\quad \quad \quad \quad x<-2$

$x\quad \varepsilon (-\infty ,-2)$

$x\quad \varepsilon (-\infty ,-2)\bigcup(-2,0)\bigcup (1,\infty )$

Solve the following inequality:
$\displaystyle\, \frac{1}{|x| - 3} < \frac{1}{2}$

$\cfrac { 1 }{ \left| x \right| -3 } <\cfrac { 1 }{ 2 }$

$(i)when\quad x>0$

$\quad \quad \cfrac { 1 }{ x-3 } -\cfrac { 1 }{ 2 } <0$

$\quad \quad \cfrac { 2-x+3 }{ 2(x-3) } <0$

$\quad \quad \cfrac { (x-5) }{ (x-3) } >0$

$\quad x\quad \varepsilon (-\infty ,3)\bigcup (5,\infty )$

$\quad x>0$

$\quad x\quad \varepsilon (0,3)\bigcup (5,\infty )$

$(ii)when\quad x<0$

$\quad \quad \cfrac { 1 }{ -x-3 } -\cfrac { 1 }{ 2 } <0$

$\quad \quad \quad \cfrac { 2-(-x-3) }{ -2(x+3) } <0$

$\quad \quad \quad \cfrac { 2+x+3 }{ x+3 } >0$

$\quad \quad \quad \cfrac { x+5 }{ x+3 } >0$

$x\quad \varepsilon (-\infty ,-5)\bigcup(-3,\infty )$

$\quad \quad \quad x<0$

$x\quad \varepsilon (-\infty ,-5)\bigcup (-3,0)$

$x\quad \varepsilon (-\infty ,-5)\bigcup(-3,0)\bigcup (0,3)\bigcup(5,\infty )$

Solve the following two- sided inequality.
$\displaystyle\, 0 < \frac{3x - 1}{2x + 5} < 1$

$(i)\cfrac { 3x-1 }{ 2x+5 } -1<0$

$\quad \cfrac { 3x-1-2x-5 }{ 2x+5 } <0$

$\quad \cfrac { x-6 }{ x+\cfrac { 5 }{ 2 } } <0$

$x\quad \varepsilon (\cfrac { -5 }{ 2 } ,6)\quad \quad -(1)$

$(ii)0<\cfrac { 3x-1 }{ 2x+5 }$

$\quad \quad \cfrac { x-\cfrac { 1 }{ 3 } }{ x+\cfrac { 5 }{ 2 } } >0$

$x\quad \varepsilon (-\infty ,-\cfrac { -5 }{ 2 } )\bigcup (\cfrac { 1 }{ 3 } ,\infty )\quad \quad -(2)$

$x\quad \varepsilon (\cfrac { 1 }{ 3 } ,\infty )\quad \quad -from(1)\quad \& \quad (2)$

Solve the following equation:
$\displaystyle\, \sqrt{2 - x} + \frac{4}{\sqrt{2 - x} + 3} = 2$

$\sqrt { 2-x } +\cfrac { 4 }{ \sqrt { 2-x } +3 } =2$

$\cfrac { 4 }{ \sqrt { 2-x } +3 } +\sqrt { 2-x } (\sqrt { 2-x } +3)=2$

$4+2-x+3\sqrt { 2-x } =2\sqrt { 2-x } +6\\ 6-x-6=-\sqrt { 2-x }$

$-x=-\sqrt { 2-x }$

$x=\sqrt { 2-x }$

${ x }^{ 2 }=2-x$

${ x }^{ 2 }+x-2=0$

${ x }^{ 2 }+2x-x-2=0$

$(x+2)(x-1)=0$

$\quad \quad x=1\quad and\quad -2$

$but\quad x=-2\quad doesn't\quad satisfy$

$\quad x=1$

Solve the following inequality:
$\displaystyle \sqrt{\frac{3x \, - \, 2}{2 \, - \, x}} \,> \, 1$

$\sqrt { \cfrac { 3x-2 }{ 2-x } } >1$

$(\cfrac { 3x-2 }{ 2-x } )>1$

$\cfrac { 3x-2 }{ 2-x } -1>0$

$\cfrac { 3x-2-2+x }{ 2-x } >0$

$\cfrac { 4(x-1) }{ -1(x-2) } >0$

$\cfrac { (x-1) }{ (x-2) } <0$

$x\quad \varepsilon (1,2)$

Solve the following inequality:
$\displaystyle \frac{2}{x} \,+ \, 3 \, \leqslant \, \sqrt{41 \, - \, \frac{16}{x}}.$

$\cfrac { 2 }{ x } +3\le \sqrt { 41-\cfrac { 16 }{ x } }$

$41-\cfrac { 16 }{ x } \ge ({ \cfrac { 2 }{ x } +3) }^{ 2 }$

$41-\cfrac { 16 }{ x } \ge \cfrac { 4 }{ { x }^{ 2 } } +9+\cfrac { 12 }{ x }$

$\cfrac { 4 }{ { x }^{ 2 } } +\cfrac { 28 }{ x } -32\le 0$

$\cfrac { 4+28x-32{ x }^{ 2 } }{ { x }^{ 2 } } \le 0$

$32{ x }^{ 2 }-28x-4\ge 0$

$8{ x }^{ 2 }-7x-1\ge 0$

$(8x+1)(x-1)\ge 0$

$x\quad \varepsilon (-\infty ,\cfrac { -1 }{ 8 } )\bigcup (1,\infty )$

Solve the following inequality:
$\displaystyle\, \left ( \dfrac{2}{5} \right )^\frac{6 - 5x}{2 + 5x} < \frac{25}{4}$

${ (\cfrac { 2 }{ 5 } ) }^{ \cfrac { 6-5x }{ 2+5x } }<\cfrac { 25 }{ 4 }$

$({ \cfrac { 2 }{ 5 } ) }^{ \cfrac { 5x-6 }{ 5x+2 } }<{ (\cfrac { 5 }{ 2 } ) }^{ 2 }$

$\cfrac { 5x-6 }{ 5x+2 } <2$

$\cfrac { 5x-6-10x-4 }{ 5x+2 } <0$

$\cfrac { -5x-10 }{ x+\cfrac { 2 }{ 5 } } <0$

$\cfrac { x+2 }{ x+\cfrac { 2 }{ 5 } } >0$

$x\quad \varepsilon (-\infty ,-2)\bigcup (\cfrac { -2 }{ 5 } ,\infty )$

Solve the following inequality:
$\displaystyle\, 2^x + 2^{-x + 1} - 3 < 0$

${ 2 }^{ x }+{ 2 }^{ -x+1 }-3<0$

${ 2 }^{ x }+\cfrac { 2 }{ { 2 }^{ x } } -3<0$

$let\quad { 2 }^{ x }=t\quad (t>0)$

$t+\cfrac { 2 }{ t } -3<0$

${ t }^{ 2 }-3t+2<0$

${ t }^{ 2 }-2t-t+2<0$

$(t-2)(t-1)<0$

$t\quad \varepsilon (1,2)$

${ 2 }^{ x }\quad \varepsilon (1,2)$

$x\quad \varepsilon (0,1)$

Solve the following inequality:
$\displaystyle\, 2^{2x + 1} - 21 \cdot \left ( \frac{1}{2} \right )^{2x + 3} + 2 \geqslant 0$

${ 2 }^{ 2x+1 }-21.{ (\cfrac { 1 }{ 2 } ) }^{ 2x+3 }+2\ge 0$

$2.{ { (2 }^{ x }) }^{ 2 }-21.{ \cfrac { 2 }{ 8 } }^{ -2x }+2\ge 0$

$2.{ 2 }^{ x }-\cfrac { 21 }{ 8 } { 2 }^{ -2x }+2\ge 0$

$let\quad { 2 }^{ 2x }=t\quad \quad (t>0)\\ 2t-\cfrac { 21 }{ 8t } +2\ge 0$

$16{ t }^{ 2 }-21+16t\ge 0$

$16{ t }^{ 2 }+16t-21\ge 0$

${ t }^{ 2 }+t-\cfrac { 21 }{ 6 } \ge 0$

$(t-\cfrac { 3 }{ 4 } )(t+\cfrac { 7 }{ 4 } )\ge 0$

$t\quad \varepsilon (-\infty ,\cfrac { -7 }{ 4 } )\bigcup (\cfrac { 3 }{ 4 } ,\infty )$

$but\quad t>0$

$t\quad \varepsilon (\cfrac { 3 }{ 4 } ,\infty )$

${ { (2 }^{ x }) }^{ 2 }\quad \varepsilon (\cfrac { 3 }{ 4 } ,\infty )$

${ 2 }^{ x }\quad \varepsilon (\cfrac { \sqrt { 3 } }{ 2 } ,\infty )$

$x\quad \varepsilon (\cfrac { \log { \cfrac { \sqrt { 3 } }{ 2 } } }{ \log { 2 } } ,\infty )$

Solve the following inequality:
$\displaystyle\, 5^{2x + 1} > 5^x + 4$

${ 5 }^{ 2x }\times 5>{ 5 }^{ x }+4$

$let\quad { 5 }^{ x }=t\quad \quad (t>0)$

$5{ t }^{ 2 }>t+4$

$5{ t }^{ 2 }-t-4>0$

$5{ t }^{ 2 }-5t+4t-4>0$

$5t(t-1)+4(t-1)>0$

$(t-1)(5t+4)>0$

$(t+\cfrac { 4 }{ 5 } )(t-1)>0$

$t\quad \varepsilon (-\infty ,\cfrac { -4 }{ 5 } )\bigcup (1,\infty )$

$but\quad t>0$

$t\quad \varepsilon (1,\infty )$

${ 5 }^{ x }\quad \varepsilon (1,\infty )$

$x\quad \varepsilon (0,\infty )$

Solve the following systems of inequality:
$|x| \geqslant 1, |x - 1| < 3$

$|x|\geq 1\implies x\in (-\infty,-1]\cup [1,\infty)$

Also,

$|x-1|<3\implies x-1\in (-3,3)\implies x\in(-2,4)$

$x\in (-2,-1]\cup [1,4)$

Solve the following inequality:

$\displaystyle\, x^2 \cdot 5^x - 5^(2 + x) < 0$

$x^2.5^x<5^{2+x} \implies x^2<5^2$

we can get equality at

$x=5$ when we compare terms on both sides

and LHS goes on decreasing on decreasing the value of x and satisfies the inequality

$\implies x \in (-\infty,5)$

Solve the following inequality:
$\displaystyle\, 4^{-x + 0.5} - 7 \cdot 2^{-x} - 4 < 0$

${ 4 }^{ -x+0.5 }-7({ 2 })^{ -x }-4<0$

$\cfrac { \sqrt { 4 } }{ { 4 }^{ x } } -\cfrac { 7 }{ { 2 }^{ x } } -4<0$

$\cfrac { 2 }{ { (2 }^{ x })^{ 2 } } -\cfrac { 7 }{ { 2 }^{ x } } -4<0$

$let\quad { 2 }^{ x }=t$

$\cfrac { 2 }{ { t }^{ 2 } } -\cfrac { 7 }{ t } -4<0$

$2-7t-4{ t }^{ 2 }<0$

$4{ t }^{ 2 }+7t-2>0$

$4{ t }^{ 2 }+8t-t-2>0$

$(4t-1)(t+2)>0$

$(t-\cfrac { 1 }{ 4 } )(t+2)>0$

$t\quad \varepsilon (-\infty ,-2)\bigcup (\cfrac { 1 }{ 4 } ,\infty )$

$but\quad t>0\\ hence$

$\quad \quad \quad t\quad \varepsilon (\cfrac { 1 }{ 4 } ,\infty )$

$\quad \quad { 2 }^{ x }\quad \varepsilon (\cfrac { 1 }{ 4 } ,\infty )$

$\quad \quad x\quad \varepsilon (-2,\infty )$

Solve the following inequality:
$\displaystyle\, 2^{3 - 6x} > 1$

$2^{3-6{x}}>1\implies 2^{3-6{x}}>2^{0}\implies 3-6{x}>0\implies x<\dfrac{1}{2}$

Solve the following inequality:
$\displaystyle\, 16^x > 0.125$

$16^{x}>0.125$

$\implies 2^{4{x}}>\dfrac{1}{8}$

$\implies 2^{4{x}}>2^{-3}$

$\implies 4{x}>-3$

$\implies x>-\dfrac{3}{4}$

Solve the following two- sided inequality.
$\displaystyle\, 1 \leqslant \frac{2 - x}{x + 1} \leqslant 2$

$1\le \cfrac { 2-x }{ x+1 } \le 2$

$(i)\cfrac { 2-x }{ x+1 } \le 2$

$\quad \cfrac { 2-x }{ x+1 } -2\le 0$

$\quad \cfrac { 2-x-2(x+1) }{ x+1 } \le$

$\quad \cfrac { 2-x-2x-2 }{ x+1 } \le 0$

$\quad \cfrac { x }{ x+1 } \ge 0$

$x\quad \varepsilon (-\infty ,-1]\bigcup [0,\infty )\quad -(1)$

$(ii)1\le \cfrac { 2-x }{ x+1 }$

$\quad \cfrac { 2-x }{ x+1 } -1\ge 0$

$\quad \cfrac { 2-x-x-1 }{ x+1 } \ge 0$

$\quad \cfrac { 1-x }{ x+1 } \ge 0$

$\quad \cfrac { 2x-1 }{ x+1 } \le 0$

$\quad \cfrac { x-\cfrac { 1 }{ 2 } }{ x+1 } \le 0$

$x\quad \varepsilon [-1,\cfrac { 1 }{ 2 } )\quad \quad -(2)$

$x\quad \varepsilon [0,\cfrac { 1 }{ 2 } ]\quad \quad -from\quad (1)\quad \& \quad (2)$

Solve the following inequality:
$\displaystyle\, (0.2)^\dfrac{2x - 3}{x - 2} > 5$

${ (\cfrac { 2 }{ 10 } ) }^{ \cfrac { 2x-3 }{ x-2 } }>{ (5) }^{ 1 }$

${ (\cfrac { 1 }{ 5 } ) }^{ \cfrac { 2x-3 }{ x-2 } }>{ 5 }^{ 1 }$

${ (5) }^{ \cfrac { 2x-3 }{ 2-x } }>{ 5 }^{ 1 }$

$\cfrac { 2x-3 }{ 2-x } -1>0$

$\cfrac { 2x-3-2+x }{ 2-x } >0$

$\cfrac { 3x-5 }{ x-2 } <0$

$\cfrac { x-\cfrac { 5 }{ 3 } }{ x-2 } <0$

$x\quad \varepsilon (\cfrac { 5 }{ 3 } ,2)$

Solve the following inequality:
$\displaystyle\, \left ( \dfrac{1}{5} \right )^\frac{2x + 1}{1 - x} > \left ( \frac{1}{5} \right )^{-3}$

${ (\cfrac { 1 }{ 5 } ) }^{ \cfrac { 2x+1 }{ 1-x } }>{ (\cfrac { 1 }{ 5 } ) }^{ -3 }$

${ (5 })^{ \cfrac { 2x+1 }{ x-1 } }>{ 5 }^{ 3 }$

$\cfrac { 2x+1 }{ x-1 } >3$

$\cfrac { 2x+1-3(x-1) }{ x-1 } >0$

$\cfrac { 2x+1-3x+3 }{ x-1 } >0$

$\cfrac { 4-x }{ x-1 } >0$

$\cfrac { x-4 }{ x-1 } <0$

$x\quad \varepsilon (1,4)$

Solve the following inequality:
$\displaystyle\, \left ( \dfrac{1}{3} \right )^{x + \dfrac{1}{2} - \dfrac{2}{x}} > \dfrac{1}{\sqrt{27}}$

${ (\cfrac { 1 }{ 3 } ) }^{ x+\cfrac { 1 }{ 2 } -\cfrac { 2 }{ x } }>\cfrac { 1 }{ \sqrt { 27 } }$

${ 3 }^{ \cfrac { 2 }{ x } -x-\cfrac { 1 }{ 2 } }>{ 3 }^{ \cfrac { -3 }{ 2 } }$

$\cfrac { 2 }{ x } -x-\cfrac { 1 }{ 2 } >\cfrac { -3 }{ 2 }$

$\cfrac { 2 }{ x } -x+1>0$

$2-{ x }^{ 2 }+x<0$

${ x }^{ 2 }-x-2<0$

${ x }^{ 2 }-2x+x-2<0$

$(x-2)(x+1)<0$

$x\quad \varepsilon (-1,2)$

Solve the following inequality:
$\displaystyle\, 2^x + 2^{| x| } \geqslant 2\sqrt{2}$

${ 2 }^{ x }+{ 2 }^{ \left| x \right| }\ge { 2 }^{ \cfrac { 3 }{ 2 } }$

$when\quad x>0$

$2\times { 2 }^{ x }\ge { 2 }^{ \cfrac { 3 }{ 2 } }$

${ 2 }^{ x+1 }\ge { 2 }^{ \cfrac { 3 }{ 2 } }$

$x+1\ge \cfrac { 3 }{ 2 }$

$x\ge \cfrac { 1 }{ 2 } \quad \quad ,\quad x\quad \varepsilon [\cfrac { 1 }{ 2 } ,\infty )\quad \quad -(i)$

$when\quad x<0$

${ 2 }^{ x }+{ 2 }^{ -x }\ge { 2 }^{ \cfrac { 3 }{ 2 } }$

${ 2 }^{ x }+\cfrac { 1 }{ { 2 }^{ x } } \ge { 2 }^{ \cfrac { 3 }{ 2 } }$

$\cfrac { { { (2 }^{ x }) }^{ 2 }+1 }{ { 2 }^{ x } } \ge { 2 }^{ \cfrac { 3 }{ 2 } }$

$let\quad { 2 }^{ x }=t\quad \quad (t>0)$

Solve the following inequality:
$\displaystyle\, 4^x - 3 \leqslant 2^{x + 1}$

${ { (2 }^{ x }) }^{ 2 }-3\le 2.{ 2 }^{ x }$

$let\quad { 2 }^{ x }=t\quad \quad (t>0)$

${ t }^{ 2 }-3\le 2t$

${ t }^{ 2 }-2t-3\le 0$

${ t }^{ 2 }-3t+t-3\le 0$

$(t-3)(t+1)\le 0$

$t\quad \varepsilon (-1,3)$

$but\quad t>0,\quad t\quad \varepsilon (0,3)$

${ 2 }^{ x }\quad \varepsilon (0,3)$

$x\quad \varepsilon (-\infty ,\cfrac { \log { 3 } }{ \log { 2 } } )$

Solve the following inequalities.
$\displaystyle\, \frac{1 \, - \, \sqrt{1 \, - \, 8x^2}}{2x} \, < \, 1$

$\Rightarrow \dfrac {1 - \sqrt {1 - 8x^{2}}}{2x} < 1$

$\Rightarrow 1 - \sqrt {1 - 8x^{2}} < 2x$

$\Rightarrow 1 - 2x < \sqrt {1 - 8x^{2}}$

Square both sides,

$\Rightarrow 1 + 4x^{2} - 4x < 1 - 8x^{2}$

$\Rightarrow 12x^{2} - 4x < 0$

$\Rightarrow 3x^{2} - x < 0$

$\Rightarrow x(3x - 1) < 0$

$x < 0, x (3x - 1) < 0$

$x = 0, x (3x - 1) = 0$

$0 < x < \dfrac {1}{3}, x (3x - 1) < 0$

$x\geq \dfrac {1}{3}, x(3x - 1) \geq 0$

$\therefore solution: 0 < x < \dfrac {1}{3}$

Interval notation :

$\left (0, \dfrac {1}{3}\right )$ .

Solve the following inequality:
$\displaystyle\, \left ( \dfrac{1}{3} \right )^ \frac{ | x + 2| }{2 - | x| } > 9$

${ (\cfrac { 1 }{ 3 } })^{ \cfrac { \left| x+2 \right| }{ 2-\left| x \right| } }>{ 3 }^{ 2 }$

${ 3 }^{ \cfrac { \left| x+2 \right| }{ \left| x \right| +2 } }>{ 3 }^{ 2 }$

$\cfrac { \left| x+2 \right| }{ \left| x \right| -2 } >2$

$\cfrac { \left| x+2 \right| -2(\left| x \right| -2) }{ \left| x \right| -2 } >0$

$\cfrac { \left| x+2 \right| -2\left| x \right| +4 }{ \left| x \right| -2 } >0$

$(i)when\quad x>0$

$\quad \cfrac { x+2-2x+4 }{ x-2 } >0$

$\quad \cfrac { x-6 }{ x-2 } <0\quad \quad ,\\x\quad \varepsilon (2,6) \quad -(1)$

$(ii)when\quad x<-2$

$\quad \cfrac { -x-2+2x+4 }{ -x-2 } >0$

$\quad \cfrac { x+2 }{ -(x+2) } >0$

$\quad 1<0\quad \quad (not\quad possible)$

$\quad x\quad \varepsilon \{ \quad \} \quad -(2)$

$(iii)when\quad -2<x<0$

$\quad \quad \cfrac { x+2-2(-x-2) }{ -x-2 } >0$

$\quad \quad \cfrac { x+2+2x+4 }{ x+2 } <0$

$\quad \quad \cfrac { x+2 }{ x+2 } <0\quad \quad (not\quad possible)$

$\quad x\quad \varepsilon \{ \quad \} \quad -(3)$

$from\quad (1),(2)\quad \& (3),\quad x\quad \varepsilon (2,6)\quad$

State which of the following are equation (with variable). Given reasons for your an mention which variable is used from the equation with a variable.
$8m<17$

$8m<17$

No It is not an equation in variable as there not equal sign in the expression

Solve the inequation $\dfrac{1}{x-2}<0$ in $R$ .

$\dfrac{1}{x-2}<0$

We have

$x-2\neq\,0$

$\Rightarrow\,x\neq\,2$

$\dfrac{1}{x-2}<0$ then

$\dfrac{1}{x-2}$ must be negative.

$x$ is less than

$2$

$\therefore\,$ Solution is

$x\in \left(-\infty,1\right)$

If $x$ and $y$ are integers, where $12 < x < 18$ and $15 < y < 27$ , then the maximum value of $x + y$ is

$x$ is integer and

$12<x<18$

then the maximum value of

$x$ is

$17$

$y$ is integer and

$15<y<27$

then the maximum value of

$y$ is

$26$

Therefore, the maximum value of

$x+y$ is

$=17+26=43$

Write the solution of $4x+3<6x+7$ in interval from.

$\displaystyle 4 x + 3< 6x + 7$

$\displaystyle 6x + 7-4 x - 3 > 0$

$\displaystyle 2x + 4 > 0$

$\displaystyle x + 2 > 0$

$\displaystyle x > -2 \quad x \in (-2 , \infty)$

Solve the inequality $\dfrac {x - 1}{x^{2} - 4x + 3} < 1$ .

$\cfrac { x-1 }{ { x }^{ 2 }-3x-x+3 } <1$

$\cfrac { (x-1) }{ (x-3)(x-1) } <1\quad \quad \quad \quad \{ x\neq 1\}$

$\cfrac { 1 }{ x-3 } -1<0$

$\cfrac { 1-x+3 }{ x-3 } <0$

$\cfrac { x-4 }{ x-3 } >0$

$x\quad \varepsilon (-\infty ,3)\bigcup(4,\infty )$

$but\quad x\neq 1$

$x\quad \varepsilon (-\infty ,1)\bigcup (1,3)\bigcup (4,\infty )$

Let $f\left(x\right)=\frac{\left(x-3\right)\left(x+2\right)\left(x+6\right)}{\left(x+1\right)\left(x-5\right)}$
Find intervals, where $f\left(x\right)$ is positive or negative.

Let

$f\left(x\right)=\dfrac{\left(x-3\right)\left(x+2\right)\left(x+6\right)}{\left(x+1\right)\left(x-5\right)}$
The critical points are

$-6,-2,-1,3,5$
For

$f\left(x\right)>0,$ for all

$x\in\left(-6,-2\right)\cup\left(-1,3\right)\cup\left(5,\infty\right)$
For

$f\left(x\right)<0,$ for all

$x\in\left(-\infty,-6\right)\cup\left(-2,-1\right)\cup\left(3,5\right)$

Solve: $\dfrac{x-2}{x+5} > 2$ .

$\dfrac{x-2}{x+5}$ > 2

$x-2$ >

$2x + 10$

$\Rightarrow$

$x$ < -12

$\Rightarrow$

$x$

$\in$

$(-\infty,-12)$

If $x:y = 6:11$ , find $(8x-3y) : (3x+2y)$ .

Given:

$x:y=6:11$

$\Rightarrow x=6k,\ y=11k$ , where

$k$ is a constant.

Therefore,

$(8x-3y):(3x+2y)=(8\times 6k-3\times 11k):(3\times 6k+2\times 11k)$

$=15k:40k$

$=3:8$

Hence, this is the required ratio.

Solve the given inequality for $x$ :
$\sqrt{\dfrac{x-2}{1- 2x}}> 1$

First of all, term inside the square root must be positive

$\Rightarrow \dfrac {x-2}{1-2x}\geq 0$

$\Rightarrow \dfrac {x-2}{x-\dfrac {1}{2}}\leq 0$

$\Rightarrow x\in \left [\dfrac {1}{2},2\right]$ .......

$(1)$

Given

$\sqrt{\dfrac {x-2}{1-2x}}>1$

Taking square on both sides ;

$\Rightarrow \dfrac {x-2}{1-2x}>1$

$\Rightarrow x-2<1-2x$ ......

$[\because 1-2x\le 0]$

$\Rightarrow 3x<3$

$\Rightarrow x<1$ .......

$(2)$

Combining both equations, we get ;

$x\in \Big[\dfrac{1}{2},1)$

Solve the following inequality: $2x - 1 < 5$

$2x-1<5$

$2x<5+1$

$2x<6$

$x<3$

The above inequality is represented by the number line in the figure.

All real numbers less than

$3$ are included.

There is a hollow circle on

$3$ , because

$3$ is not included in the solution of the inequality.

1033384_1082145_ans_e32d292558a642008b8a263694411285.jpg

Solve:
$6x^2-7x-3$ .

$6x^2-7x-3\\=6x^2-9x+2x-3\\=3x(2x-3)+1(2x-3)\\=(3x+1)(2x-3)$

Yamini and Fatima, two students of class IX of a school, together contributed Rs. $100$ towards the Prime Minister's relief fund to help the earthquake victims. Write a linear equation which this data satisfies. Draw the graph of the same.

Let

$x,y$ be the money contributed by Yamini and Fatima respectively;

$x+y=100$

1175098_1084902_ans_8c84b81fdd0d4bc68b4348be711365a0.png

Solve the given inequality for real x.
$3x-7>5x-1$

$3x-7>5x-1$

$3x-7+7>5x-1+7$

$3x>5x+6$

$3x-5x>5x+6-5x$

$-2x>6$

$x<-3$

Hence, the solution set of the given inequality is

$(-\infty, -3)$ .

Solve : $\dfrac{2x}{3} - \dfrac{x}{2} \le 6.5$

$\dfrac{2x}{3}-\dfrac{x}{2}\leq 6.5$

$\Rightarrow \dfrac{4x-3x}{3\times x}\leq \dfrac{13}{x}$

$\Rightarrow x\leq 13\times 3$

$\Rightarrow x\leq 39$ .

Solve it :-
If $A:B=5:6$ and $C=8:9$ find $A:B:C$

$A:B=5:6;B:C=8:9$

We should make the value of

$B$ same, so

$A:B=5:6$ multiply with

$8$

$A:B=40:48$

$B:C=8:9$ multiply by

$6$

$=48:54$

$A:B:C=40:48:54$

$A:B:C=20:24:27$

Solve: $\dfrac{1}{|x-2|} < 1$

$\dfrac{1}{|x-2|} < 1$

$\Rightarrow 1 < |x - 2|$

$\Rightarrow |x - 2| > 1$

$\Rightarrow x-2 < -1$ or

$x-2 > 1$

$\Rightarrow x < 1$ or

$x > 3$

$\therefore x t (-\propto , 1)\cup (3, \propto)$

Solve for real $x$ : $\dfrac{x + 8}{x + 2} > 2$

$\dfrac{x+8}{x+2}> 2$

$x+8> 2(x+2)$

$x+8> 2x+4$

$\Rightarrow x<4$

Fill in the blank with $>,\ <$ or $=$ sign
$(-21)-(-10)$ ________ $(-31)+(-11)$

According to question,

L.H.S=

$-21+10$ ----------(multiplication of signs "

$-\times-=+$ ")

$-11$

R.H.S=

$-31-11$ ----------(multiplication of signs "

$+\times-=-$ ")

$-42$

L.H.S is greater than R.H.S

So, sign

$>$ is used to fill the blank

Solve :- $18\le 7y+4$

$18\le7y+4$

$\implies 14\le7y$

$\implies \boxed{2\le y}$

Solve $5 x - 3 < 3 x + 1$ when
i) x is an integer.
ii) $x$ is a real number.

$5x-3<3x+!\\5x-3x<3+1\\2x<4\\x<2\\(1)x={-\infty,.....,-1,0,1}\\(2)x\in\>(-\infty,2)$

Solve :
$\dfrac{5x+2}{3x-1}-\dfrac{5x-2}{3x+7}<0$

Consider given the inequality,

$\dfrac{5x+2}{3x-1}-\dfrac{5x-2}{3x+7}<0$

$\dfrac{\left( 5x+2 \right)\left( 3x+7 \right)-\left( 5x-2 \right)\left( 3x-1 \right)}{\left( 3x-1 \right)\left( 3x+7 \right)}<0$

$\left( 5x+2 \right)\left( 3x+7 \right)-\left( 5x-2 \right)\left( 3x-1 \right)<0$

$\left( 15{{x}^{2}}+41x+14 \right)-\left( 15{{x}^{2}}-11x+2 \right)<0$

$52x+12<0$

$x<\dfrac{-3}{13}$

Hence,

$x\in \left( -\infty ,\dfrac{-3}{13} \right)$

Solve $30x < 200$
When
$(i)x$ is a natural no.
$(ii) x$ is an integer

$30x<200\\x<(\dfrac{200}{3})\\or\>x<6.6(approx)\\(1)\>As\>x\>is\>a\>natural\>number\>hence\>x\>=\>1,2,3,4,5,6\\(2)As\>x\>is\>an\>integer\>hence\>x\>=[-\infty,.......,-1,0,1,2,3,4,5,6]$

The least of $x$ which satisfies the inequation $- 3 \le \dfrac{{4x - 3}}{5} \le 3$ is

$-3\leq \dfrac{4x-3}{5}\leq 3$

$\dfrac{4x-3}{5}\geq -3$ and

$\dfrac{4x-3}{5}\leq 3$

$\dfrac{4x-3}{5}+3\geq 0$

$\dfrac{4x-3}{5}-3\leq 0$

$\dfrac{4x-12}{5}\geq 0$

$\dfrac{4x-12}{5}\leq 0$

$\dfrac{4(x-3)}{5}\geq 0$

$2x-9\leq 0$

$x\in[3, \infty)$

$x\in\left(-\infty, \dfrac{9}{2}\right]$

$x\in \left[3, \dfrac{9}{2}\right]$

Least value of

$x=3$ .

If $A={4,5,7,9}$ , determine the truth values of the following quantified statements:
(i) $\exists x \in A$ such that $x + 5 \ge 9$
(ii) $\forall x \in A,2x \le 17$

1338093_1294667_ans_3b6ee9aa2d5b4632953de932aef171d8.PNG

The ratio of two numbers is $\dfrac{2}{3}$ . If $2$ is subtracted from the first and $8$ from the second, the ratio becomes the reciprocal of the original ratio. Find the numbers.

let the first number be x and second be y

$\frac{x}{y} = \frac{2}{3}$

$\Rightarrow 3x = 2y \,...(1)$

$\Rightarrow \frac{x-2}{y-8} = \frac{3}{2}$

$\Rightarrow 2x-4 = 3y-24$

$\Rightarrow 2x-3y = -20$

$\Rightarrow x = \frac{3y-20}{2}$

put the value of x in equation (1)

$3(3y-20) = 4y$

$9y-60 = 4y$

$5y = 60$

$y = 12$

put

$y = 12$ in equation (1)

$x = 8$

Numbers are

$8$ and

$12$ .

1180228_1284032_ans_d0e42f69477f45dfbc6c114223ab41a0.jpg

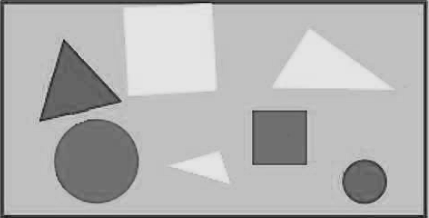
See the figure and find the ratio of
Number of triangle to the number of circle inside the rectangle.

Given that,

Number of triangle

$=3$

Number of circle

$=2$

then,

$\dfrac{Number\ of\ triangle}{Number\ of\ circle}=\dfrac{3}{2}$

$=3:2$

Hence, this is the answer.

Find the solution set of $7x - 3 \ge - 24$ and $- 11x + 10 \ge - 12$

$7x-3\geq -24$ &

$-11x+10\geq -12$

$7x+21\geq 0$

$-11x+22\geq 0$

$7(x+3)\geq 0$

$22\geq 11x$

$x+3\geq 0$

$2\geq x$

$x\geq -3$

$x\leq 2$ .

$x\in [-3, 2]$ .

The denominator of a fraction exceeds its numerator by $5$ . If $2$ is added to both numerator and the denominator, the fraction becomes $\dfrac{4}{5}.$ Find the fraction.

The denominator of a fraction exceeds its numerator by

$5$ .

$d=n+5$

$............(1)$

According to the question,

$\dfrac{n+2}{d+2}=\dfrac{4}{5}$

$5n+10=4d+8$

$5n=4d-2$

$5n=4(n+5)-2$

$From\ equation\ (1)$

$5n=4n+20-2$

$n=18$

$d=23$

Therefore, fraction will be

$\dfrac{n}{d}=\dfrac{18}{23}$

If x : y = 3;5, find the ratio $3x + 4y : 8x + 5y$

Given x : y = 3 ; 5

Let x = 3k, y = 5k

$\frac{3x+4y}{8x+5y}=\frac{3(3k)+4(5k)}{8(3k)+5(5k)}=\frac{9k+20k}{24k+25k}=\frac{29k}{49k}$

$=\frac{29}{49}$

1184064_1298864_ans_e299ca920cf34521a2cfd761d74e5e26.jpeg

Solve
$2-3x > 1$

We have

$2-3x>1$

$-3x>1-2$

$-3x>-1$

$3x>1$

$\therefore x > \dfrac{1}{3}$

If $\dfrac {a}{b}=\dfrac {c}{d}=\dfrac {e}{f}$ prove that:
$\dfrac {a^{3}+c^{3}+e^{3}}{b^{3}+d^{3}+f^{3}}=\dfrac {ace}{bdf}$

Given:-

$\cfrac{a}{b} = \cfrac{c}{d} = \cfrac{e}{f}$

To proof:-

$\cfrac{{a}^{3} + {c}^{3} + {e}^{3}}{{b}^{3} + {d}^{3} + {f}^{3}} = \cfrac{ace}{bdf}$

Proof:-

Let

$\cfrac{a}{b} = \cfrac{c}{d} = \cfrac{e}{f} = k$

$\Rightarrow a = bk, \quad c = dk, \quad e = fk$

Now,

$\cfrac{{a}^{3} + {c}^{3} + {e}^{3}}{{b}^{3} + {d}^{3} + {f}^{3}} = \cfrac{ace}{bdf}$

$\cfrac{{\left( bk \right)}^{3} + {\left( dk \right)}^{3} + {\left( fk \right)}^{3}}{{b}^{3} + {d}^{3} + {f}^{3}} = \cfrac{\left( bk \right) \left( dk \right) \left( fk \right)}{bdf}$

$\cfrac{{b}^{3} {k}^{3} + {d}^{3} {k}^{3} + {f}^{3} {k}^{3}}{{b}^{3} + {d}^{3} + {f}^{3}} = \cfrac{bdf \cdot {k}^{3}}{bdf}$

$\cfrac{{k}^{3} \left( {b}^{3} + {d}^{3} + {f}^{3} \right)}{{b}^{3} + {d}^{3} + {f}^{3}} = \cfrac{\left( bdf \right) {k}^{3}}{bdf}$

$\Rightarrow {k}^{3} = {k}^{3}$

L.H.S.

$=$ R.H.S.

Hence proved

Evaluate the following:
$\left| x \right| < \,\cfrac{a}{x}$

We have,

$\left| x \right| < \,\cfrac{a}{x}$

Case

$1$ : When

$x\ge 0$

So,

$x < \,\cfrac{a}{x}$

$x^2 <a$

$x<\pm \sqrt a$

Case

$2$ : When

$x\le 0$

So,

$-x < \,\cfrac{a}{x}$

$-x^2 <a$

$x^2 >-a$

$x>\pm \sqrt {-a}$

Hence, this is the answer.

Solve
$14-2x =6$

We have

$14-2x=6$

$\Rightarrow - 2x = 6 - 14$

$\Rightarrow - 2x = - 8$

$\ \Rightarrow 2x = 8$

$\therefore x = 4$

Hence, required value is

$4$

Solve $\dfrac{{\left| {x + 2} \right| - x}}{x} < 2$

We have,

$\dfrac{{\left| {x + 2} \right| - x}}{x} < 2$

$\left| {x + 2} \right| - x < 2x$

$\left| {x + 2} \right| < 3x$

So,

$x + 2< 3x$ or

$-(x+2)<3x$

$2< 3x-x$ or

$-x-2<3x$

$2< 2x$ or

$-2<4x$

$1< x$ or

$-\dfrac{1}{2}<x$

$x>1$ or

$x>-\dfrac{1}{2}$

Hence, this is the answer.

$3 \le (x - 1) - 2 { \le 4} .$

$3\leq(x-1)-2\leq 4$

$\text{Adding the equation by}$

$2$

$\text{to eliminate the}$

$-2$

$\text{in the centre}$

$\Rightarrow 5\leq(x-1)\leq 6$

$\text{Adding the equation by}$

$1$

$\text{to eliminate the}$

$-1$

$\text{in the centre}$

$\Rightarrow 6\leq x\leq 7$

$\textbf{The answer is}$

$\mathbf{6\leq x\leq 7}$

$\mathbf{x}$

$\textbf{lies in between}$

$\textbf{6}$

$\textbf{and}$

$\mathbf{7}$

Solve $x > \sqrt { ( 1 - x ) }$

$x > \sqrt{1-x}$

Squaring both sides,

$x^2 > 1-x$

$x^2+x-1 > 0$

For

$x^2+x-1=0$ ,

$x=\dfrac{-1\pm\sqrt{1+4}}{2}$

$=\dfrac{-1\pm \sqrt{5}}{2}$

For

$\sqrt{1-x}$ , we have

$x < 1$ .

Also

$x\in\left(\dfrac{-1-\sqrt{5}}{2}, \dfrac{-1+\sqrt{5}}{2}\right)$

Since

$\sqrt{1-x} > 0$

we get

$x > 0$

$\therefore x\in\left(0, \dfrac{\sqrt{5}-1}{2}\right)$ .

1202869_1328096_ans_c366c35cfc434c7ab63fe208df40a1ef.jpg

Express each of the following ratios as a per cent.
$1:5$

$1 : 5 = \cfrac{1}{5} = \left( \cfrac{1}{5} \times 100 \right) \% = \cfrac{100}{5} \% = 20 \%$

Find two positive numbers in the ratio $2:5$ such that their difference is $15$

Let the common multiple be

$x$ .

Therefore, the numbers are

$2x$ and

$5x$ .

According to given condition.

$5x - 2x = 15$

$3x = 15$

$x = 5$

Thus, the numbers are

$10, 25$

Hence, this is the answer.

Determine if the following ratios forms a proportion. Also, write the middle terms and extreme terms if the ratios are in proportion.
$200\ ml; \; 2.5$ litre and $Rs. 4; \; Rs. 50$

$\dfrac{200ml}{2.5litre}=\dfrac{200\times 10}{2.5\times 1000}=\dfrac{2}{25}$

$\dfrac{Rs. 4}{Rs. 50}=\dfrac{2}{25}$

Yes Ratios are in proportion

Middle terms

$=2.5$ ltr, Rs.

$4$

Extreme terms

$=200$ ml, Rs.

$50$ .

1203674_1328741_ans_d9c7f34ad2dc468f83de3fcd5310ff44.jpg

The number of solution (s) of the equation $\dfrac { 1 } { 2 } \log _ { \sqrt { 3 } } \left( \dfrac { x + 1 } { x + 5 } \right) + \log _ { 9 } ( x + 5 ) ^ { 2 } = 1$ are/is

$\frac {1}{2}log_{\sqrt{3}}\left ( \frac {x+1}{x+5} \right )+log_9(x+5)^2=1$

$\Rightarrow \frac {1}{2}log_{\sqrt{3}^{1/2}}\left ( \frac {x+1}{x+5} \right )+2 log_{3^2}(x+5)^2=1$

$\Rightarrow 2 \times \frac {1}{2}log_3 \left ( \frac {x+1}{x+5} \right )+2 \times \frac {1}{2}log_{3}(x+5)=1$

$\Rightarrow log_3 \left ( \frac {x+1}{x+5} \right )+log_{3}(x+5)=1$

$\Rightarrow log_3 [\left ( \frac {x+1}{x+5} \right )+(x+5)]=1$ {

$log a +log b = log ab$ }

$\Rightarrow (x+1)= 3$

$\Rightarrow x+1 = 3$

$\Rightarrow x=2$

$\therefore$ Number od solution = 1

Read this proportion, and complete it:
$\dfrac{8}{2}=\dfrac{20}{x}$

$\dfrac{8}{2}=\dfrac{20}{x}$

$4=\dfrac{20}{x}$

$\Rightarrow\,4x=20$

$\Rightarrow\,x=\dfrac{20}{4}=5$

$\therefore\,x=5$

Complete this proportion: $8:32$ as $9:x$

We know that product of extremes

$=$ Product of means

$\Rightarrow\,8x=32\times 9$

$\Rightarrow\,x=\dfrac{32\times 9}{8}=4\times 9=36$

$2\left( {x - 6} \right) < 3x - 7;$ $11 - 2x < 6 - x$ .

We have,

$2\left( {x - 6} \right) < 3x - 7;$

$11 - 2x < 6 - x$

$\left( 2x - 12 \right) < 3x - 7;$

$11 - 6 <2x- x$

$2x -3x < 12 - 7;$

$5<x$

$-x < 5;$

$5<x$

$x >- 5;$

$5<x$

Hence, this is the answer.

Rita gave away $\cfrac{2}{3}$ of her chocolate to $6$ of her friends. What fraction did each of her friends get?

1349816_1343061_ans_38e0e45dfbad43c79c06292c568f422e.jpg

Find the ratio of $10$ hours to a day.

We've one day

$=24$ hrs.

Now the ratio of

$10$ hrs to a day is

$\dfrac{10}{24}$

$=\dfrac{5}{12}$ .

Required ratio is

$5:12$ .

$11 - 5x > - 4;4x + 13 \le - 11$

We have,

$11 - 5x > - 4;\,\,\,\,4x + 13 \le - 11$

$- 5x > -11- 4;\,\,\,\,4x\le -13- 11$

$- 5x > -15;\,\,\,\,4x\le -24$

$x <3;\,\,\,\,x\le -6$

Hence, this is the answer.

Solve:
$\dfrac{1}{x-3}<\dfrac{1}{2}$

We have,

$\dfrac{1}{x-3}<\dfrac{1}{2}$

$2<x-3$

$x>5$

Hence, this is the answer.

If $\dfrac {a}{b}=\dfrac {c}{d}=\dfrac {e}{f}$ prove that:
$(bdf).\left(\dfrac {a+b}{a}+\dfrac {c+d}{d}+\dfrac {e+f}{f}\right)^{3}=27(a+b)(c+d)(e+f)$

Given:-

$\cfrac{a}{b} = \cfrac{c}{d} = \cfrac{e}{f}$

To proof:-

$\left( bdf \right) \cdot {\left( \cfrac{a + b}{b} + \cfrac{c + d}{d} + \cfrac{e + f}{f} \right)}^{3} = 27 \left( a + b \right) \left( c + d \right) \left( e + f \right)$

Proof:-

Let

$\cfrac{a}{b} = \cfrac{c}{d} = \cfrac{e}{f} = k$

$\Rightarrow a = bk, \quad c = dk, \quad e = fk$

Now,

$\left( bdf \right) \cdot {\left( \cfrac{a + b}{b} + \cfrac{c + d}{d} + \cfrac{e + f}{f} \right)}^{3} = 27 \left( a + b \right) \left( c + d \right) \left( e + f \right)$

$\left( bdf \right) \cdot {\left( \left( 1 + \cfrac{a}{b} \right) + \left( 1 + \cfrac{c}{d} \right) + \left( 1 + \cfrac{e}{f} \right) \right)}^{3} = 27 \left( bk + b \right) \left( dk + d \right) \left( fk + f \right)$

$\left( bdf \right) \cdot {\left( 1 + k + 1 + k + 1 + k \right)}^{3} = 27 \left( bdf \right) {\left( 1 + k \right)}^{3}$

$\left( bdf \right) \cdot {\left( 3 + 3k \right)}^{3} = 27 \left( bdf \right) \cdot {\left( 1 + k \right)}^{3}$

$\left( bdf \right) \cdot {3}^{3} {\left( 1 + k \right)}^{3} = 27 \left( bdf \right) \cdot {\left( 1 + {k}^{3} \right)}^{3}$

$27 \left( bdf \right) \cdot {\left( 1 + k \right)}^{3} = 27 \left( bdf \right) \cdot {\left( 1 + k \right)}^{3}$

L.H.S.

$=$ R.H.S.

Hence proved.

Complete this proportion $\dfrac{7}{21}=\dfrac{4}{?}$

Let the missing number be

$x$

$\dfrac{7}{21}=\dfrac{4}{x}$

$\Rightarrow \dfrac{1}{3}=\dfrac{4}{x}$

$\Rightarrow\,x=4\times 3=12$

$\therefore\,x=12$

The second third and fourth terms of the proportion are $25,30$ and $150$ . Find the first term.

Let first term be x

$\Rightarrow \dfrac{x}{30}=\dfrac{25}{150}$

$\Rightarrow x=\dfrac{1}{6}\times 30$

$\Rightarrow x=5$ .

1214447_1396051_ans_74105c79211242c8a84693bdbf7d26b7.jpg

If $A : B = 6 :7$ , $B : C = 3:5$ Find $A:B:C$

1323540_1491197_ans_40786941f1bf4c5e99d1e67dff783085.JPG

Solve the following linear inequations in $R$ .
$\dfrac {5x + 8}{4 - x} < 2$ .

1436530_1666574_ans_7a5248acec4e44bf9edfa60b80e46ea6.jpg

Solve the following linear inequations in $R$ .
Solve : $12x < 50$ , when $x\epsilon Z$

For the inequation,

$12x<50\Rightarrow x<\dfrac {50}{12}$

the set of values of

$x \forall \, \, x\in Z$

$\left \{... - 3, -2, -1, 0, 1, 2, 3, 4\right \}$ .

Find the integer values of $x$ for which $x-7\le 4x\le 5+2x$ .

$x-7 \le 4x\Rightarrow 4x \ge x - 7 \Rightarrow 3x \ge -7 \Rightarrow x \ge \dfrac{-7}{3} \simeq -2.33$

and

$4x \le 5+2x \Rightarrow 2x \le 5 \Rightarrow x \le \dfrac{5}{2} = 2.5$

$\Rightarrow$ Integral values of

$x = -2, -1, 0, 1, 2$

1226948_1398401_ans_588f104afd514cf08ffab2b2e943eaee.jpg

Solve : $\dfrac{2x+3}{5} > \dfrac{4x-1}{2},\ x\ \epsilon \ W$ .

$\dfrac{2x+3}{5}>\dfrac{4x-1}{2}\\2(2x+3)>5(4x-1)\\4x+6>20x-5\\-16x+11>0\\-16x>-11\\x<\dfrac{11}{16}$

so x=0 is the solution

Solve the following linear inequations in $R$ .
$\dfrac {x - 1}{x + 3} > 2$ .

1436532_1666576_ans_3f719c9a5dd443788512e4c92298ca19.jpg

Solve the following linear inequations in $R$ .
$\dfrac {5x - 6}{x + 6} < 1$ .

1436529_1666571_ans_facfc78faf13444793173fef01beeaab.jpg

Rationalize the denominator of $\cfrac {1}{2^\cfrac{1}{3} + 2^\cfrac{-1}{3}}$ is

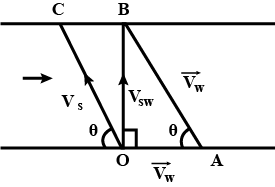
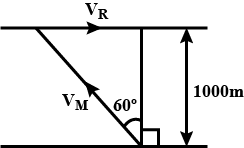
A child in danger of drowning in a river is being carried downstream by a current that flows uniformly at a speed of $2.5 km/h$ . The child is $0.6 km$ from shore and $0.8\ km$ upstream of a boat landing when a rescue boat sets out. If the boat proceeds at its maximum speed of $20 km/h$ with respect to the water, the angle (in degrees) , the boat velocity $v$ make with the shore is 37x. The value of x is:

Let boat velocity be v and we need to determine the angle boat makes with the shore.

$\vec v_b=$ velocity of boatman

$\vec v_{br}+\vec v_r$
and

$\vec v_c=$ velocity of child

$=\vec v_r$

$\therefore \vec v_{bc}=\vec v_b-\vec v_c=\vec v_{br}$

$\vec v_{br}$ should be along BC.
i.e.,

$\vec v_{br}$ should be along BC.
where,

$tan\alpha=\dfrac {0.6}{0.8}=\dfrac {3}{4}$
or

$\alpha=37^o$

If $\left | x-2 \right |< 3$ , then number of integers in the range of $x$ is

Let $x- 2= y$

$=> x - 2 < 3$

$=> x < 5$ -- (1)
And when $y < 0$ , we have $\left | y \right | = - y$
So, $-y-3 < 0$
$y > -3$

$=> x - 2 > -3$

$=> x > -1$ -- (2)
From $(1), (2) ; x \in (-1, 5)$

Solve the inequation $5(x - 2) > 4(x + 3) - 24$ and represent its solution on a number line. Given the replacement set is ${-4, -3, -2,-1, 0, 1, 2, 3, 4}.$

$5\left( x-2 \right) >4\left( x+3 \right) -24$

$5x-10>4x+12-24$

$5x-4x>-12+10$

$x>-2$
As the set

$x$ is a sub-set of the replacement set

$\left\{ -4,-3,-2,-1,0,1,2,3,4, \right\}$
set

$x$ =

$\left\{ -1,0,1,2,3,4, \right\}$
Ans: The number of numbers in the set

$x$ is 6

Solve $\displaystyle \frac{2}{3}(x - 1) + 4 < 10$ and represent its solution on a number line. Given replacement set is ${-8, -6, -4, 3, 6, 8, 12}$ .

$\dfrac { 2 }{ 3 } \left( x-1 \right) +4<10$

$\dfrac { 2 }{ 3 } x-\dfrac { 2 }{ 3 } +4<10$

$\dfrac { 2 }{ 3 } x<10-4+\dfrac { 2 }{ 3 }$

$\dfrac { 2 }{ 3 } x<6+\dfrac { 2 }{ 3 }$

$\dfrac { 2 }{ 3 } x<\dfrac { 20 }{ 3 }$

$x<\dfrac { 20 }{ 3 } \div \dfrac { 2 }{ 3 }$

$x<\dfrac { 20 }{ 3 } \times \dfrac { 3 }{ 2 }$

$x<10$
Given that the set

$x$ is a sub set of replacement set

$\left\{ -8,-6,-4,3,6,8,12 \right\}$
Ans: set

$x$ =

$\left\{ -8,-6,-4,3,6,8 \right\}$
Hence the number of integers in the set

$x$ is 6

A motorboat going downstream overcame a raft at a point A. One hour later it turned back and after sometime passed the raft at a distance 12 km from the point A. Find the river velocity (in km/hr) assuming the speed of the motorboat to be constant.

Let angle velocity of motorboat be v

From the given figure $(v + u)t_1 = u(t_1 + t_2) + (v - u)t_2 \Rightarrow t_2 =t_1$ = 1 hr

But 12 km = $u(t_1 + t_2)$ so $\displaystyle u = \frac {12 km} {2 hr}$ = 6 km/hr

Let a and b be positive real numbers such that $a + b = 1$ . Prove that $a^ab^b\, +\, a^ab^b\, \leq\, 1$

We have,

$1\, =\, a\, +\, b\, =\, a^{a\, +\,b}b^{a\, +\, b}\, =\, a^ab^b\, +\, b^ab^b$

$\therefore 1\, -\, a^ab^b\, -\, a^bb^a\, =\, a^ab^b\, +\, b^ab^b\, -\, a^ab^b\, -\, a^bb^a\, =\, (a^a\, -\, b^a)(a^b\, -\, b^b)$
Now if

$a\, \leq\, b$ , then

$a^a\, \leq\, b^a$ and

$a^b\, \leq\, b^b$ . If

$a\, \geq\, b$ , then

$a^a\, \geq\, b^a$ and

$a^b\, \geq\, b^b$ . Hence the product is non-negative for all positive a and b.

$\therefore a^ab^b\, +\, a^bb^a\, \leq\, 1$ .

Solve 4x + 3 < 6x + 13, where $x$ is natural no. less than 3.

We have

$4x + 3 < 6x + 13$
or

$4x - 6x < 6x + 10 - 6x$
or

$-2x - 10 < 0$ or

$2x + 10 > 0$

$\displaystyle \Rightarrow x + 5 > 0$
i.e. all the natural which are greater than -5 are the solutions of the given inequality Hence the solution set is

${1,2}$

Evaluate | 3 | + | -2 - 3 | - 3 - | -7 |

$\textbf{Step-1: Removing modulus}$

$\Rightarrow 3+\left| -5 \right|-3-\left( 7 \right)$

$\textbf{Step-2: Solving}$

$\Rightarrow 3+5-3-7$

$\Rightarrow 8-10$

$\Rightarrow -2$

$\textbf{Hence , The value comes out is -2}$

Find $x$ from $1 < | x | < 2$ and represent it on number line

$\displaystyle 1<|x|\Rightarrow |x|>1\Rightarrow x>1or <-1$

$\displaystyle \therefore x\in (-\infty ,-1)\cup (1,\infty )$ .....................(i)
also |x| < 2

$\Rightarrow$

$x < 2\ or\ x > - 2$

$\therefore$ x lies between

$- 2 \& 2$

$\displaystyle \Rightarrow x\in (-2,2)$ ...........(ii)
Combining the two results we get

$\displaystyle 1<|x|<2\Rightarrow {-2<x<-1}\cup {1<x<2}$ i.e.

$\displaystyle x\in (-2,-1)\cup (1,2)$
1032182_329160_ans_769407a9114744f29aa5548c5a94a4e6.bmp

Solve $3x + 8 >2,$ when (i) $x$ is an integer. (ii) $x$ is a real number

The given inequality is

$3 x +8 >2$

${\Rightarrow 3x+8 -8 > 2-8}$

${\Rightarrow 3x > -6 }$

${\Rightarrow \dfrac {3x}{3}>\dfrac {-6}{3}}$

${\Rightarrow x > -2}$
(i) The integers greater than

$-2$ are

$-1,0,1,2,.......$
Thus when

$x$ is an integer, the solutions of the given inequality are

$-1,0,1,2............$
(ii) When

$x$ is a real number, the solutions of the given inequality are all the real numbers, which are greater than

$-2$ .
Thus in this case, the solution set is

${(-2, \infty)}$

Solve the inequality for real $x$ .
$\displaystyle {\frac {x}{4}<\frac{(5x-2)}{3} -\frac{(7x-3)}{5}}$

Given,

$\displaystyle{\frac {x}{4}< \frac{(5x-2)}{3}-\frac{(7x-3)}{5}}$

$\displaystyle{\Rightarrow\frac {x}{4}< \frac{5(5x-2)-3(7x-3)}{15}}$

${\Rightarrow\displaystyle\frac {x}{4}< \frac{(25x-10-21x +9)}{15}}$

${\Rightarrow\displaystyle\frac {x}{4}< \frac{4x-1}{15}}$

${\Rightarrow \displaystyle15 x < 4(4x-1)}$

${\Rightarrow\displaystyle 15 x < 16 x -4}$

${\Rightarrow\displaystyle 4 < 16 x -15 x}$

${\Rightarrow \displaystyle x>4} \ \text{or} \ x\in (4,\infty)$

Solve $5x - 3 < 7,$ when
(i) $x$ is an integer.
(ii) $x$ is a real number.

The given inequality is,

$5x-3<7$

${\Rightarrow 5x -3 +3 <7 +3}$

${\Rightarrow 5x <10}$

${\Rightarrow \dfrac{5x}{5}< \dfrac{10}{5}}$

${\Rightarrow x<2}$
(i) The integers less than 2 are

$.......,-4,-3,-3,-1,0 ,1.$
Thus when

$x$ is an integer, the solutions of the given inequality are
all the integral values of

$x$ which are less than

$2$ .
(ii) When

$x$ is real number the solution is given by

$x <2$ ,
i.e., all real numbers

$x$ which are less than 2.
Thus, the solution set of the given inequality is

$x\in {(-\infty, 2 )}$

Solve the inequality for real $x$ .
$\displaystyle \frac{1}{2}\left ( \frac{3x}{5} +4 \right) \geq \frac{1}{3}(x-6)$

Given,

$\displaystyle {\frac{1}{2}\left ( \frac{3x}{5} +4\right )\geq\frac{1}{3}(x-6)}$

$\displaystyle{\Rightarrow 3\left ( \frac{3x}{5} +4\right )\geq 2(x-6)}$

$\displaystyle{\Rightarrow \frac{9x}{5} +12 \geq 2x-12}$

$\displaystyle{\Rightarrow 12+12 \geq 2x -\frac{9x}{5}}$

$\displaystyle{\Rightarrow 24 \geq \frac{ 10x-9x}{5}}$

$\Rightarrow \displaystyle {24 \geq \frac{x}{5}}{\Rightarrow x \leq 120} \ \text{or} \ x \in (-\infty, 120]$

Find the number of values of $x$ which satisfies the following inequality.
$\displaystyle \left | 5x-7 \right |< -18$

The modulus of any number has to be

$0$ or positive.

Thus, there are no values of

$x$ which satisfy the given inequality.

The solution set is

$\displaystyle \phi$

Find all pairs of consecutive odd positive integers both of which are smaller than $10$ such that their sum is more than $11$ .

${\textbf{Step -1: Forming an equation}}$

${\text{Let x be the small}}$

${\text{Then, the other integer is x + 2}}{\text{. Since both the integers are smaller than 10}}{\text{.}}$

${\text{x + 2 < 10}}$

$\Rightarrow {\text{x < 10 - 2}}$

$\Rightarrow {\text{x < 8 }}.....{\text{ (i)}}$

${\text{Also, the sum of the two integers is more than 11}}{\text{.}}$

$\Rightarrow {\text{x + (x + 2) > 11}}$

$\Rightarrow {\text{2x + 2 > 11}}$

$\Rightarrow {\text{2x > 11 - 2}}$

$\Rightarrow {\text{2x > 9}}$

$\Rightarrow {\text{x > }}\frac{9}{2}{\text{ }}$

$\Rightarrow {\text{x > 4}}{\text{.5 }}......{\text{ (ii)}}$

${\textbf{Step -2: Finding pairs}}$

${\text{From (i) and (ii), we obtain}}$

${\text{Since x is an odd number, x can take values, 5 and 7}}{\text{.}}$

${\text{Thus, the required possible pairs are (5,7) and (7,9)}}{\text{.}}$

${\textbf{Hence, required possible pairs are (5,7) and (7,9)}}{\text{.}}$

Solve the inequality for real $x$ .
$\displaystyle {\frac{(2x-1)}{3}\geq \frac{(3x-2)}{4}-\frac{(2-x)}{5}}$

Given,

$\displaystyle{\frac{(2x-1)}{3}\geq \frac{(3x-2)}{4}-\frac{(2-x)}{5}}$

$\displaystyle{\Rightarrow\frac{(2x-1)}{3}\geq\frac{5(3x-2)-4(2-x)}{20}}$

${\Rightarrow\displaystyle\frac{(2x-1)}{3}\geq\frac{15 x-10 -8 +4 x}{20}}$

${\Rightarrow\displaystyle\frac{(2x-1)}{3}\geq\frac{19x-18}{20}}$

${\Rightarrow\displaystyle 20(2x -1)\geq 3(19x -18)}$

${\Rightarrow \displaystyle 40 x -20 \geq 57 x -54}$

${\Rightarrow \displaystyle -20 + 54 \geq 57 x-40 x}$

${\Rightarrow \displaystyle 34 \geq 17 x}$

${\Rightarrow \displaystyle x\leq 2} \ \text{or} \ x\in (-\infty, 2]$

Ravi obtained $70$ and $75$ marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least $60$ marks.

Let

$x$ be the marks obtained by Ravi in the third unit test.
Since the student should have an average of at least

$60$ marks.

$\displaystyle {\frac{70+75+x}{3}\geq 60}$

${\Rightarrow 145 +x\geq 180}$

${\Rightarrow x\geq 180-145}$

${\Rightarrow x\geq 35}$
Thus the student must obtain a minimum of

$35$ marks to have an average of at least

$60$ marks.

Solve for $x$ : $\displaystyle \frac{-2}{x-10} < 0$ . If $x \in (a,b)$ then find $a$ .

1977996_427066_ans_7f442d57fbbe46efa4ef6ea40fb27420.jpg

Solve, and express the answer in interval notation.
$\displaystyle\frac{4x-8}{x-7} \ge 0$

Solve with an

$=$

$\displaystyle\frac{4x-8}{x-7} = 0$

$4x = 8$

$x = 2$
Critical values are

$x = 2$ and

$x = 7$ (denominator

$= 0$ )

$ck\left( 0 \right) :\displaystyle\frac { 4\left( 0 \right) -8 }{ \left( 0 \right) -7 } =\displaystyle\frac { -8 }{ -7 } =+\displaystyle\frac { 8 }{ 7 }$ ; yes

$\ge 0$

$ck\left( 5 \right) :\displaystyle\frac { 4\left( 5 \right) -8 }{ \left( 5 \right) -7 } =\displaystyle\frac { 12 }{ -2 } =-6$ ; Not

$\ge 0$

$ck\left( 8 \right) :\displaystyle\frac { 4\left( 8 \right) -8 }{ \left( 8 \right) -7 } =\displaystyle\frac { 24 }{ 1 } =24$ ; yes

$\ge 0$
Solution: (

$-\infty, 2$ ]

$\cup \left(7, +\infty\right)$

If the solution of the inequation $\displaystyle\dfrac { 3 }{ x-3 } \le \displaystyle\dfrac { 2 }{ x+2 }$ is ( $-\infty$ , $k$ ], Find the value of $k$ .

1822293_426599_ans_5417fb6898de41b7946653bf40429a51.jpg

Solve the inequalities
$6\le -3(2x-4)< 12$

$6\le -3(2x-4)< 12$

$\Rightarrow -2\ge2x-4\gt -4$

$\Rightarrow -4+4\lt2x\le-2+4$

$\Rightarrow 0\lt x\le2$

$\Rightarrow x\in(0,2]$

Solve the inequalities:
$2\le 3x-4\le 5$

$2\le3x-4\le5$

$\Rightarrow 2+4\le3x\le5+4$

$\Rightarrow 6\le3x\le9$

$\Rightarrow 2\le x\le3$

$\Rightarrow x\in [2,3]$

Solve the inequalities
$-12<4+\dfrac{3x}{5}\le 2$

$-12\lt4+\dfrac{3x}{5}\le2$

$-12-4\lt\dfrac{3x}{5}\le2-4$

$-16\times 5\lt3x\le -2\times 5$

$\dfrac{-80}{3}\lt x\le\dfrac{-10}{3}$

$\therefore x\in\left(\dfrac{-80}{3},\dfrac{-10}{3}\right]$

Solve the inequalities
$-3 \le 4-\dfrac{7x}{2}\le 18$

We have,

$-3 \le 4-\dfrac{7x}{2}\le 18$
Add

$-4$ on each of the sides, we get

$-3-4 \le -4+4-\dfrac{7x}{2}\le 18-4$

$\Rightarrow -7 \le -\dfrac{7x}{2}\le 14$
Multiply

$\dfrac{2}{7}$ on each of the sides

$\Rightarrow -2 \le -x\le 4$
Now multiply each side by

$-1$

$\Rightarrow 2\ge x\ge -4$ , since after multiplying any inequalty by negative number its sign reverses

$\Rightarrow -4\le x\le 2$

$\Rightarrow x\in [-4,2]$

Solve the inequalities
$-15<\dfrac{3(x-2)}{5}\le 0$

$-15\lt\dfrac{3(x-2)}{5}\le 0$

$-25\lt x-2\le0$

$-23\lt x\le2$

$x\in(-23,2]$

IQ of a person is given by the formula $IQ=\dfrac{MA}{CA}\times 100$
where MA is mental age and CA is chronological age. If $80 \le IQ \le 140$ for a group 12 years old children, find the range of their mental age.

$80\le \dfrac{MA}{CA}\times100\le140$

$96\le MA\times10\le14\times12$

$9.6\le MA \le16.8$

range of mental age is

$[9.6,16.8]$

Solve the inequalities
$7<\dfrac{(3x+11)}{2}\le 11$

Given :

$7<\dfrac{(3x+11)}{2}\le 11$

$14\lt 3x+11\le22$

$3\lt3x\le11$

$1\lt x\le\dfrac{11}{3}$

$\therefore x\in \left(1,\dfrac{11}{3}\right]$

Solve for $x:12-2x> 4$

Given $12-2x > 4$
Which implies $2x < 8$
therefore $x < 4$

Solve for $z:6z+1\le 3(z-2)$

Given $6z+1 \le 3(z-2)$
Which implies $6z+1\le3z-6$ , which gives $3z \le -7$
Therefore $z \le -7/3$

In a mixture $60$ litres, the ratio of milk and water $2 : 1$ . If this ratio is to be $1 : 2$ , then the quanity of water to be further added is

Quantity of milk

$=\left ( 60 \times \dfrac{2}{3} \right )$ litres

$= 40$ litres

Quantity of water in it

$= (60-40)$ litres

$= 20$ litres

New ratio

$= 1:2$

Let the quantity of water to be added further be x litres

Then milk : water

$=\left ( \dfrac{40}{20+x} \right )$

Now,

$\left ( \dfrac{40}{20+x} \right ) = \dfrac {1}{2}$

$20 + x = 80$

$x = 60$

$\therefore$ Quantity of water to be added

$= 60$ litres

Disprove, by finding a suitable counter example, the statement $x^2>y^2$ for all $x>y$ .

For negative number The statement

$x^{2}> y^{2}$ For all x > y is disprove

$x=-3$ and

$y=-4$ Then

$-3 > -4$

But in case

$x^{2}=(-3)^{2}=9$ and

$y^{2}=(-4)^{2}==16$

$x^{2}<y^{2}$

Then the statement

$x^{2}> y^{2}$ For all x > y is disprove

If the compound ratio of $5 : 8$ and $3 : 7$ is $45 : x$ . Find the value of $x$ .

$\textbf{Step - 1 : Form the compound ratio }$

$\dfrac{5}{8}\times\dfrac{3}{7}=\dfrac{45}{x}$

$\Rightarrow \dfrac{15}{56}=\dfrac{45}{x}$

$\textbf{Step - 2 : Solve for x by doing cross multiplication }$

$x\times15=56\times45$

$\Rightarrow x=56\times3$

$\Rightarrow x=168$

$\textbf{Hence, the value of x is 168 }$

If the compound ratio of $7 : 5$ and $8 : x$ is $84 : 60$ . Find $x$ .

$\textbf{Step - 1 : Simplify the compound ratio }$

${\dfrac{7}{5}\times\dfrac{8}{x}=\dfrac{84}{60}}$

$\Rightarrow {\dfrac{56}{5x}=\dfrac{84}{60}}$

$\Rightarrow {5x\times84=60\times56}$

$\Rightarrow x=8$

$\textbf{Hence, the value of x is 8}$

Restate the following statements with appropriate conditions, so that they become true statements.
For any $x, 3x+1>4$ .

The given statement is true, when

$x > 1$ .

So, if

$x=2$ , then

$3x+1= 3 \times 2+1 =7$

$x=1.5$ , then

$3x+1=3\times 1.5+1=5.5$

This is a true stetment, when

$x$ is positive number.

The compound ratio of $3 : 4$ and the inverse ratio of $4 : 5$ is $45 : x$ . Find $x$ .

$\textbf{Step - 1 : Form the compound ratio }$

$\text{Inverse ratio of } \dfrac{4}{5}= \dfrac{5}{4}$

$\dfrac{3}{4}\times\dfrac{5}{4}=\dfrac{15}{16}$

$\dfrac{15}{16}=\dfrac{45}{x}$

$\textbf{Step - 2 : Solve for x by cross multiplication }$

$x\times15=16\times45$

$x=16\times3$

$x=48$

$\textbf{Hence, the value of x is 48}$

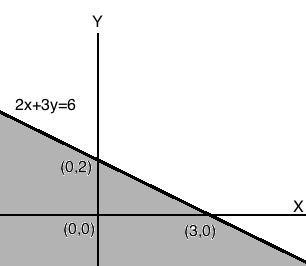
Draw the graph of the following inequation $2x+3y\le 6$ .

The shaded region in the graph shown represents the area marked by

$2x+3y≤6$ .

Solve the equations:
$\dfrac {2x^{3} - 3x^{2} + x + 1}{2x^{3} -3x^{2} - x - 1} = \dfrac {3x^{3} - x^{2} + 5x - 13}{3x^{3} - x^{2} - 5x + 13}$ .

$\dfrac { 2x^{ 3 }-3x^{ 2 }+x+1 }{ 2x^{ 3 }-3x^{ 2 }-x-1 } =\dfrac { 3x^{ 3 }-x^{ 2 }+5x-13 }{ 3x^{ 3 }-x^{ 2 }-5x+13 }$

Using dividendo and componendo

$\dfrac { 2x^{ 3 }-3x^{ 2 }+x+1+(2x^{ 3 }-3x^{ 2 }-x-1) }{ 2x^{ 3 }-3x^{ 2 }+x+1-(2x^{ 3 }-3x^{ 2 }-x-1) } =\dfrac { 3x^{ 3 }-x^{ 2 }+5x-13+(3x^{ 3 }-x^{ 2 }-5x+13) }{ 3x^{ 3 }-x^{ 2 }+5x-13-(3x^{ 3 }-x^{ 2 }-5x+13) }$

$\dfrac { 4x^{ 3 }-6x^{ 2 } }{ 2x+2 } =\dfrac { 6x^{ 3 }-2x^{ 2 } }{ 10x-26 }$

Here we see that

$x$ is common both the equations, So

$x=0$ is the solution,

$\dfrac { 2x-3 }{ x+1 } =\dfrac { 3x-1 }{ 5x-13 }$

$10x^{ 2 }-15x-26x+39=3x^{ 2 }-x+3x-1$

$7x^{ 2 }-43x+40=0$

$7x^{ 2 }-35x-8x+40=0$

$(7x-8)(x-5)=0$

$x=5,\dfrac { 8 }{ 7 },0$ are the solutions.

Find four proportionals such that the sum of the extremes is $21$ , the sum of the means $19$ , and the sum of the squares of all four numbers is $442$ .

Take proportionals as

$a:ax::b:bx$

Now three equations are given

$a+bx=21$ .....(i)

$ax+b=19$ .....(ii)

$a^2 +(ax)^2+b^2+(bx)^2=442$

$\Rightarrow (a^2+b^2)(1+x^2) = 442$ .....(iii)

Add (i) and (ii), we get

$(a+b)(1+x) = 40$ ......(iv)

Subtract (ii) from (i), we get

$(a-b)(1-x)=2$ ......(v)

Multiply (iv) and (v)

$(a^2-b^2)(1-x^2)=80$ ......(vi)

Now add (iii) and (vi) and get equation

$a^2+(bx)^2 = 261$

Now both

$a^2$ and

$(bx)^2$ are perfect squares.

Now, we have to split

$261$ into two parts such that both are perfect squares and it can be done as

$36 + 225$ .

So,

$a= 6$ and

$bx=15$

Now subtract (vi) from (iii), we get

$(ax)^2+b^2=181$

Now

$ax$ and

$b$ are also perfect square so split

$181$ in two parts which is

$81+100$ .

So,

$ax=9$ and

$b=10$

So, the proportionals are

$6,9,10,15$ .

If $x + 7 ; 2(x + 14)$ in the duplicate ratio of $5 : 8$ , find $x$ .

Duplicate ratio of two numbers, means the ratio of their squares

So the duplicate ratio of

$5:8$ is

$25:64$

Given that the duplicate ratio of

$5:8$ is

$x+7:2(x+14)$

$\Rightarrow \dfrac{x+7}{2(x+14)}=\dfrac{25}{64}$

$\Rightarrow 32(x+7)=25(x+14)$

$\Rightarrow 32x-25x=350-224$

$\Rightarrow 7x=126$

$\Rightarrow x=18$

Therefore the value of

$x$ is

$18$

$3(2x+y)=7xy; 3(x+3y)=11xy$ using elimination method.

The given system of equations is

$3(2x+y)=7xy$ (1)

$3(x+3y)=11xy$ (2)
Observe that the given system is not linear because of the occurrence of xy term. Also, note that if x = 0, then y = 0 and vice versa. So, (0, 0) is a solution for the system and any other solution would have both

$x \neq 0$ and

$y \neq 0$ .
Thus, we consider the case where

$x \neq 0, y\neq 0$ .
Dividing both sides of each equation by xy, we get

$\frac{6}{y}+\frac{3}{x}=7, i.e., \frac{3}{x}+\frac{6}{y}=7$ (3)
and

$\frac{9}{x}+\frac{3}{y}=11$ (4)
Let

$a=\frac{1}{x}$ and

$b=\frac{1}{y}$
Equations (3) and (4) become

$3a +6b=7$ (5)

$9a+3b=11$ (6)
which is a linear system in a and b.
To eliminate b, we have

$(6) \times 2 \rightarrow 18a + 6b = 22$ (7)
Subtracting (7) from (5) we get, -15a=15. That is, a=1.
Substituting a = 1 in (5) we get,

$b=\frac{2}{3}$ . Thus, a=1 and

$b=\frac{2}{3}$ .
When a=1, we have

$\frac{1}{x}=1$ , Thus x=1.
When

$a=\frac{2}{3}$ , we have

$\frac{1}{y}= \frac{2}{3}$ , Thus

$y=\frac{3}{2}$ .
Thus, the system has two solutions

$\left ( 1, \frac{3}{2} \right )$ and

$\left ( 0, 0 \right )$ .

Express the following ratio in their simplest form. $16:20$ .

HCF of 16 and 20 is 4.

By dividing both numerator and denominator by HCF 4 we get;

$\dfrac { \dfrac { 16 }{ 4 } }{ \dfrac { 20 }{ 4 } }$ =

$\dfrac { 4 }{ 5 }$

Find the number of solutions of the equation
$\sin5x \cos3x =\sin6x \cos2x, \,\, x \in [0, \pi]$

$2\sin { 5x } \cos { 3x } =\sin { (5x+3x) } +\sin { (5x-3x) } =\sin { 8x } +\sin { 2x }$

$2\sin { 6x } \cos { 2x } =\sin { (6x+2x) } +\sin { (6x-2x) } =\sin { 8x } +\sin { 4x }$

ie,

$\sin { 5x } \cos { 3x } =\sin { 6x } \cos { 2x } \Leftrightarrow \sin { 8x } +\sin { 2x } =\sin { 8x } +\sin { 4x }$

$\Rightarrow \sin { 4x } =\sin { 2x }$

But,

$\sin { 4x } =2\sin { 2x } \cos { 2x }$

$\therefore \sin { 4x } =\sin { 2x } \Rightarrow 2\cos { 2x } =1$ or

$\sin { 2x=0 }$

for

$\cos { 2x } =\dfrac { 1 }{ 2 }$ ,

$x=\dfrac { \pi }{ 6 } ,\quad \dfrac { 5\pi }{ 6 }$

for

$\sin { 2x=0 }$

$x=0,\quad \dfrac { \pi }{ 2 },\quad\pi$

Solve: $|(x^2+2x+2)+(3x+7)|<|x^2+2x+2|+|3x+7|$ .

$\left| { x }^{ 2 }+2x+2+3x+7 \right| <\left| { x }^{ 2 }+2x+2 \right| +\left| 3x+7 \right|$

$\left| { x }^{ 2 }+5x+9 \right| <\left| { x }^{ 2 }+2x+2 \right| +\left| 3x+7 \right|$

now,

$({ x }^{ 2 }+5x+9)$ and

$({ x }^{ 2 }+5x+9)$ both have D<0 and hence are >0

${ x }^{ 2 }+5x+9<{ x }^{ 2 }+2x+2$

$\left| 3x+7 \right| >3x+7$

(i) For

$x<\cfrac { -7 }{ 3 }$ ,

$3x+14$

$6x+14<0$

$x<\cfrac { -7 }{ 3 }$

$x\quad \varepsilon \quad (-\infty ,\cfrac { -7 }{ 3 } )$

(ii) For

$x>\cfrac { -7 }{ 3 }$

$3x+7>3x+7$

$x\varepsilon \quad (-\infty ,\cfrac { -7 }{ 3 } )$

Prove that ${a}^{3}b+a{b}^{3}< {a}^{4}+{b}^{4}$ .

Assume

$a^{3}b+b^{3}a<a^{4}+b^{4}$

$\Rightarrow a^{3}b+b^{3}a-a^{4}-b^{4}<0$

$\Rightarrow a^{3}(b-a)+b^{3}(a-b)<0$

$\Rightarrow (a-b)(b^{3}-a^{3})<0$

$\Rightarrow (a-b)(b-a)(a^{2}+b^{2}+ab)<0$

$\Rightarrow (a-b)^{2}(a^{2}+b^{2}+ab)>0$

We already know that

$(a-b)^{2}>0, (a^{2}+b^{2}+ab)>0$

Hence our assumption

$a^{3}b+b^{3}a<a^{4}+b^{4}$ is correct

If $\displaystyle \frac{a}{b} = \frac{c}{d}$ $=$ $\dfrac{e}{f}$ and $\dfrac{2a^4b^2 + 3a^2c^2 - 5e^4f}{2b^6 + 3 b^2d^2 - 5f^5}$ $=$ $\left (\dfrac{a}{b}\right)^n$ then find the value of $n$ .

Given,

$\displaystyle \frac{a}{b} = \frac{c}{d}$

$=$

$\dfrac{e}{f}$

and

$\dfrac{2a^4b^2+3a^2c^2-5e^4f}{2b^6+3b^2d^2-5f^5}=\left (\dfrac {a}{b}\right)^n$

Let

$\dfrac{a}{b}=k$

Putting

$a=kb, c=kd,\, e=kf$ in numerator, we get

Therefore,

$\dfrac{2k^4b^6+3k^4b^2d^2-5k^4f^5}{2b^6+3b^2d^2-5f^5}=k^4=\Bigr(\dfrac{a}{b}\Bigl)^4$

$\Rightarrow n=4$

Solve the inequality $24x<100$ if $x$ is a natural number.

$24x<100$

$\Rightarrow x<\dfrac{100}{24}=4\dfrac{1}{6}$

Thus the natural number satisfying the inequality is

$x=4$

Any other natural number less than

$4$ also satisfies the inequality.

So the solution is the set

$\{1,2,3,4\}$ .

Solve that: $\displaystyle\frac{1}{3}(2x -1)\geq \frac{1}{4}(3x-2)-\frac{1}{5}(2-x)$ for $x\epsilon N$ .

$\dfrac{1}{3}(2x-1)\geq \dfrac{1}{4}(3x-2)-\dfrac{1}{5}(2-x)$

$\implies \dfrac{2x}{3}-\dfrac{1}{3}\geq \dfrac{3x}{4}-\dfrac{2}{4}-\dfrac{2}{5}+\dfrac{x}{5}$

$\implies \dfrac{3x}{4}+\dfrac{x}{5}-\dfrac{2x}{3}\leq \dfrac{2}{4}+\dfrac{2}{5}-\dfrac{1}{3}$ (on rearranging)

$\implies \dfrac{45x+12x-40x}{60} \leq \dfrac{30+24-20}{60}$

$\implies 17x\leq 34$

$\implies x\leq 2$

This is the required solution.

Solve: $\displaystyle \frac{3x-1}{2} < -3$ and $\displaystyle \frac{3x+8}{5} + 11 < 0$

$\dfrac{3x-1}{2}<-3\implies 3x-1<-6\implies 3x<-5\implies x<-\dfrac{5}{3}$

$\dfrac{3x+8}{5}<-11\implies 3x+8<-55\implies 3x<-63\implies x<-21$

The intersection of

$x<-\dfrac{5}{3}$ and

$x<-21$ is the solution for the problem.

Hence, the solution is

$x<-21$ .

Solve the given inequality for real x :
$37 - (3x+5) \geq 9x - 8(x-3)$

$37-\left(3x+5\right)\ge 9x-8\left(x-3\right)$

$\Rightarrow 37-3x-5\ge 9x-8x+24$

$\Rightarrow 32-3x\ge x+24$

$\Rightarrow -3x-x\ge 24-32$

$\Rightarrow -4x\ge -8$

$-x\ge -2$

Since

$x$ is negative, we multiply both sides by

$-1$ and change the signs,

$\left(-1\right)\left(-x\right)\le\left(-1\right)\left(-2\right)$

$\therefore x\le 2$

Since

$x$ is a real number which is less than or equal to

$2$

Hence

$x\in\left(-\infty,2\right]$ is the solution.

Solve the system of inequality:
$2(3x - 1) < 3 (4x + 1 ) + 16, 4(2 + x) < 3x + 8$

$(1)2(3x-1)<3(4x+1)+16$

$\quad \quad \quad 6x-2<12x+3+16$

$\quad \quad \quad 6x>-5-16$

$\quad \quad \quad x>\cfrac { -21 }{ 6 }$

$\quad \quad \quad x\quad \varepsilon (\cfrac { -21 }{ 6 } ,\infty )$

$(2)4(2+x)<3x+8$

$\quad \quad 8+4x<3x+8$

$\quad \quad x<0$

$\quad \quad x\quad \varepsilon (-\infty ,0)$

$x\quad \varepsilon (\cfrac { -21 }{ 6 } ,0)$

Solve the following inequality:
$\left | x\, - \, 2 \, \right | \, \leqslant \, \left | x \, + \, 4 \, \right |$

The given equation is

$|x-2|\le |x+4|$

Therefore we have 3 cases

$i.)x\le -4\ ,ii.)-4\le x\le 2,\ iii.)x \ge 2$

Therefore the respective equations are

$i.)2-x \le -4-x$ which is equal to

$2 \le -4,$ which is not possible therefore no solution in this case

$ii.)2-x \le x+4$ which is equal to

$x\ge -1$

$iii.)x-2 \le x+4$ which is equal to

$-2\le 4$ which is possible for all values of x and also we assumed

$x \ge 2$

Hence the solution is

$x\in [-1,\infty )$

Simplify the following expression:
$\displaystyle\left ( a + \frac{ab}{a - b} \right ) \left ( \frac{ab}{a - b} - a \right ) :\frac{a^2 + b^2}{a^2 - b^2}$

$\bigg(a+\dfrac{a{b}}{a-b}\bigg)\bigg(\dfrac{a{b}}{a-b}-a\bigg)=\dfrac{a^{2}b^{2}}{(a-b)^{2}}-a^{2}=a^{2}\dfrac{b^{2}-a^{2}-b^{2}+2{a}{b}}{(a-b)^{2}}=\dfrac{a^{3}(2{b}-a)}{(a-b)^{2}}$

$\displaystyle\left(a+\dfrac{a{b}}{a-b}\right)\bigg(\dfrac{a{b}}{a-b}-a\bigg):\dfrac{a^{2}+b^{2}}{a^{2}-b^{2}}=\dfrac{a^{3}(2{b}-a)}{(a-b)^{2}}\times \dfrac{a^{2}-b^{2}}{a^{2}+b^{2}}=\dfrac{a^{3}(2{b}-a)(a+b)}{(a+b)(a^{2}+b^{2})}$

Solve the following inequality:
$\displaystyle \sqrt{3x \, - \, 10} \, > \, \sqrt{6 \, - \, x}$

$\sqrt { 3x-10 } >\sqrt { 6-x }$

$\quad 3x-10>6-x\\ 3x+x>16$

$4x>16$

$x>4$

$x\quad \varepsilon (4,\infty )\quad -(i)$

$but\quad (6-x)\quad \& \quad (3x-10)\quad can\quad not\quad be\quad negative$

$6-x>0$

$x<6\quad \quad x\quad \varepsilon (-\infty ,6)\quad -(ii)$

$3x-10>0$

$x>\cfrac { 10 }{ 3 } \quad x\quad \varepsilon (\cfrac { 10 }{ 3 } ,\infty )\quad -(iii)\\$

$x\quad \varepsilon (4,6)\quad from\quad (i),(ii)\& (iii)$

Find natural $x$ which satisfy the system of inequality:
$x + 3 < 4 + 2x, 5x - 3 < 4x - 1$

$(1)x+3<4+2x$

$\quad \quad x>-1$

$\quad x\quad \varepsilon (-1,\infty )$

$(2)5x-3<4x-1$

$\quad \quad x<2$

$x\quad \varepsilon (-\infty ,2)$

$x\quad \varepsilon (-1,2)$

Solve the inequality $\left | x\, + \, 1 \, \right | \, + \, \left | x \, - \, 4 \, \right |\, > \, 7,$ indicating the least positive integer $x$ satisfying the inequality.

given inequality is

$|x+1|+|x-4|>7$

there are 3 cases

$i.)x<-1,ii.)-1<x<4,iii.)x>4$

the respective equations in these cases are

$i.)(-1-x)+(4-x)>7,ii.)(x+1)+(4-x)>7,iii.)(x+1)+(x-4)>7$

in first case

$i.)3-2x>7$ implies

$x<5$ and we assumed

$x<-1$

therefore the solution in this case is

$x<-1$

in second case

$ii.)5>7$ which is not possible

therefore there is no solution in this case

in third case

$iii.)2x-3>7$ implies

$x>5$ and we assumed

$x>4$

therefore the solution in this case is

$x>5$

so, the solution is union of all cases which is

$x\in(-\infty,-1)\cup (4,\infty)$

$\left | 5\, - \, 2x \right | \, < 1$

The given equation is

$|5-2x|<1$

therefore we have 2 cases

$i.)x>5/2,ii.)x<5/2$

in first case the inequality becomes

$2x-5<1$ implies

$x<3$ and we assumed

$x>5/2$

therefore the solution is

$5/2<x<3$

in second case the inequality becomes

$5-2x<1$ implies

$x>2$ and we assumed

$x<5/2$

therefore the solution is

$2<x<5/2$

now the solution of the equation is the union of the two solutions

therefore the solution is

$2<x<3$

Solve the following inequality:
$\left | 3x\, - \, 2.5 \right | \, \geqslant \, 2$

The given equation is :

$|3x-2.5|\ge2$

therefore we have 2 cases

$i.)x\ge \dfrac{2.5 }{3 }$

$ii.)x\le \dfrac{2.5 }{3 }$

in first case the inequality becomes

$3x\ge 4.5$ implies

$x\ge 1.5$ and we assumed

$x\ge \dfrac{2.5 }{3 }$

therefore the solution is

$x\ge 1.5$

in second case the inequality becomes

$3x \le 0.5$ implies

$x\le \dfrac{0.5 }{3 }$ and we assumed

$x\le \dfrac{2.5 }{3 }$

therefore the solution is

$x\le \dfrac{0.5 }{3 }$

now the solution of the equation is the union of the two solutions

therefore the solution is

$x\in(-\infty ,\dfrac { 0.5 }{ 3 } ]\cup [1.5,\infty )$

Simplify the following expression:
$\displaystyle\left ( m + n - \frac{4mn}{m + n} \right ) :\left ( \frac{m}{m + n} - \frac{n}{n - m} - \frac{2mn} {m^2 - n^2}\right )$

$\displaystyle \bigg(\displaystyle \frac{(m+n)^{2}-4mn}{m+n}\bigg):\bigg(\frac{m}{m+n}+\frac{n}{m-n}-\frac{2mn}{m^{2}-n^{2}}\bigg)=\bigg(\frac{(m-n)^{2}}{m+n}\bigg):\bigg(\frac{m^{2}-mn+mn+n^{2}-2mn}{m^{2}-n^{2}}\bigg)=\bigg(\frac{(m-n)^{2}}{m+n}\bigg):\bigg(\frac{(m-n)^{2}}{m^{2}-n^{2}}\bigg)=m-n:1$

Solve the following inequality:
$\left | x\, - \, 4 \, \right | \, < \, x \, - \, 1$

The given equation is:

$|x-4|<x-1$ there are 2 possible cases

$i.)\ x<4,ii.)\ x>4$

and the respective equations in 2 cases are

$i.)4-x<x-1,ii.)x-4<x-1$

$1^st$ case:

$i.)2x>5$ implies

$x>\dfrac{5}{2}$ and we assumed

$x<4$

therefore the solution is

$\dfrac{5}{2}<x<4$

$2^nd$ case

$ii.)-4<-1$ which is possible for all values of x and we assumed

$x>4$

therefore the solution is

$x \in(\dfrac{5}{2},\infty)$

Solve the following inequality:
$\displaystyle\, \frac{4^x + 2x - 4}{x - 1} \leqslant 2$

$\cfrac { { 4 }^{ x }+2x-4 }{ x-1 } \le 2$

$\Rightarrow { 2 }^{ 2x }+2x-4\le 2x-2$

$\Rightarrow { 2 }^{ 2x }+2x-2x\le 4-2$

$\Rightarrow { 2 }^{ 2x }\le 2$

$\Rightarrow 2x\le 1$

$\therefore x\le 1$ solved

Solve the following inequalities.
$\displaystyle\, 2^{x + 2} - 2^{x + 1} + 2^{x - 1} - 2^{x - 2} \leqslant 9$

Solve the following Inequality

$1) 2^{x+2}-2^{x+1}+2^{x-1}-2^{x-2}\leq 9$

Sol From the formula

$a^{m+n} = a^{m}.a^{n}$

$\Rightarrow 2^{x+2} = 2^{x}.2^{2}$ Similarly from the given equation we

have

$\Rightarrow 2^{x}.2^{2}-2^{x}.2^{1}+2^{x}.2^{-1}-2^{x}.2^{-2}\leq 9$

$\Rightarrow 2^{x}[2^{2}-2^{1}+\dfrac{1}{2}-\dfrac{1}{4}]\leq 9$

$[\because a^{-m} = \dfrac{1}{a^{m}}]$

$\Rightarrow 2^{x}[4-2+\dfrac{1}{2}-\dfrac{1}{4}]\leq 9$

$\Rightarrow 2^{x}[2+\dfrac{1}{4}]\leq 9$

$[\because \dfrac{1}{2}-\dfrac{1}{4} = \dfrac{2-1}{4} = \dfrac{1}{4}]$

$\Rightarrow 2^{x}[\dfrac{9}{4}]\leq 9$

$\Rightarrow 2^{x}\leq 2^{2}$

$\Rightarrow \boxed{x = 2}$

$\boxed{\because a^{m} = a^{n} \Rightarrow m = n}$

1122871_887162_ans_ca44985810d94c8d9f9083e74bb46dfa.jpeg

Solve the following two- sided inequality:
$\displaystyle\, 1< \frac{3x - 1}{2x + 1} < 2$

$1<\dfrac{3{x}-1}{2{x}+1}<2\implies 1<\dfrac{3}{2}-\dfrac{5}{2(2{x}+1)}<2$

$\implies -\dfrac{1}{2}<-\dfrac{5}{2(2{x}+1)}<\dfrac{1}{2}\implies \dfrac{-1}{5}<\dfrac{1}{2{x}+1}<\dfrac{1}{5}\implies -5<2{x}+1<5\implies x\in (-3,2)$

Find the domain of definition and the range of the following function:

$\displaystyle f \, (x) \, = \, \sqrt{2 \, - \, x} \, + \, \sqrt{1 \, + \, x}$

$2-x\ge0$ and

$1+x\ge0$

$\implies x \in [-1,2]$

range

$=(\sqrt2,\sqrt6)$

Solve the following inequality:
$\displaystyle\, 4^x - 2^{2(x - 1)} + 8^\dfrac{2(x - 2)}{3} > 52$

${ 4 }^{ x }-{ 2 }^{ 2(x-1) }+{ 8 }^{ \cfrac { 2(x-2) }{ 3 } }>52$

${ { (2 }^{ x } })^{ 2 }-{ (\cfrac { { 2 }^{ x } }{ 2 } ) }^{ 2 }+{ (\cfrac { { 2 }^{ x } }{ 4 } ) }^{ 2 }>52$

$\quad \quad \quad let\quad { 2 }^{ x }=t$

${ t }^{ 2 }+\cfrac { { t }^{ 2 } }{ 16 } -\cfrac { { t }^{ 2 } }{ 4 } >52$

${ t }^{ 2 }(1+\cfrac { 1 }{ 16 } -\cfrac { 1 }{ 4 } )-52>0$

${ t }^{ 2 }(\cfrac { 13 }{ 16 } )>52$

${ t }^{ 2 }>64$

$t\quad \varepsilon (8,\infty )$

${ 2 }^{ x }\quad \varepsilon (8,\infty )$

$x\quad \varepsilon (3,\infty )$

Solve the following inequality:
$\displaystyle\, \frac{2^{x - 1} - 1}{2^{x + 1} + 1} < 2$

$\cfrac { { 2 }^{ x-1 }-1 }{ { 2 }^{ x+1 }+1 } <2$

$\cfrac { { 2 }^{ x-1 }-1-2({ 2 }^{ x+1 }+1) }{ { 2 }^{ x+1 }+1 } <0$

${ 2 }^{ x+1 }+1>0$

$\cfrac { { 2 }^{ x } }{ 2 } -1-2(2.{ 2 }^{ x }+1)<0$

$\cfrac { { 2 }^{ x } }{ 2 } -1-4.{ 2 }^{ x }-2<0$

$\quad \quad let\quad { 2 }^{ x }=t$

$\cfrac { t }{ 2 } -1-4t-2<0$

$\cfrac { t }{ 2 } -4t-3<0$

$t-8t-6<0$

$-7t<6$

$t>\cfrac { -6 }{ 7 }$

$but\quad t={ 2 }^{ x }>0$

$x\quad is\quad all\quad real\quad numbers$

Solve the following inequalities.
$\displaystyle\, 25^{-x} - 5^{-x + 1} \geqslant 50$

$25^{-x}-5^{-x+1}\geq 50$

$5^{-2x}-5^{-x}\geq 50$

$[\because a^{m+m} = a^{m}.a^{n}]$

Let

$5^{x} = a$

$\Rightarrow a^{2}-5a-50\geq 0$

$\Rightarrow a^{2}+5a-10a-50\geq 0$

$\Rightarrow a(a+5)-10(a+5)\geq 0$

$\Rightarrow (a+5)(a-10)\geq 0$

$\Rightarrow a\leq -5$ (or)

$a\geq 10$

$[\because (x-a)(x-b)> 0 a< b]$

$\Rightarrow x< a$ or

$x> b$

$\Rightarrow 5^{-x}\leq -5$ (or)

$5^{-x}\geq 10$

$\Rightarrow -xlog \leq -log5$

$\boxed{ x\leq 1 }$

$-x\,log\,5\geq log\,10$

$-x\,log5\geq 1$

$-x\geq -log\,5$

$\boxed{ x \geq log\,5}$

1125525_887171_ans_924484912bb04a42b951b67c78680798.jpeg

Solve the following inequalities.
$\displaystyle\, 2^{x + 2} - 2^{x + 3} - 2^{x + 4} > 5^{x + 1} - 5^{x + 2}$

$2^{x+2}-2^{x+3}-2^{x+4}>5^{x+1}-5^{x+2}$

$\Rightarrow 2^{x}.2^{2}-2^{x}.2^{3}-2^{x}.2^{4}> 5^{x}.5^{1}-5^{x+2}$

$[\because a^{m+n} = a^{m}.a^{n}]$

$\Rightarrow 2^{x}[4-8-16]> 5^{x}[5-25]$

$\Rightarrow 2^{x}[-20]> 5^{x}[-20]$

$\Rightarrow 1> \left ( \dfrac{5}{2} \right )^{x}$

$\Rightarrow$ Apply log on both sides

$\Rightarrow log_{1}> log\left ( \dfrac{5}{2} \right )^{x}$

$\Rightarrow log_{1}> x\,log\left ( \dfrac{5}{2} \right )$

$\Rightarrow 0> x\,log\left ( \dfrac{5}{2} \right )$

$\Rightarrow \boxed{x< 0}$

1125586_887166_ans_ad4a489eca2c44cb8d1e9e0113896c30.jpeg

Solve the following inequalities.
$\displaystyle\, 3^{72} \cdot \left ( \frac{1}{3} \right )^x \cdot \left ( \frac{1}{3} \right )^{\sqrt{x}} > 1$

$3^{72}\left ( \dfrac{1}{3} \right )^{x}.\left ( \dfrac{1}{3} \right )^{\sqrt{x}}> 1$

Sol

$\dfrac{3^{72}}{3^{x}+\sqrt{x}}> 1$

$[\because a^{m}.a^{n} = a^{m+n}]$

$\Rightarrow 3^{72}> 3^{x+\sqrt{x}}$

$\Rightarrow 72> x+\sqrt{x}$

$[\because a^{m}\geq a^{n}\Rightarrow m\geq n]$

$\Rightarrow 72-x> \sqrt{x}$

Squaring on both sides

$\Rightarrow (72-x)^{2}> (\sqrt{x})^{x}$

$\Rightarrow 5184+x^{2}-144x> x$

$\Rightarrow 5184+x^{2}-144x> 0$

$\Rightarrow 5184+x^{2}-145x> 0$

$\Rightarrow x^{2}-145x+5184> 0$

$\Rightarrow x^{2}-64x-81x+5184> 0$

$\Rightarrow x(x-64)-81(x-64)> 0$

$\Rightarrow (x-64)(x-81)> 0$

$\Rightarrow x< 64$ or

$x> 81$

$[\because (x-a)(x-b)> 0$ If

$a< b]$

$\Rightarrow x< a$ or

$x> b$

1125413_887168_ans_4066c4294c2a42ffaf090c0a8360d4fb.jpeg

Solve the following inequality:

$\displaystyle\, \left ( \dfrac{1}{3} \right )^\sqrt{x + 2} > 3^{-x}$

$\displaystyle\bigg(\dfrac{1}{3}\bigg)^{\sqrt{x+2}}>3^{-x}$

$\displaystyle3^{-\sqrt{x+2}}>3^{-x}$

$\displaystyle-\sqrt{x+2}>-x\implies \sqrt{x+2}<x\implies x^{2}-x-2>0\implies x\in (-\infty,-1)\cup (2,\infty)$

and

$x+2\geq 0\implies x\geq -2$

$x\in [-2,-1)\cup (2,\infty)$

Solve the following inequalities.
$\displaystyle\, x^22^{2x} + 9 (x + 2) 2^x + 8x^2 \leqslant (x + 2) 2^{2x} + 9x^22^x + 8x + 16$

$x^{2} (2^{2x})+9 (x+2)2^x + 8x^2 \leq (x+2)2^{2x} + 9x^{2x}2 + 8x +16$

segregating the terms as follows

$\Rightarrow x^{2}\left ( 2^{3x} \right ) + 9(x+2)2^x + 8x^{2}- (x+2)2^{2x}- 9x^{2}2^{x}-8x -16 \leq 0$

$\Rightarrow 2^{2x} \left [ x^{2}-x-2 \right ]+2^{x} [9(x+2)- 9x^{2}] + 8x^{2}- 8x -16 \leq 0.$

$\Rightarrow 2^{2x} [x^2 -x-2] + 2^{x} [ 9x+ 18-9x^{2}]+8x^{2}-8x - 16 \leq 0$

$\Rightarrow 2^{2x}[x^{2}-x-2]+2^{x} (-9) [x^{2}-x-2]+8 [x^{2}-x-2] \leq 0$

$\Rightarrow (x^{2}-x-2)(2^{2x}-9(2^{x})+8)\leq 0$

$\Rightarrow x^2 - x-2\leq 0$

$\Rightarrow x^2 -2x+x-2 \leq 0$

$\Rightarrow x(x-2)+1 (x-2)\leq 0$

$\Rightarrow (x-2)(x+1)\Rightarrow 0$

$\Rightarrow \boxed{ x\leq 2 (or) x\leq -1}$

$2^{2x}-9(2^x)+8\leq 0$

put

$2^{x} = y\Rightarrow 2^{2x} y^2$

$\Rightarrow y^2 - 9y +8\leq 0$

$y^2 -8y -y+8 \leq 0$

$\Rightarrow y(y-8)-1 (y-8) \leq 0$

$(y-8)(y-1)\leq 0 \Rightarrow \boxed{y \leq 8 \,or\, y \leq 1}$

$y \leq 8 \,or\, y\leq 1$

$2^x\leq 2^3$

$2^x \leq 1$

$\Rightarrow \downarrow$

$\downarrow$

$x\leq 3$ Not possible

$\boxed{ \therefore x\leq -1, x\leq 2 \,or \,x\leq 3}$

1122929_887193_ans_a592d189b48f4d0ab01e439551d7e5c8.jpeg

Solve the following inequalities
$\sqrt{25 - \, x^2} \, \leqslant \, \dfrac{12}{x}.$

$\sqrt {25 - x^{2}} \leq \dfrac {12}{x}$

Square both sides

$\Rightarrow 25 - x^{2} \leq \dfrac {144}{x^{2}}$

$\Rightarrow x^{4} - 25x^{2} + 144 \geq 0$

Let

$u = x^{2}$ and

$u^{2} = x^{4}$

$\Rightarrow u^{2} - 25u + 144\geq 0$

$\Rightarrow (u - 16)(u - 9) \geq 0$

$\Rightarrow (x^{2} - 16)(x^{2} - 9) \geq 0$

$\Rightarrow (x - 4)(x + 4)(x - 3)(x + 3)\geq 0$

For

$x < -4$

$(x - 4)(x + 4)(x - 3)(x + 3) > 0$

$x = -4$ , it will be zero.

For

$-4 < x < -3$ ,

$(x - 4)(x + 4)(x - 3)(x + 3) < 0$

For

$-3\leq x \leq 3$

$(x - 4)(x + 4)(x - 3)(x + 3) \geq 0$

Similarly

for

$x \geq 4$

$(x - 4)(x + 4)(x - 3)(x + 3) \geq 0$

Solution : -

$(-\infty, -4]\cup [-3, 3]\cup [4, \infty)$ .

Solve the following inequality:
$\displaystyle\, 3 \sqrt{x} > 2^a$

$3\sqrt{x}>2^{a}$

$\implies \sqrt{x}>\dfrac{2^a}{3}\implies x>\bigg(\dfrac{2^{a}}{3}\bigg)^2\implies x>\dfrac{4^a}{9}$

Solve the following inequalities.
$\displaystyle\, 8 \cdot \frac{3^{x - 2}}{3^x - 2^x} > 1 + \left ( \frac{2}{3} \right )^x$

$8. \dfrac{3^{x-2}}{3^{x}-2^{x}}> 1+\left ( \dfrac{2}{3} \right )^{x}$

$8. \dfrac{3^{x}.3^{-2}}{3^{x}-2^{x}}> 1+\left ( \dfrac{2}{3} \right )^{x}$

$\left [ \because a^{m-n} = a^{m}.a^{-n} \right ]$

$8\times \dfrac{3^{x}}{\dfrac{9}{3^{x}\left(1-\left(\dfrac{2}{3}\right )^x\right)}}> 1+\left ( \dfrac{2}{3} \right )^x$

$\dfrac{8}{9}> \left ( 1+\left ( \dfrac{2}{3} \right )^{x} \right )\left ( 1-\left ( \dfrac{2}{3} \right )^{x} \right )$

$\left [ \because (a+b)(a-b) = a^{2}-b^{2} \right ]$

$\dfrac{8}{9}> \left ( 1-\left ( \dfrac{2}{3} \right )^{2x} \right )$

$\left ( \dfrac{2}{3} \right )^{2x}> 1-\dfrac{8}{9}$

$\left ( \dfrac{4}{9} \right )^{x}> \dfrac{1}{9}$

Apply log on both sides

$ln\left ( \dfrac{4}{9} \right )^{x}> ln\left ( \dfrac{1}{a} \right )$

$|\because ln\,x^{n} = n\,ln\,x |$

$x\left ( ln\dfrac{4}{9} \right )> ln\left ( \dfrac{1}{a} \right )$

$x> \dfrac{ln(1/a)}{ln(4/9)} \Rightarrow \boxed {x> \dfrac{ln\,1-ln\,9}{ln\,4-ln\,9}}$

1126649_887184_ans_0830116e11d749ae8a4bbe5ed1311f3a.jpg

Solve the following inequality:
$\displaystyle\, \sqrt{9^x + 3^x - 2} \geqslant 9 - 3^x$

$\sqrt { { 9 }^{ x }+{ 3 }^{ x }-2 } \ge 9-{ 3 }^{ x }$

$let\quad { 3 }^{ x }=t$

$\sqrt { { t }^{ 2 }+t-2 } \ge 9-t$

${ t }^{ 2 }+t-2\ge { (9-t) }^{ 2 }$

${ t }^{ 2 }+t-2\ge { t }^{ 2 }+81-18t$

$19t\ge 83$

$t\ge \cfrac { 83 }{ 19 }$

${ 3 }^{ x }\ge \cfrac { 83 }{ 19 }$

$x\log { 3 } \ge \log { (\cfrac { 83 }{ 19 } ) }$

$x\ge \cfrac { \log { 83 } -\log { 19 } }{ \log { 3 } }$

Solve the following inequalities.
$\displaystyle\, \sqrt{9^x - 3^x + 2} > 3^x - 9$

$\sqrt{9^{x}-3^{x}+2}> 3^{x}-9$

Squaring on both sides

$\Rightarrow [\sqrt{9^{x}-3^{x}+2}]^{x}> [3^{x}-9]^{2}$

$\Rightarrow 9^{x}-3^{x}+2> (3^{x})^{2}+(a)^{x}-2\times 3^{x}\times 9$

$\Rightarrow 9^{x}-3^{x}+2> 9^{x}+81-18(3^{x})$

$\Rightarrow 18(3^{x})-3^{x}> 81-2$

$\Rightarrow 17(3^{x})> 79$

$\Rightarrow 3^{x}> \dfrac{79}{17}$

Apply

$log_{3}$ on both sides

$\Rightarrow log_{3}3^{x}> log_{3}\left ( \dfrac{79}{17} \right )$

$[\because log_{b}a^{n}=nlog_{b}^{a}]$

$\Rightarrow x\,log_{3}^{3}> log_{3}79-log_{3}^{17}$

$[\because log\left(\dfrac{a}{b} \right )= log\,a-log\,b]$

$\boxed{ \Rightarrow x> log_{3}^{79}-log_{3}^{17} }$

$[\because log_{a}^{a} = 1]$

1126610_887175_ans_4dc0b450b3f14c8ea34ae59249fe02d2.jpeg

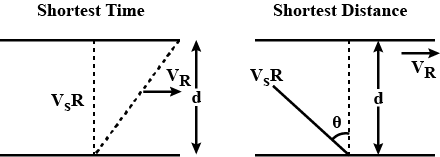
A person rows a boat across a river making an angle of $60^o$ with the downstream. Find the percentage time he would have saved, had he crossed the river in the shortest possible time.

Let

$v$ be the velocity of the boat and

$d$ the width of the river. The component of velocity along the direction perpendicular to the flow of water current is

$v$

$\sin 60^o$ ,Now if

$f_1$ be the time taken by the person to cross the river ,then

$t_1=\dfrac{d}{v\sin60^o}=\dfrac{d}{v}\left(\dfrac{2}{\sqrt{3}}\right)$

Had he crossed the river in the minimum possible time then his direction should be perpendicular to the flow of river and the corresponding time taken,

$t_2(say)=\dfrac{d}{v}$

$\therefore$ Percentage time saved

$=\dfrac{t_1-t_2}{t_2}\times 100$

$=\dfrac{\dfrac{d}{v}\left(\dfrac{2}{\sqrt{3}}\right)-\dfrac{d}{v}}{\dfrac{d}{v}}\times 100=15.47\%$

(a) Find all integral values of $x$ for which
$\begin{matrix} (5x-1)< & { \left( x+1 \right) }^{ 2 }< & (7x-3) \\ I & II & III \end{matrix}$ .
(b) $Solve\left| \dfrac { 12x }{ 4{ x }^{ 2 }+9 } \right| \le 1$ .

(a) Both the following inequalities have to hold good simultaneously.

${ x }^{ 2 }-3x+2=(x-1)(x-2)>0$ from I and II

${ x }^{ 2 }-5x+4=(x-1)(x-4)<0$ from II and III

$\therefore$

$x<1$ or

$x>2$ and

$1<x<4$

$\therefore$ From above we conclude that

$2<x<4$ satisfy both. Since x is integral therefore

$x=3$ .
(b) From the given relation we have

$-1\le \dfrac { 12x }{ 4{ x }^{ 2 }+9 } \le 1$ by definition of mod.
Since

$4{ x }^{ 2 }+9$ is

$+ive$ for all real x, we can multiply the inequality by

$4{ x }^{ 2 }+9$ .

$\therefore$

$-(4{ x }^{ 2 }+9)\le 12x\le (4{ x }^{ 2 }+9)$

${ \left( 2x+3 \right) }^{ 2 }\ge 0$ and

${ \left( 2x-3 \right) }^{ 2 }\ge 0$
Above is true for all real values of x being perfect squares.

Solve: $\dfrac{(x-1)(x-2)(x-3)}{(x+1)(x+2)(x+3)}>1$

$\cfrac { (x-1)(x-2)(x-3)-(x+1)(x+2)(x+3) }{ (x+1)(x+2)(x+3) } >0$

$\cfrac { (x-1)({ x }^{ 2 }-5x+6)-(x+1)({ x }^{ 2 }+5x+6) }{ (x+1)(x+2)(x+3) } >0$

$\cfrac { { (x }^{ 3 }-{ 5x }^{ 2 }+6x-{ x }^{ 2 }+5x-6)-({ x }^{ 3 }+{ 5x }^{ 2 }+6x+{ x }^{ 2 }+5x+6) }{ (x+1)(x+2)(x+3) } >0$

$\cfrac { { x }^{ 3 }-6{ x }^{ 2 }+11x-6-({ x }^{ 3 }+6{ x }^{ 2 }+11x+6) }{ (x+1)(x+2)(x+3) } >0$

$\cfrac { -12{ x }^{ 2 }-12 }{ (x+1)(x+2)(x+3) } >0$

$\cfrac { { x }^{ 2 }+1 }{ (x+1)(x+2)(x+3) } <0\quad \quad \quad ({ x }^{ 2 }+1>0)$

$\cfrac { 1 }{ (x+1)(x+2)(x+3) } <0$

$x \epsilon (-\infty ,-3)\cup(-2,-1)$

Let $a, b, c$ be positive real numbers, then prove that-
$\dfrac{1}{a^3(b+ c)} +\dfrac{1}{b^3( a+c)} +\dfrac{1}{c^3(a+b)} \geq \dfrac{3}{2}$ , if $abc \leq 1$ .

1827590_1035183_ans_4954917d64e34ba682e52b22d5be14d4.jpg

If the replacement set is the set of real numbers, solve : $\cfrac { x+3 }{ 8 } <\cfrac { x-3 }{ 5 }$

$\cfrac { x+3 }{ 8 } <\cfrac { x-3 }{ 5 }$

$5x+15<8x-24$

$39<3x$

$x>13\\ \Rightarrow\ x \varepsilon (13,\infty )$

A man wants to cut three lengths from a single piece of board of length $91cm$ . The second length is to be $3cm$ longer than the shortest and the third length is to be twice as long as the shortest. Find the length of the shortest piece.

Let the Length of shortest piece be

$s$

Second piece

$=s+3$

Third piece

$=2s$

Now,

$s+s+3+2s=91\Rightarrow 4s=88\Rightarrow s=22$

Find the smallest value of x for which $5 - 2x < 5{1 \over 2} - {5 \over 3}x$ , where x is an integer.

$5-2x<\cfrac { 11 }{ 2 } -\cfrac { 5x }{ 3 }$

$30-12x<33-10x$

$-3<2x$

$x>\cfrac { -3 }{ 2 }$

$x>-1.5$

$x\quad \varepsilon \quad Integers,\quad x\ge -1$

$least\quad value\quad of\quad x=-1$

Solve the inequation :
$12 + 1{5 \over 6}x \le 5 + 3x$ and $x \in R$ .

$12+\cfrac { 11x }{ 6 } \le 5+3x$

$7\le 3x-\cfrac { 11x }{ 6 }$

$7\le \cfrac { 7x }{ 6 }$

$7x\ge 7\times 6$

$x\ge 6$

$x\quad \varepsilon [6,\infty )$

If the replacement set is the set of real numbers,
solve : $5 + {x \over 4} > {x \over 5} + 9$

$5+\cfrac { x }{ 4 } >\cfrac { x }{ 5 } +9$

$\cfrac { x }{ 20 } >4$

$x>80$

$x\quad \varepsilon (80,\infty )$

Find the values of $x$
$3{x^2} - 5x + 9 \ge 3x - {x^2}$

$3{x^{2}}-5{x}+9\ge 3{x}-x^{2}$

$4{x^{2}}-8{x}+9\ge 0$

$4(x^{2}-2{x}+1)+5\ge 0$

$4(x-1)^{2}+5\ge 0\implies x\in R$

Man of weight $40$ kg standing on boat of weight $15kg$ and length $2m$ man walk one end to other what will be displacement of boat

Given,

The weight of the man is

$40kg$ and weight of the boat is

$15kg,$

length

$=2m$

Since the center of mass remain unchanged,

Thus, the mass of the man is multiplied displacement is equal to the product of the mass of the boat with the displacement of the boat,

Displacement of man

$= 2-x$

So,

$40\times(2-x)=15\times x$

$\Rightarrow x=\dfrac{80}{55}=1.45m$

where x is the displacement of the boat.

Solve:
$\dfrac{x}{4} < \dfrac{5x-2}{3} -\dfrac{(7x-4)}{5}$ .

We are given linear inequality

$\dfrac{x}{4} < \dfrac{5x-2}{3}- \dfrac{(7x-4)}{5}$

So,

$\dfrac{x}{4} < \dfrac{(5x-2)}{3} - \dfrac{(7x-4)}{5}$

$0 < \dfrac{(5x-2)}{3}- \dfrac{ (7x-4) }{5} - \dfrac{x}{4}$

$\therefore \dfrac{20 (5x-2)-12 (7x-4)-15x}{60} > 0$

$\therefore 100x -40- 84x+ 48 - 15x > 0$

$x+ 8 > 0$

So,

$x \in (-8 , \infty)$

Solve $\sqrt {x+y}\ge x; y\ge 2$

$\sqrt{x + y} \ge x; \; y \ge 2$

$\sqrt{x + y} \ge x$

Squaring both sides, we have

$x + y \ge {x}^{2}$

$\Rightarrow y \ge {x}^{2} - x$

$\Rightarrow y \ge {\left( x - \cfrac{1}{2} \right)}^{2} - \cfrac{1}{4}$

The graph for the above equation is a parabola.

Therefore, the parabola has vertex

$\left( \cfrac{1}{2}, -\cfrac{1}{4} \right)$ meeting

$x$ -axis at

$0$ and

$1$ while

$y$ -axis at

$0$ .

$y \ge 2$

The above equation will be straight line.

The shaded area will be the solution for the given system of inequality.

1051347_1063970_ans_ead6ac8ab3964bb5a74073fe7addee44.jpg

Find the complete set of values of $x$ satisfying :
(i) $\dfrac{5[x]+4}{11[x]+7} \ge 3$
(ii) $[x]^{2}-3[x]+2 \le 0$

(i)

$\dfrac{5[x] + 4}{11[x] + 7} \geq 3$

$\implies \dfrac{5[x] + 4}{11[x] + 7} - 3 \geq 0$

$\implies \dfrac{5[x] + 4 - 33[x] - 21}{11[x] + 7} \geq 0$

$\implies \dfrac{- 28[x] - 17}{11[x] + 7} \geq 0$

$\implies \dfrac{28[x] + 17}{11[x] + 7} \leq 0$

$\implies \dfrac{-17}{28} \leq [x] \leq \dfrac{- 7}{11}$

$\therefore x = \phi$

(ii)

$[x]^{2} - 3[x] + 2 \leq 0$

$\implies ([x] - 1)([x] - 2) \leq 0$

$\implies 1 \leq [x] \leq 2$

$\therefore x \in [1, 3)$

If the replacement set is the set of natural numbers, Find the set with maximum elements:
1)   $x - 5 < 0$
2)   $x + 1 \le 7$
3)   $3x - 4 > 6$
4)   $4x + 1 > 17$

(1)

$x-5<0$

$x<5$

$x=\left \{ 1,2,3,4 \right \}$

(2)

$x+1\leq 7$

$x\leq 7-1$

$x\leq 6$

$x=\left \{ 1,2,3,4,5,6 \right \}$

(3)

$3x-4>6$

$3x>6+4$

$3x>10$

$x>\cfrac{10}{3}$

$x=\left \{ 4,5,6,7,........ \right \}$

(4)

$4x+1>17$

$4x>17-1$

$4x>16$

$x>\cfrac{16}{4}$

$x>4$

$x=\left \{ 5,6,7,........ \right \}$

So, the set represented by equation (3) has maximum elements.

Mr. Goel left one-third of his property for his son, one fourth to his daughter and the remaining Rs. 2,00,000 to his wife. How much money did he leave?

Let the total amount of money be

$x$ .

So, money given to son is

$\dfrac{x}{3}$

Money given to daughter is

$\dfrac{x}{4}$

Money given to his wife is

$Rs. 2,00,000$

So,

$200000+\dfrac{x}{4}+\dfrac{x}{3} = x$

$200000 = \dfrac{5x}{12}$

$\implies \ x =Rs. 4,80,000$

The compound ratio of $3:4$ and the inverse ratio of $4:5$ is $45:x$ . Find $x$ .

1332372_1081773_ans_ffa3c648711448819c9ca5e5b1f191e5.jpg

If a, b, c, d are $4$ -distinct positive numbers, then prove that $(a+b+c+d)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{d}\right) > 16$ .

We know that for a finite number of terms (real)

A.M

$\ge$ G.M

Consider the terms to be

$a,b,c,d$

then A.M

$=\cfrac{a+b+c+d}{4}$

G.M=\sqrt [ 4 ]{ abcd } $$

A.M

$\ge$ G.M

$\cfrac{a+b+c+d}{4}\ge \sqrt [ 4 ]{ abcd } ......(1)$

Consider the terms to be

$\cfrac{1}{a},\cfrac{1}{b},\cfrac{1}{c},\cfrac{1}{d}$ then A.M

$\cfrac { \cfrac { 1 }{ a } +\cfrac { 1 }{ b } +\cfrac { 1 }{ c } +\cfrac { 1 }{ d } }{ 4 }$

G.M

$\sqrt [ 4 ]{ \cfrac { 1 }{ abcd } } ....$

A.M

$\ge$ G.M

$\Rightarrow \cfrac { \cfrac { 1 }{ a } +\cfrac { 1 }{ b } +\cfrac { 1 }{ c } +\cfrac { 1 }{ d } }{ 4 } \ge \sqrt [ 4 ]{ \cfrac { 1 }{ abcd } } ....(2)$

$(1)\times (2)$

$\cfrac { \left( a+b+c+d \right) \left( \cfrac { 1 }{ a } +\cfrac { 1 }{ b } +\cfrac { 1 }{ c } +\cfrac { 1 }{ d } \right) }{ 16 } \ge \sqrt [ 4 ]{ abcd } .\sqrt [ 4 ]{ \cfrac { 1 }{ abcd } }$

$\Rightarrow \left( a+b+c+d \right) \left( \cfrac { 1 }{ a } +\cfrac { 1 }{ b } +\cfrac { 1 }{ c } +\cfrac { 1 }{ d } \right) \ge 16$

Hence proved

Prove that $\dfrac{3x^2+1}{x}\geq 2\sqrt{3}, x > 0$ .

We know that for finite number of +ve real terms

A.M

$\ge$ G.M

Consider the terms to be

$3{x}^{2},1$ (

$x> 0$ )

$A.M=\cfrac{3{x}^{2}+1}{2}$ ,

$G.M=\sqrt { 3{ x }^{ 2 } } =\sqrt {3}x$

A.M

$\ge$ G.M

$\cfrac{3{x}^{2}+1}{2}\ge \sqrt {3}x$

$\cfrac{3{x}^{2}+1}{x}\ge 2\sqrt{3}$

If x, y, z $> 0$ , then prove that $(x+y+z)(x^3+y^3+z^3)\geq 9(xyz)^{\dfrac43}$ .

We know that for a finite number of positive real terms,

$A.M\ge G.M$

Consider the terms to be

$x,y,z$

$A.M=\cfrac{x+y+z}{3},G.M=\sqrt [ 3 ]{ xyz }$

$\Rightarrow$

$\cfrac{x+y+z}{3}\ge \sqrt [ 3 ]{ xyz } ...(1)$

Consider the terms

${x}^{3},{y}^{3},{z}^{3}$

$A.M=\cfrac{{x}^{3}+{y}^{3}+{z}^{3}}{3}$ ,

$G.M=\sqrt [ 3 ]{ { x }^{ 3 }{ y }^{ 3 }{ z }^{ 3 } } =xyz$

$\Rightarrow$

$\cfrac{{x}^{3}+{y}^{3}+{z}^{3}}{3}\ge xyz....(2)$

$(1)\times (2)$

$(x+y+z)({x}^{3}+{y}^{3}+{z}^{3})\ge 9{(xyz)}^{4/3}$

If x, y, z $> 0$ , then prove that $x^3y^3+y^3z^3+z^3x^3 \geq 3x^2y^2z^2$ .

We know that A.M

$\ge$ G.M

Consider the terms

$x^3y^3, y^3z^3, z^3x^3$

Arithmetic mean

$=\dfrac{x^3y^3+y^3z^3+z^3x^3}{3}$

Geometric mean

$=\sqrt[3]{(x^3y^3)(y^3z^3)(z^3x^3})$

$=\sqrt[3]{x^6y^6z^6}$

$=x^2y^2z^2$

$A.M\ge G.M$

$\Rightarrow \dfrac{x^3y^3+y^3z^3+z^3x^3}{3}\ge x^2y^2z^2$

$\Rightarrow x^3y^3+y^3z^3+z^3x^3 \ge 3x^2y^2z^2$

If the air is maintained at $30^o$ C and the temperature of the body cools from $80^o$ C to $60^o$ C in $12$ minutes, find the temperature of the body after $24$ minutes.

Change in temperature in

$1$ minute =

$\cfrac{20}{12} \space ^\circ C$

Change in temperature in

$24$ minute =

$\cfrac{20 \times 24}{12} \space ^\circ C = 40^\circ C$

Hence, the temperature,

$80 - 40 = 40^\circ C$

If a, b, c $> 0$ , then prove that $\dfrac{3a}{b}+\dfrac{4b}{c}+\dfrac{16c}{3a} \geq 12$ .

WE know that for a finite number of real terms

A.M

$\ge$ G.M

Consider the term to be

$\cfrac{3a}{b},\cfrac{4b}{c},\cfrac{!6c}{3a}$

A.M

$=\cfrac { \cfrac { 3a }{ b } +\cfrac { 4b }{ c } +\cfrac { 16c }{ 3a } }{ 3 }$

G.M

$=\sqrt [ 3 ]{ \cfrac { 3a }{ b } +\cfrac { 4b }{ c } +\cfrac { 16c }{ 3a } } =4$

A.M

$\ge$ G.M

$\cfrac { 3a }{ b } +\cfrac { 4b }{ c } +\cfrac { 16c }{ 3a } \ge 12$

If a, b, c $> 0$ , then prove that $\left (a^3+b^3+c^3+\dfrac{1}{a^3b^3c^3} \right )\geq 4$ .

we know that A.M

$\ge$ G.M for any set of values.

consider

$a^{3} , b^{3} , c^{3} , \dfrac{1}{a^{3}b^{3}c^{3}}$

A.M

$=\dfrac{a^{3}+b^{3}+c^{3}+\dfrac{1}{a^{3}b^{3}c^{3}}}{4}$

G.M

$=\sqrt{a^{3}.b^{3}.c^{3}.\dfrac{1}{a^{3}b^{3}c^{3}}}=1$

A.M

$\ge$ G.M

$=a^{3}+b^{3}+c^{3}+\dfrac{1}{a^{3}b^{3}c^{3}}\ge 4$

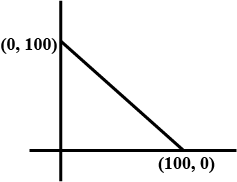
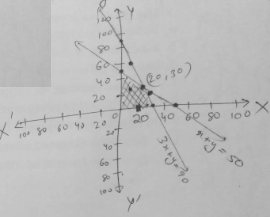
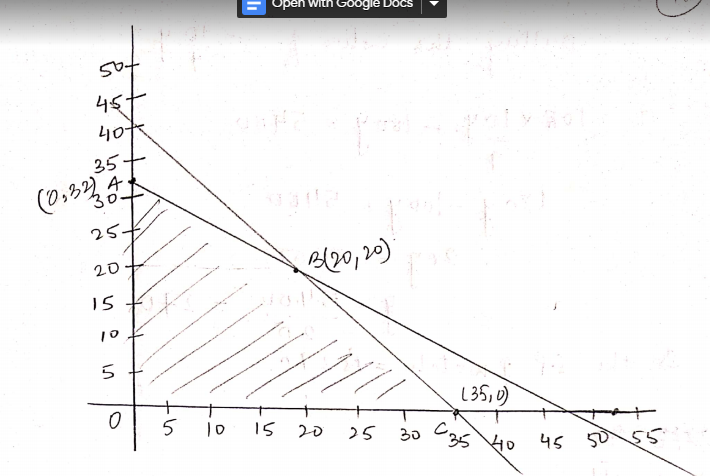
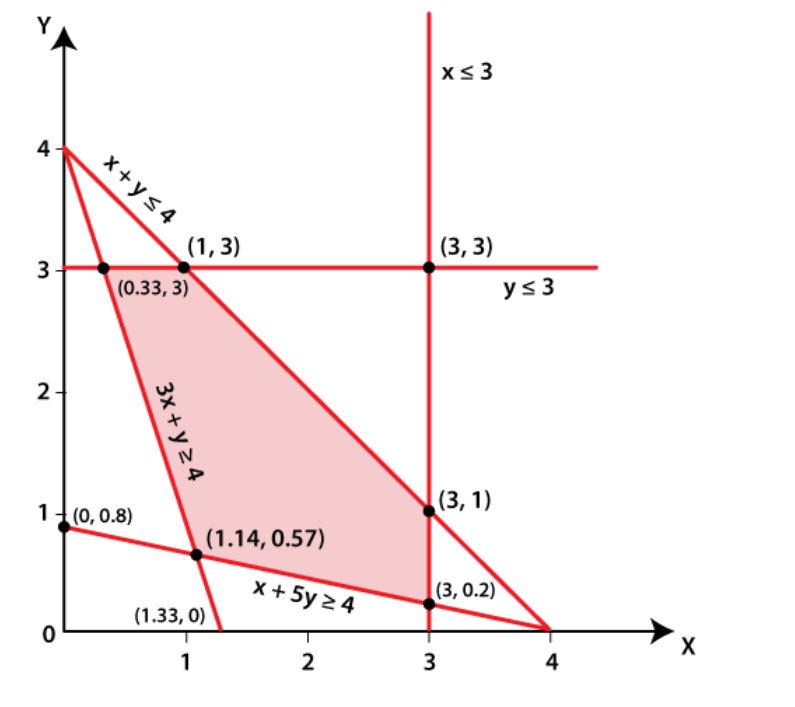
Solve the following linear programming problem graphically :
Maximize $z = 60x + 15y$ subjected to constraints:
$x + y\leq 50$
$3x + y\leq 90$
$x ,y\geq 0$

Maximize

$z=60x+15y$

$x$	$0$	$50$	$30$
$y$	$50$	$0$	$20$

$x+y\le 50$

$3x+y\le 90$

$x$	$0$	$30$	$10$
$y$	$90$	$0$	$60$

$x,y \ge 0$

$3x+y=90\\ x+y=50\\ \_ \_ \_ \_ \_ \_ \_ \_ \_ \\ 2x=40$

$x=20$

$y=30$

Optimal solution

$=60x+15y$

$=60(20)+15(30)$

$=1200+450$

$=1650$

1381694_1140516_ans_c34d076af3ac470aa3eb8d7e4f599f6c.png

A motor boat going downstream overcame a raft at a point A; $\tau = 60 \,min$ later it turned back and after some time passed the raft at a distance $l = 6.0km$ from point A. Find the flow velocity assuming the duty of the engine to be constant.

Let

$\nu_0$ be the stream velocity and

$\nu^{'}$

$the velocity of motorboat with respect to water. The motorboat reached point$

$B$

$while going downstream with velocity$

$(\nu_0+ \nu^{'})$

$and then returned with velocity$

$(\nu^{'}- \nu_0)$

$and passed the raft at point$

$C$

$. Let$

$t$

$be the time for the raft (which flows with stream with velocity$

$\nu_0$

$) to move from point$

$A$

$to$

$C$

$, during which the motorboat moves from$

$A$

$to$

$B$

$and then from$

$B$

$to$

$C$ $

Therefore

$\dfrac{l}{\nu_0}= \tau+ \dfrac{(\nu_0+\nu^{'}) \tau-l}{(v^{'}-\nu_0)}$

on solving we get

$\nu_0=\dfrac{1}{2 \tau}$

1792873_1122122_ans_2a2ccbe4208241e486eccdcb1b714c4c.png

If $a:b = 3:7$ and $b:c = 3:4$ then find $a:b:c$ .
If $a:b = 3:5$ and $b:c = 2:3$ then find $a:b:c$

Part

$(A)$

$a:b=3:7$ and

$b:c=3:4$

$a:b=9:21$ and

$b:c=21:28$

So,

$a:b:c=9:21:28$

Part

$(B)$

$a:b=3:5$ and

$b:c=2:3$

$a:b=6:10$ and

$b:c=10:15$

So,

$a:b:c=6:10:25$

Hence, this is the answer.

Solve $2 < |2x+1| < 5$

$2 < |2x+1| < 5$

$\Rightarrow 2 < |2x+1|$ and

$|2x+1| < 5$

$\Rightarrow 2x+ 1 < -2$ or

$2x+1 > 2$ and

$-5 < 2x + 1$ or

$2x+1 < 5$

$\Rightarrow 2x < -3$ or

$2x > 1$
and

$2x > -6$ or

$2x < 4$

$\Rightarrow x < \dfrac{-3}{2}$ or

$x > \dfrac{1}{2}$ and

$x > -3$ or

$x < 2$

$\Rightarrow x \in \left(-3, \dfrac{-3}{2}\right) \cup \left(\dfrac{1}{2}, 2\right)$

Solve : $||x - 1| - 5| \ge 2$

$||x-1|-5|\ge2$

$((x-1)-5)\in (-\infty,-2)\cup(2,0)$

$-\infty <|x-1|-5\le -2$

$2\le|x-1|-5<\infty$

$-\infty<|x-1|\le3$

$7\le|x-1|<\infty$

$\Rightarrow |x-1|\le3$

$\Rightarrow |x-1|\ge7$

$-3\le(x-1)\le3$

$\Rightarrow (x-1)\in(-\infty,-7)\cup[7,\infty]$

$\Rightarrow \boxed{-2\le x\le4}$

$x\in (-\infty.-6)\cup [8,\infty]$

$\therefore x\in [-\infty,-6]\cup [-2,4]\cup[8,\infty]$

Cost of a table and chair is in the ratio $2 : 3$ . If the total cost is $Rs. 2250$ , find the cost table and chair each.

Let the cost of a table be

$2x$ and cost of a chair be

$3x$ .

SInce, total cost

$=Rs. 2250$

So,

$2x+3x=2250$

$5x=2250$

$x=Rs. 450$

Therefore,

Cost of a table is

$=2\times 450=Rs. 900$

Cost of a chair is

$=3\times 450=Rs. 1350$

Hence, this is the answer.

Solve : $\left | x\ +\ \dfrac{1}{3} \right | > \dfrac{8}{3}$

Given

$\left|x+\dfrac{1}{3}\right|>\dfrac{8}{3}$

Case I :

$x+\dfrac{1}{3}\ge 0 \Rightarrow x\ge \dfrac{-1}{3}$ ......

$(1)$

$\left|x+\dfrac{1}{3}\right|=x+\dfrac{1}{3}>\dfrac{8}{3}\rightarrow x>\dfrac{7}{3}$ .....

$(2)$

From

$(1), (2) x>\dfrac{7}{3}$

Case II:

$x+\dfrac{1}{3}<0\Rightarrow x<\dfrac{-1}{3}$ .......

$(3)$

$\left|x+\dfrac{1}{3}\right|=-x-\dfrac{1}{3}>\dfrac{8}{3}\Rightarrow x<-3$ .....

$(4)$

from

$(3), (4) x<-3$

$\Rightarrow x\in (-\infty, -3)v\left(\dfrac{7}{3}, \infty\right)$

$2 \,km$ wide river flowing at the rate $5 \,km/hr$ . A man can swim is still water $10 \,km/hr$ . He wants to cross the river along the shorted path. Find-
(a) in which direction should the person swim.
(b) crossing time.

Since the man goes along the shortest path.
So,

$10 \,\cos \theta = 5$

$\cos \theta = \dfrac{1}{2}$

$\theta = 60^o$ from opposite to flow
or

$\theta = 180 - 60$ from flow

$= 120^o$

Time taken

$= \dfrac{distance}{speed} = \dfrac{2}{10 \sin 60}$

$= \dfrac{1}{5 \times \dfrac{\sqrt{3}}{2}}$

$= \dfrac{2}{5\sqrt{2}}$

Solve for : $-12<4+\dfrac{3x}{\left(-5\right)} \le 2$

$- 12 < 4 + \dfrac{3x}{(-5)} \leq 2$

Multiply with

$- 5$ we get,

$\implies - 12 \times - 5 > 4 \times (-5) + 3x \geq 2 \times (-5)$

$\implies 60 > 3x - 20 \geq - 10$

$\implies 60 + 20 > 3x - 20 + 20\geq - 10 + 20$

$\implies 80 > 3x \geq 10$

$\implies 10 \leq 3x < 80$

$\implies \dfrac{10}{3} \leq x < \dfrac{80}{3}$

$\therefore x \in \left [\dfrac{10}{3}, \dfrac{80}{3} \right )$

Minimize and maximize $Z=x+2y$ subject to constraints are $x+2y\ge 100,2x-y\ge 0,2x+y\le 200$ and $x,y\ge 0$ .

$Z=x+2y, 4$ constrats are,

$x+2y\ge 100$

$2n-y\le 0$

$2x+y\le 2$

$x,y,\ge 0$
we have of draw the 3 linear
so,at point (0,200)z\rightarrow man

$from point$

$(0,\frac { 1 }{ 2 }$

$to$

$(\frac { 1 }{ 5 } ,\frac { 2 }{ 5 } )$ $ z is min.

Prove that
$\frac { 1 } { x + 1 } - \frac { 1 } { x } \leq \frac { 1 } { x - 1 } - \frac { 1 } { x - 2 }$

Solving L.H.S,

$\dfrac { 1 }{ 1+x } -\dfrac { 1 }{ x }$

$=\dfrac { x-x-1 }{ x(x+1) }$

$=\dfrac { -1 }{ x(x+1) }$

Solving R.H.S,

$\dfrac { 1 }{ x-1 } -\dfrac { 1 }{ x-2 }$

$=\dfrac { x-2-x+1 }{ (x-1)(x-2) }$

$=\dfrac { -1 }{ (x-1)(x-2) }$

It is obvious that L.H.S is

$\le$ R.H.S

That is

$\dfrac { -1 }{ x(x+1) } \le \dfrac { -1 }{ (x-1)(x-2) }$

$\Longrightarrow \dfrac { 1 }{ 1+x } -\dfrac { 1 }{ x } \le \dfrac { 1 }{ x-1 } -\dfrac { 1 }{ x-2 }$

The present ages of A, B and C are in the ratio of 8: 14:22 respectively. The present ages of B , C and D are in the ratio of 21:33:44 respectively, which of the following represents the ratio of the present ages of A, B, C and D respectively?.

$A:B:C= 8:14:22$ ] given

$= 4:7:11$

$B:C:D = 21:33:44$

$\therefore A:B:C:D$

$= 12:21:33:44$

1115340_1200969_ans_f08132c066004adaa47f52e146c186ba.jpeg

Find three consecutive whole numbers whose sum is more than $45$ but less than $54$ .

Let no.s be

$\Rightarrow x-1, x , x+1$

$(x-1)+x+(x-1) > 45$

$\Rightarrow 3x > 45 \Rightarrow x > 15$

also,

$(x-1)+x+(x+1) < 45$

$3x < 54 \Rightarrow x < 18$

$x \in (15, 18) \therefore x$ can be

$\Rightarrow 16 , 17$

$\therefore 15, 16, 17$ or

$16, 17, 18$ .

The ratio between the prices of a scooter and a refrigerator is $4 : 1$ . If the scooter costs $Rs\ 45,000$ more than the refrigerator, find the price of the refrigerator.

It is given that
Ratio between the prices of a scooter and a refrigerator

$= 4: 1$
Cost of scooter

$= ₹ 45,000$
Consider the cost of scooter

$= 4x$
Cost of refrigerator

$= 1x$
Using the conditionCost of scooter > Cost of refrigerator

$4x – x = 45000$
On further calculation

$3x = 45000$
So we get

$x = \dfrac{45000}3 = ₹ 15000$
So the price of refrigerator

$= ₹ 15000$

Solve: $\dfrac{|x + 2| -x}{x} < 2.$

We have,

$\cfrac{|x+2|-x}{x}<2$

For

$x\ge -2$

$\cfrac{(x+2)-x}{x}<2$

$\implies \cfrac{1}{x}-1\le0$

$\implies \cfrac{x-1}{x}>0$

$x\ \epsilon\ (-\infty,0)\cup(1,\infty)$

But

$x\ge -2$

So,

$x\ \epsilon\ [-2,0)\cup(1,\infty)$

For

$x\le -2$

$\cfrac{-(x+2)-x}{x}<2$

$\implies \cfrac{-(x-1)}{x}<1$

$\implies \cfrac{2x+1}{x}>0$

$x\ \epsilon\ (-\infty,-1/2)\cup(0,\infty)$

But

$x\le -2$

$x\ \epsilon\ (-\infty,-2)$

Finally,

$x\ \epsilon\ [-\infty,0)\cup(1,\infty)$

Hence, this is the answer.

find range of x:
$x + 5 > 4 x - 10$

$\\x+5>4x-10\\5+10>3x\\15>3x\\5>x\\\therefore\>x\in (-\infty,5)$

Solve: $x + 3 < \dfrac { - 2 } { x + 2 }$

R.E.F image

$(x+3)+\dfrac{2}{(x+2)}< 0$

$\dfrac{(x+3)(x+2)+2}{(x+2)}< 0$

$\dfrac{x^{2}+2x+3x+6+2}{(x+2)}< 0$

$\dfrac{x^{2}+5x+8}{(x+2)}< 0$

$x^{2}+5x+8$ doesn't has

any Zeroos.

$\therefore x\epsilon (-\infty ,-2)$

1383070_1211327_ans_355547ec528b44099a0485fb07a97594.PNG

A factory makes cricket bats and hockey sticks. A bat takes $1.5$ hours of machine time and $2$ hours of craftsman time. While a hockey stick takes $2.5$ hour of a machine time and $1.5$ hours of craftsman time. In a day the factory is available up to $80$ hours of machine time and $70$ hours of craftsman time. Show that in order to make maximum profit the factory should produce only cricket bats given that the profits on a cricket at and a hockey stick are Rs. $50$ and Rs. $35$ respectively.

Let the number of cricket bat be

$x$ and hockey sticks be

$y$

In the factory machine time is available upto

$80$ hours

$1.5x+2.5y\le80$

In the factory craftsman time is available upto

$70$ hours

$2.6x+1.5y\le70$

Let the total profit be

$z$ .

Profit on cricket bat is

$Rs.50$ and

$Rs.35$ on hockey stick.

$z=50x+35y$

Maximize$$z=50x+35y$

Subject to

$1.5x+2.5y\le80$

$2x+1.5y\le 70$

$1.5x+2.5y\le80$

$x$	$0$	$20$
$y$	$32$	$20$

$2x+1.5y\le 70$

$x$	$35$	$20$
$y$	$0$	$20$

From the graph we can conclude the maximum profit is at

$(20,20)$ $$

So,

$20$ cricket bat and

$20$ hockey sticks should be produced for maximum profit.

1210936_1242605_ans_1c4c2e28c9a847548c1d5bd5c7745517.PNG

Evaluate values of $x$ :
$2 ( 3 - x ) \geq \dfrac { x } { 5 } + 4$

$\\2(3-x)\geq(\frac{x}{5})+4\\6-2x\geq(\frac{x}{5})+4\\6-4\geq(\frac{x}{5})+2x\\2\geq(\frac{11x}{5})\\(\frac{10}{11})\geq\>x\\\therefore\>x\in\left(-\infty,\frac{10}{11}\right]$

Solve $\dfrac{{62x + 404}}{{140}} \le \dfrac{{51 + 15x}}{{35}}$ .

1337494_1241183_ans_bb0d5a17e6cd4c18b32b96506da0c557.jpg

Solve : $9x-7\le 28+4x;$ $x \epsilon R$

$9x-7\le 28+4x$

$\Rightarrow 9x-4x\le 28+7$

$\Rightarrow 5x\le 35$

$\Rightarrow x\le 7$

Hence, solved.

The solution set for $\left(x+3\right)+4>-2x+5$ is

$x+3+4>-2x+5$

$\Rightarrow x+7>-2x+5$

$\Rightarrow x+2x>5-7$

$\Rightarrow 3x>-2$

$\Rightarrow x>\dfrac{-2}{3}$

$\therefore x\in\left(\dfrac{-2}{3},\infty\right)$

Solve
$2x \le x-1< 3x+5$ .

We have

$2x\le x-1\le 3x+5$

$(i)\quad 2x \le x-1$

$2x-x < -1$

$x< -1$

$(ii)\quad x-1\le 3x+5$

$x-3x-1\le 5$

$-2x-1\le 5$

$-2x\le 4$

$x\ge -\dfrac {4}{2}$

$x\ge -2$

$\therefore \ -2 \le x < -1$

Hence this is the answer.

Solve the inequality $\left( x-11 \right) \left( x-7 \right) \le 1$ . The number of integers satisfy this inequality is ____ .

1820500_1240823_ans_b09425530cf64ea69e531e3893aa47bd.jpg

Solve for $x$ :
$\dfrac { 7 x - 1 } { 2 } < - 3 , \dfrac { 3 x + 8 } { 5 } + 11 < 0$

$\displaystyle(\dfrac{7x-1}{2})< -3\\7x-1<-6\\7x<-6+1\\7x<-5\\x<(\dfrac{-5}{7})\ and\ (\dfrac{3x+8}{5})+11<0\\(\dfrac{3x+8+55}{5})<0\\3x+63<0\\3x<-63\\x<-21\\hence \>common \>region\> will\> be \\x\in(-\infty,-21 )$

Solve for $x$
$\dfrac { 1 } { | x | - 3 } < \dfrac { 1 } { 2 }$

$\\(\frac{1}{|x|-3})<(\frac{1}{2})\\(\frac{1}{|x|-3})-(\frac{1}{2})<0\\(\frac{2-(|x|-3)}{(|x|-3)\times2})<0\\(\frac{5-|x|}{|x|-3})<0\\(\frac{|x|-5}{|x|-3})>0\\hence\>\>\>0\leqslant\>|x|<3\>\>\cup\>5<|x|<\infty\\\therefore\>x\in(-\infty,-5)\>\cup\>(-3,3)\>\cup\>(5,\infty)$

1161688_1258537_ans_ef73c2bda22d4107aa98b975aa4abecb.png

Show that $\frac { x } { 1 + x } < \ln ( 1 + x ) < x \forall x > 0$

Let

$f(x)=\dfrac{x}{1+x}-ln (1+x)$

$f'(x)=\dfrac{1}{1+x}+\dfrac{-x}{(1+x)^2}-\dfrac{1}{1+x}$

$=\dfrac{-x}{(1+x)^2}$

Thus

$f'(x) < 0\forall x\in R$

Thus

$f(x)$ is decreasing

$fx^n$

$f(0)=0$

Thus

$f(x) < f(0)\forall x > 0$

$\Rightarrow \dfrac{x}{1+x}-ln(1+x) < 0$

$\Rightarrow \dfrac{x}{1+x} < ln(1+x)\forall x > 0$ ……(i)

Let

$g(x)=ln (1+x)-x$

$g'(x)=\dfrac{1}{1+x}-1=\dfrac{1-(1+x)}{1+x}=\dfrac{-x}{1+x} < 0\forall x > 0$

$g(x) =$ is decreasing

$fx^h \forall x > 0$

$\Rightarrow g(x) < g(0)\forall x > 0$

$\Rightarrow ln(1+x)-x < 0\forall x > 0$

$\Rightarrow ln(1+x) < x$ ……..(ii)

Proved.

1136321_1246152_ans_1c605c7b8d584cd3a8b683e3c7ed4c54.jpg

The first, second and third class railway fares in the ratio between two stations are in the ratio as 6 : 4 : 1 and the number of passenger of the three classes are 2 : 5 :If the sale of the tickets of three classes amount of Rs 12300, find total collection from each class.

Let first, second, third class fare,

$6x, 4x, x$ resp

Let no. of the passenger of first, second, third be

$2y, 5y, 50y$ resp

Total fare :

$6x \times 2y + 4x \times 5y + x \times 50 y = 12 xy + 20 xy + 50 xy$

$82 xy = 12300$

$xy = 150$

Total collection from

$1^{st} \, class = 12xy = 12 \times 150 = 1800$

$2^{nd} \, class = 20 xy = 20 \times 150 = 3000$

$3^{rd} \, class = 50 xy = 50 \times 150 = 7500$

If $a,b$ are natural numbers, prove that

$\sqrt { \dfrac { a ^ { 2 } + 2 b ^ { 2 } } { 2 } } > b$

$\sqrt{\dfrac{a^2+2b^2}{2}} > b$

Square on both sides

$\dfrac{a^2+2b^2}{2} > b^2$

$\Rightarrow a^2+2b^2 > 2b^2$

$\Rightarrow a^2 > 0$

$\Rightarrow a\in R$ ,

$b$ is arbitrary

$\Rightarrow a, b\in R$ .

Solve:
$5 ^ { \log _ { \sqrt { 5 } } x } - x - 6 < 0$

${ 5 }^{ \log _{ \sqrt { 5 } }{ x } }-x-6 < 0$

${ 5 }^{ 2\log _{ 5 }{ x } }-x-6<0$

${ 5 }^{ \log _{ 5 }{ { x }^{ 3 } } }-x-6<0$

$x^{2}-x-6<0$

$x^{2}-3x+2x-6<0$

$x(x-3)+2(x-3)<0$

${x-3}(x+2)<0$

$\Rightarrow x, \in (-2, 3)$

Find range of $x$
$\dfrac { 5 x + 8 } { 4 - x } < 2$

$(\dfrac{5x+8}{4-x})<2$

$(\dfrac{5x+8}{4-x})-2<0$

$(\dfrac{5x+8-2(4-x)}{4-x})<0$

$(\dfrac{7x}{4-x})<0$

$\therefore\>x\>\in\>(-\infty,0)\cup(4,\infty)$

1165806_1247377_ans_e6347fc4ae4a461b800b061b4ea44033.png

A number is such that it is as much greater than $65$ as it is less than $91$ .Find the number.

Let the number be

$x$

According to the question,

The number

$-65=91-$ the number

$\Rightarrow x-65=91-x$

$\Rightarrow x+x=91+65$

$\Rightarrow 2x=156$

$\therefore x=\dfrac{156}{2}=78$

Thus, the required number is

$78$

A recipe for cookies uses butter and sugar in ratio $2:3$ . If we are using $8$ cups of butter, how many cups of sugar should we use?

$I^{st}$ method

$\Rightarrow$ butter : sugar

$\Rightarrow$ 2 : 3

$II^{nd}$ method

$\Rightarrow$ butter : sugar

$\Rightarrow$ 2x : 3x

$\begin{array}{l} 2x=8 \\ x=4 \end{array}$

Then sugar

$=3x$

$= 3 \times 4 = 12$

1209137_1310792_ans_a84febb55fda4e80ab9c77cd5b8ddb0e.PNG

Find the ratio in which the line segment joining A (6,4) and B(1,-7) is divided internally by x axis.

For x-axis

$y=0$

Let the ratio be

$k:1$

Then

$\dfrac{kx_2+1\times x_1}{k+1}=a$ ,

$\dfrac{ky_2+1\times y_1}{k+1}=0$

$\Rightarrow \dfrac{k+6}{k+1}=a$ ,

$\dfrac{k(-7)+4}{k+1}=0$

$\Rightarrow -7k+4=0$

$\Rightarrow 7k=4$

$\Rightarrow k=\dfrac{4}{7}$

$\therefore$ Ratio

$=4:7$ .

1162335_1280893_ans_9723f664f229498c955348d0bd376e8d.jpg

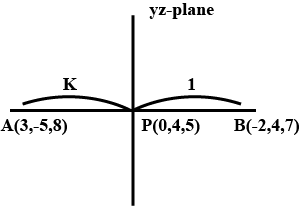
the ratio in which YZ plane divides the line segment formed by joining the points (-2,4,7) and (3,-5,8)

Let

$P \equiv \left( {o,h,s} \right)$ be the point at which

$yz$ plane interest above point

$\left[ {\because \,x - coordinate = 0\,in\,yz\,plane} \right]$

also let the ratio be

$K:1$

$0 = \dfrac{{ - 2K + 3}}{{K + 1}}$

$\Rightarrow - 2K + 3 = 0$

$\Rightarrow K = \dfrac{{ - 3}}{{ - 2}} = \dfrac{3}{2}$

$\therefore$ Required ratio is

$3:2$

1218494_1311970_ans_6f727f9df66c4dcf8e20dddb63386e79.png

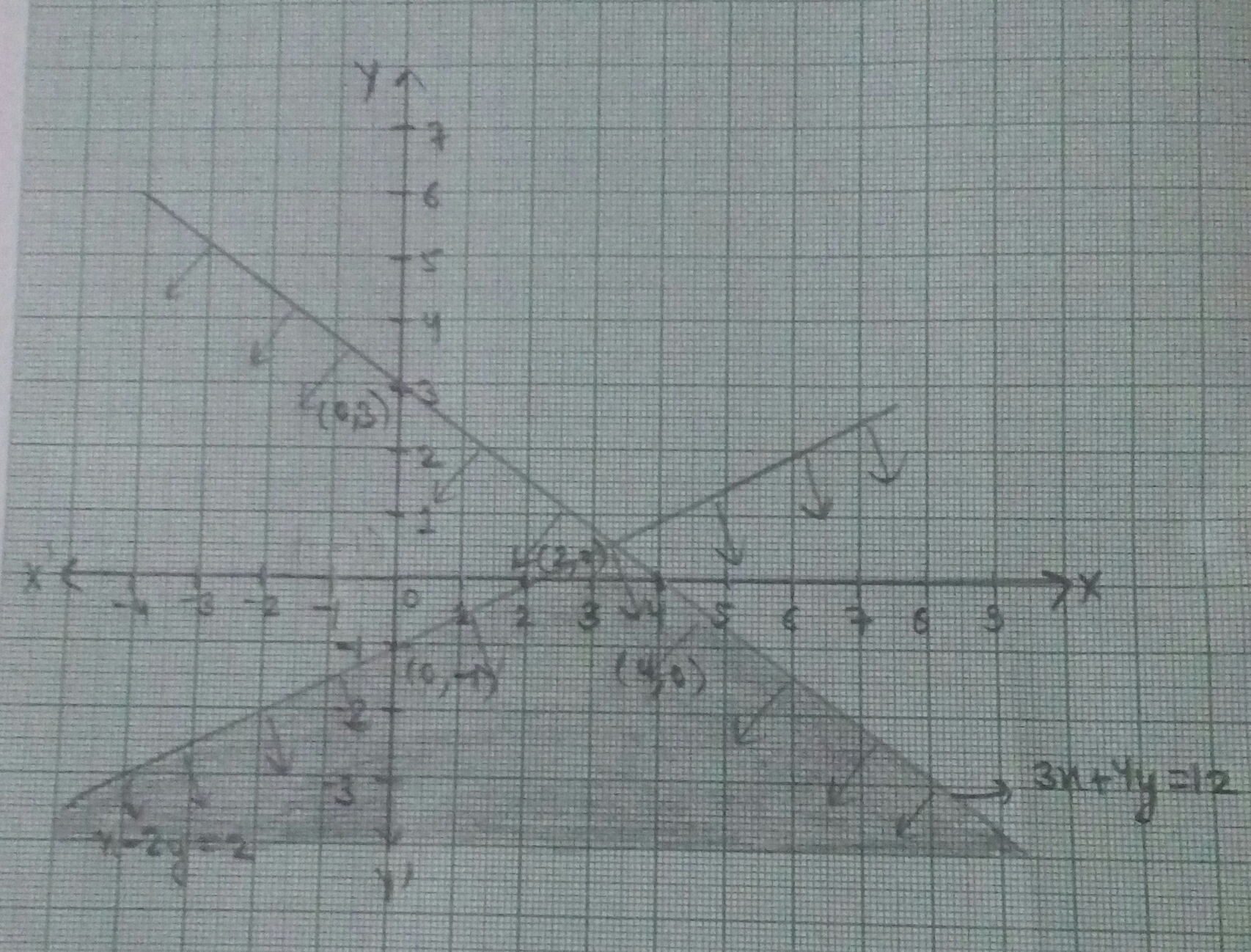
Find the graphical solution of the following in equations $3x+4y \le 12$ and $x-2y \ge2$

The shaded portion is the graphical solution of the given inequalities.

1284075_1364130_ans_6c1b985feed74d54ad6f871dfc63dd91.jpg

One kilogram of onions cost $Rs\ 12.75$ . How much will $3.5\ kg$ cost?

$1$ kg

$\rightarrow 12.75$ Rs. unitary method

$3.5$ kg

$\rightarrow 12.75 \times 3.5$

$= 44.625$ Rs.

$\simeq 44.63$ Rs.

1187798_1353133_ans_a573ea1227a245bcbd4285d8ca634329.jpg

Divide $1500$ among $A,B,C$ in the ratio $3:5:2$

We have sum of the terms of the ratio

$=3+5+2=10$

$A's$ share

$=\dfrac{3}{10}\times 1500=3\times 150=450$

$B's$ share

$=\dfrac{5}{10}\times 1500=5\times 150=750$

$C's$ share

$=\dfrac{2}{10}\times 1500=2\times 150=300$

Solve: $9x+3>2$

$9x+3>2$

$\Rightarrow\,9x>2-3$

$\Rightarrow\,9x>-1$

$\Rightarrow\,x>\dfrac{-1}{9}$

$\therefore,x\in\left(\dfrac{-1}{9},\infty\right)$

If $3:x::12:20,$ find the value of $x?$

We have

$3:x::12:20$

$\Rightarrow 3,\,x,\,12,\,20$ are in proportion.

$\Rightarrow$ Product of extremes

$=$ Product of means

$\Rightarrow 3\times 20=x\times 12$

$\Rightarrow 60=12x$

$\Rightarrow x=\dfrac{60}{12}=5$

$\left| \frac { 3 x - 4 } { 2 } \right| \leq \frac { 5 ! } { 12 }$

Consider given the expression,

$\left| \dfrac{3x-4}{2} \right|\le \dfrac{5!}{12}$

$\dfrac{\left| 3x-4 \right|}{2}\le \dfrac{5!}{12}$

$\dfrac{\left| 3x-4 \right|\times 2}{2}\le \dfrac{5!\times 2}{12}$

$\left| 3x-4 \right|\le \dfrac{5\times 4\times 3\times 2\times 1}{6}$

$\left| 3x-4 \right|\le 20$

If, $x\ge \dfrac{4}{3}$

Then, $\left| 3x-4 \right|\ge 0$

So,

$3x-4\le 20$

$x\le 8$

Hence, this is the answer.

Solve: $2x+5>3x-5$

$2x+5>3x-5$

$\Rightarrow\,2x+5-3x+5>0$

$\Rightarrow\,-x+10>0$

$\Rightarrow\,-x>-10$

$\Rightarrow\,x<10$

$\therefore\,x\in\left(-\infty,10\right)$

A sum of Rs. $84,000$ is divided among three persons $A,B$ and $C$ .If $A$ gets one-fourth of it and $B$ gets one-fifth of it.How much did $C$ get?

Total money

$=$ Rs.

$84,000$

$A$ gets

$=\dfrac{1}{4}$ of

$84,000=\dfrac{1}{4}\times\,84,000=$ Rs.

$21,000$

$B$ gets

$=\dfrac{1}{5}$ of

$84,000=\dfrac{1}{5}\times\,84,000=$ Rs.

$16,800$

$\therefore\,C$ gets the remaining money

$\therefore\,C's$ share

$=$ Rs.

$84,000-\left(Rs.21,000+Rs.\,16800\right)$

$=$ Rs.

$84,000-37,800=$ Rs.

$46,200$

Solve: $8x+9\le 3x+2$

given,

$8x+9\le 3x+2$

$\Rightarrow\,8x+9-3x-2\le \,0$

$\Rightarrow\,5x+7\le 0$

$\Rightarrow\,5x\le -7$

$\Rightarrow\,x\le \dfrac{-7}{5}$

$\therefore\,x\in\left(-\infty,\dfrac{-7}{5}\right]$

Solve for $x$ :
$10 \leq - 5 ( x - 2 ) < 20$

Consider the given inequality.

$10\le-5(x-2)<20$

$-2\ge(x-2)>-4$

$-2+2\ge x>-4+2$

$0\ge x>-2$

$-2\le x<0$

Hence, this is the answer.

A bag contains $187$ in the form of $1$ rupee, $\,50$ paise and $\,10$ paise coin in the ratio $3:4:5$ .Find the number of each type of coins?

Let the number of

$1$ rupee,

$50$ paise and

$10$ paise coins be

$3x,\,4x$ nd

$5x$ respectively.

Then,

$3x+4x\times\dfrac{50}{100}+5x\times\dfrac{10}{100}=187$

$\Rightarrow\,3x+2x+\dfrac{x}{2}=187$

$\Rightarrow\,5x+\dfrac{x}{2}=187$

$\Rightarrow\,\dfrac{10x+x}{2}=187$

$\Rightarrow\,\dfrac{11x}{2}=187$

$\Rightarrow\,x=17\times 2=34$

$\therefore\,3x=3\times 34=102$

$4x=4\times 34=136$ and

$5x=5\times 34=170$

Thus, the number of

$1$ rupee ,

$50$ paise and

$10$ paise coins are

$102,\,136$ and

$170$ respectively.

If $4x+5:3x+11=13:17$ find the value of $x$

We have

$4x+5:3x+11=13:17$

$\Rightarrow\,\dfrac{4x+5}{3x+11}=\dfrac{13}{17}$

$\Rightarrow\,17\left(4x+5\right)=13\left(3x+11\right)$

$\Rightarrow\,68x+85=39x+143$

$\Rightarrow\,68x-39x=143-85$

$\Rightarrow\,29x=58$

$\Rightarrow\,x=\dfrac{58}{29}=2$

$\therefore\,x=2$

Replace * by '<' or '>' in each of the following to make the statement true:
(i) $(-6) + (-9) * (-6) - (-9)$
(ii) $(-12) - (-12) * (-12) + (-12)$
(iii) $(-20)- (-20) * 20 - (65)$
(iv) $28- (-10) * (-16)- (-76)$

(i)

$(-6) + (-9) < (-6) - (-9)$
(ii)

$(-12) - (-12) > (-12) + (-12)$
(iii)

$(-20)- (-20) > 20 - (65)$
(iv)

$28- (-10) < (-16)- (-76)$

Solve the following minimal assignment problem
Jobs Jobs Jobs
Machines I II III
$M_1$ $1$ $4$ $5$
$M_2$ $4$ $2$ $7$
$M_3$ $7$ $8$ $3$

$\begin{matrix} & I & II & III \\ M_ 1 & 1 & 4 & 5 \\ M_ 2 & 4 & 2 & 7 \\ M_ 3 & 7 & 8 & 3 \end{matrix}$

Apply row reduction

$\begin{matrix} & I & II & III \\ M_1 & 0 & 3 & 4 \\ M_ 2 & 2 & 0 & 5 \\ M_ 3 & 4 & 5 & 0 \end{matrix}$

Apply column reduction (refer image)

Degeneracy check

$=$ No. of crossed lines

$= 3$

$=$ order of matrix

So,

$M_1 = I$

$M_2 = II$

$M_3 = III$

Minimal time

$= 1 + 2 + 3 = 6$

1186862_1424050_ans_0c39dd757c42455dbd42a23075fe6397.png

$\displaystyle \int \left [ \left ( \dfrac{x}{e} \right )^x + \left ( \dfrac{e}{x} \right )^x \right ] ln\, x$ dx

$\displaystyle \int \left [ \left ( \dfrac xe\right )^x + \left ( \dfrac{e}{x} \right )^x \right ] ln\, x$ dx

Let

$\left ( \dfrac{x}{e} \right )^x=t$

$x \ln \left ( \dfrac{x}{e} \right )= \ln t$

$x \ln x-x = \ln t$

$\left ( \dfrac{e}{x} \right )^x=\dfrac{1}{t}$

$x \ln \left ( \dfrac{e}{x} \right )= - \ln t$

$x- x \ln x = - \ln t$

also

$(\ln x +\dfrac{x}{x}-1)dx=\dfrac{1}{t}dt$

$x>8$

so we have

$x\in (8, \infty)$ .

Solve the following linear inequations in $R$ .
$\dfrac {3x - 2}{5}\leq \dfrac {4x - 3}{2}$ .

we have

$\dfrac{3x-2}{5}\le \dfrac{4x-3}{2}\quad x\in R$

$(3x-2)\times 2\le (4x-3)\times 5$

$6x-4\le 20x-15$

$15-4\le 20x-6x$

$14x\ge 11$

$x\ge \dfrac{11}{14}$

$x\in [\dfrac{11}{14}, \infty)$

Solve the following linear inequations in $R$ .
$-(x - 3) + 4 < 5 - 2x$ .

we have

$-(x-3)+4<5-2x$ where

$x\in R$

add

$(x-3)$ both side we get

$4<5-2x+x-3$

$4<2-x$

$x<2-4\Rightarrow x<-2$

$x\in (-\infty, -2)$

Solve the following linear inequations in $R$ .
$\dfrac {2x + 3}{4} - 3 < \dfrac {x - 4}{3} - 2$ .

we have

$\dfrac{2x+3}{4}-3<\dfrac{x-4}{3}-2\quad x\in R$

$\dfrac{2x}{4}+\dfrac{3}{4}-3<\dfrac{x}{3}-\dfrac{4}{3}-2$

$\dfrac{2x}{4}-\dfrac{x}{3}<-\dfrac{4}{3}-2+3-\dfrac{3}{4}$

$\dfrac{x}{2}-\dfrac{x}{3}<-\dfrac{4}{3}+1-\dfrac{3}{4}$

$\dfrac{3x-2x}{6}<\dfrac{-16+12-9}{12}$

$\dfrac{x}{6}<\dfrac{-25+12}{12}$

$x<\dfrac{-13}{2}\Rightarrow x\in \left(-\infty, \dfrac{-13}{2}\right)$

Solve the following linear inequations in $R$ .
$\dfrac {5x}{2} + \dfrac {3x}{4} \geq \dfrac {39}{4}$ .

we have

$\dfrac{5x}{2}+\dfrac{3x}{4}\ge \dfrac{39}{4}\quad x\in R$

$\dfrac{10x+3x}{4}\ge \dfrac{39}{4}$

$\dfrac{13x}{4}\ge \dfrac{39}{4}\Rightarrow 13x\ge 39$

$x\ge 3$

so we have

$x\in [3, \infty)$ .

Solve the following linear inequations in $R$ .
$\dfrac {x}{5} < \dfrac {3x - 2}{4} - \dfrac {5x - 3}{5}$ .

we have

$\dfrac{x}{5}<\dfrac{3x-2}{4}-\dfrac{5x-3}{5}\quad x\in R$

$\dfrac{x}{5}<\dfrac{5(3x-2)-4(5x-3)}{20}$

$x<\dfrac{15x-10-20x+12}{4}$

$4x<-5x+2$

$9x<2\Rightarrow x< \dfrac{2}{9}$

$x\in \left(-\infty, \dfrac{2}{9}\right)$ .

Solve the following linear inequations in $R$ .
$3x + 9 > -x + 19$ .

For the inequation,

$3x+9>19-x\Rightarrow4x>10\Rightarrow x>\dfrac52$

the set of values of

$x \forall \, \, x\in R$

$[5/2, \infty)$ .

Solve the following linear inequations in $R$ .
$\dfrac {x - 1}{3} + 4 < \dfrac {x - 5}{5} - 2$ .

we have

$\dfrac{x-1}{3}+4<\dfrac{x-5}{5}-2\quad x\in R$

$\dfrac{x}{3}-\dfrac{1}{3}+4<\dfrac{x}{5}-1-2$

$\dfrac{x}{3}-\dfrac{x}{5}<-3-4+\dfrac{1}{3}$

$\dfrac{5x-3x}{15}<-7+\dfrac{1}{3}$

$\dfrac{2x}{15}<\dfrac{-21+1}{3}$

$\dfrac{2x}{15}<\dfrac{-20}{3}\Rightarrow \dfrac{x}{15}<\dfrac{-10}{3}$

$\dfrac{x}{5}<-10\Rightarrow x<-50$

so we have

$x\in (-\infty, -50)$ .

Solve the following linear inequations in $R$ .
$2(3 - x) \geq \dfrac {x}{5} + 4$ .

we have

$2(3-x)\ge \dfrac{x}{5}+4\quad x\in R$

$10(3-x)\ge x+20$

$30-10x\ge x+20$

$10\ge 11x$

$x\le \dfrac{10}{11}$

$x\in (-\infty, \dfrac{10}{11}]$

Solve the following linear inequations in $R$ .
$\dfrac {2(x - 1)}{5}\leq \dfrac {3(2 + x)}{7}$ .

we have

$\dfrac{2(x-1)}{5}\le \dfrac{3(2+x)}{7}\quad x\in R$

$14(x-1)\le 15(2+x)$

$14x-14\le 30+15x$

$-30-14\le 15x-14x$

$x\ge -44$

so we have

$x\in [-44, \infty)$

Solve each of the following system of equations in $R$ .
$2x - 7 > 5 - x, 11 - 5x \leq 1$ .

$1) \ 2x-7>5-x\\$

$\Rightarrow3x-12>0\\$

$\Rightarrow x-4>0\\$

$\Rightarrow x>4\\$

$\therefore x\in(4,\infty)\\$

$2)\ 11-5x\leq 1\\$

$\Rightarrow10-5x\leq 0\\$

$\Rightarrow2-x\leq 0\\$

$\Rightarrow x-2\geq 0\\$

$\Rightarrow x\geq 2\\$

$\therefore x\in[2,\infty)$

Solve the following linear inequations in $R$ .
$\dfrac {2x + 3}{5} - 2 < \dfrac {3(x - 2)}{5}$ .

$\dfrac{2x + 3}{5} - 2 < \dfrac{3(x - 2)}{5} \Rightarrow \dfrac{2x + 3}{5} - \dfrac{3 (x - 2)}{5} < 2$

$\Rightarrow \dfrac{2x + 3 - 3x + 6}{5} < 2 \Rightarrow \dfrac{-x + 9}{5} < 2 \Rightarrow -x + 9 < 10$

$\Rightarrow -x < 1 \Rightarrow x > -1 \Rightarrow x \in (-1 , \infty)$

Solve the following linear inequations in $R$ .
$\dfrac {x}{x - 5} > \dfrac {1}{2}$ .

$\dfrac{x}{x-5}>\dfrac{1}{2}\\$

$\therefore\dfrac{x}{x-5}-\dfrac{1}{2}>0\\$

$\therefore\dfrac{2x-x+5}{2x-10}>0\\$

$\therefore\dfrac{x+5}{2(x-5)}>0\\$

$\therefore\dfrac{x+5}{x-5}>0\\$

So, both numerator and denominator should be positive or both should be negative.

$Case\ 1:$

Both are positive,

$\Rightarrow x+5>0\ and\ x-5>0$

$\Rightarrow x>-5\ and\ x>5$

$\Rightarrow x>5,$ it satisfies both the conditions

$Case\ 2:$

Both are negative,

$\Rightarrow x+5<0\ and\ x-5<0$

$\Rightarrow x<-5\ and\ x<5$

$\Rightarrow x<-5,$ it satisfies both the conditions

Therefore, combined solution will be

$x>5\ and x<-5$

$\therefore x\in (-\infty, -5)\cup (5, \infty)$

Solve the following linear inequations in $R$ .
$\dfrac {1}{x - 1} \leq 2$ .

1445031_1666568_ans_91f90531f4fc4cbb806ab883ce4f445b.jpg

Solve the following linear inequations in $R$ .
$x - 2\leq \dfrac {5x + 8}{3}$ .

$x - 2 \le \dfrac{5x + 8}{3} \Rightarrow 3(x - 2) \le 5x + 8$

$\Rightarrow 3x - 6 \le 5x + 8$

$\Rightarrow -8 - 6 \le 5x - 3x$

$\Rightarrow 2x \ge -14$

$\Rightarrow x \ge -7 \Rightarrow x \in [-7, \infty)$

Solve the following linear inequations in $R$ .
$\dfrac {4 + 2x}{3} \geq \dfrac {x}{2} - 3$ .

we have

$\dfrac{4+2x}{3}\ge \dfrac{x}{2}-3\quad R$

$\dfrac{4}{3}+\dfrac{2x}{3}\ge \dfrac{x}{2}-3$

$\dfrac{4}{3}+3\ge \dfrac{x}{2}-\dfrac{2x}{3}$

$\dfrac{13}{3}\ge \dfrac{3x-4x}{6}$

$\dfrac{-x}{6}\le \dfrac{13}{3}\Rightarrow \dfrac{x}{2}\ge -13$

$x\ge -26$

Hence

$x\in [-26, \infty)$ .

Solve the following linear inequations in $R$ .
$\dfrac {2x - 3}{3x - 7} > 0$ .

$\dfrac{2x - 3}{3x - 7} > 0$

$\because \dfrac{p}{q} > 0 \Rightarrow p>0 \ \& \ q > 0$

then

$2x - 3 > 0 \, \& \, 3x - 7 > 0$ and

$p < 0 \, \& \ q < 0$

$\Rightarrow x > \dfrac{3}{2} \, \& \, x > \dfrac{7}{3}$

$\Rightarrow x > \dfrac{7}{3}$

$2x - 3 < 0 \, \& \, 3x - 7 < 0$

$x < \dfrac{3}{2} \,\& \, x < \dfrac 73$

$\Rightarrow x < \dfrac{3}{2}$

Hence

$x < \dfrac{3}{2}$ or

$x > \dfrac{7}{3}$

$\Rightarrow x \in \left(-\infty , \dfrac{3}{2} \right) \cup \left(\dfrac{7}{3} , \infty\right)$

Solve the following linear inequations in $R$ .
$\dfrac {7x - 5}{8x + 3} > 4$ .

$\dfrac{7x - 5}{8x + 3} > 4$

$\Rightarrow \dfrac{7x - 5}{8x + 3} - 4 > 0 \Rightarrow \dfrac{-25x - 17}{3x + 3} > 0$

(1)

$-25x 0 17 > 0$ and

$3x + 3 > 0$

$x < \dfrac{-17}{25}$ and

$x > \dfrac{-3}{8}$

then

$x \in \{\}$ empty set

(2)

$-25x - 17 < 0$ and

$8x + 3 < 0$

$x > -\dfrac{17}{25}$ and

$x < -\dfrac{-3}{8}$

$\Rightarrow x \in \left(\dfrac{-17}{25} , \dfrac{-3}{8} \right)$

Solve the following linear inequations in $R$ .
$\dfrac {3}{x - 2} < 1$ .

$\dfrac{3}{x - 2} < 1$

$x > 2 \Rightarrow x -2 > 0$

then

$3 < x - 2 \Rightarrow x > 5$

$x < 2 \Rightarrow x - 2 < 0$

then

$3 > x - 2 \Rightarrow x < 5$

from case (1)

$x > 2 \Rightarrow x > 5$

$x > 5$

from case (2)

$x < 2 \Rightarrow x < 5$

then

$x < 2$

then

$x < 2$ or

$x > 5$

hence

$x \in (-\infty, 2) \cup (5 , \infty)$

Solve the following linear inequations in $R$ .
$\dfrac {4x + 3}{2x - 5} < 6$ .

$\dfrac{4x + 3}{2x - 5} < 6$

$\dfrac{4x + 3}{2x - 5} -6 < 0 \Rightarrow \dfrac{-3x + 33}{2x - 5} < 0$

Case (1)

$-3x + 33 > 0$ and

$2x - 5 < 0$

$x < \dfrac{33}{3}$ and

$x < \dfrac{5}{2}$

$\Rightarrow x < \dfrac{33}{8}$ and

$x < \dfrac{5}{2}$

$\Rightarrow x < \dfrac{5}{2}$

Case (2)

$-3x + 33 < 0$ and

$2x - 5 > 0$

$x > \dfrac{33}{8}$ and

$x > \dfrac{5}{2}$

$\Rightarrow x > \dfrac{33}{8}$

then

$x < \dfrac{5}{2}$ or

$x > \dfrac{33}{8}$

$\Rightarrow x \in \left(-\infty, \dfrac{5}{2} \right) \cup \left(\dfrac{33}{8} , \infty\right)$

Find the linear inequations for which the solution set is the shaded region given in Fig.

Considering the line

$6x+2y=8$ , we find that the shaded region and the origin

$(0,0)$ are on the opposite side of this line and

$(0,0)$ does not satisfy the inequation

$6x+2y\geq 8$ So, the first inequation is

$6x+2y\geq 8$

Considering the line

$x+5y=4$ , we find that the shaded region and the origin

$(0,0)$ are on the opposite side of this line and

$(0,0)$ does not satisfy the inequation

$x+5y\geq 4$ So, the corresponding inequation is

$x+5y\geq 4$

Considering the line

$x+y=4$ , we find that the shaded region and the origin

$(0, 0)$ are on the same side of this line and

$(0, 0)$ satisfies the inequation

$x+y\leq 4$ So, the corresponding inequation is

$x+y\leq 4$

Considering the line

$y = 3$ , we find that the shaded region and the origin

$(0, 0)$ are on the same side of this line and

$(0, 0)$ satisfies the inequation

$y\leq 3$ So, the corresponding inequation is

$y\leq 3$

Considering the line

$x=3$ , we find that the shaded region and the origin

$(0, 0)$ are on the same side of this line and

$(0, 0)$ satisfies the inequation

$x \leq 3$ So, the corresponding inequation is

$x \leq 3$

Also, the shaded region is in the first quadrant. Therefore, we must have

$x\geq 0$ and

$y\geq 0$

Thus, the linear inequations comprising the given solution set are given below:

$6x+2y\geq 8$ ,

$x+5y\geq 4$ ,

$x+y\leq 4$ ,

$y\leq 3$ ,

$x\leq 3$ ,

$x\geq 0$ and $$y\geq 0$
1611545_1666922_ans_ee80c0354e7f432980c5314759f9244b.JPG

Write the solution set of the inequation $x + \dfrac {1}{x} \geq 2$ .

given

$x+\dfrac{1}{x}\ge 2$

$x+\dfrac{1}{x}-2\ge 0$

$(\sqrt{x})^2+\dfrac{1}{(\sqrt{x})^2}-2\sqrt x\times \dfrac{1}{\sqrt x}\ge 0$

$\left(\sqrt x-\dfrac{1}{\sqrt x}\right)^2\ge 0$ which is always true

for

$x>0$

Hence

$x\in (0, \infty)$ .

Write the solution set of the inequation $\left |\dfrac {1}{x} - 2\right | < 4$ .

1449525_1666935_ans_f9d3dc5d84614cfc92c5b05b4f7ce19f.jpg

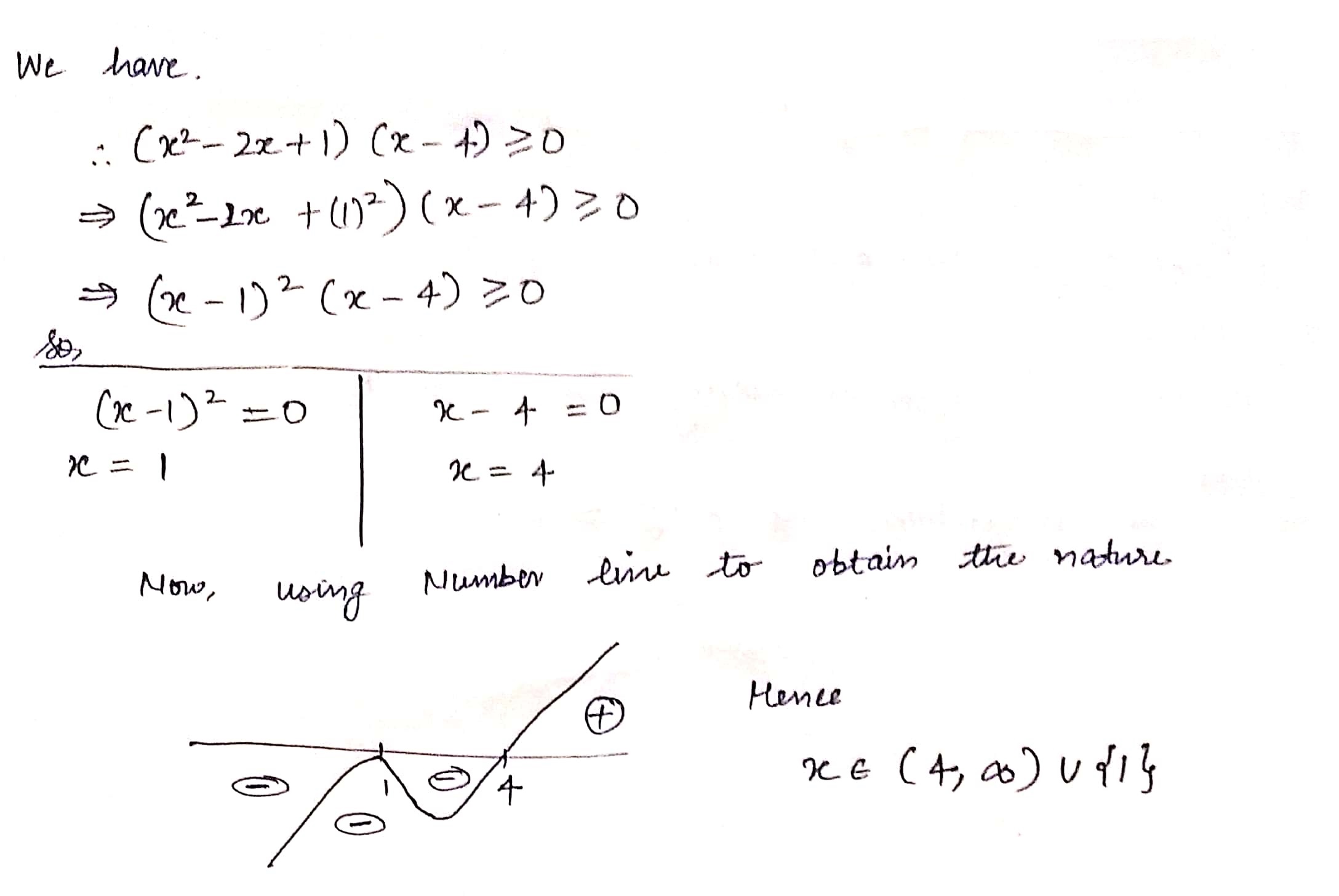
Write the set of values of $x$ satisfying the inequation $(x^{2} - 2x + 1)(x - 4)\geq 0$ .

1608223_1666932_ans_a1a95b305c6a41f6995336f114653485.jpeg

Write the solution set of the inequation $|x - 1| \geq |x - 3|$ .

$|x - 1| \ge |x - 3|$

$\Rightarrow |x - 1| - |x - 3| \ge 0$

$|x - 1| - |x - 3| = \begin{cases} -2 & if & x < 1 \\ 2x - 4 & if & 1 \le x \le 3 \\ 2 & if & x > 3 \end{cases}$

$x < 1$

$\Rightarrow -2 \ge 0$ not possible

$1 \le x \le 3$

$\Rightarrow 2x - 4 \le 0 \Rightarrow x \le 2 \Rightarrow x \in [2, \infty)$

$\because 1 \le x \le 3$

$\Rightarrow x \in [2, 3]$

$x > 3$

$\Rightarrow 2 \le 0$ is true then

$x \in (3, \infty)$

then

$x \in [2, 3] \cup (3, \infty)$

$x \in [2, \infty)$

Find the linear inequations for which the shaded ares in Fig. is the solution set. Draw the diagram of the solution set of the linear inequations.

To find the inequation we see if the shaded region and Origin are on the same side of the line or not.
So,
Considering the line

$2x+3y=6$ , we find that the shaded region and the origin

$(0,0)$ are on the opposite side of this line and

$(0,0)$ does not satisfy the inequation

$2x+3y\geq6$ So, the first inequation is

$2x+3y\geq6$

Considering the line

$4x+6y=24$ , we find that the shaded region and the origin

$(0, 0)$ are on the same side of this line and

$(0, 0)$ satisfies the inequation

$4x+6y\leq24$ So, the corresponding inequation is

$4x+6y\leq24$

Considering the line

$x − 2y = 2$ , we find that the shaded region and the origin

$(0, 0)$ are on the same side of this line and

$(0, 0)$ satisfies the inequation

$x − 2y\leq2$ So, the corresponding inequation is

$x − 2y\leq 2$

Considering the line

$-3x+2y=3$ , we find that the shaded region and the origin

$(0, 0)$ are on the same side of this line and

$(0, 0)$ satisfies the inequation

$-3x + 2y\leq3$ So, the corresponding inequation is

$-3x + 2y\leq 3$

Also, the shaded region is in the first quadrant. Therefore, we must have

$x\geq 0$ and

$y\geq 0$

Thus, the linear inequations comprising the given solution set are given below:

$2x + 3y\geq 6$ ,

$4x + 6y\leq24$ ,

$x − 2y\leq2$ ,

$-3x + 2y\leq3$ ,

$x\geq 0$ and

$y\geq 0$

Write the set of values of $x$ satisfying the inequations $5x + 2 < 3x + 8$ and $\dfrac {x + 2}{x - 1} < 4$ .

1446181_1666937_ans_b5d0e764c0ae43f8ba3184df81750392.jpg

Write the set of values of $x$ satisfying $|x - 1| \leq 3$ and $|x - 1| \leq 1$ .

1609891_1666933_ans_22798acee3b244b79533480660d53672.jpeg

Solve each of the following system of equations in $R$ .
$\dfrac {2x + 1}{7x - 1} > 5, \dfrac {x + 7}{x - 8} > 2$ .

$1) \dfrac{2x+1}{7x-1}>5\\$

$\Rightarrow \dfrac{2x+1}{7x-1}-5>0\\$

$\Rightarrow \dfrac{2x+1-35x+5}{7x-1}>0\\$

$\Rightarrow \dfrac{-33x+6}{7x-1}>0\\$

$\Rightarrow \dfrac{33x-6}{7x-1}<0\\$ , inequality changed due to multiplication of

$-1$

$\Rightarrow \dfrac{11x-2}{7x-1}<0\\$

So, out of numerator and denominator one should be positive and one should be negative.

That is possible in interval

$(\dfrac{1}{7},\dfrac{2}{11})$

$\therefore x\in (\dfrac{1}{7},\dfrac{2}{11})\\$

$2) \dfrac{x+7}{x-8}>2\\$

$\Rightarrow \dfrac{x+7}{x-8}-2>0\\$

$\Rightarrow \dfrac{x+7-2x+16}{x-8}>0\\$

$\Rightarrow \dfrac{-x+23}{x-8}>0\\$

$\Rightarrow \dfrac{x-23}{x-8}<0\\$

So, out of numerator and denominator one should be positive and one should be negative.

That is possible in interval

$(8,23)$

$\therefore x\in (8,23)$

Solve each of the following system of equations in $R$ .
$x - 2 < 0, 3x < 18$ .

$1)\ x-2<0\\$

$\Rightarrow x<2\\$

$\therefore x\in(-\infty,2)\\$

$2)\ 3x<18\\$

$\Rightarrow x<6\\$

$\therefore x\in(-\infty,6)$

Classify the given polynomial as linear, quadratic, cubic and biquadratic polynomial.
$3y$ .

1432895_1668699_ans_2fc84e818b63403691f4359155598a07.jpg

Shikha and Aarushi are sisters. The ratio of their ages is $3 : 4$ . Their parents give them Rs. $1400$ to share in the ratio of their ages. How much does each of them receive?

1511800_1674507_ans_2ebf198b5d814a9c940f080b5def48da.jpg

Fill in the blank.
If $2x = 5y$ , then $x : y=$ ________.

1498260_1674518_ans_3265ccb665364b53b80efa6db261a333.jpg

The ratio of copper and zinc in an alloy is $5 : 3$ . If the weight of copper in the alloy is $30.5$ g, find the weight of zinc in it.

Given the ratio of copper and zinc in an alloy is

$5:3$ .

Let weight of copper and zinc be

$5x$ and

$3x$ .

Then according to the problem we have,

$5x=30.5$

or,

$x=6.1$

Then weight of zinc is

$3\times 6.1=18.3$ g.

Fill in the following blanks: $\cfrac{12}{20}=\cfrac{\Box }{5}=\cfrac{9}{\Box }$

1514870_1675511_ans_1e19644e40e64175a09753b90e9bb6ad.jpg

The marks (out of $100$ ) obtained by a group of students in science tests are $85, 76, 90, 84, 39, 48, 56, 95, 81$ and $75$ . Find the highest and the lowest marks obtained by the students.

Highest mark of student

$=95,$ mark

Lowest mark of student

$=39$ mark

The marks (out of 100) obtained by a group of students in science test are 85, 76, 90, 84, 39, 48, 56, 95, 81 andFind the range of marks obtained.

Range of marks = Highest marks – Lowest marks = 95 – 39 = 56

A boat is traveling upstream in the positive direction of an $x$ axis at $14 km/h$ with respect to the water of a river. The water is flowing at $9.0 km/h$ with respect to the ground. What are the (a) magnitude and (b) direction of the boats velocity with respect to the ground? A child on the boat walks from front to rear at $6.0 km/h$ with respect to the boat. What are the (c) magnitude and (d) direction of the childs velocity with respect to the ground?

Assuming the upstream corresponds to the

$\hat { i }$ direction.
(a) where subscript

$b$ is for the boat,

$w$ is for the water, and

$g$ is for the ground.

It is clear that

$\vec { { v }_{ bg } } =\vec { { v }_{ bw } } +\vec { { v }_{ wg } }$

$=(14km/h)\hat { i } +(-9km/h)\hat { i } =(5km/h)\hat { i } .$

Thus, the magnitude is

$\left| \vec { { v }_{ bg } } \right|= 5 km/h$ .

(b) The direction of

$\left| \vec { { v }_{ bg } } \right|$ is

$+x$ , or upstream.

$c$ for the child, and obtain

$\vec { { v }_{ cg } } =\vec { { v }_{ cb } } +\vec { { v }_{ bg } } =(-6km/h)\hat { i } +(5km/h)\hat { i } =(-1km/h)\hat { i }$ .

The magnitude is

$\left| \vec { { v }_{ cg } } \right| = 1 km/h$ .

(d) The direction of

$\vec { { v }_{ cg } }$ is

$−x$ , or downstream.

Solve the following inequation :
$\dfrac{2y - 1}{5} \leq 2 , y\, \varepsilon \, N$

Given:

$\dfrac{2y - 1}{5} \leq 2$

$2y - 1 \leq 2 \times 5$

$2y - 1 \leq 10$

$2y \leq 10 + 1$

$2y \leq 11$

We get,

$y \leq \dfrac{11}{2}$

$y\, \varepsilon \, N$

Therefore , solution set

$= \left \{1 , 2 , 3 , 4, 5 \right \}$

Solve the following inequation :
$-17 \leq 9x - 8, x \, \varepsilon \, Z$

Given:

$-17 \leq 9x - 8$

$-17 + 8 \leq 9x$

$-9 \leq 9x$

$\dfrac{-9}{9} \leq x$

$-1 \leq x$

$x \geq -1$

$x \, \varepsilon \, Z$

Hence , solution set

$= \left \{ -1 , 0 , 1 , 2 , .... \right \}$

Solve the following inequation:
$4 > 3x - 11 , x \, \varepsilon \, N$

Given:

$4 > 3x - 11$

$4 + 11 > 3x$

$15 > 3x$

$\dfrac{15}{3} > x$

We get ,

$5 > x$

$x < 5$

$x \, \varepsilon \, N$

Hence , solution set

$= \left \{ 1 , 2 , 3 , 4 \right \}$

Solve the following inequation:
$3(x - 2) < 2(x - 1 ), x \, \varepsilon \, W$

Given

$3(x - 2) < 2(x - 1)$

$3x - 6 < 2x - 2$

$3x - 2x < -2 + 6$

We get ,

$x < 4$

$x \, \varepsilon \, W$

Hence , solution set

$= \left \{ 0 , 1 , 2 , 3 \right \}$

Solve the following inequation:
$-2 ( p + 3) > 5 , p\, \varepsilon \, I$

Given

$-2 ( p + 3) > 5$

$-2p - 6 > 5$

$-2p > 5 + 6$

$-2p > 11$

We get,

$-p > \dfrac{11}{2}$

$p < \dfrac{-11}{2}$

$p\, \varepsilon \, I$ ,

Therefore , solution set

$= \left \{ ..... -8 , -7 , -6 \right \}$

Solve the following inequation:
$2x - 3 < x + 2 , x \, \varepsilon \, N$

Given,

$2x - 3 < x + 2$

$2x - x < 2 + 3$

We get ,

$x < 5$

$x \, \varepsilon \, N$ ,

Hence , solution set

$= \left \{1 , 2, 3 ,4 \right \}$

Solve the following inequation:
$3 - x\leq 5 - 3x , x \, \varepsilon \, W$

Given

$3 - x\leq 5 - 3x$

$3x - x \leq 5 - 3$

$2x \leq 2$

We get,

$x \leq 1$

$x \, \varepsilon \, W$

Hence, solution set

$= \left \{0 , 1 \right \}$

Solve the following inequation :
$\dfrac{2y + 1}{3} + 1 \leq 3 , y\, \varepsilon \, W$

Given:

$\dfrac{2y + 1}{3} + 1 \leq 3$

$\dfrac{2y + 1 + 3}{3} \leq 3$

$\dfrac{2y + 4}{3} \leq 3$

$(2y + 4) \leq 3 \times 3$

$2y + 4 \leq 9$

$2y \leq 9 - 4$

$2y \leq 5$

We get ,

$y \leq \dfrac{5}{2}$

$y\, \varepsilon \, W$ ,

Therefore , solution set

$= \left \{0 , 1 , 2 \right \}$

Solve the following inequation :
$\dfrac{3}{2} - \dfrac {x}{2} > -1 , x \, \varepsilon \, N$

Given:

$\dfrac{3}{2} - \dfrac {x}{2} > -1$

$\dfrac{3}{2} + 1 > \dfrac{x}{2}$

$\dfrac{3 + 2}{2} > \dfrac{x}{2}$

$\dfrac{5}{2} > \dfrac{x}{2}$

So,

$5 > x$

$x < 5$

$x \, \varepsilon \, N$

Hence , solution set

$= \left \{ 1 , 2 , 3 , 4 \right \}$

A swimmer can swim with velocity of $10km/hr$ w.r.t. the water flowing in a river with velocity of $5 km /hr$ . In what direction should he swim to reach the point on the other bank just opposite to his starting point?

Let the angle of the swimmer be e w.r.t the horizontal

$cos \theta=\dfrac{OA}{AB}$

$=\dfrac{V_{w}}{V_{s}}$

$=\dfrac{5}{10}$

$\Rightarrow cos \theta=1/2$

$\Rightarrow \theta=60^{o}$

1768850_1844816_ans_0aa5b1ee68f94347b5cb10ac415816e0.png

Define inequality.

Two real numbers or two algebraic expressions related by the symbol '<', V, '<' or '>' form an inequality.
For example: 3 < 5, 7 > 5 are numerical inequalities x < 5, y > 2, x > 3 are literal inequalities. ax + b < 0, ax + b > 0 are strick inequalities in one variable.
ax + b < 0, ax + b > 0 are slack inequalities in one variable.
ax + by < c, ax + by > c are strick inequalities in two variables.
ax + by < c, ax + by > c are slack inequalities in two variables.

$ax^2 + by < c, ax^2 + by > c$ are quadratic inequalities in one variable.

For the following numbers write the ratio of first number to second number in the reduced form.
$138 , 161$

1810173_1854980_ans_3367130e68e640c6bb4a1028ae508789.PNG

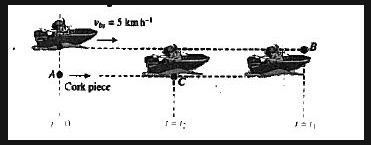
A row-boat is observed travelling downstream on a flowing river at a speed of $8 m/s$ with respect to the shore. A motor-boat comes from the opposite direction at a speed of $10 m/s$ with respect to the water. $10 seconds$ after meeting each other they are at $160 meter$ from each other.
(a) at what speed does the river flow?
(b) Find the speed of row-boat in still water.

1466097_133398_ans_109b1556cea74f7fb693dadf874d7826.jpg

A motorboat going downstream overcame a raft at a point $A$ ; $\tau = 60\:min$ later it turned back and after some time the raft is at a distance $l = 6.0\:km$ from the point $A$ . Find the flow velocity in $km/h$ assuming the duty of the engine to be constant.

Considering the given figure below.
Let

$v_0$ be the stream velocity and

$v^\prime$ the velocity of motorboat with respect to water. The motorboat reached point

$B$ while going downstream with velocity

$(v_0+v^\prime)$ and then returned with velocity

$(v^\prime-v_0)$ and passed the raft at point

$C$ . Let

$t$ be the time for the raft (which flows with stream with velocity

$v_0$ ) to move from point

$A$ to

$C$ , during which the motorboat moves from

$A$ to

$B$ and then from

$B$ to

$C$ .
Therefore

$\displaystyle\frac{l}{v_0}=\tau+\frac{(v_0+v^\prime)\tau-l}{(v^\prime-v_0)}$

On solving, we get

$\displaystyle v_0=\frac{l}{2\tau}=3 km/hr$ .

Solve the inequation $-\left| y \right| +x\sqrt { \left( { x }^{ 2 }+{ y }^{ 2 }-1 \right) } \ge 1$ . The sum of the ordinate and abscissa of the solution is

we have

$-\left| y \right| +x\sqrt { \left( { x }^{ 2 }+{ y }^{ 2 }-1 \right) } \ge 1$

$\Rightarrow x-\left| y \right| \ge 1+\sqrt { \left( { x }^{ 2 }+{ y }^{ 2 }-1 \right) } \\ if\quad x\ge \left| y \right| ,$
then squaring both sides

${ x }^{ 2 }{ y }^{ 2 }-2x\left| y \right| \ge +{ x }^{ 2 }{ +y }^{ 2 }-1+2\sqrt { \left( { x }^{ 2 }+{ y }^{ 2 }-1 \right) }$

$\Rightarrow -x\left| y \right| \ge \sqrt { \left( { x }^{ 2 }+{ y }^{ 2 }-1 \right) } ............(1)$
since

$x\ge \left| y \right| \ge 0$
then L.H.S. of (1) is non positive and R.H.S of (2) is non negative. Therefore the system is satisfied only when both sides are zero.

$\therefore$ The inequality (1) is equivalent to the system

$\begin{cases} x\left| y \right| =0 \\ { x }^{ 2 }+{ y }^{ 2 }-1=0 \end{cases}$
THe first equation gives x=0 or y=0. if x=0, then we find

$y\pm 1$ from second equation but

$x\ge \left| y \right|$ which is impossible.
If y=0 then from second equation we find

${ x }^{ 2 }=1$

$\therefore$ x=1,-1
taking x=1

$\left( \because x\ge \left| y \right| \right)$

$\therefore$ the pair (1,0) satisfies the given inequation. Hence (1,0) is the solution of the original
inequation.

Two boats, $A$ and $B$ , move away from a buoy anchored at the middle of a river along the mutually perpendicular straight lines: the boat $A$ along the river, and the boat $B$ across the river. Having moved off an equal distance from the buoy the boats returned. The ratio of times of motion of boats $\displaystyle\frac{\tau_A}{\tau_B}$ is $\dfrac{x}{10}$ if the velocity of each boat with respect to water is $\eta=1.2$ times greater than the stream velocity. Find $x$ rounded off to the nearest integer.

Let

$l$ be the distance covered by the boat

$A$ along the river as well as by the boat

$B$ across the river. Let

$v_0$ be the stream velocity and

$v^\prime$ the velocity of each boat with respect water. Therefore time taken by the boat

$A$ in its journey

$\displaystyle t_A=\frac{l}{v^\prime+v_0}+\frac{l}{v^\prime-v_0}$

and for the boat

$B$

$\displaystyle t_B=\frac{l}{\sqrt{{v^\prime}^2-v_0^2}}+\frac{l}{\sqrt{{v^\prime}^2-v_0^2}}=\frac{2l}{\sqrt{{v^\prime}^2-v_0^2}}$

Hence,

$\displaystyle\frac{t_A}{t_B}=\frac{v^\prime}{\sqrt{{v^\prime}^2-v_0^2}}=\frac{\eta}{\sqrt{\eta^2-1}}\:\left(where\:\eta=\frac{v^\prime}{v}\right)$

On substitution

$\displaystyle\frac{t_A}{t_B}=1.8$

A child in danger of drowning in a river is being carried downstream by a current that flows uniformly at a speed of $2.5\ km/h$ . The child is $0.6\ km$ from shore and $0.8\ km$ upstream of a boat landing when a rescue boat sets out. If the boat proceeds at its maximum speed of $20\ km/h$ with respect to the water, how long (in $min$ )does it take the boat to reach the child?

The boat moves on a path that makes an angle of

$\theta$ with respect to the shore line.

Call the direction of river flow the x axis and the direction across the river as the y axis.

Then the component of motion of the boat along the x axis is

$20 \cos\theta$ and y component

$20 \sin \theta$

Therefore

$20 \cos\theta \times t = 0.8$

and

$20 \sin \theta \times t = 0.6$

Divide both the equation we get

$\tan \theta = \dfrac{3}{4}$

Therefore,

$\sin \theta = \dfrac{3}{5}$

Time taken is

$20 \times \dfrac{3}{5}t = 0.6$

$t = \dfrac{0.6}{12} = 0.05\ h = (0.05 \times 60) = 3\ min$

Solve the inequality:

$\displaystyle\frac { 3x+1 }{ x+4 } \le 1$

$\dfrac{3x+1}{x+4}\leq 1$

$\Rightarrow \dfrac{3x+1}{x+4}-1\leq 0 \Rightarrow \dfrac{3x+1}{x+4}-\dfrac{x+4}{x+4}\leq 0$

$\Rightarrow \dfrac{3x-1-x-4}{x+4}\leq 0\Rightarrow \dfrac{2x-3}{x+4}\leq 0$

This means either Numerator is negative

and denominator is positive ar vice -versa

$(2x-3)\leq 0$ and

$(x+4)> 0$

$\Rightarrow x\leq 3/2$ and

$x> -4$

$\Rightarrow -4<x\leq 3/2$

$(2x-3)\geq (x+4)<0$

$\Rightarrow x\geq 3/2$ and

$x<-4$ (not feasible)

Since a number can;t be simultaneously

greater then

$(3/2)$ and less than

$(-4)$

$-4 <x\leq \dfrac{3}{2}$

1116988_426594_ans_f8fecd52b9a94f5fb955fd2cebd1480a.jpg

Find the ratio compounded of
(1) the ratio 2a, 3b, and the duplicate of $9b^2 : ab .$
(2) the subduplicate ratio of 64 : 9, and the ratio 27 : 56.
(3) the duplicate ratio of $\frac {2a}{b} : \frac {\sqrt{C}a^2}{b^2} ,$ and the ratio 3ax : 2by .

$(1)$ Duplicate of

$9b^{2}:ab$ is equal to

$81b^{4}:a^{2}b^{2}$

The compound of

$2a:3b$ and the duplicate of

$9b^{2}:ab$ is

$2a \times 81b^{4}:3b \times a^{2}b^{2}=54b:a$

$(2)$ Sub duplicate ratio of

$64:9$ is

$8:3$

The compound of the sub duplicate ratio of

$64:9$ and the ratio

$27:56$ is

$8 \times 27:3 \times 56=9:7$

$(3)$ Duplicate ratio of

$\frac{2a}{b}:\frac{ \sqrt c a^{2}}{b^{2}}$ is equal to

$\frac{4a^{2}}{b^{2}}:\frac{ca^{4}}{b^{4}}$

The compound of the duplicate of ratio

$\frac{2a}{b}:\frac{\sqrt ca^{2}}{b^{2}}$ and the ratio

$3ax:2by$ is

$\frac{4a^{2}}{b^{2}} \times 3ax:\frac{ca^{4}}{b^{4}} \times 2by=6bx:acy$

Solve the following equations:
Find the least integral value of $x$ which satisfies the equation $\left | x \, - \, 3 \right | \, + \, 2 \, \left | \, x \, + \, 1 \right | \, = \, 4.$

The given equation is

$|x-3|+2|x+1|=4$

$\therefore$ We have three cases

$i.)x<-1,ii.)-1<x<3,iii.)x>3$

Hence the respective equations in three cases are

$i.)(3-x)+2(-x-1)=4,ii.)(3-x)+2(x+1)=4,iii.)(x-3)+2(x+1)=4$

in first case the equation becomes

$i.)-3x=3$ implies

$x=-1$

in second case the equation becomes

$ii.)5+x=4$ implies

$x=-1$ but we assumed

$x>-1$ therefore no solution in this case$$

in third case the equation becomes

$3x=5$ implies

$x=5/3$ but we assumed

$x>3$ therefore no solution in this case

therefore the least integral value of x is -1

Solve the following equation:
$\left | x \right | \, - \, \left | \, x \, - \, 2\right | \, = \, 2$

given equation is

$|x|-|x-2|=2$

now it has 3 cases

$i.)x<0,ii.)0<x<2,iii.)x>2$

the respective equations in 3 cases are

$i.)-x-(2-x)=2,ii.)x-(2-x)=2,iii.)x-(x-2)=2$

therefore

in first case we get

$-2=2$ so no soution

in second case we get

$2x=4$ so

$x=2$

in third case we get

$2=2$ therefore possible for every value of x greater then 2

so the solution is

$x\ge 2$

Solve the following equation:
$\left | x \, + \, 2 \, \right | \, = \, 2 \, (3 \, - \, x)$

Given equation is:

$|x+2|=2(3-x)$

$|x+2|=6-2x$

$x+2x=6-2$

$3x=4$

$\Rightarrow x= \dfrac{4}{3}$

Solve the following equation:
$\left | 3x \, - \, 2 \right | = \, 11$

The given equation is

$|3x-2|=11$

$\Rightarrow 3x=11+2$

$\Rightarrow x=\dfrac{13}{3}$

Hence this the required solution.

Prove the, inequality $\displaystyle\, n^{n + 1} > (n + 1)^n, n \geqslant 3, n\, \epsilon \, N$ .

1170135_884078_ans_649e2c5ecf7d49f79576bd987c82f00e.jpeg

Solve the following inequalities.
$\displaystyle 2^x \, + \, 3^x \, \geqslant \, 2.$

We know that -

For

$x<0$ ,

$3^x<2^x<1$

For

$x=0$ ,

$3^x=2^x=1$

For

$x>0$ ,

$3^x>2^x>1$

Hence,

$2^x+3^x\geq1$ when

$x\geq 0$

Solution set is -

$x\in[0,\infty)$

Solve the following inequalities.
$\displaystyle\, \frac{1}{x + 2} < \frac{3}{x - 3}$

Given that

$\dfrac {1}{x+2}<\dfrac {3}{x-3}$

now we have ,

$\dfrac {1}{x+2}-\dfrac {3}{x-3}<0$

$\dfrac {1(x-3)-3(x+2)}{(x+2)(x-3)}<0$

$\dfrac {-2x-9}{(x+2)(x-3)}<0$

$\dfrac {2x+9}{(x+2)(x-3)}>0$

Now solve for

$(2x+9)=0$ and

$(x+2)(x-3)=0$

$(2x+9)=0$

$x=\dfrac {-9}{2}$

and

$(x+2)(x-3)=0$

$-2<x<3$

hence the final value for x for the equation

$\dfrac {1}{x+2}<\dfrac {3}{x-3}$ is

$x\in(3,\infty]$

Let us consider a boat which moves with a velocity $v_{bw}$ = 5 km/h relative to water. At time t=0, the boat passes through a piece of code floating in water while moving downstream. If it turns back at time t= $t_1$ when and where does the boat meet the cork again? Assume $t_1$ , = 30 min.

Time of travelling of boat from A to B (

$t_1$ ) and then B to C (

$t_1'$ ) = time of moving the cork from A to C.
Velocity of boat from A to B

$\vec{v}_{b,w} + \vec{v}_w$ = ( 5 + u ) km/h
And velocity of boat from B to C

$\vec{v}_{b,w} + \vec{v}_w$ = ( 5 - u ) km/h
Distance moved by boat in time

$t_1$ ,
AB = (5 + 4)

$t_1$ ,
And distance moved by boat in time

$t_1'$ = BC = (5 - u)

$t_1'$ ,
Distance moved by cork during this time
AC = u

$( t_1 + t_1')$
But AB = AC + BC
(5 + u)

$t_1$ = u

$(t_1 + t_1') + (5 - u)t_1'$
5

$t_1 = 5t_1'$

$t_1' = t_1$ = 30 min
Hence, the cork meets the boat again after 1 h.
1031975_991863_ans_b5fa9bc1331642e691c347a9af7e4739.png

If a, b, c $> 0$ , then prove that $\dfrac{a^3}{b^3}+\dfrac{b^3}{c^3}+\dfrac{c^3}{a^3}\geq 3$ .

We know that for a given number of real terms

A.M

$\ge$ G.M...(1)

consider the terms to be

$\cfrac { { a }^{ 3 } }{ { b }^{ 3 } } ,\cfrac { { b }^{ 3 } }{ { c }^{ 3 } } ,\cfrac { { c }^{ 3 } }{ { a }^{ 3 } }$

then A.M

$=\cfrac { \cfrac { { a }^{ 3 } }{ { b }^{ 3 } } +\cfrac { { b }^{ 3 } }{ { c }^{ 3 } } +\cfrac { { c }^{ 3 } }{ { a }^{ 3 } } }{ 3 }$

G.M

$=\sqrt [ 3 ]{ \cfrac { { a }^{ 3 } }{ { b }^{ 3 } } \times \cfrac { { b }^{ 3 } }{ { c }^{ 3 } } \times \cfrac { { c }^{ 3 } }{ { a }^{ 3 } } } =1$

applying (1)

$\cfrac { { a }^{ 3 } }{ { b }^{ 3 } } +\cfrac { { b }^{ 3 } }{ { c }^{ 3 } } +\cfrac { { c }^{ 3 } }{ { a }^{ 3 } } \ge 3$

Hence proved

If a, b, c $> 0$ then prove $(abc) \left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^3\geq 27$ .

We know that for a finite number of real terms,

A.M

$\ge$ G.M....(1)$$

Consider the terms to be

$\cfrac{1}{a},\cfrac{1}{b},\cfrac{1}{c}$

A.M

$=\cfrac { \cfrac { 1 }{ a } +\cfrac { 1 }{ b } +\cfrac { 1 }{ c } }{ 3 }$

G.M

$=\sqrt [ 3 ]{ \cfrac { 1 }{ a } .\cfrac { 1 }{ b } .\cfrac { 1 }{ c } }$

Applying (1)

$\cfrac { \cfrac { 1 }{ a } +\cfrac { 1 }{ b } +\cfrac { 1 }{ c } }{ 3 } \ge \quad \sqrt [ 3 ]{ \cfrac { 1 }{ abc } }$

$\cfrac { { \left( \cfrac { 1 }{ a } +\cfrac { 1 }{ b } +\cfrac { 1 }{ c } \right) }^{ 3 } }{ 27 } \ge \cfrac { 1 }{ abc } \left( \because a,b,c>0 \right)$

$\left( abc \right) { \left( \cfrac { 1 }{ a } +\cfrac { 1 }{ b } +\cfrac { 1 }{ c } \right) }^{ 3 }\ge 27$

Hence proved

A man can swim at a speed 2 m/s in still water. He starts swimming in a river at an angle 150 to the direction of water flow and reaches the directly the directly opposite point on the opposite bank.
(a) Find the speed of flowing water.
(b) If width od river is 1 km then calculate the time taken to cross the river.

Here

$V_R=$ velocity of river

$V_M=$ velocity of man in still water = 2m/s (given)

from figure it is clear that

$\sin\theta=\dfrac{V_R}{V_M},$ where

$\theta=60$ degree

$\implies V_R=\sqrt{3}m/s$

from figure it is evident that

$V_M\cos\theta\times t=1000m$

$\implies t=1000$ s

960033_1039054_ans_4e852f96f2bb4a8b9322eff6ebcb6c3b.png

Solve the following system of inequalities : $\dfrac{2x+1}{7x-1} > 5$

$\dfrac{2x+1}{7x-1}>5$

$\dfrac{2x+1}{7x-1}-5>0$

$\dfrac{2x+1-35x+5}{7x-1}>0$

$\dfrac{6-33x}{7x-1}>0$

$\dfrac{2-11x}{7x-1}>0$

$Case 1:$

$\quad$

$2-11x>0 \quad and \quad 7x-1>0$

$\therefore x\in\left(\dfrac{1}{7},\dfrac{2}{11}\right)$

$Case 2: \quad$

$2-11x<0 \quad and\quad 7x-1<0$

which is not possible so only set of values of x are

$\therefore x\in\left(\dfrac{1}{7},\dfrac{2}{11}\right)$

Solve the following:
$|x - 1| + |x - 2| + |x - 3| \geq 6.$

1428067_1201258_ans_e1b75609e95d47e29342d3d34ab5bd7a.jpg

Show that $\dfrac {a_{1}}{a_{2}} + \dfrac {a_{2}}{a_{3}} + \dfrac {a_{3}}{a_{4}} + ..... + \dfrac {a_{n - 1}}{a_{n}} + \dfrac {a_{n}}{a_{1}} > n$ , where $a_{1}, a_{2}, ..., a_{n}$ are different positive integers.

We know that

$AM\ge GM$

$AM=$ Arithmetic mean

$GM=$ Geometric mean

Now,

$\cfrac { \cfrac { { a }_{ 1 } }{ { a }_{ 2 } } +\cfrac { { a }_{ 2 } }{ { a }_{ 3 } } +\cfrac { { a }_{ 3 } }{ { a }_{ 4 } } +.......+\cfrac { { a }_{ n } }{ { a }_{ 1 } } }{ n } \ge { (\cfrac { { a }_{ 1 } }{ { a }_{ 2 } } +\cfrac { { a }_{ 2 } }{ { a }_{ 3 } } +\cfrac { { a }_{ 3 } }{ { a }_{ 4 } } +.......+\cfrac { { a }_{ n } }{ { a }_{ 1 } } ) }^{ 1/n }\\ =\cfrac { { a }_{ 1 } }{ { a }_{ 2 } } +\cfrac { { a }_{ 2 } }{ { a }_{ 3 } } +\cfrac { { a }_{ 3 } }{ { a }_{ 4 } } +.......+\cfrac { { a }_{ n } }{ { a }_{ 1 } } \ge { n(1) }^{ 1/n }\\ =\cfrac { { a }_{ 1 } }{ { a }_{ 2 } } +\cfrac { { a }_{ 2 } }{ { a }_{ 3 } } +\cfrac { { a }_{ 3 } }{ { a }_{ 4 } } +.......+\cfrac { { a }_{ n } }{ { a }_{ 1 } } \ge n$

Hence proved

To cross the river in shortest distance, a swimmer should swim making an angle θ with the upstream. What is the ratio of the time taken to swim across in the shortest time to that in swimming across over shortest distance. [Assume that the speed of swimmer in still water is greater than the speed of river flow]

${ t }_{ 1 }=\frac { d }{ { v }_{ s }r }$

${ V }_{ s }rsin\theta \quad ={ V }_{ R }$

$\frac { { t }_{ 1 } }{ { t }_{ 2 } } =\frac { \sqrt { { V }_{ s }{ R }^{ 2 }-{ VR }^{ 2 } } }{ { V }_{ s }{ R }^{ 2 } }$

$=\frac { \sqrt { 1-{ VR }^{ 2 } } }{ { V }_{ s }{ R }^{ 2 } }$

$=\frac { d }{ { V }_{ s }Rcos\theta }$

${ t }_{ 2 }=\frac { d }{ \sqrt { { V }_{ s }{ R }^{ 2 }-{ VR }^{ 2 } } }$

1144665_1207591_ans_4c2138bdf4cf402dbe176db82c9cdc13.png

The ratio of the number of stamps with Rahul to the number of stamps with Sahil is $4:5$ . If Rahul has $24$ stamps, how many stamps does Sahil have?

number of Sahil stamps=

$\dfrac{24\times5}{4}$

=30

1209127_1310773_ans_dfd3b69062ca48bbbec5d72ed7a471ba.PNG

The different between two whole numbers is $66$ . The ratio of the the numbers is $2:5$ . What are the two numbers?

$\begin{array}{l} Two\, \, whole\; \; numbers\, x,y \\ x-y=66\to (i) \\ \dfrac { y }{ x } =\dfrac { 2 }{ 5 } \\ 5y=2x \\ 2x-5y=0\to (ii) \\ \left( 2 \right) \, \, -\left( 1 \right) \times 2 \\ 2x-5y=0 \\ 2x-2y=66\times 2 \\ -\, \, \, \, \, \, +\, \, \, \, \, \, - \\ \overline { \, \, \, \, \, \, \, \, +3y=132 } \\ y=44 \\ put\, \, value\, \, of\, \, y\, \, in\, \, (i) \\ x-44=66 \\ x=44+66 \\ =110 \\ number=\, \, 110,\, \, 44 \end{array}$

Divide $Rs.3450$ among $A.B$ and $C$ in the ratio $3:5:7$ .

Given Ratio

$=3:5:7$

Total Ratio

$=15$

Amount of A

$=3/15\times 3450$

$=690$

Amount of B

$=\dfrac{5}{15}\times 3450$

$=1150$

Amount of C

$=\dfrac{7}{15}\times 3450$

$=1610$ .

1192609_1265624_ans_622be93297344517878bb3d4e9cfdf74.jpg

A woman can row a boat at $6.40 km/h$ in still water. (a) If she is crossing a river where the current is $3.20 km/h$ , in what direction must her boat be headed if she wants to reach a point directly opposite her starting point? (b) If the river is $6.40 km$ wide, how long will she take to cross the river? (c) Suppose that instead of crossing the river she rows $3.20 km$ down the river and then back to her starting point. How long will she take? (d) How long will she take to row $3.20 km$ up the river and then back to her starting point? (e) In what direction should she head the boat if she wants to cross in the shortest possible time, and what is that time?

1660096_1791213_ans_b1f34697c74c4c99b55966d9c27c4ffd.jpg

A river is flowing due east with a speed $3m/s$ . A swimmer can swim in still water at a speed of $4m/s$ as shown in the figure.
(a) If swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction)?
(b) If he wants to start from point A on the south bank and reaches the opposite point B on the north bank,
(i) which direction should be swim?
(ii) what will be his resultant speed?
(c) From two different cases are mentioned in (a) and (b) above, in which case will he reach opposite bank in the shorter time?

${ v }_{ s}=4m/s$ along AB(due North)

${ v }_{ R}=3m/s$ towards East
(a) Insert image 10

${ v }_{ s}=4m/s$ due North

${ v }_{ R}=4m/s$ due East
As both are perpendicular.
So

$v^{ 2 }={ { v }_{ s } }^{ 2 }+{ { v }_{ R } }^{ 2 }=4^{ 2 }+3^{ 2 }$

$V=\sqrt { 25 }=5m/s$

$tan\theta =\dfrac { { v }_{ R } }{ { v }_{ s } } =\dfrac { 3 }{ 4 } =0.75$

$tan\theta =\quad \tan{ 36 }^{ 0 }$

$\theta =\quad{ 36 }^{ 0 }{ 54 }^{ ' }$ with north direction.

(b) Let swimmer strike to swim with angle

$\theta$ with north direction towards west as again in

$\bot \Delta$ then from figure.

${ v }^{ 2 }={ { v }_{ s } }^{ 2 }-{ { v }_{ R } }^{ 2 }={ 4 }^{ 2 }-{ 3 }^{ 2 }$

${ v }^{ 2 }=16-9=7$

$v=\sqrt { 7 } m/s$

$\therefore tan\theta =\dfrac { { { v }_{ s } } }{ v } =\dfrac { 3 }{ \sqrt { 7 } } \times \dfrac { \sqrt { 7 } }{ \sqrt { 7 } }$

$tan\theta =\dfrac { 3\times2.64 }{ 7 } =\dfrac { 7.92 }{ 7 }$

$tan\theta =1.13=\tan{ 48 }^{ 0 }$

$\theta =\tan{ 48 }^{ 0 }$

$4m/s$
Let width of river

$={ { v }_{ R } }$
Time taken when he strike towards North

$\dfrac { { d }_{ R } }{ d } ={ t }_{ 1 }$
When swimmer strike at angle

${ 48 }^{ 0 }{ 29 }^{ ' }30^{ " }$ in part (b) its resultant velocity along perpendicular to river is

$v=\sqrt { 7 } m/s$

$\therefore$ Time in (b) part

$=\dfrac { { d }_{ R } }{ \sqrt { 7 } } ={ t }_{ 2 }$

$\dfrac { { t }_{ 1 } }{ { t }_{ 2 } } =\dfrac { \frac { { d }_{ R } }{ 4 } }{ \frac { { d }_{ R } }{ \sqrt { 7 } } } =\dfrac { \sqrt { 7 } }{ 4 }$

$4{ t }_{ 1 }=\sqrt { 7 } { t }_{ 2 }\quad as\quad 4>\sqrt { 7 }$

$\quad \therefore { t }_{ 1 }<{ t }_{ 2 }$
Hence, he will reach the opposite bank in the shorter time in the case(a).

A boat installed with two engines commutes between two towns P and
Q connected by a river. The boat takes $t_1 = 50.00$ min on its way from P
to Q with only one engine on and $t_2 = 25.00$ min with both the engines
on. Force of water resistance is proportional to velocity of the boat
relative to the water. Assume water flow velocity to be uniform and the
boat always moves with respect to water with its maximum possible
velocity.

(a) What minimum time will the boat take on,its way from Q to P with
one engine on?

(b) What minimum time will the boat take on its way from Q to P with
both the engines on?

1978128_1729858_ans_fef53235190b4283834d33abe43c0a58.jpg

Solve the system of inequalities: $\left| 2x-3 \right| \le 11,\left| x-2 \right| \ge 3$

$|2x-3|\leq 11, |x-2|\geq 3$

$-11\leq 2x-3\leq$ ,

$-3\geq x-2 \geq 3$

$-8\leq 2x\leq 14$ ,

$-1\geq x \geq 5$

$x\in [-4,7]$ and

$x \in(-\infty ,-1)\cup [5,\infty ]$

$\therefore x\in [-4,-1] \cup [5,7]$

A woman who can row a boat at $6.4 km/h$ in still water faces a long, straight river with a width of $6.4 km$ and a current of $3.2 km/h$ . Let $\hat { i }$ point directly across the river and $\hat { j }$ point directly downstream. If she rows in a straight line to a point directly opposite her starting position, (a) at what angle to $\hat { i }$ must she point the boat and (b) how long will she take? (c) How long will she take if, instead, she rows $3.2 km$ down the river and then back to her starting point? (d) How long if she rows $3.2 km$ up the river and then back to her starting point? (e) At what angle to $\hat { i }$ should she point the boat if she wants to cross the river in the shortest possible time? (f) How long is that shortest time?

Assume

$\hat { i }$ pointing to the far side of the river (perpendicular to the current)

and

$\hat { j }$ pointing in the direction of the current.

magnitude (presumed constant) of the velocity of the boat relative to the water is

$\left| \vec { { v }_{ bw } } \right| =6.4km/h.$

Its angle, relative to the

$x axis$ is

$θ$ . With

$km$ and

$h$ as the understood units, the velocity of the water (relative to the ground) is

$\vec { { v }_{ wg } } =(3.2m/h)\hat { j } .$

(a) To reach a point “directly opposite” means that the velocity of her boat relative to ground

$\vec { { { v }_{ bw } } } +\vec { { v }_{ wg } } =\vec { { v }_{ bg } }$

where

$\vec{v}_{bg}$ > 0 is unknown.

Thus, all

$\hat { j }$ components must cancel in the vector sum

$\vec { { v }_{ bg } } ={ v }_{ bg }\hat { i }$ ,

which means the

${ v }_{ bw } sin θ = (–3.2 km/h) \hat { j }$ , so

$θ = { sin }^{ -1 }[(–3.2 km/h)/(6.4 km/h)] = –30°.$

(b) Using the result from part (a), we find

${ v }_{ bg }={ v }_{ bw }cos\theta =5.5km/h$ .

Thus, traveling a distance of

$l= 6.4 km$ requires a time of

$(6.4 km)/(5.5 km/h) = 1.15$ h =

$69 min.$

$y$ axis (as the problem implies) then with

${ v }_{ wg }= 3.2 km/h$ (the water speed) we have

${ t }_{ total }=\dfrac { D }{ { v }_{ bw }+{ v }_{ wg } } +\dfrac { D }{ { v }_{ bw }-{ v }_{ wg } } =1.33h$ .

where

$D = 3.2 km$ . This is equivalent to

$80 min$ .

(d) Since

$\dfrac { D }{ { v }_{ bw }+{ v }_{ wg } } +\dfrac { D }{ { v }_{ bw }-{ v }_{ wg } } =\dfrac { D }{ { v }_{ bw }-{ v }_{ wg } } +\dfrac { D }{ { v }_{ bw }+{ v }_{ wg } }$

the answer is the same as in the previous part, that is,

${ t }_{ total }= 80 min$ .

(e) The shortest-time path should have

$θ = 0°.$ This can also be shown by noting that the case of general

$θ$ leads to

$\vec { { v }_{ bg } } =\vec { { v }_{ bw } } +\vec { { v }_{ wg } } ={ v }_{ bw }cos\theta \hat { i } +({ v }_{ bw }sin\theta +{ v }_{ wg })\hat { j }$

where the

$x$ component of

${ v }_{ bg }$ must equal

$l/t$ . Thus,

$t=\dfrac { 1 }{ { v }_{ bw }cos\theta }$
which can be minimized using

$dt/dθ = 0.$

(f) The above expression leads to

$t = (6.4 km)/(6.4 km/h) = 1.0 \,h, = 60 \,min.$

A $200-m$ -wide river has a uniform flow speed of $1.1 m/s$ through a jungle and toward the east. An explorer wishes to leave a small clearing on the south bank and cross the river in a powerboat that moves at a constant speed of $4.0 m/s$ with respect to the water. There is a clearing on the north bank $82 m$ upstream from a point directly opposite the clearing on the south bank. (a) In what direction must the boat be pointed in order to travel in a straight line and land in the clearing on the north bank? (b) How long will the boat take to cross the river and land in the clearing?

We construct a right triangle starting from the clearing on the south bank,

drawing a line (200 m long) due north (upward in our sketch) across the river, and then a line due west (upstream, leftward in our sketch) along the north bank for a distance

$(82 m)+(1.1 m/s) t$ ,
where the t-dependent contribution is the distance that the river will carry the boat downstream during time

$t$ .
The hypotenuse of this right triangle (the arrow in our sketch) also depends on t and on the boat’s speed (relative to the water), and we set it equal to the Pythagorean “sum” of the triangle’s sides:

$(4.0)t=\sqrt { { 200 }^{ 2 }+{ (82+1.1t) }^{ 2 } }$

which leads to a quadratic equation for

$t$

$46724+180.4t-14.8{ t }^{ 2 }=0$

(a) The angle between the northward

$(200 m)$ leg of the triangle and the hypotenuse

(which is measured “west of north”) is then given by (see image)

$\theta ={ tan }^{ -1 }\left( \dfrac { 82+1.1t }{ 200 } \right) ={ tan }^{ -1 }\left( \dfrac { 151 }{ 200 } \right) ={ 37 }^{ o }$ .

(b)

$46724+180.4t-14.8{ t }^{ 2 }=0$

We solve for t first and find a positive value:

$t = 62.6 s$ .

1646962_1783906_ans_ca95ea3299394ffb944a61b4b6d23a44.png

Write down the $3$ inequalities which define the unshaded region.

1) Consider first straight line

The line is passing through points

$\left( -2,0 \right)$ and

$\left( 0,2 \right)$

Thus, equation of line passing through two given points is,

$\frac { y-{ y }_{ 1 } }{ { y }_{ 2 }-{ y }_{ 1 } } =\frac { x-{ x }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } }$

$\therefore \frac { y-0 }{ 2-0 } =\frac { x-\left( -2 \right) }{ 0-\left( -2 \right) }$

$\therefore \frac { y }{ 2 } =\frac { x+2 }{ 0+2 }$

$\therefore \frac { y }{ 2 } =\frac { x+2 }{ 2 }$

$\therefore y=x+2$

$\therefore x-y=-2$

The inequality for unshaded region is

$\therefore x-y\le -2$

2) Consider second straight line passing through

$\left( 6,0 \right)$ and

$\left( 0,6 \right)$

The equation of line is given by,

$\frac { y-0 }{ 6-0 } =\frac { x-6 }{ 0-6 }$

$\therefore \frac { y }{ 6 } =\frac { x-6 }{ -6 }$

$\therefore y=-\left( x-6 \right)$

$\therefore y=-x+6$

$\therefore x+y=6$

The inequality for unshaded region is

$x+y\ge 6$

3) Consider third line parallel to x axis.

The equation of line is,

$y=8$

The inequality for unshaded region is

$y\le 8$

A fisherman sets out upstream on a river. His small boat, powered by an outboard motor, travels at a constant speed $v$ in still water. The water flows at a lower constant speed $v_{w}$ . The fisherman has traveled upstream for $2.00 km$ when his ice chest falls out of the boat. He notices that the chest is missing only after he has gone upstream for another $15.0 min$ . At that point, he turns around and heads back downstream, all the time traveling at the same speed relative to the water. He catches up with the floating ice chest just as he returns to his starting point. How fast is the river flowing? Solve this problem in two ways. (a) First, use the Earth as a reference frame. With respect to the Earth, the boat travels upstream at speed $v - v_{w}$ and downstream at $v + v_{w}$ . (b) A second much simpler and more elegant solution is obtained by using the water as the reference frame. This approach has important applications in many more complicated problems; examples are calculating the motion of rockets and satellites and analyzing the scattering of subatomic particles from massive targets.

(a) Reference frame: Earth
The ice chest floats downstream

$2 km$ in time interval

$\Delta t$ , so

$2 km = v_{ow}\Delta t \rightarrow \Delta t = 2 km/v_{ow}$
The upstream motion of the boat is described by

$d = (v – v_{ow})(15 min)$
and the downstream motion is described by

$d + 2 km = (v – v_{ow})(\Delta t – 15 min)$
We substitute the above expressions for

$\Delta t$ and

$d$ :

$(v-v_{ow})(15min)+2km=(v+v_{ow})\left ( \frac{2km}{v_{ow}}-15min \right )$

$v(15min)-v_{ow}(15min)+2km$

$=\frac{v}{v_{ow}}(2km)+2km-v(15min)-v_{ow}(15min)$

$v(30min)=\frac{v}{v_{ow}}(2km)$

$v_{ow}=4.00km/h$
(b) Reference frame: water
After the boat travels so that it and its starting point are

$2 km$ apart, the chest enters the water, where, in the frame of the water, it is motionless. The boat then travels upstream for

$15 min$ at speed

$v$ , and then downstream at the same speed, to return to the same point where the chest is at rest in the water. Thus, the boat travels for a total time interval of

$30 min$ . During this same time interval, the starting point approaches the chest at speed

$v_{ow}$ , traveling

$2 km$ . Thus,

$v_{ow}=\frac{\Delta x}{\Delta t_{total}}=\frac{2km}{30min}=4.00km/h$

Two swimmers, Chris and Sarah, start together at the same point on the bank of a wide stream that flows with a speed $v$ . Both move at the same speed $c$ (where $c > v$ ) relative to the water. Chris swims downstream a distance $L$ and then upstream the same distance. Sarah swims so that her motion relative to the Earth is perpendicular to the banks of the stream. She swims the distance $L$ and then back the same distance, with both swimmers returning to the starting point. In terms of $L, c$ , and $v$ , find the time intervals required (a) for Chriss round trip and (b) for Sarahs round trip. (c) Explain which swimmer returns first.

(a) For Chris, his speed downstream is

$c + v$ , while his speed upstream is

$c – v$ .
Therefore, the total time for Chris is

$\Delta t_{1}=\frac{L}{c+v}+\frac{L}{c-v}=\frac{2L/c}{1-v^{2}/c^{2}}$
(b) Sarah must swim somewhat upstream to counteract the effect from the current. As is shown in the diagram, the magnitude of her cross-stream velocity is

$\sqrt{c^{2}-v^{2}}$
Thus, the total time for Sarah is

$\Delta t_{2}=\frac{2L}{\sqrt{c^{2}-v^{2}}}=\frac{2L/c}{\sqrt{1-v^{2}/c^{2}}}$
(c) Since the term

$(1-v^{2}/c^{2})<1,\Delta t_{1}>\Delta t_{2}$ . Sarah, who swims cross-stream, returns first.
1804612_1863306_ans_7e3555b52f4642e98c88914815336860.jpg

	Jobs	Jobs	Jobs
Machines	I	II	III
$M_1$	$1$	$4$	$5$
$M_2$	$4$	$2$	$7$
$M_3$	$7$	$8$	$3$

Quantification And Numerical Applications - Class 12 Commerce Applied Mathematics - Extra Questions

One side of a triangle measures 8 cm. Of the remaining two sides, one measures 2 cm more than the other. Then, the length of each side of the triangle is greater than xx cm. Find xx?

Solve 30x < 160 when x is an integer.

Solve 3x−102≥x+16−1\displaystyle \frac{3x-10}{2}\geq \frac{x+1}{6}-1 , where xx is a ntaural no. less than 10.

Solve 30x < 160 when x is a natural number.

Solve 5x−7<2x+25x - 7 < 2x + 2, when x is a natural number

Solve the inequalities for real xx.4x+3<5x+74x + 3 < 5x + 7

Solve the inequality for real xx.x+x2+x3<11{x +\dfrac{x}{2} + \dfrac{x}{3} < 11}

Solve −12x>30-12x > 30, when (i) xx is a natural number. (ii) xx is an integer

Solve 5x−3<3x+15x - 3 < 3x + 1 when(i) xx is an integer (ii) xx is a real number

Solve 24x<10024x < 100, when (i) xx is a natural number. (ii) xx is an integer

Solve the inequality for real xx.x3>x2+1\displaystyle {\frac{x}{3}>\frac{x}{2} +1}

Solve the inequality for real xx.3(2−x)≥2(1−x)3 (2 -x) \geq 2 (1- x)

Solve the inequalities for real xx.3x−7>5x−13x - 7 > 5x -1

Solve the inequalities for real xx.3(x−1)≤2(x−3)3(x - 1) {\leq} 2 (x- 3)

Solve, and express the answer graphically.3x−2x+4<2\displaystyle\frac{3x-2}{x+4} < 2

Solve the inequality for real xx.2(2x+3)−10<6(x−2)2 (2x + 3) -10 < 6 (x -2)

Solve the inequality for real xx.37−(3x+5)≥9x−8(x−3)37- (3x + 5) \geq 9x -8 (x -3)

Solve the inequality for real xx.3(x−2)5≤5(2−x)3\displaystyle {\frac{3(x-2)}{5}\leq \frac{5(2-x)}{3}}

2x+1≥1x−2\displaystyle\frac { 2 }{ x+1 } \ge \displaystyle\frac { 1 }{ x-2 } is k,∞\infty what is the value of the k?

Solve, and express the answer in interval form.2x−8x−2≥0\displaystyle\frac{2x-8}{x-2} \ge 0

Pressure varies inversely with volume while temperatures varies directly with volume. At a time, Volume =50m3=50m^3, Temperature=25o=25^oK and Pressure=1=1 atmosphere. If the volume is increased to 200m3200m^3, then find the temperature in o^oK

Solve the given inequality for real x:x3>x2+1\dfrac{x}{3} > \dfrac{x}{2}+1

Solve the given inequality for real x :3(x−1)≤2(x−3)3(x-1) \leq 2(x-3)

Solve 3−5x≤93 - 5x \leq 9

Solve 3(5−x)>63(5 - x) > 6

Solve the following inequality:3x−2<1\displaystyle\, \frac{3}{x - 2} < 1

Solve the following inequality:6x−54x+1<0\displaystyle\, \dfrac{6x - 5}{4x + 1} < 0

Simplify the following expression:(a+3b(a−b)2+a−3ba2−b2):a2+3b2(a−b)2\displaystyle\left ( \frac{a + 3b}{(a - b)^2} + \frac{a - 3b}{a^2 - b^2} \right ) : \frac{a^2 + 3b^2}{(a - b)^2}

Solve the following inequation, write down the solution set and represent it on the real number line:−2+10x≤13x+10<24+10x-2+10x \leq 13x+10 < 24+10x, xϵ\epsilonZ.

Solve the following inequality:2x−33x−7>0\displaystyle\, \frac{2x - 3}{3x - 7} > 0

Find all values of aa for which the inequality x−2a−3x−a+2<0\displaystyle\, \frac{x - 2a - 3}{x - a + 2} < 0 is satisfied for all xx belonging to the interval 1⩽\displaystyle\, 1\leqslant x\leqslant 2.

Solve the following inequality:\displaystyle\, \frac{5x + 8}{4 - x} < 2\displaystyle\, \frac{5x + 8}{4 - x} < 2

Solve the following inequality:\displaystyle\, 2 + \frac{3}{x + 1} > \frac{2}{x}\displaystyle\, 2 + \frac{3}{x + 1} > \frac{2}{x}

Solve the following inequality:\displaystyle\, \frac{|x + 3| + x}{x + 2} > 1\displaystyle\, \frac{|x + 3| + x}{x + 2} > 1

Solve the following inequality:\displaystyle\, \left | \frac{2x - 1}{x - 1} \right | > 2\displaystyle\, \left | \frac{2x - 1}{x - 1} \right | > 2

Solve the following inequality:\displaystyle\, \frac{|x - 1|}{x + 2} < 1\displaystyle\, \frac{|x - 1|}{x + 2} < 1

Solve the following inequality:\displaystyle\, \left | \frac{2}{x - 4} \right | > 1\displaystyle\, \left | \frac{2}{x - 4} \right | > 1

Solve the following inequality:\displaystyle\, \frac{14x}{x +1} - \frac{9x - 30}{x - 4} < 0\displaystyle\, \frac{14x}{x +1} - \frac{9x - 30}{x - 4} < 0

Solve the following inequality:\displaystyle\, \frac{x + 7}{x - 5} + \frac{3x + 1}{2} \geqslant 0\displaystyle\, \frac{x + 7}{x - 5} + \frac{3x + 1}{2} \geqslant 0

Solve the following inequality:\displaystyle\, 1 + \frac{2}{x - 1} > \frac{6}{x}\displaystyle\, 1 + \frac{2}{x - 1} > \frac{6}{x}

Solve the following inequality:\displaystyle\, \frac{|x - 2|}{x - 2} > 0\displaystyle\, \frac{|x - 2|}{x - 2} > 0

Solve the following inequalities.\displaystyle x \, - \, 3 \, \sqrt{x \, - \, 3} \, - \, 1 \, > \, 0.\displaystyle x \, - \, 3 \, \sqrt{x \, - \, 3} \, - \, 1 \, > \, 0.

Solve the following inequality:\displaystyle \sqrt{\frac{x \, - \, 3}{x \, - \, 2}} \,> \, 0\displaystyle \sqrt{\frac{x \, - \, 3}{x \, - \, 2}} \,> \, 0

Solve the following inequality:\displaystyle \frac{\sqrt{a \, + \, 4}}{1 \, - \, a} \, \, < \, 0.\displaystyle \frac{\sqrt{a \, + \, 4}}{1 \, - \, a} \, \, < \, 0.

Solve the following equation:\displaystyle\, \frac{3}{\sqrt{x + 1} + 1} + 2\sqrt{x + 1} = 5\displaystyle\, \frac{3}{\sqrt{x + 1} + 1} + 2\sqrt{x + 1} = 5

Solve the following inequality:\displaystyle\, \frac{|x + 2| - x}{x} < 2\displaystyle\, \frac{|x + 2| - x}{x} < 2

Solve the following inequality:\displaystyle\, \frac{1}{|x| - 3} < \frac{1}{2}\displaystyle\, \frac{1}{|x| - 3} < \frac{1}{2}

Solve the following two- sided inequality.\displaystyle\, 0 < \frac{3x - 1}{2x + 5} < 1\displaystyle\, 0 < \frac{3x - 1}{2x + 5} < 1

Solve the following equation:\displaystyle\, \sqrt{2 - x} + \frac{4}{\sqrt{2 - x} + 3} = 2\displaystyle\, \sqrt{2 - x} + \frac{4}{\sqrt{2 - x} + 3} = 2

Solve the following inequality:\displaystyle \sqrt{\frac{3x \, - \, 2}{2 \, - \, x}} \,> \, 1\displaystyle \sqrt{\frac{3x \, - \, 2}{2 \, - \, x}} \,> \, 1

Solve the following inequality:\displaystyle \frac{2}{x} \,+ \, 3 \, \leqslant \, \sqrt{41 \, - \, \frac{16}{x}}.\displaystyle \frac{2}{x} \,+ \, 3 \, \leqslant \, \sqrt{41 \, - \, \frac{16}{x}}.

Solve the following inequality:\displaystyle\, \left ( \dfrac{2}{5} \right )^\frac{6 - 5x}{2 + 5x} < \frac{25}{4}\displaystyle\, \left ( \dfrac{2}{5} \right )^\frac{6 - 5x}{2 + 5x} < \frac{25}{4}

Solve the following inequality:\displaystyle\, 2^x + 2^{-x + 1} - 3 < 0\displaystyle\, 2^x + 2^{-x + 1} - 3 < 0

Solve the following inequality:\displaystyle\, 2^{2x + 1} - 21 \cdot \left ( \frac{1}{2} \right )^{2x + 3} + 2 \geqslant 0\displaystyle\, 2^{2x + 1} - 21 \cdot \left ( \frac{1}{2} \right )^{2x + 3} + 2 \geqslant 0

Solve the following inequality:\displaystyle\, 5^{2x + 1} > 5^x + 4\displaystyle\, 5^{2x + 1} > 5^x + 4

Solve the following systems of inequality:|x| \geqslant 1, |x - 1| < 3|x| \geqslant 1, |x - 1| < 3

Solve the following inequality:\displaystyle\, x^2 \cdot 5^x - 5^(2 + x) < 0\displaystyle\, x^2 \cdot 5^x - 5^(2 + x) < 0

Solve the following inequality:\displaystyle\, 4^{-x + 0.5} - 7 \cdot 2^{-x} - 4 < 0\displaystyle\, 4^{-x + 0.5} - 7 \cdot 2^{-x} - 4 < 0

Solve the following inequality:\displaystyle\, 2^{3 - 6x} > 1\displaystyle\, 2^{3 - 6x} > 1

Solve the following inequality:\displaystyle\, 16^x > 0.125\displaystyle\, 16^x > 0.125

Solve the following two- sided inequality.\displaystyle\, 1 \leqslant \frac{2 - x}{x + 1} \leqslant 2\displaystyle\, 1 \leqslant \frac{2 - x}{x + 1} \leqslant 2

Solve the following inequality:\displaystyle\, (0.2)^\dfrac{2x - 3}{x - 2} > 5\displaystyle\, (0.2)^\dfrac{2x - 3}{x - 2} > 5

Solve the following inequality:\displaystyle\, \left ( \dfrac{1}{5} \right )^\frac{2x + 1}{1 - x} > \left ( \frac{1}{5} \right )^{-3}\displaystyle\, \left ( \dfrac{1}{5} \right )^\frac{2x + 1}{1 - x} > \left ( \frac{1}{5} \right )^{-3}

Solve the following inequality:\displaystyle\, \left ( \dfrac{1}{3} \right )^{x + \dfrac{1}{2} - \dfrac{2}{x}} > \dfrac{1}{\sqrt{27}}\displaystyle\, \left ( \dfrac{1}{3} \right )^{x + \dfrac{1}{2} - \dfrac{2}{x}} > \dfrac{1}{\sqrt{27}}

Solve the following inequality:\displaystyle\, 2^x + 2^{| x| } \geqslant 2\sqrt{2}\displaystyle\, 2^x + 2^{| x| } \geqslant 2\sqrt{2}

Solve the following inequality:\displaystyle\, 4^x - 3 \leqslant 2^{x + 1}\displaystyle\, 4^x - 3 \leqslant 2^{x + 1}

Solve the following inequalities.\displaystyle\, \frac{1 \, - \, \sqrt{1 \, - \, 8x^2}}{2x} \, < \, 1\displaystyle\, \frac{1 \, - \, \sqrt{1 \, - \, 8x^2}}{2x} \, < \, 1

Solve the following inequality:\displaystyle\, \left ( \dfrac{1}{3} \right )^ \frac{ | x + 2| }{2 - | x| } > 9\displaystyle\, \left ( \dfrac{1}{3} \right )^ \frac{ | x + 2| }{2 - | x| } > 9

State which of the following are equation (with variable). Given reasons for your an mention which variable is used from the equation with a variable.8m<178m<17

Solve the inequation \dfrac{1}{x-2}<0\dfrac{1}{x-2}<0 in RR.

If xx and yy are integers, where 12 < x < 1812 < x < 18 and 15 < y < 2715 < y < 27, then the maximum value of x + yx + y is

Write the solution of 4x+3<6x+74x+3<6x+7 in interval from.

Solve the inequality \dfrac {x - 1}{x^{2} - 4x + 3} < 1\dfrac {x - 1}{x^{2} - 4x + 3} < 1.

Let f\left(x\right)=\frac{\left(x-3\right)\left(x+2\right)\left(x+6\right)}{\left(x+1\right)\left(x-5\right)}f\left(x\right)=\frac{\left(x-3\right)\left(x+2\right)\left(x+6\right)}{\left(x+1\right)\left(x-5\right)}Find intervals, wheref\left(x\right)f\left(x\right) is positive or negative.

Solve: \dfrac{x-2}{x+5} > 2\dfrac{x-2}{x+5} > 2.

If x:y = 6:11x:y = 6:11, find(8x-3y) : (3x+2y)(8x-3y) : (3x+2y).

Solve the given inequality for xx:\sqrt{\dfrac{x-2}{1- 2x}}> 1\sqrt{\dfrac{x-2}{1- 2x}}> 1

Solve the following inequality: 2x - 1 < 52x - 1 < 5

Solve:6x^2-7x-36x^2-7x-3.

One side of a triangle measures 8 cm. Of the remaining two sides, one measures 2 cm more than the other. Then, the length of each side of the triangle is greater than $x$ cm. Find $x$ ?

Solve $\displaystyle \frac{3x-10}{2}\geq \frac{x+1}{6}-1$ , where $x$ is a ntaural no. less than 10.

Solve $5x - 7 < 2x + 2$ , when x is a natural number

Solve the inequalities for real $x$ .
$4x + 3 < 5x + 7$

Solve the inequality for real $x$ .
${x +\dfrac{x}{2} + \dfrac{x}{3} < 11}$

Solve $-12x > 30$ , when (i) $x$ is a natural number. (ii) $x$ is an integer

Solve $5x - 3 < 3x + 1$ when
(i) $x$ is an integer (ii) $x$ is a real number

Solve $24x < 100$ , when (i) $x$ is a natural number. (ii) $x$ is an integer

Solve the inequality for real $x$ .
$\displaystyle {\frac{x}{3}>\frac{x}{2} +1}$

Solve the inequality for real $x$ .
$3 (2 -x) \geq 2 (1- x)$

Solve the inequalities for real $x$ .
$3x - 7 > 5x -1$

Solve the inequalities for real $x$ .
$3(x - 1) {\leq} 2 (x- 3)$

Solve, and express the answer graphically.
$\displaystyle\frac{3x-2}{x+4} < 2$

Solve the inequality for real $x$ .
$2 (2x + 3) -10 < 6 (x -2)$

Solve the inequality for real $x$ .
$37- (3x + 5) \geq 9x -8 (x -3)$

Solve the inequality for real $x$ .
$\displaystyle {\frac{3(x-2)}{5}\leq \frac{5(2-x)}{3}}$

$\displaystyle\frac { 2 }{ x+1 } \ge \displaystyle\frac { 1 }{ x-2 }$ is k, $\infty$ what is the value of the k?

Solve, and express the answer in interval form.
$\displaystyle\frac{2x-8}{x-2} \ge 0$

Pressure varies inversely with volume while temperatures varies directly with volume. At a time, Volume $=50m^3$ , Temperature $=25^o$ K and Pressure $=1$ atmosphere. If the volume is increased to $200m^3$ , then find the temperature in $^o$ K

Solve the given inequality for real x:
$\dfrac{x}{3} > \dfrac{x}{2}+1$

Solve the given inequality for real x :
$3(x-1) \leq 2(x-3)$

Solve $3 - 5x \leq 9$

Solve $3(5 - x) > 6$

Solve the following inequality:
$\displaystyle\, \frac{3}{x - 2} < 1$

Solve the following inequality:
$\displaystyle\, \dfrac{6x - 5}{4x + 1} < 0$

Simplify the following expression:
$\displaystyle\left ( \frac{a + 3b}{(a - b)^2} + \frac{a - 3b}{a^2 - b^2} \right ) : \frac{a^2 + 3b^2}{(a - b)^2}$

Solve the following inequation, write down the solution set and represent it on the real number line:
$-2+10x \leq 13x+10 < 24+10x$ , x $\epsilon$ Z.

Solve the following inequality:
$\displaystyle\, \frac{2x - 3}{3x - 7} > 0$

Find all values of $a$ for which the inequality $\displaystyle\, \frac{x - 2a - 3}{x - a + 2} < 0$ is satisfied for all $x$ belonging to the interval $\displaystyle\, 1\leqslant x\leqslant 2$ .

Solve the following inequality:
$\displaystyle\, \frac{5x + 8}{4 - x} < 2$

Solve the following inequality:
$\displaystyle\, 2 + \frac{3}{x + 1} > \frac{2}{x}$

Solve the following inequality:
$\displaystyle\, \frac{|x + 3| + x}{x + 2} > 1$

Solve the following inequality:
$\displaystyle\, \left | \frac{2x - 1}{x - 1} \right | > 2$

Solve the following inequality:
$\displaystyle\, \frac{|x - 1|}{x + 2} < 1$

Solve the following inequality:
$\displaystyle\, \left | \frac{2}{x - 4} \right | > 1$

Solve the following inequality:
$\displaystyle\, \frac{14x}{x +1} - \frac{9x - 30}{x - 4} < 0$

Solve the following inequality:
$\displaystyle\, \frac{x + 7}{x - 5} + \frac{3x + 1}{2} \geqslant 0$

Solve the following inequality:
$\displaystyle\, 1 + \frac{2}{x - 1} > \frac{6}{x}$

Solve the following inequality:
$\displaystyle\, \frac{|x - 2|}{x - 2} > 0$

Solve the following inequalities.
$\displaystyle x \, - \, 3 \, \sqrt{x \, - \, 3} \, - \, 1 \, > \, 0.$

Solve the following inequality:
$\displaystyle \sqrt{\frac{x \, - \, 3}{x \, - \, 2}} \,> \, 0$

Solve the following inequality:
$\displaystyle \frac{\sqrt{a \, + \, 4}}{1 \, - \, a} \, \, < \, 0.$

Solve the following equation:
$\displaystyle\, \frac{3}{\sqrt{x + 1} + 1} + 2\sqrt{x + 1} = 5$

Solve the following inequality:
$\displaystyle\, \frac{|x + 2| - x}{x} < 2$

Solve the following inequality:
$\displaystyle\, \frac{1}{|x| - 3} < \frac{1}{2}$

Solve the following two- sided inequality.
$\displaystyle\, 0 < \frac{3x - 1}{2x + 5} < 1$

Solve the following equation:
$\displaystyle\, \sqrt{2 - x} + \frac{4}{\sqrt{2 - x} + 3} = 2$

Solve the following inequality:
$\displaystyle \sqrt{\frac{3x \, - \, 2}{2 \, - \, x}} \,> \, 1$

Solve the following inequality:
$\displaystyle \frac{2}{x} \,+ \, 3 \, \leqslant \, \sqrt{41 \, - \, \frac{16}{x}}.$

Solve the following inequality:
$\displaystyle\, \left ( \dfrac{2}{5} \right )^\frac{6 - 5x}{2 + 5x} < \frac{25}{4}$

Solve the following inequality:
$\displaystyle\, 2^x + 2^{-x + 1} - 3 < 0$

Solve the following inequality:
$\displaystyle\, 2^{2x + 1} - 21 \cdot \left ( \frac{1}{2} \right )^{2x + 3} + 2 \geqslant 0$

Solve the following inequality:
$\displaystyle\, 5^{2x + 1} > 5^x + 4$

Solve the following systems of inequality:
$|x| \geqslant 1, |x - 1| < 3$

Solve the following inequality:

$\displaystyle\, x^2 \cdot 5^x - 5^(2 + x) < 0$

Solve the following inequality:
$\displaystyle\, 4^{-x + 0.5} - 7 \cdot 2^{-x} - 4 < 0$

Solve the following inequality:
$\displaystyle\, 2^{3 - 6x} > 1$

Solve the following inequality:
$\displaystyle\, 16^x > 0.125$

Solve the following two- sided inequality.
$\displaystyle\, 1 \leqslant \frac{2 - x}{x + 1} \leqslant 2$

Solve the following inequality:
$\displaystyle\, (0.2)^\dfrac{2x - 3}{x - 2} > 5$

Solve the following inequality:
$\displaystyle\, \left ( \dfrac{1}{5} \right )^\frac{2x + 1}{1 - x} > \left ( \frac{1}{5} \right )^{-3}$

Solve the following inequality:
$\displaystyle\, \left ( \dfrac{1}{3} \right )^{x + \dfrac{1}{2} - \dfrac{2}{x}} > \dfrac{1}{\sqrt{27}}$

Solve the following inequality:
$\displaystyle\, 2^x + 2^{| x| } \geqslant 2\sqrt{2}$

Solve the following inequality:
$\displaystyle\, 4^x - 3 \leqslant 2^{x + 1}$

Solve the following inequalities.
$\displaystyle\, \frac{1 \, - \, \sqrt{1 \, - \, 8x^2}}{2x} \, < \, 1$

Solve the following inequality:
$\displaystyle\, \left ( \dfrac{1}{3} \right )^ \frac{ | x + 2| }{2 - | x| } > 9$

State which of the following are equation (with variable). Given reasons for your an mention which variable is used from the equation with a variable.
$8m<17$

Solve the inequation $\dfrac{1}{x-2}<0$ in $R$ .

If $x$ and $y$ are integers, where $12 < x < 18$ and $15 < y < 27$ , then the maximum value of $x + y$ is

Write the solution of $4x+3<6x+7$ in interval from.

Solve the inequality $\dfrac {x - 1}{x^{2} - 4x + 3} < 1$ .

Let $f\left(x\right)=\frac{\left(x-3\right)\left(x+2\right)\left(x+6\right)}{\left(x+1\right)\left(x-5\right)}$
Find intervals, where $f\left(x\right)$ is positive or negative.

Solve: $\dfrac{x-2}{x+5} > 2$ .

If $x:y = 6:11$ , find $(8x-3y) : (3x+2y)$ .

Solve the given inequality for $x$ :
$\sqrt{\dfrac{x-2}{1- 2x}}> 1$

Solve the following inequality: $2x - 1 < 5$

Solve:
$6x^2-7x-3$ .

Yamini and Fatima, two students of class IX of a school, together contributed Rs. $100$ towards the Prime Minister's relief fund to help the earthquake victims. Write a linear equation which this data satisfies. Draw the graph of the same.

Solve the given inequality for real x.
$3x-7>5x-1$

Solve : $\dfrac{2x}{3} - \dfrac{x}{2} \le 6.5$