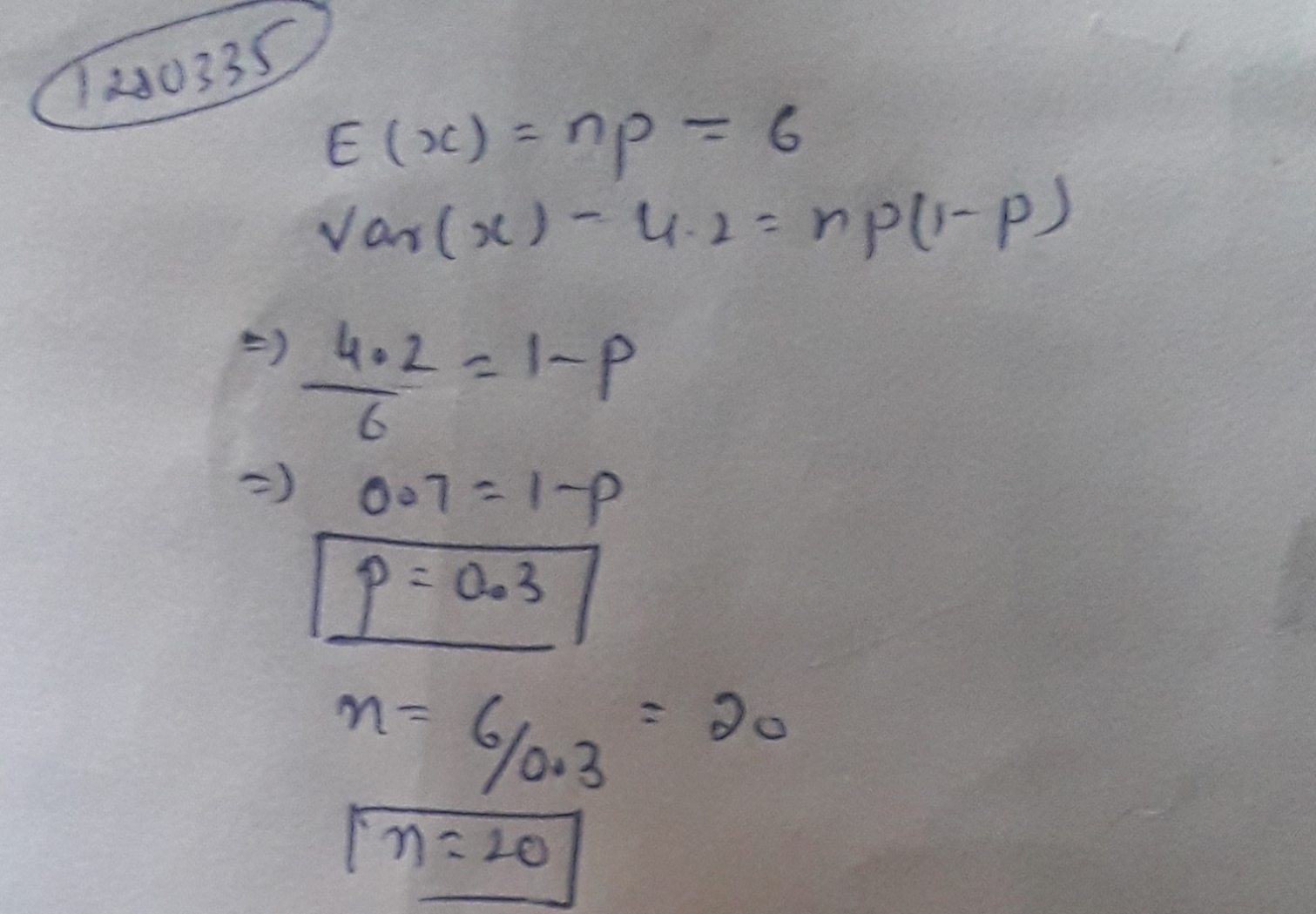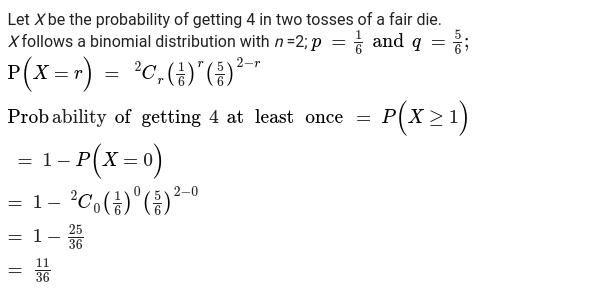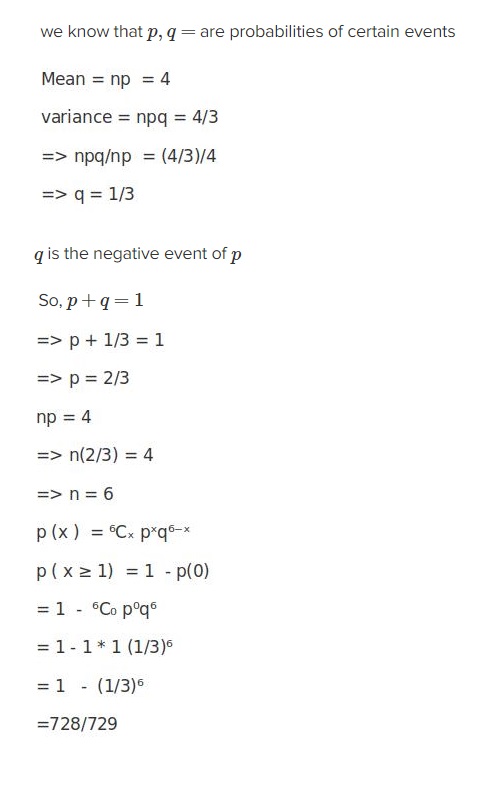Standard Probability Distributions - Class 12 Commerce Applied Mathematics - Extra Questions
If the mean and standard deviation of a binomial distribution are $$12$$ and $$2$$ respectively, then the value of its parameter $$p$$ is
In five throws with a single die what is the chance of throwing $$(1)$$ three aces exactly, $$(2)$$ three aces at least.
Prove that the total probability is one by using Poisson distribution.
The below frequency distribution table represents the blood groups of $$30$$ students of a class. Use this table to determine the probability that a student of this class, selected at random, has blood group $$AB$$.
| Blood group | Number of students |
| A | 9 |
| B | 6 |
| AB | 3 |
| O | 12 |
| Total | 30 |
It is known that $$60\%$$ mice inoculated with a serum are protected from a certain disease. If $$5$$ mice are inoculated, find the probability that none contact the disease.
The items produced by a firm are supposed to be $$5$$% defective what is the probability that a sample of $$8$$ items will contain less than $$2$$ defective items?
It is known that $$60\%$$ mice inoculated with a serum are protected from a certain disease. If $$5$$ mice are inoculated, find the probability that more than $$3$$ contact the disease.
If $$ P(X = r) = \ ^{n}C_{r} \left ( \dfrac{1}{5} \right )^{r} \left ( \dfrac{4}{5} \right )^{n-r},r = 0,1,2,...,n $$ is the binomial distribution whose mean is 20 and varianceFind the value of $$n.$$
In a binomial distribution the sum and product of the mean and the variance are $$ \dfrac{25}{3} $$ and $$ \dfrac{50}{3} $$ respectively. The distribution $$ P(X = r) = \ ^{n}C_{r} \left ( \dfrac{1}{3} \right )^{r} \left ( \dfrac{a}{3} \right )^{n-r},r = 0,1,2,...,n $$. Find value of $$n+a$$.
If the mean and variance of a binomial distribution are respectively 9 and 6, If the distribution is $$ P(X = r) = \ ^{k}C_{r} \left ( \dfrac{1}{3} \right )^{r} \left ( \dfrac{2}{3} \right )^{k-r},r = 0,1,2,...,k $$.
Find the value of $$k$$.
If the mean and variance of a binomial variable X are 2.4 and 1.44 respectively, find the perimeters of the distribution X. (Binomial)
Can the mean of a binomial distribution be less then its variance ?
Determine the binomial distribution whose mean is 4 and variance 3.
The probability that Raju arrives on time at school is $$0.72$$. Raju attends school on $$200$$ days.Work out the expected number of days he will arrive on time.
If $$ P(X = r) = ^{5}C_{r} \left ( \dfrac{a}{5} \right )^{r} \left ( \dfrac{1}{b} \right )^{5-r},r = 0,1,2,...,5 $$ is the binomial distribution when the sum of its mean and variance for 5 trials is 4.8.
What is the value of $$a+b.$$
A die is thrown thrice. A success is 1 or 6 in a throw. If the sum of the mean and variance of the number of successes is $$ \dfrac {a}{3}$$, the value of a is _____ .
The probability is 0.02 that an item produced by a factory is defective. A shipment of 10,000 items is sent to its warehouse. Find the sum of the expected number of defective items and the standard deviation.
In eight throws of a die 5 or 6 is considered a success, find the sum of the mean number of successes and the standard deviation.
If on an average 9 ships out of 10 arrive safely to ports, The sum of mean and S.D of ships returning safely out of a total of 500 ships is $$ ( x + \sqrt{k} )$$. The value of $$ x + k$$ is ____ .
If the probability of a defective bolt is 0.1,find the mean and standard deviation for the distribution of defective bolts in a total of 500 bolts.
The mean and variance of a binomial variate with parameters $$n$$ and $$p$$ are $$16$$ and $$8$$ respectively. If $$ P (X = 0) =\left ( \dfrac{1}{2} \right )^{a},P(X = 1) = \left ( \dfrac{1}{2} \right )^{b} $$ and $$ P(X\geq 2) = \left (1-\dfrac{33}{2^{\ a}} \right) $$, then value of $$ a+b $$ is ___.
If the binomial distribution whose mean is $$5$$ and variance $$ \dfrac{10}{3} $$ is $$ P(X = r) =\ ^{15}C_{r} \left ( \dfrac{1}{a} \right )^{r} \left ( \dfrac{2}{a} \right )^{15-r},r = 0,1,2,...,15 $$, then the value of $$a$$ is ____.
The mean of a binomial distribution is $$20$$, and the standard deviation $$4$$. The sum of parameters of the binomial distribution $$(n$$ and $$p)$$ is $$\dfrac{k}{5}$$. then value of $$k$$ is ______ .
An unbiased die is thrown again and again until three sixes are obtained. The probability of obtaining 3rd six in the sixth throw of the die is $$\dfrac {1250}{x^x}$$
The probability of a man hitting a target is 1/How many times must he fire so that the probability of his hitting the target at least once is greater than 2/3 ?
A perfect cubic die is thrown a large number of times in sets ofThe occurrence of 5 or 6 is called a success. If the proportion of the sets you expect 3 successes is $$x \%$$, then find $$x$$.
If the sum of the mean and variance of a binomial distribution for 6 trials is $$ \dfrac{10}{3} $$, the distribution is $$ P(X = r) = \ ^{6}C_{r} \left ( \dfrac{1}{a} \right )^{r} \left ( \dfrac{b}{3} \right )^{6-r},r = 0,1,2,...,n $$, then value of $$(a+b)$$ is____.
If $$X$$ follows binomial distribution with mean $$4$$ and variance $$2$$, and $$ P(X\geq 5) = \dfrac{93}{4^x} $$, then the value of $$'x'$$ is ______.
Prove that the mean of a binomial distribution is alway greater than the variance.
There are 5 percent defective items in a large bulk of items. The probability that a sample of 10 items will include not more than one defective item is $$ \left ( \dfrac{19^9 \times 29}{20^x} \right )$$, then what is the value of $$x.$$
A die is thrown 20 times. Getting a number greater than 4 is considered a success. If the variance = $$ \dfrac {a}{b}\times$$ Mean. The value of $$a+b$$ is ____.
If a random variable $$X$$ follows binomial distribution with mean $$3$$ and variance $$\dfrac {3}{2}$$, and $$ P(X\leq 5) = \dfrac{63}{2^x}$$, then the value of $$'x' $$ is ____ .
The expectation of the number of heads in $$15$$ tosses of a coin is $$\dfrac {x}{2}$$. The value of $$x$$ is ____.
Find the expectation of the number of heads in 15 tosses of a coin.
Five dice are thrown simultaneously. If the occurrence of an even number in a single die is considered a success and the probability of at most 3 success is $$\dfrac {13}{2^x}$$ , then the value of $$x$$ is ___ .
Six coins are tossed simultaneously. Find the probability of getting 3 heads.
If two dice are rolled 12 times, the relation between mean and the variance of the distribution of successes is $$ Variance = \dfrac {1}{x} \ Mean$$, if getting a total greater than 4 is considered a success. The value of $$'x'$$ is ____.
A die is tosses thrice. Getting an even number is considered as success. What is the variance of the binomial distribution ?
Suppose X has a binomial distribution with $$ n = 6 $$ and $$ p = \dfrac{1}{2}. $$ Show that $$ X = 3 $$ is the most likely outcome.
A bag contains 10 balls each marked with one of the digitd 0 toIf four balls are drawn successively with replacement from the bag, the probability that none is marked with the digit 0 is $$4_{C_0}(\dfrac{1}{10})(\dfrac{k}{10})^4$$, then the value of $$'k'$$ is ____.
Find the binomial distribution for which the mean is 4 and variance 3.
If the probability of defective bolts is 0.1, the sum of the mean and standard deviation for the distribution of defective volts in a total of 500 bolts is $$(a+ \sqrt{b})$$, then the value of $$a+b $$ is _____.
Six coins are tossed simultaneously. If the probability of getting no heads is $$ \dfrac{1}{2^x}$$, then the value of $$x$$ is ____.
The binomial distribution for which the mean is 4 and variance is 3 is Comparing with $$P(X=r) = n_{C_r} (\dfrac{1}{k})^r(\dfrac{3}{k})^{n-r}, r=0,1,2,..,n$$. Find the value of $$n +k.$$
Six coins are tossed simultaneously. If the probability of getting 3 heads is $$ \dfrac{5}{2^x}$$, then what is the value of $$x$$.
Six coins are tossed simultaneously. If the probability of getting at least one head is $$\dfrac{x-1}{x}$$, then what is the value of $$'x'$$.
The probability that a certain kind of component will survive a given shock test is $$ \dfrac{3}{4}.$$ If the probability that among 5 components tested exactly 2 will survive is $$\dfrac{90}{4^x}$$, then what is the value of $$x$$.
A die is thrown three times. Let X be the number of two's seen. If the expectation of X is $$\dfrac{1}{a}$$, then the value of $$a$$ is ___.
Assume that the probability that a bomb dropped from an aeroplane will strike a certain target is 0.If 6 bombs are dropped, the probability that exactly 2 will strike the target is $$\dfrac {3\times 8^a}{10^b}$$, then the value of $$a+b $$ is ____.
Assume that the probability that a bomb dropped from an aeroplane will strike a certain target is 0.If 6 bombs are dropped, the probability that at least 2 will strike the target is $$\dfrac {34464}{10^x}$$, then the value of $$x$$ is ____.
The probability that a certain kind of component will survive a given shock test is $$ \dfrac{3}{4}.$$ The probability that among 5 components tested at most 3 will survive is $$\dfrac {47}{2^x}$$, then what is the value of $$x$$.
For 6 trials of an experiment, let X be a binomial variate which satisfies the relation 9P(X=4)=P(X=2). If the probability of success is $$\dfrac{1}{x}$$, then the value of $$x$$ is ____.
The probability that a student entering a university will graduate is 0.If the probability that out of 3 students of the university, all will graduate is $$\left (\dfrac{4}{10} \right)^x$$, then the value of $$x$$ is ___.
Ina hurdles race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is $$\dfrac{5}{6}$$. What is the probability that he will knock down fewer than 2 hurdles ?
An unbiased die is thrown again and again until three sixes are obtained. Find the probability of obtaining 3rd six in the sixth throw of the die.
A factory produces bulbs. The probability that one bulb is defective is $$ \dfrac{1}{50}$$ and they are packed in boxes ofIf the probability that none of the bulbs is defective from a single box is $$(\dfrac{49}{50})^{k}$$, then value of $$k$$ is ___.
The probability that a student entering a university will graduate is 0.If the probability that out of 3 students of the university none will graduate is $$\left (\dfrac {6}{10} \right )^x$$, then what is the value of $$x$$.
A die is thrown 6 times. If getting an odd number is a success, the probability of 5 successes is $$\dfrac{3}{2^x}$$, then the value of $$x$$ is ___.
How many times must a man toss a fair coin so that the probability of having at least one head is more then 80%?
It is known that 60% of mice inoculated with a serum are protected from a certain disease.if 5 mice are inoculated, If the probability that more than 3 contract the disease is $$ \dfrac {13}{5} (\dfrac{3}{5})^x$$, then the value of $$x$$ is ___.
The probability that a student entering a university will graduate is 0.If the probability that out of 3 students of the university, only one will graduate is $$\dfrac{432}{10^x}$$, then the value of $$x$$ is ___.
A lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, what is the probability that there will be at least one defective watch ?
If the probability that in 10 throws of a fair die a score which is a multiple of 3 will be obtained in at least 8 of the throws is $$\dfrac{201}{3^{x}}$$, then what is the value of $$x$$.
A lot of 100 watches is known to have 10 defective watches. If 8 watches are selected ( one by one with replacement ) at random, the probability that there will be at least one defective watch is $$=1-(\dfrac{9}{10})^x$$, then the value of $$x$$ is ___.
A die is thrown 5 times. The probability that an odd number will come up exactly three times is $$\dfrac{5}{2^x}$$, the value of $$x$$ is ____.
A factory produces bulbs. The probability that one bulb is defective is $$ \dfrac{1}{50}$$ and they are packed in boxes ofIf the probability that exactly two bulbs are defective from a single box is $$45 \times \dfrac{(49)^k}{(50)^{m}}$$, what is the value of $$k+m$$.
The probability of a man hitting a target is 0.He shoots 7 times. The probability of his hitting at least twice is $$\dfrac{x}{8192}$$, then the value of $$x$$ is ____.
A factory produces bulbs. The probability that one bulb is defective is $$ \dfrac{1}{50}$$ and they are packed in boxes ofIf the probability that more than 8 bulbs work properly from a single box is $$\ \dfrac{(k)^8 \times 2936}{(k+1)^{10}}$$, then the value of $$k$$ is ___.
If $$X$$ follows a binomial distribution with parameters $$n=100$$ and $$p=\cfrac{1}{3}$$, then $$P(X=r)$$ is maximum when $$r=$$ _____
A fair coin is tossed $$n$$ times. If the probability that head occurs $$6$$ times is equal to the probability that head occurs $$8$$ times, then the value of $$n$$ is
If the mean and the variance of a binomial variate are $$2$$ and $$1$$ respectively, the probability that $$X$$ takes a value greater than $$1$$ is equal to $$1-k/16$$.Find the value of $$k$$.
Two cards are drawn one by one from the a pack of well shuffled cards with replacement, the probability of at least one king and no club card being chosen is $$\displaystyle \frac{25k}{2704}.$$ Find the value of $$k$$.
A bag contains a certain number of balls, some of which are white;a ball is drawn and replaced, another is then drawn and replaced' and so on. If p be the chance of white balls that is most likely to have been drawn in n trials. For $$p=\cfrac { 1 }{ 2 } $$ and $$n=12$$, the number of white balls required to be drawn is $$k$$. Find the value of $$k$$.
A shopkeeper has five customers who take cycle on rent. He has three cycles and the probability that customer will hire a cycle is $$\displaystyle \frac{3}{4}$$. If he charges rs.2 for a cycle as a rent, the probability that he earns exactly Rs.6 per day is $$\displaystyle \frac{45k}{512}$$. Find the value of $$k$$.
If on an average $$1$$ vessel in every $$10$$ is wrecked the chance that out of $$5$$ vessels expected $$4$$ at least will arrive safely is $$\displaystyle \frac{45920+k}{50000}$$. Find the value of $$k$$.
Suppose $$X$$ follows a binomial distribution with parameters $$n=6$$ and $$p$$. If $$9P(X=4)=P(X=2)$$, find $$4p$$
The probability that an archer hits the target when it is windy is 0.4; when it is not windy, her probability of hitting the target is 0.On any shot, the probability of a gust of wind is 0.If the probability that She hits the target exactly once in two shots is $$0.4x58$$. Find the value of $$x$$.
A bomber wants to destroy a bridge. Two bombs are sufficient to destroy it. If four bombs are dropped, what is the probability that it is destroyed, if the chance of a bomb hitting the target is $$0.4$$,
If the answer is $$ \dfrac{a}{b} $$ (HCF of $$a$$ and $$b$$ is $$1$$), then find $$b-a$$?
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.Find the probability that out of 5 such bulbs.
(i) none
(ii) not more than one
(iii) more than one
(iv) at least one
will fuse after 150 days of use.
A coin is tossed a times, what is the chance that the head will present itself an odd number of times?
The probability that a certain kind of component will survive a check test is $$0.6$$. Find the probability that exactly $$2$$ of the next $$4$$ tested components survive.
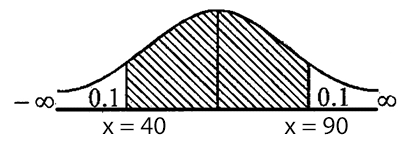
Marks in an aptitude test given to $$800$$ students of a school was found to be normally distributed. $$10\%$$ of the students scored below $$40$$ Marks and $$10\%$$ of the students scored above $$90$$ marks. Find the number of students who scored between $$40$$ and $$90$$.
Let $$X$$ denote the height of the student given
$$P(X < 40) = 10$$ $$\%$$ $$= \dfrac{10}{100} = 0.1$$
$$P(X > 90) = 10$$ $$\%$$ $$= \dfrac{10}{100} = 0.1$$
$$\therefore P(40 < X < 90) = P(- \infty < X < \infty) -\{P (X < 40) P(X > 90)\}$$
$$= 1 - 0.1 - 0.1 = 0.8$$
Out of $$800$$ students number of student scored between $$40$$ and $$90$$ $$= 800$$ $$\times$$ $$0.8 = 640$$ students.
$$P(X < 40) = 10$$ $$\%$$ $$= \dfrac{10}{100} = 0.1$$
$$P(X > 90) = 10$$ $$\%$$ $$= \dfrac{10}{100} = 0.1$$
$$\therefore P(40 < X < 90) = P(- \infty < X < \infty) -\{P (X < 40) P(X > 90)\}$$
$$= 1 - 0.1 - 0.1 = 0.8$$
Out of $$800$$ students number of student scored between $$40$$ and $$90$$ $$= 800$$ $$\times$$ $$0.8 = 640$$ students.
Find the variance of numbers obtained on thrown an unbiased die.
None of them is fuse.
The probability that a person chosen at random is left handed (in hand writing) is $$0.1$$. What is the probability that in a group of $$10$$ people, there is one who is left handed?
If $$X$$ is a Poisson variable with $$P\left( X=0 \right) =P\left( X=1 \right) =k$$, then show that $$k={ e }^{ -1 }$$.
The probability that a bomb will hit a target is $$0.8$$. Find the probability that out of $$10$$ bombs dropped, exactly $$2$$ will hit the target.
If on an average $$1$$ vessel in every $$10$$ is wrecked, find the chance that out of $$5$$ vessels expected $$4$$ at least will arrive safely.
Two numbers are selected at random(without replacement) from the first five positive integers. Let X denote the larger of the two numbers obtained. Find the mean and variance of X.
If X has Poisson distribution with parameter $$m = 1$$, find $$P[X \leq 1]$$. (Use $$e^{-1} = 0.3679$$)
A life insurance salesman sells on the average 3 life insurance policies per week. Use poisson's law to caculate the probability that in a given week he will sell 2 or more policies but less than 5 policies.
If a fair coin is tossed $$10$$ times, find the probability of
(i) Exactly six heads.
(ii) Atleast six heads.
(ii) Atleast six heads.
If the sum of the mean and variance of a binomial distribution for $$6$$ trials be $$10/3$$, find the distribution.
Determine the probability of $$3$$ successes in a binomial distribution whose mean and variance are respectively $$2$$ and $$1.5$$.
An unbiased coin is tossed 8 times . Find by using binomial distribution , the probability of getting atleast 3 heads .
A pair of dice is thrown $$6$$ times. If getting a total of $$7$$ is considered as a success then what is the probability of getting at least $$4$$ successes?
The mean and variance of a binomial distribution are $$\dfrac{4}{3}$$ and $$\dfrac{8}{9}$$ respectively. Find $$P(x\geq 1)$$.
The mean and variance of a binomial distribution are $$10$$ and $$\dfrac{5}{3}$$ respectively. Find $$P(x \geq 1)$$.
Given mean and variance of a binomial distribution are
10 and $$ \dfrac{5}{3} $$ respectively.
Let the parametrs be n,p,q
$$ \Rightarrow np = 10, npq = \dfrac{5}{3} $$
$$ \Rightarrow q = \dfrac{5}{\dfrac{3}{10}} = \dfrac{1}{6} $$
$$ p = 1-q = 1-\dfrac{1}{6} = \dfrac{5}{6} $$
$$ np = 10\Rightarrow n.\dfrac{5}{6} = 10\Rightarrow n = 12 $$
$$ p(x\geq 1) = 2^{n}-p(x = 0) $$
$$ = 2^{12}-^{12}C_{0} \left ( \dfrac{5}{6} \right )^{0}\left ( \dfrac{1}{6} \right )^{12} $$
$$ = 2^{12}-\left ( \frac{1}{6} \right )^{12} $$
a box containing$$100$$ transistors $$20$$ of which are defective.from this box,$$10$$ transistors are drawn for inspection
what is the probability that$$\left( i \right)$$ all $$10$$ are defective?$$\left( {ii} \right)$$all $$10$$ are good?$$\left( {iii} \right)$$at least one is defective?$$\left( {iv} \right)$$at most $$3$$ are
A student is given a test with $$8$$ items of true-false type. If he gets $$6$$ or more items correct, he is declared pass. Given that he guesses the answer to each item, compute the probability that he will pass in the test.
An unbiased coin is tossed 32 times . Find the probability of obtaining 2 heads .
A rat maze consists of a straight corridor, at the end of which the rats take either right or left turn. If $$10$$ rats are placed in the maze one at a time and the random variable $$X$$ denotes the number of right turns taken by the rats then what is the probability distribution of $$X$$? Find the probability that atleast $$9$$ rats will turn the same way.
In a box containing $$50$$ bulbs, $$5$$ are defective. what is the probability that out of a sample of $$5$$ bulbs at most two are defective?
In a book of 500 pages , there are 500 misprinting errors, find the probability of at most three misprinting 3 pages selected at random from the book.
Find n and p for a binomial distribution if mean = 6 and standard deviation =Also find p (x=1).
In tossing three coins together, what is the probability of getting i) at least one tail ii) at least one head ?
An examination consists of $$8$$ questions in each of which the candidate must say which one of the $$5$$ alternatives is correct one. Assuming that the student has not prepared earlier choose for each of the question any one of $$5$$ answer with equal probability.
(i) Prove that the probability that he gets more than one correct answer is $$(5^{8}-3\times\ 4^{8})/5^{8}$$
(ii) Find the probability that he gets correct answer to x or more questions.
(iii) Find the standard deviation of this distribution.
In a box containing $$100$$ bulbs, $$10$$ are defective. If $$5$$ bulbs are drawn one after another with replacement, then the probability that none is defective, is
In a binomial distribution, mean is 3 and varience is 3/Find the probability of at least 5 success ?
For a Binomial probability distribution $$E(x)=6$$ and $$Var(x)=4.2$$. Find $$n$$ and $$p$$.
$$E(x) = np = 6$$
$$V ar (x) - 4.2 = np(1-p)$$
$$\Rightarrow \frac{4.2}{6}= 1-p$$
$$\Rightarrow 0.7 = 1-p$$
$$p=0.3$$
$$n=6/0.3=20$$
$$n=20$$
In a binomial distribution, mean is $$3$$ and variance is $$3/2$$. Find the probability of at least $$4$$ success.
A] E(x)=np=3
v(x)=npq=$$\frac{3}{2}$$
$$\therefore a=\frac{1}{2}$$
$$ p=1-q=\frac{1}{2}$$
np = 3
$$\therefore np=n\times \frac{1}{2}=3\Rightarrow n=6$$
$$p(x=x)=^{n}c_{x}p^{x}q^{n-x}$$ $$(x\epsilon 64,6)$$
P(X=4)+P(X=5)+P(X=6)
$$^{6}C_{4}(\frac{1}{2})^{4}(\frac{1}{2})^{6-4}+6(\frac{1}{2})^{5}(\frac{1}{2})^{6-5}+^{6}C_{6}(\frac{1}{2})^{6}\frac{1}{2}$$
$$=\frac{6\times 5}{2}\times \frac{1}{2^{6}}+6\frac{1}{2^{6}}+1\times \frac{1}{2^{6}}$$
$$ =\frac{1}{2^{6}}[15+6+1]=\frac{1}{2^{6}}\times 22$$
$$=\frac{11}{25}=\frac{11}{32}$$
Find the mean of the binomial distribution $$B\left(4,\dfrac{1}{3}\right)$$.
The mean the variance of a binomial distribution are 4 and 2 respectively . Then the probability of 2 success is -
If the difference between the mean and the variance of a binomial variate is $$5/9$$ then find the probability for the event of $$2$$ successes when the experiment is conducted $$5$$ times.
$$P(A') = \dfrac{7}{25}$$, $$P(\dfrac{B}{A}) = \dfrac{5}{12}$$, $$P(A \cap B) = ?$$
write the formula for E(X) and Var(X).
If $$X$$ has Poisson distribution with parameter $$m=1$$. Find $$P[X\le 1] $$(use $$e^{-1}=0.367879)$$.
The probability of a shooter hitting a target is $$\frac{3}{4}$$. How many minimum number of times must he/she fire so that the probability of hitting the target at least once is more than 0.99?
Find the expectation of the number of heads in 15 tosses of a coin.
There are 6% defective items in a large bulk of items. Probability that a sample of 8 items will include not more than one defective items is $$ 1.42 \times \left ( 0.94 \right )^{x}$$. What is the value of x.
A coin is tossed 5 times. What is the probability of getting at least 3 heads.
A die is tossed twice. A'success' is getting an even number on a toss. The variance of the number of successes is $$\dfrac {1}{x}$$, the value of $$x$$ is ___.
A pair of fair dice is thrown. Let X be the random variable which denotes the minimum or equal of the two numbers which appear. Find the probability distribution, mean and variance of X.
For 6 trials of an experiment, let X be a binomial variate which satisfies the relation $$9P(X=4)=P(X=2)$$. Find the probability of success.
If the probability of defective bolts is $$0.1,$$ find the mean and standard deviation for the distribution of defective bolts in a total of $$500$$ bolts.
In roulette, the wheel has 13 numbers 0,1,2,....,12 marked on equally spaced slots. A player sets Rs. 10 on a given number. He receives Rs. 100 from the organizer of the game if the ball comes to rest in this slot; otherwise he gets nothing. If X denotes the player's net gain/loss, If $$E(X)=\dfrac{-30}{X}$$, then find X.
If $$X\sim B(n,P)$$ and $$n=10,E(X)=5$$, then find the value of $$p$$.
A coin is tossed $$6$$ times. Find the probability of getting
(i) exactly 4 heads (ii) at least 1 head (iii) at most $$4$$ head
A die is thrown $$6$$ times. If 'getting an even number' is a success, find the probability of getting
(i) exactly $$5$$ successes (ii) at least $$5$$ successes (iii) at most $$5$$ successes
$$10$$ coins are tossed simultaneously. Find the probability of getting
(i) exactly $$3$$ heads (ii) not more than $$4$$ heads (iii) at least $$4$$ heads
$$7$$ coins are tossed simultaneously. What is the probability that a tail appears an odd number of times?
Three rotten apples are mixed with seven fresh apples. Find the probability distribution of the number of rotten apples, if three apples are drawn one by with replacement. Find the mean of the number of rotten apples.
Given Rotten apples $$-3$$
Fresh apples $$-\dfrac{7}{10}$$
$$p = p(R) = \dfrac{3}{10}$$
$$q = 1 - p = 1 - \dfrac{3}{10} = \dfrac{7}{10}$$
here $$n = 3$$
$$p(x) = p(0,1,2,3)$$
$$p(0) = \ ^3c_0 \left(\dfrac{3}{10}\right)^0 \left(\dfrac{7}{10}\right)^3 = \ ^3c_0 .\dfrac{7^3}{10^3} = \dfrac{343}{1000}$$
$$p(1) = \ ^3c_1 \left(\dfrac{3}{10}\right)^1 \left(\dfrac{7}{10}\right)^2 = \ ^3c_1 . \dfrac{3.7.7}{10^3} = \dfrac{441}{1000}$$
$$p(2) = \ ^3c_2 \left(\dfrac{3}{10}\right)^2 \left(\dfrac{7}{10}\right)^1 = \dfrac{3.9.7}{100} = \dfrac{189}{1000} $$
$$p(3) = \ ^3c_3 \left(\dfrac{3}{10}\right)^3 \left(\dfrac{7}{10}\right)^0 = \dfrac{1.27}{1000} = \dfrac{27}{1000} $$
Refer image.
$$H = \sum x . p(x)$$
$$= 0. \left(\dfrac{343}{1000}\right) + 1. \left(\dfrac{441}{1000}\right) +2.\left(\dfrac{189}{1000}\right) +3.\left(\dfrac{27}{1000}\right) $$
$$= \dfrac{441 + 378 + 81}{1000} = \dfrac{9000}{1000} = \dfrac{9}{10}$$
A coin is tossed $$5$$ times. What is the probability that a head appears an even number of times?
Past records show that $$80$$% of the operations performed by a certain doctor were successful. If he performs $$4$$ operations in a day, what is the probability that at least $$3$$ operations will be successful?
In a box containing $$60$$ bulbs, $$6$$ are defective. What is the probability that out of a sample of $$5$$ bulbs (i) none is defective (ii) exactly $$2$$ are defective?
Find the probability of a $$4$$ turning up at least once in two tosses of a fair die.
A die is thrown $$4$$ times. 'Getting a $$1$$ or $$6$$' is considered a success. Find the probability of getting
(i) exactly $$3$$ successes (ii) at least $$2$$ successes (iii) at most $$2$$ successes
Three cars participate in a race. The probability that any one of them has an accident is $$0.1$$. Find the probability that all the cars reach the finishing line without any accident.
The probability of a man hitting a target is $$(1/4)$$. If he fires $$7$$ times, what is the probability of his hitting the target at least twice?
A pair of dice is thrown $$4$$ times. If 'getting a doublet' is considered a success, find the probability of getting $$2$$ successes.
Assume that on an average one telephone number out of $$15$$, called between $$3$$ p.m and $$4$$ p.m on weekdays, will be busy. What is the probability that if six randomly selected telephone numbers are called, at least $$3$$ of them will be busy?
The probability that a bulb produced by a factory will fuse after $$6$$ months of use is $$0.05$$. Find the probability that out of $$5$$ such bulbs
(i) none will fuse after $$6$$ months of use
(ii) at least one will fuse after $$6$$ months of use
(iii) not more than one will fuse after $$6$$ months of use.
A man can hit a bird, once in $$3$$ shots. On this assumption, he fires $$3$$ shots. What is the chance that at least one bird is hit?
The mean and variance of a binomial distribution are $$4$$ and $$(4/3)$$ respectively. Find $$P(X\ge 1)$$
Find the binomial distribution whose mean is $$5$$ and variance is $$2.5$$
Obtain the binomial distribution whose mean is $$10$$ and standard deviation is $$2\sqrt{2}$$
In a binomial distribution, the sum and the product of the mean and the variance are $$\dfrac {25}{3}$$ and $$\dfrac {50}{3}$$ respectively. Find the distribution.
A policeman fires $$6$$ bullets at a burglar. The probability that the burglar will be hit by a bullet is $$0.6$$. What is the probability that the burglar is still unhurt?
A bag contains $$5$$ white, $$7$$ red and $$8$$ black balls. If four balls are drawn one by one with replacement, what is the probability that (i) none is white, (ii) all are white (iii) at least one is white?
For a binomial distribution, the mean is $$6$$ and the standard deviation is $$\sqrt{2}$$. Find the probability of getting $$5$$ successes.
Determine the binomial distribution whose mean is $$9$$ and variance is $$6$$.
A die is tossed thrice. A success is $$1$$ or $$6$$ on a toss. Find the mean and variance of successes.
A die is thrown $$100$$ times. Getting an even number is considered a success. Find the mean and variance of successes.
Bring out the fallacy, if any, in the following statement.
'The mean of a binomial distribution is $$6$$ and its variance is $$9$$'
Explain why the experiment of tossing a coin three times is said to have binomial distribution.
If X follows binomial distribution with parameters n = 5, p and P(X = 2) = 9, P(X = 3), then P = _________
Suppose $$X$$ has a binomial distribution $$B(6,\cfrac{1}{2})$$. Show that $$x=3$$ is the most likely outcome.
If X has a Binomial distribution $$ B \left ( 4 , \dfrac{1}{3} \right ) $$ , then write $$ P(x = 1 ) $$ .
A die is thrown 1000 times with the frequencies for the outcomes 1, 2, 3, 4, 5 and 6 as given in the following table:
| Outcome | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency | 179 | 150 | 157 | 149 | 175 | 190 |
(i) an odd number
(ii) a prime number
(iii)a number greater than 4
(iv) a multiple of 2
The mean and variance of a binomial variable $$X$$ are $$2$$ and $$1$$ respectively. The probability that $$X$$ takes values greater than $$1$$ is $$1-\dfrac { k }{ 16 } $$.The value of $$k$$ is
If $$X$$ follows binomial distribution with parameters $$2n+1$$ and $$p=1/2$$, then the probability that $$X$$ takes odd value is $$1/k$$. Find the value of $$k$$
In a sequence of independent trials, the probability of success is 1/If $$p $$ denotes the probability that the second success occurs on the fourth trial or later trial, find $$32 p$$
The probability of a bomb hitting a bridge is $$1/2$$. Two direct hits are needed to destroy it. The number of bombs required so that the probability of the bridge being destroyed is greater that $$0.9$$
The difference between mean and variance of a binomial distribution is $$1$$ and the difference of their squares is $$11$$. Find the distribution.
On dialling certain telephone numbers, assume that on an average, one telephone number out of five is busy, ten telephone numbers are randomly selected and dialled. Find the probability that at least three of them will be busy.
An insurance agent insures lives of $$5$$ men, all of the same age and in good health. The probability that a man of this age will survive the next $$30$$ years is known to be $$\dfrac {2}{3}$$. Find the probability that in the next $$30$$ years at most $$3$$ men will survive
If the sum and the product of the mean and variance of a Binomial Distribution are $$1.8$$ and $$0.8$$ respectively, find the probability distribution and the probability of at least one success.
The probability that a person who undergoes kidney operation will recover is $$0.5$$. Find the probability that of the six patients who undergo similar operations. (a) None will recover. (b) Half of them will recover
Let $$X$$ have Poisson distribution with mean $$4$$. Find $$P\left( X\le 3 \right) $$ and $$P\left( 2\le X<5 \right)$$, $$\left( { e }^{ -4 }=0.0183 \right) $$
The probability that a bulb produced by a factory will fuse in $$100$$ days of use is $$0.05$$. Find the probability that out of $$5$$ such bulbs, after $$100$$ days of use, more than one fuses.
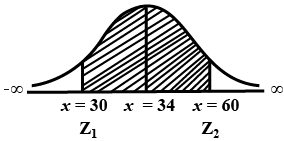
The mean score of $$1000$$ students for an examination is $$34$$ and $$S.D.$$ is $$16$$.(i) How many candidates can be expected to obtain marks between $$30$$ and $$60$$ assuming the normality of the distribution and (ii) determine the limit of the marks of the central $$70$$ $$\%$$ of the candidates:
$$\left \{P[0 < z < 0.25] = 0.0987\ P[0 < z < 1.63] = 0.4484\ P[0 < z < 1.04] = 0.35\right \}$$
$$\left \{P[0 < z < 0.25] = 0.0987\ P[0 < z < 1.63] = 0.4484\ P[0 < z < 1.04] = 0.35\right \}$$
Given, $$\mu = 34, \sigma = 16, N = 1000$$
(i) $$P(30 < X < 60); Z = \dfrac {X - \mu}{\sigma}$$
$$\therefore X = 30, Z_{1} = \dfrac {30 - \mu}{\sigma} = \dfrac {30 - 34}{16}$$
$$= \dfrac {-4}{16} = 0.25$$
$$Z_{1} = -0.25$$
$$Z_{2} = \dfrac {60 - 34}{16} = \dfrac {26}{16} = 1.625$$
$$Z_{2} = 1.63$$ [Approximately]
$$P(-0.25 < Z < 1.63) = P(0 < Z < 0.25) + P(0 < Z < 1.63)$$ (due to symmetry)
$$= 0.0987 + 0.4484 = 0.5471$$
$$\therefore$$ Number of students scoring between $$30$$ and $$60$$ $$= 0.5471\times 1000 = 547$$
(ii) limit of central $$70$$ $$\%$$ of candidates:
Values of $$Z_{1}$$ from the area label for the area $$0.35$$$$= -1.04$$
[since $$Z_{1}$$ lies the left of $$Z = 0$$]
Similarly $$Z_{2} = 1.04$$
$$\therefore Z_{1} = \dfrac {X - 34}{16} = 1.04\ Z_{2} = \dfrac {X - 34}{16} = -1.04$$
$$X_{1} = 16\times 1.04 + 34\ X_{2} = -1.04 \times 16 + 34$$
$$= 16.64 + 34\ X_{2} = -16.64 + 34$$
$$X_{1} = 50.64\ X_{2} = 17.36$$
$$\therefore 70$$ $$\%$$ of the candidates score between $$17.36$$ and $$50.64$$.
(i) $$P(30 < X < 60); Z = \dfrac {X - \mu}{\sigma}$$
$$\therefore X = 30, Z_{1} = \dfrac {30 - \mu}{\sigma} = \dfrac {30 - 34}{16}$$
$$= \dfrac {-4}{16} = 0.25$$
$$Z_{1} = -0.25$$
$$Z_{2} = \dfrac {60 - 34}{16} = \dfrac {26}{16} = 1.625$$
$$Z_{2} = 1.63$$ [Approximately]
$$P(-0.25 < Z < 1.63) = P(0 < Z < 0.25) + P(0 < Z < 1.63)$$ (due to symmetry)
$$= 0.0987 + 0.4484 = 0.5471$$
$$\therefore$$ Number of students scoring between $$30$$ and $$60$$ $$= 0.5471\times 1000 = 547$$
(ii) limit of central $$70$$ $$\%$$ of candidates:
Values of $$Z_{1}$$ from the area label for the area $$0.35$$$$= -1.04$$
[since $$Z_{1}$$ lies the left of $$Z = 0$$]
Similarly $$Z_{2} = 1.04$$
$$\therefore Z_{1} = \dfrac {X - 34}{16} = 1.04\ Z_{2} = \dfrac {X - 34}{16} = -1.04$$
$$X_{1} = 16\times 1.04 + 34\ X_{2} = -1.04 \times 16 + 34$$
$$= 16.64 + 34\ X_{2} = -16.64 + 34$$
$$X_{1} = 50.64\ X_{2} = 17.36$$
$$\therefore 70$$ $$\%$$ of the candidates score between $$17.36$$ and $$50.64$$.
If $$X$$ is normally distributed with mean $$6$$ and standard deviation $$5$$, find:
(i) $$P[0\le X\le 8]$$
(ii) $$P\left( \left| X-6 \right| <10 \right) $$
Here $$P(0< Z< 1.2)=0.3849$$
$$P(0< Z< 0.4)=0.1554$$
$$P(0< Z< 2)=0.4772$$
Not more than one fuses.
$$20\%$$ of the bolts produced in a factory are found to be defective. Find the probability that in a sample of $$10$$ bolts chosen at random exactly $$2$$ will be defective using:
(i) Binomial distribution
(ii) Poisson distribution $$[e^{-2} = 0.1353]$$
Suppose that the probability of suffering a side effect from a certain vaccine is $$0.005$$. If $$1000$$ persons are inoculated, find the probability that:
(i) atmost $$1$$ person suffers
(ii) $$4,5$$ or $$6$$ persons suffer $$[{e}^{-5}=0.0067$$]
The mean weight of $$500$$ male students in a certain college is $$151$$ pounds and the standard deviation is $$15$$ pounds. Assuming the weights are normally distributed, find the approximate number of students weighing.
(i) between $$120$$ and $$155$$ pounds,
| $$Z$$ | $$0.2667$$ | $$2.067$$ | $$2.2667$$ |
| Area | $$0.1026$$ | $$0.4803$$ | $$0.4881$$ |
(ii) more than $$185$$ pounds.
The mean score of $$1000$$ students for an examination is $$34$$ and standard deviation is $$16$$.
(i) How many candidates can be expected to obtain marks between $$30$$ and $$60$$ assuming the normality of the distribution and
(ii) Determine the limits of the marks of the central $$70\%$$ of the candidates
$$\{P[0 < z < 0.25] = 0.0987; P [0< z < 1.63] = 0.4484; P[0 < z < 1.04] = 0.35\}$$
From a bag containing n balls, all either white or black, all numbers of each being equally likely, a ball is drawn which turns out to be white; this is replaced, and another ball is drawn, which also turns out to be white. If this ball is replaced, prove that the chance of the next draw giving a black ball is $$\displaystyle\frac{1}{2}(n-1)(2n+1)^{-1}$$.
(i) Let $$Z$$ be a standard normal variate. Find the value of $$c$$ if $$P(Z< c)=0.05$$
Here $$P(Z< c)=0.05$$
Here $$P[0< Z< 1.65]=0.45$$
(ii) The difference between the mean and the variance of a Binomial distribution is $$1$$ and the difference between their squares is $$11$$. Find $$n$$
$$(i)$$
Let $$Z$$ be the standard normal variate.
We have to find the value of $$c$$ if $$P(Z<c)=0.05$$
Consider $$P(Z<c)=0.05$$
$$\Rightarrow P(-\infty < Z<c)=0.05$$
As area is $$<0.05$$, $$c$$ lies to the left of $$z=0$$
From the area table $$Z$$ value for the area $$0.45$$ is $$1.65$$
Therefore $$c=-1.65$$
$$(ii)$$
Let the mean be $$(m+1)$$ and the variance be $$m$$ from the given data [since mean $$>$$ variance in binomial distribution]
$$(m+1)^2-m^{2}=11$$
$$\Rightarrow m=5$$
$$\therefore mean=m+1=6$$
$$\Rightarrow np=6, npq=5$$
$$\therefore q=\dfrac{5}{6}, p=\dfrac{1}{6}$$
Since $$npq=5$$
Substitute $$q=\dfrac{5}{6}, p=\dfrac{1}{6}$$ we get
$$n\times \dfrac{1}{6} \times \dfrac{5}{6}=5$$
$$\Rightarrow n \times \dfrac{1}{36}=1$$
$$\therefore n=36$$
An urn contains $$25$$ balls of which $$10$$ bear a mark '$$X$$' and the remaining $$15$$ bear a mark '$$Y$$'. A ball is drawn at random from the urn, its mark noted down and it is replaced. If $$6$$ balls are drawn in this way, find the probability that
(i) All will bear mark '$$X$$'
(ii) Not more than two will bear '$$Y$$' mark
A poisson variable satisfies $$P(X=1)=P(X=2)$$, find $$P(X=5)$$
Given $$X - B(n, p)$$
If $$n = 10$$ and $$p = 0.4$$, find $$E(X)$$ and $$Var(X)$$.
A pair of disc rolled $$24\ times$$. A person wins by not getting a pair of $$6's$$ on any of the $$24$$ rolls. What is the probability of his wining?
A pair of dice is thrown $$6$$ times. If getting a total of $$9$$ is considered as a success, what is the probability of getting at least 5 successes ?
In a box containing $$15$$ bulbs, $$5$$ are defective. If $$5$$ bulbs are selected at random from the box, find the probability of the event, that
None of them is defective
Suppose that $$80\%$$ of all families own a television set. If $$5$$ families are interviewed at random,
find the probability that:
$$(i)$$ Three families own a television set.
$$(ii)$$ At least two families own a television set.
Lot of 100 items contain 10 defective items. Five items are selected at random from the lot and sent to the retail store. What is the probability thet the store will receive at most one defective item?
If $$X$$ follows a binomial distribution with parameters $$n=8$$ and $$p=\dfrac{1}{2}$$, then $$p\left(\left|x-4\right|\le 2\right)$$ is equal to
n different toys are to be distributed among n children. Find the number of ways in which these toys can be distributed so that exactly one child gets no toy
From a lot of 30 bulbs which include 6 defectives,a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulls.
If the number of incoming buses per minute at a bus terminus us a random variable having a poisson distribution with $$\lambda = 0
.9$$, find the probability that there will be:
(i) exactly 9 incoming buses during a period of 5 minutes.
(ii) fewer than 10 incoming buses during a period fo 8 minutes.
(iii) at least 10 incoming huses during a period of 11 minutes.
There are $$6$$% defective items in a large bulk of items. Find the probability that a sample of $$8$$ items will include not more than one defective item.
In a binomial distribution, mean is $$3$$ and varience is $$\dfrac{3}{2}$$. Find the probability of at least $$5$$ success ?
The mean score $$1000$$ students for an examination is $$34$$ and the standard deviation is $$16$$. Determine the limit of the marks of the central $$70\%$$of the candidates by the distribution is normal
$$P[0<Z<1.04]=0.35$$
A box contains 12 red and 6 white balls. Balls are drawn from the bag one at a time without replacement.If in 6 draws, there are at least 4 white balls,find the probability that exactly one white ball is drawn in the next two draws.(Binomial coefficients can be left as such.)
A die is rolled $$200$$ times and its outcomes are recorded as given below. Find the probability of getting (i) an even number, (ii) a multiple of $$3$$.Outcome
$$1$$
$$2$$
$$3$$
$$4$$
$$5$$
$$6$$
Frequency
$$25$$
$$35$$
$$40$$
$$28$$
$$42$$
$$30$$
| Outcome | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ |
| Frequency | $$25$$ | $$35$$ | $$40$$ | $$28$$ | $$42$$ | $$30$$ |
Class 12 Commerce Applied Mathematics Extra Questions
- Application Of Derivatives Extra Questions
- Applications Of Integrals Extra Questions
- Definite Integrals Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Indefinite Integrals Extra Questions
- Linear Equations Extra Questions
- Matrices Extra Questions
- Probability Distribution And Its Mean And Variance Extra Questions
- Quantification And Numerical Applications Extra Questions
- Standard Probability Distributions Extra Questions