Wave Optics - Class 12 Engineering Physics - Extra Questions
In YDSE, find the thickness of a glass slab $$(\mu=1.5)$$ which should be placed before the upper slit $$S1$$ so that the central maximum now lies at a point where $$5_{th}$$ bright fringe was lying earlier (before inserting the slab). Wavelength of light used is 5000 $$\mathring{A}$$.
A glass plate $$(n=1.53)$$ that is $$485\mu m$$ thick and surrounded by air is illuminated by a beam of white light normal to the plate, (a) What wavelengths in the visible spectrum $$(400$$ or $$700nm)$$ are intensified in the reflected beam? (b) What wavelengths are intensified in transmitted beam?
Match Column I and Column Ii
A certain region of a soap bubble reflects red light of vacuum wavelength $$\lambda =650nm$$ . The minimum thickness that this region of soap bubble could have is $$13\times 10^{-x}m$$. Find $$x$$. ( The index of refraction of the soap film is $$1.25$$)
For the situation shown in figure, match the entries of Column I with Column II.
Assume thickness of films to be very small compared towavelenght of incident light.
In Young's double -slit experiment performed with a source of white light, only black and white fringes are observed. Mark 0 for False and 1 for True.
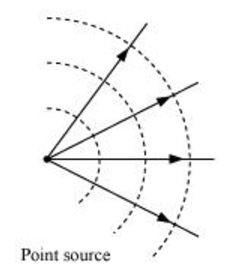
The shape of the wave diverging from a point of source is .......................
What is dual nature of light?
A water film having a refractive index of 1.33 in air is 320 nm thick. If it is illuminated with white light at normal incidence, the light of what wavelength (in nm) will appear to be in reflected light?
Interference fringes are produced by a double-slit experiment and a piece of plane parallel glass refractive index $$1.5$$ is interposed in one of the interfering beams. If the fringes are displaced through $$30$$ fringe widths for light of wavelength $$6\times {10}^{-5}cm$$, if the thickness of the plate is $$3.6\times {10}^{-X}cm$$. Find X?
A glass of refractive index $$1.5$$ is coated with a thin layer of thickness of $$t$$ of refractive index $$1.8$$ light of wavelength $$\lambda$$ tavelling at the upper and the lower surfaes of the layer and the two reflected rays interfere. If $$\lambda=648nm$$, obtain the least value of $$t$$ (in $${10}^{-8}m$$) for which the rays interfere constructively.
Let us list some of the factors, which could possibly influence the speed of wave propagation:
(i) nature of the source.
(ii) direction of propagation.
(iii) motion of the source and/or observer.
(iv) wavelength.
(v) intensity of the wave.
On which of these factors, if any, does
(a) The speed of light in vacuum(b) The speed of light in a medium (say, glass or water), depend?
(i) nature of the source.
(ii) direction of propagation.
(iii) motion of the source and/or observer.
(iv) wavelength.
(v) intensity of the wave.
On which of these factors, if any, does
For sound waves, the Doppler formula for frequency shift differs slightly between the two situations: (i) source at rest; observer moving, and (ii) source moving; observer at rest. The exact Doppler formulas for the case of light waves in vacuum are, however, strictly identical for these situations. Explain why this should be so. Would you expect the formulas to be strictly identical for the two situations in case of light travelling in a medium?
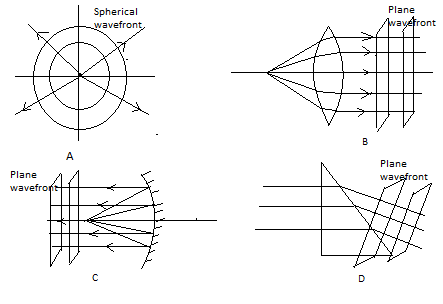
What is the shape of the wavefront in each of the following cases:
(a) Light diverging from a point source.(b) Light emerging out of a convex lens when a point source is placed at its focus.(c) The portion of the wavefront of light from a distant star intercepted by the Earth.
For a single slit of width "a", the first minimum of the interference pattern of a monochromatic light of wavelength $$\lambda$$ occurs at an angle of $$\dfrac{k}{a}$$. At the same angle of $$\dfrac{k}{a}$$, we get a maximum for two narrow slits separated by a distance "a". Explain.
Explain Doppler effect in light. Distinguish between Red shift and Blue shift.
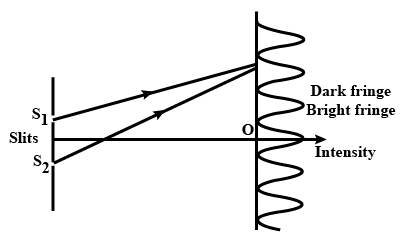
In Young's double slit experiment, show graphically how intensity of light varies with distance.
With the help of an experiment, state how will you identify whether a given beam of light is polarised or unpolarised.
Suppose white light falls on a double slit but one slit is covered by a violet filter (allowing $$\lambda = 400 nm)$$. Describe the nature of the fringe pattern observed.
The ratio of the intensities at minima to the maxima in the Young's double slit experiment is 9:Find the ratio of the widths of the two slits.
Why don't we have interference when two candles are placed close to each other and the intensity is seen at a distant screen? What happens if the candles are replaced by laser sources?
A soap film of thickness $$0.3\ \mu m$$ appears dark when seen by the reflected light of wavelength $$580\ nm$$. What is the index of reflection of the soap solution if it is known to be in between $$1.3$$ and $$1.5$$?
Explain Doppler Effect in light. Hence explain the red and blue shift. State its two applications. the number of waves in $$6\ cm$$ of vacuum is same as the number of waves in $$X\ cm$$ of a medium. If the refractive index of the medium is $$1.5$$, find X.
Can white light produce interference? What is the nature?
In a Young's double slit experiment, the separation between the slits = $$2.0$$ mm, the wavelength of the light = $$600$$ nm and the distance of the screen from the slits = $$2.0$$ m. If the intensity at the center of the central maximum is $$0.20 {Wm^{-2}}$$, what will be this intensity at a point $$0.5$$ cm away from this center along the width of the fringes?
If two waves of equal intensities $$I_1 = I_2 = I_0$$, meet at two locations $$P$$ and $$Q$$ with path differences $$\triangle_1$$ and $$\triangle_2$$, respectively. What will be the ratio of resultant intensity at points $$P$$ and $$Q$$?
State the conditions for the following to take place :
Sustained interference of light from two narrow slits.
In a $$YDSE$$,performed with a source of white light ,only black and white fringes are observed.
Write definitions of plane of vibration and plane of polarization. Explain the working process to obtain plane polarized light by Nicole Prism. Draw necessary diagram.
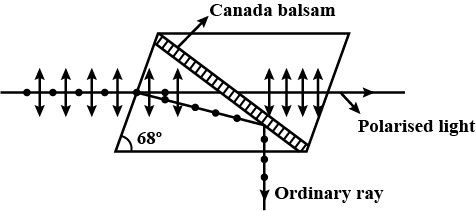
Explain how an unpolarised light gets polarised when incident on the interface separating the two transparent media.
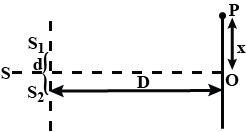
The intensity at the central maximum (O) in a Yong's double slit experimental set-up shown in the figure is $$I_O$$. If the distance $$OP$$ equals one-third of the fringe width of the pattern. show that the intensity at point P. would equal $$\dfrac{I_O}{4}$$
Green light is incident at the polarising angle on a certain transparent medium. The angle of refraction is $$30^o$$. Find
(i) polarising angle, and
(ii) refractive index of the medium.
A parallel beam of light of wavelength 500 nm falls on a narrow slit and the resulting diffraction pattern is obtained on a screen 1 m away. If the first minimum is formed at a distance of 2.5 mm from the centre of the screen, find the (i) width of the slit, and (ii) distance of first secondary maximum from the centre of the screen.
Interference fringes are produced by a double-slit experiment and a piece of plane parallel glass of refractive index $$1.5$$ is interposed in one of the interfering beam. If the fringes are displaced through $$30$$ fringe widths for light of wavelength $$6 \times 10^{-5} cm$$, find the thickness of the plate.
A plate of thickness $$t$$ made of a material of refractive index $$\mu$$ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the thickness $$t$$ which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is $$\lambda$$. Neglect any absorption of light in the plate.
A spaceship approaches Earth at a speed of $$0.42 c .$$ A light on the front of the ship appears red (wavelength $$650 \mathrm{nm}$$ ) to passengers on the ship. What (a) wavelength and (b) color (blue, green, or yellow would it appear to an observer on Earth?
A spaceship is moving away from Earth at speed 0.20c. A source on the rear of the ship emits light at wavelength 450 nm according to someone on the ship. What (a) wavelength and(b) color (blue, green, yellow, or red) are detected by someone on earth watching the ship?
A sodium light source moves in a horizontal circle at a constant speed of $$0.100 c$$ while emitting light at the proper wavelength of $$\lambda_{0}=589.00 \mathrm{nm} .$$ Wavelength $$\lambda$$ is measured for that light by a detector fixed at the center of the circle. What is the wavelength shift $$\lambda-\lambda_{0} ?$$
In what way is the diffraction from each slit related to interference pattern in double slit experiment?
Which of the above two graphs $$(a)$$ and $$(b)$$ representing the human voice is likely to be the male voice ? Give a reason for your answer.

Two slits are separated by 0.180 mm. An interference pattern is formed on a screen 80.0cm away by 656.3-nm light. Calculate the fraction of the maximum intensity a distance $$ y = 0.600 cm $$ away from the central maximum.
Two light pulses are emitted simultaneously from a source. Both pulses travel through the same total length of air to a detector, but mirrors shunt one pulse along a path that carries it through an extra length of $$ 6.20 \mathrm{m} $$ of ice along the way. Determine the difference in the pulses' times of arrival at the detector.
To reduce the light reflected by the glass surface of a camera lens, the surface is coated with a thin layer of another material which has an index of refraction $$(\mu =7 / 4)$$ smaller than that of glass. The least thickness of the layer, to ensure that light falling perpendicularly on the surface and having wavelengths, $$\lambda _ 1 = 700nm$$ and $$\lambda _ 2 = 420nm$$ will be weekly reflected for both wavelengths is $$x \times 10^{-8} m$$. Find x ?
To reduce the light reflected by the glass surface of a camera lens, the surface is coated with a thin layer of another material which has an index of refraction ($$\mu = 7/4$$) smaller than that of glass. The least thickness of the layer, to ensure that light falling perpendicularly on the surface and having wavelengths, $$\lambda_1$$ = 700 nm and $$\lambda_2$$ = 420 nm will be weekly reflected for both wavelengths is $$10^{-7}$$m. Find x ?
A narrow monochromatic beam of light of intensity $$I$$ is incident on a glass plate as shown in figure. Another identical glass plate is kept close to the first one and parallel to it. Each glass plate reflects $$25$$% of the light incident on it and transmits the remaining. Find the ratio $$\sqrt{\cfrac{{I}_{max}}{{I}_{min}}}$$ the interference pattern formed by two beams obtained after one reflection at each plate.
Explain how Corpuscular theory predicts the speed of light in a medium, say, water, to be greater than the speed of light in vacuum. Is the prediction confirmed by experimental determination of the speed of light in water? If not, which alternative picture of light is consistent with experiment?
Two coherent sources separated by distance d are radiating in phase having wavelength $$\lambda$$. A detector moved in a big circle around the two sources in the plane of the two sources. The angular position of n=4 interference maxima is given as ______.

In a modified $$ YDS$$ the two slits $$ S_3$$ and $$ S_4$$ are placed in front of the slits $$S_1$$ and $$S_2$$ ,calculate the ratio of $$max^m$$ intensity to minimum intensity produced in the screen if
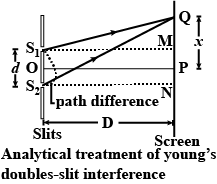
Give analytical treatment of YDSE interference bands and hence obtain the expression for fringe width.
Light of wave length $$6000A^{\circ}$$ is used to obtain interference fringes of width $$6\ mm$$ in a Young's double slit experiment. Calculate the wave length of light required to obtain fringe of width $$4\ mm$$ when the distance between the screen and slits is reduced to half of its initial value.
A parallel beam of light of wavelength 560 nm falls on a thin of oil (refractive index = 1.4) What should be the minimum thickness of the film so that it weakly transmits the light
In an interference experiment, monochromatic light is replaced by white light we will see:
A transparent paper (refractive index $$=1.45$$) of thickness $$0.02\ mm$$ is pasted on one of the slits of Young's double slit experiment which uses monochromatic light of wavelength $$620\ nm$$. How many fringes will cross through the centre if the paper is removed?
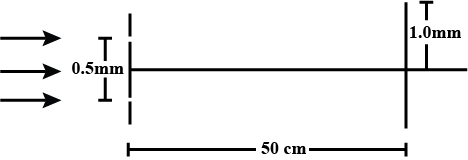
White coherent light $$(400\ nm-700\ nm)$$ is sent through the slits of a Youngs double slit experiment . The separation between the slits is 0.5 mm and the screen is $$50\ cm$$ away from the slits. There is a hole in the screen at a point $$1.0\ mm$$ away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole ? (b) which will have a strong intensity ?
The two sources of light should be close to each other for the production of the steady interference pattern. Why?
In the Young's double slit experiment ,two slits $$0.125 \,mm$$ apart are illuminated by light of wavelength $$4500 \,A^o$$. The screen is $$1 \,m$$ away from the plane of the slits. Find the separation between second bright fringes on both sides of central maxima.
Unpolarized light falls on two polarizer sheets whose axes are at right angles. (a) What fraction of the incident light intensity is transmitted ? (b) What fraction is transmitted if a third polarizer is placed between the first two so that its axis makes a $$60^{\circ}$$ angle with the axis of the first polarizer? (c) What if the third polarizer is infront of the other two?
Suppose we have $$N$$ (ideal) polarizers in the beam in see Fig. instead of three. The beam incident on polarizer $$1$$ is plane polarized, and polarizer $$1$$ has its transmission axis rotated an angle $$\theta / N$$ to the plane of polarization of the incident beam. Each subsequent polarizer has its axis rotated in the same sense by an angle of $$\theta/ N$$ to the one before it, so that the last polarizer has its axis rotated by an angle $$\theta$$ to the plane of polarization of the beam incident on polarizer $$1$$. Show that the intensity transmitted by the last polarizer is
$$I = I_{0}\left (\cos \dfrac {\theta}{N}\right )^{2N}$$
where $$I_{0}$$ is the intensity of the incident beam.
A double slit of separation 1.5mm is illuminated by white light(between 4000 and 8000 $$\mathring{A}$$) on a screen 120 cm away coloured interference pattern is formed. If a pinhole is made on this screen at a distance of 3.0 mm from the central white fringe, some wavelengths will be absent in the transmitted light. Find the second longest wavelength (in $$\mathring{A}$$) which will be absent in the transmitted light.
Some of the familiar hydrogen lines appear in the spectrum of quasar $$3 \mathrm{C} 9,$$ but they are shifted so far toward the red that their wavelengths are observed to be 3.0 times as long as those observed for hydrogen atoms at rest in the laboratory. (a) Show that the classical Doppler equation gives a relative velocity of recession greater than $$c$$ for this situation. (b) Assuming that the relative motion of $$3 \mathrm{C} 9$$ and Earth is due entirely to the cosmological expansion of the universe, find the recession speed that is predicted by the relativistic Doppler equation.
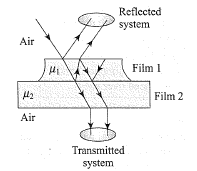
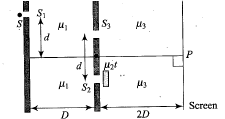
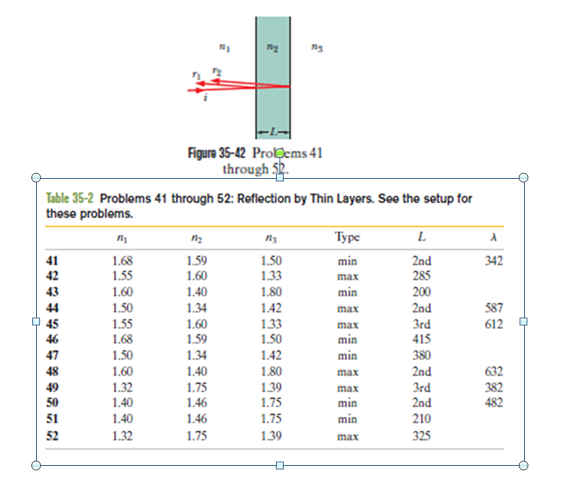
Reflection by thin layers. In Fig. 35-42, light is incident perpendicularly on a thin layer of material 2 that lies between (thicker) materials 1 and(The rays are titled only for clarity.) The waves of rays $$r_1$$ and $$r_2$$ interfere, and here we consider the type of interference to be either maximum (max) or minimum (min). For this situation, each problem in Table 35-2 refers to the indexes of refraction $$n_1, n_2$$ and $$n_3$$, the type of interference, the thin-layer thickness $$L$$ in nanometers, and the wavelength $$\lambda$$ in nanometers of the light as measured in air. Where $$\lambda$$ is missing, give the wavelength that is in the visible range. Where$$L$$ is missing, give the second least least thickness or the third least thickness as indicated.
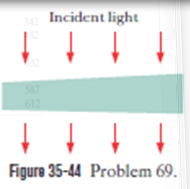
In Fig. 35-44, aboard beam of light of wavelength 630 nm is incident at $$90^{0}$$ on a thin, wedge-shaped film with index of refraction 1.Transmission gives 10 bright and 9 dark fringes along the film's length. What is the left-to-right change in film thickness?
If Superman really had x-ray vision at $$ 0.10 \mathrm{nm} $$ wavelength and a $$ 4.0 \mathrm{mm} $$ pupil diameter, at what maximum altitude could he distinguish villains from heroes, assuming that he needs to resolve points separated by $$ 5.0 \mathrm{cm} $$ to do this?
By the whole system when the planes of the polarizer are parallel.
One of the spectral lines emitted by excited $${He}^+$$ ions has a wavelength $$\lambda = 410 nm$$. Find the Doppler shift $$\Delta \lambda$$ of that lines when observed at an angle $$\theta = 30^o$$ to the beam of moving ions possessing kinetic energy T = 10 MeV.
The Doppler affect has made its possible to discover the double stars which are so distant that their resolution by means of a telescope is impossible. The spectral lines of such stars periodically become doublets indicating that the radiation does come from two stars revolving about their cantre of mass. Assuming the masses of the two stars to be equal, find the distance between them and their masses if the maximum splitting of the spectral lines is equal to $$(\Delta\lambda/\lambda)_m = 1.2.10^{-4}$$ and occurs every 30 days.
One of the spectral lines of atomic hydrogen has the wavelength $$\lambda = 656.3 nm$$. Find the Doppler shift $$\Delta \lambda$$ of that lines when observed at right angles to the beam of hydrogen atoms with kinetic energy T = 1.0 MeV ( the transverse Doppler effect).
When a spectral line of wavelength $$\lambda = 0.59 \mu m$$ is observed in the directions to the opposite edges of the solar disc along its equator, there is a difference in wavelengths equal to $$\delta \lambda = 8.0 pm$$. Find the period of the sun's revolution about its own axis.
Plane-polarized light of wavelength $$0.59 \mu$$m falls on a trihedral quartz prism P with refracting angle $$\theta = 30^o$$. Inside the prism light propagates along the optical axis whose direction is shown by hatching. Behind the Polaroid Pol an interference pattern of bright and dark fringes of width $$\Delta x = 15.0$$ mm is observed. Find the specific rotation constant of quartz and the distribution of intensity of light behind the Polaroid.
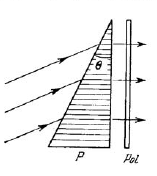
The width of the fringe $$\Delta x$$
Class 12 Engineering Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials,Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions