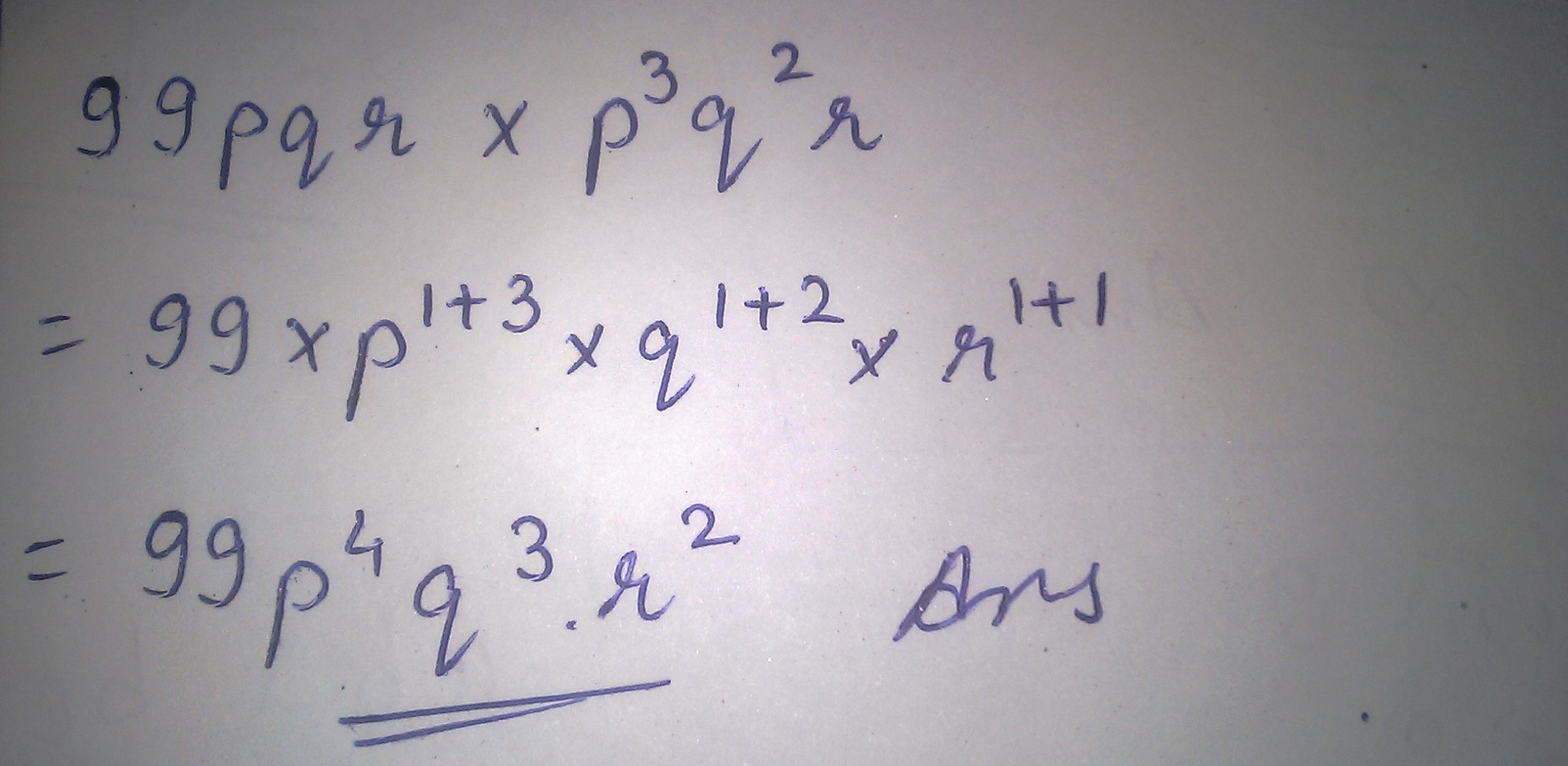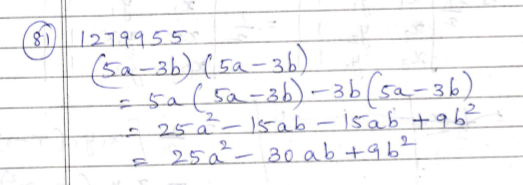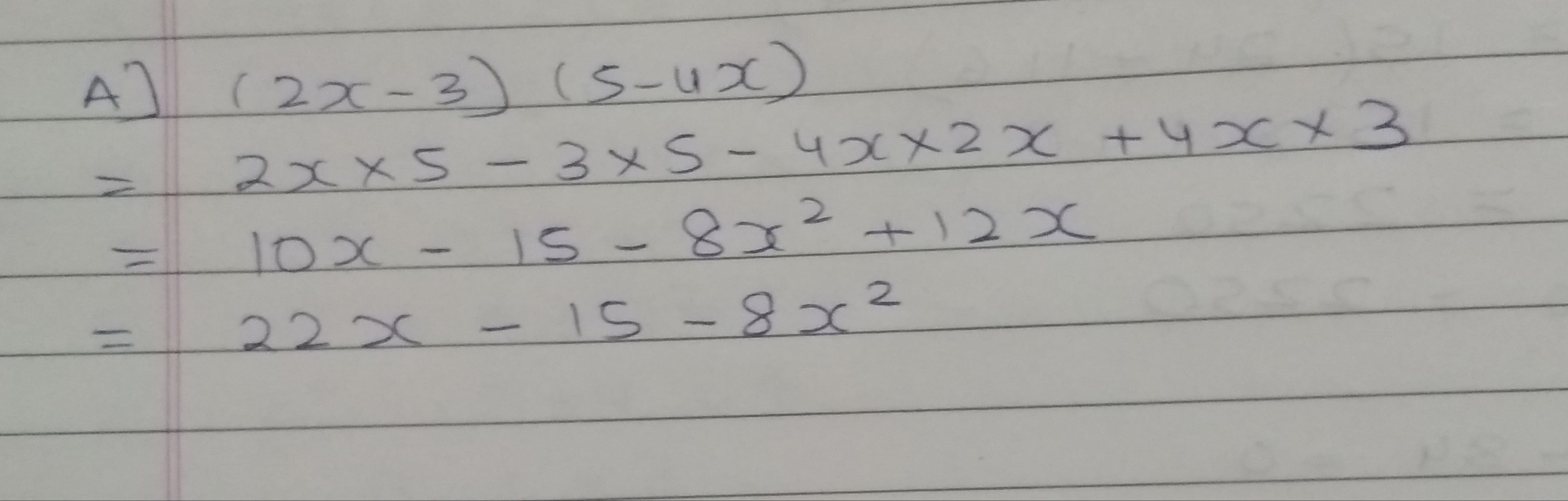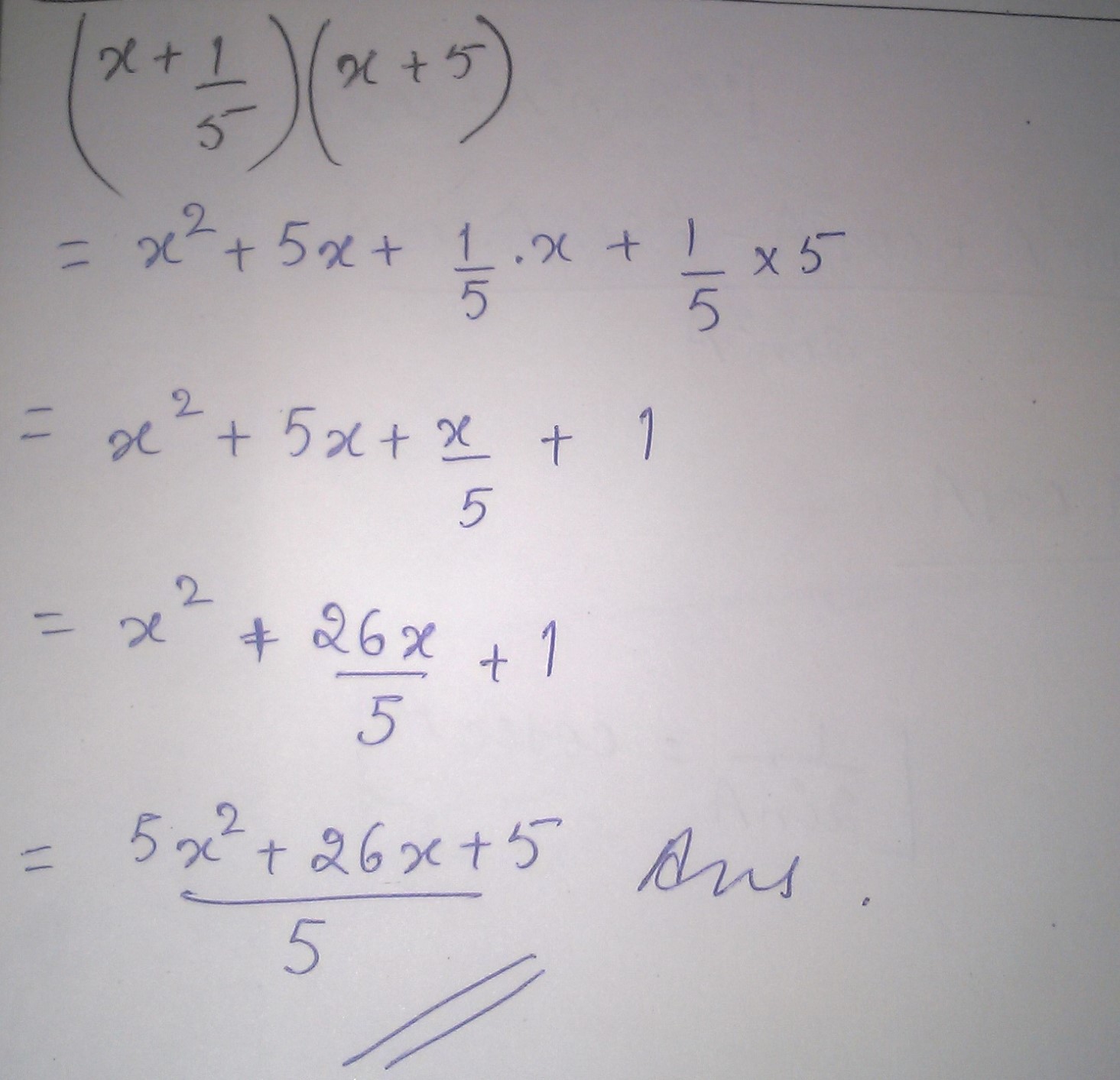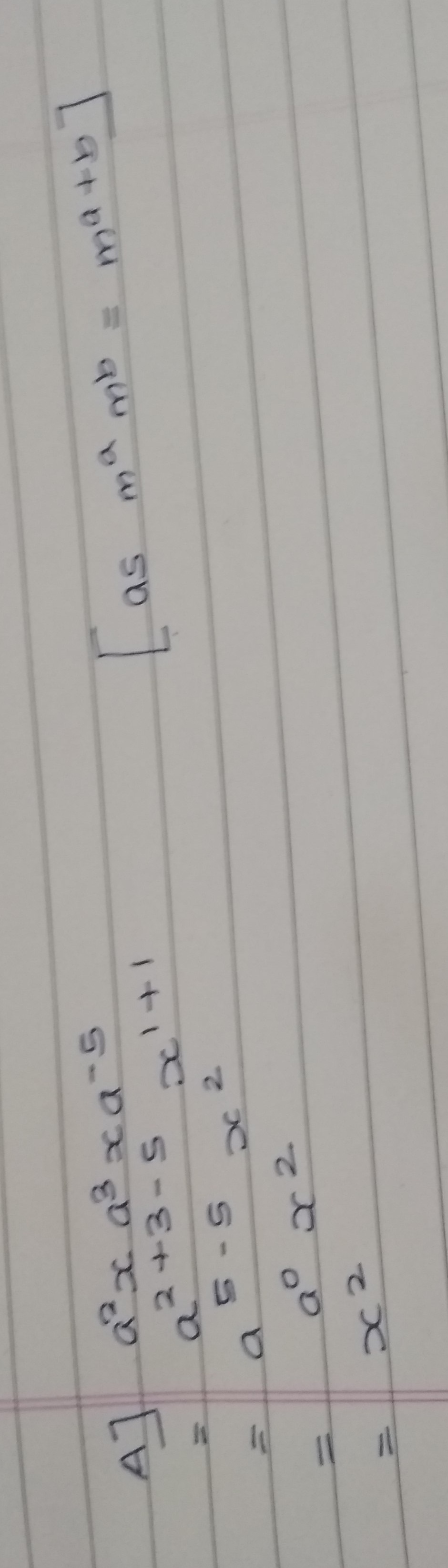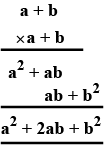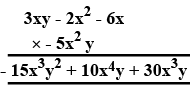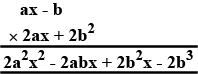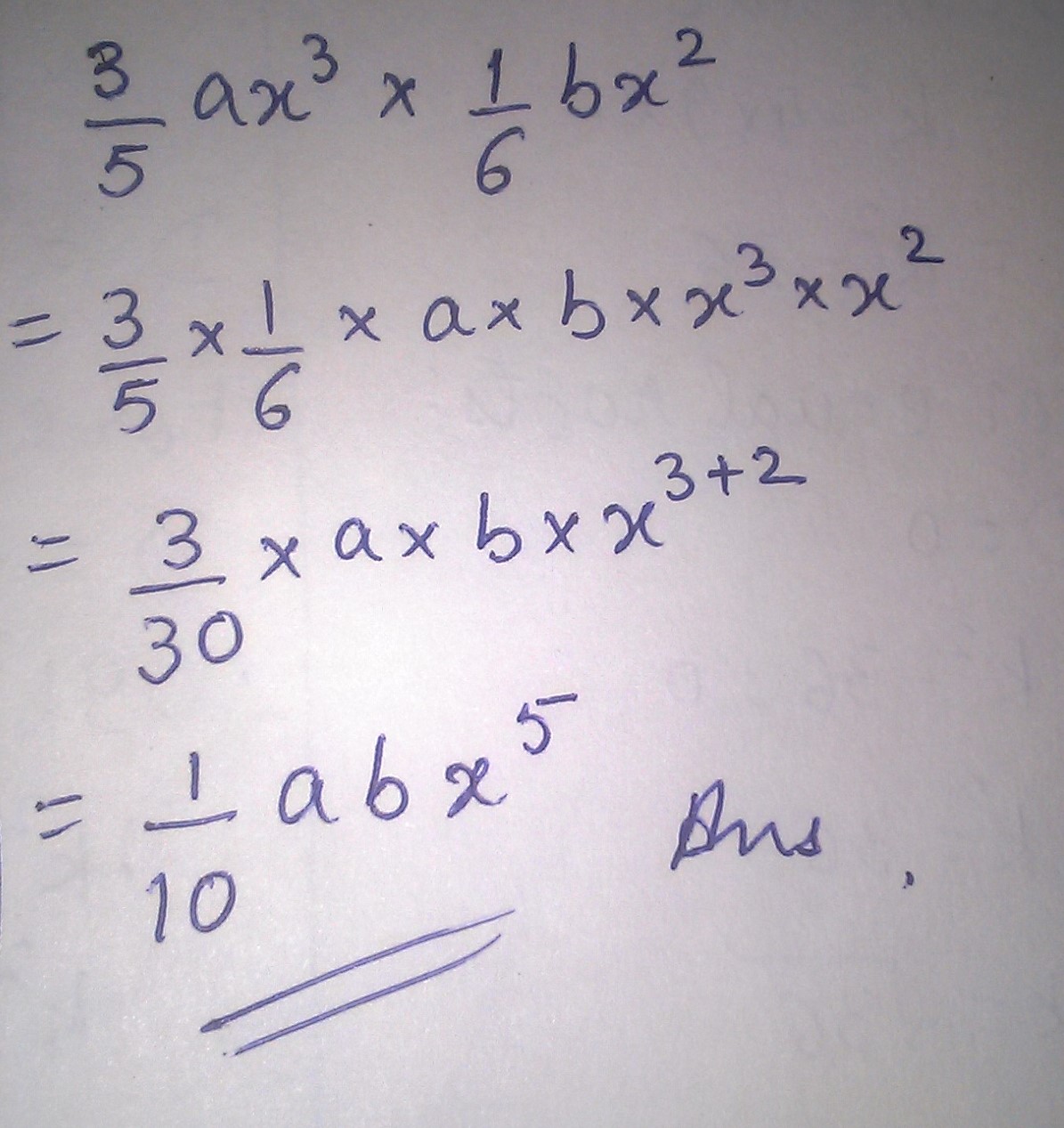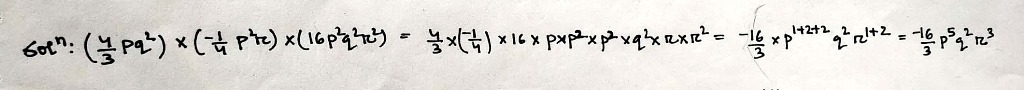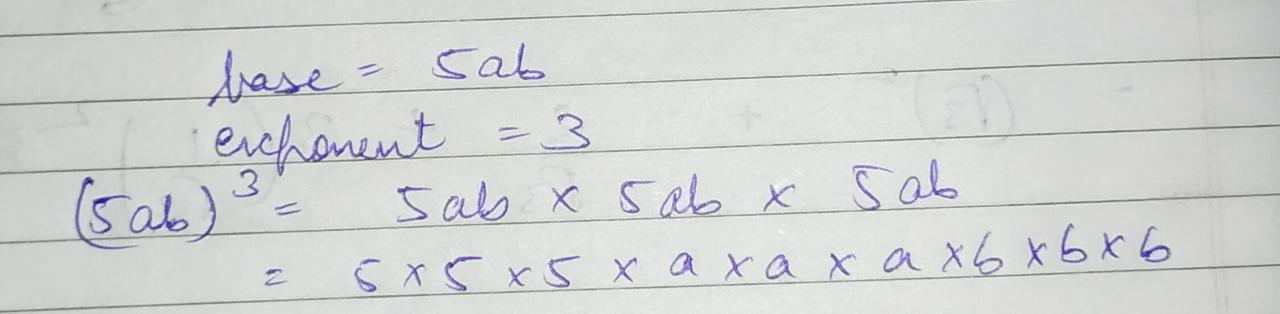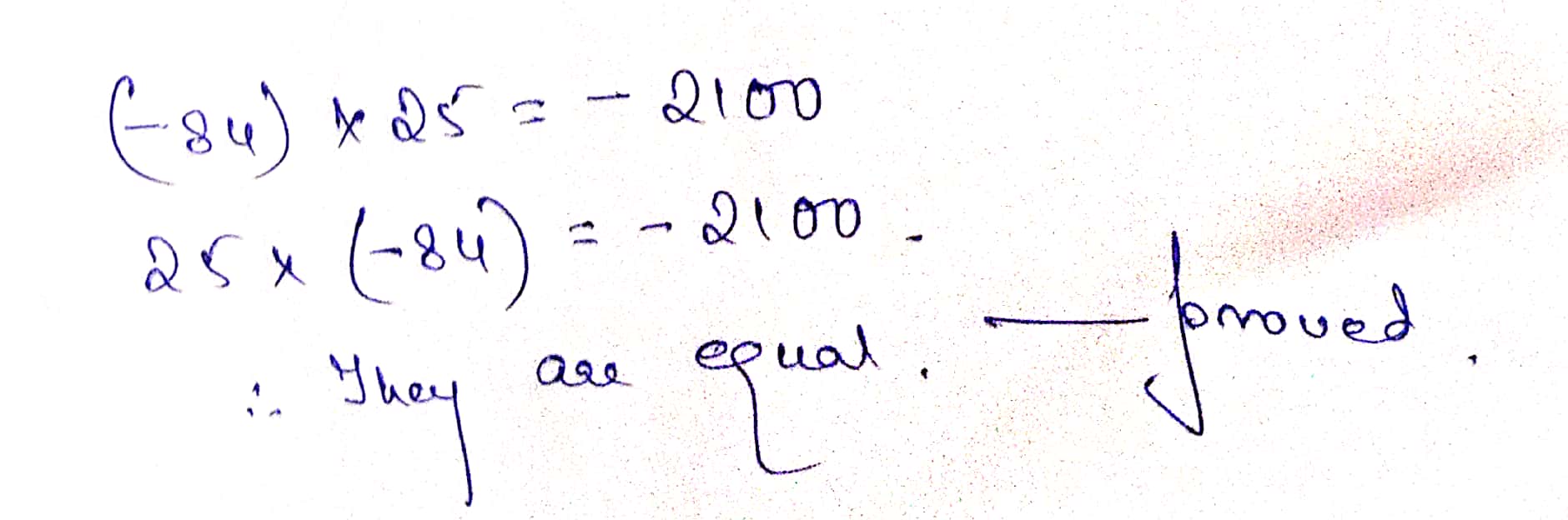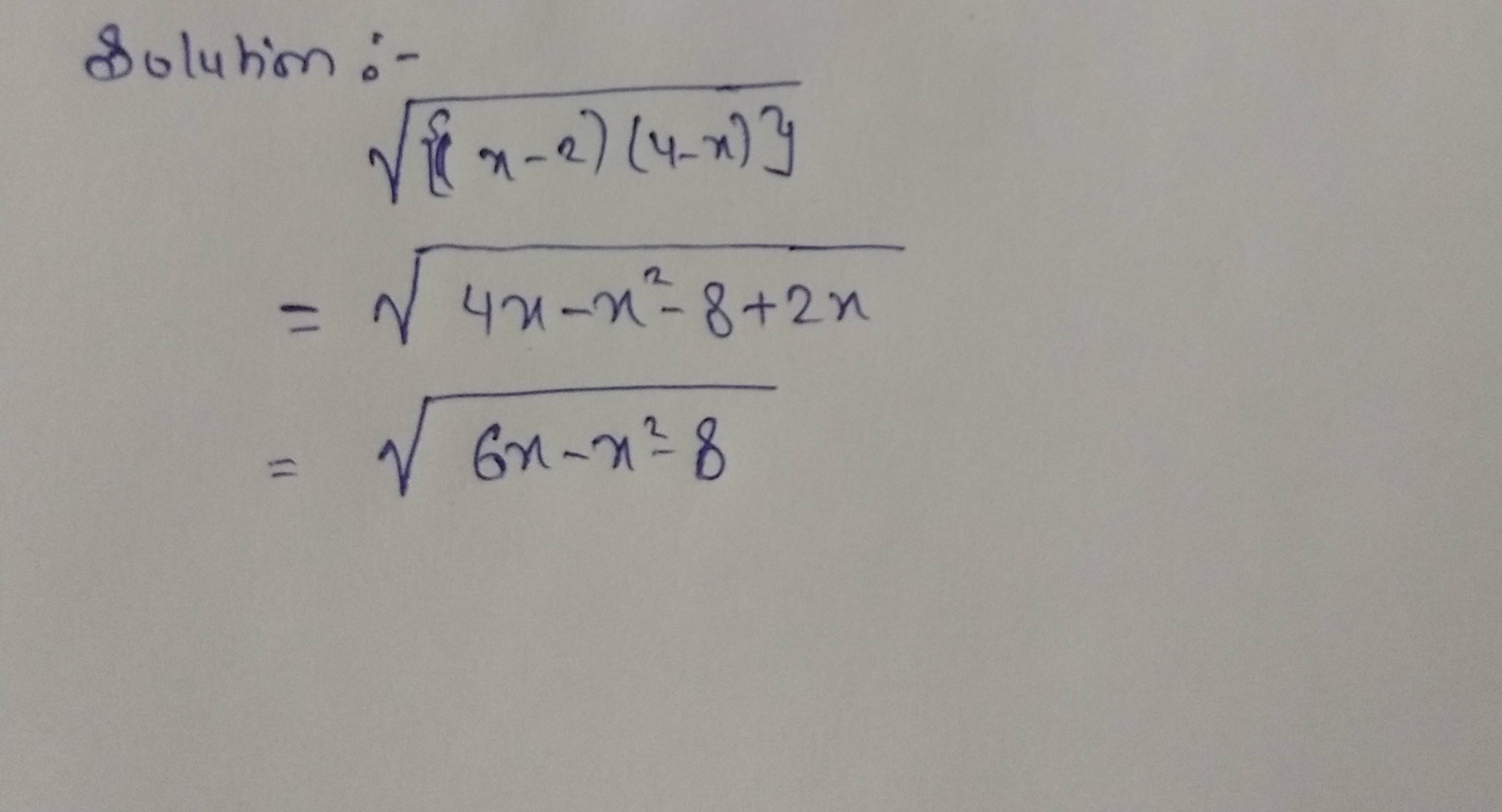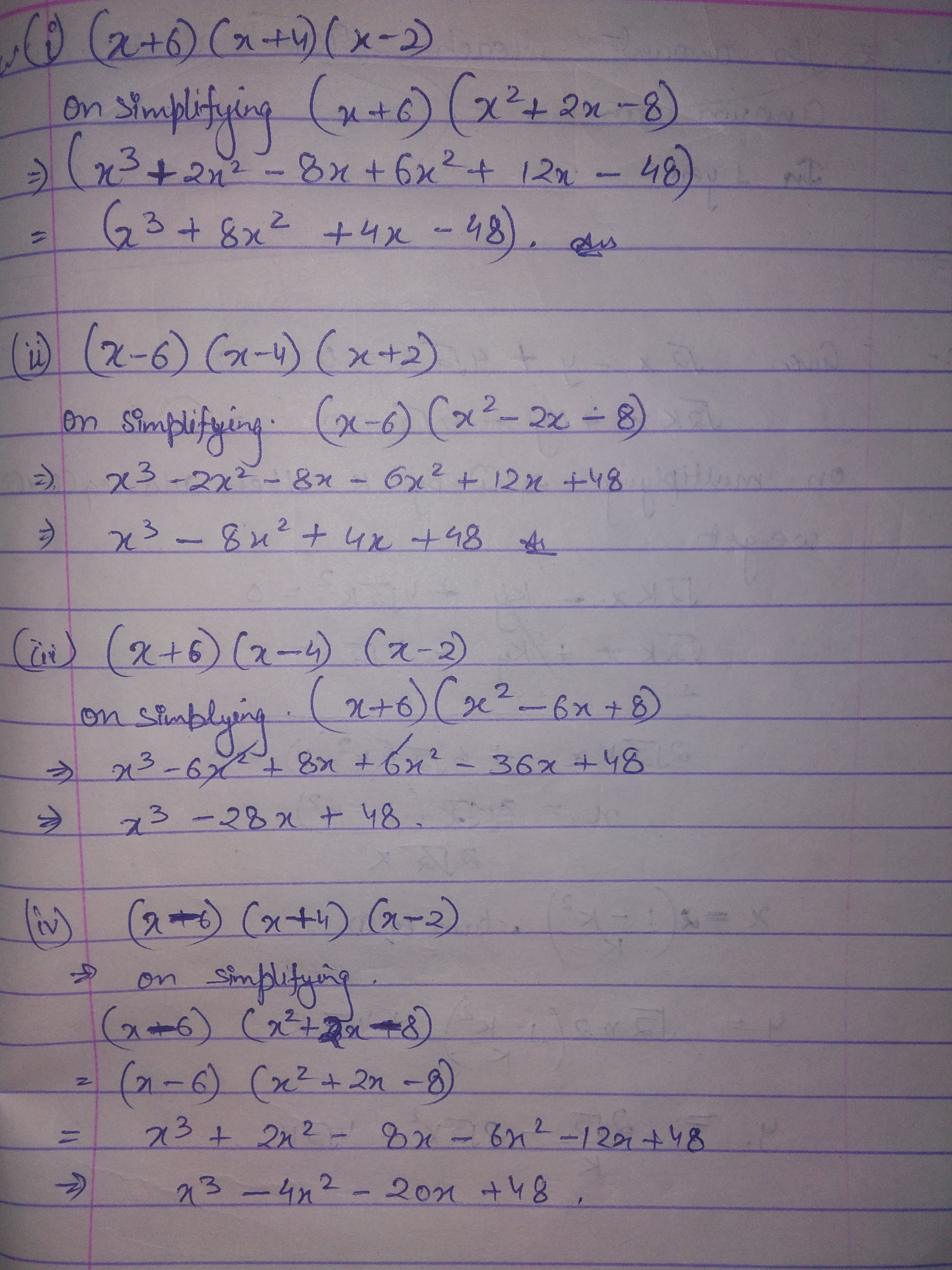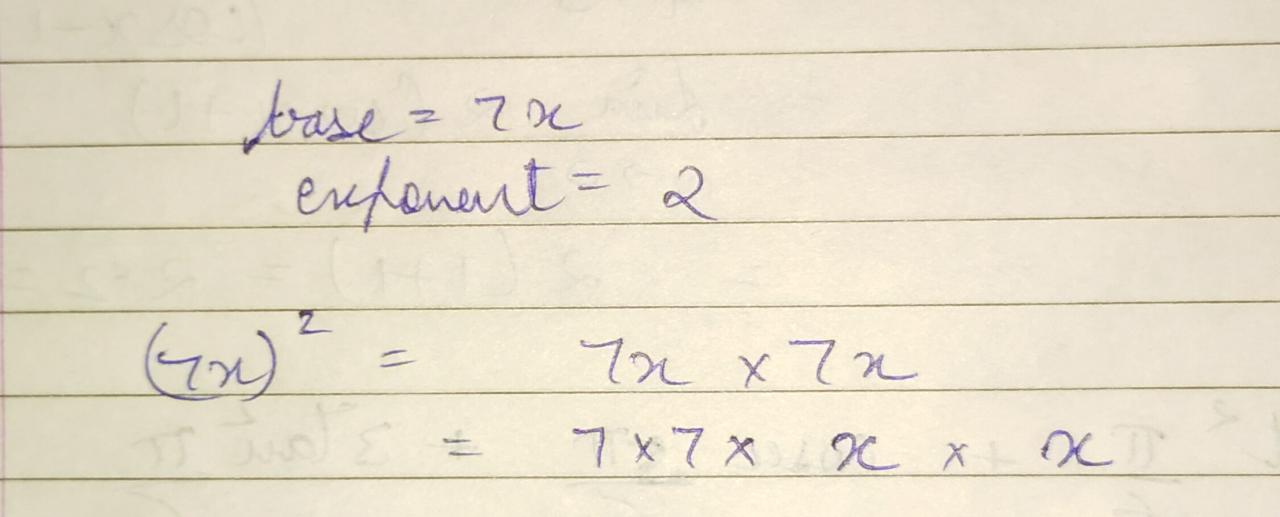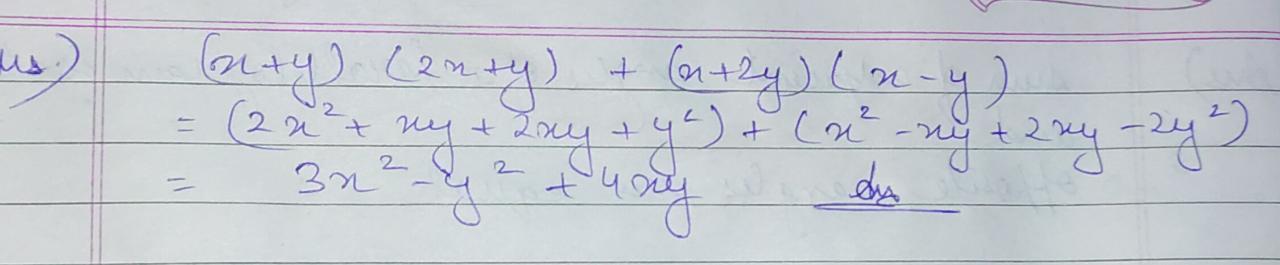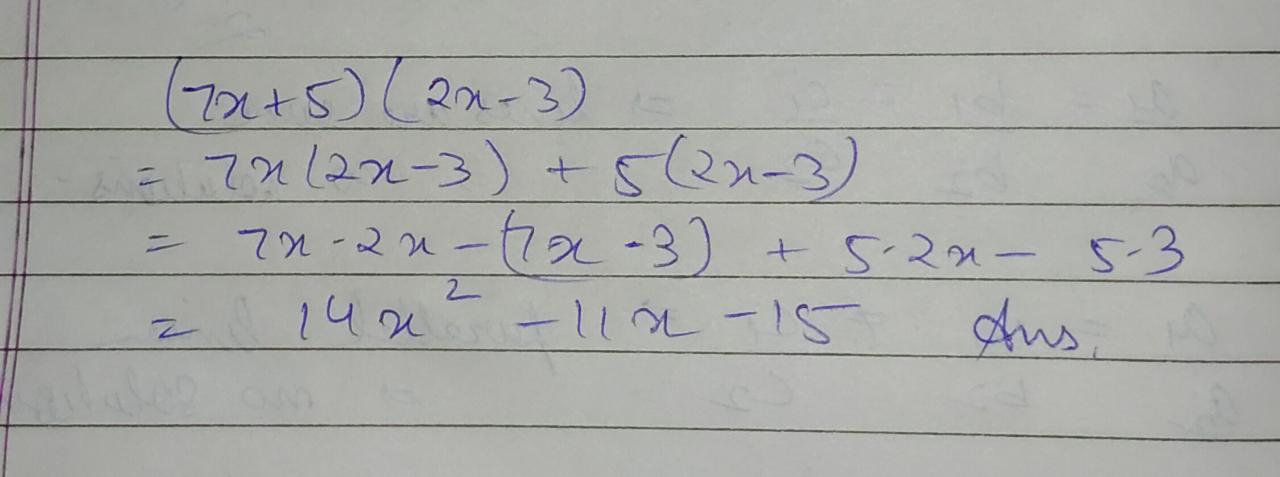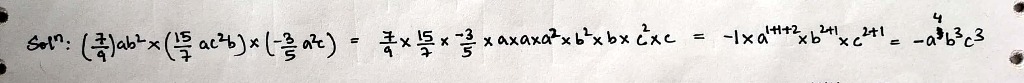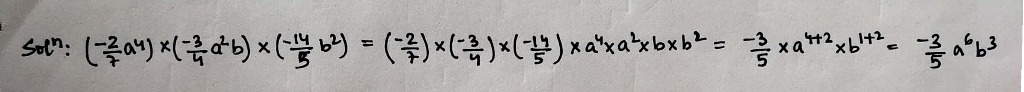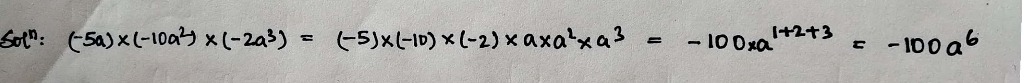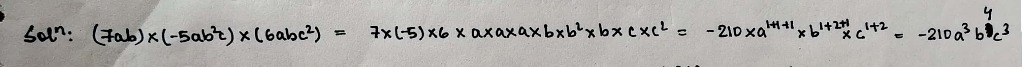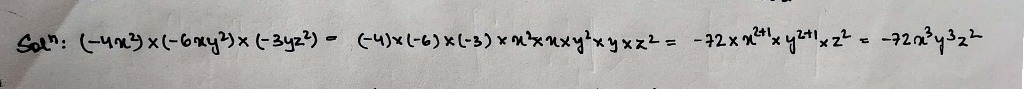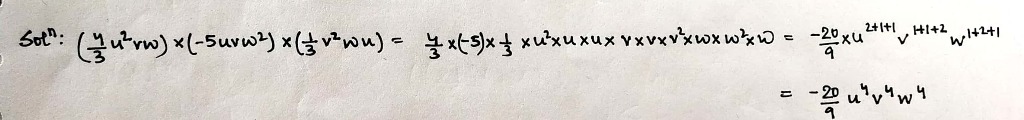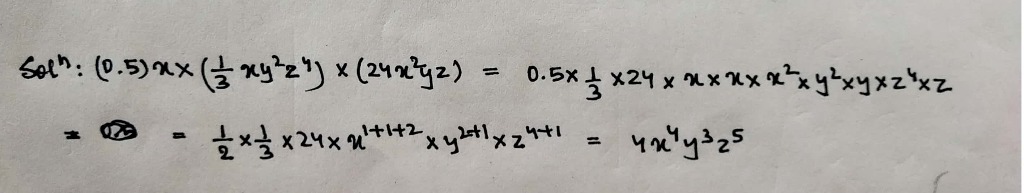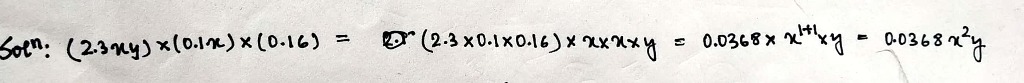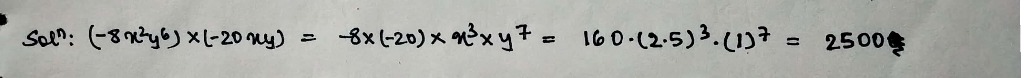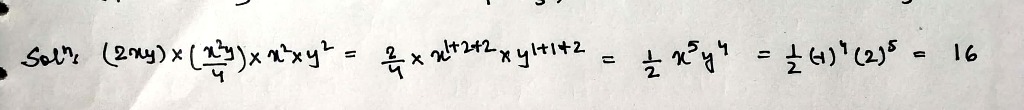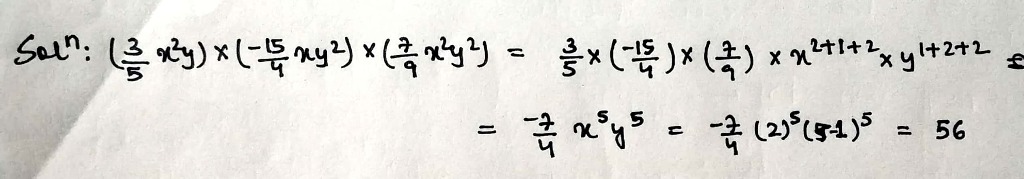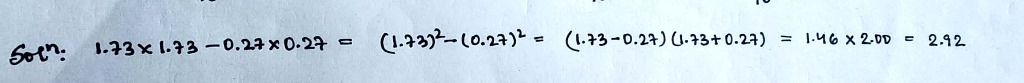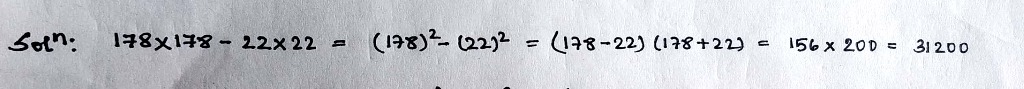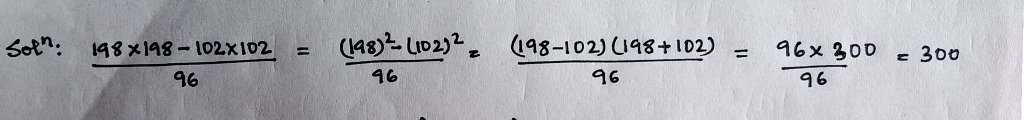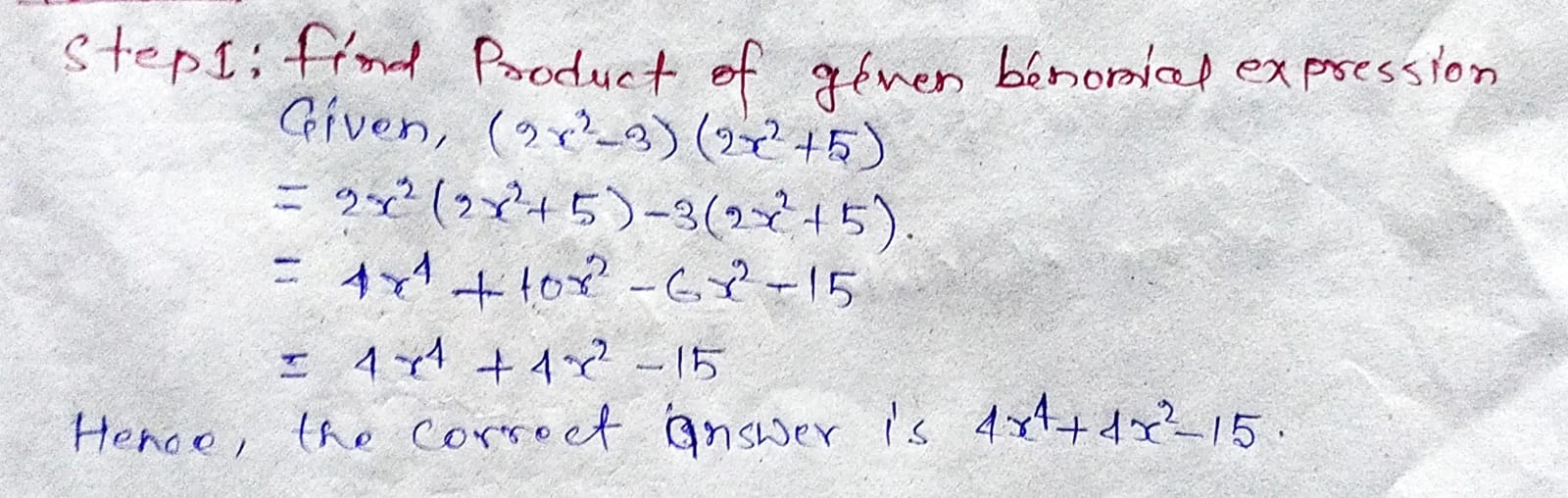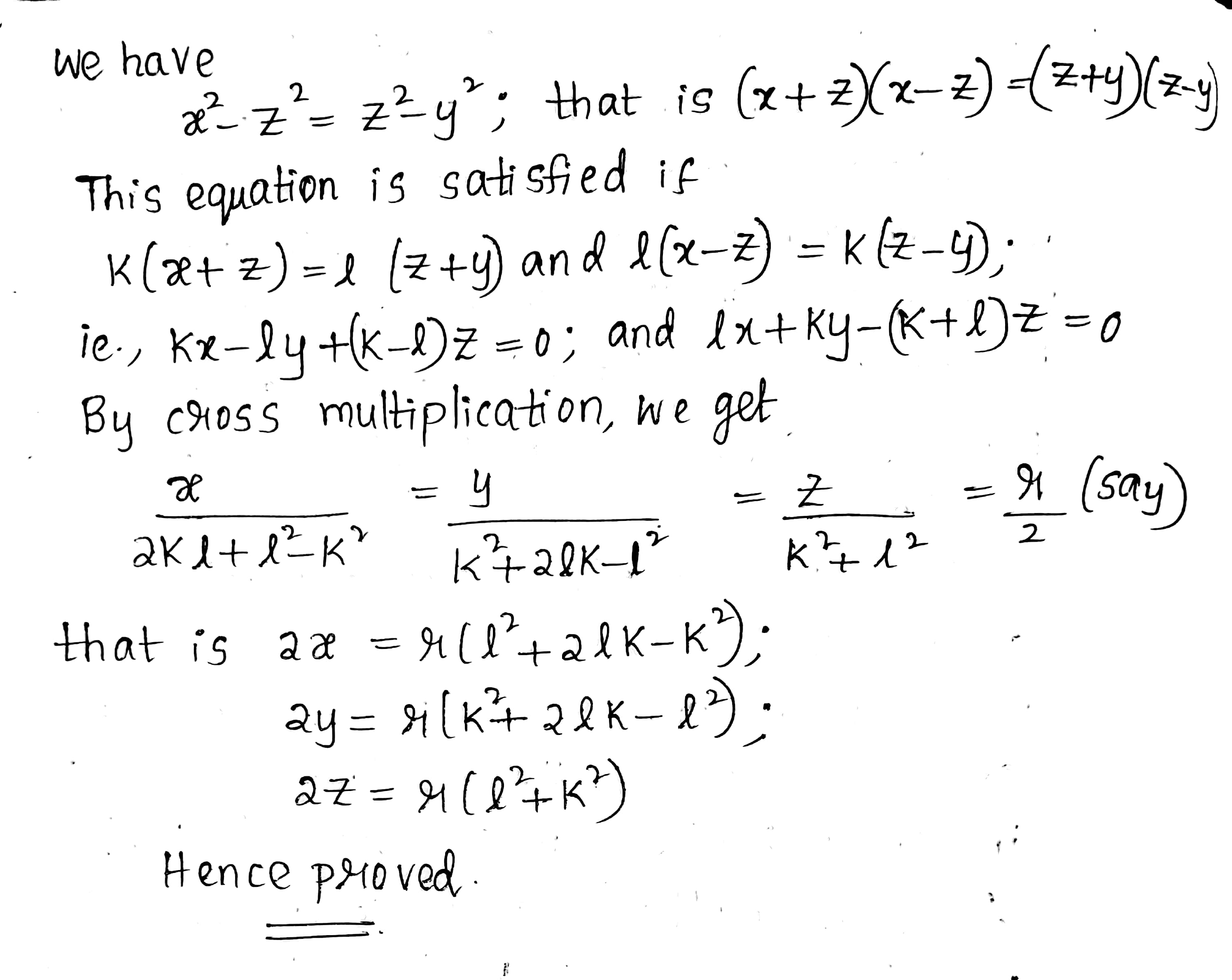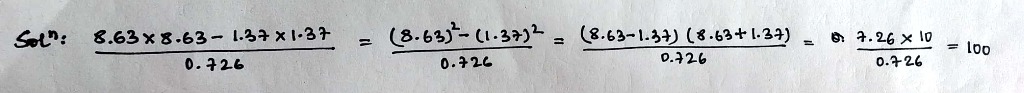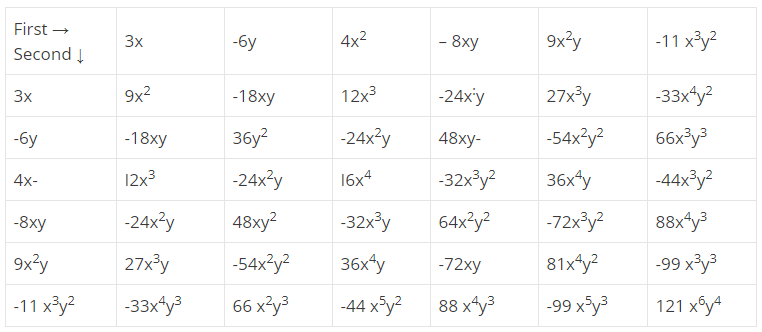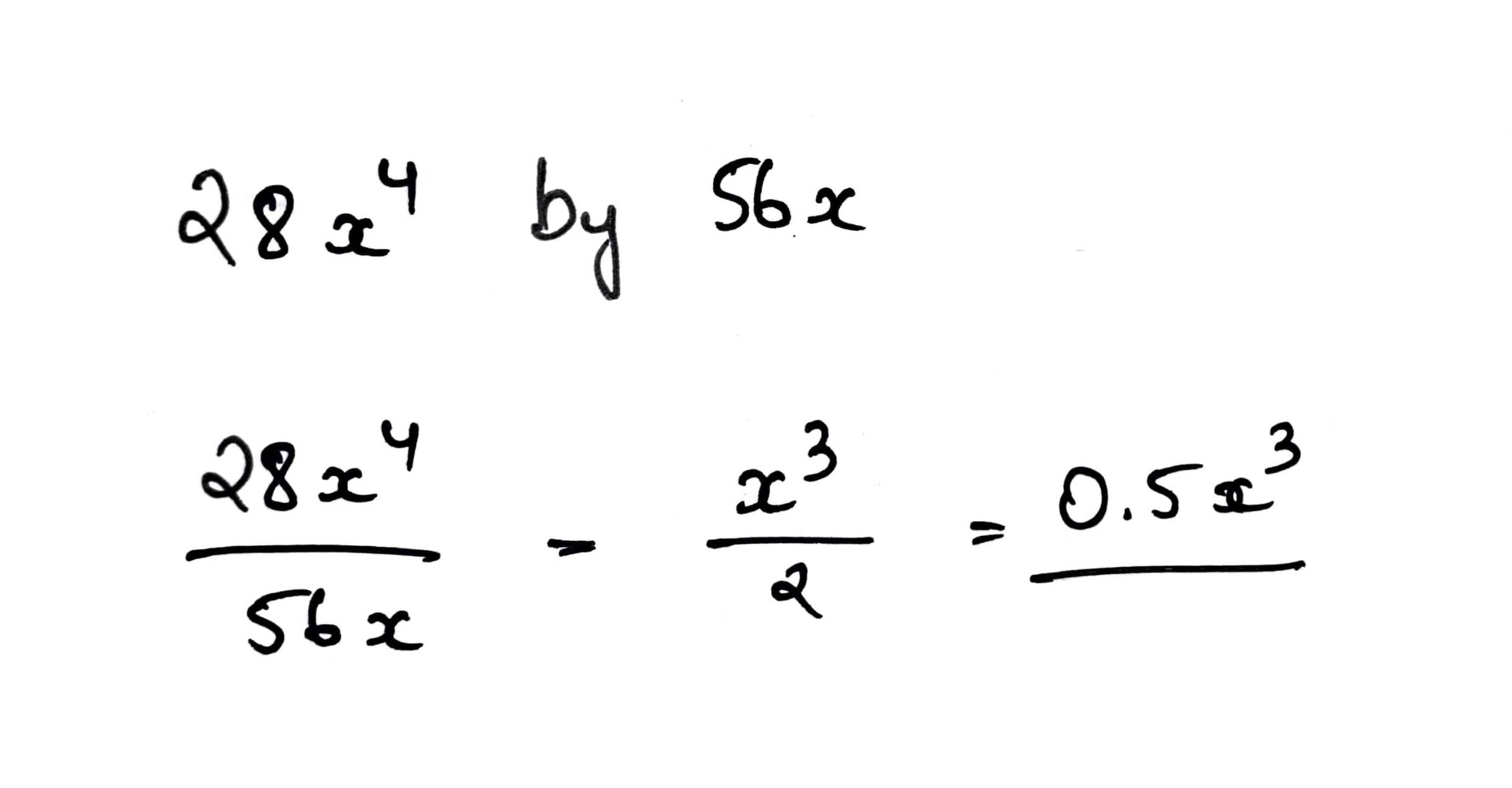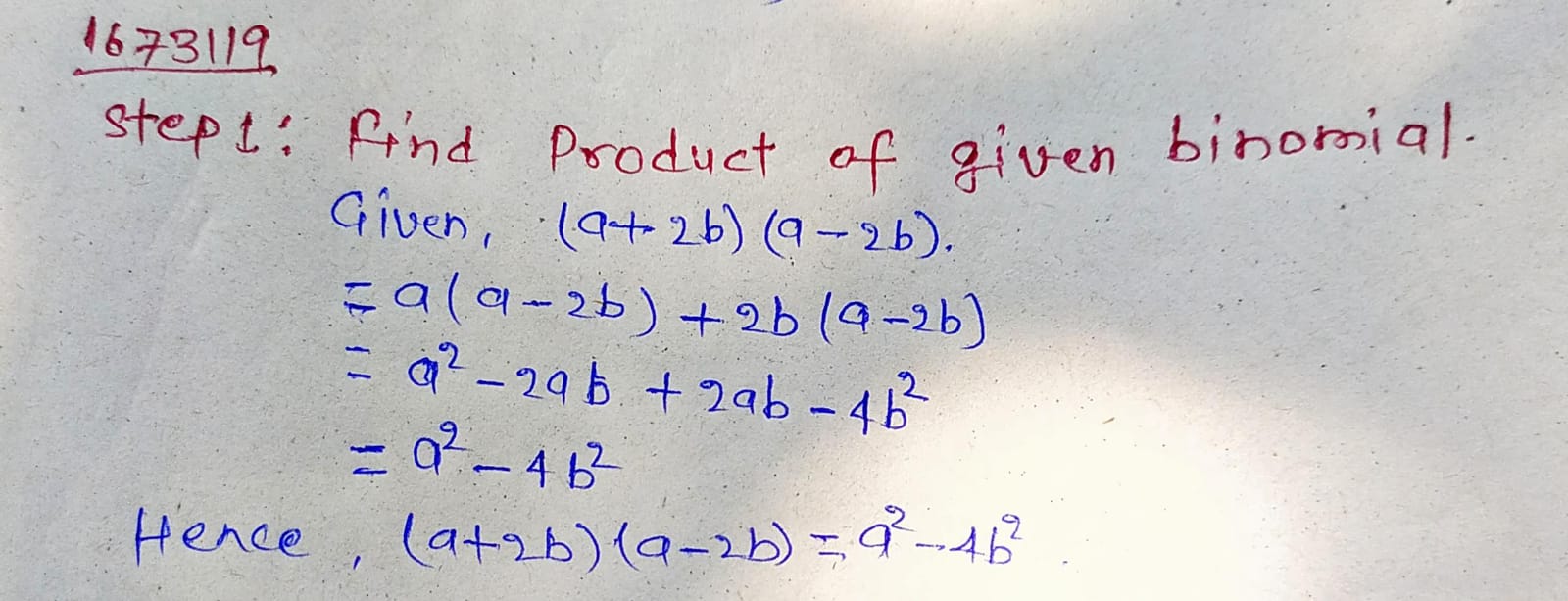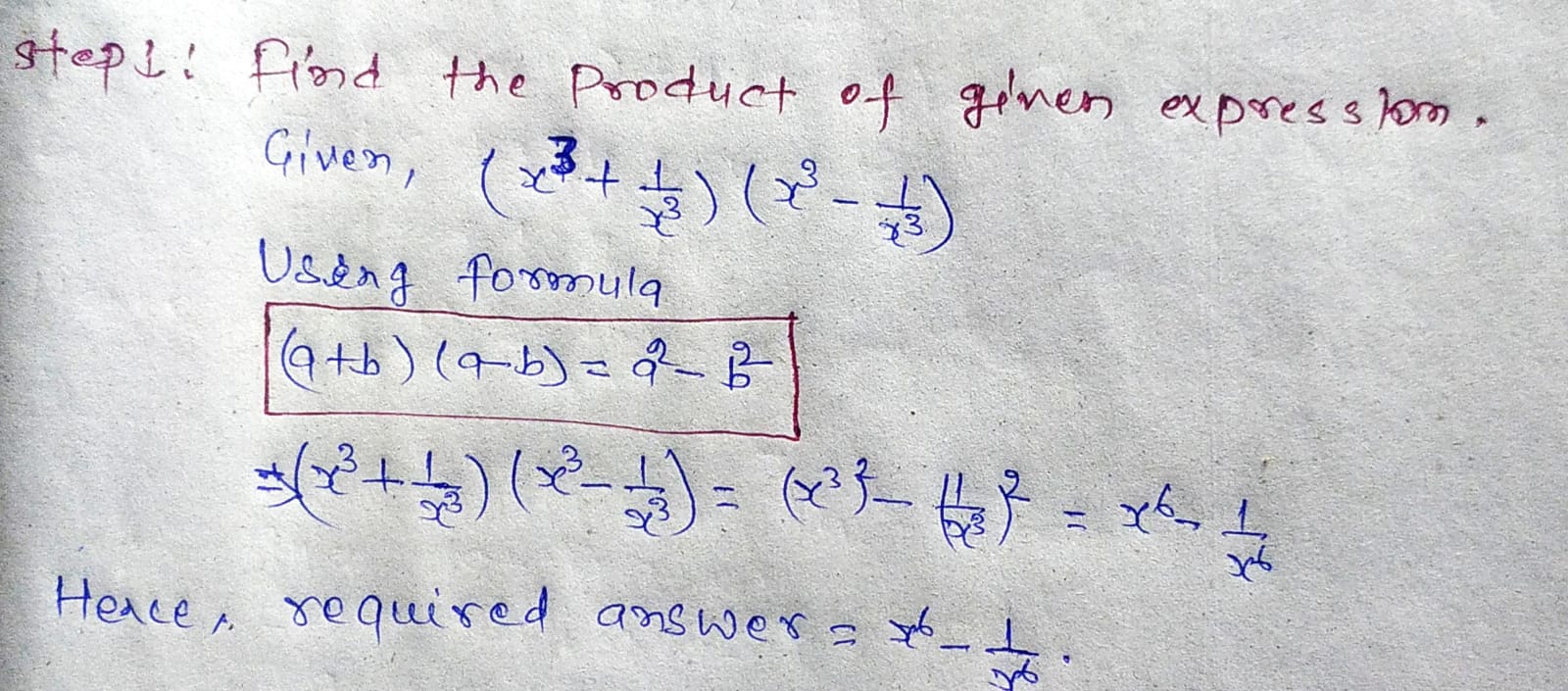Algebraic Expressions And Identities - Class 8 Maths - Extra Questions

Find the product $$4x \times 5y \times 7z$$

While multiplying three monomials, we can multiply the coefficients first and then multiply the variables.

Hence, $$4x \times 5y \times 7z = (4 \times 5 \times 7) \times (x \times y \times z)$$ 

                                      $$= 140xyz$$


Find the product : $$(-3pq)(-15p^3q^2-q^3)$$

Given: $$(-3pq)(-15p^3q^2-q^3)$$
So multiplying $$(-3pq)$$ and $$(-15p^3q^2-q^3)$$
 $$= (-3pq)$$ $$(-15p^3q^2)-(q^3)$$$$(-3pq)$$
Thus we get: $$(-3pq)(-15p^3q^2-q^3)= $$ $$ {45p^4q^3+3pq^4}$$


Find the product: $$3(5x+8)$$ 

To find: product of $$3(5x+8)$$
                           $$=3(5x)+3(8)$$
                           $$=15x+24$$


Find the product $$(x+2)$$ and $$(x+3)$$.

We use multiply term by term rule. Thus
$$(x+2)(x+3)=(x+2)x+(x+3)3=(x)(x)+2(x)+(x)(3)+(2)(3)={ x }^{ 2 }+2x+3x+6={ x }^{ 2 }+5x+6$$


Find the product of the binomials $$x+2,x+3$$ and $$x+4$$.

We use the identity
$$(x+a)(x+b)(x+c)={x}^{3}+{x}^{2}(a+b+c)+x(ab+bc+ca)+abc$$
Take $$a=2,b=3$$ and $$c=4$$. You obtain
$$a+b+c=2+3+4=9$$
$$ab+bc+ca=(2\times 3)+(3\times 4)+(4\times 2)=6+12+18=26$$,
$$abc=2\times 3\times 4=24$$.
Hence
$$(x+2)(x+3)(x+4)={ x }^{ 3 }+9{ x }^{ 2 }+26x+24$$


Find the common factors of the given terms: 
$$3a,21ab$$

We need to find common factors of $$3a$$ and $$21ab$$. Fist, we will find the factors of both the terms:
$$3a=3\times a$$
$$21ab=3\times b\times a\times 7$$
From above it can be observed that $$3$$ and $$a$$ are the common factors of both the terms.


$$40{x^2} = \left( {3.6{x^2} - 4.06x + 8{x^3} + 0.432} \right)\times 27x^{6}$$

We have,
$$40{x^2} = \left( {3.6{x^2} - 4.06x + 8{x^3} + 0.432} \right)\times 27x^{6}$$

$$40{x^2} = 97.2{x^8} - 109.62x^7 + 216{x^9} + 11.664x^6$$

$$216x^9+97.2{x^8} - 109.62x^7  + 11.664x^6-40x^2=0$$

Hence, this is gthe answer.


Multiply $$4mn$$ by $${(-1)}^{7}{p}^{2}q-4mn{p}^{2}q$$

$$(4mn)\times((-1)^{7}p^{2}q-4mnp^{2}q)$$
$$=-4mnp^{2}q-16m^{2}n^{2}p^{2}q$$
$$=-4mnp^{2}q(1+4mn)$$


Simplify $$(3x^{2}+2x)(2x^{2}+33)$$

$$(3x^{2}+2x)(2x^{2}+33)$$
$$=3x^{2}\times 2x^{2}+2x\times 2x^{2}+3x^{2}\times 33+2x\times33$$
$$=6x^{4}+4x^{3}+99x^{2}+66x$$


Find out the product:
$$2a,33a^{2},5a^{4}$$

Consider the given number.
$$2a, 33a^2, 5a^4$$

According to the question,
$$=2a\times33a^2\times5a^4$$
$$=330a^7$$

Hence, this is the answer.


Find the products:
(a) $$(-\cfrac{2}{7}{a}^{2}c)(\cfrac{16}{21}d{d}^{2})$$
(b) $$(-\cfrac{6}{8}{x}^{4}{y}^{2})(24{x}^{2}{y}^{2}{z}^{3})$$

(i) $$\left( -\cfrac { 2 }{ 7 } { a }^{ 2 }c \right) \left( \cfrac { 16 }{ 21 } d{ d }^{ 2 } \right) =\cfrac { -32 }{ 147 } { a }^{ 2 }c{ d }^{ 3 }$$
(ii) $$\left( -\cfrac { 6 }{ 8 } { x }^{ 4 }{ y }^{ 2 } \right) \left( 2y{ x }^{ 2 }{ y }^{ 2 }{ z }^{ 3 } \right) =-18{ x }^{ 6 }{ y }^{ 4 }{ z }^{ 3 }$$


Find the following product.
$$99pqr\times p^{3}q^{2}r$$ 

$$99pqr\times p^3q^2r$$
$$=99\times p^{1+3}\times q^{1+2}\times r^{1+1}$$
$$=99p^4q^3r^2$$.

1195553_1242441_ans_c3cd9a4326a243ec989df07a850eb12a.jpg


Product of $$(5a-3b)(5a-3b)=$$


1338072_1279955_ans_625d6d114d664d3e83bb0f0f695503af.PNG


Multiply : $$\left(2x-3\right)\left(5-4x\right)$$

A) $$(2x-3)(5-4x)$$
$$= 2x\times 5-3\times 5-4x\times 2x+4x\times 3$$
$$=10x-15-8x^{2}+12x$$
$$= 22x-15-8x^{2}$$

1195247_1297036_ans_fc1c0f9dc2d542d1ac135863ba46c652.jpg


Simplify the equation $$\left(2x + \dfrac{1}{3x}\right)^2$$.

We have,
$$\left(2x + \dfrac{1}{3x}\right)^2$$

$$\Rightarrow 4x^2 + \dfrac{1}{9x^2}+2\times 2x\times \dfrac{1}{3x}$$

$$\Rightarrow 4x^2 + \dfrac{1}{9x^2}+\dfrac{4}{3}$$

Hence, this is the answer.


Find each of the following products.
$$7x\times 8$$

$$7x \times 8 = \left( 7 \times 8 \right) x = 56x$$


Simplify: $$(x+\dfrac{1}{5})(x+5)$$

$$ (x+\frac{1}{5})(x+5) $$
$$ = x^{2}+5x+\frac{1}{5}.x+\frac{1}{5}\times 5 $$
$$ = x^{2}+5x+\frac{x}{5}+1 $$
$$ = x^{2}+\frac{26x}{5}+1 $$
$$ = \frac{5x^{2}+26x+5}{5} $$

1164026_1282927_ans_ceffbd576b084585aab82ed860b6e371.jpg


Simplify $$a^{2}x a^{3}x a^{-5}$$.

A]$$a^{2}xa^{3}xa^{-5}$$
$$=a^{2+3-5}  x^{1+1}$$              [as $$m^{a}m^{b}=m^{a}+b]$$
$$=a^{5-5} x^{2}$$
$$=a^{0}x^{2}$$
$$=x^{2}$$

1195139_1296423_ans_e4d6ded9930e44efa2052f5af59a5b43.jpg


Expand $$(1+x^{3}).4$$

Given that,
$$\begin{array}{l} \left( { 1+{ x^{ 3 } } } \right) .4 \\ =4\left( { 1+{ x^{ 3 } } } \right)  \end{array}$$
We know that,
$$\begin{array}{l} a\left( { b+c } \right) =ab+ac \\ a=4,b=1,c={ x^{ 3 } } \\ =4.1+4{ x^{ 3 } } \end{array}$$
$$ = 4{x^3} + 4$$
Then,
We get $$ = 4{x^3} + 4$$


Solve the following algebraic expressions by both trial and error method and balancing equation.
$$2x=5$$

Given $$2 x=5$$
Let $$x=1,LHS=2(1)=2,RHS=5$$
As $$LHS\ne RHS$$
Let $$ x=\frac{5}{2}$$
$$LHS=2\big(\frac{5}{2}\big)=5,RHS=5$$
$$LHS=RHS$$
By trial and error method 
So $$x=\frac{5}{2}$$
By balancing equation
$$2 x=5\implies x=\dfrac{5}{2}$$


Fill in the blanks:
$$6 \times 3 =$$ ………. and $$6x^2 \times  3x^3 =$$ …………

$$6 \times 3 = 18$$
Hence,
$$6x^2  \times 3 x^3 = 6  \times 3  \times x^2 \times x^3$$
$$= 18  \times x^5$$
$$= 18 x^5$$
Therefore, $$6  \times 3 = 18$$ and $$6 x^2  \times 3 x^3 = 18 x^5$$


Expand the brackets:
$$x(3x-4)$$

$$x(3 x-4)$$=$$3 x^{2}-4 x$$


Fill in the blanks:
$$6 \times 3 =$$ . and $$6x \times  3x = $$

$$6 \times 3 = 18$$
Hence,
$$6x  \times 3x = 6  \times 3  \times x  \times x$$
We get,
$$= 18  \times x^2$$
$$= 18 x^2$$
Therefore, $$6  \times 3 = 18$$ and $$6x  \times 3x = 18 x^2$$


Fill in the blanks:
$$4 \times 7 =$$ . and $$4ax \times  7x =$$

$$4 \times 7 = 28$$
Hence,
$$4 ax \times 7x = 4 \times 7 \times a \times x \times x$$
$$= 28 \times a \times x^2$$
$$= 28 ax^2$$
Therefore, $$4 \times 7 = 28$$ and $$4 ax \times 7 x = 28 ax^2$$


Fill in the blanks:
$$4x \times 6x \times 2 =$$

$$4x \times 6x \times 2 = 4 \times 6 \times 2 \times x \times x$$
$$= 48 \times x^2$$
We get,
$$= 48 x^2$$
Hence, $$4x \times 6x \times 2 = 48 x^2$$


Fill in the blanks:
$$3ab \times 6ax  =$$ ………

$$3 ab \times 6 ax = 3 \times 6 \times a \times a \times b \times x$$
$$= 18 \times a^2 \times b \times x$$
We get,
$$= 18 a^2 bx$$
Hence, $$3 ab \times 6 ax = 18 a^2 bx$$


Find the value of:
$$5 a^2 \times 7 a^7$$

$$5 a^2 \times 7 a^7$$
$$5 a^2 \times 7 a^7 = 5 \times 7 \times a^2 \times a^7$$
$$= 35 \times a^{2 + 7}$$
$$= 35 \times a^9$$
We get,
$$= 35 a^9$$
Hence, the value of $$5 a^2 \times 7 a^7$$ is $$35 a^9$$


Fill in the blanks:
$$ 6  \times 6 x^2  \times 6 x^2 y^2 =$$

$$6  \times 6 x^2  \times 6 x^2 y^2 = 6  \times 6  \times 6  \times x^2  \times x^2  \times y^2$$
$$= 216  \times x^{2+ 2}  \times y^2$$
$$= 216  \times x^4  \times y^2$$
We get, $$= 216 x^4y^2$$
Hence, $$6  \times 6 x^2  \times 6x^2y^2 = 216x^4y^2$$


Fill in the blanks:
$$ 5   \times 5\, a^3=$$

$$5 \times 5a^3 = 5 \times 5 \times a^3$$
$$= 25 \times a^3$$
We get,
$$= 25 a^3$$
Hence, $$5 \times 5 a^3 = 25 a^3$$


Fill in the blanks:
$$ x   \times 2 x^2   \times 3 x^3 =$$ ………

$$x \times 2 x^2 \times 3 x^3 = 2 \times 3 \times x \times x^2 \times x^3$$
$$= 6 \times x^{1 + 2 + 3}$$
$$= 6 \times x^6$$
$$= 6 x^6$$
Hence, $$x \times 2 x^2 \times 3 x^3 = 6 x^6$$


Fill in the blanks:
$$5 \times 4 =$$ . and $$5x \times  4y =$$

$$5 \times 4 = 20 $$ and $$5x \times 4y = 5 \times 4 \times x \times y$$
$$= 20 xy$$
Therefore, $$5 \times 4 = 20$$ and $$5x \times 4y = 20 xy$$


Find the value of:
$$3 x^3 \times 5x^4$$


$$3 x^3  \times 5 x^4 = 3  \times 5  \times x^3  \times x^4$$
$$= 15  \times x^{3 + 4}$$
We get,$$= 15  \times x^7$$
$$= 15 x^7$$
Hence, the value of $$3 x^3  \times 5 x^4$$ is $$15 x^7$$


Fill in the blanks:
$$6 \times 2 =$$ . and $$6xy \times  2xy =$$

$$6 \times 2 = 12$$
Hence,$$6 xy \times 2 xy = 6 \times 2 \times x^{1+1} \times y^{1+1} $$
$$= 12 \times x^2 \times y^2$$
$$= 12 x^2 y^2$$
Therefore, $$6 \times 2 = 12$$ and $$6 xy \times 2 xy = 12 x^2 y^2$$


Multiply:
$$4 x + 2 y$$ by $$ 3\,xy$$

The multiplication of $$4 x + 2 y$$ by $$3\,xy$$ is calculated as,
$$(4 x + 2 y) \times 3 xy = 4x \times 3 xy + 2y \times 3 xy$$
On simplification, we get
$$= 12 x^{1+1} y + 6 xy^{1+1}$$
$$= 12 x^2 y + 6 xy^2$$
Therefore, $$(4x + 2y) \times 3 xy = 12 x^2 y + 6 xy^2$$


Multiply:
$$2 xyz + 3 xy$$ and $$- 2y^2z$$

The multiplication of the given expression is calculated as,
$$(2 xyz + 3 xy) \times - 2 y^2z = 2 xyz \times - 2 y^2z + 3 xy \times - 2 y^2z$$
On further calculation, we get
$$= - 4 xy^{1+ 2} z^{1+1} - 6 xy^{1+2}z$$
$$= - 4 xy^3 z^2 - 6xy^3z$$
Hence, the multiplication of $$2 xyz + 3 xy\,\, and\,\, - 2 y^2z = - 4 xy^3 z^2 - 6 xy^3z$$


Multiply:
$$(1 + 4 x)$$ by $$x$$

The multiplication of $$(1 + 4\,x)$$ by $$x$$ is calculated as,
$$(1 + 4x) \times x = 1 \times x + 4x \times x$$
On simplification, we get
$$= x + 4 x^{1+1}$$
$$= x + 4 x^2$$
Therefore, $$(1 + 4 x)\times x = x + 4 x^2$$


Multiply:
$$- 3 xy^2 + 4 x^2y$$ and $$ - xy$$

The multiplication of the given expression is calculated as,
$$(- 3xy^2 + 4 x^2y) \times - xy = 3 x^{1+1} y^{2+1} - 4 x^{2+1}y^{1+1}$$
On calculation, we get
$$= 3 x^2y^3 - 4x^3y^2$$
Hence, the multiplication of $$- 3xy^2 + 4x^2y$$ and $$- xy = 3x^2y^3 - 4x^3y^2$$


Find the value of:
$$2 x^2 y^3 \times 5 x^3 y^4$$

$$2 x^2y^3 \times 5 x^3 y^4 = 2  \times 5  \times x^2  \times x^3  \times y^3  \times y^4$$
$$= 10  \times x^{2+3}  \times y^{3+4}$$
We get,
$$= 10  \times x^5  \times y^7$$
$$= 10 x^5 y^7$$
Hence, the value of $$2 x^2 y^3  \times 5 x^3 y^4$$ is $$10 x^5 y^7$$


Find the value of:
$$a^2b^2 \times 5 a^3 b^4$$

$$a^2b^2  \times 5 a^3b^4 = 5  \times a^2  \times a^3  \times b^2  \times b^4$$
$$= 5  \times a^{2+3}  \times b^{2+4}$$
$$= 5  \times a^5  \times b^6$$
We get,
$$= 5 a^5b^6$$
Hence, the value of $$a^2b^2  \times 5 a^3b^4$$ is $$5 a^5b^6$$


Find the value of:
$$3 abc \times 6 ac^3$$

$$3 abc \times 6 ac^3 = 3  \times 6  \times a  \times a  \times b  \times c \times c^3$$
$$=18  \times a^{1+ 1 } \times b  \times c^{1+3}$$
$$= 18  \times a^2  \times b  \times c^4$$
We get,
$$= 18 a^2 bc^4$$
Hence, the value of $$3 abc  \times 6 ac^3$$ is $$18 a^2 bc^4$$


Multiply:
$$a + b$$ by $$ab$$

The multiplication of $$(a + b)$$ by $$ab$$ is calculated as,
$$(a + b) \times ab = a \times ab + b \times ab$$
$$= a^{1+1}b + ab^{1+1}$$
We get,
$$= a^2 b + ab^2$$
Hence, $$(a + b)\times ab = a^2 b + ab^2$$


Multiply:
$$3\,ab - 4b$$ by $$3 \,ab$$

The multiplication of $$3ab – 4b$$ by $$3ab$$ is calculated as,
$$(3\,ab - 4\,b) \times 3\,ab = 3\,ab  \times 3\,ab - 4b  \times 3\,ab$$
$$= 9\,a^{1+1}\,b^{1+1} - 12\,ab^{1+1}$$
We get,
$$= 9\,a^2\,b^2 - 12\,ab^2$$
Therefore, $$(3\,ab - 4\,b) $$ by $$3\,ab = 9 a^2b^2 - 12\,ab^2$$


Multiply:
$$- x + y - z$$ and $$- 2\,x$$

The multiplication of the given expression is calculated as,
$$(- x + y - z) \times - 2 x = - x \times - 2x + y \times - 2x - z \times - 2x$$
On further calculation, we get
$$= 2 x^{1+1} - 2 xy + 2 xz$$
$$= 2 x^2 - 2 xy + 2 xz$$
Hence, the multiplication of $$(- x + y - z)$$ and $$- 2x$$ is $$2x^2 - 2xy + 2xz$$


Multiply: 
$$3x, 5x^{2}$$y and $$2 y $$

$$3x, 5x^{2}$$y and $$2y$$ 
Product $$=  3x\times 5x^{2}y$$ and $$2y$$ 
We can write it as $$3\times 5\times 2\times x\times x^{2}\times y\times y$$
So we get $$= 30x^{3}y^{2}$$


Multiply:
$$ x + 2\,\, and \,\,x + 10$$

$$x + 2\,\, and\,\, x + 10$$
The given expression is calculated as follows
$$(x + 2) \times (x + 10) = x \times (x + 10) + 2 \times (x + 10)$$
We get,
$$= x^2 + 10x + 2x + 20$$
$$= x^2 + 12x + 20$$
Hence, the multiplication of $$(x + 2)$$ and $$(x + 10) = x^2 + 12x + 20$$


Fill in the blanks :
$$ 6xy^{2}+9xy^{2} $$ = ........

$$6xy^{2}+9xy^{2} = 15xy^{2}$$


Multiply:
$$5, 3a$$ and $$2ab^{2}$$ 

$$5,3a$$ and $$2 ab^{2}$$
Product $$=  5\times 3a\times 2ab^{2}$$
We can write it as $$=5\times 3\times 2\times a\times ab^{2}$$
So we get $$= 30a^{2}b^{2}$$


Simplify :
$$-5m (-2m + 3n - 7p)$$

$$-5m (-2m + 3n - 7p)$$
We can write it as
$$= 10m^{2} - 15mn + 35mp$$


Multiply:
$$ x + 5 \,\,and\,\, x - 3$$

$$x + 5\,\, and\,\, x - 3$$
The given expression is calculated as follows
$$(x + 5) \times (x - 3) = x \times (x - 3) + 5 \times (x - 3)$$
On simplification, we get
$$= x^2 - 3x + 5x - 15$$
$$= x^2 + 2x - 15$$
Hence, the multiplication of $$(x + 5)$$ and $$(x - 3) = x^2 + 2x - 15$$


Simplify :
$$9a (2b - 3a + 7c)$$

$$9a (2b - 3a + 7c)$$
We can write it as
$$= 18ab - 27a^{2} + 63ca$$


Multiply:
$$ x - 5 \,\,and\,\, x + 3$$

$$x - 5\,\,\, and\,\, x + 3$$
The given expression is calculated as follows
$$(x - 5) \times (x + 3) = x \times (x + 3) - 5 \times (x + 3)$$
On further calculation, we get
$$= x^2 + 3x - 5x - 15$$
$$= x^2 - 2x - 15$$
Hence, the multiplication of $$(x - 5)$$ and $$(x + 3) = x^2 - 2x - 15$$


Multiply:
$$- 5xy$$ and $$ - xy^2 - 6x^2y$$

The multiplication of the given expression is calculated as,
$$-5 xy \times (- xy^2 - 6 x^2 y) = - 5 xy \times - xy^2 - 5 xy \times - 6 x^2 y$$
On further calculation, we get
$$= 5x^{1+1}y^{1+2} + 30x^{1+2}y^{1+1}$$
$$= 5x^2y^3 + 30x^3y^2$$
Therefore, the multiplication of $$- 5 xy\,\, and\,\, - xy^2 - 6x^2y = 5 x^2 y^3 + 30x^3y^2$$


Multiply:
$$4\,xy$$ and $$- x^2y - 3x^2 \,y^2$$

The multiplication of the given expression is calculated as,
$$(- x^2y - 3x^2y^2) \times 4 xy = - x^2y \times 4 xy - 3x^2y^2 \times 4xy$$
On further calculation, we get
$$= - 4x^{ 2+1}y^{1+1} - 12x^{2+1}y^{2+1}$$
$$= - 4x^3y^2 - 12x^3y^3$$
Hence, the multiplication of $$4xy$$ and $$- x^2y - 3x^2\, y^2 = - 4x^3y^2 - 12x^3y^3$$


Copy and  complete the following multiplication :

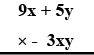
1826900_a86324a2019244e3b9f7c838d8e428da.png


1742314_1826900_ans_eda8b815bde54dc4b1660bbeb6a5f2c2.png


Evaluate: 
$$(3c-5d) (4c-6d)$$

It can written as $$= 3c (4c -6d) -5d( 4c - 6d) $$
By further calculation $$=12c^{2}-18cd-20cd+30d^{2}$$
=$$12c^{2}-38cd+30d^{2}$$


Evaluate: 
$$(c+5) ( c -3) $$

$$(c+5) (c-3)$$
It can be written as $$= c (c-3) +5 ( c-3)$$
By further calculation $$=c^{2}-3c+5c-15$$ 
$$=c^{2}+2c-15$$


Multiply:
 $$4a + 5b$$ and $$4a - 5b$$

$$4a + 5b$$ and $$4 a - 5b$$
Product $$ = ( 4a + 5b) ( 4a -5b)$$
So we get  $$= 16a^{2}-25b^{2}$$

1739820_1826882_ans_3cd91fb6e3a14ca9ae5eec5772411f3a.png


Multiply: 
$$5x + 2 y$$ and $$3 xy $$

$$5x + 2 y$$ and $$3xy$$ 
Product  $$= 3xy (5x+2y) $$
We can write it $$=3xy\times 5x+3x\times 2y$$
So we get  $$=15x^{2}y+6xy^{2}$$


Copy and  complete the following multiplication :

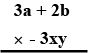
1826897_19bb939b086d4b1c8c952fac36830397.png



1742368_1826897_ans_33e3030b02e5498ba4e755c43ddab5ad.png


Copy and  complete the following multiplication :

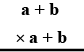
1826903_5010532f4db74dbf8f336fd4e112aaf1.png


1742312_1826903_ans_937e3952aece487083f2e4fa9d18ae0d.png


Copy and  complete the following multiplication :

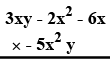
1826902_ee81de63bd784c5ea7b0225dfb8caa6f.png


1742317_1826902_ans_23b3d49baf5e4d3691461b08428ff7e1.png


Multiply:
$$6a - 5 b$$ and $$- 2a$$

$$6a -  5b$$ and $$- 2a$$
Product $$=  - 2a ( 6a - 5b)$$
We can write it as $$ =-2a\times 6a+2a\times 5b$$ 
So we get $$=-12a^{2}+10ab$$


Copy and  complete the following multiplication :

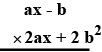
1826906_7ae41a13a6de4dea9d4b95cee1871b4f.png


1742328_1826906_ans_42b0ca51577d4fe593860aece7e41992.png


Multiplying: 
$$a^{3}-4ab$$ and $$ 2a^{2}b$$ 

$$a^{3}-4ab$$ and $$ 2a^{2}b$$ 
It can be written as $$= 2a^{2}b \times  (a^{3}-4ab)$$
By further calculation $$=2a^{5}b-8a^{3}b^{2}$$


Multiplying:
$$pq-pm$$ and $$p^{2}m$$ 

$$pq-pm$$ and $$p^{2}m$$ 
It can be  written as $$p^{2}m\times (pq-pm)$$
So we get = $$p^{3}qm-p^{3}-p^{3}m^{2}$$


Use direct method to evaluate :
$$(x+1)(x-1)$$

$$(x+1)(x-1)=x\times x+x\times (-1)+1\times (x)+1\times (-1)$$
$$=(x^2)-x+x-1^2$$
$$=x^2-1$$


Multiplying:
$$ mn^{4},mn$$ and $$5m^{2}n^{3}$$

$$ mn^{4},mn$$ and $$5m^{2}n^{3}$$ 
It can be written as $$= 5m^{2}n^{3} \times mn^{4} \times m^{3}n$$
By further calculation $$= 5m^{2+1+3}n^{3+4+1}$$
$$=5 m^{6}n^{8}$$


Use direct method to evaluate :
$$(2+a)(2-a)$$

$$(2+a)(2-a)=(2)^2-(a^2)=4-a^2$$   $$[\because (a+b)(a-b)=a^2-b^2]$$


Use direct method to evaluate :
$$(2a+3)(2a-3)$$

$$(2a+3)(2a-3)=2a^2-3^2=4a^2-9$$


Multiplying: 
$$2mnpq,4mnpq$$  and $$5mnpq$$

$$2mnpq, 4 mnpq$$  and $$5 mnpq  $$
It can be written as $$= 5\times 2\times 4m^{1+1+1}n^{1+1+1}p^{1+1+1}q^{1+1+1}= 40m^{3}n^{3}p^{3}q^{3}$$


Multiplying:
$$x^{3}-3y^{3}$$ and $$4x^{2}y^{2}$$

$$x^{3}-3y^{3}$$ and $$4x^{2}y^{2}$$
It can be  written as  $$=x^3(4x^2y^2)-3y^3(4x^2y^2)=4x^{5}y^{2}-12x^{2}y^{5}$$


Use direct method to evaluate :
$$(4+5x)(4-5x)$$

$$(4+5x)(4-5x)=(4)^2-(5)^2=16-25x^2$$         [$$\because (a+b)(a-b)=a^2-b^2$$]


Use direct method to evaluate :
$$(3b-1)(3b+1)$$

$$(3b-1)(3b+1)=(3b)^2-(1)^2=9b^2-1$$      $$[\because (a+b)(a-b)=a^2-b^2]$$


Use direct method to evaluate :
$$\left(\dfrac{a}{2}- \dfrac{2}{3} \right) \left(\dfrac{a}{2}+\dfrac{2}{3} \right)$$

$$\left(\dfrac{a}{2}- \dfrac{2}{3} \right) \left(\dfrac{a}{2}+\dfrac{2}{3} \right)$$ $$=\dfrac{a^2}{4} - \dfrac{4}{9} $$        [$$\because (a+b)(a-b)=a^2-b^2$$]


Use direct method to evaluate :
$$\left(\dfrac{3}{5}a+\dfrac{1}{2}\right)\left(\dfrac{3}{5}a-\dfrac{1}{2}\right)$$

$$\left(\dfrac{3}{5}a+\dfrac{1}{2}\right)\left(\dfrac{3}{5}a-\dfrac{1}{2}\right)$$ $$=\left(\dfrac{3}{5}a \right) -\left(\dfrac{1}{2} \right)^2=\dfrac{9}{25} a^2-\dfrac{1}{4}$$      [$$\because (a+b)(a-b)=a^2-b^2$$]


Use direct method to evaluate :
$$(xy+4)(xy-4)$$

$$(xy+4)(xy-4)=xy^2-4^2=x^2y^2-16$$


Find the products
$$ -x^{2}(x-15) $$

$$ -x^{2}(x-15) $$
$$=\left(-x^{2}\right) x-\left(-x^{2}\right) 15 $$
$$ =-x^{3}+15 x^{2} $$


Use direct method to evaluate :
$$(3x^2+5y^2)(3x^2-5y^2)$$

$$(3x^2+5y^2)(3x^2-5y^2)=(3x^2)^2-(5y^2)^2=9x^4-25y^4$$


Use direct method to evaluate :
$$\left(z-\dfrac{2}{3}\right)\left(z+\dfrac{2}{3}\right)$$

$$\left(z-\dfrac{2}{3}\right)\left(z+\dfrac{2}{3}\right)=(z)^2-\left(\dfrac{2}{3}\right)^2=z^2-\dfrac{4}{9}$$


Find the products
$$ (5 x+8) 3 x $$

$$ (5 x+8) 3 x $$
$$ 5 x \times 3 x+8\times3 x=15 x^{2}+24 x $$


Use direct method to evaluate :
$$(0.5-2a)(0.5+2a)$$

$$(0.5-2a)(0.5+2a)$$ $$=(0.5)^2-(22a)^2=0.25-4a^2$$        [$$\because (a+b)(a-b)=a^2-b^2$$]


Use direct method to evaluate :
$$(ab+x^2)(ab-x^2)$$

$$(ab+x^2)(ab-x^2)=(ab)^2-(x^2)^2=a^2b^2-x^4$$


Multiply:
$$ -8x$$  and  $$ 4-2x-x^2 $$ , then answer is $$ -32x+16x^2+8x^3 $$
If true then enter $$1$$ and if false then enter $$0$$

$$\\ -8x\times (4-2x-{ x }^{ 2 })\\ =-32x+16{ x }^{ 2 }+8{ x }^{ 3 }\\ \\ $$


Multiply the binomials
 $$\left( i \right)\,\left( {2x + 5} \right)\,and\,\left( {4x - 3} \right)$$
$$\left( {ii} \right)\,\left( {2.5l - 0.5m} \right)\,and\,\left( {2.2l + 0.5m} \right)$$

(i) $$(2x+5)\times (4x-3)$$

$$\Rightarrow 8x^2-6x+20x-15$$

$$\Rightarrow 8x^2+14x-15$$

(ii) $$(2.5l-0.5m)\times (2.2l+0.5m)$$

$$\Rightarrow 5.5l^2+1.25ml-1.5ml-0.25m^2$$

$$\Rightarrow 5.5l^2+2.75ml-0.25m^2$$.


Find the square of: $$(x - 5)$$

Square of $$ (x-5) $$ is $$ (x-5)^{2} $$

then $$ (x-5)^{2} = x^{2}-2.x.5+(5)^{2} $$

$$ = x^{2}-10x+25 $$


obtain the product of 
$$\left( i \right)\,xy,\,yz,\,zx$$    $$\left( {ii} \right)\,a,\, - {a^2},{a^3}$$    $$\left( {iii} \right)\,2,\,4y,\,8{y^2},\,16{y^2}$$    $$\left( {iv} \right)\,a,\,2b,\,3c,\,6abc$$    $$\left( v \right)\,m,\, - mn,\,mnp$$



1142675_1224977_ans_30df393b044f4db8a583992de784ad01.jpg


Multiply $$xy + 5x$$ with $$y + 7x$$

$$(xy+5x)\times (y+7x)$$
$$\Rightarrow xy^2+7x^2y+5xy+35x^2$$
$$\Rightarrow 35x^2+(y+7x)xy+5xy$$.


Find the following product.
$$\dfrac{3}{5}ax^{3}\times \dfrac{1}{6}bx^{2}$$

$$\dfrac{3}{5}ax^3\times \dfrac{1}{6}bx^2$$
$$=\dfrac{3}{5}\times \dfrac{1}{6}\times a\times b\times x^3\times x^2$$
$$=\dfrac{3}{30}\times a\times b\times x^{3+2}$$
$$=\dfrac{1}{10}abx^5$$.

1195550_1242435_ans_25b8ca13ab3c434f9d3c253c2c8d7fd5.jpg


Multiply $${y^2} - 3y + 5$$ with $$12{y^2} - 6y$$

$$ (y^2-3y+5)\times (12y^2-6y)$$

$$\Rightarrow 12y^4-36y^3+60y^2-6y^3+18y^2-30y$$

$$\Rightarrow 12y^4-42y^3+60y^2+18y^2-30y$$

$$=12y^4-42y^3+78y^2-30y$$.


Simplify
$$( x + y ) ( 2 y + 3 x ) + ( 3 x + y ) ( y + 2 x )$$

$$(x+y)(2y+3x)+(3x+y)(y+2x)$$

$$=x(2y+3x)+y(2y+3x)+3x(y+2x)+y(y+2x)$$

$$=2xy+3x^{2}+2y^{2}+3xy+3xy+6x^{2}+y^{2}+2xy$$

$$=9x^{2}+10xy+3y^{2}$$


Multiple the binomials.
$$\left(\dfrac{3}{4}a^2+3b^2\right)$$ and $$4\left(a^2-\dfrac{2}{3}b^2\right)$$ 

$$\left(\dfrac{3}{4} a^2 + 3b^2\right) * 4 \left(a^2 - \dfrac{2}{3} b^2 \right)$$
$$= \left(\dfrac{3a^2 + 12b^2}{4} \right) \times 4 \left(\dfrac{3a^2 - 2b^2}{3} \right)$$
$$= 3(a^2 + 4b^2) \dfrac{(3a^2 - 2b^2)}{3}$$
$$= (a^2 + 4b^2) (3a^2 - 2b^2)$$
$$= 3a^4 - 2b^2 a^2 + 12a^2 b^2 - 8 b^4$$
$$= 3a^2 + 10 a^2 b^2 - 8 b^4$$


Multiple the binomials.
$$(y-8)$$ and $$(3y-4)$$

Given binomials
$$(y - 8)$$ and $$(3y - 4)$$
$$(y - 8) \times (3y - 4) - 3y^2 - 4y - 24y + 32$$
$$= 3y^2 - 28y + 32$$


Degree of the polynomial of $$(x^{2}+1)(x+2)$$ is___________.

$$\left(x^2+1\right)\left(x+2\right)=x^3+2x^2+x+2$$
$$\Rightarrow$$ Degree $$=3.$$
Hence, the answer is $$3.$$



Multiple the binomials.
$$(2pq+3q^{2})$$ and $$(3pq-2q^{2})$$

Given Binomials
$$(2pq + 3q^2)$$ and $$(3pq - 2q^2)$$
$$(2pq + 3q^2) \times (3pq - 2q^2)$$
$$6 p^2q^2 - 2 pq^3 + 9pq^3 - 6 q^4$$
$$= 6p^2q^2 + 5 pq^3 - 6 q^4$$


Express the following product as a monomial and verify the result in case for $$x=1$$.
$$(4x^2)\times (-3x)\times \left(\dfrac{4}{5}x^3\right)$$.

Now,
$$(4x^2)\times (-3x)\times \left(\dfrac{4}{5}x^3\right)$$

$$=\dfrac{4\times (-3)\times 4}{5}x^{2+1+3}$$

$$=-\dfrac{48}{5}x^6$$.

Now for $$x=1$$ the value will be $$-\dfrac{48}{5}\times(1)^6=-\dfrac{48}{5}=-9.6$$.


If the product of $$\left(\dfrac{4}{3}pq^2\right)\times \left(-\dfrac{1}{4}p^2r\right)\times (16p^2q^2r^2)$$ is $$\dfrac{-a}{3}p^5q^4r^3$$, then value of $$a$$ is 


1510162_1673021_ans_775d9159b78a4304b3cc05ceb3859955.jpg


Use suitable identities to find the following products:
$$\left ( x^{2} + \dfrac{3}{5} \right ) \left ( x^{2} - \dfrac{3}{5} \right )$$

$$\left ( x^{2} + \dfrac{3}{5} \right ) \left ( x^{2} - \dfrac{3}{5} \right )$$
$$\because (a + b)(a - b) = a^{2} - b^{2}$$
$$\therefore \left ( x^{2} + \dfrac{3}{5} \right ) \left ( x^{2} - \dfrac{3}{5} \right ) = (x^{2})^{2} - \left ( \dfrac{3}{5} \right )^{2}$$
$$= x^{4} - \dfrac{9}{25}$$


Simplify: $$(y - 7) (y + 3)$$

$$(y-7)(y+3)$$
$$= \{y+(-7)\}(y+3)$$
      [Using $$(x-a)(x+ b)=x^2 + (b-a)x-ab$$]
$$  =y^2+(-7+3)y+(-7) \times 3$$
$$= y^2 - 4y-21$$


Find and correct errors of the following mathematical expressions:
$$ (2x)^{2}+4(2x)+7 = 2x^{2} +8x+7 $$

The given statement is incorrect.
Only the first term is written incorrect.
Correct statement is 
$$ (2x)^{2}+4(2x) +7 = 4x^{2}+8x+7 $$


Find and correct errors of the following mathematical expressions:
$$x(3x+2) =$$ $$ 3x^{2} +2 $$ 

The given statement is incorrect. 
The correct statement is 
$$x(3x+2) =$$ $$ 3x^{2} +2x $$


Simplify:
$$(x+5) (x -2)$$

[Using $$(x + a) (x - b)=x^2+(a -b)x-ab$$]

$$(x+5)(x-2)$$
Using $$(x+a) (x + b) = x^2+(a+ b)x +ab$$
$$= x^2 + \{5 + (-2)\} x-5 \times 2$$
$$ = x^2+ (5 -2)x-10$$
$$ =x^2+3x-10$$


Multiply the binomials
$$(2.5~l-0.5~m)$$ and $$(2.5~l+0.5~m)$$

$$\left(2.5~l-0.5~m\right)\left(2.5~l+0.5~m\right)$$ is of the form $$\left(a-b\right)\left(a+b\right)={a}^{2}-{b}^{2}$$
$$={\left(2.5~l\right)}^{2}-{\left(0.5~m\right)}^{2}$$
$$=6.25‬{l}^{2}-0.25‬{m}^{2}$$


$$(a+b)^{2} = $$

$$(a+b)^{2} = a^{2} +b^{2} + 2ab$$


If $$a=3,\,q=1$$ then find the value of $$8{a}^{4}{q}^{5}$$

$$8{a}^{4}{q}^{5}=8\times {1}^{4}\times{3}^{5}=8\times 243=1944‬$$


If $$a=6,\,p=4$$ find the value of $$ap$$

$$ap=6\times 4=24$$


Multiply:
$$(3x - 5y + 7z)$$ by $$- 3xyz$$ 

$$- 3xyz \times (3x - 5y + 7z)$$ 
= $$(- 3xyz) \times 3x + (- 3xyz) \times (- 5y) + (- 3xyz) \times (7z)$$ 
= $$- 9x^2yz + 15xyz^2 - 21xyz^2$$ 


Write the base and the exponent in each case. Also, write the term in the expanded from.
$$\left( 5ab \right) ^{ 3 }$$


1306404_1436557_ans_811cb17b9044401ebe71a09c56f3ee12.jpeg


Find the product of $$\left( x-2 \right) \left( x+2 \right) \left( { x }^{ 2 }+4 \right) \left( { x }^{ 4 }+16 \right) $$

use the identity $$(a-b)(a+b)=(a^2-b^2)$$
we have
$$(x-2)(x+2)=x^2-4$$

$$(x^2-4)(x^2+4)=(x^4-16)$$

$$(x^4-16)(x^4+16)=(x^8-256)$$

hence $$(x-2)(x+2)(x^2+4)(x^4+16)=(x^8-256)$$


Find the product of $$6x$$ and $$-7x^2y$$

We have $$(6x) (7x^2y) =6 \times 7\times x \times x^2y$$

                                     $$= 42\ x^3y$$


What is the product $$2l^2m\times 3lm^2$$?

We have $$2l^2m\times 3lm^2= (2\times 3)\times (l^2 \times l)\times (m\times m^2) = 6l^3m^3$$. .....[using the law of indices: $$a^k \times a^l = a^{k+l}$$.]



Show that - 
(i) $$(2a+3b)^{2}-(2a-3b)^{2}=24ab$$
(ii) $$(4x+5)^{2}-80x=(4x-5)^{2}$$

As we know that 
$$(a+b)^2-(a-b)^2=4 a b$$ and also $$(a+b)^2=(a-b)^2+4 a b$$
(i)$$(2 a+3 b)^2-(2 a-3 b)^2=4(2 a)(3 b)=24 a b$$
(ii)$$(4 x+5)^2-80 x=(4 x-5)^2+4(4 x)(5)-80 x=(4 x-5)^2+80 x-80 x=(4 x-5)^2$$


Find the product : $$\dfrac{6x}{5}(a^3-b^3)$$

We need to find product of $$\dfrac{6x}{5}{(a^3-b^3)}$$,

Now by multipling monomial outside the brackets to inside binomial, we get
$$\dfrac {6x}{5}\times a^3-\dfrac {6x}{5}\times b^3$$
$$\Rightarrow \dfrac {6xa^3}{5}-\dfrac {6xb^3}{5}$$
This is the required result.


Expand the following using identities
$$(x + 7)(y + 5)$$

$$(x + 7)(y + 5) = y^2 + (7 + 5) y + (7) (5)$$
                    
                           $$= y^2 + 12y + 35$$


Expand the following using identities
$$(3x - 4y)^2$$

$$(3x - 4y)^2 = (3x)^2 - 2(3x)(4y) + (4y)^2$$

                     $$= 9x^2 - 24xy + 16 y^2$$


Expand:
$${ a }^{ 4 }-16{ b }^{ 4 }$$

$$a^{4}-16{b^4}=(a^2)^2-(4 b^2)^{2}=(a^2+4{b^2})(a^{2}-4{b^2})$$
                                                 $$=(a^{2}+4{b^2})(a^{2}-(2 b)^2)=(a^2+4{b^2})(a-2{b})(a+2{b})$$


Verify the following : $$(-84)\times (25)=25\times (-84)$$


1326925_1589611_ans_6702ddcc239e478b89caa8d1241503bd.jpg


Simplify:
$$(x^2 + 3) (x - 3) + 9$$ 

$$(x^2 + 3) (x - 3) + 9$$
= $$x^2(x - 3) + 3(x - 3) + 9$$ 
= $$x^2 - 3x^2 + 3x - 9 + 9$$ 
= $$x^3 - 3x^2 + 3x$$


Multiply:
$$(ax + b)$$ by $$(cx + d)$$ 

$$(ax + b)$$ by $$(cx + d)$$ 
= $$(ax + b) \times (cx + d)$$ 
= $$ax (cx + d) + b (cx + d)$$ 
= $$acx^2 + adx + bcx + bd$$ 


Find the product of given monomials:
$$2a, 3a^{2}$$ and $$ 5a^{4}$$

Given monomials are $$2a, 3a^2, 5a^4$$
Their product $$= 2a\times 3a^2\times 5a^4$$
                        $$=2\times 3\times 5\times a^{1+2+4}$$
                        $$=30a^{7}$$


Find the product of given monomials:
$$(a^{2}) \times (2a^{5})\times (4a^{15})$$

Given monomials are $$a^2, 2a^5, 4a^{15}$$
Their product is $$a^2\times 2a^5\times 4a^{15}$$
$$=(1\times 2\times 4)(a^{2+5+15})$$
$$=8a^{22}$$


Find the product of given monomials:
$$xyz, y^{2}z$$ and $$ yx^{2}$$

Given monomials are $$xyz, y^2z, yx^2$$
Their product is $$xyz\times y^2z\times yx^2$$
$$=(x^{1+2})(y^{1+2+1})(z^{1+1})$$
$$=x^3y^4z^2$$


Find the product of given monomials:
$$-2p, -3q, -5p^{2}$$

Given monomials are $$-2p, -3q, -5p^2$$
Their product is $$(-2p)\times (-3q)\times (-5p^2)$$
$$=-(2\times 3\times 5)(p^{1+2}\times q)$$
$$=-30p^3q$$


Find the product of given monomials:
$$2x, 4y, 9z$$

Given monomials are $$2x, 4y, 9z$$
Their product is $$2x\times 4y\times 9z$$
$$=2\times 4\times 9\times xyz$$
$$=72xyz$$


For the above expression, keeping $$a=2m$$ and $$b = 3$$, we get
$$\left (\dfrac {3}{4} - x\right )\left (\dfrac {3}{4} +x\right )$$

using $$(a+b)(a-b)=a^2-b^2$$
For the above expression, keeping $$a=\dfrac{3}{4}$$ and $$b = x$$, we get
$$\left(\dfrac{3}{4}-x\right)\left(\dfrac{3}{4}+x\right)=\left(\dfrac{9}{16}-x^2\right)$$


Using a suitable identity, find the following product:
$$(5a - 3b)(5a - 3b)$$

using $$(a-b)(a-b)=a^2+b^2-2ab$$
For the above expression, keeping $$a=5a$$ and $$b = 3b$$, we get
$$(5a-3b)(5a-3b)=(25a^2+9b^2-30ab)$$


If  $$x + y - 1 = 0$$, prove that $$x^3 + y^3 + 3xy = 1$$

$$x+y-1=0$$
$$\Rightarrow x+y=1\quad\quad\quad\dots(i)$$

Now, on taking cube both sides of the equation $$(i)$$ we get,
$$\begin{aligned}{}{(x + y)^3} &= 1\\{x^3} + {y^3} + 3xy(x + y) &= 1\\{x^3} + {y^3} + 3xy &= 1\end{aligned}$$

Hence proved.


$$(x-4)^{2}=$$

$$ \textbf {Hint : Use the following algebraic identity} $$
$$ {(a-b)}^{2} = a^2 - 2ab + b^2 $$
$$ \textbf {Step 1 : Expansion by using algebraic identity} $$
$$ {(x-4)}^{2} = x^2 - (2 \times x \times 4) + 4^2 $$
                $$ = x^2 - 8x + 16 $$
$$ \textbf {Final step :}$$ $$ {(x-4)^{2}} = x^2 - 8x + 16 $$


Find the product:$$\dfrac{m}{d}\times\dfrac{m}{l}$$

$$\dfrac{m}{d}\times\dfrac{m}{l}=\dfrac{{m}^{2}}{dl}$$


Find the product of  $$-4p, 7pq$$

 We have to find $$-4p\times7pq$$
$$=-4 \times 7\times p^2q$$
$$=-28p^2q$$


Find the product of the following pairs of monomials $$4p^{3}, -3p$$

  $$4p^3\times(-3p)$$
$$=4 \times (-3)\times p^4$$
$$=-12p^4$$


Simplify $$\displaystyle \sqrt{8a^{5}b}\times \sqrt{4a^{2}b^{2}}$$.

$$\sqrt{8a^5b}\times \sqrt{4a^2b^2}=\sqrt{32a^7b^3}=4a^3b\sqrt{2ab}$$


Simplify:
$$(x + 3)(x + 5) $$
 [Using $$(x+a) (x + b) = x^2+(a+ b)x +ab$$]

$$(x+3)(x+5)$$
Using $$(x+a) (x + b) = x^2+(a+ b)x +ab$$
$$=x^2+(3+5) x+3 \times 5$$
$$ =x^2+8x+15$$


Multiply: $$\left(\displaystyle \frac{1}{5}  -\frac{1}{4}y \right) $$ and $$(5x^2-4y^2)$$

We have
$$\left( \displaystyle \frac{1}{5} x -\frac{1}{4}y \right) \times (5x^2 - 4y^2)$$
$$= \displaystyle \frac{1}{5} x \times (5x^2 - 4y^2) -\frac{1}{4}y \times (5x^2 -4y^2)$$
$$= \displaystyle \frac{1}{5} x \times 5x^2 - \frac{1}{5} x \times 4y^2 - \frac{1}{4}y \times 5x^2 +\frac{1}{4}y\times 4y^2$$
$$=x^3 -\displaystyle \frac{4}{5}xy^2 - \frac{5}{4}x^2y + y^3$$


Multiply: $$2x$$ and $$(3y+2)$$

$$2x \times (3y+2)$$
$$2x \times 3y + 2x \times 2 $$
$$= 6xy + 4x$$


Multiply: $$(3x^2+y^3)$$ by $$(x^2+2y^2)$$


$$(3x^2 + y^2) (x^2 + 2y^2)$$
$$=3x^2 \times  (x^2+2y^2)+y^2 \times (x^2 + 2y^2)$$
$$=3x^2 \times x^2+3x^2 \times 2y^2+y^2 \times x^2+ y^2 \times 2y^2$$
$$=3x^4 +6x^2y^2+x^2y^2+ 2y^4$$
$$=3x^4+ 7x^2y^2+ 2y^4$$


Simplify:
$$(x -5)(x -3)$$

[Using $$(x-a)(x-b)=x^2-(a+ b)x+ab$$]

$$(x-5)(x-3)$$
Using $$(x+a) (x + b) = x^2+(a+ b)x +ab$$
$$=x^2-(5+3) x +(-5) \times (-3)$$
$$ =x^2-8x+15$$


Find the product $$\left( \sqrt { 3 } x+a \right) \left( 2+\pi x \right) $$.

We expand term by term to get:
$$\left( \sqrt { 3 } x+a \right) \left( 2+\pi x \right) =\left( \sqrt { 3 } x \right) 2+\left( \sqrt { 3 } x \right) \left( \pi x \right) +\left( a \right) 2+\left( a \right) \pi x$$
                                     $$=2\sqrt { 3 } x+\pi \sqrt { 3 } { x }^{ 2 }+2a+\pi ax=\pi \sqrt { 3 } { x }^{ 2 }+\left( 2\sqrt { 3 } +\pi a \right) x+2a$$


Find the product: $$-x(x-15)$$

GIven that : $$ -x(x -15)$$
On multiplication we get: $$-x(x-15)$$ = $$-x(x)-15(-x)$$
The correct answer is $$ {-x^2+15x}$$


Find the product of $$(y - 1)(y - 1)$$ using appropriate identity.

We need to find value of $$(y-1)(y-1)$$
Thus $$y-1)(y-1)$$ $$=(y-1)^{2}$$
Using identity  $$(x-y)^{2}=x^{2}-2xy+y^{2}$$
Therefore, $$ (y-1)^{2}$$
$$=(y)^{2}-2\times y\times 1+(1)^{2}$$
$$=y^{2}-2y+1$$


Find the product of $$(x + 5)(x + 5)$$ using appropriate identity.

$$(x+5)(x+5)=(x+5)^2$$

                           $$= x^{2}+10x+25$$                        $$\bigg[$$ Using the identity: $$(x+y)^2=x^2+2xy+y^2 \bigg]$$


Find the product of $$(t + 2)(t + 4)$$ using appropriate identity.

Lets use the identity $$(x+a)(x+b)=x^2+(a+b)x+b^2$$
Here $$a=2, b=4$$
The value of $$(t+2)(t+4)$$ is
$$=t^2+(2+4)t+2(4)$$
$$=t^2+6t+8$$


Find the product of $$(p - 3)(p + 3)$$ using appropriate identity.

We need to find value of $$(p-3)(p+3)$$
Using identity  $$(x-y)(x+y)=x^{2}-y^{2}$$
Therefore, $$ (p-3)(p+3)=(p)^{2}-(3)^{2}=p^{2}-9$$


Find the product of $$5x,6y$$ and $$7z$$

$$5x\times 6y\times 7z=(5x\times 6y)\times 7z$$
$$=30xy\times 7z$$
$$=210xy$$


Factorise $$a^{3} - 8b^{3} - 64c^{3} - 24abc$$

Here the given expression can be written as,
$$a^{3} - 8b^{3} - 64c^{3} - 24abc = (a)^{3} + (-2b)^{3} + (-4c)^{3} - 3(a)(-2b)(-4c)$$
Comparing with the given identity, 
$$x^{3} + y^{3} + z^{3} - 3xyz \equiv (x + y + z)(x^{2} + y^{2} + z^{2} - xy - yz - xz)$$
We get factor as
$$= (a - 2b - 4c)[(a)^{2} - (-2b)^{2} + (-4c)^{2} - (a) (-2b) - (-2b) (-4c) - (-4c)(a)]$$
$$= (a - 2b - 4c)(a^{2} + 4b^{2} + 16c^{2} + 2ab - 8bc + 4ca)$$


Simplify: $$4y(3y+4)$$

Given expression is , 
$$4y(3y+4)$$
Multiplying the factors, we get,
$$=4y\times 3y+4y\times 4$$
$$=12y^2+16y$$

Hence,  $$4y(3y+4)=12y^2+16y  $$


Find the product of given monomials:
$$abc, abc$$

Given monomials are $$abc, abc$$
Their product is $$abc\times abc$$
$$\Rightarrow (a\times a)(b\times b)(c\times c)$$
$$\Rightarrow a^2b^2c^2$$

Hence, the product of given monomials is $$a^2b^2c^2$$.


Find the product of the following pairs of monomials:
$$5a^{2}, -4a$$

Given monomials are $$5a^2, -4a$$
Their product is $$5a^2\times (-4a)=-20a^3$$.


Find the product of the following pairs of monomials:
$$\dfrac {3}{7}x^{5}, \dfrac {14}{9}x^{2}$$

Given monomials are $$\dfrac {3}{7}x^5, \dfrac {14}{9}x^2$$
Here we will use identity $$x^m\times x^n=x^{m+n}$$
Their product is $$\dfrac {3}{7}x^5\times \dfrac {14}{9}x^2=\dfrac {2}{3}x^7$$.


Find the product of the following pairs of monomials:
$$-3a, 5ab$$

We need to find product of the monomials $$-3a$$ and $$5ab$$
Their product is $$(-3a\times 5ab)=-15a^2b$$


Find the product of the following pairs of monomials:
$$-7x, 3y$$

We need to find product of the monomials $$-7x$$ and $$3y$$
Their product is $$(-7x\times 3y)=-21xy$$


Find the product of the following pairs of monomials:
$$3, 7x$$

Given monomials are $$3,7x$$.
Their product is $$3\times 7x=21x$$.


Find the product of the following pairs of monomials:
$$xy^{2}, x^{2}y$$

Given monomials are $$xy^2, x^2y$$
Here using identity $$x^m\times x^n=x^{m+n}$$
Their product is $$xy^2\times x^2y=x^3y^3$$.


Find the product of given monomials:
$$x^{3}y^{5}, xy^{2}$$

Given monomials are $$x^3y^5, xy^2$$
Their product is $$x^3y^5\times xy^2$$
$$=x^{3+1}y^{5+2}$$
$$=x^4y^7$$


Find the product of given monomials:
$$m, 4m, 3m^{2}$$ and $$ -6m^{2}$$

Given monomials are $$m, 4m, 3m^2, -6m^2$$
Their product is $$m\times 4m\times 3m^2\times (-6m^2)$$
$$=1\times 4\times 3\times (-6)\times m^{1+1+2+2}$$
$$=-72m^{6}$$


Find the product of given monomials:
$$ab, bc$$ and $$ca$$

Given monomials are $$ab,bc.ca$$
Their product is $$ab\times bc\times ca$$
$$=(a\times a)(b\times b)(c\times c)$$
$$=a^2b^2c^2$$


Find the product of given monomials:
$$a^{2}b^{2}c^{3}$$ and $$ abc^{2}$$

Given monimials are $$a^2b^2c^3, abc^2$$
Their product is $$a^2b^2c^3\times  abc^2$$
$$=(a^{2+1})(b^{2+1})(c^{3+2})$$
$$=a^3 b^3c^5$$


Find the product of given monomials:
$$xyz$$ and $$ x^{2}yz$$

Given monomials are $$xyz, x^2yz$$
Their product is $$xyz\times x^2yz$$
$$=(x\times x^2)(y\times y)(z\times z)$$
$$=x^3y^2z^2$$


Find the product of given monomials:
$$lm^{2}, mn^{2}$$ and $$ ln^{2}$$

Given monomials are $$lm^2, mn^2, ln^2$$
Their product is $$lm^2\times mn^2\times ln^2$$
$$=l^{1+1}m^{2+1}n^{2+2}$$
$$=l^2m^3n^4$$


Simplify: 
$$21py^{2}-56py$$

Now,
$$21py^{2}-56py$$
$$=7py(3y-8)$$.


Find the product of $$(x + y + z)$$ and $$(x + y - z)$$.

$${\textbf{Step -1: Rearranging .}}$$

                  $$\therefore \left( {x + y+z} \right)\times \left( {x + y-z} \right).$$ 

                  $$ = (\left( {x + y } \right)+z)\times (\left( {x+y} \right)-z)$$

$${\textbf{Step -2: Now use identity of algebra .}}$$

                  $$\therefore (\left( {x + y } \right)+z)\times (\left( {x+y} \right)-z)$$  

                  $$= {\left( {x + y } \right)^2}  - {z^2}$$  $$\textbf{[Using (a+b) (a-b) = }$$ $$\mathbf{ {\left ({a} \right)^2}  - {b^2}]}$$

$${\textbf{Thus, the product value  is }}\mathbf{ {\left( {x + y } \right)^2}  - {z^2}.}$$



Find the product of $$(x + 3y)$$ and $$(3x - y)$$

We need to simplify the given product as follows:
$$(x+3y)(3x-y)$$$$=x(3x-y)+3y(3x-y)$$
                               $$=3x^2-xy+9xy-3y^2$$
                               $$=3x^2+8xy-3y^2$$


Using the identity $$(x + a)(x + b) = x^{2} + (a + b)x + ab$$, find out the following product:
$$(x + 4)(x + 7)$$

using $$(x+a)(x+b)=x^2+ba+(a+b)x$$
For the above expression, keeping $$a=4$$ and $$b = 7$$, we get
$$(x+4(x+7)=(x^2+7\times4+(7+4)x)=x^2+28+11x$$


Using a suitable identity, find each of the following products:
$$\left (\dfrac {1}{x} + \dfrac {1}{y}\right )\left (\dfrac {1}{x} - \dfrac {1}{y}\right )$$

using $$(a+b)(a-b)=a^2-b^2$$
$$(\dfrac{1}{x}-\dfrac{1}{y})(\dfrac{1}{x}+\dfrac{1}{y})=(\dfrac{1}{x^2}-\dfrac{1}{y^2})$$


Find the product of $$(3x + 2)$$ and $$(4x - 3)$$.

We need to simplify: $$(3x+2).(4x-3)$$
It can be simplified as; $$3x(4x-3)+2(4x-3)$$
                                     $$=12x^2-9x+8x-6$$
                                     $$=12x^2-x-6$$


Using a suitable identity, find each of the following products:
$$(100 + 3)(100 - 3)$$

using $$(a+b)(a-b)=a^2-b^2$$
$$(100^2-3^2)=(10000-9)=9996$$


Find out the product of:
$$\left (\dfrac {2}{3}ab\right )$$ and $$\left (\dfrac {-15}{8}a^{2}b^{2}\right )$$

We need to find product of $$\left (\dfrac {2}{3}ab\right )$$ and $$\left (\dfrac {-15}{8}a^{2}b^{2}\right )$$
Their product is $$\dfrac {2}{3}\times \left(-\dfrac {15}{8}\right)(a\times a^2)(b\times b^2)$$
$$=\dfrac {2}{3}\times \left(-\dfrac {15}{8}\right)a^{1+2}b^{1+2}$$
$$=-\dfrac {5}{4}a^3b^3$$


Using the identity $$(x + a)(x + b) = x^{2} + (a + b)x + ab$$, find out the following products:
$$(2m + 3n)(2m + 4n)$$

using $$(x+a)(x+b)=x^2+ba+(a+b)x$$
For the above expression, keeping $$a=3n$$ and $$b = 4n$$, we get
$$(2m+3n)(2m+4n)=(2x)^2+(3n+4n)2m+3n\times 4n=4x^2+14mn+12n^2$$


Using the identity $$(x + a)(x + b) = x^{2} + (a + b)x + ab$$, find the product of $$(7x + 3y)(7x - 3y)$$.

Given identity is $$(x+a)(x+b)=x^2+(a+b)x+ab$$
We need to use this identity to expand $$(7x+3y)(7x-3y)$$
Here $$a=3y, b=-3y$$ 
Thus we have $$(7x+3y)(7x-3y)=(7x)^2+[7x(3y-3y)]+3y(-3y)$$
$$=49x^2+7x\times 0-9y^2$$
$$=49x^2-9y^2$$


Using the identity $$(x + a)(x + b) = x^{2} + (a + b)x + ab$$, find the product of
$$(5x + 3)(5x + 4)$$.

Given identity is $$(x+a)(x+b)=x^2+(a+b)x+ab$$
We need to find product of $$(5x+3)(5x+4)$$
Here $$a=3, b=4$$
Hence, it can be simplified as $$(5x+3)(5x+4)$$
$$=(5x)^2+(3+4)5x+3(4)$$
$$=25x^2+35x+12$$


Simplify: $$(2x)\times (3x + 5)$$

We need to simplify the expression $$(2x)\times (3x+5)$$
It can be written as $$2x(3x+5)=2x\times 3x+2x\times 5$$
$$=6x^2+10x$$
This is the required answer.


Using the identity $$(x + a)(x + b) = x^{2} + (a + b)x + ab$$, find out the following product:
$$(8x - 5)(8x - 2)$$

using $$(x+a)(x+b)=x^2+ba+(a+b)x$$
For the above expression, keeping $$a=8x$$ and $$b = 2$$, we get
$$(8x-5)(8x-2)=(8x)^2+10+(-5-2)8x=64x^2+10-56x$$


Using the identity $$(x + a)(x + b) = x^{2} + (a + b)x + ab$$, find out the following product:
$$(xy - 3)(xy - 2)$$

using $$(x+a)(x+b)=x^2+ba+(a+b)x$$
For the above expression, keeping $$a=3$$ and $$b = 2$$, we get
$$(xy-3)(xy-2)=(xy)^2+(-3)(-2)+(-2-3)xy=(xy)^2+6-5xy$$


Simplify: $$(-2x)\times (4 - 5y)$$

We need to simplify $$(-2x)\times (4-5y)$$
It can be written as $$(-2x)\times (4-5y)=-2x(4)-(-2x)(5y)$$
$$=-8x+10xy$$


Simplify:
$$(a-b)(a^{2} +ab + b^{2})$$

$$(a-b)(a^2 + ab + b^2) = a^3 - b^3$$

Formula:
$$(x - y)(x^2 + xy + y^2)= x^3 - y^3$$


Simplify $$14\left( {12yz} \right) = \_\_\_\_\_$$

$$ 14( 12 yz) = 14 \times 12 \times yz $$

                   $$ = 168 yz$$



Solve $$5x - ( 4x - 7 ) ( 3x - 5 ) =  6 - 3( 4x - 9 ) ( x - 1 )$$

$$5x - (4x - 7)(3x - 5) = 6 - 3(4x - 9)(x - 1)$$

$$5x - \left( {12{x^2} - 20x - 21x + 35} \right) = 6 - 3\left( {4{x^2} - 4x - 9x + 9} \right)$$

$$5x - 12{x^2} + 41x - 35 = 6 - 12{x^2} + 39$$

$$46x - 35 = 39x - 21$$

$$7x = 14$$

$$x = 2$$



Simplify $$\left(\dfrac{2}{x}-\dfrac{x}{2}\right)^{2}$$

We have,

$$ {{\left( \dfrac{2}{x}-\dfrac{x}{2} \right)}^{2}} $$

$$ =\left( \dfrac{2}{x}-\dfrac{x}{2} \right)\left( \dfrac{2}{x}-\dfrac{x}{2} \right) $$

$$ =\dfrac{4}{{{x}^{2}}}-\dfrac{x}{2}\times \dfrac{2}{x}-\dfrac{2}{x}\times \dfrac{x}{2}+\dfrac{{{x}^{2}}}{4} $$

$$ =\dfrac{4}{{{x}^{2}}}+\dfrac{{{x}^{2}}}{4}-2 $$


Hence, this is the answer.


Multiply $$\left( {a + 2} \right)\left( {a - 1} \right)$$

$$\left( {a + 2} \right)\left( {a - 1} \right) \Rightarrow a\left( {a - 1} \right) + 2\left( {a - 1} \right)$$

$${a^2} - a + 2a - 2$$

$${a^2} + a - 2$$


Expand $$(5x+3)(x-1)(3x-2)$$

Solution:-
$$\left( 5x + 3 \right) \left( x - 1 \right) \left( 3x - 2 \right)$$
$$= \left( 5x \left( x - 1 \right) + 3 \left( x - 1 \right) \right) \left( 3x - 2 \right)$$
$$= \left( 5 {x}^{2} - 5x + 3x - 3 \right) \left( 3x - 2 \right)$$
$$= \left( 5{x}^{2} - 2x - 3 \right) \left( 3x - 2 \right)$$
$$= \left( 5{x}^{2} \left( 3x - 2 \right) - 2x \left( 3x - 2 \right) - 3 \left( 3x - 2 \right) \right)$$
$$= \left( 15 {x}^{3} - 10 {x}^{2} - 6{x}^{2} + 4x - 9x + 6 \right)$$
$$= 15 {x}^{3} - 16 {x}^{2} - 5x + 6$$


Multiply : $$(a^2 + 2c^2) (3a - 3c)$$

$$(a^2+2c^2)(3a-3c)$$
$$\therefore a^2(3a-3c)+2c^2(3a-3c)$$
$$\therefore 3a^3-3a^2c+6ac^2-6c^3$$
$$\therefore \boxed{3(a^3-a^2c+2ac^2-2c^3)}$$


Find $$\dfrac{1}{2}x(1+1\cdot 2)$$.

$$\cfrac{1}{2}x(1+1\cdot 2)$$
$$=\cfrac{1}{2}x(1+ 2)\\=\cfrac{3x}{2}$$



Find the product of $$(7x - 4y)$$ and $$(3x - 7y)$$

product of $$(7x-4y)$$ and $$(3x-7y)$$
$$(7x-4y)$$ $$(3x-7y)$$
$$\Rightarrow (7x)(3x)-(7x)(7y)-(4y)(3x)+(4y)(7y)$$
$$\Rightarrow 21x^2-49xy-12xy+28y^2$$
$$\Rightarrow {21x^2+28y^2-61xy}$$


Multiply $$x\left[1+\dfrac {1}{x}\right]\left[1-\dfrac {1}{x}\right]$$

We have,
$$\Rightarrow x(1+\dfrac{1}{x})(1-\dfrac{1}{x})$$
$$\Rightarrow x(1^1-\dfrac{1}{x^2})$$                          $$(a^2-b^2)=(a+b)(a-b)$$
$$\Rightarrow x-\dfrac{1}{x}$$

Hence, this is the answer.


Solve:
$$(\sqrt x  - 3x)\left( {x + \frac{1}{x}} \right)$$

$$(\sqrt { x } -{ 3x })({ x }+\dfrac { 1 }{ x } )\\ ={ x\sqrt { x }  }-{ { 3x }^{ 2 } }+\dfrac { \sqrt { x }  }{ x } -{ 3 }\\ ={ x }^{ \frac { 3 }{ 2 }  }-{ 3x }^{ 2 }+{ x }^{ -\frac { 1 }{ 2 }  }-{ 3 }$$


Multiply $$-a^2b $$ by $$a^3 b^2 $$ and verify your result for $$a = 2, b = 3$$.

Multiplying ;$$-a^{2}b\times a^{3}b^{2}$$

                   $$=-a^{2+3}b^{1+2}$$

                   $$=-a^{5}b^{3}$$

Verify:
If $$a=2$$  and  $$b=3$$

$$-a^{2}b=-(2)^{2}\times 3$$$$=-4\times 3$$$$=-12$$

  $$a^{3}b^{2}=(2)^{3}\times (3)^{2}$$$$=8\times 9$$$$=72$$

$$-a^{2}b\times a^{3}b^{2}=-12\times 72=-864$$

$$-a^{5}b^{3}=-(2)^{5}\times (3)^{3}$$
            $$=-32\times 27$$
            $$=-864$$

Hence, verified.


Multiply: $$\left[ {x + \frac{2}{3}} \right]\left[ {x + \frac{3}{4}} \right]$$

$$\left(x+\dfrac{2}{3}\right)\left(x+\dfrac{3}{4}\right)$$

$$=x\left(x+\dfrac{3}{4}\right)+\dfrac{2}{3}\left(x+\dfrac{3}{4}\right)$$

$$={x}^{2}+\dfrac{3}{4}x+\dfrac{2}{3}x+\dfrac{1}{2}$$

$$={x}^{2}+\dfrac{9x+8x}{12}+\dfrac{1}{2}$$

$$={x}^{2}+\dfrac{17x}{12}+\dfrac{1}{2}$$


Solve:
$$\sqrt {\{ \left( {x - 2} \right)\left( {4 - x} \right)\} } $$

Solution :- 
$$ \sqrt{\left \{ (x-2)(4-x) \right \}}$$
$$= \sqrt{4x-x^{2}-8+2x}$$
$$ = \sqrt{6x-x^{2}-8}$$

1113646_1183959_ans_d24140ab0fc64c44b15b0f7c66c26cdc.jpg


Solve: $$\dfrac{x+1}{2}=12$$ find x

$$\dfrac{x+1}{2}=12\Rightarrow x+1=24\Rightarrow x=24-1=23$$


Solve the equation:-
$$\left ( x^{2}-5 \right )\left ( x+5 \right )+25=0$$

$$(x^{2}-5)(x+5)+25=0$$
$$x^{3}-5{x}+5{x^{2}}-25+25=0$$
$$x^{3}+5{x^{2}}-5{x}=0$$
$$x(x^{2}+5{x}-5)=0$$
$$x=0$$ or $$x^{2}+5{x}-5=0$$
$$x=0$$ or $$x=\dfrac{-5\pm\sqrt{25+20}}{2}=\dfrac{-5\pm3\sqrt{5}}{2}$$


solve:
$$2x \times 3x$$

$$2x \times 3x$$
$$= 6x^2$$


If * represent 7 mangoes and @ represents 4 apples, then what does " *@ *@ " represent?

then it is equal to $$ 7\times4\times7\times4$$ $$=784$$


Find the product of $$3x(2y-3)$$.

$$3x(2y-3)=3x\times 2y-3x\times 3$$
                 $$=6xy-9x$$


simplify: $$\left( x ^ { 3 } + \frac { 1 } { x ^ { 3 } } \right) \left( x ^ { 3 } - \frac { 1 } { x ^ { 3 } } \right)$$

$$(x^3+(\frac{1}{x^3}))(x^3-(\frac{1}{x^3}))\\use (a+b)(a-b)=a^2-b^2\\\therefore value =(x^3) ^2-(x(\frac{1}{x^3})^2)\\=x^6-(\frac{1}{x^6})$$



Find the product:
$$\left( \frac { 4 x } { 5 } - \frac { 3 y } { 4 } \right) \left( \frac { 4 x } { 5 } + \frac { 3 y } { 4 } \right)$$

$$(a-b)(a+b)=a^2-b^2\\\therefore(4x/5-3y/4)(4x/5+3y/4)\\=(\dfrac{4x}{5})^2-(\dfrac{3y}{4})^2\\=(\dfrac{16x^2}{25})-(\dfrac{9y^2}{16})$$



Solve: $$2\times5x(10x^2y-100xy^2)$$

$$2\times5x(10x^2y-100xy^2)=10\times x(10x^2y-100xy^2)=100x*x^2y-1000x*xy^2=100x^3y-1000x^2y^2$$


Obtain the product of $$x y , y z , z x$$ 

$$\textbf{Step -1: Multiplying the first two values.}$$
                 $$xy\times yz=?$$
                 $$\text{We know that}$$ $$a^x.a^y=a^{x+y}$$
                 $$\text{Hence, the product is}$$ $$xy^2z$$
$$\textbf{Step -2: Multiplying obtained product with the next term.}$$
                 $$xy^z\times xz=x^2y^2z^2$$ $$\text{(Using laws of indices)}$$
$$\textbf{Hence , the required product is}$$ $$\mathbf{x^2y^2z^2.}$$


Find the product of the following pairs of monomials:
( i )  $$\quad ( 2,4 x )$$
( i i )  $$( - 3 x , 2 x )$$

We have,
$$(1)\,2\times 4x=8x$$
$$(2)\,-3x\times 2x=-6x^2$$

Hence, this is the answer.


If $${\rm{A}} = xy,\,B = yz$$ and $$C = zx,$$ then find $${\rm{ABC = }}.........$$

We have,
$$A=xy, B=yz, C=zx$$

So,
$$ABC=xy\times yz\times zx$$

$$ABC=(xyz)^2$$

Hence, this is the answer.


Find each of the following products.
$$6a \times 4b^{2}$$

$$6a \times 4 {b}^{2} = \left( 6 \times 4 \right) \times \left( a {b}^{2} \right) = 24 a {b}^{2}$$


Solve 
(i) $$\left( x+6 \right) \left( x+6 \right) $$
(ii) $$\left( \dfrac { 2 }{ 3 } x+\dfrac { 4 }{ 5 } y \right) \left( \dfrac { 2 }{ 3 } x+\dfrac { 4 }{ 5 } y \right) $$

  1. $$\left( x + 6 \right) \left( x + 6 \right) \\ = x \cdot x + 6x + 6x + 6 \cdot 6 \\ = {x}^{2} + 12x + 36$$
  2. $$\left( \cfrac{2}{3} x + \cfrac{4}{5} y \right) \left( \cfrac{2}{3} x + \cfrac{4}{5} y \right) \\ = \left( \cfrac{2}{3} x \right) \cdot \left( \cfrac{2}{3} x \right) + \left( \cfrac{2}{3}x \right) \left( \cfrac{4}{5} y \right) + \left( \cfrac{4}{5} y \right) \left( \cfrac{2}{3} x \right) + \left( \cfrac{4}{5} y \right) \cdot \left( \cfrac{4}{5} y \right) \\ = \cfrac{4}{9} {x}^{2} + \cfrac{8}{15} xy + \cfrac{8}{15} xy + \cfrac{!6}{25} {y}^{2} \\ = \cfrac{4}{9} {}^{2} + \cfrac{16}{15} xy + \cfrac{16}{25} {y}^{2}$$


Fill in the blank
$$5m^{2}\times 3m^{2}=\square$$

$$\begin{aligned}{}5{m^2} \times 3{m^2} &= \left( {5 \times 3} \right) \times \left( {{m^2} \times {m^2}} \right)\\ &= \left( {15} \right)\left( {{m^4}} \right)\\ &= \boxed{15{m^4}}\end{aligned}$$


Fill in the blank
$$(3x^{2}+4y)(2x+3y)=\square$$

$$(3x^{2}+4y)(2x+3y)$$
$$=6x^{3}+9x^{2}y+8xy+12y^{2}$$
$$=6x^{3}+12y^{2}+xy(9x+8)$$


Simplify the following:
$$\left (i\right)\left (x+6\right)\left (x+4\right) \left(x-2\right)$$
$$\left(ii\right)\left (x-6\right)\left (x-4\right)\left (x+2\right)$$
$$\left(iii\right)\left (x+6\right) \left(x-4\right)\left (x-2\right)$$
$$\left(iv\right)\left (x+6\right)\left (x-4\right)\left (x-2\right)$$ 

(i)(X+6)(X+4)(X-2)
on simplifying$$ (x+6)(x^{2}+2x-8)$$
$$\Rightarrow (x^{3}+2x^{2}-8x+6x^{2}+12x-48)$$
$$\Rightarrow(x^{3}+8x^{2}+4x-48)$$
(ii)(x-6)(x-4)(x+2)
on simplifying$$ (x-6)(x^{2}-2x-8)$$
$$\Rightarrow x^{3}-2x^{2}-8x-6x^{2}+12x+48$$
$$\Rightarrow x^{3}-8x^{2}+4x+48$$
(iii)(x+6)(x-4)(x-2)
on simplifying $$ (x+6)(x^{2}-6x+8)$$
$$\Rightarrow x^{3}-6x^{2}+8x+6x^{2}-36+48$$
$$\Rightarrow x^{3}-28+48.$$
(iv)(x-6)(x+4)(x-2)
on simplifying 
 (x-6)$$(x^{2}+2x-8)$$
$$\Rightarrow (x-6)(x^{2}2x-8)$$
$$\Rightarrow x^{3}+2x^{2}-8x-6x^{2}-12x-48$$
$$\Rightarrow x^{3}-4x^{2}-20x+48$$.

1194292_1369375_ans_5c34534760fa4fcfb4b27745ed780deb.jpg


Simplify:
$$(a^{2}+5)(b^{3}+3)+5$$

$$\left({a}^{2}+5\right)\left({b}^{3}+3\right)+5$$

$$={a}^{2}{b}^{3}+3{a}^{2}+5{b}^{3}+15+5$$

$$={a}^{2}{b}^{3}+3{a}^{2}+5{b}^{3}+20$$



Solve:
$$4a^{2}b^{2}-12abc+9c^{2}$$

$$4 {a}^{2} {b}^{2} - 12 abc + 9 {c}^{2}$$

$$= {\left( 2ab \right)}^{2} - 2 \cdot 2ab \cdot 3c + {\left( 3c \right)}^{2}$$

$$= {\left( 2ab - 3c \right)}^{2} \quad \left( \because {\left( x - y \right)}^{2} = {x}^{2} - 2xy + {y}^{2} \right)$$


Expand $$(3x+9)(3x-9)$$

$$\left(3x+9\right)\left(3x-9\right)$$
$$= 9{x}^{2}-81$$ using the identity $$\left(a-b\right)\left(a+b\right)={a}^{2}-{b}^{2}$$



Solve:
$$ab - {c^2} = \cfrac{(bc - a^2)^2}{ac - b^2}$$

We have,
$$ab - {c^2} = \cfrac{(bc - a^2)^2}{ac - b^2}$$

$$(ab - c^2)(ac-b^2)= (bc - a^2)^2$$

$$a^2bc-ab^3-ac^3+b^2 c^2=b^2c^2+a^4-2a^2bc$$

$$-ab^3-ac^3=a^4-3a^2bc$$

$$a^3+b^3+c^3=3abc$$

Hence, this is the answer.


Simplify:
$$25abc^{2}-15a^{2}b^{2}c$$

Now,
$$25abc^{2}-15a^{2}b^{2}c$$
$$=5abc(5c-3ab)$$.


$$(a+b)^{2}=?$$

$${\textbf{Step -1: Simplify the equation to find the value}}{\textbf{.}}$$
               $${\left( {a + b} \right)^2}$$
                $$ = \left( {a + b} \right)\left( {a + b} \right)$$
                $$ = a\left( {a + b} \right) + b\left( {a + b} \right)$$
                $$ = {a^2} + ab + ab + {b^2}$$
                $$ = {a^2} + 2ab + {b^2}$$
$${\textbf{ Hence, the value of }}{\mathbf{\left( {a + b} \right)^2}}{\textbf{ is }}\mathbf{{a^2} + 2ab + {b^2}.}$$


Multiply the binomials:
$$(2x+5)$$ and $$(4x-3)$$

If we multiply the binomials $$(2x+5)$$ and $$(4x-3)$$ we'll get,

$$(2x+5)(4x-3)$$$$=8x^2-6x+20x-15$$

$$(2x+5)(4x-3)$$$$=8x^2+14x-15$$.


Complete the table of products
$$\displaystyle \underset{\downarrow Second monomial}{\xrightarrow{\displaystyle First monomial \rightarrow}}$$2x-5y$$3x^2$$-4xy$$7x^2y$$$$-9x^2y^2$$
2x$$4x^2$$-----
- 5y--$$- 15 x^2 y$$---
$$3x^2$$------
- 4xy------
$$7x^2 y$$------
$$- 9x^2 y^2$$------

Complete table is --
$$\displaystyle \underset{\downarrow Second monomial}{\xrightarrow{\displaystyle First monomial \rightarrow}}$$$$2x$$$$-5y$$$$3x^2$$$$-4xy$$$$7x^2y$$$$-9x^2y^2$$
$$2x$$
$$4x^2$$$$ -10xy$$$$6x^3$$$$-8x^2y$$$$14x^3 y$$$$-18 x^3 y^2$$
$$- 5y$$$$ -10xy$$
$$25 y^2$$$$- 15 x^2 y$$$$20xy^2$$$$-35x^2 y^2$$$$45x^2 y^3$$
$$3x^2$$$$6x^3$$$$-15x^2y$$$$9x^4$$$$-12x^3 y$$$$21x^4 y$$$$-27x^4 y^2$$
$$- 4xy$$$$-8x^2 y$$$$20 xy^2$$$$-12x^3 y$$$$16 x^2 y^2$$$$-28 x^3 y^2$$$$36 x^3 y^3$$
$$7x^2 y$$$$14x^3 y$$$$-35x^2 y^2$$$$21 x^4 y$$$$-28 x^3 y^2$$$$49 x^4 y^2$$$$-63 x^4 y^3$$
$$- 9x^2 y^2$$$$-18 x^3 y^2$$
$$45 x^2 y^3$$
$$-27 x^4 y^2$$
$$36 x^3 y^3$$
$$-63 x^4 y^3$$
$$81x^4 y^4$$


Find and correct errors of the following mathematical expressions:
$$ (a+4)(a+2) = a^{2} +8 $$

The given statement is incorrect.
Correct statement is
$$ (a+4)(a+2) = a^{2} +6a+8 $$


Find and correct errors of the following mathematical expressions:
$$ (2a+3b)(a-b) = 2a^{2} -3b^{2} $$ 

The given statement is incorrect. Middle term is missing in the expression.
Correct statement is
$$ (2a+3b)(a-b) = 2a^{2} +ab-3b^{2} $$


Find areas of rectangles with following pairs of monomials as their length and breadth respectively.
(i) $$(p,\,q)$$
(ii) $$10m,\,5n$$
(iii) $$20x^2,\,5y^2$$
(iv) $$(4x,\,3x^2)$$
(v) $$3mn,\,4np$$

Area of rectangle, $$A= \text{Length}\times \text{Breadth}$$
(i) $$A=l\times b=p \times q=pq$$ 

(ii) $$A=l\times b=5n\times10m=50mn$$

(iii) $$A=l\times b=20x^2\times5y^2=100x^2y^2$$

(iv) $$A=l\times b=4x\times3x^2=12x^3$$

(v) $$A=l\times b=3mn\times4np=12mn^2p$$


Find product of following pairs of monomials
(i) $$4,\,7p$$
(ii) $$-4p,\,7p$$
(iii) $$-4p,\,7pq$$
(iv) $$4p^3,\,-3p$$
(v) $$4p,\,0$$

(i) $$4\times7\times p=28p$$

(ii) $$-4p\times7p=-28p^2$$

(iii) $$-4p\times7pq=-28p^2q$$

(iv) $$4p^3\times3p=-12p^4$$

(v) $$4p\times0=0$$


Find and correct errors of the following mathematical expressions:
$$ (a-4)(a-2) = a^{2} -8 $$

The given statement is incorrect. Middle term is missing in this expression.
Correct statement is
$$ (a-4)(a-2) = a^{2} -6a+8 $$


Find the product.
(i) $$a^2\times(2a^{22})\times(4a^{26})$$

(ii) $$\left(\dfrac23xy\right)\times\left(-\dfrac9{10}x^2y^2\right)$$

(iii) $$\begin{pmatrix}\dfrac{-10}{3}pq^3\end{pmatrix}\times\begin{pmatrix}\dfrac{6}{5}p^3q\end{pmatrix}$$

(iv) $$x\times x^2\times x\times x^3\times x^4$$

(i) As all the terms are having same base, then we can add the powers.
$$\therefore 8a^{2+22+26}$$ $$=8a^{50}$$

(ii) $$\left (\dfrac {2}{3}\times y \right )\left (\dfrac {-9}{10}x^2y^2 \right )=\dfrac{-3}{5}x^3y^3$$

(iii) $$\left ( \dfrac {-10}{3}p q^3\right) \times \left (\dfrac {6}{5}p^3 q\right )=-4p^4q^4$$

(iv) $$x\times x^2 \times x\times x^3 \times x^4=x^{2+3+4}=x^{10}$$


Obtain the product of
(i) $$xy,\,yz,\,zx$$
(ii) $$a,\,-a^2,\,a^3$$
(iii) $$2,\,4y,\,8y^2,\,16y^3$$
(iv) $$a,\,2b,\,3c,\,6abc$$
(v) $$m,\,-mn,\,mnp$$

(i) $$xy\times yz\times zx=x^2y^2z^2$$

(ii) $$a\times -a^2\times a^3=-a^6$$

(iii) $$2\times4y\times8y^2\times16y^3=1024y^6$$

(iv) $$a\times2b\times3c\times6abc=36a^2b^2c^2$$

(v) $$m\times-mn\times mnp=-m^3n^2p$$


Multiply the binomials
(i) $$(2x+5)$$ and $$(4x-3)$$

(ii) $$(y-8)$$ and $$(3y-4)$$

(iii) $$(2.5l-0.5m)$$ and $$(2.5l+0.5m)$$

(iv) $$(a+3b)$$ and $$(x+5)$$

(v) $$(2pq+3q^2)$$ and $$(3pq-2q^2)$$

(vi) $$\begin{pmatrix}\dfrac{3}{4}a^2+3b^2\end{pmatrix}$$ and $$\begin{pmatrix}a^2-\dfrac{2}{3}b^2\end{pmatrix}$$

Multiplying the given polynomials one by one:

$$(i)$$ 
$$(2x+5)(4x-3)$$
$$=2x\times(4x-3)+5\times(4x-3)$$
$$=8x^2-6x+20x-15$$
$$=8x^2+14x-15$$

Hence, $$(2x+5)(4x-3)=8x^2+14x-15$$.

$$(ii)$$ 
$$(y-8)(3y-4)$$
$$=y(3y-4)-8(3y-4)$$
$$=3y^2-4y-24y+32$$
$$=3y^2-28y+32$$

Hence, $$(y-8)(3y-4)=3y^2-28y+32$$

$$(iii)$$
$$(2.5l-0.5m)(2.5l+0.5m)$$
We know that, $$(a+b)(a-b)=a^2-b^2$$
So, $$(2.5l-0.5m)(2.5l+0.5m)=(2.5l)^2-(0.5m)^2$$
$$=6.25\ell^2-0.25m^2$$

Hence, $$(2.5l-0.5m)(2.5l+0.5m)=6.25\ell^2-0.25m^2$$

$$(iv)$$
$$(a+3b)(x+5)$$
$$=a(x+5)+3b(x+5)$$
$$=ax+5a+3bx+15b$$
$$=ax+3bx+5a+15b$$

Hence, $$(a+3b)(x+5)=ax+3bx+5a+15b$$

$$(v)$$ 
$$(2pq+3q^2)(3pq-2q^2)$$
$$=2pq(3pq-2q^2)+3q^2(3pq-2q^2)$$
$$=6p^2q^2-4pq^3+9pq^3-6q^4$$
$$=6p^2q^2+5pq^3-6q^4$$

Hence, $$(2pq+3q^2)(3pq-2q^2)=6p^2q^2+5pq^3-6q^4$$

$$(vi)$$ 

$$\left(\dfrac34a^2+3b^2\right)\left(a^2-\dfrac23b^2\right)$$

$$=\dfrac{3}{4}a^2\begin{pmatrix}a^2-\dfrac{2}{3}b^2\end{pmatrix}+3b^2\begin{pmatrix}a^2-\dfrac{2}{3}b^2\end{pmatrix}$$

$$=\dfrac34a^4-\dfrac12a^2b^2+3a^2b^2-2b^4$$

$$=\dfrac34a^4-2b^4+\dfrac52a^2b^2$$

Hence, $$\left(\dfrac34a^2+3b^2\right)\left(a^2-\dfrac23b^2\right)=\dfrac34a^4-2b^4+\dfrac52a^2b^2$$


Complete the table.

 First expression Second expression Product
 (i) $$a$$ $$b+c+d$$.....
 (ii) $$x+y-5$$ $$5xy$$.....
 (iii) $$p$$ $$6p^2-7p+5$$.....
 (iv) $$4p^2q^2$$ $$p^2-q^2$$..... 
 (v) $$a+b+c$$ $$abc$$..... 

(i) $$a(b+c+d)=ab+ac+ad$$

(ii) $$(x+y-5)5xy=5x^2y+5xy^2-25xy$$

(iii) $$p(6p^2-7p+5) = 6p^3-7p^2+5p$$

(iv) $$4p^2q^2(p^2-q^2) = 4p^4q^2-4p^2q^4$$

(v) $$(a+b+c)abc = a^2bc+ab^2c+abc^2$$


Find the products:
(i) $$(5-2x)\;(3+x)$$
(ii) $$(x+7y)\;(7x-y)$$
(iii) $$(a^2+b)\;(a+b^2)$$
(iv) $$(p^2-q^2)\;(2p+q)$$

(i) $$(5-2x)\;(3+x)$$
$$=5(3+x)\;-2x(3+x)$$
$$=15+5x-6x-2x^2$$
$$=15-x-2x^2$$

(ii) $$(x+7y)\;(7x-y)$$
$$=x(7x-y)+7y(7x-y)$$
$$=7x^2-xy+49xy-7y^2$$
$$=7x^2+48xy-7y^2$$

(iii) $$(a^2+b)\;(a+b^2)$$
$$=a^2(a+b^2)+b(a+b^2)$$
$$=a^3+a^2b^2+ab+b^3$$

(iv) $$(p^2-q^2)\;(2p+q)$$
$$=p^2(2p+q)-q^2(2p+q)$$
$$=2p^3+p^2q-2pq^2-q^3$$




Obtain the volume of rectangular boxes with following length, breadth and height given respectively.
(i) $$5a,\,3a^2,\,7a^4$$
(ii) $$2p,\,4q,\,8r$$
(iii) $$xy,\,2x^2y,\,2xy^2$$
(iv) $$a,\,2b,\,3c$$

Volume $$= \text{Length}\times\text{Breadth}\times\text{Height}$$
$$V=l\times b\times h$$
(i) $$V=5a\times3a^2\times7a^4=105 a^{(1+2+4)} = 105a^7$$

(ii) $$V=2p\times4q\times8r=64pqr$$

(iii) $$V=xy\times2x^2y\times2xy^2$$ $$ =4x^{(1+2+1)}y^{(1+1+2)} =4x^4y^4$$

(iv) $$V=a\times2b\times3c=6abc$$


Complete the table of products

 1st monomial $$\longrightarrow$$
2nd monomial $$\downarrow$$		 $$2x$$$$-5y$$ $$3x^2$$ $$-4xy $$$$7x^2y$$ $$-9x^2y^2$$ 
 $$2x$$ $$4x^2$$ ........ .... .... .... 
 $$-5y$$ .... ....  $$-15x^2y$$ ........ ... 
 $$3x^2$$ .... .... .... ........ .... 
 $$-4xy $$.... .... .... .... .... .... 
 $$7x^2y$$ .... .... .... .... .... .... 
 $$-9x^2y^2$$ .... .... .... ....  ........ 


 1st monomial $$\longrightarrow$$
2nd monomial $$\downarrow$$		 $$2x$$$$-5y$$ $$3x^2$$ $$-4xy $$$$7x^2y$$ $$-9x^2y^2$$ 
 $$2x$$ $$4x^2$$$$-10xy$$$$6x^3$$ $$-8x^2y$$$$14x^3y$$$$-18x^3y^2$$
 $$-5y$$ $$-10xy$$$$25y^2$$ $$-15x^2y$$$$20xy^2$$$$-35x^2y^2$$$$45x^2y^3$$
 $$3x^2$$ $$6x^3$$$$-15x^2y$$$$9x^4$$$$-12x^3y$$$$21x^4y$$$$-27x^4y^2$$
 $$-4xy $$$$-8x^2y$$$$20xy^2$$$$-12x^3y$$$$16x^2y^2$$$$-28x^3y^2$$$$36x^3y^3$$
 $$7x^2y$$ $$14x^3y$$$$-35x^2y^2$$$$21x^4y$$$$-28x^3y^2$$$$49x^4y^2$$$$-63x^4y^3$$
 $$-9x^2y^2$$ $$-18x^3y^2$$$$45x^2y^3$$$$-27x^4y^2$$$$36x^3y^3$$$$-63x^4y^3$$$$81x^4y^4$$



Determine the product:
$$(8y + 3) \times 4x$$

We have,
$$(8y + 3) \times (4x) = (4x) \times (8y + 3)$$
                             $$= (4x \times 8y) + (4x) \times 3$$
                             $$= 32xy + 12x$$.


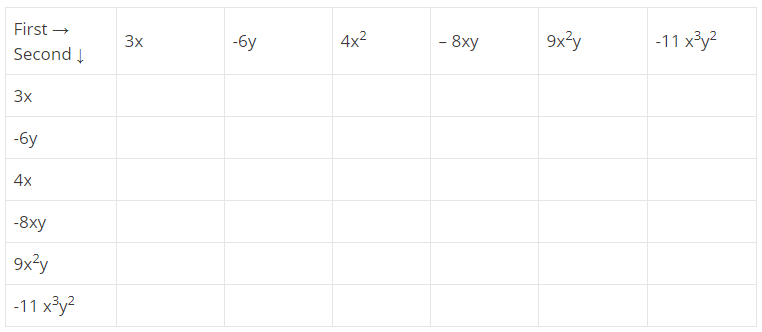
Complete the following table of products of two monomials:
First $$\rightarrow$$
Second $$\downarrow$$		$$3x$$$$-6y$$$$4x^2$$$$-8xy$$$$9x^2y$$$$-11x^3y^2$$
$$3x$$
$$-6y$$
$$4x^2$$
$$-8xy$$
$$9x^2y$$
$$-11x^3y^2$$

 First $$\rightarrow$$
Second 		 $$3x$$ $$-6y$$$$4x^2$$ $$-8xy$$ $$9x^2y$$ $$-11x^3y^2$$ 
 $$3x$$ $$9x^2$$$$-18xy$$$$12x^3$$ $$-24x^2y$$  $$27x^3y$$ $$-33x^4y^2$$
 $$-6y$$ $$-18xy$$ $$36y^2$$ $$-24x^2y$$  $$43xy^2$$  $$-54x^2y^2$$  $$66x^3y^3$$ 
 $$4x^2$$ $$12x^3$$ $$-24x^2y$$ $$16x^4$$  $$-32x^3y$$  $$36x^4y$$  $$-44x^5y^2$$ 
 $$-8xy$$ $$-24x^2y$$ $$48xy^2$$ $$-32x^3y$$  $$64x^2y^2$$  $$-72x^3y^2$$  $$88x^4y^3$$ 
 $$9x^2y$$ $$27x^3y$$ $$-54x^2y^2$$ $$36x^4y$$  $$-72x^3y^2$$  $$81x^4y^2$$  $$-99x^5y^3$$ 
 $$-11x^3y^2$$ $$-33x^4y^2$$ $$66x^3y^3$$ $$-44x^5y^2$$  $$88x^4y^3$$  $$-99x^5y^3$$  $$121x^6y^4$$ 


Evaluate the following product of  $$a{ x }^{ 2 }(bx+c)$$

Consider the polynomials $$ax^2$$ and $$bx+c$$ and multiply as follows:

$$(ax^2)(bx+c)=(ax^2\times bx)+(ax^2\times c)=abx^3+acx^2$$


Multiply $${ c }^{ 2 }a$$ and $${ b }^{ 2 }+2bc$$.

Consider the polynomials $$c^2a$$ and $$b^2+2bc$$ and multiply as follows:

$$(c^2a)(b^2+2bc)=(c^2a\times b^2)+(c^2a\times 2bc)=ab^2c^2+2abc^3$$


Expand $${ \left( x+\cfrac { 1 }{ x }  \right)  }^{ 2 }$$ using appropriate identity

Using the identity: $$(a+b)^{ 2 }=a^{ 2 }+b^{ 2 }+2ab$$.

Given:$$\left( x+\frac { 1 }{ x }  \right) ^{ 2 }$$ and apply the above identity by taking $$a = x$$ and $$b = \dfrac{1}{x}$$ in the given identity.
We get, $$\left( x+\dfrac { 1 }{ x }  \right) ^{ 2 }=x^{ 2 }+\left( \dfrac { 1 }{ x }  \right) ^{ 2 }+\left( 2\times x\times \dfrac { 1 }{ x }  \right) =x^{ 2 }+\dfrac { 1 }{ x^{ 2 } } +2$$
 
Hence, $$\left( x+\dfrac { 1 }{ x }  \right) ^{ 2 }=x^{ 2 }+2+\dfrac { 1 }{ x^{ 2 } }$$.


Expand $${ \left( 2a+3 \right)  }^{ 2 }$$ using appropriate identity

We know that the identity: $$(x+y)^{ 2 }=x^{ 2 }+y^{ 2 }+2xy$$.

Consider $$(2a+3)^2$$ and apply the above identity as follows:
Taking $$x = 2a$$ and $$y =3$$ in the above identity.
We get, $$(2a+3)^2=2a^2+3^2+(2\times 2a\times 3)=4a^2+9+12a$$
Hence, $$(2a+3)^2=4a^2+12a+9$$.


Find the product of the pair of monomial: $$4p^3, -3p$$

Let us multiply the given monomials $$4p^3$$ and $$-3p$$:

$$4p^{ 3 }\times (-3p)\\ =(4\times -3)\times (p^{ 3 }\times p)\\ =-12\times ({ p }^{ 3+1 })\quad \quad \quad (\because \quad a^{ x }\times a^{ y }=a^{ x+y })\\ =-12{ p }^{ 4 }$$

Hence, $$4p^{ 3 }\times (-3p)=-12{ p }^{ 4 }$$


Simplify: $${ \left( x+\cfrac { 1 }{ x }  \right)  }^{ 2 }-{ \left( x-\cfrac { 1 }{ x }  \right)  }^{ 2 }$$

Formula:
$$a^2-b^2=(a+b)(a-b)$$

$$(x+\dfrac{1}{x})^2-(x-\dfrac{1}{x})^2$$ is of the form $$a^2-b^2$$

$$\Rightarrow (x+\dfrac{1}{x})^2-(x-\dfrac{1}{x})^2=[(x+\dfrac{1}{x})+(x-\dfrac{1}{x})][(x+\dfrac{1}{x})-(x-\dfrac{1}{x})]$$

$$\Rightarrow (x+\dfrac{1}{x}+x-\dfrac{1}{x})(x+\dfrac{1}{x}-x+\dfrac{1}{x})$$

$$\Rightarrow (x+x)(\dfrac{1}{x}+\dfrac{1}{x})$$

$$\Rightarrow (2x)(\dfrac{2}{x})$$(Cancel $$x$$)
$$\Rightarrow 2\times 2=4$$


Expand $$(3x-5y)(3x+5y)$$

Using the identity is $$(a+b)(a-b)=a^{ 2 }-b^2$$.

Given: $$(3x-5y)(3x+5y)$$ we apply the above identity by taking 
$$a = 3x$$ and $$b = 5y$$ 
We get, $$(3x-5y)(3x+5y)={ \left( 3x \right)  }^{ 2 }-{ \left( 5y \right)  }^{ 2 }=9x^{ 2 }-25y^{ 2 }$$

Hence, $$(3x-5y)(3x+5y)=9x^{ 2 }-25y^{ 2 }$$.


Expand (2x+3)(2x+5) using appropriate identity.

Using the identity $$(m+a)(m+b)=m^{ 2 }+m(a+b)+ab$$.
Given, $$(2x+3)(2x+5)$$ 
We can apply the above identity by taking
$$m = 2x$$, $$a = 3$$ , $$b =5$$.
Hence, we get, 
$${ \left( 2x+3 \right)  }\left( 2x+5 \right) ={ \left( 2x \right)  }^{ 2 }+\left( 2x \right) \left( 3+5 \right) +\left( 3\times 5 \right)$$
$$\Rightarrow 4x^{ 2 }+\left( 2x \right) \left( 8 \right) +15$$
$$\Rightarrow 4x^{ 2 }+16x+15$$

Hence, $${ \left( 2x+3 \right)  }\left( 2x+5 \right) =4x^{ 2 }+16x+15$$.


Evaluate the product of $${ b }^{ 4 }({ b }^{ 6 }+{ b }^{ 8 })$$

The given polynomials are $$b^4$$ and $$b^6+b^8$$ we multiply them as follows:

$$(b^4)(b^6+b^8)=(b^4\times b^6)+(b^4\times b^8)={b}^{10}+{b}^{12}$$

Hence, $$(b^4)(b^6+b^8)={b}^{10}+{b}^{12}$$.


Evaluate the product of $$ { a }^{ 2 }{ b }^{ 2 }(a{ b }^{ 2 }+{ a }^{ 2 }b)$$

The given polynomials are $$a^2b^2$$ and $$ab^2+a^2b$$ we multiply them as follows:

$$(a^2b^2)(ab^2+a^2b)=(a^2b^2\times ab^2)+(a^2b^2\times a^2b)=a^3b^4+a^4b^3$$

Hence, $$(a^2b^2)(ab^2+a^2b)=a^3b^4+a^4b^3$$.


Evaluate the product of $$(x+3)(x+2)$$

The given polynomials are $$x+3$$ and $$x+2$$ we multiply them as follows:

$$(x+3)(x+2)=(x\times x)+(2\times x)+(3\times x)+(3\times 2)=x^2+3x+2x+6=x^2+5x+6$$

Hence, $$(x+3)(x+2)=x^2+5x+6$$.


Evaluate the product of $$ab(a+b)$$

The given polynomials are $$ab$$ and $$a+b$$ we multiply them as follows:

$$(ab)(a+b)=(ab\times a)+(ab\times b)=a^2b+ab^2$$

Hence, $$(ab)(a+b)=a^2b+ab^2$$.


Find the coefficients of $${x}^{2}$$ and $$x$$ in $$(x+4)(x+1)(x+2)$$

The given binomials $$(x+4)$$, $$(x+1)$$ and $$(x+2)$$.

Firstly multiply the first and second term as follows:

$$(x+4)(x+1)(x+2)=\left[ (x\times x)+(x\times 1)+(4\times x)+(4\times 1) \right] (x+2)=(x^{ 2 }+x+4x+4)(x+2)$$
$$=(x^{ 2 }+5x+4)(x+2)$$

Now multiply the resulting expression:

$$(x^{ 2 }+5x+4)(x+2)=(x^{ 2 }\times x)+(x^{ 2 }\times 2)+(5x\times x)+(5x\times 2)+(4\times x)+(4\times 2)$$
$$=x^{ 3 }+2x^{ 2 }+5x^{ 2 }+10x+4x+8=x^{ 3 }+7x^{ 2 }+14x+8$$

Therefore, $$(x+4)(x+1)(x+2)=x^{ 3 }+7x^{ 2 }+14x+8$$.

Hence, the coefficient of $$x^2$$ is $$7$$ and coefficient of $$x$$ is $$14$$.






Find the coefficients of $${x}^{2}$$ and $$x$$ in $$(2x+1)(2x-2)(2x-5)$$

The given binomials are $$(2x+1)$$, $$(2x-2)$$ and $$(2x-5)$$.

Firstly multiply the first and second term as follows:

$$(2x+1)(2x-2)(2x-5)=\left[ (2x\times 2x)+(2x\times -2)+(1\times 2x)+(1\times -2) \right] (2x-5)=(4x^{ 2 }-4x+2x-2)(2x-5)$$
$$=(4x^{ 2 }-2x-2)(2x-5)$$

Now multiply the resulting expression:

$$(4x^{ 2 }-2x-2)(2x-5)=(4x^{ 2 }\times 2x)+(4x^{ 2 }\times -5)+(-2x\times 2x)+(-2x\times -5)+(-2\times 2x)+(-2\times -5)$$
$$=8x^{ 3 }-20x^{ 2 }-4x^{ 2 }+10x-4x+10=8x^{ 3 }-24x^{ 2 }+6x+10$$

Therefore, $$(2x+1)(2x-2)(2x-5)=8x^{ 3 }-24x^{ 2 }+6x+10$$.

Hence, the coefficient of $$x^2$$ is $$-24$$ and coefficient of $$x$$ is $$6$$.




p(x) = $${x^3} + 4{x^2} - 5x + 6$$
g(x) = x + 1
and verify with $$p(x)[g(x) \times q(x)] + r(x)$$

considering the question to be:

To prove  $$p(x) = g(x)q(x)+r(x)$$

$$\dfrac{x^3+4x^2-5x+6}{x+1}$$

$$=x^2+\dfrac{3x^2-5x+6}{x+1}$$

$$=x^2+3x+\dfrac{-8x+6}{x+1}$$

$$=x^2+3x-8+\dfrac{14}{x+1}$$

$$p(x)=x^3+4x^2-5x+6, g(x)=x+1, q(x)=x^2+3x-8, r(x)=14$$

To prove

$$p(x) = g(x)q(x)+r(x)$$

$$g(x)q(x)+r(x)$$

$$=(x+1)(x^2+3x-8)+14$$

$$=x^3+3x^2-8x+x^2+3x-8+14$$

$$=x^3+4x^2-5x+6$$

$$=p(x)$$


The length and breadth and height of a cuboid are $$(x+3),(x-2)$$ and $$(x-1)$$ respectively. Find its volume.

Volume of cuboid is length $$\times$$ breadth $$\times$$ height

Here, the length is $$(x+3)$$, breadth is $$(x-2)$$ and height is $$(x-1)$$.
 
Therefore, the volume of cuboid is:

length$$\times$$ breadth $$\times$$ height $$=$$ $$\left( x+3 \right) \left( x-2 \right) \left( x-1 \right)$$

Firstly multiply the first and second term as follows:

$$\left( x+3 \right) \left( x-2 \right) \left( x-1 \right) =\left[ \left( x\times x \right) +\left( x\times -2 \right) +\left( 3\times x \right) +\left( 3\times -2 \right)  \right] \left( x-1 \right) $$
$$=(x^{ 2 }-2x+3x-6)\left( x-1 \right)$$
$$=(x^{ 2 }+x-6)\left( x-1 \right)$$ 

Now multiply the resulting expression:

$$(x^{ 2 }+x-6)\left( x-1 \right) =\left( x^{ 2 }\times x \right) +\left( x^{ 2 }\times -1 \right) +\left( x\times x \right) +\left( x\times -1 \right) +\left( -6\times x \right) +\left( -6\times -1 \right) $$
$$=x^{ 3 }-x^{ 2 }+x^{ 2 }-x-6x+6$$
$$=x^{ 3 }-7x+6$$

Hence, volume of cuboid id $$x^3-7x+6$$.






Solve $$(4x+5y)(4x-5y)$$

$$\left( {4x + 5y} \right)\left( {4x - 5y} \right) = {\left( {4x} \right)^2} - {\left( {5y} \right)^2}$$

$$ = 16{x^2} - 25{y^2}$$



Complete the following table of products:
First monomial $$\rightarrow$$
Second Monomial $$\downarrow$$		$$2x$$$$-3y$$$$4x^{2}$$$$-5xy$$$$7x^{2}y$$$$-6x^{2}y^{2}$$
$$2x$$$$4x^{2}$$........
$$-3y$$
$$4x^{2}$$
$$-5xy$$$$25x^{2}y^{2}$$
$$7x^{2}y$$
$$-6x^{2}y^{2}$$$$18x^{2}y^{2}$$

We can complete the given table by multiplying the monomials, as shown below:

First Monomial $$\rightarrow$$
Second monomial $$\downarrow$$ 		 $$2x$$$$-3y$$ $$4x^2 $$$$-5xy $$$$7x^2y$$ $$-6x^2y^2 $$
 $$2x$$ $$4x^2$$ $$-6xy$$$$8x^3$$ $$-10x^2y$$ $$14x^3y $$$$-12x^3y^2 $$
 $$-3y$$ $$-6xy$$ $$9y^2$$$$-12x^2y $$$$15xy^2 $$$$-21x^2y^2 $$$$ 18x^2y^3$$
 $$4x^2$$$$ 8x^3$$$$-12x^2y$$$$16x^4 $$$$-20x^3y $$$$28x^4y$$ $$-24x^4y^2 $$
$$ -5xy$$$$ -10x^2y$$$$15xy^2$$ $$-20x^3y $$ $$25 x^2y^2$$$$-35x^3y^2 $$$$ 30x^3y^3$$
 $$7x^2y$$$$ 14x^3y$$ $$-21x^2y^2$$$$ 28x^4y$$$$ -35x^3y^2$$ $$49x^4y^2$$$$ -42x^4y^3$$
$$ -6x^2 y^2$$$$ -12x^3y^2$$$$18x^2 y^3$$ $$ -24x^4y^2$$$$ 30x^3y^3$$$$ -42x^4y^3$$ $$36x^4y^4$$


Find the product of the following:
$$(m - n)(m^{2} + mn + n^{2})$$

Product of $$\left( m-n \right) \left( m^2+mn+n^2 \right) $$
$$=m\left( m^2+mn+n^2 \right)-n\left( m^2+mn+n^2 \right)$$
$$=m^3+m^2n+mn^2-m^2n-mn^2-n^3$$
$$=m^3-n^3$$
Hence, the answer is $$m^3-n^3.$$


Find out the following squares by using the identities:
$$0.54\times 0.54 - 0.46\times 0.46$$

$$\left( 0.54\times 0.54 \right) -\left( 0.46\times 0.46 \right) $$
$${ \left( 0.54 \right)  }^{ 2 }-{ \left( 0.46 \right)  }^{ 2 }$$
$$\Rightarrow$$ using $$a^2-b^2=\left( a+b \right) \left( a-b \right) $$
                              $$=\left( 0.54+0.46 \right) \left( 0.54-0.46 \right) $$
                              $$=1\left( 0.08 \right) $$
                              $$=\left( 0.08 \right) .$$
Hence, the answer is $$0.08.$$


Using the identity $$(x + a)(x + b) = x^{2} + (a + b)x + ab$$, find out the following products:
$$(2 + x)(2 - y)$$

$$\left( 2+x \right) \left( 2-y \right) $$
using, $$\left( x+a \right) \left( a+b \right) =x^2+\left( a+b \right) x+ab$$
$$\Rightarrow \left( 2+x \right) \left( 2-y \right) =2^2+\left( x-y \right)2- \left( xy \right) $$
                                  $$=4+2x-2y-xy.$$
Hence, the answer is $$4+2x-2y-xy.$$


Find out the following squares by using the identities:
$$(p - q)^{2}$$

$${ \left( p-q \right)  }^{ 2 }=p^2+q^2-2pq$$
Hence, the answer is $$p^2+q^2-2pq.$$


Find out the following square by using the identity $$(a-b)^2=a^2+b^2-2ab$$:
$$(5x - 4)^{2}$$

$${ \left( 5x -4 \right)  }^{ 2 }={ \left( 5x \right)  }^{ 2 }-2{ \left( 5x \right)  }{ \left( 4 \right)  }+{ \left( 4 \right)  }^{ 2 }$$
                    $$=25x^2-40x+16$$
Hence, the answer is $$25x^2-40x+16.$$


If $$x$$ and $$y$$ are positive integers, and it $$x - y$$ is even, show that $$x^{2} - y^{2}$$ is divisible by $$4$$.

Given $$x-y$$ is even ; 
Every number is of the form $$2k$$ or $$2k+1$$. For difference of two numbers to be even both should be either $$2k$$ form or $$2k+1$$ form.
ie. both $$x$$ and $$y$$ are even or both $$x,y$$ are odd. 
Both $$x,y$$ are even say $$ x=2k_1;y=2k_2$$
$$x^2-y^2=4k_1^2-4k_2^2=4(k_1^2-k_2^2)$$ which is divisible by 4.
Both $$x,y$$ are odd say $$ x=2k_1+1;y=2k_2+1$$
$$x^2-y^2=4k_1^2+4k_1+1-4k_2^2-4k_2-1=4(k_1^2+k_1-k_2^2-k_2)$$ which is divisible by $$4$$.
Thus if $$x-y$$ is even $$x^2-y^2$$ is divisible by $$4$$


Expand the following using standard identities:
$$(4x + 5y) (4x - 5y)$$

We know that $$(a+b)(a-b)=a^2-b^2$$

Using the above identity we get,

$$(4x + 5y) (4x - 5y) = (4x)^2 - (5y)^2$$
                             
                                    $$= 16x^2 - 25y^2$$


$$(a-b)(a+b)+(b-c)(b+c)+(c-a)(c+a)=0$$


$${\textbf{Step -1: Multiply these monomials}}{\textbf{.}}$$

                  $${\text{So, }}\left( {a - b} \right)\left( {a + b} \right) + \left( {b - c} \right)\left( {b + c} \right) + \left( {c - a} \right)\left( {c + a} \right).$$

                  $$ = a \times \left( {a + b} \right) - b \times \left( {a + b} \right) + b \times \left( {b + c} \right) - c \times \left( {b + c} \right) + c \times \left( {c + a} \right) - a \times \left( {c + a} \right).$$

                  $$ = {a^2} + ab - ba - {b^2} + {b^2} + bc - cb - {c^2} + {c^2} + ca - ac - {a^2}.$$

$${\textbf{Step -2: Simplify by cancelling out the same terms}}{\textbf{.}}$$

                  $$ = {a^2} - {a^2} + ab - ba - {b^2} + {b^2} + bc - cb - {c^2} + {c^2} + ca - ac.$$

                  $$ = 0.$$                    

$${\textbf{Hence, The value of }} \mathbf{\left( {a - b} \right)\left( {a + b} \right) + \left( {b - c} \right)\left( {b + c} \right) + \left( {c - a} \right)\left( {c + a} \right) = 0 .}$$

 



Solve
$$\left( x+\dfrac { 1 }{ x }  \right) \left( \sqrt { x } +\frac { 1 }{ \sqrt { x }  }  \right) $$

$$(x+\cfrac{1}{x}) (\sqrt{x} + \cfrac{1}{\sqrt{x}})$$
$$ = x \sqrt x + \cfrac{x}{\sqrt x} + \cfrac{\sqrt x}{x} + \cfrac{1}{x \sqrt x}$$
$$ = x\sqrt x  + \sqrt x  + \cfrac{1}{\sqrt x} + \cfrac{1}{x \sqrt x}$$


Find the product $$-3y(xy+y^2)$$ and find its value at $$x=4$$ and $$y=5$$

We simply substitute $$x=4,y=5$$ in the given product $$-3y(xy+y^2)$$ as follows:

$$-3y(xy+y^{ 2 })\\ =-(3\times 5)((4\times 5)+5^{ 2 })\\ =-15(20+25)\\ =-15\times 45\\ =-675$$

Hence, $$-3y(xy+y^2)=-675$$ when $$x=4,y=5$$.


Expand the following and collect like terms:
$$\begin{array}{l}\left( a \right)\,\,\,\,\left( {x + 5} \right)\left( {x + 5} \right)\\\left( b \right)\,\,\,\,\,\left( {x + 9} \right)\,\left( {x + 9} \right)\end{array}$$

(a) The given product $$(x+5)(x+5)$$ can be expanded as follows:

$$(x+5)(x+5)\\ =x(x+5)+5(x+5)\\ =(x\times x)+(x\times 5)+(5\times x)+(5\times 5)\\ =x^{ 2 }+5x+5x+25\\ =x^{ 2 }+10x+25$$

Hence, $$(x+5)(x+5)=x^{ 2 }+10x+25$$.

(b) The given product $$(x+9)(x+9)$$ can be expanded as follows:

$$(x+9)(x+9)\\ =x(x+9)+9(x+9)\\ =(x\times x)+(x\times 9)+(9\times x)+(9\times 9)\\ =x^{ 2 }+9x+9x+81\\ =x^{ 2 }+18x+81$$

Hence, $$(x+5)(x+5)=x^{ 2 }+18x+81$$.


Simplify $$\left(y^{2}+\dfrac {3}{2}\right) \left(y^{2}+\dfrac {3}{2}\right)$$

Simplifying $$\left( {{y^2} + \cfrac{3}{2}} \right)\left( {{y^2} + \cfrac{3}{2}} \right)$$


$$\left( {{y^2} + \cfrac{3}{2}} \right)\left( {{y^2} + \cfrac{3}{2}} \right) = {\left( {{y^2} + \cfrac{3}{2}} \right)^2}$$


$$ = {y^4} + {\left( {\cfrac{3}{2}} \right)^2} + 2\left( {\cfrac{3}{2}} \right){y^2}$$


$$ = {y^4} + \cfrac{9}{4} + 3{y^2}$$


$$ = {y^4} + 3{y^2} + \cfrac{9}{4}$$



Find the expression for the product $$(x+a)(x+b)(x+c)$$ using the identity $$(x+a)(x+b)=x^{2}+(a+b)x+ab$$

$$\left( {x + a} \right)\left( {x + b} \right)\left( {x + c} \right)$$
$$ = \left[ {{x^2} + \left( {a + b} \right)x + ab} \right]\left( {x + c} \right)$$
$$ = {x^2}\left( {x + c} \right) + \left[ {\left( {a + b} \right)x + ab} \right]\left( {x + c} \right)$$
$$ = {x^3} + {x^2}c + a{x^2} + b{x^2} + acx + bcx + abx + a$$
$$ = {x^3} + \left( {a + b + c} \right){x^2} + \left( {ab + bc + ca} \right)x + abc$$


Find the product of the following pair of monomials.
$$4, 7p$$

Let us multiply the given monomials $$4$$ and $$7p$$ as shown below:

$$4\times 7p\\ =(4\times 7)\times p\\ =28p$$

Hence, $$4\times 7p=28p$$.


Find the product of the following pair of monomials.
$$-4p, 7pq$$

Let us multiply the given monomials $$-4p$$ and $$7pq$$ as shown below:

$$(-4p)\times 7pq\\ =(-4\times 7)\times (p\times p)\times q\\ =(-28)\times ({ p }^{ 1+1 })\times q\quad \quad \quad [\because a^{ x }\times a^{ y }=a^{ x+y }]\\ =-28{ p }^{ 2 }q$$

Hence, $$(-4p)\times 7pq=-28{ p }^{ 2 }q$$.


$$(4x+5y)(4x+5y)$$

Simplifying $$\left( {4x + 5y} \right)\left( {4x + 5y} \right)$$.

$$\left( {4x + 5y} \right)\left( {4x + 5y} \right)$$

$$ = {\left( {4x + 5y} \right)^2}$$

$$ = {\left( {4x} \right)^2} + {\left( {5y} \right)^2} + 2\left( {4x} \right)\left( {5y} \right)$$

$$ = 16{x^2} + 25{y^2} + 40xy$$



Find the product of the following pair of monomial.
$$-4p, 7p$$

Let us multiply the given monomials $$-4p$$ and $$7p$$ as shown below:

$$-4p\times 7p\\ =(-4\times 7)\times (p\times p)\\ =-28\times ({ p }^{ 1+1 })\quad \quad \quad (\because \quad a^{ x }\times a^{ y }=a^{ x+y })\\ =-28{ p }^{ 2 }$$

Hence, $$-4p\times 7p=-28{ p }^{ 2 }$$.


Factorise: $${ a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 }-3abc$$

To factorise: $${ a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 }-3abc$$

From the standard identity,

$${ a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 }=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)+3abc$$
$$\Rightarrow { a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 }-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$$

Hence, the factorised form is, 
$$(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$$




$$(2x^2-5y^2)\times(x^2+3y^2)$$.

Let us multiply the given binomials $$(2x^2-5y^2)$$ and $$(x^2+3y^2)$$ as shown below:

$$(2x^{ 2 }-5y^{ 2 })(x^{ 2 }+3y^{ 2 })\\ =2x^{ 2 }(x^{ 2 }+3y^{ 2 })-5y^{ 2 }(x^{ 2 }+3y^{ 2 })\\ =(2x^{ 2 }\times x^{ 2 })+(2x^{ 2 }\times 3y^{ 2 })-(5y^{ 2 }\times x^{ 2 })-(5y^{ 2 }\times 3y^{ 2 })\\ =2x^{ 4 }+6x^{ 2 }y^{ 2 }-5x^{ 2 }y^{ 2 }-15y^{ 4 }\\ =2x^{ 4 }+(6x^{ 2 }y^{ 2 }-5x^{ 2 }y^{ 2 })-15y^{ 4 }\quad \quad \quad \quad (Combining\quad like\quad terms)\\ =2x^{ 4 }+x^{ 2 }y^{ 2 }-15y^{ 4 }$$

Hence, $$(2x^{ 2 }-5y^{ 2 })\times (x^{ 2 }+3y^{ 2 })=2x^{ 4 }+x^{ 2 }y^{ 2 }-15y^{ 4 }$$.


Find the product of the following pair of monomials.
$$4p$$ and $$ 0$$

Let us multiply the given monomials $$4p$$ and $$0$$ as shown below:

$$4p\times 0\\ =(4\times 0)\times p\\ =0\times p\\ =0$$

Hence, $$4p\times 0=0$$.


$$\left(\dfrac{3}{5}x+\dfrac{1}{2}y\right)$$ by $$\left(\dfrac{5}{6}x+4y\right)$$.

Let us find the product of $$\left( \dfrac { 3 }{ 5 } x+\dfrac { 1 }{ 2 } y \right)$$ and $$\left( \dfrac { 5 }{ 6 } x+4y \right)$$ as shown below:

$$\left( \dfrac { 3 }{ 5 } x+\dfrac { 1 }{ 2 } y \right) \left( \dfrac { 5 }{ 6 } x+4y \right) \\ =\left( \dfrac { 3 }{ 5 } x\times \dfrac { 5 }{ 6 } x \right) +\left( \dfrac { 3 }{ 5 } x\times 4y \right) +\left( \dfrac { 1 }{ 2 } y\times \dfrac { 5 }{ 6 } x \right) +\left( \dfrac { 1 }{ 2 } y\times 4y \right) \\ =\dfrac { 1 }{ 2 } x^{ 2 }+\dfrac { 12 }{ 5 } xy+\dfrac { 5 }{ 12 } xy+2y^{ 2 }\\ =\dfrac { 1 }{ 2 } x^{ 2 }+2y^{ 2 }+\left( \dfrac { 12 }{ 5 } xy+\dfrac { 5 }{ 12 } xy \right) \quad \quad \quad \quad \quad \left( Combining\quad like\quad terms \right)$$
$$=\dfrac { 1 }{ 2 } x^{ 2 }+2y^{ 2 }+\left( \dfrac { 12 }{ 5 } +\dfrac { 5 }{ 12 }  \right) xy\\ =\dfrac { 1 }{ 2 } x^{ 2 }+2y^{ 2 }+\left( \dfrac { 144+25 }{ 60 }  \right) xy\\ =\dfrac { 1 }{ 2 } x^{ 2 }+2y^{ 2 }+\dfrac { 169 }{ 60 } xy$$ 

Hence, $$\left( \dfrac { 3 }{ 5 } x+\dfrac { 1 }{ 2 } y \right) \left( \dfrac { 5 }{ 6 } x+4y \right) =\dfrac { 1 }{ 2 } x^{ 2 }+2y^{ 2 }+\dfrac { 169 }{ 60 } xy$$.


Solve : i) (z + 19 ) (z + 7)
ii) (9 + 4a) (7 + 4a)

i) $$(z+19)(z+7)=0$$

$$\implies z+19=0$$ or $$z+7=0$$

$$\implies z=-19$$ or $$z=-7$$

ii) $$(9+4a)(7+4a)=0$$

$$\implies 9+4a=0$$ or $$7+4a=0$$

$$\implies a=-\dfrac 94$$ or $$a=-\dfrac 74$$


Find: $$(x^{2}-y^{2})(x^{2}+y^{2})$$

We know that one of the identity is $$(a-b)(a+b)=a^2-b^2$$.

Here, $$a=x^2$$ and $$b=y^2$$. Now applying the identity we get:

$$(x^{ 2 }-y^{ 2 })(x^{ 2 }+y^{ 2 })\\ =(x^{ 2 })^{ 2 }-(y^{ 2 })^{ 2 }\\ =(x^{ 2\times 2 })-(y^{ 2\times 2 })\\ =x^{ 4 }-y^{ 4 }$$

Hence, $$(x^{ 2 }-y^{ 2 })(x^{ 2 }+y^{ 2 })=x^{ 4 }-y^{ 4 }$$.


Solve: $$(30x^{2}+15-10)\times (2x+3)$$


1356429_1132054_ans_2f2f154f7222487c9c02f24d9b7f0692.jpeg


$$\left(y^2+\dfrac{3}{2}\right)\left(y^2-\dfrac{3}{2}\right)$$

We know that one of the identity is $$(a-b)(a+b)=a^2-b^2$$.

Here, $$a=y^2$$ and $$b=\dfrac {3}{2}$$. Now applying the identity we get:

$$\left( y^{ 2 }+\dfrac { 3 }{ 2 }  \right) \left( y^{ 2 }-\dfrac { 3 }{ 2 }  \right) \\ =\left( y^{ 2 } \right) ^{ 2 }-\left( \dfrac { 3 }{ 2 }  \right) ^{ 2 }\\ =y^{ 4 }-\left( \dfrac { 3^{ 2 } }{ 2^{ 2 } }  \right) \\ =y^{ 4 }-\dfrac { 9 }{ 4 }$$

Hence, $$\left( y^{ 2 }+\dfrac { 3 }{ 2 }  \right) \left( y^{ 2 }-\dfrac { 3 }{ 2 }  \right) =y^{ 4 }-\dfrac { 9 }{ 4 }$$.


Solve : $$(x^2 - y^2) \times (x + 2y)$$

Let us multiply the given binomials $$(x^2-y^2)$$ and $$(x+2y)$$ as shown below:

$$(x^{ 2 }-y^{ 2 })(x+2y)\\ =x^{ 2 }(x+2y)-y^{ 2 }(x+2y)\\ =(x^{ 2 }\times x)+(x^{ 2 }\times 2y)-(y^{ 2 }\times x)-(y^{ 2 }\times 2y)\\ =x^{ 3 }+2x^{ 2 }y-xy^{ 2 }-2y^{ 3 }$$

Hence, $$(x^{ 2 }-y^{ 2 })\times (x+2y)=x^{ 3 }+2x^{ 2 }y-xy^{ 2 }-2y^{ 3 }$$.


If $$x:y=1:7$$ and $$y:z=4:5$$, find 
$$x:y:z$$

Given 
$$\dfrac{x}{y}=\dfrac{1}{7}...........(1)$$
$$\dfrac{y}{z}=\dfrac{4}{5}...........(2)$$
Multiply (1) and (2)
$$\dfrac{x}{y}\times\dfrac{y}{z}=\dfrac{1}{7}\times\dfrac{4}{5}$$
$$\dfrac{x}{z}=\dfrac{4}{35}$$
Now,
$$x=\dfrac{4z}{35}$$
$$y=\dfrac{4z}{5}$$
$$x:y:z=\dfrac{4z}{35}:\dfrac{4z}{5}:z$$
Multiplying with $$\dfrac{35}{z}$$
$$x:y:z=4:28:35$$


Find the product $$-5x^2y$$ and $$2xy^2$$.

$$\begin{matrix} -5{ x^{ 2 } }y\, \, and\, \, 2x{ y^{ 2 } } \\ \Rightarrow \left( { -5{ x^{ 2 } }y } \right) \left( { 2x{ y^{ 2 } } } \right)  \\ \Rightarrow -10{ x^{ 3 } }{ y^{ 3 } } \\ \Rightarrow -10{ \left( { xy } \right) ^{ 3\, \, \,  } }\, \, \, \, \, \, Ans. \\  \end{matrix}$$


Multiply the binomials.
$$(2x+5)$$ and $$(4x-3)$$

$$(2x+5)(4x-3)=8x^2-6x+20x-15=8x^2+14x-15$$


$$a(3x - 2y) + b(2y - 3x)=?$$.

$$3ax-2ay+2by-3bx$$


Find the product of :
$$\left( {3{x^2} - 4xy} \right)\left( {3{x^2} - 4xy} \right)$$

Solution :-
$$ (3x^{2}-4xy)(3x^{2}-4xy)$$

$$ \Rightarrow 3x^{2}(3x^{2}-4xy)-4xy(3x^{2}-4xy)$$

$$ \Rightarrow 9x^{4}-12x^{3}y-12x^{3}y+16x^{2}y^{2}$$

$$\Rightarrow 9x^{4}-24x^{3}y+16x^{2}y^{2}$$


Multiply: $$16xy\times 18xy$$

$$\begin{matrix} 16xy\times 18xy \\ 288{ x^{ 2 } }{ y^{ 2 } }\, \, \, \, \, Ans. \\  \end{matrix}$$


Find the product $$\left( {x + y - z} \right)\left( {{x^2} + {y^2} + {z^2} - xy + yz + zx} \right)$$.

$$\left(x+y−z\right)\left({x}^{2}+{y}^{2}+{z}^{2}−xy+yz+zx\right)$$
$$=x\left({x}^{2}+{y}^{2}+{z}^{2}−xy+yz+zx\right)+y\left({x}^{2}+{y}^{2}+{z}^{2}−xy+yz+zx\right)-z\left({x}^{2}+{y}^{2}+{z}^{2}−xy+yz+zx\right)$$
$$={x}^{3}+x{y}^{2}+x{z}^{2}−{x}^{2}y+xyz+z{x}^{2}+y{x}^{2}+{y}^{3}+y{z}^{2}−x{y}^{2}+{y}^{2}z+zxy-z{x}^{2}-z{y}^{2}-{z}^{3}+xyz-y{z}^{2}-{z}^{2}x$$
$$={x}^{3}+{y}^{3}-{z}^{3}+3xyz$$


Multiply :
$$3{x^2} - {x^3} + x + 1$$ by $$(1+x)$$

Here we need to multiply $$3x^2-x^3+x+1$$ by $$(1+x)$$

$$(3x^2-x^3+x+1)(1+x)=3x^2-x^3+x+1+3x^3-x^4+x^2+x$$

                                                $$=4x^2+2x^3+2x+1-x^4$$

                                                $$=-x^4+2x^3+4x^2+2x+1$$


Multiply  $$ \left( 3p - q^ { 2 } \right) \left( 7 q + 4 p ^ { 4 } \right)$$

$$(3p-q^{2})(7q+4p^{4})$$

$$=3p(7q+4p^{4})-q^{2}(7q+4p^{4})$$

$$=21pq+12p^{5}-7q^{3}-4p^{4}q^{2}$$


If the polynomial $$6x^{4}+8x^{3}-5x^{2}+ax+b$$ is exactly divisible by the polynomial $$2x^{2}-5$$, then find the value of $$a$$ and $$b$$.

Given polynomial

$$p\left( x \right)=6{{x}^{4}}+8{{x}^{3}}-5{{x}^{2}}+ax+b$$

And $$g\left( x \right)=2{{x}^{2}}-5$$

So,

On divide $$p(x)$$ to $$g(x)$$ and we get,

Quotient $$=3{{x}^{2}}+4x+5$$

Reminder$$=\left( 20+a \right)x+\left( 25+b \right)$$


Given that,

The polynomial $$6{{x}^{4}}+8{{x}^{3}}-5{{x}^{2}}+ax+b$$ is exactly divisible by the polynomial $$2{{x}^{2}}-5$$.


Hence,

$$ \left( 20+a \right)x+\left( 25+b \right)=0 $$

$$ \Rightarrow 20+a=0 $$

$$ \Rightarrow a=-20 $$


And $$25+b=0$$

$$b=-25$$


Hence, this is the answer.


Multiple the binomials.
$$(a+3b)$$ and $$(x+5)$$

Given binomials are $$(a + 3b)$$ and $$(x + 5)$$

On multiplying them, we get:
$$(a + 3b) \times (x + 5)\\$$
$$=a(x + 5) + 3b(x + 5)\\$$
$$=ax + 5a + 3bx + 15b\\$$
$$=ax+3bx+5a+15b$$

Hence, $$(a + 3b) \times (x + 5)=ax + 3bx+5a+ 15b$$.


Form a cubic polynomial whose zeros are $$-3,-1$$ and $$2$$.

The given zeros are $$-3,-1$$ and $$2$$
So, the factors of the polynomial are $$(x-(-3)),(x-(-1))$$ and $$(x-2)$$

Then the polynomial
$$P(x)=(x-(-3))(x-(-1))(x-2)$$
          $$=(x+3)(x+1)(x-2)$$
          $$=(x^2+4x+3)(x-2)$$
          $$=x^3-2x^2+4x^2-8x+3x-6$$
          $$=x^3+2x^2-5x-6$$

Hence, the polynomial is $$x^3+2x^2-5x-6$$


Solve for $$x$$
$$\dfrac{1}{2(2x+3x)}+\dfrac{12}{7(3x-2x)}=\dfrac{1}{2}$$

We have,

$$ \dfrac{1}{2\left( 2x+3x \right)}+\dfrac{12}{7\left( 3x-2x \right)}=\dfrac{1}{2} $$

$$ \Rightarrow \dfrac{1}{10x}+\dfrac{12}{7x}=\dfrac{1}{2} $$

$$ \Rightarrow \dfrac{7+120}{70x}=\dfrac{1}{2} $$

$$ \Rightarrow \dfrac{127}{70x}=\dfrac{1}{2} $$

$$ \Rightarrow 254=70x $$

$$ \Rightarrow x=\dfrac{254}{70} $$

$$ \Rightarrow x=\dfrac{127}{35} $$


Hence, this is the answer.



Simplfy:
$${ ax }^{ 2 }y+{ bxy }^{ 2 }+cxyz$$

Simplify $$ax^2y+bxy^2+cxyz$$ on simplifying we get

$$=xy(ax+by)+cxyz$$

$$=xy[ax+by+cz]$$.


Find the product of the following pairs of monomials.
i) - 4p, 7p  ii) 4p$$^3$$, - 3p

i)  $$-4p,7p$$
The product of the above monomials is $$-4p\times 7p=-28{ p }^{ 2 }$$
ii)  $${ 4p }^{ 3 },-3p$$
The product of the above monomial is $$-4{ p }^{ 3 }\times 3p=-12{ p }^{ 4 }$$


solve the equation by cross multiplication
$$x+ay=b$$ 
$$ax-by=c$$

$$x+ay=b \\ ax-by=c $$

$$we\, \, can\, write\,$$

$$ x+ay-b=0 \\ ax-by-c=0 $$

$$then,\, by\, cross\, multiplication$$

$$ \dfrac { x }{ { a\left( { -c } \right) -\left( { -b } \right) \left( { -b } \right)  } } $$$$=\dfrac { y }{ { \left( { -b } \right) \left( a \right) -\left( { -c } \right) \left( 1 \right)  } } $$$$=\dfrac { 1 }{ { \left( { -b } \right) \left( 1 \right) -\left( a \right) \left( a \right)  } } $$

$$\dfrac { x }{ { -ac-{ b^{ 2 } } } } =\dfrac { y }{ { -ab+c } } =\dfrac { 1 }{ { -b-{ a^{ 2 } } } }$$

$$hence, \\ x=\dfrac { { ac+{ b^{ 2 } } } }{ { b+{ a^{ 2 } } } } ,\, \, \, \, y=\dfrac { { -ab+c } }{ { -b-{ a^{ 2 } } } } $$


Evaluate the following product

(1)     $$\left( { X }^{ 2 }+3 \right) \left( { X }^{ 2 }+4 \right) $$


2040821_1340117_ans_7d33976841da448fad9ac303b64f7c28.jpg


Divide and write the quotient and the remainder.
$$(a^{3}+5)\div (a^{3}+2)$$

$$quotient=1\\ remainder=1$$


select a suitable identity and find the following products
$$(ax^{2}+by^{2})(ax^{2}+by^{2})$$

$$\left( a {x}^{2} + b{y}^{2} \right) \left( a{x}^{2} + b{y}^{2} \right)= {\left( a{x}^{2} + b{y}^{2} \right)}^{2}\\$$
                                             $$= {\left( a{x}^{2} \right)}^{2} + {\left( b{y}^{2} \right)}^{2} + 2 \left( a{x}^{2} \right) \left( b{y}^{2} \right) \quad \left[ \text{Using identity: } {\left( a + b \right)}^{2} = {a}^{2} + {b}^{2} + 2ab \right]\\$$
                                              $$= {a}^{2} {x}^{4} + {b}^{2} {y}^{4} + 2ab{x}^{2}{y}^{2}$$


Prove that:
$$(a^{2}+b^{2})(a^{2}+b^{2})-(a^{2}-b^{2})(a^{2}-b^{2})=4{a}^{2}{b}^{2}$$

$$\left({a}^{2}+{b}^{2}\right)\left({a}^{2}+{b}^{2}\right)-\left({a}^{2}-{b}^{2}\right)\left({a}^{2}-{b}^{2}\right)$$
$$={\left({a}^{2}+{b}^{2}\right)}^{2}-{\left({a}^{2}-{b}^{2}\right)}^{2}$$
$$=\left({a}^{2}+{b}^{2}+{a}^{2}-{b}^{2}\right)\left({a}^{2}+{b}^{2}-{a}^{2}+{b}^{2}\right)$$
$$=\left(2{a}^{2}\right)\left(2{b}^{2}\right)$$
$$=4{a}^{2}{b}^{2}$$
Hence proved


Multiply the binomials
$$(2pq+3q^{2})$$ and $$(2pq-2q^{2})$$

$$\left(2pq+3{q}^{2}\right)\left(2pq-2{q}^{2}\right)$$
$$=2pq\left(2pq-2{q}^{2}\right)+3{q}^{2}\left(2pq-2{q}^{2}\right)$$
$$=4{p}^{2}{q}^{2}-4p{q}^{3}+6p{q}^{3}-6{q}^{4}$$
$$=4{p}^{2}{q}^{2}+2p{q}^{3}-6{q}^{4}$$


Expand:$${ \left(x-\dfrac { 2 }{ 3 } y\right)}^{ 3 }$$

$${\left(x-\dfrac{2y}{3}\right)}^{3}$$ is of the form $${\left(a-b\right)}^{3}={a}^{3}-{b}^{3}-3ab\left(a-b\right)$$ where $$a=x,b=\dfrac{2y}{3}$$

$$={\left(x\right)}^{3}-{\left(\dfrac{2y}{3}\right)}^{3}-3\left(x\right)\left(\dfrac{2y}{3}\right)\left(x-\dfrac{2y}{3}\right)$$

$$={x}^{3}-\dfrac{8y^3}{27}-2xy\left(x-\dfrac{2y}{3}\right)$$

$$={x}^{3}-\dfrac{8y^3}{27}-2{x}^{2}y+\dfrac{4x{y}^{2}}{3}$$

$$=\dfrac{1}{27}\left(27{x}^{3}-8{y}^{3}-54{x}^{2}y+36x{y}^{2}\right)$$


Find the product of $$\left(7x+3y\right)\left(7x-y\right)$$

given, $$\left(7x+3y\right)\left(7x-y\right)$$

$$=7x\left(7x-y\right)+3y\left(7x-y\right)$$

$$=49{x}^{2}-7xy+21xy-3{y}^{2}$$

$$=49{x}^{2}+14xy-3{y}^{2}$$


Find cubic polynomial whose zeroes are 3, $$\dfrac { 1 }{ 2 } $$ & $$-1$$

Given: zeroes of a cubic polynomial $$3,\dfrac{1}{2},-1$$

By factor theorem,

$$\left(x-3\right)\left(x-\dfrac{1}{2}\right)\left(x+1\right)$$ are the factors of the cubic polynomial.

We know that $$\left(x+a\right)\left(x+b\right)={x}^{2}+\left(a+b\right)x+ab$$ 

Using the factors $$\left(x-3\right)\left(x-\dfrac{1}{2}\right)$$ we have as

$${x}^{2}+\left(-3-\dfrac{1}{2}\right)x+\dfrac{3}{2}$$

$$={x}^{2}-\dfrac{-7}{2}x+\dfrac{3}{2}$$

Again $$\left(x+1\right)\left({x}^{2}-\dfrac{7}{2}x+\dfrac{3}{2}\right)={x}^{3}-\dfrac{7{x}^{2}}{2}+\dfrac{3x}{2}+{x}^{2}-\dfrac{7}{2}x+\dfrac{3}{2}$$

$$={x}^{3}+\dfrac{2{x}^{2}-7{x}^{2}}{2}+\dfrac{3x-7x}{2}+\dfrac{3}{2}$$

$$={x}^{3}-\dfrac{5{x}^{2}}{2}-2x+\dfrac{3}{2}$$

$$=2{x}^{3}-5{x}^{2}-4x+3$$ is the required cubic polynomial.


Evaluate: $$(x+2y)(-3x-y)-(x+y)(x-y)+(x-2y)(-2x+y)$$

$$\left(x+2y\right)\left(-3x-y\right)-\left(x+y\right)\left(x-y\right)+\left(x-2y\right)\left(-2x+y\right)$$
$$=-3{x}^{2}-xy-6xy-2{y}^{2}-{x}^{2}+{y}^{2}-2{x}^{2}+xy+4xy-2{y}^{2}$$
$$=-6{x}^{2}-3{y}^{2}-2xy$$
$$=-\left(6{x}^{2}+2xy-3{y}^{2}\right)$$


Simplify:$${\left({l}^{2}+{m}^{2}\right)}^{2}+{\left({l}^{2}-{m}^{2}\right)}^{2}$$

$${\left({l}^{2}+{m}^{2}\right)}^{2}+{\left({l}^{2}-{m}^{2}\right)}^{2}$$

$$={l}^{4}+{m}^{4}+2{l}^{2}{m}^{2}+{l}^{4}+{m}^{4}-2{l}^{2}{m}^{2}$$

$$={l}^{4}+{m}^{4}+{l}^{4}+{m}^{4}$$

$$=2\left({l}^{4}+{m}^{4}\right)$$


Simplify: $$2{p}^{3}-3{p}^{2}+4p-5-6{p}^{3}+2{p}^{2}-8p-2+6p+8$$

Given, $$2{p}^{3}-3{p}^{2}+4p-5-6{p}^{3}+2{p}^{2}-8p-2+6p+8$$

$$=2{p}^{3}-6{p}^{3}-3{p}^{2}+2{p}^{2}+4p-8p+6p+8-5-2$$    (combining like terms)

$$=-4{p}^{3}-{p}^{2}+2p+1$$


Find the product of $$2x$$ and $$\left(x+y\right)$$

$$2x\left(x+y\right)$$

$$=2{x}.x+2x.y$$

$$=2{x}^{2}+2xy$$


Write the base and the exponent in each case. Also, write the term in the expanded from.
$$\left( 7x \right) ^{ 2 }$$


1306396_1436552_ans_784753611c244973b615eadca2fcef28.jpeg


Divide $$2a^2+6ab$$ by $$a+3b$$.

If we divide $$2a^2+6ab$$ by $$a+3b$$ then we've,
$$\dfrac{2a^2+6ab}{a+3b}$$
$$=\dfrac{2a(a+3b)}{a+3b}$$
$$=2a$$.
So quotient is $$2a$$ and remainder is $$0$$.


Solve : $$\dfrac { { x }^{ 2 }-5x-24 }{ (x+3)(x+8) } \times\dfrac { { x }^{ 2 }-64 }{ { (x-8) }^{ 2 } } $$

$$\dfrac{{x}^{2}-5x-24}{\left(x+3\right)\left(x+8\right)}\times\dfrac{{x}^{2}-64}{{\left(x-8\right)}^{2}}$$
$$=\dfrac{{x}^{2}-8x+3x-24}{\left(x+3\right)\left(x+8\right)}\times\dfrac{\left(x-8\right)\left(x+8\right)}{{\left(x-8\right)}^{2}}$$
$$=\dfrac{x\left(x-8\right)+3\left(x-8\right)}{\left(x+3\right)\left(x+8\right)}\times\dfrac{\left(x+8\right)}{\left(x-8\right)}$$
$$=\dfrac{\left(x-8\right)\left(x+3\right)}{\left(x+3\right)\left(x+8\right)}\times\dfrac{\left(x+8\right)}{\left(x-8\right)}$$
$$=1$$


Simplify: 
$$\left( 1.5x-4y \right) \left( 1.5x+4y+3 \right) -4.5x$$


1305769_1412371_ans_f184a425fa064a19b425df48f17db9bf.jpeg


Evaluate:$$\left( x+y \right) \left( 2x+y \right) \left( 2x-y \right) \left( x-y \right) $$

$$\left(x+y\right)\left(2x+y\right)\left(2x-y\right)\left(x-y\right)$$
$$=\left(x+y\right)\left(x-y\right)\left(2x+y\right)\left(2x-y\right)$$
$$=\left({x}^{2}-{y}^{2}\right)\left(4{x}^{2}-{y}^{2}\right)$$ using $$\left(a+b\right)\left(a-b\right)={a}^{2}-{b}^{2}$$
$$={x}^{2}\left(4{x}^{2}-{y}^{2}\right)-{y}^{2}\left(4{x}^{2}-{y}^{2}\right)$$
$$=4{x}^{4}-{x}^{2}{y}^{2}-4{x}^{2}{y}^{2}+{y}^{4}$$
$$=4{x}^{4}-5{x}^{2}{y}^{2}+{y}^{4}$$


Solve:
$$\dfrac{2}{5x}-\dfrac{5}{3x}=\dfrac{1}{15}$$

Given $$\dfrac{2}{5 x}-\dfrac{5}{3 x}=\dfrac{1}{15}$$
$$\implies \dfrac{2}{5}-\dfrac{5}{3}=\dfrac{x}{15}$$
$$\implies \dfrac{6-25}{15}=\dfrac{x}{15}$$
$$\implies \dfrac{-19}{15}=\dfrac{x}{15}$$
$$\implies x=-19$$


Solve:
$$\dfrac{x+2}{6}-\left(\dfrac{11-x}{3}-\dfrac{1}{4}\right)=\dfrac{3x-4}{12}$$

Given $$\dfrac{x+2}{6}-\left(\dfrac{11-x}{3}-\dfrac{1}{4}\right)=\dfrac{3x-4}{12}$$
$$\implies \dfrac{2{x}+4-44+4{x}+3}{12}=\dfrac{3 x-4}{12}$$
$$\implies \dfrac{6 x-37}{12}=\dfrac{3 x-4}{12}$$
$$\implies 6{x}-37=3{x}-4$$
$$\implies 3 x=33\implies x=11$$


Simplify 
$$\left( x+y \right) \left( 2x+y \right) +\left( x+2y \right) \left( x-y \right) $$


1305774_1416170_ans_4fe1d26341ad48a48582b3c286bce2d7.jpeg


Multiply : $$3ab\times \left( { 5a }^{ 2 }+{ 4b }^{ 2 } \right) $$

$$3ab\times\left(5{a}^{2}+4{b}^{2}\right)$$
$$=(3ab\times 5a^2)+(3ab\times 4b^2)$$
$$=15{a}^{3}b+12a{b}^{3}$$


Prove that : 
$$ \left ( \dfrac{x^{a}}{x^{b}} \right )^{c}\times \left ( \dfrac{x^{b}}{x^{c}} \right )^{a}\times \left ( \dfrac{x^{c}}{x^{a}} \right )^{b} = 1 $$ 

Given,

$$\left (\dfrac{x^a}{x^b}  \right )^c\times \left (\dfrac{x^b}{x^c}  \right )^a\times \left (\dfrac{x^c}{x^a}  \right )^b$$

$$=\left (x^{a-b}  \right )^c\times \left ( x^{b-c} \right )^a\times \left ( x^{c-a} \right )^b$$

$$=x^{ac-bc}\times x^{ab-bc}\times x^{bc-ab}$$

$$=x^{ac-bc+ab-bc+bc-ab}$$

$$=x^0$$

$$=1$$    $$[hence \, proved]$$


Find the product of $$(7x+5) (2x-3)$$


1312313_1538160_ans_45ff17894a304bbab9993d4a8b9aed93.jpeg


Evaluate the following using identities
$$117\times 83$$

Given,

$$117 \times 83$$

$$=(100+17)(100-17)$$

 By using $$(a+b)(a-b)=a^2-b^2$$

$$=100^2-17^2$$

$$=10000-289=9711$$


Find the following product:
$$\left( \cfrac { 3 }{ x } -\cfrac { 5 }{ y }  \right) \left( \cfrac { 9 }{ { x }^{ 2 } } +\cfrac { 25 }{ { y }^{ 2 } } +\cfrac { 15 }{ xy }  \right) $$

Formula,

$$a^3-b^3=(a-b)(a^2+ab+b^2)$$

$$a^3+b^3=(a+b)(a^2-ab+b^2)$$

Given,

$$\left ( \dfrac{3}{x}-\dfrac{5}{y} \right )\left ( \dfrac{9}{x^2}-\dfrac{15}{xy}+\dfrac{25}{y^2} \right )$$

$$=\left (\dfrac{3}{x}\right )^3-\left (\dfrac{5}{y}\right )^3$$

$$=\dfrac{27}{x^3}-\dfrac{125}{y^3}$$ 


Find the product of the following:
$$\left( \cfrac { 3 }{ x } -2{ x }^{ 2 } \right) \left( \cfrac { 9 }{ { x }^{ 2 } } +4{ x }^{ 4 }-6x \right) $$

Formula,

$$a^3-b^3=(a-b)(a^2+ab+b^2)$$

$$a^3+b^3=(a+b)(a^2-ab+b^2)$$

Given,

$$\left (\dfrac{3}{x}-2x^2 \right )\left (\dfrac{9}{x^2}+4x^4-6x \right )$$

$$=\left (\dfrac{3}{x}\right )^3-(2x^2)^3$$

$$=\dfrac{27}{x^3}-8x^6$$ 


Find the product of the following:
$$(1+x)(1-x+{x}^{2})$$

Given,

$$\left(1+x\right)\left(1-x+x^2\right)$$

$$=1\cdot \:1+1\cdot \left(-x\right)+1\cdot \:x^2+x\cdot \:1+x\left(-x\right)+xx^2$$

$$=1\cdot \:1-1\cdot \:x+1\cdot \:x^2+1\cdot \:x-xx+x^2x$$

$$=x^3+1$$


Find the product of the following:
$$(1-x)(1+x+{x}^{2})$$

Given,

$$\left(1-x\right)\left(1+x+x^2\right)$$

$$=1\cdot \:1+1\cdot \:x+1\cdot \:x^2+\left(-x\right)\cdot \:1+\left(-x\right)x+\left(-x\right)x^2$$

$$=1\cdot \:1+1\cdot \:x+1\cdot \:x^2-1\cdot \:x-xx-x^2x$$

$$=1-x^3$$


Evaluate the following using identities
$$991\times 1009$$

Given,

$$991 \times 1009$$

$$=(1000-9)(1000+9)$$

By using $$(a+b)(a-b)=a^2-b^2$$

$$=1000^2-9^2$$

$$=1000000-81=999919$$


Evaluate the following using identities:
$$(2x+y)(2x-y)$$

Given,

$$(2x+y)(2x-y)$$

formula: $$(a+b)(a-b)=a^2-b^2$$

$$=(2x)^2-y^2$$

$$=4x^2-y^2$$


Find the product of the following:
$$\left( \cfrac { 2 }{ x } +3x \right) \left( \cfrac { 4 }{ { x }^{ 2 } } +9{ x }^{ 2 }-6 \right) $$

Formula,

$$a^3-b^3=(a-b)(a^2+ab+b^2)$$

$$a^3+b^3=(a+b)(a^2-ab+b^2)$$

Given,

$$\left (\dfrac{2}{x}+3x \right )\left (\dfrac{4}{x^2}-6+9x^2 \right )$$

$$=(3x)^3+\left (\dfrac{2}{x}\right )^3$$

$$=27x^3+\dfrac{8}{x^3}$$ 


Find the product of the following:
$$\left( 3+\cfrac { 5 }{ x }  \right) \left( 9-\cfrac { 15 }{ x } +\cfrac { 25 }{ { x }^{ 2 } }  \right) $$

Formula,

$$a^3-b^3=(a-b)(a^2+ab+b^2)$$

$$a^3+b^3=(a+b)(a^2-ab+b^2)$$

Given,

$$\left (3+\dfrac{5}{x} \right )\left (9-\dfrac{15}{x}+\dfrac{25}{x^2} \right )$$

$$=(3)^3+\left (\dfrac{5}{x}\right )^3$$

$$=27+\dfrac{125}{x^3}$$ 


Write the following in the expanded form:
$${({a}^{2}+{b}^{2}+{c}^{2})}^{2}$$

Given,

$$(a^2+b^2+c^2)^2$$

Formula,

$$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$$

$$\Rightarrow (a^2+b^2+c^2)^2=(a^2)^2+(b^2)^2+(c^2)^2+2(a^2b^2)+2(b^2c^2)+2(c^2a^2)$$

$$=a^4+b^4+c^4+2a^2b^2+2c^2b^2+2a^2c^2$$



If the product of $$\left(\dfrac{7}{9}ab^2\right)\times \left(\dfrac{15}{7}ac^2b\right)\times \left(-\dfrac{3}{5}a^2c\right)$$ is $$\dfrac{-1}xa^4b^3c^3$$, then what is the value of $$x$$?


1510159_1673015_ans_0e944c19272e428ea3750a23d94d360f.jpg


If the product of $$\left(-\dfrac{2}{7}a^4\right)\times \left(-\dfrac{3}{4}a^2b\right)\times \left(-\dfrac{14}{5}b^2\right)=\dfrac{-3}{z}a^6b^3$$, then value of $$z$$ is


1510158_1673012_ans_342d237910b34955becb838f6ec55f07.jpg


If the product of $$(-5a)\times (-10a^2)\times (-2a^3)=-100a^b$$, then what is the value of $$b?$$


1510156_1673010_ans_eb0de303068a439c91671c46e35cf7f7.jpg


If the product of $$(7ab)\times (-5ab^2c)\times (6abc^2)=-la^3b^4c^3$$, then what is the value of $$l?$$


1510155_1673009_ans_b63414aed6064d2e9b0faa299301216d.jpg


If $$x=3$$ and $$y=-1$$, find the values of the following using in identity:
$$\left( \cfrac { 5 }{ x } +5x \right) \left( \cfrac { 25 }{ { x }^{ 2 } } -25+25{ x }^{ 2 } \right) $$

Formula,

$$a^3-b^3=(a-b)(a^2+ab+b^2)$$

$$a^3+b^3=(a+b)(a^2-ab+b^2)$$

Given,

$$\left ( \dfrac{5}{x}+5x \right )\left ( \dfrac{25}{x^2}+25x^2-25 \right )$$

$$=\dfrac{125}{x^3}+125x^3$$

$$=\dfrac{125}{3^3}+125(3)^3$$

$$=\dfrac{91250}{27}$$


Find the product of the following:
$$({x}^{2}-1)({x}^{4}+{x}^{2}+1)$$

Given,

$$\left(x^2-1\right)\left(x^4+x^2+1\right)$$

$$=x^2x^4+x^2x^2+x^2\cdot \:1+\left(-1\right)x^4+\left(-1\right)x^2+\left(-1\right)\cdot \:1$$

$$=x^4x^2+x^2x^2+1\cdot \:x^2-1\cdot \:x^4-1\cdot \:x^2-1\cdot \:1$$

$$=x^6-1$$


If $$x=3$$ and $$y=-1$$, find the values of the following using in identity:
$$\left( \cfrac { x }{ 4 } -\cfrac { y }{ 3 }  \right) \left( \cfrac { { x }^{ 2 } }{ 16 } +\cfrac { xy }{ 12 } +\cfrac { { y }^{ 2 } }{ 9 }  \right) $$

Formula,

$$a^3-b^3=(a-b)(a^2+ab+b^2)$$

$$a^3+b^3=(a+b)(a^2-ab+b^2)$$

Given,

$$\left ( \dfrac{x}{4}-\dfrac{y}{3} \right )\left ( \dfrac{x^2}{64}+\dfrac{y^2}{9}+\dfrac{xy}{12} \right )$$

$$=\dfrac{x^3}{64}-\dfrac{y^3}{27}$$

$$=\dfrac{3^3}{64}-\dfrac{(-1)^3}{27}$$

$$=\dfrac{665}{1728}$$


Find the product of the following:
$$({x}^{3}+1)({x}^{6}-{x}^{3}+1)$$

Given,

$$\left(x^3+1\right)\left(x^6-x^3+1\right)$$

$$=x^3x^6+x^3\left(-x^3\right)+x^3\cdot \:1+1\cdot \:x^6+1\cdot \left(-x^3\right)+1\cdot \:1$$

$$=x^6x^3-x^3x^3+1\cdot \:x^3+1\cdot \:x^6-1\cdot \:x^3+1\cdot \:1$$

$$=x^9+1$$


If the product of $$(-4x^2)\times (-6xy^2)\times (-3yz^2)=-kx^3y^3z^2$$, then value of $$k?$$ 


1510157_1673011_ans_5145a9c3962040129865989f6f3013d1.jpg


If $$x=3$$ and $$y=-1$$, find the values of the following using in identity:
$$\left( \cfrac { x }{ 7 } -\cfrac { y }{ 3 }  \right) \left( \cfrac { { x }^{ 2 } }{ 49 } +\cfrac { { x }^{ 2 } }{ 9 } +\cfrac { xy }{ 21 }  \right) $$

Formula,

$$a^3-b^3=(a-b)(a^2+ab+b^2)$$

$$a^3+b^3=(a+b)(a^2-ab+b^2)$$

Given,

$$\left ( \dfrac{x}{7}-\dfrac{y}{3} \right )\left ( \dfrac{x^2}{49}+\dfrac{x^2}{9}+\dfrac{xy}{21} \right )$$

$$=\dfrac{x^3}{343}-\dfrac{y^3}{27}$$

$$=\dfrac{3^3}{343}-\dfrac{(-1)^3}{27}$$

$$=\dfrac{386}{9261}$$


Express the following product as a monomial and find the value of A. Also, verify the result in the case of $$x=1$$.
$$(3x)\times (4x)\times (-5x)=-Ax^3$$.

We have to find the product of the expression in order to express it as a monomial.
Now, We have $$(3x)\times(4x)\times(-5x)$$

$$=[(3\times4\times(-5)]\times(x \times x\times x)$$

$$=-60\times x^{(1+1+1)}\quad[\because a^m a^n=a^{m+n}]$$

$$=-60x^3$$

Therefore, Value of $$A=60$$.

Verification for $$x=1$$:

LHS$$=(3x)\times(4x)\times(-5x)$$

$$=3(1)\times4(1)\times(-5)(1)$$

$$=3\times4\times(-5)$$

$$=-60$$

RHS$$=-60x^3$$

$$=-60(1)^3$$

$$=-60$$

$$\therefore$$ LHS$$=$$RHS

Hence verified.


If the product of $$\left(\dfrac{4}{3}u^2vw\right)\times \left(-5uvw^2\right)\times \left(\dfrac{1}{3}v^2wu\right)$$ is $$\dfrac{-20}{a}u^4v^4w^4$$, then what is the value of $$a$$?


1510160_1673018_ans_344774e1ef944c8d962e5f533d6a96b1.jpg


If the product of $$(0.5x)\times \left(\dfrac{1}{3}xy^2z^4\right)\times (24x^2yz)$$ is $$cx^4y^3z^5$$, then the value of $$c$$ is 


1510161_1673020_ans_006901a0fa794e3eb3618456c0720d94.jpg


Write down the product of $$-8x^2y^6$$ and $$-20xy$$. Verify the product for $$x=2.5, y=1$$.

If we multiply $$(-8x^2y^6)$$ to $$ (-20xy)$$ then we get,
$$(-8x^2y^6)$$$$\times  (-20xy)$$
$$=(-20)\times (-8)\times x^3\times y^7$$
$$=160x^3y^7$$.
Now if $$x=2.5=\dfrac{5}{2}$$ and $$y=1$$ then we get,
$$160\times \dfrac{5^3}{2^3}\times 1^7$$
$$=160\times \dfrac{125}{8}\times 1$$
$$=20\times 125$$
$$=5,000$$.


Express the following product as a monomial and verify the result in case for $$x=1$$.
$$(x^2)^3\times (2x)\times (-4x)\times (5)$$.

Now,
$$(x^2)^3\times (2x)\times (-4x)\times (5)$$
$$=x^6\times (2x)\times (-4x)\times (5)$$
$$=(2\times -4\times 5)\times x^6\times x\times x$$
$$=-40x^8$$.
Now for $$x=1$$ we get,
$$-40\times (1)^8$$
$$=-40$$.


If the product of $$(2.3xy)\times (0.1x)\times (0.16)$$ is $$0.036bx^2y$$, then what is the value of $$b$$?


1510163_1673022_ans_a4ffe5afdb334c17828eb1b3b02763ca.jpg


Evaluate $$(3.2x^6y^3)\times (2.1x^2y^2)$$ when $$x=1$$ and $$y=0.5$$.

Value of $$(3.2x^6y^3)\times (2.1x^2y^2)$$ when $$x=1$$ and $$y=0.5$$ is given as
$$(3.2x^6y^3)\times (2.1x^2y^2)=(3.2\times2.1 x^8y^5)$$
$$=3.2\times 2.1\times 1^8\times 0(0.5)^5$$     (on putting $$x=1$$ and $$y=0.5$$)
$$=0.21$$


Evaluate $$(-8x^2y^6)\times (-20xy)$$ for $$x=2.5$$ and $$y=1$$.


1511568_1673031_ans_af340adf89334ab6a53e5e6021ffb848.jpg


Multiply $$(2x^2y^2-5xy^2)$$ by $$(x^2-y^2)$$.

$$\textbf{Step-1: Apply the concept of multiplication}$$
                 $$\text{We have to multiply}$$ $$(2x^2y^2-5xy^2)$$ $$\text{by}$$ $$(x^2-y^2)$$
                 $$= 2x^2y^2(x^2 - y^2)- 5xy^2(x^2-y^2)$$
                 $$= 2x^4y^2-2x^2y^4- 5x^3y^2+ 5xy^4$$
$$\textbf{Hence, answer is }\boldsymbol{2x^4y^2 - 2x^2y^4 - 5x^3y^2 + 5xy^4}$$


Find the following product.
$$0.1y(0.1x^5+0.1y)$$

$$\textbf{Step-1: Apply multiplication rule}$$
                 $$\text{We have,}$$
                 $$0.1y\times (0.1x^5+0.1y)$$$$=0.1y\times 0.1x^5+0.1y\times 0.1y$$
                                                        $$= 0.01x^5y+0.01y^2$$

$$\textbf{Hence, answer}$$


Evaluate the following when $$x=2, y=-1$$.
$$(2xy)\times \left(\dfrac{x^2y}{4}\right)\times (x^2)\times (y^2)$$.


1511579_1673037_ans_8955ce4fa77b4e4e931573811a6677f5.jpg


Evaluate the following when $$x=y=-1$$.
$$\left(\dfrac{3}{5}x^2y\right)\times \left(-\dfrac{15}{4}xy^2\right)\times \left(\dfrac{7}{9}x^2y^2\right)$$.


1511581_1673038_ans_05f67836d97b43f58e4d2ac96c05d09f.jpg


Find the following product.
$$2a^3(3a+5b)$$.

$$\textbf{Step-1: Apply multiplication rule}$$
                 $$\text{We have,}$$
                 $$2a^3(3a+5b)$$$$=2a^3\times 3a+2a^3\times 5b$$
                                        $$= 6a^4+10a^3b$$
$$\textbf{Hence, answer}$$


Simplify the following using the identity.
$$1.73\times 1.73-0.27\times 0.27$$.


1514413_1673142_ans_f5587bc8f5314e1a9bb47f3f5c86c9ea.jpg


Find the following product.
$$(x+4)(x+7)$$.

$$\textbf {Step1- Find  the product of given binomial expression}$$
               $$\text{Consider, }$$
               $$(x+4)(x+7)$$$$=x(x+7)+4(x+7)$$
                                         $$= x^2+ 7x+4x+28$$
                                         $$=x^2+11x+28$$

$$\textbf{Hence, the required product =}$$$$\boldsymbol{x^2+11x+28}$$


Find each of the following products:
$$(x^{4}+(1/x^{4})\times (x+(1/x))$$

Given $$(x^{4}+(1/x^{4})\times (x+(1/x))$$
To find the product of given expression we have to use horizontal method.
In that we have to multiply each term of one expression with each term of another
Expression so by multiplying we get,
$$(x^{4}+(1/x^{4})\times (x+(1/x))$$
$$\Rightarrow x^{4}(x+(1/x))+(1/x^{4})(x+(1/x))$$
$$\Rightarrow x^{5}+x^{3}+(1/x^{3})+(1/x^{5})$$


Simplify the following using the identity.
$$178\times 178-22\times 22$$.


1514411_1673140_ans_371cf6e402f346c38ab38c42467654df.jpg


Simplify the following using the identity.
$$\dfrac{198\times 198-102\times 102}{96}$$.


1514412_1673141_ans_7c4f3c51d08e4bf7b5412a74afc1c179.jpg


Given that $$ x^{2}-3 x+1=0, $$ then the value of the expression $$ y=x^{9}+x^{7}+x^{9}+x^{-7} $$ is divisible by prime number.

 The given equation is $$ x^{2}-3 x+1=0 $$

$$ x+\dfrac{1}{x}=3 $$

$$ \therefore x^{2}+\dfrac{1}{x^{2}}=7 \Rightarrow x^{4}+\dfrac{1}{x^{4}}=47 \Rightarrow x^{8}+\dfrac{1}{x^{8}}=(47)^{2}-2 $$

$$ \therefore x^{8}+x^{-8} =2207 $$

  Now 

$$ E =x^{9}+x^{7}+x^{-9}+x^{-7} $$

$$= x^{8}\left(x+\dfrac{1}{x}\right)+x^{-9}+x^{-7}=x^{8}\left(x+\dfrac{1}{x}\right)+x^{-8}\left(x+\dfrac{1}{x}\right) $$

$$ E=\left(x+\dfrac{1}{x}\right)\left(x^{8}+x^{-8}\right) $$

Substitute the value of $$ x^{8}+x^{-8}=2207 $$

 from (1) and $$ x+\dfrac{1}{x}=3 $$

$$ E=(3)(2207)=6621 $$


Find the following product.
$$(2x^2-3)(2x^2+5)$$.


2184815_1673255_ans_5265aa845fbe405bbe71cb391b35c396.jpeg


Show that if $$x^{2}+y^{2}=2z^{2}$$, where $$x, y, z$$ integers then $$2x=r(l^{2}+2lk -k^{2}), 2y=r(k^{2}+2lk-l^{2}), 2z=r(l^{2}+k^{2})$$ where $$r, l,$$ and $$k$$ are integers.


1579682_1747399_ans_d3ab67696b0a49e7ac62f779ac6579f0.jpg


Simplify the following using the identity.
$$\dfrac{8.63\times 8.63-1.37\times 1.37}{0.726}$$.


1514414_1673143_ans_32054dff997b4efe9b44a345fdafed20.jpg


Find the product of $$\dfrac{-1}{2}x^2,\  - \dfrac{3}{5}xy,\ \dfrac{2}{3}yz$$ and $$\dfrac{5}{7}xyz$$ 

$$\Big(-\dfrac{1}{2}x^2\Big) \times \Big(-\dfrac{3}{5}xy\Big) \times \Big(\dfrac{2}{3}yz\Big) \times \Big(\dfrac{5}{7}xyz\Big)$$

       $$=\Big(-\dfrac{1}{2}\Big) \times \Big(-\dfrac{3}{5}\Big) \times \Big(\dfrac{2}{3}\Big) \times \Big(\dfrac{5}{7}\Big) \times x^2 \times xy \times yz \times xyz$$

       $$=\dfrac{1}{7}x^4y^3z^2$$


Find product of the following expressions:
$$(x^{4}+y^{4}),  (x^{2}-y^{2})$$

Given: $$(x^{4}+y^{4}), (x^{2}-y^{2})$$

To find the product of the given expression we have to use the horizontal method.
In that, we have to multiply each term of one expression with each term of another expression.

So by multiplying we get,

$$(x^{4}+y^{4})\times (x^{2}-y^{2})$$

$$\Rightarrow x^{4}(x^{2}-y^{2})+y^{4}(x^{2}-y^{2})$$

$$\Rightarrow x^{6}-x^{4}y^{2}+x^{2}y^{4}-y^{6}$$


Find the following product:
$$8a^2(2a+5b)$$

By distributive law of multiplication over addition, we have:
$$p\times (q+r)=(p\times q)+(p\times r)$$
where $$p, q$$ and $$r$$ be three monomials.

$$\therefore8a^2(2a+5b)$$
$$=(8a^2\times 2a)+(8a^2\times 5b)$$
$$=(16a^{2+1}+40a^2b) \hspace{1cm}[\because a^m \times a^n=a^{m+n}]$$
$$=(16a^3+40a^2b)$$


Find the following product:
$$9x^2(5x+7)$$

By distributive law of multiplication over addition, we have:
$$p\times (q+r)=(p\times q)+(p\times r)$$
where $$p, q$$ and $$r$$ be three monomials.

$$\therefore 9x^2(5x+7)$$
$$=(9x^2\times 5x)+(9x^2\times 7)$$
$$=(45x^{2+1}+63x^2)$$          $$[\because a^m \times a^n=a^{m+n}]$$
$$=(45x^3+63x^2)$$


Find the following product:
$$\dfrac{2}{3}x^2y \times \dfrac{3}{5}xy^2$$

We know that,
The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part in the product of two monomials is equal to the product of the variables in the given monomials. 

$$\therefore\dfrac{2}{3}x^2y\times\dfrac{3}{5}xy^2$$
$$=\left(\dfrac{2}{3}\times \dfrac{3}{5}\right)\times (x^2 \times x)\times (y^2 \times y)$$
$$=\left(\dfrac{2\times 3}{3\times 5}\right)\times (x^{2+1})\times (y^{1+2})$$ $$\hspace{1cm}[\because a^{m}\times a^{n}=a^{m+n}]$$
$$=\left(\dfrac{2}{5}\right)\times (x^{3})\times (y^{3})$$
$$=\dfrac{2}{5}x^3 y^3$$


Find the following product:
$$(-4ab) \times (-3a^2bc)$$

We know that,
The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part in the product of two monomials is equal to the product of the variables in the given monomials. 

$$\therefore(-4ab)\times(-3a^2bc)$$
$$=((-4)\times (-3))\times (a\times b\times a^2\times b\times c)$$
$$=((-4)\times (-3))\times (a\times a^2) \times (b\times b)\times c$$
$$=(12)\times (a^{1+2})\times (b^{1+1})\times c\hspace{1cm}  [\because a^m \times a^n =a^{m+n}]$$
$$=(12)\times (a^3)\times (b^2)\times c$$
$$=12\ a^{3}b^2 c$$

Hence, the product $$=12\ a^{3}b^2 c$$


Find the following product:
$$4a(3a+7b)$$

By distributive law of multiplication over addition, we have:
$$p\times (q+r)=(p\times q)+(p\times r)$$
where $$p, q$$ and $$r$$ be three monomials.

$$\therefore\ 4a(3a+7b)$$
$$=(4a\times 3a)+(4a\times 7b)$$
$$=(12a^{1+1}+28ab)$$     $$[\because a^m \times a^n=a^{m+n}]$$
$$=(12a^2+28ab)$$

Hence, $$4a(3a+7b)=12a^2+28ab$$.


Find the product:
$$-6x^3 \times 5x^2$$

We know that,
The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part in the product of two monomials is equal to the product of the variables in the given monomials. 

$$\therefore-6x^3\times5x^2$$
$$=(-6\times 5)\times (x^3 \times x^2)$$
$$=(-30)\times (x^{3+2})\hspace{1cm}  [\because a^m \times a^n =a^{m+n}]$$
$$=(-30)\times (x^5)$$
$$=-30\ x^{5}$$


Find the following product:
$$5a(6a-3b)$$

By distributive law of multiplication over subtraction, we have:
$$p\times (q-r)=(p\times q)-(p\times r)$$
where $$p, q$$ and $$r$$ be three monomials.

$$\therefore 5a(6a-3b)$$
$$=(5a\times 6a)-(5a\times 3b)$$
$$=(30a^{1+1}-15ab)$$     $$[\because a^m \times a^n=a^{m+n}]$$
$$=(30a^2-15ab)$$

Hence, the product is $$(30a^2-15ab)$$


Find the product:
$$3a^2 \times 8a^4$$

The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part is equal to the product of the variables in the given monomials. Hence,

$$3a^2\times8a^4=(3\times 8)\times (a^2 \times a^4)$$
                   $$=(24)\times (a^{2+4})$$  $$\hspace{1cm}[\because a^m \times a^n =a^{m+n}]$$
                   $$=(24)\times (a^6)$$
                   $$=24 a^{6}$$


Find the following product:
$$(2a^2b^3) \times (-3a^3b)$$

Given: $$(2a^2b^3) \times (-3a^3b)$$
$$=(2\times -3)\times (a^2\times a^3) \times (b^3\times b)$$
$$=(-6)\times (a^{2+3})\times (b^{3+1})...  [\because a^m \times a^n =a^{m+n}]$$
$$=(-6)\times (a^5)\times (b^4)$$
$$=-6\ a^{5}b^4$$



Find the following product:
$$ab(a^2-b^2)$$

By distributive law of multiplication over subtraction, we have:
$$p\times (q-r)=(p\times q)-(p\times r)$$
where $$p, q$$ and $$r$$ be three monomials.

$$\therefore ab(a^2-b^2)$$
$$=(ab\times a^2)-(ab\times b^2)$$
$$={(a^{1+2}b)-(ab^{1+2})}$$    $$ [ \because a^m \times a^n=a^{m+n}]$$
$$=(a^3b-ab^3)$$


Simplify:  $$ (- 4a 8a)$$.

$$– (- 4a – 8a)$$,
The simplified form of the expression $$– (- 4a – 8a)$$ is calculated as below,
$$– (- 4a – 8a) = - (- 12a)$$
We get,
$$= 12a$$.


Find the following product:
$$\dfrac{-13}5ab^2c \times \dfrac73a^2 bc^2$$

We know that,
The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part is equal to the product of the variables in the given monomials. 

$$\therefore\dfrac{-13}5ab^2c\times \dfrac73a^2bc^2$$
$$=\left(\dfrac{-13}5\right)\times \left(\dfrac73\right)\times (a \times a^2)\times (b^2 \times b)\times (c\times c^2)$$
$$=\dfrac{(-13\times 7)}{(5\times 3)}\times (a^{1+2})\times (b^{2+1})\times (c^{1+2})$$ $$\hspace{1.5cm}[\because a^m\times b^n=a^{m+n}]$$
$$=\left(\dfrac{-91}{15}\right)\times(a^3)\times (b^3) \times (c^3)$$
$$=\left(\dfrac{-91}{15}\right)a^3 b^3 c^3$$


Find the following product:
$$\dfrac72x^2(\dfrac47x+2)$$

Let $$p, q$$ and $$r$$ be three monomials.
Then, by distributive law of multiplication over addition, we have:
$$p\times (q+r)=(p\times q)+(p\times r)$$

$$\therefore \dfrac72x^2\times\left(\dfrac47x+2\right)$$
$$=\left(\dfrac72x^2 \times \dfrac47x\right)+\left(\dfrac72x^2\times 2\right)$$
$$=\left\{\dfrac{(7\times 4)}{(2\times 7)}\times x^{2+1}\right\}+ \left\{\dfrac{(7\times 2)}{(2\times 1)}x^2\right\}$$         $$[\because a^m \times a^n=a^{m+n}]$$
$$=\left(\dfrac{(1\times 2)}{(1\times 1)}\times x^3\right)+\left(\dfrac{(7\times 1)}{(1\times 1)}\times x^2\right)$$
$$=2x^3+7x^2$$


Find the following product:
$$\dfrac35m^2n(m+5n)$$

By distributive law of multiplication over addition, we have:
$$p\times (q+r)=(p\times q)+(p\times r)$$
where $$p, q$$ and $$r$$ be three monomials.

$$\therefore \dfrac35m^2n(m+5n)$$
$$=\left(\dfrac35m^2n \times m\right)+\left(\dfrac35m^2n\times 5n\right)$$
$$=\left(\dfrac35m^{2+1}n+3m^2n^{1+1}\right)$$       $$[\because a^m \times a^n=a^{m+n}]$$
$$=\left(\dfrac35m^3n+3m^2n^2\right)$$


Find the following product:
$$2x^2(3x-4x^2)$$

By distributive law of multiplication over subtraction, we have:
$$p\times (q-r)=(p\times q)-(p\times r)$$
where $$p, q$$ and $$r$$ be three monomials.

$$\therefore 2x^2(3x-4x^2)$$
$$=(2x^2\times 3x)-(2x^2\times 4x^2)$$
$$=(6x^{2+1}-8x^{2+2})$$    $$ [ \because a^m \times a^n=a^{m+n}]$$
$$=(6x^3-8x^4)$$


Find the following product:
$$(-1/27)a^2 b^2 \times (-9/2)a^3 bc^2$$

We know that,
The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part is equal to the product of the variables in the given monomials. 

$$\therefore\left(\dfrac{-1}{27}\right)a^2b^2\times\left(\dfrac{-9}{2}\right)a^3bc^2$$
$$=\left[\left(\dfrac{-1}{27}\right)\times \left(\dfrac{-9}2\right)\right]\times (a^2 \times a^3)\times (b^2 \times b)\times c^2$$
$$=\dfrac{(1\times 9)}{(27\times 2)}\times (a^{2+3})\times (b^{2+1})\times c^2$$ $$\hspace{1cm}[\because a^m\times a^n=a^{m+n}]$$
$$=\dfrac{(1\times 1)}{(3\times 2)}\times (a^{5})\times (b^{3})\times c^2$$
$$=\dfrac16a^5 b^3 c^2$$


Find the following product:
$$\dfrac{-3}{4}ab^3 \times \dfrac{-2}3a^2 b^4$$

We know that,
The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part is equal to the product of the variables in the given monomials. 

$$\therefore\dfrac{-3}4ab^3\times \dfrac{-2}3a^2b^4$$
$$=\left(\dfrac{-3}4\times \dfrac{-2}3\right)\times (a \times a^2)\times (b^3 \times b^4)$$
$$=\left(\dfrac{-1\times-1}{2\times1}\right)\times (a^{1+2})\times (b^{3+4})$$
$$=\dfrac12\times (a^{3})\times (b^{7})$$
$$=\dfrac12a^3 b^7$$


Find the following product:
$$-4x^2y(3x^2-5y)$$

Let $$p, q$$ and $$r$$ be three monomials.
Then, by distributive law of multiplication over subtraction, we have:
$$p\times (q-r)=(p\times q)-(p\times r)$$

$$\therefore -4x^2y \times (3x^2-5y)$$
$$=(-4x^2y \times 3x^2)-(-4x^2y \times 5y)$$ 
$$=(-12x^{2+2}y+20x^2y^{1+1})$$           $$[\because a^m\times a^n=a^{m+n}]$$
$$=(-12x^4y+20x^2y^2)$$


Find the following product:
$$-17x^2(3x-4)$$

Let $$p, q$$ and $$r$$ be three monomials.
Then, by distributive law of multiplication over subtraction, we have:
$$p\times (q-r)=(p\times q)-(p\times r)$$

$$\therefore-17x^2(3x-4)$$
$$=(-17x^2 \times 3x)-(-17x^2\times 4)$$
$$=(-51x^{2+1}+68x^2)$$           $$[\because a^m \times a^n=a^{m+n}]$$
$$=(-51x^3+68x^2)$$


Find the following product:
$$\left(\dfrac{-18}{5}\right)x^2z \times \left(\dfrac{-25}{6}\right)xz^2y$$

We know that,
The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part is equal to the product of the variables in the given monomials. 

$$\therefore \dfrac{-18}5x^2z\times \dfrac{-25}6xz^2y$$
$$=\left(\dfrac{-18}5\times \dfrac{-25}6\right)\times (x^2 \times x)\times (z \times z^2)\times (y)$$
$$=\left(\dfrac{-3\times 5}{1\times 1}\right)\times (x^{2+1})\times (z^{1+2})\times (y)$$           $$[\because a^m\times a^n=a^{m+n}]$$
$$=(-15)\times (x^3) \times (z^3)\times y$$
$$=-15x^3 y z^3$$


Find the following product:
$$\dfrac{-4}{27}xyz(\dfrac92x^2yz-\dfrac34xyz^2)$$

Let $$p, q$$ and $$r$$ be three monomials.
Then, by distributive law of multiplication over subtraction, we have:
$$p\times (q-r)=(p\times q)-(p\times r)$$

$$\therefore \dfrac{-4}{27}xyz \times \left(\dfrac92x^2yz-\dfrac34xyz^2\right)$$
$$=\left(\dfrac{-4}{27}xyz\times \dfrac92x^2yz\right)-\left(\dfrac{-4}{27}xyz\times\dfrac34xyz^2\right)$$
$$=\dfrac{(-4\times 9)}{(27\times 2)}x^{1+2}y^{1+1}z^{1+1}+\dfrac{(-4\times -3)}{(27\times 4)}x^{1+1}y^{1+1}z^{1+2}$$            $$[\because a^m \times a^n=a^{m+n}]$$
$$=\dfrac{(-2\times 1)}{(3\times 1)}x^3y^2z^2+\dfrac{(-1\times -1)}{(9\times 1)}x^2y^2z^3$$
$$=\dfrac{-2}3x^3y^2z^2+\dfrac19x^2y^2z^3$$


Find the product:
$$2a^2b \times (-5)ab^2c \times (-6)bc^2$$

We know that,
The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part is equal to the product of the variables in the given monomials. 

$$\therefore 2a^2b\times (-5)ab^2c\times (-6)bc^2$$
$$=\{2\times (-5)\times (-6)\}\times (a^2 \times a)\times (b\times b^2 \times b)\times (c\times c^2)$$
$$=60\times (a^{2+1})\times (b^{1+2+1})\times (c^{1+2})$$    $$[\because a^p\times a^q\times a^r=a^{p+q+r}$$ and $$ a^m\times a^n=a^{m+n}]$$
$$=60\times (a^3)\times (b^4)\times (c^3)$$
$$=60a^3b^4 c^3$$


Volume of a rectangular box with length $$2x$$, breadth $$3y$$ and height $$4z$$ is __________ .

Given
Length of box = $$2x$$
Breadth of box = $$3y$$
Height of box = $$4z$$

We know that,
Volume of cuboid $$= length \times breadth \times height$$
$$= (2x) \times (3y) \times (4z)$$
$$= 24xyz$$

Hence, volume of the box is $$24xyz$$


Find the following product:
$$\left(\dfrac{-3}{14}\right)xy^4 \times \left(\dfrac76\right)x^3y$$

We know that
The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part is equal to the product of the variables in the given monomials. 

$$\therefore \left(\dfrac{-3}{14}\right)xy^4\times \left(\dfrac76\right)x^3y$$
$$=\left(\dfrac{-3}{14}\times \dfrac76\right)\times (x \times x^3)\times (y^4 \times y)$$
$$=\left(\dfrac{-3\times 7}{14\times 6}\right)\times (x^{1+3})\times (y^{4+1})$$            $$[\because a^m\times a^n=a^{m+n}]$$
$$=\dfrac{(-1\times 1)}{(2\times 2)}\times (x^4) \times (y^5)$$
$$=\left(\dfrac{-1}4\right)x^4 y^5$$


$$(x + a) (x +b) =x^{2}+(a+b) x+$$ __________ .

Expanding $$(x + a)(x + b)$$,

$$(x+a)(x+b) \\= x(x + a) + b(x + a)\\=x^{2}+ax + bx + ab\\ = x^{2} + (a + b)x + ab$$

Hence, $$(x+a)(x+b) = x^{2} + (a + b)x + ab$$


Find the product:
$$\left(\dfrac{-7}5\right)x^2y \times \left(\dfrac32\right)xy^2 \times \left(\dfrac{-6}5\right)x^3 y^3$$

We know that
The coefficient of the product of two monomials is equal to the product of their coefficients. And the variable part is equal to the product of the variables in the given monomials. 

$$\therefore \left(\dfrac{-7}5\right)x^2y \times \left(\dfrac32\right)xy^2 \times \left(\dfrac{-6}5\right)x^3 y^3$$
$$=\left(\dfrac{-7}5\times \dfrac32\times \dfrac65\right)\times (x^2 \times x\times x^3)\times (y\times y^2 \times y^3)$$
$$=\left(\dfrac{-7\times 3\times -6}{5\times 2\times 5}\right)\times (x^{2+1+3})\times (y^{1+2+3})$$            $$[\because a^p\times a^q\times a^r=a^{p+q+r}]$$
$$=\left(\dfrac{-7\times 3\times -3}{5\times 1\times 5}\right)\times (x^6) \times (y^6)$$
$$=\dfrac{63}{25}x^6 y^6$$


Find the following product:
$$10a^2(0.1a-0.5b)$$

Let $$p, q$$ and $$r$$ be three monomials.
Then, by distributive law of multiplication over subtraction, we have:
$$p\times (q-r)=(p\times q)-(p\times r)$$

$$\therefore 10a^2(0.1a-0.5b)$$
$$=(10a^2\times 0.1a)-(10a^2\times 0.5b)$$
$$=(1a^{2+1}-5a^2b)$$              $$[\because a^m \times a^n=a^{m+n}]$$
$$=(a^3-5a^2b)$$


Find the following product:
$$9t^2(t+7t^3)$$

Let $$p, q$$ and $$r$$ be three monomials.
Then, by distributive law of multiplication over addition, we have:
$$p\times (q+r)=(p\times q)+(p\times r)$$

$$\therefore 9t^2(t+7t^3)$$
$$=(9t^2\times t)+(9t^2\times 7t^3)$$
$$=9t^{2+1}+63t^{2+3}$$        $$[\because a^m \times a^n=a^{m+n}]$$
$$=9t^3+63t^5$$


Volume of a rectangular box with $$l = b = h = 2x$$ is __________ .

Given, length, breadth and height are same.
So, $$l = b =h = 2x$$

$$\therefore$$  Volume of rectangular plot $$=l \times b \times h$$
                                                    $$= 2x \times 2x \times 2x$$
                                                    $$=8x^{3}$$.
Hence, volume of rectangular plot $$=8x^{3}$$.


Area of a rectangular plot with sides $$4x^{2}$$ and $$3y^{2}$$ is __________ .

Given
Length of rectangular plot $$= l = 4x^{2}$$
Breadth of rectangular plot $$= b = 3y^{2}$$

$$\therefore$$  Area of rectangular plot = $$l \times b$$
$$= 4x^{2} \times 3y^{2}$$
$$= 12x^{2}y^{2}$$



Multiply: $$-5a^{2}bc$$ , $$11ab$$ and $$13abc^{2}$$.

The required multiplication is as follows:
$$-5a^{2}bc \times 11ab \times 13abc^{2}$$

$$=(-5 \times 11 \times 13) \times a^{2+1+1}b^{1+1+1}c^{1+0+2}$$

$$=-715a^{4}b^{3}c^{3}$$


Multiply $$15xy^{2}$$ and $$17yz^{2}$$

The required multiplication is as follows:
$$15xy^{2} \times 17yz^{2}$$
$$= (15 \times 17) \times xy^{3}z^{2}$$
$$=255 xy^{3}z^{2}$$


Multiply  $$-7pq^{2}r^{3}$$ and $$-13p^{3}q^{2}r$$

The required multiplication is as follows,
$$7pq^{2}r^{3} \times 13p^{3}q^{2}r$$
$$=(-7 \times -13 \times 3) \times pq^{2}r^{3} \times pq^{2}r$$
$$=273p^{4}q^{4}r^{4}$$


Multiply $$3x^{2}y^{2}z^{2}$$ and $$17xyz$$

The required multiplication is as follows,
$$3x^{2}y^{2}z^{2} \times 17xyz$$
$$=(3 \times 17) \times x^{3}y^{3}z^{3}$$
$$=51x^{3}y^{3}z^{3}$$


Find the product of:
$$-7ab, -3a^3$$ and $$-(2/7)ab^2$$

Product of:
$$(-7ab) \times (-3a^3) \times \Big(-\dfrac{2}{7}ab^2\Big)$$
= $$(-7) \times (-3) \times \Big(-\dfrac{2}{7}\Big) \times ab \times a^3 \times ab^2$$
= $$-6a^5b^3$$.


Find the product of $$4x^3$$ and $$-3xy$$

$$ 4x^3 \times (-3xy) = -12\times x^{3 + 1}\times y $$

                          $$= -12x^4y$$


Multiply:
$$(4p - 7)$$ by $$(2 - 3p)$$

$$(4P - 7)$$ by $$(2 - 3p)$$$$=(4p - 7) \times (2 - 3p)$$ 
                                     $$=4p(2 - 3p) - 7(2 - 3p)$$ 
                                     $$=8p- 12p^2 - 14 + 21p$$ 
                                     $$=29p - 12p^2 - 14$$ 


Multiply:
$$(5x - 2)$$ by $$(3x + 4)$$ 

$$(5x - 2)$$ by $$(3x + 4)$$ 
= $$(5x - 2) \times (3x + 4)$$ 
= $$5x (3x + 4) - 2 (3x + 4)$$ 
= $$15x^2 + 20x - 6x - 8$$ 
= $$15x^2 + I4x - 8$$ 


Multiply:
$$(2x^2 + 3)$$ by $$(3x - 5)$$

 $$(2x^2 + 3)$$ by $$(3x - 5)$$ 
= $$(2x^2 + 3) (3x - 5)$$ 
= $$2x^2(3x - 5) + 3(3x - 5)$$ 
= $$6x^3 - 10x^2 + 9x - 15$$ 


Multiply: 
$$(2p^2 - 3pq + 5q^2 + 5)$$ by $$- 2pq$$ 

$$-2pq \times (2p^2 - 3pq + 5q^2 + 5)$$
$$=(-2pq) \times 2p^2 + (-2pq) \times (-3pq) + (- 2pq) \times (5q^2) + (-2pq) \times 5$$ 
$$=-4p^3q + 6p^2q^2 - 10pq^3 - 10pq$$ 


Find the product of:
$$2xyz$$ and $$0$$

Product of:
$$2xyz$$ and $$0 = 2xyz \times 0 = 0$$


Simplify:  $$12x (5x + 2x)$$.

$$12x – (5x + 2x)$$,
The simplified form of the expression $$12x – (5x + 2x)$$ is calculated as below,
$$12x – (5x + 2x) = 12x – 7x$$
We get,
$$= 5x$$.


Find the product of $$-4.5xy, \ \dfrac{5}{7}yz$$  and $$-\dfrac{14}{9}zx$$.

To find: Product of $$-4.5xy, \ \dfrac{5}{7}yz$$  and $$-\dfrac{14}{9}zx$$.

$$=-4.5xy\times \dfrac{5}{7}yz$$ $$\times \left(\dfrac{-14}{9}\right)zx$$.

$$=-4.5\times \dfrac{5}{7}$$ $$\times \left(\dfrac{-14}{9}\right)xy\times yz\times zx$$.

$$=-5$$ $$\times \left(\dfrac{-2}{2}\right)x^2y^2z^2$$.

$$ = 5x^2y^2z^2$$


Evaluate:  $$35b (16b + 9b)$$.

$$35b – (16b + 9b)$$,
The value of the expression $$35b – (16b + 9b)$$ is calculated as follows,
$$35b – (16b + 9b) = 35b – 25b$$
We get,
$$= 10b$$.
Hence, the value of the expression $$35b – (16b + 9b) = 10b$$.


Evaluate:  $$6m (4m m)$$.

$$6m – (4m – m)$$
The value of the expression $$6m – (4m – m)$$ is calculated as follows,
$$6m – (4m – m) = 6m – 3m$$
We get,
$$= 3m$$.
Hence, the value of the expression $$6m – (4m – m) = 3m$$.


Find the product of
$$3x^2y $$ and $$-4xy^2$$

Product of
$$3x^2y $$ and $$-4xy^2$$
$$ = 3x^2 \times (-4xy^2)$$
$$ = -12x^{2+1} y^{1+2}$$
$$=12x^3y^3$$


$$6p 5x + q = 6p (.)$$

$$6p – 5x + q = 6p – (5x – q)$$.


Multiply:
$$3a + 4b- 5c$$ and $$ 3 a$$

The multiplication of the given expression is calculated as,
$$(3a + 4b - 5c) \times 3a = 3a \times 3a + 4b \times 3a - 5c \times 3a$$
On further calculation, we get
$$= 9a^{1+1} + 12 ab - 15 ac$$
$$= 9 a^2 + 12 ab - 15 ac$$
Therefore, the multiplication of $$3 a + 4b - 5c$$ and $$3 a = 9a^2 + 12 ab - 15 ac$$


Simplify:  $$10m + (4n 3n) 5n$$.

$$10m + (4n – 3n) – 5n$$,
The simplified form of the expression $$10m + (4n – 3n)$$ is calculated as below,
$$10m + (4n – 3n) – 5n = 10m + n – 5n$$
We get,
$$= 10m – 4n$$.


Simplify:  $$x (x y) (- x + y)$$.

$$x – (x – y) – (- x + y)$$,
The simplified form of the expression $$x – (x – y) – (- x + y)$$ is calculated as below,
$$x – (x – y) – (- x + y) = x – x + y + x – y$$
We get,
$$= x$$.


Simplify:  $$2 (3a b) 5 (a 3b)$$.

$$2 (3a – b) – 5 (a – 3b) = 6a – 2b – 5a + 15b$$
                                  $$= 6a - 5a – 2b + 15b$$
                                  $$= a + 13b$$


$$x 2y = - ()$$

$$x – 2y = - (2y – x)$$.


Multiply:
$$xy- yz$$ and $$x^2\,yz^2$$

The multiplication of the given expression is calculated as,
$$(xy - yz) \times (x^2 yz^2) = xy \times x^2 yz^2 - yz \times x^2 yz^2$$
We get,
$$= x^{1+2}y^{1+1}z^2 - x^2y^{1+1}z^{1+2}$$
$$= x^3 y^2 z^2 - x^2 y^2 z^3$$
Hence, the multiplication of $$(xy - yz)$$ and $$x^2 yz^2 = x^3 y^2 z^2 - x^2 y^2 z^3$$


Multiply:
$$ 3\,abc\,\, and\,\, - 5 a^2b^2c$$ 

We have to multiply $$3\,abc\,\, and\,\, - 5 a^2b^2c$$
The given expression is calculated as follows,
$$3 abc \times - 5 a^2b^2c = 3 \times - 5 \times a \times a^2 \times b \times b^2 \times c \times c$$
On further calculation, we get
$$= - 15 \times a^{(1+2)} \times b^{(1+2)} \times c^{(1+1)}$$
$$= - 15 \times a^3 \times b^3 \times c^2$$
$$= - 15 a^3 b^3 c^2$$
Therefore, the multiplication of $$3 abc$$ and $$- 5 a^2 b^2c = - 15 a^3 b^3 c^2$$


Simplify:  $$(15b 6b) (8b + 4b)$$.

$$(15b – 6b) – (8b + 4b)$$,
The simplified form of the expression $$(15b – 6b) – (8b + 4b)$$ is calculated as below,
$$(15b – 6b) – (8b + 4b) = 9b – 12b$$
We get,
$$= - 3b$$.


Evaluate:
$$\big (\dfrac{1}{2}a + \dfrac{1}{2} b \big) \big(\dfrac{1}{2} a- \dfrac{1}{2}b \big)$$

$$\big (\dfrac{1}{2}a + \dfrac{1}{2} b \big) \big(\dfrac{1}{2} a- \dfrac{1}{2}b \big)$$

It can written as 
$$= \dfrac{1}{2} \big (\dfrac{1}{2}a + \dfrac{1}{2} b \big)+ \dfrac{1}{2}  \big (\dfrac{1}{2}a - \dfrac{1}{2} b \big)$$

By further calculation $$ =  \dfrac{1}{4} a^{2}-\dfrac{1}{4}  ab+\dfrac{1}{4}  ab-\dfrac{1}{4}  b^{2}$$

$$=\dfrac{1}{4} a^{2}-\dfrac{1}{4} b^{2}$$


Multiply:
$$ x - y + z \,\,and\,\, -2x$$

We have to multiply $$x - y + z\,\, and\,\, -2x$$
The given expression is calculated as follows,
$$(x - y + z) \times – 2x = x \times - 2x - y \times - 2x + z \times - 2x$$
On simplification, we get
$$= - 2x^{(1+1)} + 2xy - 2xz$$
$$= - 2x^2 + 2xy - 2xz$$
Therefore, the multiplication of $$x - y + z$$ and $$-2x = - 2 x^2 + 2 xy - 2xz$$


Find the product: 
(a - 8)(a + 2)

$$  {\textbf{Step -1: Form an equation}} $$

                  $$  {\text{This is in the form}}{\text{.}} $$

                  $$   \Rightarrow (x + a)(x + b) $$

                  $$   = {x^2} + ax + bx + ab $$

                  $$   = {x^2} + (a + b)x + ab $$

$$  {\textbf{Step -2: Calculation}} $$

                 $$  {\text{Given,(a - 8)(a + 2)}} $$

                 $$  {\text{Here x = a, a =  - 8,}} $$

                 $$  b =  2$$

                 $$ \Rightarrow (a - 8)(a + 2) $$

                 $$   = {a^2} + ( - 8 + 2)a + ( - 8)( 2) $$

                 $$   = {a^2} + ( - 6)a - 16 $$

                 $$   = {a^2} - 6a - 16 $$

$$  {\textbf{Hence, the correct answer is }}\mathbf{{a^2} - 6a - 16.} $$ 



Multiply:
$$ - 8xyz + 10 x^2yz^3 \,\,and\,\, xyz$$

We have to multiply $$- 8\,xyz + 10 x^2yz^3\,\, and\,\, xyz$$
The given expression is calculated as follows,
$$(- 8xyz + 10x^2yz^3) \times xyz = - 8xyz \times xyz + 10x^2yz^3 \times xyz$$
On further calculation, we get
$$= - 8x^{(1+1)}y^{(1+1)}z^{(1+1)} + 10x^{(2+1)}y^{(1+1)}z^{(3+1)}$$
$$= - 8x^2y^2z^2 + 10x^3y^2z^4$$
Therefore, the multiplication of $$- 8xyz + 10 x^2yz^3$$ and $$xyz = - 8x^2y^2z^2 + 10x^3y^2z^4$$


$$\text { Complete the following table of products of two monomials }$$

1870403_a241967f5ed3420ba0fca8ca59f56f19.png


1842033_1870403_ans_cd300b5acac846848c0e75231cd59c05.PNG


Multiply the given polynomial 
$$2x; x^{2} - 2x - 1 $$

$$2x(x^{2} -2x - 1)$$
$$=2x \times x^{2} + 2x \times  ( -2x) + 2x (-1)$$
$$=2x^{3} - 4x^{2} -2x$$


Find the product: (a - 6)(a - 2)

$$  {\textbf{Step 1: Form an equation}} $$

                $$  {\text{This is in the form}}{\text{.}} $$

                $$   \Rightarrow (x + a)(x + b) $$

                $$   = {x^2} + ax + bx + ab $$

                $$   = {x^2} + (a + b)x + ab $$

$$  {\textbf{Step 2: Calculation}} $$

                $$  {\text{Given, (a - 6)(a - 2)}} $$

                $$  {\text{Here x = a,a =  - 6,}} $$

                $$  b =  - 2$$

                $$ \Rightarrow (a - 6)(a - 2) $$

                $$   = {a^2} + ( - 6 - 2)a + ( - 6)( - 2) $$

                $$   = {a^2} + ( - 8)a + 12 $$

                $$   = {a^2} - 8a + 12 $$

$$  {\textbf{Hence, the correct answer is }}\mathbf{{a^2} - 8a + 12.} $$ 



Multiply:
$$xyz\,\, and\,\, - 13 xy^2z + 15x^2yz - 6xyz^2$$

We have to multiply $$xyz\,\, and\,\, - 13 xy^2z + 15x^2yz - 6xyz^2$$
The given expression is calculated as follows,
$$xyz \times (- 13 xy^2z + 15x^2yz - 6xyz^2) = xyz \times - 13xy^2z + xyz \times15x^2yz - xyz \times 6xyz^2$$
On simplification, we get
$$= - 13x^{(1+1)}y^{(1+2)}z^{(1+1)} + 15x^{(1+2)}y^{(1+1)}z^{(1+1)} - 6x^{(1+1)}y^{(1+1)}z^1+2$$
We get,
$$= - 13x^2y^3z^2 + 15x^3y^2 z^2 - 6x^2y^2z^3$$
Therefore, the multiplication of $$xyz$$ and $$- 13xy^2z + 15x^2yz - 6xyz^2 = - 13x^2y^3z^2 + 15x^3y^2z^2 - 6x^2y^2z^3$$


Multiply:
$$ 2x -3y - 5z\,\, and\,\, -2y$$

We have to multiply $$2x - 3y - 5z\,\, and\,\, -2y$$
The given expression is calculated as follows,
$$(2x - 3y - 5z) \times - 2y = 2x \times - 2y - 3y \times - 2y - 5z \times - 2y$$
On further calculation, we get
$$= - 4xy + 6y^{(1+1)} + 10 yz$$
$$= - 4xy + 6y^2 + 10yz$$
Therefore, the multiplication of $$2x - 3y - 5z$$ and $$-2y $$ is $$ - 4xy + 6y^2 + 10yz$$


Find the products
$$ \dfrac{2 x}{5}\left(3 a^{3}-3 b^{3}\right) $$

$$ \dfrac{2 x}{5}\left(3 a^{3}-3 b^{3}\right) $$
$$\Rightarrow \dfrac{2 x}{5} \times 3 a^{3}-\dfrac{2 x}{5} \times 3 b^{3}=\dfrac{6 x a^{3}}{5}-\dfrac{6 x b^{3}}{5} $$


Find the products
$$ (-3 \mathrm{pq})\left(-15 \mathrm{p}^{3} \mathrm{q}^{2}-\mathrm{q}^{3}\right) $$

$$ (-3 \mathrm{pq})\left(-15 \mathrm{p}^{3} \mathrm{q}^{2}-\mathrm{q}^{3}\right) $$
$$ =(-3 p q)\left(-15 p^{3} q^{2}\right)-(-3 p q)\left(q^{3}\right) $$
$$ =45 \mathrm{p}^{4} \mathrm{q}^{3}+3 \mathrm{pq}^{4} $$


Use suitable identities to find the following products:
$$(x + 2)(x - 5)$$

$$(x + 2)(x - 5)$$
$$\because (x + a)(x + b) = x^{2} + (a + b)x + ab$$
$$\therefore (x + 2)(x - 5)$$
$$= x^{2} + (2 + (-5))x + 2 \times (-5)$$
$$= x^{2} - 3x - 10$$


Use suitable identities to find the following products:
$$(x - 5)(x + 8)$$

$$\because (x + a)(x + b) = x^{2} + (a + b)x + ab$$
$$\therefore (x + (-5)) (x + 8)$$
$$= x^{2} + (-5 + 8)x + (-5) \times (8)$$
$$= x^{3} + 3x - 40$$


The base and altitutde of a triangle are $$ (3 x-4 y) $$ and $$ (6 x+5 y) $$ respectively. Find its area.

Area of a triangle $$ =\dfrac{1}{2} \times $$ base $$ \times $$ height $$ =\dfrac{1}{2} (3 x-4 y)(6 x+5 y) $$
$$ =\dfrac{1}{2}[(3 x(6 x+5 y)-4 y(6 x+5 y)]] $$
$$ \left.=\dfrac{1}{2}\left[18 x^{2}+15 y\right)-24 y-20 y^{2}\right] $$
$$ =\dfrac{1}{2}\left[18 x^{2}-9 x y-20 y^{2}\right] $$


Use suitable identities to find the following products:
$$(x + 3)(x + 7)$$

$$\because (x + a)(x + b) = x^{2} + (a + b)x + ab$$
$$\therefore (x + 3)(x + 7) = x^{2} + (3 + 7)x + 3 \times 7$$
$$= x^{2} + 10x + 21$$


Use suitable identities to find the following products:
$$(2x + 7)(3x - 5)$$

We have, $$(2x + 7)(3x + 5)$$
$$= 2\left ( x + \dfrac{7}{2} \right ) . 3\left ( x - \dfrac{5}{3} \right )$$
$$= 6\left (x + \dfrac{7}{2} \right ) \left (x - \dfrac{5}{3} \right )$$
$$= 6 \left [ x^{2} + \left ( \dfrac{7}{2} - \dfrac{5}{3} \right ) x + \dfrac{7}{2} \times \dfrac{-5}{3} \right ]$$
$$[\because (x + a)(x + b) = x^{2} + (a + b)x + ab]$$
$$= 6 \left [ x^{2} + \left ( \dfrac{21 - 10}{6} \right )x - \dfrac{35}{6} \right ]$$
$$= 6x^{2} + 11x - 35$$


Use suitable identities to find the following products:
$$(5 - 3x)(3 + 2x)$$

$$(5 - 3x)(3 + 2x)$$
$$= 3\left ( \dfrac{5}{3} - x \right ) \times 2 \left ( \dfrac{3}{2} + x \right )$$
$$= 6 \left ( \dfrac{5}{3} - x \right ) \left ( \dfrac{3}{2} + x \right )$$
$$ = -6 \left [ \left ( x - \dfrac{5}{3} \right ) \left ( x + \dfrac{3}{2} \right ) \right ]$$
$$= -6\left [ x^{2} + \left ( \dfrac{-5}{3} + \dfrac{3}{2} \right )x + \left ( \dfrac{-5}{3} \right ) \times \left ( \dfrac{3}{2} \right ) \right ]$$
$$= -6 \left [ \left ( x^{2} + \left ( \dfrac{-10 + 9}{6} \right )x - \dfrac{5}{2} \right ) \right ]$$
$$= -6 \left [ x^{2} - \dfrac{x}{6} - \dfrac{5}{2} \right ] = -6x^{2} + x + 15$$


Expand $${ \left( \pi +\cfrac { 22 }{ 7 }  \right)  }^{ 2 }$$ using appropriate identity

Using the identity is $$(x+y)^{ 2 }=x^{ 2 }+y^{ 2 }+2xy$$.

Given: $$\left( π+\frac { 22 }{ 7 }  \right) ^{ 2 }$$, apply the above identity by taking $$x=\pi$$ and $$y = \dfrac{22}{7}$$.
We get, $$\left( π+\dfrac { 22 }{ 7 }  \right) ^{ 2 }={ \left( π \right)  }^{ 2 }+\left( \dfrac { 22 }{ 7 }  \right) ^{ 2 }+\left( 2\times π\times \dfrac { 22 }{ 7 }  \right) =π^{ 2 }+\dfrac { 484 }{ 49 } +\dfrac { 44 }{ 7 } π$$ 
 
Hence, $$\left( π+\dfrac { 22 }{ 7 }  \right) ^{ 2 }=π^{ 2 }+\dfrac { 44 }{ 7 } π+\dfrac { 484 }{ 49 }$$.


Expand $${ \left( \sqrt { 12 } a+\sqrt { 6 } b \right)  }^{ 2 }$$ using appropriate identity

Using the identity $$(x+y)^{ 2 }=x^{ 2 }+y^{ 2 }+2xy$$.

Given:$${ \left( \sqrt { 12 } a+\sqrt { 6 } b \right)  }^{ 2 }$$, apply the above identity taking $$x = \sqrt{12} a $$ and $$y = \sqrt{6} b$$
We get, $${ \left( \sqrt { 12 } a+\sqrt { 6 } b \right)  }^{ 2 }={ \left( \sqrt { 12 } a \right)  }^{ 2 }+\left( \sqrt { 6 } b \right) ^{ 2 }+\left( 2\times \sqrt { 12 } a\times \sqrt { 6 } b \right) =12a^{ 2 }+6b^{ 2 }+12\sqrt { 2 } ab$$

Hence, $${ \left( \sqrt { 12 } a+\sqrt { 6 } b \right)  }^{ 2 }=12a^{ 2 }+12\sqrt { 2 } ab+6b^{ 2 }$$.


Expand $${ \left( \pi -\cfrac { 22 }{ 7 }  \right)  }^{ 2 }$$ using appropriate identity

Using the identity is $$(x-y)^{ 2 }=x^{ 2 }+y^{ 2 }-2xy$$.

Given: $${ \left( \sqrt { 10 } x-\sqrt { 5 } y \right)  }^{ 2 }$$ we apply the above identity by taking $$x = \pi$$ and $$y = -\dfrac{22}{7}$$
We get, $${ \left( π-\frac { 22 }{ 7 }  \right)  }^{ 2 }={ \left( π \right)  }^{ 2 }+\left( \dfrac { 22 }{ 7 }  \right) ^{ 2 }-\left( 2\times π\times \dfrac { 22 }{ 7 }  \right) =π^{ 2 }+\dfrac { 484 }{ 49 } -\dfrac { 44 }{ 7 } π$$

Hence, $${ \left( π-\dfrac { 22 }{ 7 }  \right)  }^{ 2 }=π^{ 2 }+\dfrac { 484 }{ 49 } -\dfrac { 44 }{ 7 } π$$.


Expand $${ \left( 3a-2b \right)  }^{ 2 }$$ using appropriate identity

Using  the identity is $$(x-y)^{ 2 }=x^{ 2 }+y^{ 2 }-2xy$$.

Given: $${ \left( 3a-2b \right)  }^{ 2 }$$ we apply the above identity by taking 
$$x = 3a $$ and $$ y = -2b$$
We get, $${ \left( 3a-2b \right)  }^{ 2 }={ \left( 3a \right)  }^{ 2 }+\left( 2b \right) ^{ 2 }-\left( 2\times 3a\times 2b \right) =9a^{ 2 }+4b^{ 2 }-12ab$$

Hence, $${ \left( 3a-2b \right)  }^{ 2 }=9a^{ 2 }-12ab+4b^{ 2 }$$.


Expand $$(3x-3)(3x+4)$$ using appropriate identity

Using the identity is $$(m+a)(m+b)=m^{ 2 }+m(a+b)+ab$$.

Given: $$(3x-3)(3x+4)$$ we apply the above identity by taking 
$$m = 3x$$, $$a = -3$$ and $$b = 4$$
We get,
$$(3x-3)(3x+4)={ \left( 3x \right)  }^{ 2 }+\left( 3x \right) \left( -3+4 \right) +\left( -3\times 4 \right) =9x^{ 2 }+\left( 3x \right) \left( 1 \right) -12=9x^{ 2 }+3x-12$$

Hence, $$(3x-3)(3x+4)=9x^{ 2 }+3x-12$$.


Expand $${ \left( \sqrt { 10 } x-\sqrt { 5 } y \right)  }^{ 2 } $$ using appropriate identity

Using the identity is $$(x-y)^{ 2 }=x^{ 2 }+y^{ 2 }-2xy$$.

Given: $${ \left( \sqrt { 10 } x-\sqrt { 5 } y \right)  }^{ 2 }$$ we apply the above identity by taking $$x =\sqrt{10}x$$ and $$y= -\sqrt{5}y$$:
We get, $${ \left( \sqrt { 10 } x-\sqrt { 5 } y \right)  }^{ 2 }={ \left( \sqrt { 10 } x \right)  }^{ 2 }+\left( \sqrt { 5 } y \right) ^{ 2 }-\left( 2\times \sqrt { 10 } x\times \sqrt { 5 } y \right) =10x^{ 2 }+5y^{ 2 }-2\sqrt { 50 } xy=10x^{ 2 }+5y^{ 2 }-10\sqrt { 2 } xy$$

Hence, $${ \left( \sqrt { 10 } x-\sqrt { 5 } y \right)  }^{ 2 }=10x^{ 2 }-10\sqrt { 2 } xy+5y^{ 2 }$$.


Expand: $$\left( \cfrac { x }{ 3 } +\cfrac { y }{ 2 }  \right) \left( \cfrac { x }{ 3 } -\cfrac { y }{ 2 }  \right) $$

Using the identity is $$(a+b)(a-b)=a^{ 2 }-b^2$$.

Given: $$\left( \frac { x }{ 3 } +\frac { y }{ 2 }  \right) \left( \frac { x }{ 3 } -\frac { y }{ 2 }  \right)$$ we apply the above identity by taking $$ a = \dfrac{x}{3}$$ and $$b =\dfrac{y}{2}$$
We get, $$\left( \dfrac { x }{ 3 } +\dfrac { y }{ 2 }  \right) \left( \dfrac { x }{ 3 } -\dfrac { y }{ 2 }  \right) ={ \left( \dfrac { x }{ 3 }  \right)  }^{ 2 }-{ \left( \dfrac { y }{ 2 }  \right)  }^{ 2 }=\dfrac { x^{ 2 } }{ 9 } -\dfrac { y^{ 2 } }{ 4 }$$ 
 
Hence, $$\left( \dfrac { x }{ 3 } +\dfrac { y }{ 2 }  \right) \left( \dfrac { x }{ 3 } -\dfrac { y }{ 2 }  \right) =\dfrac { x^{ 2 } }{ 9 } -\dfrac { y^{ 2 } }{ 4 }$$.


Expand $$\left( y-\cfrac { 1 }{ y }  \right) ^{ 2 }$$ using appropriate identity

Using the identity is $$(a-b)^{ 2 }=a^{ 2 }+b^{ 2 }-2ab$$.

Given: $$\left( y-\frac { 1 }{ y }  \right) ^{ 2 }$$ we apply the above identity By taking $$a = y$$ and $$b = -\dfrac{1}{y}$$ 
We get, $$\left( y-\frac { 1 }{ y }  \right) ^{ 2 }={ \left( y \right)  }^{ 2 }+\left( \dfrac { 1 }{ y }  \right) ^{ 2 }-\left( 2\times y\times \frac { 1 }{ y }  \right) =y^{ 2 }+\dfrac { 1 }{ y^{ 2 } } -2$$ 

Hence, $$\left( y-\frac { 1 }{ y }  \right) ^{ 2 }=y^{ 2 }-2+\dfrac { 1 }{ y^{ 2 } }$$.


Expand: $$\left( { a }^{ 2 }+4{ b }^{ 2 } \right) \left( a+2b \right) \left( a-2b \right) $$

Using the identity is $$(x+y)(x-y)=x^{ 2 }-y^2$$.

Given: $$\left( a^{ 2 }+4b^{ 2 } \right) \left( a+2b \right) \left( a-2b \right)$$ we apply the above identity in 2nd and 3rd term as follows:

$$\left( a^{ 2 }+4b^{ 2 } \right) \left( a+2b \right) \left( a-2b \right) =\left( a^{ 2 }+4b^{ 2 } \right) [{ \left( a \right)  }^{ 2 }-{ \left( 2b \right)  }^{ 2 }]=\left( a^{ 2 }+4b^{ 2 } \right) \left( a^{ 2 }-4b^{ 2 } \right)$$

Again using the identity $$(x+y)(x-y)=x^{ 2 }-y^2$$:
 
$$\left( a^{ 2 }+4b^{ 2 } \right) \left( a^{ 2 }-4b^{ 2 } \right) ={ \left( a^{ 2 } \right)  }^{ 2 }-{ \left( 4b^{ 2 } \right)  }^{ 2 }=a^{ 4 }-16b^{ 4 }$$

Hence, $$\left( a^{ 2 }+4b^{ 2 } \right) \left( a+2b \right) \left( a-2b \right) =a^{ 4 }-16b^{ 4 }$$.


Expand $$\left( { x }^{ 2 }+{ y }^{ 2 } \right) \left( { x }^{ 2 }-{ y }^{ 2 } \right) $$

Using the identity is $$(a+b)(a-b)=a^{ 2 }-b^2$$.

Given: $$\left( \frac { x }{ 3 } +\frac { y }{ 2 }  \right) \left( \frac { x }{ 3 } -\frac { y }{ 2 }  \right)$$ we apply the above identity by taking $$ a = x^2$$ and $$b = y^2$$ :

We get, $$\left( x^{ 2 }+y^{ 2 } \right) \left( x^{ 2 }-y^{ 2 } \right) ={ \left( x^{ 2 } \right)  }^{ 2 }-{ \left( y^{ 2 } \right)  }^{ 2 }=x^{ 4 }-y^{ 4 }$$ 
 
Hence, $$\left( x^{ 2 }+y^{ 2 } \right) \left( x^{ 2 }-y^{ 2 } \right) =x^{ 4 }-y^{ 4 }$$.


Simplify: $${ (4a-7b) }^{ 2 }-{ (3a) }^{ 2 }$$

Given expression is $${ \left( 4a-7b \right)  }^{ 2 }-{ \left( 3a \right)  }^{ 2 }$$

Using the identity $$(x-y)^{ 2 }=x^{ 2 }+y^{ 2 }-2xy$$, we get:

$${ \left( 4a-7b \right)  }^{ 2 }-{ \left( 3a \right)  }^{ 2 }=\left[ { \left( 4a \right)  }^{ 2 }+\left( 7b \right) ^{ 2 }-\left( 2\times 4a\times 7b \right)  \right] -9a^{ 2 }$$

$$=16a^{ 2 }+49b^{ 2 }-56ab-9a^{ 2 }$$

$$=7a^{ 2 }+49b^{ 2 }-56ab$$

$$=7(a^{ 2 }+7b^{ 2 }-8ab)$$

Hence, $${ \left( 4a-7b \right)  }^{ 2 }-{ \left( 3a \right)  }^{ 2 }=7(a^{ 2 }+7b^{ 2 }-8ab)$$.


Suppose $$x$$ and $$y$$ are positive real numbers such that $$x \sqrt x\,+\,y \sqrt y=\,183$$ and $$ x \sqrt y\, =y \sqrt x=182$$ then value of $$\frac{18}{5}(x+y)$$ is : 

Given, 
$$x\sqrt{x}+y\sqrt{y}=183$$   .......$$(1)$$
$$x\sqrt{y}+y\sqrt{x}=182$$   ........$$(2)$$
$$\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)=182$$
Let $$u=\sqrt{x}$$ and $$v=\sqrt{y}$$
$$\Rightarrow\,x={u}^{2}$$ and $$y={v}^{2}$$
$$(1)\Rightarrow\,{u}^{2}u+{v}^{2}v=183$$
$$\Rightarrow\,{u}^{3}+{v}^{3}=183$$    ......$$(3)$$
and $$uv\left(u+v\right)=182$$     .....$$(4)$$
$$\therefore\,3uv\left(u+v\right)=3\times 182=546$$     .......$$(5)$$
$$(u+v)^3={u}^{3}+{v}^{3}+3uv\left(u+v\right)$$
$$(u+v)^3=728$$
We then claim that, $$u+v=9$$.

From $$(3)$$ we have
$${u}^{3}+{v}^{3}=183$$ 
$$\Rightarrow\,\left(u+v\right)\left({u}^{2}+{v}^{2}-uv\right)=183$$
$$\Rightarrow\,\left(u+v\right)\left({u}^{2}+{v}^{2}\right)-uv\left(u+v\right)=183$$
$$\Rightarrow\,\left(u+v\right)\left({u}^{2}+{v}^{2}\right)-182=183$$ where $$uv\left(u+v\right)=182$$
$$\Rightarrow\,\left(u+v\right)\left({u}^{2}+{v}^{2}\right)=183+182=365$$
$$\Rightarrow\,\left({u}^{2}+{v}^{2}\right)=\dfrac{365}{\left(u+v\right)}=\dfrac{365}{9}$$
Then the required expression $$=\dfrac{18}{5}\left({u}^{2}+{v}^{2}\right)=\dfrac{18}{5}\times\dfrac{365}{9}=146$$
$$\therefore\,\dfrac{18}{5}\left(x+y\right)=146$$


Find the product : $$6x^{2}\times 4xy$$

We multiply $$6x^2$$ and $$4xy$$ as shown below:

$$6x^{ 2 }\times 4xy\\ =(6\times x\times x)\times (4\times x\times y)\\ =(6\times 4)\times (x\times x\times x)\times y\quad \quad \quad \quad (Combining\quad like\quad terms)\\ =24\times x^{ 3 }\times y\\ =24x^{ 3 }y$$

Hence, $$6x^{ 2 }\times 4xy=24x^{ 3 }y$$.


Simplify: $$\left( { m }^{ 2 }+2{ n }^{ 2 } \right) ^{ 2 }-4{ m }^{ 2 }{ n }^{ 2 }$$

Using $$(x+y)^{ 2 }=x^{ 2 }+y^{ 2 }+2xy$$.

Given:$${ \left( { m^{ 2 } }+{ 2n^{ 2 } } \right)  }^{ 2 }-4{ m^{ 2 } }{ n^{ 2 } }$$ we apply the above identity as follows:

$${ \left( { m^{ 2 } }+{ 2n^{ 2 } } \right)  }^{ 2 }-4{ m^{ 2 } }{ n^{ 2 } }={ \left( { m^{ 2 } } \right)  }^{ 2 }+\left( 2n^{ 2 } \right) ^{ 2 }+\left( 2\times { m^{ 2 } }\times 2n^{ 2 } \right) -4{ m^{ 2 } }{ n^{ 2 } }=m^{ 4 }+4n^{ 4 }+4{ m^{ 2 } }n^{ 2 }-4{ m^{ 2 } }{ n^{ 2 } }=m^{ 4 }+4n^{ 4 }$$

Hence, $${ \left( { m^{ 2 } }+{ 2n^{ 2 } } \right)  }^{ 2 }-4{ m^{ 2 } }{ n^{ 2 } }=m^{ 4 }+4n^{ 4 }$$.


Simplify: $${ \left( 3a-2 \right)  }^{ 2 }-{ \left( 2a-3 \right)  }^{ 2 }$$

Using the identity: $$(x-y)^{ 2 }=x^{ 2 }+y^{ 2 }-2xy$$.

Given: $${ \left( 3a-2 \right)  }^{ 2 }-{ \left( 2a-3 \right)  }^{ 2 }$$ ,  we apply the above identity as follows:

$${ \left( 3a-2 \right)  }^{ 2 }-{ \left( 2a-3 \right)  }^{ 2 }$$

$$=\left[ { \left( 3a \right)  }^{ 2 }+\left( 2 \right) ^{ 2 }-\left( 2\times 3a\times 2 \right)  \right] -\left[ { \left( 2a \right)  }^{ 2 }+\left( 3 \right) ^{ 2 }-\left( 2\times 2a\times 3 \right)  \right]$$ 

$$=(9a^{ 2 }+4-12a)-(4a^{ 2 }+9-12a)$$

$$=9a^{ 2 }+4-12a-4a^{ 2 }-9+12a$$

$$=5a^{ 2 }-5$$

$$=5(a^{ 2 }-1)$$

Hence, $${ \left( 3a-2 \right)  }^{ 2 }-{ \left( 2a-3 \right)  }^{ 2 }=5(a^{ 2 }-1)$$.


$$ {28x}^{4} by 56 x $$


2039348_1264222_ans_38230ee4ac71492986c3f6b5dc9ef369.JPG


Expand : $$( x + a ) ( x + b )$$

Hint: To expand the given expression, multiply both the binomials.

 

The given expression can be written as:

$$(x+a)(x+b)=x(x+b)+a(x+b)$$ (here, $$x$$ is a constant and $$a$$ and $$b$$ are variables)

$$\Rightarrow(x+a)(x+b)=x^2+xb+ax+ab$$

$$\Rightarrow(x+a)(x+b)=x^2+x(b+a)+ab$$

 

Hence, expanding $$(x+a)(x+b)$$, we get $$x^2+x(b+a)+ab$$



Expand : $$( a + b ) ( a - b )$$

Hint: To expand the given expression, multiply both the binomials.

 

The given expression can be written as:

$$(a+b)(a-b)=a(a-b)+b(a-b)$$

$$\Rightarrow(a+b)(a-b)=a^2-ab+ba-b^2$$

$$\Rightarrow(a+b)(a-b)=a^2-b^2$$

 

Hence, expanding $$(a+b)(a-b)$$, we get $$a^2-b^2$$



Find the product of the following binomial.
$$(a+2b)(a-2b)$$.


2184388_1673119_ans_4320253589da424ca684fad24c09060a.jpeg


Find the product of the following binomial.
$$\left(x^3+\dfrac{1}{x^3}\right)\left(x^3-\dfrac{1}{x^3}\right)$$.


2184425_1673125_ans_6c322f38d6b94732901191d2263bb0a6.jpeg


Simplify.
$$6uw^{-3} \times 4uw^{6}$$

Given algebraic expression is,
$$6u{ w }^{ -3 }\times 4u{ w }^{ 6 }$$

$$=24\times \left( u\times u \right) \times \left( { w }^{ -3 }\times { w }^{ 6 } \right) $$

$$=24\times \left( { u }^{ 2 } \right) \times \left( { w }^{ 3 } \right) $$              $$\left[ { a }^{ m }\times { a }^{ n }={ a }^{ m+n } \right] $$

$$=24{ u }^{ 2 }{ w }^{ 3 }$$


Find:
$${(x^2-7x)(x+5)}$$


2044828_1568356_ans_b21adc9a05454a3d9b294efcf9114c5f.jpg


Find the following product.
$$\left(z+\dfrac{3}{4}\right)\left(z+\dfrac{4}{3}\right)$$.


2184800_1673263_ans_1eea06bb83f847729f521cb4b0e99ce7.jpeg


Class 8 Maths Extra Questions