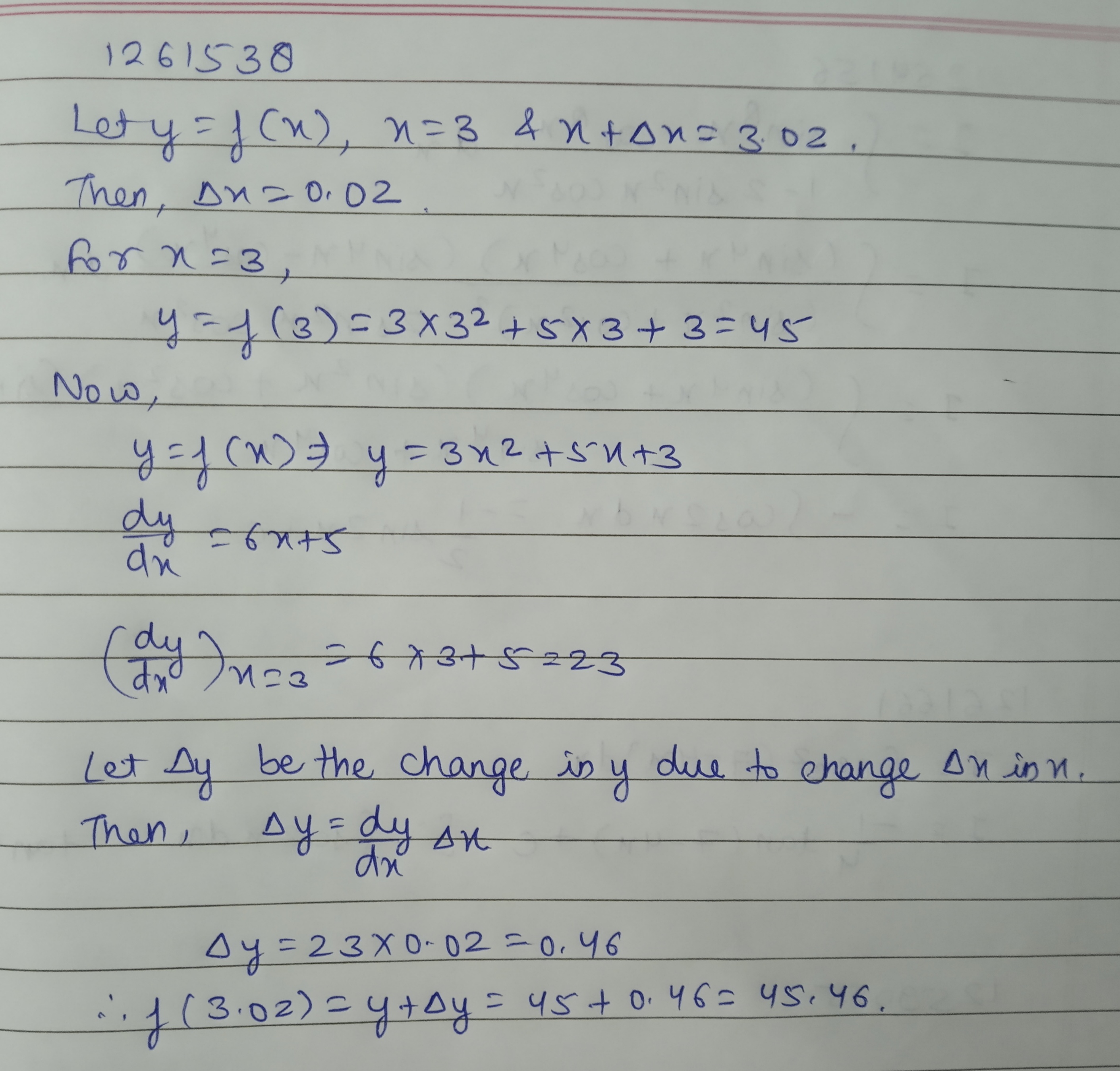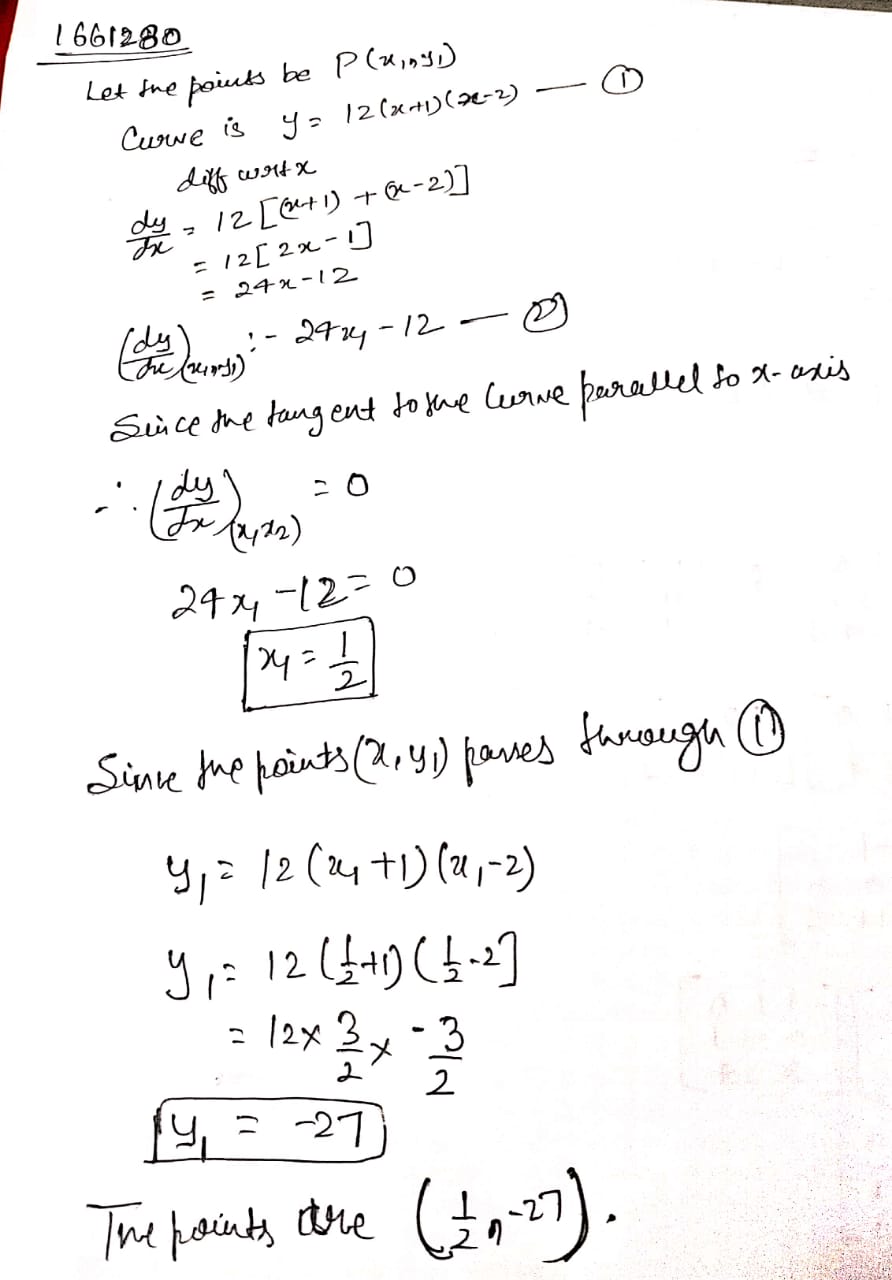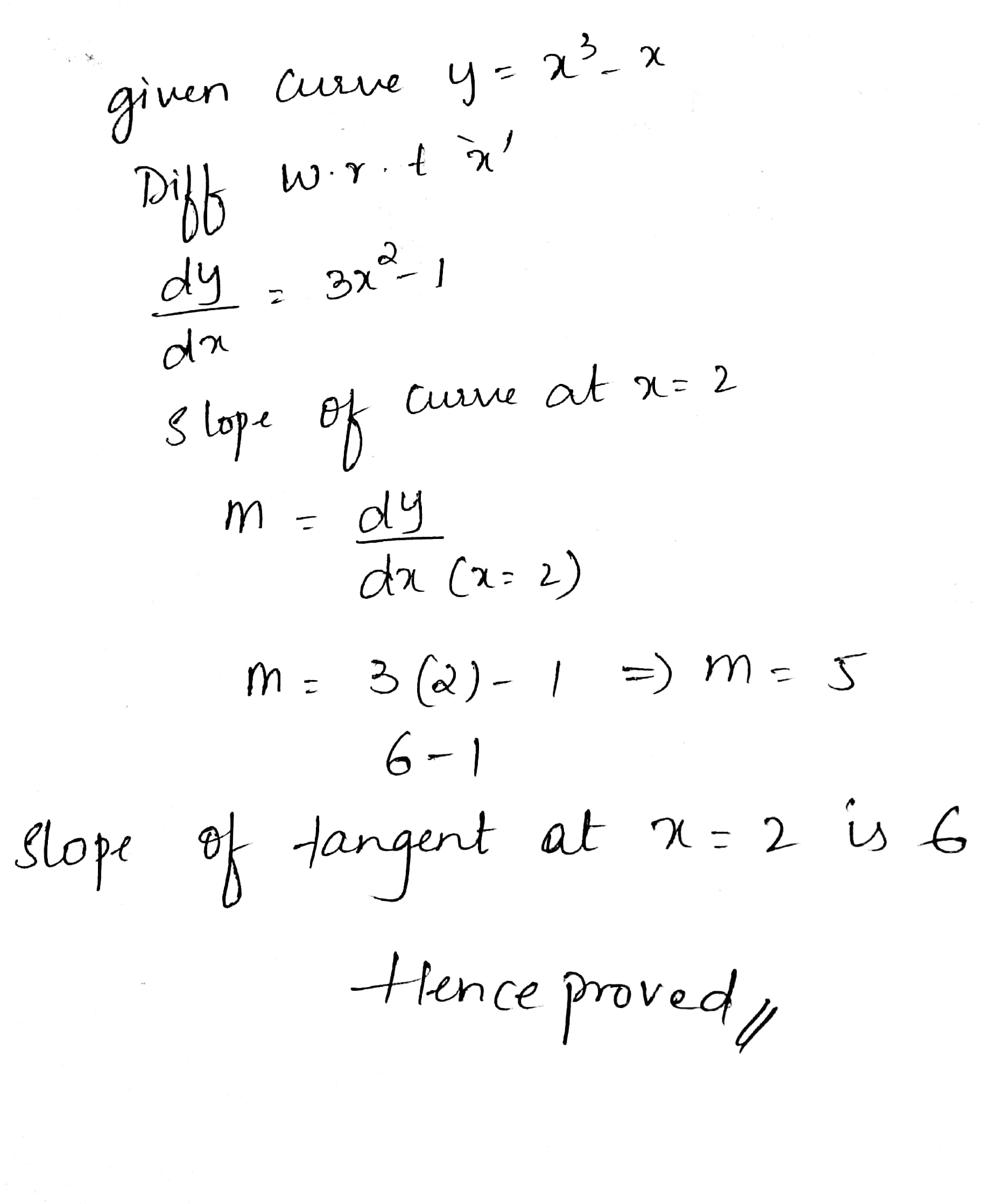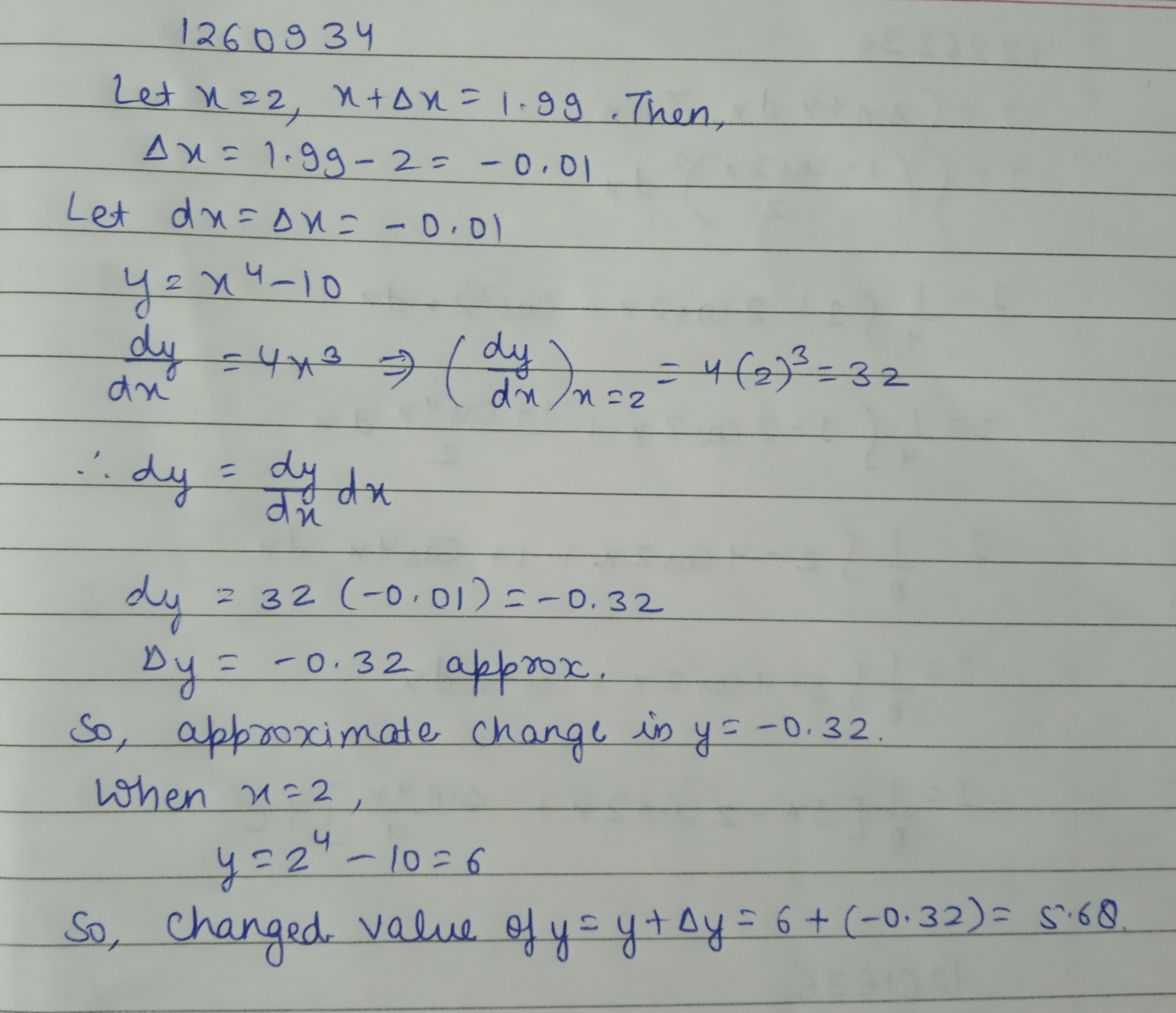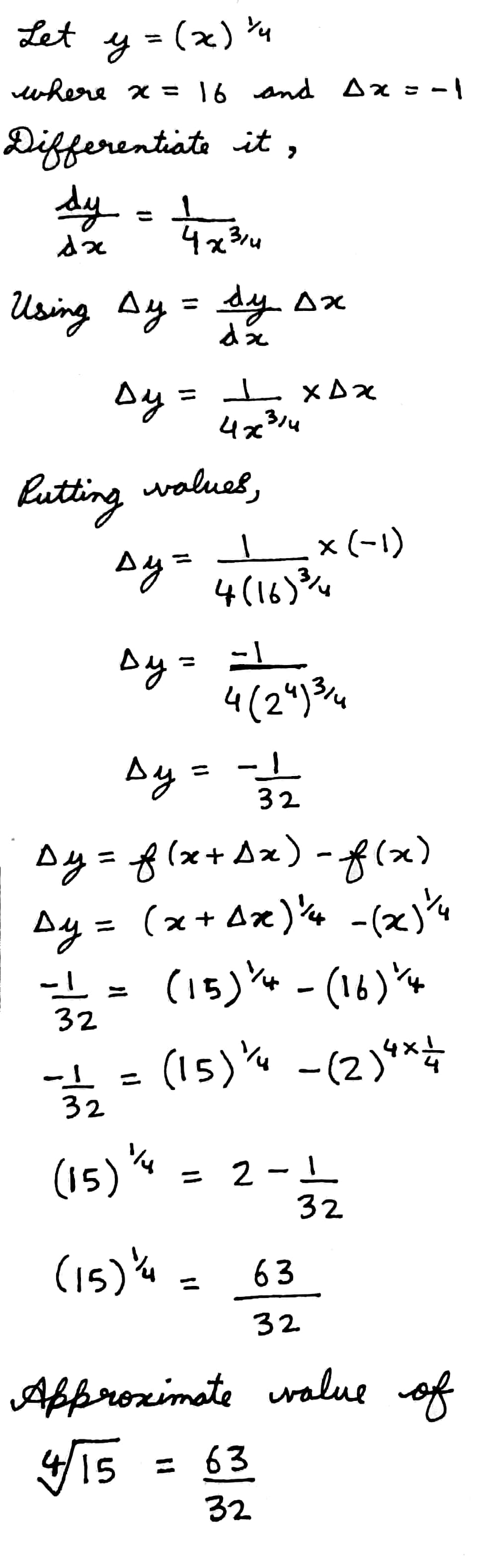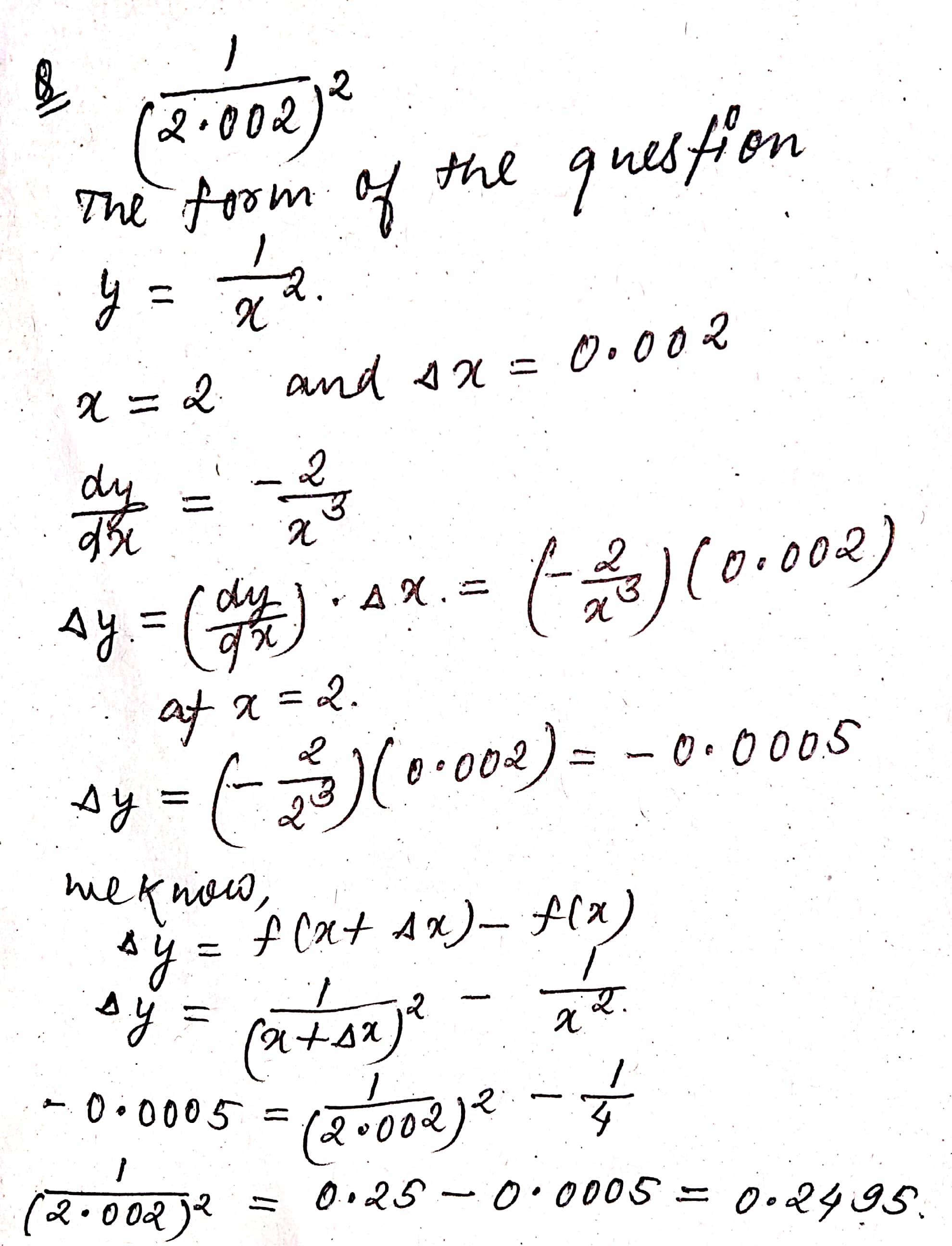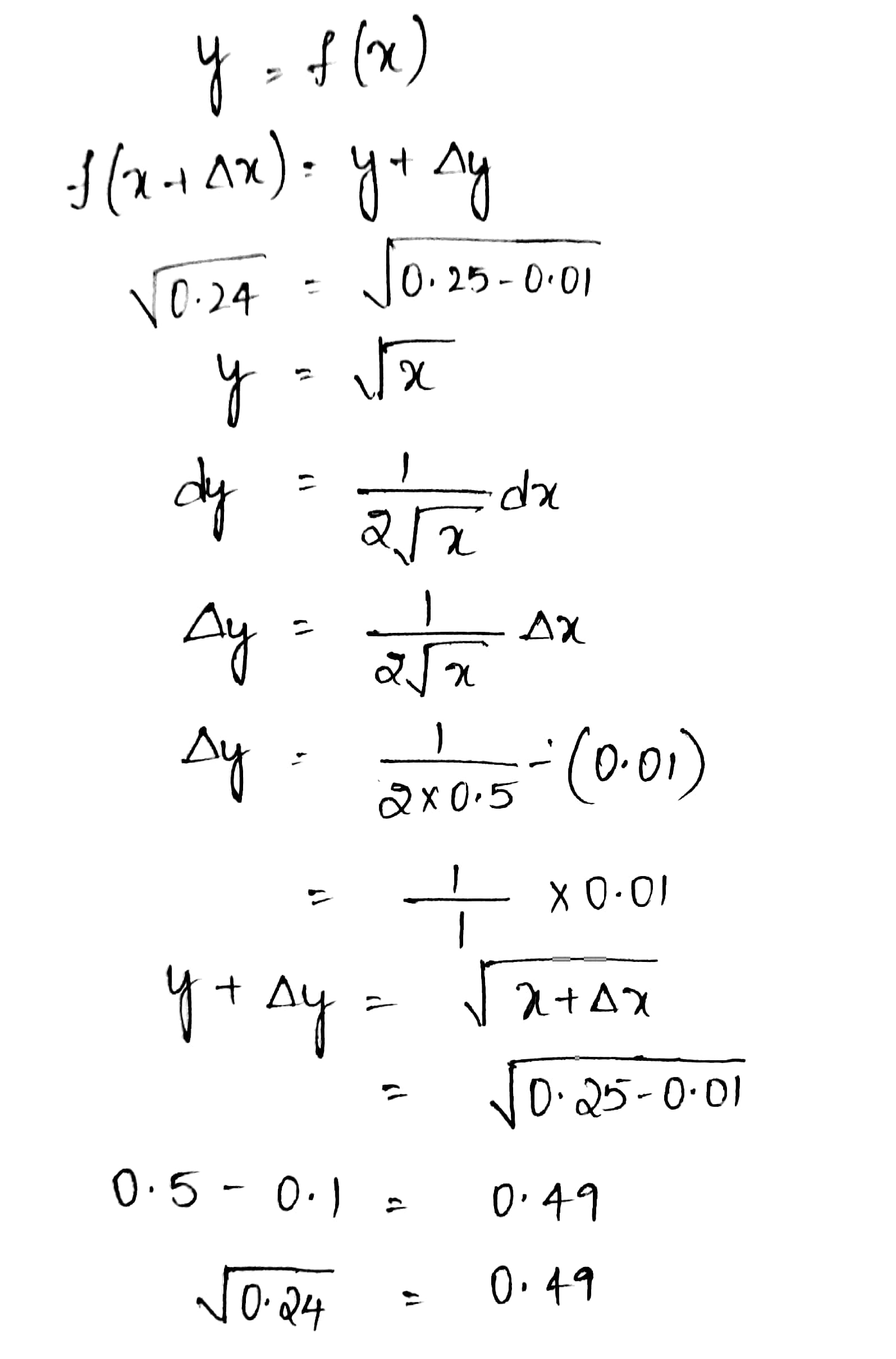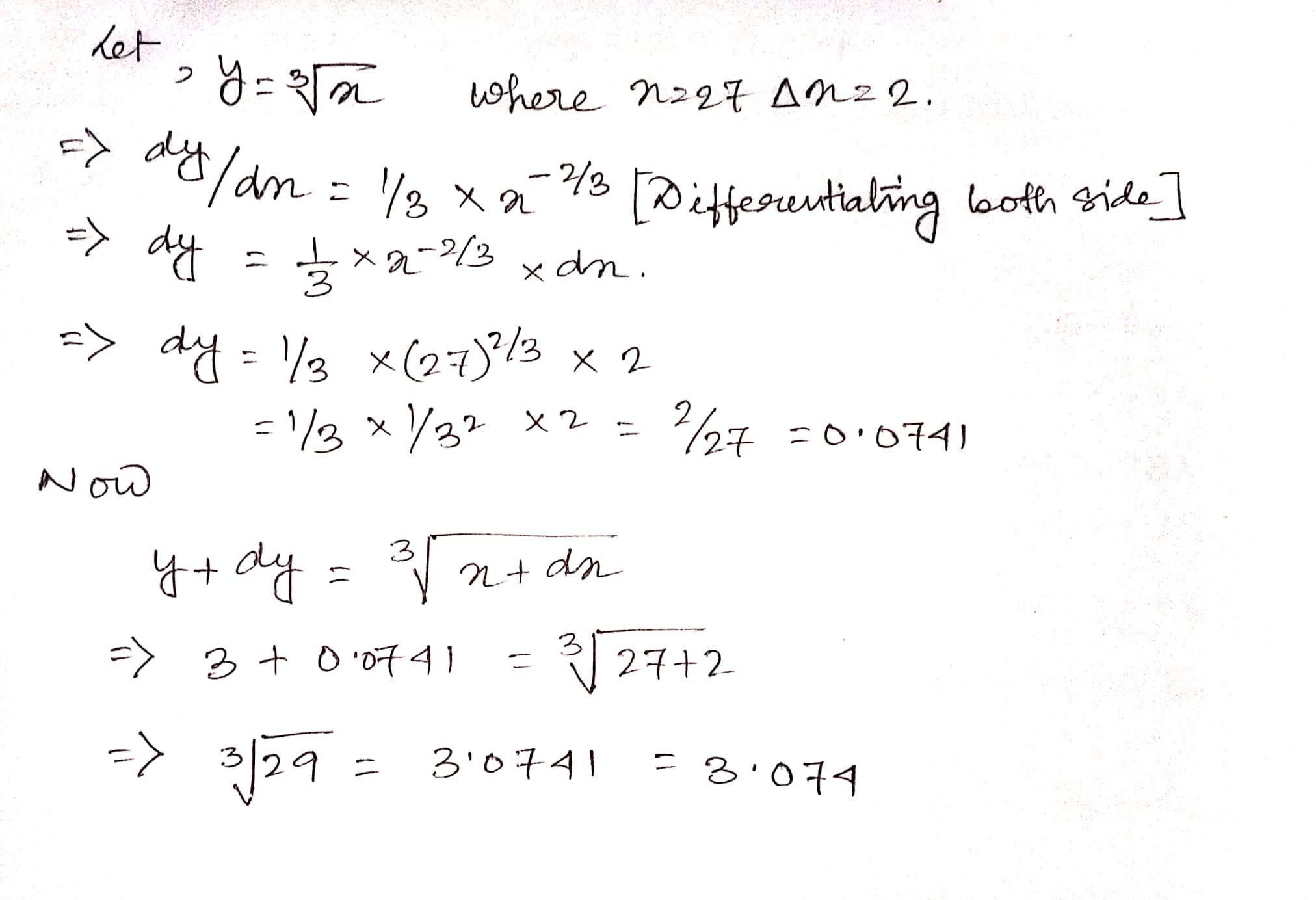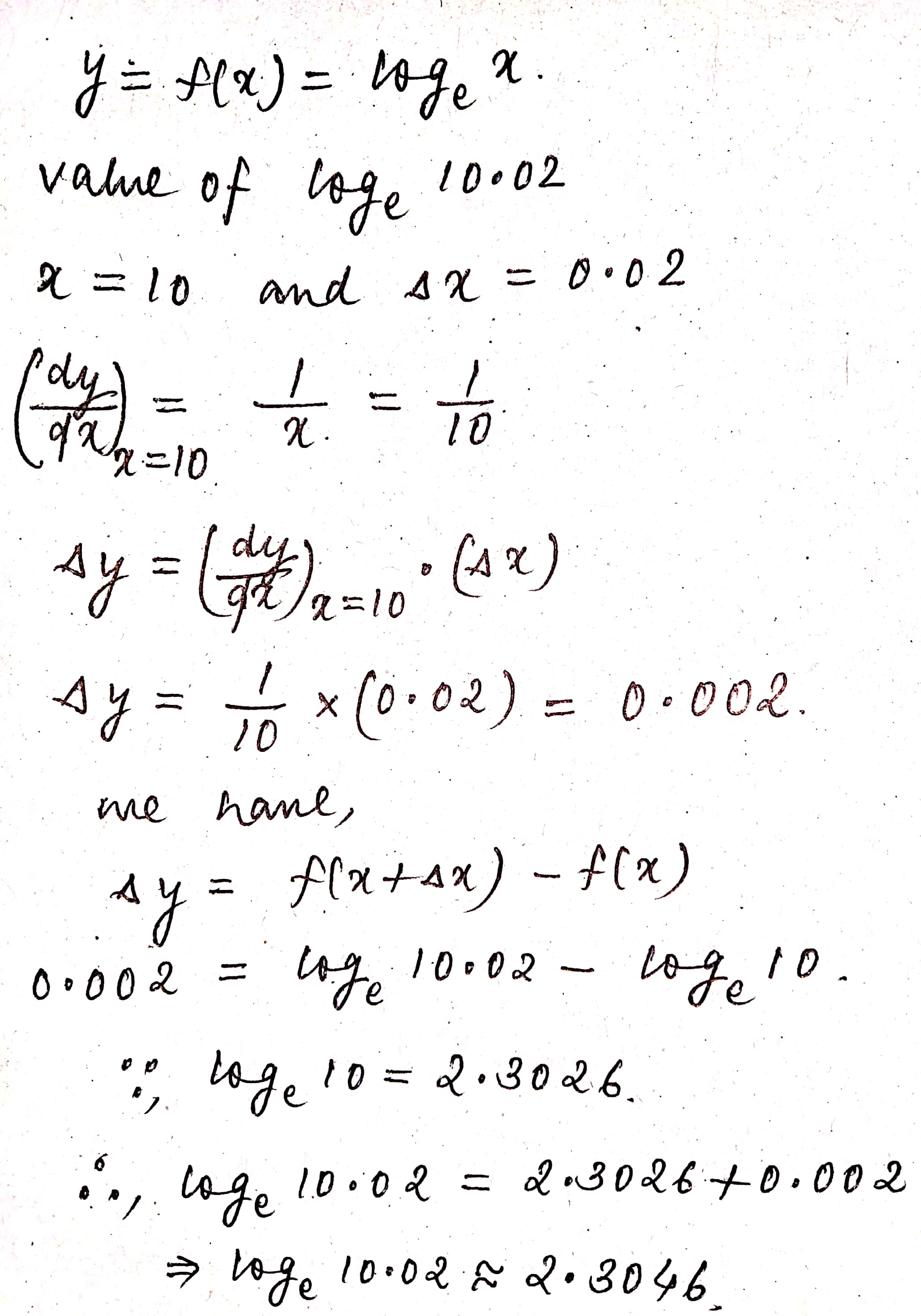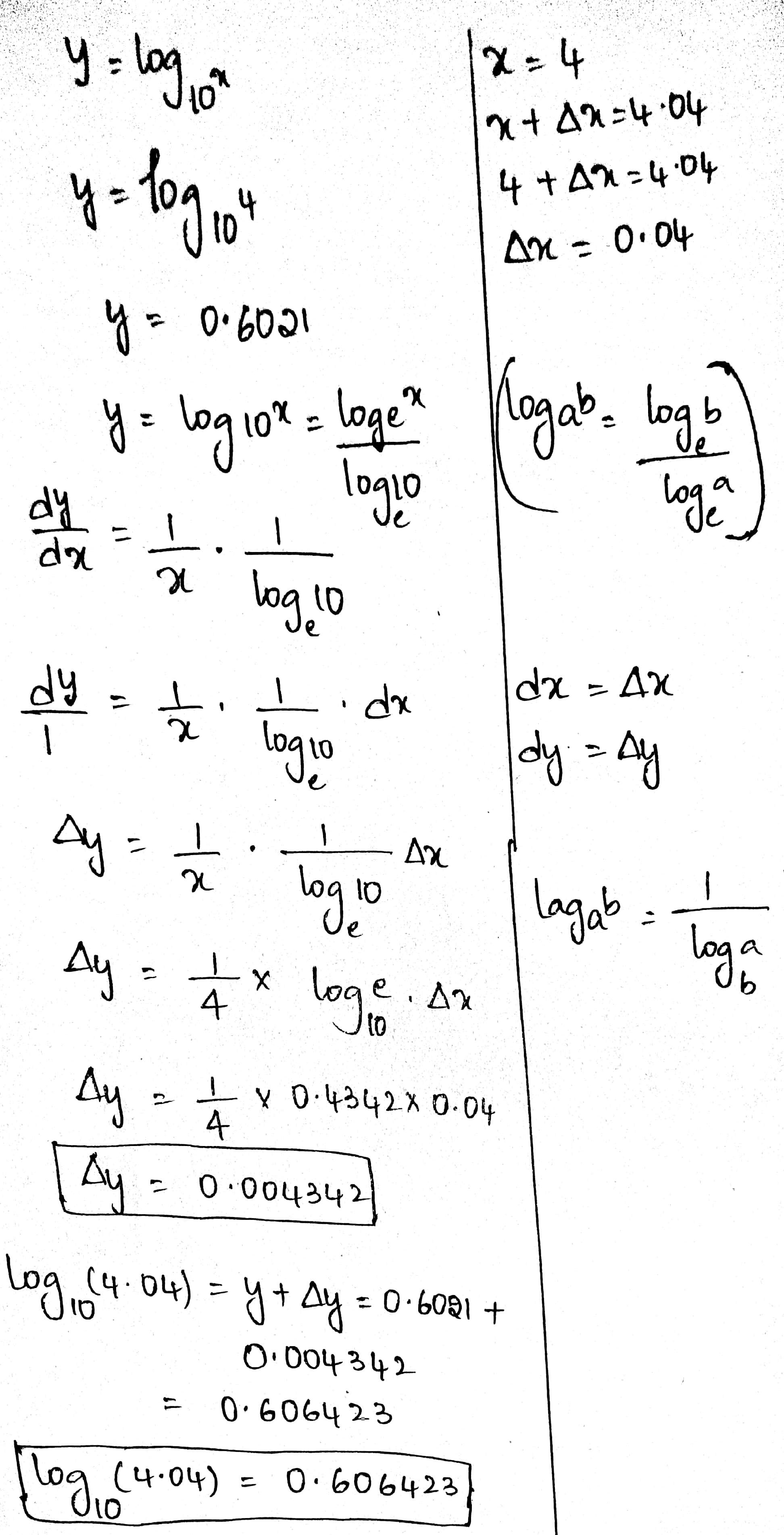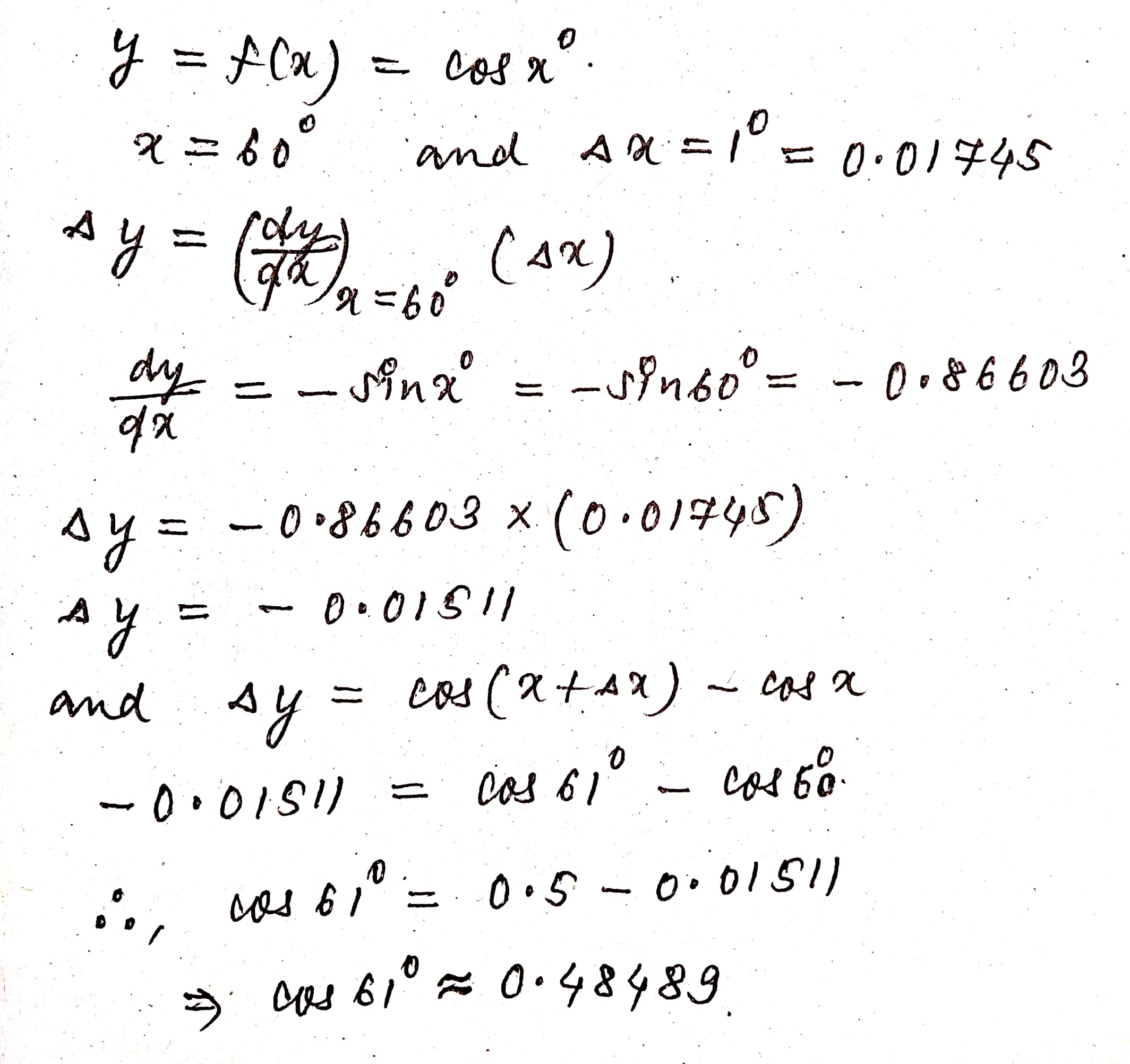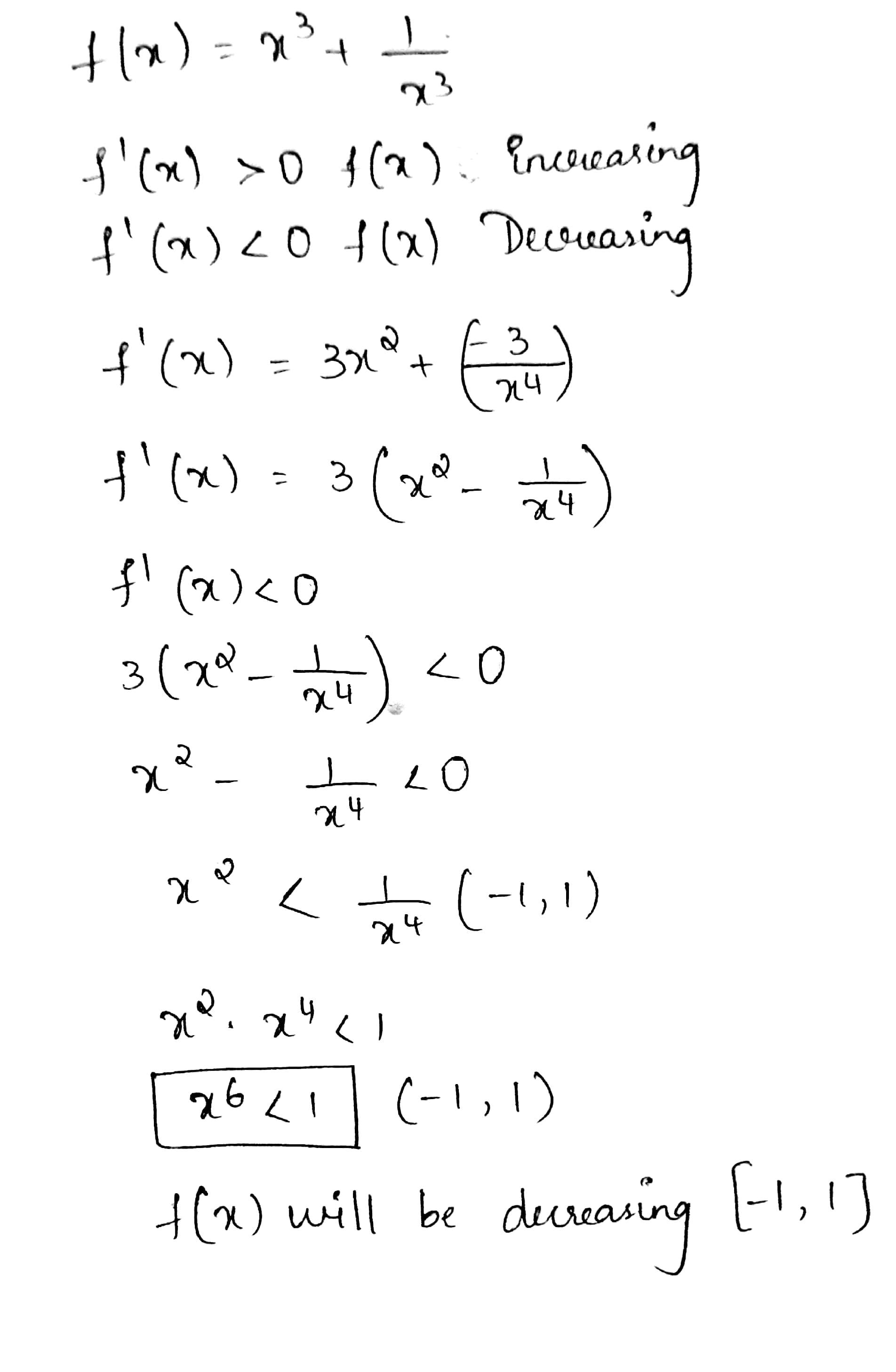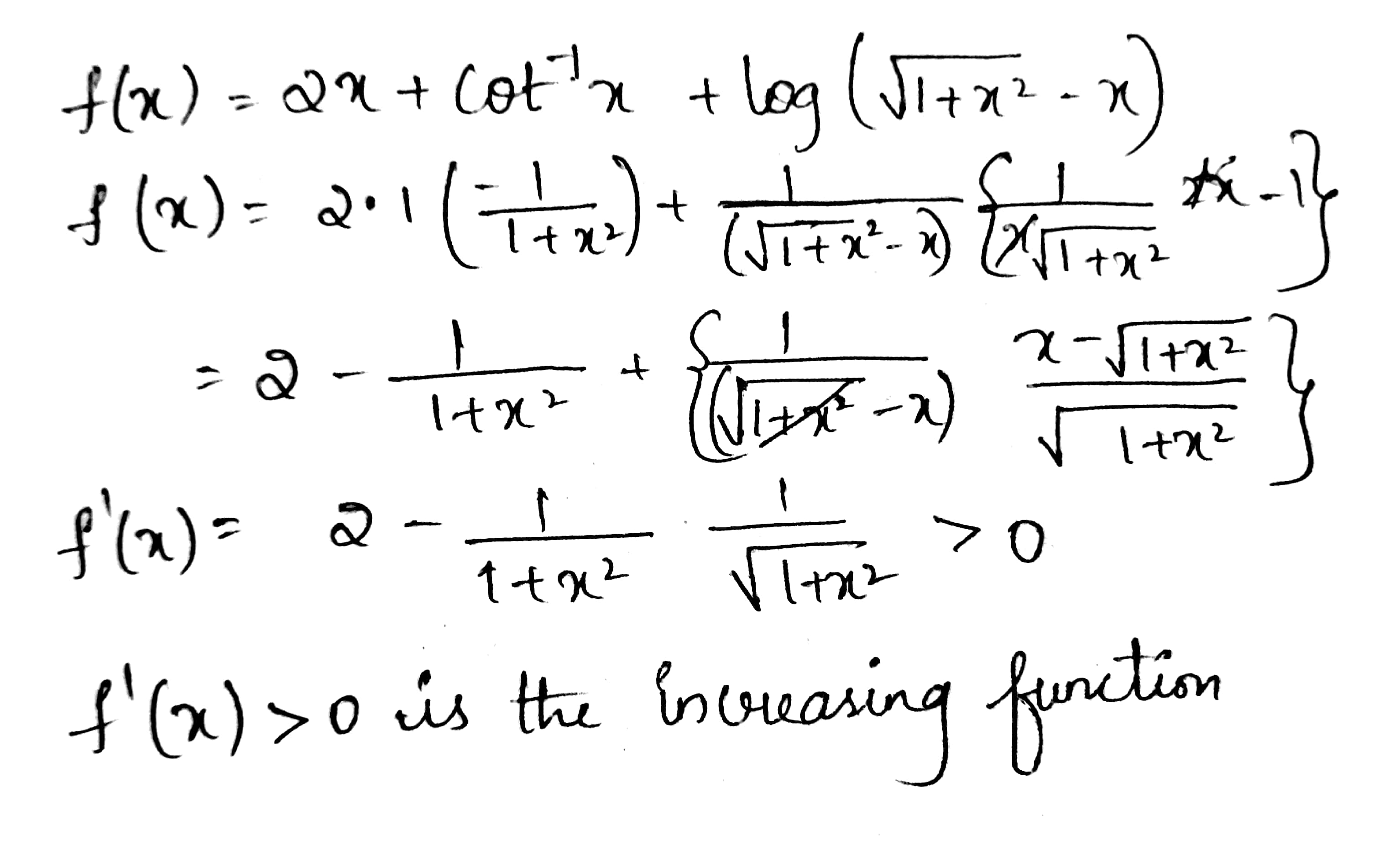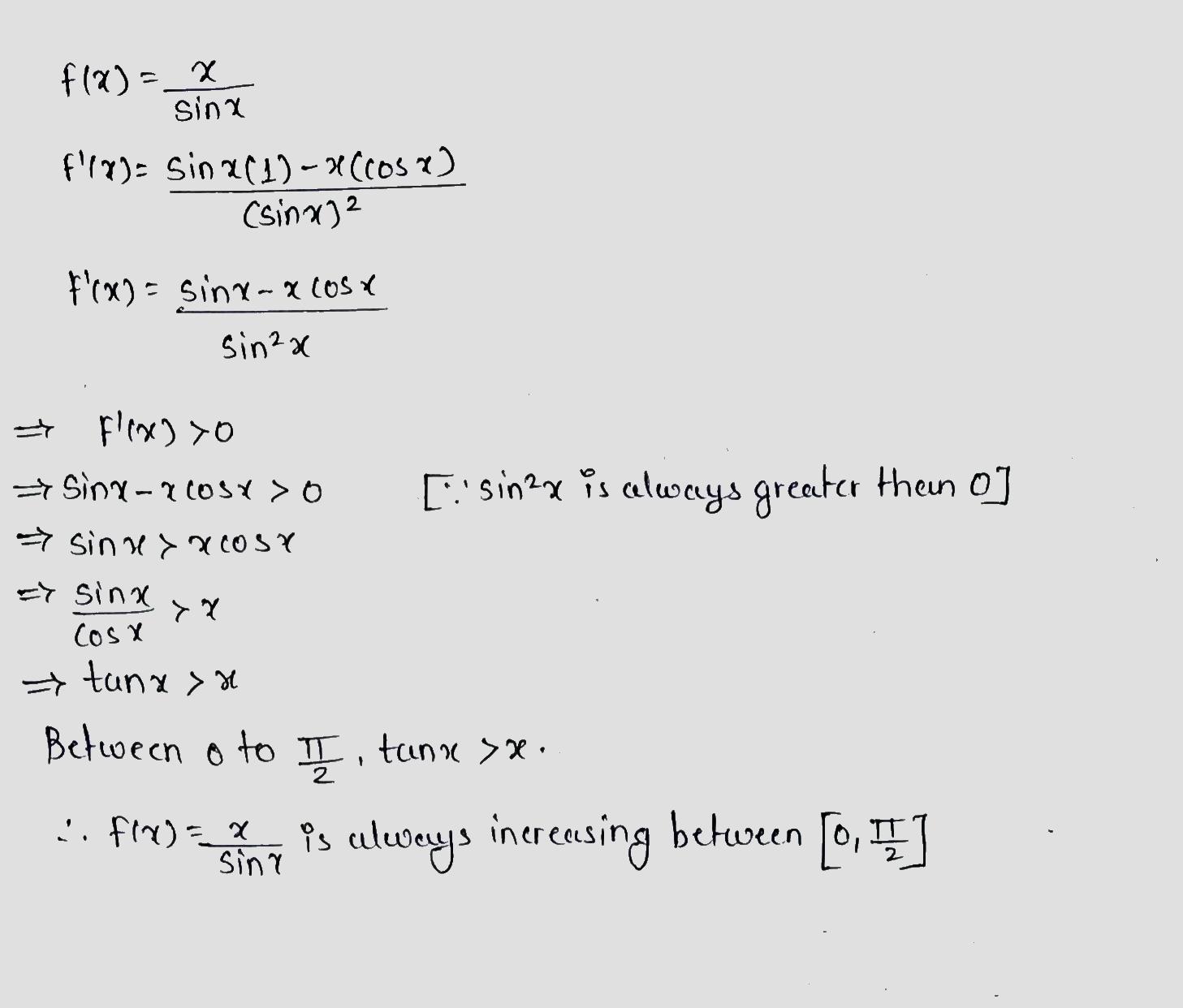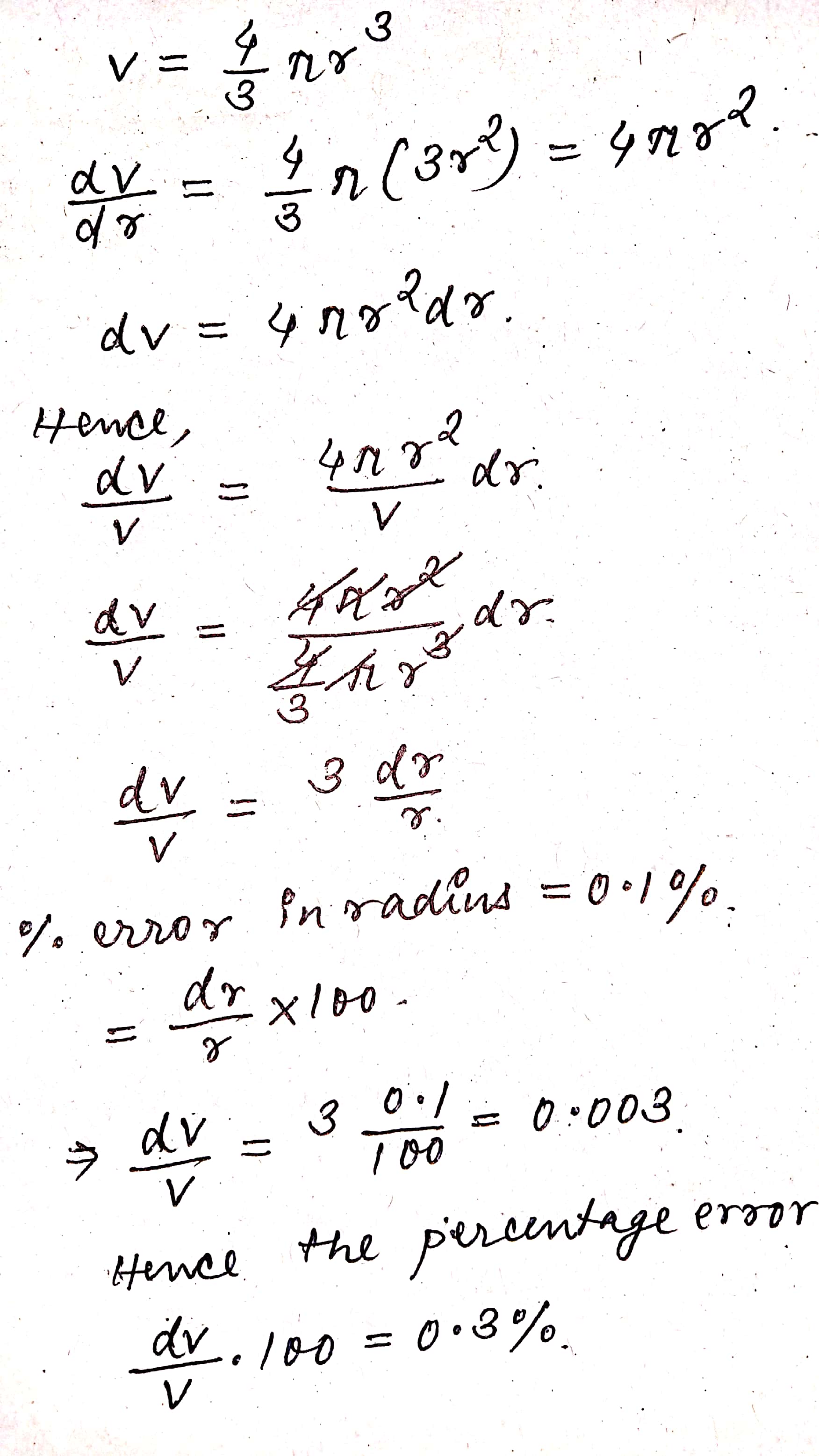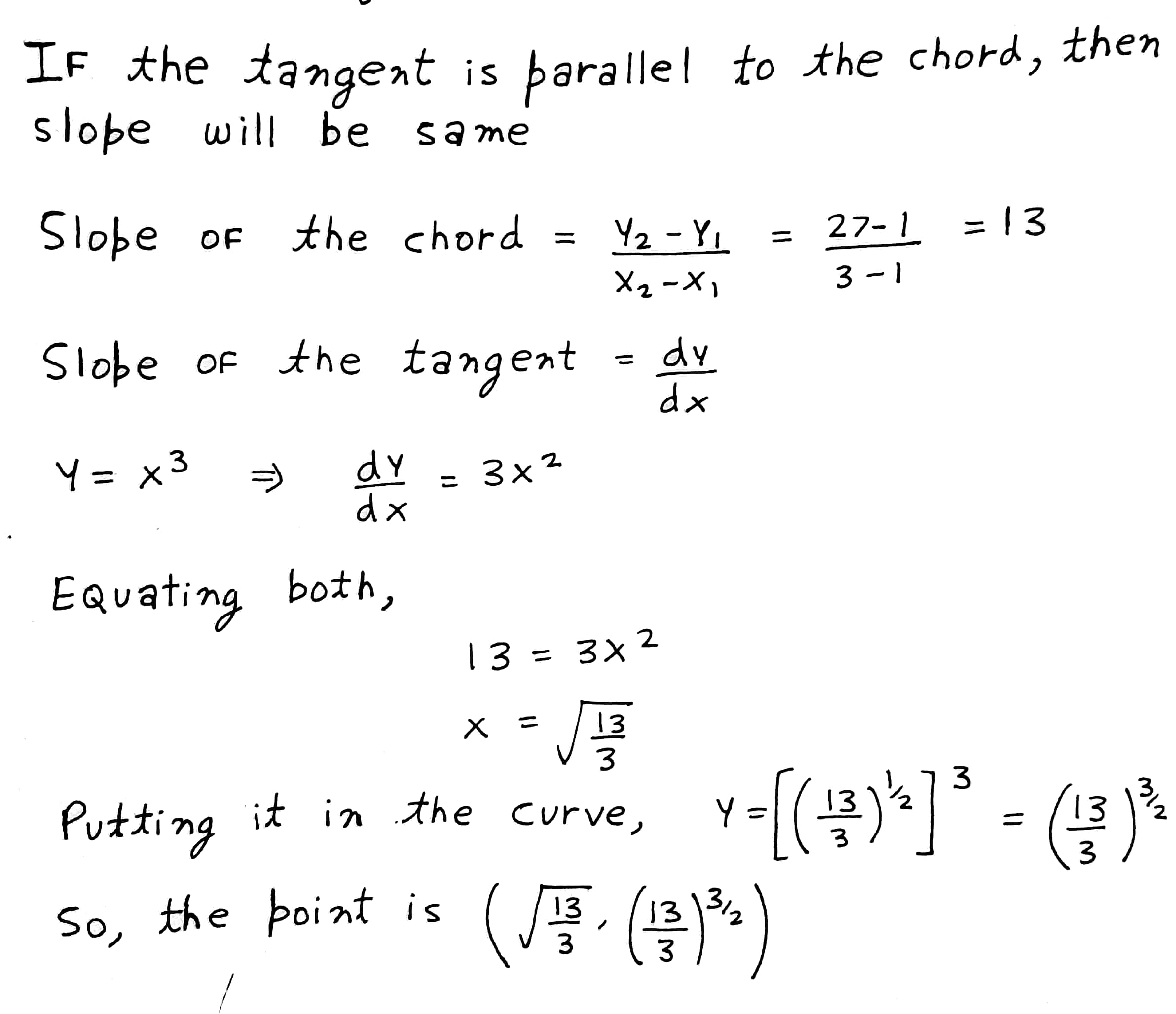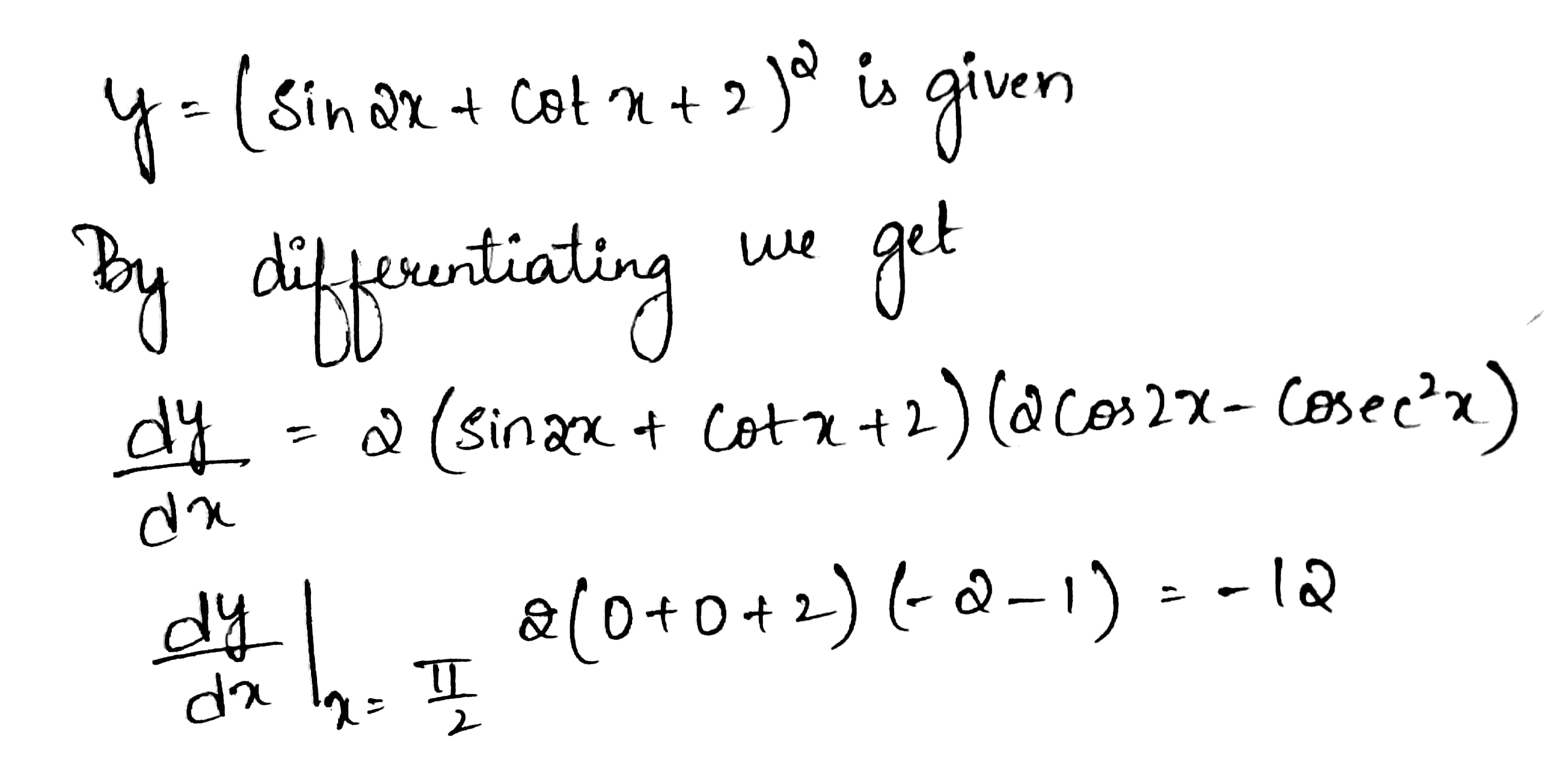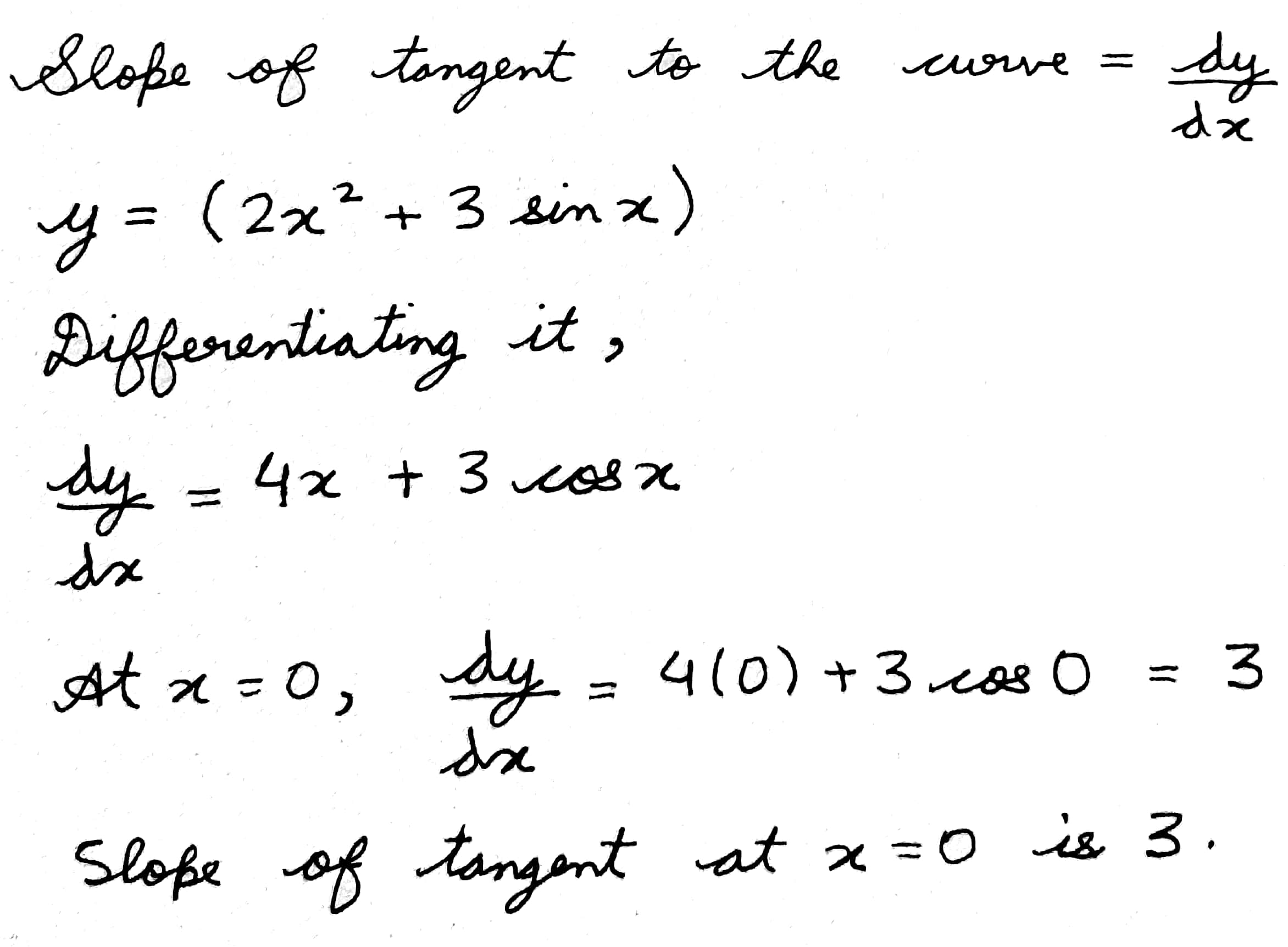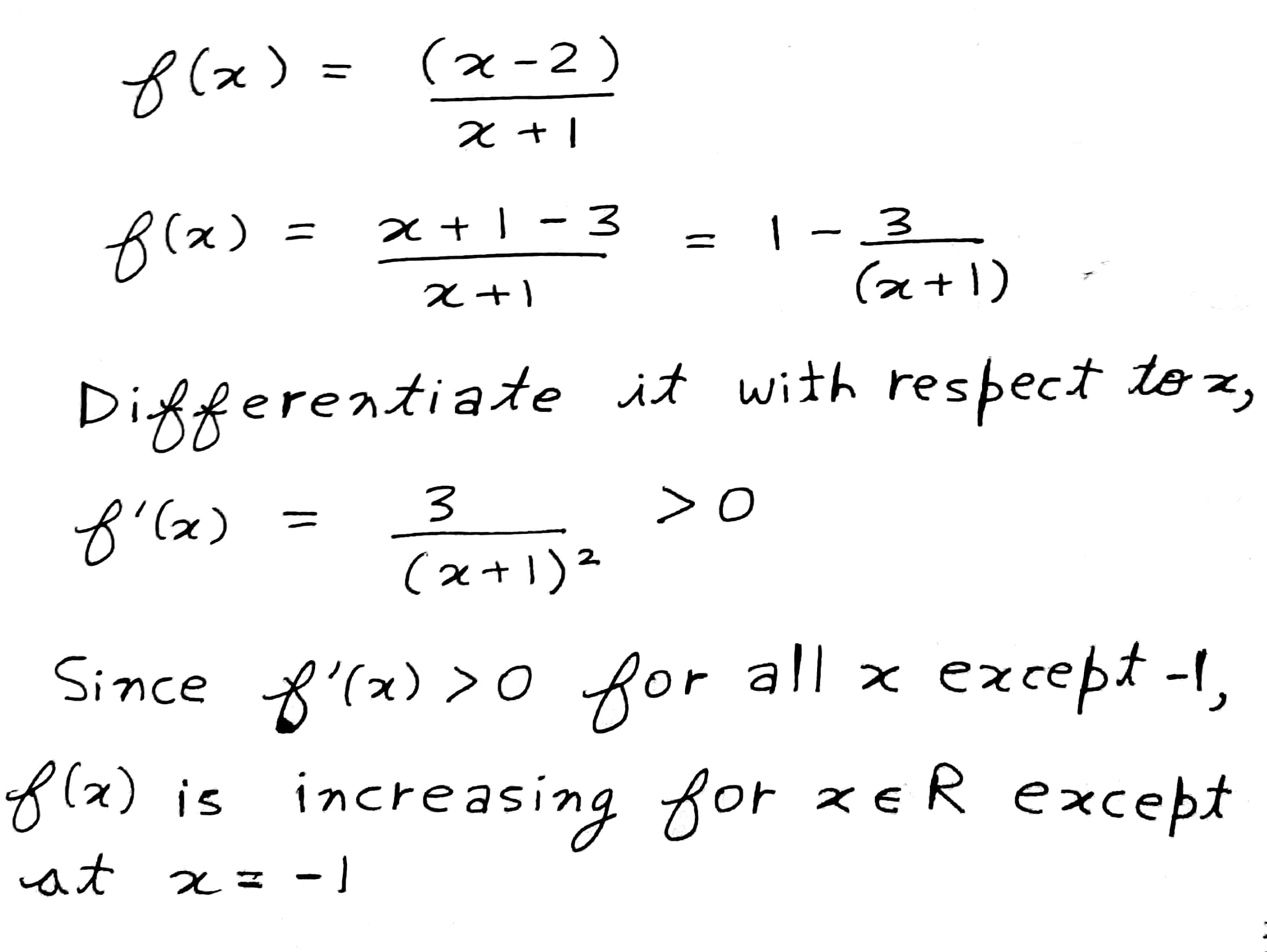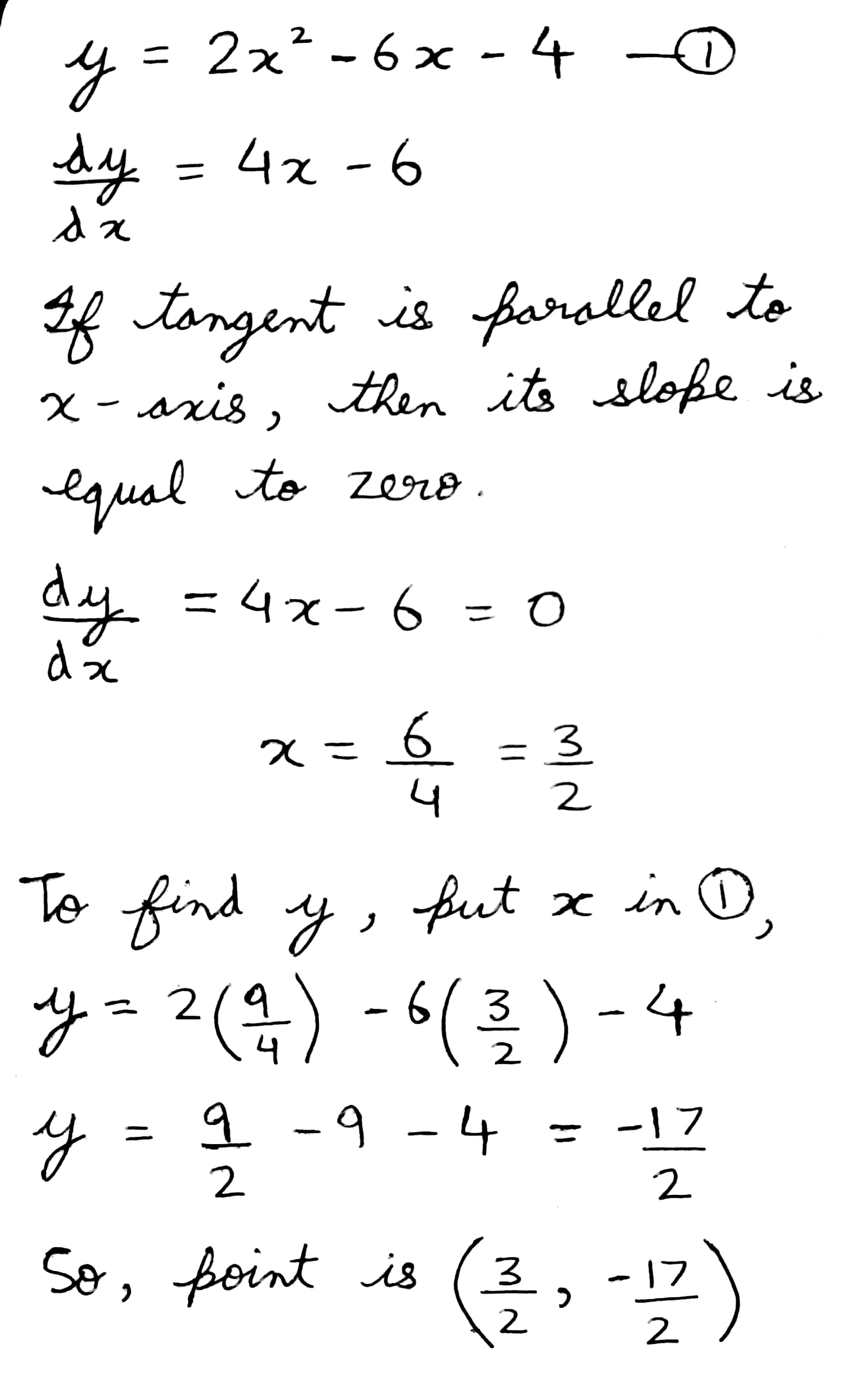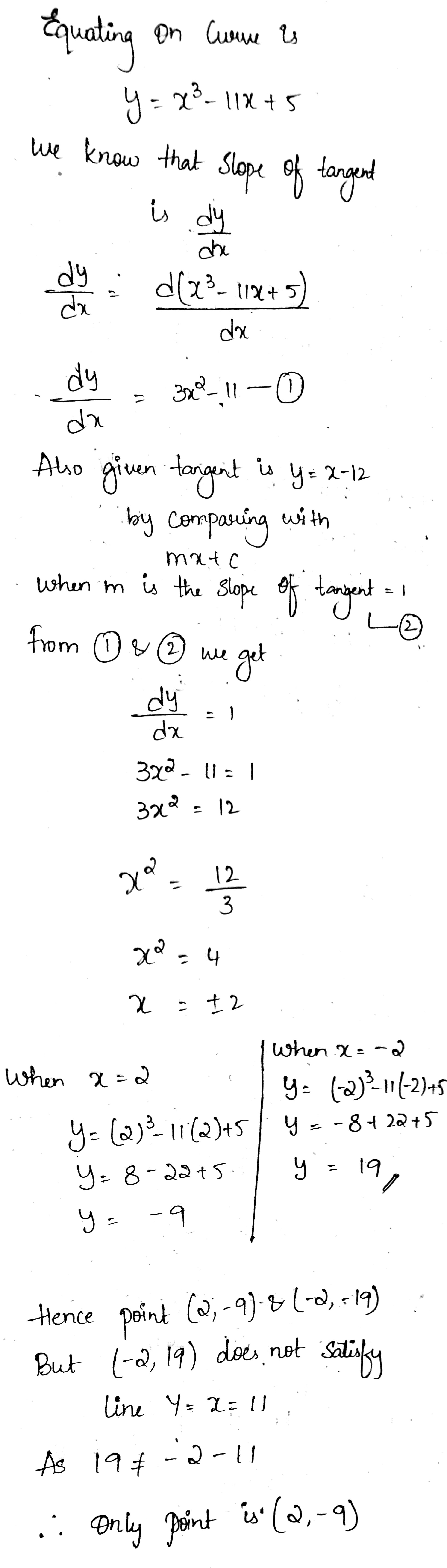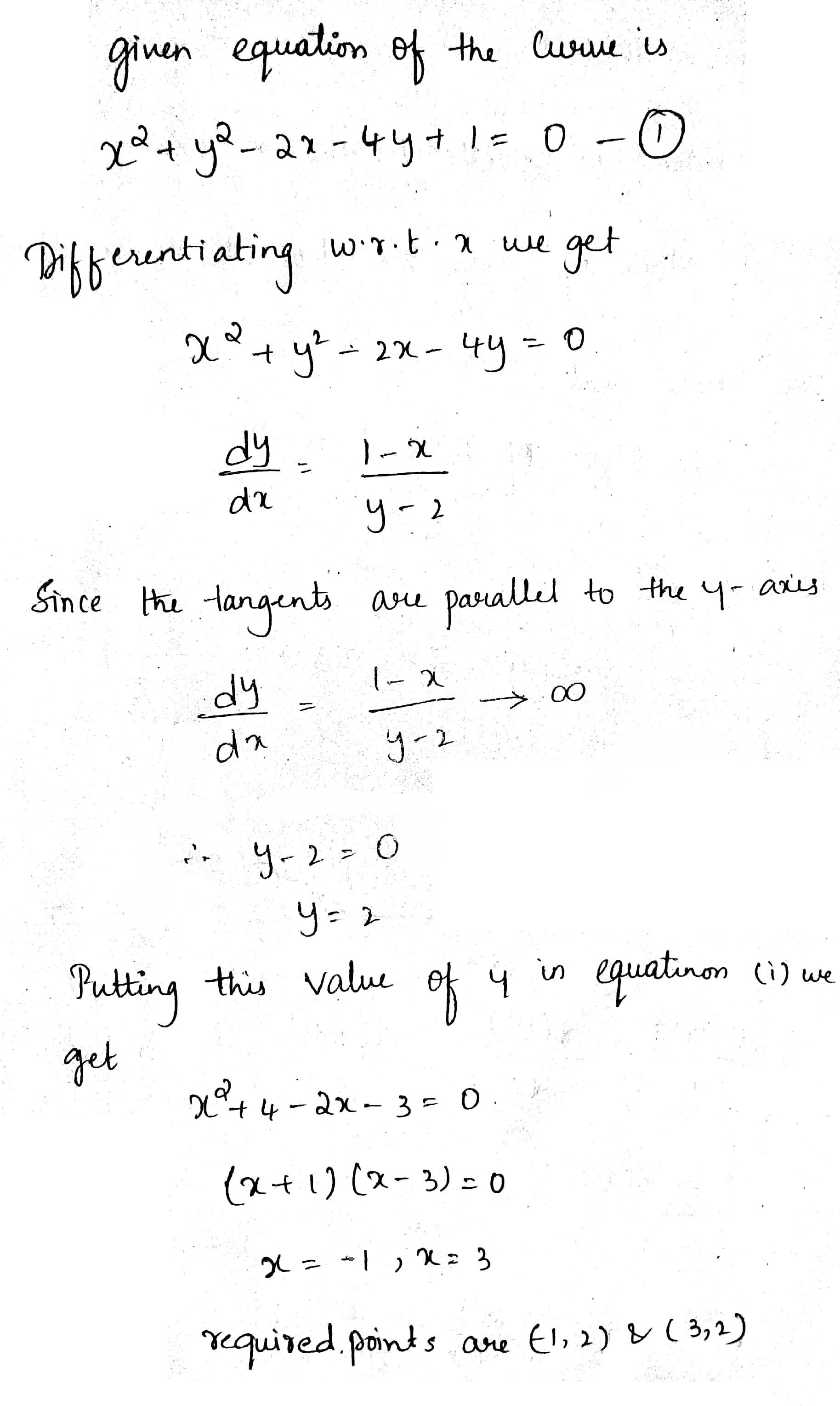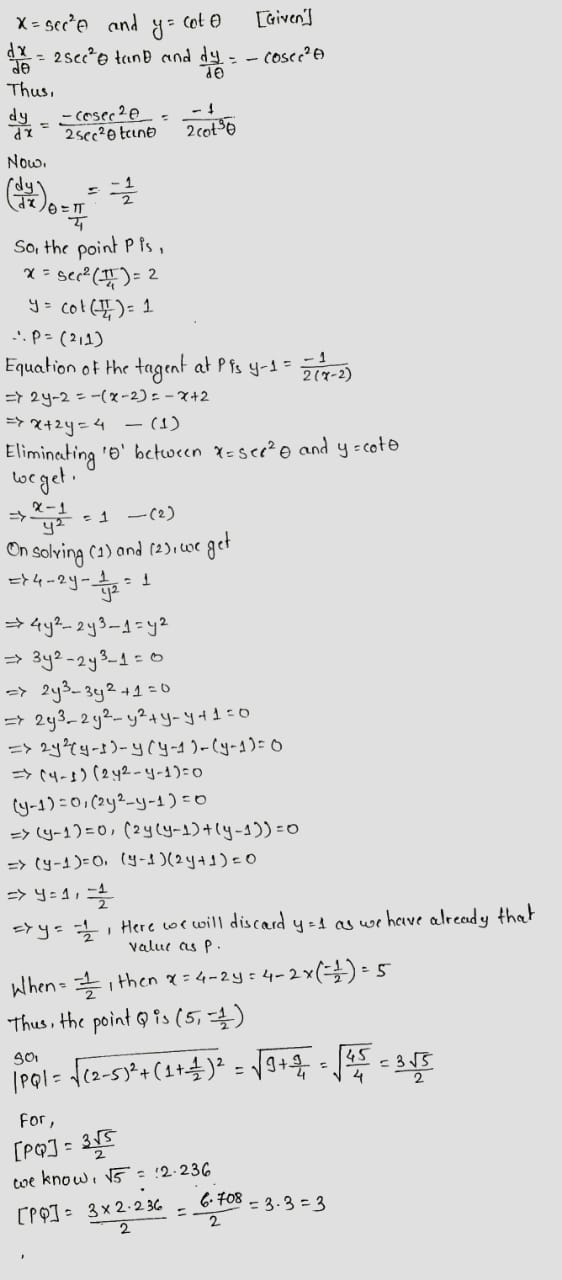Class 12 Commerce Maths - Application Of Derivatives

Find the equation of tangent in $$1^{\mathrm{s}\mathrm{t}}$$ quadrant to the circle $$\mathrm{x}^{2}+\mathrm{y}^{2}=16$$ at $$(2,2 \sqrt 3)$$

The given circle is $$x^2+y^2=16$$

The slope of tangent of circle is $$2x+2y\dfrac {dy}{dx}=0\\\dfrac {dy}{dx}=\dfrac{-x}y\\\left.\dfrac {dy}{dx}\right|_{(2,2\sqrt 3)}=\dfrac {-1}{\sqrt 3}$$

The equation of tangent is $$y-2\sqrt 3=\dfrac {-1}{\sqrt 3}(x-2)\\\sqrt 3 y-6=-x+2\\x+\sqrt 3y-8=0$$

Find the slope of the tangent to curve $$y = x^3- x + 1$$ at the point whose $$x$$-coordinate is $$2$$.

The given curve is $$y = x^3 - x + 1$$

$$\therefore \displaystyle \frac{dy}{dx}=3x^2-1$$

The slope of the tangent to the curve at $$x=2$$ is given by,

$$\displaystyle \left(\frac{dy}{dx} \right)_{x=2}=\left(3x^2-1\right)_{x=2}=3(2)^2-1=11$$

Find the slope of the tangent to the curve $$y = 3x^4- 4x$$ at x = 4.

The given curve is $$y = 3x ^4-4x$$.
Thus, the slope of the tangent to the given curve at $$x = 4$$ is given by,
$$\displaystyle \left[\frac{dy}{dx}\right]_{x=4} =\left[12x^3-4\right]_{x=4}$$=$$ 12(4)^3-4=12(64)-4=764$$

Show that the function given by $$f(x) = \sin x$$ is (a) strictly increasing in $$\left ( 0, \dfrac{\pi}{2} \right )$$ (b) strictly decreasing in $$\left ( \dfrac{\pi}{2}, \pi \right )$$ (c) neither increasing nor decreasing in $$(0, \pi)$$.

The given function is $$f(x) = \sin x.$$
$$\therefore f'(x)=\cos x$$
(a) Since for each $$x \in \left ( 0,\dfrac{\pi}{2}, \right ), \cos x>0\Rightarrow f'(x)>0.$$
Hence, $$f$$ is strictly increasing in $$ \left ( 0,\dfrac{\pi}{2} \right )$$.
(b) Since for each $$x \in \left ( \dfrac{\pi}{2}, \pi \right ), \cos x<0\Rightarrow f'(x)<0$$.
Hence, $$f$$ is strictly decreasing in $$ \left ( \dfrac{\pi}{2}, \pi \right )$$.
(c) From the results obtained in (a) and (b), it is clear that $$f$$ is neither increasing nor
decreasing in $$(0, \pi)$$.

Show that the tangents to the curve $$y = 7x^3+ 11$$ at the points where $$x = 2$$ and $$x = -2$$ are parallel.

The equation of the given curve is $$y = 7x^3+ 11$$.
$$\therefore \cfrac{dy}{dx}=21x^2$$
Thus slope of the tangent to a curve at $$x=2$$ is $$= \left(\cfrac{dy}{dx}
\right )_{x=2}=(21x^2)_{x=2}=84$$
and slope of the tangent to a curve at $$x=-2$$ is $$= \left(\cfrac{dy}{dx}
\right )_{x=-2}=(21x^2)_{x=-2}=84$$
It is observed that the slopes of the tangents at both the are equal.
Hence, the two tangents are parallel.

Find the slope of the tangent to the curve $$y = x^3-3x + 2$$ at the point whose $$x$$ coordinate is $$3$$.

The given curve is $$y = x^3 - 3 x + 2$$
$$\Rightarrow \displaystyle \frac{dy}{dx}=3x^2-3$$
Thus slope of the tangent to the given curve at $$x=3$$ is
$$\displaystyle \left(\frac{dy}{dx} \right)_{x=3}=\left(3x^2-3 \right)_{x=3}=3(3)^2-3=24$$

Find the slope of the tangent at $$(1,2)$$ on the curve $$y={ x }^{ 2 }-4x+5$$.

Slope of the tangent to a curve at $$(x,y)$$ is the value of $$\dfrac { dy }{ dx } $$ at $$(x,y)$$

$$\Longrightarrow \dfrac { dy }{ dx } =\dfrac { d({ x }^{ 2 }-4x+5) }{ dx } \\ \\ \Longrightarrow \dfrac { dy }{ dx } =2x-4$$

At $$(1,2), \dfrac { dy }{ dx } =2(1)-4=-2$$

Slope of the tangent $$=-2$$

Find the slope of tangent to the curve $$y=3x^2-6$$ at the point on it whose x-coordinate is 2.

$$y=3x^2-6$$

$$\dfrac{dy}{dx}=6x$$

Thus, $$\left [\dfrac{dy}{dx}\right ]_{x=2}=6(2)=12$$

Write the differential equation representing the family of curves $$y=mx$$, where m is an arbitrary constant.

Given, family of curves is $$y=mx$$. ........(1)

Now, differentiating w.r.t. x, we get,

$$\dfrac{dy}{dx}=m$$

On putting $$m=\dfrac{dy}{dx}$$ in equation 1, we get,

$$y=x \dfrac{dy}{dx}$$ which is the required differential equation.

Find the slope of the tangent to the curve $$y=\dfrac{x-1}{x-2}, x\ne 2$$ at $$x=10$$.

$$\dfrac { du(x) }{ v(x) } =\dfrac { \dfrac { d(u(x)) }{ dx } v(x)-u(x)\dfrac { d(v(x)) }{ dx } }{ { v(x) }^{ 2 } } $$

$$\dfrac { dy }{ dx } =\dfrac { (x-2)\dfrac { d(x-1) }{ dx } -(x-1)\dfrac { d(x-2) }{ dx } }{ { (x-2) }^{ 2 } } $$

$$=\dfrac { x-2-x+1 }{ { (x-2) }^{ 2 } } =\dfrac { -1 }{ { (x-2) }^{ 2 } } $$

at $$x =10$$ we get $$\dfrac{-1}{64}$$

If the tangent to the curve $$y = {x}^{3} + ax + b$$ at $$(1, -6)$$ is parallel to the line $$x - y + 5 = 0$$, find $$a$$ and $$b$$.

Given: $$y= x^3+ax+b$$ ........(i)

Tangent to the curve= $$\dfrac{dy}{dx}=3x^2+a$$

Tangent to the curve at point $$(1,-6)$$ $$=$$ $$\dfrac{dy}{dx}_{(1,-6)}=3(1)^2+a=3+a$$

Now, $$x-y+5=0$$

$$\Rightarrow y=x+5$$

Comparing it with $$y=mx+c $$, where $$m=$$ slope, we get $$m=1$$

Therefore, slope of the above line is $$1$$.

Given tangent is parallel to the line $$x-y+5=0$$.

Thus slope will be equal.

Therefore, $$ 3+a=1$$

$$\Rightarrow a=1-3=-2$$

Substituting $$a=-2$$ in eqn (i) we get

$$-6=1^3+(-2)(1)+b$$

$$\Rightarrow -6=1-2+b$$

$$\Rightarrow -6+1=b$$

$$\Rightarrow b=-5$$

$$\Rightarrow a=-2, b=-5$$

Find the points on curve $$y=x^3-11x+5$$ at which equation of tangent is $$y=x-11$$.

Given equation of curve is $$y=x^3-11x+5$$.

Slope of tangent to the given curve is $$\dfrac{dy}{dx}$$.

Therefore,

$$\dfrac{dy}{dx}=3x^2-11$$

Also, slope of the tangent $$y=x-11$$ is $$1$$.

$$\dfrac{dy}{dx}=1$$

$$3x^2-11=1$$

$$3x^2=12$$

$$x^2=4$$
$$x=\pm 2$$

Then, when $$x=2$$

Then, $$y=(2)^3-11(2)+5=-9$$

When $$x=-2, y=19$$.

Hence, the required points on the curve are $$(2,-9)$$ and $$(-2,19)$$.

Find the equations of the common tangents to the parabolas $$\displaystyle y \, = \, x^2 \, - \, 5x \, + \, 6 \, and \, y \, = \, x^2 \, + \, x \, + \, 1.$$

$$x^2-5x+6=y=f(x)$$

$$x^2+x+1=y=g(x)$$

$$y=mx+c=tangent$$

$$f'(x_1)=2x_15=m$$

$$f'(x_2)=2x_2+1=m$$

$$2x_1-5.2x_2+1$$

$$\boxed{x_1-x_2=3}\Rightarrow x_1=x_2+3$$

$$y_1=x^2_1-5x_1+6$$

$$y_2=x^2_2+x+1$$

$$=(x_1-3)+x_1-3+7$$

$$=x_1^2-5x_1+7$$

$$y_1=mx_1+c$$

$$\Rightarrow y_1=(2x_1-5)x_1+c$$

$$\Rightarrow x^2_1-5x_1+6=2x^2_1-5x+c$$

$$C=6-x^2_1$$

also, $$y_2=mx_2+c$$

$$x^2_1-5x_1+7=(2x_1-5)(x_1-3)+c$$

$$x^2_1-5x_1+7=2x^2_1-11x_1+5+6-x^2_1$$

$$6x_1=14$$

$$x_1=\dfrac{7}{3},x_2=\dfrac{-2}{3}$$

$$\boxed{\therefore common\,\, tangent=y=\dfrac{-1}{3}x+\dfrac{5}{9}}$$

Find the equation of the tangent at origin to the curve $$y=x^{{\cfrac{3}{2}}}$$.

Given the curve $$y=x^{\large{\cfrac{3}{2}}}$$.

Now $$\dfrac{dy}{dx}=\dfrac{3}{2}x^{\large{\cfrac{1}{2}}}$$.

Now,$$\left.\dfrac{dy}{dx}\right|_{(0,0)}=0$$.

So the equation of tangent at $$(0,0)$$ to the given curve is

$$(y-0)=$$$$\left.\dfrac{dy}{dx}\right|_{(0,0)}$$ $$(x-0)$$

or, $$y=0$$.

Find the points at which the tangent to the curve $$\displaystyle y \, = \, x \, - \, 0.5 \, sin \, 2x \, - \, 0.5 \, cos \, 2x \, + \, 16 \, cos \, x$$ is parallel to the abscissa axis.

$$y=x-0.5\sin 2x-0.5\cos 2x+16\cos x$$

absaissa axis $$\rightarrow x-axis$$

$$slope=0$$

Tangent equation $$: \dfrac{dy}{dx}|(x,y)=\dfrac{y-y_1}{x-x_1}$$

Points at which is $$0\rightarrow $$ Tangent are parallel to x-axis

$$\dfrac{dy}{dx}=\dfrac{d}{dx}[x-0.5(\sin2x+\cos 2x)+16\cos x]$$

$$0=1-0.5(\cos2x-\sin2x).2-16\cos x$$

$$0=1-\sqrt{2}(\sin(\dfrac{\pi}{4})-2x)-16\sin x$$

$$0=1-(\cos^2x-\sin^2x-2\sin x\,\cos x)-16\sin x$$

$$=1-(\cos^2x-\sin^2x+2\sin x\cos x)-16\sin x$$

$$0=25sin^2x+2\sin x\cos x-16\sin x$$

For zero $$:\sin x=0$$

$$x=x\pi$$ where $$n=0,1,2....$$

$$y=n\pi-0.5+16(-1)^n$$

$$(n\pi,n\pi-0.5+16(-1)^n)$$ where $$n=0,1,2.....$$

are the points where the curve is parallel to absaissa axis.

Find the co-ordinates of the points on the ellipse $$x^2+2y^2=9$$ at which tangent has slope $$\dfrac{1}{4}$$. Also find the equation of normal.

$$x^2+2y^2=9$$
$$\therefore 2x+4y\dfrac{dy}{dx}=0$$
$$\therefore x+2y\dfrac{dy}{dx}=0$$
$$\therefore \dfrac{dy}{dx}=-\dfrac{x}{2y}$$
Now slope of tangent $$=\dfrac{1}{4}$$
$$\therefore -\dfrac{x}{2y}=\dfrac{1}{4}$$
$$\therefore x=-\dfrac{y}{2}$$ $$(1)$$
Put $$x=-\dfrac{y}{2}$$ in equation $$x^2+2y^2=9$$
$$\therefore \dfrac{y^2}{4}+2y^2=9$$
$$\therefore y^2+8y^2=36$$
$$\therefore 9y^2=36$$
$$\therefore y^2=4$$
$$\therefore y=\pm 2$$
Substitute this value in result $$(1)$$
$$\therefore x=\dfrac{\pm 2}{2}$$
$$\therefore x=\pm 1$$
$$\therefore$$ Required points means co-ordinates of the point of contact $$(1, 2)$$ and $$(-1, 2)$$
Now slope of tangent $$\displaystyle\frac{dy}{dx}=\dfrac{x}{2y}$$
$$\therefore \left(\dfrac{dy}{dx}\right)_{P(1, 2)}=\dfrac{1}{4}$$
$$\therefore$$ Slope of Normal $$=-4$$
$$\therefore$$ We get equation of Normal using equation
$$y=y_1=m(x-x_1)$$
$$\therefore y+2=-4(x-1)$$
$$\therefore y+2=-4x+4$$
$$\therefore 4x+y=2$$ .$$(1)$$
$$\therefore$$ Now equation of normal at point
$$(-1, 2) y-2=-4(x+1)$$
$$\therefore y-2=-4x-4$$
$$\therefore 4x+y=-2$$ .$$(2)$$
$$\therefore$$ Result $$(1)$$ and $$(2)$$ shows equation of Normal.

If the slope of tangent of $$xy+ax+by=2$$ at point $$(1,1)$$ is $$5$$ then find the values of $$a$$ and $$b$$.

$$x+ax-by=2$$
Now differrentiate w.r.to $$x$$
$$x\cfrac { dy }{ dx } +y+a+b\cfrac { dy }{ dx } =0$$
$$\therefore \left( x+b \right) \cfrac { dy }{ dx } =-(y+a)\quad $$
$$\therefore \cfrac { dy }{ dx } =-\cfrac { y+a }{ x+b } $$
Slope of a tangent at $$(1,1)$$ is $$5$$
$$\therefore { \left( \cfrac { dy }{ dx } \right) }_{ (1,1) }=\cfrac { a+1 }{ b+1 } =5\quad $$
$$-a-1=5b+5$$
$$a+5b=-6....(1)$$
Also point $$(1,1)\in xy+ax+by=2$$
$$-a-5b=5+1$$
$$a+5b=-6....(2)$$
By solving eqn (1) and (2)
we get $$a=\cfrac { 11 }{ 4 } ,b=-\cfrac { 7 }{ 4 } $$

Using differentiation, find the approximate value of each of the following:
a) $${\dfrac {17}{81}}^{\dfrac {1}{4}}$$
b) $${(33)}^{-\dfrac {1}{5}}$$

$$a)$$ let $$x=\cfrac { 16 }{ 81 } \quad ,\quad \quad \triangle x=\cfrac { 1 }{ 81 } \quad ,\quad \quad f(x)={ x }^{ \frac { 1 }{ 4 } }\\ f(x+\triangle x)=f(x)+f'(x)\triangle x\\ f(\cfrac { 17 }{ 81 } )=\sqrt [ 4 ]{ \cfrac { 16 }{ 81 } } +\cfrac { 1 }{ 4 } (\cfrac { 16 }{ 81 } )^{ \cfrac { -3 }{ 4 } }\times \cfrac { 1 }{ 81 } \\ \quad \quad =0.677$$

$$b$$) let $$x=32\quad ,\quad \quad \triangle x=1\quad ,\quad \quad f(x)={ x }^{ \cfrac { -1 }{ 5 } }\quad f'(x)=\cfrac { -1 }{ 5 } \\ f(x+\triangle x)=f(x)+f'(x)\triangle x\\ f(33)={ (32) }^{ \cfrac { -1 }{ 5 } }-\cfrac { { (32) }^{ \cfrac { -6 }{ 5 } } }{ 5 } \\ \quad \quad =0.497$$

Find the equation of the tangent to the curve $$y\, = \,\sqrt {3x\, - \,2} $$ which is parallel to the line $$4x\, - \,2y\, + \,5\, = 0$$.
Further find the equation of the normal to the curve.

Equation of tangent is $$\dfrac{dy}{dx}=\dfrac{1}{2\sqrt{3x-2}}\times 3\ at\ (h,k)\,\hbox{slope of tangent}=\dfrac{3}{2\sqrt{3h-2}}$$ Given tangent is parallel to line $$4x-2y+5\hbox{ so slope of tangent}=\hbox{slope of line}$$

$$\Rightarrow \dfrac{3}{2\sqrt{3h-2}}=2$$

$$\Rightarrow 9=16(3h-2)$$

$$\Rightarrow 3h=2+\dfrac{9}{16}$$

$$\Rightarrow h=\dfrac{41}{48}$$

$$\because (h_1k)$$ lies on curve so

$$k=\sqrt{3h-2}=\sqrt{3\times\dfrac{41}{48}-2}=\sqrt{\dfrac{9}{16}}=\dfrac{3}{4}$$

$$\therefore (h_1k)=\left(\dfrac{41}{48},\dfrac{3}{4}\right )$$

$$\hbox{eqn of tangent is }y-\dfrac{3}{4}=2\left(x-\dfrac{41}{48}\right)$$

$$\Rightarrow 4y-3=\dfrac{8}{48}(48x-41)$$

$$\Rightarrow 24y-18=40x-41$$

$$\Rightarrow \fbox{$48x-24y=23$}$$

$$\hbox{eqn of normal is }y-\dfrac{3}{4}=\dfrac{-1}{2}\left(x-\dfrac{41}{48}\right)$$

$$\Rightarrow 4y-3=\dfrac{-2}{48}(48x-41)$$

$$\Rightarrow 96y-72=-48x+41$$

$$\Rightarrow \fbox{$48x+96y=113$}$$

Find the maxima of function $$8-7x^2$$

The function has extreme value at $$f^{\prime}(x)=0$$

$$\implies f^{\prime}(x)=\dfrac{d}{dx}8-7x^2\\-14x=0\\x=0$$

At $$x=0$$

The maxima of function is $$8-7(0)=8$$

If $$ a,b,c$$ are real number, then find the intervals in which $$f\left( x \right) = \left| {\begin{array}{*{20}{c}} {x + {a^2}}&{ab}&{ac} \\ {ab}&{x + {b^2}}&{bc} \\ {ac}&{bc}&{x + {c^2}} \end{array}} \right|$$ is increasing or decreasing.

Finding the value of the determinant

$$f(x) = (x+a^2)(x^2+xc^2+xb^2+b^2c^2-b^2c^2)-ab(abx+abc^2-abc^2) + ac(ab^2c - ab^2c-acx)$$

$$f(x) = (x+a^2)(x^2+x(b^2+c^2)) -a^2b^2x - a^2c^2x$$

$$f(x) = x^3+x^2(a^2+b^2+c^2)$$

Hence the function is an increasing function

Find the slope of tangent and normal to the curve $${x^2} + 2y + {y^2} = 0$$ at $$(-1 , 2)$$

1322201_1080394_ans_e6e00fef81a5471d868821f3fe04e891.jpg

Find the equation of the tangent and normal to the curves

(i) $$y = {x^2} - 4x - 5$$ at $$x = - 2$$
(ii) $$y = x - \sin x\cos x$$
(iii) $$y = 2{\sin ^2}3x\,$$ at $$x = \frac{\pi }{6}$$

$$(i)$$

$$y=x^{2}-4x-5$$

at $$x=-2$$

$$y= (-2)^{2}+ 8-5= 7$$

$$\dfrac{dy}{dx}= 2x-4$$

at $$x=-2, \dfrac{dy}{dx}=-8$$

eq of tangent :

$$(y-7)=-8 (x+2)$$

$$\Rightarrow y+8x+9=0$$

$$\dfrac{eq\ of\ normal}{(y-7)= \dfrac{1}{8} (x+2)}$$

$$\Rightarrow x-8y+58=0$$

$$(ii)$$

$$y=x- \sin x\ ws\ x $$

$$at $$x= \dfrac{x}{6}$$

$$y= \dfrac{\pi}{6}- \dfrac{1}{2}. \dfrac{\sqrt{3}}{2}$$

$$=\dfrac{\pi}{6}- \dfrac{\sqrt{3}}{4}$$

$$\dfrac{dy}{dx}= 1- \cos^{2} x+ \sin^{2} x$$

$$=2 \sin^{2} x$$

at $$x=\dfrac{\pi}{6}, \dfrac{dy}{dx}= 2.\dfrac{1}{4}= \dfrac{1}{2}$$

eq of tangent :

$$\left(y- \dfrac{\pi}{6}+ \dfrac{\sqrt{3}}{4} \right) = \dfrac{1}{2} \left( x - \dfrac{\pi}{6} \right)$$

eq of normal

$$\left( y- \dfrac{\pi}{6} + \dfrac{\sqrt{3}}{4} \right) =-2 \left( x - \dfrac{\pi}{6} \right)$$

$$(iii)$$

$$y= 2 \sin^{2} 3x$$

at $$x =\dfrac{\pi}{6}$$

$$y= 2 \sin^{2} \dfrac{\pi}{2}= 2$$

$$\dfrac{dy}{dx} = 4 \sin 3x , \cos 3x$$

at $$x =\dfrac{\pi}{6}, \dfrac{dy}{dx}=0$$.

eq of tangent :

$$(y-2)=0$$

$$\Rightarrow y=2$$

eq of normal

$$x- \dfrac{\pi}{6}= 0$$

$$\Rightarrow x=\dfrac{\pi}{6}$$

Find the stationary point of $$y=x^2+5x-6$$.

The stationary point is given at $$\dfrac{dy}{dx}=0$$

The relation is

$$y=x^2+5x-6\\\dfrac{dy}{dx}=2x+5=0\\x=\dfrac{-5}2$$

So the point is given as

$$y=\left(\dfrac {-5}2\right)^2+5\left(\dfrac{- 5}2\right)-6 $$

$$y=\dfrac {25}4-\dfrac {25}2-6$$

$$y=\dfrac {-25}4-6=\dfrac{-49}4$$

So the point is $$\left(\dfrac {-5}2,\dfrac {-49}4 \right)$$.

Slope of the normal to the curve $$6y^{4}=ax^{3}+bx$$ at $$(1,-1)$$ is $$\dfrac{1}{2}$$. Solve the values of $$a$$ and $$b$$.

Consider the given equation,

$$6{{y}^{4}}=a{{x}^{3}}+by$$ ….(1)

Differentiate equation (1) with respect to x, we get

$$ 24\dfrac{dy}{dx}=3a{{x}^{2}}+b $$

$$ \dfrac{dy}{dx}=\dfrac{3a{{x}^{2}}}{24}+\dfrac{b}{24} $$

Given the slop is $$\dfrac{1}{2}$$at (1-1) ,

Hence,

$$ {{\left( \dfrac{dy}{dx} \right)}_{1,-1}}=\dfrac{3a{{.1}^{2}}}{24}+\dfrac{b}{24}=\dfrac{1}{2} $$

$$ 3a+b=12 $$ ……(2)

Put , point (1,-1) in equation (1),

$$a-b=6$$ ….(3)

On solving equation (2) and (3),we get

$$a=\dfrac{9}{2}$$ ,$$b=\dfrac{-3}{2}$$

Hence, this is the answer.

Find Stationary points of $$f\left( x \right) = \sin x$$, where $$0 < x < 2\pi $$

$$f(x)=\sin x \\f^{\prime}(x)=\cos x $$

For Stationary points $$f(x)=0\\\cos x=0\\x=\dfrac{\pi}{2},\dfrac{3\pi}{2}$$

Show that the tangents to the curve $$y=2x^3-3$$ at the points where $$x=2$$ and $$x=-2$$ are parallel.

The equation of the curve is $$y = 2x^3-3$$.

Differentiating w.r.t. $$x$$, we get,

$$\dfrac{dy}{dx} = 6x^2$$

Now, $$m_1 = $$ (slope of tangent $$x=2) = \left(\dfrac{dy}{dx}\right)_{x=2} = 6\times (2)^2 = 24$$

and $$m_2 = $$ (slope of tangent at $$x = -2)= \left(\dfrac{dy}{dx}\right)_{x=-2} = 6(-2)^2 = 24$$

Clearly, $$m_1=m_2$$

Thus, the tangents to the given curve at the points where $$x=2$$ and $$x=-2$$ are parallel.

Find the equation of all lines having slope 2 which are tangents to the curve $$y=\dfrac{1}{x-3}, x\neq 3$$.

The equation of the given curve is $$y=\dfrac{1}{x-3}, x\neq 3$$

Slope of tangent,

$$\dfrac{dy}{dx}=\dfrac{-1}{(x-3)^2}$$

If the slope of tangent is 2, then,

$$\dfrac{-1}{(x-3)^2}=2$$

$$(x-3)^2=\dfrac{-1}{2}$$

This is not possible.

Hence, there is no tangent to the curve having slope 2.

The normal lines to a given curve at each point pass through (2,0). The curve passes through (2,3). Formulate the differential equation and hence find out the equation of the curve.

Let P(x,y) be any point on the curve. The equation of the normal at P(x,y) to the given curve is

$$Y-y=-\dfrac{1}{\dfrac{dy}{dx}}(X-x)$$

Normal at each point pases through (2,0). Hence,

$$0-y=-\dfrac{1}{\dfrac{dy}{dx}}(2-x)$$

$$y\dfrac{dy}{dx}=2-x$$

$$ydy=(2-x)dx$$

$$\dfrac{y^2}{2}=-\dfrac{(2-x)^2}{2}+C$$

$$y^2=-(2-x)^2+2C$$

This passes through (2,3). Therefore,

$$9=0+2C$$

$$C=\dfrac{9}{2}$$

Therefore, the equation of the required curve is $$y^2=-(2-x)^2+9$$

Prove that the tangent drawn at any point to the curve $$f(x)= x^{5}+3x^{3}+4x+8$$ would make an acute angle with $$x$$-axis.

$$f(x)= x^{5}+3x^{3}+4x+8$$

$$f(x)= 5x^{4}+9x^{2}+y$$

for all valume of x the f(x)fx

in increasing

$$tan\theta =5x^{4}+9x^{2}+y$$

The angle will always between

0 to 90$$^{\circ}$$

so the angle in acute angle for all value.

1214589_1359071_ans_c44699efbe2a410a91639bb78dc7a93b.jpeg

Find the approximate value of f(3.02), where $$f(x)=3x^2+5x+3$$.

1346791_1261538_ans_8a2de60022934931be621fb2f6c14ace.jpg

The slope of the tangent to a curve at any point is reciprocal of twice the ordinate of that point. The curve passes through (4,3). Formulate the differential equation and hence find the equation of the curve.

Let P(x,y) be any point on the curve.

Slope of tangent at P(x,y) = $$\dfrac{dy}{dx}$$

Therefore, according to question,

$$\dfrac{dy}{dx}=\dfrac{1}{2y}$$

$$2y dy = dx$$

Integrating both sides,

$$y^2=x+C$$

Since, the curve passes through (4,3), then,

$$9=4+C$$

$$C=5$$

Hence, the required equation of the curve is $$y^2=x+5$$.

Find the intervals in which $$f(x)=2x^3+x^2-20x$$ is increasing and decreasing.

1207794_1505965_ans_9cbea81e80dc405ab582f701d378ed67.jpg

Prove that $$f(x)=ax+b$$, where $$a,b$$ are constants and $$a<0$$ is strictly decreasing function on $$R$$.

Given $$f(x)=ax+b$$ for $$x\in {R}$$.

Now $$f'(x)=a<0$$. [ Since $$a<0$$ given]

So the function is strictly decreasing on $${R}$$.

A stone is dropped into a quiet lake and waves move in a circle at a speed of $$3.5$$ cm/sec. At the instant when the radius of the circular wave is $$7.5$$ cm, how fast is the enclosed area increasing ?

Let r be the radius and A be the area of the circular wave at any time t. Then,

$$A=\pi r^2$$ and $$\dfrac{dr}{dt}=3.5 \ cm/sec.$$

Now, $$A=\pi r^2$$

$$\dfrac{dA}{dt}=\pi(2r \dfrac{dr}{dt})=2\pi r \dfrac{dr}{dt}$$

$$\dfrac{dA}{dt}=2\pi r (3.5)=7\pi r$$

$$(\dfrac{dA}{dt})_{r=7.5}=7\pi(7.5)=52.5 \pi \ cm^2/sec.$$

At what point of the curve $$y=x^2$$ does the tangent make an angle of $$45^o$$ with the $$x$$-axis?

The required point be $$(x,y)$$

The tangent makes an angle of $$45^o$$ with the $$x-$$axis.

$$\therefore$$ Slop of the tangent $$=\tan 45^o=1$$

Since, the point lies on the curve.

Now, $$y=x^2$$

Differentiate w.r.t $$x,$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=2x$$

Slop of the tangent $$=\left(\dfrac{dy}{dx}\right)_{(x,y)}=2x$$

$$\Rightarrow$$ $$2x=1$$ [ Given ]

$$\Rightarrow$$ $$x=\dfrac{1}{2}$$

Now,

$$\Rightarrow$$ $$y=x^2=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}$$

$$\therefore$$ $$(x,y)=\left(\dfrac{1}{2},\dfrac{1}{4}\right)$$

Find the slopes of the tangent and the normal to the following curves at the indicated points.
$$x=a\cos^3\theta, y=a\sin^3\theta$$ at $$\theta =\pi/4$$.

We have,

$$x=a\cos^3\theta$$ and $$y=a\sin^3\theta$$

Now, differentiate w.r.t $$\theta$$, we get

$$\dfrac{dx}{d\theta}=a(3\cos^2\theta)(-\sin \theta)$$ and $$\dfrac{dy}{d\theta}=a(3\sin^2\theta)(\cos \theta)$$

$$\dfrac{dx}{d\theta}=-3a\cos^2\theta\sin \theta$$ and $$\dfrac{dy}{d\theta}=3a\sin^2\theta\cos \theta$$

Therefore,

$$\dfrac{\dfrac{dy}{d\theta}}{\dfrac{dx}{d\theta}}=\dfrac{3a\sin^2\theta\cos\theta}{-3a\cos^2\theta\sin\theta}$$

$$\dfrac{dy}{dx}=-\dfrac{\sin\theta}{\cos\theta}$$

$$\dfrac{dy}{dx}=m=-\tan\theta$$

Put $$\theta =\dfrac{\pi}{4}$$

So,

$$m=-\tan\dfrac{\pi}{4}$$

$$m=-1$$

Therefore,

The slope of the tangent of the curve

$$=m=-1$$

And the slope of the normal the curve

$$=-\dfrac{1}{m}$$

$$=-\dfrac{1}{-1}=1$$

Hence, this is the answer.

Prove that $$f(x)=ax+b$$, where $$a,b$$ are constants and $$a> 0$$ is an increasing function on $$R$$.

$$f(x)=ax+b$$

diff wrt x

$$f'(x)=a(1)+0$$

$$=a$$

if $$a > 0$$

then $$f'(x) > 0$$

$$\therefore f(x)$$ is increasing function $$a > 0$$.

Find the slope of the tangent to the curve $$x=t^2+3t-8, y=2t^2-2t-5$$ at $$t=2$$.

Given $$x=t^2+3t-8, y=2t^2-2t-5$$

Slope of curve at t=2,

$$\dfrac{dy}{dx}$$

$$=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}$$

$$=\dfrac{\dfrac{d(2t^2-2t-5)}{dt}}{\dfrac{d(t^2+3t-8)}{dt}}$$

$$=\dfrac{4t-2}{2t+3}$$

as $$t=2$$

$$=\dfrac{6}{7}$$

Find the slopes of the tangent and the normal to the following curves at the indicated points.
$$x=a(1-\cos\theta)$$ and $$y=a(\theta+\sin\theta)$$ at $$\theta =\pi/2$$.

We have,

$$x=a(1-\cos\theta)$$ and $$y=a(\theta+\sin\theta)$$

Now, differentiate w.r.t $$\theta$$, we get

$$\dfrac{dx}{d\theta}=a(0-(-\sin\theta))$$ and $$\dfrac{dy}{d\theta}=a(1+\cos\theta)$$

$$\dfrac{dx}{d\theta}=a\sin\theta$$ and $$\dfrac{dy}{d\theta}=a(1+\cos\theta)$$

Therefore,

$$\dfrac{\dfrac{dy}{d\theta}}{\dfrac{dx}{d\theta}}=\dfrac{a(1+\cos\theta)}{a\sin\theta}$$

$$\dfrac{dy}{dx}=m=\dfrac{(1+\cos\theta)}{\sin\theta}$$

Put $$\theta =\dfrac{\pi}{2}$$

So,

$$\dfrac{dy}{dx}=m=\dfrac{(1+\cos\dfrac{\pi}{2})}{\sin\dfrac{\pi}{2}}$$

$$\dfrac{dy}{dx}=m=\dfrac{1+0}{1}$$

$$\dfrac{dy}{dx}=m=1$$

Therefore,

The slope of the tangent of the curve

$$=m=1$$

And the slope of the normal the curve

$$=-\dfrac{1}{m}$$

$$=-\dfrac{1}{1}=-1$$

Hence, this is the answer.

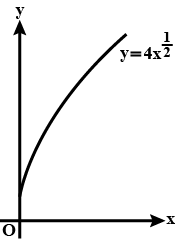
The diagram shows the curve with equation $$y=4x^{\frac{1}{2}}$$.
The tangent to the curve at a point T is parallel to AB. Find the coordinates of T.Equation of line AB is is y=x+3.

Given equation of the curve is $$y=4 x^{1/2}$$

As $$AB$$ lies on the line $$y=x+3$$

So slope of $$AB$$ is $$1$$

As tangent at point $$T$$ is parallel to $$AB$$ so slope of tangent at point $$T$$ is $$1$$

Let the point $$T$$ be $$(x_1,y_1)$$

$$\implies y_1=4 x_1^{1/2}$$

Slope at point $$T$$ is $$\dfrac{d y}{d x}=4 \times \dfrac{1}{2} \times {x_1}^{1/2-1}=2 {x_1}^{-1/2}=1$$

$${x_1}^{1/2}=2\implies x_1=4\implies y_1=4\times 2=8$$

So coordinates of $$T$$ is $$(4,8)$$

Find the slopes of the tangent and the normal to the following curves at the indicated points.
$$xy=6$$ at $$(1, 6)$$.

We have,

$$xy=6$$

Now, differentiate w.r.t $$x$$, we get

$$y+x\dfrac{dy}{dx}=0$$

$$x\dfrac{dy}{dx}=-y$$

$$\dfrac{dy}{dx}=-\dfrac{y}{x}$$

Put $$x=1, y=6$$

So,

$${\dfrac{dy}{dx}}_{(1,6)}=-\dfrac{6}{1}$$

$${\dfrac{dy}{dx}}_{(1,6)}=-6$$

Therefore,

The slope of the tangent of the curve

$$=-6$$

And the slope of the normal the curve

$$=-\dfrac{1}{m}$$

$$=-\dfrac{1}{-6}$$

$$=\dfrac{1}{6}$$

Hence, this is the answer.

Find the slopes of the tangent and the normal to the following curves at the indicated points.
$$x^2+3y+y^2=5$$ at $$(1, 1)$$.

We have,

$$x^2+3y+y^2=5$$

Now, differentiate w.r.t $$x$$, we get

$$2x+3\dfrac{dy}{dx}+2y\dfrac{dy}{dx}=0$$

$$2x+(3+2y)\dfrac{dy}{dx}=0$$

$$(3+2y)\dfrac{dy}{dx}=-2x$$

$$\dfrac{dy}{dx}=-\dfrac{2x}{3+2y}$$

Put $$x=1, y=1$$

So,

$${\dfrac{dy}{dx}}_{(1,1)}=-\dfrac{2(1)}{3+2(1)}$$

$${\dfrac{dy}{dx}}_{(1,1)}=-\dfrac{2}{5}$$

Therefore,

The slope of the tangent of the curve

$$=-\dfrac{2}{5}$$

And the slope of the normal the curve

$$=-\dfrac{1}{m}$$

$$=-\dfrac{1}{-\dfrac{2}{5}}$$

$$=\dfrac{5}{2}$$

Hence, this is the answer.

Find the slope of the normal to the curve $$x=a\cos^3 \theta, y=a\sin^3 \theta$$ at $$\theta =\dfrac{\pi}{4}$$.

We have,

$$x=a\cos ^3 \theta, y=a\sin^3 \theta$$

$$\dfrac{dx}{d\theta}=-3a\cos^2 \theta \sin \theta$$

$$\dfrac{dy}{d\theta}=3a\sin^2 \theta \cos \theta$$

Now, $$\dfrac{dy}{dx}=\dfrac{3a\sin^2 \theta \cos \theta}{-3a\cos^2 \theta \sin \theta}=-\tan \theta$$

Therefore, slope of the normal at any point on the curve = $$-\dfrac{1}{\dfrac{dy}{dx}}=-\dfrac{1}{-\tan \theta}=\cot \theta$$

Hence, Slope of the normal at $$\theta =\dfrac{\pi}{4}=\cot \dfrac{\pi}{4}=1$$

At what points on the following curve, is the tangent parallel to $$x$$-axis?
$$y=12(x+1)(x-2)$$ on $$[-1,2]$$

1407211_1661280_ans_537a5b0b10994940877a335744f7334a.jpg

Find the slope of the tangent to the curve
$$y=(x^{3}-x)$$ at $$x=2$$

1546026_1706763_ans_c384679878a94efabe31ee400e321b00.jpg

Find the slope of the tangent to the curve $$y=x^3-3x+2$$ at the point whose $$x$$ coordinate is 3.

Given equation of the curve is

$$y=x^3-3x+2$$ ......(1)

When $$x=3$$,

$$y=(3)^3-9+2=20$$

Therefore, the point on the curve is $$(3,20).$$

Differentiating equation 1 w.r.t. x, we get,

$$(\dfrac{dy}{dx})=3x^2-3$$

Therefore, the slope of the tangent at $$(3,20)$$

$$=3(3)^3-3=27-3=24$$

Find the values of $$b$$ for which the function $$f(x)=\sin x-bx+c$$ is a decreasing function on $$R$$.

Since, $$f(x)$$ is decreasing on $$R$$
$$\therefore$$ $$f'(x)< 0$$ for all $$x\in R$$
$$\Rightarrow \cos x-b< 0$$ for all $$x\in R$$
$$\Rightarrow \cos x< b$$ for all $$x\in R$$
$$\Rightarrow b\ge 1$$

Find $$a$$ for which $$f(x)=a(x+\sin x)+a$$ is increasing on $$R$$.

Given the function,

$$f(x)=a(x+\sin x)+a$$.

Now,

$$f'(x)$$

$$=a(1+\cos x)$$.

Now,

$$-1\le\cos x\le 1$$

Then,

$$1+\cos x\ge 0$$.

Then $$f(x)$$ will be $$\ge 0$$ if $$a\ge 0$$.

So $$a\in [0,\infty)$$.

If the tangent line at a point $$(x, y)$$ on the curve $$y=f(x)$$ is parallel to y-axis, find the value of $$\dfrac{dx}{dy}$$.

$$\dfrac{dy}{dx}=\infty\Rightarrow \tan\theta=\tan90^o\Rightarrow\theta=90^o$$

$$\dfrac{dx}{dy}$$ $$=cot\theta$$ where $$\theta$$ is angle made by tangent with x-axis

$$=cot(90^o)$$

$$=0$$

Find the equation of the normal to the curve $$y=2x^2+3 \sin x $$at $$x=0$$.

The equation of the given curve is $$y=2x^2+3 \sin x$$ .........(1)

Putting $$x=0$$ in 1, we get, $$y=0$$.

So, the point of contact is $$(0,0)$$.

Now, $$y=2x^2+3\sin x$$

$$\dfrac{dy}{dx}=4x+3\cos x$$

$$(\dfrac{dy}{dx})_{(0,0)}=4 \times 0 +3\cos 0 =3$$

So, the equation of the normal at (0,0) is :

$$y-0=-\dfrac{1}{3}(x-0)$$

$$x+3y=0$$

Let $$f(x)=ax^3+bx^2+cx+d \sin x$$. If the condition that f(x) is always one-one function is $$b^t < ka(c-|d|)$$ Find $$k+t$$

$$f(x)=ax^3+bx^2+cx+d \sin x$$
$$f'(x)=3ax^2+2bx+c-d \cos x$$
For $$f(x)$$ to be one-one function,$$f'(x)> 0\forall x\in R$$
$$3ax^2+2bx+c-d \cos x>0\Rightarrow 3ax^2+2bc+c-|d|>0$$
$$\Rightarrow (2b)^2-4.3a(c-|d|)<0\Rightarrow b^2<3a(c-|d|)$$

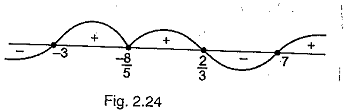
The number of critical points for $$ \left( x+3 \right) { \left( 3x-2 \right) }^{ 5 }{ \left( 7-x \right) }^{ 3 }{ \left( 5x+8 \right) }^{ 2 }\ge 0$$ is

We have $$ \left( x+3 \right) { \left( 3x-2 \right) }^{ 5 }{ \left( 7-x \right) }^{ 3 }{ \left( 5x+8 \right) }^{ 2 }\ge \quad 0$$
$$- \left( x+3 \right) { \left( 3x-2 \right) }^{ 5 }{ \left( x-7 \right) }^{ 3 }{ \left( 5x+8 \right) }^{ 2 }\ge \quad 0$$
$$ \Rightarrow \quad \left( x+3 \right) { \left( x-\dfrac { 2 }{ 3 } \right) }^{ 5 }{ \left( x-7 \right) }^{ 3 }{ \left( x+\dfrac { 8 }{ 5 } \right) }^{ 2 }\le \quad 0$$
$$\therefore$$ The critical points are
-3,$$ -\dfrac { 8 }{ 5 } $$, $$\dfrac { 2 }{ 3 }$$ , 7
$$ \therefore \quad x\quad \in \quad \left( -\infty ,-3 \right) \cup \left[ \dfrac { 2 }{ 2 } ,7 \right] \cup \left\{ -\dfrac { 8 }{ 5 } \right\} $$.

$$\displaystyle y^{2}=8x$$ and $$\displaystyle x^{2}=4y-12.$$ both touch each other at (k,m).Find $$k+m$$?

$$\displaystyle y^{2}=8x,$$ $$\displaystyle x^{2}=4y-12.
$$ Eliminate x.
$$\displaystyle \left ( \frac{y^{2}}{8} \right )^{2}=4y-12$$
Clearly $$y=4$$ satisfies it and putting in $$\displaystyle y^{2}=8x,$$ we get $$x=2$$.
$$\displaystyle \therefore $$ Point is $$(2, 4).$$
Now $$\displaystyle 2y\frac{dy}{dx}= 8$$
$$\displaystyle \therefore \left ( \frac{dy}{dx} \right )= \frac{8}{2y}= 1$$ at $$\displaystyle \left ( 2, 4 \right )$$ and $$\displaystyle2x=4\frac{dy}{dx}$$
$$\displaystyle \therefore \left ( \frac{dy}{dx} \right )= \frac{x}{2}= 1$$ at $$\displaystyle \left ( 2, 4 \right ).$$
Thus their slopes are same and hence the two curves touch at the point (2, 4).

Let the abscissa of the point on the curve $$\displaystyle ay^{2}= x^{3},$$ the normal at which cuts off equal intercepts from the axes be ka/m. Find $$m-k$$?

$$\displaystyle ay^{2}= x^{3}$$ ...(1)
$$\displaystyle \therefore 2ay\frac{dy}{dx}=3x^{2}$$ or $$\displaystyle \frac{dy}{dx}=\frac{3x^{2}}{2ay}$$
Hence slope of the normal is $$-\displaystyle \frac{1}{dy/dx}=\frac{-2ay}{3x^{2}}$$
Since the normal makes equal intercepts on the axes its inclination to axis of x either $$\displaystyle 45^{\circ}$$ or $$\displaystyle

135^{\circ}.$$
In other words its slope is $$\displaystyle \tan

45^{\circ}$$ or $$\displaystyle \tan 135^{\circ}.$$ or $$1, -1$$.
$$\displaystyle \therefore -\frac{2ay}{3x^{2}}=\pm 1$$ or $$\displaystyle 4a^{2}y^{2}= 9x^{4}$$
$$\Rightarrow \displaystyle 4a\cdot x^{3}= 9x^{4}\therefore x= 4a/9$$

If the critical point as well as stationary point of the function $$f(x)\, =\, \displaystyle \frac{e^x}{x}$$ is $$x=a$$, then value of $$a$$ is:

$$f(x)=\dfrac {e^x}x $$
The above function is not defined at $$x=0$$.
Differentiating the function and equating it to zero.
$$\dfrac {{ (e }^{ x }x-{ e }^{ x })}{{ x }^{ 2 }}=0$$
$$\dfrac {{ e }^{ x }(x-1)}{{ x }^{ 2 }}=0$$
$${ e }^{ x }$$ is positive for all $$x$$.
Therefore $$x=1$$ is critical point

Find the intervals in which the following functions are strictly increasing or decreasing:
(a) $$x^2 + 2x - 5$$
(b) $$ 10- 6x -2x^ 2$$
(c) $$-2x^3 - 9x^2 - 12x + 1$$
(d) $$6-9x-x^2$$
(e) $$f(x)=(x + 1)^3(x - 3)^3 $$

(a)

We have,
$$f(x)=x^2+2x-5$$
$$\therefore f'(x)=2x+2$$
Now, $$ f'(x)=0\Rightarrow x=-1$$
The point $$x = -1$$ divides the real line into two disjoint intervals
i.e., $$(-\infty ,-1) $$ and $$(-1,\infty )$$.
In interval $$(-\infty ,-1) , f'(x)=2x+ 2<0$$
$$\therefore $$ $$f$$ is strictly decreasing in interval $$(-\infty ,-1)$$.
And in interval $$(-1,\infty) , f'(x)=2x+ 2>0$$
Thus, $$f$$ is strictly increasing for $$x > 1.$$

(b)

$$f(x) = 10 -6x -2x^ 2$$
$$\therefore f'(x)=-6-4x$$
Now, $$f'(x)= 0\Rightarrow x=-\dfrac{3}{2}$$
The point $$x =-\dfrac{3}{2}$$ divides the real line into two disjoint intervals i.e., $$\left ( -\infty , -\dfrac{3}{2}\right )$$ and $$\left ( -\dfrac{3}{2}, \infty \right )$$.
In interval $$\left ( -\infty , -\dfrac{3}{2}\right )$$ i.e., when $$x<-\dfrac{3}{2}, f'(x)=-6-4x<0.$$
$$\therefore $$ $$f$$ is strictly decreasing for $$x<-\dfrac{3}{2}$$ and in interval $$\left ( -\dfrac{3}{2}, \infty \right ), f'(x)>0$$
Thus $$f$$ is strictly increasing in this interval.

(c)

$$f(x)= -2x^3- 9x^2 -12x + 1$$
$$\therefore f'(x)=-6x^3 -18x^2 -12=-6(x^2+3x+2)=-6(x+1)(x+2)$$
Now,
$$f'(x)= 0\Rightarrow x=-1\,\,$$ and $$\,\, x=-2$$
Points $$x = -1$$ and $$x = -2$$ divide the real line into three disjoint intervals
i.e., $$(-\infty, -2 ) (-2, -1 )$$ and $$(-1, -\infty )$$.
In intervals $$(-\infty, -2 ) $$ and $$(1, -\infty )$$ i.e., when $$x < -2$$ and $$x > -1,$$
$$f'(x)=-6(x+1)(x+2)<0$$
$$\therefore$$ $$f$$ is strictly decreasing for $$x < -2$$ and $$x > -1$$.
Now, in interval $$(-2, -1)$$ i.e., when $$-2 < x <- 1, f'(x)=-6(x+1)(x+2)>0$$
$$\therefore$$ $$f$$ is strictly increasing for $$-2 < x < -1.$$

(d)

$$f(x) = 6-9x-x^2$$
$$f'(x) =-9-2x$$

For f to be strictly increasing $$f'(x)>0\Rightarrow 2x+9<0\Rightarrow x<-\dfrac{9}{2}$$
And for f to be strictly decreasing, $$f'(x)<0\Rightarrow 2x+9>0\Rightarrow x>-\dfrac{9}{2}$$

(e)

We have,
$$ f(x) = (x + 1)^3(x- 3)^3 $$
$$f'(x)=3(x+1)^2(x-3)^3+3(x-3)^2(x+1)^3$$
$$=3(x+1)^2(x-3)^2[x-3+x+1]$$
$$=3(x+1)^2(x-3)^2(2x-2)$$
$$=6(x+1)^2(x-3)^2(x-1)$$
Now,
$$f'(x)=0\Rightarrow x=-1, 3, 1$$
The points $$x =- 1, x = 1,$$ and $$x = 3$$ divide the real line into four disjoint intervals
i.e.,$$(-\infty , -1), (-1,1), (1, 3)$$ and $$(3, \infty)$$.
In intervals $$(-\infty , -1)$$ and $$(-1, 1)$$, $$f'(x)=6(x+1)^2(x-3)^2(x-1)<0$$
$$\therefore $$ $$f$$ is strictly decreasing in intervals $$(-\infty , -1)$$ and $$(-1, 1).$$
In intervals $$(1, 3)$$ and $$(3,\infty ) f'(x)=6(x+1)^2(x-3)^2(x-1)>0$$
$$\therefore$$ $$f$$ is strictly increasing in intervals $$(1, 3)$$ and $$(3,\infty )$$.

Find the intervals in which the function $$f$$ given by $$f(x) = 2x^3- 3x^2 -36x + 7$$ is (a) strictly increasing (b) strictly decreasing.

The given function is $$f (x) = 2x^3- 3x^2- 36x + 7$$

$$f'(x)=6x^2-6x-36=6(x^2-x-6)=6(x+2)(x-3)$$

$$\therefore f'(x)=0\Rightarrow x = -2, 3 $$

The points $$x = 2$$ and $$x = 3$$ divide the real line into three disjoint intervals

i.e., $$(-\infty , -2), (-2, 3),$$ and $$(3, \infty ).$$

In intervals $$(-\infty,-2)$$ and $$( 3, \infty), f'(x)>0$$

while in interval $$(-2, 3), f'(x)<0$$

Hence, the given function $$(f)$$ is strictly increasing in intervals

$$(-\infty , -2)$$ and $$(3, \infty )$$ while function (f) is strictly decreasing in interval $$(-2, 3).$$

Find the slope of the normal to the curve $$x =1 - a \sin \theta, y = b \cos^2 \theta $$ at $$\theta =\dfrac{\pi}{2}$$.

It is given that $$x = 1 - a \sin \theta$$ and $$y = b \cos^2 \theta$$.

$$\therefore \cfrac{dx}{d\theta }=-a \cos \theta$$

and $$\dfrac{dy}{d \theta}=2b \cos \theta (-\sin \theta )=-2b \sin \theta
\cos \theta$$

$$\displaystyle \frac{dy}{dx}=\frac{\left ( \frac{dy}{d\theta } \right )}{\left ( \frac{dx}{d\theta } \right )}=\frac{-2b \sin \theta \cos \theta}{-a \cos \theta} =\frac{2b }{a } \sin \theta $$

Therefore, the slope of the tangent at $$\theta =\dfrac{\pi}{2}$$ is given by,

$$\displaystyle \left(\frac{dy}{dx}\right)_{\theta=\frac{\pi}{4}}=\frac{2b}{a}$$

Hence, the slope of the normal at $$\theta =\dfrac{\pi}{2}$$ is given by,

$$\displaystyle -\frac{1}{\text{slope of the tangent at} \theta =\frac{\pi}{4}}=\frac{-1}{\frac{2b}{a}}=-\frac{a}{2b}$$

Find points at which the tangent to the curve $$y = x^3 - 3x^2 -9x + 7$$ is parallel to the $$x$$-axis.

The equation of the given curve is $$y = x^3 -3x^2 -9x + 7$$ .

$$\cfrac{dy}{dx}=3x^2-6x-9$$

Now, the tangent is parallel to the $$x$$-axis if the slope of the tangent is zero.

$$\therefore 3x^2-6x-9 \Rightarrow x^2-2x-3=0$$

$$\Rightarrow (x-3)(x+1)=0$$

$$\Rightarrow x=3 \,\,or \,\, x=-1$$

When $$x = 3, y = (3)^3- 3 (3)^2- 9 (3) +7 = 27- 27- 27 + 7 = -20$$.

When $$x = 1, y = (1)^3 - 3 (1)^2 -9 (1) + 7 = 1- 3 - 9 + 7 = -4$$.

Hence, the points at which the tangent is parallel to the x-axis are $$(3, -20)$$ and $$(1, -4)$$.

Find a point on the curve $$y = (x - 2)^2$$ at which the tangent is parallel to the chord joining the points $$(2, 0)$$ and $$(4, 4)$$.

If a tangent is parallel to the chord joining the points $$(2, 0)$$ and $$(4, 4)$$, then,

The slope of the tangent $$=$$ the slope of the chord.

The slope of the chord is $$\displaystyle \frac {4-0}{4-2}=\frac{4}{2}=2$$.

Now, the slope of the tangent to the given curve at a point $$(x, y)$$ is given by, $$\cfrac{dy}{dx}=2(x-2 )$$

Since the slope of the tangent $$=$$ slope of the chord, we have:

$$2(x-2)=2\Rightarrow x-2 =1\Rightarrow x=3$$

When $$x=3, y=(3-2)^2=1$$

Hence, the required point is $$(3, 1). $$

Find points on the curve $$\displaystyle \frac{x^2}{9}+\frac{y^2}{16}=1$$ at which the tangents are
(i) Parallel to $$x$$-axis .
(ii) Parallel to $$y$$-axis.

The equation of the given curve is $$\displaystyle \frac{x^2}{9}+\frac{y^2}{16}=1$$

On differentiating both sides with respect to $$x$$, we have:
$$\displaystyle \frac{2x}{9}+\frac{2y}{16}\frac{dy}{dx}=0$$
$$\Rightarrow\displaystyle \frac{dy}{dx}=\frac{-16x}{9y}$$

(i)
The tangent is parallel to the $$x$$-axis if the slope of the tangent is $$0.$$
i.e.,$$\cfrac{-16x}{9y}=0$$, which is possible if $$x = 0.$$.
Then, $$\displaystyle \frac{x^2}{9}+\frac{y^2}{16}=1$$
for $$x = 0,$$ $$\Rightarrow =y^2=16\Rightarrow y=\pm 4$$
Hence, the points at which the tangents are parallel to the $$x$$-axis are $$(0, 4)$$ and $$(0,-4)$$.

(ii)

The tangent is parallel to the $$y$$-axis if the slope of the normal is $$0$$,
which gives $$\displaystyle \frac{-1}{\left ( \frac{-16}{9y} \right )}=\frac{9y}{16x}=0$$ $$\Rightarrow y=0$$
Then, $$\displaystyle \frac{x^2}{9}+\frac{y^2}{16}=1$$ for $$y = 0$$, $$\Rightarrow x=\pm 3$$
Hence, the points at which the tangents are parallel to the $$y$$-axis are $$(3, 0)$$ and $$(-3, 0)$$.

Prove that the function $$f$$ given by $$f (x) = \log \cos x$$ is strictly decreasing on $$\left ( 0, \dfrac{\pi}{2} \right )$$and strictly increasing on $$\left ( \dfrac{\pi}{2}, \pi \right )$$.

We have $$f\left( x \right) =\log { \cos { x } } $$

Differentiate both sides wrt x to get

$$f^{ ' }\left( x \right) =\displaystyle\frac { -\sin { x } }{ \cos { x } } =-\tan { x } $$

comparing it to the graph of $$h\left( x \right)=\tan { x } $$ in the intervals $$\left( 0,\displaystyle\frac { \pi }{ 2 } \right) and\left( \displaystyle\frac { \pi }{ 2 } ,\pi \right) $$

we can say that the given function is strictly decreasing on $$\left( 0,\displaystyle\frac { \pi }{ 2 } \right) $$ and strictly increasing on $$\left( \displaystyle\frac { \pi }{ 2 } ,\pi \right) $$

Find the points on the curve $$y = x^3$$ at which the slope of the tangent is equal to the $$y$$ coordinate of the point.

The equation of the given curve is $$y = x^3$$.

$$\therefore\displaystyle \frac{dy}{dx}=3x^2$$

When the slope of the tangent is equal to the $$y$$-coordinate of the point,

then $$\displaystyle \frac{dy}{dx}=y = 3x^2$$ .

Also, we have $$y = x^3$$ .

$$3x^2= x^3\Rightarrow x^2(x -3) = 0\Rightarrow x = 0, x = 3$$

When $$x = 0$$, then $$y = 0$$ and when $$x = 3$$, then $$y = 3(3)^2= 27$$.

Hence, the required points are $$(0, 0)$$ and $$(3, 27).$$

Find the slope of the normal to the curve $$x = a \cos^3 \theta , y = a \sin^3 \theta$$ at $$\theta =\cfrac{\pi}{4}$$.

It is given that $$x = a \cos^3 \theta , y = a \sin^3 \theta $$

$$\displaystyle \Rightarrow \frac{dx}{d\theta }=3a \cos^2\theta (-\sin \theta )=-3a \cos^2\theta \sin \theta $$

& $$\displaystyle \frac{dy}{d\theta}=3a \sin^2\theta (\cos \theta )$$

$$\Rightarrow \displaystyle \frac{dy}{dx}=\frac{\left

( \dfrac{dy}{d\theta } \right )}{\left ( \dfrac{dx}{d\theta } \right

)}=\dfrac{3a \sin^2\theta \cos \theta }{-3a \cos^2\theta \sin \theta}

=\frac{\sin \theta }{\cos \theta} =-\tan \theta $$

Therefore, the slope of the tangent at $$\theta =\dfrac{\pi}{4}$$ is given by,

$$\displaystyle \left(\frac{dy}{dx}\right)_{\theta=\pi/4}=\left(-\tan\theta\right)_{\theta=\pi/4}=-1$$

Hence, the slope of the normal at $$\theta =\dfrac{\pi}{4}$$ is ,

$$= \displaystyle -\frac{1}{\text{slope of the tangent at} \theta =\frac{\pi}{4}}=\frac{-1}{-1}=1$$

Find the point on the curve $$y = x^3-11x + 5$$ at which the tangent is $$y = x -$$

The equation of the given curve is $$y = x^3 - 11x + 5$$.

The equation of the tangent to the given curve is given as $$y = x -11$$
(which is of the form $$y = mx + c$$).

$$\therefore$$ Slope of the tangent $$= 1$$

Now, the slope of the tangent to the given curve at the point $$(x, y)$$ is given by,

$$\cfrac{dy}{dx}=3x^2-11$$

Then, we have:

$$3x^2-11=1\Rightarrow 3x^2=12$$

$$\Rightarrow x^2=4$$

$$\Rightarrow x=\pm 2$$

When $$x = 2, y = (2)^3- 11 (2) + 5 = 8 -22 + 5 = -9$$.

When $$x = -2, y = (-2)^3- 11 (-2) + 5 = -8 + 22 + 5 = 19$$.

Hence, the required points are $$(2, 9)$$ and $$(2, 19).$$

Find the slope of the tangent to the curve $$y=\cfrac{x-1}{x-2}, x\neq 2$$ at $$x=10.$$

The given curve is $$y=\cfrac{x-1}{x-2}, x\neq 2$$.

$$\therefore\displaystyle \frac{dy}{dx}=\frac {(x-2)(1)-(x-1)(1)}{(x-2)^2}$$

$$\displaystyle =\frac{x-2-x+1}{(x-2)^2}=\frac{-1}{(x-2)^2}$$

Thus, the slope of the tangent at $$x = 10$$ is given by,

$$\displaystyle \left(\frac{dy}{dx}\right)_{x=10}=\left(\frac{-1}{(x-2)^2} \right)_{x=10}=-\frac{1}{(10-2)^2}=-\frac{1}{64}$$

Find the values of $$x$$ for which $$y = [x(x - 2)]^2$$ is an increasing function.

$$y = [x(x - 2)]^2=[x^2-2x]^2$$
$$\therefore \cfrac{dy}{dx}=y'=2(x^2-2x)(2x-2)=4x(x-2)(x-1)$$
$$\therefore \cfrac{dy}{dx}=0\Rightarrow x =0, x=2, x=1$$
The points $$x = 0, x = 1,$$ and $$x = 2$$ divide the real line into four disjoint intervals
i.e., $$(-\infty ,0), (0, 1),(1, 2)$$ and $$(2, \infty )$$.
In intervals $$(-\infty ,0)$$ and $$(1, 2)$$ , $$\cfrac{dy}{dx}<0$$
$$\therefore $$ $$y$$ is strictly decreasing in intervals $$(-\infty ,0)$$ and $$(1, 2) $$
However, in intervals $$(0, 1)$$ and $$(2, \infty), \cfrac{dy}{dx}>0$$.
$$\therefore $$ $$y$$ is strictly increasing in intervals $$(0, 1)$$ and $$(2, \infty )$$.
$$\therefore $$ $$y$$ is strictly increasing for $$0 < x < 1$$ and $$x > 2. $$

If the radius of a sphere is measured as $$9\ m$$ with an error of $$0.03\ m$$, then find the approximate error in calculating in surface area.

Let $$r$$ be the radius of the sphere and $$\Delta r$$ be the error in measuring the radius.
Then, $$r = 9$$ m and $$\Delta r = 0.03$$ m
Now, the surface area of the sphere $$(S)$$ is given by,
$$S = 4\pi r^2$$
$$\Rightarrow \dfrac{dS}{dr}=8 \pi r^2$$
$$\therefore dS=\left ( \dfrac{dS}{dr} \right ) \Delta r$$
$$=(8 \pi r^2)\Delta r$$
$$=8 \pi(9)^2(0.03)$$ $$m^2$$ $$=2.16 \pi$$ $$m^2$$
Hence, the approximate error in calculating the surface area is $$2.16 \pi$$ $$m^2 $$

Find the points on the curve $$x^2+ y ^2-2x -3 = 0$$ at which the tangents are parallel to the $$x$$-axis.

The equation of the given curve is $$ x^2+ y^2-2x -3 = 0$$.
On differentiating with respect to $$x$$, we have:
$$\displaystyle 2x+2y \frac{dy}{dx}-2=0$$
$$\Rightarrow\displaystyle y \frac{dy}{dx}=1-x$$
$$\Rightarrow\displaystyle \frac {dy}{dx}=\frac{1-x}{y}$$
Now, the tangents are parallel to the $$x$$-axis if the slope of the tangent is $$0$$.
$$\displaystyle \therefore \frac{1-x}{y}=0\Rightarrow 1-x=0\Rightarrow x=1$$
Putting $$x=1$$ in $$ x^2+ y^2-2x -3 = 0$$
$$\Rightarrow y^2=4$$

$$\Rightarrow y=\pm 2$$

Hence, the points at which the tangents are parallel to the $$x$$-axis are $$(1, 2)$$ and $$(1, 2).$$

Using differentials, find the sum of digits approximate value of the following up to $$3$$ places of decimal.
$$(0.999)^{\tfrac{1}{10}}$$

Consider $$y=x ^{\tfrac{1}{10}}$$. Let $$x = 1$$ and $$\Delta x = 0.001.$$

Then,

$$\Delta y=(x+\Delta x)^{\tfrac{1}{10}}-x^{\tfrac{1}{10}}=(0.009)^{\tfrac{1}{10}}-)-1$$

$$\Rightarrow (0.009)^{\tfrac{1}{10}}=1+\Delta y$$

Now, $$dy$$ is approximately equal to $$\Delta $$y and is given by,

$$dy=\left ( \dfrac{dy}{dx} \right )\Delta x=\tfrac{1}{3(x)^{\tfrac{9}{10}}}(\Delta x)$$ [as $$y= x^{{\tfrac{1}{10}}}$$]

$$=\dfrac{1}{10}(-0.001)=-0.0001$$

Hence, the approximate value of $$(0.999)^{\tfrac{1}{10}}$$ is $$1 + (-0.0001) = 0.9999. $$

If the radius of a sphere is measured as $$7 m$$ with an error of $$0.02m$$, then find the approximate error in calculating its volume.

Let $$r$$ be the radius of the sphere and $$\Delta r$$ be the error in measuring the radius.
We have given, $$r = 7$$ m and $$\Delta r = 0.02$$ m
Now, the volume $$V$$ of the sphere is given by,
$$\displaystyle V=\frac{4}{3}\pi r^2$$
$$\Rightarrow \displaystyle \frac{dV}{dr}=4\pi r^2$$
$$\therefore\displaystyle \Delta V\approx dV=\left ( \frac{dV}{dr} \right ) \Delta r$$
$$=(4 \pi r^2)\Delta r$$
$$=4 \pi(7)^2(0.02)m^3=3.92 \pi$$ m$$^3$$
Which is approximate error in measuring volume

Using differentials, find the approximate value of the following up to $$3$$ decimal places.
$$\sqrt {49.5}$$

Consider $$y=\sqrt x$$.

Let $$x = 49$$ and $$\Delta x = 0.5$$.

Then,

$$\Delta y=\sqrt{x+\Delta x}-\sqrt x=\sqrt{49.5}-\sqrt{49}=\sqrt{49.5}-7$$

$$\Rightarrow \sqrt{49.5}=7+\Delta y$$

Now, dy is approximately equal to $$\Delta $$y and is given by,

$$dy=\left ( \dfrac{dy}{dx} \right )\Delta x=\dfrac{1}{2 \sqrt x}(0.5)$$ [as $$y=\sqrt x$$]

$$=\dfrac{1}{2\sqrt {49}}(0.5)=(0.5)=\dfrac{1}{14}(0.5)=0.035=\Delta y$$

Hence, the approximate value of $$\sqrt{49.5}$$ is $$7+.035=7.035$$

Show that $$y=\log { \left( 1+x \right) } -\cfrac { 2x }{ 2+x } ,x>-1$$, is an increasing function of $$x$$ throughout its domain.

By watching slope of a function, it can be observed that a function is increasing or decreasing.
If slope is always positive then it means that the function is always increasing.

Here $${f}^{'}(x)=\dfrac { 1 }{ 1+x } -\dfrac { 4 }{ { (2+x) }^{ 2 } } $$

$$=\dfrac{{x}^{2}}{{(x+2)}^{2}.(1+x)}$$

$${f}^{'}(x)=0$$ at $$x=0$$ and is not defined at $$x=-1, -2$$; it is also clear that it is $$>0$$ for all $$x>-1$$.

As function is always positive in given domain, so this function is increasing in its domain.

Using differentials, find the sum of digits approximate value of the following up to $$3$$ places of decimal.
$$(0.999)^{\tfrac{1}{3}}$$

Consider $$y=x ^{\tfrac{1}{3}}$$.

Let $$x=0.008, \Delta x=0.001$$

$$\Delta y=(x+\Delta x)^{\dfrac{1}{3}}-x^{\dfrac{1}{3}}=(0.009)^{\dfrac{1}{3}}-0.2$$

$$\Rightarrow (0.009)^{\dfrac{1}{3}}=0.2+\Delta y$$

Now, $$dy$$ is approximately equal to $$\Delta $$y and is given by,

$$dy=\left ( \dfrac{dy}{dx} \right )\Delta x=\dfrac{1}{3(x)^{\tfrac{2}{3}}}(\Delta x)$$ [as y=$$ x^{{\tfrac{1}{3}}}$$]

$$=\dfrac{1}{3 \times 0.04}(0.001)=\dfrac{0.001}{0.12}=0.008$$

Hence, the approximate value of $$(0.999)^{\tfrac{1}{3}}$$ is $$0.2 + 0.008 = 0.208 \approx 0.21$$.

Using differentials, find the sum of digits approximate value of the following up to $$3$$ places of decimal.
$$(26)^{\tfrac{1}{3}}$$

Consider $$y=x ^{\tfrac{1}{3}}$$.

Let $$x = 27 $$and $$\Delta x = -1.$$

Then,

$$\Delta y={x+\Delta x}^{\tfrac{1}{3}}-x^{\tfrac{1}{3}}=(26)^{\tfrac{1}{3}}-(27)^{\tfrac{1}{3}}=(26)^{\tfrac{1}{3}}-3$$

$$\Rightarrow (26)^{\tfrac{1}{3}}-)=3+\Delta y$$

Now, $$dy$$ is approximately equal to $$\Delta y$$ and is given by,

$$dy=\left ( \dfrac{dy}{dx} \right )\Delta x=\dfrac{1}{3(x)^{\tfrac{2}{3}}}(\Delta x)$$ [as $$y= x^{{\tfrac{1}{3}}}$$]

$$=\displaystyle \frac{1}{3(27)^{2/3}}(-1)=-\frac{1}{27}=-.037$$

Hence, the approximate value of $$(26)^{\frac{1}{3}}$$ is $$3+ (-0.0370) = 2.9629\approx 2.963 $$

Find the approximate value of $$f (2.01)$$, where $$f (x) = 4x^2 + 5x + 2$$.

Let $$x = 2$$ and $$\Delta x = 0.01$$.
Now, $$\Delta y = f(x +\Delta x)- f(x)$$
$$f(x + \Delta x) = f(x) + \Delta y$$
$$\simeq f(x)+f'(x)\cdot \Delta x$$, as $$( dx\simeq \Delta x)$$
$$\Rightarrow f(2.01)\approx (4x^2+5x+2)+(8x+5)\Delta x$$
$$=[4(2)^2+5(2)+2]+[8(2)+5](0.01)$$
$$=28+(21)(0.01)=28+0.21=28.21$$
Hence, the approximate value of $$f (2.01)$$ is $$28.21. $$

Find the intervals in which the function $$f$$ given by $$f(x) ={x}^{3}+\cfrac{1}{{x}^{3}}$$, $$x\ne 0$$ is
(i) increasing (ii) decreasing.

A function $$f(x)$$ is increasing if $$f'(x)>0$$ and decreasing if $$f'(x)<0$$
$$f(x)= x^3+\dfrac{1}{x^3}\\
f'(x)= 3x^2-\dfrac{3}{x^4}= \dfrac{3x^6-3}{x^4}$$
Now,
$$f'(x)>0\;\; x\in (-1,0)\;\; and\;(1,\infty)\\
f'(x)<0 \;\; x\in(-\infty,-1)\;and\;x\in(0,1)$$

Let $$f$$ be function defined on $$[a,b]$$ such that $$f'(x)> 0$$, for all $$x\in (a,b)$$. Then prove that $$f$$ is an increasing function on $$(a,b)$$.

Let us take any $$2$$ points $$c_1$$ and $$c_2$$ such that $$\{c_1,c_2\} \in (a,b)$$ and $$c_2 = c_1+h$$, where $$h\rightarrow 0$$

Now, $$f'(c_1) =\displaystyle \lim_{h\rightarrow 0}\cfrac{f(c_1+h) - f(c_1)}{h} = \cfrac{f(c_2) - f(c_1)}{c_2-c_1}$$

Now, it is given that $$f'(x) > 0\quad \forall x\in(a,b)$$.

Therefore, $$f'(c_1) > 0$$

$$\Rightarrow \cfrac{f(c_2)-f(c_1)}{c_2-c_1} > 0$$

From the above fraction, we can conclude that:

1. For $$c_2 > c_1, f(c_2) > f(c_1)$$

2. For $$c_1> c_2, f(c_1) > f(c_2)$$

Hence, $$f(x)$$ is an increasing function in $$(a,b)$$.

Show that the normal at any point $$\theta$$ to the curve
$$x=a\cos{\theta}+a\theta \sin{\theta}$$, $$y=a\sin{\theta}-a\theta \cos{\theta}$$ is at constant distance from the origin.

First, let us find the slope of the tangent to the curve at a point $$\theta$$.

$$m_T =\cfrac{dy}{dx} = \cfrac{\dfrac{dy}{d\theta}}{\dfrac{dx}{d\theta}} = \cfrac{a\cos \theta - a\cos \theta + a\theta \sin \theta}{-a\sin \theta + a\sin \theta +a\theta\cos\theta}=\cfrac{\sin\theta}{\cos\theta}$$

Since, normal is always perpendicular to the tangent, slope of the normal will be

$$m_N = -\cfrac{\cos \theta}{\sin \theta}$$

Normal passes through the point $$(x,y)$$ given in the question. Using the equation of the line in slope-point form,

$$\cfrac{y - a\sin\theta+a\theta\cos\theta}{x-a\cos\theta-a\theta\sin\theta} = -\cfrac{\cos\theta}{\sin\theta}$$

$$\Rightarrow y\sin\theta-a\sin^2\theta+a\theta\sin\theta\cos\theta=a\cos^2\theta+a\theta\sin\theta\cos\theta-x\cos\theta$$

$$\Rightarrow x\cos\theta+y\sin\theta=a(\cos^2\theta+\sin^2\theta) = a$$

Distance of origin from this line will be

$$d$$ $$=\cfrac{|0+0-a|}{\sqrt{\sin^2\theta+\cos^2\theta}}\\=|a|$$

Hence, the distance from origin to the normal at any point $$\theta$$ is a constant.

Using differentials, find the approximate value of $${ \left( \cfrac { 17 }{ 81 } \right) }^{ \tfrac { 1 }{ 4 } }$$

Here we will assume a function $$f(x)={x}^{\tfrac{1}{4}}$$

Formula for approximation is given by

$$f(x+\triangle x)=f(x)+{f}^{'}(x).\triangle x$$

$${f}^{'}(x)=\dfrac{1}{4}{(x)}^{\tfrac{-3}{4}}$$

Now most important step is to find $$\triangle x$$ and for this we need to refer to question.

We need to choose $$x$$ and one important thing which we need to keep in mind is that $$x$$ when inserted in $$f(x)$$ should give a perfect outcome, here $$x$$ should be the nearest number to $$\dfrac{17}{81}$$ and should give a perfect fourth root.

Best number which can be seen is $$\dfrac{16}{81}$$ so from here we can conclude that $$\triangle x =\dfrac{1}{81}$$

Plugging all the value in formula $$f(x+\triangle x)=f(x)+{f}^{'}(x).\triangle x$$

We get $${\left (\dfrac{16}{81}\right)}^{\tfrac{1}{4}}+$$ $$\dfrac{1}{4}{\left (\dfrac{16}{81}\right)}^{\tfrac{-3}{4}}.\dfrac{1}{81}$$

This is equal to $$\dfrac{65}{96}$$.

At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (-4, -3). Find the equation of the curve given that it passes through (-2, 1).

According to question, we have
$$\dfrac{dy}{dx}= 2 \dfrac{y+3}{x+4}\\
\dfrac{dy}{(y+3)}= 2 \dfrac{dx}{(x+4)}\\
ln(y+3)=2ln(x+4)+lnc\\
ln(y+3)=ln(x+4)^2+lnc\\
(y+3)=c.(x+4)^2$$
and it passes through $$(-2,1)$$
$$(1+3)=c(-2+4)^2\\
4=c4\\
c=1$$
equation of curve is $$(y+3)=(x+4)^2$$

Using differentials, find the approximate value of $${(33)}^{\tfrac { 1 }{ 5 } }$$

Here we will assume a function $$f(x)={x}^{\tfrac{1}{5}}$$

Formula for approximation is given by

$$f(x+\triangle x)=f(x)+{f}^{'}(x).\triangle x$$

$${f}^{'}(x)=\dfrac{1}{5}{(x)}^{\tfrac{-4}{5}}$$

Now most important step is to find $$\triangle x$$ and for this we need to refer to question.

We need to choose $$x$$ and one important thing which we need to keep in mind is that $$x$$ when inserted in $$f(x)$$ should give a perfect outcome, here $$x$$ should be nearest number to $$33$$ and should give a perfect fifth root.

Best number which can be seen is $$32$$ so from here we can conclude that $$\triangle x =1$$

Plugging all the value in formula $$f(x+\triangle x)=f(x)+{f}^{'}(x).\triangle x$$

We get $${(32)}^{\tfrac{1}{5}}+$$ $$\dfrac{1}{5}{(32)}^{\tfrac{-4}{5}}.1$$

This is equal to $$\dfrac{161}{80}$$

Find the equation of a curve passing through the origin given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the coordinates of the point.

According to question, we have
$$\dfrac{dy}{dx}=x+y$$
$$\dfrac{dy}{dx}-y=x$$
IF $$= e^{\int { -1dx}}=e^{-x}\\
y\times e^{-x}=\int{ e^{-x} \times x dx}\\
y\times e^{-x}=(-x-1)e^{-x}+c\\
y=(-x-1)+ce^x$$

Find the equation of a curve passing through the point (0, 2) given that the sum of the coordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.

According to question, we have
$$\dfrac{dy}{dx}+5=x+y$$
$$\dfrac{dy}{dx}-y=x-5$$
IF $$= e^{\int { -1dx}}=e^{-x}\\
y\times e^{-x}=\int{ e^{-x} \times (x-5) dx}\\
y\times e^{-x}=-(x-4)e^{-x}+c\\
y=-(x-4)+ce^x$$
and it is passing through $$(0,2)$$
$$2=4+c\\
c=-2$$
Equation of curve is $$y=-(x-4)-2e^x$$

Find the coordinates of the points on the curve $$y = x - \dfrac{4}{x}$$, where the tangents are parallel to the line $$y = 2x$$.

Equation of line is given by,
$$y = 2x$$ .......... (1)
We know that
$$y = mx + c$$ .......... (2)
On comparing equation (2) with (1),
We get, $$m = 2$$
Given, $$y = x - \dfrac{4}{x}$$
Differentiating w.r.t.$$x$$, we get
$$\dfrac{dy}{dx} = 1 - 4 (-1) .\dfrac{1}{x^2}$$
$$= 1 + \dfrac{4}{x^2} = m$$ ......... (3)
Slope of the tangent, $$m = 1 + \dfrac{4}{x^2}$$
$$\Rightarrow 1 + \dfrac{4}{x^2} = 2$$
$$\Rightarrow x^2 + 4 = 2x^2$$
$$\Rightarrow x = \pm 2$$ and $$y=2x$$
$$\Rightarrow x_1 = 2, x_2 = - 2$$
$$\Rightarrow y_1 = 4, y_2 = - 4$$
Co-ordinates of the point of contact are $$(2, 4) $$ and $$(-2, -4)$$.

If the radius of a sphere is measured as $$9\ cm$$ with an error of $$0.02\ cm$$, then find the approximate error in calculating its volume.

Volume of a sphere is given by $$V = \cfrac{4\pi R^3}{3}$$

$$\therefore \cfrac{\Delta V}{V} = \cfrac{3\Delta R}{R}$$

$$\therefore \Delta V = 3V \times \cfrac{\Delta R}{R}$$

$$= 4\pi R^3 \times \cfrac{\Delta R}{R}$$

$$= 4\pi R^2 \times \Delta R$$

$$= 4\pi \times 81 \times 0.02$$

$$= 20.357 cm^3$$ approximately

If the normal to the curve $$x^{\tfrac{2}{3}} + y^{\tfrac{2}{3}} = a^{\tfrac{2}{3}}$$ makes an angle $$\theta$$ with $$x$$-axis then the slope of the normal is:

$$x^{\tfrac{2}{3}}+y^{\tfrac{2}{3}}=a^{\tfrac{2}{3}}$$.

Differentiating with respect to $$x$$ give us

$$\dfrac{2}{3}\left(x^{-\tfrac{1}{3}}+y'.y^{\tfrac{-1}{3}}\right)=0$$

$$x^{-\tfrac{1}{3}}+y'.y^{\tfrac{-1}{3}}=0$$

$$x^{-\tfrac{1}{3}}=-y'.y^{\tfrac{-1}{3}}$$

$$y'=\left(\dfrac{y}{x}\right)^{\tfrac{1}{3}}$$

Therefore slope of normal

$$=\left(\dfrac{-x}{y}\right)^{\tfrac{1}{3}}$$

Since it makes an angle $$\theta$$ with the positive x axis,

$$\tan\theta=\left(\dfrac{-x}{y}\right)^{\tfrac{1}{3}}$$

Show that the percentage error in the $$n^{th}$$ root of a number is approximately $$\dfrac{1}{n}$$ times the percentage error in the number.

Let $$x$$ be the number
Let $$y = f(x) = x^{1/n}$$
Then $$\log y = \dfrac {1}{n} \log x$$
Taking differential on the both sides, we have
$$\dfrac{1}{y} dy = \dfrac{1}{n} . \dfrac{1}{x} dx$$
$$\dfrac{\Delta y}{y} \approx \dfrac{1}{y} dy = \dfrac{1}{n} . \dfrac{1}{x} dx$$
$$\dfrac{\Delta y}{y} \times 100 \approx \dfrac{1}{n} \left( \dfrac{dx}{x} \times 100 \right )$$
$$= \dfrac{1}{n}$$ times the percentage error in the number

Let $$P$$ be a point on the curve $$y={x}^{3}$$ and suppose that the tangent line at $$P$$ intersects the curve again at $$Q$$. Prove that the slope at $$Q$$ is four times the slope at $$P$$.

Let $$\left( a,{ a }^{ 3 } \right) $$ be a point on the curve $$y={x}^{3}$$ .....$$(1)$$
$$\cfrac { dy }{ dx } =3{ x }^{ 2 }\cfrac { dy }{ dx } $$ at $$\left( a,{ a }^{ 3 } \right) =3{a}^{2}=m=$$ Slope of tangent
Equation of tangent at $$P$$ is
$$y-{ a }^{ 3 }=3{ a }^{ 2 }(x-a)$$
(i.e.,) $$\quad y-{ a }^{ 3 }=3{ a }^{ 2 }x-3{ a }^{ 3 }$$
$$y=3{ a }^{ 2 }x-2{ a }^{ 3 }$$ .....$$(2)$$

Solving $$(1)$$ and $$(2)$$, we get
$$ { x }^{ 3 }=3{ a }^{ 2 }x-2{ a }^{ 3 }\Rightarrow { x }^{ 3 }-3{ a }^{ 2 }x-2{ a }^{ 3 }=0\quad $$
$${ \left( x-a \right) }^{ 2 }\left( x+2a \right) =0$$
$$x=a$$ or $$2a$$

At $$x=a;y={a}^{3}$$ at $$x=-2a,y=-8{a}^{3}$$
But $$\left( a,{ a }^{ 3 } \right) $$ is the point $$P$$
$$\therefore$$ $$Q=(-2a,-8{a}^{3})$$

$$\cfrac { dy }{ dx } $$ at $$Q$$ $$(-2a,-8{a}^{3})=3(-2{a}^{2})=12{a}^{2}$$
$$\cfrac { dy }{ dx } $$ at $$P\left( a,{ a }^{ 3 } \right) =3{ (a }^{ 2 })=3{ a }^{ 2 }\quad $$
$$\therefore $$ the slope of $$Q=4$$ (slope at $$P$$).

Find the intervals of convexity and concavity of the Gaussian curve $$y = e^{-x^{2}}$$ and also find the point of inflection

$$y={ e }^{ { -x }^{ 2 } }$$

$$y'=-2x{ e }^{ { -x }^{ 2 } }$$

$$y''={ e }^{ { -x }^{ 2 } }(4{ x }^{ 2 }-2)$$

$$y''=0,x=\pm \dfrac { 1 }{ \sqrt { 2 } } $$

$$y''>0\ for\ x<\dfrac { -1 }{ \sqrt { 2 } } \ and\ x>\dfrac { 1 }{ \sqrt { 2 } } $$

$$y''<0\ for\ x\in (\dfrac { -1 }{ \sqrt { 2 } } ,\dfrac { 1 }{ \sqrt { 2 } } )$$

So it is concave up in $$x\in (-\infty ,\dfrac { -1 }{ \sqrt { 2 } } )\cup (\dfrac { 1 }{ \sqrt { 2 } } ,\infty )$$

Concave downwards in $$x\in (\dfrac { -1 }{ \sqrt { 2 } } ,\dfrac { 1 }{ \sqrt { 2 } } )$$

And $$x=\dfrac { -1 }{ \sqrt { 2 } } ,\dfrac { 1 }{ \sqrt { 2 } } $$ are inflection points.

So $$(\dfrac { -1 }{ \sqrt { 2 } } ,{ e }^{ \frac { -1 }{ 2 } }),(\dfrac { 1 }{ \sqrt { 2 } } ,{ e }^{ \frac { -1 }{ 2 } })$$ are inflection points.

Show that the function $$f(x) = x^3 - 3x^2 + 6x - 100$$ is increasing on R.

$$\cfrac { d }{ dx } (f(x))= 3{ x }^{ 2 }-6x+6$$

Discriminant of $$\cfrac { d }{ dx } (f(x))$$ $$=36-4(6)(3)=-36<0$$

The coefficient of $${ x }^{ 2 }=3>0$$

Test whether the function, $$f(x) = x - \dfrac {1}{x}, x\epsilon R, x\neq 0$$, is increasing or decreasing

Given function is $$f(x)=x-\frac{1}{x}$$ and $$x \neq0$$ , $$x\in R$$

Now differentiate the given function , we get $$f^{ 1 }\left( x \right) =1+\frac { 1 }{ { x }^{ 2 } } $$

For $$x\in R$$ and $$x \neq 0$$ , $$1+\frac{1}{x^{2}} >0$$

Therefore $$f^{1}(x)$$ is always greater than zero for all $$x \in R$$ and $$x \neq 0$$

So the function $$f(x)$$ is increasing function in the given domain

Find the equation of the curve passing through the point (1, 1), given that the slope of the tangent to the curve to the any point is $$\dfrac{y}{x}+1$$

Let the curve be $$F(x,y)$$ and $$\dfrac{dy}{dx}$$ be the slope.

Hence, the equation is $$\dfrac{dy}{dx}=\dfrac{y}{x}+1$$

$$\implies \dfrac{dy}{dx}-\dfrac{y}{x}=1$$ is the first order linear equation, where $$P(x)=-\dfrac{1}{x}$$ and $$Q(x)=1$$

$$\therefore \text{I.F.}=e^{-\int \frac{1}{x}} dx=e^{-\log x}$$

$$\therefore$$ Solution is $$ye^{-\log x}=\int 1. e^{-\log x} dx$$

$$=\int x^{-1}dx$$

$$=\log x +c$$

$$\implies yx^{-1}=\log x+c$$ ........ $$(i)$$

To find $$c$$, substitute the values of $$x$$ and $$y$$ we get

$$1\cdot 1=\log 1+c$$

$$\implies c=1$$

Put in $$(i)$$, we get

$$yx^{-1}=\log x+1$$

$$\implies y=x(\log x +1)$$ is the required equation.

Prove that, $$f(x) = x^{3} - 3x^{2} + 3x - 100$$ is an increasing function in $$R$$.

Given function $$f(x) = x^{3} - 3x^{2} + 3x - 100$$
$$\therefore \dfrac {d}{dx}[f(x)] = \dfrac {d}{dx}[x^{3} - 3x^{2} + 3x - 100]$$
$$\Rightarrow f'(s) = 3x^{2} - 6x + 3$$
$$\Rightarrow f'(x) = 3(x^{2} - 2x + 1)$$
$$\Rightarrow f'(x) = 3(x - 1)^{2}$$
It is clear that value $$3(x - 1)^{2}$$ can not be negative. So $$f'(x) > 0$$
$$\therefore f(x)$$, so it is an increasing function in $$R$$.

Find limits of the error when $$\displaystyle\frac{916}{191}$$ is taken for $$\sqrt{23}$$.

We know $$ \sqrt { 23 } =4+\sqrt { 23 } -4$$
$$\Rightarrow 4+\cfrac { 7 }{ \sqrt { 23 } +4 } $$
$$\Rightarrow \cfrac { \sqrt { 23 } +4 }{ 7 } =1+\cfrac { \sqrt { 23 } -3 }{ 7 } =1+\cfrac { 2 }{ \sqrt { 23 } +3 } $$
$$\Rightarrow \cfrac { \sqrt { 23 } +3 }{ 2 } =3+\cfrac { \sqrt { 23 } +3 }{ 2 } =3+\cfrac { 7 }{ \sqrt { 23 } +3 } $$
$$\therefore $$ the continued fraction is:-
$$=4+\cfrac { 1 }{ 1+\cfrac { 1 }{ 3+\cfrac { 1 }{ 1+... } } } $$
and the convergents are :-
$$\Rightarrow \cfrac { 4 }{ 1 } ,\cfrac { 5 }{ 1 } ,\cfrac { 19 }{ 4 } ,\cfrac { 24 }{ 5 } ,\cfrac { 211 }{ 44 } ,\cfrac { 235 }{ 49 } ,\cfrac { 916 }{ 191 } ,\cfrac { 1151 }{ 240 } ,....$$
Therefore, the error in taking $$\cfrac { 916 }{ 191 } $$ is less than $$\cfrac { 1 }{ { \left( 191 \right) }^{ 2 } } $$ and greater than $$\cfrac { 1 }{ { 2\left( 240 \right) }^{ 2 } } $$.

(i) Find the critical numbers of $${ x }^{ \frac { 3 }{ 5 } }\left( 4-x \right) $$
(ii) Determine the domain of convexity of $$y={ e }^{ x }$$

$$(1)$$ To determine the critical point, first find the derivative of the given function $$f(x)$$,

$$f'(x)=\dfrac{d}{dx}x^{3/5}(4-x)=\dfrac{4\times 3}{5x^{2/5}}-\dfrac{8}{5}x^{3/5}=\dfrac{12-8x^{}}{5x^{2/5}}$$

Now, put $$f'(x)=0\Rightarrow x=\dfrac{3}{2}$$

$$\therefore $$ Critical number for $$x$$ is $$3$$.

$$(2)$$ A function $$f(x)$$ is convex, if $$f''(x)>0$$

$$\Rightarrow y=e^x\Rightarrow y''=e^x$$, which is always greater than zero

$$\therefore $$ domain of convexity $$\in R$$

Find the critical points of the following functions and test them for their maxima and minima.
$$\displaystyle\, f(x) \, =\, \frac{x^2 \, -\, 3x\, +\, 2}{x^2\, +\, 3x\, +\, 2}$$

$$f(x)=\dfrac { { x }^{ 2 }-3x+2 }{ { x }^{ 2 }+3x+2 } \\ \quad \quad \quad =\dfrac { (x-2)(x-1) }{ (x+2)(x+1) } \\ f'(x)=\dfrac { (2x-3)({ x }^{ 2 }+3x+2)-{ (x }^{ 2 }-3x+2)(2x+3) }{ { ({ { x }^{ 2 }+3x+2) }^{ 2 } } } \\ f'(x)=0$$

$$2x^3+6x^2+4x-3x-9x-6=2x^3-3x^2-5x+6$$

$$6x^2=12$$

$$x=\pm \sqrt { 2 } $$

$$f(\sqrt { 2 } )=\dfrac { (\sqrt { 2 } -2)(\sqrt { 2 } -1) }{ (\sqrt { 2 } +2)(\sqrt { 2 } +1) }=-17+12\sqrt{2} $$

$$f(-\sqrt { 2 } )=\dfrac { (-\sqrt { 2 } -2)(-\sqrt { 2 } -1) }{ (-\sqrt { 2 } +2)(-\sqrt { 2 } +1) } =-17-12\sqrt { 2 } $$

Find the critical points of the following functions.
$$y \, = \, \dfrac{x^3}{3} \, + \, 2x^2 \, - \, 5x \, + \, 4$$

$$y=\dfrac{x^3}{3}+2x^2-5x+4$$

$$\implies \dfrac{dy}{dx}=x^2+4x-5$$

For critical points-

$$\dfrac{dy}{dx}=0$$

$$\implies x^2+4x-5=0$$

$$\implies (x+5)(x-1)=0$$

$$\implies x=-5,1$$

Hence, critical points are $$x=-5 $$ and $$x=1$$

Find the critical points of the following functions and test them for their maxima and minima.
$$\displaystyle\, f(x) = \frac{x^2}{17} - \ln(x^28)$$

Given: $$\displaystyle\, f(x) = \frac{x^2}{17} - \ln(x^28)$$

$$f(x)$$ is not defined as $$x=0$$ since $$\ln 0$$ is not defined

$$f'(x) = \dfrac {2x}{17} - \dfrac {1}{x^{2}.8} \cdot 8.2x = 10$$

$$\Rightarrow \dfrac {2x}{17} - \dfrac {2}{x} = 0$$

$$\Rightarrow \dfrac {x}{17} - \dfrac {1}{x} = 0$$

$$\Rightarrow x^{2} - 17 = 0\Rightarrow x = \pm \sqrt {17}$$

here $$f''(x) = \dfrac {2}{17} + \dfrac {2}{x^{2}}$$

at $$x = \sqrt {17}$$ and $$x = -\sqrt {17}$$

So $$f''(x) > 0$$ (So minima at $$x = \sqrt {17}$$ and $$-\sqrt {17})$$

Find the critical points of the following function and test them for their maxima and minima.
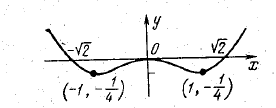
$$\displaystyle\, y \, = \, x^4 \, -\, 10x^2 \, +\, 9$$

$$y=x^4-10x^2+9$$

$$\dfrac{dy}{dx}=4x^3-20x=0\Rightarrow x=\pm \sqrt5$$

$$\dfrac{d^2y}{dx^2}=12x^2-20$$

At $$x=\pm \sqrt5,\dfrac{d^2y}{dx^2}>0$$, Hence y has its minimum at $$x=\pm \sqrt 5$$ and increases after that ,i.e no maximums.

Find the critical points of the following function and test them for their maxima and minima.
$$\displaystyle f(x) \, = \, 3x^4 \, - \, 4x^3$$

f(x)=3x4−4x3 Hence it is a point where f(x) is minimum.

Given a function y = $$x^4 \, - \, 10x^2 \, + \, 9$$. Investigate its behaviour and construct a rough drawing of the graph.

1130623_890131_ans_4b1913fc3f574f99885e321f92b0a801.jpg

Show that $$y=log(1+x)-\dfrac{2x}{2+x},x>-1$$, is an increasing function of x throughout its domain.

Given, $$y=\log (1+x)-\dfrac{2x}{2+x}$$

$$\dfrac{dy}{dx}=\dfrac{1}{1+x}-\dfrac{2(2+x)-2x}{(2+x)^2}$$ [ Product/ quotient- rule]

$$=\dfrac{1}{1+x}-\dfrac{4}{(x+2)^2}$$

$$=\dfrac{(x+2)^2-4(1+x)}{(x+2)^2(x+1)}$$

$$=\dfrac{x^2+4+4x-4-4x}{(x+2)^2(x+1)}$$

$$=\dfrac{x^2}{(x+2)^2(x+1)}$$

for increasing function $$\dfrac{dy}{dx}>0$$

$$\Rightarrow \dfrac{x^2}{(x+2)^2(x+1)}>0\quad \left[\because \left(\dfrac{x}{x+2}\right)^2>0\right]$$

$$x+1>0$$

$$x>-1$$

$$\therefore$$ for $$x>-1$$, given function is always increasing

Check monotonocity at following points for
(i) $$f(x) = x^3-3x +1$$ at $$x= -1, 2$$
(ii)$$ f(x) =|x -1| +2 | x- 3| -| x+2| $$at $$ x= -2, 0, 3, 5$$

1076506_1025138_ans_c67ee20dc08243d9a3388bba89ebc71f.png

Find the abscissa of point $$P$$ and $$Q$$ on the curve $$y=e^{x}+e^{-x}$$ such that tangents at $$P$$ and $$Q$$ make $$60^{o}$$ with $$x-axis$$.

Slope at point $$P$$ is

$$m_1=\tan 60^o=\sqrt{3}$$

Slope at point $$Q$$ is

$$m_2=\tan 60^o=\sqrt{3}$$

$$\dfrac{dy}{dx}=e^x-e^{-x}=\tan 60^o=\sqrt{3}$$

$$\Rightarrow$$ $$e^x-\dfrac{1}{e^x}=\sqrt{3}$$

$$\Rightarrow$$ $$e^{2x}-1=\sqrt{3}e^x$$

$$\Rightarrow$$ $$e^{2x}-\sqrt{3}e^x-1=0$$

let $$e^x=t$$ we get,

$$\Rightarrow$$ $$t^2-\sqrt{3}t-1=0$$

$$t=\dfrac{\sqrt{3}\pm\sqrt{3+4}}{2}$$

$$t=\dfrac{\sqrt{3}\pm\sqrt{7}}{2}$$

$$\Rightarrow$$ $$e^x=\dfrac{\sqrt{3}\pm\sqrt{7}}{2}$$

$$\Rightarrow$$ $$x=ln\left(\dfrac{\sqrt{3}\pm\sqrt{7}}{2}\right)$$

We know that value under $$ln$$ must be greater than $$0$$.

$$\therefore$$ $$x=ln\left(\dfrac{\sqrt{3}+\sqrt{7}}{2}\right)$$

Show that $$f\left( x \right) =2x+\cot ^{ -1 }{ x } +\log { \left( \sqrt { 1+{ x }^{ 2 } } -x \right) } $$ is increasing in $$R$$.

Consider the given function.

$$f\left( x \right)=2x+{{\cot }^{-1}}x+\log \left( \sqrt{1-{{x}^{2}}}-x \right)$$

On differentiating with respect to $$x$$, we get

$$ f'\left( x \right)=2-\dfrac{1}{1+{{x}^{2}}}+\dfrac{1}{\sqrt{1+{{x}^{2}}}-x}\left( \dfrac{d\left( \sqrt{1+{{x}^{2}}}-x \right)}{dx} \right) $$

$$ f'\left( x \right)=2-\dfrac{1}{1+{{x}^{2}}}+\dfrac{1}{\sqrt{1+{{x}^{2}}}-x}\left( \dfrac{2x}{2\sqrt{1+{{x}^{2}}}}-1 \right) $$

$$ f'\left( x \right)=2-\dfrac{1}{1+{{x}^{2}}}+\dfrac{1}{\sqrt{1+{{x}^{2}}}-x}\left( \dfrac{x-\sqrt{1+{{x}^{2}}}}{\sqrt{1+{{x}^{2}}}} \right) $$

$$ f'\left( x \right)=2-\dfrac{1}{1+{{x}^{2}}}-\dfrac{1}{\sqrt{1+{{x}^{2}}}} $$

$$ f'\left( x \right)=2-\left[ \dfrac{1+\sqrt{1+{{x}^{2}}}}{1+{{x}^{2}}} \right]>0 $$

Hence, $$f\left( x \right)$$ is increasing in $$R$$.

Find the intervals in which the function $$f(x) = \log (1 + x) - \dfrac{{2x}}{{2 + x}}$$ is increasing or decreasing.

from the given function if we write domain it becomes;

for $$\log x$$ condition is $$x>0$$ from this we get

$$(1+x)>0$$

$$x>-1$$

from $$\dfrac{2x}{2+x}$$

we get $$(2+x)=0$$ that is $$x=-2$$ is not in our domain

so our domain is $$x>-1$$

for checking increasing or decreasing we need $$f'(x)$$

$$f' (x)=\dfrac{1}{1+x}-\dfrac{2(2+x)-2x(1)}{(2+x)^{2}}$$

$$f'(x)=\bigg(\dfrac{1}{1+x}\bigg)\times\bigg(\dfrac{x}{2+x}\bigg)^{2}$$

we know that any squared expression is greater than or equal to zero;

$$\bigg(\dfrac{x}{2+x}\bigg)^{2}>0$$,equality occurs when $$x=0$$

and from domain $$(1+x)>0$$ which also means $$\dfrac{1}{1+x}>0$$

so from this we can say that $$f'(x)>0$$ for all $$x>-1$$,except for $$x=0$$ it becomes $$0$$.

so therefore we conclude that $$f(x)$$ increases in the intervals $$x\epsilon(-1,0)$$ and $$x\epsilon(0,\infty)$$

A particle moves along the curve $$6y = {x^3} + 2$$. Find the points on the curve at which y - coordinate is changing 2 times as fast as x - coordinate.

we need to find coordinates of point where $$\dfrac{dy}{dt}=2\dfrac{dx}{dt}$$

$$6y=x^3+2$$

Differentiating on both sides

$$6\dfrac{dy}{dt}=3x^2\dfrac{dx}{dt}$$

$$6\times 2\dfrac{dx}{dt}=3x^2\dfrac{dx}{dt}$$

$$x^2=4$$

$$x=\pm 2$$

If $$x=2\Rightarrow y=\dfrac{5}{3}$$

if $$x=-2\Rightarrow y=-1$$

Find the condition tht the curves $$2x=y^{2}$$ and $$2xy=k$$ intersect orthogonally.

Given curves,

$$2x=y^2$$ .....$$(1)$$

$$2xy=k$$ .....$$(2)$$

From $$(1)$$, $$x=\dfrac{y^2}{2}$$

Substitute this value of $$x$$ in $$(2)$$, we get

$$\Rightarrow2(\dfrac{y^2}{2})y=k$$

$$\Rightarrow y^3=k$$

$$\Rightarrow y=(k)^\dfrac{1}{3}$$

$$\Rightarrow x=\dfrac{y^2}{2}=\dfrac{(k)^\dfrac{2}{3}}{2}$$

So the two curves intersect at $$(\dfrac{(k)^\dfrac{2}{3}}{2},(k)^\dfrac{1}{3})$$

Now, Consider $$2x=y^2$$

Differentiate w.r.t $$x$$

$$\Rightarrow 2=2y\dfrac{dy}{dx}$$

$$\Rightarrow 1=y\dfrac{dy}{dx}$$

$$\Rightarrow \dfrac{dy}{dx}=\dfrac{1}{(k)^\dfrac{1}{3}}=(k)^\dfrac{-1}{3}$$

Let this $$\dfrac{dy}{dx}=m_{1}$$

$$\Rightarrow m_{1}=(k)^\dfrac{-1}{3}$$

Now, Consider $$2xy=k$$

Differentiate w.r.t $$x$$

$$\Rightarrow 2y+2x\dfrac{dy}{dx}=0$$

$$\Rightarrow y+x\dfrac{dy}{dx}=0$$

$$\Rightarrow \dfrac{dy}{dx}=\dfrac{-y}{x}$$

$$\Rightarrow \dfrac{dy}{dx}=\dfrac{-(k)^\dfrac{1}{3}}{\dfrac{(k)^\dfrac{2}{3}}{2}}$$

On simplifying we get,

$$\Rightarrow \dfrac{dy}{dx}=-2(k)^\dfrac{-1}{3}$$

Let this $$\dfrac{dy}{dx}=m_{2}$$

$$\Rightarrow m_{2}=-2(k)^\dfrac{-1}{3}$$

Since these 2 curves cut at Right angles,

$$\Rightarrow m_{1}m_{2}=-1$$

$$\Rightarrow (k)^\dfrac{-1}{3}\times (-2k^\dfrac{-1}{3})=-1$$

On simplifying we get,

$$\Rightarrow -2k^\dfrac{-2}{3}=-1$$

$$\Rightarrow k^{\dfrac{-2}{3}}=\dfrac{1}{2}$$

cubing on both sides, we get

$$\Rightarrow k^{-2}=\dfrac{1}{8}$$

$$\Rightarrow k^{2}=8$$

Therefore, $$\Rightarrow k=2\sqrt2$$

Hence, the condition that the 2 curves intersect orthogonally is $$k=2\sqrt2$$

Find the co-ordinates of the point on the curve $$\sqrt {x} + \sqrt {y}=4$$ at which tangent is equally inclined to the axes.

Let the required point be $$(x_1,y_1)$$

Given equation of curve is $$\sqrt x+ \sqrt y=4$$

Since $$(x_1,y_1)$$ lies on the curve we get,

$$\Rightarrow \sqrt {x_1}+ \sqrt {y_1}=4$$ ...$$(1)$$

Consider the curve $$\sqrt x+ \sqrt y=4$$

On differentiating w.r.t x we get

$$\Rightarrow \dfrac{1}{2\sqrt x}+\dfrac{1}{2\sqrt y}\dfrac{dy}{dx}=0$$

$$\Rightarrow \dfrac{dy}{dx}=-\sqrt {\dfrac{y}{x}}$$

Given that tangent is equally inclined to the axes

$$\theta=45^0\space \Rightarrow tan\theta=1$$

$$\Rightarrow (\dfrac{dy}{dx})_{(x_1,y_1)}=1$$

$$\Rightarrow -\sqrt {\dfrac{y_1}{x_1}}=1$$

Squaring on both sides, we get

$$\Rightarrow x_1=y_1$$

From $$(1)$$ we have

$$\Rightarrow \sqrt {x_1}+ \sqrt {y_1}=4$$

$$\Rightarrow \sqrt {x_1}+ \sqrt {x_1}=4$$

$$\Rightarrow 2\sqrt {x_1}=4$$

$$\Rightarrow \sqrt {x_1}=2$$

$$\Rightarrow {x_1}=y_1=4$$

Hence the required point is $$(4,4)$$

If a variable tangent to the curve $${x}^{2}y={c}^{3}$$ makes intercepts $$a,b$$ on $$x$$ and $$y$$ axis respectively, then prove that $${a}^{2}b=(27/4){C}^{3}$$.

$$\begin{array}{l} { x^{ 2 } }y={ c^{ 3 } } \\ y=\frac { { { c^{ 3 } } } }{ { { x^{ 2 } } } } \\ \frac { { dy } }{ { dx } } =\frac { { -2{ c^{ 3 } } } }{ { { x^{ 3 } } } } \end{array}$$

The tangent into the point

$$\left( {{x_1},\frac{{{c^3}}}{{x_1^2}}} \right)\,\,is\,\,{y^1} = \frac{{ - 2{c^3}}}{{{x^3}}}$$

The tangent crossing the point of the $$f(x)$$

$$y - \frac{{{c^3}}}{{x_1^2}} = \frac{{ - 2{c^3}}}{{x_1^2}}\left( {x - {x_1}} \right)$$

a is where tangent cross x-axis

$$i.e\,\,y = 0$$

Similarly $${b_1}\,\,i.e\,\,x = 0$$

$$\begin{array}{l} y=0\Rightarrow a=\frac { 3 }{ 2 } { x_{ 1 } }\to \left( 1 \right) \\ x=0\Rightarrow b=3\frac { { { c^{ 3 } } } }{ { x_{ 1 }^{ 2 } } } \to \left( { ii } \right) \\ From\, \, \left( i \right) \, and\, \left( { ii } \right) \\ { a^{ 2 } }b=\frac { { 27 } }{ 4 } { c^{ 3 } } \end{array}$$

Find the slope of the tangent to the curve $$x=at^{2},\ y=2at$$ at $$t=1$$

Consider the following equation.

$$ x=a{{t}^{2}},\text{ }\!\!~\!\!\text{ }y=2at\,\,\,at\,\,t=1$$

Differentiate both side w.r.t x and y we get.

$$ \dfrac{dx}{dt}=2at\,\,\,\,\,\,\,\,\,.....\left( 1 \right) $$

$$ \dfrac{dy}{dt}=2a\,\,\,\,\,\,\,..........\left( 2 \right) $$

Divide eq.(1)in eq. (2) we get.

$$ \dfrac{dy}{dx}=\dfrac{2at}{2a}\,\,\,\,\,\,\,\,......\left( 3 \right) $$

$$ \dfrac{dy}{dx}=t $$

Put the value of $$'t'$$ in eq. (3) we get.

$$ \dfrac{dy}{dx}=1 $$

$$ dy=dx $$

Hence, this is the correct answer

For the curve $$y=4x-2x^2$$, find the equation of tangent passes through the origin.

The equation is $$y=4x-2x^2$$

The slope of tangent is given as $$\dfrac {dy}{dx}=\dfrac d{dx}4x-2x^2\\\dfrac {dy}{dx}=4-4x\\\left.\dfrac {dy}{dx}\right|_{(0.0)}=4$$

The equation of tangent passing through origin is $$y-0= 4(x-0)\\y=4x$$

Tangent at a point $$P_{1}$$ (other then $$(0,0)$$ on the curve $$y=x^3$$ meets it again at $$P_{2}$$. The tangent at $$P_{2}$$ meets the curve at $$P_{3}$$ & so on. Show that the abscissa of $$P_{1},P_{2},P_{3},......P_{n}$$ form a $$G.P$$. Also find the ratio $$\dfrac {area of \Delta(P_{1}P_{2}P_{3})}{area of \Delta (P_{2}P_{3}P_{4})}$$

Let a point $${P}_{1}$$ on $$y = {x}^{3}$$ be $$\left( h, {h}^{3} \right)$$.

Tangent at $${P}_{1}$$ is $$y - {h}^{3} = 3{h}^{2} \left( x - h \right)$$, it meets $$y = {x}^{3}$$ at $${P}_{2}$$.

$$\therefore \; {x}^{3} - {h}^{3} = 3{h}^{2} \left( x - h \right)$$

$$\Rightarrow \; \left( x - h \right) \left( {x}^{2} + xh + {h}^{2} \right) = 3 {h}^{2} \left( x - h \right) \; \left[ \because {a}^{3} - {b}^{3} = \left( a - b \right) \left( {a}^{2} + ab + {b}^{2} \right) \right]$$

$$\Rightarrow \; {x}^{2} + xh + {h}^{2} - 3{h}^{2}$$

$$\Rightarrow \; {x}^{2} + xh - 2{h}^{2} = 0$$

$$\Rightarrow \; \left( x - h \right) \left( x + 2h \right) = 0$$

$$\therefore \; x = -2h$$ for $${P}_{2}$$ $$x = h$$ is for point $${P}_{1}$$

$$\therefore \; {P}_{2}$$ is $$\left( -2h, -8{h}^{3} \right)$$

Again, tangent at $${P}_{2}$$ is $$y + 8{h}^{3} = 3{\left( 2h \right)}^{2} \left( x + 2h \right)$$, it meets $$y = {x}^{3}$$ at $${P}_{3}$$.

$$\therefore \; {x}^{3} + 8{h}^{3} = 12{h}^{2} \left( x + 2h \right)$$

$$\Rightarrow \; \left( x + 2h \right) \left( {x}^{2} - 2xh + 4{h}^{2} \right) = 12 {h}^{2} \left( x - h \right) \; \left[ \because {a}^{3} + {b}^{3} = \left( a + b \right) \left( {a}^{2} - ab + {b}^{2} \right) \right]$$

$$\Rightarrow \; {x}^{2} - 2xh + 4{h}^{2} - 12{h}^{2}$$

$$\Rightarrow \; {x}^{2} - 2xh - 8{h}^{2} = 0$$

$$\Rightarrow \; \left( x - 4h \right) \left( x + 2h \right) = 0$$

$$\therefore \; x = 4h$$ for $${P}_{3}$$ $$x = -2h$$ is for point $${P}_{2}$$

$$\therefore \; {P}_{3}$$ is $$\left( 4h, 64{h}^{3} \right)$$

Similarly, we get

$$x = -8h$$ for $${P}_{4} ........$$

Hence, the abscissa for $${P}_{1}, {P}_{2}, {P}_{3}, .......$$ are $$h, -2h, 4h, .......$$ respectively, which are in G.P.. [Hence proved]

Now for $$\triangle{\left( {P}_{1}{P}_{2}{P}_{3} \right)}$$

$$ar{\left( \triangle{\left( {P}_{1}{P}_{2}{P}_{3} \right)} \right)} = \cfrac{1}{2}\begin{vmatrix} h & {h}^{3} & 1 \\ -2h & -8{h}^{3} & 1 \\ 4h & 64{h}^{3} & 1 \end{vmatrix}$$

Again for $$\triangle{\left( {P}_{2}{P}_{3}{P}_{4} \right)}$$

$$ar{\left( \triangle{\left( {P}_{2}{P}_{3}{P}_{4} \right)} \right)} = \cfrac{1}{2}\begin{vmatrix} -2h & -8{h}^{3} & 1 \\ 4h & 64{h}^{3} & 1 \\ -8h & -512{h}^{3} & 1 \end{vmatrix} = \cfrac{1}{2} \left( -2 \right) \left( -8 \right) \begin{vmatrix} h & {h}^{3} & 1 \\ -2h & -8{h}^{3} & 1 \\ 4h & 64{h}^{3} & 1 \end{vmatrix}$$

$$\therefore \; \cfrac{ar{\left( \triangle{\left( {P}_{1}{P}_{2}{P}_{3} \right)} \right)}}{ar{\left( \triangle{\left( {P}_{2}{P}_{3}{P}_{4} \right)} \right)}} = \cfrac{\cfrac{1}{2}\begin{vmatrix} h & {h}^{3} & 1 \\ -2h & -8{h}^{3} & 1 \\ 4h & 64{h}^{3} & 1 \end{vmatrix}}{\cfrac{1}{2} \left( -2 \right) \left( -8 \right) \begin{vmatrix} h & {h}^{3} & 1 \\ -2h & -8{h}^{3} & 1 \\ 4h & 64{h}^{3} & 1 \end{vmatrix}}$$

$$\Rightarrow \; \cfrac{ar{\left( \triangle{\left( {P}_{1}{P}_{2}{P}_{3} \right)} \right)}}{ar{\left( \triangle{\left( {P}_{2}{P}_{3}{P}_{4} \right)} \right)}} = \cfrac{1}{16}$$

If $$g(x)=f(x)+f(2a-x)$$ and $$f''(x)> 0$$ for all $$x\in [0,a]$$, then shown that $$g(x)$$ is decreasing on $$[0,a]$$

$${g}^{\prime} (x)=f\prime (x)-f\prime (2a-x)$$

Given $${ f }^{ \prime \prime } > 0$$

$${ f }^{ \prime }$$ is increasing function

Now,

if $$x\in (0,a)$$

$$\Rightarrow$$ $$2a-x\in [a,2a]$$

for all $${x}_{1}\in (0,a)$$ and for all $${x}_{2}\in(2a-x)$$

$$\Rightarrow$$ $${x}_{2}> {x}_{1}$$

$${ f }^{ \prime } ({x}_{2})> f\prime ({x}_{1})$$

$$\Rightarrow$$ $${ f }^{ \prime } (2a-x)> f\prime (x)$$

$$\Rightarrow$$ $${ f }^{ \prime } (x)-{ f }^{ \prime } (2a-x)< 0$$

$$\Rightarrow$$ $${ g }^{ \prime } (x)< 0$$

$$g$$ is a decreasing function

Prove that $$\sin x < x < \tan x \forall x \in (0, \pi/2)$$.

Solution:

The blue line is for $$y=\tan x$$. The red line is for $$y=x$$ . The green line is for $$y=\sin x$$. As you can see, in the given interval the blue line is above the other two. So $$\tan x$$ is the greatest. The red line is in the middle while the green line is the lowest.

So $$\sin x<x<\tan x$$

1111066_1099346_ans_8ea93f8de41c4b5e9bd82bf73f5541d8.png

Find the critical points of the function $$g(x) = \sqrt{x^2 - 2x - 3}$$

The critical points of a function are those points in its domain, where

its derivative is $$0$$ or the derivative is not defined.

$$g(x)=\sqrt{x^{2}-2x-3}$$

$${g}'(x)=\cfrac{2x-2}{2\sqrt{x^{2}-2x-3}}$$

$${g}'(x)=\cfrac{x-1}{\sqrt{x^{2}-2x-3}}$$

Put $${g}'(x)=0$$

$$\Rightarrow x-1=0$$

$$x=1$$

So, $$x=1$$ is a critical point.

Also $${g}'(x)$$ is not defined at those points, where the denominator $$\sqrt{x^{2}-2x-3}=0$$

$$\Rightarrow x^{2}-2x-3=0$$

$$x=-1,3$$

So, the critical points are $$x=-1,1,3$$

Find the points on the curve $$y=x^3-2x^2-x$$, where the tangents are parallel to $$3x-y+1=0$$.

$$\begin{matrix} y=x3-2x2-x...\left( 1 \right) \\ let\, po{ int }s\, curve\, os\, \left( { { x_{ 1 } },{ y_{ 1 } } } \right) \\ differentiate\, w.r.t.\, x \\ \dfrac { { dy } }{ { dx } } =\dfrac { { d\left( { x3-2x2-x } \right) } }{ { dx } } \\ \dfrac { { dy } }{ { dx } } =3{ x^{ 2 } }-4x-1 \\ slope=\dfrac { { dy } }{ { dx } } \\ 3x-y+1=0....\left( 1 \right) \\ y=3x+1 \\ slop=3 \\ which\, is\, parallel \\ then \\ 3{ x^{ 2 } }-4x-1=3 \\ 3{ x^{ 2 } }-4x-4=0 \\ 3{ x^{ 2 } }-6x+2x-4=0 \\ 3x\left( { x-2 } \right) +2\left( { x-2 } \right) =0 \\ \left( { 3x+2 } \right) \left( { x-2 } \right) =0 \\ x=-\dfrac { 2 }{ 3 } .or\, x=2 \\ putting\, x=-\dfrac { 2 }{ 3 } \, or\, x=2\, in\, equatin\, \left( 1 \right) \\ y=-\dfrac { 8 }{ { 27 } } -\dfrac { 8 }{ 9 } +\frac { 2 }{ 3 } \\ y=-\dfrac { { 14 } }{ { 27 } } \\ and\, \, \\ y=-2 \\ the\, req\, po{ int }s\, are\, \\ \left( { -\dfrac { 2 }{ 3 } ,-\frac { { 14 } }{ { 27 } } } \right) and\left( { 2,-2 } \right) \\ \end{matrix}$$

The number of distinct line(s) which is/ are tangent at a point on curve $$4x^{3} = 27 y^{2}$$ and normal at other point, is

Find the values of a for which $$f(x)=ax^3-9ax^2+9x+25$$ is increasing on R.

Given $$f(x)=ax^3-9ax^2+9x+25$$

The given function is increasing on $$R$$

If $$f' (x) > 0$$ on $$R$$

$$f'(x)=3ax^2-18ax+9$$

$$=3(ax^2-6ax+3)>0$$ for $$x\in(-\infty,\infty)$$

The only possible case is that determinant is less than zero and coefficient of $$x^2$$ is positive.

$$\Delta=9(36a^2-4.a.3)<0$$

$$\Rightarrow 3a^2-a<0$$

$$\Rightarrow a(3a-1)<0$$

$$\Rightarrow 0< a< \dfrac{1}{3}$$.

and $$3a>0 \Rightarrow a>0$$

$$\therefore $$ The value of a must be such that

$$0 < a < \frac{1}{3}$$

The diameter of a sphere is measured to be $$40\ cm$$. If an error of $$0.02\ cm$$ is made in it, then find approximate errors in volume and surface area of the sphere.

1360996_1129349_ans_dd056cf37ed94caebe290e94b76406e7.jpg

The function $$y=\dfrac {ax+b}{(x-1)(x-4)}$$ has turning point at $$P(2,-1) $$. Then find the value of $$a$$ and $$b$$.

1298840_1142641_ans_6e7c7e5b4ef445b08b3fd39a271e79e6.jpg

Prove that $$f(x)=a^x, 0 < a < 1$$, is decreasing in R.

$$\begin{array}{l} f\left( x \right) ={ a^{ x } }0<a<1\, \, is\, \, decrea\sin g\, in\, R \\ Taking\, \, \log \, \, both\, \, sides \\ \log f\left( x \right) =x\log a \\ \frac { { f'\left( x \right) } }{ { { a^{ x } } } } =\log a \\ f'\left( x \right) ={ a^{ x } }\log a\, \, \, \, \, \, \left[ { { a^{ x } }>0x\in R } \right] \\ f;\left( x \right) <0x\in R \\ \Rightarrow f\left( x \right) \, \, is\, \, decre\sin g\, \, fun\, \, \, \, \left[ { \log a<0 } \right] \, \, because\, \, 0<a<1 \end{array}$$

Find the values of $$x$$, for which the function $$f(x)=x^{3}+12x^{2}+36x+6$$ is increasing.

Let

$$f(x)=x^3+12x^2+36x+6$$

Differentiate it w.r.t $$x$$

$$f'(x)=3x^2+24x+36$$

The function increases when $$f'(x)>0$$

So,

$$3x^2+24x+36>0$$

$$x^2+8x+12>0$$

$$x^2+6x+2x+12>0$$

$$x(x+6)+2(x+6)>0$$

$$(x+2)(x+6)>0$$

$$x<-2 $$

$$x<-6$$

So, for $$x<-2$$ and $$x<-6$$ the function is increasing\

Find the slope of the tangent and normal to the curve $$y=(\sin 2x+\cot x +2)^2$$ at $$x=\dfrac{\pi}{2}$$.

We have,

$$y=(\sin 2x+\cot x +2)^2$$

On differentiating both sides w.r.t. x, we get,

$$\dfrac{dy}{dx}=2(\sin 2x+\cot x +2)\dfrac{d}{dx}(\sin 2x+\cot x +2)$$

$$\dfrac{dy}{dx}=2(\sin 2x+\cot x +2)(2\cos 2x-cosec^2x)$$

Therefore, $$(\dfrac{dy}{dx})_{x=\pi/2}=\sin \pi +\cot \dfrac{\pi}{2}+2$$

$$=2[0+0+2][-2-1]=-12$$

Therefore, slope of tangent = -12

And, slope of normal $$=\dfrac{1}{12}$$

If $$f(x)=\tan ^{ -1 }{ x } -(1/2)\log { x } $$. Then comment on the nature of curve of f(x).

$$f(x)=\tan^{-1}x=(1/2)ln x$$

Domain: $$x > 0$$

$$f'(x)=\dfrac{1}{1+x^2}-\dfrac{1}{2x}$$

$$=\dfrac{2x-1-x^2}{2x(1+x^2)}$$

$$=\dfrac{-(x-1)^2}{2x(1+x^2)}$$

$$\therefore$$ for $$x > 0$$, $$f(x)$$ is decreasing.

1053037_1156732_ans_3f08a7b2580d4be5815d8c4d3c35aba9.jpg

For the curve $$y =4x^{3}-2x^{5}$$, fnd all the points on the curve at which the tangent passes through the original.

Consider the given function:

$$ y=4{{x}^{3}}-2{{x}^{5}} $$

$$ \dfrac{dy}{dx}=\dfrac{d}{dx}\left( 4{{x}^{3}}-2{{x}^{5}} \right) $$

$$ =3*4{{x}^{2}}-5*2{{x}^{4}} $$

$$ po\operatorname{int}\left( x,y \right) $$

$$ {{y}_{1}}=m{{x}_{1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}}eq...1 $$

$$ y=4{{x}^{3}}-2{{x}^{5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}}\,\,eq...2 $$

$$ m=12{{x}^{2}}-10{{x}^{4}} $$

$$ $$

putting the value eq….(1)

$$ {{y}_{1}}=(4{{x}^{2}}-2{{x}^{4}})x $$

$$ {{y}_{1}}=(4{{x}^{3}}-2{{x}^{5}}) $$ eq...3

Solving for the from (2) and (3 )

$$ \therefore 4{{x}_{1}}^{3}+10{{x}_{1}}^{4} $$

$$ \therefore \,4{{x}_{1}}^{3}-2{{x}_{1}}^{5} $$

$$ [{{x}_{1}}=\pm 1] $$

$$ \,\,\,\,\,\,\,\,\,\,\,\,\,\,for\,\,\,{{x}_{1}}=\pm 1\,\,put\,\,in\,\,eq..y=4{{x}^{3}}-2{{x}^{5}} $$

$$ {{x}_{1}}=+1\, $$

$$ y=4{{(1)}^{3}}+2{{\left( 1 \right)}^{5}}\,\,\,\,=6 $$

$$ {{x}_{1}}=-1\, $$

$$ y=4{{(-1)}^{3}}+2{{\left( -1 \right)}^{5}}\,\,=-6\, $$

$$ po\operatorname{int}\,\,are\,\,(1,6)(-1,-6)\,\,\, $$

Hence this is the answer.

Find the condition for the line $$y = m x + c$$ to be a tangent to the parabola $$x ^ { 2 } = 4 a y$$.

$$y = mx + c$$

$$x^2 = 4ay$$

for line $$y = mx + c$$ to be tangent to $$x^2 = 4ay$$

slope of $$y = mx + c$$ should be equal to

slope of $$x^2 = 4ay$$ at point of tang ency

Let point of tangency $$ = (x_1, y_1)$$

$$\left.\begin{matrix}\frac{dy}{dx}\end{matrix}\right|_{(x_1, y_1)}$$ of $$x^2=4ay$$ should be equal to $$m$$

$$\Rightarrow \dfrac{2x_1}{4a} = m$$

$$\Rightarrow x_1 = 2am$$

putting $$x_1 = 2am$$ in $$x^2 = 4ay$$ we get, $$y_1 = am^2$$

putting $$(x_1, y_1)$$ in line $$y = mx + c$$ we get $$am^2 = 2am^2+c$$

$$\boxed {c = - am^2}$$

Equation of the curve whose sub tangent is constant is

$$\textbf{Step-1: Assume the given function to be equal to some variable}$$

$$\textbf{and then apply all information given.}$$

$$\text{Let,}$$ $$y=f(x)$$ $$\text{be the curve.}$$

$$\text{Then its subtangent is}$$ $$\dfrac{y}{\left(\dfrac{dy}{dx}\right)}$$

$$\text{According to the problem,}$$

$$\dfrac{y}{\left(\dfrac{dy}{dx}\right)}=(1/e) \text{[constant]}$$

$$\text{or,}$$ $$\dfrac{dy}{dx}=cy$$

$$\text{or,}$$ $$\dfrac{dy}{y}=cdx$$

$$\text{On Integrating we get,}$$

$$log|y|=cx+log|c_1|$$ $$[c_{1}\text{ is an integrating constant]}$$

$$\text{or,}$$ $$y=c_1e^{cx}$$.

$$\textbf{Hence,the equation is }$$$$\boldsymbol{y=c_1e^{cx}}$$.

The $$x-$$intercept of the tangent at any arbitrary point of the curve $$\dfrac { a } { x ^ { 2 } } + \dfrac { b } { y ^ { 2 } } = 1$$ is proportional to

$$\dfrac{a}{x^{2}}+\dfrac{b}{y^{2}}=1$$

Now, differentiating above equation we get

$$\dfrac{dy}{dx}=-\dfrac{ay^{3}}{bx^{3}}$$

Let $$(p,q)$$ be any arbitrary point of $$\tan$$ gency on the curve, then equation of tangent at $$(p,q)$$ is

$$y-q=-\dfrac{aq^{3}}{bp^{3}}(x-p)$$

So, the $$x-$$ intercept of the tangent at $$(p,q)$$ is obtained by putting $$y=0$$ in the above equation

$$i.e, x=\dfrac{bp^{3}}{aq^{2}}+p$$........$$(1)$$

Now as $$(p,q)$$ lies on the given curve so it satisfies the equation $$\dfrac{a}{x^{2}}+\dfrac{b}{y^{2}}=1$$

$$i.e, aq^{2}+bp^{2}=p^{2}q^{2}$$......$$(2)$$

From $$(1)$$ and $$(2)$$, we get

$$x=\dfrac{bp^{3}+paq^{2}}{aq^{2}}=\dfrac{p(aq^{2}+bp^{2})}{aq^{2}}=\dfrac{p^{2}q^{2}}{aq^{2}}=\dfrac{p^{3}}{a}$$

Hence, $$x$$ is proportional to $$p^{3}$$

The radius of a sphere is measured as $$14\ cm$$. Later it was found that there is an error $$0.02\ cm$$ in measuring the radius. Find the approximate error in surface area of the sphere.

Radius of the sphere $$= 14 m$$

Error in measurement of radius = $$\triangle r = 0.02 m$$

Volume of the sphere $$V= \dfrac{4}{3}\pi r^{3}$$

$$\triangle V =\dfrac{dV}{dr} \triangle r$$ ___ (1)

$$\dfrac{dV}{dx}= \dfrac{4}{3}\times 3r^{2}\times \pi \triangle r$$ (Diff with respect to x)

substitute the value of $$\dfrac{dv}{dx}$$ and $$\triangle r$$ in eq (1)

$$\triangle v = \dfrac{4}{3}\times 3r^{2}\times \pi \times 0.02$$

$$=4\pi r^{2}\times 0.02= 4\pi 14^{2}\times 0.02$$

$$= 784\pi \times 0.02$$

$$= 15.68 \pi m^{3}$$

Find the stationary points of $$f(x)=\cos x $$ where $$0<x<2\pi$$

$$f(x)=\cos x \\f^{\prime}(x)=-\sin x $$

For Stationary points $$f'(x)=0$$

$$-\sin x=0$$

$$x=0,\pi$$

The point on the curve $$y = 5x - {x^2}$$ at which normal is perpendicular to the line $$x + y = 0$$ is

Given curve is $$y=5x-x^2$$

$$\cfrac{dy}{dx}=5-2x\Rightarrow \cfrac{-dx}{dy}=\cfrac{-1}{5-2x}$$

Given that slope of normal is perpendicular to $$x+y=0$$

Slope of $$x+y=0$$ is $$-1$$

A/Q $$\cfrac{-1}{5-2x}\times -1=-1\\ \Rightarrow 1=5-2x\Rightarrow 2x=4\Rightarrow x=2\\ \therefore y=5x-x^2=5\times 2-2\times 2=10-4=6$$

$$\therefore$$ Required point is $$(2,6)$$

The stationary points of $$f ( x ) = x ^ { 3 } - 9 x ^ { 2 } + 24 x - 12$$ are

$$f'(x)=3x^2-18x+24\\=3(x^2-x+8)\\=3(x-4)(x-2)\\for\>stationary\>points\>f'(x)=0\\\therefore\>x\>=\>2,4$$

If line $$y=4x-5$$ touches curve $$y^2=ax^3+b$$ at point $$(2, 3)$$ then find the values of a and b.

1178850_1294298_ans_16f6f8ac71754a718db0f041e0dbb565.jpg

A circular metal plate expands under heating so that it radius increases by 2%. Find the approximate increase in the area of the plate if the radius of the plate before heating is 10 cm.

1346783_1259067_ans_7773b11788b744d5a4a031d1d9fb1230.jpg

If $$y=x^4-10$$ and if x changes from 2 to 1.99, what is the approximate change in y ? Also, find the changed value of y.

1346781_1260934_ans_742b7771f96945e0a307b34b02517d0b.jpg

The equation of tangent at $$(1,2)$$ to $$x^2+y^2=5$$

The given point is $$(1,2)$$

The equation is $$x^2+y^2=5$$

The slope of tangent is $$2x+2y\dfrac{dy}{dx}=0\\\dfrac{dy}{dx}=\dfrac{-x}{y}\\\left.\dfrac{dy}{dx}=\right|_{(1,2)}=\dfrac{-1}{2}$$

Equation of line is given as $$y-2=\dfrac{-1}{2}(x-1)\\2y-4=-x+1\\x+2y-5=0$$

Show that $$\dfrac{x}{p} + \dfrac{y}{q} = 1$$ touches the curve $$y = qe^{\frac{-x}{p}}$$ at the point, where the curve crosses the axis of $$y-$$axis.

$$\begin{array}{l} y=q{ e^{ -\frac { x }{ p } } } \\ \Rightarrow \dfrac { { dy } }{ { dx } } =-\dfrac { q }{ p } { e^{ -\frac { x }{ p } } } \\ when\, the\, curves\, crosses\, the\, y-axis,\, x=0 \\ At\, x=0,\, y=q{ e^{ -\frac { 0 }{ p } } }\, \, ,\, \, i.e.\, y=q \\ So,\, the\, curve\, crosses\, the\, y-axis\, at\, \left( { 0,q } \right) \, is \\ y-q=-\dfrac { q }{ p } \left( { x-0 } \right) \\ \dfrac { x }{ p } +\dfrac { y }{ q } =1 \\ \end{array}$$

Hence, proved.

Find points on the curve $$\dfrac {x^{2}}{9}+\dfrac {y^{2}}{16}=1$$at which tangents are
parallel to $$y-$$axis

$$\dfrac{{x}^{2}}{9}+\dfrac{{y}^{2}}{16}=1$$

Differentiating both sides w.r.t $$x$$ we get

$$\dfrac{2x}{9}+\dfrac{2y}{16}\dfrac{dy}{dx}=0$$

$$\Rightarrow \dfrac{2y}{16}\dfrac{dy}{dx}=\dfrac{-2x}{9}$$

$$\Rightarrow \dfrac{dy}{dx}=\dfrac{-16x}{9y}$$

Given:The line is parallel to $$y-$$axis

$$\Rightarrow$$ Angle with $$x-$$axis$$={90}^{\circ}$$

$$\Rightarrow \theta={90}^{\circ}$$

Slope$$=\tan{\theta}=\tan{{90}^{\circ}}=\infty$$

Hence $$\dfrac{dy}{dx}=\infty$$

$$\Rightarrow \dfrac{-16x}{9y}=\infty$$

$$\Rightarrow \dfrac{16x}{9y}=\dfrac{1}{0}$$

This will be possible only if the denominator is $$0$$

$$\Rightarrow 9y=0$$

$$\Rightarrow y=0$$

Put $$y=0$$ in $$\dfrac{{x}^{2}}{9}+\dfrac{{y}^{2}}{16}=1$$ we get

$$\dfrac{{x}^{2}}{9}=1$$

$$\Rightarrow {x}^{2}=9$$

$$\Rightarrow x=\pm 3$$

Hence the points at which tangent is parallel to $$y-$$axis are $$\left(3,0\right)$$ and $$\left(-3,0\right)$$

Find the slope of a line. Which bisects the first quadrant angle.

As we know , the angle between coordinate axes is $$\dfracπ2.$$

It is given that the line bisects the first quadrant angle.

Hence , the inclination of the given line with the positive x-axis is equal to $$\dfrac{1}{2}\cdot \dfrac{π}{2} = \dfracπ4 .$$

Therefore, slope of the line $$= \tan \left(\dfrac{\pi}{4}\right) = 1.$$

Find the value of $$x$$ such that $$f(x)=2x^3-15x^2+36x+1$$ is an increasing function.

$$f(x)=2x^3-15x^2+36x+1$$
$$\therefore f'(x)=6x^2-30x+36$$
$$\therefore f'(x)=6(x^2-5+6)$$
i,e. $$f'(x)=6(x-3)(x-2)$$
$$\because f(x)$$ is increasing function.
$$\therefore f'(x)\ge 0$$
$$6(x-3)(x-2)\ge 0$$
$$\therefore x\gt 3$$ or $$x \lt 2$$
$$\therefore f(x)$$ is increasing $$x\gt 3$$ or $$x \lt 2$$.

Find the equation of a curve passing through $$\left( 1,\dfrac { \pi }{ 4 } \right) $$ if the slope of the tangent to the curve at any point $$p\left( x,y \right) $$ is $$\dfrac { y }{ x } -\cos { ^{ 2 } } \dfrac { y }{ x } $$.

According to the given condition
slope of tangent, $$m=dy/dx$$
$$\dfrac{dy}{dx}=\dfrac{y}{x}- \cos ^2 \dfrac{y}{x}....(i)$$
This is a homogeneous differential equation. Substituting $$y=vx$$, we get
$$v+x\dfrac{dv}{dx}=v- \cos^2v \Rightarrow x\dfrac{dv}{dx}=- \cos^2v$$
$$\displaystyle \Rightarrow \sec^2 vdv=-\dfrac{dx}{x} \Rightarrow\tan v=- \log x+ c \int \sec^2 vdv= \int - \dfrac{dx}{x}$$
$$\Rightarrow \tan \dfrac{y}{x}+ \log x=c...(ii)$$
Substituting $$x=1,\ y=\dfrac{\pi}{4},$$ we get $$c=1$$.
Thus, we get
$$\tan \left(\dfrac{y}{x}\right)+ \log x=1$$, which is the required equation.

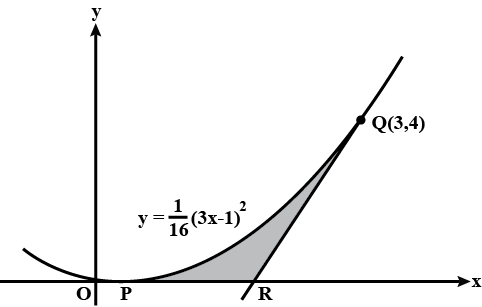
The diagram shows part of the curve $$y=\dfrac{1}{16}(3x-1)^2$$, which touches the x-axis at the point P. The point $$Q(3,4)$$ lies on the curve and the tangent to the curve at $$Q$$ crosses the x-axis at $$R$$.
State the x-coordinate of $$P$$.

The slope of tangent is given as $$\dfrac{dy}{dx}=\left[\dfrac{6}{16}(3x-1)\right]$$
At $$P$$ Slope is $$0$$

$$\implies \dfrac {dy}{dx}=0\\\dfrac 6{16}(3x-1)=0\\x=\dfrac 13$$

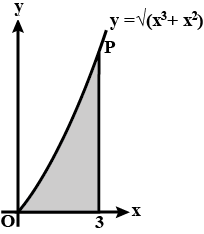
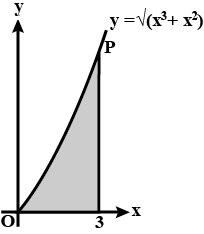
The diagram shows part of the curve with equation $$y=\sqrt{(x^3+x^2)}$$. The shaded region is bounded by the curve, the x-axis and the line $$x=3$$.
P is the point on the curve with x-coordinate $$3$$. Find the y-coordinate of the point where the normal to the curve at P crosses the y-axis.

$$y=\sqrt {x^3+x^2}\\\dfrac{dy}{dx}=\dfrac{1}{2}(x^3+x^2)^{-1/2}\times (3x^2+2x)$$

At $$x=3$$

$$\implies y=\sqrt {3^3+3^2}\\y=\sqrt {36}$$

$$y=6$$
At $$x=3,$$

Slope of tangent is $$m=\dfrac{1}{2}\times \dfrac{1}{6}\times 33=\dfrac{11}{4}$$
Equation of normal is $$y-6=-\dfrac{4}{11}(x-3)$$

Condition to cross $$y$$ axis $$x=0,$$

$$\implies y-6=\dfrac{-4}{11}(-3)\\y=7\dfrac 1{11} $$

A curve has equation $$y=(2x-1)^{-1}+2x$$. $$x\neq\dfrac{1}{2}$$
Find the x-coordinates of the stationary points

$$y=(2x-1)^{-1}+2x$$

$$\dfrac{dy}{dx}=\dfrac d{dx}(2x-1)^{-1}+2x$$

$$\dfrac{dy}{dx}=-2(2x-1)^{-2}+2$$

For stationary points

$$\dfrac {dy}{dx}=0\\-2(2x-1)^{-2}+2=0\\(2x-1)^{-2}=1\\2x-1=1\\x=1$$

Find the value of p for when the curves $$x^{2}=9p(9-y)$$ and $$x^{2}=P(y+1)$$ cut each other at right angles .

1297533_1585062_ans_fea4ce8a56ba410d832432c3c04db2a4.jpg

Find the slopes of the tangent and the normal to the following curve at the indicated point.
$$y=\sqrt{x^3}$$ at $$x=4$$.

$$y=\sqrt{x^3}$$ [ Given ]

$$\Rightarrow$$ $$y=x^{\frac{3}{2}}$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=\dfrac{3}{2}x^{\frac{1}{2}}$$ [ Differentiating both sides ]

$$\therefore$$ $$\dfrac{dy}{dx}=\dfrac{3}{2}\sqrt{x}$$

When $$x=4,$$

$$\Rightarrow$$ $$y=\sqrt{x^3}$$

$$=\sqrt{(4)^3}$$

$$=\sqrt{64}$$

$$=8$$

Now,

Slop of the tangent $$(m)=\left(\dfrac{dy}{dx}\right)_{(4,8)}=\dfrac{3}{2}\sqrt{4}$$

$$=\dfrac{3}{2}\times 2$$

$$=3$$

Slop of the normal $$=\dfrac{-1}{m}=\dfrac{-1}{3}$$

Find the slopes of the tangent and the normal to the following curve at the indicated point.
$$y=\sqrt{x}$$ at $$x=9$$.

$$y=\sqrt{x}$$

$$\Rightarrow$$ $$y=\sqrt{9}$$

$$\Rightarrow$$ $$y=3$$

The point has co-ordinates $$(9,3)$$.

Now, the slop of tangent $$\dfrac{dy}{dx}$$ at any point to the function $$f(x)=\sqrt{x}$$ is given as

$$\Rightarrow$$ $$\dfrac{dy}{dx}=f'(x)$$

$$=\dfrac{d}{dx}(\sqrt{x})$$

$$=\dfrac{1}{2\sqrt{x}}$$

Now, the slop $$m$$ of tangent at the given point $$(9,3)$$ is given as

$$\Rightarrow$$ $$m=f'(9)$$

$$\Rightarrow$$ $$m=\dfrac{1}{2\sqrt{9}}$$

$$\Rightarrow$$ $$m=\dfrac{1}{6}$$

$$\Rightarrow$$ Slopes of the normal $$=\dfrac{-1}{\dfrac{dx}{dy}}=\dfrac{-1}{\dfrac{1}{2\sqrt{x}}}=-2\sqrt{x}$$

$$\Rightarrow$$ Slopes of the normal $$=-2\sqrt{9}=-6$$

The diagram shows part of the curve with equation $$y=\sqrt{(x^3+x^2)}$$. The shaded region is bounded by the curve, the x-axis and the line $$x=3$$.
Find the y-coordinate of the point where the normal to the curve at P crosses the y-axis.

$$y=\sqrt {x^3+x^2}\\\dfrac{dy}{dx}=\dfrac{1}{2}(x^3+x^2)^{-1/2}\times (3x^2+2x)$$

At $$x=3$$

$$\implies y=\sqrt {3^3+3^2}\\y=\sqrt {36}$$

$$y=6$$
At $$x=3,$$

Slope of tangent is $$m=\dfrac{1}{2}\times \dfrac{1}{6}\times 33=\dfrac{11}{4}$$
Equation of normal is $$y-6=-\dfrac{4}{11}(x-3)$$

Condition to cross $$y$$ axis $$x=0,$$

$$\implies y-6=\dfrac{-4}{11}(-3)\\y=7\dfrac 1{11} $$

If the tangent to the curve $$y=x^3+ax+b$$ at $$(1, -6)$$ is parallel to the line $$x-y+5=0$$, find $$a$$ and $$b$$.

$$x-y+5=0$$

$$\Rightarrow$$ $$y=x+5$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=1$$

Now,

$$\Rightarrow$$ $$y=x^3+ax+b$$ ---- ( 1 )

$$\Rightarrow$$ $$\dfrac{dy}{dx}=3x^2+a$$

Slop of the tangent at $$(1,-6)=$$ Slop of the given line

$$\Rightarrow$$ $$\left(\dfrac{dy}{dx}\right)_{(1,-6)}=1$$

$$\Rightarrow$$ $$3(1)^2+a=1$$

$$\Rightarrow$$ $$3+a=1$$

$$\Rightarrow$$ $$a=-2$$

On substituting $$a=-2,x=1$$ and $$y=-6$$ in equation ( 1 ), we get

$$\Rightarrow$$ $$-6=1-2+b$$

$$\Rightarrow$$ $$b=-5$$

$$\therefore$$ $$a=-2$$ and $$b=-5$$

Find the equation of the tangent and the normal to the following curves at the indicated points.
$$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$$ at $$(a\sec\theta, b\tan\theta)$$.

$$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$$

Differentiating both sides w.r.t. $$x,$$

$$\Rightarrow$$ $$\dfrac{2x}{a^2}-\dfrac{2y}{b^2}\dfrac{dy}{dx}=0$$

$$\Rightarrow$$ $$\dfrac{2y}{b^2}\dfrac{dy}{dx}=\dfrac{2x}{a^2}$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=\dfrac{xb^2}{ya^2}$$

Slope of tangent, $$m=\left(\dfrac{dy}{dx}\right)_{(a\sec\theta, b\tan\theta)}=\dfrac{a\sec\theta(b^2)}{b\tan\theta(a^2)}$$

$$=\dfrac{b}{a\sin\theta}$$

$$\Rightarrow$$ $$(x_1,y_1)=(a\sec\theta,b\tan\theta)$$ [ Given ]

Equation of tangent :

$$y-y_1=m(x-x_1)$$

$$\Rightarrow$$ $$y-b\tan\theta=\dfrac{b}{a\sin\theta}(x-a\sec\theta)$$

$$\Rightarrow$$ $$ay\sin\theta-ab\dfrac{\sin^2\theta}{\cos\theta}=bx-\dfrac{ab}{\cos\theta}$$

$$\Rightarrow$$ $$\dfrac{ay\sin\theta\cos\theta-ab\sin^2\theta}{\cos\theta}=\dfrac{bx\cos\theta-ab}{\cos\theta}$$

$$\Rightarrow$$ $$ay\sin\theta\cos\theta-ab\sin^2\theta=bx\cos\theta-ab$$

$$\Rightarrow$$ $$bx\cos\theta-ay\sin\theta\cos\theta=ab(1-\sin^2\theta)$$

Dividing by $$ab\cos^2\theta,$$

$$\Rightarrow$$ $$\dfrac{x}{a}\sec\theta-\dfrac{y}{b}\tan\theta=1$$

Equation of normal :

$$y-y_1=\dfrac{-1}{m}(x-x_1)$$

$$\Rightarrow$$ $$y-b\tan\theta=\dfrac{-a\sin\theta}{b}(x-a\sec\theta)$$

$$\Rightarrow$$ $$yb-b^2\tan\theta=-ax\sin\theta+a^2\tan\theta$$

$$\Rightarrow$$ $$ax\sin\theta+by=(a^2+b^2)\tan\theta$$

Dividing by $$\tan\theta,$$

$$\Rightarrow$$ $$ax\cos\theta+by\cot\theta=(a^2+b^2)$$

Find the slopes of the tangent and the normal to the following curve at the indicated point.
$$y=(\sin 2x+\cot x+2)^2$$ at $$x=\dfrac {\pi}{2}$$.

$$y=(\sin 2x+\cot x+2)^2$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=2(\sin 2x+\cot x+2)(2\cos 2x-cosec^2x)$$

Now,

$$\Rightarrow$$ Slop of the tangent $$=\left(\dfrac{dy}{dx}\right)_{x=\frac{x}{2}}$$

$$=2\left[\sin 2\left(\dfrac{\pi}{2}\right)+\cot\left(\dfrac{\pi}{2}\right)+2\right]\left[2\cos2\left(\dfrac{\pi}{2}\right)-cosec^2\left(\dfrac{\pi}{2}\right)\right]$$

$$=2(0+0+2)(-2-1)$$

$$=-12$$

$$\Rightarrow$$ Slop of the normal $$=\dfrac{-1}{\left(\dfrac{dy}{dx}\right)_{x=\frac{\pi}{2}}}=\dfrac{-1}{-12}=\dfrac{1}{12}$$

Find the slope of the tangent and the normal to the following curve at the indicated point.
$$y=2x^2+3\sin x$$ at $$x=0$$.

Slope of tangent is $$\dfrac{dy}{dx}$$

$$y=2x^2+3\sin x$$

Differentiating w.r.t. $$x$$,

$$\dfrac{dy}{dx}=\dfrac{d(2x^2+3\sin x)}{dx}$$

$$\dfrac{dy}{dx}=4x+3\cos x$$

We know that

$$\Rightarrow$$ Slop of tangent $$x$$ slop of normal $$=-1$$

$$\Rightarrow$$ $$(4x+3\cos x)\times $$ slop of normal $$=-1$$

Slop of normal $$=\dfrac{-1}{4x+3\cos x}$$

We need to find slop of normal at $$x=0$$

Slop of normal at $$(x=0)=\dfrac{-1}{4(0)+3\cos 0^o}=\dfrac{-1}{0+3(1)}=\dfrac{-1}{3}$$

Find the point on the curve $$y=x^2$$, where the slope of the tangent is equal to the $$x$$-coordinate of the point.

Let the required point be $$(x_1,y_1).$$

$$\Rightarrow$$ $$y=x^2$$

Point $$(x_1,y_1)$$ lies on a curve.

$$\therefore$$ $$y_1=x_1^2$$ ----- ( 1 )

Now,

$$y=x^2\Rightarrow \dfrac{dy}{dx}=2x$$

$$\Rightarrow$$ Slope of the tangent at $$(x_1,y_1)=\left(\dfrac{dy}{dx}\right)_{(x_1,y_1)}=2x_1$$

$$\Rightarrow$$ Slope of the tangent $$=x-coordinate$$ of the point [ given ]

$$\therefore$$ $$2x_1=x_1$$

This happens only when $$x_1=0$$

On putting $$x_1=0$$ in equation ( 1 ), we get

$$y_1=x_1^2=0^2=0$$

Thus, the required point is $$(0,0).$$

Find the slope of the tangent and the normal to the following curves at the indicated points.
$$y=x^3-x$$ at $$x=2$$.

The equation of the curve is $$y=x^3-x$$.
$$\therefore \dfrac{dy}{dx}=3x^2-1$$
At $$x=2$$, we get: $$\dfrac{dy}{dx}=3\times 2^2-1=11$$
Hence, slope of the tangent at $$x=2$$ is $$11$$ and that of the normal is $$-\dfrac{1}{11}$$.

Find the slopes of the tangent and the normal to the following curve at the indicated point.
$$x=a(\theta -\sin\theta), y=a(1+\cos\theta)$$ at $$\theta =-\dfrac {\pi}{2}$$.

$$x=a(\theta-\sin\theta)$$

$$\Rightarrow$$ $$\dfrac{dx}{d\theta}=a(1-\cos\theta)$$

$$y=a(1+\cos\theta)$$

$$\Rightarrow$$ $$\dfrac{dy}{d\theta}=a(-\sin\theta)$$

$$\therefore$$ $$\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{d\theta}}{\dfrac{dx}{d\theta}}=\dfrac{a(-\sin\theta)}{a(1-\cos\theta)}$$

$$=\dfrac{-2\sin\dfrac{\theta}{2}\cos\dfrac{\theta}{2}}{2\sin^2\dfrac{\theta}{2}}$$

$$=-\cos\dfrac{\theta}{2}$$

Now,

Slop of the tangent $$(m)=\left(\dfrac{dy}{dx}\right)_{\theta=\frac{-\pi}{2}}=-\cot\left(\dfrac{-\pi}{4}\right)=1$$

Slop of the normal $$=\dfrac{-1}{m}=\dfrac{-1}{1}=-1$$

Find the values of $$a$$ and $$b$$, if the slope of the tangent to the curve $$xy+ax+by=2$$ at $$(1, 1)$$ is $$2$$.

$$xy+ax+by=2$$ ----- ( 1 )

On differentiating both sides w.r.t. $$x,$$ we get

$$x\dfrac{dy}{dx}+y+a+b\dfrac{dy}{dx}=0$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}(x+b)=-a-y$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=\dfrac{-a-y}{x+b}$$

Now,

The slope of the tangent $$=2$$

$$\left(\dfrac{dy}{dx}\right)_{(1,1)}=2$$

$$\Rightarrow$$ $$\dfrac{-a-1}{1+b}=2$$

$$\Rightarrow$$ $$-a-1=2+2b$$

$$\Rightarrow$$ $$-a=3+2b$$

$$\Rightarrow$$ $$a=-(3+2b)$$

On substituting $$a=-(3+2b),\,x=1$$ and $$y=1$$ in equation ( 1 ), we get

$$\Rightarrow$$ $$1-(3+2b)+b=2$$

$$\Rightarrow$$ $$1-3-2b+b=2$$

$$\Rightarrow$$ $$b=-4$$

And

$$\Rightarrow$$ $$a=-(3+2b)=-(3-8)=5$$

$$\therefore$$ $$a=5$$ and $$b=-4$$

Find the points on the curve $$xy+4=0$$ at which the tangents are inclined at an angle of $$45^o$$ with the $$x$$-axis.

Given the curve is $$xy+4=0$$

or, $$y=-\dfrac{4}{x}$$.

Now $$\dfrac{dy}{dx}=\dfrac{4}{x^2}$$.

We've the slope of the tangent at $$(x,y)$$ is $$\dfrac{dy}{dx}$$.

According to the problem,

$$\dfrac{dy}{dx}=\tan 45^o$$

or, $$\dfrac{4}{x^2}=1$$

or, $$x^2=4$$

or, $$x=\pm 2$$.

If $$x=\pm 2$$ then $$y$$ will be $$\mp 2$$.

So the points are $$(\pm 2,\mp 2)$$.

Find the points on the curve $$y^2=2x^3$$ at which the slope of the tangent is $$3$$.

Let $$(x_1,y_1)$$ be the required point

$$\Rightarrow$$ $$y^2=2x^3$$ [ Given ]

Since, $$(x_1,y_1)$$ lies on a curve, $$y_1^2=2x_1^3$$ ---- ( 1 )

$$\Rightarrow$$ $$2y\dfrac{dy}{dx}=6x^2$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=\dfrac{6x^2}{2y}=\dfrac{3x^2}{y}$$

Slope of the tangent at $$(x_1,y_1)=\left(\dfrac{dy}{dx}\right)_{(x_1,y_1)}=\dfrac{3x_1^2}{y_1}$$

Slope of the tangent $$=3$$

$$\therefore$$ $$\dfrac{3x_1^2}{y_1}=3$$ ---- ( 2 )

$$\Rightarrow$$ $$y_1=x_1^2$$

On substituting the value of $$y_1$$ in equation ( 1 ), we get

$$\Rightarrow$$ $$x_1^4=2x_1^3$$

$$\Rightarrow$$ $$x_1^3(x_1-2)=0$$

$$\Rightarrow$$ $$x_1=0,2$$

$$Case\,I:$$

When $$_1=0,\,y_1=x^2=0.$$

Thus, we get the point $$(0,0).$$ But, it does not satisfy equation ( 2 ).

So, we can ignore $$(0,0).$$

$$Case\,II:$$

When $$x_1=2,$$ $$y_1=x_1^2=4.$$

Thus, we get the point $$(2,4).$$

Prove that the function $$f(x)=\log _{ e }{ x } $$ is increasing on $$(0,\infty)$$.

$$f(x)=log x$$

we need to prove $$f(x)$$ is increasing on $$x\in(0, \infty)$$

i.e., we need to show $$f'(x) > 0$$ for $$x\in (0, \infty)$$

Now,

$$f(x)=log x$$

$$f'(x)=\dfrac{1}{x}...$$ [we differentiate w.r.t x]

when $$x > 0$$

$$\Rightarrow \dfrac{1}{x} > 0$$

$$\Rightarrow f'(x) > 0$$

Hence $$f(x)$$ is an increasing function for $$x > 0$$

Hence proved.

Using differential, find the approximate value of the following:
$$\sqrt{401}$$

$$y=\sqrt{x}$$

$$x=400\, \ \ \ \ \Delta x=1$$

$$\dfrac{dy}{dx}=\dfrac{1}{2\sqrt{x}}$$

$$\Delta y=\dfrac{dy}{dx}\times \Delta x=\dfrac{dy}{2\sqrt{x}}\times \Delta x$$

$$\Delta y=\dfrac{1}{2\sqrt{400}}\times (1)$$

$$\Delta y=\dfrac{1}{2\times 20}=0.025$$

$$\Delta y=f(x+\Delta x)-f(x)$$

$$=(x+\Delta x)^{1/2}-x^{1/2}$$

Putting value

$$\Delta y=(401)^{1/2}-(20)^{2\times \tfrac{1}{2}}$$

$$0.025=(401)^{1/2}-(20)^{2\times \tfrac{1}{2}}$$

$$(401)^{1/2}=20+0.025=20.025$$

Prove that $$\left(\dfrac{x}{a}\right)^n+\left(\dfrac{y}{b}\right)^n=2$$ touches the straight line $$\dfrac{x}{a}+\dfrac{y}{b}=2$$ for all $$n\in N$$, at the point (a, b).

We have, $$\left(\dfrac{x}{a}\right)^n+\left(\dfrac{y}{b}\right)^n=2$$

Differentiating both sides with respect to x, we get

$$n\left(\dfrac{x}{a}\right)^{n-1}\dfrac{1}{a}+n\left(\dfrac{y}{b}\right)^{n-1}\dfrac{1}{b}\dfrac{dt}{dx}=0$$

$$\Rightarrow \dfrac{dy}{dx}=\dfrac{-b}{a}\left(\dfrac{x}{a}\right)^{n-1}\left(\dfrac{b}{y}\right)^{n-1}$$

$$\Rightarrow \left(\dfrac{dy}{dx}\right)_{(a, b)}=\dfrac{-b}{a}$$

The equation of the tangent at $$(a, b)$$ is

$$y-b=\dfrac{-b}{a}(x-a)$$

$$\Rightarrow ay-ab=-bx+ab$$

$$\Rightarrow bx+ay=2ab$$

$$\Rightarrow \dfrac{x}{a}+\dfrac{y}{b}=2$$

Hence, $$\dfrac{x}{b}+\dfrac{y}{b}=2$$ touches the given curve at $$(a, b)$$ for all $$n\in N$$.

A stone is dropped into a quiet lake and waves move in circles at a speed of $$4$$ cm/sec. At the instant when the radius of the circular wave is $$10$$ cm, how fast is the enclosed area increasing?

Let $$r$$ be radius of circular region

$$A$$ be area

$$A = \pi r^2$$ $$\left[\dfrac{dr}{dt} = 4cm/sec\right]$$

$$\dfrac{dA}{dt} = 2\pi r \dfrac{dr}{dt}$$

$$= 2\pi r \times 4$$

$$\dfrac{dA}{dt} = 8\pi r$$

$$\left(\dfrac{dA}{dt}\right)_{r=10}$$ $$= 8\pi \times 10 = 80\pi \ cm^2/sec$$

Prove that the function $$f(x)=\log _{ a }{ x } $$ is increasing on $$(0,\infty )$$, if $$a> 1$$ and decreasing on $$(0,\infty )$$, if $$0< a< 1$$.

SHP$$(1)$$ $$f(x)=log_ax$$

$$f(x)=\dfrac{log_ex}{log_ea}$$

diff wrt x

$$f'(x)=\dfrac{1}{log_e(a)}\times \dfrac{1}{x}$$

$$f'(x)=\dfrac{1}{x log(a)}$$

if $$a > 1$$

then

$$f'(x) > 0$$

$$\therefore f(x)$$ is increasing function for $$a > 1$$

SHP $$(2)$$ $$f'(x)=\dfrac{1}{x log a}$$

if $$a > 0$$ & $$a < 1$$

then $$f'(x)$$ is not greater than zero.

$$\therefore f(x)$$ is decreasing function $$0 < a < 1$$.

The pressure $$P$$ and the volume $$v$$ of a gas are connected by the relation $$pv^{1.4}=$$ const. Find the percentage error in $$p$$ corresponding to a decrease of $$\dfrac {1}{2}\%$$ in $$v$$.

The given relation is

$$p{ v }^{ 1.4 }=const.$$

$$p=\dfrac { c }{ { v }^{ 1.4 } } $$

Differentiate with respect to $$v$$

$$\dfrac { dp }{ dv } =\dfrac { c\left( -1.4 \right) }{ { v }^{ 2.4 } } $$

Rearrange above and dividing both sides by $$p$$

$$\dfrac { dp }{ p } =\dfrac { c\left( -1.4 \right) }{ { v }^{ 2.4 } } \cdot \dfrac { dv }{ p } $$

Substituting value of $$p$$ in above from given equation,

$$\dfrac { dp }{ p } =\dfrac { c\left( -1.4 \right) }{ { v }^{ 2.4 } } \cdot \dfrac { dv\cdot { v }^{ 1.4 } }{ c } $$

$$\dfrac { dp }{ p } =\left( -1.4 \right) \cdot \dfrac { dv }{ v } $$

$$\% $$error in $$p$$

(-)ve sign cancels out as we consider decrease in volume $$v$$

$$\dfrac { dp }{ p } \times 100=\left( 1.4 \right) \left( \dfrac { 1 }{ 200 } \right) \times 100$$

$$ \quad \quad \quad \quad \quad \quad \quad \quad =\dfrac { 7 }{ 10 } =0.7%$$

lf there is an error of $$0.1\%$$ in the measurement of the radius of a sphere, find approximately the percentage error in the calculation of the volume of the sphere.

The volume of a sphere of radius $$r$$is $$V=\dfrac { 4 }{ 3 } \pi { r }^{ 3 }$$.

Thus,

$$dV=\dfrac { 4 }{ 3 } \pi \cdot 3{ r }^{ 2 }=4\pi { r }^{ 2 }dr$$

Divide both sides of the equation by $$V$$.

Hence,

$$\dfrac { dV }{ V } =\dfrac { 4\pi { r }^{ 2 } }{ V } dr\\ \dfrac { dV }{ V } =\dfrac { 4\pi { r }^{ 2 } }{ \dfrac { 4 }{ 3 } \pi { r }^{ 3 } } dr\\ \dfrac { dV }{ V } =3\dfrac { dr }{ r }...(i) $$

The percentage error in radius of sphere $$=0.1 \%$$.

Percentage error=$$\dfrac { dr }{ r }\cdot100$$

Percentage error in volume=$$\dfrac{dV}{V}\cdot100$$

From (i),

$$\dfrac { dV }{ V } =3\dfrac { 0.1 }{ 100 } =0.003$$

Hence the percentage error,

$$\dfrac { dV }{ V } \cdot 100=0.3%$$

Find the equation of all lines of slope zero and that are tangent to the curve $$y=\dfrac{1}{x^2-2x+3}$$.

$$y=\dfrac{1}{x^2-2x+3}$$ [ Given ]

Differentiating both sides w.r.t. $$x,$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=\dfrac{d}{dx}(x^2-2x+3)^{-1}$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=-(x^2-2x+3)^{-2}(2x-2)$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=-2(x^2-2x+3)^{-2}(x-1)$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=\dfrac{-2(x-1)}{(x^2-2x+3)^2}$$

$$\therefore$$ Slope of tangent $$=\dfrac{-2(x-1)}{(x^2-2x+3)^2}$$

Slope of tangent is $$0$$

$$\Rightarrow$$ $$\dfrac{-2(x-1)}{(x^2-2x+3)^2}=0$$

$$\Rightarrow$$ $$-2(x-1)=0$$

$$\Rightarrow$$ $$x-1=0$$

$$\Rightarrow$$ $$x=1$$

Now,

$$y=\dfrac{1}{x^2-2x+3}$$ [ Given ]

$$\Rightarrow$$ $$y=\dfrac{1}{(1)^2-2(1)+3}$$ [ Substituting $$x=1$$ ]

$$\Rightarrow$$ $$y=\dfrac{1}{1-2+3}$$

$$\Rightarrow$$ $$y=\dfrac{1}{2}$$

Tangent passes through points $$\left(1,\dfrac{1}{2}\right)$$

Equation of tangent :

$$(y-y_1)=m(x-x_2)$$

Equation of tangent at $$\left(1,\dfrac{1}{2}\right)$$ and having slope zero is

$$\left(y-\dfrac{1}{2}\right)=0(x-1)$$

$$\Rightarrow$$ $$y-\dfrac{1}{2}=0$$

$$\therefore$$ $$y=\dfrac{1}{2}$$

Hence equation of tangent is $$y=\dfrac{1}{2}$$

Using differentials, find the approximate value of the following:
$$\sqrt{37}$$

Let $$y=f(x)=\sqrt{x}$$

This gives $$\dfrac{dy}{dx}=\dfrac{1}{2\sqrt{x}}$$.

Now, we've,

$$\Delta y=\dfrac{dy}{dx} \Delta x$$

or, $$\Delta y=\dfrac{1}{2\sqrt x} \Delta x$$ [ For $$y=\sqrt{x}$$].......(1)

Now, let us take $$x=36$$ and $$\Delta x=1$$, then we've from (1),

$$\Delta y=\dfrac{1}{12}.1$$

or, $$\Delta y=\dfrac{1}{12}$$.

Again we've,

$$\Delta y=f(x+\Delta x)-f(x)$$

or, $$\dfrac{1}{12}=\sqrt{37}-6$$ [ For $$x=36$$ and $$\Delta x=1$$]

or, $$\sqrt{37}=\dfrac{73}{12}$$.

A man $$160$$ cm tall, walks away from a source of light situated at the top of a pole $$6$$ m high, at the rate of $$1.1$$ m/sec. How fast is the length of his shadow increasing when he is $$1$$ m away from the pole?

Let x$$=$$ distance of man from pole

Given $$\dfrac{dx}{dt}=1.1$$ m/s

$$\Delta ABC \sim \Delta PRC$$ (By AA rule)

$$\dfrac{AB}{PR}=\dfrac{BC}{RC}$$

$$\Rightarrow \dfrac{6}{1.6}=\dfrac{x+y}{y}$$

$$\Rightarrow 6y=1.6x+1.6y$$

$$\Rightarrow 4.4y=1.6x$$

$$\Rightarrow y=\dfrac{4}{11}x$$ we have to find $$\left.\dfrac{dy}{dx}\right|_{x=1m}$$

$$\therefore \dfrac{dy}{dt}=\dfrac{4}{11}\times \dfrac{dx}{dt}$$

$$\Rightarrow \dfrac{dy}{dt}=\dfrac{4}{11}\times 1.1$$ m/s

$$=0.4$$ m/s

at $$x=1$$m, $$\dfrac{dy}{dt}=0.4$$ m/s.

If $$y = 7x-x^{3}$$ and $$x$$ increases at the rate of $$4$$ units per second, how fast is the slope of the curve changing when $$x = 2$$?

$$y=7x-x^3$$ [ Given ]

Differentiate both sides w.r.t. $$x,$$ we get

$$\Rightarrow$$ $$\dfrac{dy}{dx}=7-6x^2$$

Let $$s$$ be the slope. Then,

$$s=7-3x^2$$

Differentiating both sides w.r.t. $$t,$$ we get

$$\Rightarrow$$ $$\dfrac{ds}{dt}=-6x\dfrac{dx}{dt}$$

It is given that $$\dfrac{dx}{dt}=4\,units/sec$$ and $$x=2$$

$$\Rightarrow$$ $$\dfrac{ds}{dt}=-6(4)(2)$$

$$\therefore$$ $$\dfrac{ds}{dt}=-48$$

A particle moves along the curve $$ y = x^3.$$ Find the points on the curve at which the y-coordinate changes three times more rapidly than the x-coordinate.

Given: Particle moves in along the curve;

$$y = x^3$$

Change in y-coordinate $$= 3\times$$ (change in x-coordinate)

$$dy = 3dx$$

$$\dfrac{dy}{dx} = 3$$

$$\text{To find:}$$ The point at which $$\dfrac{dy}{dx} = 3$$

$$\text{then :}$$

consider $$y = x^3$$

Differentiate w.r.t. 'x'

$$\dfrac{dy}{dx} = 3x^2$$

$$\therefore 3x^2 = 3 \left[\because \dfrac{dy}{dx} = 3\right]$$

$$x^2 = 1$$

$$x = \pm 1$$

If $$x = +1$$

$$y=1$$

If $$x = -1$$

$$y = -1$$

$$\therefore$$ The required are $$(1,1)$$ and $$(-1,-1)$$

Write the coordinates of the point on the curve $$y^2=x$$ where the tangent line makes an angle $$\dfrac{\pi}{4}$$ with x-axis.

Let the point be $$P(x_1,y_1)$$

The eqn of curve is $$y^2 = x$$ ...(1)

$$2y \dfrac{dy}{dx} = 1$$

$$\left(\dfrac{dy}{dx}\right)_{x_1y_1} = \dfrac{1}{2y_1}$$

Since tangent line makes angle $$\dfrac{\pi}{4}$$ units x-axis

slope of $$P(x,y)=$$ Slope pf line at angle $$\dfrac{\pi}{4}$$

$$\left(\dfrac{dy}{dx}\right)_{x_1y_1} = \tan\dfrac{\pi}{4}$$

$$\dfrac{1}{2y_1} = 1$$

$$y_1 = \dfrac{1}{2}$$

Also line passes through (1)
$$y_1^2=x_1$$

$$x_1 = \dfrac{1}{4}$$

Coordinate of the point are $$\left(\dfrac{1}{4}, \dfrac{1}{2}\right)$$

Let $$C$$ be a curve defined parametrically as $$x=a\cos^{3}\theta, y=a\sin^{3}\theta, 0\le \theta \le \dfrac{\pi}{2}$$. Determine a point $$P$$ on $$C$$, where the tangent to $$C$$ is parallel to the chord joining the points $$(a,0)$$ and $$(0,a)$$

Let point be $$p(x, y)$$
Slope of tangent $$= \dfrac{dy}{dx}$$

Given equations

$$x = a \cos^3 \theta$$

$$y = a \sin^3 \theta$$

$$\dfrac{dx}{d\theta} = -3a \cos^2 \theta \sin \theta$$

$$\dfrac{dy}{d\theta} = 3a \sin^2 \theta \cos \theta$$

$$\therefore \dfrac{dy}{dx} = \dfrac{dy/d\theta}{dx/ d \theta} = \dfrac{3 a \sin^2 \theta \cos \theta}{-3a \cos^2 \sin \theta} = - \tan \theta=$$ slope of tangent

Given two points $$(a, 0)$$ and $$(0, a)$$

$$\therefore $$ Slope of chord, $$m = \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{a - 0}{0 - a} = \dfrac{a}{-a} = -1$$

$$\because $$ it is given that tangent to c is parallel to chord

$$\therefore $$ slope of tangent = slope of chord

$$\Rightarrow -\tan \theta = -1 $$

$$\theta = \pi/4$$

$$\therefore x = a \cos^3 \theta$$

$$x = a \cos^3 \pi/4$$

$$x = a \left(\dfrac{1}{\sqrt{2}}\right)^3 = \dfrac{a}{2 \sqrt{2}}$$

$$y = a \sin^3 \theta$$

$$y = a \sin^3 \pi/4$$

$$y = a \left(\dfrac{1}{\sqrt{2}} \right)^3 = \dfrac{a}{2 \sqrt{2}}$$

$$\therefore $$ point P is $$\left(\dfrac{a}{2 \sqrt{2}} , \dfrac{a}{2\sqrt{2}} \right)$$

If the radius of a sphere is measured as $$7$$ m with an error of $$0.02$$ m, find the approximate error in calculating its volume.

Let $$r$$ be the radius and $$v$$ be the volume of the sphere, then

$$v = \dfrac{4}{3} \pi r^3 \Rightarrow \dfrac{dv}{dr} = 4\pi r^2$$

Let $$\Delta r$$ be the error in $$R$$ and the corresponding error in $$v$$ be $$\Delta v$$, then

$$\Delta V = \dfrac{dv}{dr} \Delta r = 4\pi r^2\Delta r$$

If $$r$$ given that $$r=7$$ and $$\Delta r = 0.02$$

$$\therefore \Delta v = 4\pi \times 7^2 \times 0.02$$

$$= 3.92 \pi$$

Hence, approximate error in calculating volume is $$3.92\pi m^3$$

Find the slope of the normal at the point '$$t$$' on the curve $$x=\dfrac{1}{t}, y=t$$.

$$x=\dfrac{1}{t}\quad y = t$$

$$\dfrac{dx}{dt} = - \dfrac{1}{t^2}\quad \dfrac{dy}{dt}=1$$

Now slope of tangent $$\dfrac{dy}{dx} = \dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}} = \dfrac{1}{-\dfrac{1}{t^2}}=-t^2$$

For calculating slope of normal

Let slope of normal is $$m_2$$ and slope of tngent is $$m_1$$ and they are perpendicular to each other.

$$m_1\times m_2 = -1$$

$$-t^2 \times m_2 = -1$$

or, $$m_2= \dfrac{-1}{-t^2} = \dfrac{1}{t^2}$$

So, slope of normal is $$\dfrac{1}{t^2}$$

Show that the curves $$4x=y^2$$ and $$4xy=k$$ cut at right angles, if $$k^2=512$$.

The given curves are,

$$\Rightarrow$$ $$4x=y^2$$ ----- ( 1 )

$$\Rightarrow$$ $$4xy=k$$ ----- ( 2 )

We have to prove that two curves cut at right angles if $$k^2=512$$

Now,

$$4x=y^2$$

Differentiating both sides w.r.t.$$x,$$ we get

$$\Rightarrow$$ $$4=2y.\dfrac{dy}{dx}$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=\dfrac{2}{y}$$

$$\Rightarrow$$ $$m_1=\dfrac{2}{y}$$ ----- ( 3 )

$$4xy=k$$

Differentiating both sides w.r.t.$$x,$$ we get

$$\Rightarrow$$ $$4\left(1\times y+x\dfrac{dy}{dx}\right)=0$$

$$\Rightarrow$$ $$y+x\dfrac{dy}{dx}=0$$

$$\Rightarrow$$ $$\dfrac{dy}{dx}=\dfrac{-y}{x}$$

$$\Rightarrow$$ $$m_2=\dfrac{-y}{x}$$ ----- ( 4 )

It is given that two curves intersect orthogonally.

$$\therefore$$ $$m_1.m_2=-1$$

$$\Rightarrow$$ $$\dfrac{2}{y}\times \dfrac{-y}{x}=-1$$ [ From ( 3 ) and ( 4 ) ]

$$\Rightarrow$$ $$\dfrac{-2}{x}=-1$$

$$\Rightarrow$$ $$x=2$$

Now,

$$4xy=k$$

$$\Rightarrow$$ $$(y^2)y=k$$ [ Since, $$4x=y$$ ]

$$\Rightarrow$$ $$y^3=k$$

$$\Rightarrow$$ $$y=k^{\frac{1}{3}}$$

Substituting $$y=k^{\frac{1}{3}}$$ in equation ( 1 ) we get,

$$\Rightarrow$$ $$4x=\left(k^{\frac{1}{3}}\right)^2$$

$$\Rightarrow$$ $$4\times 2=k^{\frac{2}{3}}$$

$$\Rightarrow$$ $$8=k^{\frac{2}{3}}$$

$$\Rightarrow$$ $$k^2=(8)^3$$ [ Taking cube on both sides ]

$$\Rightarrow$$ $$k^2=512$$

If the straight line $$x\cos \alpha +y\sin \alpha =p$$ touches the curve $$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$$, then prove that $$a^2\cos^2\alpha -b^2\sin^2\alpha =p^2$$.

Let the line $$x \cos \alpha + y \sin \alpha = p$$ touches the curve at point $$P(x_1, y_1)$$

The equation of tangent at $$P(x_1 , y_1)$$

$$\dfrac{x x_1}{a^2} - \dfrac{y y_1}{b^2} = 1$$ ...(1)

Here both the equation represent same line

Now the equation $$x \cos \alpha + y \sin \alpha = p$$

or $$\dfrac{x}{\alpha} \cos \alpha + y \dfrac{\sin \alpha}{p} = 1$$....(2)

Now coefficient of line (1) and (2) are same

$$\therefore \dfrac{x_1}{a^2} = \dfrac{\cos \alpha}{p}$$ and $$\dfrac{-y_1}{b^2} = \dfrac{\sin \alpha}{p}$$

or, $$x_1 = \dfrac{a^2 \cos \alpha}{p}$$ and $$y_1 = \dfrac{-b^2 \sin \alpha}{p}$$

$$\because$$ These two points lies on the equation of straight line

$$\therefore \dfrac{a^2 \cos^2 \alpha}{p} - \dfrac{b^2 \sin^2 \alpha}{p} = p$$

or, $$a^2 \cos^2 \alpha - b^2 \sin^2 \alpha = p^2$$ hence prove

Show that the curves $$2x=y^2$$ and $$2xy=k$$ cut at right angles, if $$k^2=8$$.

Let it cut at $$(a, b)$$

Given equations are $$2x = y^2$$__(1) and $$2xy = k $$ __(2)

$$2x = y^2$$

or, $$x = \dfrac{y^2}{2} \Rightarrow$$ put value of x in (2)

$$\dfrac{2y^3}{2} = k$$ or, $$y = k^{1/3}$$

or $$b = k^{1/3}$$

$$\Rightarrow x = \dfrac{k}{2}^{2/3} $$ or , $$a = \dfrac{k}{2}^{2/3}$$

$$\therefore$$ point of intersection are $$\left(\dfrac{k^{2/3}}{2} , k^{1/3} \right)$$ __(3)

$$[a, b]$$

we have to prove slope of tangent x slope of parabola $$= -1$$

i.e. $$m_1 m_2 = -1$$

$$\Rightarrow $$ Now $$m_1 : 2x = y^2$$

$$2 = 2y\dfrac{dy}{dx}$$

$$m_1 = \dfrac{1}{y}$$

or, $$m_1 = k^{-1/3}$$ __(4)

$$m_2 : 2\times y = k$$

$$y = \dfrac{k}{2x}$$

$$\dfrac{dy}{dx} = \dfrac{-k}{2x^2}$$

$$m_2 = \dfrac{-k}{2 \left[\dfrac{k^{2/3}}{2} \right]^2}$$

$$m_2 = \dfrac{-2k}{k^{4/3}}$$

$$m_2 = -2 k^{-1/3}$$ __(5)

Now $$m_1 \times m_2$$

$$(k^{-1/3}) (-2k^{-1/3})$$

$$= -2k^{-2/3} = (-2) (8^{-1/3})$$ $$[\because k^2 = 8\, given]$$

$$= (-2) (2^{-1})$$

$$= -1$$

$$\therefore m_1 \times m_2 = -1$$

Write the slope of the normal to the curve $$y=\dfrac{1}{x}$$ at the point $$\left(3, \dfrac{1}{3}\right)$$.

Given,

The equation of curve $$y=\dfrac{1}{x}$$

We know that,

The slope of normal at a point (x, y) on the curve

$$y=f(x)$$ is

$$m=\dfrac{-1}{\left(\dfrac{dy}{dx}\right)_{at(x, y)}}$$

$$\therefore y=\dfrac{1}{x}$$

$$\Rightarrow \dfrac{dy}{dx}=\dfrac{-1}{x^2}$$

Slope of normal at a point $$\left(3, \dfrac{1}{3}\right)$$ on the curve $$\left(3, \dfrac{1}{3}\right)$$ is

$$m=\dfrac{-1}{\left(\dfrac{-1}{x^2}\right)_{\left(3, \frac{1}{3}\right)}}=\dfrac{-1}{\dfrac{-1}{(3)^2}}=9$$

$$\therefore$$ The slope of the normal to the curve $$y=\dfrac{1}{x}$$ at a point $$\left(3, \dfrac{1}{3}\right)$$ is $$9$$.

What are the values of $$a$$ for which $$f(x)={a}^{x}$$ is decreasing on $$R$$?

$$f(x)=a^x$$

Differentiate both sides, we get

$$\Rightarrow$$ $$f'(x)=a^x\log a$$

It is given that $$f(x)$$ is decreasing on $$R.$$

$$\Rightarrow$$ $$f'(x)<0,\,\forall x\in R$$

$$\Rightarrow$$ $$a^x\log a<0,\,\forall x\in R$$

Here, logarithmic function is not defined for negative values of $$a.$$

$$\Rightarrow$$ $$a^x>0$$

$$\therefore$$ $$a^x\log a<0$$ can be possible when $$\log a<0,\,\forall x\in R$$

Here, logarithmic function is not defined for negative values of $$a.$$

$$\Rightarrow$$ $$a^x>0$$

$$\therefore$$ $$a^x\log a<0$$ can be possible when $$\log a<0,\,\forall x\in R.$$

$$\Rightarrow$$ $$0<a<1.$$

What are the values of $$a$$ for which $$f(x)={a}^{x}$$ is increasing on $$R$$?

$$f(x)=a^x$$ [ Given ]

Differentiating both sides, we get

$$\Rightarrow$$ $$f'(x)=a^x\log a$$

It is given that $$f(x)$$ is increasing on $$R.$$

$$\Rightarrow$$ $$f'(x)>0$$

$$\Rightarrow$$ $$a^x\log a>0$$

Logarithmic function is defined for positive values of $$a.$$

$$\Rightarrow$$ $$a>0$$

$$\Rightarrow$$ $$a^x>0$$

We know,

$$a^x\log a>0$$

It can be possible when $$a^x>0$$ and $$\log a>0$$ or $$a^x<0$$ and $$\log a<0$$.

$$\Rightarrow$$ $$\log a>0$$

$$\Rightarrow$$ $$a>1$$

So, $$f(x)$$ is increasing when $$a>1.$$

Write the set of values of $$a$$ for which $$f(x)=\log _{ a }{ { x }_{ } } $$ is increasing in its domain.

$$f(x)=\log_a x$$

Let $$x_1,x_2\in (0,\infty)$$ such that $$x_1<x_2.$$

Since given function is logarithmic, either $$a>1$$ or $$0<a<1.$$

$$Case\,I:$$ Let $$a>1$$

Here, $$x_1<x_2$$

$$\Rightarrow$$ $$\log_a x_1<\log_a x_2$$

$$\Rightarrow$$ $$f(x_1)<f(x_2)$$

$$\therefore$$ $$x_1<x_2\Rightarrow f(x_1)<f(x_2),\,\forall x_1, x_2\in(0,\infty)$$

So, $$f(x)$$ is increasing on $$(0,\infty).$$

$$Case\,II:$$ Let $$0<a<1$$

Here,

$$x_1<x_2$$

$$\Rightarrow$$ $$\log_a x_1>\log_a x_2$$

$$\Rightarrow$$ $$f(x_1)>f(x_2)$$

$$\therefore$$ $$x_1<x_2\Rightarrow f(x_1)>f(x_2),\,\forall x_1,x_2\in(0,\infty)$$

$$\therefore$$ For $$a>1,$$ $$f(x)$$ is increasing in its domain.

Find the set of values of $$a$$ for which $$f(x)=x+\cos x+ax+b$$ is increasing on $$R$$.

$$A = \begin{bmatrix}1 & 1\\ 1 & 1\end{bmatrix}$$

$$\Rightarrow$$ $$A^2 = \begin{bmatrix}1 & 1\\ 1 & 1\end{bmatrix}$$ $$ \begin{bmatrix}1 & 1\\ 1 & 1\end{bmatrix}$$

$$=\begin{bmatrix}1+1&1+1\\1+1&1+1\end{bmatrix}$$

$$=\begin{bmatrix}2&2\\2&2\end{bmatrix}$$

$$\Rightarrow$$ $$A^2=\begin{bmatrix}2&2\\2&2\end{bmatrix}$$

$$\Rightarrow$$ $$A^4=A^2A^2$$

$$=\begin{bmatrix}2&2\\2&2\end{bmatrix}$$ $$\begin{bmatrix}2&2\\2&2\end{bmatrix}$$

$$=\begin{bmatrix}4+4&4+4\\4+4&4+4\end{bmatrix}$$

$$=\begin{bmatrix}8&8\\8&8\end{bmatrix}$$

$$\Rightarrow$$ $$A^4=\begin{bmatrix}8&8\\8&8\end{bmatrix}$$

$$A^4=\lambda A$$

$$\Rightarrow$$ $$\begin{bmatrix}8&8\\8&8\end{bmatrix}=\lambda\begin{bmatrix}1&1\\1&1\end{bmatrix}$$

$$\Rightarrow$$ $$\begin{bmatrix}8&8\\8&8\end{bmatrix}=\begin{bmatrix}\lambda&\lambda\\ \lambda&\lambda\end{bmatrix}$$

$$\therefore$$ $$\lambda=8$$

Find the set of values of $$b$$ for which $$f(x)=b(x+\cos x)+4$$ is decreasing on $$R$$.

$$f(x)=b(x+\cos x)+4$$

$$f'(x)=b(1-\sin x)$$

for decreasing function

$$f'(x) \leq 0$$

$$b(1-\sin x)\leq 0$$

As, $$\sin x\leq 1$$ $$\forall x\in R$$

and $$1-\sin x\geq 0\forall x\in R$$

So b should be negative

$$\therefore b\in(-\infty, 0)$$.

Write the set of values of $$a$$ for which $$f(x)=\log _{ a }{ { x }_{ } } $$ is decreasing in its domain.

$$f(x)=\log_a x$$

Domain of the given function is $$(0,\infty).$$

Let $$x_1,x_2\in(0,\infty)$$ such that $$x_1<x_2.$$

Since, the given function is logarithmic, either $$a>1$$ or $$0<a<1.$$

$$Case\,I:$$ Let $$a>1$$

Here, $$x_1<x_2$$

$$\Rightarrow$$ $$\log_a x_1<\log_a x_2$$

$$\Rightarrow$$ $$f(x_1)<f(x_2)$$

$$\therefore$$ $$x_1<x_2\Rightarrow f(x_1)<f(x_2),\forall x_1, x_2\in(0,\infty)$$

So, $$f(x)$$ is increasing on $$(0,\infty).$$

$$Case\,II:$$ Let $$0<a<1$$

Here, $$x_1<x_2$$

$$\Rightarrow$$ $$\log_a x_1>\log_a x_2$$

$$\Rightarrow$$ $$f(x_1)>f(x_2)$$

$$\therefore$$ $$x_1<x_2\Rightarrow f(x_1)>f(x_2),\,\forall x_1,x_2\in(0,\infty)$$

So, $$f(x)$$ is decreasing on $$(0,\infty)$$

$$\therefore$$ For $$0<a<1,$$ $$f(x)$$ is decreasing in its domain.

Write the set of values of $$k$$ for which $$f(x)=kx-\sin x$$ is increasing on $$R$$.

$$f(x) = kx - \sin x$$

$$f'(x) = k - \cos x$$

for increasing $$f'(x) \ge 0$$

$$k - \cos x \ge 0 \,\, \forall x \in R$$

$$k- \cos x \ge 0$$

$$k \ge \cos x$$

$$k = \max (\cos x)$$

$$k = 1$$

$$\therefore k \in (1, \infty)$$

Write the set of values of $$a$$ for which the function $$f(x)=ax+b$$ is decreasing for all $$x\in R$$.

Given the function,

$$f(x)=ax+b$$.

Now,

$$f'(x)=a$$.

The function $$f(x)$$ will be decreasing if,

$$f'(x)\le 0$$

or, $$a\le 0$$.

The function $$f(x)$$ will be decreasing if $$a$$ belongs to $$ (-\infty, 0]$$.

At what points on the following curve, is the tangents parallel to $$x$$-axis?
$$y=x^{2}$$ on $$[-2,2]$$

1407218_1661277_ans_319246ec012940c085bb7d74e294ab47.jpg

Solve the following equation:
$$\tan 3x+\tan x=2\tan 2x$$

$$\tan 3x+\tan x=2\tan 2x$$

$$\tan 3x-\tan 2x=\tan 2x-\tan x$$

$$\Rightarrow \ \dfrac {\sin (3x -2x)}{\cos 3x \cos 2x}=\dfrac {\sin (2x-x)}{\cos 2x \cos x}$$

$$\Rightarrow \ \dfrac {\sin x}{\cos 3x \cos 2x}=\dfrac {\sin x}{\cos 2x \cos x}$$

$$\Rightarrow \ \sin x \cos 2x (\cos 3x -\cos x)=0$$

$$\Rightarrow \ -2\sin x\cos 2x \sin 2x \sin x=0$$

$$\Rightarrow \ 2\sin^2x \sin 2x=0$$ $$\because cos2x=0$$ is not possible because initial equation will not satisfy.

$$\Rightarrow \ \sin x=0$$ or, $$\sin 2x=0\Rightarrow x=n\pi$$ or, $$2x=m\pi \Rightarrow x=n\pi $$ or, $$x=\dfrac {m\pi}{2}$$, where $$n, m\in Z$$

Find the slope of the tangent and the normal to the curve $$2{x}^{2}+4y-3{y}^{2}=3$$ at $$\left(-1,1\right)$$

The equation of the curve is $$2{x}^{2}+4y-3{y}^{2}=3$$

Differentiating w.r.t $$x$$ we get

$$\Rightarrow\,4x+4\dfrac{dy}{dx}-6y\dfrac{dy}{dx}=0$$

$$\Rightarrow\,2x+2\dfrac{dy}{dx}-3y\dfrac{dy}{dx}=0$$

$$\Rightarrow\,2\dfrac{dy}{dx}-3y\dfrac{dy}{dx}=-2x$$

$$\Rightarrow\,\left(2-3y\right)\dfrac{dy}{dx}=-2x$$

$$\Rightarrow\,\dfrac{dy}{dx}=\dfrac{-2x}{\left(2-3y\right)}$$

$$\Rightarrow\,\left[\dfrac{dy}{dx}\right]_{\left(-1,1\right)}=\dfrac{-2\times -1}{\left(2-3\right)}=\dfrac{2}{-1}=-2$$

$$\therefore\,$$Slope of the tangent$$=-2$$

And ,slope of the normal at $$\left(-1,1\right)=\dfrac{-1}{\left[\dfrac{dy}{dx}\right]_{\left(-1,1\right)}}=\dfrac{-1}{-2}=\dfrac{1}{2}$$

Differentiate the following function with respect to x.
$$x^{-4}(3-4x^{-5})$$.

Given expression

$$=x^{-4}(3-4x^{-5})$$

$$=3x^{-4}-4x^{-9}$$

differentiating with resspect to x

$$=\dfrac d{dx}(3x^{-4}-4x^{-9})$$

$$=\dfrac d{dx}(3x^{-4})-\dfrac d{dx}({4x^{-9}})$$

$$\implies -12x^{-5}+36x^{-10}$$

At what points on the following curve, is the tangent parallel to $$x$$-axis?
$$y=e^{1-x^{2}}$$ on $$[-1,1]$$

Given,

$$y=e^{1-x^{2}}$$ on $$[-1,1]$$

Then,

$$\dfrac{dy}{dx}=e^{1-x^2}.(-2x)$$.

Now if the given curve is parallel to the $$x-$$ axis then we've,

$$\dfrac{dy}{dx}=0$$

or, $$-2xe^{1-x^2}=0$$

or, $$x=0$$ [ Since $$e^{1-x^2}\ne 0$$ for $$x\in \mathbb{R}$$]

When $$x=0$$ then $$y=1$$.

So the required point is $$(0,1)$$.

Find the derivative of the following function at the indicated points.
$$\sin x$$ at $$x=\dfrac{\pi}{2}$$.

$$f(x)=\sin x$$

$$\dfrac{d(f(x))}{dx}=\cos x\left.\dfrac{}{}\right|_{x=\dfrac{\pi}{2}}=0$$

Find the slope of the tangent and the normal to the curve $${x}^{2}+y-{y}^{2}=5$$ at $$\left(-1,2\right)$$

To find the slope of the tangent differentiate the above equation with respect to x.

Thus differentiate,

$${ x }^{ 2 }+y-{ y }^{ 2 }=5$$

Hence,

$$2x+{ y }^{ \prime }-{ 2y }^{ \prime }y=0\\ { y }^{ \prime }=-\frac { 2x }{ 1-2y } =\frac { 2x }{ 2y-1 }$$

Thus the slope of the tangent at (-1,2).

$${ y }^{ \prime }=-\frac { 2(-1) }{ 1-2\times 2 } =-\frac { 2 }{ 3 }$$

and slope of normal at (-1,2) is =$$\frac{3}{2}$$

Find the slope of the tangent and the normal to the curve $${x}^{2}-2y-{y}^{2}=1$$ at $$\left(-1,-2\right)$$

The equation of the curve is $${x}^{2}-2y-{y}^{2}=1$$

Differentiating w.r.t $$x$$ we get

$$\Rightarrow\,2x-2\dfrac{dy}{dx}-2y\dfrac{dy}{dx}=0$$

$$\Rightarrow\,-2\dfrac{dy}{dx}-2y\dfrac{dy}{dx}=-2x$$

$$\Rightarrow\,\left(1+y\right)\dfrac{dy}{dx}=x$$

$$\Rightarrow\,\dfrac{dy}{dx}=\dfrac{x}{\left(1+y\right)}$$

$$\Rightarrow\,\left[\dfrac{dy}{dx}\right]_{\left(-1,-2\right)}=\dfrac{-1}{\left(1-2\right)}=1$$

$$\therefore\,$$Slope of the tangent$$=1$$

And ,slope of the normal at $$\left(-1,-2\right)=\dfrac{-1}{\left[\dfrac{dy}{dx}\right]_{\left(-1,-2\right)}}=\dfrac{-1}{1}=-1$$

Find the derivative of $$f(x)=3x$$ at $$x=2$$.

$$f(x)=3x$$

$$f^{\prime}(x)=\dfrac d{dx}(3x)$$

$$f^{\prime}(x)=3$$

$$for \, x=2\implies f^{\prime}(2)=3$$

Find the derivative of $$f(x)=\tan x$$ at $$x=0$$.

$$f(x)=\tan x$$

$$\dfrac{d(f(x))}{dx}=\sec^{2}x\left.\dfrac{}{}\right|_{x=0}=1$$

Find the derivative of the following function at the indicated points.
$$\sin 2x$$ at $$x=\dfrac{\pi}{2}$$.

$$f(x)=\sin 2 x$$

$$\dfrac{d(f(x))}{dx}=\left.2(\cos 2x)\right|_{x=\dfrac{\pi}{2}}=2\cos \pi=-2$$

Find the derivative of the following function at the indicated points.
$$2\cos x$$ at $$x=\dfrac{\pi}{2}$$.

$$f(x)=2\cos x$$

$$\dfrac{d(f(x))}{dx}=\left.-2\sin x\right|_{x=\dfrac{\pi}{2}}=-2$$

Find the derivative of the following function at the indicated points.
$$x$$ at $$x=1$$.

$$f(x)=x$$

$$\dfrac{d(f(x))}{dx}=\left.1\right|_{x=1}=1$$

Find the derivative of $$f(x)=\cos x$$ at $$x=0$$.

$$f(x)=\cos x$$

$$\dfrac{d(f(x))}{dx}=-\sin x\left.\dfrac{}{}\right|_{x=0}=0$$

Using differentials, find the approximate value of :
$$\sqrt[4]{15}$$

1560929_1706430_ans_3b7dcbffc515400fabad4e545ba0786e.jpg

Using differentials, find the approximate value of :
$$\sqrt{49.5}$$

1550899_1706428_ans_58db4a1147bc4beaad21993cba64b219.jpg

Using differentials, find the approximate value of :
$$\dfrac{1}{(2.002)^2}$$

1567985_1706432_ans_acbb08cd3192436e95a1d1a492f898e6.jpg

Using differentials, find the approximate value of :
$$\sqrt{0.24}$$

1555370_1706427_ans_5fedec569f764bf4932edfe2fd80a2e3.jpg

Using differentials, find the approximate value of :
$$\sqrt{37}$$

1550801_1706422_ans_b9679256265a4d41af609b91581c6667.jpg

Using differentials, find the approximate value of :
$$\sqrt[3]{29}$$

1550819_1706424_ans_15d85de6bc6e49ecaa81b41d75557dd7.jpg

Using differentials, find the approximate value of :
$$\sqrt[3]{27}$$

1553082_1706425_ans_a8590f253ace462497910c85f4782884.jpg

Using differentials, find the approximate value of :
$$\log_e 10.02$$, given that $$\log_e 10=2.3026$$

1567987_1706435_ans_ead155a3af3a4279a34fd60abf8de947.jpg

Using differentials, find the approximate value of :
$$\log_{10}(4.04)$$, it being given that $$\log_{10}4=0.6021$$ and $$\log_{10}e=0.4343$$

1553090_1706442_ans_9b6db90f48f3473abc15eb34d983e72f.jpg

Find the points on the curve $$y=x^3-3x$$, where the tangent to the curve is parallel to the chord joining $$(1, -2)$$ and $$(2, 2)$$.

1554512_1706588_ans_f3ea0f44f6a54af79c093c055c021b12.jpg

Using differentials, find the approximate value of :
$$\cos 61^o$$, it being given that $$\sin 60^o=0.86603$$ and $$1^o=0.01745$$ radian

1567988_1706446_ans_4177ae08d5f14f228da448bb8fb45fa7.jpg

Show that $$f(x)=\left(x^3+\dfrac{1}{x^3}\right)$$ is decreasing on $$(-1, 1)$$.

1556454_1706674_ans_3929ae9b7afd41379844a98cb1885b8b.jpg

Prove that the function $$f(x)=\log (1+x)-\dfrac{2x}{(x+2)}$$ is increasing for all $$x>-1$$.

1558116_1706682_ans_d7d3ad67137341ac904fd1c7623684d9.jpg

Show that $$f(x)=\dfrac{x}{\sin x}$$ is increasing on $$\left[ 0, \dfrac{\pi}{2}\right].$$

1672888_1706679_ans_00fe90c5f6414a93a4145d87bf6c9877.jpeg

If there is an error of $$0.1\%$$ in the measurement of the radius of a sphere, find approximately the percentage error in the calculation of the volume of the sphere.

1568042_1706465_ans_cf6f110b07a24e819617d05fe26ca641.jpg

Show that the relative error in the volume of a sphere, due to an error in measuring the diameter, is three times the relative error in the diameter.

1553160_1706466_ans_156152893f174dcb958d10015d0bdc9b.jpg

Find a point of the curve $$y=x^3$$, where the tangent to the curve is parallel to the chord joining the points $$(1, 1)$$ and $$(3, 27)$$.

1565812_1706583_ans_562add3140634ba08137d736093eca6c.jpg

Find the slope of the tangent to the curve
$$y=(\sin 2x+\cot x+2)^{2}$$ at $$x=\dfrac{\pi}{2}$$

1546039_1706768_ans_c15489c4f51246d19c32cd6a8a2e1b65.jpg

Find the slope of the tangent to the curve
$$y=(2x^{2}+3\sin x)$$ at $$x=0$$

1563133_1706764_ans_cdbb7b13f1dc48d88ec3329a046d8125.jpg

Find the points on the curve $$y=x^{2}+3x+4$$ at which the tangent passes through the origin.

1570193_1706865_ans_cde99d05580a45ad885a007cad74d104.png

Find a point on the parabola $$y=(x-3)^{2}$$, where the tangent is parallel to the chord joining the points $$(3,0)$$ and $$(4,1)$$.

Let the required point be $$P(x_{1},y_{1})$$

Slope of the chord joining $$A(3,0)$$ and $$B(4,1)$$ is $$\dfrac{(1-0)}{(4-3)}=1$$

Now, $$y=(x-3)^{2}$$

$$\Rightarrow \dfrac{dy}{dx}=2(x-3)\\$$
$$\Rightarrow \left(\dfrac{dy}{dx}\right)_{x_{1}, y_{1}}=2(x_1-3)$$

As tangent is parallel to chord there slopes will be equal.

$$\Rightarrow 2(x_{1}-3)=1$$
$$\Rightarrow x_{1}=\dfrac{7}{2}$$

$$\therefore y=(x-3)^{2}$$
$$\Rightarrow y_{1}=(x_1-3)^{2}=\left(\dfrac{7}{2}-3\right)^{2}=\dfrac{1}{4}$$

Hence, the required point is $$\left(\dfrac{7}{2},\dfrac{1}{4}\right)$$

Show that $$f(x)=\dfrac{(x-2)}{(x+1)}$$ is increasing for all $$x\in R$$, except at $$x=-1$$.

1566778_1706689_ans_78a65a88ecdd4ecd9b141540269b3954.jpg

Find the points on the parabola $$y=2x^{2}-6x-4$$ at which the tangent is parallel to the $$x-$$ axis:

1557633_1706883_ans_5fd4dfb7435f43fe8bd745e1f743bc88.jpg

Prove that the tangents to the curve $$y=x^{2}-5x+6$$ at the points $$(2,0)$$ and $$(3,0)$$ are at right angles.

1546675_1706860_ans_6ec06887ab724839af316a7c24e793e2.jpg

Find the points on the curve $$x^{2}+y^{2}-2x-3=0$$ where the tangent is parallel to the $$x-$$ axis

1570192_1706859_ans_e3c38f63d7b647fa8120c8ba2b84ab86.png

Find the points on the curve $$y=x^{3}-11x+5$$ at which the equation of tangent is $$y=x-11$$

1546704_1706868_ans_acaf648570074bb58f46f08496ec37e4.jpg

At what points on the curve $$x^{2}+y^{2}-2x-4y+1=0$$, is the tangent parallel to the $$y-$$ axis?

1546280_1706856_ans_1e71fb48d89b4c5a852adaff5b10a267.jpg

Tangents are drawn from the origin to curve $$y= \sin x.$$ Prove that portion of contact lie on $$y^{2}= \dfrac{x^{2}}{1+x^{2}}$$

Let P(h, k) be a point of contact of tangents from the origin (0, 0) on the curve $$y = \sin h..................$$ (i)

Also $$\dfrac{dy}{dx} = \cos x\Rightarrow \left ( \dfrac{dy}{dx} \right )_{(h,k)}=\cos h$$

Slope of the line joining $$O(0,0)$$ and $$P(h, k )$$ is $$\dfrac{k}{h}$$

Given that $$\cos h = \dfrac{k}{h}.....................$$ (ii)

squaring and adding (i) and (ii), $$k^{2} + \dfrac{k^{2}}{h^{2}} = 1\Rightarrow h^{2}k^{2}+k^{2}=h^{2}\Rightarrow k^{2}=\dfrac{h^{2}}{1+h^{2}}\Rightarrow y^{2}=\dfrac{x^{2}}{1+x^{2}}$$

Let $$f$$ be a twice differentiable function such that $$f^{''} (x) = -f(x)$$, and $$f^{'} (x) = g(x)$$, $$h(x) = \left [f(x)^{2} \right ] + \left [g(x)^{2} \right ]$$. Find $$h(10)$$ if $$h(5) = 11$$. (IIT-JEE, 1982)

Given that $$f$$ is twice differentiable function such that $$f^{''} (x)$$

$$f^{''} (x) = -f(x)$$, and $$f^{'} (x) = g(x)$$, $$h(x) = \left [f(x)^{2} \right ] + \left [g(x)^{2} \right ]$$

$$\Rightarrow h^{'}(x) = 2f(x)f^{'}(x) + 2g(x) g^{'} (x)$$

$$ = 2f(x) g(x) + 2g(x)f^{''}(x)$$ $$\left [ \therefore g(x) - f^{'}(x) \Rightarrow g^{'}(x) = f^{''} (x) \right ]$$

$$ = 2f(x)g(x) + 2g(x) (-f(x))$$

$$= 2f(x) g(x) - 2f(x) g(x)$$

$$= 0$$

$$\therefore h^{'} (x) = 0, \space \forall \space x$$

$$\Rightarrow h$$ is a constant function.

$$\therefore h(5=h(10)=11 $$

At the point $$P(a, a^{n})$$ on the graph of $$y= x^{n} (n \epsilon N)$$ in the first quadrant a normal is drawn. The normal interersects the y-axis at the point (o, b). If $$\underset{a\rightarrow 0}{\lim}b=\dfrac{1}{2}$$, then n equals

1789844_1758727_ans_74221e0b554a46f4b36f64936896cdb1.jpeg

A curve is given by the equations $$x = \sec ^{2} \theta,\,y=\cot \theta$$. If the tangent at P where $$\theta=\dfrac{\pi}{4}$$ meets the curve again at Q, then [PQ] is, where [ . ] represents the greatest integer function,

1771455_1758733_ans_2da7f8baeada46059b60de1d78dd8474.jpeg

There is a point (p, q) on the graph of $$f(x)= x^{2}$$ and a point (r, s) on the graph of $$g(x)= \dfrac{-8}{x}$$ , where $$p> 0$$ and $$r> 0$$. if the line through (p, q) and (r, s) is also tangent to both the curves at these points, respectively, then value of p+r is

1712239_1758704_ans_727dffc4998e4c88b6e1df8c4b4b1cb9.PNG

If the slope of line through the origin which is tangent to the curve $$y = x^{3}+x+16$$ is m, then the value of m-4 is

1975550_1758736_ans_3121766dced74d0a858d907e0bf7a05c.jpg

Suppose a, b, care such that the curve $$y = ax^{2}+ bx + c$$ is tangent to y = 3x- 3 at (1, 0) and is also tangent to y = x+1 at (3, 4) then the value of (2a - b - 4c) equals

1787304_1758749_ans_43563447b0a8465db675c5a9ee4adfc5.jpeg

Let $$y=f(x)$$ be drawn with $$f(0) = 2$$ and for each real number the tangent to $$y = f(x)$$ at $$(a, f(a)),$$ has $$x$$ intercept $$(a-2).$$ If $$f(x)$$ is of the form of $$k e^{px},$$ then $$\left ( \dfrac{k}{p} \right )$$ has the value equal to

1789925_1758744_ans_17a06fe5407248879350bef1c5f58406.jpeg

Let C be a curve defined by $$y = e^{a+bx^{2}}$$.The curve C passes through the point O(1, 1) and the slope of the tangent at P is (-2). Then the value of 2a- 3b is

1776363_1758752_ans_f73e05c7a3164329a56f606997645ac8.jpeg

Let $$-1\le p\le 1$$. Show that the equation $$4x^{2}-3x-p=0$$ has a unique root in the interval $$[1/2,1]$$ and identify it.

Given $$-1\le p\le 1$$ and equation $$4x^{3}-3x-p=0$$
Also, $$\cos 3\theta=4\cos^{3}\theta-3\cos\theta$$
Then let $$x=\cos \theta$$
Then $$4x^{3}-3x-p=0\Rightarrow 4\cos^{3}\theta-3\cos \theta-p=0$$
$$\Rightarrow \cos 3\theta=p$$
Since, $$x=\cos \theta\in [1/2,1]$$
$$\Rightarrow \theta\in [0, \pi/3]$$
$$\Rightarrow 3\theta\in [0,\pi]$$ for which $$\cos 3\theta=p\in [-1,1]$$
Hence proved.
Also $$\cos 3\theta=p$$
$$\Rightarrow 3\theta=\cos^{-1}p$$
$$\Rightarrow \theta=\dfrac{1}{3}\cos^{-1}(p)$$
$$\Rightarrow x=\cos \theta=\cos\left(\dfrac{1}{3}\cos^{-1}(p)\right)$$

Find all the tangents to the curve $$y =\cos (x + y )$$, where $$-2\pi \leq x\leq 2\pi $$, that are parallel to the line x + 2y = 0.

1794379_1758796_ans_cc28d551057040d8af464b7c3f0b02f4.jpg

Find the coordinates of the point on the curve $$y=\dfrac{x}{1+x^{2}}$$ where the tangent to the curve has the greatest slope.

$$y=\dfrac{x}{1+x^{2}}$$ is an odd function.
Also, $$x > 0\Rightarrow u > 0$$ and $$x < 0\Rightarrow y<0$$
When $$x\rightarrow \pm \infty, y\rightarrow 0$$
$$\dfrac{dy}{dx}=\dfrac{1+x^{2}-x(2x)}{(1+x^{2})^{2}}=\dfrac{1-x^{2}}{(1+x^{2})^{2}}$$ which has value at $$x=0$$.
1976709_1759278_ans_3d60b71bec7a49b0a9889c7729a57a72.png

1976709_1759278_ans_3d60b71bec7a49b0a9889c7729a57a72.png

Find the point on the curve $$4x^{2}+a^{2}y^{2}=4a^{2}, 4 < a^{2} < 8$$ that is farthest from the point $$(0,-2)$$

Given curve is $$4x^{2}+a^{2}y^{2}=4a^{2}$$
$$\Rightarrow \dfrac{x^{2}}{a^{2}}+\dfrac{y^{4}}{4}=1$$
Let point $$P(a\cos \phi, 2\sin \phi)$$ be on $$(1)$$, also given a point
$$Q(0,-2)$$.
Let $$u=(PQ)^{2}=(a\cos\phi)^{2}+(2\sin \phi+2)^{2}$$
Differentiating both sides w.r.t. $$\phi$$, we have
$$\dfrac{du}{d\phi}=\cos\phi[(8a-2a^{2})\sin \phi+8]$$
For the extremum value of $$u, \dfrac{du}{d\phi}=0$$
$$\Rightarrow \phi=\dfrac{\pi}{2}$$ and $$\sin \phi=\dfrac{4}{a^{2}-4}$$
$$\because 4 < a^{2} < 8\Rightarrow 0 < a^{2}-4 < 4$$
$$\Rightarrow \dfrac{a^{2}-4}{4} < 1\Rightarrow \dfrac{4}{a^{2}-4} > 1$$
$$\Rightarrow \sin \phi > 1$$ (not possible)
$$\therefore \phi=\pi/2$$
Again, $$\dfrac{d^{2}u}{d\phi^{2}}=(8-20a^{2})\cos^{2}\phi+(2a^{2}-8)\sin^{2}\phi-8\sin \phi$$
$$\therefore \left.\dfrac{d^{2}u}{d\phi^{2}}\right|_{\phi=\pi/2}=0+(2a^{2}-8)-8=2(a^{2}-8) < 0$$ $$(\because 4 < a^{2} < 8)$$
$$\therefore u$$ is maximum at $$\phi=\pi/2$$
So, $$\sqrt{PQ}$$ is also maximum at $$\phi=\pi/2$$
Hence, co-ordinates of point $$P$$ are $$(0,2)$$.

Fill in the blanks
Let C be the curve $$y^{3}-3xy+2=0$$. If H is the set of points on the curve C where the tangent is horizontal and V is the set of points on the curve C where the tangent is vertical is vertical, then
H= _ and V= ___

1859190_1759500_ans_03ddec26e6b549438f7e4d6d4d1aa33f.jpg

Find the points on the curve $$y=x^{3}$$ at which the slope of the tangent is equal to the y- coordinates of the point.

Let p($$x_{1}, y_{1})$$ be the required point on the curve
$$y=x^{3}$$ ....(i)
$$\dfrac{dy}{dx}= 3x^{2}$$
$$\implies\, [\dfrac{dy}{dx}]_{x_{1}, y_{1}}= 3x_{1}^{2}$$
$$\implies\, Slope of tangent at (x_{1}, y_{1})= 3x_{1}^{2}$$
According to the question,
$$3x_{1}^{2}= y_{1}$$ .....(ii)
Also $$(x_{1}, y_{1})$$ lies on (i)
$$\implies\, y_{1}= x_{1}^{3}$$ ...(iii)
From (ii) and (iii), we get
$$3x_{1}^{2}= x_{1}^{3}$$
$$\implies\, x_{1}^{3}- 3x_{1}^{2}=0$$
$$\implies\, x_{1}^{2}(x_{1}-3)=0$$
$$\implies\, x_{1}=0\, or x_{1}=3$$
$$\implies\, y_{1}=0\, or \, y_{1}=27$$
Hence, required points are $$(0,0)$$ and $$(3,27).$$

Using differentials, find the approximate value of $$\sqrt{49.5}.$$

Let $$f(x)= \sqrt{x}$$, where $$x=49\, and\, \delta x =0.5$$

$$\therefore\, f(x+ \delta x)= \sqrt{x+ \delta x}= \sqrt{49.5}$$

Now by definition , approximately we can write

$$f'(x)= \dfrac{f(x+ \delta x)- f(x)}{\delta x}$$ ...(i)

Here $$f(x)= \sqrt{x}= \sqrt{49}= 7\, and\, \delta x=0.5$$

$$\implies\, \, f'(x)= \dfrac{1}{2 \sqrt{x}}= \dfrac{1}{2 \sqrt{49}}= \dfrac{1}{14}$$

Putting these values in (i), we get

$$\Rightarrow \dfrac{1}{14}= \dfrac{\sqrt{49.5}- 7}{0.5}$$

$$\Rightarrow \sqrt{49.5}= \dfrac{0.5}{14}+ 7$$

$$\Rightarrow \dfrac{0.5+ 98}{14}= \dfrac{98.5}{14}= 7.036$$

Find the slope of the tangent to the curve $$x=t^{2}+ 3t - 8, y= 2t^{2}- 2t- 5\, at\, t=2$$

Slope of tangent =$$\dfrac{dy}{dx}= \dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}$$= $$\dfrac{4t-2}{2t+3}$$
$$\implies \, \dfrac{dy}{dx}\, at\, t=2=(\dfrac{4t-2}{2t+3})_{at\, t=2}=\dfrac{4(2)-2}{2(2)+3}=\dfrac{6}{7}$$

Find the point at which the tangent to the curve $$y=\sqrt{4x-3}-1 $$ has its slope $$\dfrac{2}{3}$$.

Slope of tangent to the given curve
$$y= \sqrt{4x-3}-1 \, at(x,y)=\dfrac{dy}{dx}$$
$$\implies \, \dfrac{2}{3}=\dfrac{1 \times 4}{2 \sqrt{4x-3}}-0$$
$$ \implies \, 4\sqrt{4x-3}= 3 \times 4$$
$$\implies \, \, \sqrt{4x-3}=3$$
$$\implies\,\, 4x-3=9$$
$$\implies\, \, x=\dfrac{12}{4}$$
$$\implies \, \, \, x=3$$
$$If x=3\, then \, y=\sqrt{4 \times 3-3}-1 = 3-1=2$$
Therefore, required points is $$(3,2)$$

If the radius of a sphere is measured as $$9\, cm$$ with an error of $$0.03\, cm$$, find the approximate error in calculating its surface area.

Here, radius of the sphere r =$$9\, cm$$Error in calculating radius $$\delta r=0.03\, cm$$
Let $$\delta s $$ be approximate error in calculating surface area.
If S be the surface area of sphere, then S =$$4 \pi r^{2}$$
$$\implies \dfrac{ds}{dr}= 4 \pi. 2r= 8 \pi r$$
Now by definition, approximately
$$\dfrac{ds}{dr}= \dfrac{\delta s}{\delta r}$$
[$$\therefore \dfrac{ds}{dr}= \lim_{\delta r ->0} \dfrac{\delta s}{\delta r}]$$
$$\implies \delta s=(\dfrac{sd}{dt}). \delta r$$ $$\implies\,\, \, \delta s=8 \pi r. \delta r$$
=$$8 \pi\times 9 \times 0.03 \, cm^{2}= 2.16p\, cm^{2}$$
$$[\therefore\, r=9\, cm]$$

Show that the normal at any point to the curve $$x= a cos \theta+ a \theta sin \theta, y= a sin \theta- a \theta cos \theta$$ is at a constant distance from the origin.

$${\textbf{Step 1: Find slope of tangent}} $$

$${\text{Now,}}\dfrac{{dx}}{{d\theta }} = - a\sin \theta + a\sin \theta + a\theta \cos \theta $$

$$ = a\theta \cos \theta $$

$${\text{And,}}\dfrac{{dy}}{{d\theta }} = a\cos \theta - a\cos \theta + a\theta \sin \theta $$

$$ = a\theta \sin \theta $$

$${\text{Now,}}\dfrac{{dy}}{{dx}} = \dfrac{{dy}}{{d\theta }}\dfrac{{d\theta }}{{dx}}$$

$$ \Rightarrow $$ $$ = \dfrac{{dy}}{{dx}} = \dfrac{{a\theta \sin \theta }}{{a\theta \cos \theta }} = \tan \theta $$

$${\textbf{Step 2: Find slope of normal}}$$

$${\text{Slope of normal}} = - \dfrac{1}{{{\text{Slope of tangent}}}} = - \cot \theta $$

$${\textbf{Step 3: Find the equation of normal}}$$

$${\text{The equation of the normal at a given point }}(x,y){\text{ is given by }}$$

$$y - a\sin \theta + a\theta \cos \theta = \dfrac{{ - 1}}{{\tan \theta }}\left( {x - a\cos \theta - a\theta \sin \theta } \right)$$

$$ \Rightarrow y\sin \theta - a{\sin ^2}\theta + a\theta \sin \theta \cos \theta = - x\cos \theta + a{\cos ^2}\theta + a\theta \sin \theta \cos \theta $$

$$ \Rightarrow x\cos \theta + y\sin \theta - a({\sin ^2}\theta + {\cos ^2}\theta ) = 0$$

$$ \Rightarrow x\cos \theta + y\sin \theta - a = 0$$

$${\textbf{Step 4: Find the perpendicular distance using formula}}$$

$${\text{Now, the perpendicular distance of the normal from the origin is}}$$

$$\dfrac{{| - a|}}{{\sqrt {{{\cos }^2}\theta + {{\sin }^2}\theta } }} = \dfrac{{| - a|}}{1},{\text{which is independent of }}\theta $$

$${\textbf{Thus, the perpendicular distance of the normal from the origin is constant}}$$

The values of $$ a $$ for which $$ y=x^2+ax+25 $$ touches the axis of $$ x$$ are______.

As the curve touches x- axis

$$\dfrac{dy}{dx}=0$$

$$ y=x^2+ax+25 $$

$$ \dfrac{dy}{dx}=0 \Rightarrow 2x+a=0$$

i.e. $$x=-\dfrac{a}{2}, $$

Therefore, $$ \dfrac{a^2}{4}+a \left( -\dfrac { a }{ 2 } \right) +25=0 \Rightarrow a= \pm 10 $$

Hence, the values of $$ a $$ are $$ \pm 10 $$.

Find the equation of a curve whose tangent at any point on it, different from origin, has slope $$y+\dfrac {y}{x}$$.

Given $$\dfrac {dy}{dx}=y+\dfrac {y}{x}=y\left(1+\dfrac {1}{x}\right)$$
$$\Rightarrow \dfrac {dy}{y}=\left(1+\dfrac {1}{x}\right)dx$$
Integrating on both sides, we get
$$\displaystyle \int \dfrac {dy}{y} =\displaystyle \int \left(1+\dfrac {1}{x}\right)$$
$$\log y=x+\log x+c\Rightarrow \log \left(\dfrac {y}{x}\right)=x+c$$
$$\Rightarrow \ \dfrac {y}{x}=e^{x+c}=e^x. e^x \Rightarrow \dfrac {y}{x}=ke^x$$
$$\Rightarrow y=kx.e^x$$

Find a pair of curves such that
a. the tangent drawn at points with equal abscissas intersect on the y-axis.
b. the normal drawn at points with equal abscissa intersect on the x-axis.
c. one curve passes through (1,1) and other passes through (2, 3).

Let the curve be $$y = f_1(x)$$ and $$y=f_2(x)$$ equation of tangents with equal abscissa, $$x$$ are
$$Y - f_1(x)=f'(x) (X - x)$$ and $$Y - f_2(x) = f'(x) (X- x)$$
These tangent intersect at y-axis,
so their Y-intercept are same.
$$\Rightarrow -xf'_1(x) + f_1(x) = -xf'_2 (x) + f_2(x)$$
$$\Rightarrow f_1(x) - f_2(x) = x(f'_1(x) - f'_2(x))$$

$$\Rightarrow \int \dfrac{f'_1(x) - f'_2(x)}{f_1(x) - f_2(x)} = \int\dfrac{dx}{x}$$

$$\Rightarrow ln |f_1 (x) - f_2(x)| = ln |x| + ln\ C_1$$

$$\Rightarrow f_1(x) - f_2(x) = \pm C_1x$$ (1)
Now equation of normal with equal abscissa $$x$$ are
$$(Y - f_1(x)) = - \dfrac{1}{f'_1(x)} (X - x)$$, and

$$(Y - f_2(X)) = - \dfrac{1}{f'_2(x)} (X - x)$$
As these normal intersect on the x-axis
$$\Rightarrow x + f_1(x) f_1'(x) + x + f_2(x) . f'_2(x)$$
$$\Rightarrow f_1(x) f_1'(x) - f_2(x)f'_2(x) = 0$$

Integrating, we get $$f_1^2(x) - f^2_1(x) = C_2$$

$$\Rightarrow f_1(x) + f_2(x) = \dfrac{C_2}{f_1(x) - f_2(x)}$$

$$= \pm \dfrac{C_2}{C_1x} = \dfrac{\pm \lambda_2}{x}$$ (2)
From equation (1) and (2), we get $$2f_1(x) = \pm \left( \dfrac{\lambda_2}{x} + C_1x\right)$$,

$$2f_2(x) = \pm \left(\dfrac{\lambda_2}{x} - C_1x\right)$$
We have $$f_1 (1) = 1$$ and $$f(2) = 3$$

$$\Rightarrow f_1(x) = \dfrac{2}{x} - x,\ f_2(x) = \dfrac{2}{x} + x$$

Given two curves: $$y = f(x)$$ passing through the point $$(0, 1)$$ and $$g(x) = \int_{-\infty}^x f(t)dt$$ passing through the point $$\left(0, \dfrac{1}{n}\right)$$. The tangents drawn to both the curves at the points with equal abscissa intersect on the x-axis. Find the curve $$y = f(x)$$.

Equation of tangent to the curve $$y = f(x)$$ is
$$Y- y= f'(x) (X - x)$$

Equation of tangents to the curve $$g(x) = y_1 = \int_{-\infty}^x f(t) dt$$

is $$Y - y = f(x) (X - x)$$ $$\left( \dfrac{dy_1}{dx} = g' (x) = f(x) \right)$$

Since the tangent with equal abscissa intersect on the x-axis

$$\Rightarrow x - \dfrac{y}{f'(x)} = x - \dfrac{y_1}{f(x)}$$

$$\Rightarrow \dfrac{f(x)}{f'(x)} = \dfrac{y_1}{f(x)}$$

$$\Rightarrow \dfrac{g'(x)}{g(x)} = \dfrac{g"(x)}{g'(x)}$$

$$\Rightarrow ln\ g(x) = ln\ cg'(x)$$

$$\Rightarrow g(x) = c g'(x)$$

$$\Rightarrow \dfrac{g'(x)}{g(x)}= c$$

$$\Rightarrow g(x) = ke^{cx}$$

$$\Rightarrow f(x) = g'(x) = kce^{cx}$$
The curve $$y = f(x)$$ passes through $$(0, 1) \Rightarrow kc = 1$$

The curve $$y = g(x) $$ passes through $$\left(0, \dfrac{1}{n}\right)$$

$$\Rightarrow k = \dfrac{1}{n} \Rightarrow c = n \Rightarrow f(x) = e^{nx}$$

Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point $$(x, y)$$ is equal to the square of the difference of the abscissa and ordinate of the point.

Slope of tangent to the curve $$=\dfrac{dy}{dx}$$

and difference of abscissa and ordinate $$=x-y$$

According to the question $$\dfrac{dy}{dx}=(x-y)^{2}$$ ...(i)

Put $$x-y=z$$

$$\Rightarrow 1.\dfrac{dy}{dx}=\dfrac{dz}{dx}$$

$$\Rightarrow \dfrac{dy}{dx}=1-\dfrac{dz}{dx}$$

On substituting these value in Eq (i), we get

$$1-\dfrac{dz}{dx}=z^{2}$$

$$\Rightarrow 1-z^{2}=\dfrac{dz}{dx}$$

$$\Rightarrow dx=\dfrac{dz}{1-z^{2}}$$

On integrating both sides, we get

$$\displaystyle\int dx=\int \dfrac{dz}{1-z^{2}}$$

$$\Rightarrow x=\dfrac{1}{2}\log \left|\dfrac{1+z}{1-z}\right|+C$$

$$\Rightarrow tx=\dfrac{1}{2}\log \left|\dfrac{1+x-y}{1-x+y}\right|+C$$ .... (iii) $$x=\dfrac{1}{2}\log \left|\dfrac{1+x-y}{1-x+y}\right|+C$$ Since, the curve through the origin

$$\therefore 0=\dfrac{1}{2}\log \left|\dfrac{1+0-0}{1-0+0}\right|+C$$

$$\Rightarrow C=0$$

On substituting the value of $$C$$ in Eq (ii), we get

$$x=\dfrac{1}{2}\log \left|\dfrac{1+x-y}{1-x+y}\right|$$

$$\Rightarrow 2x=\log \left|\dfrac{1+x-y}{1-x+y}\right|$$

$$\Rightarrow e^{2x}=\left|\dfrac{1+x-y}{1-x+y}\right|$$

$$\Rightarrow (1-x+y)e^{2x}=1+x-y$$

Find the equation of a curve passing through the point $$(1,1)$$. If the tangent drawn at any point $$P(x, y)$$ on the curve meets the co-ordinates axes at $$A$$ and $$B$$ such that $$P$$ is the mid-point of $$AB$$.

The below figure obtained by the given information
Let the coordinates of the point $$P$$ is $$(x, y)$$. It is given that, $$P$$ is mid-point of $$AB$$.
So, the coordinates of point $$A$$ and $$B$$ are $$(2x,0)$$ and $$(0,2y)$$, respectively.
$$\therefore$$ Slope of $$AB=\dfrac{0-2y}{2x-0}=-\dfrac{y}{x}$$
Since, the segment $$AB$$ is a tangent to the curve at $$P$$.
$$\therefore \dfrac{dy}{dx}=-\dfrac{y}{x}$$
$$\Rightarrow \dfrac{dy}{y}=-\dfrac{dx}{x}$$
On integrating both sides, we get
$$\log y=-\log x+\log C$$
$$\log y=\log \dfrac{C}{x}$$ ...(i)
Since, the given curve passes through $$(1,1)$$
$$\therefore \log 1=\log \dfrac{C}{1}$$
$$\Rightarrow 0=1\log C$$
$$\Rightarrow c=1$$
$$\therefore \log y=\log \dfrac{1}{x}$$
$$\Rightarrow y=\dfrac{1}{x}$$
$$\Rightarrow xy=1$$
1768282_1797809_ans_9e49336c0d7249fa9592af5cb6809a67.png

1768282_1797809_ans_9e49336c0d7249fa9592af5cb6809a67.png

Solve the following: Determine the area of the triangle formed by the tangent to the graph of the function $$y=3-x^{2}$$ drawn at the point $$(1,2)$$ and the coordinate axes.

$$y=3-x^{2}$$
$$\therefore \dfrac{dy}{dx}=\dfrac{d}{dx}(3-x^{2})=0-2x=-2x$$
$$\therefore \left(\dfrac{dy}{dx}\right)_{at\ (1,2)}=-2(1)=-2$$
=slope of the tangent at $$(1\ 2)$$
$$\therefore$$ equation of the tangent at $$(1,2)$$ is
$$y-2=2(x-1)$$
$$\therefore y-2=-2x+2$$
$$\therefore 2x+y=4$$
Let this tangent cuts the coordinate axes at $$A(a, 0)$$ and $$B(0,b)$$.
$$\therefore 2a+0=4$$ and $$2(0)+b=4$$
$$\therefore a=2$$ and $$b=4$$
are of required triangle
$$=\dfrac{1}{2}\times l(OA)\times l(OB)$$
$$=\dfrac{1}{2}ab$$
$$=\dfrac{1}{2}(2)(4)$$
$$=4\ sq\ units.$$

Find the equation of the curve through the point $$91,0)$$ if the slope of the tangent to the curve at any point $$(x, y)$$ is $$\dfrac{y-1}{x^{2}+x}$$

It is given that, slope of tangent to the curve at any point $$(x, y)$$ is $$\dfrac{y-1}{x^{2}+x}$$

$$\therefore \left(\dfrac{dy}{dx}\right)_{(x,y)}=\dfrac{y-1}{x^{2}+x}$$

$$\Rightarrow \dfrac{dy}{dx}=\dfrac{y-1}{x^{2}+x}$$

$$\Rightarrow \dfrac{dy}{y-1}=\dfrac{dx}{x^{2}+x}$$

On integrating both sides, we get

$$\displaystyle\int \dfrac{dy}{y-1}=\int \dfrac{dx}{x^{2}+x}$$

$$\Rightarrow \displaystyle\int \dfrac{dy}{y-1}=\int \dfrac{dx}{x(x+1)}$$

$$\Rightarrow \displaystyle\int \dfrac{dy}{y-1}=\int \left(\dfrac{1}{x}-\dfrac{1}{x+1}\right)dx$$

$$\Rightarrow \log (y-1)=\log x-\log (x+1)+\log C$$

$$\Rightarrow \log (y-1)=\log \left(\dfrac{xC}{x+1}\right)$$

Since, the given curve passes through point $$(1,0)$$

$$\therefore 0-1=\dfrac{1.C}{1+1}\Rightarrow C=-2$$

The particular solution is $$y-1=\dfrac{-2}{x+1}$$

$$\Rightarrow (y-1)(x+1)=-2x$$

$$\Rightarrow (y-1)(x+1)+2x=0$$

Find the equation of a curve passing through $$(2,1)$$ if the slope of the tangent to the curve at any point $$(x,y)$$ is $$\dfrac{x^{2}+y^{2}}{2xy}$$.

It is given that, the slope of tangent to the curve at point $$(x, y)$$ is $$\dfrac{x^{2}+y^{2}}{2xy}$$

$$\therefore \left(\dfrac{dy}{dx}\right)_{(x, y)}=\dfrac{x^{2}+y^{2}}{2xy}$$

$$\Rightarrow \dfrac{dy}{dx}=\dfrac{1}{2}\left(\dfrac{x}{y}+\dfrac{y}{x}\right)$$ .... (i)

Which is homogeneous differential equation

Put $$y=vx$$

$$\Rightarrow \dfrac{dy}{dx}=v+x\dfrac{dv}{dx}$$

On substituting these values in Eq (i) we get

$$v+x\dfrac{dv}{dx}=\dfrac{1}{2}\left(\dfrac{1}{v}+v\right)$$

$$\Rightarrow v+x\dfrac{dv}{dx}=\dfrac{1}{2}\left(\dfrac{1+v^{2}}{v}\right)$$

$$\Rightarrow x\dfrac{dv}{dx}=\dfrac{1+v^{2}}{2v}-v$$

$$\Rightarrow x\dfrac{dv}{dx}=\dfrac{1+v^{2}-2v^{2}}{2v}$$

$$\Rightarrow x\dfrac{dv}{dx}=\dfrac{1-v^{2}}{2v}$$

$$\Rightarrow \dfrac{2v}{1-v^{2}}dv=\dfrac{dx}{x}$$

On integrating both sides, we get

$$\displaystyle\int \dfrac{2v}{1-v^{2}}dv=\int \dfrac{dx}{x}$$

Put $$1-v^{2}=t$$ in $$LHS$$, we get

$$-2v\ dv=dt$$

$$\Rightarrow -\displaystyle\int \dfrac{dt}{t}=\int \dfrac{dx}{x}$$

$$\Rightarrow -\log t=\log x+\log C$$

$$\Rightarrow -\log (1-v^{2})=\log x+\log C$$

$$\Rightarrow -\log \left(1-\dfrac{y^{2}}{x^{2}}\right)=\log x+\log C$$

$$\Rightarrow \log \left(\dfrac{x^{2}-y^{2}}{x^{2}}\right)=\log x+\log C$$

$$\Rightarrow \log\left(\dfrac{x^{2}}{x^{2}-y^{2}}\right)=\log c+\log C$$

$$\Rightarrow \dfrac{x^{2}}{x^{2}-y^{2}}=Cx$$

Since, the curve passes through the point $$(2,1)$$

$$\therefore\dfrac{(2)^{2}}{(2)^{2}-(1)^{2}}=C(2)\Rightarrow C=\dfrac{2}{3}$$

So, the required solution is $$2(x^{2}-y^{2})=3x$$

Find the $$ x $$ co-ordinates of all the points on the curve $$ y=\sin 2 x-2 \sin x, 0 \leq x<2 \pi, $$ where $$ \dfrac{d y}{d x}=0 $$

$$\begin{array}{l}y=\sin 2 x-2 \sin x, 0 \leq x<2 \pi \\\therefore \dfrac{d y}{d x}=\dfrac{d}{d x}(\sin 2 x-2 \sin x) \\=\dfrac{d}{d x}(\sin 2 x)-2 \dfrac{d}{d x}(\sin x) \\=\cos 2 x \cdot \dfrac{d}{d x}(2 x)-2 \cos x \\=\cos ^{2} x \times 2-2 \cos x \\=2\left(2 \cos ^{2} x-1\right)-2 \cos x \\=4 \cos ^{2} x-2-2 \cos x \\=4 \cos ^{2} x-2 \cos x-2 \\\text { If } \dfrac{d y}{d x}=0, \text { then } 4 \cos ^{2} x-2 \cos x-2=0 \\\therefore 4 \cos ^{2} x-4 \cos x 2 \cos x-2=0 \\\therefore 4 \cos x(\cos x-1)+2(\cos x-1)=0 \\\therefore(\cos x-1)(4 \cos x+2)=\end{array}$$
$$ \therefore \cos x-1=0 $$ or $$ 4 \cos x+2=0 $$
$$ \therefore \cos x=1 $$ or $$ \cos x=-\dfrac{1}{2} $$
$$ \therefore \cos x=\cos 0 $$
Or
$$ \cos x=-\cos \dfrac{\pi}{3} $$
$$ =\cos \left(\pi-\dfrac{\pi}{3}\right) $$
$$ =\dfrac{\cos 2 \pi}{3} $$
Or
$$ \cos x=-\cos \dfrac{\pi}{3} $$
$$ =\cos \left(\pi-\dfrac{\pi}{3}\right) $$
$$ =\dfrac{\cos 4 \pi}{3} \quad \ldots[\because 0 \leq x<2 \pi] $$
$$ \therefore \mathrm{x}=0 $$ or $$ x=\dfrac{2 \pi}{3} $$ or $$ x=\dfrac{4 \pi}{3} $$
$$ \therefore x=0 $$ or $$ \dfrac{2 \pi}{3} $$ or $$ \dfrac{4 \pi}{3} $$

Find the values of $$x$$ for which the function $$f(x)=x^{3}-12x^{2}-144x+13$$ (a) increasing (b) decreasing

$$f(x)=x^{3}-12x^{2}-144x+13$$
$$\therefore f'(x)=\dfrac{d}{dx}x^{3}-12x^{2}-144x+13$$
$$=3x^{2}-12\times 2x-144\times 1+0$$
$$=3x^{2}-24x-144$$
$$=3(x^{2}-8x-48)$$
(a) if is increasing if $$f'(x)\ge 0$$
i.e. if $$3(x^{2}-8x-48)\ge 0$$
i.e. if $$x^{2}-8x-48\ge 0$$
i.e. if $$x^{2}-8x\ge 48$$
i.e. if $$x^{2}-8x+16\ge 48+16$$
i.e. if $$(x-4)^{2}\ge 64$$
i.e. if $$x-4\ge 8$$ or $$x-4\le -8$$
i.e. if $$x\ge 12$$ or $$x\le -4$$
$$\therefore f$$ is increasing if $$x\le -4$$ or $$x\ge 12,$$
i.e. $$x\in (-\infty,-4]\cup [12,\infty).$$
(b) if is increasing if $$f'(x)\le 0$$
i.e. if $$3(x^{2}-8x-48)\le 0$$
i.e. if $$x^{2}-8x-48\le 0$$
i.e. if $$x^{2}-8x\le 48$$
i.e. if $$x^{2}-8x+16\le 48+16$$
i.e. if $$(x-4)^{2}\le 64$$
i.e. if $$-8\le x-4\le 8$$
i.e. if $$-4\le x\le 12$$
$$\therefore f$$ is decreasing if $$-4\le x\le 12,$$ i.e $$x\in [-4,12].$$

Test whether the following function are increasing or decreasing : $$f(x)=2-3x+3x^{2}-x^{3},x\in R.$$

$$f(x)=2-3x^{2}+3x^{2}-x^{3}$$
$$\therefore f'(x)=\dfrac{d}{dx}(2-3x+3x^{2}-x^{3})$$
$$0-3\times 1+3\times 2x-3x^{2}$$
$$-3+6x-3x^{2}$$
$$-3(x^{2}-2x+1)$$
$$=-3(x-1)^{2}\le 0$$ for all $$x\in R$$
$$\therefore f'(x)\le 0$$ for all $$x\in R$$
$$\therefore f$$ is decreasing for all $$x\in R.$$

Find the slope of the tangent to the curve
$$y = \dfrac{x - 1}{x - 2} , x \neq 2 $$ at $$x = 10$$

$$Slope \space of \space tangent \space of \space y=f(x) \space is \space f'(x)$$

$$Using \space chain \space rule$$

$$Slope=$$ $$\dfrac{dy}{dx} = \dfrac{(x -2)(1)-(x-1)(1)}{(x-2)^{2}}=\dfrac{-1}{(x-2)^2}$$

$$Slope \space at \space x=10 \space \dfrac{-1}{(10-2)^2}=\dfrac{-1}{64}$$

Find the slope of the tangent to the curve $$y = x^{3} - 3x +2 $$ at the point whose x - coordinates is 3

$$y=x^3-3x+2$$

$$Slope \space of \space tangent =\dfrac{dy}{dx}$$

$$y=x^3-3x+2$$

$$\dfrac{dy}{dx}=3x^2-3$$

$$\dfrac{dy}{dx}|x=3=3(3)^2-3=24$$

$$Slope \space of \space tangent=24$$

Find the slope of the tangent to curve $$y = x^{3}-x + 1 $$ at the point whose x - coordinate is 2

$$y = x ^{3} - x +1$$

$$\dfrac{dy}{dx}=3x^2-1$$

$$Slope \space of \space tangent=\dfrac{dy}{dx}$$

$$Slope \space tangent \space at \space (x=2) = \space \dfrac{dy}{dx}|{x=2}$$

$$Slope \space of \space tangent=3(2)^2-1=11$$

Solve the following: Find all points on the ellipse $$9x^{2}+16y^{2}=400$$, at which the $$y-$$ coordinate is decreasing and the coordinate is increasing at the same rate.

$$L\ P(x_{1}, y_{1})$$ be the point on the ellipse $$9x^{2}+16y^{2}=400$$, at which the $$y-$$ coordinates decreasing and the $$x-$$ coordinate is increasing at the same rate...
Then $$-\left(\dfrac{dy}{dt}\right)_{at\ (x_{1}, y_{1})}=\left(\dfrac{dx}{dy}\right)_{at\ (x_{1}, y_{1})}$$ $$...(1)$$
Differentiating $$9x^{2}+16y^{2}=400$$ w.r.t. $$t$$, we get
$$9\times 2x\dfrac{dx}{dt}+16\times 2y\dfrac{dy}{dx}=0$$
$$\therefore 9x\dfrac{dx}{dt}+16y\dfrac{dy}{dt}=0$$
$$\therefore 9x_{1}\left(\dfrac{dx}{dt}\right)_{at\ (x_{1}y_{1})}+16y_{1}\left(\dfrac{dy}{dt}\right)_{at\ (x_{1}, y_{1})}=0$$
$$\therefore 9x_{1}\left(\dfrac{dx}{dt}\right)_{at\ (x_{1}, y_{1})}-16y_{1}\left(\dfrac{dy}{dt}\right)_{at\ (x_{1}, y_{1})}=0$$ ...[By $$(1)$$]
$$\therefore 9x1-116y1=0$$ $$...(2)$$
Now, $$(x1, y1)$$ lies on the ellipse $$9x^{2}+16y^{2}=400$$
$$\therefore 9x_{1}^2+16y_1^2=400$$
From $$(2), x_1=\dfrac{16y_1}{9}$$
Substitute $$x_1=\dfrac{16y_1}{9}$$in $$(3)$$, we get
$$\therefore 9\left(\dfrac{16y_1}{9}\right)^{2}+16_1^2=400$$
$$\therefore 16y_1^2+9y_1^2=225$$
$$\therefore 25y_1^2=225$$
$$\therefore y_1^2=9$$
$$\therefore y_1=\pm 3$$
When $$y_1=3, x_1=\dfrac{16(3)}{9}=\dfrac{16}{3}$$
When $$y_1=-3, x_1=\dfrac{16(-3)}{9}=-\dfrac{16}{3}$$
Hence, the required points on the ellipse are
$$\left(\dfrac{16}{3}, 3\right)$$ and $$\left(-\dfrac{16}{3}, -3\right)$$

Test whether the following function are increasing or decreasing : $$f(x)=\dfrac{1}{x},x\in R,\ x\neq0$$

$$f(x)=\dfrac{1}{x}$$
$$\therefore f'(x)=\dfrac{d}{dx}(x-\dfrac{1}{x})$$
$$=1-\left(\dfrac{-1}{x^{2}}\right)$$
$$=1+\dfrac{1}{x^{2}} > $$ for all $$x\in R, x\neq 0$$
$$\therefore f'(x) > 0$$ for all $$x\in R,$$ where $$x\neq 0$$
$$\therefore f$$ is increasing for all $$x\in R,$$ where $$x\neq 0.$$

Find the slope of the tangent to the curve $$ 3x^{4} - 4x $$ at $$x = 4$$

$$Slope \space of \space tangent \space =$$$$\dfrac{dy}{dx}$$

$$For \space given \space f(x) \space $$

$$\dfrac{dy}{dx}=12x^3-4$$

$$\dfrac{dy}{dx} at x=4$$

$$Slope= \space 12(4)^3-4=764$$

Prove that the function given by $$ f (x) = x^{3} - 3x^{2} + 3x - 100$$ is increasing in R

1910458_1858638_ans_559026e62dab493fa11e1d21733e7da8.jpg

Find points at which the tangent to the curve $$y = x^{3} - 3x^{2} - 9x + 7$$ is parallel to the x-axis

$$y = x^{3} - 3x^{2} - 9x + 7$$

$$ slope \space of \space tangent=$$ $$\dfrac{dy}{dx} = 3x^{2} - 6x -9$$

$$Given$$ $$ tangent $$ $$parallel$$ $$to$$ $$x-axis$$

$$ \therefore slope=0 \implies 3x^2-6x-9=0$$

$$3(x^2-2x-3)=0$$

$$(x-3)(x+1)=0$$

$$x=3 \space or \space x=-1$$

$$So \space the \space points \space (3,-20) \space or \space(-1,18)$$

Find the points of curve $$\dfrac{x^{2}}{9} + \dfrac{y ^{2}}{16} = 1 $$ which the tangents are
parallel to x- axis

$$ 16 x ^{2} + 9y^{2} = 144$$
$$16 \times 2 x + 9\times 2y \times \dfrac{dy}{dx} = 0$$
$$\Rightarrow \dfrac{dy}{dx} = \dfrac{-32 x}{18 y} = \dfrac{-16}{9} \dfrac{x}{y} $$
$$for\space tangents \space parallel \space to \space x - axis$$ , $$\dfrac{dy}{dx} = 0 $$
$$\dfrac{-16x}{9y} = 0 \Rightarrow x = 0 $$
$$when$$ $$x = 0,$$

$$\dfrac{0}{9} + \dfrac{y^{2}}{16} = 1 , y = \pm 4$$
$$( 0 , 4)$$ and $$ ( 0, -4) $$ $$are\space the\space points \space on\space the \space curve\space at \space which \space tangents \space is \space parallel \space to \space x -axis \space $$

Show that the normal at any point 6, to the curve $$x = a \cos \theta + a \theta \sin \theta, y = a \sin \theta - a \theta \cos \theta$$ is at a constant distance from the origin.

$${\textbf{Step 1: Differentiate both the equation of curves w.r.t. }}\mathbf \theta .$$

$${\text{We have,}}$$

$$x = a\cos \theta + a\theta \sin \theta $$

$${\text{Differentiating w}}{\text{.r}}{\text{.t}}{\text{. }}\theta {\text{ we get,}}$$

$$\dfrac{d}{{d\theta }}\left( x \right) = \dfrac{d}{{d\theta }}\left( {a\cos \theta + a\theta \sin \theta } \right)$$

$$ \Rightarrow \dfrac{{dx}}{{d\theta }} = \dfrac{d}{{d\theta }}\left( {a\cos \theta } \right) + \dfrac{d}{{d\theta }}\left( {a\theta \sin \theta } \right)$$

$$ \Rightarrow \dfrac{{dx}}{{d\theta }} = - a\sin \theta + a\sin \theta + a\theta \cos \theta $$ $$\left( {{\textbf{by product rule}}} \right)$$

$$ \Rightarrow \dfrac{{dx}}{{d\theta }} = a\theta \cos \theta \ldots \left( 1 \right)$$

$$y = a\sin \theta - a\theta \cos \theta $$

$${\text{Differentiating w}}{\text{.r}}{\text{.t}}{\text{. }}\theta {\text{ we get,}}$$

$$\dfrac{d}{{d\theta }}\left( y \right) = \dfrac{d}{{d\theta }}\left( {a\sin \theta - a\theta \cos \theta } \right)$$

$$ \Rightarrow \dfrac{{dy}}{{d\theta }} = \dfrac{d}{{d\theta }}\left( {a\sin \theta } \right) - \dfrac{d}{{d\theta }}\left( {a\theta \cos \theta } \right)$$

$$ \Rightarrow \dfrac{{dy}}{{d\theta }} = a\cos \theta + a\theta \sin \theta - a\cos \theta $$

$$ \Rightarrow \dfrac{{dy}}{{d\theta }} = a\theta \sin \theta \ldots \left( 2 \right)$$

$${\text{Dividing equation }}\left( 2 \right){\text{ by }}\left( 1 \right){\text{ we get,}}$$

$$\dfrac{{\dfrac{{dy}}{{d\theta }}}}{{\dfrac{{dx}}{{d\theta }}}} = \dfrac{{a\theta sin\theta }}{{a\theta \cos \theta }}$$

$$ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{sin\theta }}{{\cos \theta }}$$

$$ \Rightarrow \dfrac{{dy}}{{dx}} = \tan \theta $$

$$\therefore {\text{Slope of normal}} = - \dfrac{1}{{\tan \theta }}$$

$${\textbf{Step 2: Write the equation of normal using the known values.}}$$

$${\text{Equation of normal}}$$

$$y - \left( {a\sin \theta - a\theta \cos \theta } \right) = \dfrac{{ - 1}}{{\dfrac{{\sin \theta }}{{\cos \theta }}}}\left( {x - \left( {a\cos \theta + a\theta \sin \theta } \right)} \right)$$

$$\left(\mathbf {{\textbf{Using equation of normal: }}\mathbf{y - {y_1}} =\mathbf{ \dfrac{{ - 1}}{{\dfrac{{dy}}{{dx}}}}\left( {x - {x_1}} \right)}} \right)$$

$$ \Rightarrow y - a\sin \theta + a\theta \cos \theta = \dfrac{{ - \cos \theta }}{{\sin \theta }}\left( {x - a\cos \theta - a\theta \sin \theta } \right)$$

$$ \Rightarrow y\sin \theta - a{\sin ^2}\theta + a\theta \cos \theta \sin \theta = - x\cos \theta + a{\cos ^2}\theta + a\theta \cos \theta \sin \theta $$

$$ \Rightarrow y\sin \theta + x\cos \theta = a{\cos ^2}\theta + a{\sin ^2}\theta $$

$$ \Rightarrow y\sin \theta + x\cos \theta = a\left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right)$$

$$ \Rightarrow y\sin \theta + x\cos \theta = a \ldots \left( 3 \right)$$ $$\left( {\because {{\cos }^2}\theta + {{\sin }^2}\theta = 1} \right)$$

$${\textbf{Step 3: Find distance of a normal from the origin}}{\text{.}}$$

$${\text{Comapring equation }}\left( {\text{3}} \right){\text{ with }}a{x_1} + b{y_1} + C$$ $${\text{we get,}}$$

$$a = \cos \theta ,b = \sin \theta ,c = - a$$ $${\text{and }}\left( {{x_1},{y_1}} \right) = \left( {0,0} \right)$$

$${\text{So, the perpendicular distance from the origin is,}}$$

$$d = \dfrac{{\left| {\cos \theta \left( 0 \right) + \sin \theta \left( 0 \right) - a} \right|}}{{\sqrt {{{\cos }^2}\theta + {{\sin }^2}\theta } }}$$ $$\left(\mathbf {{\textbf{Using formula: }}d = \dfrac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}} \right)$$

$$d = \dfrac{{\left| { - a} \right|}}{{\sqrt 1 }}$$ $$\left(\mathbf {\because {{\textbf{cos} }^2}\theta + {{\textbf{sin }}^2}\theta = 1} \right)$$

$$d = a$$

$${\textbf{Hence, distance of normal from origin is constant.}}$$

At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point $$(- 4, -3)$$. Find the equation of the curve given that it passes through $$(-2, 1)$$.

Given $$\dfrac{dy}{dx}=2\Bigg(\dfrac{y+3}{x+4}\Bigg)$$, slope is $$\dfrac{y-y_1}{x-x_1}$$

$$\int \dfrac{dy}{y+3}=2\int \dfrac{dx}{x+4}$$

$$\log |y+3|=2\log |x+4|+\log C$$

$$y + 3 = (x + 4)^2 C$$

when $$x = -2, y = 1, 4 = (2)^2\,C$$

$$\Rightarrow C = 1$$ Required equation is $$y + 3 = (x + 4)^2$$

Find a point on the curve $$y = (x - 2) ^{2} $$ at which the tangent is parallel to the chord joining the point $$( 2 ,0) $$ and $$(4, 4)$$

1994106_1858765_ans_44b57c74d0a940f0975411f11ea96fb0.png

Find the points of curve $$\dfrac{x^{2}}{9} + \dfrac{y ^{2}}{16} = 1 $$ which the tangents are parallel to y- axis.

Given, $$ 16 x ^{2} + 9y^{2} = 144$$

differentiate

$$16 \times 2 x + 9\times 2y \times \dfrac{dy}{dx} = 0$$

$$\Rightarrow \dfrac{dy}{dx} = \dfrac{-32 x}{18 y} = \dfrac{-16}{9} \dfrac{x}{y} $$

For tangents parallel to y - axis $$\dfrac{dy}{dx} = \dfrac{1}{0}\dfrac{-16x}{9y} = \dfrac{1}{0} \Rightarrow y = 0 $$

when $$ y = 0 , x^{2} = 9 \implies x = \pm 3 $$ point is $$ (3,0) $$ and $$(-3 , 0)$$

$$ (3,0) $$ and $$(-3 , 0) $$ are the points at which the curve is parallel to y -axis.

Find the slope of the tangent to the curve
$$x = a \cos ^{3} \theta , y = a \sin ^{3} \theta = \dfrac{\pi }{4}$$

$$x=acos^3\theta$$

$$\dfrac{dx}{d\theta}=-3acos^2\theta sin\theta$$

$$y=asin^3\theta \implies \dfrac{dy}{d\theta}=3asin^{2}\theta cos\theta$$

$$Slope \space of \space tangent =\dfrac{dy}{dx}$$

$$\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{d\theta}}{\dfrac{dx}{d\theta}}$$

$$\dfrac{dy}{dx}=\dfrac{3asin^2\theta cos\theta}{-3acos^2\theta sin\theta}$$

$$\dfrac{dy}{dx}=-tan\theta$$

$$\dfrac{dy}{dx}|_{\theta=\frac{\pi}{4}}=-tan\dfrac{\pi}{4}=-1$$

$$Slope \space of \space tangent=-1$$

Find the slope of the normal to the curve
$$x = 1 - a \sin \theta , y = b \cos ^{2} \theta at \theta = \dfrac{\pi }{2}$$

$$x = 1 - a \ sin \theta , y = b \cos^{2} \theta at \theta = \dfrac{\pi }{2}$$

In the radius of sphere is measured as $$9 cm$$ with an error of $$0.03 cm$$, find the apps error in. Calculating its surface area,

$$Given \space \Delta r = 0.03 cm$$
$$Surface \space area\space of \space sphere=A = 4 \pi r^{2}$$
$$\dfrac{dA}{dr} = 8\pi r$$
$$\Delta A =8 \pi r \times (\Delta r)$$
$$= 8 \pi \times 9 \times .03$$$$= 2.16 \pi cm^{2}$$
$$\therefore $$$$Error\space in\space calculating\space surface\space Area =$$ $$2.16 \pi cm^{2}$$

For the curve $$4x^{3} - 2x^{5}$$ , find all the points at which tangents passes through the origin .

$$y=4x^{3} - 2x^{5} $$

$$Slope \space of \space tangent \space =\dfrac{dy}{dx}$$
$$\dfrac{dy}{dx} = 12x^{2} - 10x^{4} $$
$$Let\space (a,b)\space be\space the\space point\space on\space the\space curve\space at\space which\space the\space tangent\space passes\space through\space the\space origin.$$ .
$$\therefore $$ $$Equation\space of\space tangent\space is$$
$$ y -b = ( 12 a ^{2} - 10 a^{2} )(x - a)$$
$$but\space this\space passes\space through\space the\space origin$$
$$\therefore 0 -b= (12a^{2} - 10a^{4}) (-a)$$

$$b = 12a^{3} - 10a ^{5} ... (1)$$
$$Also\space from\space the\space equation\space since \space (a,b) \space lies \space on \space curve\space$$$$b = 4a^{3} - 2a^{5} ...(2) $$
$$from\space (1)\space and\space (2)$$ $$12a^{3} - 10a^{5} = 4a^{3} - 2a^{5}$$
$$8a^{3} = 8a^{5} $$
$$a^{3} (1 - a^{2}) = 0 \Rightarrow a = 0 , a = \pm1$$
$$when$$ $$a = 0 , b = 0 , (0,0)$$
$$a = 1 , b = 12 (1) -10 (1) = 2 , (1,2) $$
$$a - 1 , b = 12 (-1) -10 (-1) = -2 , (-1,-2)$$
$$Hence\space the\space required\space points\space are$$ $$(0,0) , (1,2) , (1,-2)$$

Prove that the curves $$ x = y ^{2} $$ and $$xy= k $$ cut at right angles if $$ 8k^{2} = 1 $$

Given, $$x = y ^{2}$$ and $$xy = k$$
$$\Rightarrow y^{2}\times y = k \Rightarrow y = k^{1/3}$$

when $$ y = k ^{1/3} \Rightarrow x = k ^{2/3}$$

point $$(k^{2/3}, k^{1/3})$$

$$m_1=\dfrac{1}{2y}_{(k^{2/3}, k^{1/3})} = \dfrac{1}{2k^{2/3}},m_2=\dfrac{-y}{x}_{(k^{2/3}, k^{1/3})}=\dfrac{-1}{k^{1/3}} $$

Since the curve cuts at right angles

$$m_{1}\times m_{2} = -1$$

$$\dfrac{1}{2k^{2/3}}\times \dfrac{-1}{k^{1/3}} =- 1$$

$$\dfrac{1}{2k^{2/3}} = 1 \Rightarrow 2k^{2/3} = 1 $$

cubing $$8 k ^{2} = 1$$

Find the points on the curve $$ y = x^{3} $$ at which the slope of the tangents is equal to the y - coordinates of the point

Given, $$ y = x^{3} $$

$$\dfrac{dy}{dx} = 3x, ^{2} $$

Given that $$\dfrac{dy}{dx} = y = x ^{3} $$

$$\therefore 3x^{2} = x ^{3} \Rightarrow x^{2} ( 3 - x) = 0 \Rightarrow x = 0 $$ or $$x = 3 $$

when $$x = 3 , y = 3^{3} = 27 , $$ when $$x = 0 , y = 0 $$

$$\therefore $$ The required points are $$ (0,0) , (3,27) $$

Show that the tangents to the curve $$ y = 7x ^{3} + 11 $$ at the point where $$x = 2 $$ and $$ x = -2 $$ are parallel.

Given, $$ y = 7x ^{3} + 11 $$

$$\dfrac{dy}{dx} = 21 x^{2} $$

$$\dfrac{dy}{dx} |_{x = 2} = 84 $$

Also $$\dfrac{dy}{dx} |_{x = -2} = 21 (-2)^{2} = 84 $$

since slopes are equal tangents at $$x = 2 $$ and $$x$$$$=-2 $$ are parallel

Find the points on the curve $$ x ^{2} + y ^{2} - 2x - 3 = 0 $$ at which the tangents are parallel to the x-axis

Given, $$ x ^{2} + y ^{2} - 2x - 3 = 0 $$

$$ 2x + 2y \times \dfrac{dy}{dx} - 2 = 0 \Rightarrow \dfrac{dy}{dx} =\dfrac{1 - x}{y}$$

Since tangents are parallel to x - axis , slope $$ =0$$

$$\therefore \dfrac{dy}{dx} = 0 $$

$$\dfrac{1 -x}{y} = 0 \Rightarrow x = 1 $$

when $$ x = 1 $$

$$\therefore y ^{2} + 1 -2 (1) -3 = 0 , y ^{2} = 4 , y = \pm 2 $$

$$\therefore $$

The points are $$(1,2) $$ and $$(1 ,-2) $$

Prove that $$ f(X) = a^x, 0 < a < 1$$, is decreasing in $$R$$.

Let $$ x_1, x_2 \epsilon R$$ is such that

$$ x_1 < _2$$

Then, $$ x_1 < _2$$

$$\Rightarrow a^{x1} > a^{x2}$$

$$[\because 0 < a < 1 and x < x_2 \Rightarrow a^{x1} > a^{x2}]$$

$$\Rightarrow f (x_1) > f (x_2)$$

$$\therefore x_1 < x_2$$

$$ \Rightarrow f(x_1) > f(x_2) \forall x_1, x_2 \epsilon R$$

Hence, function $$f(x) = a^x, 0 < a < 1, R$$ is decreasing in $$R$$.

For curve $$ y = \frac{x - 1}{x - 2}, X \neq 2$$ find slope of tangent at $$ X = 10$$.

Given,

$$ y = \frac{x - 1}{x - 2}$$

Diff. w.r.t. x,

$$ \frac{dy}{dx} = \frac{1 (x - 2) - 1 (x - 1)}{(x - 2)^2}$$

$$= \frac{x - 2 - x + 1}{(x - 2)^2} = - \frac{1}{(x - 2)^2}$$

At, $$ x = 10$$

$$\frac{dy}{dx} = - \frac{1}{(10 - 2)^2}$$

$$ = - \frac{1}{8^2} = - \frac{1}{64}s$$

$$\therefore (\frac{dy}{dx})_{(x = 10)} = - \frac{1}{64}$$.

So, at $$ x = 10$$ slope of tangent $$ = - \frac{1}{64}$$.

Prove that exponential function $$(e^x)$$ is an increasing function,

$$y = e^x$$
Then, $$\frac{dy}{dx} = e^x$$
$$= + ve \forall x \epsilon R$$
So, for $$x \epsilon R, e^x$$ is an increasing function.

For curve $$ y = x^3 - x$$ find slope of tangent at $$ x = 2$$.

Given , $$y = x^3 - x$$

Diff. w.r.t. x,

$$ \frac{dy}{dx} = 3x^2 - 1$$ ...(i)

Putting x = 2 in eq. (i),

$$(\frac{dy}{dx})_{(x = 2)} = 3 (2)^2 - 1 = 11$$

So, slope of tangent $$ = 11$$.

Find all points where slope of tangent to the curve
$$ y = \sqrt{(4x - 3)} - 1$$ is $$\frac{2}{3}$$.

Given curve,

$$ y = \sqrt{(4x - 3)} - 1$$ ...(i)

Diff. w.r.t. x,

$$\frac{dy}{dx} = \frac{1}{2\sqrt{(4x - 3)}} \frac{d}{dx} (4x - 3) - 0$$

$$\Rightarrow \frac{dy}{dx} = \frac{1}{2\sqrt{4x - 3}}. (4)$$

$$\Rightarrow \frac{dy}{dx} = \frac{2}{\sqrt{4x - 3}}$$

As, given, slope $$ = \frac{2}{3}$$

Then, $$\frac{2}{\sqrt{4x - 3}} = \frac{2}{3}$$

$$\Rightarrow \sqrt{4x - 3} = 3$$

$$\Rightarrow 4x - 3 = 9$$

$$\Rightarrow 4x = 12$$

$$\Rightarrow x = 3$$

Putting $$ x = 3$$ in eq. (i)

$$ y = \sqrt{4(3) - 3 - 1}$$

$$\Rightarrow y = \sqrt{12 - 3}-1$$

$$\Rightarrow y = \sqrt{9} - 1$$

$$\Rightarrow y = 3 - 1$$

$$\Rightarrow y = 2$$

So, required point is $$(3, 2)$$.

If tangent $$OX$$ and $$OY$$ of curve $$ \sqrt{x} - \sqrt{y} = \sqrt{a}$$ at some point cut the axis at point $$P$$ and $$Q$$, then show that $$ OP + OQ - a$$, when $$O$$ is origin.

Given
Equation $$\sqrt{x} - \sqrt{y} = \sqrt{a}$$ ...(i)
Let, tangent cut the axis $$OX$$ and $$OY$$ at point $$P$$ and $$Q$$, point on curve contact with tangent is $$(h, k)$$.
Since, $$(h, k)$$ situated to curve.
So, $$\sqrt{x} - \sqrt{y} = \sqrt{a}$$ ...(ii)
DifF. (i) w.r.t. x,
$$ \frac{1}{2\sqrt{x} - \frac{1}{2\sqrt{y}}} \frac{dy}{dx} = 0$$
$$\Rightarrow \frac{dy}{dx} = \frac{\sqrt{y}}{\sqrt{x}}$$
$$\therefore$$ Slope of tangent at point $$(h, k)$$ of curve.
$$ m = [\frac{dy}{dx}]_{(h, k)} = \frac{\sqrt{k}}{\sqrt{h}}$$
So, from $$ y - y_1 = m (x - x_1)$$ equation of tangent at the point $$(h, k)$$
$$ y - k = \frac{\sqrt{y}}{\sqrt{x}} ( x - h)$$
$$\Rightarrow \frac{y - k}{\sqrt{k}} = \frac{y - k}{\sqrt{h}}$$
$$\Rightarrow \frac{y}{\sqrt{k}} - \sqrt{k} = \frac{x}{\sqrt{h}} - \sqrt{h}$$
$$\Rightarrow \frac{x}{\sqrt{h}} - \frac{y}{\sqrt{k}} = \sqrt{h} - \sqrt{k}$$
$$\Rightarrow \frac{x}{\sqrt{h}} - \frac{y}{\sqrt{k}} = \sqrt{a}$$ ...(iii) [using (ii)]
$$\Rightarrow \frac{x}{\sqrt{ah}} - \frac{y}{\sqrt{ak}} = 1$$
which is form of (i)
$$ A = \sqrt{ah}, B = \sqrt{ak}$$
Hence, $$OP = A = \sqrt{ah}$$
and $$OQ = B = - \sqrt{ak}$$
$$\Rightarrow OP + OQ = \sqrt{ah} - \sqrt{ak}$$
$$= \sqrt{a} (\sqrt{h} - \sqrt{k})$$
$$= \sqrt{a}. \sqrt{a} = a$$ [Using (ii)]

Find the percentage error in calculating the volume of a cubical box if an error of $$5$$% is made in measuring the length of edge of the cube.

Let side of cube is $$x$$ and volume is $$V$$.

$$\frac{\Delta x}{x} \times 100 = 5$$

Volume of cube $$V = x^3$$

$$\frac{dV}{dx} = 3x^2$$

$$\Rightarrow \Delta V = \frac{dV}{dx} \times \Delta x$$

$$\Rightarrow \Delta V = 3x^2 \Delta x$$

$$\Rightarrow \frac{\Delta V}{V} = \frac{3x^2\Delta x}{V}$$

$$\Rightarrow \frac{\Delta V}{V} = \frac{3x^2\Delta x}{V} = 3 \frac{\Delta x}{x}$$

$$\Rightarrow \frac{\Delta V}{V} \times 100 = 3 \frac{\Delta x}{x} \times 100$$

Percentage error in volume $$= 3 \times 5$$% $$=15$$%

Hence, required percentage error is $$15$$%

For curve
$$\frac{x^2}{4} + \frac{y^2}{25} = 1$$,,
find those points where tangent is
(i) Parallel to x-axis
(ii) Parallel to y-axis

Given curve, $$\frac{x^2}{4} + \frac{y^2}{25} = 1$$

Diff. w.r.t. x,

$$\frac{2x}{4} + \frac{2y}{25} \frac{dy}{dx} = 0$$

$$\Rightarrow \frac{dy}{dx} = \frac{-2x}{4} \times \frac{25}{2y}$$

$$\Rightarrow \frac{dy}{dx} = - \frac{25x}{4y}$$

(i) When tangent is parallel to x-axis then,

$$\frac{dy}{dx} = 0$$

$$ - \frac{25}{4} \frac{x}{y} = 0 \Rightarrow x = 0$$

Putting $$x = 0$$ in eq. $$\frac{x^2}{4} + \frac{y^2}{25} = 1$$

$$ y^2 = 25 \Rightarrow y = \pm 5$$

Hence, tangents are parallel to x-axis at points $$(0, \pm 5)$$.

(ii) When tangent is parallel to u-axis then,

$$ - \frac{1}{dy/dx} = 0$$

$$\Rightarrow - \frac{1}{- \frac{25x}{4y}} = 0$$

$$\Rightarrow \frac{4y}{25x} = 0 \Rightarrow y = 0$$

Putting $$ y = 0$$ in eq. (i) $$\frac{x^2}{4} + \frac{y^2}{25} = 1$$

$$ \frac{x^2}{4} + 0 = 0 \Rightarrow x^2 = 4 \Rightarrow x = \pm 2$$

Hence, tangents are parallel to 7-axis at points $$(\pm, 2)$$

Number of critical points of the function $$f(x)=\left ( x-2 \right )^{\frac{2}{3}}\left ( 2x+1 \right )$$ is equal to

$$f(x)=(x-2)^{\displaystyle \frac{2}{3}}(2x+1)$$

$${f}'(x)=\displaystyle \dfrac{2}{3}\left ( x-2 \right )^{-\dfrac{1}{3}}\left ( 2x+1 \right )+\left ( x-2 \right )^{\dfrac{2}{3}}(2)$$

$$=\displaystyle \dfrac{2\left ( \dfrac{2x+1}{3}+(x-2) \right )}{\left ( x-2 \right )^{\dfrac{1}{3}}}$$

For critical point $${f}'(x)=0 \ or \ {f}'(x)$$ is not defined so $$x=2 \ and \ 2x+1+3x-6=0$$
$$\Rightarrow x=1$$
Therefore, number of critical points are $$ 2 $$

The slope of the tangent to the curve $$(y - x^5)^2 = x(1+x^2)^2$$ at the point $$(1, 3)$$ is ..................

Taking derivative with respect to 'x' on both sides ( Using Product rule in RHS)

$$2(y-x^{5}_{})( \dfrac{dy}{dx} - 5x^{4}_{} ) = (1+x^{2}_{})^{2}_{} + 2x(1+x^{2}_{})\times 2x $$

Putting x=1 and y=3 and finding the value of $$\dfrac{dy}{dx}$$

$$4\times (\dfrac{dy}{dx} - 5)= 12$$

$$\dfrac{dy}{dx} = 8$$

Slope of tangent is $$8$$ units

Number of normals at the points on the curve $$y=\dfrac{x}{\displaystyle (1-x^{2})}$$ where the tangents makes an angle of $$\displaystyle \dfrac{\pi} {4}$$ with x-axis

Given eqn of curve is
$$y=\dfrac{x}{1-x^2}$$
Also, given slope of tangent to curve is $$\tan \frac{\pi }{4}=1$$
$$\displaystyle \frac{dy}{dx}=\frac{1.(1-x^{2})-(-2x)x}{(1-x^{2})^{2}}$$
$$\Rightarrow 1=\dfrac{1+x^2}{(1-x^2)^2}$$
$$ \therefore (1+x^{2})=(1-x^{2})^{2}$$
$$\displaystyle x^{4}-3x^{2}=0$$
$$\displaystyle\Rightarrow x=0, -\sqrt{3},\sqrt{3}$$
At $$x=0 \Rightarrow y=0$$
At $$x=\sqrt{3}\Rightarrow y=\dfrac{-\sqrt{3}}{2}$$
At $$x=-\sqrt{3}\Rightarrow y=\dfrac{\sqrt{3}}{2}$$
Hence the points are : $$\displaystyle (0,0),(-\sqrt{3},\dfrac{\sqrt{3}}{2}) and (\sqrt{3},-\dfrac{\sqrt{3}}{2})$$.

Eqn of normal at (0,0) is
$$y-0=-1(x-0)$$
$$x+y=0$$

Eqn of normal at $$(\sqrt{3},-\dfrac{\sqrt{3}}{2})$$ is
$$y+\dfrac{\sqrt{3}}{2}=-1(x-\sqrt{3})$$
$$2y+2x=\sqrt{3}$$

Eqn of normal at $$(-\sqrt{3},\dfrac{\sqrt{3}}{2})$$ is
$$y-\dfrac{\sqrt{3}}{2}=-1(x+\sqrt{3})$$
$$2y+2x=-\sqrt{3}$$

Table

A) $$(x - 3)^2y' + y = 0$$
$$\displaystyle \Rightarrow \frac {dy}{y} = - \frac {dy}{(x - 3)^2}$$
Integrating we get $$\displaystyle \log | y | = \frac {1}{x - 3} + const$$
$$\displaystyle \Rightarrow y = Ce^{1/(x - 3)}$$
The solution is defined for x in R ~ [3]. This contains $$\displaystyle (- \pi /2), \pi / 2); (0, \pi /2)$$ and $$\displaystyle (0, \pi /8)$$

B) Put $$x - 3 = t$$, then
$$\displaystyle I = \int^2_{-2} (t + 2)(t + 1)^t (t - 1) (t - 2) dt = 0$$
(the integrand is an odd function)
This lies in $$\displaystyle (-\pi / 2, \pi / 2)$$ and $$\displaystyle (- \pi, \pi)$$

C) $$ f(x) = \cos^2x + \sin x \: f'(x) = -2 \cos x \sin x + \cos x = \cos x (1 - 2 \sin x)$$
For local maximum, $$\displaystyle f'(x) = 0$$
$$\displaystyle \Rightarrow x = \pi / 2, - \pi / 2, \pi / 6 \: 5 \pi / 6 $$ within $$\displaystyle (- \pi, \pi) f'' (x) = -\sin x (1 - 2 \sin x) + \cos x (-2 \cos x)$$
$$\displaystyle f'' (\pi / 2) = 1 > 0, f'' (-\pi / 2) = 3 > 0$$
$$\displaystyle f''(\pi / 6) = -3 / 2 < 0, f'' (5 \pi / 6) = - 3 / 2 < 0$$
Thus f(x) has a local maximum at $$\displaystyle x = \pi / 6$$ and $$\displaystyle 5 \pi / 6$$. These value lie in $$\displaystyle (-\pi/2), (0, \pi/2), (\pi/8, 5 \pi/2)$$ and $$\displaystyle (-\pi, \pi)$$.

D) $$ f(x) = \tan^{-1} (\sin x + \cos x)$$
$$\displaystyle f'(x) = \frac {\cos x - \sin x}{1 + (\sin x + \cos x)^2} = \frac {\sqrt 2 \sin (\pi / 4 - x)}{1 + (\sin x + \cos x)^2}$$
$$\displaystyle (f'(x) > 0$$ for $$\displaystyle 0 < x < (0, \pi / 8)$$
$$\displaystyle \Rightarrow f$$ is strictly increasing on $$\displaystyle (0, \pi / 8)$$.

Column-I Column-II

A) Given curve $$\displaystyle 2y^{2}=ax^{2}+b$$

$$\displaystyle 4y\dfrac{dy}{dx}=2ax$$

$$\Rightarrow \dfrac{dy}{dx}=\dfrac{ax}{2y}$$

$$\Rightarrow \dfrac{dy}{dx}=\dfrac{-a}{2}=-1$$ at $$(1,-1)$$

$$\Rightarrow a=2$$

$$\displaystyle 2y^{2}=ax^{2}+b$$

Since, (1,-1) lies on the curve,

$$\displaystyle 2=a+b$$

$$\displaystyle \Rightarrow b=0$$

$$\Rightarrow a-b=2$$

(B) Given curve $$9y^2=x^3$$

Slope of normal = -1 (since the normal makes equal intercept with axes)

Slope of tangent =1

$$\displaystyle 18y\dfrac{dy}{dx}=3x^{2}$$

$$18b =3a^{2} $$ (Slope of tangent at (a,b) is 1)

$$\Rightarrow b=\dfrac{a^{2}}{6}$$

Since, $$(a,b)$$ lies on the curve

$$\;9b^{2}=a^{3}$$

$$\:9.\dfrac{a^{4}}{36}=a^{3}$$

$$\Rightarrow a=4 $$

$$\Rightarrow b=\dfrac{16}{6}=\dfrac{8}{3}$$

$$\Rightarrow a-b=4-\dfrac{8}{3}=\dfrac{4}{3}$$

Since, (1, 2) lies on the curve

$$\Rightarrow 2=a+b+\dfrac{7}{2}$$

$$\Rightarrow a+b=\dfrac{-3}{2} $$ ......(1)

Now, $$\dfrac{dy}{dx}=2ax+b $$

Slope of tangent at (1,2) is $$2a+b$$

Now equation of the second curve is

$$y=x^2+6x+10$$

$$\displaystyle \dfrac{dy}{dx}=2x+6$$

Slope of tangent at (-2,2) is 2.

Slope of normal $$\displaystyle =-\dfrac{1}{2}$$

Given slope of normal to second curve = Slope of tangent to first curve.

$$\:2a+b=-\dfrac{1}{2}$$ ....(2)

Solving (1) and (2), we get

$$a=1, b=-\dfrac{5}{2}$$

$$\Rightarrow a-b=\dfrac{7}{2}$$

(D) Given curve is $$xy+ax+by=0$$

Since, (1,1) is a point on the curve

$$\Rightarrow 1+a+b=0$$ ... (3)

$$\displaystyle \dfrac{dy}{dx}=\dfrac{-(a+y)}{b+x}$$

Slope of tangent at (1,1) is given 2

$$2=\dfrac{-a-1}{b+1}$$

$$\Rightarrow a+2b=-3$$ .....(4)

Solving (3) and (4), we get

$$b=-2, a =1$$

$$\Rightarrow a-b=3$$

Find the point on the curve $$y = x^{3} - 11x + 5$$ at which the equation of tangent is $$y = x - 11$$

Let the required point of contact be (x, y)
Given: The equation of the curve is $$y= x^3-11x+5$$
The equation of the tangent to the circle as $$y=x-11$$ (which is of the form y = mx + c)
Therefore, Slope of the tangent = 1
Now, the slope of the tangent to the given circle at the point (x, y) is given by $$\frac{dy}{dx}=3x^2-11$$
Then, we have:
$$3x^2-11=1$$
$$3x^2=12$$
$$x^2=4$$
$$x=\pm 2$$
When$$ x = 2, y = (2)^3 - 11(2) + 5 = 8 - 22 + 5 = -9$$.
When $$x = -2, y = (-2)^3 - 11(-2) + 5 = -8 + 22 + 5 = 19$$.
So, the required point are $$ (2, -9)$$ and $$ (-2, 19)$$
But (2, -19) does not satisfy the line y = x - 11
Therefore, (2, -9) is required point of curve at which tangent is $$y = x - 11.$$

Find the equation of tangents to the curve $$\displaystyle y={ x }^{ 3 }+2x-4$$, which are perpendicular to the line $$\displaystyle x+14y+3=0$$.

The slope of line $$x+14y+3=0$$ is $$\dfrac{-1}{14}$$ , so the slope of line perpendicular to given line is $$14.$$
Given curve is $$y = {x}^{3}+2x-4$$ , the slope of tangent to given curve is $$\dfrac { dy }{ dx } =3{ x }^{ 2 }+2 = 14$$
we get $${x}^{2} = 4$$ , which gives $$x = \pm2$$
At $$x=2$$ , we get $$y = 8$$ and at$$x=-2$$ , we get $$y=-16$$
Therefore there are two tangents having slope $$14$$ and one passing through $$(2,8)$$ and the other passing through $$(-2,-16)$$
the equation of tangent passing through point $$(2,8)$$ is $$y-8 = 14(x-2)$$ , which gives $$14x-y-20=0$$
The equation of line passing through point $$(-2,-16)$$ is $$y+16=14(x+2)$$ , which gives $$14x-y+12=0.$$

On lighting a rocket cracker it gets projected in a parabolic path and reaches a maximum height of $$4\ m$$ when it is $$6\ m$$ away from the point of projection. Finally it reaches the ground $$12\ m$$ away from the salting point. Find the angle of projection.

The equation of the parabola is of the form $${ x }^{ 2 }=-4ay$$
It passes through $$(6,-4)$$
$$\therefore$$ $$36=16a\Rightarrow$$ $$a=\cfrac{9}{4}$$
The equation is $${x}^{2}=-9y$$ .....$$(1)$$
To find the solpe at $$(-6,-4)$$
Differentiating $$(1)$$ w.r.t $$x$$, we get
$$2x=-9\cfrac { dy }{ dx } \Rightarrow \cfrac { dy }{ dx } =\cfrac { -2 }{ 9 } x$$
at $$(-6,-4)$$, $$\cfrac { dy }{ dx } =\cfrac { -2 }{ 9 } \times (-6)=\cfrac { 4 }{ 3 } $$
(i.e.,) $$\tan { \theta } =\cfrac { 4 }{ 3 } ;\theta =\tan ^{ -1 }{ \cfrac { 4 }{ 3 } } $$
$$\therefore$$ the angle of projection is $$\tan ^{ -1 }{ \cfrac { 4 }{ 3 } } $$.

If $$x = a\sin 2t (1 + \cos 2t)$$ and $$y = b\cos 2t (1 - \cos 2t)$$, show that at $$t = \dfrac {\pi}{4}, \left (\dfrac {dy}{dx}\right ) = \dfrac {b}{a}.$$

We have, $$x = a sin 2t (1 + cos 2t)$$

Therefore, $$\dfrac{dx}{dt} = a. [2 cos 2t (1 + cos 2t) + sin 2t (– 2sin 2t)]$$

$$= 2a [cos 2t + cos^2 2t – sin^2 2t]$$

$$= 2a [cos 2t + cos 4t]$$

and $$y = b cos 2t (1 – cos 2t)$$

then $$\dfrac{dy}{dt} = b [– 2 sin 2t (1 – cos 2t) + cos 2t. 2 sin 2t]$$

$$= 2b [– sin 2t + 2 sin 2t cos 2t]$$

$$= 2b [– sin 2t + sin 4t]$$

Therefore, $$\dfrac{dy}{dx} = \dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}$$

$$=\dfrac{ 2b(-sin2t+sin4t) }{2a(cos2t+cos4t)}$$

Therefore, $$[\dfrac{dy}{dx}]$$ at $$t =\dfrac{\pi}{4} = \dfrac{b}{a} \left [ \dfrac{sin\pi-sin\dfrac{\pi}{2}}{cos\pi+cos\dfrac{\pi}{2}} \right ]$$

$$=\dfrac{b}{a}\times\dfrac{-1}{-1}$$

$$=\dfrac{b}{a}$$

Find the value of $$\dfrac {dy}{dx}$$ at $$\theta = \dfrac {\pi}{4}$$ if $$x = ae^{\theta} (\sin \theta - \cos \theta)$$ and $$y = ae^{\theta} (\sin \theta + \cos \theta).$$

$$y=ae^\theta(sin\theta+cos\theta)$$
$$x=ae^\theta(sin\theta-cos\theta)$$
Applying parametric differentiation,
$$\frac{dy}{dx}=\frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}$$----(1)
Now, $$\dfrac{dy}{d\theta}=ae^\theta(cos\theta-sin\theta)+ae^\theta(sin\theta+cos\theta)$$
Applying product rule: we get
$$=2ae^\theta(cos\theta)$$
$$\dfrac{dx}{d\theta}=ae^\theta(cos\theta+sin\theta)+ae^\theta(sin\theta-cos\theta)$$
$$=2ae^\theta(sin\theta)$$
Substituting the values of $$\dfrac{dy}{d\theta}$$ and $$\dfrac{dx}{d\theta}$$ in (1),
$$\dfrac{dy}{dx}=\dfrac{2ae^\theta cos\theta}{2ae^\theta sin\theta}=cot\theta$$

Now, $$\dfrac{dy}{dx}$$ at $$\theta=\dfrac{pi}{4}$$

$$[cot\theta]_{\theta=\dfrac{pi}{4}}=cot\dfrac{\pi}{4}=1.$$

The radius of a circular disc is given as $$24cm$$ with a maximum error in measurement of $$0.02cm$$. Estimate the maximum error in the calculated area of the disc and compute the relative error by using differentials.

Area of the circular disc is given by $$A=\pi r^2$$.

Consider $$A=\pi r^2$$

Differentiate both sides with respect to $$r$$, we get

$$\dfrac{dA}{dr}=2\pi r$$

$$\Rightarrow dA=2\pi r\:dr$$

Calculated area: $$A=\pi(24)^2=576\pi \:cm^2 \approx 1809.6\:cm^2 $$

Because of an error in measurement, the radius might actually be as big as $$24+0.02$$

If $$r$$ is increased from $$24$$ by an amount $$\Delta r=dr=0.02$$.

Then the actual change in the calculated area would be $$\Delta A=A(24+\Delta r)-A(24)=A(24.02)-A(24)$$.

$$\therefore \Delta A \approx dA = A(24.02)-A(24)=\pi(24.02)^2-576\pi=576.96\pi-576\pi=0.96\pi \:cm^2$$.

So we estimated the maximum error in calculated area as $$0.96\pi cm^2 \approx 3.01718 \: cm^2\approx 3.02 \:cm^2$$

The maximum relative error in calculated area is $$\dfrac{\Delta A}{A}\approx \dfrac{dA}{A}=\dfrac{0.96 \pi}{576 \pi}=\dfrac{0.96}{576}\approx 0.0017$$

The maximum $$\%$$ relative error in calculated area is about $$0.17 \%$$

Find the critical points of the following function and test them for their maxima and minima.
$$\displaystyle\, y \, =\, x^5 \, \, x^2 \, +\, 8$$

$$y=x^5-x^2+8$$

$$\dfrac{dy}{dx}=5x^4-2x=0$$

$$x=0,(\dfrac{2}{5})^\frac{1}{3}$$

$$\dfrac{d^2y}{dx^2}=20x^3-2$$

For $$x=0,\dfrac{d^2y}{dx^2}<0$$ Hence it is a maximum.

For $$x=(\dfrac{2}{5})^{\frac{1}{3}},\dfrac{d^2y}{dx^2}>0$$,Hence it is a minimum.

Find the critical points of the following function and test them for their maxima and minima.
$$\displaystyle\, y\, =\, x \cdot e^x$$

$$y=x.e^x$$

$$\dfrac{dy}{dx}=e^x+xe^x=0\Rightarrow x=-1$$

$$\dfrac{d^2y}{dx^2}=2e^x+xe^x$$

For $$x=-1,\dfrac{d^2y}{dx^2}>0$$,Hence it has minimum at $$x=-1$$ and increases continously in $$(-1,\infty)$$

Given a function y = $$x^2$$/(x - 2). Investigate its behaviour and make a rough drawing
of the graph.

1130895_890134_ans_de2976606e5940b495dab8e0f4e7d45e.jpg

Find the critical points of the following function and test them for their maxima and minima.
$$\displaystyle\, y\, =\, x \cdot e^{\, -\, x2}$$

$$y=x.e^{-x^2}$$

$$\dfrac{dy}{dx}=e^{-x^2}+xe^{-x^2}(-2x)=e^{-x^2}(1-2x^2)=0$$

$$e^{-x^2}\ne 0 \ and \ x=\pm \dfrac{1}{\sqrt2}$$

$$\dfrac{d^2y}{dx^2}=e^{-x^2}(-6x+4x^3)$$

For $$x=-\dfrac{1}{\sqrt 2},\dfrac{d^2y}{dx^2}>0$$,Hence y is minimum here

For $$x=+\dfrac{1}{\sqrt 2},\dfrac{d^2y}{dx^2}<0$$,Hence y is maximum here

Find the critical points of the following functions and test them for their maxima and minima.$$\displaystyle\, y \, =\, (x \, -\, 3)^2 (x \, -\, 2)^2.$$

$$y = (x -3)^{2} (x - 2)^{2}$$

$$\dfrac {dy}{dx} = (x - 3)^{2} \dfrac {d}{dx} (x - 2)^{2} + (x - 2)^{2}\dfrac {d}{dx} (x - 3)^{2}$$

[Using product Rule]

$$= (x -3)^{2} 2(x - 2) + (x - 2)^{2} \cdot 2(x -3)$$

$$= 2(x - 2) (x - 3) [x - 3 + x - 2]$$

$$= 2(x - 2) (x - 3)(2x - 5)$$

for maximum and minimum $$\dfrac {dy}{dx} = 0$$

so $$x = 2, 3, \dfrac {5}{2}$$

Second derivative test

$$\dfrac {dy}{dx} - 2[x^{2} - 5x + 6] (2x - 5)$$

$$= 2[2x^{3} - 5x^{2} - 10x^{2} + 25x + 12x - 30]$$

$$= 4x^{3} - 10x^{2} - 20x^{2} + 50x + 24x - 30]$$

at $$x = 2, x = 3$$ $$\dfrac {d^{2}y}{dx} > 0$$ Point of local minima and

$$\dfrac {d^{2}y}{dx} < 0$$ for $$x = \dfrac {5}{2}$$ Point of local maxima

Find the critical points of the following function and test them for their maxima and minima.
$$\displaystyle\, y \, =\, 2x^2 \, +\, x \, +\, 2$$

$$y=2x^2+x+2$$

$$\dfrac{dy}{dx}=4x+1=0\Rightarrow x=-\dfrac{1}{4}$$

$$\dfrac{d^2y}{dx^2}=4>0(always)$$

The function increases continously from $$[-\dfrac{1}{4},\infty]$$ and decreases continously from $$[-\infty,-\dfrac{1}{4}]$$ and the minimum at $$x=-\dfrac{1}{4}$$

Given a function y = $$x^4 \, - \, 2x^2 \, + \, 5$$. Investigate its behaviour with the aid of the
derivative and construct its graph.

1130554_890130_ans_da4dabdb06054de38e448a738ec4d66c.jpg

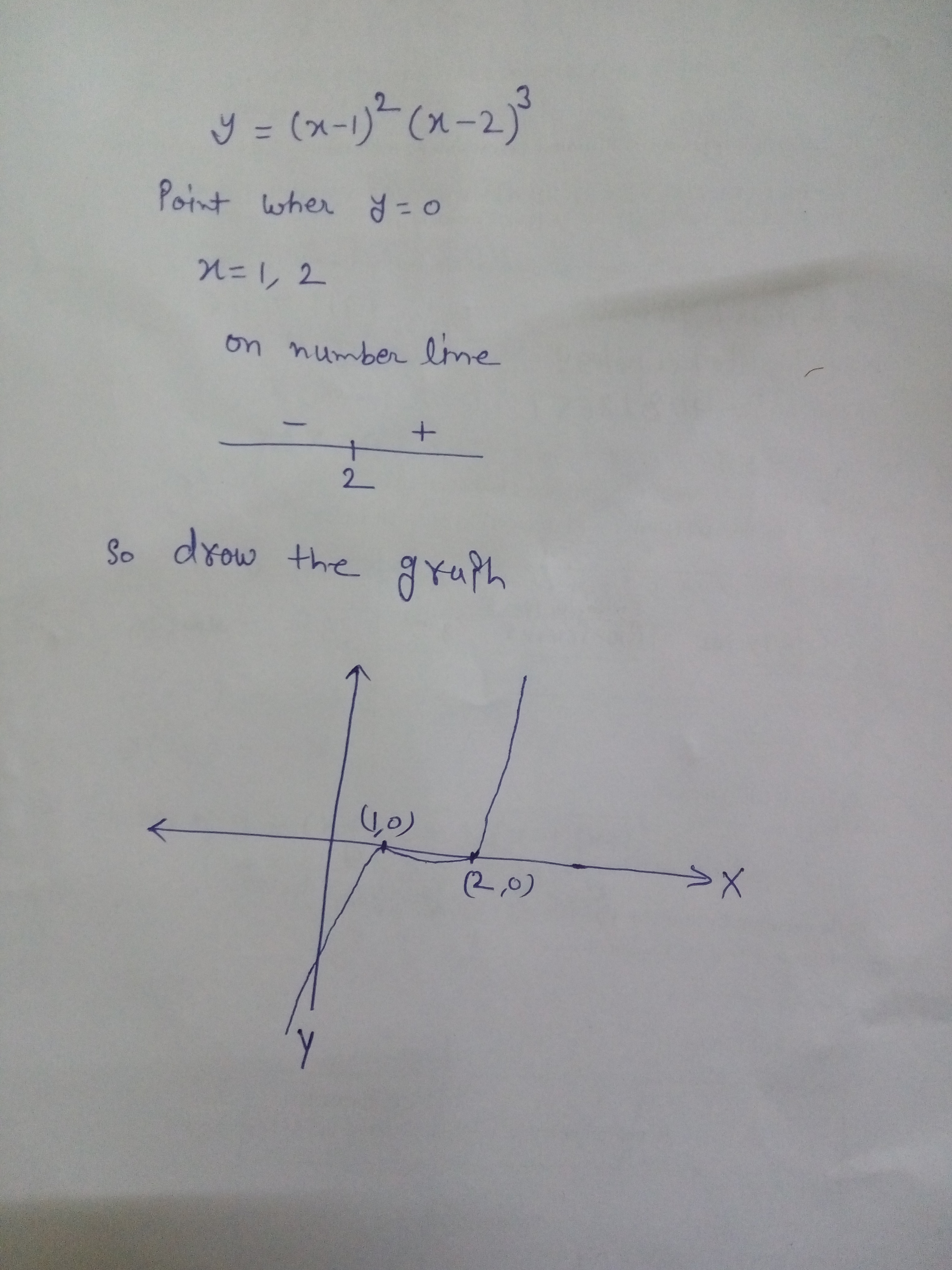
Given a function y = $$(x \, \, 1)^2 (x \, - \, 2)^3$$. Investigate its variation and construct its graph.

1130717_890132_ans_89ed6e003cf74bb1b1a733a7cf26f6b2.jpg

Find the critical points of the following function and test them for their maxima and minima.
$$\displaystyle\, y \, =\, \frac{1}{5}\, x^5\, -\, 4x^2$$

$$y=\dfrac{1}{5}x^5-4x^2$$

$$\dfrac{dy}{dx}=x^4-8x=0$$

$$x(x^3-8)=0$$

$$x=0;x=2$$

$$\dfrac{d^2y}{dx^2}=4x^3-8$$

for $$x=0,4x^3-8<0 $$ Hence $$x=0$$ is a maximum for this function

For $$x=2,4x^{3}-8>0$$ Hence $$x=2$$ is a minimum for this function

Investigate the behaviour of the function y =$$ (x^4 \, - \, 2x^2)/4$$ with the aid of the derivative and construct its graph.

1116747_890127_ans_b1d0085baeb4458d9d9087d302b2f0a5.png

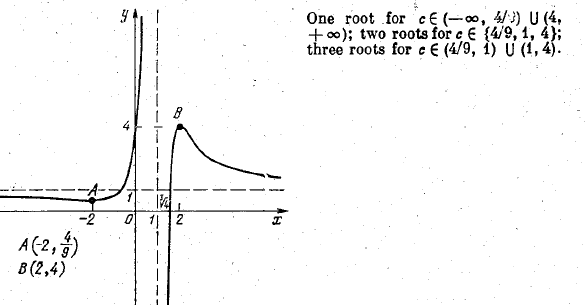
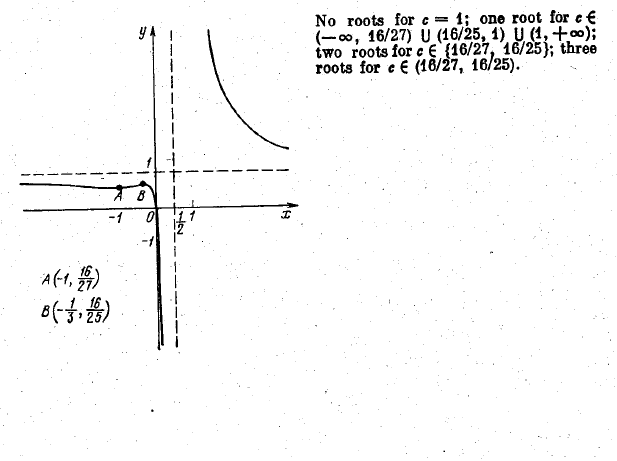
Investigate the behaviour of the function y = $$(x^3 \, - \, 4) / (x \, - \, 1)^3$$ and construct its graph. How many roots does the equation $$(x^3 \, - \, 4) / (x \, - \, 1)^3$$ = c possess?

1116755_890161_ans_d1f8342baba44d1ba66e69ccd51ecbae.png

Tangents to Curves
Find the slope of the tangent drawn to the graph of the function y = tan x at the point with abscissa $$x_0 \, = \, \pi/4.$$

$$y=\tan x$$

$$\dfrac{dy}{dx}=\sec^2x$$

At $$x=\dfrac{\pi}{4}$$

slope$$=\sec^2\dfrac{\pi}{4}=2$$

Construct the graphs of the following functions and carry out a complete investigation .
y = $$|x^2$$ - 4x + 3| + 2x.

1116768_890169_ans_edc84a9384cd4a72aa331e83e68939fa.png

Construct the graphs of the following functions and carry out a complete investigation .
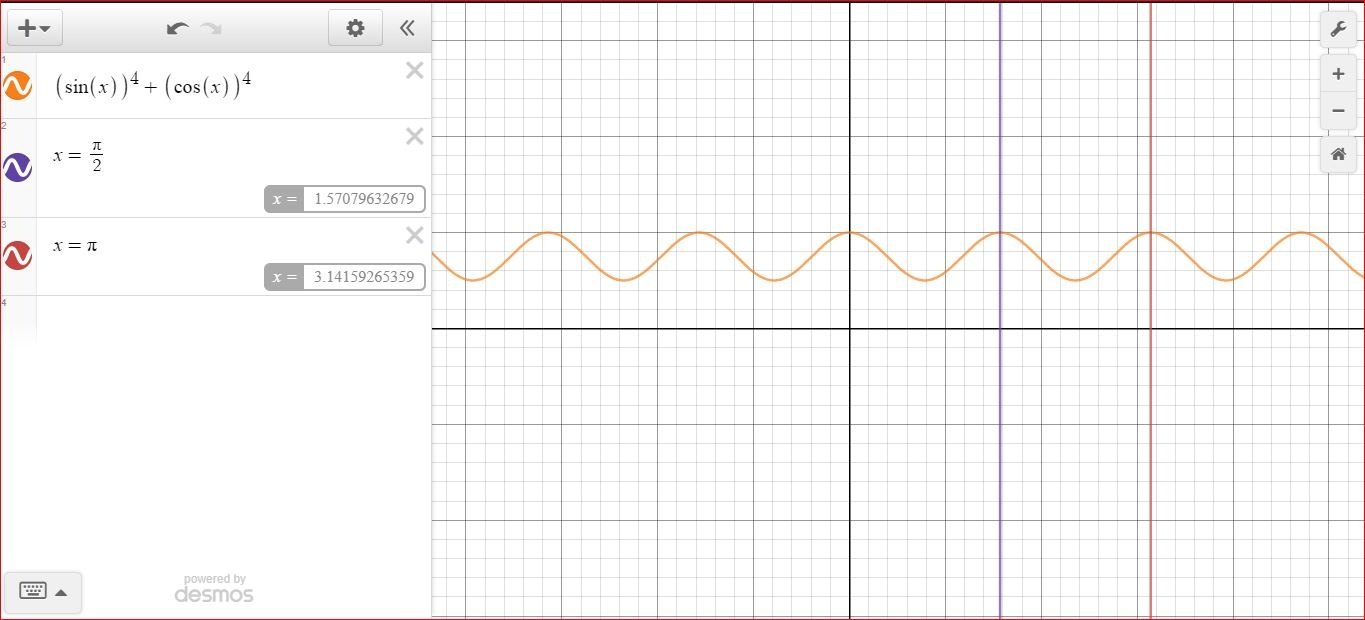
y = $$sin^4 x \, + \, cos^4 x$$

$$y={{\sin }^{4}}x+{{\cos }^{4}}x$$

$$ ={{\left( {{\sin }^{2}}x+{{\cos }^{2}}x \right)}^{2}}-2{{\sin }^{2}}x{{\cos }^{2}}x $$

$$=1-\dfrac{1}{2}{{\sin }^{2}}2x $$

We know that the period of $$\sin x$$ is $$2\pi $$ so, the period of $$\sin 2x$$ is $$\pi $$

Hence, it is clear that the period of $${{\sin }^{2}}\left( 2x \right)$$ is $$\dfrac{\pi }{2}$$

So, the period of the given function will be $$\dfrac{\pi }{2}$$

1178575_890166_ans_6f0e64c5c9734e81bdf0a9323368ca1a.jpg

Find the critical points of the following functions.
$$f(x) \, = \, (x^2 \, - \, 4)^{10}$$

$$f(x)=(x^2-4)^{10}$$

$$\implies f'(x)=10(x^2-4)(2x)$$

For, critical points, we put $$f'(x)=0$$

$$\implies x=0$$ and $$x^2-4=0$$

$$\implies x=-2,0,2$$

These points that are -2,0,2 are the critical points

Investigate the behaviour of the function y = 8($$x^3$$ + x) / $$(2x \, - \, 1)^3$$ and construct its graph. How many roots does the equation 8($$x^3$$ + x) / $$(2x \, - \, 1)^3$$ = c possess?

1116758_890163_ans_81666d7471e241689aeda2770740d696.png

Construct the graphs of the following functions and carry out a complete investigation.
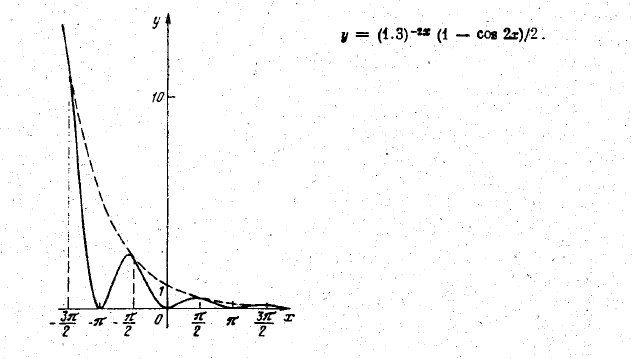
y = $$(1.3)^ { -2x} sin^2 x$$

1116765_890167_ans_55e2cb22beb845fcaac6e582dc757faf.png

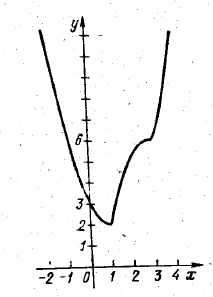
Given a function y = $$(-x^2$$ + 3x - l)/x. Investigate its behaviour and make a rough drawing of the graph

1130888_890135_ans_36cbeb0e0d224cca9687947f7a5d881a.jpg

Construct the graphs of the following functions and carry out a complete investigation .
y = $$\dfrac{x^3}{6} \, - \, x^2$$

1116774_890170_ans_5550dd070a4c48fea27ee8529687e8a9.png

Show that $$f(x) =\frac{x}{\sqrt{1+x}}- \ln(1+x)$$ is an increasing function for x > -1.

$$X=\dfrac{x}{\sqrt{1+x}}\ln (1+x)$$

$$Y^{1}=\dfrac{1}{\sqrt{1+x}}+x\left(\dfrac{-1}{2}\right)(x+1)^{\dfrac{-3}{2}}-\dfrac{1}{(1+x)}$$

$$Y^{1}=0$$

$$\Rightarrow \dfrac{1}{\sqrt{1+x}}-\dfrac{x}{2(x+1)^{\dfrac{3}{2}}}-\dfrac{1}{(1+x)}=0$$

$$\Rightarrow 1-\dfrac{x}{(x+1)^{\dfrac{3}{2}}}-\dfrac{1}{\sqrt{1+x}}=0$$

$$\Rightarrow -1\dfrac{x}{x+1}-\dfrac{1}{\sqrt{1+x}}=0$$

$$\Rightarrow \dfrac{x+1-x}{x+1}=\dfrac{1}{\sqrt{x+1}}$$

$$\Rightarrow \sqrt{x+1}=x+1$$

$$\Rightarrow x+1=x^{2}+2x+1$$

$$\Rightarrow x^{2}+x=0$$

$$x(x+1)=0$$

Hence, function is increasing for $$x> -1$$

Prove that $$f(x)=\dfrac{4\sin x}{2+\cos x}-x$$ is an increasing function for $$x\epsilon\Bigg(0,\dfrac{\pi}{2}\Bigg)$$ .

$$y=\dfrac{4\sin x}{2+\cos x}-x$$

$$\dfrac{dy}{dx}=\dfrac{4\cos x(2+\cos x)-(-\sin x)(4\sin x)}{(2+\cos x)^2}-1$$

$$\dfrac{dy}{dx}=\dfrac{8\cos x+4(\cos x^2+\sin x^2)}{(2+\cos x)^2}-1$$

$$=\dfrac{8\cos x+4}{(2+\cos x)^2}-1$$

$$=\dfrac{8\cos x+4-(2+\cos x)^2}{(2+\cos x)^2}$$

$$=\dfrac{8\cos x-4\cos x+4-4-\cos ^2x}{(2+\cos x)^2}$$

$$\dfrac{dy}{dx}=\dfrac{4\cos x-\cos ^2x}{(2+\cos x)^2}$$

For function to be increa\sin g,

$$\dfrac{dy}{dx}=\dfrac{\cos x(4-\cos x)}{(2+\cos x)^2} x>0$$

Therefore, $$\cos x(4-\cos x) >\,0 for x\epsilon[0,\dfrac{\pi}{2}]$$

$$0\leq \cos x\leq1$$...................(i)

Adding 4 both sides,

$$3\leq4-\cos x\leq4$$

Therefore $$4-\cos x$$ is positive.

Therefore$$\cos x(4-\cos x)>0\, for \theta\epsilon[0,\dfrac{\pi}{2}]$$

Hence, $$y=\dfrac{4\sin x}{2+\cos x}-x$$ is increa\sin g function for $$x\epsilon[0,\dfrac{\pi}{2}]$$

At what point on the curve $${x^2} + {y^2} - 2x - 4y + 1 = 0$$, the tangents are parallel to the y axis

$$x^2+y^2-2x-4y+1$$

$$\Rightarrow 2x+2y\dfrac { dy }{ dx } -2-4\dfrac { dy }{ dx } =0\\ \Rightarrow x+y\dfrac { dy }{ dx } -1-2\dfrac { dy }{ dx } =0\ \Rightarrow \ \left( y-2 \right) \dfrac { dy }{ dx } =\left( 1-x \right) \\ \dfrac { dy }{ dx } =\dfrac { \left( y-2 \right) }{ \left( 1-x \right) } $$

for the tangents to be parallel to $$y-$$ axis, $$\dfrac { dy }{ dx } =0$$

$$\therefore \dfrac { dy }{ dx } =\dfrac { \left( y-2 \right) }{ \left( 1-x \right) } =0\ \Rightarrow y=2$$

When $$y=2$$

$${ x }^{ 2 }+{ 2 }^{ 2 }-2x-4(2)+1=0\ \Rightarrow { x }^{ 2 }+4-2x-8+1=0\\ \Rightarrow { x }^{ 2 }-2x-3=0\ \Rightarrow \left( x-1 \right) \left( x-3 \right) =0\ \Rightarrow x=-1\ or\ 3$$

So, the points where tangents are parallel to $$y-$$ axis

$$={ (-1,2),(3,2) } $$

If the distance of the point on $$y=x^4+3x^2+2x$$ which is nearest to the line $$y=2x-1$$ is p, Find $$5p^2$$.

$$y=x^4+3x^2+2x$$ and $$y=2x-1$$

The distance between the points lying on two curves which is shortest.

$$D=\dfrac { { x }^{ 4 }+{ 3 }x^{ 2 }+2x-2x+1 }{ \sqrt { \left( -2 \right) ^{ 2 }+\left( 1 \right) ^{ 2 } } }$$ ........ (Substitute $$y={ x }^{ 4 }+{ 3 }x^{ 2 }+2x\ in\ y=2x-1)$$

$$ D=\dfrac { { x }^{ 4 }+{ 3 }x^{ 2 }+1 }{ \sqrt { 5 } } $$

Since $$x^4$$ & $$x^2$$ both are squared terms, $$x^4 \ge 0$$ & $$3x^2 \ge 0$$

$$\therefore { D }_{ min }=\dfrac { 0+0+1 }{ \sqrt { 5 } } =\dfrac { 1 }{ \sqrt { 5 } } \\ So,\ p=\dfrac { 1 }{ \sqrt { 5 } } \\ \therefore { 5p }^{ 2 }=5\left( \dfrac { 1 }{ \sqrt { 5 } } \right) ^{ 2 }=5\left( \dfrac { 1 }{ 5 } \right) ={ 1 } $$

If the straight line $$x \ \cos \alpha + y \sin \alpha = p$$ touches the curve $$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1,$$ then prove that $$a^2 \cos^2 \alpha + b^2 \sin^2 \alpha = p^2$$

$$x\cos \alpha +y\sin \alpha =P$$ touches $$\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1$$

then also at that point should be same

$$\to \ \cos \alpha +m \sin \alpha =0$$ or $$\boxed {m=\cot \alpha}---(1)$$

$$\to \ \dfrac {2x}{a^2}+\dfrac {2ym}{b^2}=0$$ or $$\boxed {x=a^2 \dfrac {\cot \alpha y}{b^2}}---(2)$$

put $$(2)$$ in $$(1)$$

$$y\left (\dfrac {a^2 \cos^2 \alpha}{b^2 \sin \alpha} + \sin \alpha \right)=P$$

$$\Rightarrow \ \dfrac {y}{b^2 \sin \alpha} [a^2 \cos^2 \alpha +b^2 \sin^2 \alpha ]=P$$

or $$\boxed {y=\dfrac {Pb^2 \sin \alpha}{a^2 \cos^2 \alpha +b^2 \sin^2 \alpha}} \Rightarrow \ \boxed {x=Pa^2 \cos \alpha \left (\dfrac {1}{a^2 \cos^2 \alpha +b^2 \sin^2 \alpha}\right)}----(3)$$

Put $$(3)$$ back in $$(2)$$

$$\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1\Rightarrow \ \dfrac {P^2a^4 \cos^2 \alpha }{(a^2 \cos^2 \alpha +b^2 \sin^2 \alpha)^2 a^2}+\dfrac {P^4 b^2\sin^2 \alpha}{b^2 (a^2\cos^2\alpha +b^2\sin^2 \alpha)^2}=1$$

$$\Rightarrow \ P^2 (a^2\cos^2\alpha +b^2 \sin^2 \alpha)=(a^2\cos^2\alpha +b^2\sin^2 \alpha )^2$$

$$\Rightarrow \ \boxed {a^2\cos^2\alpha +b^2\sin^2 \alpha =P^2}$$

Prove that the curves $$xy=4$$ and $$x^{2}+y^{2}=8$$ touch each other.

Given curves are

$$xy=4$$ ......$$(1)$$

$$ x^2+y^2=8$$ .....$$(2)$$

We need to find the point of intersection of curves.

From $$(1)$$ $$y=\dfrac{4}{x}$$

Substituting this in $$(2)$$ we get,

$$\Rightarrow x^2+\dfrac{16}{x^2}=8$$

$$\Rightarrow x^4-8x^2+16=0$$

$$\Rightarrow (x^2-4)^2=0$$

$$\Rightarrow x^2=4$$

$$\Rightarrow x=\pm 2$$

Using $$(1)$$ we get $$y=\pm 2$$

Therefore points of intersection are $$(2,2), (-2,-2)$$

Differentiating curve 1 we get

$$\Rightarrow y+x(\dfrac{dy}{dx})=0$$

$$\Rightarrow (\dfrac{dy}{dx})=\dfrac{-y}{x}$$

At $$(2,2),(-2,-2)$$ $$\Rightarrow (\dfrac{dy}{dx})=-1$$

Differentiating curve 2 we get

$$\Rightarrow 2x+2y(\dfrac{dy}{dx})=0$$

$$\Rightarrow (\dfrac{dy}{dx})=\dfrac{-x}{y}$$

At $$(2,2),(-2,-2)$$ $$\Rightarrow (\dfrac{dy}{dx})=-1$$

Thus we can say that the 2 curves touch each other at their point of intersection.

The first derivative of the function
$$\left[ {{{\cos }^{ - 1}}\left( {\sin \sqrt {\frac{{1 + x}}{2}} } \right) + {x^x}} \right]$$
with respect to$$x$$ at $$x=1$$ is

$$u = {\cos ^{ - 1}}\left( {90 - \frac{{{{\cos }^{ - 1/4}}}}{2}} \right)$$
$$ = \frac{1}{{{{\sqrt {1 - \left( {\frac{{90{{\cos }^{ - 1/4}}}}{2}} \right)} }^2}}} \times dx\left( {\frac{{90 - {{\cos }^{ - 1/4}}}}{2}} \right)$$\[V = {x^4}\]
$$ = \frac{{ - 2}}{{\sqrt {4 - {{\left( {90 - {{\cos }^{ - 1/4}}} \right)}^2}} }}\left( {\frac{1}{{\sqrt {1 - {x^2}} }}} \right)$$
$$V = {x^4}$$
$$\log V = x\log x$$
$$\frac{1}{v}\frac{{dv}}{{dx}} = x \times \frac{1}{x} + \log x$$
$$\frac{{dv}}{{dx}} = {x^4}(1 + \log x)$$
$$\frac{{dy}}{{dx}} = \frac{{du}}{{dx}} + \frac{{dv}}{{dx}} = \frac{{ - 2}}{{\sqrt {4 - {{(90 - {{\cos }^{ - 1/4}})}^2}\sqrt {1 - {x^2}} } }} + {x^4}(1 + \cos )$$

Find the value of a for which the function $$f(x)=ax^3-3(a+2)x^2+9(a+2)x-1$$ is decreasing for all $$x\in R$$.

Given, $$f(x)=ax^{3}-3(a+2)x^{2}+a(a+2)x-1$$

A function is decreasing $$\forall x \in \mathbb{R}$$ if $$f'(x) < 0 \forall x\in \mathbb{R}$$

$$f'(x)= 3ax^{2}-6(a+2)x+9(a+2)$$

$$3ax^{2}-6(a+2)x+9(a+2) < 0$$

$$\Rightarrow ax^{2}-2(a+2)x+3(a+2) < 0 \forall x\in \mathbb{R}$$

This is possible only where its discriminant

is less than zero and coefficient of $$x^{2}$$ is less

than zero.

$$\Rightarrow \triangle < 0$$ & $$a < 0$$

$$\Rightarrow 4(a+2)^{2}-4a.3(a+2) < 0$$ & $$a < 0$$

$$\Rightarrow a^{2}+4a+4-3a^{2}-6a < 0$$ & $$a < 0$$

$$\Rightarrow -2a^{2}-2a+4 < 0$$ & $$a < 0$$

$$\Rightarrow a^{2}+a-2 > 0$$ & $$a < 0$$

$$\Rightarrow a^{2}+2a- a-2 > 0$$ & $$a < 0$$

$$\Rightarrow (a+2)(a-1) > 0$$ & $$a < 0$$

$$\Rightarrow a < -2$$ or $$a > 1$$ & $$a < 0$$.

$$\Rightarrow a < -2$$.

$$\therefore a < -2$$ makes $$f(x)$$ decreasing function

$$\forall x \in \mathbb{R}$$

1104137_1111147_ans_b086f4f92288496fa80c0bbb9b681206.jpg

To find the point on the curve $$y=x^3-9x^2+15x+3$$ at which the tangents are parallel to the x-axis.

$$y={ x^{ 3 } }-q{ x^{ 2 } }+15x+3\to (i) \\ when\, \, \tan gent\, \, are\, \, parallel\, to\, \, x-axis \\ Then,\, \, dy/dx=0 \\ differentiate\, \, w.r\, \, to\, x \\ \Rightarrow dy/dx=3{ x^{ 2 } }-18x+15+0 \\ \Rightarrow dy/dx=0,\, \, 3{ x^{ 2 } }-18x+15=0,\, \, { x^{ 2 } }-6x+5=0 \\ \Rightarrow { x^{ 2 } }-5x-x+5=0x\left( { x-5 } \right) -1\left( { x-5 } \right) =0 \\ at\, x=1 \\ x=1\, \, or\, \, x=5 \\ Putting\, \, in\, \, equation\, \, (i) \\ y=1-9\times 1+15\times 1+3=10\, \, and \\ y={ 5^{ 3 } }-9\times 25+15\times 5+3=22\, \, \, \, $$

The normal to the curve $$5x^{5}-10x^{3}+x+2y+6=0$$ at the point $$P\left(0,-3\right)$$ is tangent to the curve at some other points. Find those points?

$$Y=5x^{5}+10x^{3}+x+2y+6$$

let y=$$\frac{5x^{5}}{2}+5x^{3}-\frac{x}{2}-3$$

Differentiating w.r.tx

$$y= \frac{-25x^{4}}{2}+15x^{2}-\frac{1}{2}$$

substituting (0,-3)

$$y=\frac{25(0)}{2}^{4}+15(0)\frac{-1}{2}$$

$$=\frac{-1}{2}$$

slope of tangent is $$\frac{-1}{2}$$

equation is

$$y=\frac{-1}{2}x+c$$

It passes through$$ (0,-3)$$

$$\therefore c = -3$$

$$\Rightarrow y $$=\frac-1}{2}$$ x-3$$

solving equation with the carve, we obtain

$$5x^{5}-10x^{3}=0$$

$$\Rightarrow x^{3}(x^{2})=0$$

$$so, x=0,\sqrt{2},\sqrt{-2}$$

points are

$$(0,-3,) (\sqrt{2},\frac{-1 } {\sqrt{2}}-3),(\sqrt{-2},\frac{1}{\sqrt{2}}-3)$$

1211709_1376008_ans_adbb03e191794a699fc3751edbdc905c.jpg

Prove that the function $$f$$ given by $$f(x)=x^{2}-x+1$$ is neither strictly increasing nor strictly decreasing on $$(-1,1)$$.

Let $$f\left(x\right)={x}^{2}-x+1$$ for $$x\in\left(-1,1\right)$$

$$\Rightarrow {f}^{\prime}{\left(x\right)}=2x-1$$

$$\Rightarrow {f}^{\prime}{\left(x\right)}=0\Rightarrow 2x-1=0$$

$$\Rightarrow x=\dfrac{1}{2}$$

Since $$x\in\left(-1,1\right)$$.The point $$x=\dfrac{1}{2}$$ divide the intervals $$\left(-1,1\right)$$ into two disjoint intervals.

$$\left(-1,\dfrac{1}{2}\right)$$ and $$\left(\dfrac{1}{2},1\right)$$

Let $$-1<x<\dfrac{1}{2}\Rightarrow x=0\in\left(-1,\dfrac{1}{2}\right)$$

$$\Rightarrow {f}^{\prime}{\left(0\right)}=2\left(0\right)-1=-1<0$$

$$\therefore f\left(x\right)$$ is strictly decreasing.

$$\left(\dfrac{1}{2},1\right)$$ and $$\left(\dfrac{1}{2},1\right)$$

Let $$-1<x<\dfrac{1}{2}\Rightarrow x=0.7\in\left(\dfrac{1}{2},1\right)$$

$$\Rightarrow {f}^{\prime}{\left(0.7\right)}=2\left(0.7\right)-1=0.4>0$$

$$\therefore f\left(x\right)$$ is strictly increasing.

Hence $${f}^{\prime}{\left(x\right)}<0$$ for $$x\in\left(-1,\dfrac{1}{2}\right)$$

and $${f}^{\prime}{\left(x\right)}>0$$ for $$x\in\left(\dfrac{1}{2},1\right)$$

Hence $$f\left(x\right)$$ is neither decreasing nor increasing on $$\left(-1,1\right)$$

Hence proved.

If the area of the triangle included between the axes and any tangent to the curve $$x^{n}y=a^{n}$$ is constant, then find the value of n .

1769125_1757335_ans_ce1b6d9e66574ceca35f088e0f39587b.jpg

A curve is defined parametrically be equations $$x=t^2$$ and $$y=t^3 .$$ A variable pair of perpendicular lines through the origin $$O$$ meet the curve of $$P$$ and $$Q .$$ If the locus of the point of intersection of the tangents at $$P$$ and $$Q$$ is $$ay^2=bx-1$$, then the value of $$(a+b)$$ is

1782045_1758709_ans_01af341906454f9583d3616628f911b5.jpeg

Find the equation of a curve which is passing through the point $$(1,1)$$. If the perpendicular distance of the origin from the normal at any point $$P(x,\ y)$$ of the curve is equal to the distance of $$P$$ form the $$x-axis.$$

Let the equation of normal at $$P(x,y)$$ be $$Y-y=\dfrac{-dx}{dy}(X-x),$$i.e.,

$$Y+X \dfrac{dx}{dy} - \left(y+x\dfrac{dx}{dy} \right)=0....(1)$$

Therefore, the length of perpendicular from origin to $$(1)$$ is $$\dfrac{ y+x\dfrac{dx}{dy} }{\sqrt{1+ \left(\dfrac{dx}{dy}\right)^2 } }...(2)$$

Also, distance between $$P$$ and $$x-axis$$ is $$|y|$$. Thus, we get

$$\dfrac{ y+x\dfrac{dx}{dy} }{\sqrt{1+ \left(\dfrac{dx}{dy}\right)^2 } }=|y|$$

$$\Rightarrow \left(y+x\dfrac{dx}{dy} \right)^2$$=$$y^2 \left[1+\left(\dfrac{dx}{dy}\right)^2 \right]$$

$$\Rightarrow \dfrac{dx}{dy} \left[ \dfrac{dx}{dy} (x^2-y^2)+2xy \right]=0 \Rightarrow \dfrac{dx}{dy}=0$$

or $$ \dfrac{dx}{dy}=\dfrac{2xy}{y^2-x^2}$$

Case $$i:$$ $$\dfrac{dx}{dy}=0\Rightarrow dx =0$$

Integrating both sides, we get $$x=k,$$ subsituting $$x=1$$, we get $$k=1$$.

Therefore, $$x=1$$ is the equation of curve (not possible, so rejected).

Case $$II:$$ $$\dfrac{dx}{dy}=\dfrac{2xy}{y^2-x^2} \Rightarrow \dfrac{dx}{dy}=\dfrac{y^2-x^2}{2xy}$$

substituting $$y=vx$$, we get

$$v+x \dfrac{dv}{dx}=\dfrac{v^2 x^2 -x^2}{2vx^2} \Rightarrow x.\dfrac{dv}{dx}- \dfrac{v^2-1}{2v}-v\ \ x.\dfrac{dv}{dx}= \dfrac{v^2-1}{2v}-v$$

$$=\dfrac{-(1+v^2)}{2v} \Rightarrow\dfrac{2v}{1+v^2}dv=\dfrac{-dx}{x}$$

Integrating both sides, we get

$$\log (1+v^2)= - \log x+ \log c \Rightarrow \log (1+v^2)(x)=\log c (1+v^2)x=c$$

$$\Rightarrow x^2+y^2=cx$$. Subsituting $$x=1,\ y=1,$$ we get $$c=2$$

Therefore, $$x^2+y^2-2x=0$$ is the required equation.

Find the critical numbers of $$f(x)=\sin\,x$$

Given: $$f(x)=\sin\,x$$

To find: critical numbers

In order to find critical number, we equate derivatives of function to $$0$$.

$$\therefore f'(x)=\cos \,x$$

$$\cos x=0$$ $$\therefore x=(2x+1)\dfrac{\pi}{2}$$, $$n\epsilon I$$

Therefore, $$\dfrac{\pi}{2},\dfrac{3\pi}{2},\dfrac{-5\pi}{2},\dfrac{-7\pi}{2},------$$ etc.

Application Of Derivatives - Class 12 Commerce Maths - Extra Questions

Find the equation of tangent in $$1^{\mathrm{s}\mathrm{t}}$$ quadrant to the circle $$\mathrm{x}^{2}+\mathrm{y}^{2}=16$$ at $$(2,2 \sqrt 3)$$

Find the slope of the tangent to curve $$y = x^3- x + 1$$ at the point whose $$x$$-coordinate is $$2$$.

Find the slope of the tangent to the curve $$y = 3x^4- 4x$$ at x = 4.

Show that the function given by $$f(x) = \sin x$$ is (a) strictly increasing in $$\left ( 0, \dfrac{\pi}{2} \right )$$ (b) strictly decreasing in $$\left ( \dfrac{\pi}{2}, \pi \right )$$ (c) neither increasing nor decreasing in $$(0, \pi)$$.

Show that the tangents to the curve $$y = 7x^3+ 11$$ at the points where $$x = 2$$ and $$x = -2$$ are parallel.

Find the slope of the tangent to the curve $$y = x^3-3x + 2$$ at the point whose $$x$$ coordinate is $$3$$.

Find the slope of the tangent at $$(1,2)$$ on the curve $$y={ x }^{ 2 }-4x+5$$.

Find the slope of tangent to the curve $$y=3x^2-6$$ at the point on it whose x-coordinate is 2.

Write the differential equation representing the family of curves $$y=mx$$, where m is an arbitrary constant.

Find the slope of the tangent to the curve $$y=\dfrac{x-1}{x-2}, x\ne 2$$ at $$x=10$$.

If the tangent to the curve $$y = {x}^{3} + ax + b$$ at $$(1, -6)$$ is parallel to the line $$x - y + 5 = 0$$, find $$a$$ and $$b$$.

Find the points on curve $$y=x^3-11x+5$$ at which equation of tangent is $$y=x-11$$.

Find the equations of the common tangents to the parabolas $$\displaystyle y \, = \, x^2 \, - \, 5x \, + \, 6 \, and \, y \, = \, x^2 \, + \, x \, + \, 1.$$

Find the equation of the tangent at origin to the curve $$y=x^{{\cfrac{3}{2}}}$$.

Find the points at which the tangent to the curve $$\displaystyle y \, = \, x \, - \, 0.5 \, sin \, 2x \, - \, 0.5 \, cos \, 2x \, + \, 16 \, cos \, x$$ is parallel to the abscissa axis.

Find the co-ordinates of the points on the ellipse $$x^2+2y^2=9$$ at which tangent has slope $$\dfrac{1}{4}$$. Also find the equation of normal.

If the slope of tangent of $$xy+ax+by=2$$ at point $$(1,1)$$ is $$5$$ then find the values of $$a$$ and $$b$$.

Using differentiation, find the approximate value of each of the following:a) $${\dfrac {17}{81}}^{\dfrac {1}{4}}$$b) $${(33)}^{-\dfrac {1}{5}}$$

Find the equation of the tangent to the curve $$y\, = \,\sqrt {3x\, - \,2} $$ which is parallel to the line $$4x\, - \,2y\, + \,5\, = 0$$.Further find the equation of the normal to the curve.

Find the maxima of function $$8-7x^2$$

If $$ a,b,c$$ are real number, then find the intervals in which $$f\left( x \right) = \left| {\begin{array}{*{20}{c}} {x + {a^2}}&{ab}&{ac} \\ {ab}&{x + {b^2}}&{bc} \\ {ac}&{bc}&{x + {c^2}} \end{array}} \right|$$ is increasing or decreasing.

Find the slope of tangent and normal to the curve $${x^2} + 2y + {y^2} = 0$$ at $$(-1 , 2)$$

Find the equation of the tangent and normal to the curves(i) $$y = {x^2} - 4x - 5$$ at $$x = - 2$$(ii) $$y = x - \sin x\cos x$$(iii) $$y = 2{\sin ^2}3x\,$$ at $$x = \frac{\pi }{6}$$

Find the stationary point of $$y=x^2+5x-6$$.

Slope of the normal to the curve $$6y^{4}=ax^{3}+bx$$ at $$(1,-1)$$ is $$\dfrac{1}{2}$$. Solve the values of $$a$$ and $$b$$.

Find Stationary points of $$f\left( x \right) = \sin x$$, where $$0 < x < 2\pi $$

Show that the tangents to the curve $$y=2x^3-3$$ at the points where $$x=2$$ and $$x=-2$$ are parallel.

Find the equation of all lines having slope 2 which are tangents to the curve $$y=\dfrac{1}{x-3}, x\neq 3$$.

The normal lines to a given curve at each point pass through (2,0). The curve passes through (2,3). Formulate the differential equation and hence find out the equation of the curve.

Prove that the tangent drawn at any point to the curve $$f(x)= x^{5}+3x^{3}+4x+8$$ would make an acute angle with $$x$$-axis.

Find the approximate value of f(3.02), where $$f(x)=3x^2+5x+3$$.

The slope of the tangent to a curve at any point is reciprocal of twice the ordinate of that point. The curve passes through (4,3). Formulate the differential equation and hence find the equation of the curve.

Find the intervals in which $$f(x)=2x^3+x^2-20x$$ is increasing and decreasing.

Prove that $$f(x)=ax+b$$, where $$a,b$$ are constants and $$a<0$$ is strictly decreasing function on $$R$$.

A stone is dropped into a quiet lake and waves move in a circle at a speed of $$3.5$$ cm/sec. At the instant when the radius of the circular wave is $$7.5$$ cm, how fast is the enclosed area increasing ?

At what point of the curve $$y=x^2$$ does the tangent make an angle of $$45^o$$ with the $$x$$-axis?

Find the slopes of the tangent and the normal to the following curves at the indicated points.$$x=a\cos^3\theta, y=a\sin^3\theta$$ at $$\theta =\pi/4$$.

Prove that $$f(x)=ax+b$$, where $$a,b$$ are constants and $$a> 0$$ is an increasing function on $$R$$.

Find the slope of the tangent to the curve $$x=t^2+3t-8, y=2t^2-2t-5$$ at $$t=2$$.

Find the slopes of the tangent and the normal to the following curves at the indicated points.$$x=a(1-\cos\theta)$$ and $$y=a(\theta+\sin\theta)$$ at $$\theta =\pi/2$$.

The diagram shows the curve with equation $$y=4x^{\frac{1}{2}}$$.The tangent to the curve at a point T is parallel to AB. Find the coordinates of T.Equation of line AB is is y=x+3.

Find the slopes of the tangent and the normal to the following curves at the indicated points.$$xy=6$$ at $$(1, 6)$$.

Find the slopes of the tangent and the normal to the following curves at the indicated points.$$x^2+3y+y^2=5$$ at $$(1, 1)$$.

Find the slope of the normal to the curve $$x=a\cos^3 \theta, y=a\sin^3 \theta$$ at $$\theta =\dfrac{\pi}{4}$$.

At what points on the following curve, is the tangent parallel to $$x$$-axis?$$y=12(x+1)(x-2)$$ on $$[-1,2]$$

Find the slope of the tangent to the curve$$y=(x^{3}-x)$$ at $$x=2$$

Find the slope of the tangent to the curve $$y=x^3-3x+2$$ at the point whose $$x$$ coordinate is 3.

Find the values of $$b$$ for which the function $$f(x)=\sin x-bx+c$$ is a decreasing function on $$R$$.

Find $$a$$ for which $$f(x)=a(x+\sin x)+a$$ is increasing on $$R$$.

If the tangent line at a point $$(x, y)$$ on the curve $$y=f(x)$$ is parallel to y-axis, find the value of $$\dfrac{dx}{dy}$$.

Find the equation of the normal to the curve $$y=2x^2+3 \sin x $$at $$x=0$$.

Let $$f(x)=ax^3+bx^2+cx+d \sin x$$. If the condition that f(x) is always one-one function is $$b^t < ka(c-|d|)$$ Find $$k+t$$

The number of critical points for $$ \left( x+3 \right) { \left( 3x-2 \right) }^{ 5 }{ \left( 7-x \right) }^{ 3 }{ \left( 5x+8 \right) }^{ 2 }\ge 0$$ is

$$\displaystyle y^{2}=8x$$ and $$\displaystyle x^{2}=4y-12.$$ both touch each other at (k,m).Find $$k+m$$?

Let the abscissa of the point on the curve $$\displaystyle ay^{2}= x^{3},$$ the normal at which cuts off equal intercepts from the axes be ka/m. Find $$m-k$$?

If the critical point as well as stationary point of the function $$f(x)\, =\, \displaystyle \frac{e^x}{x}$$ is $$x=a$$, then value of $$a$$ is:

Find the intervals in which the following functions are strictly increasing or decreasing: (a) $$x^2 + 2x - 5$$(b) $$ 10- 6x -2x^ 2$$(c) $$-2x^3 - 9x^2 - 12x + 1$$(d) $$6-9x-x^2$$(e) $$f(x)=(x + 1)^3(x - 3)^3 $$

Find the intervals in which the function $$f$$ given by $$f(x) = 2x^3- 3x^2 -36x + 7$$ is (a) strictly increasing (b) strictly decreasing.

Find the slope of the normal to the curve $$x =1 - a \sin \theta, y = b \cos^2 \theta $$ at $$\theta =\dfrac{\pi}{2}$$.

Find points at which the tangent to the curve $$y = x^3 - 3x^2 -9x + 7$$ is parallel to the $$x$$-axis.

Find a point on the curve $$y = (x - 2)^2$$ at which the tangent is parallel to the chord joining the points $$(2, 0)$$ and $$(4, 4)$$.

Find points on the curve $$\displaystyle \frac{x^2}{9}+\frac{y^2}{16}=1$$ at which the tangents are(i) Parallel to $$x$$-axis .(ii) Parallel to $$y$$-axis.

Prove that the function $$f$$ given by $$f (x) = \log \cos x$$ is strictly decreasing on $$\left ( 0, \dfrac{\pi}{2} \right )$$and strictly increasing on $$\left ( \dfrac{\pi}{2}, \pi \right )$$.

Find the points on the curve $$y = x^3$$ at which the slope of the tangent is equal to the $$y$$ coordinate of the point.

Find the slope of the normal to the curve $$x = a \cos^3 \theta , y = a \sin^3 \theta$$ at $$\theta =\cfrac{\pi}{4}$$.

Find the point on the curve $$y = x^3-11x + 5$$ at which the tangent is $$y = x -$$

Find the slope of the tangent to the curve $$y=\cfrac{x-1}{x-2}, x\neq 2$$ at $$x=10.$$

Find the values of $$x$$ for which $$y = [x(x - 2)]^2$$ is an increasing function.

If the radius of a sphere is measured as $$9\ m$$ with an error of $$0.03\ m$$, then find the approximate error in calculating in surface area.

Find the points on the curve $$x^2+ y ^2-2x -3 = 0$$ at which the tangents are parallel to the $$x$$-axis.

Using differentials, find the sum of digits approximate value of the following up to $$3$$ places of decimal.$$(0.999)^{\tfrac{1}{10}}$$

If the radius of a sphere is measured as $$7 m$$ with an error of $$0.02m$$, then find the approximate error in calculating its volume.

Using differentials, find the approximate value of the following up to $$3$$ decimal places.$$\sqrt {49.5}$$

Show that $$y=\log { \left( 1+x \right) } -\cfrac { 2x }{ 2+x } ,x>-1$$, is an increasing function of $$x$$ throughout its domain.

Using differentials, find the sum of digits approximate value of the following up to $$3$$ places of decimal.$$(0.999)^{\tfrac{1}{3}}$$

Using differentials, find the sum of digits approximate value of the following up to $$3$$ places of decimal.$$(26)^{\tfrac{1}{3}}$$

Find the approximate value of $$f (2.01)$$, where $$f (x) = 4x^2 + 5x + 2$$.

Find the intervals in which the function $$f$$ given by $$f(x) ={x}^{3}+\cfrac{1}{{x}^{3}}$$, $$x\ne 0$$ is(i) increasing (ii) decreasing.

Let $$f$$ be function defined on $$[a,b]$$ such that $$f'(x)> 0$$, for all $$x\in (a,b)$$. Then prove that $$f$$ is an increasing function on $$(a,b)$$.

Using differentiation, find the approximate value of each of the following:
a) $${\dfrac {17}{81}}^{\dfrac {1}{4}}$$
b) $${(33)}^{-\dfrac {1}{5}}$$

Find the equation of the tangent to the curve $$y\, = \,\sqrt {3x\, - \,2} $$ which is parallel to the line $$4x\, - \,2y\, + \,5\, = 0$$.
Further find the equation of the normal to the curve.

Find the equation of the tangent and normal to the curves

(i) $$y = {x^2} - 4x - 5$$ at $$x = - 2$$
(ii) $$y = x - \sin x\cos x$$
(iii) $$y = 2{\sin ^2}3x\,$$ at $$x = \frac{\pi }{6}$$

Find the slopes of the tangent and the normal to the following curves at the indicated points.
$$x=a\cos^3\theta, y=a\sin^3\theta$$ at $$\theta =\pi/4$$.

Find the slopes of the tangent and the normal to the following curves at the indicated points.
$$x=a(1-\cos\theta)$$ and $$y=a(\theta+\sin\theta)$$ at $$\theta =\pi/2$$.

The diagram shows the curve with equation $$y=4x^{\frac{1}{2}}$$.
The tangent to the curve at a point T is parallel to AB. Find the coordinates of T.Equation of line AB is is y=x+3.

Find the slopes of the tangent and the normal to the following curves at the indicated points.
$$xy=6$$ at $$(1, 6)$$.

Find the slopes of the tangent and the normal to the following curves at the indicated points.
$$x^2+3y+y^2=5$$ at $$(1, 1)$$.

At what points on the following curve, is the tangent parallel to $$x$$-axis?
$$y=12(x+1)(x-2)$$ on $$[-1,2]$$

Find the slope of the tangent to the curve
$$y=(x^{3}-x)$$ at $$x=2$$

Find the intervals in which the following functions are strictly increasing or decreasing:
(a) $$x^2 + 2x - 5$$
(b) $$ 10- 6x -2x^ 2$$
(c) $$-2x^3 - 9x^2 - 12x + 1$$
(d) $$6-9x-x^2$$
(e) $$f(x)=(x + 1)^3(x - 3)^3 $$

Find points on the curve $$\displaystyle \frac{x^2}{9}+\frac{y^2}{16}=1$$ at which the tangents are
(i) Parallel to $$x$$-axis .
(ii) Parallel to $$y$$-axis.

Using differentials, find the sum of digits approximate value of the following up to $$3$$ places of decimal.
$$(0.999)^{\tfrac{1}{10}}$$

Using differentials, find the approximate value of the following up to $$3$$ decimal places.
$$\sqrt {49.5}$$

Using differentials, find the sum of digits approximate value of the following up to $$3$$ places of decimal.
$$(0.999)^{\tfrac{1}{3}}$$

Using differentials, find the sum of digits approximate value of the following up to $$3$$ places of decimal.
$$(26)^{\tfrac{1}{3}}$$

Find the intervals in which the function $$f$$ given by $$f(x) ={x}^{3}+\cfrac{1}{{x}^{3}}$$, $$x\ne 0$$ is
(i) increasing (ii) decreasing.

Show that the normal at any point $$\theta$$ to the curve
$$x=a\cos{\theta}+a\theta \sin{\theta}$$, $$y=a\sin{\theta}-a\theta \cos{\theta}$$ is at constant distance from the origin.

(i) Find the critical numbers of $${ x }^{ \frac { 3 }{ 5 } }\left( 4-x \right) $$
(ii) Determine the domain of convexity of $$y={ e }^{ x }$$

Find the critical points of the following functions and test them for their maxima and minima.
$$\displaystyle\, f(x) \, =\, \frac{x^2 \, -\, 3x\, +\, 2}{x^2\, +\, 3x\, +\, 2}$$

Find the critical points of the following functions.
$$y \, = \, \dfrac{x^3}{3} \, + \, 2x^2 \, - \, 5x \, + \, 4$$

Find the critical points of the following functions and test them for their maxima and minima.
$$\displaystyle\, f(x) = \frac{x^2}{17} - \ln(x^28)$$

Find the critical points of the following function and test them for their maxima and minima.
$$\displaystyle\, y \, = \, x^4 \, -\, 10x^2 \, +\, 9$$

Find the critical points of the following function and test them for their maxima and minima.
$$\displaystyle f(x) \, = \, 3x^4 \, - \, 4x^3$$

Check monotonocity at following points for
(i) $$f(x) = x^3-3x +1$$ at $$x= -1, 2$$
(ii)$$ f(x) =|x -1| +2 | x- 3| -| x+2| $$at $$ x= -2, 0, 3, 5$$

Find points on the curve $$\dfrac {x^{2}}{9}+\dfrac {y^{2}}{16}=1$$at which tangents are
parallel to $$y-$$axis

The diagram shows part of the curve $$y=\dfrac{1}{16}(3x-1)^2$$, which touches the x-axis at the point P. The point $$Q(3,4)$$ lies on the curve and the tangent to the curve at $$Q$$ crosses the x-axis at $$R$$.
State the x-coordinate of $$P$$.

The diagram shows part of the curve with equation $$y=\sqrt{(x^3+x^2)}$$. The shaded region is bounded by the curve, the x-axis and the line $$x=3$$.
P is the point on the curve with x-coordinate $$3$$. Find the y-coordinate of the point where the normal to the curve at P crosses the y-axis.

A curve has equation $$y=(2x-1)^{-1}+2x$$. $$x\neq\dfrac{1}{2}$$
Find the x-coordinates of the stationary points

Find the slopes of the tangent and the normal to the following curve at the indicated point.
$$y=\sqrt{x^3}$$ at $$x=4$$.