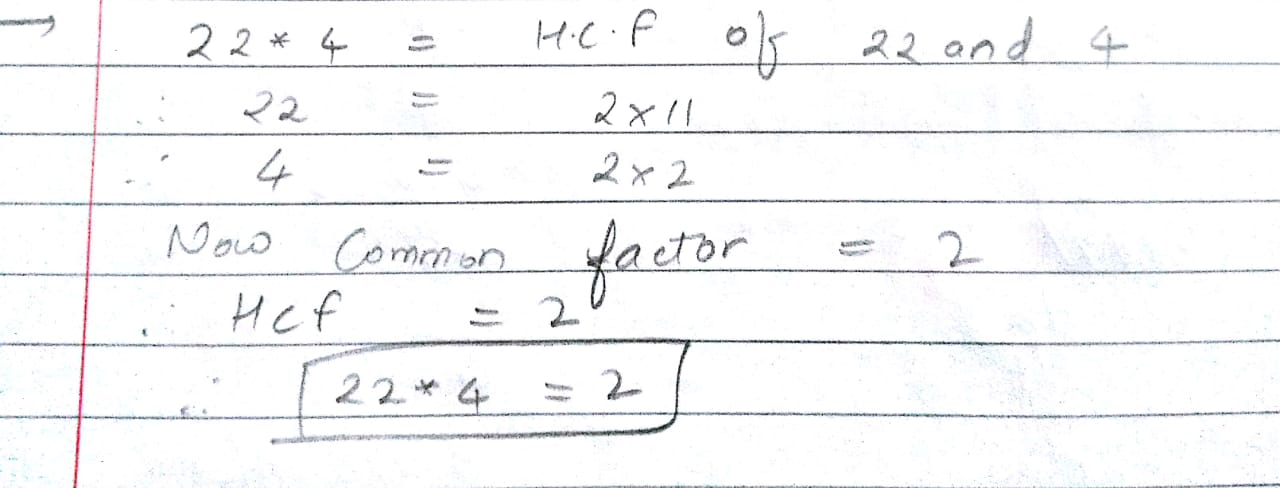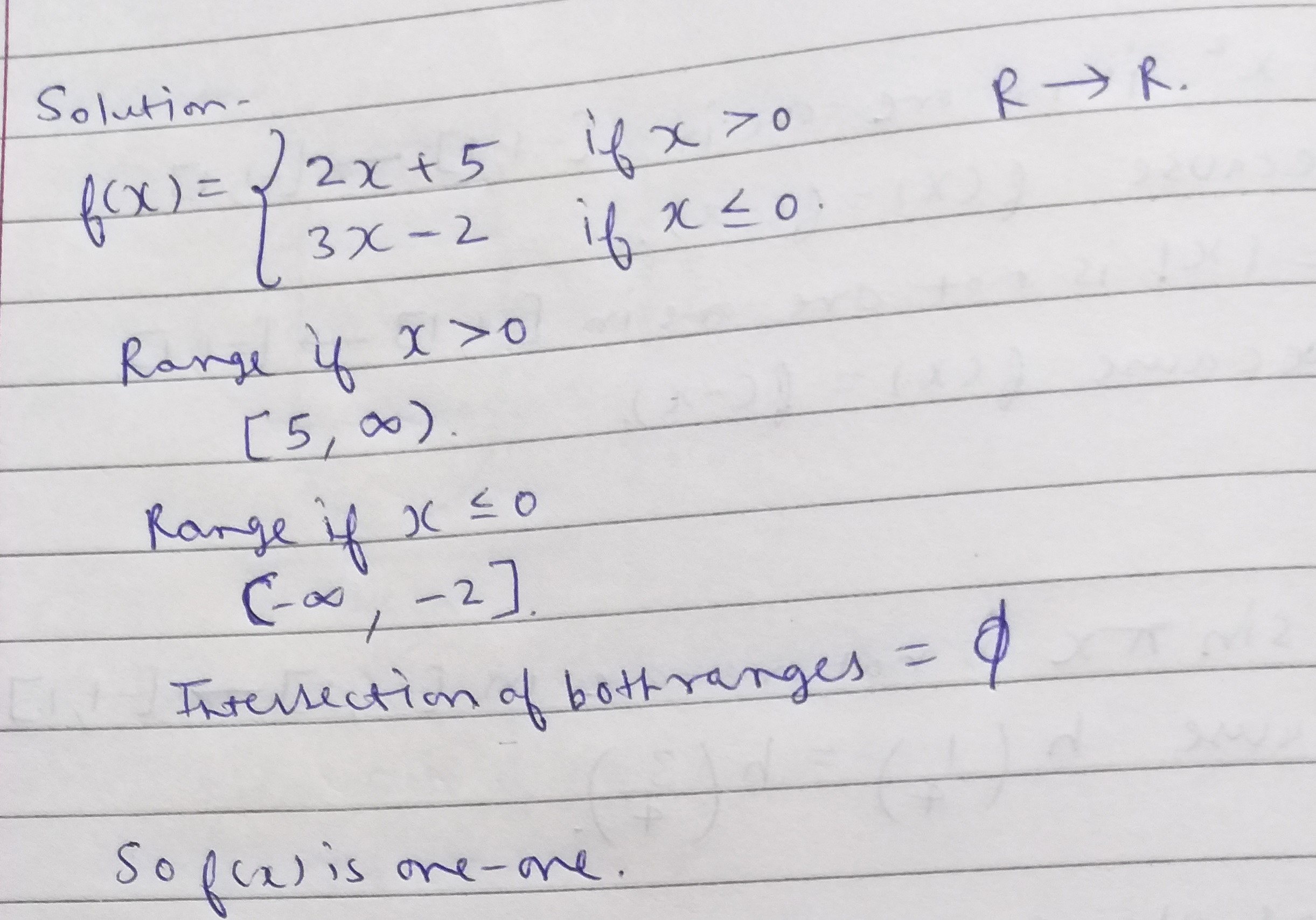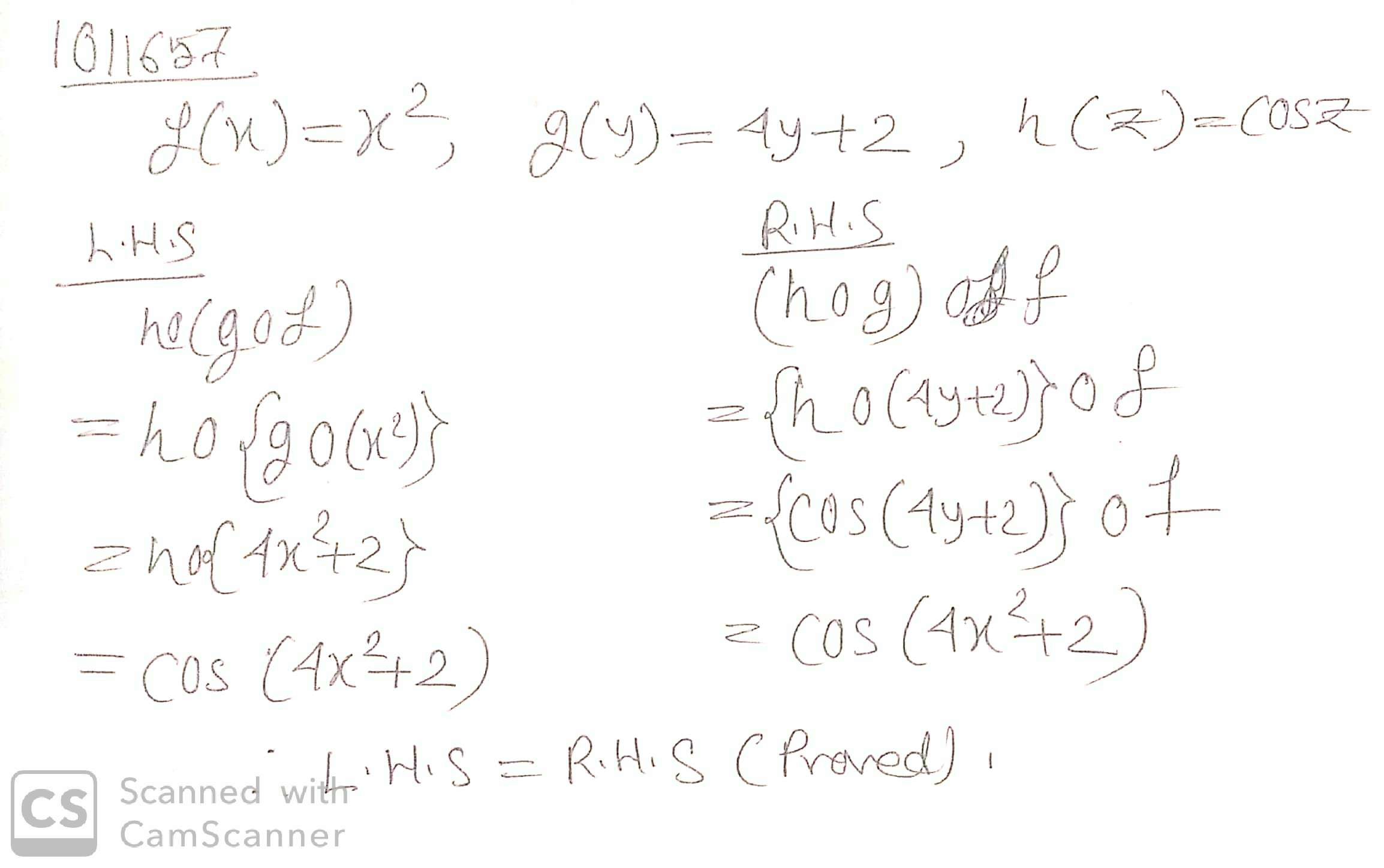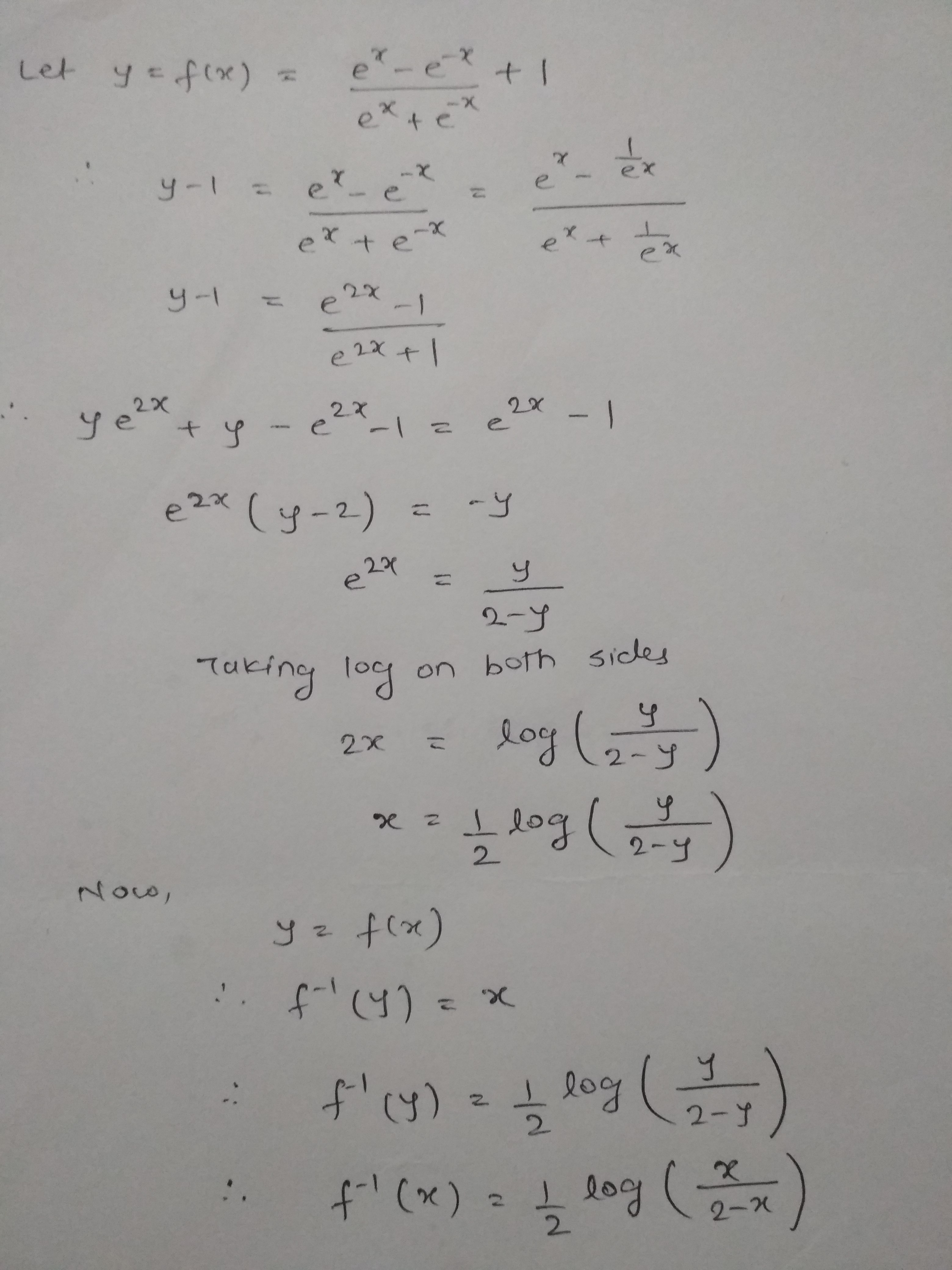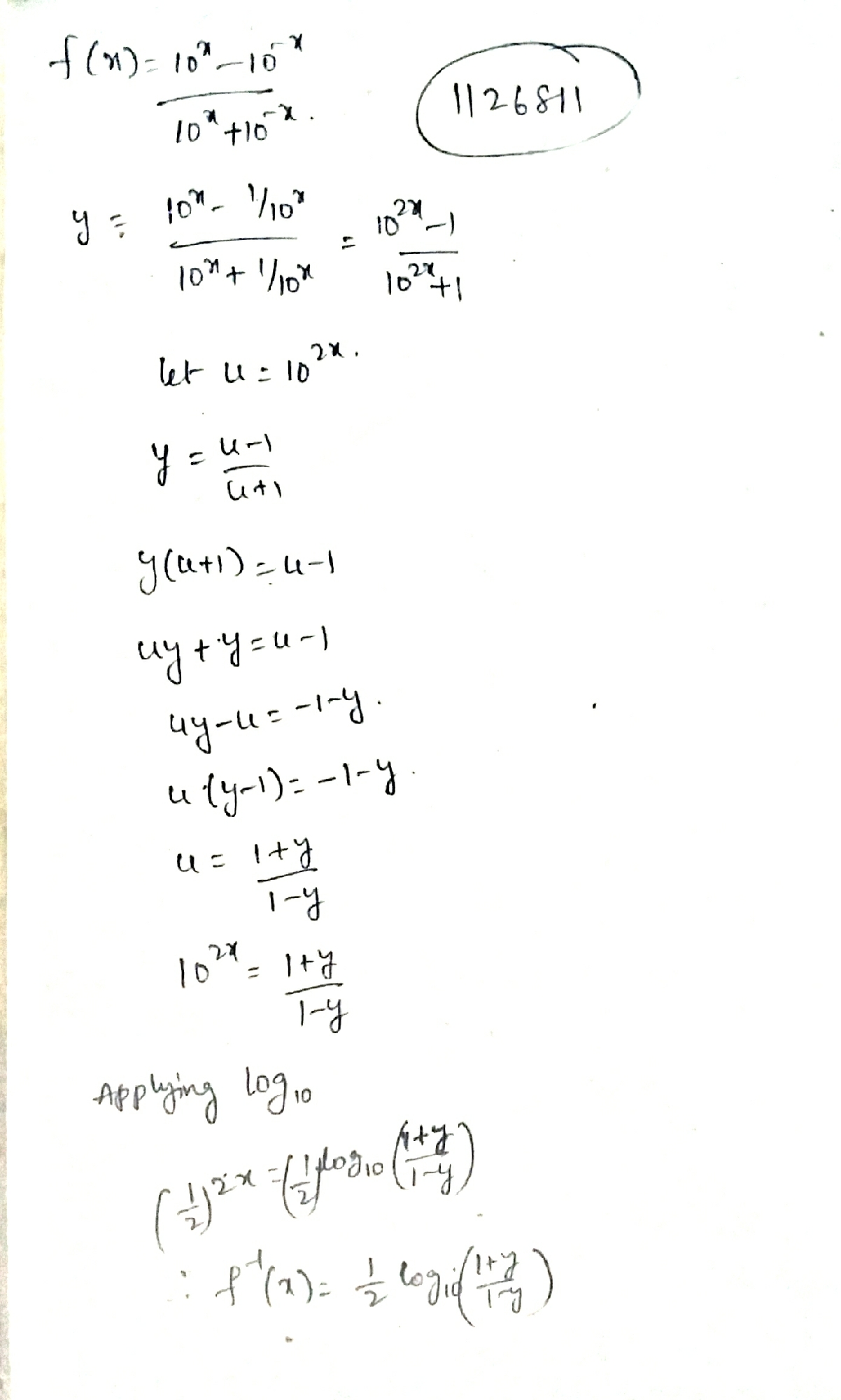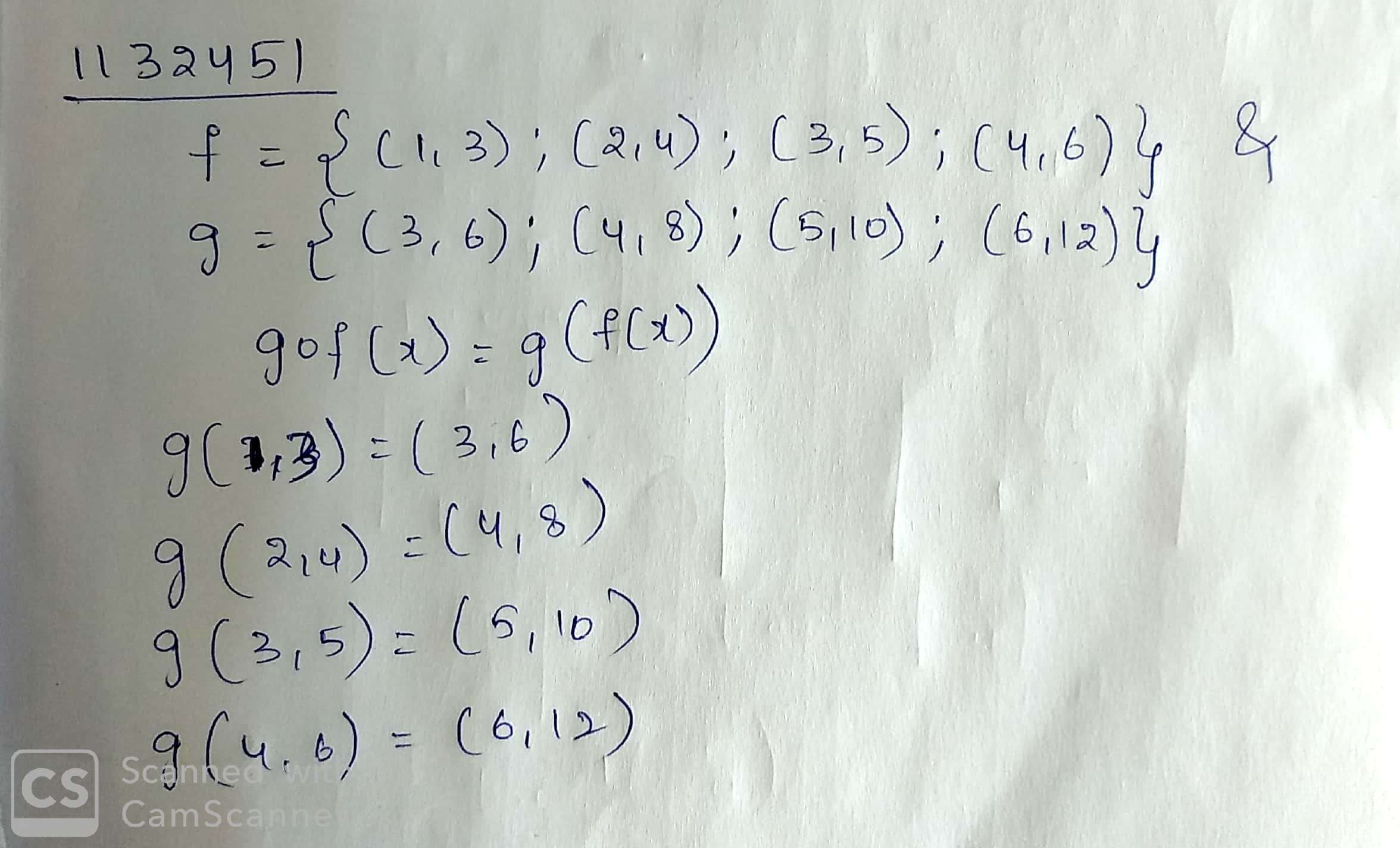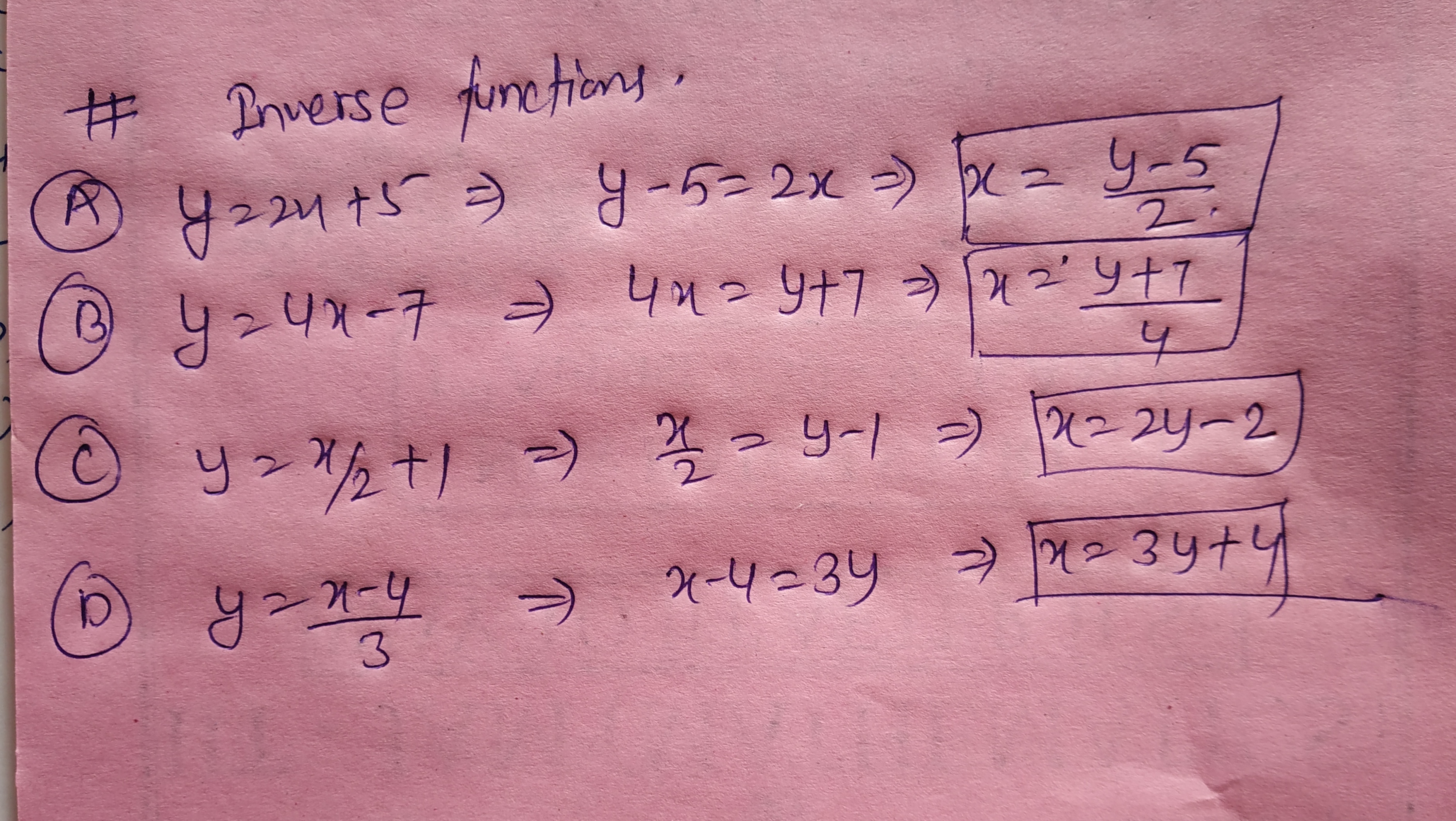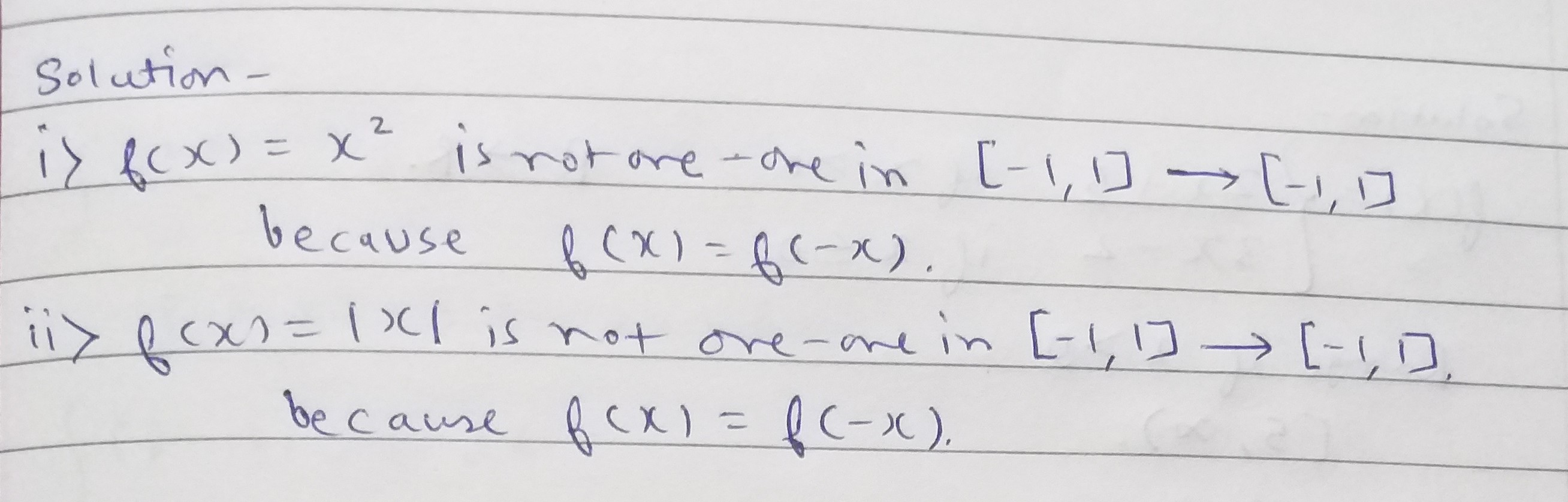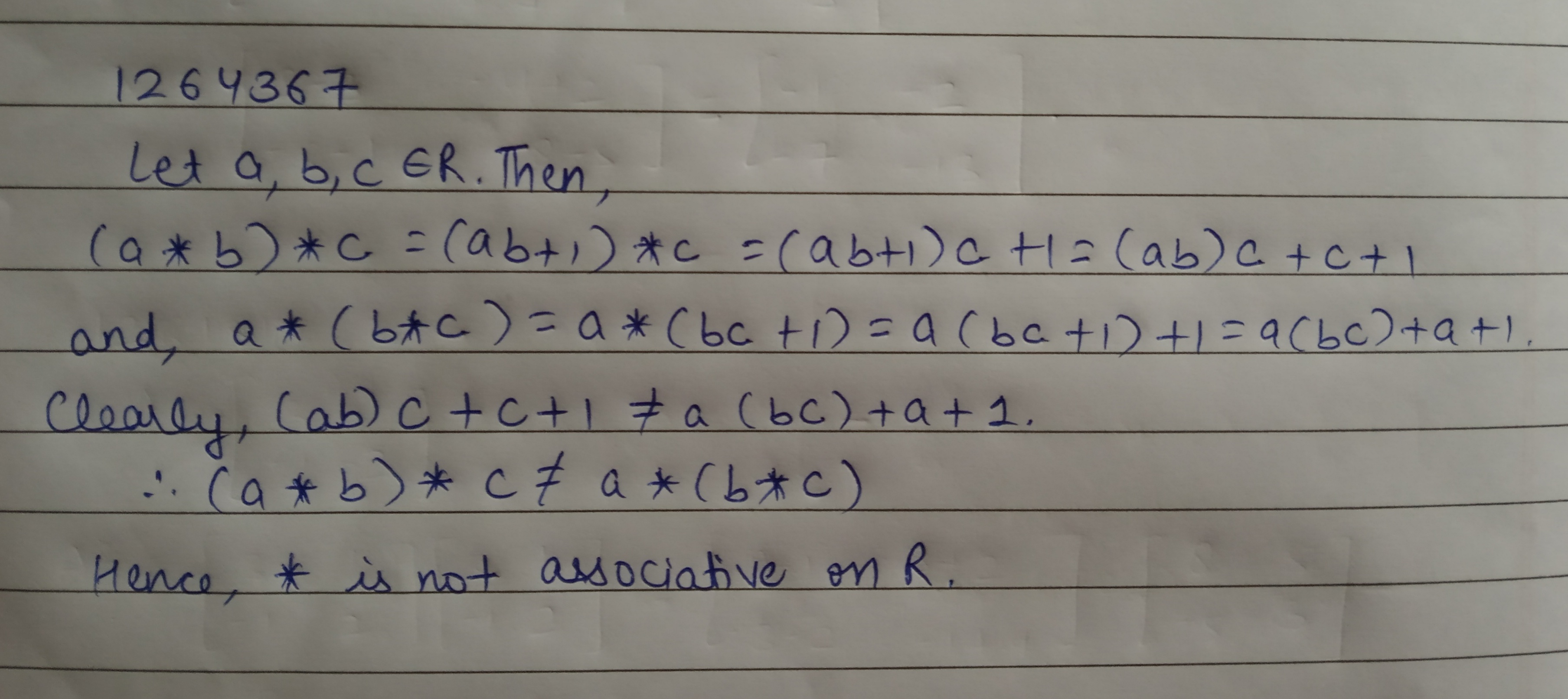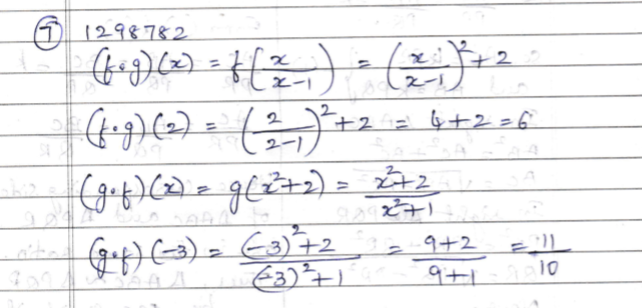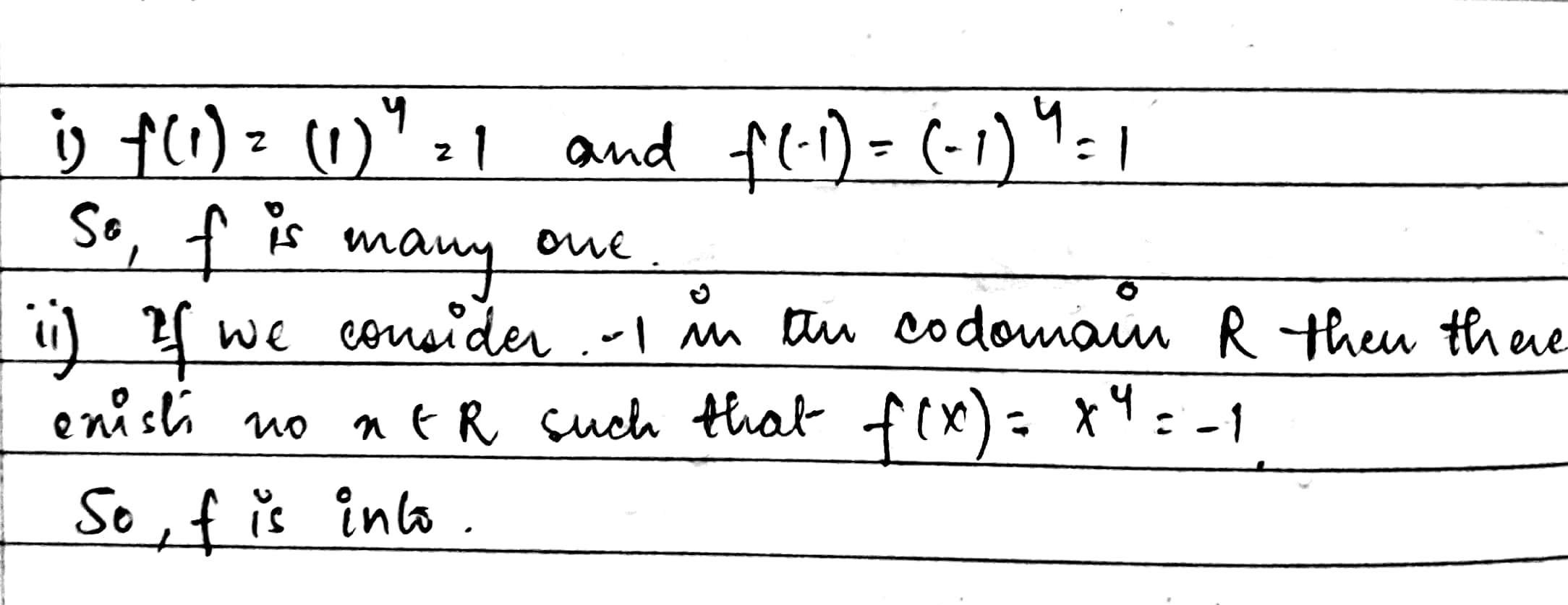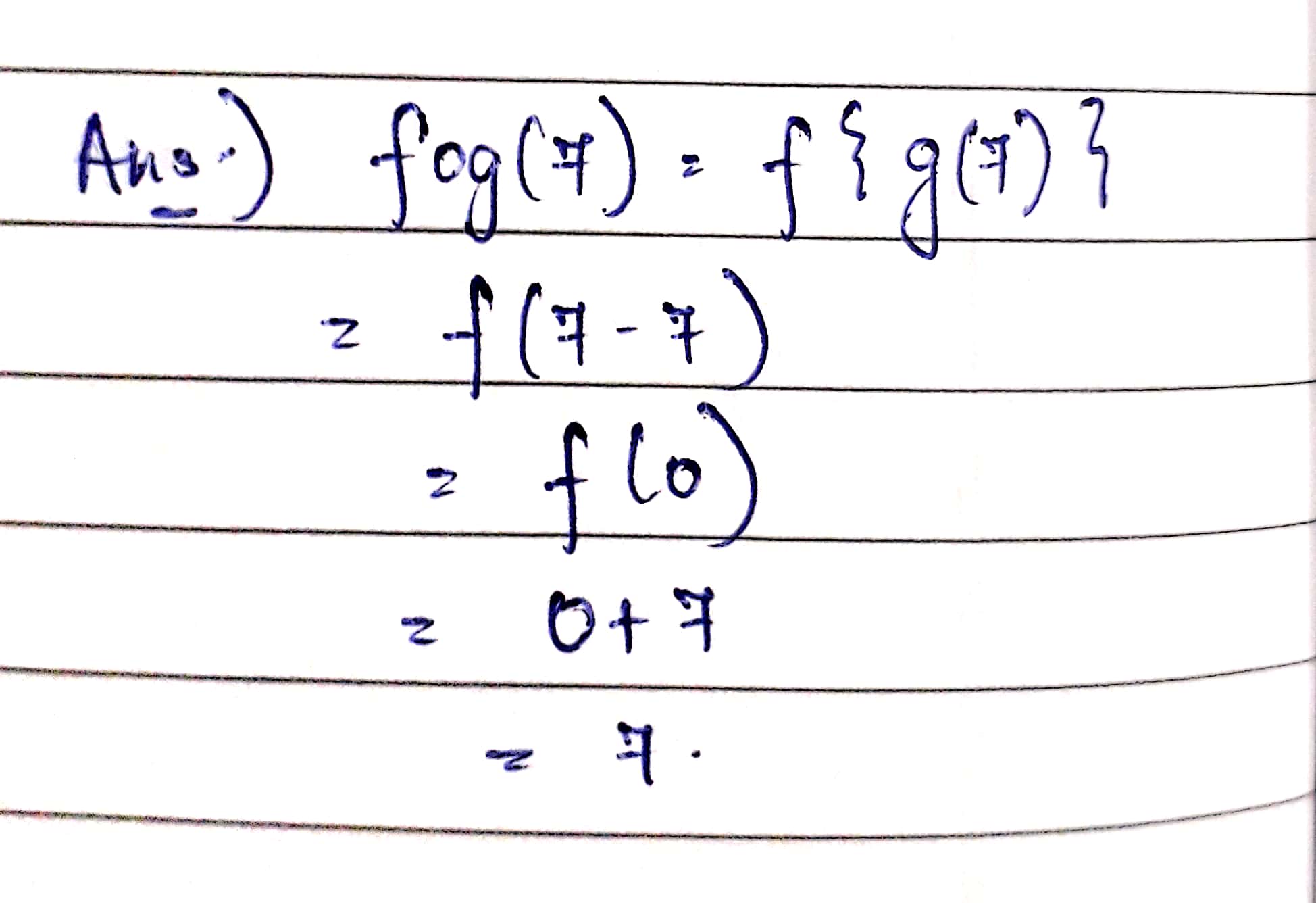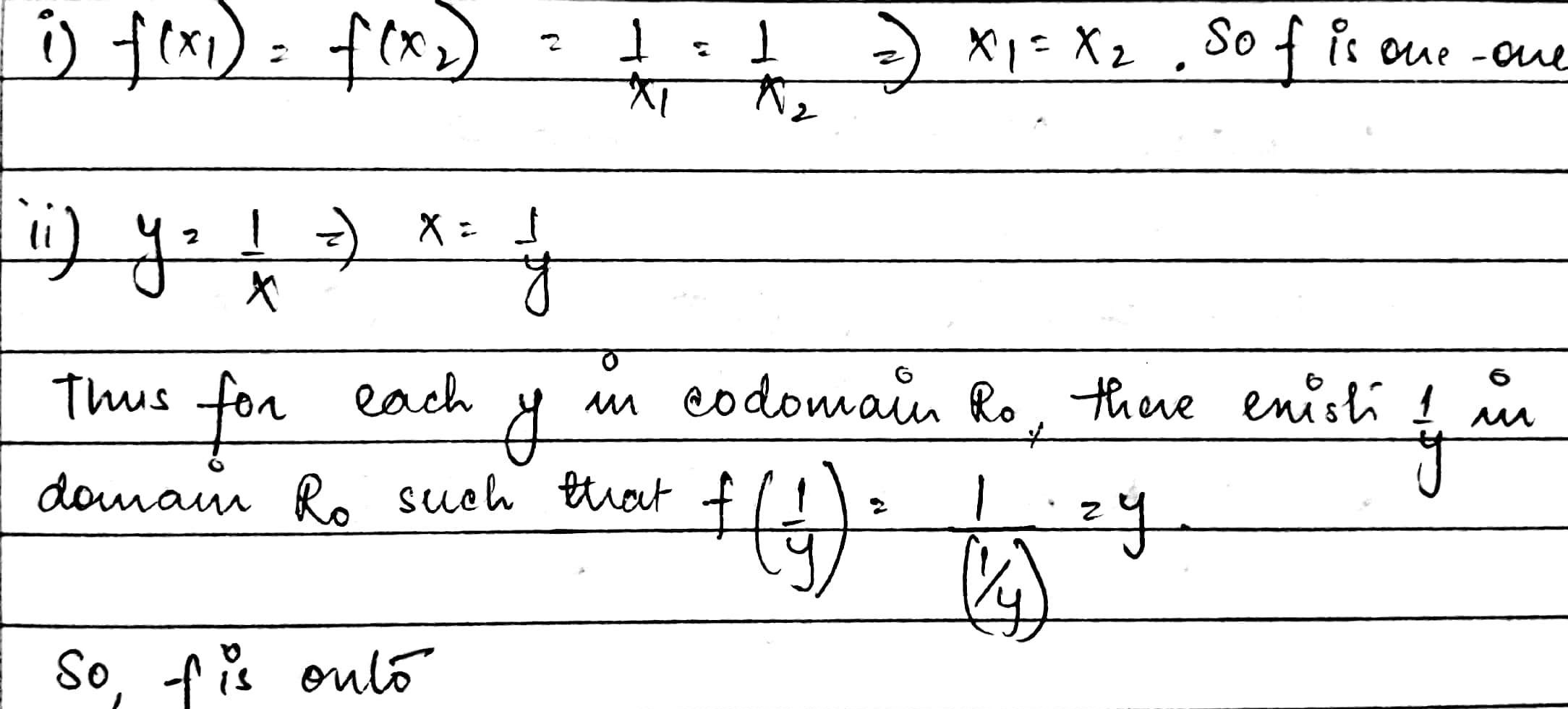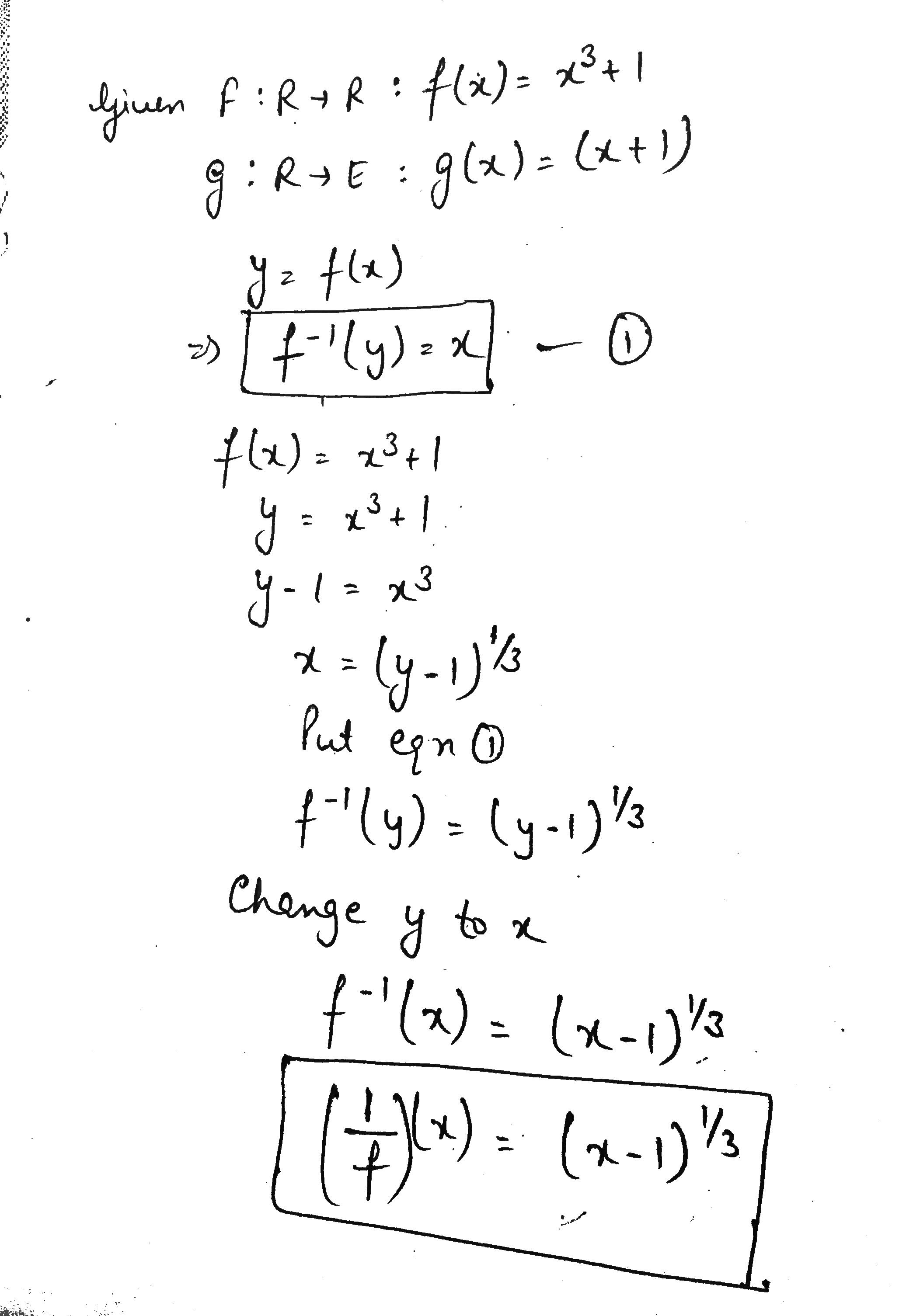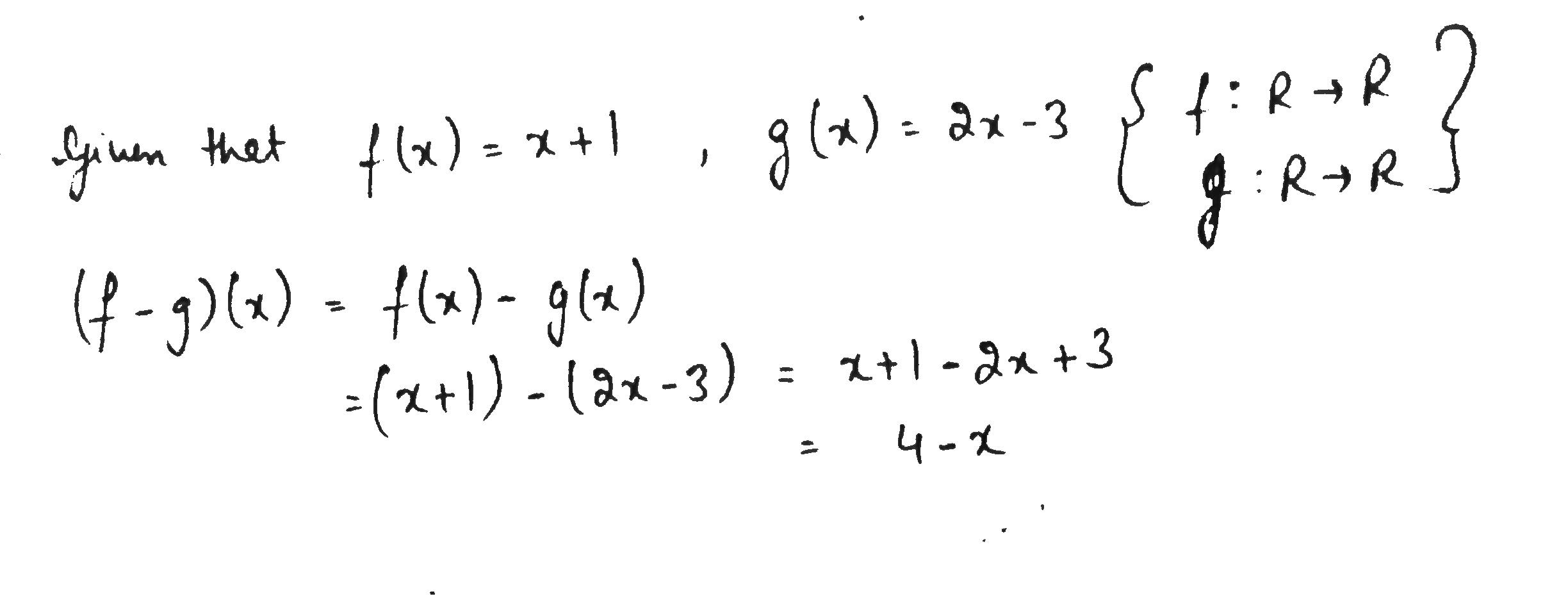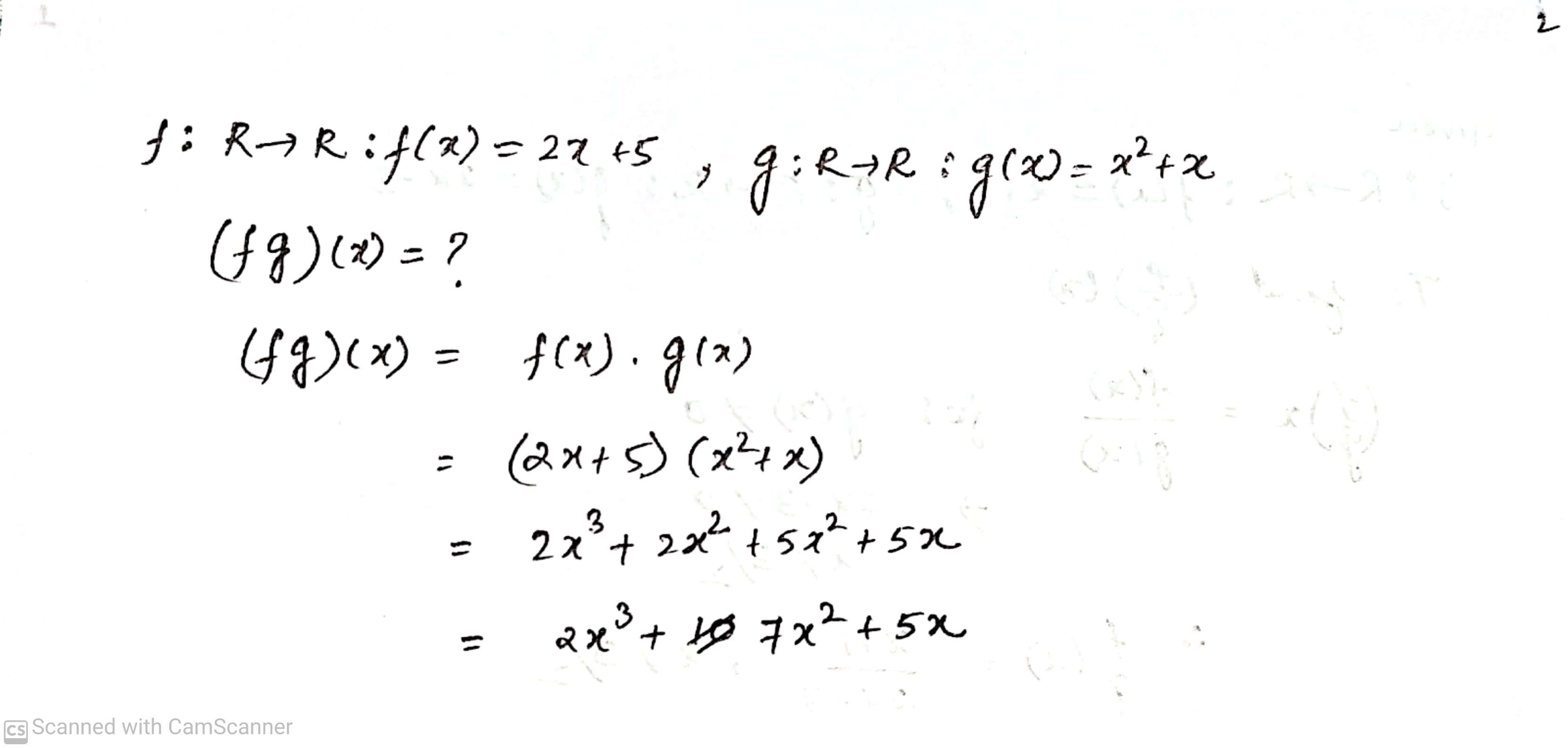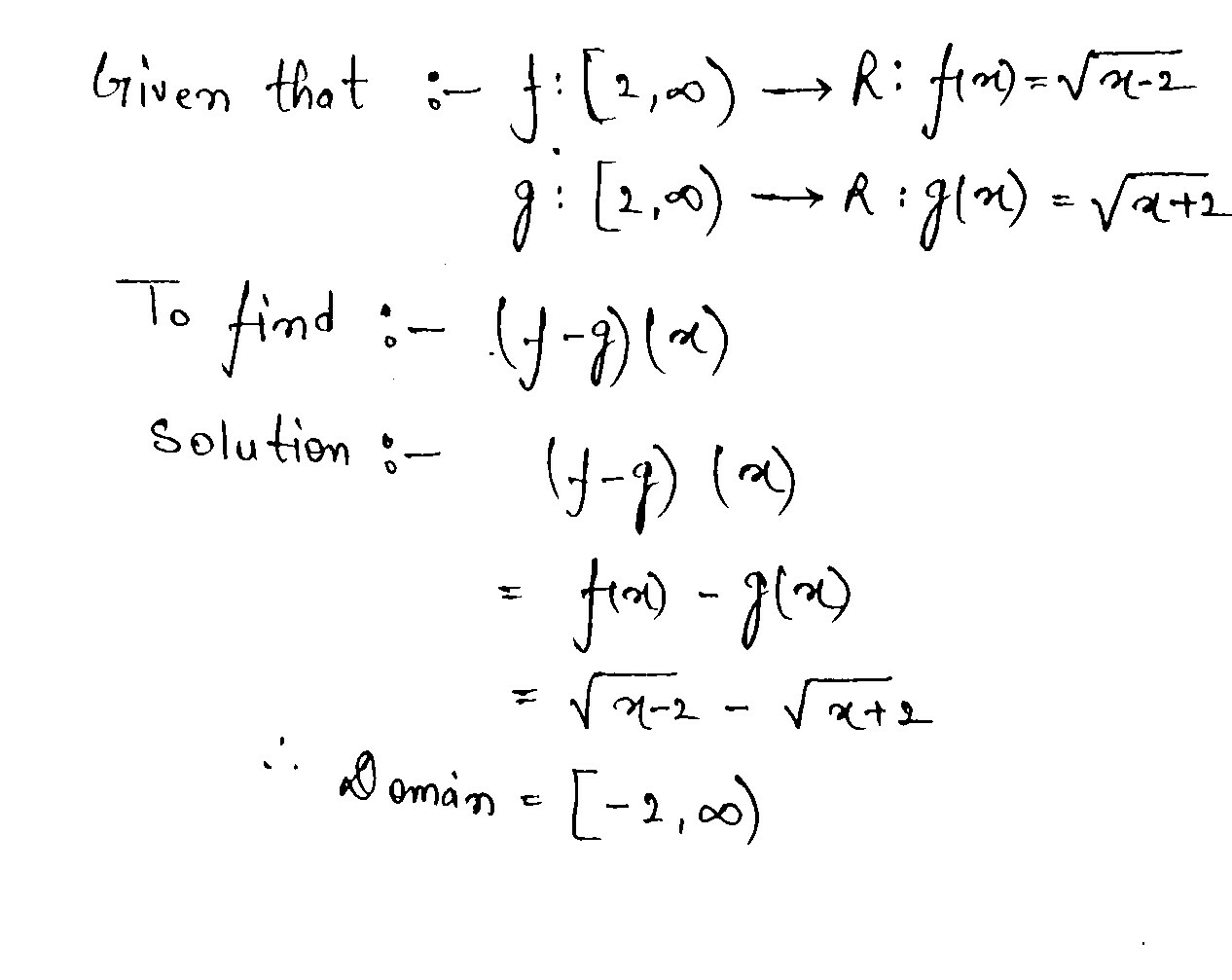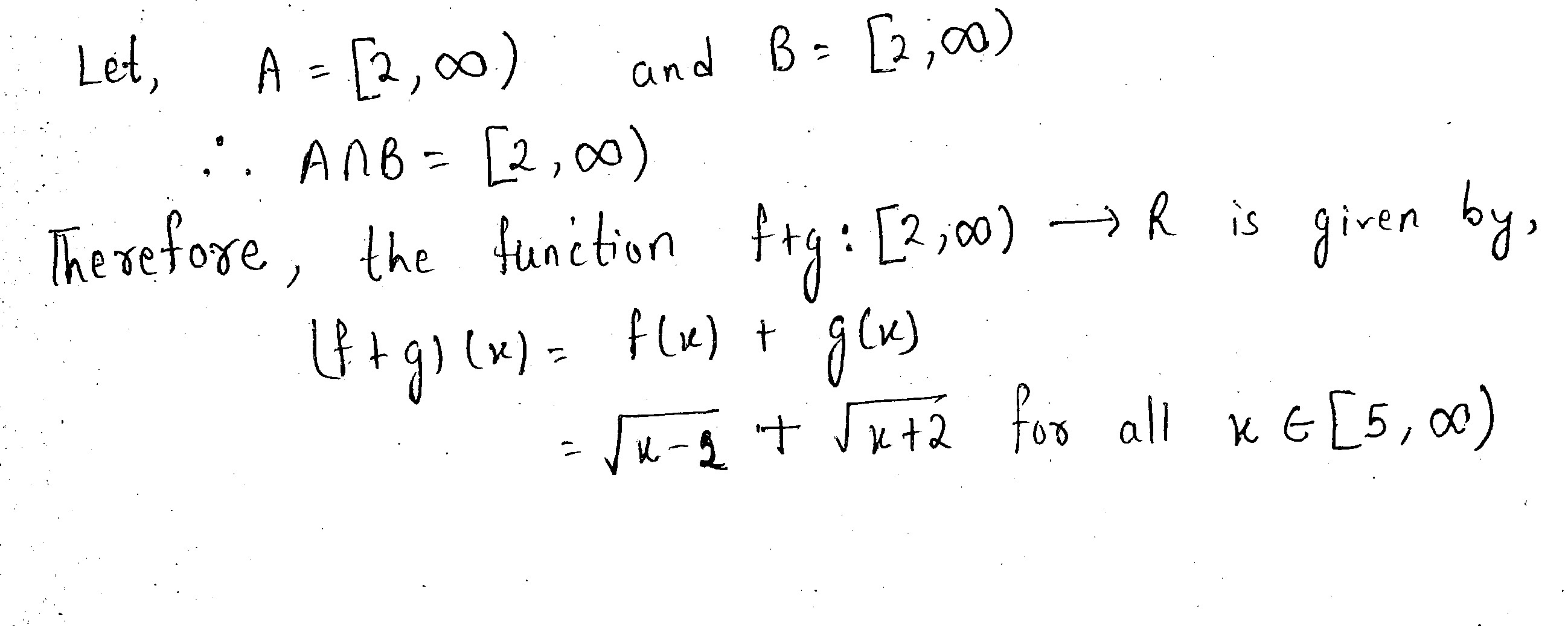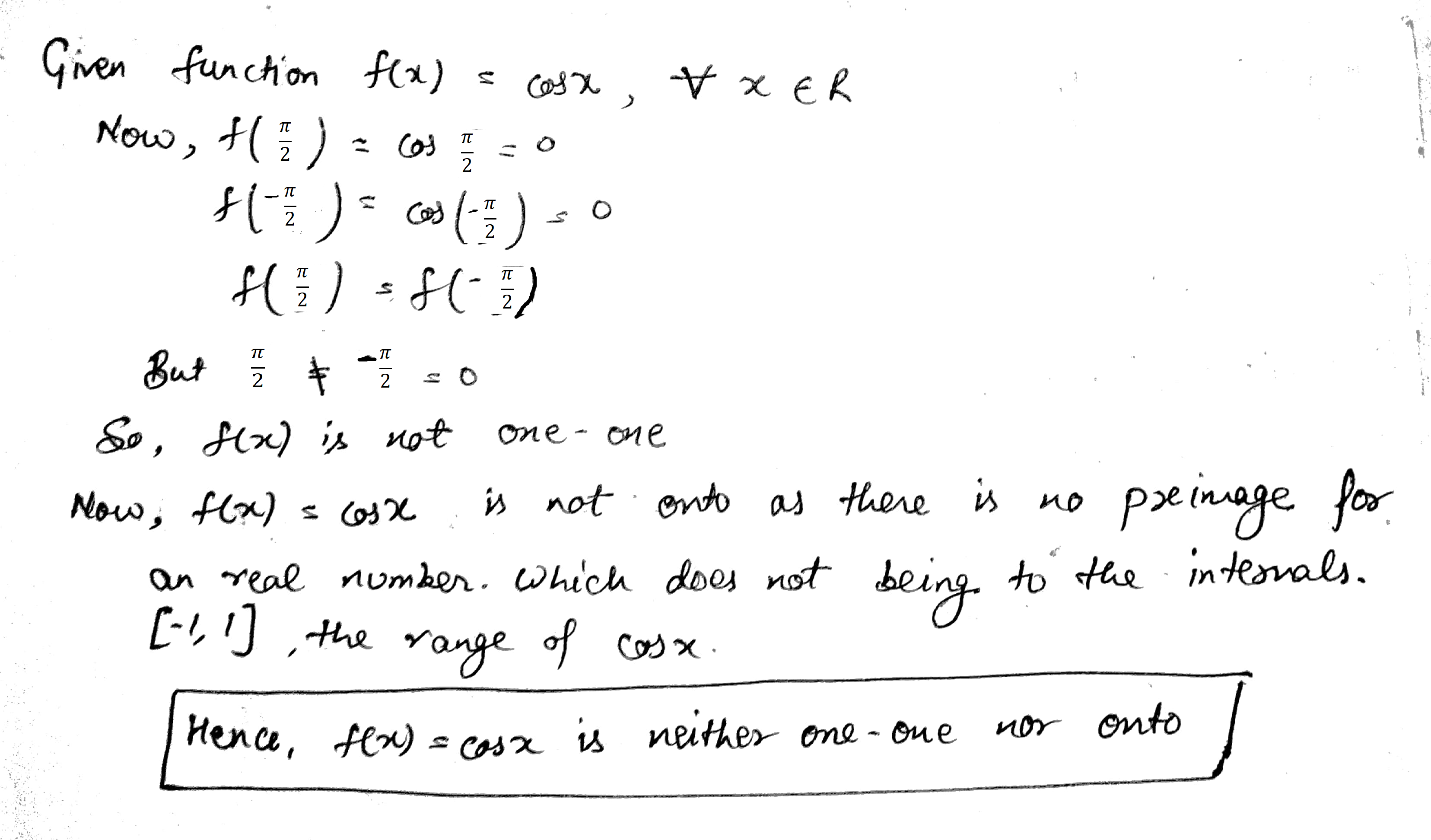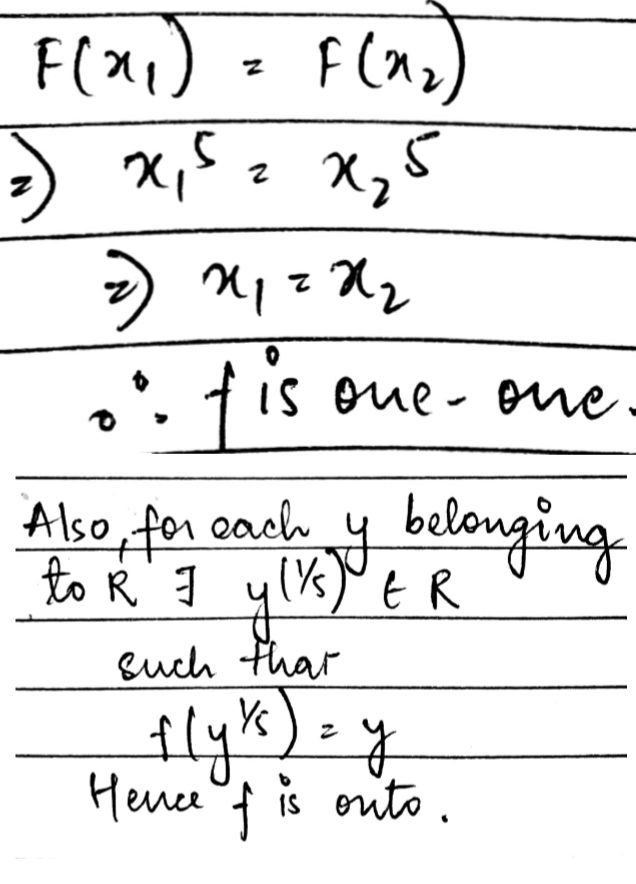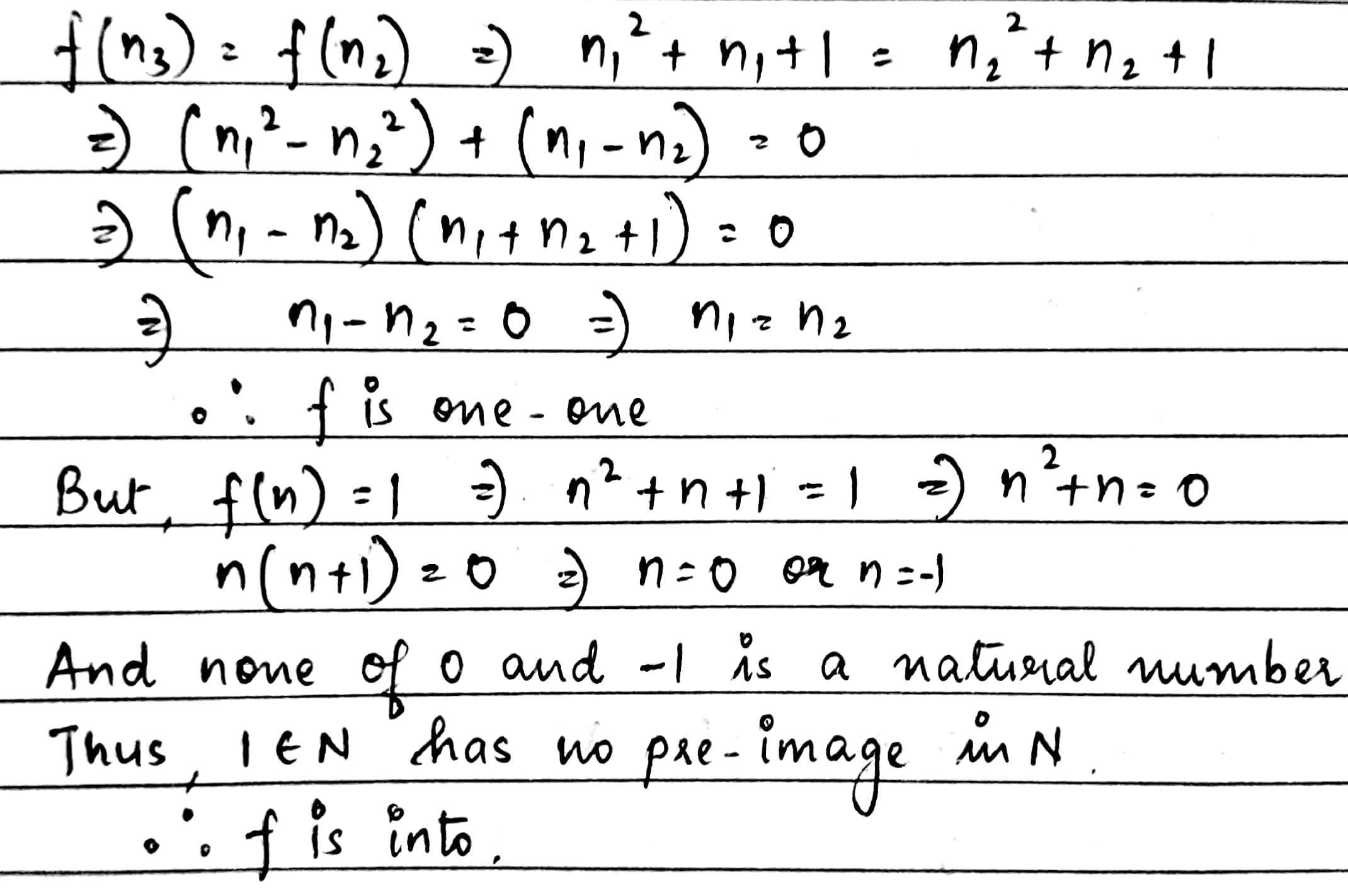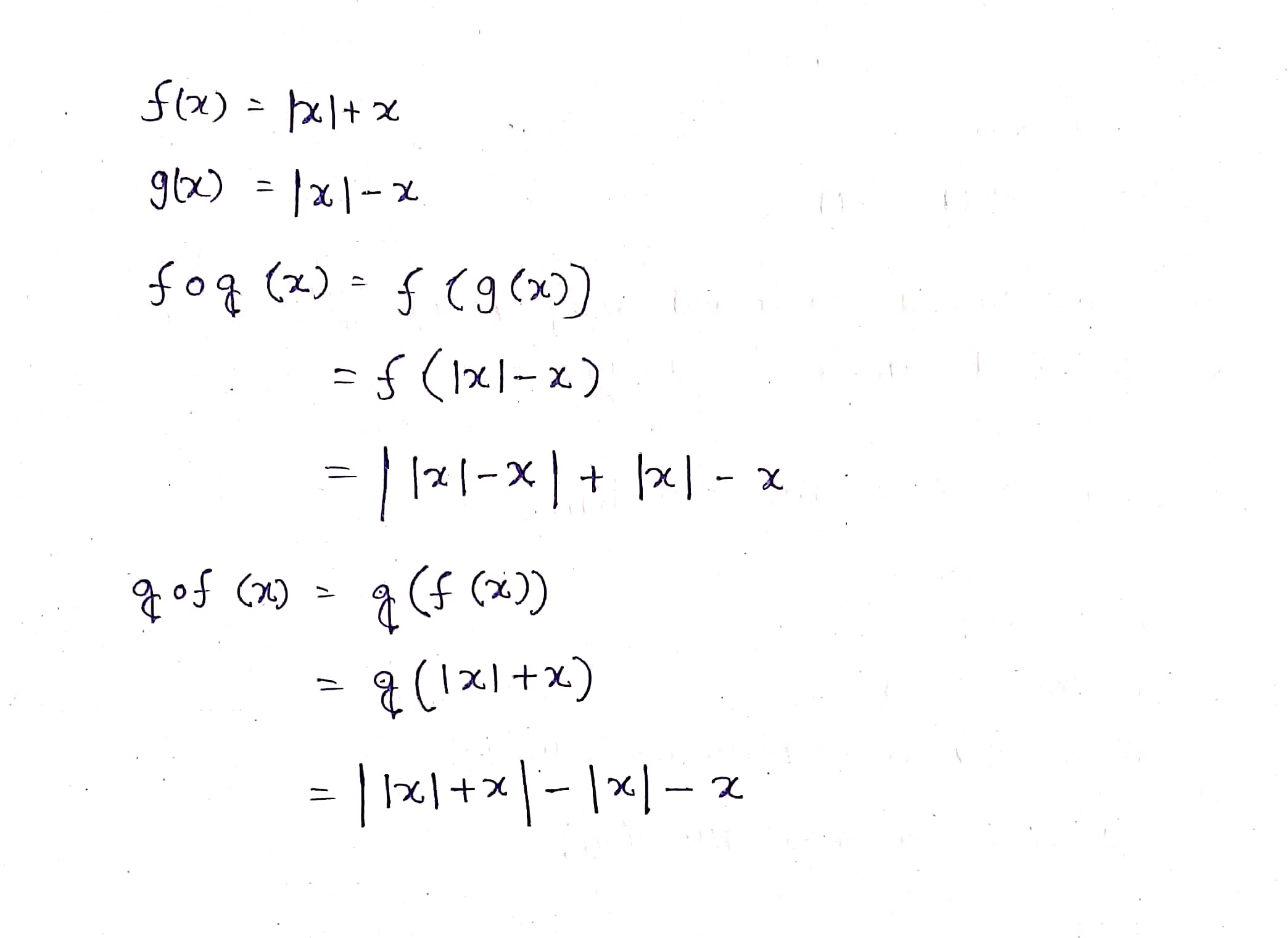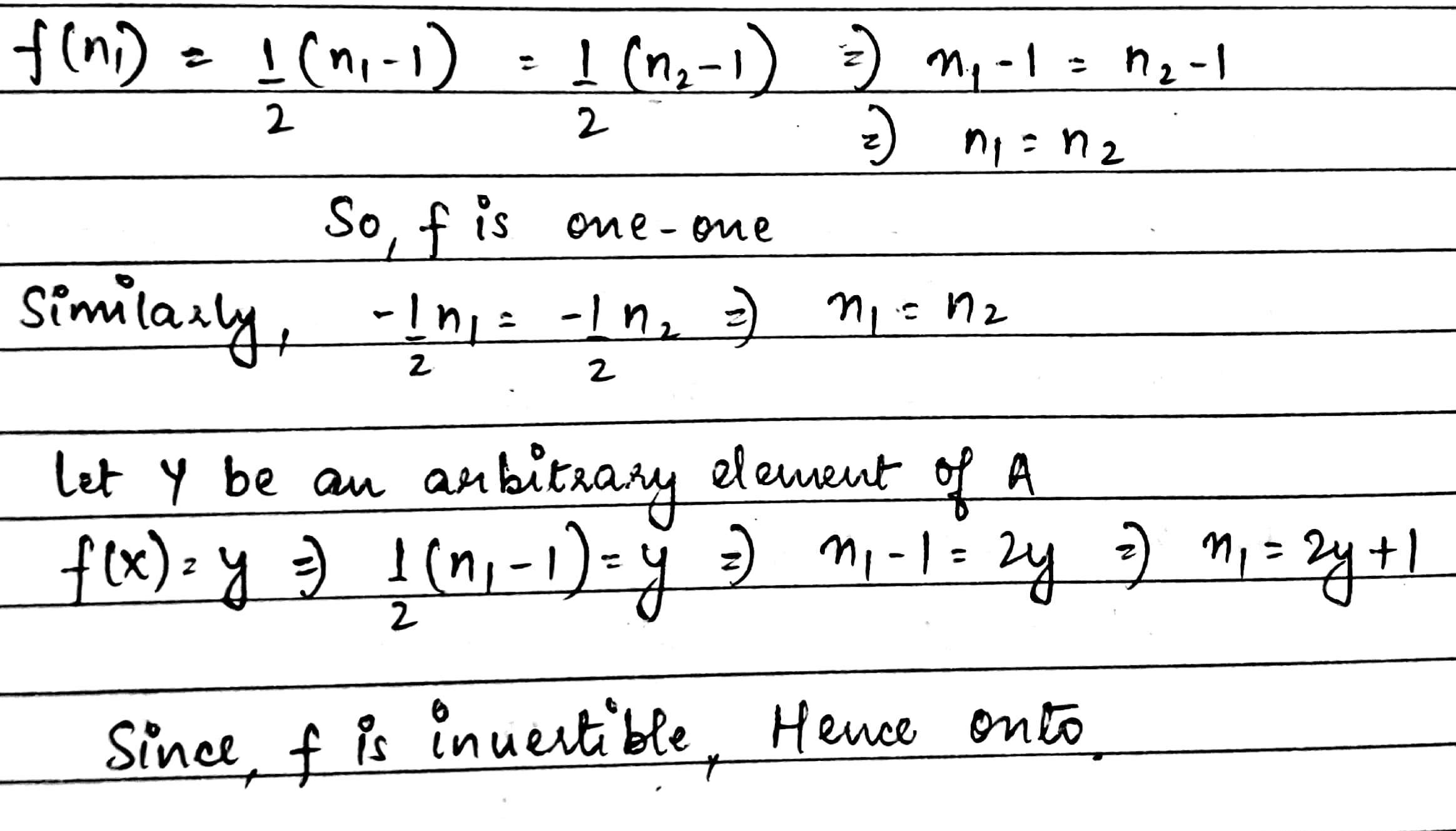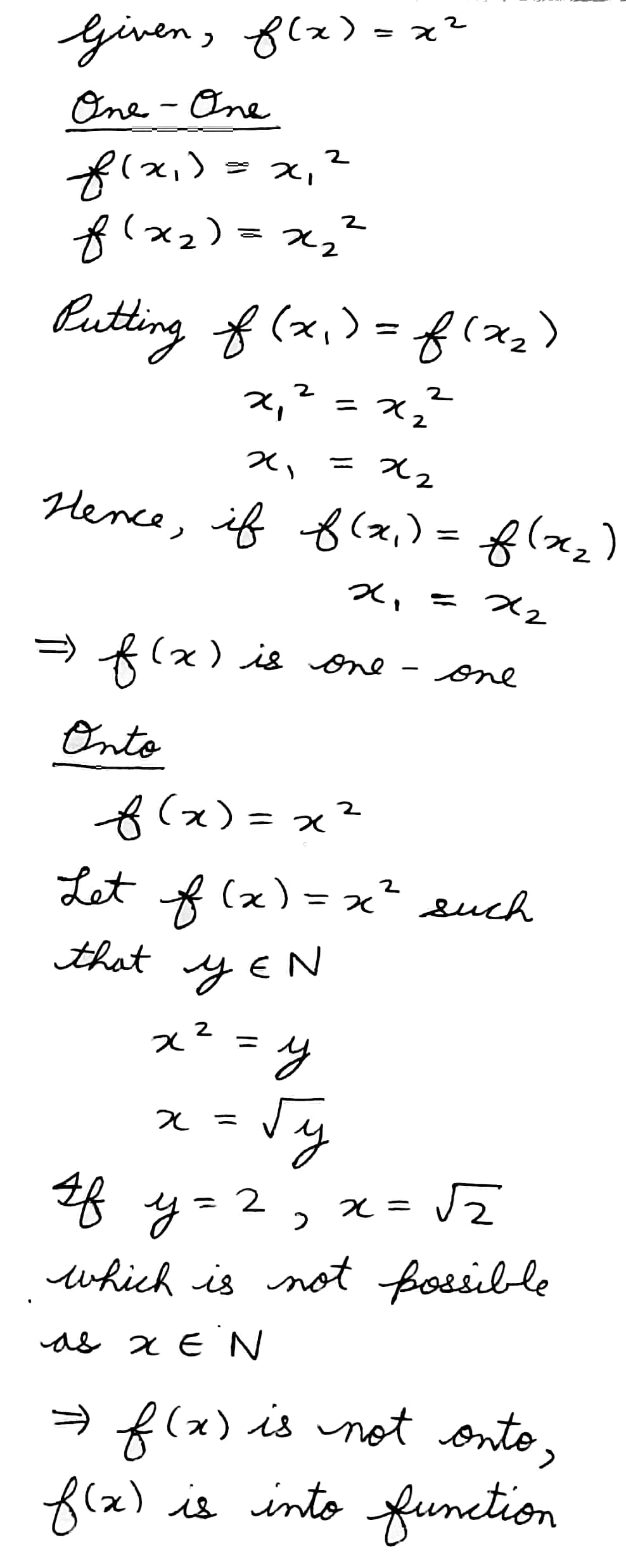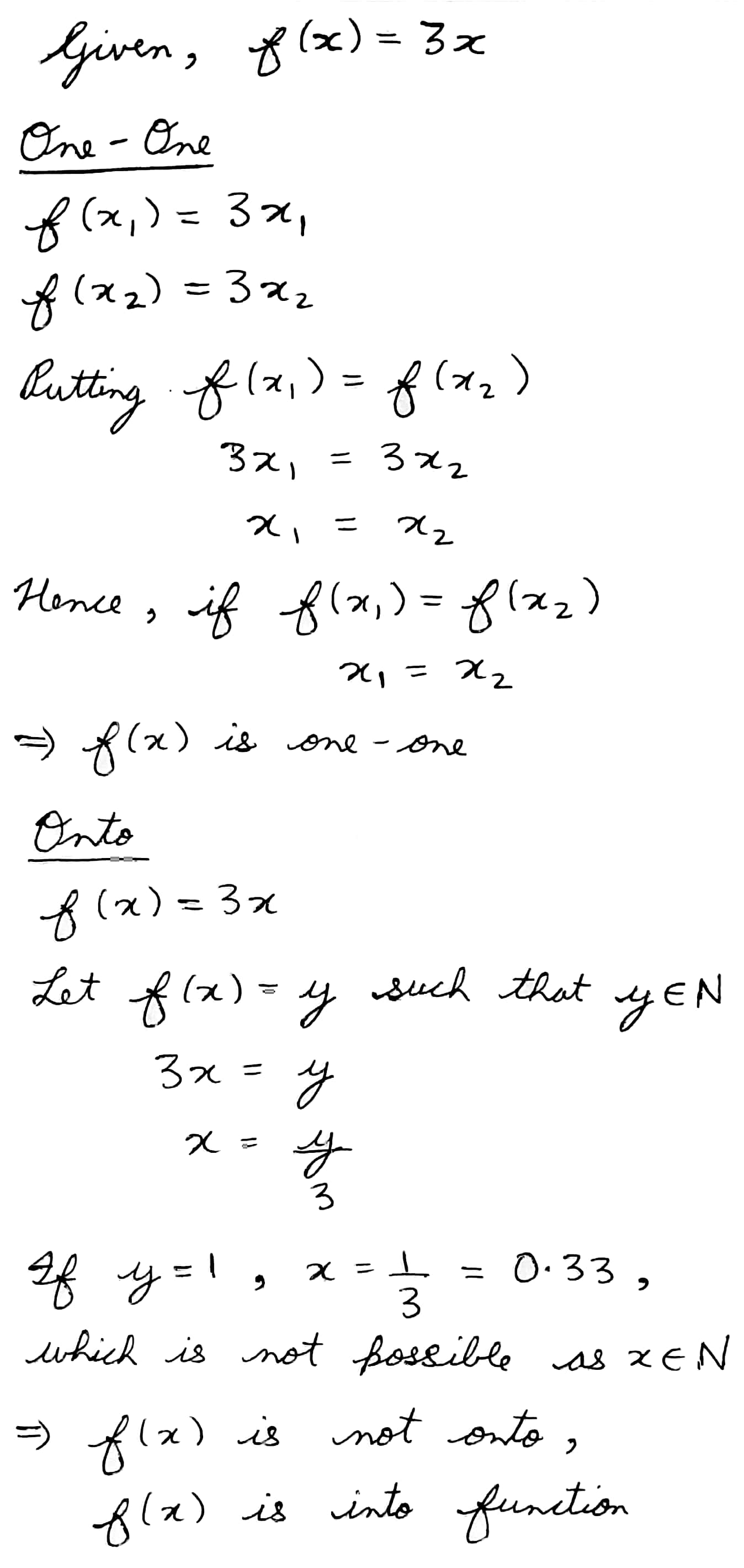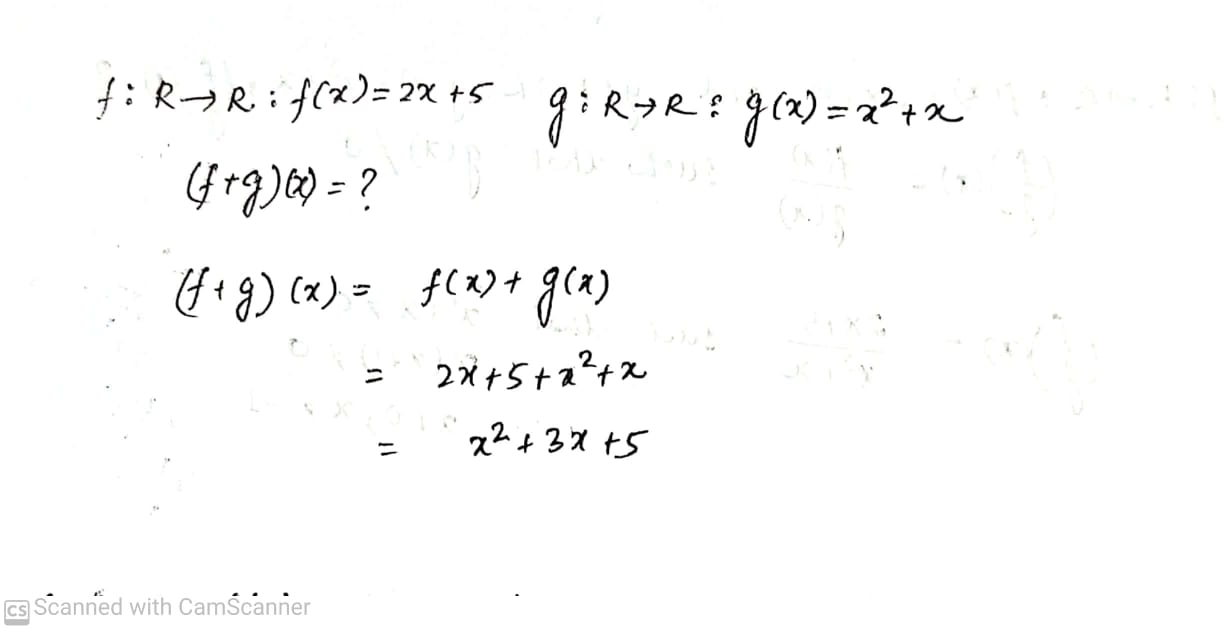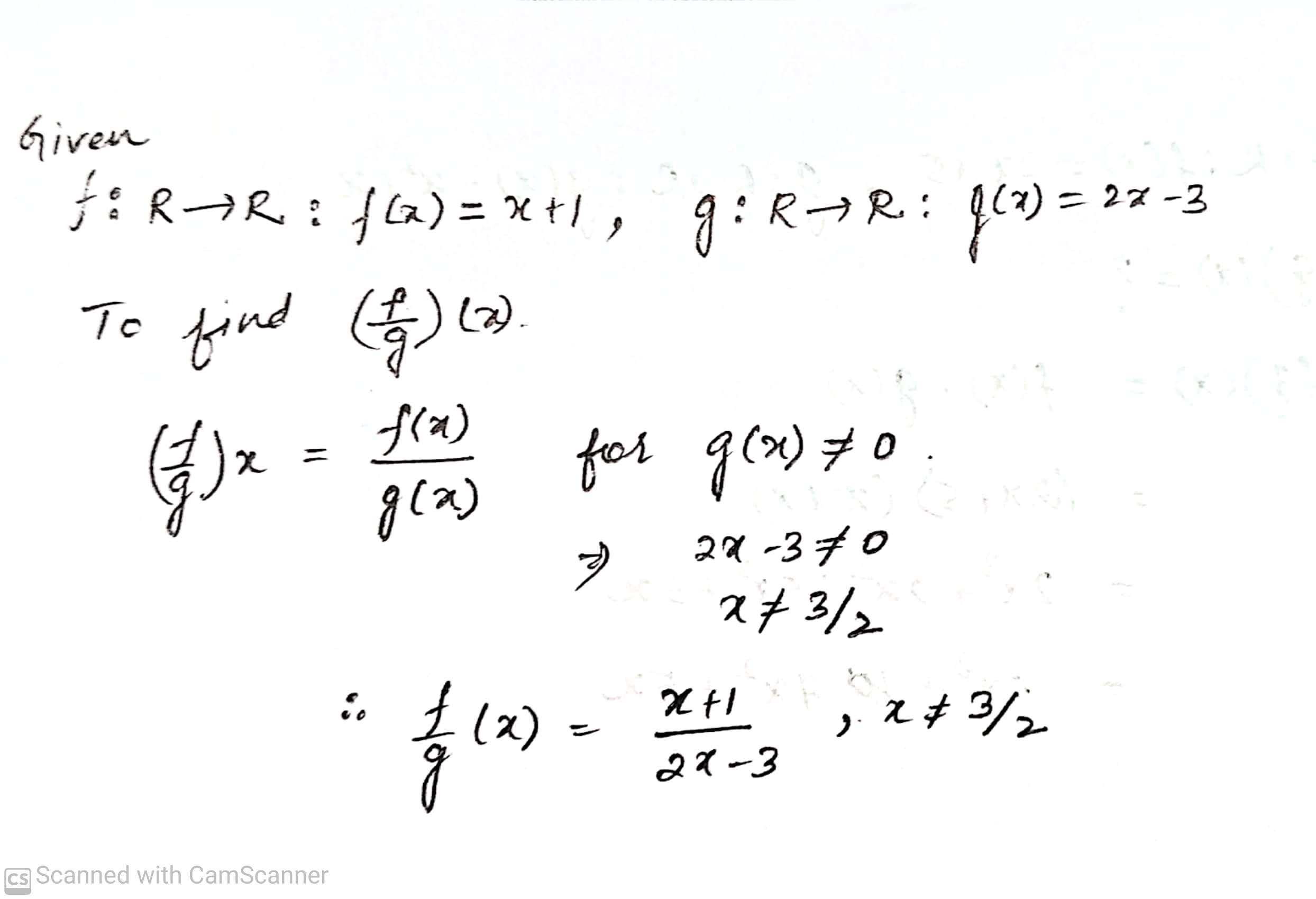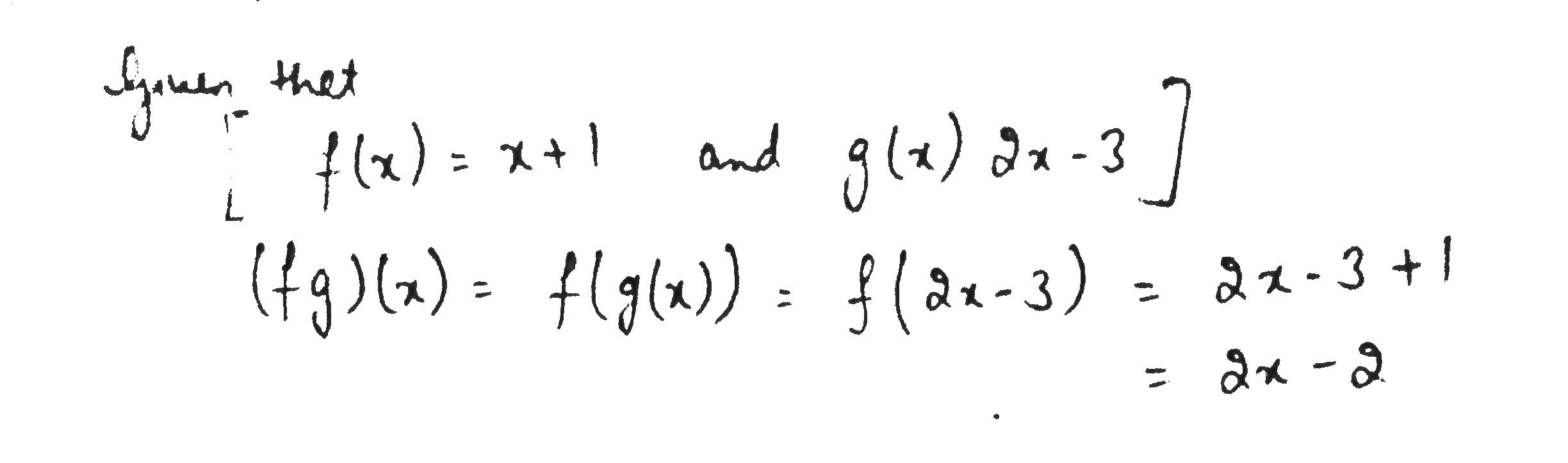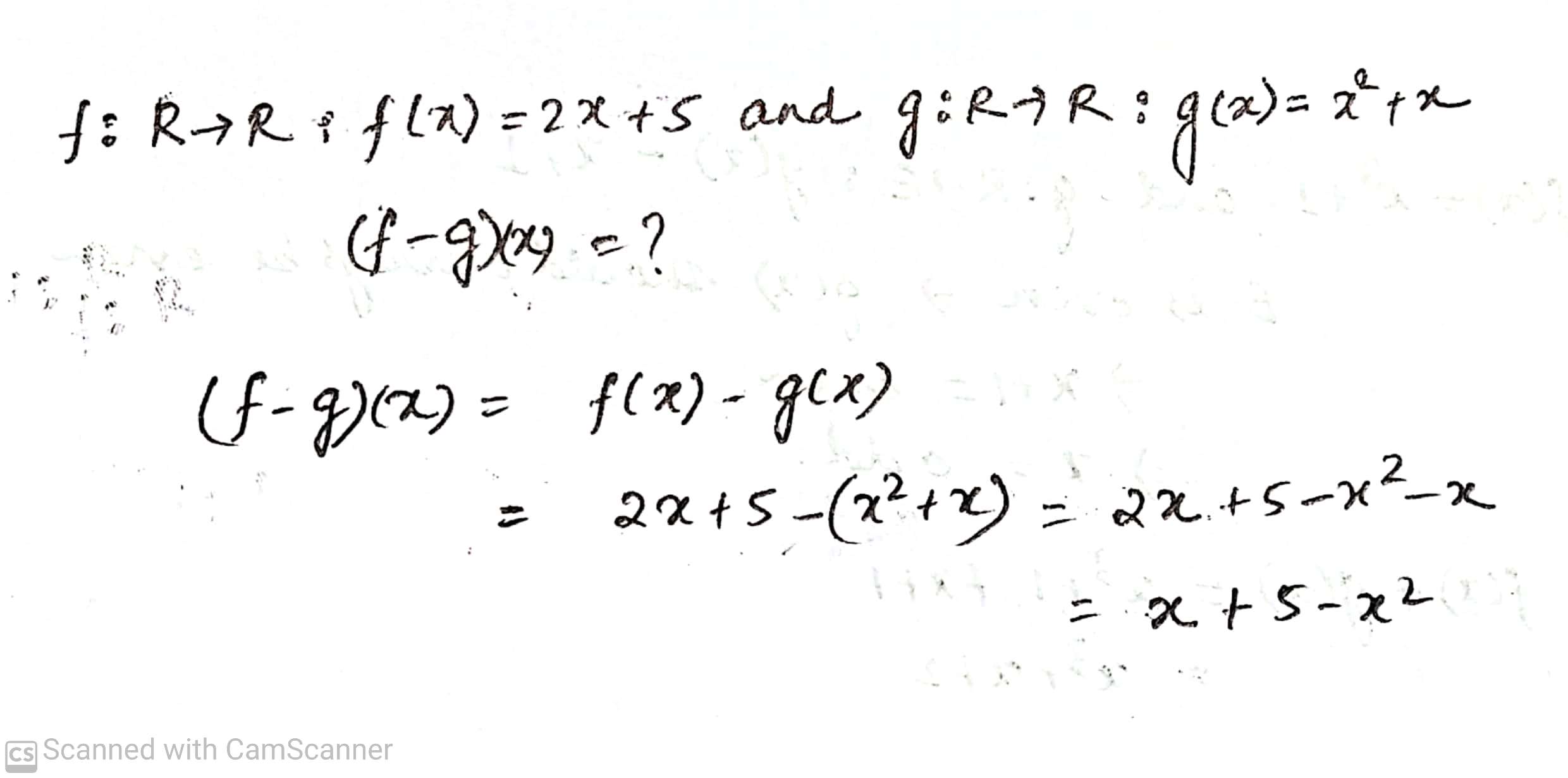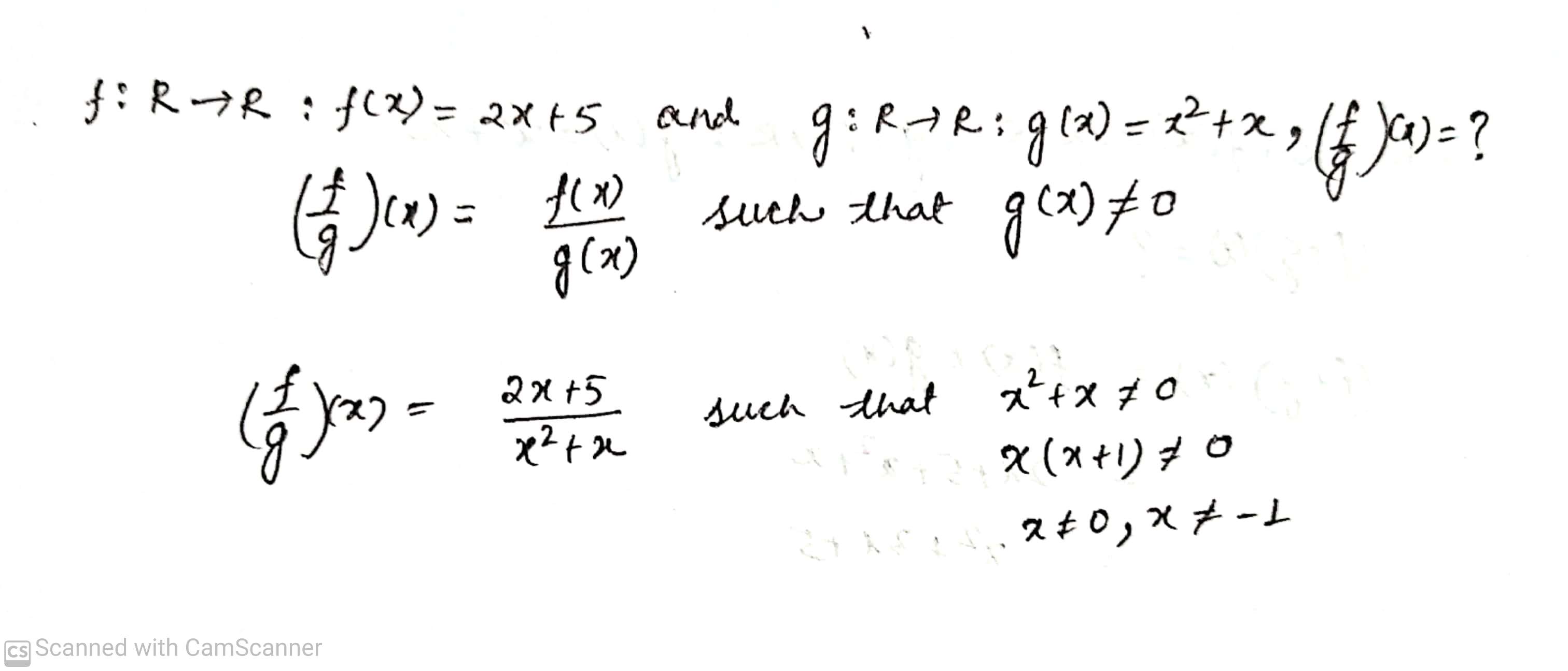Relations And Functions - Class 12 Commerce Maths - Extra Questions
Let the functions f:(−1,1)→R and g:(−1,1)→(−1,1) be defined by f(x)=|2x−1|+|2x+1| and g(x)=x−[x], where [x] denotes the greatest integer less than or equal to x. Let f∘g:(−1,1)→R be the composite function defined by (f∘g)(x)=f(g(x)). Suppose c is the number of points in the interval (−1,1) at which f∘g is NOT continuous, and suppose d is the number of points in the interval (−1,1) at which f∘g is NOT differentiable. Then the value of c+d is _____.
Let A={2,3,5,7,10} show that the relation
(i) R1 is A defined as "is equal to" is an identify relation. (ii) R2 is A defined as "difference is an integer" is the universal relation in A.
If the function f(x)={x,x<1x2,1≤x≤48√x,x>4
then find f−1(9)=
If f(x)=x6+3x3+1 then find f(1x) in terms of f(x)
Is function g defined by
g(x)={()}
a one to one function?
If f(x)=3x−1 and g(x)=4x+2, what if the value of g(f(0)+2)?
If a function f:R\rightarrow R is defined by f(x)=3x+4 show that {f}^{-1} (the inverse function of f) exists and find it.
If f(x) = \log x and g(x) =x^3 find fog(a) + fog(b).
Let A = { 1, 2, 3, 4, 5 }, B = N and f: A \rightarrow B be defined byf(x)=x^2.
Find the range of f. Identify the type of function.
Given f(x)=\dfrac{8}{x}, x\neq 0 and \text{fog}(x)=4x, find the (i) g(x) (ii) the value of x, when \text{gof} (x)=3.
Given the function f(x) =\dfrac{x-2}{5} and \text{gof}(x)=x-3. Find the component function g.
Let * be a operation defined on the set of rational numbers by a*b=\dfrac{ab}{4}, find the identity element.
Let f : N\rightarrow Y be a function defined as f(x) = 4x + 3, where, Y = \left \{y\epsilon N : y = 4x + 3 \text {for some}x\epsilon N\right \}. Show that f is invertible. Find the inverse function
If function f : R\rightarrow R and g : R\rightarrow R are given by f(x) = |x| and g(x) = [x], (where [x] is greatest integer function) find f\circ g\left(-\dfrac{1}{2}\right) and g\circ f \left(-\dfrac{1}{2}\right).
An equation * on Z^+ (the set of all non-negative integers) is defined as a*b=a-b, \forall a, b \in Z^+. Is * a binary operation on Z^+ ?
Let \ast be an operation such that a \ast b = LCM of a and b defined on the set A = \left\{ 1,2,3,4,5 \right\}. Is \ast a binary operation? Justify your answer.
If g:N\rightarrow N is given by g(n)=2n+3, and f:N\rightarrow N is given by f(n)=n+1, then find g\circ f, f\circ g and g\circ g
Find gof\left( x \right), if f\left( x \right) =8{ x }^{ 3 } and g\left( x \right) ={ x }^{ { 1 }/{ 3 } }.
If a\ast b denotes the larger of 'a' and 'b' and if aob=(a\ast b) +3, then write the value of (5 o 10), where \ast and o are binary operations.
Let f:N\rightarrow R be a function defined as f(x)=4{x}^{2}+12x+15 that f:N\rightarrow S where S is range of {f}_{a} is invariable. Find the inverse f(x).
Prove that the function f(x)=x+|x|, x\in \mathbb{R}. is not injective.
If a\ast b=\cfrac { ab }{ 10 } on {Q}^{+}, then find the identity for \ast.
The function f:\mathbb{R}\to \mathbb{R} be defined by f(x)=(x^2+1)^{35}. Prove that the function f(x) is not one-one.
If h(x)=2x, g(x)=x^2, f(x)=2, then find (f \circ g \circ h)(x).
Define a binary operation on a set.
Consider functions f and g such that composite gof is defined and is one are g both necessarily one-one.
Given that f(x) = {\left( {a - {x^n}} \right)^{\cfrac{1}{n}}};2 > 0,n \in N, show that f\left( {f(x)} \right) = x.
If f : R \rightarrow R defined by f(x) = (3 - x^3)^{\dfrac{1}{3}}, then find (fof) (x).
Show that the function f in A =R = \dfrac{2}{3} defined by f\left( x \right) = \dfrac{{3x + 2}}{{5x + 3}}, \ne \dfrac{{ - 3}}{5} is one-one and onto.Hence find {f^{ - 1}}\left( x \right)
Let \ast be a binary operation on the set of all non zero real numbers, given by a\ast b=\cfrac{ab}{5}\forall a,b\in R-\left\{ 0 \right\} , find the value of x, given that 2\ast(x\ast 5)=10
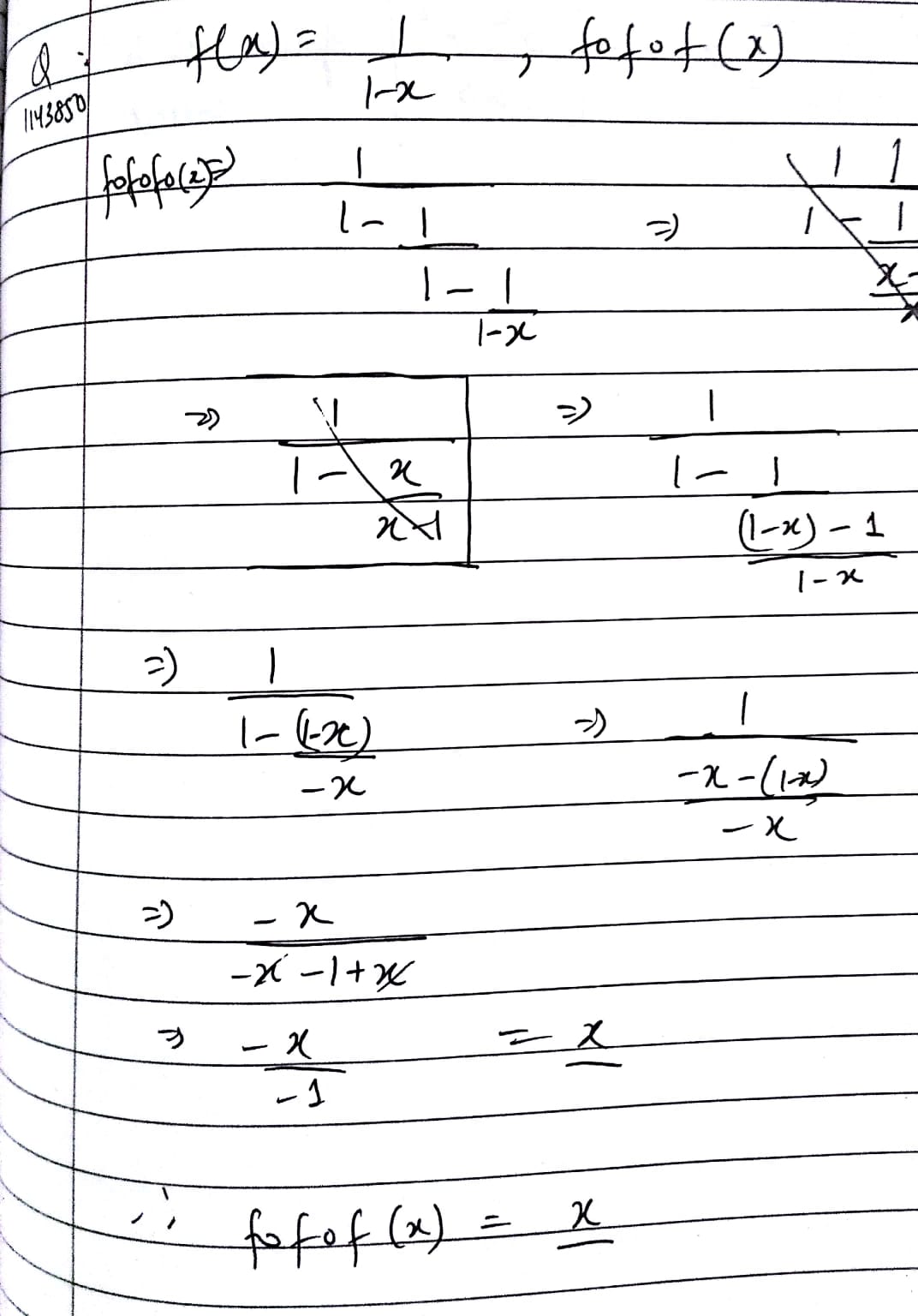
If f(x) = \dfrac{1}{1-x}, then (f \,o \,f \, o \,f)(x) is
If f ( x ) = \dfrac { x + 1 } { x - 1 } , then show that f ( x ) + f \left( \begin{array} { l } { 1 } \\ { x } \end{array} \right) = 0.
If f ( x ) = 2 x + 1 and g ( x ) = x - 3 find fog.
Let * be a binary operation on N given by a*b=HCF*(a,b) find 22*4
Solve: If f(x)=(x-1)(2x+1) Find f(1),f(2)and f(-3)
Show that the function f:N\rightarrow N, given by f(1)=f(2)=1 and f(x)=x-1 for every x>2, is onto but not one-one.
f from R into R is defined as
f\left( x \right) = \left\{ \begin{array}{l}2x + 5,\,\,if\,x > 0\\3x - 2,\,if\,x \le 0\end{array} \right. Show that F is one -one.
Let *:R\times R \rightarrow R given by (a,b)\rightarrow a+4b^2 is a binary operation, compute (-5)*(2*0).
If f(x) =x^{ 2 } and g(x)=2x+1 be two real valued function. Find f\left(g\left(x\right)\right) and \dfrac{f\left(x\right)}{g\left(x\right)}
Let 'o' be a binary operation on the set Q_{0} of all non-zero rational numbers defined by a\, o\, b= \dfrac{ab}{2}, for all a,b \in Q_{0}. Show that 'o' is commutative.
For what value of k, the matrix \begin{bmatrix} 2-k & 4 \\ -5 & 1 \end{bmatrix} is not invertible?
Let A= R_{0}\times R, where R_{0} denote the set of all non-zero real numbers. A binary operation 'O' is defined on A as follows: (a,b)O(c,d)= (ac, bc+d) for all (a,b)(c,d)\in R_{0}\times R
Find the invertible elements in A.
Check the commutativity and associativity of the following binary operation:
'\ast ' on Q defined by a \ast b= ab+1 for all a,b \in Q.
If f(x)=\left [4-(x-7)^3 \right], then f^{-1}(x)= .......
Using the definition, prove that the function f:A\to B is invertible if and only if f is both one-one and onto.
Let R be the set of real numbers and ^*be the binary operation defined on R as a^*b=a+b-ab \ \forall\ a,b\ \in R Then, the identity element with respect to the binary operation * is _______.
State how many of (1, 0)\ (-2, -1)\ (7, -6)\ (-3, 4)\ (0, 2) \left (\dfrac{-1}{2}, \dfrac{1}{2} \right ) are not the elements of the relation:
\left \{ (x, y):y=1-\left | x \right |; x, y\in Q \right \}
A mapping is defined as f: R\rightarrow R, f(x)= \cos x. Show that it is neither one-one nor surjective.
\displaystyle f:R\rightarrow R defined as under: \displaystyle f\left ( x \right )=\left\{\begin{matrix}x-4, &x< -9 \\x^{2}-1, &x\epsilon \left [ -9, 9 \right ] \\2x+5 &x> 9 \end{matrix}\right. Evaluate \displaystyle \left ( f\: o\: f \right )5
if \displaystyle f\left ( x \right )=\left\{\begin{matrix}1+x; &0\leq x\leq 2 \\3-x; &2< x\leq 3 \end{matrix}\right. then determine \displaystyle \left ( fof \right )(2).
If the functions \displaystyle f:R\rightarrow R and \displaystyle g:R\rightarrow R be defined by \displaystyle f\left ( x \right )= 2x+1,g\left ( x \right )=x^{2}-2Find the formulae for f o g.(2)
\displaystyle y= \frac{1}{\sqrt{\left ( 4+3\cos x \right )}} Is the function one-one ? Explain
Let A = {1, 2, 3, 4} and B = {a, b, c}. State, which of the given are relations from A to B.
{ (1, a), (1, b), (2, b), (3, c), (4, c) }
Given A={2,3,4}, B={2,5,6,7}.
A mapping from A to B \displaystyle g= \left \{ \left ( 2,2 \right ), \left ( 3,5 \right ), \left ( 4,2 \right ) \right \}.
Is it one-one
Let A = {1, 2, 3, 4} and B = {a, b, c}. State, which of the given are relations from A to B.
{ (1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (3, 1) }.
Let A = {1, 2, 3, 4} and B = {a, b, c}. State, which of the given are relations from A to B.
{ (a, 1), (b, 2), (c, 3), (b, 3), (b, 4) }
Let A = {1, 2, 3, 4} and B = {a, b, c}. State, which of the given are relations from A to B.
{ (a, b), (a, c), (b, a), (b, c), (c, a) }
Let A = {a, b, c} and B = {5, 7, 9}. State, which of the given are relations from B to A.
{ (a, 5), (a, 7), (b, 7), (c, 9) }
Let A = {a, b, c} and B = {5, 7, 9}. State, which of the given are relations from B to A.
{ (5, b), (7, c), (7, a), (9, b) }
If f\left ( x \right )=\sin ^{2}x+\sin ^{2}\left ( x+\dfrac{\pi}3 \right )+\cos x\cos \left ( x+\dfrac{\pi}3 \right ) and g\left(\dfrac54\right)=1, then gof(x) is equal to
Let A = {a, b, c} and B = {5, 7, 9}. State, which of the given are relations from B to A.
{ (5, 7), (9, 9), (7, 5) }
Given A = {3, 4, 5, 6} and B = {8, 9}. State, giving reason, whether { (3, 8), (4, 9), (5, 8) } is a mapping from A to B or not. Type 1 if it is a mapping and 0 if it is not
If f\left( x \right)=\left| x-2 \right| and g\left( x \right)=f\left( f\left( x \right) \right) , then g'\left( x \right) for x>2 is
Let A = {a, b, c} and B = {5, 7, 9}. State, which of the given are relations from B to A.
{ (5, a), (5, b), (5, c) }
Let two functions are defined as \displaystyle g(x)= \left\{\begin{matrix} x^{2}, &-1\leq x\leq 2\\x+2, &2 \leq x \leq 3\end{matrix}\right., and f(x)=\left\{\begin{matrix}x+1&x\leq 1\\2x+1&1<x\leq 2,\end{matrix}\right. then find g of(1)
Let A = \{1, 2, 3, 4\}, B = \{ 1, 5, 9, 11, 15, 16\} and f = \{(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)\} Are the following true?
(i) f is a relation from A to B
(ii) f is a function from A to B
Justify your answer in each case
Let f: {1,3,4} \rightarrow {1,2,5} and g: {1,2,5}\rightarrow {1,3} be given by f={(1,2), (3,5), (4,1)} and g= {(1,3), (2,3), (5,1)}. Write down gof.
Show that the Signum function f:R \rightarrow R, given by
\displaystyle f(x)=\begin{cases}1,\ if\ x > 0 \\0,\ if\ x = 0 \\ -1,\ if\ x < 0 \end{cases}is neither one-one nor onto.
Let A={1,2,3}, B={4,5,6,7} and let f={(1,4), (2,5),(3,6)} be a function from A to B. Show that f is one-one.
Let f,g and h be functions from R to R. Show that
(i) (f+g)oh=foh+goh
(ii) (f.g)oh=(foh).(goh)
Find gof and fog, if (i) f(x)=|x| and g(x)=|5x-2|
ii)f(x)=8x^3 and \displaystyle g(x)=x^{\frac {1}{3}}
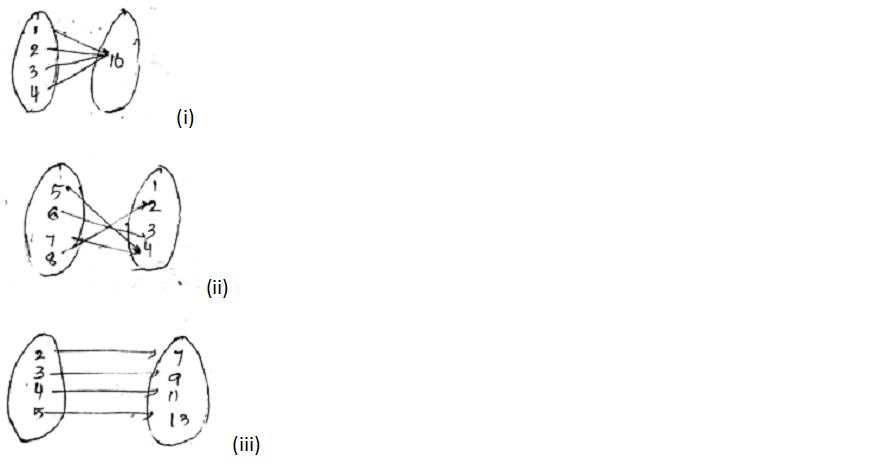
State with reason whether following functions have inverse
(i) f:\left \{1, 2, 3, 4\right \}\rightarrow \left \{10\right \} with
f = \left \{(1, 10), (2, 10), (3, 10), (4, 10)\right \}
(ii) g: \left \{5, 6, 7, 8\right \}\rightarrow \left \{1, 2, 3, 4\right \} with
g = \left \{(5, 4), (6, 3), (7, 4), (8, 2)\right \}
(iii) h: \left \{2, 3, 4, 5\right \}\rightarrow \left \{7, 9, 11, 13\right \} with
h = \left \{(2, 7), (3, 9), (4, 11), (5, 13)\right \}
If f(x) = \dfrac {4x + 3}{6x - 4}, x\neq \dfrac {2}{3}, show that fof (x) = x, for all x\neq \dfrac {2}{3}. What is the inverse of f?
Let f: X\rightarrow Y be an invertible function. Show that f has unique inverse
Consider f: R^{+} \in [-5, \infty) given by f(x) = 9x^{2} + 6x - 5. Show that f is invertible with f^{-1} (y) = \left (\dfrac {(\sqrt {y + 6})- 1}{3}\right )
If g(x)=3x+\sqrt {x}, find g({d}^{2}+6d+9).
Given a non-empty set X, consider the binary operation * : P(X) \times P(X) \rightarrow P(X) given by A * B = A\cap B\forall A, B in P(X), where P(X) is the power set of X. Show that X is the identity element for this operation and X is the only invertible element in P(X) with respect to the operation *
Show that the function f: R\rightarrow R given by f(x) = x^{3} is injective
Let f: W\rightarrow W be defined as f(x) = x - 1, if x is odd and f(x) = x + 1, if n is even. Show that f is invertible. Find the inverse of f, where, W is the set of all whole numbers.
Consider f: \left \{1, 2, 3\right \}\rightarrow \left \{a, b, c\right \} given by f(1) = a, f(2) = b and f(3) = c. Find f^{-1} and show that (f^{-1})^{-1} = f
Let f: X \rightarrow Y be an invertible function. Show that the inverse of f^{-1} is f, i.e., (f^{-1})^{-1} = f
Give examples of two functions f: N \rightarrow Z and g: Z \rightarrow Z such that gof is injective but g is not injective
Given a non-empty set X, let *: P(X) \times P(X) \rightarrow P(X) be defined as A * B = (A - B) \cup (B - A), \forall A, B\epsilon P(X). Show that the empty set \phi is the identity for the operation * and all the elements A of P(X) are invertible with A^{-1} = A
Let S = \left \{a, b, c\right \} and T = \left \{1, 2, 3\right \}. Find F^{-1} of the following functions F from S to T, if it exists
(i) F = \left \{(a, 3), (b, 2), (c, 1)\right \} (ii) F = \left \{(a, 2), (b, 1), (c, 1)\right \}
Give examples of two functions f: N\rightarrow N and g: N\rightarrow N such that gof is onto but f is not onto
Consider the binary operation \wedge on the set \left \{1, 2, 3, 4, 5\right \} defined by a\wedge b = min \left \{a, b\right \}. Write the operation table of the operation \wedge
Is \ast defined on the set \left \{1, 2, 3, 4, 5\right \} by a\ast b = L.C.M. of a and ba binary operation? Justify your answer
Let \ast' be the binary operation on the set \left \{1, 2, 3, 4, 5\right \} defined by a\ast' b = H.C.F. of a and b. Is the operation \ast' same as the operation \ast$ defined in above? Justify your answer
If the inverse of the rational function f(x)=\dfrac{x+1}{x-1} is \dfrac{x+m}{x-m}.Find the value of m
Let \ast be a 'binary' operation of N given by a\ast b = LCM (a, b) for all a, b\in N. Find 5\ast 7.
If the function f : R\rightarrow R be given by f(x) = x^{2} + 2 and g : R\rightarrow R be given by g(x) = \dfrac {x}{x - 1}, x\neq 1, find fog and gof and hence find fog(2) and gof(-3)
Let A = Q \times Q, where Q is the set of all rational numbers, and * be a binary operation on A defined by (a, b) * (c, d) = (ac, b + ad) for (a, b), (c, d) \epsilon A. Then find
(i) The identify element of * in A.
(ii) Invertible elements of A, and hence write the inverse of elements (5, 3) and \left ( \dfrac{1}{4}, 4 \right ).
Consider f:R^{+} \rightarrow [-9, \infty] given by f(x) = 5x^2 + 6x - 9. Prove that f is invertible with f'(y) =(\dfrac{\sqrt{54+5y}-3}{5}).
Show that f : N\rightarrow N, given byf(x) = \begin{cases}x + 1, \ \ \ \text{if} \ x \ \text{is} \ \text{odd} \\ x - 1, \ \ \ \text{if} \ x \ \text{is} \ \text{even} \end{cases} is both one-one and onto.
Let \ast be binary operation on the set of all non-zero real numbers, given by a\ast b = \dfrac {ab}{5} for all a, b, \in R - \left \{0\right \}. Find the value of x, given that 2\ast (x \ast 5) = 10.
Given f: x\rightarrow 2x+p and f^{-1} : x \rightarrow m (4x + 3), where p and m are constants. Find the value of p and value of m.
(f\circ f)(x)
If x\ \lambda\ y = 2x - y and x\nu y = 3x \times y, then (5\ \nu\ 2)\lambda\ 9
Consider f : R \rightarrow R given by f(x) = 2x + 3. Show that f is invertible. Find also the inverse of function f.
A function f : (-3, 7)\rightarrow R is defined as follows:
f(x) = \left\{\begin{matrix} 4x^{2} -1;& -3 \leq x < 2\\ 3x - 2; & 2\leq x \leq 4\\ 2x - 3; & 4 < x \leq 6\end{matrix}\right.
Find: f(5) + f(6)
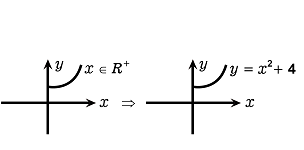
Let R_+ be the set of all non-negative real numbers. Show that the function f:R_+ \rightarrow [4, \infty) given by f(x)=x^2+4 is invertible and write the inverse of f.
A function f : [3, 7) \rightarrow R is defined as follows
f(x) = \left\{\begin{matrix}4x^2 - 1; &-3 \le x < 2 \\ 3x - 2; & 2 \leq x \leq 4\\ 2x -3; & 4 < x < 7\end{matrix}\right.
Find f(-2) - f(4)
Let f,g,h are functions defined by f(x)=x; \,g(x)=1-x; \,h(x)=x+1; then show that h\circ (g\circ f)=(h\circ g)\circ f.
Find g o f and f o g if f : R\rightarrow R and g: R\rightarrow R are given by f(x)=\cos x and g(x) = 3x^2. Show that g o f \ne f o g.
Prove that the function f:N\rightarrow Y defined by f(x)=4x+3, where Y={y=4x+3, x\epsilon N} is invertible. Also write the inverse of f(x).
Let f: \left \{x, y, z\right \} \rightarrow \left \{a, b, c\right \} be an one-one function. It is known that only one of the following statements is true:
(i) f(x) \neq b (ii) f(y) = b (iii) f(z) \neq a.
Find the function f.
Show that the function f: R_{\ast} \rightarrow R_{\ast} defined by f(x) = \dfrac {1}{x} is one-one, where R_{\ast} is the set of all non-zero real numbers. Is the result true, if the domain R_{\ast} is replaced by N with co-domain being same as R_{\ast}?
The binary operation \ast : R \times R \rightarrow R is defined as a a\ast b=2a+b. Find (2\ast 3)\ast 4.
Solve the equation. f'(x) \, g'(x) if f(x) \, = \, 3 \, + \, 2x^2 \, and \, g(x) \, 3x^2 \, - \, (5x \, - \, 3)\, (2 \, - \, x)
If f(x) = 4x+2, g(x) = 3x^2, h(x) = 3x -2 such that fo(goh) = (fog)o h
Let f : [0,3] is defined by f(x) = {x^2} + x + 1 then {f^{ - 1}}(x)
f: N \rightarrow N, g: N \rightarrow N, and h: N \rightarrow R defined and f(x) = x^2, g(y) = 4y+2, h(z) = \ cosz such that ho(gof) = (hog)of
Let f : R \rightarrow R be defined by f(x) = 3x + 4, x \epsilon R. Is f invertible? If so, give a formula for f^{-1}.
Let f\left( x \right) =\left[ x \right] and g\left( x \right) =\left| x \right| , find (g+f)(2.3)
If f:R \to \left( {0,2} \right) defined by f\left( x \right) = \dfrac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}} + 1 is invertible, find {f^{ - 1}}
Show that if f: A \rightarrow B and g: B \rightarrow C are 1-1, then gof:A \rightarrow C is also 1-1
Show that the function f: R \rightarrow R is defined by f(x) = 4x+3 is invertible. Hence write the inverse of f.
Let f(x+\frac{1}{2}) =f(x). If f(2)= 5 and f(\frac{9}{4}) =2. Find f(-3) and f(\frac{1}{4}).
Let * be a binary operation on the set Q of rational numbers as follows:
a*b={ \left( a-b \right) }^{ 2 }
Find which of the binary operations are commutative and which are associative.
Let * be a binary operation on the set Q of rational numbers as follows:
a*b={ ab }^{ 2 }
Find which of the binary operations are commutative and which are associative.
Let * be a binary operation on the set Q of rational numbers as follows:
a*b=a+ab
Find which of the binary operations are commutative and which are associative.
Let * be a binary operation on the set Q of rational numbers as follows:
a*b=\dfrac { ab }{ 4 }
Find which of the binary operations are commutative and which are associative.
Let F(x)={x}^{3}-3x+1
find no. of real soln, of F(F(x))=0.
f(x)=3x^{4}+17x^{3}+9x^{2}-7x-10; g(x)=x+5
If f(x)=\dfrac{3x+2}{4x-1} and g(x)=\dfrac{x+2}{4x-3}, prove that (gof)(x)=(fog)(x)=x.
Let F(x)={x^3} - 3x + 1
Find no of real solutions of F\left( {F\left( x \right)} \right) = 0
f:R \rightarrow R,f(x)=x^{2},g:R \rightarrow R,g(x)=2^{x}, then {x|(fog)(x)=(gof))(x)}=.........
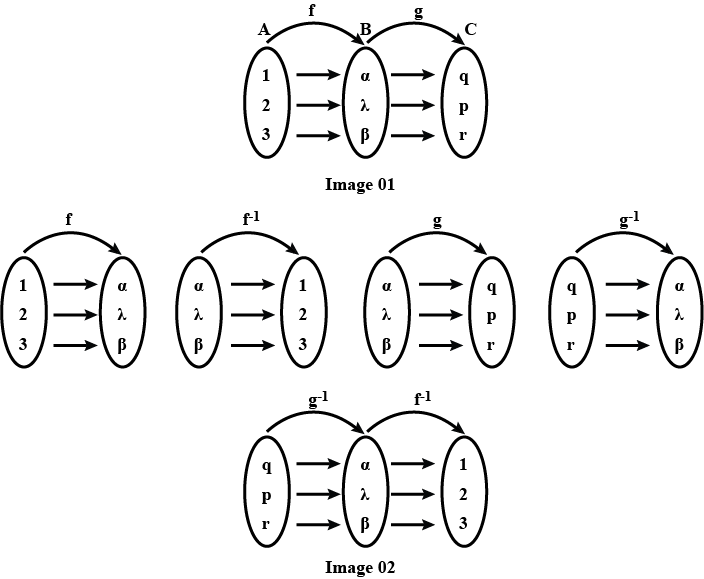
If A = \{ 1,2,3\} ,B = \{ \alpha ,\beta ,\lambda \} C = \{ p,q,r\} and f:A \to B,\,g:B \to C are defined by f = \left\{ {\left( {1,\alpha } \right),\left( {2,\lambda } \right)\left( {3,\beta } \right)} \right\} and g = \left\{ {\left( {\alpha ,q} \right),\left( {\beta ,r} \right),\left( {\lambda ,p} \right)} \right\} Show that f and g are bijective functions and {\left( {gof} \right)^{ - 1}} = {f^{ - 1}}o{g^{ - 1}}
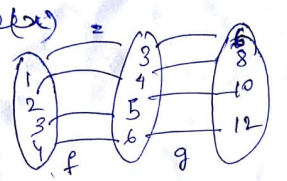
Find composite of f and g and express it by formula :
f=\{(1,3),(2,4),(3,5),(4,6)\}
g=\{(3,6),(4,8),(5,10),(6,12)\}
f : R\rightarrow (-1, 1), f(x) = \dfrac {10^{x} - 10^{-x}}{10^{x} + 10^{-x}}. Find f^{-1}, if it exists.
If the binary operation on the set of integers Z, defined by a\times b=a+3{ b }^{ 2 }, then find the value of 8\times 3.
If f(x)=\dfrac {1}{(1-x)} find (fofof)(x)=?
If f:R\rightarrow R be given by f\left( x \right) =\left( 3-{ x }^{ 3 } \right) , find the value of fof\left( x \right)
If g\ {(x)}={e}^{2x}+{e}^{x}-{1} and h\ {(x)}={3x}^{2}-{1}, the value of g\ {(h(0))} is
Find composite function g \, o f(x) of f and g.
f = \{(1,3) ; (2, 4) ; (3, 5) ; (4, 6) \} & g = \{(3, 6) ; (4, 8); (5, 10) ; (6, 12)\}.
If f:R\rightarrow R is given by f(x)=(3-x^3)^{1/3}, find fof(x).
If f (x) =\cfrac{x^{2}-x}{x^{2}+2x}, find the domain of f(x). Show that f is one-one.
(ii) Let * be the binary operation on N given by a * b= ab
(a) Find 20 * 16
(b) Find the identity of * in N
Find inverse function of \,f(x) = 9{x^2} + 6x - 5
f:R \to R\;given by f\left( x \right) = 4x + 3, show that f is invertable. Find the inverse of f.
Show that subtraction are not binary operation on natural number N
If y=f(x)=\dfrac{px+q}{px-p}, then find f(y) in terms of x.
Let A be a finite set, If f:A \to A is onto. Show that f is one-one
Work out the inverse function for each equation.a)y = 2 x + 5b)y = 4 x - 7c)y = \frac { x } { 2 } + 1d)y = \frac { x - 4 } { 3 }
Give one example for One one function.
If f= \{(2,4)(3,6)(4,8)(5,10)(6,12)\},
g=\{(4,13)(6,19)(8,25)(10,31)(12,37)\},
Find (gof) ?
Let A=B=[-1,1]. State whether the following functions from A into B are one-one.
i)f\left( x \right) = {x^2}
ii)g\left( x \right) = \left| x \right|
Prove that the function f:R\to R be defined by f(x)=(x^2+1)^{35} is not one one.
Prove that the function f(x)=x+|x|, x\in R is not one-one.
If the functions f and g are given by f ={(1,2)(3,5)(4,1)} & g={(2,3)(5,1)(1,3)}. Find the range of f and g . Also find fog(2).
If * is a binary operation on set N,of natural no defined as a*b=HCF of (a,b). Evaluate 3*(2*5).
A binary operation * on the set {0,1,2,3,4,5} is defined as
a*b = \left\{ \matrix{ a + b{\rm{\ , if\ a + b < 6}} \hfill \cr {\rm{a + b - 6\, if\ a + b}} \ge {\rm{6}} \hfill \cr} \right\} show that zero is the identity element of this operational each element 'a' of the set is invertible with 6-a being the inverse of 'a'
Find the inverse of the following functions.
f:R\rightarrow (0,\infty) defined by f(x)=5^{x}.
Prove that the function f : R \rightarrow R defined by f ( x ) = 4 x + 3 , is invertible and find the inverse of f .
If y=f(x)=\dfrac{x-5}{5x-1}, show that f(y)=x.
Show that the function f:R \rightarrow R defined by f(x) = \dfrac{x}{{x}^{2}+1} for all x\in R is neither one-one nor onto.
Examine whether the binary operation * defined on R by a*b=ab+1 is associative or not.
Find the equation of two straight lines through the point (4,5) which makes an acute angle of 45 degree with 2x-y+7=0.
On the set W of all non-negative integers * is defined by a*b=a^b. Prove that * is not a binary operation on W.
If * is defined on the set R of all real numbers by a*b=\sqrt{a^2+b^2}, find the identity element in R with respect to *.
If the function f : R \rightarrow R be given by f(x) = {x}^{2}+2 and g : R → R be given g(x) =\dfrac{x}{x-1},\,\, x \neq 1, find f. g and g.f and hence fog\left(2\right) and gof\left(-3\right).
f(x) = \dfrac{1}{x^{3}} then f^{'}(x)=
If f(x)=x+1 and g(x)=x^{2} Find
Fog\ (1)
Gof\ (-1)
Fog\ (2)
Gof\ (3)
If f(x)=x, g(x)=x^2 and h(x)=x^3, then find [(hog) of] (x).
Is the binary operation * defined on the set of integer z by the rule a * b = a - b + 2 commutative ?
Check whatever there is a direct or an inverse proportion in the following cases. Give reason to support your answer.i) Number of water bottles and their costii) Time taken and the distance covered at a uniform speed of vehicleiii) Distance traveled and there fare charge for itiv) Number of person and the number of days for which the food should last
Let A=\left\{1,2,3\right\},B=\left\{4,5,6,7\right\} and let f=\left\{\left(1,4\right),\left(2,5\right),\left(3,6\right)\right\} be a function from A to B.Show that f is one-one.
Let f(x)=3x^2-5 and g(x)=\dfrac{x}{x^2+1}. Then find (gof)(x).
The function f is defined for x\le 0 by f\left( x \right) =\frac { { x }^{ 2 }-1 }{ { x }^{ 2 }+1 } . Find its inverse
If f\left( x \right) ={ x }^{ 2 } and g\left( x \right) =2x+1 be two real valued function. Find \left( fg \right) \left( x \right) and \left( \dfrac { f }{ g } \right) \left( x \right) .
Let f : N \rightarrow N be a function defined as f(x) =4x^2+12x+15. Show that f : N \rightarrow S is invertible, where S is range of f. Also find the inverse of f.
Let x be non-empty set. P ( x ) be its power set. Let * be an operation defined on element of P ( x ) b y , A * B =
A \cap B \forall A , B \in P ( x ) . Then
(i) Prove that * is a binary operation in P ( x )
(ii) is * associative?
(iii) Is * commutative?
Let f(x)=3x+1 and g(x)=x^2+2 then find fog.
Show that function f : N \rightarrow N given by f ( x ) = 3 x is one-one but not onto.
The function f and g as defined for x \ge 0 by
f (x) = 2x^2 + 3,
g(x) = 3x+2.
Show that g(f(x)) = 6x^2 + 11
Show that function f:R\rightarrow R, f(x)=\frac { 2x+5 }{ 8 } is invertible. Also find inverse of f.
Given an example to show that \ast : N\times N \rightarrow N, given by (a, b) = a - b is not a binary operation.
Give examples of two one-one functions {f}_{1} and {f}_{2} from R to R such that {f}_{1}+{f}_{2}:R\rightarrow R, defined by ({f}_{1}+{f}_{2})(x)={f}_{1}(x)+{f}_{2}(x) is not one-one.
Find the number of all onto functions from the set A=\left\{ 1,2,3,....n \right\} to itself.
If f:A\rightarrow B and g:B\rightarrow C are one-one functions, show that g\circ f is a one-one function.
Let A=\left\{ 1,2,3 \right\} . Write all one-one from A to itself.
Let f=\left\{ \left( 3,1 \right) ,\left( 9,3 \right) ,\left( 12,4 \right) \right\} and g=\left\{ \left( 1,3 \right) ,\left( 3,3 \right) ,\left( 4,9 \right) ,\left( 5,9 \right) \right\} . Show that g\circ f and f\circ g are both defined. Also, find f\circ g and g\circ f.
Show that if {f}_{1} and {f}_{2} are one-one maps from R to R, then the product {f}_{1}\times {f}_{2}:R\rightarrow R defined by ({f}_{1}\times {f}_{2})(x)={f}_{1}(x){f}_{2}(x) need not be one-one.
Give examples of two functions f:N\rightarrow N and g:N\rightarrow N such that g\circ f is onto, but f is not onto.
Show that the exponential function f:R\rightarrow R, given by f(x)={e}^{x}, is one-one but not onto. What happens, if the co-domain is replaced by {R}_{0}^{+} (Set of all positive real numbers)?
Prove that the function F:N\rightarrow N, defined by f(x)={x}^{2}+x+1 is one-one but not onto.
Let f=\left\{ \left( 1,-1 \right) ,\left( 4,-2 \right) ,\left( 9.-3 \right) ,\left( 16,4 \right) \right\} and g=\left\{ \left( -1,-2 \right) ,\left( -2,-4 \right) ,\left( -3,-6 \right) ,\left( 4,8 \right) \right\} . Show that g\circ f is defined while f\circ g is not defined. Also, find g\circ f.
Consider f:R\rightarrow R given by f(x)=4x+3. Show that f is invertible. Find the inverse f.
Determine whether the operation '\ast ' on N defined by a\ast b = a^{b} for all a,b \in N is a binary operation or not :
If f:R\rightarrow (-1,1) defined by f(x)=\cfrac{{10}^{x}-{10}^{-x}}{{10}^{x}+{10}^{-x}} is invertible, find {f}^{-1}.
Let f(x)={x}^{2}+x+1 and g(x)=\sin x. Show that f\circ g\ne g\circ f.
If f(x)=\left| x \right| , prove that f\circ f=f.
Let f:[-1,\infty)\rightarrow [-1,\infty) is given by f(x)={(x+1)}^{2}-1. Show that f is invertible. Also, find the set S\left\{ x:f(x)={ f }^{ -1 }(x) \right\} .
Let f be a function from R to R, such that f(x)=\cos(x+2). Is f invertible? Justify your answer.
If f(x)=\cfrac{4x+3}{6x-4},x\ne \cfrac{2}{3}, show that f\circ f(x)=x for all x\ne \cfrac{2}{3}. What is the inverse of f?
Determine whether the operation 'O ' on Z defined by aO b = a^{b} for all a,b \in Z is a binary operation or not :
If f:R\rightarrow (0,2) is defined by f(x)=\cfrac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}} is invertible, then find {f}^{-1}.
Determine whether the following operation define a binary operation on the given set or not :
'x_{6}' on S=\left \{ 1,2,3,4,5 \right \} defined by a\times _{6}b= Remainder when ab is divided by 6.
Let \ast be a binary operation on the set I of integers, defined by a\ast b= 2a+b-3. Find the value of 3\ast 4.
Determine whether or not the definition of \ast On Z^{+}, define \ast by a\ast b= a. gives a binary operation.If the event that \ast is not a binary operation give justification of this.
Determine whether or not the definition of \ast On Z^{+} define \ast by a\ast b= \left | a-b \right | gives a binary operation. If the event that \ast is not a binary operation give justification of this.
Determine whether the following operation define a binary operation on the given set or not:
'\bigodot ' on N defined by a\bigodot b= a^{b}+b^{a} for all a,b \in N.
Determine whether or not the definition of \ast On Z^{+}, defined by a\ast b= ab. gives a binary operation. If the event is not a binary operation give justification of this.
Determine whether the operation '\ast ' on N defined by a\ast b = a+b-2 for all a,b \in N is a binary operation or not :
Determine whether the following operation define a binary operation on the given set or not:
'\ast ' on Q defined by a\ast b= \dfrac{a-1}{b+1} for all a,b \in Q.
Determine whether or not the definition of \ast On Z^{+}, defined by a\ast b= a-b gives a binary operation. If the event \ast is not a binary operation give justification of this.
Determine whether or not the definition of \ast On R, defined by a\ast b= ab^{2}. gives a binary operation. If the event that \ast is not a binary operation give justification of this.
Write the total number of one-one functions from set A=\left\{ 1,2,3,4 \right\} to set B=\left\{ a,b,c \right\} .
Let S be the set of all rational number of the form \dfrac{m}{n}, where m\in Z and n= 1,2,3. Prove that \ast on S defined by a\ast b=ab is not a binary operation.
If f:R\rightarrow R is given by f(x)={x}^{3}, write {f}^{-1}(1).
Find the total number of binary operations on \left \{ a,b \right \}.
If A=\left\{ a,b,c \right\} and B=\left\{ -2,-1,0,1,2 \right\} , write total number of one-one functions from A to B.
If f:R\rightarrow R is defined by f(x)={x}^{2}, write {f}^{-1}(25).
The binary operation \ast : R\times R\rightarrow R is defined as a\ast b= 2a+b. Find (2\ast 3)\ast 4.
Let \ast be a binary operation on N given by a\ast b= \text{LCM}(a,b) for all a,b \in N. Find 5\ast 7.
Let S= \left \{ a,b,c \right \}. Find the total number of binary operations on S.
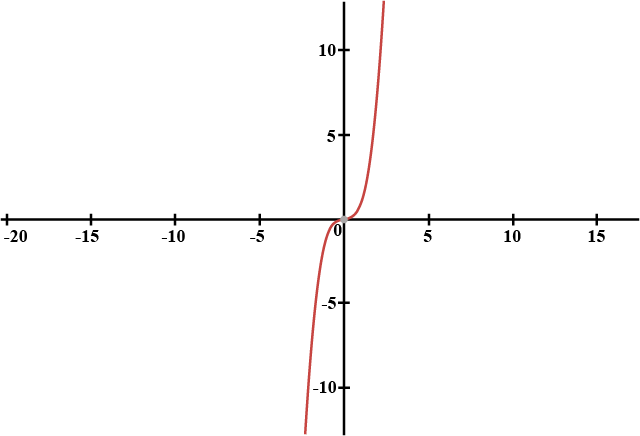
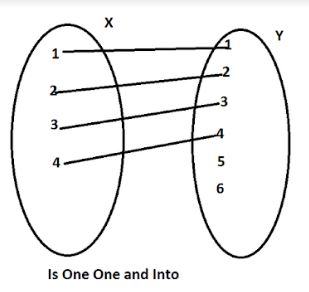
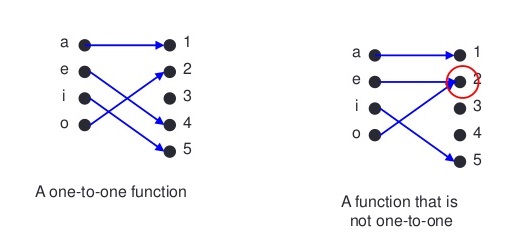
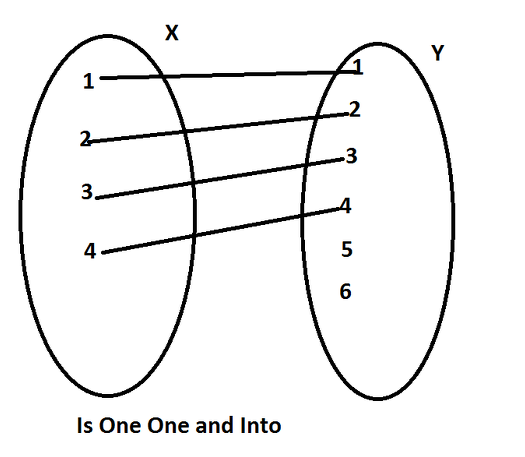
Which one of the given graphs represents a one-one function?

Check the commutativity and associativity of the following binary operation:
'\ast ' on Q defined by a \ast b= ab^{2} for all a,b \in Q.
Let A=\left\{ 1,2,3,4 \right\} and B=\left\{ a,b \right\} be two sets. Write total number of onto functions from A to B.
Check the commutativity and associativity of the following binary operation:
'\ast ' on Q defined by a \ast b= (a-b)^{2} for all a,b \in Q.
Let '\ast ' be a binary operation on N defined by a\ast b= \text{LCM}(a,b) for all a,b \in N. Find 2\ast 4, 3\ast 5, 1\ast 6.
Check the commutativity and associativity of the following binary operation:
'\ast ' on Z a \ast b= a-b for all a,b \in Z.
Check the commutativity and associativity of the following binary operation:
'\ast ' on N, defined by a \ast b= a^{b} for all a,b \in N.
Let f be an invertible real function. Write ({f}^{-1} \circ f)(1)+({f}^{-1} \circ f(2)+.....+({f}^{-1} \circ f)(100).
Check the commutativity and associativity of the following binary operation:
'\ast ' on R defined by a \ast b= a+b-7 for all a,b \in Q.
Check the commutativity and associativity of the following binary operation:
'\ast ' on Q defined by a \ast b= a+ab for all a,b \in Q.
Check the commutativity and associativity of the following binary operation:
'o ' on Q defined by a o b= \dfrac{ab}{2} for all a,b \in Q.
Check the commutativity and associativity of the following binary operation:
'\ast ' on Q defined by a \ast b= \dfrac{ab}{4} for all a,b \in Q.
Let A=\left\{ 1,2,3 \right\} , B=\left\{ 4,5,6,7 \right\} and let f=\left\{ \left( 1,4 \right) ,\left( 2,5 \right) ,\left( 3,6 \right) \right\} be a function from A to B. State whether f is one-one or not.
If f:R\rightarrow R be defined by f(x)={(3-{x}^{3})}^{1/3}, then find f\circ f(x).
If f:R\rightarrow R be defined by f(x)=3x+2, find f(f(x)).
Let \ast be a binary operation on Z defined by a\ast b= a+b-4 for all a,b\in Z. Find the invertible elements in Z.
Let f,g:R\rightarrow R be defined by f(x)=2x+1 and g(x)={x}^{2}-2 for all x\in R, respectively. Then, find g\circ f.
If f(x)=x+7 and g(x)=x-7, x\in R, write f\circ g(7).
Let S be the set of all rational numbers except 1 and \ast be defined on S by a\ast b= a+b- ab, for all a,b \in S. Prove that \ast is commutative as well as associative.
Let S be the set of all rational numbers except 1 and \ast be defined on S by a\ast b= a+b- ab, for all a,b \in S. Prove that \ast is a binary operation on S.
Let \ast be a binary operation on Z defined by a\ast b= a+b-4 for all a,b\in Z.
Show that '\ast ' is commutative.
For the binary operation \times _{7} on set S=\left \{ 1,2,3,4,5,6 \right \}, compute 3^{-1}\times _{7}4.
Let R_{0} denote the set of all non-zero real numbers and let A= R_{0}\times R_{0}. If '\ast ' is a binary operation on A defined by (a,b)\ast (c,d)= (ac, bd) for all (a,b)(c,d) \in A.
Show that '\ast ' is both commutative and associative on A
Let 'o' be a binary operation on the set Q_{0} of all non-zero rational numbers defined by a\, o\, b= \dfrac{ab}{2}, for all a,b \in Q_{0}. Find the invertible elements of Q_{0}.
Let \ast a binary operation on Q-\left \{ -1 \right \} defined by a\ast b= a+b+ab for all a,b \in Q -\left \{ -1 \right \}.
Then, show that '\ast ' is commutative on Q-\left \{ -1 \right \}.
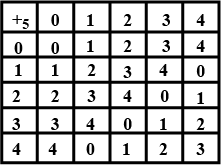
Construct the composition table for +_{5} on set S= \left \{ 0,1,2,3,4 \right \}.
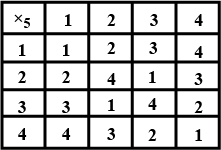
Construct the composition table for \times_{5} on Z= \left \{ 1,2,3,4 \right \}.
Let R_{0} denote the set of all non-zero real numbers and let A= R_{0}\times R_{0}. If '\ast ' is a binary operation on A defined by (a,b)\ast (c,d)= (ac, bd) for all (a,b)(c,d) \in A.
Find the invertible element in A.
Find f\circ g and g\circ f, if f(x)={x}^{2},g(x)=\cos x.
Find f\circ g and g\circ f, if f(x)=\sin ^{ -1 }{ x } , g(x)={x}^{2}.
Find f\circ g and g\circ f, if f(x)=c,c\in R, g(x)=\sin {x}^{2}.
For the relation R_1 defined on R by the rule (a, b)\in R_1\Leftrightarrow 1+ab > 0. Prove that: (a, b)\in R_1 and (b, c)\in R_1\Rightarrow (a, c)\in R_1 is not true for all a, b, c \in R.
Find g\circ f and f\circ g when f:R\rightarrow R and g:R\rightarrow R are defined by f(x)=8{x}^{3} and g(x)={x}^{1/3}.
Find f\circ g and g\circ f, if f(x)={x}^{2}-2, g(x)=1-\cfrac{1}{1-x}.
Find f\circ g and g\circ f, if f(x)={e}^{x},g(x)=\log _{ e }{ x } .
Find f\circ g and g\circ f, if f(x)=x+1, g(x)=2x+3.
Find f\circ g and g\circ f, if f(x)=\left| x \right| , g(x)=\sin x.
Find f\circ g and g\circ f, if f(x)=x+1; g(x)={e}^{x}.
Give an example of a function which is one-one and onto.
If f(x) = \dfrac{4x + 3}{6x -4}, \, x \neq \dfrac{2}{3}, then show that (fof) (x) = x, for all x \neq \dfrac{2}{3}. Also, write inverse of f.
Give an example of a function which is one-one but not onto.
Show that the function f: R\rightarrow R: f(x)=x^4 is neither one-one nor onto.
Let R be a relation on N\times N defined by (a, b) R(c, d)\Leftrightarrow a+d=b+c for all (a, b), (c, d)\in N\times N
Show that (a, b) R (a, b) for all (a, b)\in N\times N.
Show that the function f: N\rightarrow N:f(x)=x^2 is one-one into.
The binary operation ^\star on R is defined by a^{\star} b=2a+b. Find (2^{\star} 3)\star 4.
Let f(x)=x+7 and g(x)=x-7, x\in R. Find (f o g)(7).
Let R_0 be the set of all non zero real numbers. Then, show that the function f: R_0\rightarrow R_0:f(x)=\dfrac{1}{x} is one-one and onto.
Let f: R\rightarrow R:f(x)=(3-x^3)^{1/3}. Find f o f.
Let \star be a binary operation on the set I of all integers, defined by a^{\star}b=3a+4b-2. Find the value of 4\star 5.
Let ^{\star} be a binary operation on the set of all non zero real numbers, defined by a^{\star}b=\dfrac{ab}{5}. Find the value of x given that 2^{\star}(x^{\star}5)=10.
Let A=\{1, 2, 3\}, B=\{4, 5, 6, 7\} and let f=\{(1, 4), (2, 5), (3, 6)\} be a function from A to B. State whether f is one-one.
Let f: R\rightarrow R and g: R\rightarrow R defined by f(x)=x^2 and g(x)=(x+1). Show that g o f\neq f o g.
Let ^{\star}: R\times R\rightarrow R be a binary operation given by a^{\star}b=a+4b^2. Then, compute (-5)^{\star}(2^{\star}0).
Show that \star on Z^+ defined by a\star b=|a-b| is not a binary operation.
Let F : R \rightarrow R : f(x) = x^3 + 1 and g: R \rightarrow E : g (x) = (x+ 1) .
Find ( \frac {1}{f})(x) .
Let f : R \rightarrow R : f(x) =x +1 and g : R \rightarrow R : g(x) = 2x -3 .
Find (f -g)(x) .
Let ^{\star} be a binary operation on the set Q of all rational numbers given as a^{\star}b=(2a-b)^2 for all a, b\inQ. Find 3^{\star}5 and 5^{\star}3. Is 3^{\star}5=5^{\star}3?
Let Q^+ be the set of all positive rational numbers. Show that the operation \star on Q^+ defined by a\star b=\dfrac{1}{2}(a+b) is a binary operation.
If \star be the binary operation on the set Z of all integers defined by a^{\star}b=(a+3b^2), find 2^{\star}4.
Let f : R \rightarrow R : f(x) = 2x +5 and g : R \rightarrow R : g(x) =x^2 + x.
Find (fg)(x).
Let A=N\times N. Define \star on A by (a, b)\star (c, d)=(a+c, b+d). Show that A is closed for \star.
Let f(x) and g(x) be two continuous functions and h(x) =\underset{h\rightarrow \infty }{\lim}\dfrac{x^{2n}f(x)+x^{2n}g(x)}{(x^{2n}+1)} if limit of h(x) exists x=1 then one root of f(x)-g(x)=0 is
Let f : [ 2 , \infty ) \rightarrow R : f(x) = \sqrt {x-2} and g: [2, \infty) \rightarrow R : g (x) = \sqrt {x +2}
Find (f-g)(x).
Let f : [ 2 , \infty ) \rightarrow R : f(x) = \sqrt {x-2} and g: [2, \infty) \rightarrow R : g (x) = \sqrt {x +2}
Find ( f+g)(x).
Find the set of values for which the function f(x) = x +3 and g(x) = 3x^2 -1 are equal.
Given f(\dfrac{1}{e})=0 \dfrac{\int_{f(y)}^{f(y)}e'dt}{\int_{y}^{x}(1/2)dt}=1,\forall x,y\epsilon (\dfrac{1}{e^{2}}\infty ) Where f(x) is Continuous and differentiable function and f\left ( \dfrac{1}{e} \right )=0 if then the value of K' for which f(g(x)) is continuous \forall x\epsilon R^{+} is
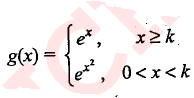
Let f : R\to R be the function defined by f(x)=2x-3, \forall c \in R. write f^{-1}.
A table of values of \mathrm{f}, \mathrm{g}, \mathrm{f}^{\prime} and \mathrm{g}^{\prime} is given :
If \mathrm{r}(\mathrm{x})=\mathrm{f}[\mathrm{g}(\mathrm{x})] find \mathrm{r}^{\prime}(2)
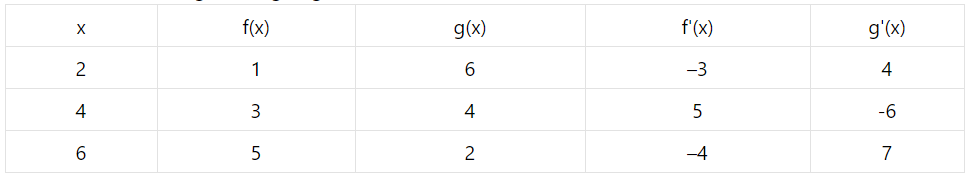
Let f, g:R\to R be defined by f(x)=2x+1 and g(x)=x^2 -2 respectively.
Then find g\ o\ f.
A table of values of \mathrm{f}, \mathrm{g}, \mathrm{f}^{\prime} and \mathrm{g}^{\prime} is given:
If \mathrm{R}(\mathrm{x})=\mathrm{g}[3+\mathrm{f}(\mathrm{x})] find \mathrm{R}^{\prime}(4)
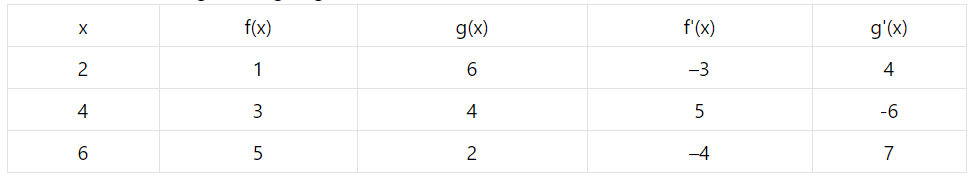
If A=\left\{a,b,c,d \right\} and the function f=\left\{(a,b),(b,d),(c,a),(d,c) \right\}, write f^{-1}.
Consider the binary operation * on the set {1,2,3,4,5} defined by a*b=min. {a,b}. Write the operation table of the operation *.
If f(x)=x^{3}+x-2, find \left(f^{-1}\right)^{\prime}(-2)
Determine whether or not each of the definitions given below gives a binary operation. In the event that is not a binary operation, give justification for this.
OnZ^+,* defined by a*b=|a-b|
Determine whether or not each of the definition of given below gives a binary operation. In the even that is not a binary operation, give justification for this.
On\ R,* defined by a*b=ab^2
Determine whether or not each of the definition of given below gives a binary operation. In the even that is not a binary operation, give justification for this.
OnZ^+,* defined by a*b=ab
Determine whether or not each of the definition of given below gives a binary operation. In the even that is not a binary operation, give justification for this.
OnZ^+,* defined by a*b=a
Determine whether or not each of the definition of given below gives a binary operation. In the even that is not a binary operation, give justification for this.
OnZ^+,* defined by a*b=a-b
A table of values of f, g, f^{\prime} and g^{\prime} is given:
If S(x)=g[g(x)] find S^{\prime}(6)
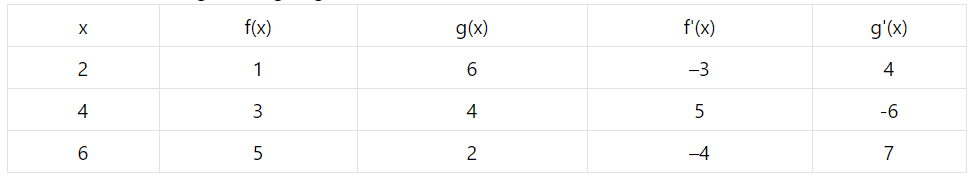
If h(x)=\sqrt{4 f(x)+3 g(x)}, f(1)=4, g(1)=3, f \prime(1)=3, g \prime(1)=4, find h ^{\prime}(1)
A table of values of f, g, f^{\prime} and g^{\prime} is given:
If s(x)=f[9-f(x)] find s^{\prime}(4)
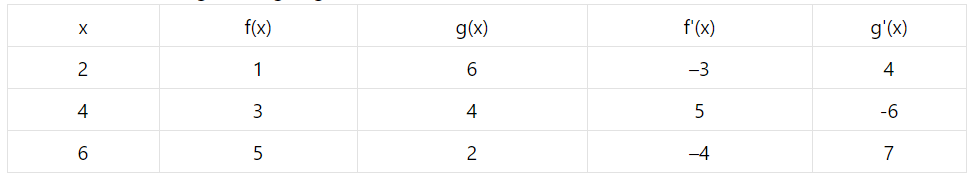
Let S= \left\{a,b,c\right\} and T=\left\{1,2,3,\right\} Find F^{-1} of the folowing function F from S to T if it exists.
F=\left\{(a,2), (i,1), (c,1) \right\}
Let S= \left\{a,b,c\right\} and T=\left\{1,2,3,\right\} Find F^{-1} of the folowing function F from S to T if it exists.
F=\left\{(a,3), (b,2), (c,1) \right\}
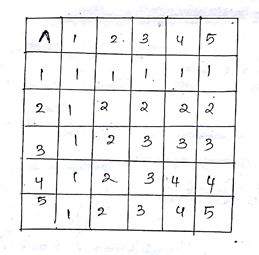
Consider a binary * operation on the set {1,2,3,4,5} given by the following multiplication table
Compute (2*3)*4 and 2*(3*4)
| * | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 1 | 3 | 1 | 1 |
| 4 | 1 | 2 | 1 | 4 | 1 |
| 5 | 1 | 1 | 1 | 1 | 5 |
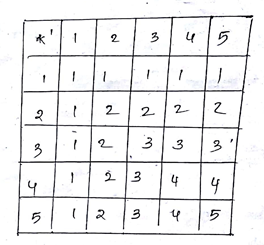
Consider a binary * operation on the set {1,2,3,4,5} given by the following multiplication table
Compute (2*3)*(4*5) .
| * | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 1 | 3 | 1 | 1 |
| 4 | 1 | 2 | 1 | 4 | 1 |
| 5 | 1 | 1 | 1 | 1 | 5 |
Consider f:\left\{1,2,3\right\}\rightarrow \left\{a, b, c\right\} given by f(1)=a, f(2)=b and f(3)=c. Find f^{-1} and show that (f^{-1})^{-1}=f.
*' Let be the binary operation on the set {1,2,3,4,5} defined by a*'b=H.C.F of a band b. Is the *' operation same as the * operation defined in Exercise 4 above? Justify your answer.
Consider a binary * operation on the set {1,2,3,4,5} given by the following multiplication table
* Is commutative?
| * | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 1 | 3 | 1 | 1 |
| 4 | 1 | 2 | 1 | 4 | 1 |
| 5 | 1 | 1 | 1 | 1 | 5 |
Let f: W \rightarrow W be defined as f(n)=-1 i fn is odd and f(n)=n-1, if n is even. Show that
f is invertible. Find the inverse of f. Here, W is the set of all whole numbers.
Let A= \left\{-1,0,1,2 \right\},\ B=\left\{-4,-2,0,2 \right\} and f, g : A \rightarrow B be functions defined by
f(x)=x^2-x, x \in A and g(x)=-1, x \in A Are f and g equal? Justify your answer.
Consider the binary \wedge operation on the set \left\{1,2,3,4,5\right\}
defined by a \wedge b=min\left\{a,b\right\}. Write operation table of the operation \wedge
Determine whether each of the following operation define a binary on the given set or not. Also, Justify your answer.
a*b =a+3b, on N
Define a relation.
Determine whether each of the following operation define a binary on the given set or not. Also, Justify your answer.
a*b =a, on N
Determine whether each of the following operation define a binary on the given set or not. Also, Justify your answer.
a*b =a/b, on Q
Let f, g: R\to R be defined, respectively by f(x)=x+1, g(x)=2x-3 Find f+g, f-g and \cfrac{f}{g}
Show that the function f: R \rightarrow R defined by f(n)=\dfrac{2n-1}{3}, n \in R is one-one onto function. Also find the inverse of f
Determine whether each of the following operation define a binary on the given set or not. Also, Justify your answer.
a*b =a+b-3, on N
Let f(x)=\sqrt x and g(x)=x be two function defined over the set of non-negative real numbers. Find f(+g)(x), (f-g)(x)(fg)(x) and \left( \dfrac fg \right)(x)
State whether the following statements are true or false. Justify.
For an arbitrary binary operation * on a set N,a*a=a \forall a\epsilon N
If A=\left\{ -1, 1\right\}f and g are two functions defined on A, where f(x)=x^2, g(x)=\sin ( \pi x/2), prove that g^{-1} exists but f^{-1} does not exist, also find g^{-1}.
Give one example of each of the following function :
One-one into
Four function are defined on set R_0. Such that,
f_1(x)=x, f_2(x)=-x, f_3(x)=1/x, f_4(x)=-1/x Construct the composition table for the composition of functions f_1, f_2, f_3, f_4. Also find identify element and inverse of every element.
If f:R\rightarrow R,f(x)=\cos (x+2), is f^{-1} exists.
Determine whether each of the following operation define a binary on the given set or not. Also, Justify your answer.
a*b =a-b, on R
If f : C \rightarrow C , f ( x + iy) = ( x - iy) , then prove that if is an one-one onto function.
Verify the associative law for the composite function of following three functions:
f:N \to Z_0, f(x)=2x
g: Z_0 \to Q, g(x)=1/x
h: Q \to R, h(x)=e_x
Give one example of each of the following function :
Onto but not one-one
Verify or prove whether the given functions are inverses of each other or not:
f(x)=4x-2 and g(x)=\dfrac{x+2}{4}
Let A=\{a,b,c\},B=\{u,v,w\} and f and g be two function from A to B and from B to A respectively defined as f = \{(a,v),(b,u),(c,w)\} and g=\{(u,b),(v,a),(w,c)\}.
Show that f and g both are bijections and find fog and gof.
Give one example of each of the following function :
One - one but not onto
If the function {f}({x})={x}^{3}+{e}^{{x}/2} and {g}({x})={f}^{-1}({x}), then the value of {g}'(1) is
Let f(x)=x+\dfrac{1}{x} and g(x)=\dfrac{x+1}{x+2}
Determine whether or not each of the definition of * given below gives a binary operation. In the event that * is not a binary operation, given justification for this
(i) On Z^{+}, define * by a * b = a - b
(ii) On Z^{+}, define * by a * b = ab
(iii) On R, define * by a * b = ab^{2}
(iv) On Z^{+}, define * by a * b = |a - b|
On Z^{+}, define * by a * b = a
Find the inverse of the rational function f.
f(x)=\dfrac2x
If the function f:R\rightarrow A, given by \displaystyle f(x)=\frac{x^{2}}{x^{2}+1} is surjection, then A\in [k,m). Find k+m.
If the function f:R\rightarrow A, given by \displaystyle f(x)=\frac{e^{x}-e^{-\left|x\right|}}{e^{x}+e^{\left|x\right|}} is surjection,then \displaystyle A\in \left[ m,k.\right),Find 2(m+k) ?
Let \displaystyle A=R\times R and \displaystyle * be a binary operation on A defined by
\displaystyle \left( a,b \right) \ast \left( c,d \right) =\left( a+c,b+d \right)
Show that \displaystyle * is commutative and associative. Find the identity element for \displaystyle * on A. Also find the inverse of every element \displaystyle \left( a,b \right) \in A.
Show that the function f in A=R-\left\{\dfrac{2}{3}\right\} defined as f(x)=\dfrac{4x+3}{6x-4} is one-one and onto. Hence find f^{-1}.
The binary operation \ast : R\times R \rightarrow R is defined as a\ast b = 2a + b. Find (2\ast 3)\ast 4.
Consider f:R+\rightarrow [4, \infty] given by f(x) = x^2+4. Show
that f is invertible with the inverse f^{-1} of f given by f^{-1}(y) = \sqrt{y-4} where R_+ is the set of all non-negative real numbers.
Consider the binary operations \ast : R\times R \rightarrow R and o : R\times R \rightarrow R defined as a\ast b = |a - b| and aob = a for all a, b\in R. Show that '\ast' is commutative but not associative, 'o' is associative but not commutative.
If f(x) = \sqrt{x^2+1}, g(x)=\dfrac{x+1}{x^2+1} and h(x) = 2x - 3, then find f'[h'|g'(x)|].
Let f,g,h are functions defined by f(x)=x-1,g(x)={ x }^{ 2 }-2 and h(x)={ x }^{ 3 }-3, show that \left( f\circ g \right) \circ h=f\circ \left( g\circ h \right) .
If f:R-\left\{ 3 \right\} \rightarrow R is defined by f(x)=\cfrac { x+3 }{ x-3 } , show that f\left[ \cfrac { 3x+3 }{ x-1 } \right] =x for x\ne 1.
If functions f, g : R \rightarrow R are defined as f(x) = x^{2} + 1, g(x) = 2x - 3, then find f\ o\ g(x), g\ o\ f(x) and g\ o\ g(3)
If f(x)={x}^{2} and g(x)=2x-6, find the following functions:
(f+g)(x), (f\times g)(x), (f\circ g)(x), (f\circ f)(x), {g}^{-1}(x)
Let f:A \to B and g:B \to C be one-one onto functions. prove that \left( {gof} \right):A \to C which is one-one onto
Let f:[0,\infty )\rightarrow R be a function defined by f(x)=9{ x }^{ 2 }+6x-5. Prove that f is not invertible and then find its inverse.
Let f:\left\{1,3,4\right\} \rightarrow \left\{1,2,5\right\} and g:\left\{1,2,5\right\} \rightarrow \left\{1,3\right\}
given by f=\left\{(1,2),(3,5),(4,1)\right\} and g=\left\{(1,3),(2,3),(5,1)\right\} write down gof
If f(x)=(a-x^n)^{\dfrac{1}{n}} then fof(x) is?
Let f:W\longrightarrow W be defined as f(x)=x-1, if x is odd and f(x)=x+1, if x is even, then show that f is invertible. Also, find the inverse of f, where W is the set of all whole numbers.
Let f:R\rightarrow R be defined by f\left( x \right) =2x+\left| x \right| Then prove that f\left( 2x \right) +f\left( -x \right) -f\left( x \right) =2\left| x \right|.
If f\left( x \right)=\dfrac { 2x-1 }{ x-2 }
what is the inverse function of f\left( x \right)
Show that the binary operation on Q - \{1\}, defined by a \times b = a + b - ab for all a, b \in Q - \{1\} satisfies (i) the closure property, (ii) the associative law
(iii) the commutative law
(iv) What is the identity element ?
(v) For each a \in Q - \{1\}, find the inverse of a.
If f\left( x \right) =2{ x }^{ 2 }-3x-1, Find f\left( x+2 \right)
Given f(x)=x+2,g(x)=2x+3,h(x)=3x^4 for x \epsilon R . Find
fo(goh)
Let * be the binary operation on N , given by a * b = L C M of a and b . Find 20 * 16.
0.25\ (4-f-3)=0.05\ (10f-9)
Let A=Z\times Z and * be a binary operation on A defined by (a, b)*(c, d)=(ad+bc, bd).
Find the identity element for * in the set A.
If f(x)=3x-2 and (gof)^{-1}(x)=x-2, then find the function g(x)
A,B,C are three sets such that n(A)=2,n(B)=3,n(C)=4, If P(x) denotes power set of X,k=\dfrac{n\left(P\left(P\left(C\right)\right)\right)}{n\left(P\left(P\left(A\right)\right)\right)\times n\left(P\left(P\left(B\right)\right)\right)}.then find the Sum of digits of k
Let the function f:R\longrightarrow R be defined by f(x)=\cos { x } ,\forall x\in R. Show hat f is neither one-one nor onto.
Let A=Q\times Q and let* be a binary operation on A defined by \left( a,b \right) *\left( c,d \right) =\left( ac,b+ad \right) for\left( a,b \right) ,\left( c,d \right) \epsilon A. Determine, whether * is commutative and associative. Then, with respect to * on A
Find the invertible elements of A.
Find {f}^{-1}, if it exists:f:A\rightarrow B, where
(i) A=\left\{ 0,-1,-3,2 \right\} ;B=\left\{ -9,-3,0,6 \right\} and f(x)=3x
(ii) A=\left\{ 1,3,5,7,9 \right\} ;B=\left\{ 0,1,9,25,49,81 \right\} and f(x)={x}^{2}
State with reasons whether given functions have inverse:
(i) f:\left\{ 1,2,3,4 \right\} \rightarrow \left\{ 10 \right\} with f=\left\{ \left( 1,10 \right) ,\left( 2,10 \right) ,\left( 3,10 \right) ,\left( 4,10 \right) \right\}
(ii) g:\left\{ 5,6,7,8 \right\} \rightarrow \left\{ 1,2,3,4 \right\} with g=\left\{ \left( 5,4 \right) ,\left( 6,3 \right) ,\left( 7,4 \right) ,\left( 8,2 \right) \right\}
(iii) h:\left\{ 2,3,4,5 \right\} \rightarrow \left\{7,9,11,13 \right\} with h=\left\{ \left( 2,7 \right) ,\left( 3,9 \right) ,\left( 4,11 \right) ,\left( 5,13 \right) \right\}
Let f:R\rightarrow R and g:R\rightarrow R be defined by f(x)={x}^{2} and g(x)=x+1. Show that f\circ g\ne g\circ f.
Show that the function f:Q\rightarrow Q defined by f(x)=3x+5 is invertible. Also, find {f}^{-1}.
Which of the following functions from A to B are one-one and onto?
(i) {f}_{1}=\left\{ \left( 1,3 \right) ,\left( 2,5 \right) ,\left( 3,7 \right) \right\} ; A=\left\{ 1,2,3 \right\} ,B=\left\{ 3,5,7 \right\}
(ii) {f}_{2}=\left\{ \left( 2,a \right) ,\left( 3,b \right) ,\left( 4,c \right) \right\} ; A=\left\{ 2,3,4 \right\} ,B=\left\{ a,b,c \right\}
(iii) {f}_{3}=\left\{ \left( a,x \right) ,\left( b,x \right) ,\left( c,z \right) \right\} ; A=\left\{ a,b,c,d \right\} ;B=\left\{ x,y,z \right\}
Suppose {f}_{1} and {f}_{2} are non-zero one-one functions from R to R. Is \cfrac{{f}_{1}}{{f}_{2}} necessarily one-one. Justify your answer. Here \cfrac{{f}_{1}}{{f}_{2}}:R\rightarrow R is given by \left( \cfrac { { f }_{ 1 } }{ { f }_{ 2 } } \right) \left( x \right) =\cfrac { { f }_{ 1 }(x) }{ { f }_{ 2 }(x) } for all x\in R.
Let f:R\rightarrow R and g:R\rightarrow R be defined by f(x)=x+1 and g(x)=x-1. Show that f\circ g=g\circ f={R}_{R}.
Let f(x)=\begin{cases} 1+x,\quad 0\le x\le 2 \\ 3-x,\quad 2<x\le 3 \end{cases}. Find f\circ f.
Consider the function f:{R}^{+}\rightarrow [-9,\infty) given by f(x)=5{x}^{2}+6x-9. Prove that f is invertible with {f}^{-1}(y)=\cfrac { \sqrt { 54-5y } -3 }{ 5 } .
Let A=R-\left\{ 3 \right\} and B=R-\left\{ 1 \right\} . Consider the function f:A\rightarrow B defined by f(x)=\cfrac{x-2}{x-3}. Show that f is one-one and onto and hence find {f}^{-1}.
Consider f:{R}^{+}\rightarrow [-5,\infty) given by f(x)=9{x}^{2}+6x-5. Show that f is invertible with {f}^{-1}(x)=\cfrac{\sqrt{x+6}-1}{3}.
Show that the function f: R\rightarrow R:f(x)=x^5 is one-one and onto.
Show that the function f: Z\rightarrow Z:f(x)=x^3 is one-one into.
Prove that the function f: N\rightarrow N:f(n)=(n^2+n+1) is one-one but not onto.
If the mapping f:\left\{ 1,3,4 \right\} \rightarrow \left\{ 1,2,5 \right\} and g:\left\{ 1,2,5 \right\} \rightarrow \left\{ 1,3 \right\} , given by f=\left\{ \left( 1,2 \right) ,\left( 3,5 \right) ,\left( 4,1 \right) \right\} and g=\left\{ \left( 2,3 \right) ,\left( 5,1 \right) ,\left( 1,3 \right) \right\} , write f\circ g.
Consider f:{R}^{+}\rightarrow [4,\infty) given by f(x)={x}^{2}+4. Show that f is invertible with inverse {f}^{-1} of f given by {f}^{-1}(x)=\sqrt{x-4}, where {R}^{+} is the set of all non-negative real numbers.
Let f:\left[0, \dfrac{\pi}{2}\right]\rightarrow R:f(x)=\sin x and g:\left[0, \dfrac{\pi}{2}\right]\rightarrow R: g(x)=\cos x. Show that each one of f and g is one-one but (f+g) is not one-one.
Show that the function f: N\rightarrow N:f(x)=x^3 is one-one into.
Let A=\{1, 2, 3, 4\} and f=\{(1, 4), (2, 1), (3, 3), (4, 2)\}. Write down (f o f).
Let f(x)=8x^3 and g(x)=x^{1/3}. Find g o f and f o g.
Let f and g be two functions from R into R, defined by f(x)=|x|+x and g(x)=|x|-x for all x\in R. Find f o g and g o f.
Show that the function f:Z\rightarrow Z:f(x)=x^3 is one-one and into.
Let f=\{(1, 2), (3, 5), (4, 1)\} and g=\{(1, 3), (2, 3), (5, 1)\}. Write down g o f.
Prove that the function f: R\rightarrow R: f(x)=2x is one-one and onto.
Show that the function f: N\rightarrow Z, defined by
f(n)=\left\{\begin{matrix} \dfrac{1}{2}(n-1), & \text{when} \,n \,\text{is odd}\\ -\dfrac{1}{2}n, & \text{when} \, n \, \text{is even}\end{matrix}\right. is both one-one and onto.
Show that the function f: N\rightarrow N:f(x)=x^2 is one-one and into.
Prove that the function f: N\rightarrow N:f(x)=3x is one-one and into.
Let Q be the set of all rational numbers. Define an operation \star on Q-\{-1\} by a\star b=a+b+ab.
Show that \star is a binary operation on Q-\{-1\}.
Let f : R \rightarrow R : f(x) = 2x +5 and g : R \rightarrow R : g(x) =x^2 + x.
Find (f +g)(x) .
Let f : R \rightarrow R : f(x) =x +1 and g : R \rightarrow R : g(x) = 2x -3 .
Find (\frac {f}{g} )(x) .
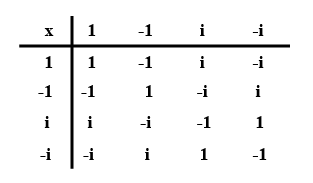
Let A=\{1, -1, i, -i\} be the set of four 4th roots of unity. Prepare the composition table for multiplication on A and show that
(i) A is closed for multiplication,
(ii) multiplication is associative on A,
(iii) multiplication is commutative on A,
(iv) 1 is the multiplication identity,
(v) every element in A has its multiplicative inverse.
Let f : R \rightarrow R : f(x) =x +1 and g : R \rightarrow R : g(x) = 2x -3 . Find (fg)(x).
Let f : R \rightarrow R : f(x) = 2x +5 and g : R \rightarrow R : g(x) =x^2 + x.
Find (f-g)(x).
Find the set of values for which the function f(x) = 1 -3x and g(x) = 2x^2 -1 are equal.
Let f : R \rightarrow R : f(x) = 2x +5 and g : R \rightarrow R : g(x) =x^2 + x.
Find ( \frac {f}{g})(x) .
Let F : R \rightarrow R : f(x) = x^3 + 1 and g: R \rightarrow E : g (x) = (x+ 1) .
Find (f +g)(x)
Let \displaystyle A = \{3, 5 \} and \displaystyle B = \{ 7, 9 \}. Let \displaystyle R = \{ (a, b) : a \in A, b \in B and \displaystyle (a - b) is odd \displaystyle \}.
Show that \displaystyle R is an empty relation from \displaystyle A to \displaystyle B.
Let F : R \rightarrow R : f(x) = x^3 + 1 and g: R \rightarrow E : g (x) = (x+ 1) .
Find ( \frac {f}{g} ) (x) .
Let f : [ 2 , \infty ) \rightarrow R : f(x) = \sqrt {x-2} and g: [2, \infty) \rightarrow R : g (x) = \sqrt {x +2}
Find (fg)(x).
Let F : R \rightarrow R : f(x) = x^3 + 1 and g: R \rightarrow E : g (x) = (x+ 1) .
Find (f-g)(x).
Consider the set A containing n elements. Then, the total number of injective functions from A onto itself is _______.
Class 12 Commerce Maths Extra Questions
- Application Of Derivatives Extra Questions
- Application Of Integrals Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Linear Programming Extra Questions
- Matrices Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions