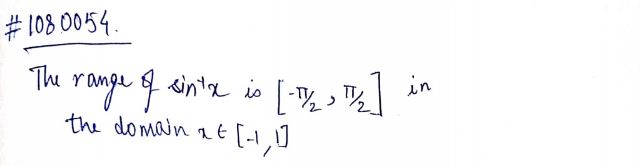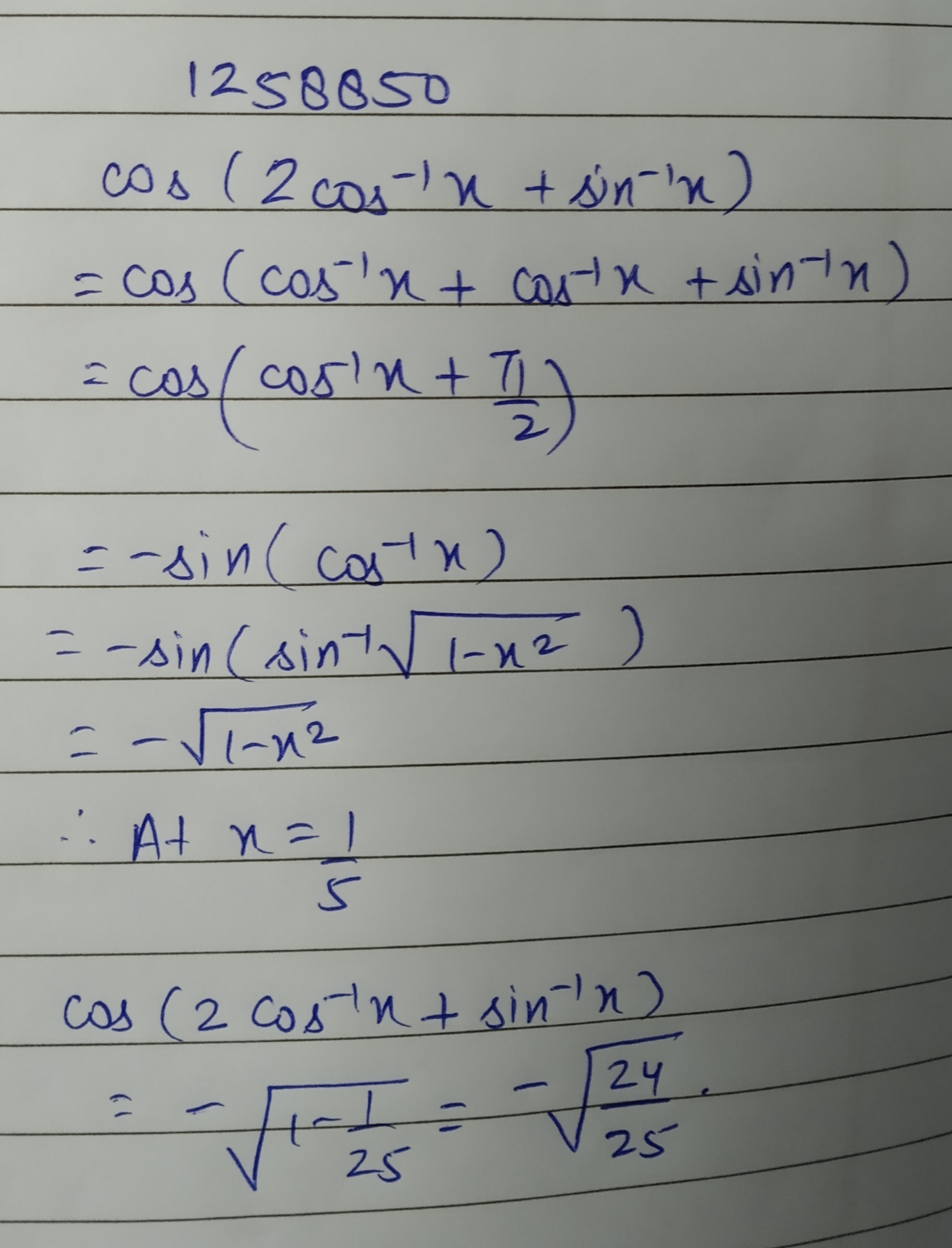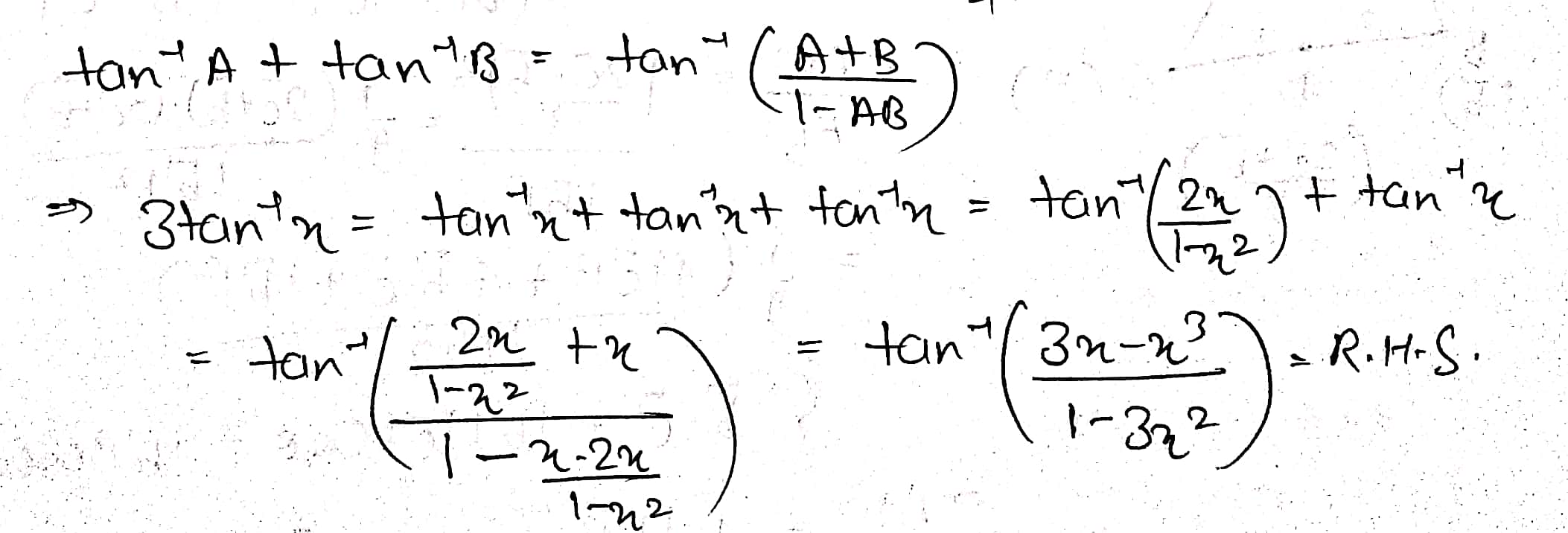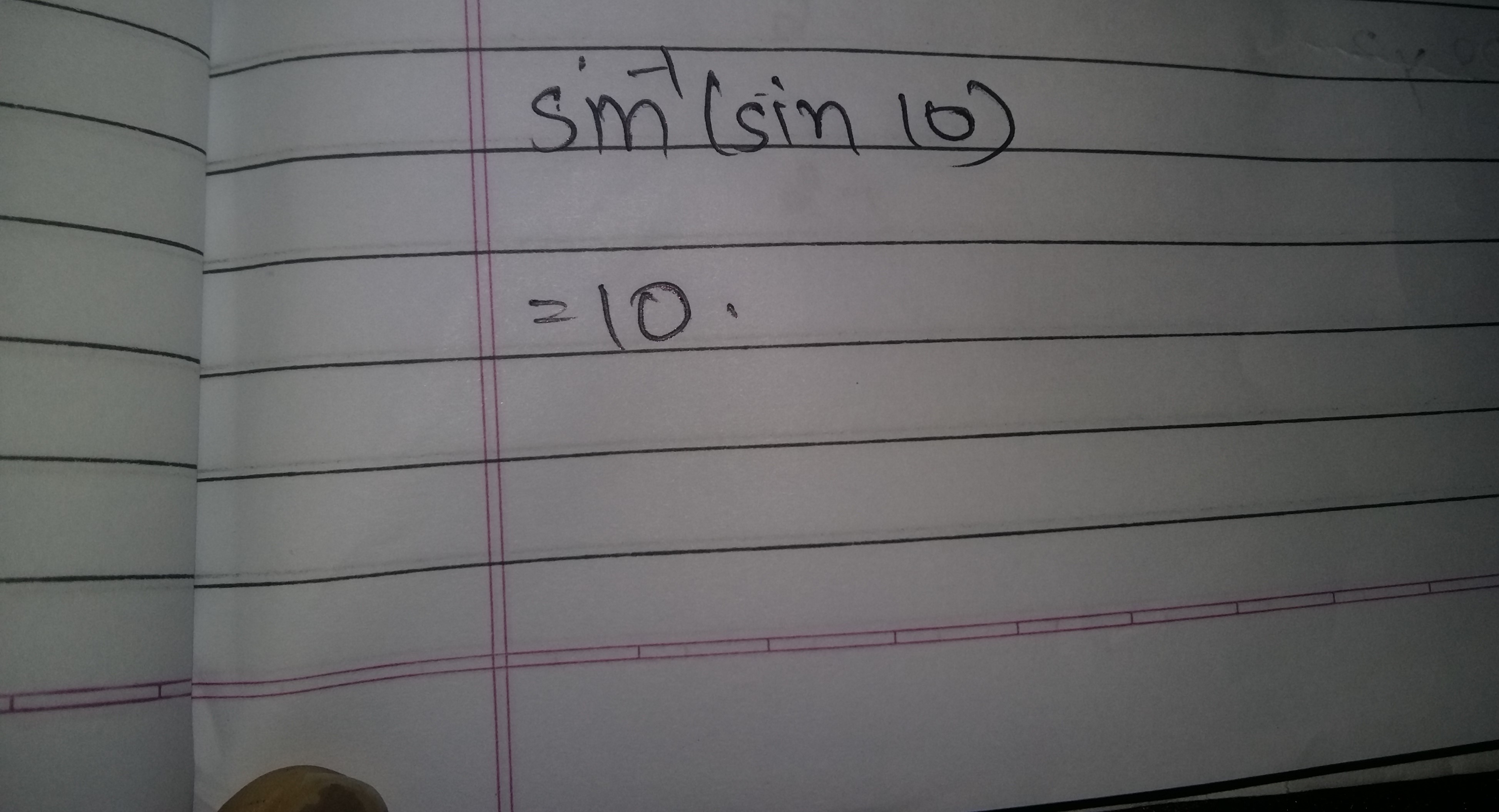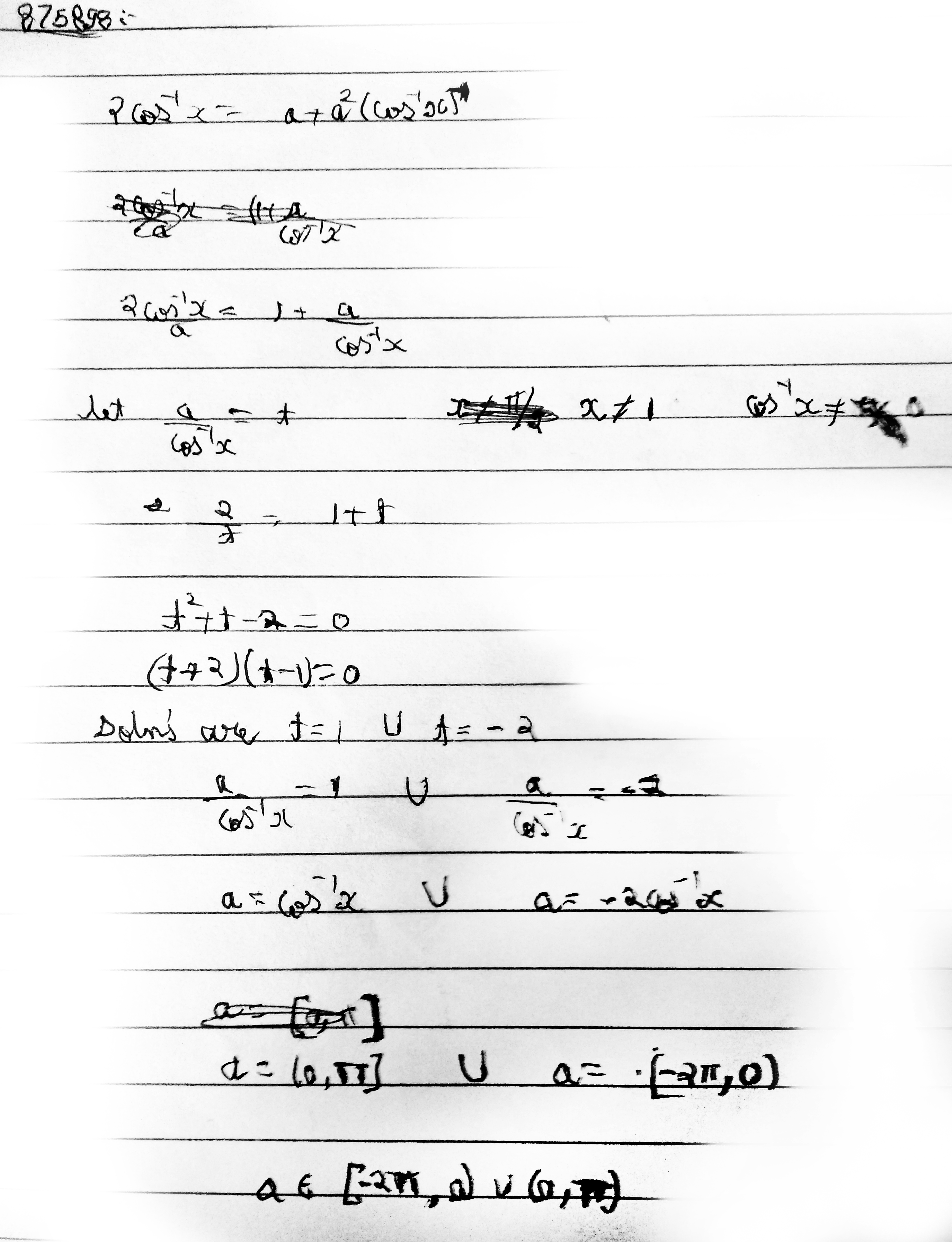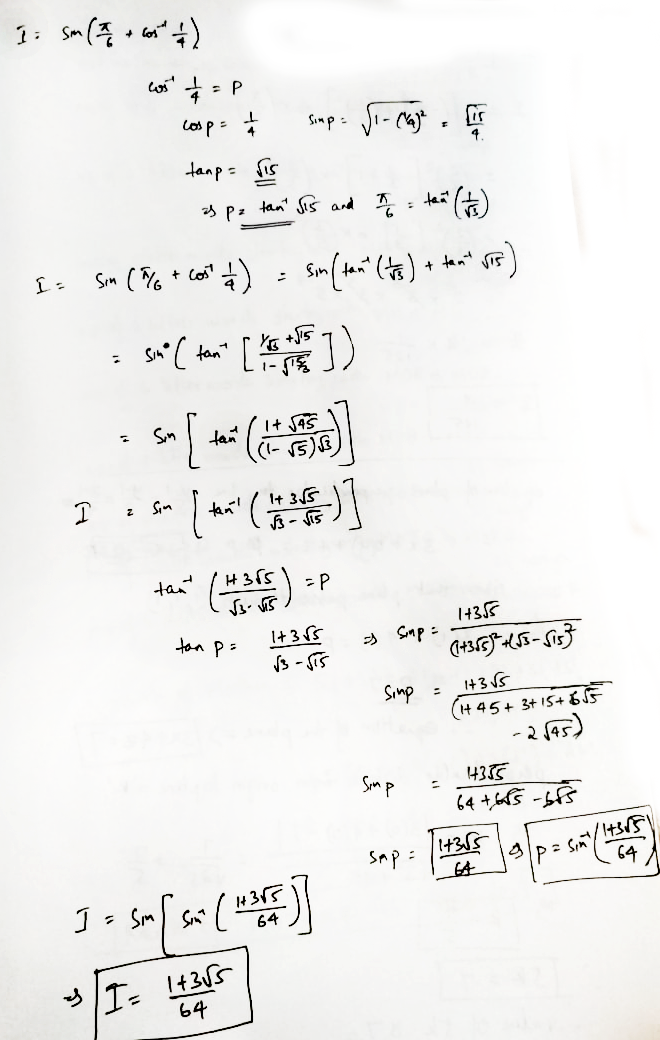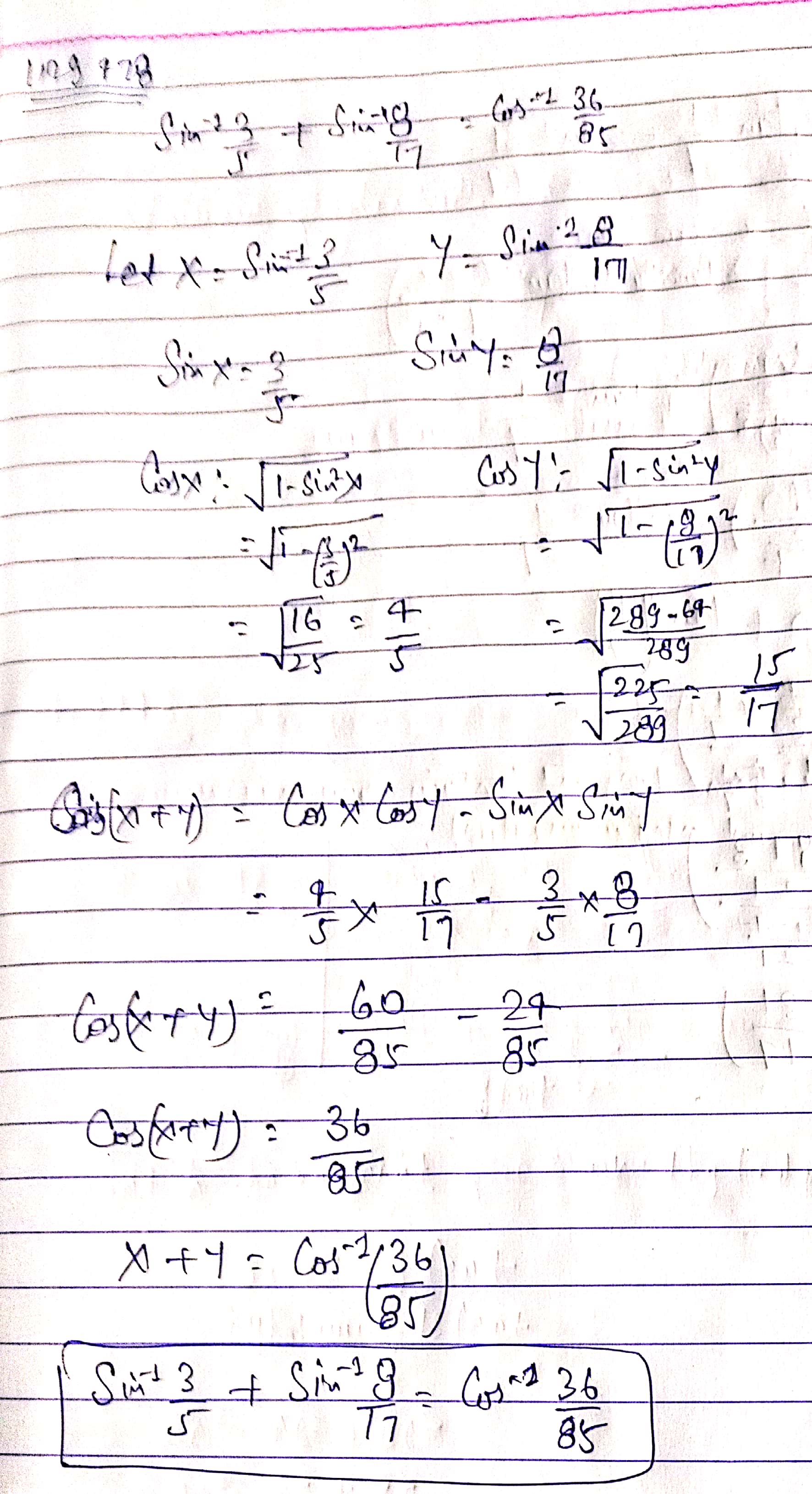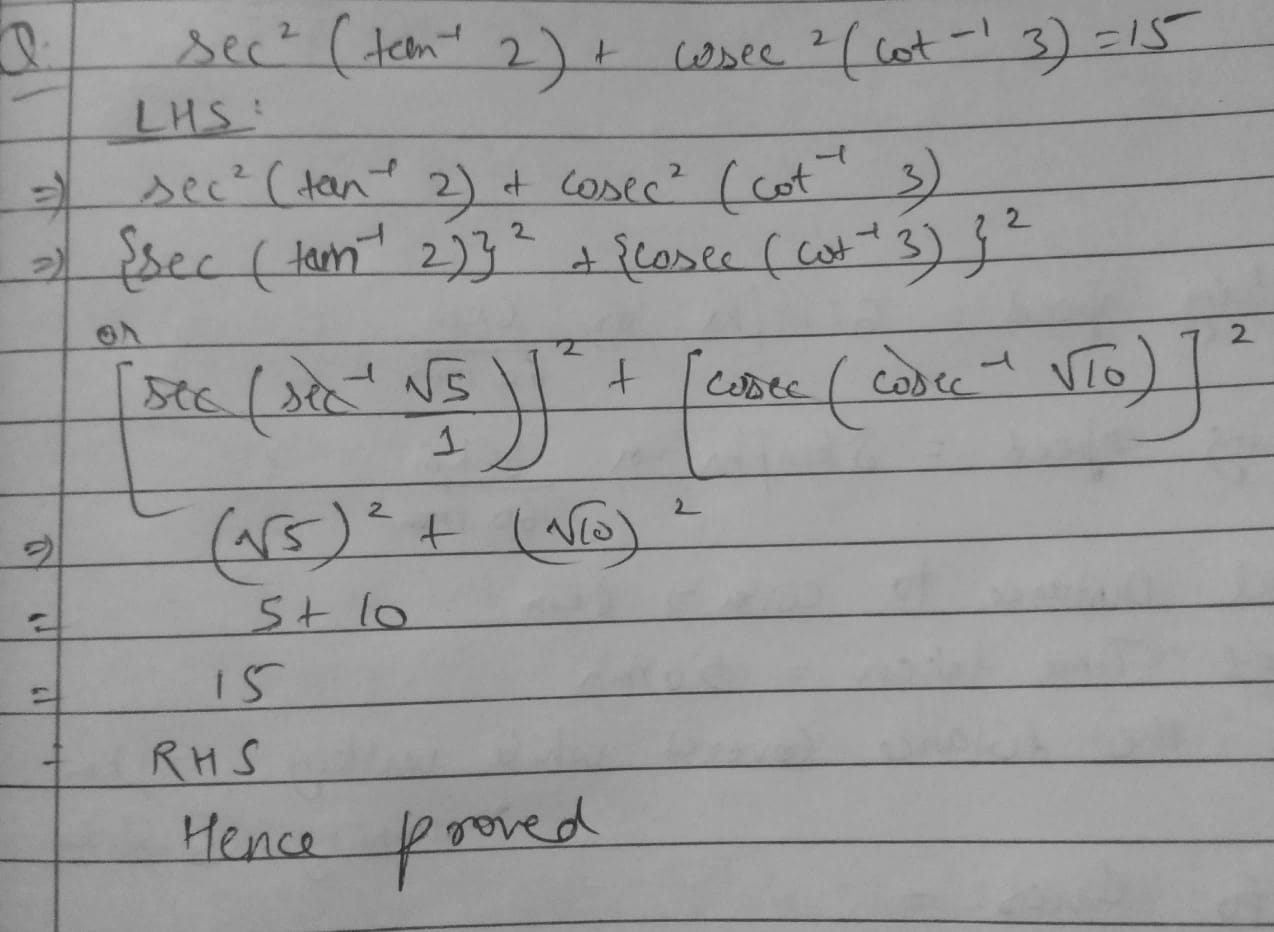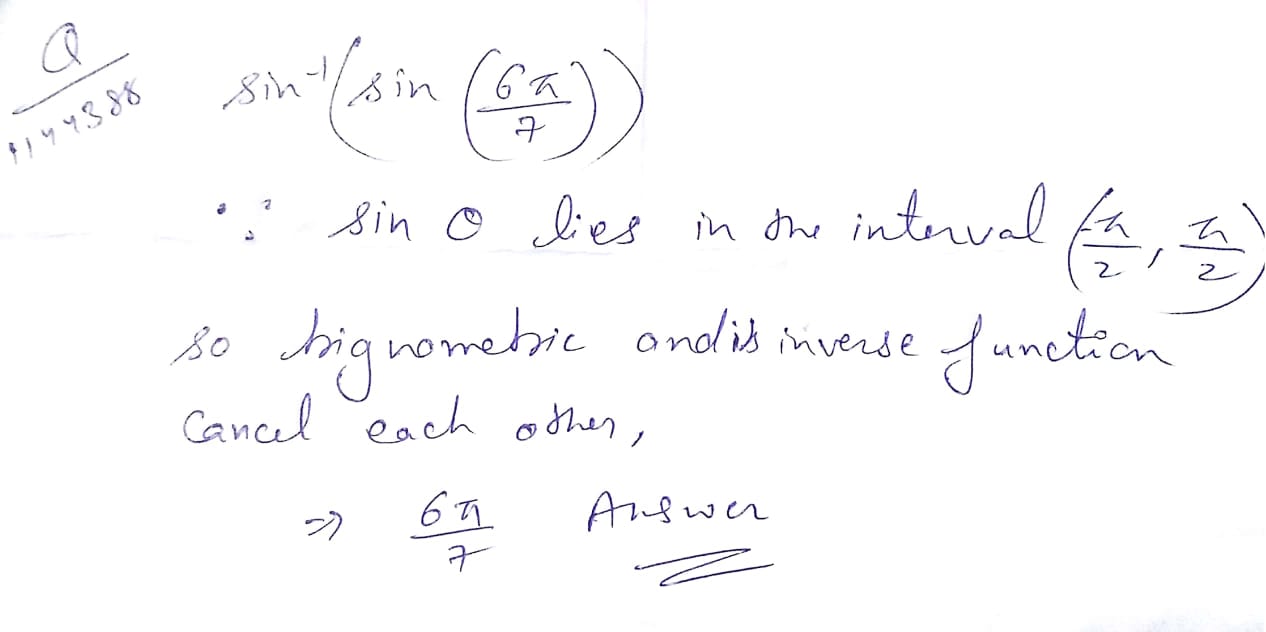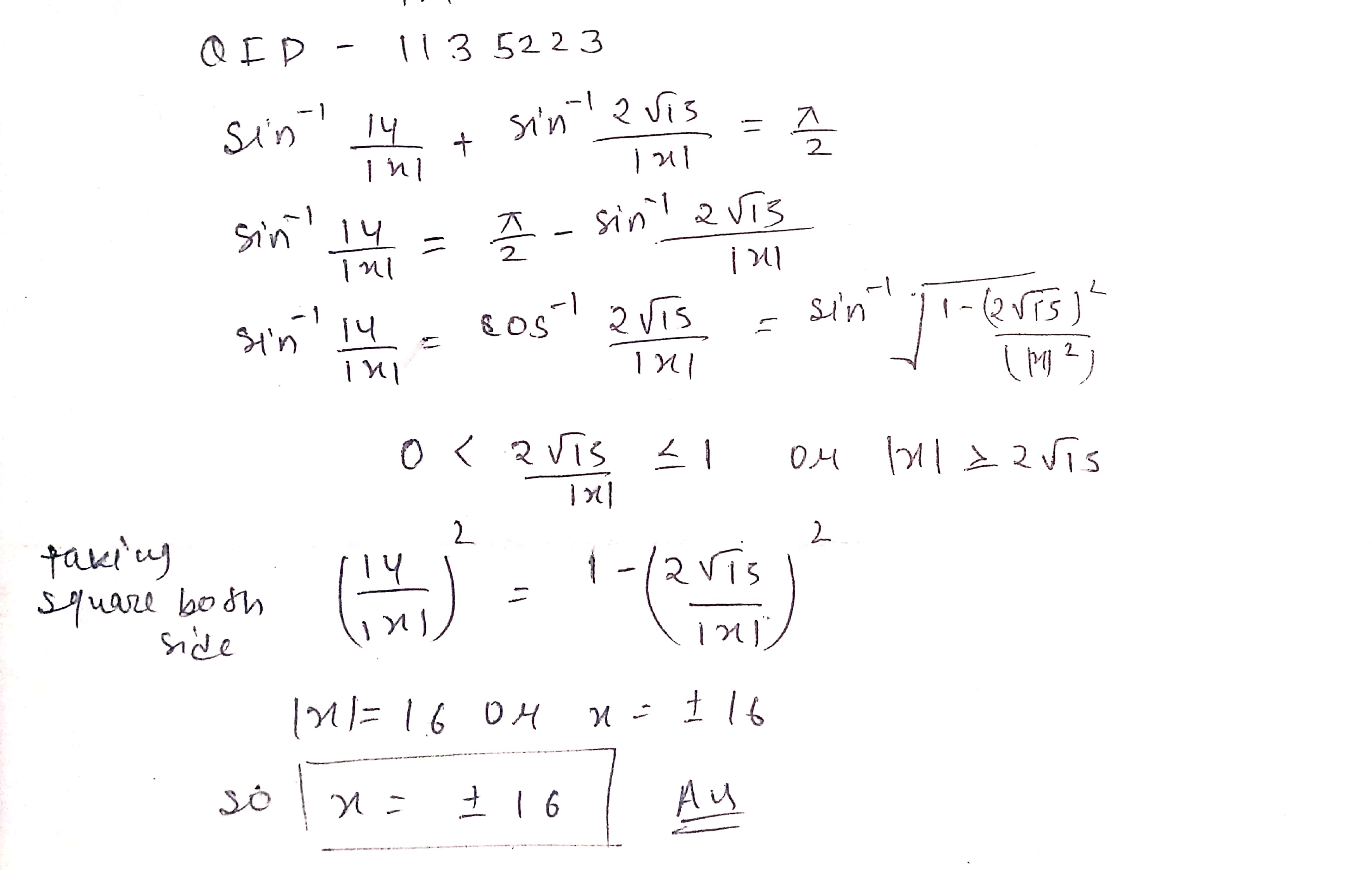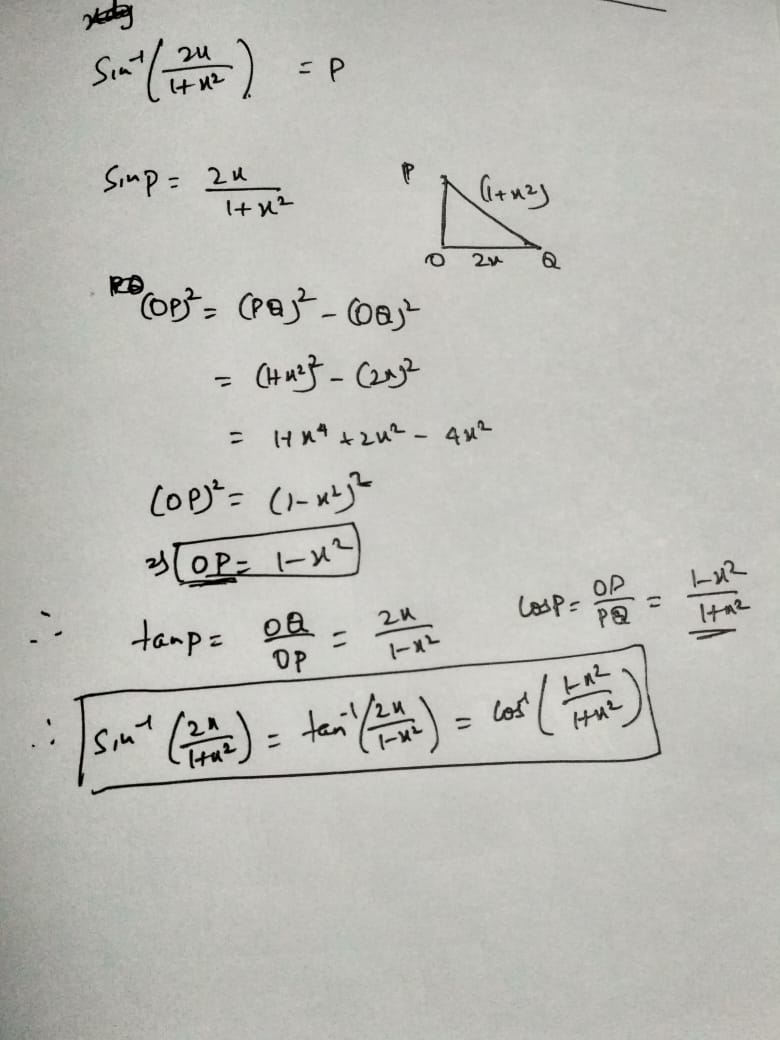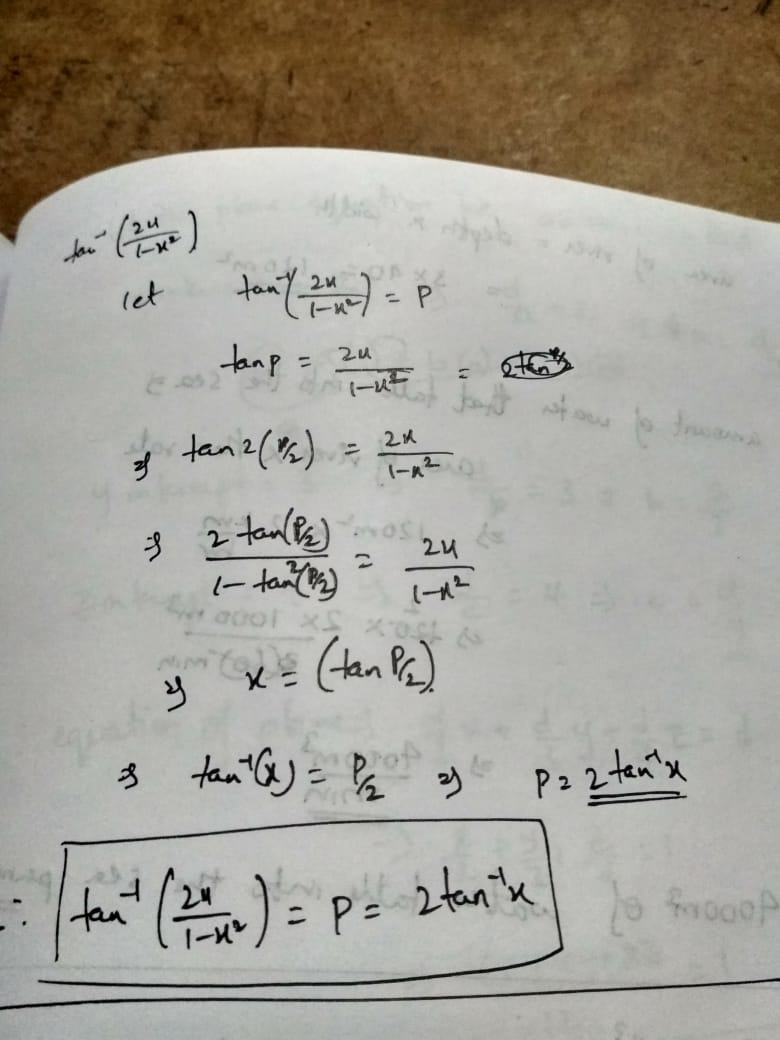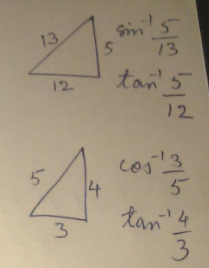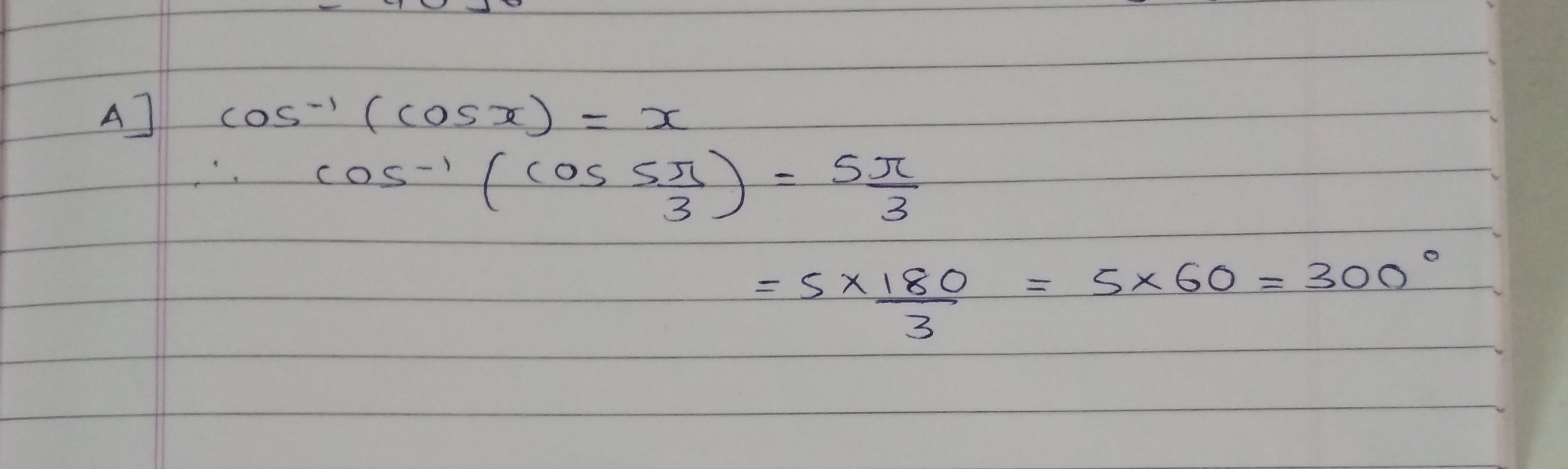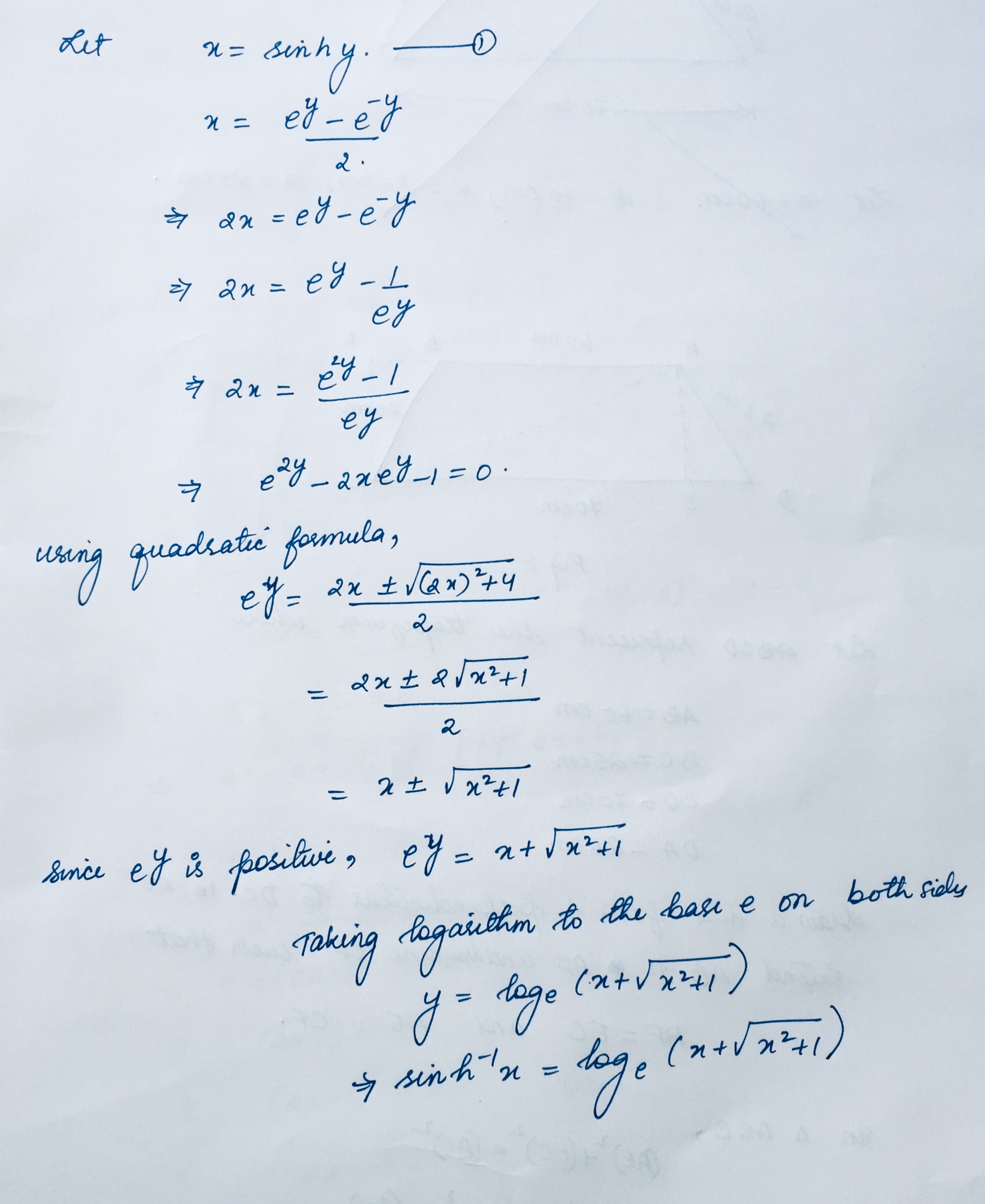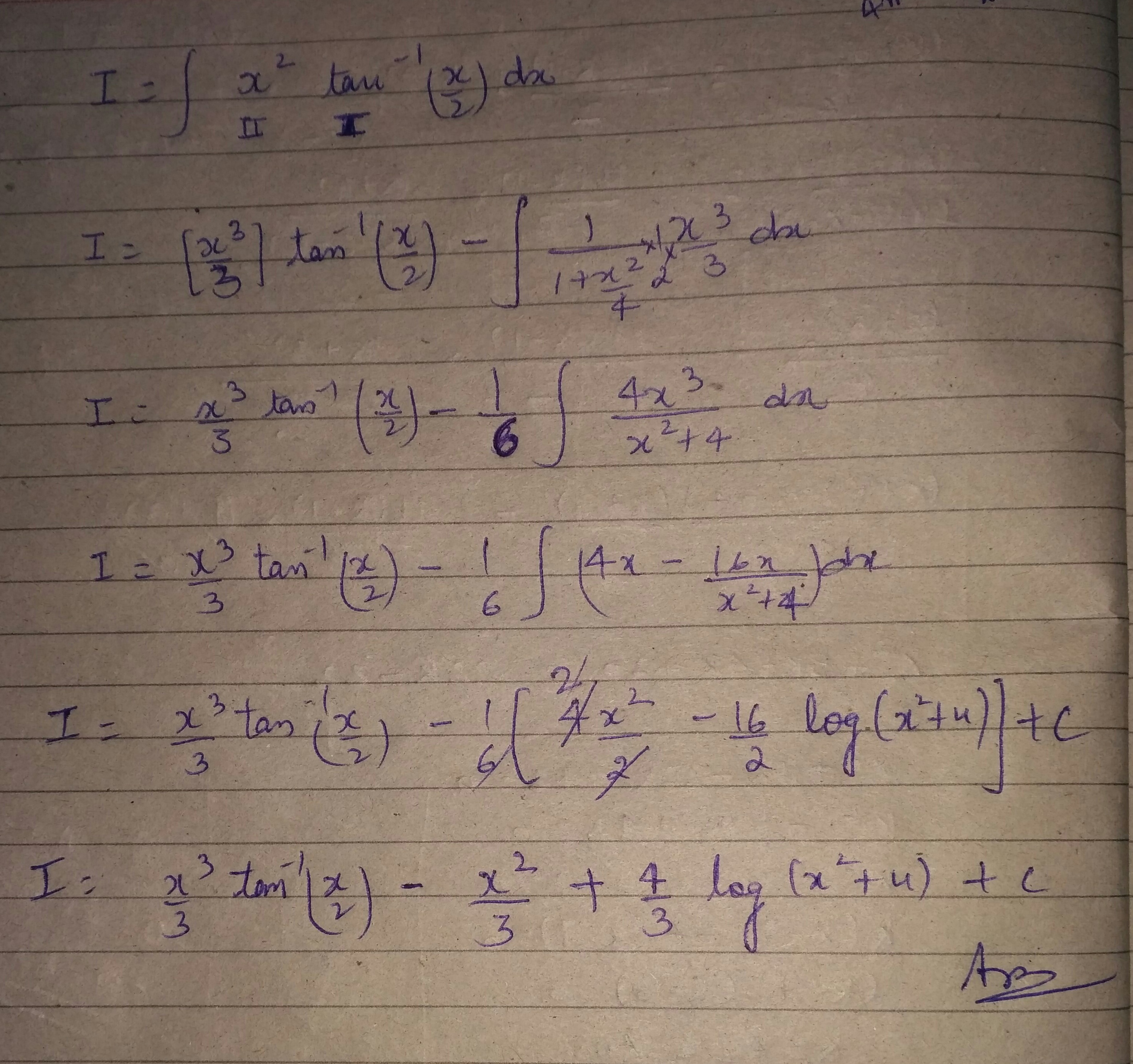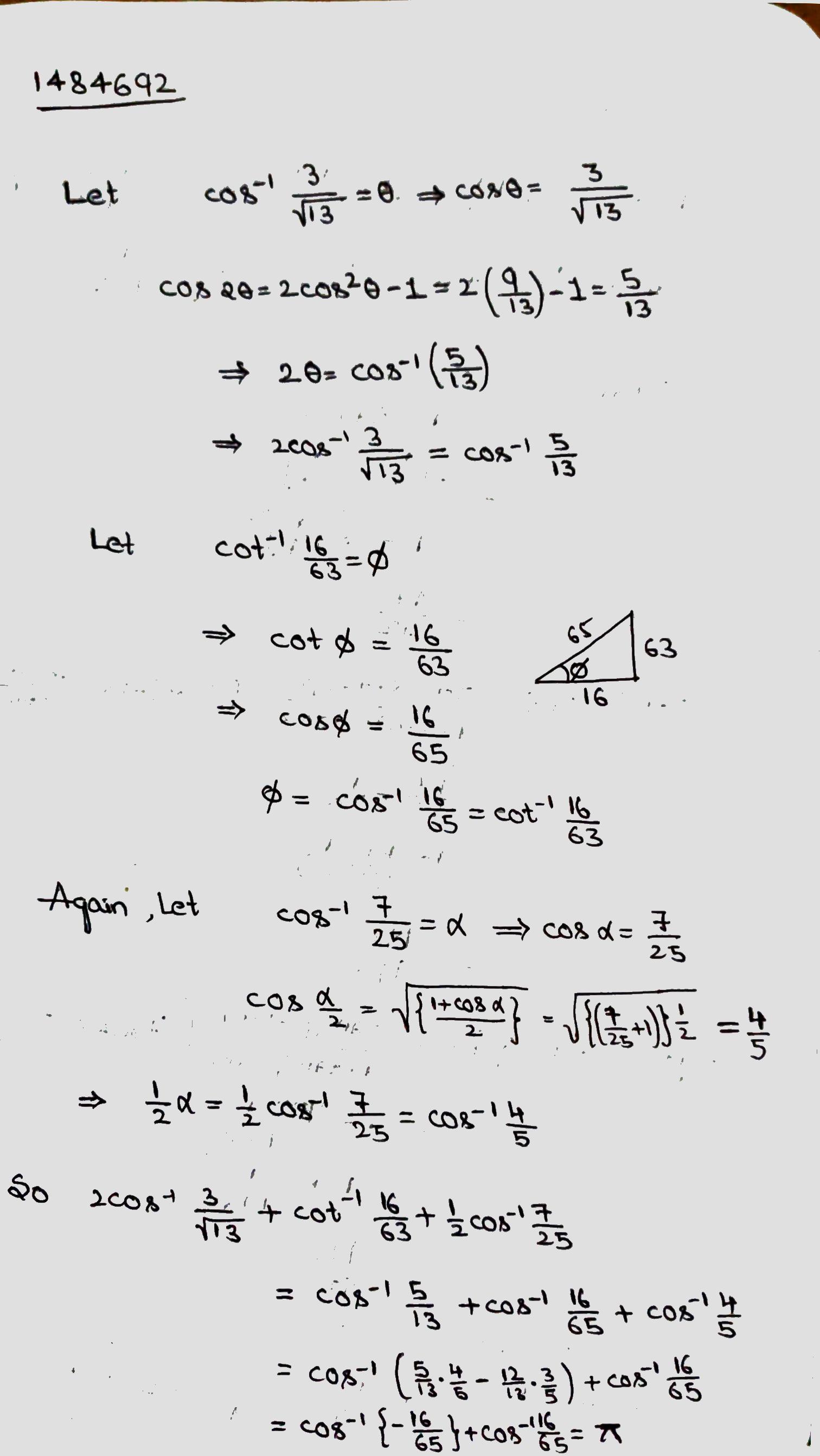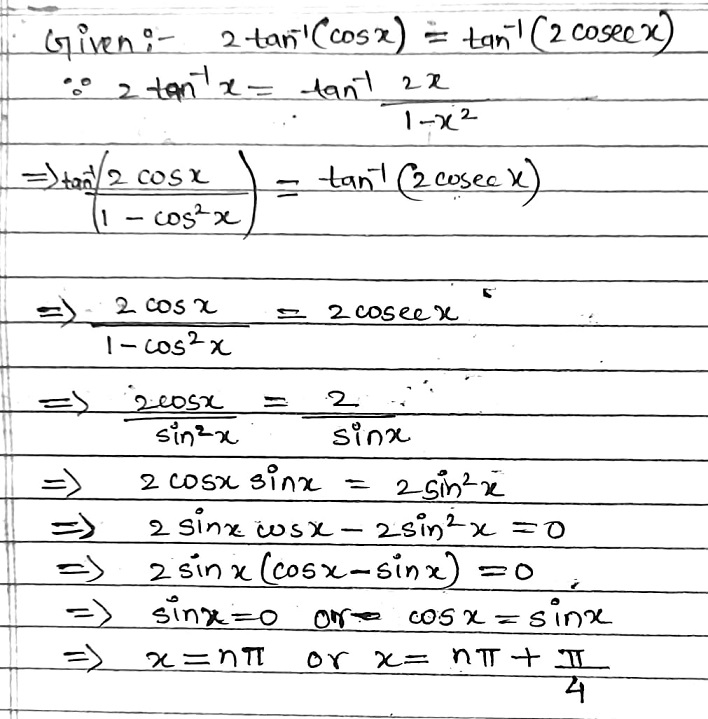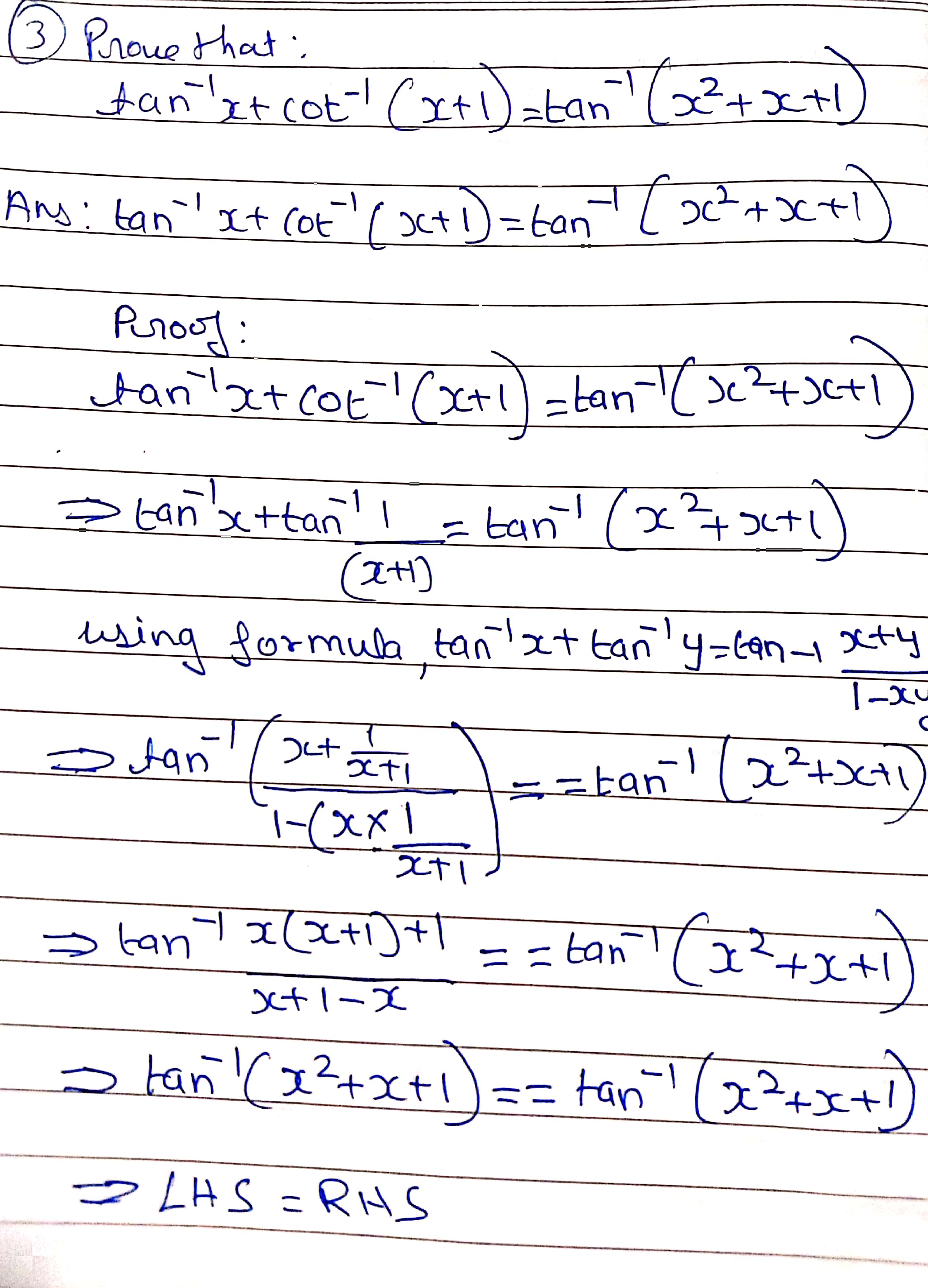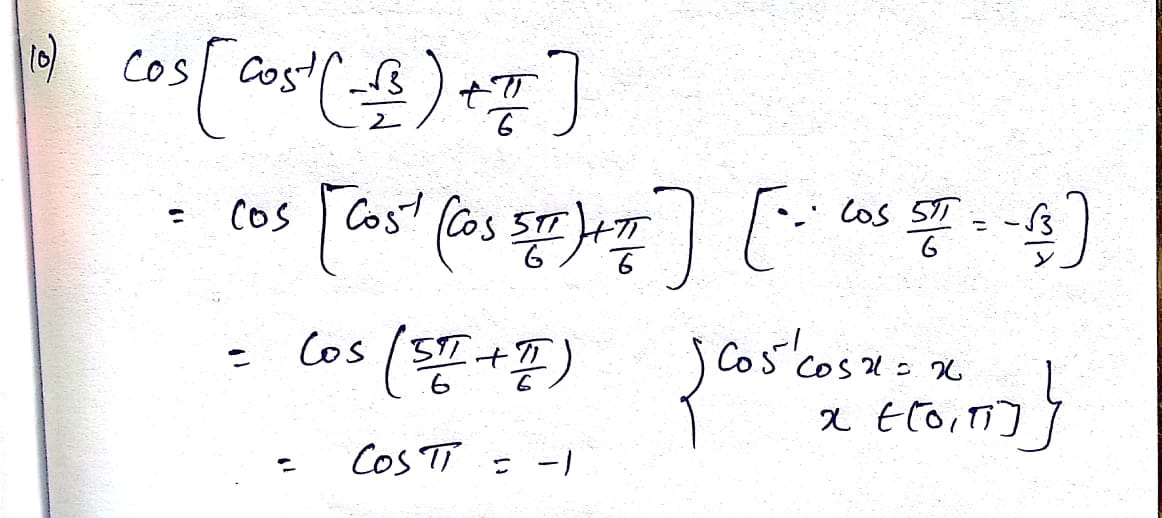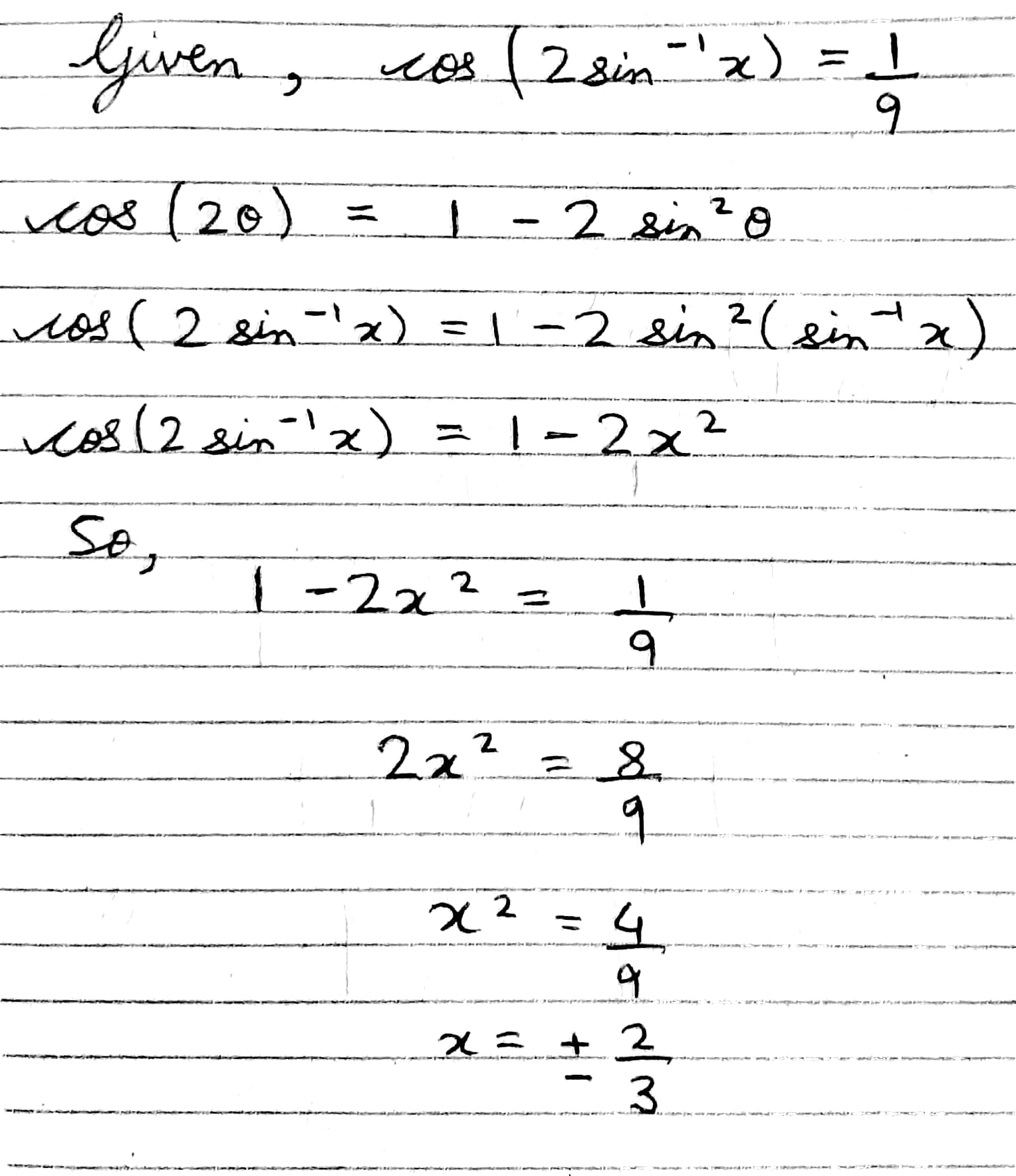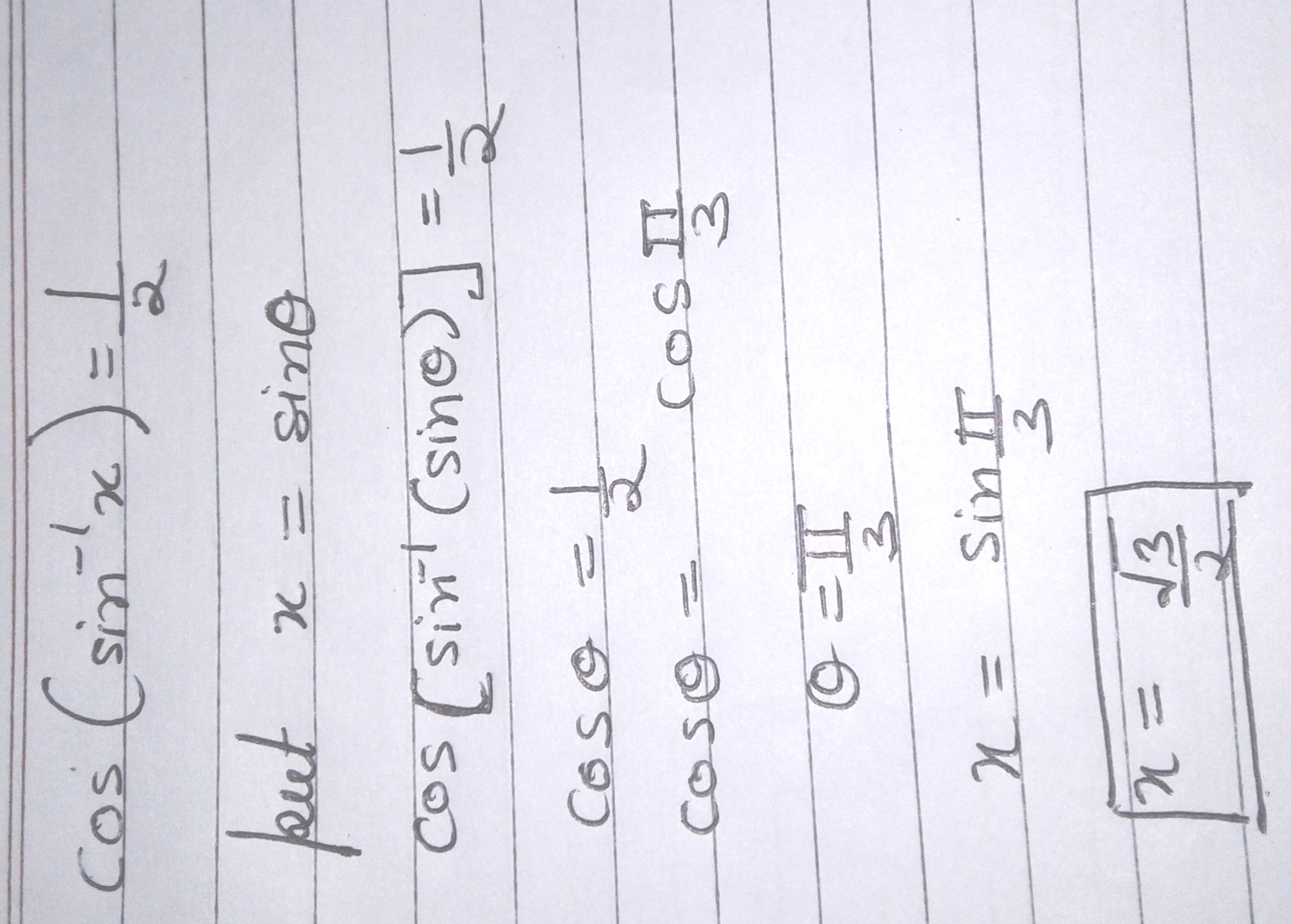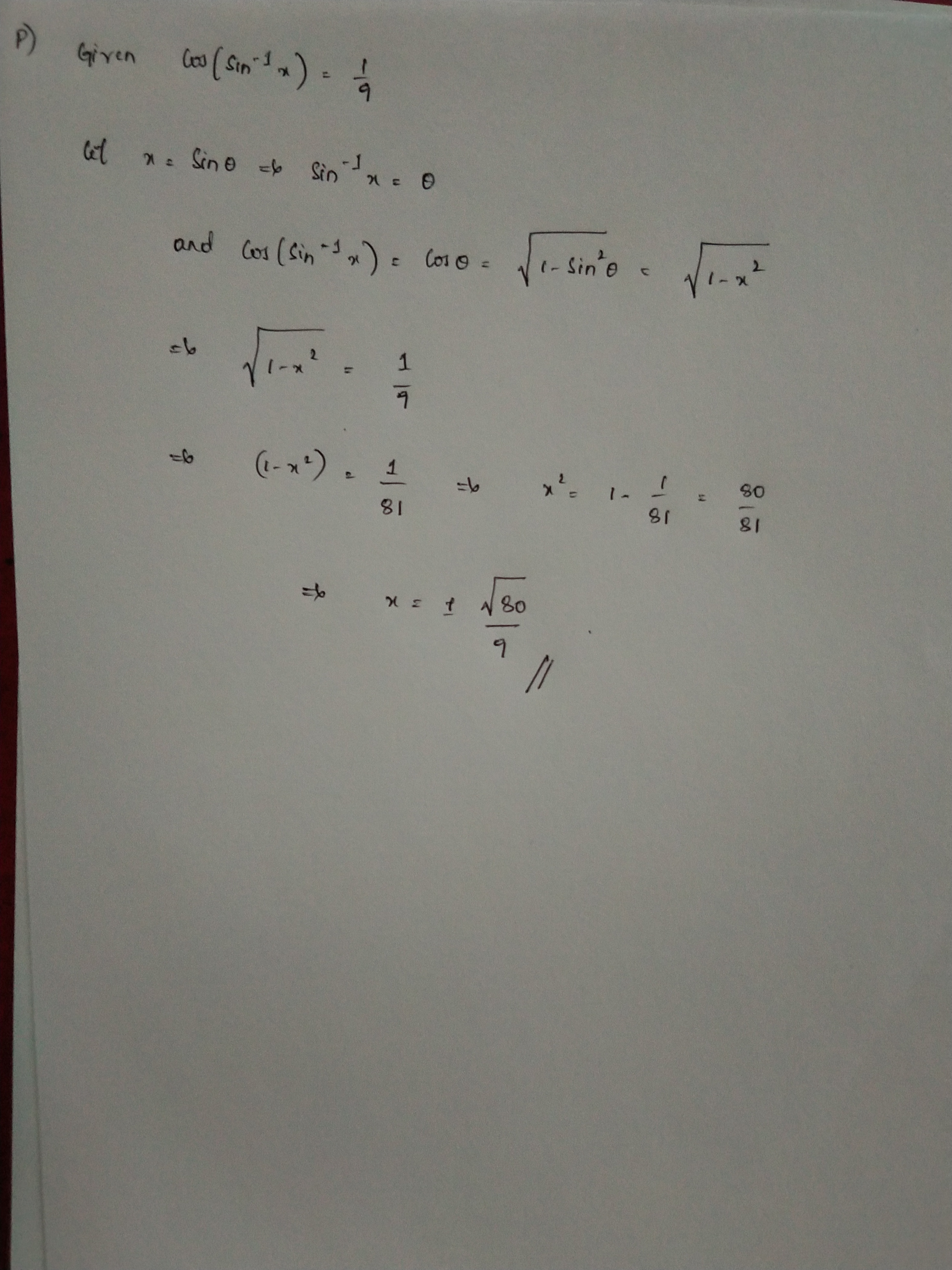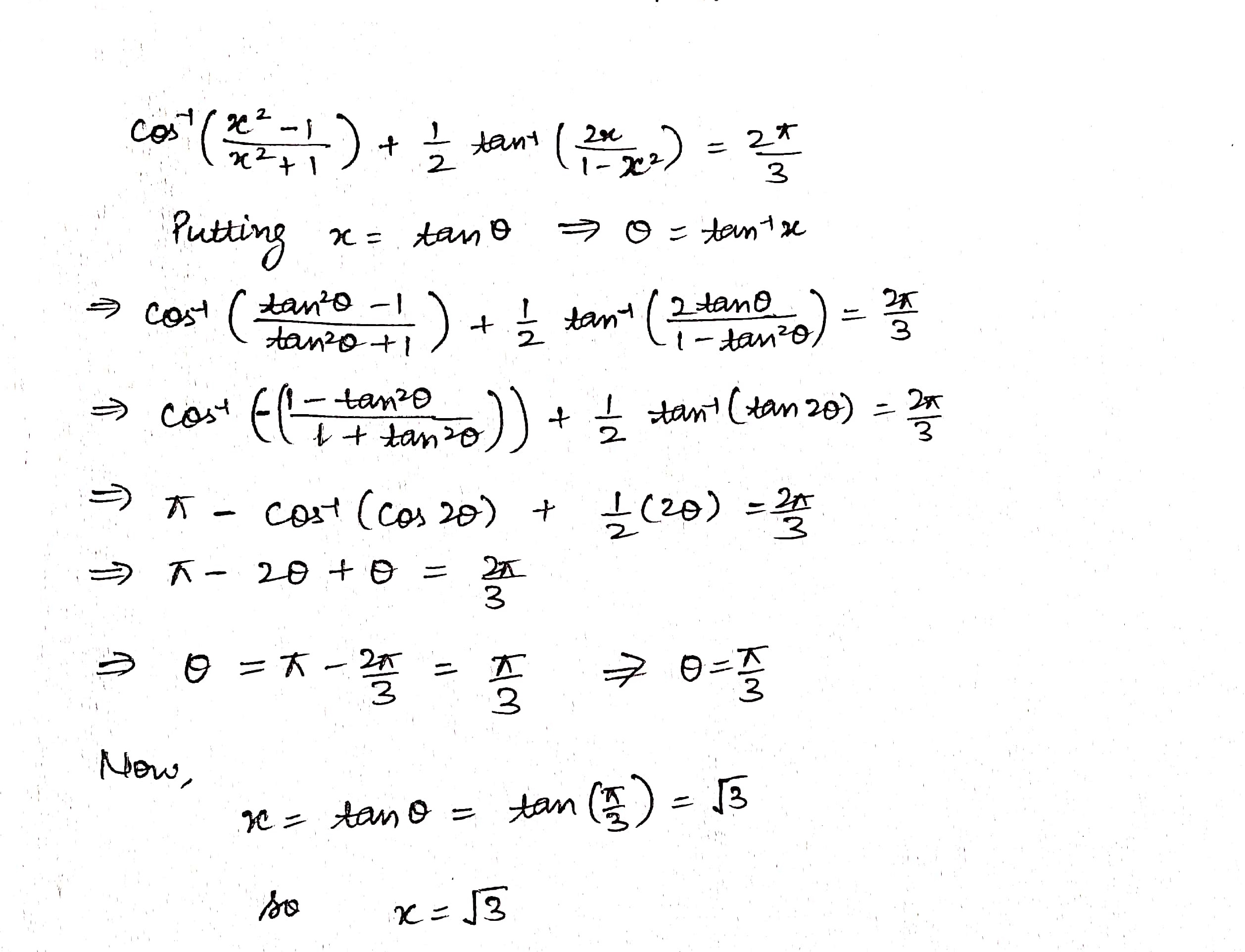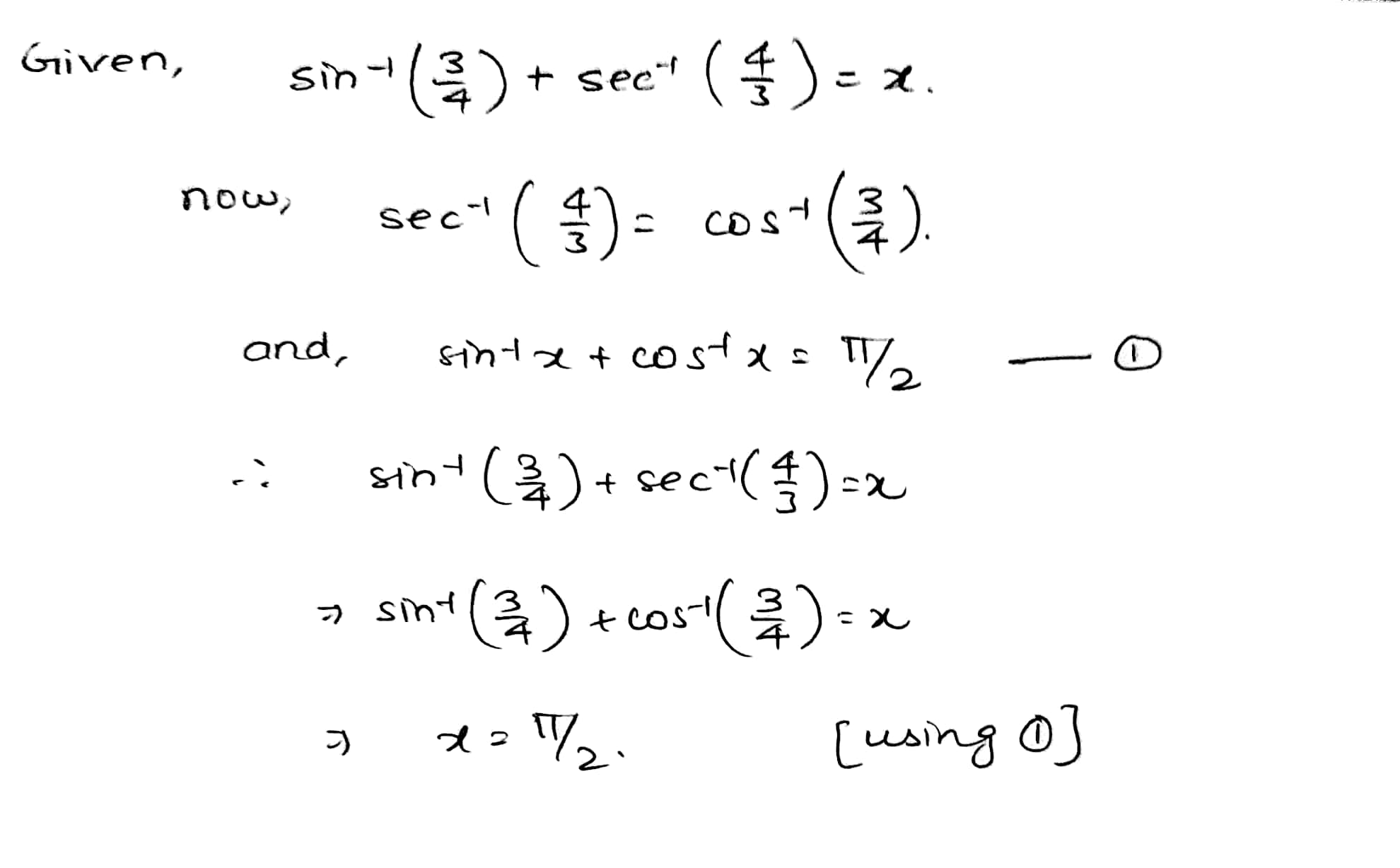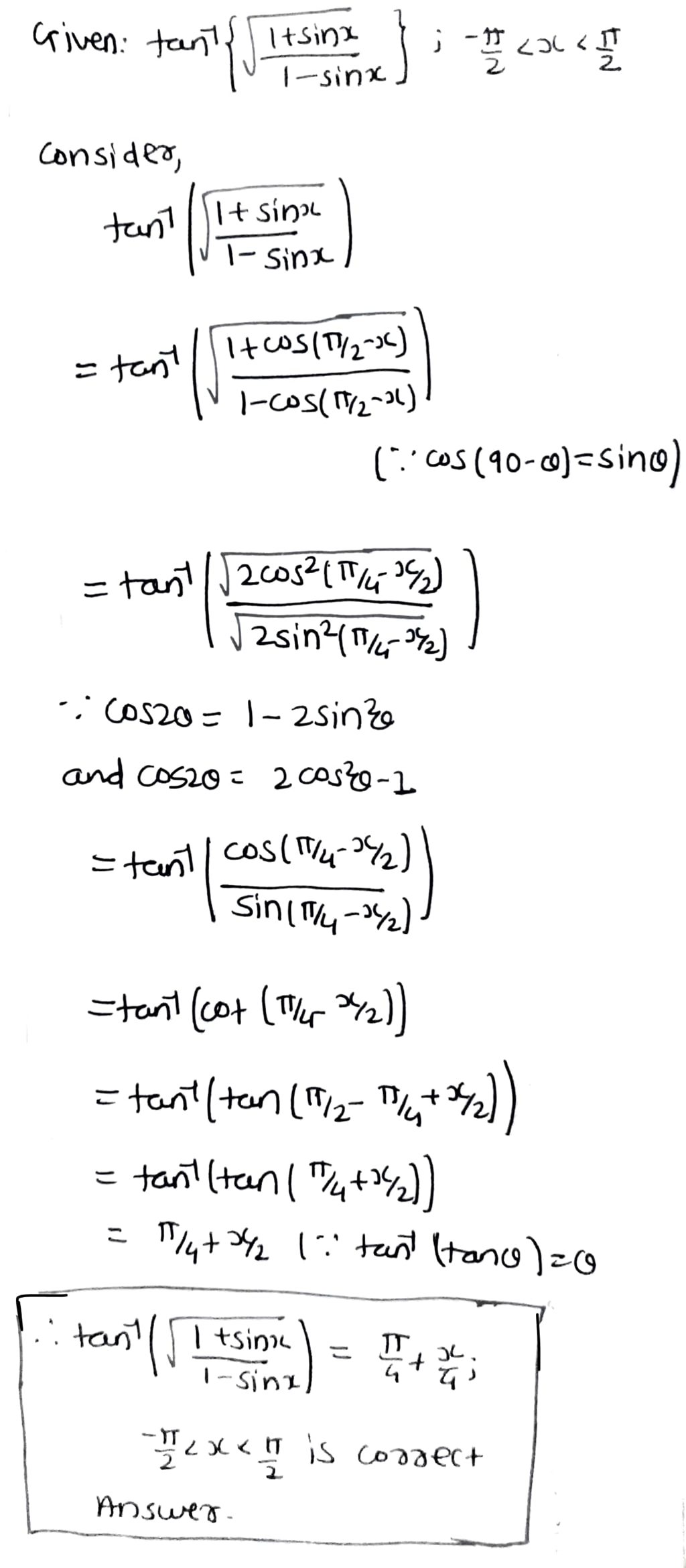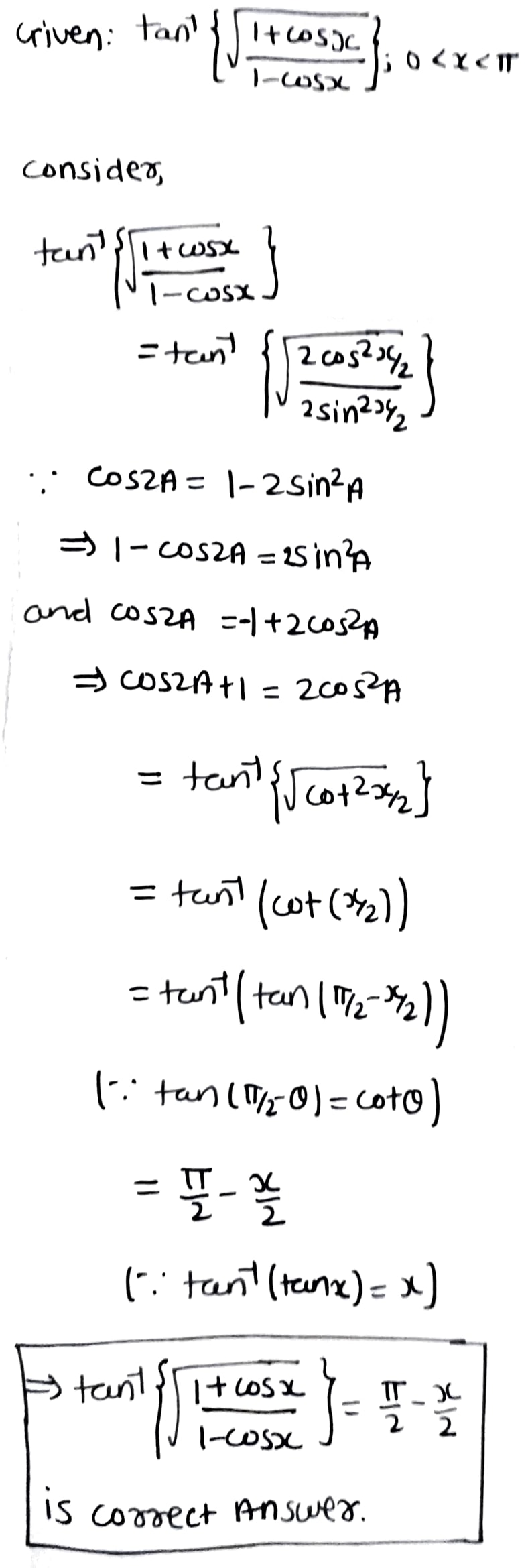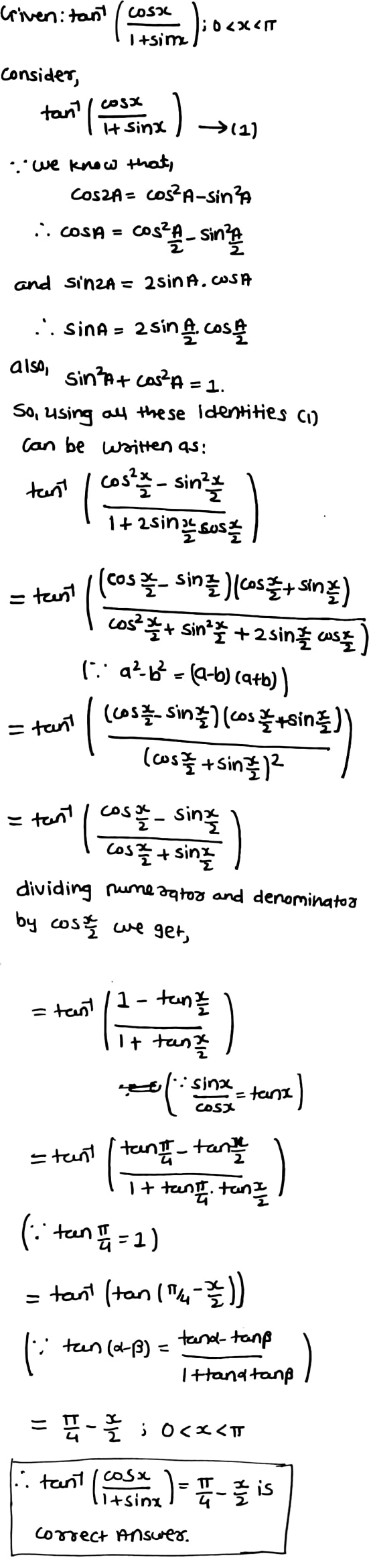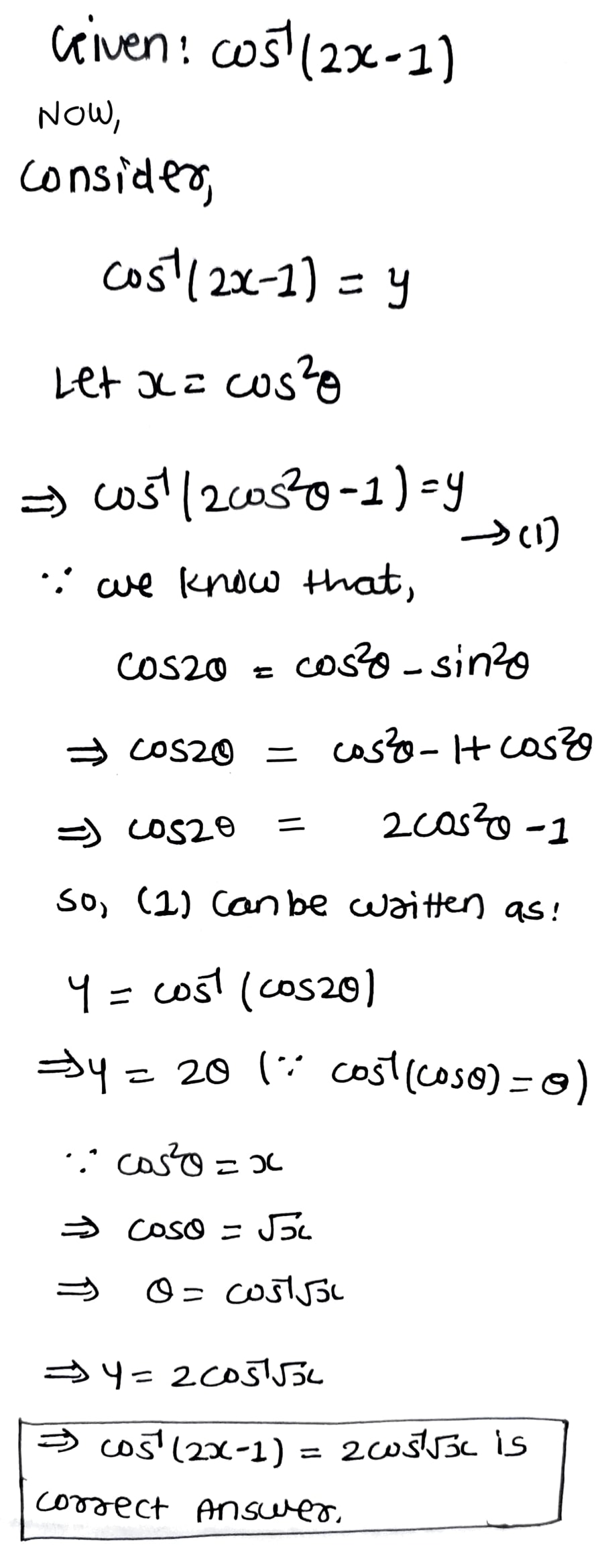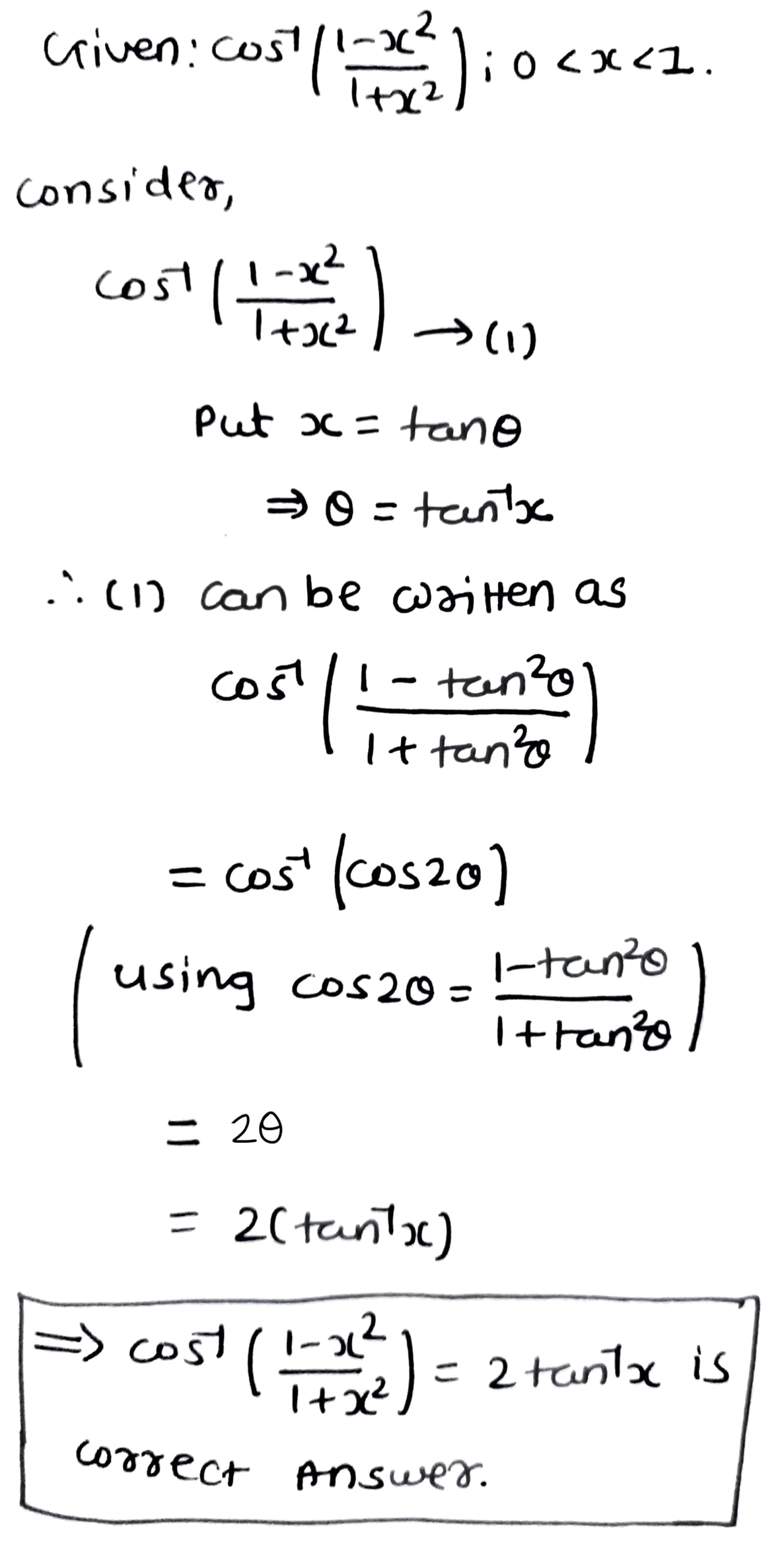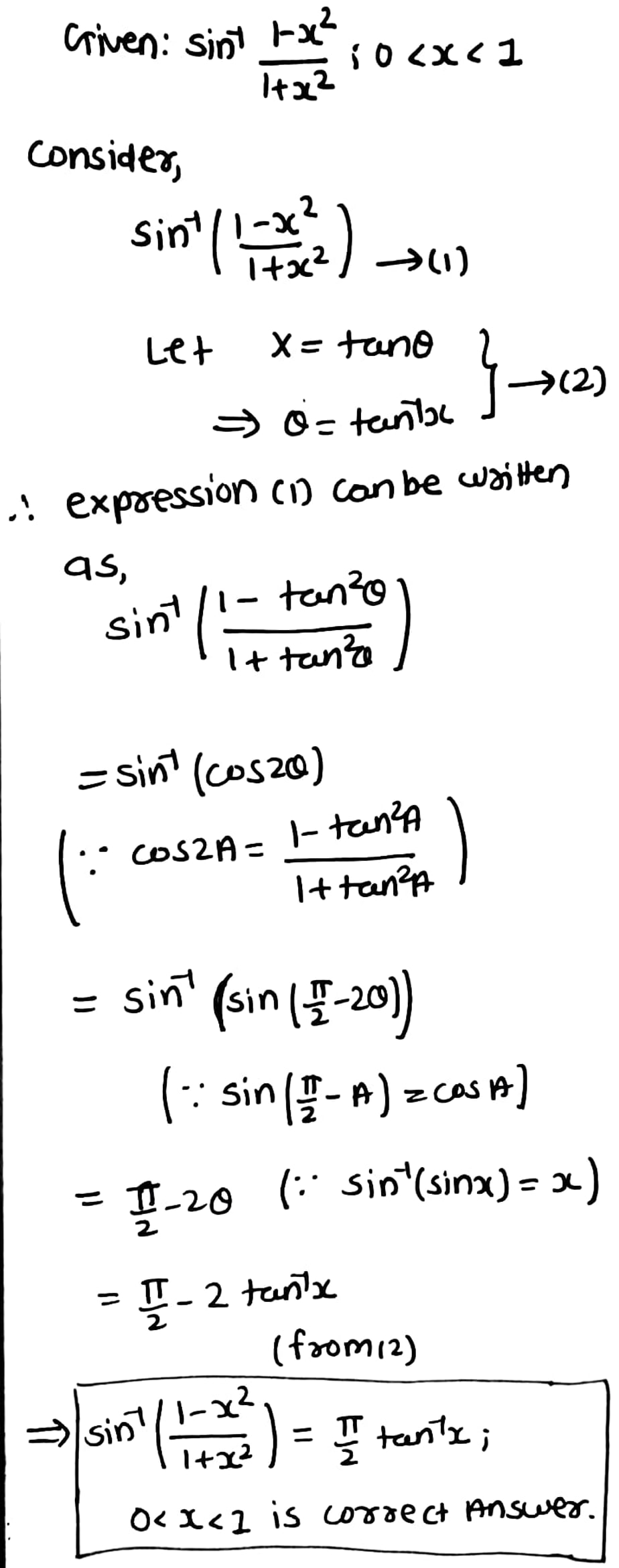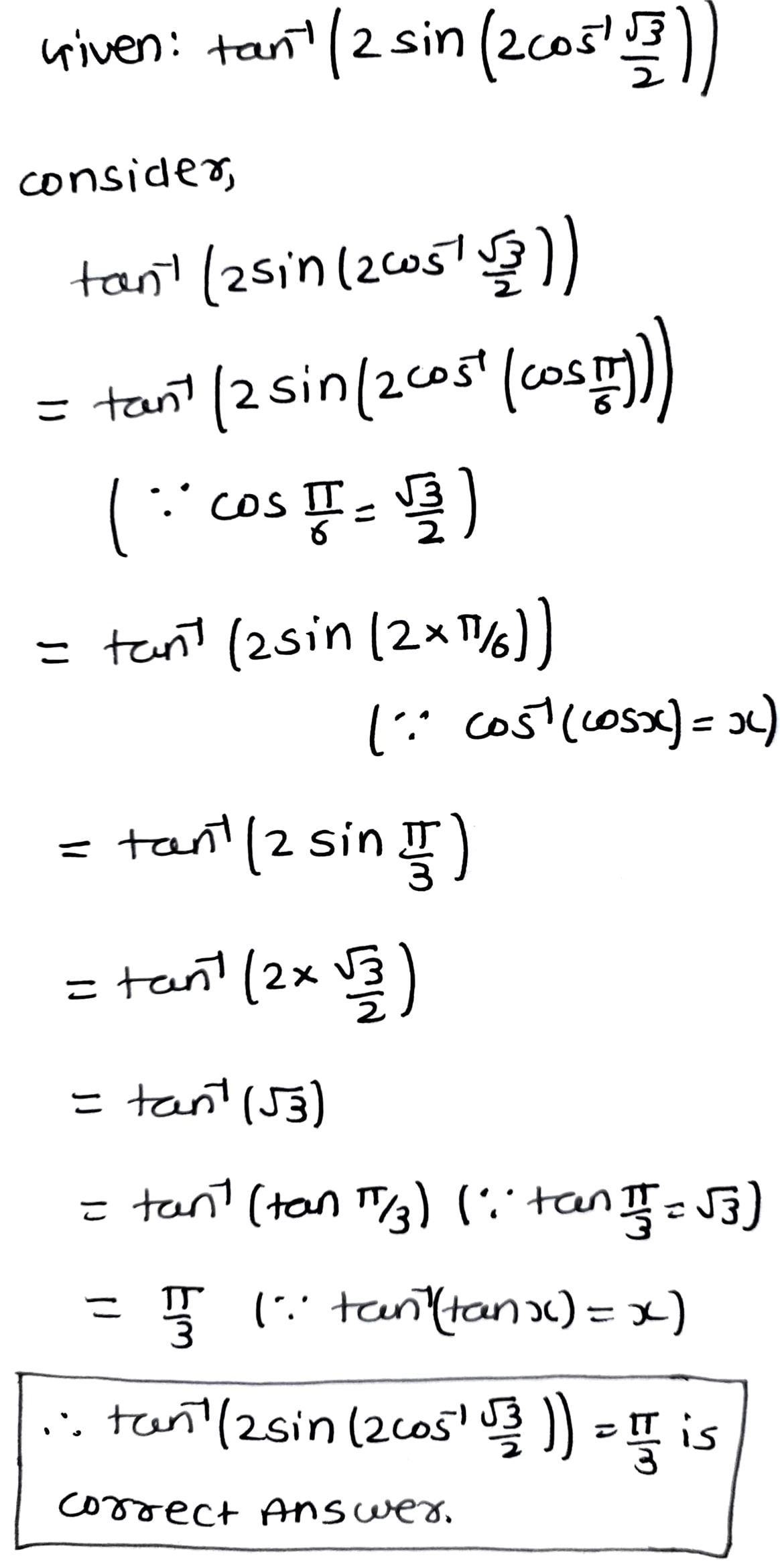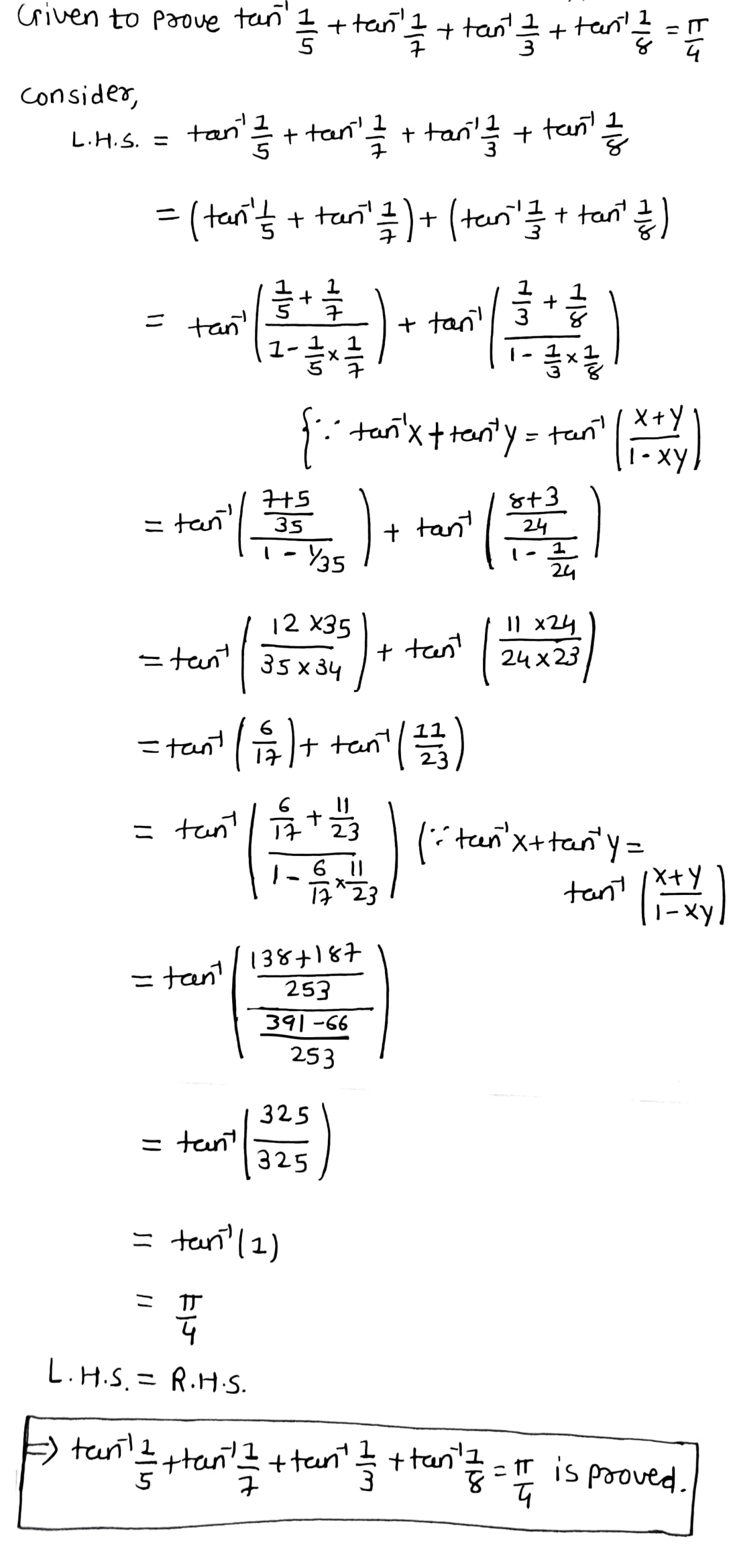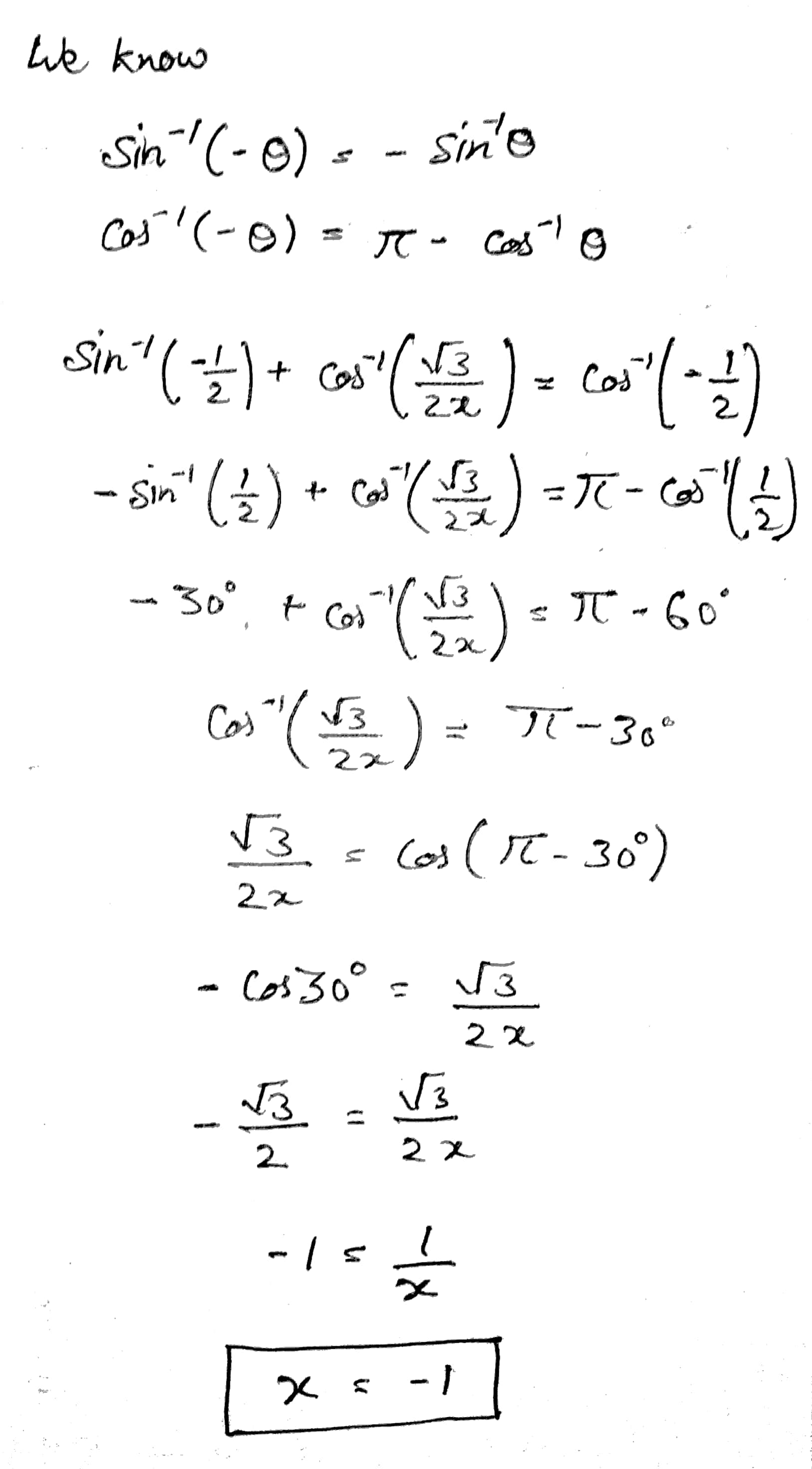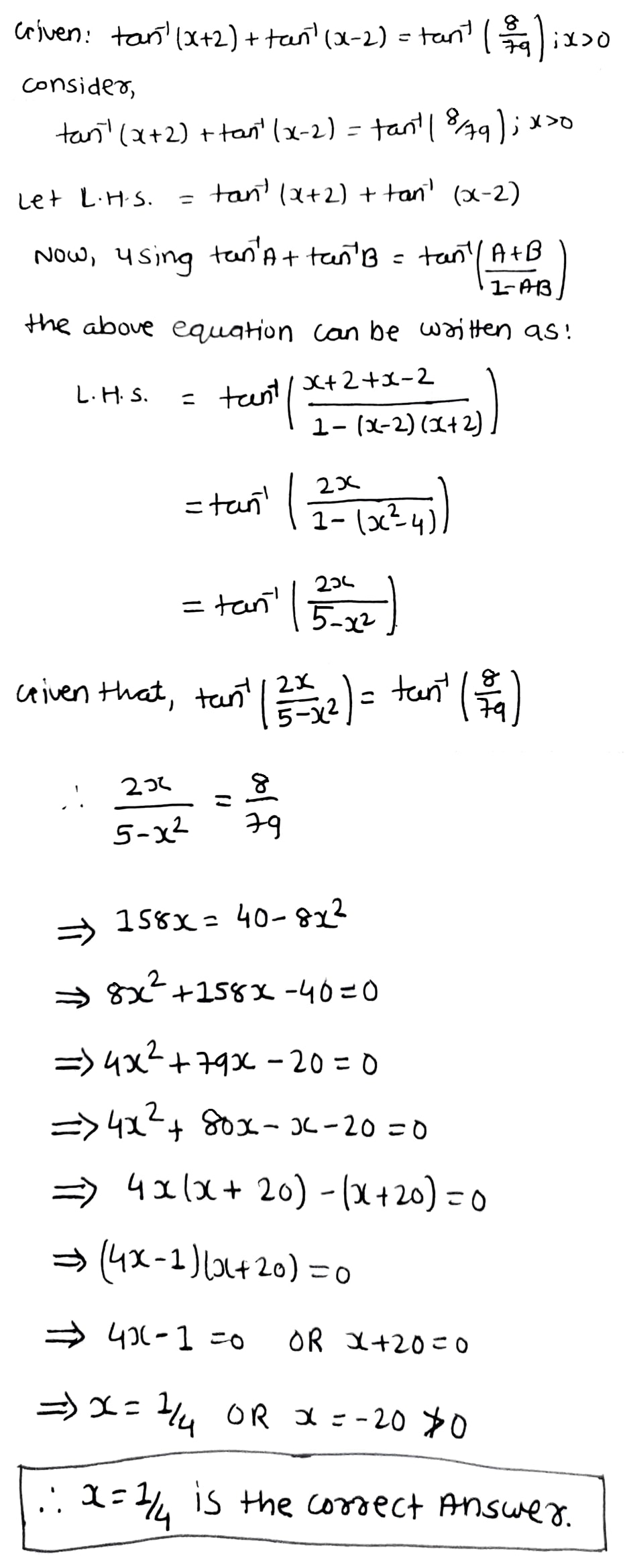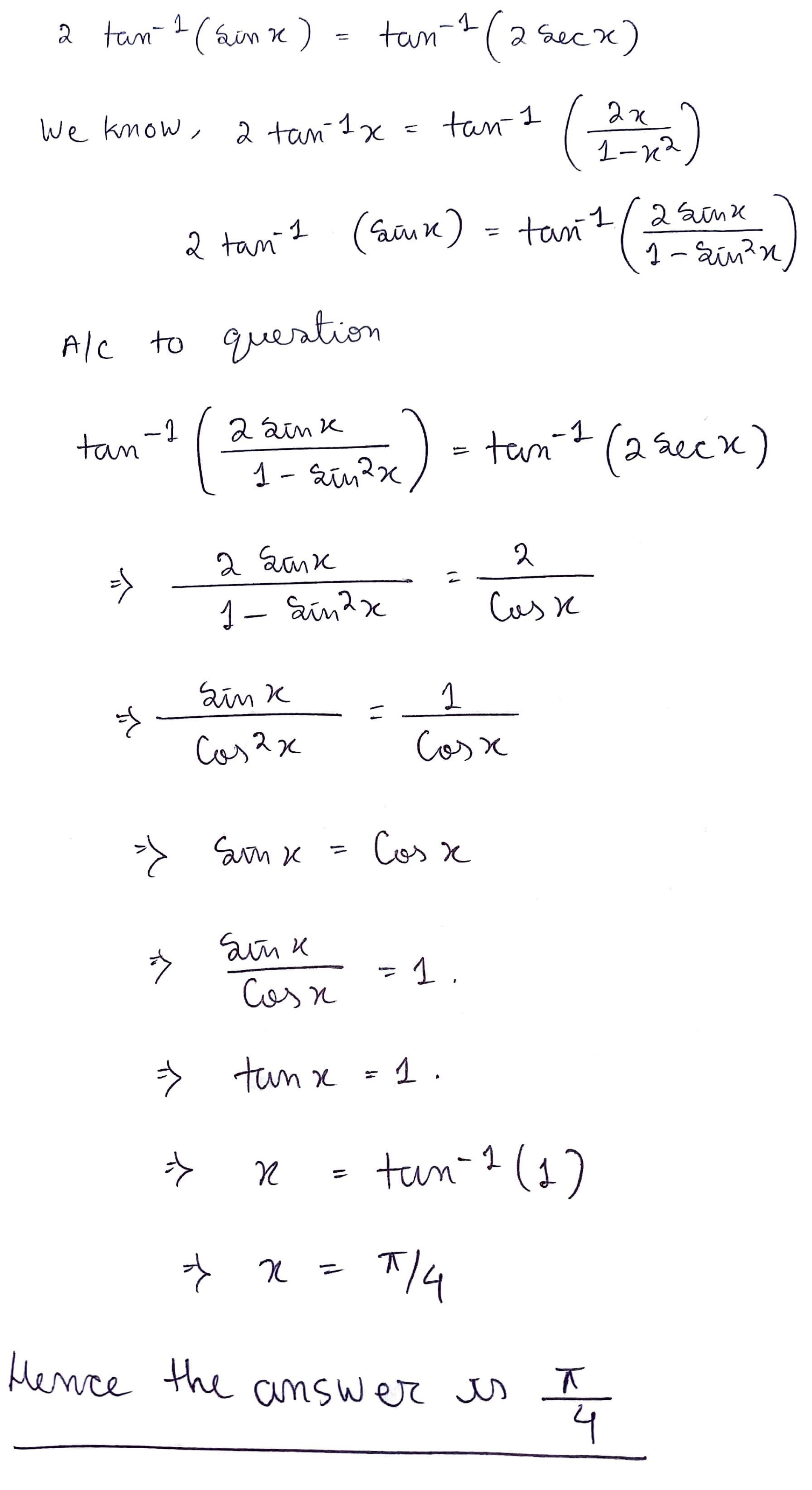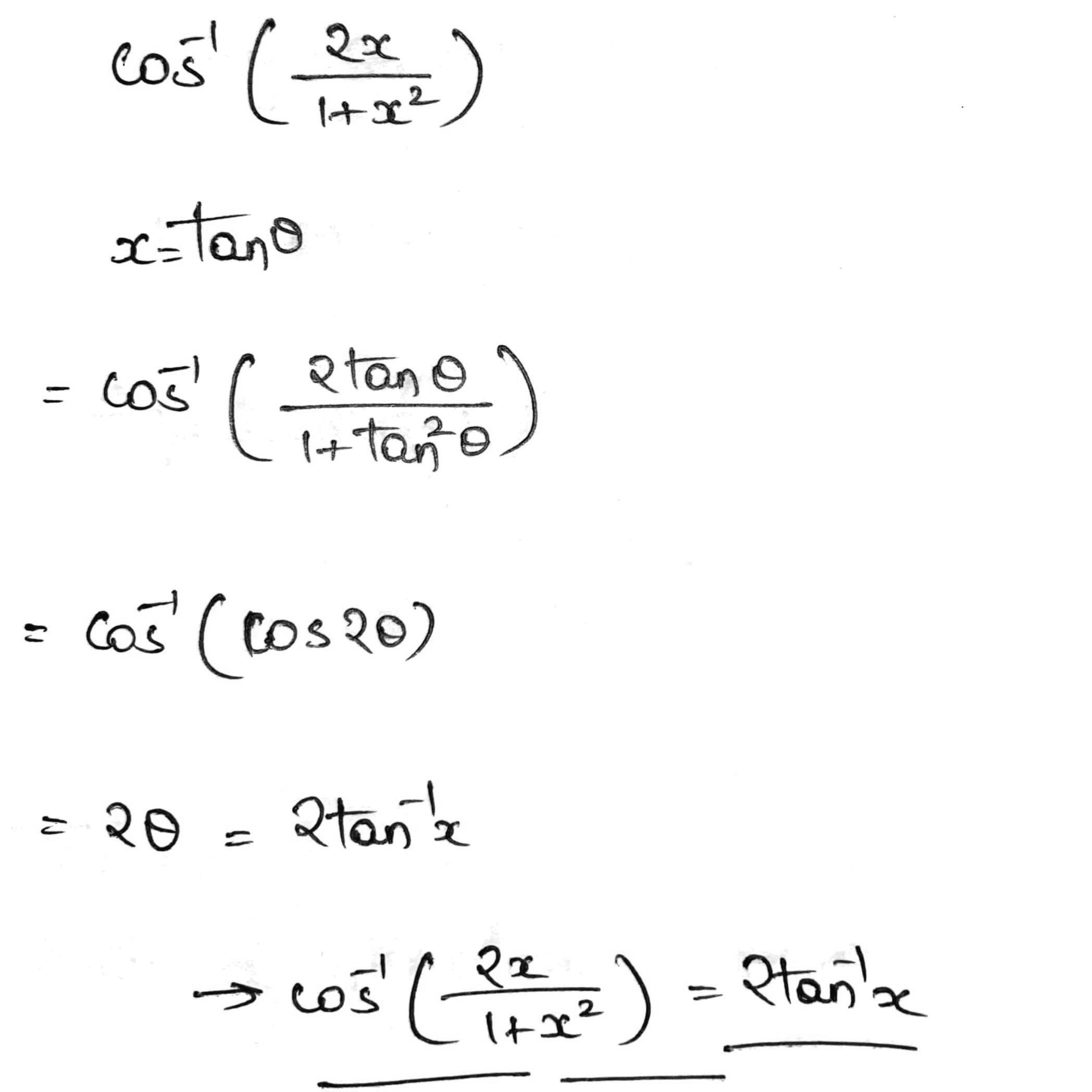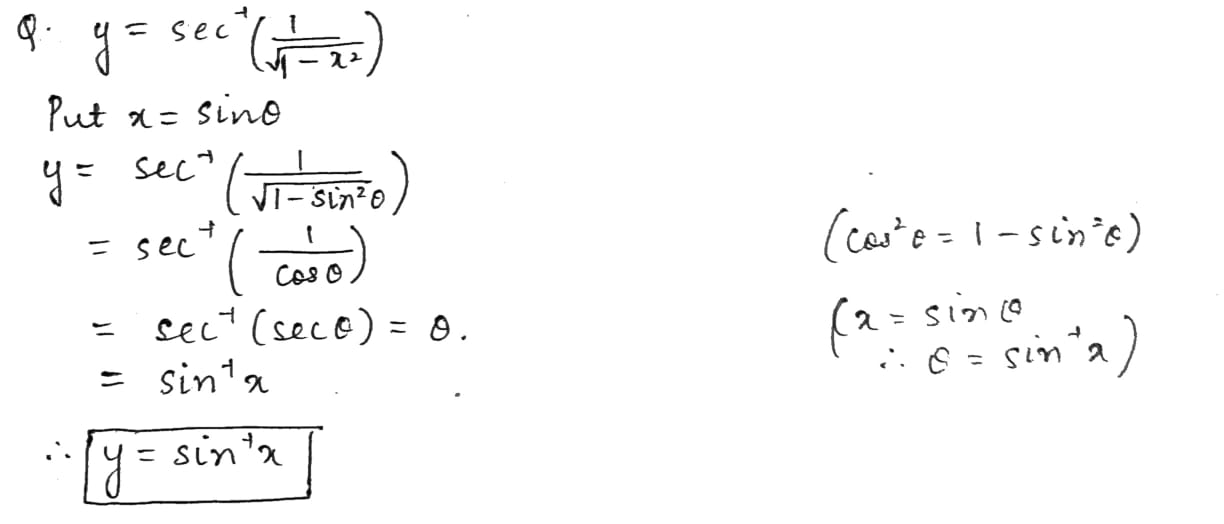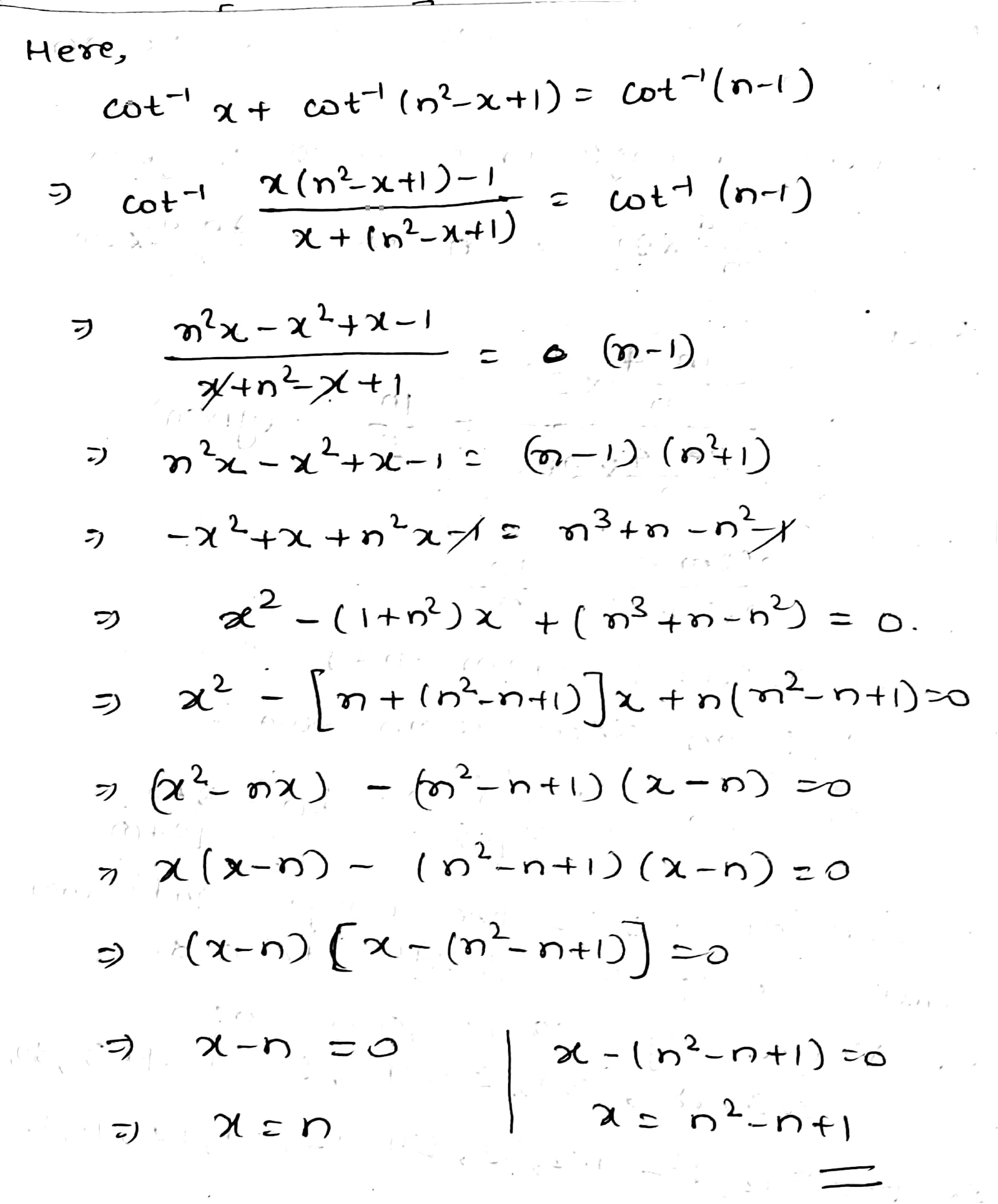Class 12 Commerce Maths - Inverse Trigonometric Functions

Solve $\displaystyle \tan^{-1} \left ( \frac{1-x}{1+x} \right ) = \frac{1}{2} \tan^{-1} x, \: \: \left( 0<x<1 \right)$

$\displaystyle \tan ^{ -1 } \left( \frac { 1-x }{ 1+x } \right) =\frac { 1 }{ 2 } \tan ^{ -1 } x\Rightarrow 2\tan ^{ -1 } \left( \frac { 1-x }{ 1+x } \right) =\tan ^{ -1 }{ x }$

$\displaystyle \Rightarrow \tan ^{ -1 }{ \left( \frac { 2\left( \frac { 1-x }{ 1+x } \right) }{ 1-{ \left( \frac { 1-x }{ 1+x } \right) }^{ 2 } } \right) } =\tan ^{ -1 }{ x } \Rightarrow \tan ^{ -1 }{ \left( \frac { 1-{ x }^{ 2 } }{ 2x } \right) } =\tan ^{ -1 }{ x }$

$\displaystyle \Rightarrow \frac { 1-{ x }^{ 2 } }{ 2x } =x\Rightarrow 1-{ x }^{ 2 }=2{ x }^{ 2 }\Rightarrow x=\pm \frac { 1 }{ \sqrt { 3 } }$
Neglecting

$\displaystyle x=-\frac { 1 }{ \sqrt { 3 } }$
We get

$\displaystyle x=\frac { 1 }{ \sqrt { 3 } }$

Solve for $\displaystyle x$ and $\displaystyle y$ ; $\displaystyle \sin^{-1} x + \sin^{-1} y = \frac{2 \pi}{3}$ and $\displaystyle \cos^{-1} x - \cos^{-1} y = \frac{\pi}{3}$

Adding,

$\displaystyle \frac { \pi }{ 2 } +\sin ^{ -1 }{ y } -\cos ^{ -1 }{ y } =\pi$

$\displaystyle \Rightarrow \pi -2\cos ^{ -1 }{ y } =\pi$ or

$\displaystyle \cos ^{ -1 }{ y } =0 \Rightarrow y=1$

$\displaystyle \therefore \sin ^{ -1 }{ x } + \sin ^{ -1 }1 =\frac { 2\pi }{ 3 }$
or

$\displaystyle \sin ^{ -1 }{ x } =\frac { 2\pi }{ 3 } -\frac { \pi }{ 2 } =\frac { \pi }{ 6 } \quad \Rightarrow x=\frac { {1 } }{ 2 }$
So, there is one solution.

Solve $\displaystyle \tan x< 2$

$\tan x<2$

$\Rightarrow x < n\pi+\tan^{-1}(2) \forall n \in I$

Find the inverse of the following functions:
$\displaystyle f(x)=\sin ^{-1}\left(\frac{x}{3}\right),x\in [-3,3]$
then $f^{-1}(\pi/2)$

$\displaystyle f(x)=\sin ^{-1}\left(\frac{x}{3}\right) =y$ (say)

$\Rightarrow \dfrac{x}{3}=\sin y\Rightarrow x =3\sin y$

$\therefore f^{-1}(x) = f(y) =3\sin y$
Hence

$f^{-1}(\pi/2) = 3$

Prove: $\displaystyle { \cos }^{ -1 }\frac { 4 }{ 5 } +{ \cos }^{ -1 }\frac { 12 }{ 13 } ={ \cos }^{ -1 }\frac { 33 }{ 65 }$

Let

$\displaystyle { \cos }^{ -1 }\frac { 4 }{ 5 }=x \Rightarrow \cos { x } =\frac { 4 }{ 5 } \Rightarrow \sin { x } =\sqrt { 1-{ \left( \frac { 4 }{ 5 } \right) }^{ 2 } } =\frac { 3 }{ 5 }$

$\displaystyle \therefore \tan { x } =\frac { 3 }{ 4 } \Rightarrow x={ \tan }^{ -1 }\frac { 3 }{ 4 }$

$\displaystyle \therefore { \cos }^{ -1 }\frac { 4 }{ 5 } ={ \tan }^{ -1 }\frac { 3 }{ 4 } .....(1)$
Now, let

$\displaystyle { \cos }^{ -1 }\frac { 5 }{ 12 } =y\Rightarrow \cos { y } =\frac { 12 }{ 13 } \Rightarrow \sin { y } =\frac { 5 }{ 13 }$

$\displaystyle \therefore \tan { y } =\frac { 12 }{ 13 } \Rightarrow y={ \tan }^{ -1 }\frac { 5 }{ 12 }$

$\displaystyle \therefore { \cos }^{ -1 }\frac { 12 }{ 13 } ={ \tan }^{ -1 }\frac { 5 }{ 12 } .....(2)$
Let

$\displaystyle { \cos }^{ -1 }\frac { 33 }{ 65 } =z\Rightarrow \cos { z } =\frac { 33 }{ 65 } \Rightarrow \sin { z } =\frac { 56 }{ 65 }$

$\displaystyle \therefore \tan { z } =\frac { 56 }{ 33 } \Rightarrow z={ \tan }^{ -1 }\frac { 56 }{ 33 }$

$\displaystyle \therefore { \cos }^{ -1 }\frac { 33 }{ 65 } ={ \tan }^{ -1 }\frac { 56 }{ 33 } .....(3)$
Now,
L.H.S.

$\displaystyle { =\cos }^{ -1 }\frac { 4 }{ 5 } +{ \cos }^{ -1 }\frac { 12 }{ 13 }$

$\displaystyle ={ \tan }^{ -1 }\frac { 3 }{ 4 } +{ \tan }^{ -1 }\frac { 5 }{ 12 }$ [using (1) and (2)]

$\displaystyle ={ \tan }^{ -1 }\frac { \frac { 3 }{ 4 } +\frac { 5 }{ 12 } }{ 1-\frac { 3 }{ 4 } .\frac { 5 }{ 12 } }, [\because { \tan }^{ -1 }x+{ \tan }^{ -1 }y={ \tan }^{ -1 }\frac { x+y }{ 1-xy } ]$

$\displaystyle ={ \tan }^{ -1 }\frac { 36+20 }{ 48-15 }$

$\displaystyle ={ \tan }^{ -1 }\frac { 56 }{ 33 }$ [By 3]

$=$ R.H.S.

$\dfrac {1}{2}\tan^{-1} x = \cos^{1} \left \{\dfrac {1 + \sqrt {1 + x^{2}}}{2\sqrt {1 + x^{2}}} \right \}^{\dfrac {1}{2}}$ .

$\cfrac { 1 }{ 2 } \tan ^{ -1 }{ x } =\cos ^{ -1 }{ { \left\{ \cfrac { 1+\sqrt { 1+{ x }^{ 2 } } }{ 2\sqrt { 1+{ x }^{ 2 } } } \right\} }^{ \cfrac { 1\\ }{ 2 } } }$

R.H.S Let $x=\tan { \theta } \quad \theta =\tan ^{ -1 }{ x } \\ =\cos ^{ -1 }{ { \left\{ \cfrac { 1+\sqrt { 1+{ x }^{ 2 } } }{ 2\sqrt { 1+{ x }^{ 2 } } } \right\} }^{ \cfrac { 1\\ }{ 2 } } } \\ =\cos ^{ -1 }{ { \left\{ \cfrac { 1+\sec { \theta } }{ 2\sec { \theta } } \right\} }^{ \cfrac { 1 }{ 2 } } } \\ =\cos ^{ -1 }{ { \left\{ \cfrac { 1+\cos { \theta } }{ 2 } \right\} }^{ \cfrac { 1 }{ 2 } } } \\ =\cos ^{ -1 }{ { \left\{ \cfrac { 2\cos ^{ 2 }{ \cfrac { \theta }{ 2 } } }{ 2 } \right\} }^{ \cfrac { 1 }{ 2 } } } =\cos ^{ -1 }{ \cos { \cfrac { \theta }{ 2 } } }$

So, $=\cfrac { \tan ^{ -1 }{ x } }{ 2 } =L.H.S$

Proved

$\displaystyle\, \tan^{-1}\frac{2}{11} + \tan^{-1}\frac{7}{24} = \tan^{-1}\frac{1}{2}$

Now,

$\tan^{-1}\dfrac{2}{11}+\tan^{-1} \dfrac{7}{24}$

$=\tan^{-1}\dfrac{\dfrac{2}{11}+\dfrac{7}{24}}{1-\dfrac{2}{11}.\dfrac{7}{24}}$

$=\tan^{-1}\dfrac{125}{250}$

$=\tan^{-1}\dfrac{1}{2}$

Find the value of $\sin\left\{2\sin^{-1}\dfrac{3}{5}\right\}$

$=sin^{-1}\dfrac{3}{5}=\theta$

$=sin\theta=\dfrac{3}{5}$

$=sin2\theta=2sin\dfrac{\theta}{2} cos\dfrac{\theta}{2}$

$=cos\dfrac{\theta}{2}=\dfrac{4}{5}$

$=sin2\theta=2\times \dfrac{3}{5}\times \dfrac{4}{5}$

$\sin({2sin^{-1}{\dfrac{3}{5}}}) =\dfrac{24}{25}$

The range of $arc\sin { x } +arc\cos { x } +arc\tan { x }$ is

Let,

$y=\sin^{-1}x+\cos^{-1}x+\tan^{-1}x$

or,

$y=\large{\frac{\pi}{2}}$

$+\tan ^{-1}x$ . [Since

$\sin^{-1}x+\cos^{-1}x=\large{\frac{\pi}{2}}$ ]

As range of

$\tan^{-1}x$ is

$\left(\large{-\frac{\pi}{2}},\frac{\pi}{2}\right)$ , so range of

$y$ is

$(0,\pi)$ .

Prove that $\displaystyle\, \tan^{-1}\frac{\sqrt{1 + x^2} - 1}{x}=\dfrac{1}{2}\tan^{-1}x, x \neq 0$

To find the value of

$\tan^{-1}\dfrac{\sqrt{1+x^2}-1}{x}$ let

$x=\tan \theta$ .....(1)

$\therefore \tan^{-1}\dfrac{\sqrt{1+x^2}-1}{x}$

$=\tan^{-1}\dfrac{\sec \theta-1}{\tan \theta}$

$=\tan^{-1}\dfrac{1-\cos \theta}{\sin \theta}$

$=\tan^{-1}\tan \dfrac{\theta}{2}$

$=\dfrac{1}{2}\theta$

$=\dfrac{1}{2}\tan^{-1}x$ [Using (1)]

Evaluate $\sin ^{ -1 }{ \left( \cos { x } \right) }$

We know that the cosine function, is nothing more than the sine $\dfrac{\pi}{2}$ radians out of phase, as proved below:

$cos\left (\theta- \dfrac{\pi}{2} \right ) = cos\left (\theta \right )cos\left (- \dfrac{\pi}{2} \right ) - sin\left (\theta \right )sin\left (- \dfrac{\pi}{2} \right )$

$cos\left (\theta- \dfrac{\pi}{2} \right ) = cos\left (\theta \right )\times 0 - \left ( sin\left (\theta \right )sin\left (\dfrac{\pi}{2} \right ) \right )$

$cos\left (\theta- \dfrac{\pi}{2} \right ) = sin\left (\theta \right ) \times 1 = sin\left (\theta \right )$

It's clear that

$cos\left (\theta \right ) = sin \left (x + \dfrac{\pi}{2} \right )$

$sin^{-1} \left ( sin \left (x + \dfrac{\pi}{2} \right ) \right )$

$= \left (x + \dfrac{\pi}{2} \right )$

Write the range of $\sin^{-1}x$ .

1322207_1080054_ans_0910c1c0563c4b3ba6b48b32f452275f.JPG

Solve for x :
${\left( {{{\tan }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2} = \dfrac{{5{\pi ^2}}}{8}$

${\left( {{{\tan }^{ - 1}}x} \right)^2} + \left( {{{\cot }^{ - 1}}x} \right) = {{5{\pi ^2}} \over 8}$

${\left( {{{\tan }^{ - 1}}x} \right)^2} + \left( {{\pi \over 2} - {{\tan }^{ - 1}}{x^2}} \right) = {{5{\pi ^2}} \over 8}$

Let ${\tan ^{ - 1}}x = k$

Then ${k^2} + {\left( {{\pi \over 2} - k} \right)^2} = {{5{\pi ^2}} \over 8}$

${k^2} + {{{\pi ^2}} \over 4} + {k^2} - \pi k = {{5{\pi ^2}} \over 8}$

$= 2{k^2} - \pi k + {{{\pi ^2}} \over 4} - {{5{\pi ^2}} \over 8} = 0$

$= 2{k^2} - \pi k - {{3{\pi ^2}} \over 8} = 0$

$= 16{k^2} - 8\pi k - 3{\pi ^2} = 0$

$= \left( {4k - 3\pi } \right)\left( {4k + \pi } \right)$

$k = {{3\pi } \over 4},k = {{ - \pi } \over 4}$

$x = \tan \left( {{{3\pi } \over 4}} \right);x = \tan \left( { - {\pi _4}} \right)$

$x = - 1$

If $y=$ ${\cot ^{ - 1}}\,\left( {\sqrt {\cos x} } \right) - {\tan ^{ - 1}}\,\left( {\sqrt {\cos x} } \right)$ , then prove that $\sin y = {\tan ^2}\dfrac{x}{2}.$

$y = {\cot ^{ - 1}}\left( {\sqrt {\cos } x} \right) - {\tan ^{ - 1}}\left( {\sqrt {\cos } x} \right)\,.$

$taking\,\sin \,both\,side$

$\sin y = \sin \left[ {{{\cot }^{ - 1}}\left( {\sqrt {\cos } x} \right) - {{\tan }^{ - 1}}\left( {\sqrt {\cos } x} \right)} \right]$

$\sin \left[ {{{\tan }^{ - 1}}\left( {\dfrac{1}{{\sqrt {\cos } x}}} \right) - {{\tan }^{ - 1}}\left( {\sqrt {\cos } x} \right)} \right]$

$\sin \left[ {{{\tan }^{ - 1}}\dfrac{{\left( {\dfrac{1}{{\sqrt {\cos } x}} - \sqrt {\cos } x} \right)}}{{1 + \dfrac{1}{{\sqrt {\cos } x}} \times \sqrt {\cos } x}}} \right]$

$\sin \left[ {{{\tan }^{ - 1}}\dfrac{{\left( {1 - \cos x} \right)}}{{2\sqrt {\cos } x}}} \right]$

$\sin \left[ {{{\sin }^{ - 1}}\left( {\dfrac{{1 - \cos x}}{{1 + \cos x}}} \right)} \right]$

$=\dfrac{{1 - \cos x}}{{1 + \cos x}}$

$=\dfrac{{2{{\sin }^2}\dfrac{x}{2}}}{{2{{\cos }^2}\dfrac{x}{2}}}$

$\sin y = {\tan ^2}\dfrac{x}{2}$

Simplify: $\tan^{-1}\left(\dfrac{a - x}{1 + ax}\right)$

$\tan^{-1}\left(\dfrac{a - x}{1 + ax}\right)$

$=\tan^{-1}a-\tan^{-1}x$ [ Using direct formula]

Write the function in simplest form : $\tan^{-1} \left ( \dfrac{x}{\sqrt{a^2-x^2}} \right ) where, |x|<a$ .

$\tan^{-1} \dfrac{x}{\sqrt{a^2-x^2}}$

Let

$x=a\sin \theta$

$\dfrac{x}{a}=\sin \theta \implies \theta = \sin^{-1} \dfrac{x}{a}$

Therefore,

$\tan^{-1} \dfrac{x}{\sqrt{a^2-x^2}}$

$\tan^{-1} \left ( \dfrac{asin \theta}{\sqrt{a^2-a^{2}{sin^{2}\theta}}} \right )$ .............(since

$x= asin \theta$ )

$\tan^{-1} \left ( \dfrac{asin \theta}{a \sqrt{1-{sin^{2}\theta}}} \right )$

$\tan^{-1} \left ( \dfrac{asin \theta}{a \sqrt{{cos^{2}\theta}}} \right )$

$\tan^{-1} \left (\dfrac{a\sin \theta}{a\cos \theta} \right )$

$=\tan^{-1}(\tan \theta)$

$=\theta$

$= \sin^{-1} \left (\dfrac{x}{a} \right )$ .............(since

$\theta= \dfrac {x}{a}$ )

Calculating the principal value, find the value of $\cos\left[\sin^{-1}\left(\dfrac{3}{5}\right)\right]$ .

We are to find

$cos \left [ sin^{-1}\left ( \dfrac{3}{5} \right ) \right ]$

Let

$sin^{-1}\left ( \dfrac{3}{5} \right ) = \theta$

where

$\theta \epsilon \left [ -\dfrac{\pi }{2}, \dfrac{\pi}{2} \right ]$

So,

$sin \theta = \dfrac{3}{5}$

so,

$= cos\left [ sin^{-1}\left ( \dfrac{3}{5} \right ) \right ]$

$= cos \theta$

$= \sqrt{1-sin^{2}\theta}$

$= \sqrt{1-\left ( \dfrac{3}{5} \right )^2}$

$= \sqrt{1-\dfrac{9}{25}}$

$= \sqrt{\dfrac{16}{25}}$

$= \dfrac{4}{5}$

So,

$cos \left [ sin^{-1} \left(\dfrac{3}{5} \right)\right ] = \dfrac{4}{5}$

1213004_1069982_ans_30145d3e7a8e4fbe88b3933dd0968bf2.jpg

Solve for x : $\cos^{-1} x + \sin^{-1} \left(\dfrac{x}{2} \right) = \dfrac{\pi}{6}$

$\sin^{-1}(\dfrac{x}{2})=2$

$\cos^{-1}x=q$

$\dfrac{x}{2}=\sin P$

$\cos q=x$

$x=2\,sin P$

$\boxed{\cos Q=2 \sin p}$ ....(2)

$p+q=\dfrac{\pi}{6}$

$\boxed{P=\dfrac{\pi}{6}-Q}$

$\sin p=\sin\dfrac{\pi}{6}-q)$

$=\sin\dfrac{\pi}{6}\cos Q-\cos\dfrac{\pi}{6}\sin q$

$=\dfrac{\cos q}{2}-\dfrac{\sqrt{3}}{2}\sin q$

$=\boxed{2 \sin p=(\cos q-\sqrt{3}\sin q)}$ ....(1)

From (1) and (2)

$=\cos Q=\cos Q-\sqrt{3}\sin Q$

$\therefore \sin q=0\,\, \therefore q=o$

$\cos q=2\sin P$

$\cos(O)=2 \sin P$

$\dfrac{1}{2}=\sin p\Rightarrow \boxed{P=\dfrac{\pi}{6}}$

$\boxed{x=2 \sin p=2 \sin (\dfrac{\pi}{6})=1}$

Prove that: $\cot \left(\dfrac {\pi}{2}-2\ \cot^{-1}3\right)=\dfrac{3}{4}$

L.H.S

$\cot \left( \dfrac{\pi }{2}-2{{\cot }^{-1}}3 \right)$

We know that

$\cot \left( \dfrac{\pi }{2}-\theta \right)=\tan \theta$

Therefore,

$\Rightarrow \tan \left( 2{{\cot }^{-1}}3 \right)$

$\Rightarrow \tan \left( 2{{\tan }^{-1}}\left( \dfrac{1}{3} \right) \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ \because {{\cot }^{-1}}x={{\tan }^{-1}}\left( \dfrac{1}{x} \right) \right]$

$\Rightarrow \tan \left( {{\tan }^{-1}}\left( \dfrac{2\times \dfrac{1}{3}}{1-{{\left( \dfrac{1}{3} \right)}^{2}}} \right) \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ 2{{\tan }^{-1}}x={{\tan }^{-1}}\left( \dfrac{2x}{1-{{x}^{2}}} \right) \right]$

$\Rightarrow \dfrac{\dfrac{2}{3}}{1-\dfrac{1}{9}}$

$\Rightarrow \dfrac{\dfrac{2}{3}}{\dfrac{8}{9}}$

$\Rightarrow \dfrac{2\times 9}{3\times 8}$

$\Rightarrow \dfrac{3}{4}$

Hence, this is the answer.

Evaluate: $sec^{-1}(-2)$

$sec^{-1}(-2)\\=cos^{-1}((\frac{-1}{2}))\\=\pi-cos^{-1}((\frac{1}{2}))\\=\pi -(\frac{\pi}{3})\\=(\frac{2\pi}{3})$

Solve ${\tan ^{ - 1}}\left( {\tan \frac{{2\pi }}{3}} \right)$

Given that, ${\tan ^{ - 1}}\left( {\tan \dfrac{{2\pi }}{3}} \right)$ ………. (1)

First solve that,

$\tan \left( \dfrac{2\pi }{3} \right)$

$=\tan \left( \pi -\dfrac{\pi }{3} \right)$

$=\tan \left( \dfrac{-\pi }{3} \right)$

$=-\tan \dfrac{\pi }{3}$

$=-\sqrt{3}$

By equation (1),

$=\tan \left( -\sqrt{3} \right)$

Let

$\tan \left( -\sqrt{3} \right)=x$

$\tan x=-\sqrt{3}$

Then, $-\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2}$

Hence, this is the answer.

Evaluate
${\cos ^{ - 1}}\dfrac{1}{2} + 2{\sin ^{ - 1}}\dfrac{1}{2}$

$\begin{array}{l}{\cos ^{ - 1}}\cfrac{1}{2} = \cfrac{\pi }{3}\\{\sin ^{ - 1}}\cfrac{1}{2} = \cfrac{\pi }{6}\\{\cos ^{ - 1}}\cfrac{1}{2} + 2{\sin ^{ - 1}}\cfrac{1}{2}\\\cfrac{\pi }{3} + \cfrac{2\pi }{6}\\ = \cfrac{{2\pi }}{3}\end{array}$

Solve: ${\sin ^{ - 1}}\left( {\frac{{1 - {x^2}}}{{1 + {x^2}}}} \right)$

Consider the given function $={{\sin }^{-1}}\left( \dfrac{1-{{x}^{2}}}{1+{{x}^{2}}} \right)$

Let, put $x=\tan A$ then $A={{\tan }^{-1}}x$ ……. (1)

Then,

${{\sin }^{-1}}\left( \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A} \right)$

$={{\sin }^{-1}}\left( \dfrac{1-\dfrac{{{\sin }^{2}}A}{{{\cos }^{2}}A}}{1+\dfrac{{{\sin }^{2}}A}{{{\cos }^{2}}A}} \right)$

$={{\sin }^{-1}}\left( \dfrac{{{\cos }^{2}}A-{{\sin }^{2}}A}{{{\cos }^{2}}A+{{\sin }^{2}}A} \right)$

$={{\sin }^{-1}}\left( \dfrac{\cos 2A}{1} \right)$

$={{\sin }^{-1}}\cos 2A$

$={{\sin }^{-1}}\sin \left( {{90}^{0}}-2A \right)$

$={{90}^{0}}-2A$

By equation (1) and we get,

$={{90}^{0}}-2{{\tan }^{-1}}x$

Hence, this is the answer.

Solve:-
${\cos ^{ - 1}}\left( {\frac{1}{2}} \right) - 2{\sin ^{ - 1}}\left( { - \frac{1}{2}} \right)$

$\cos ^{ -1 }{ \dfrac { 1 }{ 2 } } -2\sin ^{ -1 }{ \dfrac { -1 }{ 2 } }$

$\\ =\dfrac { \pi }{ 3 } -2\times (\dfrac { -\pi }{ 6 } )$

$\\ =\dfrac { 2\pi }{ 3 }$

Differentiate $\tan^{-1}\left(\dfrac{a\cos x-b\sin x}{b\cos x+a\sin x}\right)$ .

$d(a\cos x - b \sin x) = -a\sin x - b \sin x = -(a\sin x + b \cos x)$

$d(b\cos x + a \sin x) = -b\sin x + a \cos x$

$d\Bigg(\cfrac{a\cos x - b\sin x}{b \cos x + a\sin x}\Bigg) = dy = -\cfrac{(a\sin x + b\cos x)^2 + (a\cos x - b\sin x)^2}{(b\cos x + a \sin x)^2} = -(1 + y^2)$ where

$y = \cfrac{a\cos x - b \sin x}{b \cos x + a \sin x}$

$d(tan^{-1} y) = \cfrac{1}{1+y^2} dy$

$\implies -1$

$\sin\left(2\tan^{-1}\sqrt{\dfrac{1-x}{1+x}}\right)$ .

Putting

$x =\cos 2\theta$

$\sin \Bigg(2\tan^{-1} \sqrt{\cfrac{1-\cos 2\theta}{1+\cos 2 \theta}}\Bigg)$

$\sin (2\tan^{-1} \tan \theta)$

$\sin 2 \theta$

$\sqrt{1-\cos^2 2\theta}$

$\sqrt{1-x^2}$

Solve:
${\sin ^{ - 1}}(\cos x)$

${ sin^{ -1 }{ cos{ x } } }\\ =sin^{ -1 }{ sin{ { (\dfrac { \pi }{ 2 } +{ x) } } } }\\ =(\dfrac { \pi }{ 2 } +{ x })$

$sin^{-1}(cosx)$

As we know that,

$\sin{\left( \dfrac{\pi}{2} + \theta \right)} = \cos{\theta}$

Therefore,

$\sin^{-1}{\left( \cos{x} \right)}$

$= \sin^{-1}{\left( \sin{\left( \dfrac{\pi}{2} + \theta \right)} \right)}$

$= \dfrac{\pi}{2} + \theta \; \left[ \because f^{-1}{\left( f{\left( x \right)} \right)} = x \right]$

Hence the correct answer is

$\left( \dfrac{\pi}{2} + \theta \right)$ .

Solve:
${\sin ^{ - 1}}(\cos x)$

${ sin^{ -1 }{ cos{ x } } }\\ =sin^{ -1 }{ sin{ { (\dfrac { \pi }{ 2 } +{ x) } } } }\\ =(\dfrac { \pi }{ 2 } +{ x })$ d

$sin^{-1}sin15+cos^{-1}cos20+tan^{-1}tan 25=$

We have,

${{\sin }^{-1}}\sin {{15}^{o}}+{{\cos }^{-1}}\cos {{20}^{o}}+{{\tan }^{-1}}\tan {{25}^{o}}$

$\Rightarrow {{15}^{o}}+{{20}^{o}}+{{25}^{o}}$

$\Rightarrow {{60}^{o}}=\dfrac{\pi }{3}$

Hence, this is the answer.

Prove $\tan ^ { - 1 } \dfrac { 1 } { 2 } + \tan ^ { - 1 } \dfrac { 2 } { 11 } = \tan ^ { - 1 } \dfrac { 3 } { 4 }$

$LHS=\tan^{-1}\dfrac{1}{2}+\tan^{-1}\dfrac{2}{11}\\=\tan^{-1}[(\dfrac{\dfrac{1}{2}+\dfrac{2}{11}}{1-(\dfrac{1}{2})(\dfrac{2}{11})})]\\=\tan^{-1}(\dfrac{(\dfrac{11+4}{22})}{(\dfrac{22-2}{22})})\\=\tan^{-1}\dfrac{15}{20}=\tan^{-1}\dfrac{3}{4}=RHS$

$\sin ^ { - 1 } \left( \dfrac { 2 x } { 1 + x ^ { 2 } } \right)$

Let $\>x\>=\>tan\theta\>or\>\theta\>=\>tan^{-1}x\\ =\> sin^{-1}(\dfrac{2tan\theta\>}{1+tan^2\theta\>})\\=sin^{-1}(sin2\theta)\\=2\theta\\=2tan^{-1}x$

Differentiating w.r.t x, We get:

$\>(\dfrac{2}{1+x^2})$

Find the value of $\cot ^ { - 1 } ( - \sqrt { 3 } )$

The range for

$\cot^{-1} x$ is

$\dfrac{-\pi}{2}$ to

$\dfrac{\pi}{2}$

$\cot(\dfrac{-\pi}{6})=-\sqrt{3}$

$\cot^{-1}(-\sqrt{3})=\dfrac{-\pi}{6}$

${\tan ^{ - 1}}\left( 2 \right) + {\tan ^{ - 1}}\left( 3 \right) =$

Solution :-

$tan^{-1}(2)+ tan^{-1}(3)$

$= tan^{-1}(\dfrac{2+3}{1-2\times 3})$

$=tan^{-1}(\dfrac{5}{1-6})$

$= tan^{-1}(\dfrac{5}{-5})$

$= tan^{-1}(-1)$

$=-tan^{-1}(1)$

$=\dfrac{-\pi }{4}$

Solve:
$\dfrac { \sin ^{ -1 }{ \sqrt { x } - } \cos ^{ -1 }{ \sqrt { x } } }{ \sin ^{ -1 }{ \sqrt { x } - } \cos ^{ -1 }{ \sqrt { x } } } ,x\epsilon \left[ 0,1 \right]$

$\dfrac { {sin}^{-1} { \sqrt { x } } -{cos}^{-1} { \sqrt { x } } }{ {sin}^{-1} { \sqrt { x } } -{cos}^{-1} { \sqrt { x } } } =1$ for x

$\epsilon [0,1]$

Solve:
${\sin ^{ - 1}}x + {\sin ^{ - 1}}\sqrt {1 - {x^2}}$

REF.Image.

$I = sin^{-1}x+sin^{-1}\sqrt{1-x^{2}}$

$\triangle ABC$

$\Rightarrow sinA = (\frac{x}{1})$

$\Rightarrow A = sin^{-1}(x)$

$sin C = \frac{\sqrt{1-x^{2}}}{1}$

$\Rightarrow C = sin^{-1}(\sqrt{1-x^{2}})$

$\therefore A+C = sin^{-1}(x)+sin^{-1}(\sqrt{1-x^{2}})$

$A+B+C = 180^{\circ}\Rightarrow$

$A+90+C = 180^{\circ} \Rightarrow A+C = 90^{\circ}= \pi/2$

$\therefore sin^{-1}(x)+sin^{-1}(\sqrt{1-x^{2}}) = \pi /2$

1108491_1189428_ans_037e75b3d1ae4537886ed2781609b139.jpeg

Prove:
$\tan^{-1}\sqrt{x}=\dfrac{1}{2}\cos^{-1}\left (\dfrac{1-x}{1+x}\right),x\epsilon [0,1]$

1203339_1249093_ans_ca074aa4e040461f9ccbde5af185938f.jpg

$tan^{-1}(tan\,5)$

Consider the given expression,

$\Rightarrow {{\tan }^{-1}}\left( \tan 5 \right)$

$\Rightarrow 5$

Hence, this is the answer.

Solve:
${ \cos }^{ -1 }\left( \dfrac { 3\cos x-4\sin x }{ 5 } \right)$

Given,

$\cos ^{-1}\left ( \dfrac{3\cos x-4\sin x}{5} \right )$

$=\cos ^{-1}\left ( \dfrac{3}{5}\cos x-\dfrac{4}{5}\sin x \right )$

Let

$\dfrac{3}{5}=\cos \alpha ,\dfrac{4}{5}=\sin \alpha$

Therefore,

$=\cos ^{-1}\left ( \cos \alpha \cos x-\sin \alpha\sin x \right )$

$=\cos ^{-1}(\cos (x+\alpha ))$

$=x+\alpha \,\,\,\,\,$ where

$\alpha=\cos^{-1}\dfrac{3}{5}$

Hence, this is the answer.

Evaluate :
$\cos(2\cos^{-1}x+\sin^{-1}x)$ at $x=\dfrac{1}{5}$ .

1345955_1258850_ans_11befa7ee49348aa97fba95eebd613fa.jpg

Simplify ${\sin ^{ - 1}}\left( {\sin \dfrac{{2\pi }}{3}} \right)$

We have,

${\sin ^{ - 1}}\left( {\sin \cfrac{{2\pi }}{3}} \right)$

$=\left( { \cfrac{{2\pi }}{3}} \right)$

Hence, this is the answer.

Prove that : ${ cos }^{ -1 }\left( \dfrac { 3 }{ 5 } \right) +{ cos }^{ -1 }\left( \dfrac { 4 }{ 5 } \right) =\dfrac { \pi }{ 2 }$

Let,

$\cos^{-1}\left ( \dfrac{3}{5} \right )=x$

$\Rightarrow \cos x=\dfrac{3}{5}$

From Pythagorus theorem, we have,

$\sin x =\dfrac{4}{5}$

Given,

$\cos^{-1}\left ( \dfrac{3}{5} \right )+\cos^{-1}\left ( \dfrac{4}{5} \right )$

$=\sin^{-1}\left ( \dfrac{4}{5} \right )+\cos^{-1}\left ( \dfrac{4}{5} \right )$

we have general formula,

$\sin ^{-1}x+\cos ^{-1}x=\dfrac{\pi}{2}$

$=\dfrac{\pi}{2}$

Hence proved.

${\cos ^{ - 1}}\left( { - \cfrac{{\sqrt 3 }}{2}} \right)$

We have,

${\cos ^{ - 1}}\left( { - \cfrac{{\sqrt 3 }}{2}} \right)$

$\Rightarrow {\cos ^{ - 1}}\left(\cos \dfrac{5\pi}{6}\right)$

$\Rightarrow \dfrac{5\pi}{6}$

Hence, this is the answer.

Simplify: $\sin.{ \cot }^{ -1 }{ \cot x }$

We have,

$\sin {{\cot }^{-1}}\cot x$

$\Rightarrow \sin x$

Hence, this is the answer.

Solve for $x$ :
$4\sin^{-1}x+\cos^{-1}x=\pi$ .

Given,

$4\sin^{-1}x+\cos^{-1}x=\pi$

$\Rightarrow 3\sin^{-1}x+(\sin^{-1}x+\cos^{-1}x)=\pi$

$\Rightarrow 3\sin^{-1}x+\dfrac{\pi}{2}=\pi$

$\Rightarrow 3\sin^{-1}x=\dfrac{\pi}{2}$

$\Rightarrow \sin^{-1}x=\dfrac{\pi}{6}$

$\Rightarrow x=\sin \dfrac{\pi}{6}$

$\Rightarrow x=\dfrac{1}{2}$ .

If $\sin^{-1}x=\tan^{-1}y$ then prove that $\dfrac{1}{x^2}-\dfrac{1}{y^2}=1$ .

Given,

Let

$\sin^{-1}x=\tan^{-1}y=\theta$

or,

$x=\sin \theta$ and

$y=\tan \theta$

or,

$\dfrac{1}{x}=cosec \theta$ ......(1) and

$\dfrac{1}{y}=\cot \theta$ .....(2).

Now,

$\dfrac{1}{x^2}-\dfrac{1}{y^2}$

$=cosec^2 \theta-\cot^2 \theta$ [ Using (1) and (2)]

$\dfrac{1}{x^2}-\dfrac{1}{y^2}$

$=1$ .

Prove that 3 $sin^{-1}=sin^{-1} (3x-4x^{3}),x\epsilon[\frac{-1}{2},\frac{1}{2}]$

Let

$x=sin\theta$

RHS :

$=sin^{-1}(3x-4x^{3})$

$=sin^{-1}(3sin\theta-4sin^{3}\theta)$

$=sin^{-1}sin3\theta$

$=3\theta$

$=3sin^{-1}x$ = LHS

Find the value of $\tan^{-1}{\left(\tan{\dfrac{2\pi}{3}}\right)}$

$\tan^{-1}{\left( \tan{\cfrac{2 \pi}{3}} \right)}\\$

$= \tan^{-1}{\left( \tan{\left( \pi - \cfrac{\pi}{3} \right)} \right)}\\$

$= \tan^{-1}{\left( \tan{\left( - \cfrac{\pi}{3} \right)} \right)}\\$

$= - \cfrac{\pi}{3}$

Solve:
$3\tan ^{ -1 }{ x } =\tan ^{ -1 }{ \left( \dfrac { 3x-{ x }^{ 3 } }{ 1-3{ x }^{ 2 } } \right) }$

$\tan^{-1}A+\tan^{-1}B=\tan^{-1}\left(\dfrac{A+B}{1-AB}\right)$

$\Rightarrow 3\tan^{-1}x=\tan^{-1}x+\tan^{-1}x+\tan^{-1}x=\tan^{-1}\left(\dfrac{2x}{1-x^2}\right)+\tan^{-1}x$

$=\tan^{-1}\left(\dfrac{\dfrac{2x}{1-x^2}+x}{1-\dfrac{x-2x}{1-x^2}}\right)=\tan^{-1}\left(\dfrac{3x-x^3}{1-3x^2}\right)=$ R.H.S.

1214406_1395703_ans_bacd02c48cf74529a2192acb8cfbcdfb.jpg

Evaluate the following :
$\sin^{-1} (\sin 10)$

$sin^{-1}(sin 10)$

= 10

1208345_1348323_ans_5711938fe87e418484ab4eb104047749.jpg

if $\sin x=1$ then find $\sin 2x$

$\sin x=1\\x=\sin^{-1}1\\x=\dfrac{\pi}{2}\\2x=\pi\\\sin 2x=\sin \pi\\\sin x=0$

$y = \sin ^ { - 1 } \left( \frac { 2 n } { 1 + n ^ { 2 } } \right) + \sec ^ { - 1 } \left( \frac { 1 + n ^ { 2 } } { 2 n } \right)$

$y=\sin^{-1}\left(\dfrac{2n}{1+n^2}\right)+\sec^{-1}\left(\dfrac{1+n^2}{2n}\right)\\y=\sin^{-1}\left(\dfrac{2n}{1+n^2}\right)+\cos ^{-1}\left(\dfrac{2n}{1+n^2}\right)\\\sin^{-1}x+\cos^{-1}x=\dfrac{\pi}{2}\\\implies y=\dfrac{\pi}{2}$

If ${\left( {{{\tan }^{ - 1}}x} \right)^2} + {\left( {{{\cot }^{ - 1}}x} \right)^2} = \dfrac{{5{\pi ^2}}}{8}$ , then find $x.$

$(tan^{2}1)^{2}+(cot^{-1})^{2}=\dfrac{5\pi ^{2}}{8}$

$(tan^{-1}x)^{2}+(\dfrac{\pi }{2}-tan^{-1}x)^{2}=\dfrac{5\pi ^{2}}{8}$

$k=tan^{-1}x$

$2k^{2}-\pi k+\dfrac{\pi ^{2}}{4}-\dfrac{5\pi ^{2}}{8}=0$

$16k^{2}-3\pi k-3\pi ^{2}=0$

$(4k-3\pi )(4k+\pi )=0$

$x= tan \dfrac{3\pi }{4}, tan\dfrac{-\pi }{4}$

$x=-1$

Prove that :
$\cos^{-1}\left(\dfrac{12}{13}\right)+\sin^{-1}\left(\dfrac{3}{5}\right)=\sin^{-1}\left(\dfrac{56}{65}\right)$ .

1443580_1688044_ans_65e2dae7b4864972bd44f2b5bc20707f.jpeg

Find the value of $\sin^{-1}\left (\sin \dfrac{3\pi}{5}\right)$ .

$\sin^{-1} (\sin \dfrac{3\pi}{5})=\sin^{-1}(\sin (\pi-\dfrac{2\pi}{5}))$

$=\sin^{-1}(\sin \dfrac{2\pi}{5})$

$=\dfrac{2\pi}{5}$

Write the value of $\cos^{-1} (\cos 6)$ .

$cos^{-1}(cos6)$

Since,

$cos(2\pi-\theta)=cos(\theta)$

$=cos^{-1}(cos6)\\=cos^{-1}(cos(2\pi-6))\\=2\pi-6$ as

$0\leq(2\pi-6)\leq\pi$

Prove that :
$\tan^{-1} 1 +\tan^{-1} 2 +\tan^{-1} 3=\pi$

arctan(x) + arctan(y) = π + arctan({x+y}/{1−xy}), if x > 0, y > 0 and xy > 1

$\tan^{-1}1+\tan^{-1}2 +\tan^{-1} 3$

$=\tan^{-1} 1 +(\tan^{-1} 2 +\tan^{-1}3)$

$=\tan^{-1}1+\pi+\tan^{-1}{\dfrac{2+3}{1-2\times3}}$

$=\tan^{-1}1+tan^{-1}{-1}+\pi$

$=\dfrac{\pi}{4}+\dfrac{-\pi}{4}+\pi$

$=\pi$

If $\tan^{-1} 2 +\tan^{-1} 3 +\theta =\pi$ , find the value of $\theta$ .

$\tan^{-1}2+\tan^{-1} 3 +\theta = \pi$

$\Rightarrow \tan^{-1} 2 +\tan^{-1} 3 =\pi-\theta$

$\Rightarrow \pi+\tan^{-1}\left(\dfrac{2+3}{1-2\times 3}\right)=\pi-\theta$

$\left[\because ab>1,\ tan^{-1} a+tan^{-1} b=\pi+tan^{-1} {\dfrac{a+b}{1-ab}}\right]$

$\Rightarrow \pi+\tan^{-1}(-1)=\pi-\theta$

$\Rightarrow \pi-\dfrac{\pi}{4}=\pi-\theta$

$\therefore\ \theta =\dfrac{\pi}{4}$

Prove that :
$\tan^{-1} 2 +\tan^{-1}3=\dfrac{3\pi}{4}$

$\tan^{-1} 2 +\tan^{-1}3=\pi+\tan^{-1}[\dfrac{2+3}{1-2\times 3}]$

$=\pi+\tan^{-1}(-1)$

$=\pi-\dfrac{\pi}{4}=\dfrac{3\pi}{4}$

Solve
${\sin }^{ -1 }(\cos x)$ .

We have

$\sin^{-1} (\cos x)$

We know

$\cos x = \sin \left(\dfrac{\pi}{2} - x\right)$ .

Also

$\sin^{-1}(\sin x ) = x$ .

Put

$\cos x = \sin \left(\dfrac{\pi}{2}-x\right)$ and get

$\sin^{-1} (\cos x) = \sin^{-1} \sin \left(\dfrac{\pi}{2}-x\right)$

$= \dfrac{\pi}{2}-x$

Evaluate
$\tan (\tan^{-1}(-4))$

$\tan (\tan^{-1}x)=x, \forall x\in R, \tan (\tan^{-1}(-4))=-4$ .

Evaluate $\cos \left[\cos^{-1}\left (\dfrac {-\sqrt 3}{2}\right) +\dfrac {\pi}{6}\right]$

$\cos \left[\cos^{-1}\left (\dfrac {-\sqrt 3}{2}\right) +\dfrac {\pi}{6}\right]$

$=\cos \left[\cos^{-1}\left(\cos \dfrac {5\pi}{6}\right) \right] \left[\because \cos \dfrac {5\pi}{6}=\dfrac {-\sqrt 3}{2}\right]$

$=\cos \left(\dfrac {5\pi}{6}+\dfrac {\pi}{6}\right) \left\{\cos^{-1} \cos x=x, x\in [0,\pi]\right\}$

$=\cos \left(\dfrac {6\pi}{6}\right)$

$=\cos (\pi)=-1$

Find the value of $\tan^{-1}\left(\tan \dfrac {5\pi}{6}\right)+ \cos^{-1} \left(\cos \dfrac {13\pi}{6}\right)$ .

We know that,

$\tan^{-1} (\tan x)=x; x\in \left(-\dfrac {\pi}{2},\dfrac {\pi}{2}\right)$ and

$\cos^{-1}(\cos x)=x; x\in [0,\pi]$

$\therefore \tan^{-1}\left(\tan \dfrac {5\pi}{6}\right)+\cos^{-1}\left(\cos \dfrac {13\pi}{6}\right)$

$=\tan^{-1}\left[\tan \left(\pi- \dfrac {\pi}{6}\right)\right] +\cos^{-1}\left[\cos \left(\pi+ \dfrac {7\pi}{6}\right)\right]$

$=\tan^{-1}\left(-\tan \dfrac {\pi}{6}\right)+\cos^{-1}\left(-\cos \dfrac {7\pi}{6}\right) [\cos (\pi +\theta)=- \cos \theta]$

$=\tan^{-1} \left(\tan \dfrac {\pi}{6}\right)+\pi -\left[\cos^{-1} \cos \left(-\tan \dfrac {7\pi}{6}\right)\right]$

$\left\{\because \tan^{-1}(-x)=-\tan^{-1} x, x\in R\ and\ \cos^{-1} (-x) =\pi -\cos^{-1}x, x\in [-1,1]\right\}$

$=\tan^{-1}\left(\tan \dfrac {\pi}{6}\right)+\pi -\cos^{-1} \left[\cos \left(\pi +\dfrac {\pi}{6}\right)\right]$

$\tan^{-1}\left(\tan \dfrac {\pi}{6}\right) +\pi - \left[\cos^{-1} \left(-\cos \dfrac {\pi}{6}\right)\right] [\because \cos (\pi +\theta)=- \cos \theta]$

$=\tan^{-1} \left(\tan \dfrac {\pi}{6}\right)+\pi -\pi +\cos^{-1} \left(\cos \dfrac {\pi}{6}\right) [\because \cos^{-1} (-x)=\pi -\cos^{-1}x]$

$=-\dfrac {\pi}{6}+0+\dfrac {\pi}{6}=0$

Note: Remember that

$\tan^{-1}\left(\tan \dfrac {5\pi}{6}\right)=\dfrac {5\pi}{6}$ and

$\cos^{-1}\left(\cos \dfrac {13\pi}{6}\right) \dfrac {13\pi}{6}$

Since,

$\dfrac {5\pi}{6}\notin \left(-\dfrac {\pi}{2}, \dfrac {\pi}{2}\right)$ and

$\dfrac {13\pi}{6} \notin [0, \pi]$

Prove that $\cos \left(\dfrac {\pi}{4}-2\cot^{-1} 3\right)=7$ .

We have

$\cot \left(\dfrac {\pi}{4}-2\cot^{-1}3\right)=7$

$\Rightarrow \ \left(\dfrac {\pi}{4} -2\cot^{-1}3\right)=\cot^{-1}7$

$\Rightarrow \ (2\cot^{-1}3)=\dfrac {\pi}{4}-\cot^{-1}7$

$\Rightarrow \ 2\tan^{-1}\dfrac {1}{3} =\dfrac {\pi}{4} -\tan^{-1} \dfrac {1}{7}$

$\Rightarrow \ \tan^{-1} \dfrac {1}{3} +\tan^{-1} =\dfrac {\pi}{4}$

$\tan^{-1} \dfrac {2/3}{1-(1/3)^3}+\tan^{-1}\dfrac {1}{7}=\dfrac {\pi}{4}$

$\Rightarrow \ \tan^{-1}\dfrac {2/3}{8/9}+\tan^{-1}\dfrac 17 =\dfrac {\pi}{4}$

$\Rightarrow \ \tan^{-1}\dfrac 34 +\tan^{-1}\dfrac 17 =\dfrac {\pi}{4}$

$\Rightarrow \ \tan^{-1} \dfrac {\dfrac {3}{4}+\dfrac {1}{7}}{1-\dfrac {3}{4}.\dfrac {1}{7}} =\dfrac {\pi}{4}$

$\Rightarrow \ \tan^{-1}\dfrac {(21+4)/28}{(28-3)/28}=\dfrac {\pi}{4}$

$\Rightarrow \ \tan^{-1} \dfrac {25}{25}=\dfrac {\pi}{4}$

$\Rightarrow \ 1=\tan \dfrac {\pi}{4}$

$1=1$

$\Rightarrow \ LHS=RHS$ Hence Proved.

If $\displaystyle x > y > 0$ then find the value of $\displaystyle \tan^{-1} \frac{x}{y} + \tan^{-1} \left [ \frac{x + y}{x - y} \right ]$ ,

Given,

$\displaystyle \tan ^{ -1 }{ \left( \frac { x }{ y } \right) } +\tan ^{ -1 }{ \left( \frac { x+y }{ x-y } \right) }$

$=\tan ^{ -1 }{ \left( \frac { \frac { x }{ y } +\frac { x+y }{ x-y } }{ 1-\frac { x }{ y } \times \frac { x+y }{ x-y } } \right) }$

$\displaystyle =\tan ^{ -1 }{ \left( \frac { x\left( x-y \right) +\left( x+y \right) y }{ y\left( x-y \right) -x\left( x+y \right) } \right) }$

$=\tan ^{ -1 }{ \left( \frac { { x }^{ 2 }-xy+xy+{ y }^{ 2 } }{ xy-{ y }^{ 2 }-{ x }^{ 2 }-xy } \right) }$

$\displaystyle =\tan ^{ -1 }{ \left( \frac { { x }^{ 2 }+{ y }^{ 2 } }{ -\left( { x }^{ 2 }+{ y }^{ 2 } \right) } \right) }$

$=\tan ^{ -1 }{ \left( -1 \right) } =\dfrac { 3\pi }{ 4 }$

If $\displaystyle x + y + z = xyz$ , and $\displaystyle x, \: y, \: z > 0$ , then find the value of $\displaystyle \tan^{-1}x + \tan^{-1} y + \tan^{-1} z$

Let

$x=tanA$ ,

$y=tanB$ and

$z=tanC$ such that

$A+B+C=\pi$ .
Then

$x+y+z$

$=tanA+tanB+tanC$

$=(tanA+tanB)+tanC$

$=tan(A+B)(1-tanA.tanB)+tanC$

$=tan(\pi-C)(1-tanA.tanB)+tanC$

$=tanC-tanC(1-tanA.tanB)$

$=tanC(1-1+tanA.tanB)$

$=tanA.tanB.tanC$

$=xyz$ .
Hence

$tan^{-1}(x)+tan^{-1}(y)+tan^{-1}(z)$

$=tan^{-1}(tanA)+tan^{-1}(tanB)+tan^{-1}(tanC)$

$=A+B+C$

$=\pi$ ... (as taken).

Prove: $\displaystyle { \tan }^{ -1 }\sqrt { x } =\frac { 1 }{ 2 } { \cos }^{ -1 }\left( \frac { 1-x }{ 1+x } \right) ,x\in \left[ 0,1 \right]$

Let

$\displaystyle x={ \tan }^{ 2 }\theta$

$\Rightarrow \sqrt { x } =\tan { \theta }$

$\Rightarrow \theta ={ \tan }^{ -1 }\sqrt {x }$

$\displaystyle \therefore \frac { 1-x }{ 1+x } =\frac { 1-{ \tan }^{ 2 }\theta }{ 1+{ \tan }^{ 2 }\theta } =\cos { 2\theta }$

Now, we have:

$\displaystyle R.H.S.=\frac { 1 }{ 2 } { \cos }^{ -1 }\left( \frac { 1-x }{ 1+x } \right)$

$=\dfrac { 1 }{ 2 } { \cos }^{ -1 }\left( \cos { 2\theta } \right)$

$=\dfrac { 1 }{ 2 } \times 2\theta =\theta$

$={ \tan }^{ -1 }\sqrt {x } =L.H.S.$

Write the function in the simplest form:
$\displaystyle { \tan }^{ -1 }\frac { \sqrt { 1+{ x }^{ 2 } } -1 }{ x } ,x\neq 0$

$\displaystyle { \tan }^{ -1 }\frac { \sqrt { 1+{ x }^{ 2 } } -1 }{ x }$

Put

$\displaystyle x=\tan { \theta } \Rightarrow \theta ={ \tan }^{ -1 }x$

$\displaystyle \therefore \quad { \tan }^{ -1 }\frac { \sqrt { 1+{ x }^{ 2 } } -1 }{ x } ={ \tan }^{ -1 }\left( \frac { \sqrt { 1+{ \tan }^{ 2 }\theta} -1 }{ \tan { \theta } } \right)$

$\displaystyle ={ \tan }^{ -1 }\left(\frac { \sec { \theta -1 } }{ \tan { \theta } } \right) ={ \tan }^{ -1 }\left( \frac { 1-\cos { \theta } }{ \sin { \theta } } \right)$

$\displaystyle ={ \tan }^{ -1 }\left( \frac { 2{ \sin }^{ 2}\frac { \theta }{ 2 } }{ 2\sin { \frac { \theta }{ 2 } \cos { \frac{ \theta }{ 2 } } } } \right)$

$\displaystyle ={ \tan }^{ -1 }\left( \tan { \dfrac { \theta }{ 2 } } \right) =\dfrac { \theta }{ 2 }$

$=\dfrac { 1 }{ 2 } { \tan }^{ -1 }x$

If $y = \sin (\cos^{-1} x)$ and $x = 99$ , then $1/y^2$ is equal to

$y = \displaystyle \sin \sin^{-1} \frac{1}{\sqrt{1 + x^2}} = \frac{1}{\sqrt{1 + x^2}}$

$\therefore \displaystyle \frac{1}{y^2} = 1 + x^2 = 1 + (99)^2 = 9802$

Write the function in the simplest form:
$\displaystyle { \tan }^{ -1 }\left( \sqrt { \frac { 1-\cos { x } }{ 1+\cos { x } } } \right) ,x<\pi$

$\displaystyle { \tan }^{ -1 }\left( \sqrt { \frac { 1-\cos { x } }{ 1+\cos { x } } } \right)$ and

$x<\pi$

$\displaystyle{ \tan }^{ -1 }\left( \sqrt { \frac { 1-\cos { x } }{ 1+\cos { x } } } \right) ={ \tan }^{ -1 }\left( \sqrt { \frac { 2{ \sin }^{ 2 }\frac { x}{ 2 } }{ 2{ \cos }^{ 2 }\frac { x }{ 2 } } } \right)$

$\displaystyle={ \tan }^{ -1 }\left( \frac { \sin\frac { x }{ 2 } }{ \cos\frac { x }{ 2} } \right) ={ \tan }^{ -1 }\left( \tan\frac { x }{ 2 } \right) =\frac { x }{ 2 }$

Prove that : $\displaystyle { \sin }^{ -1 }\frac { 5 }{ 13 }+{ \cos }^{ -1 }\frac { 3 }{ 5 }={ \tan }^{ -1 }\frac { 63 }{ 16 }$

Let

$\displaystyle { \sin }^{ -1 }\frac { 5 }{ 13 } =x\Rightarrow \sin { x } =\frac { 5 }{ 13 } \Rightarrow \cos{ x }=\frac { 12 }{ 13 }$

$\displaystyle \therefore \quad \tan { x } =\frac { 5 }{ 12 } \Rightarrow x={ \tan }^{ -1 }\frac { 5 }{ 12 }$ .........(1)

Let

$\displaystyle { \cos }^{ -1 }\frac { 3 }{ 5 }=y \Rightarrow \cos { y } =\frac { 3 }{ 5 } \Rightarrow \sin { y }=\frac { 4 }{ 5 }$

$\displaystyle \therefore \quad \tan { y } =\frac { 4 }{ 3 } \Rightarrow y={ \tan }^{ -1 }\frac { 4 }{ 3 }$ .......(2)

Using (1) and (2), we have

$\displaystyle \text{L.H.S.}={ \sin }^{ -1 }\frac { 5 }{ 13 } +{ \cos }^{ -1 }\frac { 3 }{ 5 }$

$\displaystyle ={ \tan }^{ -1 }\frac { 5 }{ 12 } +{ \tan }^{ -1 }\frac { 4 }{ 3 }$

$\displaystyle={ \tan }^{ -1 }\left( \frac { \frac { 5 }{ 12 } +\frac { 4 }{ 3 } }{ 1-\frac { 5 }{ 12 } \times \frac { 4 }{ 3 } } \right)$

$\displaystyle ={ \tan }^{ -1 }\left( \frac { 15+48 }{ 36-20 } \right)$

$\displaystyle ={ \tan }^{ -1 }\frac { 63 }{ 16 } =\text{R.H.S.}$

Write the function in the simplest form:
$\displaystyle { \tan }^{ -1 }\left( \frac { 3{ a }^{ 2 }x-{ x }^{ 3 } }{ { a }^{ 3 }-3{ ax }^{ 2 } } \right) ,a>0;\frac { -a }{ \sqrt { 3 } } \le x\le \frac { a }{ \sqrt { 3 } }$

$\displaystyle { \tan }^{ -1 }\left( \frac { 3{ a }^{ 2 }x-{ x }^{ 3 } }{ { a }^{ 3 }-3{ ax }^{ 2 } } \right)$

Put

$\displaystyle x=a\tan { \theta } \Rightarrow \frac { x }{ a } =\tan {\theta } \Rightarrow \theta ={ \tan }^{ -1 }\frac { x }{ a }$

$\therefore \displaystyle { \tan }^{ -1 }\left( \frac { 3{ a }^{ 2 }x-{ x }^{ 3 } }{ { a }^{ 3 }-3{ ax }^{ 2 } } \right) ={ \tan }^{ -1 }\left( \frac { 3{ a }^{ 2 }.a\tan { \theta } -{ a }^{ 3 }{ \tan }^{ 3 }\theta }{ { a }^{ 3 }-3a.{a }^{ 2 }{ \tan }^{ 2 }\theta } \right)$

$\displaystyle ={ \tan }^{ -1 }\left( \frac { 3{ a }^{ 2 }\tan { \theta } -{ a }^{ 3 }{ \tan }^{ 3 }\theta }{ { a }^{ 3 }-3{ a }^{ 3 }{ \tan }^{ 2 }\theta } \right)$

$\displaystyle ={ \tan }^{ -1 }\left( \frac { 3\tan { \theta } -{ \tan }^{ 3 }\theta }{ 1-3{ \tan }^{ 2 }\theta } \right)$

$\displaystyle ={ \tan }^{ -1 }\left( \tan { 3\theta } \right)$

$\displaystyle =3\theta =3{ \tan }^{ -1 }\frac { x }{ a }$

Prove the following:
$\cos^{-1}\left (\dfrac {12}{13}\right )+ \sin^{-1}\left (\dfrac {3}{5}\right ) = \sin^{-1}\left (\dfrac {56}{65}\right )$

$sin \left ( cos^{-1}\left ( \cfrac{12}{13} \right ) + sin^{-1} \left( \cfrac{3}{5} \right ) \right )$

$= sin\left ( cos^{-1} \left( \cfrac{12}{13} \right ) \right ) cos \left ( sin^{-1} \left ( \cfrac{3}{5} \right) \right ) + cos \left ( cos^{-1} \left ( \cfrac{12}{13} \right )\right ) sin\left ( sin^{-1} \left ( \cfrac{3}{5} \right ) \right )$

$= \cfrac{\sqrt{169 - 144}}{13} \times \cfrac{\sqrt{25 - 9}}{5} + \cfrac{12}{13} \times \cfrac{3}{5}$

$= \cfrac{5}{13} \times \cfrac{4}{5} + \cfrac{36}{65}$

$= \cfrac{20}{65} + \cfrac{36}{65}$

$= \cfrac{56}{65}$

Hence proved

If $\tan^{-1}x + \tan^{-1} y = \dfrac {\pi}{4}, xy < 1$ , then write the value of $x + y + xy.$

$\tan ^{ -1 }{ x } +\tan ^{ -1 }{ y } =\dfrac{\pi}{4}$ , which gives

$\tan ^{ -1 }{ \dfrac { x+y }{ 1-xy } } =\dfrac{\pi}{4}$ , which gives

$\dfrac { x+y }{ 1-xy } =1$

Therefore

$x+y+xy=1.$

Write the principal value of $\cos^{-1}\left (\dfrac {1}{2}\right )-2 \sin^{-1} \left (-\dfrac {1}{2}\right ).$

The principal value of

$cos^{-1}x$ lies in

$[0,\pi]$ and that of

$sin^{-1}x$ lies in

$\left [-\cfrac{\pi}{2}, \cfrac{\pi}{2} \right ]$

$\Rightarrow cos^{-1} \left ( \cfrac{1}{2} \right ) = \cfrac{\pi}{3}$ and

$sin^{-1} \left( -\cfrac{1}{2} \right ) = \cfrac{-\pi}{6}$

Substituting these values in the final equation, we get

$\cfrac{\pi}{3} - 2\times \cfrac{-\pi}{6}$

$= \cfrac{\pi}{3} + \cfrac{\pi}{3}$

$= \cfrac{2\pi}{3}$

Prove that: $\tan^{-1} \dfrac {1}{5} + \tan^{-1} \dfrac {1}{7} + \tan^{-1} \dfrac {1}{3} + \tan^{-1} \dfrac {1}{8} = \dfrac {\pi}{4}$

$\tan^{-1}a + \tan^{-1}b = \tan^{-1}\left (\cfrac{a + b}{1 - ab}\right)$

$\therefore \tan^{-1}\cfrac{1}{5} + \tan^{-1}\cfrac{1}{7} = \tan^{-1}\cfrac{5 + 7}{35 - 1} = \tan^{-1}\cfrac{6}{17}$

$\tan^{-1}\cfrac{6}{17} + \tan^{-1}\cfrac{1}{3} = \tan^{-1}\cfrac{18 + 17}{51 - 6} = \tan^{-1}\cfrac{7}{9}$

$\tan^{-1}\cfrac{7}{9} + \tan^{-1}\cfrac{1}{8} = \tan^{-1}\cfrac{56 + 9}{72 - 7} = \tan^{-1}1 = \cfrac{\pi}{4}$

Hence proved

If $\sin^{-1}x + \sin^{-1} y = \pi$ and $x = ky,$ then find the value of $39^{2k} + 5^k$

for

$Sin^{-1}(x)+Sin^{-1}(y)=\pi$

$x=1$

$y=1$

$x=ky$

$1=k(1)$

$k=1$

Value of

$39^{2k}+5^{k}$

$=39^{2}+5$

$=1521+5$

$=1526$

Show that:
$\cos ^{ -1 }{ \left[ \dfrac { \cos { \alpha } +\cos { \beta } }{ 1+\cos { \alpha } \cos { \beta } } \right] } =2\tan ^{ -1 }{ \left( \tan { \dfrac { \alpha }{ 2 } } \tan { \dfrac { \beta }{ 2 } } \right) }$

$\cos ^{ -1 }{ \left[ \dfrac { \cos { \alpha } +\cos { \beta } }{ 1+\cos { \alpha } \cos { \beta } } \right] } =2\tan ^{ -1 }{ \left( \tan { \dfrac { \alpha }{ 2 } } \tan { \dfrac { \beta }{ 2 } } \right) }$

RHS

$\displaystyle = 2\,tan_{-1}\left [ tan\frac{\alpha }{2}tan\frac{\beta }{2} \right ]$

$\displaystyle = cos_{-1}\left [ \dfrac{1-tan^{2}\alpha /2\,tan^{2}\beta /2}{1+tan^{2}\alpha /2\,tan^{2}\beta /2} \right ]$

$\displaystyle = cos^{-1} \left [ \dfrac{\dfrac{1-sin^{2}\alpha /2\,sin^{2}\beta /2}{cos^{2}\alpha /2\,cos^{2}\beta /2}}{1+\dfrac{sin^{2}\alpha /2\,sin^{2}\beta /2}{cos^{2}\alpha /2\,cos^{2}\beta /2}} \right ]$

$\displaystyle = cos^{-1}\left [ \frac{cos^{2}\alpha /2\,cos^{2}\beta /2-sin^{2}\alpha /2\,sin^{2}\beta /2}{cos^{2}\alpha /2\,cos^{2}\beta /2+sin^{2}\alpha /2\,sin^{2}\beta /2} \right ]$

$\displaystyle = cos^{-1}\left [ \dfrac{2cos^{2}\alpha /2\,cos^{2}\beta /2-sin^{2}\alpha /2\,sin^{2}\beta /2}{2cos^{2}\alpha /2\,cos^{2}\beta /2+2sin^{2}\alpha /2\,sin^{2}\beta /2} \right ]$

$\displaystyle = cos^{-1}\left [ \dfrac{(1+cos\alpha )(1+cos\beta )-(1-cos\alpha )(1-cos\beta )}{(1+cos\alpha )(1+cos\beta )+(1-cos\alpha )(1-cos\beta )} \right ]$

$\displaystyle = cos^{-1}\left [ \dfrac{cos\alpha +cos\beta }{1-cos\alpha \,cos\beta } \right ]$

$= LHS$

1129344_872312_ans_f04af259706d4b2dbf18f62a9e8e66c5.jpg

$\sin ^{ -1 }{ \left( \dfrac { 2\sec { x } }{ 1+\sec ^{ 2 }{ x } } \right) =y }$

$\sin ^{ -1 }{ \left( \dfrac { 2\sec { x } }{ 1+\sec ^{ 2 }{ x } } \right) =y } \\ \Rightarrow \sin ^{ -1 }{ \left( \frac { 2\cos { x } }{ 1+\cos ^{ 2 }{ x } } \right) =y }$

$\Rightarrow \sin ^{ -1 }\left( \dfrac { 2 }{ \cos { x } +\frac { 1 }{ \cos { x } } } \right) =y$

$\Rightarrow \left( \dfrac { 2 }{ \cos { x } +\frac { 1 }{ \cos { x } } } \right) =\sin y$

We know that

$-1\le \sin y\le 1$

Thus, the value of

$\dfrac { 2 }{ \cos { x } +\frac { 1 }{ \cos { x } } }$ can be

$1$ or

$-1$ only

So value of

$\sin ^{ -1 }{ \left( \dfrac { 2\sec { x } }{ 1+\sec ^{ 2 }{ x } } \right) }$ can be

$\dfrac { \pi }{ 2 }$ or

$\dfrac { -\pi }{ 2 }$

Solve for $x: \cos { \left( \sin ^{ -1 }{ x } \right) } =\dfrac{ 1 }{ 7 }$ .

Given

$\cos(\sin^{-1}x)=\dfrac{1}{7}$

now we know that

$\sin^{-1}x=\cos^{-1}\sqrt{1-x^{2}}$

substituting this property in the given question

$\cos(\cos^{-1}\sqrt{1-x^{2}})=\dfrac{1}{7}$

$\Rightarrow$

$\sqrt{1-x^{2}}=\dfrac{1}{7}$

squaring on both sides

$1-x^{2}=\dfrac{1}{7}$

$x^{2}=\dfrac{48}{49}$

$\Rightarrow$

$x=\dfrac{4\sqrt{3}}{7}$

This is the required answer

Solve: $\tan^{-1}2x+\tan^{-1}3x=\displaystyle\frac{\pi}{4}$ .

$\tan^{-1}{x}+\tan^{-1}{y}=\tan^{-1}{\left[\dfrac{x+y}{1-xy}\right]}$

$\rightarrow$ Identity

$tan^{-1}{2x}+tan^{-1}{3x}=\dfrac{\pi}{4}$

$\Rightarrow tan^{-1}{\left[\dfrac{2x+3x}{1-2x\times{3x}}\right]}=tan^{-1}{(1)}$

$\Rightarrow \dfrac{5x}{1-6x^2}=1$

$\Rightarrow 6x^2+5x-1=0$

$\Rightarrow (6x-1)(x+1)=0$

$\Rightarrow x=-1$ or

$x=\dfrac{1}{6}$

Putting

$x=-1 \Rightarrow tan^{-1}{-2}+tan^{-1}{-3}=\dfrac{5\pi}{4}$

Putting

$x=\dfrac{1}{6} \Rightarrow tan^{-1}{\dfrac{1}{3}}+tan^{-1}{\dfrac{1}{2}}=\dfrac{\pi}{4}$

$\therefore x=-1$ is not a solution.

So,

$x=\dfrac{1}{6}$ .

Solve: $3\tan^{-1}x+\cot^{-1}x=\pi$ .

We know that

$tan^{-1}x+cot^{-1}x=\dfrac{\pi}{2}\space(x\space\epsilon \space R)$

$\therefore 3 tan^{-1}x+cot^{-1}x=\pi\Rightarrow 2tan^{-1}x+tan^{-1}+cot^{-1}x=\pi$

$\Rightarrow 2tan^{-1} x+\dfrac{\pi}{2}=\pi\Rightarrow tan^{-1}x=\dfrac{\pi}{4}$

$x=tan\dfrac{\pi}{4}=1$

$x=1$ .

Prove that $\cos ^{ -1 }{ \left( -x \right) } =\pi -\cos ^{ -1 }{ \left( x \right) }$ , $-1\le x\le 1$ .

Let $\cos A=x$ then $\cos(\pi-A)=-\cos A=-x$

Hence, $\cos^{-1}x=A$

$\cos^{-1}(-x)=\pi-A$

Adding them,

$\cos^{-1}x+\cos^{-1}(-x)=A+\pi-A\Rightarrow \cos^{-1}x+\cos^{-1}(-x)=\pi\\ \Rightarrow \cos^{-1}(-x)=\pi-\cos^{-1}(x)$

Solve : $\cos^{-1}\sqrt{\dfrac{1+\cos x}{2}}$

$\displaystyle \cos^{-1}\sqrt{\dfrac{1+\cos x}{2}}=\cos^{-1}\sqrt{\dfrac{\cos^2 \dfrac{x}{2}+\sin^2\dfrac{x}{2}+\cos^2 \dfrac{x}{2}-\sin^2\dfrac{x}{2}}{2}}$

$=\cos^{-1}\sqrt{\dfrac{2\cos^2 \dfrac{x}{2}}{2}}$

$=\cos^{-1}\sqrt{\cos^2 \dfrac{x}{2}}$

$=\cos^{-1}\left(\cos \dfrac{x}{2}\right)$

$=\dfrac{x}{2}$

This is the required solution.

Prove that
$\tan^{-1} \left (\dfrac {\cos x}{1 + \sin x}\right ) = \dfrac {\pi}{4} - \dfrac {x}{2}$ .

$\tan ^{ -1 }{ \left( \cfrac { \cos { x } }{ 1+\sin { x } } \right) } \\ =\tan ^{ -1 }{ \left( \cfrac { \cos ^{ 2 }{ \cfrac { x }{ 2 } } -\sin ^{ 2 }{ \cfrac { x }{ 2 } } }{ \sin ^{ 2 }{ \cfrac { x }{ 2 } } +\cos ^{ 2 }{ \cfrac { x }{ 2 } } +2\sin { \cfrac { x }{ 2 } \cos { \cfrac { x }{ 2 } } } } \right) } \\ =\tan ^{ -1 }{ \left[ \cfrac { \left( \cos { \cfrac { x }{ 2 } } -\sin { \cfrac { x }{ 2 } } \right) \left( \cos { \cfrac { x }{ 2 } } +\sin { \cfrac { x }{ 2 } } \right) }{ { \left( \cos { \cfrac { x }{ 2 } } +\sin { \cfrac { x }{ 2 } } \right) }^{ 2 } } \right] } \\ =\tan ^{ -1 }{ \left[ \cfrac { \cos { \cfrac { x }{ 2 } } -\sin { \cfrac { x }{ 2 } } }{ \cos { \cfrac { x }{ 2 } } +\sin { \cfrac { x }{ 2 } } } \right] } \\ =\tan ^{ -1 }{ \left[ \cfrac { 1-\tan { \cfrac { x }{ 2 } } }{ 1+\tan { \cfrac { x }{ 2 } } } \right] } \\ =\tan ^{ -1 }{ \left[ \cfrac { \tan { \cfrac { \pi }{ 4 } - } \tan { \cfrac { x }{ 4 } } }{ 1+\tan { \cfrac { \pi }{ 4 } \tan { \cfrac { x }{ 2 } } } } \right] } \\ =\tan ^{ -1 }{ \left[ \tan { \left( \cfrac { \pi }{ 4 } -\cfrac { x }{ 2 } \right) } \right] } =\cfrac { \pi }{ 4 } -\cfrac { x }{ 2 }$

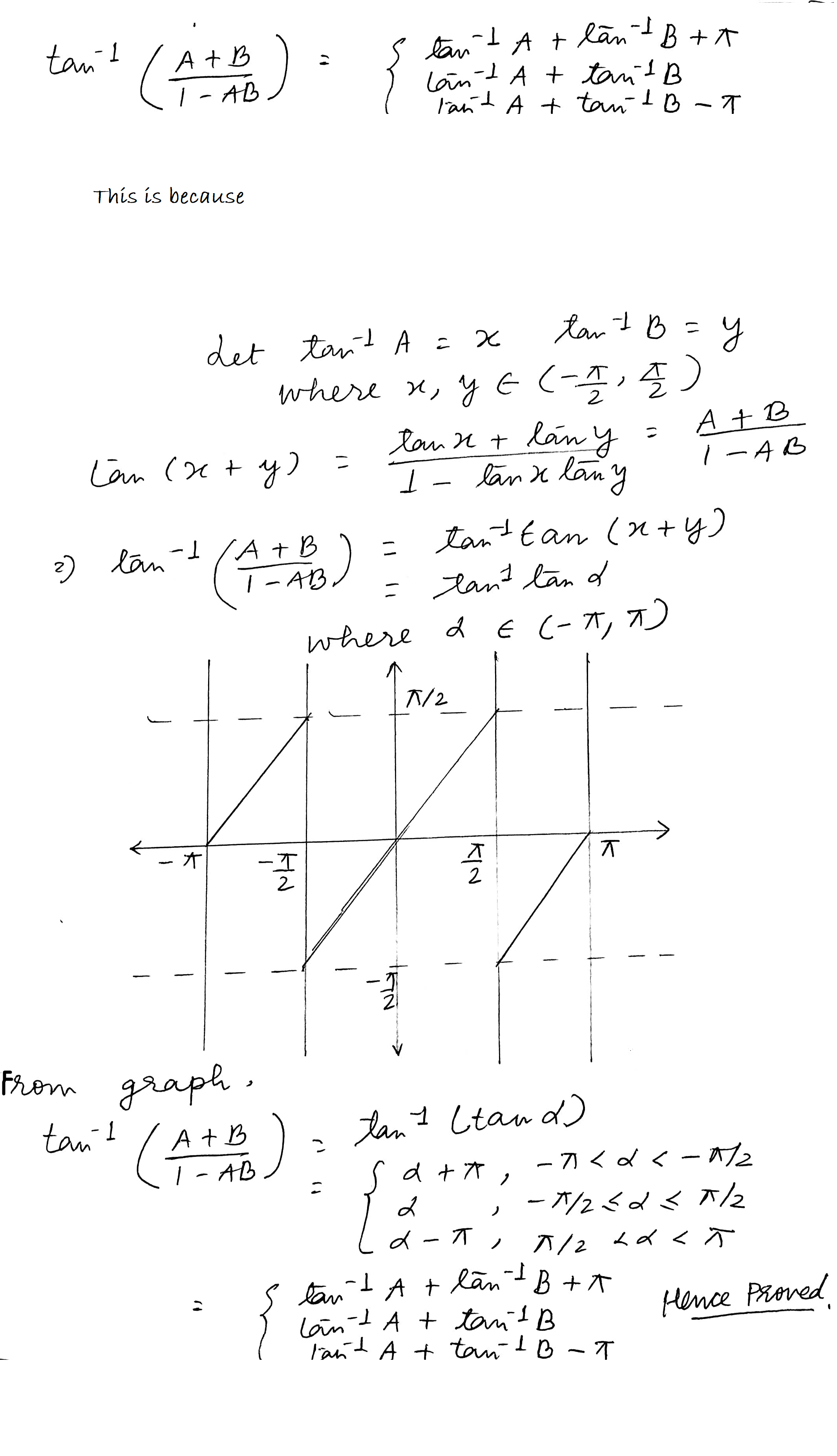
Inverse circular functions,Principal values of ${ sin }^{ -1 }x,{ cos }^{ -1 }x,{ tan }^{ -1 }x$ .
${ tan }^{ -1 }x+{ tan }^{ -1 }y={ tan }^{ -1 }\dfrac { x+y }{ 1-xy }$ , $xy<1$
$\pi +{ tan }^{ -1 }\dfrac { x+y }{ 1-xy }$ , $xy>1$ .
Prove
(a) ${ sin }^{ -1 }\dfrac { 4 }{ 5 } +{ sin }^{ -1 }\dfrac { 5 }{ 13 } +{ sin }^{ -1 }\dfrac { 16 }{ 65 } =\dfrac { \pi }{ 2 }$
(b) ${ sin }^{ -1 }\dfrac { 3 }{ 5 } +{ sin }^{ -1 }\dfrac { 8 }{ 17 } ={ cos }^{ -1 }\dfrac { 36 }{ 85 }$
(c) ${ sin }^{ -1 }\dfrac { 3 }{ 5 } +{ cos }^{ -1 }\dfrac { 12 }{ 13 } ={ cos }^{ -1 }\dfrac { 33 }{ 65 }$

To prove

${ sin }^{ -1 }(4/5)+{ sin }^{ -1 }(5/13)$

$\dfrac { \pi }{ 2 } -{ sin }^{ -1 }\dfrac { 16 }{ 65 } ={ cos }^{ -1 }\left( \dfrac { 16 }{ 65 } \right)$ .

Now

${ sin }^{ -1 }x\pm { sin }^{ -1 }y$

$={ sin }^{ -1 }[x\sqrt { 1-{ y }^{ 2 } } \pm y\sqrt { 1-{ x }^{ 2 } } ]$ .

L.H.S.

$={ sin }^{ -1 }\left[ \dfrac { 4 }{ 5 } \sqrt { \left( 1-\dfrac { 25 }{ 169 } \right) } +\dfrac { 5 }{ 12 } \sqrt { \left( 1-\dfrac { 16 }{ 25 } \right) } \right]$

$={ sin }^{ -1 }\left( \dfrac { 4 }{ 5 } ,\dfrac { 12 }{ 13 } +\dfrac { 5 }{ 13 } ,\dfrac { 3 }{ 5 } \right) ={ sin }^{ -1 }\left( \dfrac { 48 }{ 65 } +\dfrac { 15 }{ 65 } \right)$

$={ sin }^{ -1 }\dfrac { 63 }{ 65 }$

and R.H.S.

$={ cos }^{ -1 }(16/65)={ sin }^{ -1 }(63/65)$

Solve the equation $\tan ^{ -1 }{ \left( \cfrac { 1-x }{ 1+x } \right) } =\cfrac { 1 }{ 2 } \tan ^{ -1 }{ x } ,\,x > 0$

$\tan ^{ -1 }{ \left( \cfrac { 1-x }{ 1+x } \right) } =\cfrac { 1 }{ 2 } \tan ^{ -1 }{ x }$

$\tan ^{ -1 }{ \left( 1 \right) } -\tan ^{ -1 }{ x } =\cfrac { 1 }{ 2 } \tan ^{ -1 }{ x }$
Let

$\tan ^{ -1 }{ x } =\theta$

$\cfrac { \pi }{ 4 } -\theta =\cfrac { \theta }{ 2 } \Rightarrow \theta +\cfrac { \theta }{ 2 } =\cfrac { \pi }{ 4 }$

$3\cfrac { \theta }{ 2 } =\cfrac { \pi }{ 4 }$

$\theta =\cfrac { \pi }{ 6 }$

$x=\tan { \cfrac { \pi }{ 6 } } =\cfrac { 1 }{ \sqrt { 3 } }$

Inverse circular functions,Principal values of ${ \sin }^{ -1 }x,{ cos }^{ -1 }x,{ \tan }^{ -1 }x$ .
${ \tan }^{ -1 }x+{ \tan }^{ -1 }y={ \tan }^{ -1 }\dfrac { x+y }{ 1-xy }$ , $xy<1$
$\pi +{ \tan }^{ -1 }\dfrac { x+y }{ 1-xy }$ , $xy>1$ .
Evaluate the following :
(a) $\sin\left[ \dfrac { \pi }{ 3 } -{ \sin }^{ -1 }\left( -\dfrac { 1 }{ 2 } \right) \right]$
(b) $\sin\left[ \dfrac { \pi }{ 2 } -{ \sin }^{ -1 }\left( -\dfrac { \sqrt { 3 } }{ 2 } \right) \right]$

(a)

$sin\left[ \frac { \pi }{ 3 } -{ sin }^{ -1 }\left( -\frac { 1 }{ 2 } \right) \right]$

$=sin\left[ \frac { \pi }{ 3 } +{ sin }^{ -1 }\left( -\frac { 1 }{ 2 } \right) \right] =sin\left( \frac { \pi }{ 3 } +\frac { \pi }{ 6 } \right) =sin\frac { \pi }{ 2 } =1$

$\because$

${ sin }^{ -1 }(-x)={ sin }^{ -1 }x.$ .
(b) Just as part (a).

$sin\left( \frac { \pi }{ 2 } +\frac { \pi }{ 3 } \right) =cos\frac { \pi }{ 3 } =\frac { 1 }{ 2 }$

Show that: $\sin ^{ -1 }{ \left( 2x\sqrt { 1-{ x }^{ 2 } } \right) } =2\cos ^{ -1 }{ x },\, \cfrac { 1 }{ \sqrt { 2 } } \le x\le 1\quad$

Let

$\cos ^{ -1 }{ x } =\theta \Rightarrow \cos { \theta } =x$
LHS

$\sin ^{ -1 }{ \left( 2\sin { \theta } \cos { \theta } \right) } =\sin ^{ -1 }{ \left( \sin { 2\theta } \right) }$

$=2\theta =2\cos ^{ -1 }{ x }$

Find the set of values of $'a'$ for which the equation $2\cos^{-1} x = a + a^{2}(\cos^{-1} x)^{-1}$ posses a solution.

$2 \cos^{-1} x = a + a^2 (\cos^{-1} x)$

$\dfrac{2\cos^{-1} x}{a} = 1 + \dfrac{a}{\cos^{-1} x}$

let

$\dfrac{a}{\cos^{-1} x} = t$

$x \neq 1$

$\cos^{-1} x \neq a$

$\dfrac{2}{t} = 1 + t$

$t^2 + t - 2 = 0$

$(t + 2)(t - 1) = 0$

solution are

$t = 1 \cup t= -2$

$\dfrac{a}{cos^{-1}x} \cup \dfrac{a}{\cos^{-1} x} = -2$

$a = \cos^{-1} x \cup a = -2 \cos^{-1} x$

$a = [0, \pi] \cup a = [-2\pi, 0]$

$a \in [-2 \pi , 0] \cup ( a, \pi]$

1068558_875898_ans_92f4810f27824cb192dfeed64868f25d.png

If $\theta = \sin^{-1} x + \cos^{-1} x - \tan^{-1} x, 1 \le x < \infty$ , the smallest interval in which $\theta$ lies is

Domain of the given function is

$1\le x\le 1$

it is also given that

$1\le x<\infty$

the only possible value of

$x$ is

$1$

$\sin^{-1}1+\cos^{-1}-\tan^{-1}1$

$\dfrac{\pi}{4}$

Inverse circular functions,Principal values of ${ sin }^{ -1 }x,{ cos }^{ -1 }x,{ tan }^{ -1 }x$ .
${ tan }^{ -1 }x+{ tan }^{ -1 }y={ tan }^{ -1 }\frac { x+y }{ 1-xy }$ , $xy<1$
$\pi +{ tan }^{ -1 }\frac { x+y }{ 1-xy }$ , $xy>1$ .
Solve
(a) $cos(2{ sin }^{ -1 }x)=1/9$
(b) ${ cos }^{ -1 }(3/5)-{ sin }^{ -1 }(4/5)={ cos }^{ -1 }x$
(c) If $sin({ sin }^{ -1 }\frac { 1 }{ 5 } +{ cos }^{ -1 }x)=1$ , then prove that x is equal to $1/5$ .

(a) Put

${ sin }^{ -1 }x=\theta$ so that

$sin\theta =x$ .

Then the equation

$cos(2{ sin }^{ -1 }x)=1/9$ takes the form

$cos2\theta =1/9$

$1-2{ sin }^{ 2 }\theta =1/9$ or

${ sin }^{ 2 }\theta =4/9$

${ x }^{ 2 }=4/9$ , giving

$x=\pm 2/3$ .

(b)

$\because$

${ sin }^{ -1 }(4/5)={ cos }^{ -1 }(3/5)$ .

the given equation can be written as

${ sin }^{ -1 }(4/5)-{ sin }^{ -1 }(4/5)={ cos }^{ -1 }x$

${ cos }^{ -1 }x=0\Rightarrow x=cos0=1$

$\therefore$

$x=1$ .

(c)

${ sin }^{ -1 }\dfrac { 1 }{ 5 } +{ cos }^{ -1 }x=\dfrac { \pi }{ 2 }$

$\therefore$

${ sin }^{ -1 }\dfrac { 1 }{ 5 } =\dfrac { \pi }{ 2 } -{ cos }^{ -1 }x={ sin }^{ -1 }x$

$\therefore$

$x=1/5$ .

Find the value of $\ \tan^2(\dfrac{1}{2} \ \sin^{-1} \dfrac 2 3)$

$\cos 2\theta=\cfrac{1-\tan^{2}\theta}{1+\tan^{2}\theta}$

$\Rightarrow \cos 2\theta+\cos 2\theta\tan^{2}\theta=1-\tan^{2}\theta$

$\Rightarrow \tan^{2}\theta(\cos2\theta+1)=1-\cos2\theta$

$\Rightarrow \tan^{2}\theta=\cfrac{1-\cos 2\theta}{1+\cos 2\theta}$

Now,

$\tan^{2}(\cfrac{1}{2}\sin^{-1}\cfrac{2}{3})=\cfrac{1-\cos(2\times\cfrac{1}{2}\sin^{-1}\cfrac{2}{3})}{1+\cos(2\times\cfrac{1}{2}\sin^{-1}\cfrac{2}{3})}$

$=\cfrac{1-\cos(\sin^{-1}\cfrac{2}{3})}{1+\cos(\sin^{-1}\cfrac{2}{3})}$

Let

$\sin^{-1}\cfrac{2}{3}=m$

$\Rightarrow \cfrac{2}{3}=\sin m$

$\Rightarrow \cos m=\sqrt {1-\cfrac{4}{9}}=\cfrac{\sqrt 5}{3}$

$\Rightarrow m=\cos^{-1}(\cfrac{\sqrt 5}{3})$

So, by using the value we get

$=\cfrac{1-\cos(\cos^{-1}\cfrac{\sqrt 5}{3})}{1+\cos(\cos^{-1}\cfrac{\sqrt 5}{3})}$

$=\cfrac{1-\cfrac{\sqrt 5}{3}}{1+\cfrac{\sqrt 5}{3}}=\cfrac{3-\sqrt 5}{3+\sqrt 5}$ .

If $\tan \left( {\dfrac{\pi }{4} + \dfrac{1}{2}{{\cos }^{ - 1}}\dfrac{a}{b}} \right) + \tan \left( {\dfrac{\pi }{4} - \dfrac{1}{2}{{\cos }^{ - 1}}\dfrac{a}{b}} \right) = \dfrac{{mb}}{a}$ .Find $m$

L.H.S

$\tan (A \pm B) = \dfrac{{\tan A \pm \tan B}}{{1 \pm \tan A\tan B}}$

$\dfrac{{1 + \tan \left( {\dfrac{1}{2}{{\cos }^{ - 1}}\dfrac{a}{b}} \right)}}{{1 - \tan \left( {\dfrac{1}{2}{{\cos }^{ - 1}}\left( {\dfrac{a}{b}} \right)} \right)}} + \dfrac{{1 - \tan \left( {\dfrac{1}{2}{{\cos }^{ - 1}}\left( {\dfrac{a}{b}} \right)} \right)}}{{1 + \tan \left( {\dfrac{1}{2}{{\cos }^{ - 1}}\left( {\dfrac{a}{b}} \right)} \right)}}$

$\dfrac{{1 + \tan x}}{{1 - \tan x}} + \dfrac{{1 - \tan x}}{{1 + \tan x}},x = \dfrac{1}{2}{\cos ^{ - 1}}\left( {\dfrac{a}{b}} \right)$

$= \dfrac{{{{\left( {1 + \tan } \right)}^2} + {{\left( {1 - \tan x} \right)}^2}}}{{1 - {{\tan }^2}x}}$

$= 2\dfrac{{\left( {1 + {{\tan }^2}x} \right)}}{{1 - {{\tan }^{2x}}}} = \dfrac{{2{{\sec }^2}x}}{{1 - {{\tan }^2}x}}$

$=\dfrac{2}{{{{\cos }^2}x\left( {1 - \dfrac{{{{\sin }^2}x}}{{co{x^2}x}}} \right)}} = \dfrac{2}{{{{\cos }^2}x-{{\sin }^2}x}} = \dfrac{2}{{\cos 2x}} = \dfrac{{2b}}{a}$

$\therefore\ m=2$

Solve $\sin^{-1}(\cos \dfrac {2\pi}{3})$

$\begin{array}{l} { \sin ^{ -1 } }\left( { \cos \dfrac { { 2\pi } }{ 3 } } \right) \\ ={ \sin ^{ -1 } }\left( { \cos \left( { \pi -\dfrac { \pi }{ 3 } } \right) } \right) \\ ={ \sin ^{ -1 } }\left( { -\cos \dfrac { \pi }{ 3 } } \right) \\ =-{ \sin ^{ -1 } }\left( { \cos \dfrac { \pi }{ 3 } } \right) \\ =-{ \sin ^{ -1\left[ { \sin \left( { \dfrac { \pi }{ 2 } -\dfrac { \pi }{ 3 } } \right) } \right] } } \\ =-{ \sin ^{ -1 } }\left[ { \sin \left( { \dfrac { \pi }{ 6 } } \right) } \right] \\ =-{ \sin ^{ -1 } }\left( { \sin \dfrac { \pi }{ 6 } } \right) \\ =-\dfrac { \pi }{ 6 } \end{array}$

Simplify : $\tan^{-1} \left[\dfrac{\sqrt{1 + x^2} - 1}{x}\right]$

Let

$x=\tan { \theta }$ , then

$\theta =\tan ^{ -1 }{ x }$

$\tan ^{ -1 }{ \left( \frac { \sqrt { 1+{ x }^{ 2 } } -1 }{ x } \right) } =\tan ^{ -1 }{ \left( \frac { \sqrt { 1+\tan ^{ 2 }{ \theta } } -1 }{ \tan { \theta } } \right) }$

$=\tan ^{ -1 }{ \left( \frac { \sqrt { \sec ^{ 2 }{ \theta } } -1 }{ \tan { \theta } } \right) }$

$=\tan ^{ -1 }{ \left( \frac { \sec { \theta } -1 }{ \tan { \theta } } \right) }$

$=\tan ^{ -1 }{ \left[ \frac { \frac { 1 }{ \cos { \theta } } -1 }{ \frac { \sin { \theta } }{ \cos { \theta } } } \right] }$

$=\tan ^{ -1 }{ \left[ \frac { 1-\cos { \theta } }{ \sin { \theta } } \right] }$

$=\tan ^{ -1 }{ \left[ \frac { 2\sin ^{ 2 }{ \frac { \theta }{ 2 } } }{ 2\sin { \frac { \theta }{ 2 } } \cos { \frac { \theta }{ 2 } } } \right] }$

$=\tan ^{ -1 }{ \left[ \frac { \sin { \frac { \theta }{ 2 } } }{ \cos { \frac { \theta }{ 2 } } } \right] }$

$=\tan ^{ -1 }{ \left[ \tan { \frac { \theta }{ 2 } } \right] }$

$=\frac { \theta }{ 2 }$

$=\frac { \tan ^{ -1 }{ x } }{ 2 }$

Let $\sin^{-1}x=\theta$ then the value of $cosec^{-1}\dfrac{1}{\sqrt{1-x^2}}$ .

Given,

$\sin^{-1}x=\theta$

or,

$\sin \theta=x$

or,

$\cos \theta=\sqrt{1-x^2}$

or,

$\sec\theta=\dfrac{1}{\sqrt{1-x^2}}$

or,

$cosec (90^o-\theta)=\dfrac{1}{\sqrt{1-x^2}}$

or,

$\dfrac{\pi}{2}-\theta=cosec^{-1}\dfrac{1}{\sqrt{1-x^2}}$ .

Find the approximate value of $\tan^{-1}{[1.001]}$ .

1310756_1034044_ans_8c0cc8cdfc1c495cb82442cbeb557e84.jpeg

Find the value of ${\sin ^{ - 1}}\left\{ {\sin \left( { - {{600}^0}} \right)} \right\}$ .

Given,

$\sin \left( { - {{600}^0}} \right)$

$= - \sin \left( {{{540}^0} + {{60}^0}} \right)$

$= - \sin \left( {3\pi + {{60}^0}} \right)$

$= \sin \left( {{{60}^0}} \right)\left[ {{3^{rd}}qaudrant} \right]$

$={\sin ^{ - 1}}\left\{ {\sin \left( { - {{600}^0}} \right)} \right\}$

$= {\sin ^{ - 1}}\left\{ {\sin \left( {{{60}^0}} \right)} \right\}\\ = {60^0}$

If $\sin^{-1} \left(\dfrac{x}{5}\right) + cosec^{-1} \left(\dfrac{5}{4}\right) = \dfrac{\pi}{2}$ then a value of $x$ is

Given,

$\sin^{-1} \left(\dfrac{x}{5}\right) + cosec^{-1} \left(\dfrac{5}{4}\right) = \dfrac{\pi}{2}$

or,

$\sin^{-1} \left(\dfrac{x}{5}\right) + \sin^{-1} \left(\dfrac{4}{5}\right) = \dfrac{\pi}{2}$

or,

$\sin^{-1} \left(\dfrac{x}{5}\right) =\dfrac{\pi}{2}- \sin^{-1} \left(\dfrac{4}{5}\right)$

or,

$\sin^{-1} \left(\dfrac{x}{5}\right) = \cos^{-1} \left(\dfrac{4}{5}\right)$ [ Since

$\sin^{-1}x+\cos^{-1}x=\dfrac{\pi}{2}$ for

$|x|\le 1$ ]

or,

$\sin^{-1} \left(\dfrac{x}{5}\right) = \sin^{-1} \left(\dfrac{3}{5}\right)$ [ Since

$\sin^{-1}\dfrac{3}{5}=\cos^{-1}\dfrac{4}{5}$ ]

or,

$x=3$ .

Solve the equation $3{\sin ^{ - 1}}\left( {\frac{{2x}}{{1 + {x^2}}}} \right) - 4{\cos ^{ - 1}}\left( {\frac{{1 - {x^2}}}{{1 + {x^2}}}} \right) + 2{\tan ^{ - 1}}\left( {\frac{{2x}}{{1 - {x^2}}}} \right) = \dfrac{\pi }{3}$

If we put x =

$\tan \cfrac{\theta}{2}$

we get ,

$3 sin^{-1} (\cfrac{2\tan (\cfrac{\theta}{2})}{1+\tan^2 \cfrac{\theta}{2}})$ =

$3\sin^{-1}(sin\theta)$ =

$\theta$

Similarly, putting in half tan formula we get

$\theta$ for all three cases.

Hence

$3\theta - 4\theta + 2\theta = \cfrac{\pi}{3}$

or,

$\theta = \cfrac{\pi}{3}$

$x = \tan(\cfrac{\pi}{6})$

or,

$x = \dfrac{1}{\sqrt{3}}$

$\cot^{-1} 9+cosec^{-1} \dfrac{41}{4}=\dfrac{\pi}{4}$

$LHS$

$cot^{-1}9=tan^{-1}\dfrac{1}{9}$ and

$cosec^{-1}\dfrac{\sqrt 41}{4}=tan^{-1}\frac{4}{5}$

$cot^{-1}9+cosec^{-1}\dfrac{\sqrt 41}{4}= tan^{-1}\dfrac{1}{9}+tan^{-1}\dfrac{4}{5}=tan^{-1}\left(\dfrac{\frac{1}{9}+\dfrac{4}{5}}{1-\dfrac{1}{9}\times \dfrac{4}{5}}\right)$

$=tan^{-1}(1)=\dfrac{\pi}{4}=RHS$

$\text{hence proved}$

If $\cot { \left( \cos ^{ -1 }{ \dfrac { 3 }{ 5 } +\sin ^{ -1 }{ x } } \right) } =0$ , find the value of $x$ .

$\begin{array}{l} \cot \left( { { { \cos }^{ -1 } }\dfrac { 3 }{ 5 } +{ { \sin }^{ -1 } }x } \right) =0 \\ \Rightarrow { \cos ^{ -1 } }\dfrac { 3 }{ 5 } +{ \sin ^{ -1 } }x={ \cot ^{ -1 } }0 \\ { \cos ^{ -1 } }\dfrac { 3 }{ 5 } +{ \sin ^{ -1 } }x=\dfrac { \pi }{ 2 } \\ { \sin ^{ 1 } }x=\dfrac { \pi }{ 2 } -{ \cos ^{ -1 } }\dfrac { 3 }{ 5 } \\ { \sin ^{ -1 } }x={ \sin ^{ -1 } }\dfrac { 3 }{ 5 } \\ x=\dfrac { 3 }{ 5 } \end{array}$

${({\tan ^{ - 1}}x)^2}\, + \,{({\cot ^{ - 1}}x)^2} = 5\pi$ . Find the value of $x$ .

Given that

$(tan^{-1}x)^2+(cot^{-1}x)^2=\dfrac{5\pi^2}{8}$

We know that,

$tan^{-1}x+cot^{-1}x=\dfrac{\pi}{2}$ ..... $(1)$

Squaring on both sides

$\Rightarrow (tan^{-1}x+cot^{-1}x)^2=(\dfrac{\pi}{2})^2$

$\Rightarrow (tan^{-1}x)^2+(cot^{-1}x)^2+2(tan^{-1}x)(cot^{-1}x)=\dfrac{\pi^2}{4}$ .... $(2)$

from the given information,

$(tan^{-1}x)^2+(cot^{-1}x)^2=\dfrac{5\pi^2}{8}$

Substituting this in $(2)$ , we get

$\Rightarrow \dfrac{5\pi^2}{8}+2(tan^{-1}x)(cot^{-1}x)=\dfrac{\pi^2}{4}$

$\Rightarrow 2(tan^{-1}x)(cot^{-1}x)=\dfrac{-3\pi^2}{8}$ .... $(3)$

We know that $(a-b)^2=(a+b)^2-4ab$

Using this formula, we obtain

$(tan^{-1}x-cot^{-1}x)^2=(tan^{-1}x+cot^{-1}x)^2-4(tan^{-1}x)(cot^{-1}x)$

$\Rightarrow (tan^{-1}x-cot^{-1}x)^2=\dfrac{\pi^2}{4}-2(\dfrac{-3\pi^2}{8})$ $(from (2),(3))$

$\Rightarrow (tan^{-1}x-cot^{-1}x)^2=\dfrac{\pi^2}{4}+\dfrac{3\pi^2}{4}$

$(tan^{-1}x-cot^{-1}x)^2=\pi^2$

Taking square root,

$\Rightarrow tan^{-1}x-cot^{-1}x=\pi$ ..... $(4)$

On solving $(1)$ and $(4)$ , we get

$\Rightarrow 2tan^{-1}x=\dfrac{3\pi}{2}$

$\Rightarrow tan^{-1}x=\dfrac{3\pi}{4}$

$\Rightarrow x=tan(\dfrac{3\pi}{4})$

$\Rightarrow x=-1$

Let $y=\tan^{-1}\dfrac{1-\cos 2x}{\sin 2x}$ , then prove that $\dfrac{dy}{dx}=-1$ .

Given,

$y=\tan^{-1}\dfrac{1-\cos 2x}{\sin 2x}$

or,

$y=\tan^{-1}\dfrac{2cos^2x}{2\sin x.\sin x}$

or,

$y=\tan^{-1}\dfrac{\cos x}{\sin x}$

or,

$y=\tan^{-1}\tan\left(\dfrac{\pi}{2}-x\right)$

or,

$y=\dfrac{\pi}{2}-x$

Now differentiating both sides with respect to

$x$ we get,

$\dfrac{dy}{dx}=-1$ .

If $(\sin^{-1}x)^{2}+(\cos^{-1}x)^{2}=\dfrac {17\pi^{2}}{36}$ , find $x$ .

Let,

$\dfrac{17\pi^2}{36}=(sin^{-1}x+cos^{-1}x)^2-2sin^{-1}xcos^{-1}x$ ( $a^2+b^2=(a+b)^2-2ab$ )

$\dfrac{{17{\pi ^2}}}{{36}}=\dfrac{\pi^2}{4}-2sin^{-1}[\dfrac{\pi}{2}-sin^{-1}x]$

$(sin^{-1})^2-\dfrac{\pi}{2}(sin^{-1}x)-\dfrac{\pi^2}{9}=0$

$sin^{-1}x=\dfrac{\dfrac{\pi}{2} \pm \sqrt{\dfrac{\pi^2}{4}+\dfrac{4\pi^2}{9}}}{2 (1)}$

$sin^{-1}x=\dfrac{\pi}{2},-\dfrac{\pi}{6}$

$sin^{-1}x=-\dfrac{\pi}{6}$

$x=-\dfrac{1}{2}$

Simplify $sin^{-1}(2x \sqrt{1-x^2}), \frac{1}{\sqrt{2}}\leq x \leq 1$

$let x=sin\theta \> then\> \theta =sin^{-1}x\\then \>sin^{-1}(2sin\theta \sqrt{1-sin^2\theta })\\=sin^{-1}(2sin\theta cos\theta )\\=sin^{-1}(sin2\theta )\\=2\theta \\=2sin^{-1}x$

Find the value of $\tan { \left\{ \dfrac { 1 }{ 2 } \sin ^{ -1 }{ \left( \dfrac { 2x }{ 1+{ x }^{ 2 } } \right) +\dfrac { 1 }{ 2 } \cos ^{ -1 }{ \left( \dfrac { 1-{ y }^{ 2 } }{ 1+{ y }^{ 2 } } \right) } } \right\} }$ ; if $x> y> 1$ .

We have,

$\tan \left\{ \dfrac{1}{2}{{\sin }^{-1}}\left( \dfrac{2x}{1+{{x}^{2}}} \right)+\dfrac{1}{2}{{\cos }^{-1}}\left( \dfrac{1-{{y}^{2}}}{1+{{y}^{2}}} \right) \right\}$

Put $x=y=\tan \theta$

Then, $\theta ={{\tan }^{-1}}x={{\tan }^{-1}}y$

$\tan \left\{ \dfrac{1}{2}{{\sin }^{-1}}\left( \dfrac{2x}{1+{{x}^{2}}} \right)+\dfrac{1}{2}{{\cos }^{-1}}\left( \dfrac{1-{{y}^{2}}}{1+{{y}^{2}}} \right) \right\}$

$=\tan \left\{ \dfrac{1}{2}{{\sin }^{-1}}\left( \dfrac{2\tan \theta }{1+{{\tan }^{2}}\theta } \right)+\dfrac{1}{2}{{\cos }^{-1}}\left( \dfrac{1-{{\tan }^{2}}\theta }{1+{{\tan }^{2}}\theta } \right) \right\}$

$=\tan \left\{ \dfrac{1}{2}{{\sin }^{-1}}\sin 2\theta +\dfrac{1}{2}{{\cos }^{-1}}\cos 2\theta \right\}$

$=\tan \left\{ \dfrac{1}{2}\times 2\theta +\dfrac{1}{2}\times 2\theta \right\}$

$=\tan 2\theta$

$=\dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }$

$=\dfrac{2x}{1-{{x}^{2}}}=\dfrac{2y}{1-{{y}^{2}}}$

Hence, this is the answer.

Find the derivative of $f$ given by $f(x)=\sin ^{ -1 }{ x }$ assuming it exists.

Given that

$f(x)=\sin^{-1}x$

$\Rightarrow f'(x)=\dfrac{1}{\sqrt {1-x^2}}$

If $y=\tan^{-1}\left(\dfrac{x\sin \alpha}{1-x\cos\alpha}\right)$ . Find $\cot y$

$y=\tan^{-1}\left(\dfrac{x\sin \alpha}{1-x\cos \alpha}\right)$

$\tan y=\dfrac{x\,\sin \alpha}{1-x\cos \alpha}$

$\cot y=\dfrac{1-x\,\cos \alpha}{x\,sin \alpha}$

$\cot y=\dfrac{1}{x\sin \alpha}-\cot \alpha$

Show that $\tan ^{ -1 }{ \cfrac { 2 }{ 11 } } +\tan ^{ -1 }{ \cfrac { 7 }{ 24 } } =\tan ^{ -1 }{ \cfrac { 1 }{ 2 } }$

$\text{tan}^{-1}x+\text{tan}^{-1}y=\text{tan}^{-1}\bigg(\dfrac{x+y}{1-{x}{y}}\bigg)$

$\text{tan}^{-1}\dfrac{2}{11}+\text{tan}^{-1}\dfrac{7}{24}=\text{tan}^{-1}\bigg(\dfrac{\dfrac{2}{11}+\dfrac{7}{24}}{1-\dfrac{2}{11}\times \dfrac{7}{24}}\bigg)=\text{tan}^{-1}\bigg(\dfrac{\dfrac{48+77}{11\times 24}}{\dfrac{264-14}{11\times 24}}\bigg)=\text{tan}^{-1}\bigg(\dfrac{125}{250}\bigg)=\text{tan}^{-1}\dfrac{1}{2}=RHS$

Hence Proved

Find the value of $\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$ .

Now,

$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$

$=\tan^{-1}1+\tan^{-1}\dfrac{2+3}{1-6}$

$=\dfrac{\pi}{4}+\tan^{-1}(-1)$

$=\dfrac{\pi}{4}+\dfrac{3\pi}{4}$

$=\pi$ .

$\tan^{-1}(1)+\cos^{-1}(-\dfrac {1}{2})+\sin^{-1}(-\dfrac {1}{2})$

We have,

${{\tan }^{-1}}\left( 1 \right)+{{\cos }^{-1}}\left( -\dfrac{1}{2} \right)+{{\sin }^{-1}}\left( -\dfrac{1}{2} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \tan \dfrac{\pi }{4} \right)+{{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)+{{\sin }^{-1}}\left( \sin \dfrac{7\pi }{6} \right)$

$\Rightarrow \dfrac{\pi }{4}+\dfrac{2\pi }{3}+\dfrac{7\pi }{6}$

$\Rightarrow \dfrac{3\pi +8\pi +14\pi }{12}$

$\Rightarrow \dfrac{25\pi }{12}$

Hence, this is the answer.

If $\sec ^{ -1 }{ x } =cosec ^{ -1 }{ y }$ , then find the value of $\cos ^{ -1 }{ \cfrac { 1 }{ x } } +\cos ^{ -1 }{ \cfrac { 1 }{ y } }$

Given equation

$\sec^{-1}x =\csc^{-1}y$

Now Taking

$=\cos^{-1}\dfrac {1}{x} +\cos^{-1}\dfrac {1}{y}\quad$ [using property

$\cos^{-1}\left (\dfrac {1}{x}\right) =\sec^{-1}x$ ]

$=\sec^{-1}x+\sec^{-1}y\quad$ Putting

$\sec^{-1}x=\csc ^{-1}y$

$=\csc^{-1}y+\sec^{-1}y$

$=\dfrac {\pi}{2}$

The value of $a$ for which $a{x^2} + {\sin ^{ - 1}}\left( {{x^2} - 2x + 2} \right) + \cos^{ - 1}\left( {{x^2} - 2x + 2} \right) = 0$ has real solution is

$a{x}^{2}\sin ^{ -1 }{ \left( { x }^{ 2 }-2x+2 \right) } +\cos ^{ -1 }{ \left( { x }^{ 2 }-2x+2 \right) } =0$

we know that

$\sin ^{ -1 }{ \left( f(x) \right) } +\cos ^{ -1 }{ \left( f(x) \right) } =\cfrac { \pi }{ 2 }$

$a{ x }^{ 2 }+\cfrac { \pi }{ 2 } =0\Rightarrow a{ x }^{ 2 }=-\cfrac { \pi }{ 2 }$

$a$ must be negative

$a\in (-\infty,0)$

Find the value of x
If, $\sin ^{ -1 }{ x } +\sin ^{ -1 }{ 2x= } \frac { \pi }{ 3 }$

Given,

${\sin}^{-1}{x}+{\sin}^{-1}{2x}=\dfrac{\pi}{3}$

$\Rightarrow\,{\sin}^{-1}{2x}=\dfrac{\pi}{3}-{\sin}^{-1}{x}$

$\Rightarrow\,2x=\sin{\left(\dfrac{\pi}{3}-{\sin}^{-1}{x}\right)}$

$\Rightarrow\,2x=\sin{\dfrac{\pi}{3}}\cos{\left({\sin}^{-1}{x}\right)}-\cos{\dfrac{\pi}{3}}\sin{\left({\sin}^{-1}{x}\right)}$

$\Rightarrow\,2x=\dfrac{\sqrt{3}}{2}\cos{\left({\cos}^{-1}{\sqrt{1-{x}^{2}}}\right)}-\dfrac{x}{2}$

$\Rightarrow\,2x+\dfrac{x}{2}=\dfrac{\sqrt{3}}{2}\cos{\left({\cos}^{-1}{\sqrt{1-{x}^{2}}}\right)}$

$\Rightarrow\,\dfrac{4x+x}{2}=\dfrac{\sqrt{3}}{2}\cos{\left({\cos}^{-1}{\sqrt{1-{x}^{2}}}\right)}$

$\Rightarrow\,\dfrac{5x}{2}=\dfrac{\sqrt{3}}{2}\cos{\left({\cos}^{-1}{\sqrt{1-{x}^{2}}}\right)}$

$\Rightarrow\,5x=\sqrt{3}\sqrt{1-{x}^{2}}$

squaring both sides, we get

$\Rightarrow\,25{x}^{2}=3\left(1-{x}^{2}\right)$

$\Rightarrow\,25{x}^{2}=3-3{x}^{2}$

$\Rightarrow\,28{x}^{2}=3$

$\Rightarrow\,{x}^{2}=\dfrac{3}{28}$

$\therefore\,x=\pm\sqrt{\dfrac{3}{28}}$

Evaluate $\sin \left(\dfrac{\pi}{6} + \cos^{-1} \dfrac{1}{4} \right)$

$I = sin \left ( \dfrac{\pi}{6} + cos^-1 \dfrac{1}{4}\right )$

$cos^{-1} \dfrac{1}{4} = P$

$cos p = \dfrac{1}{4}$

$sin\, p = \sqrt{1-(\dfrac{1}{4})^2} = \dfrac{\sqrt{15}}{4}$

$tanp = \sqrt{15}$

$\Rightarrow p = tan^{-1} \sqrt{15}$ and

$\dfrac{\pi}{6} = tan^{-1} (\dfrac{1}{\sqrt{3}})$

$I = sin (\dfrac{\pi}{6} + cos^{-1} \dfrac{1}{4}) = sin (tan^{-1}(\dfrac{1}{\sqrt{3}}) + tan^{-1} \sqrt{15})$

$= sin \left(tan^{-1} \left [ \dfrac{\dfrac{1}{\sqrt{3}}+\sqrt{15}}{1-\sqrt{15}/3} \right ]\right)$

$= sin \left [ tan^{-1} \left ( \dfrac{1+\sqrt{45}}{(1-\sqrt{5})\sqrt{3}} \right ) \right ]$

$I = sin \left [ tan^{-1} \left ( \dfrac{1+3\sqrt{5}}{\sqrt{3}- \sqrt{15}} \right ) \right ]$

$tan^{-1} \left ( \dfrac{1+3\sqrt{5}}{\sqrt{3}-\sqrt{15}} \right ) = P$

$tan\, p = \dfrac{1+3\sqrt{5}}{\sqrt{3}-\sqrt{15}} \Rightarrow sinp = \dfrac{1+3\sqrt{5}}{(1+3\sqrt{5})^2 + (\sqrt{3}-\sqrt{15})^2}$

$sin p = \dfrac{1+3\sqrt{5}}{(1+45+3+15+6\sqrt{5} -2 \sqrt{45})}$

$sin p = \dfrac{43 \sqrt{5}}{64+6\sqrt{5}-6\sqrt{5}}$

$sinp = \boxed{\frac{1+3\sqrt{5}}{64}} \Rightarrow \boxed{ p = sin^{-1}(\frac{1+3\sqrt{5}}{64})}$

$I = sin \left [ sin^{-1} \left ( \dfrac{1+3\sqrt{5}}{64} \right ) \right ]$

$\Rightarrow \boxed{ I = \dfrac{1+3\sqrt{5}}{64}}$

1074126_1116445_ans_b3b46e274181452dac0404a96c6dab16.png

Find the range of $f(x)=\sin^{-1}x+\cos^{-1}x+\tan^{-1}x$ .

$\tan^{-1}x$ is defined for

$x\in (-\infty ,\infty )$

$\sin^{-1}x+\cos^{-1}x$ are defined for

$x\in [-1,1]$

so,

$f(x)$

$\sin^{-1}x+\cos^{-1}x+\tan^{-1}x$ is defined for

$x\in [-1,1]$

for

$x\in [-1,1]$ ,

$\sin^{-1}x+\cos^{-1}x=\pi /2$

and

$-\dfrac{\pi }{4} \le \tan^{-1}x \leq \dfrac{\pi }{4}$

$\Rightarrow$

$\dfrac{\pi }{2}-\dfrac{\pi }{4} \leq \sin^{-1}x+\cos^{-1}x+\tan^{-1}x\leq \dfrac{\pi }{2}+\dfrac{\pi }{4}$

$\Rightarrow$ Range =

$\left [ \dfrac{\pi }{4},\dfrac{3\pi }{4} \right ]$

Solve : $\sin^{-1} \left\{ \dfrac{\sin \, x + \cos \, x}{\sqrt{2}} \right \} , - \dfrac{3 \pi}{4} < x < \dfrac{\pi}{4}$

$\sin^{-1}\left \{ \dfrac{\sin x+\cos x}{\sqrt{2}} \right \}$

$=\sin^{-1}\left \{ \dfrac{1}{\sqrt{2}}\sin x+\dfrac{1}{\sqrt{2}}\cos x \right \}$

$=\sin^{-1}\left \{ \cos \dfrac{\pi }{4}\sin x+\sin \dfrac{\pi }{4}\cos x \right \}$

$=\sin^{-1}\left \{ \sin \left ( x+\dfrac{\pi }{4} \right )\right \}$

$=x+\dfrac{\pi }{4}$

It is given that,

$\dfrac{-3\pi }{4} <x<\dfrac{\pi }{4}$

So,

$\dfrac{-3\pi }{4}+\dfrac{\pi }{4} <x+\dfrac{\pi }{4} <\dfrac{\pi }{4} + \dfrac{\pi }{4}$

$\dfrac{-\pi }{2} <x+\dfrac{\pi }{4} <\dfrac{\pi }{2}$

Solve :
$\displaystyle \tan^{-1} \left(\dfrac { \frac { 1 }{ 2 } +\frac { 2 }{ 11 } }{ 1-\frac { 1 }{ 2 } \times \frac { 2 }{ 11 } } \right)$

1356431_1132076_ans_308b4dda788e422e8497671310682a78.jpeg

Prove that $\sin ^{ -1 }{ \dfrac { 3 }{ 5 } } +\sin ^{ -1 }{ \dfrac { 8 }{ 17 } } =\cos ^{ -1 }{ \dfrac { 36 }{ 85 } }$

1361014_1129478_ans_b42dc1a02ad04a1c9338208ea1bacef3.jpg

$2\tan ^{ -1 }{ \dfrac { 1 }{ 2 } } +\tan ^{ -1 }{ \dfrac { 1 }{ 7 } } =\tan ^{ -1 }{ \dfrac { 31 }{ 17 } }$

1361016_1129488_ans_d5103a216d334bd6b41be016265ff961.jpg

If $\tan^{-1} \left\{2\cos \left(2\sin^{-1}\dfrac{1}{2}\right)\right\}$

1349019_1134696_ans_fd48d7ec82a84a4983da36f2b879ec29.jpg

Find the domain of the function:
$y=\sin^{-1}(2x-3)$

1356736_1128377_ans_1a320167c3d34b0390668c7128b300b4.jpg

If $y=\cot^{-1}(\sqrt{\cos x})-\tan^{-1}(\sqrt{cos x})$ , prove that $\sin y =\tan^2 \dfrac{x}{2}$ .

Given,

$y=\cot^{-1}(\sqrt{\cos x})-\tan^{-1}(\sqrt{\cos x})$

$y=\dfrac{\pi}{2}-2\tan^{-1}(\sqrt{\cos x})$

$y=\dfrac{\pi}{2}-\cos^{-1}[\dfrac{1-\cos x}{1+\cos x}]$

$y=\dfrac{\pi}{2}-\cos^{-1}(\tan^2 \dfrac{x}{2})$

$\cos^{-1}(\tan^2 \dfrac{x}{2})=\dfrac{\pi}{2}-y$

$\tan^2 \dfrac{x}{2}=\cos(\dfrac{\pi}{2}-y)$

Therefore,

$\tan^2 \dfrac{x}{2}=\sin y$

$\tan ^{ -1 }{ \left[ \frac { \frac { 2y+1+2x+1 }{ \sqrt { 3 } } }{ 1-\left( \frac { 4xy+2x2y+1 }{ 3 } \right) } \right] } =k$

Consider

$\dfrac{\dfrac{2y+1+2x+1}{\sqrt{3}}}{1-\left(\dfrac{4xy+2x+2y+1}{3}\right)}$

$=\dfrac{\dfrac{2x+1}{\sqrt{3}}+\dfrac{2y+1}{\sqrt{3}}}{1-\left(\dfrac{2x\left(2y+1\right)+1\left(2y+1\right)}{{\left(\sqrt{3}\right)}^{2}}\right)}$

$=\dfrac{\dfrac{2x+1}{\sqrt{3}}+\dfrac{2y+1}{\sqrt{3}}}{1-\dfrac{\left(2x+1\right)}{\sqrt{3}}\dfrac{\left(2y+1\right)}{\sqrt{3}}}$

Now,

${\tan}^{-1}{\left[\dfrac{\dfrac{2y+1+2x+1}{\sqrt{3}}}{1-\left(\dfrac{4xy+2x+2y+1}{3}\right)}\right]}=k$

${\tan}^{-1}\tan\left[{{\dfrac{\dfrac{2x+1}{\sqrt{3}}+\dfrac{2y+1}{\sqrt{3}}}{1-\dfrac{\left(2x+1\right)}{\sqrt{3}}\dfrac{\left(2y+1\right)}{\sqrt{3}}}}}\right]=k$

$\Rightarrow {\tan}^{-1}\tan{\left[\dfrac{2x+1}{\sqrt{3}}+\dfrac{2y+1}{\sqrt{3}}\right]}=k$

$\Rightarrow 2x+1+2y+1=k\sqrt{3}$

$\Rightarrow 2x+2y=k\sqrt{3}-2$

$x+y=\dfrac{k\sqrt{3}-2}{2}$

Prove that $\sec^{2} (\tan^{-1}2)+ \csc^{2} (\cot^{-1} 3)=15$ .

$sec^{2}(tan^{-1}2)+cosec^{2}(cot^{-1}3) = 15$

LHS :

$\Rightarrow sec^{2}(tan^{1}2)+cosec^{2}(cot^{-1}3)$

$\Rightarrow \left \{ sec(tan^{1}2)\right \}^{2}+\left \{ cosec(cot^{1}3) \right \}^{2}$

$[sec(sec^{-1}\frac{\sqrt{5}}{1})]^{2}+[cosec(cosec^{-1}\sqrt{10})]^{2}$

$= (\sqrt{5})^{2}+(\sqrt{10})^{2}$

$= 5+10$

$= 15$

= RHS

Hence proved

1121156_1140095_ans_032fcd4efbe146669e5f4ecc1043401d.jpeg

Evaluate
$\sin^{-1}x+\sin^{-1}y=\cos^{-1}$ { $\sqrt{(1-x^{2})(1-y^{2})}-xy$ }

$\sin^{-1}x+\sin^{-1}y =\cos^{-1}\left\{\sqrt {(1-x^2)(1-y^2)}-xy\right\}$

$\sin^{-1}x \cos^{1}x =\dfrac {\pi}{2}$

$\therefore \ \sin^{-1}x =\dfrac {\pi}{2}-\cos x$

and

$\sin^{-1}y=\dfrac {\pi}{2}-\cos^{-1}y$

$\therefore \ \dfrac {\pi}{2}-\cos^{-1}x+\dfrac {\pi}{2}-\cos^{-1}y$

$\Rightarrow \ \pi -(\cos^{-1}x \cos^{-1}y)$

$\Rightarrow \ \pi -(\cos^{-1} (xy -\sqrt {(1-x^2)(1-y^2)}))$

$\Rightarrow \ \cos^{-1} \left\{(\sqrt {(1-x^2)(1-y^2)}) -xy\right\}$

$RHS$

Hence proved

Evaluate $\sin^{-1} (\sin\dfrac{6\pi}{7})$ .

$sin^{-1}(sin(\dfrac{6\pi}{7}))$

$\because sin \theta$ lies in the interval

$(\dfrac{-\pi}{2},\dfrac{\pi}{2})$

so trigonometric and is inverse function

cancel each other,

$\Rightarrow \dfrac{6\pi}{7}$ Answer

1159634_1144388_ans_7bc8389c59c44a2aaa140fda733175c3.jpg

Solve $\sin^{-1}\dfrac{14}{|x|}+\sin^{-1}\dfrac{2\sqrt{15}}{|x|}=\dfrac{\pi}{2}$ .

1358417_1135223_ans_930dc36ebaec4099b466a18fe8507589.jpg

$\tan ^{ -1 }{ \left( \frac { 1 }{ 2 } \tan { 2A } \right) } +\tan ^{ -1 }{ \left( \cot { A } \right) } +\tan ^{ -1 }{ \left( \cot ^{ 3 }{ A } \right) } =\begin{cases} 0,if\frac { \pi }{ 4 } <A<\frac { \pi }{ 2 } \\ \pi ,if0<A<\frac { \pi }{ 2 } \end{cases}$

$\tan^{-1}\left(\dfrac{1}{2}\tan 2A\right)+\tan^{-1}\left(\dfrac{\cot A+\cot 3A}{1-\cot 4A}\right)$

$\tan^{-1}\left(\dfrac{2\tan A}{2(1-\tan^{2}x)}\right)+\tan^{1}\left(\dfrac{\cot A}{1-\cot^{2}}\right)$

$\Rightarrow \tan^{-1}\left(\dfrac{\tan A}{1-\tan^{2}A}\right)+\tan^{-1}\left(\dfrac{\dfrac{1}{\tan A}}{\dfrac{\tan^{2}A-1}{\tan^{2}A}}\right)$

$\Rightarrow \tan^{-1}\left(\dfrac{\tan A}{1-\tan^{2}A}\right)+\tan^{-1}\left(\dfrac{\tan A}{\tan^{2}A-1}\right)$

$\Rightarrow$ if

$\dfrac{\pi}{4}<A<\dfrac{\pi}{2}$

$\Rightarrow \tan^{-1}\left(\dfrac{\tan A}{1-\tan^{2}A}\right)-\tan^{-1}\left(\dfrac{\tan A}{1-\tan^{2}A}\right)=0$

$0<A<\dfrac{\pi}{2}$

$\Rightarrow \tan^{-1}\left(\dfrac{\tan A}{1-\tan^{2}A}\right)+\cot^{-1}\left(\dfrac{\tan A}{1-\tan^{2}A}\right)$

$=\pi$

If ${\tan ^{ - 1}}\left( {\dfrac{{x - 1}}{{x - 2}}} \right) + {\tan ^{ - 1}}\left( {\dfrac{{x + 1}}{{x + 2}}} \right) = \dfrac{\pi }{4}$ . Find the value of x.

Using the formula,

${\tan}^{-1}{x}+{\tan}^{-1}{y}={\tan}^{-1}{\left(\dfrac{x+y}{1-xy}\right)}$

${\tan}^{-1}{\left(\dfrac{x-1}{x-2}\right)}+{\tan}^{-1}{\left(\dfrac{x+1}{x+2}\right)}=\dfrac{\pi}{4}$

$\Rightarrow\,{\tan}^{-1}{\left(\dfrac{\dfrac{x-1}{x-2}+\dfrac{x+1}{x+2}}{1-\left(\dfrac{x-1}{x-2}\right)\left(\dfrac{x+1}{x+2}\right)}\right)}=\dfrac{\pi}{4}$

$\Rightarrow\,\dfrac{\dfrac{\left(x-1\right)\left(x+2\right)+\left(x-2\right)\left(x+1\right)}{{x}^{2}-4}}{\dfrac{{x}^{2}-4-{x}^{2}+1}{{x}^{2}-4}}=\tan{\dfrac{\pi}{4}}$

$\Rightarrow\,\dfrac{{x}^{2}-x+2x-2+{x}^{2}-2x+x-2}{-3}=1$

$\Rightarrow\,2{x}^{2}-4=-3$

$\Rightarrow\,2{x}^{2}=-3+4=1$

$\Rightarrow\,{x}^{2}=\dfrac{1}{2}$

$\therefore\,x=\pm\dfrac{1}{\sqrt{2}}$

Is $\dfrac{{{{\sin }^{ - 1}}}}{{{{\tan }^{ - 1}}}} = {\cot ^{ - 1}}$ a valid relation?

Solution :-

No,

$\dfrac{sin^{-1}}{tan^{-1}} = cot^{-1}$ is not a valid relation.

$\Rightarrow$ We know inverse of triangular function return an angle and ratio of 2 angle (say

$\dfrac{sin^{-1}}{tan^{-1}})$ can not be equal to another

angle (say

$cot^{-1})$

$sin^{-1}(sin(4))$ =?

$\sin^{-1}{\left( \sin{\left( 4 \right)} \right)} = ?$

As we know that,

$n$ radian

$= \left( n \times \cfrac{180°}{\pi} \right)$

Therefore,

$1$ radian

$\approx 60°$

$\Rightarrow 4$ radian

$\approx 240°$

Therefore,

$4$ radian will lie in

${3}^{rd}$ quadrant.

Therefore,

$4$ radian

$= \pi + x \Rightarrow x = \left( 4 - \pi \right)$

Whereas,

$x$ is an acute angle

$\therefore \sin{4} = \sin{\left( \pi + x \right)} = - \sin{x}$

$\therefore \sin^{-1}{\sin{4}} = \sin^{-1}{\left( -\sin{x} \right)} = -x = -\left( 4 - \pi \right) = \left( \pi - 4 \right)$

Therefore,

$\sin^{-1}{\left( \sin{\left( 4 \right)} \right)} = \left( \pi - 4 \right)$

Hence the correct answer is

$\left( \pi - 4 \right)$ .

Write ${\tan ^{ - 1}}\left( {\dfrac{{\sqrt {1 + {x^2}} - 1}}{{ - x}}} \right), x \ne 0$ in the simplest form

let

${ x }={ \tan { a } }\Rightarrow a=\tan ^{ -1 }{ x }$

$\\ =\tan ^{ -1 }({ \dfrac { \sqrt { 1+{ x }^{ 2 } } -1 }{ -x } } )$

$\\ =\tan ^{ -1 }({ \dfrac { \sqrt { 1+\tan ^{ 2 }{ a } } -1 }{ -tana } })$

$\\ =\tan ^{ -1 }({ \dfrac { \sec { a } -1 }{ -tana } })$

$\\ =\tan ^{ -1 }({ \dfrac { \dfrac { 1-\cos { a } }{ \cos { a } } }{ \dfrac { -\sin { a } }{ \cos { a } } } })$

$\\ =\tan ^{ -1 }({ \dfrac { 1-cosa }{ -sina } } )$

$\\ =\tan ^{ -1 }({ \dfrac { 2\sin ^{ 2 }{ \dfrac { a }{ 2 } } }{ -2\sin { \dfrac { a }{ 2 } } \cos { \dfrac { a }{ 2 } } } } )$

$=\tan ^{ -1 }{ (-\tan { \dfrac { a }{ 2 } } ) } \\ =\dfrac { a }{ 2 }$

$=-\dfrac { \tan ^{ -1 }{ x } }{ 2 }$

Is $\frac{{{{\sin }^{ - 1}}}}{{{{\cos }^{ - 1}}}} = {\tan ^{ - 1}}$ a valid relation?

Solution :-

No,

$\dfrac{sin^{-1}}{cos^{-1}} = tan^{-1}$ is not a

valid relation.

$\Rightarrow$ We know inverse of every triangular

function returns an angle say

the angle is

$\theta$

$sin^{-1}$ will return an angle

$cos^{-1}$ will return an angle

as well

$tan^{-1}$ will also return an angle

So ratio of 2 angle can not be

equal to another angle (Ans)

Solve:-
${\tan ^{ - 1}}\left( {\dfrac{{6x}}{{1 - 8{x^2}}}} \right)$

$\tan ^{ -1 }{ \dfrac { 6x }{ 1-{ 8x }^{ 2 } } } \\ =\tan ^{ -1 }{ (\dfrac { 2x+4x }{ 1-{ 2x }\times { 4x } } ) } \quad \quad (\tan ^{ -1 }{ x } +\tan ^{ -1 }{ y } =\tan ^{ -1 }{ \dfrac { x+y }{ 1-xy } } )\\ =\tan ^{ -1 }{ 2x } +\tan ^{ -1 }{ 4x }$

Evaluate :
${\tan ^{ - 1}}\left( {\frac{{4x}}{{1 + 5{x^2}}}} \right) + {\tan ^{ - 1}}\left( {\frac{{2 + 3x}}{{3 - 2x}}} \right)$

$\tan ^{ -1 }{ \left( \dfrac { 4 }{ 1+5{ x }^{ 2 } } \right) } +\tan ^{ -1 }{ \left( \dfrac { 2+3x }{ 3-2x } \right) }$

we know that

$\tan ^{ -1 }{ a } +\tan ^{ -1 }{ b } =\tan ^{ -1 }{ \left( \dfrac { a+b }{ 1-ab } \right) }$

$\tan ^{ -1 }{ \left( \dfrac { 4 }{ 1+5{ x }^{ 2 } } \right) } +\tan ^{ -1 }{ \left( \dfrac { 2+3x }{ 3-2x } \right) } =\left( \dfrac { \dfrac { 4 }{ 1+5{ x }^{ 2 } } +\dfrac { 2+3x }{ 3-2x } }{ 1-\left( \dfrac { 4 }{ 1+5{ x }^{ 2 } } \right) \left( \dfrac { 2+3x }{ 3-2x } \right) } \right)$

$=\tan ^{ -1 }{ \left( \dfrac { 4\left( 3-2x \right) +\left( 2+3x \right) \left( 1+5{ x }^{ 2 } \right) }{ \left( 1+5{ x }^{ 2 } \right) \left( 3-2x \right) -4\left( 2+3x \right) } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { 12-8x+2+10{ x }^{ 2 }+3x+15{ x }^{ 3 } }{ 3-2x+15{ x }^{ 2 }-10{ x }^{ 3 }-8-12x } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { 15{ x }^{ 3 }+10{ x }^{ 3 }-5x+14 }{ -10{ x }^{ 3 }+15{ x }^{ 2 }-14x-5 } \right) }$

$\cos \left( {{{\cos }^{ - 1}}\left( {\frac{{\sqrt 3 }}{2}} \right) + \frac{\pi }{6}} \right)$

You should know trignometric values of functions

${{\cos}^{-1}}\left(\dfrac{\sqrt 3}{2}\right)$

${{\cos}^{-1}}\left(\dfrac{\sqrt 3}{2}\right)$ =30

30+30=60.

And

$\cos(60) = \dfrac{1}{2}$

Evaluate: ${\sec ^{ - 1}}\left( {\dfrac{{x + 1}}{{x - 1}}} \right) + {\sin ^{ - 1}}\left( {\dfrac{{x - 2}}{{x + 1}}} \right)$

Solution :-

$\displaystyle sec^{-1}(\frac{x+1}{x-1})+sin^{-1}(\frac{x-1}{x+1})$

$\displaystyle \Rightarrow cos^{-1}(\frac{x-1}{x+1})+sin^{-1}(\frac{x-1}{x+1})$

$\displaystyle \Rightarrow \frac{\pi }{2}$

Solve : $\text{cosec}^{-1} \left(\dfrac{1 + x^2}{2x} \right) + \tan^{-1} \left(\dfrac{1 - x^2}{2x} \right) = \dfrac{x}{2}$

$\csc^{-1}\left ( \dfrac{1+x^2}{2x} \right )+\tan^{-1}\left ( \dfrac{1-x^2}{2x} \right )=\dfrac{x}{2}$

$2\tan^{-1}x+\tan^{-1}\left ( \dfrac{1-x^2}{2x} \right )=\dfrac{x}{2}$

$\tan^{-1}x+\tan^{-1}x+\tan^{-1}\left ( \dfrac{1-x^2}{2x} \right )=\dfrac{x}{2}$

$\tan^{-1}\left ( \dfrac{2x}{1-x^2} \right )+\tan^{-1}\left ( \dfrac{1-x^2}{2x} \right )=\dfrac{x}{2}$

$\tan^{-1}\left ( \dfrac{2x}{1-x^2} \right )+\cot^{-1}\left ( \dfrac{2x}{1-x^2} \right )=\dfrac{x}{2}$

$\dfrac{\pi}{2}=\dfrac{x}{2}$

$\therefore x=\pi$

Solve : ${\cos ^{ - 1}}\left( {\cos \frac{{7\pi }}{6}} \right)$

${\cos}^{-1}{\cos{\dfrac{7\pi}{6}}}$

$={\cos}^{-1}{\cos{\left(\pi+\dfrac{\pi}{6}\right)}}$

$={\cos}^{-1}{\cos{\left(-\dfrac{\pi}{6}\right)}}$

$={\cos}^{-1}{\dfrac{\sqrt{3}}{2}}$

$=\dfrac{\pi}{6}$

Solve: ${\tan ^{ - 1}}\left( {\tan \frac{{2\pi }}{3}} \right)$

${\tan}^{-1}{\tan{\dfrac{2\pi}{3}}}$

$={\tan}^{-1}{\tan{\left(\pi-\dfrac{\pi}{3}\right)}}$

$={\tan}^{-1}{\left(-\tan{\left(\dfrac{\pi}{3}\right)}\right)}$

$={\tan}^{-1}{\left(-\sqrt{3}\right)}$

$=-\dfrac{\pi}{3}$

The numerical value of tan $\left( {2{{\tan }^{ - 1}}\dfrac{1}{5} - \dfrac{\pi }{4}} \right)$ is

Solution :-

Let

$A= tan [2 tan^{-1}(\dfrac{1}{5})-\dfrac{\pi }{4}]$

Let

$2tan^{-1}(\dfrac{1}{5})=\theta$

$\therefore A= tan (\theta -\pi /4)= \dfrac{tan\theta -tan\pi /4}{1+tan\theta \, tan\pi /4}= \dfrac{tan\theta -1}{tan\theta +1}$

$\dfrac{\theta }{2}=\dfrac{2tan^{-1}}{2}(\dfrac{1}{5})= tan^{-1}(\frac{1}{5})=\dfrac{\theta }{2}\Rightarrow tan\dfrac{\theta }{2}=\dfrac{1}{5}$

But

$tan\theta =\dfrac{2tan \theta /2}{1-tan^{2}\theta /2}=\dfrac{2\cdot 1/5}{1-1/25}=\dfrac{2/5}{24/25}=\dfrac{5}{12}$

$\therefore A=\dfrac{tan\theta -1}{tan\theta +1}=\dfrac{5/12-1}{5/12+1}=\dfrac{-7}{17}$

$\therefore$ Numerical Value =

$\left | \dfrac{-7}{17} \right |= 7/17$

Prove that
${\tan ^{ - 1}}\dfrac{1}{5} + {\tan ^{ - 1}}\dfrac{1}{7} = {\tan ^{ - 1}}\dfrac{6}{{17}}$

$\tan^{-1}\left (\dfrac {1}{5}\right)+\tan^{-1}\left (\dfrac {1}{7}\right)$

$=\tan ^{ -1 }{ \left( \dfrac { \dfrac { 1 }{ 5 } +\dfrac { 1 }{ 7 } }{ 1-\dfrac { 1 }{ 5 } .\dfrac { 1 }{ 7 } } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { \dfrac { 12 }{ 35 } }{ \dfrac { 34 }{ 35 } } \right) }$

$=\tan ^{ -1 }{ \left(\dfrac{12}{34}\right)}$

$=\tan ^{ -1 }{ \left(\dfrac{6}{17}\right)}$

Solve $\sin^{-1}\left\{\dfrac{\sin\:x+\cos\:x}{\sqrt{2}}\right\},\:-\dfrac{3\pi }{4}<x<\dfrac{\pi }{4}$

Let

${\sin}^{-1}\left\{\dfrac{\sin{x}+\cos{x}}{\sqrt{2}}\right\}=\theta$

$\Rightarrow \dfrac{\sin{x}+\cos{x}}{\sqrt{2}}=\sin{\theta}$

$\Rightarrow \sin{x}\cos{\dfrac{\pi}{4}}+\cos{x}\sin{\dfrac{\pi}{4}}=\sin{\theta}$ where

$\dfrac{1}{\sqrt{2}}=\sin{\dfrac{\pi}{4}}$ and

$\dfrac{1}{\sqrt{2}}=\cos{\dfrac{\pi}{4}}$

$\Rightarrow \sin{\left(x+\dfrac{\pi}{4}\right)}=\sin{\theta}$ where

$\sin{A}\cos{B}+\cos{A}\sin{B}=\sin{\left(A+B\right)}$

LHS and RHS are positive.Hence

$\sin{\theta}$ is positive in first quadrant and second quadrant.

$\sin{\left(x+\dfrac{\pi}{4}\right)}$ is positive when

$x=\dfrac{\pi}{4}$

and

$x=\pi-\dfrac{\pi}{4}=\dfrac{3\pi}{4}$

and

$x=-\pi+\dfrac{\pi}{4}=\dfrac{-3\pi}{4}$ in clockwise direction.

Hence

${\sin}^{-1}{\left\{\dfrac{\sin{x}+\cos{x}}{\sqrt{2}}\right\}}={\sin}^{-1}\left\{\sin{\left(x+\dfrac{\pi}{4}\right)}\right\}=x+\dfrac{\pi}{4}$

Solve:
${\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)$

1101237_1185821_ans_0e0e3a059aae4f398ebe7d1d2d35cfaa.jpeg

$2\;{\tan ^{ - 1}}\left( {\sqrt {\dfrac{{a - b}}{{a + b}}}\tan \dfrac{x}{2}} \right)$

1146407_1193010_ans_fc12b8efca0f40ffa3ee920d71939225.jpg

Solve:
${\tan ^{ - 1}}\left( {\frac{{2x}}{{1 - {x^2}}}} \right)$

$tan -(\frac{2x}{1-x^{2}})$

let

$tan^{-1}(\frac{2x}{1-x^{2}}) = P$

$tan p = \frac{2x}{1-x^{2}} =$

$\Rightarrow tan2(\frac{p}{2}) = \frac{2x}{1-x^{2}}$

$\Rightarrow \frac{2tan(\frac{p}{2})}{1-tan^{2}(\frac{p}{2})} = \frac{2x}{1-x^{2}}$

$\Rightarrow x = (tan\frac{p}{2})$

$\Rightarrow tan^{1}(x) = \frac{p}{2} \Rightarrow p = 2tan^{-1}x$

$\therefore tan^{-1}(\frac{2x}{1-x^{2}}) = P = 2tan^{-1}x$

1108501_1189524_ans_67a7859c25844b2097fcf5c197a45ed7.jpeg

Prove that :
${\cos ^{ - 1}}x = 2{\sin ^{ - 1}}\left(\sqrt{\dfrac{1-x}{2}} \right).$

R.E.F image

Solution -

$cos^{-1}x = 2\,sin^{-1}\sqrt{\dfrac{1-x}{2}}$

R.H.S

Let

$y = 2\, sin^{-1}\sqrt{\dfrac{1-x}{2}}$

$\dfrac{y}{2} = cos^{-1}(\dfrac{\sqrt{1+x}}{\sqrt{2}})$

$cos^{2}(\dfrac{y}{2}) = \dfrac{1+x}{2}$

$cos\,y = 2\,cos^{2}\dfrac{y}{2}-1 = 1+x-1$

$cos\,y = x$

$y = cos^{-1}x$

$= LHS$

Solve $Cos^{-1}\left[Cos\:\frac{5\pi }{4}\right]$

Let

${\cos}^{-1}\left[\cos{\dfrac{5\pi}{4}}\right]=\theta$

$\Rightarrow \cos{\dfrac{5\pi}{4}}=\cos{\theta}$

$\Rightarrow \cos{\left(\pi+\dfrac{\pi}{4}\right)}=\cos{\theta}$

since

$\pi+\theta$ is in third quadrant, cosine of the angle

$\theta$ is negative.

Hence

$\cos{\left(\pi+\dfrac{\pi}{4}\right)}=-\cos{\dfrac{\pi}{4}}=\cos{\theta}$

$\Rightarrow \cos{\theta}=\dfrac{-1}{\sqrt{2}}$

$\cos{\theta}$ is negative in second and third quadrant.

$\therefore \theta=\pi-\dfrac{\pi}{4}, \pi+\dfrac{\pi}{4}$

Hence

$\theta=\dfrac{3\pi}{4}, \dfrac{5\pi}{4}$

If $\cos c=\dfrac {\sin \left(2\pi+\dfrac {\pi}{2}\right)-\sin \pi/2}{\pi}$ , find the value of $c$ .

$\sin { \left( 2\pi +\theta \right) } =\sin { \theta }$

$\therefore \cos { c } =\cfrac { \sin { \pi /2 } -\sin { \pi /2 } }{ \pi } =0$

$c=\cos ^{ -1 }{ \left( 0 \right) } =\pi /2$

Integrate the function $\tan^{-1} \big({\sqrt{\dfrac{1 - \sin x}{ 1 + \sin x}}}\big)$ w.r.t dx.

$I=\displaystyle\int\tan^{-1}\sqrt{\dfrac{1-\sin x}{1+\sin x}}d x_n$

$=\displaystyle\int \tan^{-1}\sqrt{\dfrac{\cos^2x/2+\sin^2x/2-2\cos x/2\sin x/2}{\cos^2x/2+\sin^2x/2+2\cos x/2\sin x/2}}dx$

$=\displaystyle\int \tan^{-1}\sqrt{\dfrac{(\cos x/2+\sin x/2)^2}{(\cos x/2+\sin x)^2}}dx$

$=\displaystyle\int \tan^{-1}\left(\dfrac{\cos x/2-\sin x/2}{\cos x/2+\sin x/2}\right)dx$

$=\displaystyle\int \tan^{-1}\left(\tan\left(\dfrac{\pi}{4}-\dfrac{x}{2}\right)\right)dx$

$=\displaystyle\int \dfrac{\pi}{4}-\dfrac{x}{2}dx$

$=\left[\dfrac{\pi}{4}x-\dfrac{x^2}{4}\right]$ .

Evaluate: $\tan^{-1}\left(1\right)+ \cos^{-1}\left(\dfrac{1}{2}\right)+ \sin^{-1}\left(\dfrac{1}{2}\right)$ which lies in the interval $\left[0,\pi\right]$

$\tan^{-1}+\cos^{-1}(1/2)+\sin^{-1}(1/2)\quad 0\le x \le \pi$

Let

$x=\tan^{-1}1\Rightarrow \tan x=1$

$\Rightarrow x=\pi /4$

Let

$y=\cos^{-1}(1/2)\Rightarrow \cos y=1/2$

$y=\pi /3$

Let

$=\sin^{-1}(1/2)\Rightarrow \sin z=1/2$

$\Rightarrow z=\pi /6$

$\therefore \ x+y+z=\pi /4 +\pi /3 + \pi /6$

$=\dfrac {3\pi +4\pi +2\pi}{12}$

$=\dfrac {9\pi}{12}=\dfrac {3\pi}{4}$

The value of $\cos\left(\sin^{-1}\dfrac{1}{2}+\sec^{-1}2\right)$ .

Now,

$\cos\left(\sin^{-1}\dfrac{1}{2}+\sec^{-1}2\right)$

$=\cos\left(\sin^{-1}\dfrac{1}{2}+\cos^{-1}\dfrac{1}{2}\right)$

$=\cos \dfrac{\pi}{2}$ [ Since

$\sin^{-1}\dfrac{1}{2}+\cos^{-1}\dfrac{1}{2}=\dfrac{\pi}{2}$ ]

$=0$ .

Write in simplest form $\sin^{-1}{\left[\dfrac{\sqrt{1+x}+\sqrt{1-x}}{2}\right]}$

$\begin{array}{l} { \sin ^{ -1 } }\left[ { \frac { { \sqrt { 1+x } +\sqrt { 1-x } } }{ 2 } } \right] \\ let\, \, x={ \left[ { { { \cos }^{ 2 } }\theta } \right] } \\ \Rightarrow { \sin ^{ -1 } }\left( { \frac { { \sqrt { 1+{ { \cos }^{ 2 } }\theta } +\sqrt { { { \cos }^{ 2 } }\theta } } }{ 2 } } \right) \\ \Rightarrow { \sin ^{ -1 } }\left[ { \frac { { \cos \theta } }{ { \sqrt { 2 } } } +\frac { { \sin \theta } }{ { \sqrt { 2 } } } } \right] \\ \Rightarrow { \sin ^{ -1 } }\left[ { \cos \theta \cdot \sin { { 45 }^{ 0 } } +\sin \theta \cdot \cos { { 45 }^{ 0 } } } \right] \\ \Rightarrow { \sin ^{ -1 } }\left[ { \sin \left( { \theta +{ { 45 }^{ 0 } } } \right) } \right] \\ \therefore \theta +{ 45^{ 0 } } \\ \Rightarrow \frac { { { { \cos }^{ -1 } }x } }{ 2 } +{ 45^{ 0 } } \end{array}$

The value of $\sin \left( {{{\cos }^{ - 1}}\dfrac{3}{5}} \right)$

$\sin (\cos^{-1}\dfrac{3}{5})$

$\therefore\cos \theta =\dfrac{3}{5}\Rightarrow \sin \theta=\sqrt{1-\cos^2 \theta}=\dfrac45$

$= \sin (\sin^{-1}\dfrac{4}{5})$

$= \dfrac{4}{5}$

Evaluate the given expression:
$\cos \left(\sin^{-1}\dfrac {3}{5}+\sin^{-1}\dfrac {5}{13}\right)$

$\cos{\left({\sin}^{-1}{\dfrac{3}{5}}+{\sin}^{-1}{\dfrac{5}{13}}\right)}$

Let

${\sin}^{-1}{\dfrac{3}{5}}=a,\,\,\,\,{\sin}^{-1}{\dfrac{5}{13}}=b$

$\Rightarrow\,\sin{a}=\dfrac{3}{5},\,\,\,\,\sin{b}=\dfrac{5}{13}$

$\Rightarrow\,{\sin}^{2}{a}=\dfrac{9}{25},\,\,\,\,{\sin}^{2}{b}=\dfrac{25}{169}$

$\Rightarrow\,{\cos}^{2}{a}=1-{\sin}^{2}{a}=1-\dfrac{9}{25}=\dfrac{25-9}{25}=\dfrac{16}{25},\,\,\,\,{\cos}^{2}{b}=1-{\sin}^{2}{b}=1-\dfrac{25}{169}=\dfrac{169-25}{169}=\dfrac{144}{169}$

$\Rightarrow\,\cos{a}=\dfrac{4}{5},\,\,\,\,\cos{b}=\dfrac{12}{13}$

Now,

$\cos{\left({\sin}^{-1}{\dfrac{3}{5}}+{\sin}^{-1}{\dfrac{5}{13}}\right)}$

$=\cos{\left(a+b\right)}$

$=\cos{a}\cos{b}-\sin{a}\sin{b}$

$=\dfrac{4}{5}\times\dfrac{12}{13}-\dfrac{3}{5}\times\dfrac{5}{13}$

$=\dfrac{48}{65}-\dfrac{15}{65}$

$=\dfrac{48-15}{65}=\dfrac{33}{65}$

Evaluate $\cos^{-1}{[\cos{11\pi/6}]}$

$\begin{array}{l} { \cos ^{ -1 } }\left[ { \cos 11\pi /6 } \right] \\ \Rightarrow { \cos ^{ -1 } }\left[ { \cos \left( { 2\pi -\frac { \pi }{ 6 } } \right) } \right] \\ \Rightarrow { \cos ^{ -1 } }\left[ { \cos \left( { \pi /6 } \right) } \right] \, \, \, \left[ { 0<\pi /6\pi } \right] \\ =\pi /6 \end{array}$

Evaluate $\cos \left[\cos^{-1}\left(-\dfrac {\sqrt {3}}{2}\right)+\dfrac {\pi}{6}\right]$ .

$\cos { [{ \cos }^{ -1 }(\cfrac { \sqrt { -3 } }{ 2 } )+\cfrac { \pi }{ 6 } ] } =\cos { [{ { \cos }^{ -1 } }(\cos { \cfrac { 5\pi }{ 6 } } )+\cfrac { \pi }{ 6 } ] } \\ =\cos { (\cfrac { 5\pi }{ 6 } +\cfrac { \pi }{ 6 } )\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \{ \because \cos { \cfrac { 5\pi }{ 6 } } =\cfrac { -\sqrt { 3 } }{ 2 } \} } \\ =\cos { \text{ }\pi=-1 }$

Solve:
${\tan ^{ - 1}}\left( {\tan \frac{{7\pi }}{6}} \right)$

$\dfrac{7\pi}{6}\in (\pi,\dfrac{3\pi}{2})$

So tan

$^{-1}\dfrac{7\pi}{6}=\dfrac{7\pi}{6}-\pi=\dfrac{\pi}{6}$

The reason we do so is that

$tan^{-1}m\in (\dfrac{-\pi}{2},\dfrac{\pi}{2})$ So we have to find the angle m in

$(\dfrac{-\pi}{2},\dfrac{\pi}{2})$ for which

$tan m = tan \dfrac{7\pi}{6}$

Prove that : $\tan ^ { - 1 } \frac { 1 } { 3 } + \tan ^ { - 1 } \frac { 1 } { 7 } + \tan ^ { - 1 } \frac { 1 } { 5 } + \tan ^ { - 1 } \frac { 1 } { 8 } = \frac { \pi } { 4 }$

$tan^{-1}(\frac{(\frac{1}{3})+(\frac{1}{7})}{1-(\frac{1}{21})})+tan^{-1}(\frac{(\frac{1}{5})+(\frac{1}{8})}{1-(\frac{1}{40})})\\=tan^{-1}(\frac{10}{20})+tan^{-1}(\frac{13}{39})\\=tan^{-1}(\frac{1}{2})+tan^{-1}(\frac{1}{3})\\=tan^{-1}(\frac{(\frac{1}{2})+(\frac{1}{3})}{1-(\frac{1}{20})})\\tan^{-1}(\frac{5}{5})=tan^{-1}1=(\frac{\pi}{4})$

Prove that ${\tan ^{ - 1}}\frac{1}{5} + {\tan ^{ - 1}}\frac{1}{7} + {\tan ^{ - 1}}\frac{1}{3} + {\tan ^{ - 1}}\frac{1}{8} = \dfrac{\pi }{4}$

$\tan^{-1} \left(\dfrac{1}{5} \right) + \tan^{-1} \left(\dfrac{1}{7} \right) + \tan^{-1} \left(\dfrac{1}{3} \right) + \tan^{-1} \left(\dfrac{1}{8} \right)$

$\Rightarrow \tan^{-1} \left(\dfrac{\dfrac{1}{5} + \dfrac{1}{7}}{1 - \dfrac{1}{5} \times \dfrac{1}{7}} \right) + \tan^{-1} \left(\dfrac{\dfrac{1}{3} + \dfrac{1}{2}}{1 - \dfrac{1}{3} \times \dfrac{1}{8}} \right)$

On application of

$\tan^{-1} x + \tan^{-1} y = \tan^{-1} \left(\dfrac{x + y}{1 - xy} \right)$

$= \tan^{-1} \left(\dfrac{12}{34} \right) + \tan^{-1} \left(\dfrac{11}{23} \right)$

$= \tan^{-1} \left(\dfrac{\dfrac{6}{17} + \dfrac{11}{23}}{1 - \dfrac{6}{17} \times \dfrac{11}{23}} \right) = \tan^{-1} \left(\dfrac{138 + 187}{391 - 66} \right)$

$= \tan^{-1} \left(\dfrac{325}{325} \right) = \tan^{-1} (1) = \dfrac{\pi}{4}$

hence proved

$\tan^{-1}\left(\dfrac{1}{4}\right)+2\tan^{-1}\left(\dfrac{1}{5}\right)+\tan^{-1}\left(\dfrac{1}{6}\right)+\tan^{-1}\left(\dfrac{1}{x}\right)=\dfrac{\pi}{4}$ .

$\tan \left( \dfrac{\dfrac{1}{x}+\dfrac{1}{4}}{1-\dfrac{1}{x} \times \dfrac{1}{4}}\right) + \tan^{-1} \left\{ \dfrac{2 \times \dfrac{1}{5}}{1- \left( \dfrac{1}{5}\right)^2}\right\}+ \tan^{-1} \dfrac{1}{6}=\dfrac{\pi}{4}$

$\Rightarrow \tan^{-1} \left( \dfrac{4+x}{4x-1} \right)+\tan^{-1}\left( \dfrac{5}{12} \right)+\tan^{-1}\dfrac{1}{6}=\dfrac{\pi}{4}$

$\Rightarrow \tan^{-1} \left( \dfrac{4+x}{4x-1} \right) + \tan^{-1}\left\{ \dfrac{\dfrac{6}{12}+\dfrac{1}{6}}{1-\dfrac{5}{12} \times \dfrac{1}{6}}\right\} =\dfrac{\pi}{4}$

$\Rightarrow \tan^{-1} \left( \dfrac{4+x}{4x-1} \right) + \tan^{-1}\left(\dfrac{30+12}{72-5}\right)=\dfrac{\pi}{4}$

$\Rightarrow \tan^{-1} \left( \dfrac{4+x}{4x-1} \right) + \tan^{-1}\left(\dfrac{42}{67} \right)=\dfrac{\pi}{4}$

$\Rightarrow \tan^{-1} \left\{ \dfrac{\dfrac{4+x}{4x-1}+\dfrac{42}{67}}{1-\left(\dfrac{4+x}{4x-1}\right) \left(\dfrac{42}{67}\right)}\right\}=\dfrac{\pi}{4}$

$\Rightarrow \dfrac{67(4+x)+42(4x-1)}{(4x-1)67-42(4+x)}=\tan \dfrac{\pi}{4}$

$\Rightarrow \dfrac{268+67x+167x-42}{268x-67-168-42x}=1$

$\Rightarrow 267+67x+168x-42=268x-67-168-42x$

$\Rightarrow 9x=-461$

$\Rightarrow x=\dfrac{-461}{9}$

$3\tan^{-1}\dfrac{1}{2+\sqrt{3}}-\tan^{-1}\dfrac{1}{x}=\tan^{-1}\dfrac{1}{3}$ .

$3\tan^{-1} \left(\dfrac{1}{2+\sqrt{3}} \right)-\tan^{-1} \left(\dfrac{1}{x} \right)=\tan^{-1} \left(\dfrac{1}{3} \right)$

$3 \tan^{-1} \left[ \dfrac{2- \sqrt 3}{(2+ \sqrt 3)(2- \sqrt 3)}\right]= \tan^{-1} \left(\dfrac{1}{3} \right)$

$3 \tan^{-1} \left[ \dfrac{2- \sqrt 3}{4- (\sqrt 3)^2}\right]= \tan^{-1} \left[ \dfrac{\dfrac{1}{x}+\dfrac{1}{3}}{1-\dfrac{1}{x} \times \dfrac{1}{3}} \right]$

$\Rightarrow 3 \tan^{-1} (2- \sqrt 3) =\tan^{-1} \left( \dfrac{3+x}{3x-1}\right)$

$\Rightarrow \tan^{-1} \left\{ \dfrac{3 (2-sqrt 3)- (2-\sqrt{3}^3)}{1-3 (2- \sqrt 3)^2}\right\} =\dfrac{3+x}{3x-1}$

$\left[ \because 3 \tan^{-1} x= \tan^{-1} \left( \dfrac{3x-x^3}{1-3x^2}\right) \right]$

$\Rightarrow \dfrac{3+x}{3x-1} \left[ \dfrac{2 (2- \sqrt 3)- (8-3 \sqrt 3-12 \sqrt 3+18)}{1-3 (4+3-4 \sqrt 3)}\right]$

$\Rightarrow \dfrac{3+x}{3x-1} =\dfrac{6-3 \sqrt 3-8+3 \sqrt 3-18+12 \sqrt 3}{1-3 (7-4 \sqrt 3)}$

$\Rightarrow \dfrac{3+x}{3x-1} =\dfrac{-20+12 \sqrt 3}{-20+12 \sqrt 3}$

$\Rightarrow \dfrac{3+x}{3x-1}=1$

$\Rightarrow 3+x=3x-1$

$\Rightarrow 2x=4$

$\Rightarrow x=2$

Solve : $\cos ^ { - 1 } \left( - \frac { 1 } { 2 } \right)$

$cos^{-1}(\frac{-1}{2})=\pi-cos^{-1}(\frac{1}{2})\\=\pi-(\frac{\pi}{3})=(\frac{2\pi}{3})$

Write the value of $2 sin^{-1} \dfrac{1}{2} + cos^{-1} (-\dfrac{1}{2})$

$2\sin^{-1}\left ( \dfrac{1}{2} \right )+\cos^{-1}\left ( \dfrac{-1}{2} \right )$

$=2\times \dfrac{\pi}{6}+\dfrac{2\pi}{3}$

$=\dfrac{\pi}{3}+\dfrac{2\pi}{3}$

$=\dfrac{3\pi}{3}$

$=\pi$

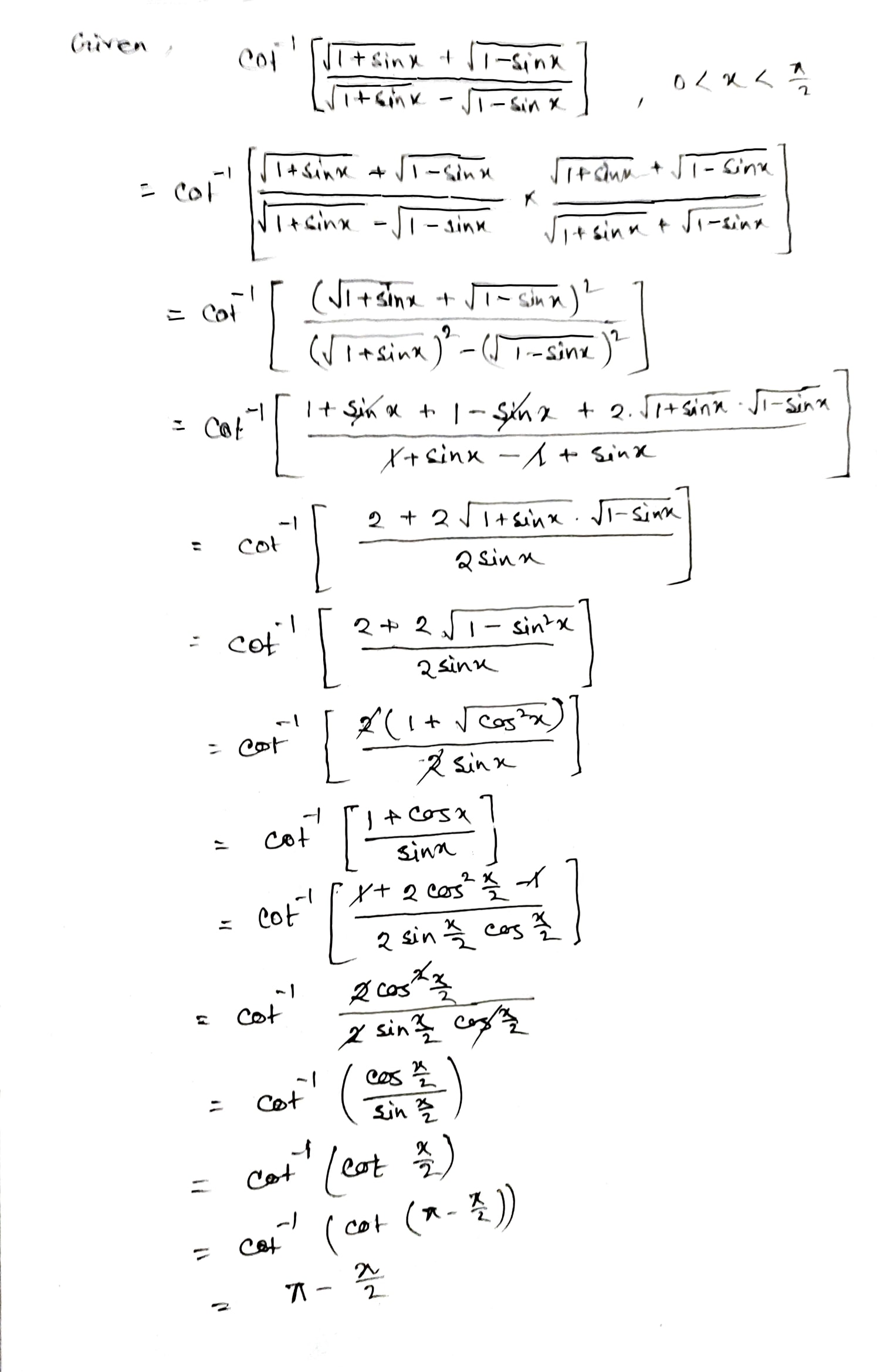
Prove that $\tan^{-1}\left(\frac { \sqrt { 1+\cos { x } } +\sqrt { 1-\cos { x } } }{ \sqrt { 1+\cos { x } } -\sqrt { 1-\cos { x } } }\right)=\dfrac{\pi}{4}-\dfrac{x}{2}$ if $\pi < x < \dfrac{3\pi}{2}$

$\tan ^{ -1 }{ \left( \dfrac { \sqrt { 1+\cos { x } } +\sqrt { 1-\cos { x } } }{ \sqrt { 1+\cos { x } } -\sqrt { 1-\cos { x } } } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { { \left( \sqrt { 1+\cos { x } } +\sqrt { 1-\cos { x } } \right) }^{ 2 } }{ { \left( \sqrt { 1+\cos { x } } \right) }^{ 2 }-{ \left( \sqrt { 1-\cos { x } } \right) }^{ 2 } } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { { 1+\cos { x } +1-\cos { x } }+2\sqrt { 1-\cos { ^{ 2 }x } } }{ 1+\cos { x } -1+\cos { x } } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { 2+2\sqrt { 1-\sin { ^{ 2 }x } } }{ 2\cos { x } } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { 1+\sin { x } }{ \cos { x } } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { 1+\dfrac { 2\tan { \dfrac { x }{ 2 } } }{ 1+\tan ^{ 2 }{ \dfrac { x }{ 2 } } } }{ \dfrac { 1-\tan ^{ 2 }{ \dfrac { x }{ 2 } } }{ 1+\tan ^{ 2 }{ \dfrac { x }{ 2 } } } } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { \left( 1+\tan { \dfrac { x }{ 2 } } \right) ^{ 2 }\left( 1+\tan { \dfrac { x }{ 2 } } \right) }{ \left( 1-\tan { \dfrac { x }{ 2 } } \right) ^{ 2 }\left( 1+\tan { \dfrac { x }{ 2 } } \right) } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { 1+\tan { \dfrac { x }{ 2 } } }{ 1-\tan { \dfrac { x }{ 2 } } } \right) }$

$=\tan ^{ -1 }{ \left( \dfrac { \tan { \dfrac { \pi }{ 4 } } +\tan { \dfrac { x }{ 2 } } }{ 1-\tan { \dfrac { x }{ 4 } } \tan { \dfrac { x }{ 2 } } } \right) }$

$\pi<x<\dfrac{3x}{2}$

$=\tan ^{ -1 }{ \left( \tan { \left( \dfrac { \pi }{ 4 } -\dfrac { x }{ 2 } \right) } \right) }$

$=\dfrac { \pi }{ 4 } -\dfrac { x }{ 2 }$

Hence, the answer is

$\dfrac{\pi}{4}-\dfrac{x}{2}.$

solve
$\sin ^{ -1 }{ x } +\sin ^{ -1 }{ 2x } =\dfrac { \pi }{ 3 }$ then $x=?$

$\sin^{-1}x+\sin^{-1}2x=\pi/3$

$\theta=\sin^{-1}x; \phi =\sin^{-1}2x$ .

$\theta+\phi=\pi/3$

$\phi=\pi/3-\theta$

$\sin \phi =\sin \left(\pi/3-\theta\right)$

$2x=\sin \dfrac{\pi}{3}\cos \theta-\cos \dfrac{\pi}{3}\sin\theta$ .

$2x=\dfrac{\sqrt{3}}{2}\sqrt{1-x^2}-\dfrac{x}{2}$

$\dfrac{5x}{2}=\dfrac{\sqrt{3}\times \sqrt{1-x^2}}{2}$

$25x^2=3(1-x^2)$

$25x^2-3+3x^2=0$

$28x^2=3$

$x^2=3/28$

$x=\pm 3/28$

Evaluate:
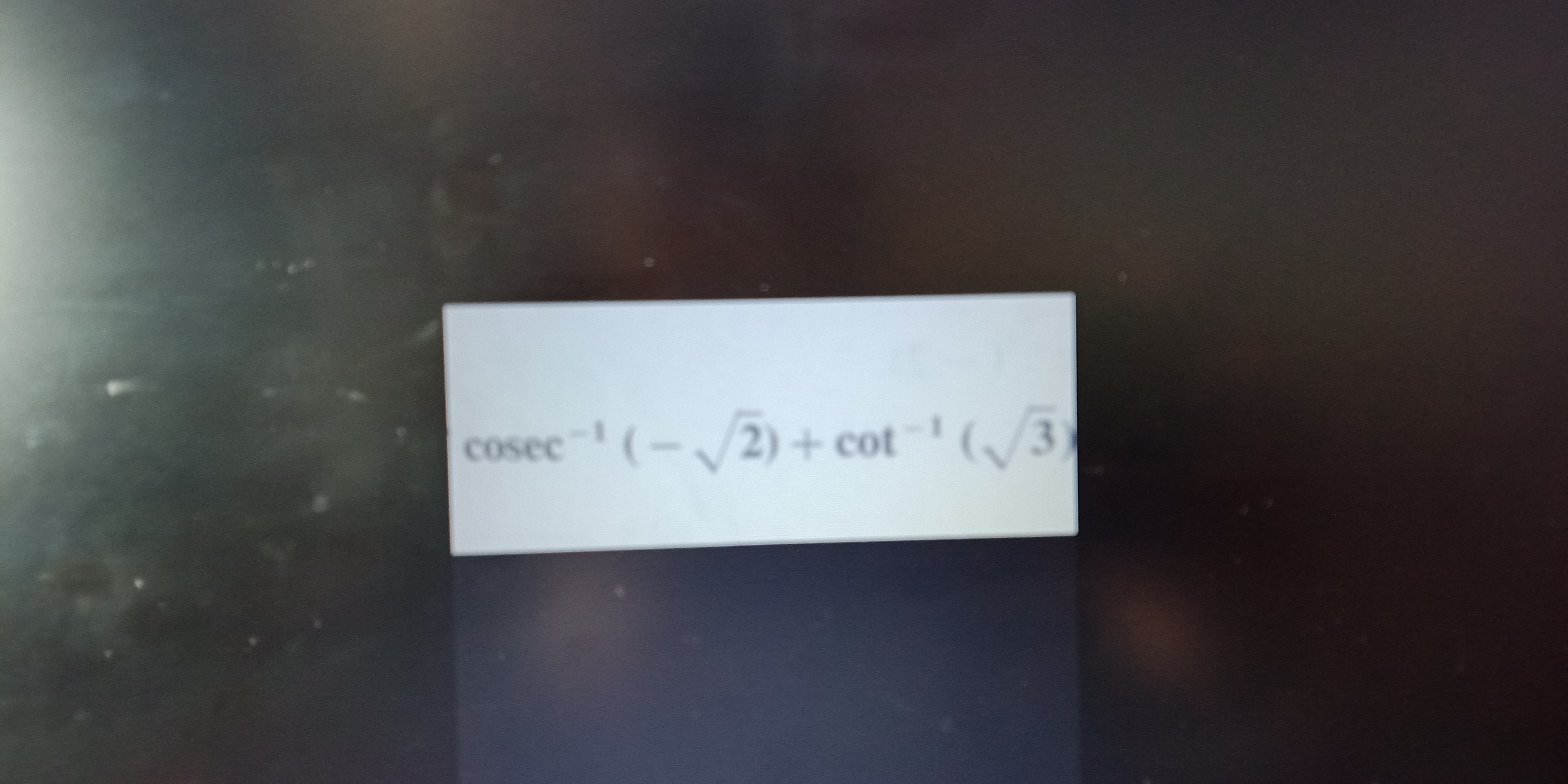
$\csc^{ - 1}\left( { - \sqrt 2 } \right)$

$cosec^{-1} (-\sqrt{2})= \theta$

$cosec \theta= -\sqrt{2}$

$\sin \theta= -\dfrac{1}{\sqrt{2}}$

$\theta=-\dfrac{\pi}{4}$

Show that $tan^{-1}\frac{63}{16}=sin^{-1}\frac{5}{13}+cos^{-1}\frac{3}{5}$

To prove :

$\tan^{-1}\dfrac{63}{16}=\sin^{-1}\dfrac{5}{13}+\cos^{-1}\dfrac{3}{5}$

R.H.S:

$\tan^{-1}\dfrac{5}{12}+\tan^{-1}\dfrac{4}{3}$

$\left[\tan^{-1}x+\tan^{-1}y=\tan^{-1}\dfrac{x+y}{1-xy}\right]$

$=\tan^{-1}\left[\dfrac{\dfrac{5}{12}+\dfrac{4}{3}}{1-\dfrac{5}{12}\times \dfrac{4}{3}}\right]=\tan^{-1} \left[\dfrac{\dfrac{5+16}{12}}{1-\dfrac{5}{9}}\right]$

$=\tan ^{-1}\dfrac{\dfrac{21}{12}}{\dfrac{4}{9}}=\tan^{-1}\dfrac{63}{16}=$ L.H.S

1346298_1239593_ans_8e1b7954365e442e8971201f7710f5bc.png

solve
$\displaystyle {\tan ^{ - 1}}\left( {{{\sin x} \over {1 + \cos x}}} \right)$

given,

$\displaystyle {\tan ^{ - 1}}\left( {{{\sin x} \over {1 + \cos x}}} \right)$

$\displaystyle = {\tan ^{ - 1}}\left[ {{{2\sin \left( {{x \over 2}} \right)\cos \left( {{x \over 2}} \right)} \over {2{{\cos }^2}{x \over 2}}}} \right]$

$\displaystyle = {\tan ^{ - 1}}\left[ {\tan \left( {{x \over 2}} \right)} \right] = {x \over 2}$

Find the value of the expression ${ \sec }^{ -1 }\left( \dfrac { x+1 }{ x-1 } \right) +{ \sin }^{ -1 }\left( \dfrac { x-1 }{ x+1 } \right)$ .

$={ \sec }^{ -1 }\left( \dfrac { x+1 }{ x-1 } \right) +{ \sin }^{ -1 }\left( \dfrac { x-1 }{ x+1 } \right)$

$={ \cos }^{ -1 }\left( \dfrac { x-1 }{ x+1 } \right) +{ \sin }^{ -1 }\left( \dfrac { x-1 }{ x+1 } \right)$

$=\dfrac { \pi }{ 2 }$ (Answer)

Find the value of $\tan ^ { - 1 } \left( \tan \frac { 5 \pi } { 6 } \right) + \cos ^ { - 1 } \left( \cos \frac { 13 \pi } { 6 } \right)$

$\tan\left(\dfrac{5\pi}{6}\right)=\tan\left(\pi -\dfrac{\pi}{6}\right)$

$=-\tan\dfrac{\pi}{6}$

$=-\dfrac{1}{\sqrt{3}}$

$\cos\left(13\dfrac{\pi}{6}\right)=\cos\left(2\pi +\dfrac{\pi}{6}\right)$

$=\cos\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}$

$\therefore \tan^{-1}\left(\dfrac{-1}{\sqrt{3}}\right)+\cos^{-1}\left(\dfrac{\sqrt{3}}{2}\right)$

$=-\dfrac{\pi}{6}+\dfrac{\pi}{6}=0$ .

What is the value of $\cos \left[ \cos ^ { - 1 } \left( \frac { - \sqrt { 3 } } { 2 } \right) + \frac { \pi } { 6 } \right]$ ?

${ \cos \left[ \cos ^ { - 1 } \left( \dfrac { - \sqrt { 3 } } { 2 } \right) + \dfrac { \pi } { 6 } \right] }$

${ = \cos \left[ \cos ^ { - 1 } \left( \cos \dfrac { 5 \pi } { 6 } \right) + \dfrac { \pi } { 6 } \right] \quad \left( \because \cos \dfrac { 5 \pi } { 6 } = \dfrac { - \sqrt { 3 } } { 2 } \right) }$

${ = \cos \left( \dfrac { 5 \pi } { 6 } + \dfrac { \pi } { 6 } \right) \quad \left( \because \cos ^ { - 1 } \cos x = x ; x \in [ 0 , \pi ] \right) }$

${ = \cos ( \pi ) = - 1 }$

Express the following in the simplest form
${\tan ^{ - 1}}\left( {\dfrac{{\cos x}}{{1 + \sin x}}} \right),\dfrac{{ - \pi }}{2} < x < \dfrac{\pi }{2}$

$\tan^{-1}(\cfrac{\cos x}{1+\sin x}),\cfrac{-\pi}{2}<2<\cfrac{\pi}{2}$

$\implies \tan^{-1}(\cfrac{\cos^(x/2)-\sin^(x/2)}{1-2\sin (x/2)\cos (x/2)})$

$\implies \tan^{-1}(\cfrac{\cos (x/2)+\sin (x/2}{\cos (x/2)-\sin(x/2)})$

Dividing numerator and denominator by

$\cos (x/2)$

we get

$\tan^{-1}(\cfrac{1+\tan^{-1}(x/2)}{1-\tan^{-1}(x/2)})$

$\implies \tan^{-1}(\tan(\pi/4)+(x/2))=\cfrac{\pi}{4}+\cfrac{x}{2}$

Solve for $x:2\tan^{-1}(\cos x)=\tan^{-1}(2\text{cosec} x)$ .

$2{ \tan }^{ -1 }\left( cosx \right) ={ \tan }^{ -1 }\left( 2cosecx \right)$

${ 2\tan }^{ -1 }x={ \tan }^{ -1 }\dfrac { 2x }{ 1-{ x }^{ 2 } }$

So,

${ \tan }^{ -1 }\left( \dfrac { 2cosx }{ 1-{ \cos }^{ 2 }x } \right) ={ \tan }^{ -1 }\left( 2cosecx \right)$

$\dfrac { 2cosx }{ { \sin }^{ 2 }x } =2cosecx$

$2cosx=2sinx$

$cosx=sinx$

$tanx=1$

$x=\pm \dfrac { \pi }{ 4 }$

Solve:
$\cot^{-1}x+\cot^{-1} 2=\dfrac{\pi}{2}$ .

Given,

$\cot^{-1}x+\cot^{-1} 2=\dfrac{\pi}{2}$

$\cot^{-1}x=\dfrac{\pi}{2}-\cot^{-1} 2$

$\cot^{-1}x=\tan^{-1} 2$

$\cot^{-1}x=\cot^{-1} \dfrac{1}{2}$

$x=\dfrac{1}{2}$ .

Solve for $x$ :
$2\tan^{-1}\dfrac{2x}{1-x^2}=\pi$ .

Given,

$2\tan^{-1}\dfrac{2x}{1-x^2}=\pi$

$2\times 2\tan^{-1} x=\pi$ [ Using direct formula for

$2\tan^{-1}x$ ]

$4\tan^{-1}x=\pi$

$\tan^{-1} x=\dfrac{\pi}{4}$

$x=\tan \dfrac{\pi}{4}$

$x=1$ .

Prove:
$\sin ^ { - 1 } \left( \dfrac { 1 } { x } \right) = \ cosec ^ { - 1 } x , \forall x \geq 1 \text { or } x \leq - 1$

$\cos ^ { - 1 } \left( \dfrac { 1 } { x } \right) = \sec ^ { - 1 } x , \forall x \geq 1 \text { or } x \leq - 1$

$\tan ^ { - 1 } \left( \dfrac { 1 } { x } \right) = \cot ^ { - 1 } x , \quad \forall x > 0$

$\cos^{-1}{\left(\dfrac{1}{x}\right)}=\theta \implies \cos\theta=\dfrac{1}{x}\implies \text{sec}\theta =x\implies\text{sec}^{-1}x$

Similarly

$\tan^{-1}\dfrac{1}{x}=\cot^{-1}x$

Solve: $\dfrac { { a }^{ 2 }-{ b }^{ 2 } }{ 4 }$ ${ \sin }^{ -1 }\dfrac { a-b }{ \sqrt { { a }^{ 2 }-{ b }^{ 2 } } }$

We have,

$\dfrac{{{a}^{2}}-{{b}^{2}}}{4}{{\sin }^{-1}}\dfrac{a-b}{\sqrt{{{a}^{2}}-{{b}^{2}}}}$

$\Rightarrow \dfrac{{{a}^{2}}-{{b}^{2}}}{4}{{\sin }^{-1}}\dfrac{a-b}{\sqrt{\left( a+b \right)\left( a-b \right)}}$

$\Rightarrow \dfrac{{{a}^{2}}-{{b}^{2}}}{4}{{\sin }^{-1}}\dfrac{\sqrt{a-b}\sqrt{a-b}}{\sqrt{a+b}\sqrt{a-b}}$

$\Rightarrow \dfrac{{{a}^{2}}-{{b}^{2}}}{4}{{\sin }^{-1}}\dfrac{\sqrt{a-b}}{\sqrt{a+b}}$

Hence, this is the answer.

Find the value of $\cos^{-1}\left(\cos {\dfrac {5\pi}{3}}\right)$

$cos^{-1}(cos x)=x$

$\therefore cos^{-1}(cos\frac{5\pi }{3})=\frac{5\pi }{3}$

$=5\times \frac{180}{3}=5\times 60=300^{\circ}$

1196615_1297910_ans_07c378aa60c24a7c8ed8d6cb34dde43e.jpg

Solve
$\sin^{-1} \left[\dfrac{\sqrt{1+x}+\sqrt{1-x}}{2}\right]$

We have,

${{\sin }^{-1}}\left( \dfrac{\sqrt{1+x}+\sqrt{1-x}}{2} \right)$

Let put $x=\cos 2\theta$

So,

${{\sin }^{-1}}\left( \dfrac{\sqrt{1+\cos 2\theta }+\sqrt{1-\cos 2\theta }}{2} \right)$

$\Rightarrow {{\sin }^{-1}}\left( \dfrac{\sqrt{1+2{{\cos }^{2}}\theta -1}+\sqrt{1-1+2{{\sin }^{2}}\theta }}{2} \right)$

$\Rightarrow {{\sin }^{-1}}\left( \dfrac{\sqrt{2{{\cos }^{2}}\theta }+\sqrt{2{{\sin }^{2}}\theta }}{2} \right)$

$\Rightarrow {{\sin }^{-1}}\left( \dfrac{\cos \theta +\sin \theta }{\sqrt{2}} \right)$

$\Rightarrow {{\sin }^{-1}}\left( \dfrac{\cos \theta }{\sqrt{2}}+\dfrac{\sin \theta }{\sqrt{2}} \right)$

$\Rightarrow {{\sin }^{-1}}\left( sin{{45}^{o}}\cos \theta +cos{{45}^{o}}\sin \theta \right)$

$\Rightarrow {{\sin }^{-1}}\sin \left( {{45}^{o}}+\theta \right)$

$\Rightarrow {{45}^{o}}+\theta$

$\Rightarrow {{45}^{o}}+\dfrac{1}{2}{{\cos }^{-1}}x$

Hence, this is the answer.

Prove that: $\tan^{-1} \left[\sqrt{\dfrac{1 - \cos x}{1 + \cos x}} \right] = \dfrac{x}{2}$

Take =

$cos x = \frac{1- tan^{2}x/2}{1+ tan^{2}x/2}$

$\frac{1- cos x}{1+ cos x}=\frac{1-\frac{1-tan^{2}x/2}{1+ tan^{2}x/2}}{1+\frac{1-tan^{2}x/2}{1+tan^{2}x/2}}$

$=\frac{1+tan^{2}x/2-1+tan^{2}x/2}{1+tan^{2}x/2+1-tan^{2}x/2}$

$=\frac{2 tan^{2}x/2}{2}= tan^{2}x/2$

$\sqrt{\frac{1-cos x}{1+cos x}}=\sqrt{tan^{2}x/2}= tan x/2$

Now,

$tan^{-1}[tan (\frac{x}{2})]=\frac{x}{2}$

1218687_1297979_ans_acf5b77116f241a0bba27a87d4497e9e.PNG

Solve the equation $\tan^{-1}\left[\dfrac {1-x}{1+x}\right]=\dfrac {1}{2}\tan^{-1}x,(x > 0)$

We have,

$\begin{array}{l} { \tan ^{ -1 } }\left[ { \dfrac { { 1-x } }{ { 1+x } } } \right] =\dfrac { 1 }{ 2 } { \tan ^{ -1 } }x \\ 2{ \tan ^{ -1 } }\dfrac { { 1-x } }{ { 1+x } } ={ \tan ^{ -1 } }x\, \, \to \left( i \right) \end{array}$

We know that,

$\begin{array}{l} 2{ \tan ^{ -1 } }x={ \tan ^{ -1 } }\left( { \dfrac { { 2x } }{ { 1-{ x^{ 2 } } } } } \right) \\ 2{ \tan ^{ -1 } }\left( { \dfrac { { 1-x } }{ { 1+x } } } \right) ={ \tan ^{ -1 } }\left[ { \dfrac { { 2\left( { \dfrac { { 1-x } }{ { 1+x } } } \right) } }{ { 1-{ { \left( { \dfrac { { 1-x } }{ { 1+x } } } \right) }^{ 2 } } } } } \right] \\ ={ \tan ^{ -1 } }\left[ { \dfrac { { 2\left( { \dfrac { { 1-x } }{ { 1+x } } } \right) } }{ { \dfrac { { { { \left( { 1+x } \right) }^{ 2 } }-{ { \left( { 1-x } \right) }^{ 2 } } } }{ { { { \left( { 1+x } \right) }^{ 2 } } } } } } } \right] \\ ={ \tan ^{ -1 } }\left[ { \dfrac { { 2\left( { 1-x } \right) \left( { 1+x } \right) } }{ { { { \left( { 1+x } \right) }^{ 2 } }-{ { \left( { 1-x } \right) }^{ 2 } } } } } \right] \\ { { using } }\, \, \left( { a+b } \right) \left( { a-b } \right) ={ a^{ 2 } }-{ b^{ 2 } } \\ ={ \tan ^{ -1 } }\left[ { \dfrac { { 2\left( { 1-{ x^{ 2 } } } \right) } }{ { \left( { 1+x+1-x } \right) \left( { 1+x-1+x } \right) } } } \right] \\ ={ \tan ^{ -1 } }\left[ { \dfrac { { 2\left( { 1-{ x^{ 2 } } } \right) } }{ { 4x } } } \right] \\ ={ \tan ^{ -1 } }\left[ { \dfrac { { 1-{ x^{ 2 } } } }{ { 2x } } } \right] \\ 2{ \tan ^{ -1 } }\left( { \dfrac { { 1-x } }{ { 1+x } } } \right) ={ \tan ^{ -1 } }\left[ { \dfrac { { 1-{ x^{ 2 } } } }{ { 2x } } } \right] \\ from\, \, equation\, \, \left( i \right) \\ 2{ \tan ^{ -1 } }\left( { \dfrac { { 1-x } }{ { 1+x } } } \right) ={ \tan ^{ -1 } }x \\ { \tan ^{ -1 } }\left( { \dfrac { { 1-{ x^{ 2 } } } }{ { 2x } } } \right) ={ \tan ^{ -1 } }x \\ \dfrac { { 1-{ x^{ 2 } } } }{ { 2x } } =1 \\ 1-{ x^{ 2 } }=2{ x^{ 2 } } \\ 1-{ x^{ 2 } }-2{ x^{ 2 } }=0 \\ 1-3{ x^{ 2 } }=0 \\ 3{ x^{ 2 } }=0 \\ 3{ x^{ 2 } }=1 \\ x=\pm \dfrac { 1 }{ { \sqrt { 3 } } } \end{array}$

$x = \dfrac{{ - 1}}{{\sqrt 3 }}$ is not possible because

$x > 0$

Taken only

$x = \dfrac{1}{{\sqrt 3 }}$

Hence, this is the answer.

How do you simplify
$\sin x + \cot x.\cos x$

$\sin x+\cot x.\cos x$

$=\sin x+\left( { \dfrac { { \cos x } }{ { \sin x } } } \right) .\cos x$

$=\dfrac { { { { \sin }^{ 2 } }x+{ { \cos }^{ 2 } }x } }{ { \sin x } }$

$=\dfrac { 1 }{ { \sin x } }$

$=\cos ecx$ which is the required answer.

$y={ cot }^{ -1 }\dfrac { 2x }{ 1-{ x }^{ 2 } }, x\neq \pm 1$

We have,

$y={{\cot }^{-1}}\dfrac{2x}{1-{{x}^{2}}}$

Let put $x=\tan \theta$

Then

$\theta ={{\tan }^{-1}}x$

$y={{\cot }^{-1}}\dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }$

$y={{\cot }^{-1}}\tan 2\theta \,\,\,\,\,\,\,\left( \therefore \tan 2\theta =\dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta } \right)$

$y={{\cot }^{-1}}\cot \left( \dfrac{\pi }{2}-2\theta \right)$

$y=\dfrac{\pi }{2}-2\theta$

$y=\dfrac{\pi }{2}-2{{\tan }^{-1}}x$

Hence, this is the answer.

Solve :
$\cos^{-1}(\log_{2}x)=0$

We have,

${\cos ^{ - 1}}\left( {{{\log }_2}x} \right) = 0$

Now,

$\begin{array}{l} \cos \, 0={ \log _{ 2 } }x \\ \Rightarrow 1={ \log _{ 2 } }x \\ \Rightarrow { 2^{ 1 } }=x \\ \therefore x=2 \end{array}$

Hence, this is the answer.

Simplify: ${ tan }^{ -1 }(1/2)+{ tan }^{ -1 }(1/3).$

We have,

${{\tan }^{-1}}\dfrac{1}{2}+{{\tan }^{-1}}\dfrac{1}{3}$

We know that,

${{\tan }^{-1}}x+{{\tan }^{-1}}y={{\tan }^{-1}}\left( \dfrac{x+y}{1-xy} \right)$

So,

${{\tan }^{-1}}\dfrac{1}{2}+{{\tan }^{-1}}\dfrac{1}{3}={{\tan }^{-1}}\left( \dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{1-\dfrac{1}{2}\times \dfrac{1}{3}} \right)$

$={{\tan }^{-1}}\left( \dfrac{\dfrac{3+2}{6}}{1-\dfrac{1}{6}} \right)$

$={{\tan }^{-1}}\left( \dfrac{5}{5} \right)$

$={{\tan }^{-1}}1$

$={{\tan }^{-1}}\tan \dfrac{\pi }{4}$

$=\dfrac{\pi }{4}$

Hence, this is the answer.

${ \tan }^{ -1 }\left( \dfrac { a\cos x-b\sin x }{ b\cos x+a\sin x } \right) =$

We have,

${{\tan }^{-1}}\left( \dfrac{a\cos x-b\sin x}{b\cos x+a\sin x} \right)$

On divide numerator and denominator by cosx and we get,

${{\tan }^{-1}}\left( \dfrac{a\cos x-b\sin x}{b\cos x+a\sin x} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{\dfrac{a\cos x-b\sin x}{\cos x}}{\dfrac{b\cos x+a\sin x}{\cos x}} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{\dfrac{a\cos x}{\cos x}-\dfrac{b\sin x}{\cos x}}{\dfrac{b\cos x}{\cos x}+\dfrac{a\sin x}{\cos x}} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{a-b\operatorname{tanx}}{b+a\tan x} \right)$

$\Rightarrow {{\tan }^{-1}}\dfrac{b}{b}\left( \dfrac{\dfrac{a}{b}-\tan x}{1+\dfrac{a}{b}\tan x} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{\tan y-\tan x}{1+\tan y\tan x} \right)\,\,\,\,\,\therefore let\,\,\tan y\,=\dfrac{a}{b}$

$\Rightarrow {{\tan }^{-1}}\tan \left( y-x \right)\,\,\,\,\,\therefore So,\,y\,={{\tan }^{-1}}\dfrac{a}{b}$

$\Rightarrow \left( y-x \right)$

$\Rightarrow {{\tan }^{-1}}\dfrac{a}{b}-x$

Hence, this is the answer.

If ${ \cos }^{ -1 }x+{\cos}^{-1}y+{ \cos }^{ -1 }z=\pi$ then, prove that ${ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2xyz=1$

We have,

${{\cos }^{-1}}x+{{\cos }^{-1}}y+{{\cos }^{-1}}z=\pi \,\,\,.....\,\,\left( 1 \right)$

${{\cos }^{-1}}x+{{\cos }^{-1}}y=\pi -{{\cos }^{-1}}z$

$\Rightarrow {{\cos }^{-1}}\left[ xy-\sqrt{\left( 1-{{x}^{2}} \right)\left( 1-{{y}^{2}} \right)} \right]=\pi -{{\cos }^{-1}}z$

$\therefore \,\,{{\cos }^{-1}}A+{{\cos }^{-1}}B={{\cos }^{-1}}\left[ AB-\sqrt{\left( 1-{{A}^{2}} \right)\left( 1-{{B}^{2}} \right)} \right]$

$\Rightarrow \left[ xy-\sqrt{\left( 1-{{x}^{2}} \right)\left( 1-{{y}^{2}} \right)} \right]=\cos \left( \pi -{{\cos }^{-1}}z \right)$

$\Rightarrow xy-\sqrt{\left( 1-{{x}^{2}} \right)\left( 1-{{y}^{2}} \right)}=-\cos {{\cos }^{-1}}z$

$\Rightarrow xy-\sqrt{\left( 1-{{x}^{2}} \right)\left( 1-{{y}^{2}} \right)}=-z$

$\Rightarrow xy+z=\sqrt{\left( 1-{{x}^{2}} \right)\left( 1-{{y}^{2}} \right)}$

On squaring both side and we get,

${{\left( xy+z \right)}^{2}}=\left( 1-{{x}^{2}} \right)\left( 1-{{y}^{2}} \right)$

$\Rightarrow {{x}^{2}}{{y}^{2}}+{{z}^{2}}+2xyz=1-{{x}^{2}}-{{y}^{2}}+{{x}^{2}}{{y}^{2}}$

$\Rightarrow {{x}^{2}}+{{y}^{2}}+{{z}^{2}}+2xyz=1$

Hence proved.

Solve $\left( { \tan }^{ -1 }x \right) ^{ 2 }+\left( { \tan }^{ -1 }x \right) ^{ 2 }=\dfrac { 5{ \pi }^{ 2 } }{ 8 }$

We have,

${{\left( {{\tan }^{-1}}x \right)}^{2}}+{{\left( {{\tan }^{-1}}x \right)}^{2}}=\dfrac{5{{\pi }^{2}}}{8}$

$\Rightarrow 2{{\left( {{\tan }^{-1}}x \right)}^{2}}=\dfrac{5{{\pi }^{2}}}{8}$

$\Rightarrow {{\left( {{\tan }^{-1}}x \right)}^{2}}=\dfrac{5{{\pi }^{2}}}{16}$

$\Rightarrow {{\tan }^{-1}}x=\sqrt{\dfrac{5{{\pi }^{2}}}{16}}$

$\Rightarrow {{\tan }^{-1}}x=\sqrt{5}\dfrac{\pi }{4}$

$\Rightarrow x=\tan \dfrac{\sqrt 5 \pi }{4}$

Hence, this is the answer.

If ${ \sin }^{ -1 }x=\dfrac { \pi }{ 5 }$ for some $x\in \left[ -1,1 \right]$ then, find the value of ${ \cos }^{ -1 }x.$

We have,

${{\sin }^{-1}}x=\dfrac{\pi }{5}$

We know that,

${{\sin }^{-1}}x+{{\cos }^{-1}}x=\dfrac{\pi }{2}$

Now,

${{\sin }^{-1}}x+{{\cos }^{-1}}x=\dfrac{\pi }{2}$

$\Rightarrow \dfrac{\pi }{5}+{{\cos }^{-1}}x=\dfrac{\pi }{2}$

$\Rightarrow {{\cos }^{-1}}x=\dfrac{\pi }{2}-\dfrac{\pi }{5}$

$\Rightarrow {{\cos }^{-1}}x=\dfrac{5\pi -2\pi }{10}$

$\Rightarrow {{\cos }^{-1}}x=\dfrac{3\pi }{10}$

Hence, this is the answer.

If ${ \cos }^{ -1 }x+{ \cos }^{ -1 }y+{ \cos }^{ -1 }z=\pi$ then, prove that ${ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2xy=1$

We have,

${{\cos }^{-1}}x+{{\cos }^{-1}}y+{{\cos }^{-1}}z=\pi \,\,......\,\,\left( 1 \right)$

$\Rightarrow {{\cos }^{-1}}x+{{\cos }^{-1}}y=\pi -{{\cos }^{-1}}z$

We know that,

${{\cos }^{-1}}A+{{\cos }^{-1}}B={{\cos }^{-1}}\left[ AB-\sqrt{1-{{A}^{2}}}\sqrt{1-{{B}^{2}}} \right]$

Therefore,

${{\cos }^{-1}}\left[ xy-\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right]=\pi -{{\cos }^{-1}}z$

$\Rightarrow \left[ xy-\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right]=\cos \left( \pi -{{\cos }^{-1}}z \right)$

$\Rightarrow \left[ xy-\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right]=\cos \left( \pi -{{\cos }^{-1}}z \right)\,\,\,\,\therefore \cos \left( \pi -\theta \right)=-\cos \theta$

$\Rightarrow \left[ xy-\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right]=-\cos {{\cos }^{-1}}z$

$\Rightarrow \left[ xy-\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}} \right]=-z$

$\Rightarrow xy+z=\sqrt{1-{{x}^{2}}}\sqrt{1-{{y}^{2}}}$

On squaring both side and we get$$\begin{align}

${{\left( xy+z \right)}^{2}}=\left( 1-{{x}^{2}} \right)\left( 1-{{y}^{2}} \right)$

$\Rightarrow {{x}^{2}}{{y}^{2}}+{{z}^{2}}+2xyz=1-{{x}^{2}}-{{y}^{2}}+{{x}^{2}}{{y}^{2}}$

$\Rightarrow {{z}^{2}}+2xyz=1-{{x}^{2}}-{{y}^{2}}$

$\Rightarrow {{x}^{2}}+{{y}^{2}}+{{z}^{2}}+2xyz=1$

Hence proved.

If ${ \sin }^{ -1 }x=\dfrac { \pi }{ 5 } x\in \left[ -1,1 \right]$ then, the value of ${ \cos }^{ -1 }x$

We have,

${{\sin }^{-1}}x=\dfrac{\pi }{5}$

We know that,

${{\sin }^{-1}}x+{{\cos }^{-1}}x=\dfrac{\pi }{2}$

${{\cos }^{-1}}x=\dfrac{\pi }{2}-{{\sin }^{-1}}x$

Now,

${{\cos }^{-1}}x=\dfrac{\pi }{2}-\dfrac{\pi }{5}$

$=\dfrac{5\pi -2\pi }{10}$

$=\dfrac{3\pi }{10}$

Hence, this is the answer.

Prove that: $2\tan^{-1}x=\tan^{-1}\dfrac {2x}{1-x^{2}}$

$\begin{array}{l} Let\, \, { \tan ^{ -1 } }x=\theta \\ \Rightarrow \tan \theta =x \\ we\, \, know\, \, that\, \, \\ { \tan ^{ 2 } }\theta =\cfrac { { 2\tan \theta } }{ { 1-{ { \tan }^{ 2 } }\theta } } \\ \Rightarrow { \tan ^{ 2 } }\theta =\cfrac { { 2x } }{ { 1-{ x^{ 2 } } } } \\ \Rightarrow 2\theta ={ \tan ^{ -1 } }\left( { \cfrac { { 2x } }{ { 1-{ x^{ 2 } } } } } \right) \\ \Rightarrow 2{ \tan ^{ -1 } }x={ \tan ^{ -1 } }\left( { \cfrac { { 2x } }{ { 1-{ x^{ 2 } } } } } \right) \end{array}$

Hence, proved.

Theorem: For any $x\in R$ $\quad { sinh }^{ -1 }x={ log }_{ e }(x+\sqrt { x^{ 2 }+1 } )$

Let

$x=\sin hy$ …………

$(1)$

$x=\dfrac{e^y-e^{-y}}{2}$

$\Rightarrow 2x=e^y-e^{-y}$

$\Rightarrow 2x=e^y-\dfrac{1}{e^y}$

$\Rightarrow 2x=\dfrac{e^{2y}-1}{ey}$

$\Rightarrow e^{2y}-2xe^y-1=0$

Using quadratic formula,

$e^y=\dfrac{2x\pm\sqrt{(2x)^2+4}}{2}$

$=\dfrac{2x\pm 2\sqrt{x^2+1}}{2}$

$=x\pm\sqrt{x^2+1}$

Since

$e^y$ is positive,

$e^y=x+\sqrt{x^2+1}$

Taking logarithm to the base e on both sides.

$y=log_e(x+\sqrt{x^2+1})$

$\Rightarrow \sin h^{-1}x=log_e(x+\sqrt{x^2+1})$ .

1186889_1314689_ans_7f9d50866041429aa5df59c25ec69a8f.JPG

Evaluate the following :
$\sin^{-1} (\sin 5)$

We have,

$\sin(\sin^{-1}5)$

$=5$

Hence, this is the answer.

Find the value of x if,

$sin\left\{ { sin }^{ -1 }\cfrac { 1 }{ 5 } +{ cos }^{ -1 }x \right\} =1$

$\sin{\left\{{\sin}^{-1}{\dfrac{1}{5}}+{\cos}^{-1}{x}\right\}}=1$

$\Rightarrow\,{\sin}^{-1}{\dfrac{1}{5}}+{\cos}^{-1}{x}={\sin}^{-1}{1}$

$\Rightarrow\,{\sin}^{-1}{\dfrac{1}{5}}+{\cos}^{-1}{x}=\dfrac{\pi}{2}$

$\Rightarrow\,{\sin}^{-1}{\dfrac{1}{5}}=\dfrac{\pi}{2}-{\cos}^{-1}{x}$

We know that

${\sin}^{-1}{x}+{\cos}^{-1}{x}=\dfrac{\pi}{2}$

$\Rightarrow\,{\sin}^{-1}{\dfrac{1}{5}}={\sin}^{-1}{x}$

$\therefore\,x=\dfrac{1}{5}$

Evaluate the following :
$\cos^{-1} (\cos 10)$

We have,

$\cos(\cos ^{-1} 10)$

$=10$

Hence, this is the answer.

If $x={ sin }^{ -1 }(sin10)$ and $y={ cos }^{ -1 }(cos10)$ , then y - x is equal to :

$x=sin^{-1}(sin 10)$

$x=3\pi -10$

Also,

$y=cos^{-1}(cos 10)$

$y=4\pi - 10$

Therefore,

$y-x=4\pi-10-3\pi+10 = \pi$

Find the value of $\cos(\sec^{-1}x+\csc^{-1}x), |x|\ge 1$

$sec^{-1}x + \cos^{-1}x = \dfrac{\pi}{2}$

$\cos(\sec^{-1}x + \cos^{-1}x) = \cos \dfrac{\pi}{2} = 0$

1227000_1398649_ans_2d5711b3e3b74665a5fe449d1d9d2d84.jpg

Solve the following equation
$\cos^{-1}\dfrac{x^2-1}{x^2+1}+\tan^{-1}\dfrac{2x}{x^2-1}=\dfrac{2\pi}{3}$ .

$\cos^{-1} \left(\dfrac{x^2-1}{x^2+1}\right)+\tan^{-1} \left(\dfrac{2x}{x^2-1}\right)=\dfrac{2\pi}{3}$ .

$\pi - \cos^{-1} \left(\dfrac{x^2-1}{x^2+1}\right)+\tan^{-1} \left(\dfrac{2x}{x^2-1}\right)=\dfrac{2\pi}{3}$ .

$[\because \cos^{-1} (-x)= \pi -\cos^{-1}x \tan^{-1} (-x)=- \tan^{-1}x]$

$\Rightarrow \pi -2 \tan^{-1} x-2\tan^{-1} x=\dfrac{2 \pi}{3}$

$\Rightarrow 4\tan^{-1} x=\pi -\dfrac{2 \pi}{3}$

$\Rightarrow 4\tan^{-1} x=\dfrac{ \pi}{3}$

$\Rightarrow \tan^{-1} x=\dfrac{ \pi}{12} \Rightarrow x =\tan \dfrac{\pi}{12} \Rightarrow x=\tan \left(\dfrac{\pi}{12} \right)$

If $\tan^{-1}x=\dfrac{\pi}{10}$ for some $x\in R$ , then find the value of $\cot^{-1}x$ .

We know that

${\tan}^{-1}{x}+{\cot}^{-1}{x}=\dfrac{\pi}{2}$

${\cot}^{-1}{x}=\dfrac{\pi}{2}-\dfrac{\pi}{10}$

$=\dfrac{5\pi-\pi}{10}$

$=\dfrac{4\pi}{10}$

$=\dfrac{2\pi}{5}$

Evaluate:
$\sec^2(\tan^{-1}2)+cosec^2(\cot^{-1}3)$

Now,

$\sec^2(\tan^{-1}2)+cosec^2(\cot^{-1}3)$

$=1+\tan^2(\tan^{-1}2)+1+\cot^2(\cot^{-1}3)$ [ Since

$\sec^2 \theta=1+tan^2 \theta$ and

$cosec^2 \theta=1+\cot^2 \theta$ ]

$=1+(\tan(\tan^{-1}2))^2+1+(\cot(\cot^{-1}3))^2$

$=1+2^2+1+3^2$

$=15$ .

Evaluate :
$\int { { x }^{ 2 }{ \tan }^{ -1 } } \dfrac{x}{2}dx$

$I=\displaystyle\int \underset{II}{x^2}\underset{I}{\tan^{-1}}\left(\dfrac{3}{2}\right)dx$

$I=\left[\dfrac{x^3}{3}\right]\tan^{-1}\left(\dfrac{x}{2}\right)-\displaystyle\int \dfrac{1}{1+\dfrac{x^2}{4}}\times \dfrac{x^3}{3}dx$

$I=\dfrac{x^3}{3}\tan^{-1}\left(\dfrac{x}{2}\right)-\dfrac{1}{6}\displaystyle\int \dfrac{4x^3}{x^2+4}dx$

$I=\dfrac{x^3}{3}\tan^{-1}\left(\dfrac{x}{2}\right)-\dfrac{1}{6}\displaystyle\int \left(4x-\dfrac{16x}{x^2+4}\right)dx$

$I=\dfrac{x^3}{3}\tan^{-1}\left(\dfrac{x}{2}\right)-\dfrac{1}{6}\left[\dfrac{4x^2}{2}-\dfrac{16}{2}log(x^2+4)\right]+c$

$I=\dfrac{x^3}{3}\tan^{-1}\left(\dfrac{x}{2}\right)-\dfrac{x^2}{3}+\dfrac{4}{3}log(x^2+4)+c$ .

1211867_1400637_ans_a762b5fa479c4a019bb7914effb16080.jpg

If $y={ cos }^{ -1 }\left( \dfrac { sinx+cosx }{ \sqrt { 2 } } \right)$ where $\dfrac { \pi }{ 4 } <x<\dfrac { \pi }{ 4 }$ then find $\dfrac { dy }{ dx }$

$y={\cos}^{-1}{\left(\dfrac{\sin{x}+\cos{x}}{\sqrt{2}}\right)}$

$\Rightarrow \cos{y}=\dfrac{\sin{x}+\cos{x}}{\sqrt{2}}$

$\Rightarrow \cos{y}=\cos{x}\cos{\dfrac{\pi}{4}}+\sin{x}\sin{\dfrac{\pi}{4}}$

$\Rightarrow \cos{y}=\cos{\left(x-\dfrac{\pi}{4}\right)}$

$\Rightarrow y=x-\dfrac{\pi}{4}$

$\Rightarrow \dfrac{dy}{dx}=1-0=1$

$\therefore \dfrac{dy}{dx}=1$

Solve : $\displaystyle\int { \dfrac { \tan { ^{ -1 } } x }{ 1+{ x }^{ 2 } } } dx$

$\displaystyle\int{\dfrac{{\tan}^{-1}{x}dx}{1+{x}^{2}}}$

Let

$t={\tan}^{-1}{x}\Rightarrow dt=\dfrac{dx}{1+{x}^{2}}$

$=\displaystyle\int{t.dt}$

$=\dfrac{{t}^{2}}{2}+c$ where

$c$ is the constant of integration.

$=\dfrac{1}{2}{\left({\tan}^{-1}{x}\right)}^{2}+c$ where

$t={\tan}^{-1}{x}$

Prove that :-
${\tan ^{ - 1}}\sqrt x = \dfrac{1}{2}{\cos ^{ - 1}}\left( {\dfrac{{1 - x}}{{1 + x}}} \right),x \in [0,1]$

Taking R.H.S

$\dfrac{1}{2}cos^{-1}(\dfrac{1-x}{1+x})$

putting

$x.tan^{2}\theta$

$=\dfrac{1}{2}cos^{-1}(\dfrac{1-tan^{2}\theta }{1+tan^{2}\theta })$

$=\dfrac{1}{2}(\dfrac{1-\dfrac{sin^{2}\theta }{cos^{2}\theta }}{1+\dfrac{sin^{2}\theta }{cos^{2}\theta }})$

$=\dfrac{1}{2}cos^{-1}(\dfrac{\dfrac{cos^{2}\theta -sin^{2}\theta }{cos^{2}\theta }}{\dfrac{cos^{2}\theta +sin^{2}\theta }{cos^{2}\theta }})$

$=\dfrac{1}{2}cos^{-1}(\dfrac{cos^{2}\theta -sin^{2}\theta }{cos^{2}\theta }\times \dfrac{cos^{2}\theta }{sin^{2}\theta +cos^{2}\theta })$

$=\dfrac{1}{2}.cos^{-1}(\dfrac{cos^{2}\theta .sin^{2}\theta }{sin^{2}\theta +cos^{2}\theta })$

$=\dfrac{1}{2}.cos^{-1}(\frac{cos^{2}\theta -sin^{2}\theta }{1})$ [

$\therefore$ using

$sin^{2}\theta +cos^{2}\theta =1]$

$\dfrac{1}{2}.cos^{-1}(cos2\theta )$ (using

$cos2\theta -cos^{2}\theta -sin^{2}\theta )$

$=\dfrac{1}{2}.\theta$

$=\theta$

we assume that

$x=tan^{2}\theta$

$\sqrt{x}=tan \theta$

$tan^{-1}\sqrt{x}=\theta$

Hence,

$\dfrac{1}{2}.cos^{-1}(\dfrac{1-x}{1+x})=0$

$\dfrac{1}{2}.cos^{-1}(\dfrac{1-x}{1+x})=tan^{-1}\sqrt{x}$

L.H.S = R.H.S

Hence proved.

1211829_1428536_ans_851ae857144040d580db1c35281884dc.jpg

Find the value of $\sec^{-1}\left ( \dfrac{2}{\sqrt{3}} \right )$

Let

$sec^{-1}\left ( \dfrac{2}{\sqrt{3}} \right )=x$

$\therefore secx=\dfrac{2}{\sqrt{3}}$

We know that

$cos\dfrac{\pi }{6}=\dfrac{\sqrt{3}}{2}$

$\therefore sec\theta =\dfrac{1}{cos\theta }$

$\therefore sec\dfrac{\pi }{6}=\dfrac{2}{\sqrt{3}}$

$\therefore$ comparing with

$sec x =\dfrac{2}{\sqrt{3}}$

$x=\dfrac{\pi }{6}$

$\therefore sec^{-1}\left ( \frac{2}{\sqrt{3}} \right )=\dfrac{\pi }{6}$

Find the value of x,
if $\tan^{-1}x+2\cot^{-1}x=\dfrac {2\pi}{3}$ .

${\tan}^{-1}{x}+2{\cot}^{-1}{x}=\dfrac{2\pi}{3}$

We know that

${\cot}^{-1}{x}=\dfrac{\pi}{2}-{\tan}^{-1}{x}$

$\Rightarrow\,{\tan}^{-1}{x}+2\left(\dfrac{\pi}{2}-{\tan}^{-1}{x}\right)=\dfrac{2\pi}{3}$

$\Rightarrow\,{\tan}^{-1}{x}+\pi-2{\tan}^{-1}{x}=\dfrac{2\pi}{3}$

$\Rightarrow\,{\tan}^{-1}{x}-2{\tan}^{-1}{x}=\dfrac{2\pi}{3}-\pi$

$\Rightarrow\,-{\tan}^{-1}{x}=\dfrac{2\pi-3\pi}{3}$

$\Rightarrow\,-{\tan}^{-1}{x}=\dfrac{-\pi}{3}$

$\Rightarrow\,{\tan}^{-1}{x}=\dfrac{\pi}{3}$

$\Rightarrow\,x=\tan{\dfrac{\pi}{3}}=\sqrt{3}$

$\therefore\,x=\sqrt{3}$

Find the value of x which satisfy the equation ${ sin }^{ -1 }x+{ sin }^{ -1 }(1-x)={ cos }^{ -1 }x$

From the given equation, we have

$\sin ({ sin }^{ -1 }x+{ sin }^{ -1 }(1-x))= \sin ({ cos }^{ -1 }x)$

$\Rightarrow \sin (\sin^{-1}x)\cos (\sin^{-1}(1-x))+\cos (-sin^{-1} x)\sin (\sin^{-1}(1-x))=\sin (\cos ^{-1}x)$

$\Rightarrow x \sqrt{1-(1-x)^2}+(1-x)\sqrt{1-x^2}=\sqrt{1-x^2}$

$\Rightarrow x \sqrt{2x-x^2}+\sqrt{1-x^2}(1-x-1)=0$

$\Rightarrow x \left(\sqrt{2x-x^2}-\sqrt{1-x^2}\right)=0$

$\Rightarrow x=0$ or

$2x-x^2=1-x^2$

$\Rightarrow x=0$ or

$x=\dfrac{1}{2}$

Prove that ${ \cos }^{ -1 }\left( \dfrac { 4 }{ 5 } \right) +{ \tan }^{ -1 }\left( \dfrac { 3 }{ 5 } \right) ={ \tan }^{ -1 }\left( \dfrac { 27 }{ 11 } \right)$

L.H.S

$=\cos^{-1}\left(\dfrac{4}{5}\right)+\tan^{-1}\left(\dfrac{3}{5}\right)$

$=\tan^{-1}\left(\dfrac{3}{4}\right)+\tan^{-1}\left(\dfrac{3}{5}\right)$

Since,

$\tan^{-1}x+\tan^{-1}{y}=\tan^{-1}\dfrac{x+y}{1-xy}$

Therefore,

$=\tan^{-1}\left(\dfrac{\dfrac{3}{4}+\dfrac{3}{5}}{1-\dfrac{3}{4}\times \dfrac{3}{5}}\right)$

$=\tan^{-1}\left(\dfrac{15+12}{20-9}\right)$

$=\tan^{-1}\left(\dfrac{27}{11}\right)$

$=$ R.H.S

Hence, proved.

Evaluate: $\sin ^{-1}\dfrac 35+\sin ^{-1}\dfrac 8{17}$

$\sin ^{-1}\dfrac 35+\sin ^{-1}\dfrac 8{17} \\\sin ^{-1}\left\{ \dfrac 35\sqrt {1- \left(\dfrac 8{17}\right)^2}+\dfrac 8{17}\sqrt {1-\left(\dfrac35 \right)^2}\right\}\\\sin ^{-1}\left\{ \dfrac 35\times \dfrac {15}{17} +\dfrac 8{17}\times \dfrac 45\right\}\\\sin ^{-1} \left\{\dfrac {45+32}{85} \right\}=\sin ^{-1}\dfrac {77}{85}$

Prove that:
$2 cos^{-1}\dfrac{3}{\sqrt {13}} + cot^{-1}\dfrac{16}{63} + \dfrac{1}{2}cos^{-1}\dfrac{7}{25} = \pi$

1585090_1484692_ans_707e13c2d7844f3c8427c72efeaef96e.jpg

If ${\sin ^{ - 1}}x - {\cos ^{ - 1}}x = \dfrac{\pi }{6}$ , then solve for $x$ .

We have

$\sin^{-1}x-\cos^{-1}x=\pi/6$

$\Rightarrow \sin^{-1}x+\cos^{-1}x-2\cdot \cos^{-1}x=\pi/6$

$\Rightarrow \pi/2-2\cdot \cos^{-1}x=\pi/6$

$\Rightarrow -2\cdot \cos^{-1}x=\pi/6-\pi/2$

$\Rightarrow -2\cdot \cos^{-1}x=\dfrac{\pi -3\pi}{6}$

$\Rightarrow -2\cdot \cos^{-1}x=\dfrac{\pi}{6}-\dfrac{3\pi}{6}$

$\Rightarrow 2\cdot \cos^{-1}x=2\pi/6$

$\Rightarrow \cos^{-1}x=\dfrac{2\pi}{6.2}$

$\Rightarrow \cos^{-1}x=\pi/6$

$\Rightarrow x=\cos\pi/6$

$\Rightarrow x=\sqrt{3}/2$ .

Evaluat the following:
$\sin^{-1} (\sin 4)$

We know,

$\Rightarrow$

$\sin^{-1}(\sin\theta)=\theta,$ If

$\left(-\dfrac{\pi}{2}\le \theta\le \dfrac{\pi}{2}\right)$

We know,

$\Rightarrow$

$\sin^{-1}(\sin 4)=\sin^{-1}\{\sin(\pi-4)\}$

$=\pi-4$

$\therefore$

$\sin^{-1}(\sin 4)=\pi-4$

Find the value of x, if $sin\left [ cot^{-1}(x+1) \right ]=cos(tan^{-1}x)$

1311041_1585521_ans_379420f7a2794420a401a7b2a30f1708.jpg

$sec^{2}(tan^{-1}2)+cosec^{2}(cot^{-1}3)$

$\text{sec}^2(\text{tan}^{-1} 2)+\text{cosec}^2(\text{cot}^{-1} 3)=1+\tan^2 (\text{tan}^{-1} 2)+1+\cot^2 (\text{cot}^{-1} 3)$

$=2+(\tan (\text{tan}^{-1} 2))^2+(\cot(\text{cot}^{-1}3)))^2=2+(2)^2+(3)^2=15$

If $tan^{-1} x - cot^{-1} x = tan^{-1} \left(\dfrac{1}{\sqrt{3}} \right), x > 0$ , find the value of $x$ and hence find the value of $sec^{-1} \left(\dfrac{2}{x}\right)$

$\text{tan}^{-1}x-\text{cot}^{-1}x\\=\text{tan}^{-1}\bigg(\dfrac{1}{\sqrt{3}}\bigg)\implies 2\text{tan}^{-1} x-\dfrac{\pi}{2}=\dfrac{\pi}{6}\\\implies \text{tan}^{-1}x=\dfrac{\pi}{3}\\\implies x=\sqrt{3}$

$\text{sec}^{-1}\bigg(\dfrac{2}{x}\bigg)=\text{sec}^{-1} \bigg(\dfrac{2}{\sqrt{3}}\bigg)=\dfrac{\pi}{6}$

Evaluate the following:
$\sin^{-1} (\sin 3)$

We know,

$\Rightarrow$

$\sin^{-1}(\sin\theta)=\theta,$ If

$\left(-\dfrac{\pi}{2}\le \theta\le \dfrac{\pi}{2}\right)$

We have,

$\Rightarrow$

$\sin^{-1}(\sin 3)=\sin^{-1}\{\sin(\pi-3)\}$

$=\pi-3$

$\therefore$

$\sin^{-1}(\sin 3)=\pi-3$

Evaluate the following :
$\sin\left( \dfrac { 1 }{ 2 } { \cos }^{ -1 }\left( \dfrac { 4 }{ 5 } \right) \right)$

Given:

$\sin{\left(\dfrac{1}{2}{\cos}^{-1}{\dfrac{4}{5}}\right)}$

Let

$x={\cos}^{-1}{\dfrac{4}{5}}$

$\Rightarrow\,\cos{x}=\dfrac{4}{5}$

$\Rightarrow\,\sin{x}=\sqrt{1-{\cos}^{2}{x}}=\sqrt{1-\dfrac{16}{25}}=\sqrt{\dfrac{25-16}{25}}=\sqrt{\dfrac{9}{25}}=\dfrac{3}{5}$

$\Rightarrow\,x={\cos}^{-1}{\dfrac{4}{5}}={\sin}^{-1}{\dfrac{3}{5}}$

Now,

$\sin{\left(\dfrac{1}{2}{\cos}^{-1}{\dfrac{4}{5}}\right)}$

$=\sin{\left(\dfrac{1}{2}x\right)}$

$=\sin{\left(\dfrac{x}{2}\right)}$

We Know that

$\cos{x}=1-2{\sin}^{2}{\dfrac{x}{2}}$

$\Rightarrow\,\dfrac{4}{5}=1-2{\sin}^{2}{\dfrac{x}{2}}$

$\Rightarrow\,2{\sin}^{2}{\dfrac{x}{2}}=1-\dfrac{4}{5}=\dfrac{5-4}{5}=\dfrac{1}{5}$

$\Rightarrow\,{\sin}^{2}{\dfrac{x}{2}}=\dfrac{1}{10}$

$\Rightarrow\,\sin{\dfrac{x}{2}}=\dfrac{1}{\sqrt{10}}$

$\therefore\,\sin{\left(\dfrac{1}{2}{\cos}^{-1}{\dfrac{4}{5}}\right)}$

$=\sin{\dfrac{x}{2}}=\dfrac{1}{\sqrt{10}}$

$2\tan^{-1}(\cos x)=\tan^{-1}(2 cosec x)$ .

1699077_1602543_ans_93a50df4e6144cea945c5f1d062d7b24.jpeg

Evaluate the following:
$\sin^{-1} (\sin 2)$

We know,

$\Rightarrow$

$\sin^{-1}(\sin\theta)=\theta,$ If

$\left(-\dfrac{\pi}{2}\le \theta\le \dfrac{\pi}{2}\right)$

We know,

$\Rightarrow$

$\sin^{-1}(\sin 2)=\sin^{-1}\{\sin(\pi-2)\}$

$=\pi-2$

$\therefore$

$\sin^{-1}(\sin 2)=\pi-2$

Evaluate:

$\tan^{-1} (\tan 1)$

${\tan}^{-1}{\left(\tan{1}\right)}$

Let

${\tan}^{-1}{\left(\tan{1}\right)}=\theta$

$\Rightarrow\,\tan{\theta}=\tan{1}$

$\Rightarrow\,\theta=1$

Hence,

${\tan}^{-1}{\left(\tan{1}\right)}=1$

Evaluate the following:
$\cos^{-1} (\cos 5)$

We know,

$cos^{-1}(\cos\theta)=\theta$ if

$(0\le \theta\le \pi)$

$\cos(2\pi-\theta)=\cos\theta$

We have

$cos^{-1}(\cos 5)=\cos^{-1}\{\cos(2\pi-5)\}$ Where,

$0\le 2\pi-5\le \pi$

$=2\pi-5$

$\therefore$

$cos^{-1}(\cos 5)=2\pi-5$

Evaluate $\cos^{-1} (\cos 3)$

${\cos}^{-1}{\left(\cos{3}\right)}$

Let

${\cos}^{-1}{\left(\cos{3}\right)}=\theta$

$\Rightarrow\,\cos{\theta}=\cos{3}$

$\Rightarrow\,\theta=3$

Hence,

${\cos}^{-1}{\left(\cos{3}\right)}=3$

Evaluate the following:
$\tan^{-1} (\tan 4)$

We know that,

$\tan^{-1}(\tan \theta)=\theta,$

$\left[-\dfrac{\pi}{2}<\theta<\dfrac{\pi}{2}\right]$

We have.

$\Rightarrow$

$\tan^{-1}(\tan 4)=\tan^{-1}[\tan(-\pi+4)]$

$=-\pi+4$

$=4-\pi$

Evaluate the following:
$\tan^{-1} (\tan 2)$

We know that,

$\tan^{-1}(\tan \theta)=\theta,$

$\left[-\dfrac{\pi}{2}<\theta<\dfrac{\pi}{2}\right]$

We have.

$\Rightarrow$

$\tan^{-1}(\tan 2)=\tan^{-1}[\tan(-\pi+2)]$

$=-\pi+2$

$=2-\pi$

Evaluate the following:
$\cos^{-1} (\cos 4)$

We know,

$cos^{-1}(\cos\theta)=\theta$ if

$(0\le \theta\le \pi)$

$\cos(2\pi-\theta)=\cos\theta$

We have

$cos^{-1}(\cos 4)=\cos^{-1}\{\cos(2\pi-4)\}$

$=2\pi-4$

$\left[{\because 0\le(2\pi-4)\le\pi }\right]$

$\therefore$

$cos^{-1}(\cos 4)=2\pi-4$

Evaluate the following:
$\sin^{-1} (\sin 12)$

$sin^{-1}(sin12)$

$=sin^{-1}(sin(12-4\pi))$

$=12-4\pi$ as

$\dfrac{-\pi}{2}\leq12-4\pi\leq \dfrac{\pi}{2}$

Evaluate the following:
$\cos^{-1} (\cos 12)$

We know,

$cos^{-1}(\cos\theta)=\theta$ if

$(0\le \theta\le \pi)$

We have

$cos^{-1}(\cos 12)=\cos^{-1}\{\cos(4\pi-12)\}$ Where

$(0\le 4\pi-12\le \pi)$

$=4\pi-12$

$\therefore$

$cos^{-1}(\cos 12)=4\pi-12$

Evaluate the following:
$\tan^{-1} (\tan 12)$

We know that,

$\tan^{-1}(\tan \theta)=\theta,$

$\left[-\dfrac{\pi}{2}<\theta<\dfrac{\pi}{2}\right]$

We have.

$\Rightarrow$

$\tan^{-1}(\tan 12)=\tan^{-1}[\tan(-4\pi+12)]$

$=-4\pi+12$

$=12-4\pi$

Show that $2\tan^{-1} x + \sin^{-1} \dfrac {2x}{1 + x^{2}}$ is constant for $x \geq 1$ . Also find that constant.

We have

$2{\tan}^{-1}{x}+{\sin}^{-1}{\left(\dfrac{2x}{1+{x}^{2}}\right)}$ for

$x>1$

$=\pi-{\sin}^{-1}{\left(\dfrac{2x}{1+{x}^{2}}\right)}+{\sin}^{-1}{\left(\dfrac{2x}{1+{x}^{2}}\right)}\,\,\,\,\,\,\,\because 2{\tan}^{-1}{x}=\pi-{\sin}^{-1}{\left(\dfrac{2x}{1+{x}^{2}}\right)},x>1$

$=\pi$

For

$x=1,\,\,2{\tan}^{-1}{x}+{\sin}^{-1}{\left(\dfrac{2x}{1+{x}^{2}}\right)}$

$=2{\tan}^{-1}{1}+{\sin}^{-1}{\left(\dfrac{2}{1+{1}^{2}}\right)}$

$=2{\tan}^{-1}{1}+{\sin}^{-1}{\left(\dfrac{2}{2}\right)}$

$=2{\tan}^{-1}{1}+{\sin}^{-1}{1}$

$=2\times\dfrac{\pi}{4}+\dfrac{\pi}{2}$

$=\dfrac{\pi}{2}+\dfrac{\pi}{2}=\pi$

$\therefore\,$ the constant is

$\pi$

Write the value of $\cos \left (2\sin^{-1}\dfrac {1}{3}\right )$ .

$\cos{\left(2{\sin}^{-1}{\dfrac{1}{3}}\right)}$

Let

${\sin}^{-1}{\dfrac{1}{3}}=\theta$

$\Rightarrow\,\sin{\theta}=\dfrac{1}{3}$

$\Rightarrow\,{\sin}^{2}{\theta}=\dfrac{1}{9}$

$\therefore\,\cos{\left(2{\sin}^{-1}{\dfrac{1}{3}}\right)}$

$=\cos{\left(2\theta\right)}$

$=1-2{\sin}^{2}{\theta}$

$=1-2\times\dfrac{1}{9}$

$=\dfrac{9-2}{9}=\dfrac{7}{9}$

$\therefore\,\cos{\left(2{\sin}^{-1}{\dfrac{1}{3}}\right)}=\dfrac{7}{9}$

Find the values of the following:
$\tan^{-1} \left \{2\cos \left (2\sin^{-1} \dfrac {1}{2}\right )\right \}$ .

${\tan}^{-1}\left\{2\cos{\left(2{\sin}^{-1}{\dfrac{1}{2}}\right)}\right\}$

$={\tan}^{-1}\left\{2\cos{\left(2\times\dfrac{\pi}{6}\right)}\right\}$

$={\tan}^{-1}\left\{2\cos{\left(\dfrac{\pi}{3}\right)}\right\}$

$={\tan}^{-1}\left\{2\times\dfrac{1}{2}\right\}$

$={\tan}^{-1}\left\{1\right\}$

$=\dfrac{\pi}{4}$

Write the value of $\cos \left (2\sin^{-1} \dfrac {1}{2}\right )$ .

$\cos{\left(2{\sin}^{-1}{\dfrac{1}{2}}\right)}$

$=\cos{\left(2\times\dfrac{\pi}{6}\right)}$

$=\cos{\left(\dfrac{\pi}{3}\right)}$

$=\dfrac{1}{2}$

Find the value of x, if:

$\tan^{-1} \left (\dfrac {x - 2}{x - 1}\right ) + \tan^{-1} \left (\dfrac {x + 2}{x + 1}\right ) = \dfrac {\pi}{4}$ .

${\tan}^{-1}{\left(\dfrac{x-2}{x-1}\right)}+{\tan}^{-1}{\left(\dfrac{x+2}{x+1}\right)}=\dfrac{\pi}{4}$

We know that

${\tan}^{-1}{A}+{\tan}^{-1}{B}={\tan}^{-1}{\left(\dfrac{A+B}{1-AB}\right)}$

$\Rightarrow\,{\tan}^{-1}{\left(\dfrac{\dfrac{x-2}{x-1}+\dfrac{x+2}{x+1}}{1-\dfrac{x-2}{x-1}\times\dfrac{x+2}{x+1}}\right)}=\dfrac{\pi}{4}$

$\Rightarrow\,{\tan}^{-1}{\left(\dfrac{\dfrac{\left(x-2\right)\left(x+1\right)+\left(x-1\right)\left(x+2\right)}{{x}^{2}-1}}{1-\dfrac{{x}^{2}-4}{{x}^{2}-1}}\right)}=\dfrac{\pi}{4}$

$\Rightarrow\,{\tan}^{-1}{\left(\dfrac{\dfrac{{x}^{2}-x-2+{x}^{2}+x-2}{{x}^{2}-1}}{\dfrac{{x}^{2}-1-{x}^{2}+4}{{x}^{2}-1}}\right)}=\dfrac{\pi}{4}$

$\Rightarrow\,{\tan}^{-1}{\left(\dfrac{\dfrac{2{x}^{2}-4}{{x}^{2}-1}}{\dfrac{3}{{x}^{2}-1}}\right)}=\dfrac{\pi}{4}$

$\Rightarrow\,{\tan}^{-1}{\dfrac{2{x}^{2}-4}{3}}=\dfrac{\pi}{4}$

$\Rightarrow\,\dfrac{2{x}^{2}-4}{3}=\tan{\dfrac{\pi}{4}}=1$

$\Rightarrow\,2{x}^{2}-4=3$

$\Rightarrow\,2{x}^{2}=3+4=7$

$\Rightarrow\,{x}^{2}=\dfrac{7}{2}$

$\therefore\,Answer \,is\, x=\sqrt{\dfrac{7}{2}}$

$\,Because \, x=-\sqrt{\dfrac{7}{2}} \,does\,\,not\,\,satisfy\,\,above\,equation$

If $x < 0$ , then write the value of $\cos^{-1} \left (\dfrac {1 - x^{2}}{1 + x^{2}}\right )$ in terms of $\tan^{-1} x$ .

Let

$x=\tan{\theta}$

$\Rightarrow\,{\cos}^{-1}{\left(\dfrac{1-{x}^{2}}{1+{x}^{2}}\right)}$

$={\cos}^{-1}{\left(\dfrac{1-{\tan}^{2}{\theta}}{1+{\tan}^{2}{\theta}}\right)}$

$={\cos}^{-1}{\left(\cos{2\theta}\right)}$

$=2\theta$

$=2{\tan}^{-1}{x}$ where

$x=\tan{\theta}$

Find the value of x, if:

$\cos^{-1} x + \sin^{1}\dfrac {x}{2} - \dfrac {\pi}{6} = 0$

${\cos}^{-1}{x}+{\sin}^{-1}{\dfrac{x}{2}}=\dfrac{\pi}{6}$

We know that

${\cos}^{-1}{x}+{\sin}^{-1}{x}=\dfrac{\pi}{2}$

$\Rightarrow\,\dfrac{\pi}{2}-{\sin}^{-1}{x}+{\sin}^{-1}{\dfrac{x}{2}}=\dfrac{\pi}{6}$

$\Rightarrow\,-{\sin}^{-1}{x}+{\sin}^{-1}{\dfrac{x}{2}}=\dfrac{\pi}{6}-\dfrac{\pi}{2}$

$\Rightarrow\,-{\sin}^{-1}{x}+{\sin}^{-1}{\dfrac{x}{2}}=\dfrac{2\pi-6\pi}{12}$

$\Rightarrow\,-{\sin}^{-1}{x}+{\sin}^{-1}{\dfrac{x}{2}}=\dfrac{-4\pi}{12}$

$\Rightarrow\,-{\sin}^{-1}{x}+{\sin}^{-1}{\dfrac{x}{2}}=\dfrac{-\pi}{3}$

$\Rightarrow\,{\sin}^{-1}{\dfrac{x}{2}}=\dfrac{-\pi}{3}+{\sin}^{-1}{x}$

$\Rightarrow\,\dfrac{x}{2}=\sin{\left(\dfrac{-\pi}{3}+{\sin}^{-1}{x}\right)}$

$\Rightarrow\,\dfrac{x}{2}=\sin{\dfrac{-\pi}{3}}\cos{{\sin}^{-1}{x}}+\cos{\dfrac{-\pi}{3}}\sin{{\sin}^{-1}{x}}$

$\Rightarrow\,\dfrac{x}{2}=-\sin{\dfrac{\pi}{3}}\cos{{\cos}^{-1}{\sqrt{1-{x}^{2}}}}+\cos{\dfrac{-\pi}{3}}\sin{{\sin}^{-1}{x}}$

$\Rightarrow\,\dfrac{x}{2}=-\dfrac{\sqrt{3}}{2}\sqrt{1-{x}^{2}}+\dfrac{1}{2}x$

$\Rightarrow\,0=-\dfrac{\sqrt{3}}{2}\sqrt{1-{x}^{2}}$

$\Rightarrow\,1-{x}^{2}=0$

$\Rightarrow\,{x}^{2}=1$

$\therefore\,x=1$ is the only answer because

$x=-1$ will not satisfy above question.

Solve the following equation for $x$ :
$\tan^{-1} \dfrac {1}{4} + 2\tan^{-1} \dfrac {1}{5} + \tan^{-1} \dfrac {1}{6} + \tan^{-1} \dfrac {1}{x} = \dfrac {\pi}{4}$ .

We know that

$2{\tan}^{-1}{x}={\tan}^{-1}{\left(\dfrac{2x}{1-{x}^{2}}\right)}$

$\Rightarrow\,2{\tan}^{-1}{\dfrac{1}{5}}={\tan}^{-1}{\left(\dfrac{2\times\dfrac{1}{5}}{1-{\left(\dfrac{1}{5}\right)}^{2}}\right)}$

$\Rightarrow\,2{\tan}^{-1}{\dfrac{1}{5}}={\tan}^{-1}{\left(\dfrac{\dfrac{2}{5}}{1-\dfrac{1}{25}}\right)}$

$\Rightarrow\,2{\tan}^{-1}{\dfrac{1}{5}}={\tan}^{-1}{\left(\dfrac{\dfrac{2}{5}}{\dfrac{25-1}{25}}\right)}$

$\Rightarrow\,2{\tan}^{-1}{\dfrac{1}{5}}={\tan}^{-1}{\left(\dfrac{\dfrac{2}{5}}{\dfrac{24}{25}}\right)}$

$\Rightarrow\,2{\tan}^{-1}{\dfrac{1}{5}}={\tan}^{-1}{\dfrac{50}{120}}$

$\Rightarrow\,2{\tan}^{-1}{\dfrac{1}{5}}={\tan}^{-1}{\dfrac{5}{12}}$

Solving for

$x$ using the formula,

${\tan}^{-1}{A}+{\tan}^{-1}{B}={\tan}^{-1}{\left(\dfrac{A+B}{1-AB}\right)}$

${\tan}^{-1}{\dfrac{1}{4}}+2{\tan}^{-1}{\dfrac{1}{5}}+{\tan}^{-1}{\dfrac{1}{6}}+{\tan}^{-1}{\dfrac{1}{x}}=\dfrac{\pi}{4}$

${\tan}^{-1}{\dfrac{1}{4}}+{\tan}^{-1}{\dfrac{5}{12}}+{\tan}^{-1}{\dfrac{1}{6}}+{\tan}^{-1}{\dfrac{1}{x}}=\dfrac{\pi}{4}$

${\tan}^{-1}{\left(\dfrac{\dfrac{1}{4}+\dfrac{5}{12}}{1-\dfrac{1}{4}\times\dfrac{5}{12}}\right)}+{\tan}^{-1}{\dfrac{1}{6}}+{\tan}^{-1}{\dfrac{1}{x}}=\dfrac{\pi}{4}$

${\tan}^{-1}{\left(\dfrac{\dfrac{12+20}{48}}{1-\dfrac{5}{48}}\right)}+{\tan}^{-1}{\left(\dfrac{\dfrac{1}{6}+\dfrac{1}{x}}{1-\dfrac{1}{6}\times\dfrac{1}{x}}\right)}=\dfrac{\pi}{4}$

${\tan}^{-1}{\left(\dfrac{\dfrac{32}{48}}{\dfrac{48-5}{48}}\right)}+{\tan}^{-1}{\left(\dfrac{\dfrac{x+6}{6x}}{1-\dfrac{1}{6x}}\right)}=\dfrac{\pi}{4}$

${\tan}^{-1}{\left(\dfrac{32}{43}\right)}+{\tan}^{-1}{\left(\dfrac{\dfrac{x+6}{6x}}{\dfrac{6x-1}{6x}}\right)}=\dfrac{\pi}{4}$

${\tan}^{-1}{\left(\dfrac{32}{43}\right)}+{\tan}^{-1}{\dfrac{x+6}{6x-1}}=\dfrac{\pi}{4}$

${\tan}^{-1}{\left(\dfrac{\dfrac{32}{43}+\dfrac{x+6}{6x-1}}{1-\dfrac{32}{43}\times\dfrac{x+6}{6x-1}}\right)}=\dfrac{\pi}{4}$

$\Rightarrow\,\left(\dfrac{\dfrac{32}{43}+\dfrac{x+6}{6x-1}}{1-\dfrac{32}{43}\times\dfrac{x+6}{6x-1}}\right)=\tan{\dfrac{\pi}{4}}=1$

$\Rightarrow\,32\left(6x-1\right)+43\left(x+6\right)=43\left(6x-1\right)-32\left(x+6\right)$

$\Rightarrow32\left(6x-1+x+6\right)=43\left(6x-1-x-6\right)$

$\Rightarrow\,32\left(7x+5\right)=43\left(5x-7\right)$

$\Rightarrow\,224x+160=215x-301$

$\Rightarrow\,224x-215x=-301-160$

$\Rightarrow\,9x=-461$

$\therefore\,x=\dfrac{-461}{9}$

Write the difference between maximum and minimum values of $\sin^{-1} x$ of $x \epsilon [-1, 1]$ .

We know that Range of

${\sin}^{-1}{x}$ is

$\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$

$\Rightarrow\,$ Minimum value

$=\dfrac{-\pi}{2}$ and Maximum value

$=\dfrac{\pi}{2}$

Difference

$=\dfrac{\pi}{2}-\left(-\dfrac{\pi}{2}\right)=\dfrac{\pi}{2}+\dfrac{\pi}{2}=\pi$

Write the value of $\cos^{2} \left (\dfrac {1}{2}\cos^{-1} \dfrac {3}{5}\right )$ .

${\cos}^{2}{\left(\dfrac{1}{2}{\cos}^{-1}{\dfrac{3}{5}}\right)}$

Let

${\cos}^{-1}{\dfrac{3}{5}}=2\theta$

$\Rightarrow\,\cos{2\theta}=\dfrac{3}{5}$

$\Rightarrow\,1-2{\sin}^{2}{\theta}=\dfrac{3}{5}$

$\Rightarrow\,-2{\sin}^{2}{\theta}=\dfrac{3}{5}-1$

$\Rightarrow\,-2{\sin}^{2}{\theta}=\dfrac{3-5}{5}$

$\Rightarrow\,-2{\sin}^{2}{\theta}=\dfrac{-2}{5}$

$\Rightarrow\,{\sin}^{2}{\theta}=\dfrac{1}{5}$

$\therefore\,{\cos}^{2}{\left(\dfrac{1}{2}{\cos}^{-1}{\dfrac{3}{5}}\right)}$

$={\cos}^{2}{\left(\dfrac{1}{2}\times 2\theta\right)}$

$={\cos}^{2}{\theta}$

$=1-{\sin}^{2}{\theta}$

$=1-\dfrac{1}{5}$ Since

${\sin}^{2}{\theta}=\dfrac{1}{5}$

$=\dfrac{5-1}{5}=\dfrac{4}{5}$

$\therefore\,{\cos}^{2}{\left(\dfrac{1}{2}{\cos}^{-1}{\dfrac{3}{5}}\right)}=\dfrac{4}{5}$

Write the value of $\sin^{-1} \left (\cos \dfrac {\pi}{9}\right )$ .

${\sin}^{-1}{\left(\cos{\dfrac{\pi}{9}}\right)}$

$={\sin}^{-1}{\left(\sin{\left(\dfrac{\pi}{2}-\dfrac{\pi}{9}\right)}\right)}$

$=\dfrac{\pi}{2}-\dfrac{\pi}{9}$

$=\dfrac{9\pi-2\pi}{18}=\dfrac{7\pi}{18}$

If $\sin^{-1} \left (\dfrac {1}{3}\right ) + \cos^{-1}x = \dfrac {\pi}{2}$ , then find $x$ .

${\sin}^{-1}{\dfrac{1}{3}}+{\cos}^{-1}{x}=\dfrac{\pi}{2}$

$\Rightarrow\,{\cos}^{-1}{x}=\dfrac{\pi}{2}-{\sin}^{-1}{\dfrac{1}{3}}$

$\Rightarrow\,x=\cos{\left(\dfrac{\pi}{2}-{\sin}^{-1}{\dfrac{1}{3}}\right)}$

$\Rightarrow\,x=\sin{\left({\sin}^{-1}{\dfrac{1}{3}}\right)}$

$\therefore\,x=\dfrac{1}{3}$

Write the value of $\sin^{-1} \left (\dfrac {1}{3}\right ) - \cos^{-1} \left (-\dfrac {1}{3}\right )$ .

${\sin}^{-1}{\dfrac{1}{3}}-{\cos}^{-1}{\left(-\dfrac{1}{3}\right)}$

$=\dfrac{\pi}{2}-{\cos}^{-1}{\dfrac{1}{3}}-{\cos}^{-1}{\left(-\dfrac{1}{3}\right)}$

$=\dfrac{\pi}{2}-{\cos}^{-1}{\dfrac{1}{3}}-{\pi}+{\cos}^{-1}{\left(\dfrac{1}{3}\right)}$

$=-\dfrac{\pi}{2}$

Write the value of $\cos^{-1} \left (\cos \dfrac {5\pi}{4}\right )$ .

${\cos}^{-1}{\left(\cos{\dfrac{5\pi}{4}}\right)}$

$={\cos}^{-1}{\left(\cos{\left(\pi+\dfrac{\pi}{4}\right)}\right)}$

$={\cos}^{-1}{\left(-\cos{\left(\dfrac{\pi}{4}\right)}\right)}$

$={\cos}^{-1}{\left(-\dfrac{1}{\sqrt{2}}\right)}$

$={\pi}-\dfrac{\pi}{4}=\dfrac{3\pi}{4}$

Evaluate : $\sin^{-1} \left (\sin \dfrac {3\pi}{5}\right )$ .

${\sin}^{-1}{\left(\sin{\dfrac{3\pi}{5}}\right)}$

$={\sin}^{-1}{\left(\sin{\left(\pi-\dfrac{2\pi}{5}\right)}\right)}$

$={\sin}^{-1}{\left(\sin{\left(\dfrac{2\pi}{5}\right)}\right)}$

$=\dfrac{2\pi}{5}$

Write the value of $\sin \left \{\dfrac {\pi}{3} - \sin^{-1} \left (-\dfrac {1}{2}\right )\right \}$ .

$\sin{\left\{\dfrac{\pi}{3}-{\sin}^{-1}{\left(\dfrac{-1}{2}\right)}\right\}}$

$=\sin{\left\{\dfrac{\pi}{3}-\left(\dfrac{-\pi}{6}\right)\right\}}$

$=\sin{\left\{\dfrac{2\pi}{6}+\dfrac{\pi}{6}\right\}}$

$=\sin{\left\{\dfrac{2\pi+\pi}{6}\right\}}$

$=\sin{\left\{\dfrac{3\pi}{6}\right\}}$

$=\sin{\left\{\dfrac{\pi}{2}\right\}}$

$=1$

Write the value of $\tan^{-1} \dfrac {a}{b} - \tan^{-1} \left (\dfrac {a - b}{a + b}\right )$ .

${\tan}^{-1}{\dfrac{a}{b}}-{\tan}^{-1}{\left(\dfrac{a-b}{a+b}\right)}$

$={\tan}^{-1}{\dfrac{a}{b}}-{\tan}^{-1}{\left(\dfrac{b\left(\dfrac{a}{b}-1\right)}{b\left(\dfrac{a}{b}+1\right)}\right)}$

$={\tan}^{-1}{\dfrac{a}{b}}-{\tan}^{-1}{\left(\dfrac{\dfrac{a}{b}-\tan{\dfrac{\pi}{4}}}{1+\tan{\dfrac{\pi}{4}}\times\dfrac{a}{b}}\right)}$

$={\tan}^{-1}{\dfrac{a}{b}}-\left[{\tan}^{-1}{\dfrac{a}{b}}-{\tan}^{-1}{\left(\tan{\dfrac{\pi}{4}}\right)}\right]$

$={\tan}^{-1}{\dfrac{a}{b}}-{\tan}^{-1}{\dfrac{a}{b}}+{\tan}^{-1}{\left(\tan{\dfrac{\pi}{4}}\right)}$

$=\dfrac{\pi}{4}$

If $x < 0, y < 0$ such that $xy = 1$ , then write the value of $\tan^{-1} x + \tan^{-1} y$ .

${\tan}^{-1}{x}+{\tan}^{-1}{y}$

$={\tan}^{-1}{\left(\dfrac{x+y}{1-xy}\right)}$

$={\tan}^{-1}{\left(\dfrac{x+y}{1-1}\right)}$ given

$xy=1$

$={\tan}^{-1}{\left(\dfrac{x+y}{0}\right)}$

$={\tan}^{-1}{\left(\infty\right)}$

$=\dfrac{\pi}{2}$

Write the value of $2\sin^{-1} \dfrac {1}{2} + \cos^{1} \left (-\dfrac {1}{2}\right )$ .

$2{\sin}^{-1}{\dfrac{1}{2}}+{\cos}^{-1}{\left(-\dfrac{1}{2}\right)}$

$=2\times\dfrac{\pi}{6}+\pi-\dfrac{\pi}{3}$

$=\dfrac{\pi}{3}+\pi-\dfrac{\pi}{3}=\pi$

Write the value of $\tan^{-1} \left \{\tan \left (\dfrac {15\pi}{4}\right )\right \}$ .

${\tan}^{-1}{\left\{\tan{\left(\dfrac{15\pi}{4}\right)}\right\}}$

$={\tan}^{-1}{\left\{\tan{\left(4\pi-\dfrac{\pi}{4}\right)}\right\}}$

We know that

$4\pi$ is in

$2\times{360}^{\circ}$ and

${720}^{\circ}-{45}^{\circ}$ is in fourth quadrant.

$\therefore\,\tan{\left(4\pi-\dfrac{\pi}{4}\right)}=-\tan{\dfrac{\pi}{4}}=-1$

$\therefore\,{\tan}^{-1}{\left\{\tan{\left(4\pi-\dfrac{\pi}{4}\right)}\right\}}$

$={\tan}^{-1}{\left(-1\right)}=-\dfrac{\pi}{4}$ since range of

${\tan}^{-1}$ is

$\left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$

Prove that:
$\tan^{-1}\left(\dfrac{1+x}{1-x}\right)=\dfrac{\pi}{4}+\tan^{-1}x,x<1$

$LHS=\tan^{-1}\left(\dfrac{1+x}{1-x}\right)$

$=\tan^{-1}\left(\dfrac{1+\tan\theta}{1-\tan\theta}\right)$ Put

$x=\tan \theta$

$=\tan^{-1}\left(\dfrac{\tan\dfrac{\pi}{4}+\tan\theta}{1-\tan\dfrac{\pi}{4}\cdot\tan\theta}\right)$

$[\because\,\tan\dfrac{\pi}{4}=1]$

$=\tan^{-1}\left({\tan(\dfrac{\pi}{4}+\theta)}\right)$

$=\dfrac{\pi}{4}+\theta$

$=\dfrac{\pi}{4}+\tan^{-1}x$

$[\because\,\tan\theta=x\Rightarrow \theta=\tan^{-1}x]$

$=RHS$

$\therefore LHS=RHS$ ......proved

Prove that
$\sin^{-1}(2x\sqrt{1-x^{2}})=2\sin^{-1}x, |x|\le \dfrac{1}{\sqrt{2}}$

1538129_1705162_ans_45b969825a704282bd1fa3736abf393c.jpg

Prove that:
$\tan^{-1}x+\cot^{-1}(x+1)=\tan^{-1}(x^{2}+x+1)$

1538112_1705157_ans_e7375649f5424143a3efc2d286d04f45.jpg

Evaluate $\sin \left\{\dfrac {\pi}{2}-\sin^{-1} \left(\dfrac {-\sqrt 3}{2}\right)\right\}$

1545850_1705193_ans_123ccc91af3644c88fdc34bd60580507.pdf

Write the value of $\cot^{-1} (-x)$ for all $x\epsilon R$ in terms of $\cot^{-1} x$ .

Let

${\cot}^{-1}{\left(-x\right)}=\theta$

$\Rightarrow\,\cot{\theta}=-x$

$\Rightarrow\,\cot{\left(\pi-\theta\right)}=x$

$\Rightarrow\,\pi-\theta={\cot}^{-1}{x}$

$\Rightarrow\,\theta=\pi-{\cot}^{-1}{x}$

$\therefore\,{\cot}^{-1}{\left(-x\right)}=\pi-{\cot}^{-1}{x}$ for

$x\in \,R$

Hence proved.

Prove that:
$\sin^{-1}(3x-4x^{3})=3\sin^{-1}x, |x|\le \dfrac{1}{2}$

1538137_1705168_ans_6ec0cbcfb3664ba5968d65e4f45cb9c3.jpg

Evaluate $\cos \left\{\cos^{-1}\left(\dfrac {-\sqrt 3}{2}\right) +\dfrac {\pi}{6}\right\}$

1545530_1705183_ans_824389ff989b4145af2ff209ebcbacce.jpg

Prove that:
$\tan^{-1}\left(\dfrac{3x-x^{3}}{1-3x^{2}}\right)=3\tan^{-1}x,|x|<\dfrac{1}{\sqrt{3}}$

1538584_1705178_ans_e1869f0585c94ae9acb793610bbba2d6.jpg

Solve for $x$ :
$\cos (2\sin^{-1}x)=\dfrac{1}{9}$

1553990_1705281_ans_45a210c9e99e4768b9bd43f012977769.jpg

Solve for $x$ :
$\cos(\sin^{-1}x)=\dfrac{1}{2}$

1546176_1705284_ans_4fdfb176fe154a4c847d63c4c61c36c0.jpg

Solve for $x$ :
$\cos(\sin^{-1}x)=\dfrac{1}{9}$

1545726_1705279_ans_928c2478e82d4d6dae9b9747d63b0fca.JPG

Prove that:
$\cos^{-1} x = 2 \sin^{-1} \sqrt{\dfrac{1 -x}{2}} = 2 \cos^{-1} \sqrt{\dfrac{1 + x}{3}}$

Let

$\text{sin}^{-1} \sqrt{\dfrac{1-x}{2}}=\theta\implies \sin \theta=\sqrt{\dfrac{1-x}{2}}$

As we know that

$\cos 2 A=1-2\sin^2 A$

$\cos 2\theta=1-2\sin^2 \theta=1-2\times \bigg(\sqrt{\dfrac{1-x}{2}}\bigg)^2=1-2\times \dfrac{1-x}{2}=1-(1-x)=x$

$\implies 2\theta=\text{cos}^{-1} x$

$\implies 2 \text{sin}^{-1} \sqrt{\dfrac{1-x}{2}}=\text{cos}^{-1} x\cdots(1)$

Let

$\text{cos}^{-1} \sqrt{\dfrac{1+x}{2}}=\phi\implies \cos \phi=\sqrt{\dfrac{1+x}{2}}$

As we know that

$\cos 2 A=2\cos^2 A-1$

$\cos 2\phi=2\cos^2 \phi-1=2\times \bigg(\sqrt{\dfrac{1+x}{2}}\bigg)^2-1=2\times \dfrac{1+x}{2}-1=1+x-1=x$

$\implies 2\phi=\text{cos}^{-1} x$

$\implies 2 \text{cos}^{-1} \sqrt{\dfrac{1+x}{2}}=\text{cos}^{-1} x\cdots(2)$

From

$(1)\ \&\ (2)$

$\text{cos}^{-1} x=2\text{sin}^{-1} \sqrt{\dfrac{1-x}{2}}=2\text{cos}^{-1} \sqrt{\dfrac{1+x}{2}}$

Prove that:
$\tan^{-1} \dfrac{1}{2} + \tan^{-1} \dfrac{1}{3} = \sin^{-1} \dfrac{1}{\sqrt{5}} + \cot^{-1} 3 = 45^{\circ}$

As we know that

$\text{tan}^{-1} a+\text{tan}^{-1} b=\text{tan}^{-1} \dfrac{a+b}{1-a b},ab <1$

$\text{tan}^{-1} \dfrac{1}{2}+\text{tan}^{-1} \dfrac{1}{3}=\text{tan}^{-1} \dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{1-\dfrac{1}{2}\times \dfrac{1}{3}}=\text{tan}^{-1} \dfrac{2+3}{6-1}=\text{tan}^{-1} \dfrac{5}{5}=\text{tan}^{-1} 1=45^{\circ}\cdots(1)$

Now

$\text{sin}^{-1} \dfrac{1}{\sqrt{5}}=\text{sin}^{-1} \dfrac{1}{\sqrt{1^2+2^2}}=\text{tan}^{-1} \dfrac{1}{2}$

$\bigg(\because \text{sin}^{-1} \dfrac{a}{\sqrt{a^2+b^2}}=\text{tan}^{-1} \dfrac{a}{b}\bigg)$

$\text{cot}^{-1} 3=\text{tan}^{-1} \dfrac{1}{3}$

$\bigg(\because \text{tan}^{-1} a=\text{cot}^{-1} \dfrac{1}{a}\bigg)$

$\text{sin}^{-1} \dfrac{1}{\sqrt{5}}+\text{cot}^{-1} 3=\text{tan}^{-1} \dfrac{1}{2}+\text{tan}^{-1} \dfrac{1}{3}=45^{\circ}$

$(\because \text{from} (1)\ )$

$\text{tan}^{-1} \dfrac{1}{2}+\text{tan}^{-1} \dfrac{1}{3}=\text{sin}^{-1} \dfrac{1}{\sqrt{5}}+\text{cot}^{-1} 3=45^{\circ}$

Hence Proved

Prove that:
$2 \tan^{-1} \dfrac{1}{5} + \tan^{-1} \dfrac{1}{7} + 2 \tan^{-1} \dfrac{1}{8} = \dfrac{\pi}{4}$

As we know that

$\text{tan}^{-1} a+\text{tan}^{-1} b=\text{tan}^{-1} \dfrac{a+b}{1-a b},ab <1$

$2\text{tan}^{-1} \dfrac{1}{5}+\text{tan}^{-1} \dfrac{1}{7}+2\text{tan}^{-1} \dfrac{1}{8}=2\bigg(\text{tan}^{-1} \dfrac{1}{5}+\text{tan}^{-1} \dfrac{1}{8}\bigg)+\text{tan}^{-1} \dfrac{1}{7}$

$=2\text{tan}^{-1} \dfrac{\dfrac{1}{5}+\dfrac{1}{8}}{1-\dfrac{1}{5}\times \dfrac{1}{8}}+\text{tan}^{-1} \dfrac{1}{8}$

$=2\text{tan}^{-1} \dfrac{1}{3}+\text{tan}^{-1} \dfrac{1}{8}$

$=\text{tan}^{-1} \dfrac{2\times \dfrac{1}{3}}{1-\bigg(\dfrac{1}{3}\bigg)^2}+\text{tan}^{-1} \dfrac{1}{8}$

$\bigg(\because 2\text{tan}^{-1} a=\text{tan}^{-1} \dfrac{2 a}{1- a^2},a<1\bigg)$

$=\text{tan}^{-1} \dfrac{3}{4}+\text{tan}^{-1} \dfrac{1}{8}$

$=\text{tan}^{-1} \dfrac{\dfrac{3}{4}+\dfrac{1}{7}}{1-\dfrac{3}{4}\times \dfrac{1}{7}}$

$\bigg(\because \text{tan}^{-1} a+\text{tan}^{-1} b=\text{tan}^{-1} \dfrac{a+b}{1-a b},ab <1\bigg)$

$=\text{tan}^{-1} 1=\dfrac{\pi}{4}$

$2\text{tan}^{-1} \dfrac{1}{5}+\text{tan}^{-1} \dfrac{1}{7}+2\text{tan}^{-1} \dfrac{1}{8}=\dfrac{\pi}{4}$

Hence Proved

Prove that:
$\sin^{-1} \dfrac{5}{13} + \sin^{-1} \dfrac{7}{25} = \cos^{-1} \left(\dfrac{253}{325} \right)$ .

Let

$\text{sin}^{-1} \dfrac{5}{13}=\theta\implies \sin \theta=\dfrac{5}{13}$

$\cos \theta=\sqrt{1-\sin^2 \theta}=\sqrt{1-\bigg(\dfrac{5}{13}\bigg)^2}=\dfrac{12}{13}$

And also let

$\text{sin}^{-1} \dfrac{7}{25}=\phi\implies \sin \phi=\dfrac{7}{25}$

$\cos \phi=\sqrt{1-\sin^2 \phi}=\sqrt{1-\bigg(\dfrac{7}{25}\bigg)^2}=\dfrac{24}{25}$

As we know that

$\cos (A+B)=\cos A\cos B-\sin A\sin B$

$\cos (\theta+\phi)=\cos \theta\cos \phi-\sin \theta\sin \phi=\dfrac{12}{13}\times \dfrac{24}{25}-\dfrac{5}{13}\times \dfrac{7}{25}=\dfrac{253}{325}$

$\implies \theta+\phi=\text{cos}^{-1} \bigg(\dfrac{253}{325}\bigg)$

$\implies \text{sin}^{-1} \dfrac{5}{13}+\text{sin}^{-1} \dfrac{7}{25}=\text{cos}^{-1} \bigg(\dfrac{253}{325}\bigg)$

Hence Proved

Prove that:
$4 \tan^{-1} \dfrac{1}{5} - \tan^{-1} \dfrac{1}{70} + \tan^{-1} \dfrac{1}{99} = \dfrac{\pi}{4}$

Let

$\text{tan}^{-1} \dfrac{1}{5}=\theta\implies \tan \theta=\dfrac{1}{5}$

As we know that

$\tan 2 A=\dfrac{2\tan A}{1-\tan^2 A}$

$\tan 2\theta=\dfrac{2\tan A}{1-\tan^2 A}=\dfrac{2\times \dfrac{1}{5}}{1-\bigg(\dfrac{1}{5}\bigg)^2}=\dfrac{\dfrac{2}{5}}{1-\dfrac{1}{25}}=\dfrac{5}{12}$

$\implies \tan 4\theta=\dfrac{2\tan 2\theta}{1-\tan^2 2\theta}=\dfrac{2\times \dfrac{5}{12}}{1-\bigg(\dfrac{5}{12}\bigg)^2}=\dfrac{120}{119}$

$\implies 4\theta=\text{tan}^{-1}\bigg(\dfrac{120}{119}\bigg)$

$\implies 4\ \text{tan}^{-1} \dfrac{1}{5}=\text{tan}^{-1} \dfrac{120}{119}$

$4\text{tan}^{-1} \dfrac{1}{5}-\text{tan}^{-1} \dfrac{1}{70}+\text{tan}^{-1} \dfrac{1}{99}=\text{tan}^{-1} \dfrac{120}{119}-\text{tan}^{-1} \dfrac{1}{70}+\text{tan}^{-1} \dfrac{1}{99}$

$=\text{tan}^{-1} \dfrac{\dfrac{120}{119}-\dfrac{1}{70}}{1+\dfrac{120}{119}\times \dfrac{1}{70}}+\text{tan}^{-1} \dfrac{1}{99}$

$\bigg(\because \text{tan}^{-1} a-\text{tan}^{-1} b=\text{tan}^{-1} \dfrac{a-b}{1+a b},ab>-1\bigg)$

$=\text{tan}^{-1} \dfrac{49}{50}+\text{tan}^{-1} \dfrac{1}{99}$

$=\text{tan}^{-1} \dfrac{\dfrac{49}{50}+\dfrac{1}{99}}{1-\dfrac{49}{50}\times \dfrac{1}{99}}$

$\bigg(\because \text{tan}^{-1} a+\text{tan}^{-1} b=\text{tan}^{-1} \dfrac{a+b}{1-a b},ab<1\bigg)$

$=\text{tan}^{-1} 1=\dfrac{\pi}{4}$

$\therefore$

$4\text{tan}^{-1} \dfrac{1}{5}-\text{tan}^{-1} \dfrac{1}{70}+\text{tan}^{-1} \dfrac{1}{99}=\dfrac{\pi}{4}$

Hence Proved

Solve the equation.
$\sin^{-1} \dfrac{5}{x} + \sin^{-1} \dfrac{12}{x} = \dfrac{\pi}{2}$

$sin^{-1}\dfrac{5}{x}+sin^{-1}\dfrac{12}{x}=\dfrac{\pi}{2}$

$sin^{-1}\dfrac{5}{x}=\dfrac{\pi}{2}-sin^{-1}\dfrac{12}{x}$

we know

$sin^{-1}x=\dfrac{\pi}{2}-cos^{-1}x$

$sin^{-1}\dfrac{5}{x}=cos^{-1}\dfrac{12}{x}$

$cos^{-1}\dfrac{\sqrt{x^2-25}}{x}=cos^{-1}\dfrac{12}{x}$

$\dfrac{\sqrt{x^2-25}}{x}=\dfrac{12}{x}$

$x \neq 0$

$\implies$

$\sqrt{x^2-25}=12$

Squaring on both sides

$x^2-25=144$

$x^2=144+25$

$x^2=169$

$x=13$

$x \neq -13$ because The given satisifies for only

$x>0$

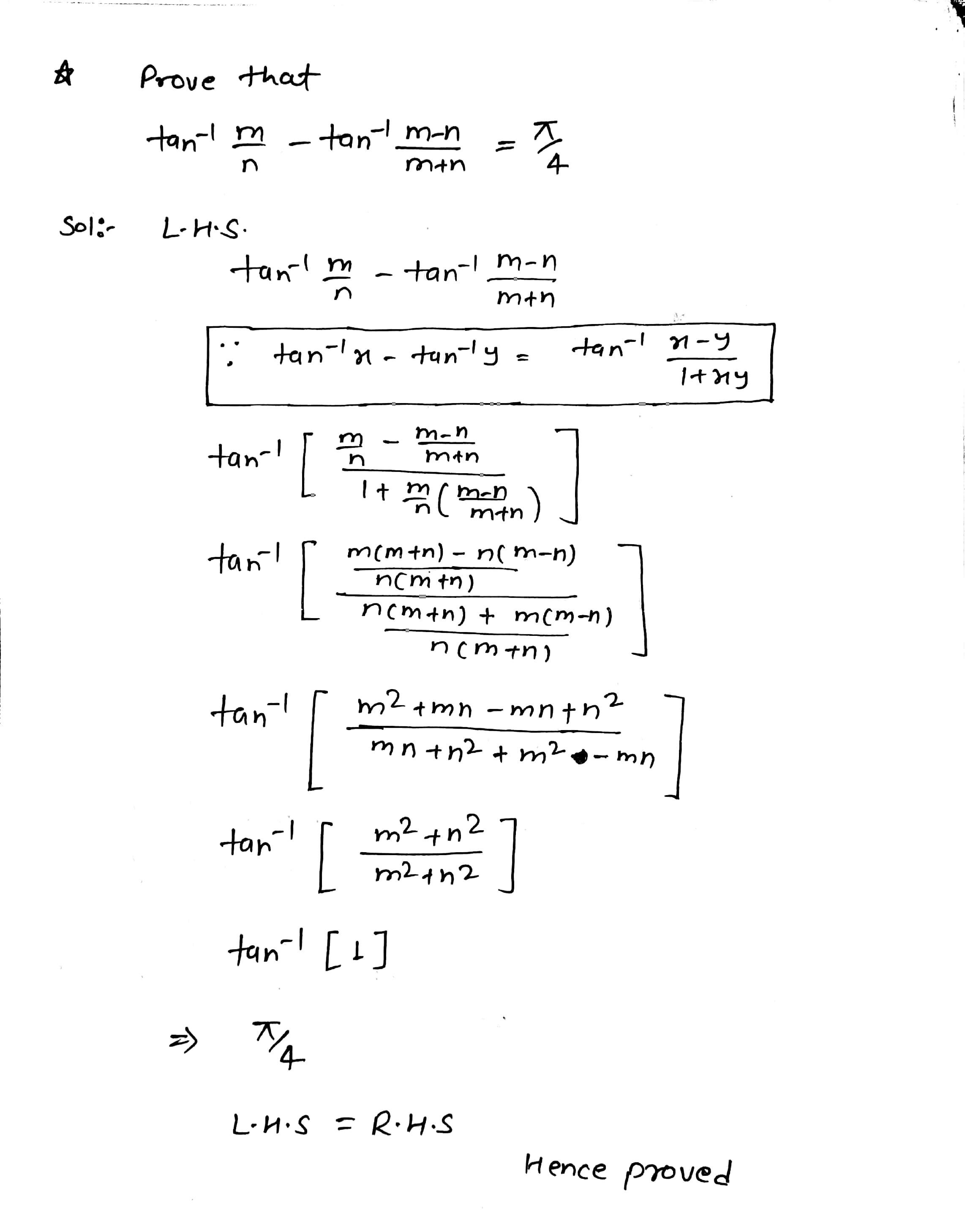
Prove that:
$\tan^{-1} \dfrac{m}{n} - \tan^{-1} \dfrac{m - n}{m + n} = \dfrac{\pi}{4}$

1588758_1733683_ans_31fc501929924d6b939dd1a7bff14821.jpg

Solve the equation.
$\cos^{-1} \dfrac{x^2 - 1}{x^2 + 1} + \tan^{-1} \dfrac{2x}{x^2 - 1} = \dfrac{2\pi}{3}$

1714986_1733752_ans_a2431f11c60e4bd89ae306c127969e7d.jpeg

Solve the equation.
$2 \tan^{-1} x = \cos^{-1} \dfrac{1 - a^2}{1 + a^2} - \cos^{-1} \dfrac{1 - b^2}{1 + b^2}$

$2tan^{-1}x=cos^{-1}\dfrac{1-a^2}{1+a^2}-cos^{-1}\dfrac{1-b^2}{1+b^2}$

$2tan^{-1}a-2tan^{-1}b=2tan^{-1}x$ because we know that

$2tan^{-1}x=cos^{-1}\dfrac{1-x^2}{1+x^2}$

$2(tan^{-1}a-tan^{-1}b)=2tan^{-1}x$

$tan^{-1}a-tan^{-1}b=tan^{-1}x$

We know that

$tan^{-1}x-tan^{-1}y=tan^{-1}({\dfrac{x-y}{1+xy}})$

$\implies$

$tan^{-1}\dfrac{a-b}{1+ab}=tan^{-1}x$

$\implies$

$x=\dfrac{a-b}{1+ab}$

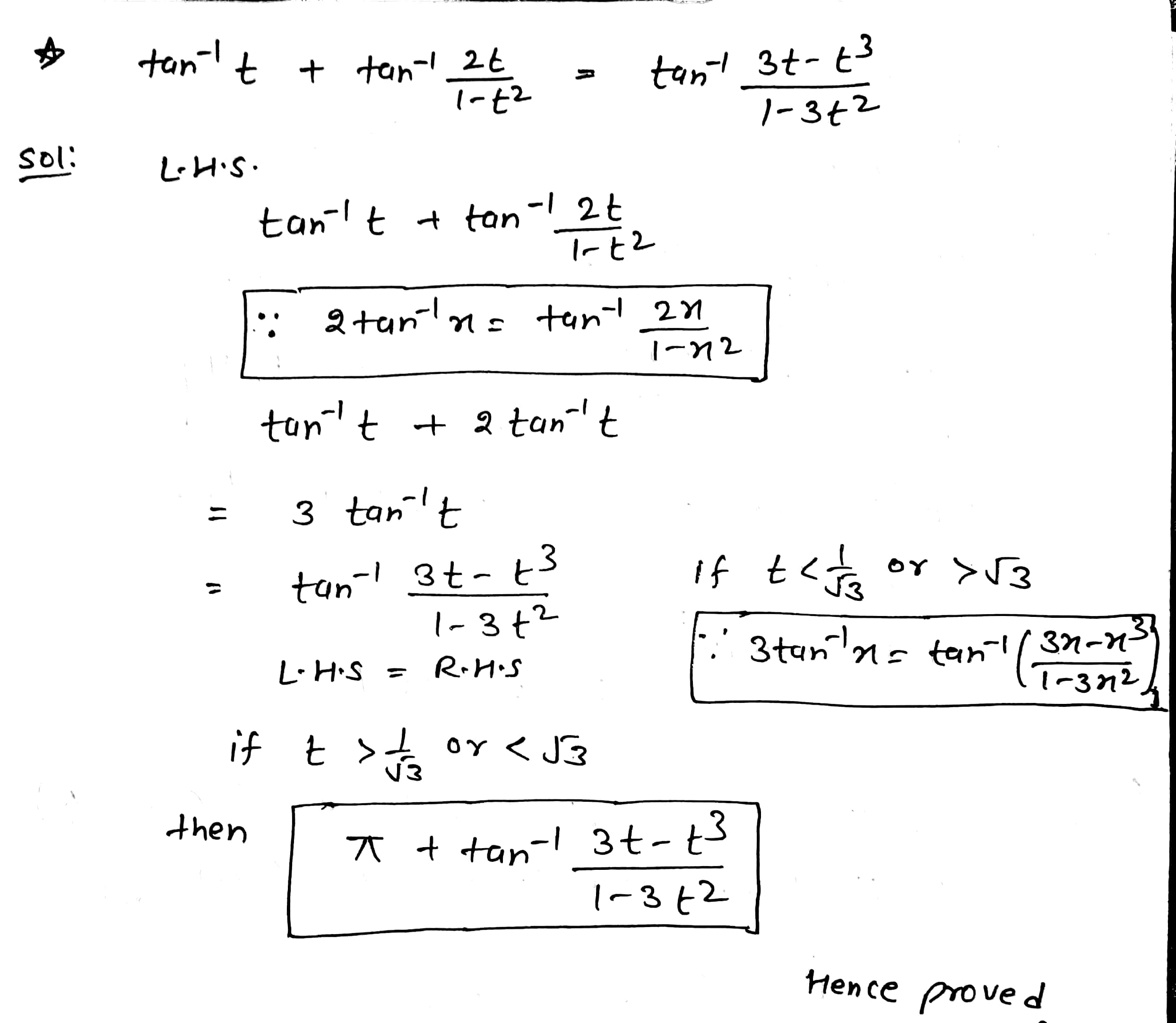
Prove that:
$\tan^{-1} t + \tan^{-1} \dfrac{2t}{1 - t^2} = \tan^{-1} \dfrac{3t - t^3}{1 - 3t^2} , t$ being positive, if $t < \dfrac{1}{\sqrt{3}}$ or $> \sqrt{3}$ ,
and
$\tan^{-1} t + \tan^{-1} \dfrac{2t}{1 - t^2}= \pi + \tan^{-1} \dfrac{3t - t^3}{1 - 3t^2}$ if $t > \dfrac{1}{\sqrt{3}}$ and $< \sqrt{3}$

1588760_1733688_ans_4191b0cfd94c4254aab6523630ddfc70.jpg

Prove that:
$\tan^{-1} \dfrac{1}{3} + \tan^{-1} \dfrac{1}{5} + \tan^{-1} \dfrac{1}{7} + \tan^{-1} \dfrac{1}{8} = \dfrac{\pi}{4}$

As we know that

$\text{tan}^{-1} a+\text{tan}^{-1} b=\text{tan}^{-1} \dfrac{a+b}{1-a b},ab <1$

$\text{tan}^{-1} \dfrac{1}{3}+\text{tan}^{-1} \dfrac{1}{5}+\text{tan}^{-1} \dfrac{1}{7}+\text{tan}^{-1} \dfrac{1}{8}=\text{tan}^{-1} \dfrac{\dfrac{1}{3}+\dfrac{1}{5}}{1-\dfrac{1}{3}\times \dfrac{1}{5}}+\text{tan}^{-1} \dfrac{\dfrac{1}{7}+\dfrac{1}{8}}{1-\dfrac{1}{7}\times \dfrac{1}{8}}$

$=\text{tan}^{-1} \dfrac{4}{7}+\text{tan}^{-1} \dfrac{3}{11}$

$=\text{tan}^{-1} \dfrac{\dfrac{4}{7}+\dfrac{3}{11}}{1-\dfrac{4}{7}\times \dfrac{3}{11}}$

$=\text{tan}^{-1} 1=\dfrac{\pi}{4}$

$\therefore \text{tan}^{-1} \dfrac{1}{3}+\text{tan}^{-1} \dfrac{1}{5}+\text{tan}^{-1} \dfrac{1}{7}+\text{tan}^{-1} \dfrac{1}{8}=\dfrac{\pi}{4}$

Hence Proved

If $\phi = \tan^{-1} \dfrac{x\sqrt{3}}{2k - x}$ , and $\theta = \tan^{-1}\dfrac{2x-k}{k\sqrt{3}}$ , prove that one value of $\phi -\theta$ is $30^o$ .

1714556_1733744_ans_f31b7d69640549b8ad3b29cf1cc1c0a9.jpeg

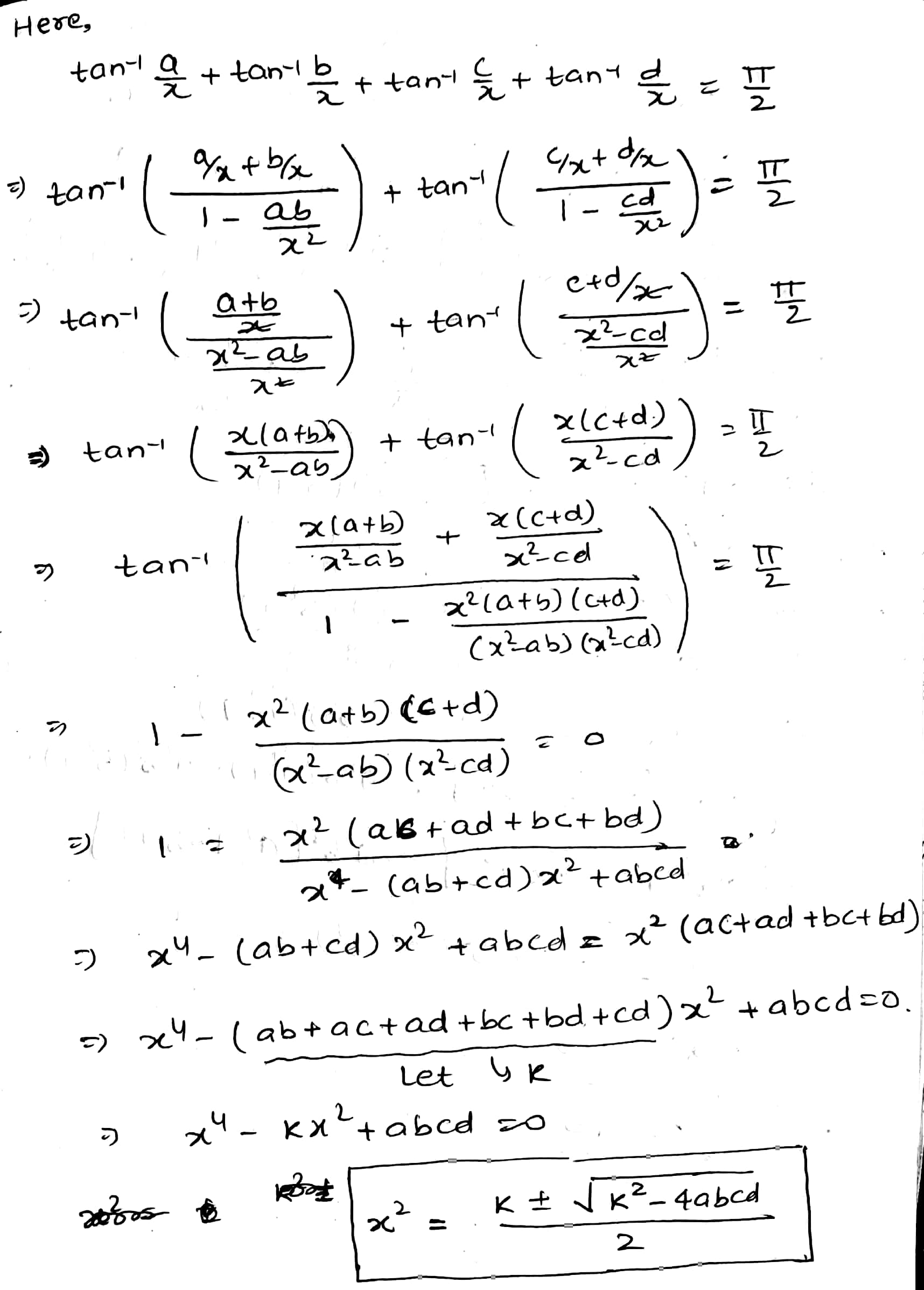
Solve the equation.
$\tan^{-1} \dfrac{a}{x} + \tan^{-1} \dfrac{b}{x} + \tan^{-1} \dfrac{c}{x} + \tan^{-1} \dfrac{d}{x} = \dfrac{\pi}{2}$

1714537_1733764_ans_347c4ef4b70e45cebb1efb88ce4f1a53.jpeg

Find the range of $f(x) =\cot^{-1}(2x-x^{2})$

Let

$\theta=\cot^{-1}(2x-x^{2})$ , where

$\theta\in(0,\pi)$

$\Rightarrow\cot\theta=2x-x^{2}$ , where

$\theta\in(0,\pi)$

$=1-(1-2x+x^{2})$ , where

$\theta\in(0,\pi)$

$=1-(1-x)^2$ , where

$\theta\in(0,\pi)$

$\Rightarrow\cot\theta\leq1$ , where

$\theta\in(0,\pi)\Rightarrow \dfrac{\pi}{4}\leq\theta<\pi\Rightarrow$ Range of f(x} is

$\bigg[\dfrac{\pi}{4},\pi\bigg)$

Find the set of values of parameter a so that the equation $(sin^{-1}x)^3+(cos^{-1}x)^3=a\pi^2$ has a solution

Let

$y = (\sin^{-1}x)^{3}+(\cos^{-1}x)^{3} = (\sin^{-1}x+\cos^{-1}x)[(\sin^{-1}x)^2+(\cos^{-1}x)^2-\sin^{-1}x.\cos^{-1}x]$

$\Rightarrow y = \cfrac{\pi}{2}[(\sin^{1-}x+\cos^{-1}x)^2-3\sin^{-1}x.\cos^{-1}x]$

$\Rightarrow y = \cfrac{\pi}{2}\left[\cfrac{\pi^2}{4}-3\sin^{-1}x\left(\cfrac{\pi}{2}-\sin^{-1}x\right)\right ]$

$\Rightarrow y = \cfrac{\pi}{2}\left[\cfrac{\pi^2}{16}+3\left(\cfrac{\pi}{4}-\sin^{-1}x\right)^2\right ]$
Now we know,

$-\cfrac{\pi}{2} \leq \sin^{-1}x \leq \cfrac{\pi}{2}$
Thus range of y is

$\left[\cfrac{\pi^3}{32}, \cfrac{7\pi^3}{8}\right]$
Thus given equation to have a solution

$a \in \left[\cfrac{1}{32}, \cfrac{7}{8}\right]$

If the roots of the equation $x^3 - 10x+ 11 = 0$ are u,v and w. Then the value of $3cosec^2(\tan^{-1}u+\tan^{-1}v+\tan^{-1}w)$ is

Let

$\tan^{-1}u=\alpha\Rightarrow\tan\alpha=u$

$\tan^{-1}v=\beta\Rightarrow\tan\beta=v$

$\tan^{-1}w=\gamma\Rightarrow\tan\gamma=w$

$\tan(\alpha+\beta+\gamma)=\dfrac{s_1-s_3}{1-s_2}=\dfrac{0-(-11)}{1-(-10)}=1$

$\therefore\alpha+\beta+\gamma=\dfrac{\pi}{4}$

$\Rightarrow3cosec^2(\tan^{-1}u+\tan^{-1}v+\tan^{-1}w)=6$

Find the sum $cosec^{-1}\sqrt{10}+cosec^{-1}\sqrt{50}+cosec^{-1}\sqrt{170}+...+cosec^{-1}\sqrt{(n^2+1)(n^2+2n+2)}.$

Let

$\theta =cosec^{-1}\sqrt{(n^2+1)(n^2+2n+2)}$

$\Rightarrow cosec^2\theta=(n^2+1)(n^2+2n+2)= (n^2 + 1)^2 +2n(n^2 + 1)+n^2 + 1=(n^2+n+ 1)^2 +1$

$\Rightarrow cot^2\theta=(n^2+n+ 1)^2$

$\Rightarrow tan\theta=\dfrac{1}{(n^2+n+ 1)}=\dfrac{(n+1)-n}{1+(n+1)n}$

$\Rightarrow \theta=\tan^{-1}\dfrac{1}{(n^2+n+ 1)}=\dfrac{(n+1)-n}{1+(n+1)n}=\tan^{-1}(n+1)-tan^{-1}n$

Thus, the sum of n terms of the given series

$=(tan^{- 1}2 -tan^{-1}1)+(tan^{- 1}3 -tan^{-1}2)+(tan^{- 1}4 -tan^{-1}3)+ ... +\tan^{-1}(n+1)-tan^{-1}n$

$=\tan^{-1}(n+1)-\dfrac{\pi}{4}$

If $tan^{-1}(x+\dfrac{3}{x})-tan^{-1}(x-\dfrac{3}{x})=tan^{-1}\dfrac{6}{x}$ , then the value of $x^4$ is

$\tan^{-1}(x+\dfrac{3}{x})-tan^{-1}(x-\dfrac{3}{x})=tan^{-1}\dfrac{6}{x}$

$\Rightarrow\tan^{-1}\dfrac{(x+\dfrac{3}{x})-(x-\dfrac{3}{x})}{1+(x+\dfrac{3}{x})(x-\dfrac{3}{x})}=tan^{-1}\dfrac{6}{x}$

$\Rightarrow x^2-\dfrac{9}{x^2}=0\,\Rightarrow x^4=9$

If $tan^{-1}y=4tan^{-1}x\,(|x|<tan\dfrac{\pi}{8})$ , find y as an algebraic function of x, and hence, prove that $\tan \pi/8$ is a root of the equation $x^4 - 6x + 1 = 0$ $$

We have

$tan^{-1}y=4tan^{-1}x$

$\Rightarrow\tan^{-1}y=2\tan^{-1}\dfrac{2x}{1-x^2}(as\,|x|<1)$

$=\tan^{-1}\dfrac{\dfrac{4x}{1-x^2}}{1-\dfrac{4x^2}{(1-x^2)^2}}$

$=\tan^{-1}\dfrac{4x(1-x^2)}{x^4-6x^2+1}$

$\Rightarrow y=\dfrac{4x(1-x^2)}{x^4-6x^2+1}$

if

$x=\dfrac{\pi}{8}\Rightarrow tan^{-1}y=4\tan^{-1}x=\dfrac{\pi}{2}\Rightarrow y\rightarrow\infty\Rightarrow x^4-6x^2+1=0$

Hence,

$\tan\dfrac{\pi}{8}$ is a root of

$x^4-6x^2+1=0$

Solve for real values of $x:\dfrac{(sin^{-1}x)^3+(cos^{-1}x)^3}{(tan^{-1}x+cot^{-1}x)^3}=7$

$\displaystyle \frac{(\sin^{-1}x)^{3}+(\cos^{-1}x)^{3}}{(\tan^{-1}x+\cot^{-1}x)^{3}}=7$

We know,

$\tan^{-1}x+\cot^{-1}x =\cfrac{\pi}{2}$

$\Rightarrow (\sin ^{ -1 } x)^{ 3 }+(\cos ^{ -1 } x)^{ 3 }=\frac { 7\pi ^{ 3 } }{ 8 }$

Now Let,

$y = (\sin^{-1}x)^{3}+(\cos^{-1}x)^{3} = (\sin^{-1}x+\cos^{-1}x)[(\sin^{-1}x)^2+(\cos^{-1}x)^2-\sin^{-1}x.\cos^{-1}x]$

$\Rightarrow y = \cfrac{\pi}{2}[(\sin^{1-}x+\cos^{-1}x)^2-3\sin^{-1}x.\cos^{-1}x]$

$\Rightarrow y = \cfrac{\pi}{2}\left[\cfrac{\pi^2}{4}-3\sin^{-1}x\left(\cfrac{\pi}{2}-\sin^{-1}x\right)\right ]$

$\Rightarrow y = \cfrac{\pi}{2}\left[\cfrac{\pi^2}{16}+3\left(\cfrac{\pi}{4}-\sin^{-1}x\right)^2\right ]=\cfrac{7\pi^3}{8}$

After Simplification

$\Rightarrow \sin^{-1}x =-\cfrac{\pi}{2} \Rightarrow x= -1$

Prove that: $2\tan^{-1}{\left(\dfrac{1}{2}\right)}+\tan^{-1}{\left(\dfrac{1}{7}\right)}=\sin^{-1}{\left(\dfrac{31}{25\sqrt{2}}\right)}$

$LHS=2\tan^{-1}{\left(\dfrac{1}{2}\right)}+\tan^{-1}{\left(\dfrac{1}{7}\right)}$

$=\tan^{-1}{\left(\dfrac{2\times\dfrac{1}{2}}{1-\left(\dfrac{1}{2}\right)^{2}}\right)}+\tan^{-1}{\left(\dfrac{1}{7}\right)} \, \, \, \, \,\left[\because 2\tan^{-1}{x}=\tan{\dfrac{2x}{1-x^{2}}}\right]$

$=\tan^{-1}{\left(\dfrac{4}{3}\right)}+\tan^{-1}{\left(\dfrac{1}{7}\right)}$

$=tan^{-1}{\left(\dfrac{\dfrac{4}{3}+\dfrac{1}{7}}{1-\dfrac{4}{3}\times\dfrac{1}{7}}\right)} \, \, \, \, \, \,\left[\because \tan^{-1}{x}+\tan^{-1}{y}=\tan\dfrac{x+y}{1-xy}and \, \,xy<1\right]$

$=\tan^{-1}{\left(\dfrac{28+3}{21}\times\dfrac{21}{21-4}\right)}$

$=\tan^{-1}{\left(\dfrac{31}{17}\right)}$
(Refer image)
Let:

$\tan^{-1}{\left(\dfrac{31}{17}\right)}=\theta \, \, \,\Rightarrow \, \, \, \,\tan\theta=\dfrac{31}{17}$

$\Rightarrow \sin{\theta}=\dfrac{31}{25\sqrt{2}} \, \, \, \,\Rightarrow \theta=\sin^{-1}\left(\dfrac{31}{25\sqrt{2}}\right)$

$\Rightarrow \tan^{-1}{\left(\dfrac{31}{17}\right)}=\sin^{-1}\left(\dfrac{31}{25\sqrt{2}}\right)$

$LHS=RHS$

1639543_1781813_ans_2cfe892bdeb147cbb5439dd5a9fa99e5.JPG

If $\tan^{-1}a+\tan^{-1}b+\tan^{-1}c=\pi$ , then prove that $a+b+c=abc$ .

Firstly, let us assume

$\tan^{-1}a=\alpha \, \, \, \,\Rightarrow \, \, \, \tan\alpha=a$

$\tan^{-1}b=\beta\, \, \, \,\Rightarrow \, \, \, \tan\beta=b$

$\tan^{-1}c=\gamma\, \, \, \,\Rightarrow \, \, \, \tan\gamma=c$

Now, given that

$\tan^{-1}a+\tan^{-1}b+\tan^{-1}c=\pi \, \, \,\Rightarrow \, \,\alpha+\beta+\gamma=\pi$

$\therefore \alpha+\beta=\pi-\gamma$

Taking tangent on both sides, we have

$\tan(\alpha+\beta)=\tan(\pi-\gamma)$

$\Rightarrow \dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha.\tan\beta}= -\tan\gamma$ ......

$\{\because\tan(\pi-\theta)=-\tan\theta\}$

$\Rightarrow \tan\alpha+\tan\beta= -\tan\gamma(1-\tan\alpha.\tan\beta)$

$\Rightarrow \tan\alpha+\tan\beta= -\tan\gamma+\tan\alpha.\tan\beta.\tan\gamma$

$\Rightarrow \tan\alpha+\tan\beta+\tan\gamma=\tan\alpha.\tan\beta.\tan\gamma$

Thus,

$a+b+c=2abc \, \, \,$ Hence proved.

Simplify: $tan^{-1}\left(\dfrac{3sin 2\alpha}{5+3\cos2\alpha}\right)+\tan^{-1}\left(\dfrac{1}{4}\tan\alpha\right)$ , where $-\dfrac{x}{2}<\alpha<\dfrac{x}{2}$

We have,

$\tan^{-1}\left[\dfrac{3\times\dfrac{2\tan\alpha}{1+\tan^{2}\alpha}}{5+3\left(\dfrac{1 \, \,\tan^2\alpha}{1+\tan^2\alpha}\right)}\right]+\tan^{-1}\left(\dfrac{1}{4}\tan\alpha\right)$

$=\tan^{-1}\left[\dfrac{6\tan\alpha}{8+2\tan^{2}\alpha}\right]+\tan^{-1}\left(\dfrac{1}{4}\tan\alpha\right)$

$=\tan^{-1}\left[\dfrac{3\tan\alpha}{4+\tan^{2}\alpha}\right]+\tan^{-1}\left(\dfrac{1}{4}\tan\alpha\right)$

$=\tan^{-1}\left[\dfrac{\dfrac{3\tan\alpha}{4+\tan^{2}\alpha}+\dfrac{1}{4}\tan\alpha}{1-\dfrac{3\tan\alpha}{4+\tan^{2}\alpha}\times\dfrac{1}{4}\tan\alpha}\right]=\tan^{-1} \left[\dfrac{16\tan\alpha+\tan^{2}\alpha}{16+\tan^{2}\alpha}\right]$

$=\tan^{-1}\left[\dfrac{\tan\alpha(16+\tan^{2}\alpha)}{(16+\tan^{2}\alpha)}\right]$

$=\tan^{-1}(\tan\alpha)=\alpha \, \, \, \, \, \, \,\left[\because \alpha \in\left(-\dfrac{x}{2},\dfrac{x}{2}\right)\right]$

Write the simplest form of $\tan^{-1} \left[\dfrac{\sqrt{1 + x^2} - 1}{x}\right]$ .

Let

$x = \tan \theta \Longrightarrow \theta = \tan^{-1} x$

$\Longrightarrow \tan^{-1} \left[\dfrac{\sqrt{1 + x^2} - 1}{x}\right] = \tan^{-1} \left[\dfrac{\sqrt{1 + \tan^2 \theta} - 1}{\tan \theta}\right]$

$= \tan^{-1} \left[\dfrac{\sqrt{\sec^2 \theta} - 1}{\tan \theta}\right] = \tan^{-1} \left[\dfrac{\sec \theta - 1}{\tan \theta}\right]$

$= \tan^{-1} \left[\dfrac{\dfrac{1}{\cos \theta} - 1}{\dfrac{\sin \theta}{\cos \theta}} \right] = \tan^{-1} \left[\dfrac{1 - \cos \theta}{\cos \theta} \times \dfrac{\cos \theta}{\sin \theta}\right]$

$= \tan^{-1} \left[\dfrac{2 \sin^2 \dfrac{\theta}{2}}{2\sin \dfrac{\theta}{2} \cdot \cos \dfrac{\theta}{2}}\right] = \tan^{-1} \left(\tan \dfrac{\theta}{2} \right) = \dfrac{\theta}{2} = \dfrac{1}{2} (\tan^{-1} x)$

Prove that: $\tan^{-1}\left(\dfrac{63}{16}\right)=\sin^{-1}\left(\dfrac{5}{13}\right)+\cos^{-1}\left(\dfrac{3}{5}\right)$

Let

$\sin^{-1}\dfrac{5}{13}=\theta$ and

$\cos^{-1}\dfrac{3}{5}=\varphi$

$\Rightarrow \sin\theta=\dfrac{5}{13} \, \,and \, \,\cos\varphi=\dfrac{3}{5} \, \, \, \, \,\left[\theta\in\left(-\dfrac{x}{2},\dfrac{x}{2}\right)and \, \,\varphi\in/0,\pi/\right]$

$\Rightarrow \cos\theta=+\sqrt{1-\left(\dfrac{5}{13}\right)^{2}}$
and

$\sin\varphi=+\sqrt{1-\left(\dfrac{3}{5}\right)^{2}} \, \, \, \, \,\begin{bmatrix} \because \theta\in\left[-\dfrac{x}{2},\dfrac{x}{2}\right]and \, \,\varphi\in/0,\pi/\\ \Rightarrow \cos\theta \,and \,\sin\varphi \,are \,+ve \end{bmatrix}$

$\Rightarrow \cos\theta=\dfrac{12}{13} \, \,and \, \,\sin\varphi=\dfrac{4}{5}$

$\therefore \tan\theta=\dfrac{5}{13}\times\dfrac{13}{12}=\dfrac{5}{12}, \, \, \,\tan\varphi=\dfrac{4}{5}\times\dfrac{5}{3}=\dfrac{4}{3}$

Now

$\tan(\theta+\varphi)=\dfrac{\tan\theta+\tan\varphi}{1-tan\theta,\tan\varphi}=\dfrac{\dfrac{5}{12}+\dfrac{4}{3}}{1-\dfrac{5}{13}\times\dfrac{4}{2}}=\dfrac{15+48}{36}\times\dfrac{36}{36-20}=\dfrac{63}{16}$

$\Rightarrow \tan(\theta+\varphi)=\dfrac{63}{16} \Rightarrow \, \,\theta+\varphi=\tan^{-1}\dfrac{63}{16}$

If $\sin^{-1}x+\sin^{-1}y+\sin^{-1}z=\pi,$ then prove that:
$x\sqrt{1-x^{2}}+y\sqrt{1-y^{2}}+z\sqrt{1-z^{2}}=2xyz$

Let

$\sin^{-1}x=A \, \, \, \,\Rightarrow \, \, \, \,\sin{A}=x$

$\sin^{-1}y=B \, \, \, \,\Rightarrow \, \, \,\sin{B}=y$

$\sin^{-1}z=C \, \, \, \,\Rightarrow \, \, \,\sin{C}=z$

Given,

$\sin^{-1}x+\sin^{-1}y+\sin^{-1}z=\pi$

$\Rightarrow A+B+C=p \, \,\Rightarrow 2A+2B+2C=2\pi$

So, using trigonometric property,

$\sin2A+\sin2B+\sin2C=4\sin A\sin B\sin C \, \, \, \, \,$

We can write,

$\Rightarrow 2\sin A \cos A+2\sin B \cos B +2\sin C \cos C =4\sin A\sin B\sin C$

$\Rightarrow 2\sin A.\sqrt{1-\sin^{2}A}+2\sin B.\sqrt{1-\sin^{2}B}+\sin C.\sqrt{1-\sin^{2}C}=4\sin A\sin B\sin C$

$2x\sqrt{1-x^{2}}+2y\sqrt{1-y^{2}}+2z\sqrt{1-z^{2}}=4xyz$

$x\sqrt{1-x^{2}}+y\sqrt{1-y^{2}}+z\sqrt{1-z^{2}}=2xyz$

Hence proved

Simplify: $\tan^{-1} \{ \sqrt{1+x^2} - x \}, x\in R$

Let

$x = \cot \theta \Longrightarrow \cot^{-1} x$

Now,

$\tan^{-1} \{\sqrt{1 + x^2} - x \} = \tan^{-1} \{ \sqrt{1 + \cot^2 \theta} - \cot \theta \}$

$= \tan^{-1} \{ \sqrt{cosec^2 \,\theta} - \cot \theta \}$

$= \tan^{-1} \{ cosec \,\theta - \cot \theta \}$

$= \tan^{-1} \left \{ \dfrac{1}{\sin \theta} - \dfrac{\cos \theta}{\sin \theta} \right \}$

$= \tan^{-1} \left \{ \dfrac{1 - \cos \theta}{\sin \theta} \right \}$

$= \tan^{-1} \left \{\dfrac{2 \sin^2 \dfrac{\theta}{2}}{2 \sin \dfrac{\theta}{2} \cos \dfrac{\theta}{2}} \right \}$

$= \tan^{-1} \left \{ \dfrac{\sin \dfrac{\theta}{2}}{\cos \dfrac{\theta}{2}} \right \}$

$= \tan^{-1} \left(\tan \dfrac{\theta}{2} \right) = \dfrac{\theta}{2} = \dfrac{1}{2} \cot^{-1} x$

Solve the equation $\tan^{-1}\dfrac{x+1}{x-1}+\tan^{-1}\dfrac{x+1}{x}=tan^{-1}(-7)$

$\dfrac{tan\Bigg[\tan^{-1}\dfrac{x+1}{x-1}\Bigg]+tan\Bigg[\tan^{-1}\dfrac{x+1}{x}\Bigg]}{1-tan\Bigg[\tan^{-1}\dfrac{x+1}{x-1}\Bigg]tan\Bigg[\tan^{-1}\dfrac{x+1}{x}\Bigg]}=tan(tan^{-1}(-7))=-7$

$\Rightarrow\dfrac{\Bigg[\dfrac{x+1}{x-1}\Bigg]+\Bigg[\dfrac{x+1}{x}\Bigg]}{1-\Bigg[\dfrac{x+1}{x-1}\Bigg]\Bigg[\dfrac{x+1}{x}\Bigg]}=-7$

$\Rightarrow\dfrac{2x^2-x+1}{1-x}=-7$

so that x = 2. ·

This value ll)akes the left-hand side of the given equation positive, ·so there is no value of x strictly
satisfying the given equation.
The value x = 2 ts a solution of the equation

$\tan^{-1}\dfrac{x+1}{x-1}+\tan^{-1}\dfrac{x+1}{x}=\pi+tan^{-1}(-7)$

Does the following trigonometric equatio have any solutions? If yes, obtain the soultions(s):
$\tan^{-1}\left(\dfrac{x+1}{x-1}\right)+\tan^{-1}\left(\dfrac{x-1}{x}\right)=-tan^{-1}7$

$\tan^{-1}\left(\dfrac{x+1}{x-1}\right)+\tan^{-1}\left(\dfrac{x-1}{x}\right)= -\tan^{-1}7$

$\Rightarrow \tan^{-1}\left[\dfrac{\left(\dfrac{x+1}{x-1}\right)+\left(\dfrac{x-1}{x}\right)}{1-\left(\dfrac{x+1}{x-1}\right)\left(\dfrac{x-1}{x}\right)}\right]= -\tan^{-1}7, if \left(\dfrac{x+1}{x-1}\right)\left(\dfrac{x-1}{x}\right)<1.....(*)$

$\Rightarrow \tan^{-1}\left[\dfrac{x(x+1)+(x-1)^2}{(x-1)x-(x+1)(x-1)}\right]= -\tan^{-1} 7$

$\Rightarrow \dfrac{(x^2+x)+(x^2+1-2x)}{(x^2-x)-(x^2-1)}=\tan [-\tan^{-1}7]$

$\Rightarrow \dfrac{2x^2-x+1}{x+1}=-7 \, \, \, \,\Rightarrow 2x^2=8x+8=0 \, \, \, \, \, \,\Rightarrow 2(x^2-4x+4)=0$

$\Rightarrow (x-2)^{2}=0 \, \, \, \, \, \, \, \Rightarrow x=2$
Let us now verify whether

$x=2$ satisfies the condition (*)
For

$x=2$ ,

$\left(\dfrac{x+1}{x-1}\right)\left(\dfrac{x-1}{x}\right)=3\times\dfrac{1}{2}=\dfrac{3}{2}$ which is not less than

$1$ .
Hence, this value does not satisfy the condition(*)
i.e., there is no solution of the given trigonometric equation.

Express in the simplest form:
$\tan - 1 \left(\dfrac{\cos x - \sin x}{\cos x + \sin x}\right), -\dfrac{\pi}{4} < x < \dfrac{\pi}{4}$

We have,

$\tan^{-1} \left(\dfrac{\cos x - \sin x}{\cos x + \sin x}\right)$

Dividing numerator and denominator by

$\cos x$ we get

$\tan^{-1} \left(\dfrac{\cos x - \sin x}{\cos x + \sin x}\right)$

$= \tan^{-1} \left(\dfrac{1 - \tan x}{1 + \tan x}\right)$

$\tan^{-1} \left \{ \tan \left(\dfrac{\pi}{4} - x\right) \right \} = \dfrac{\pi}{4} - x$

$\begin{bmatrix} \because - \dfrac{\pi}{4} < x < \dfrac{\pi}{4}\\ \Longrightarrow \dfrac{\pi}{4} > - x > -\dfrac{\pi}{4}\\ \Longrightarrow \dfrac{\pi}{4} + \dfrac{\pi}{4} > \dfrac{\pi}{4} - x > - \dfrac{\pi}{4} + \dfrac{\pi}{4}\\ \Longrightarrow \left(\dfrac{\pi}{4} - x\right) \in \left(0, \dfrac{\pi}{2}\right)\end{bmatrix}$

Prove that: $\tan^{-1} \left(\dfrac{1}{2}\right) + \tan^{-1} \left(\dfrac{1}{5}\right) + \tan^{-1} \left(\dfrac{1}{8}\right) = \dfrac{\pi}{4}$

$= \tan^{-1} \left(\dfrac{1}{2}\right) + \tan^{-1} \left(\dfrac{1}{5}\right) + \tan^{-1} \left(\dfrac{1}{8}\right)$

$= \tan^{-1} \dfrac{\dfrac{1}{2} + \dfrac{1}{5}}{1 - \dfrac{1}{2} \times \dfrac{1}{5}} + \tan^{-1} \left(\dfrac{1}{8}\right)$

$\left[ \because \dfrac{1}{2} \times \dfrac{1}{5} = \dfrac{1}{10} < 1 \right]$

$= \tan^{-1} \left(\dfrac{7}{9}\right) + \tan^{-1} \left(\dfrac{1}{8}\right) = \tan^{-1} \left(\dfrac{\dfrac{7}{9} + \dfrac{1}{8}}{1 - \dfrac{7}{9} \times \dfrac{1}{8}}\right) = \tan^{-1} \left(\dfrac{65}{72} \times \dfrac{72}{65} \right)$

$=\tan^{-1} (1) = \dfrac{\pi}{4} = RHS$

Prove the following:
$\cot^{-1} \left(\dfrac{xy + 1}{x - y}\right) + \cot^{-1} \left(\dfrac{yz + 1}{y - z}\right) + \cot^{-1} \left(\dfrac{zx + 1}{z - x}\right) = 0$ $(0 < xy, yx, zx < 1)$

$LHS = \cot^{-1} \left(\dfrac{xy + 1}{x - y}\right) + \cot^{-1} \left(\dfrac{yz + 1}{y - z}\right) + \cot^{-1} \left(\dfrac{zx + 1}{z - x}\right) = 0$

$= \tan^{-1} \left(\dfrac{x - y}{1 - xy}\right) + \tan^{-1} \left(\dfrac{y - z}{1 + yz}\right) + \tan^{-1} \left(\dfrac{z - x}{1 + zx}\right) = 0$

$= \tan^{-1} x - \tan^{-1} y + \tan^{-1} y - \tan^{-1} z + \tan^{-1} z + \tan^{-1} x$

$= 0 = RHS$

Write the value of $\cot(\tan^{-1}a+\cot^{-1}a)$ .

$\cot(\tan^{-1}a + \cot^{-1}a)=\cot\dfrac{\pi}{2}=0$

$\left[Note:\tan^{-1}x + \cot^{-1}x= \dfrac{\pi}{2}\forall \,x \in \,R\right]$

Prove that: $\tan^{-1} \left(\dfrac{1}{4}\right) + \tan^{-1} \left(\dfrac{2}{9}\right) = \dfrac{1}{2} \cos ^{-1}\left(\dfrac{3}{5}\right)$

$LHS = \tan^{-1} \left(\dfrac{1}{4}\right) + \tan^{-1} \left(\dfrac{2}{9}\right)$

$= \tan^{-1} \dfrac{\dfrac{1}{4}} + \dfrac{2}{9}{1 - \dfrac{1}{4} - \dfrac{2}{9}}$

$\left[\because \dfrac{1}{4} \times \dfrac{2}{9} < 1 \right]$

$= \tan^{-1} \left(\dfrac{17}{36} \times \dfrac{36}{34}\right) = \tan^{-1} \left(\dfrac{1}{2}\right) = \dfrac{1}{2} \cdot 2 \tan^{-1} \left(\dfrac{1}{2}\right)$

$\dfrac{1}{2} \cos^{-1} \dfrac{1 - \left(\dfrac{1}{2}\right)^2}{1 + \left(\dfrac{1}{2}\right)^2}$

$\begin{bmatrix} \because \dfrac{1}{2} \ge 0\\ \text{and} \,\,2 \tan^{-1} x = \cos^{-1} \dfrac{1 - x^2}{1 + x^2}, x \ge 0 \end{bmatrix}$

$=\dfrac{1}{2} \cos^{-1} \left(\dfrac{3}{4} \times \dfrac{4}{5}\right) = \dfrac{1}{2} \cos^{-1} \left(\dfrac{3}{5}\right) = RHS$

Write the range of one branch of $\sin^{-1}x$ , other than the principal branch

$\left[\dfrac{\pi}{2},\dfrac{3\pi}{2}\right]$

Evaluate: $\tan(\tan^{-1}(-4))$

$\tan(\tan^{-1}(-4))=-4 \, \, \, \, \, \, \,[\because\tan(\tan^{-1}x)=x \, \, \,if \, \,x\in \,R \,and \,-4\in \,R]$

Find the value of $\sin^{-1}\left(\sin\dfrac{4\pi}{5}\right)$

We are given

$\sin^{-1}\left(\sin \dfrac{4\pi}{5}\right)=\sin^{-1}\left(\sin\left(\pi-\dfrac{\pi}{5}\right)\right)=\sin^{-1}\left(\sin\dfrac{\pi}{5}\right)=\dfrac{\pi}{5}$

If $\sin(\sin^{-1}\dfrac{1}{2}+\cos^{-1}x)=1$ , then find the value of $x$ .

We have

$\sin\left(\sin^{-1}\dfrac{1}{2}+\cos^{-1}x\right)=1 \, \, \, \,\Rightarrow \, \, \, \,\sin\left(\sin^{-1}\dfrac{1}{2}+\cos^{-1}x\right)=\sin\dfrac{\pi}{2}$

$\Rightarrow \, \,\sin^{-1}\dfrac{1}{2}+\cos^{-1}x=\dfrac{\pi}{2} \, \, \, \, \,\Rightarrow \, \, \,\dfrac{\pi}{6}+\cos^{-1}x=\dfrac{\pi}{2}$

$\therefore \cos^{-1}x=\dfrac{\pi}{3} \, \, \, \, \, \,\therefore \, \,x=\cos\dfrac{\pi}{3}=\dfrac{1}{2}$

Find the value of $\sin^{-1}\left(\cos\left(\dfrac{43\pi}{5}\right)\right)$ .

$\sin^{-1}\left(\cos\left(8\pi+\dfrac{3\pi}{5}\right)\right)=\sin^{-1}\left(\cos\dfrac{3\pi}{5}\right)$

$=\sin^{-1}\left(\sin\left(\dfrac{\pi}{2}-\dfrac{3\pi}{5}\right)\right)$

$=\sin^{-1}\left(\sin\left(-\dfrac{\pi}{10}\right)\right)=-\dfrac{\pi}{10} \, \, \, \, \,\left[\because -\dfrac{\pi}{10}\in\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\right]$

If $0 < x <1$ , then solve the following for $x$ .
$tan^{-1}(x+1)+tan^{-1}(x-1)=tan^{-1}\left(\dfrac{8}{31}\right)$

Given

$\tan^{-1}(x+1)+\tan^{-1}(x-1)=\tan^{-1}\dfrac{8}{31}$

$\Rightarrow \tan^{-1}\dfrac{-x+1+x-1}{1-(x+1)(x-1)}=\tan^{-1}\dfrac{8}{31} \quad \, \, \,[\because 0<x<1 \, \, \, \,\Rightarrow (x+1)(x-1)<1]$

$\Rightarrow \tan^{-1}\dfrac{2x}{1-x^{2}+1}=\tan^{-1}\dfrac{8}{31} \, \, \, \\\Rightarrow \, \,\tan^{-1}\dfrac{2x}{2-x^2}=\tan^{-1}\dfrac{8}{31}$

$\Rightarrow \dfrac{2x}{2-x^2}=\dfrac{8}{31} \, \\ \Rightarrow 16-8x^2=62x\\ \Rightarrow 4x^2+31x-8=0\\ \Rightarrow 4x^2+32x-x-8=0 \\ \Rightarrow 4x(x+8)-1(x+8)=0\\ \Rightarrow (x+8)(4x-1)=0 \, \\\Rightarrow x=-8 \,or \,x=\dfrac{1}{4}$

$\Rightarrow x=\dfrac{1}{4} \, \, \, \,[\because x=-8$ is not acceptable

$]$

Show that
$2\tan^{-1}(-3)=\dfrac {-\pi}{2}+\tan^{-1}\left(\dfrac {-4}{3}\right)$ .

$LHS=2\tan^{-1}(-3)=-2 \tan^{-1}3 [\because \tan^{-1} (-x) =-\tan^{-1} x, x\in R]$

$=-\left[\cos^{-1}\dfrac {1-3^2}{1+3^2}\right] \quad \left[\because 2\tan^{-1}x=\cos^{-1} \dfrac {1-x^2}{1+x^2} x\ge 0 \right]$

$=-\left[\cos^{-1}\left(\dfrac {-8}{10}\right)\right] =- \left[\cos^{-1} \left(\dfrac {-4}{5}\right)\right]$

$=-\left[\pi -\cos^{-1} \left(\dfrac {4}{5}\right)\right]\ \left\{\because \cos^{-1} (-x) =\pi -\cos^{-1} x, x\in [-1,1] \right\}$

$=-\pi +\cos^{-1} \left(\dfrac 45 \right) \left[let\ \cos^{-1}\ \left(\dfrac 45 \right)=\theta =\dfrac 45 \Rightarrow \tan \theta =\dfrac 34 \Rightarrow \tan^{-1} \dfrac 34\right]$

$=-\pi +\tan^{-1} \left(\dfrac 34 \right)=-\pi +\left[\dfrac {\pi}{2}-\cot^{-1} \left(\dfrac 34 \right)\right]$

$=-\dfrac {\pi}{2}-\cot^{-1} \dfrac {3}{4}=-\dfrac {\pi}{2}-\tan^{-1} \dfrac {4}{3}$

$=- \dfrac {\pi}{2}+\tan^{-1}\left(\dfrac {-4}{3}\right)\quad [\because \tan^{-1}(-x)=-\tan^{-1}x]$

$=RHS$ Hence proved.

If $2\tan^{-1}(\cos \theta)=\tan^{-1}(2\csc \theta)$ , then show that $\theta =\dfrac {\pi}{4}$ , where $n$ is any integer.

We have,

$2\tan^{-1}(\cos \theta)=\tan^{-1}(2\csc \theta)$ ,

$\Rightarrow \ \tan^{-1} \left(\dfrac {2\cos \theta}{1-\cos^2 \theta}\right) =\tan^{-1} (2\csc \theta)$

$\left[\because 2\tan^{-1} x=\tan^{-1} \left(\dfrac {2x}{1-x^2}\right)\right]$

$\Rightarrow \ \left(\dfrac {2\cos \theta}{\sin^2 \theta}\right) =(2\csc \theta)$

$\Rightarrow \ (\cot \theta .2 \csc \theta )=(2\csc \theta )\Rightarrow \cot \theta =1$

$\Rightarrow \ \cot \theta \cot \dfrac {\pi}{2}\Rightarrow \theta =\dfrac {\pi}{4}$

Show that $\cos \left(2\tan^{-1}\dfrac 17 \right) =\sin \left(4\tan^{-1}\dfrac 13 \right)$ .

We have,

$\cos \left(2\tan^{-1}\dfrac 17 \right) =\sin \left(4\tan^{-1}\dfrac 13 \right)$ .

$LHS$

$=\ \cos \left[\cos^{-1}\left(\dfrac {1-\left(\dfrac {1}{7}\right)^2}{1+\left(\dfrac {1}{7}\right)^2}\right) \right]$

$= \ \cos \left[\cos^{-1} \left(\dfrac {\dfrac {48}{48}}{\dfrac {50}{49}} \right) \right]$

$= \ \cos \left[\cos^{-1}\left(\dfrac {48\times 49}{50\times 49}\right) \right]$

$= \ \cos \left[\cos^{-1}\left(\dfrac {24}{25}\right) \right]$

$= \ \cos \left[\cos^{-1} \left(\dfrac {24}{25}\right)\right]$

$= \ \dfrac {24}{25}$

$RHS$

$\sin \left(2.2 \tan^{-1} \dfrac {1}{3}\right) \left[\because 2\tan^{-1} x=\cos^{_1} \left(\dfrac {1-x^2}{1+x^2}\right)\right]$

$=\sin \left[2. \left(\tan^{-1}\dfrac {\dfrac {2}{3}}{1-\left(\dfrac {1}{3}\right)^2} \right)\right]$

$=\sin \left[2\tan^{-1}\left(\dfrac {18}{28}\right) \right]$

$=\sin \left(2\tan^{-1}\dfrac {2}{3}\right)$

$=\sin \left(\sin^{-1} \dfrac {2\times \dfrac {3}{4}}{1+\dfrac {9}{16}}\right)\ \left [\because 2\tan^{-1} x=\sin^{-1} \dfrac {2x}{1+x^2}\right]$

$=\sin \left(\sin^{-1} \dfrac {3/2}{25/16}\right)$

$=\dfrac{48}{50}=\dfrac{24}{25}$

$\because LHS=RHS$ Hence proved

Solve the following for $x:\cos^{-1}\left(\dfrac{x^{2}-1}{x^{2}+1}\right)+\tan^{-1}\left(\dfrac{2x}{x^{2}-1}\right)=\dfrac{2\pi}{3}$

1652830_1783033_ans_85ff59f5a7de4d41af213b4f7c1eff50.jpeg

Find the value of $\tan^{-1}\left(-\dfrac {1}{\sqrt 3}\right)+\cot^{-1}\left(-\dfrac {1}{\sqrt 3}\right)+\tan^{-1}\left[\sin \left(-\dfrac {-\pi}{2}\right)\right]$ .

$\tan^{-1}\left(-\dfrac {1}{\sqrt 3}\right)+\cot^{-1}\left(-\dfrac {1}{\sqrt 3}\right)+\tan^{-1}\left[\sin \left(-\dfrac {-\pi}{2}\right)\right]$ .

$=\tan^{-1}\left(\tan \dfrac {5\pi}{6}\right)+\cot^{-1}\left(\cot \dfrac {\pi}{3}\right)+\tan^{-1}(-1)$

$=\tan^{-1}\left[\tan \left(\pi - \dfrac {\pi}{6}\right)\right]+ \cot^{-1}\left[\cot \left(\dfrac {\pi}{3}\right)\right]+ \tan^{-1}\left[\tan \left(\pi - \dfrac {\pi}{4}\right)\right]$

$=\tan^{-1}\left(-\tan \dfrac {\pi}{6}\right)+ \cot^{-1}\left(\cot \dfrac {\pi}{3}\right) +\tan^{-1}\left(-\tan \dfrac {\pi}{4}\right)$

$\left[ \begin{matrix} \because \tan ^{ -1 }{ \left( \tan { x } \right) } =x,x\in \left( -\dfrac { \pi }{ 2 } ,\dfrac { \pi }{ 2 } \right) , \\ \cot ^{ -1 }{ \left( \cot { x } \right) } =x,x\in \left( 0,\pi \right) \\ and\tan ^{ -1 }{ \left( -x \right) =-\tan ^{ -1 }{ x } } \end{matrix} \right]$

$=-\dfrac {\pi}{6}+\dfrac {\pi}{3}-\dfrac {\pi}{4}=\dfrac {-2\pi +4\pi -3\pi}{12}$

$=\dfrac {-5\pi +4\pi}{12}=\dfrac {-\pi}{12}$

Find the value of $\sin \left(2\tan^{-1}\dfrac 13 \right)+\cos (\tan^{-1} 2\sqrt 2)$

We have,

$\sin \left(2\tan^{-1}\dfrac 13 \right)+\cos (\tan^{-1} 2\sqrt 2)$

$=\sin \left[\sin^{-1}\left\{\dfrac {2\times \dfrac 13}{1+\left(\dfrac 13 \right)^2} \right\} \right]+\cos \left(\cos^{-1} \dfrac 13 \right) \left[\because \tan^{-1} x=\cos^{-1}\dfrac {1}{\sqrt {1+x^2}}\right]$

$\left[ \because 2\tan^{-1}x=\sin^{-1} \dfrac {2x}{1+x^2}, 1\le x \le 1\ and\ \tan^{-1} (2\sqrt 2)=\cos^{-1} \dfrac 13 \right]$

$=\sin \left[\sin^{-1} \left(\dfrac {\dfrac 23}{1+\dfrac 19}\right) \right]+\dfrac 13 \quad \left\{\because \cos (\cos^{-1 x})=x, x\in [-1,1]\right\}$

$=\sin \left[\sin^{-1} \left(\dfrac {2\times 9}{3\times 10}\right)\right]+\dfrac 13 =\sin \left[\sin^{-1} \left(\dfrac {3}{5}\right)\right]+\dfrac 13 [\because \sin (\sin^{-1} x=x)]$

$=\dfrac {3}{5}+\dfrac {1}{3}=\dfrac {9+5}{15}=\dfrac {14}{15}$

Find the value of $\tan\dfrac{1}{2}\left[\sin^{-1}\dfrac{2x}{1+x^{2}}+\cos^{-1}\dfrac{1-y^2}{1+y^2}\right], |x|<1, y>0$ and $xy<1$ .

1652832_1783066_ans_d9aa6b7b51fd4bc9939aa88e0dff04f9.JPG

Find the value of $\tan^{-1}\left(\tan \dfrac {2\pi}{3}\right)$ .

We have,

$\tan^{-1}\left(\tan \dfrac {2\pi}{3}\right) =\tan^{-1} \tan \left(\pi -\dfrac {\pi}{3}\right)$ .

$=\tan^{-1}\left(-\tan \dfrac {\pi}{3}\right) \quad [\because \tan^{-1}(-x) =-\tan^{-1}x]$ .

$=\tan^{-1} \tan \dfrac {\pi}{3} =-\dfrac {\pi}{3}\quad \left[\because \tan^{-1} (\tan x)=x,x\in \left(\dfrac {-\pi}{2}, \dfrac {\pi}{2}\right)\right]$

Note: Remember that,

$\tan^{-1} \left(\tan \dfrac {2\pi}{3}\right)\neq \dfrac {2\pi}{3}$

Since,

$\tan^{-1} (\tan x) =x,$ if

$x\in \left(-\dfrac {\pi}{3}, \dfrac {\pi}{3}\right)$ and

$\dfrac {2\pi}{3}\neq \left(\dfrac {-\pi}{2}, \dfrac {\pi}{2}\right)$

Solve the following equation $\cos (\tan^{-1}x)=\sin \left(\cot^{-1} \dfrac 34 \right)$

We have,

$\cos (\tan^{-1}x)=\sin \left(\cot^{-1} \dfrac 34 \right)$

$\Rightarrow \ \cos \left(\cos^{-1} \dfrac {1}{\sqrt {x^2 +1}}\right)=\sin \left(\sin^{-1}\dfrac {4}{5}\right)$

Let

$\tan^{-1}x=\theta_1 \ \Rightarrow \tan \theta_1 =\dfrac {x}{1}$

$\Rightarrow \ \cos \theta_1 =\dfrac {1}{\sqrt {x^2 +1}}\Rightarrow \theta_1 =\cos^{-1}\dfrac {1}{\sqrt {x^2 +1}}$

And

$\cot^{-1}\dfrac {3}{4}=\theta_2 \Rightarrow \cot \theta_2 =\dfrac {3}{4}$

$\Rightarrow \ \sin \theta_2 \dfrac {4}{5} \Rightarrow \theta_2 \sin^{-1} \dfrac {4}{5}$

$\Rightarrow \ \dfrac {1}{\sqrt {x^2 +1}}=\dfrac {4}{5}$

$\left\{\because \cos (\cos^{-1}x) =x, x\in [-1,1]\ and\ \sin (\sin^{-1}x) =x,x\ \in [-1,1]\right\}$

On squaring both sides, we get

$\Rightarrow \ 16(x^2 +1)=25$

$\Rightarrow \ 15x^2=9$

$\Rightarrow \ x^2 =\left(\dfrac {3}{4}\right)^2$

$\therefore x=\pm \dfrac {3}{4}=\dfrac {-3}{4}, \dfrac {3}{4}$

Evaluate:
$\sin^{-1}\left[\cos \left(\sin^{-1}\dfrac{\sqrt{3}}{2}\right)\right]$

$\sin^{-1}\left[\cos\left(\sin^{-1}\dfrac{\sqrt{3}}{2}\right)\right]$

$=\sin^{-1}\left[\cos\left(\dfrac{\pi}{3}\right)\right]$

$=\sin^{-1}\left[\dfrac{1}{2}\right]=\dfrac{\pi}{6}$

Evaluate:
$\tan^{-1}\sqrt{3}-\sec^{-1}(-2)$

$\tan^{-1}\sqrt{3}-\sec^{-1}(-2)=\tan^{-1}\sqrt{3}-[\pi -\sec^{-1}2]$

$=\dfrac{\pi}{3}-\pi+\cos^{-1}\left(\dfrac{1}{2}\right)$

$=-\dfrac{2\pi}{3}+\dfrac{\pi}{3}=-\dfrac{\pi}{3}$

Find the value of
$\sin \left[2\cot^{-1}\left(\dfrac{-5}{12}\right)\right]$

Let

$\cot^{-1}\left(\dfrac{-5}{12}\right)=y$ . Then

$\cot y=\dfrac{-5}{12}$
Now

$\sin \left[2\cot^{-1}\left(\dfrac{-5}{12}\right)\right]=\sin 2y$

$=2\sin y\cos y=2\left(\dfrac{12}{13}\right)\left(\dfrac{-5}{13}\right)\left[since\ \cot y < 0,\ so\ y\in \left(\dfrac{\pi}{2}, \pi\right)\right]$

$=\dfrac{-120}{196}$

Find the value of
$\sec\left(\tan^{-1}\dfrac{y}{2}\right)$

$\tan^{-1}\dfrac{y}{2}=\theta$ , where

$\theta \in \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$ . So,

$\tan\theta=\dfrac{y}{2}$ , which gives

$\sec\theta=\dfrac{\sqrt{4+y^{2}}}{2}$
Therefore,

$\sec\left(\tan^{-1}\dfrac{y}{2}\right)=\sec\theta=\dfrac{\sqrt{4+y^{2}}}{2}$

Find the value of
$\cos^{-1}\left(\cos\dfrac{13\pi}{6}\right)$

$\cos^{-1}\left(\cos\dfrac{13\pi}{6}\right)=\cos^{-1}\left(\cos\left(2\pi+\dfrac{\pi}{6}\right)\right)=\cos^{-1}\left(\cos \dfrac{\pi}{6}\right)$

$=\dfrac{\pi}{6}$

Find the value of
$\tan^{-1}\left(\tan\dfrac{9\pi}{8}\right)$

$\tan^{-1}\left(\tan\dfrac{9\pi}{8}\right)=\tan^{-1}\tan\left(\pi+\dfrac{\pi}{8}\right)$

$=\tan^{-1}\left(\tan \left(\dfrac{\pi}{8}\right)\right)=\dfrac{\pi}{8}$ .

Evaluate
$\tan^{-1}\left(\sin\left(\dfrac{-\pi}{2}\right)\right)$

$\tan^{-1}\left(\sin \left(\dfrac{-\pi}{2}\right)\right).=\tan^{-1}\left(-\sin \left(\dfrac{\pi}{2}\right)\right)=\tan^{-1}(-1)=-\dfrac{\pi}{4}$

Find value of $\tan (\cos^{-1}x)$ and hence evaluate
$\tan\left(\cos^{-1}\dfrac{8}{17}\right)$

Let

$\cos^{-1}x=\theta$ , then

$\cos \theta=x$ , where

$\theta\in [0, \pi]$
Therefore,

$\tan(\cos^{-1}x)=\tan \theta=\dfrac{\sqrt{1-\cos^{2}\theta}}{\cos\theta}=\dfrac{\sqrt{1-x^{2}}}{x}$
Hence,

$\tan\left(\cos^{-1}\dfrac{8}{17}\right)=\dfrac{\sqrt{1-\left(\dfrac{8}{17}\right)^{2}}}{\dfrac{8}{17}}=\dfrac{15}{8}$

Prove that $\tan (\cot^{-1}x)=\cot (\tan^{-1}x)$ . State with reason whether the equality is valid for all values of $x$ .

Let

$\cot^{-1}x=\theta$ . Then

$\cot\theta=x$
Or,

$\tan\left(\dfrac{\pi}{2}-\theta\right)=x\Rightarrow \tan^{-1}x=\dfrac{\pi}{2}-\theta$
So

$\tan (\cot^{-1}x)=\tan \theta=\cot \big(\dfrac{\pi}{2}-\theta\big)$

$=\cot\left(\dfrac{\pi}{2}-\cot^{-1}x\right)=\cot (\tan^{-1}x)$
The equality is valid for all values of

$x$ since

$\tan^{-1}x$ and

$\cot^{-1}x$ are true for

$x\in R$ .

Evaluate
$\cos\left[\sin^{-1}\dfrac{1}{4}+\sec^{-1}\dfrac{4}{3}\right]$

$=\cos\left[\sin^{-1}\dfrac{1}{4}+\cos^{-1}\dfrac{3}{4}\right]$

$\cos\left(\sin^{-1}\dfrac{1}{4}\right)\cos \left(\cos^{-1}\dfrac{3}{4}\right)-\sin \left(\sin^{-1}\dfrac{1}{4}\right)\sin \left(\cos^{-1}\dfrac{3}{4}\right)$

$=\dfrac{3}{4}\sqrt{1-\dfrac{1^{2}}{4}}-\dfrac{1}{4}\sqrt{1-\dfrac{3^{2}}{4}}$

$=\dfrac{3}{4}\dfrac{\sqrt{15}}{4}-\dfrac{1}{4}\dfrac{\sqrt{7}}{4}=\dfrac{3\sqrt{15}-\sqrt{7}}{16}$

Find the simplified form of
$\cos^{-1}\left(\dfrac{3}{5}\cos x+\dfrac{4}{5}\sin x\right)$ , where $x\in \left[\dfrac{-3\pi}{4}, \dfrac{\pi}{4}\right]$

To find: Simplified form of

$\cos^{-1}\left(\dfrac{3}{5}\cos x+\dfrac{4}{5}\sin x\right), x\in \left[\dfrac{-3\pi}{4}, \dfrac{\pi}{4}\right]$

Let

$\cos y=\dfrac{3}{5}$

$\Rightarrow \sin y=\dfrac{4}{5}$

$\Rightarrow y=\cos^{-1}\dfrac{3}{5}=\sin^{-1}\dfrac{4}{5}=\tan^{-1}\left(\dfrac{4}{3}\right)$

$\therefore \cos^{-1}\left(\dfrac{3}{5}\cos x+\dfrac{4}{5}\sin x\right)\\=\cos^{-1}(\cos y.\cos x+\sin y.\sin x)\\$

$=\cos^{-1}[\cos (y-x)]\quad [\because \cos (A-B)=\cos A\cos B+\sin A\sin B]\\$

$=y-x\\=\tan^{-1}\dfrac{4}{3}-x\qquad \left[\because y=\tan^{-1}\dfrac{4}{3}\right]$

1658341_1796223_ans_90239dea9bcb493d8b4b7fc1391b307a.png

Show that $\tan \left(\dfrac{1}{2}\sin^{-1}\dfrac{3}{4}\right)=\dfrac{4-\sqrt{7}}{3}$ and justify why the other value $\dfrac{4+\sqrt{7}}{3}$ is isgnored?

To prove :

$\tan\left(\dfrac{1}{2}\sin^{-1}\dfrac{3}{4}\right)=\dfrac{4-\sqrt{7}}{3}$

Proof :

Let

$\dfrac{1}{2}\sin ^{-1}\dfrac{3}{4}=\theta\Rightarrow \sin^{-1}\dfrac{3}{4}=2\theta$

$\Rightarrow \sin 2\theta=\dfrac{3}{4}\Rightarrow \dfrac{2\tan \theta}{1+\tan^{2}\theta}=\dfrac{3}{4}$

$\Rightarrow 3+3\tan^{2}\theta=8\tan \theta$

$\Rightarrow 3\tan^{2}\theta-8\tan \theta+3=0$

Let

$\tan \theta=y$

$\therefore 3y^{2}+8y+3=0\\$

$\Rightarrow y=\dfrac{+8\pm \sqrt{64-4\times 3\times 3}}{2\times 3}=\dfrac{8\pm \sqrt{28}}{6}\\$

$\Rightarrow y=\dfrac{2[4\pm \sqrt{7}]}{23}\\$

$\Rightarrow \tan \theta=\dfrac{4\pm \sqrt{7}}{3}$

Since,

$-\dfrac{\pi}{2}\le \sin^{-1}\dfrac{3}{4}\le \dfrac{\pi}{2}$

$\Rightarrow -\dfrac{\pi}{4}\le \dfrac{1}{2}\sin^{-1}\dfrac{3}{4}\le \dfrac{\pi}{4}$

$\Rightarrow -\dfrac{\pi}{4}\le\theta\le \dfrac{\pi}{4}$

$\therefore \tan \left(\dfrac{-\pi}{4}\right)\le \tan\theta\le \tan \dfrac{\pi}{4}$

$\Rightarrow -1\le \tan \theta\le 1$

Ignoring

$\dfrac{4+\sqrt{7}}{3}$ as

$\dfrac{4+\sqrt{7}}{3}>1$ , We get

$\theta=\tan^{-1}\left[\dfrac{4\pm \sqrt{7}}{3}\right]$

$\therefore LHS=\tan\left[\dfrac{1}{2}\sin^{-1}\left(\dfrac{3}{4}\right)\right]$

$=\tan \tan^{-1}\left(\dfrac{4-\sqrt{7}}{3}\right)\\=\dfrac{4-\sqrt{7}}{3}=RHS$

Prove that $\sin^{-1}\dfrac{18}{7}+\sin^{-1}\dfrac{3}{5}=\sin^{-1}\dfrac{77}{85}$

To prove :

$\sin^{-1}\dfrac{8}{17}+\sin^{-1}\dfrac{3}{5}=\sin^{-1}\dfrac{77}{85}$

Proof :

Let

$\sin^{-1}\dfrac{8}{17}=\theta_{1}\Rightarrow \sin \theta_{1}=\dfrac{8}{17}$

$\Rightarrow \tan\theta_{1}=\dfrac{8}{15}\Rightarrow \theta_{1}=\tan^{-1}\dfrac{8}{15}$

And

$\sin^{-1}\dfrac{3}{5}=\theta_{2}\Rightarrow \sin \theta_{2}=\dfrac{3}{5}$

$\Rightarrow \tan\theta_{2}=\dfrac34\Rightarrow \theta_{2}=\tan^{-1}\dfrac34$

$\therefore LHS=\sin^{-1}\dfrac{8}{17}+\sin^{-1}\dfrac{3}{5}=\theta_1+\theta_2$

$=\tan^{-1}\dfrac{8}{15}+\tan^{-1}\dfrac{3}{4}\\$

$=\tan^{-1}\left[\dfrac{\dfrac{8}{15}+\dfrac{3}{4}}{1+\dfrac{8}{15}\times \dfrac{3}{4}}\right]\qquad\left[\because \tan^{-1}x+\tan^{-1}y=\tan^{-1}\left(\dfrac{x+y}{1-xy}\right)\right]\\$

$=\tan^{-1}\left[\dfrac{\dfrac{32+45}{60}}{\dfrac{60-24}{60}}\right]=\tan^{-1}\left(\dfrac{77}{36}\right)\\$

Let

$\theta_{3}=\tan^{-1}\dfrac{77}{36}\Rightarrow \tan \theta_{3}=\dfrac{77}{36}$

$\Rightarrow \sin \theta_{3}=\dfrac{77}{\sqrt{5929}+1296}=\dfrac{77}{85}$

$\therefore \theta_{3}=\sin^{-1}\dfrac{77}{85}$

$\therefore LHS=\theta_3=\sin^{-1}\dfrac{77}{85}=RHS$ Hence proved.

$\text{Alternate Method}$

To prove:

$\sin^{-1}\dfrac{8}{17}+\sin^{-1}\dfrac{3}{5}=\sin^{-1}\dfrac{77}{85}$

Proof:

Let

$\sin^{-1}\dfrac{8}{17}=x$

$\Rightarrow \sin x=\dfrac{8}{17}$

$\Rightarrow \cos x=\sqrt{1-\sin^{2}x}=\sqrt{1-\left(\dfrac{8}{17}\right)^{2}}$

$=\sqrt{\dfrac{289-64}{289}}=\sqrt{\dfrac{225}{289}}=\dfrac{15}{17}$

And

$\sin^{-1}\dfrac{3}{5}=y$

$\Rightarrow \sin y=\dfrac{3}{5}\Rightarrow \sin^{2}y=\dfrac{9}{25}$

$\therefore \cos^{2}y=1-\dfrac{9}{25}$

$\Rightarrow \cos^{2}y=\left(\dfrac{4}{5}\right)^{2}\Rightarrow \cos y=\dfrac{4}{5}$

Now,

$\sin (x+y)=\sin x.\cos y+\cos x.\sin y$

$=\dfrac{8}{17}.\dfrac{4}{5}+\dfrac{15}{17}.\dfrac{3}{5}$

$=\dfrac{32}{85}+\dfrac{45}{85}=\dfrac{77}{85}$

$\Rightarrow (x+y)=\sin^{-1}\left(\dfrac{77}{85}\right)$

$\Rightarrow \sin^{-1}\dfrac{8}{17}+\sin^{-1}\dfrac{3}{5}=\sin^{-1}\dfrac{77}{85}$

The set of values of $\sec^{-1}\dfrac 12$ is _________.

Since, domain of

$\sec^{-1}x$ is

$R- (-1, 1)$

i.e.,

$( -\infty, -1) \cup [ 1, \infty)$

So, no set of values exist for

$\sec^{-1}\dfrac 12$ .

So,

$\phi$ is the answer.

Fill in the blanks in the following:
If $\cos ( \tan^{-1}x+\cot^{-1}\sqrt 3)=0$ , then the value of $x$ is ............

We have,

$\cos ( \tan^{-1}x+\cot^{-1}\sqrt 3 )=0\\\Rightarrow \tan^{-1}x+\cot^{-1}\sqrt 3=\cos^{-1}0\\\Rightarrow \tan^{-1}x+\cot^{-1}\sqrt 3 =\cos^{-1}\cos \dfrac {\pi}{2}\\ \Rightarrow \tan^{-1}x+\cot^{-1}\sqrt 3 =\dfrac{\pi}{2}\\ \Rightarrow \tan^{-1}x=\dfrac {\pi}{2}-\cot^{-1}\sqrt 3\\ \Rightarrow \tan^{-1}x=\tan^{-1}\sqrt 3 \qquad\left[ \because\tan^{-1}x+ \cot^{-1}x=\dfrac {\pi}{2}\right]\\ \therefore x=\sqrt 3$

Fill in the blanks in the following:
The value of $\sin^{-1}\left( \sin \dfrac{3\pi}{5}\right)$ is .........

$\because -\dfrac {\pi}{2} \le \sin^{-1}x \le \dfrac{\pi}{2}$

$\therefore \sin^{-1}\left( \sin \dfrac {3\pi}{5}\right) =\sin^{-1}\sin \left( \pi -\dfrac{2\pi}{5}\right)$

$=\sin^{-1}\left( \sin \dfrac {2\pi}{5}\right) =\dfrac{2\pi}{5}$

Find the value of $4\tan^{-1}\dfrac{1}{5}-\tan^{-1}\dfrac{1}{239}$

We have

$4\tan^{-1}\dfrac{1}{5}-\tan^{-1}\dfrac{1}{239}$

$\\=2\cdot2\tan^{-1}\dfrac{1}{5}-\tan^{-1}\dfrac{1}{239}$

$\\=2\cdot\left[\tan^{-1}\dfrac{\dfrac{2}{5}}{1-\left(\dfrac{1}{5}\right)^{2}}\right]-\tan^{-1}\dfrac{1}{239}\qquad\left[\because 2\tan^{-1}x=\tan^{-1}\left(\dfrac{2x}{1-x^{2}}\right)\right]$

$\\=2\cdot\left[\tan^{-1}\left(\dfrac{\dfrac{2}{5}}{1-\dfrac{1}{25}}\right)\right]-\tan^{-1}\dfrac{1}{239}$

$=2\cdot\left[\tan^{-1}\left(\dfrac{\dfrac{2}{5}}{\dfrac{24}{25}}\right)\right]-\tan^{-1}\dfrac{1}{239}\\$

$=2\tan^{-1}\dfrac{5}{12}-\tan^{-1}\dfrac{1}{239}\\$

$=\tan^{-1}\left(\dfrac{2\dfrac{5}{12}}{1-\left(\dfrac{5}{12}\right)^{2}}\right)-\tan^{-1}\dfrac{1}{239}\qquad\left[\because 2\tan^{-1}x=\tan^{-1}\left(\dfrac{2x}{1-x^{2}}\right)\right]\\$

$=\tan^{-1}\left(\dfrac{\dfrac{5}{6}}{1-\dfrac{25}{144}}\right)-\tan^{-1}\dfrac{1}{239}$

$=\tan^{-1}\left(\dfrac{144\times 5}{119\times 6}\right)-\tan^{-1}\dfrac{1}{239}$

$=\tan^{-1}\left(\dfrac{120}{199}\right)-\tan^{-1}\dfrac{1}{239}$

$=\tan^{-1}\left(\dfrac{\dfrac{120}{119}-\dfrac{1}{139}}{1+\dfrac{120}{199}.\dfrac{1}{239}}\right)\qquad\left[\because \tan^{-1}x-\tan^{-1}y=\tan^{-1}\left(\dfrac{x-y}{1+xy}\right)\right]\\$

$=\tan^{-1}\left(\dfrac{120\times 239-119}{119\times 239+120}\right)\\$

$=\tan^{-1}\left[\dfrac{28680-119}{28441+120}\right]=\tan^{-1}\dfrac{28561}{28561}\\$

$=\tan^{-1}(1)=\tan^{-1}\left(\tan\dfrac{\pi}{4}\right)=\dfrac{\pi}{4}$

Prove that $\tan^{-1}\dfrac{1}{4}+\tan^{-1}\dfrac{2}{9}=\sin^{-1}\dfrac{1}{\sqrt{5}}$

To prove:

$\tan^{-1}\dfrac{1}{4}+\tan^{-1}\dfrac{2}{9}=\sin^{-1}\dfrac{1}{\sqrt{5}}$

Proof:

Let

$\tan^{-1}\dfrac{1}{4}=x\Rightarrow \tan x=\dfrac{1}{4}$

$\Rightarrow \cos x=\dfrac{4}{\sqrt{17}}$

$\Rightarrow \sin x=\dfrac{1}{\sqrt{17}}$

Again, let

$\tan^{-1}\dfrac{2}{9}=y\Rightarrow \tan y=\dfrac{2}{9}$

$\Rightarrow \cos y=\dfrac{9}{\sqrt{85}}$

$\Rightarrow \sin y=\dfrac{2}{\sqrt{85}}$

We know that

$\sin (x+y)=\sin x.\cos y+\cos x.\sin y$

$=\dfrac{1}{\sqrt{17}}.\dfrac{9}{\sqrt{85}}+\dfrac{4}{\sqrt{17}}.\dfrac{2}{\sqrt{85}}$

$=\dfrac{17}{\sqrt{17}.\sqrt{85}}=\dfrac{\sqrt{17}}{\sqrt{17}.\sqrt{5}}=\dfrac{1}{\sqrt{5}}$

$\Rightarrow (x+y)=\sin^{-1}\dfrac{1}{\sqrt{5}}$

$\Rightarrow \tan^{-1}\dfrac{1}{4}+\tan^{-1}\dfrac{2}{9}=\sin^{-1}\dfrac{1}{\sqrt{5}}$ Hence proved.

Fill in the blanks in the following:
If $y=2\tan^{-1}x+\sin^{-1}\left( \dfrac{2x}{1+x^2}\right)$ , then .... $< y <$ ....

We have,

$y=2\tan^{-1}x+\sin^{-1}\dfrac {2x}{1+x^2}$

Let

$x=\tan \theta$

$\therefore y=2\tan^{-1}\tan \theta +\sin^{-1}\dfrac {2\tan \theta }{1+\tan^2 \theta }$

$\Rightarrow y=2\theta +\sin^{-1}\sin 2\theta \quad\left[ \because \sin 2\theta =\dfrac {2\tan \theta }{1+\tan^2 \theta}\right]$

$\Rightarrow y=2\theta +2\theta =4\theta$

$\Rightarrow y=4\tan^{-1}x\qquad [ \because \theta =\tan^{-1}x]$

Now,

$\dfrac{\pi}2 < \tan^{-1}x < \dfrac{\pi }2$

$\therefore -\dfrac {4\pi}{2} < 4\tan^{-1}x < 2\pi\\ \Rightarrow -2\pi < 4\tan^{-1}x < 2\pi\\ \Rightarrow -2\pi < y < 2\pi\qquad [ \because y=\tan^{-1}x]$

Fill in the blanks in the following:
The value of $\cos^{-1}\left( \cos \dfrac{14\pi}{3}\right)$ is ________.

We have

$\cos^{-4}\left( \cos \dfrac {14\pi}{3}\right)=\cos^{-1}\cos \left( 4\pi +\dfrac {2\pi}{3}\right)$

$=\cos^{-1}\cos \dfrac{2\pi}{3}\qquad[ \because \cos (2n\pi +\pi ) =\cos \theta ]$

$=\dfrac {2\pi}{3} \qquad\left[ \because \cos^{-1}( \cos x )=x, x \in [0, \pi ] \right]$

Remember that,

$\cos^{-1}\left( \cos \dfrac {14\pi}{3}\right) \neq \dfrac {14\pi}{3}$

since,

$\dfrac {14\pi}{3} \notin [0, \pi]$

Fill in the blanks in the following:
The value of $\cot^{-1}(-x)x\in R$ in terms of $\cot^{-1}x$ is .........

$\cot^{-1}(-x)=\pi -\cot^{-1}x, x \in R$

Show that $\sin^{-1} \left ( 2x \sqrt{1 - x^{2}} \right ) = 2 \sin^{-1} x$

Let

$x = \sin \theta \Rightarrow \theta = \sin^{-1}x$

$2 x\sqrt{1 - x^{2}} = 2 \sin \theta \sqrt{1 - \sin^{2} \theta}$

$2 \sin \theta \cos \theta = \sin 2 \theta$

$\sin^{-1} \left ( 2x \sqrt{1 - x^{2}} \right ) = \sin^{-1} 2 \theta = 2\sin^{-1} x$

Fill in the blanks in the following:
The result $\tan^{-1}x-\tan^{-1}y=\tan^{-1}\left( \dfrac{x-y}{1+xy}\right)$ is true when value of $xy$ is .......

We know that

$\tan^{-1}x-\tan^{-1}y=\tan^{-1}\left( \dfrac {x-y}{1+xy}\right)$

when,

$xy > -1$

Find the value of $\tan \left ( \tan^{-1} x + \cot^{-1}x\right )$

$\tan^{-1}x + \cot^{-1} x = \dfrac{ \pi}{2}$

$\tan (\tan^{-1}x + \cot^{-1}x)$

$= \tan \dfrac{\pi}{2} = \varphi$ (not defined)

Prove the following: $\tan^{-1}\left[\dfrac{\cos\theta+\sin\theta}{\cos\theta-\sin\theta}\right]=\dfrac{\pi}{4}+\theta$ , if $\theta \epsilon \left(-\dfrac{\pi}{4},\dfrac{\pi}{4}\right)$

$L.H.S.=\tan^{-1}\left[\dfrac{\cos\theta+\sin\theta}{\cos\theta-\sin\theta}\right]$

$=\tan\left[\dfrac{\frac{\cos\theta}{\cos\theta}+\frac{\sin\theta}{\cos\theta}}{\frac{\cos\theta}{\cos\theta}-\frac{\sin\theta}{\cos\theta}}\right]$

$=\tan^{-1}\left(\dfrac{1+\tan\theta}{1-\tan\theta}\right)$

$=\tan^{-1}\left[\dfrac{\tan\dfrac{\pi}{4}+\tan\theta}{1-\tan\dfrac{\pi}{4}\tan\theta}\right]$

$=\tan^{-1}\left[\tan\left(\dfrac{\pi}{4}+\theta\right)\right]$

$=\dfrac{\pi}{4}+\theta \, \, \, \, \,....[\because \tan^{-1}(\tan \theta)=\theta]$

$=R.H.S.$

Fill in the blanks in the following:
The value of $\cos ( \sin^{-1}x+\cos^{-1}x)$ , where $|x| \le 1$ , is .............

We know that

$\sin^{-1}x+\cos^{-1}x=\dfrac {\pi}{2}$ , where

$|x| \le 1$

$\therefore \cos (\sin^{-1}x+\cos^{-1})\\$

$=\cos \dfrac {\pi}{2}=0$

Fill in the blanks in the following:
The value of $\tan \left( \dfrac{\sin^{-1}x+\cos^{-1}x}{2}\right)$ , where $x=\dfrac{\sqrt 3}{2}$ , is ............

We know that

$\sin^{-1}x+\cos^{-1}x=\dfrac {\pi}{2}$ , where

$|x| \le 1$

$\therefore \tan \left( \dfrac {\sin^{-1}x+\cos^{-1}x}{2}\right) =\tan \left( \dfrac {\pi /2}{2}\right)$

$=\tan \dfrac {\pi}{4}=1$

Prove the following: $\tan^{-1}\left[\sqrt{\dfrac{1-\cos\theta}{1+\cos\theta}} \,\right]=\dfrac{\theta}{2}$ ,if $\theta \,\epsilon (-\pi, \pi)$

$\dfrac{1-\cos \theta}{1+\cos \theta}=\dfrac{2\sin^{2}\left(\frac{\theta}{2}\right)}{2\cos^2\left(\frac{\theta}{2}\right)}$

$=\tan^{2}\left(\dfrac{\theta}{2}\right)$

$\therefore \sqrt{\dfrac{1-\cos\theta}{1+\cos\theta}}=\sqrt{\tan^{2}\left(\dfrac{\theta}{2}\right)}$

$=\tan^{2}\left(\dfrac{\theta}{2}\right)$

$\therefore \,L.H.S.=\tan^{-1}[\sqrt{\dfrac{1-\cos\theta}{1+\cos\theta}}$

$=\tan^{-1}\left[\tan\left(\dfrac{\theta}{2}\right)\right]$

$=\dfrac{\theta}{2} \, \, \, \,....[\because \tan^{-1}(\tan \,\theta)=\theta]$

$=R.H.S.$

Prove that $\tan ^{-1} x + \tan^{-1} \dfrac{2x}{1 - x^{2}} = tan^{-1} \left ( \dfrac{3x - x^{3}}{1 - 3x^{2}} \right )$

Let

$\tan^{-1} x = y \Rightarrow x = \tan y \rightarrow (1)$

$\tan^{1}\dfrac{2x}{1-x^{2}}=\tan^{-1} \left ( \dfrac{2 \tan y }{1 - \tan^{2}} \right ) = \tan^{1}(\tan 2y ) = 2y \rightarrow (2)$

$\tan -1 \left ( \dfrac{3x - x^{3}}{1 - 3x^{2}} \right ) = \tan^{1}\left ( \dfrac{3 \tan y - \tan^{3} y}{1 - 3 \tan^{2} y} \right )$

$=\tan^{1} \tan (3y) = 3y \rightarrow (3)$

$LHS (1) + (2) \Rightarrow y + 2y = 3y$

$RHS (3) \Rightarrow 3y$
from (1) + (2) and (3) LHS = RHS

$2 \tan ^{-1} \dfrac{1}{2} + \tan ^{-1} \dfrac{1}{7} = \tan^{-1} \dfrac{31}{17}$

$2 \tan^{-1} x = \tan^{-1} \dfrac{2x}{1 - x^{2}} fro |x| < 1$

$\therefore LHS = \tan^{-1} \left [ \dfrac{2 \times 1 /2}{1 - (1/2)^{2}} \right ]$

$= \tan^{1}\left ( \dfrac{1}{3/4} \right ) + \tan^{-1} \dfrac{1}{7} \Rightarrow \tan^{-1} \dfrac{4}{3} + \tan^{-1}\dfrac{1}{7}$
Now

$\tan^{-1} \dfrac{4}{3} + \tan^{-1} \dfrac{1}{7}$

$\tan^{-1}x + \tan^{-1} y = \tan^{-1} \left [ \dfrac{x + y}{1 - yx} \right ]$
applying this formula

$\tan^{-1}\dfrac{4}{3} + \tan^{-1} \dfrac{1}{7} = \tan^{-1} \dfrac{4}{3} + \tan^{-1} \dfrac{1}{7} = \tan^{-1} \left [ \dfrac{\frac{4}{3}+ \dfrac{1}{7}}{1-\dfrac{4}{3}\times\dfrac{1}{7}} \right ]=tan^{-1}\dfrac{31}{17}$

$\therefore$ LHS = RHS
Hence proved .

$\tan^{-1} \dfrac{2}{11} + \tan ^{-1} \dfrac{7}{14} = \tan ^{-1} \dfrac{1}{2}$

$\tan^{-1} A + \tan^{-1} B = \tan^{-1} \left [ \dfrac{A + B}{1 - AB} \right ]$
For AB > 1
Applying formula

$\tan^{-1} \dfrac{2}{11} + \tan^{-1} \dfrac{7}{24} = \tan^{-1} \left [ \dfrac{\dfrac{2}{11}+ \dfrac{7}{24}}{11 - \dfrac{2}{11}\times\dfrac{7}{24}} \right ]$

$= \tan^{-1} \left [ \dfrac{\left ( 48 + 77 \right )}{\left ( 24 \times 11 \right ) - 14} \right ] =tan^{-1}\dfrac{125}{250}$

$=tan^{-1}\dfrac{1}{2}$

$\therefore$ LHS = RHS
Hence proved.

$3 \sin^{-1} x = \sin^{-1} ( 3x - 4x^{3}) , x \epsilon \left [ -\dfrac{1}{2},\dfrac{1}{2} \right ]$

Let

$\sin^{-1} x be \theta \Rightarrow x = \sin \theta$
In RHS putting the value of x

$\sin^{-1} (3x - 4x^{3}) \Rightarrow \sin^{-1} ( 3 \sin \theta - 4 \sin^{3}\theta)$

$= \sin^{-1} ( \sin 3 \theta)=3\theta$
In LHS putting the value of x

$3\sin^{-1}\sin\theta=3\theta$
LHS=RHS

Hence proved

Find the values of the following :
$\tan^{-1} (1) + \cos ^{-1} (-\dfrac{1}{2}) + \sin ^{-1} ( -\dfrac{1}{2})$

$\tan^{-1} (1) + \left \{ \cos ^{-1} (-\dfrac{1}{2}) + \sin ^{-1} ( -\dfrac{1}{2}) \right \}$
since

$\cos^{-1} x + \ sin^{-1} x = \dfrac{\pi }{2}$

$\Rightarrow \tan^{-1} (1) + \dfrac{\pi }{2}$

$\tan^{-1} (1) = \dfrac{\pi}{4}$

$\Rightarrow \dfrac{\pi}{4} + \dfrac{\pi}{2} = \dfrac{3\pi}{4}$

$3 \cos^{-1} x = \cos^{-1} ( 4x^{3} - 3x) , x \epsilon \left [ \dfrac{1}{2}, 1 \right ]$

Let

$\cos^{-1} x = \theta \Rightarrow x = \cos \theta$
In RHS , putting the value of x

$\cos^{-1}(4x^{3} - 3x) \Rightarrow \cos^{-1} ( 4 \cos^{3} \theta - 3 \cos \theta )$

$\Rightarrow \cos^{-1} ( \cos 3 \theta)$

$\left [ \because 4 \cos^{3}\theta - 3 \cos \theta = \cos 3 \theta \right ]$

$= 3\theta$
Putting the value of

$x=cos\theta$ in LHS

$\Rightarrow 3 \cos^{-1} x = LHS$

$\Rightarrow 3cos^{-1}cos\theta=3\theta$
LHS = RHS
Hence proved .

Find the values of the following :
$\cos^{-1}(\dfrac{1}{2}) + 2 \ sin ^{-1} (\dfrac{1}{2})$

$\cos^{-1} \left ( \dfrac{1}{2} \right ) = \dfrac{\pi }{3}$

$\sin^{-1} \left ( \dfrac{1}{2} \right ) = \dfrac{\pi }{6} \Rightarrow 2 \sin ^{-1} \left ( \dfrac{1}{2} \right ) = \dfrac{\pi }{3}$

$\therefore \cos ^{-1} \left ( \dfrac{1}{2} \right ) + 2 \sin ^{-1} \left ( \dfrac{1}{2} \right ) = \dfrac{\pi }{3} + \dfrac{\pi }{3}$

$= \dfrac{2\pi }{3}$

Solve $\tan ^{-1} \left \{ \dfrac{\sqrt{1 +x^{2} - \sqrt{1 - x^{2}}}}{\sqrt{1 + x^{2} + \sqrt{1 - x^{2}}}} \right \}$

Let

$x^{2} = \cos 2 \theta$

$\Rightarrow 2 \theta = \cos^{-1} x^{2} \Rightarrow \theta = \dfrac{1}{2} \cos^{-1} x^{2}$

$=\tan^{1} \left \{ \dfrac{\sqrt{1 + \cos 2\theta } - \sqrt{1 - \cos 2 \theta }}{\sqrt{1 + \cos 2\theta } + \sqrt{1 - \cos 2 \theta }} \right \}$

$=\tan^{-1} \left \{ \dfrac{\sqrt{2} \cos \theta - \sqrt{2} \sin \theta }{\sqrt{23} \cos \theta + \sqrt{2} \sin \theta } \right \}$
divided each them by

$\sqrt{2} \cos \theta$

$= \tan ^{-1} \left \{ \dfrac{1 - \tan\theta }{1 + \tan\theta } \right \}$

$=\tan ^{-1} \tan \left ( \dfrac{\pi }{4} - \theta \right )$

Find the values of each of the following .
$\tan \dfrac{1}{2} \left [ \sin^{-1} \dfrac{2x}{1 + x^{2}}+ \cos^{-1}\dfrac{1 - y^{2}}{1 + y^{2}} \right ]$

Put

$x = \tan u , \ and\ y = \tan v$

$\Rightarrow u = \tan^{-1} x\ and\ v = \tan^{-1} y$

$\sin \dfrac{2x}{1 + x^{2}} = \sin^{-1} \left ( \dfrac{2 \tan u}{1 + \tan^{2}u} \right )$

$= \sin^{-1} \sin (2u) = 2 u = 2 \tan^{-1} x$

$= \tan \left ( \tan^{-1}\left ( \dfrac{x + y}{1 - xy} \right ) \right ) = \dfrac{x + y}{1 - xy}$

Find the values of each of the following .
$\tan^{-1} \left [ 2 \cos\left ( 2 \sin^{-1}\dfrac{1}{2} \right ) \right ]$

Let

$\sin^{-1} \dfrac{1}{2} = \theta \Rightarrow \sin \theta = \dfrac{1}{2}$

then

$\tan^{-1} \left [ 2 \cos (2 \theta) \right ]$

$\Rightarrow \tan^{-1} (2 [1-2 \sin^{2}\theta])$

since ,

$\sin \theta = \dfrac{1}{2}$

$\Rightarrow \tan^{-1} (2 [1-\dfrac12])$

$\Rightarrow \tan^{-1} (1)=\dfrac{\pi}{4}$

Find the values of each of the following .
$\cot \left ( \tan^{-1} a + \cot^{-1} a \right )$

$\cot \left ( \tan^{-1} a + \cot^{-1} a \right )$

$\tan^{-1} a + \cot^{-1} a = \dfrac{\pi}{2}$

$\therefore \cot ( \tan^{-1} a + \cot^{-1}a)$

$= \cot\left ( \dfrac{\pi}{2} \right ) = 0$

Write the following function in the simplest form :
$\tan^{-1} \dfrac{\sqrt{1 + x^{2} -1}}{x} , x\neq 0$

Let

$\tan^{-1} x = \theta$

$x\Rightarrow \tan \theta$

$\left [ \dfrac{-\pi}{2} \leq \theta \leq \dfrac{\pi}{2} \right ]$

$\tan^{-1} \left [ \dfrac{\sec \theta - 1}{\tan \theta} \right ]$

$\Rightarrow \tan ^{-1} \left [ \dfrac{\sec \theta - 1}{\tan \theta} \right ] \left [ \sqrt{1 + \tan^{2}\theta} = \sec \theta \right ]$

$\Rightarrow \tan^{-1} \left [ \dfrac{1 / \cos \theta - 1}{\sin \theta / \cos \theta} \right ] \Rightarrow \tan^{-1}\left [ \dfrac{\left ( 1 - \cos \theta \right )/cos \theta}{\sin \theta / \cos \theta} \right ]$

$\tan^{-1}\sqrt{ \dfrac{1- \cos x}{1 + \cos x}} , 0 < x < \pi$

$1 - \cos x = 2 \sin^{2} (x/2)$

$1 + \cos x = 2 \cos^{2} (x/2)$

$\therefore tan^{-1} \left [ \sqrt{\dfrac{2 \sin^{2}(x/2)}{2 \cos^{2}(x/2)}} \right ] \Rightarrow \tan^{-1} (\tan(x/2))$

$= \dfrac{x}{2}$

Write the following function in the simplest form :
$\tan^{-1} \dfrac{1}{\sqrt{x^{2}-1}} , |x| > 1$

Let

$cosec^{-1} x = \theta$

$\Rightarrow x = cosec \theta$

$\Rightarrow \tan^{-1}\dfrac{1}{\sqrt{x^{2}-1}}$

$\tan^{-1} \dfrac{1}{\sqrt{cosec^{2}\theta - 1}}$

$\Rightarrow \tan^{-1}\dfrac{1}{|\cot \theta |}$

$\Rightarrow tan^{-1}tan\theta=\theta$

$\Rightarrow \theta=cosec^{-1}x$

$\tan^{-1} \dfrac{\cos x - \sin x}{\cos x + \sin x} , \dfrac{- \pi}{4} < x < \dfrac{3\pi}{4}$

Divide each term of numerator inside the brackets by

$\cos x$

$\tan^{-1} \left [ \tan\left ( \dfrac{\pi}{4}-x \right ) \right ] \left [ \because \dfrac{1 - \tan x }{1 + \tan x} = \tan \left ( \dfrac{\pi}{4} -x \right ) \right ]$

$\Rightarrow \dfrac{\pi}{4} - x$

In $\sin \left ( \sin^{-1}\dfrac{1}{5} + \cos^{-1} x \right ) = x$

$\sin (x + y) = \sin x \cos y + \cos x \sin y$

$\sin \left ( \sin^{-1}\dfrac{1}{5} \right ) \cos (\cos^{-1} x) + \cos \left ( \sin\left ( \dfrac{1}{5} \right ) \right )$

$24 - 24x^{2} = 25 + x^{2} - 10x$

$(5x - 1)^{2} = 0 \Rightarrow x = \dfrac{1}{5}$

Find the value of the following :
$\tan ^{-1} \left ( \dfrac{\sqrt{1 + x}- \sqrt{1 - x}}{\sqrt{1 + x } + \sqrt{1 - x}} \right )= \dfrac{x}{4} - \dfrac{1}{2} \cos^{-1} x$
$-\dfrac{1}{\sqrt{2}}\leq x \geq [Hint : put x = \cos 2\theta ]$

put

$x = \cos 2\theta , \sqrt{1 + \cos 2\theta } = \sqrt{2} \cos \theta$

$\sqrt{1 - \cos 2\theta } = \sqrt{2} \sin \theta$

$LHS tan ^{-1} \left [ \dfrac{\sqrt{1 + \cos 2\theta }- \sqrt{1 - \cos\theta }}{\sqrt{1 + \cos 2\theta } + \sqrt{1 - \cos 2\theta } } \right ]$

$\tan^{-1} \left [ \dfrac{\sqrt{2}\cos \theta - \sqrt{2} \sin\theta }{\sqrt{2 \cos \theta }+ \sqrt{2}\sin\theta } \right ]$ dividing by

$\sqrt{2} \cos \theta$

$tan^{-1} \left [ \dfrac{1 - \tan\theta }{1 + \tan\theta } \right ] = \tan^{-1} \left [ \tan \left ( \dfrac{\pi }{4} - \theta \right ) \right ]$

$\dfrac{\pi }{4}-\theta$

$but x = \cos 2 \theta , \Rightarrow = \dfrac{1}{2} \cos^{-1} x$

$= \dfrac{\pi }{4} - \dfrac{1}{2} \cos^{-1} x = RHS$

If $\tan^{-1} \dfrac{x - 1}{x - 2} + \tan^{-1} \dfrac{x +1}{x +2} = \dfrac{\pi}{4}$ Then find the value of x

$\tan^{-1} \left [ \dfrac{\dfrac{x - 1}{x + 2} +\dfrac{x + 1}{x + 2}}{1 - \dfrac{x - 1}{x - 2} \times\dfrac{x + 1}{ x + 2}} \right ] = \dfrac{\pi}{4}$

$= \tan^{-1} \left [ \dfrac{(x+ 2)(x - 1)+ (x + 1)(x-2)}{(x-2)(x + 2)- (x - 1) (x + 1)} \right ] = \dfrac{\pi}{4}$

$= \tan^{-1} \left [ \dfrac{x^2+x-2+ x^2-x-2}{x^2-4- x^2+1} \right ] = \dfrac{\pi}{4}$

$= \tan^{-1} \left [ \dfrac{2x^2-4}{-3} \right ] = \dfrac{\pi}{4}$

$\dfrac{2x^2-4}{-3}=1$

$\Rightarrow 2x^{2} - 1=0$

$\Rightarrow 2x^{2} = 1 \Rightarrow x = \pm \dfrac{1}{\sqrt{2}}$

Find the values of each of the expressions.
$\sin^{-1} \left ( \sin\dfrac{2\pi}{3} \right )$

$Range \space of \space sin^{-1}x\space is [-\frac{\pi}{2},\frac{\pi}{2}]$

$sin^{-1}(sin\dfrac{2\pi}{3})=sin^{-1}\frac{\sqrt3}{2}=\dfrac{\pi}{3}$

$\dfrac{9\pi }{8} - \dfrac{9}{4} \sin^{-1} \dfrac{1}{3} = \dfrac{9}{4} \sin^{-1} \dfrac{2\sqrt{2}}{3}$

$LHS \dfrac{9}{4} \left ( \dfrac{\pi }{2}- \sin^{-1} \dfrac{1}{3} \right )$

$=\dfrac{9}{4} \cos^{-1} \left ( \dfrac{1}{3} \right )$

$=\dfrac{9}{4}\sin^{-1} \left [ \sqrt{1-\left ( \dfrac{1}{3} \right )^{2}} \right ] = \dfrac{9}{4} \sin^{-1} \left ( \sqrt{\dfrac{8}{9}}\right )$

$= \dfrac{9}{4} \sin^{-1} \left ( \dfrac{2\sqrt{2}}{3} \right ) = RHS$

Find the values of each of the expressions.
$\tan \left ( \sin^{-1}\dfrac{3}{5} + \cot^{-1}\left ( \dfrac{3}{2} \right ) \right )$

$\sin^{-1} \left ( \dfrac{3}{5} \right ) = \tan^{-1} \left ( \dfrac{3}{4} \right ) \ and\\ \cot^{-1} \left ( \dfrac{3}{2} \right ) = \tan^{-1} \left ( \dfrac{2}{3} \right )$

$\therefore \tan \left [ \tan^{-1} \dfrac{3}{4} + \tan^{-1} \left ( \dfrac{2}{3} \right ) \right ]$

$\Rightarrow \tan \left [tan^{-1} \dfrac{17}{6}\right]$

$= \dfrac{17}{6}$

Find the values of each of the expressions .
$\tan^{-1} \left ( \tan \dfrac{3\pi}{4} \right )$

$\tan^{-1} \tan \left ( \tan\dfrac{3 \pi}{4} \right )$

$= \tan^{-1} \tan\left ( \ pi - \dfrac{\pi}{4} \right )$

$= \tan^{-1} \left ( -\tan\dfrac{ \pi}{4} \right )$

$=-\dfrac{\pi}4$

Prove the following
$\tan^{-1} \sqrt{\dfrac{ax}{bc}}+\tan^{-1} \sqrt{\dfrac{bx}{ca}}+\tan^{-1} \sqrt{\dfrac{cx}{ab}}=\pi, where\ a+b+c=x$

$=\tan^{-1} \left( \dfrac{ax}{bc} \right)+\tan^{-1} \left( \dfrac{bx}{ca} \right)+\tan^{-1} \left( \dfrac{cx}{ab} \right)$

$=\tan^{-1} \left[ \dfrac { \sqrt { \dfrac { ax }{ bc } } +\sqrt { \dfrac { bx }{ ca } } +\sqrt { \dfrac { cx }{ ab } } -\sqrt { \dfrac { ax }{ bc } } .\sqrt { \dfrac { bx }{ ca } } .\sqrt { \dfrac { cx }{ ac } } }{ 1-\sqrt { \dfrac { ac }{ bc } } \sqrt { \dfrac { bx }{ ca } } -\sqrt { \dfrac { bx }{ ca } } .\sqrt { \dfrac { cx }{ ab } } -\sqrt { \dfrac { cx }{ ab } } \sqrt { \dfrac { ax }{ bc } } } \right]$

$\left( \because \tan^{-1}x+ \tan^{-1}y+\tan^{-1}x =\tan^{-1} \dfrac{x+y+x-xyz}{1-xy-yz-zx}\right)$

$=\tan^{-1} \left[ \dfrac { \dfrac { a\sqrt { x } +b\sqrt { x } +c\sqrt { x } }{ \sqrt { abc } } -\dfrac { \sqrt { x } \sqrt { x } \sqrt { x } }{ \sqrt { abc } } }{ 1-\dfrac { x }{ c } -\dfrac { x }{ a } -\dfrac { x }{ b } } \right]$

$=\left[ \dfrac { \dfrac { x\sqrt { x } -x\sqrt { x } }{ \sqrt { abc } } }{ \left( 1-\dfrac { x }{ a } -\dfrac { x }{ b } -\dfrac { x }{ c } \right) } \right] (\because a+b+c=x)$

$=\tan^{-1}(0)=tan^{-1}(\tan \pi)$

$=\pi =R.H.S$

Hence proved

Prove the following
$2 \tan^{-1}x= \sin^{-1}\dfrac{2x}{1+x^2}=\cos^{-1} \dfrac{1-x^2}{1+x^2}$

$(i)$

$2 \tan^{-1}x= \sin^{-1}\dfrac{2x}{1+x^2}$

Let

$\tan^{-1}x =\theta$

$\therefore x= \tan \theta$

$R.H.S=\sin^{-1}\dfrac{2x}{1+x^2}$

$\sin^{-1}\left( \dfrac{2 \tan \theta}{1+ \tan^2 \theta}\right)$

$\sin^{-1}\left( \dfrac{2 \tan \theta}{\sec^2 \theta}\right)$

$=\sin^{-1} (2 \sin \theta \cos \theta)$

$=\sin^{-1} (\sin 2 \theta)$

$= 2 \theta$

$= 2 \tan^{-1}x=L.H.S$

$(ii)$ R.H.S

$= \cos^{-1} \left( \dfrac{1-x^2}{1+x^2}\right)$

$= \cos^{-1} \left( \dfrac{1-\tan^2 \theta}{1+\tan^2 \theta}\right)$

$= \cos^{-1} \left( \dfrac{\cos^2 \theta - \sin^2 \theta}{\cos^2 \theta + \sin^2 \theta} \right)$

$=\cos^{-1} (\cos 2 \theta)$

$=2 \theta$

$=1 \tan^{-1}x=L.H.S$ .

So,

$2 \tan^{-1}x=\sin^{-1} \dfrac{2x}{1+x^2}$

$=\cos^{-1} \dfrac{1-x^2}{1+x^2}$

Hence proved

Prove the following
$2 \tan^{-1}\dfrac{1}{2} - \tan^{-1}\dfrac{1}{7}=\dfrac{\pi}{4}$

L.H.S

$=2 \tan^{-1}\dfrac{1}{2} - \tan^{-1}\dfrac{1}{7}$

$=\tan^{-1} \dfrac{2 \times \dfrac{1}{2}}{1- \left( \dfrac{1}{2} \right)^2}- \tan^{-1}\dfrac{1}{7}$

$\left[ \because 2 \tan^{-1} x=\tan^{-1} \dfrac{2x}{1-x^2}\right]$

$=\tan^{-1} \dfrac{1}{1-\dfrac{1}{4}}-\tan^{-1} \dfrac{1}{7}$

$=\tan^{-1} \dfrac{4}{3}-\tan^{-1} \dfrac{1}{7}$

$=\tan^{-1} \dfrac{\dfrac{4}{3}-\dfrac{1}{7}}{1+\dfrac{4}{3} \times \dfrac{1}{7}}$

$\left[ \because \tan^{-1} x-\tan^{-1} y=\tan^{-1} \dfrac{x-y}{1+xy}\right]$

$=\tan^{-1} \dfrac{28-3}{21+4}=\tan^{-1} \dfrac{25}{25}$

$\tan^{-1} (1)=\tan^{-1} \left( \tan \dfrac{\pi}{4} \right)$

$=\dfrac{\pi}{4}=R.H.S$

Hence proved

$\tan ^{-1} \dfrac{1 -x}{1 + x} = \dfrac{1}{2} \tan^{-1} x, (x>0)$

$\therefore \tan^{-1} \left ( \dfrac{1 -x}{1 +x} \right ) = \tan^{-1} x$

$\tan^{-1}\left \{ \dfrac{2\left ( \dfrac{1-x}{1-\left ( \dfrac{1-x}{1 + x} \right )^{2}} \right )}{1-\left ( \dfrac{1 -x}{1 + x } \right )} \right \}= \tan^{-1} x$

$\tan^{-1}\left \{ \dfrac{2(1 -x)}{(1 +x)}\times \dfrac{(1 + x)^{2}}{(1 + x) ( 1 + x)^{2} - (1 - x)^{2}} \right \}= \tan^{-1} x$

$\dfrac{2 (1 -x) (1 + x)}{4x}=x$

$2 ( 1 - x^{2}) = 4x^{2} \Rightarrow 2 . 2x^{2} = 4x^{2}$

$6x^{2} , x^{2} = \dfrac{1}{3}$

$x = \pm \dfrac{1}{\sqrt{3}}$

$Since x > 0 , x = \dfrac{1}{\sqrt{3}}$

1816008_1857306_ans_1e03e2127034425aa608776b64df2dc1.png

Prove the following
$2 \tan^{-1}\dfrac{17}{19} - \tan^{-1}\dfrac{2}{3}=\tan^{-1} \dfrac{1}{7}$

L.H.S

$=2 \tan^{-1}\dfrac{17}{19} - \tan^{-1}\dfrac{2}{3}$

$=\tan^{-1} \dfrac{\dfrac{17}{19}-\dfrac{2}{3}}{1+\dfrac{17}{19} \times \dfrac{2}{3}}$

$\left[\tan^{-1} x-\tan^{-1} y=\tan^{-1} \left( \dfrac{x-y}{1+xy}\right) \right]$

$=\tan^{-1} \dfrac{\dfrac{51-38}{19 \times 3}}{\dfrac{57+34}{19 \times 3}}$

$=\tan^{-1} \dfrac{13}{91}=\tan^{-1} \dfrac{1}{7}$

$=R.H.S$

Hence proved

$2 \tan ^{-1} (\cos^{ x}) = \tan^{-1} (2 cosec x)$

$2 \ tan ^{-1} x = \tan ^{-1} \dfrac{2x}{1 - x^{2}}$

$\tan^{-1} \left ( \dfrac{2 \cos x}{1 - \cos ^{2} x} \right ) = \tan^{-1} (2 cosec x)$

$\dfrac{2 \cos x}{\sin^{2} x} = \dfrac{2}{\sin x}$

$\cos x = \sin x$

$\Rightarrow \dfrac{sin\ x}{cos\ x} =1$

$\tan x = \tan \dfrac{\pi }{4}$
or

$x = \dfrac{\pi }{4} x\epsilon I$

If $\sin^{-1}\left(\dfrac{3}{4}\right)+\sec^{-1}\left(\dfrac{4}{3}\right)=x$ , then find $x$ .

1894778_1871649_ans_a681a617bce64699af721ef5840bc784.jpeg

Solve the following equation
$\sec^{-1} \left(\dfrac{x}{a} \right)-\sec^{-1} \left(\dfrac{x}{b} \right)= \sec^{-1}b-\sec^{-1}a$

$\sec^{-1} \left(\dfrac{x}{a} \right)-\sec^{-1} \left(\dfrac{x}{b} \right)= \sec^{-1}b-\sec^{-1} (a)$

$\sec^{-1} \left(\dfrac{x}{a} \right)-\sec^{-1} (a) =\sec^{-1} \left(\dfrac{x}{b} \right)-\sec^{-1} (b)$

$\Rightarrow \cos^{-1} \left(\dfrac{a}{x} \right) + \cos^{-1} \left(\dfrac{1}{a} \right)=\cos^{-1} \left(\dfrac{b}{x} \right) +\cos^{-1} \left(\dfrac{1}{b} \right)$

$\Rightarrow \cos^{-1} \left[ \dfrac { a }{ x } .\dfrac { 1 }{ a } \sqrt { 1-{ \left( \dfrac { a }{ x } \right) }^{ 2 } } \sqrt { 1-{ \left( \dfrac { 1 }{ a } \right) }^{ 2 } } \right] = \cos^{-1}\left[ \dfrac { b }{ x } .\dfrac { 1 }{ b } \sqrt { 1-{ \left( \dfrac { b }{ x } \right) }^{ 2 } } \sqrt { 1-{ \left( \dfrac { 1 }{ b } \right) }^{ 2 } } \right]$

$\Rightarrow \dfrac{1}{x} - \sqrt{1- \dfrac{a^2}{x^2}-\dfrac{1}{a^2}+\dfrac{1}{x^2}}=\dfrac{1}{x}- \sqrt{1-\dfrac{b^2}{x^2}-\dfrac{1}{b^2}+\dfrac{1}{x^2}}$

$\Rightarrow 1-\dfrac{a^2}{x^2}-\dfrac{1}{a^2}+\dfrac{1}{x^2} =1-\dfrac{b^2}{x^2}-\dfrac{1}{b^2}+\dfrac{1}{x^2}$

$\Rightarrow \dfrac{b^2}{x^2}+\dfrac{1}{b^2}=\dfrac{a^2}{x^2}+\dfrac{1}{a^2}$

$\Rightarrow \dfrac{b^2}{x^2}-\dfrac{a^2}{x^2}=\dfrac{1}{a^2}-\dfrac{1}{b^2}$

$\Rightarrow (b^2-a^2)=x^2 \left( \dfrac{b^2-a^2}{a^2b^2}\right)$

$\Rightarrow x^2=a^2b^2$

$\Rightarrow x= \pm ab$

Find : $\sin^{-1}\left(\dfrac{4}{5}\right)+2\tan^{-1}\left(\dfrac{1}{3}\right)$

$\sin^{-1}\left(\dfrac{4}{5}\right)+2\tan^{-1}\left(\dfrac{1}{3}\right)$

$=\sin^{-1}\left(\dfrac{4}{5}\right)+\cos^{-1}\left\{\dfrac{1-\left(\dfrac{1}{3}\right)^{2}}{1+\left(\dfrac{1}{3}\right)^{2}}\right\}$

$\left[\because 2\tan^{-1}x=\cos^{-1}\left\{\dfrac{1-x^{2}}{1+x^{2}}\right\}\right]$

$=\sin^{-1}\left(\dfrac{4}{5}\right)+\cos^{-1}\left(\dfrac{\dfrac{8}{9}}{\dfrac{10}{9}}\right)$

$=\sin^{-1}\left(\dfrac{4}{5}\right)+\cos^{-1}\left(\dfrac{4}{5}\right)$

$=\dfrac{\pi}{2}\left[\because \sin^{-1}x+\cos^{-1}x=\dfrac{\pi}{2}\right]$

If $4\sin^{-1}x+\cos^{-1}x=\pi$ , then find $x$ .

$4\sin^{-1}x+\cos^{-1}x=\pi$

$\Rightarrow 4\sin^{-1}x+\dfrac{\pi}{2}-\sin^{-1}x=\pi$

$\left[\because \sin^{-1}x+\cos^{-1}x=\dfrac{\pi}{2}\right]$

$\Rightarrow 3\sin^{-1}x=\pi-\dfrac{\pi}{2}$

$\Rightarrow 3\sin^{-1}x=\dfrac{\pi}{2}\Rightarrow \sin^{-1}x=\dfrac{\pi}{6}$

$\Rightarrow x=\sin\dfrac{\pi}{6}\Rightarrow x=\dfrac{1}{2}$

Prove the following
$\dfrac{1}{2} \tan^{-1} x=\cos^{-1} \left\{ \dfrac{1+ \sqrt{1+x^2}}{2 \sqrt{1+x^2}} \right\}^{\dfrac{1}{2}}$

Let

$\tan^{-1}x= \theta,$ then

$x= \tan \theta$ =

R.H.S

$\cos^{-1} \left\{ \dfrac{1+ \sqrt{1+x^2}}{2 \sqrt{1+x^2}} \right\}^{\dfrac{1}{2}}$

$=\cos^{-1} \left\{ \dfrac{1+\sec \theta}{2 \sec \theta} \right\}^{\dfrac{1}{2}}$

$=cos^{-1} \left( \dfrac{\cos \theta+1}{2}\right)^{\dfrac{1}{2}}$

$=\cos^{-1} \left( \dfrac{2 \cos^2 \dfrac{\theta}{2}}{2} \right)^{\dfrac{1}{2}}$

$=\cos^{-1} \cos \dfrac{\theta}{2}=\dfrac{\theta}{2}$

$=\dfrac{1}{2} \tan^{-1}x=L.H.S$ .

Hence proved

If $\sin^{-1}\left(\dfrac{5}{13}\right)+\sin -1\left(\dfrac{12}{x}\right)=90^o$ , then find $x$ .

$\sin^{-1} \left(\dfrac{5}{13}\right)+\sin^{-1}\left(\dfrac{12}{x}\right)=90^{o}$

$\Rightarrow \sin^{-1}\left(\dfrac{15}{13}\right)+\sin^{-1}\left(\dfrac{12}{x}\right)=\sin^{-1}\left(\dfrac{5}{13}\right)+\cos^{-1}\left(\dfrac{5}{13}\right)$

$\left[\because \sin^{-1}\left(\dfrac{5}{13}\right)+\cos^{-1}\left(\dfrac{5}{13}\right)=\dfrac{\pi}{2}\right]$

$\Rightarrow \sin^{-1}\dfrac{12}{x}=\cos^{-1}\dfrac{5}{13}$

$\Rightarrow \sin^{-1}\dfrac{12}{x}=\sin^{-1}\sqrt{1-\left(\dfrac{5}{13}\right)^{2}}$

$\left[\because \cos^{-1}x=\sin^{-1}\sqrt{1-x^{2}}\right]$

$\Rightarrow \sin^{-1}\dfrac{12}{x}=\sin^{-1}\dfrac{12}{13}$

here,

$x=13$

Prove that $\tan^{-1}(\dfrac{1}{2}\tan 2A)+\tan^{-1}(\cot A)+\tan^{-1}(\cot^2A)=0$

$\tan^{-1}\left(\dfrac{1}{2}\tan 2A\right)+\tan^{-1}(\cot A)+\tan^{-1}(\cot^{2}A)=0$

$L.H.S$

$=\tan^{-1}\left(\dfrac{1}{2}\times \dfrac{2\tan A}{1-\tan^{2}A}\right)+\tan^{-1}\left(\dfrac{1}{\tan A}\right)+\tan^{-1}\left(\dfrac{1}{\tan^{2}A}\right)$

Let

$\tan A=x$

$=\tan^{-1}\left(\dfrac{x}{1-x^{2}}\right)+\tan^{-1}\left(\dfrac{1}{x}\right)+\tan^{-1}\left(\dfrac{1}{x^{2}}\right)$

$=\tan^{-1}\left\{\dfrac{\dfrac{x}{1-x^{2}}+\dfrac{1}{x}}{1-\left(\dfrac{x}{1-x^{2}}\right)\dfrac{1}{x}}\right\}+\tan^{-1}\left(\dfrac{1}{x^{2}}\right)$

$=\tan^{-1}\left\{\dfrac{\dfrac{x^{2}+1-x^{2}}{x(1-x^{2})}}{\dfrac{1-x^{2}-1}{x(1-x^{2})}}\right\}\tan^{-1}\left(\dfrac{1}{x^{2}}\right)$

$=\tan^{-1}\left(\dfrac{1}{-x^{2}}\right)+\tan^{-1}\left(\dfrac{1}{x^{2}}\right)$

$=-\tan^{-1}\left(\dfrac{1}{x^{2}}\right)+\tan^{-1}\left(\dfrac{1}{x^{2}}\right)$

$[\because \tan^{-1}(-\theta)=-\tan^{-1}\theta]$

$=0$

$=R.H.S$ Hence proved.

Solve : $\tan^{-1} 4x + \tan^{-1} 6x = \dfrac{\pi}{4}$ .

$\tan^{-1} 4x + \tan^{-1} 6x = \dfrac{\pi}{4}$

$\because \tan^{-1}A+\tan^{-1}B=\tan^{-1}\left(\dfrac{A+B}{1-AB}\right)$

$\therefore \tan^{-1}\left(\dfrac{4x+6x}{1-24x^2}\right)=\dfrac{\pi}{4}\Rightarrow \tan^{-1}\left(\dfrac{10x}{1-24x^2}\right)=\dfrac{\pi}{4}$

$\Rightarrow \dfrac{10x}{1-24x^2}=\tan (\dfrac{\pi}{4})\Rightarrow \dfrac{10x}{1-24x^2}=1\Rightarrow 1-24x^2=10x$

$\Rightarrow 24x^2+10-1=0\Rightarrow 24x^2+12x-2x-1=0$

$\Rightarrow 12x(2x+1)-1(2x+1)=0\Rightarrow (12x-1)(2x+1)=0$

$\Rightarrow x=\dfrac{-1}{2}$ or

$x=\dfrac{1}{12}$

$\because x=-\dfrac{1}{2}$ , LHS

$=\tan^{-1}(-2)+\tan^{-1}(-3)$ = negative

$\neq$ RHS

$\therefore \boxed{x=\dfrac{1}{12}}$

Prove that:
$2\tan^{-1}\left[\tan (45^o -\alpha)\tan \dfrac{\beta}{2}\right]=\cos^{-1}\left(\dfrac{\sin 2\alpha +\cos \beta}{1+\sin 2\alpha \cos \beta}\right)$

$L.H.S$

$=2\tan^{-1}[\tan (45^o-\alpha )\tan \beta/2]$

$=2\tan^{-1}\left[\left(\dfrac{\tan 45^o-\tan \alpha}{1+\tan 45^o\tan \alpha}\right)\tan \dfrac{\beta}{2}\right]$

$=2\tan^{-1}\left[\left(\dfrac{1-\tan \alpha}{1+\tan \alpha}\right)\tan \dfrac{\beta}{2}\right]$

$=2\tan^{-1}\left[\left(\dfrac{\cos \alpha-\sin \alpha}{\cos \alpha+\sin \alpha}\right)\tan \dfrac{\beta}{2}\right]$

$=\cos^{-1}\left[\dfrac{1-\left\{\left(\dfrac{\cos \alpha -\sin \alpha}{\cos \alpha +\sin \alpha}\right)\tan \dfrac{\beta}{2}\right\}^2}{1+\left\{\left(\dfrac{\cos \alpha -\sin \alpha}{\cos \alpha +\sin \alpha}\right)\tan \dfrac{\beta}{2}\right\}^2}\right]$

$\left[\because 2 tan^{-1}x=\cos ^{-1}\left\{\dfrac{1-x^2}{1+x^2}\right\}\right]$

$=\cos^{-1}\left[\dfrac{(\cos \alpha +\sin \alpha)^2\cos^2\dfrac{\beta}{2}-(\cos \alpha -\sin \alpha )^2\sin^2\dfrac{\beta}{2}}{(\cos \alpha +\sin \alpha)^2\cos^2\dfrac{\beta}{2}+(\cos \alpha -\sin \alpha )^2\sin^2 \dfrac{\beta}{2}}\right]$

$=\cos^{-1}\left[\dfrac{(1+\sin 2\alpha )\left(\dfrac{1+\cos \beta}{2}\right)-(1-\sin 2\alpha )\left(\dfrac{1-\cos \beta}{2}\right)}{(1+\sin 2\alpha )\left(\dfrac{1+\cos \beta}{2}\right)+(1-\sin 2\alpha )\left(\dfrac{1-\cos \beta}{2}\right)}\right]$

$=\cos^{-1}\left[\dfrac{\dfrac{1}{2}\left\{(1+\sin 2\alpha +\cos \beta +\sin 2 \alpha \cos \alpha)-(1-\sin 2\alpha -\cos \beta +\sin 2 \alpha \cos \beta)\right\}}{\dfrac{1}{2}\left\{(1+\sin 2\alpha +\cos \beta +\sin 2 \alpha \cos \alpha)+(1-\sin 2\alpha -\cos \beta +\sin 2 \alpha \cos \beta)\right\}}\right]$

$\cos^{-1}\left[\dfrac{1-\sin 2\alpha +\cos \beta +\sin 2 \alpha \cos \beta -1+\sin 2\alpha +\cos \beta -\sin 2 \alpha \cos \beta }{1-\sin 2\alpha +\cos \beta +\sin 2 \alpha \cos \beta -1-\sin 2\alpha +\cos \beta -\sin 2 \alpha \cos \beta}\right]$

$=\cos^{-1}\left[\dfrac{2(\sin 2 \alpha +\cos \beta)}{2+2\sin 2 \alpha \cos \beta}\right]$

$=\cos^{-1}\left(\dfrac{\sin 2 \alpha +\cos \beta}{1+\sin 2 \alpha \cos \beta}\right)=R.H.S$

Hence proved .

$\phi =\tan^{-1}\dfrac{x\sqrt{3}}{2K-x}$ and $\theta =\tan^{-1}\dfrac{2x-K}{K\sqrt{3}}$
then prove that value of $\phi -\theta$ is $30^o$ .

Given,

$\phi=\tan^{-1}\dfrac{x\sqrt{3}}{2K-x}$

$\therefore \tan \phi=\dfrac{x\sqrt{3}}{2K-x}$

and

$\theta=\tan^{-1}\dfrac{2x-K}{K\sqrt{3}}$

$\therefore \tan \theta=\dfrac{2x-K}{K\sqrt{3}}$

$\because \tan (\phi-\theta)=\dfrac{\tan \phi-\tan \theta}{1+\tan \phi \tan \theta}$

$\tan (\phi-\theta)=\dfrac{\dfrac{x\sqrt{3}}{2K-x}-\dfrac{2x-K}{K\sqrt{3}}}{1+\left(\dfrac{x\sqrt{3}}{2K-x}\right)\left(\dfrac{2x-K}{K\sqrt{3}}\right)}$

$\Rightarrow \tan (\phi-\theta)=\dfrac{\dfrac{3Kx-(2K-x)(2x-K)}{(2K-x)K\sqrt{3}}}{\dfrac{(2K-x)K\sqrt{3}+x\sqrt{3}(2x-K)}{(2K-x)K\sqrt{3}}}$

$\Rightarrow \tan (\phi-\theta)=\dfrac{3Kx-(4xK-2K^{2}-2x^{2}+Kx)}{2\sqrt{3}K^{2}-\sqrt{3}Kx+2\sqrt{3}x^{2}-\sqrt{3}Kx}$

$\Rightarrow \tan (\phi-\theta)=\dfrac{3Kx-4Kx+2K^{2}+2x^{2}-Kx}{2\sqrt{3}K^{2}-2\sqrt{3}Kx+2\sqrt{3}x^{2}}$

$\Rightarrow \tan (\phi-\theta)=\dfrac{2K^{2}+2x^{2}-2Kx}{2\sqrt{3}K^{2}+2\sqrt{3}x^{2}-2\sqrt{3}Kx}$

$\Rightarrow \tan (\phi-\theta)=\dfrac{2(K^{2}+x^{2}-Kx)}{2\sqrt{3}(K^{2}+x^{2}-Kx)}$

$\Rightarrow \tan (\phi-\theta)=\dfrac{1}{\sqrt{3}}$

$\Rightarrow \tan (\phi-\theta)=\tan 30^{o}$

$\therefore \phi-\theta=30^{o}$ Hence proved.

Prove that $\tan^{-1}x=2\tan^{-1}(\csc (\tan^{-1}x)-\tan (\cot^{-1}x)$ .

Let

$\tan^{-1}x=\theta$

$\Rightarrow x=\tan\theta=\cot \left(\dfrac{\pi}{2}-\theta\right)$

$\Rightarrow \cot^{-1}x=\dfrac{\pi}{2}-\theta$ .....(i)

$R.H.S.=2\tan^{-1}\left[\csc\theta-\tan \left(\dfrac{\pi}{2}-\theta\right)\right]$ [From eq

$(i)$ ]

$=2\tan^{-1}[\csc\theta-\cot \theta]$

$=2\tan^{-1}\left(\dfrac{1}{\sin\theta}-\dfrac{\cos \theta}{\sin \theta}\right)$

$=2\tan^{-1}\left(\dfrac{1-\cos \theta}{\sin \theta}\right)$

$=2\tan^{-1}\left(\dfrac{2\sin^{2}\dfrac{\theta}{2}}{2\sin \dfrac{\theta}{2}\cos \dfrac{\theta}{2}}\right)$

$=2\tan^{-1}\left(\dfrac{\sin\dfrac{\theta}{2}}{\cos\dfrac{\theta}{2}}\right)=2\tan^{-1}\left(\tan \dfrac{\theta}{2}\right)$

$=2\times \dfrac{\theta}{2}=\theta=\tan^{-1}x=L.H.S.$ Hence proved.

The number of solutions of the equation $\displaystyle \sin^{-1}\left (\dfrac{1+x^{2}}{2x}\right)=\dfrac{\pi}{2}\sec(x-1)$ is

Since, domain of

$\sin^{-1}x$ is

$[-1,1]$
Therefore,

$-1\leq\dfrac{1+x^2}{2x}\leq1$

$1+2x+x^2\geq0$ and

$1-2x+x^2\leq0$

$(1+x)^{2}\geq0$ and

$(1-x)^{2}\leq0$

$-1\leq x\leq1$
However, only

$x=1$ satisfies the above equation.
Therefore, only one solution exists.

Prove that $\tan^{-1}\left (\dfrac {\cos x}{1 + \sin x}\right ) = \dfrac {\pi}{4} - \dfrac {x}{2}, x\epsilon \left (-\dfrac {\pi}{2}, \dfrac {\pi}{2}\right )$

$tan^{-1}\left ( \dfrac{cos x}{1+sinx} \right )=tan^{-1}\left ( \dfrac{cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}}{cos^2\dfrac{x}{2}+sin^2\dfrac{x}{2}+2.cos\dfrac{x}{2}.sin\dfrac{x}{2}} \right )$
$=tan^{-1}\left [ \dfrac{\left ( cos\dfrac{x}{2}-sin\dfrac{x}{2} \right )\left ( cos\dfrac{x}{2}+sin\dfrac{x}{2}\right )}{\left ( cos\dfrac{x}{2}+\sin\dfrac{x}{2} \right )^2} \right ]$
$=tan^{-1} \left ( \dfrac{cos\dfrac{x}{2}-sin\dfrac{x}{2}}{cos\dfrac{x}{2}+sin\dfrac{x}{2}} \right )=tan^{-1}\left ( \dfrac{\dfrac{cos\dfrac{x}{2}}{cos\dfrac{x}{2}}-\dfrac{sin\dfrac{x}{2}}{cos\dfrac{x}{2}}}{\dfrac{cos\dfrac{x}{2}}{cos\dfrac{x}{2}}+\dfrac{sin\dfrac{x}{2}}{cos\dfrac{x}{2}}} \right )$
$=tan^{-1}\left ( \dfrac{1-tan\dfrac{x}{2}}{1+tan\dfrac{x}{2}} \right )=tan^{-1}\left ( \dfrac{tan\dfrac{\pi}{4}-tan\dfrac{x}{2}}{1+tan\dfrac{\pi}{2}tan\dfrac{x}{2}} \right )$
$=tan^{-1}\left [ tan\left ( \dfrac{\pi}{4}-\dfrac{x}{2} \right ) \right ]$
$=\dfrac{\pi}{4}-\dfrac{x}{2}$

Prove that $\sin^{-1}\left (\dfrac {8}{17}\right ) + \sin^{-1}\left (\dfrac {3}{5}\right ) = \cos^{-1} \left (\dfrac {36}{85}\right )$

Let $sin^{-1}\left ( \dfrac{8}{17} \right )=\alpha$ and $sin^{-1}\left ( \dfrac{3}{5} \right )=\beta$
$sin\alpha =\dfrac{8}{17}$ and $sin\beta=\dfrac{3}{5}$
$\Rightarrow cos\alpha=\sqrt{1-sin^2\alpha}$ and $cos\beta=\sqrt{1-sin^2\beta}$
$\Rightarrow cos\alpha=\sqrt{1-\dfrac{64}{289}}$ and $cos\beta=\sqrt{1-\dfrac{9}{25}}$
$\Rightarrow cos\alpha=\sqrt{\dfrac{289-64}{289}}$ and $cos\beta=\sqrt{\dfrac{25-9}{25}}$
$\Rightarrow cos\alpha=\sqrt{\dfrac{225}{289}}$ and $cos\beta=\sqrt{\dfrac{16}{25}}$
$\Rightarrow cos\alpha=\dfrac{15}{17}$ and $cos\beta=\dfrac{4}{5}$
Now, $cos(\alpha +\beta)=cos\alpha.cos\beta-sin \alpha. sin\beta$
$\Rightarrow cos(\alpha +\beta)=\dfrac{15}{17}\times \dfrac{4}{5}-\dfrac{8}{17}\times\dfrac{3}{5}$
$\Rightarrow cos(\alpha +\beta)= \dfrac{60}{85}-\dfrac{24}{85}$
$\Rightarrow cos(\alpha +\beta)= \dfrac{36}{85}$
$\Rightarrow \alpha +\beta=cos^{-1} \dfrac{36}{85}$
Therefore, $\Rightarrow sin^{-1}\dfrac{8}{17}+sin^{-1}\dfrac{3}{5}=cos^{-1}\dfrac{36}{85}$
Hence proved.

Prove the following:
$\cos^{-1}\left (\dfrac {4}{5}\right ) + \cos^{-1}\left (\dfrac {12}{13}\right ) = \cos^{-1}\left (\dfrac {33}{65}\right )$

$cos \left ( cos^{-1}\cfrac{4}{5} + cos^{-1}\cfrac{12}{13} \right )$

$= cos \left ( cos^{-1}\cfrac{4}{5} \right ) \times cos \left ( cos^{-1}\cfrac{12}{13} \right ) - sin \left ( cos^{-1}\cfrac{4}{5} \right ) \times sin \left ( cos^{-1}\cfrac{12}{13} \right )$

$= \cfrac{4}{5} \times \cfrac{12}{13} - \cfrac{\sqrt{25 - 16}}{5} \times \cfrac{\sqrt{169 - 144}}{13}$

$= \cfrac{48}{65} - \cfrac{3}{5} \times \cfrac{5}{13}$

$= \cfrac{48 - 15}{65}$

$= \cfrac{33}{65}$

$\Rightarrow cos^{-1}\left ( \cfrac{4}{5} \right ) + cos^{-1}\left ( \cfrac{12}{13}\right ) = cos^{-1}\left (\cfrac{33}{65} \right )$

If $\sin \left (\sin^{-1} \dfrac {1}{5} + \cos^{-1}x \right ) = 1$ , then find the value of $x.$

$\sin \left(\sin^{-1}\dfrac 15 + \cos^{-1}x \right) = 1$

$\sin \left(\sin^{-1}\dfrac 15 + \cos^{-1}x \right) = \sin \dfrac {\pi}{2}$

$\therefore \sin^{-1}\dfrac 15 + \cos^{-1}x = \dfrac {\pi}{2}$

Let

$\sin ^{ -1 }{ \dfrac { 1 }{ 5 } } =\theta$ , so

$\sin \theta = \dfrac 15$ ...(1)

$\therefore \theta +\cos^{-1}x=\dfrac {\pi}{2}$

$\cos^{-1}x = \dfrac {\pi}{2} - \theta$

$x=\cos \left( \dfrac {\pi}{2} - \theta\right)$

$x = \sin \theta = \dfrac 15$ ...from (1)

Write the value of $\displaystyle \tan\left(2\tan^{-1}\frac{1}{5}\right)$

$\tan{\left(2{\tan}^{-1}{\dfrac{1}{5}}\right)}$

$=\tan{\left[{\tan}^{-1}{\left(\dfrac{2\times \dfrac{1}{5}}{1-{\left(\dfrac{1}{5}\right)}^{2}}\right)}\right]}$

$=\tan{\left[{\tan}^{-1}{\left(\dfrac{\dfrac{2}{5}}{1-\dfrac{1}{25}}\right)}\right]}$

$=\tan{\left[{\tan}^{-1}{\left(\dfrac{\dfrac{2}{5}}{\dfrac{25-1}{25}}\right)}\right]}$

$=\tan{\left[{\tan}^{-1}{\left(\dfrac{\dfrac{2}{5}}{\dfrac{24}{25}}\right)}\right]}$

$=\tan{\left[{\tan}^{-1}{\left(\dfrac{5}{12}\right)}\right]}$

$=\dfrac{5}{12}$

If $\tan^{-1} \dfrac{x-1}{x-2}+\tan^{-1}\dfrac{x+1}{x+2}=\dfrac{\pi}{4}$ , then find the value of $x$ .

Let

$A=\tan^{-1}\dfrac{x-1}{x-2}$ and

$B=\tan^{-1}\dfrac{x+1}{x+2}$

Now,

$\tan(A+B)=\tan\dfrac{\pi}{4}$

$\therefore \dfrac{\tan A + \tan B}{1-\tan A\tan B}=1$

$\therefore \tan A + \tan B=1-\tan A\tan B$

$\therefore \dfrac{x-1}{x-2} + \dfrac{x+1}{x+2} = 1-\dfrac{x-1}{x-2}\times\dfrac{x+1}{x+2}$

$\therefore (x-1)(x+2) + (x+1)(x-2) = 1-(x-1)(x+1)$

$\therefore x^2+x-2 + x^2-x-2 = x^{2}-4-x^2+1$

$\therefore 2x^2=1$

$\therefore x=\pm \dfrac{1}{\sqrt{2}}$

This is the required solution.

If $\displaystyle cos^{-1} x + cos^{-1} y = \frac{\pi}{2}$ then prove that $cos^{-1} x = sin^{-1} y$

Given

$cos^{-1}x+cos^{-1}y=\dfrac{\pi}{2}$

To prove:

$cos^{-1}x=sin^{-1}y$

Consider

$cos^{-1}x+cos^{-1}y=\dfrac{\pi}{2}$

$\Rightarrow cos^{-1}y=\dfrac{\pi}{2}-cos^{-1}x$

$\Rightarrow y=cos\left(\dfrac{\pi}{2}-cos^{-1}x\right)$

$\Rightarrow y=sin(cos^{-1}x)$ (Since

$cos\left(\dfrac{\pi}{2}-\theta\right)=sin\theta$ )

$\Rightarrow sin^{-1}y=cos^{-1}x$

Hence proved.

Solve: $\displaystyle \sin^{-1} \frac{5}{x} + \sin^{-1} \frac{12}{x} = \frac{\pi}{2}$

$\sin^{-1}\dfrac{5}{x}+\sin^{-1}\dfrac{12}{x}=\dfrac{\pi}{2}$

Let

$\beta=\sin^{-1}\dfrac{12}{x}$

$\Rightarrow \sin \:\beta=\dfrac{12}{x}$

We know that

$\cos^2\beta=1-\sin^2\beta$

$\Rightarrow \cos^2\beta=1-\dfrac{144}{x^2}$

$\Rightarrow \cos\:\beta=\sqrt{1-\dfrac{144}{x^2}}$

$\Rightarrow \beta=\cos^{-1}\dfrac{\sqrt{x^2-144}}{x}$

Thus

$\sin^{-1}\dfrac{5}{x}+\cos^{-1}\dfrac{\sqrt{x^2-144}}{x}=\dfrac{\pi}{2}$

$\Rightarrow \sin^{-1}\dfrac{5}{x}=\dfrac{\pi}{2}-\cos^{-1}\dfrac{\sqrt{x^2-144}}{x}$

$\Rightarrow \dfrac{5}{x}=\sin\left(\dfrac{\pi}{2}-\cos^{-1}\dfrac{\sqrt{x^2-144}}{x}\right)$

We know that

$\sin\left(\dfrac{\pi}{2}-\theta\right)=\cos\:\theta$

$\Rightarrow \dfrac{5}{x}=\cos\left(\cos^{-1}\dfrac{\sqrt{x^2-144}}{x}\right)$

$\Rightarrow \dfrac{5}{x}=\dfrac{\sqrt{x^2-144}}{x}$

$\Rightarrow \sqrt{x^2-144}=5$

$\Rightarrow x^2-144=5^2$

$\Rightarrow x^2-144=25$

$\Rightarrow x^2=144+25$

$\Rightarrow x^2=169$

$\Rightarrow x=13$

Prove that:
$2\tan^{-1} \left (\dfrac {1}{5}\right ) + \sec^{-1} \left (\dfrac {5\sqrt {2}}{7}\right ) + 2\tan^{-1} \left (\dfrac {1}{8}\right ) = \dfrac {\pi}{4}.$

$2tan^{-1}\left ( \dfrac{1}{5} \right )+sec^{-1}\left ( \dfrac{5\sqrt{2}}{7} \right )+2tan^{-1}\left ( \dfrac{1}{8} \right )$

$=2\left [ tan^{-1}\left ( \dfrac{\dfrac{1}{5}+\dfrac{1}{8}}{1-\dfrac{1}{40}} \right ) \right ]+sec^{-1}\left ( \dfrac{5\sqrt{2}}{7} \right )$

$=2\left [ tan^{-1}\left ( \dfrac{1}{3} \right ) \right ]+sec^{-1}\left ( \dfrac{5\sqrt{2}}{7} \right )$

$=tan^{-1}\dfrac{3}{4}+sec^{-1}\left ( \dfrac{5\sqrt{2}}{7} \right )$

$=tan^{-1}\dfrac{3}{4}+tan^{-1}\dfrac{1}{7}$

$=tan^{-1}(1)=\dfrac{\pi}{4}$

Evaluate: $\sum _{ r=1 }^{ \infty }{ \tan ^{ -1 }{ \left( \cfrac { 2 }{ 1+(2r+1)(2r-1) } \right) } }$

$\sum_{r=1}^{\infty}tan^{-1}\left( \dfrac{2}{1+(2r+1)(2r-1)} \right)$

Divide numerator and denomenator by

$(2r+1)(2r-1)$

$\sum_{r=1}^{\infty}tan^{-1}\left( \dfrac{\dfrac{2}{(2r+1)(2r-1)}}{\dfrac{1}{(2r+1)(2r-1)}+1} \right)$

$\sum_{r=1}^{\infty}tan^{-1}\left( \dfrac{\dfrac{1}{2r-1}-\dfrac{1}{2r+1}}{\dfrac{1}{(2r+1)(2r-1)}+1} \right)$

$tan^{-1}\dfrac{a-b}{1+ab}=tan^{-1}a-tan^{-1}b$

$\therefore$

$\sum_{r=1}^{\infty}tan^{-1}\left( \dfrac{\dfrac{1}{2r-1}-\dfrac{1}{2r+1}}{\dfrac{1}{(2r+1)(2r-1)}+1} \right)=\sum_{r=1}^{\infty}\left(tan^{-1}\dfrac{1}{2r-1}-tan^{-1}\dfrac{1}{2r+1}\right)$

Open the summation we get,

$\left(tan^{-1}1-tan^{-1}\dfrac{1}{3}\right)+\left(tan^{-1}\dfrac{1}{3}-tan^{-1}\dfrac{1}{5}\right)+\left(tan^{-1}\dfrac{1}{5}-tan^{-1}\dfrac{1}{7}\right)...........\infty$

At infinity

$tan^{-1}\dfrac{1}{\infty}=0$

And other terms all cancel out each other, only

$tan^{-1}1$ remains.

$\therefore$ Ans is

$tan^{-1}1=\dfrac{\pi}{4}$

If $\tan^{-1} x + \tan^{-1} y + \tan^{-1} z = \pi$ then prove that:
$x+y+z = xyz$

Given

$\tan^{-1}x+\tan^{-1}y+\tan^{-1}z=\pi$

To prove:

$x+y+z=xyz$

Consider

$\tan^{-1}x+\tan^{-1}y+\tan^{-1}z=\pi$

We know that,

$\tan^{-1}x+\tan^{-1}y=\tan^{-1}\dfrac{x+y}{1-xy} \quad ...(1)$

$\Rightarrow \tan^{-1}\dfrac{x+y}{1-xy}+\tan^{-1}z=\pi$

Again use

$(1)$ we get

$\Rightarrow \tan^{-1}\dfrac{\dfrac{x+y}{1-xy}+z}{1-\dfrac{x+y}{1-xy}z}=\pi$

$\Rightarrow \tan^{-1}\dfrac{\dfrac{x+y+z-xyz}{1-xy}}{\dfrac{1-xy-xz-yz}{1-xy}}=\pi$

$\Rightarrow \tan^{-1}\dfrac{x+y+z-xyz}{1-xy-yz-xz}=\pi$

$\Rightarrow \dfrac{x+y+z-xyz}{1-xy-yz-xz}=\tan\:\pi$

$\Rightarrow \dfrac{x+y+z-xyz}{1-xy-yz-xz}=0$

$\Rightarrow x+y+z-xyz=0$

$\Rightarrow x+y+z=xyz$

Hence proved.

Calculate (192 - 214)
$\sin ^{-1}$ + 2 $\tan^{-1}$ (- $\sqrt{3}$ ).

$\arcsin(-1)+2\arctan(-\sqrt{3})$

$=-\dfrac{\pi}{2}+2\dfrac{-\pi}{3}$

$=\dfrac{-7\pi}{6}$

Simplify
$\cos^{-1}$ (cos $\dfrac{8\pi}{7}$ ).

we know that the range of

$\cos^{-1}x$ is

$[0,\pi]$

Now,

$\cos^{-1}(\cos(8\pi/7))$

$=\cos^{-1}(\cos(\pi+\pi/7))$

$=\cos^{-1}(-\cos(\pi/7))$

$=\cos^{-1}(\cos(\pi-\pi/7))$

$=\cos^{-1}(\cos(6\pi/7))$

$=\dfrac{6\pi}{7}$

Show that
$\tan^{-1} (\frac{1}{2}) + \tan^{-1} (\frac{1}{3}) = \cfrac{\pi}{4}$

$\tan^{ -1 }\cfrac { 1 }{ 2 } +\tan^{ -1 }\cfrac { 1 }{ 3 } \\ =\tan^{ -1 }\left( \cfrac { \cfrac { 1 }{ 2 } +\cfrac { 1 }{ 3 } }{ 1-\cfrac { 1 }{ 2 } \times \cfrac { 1 }{ 3 } } \right) \\ = \tan^{ -1 }\left( \cfrac { \cfrac { 5 }{ 6 } }{ \cfrac { 5 }{ 6 } } \right) \\ =\tan^{ -1 }(1)\\ =\cfrac { \pi }{ 4 }$

Simplify
$\tan^{-1}$ (tan $\dfrac{8\pi}{7}$ ).

We know that range of

$tan^{-1}x$ is

$\left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$

$\tan\left(\dfrac{8\pi}{7}\right)$

$=\tan\left(\pi+\dfrac{\pi}{7}\right)$

$=\tan\left(\dfrac{\pi}{7}\right)$

Hence-

$\tan^{-1}\left(\tan\left(\dfrac{8\pi}{7}\right)\right)$

$=\tan^{-1}\left(\tan\left(\dfrac{\pi}{7}\right)\right)$

$=\dfrac{\pi}{7}$

Simplify
$\tan^{-1}$ $\sqrt{2}$ - $\cot^{-1}$ (1/ $\sqrt{2}$ )

Let

$\tan x=\sqrt{2}\implies \arctan{\sqrt{2}}=x$

$\implies \cot{x}=\dfrac{1}{\sqrt{2}}\implies arccot(1/\sqrt{2})=x$

Hence final result is

$=x-x=0$

Prove that: $\sin^{-1}\left (\dfrac {3}{5}\right ) + \cos^{-1} \left (\dfrac {12}{13}\right ) = \sin^{-1}\left (\dfrac {56}{65}\right )$ .

Let

$\cos^{-1} \left(\dfrac{12}{13}\right)=x$

$\Rightarrow \dfrac{12}{13}=\cos\: x$

$\therefore \sin\:x=\dfrac{5}{13}$

Let

$\sin^{-1} \left(\dfrac{3}{5}\right)=y$

$\Rightarrow \dfrac{3}{5}=\sin\: y$

$\therefore \cos\:y=\dfrac{4}{5}$

We know that,

$\sin(x+y)=\sin\:x\:\cos\:y+\cos\:x\:\sin\:y$

$\sin(x+y)=\dfrac{5}{13} \times \dfrac{4}{5}+\dfrac{12}{13} \times \dfrac{3}{5}$

$\sin(x+y)=\dfrac{56}{65}$

$\therefore x+y=\sin^{-1} \left(\dfrac{56}{65}\right)$

$\cos^{-1} \left(\dfrac{12}{13}\right) +\sin^{-1} \left(\dfrac{3}{5}\right)=\sin^{-1} \left(\dfrac{56}{65}\right)$

Hence proved.

Prove $2 \sin^{-1} \left(\dfrac{5}{13}\right)=\cos^{-1}\left(\dfrac{119}{169}\right)$

Applying the trigonometric identities in the LHS of $2{\sin ^{ - 1}}\left( {\dfrac{5}{{13}}} \right) = {\cos ^{ - 1}}\left( {\dfrac{{119}}{{169}}} \right)$ .

$2{\sin ^{ - 1}}\left( {\dfrac{5}{{13}}} \right) = {\sin ^{ - 1}}\left( {2\left( {\dfrac{5}{{13}}} \right)\sqrt {1 - {{\left( {\dfrac{5}{{13}}} \right)}^2}} } \right)$

$= {\sin ^{ - 1}}\left( {\dfrac{{10}}{{13}}\sqrt {1 - \dfrac{{25}}{{169}}} } \right)$

$= {\sin ^{ - 1}}\left( {\dfrac{{10}}{{13}}\sqrt {\dfrac{{144}}{{169}}} } \right)$

$= {\sin ^{ - 1}}\left( {\left( {\dfrac{{10}}{{13}}} \right)\left( {\dfrac{{12}}{{13}}} \right)} \right)$

$= {\sin ^{ - 1}}\left( {\dfrac{{120}}{{169}}} \right)$

Let ${\sin ^{ - 1}}\left( {\dfrac{{120}}{{169}}} \right) = \theta$ ,

$\dfrac{{120}}{{169}} = \sin \theta$

$\cos \theta = \dfrac{{119}}{{169}}$

$\theta = {\cos ^{ - 1}}\left( {\dfrac{{119}}{{169}}} \right)$

${\sin ^{ - 1}}\left( {\dfrac{{120}}{{169}}} \right) = {\cos ^{ - 1}}\left( {\dfrac{{119}}{{169}}} \right)$

Therefore, $2{\sin ^{ - 1}}\left( {\dfrac{5}{{13}}} \right) = {\cos ^{ - 1}}\left( {\dfrac{{119}}{{169}}} \right)$ .

Hence proved.

Write $\tan^{-1} \left( \cfrac{\sqrt{1+\cos x}}{\sqrt{1-\cos x}} \right)$ in its simplest form.

$\tan ^{ -1 } \left( \cfrac { \sqrt { 1+\cos x } }{ \sqrt { 1-\cos x } } \right) \\ =\tan ^{ -1 } \left( \cfrac { \sqrt { 2\cos ^{ 2 } \dfrac{x}{2} } }{ \sqrt { 2\sin ^{ 2 } \dfrac{x}{2} } } \right) \\ =\tan ^{ -1 } \left( \sqrt { \cfrac { 2\cos ^{ 2 } \dfrac{x}{2} }{ 2\sin ^{ 2 } \dfrac{x}{2} } } \right) \\ =\tan ^{ -1 } \left( \sqrt { \cot ^{ 2 }{ \dfrac{x}{2} } } \right) \\ =\tan ^{ -1 } \left( \cot { \dfrac{x}{2} } \right) \\ =\tan ^{ -1 } \left( \tan { \left( \cfrac { \pi }{ 2 } -\cfrac { x }{ 2 } \right) } \right) \\ =\cfrac { \pi }{ 2 } -\cfrac { x }{ 2 }$

$\sin^{-1} ( \dfrac{\sqrt{1+x} + \sqrt{1-x} }{2})$

$\sin^{-1}(\cfrac{\sqrt{1+x}+\sqrt{1-x}}{2})$

$\Rightarrow \sin^{-1}(\cfrac{\sqrt{1+\sin \theta}+\sqrt{1-\sin \theta}}{2})$

$\Rightarrow \sin^{-1}(\cfrac{\sqrt{1+2\sin\cfrac{\theta}{2}\cos \cfrac{\theta}{2}}+\sqrt{1-2\sin\cfrac{\theta}{2}\cos\cfrac{\theta}{2}}}{2})$

$\Rightarrow \sin^{-1}\cfrac{\sqrt{(\sin\cfrac{\theta}{2}+\cos \cfrac{\theta}{2})^{2}}+\sqrt{(\sin\cfrac{\theta}{2}-\cos \cfrac{\theta}{2})^{2}}}{2}$

$\Rightarrow \sin^{-1}(\cfrac{\sin \cfrac{\theta}{2}+\cos \cfrac{\theta}{2}+\sin\cfrac{\theta}{2}-\cos\cfrac{\theta}{2}}{2})$

$\Rightarrow \sin^{-1}(\cfrac{2\sin\cfrac{\theta}{2}}{2})$

$\Rightarrow \sin^{-1}(\sin \cfrac{\theta}{2})=\cfrac{\theta}{2}=\cfrac{1}{2}\sin^{-1}x$

Find the value of ${\sin}^{-1}{(\sin{\dfrac{3\pi}{5}})}$ .

${\sin ^{ - 1}}\left( {\sin \dfrac{{3\pi }}{5}} \right)$

$= {\sin ^{ - 1}}\left( {\sin \left( {\pi - \dfrac{{2\pi }}{5}} \right)} \right)$

$= {\sin ^{ - 1}}\left( {\sin \left( {\dfrac{{2\pi }}{5}} \right)} \right)$

$= \dfrac{{2\pi }}{5}$

Let (x, y) be such that $sin^{-1} ax + cos^{-1} y + cos^{-1} (bxy) = \frac{\pi}{2}$

2037910_1008637_ans_835d8e0a40fc485a974a11dc17b6fe88.jpg

The sum $\sum_\limits{n=1}^{\infty} \tan^{-1}\left(\dfrac{2}{n^2}\right)$ equals $\dfrac{\pi}{m}$ .Find $m$

Given

$\displaystyle \sum_{n=1}^{\infty} \tan^{-1} \left(\dfrac{1}{2n^2}\right) = \dfrac{\pi}{m}$

Let us consider

$\tan^{-1} \left(\dfrac{1}{2n^2}\right) = \tan^{-1} \left(\dfrac{1\times2}{2n^2 \times 2}\right)$

$=\tan^{-1} \left[\dfrac{2}{4n^2}\right]$

$=\tan^{-1} \left[\dfrac{2}{1+4n^2-1}\right]$

$=\tan^{-1} \left[\dfrac{2}{1+(2n+1)(2n-1)}\right]$

$=\tan^{-1} \left[\dfrac{(2n+1)-(2n-1)}{1+(2n+1)(2n-1)}\right]$

$=\tan^{-1} (2n+1) - \tan^{-1} (2n-1)\left[\tan^{-1}[\dfrac{x-y}{1+xy} = \tan^{-1}x - \tan^{-1}y\right]$

$\displaystyle \sum_{n=1}^{\infty} \tan^{-1} \left(\dfrac{1}{2n^2}\right) = \sum_{n=1}^{\infty} \tan^{-1} (2n+1) - \sum_{n=1}^{\infty} \tan^{-1} (2n-1)$

$=[\tan^{-1}(3) - \tan^{-1} (1)] + [\tan^{-1} (5) - \tan^{-1} (3)] + [ \tan^{-1}(7) - \tan^{-1} (5)]+[\tan^{-1}(2n+1)-\tan^{-1}(2n-1)]$

$= \tan^{-1}(2n+1) - \tan^{-1}(1)$

$=\underset{n\to \infty}{Lt} [\tan^{1} (2n+1) \tan^{-1}(1)]$

$=\tan^{-1} (\infty) -\tan^{-1} (1)$

$=\dfrac{\pi}{2} - \dfrac{\pi}{4}$

$=\dfrac{\pi}{4}$

Given

$\displaystyle \sum_{n=1}^{\infty} \tan^{-1} \left(\dfrac{1}{2n^2}\right) = \dfrac{\pi}{m} = \dfrac{\pi}{4}$

Find the value of $\sin ^{ -1 }{ \left( \cos { \cfrac { 33\pi }{ 5 } } \right) }$

We need to find the value of

$\sin^{-1}\left(\cos\left(\dfrac{33\pi}{5}\right)\right)$

$\sin^{-1}\left(\cos\left(\dfrac{33\pi}{5}\right)\right)=\sin^{-1}\left(\cos\left(\dfrac{30\pi+3\pi}{5}\right)\right)$

$=\sin^{-1}\left(\cos\left(6\pi+\dfrac{3\pi}{5}\right)\right)$

$=\sin^{-1}\left(\cos\left(\dfrac{3\pi}{5}\right)\right)$

$=\sin^{-1}\left(\sin\left(\dfrac{\pi}{2}-\dfrac{3\pi}{5}\right)\right)$

$=\sin^{-1}\left(\sin\left(-\dfrac{\pi}{10}\right)\right)$

$=-\dfrac{\pi}{10}\quad \left\{\because \sin^{-1}(\sin\:x)=x, for\:x\in\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\right\}$

$\therefore \sin^{-1}\left(\cos\left(\dfrac{33\pi}{5}\right)\right)=-\dfrac{\pi}{10}$

Find m if the following equation holds true
$\tan \left(\dfrac{1}{2} \sin^{-1} \dfrac{3}{4} \right) = \dfrac{4 - \sqrt{m}}{3}$

Let,

$\tan \left ( \cfrac{1}{2}\sin^{-1}\cfrac{3}{4} \right )=x$

$\cfrac{1}{2}\sin^{-1}\cfrac{3}{4}=\tan^{-1}x$

$\sin^{-1}\cfrac{3}{4}=2\tan^{-1}x$

$\tan^{-1}\left ( \cfrac{\frac{3}{4}}{\sqrt{1-\left ( \frac{3}{4}\right )^{2}}} \right )=2\tan^{-1}x$

$\tan^{-1}\left ( \cfrac{3}{\sqrt{7}} \right )=\tan^{-1}\left ( \cfrac{2x}{1-x^{2}} \right )$

$\Rightarrow \cfrac{3}{\sqrt{7}}=\cfrac{2x}{1-x^{2}}$

$3x^{2}+2\sqrt{7}x-3=0$

$x=\cfrac{-2\sqrt{7}\pm \sqrt{64}}{6}$

$x=\cfrac{-2\sqrt{7}\pm 8}{6}$

$x=\cfrac{-\sqrt{7}\pm 4}{3}$

$x$ cannot be negative because,

$0<\sin^{-1}\cfrac{3}{4}<\cfrac{\pi }{2}$

$0<\cfrac{1}{2}\sin^{-1}\cfrac{3}{4}<\cfrac{\pi }{4}$

$\tan 0<\tan \left ( \cfrac{1}{2}\sin^{-1}\cfrac{3}{4} \right )<\tan \cfrac{\pi }{4}$

$0<\tan \left ( \cfrac{1}{2}\sin^{-1}\cfrac{3}{4} \right )<1$

So,

$x=\cfrac{4-\sqrt{7}}{3}$

$\Rightarrow m=7$

$Show \>that$ $cot^{-1}\left( \frac{\sqrt{1+ sinx}+ \sqrt{1-sinx}}{\sqrt{1+ sinx}- \sqrt{1-sinx}}\right) =\frac{x}{2}$ $for\>x\in\>(0,\frac{\pi}{2})$

$\sqrt{1+sinx}=\sqrt{sin^2(\frac{x}{2})+cos^2(\frac{x}{2})+2sin^2(\frac{x}{2})cos^2(\frac{x}{2})}\\=\>\sqrt{{(sin(\frac{x}{2})+cos(\frac{x}{2}))^2}}=(sin(\frac{x}{2})+cos(\frac{x}{2})\\\sqrt{1-sinx}=\sqrt{sin^2(\frac{x}{2})+cos^2(\frac{x}{2})-2sin^2(\frac{x}{2})cos^2(\frac{x}{2})}\\=\sqrt{{(cos(\frac{x}{2})-sin(\frac{x}{2}))^2}}=\>(cos(\frac{x}{2})-sin(\frac{x}{2}))\\\>\therefore\>cot^{-1}((\frac{(cos(\frac{x}{2})+sin(\frac{x}{2})+cos(\frac{x}{2})-sin(\frac{x}{2})}{(cos(\frac{x}{2})+sin(\frac{x}{2})-(cos(\frac{x}{2})+sin(\frac{x}{2})}))\\=cot^{-1}(cot(\frac{x}{2}))\\but\>this\>valid\>only\>for\>x\in\>(0,(\frac{\pi}{2}))$

$\sin^{-1}(1-x)-2\sin^{-1}x=\cfrac{\pi}{2}$ , then $x$ is equal to:

Given that

${\sin}^{-1}{\left(1-x\right)}-2{\sin}^{-1}x=\dfrac{\pi}{2}$

let

$x=\sin{y}$

$\therefore {\sin}^{-1}\left(1-\sin{y}\right)-2y=\dfrac{\pi}{2}$

$\Rightarrow {\sin}^{-1}\left(1-\sin{y}\right)=\dfrac{\pi}{2}+2y$

$\Rightarrow 1-\sin{y}=\sin{\left(\dfrac{\pi}{2}+2y\right)}$

$\Rightarrow 1-\sin{y}=\cos{2y}$

$\Rightarrow 1-\sin{y}=1-2{\sin}^{2}{y}$ as

$\cos{2y}=1-2{\sin}^{2}{y}$

$\Rightarrow 2{\sin}^{2}{y}-\sin{y}=0$

$\Rightarrow 2{x}^{2}-x=0$

$\Rightarrow x\left(2x-1\right)=0$

$\Rightarrow x=0, 2x-1=0$

$\Rightarrow x=0, 2x=1$

$\Rightarrow x=0, x=\dfrac{1}{2}$

But

$x=\dfrac{1}{2}$ does not satisfy the given equation

$\therefore x=0$ is the solution of the given equation.

If $\sin^{-1}x+\sin^{-1}y+\sin^{-1}z =\pi$ , prove that $x\sqrt{1-x^2}+y\sqrt{1-y^2}+z\sqrt{1-z^2}=2xyz$ .

We are given,

$\sin^{-1}x+ \sin^{-1} y+ \sin^{-1} z = \pi$ .

let,

$\sin^{-1} x= A \Rightarrow \sin A =x$

$\sin^{-1} y= B \Rightarrow \sin B= y$

$\sin^{-1} z = C \Rightarrow \sin C= z$ .

here,

$A,B, C \in [-\pi/2, \pi/2]$

$\therefore A+B+ C = \pi$ ........

$(1)$

now,

$LHS$

$= x \sqrt{1-x^{2}}+y \sqrt{1-y^{2}}+ z \sqrt{1-z^{2}}$

$= \sin A. \sqrt{1- \sin^{2} A}+ \sin B \sqrt{1- \sin^{2} B}+ \sin C. \sqrt{1- \sin^{2} C}$

$= \sin A. \cos A+ \sin B \cos B+ \sin C. \cos C$

[Multiply & Divide by

$2$ ]

$=\dfrac{2}{2} [\sin A \cos A+ \sin B \cos B]+ \sin C. \cos C$

$=\dfrac{ [2 \sin A \cos A+ 2 \sin B \cos B] }{2}+ \sin C. \cos C (2 \sin \theta \cos \theta = \sin 2 \theta)$

$=\dfrac{(\sin A+ \sin 2B)}{2}+ \sin C. \cos C$

$=\dfrac{2 \sin \left( \dfrac{2A+ 2B}{2} \right) \cos \left( \dfrac{2A-2B}{2} \right) }{2}+ \sin C. \cos C$

$= \sin (A+B) \cos (A-B)+ \sin C. \cos C$

$=\sin (\pi- C) \cos (A-B)+ \sin C. \cos (\pi- (A+B))$

$= \sin C [\cos (A-B)- \cos (A+B)]$

$= \sin C [-2 \sin \left( \dfrac{-2B}{2} \right)\sin \left( \dfrac{3A}{2} \right) ]$

$=2 \sin A \sin B \sin C$

$=2 xyz$

$= RHS$ .

Find the value of $\cos^{-1} (\cos \dfrac {2\pi}{3}) + \sin^{-1} \left (\sin \dfrac {2\pi}{3}\right )$ .

Given,

${\cos}^{-1}{\left(\cos{\dfrac{2\pi}{3}}\right)}+{\sin}^{-1}{\left(\sin{\dfrac{2\pi}{3}}\right)}$

$={\cos}^{-1}{\left(\cos{\left(\pi-\dfrac{\pi}{3}\right)}\right)}+{\sin}^{-1}{\left(\sin{\left(\pi-\dfrac{\pi}{3}\right)}\right)}$

$={\cos}^{-1}{\left(-\cos{\left(\dfrac{\pi}{3}\right)}\right)}+{\sin}^{-1}{\left(\sin{\dfrac{\pi}{3}}\right)}$

$={\cos}^{-1}{\left(\dfrac{-1}{2}\right)}+{\sin}^{-1}{\left(\dfrac{\sqrt{3}}{2}\right)}$

$=\pi-\dfrac{\pi}{3}+\dfrac{\pi}{3}$

$=\pi$

Solve the following equation $cos(tan^{-1}x)=sin \left(cot^{-1}\dfrac{3}{4}\right)$

$\cos(tan^{-1}x)=\sin(\cot^{-1}\cfrac{3}{4})\\ \therefore let \theta_1=\tan^{-1}x\&\theta_2=\cot^{-1}\cfrac{3}{4}\\ \therefore x=\tan\theta,\&\cfrac{3}{4}=\cot\theta_2\\ \Rightarrow\cfrac{\sin\theta_1}{\cos\theta_1}=x\&\cfrac{\cos\theta_2}{\sin\theta_2}=\cfrac{3}{4}\\ \Rightarrow\cfrac{\sin^2\theta_1}{\cos^2\theta_1}=x^2\&\cfrac{\cos^2\theta_2}{\sin^2\theta_2}=\cfrac{9}{16}\\ \Rightarrow\cfrac{1-\cos^2\theta_1}{\cos^2\theta_1}=x^2\&\cfrac{1-\sin^2\theta_2}{\sin^2\theta_2}=\cfrac{9}{16}\\ \Rightarrow \cos\theta_1=\cfrac{1}{\sqrt{1+x^2}}\&\sin\theta_2=\cfrac{4}{5}\\ \therefore\theta_1=\cos^{-1}\cfrac{1}{\sqrt{1+x^2}}\& \theta_2=\sin^{-1}\cfrac{4}{5}\\ \therefore \cos(\cos^{-1}\cfrac{1}{\sqrt{1+x^2}})=\sin(\sin^{-1}\cfrac{4}{5})\\ \Rightarrow\cfrac{1}{\sqrt{1+x^2}}=\cfrac{4}{5} (\because\cos\cos^{-1}\theta=\theta\&\sin\sin^{-1}\theta=\theta)\\ \therefore x^2+1=\cfrac{25}{16}\\ \therefore x=\cfrac{3}{4}$

Solve:
$\tan \left( {{{\cos }^{ - 1}}\frac{1}{x}} \right) = \sin \left( {{{\cot }^{ - 1}}\frac{1}{x}} \right)$

$\tan \left( {{\cos }^{-1}}\dfrac{1}{x} \right)=\sin \left( {{\cot }^{-1}}\dfrac{1}{x} \right)$

We know that, ${{\cos }^{-1}}x={{\tan }^{-1}}\left( \dfrac{\sqrt{1-{{x}^{2}}}}{x} \right)$ and ${{\tan }^{-1}}x={{\sin }^{-1}}\left( \dfrac{x}{\sqrt{1+{{x}^{2}}}} \right)$

Now,

$\tan \left( {{\cos }^{-1}}\dfrac{1}{x} \right)=\sin \left( ta{{n}^{-1}}x \right)$

$\Rightarrow \tan {{\tan }^{-1}}\left( \dfrac{\sqrt{1-\dfrac{1}{{{x}^{2}}}}}{\dfrac{1}{x}} \right)=\sin {{\sin }^{-1}}\left( \dfrac{x}{\sqrt{1+{{x}^{2}}}} \right)$

$\Rightarrow \dfrac{\sqrt{{{x}^{2}}-1}}{1}=\dfrac{x}{\sqrt{{{x}^{2}}+1}}$

$\Rightarrow \sqrt{{{x}^{2}}-{{1}^{2}}}.\sqrt{{{x}^{2}}+{{1}^{2}}}=x$

$\Rightarrow \sqrt{{{x}^{4}}-{{1}^{4}}}=x$

Squaring both side and we get

$\Rightarrow {{x}^{4}}-1={{x}^{2}}$

$\Rightarrow {{x}^{4}}-1-{{x}^{2}}=0$

$\Rightarrow {{x}^{4}}-{{x}^{2}}-1=0$

Let ${{x}^{2}}=y$

$\Rightarrow {{y}^{2}}-y-1=0$

Comparing that, $a{{y}^{2}}+by+c=0$

$a=1,b=-1,c=-1$

Using quadratic equation formula, and we get

$y=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$

$y=\dfrac{-\left( -1 \right)\pm \sqrt{{{\left( -1 \right)}^{2}}-4\times 1\times \left( -1 \right)}}{2\times 1}$

$y=\dfrac{1\pm \sqrt{5}}{2}$

And

$y={{x}^{2}}=\dfrac{1\pm \sqrt{5}}{2}$

$x=\sqrt{\dfrac{1\pm \sqrt{5}}{2}}$

Hence, this is the answer.

Solve : $y=\sin^{-1}(\sec x)$

$y=\sin^{-1} \left(\sec {x}\right)$

or,

$\sin {y} = \sec {x}$

or,

$\sin {y} = \dfrac {1}{\cos {x}}$

or,

$\boxed {\sin {y}. \cos x = 1}$

Evaluate: ${{\tan }^{-1}}\left( \dfrac{\sqrt{1+\cos x}-\sqrt{1-\cos x}}{\sqrt{1+\cos x}+\sqrt{1-\cos x}} \right)$

We have,

${{\tan }^{-1}}\left( \dfrac{\sqrt{1+\cos x}-\sqrt{1-\cos x}}{\sqrt{1+\cos x}+\sqrt{1-\cos x}} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{\sqrt{1+2{{\cos }^{2}}\dfrac{x}{2}-1}-\sqrt{1-1+2si{{n}^{2}}\dfrac{x}{2}}}{\sqrt{1+2{{\cos }^{2}}\dfrac{x}{2}-1}+\sqrt{1-1+2si{{n}^{2}}\dfrac{x}{2}}} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{\sqrt{2{{\cos }^{2}}\dfrac{x}{2}}-\sqrt{2si{{n}^{2}}\dfrac{x}{2}}}{\sqrt{2{{\cos }^{2}}\dfrac{x}{2}}+\sqrt{2si{{n}^{2}}\dfrac{x}{2}}} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{\sqrt{2}\cos \dfrac{x}{2}-\sqrt{2}sin\dfrac{x}{2}}{\sqrt{2}\cos \dfrac{x}{2}+\sqrt{2}sin\dfrac{x}{2}} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{\cos \dfrac{x}{2}-sin\dfrac{x}{2}}{\cos \dfrac{x}{2}+sin\dfrac{x}{2}} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{\cos \dfrac{x}{2}-sin\dfrac{x}{2}}{\cos \dfrac{x}{2}+sin\dfrac{x}{2}} \right)\times \left( \dfrac{\cos \dfrac{x}{2}-sin\dfrac{x}{2}}{\cos \dfrac{x}{2}-sin\dfrac{x}{2}} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{{{\left( \cos \dfrac{x}{2}-sin\dfrac{x}{2} \right)}^{2}}}{{{\cos }^{2}}\dfrac{x}{2}-si{{n}^{2}}\dfrac{x}{2}} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{\left( {{\cos }^{2}}\dfrac{x}{2}+si{{n}^{2}}\dfrac{x}{2}-2sin\dfrac{x}{2}\cos \dfrac{x}{2} \right)}{{{\cos }^{2}}\dfrac{x}{2}-si{{n}^{2}}\dfrac{x}{2}} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{1-\sin x}{\cos x} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \dfrac{1}{\cos x}-\dfrac{\sin x}{\cos x} \right)$

$\Rightarrow {{\tan }^{-1}}\left( \sec x-\tan x \right)$

Hence, this is the answer.

Find the values of $\sin\left(\cos^{-1}\dfrac{3}{5}+\cos^{-1}\dfrac{12}{13}\right)$ .

${ Sin }.\left( { { { \cos }^{ -1 } }\left( { \frac { 3 }{ 5 } } \right) +{ { \cos }^{ -1 } }\frac { { 12 } }{ { 13 } } } \right) \\ Let\, \, \, \, { \cos ^{ -1 } }\frac { 3 }{ 5 } =\theta ,\, \, \, \, \, \, \, \, \, { \cos ^{ -1 } }\frac { { 12 } }{ { 13 } } ={ 0 } \\ \Rightarrow \cos \theta =\frac { 3 }{ 5 } \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \Rightarrow \cos { 0 } =\frac { { 12 } }{ { 13 } } \\ \therefore \sin \theta =\sqrt { 1-{ { \left( { \frac { 3 }{ 5 } } \right) }^{ 2 } } } \, \, \, \, \, \, \, \, \Rightarrow \sin { 0 } =\sqrt { 1-{ { \left( { \frac { { 12 } }{ { 13 } } } \right) }^{ 2 } } } \\ \Rightarrow \sin \theta =\sqrt { \frac { { 25-9 } }{ { 25 } } } \, \, \, \, \, \, \, \, \, \, \Rightarrow \sin { 0 } =\sqrt { \frac { { 169-144 } }{ { 169 } } } \\ \, \, \, \, \, \, \, \sin \theta =\frac { 4 }{ 5 } \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \sin { 0 } =\frac { 5 }{ { 13 } } \\ \Rightarrow \sin \left( { \theta +{ 0 } } \right) =\sin \theta .\cos { 0 } +\sin { 0 } .\cos \theta \\ \therefore \sin \left( { \theta +{ 0 } } \right) =\frac { 4 }{ 5 } .\frac { { 12 } }{ { 13 } } +\frac { 5 }{ { 13 } } \times \frac { 3 }{ 5 } \, \, \, \, \, \, =\frac { { 48 } }{ { 65 } } +\frac { { 15 } }{ { 65 } } =\frac { { 63 } }{ { 65 } } \,$

Find the value of $x$ for which ${\sec ^{ - 1}}x + {\sin ^{ - 1}}x = \dfrac{\pi }{2}.$

Solution: given,

$\Rightarrow \ \sec^{-1}x+\sin^{-1}x=\dfrac {\pi}{2}$

We know

$\sin^{-1}x+\cos^{-1}x=\dfrac {\pi}{2}$

and

$\sec^{-1}x=\cos^{-1}\dfrac {1}{x}$

$\Rightarrow \ \cos^{-1}\dfrac {1}{x}+\sin^{-1}x=\dfrac {\pi}{2}$

$\Rightarrow \ \dfrac {\pi}{2}-\sin^{-1}\dfrac {1}{x}+\sin^{-1}x=\dfrac {\pi}{2}$

$\Rightarrow \ \sin^{-1}x-\sin^{-1}\dfrac {1}{x}=0$

$\Rightarrow \ \sin^{-1} \left (x\sqrt {1-\dfrac {1}{x^2}} -\dfrac {1}{x}\sqrt {1-x^2}\right)=0$

$\Rightarrow \ x\times \dfrac {\sqrt {x^2-1}}{x}-\dfrac {1}{x}\sqrt {1-x^2}=\sin 0$

$\Rightarrow \sqrt{x^2-1}-\dfrac{1}{x}\sqrt{1-x^2}=0$

$\Rightarrow \ \sqrt {x^2-1}=\dfrac {\sqrt {1-x^2}}{x}$ squaring both side

$\Rightarrow \ (x^2-1)=\dfrac {1-x^2}{x^2}$

$\Rightarrow \ (x^2-1)=\dfrac {-(x^2-1)}{x^2}$

$\Rightarrow \ x^2=-1$

$\Rightarrow \ x=\pm i$ Ans (here

$i^2=-1$ )

Solve the equation
${\tan ^{ - 1}}\frac{{1 - x}}{{1 + x}} - \frac{1}{2}{\tan ^{ - 1}}x = 0,x > 0$

${\tan}^{-1}{\dfrac{1-x}{1+x}}-\dfrac{1}{2}{\tan}^{-1}{x}=0$

$\Rightarrow\,2{\tan}^{-1}{\dfrac{1-x}{1+x}}-{\tan}^{-1}{x}=0$ multiply both sides by

$2$

We know that

$2{\tan}^{-1}{x}={\tan}^{-1}{\left(\dfrac{2x}{1-{x}^{2}}\right)}=0$

$\Rightarrow\,{\tan}^{-1}{\left(\dfrac{2\dfrac{1-x}{1+x}}{1-{\left(\dfrac{1-x}{1+x}\right)}^{2}}\right)}-{\tan}^{-1}{x}=0$

$\Rightarrow\,{\tan}^{-1}{\left[\dfrac{2\left(1-x\right)}{\left(1+x\right)}\times\dfrac{\left(1+x\right)}{{\left(1+x\right)}^{2}-{\left(1-x\right)}^{2}}\right]}={\tan}^{-1}{x}$

$\Rightarrow\,{\tan}^{-1}{\left[\dfrac{2\left(1-x\right)\left(1+x\right)}{\left(1+x+1-x\right)\left(1+x-1+x\right)}\right]}={\tan}^{-1}{x}$

$\Rightarrow\,{\tan}^{-1}{\left[\dfrac{2\left(1-x\right)\left(1+x\right)}{2\left(2x\right)}\right]}={\tan}^{-1}{x}$

$\Rightarrow\,{\tan}^{-1}{\left[\dfrac{\left(1-{x}^{2}\right)}{2x}\right]}={\tan}^{-1}{x}$

$\Rightarrow\,\dfrac{\left(1-{x}^{2}\right)}{2x}=x$

$\Rightarrow\,1-{x}^{2}=2{x}^{2}$

$\Rightarrow\,3{x}^{2}=1$

$\Rightarrow\,{x}^{2}=\dfrac{1}{3}$

$\Rightarrow\,x=\pm\dfrac{1}{\sqrt{3}}$

Given that

$x>0$ the value

$x$ should be positive.

$\therefore\,x=\dfrac{1}{\sqrt{3}}$

Express $\tan^{-1}\left(\dfrac{\cos x}{1-\sin x}\right), -\dfrac{\pi}{2}<x<\dfrac{\pi}{2}$ in the simplest form.

$tan^{-1}\frac{cos x}{1-sinx}$

Calculate cos x & 1-sin x .

$cos \,2 x = cos^{2}\,x-sin^{2}\,x.$

$cos \,2 (\frac{x}{2}) = cos^{2}\frac{x}{2}-sin^{2}\frac{x}{2}$

$cos \,x = cos^{2}\frac{x}{2}-sin^{2}\frac{x}{2}$

Similarly

$sin \,x = 2 sin \frac{x}{2}cos\frac{x}{2}$

Now

$tan^{-1}\left [ \frac{cos^{2}\frac{x}{2}-sin^{2}\frac{x}{2}}{1-(2sin\frac{x}{2}\,cos\frac{x}{2})} \right ]$

$tan^{-1}\left [ \frac{cos^{2}\frac{x}{2}-sin^{2}\frac{x}{2}}{cos^{2}\frac{x}{2}+sin^{2}\frac{x}{2}-2sin\frac{x}{2}\,cos\frac{x}{2}} \right ]$

$tan^{-1}\left [ \frac{(cos\frac{x}{2}+sin\frac{x}{2})\,(cos\frac{x}{2}-sin\frac{x}{2})}{(cos\frac{x}{2}-sin\frac{x}{2})^{2}} \right ]$

$tan^{-1}\left [ \frac{cos\frac{x}{2}+sin\frac{x}{2}}{cos\frac{x}{2}-sin\frac{x}{2}} \right ]$

$tan^{-1}\left [ \frac{cos\frac{x}{2}+sin\frac{x}{2}/cos\frac{x}{2}}{cos\frac{x}{2}-sin\frac{x}{2}/cos\frac{x}{2}} \right ]$

$tan^{-1}\left [ \frac{1+tan\frac{x}{2}}{1-tan\frac{x}{2}} \right ]$

$tan^{-1}(\frac{tan\frac{\pi }{4}+tan\frac{x}{2}}{1-tan\frac{\pi }{4}tan\frac{x}{2}})$

$= tan^{-1}\left [ tan(\frac{\pi }{4}+\frac{x}{2}) \right ]$

$= \frac{\pi }{4}+\frac{x}{2}.$

1203887_1283163_ans_8b4ca1f01dab4870a288437f57fa7bf1.jpg

Solve : $\tan^{-1}\sqrt{\dfrac{1+\sin x}{1-\sin x}}$ , $-\dfrac{\pi}{2} < x < \dfrac{\pi}{2}$

2039464_1286531_ans_0071acc831804c5d82246fa6b04defc4.jpg

Tan $^{-1}$ { $\dfrac{\sqrt{1 + cos x}}{1 - cos x}$ , 0 < x < $\pi$

2039456_1286318_ans_5fff67ce936f41dba34fff6c42ac5eb0.jpg

tan $^{-1}$ { $\dfrac{cos x}{1 + sin x}$ }, 0 < x < $\pi$

2039458_1286415_ans_d043a90ba82844ee9e60b7ca5bbab0b6.jpg

$cos^{-1}(2x-1)= ?$

2039412_1284826_ans_52bd02577ea3458ea19b328bec62c636.jpg

cos $^{-1}$ ( $\dfrac{1 - x^2}{1 + x^2}$ ), 0 < x < 1

2039452_1286265_ans_915e85c7bca34ee5a35d48dbd2434691.jpg

sin $^{-1}$ $\dfrac{1 - x^2}{1 + x^2}$ , 0 < x < 1

2039455_1286307_ans_4b084b493d02491dab8ccd554dc86b40.jpg

Solve: $\left( { tan }^{ -1 }x \right) ^{ 2 }+\left( { cot }^{ -1 }x \right) ^{ 2 }=\dfrac { 5{ \pi }^{ 2 } }{ 8 }$

We have,

${{\left( {{\tan }^{-1}}x \right)}^{2}}+{{\left( {{\cot }^{-1}}x \right)}^{2}}=\dfrac{5{{\pi }^{2}}}{8}$

$\Rightarrow {{\left( {{\tan }^{-1}}x \right)}^{2}}+{{\left( {{\cot }^{-1}}x \right)}^{2}}+2{{\tan }^{-1}}x{{\cot }^{-1}}x-2{{\tan }^{-1}}x{{\cot }^{-1}}x=\dfrac{5{{\pi }^{2}}}{8}$

$\Rightarrow {{\left( {{\tan }^{-1}}x+{{\cot }^{-1}}x \right)}^{2}}-2{{\tan }^{-1}}x{{\cot }^{-1}}x=\dfrac{5{{\pi }^{2}}}{8}$

$\Rightarrow {{\left( \dfrac{\pi }{2} \right)}^{2}}-2{{\tan }^{-1}}x{{\cot }^{-1}}x=\dfrac{5{{\pi }^{2}}}{8}$

$\Rightarrow \dfrac{{{\pi }^{2}}}{4}-2{{\tan }^{-1}}x{{\cot }^{-1}}x=\dfrac{5{{\pi }^{2}}}{8}$

$\Rightarrow \dfrac{{{\pi }^{2}}}{4}-\dfrac{5{{\pi }^{2}}}{8}=2{{\tan }^{-1}}x{{\cot }^{-1}}x$

$\Rightarrow \dfrac{2{{\pi }^{2}}-5{{\pi }^{2}}}{8}=2{{\tan }^{-1}}x\left( \pi -{{\tan }^{-1}}x \right)$

$\Rightarrow \dfrac{-3{{\pi }^{2}}}{8}=2\pi {{\tan }^{-1}}x-2{{\left( {{\tan }^{-1}}x \right)}^{2}}$

$\Rightarrow 2{{\left( {{\tan }^{-1}}x \right)}^{2}}-2\pi {{\tan }^{-1}}x-\dfrac{3{{\pi }^{2}}}{8}=0$

${{\tan }^{-1}}x=\dfrac{2\pi \pm \sqrt{4{{\pi }^{2}}+4\times 2\times \dfrac{3{{\pi }^{2}}}{8}}}{2\times 2}$

${{\tan }^{-1}}x=\dfrac{2\pi \pm \sqrt{4{{\pi }^{2}}+3{{\pi }^{2}}}}{2\times 2}$

${{\tan }^{-1}}x=\dfrac{2\pi \pm \sqrt{7{{\pi }^{2}}}}{4}$

${{\tan }^{-1}}x=\dfrac{2\pi \pm \sqrt{7}\pi }{4}$

$Now,$

$x=\tan \dfrac{2\pi \pm \sqrt{7}\pi }{4}$

It is quadratic equation

Let y = ${ sin }^{ -1 }\left( \dfrac { \sqrt { 1+x } +\sqrt { 1-x } }{ 2 } \right)$ put $x=cos\theta .\quad then\theta ={ cos }^{ -1 }x$

We have,

$y={{\sin }^{-1}}\left( \dfrac{\sqrt{1+x}+\sqrt{1-x}}{2} \right)$

Let put $x=\cos 2\theta$

Then, $\theta ={{\tan }^{-1}}x$

So,

$y={{\sin }^{-1}}\left( \dfrac{\sqrt{1+\cos 2\theta }+\sqrt{1-\cos 2\theta }}{2} \right)$

$={{\sin }^{-1}}\left( \dfrac{\sqrt{1+2{{\cos }^{2}}\theta -1}+\sqrt{1-1+2{{\sin }^{2}}\theta }}{2} \right)$

$={{\sin }^{-1}}\left( \dfrac{\sqrt{2}\cos \theta +\sqrt{2}\sin \theta }{2} \right)$

$={{\sin }^{-1}}\left( \dfrac{\cos \theta +\sin \theta }{\sqrt{2}} \right)$

$={{\sin }^{-1}}\left( \dfrac{1}{\sqrt{2}}\cos \theta +\dfrac{1}{\sqrt{2}}\sin \theta \right)$

$={{\sin }^{-1}}\left( \sin \dfrac{\pi }{4}\cos \theta +\cos \dfrac{\pi }{4}\sin \theta \right)$

$={{\sin }^{-1}}\sin \left( \dfrac{\pi }{4}+\theta \right)$

$=\left( \dfrac{\pi }{4}+\theta \right)$

$=(\dfrac{\pi}{4}+tan^{-1}x)$

Hence, this is the answer..

${ cot }^{ -1 }\left[ \frac { \sqrt { 1+sinx } +\sqrt { 1-sinx } }{ \sqrt { 1+sinx } -\sqrt { 1-sinx } } \right] ,0<x<\frac { \pi }{ 2 }$

2045124_1326652_ans_06850b5e21a94594841adc0a7cdf5ece.jpg

Find the value of x if,
${ \cos }^{ -1 }\dfrac { a }{ x } -\cos^{ -1 }\dfrac { b }{ x } =\cos^{ -1 }\dfrac { 1 }{ b } -{ \cos }^{ -1 }\dfrac { 1 }{ a }$

${\cos}^{-1}{\dfrac{a}{x}}-{\cos}^{-1}{\dfrac{b}{x}}={\cos}^{-1}{\dfrac{1}{a}}-{\cos}^{-1}{\dfrac{1}{b}}$

$\Rightarrow\,{\cos}^{-1}{\dfrac{a}{x}}+{\cos}^{-1}{\dfrac{1}{b}}={\cos}^{-1}{\dfrac{1}{a}}+{\cos}^{-1}{\dfrac{b}{x}}$

We know that

${\cos}^{-1}{x}+{\cos}^{-1}{y}={\cos}^{-1}{\left(xy-\sqrt{1-{x}^{2}}\sqrt{1-{y}^{2}}\right)}$ if

$x,y>0$ and

${x}^{2}+{y}^{2}\le 1$

$\Rightarrow\,{\cos}^{-1}{\left(\dfrac{a}{x}\times\dfrac{1}{a}-\sqrt{1-\dfrac{{a}^{2}}{{x}^{2}}}\sqrt{1-\dfrac{{a}^{2}}{{x}^{2}}}\right)}={\cos}^{-1}{\left(\dfrac{b}{x}\times\dfrac{1}{b}-\sqrt{1-\dfrac{{b}^{2}}{{x}^{2}}}\sqrt{1-\dfrac{{b}^{2}}{{x}^{2}}}\right)}$

$\Rightarrow\,\dfrac{1}{x}-\sqrt{\left(\dfrac{{x}^{2}-{a}^{2}}{{x}^{2}}\right)\left(\dfrac{{a}^{2}-1}{{a}^{2}}\right)}=\dfrac{1}{x}-\sqrt{\left(\dfrac{{x}^{2}-{b}^{2}}{{x}^{2}}\right)\left(\dfrac{{b}^{2}-1}{{b}^{2}}\right)}$

$\Rightarrow\,-\sqrt{\left(\dfrac{{x}^{2}-{a}^{2}}{{x}^{2}}\right)\left(\dfrac{{a}^{2}-1}{{a}^{2}}\right)}=-\sqrt{\left(\dfrac{{x}^{2}-{b}^{2}}{{x}^{2}}\right)\left(\dfrac{{b}^{2}-1}{{b}^{2}}\right)}$

Squaring both sides, we get

$\Rightarrow\,\dfrac{\left({x}^{2}-{a}^{2}\right)\left({a}^{2}-1\right)}{{x}^{2}{a}^{2}}=\dfrac{\left({x}^{2}-{b}^{2}\right)\left({b}^{2}-1\right)}{{x}^{2}{b}^{2}}$

$\Rightarrow\,\dfrac{\left({x}^{2}-{a}^{2}\right)\left({a}^{2}-1\right)}{{a}^{2}}=\dfrac{\left({x}^{2}-{b}^{2}\right)\left({b}^{2}-1\right)}{{b}^{2}}$

$\Rightarrow\,{b}^{2}\left({x}^{2}-{a}^{2}\right)\left({a}^{2}-1\right)={a}^{2}\left({x}^{2}-{b}^{2}\right)\left({b}^{2}-1\right)$

$\Rightarrow\,{b}^{2}\left({x}^{2}{a}^{2}-{x}^{2}-{a}^{4}+{a}^{2}\right)={a}^{2}\left({x}^{2}{b}^{2}-{x}^{2}-{b}^{4}+{b}^{2}\right)$

$\Rightarrow\,{b}^{2}{x}^{2}{a}^{2}-{b}^{2}{x}^{2}-{b}^{2}{a}^{4}+{b}^{2}{a}^{2}={a}^{2}{x}^{2}{b}^{2}-{a}^{2}{x}^{2}-{a}^{2}{b}^{4}+{a}^{2}{b}^{2}$

$\Rightarrow\,{a}^{2}{x}^{2}-{b}^{2}{x}^{2}={b}^{2}{a}^{4}-{a}^{2}{b}^{4}$

$\Rightarrow\,\left({a}^{2}-{b}^{2}\right){x}^{2}={a}^{2}{b}^{2}\left({a}^{2}-{b}^{2}\right)$

$\Rightarrow\,{x}^{2}={a}^{2}{b}^{2}$

$\therefore\,x=ab$

write the value of ${ tan }^{ -1 }\left\{ 2sin\left( 2co{ s }^{ -1 }\frac { \sqrt { 3 } }{ 2 } \right) \right\}$

2040807_1333170_ans_de9c378aa4884ccb8c1651882de64041.jpg

Evaluate

${\textbf{Step-1: Calculate values of inverse trigonometric function.}}$

${\text{Let,}}$

$cosec^{-1}(-\sqrt2)=\infty$

${\text{ Where}}$

$\dfrac{-\pi}{2}\le y\le \dfrac{\pi}{2},y\neq0$

$cosec\infty=\sqrt2=-cosec\dfrac{\pi}{4}$

$\therefore cosec\infty =cosec(-\dfrac{\pi}{4})...[\because cosec(-\theta)=-cosec\theta]$

$\therefore\infty=\dfrac{\pi}{4}$

$.. ...[\because\dfrac{-\pi}{2}\le\dfrac{-\pi}{4}\le\dfrac{\pi}{2}]$

$\therefore cosec^{-1}(\sqrt2)=\dfrac{\pi}{4}.....(i)$

${\text{Let}}$

$cot^{-1}(\sqrt3)=\beta$

${\text{Where}}$

$0<\beta<\pi$

$\therefore cot\beta=\sqrt3=cot\dfrac{\pi}{6}$

$\therefore \beta =\dfrac{\pi}{6}...[0<\dfrac{\pi}{6}<\pi]$

$\therefore cot^{-1}(\sqrt3)=\dfrac{\pi}{6}...(ii)$

$\therefore cosec^{-1}(-\sqrt2)+cot^{-1}(\sqrt3)$

$=-\dfrac{\pi}{4}+\dfrac{\pi}{6}$

${\text{..[By (i) and (ii)]}}$

$=\dfrac{-3\pi+2\pi}{12}$

$=-\dfrac{\pi}{12}$

${\textbf{Hence ,}}$

$\mathbf{cosec^{-1}(-\sqrt2)+cot^{-1}(\sqrt3)=-\dfrac{\pi}{12}.}$

If $\tan^{-1}{(x+2)}+\tan^{-1}{(x-2)}=\tan^{-1}{(\cfrac{1}{2})}$ , then sum of value(s) of $x$ is equal to ?

2045126_1456076_ans_0d74e71b77684132bc6092d2f4057b9f.jpg

$solve\quad for\quad x,\\ 2{ tan }^{ -1 }\left( cos\quad x \right) ={ tan }^{ -1 }\left( 2\quad cosec\quad x \right)$

2042432_1467312_ans_1aa92b05d42e46adaa728b74087d07c8.jpg

Prove that : $\tan^{-1}{\cfrac{1}{5}}+\tan^{-1}{\cfrac{1}{7}}+\tan^{-1}{\cfrac{1}{3}}+\tan^{-1}{\cfrac{1}{8}}=\cfrac{\pi}{4}$

2042485_1471717_ans_01bd91655f5b49ccba140239da555ec1.jpg

Let $y=\sin^{-1}{(\sin{8})}-\tan^{-1}{(\tan{10})}+\cos^{-1}{(\cos{12})}-\sec^{-1}{(sec{9})}+\cot^{-1}{(\cot{6})}-cosec^{-1}{(cosec{7})}$ . If simplifies to $a\pi+b$ , then find $(a-b)$ .

$\textbf{Step 1: Changing angles based on range of inverse trigonometric function}$

$y = \sin^{-1}(\sin 8) - \tan^{-1}(\tan 10) + \cos^{-1}(\cos 12) - \sec^{-1}(\sec 9) - \cot^{-1}(\cot 6) - \csc^{-1}(\csc 7)$

$= \sin^{-1}(\sin(3\pi - 8)) - \tan^{-1}(\tan(10 - 3\pi)) + \cos^{-1}(\cos(4\pi - 12)) - \sec^{-1}(\sec(9 - 2\pi))$

$- \cot^{-1}(\cot(6 - \pi)) - \csc^{-1}(\csc(7 - 2\pi))$

$\textbf{Step 2: Simplifying}$

$y = 3\pi - 8 - 10 + 3\pi + 4\pi - 12 - 9 + 2\pi - 6 + \pi - 7 + 2\pi$

$\Rightarrow y = 13\pi - 40 = a\pi + b$

$\Rightarrow a = 13, b = -40$

$\Rightarrow a - b = 13 + 40 = 53$

$\textbf{Hence value of a - b is 53.}$

Show that: $\sin ^ { - 1 } \left( - \frac { 1 } { 2 } \right) + \cos ^ { - 1 } \left( \frac { \sqrt { 3 } } { 2 x } \right) = \cos ^ { - 1 } \left( - \frac { 1 } { 2 } \right)$

2044431_1564722_ans_0c084fb627a246e8ae1774f79a2d98c1.jpg

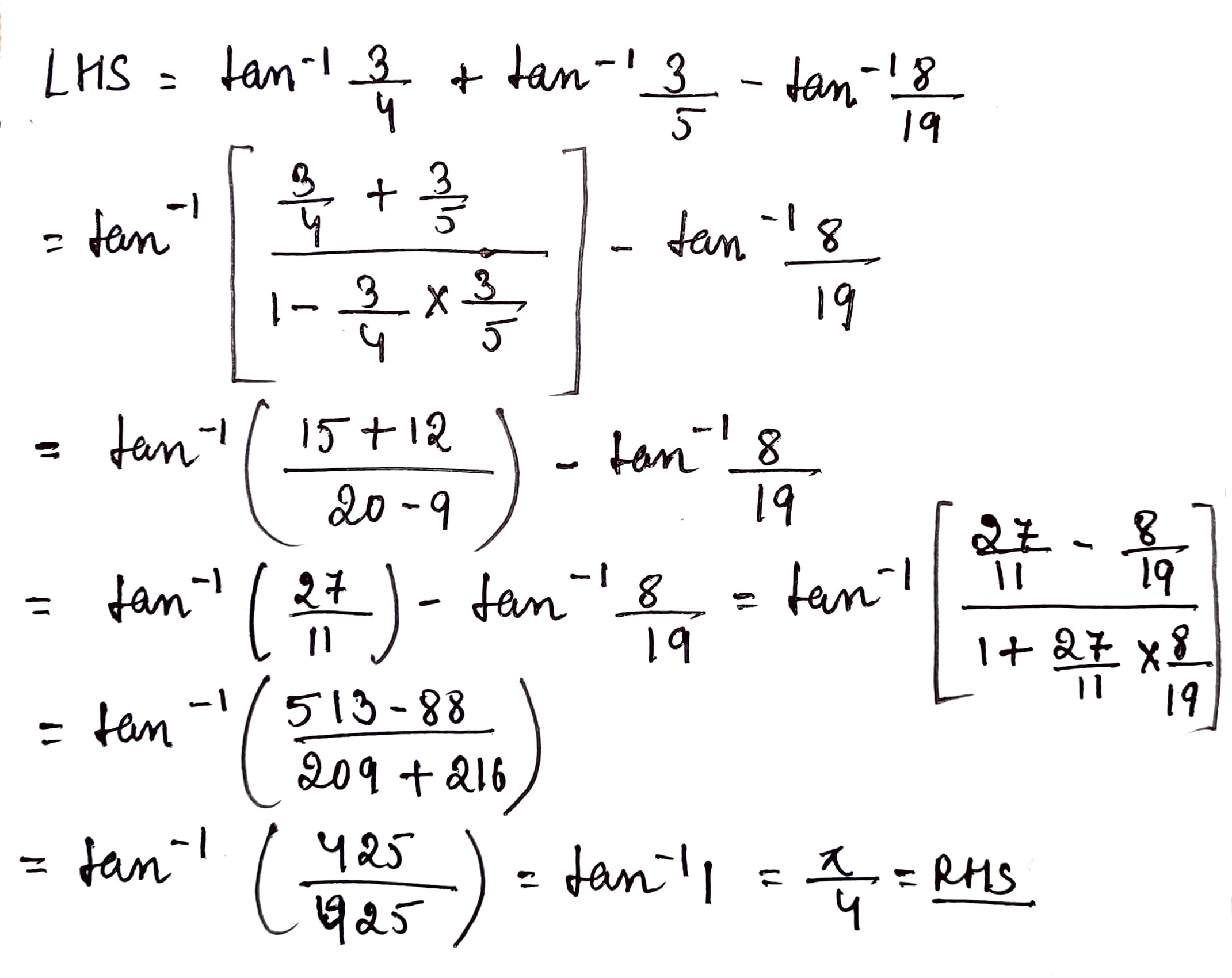
$\tan ^{ -1 }{ \left(\dfrac { 3 }{ 4 } \right) } +\tan ^{ -1 }{ \left(\dfrac { 3 }{ 5 } \right) } -\tan ^{ -1 }{ \left( \dfrac { 8 }{ 19 } \right) =\dfrac { \pi }{ 4 } }$

2043983_1553217_ans_9e8078bf8f1b4567b91b48a3309fa2e8.jpg

Find $x$ if ${ tan }^{ -1 }(x+2)+{ tan }^{ -1 }(x-2)={ tan }^{ -1 }\left( \frac { 8 }{ 79 } \right) ;x>0$

2043896_1539346_ans_655a148625fe472bbc6ac77461da2d27.png

Solve for $x , 2 \tan ^ { - 1 } ( \sin x ) = \tan ^ { - 1 } ( 2 \sec x ) , 0 < \frac { \pi } { 2 }$

2044538_1565950_ans_8614979ba07f405989459e47a4891d69.JPG

$tan^{-1} A + tan^{-1} B= ?$

2042844_1535503_ans_26d65fa21c8246d488dabaa759ef4876.png

Solve:
$cos^{-1}{(\dfrac{2x}{1+x^2})}$

2044844_1568485_ans_e7983e4c3530474d8e8cd386bd24b5b8.jpg

Show that $\tan ^ { - 1 } ( 1 / 4 ) + \tan ^ { - 1 } ( 2 / 9 ) = \frac { 1 } { 2 } \cos ^ { - 1 } \left( \frac { 3 } { 5 } \right)$

2043891_1539290_ans_4ad7ee610dc349cf8b34b1d1e9831edb.jpg

Solve -
If y = $sec^-1 (\frac{1}{\sqrt{1 - x^2}})$

2044869_1568571_ans_cc254499f6384a7a9b07d792a0347c07.jpeg

Solve the equation.
$\cot^{-1} x + \cot^{-1} (n^2 - x + 1) = \cot^{-1} (n - 1)$

1714539_1733756_ans_05e7656bd3f54e2c8660c1044141e4aa.jpeg

Write the value of $\cos^{-1} (\cos 1540^{\circ})$ .

given,

${\cos}^{-1}{\left(\cos{{1540}^{\circ}}\right)}$

$={\cos}^{-1}{\left(\cos{\left({360}^{\circ}\times 4+{100}^{\circ}\right)}\right)}$

$\because \cos(360^o \times 4 + x^o)=\cos{x^o}$

$={\cos}^{-1}{\left(\cos{{100}^{\circ}}\right)}$

$={100}^{\circ}$

Find the simplest values of
$\tan^{-1} \dfrac{\sqrt{1+x^2} - 1}{x}$ , and $\tan \left(\dfrac{1}{2}\sin^{-1} \dfrac{2x}{1 + x^2}+\dfrac{1}{2} \cos^{-1} \dfrac{1-y^2}{1+y^2}\right)$ .

undefined

1987520_1734550_ans_2a24b594e687465494430ee4da86b991.jpg

Express $tan^-1 (\frac{cosx}{1-sin x})$ , $-\frac{\pi}{2} < x < \frac{3\pi}{2}$ in the simplest form.

2045279_1569299_ans_6d5800ae218543af8851771777b64ac9.jpg

Write the value of $\tan^{-1} \left (\dfrac {1}{x}\right )$ for $x < 0$ in terms of $\cot^{-1} (x)$ .

Let

${\cot}^{-1}{\left(x\right)}=\theta$

$\Rightarrow\,\cot{\theta}=x$

Now, we have

$\tan{\left(-\pi+\theta\right)}=-\tan{\left(\pi-\theta\right)}$

$\Rightarrow\,\tan{\left(-\pi+\theta\right)}=\tan{\theta}=\dfrac{1}{\cot{\theta}}$

$\Rightarrow\,\tan{\left(-\pi+\theta\right)}=\dfrac{1}{x}$

$\Rightarrow\,-\pi+\theta={\tan}^{-1}{\dfrac{1}{x}}$

$\Rightarrow\,-\pi+{\cot}^{-1}{x}={\tan}^{-1}{\dfrac{1}{x}}$

$\therefore\,{\tan}^{-1}{\dfrac{1}{x}}=-\pi+{\cot}^{-1}{x}$

If $ax+b(sec(\tan^{-1}x))=c$ and $ay+b(sec(\tan^{-1}y))=c$ , then find the value of $\dfrac{x+y}{1-xy}$ .

Let

$tan^{-1}x=\alpha$ and

$tan^{-1}y=\beta$

$\Rightarrow \tan\alpha =x$ and

$\tan \beta=y$

Now, given equation beomes

$a \tan \alpha+b(\sec \alpha)=c$ and

$a \tan \beta+b(\sec \beta)=c$

$\Rightarrow a \tan \alpha+b\sec \alpha=c$ and

$a \tan \beta+b \sec \beta=c$

$\Rightarrow \alpha$ and

$\beta$ are the roots of

$a \tan \theta+b \sec \theta=c$ ....

$(1)$

Again

$\because a\tan \theta + b \sec \theta=c \, \, \, \, \,\Rightarrow \, \, \,b\sec \theta=c-a \tan \theta$

$\Rightarrow b^{2}\sec^{2}\theta=(c-a\tan\theta)^{2} \quad[Squaring \, \,both \, \,side]$

$\Rightarrow b^{2}sec^{2}\theta=c^{2}-2ac\tan\theta+a^{2}\tan^{2}\theta$

$\Rightarrow b^{2}(1+\tan^{2}\theta)=c^{2}-2ac\tan\theta+a^{2}\tan^{2}\theta$

$\Rightarrow -b^{2}-b^{2}\tan^{2}\theta+c^{2}-2ac\tan\theta+a^{2}\tan^{2}\theta=0$

$\Rightarrow(a^{2}-b^{2})\tan^{2}\theta-2ac\tan\theta+(c^{2}-b^{2})=0$ ...

$(2)$

Since

$\alpha, \beta$ are roots of quadratic equation

$(1)$

they also satisfy equation

$(2)$

$\therefore tan\alpha+tan\beta=\cfrac{-(-2ac)}{(a^2-b^2)}$

$\therefore x+y=\cfrac{2ac}{(a^2-b^2)}$

And,

$tan\alpha\cdot tan\beta=\cfrac{(c^2-b^2)}{(a^2-b^2)}$

$\therefore xy=\cfrac{(c^2-b^2)}{(a^2-b^2)}$

Now,

$\cfrac{x+y}{1-xy}=\cfrac{\frac{2ac}{(a^2-b^2)}}{\frac{(c^2-b^2)}{(a^2-b^2)}}$

$\therefore \cfrac{x+y}{1-xy}=\cfrac{2ac}{c^2-b^2}$

Prove that $\tan^{-1}\left(\dfrac{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}\right)=\dfrac{\pi}{4}+\dfrac{1}{2}\cos^{-1}x^{2}$

To prove:

$\tan^{-1}\left(\dfrac{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}\right)=\dfrac{\pi}{4}+\dfrac{1}{2}\cos^{-1}x^{2}$

Proof:

Let,

$x^{2}=\cos 2\theta=(\cos^{2}\theta-\sin^{2}\theta)=1-2\sin^{2}\theta=2\cos^{2}\theta-1$

$\Rightarrow \cos^{-1}x^{2}=2\theta\\\Rightarrow \theta=\dfrac{1}{2}\cos^{-1}x^{2}$

$\therefore \sqrt{1+x^{2}}=\sqrt{1+\cos 2\theta}\\$

$=\sqrt{1+2\cos^{2}\theta-1}\\=\sqrt{2}\cos \theta\\$

And

$\sqrt{1-x^{2}}=\sqrt{1-\cos 2\theta}$

$\\=\sqrt{1-+2\sin^{2}\theta}\\=\sqrt{2}\sin \theta$

$\therefore LHS=\tan^{-1}\left(\dfrac{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}\right)$

$=\tan^{-1}\left(\dfrac{\sqrt{2}\cos\theta+\sqrt{2}\sin \theta}{\sqrt{2}\cos \theta-\sqrt{2}\sin \theta}\right)$

$=\tan^{-1}\left(\dfrac{\cos\theta+\sin \theta}{\cos\theta-\sin \theta}\right)$

$=\tan^{-1}\left(\dfrac{1+\tan\theta}{1-\tan \theta}\right)=\tan^{-1}\left(\dfrac{\tan \left(\dfrac{\pi}{4}\right)+\tan \theta}{1-\tan \dfrac{\pi}{4}\tan \theta}\right)$

$=\tan^{-1}\left[\tan\left(\dfrac{\pi}{4}+\theta\right)\right]\qquad\left[\because \tan (x+y)=\dfrac{\tan x+\tan y}{1-\tan x.\tan y}\right]$

$=\dfrac{\pi}{4}+\theta\\=\dfrac{\pi}{4}+\dfrac{1}{2}\cos^{-1}x^{2}$

$=RHS$ Hence proved.

Find the real Solution of the equation
$\tan^{-1}\sqrt {x(x+1)}+\sin^{-1}\sqrt {x^2 +x+x}=\dfrac {\pi}{2}$ .

We have

$\tan^{-1}\sqrt {x(x+1)}+\sin^{-1}\sqrt {x^2 +x+x}=\dfrac {\pi}{2} ......(i)$ .

Let

$\sin^{-1}\sqrt {x^2+x+1}=\theta$

$\Rightarrow \ \sin \theta \sqrt {\dfrac {x^2+x+1}{1}}$

$\Rightarrow \ \tan \theta =\dfrac {\sqrt {x^2+x+1}}{\sqrt {-x^2 -x}}\ \left[\because \tan \theta =\dfrac {\sin \theta}{\cos \theta}\right]$

$\because \theta =\tan^{-1}\dfrac {\sqrt {x^2+x+1}}{\sqrt {-x^2 -x}}$

$=\sin^{-1} \sqrt {x^2 +x+1}$

On putting the value of

$\theta$ in equ (i) we get

$\tan^{-1}\sqrt {x(x+1)}+\tan^{-1} \dfrac {\sqrt {x^2+x+1}}{\sqrt {-x^2 -x}}=\dfrac {\pi}{2}$

We know that,

$\tan^{-1} x+\tan^{-1} \left(\dfrac {x+y}{1-xy}\right), xy < 1$

$\tan^{-1}\left[\dfrac {\sqrt {x(x+1)}+\sqrt {\dfrac {x^2+x+1}{-x^2 -x}}}{1-\sqrt {x(x+1)}\sqrt {\dfrac {x^2 +x+1}{-x^2 -x}}}\right] =\dfrac {\pi}{2}$

$\tan^{-1}\left[\dfrac {\sqrt {x^2+x}+\sqrt {\dfrac {x^2+x+1}{-1(x^2 +x)}}}{1-\sqrt {x^2+x}\sqrt {\dfrac {x^2 +x+1}{-1(x^2+x)}}}\right] =\dfrac {\pi}{2}$

$\Rightarrow \ \dfrac {x^2 +x+\sqrt {-(x^2 +x+1)}}{[1-\sqrt {-(x^2 +x+1)} \sqrt {(x^2+x)}]} =\tan \dfrac {\pi}{2}=\dfrac 10$

$\Rightarrow \ [1-\sqrt {-(x^2 +x+1)}] \sqrt {(x^2 +x)} =0\Rightarrow =(x^2 +x+1)=1$ or

$x^2 +x=0$

$\Rightarrow \ -x^2 -x-1=1$ or

$x(x+1)=0$

$\Rightarrow \ x^2+x+2=0$ or

$x(x+1)=0$

$\therefore x=\dfrac {1\pm \sqrt {1-4\times 2}}{2}$

$\Rightarrow \ x=0$ or

$x=-1$

For real solution, we have

$x=0, 1$ .

Solve the equation
$\theta = \tan^{-1} (2 \tan^2 \theta) - \dfrac{1}{2} \sin^{-1}\dfrac{3\sin 2\theta}{5+4\cos 2\theta}$ .

1697186_1734974_ans_db6587747d814be8aa0e3946ae08992f.jpg

Show that
$\sin^{-1}\dfrac{5}{13}+\cos^{-1}\dfrac{3}{5}=\tan^{-1}\dfrac{63}{16}$

To prove:

$\sin^{-1}\dfrac{5}{13}+\cos^{-1}\dfrac{3}{5}=\tan^{-1}\dfrac{63}{16}$

Proof:

Let

$\sin^{-1}\dfrac{5}{13}=x\Rightarrow \sin x=\dfrac{5}{13}$

$\therefore\cos^{2}x=1-\sin^{2}x=1-\dfrac{25}{169}=\dfrac{144}{169}$

$\Rightarrow \cos x=\sqrt{\dfrac{144}{169}}=\dfrac{12}{13}$

$\Rightarrow \tan x=\dfrac{\sin x}{\cos x}=\dfrac{5/13}{12/13}=\dfrac{5}{12}$

Again, let

$\cos^{-1}\dfrac{3}{5}=y\Rightarrow \cos y=\dfrac{3}{5}$

$\therefore \sin y=\sqrt{1-\cos^{2}y}=\sqrt{1-\left(\dfrac{3}{5}\right)^{2}}=\sqrt{1-\dfrac{9}{25}}$

$\Rightarrow\sin y=\sqrt{\dfrac{16}{25}}=\dfrac{4}{5}$

$\Rightarrow \tan y=\dfrac{\sin y}{\cos y}=\dfrac{4/5}{3/5}=\dfrac{4}{3}$

We know that,

$\\\tan(x+y)=\dfrac{\tan x+\tan y}{1-\tan x.\tan y}$

$\\\Rightarrow \tan (x+y)=\dfrac{\dfrac{5}{12}+\dfrac{4}{3}}{1-\dfrac{5}{12}.\dfrac{4}{3}}$

$\\\Rightarrow \tan (x+y)=\dfrac{\dfrac{15+48}{36}}{\dfrac{36-20}{36}}$

$\\\Rightarrow \tan (x+y)=\dfrac{63/36}{16/36}$

$\\\Rightarrow \tan (x+y)=\dfrac{63}{16}$

$\\\Rightarrow x+y=\tan^{-1}\dfrac{63}{16}$

$\\\Rightarrow \tan^{-1}\dfrac{5}{12}+\tan^{-1}\dfrac{4}{3}=\tan^{-1}\dfrac{63}{16}$

Hence proved.

If $\dfrac{1}{2}\sin^{-1} \dfrac{2x}{1-x^2}+\dfrac{1}{2} \cos^{-1}\dfrac{1-y^2}{1+y^2}+\dfrac{1}{3}\tan^{-1}\dfrac{3z-z^3}{1-3z^2}=5 \pi$
then prove that $x+y+x=xyz$

Let

$x=\tan A, y=\tan B, z=\tan C$

$\dfrac{1}{2}\sin^{-1} \left(\dfrac{2x}{1-x^2}\right)+\dfrac{1}{2} \cos^{-1} \left(\dfrac{1-y^2}{1+y^2}\right)+\dfrac{1}{3} \tan^{-1} \left(\dfrac{3z-z^3}{1-3z^2}\right)=5 \pi$

$\dfrac{1}{2}\sin^{-1} \left(\dfrac{2\tan A}{1-\tan^2 A}\right)+\dfrac{1}{2} \cos^{-1} \left(\dfrac{1-\tan^2 B}{1+\tan^2 B}\right)+\dfrac{1}{3} \tan^{-1} \left(\dfrac{3 \tan C-\tan^3 C}{1-3\tan ^2 C}\right)=5 \pi$

$\Rightarrow \dfrac{1}{2} \sin^{-1} (\sin 2A)+\dfrac{1}{2} \cos^{-1} (\cos 2 B)+\dfrac{1}{3} \tan^{-1} (\tan 3C)=5 \pi$

$\dfrac{1}{2} (2A)+\dfrac{1}{2} (2B)+\dfrac{1}{3} (3C)=5 \pi$

$\Rightarrow A+B+C=5 \pi$

$\Rightarrow A+B=5\pi -C$

$\tan (A+B)=\tan (5 \pi-C)$

$\Rightarrow \dfrac{\tan A+ \tan B}{1- \tan A \tan B}=- \tan C$

$\Rightarrow \dfrac{x+y}{1-xy}=-z$

Putting the value of

$\tan A, \tan B$ and

$\tan C$ get

$\Rightarrow x+y=-z(1-xy)=-z+xyz$

$\Rightarrow x+y+x=xyz$

Hence proved.

Inverse Trigonometric Functions - Class 12 Commerce Maths - Extra Questions

Solve tan−1(1−x1+x)=12tan−1x,(0<x<1)\displaystyle \tan^{-1} \left ( \frac{1-x}{1+x} \right ) = \frac{1}{2} \tan^{-1} x, \: \: \left( 0<x<1 \right)

Solve for x\displaystyle x and y\displaystyle y; sin−1x+sin−1y=2π3\displaystyle \sin^{-1} x + \sin^{-1} y = \frac{2 \pi}{3} and cos−1x−cos−1y=π3\displaystyle \cos^{-1} x - \cos^{-1} y = \frac{\pi}{3}

Solve \displaystyle \tan x< 2\displaystyle \tan x< 2

Find the inverse of the following functions:\displaystyle f(x)=\sin ^{-1}\left(\frac{x}{3}\right),x\in [-3,3]\displaystyle f(x)=\sin ^{-1}\left(\frac{x}{3}\right),x\in [-3,3]then f^{-1}(\pi/2)f^{-1}(\pi/2)

Prove: \displaystyle { \cos }^{ -1 }\frac { 4 }{ 5 } +{ \cos }^{ -1 }\frac { 12 }{ 13 } ={ \cos }^{ -1 }\frac { 33 }{ 65 } \displaystyle { \cos }^{ -1 }\frac { 4 }{ 5 } +{ \cos }^{ -1 }\frac { 12 }{ 13 } ={ \cos }^{ -1 }\frac { 33 }{ 65 }

\dfrac {1}{2}\tan^{-1} x = \cos^{1} \left \{\dfrac {1 + \sqrt {1 + x^{2}}}{2\sqrt {1 + x^{2}}} \right \}^{\dfrac {1}{2}}\dfrac {1}{2}\tan^{-1} x = \cos^{1} \left \{\dfrac {1 + \sqrt {1 + x^{2}}}{2\sqrt {1 + x^{2}}} \right \}^{\dfrac {1}{2}}.

\displaystyle\, \tan^{-1}\frac{2}{11} + \tan^{-1}\frac{7}{24} = \tan^{-1}\frac{1}{2}\displaystyle\, \tan^{-1}\frac{2}{11} + \tan^{-1}\frac{7}{24} = \tan^{-1}\frac{1}{2}

Find the value of \sin\left\{2\sin^{-1}\dfrac{3}{5}\right\}\sin\left\{2\sin^{-1}\dfrac{3}{5}\right\}

The range of arc\sin { x } +arc\cos { x } +arc\tan { x }arc\sin { x } +arc\cos { x } +arc\tan { x } is

Prove that \displaystyle\, \tan^{-1}\frac{\sqrt{1 + x^2} - 1}{x}=\dfrac{1}{2}\tan^{-1}x, x \neq 0\displaystyle\, \tan^{-1}\frac{\sqrt{1 + x^2} - 1}{x}=\dfrac{1}{2}\tan^{-1}x, x \neq 0

Evaluate \sin ^{ -1 }{ \left( \cos { x } \right) } \sin ^{ -1 }{ \left( \cos { x } \right) }

Write the range of \sin^{-1}x\sin^{-1}x.

Solve for x :{\left( {{{\tan }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2} = \dfrac{{5{\pi ^2}}}{8}{\left( {{{\tan }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2} = \dfrac{{5{\pi ^2}}}{8}

If y=y= {\cot ^{ - 1}}\,\left( {\sqrt {\cos x} } \right) - {\tan ^{ - 1}}\,\left( {\sqrt {\cos x} } \right){\cot ^{ - 1}}\,\left( {\sqrt {\cos x} } \right) - {\tan ^{ - 1}}\,\left( {\sqrt {\cos x} } \right), then prove that \sin y = {\tan ^2}\dfrac{x}{2}.\sin y = {\tan ^2}\dfrac{x}{2}.

Simplify: \tan^{-1}\left(\dfrac{a - x}{1 + ax}\right)\tan^{-1}\left(\dfrac{a - x}{1 + ax}\right)

Write the function in simplest form : \tan^{-1} \left ( \dfrac{x}{\sqrt{a^2-x^2}} \right ) where, |x|<a\tan^{-1} \left ( \dfrac{x}{\sqrt{a^2-x^2}} \right ) where, |x|<a.

Calculating the principal value, find the value of \cos\left[\sin^{-1}\left(\dfrac{3}{5}\right)\right]\cos\left[\sin^{-1}\left(\dfrac{3}{5}\right)\right].

Solve for x : \cos^{-1} x + \sin^{-1} \left(\dfrac{x}{2} \right) = \dfrac{\pi}{6}\cos^{-1} x + \sin^{-1} \left(\dfrac{x}{2} \right) = \dfrac{\pi}{6}

Prove that: \cot \left(\dfrac {\pi}{2}-2\ \cot^{-1}3\right)=\dfrac{3}{4}\cot \left(\dfrac {\pi}{2}-2\ \cot^{-1}3\right)=\dfrac{3}{4}

Evaluate: sec^{-1}(-2)sec^{-1}(-2)

Solve {\tan ^{ - 1}}\left( {\tan \frac{{2\pi }}{3}} \right){\tan ^{ - 1}}\left( {\tan \frac{{2\pi }}{3}} \right)

Evaluate {\cos ^{ - 1}}\dfrac{1}{2} + 2{\sin ^{ - 1}}\dfrac{1}{2}{\cos ^{ - 1}}\dfrac{1}{2} + 2{\sin ^{ - 1}}\dfrac{1}{2}

Solve:{\sin ^{ - 1}}\left( {\frac{{1 - {x^2}}}{{1 + {x^2}}}} \right){\sin ^{ - 1}}\left( {\frac{{1 - {x^2}}}{{1 + {x^2}}}} \right)

Solve:-{\cos ^{ - 1}}\left( {\frac{1}{2}} \right) - 2{\sin ^{ - 1}}\left( { - \frac{1}{2}} \right){\cos ^{ - 1}}\left( {\frac{1}{2}} \right) - 2{\sin ^{ - 1}}\left( { - \frac{1}{2}} \right)

Differentiate \tan^{-1}\left(\dfrac{a\cos x-b\sin x}{b\cos x+a\sin x}\right)\tan^{-1}\left(\dfrac{a\cos x-b\sin x}{b\cos x+a\sin x}\right).

\sin\left(2\tan^{-1}\sqrt{\dfrac{1-x}{1+x}}\right)\sin\left(2\tan^{-1}\sqrt{\dfrac{1-x}{1+x}}\right).

Solve:{\sin ^{ - 1}}(\cos x){\sin ^{ - 1}}(\cos x)

sin^{-1}(cosx)sin^{-1}(cosx)

Solve:{\sin ^{ - 1}}(\cos x){\sin ^{ - 1}}(\cos x)

sin^{-1}sin15+cos^{-1}cos20+tan^{-1}tan 25=sin^{-1}sin15+cos^{-1}cos20+tan^{-1}tan 25=

Prove \tan ^ { - 1 } \dfrac { 1 } { 2 } + \tan ^ { - 1 } \dfrac { 2 } { 11 } = \tan ^ { - 1 } \dfrac { 3 } { 4 }\tan ^ { - 1 } \dfrac { 1 } { 2 } + \tan ^ { - 1 } \dfrac { 2 } { 11 } = \tan ^ { - 1 } \dfrac { 3 } { 4 }

\sin ^ { - 1 } \left( \dfrac { 2 x } { 1 + x ^ { 2 } } \right)\sin ^ { - 1 } \left( \dfrac { 2 x } { 1 + x ^ { 2 } } \right)

Find the value of \cot ^ { - 1 } ( - \sqrt { 3 } )\cot ^ { - 1 } ( - \sqrt { 3 } )

{\tan ^{ - 1}}\left( 2 \right) + {\tan ^{ - 1}}\left( 3 \right) = {\tan ^{ - 1}}\left( 2 \right) + {\tan ^{ - 1}}\left( 3 \right) =

Solve:{\sin ^{ - 1}}x + {\sin ^{ - 1}}\sqrt {1 - {x^2}} {\sin ^{ - 1}}x + {\sin ^{ - 1}}\sqrt {1 - {x^2}}

Prove:\tan^{-1}\sqrt{x}=\dfrac{1}{2}\cos^{-1}\left (\dfrac{1-x}{1+x}\right),x\epsilon [0,1]\tan^{-1}\sqrt{x}=\dfrac{1}{2}\cos^{-1}\left (\dfrac{1-x}{1+x}\right),x\epsilon [0,1]

tan^{-1}(tan\,5)tan^{-1}(tan\,5)

Solve:{ \cos }^{ -1 }\left( \dfrac { 3\cos x-4\sin x }{ 5 } \right) { \cos }^{ -1 }\left( \dfrac { 3\cos x-4\sin x }{ 5 } \right)

Evaluate :\cos(2\cos^{-1}x+\sin^{-1}x)\cos(2\cos^{-1}x+\sin^{-1}x) at x=\dfrac{1}{5}x=\dfrac{1}{5}.

Simplify {\sin ^{ - 1}}\left( {\sin \dfrac{{2\pi }}{3}} \right){\sin ^{ - 1}}\left( {\sin \dfrac{{2\pi }}{3}} \right)

Prove that : { cos }^{ -1 }\left( \dfrac { 3 }{ 5 } \right) +{ cos }^{ -1 }\left( \dfrac { 4 }{ 5 } \right) =\dfrac { \pi }{ 2 } { cos }^{ -1 }\left( \dfrac { 3 }{ 5 } \right) +{ cos }^{ -1 }\left( \dfrac { 4 }{ 5 } \right) =\dfrac { \pi }{ 2 }

{\cos ^{ - 1}}\left( { - \cfrac{{\sqrt 3 }}{2}} \right){\cos ^{ - 1}}\left( { - \cfrac{{\sqrt 3 }}{2}} \right)

Simplify: \sin.{ \cot }^{ -1 }{ \cot x }\sin.{ \cot }^{ -1 }{ \cot x }

Solve for xx:4\sin^{-1}x+\cos^{-1}x=\pi4\sin^{-1}x+\cos^{-1}x=\pi.

If \sin^{-1}x=\tan^{-1}y\sin^{-1}x=\tan^{-1}y then prove that \dfrac{1}{x^2}-\dfrac{1}{y^2}=1\dfrac{1}{x^2}-\dfrac{1}{y^2}=1.

Prove that 3sin^{-1}=sin^{-1} (3x-4x^{3}),x\epsilon[\frac{-1}{2},\frac{1}{2}]sin^{-1}=sin^{-1} (3x-4x^{3}),x\epsilon[\frac{-1}{2},\frac{1}{2}]

Find the value of \tan^{-1}{\left(\tan{\dfrac{2\pi}{3}}\right)}\tan^{-1}{\left(\tan{\dfrac{2\pi}{3}}\right)}

Solve:3\tan ^{ -1 }{ x } =\tan ^{ -1 }{ \left( \dfrac { 3x-{ x }^{ 3 } }{ 1-3{ x }^{ 2 } } \right) } 3\tan ^{ -1 }{ x } =\tan ^{ -1 }{ \left( \dfrac { 3x-{ x }^{ 3 } }{ 1-3{ x }^{ 2 } } \right) }

Evaluate the following :\sin^{-1} (\sin 10)\sin^{-1} (\sin 10)

if \sin x=1\sin x=1 then find \sin 2x\sin 2x

y = \sin ^ { - 1 } \left( \frac { 2 n } { 1 + n ^ { 2 } } \right) + \sec ^ { - 1 } \left( \frac { 1 + n ^ { 2 } } { 2 n } \right)y = \sin ^ { - 1 } \left( \frac { 2 n } { 1 + n ^ { 2 } } \right) + \sec ^ { - 1 } \left( \frac { 1 + n ^ { 2 } } { 2 n } \right)

If {\left( {{{\tan }^{ - 1}}x} \right)^2} + {\left( {{{\cot }^{ - 1}}x} \right)^2} = \dfrac{{5{\pi ^2}}}{8}{\left( {{{\tan }^{ - 1}}x} \right)^2} + {\left( {{{\cot }^{ - 1}}x} \right)^2} = \dfrac{{5{\pi ^2}}}{8}, then find x.x.

Prove that :\cos^{-1}\left(\dfrac{12}{13}\right)+\sin^{-1}\left(\dfrac{3}{5}\right)=\sin^{-1}\left(\dfrac{56}{65}\right)\cos^{-1}\left(\dfrac{12}{13}\right)+\sin^{-1}\left(\dfrac{3}{5}\right)=\sin^{-1}\left(\dfrac{56}{65}\right).

Find the value of \sin^{-1}\left (\sin \dfrac{3\pi}{5}\right)\sin^{-1}\left (\sin \dfrac{3\pi}{5}\right).

Write the value of \cos^{-1} (\cos 6)\cos^{-1} (\cos 6).

Prove that :\tan^{-1} 1 +\tan^{-1} 2 +\tan^{-1} 3=\pi\tan^{-1} 1 +\tan^{-1} 2 +\tan^{-1} 3=\pi

If \tan^{-1} 2 +\tan^{-1} 3 +\theta =\pi\tan^{-1} 2 +\tan^{-1} 3 +\theta =\pi, find the value of \theta\theta.

Prove that :\tan^{-1} 2 +\tan^{-1}3=\dfrac{3\pi}{4}\tan^{-1} 2 +\tan^{-1}3=\dfrac{3\pi}{4}

Solve {\sin }^{ -1 }(\cos x){\sin }^{ -1 }(\cos x).

Evaluate\tan (\tan^{-1}(-4))\tan (\tan^{-1}(-4))

Evaluate \cos \left[\cos^{-1}\left (\dfrac {-\sqrt 3}{2}\right) +\dfrac {\pi}{6}\right]\cos \left[\cos^{-1}\left (\dfrac {-\sqrt 3}{2}\right) +\dfrac {\pi}{6}\right]

Find the value of \tan^{-1}\left(\tan \dfrac {5\pi}{6}\right)+ \cos^{-1} \left(\cos \dfrac {13\pi}{6}\right)\tan^{-1}\left(\tan \dfrac {5\pi}{6}\right)+ \cos^{-1} \left(\cos \dfrac {13\pi}{6}\right).

Prove that \cos \left(\dfrac {\pi}{4}-2\cot^{-1} 3\right)=7\cos \left(\dfrac {\pi}{4}-2\cot^{-1} 3\right)=7.

If \displaystyle x > y > 0\displaystyle x > y > 0 then find the value of \displaystyle \tan^{-1} \frac{x}{y} + \tan^{-1} \left [ \frac{x + y}{x - y} \right ]\displaystyle \tan^{-1} \frac{x}{y} + \tan^{-1} \left [ \frac{x + y}{x - y} \right ],

If \displaystyle x + y + z = xyz\displaystyle x + y + z = xyz, and \displaystyle x, \: y, \: z > 0\displaystyle x, \: y, \: z > 0, then find the value of \displaystyle \tan^{-1}x + \tan^{-1} y + \tan^{-1} z\displaystyle \tan^{-1}x + \tan^{-1} y + \tan^{-1} z

Prove: \displaystyle { \tan }^{ -1 }\sqrt { x } =\frac { 1 }{ 2 } { \cos }^{ -1 }\left( \frac { 1-x }{ 1+x } \right) ,x\in \left[ 0,1 \right] \displaystyle { \tan }^{ -1 }\sqrt { x } =\frac { 1 }{ 2 } { \cos }^{ -1 }\left( \frac { 1-x }{ 1+x } \right) ,x\in \left[ 0,1 \right]

Write the function in the simplest form:\displaystyle { \tan }^{ -1 }\frac { \sqrt { 1+{ x }^{ 2 } } -1 }{ x } ,x\neq 0\displaystyle { \tan }^{ -1 }\frac { \sqrt { 1+{ x }^{ 2 } } -1 }{ x } ,x\neq 0

If y = \sin (\cos^{-1} x) y = \sin (\cos^{-1} x) and x = 99x = 99, then 1/y^2 1/y^2 is equal to

Write the function in the simplest form:\displaystyle { \tan }^{ -1 }\left( \sqrt { \frac { 1-\cos { x } }{ 1+\cos { x } } } \right) ,x<\pi \displaystyle { \tan }^{ -1 }\left( \sqrt { \frac { 1-\cos { x } }{ 1+\cos { x } } } \right) ,x<\pi

Prove that : \displaystyle { \sin }^{ -1 }\frac { 5 }{ 13 }+{ \cos }^{ -1 }\frac { 3 }{ 5 }={ \tan }^{ -1 }\frac { 63 }{ 16 } \displaystyle { \sin }^{ -1 }\frac { 5 }{ 13 }+{ \cos }^{ -1 }\frac { 3 }{ 5 }={ \tan }^{ -1 }\frac { 63 }{ 16 }

Prove the following:\cos^{-1}\left (\dfrac {12}{13}\right )+ \sin^{-1}\left (\dfrac {3}{5}\right ) = \sin^{-1}\left (\dfrac {56}{65}\right )\cos^{-1}\left (\dfrac {12}{13}\right )+ \sin^{-1}\left (\dfrac {3}{5}\right ) = \sin^{-1}\left (\dfrac {56}{65}\right )

If \tan^{-1}x + \tan^{-1} y = \dfrac {\pi}{4}, xy < 1\tan^{-1}x + \tan^{-1} y = \dfrac {\pi}{4}, xy < 1, then write the value of x + y + xy.x + y + xy.

Write the principal value of \cos^{-1}\left (\dfrac {1}{2}\right )-2 \sin^{-1} \left (-\dfrac {1}{2}\right ).\cos^{-1}\left (\dfrac {1}{2}\right )-2 \sin^{-1} \left (-\dfrac {1}{2}\right ).

Prove that: \tan^{-1} \dfrac {1}{5} + \tan^{-1} \dfrac {1}{7} + \tan^{-1} \dfrac {1}{3} + \tan^{-1} \dfrac {1}{8} = \dfrac {\pi}{4}\tan^{-1} \dfrac {1}{5} + \tan^{-1} \dfrac {1}{7} + \tan^{-1} \dfrac {1}{3} + \tan^{-1} \dfrac {1}{8} = \dfrac {\pi}{4}

If \sin^{-1}x + \sin^{-1} y = \pi \sin^{-1}x + \sin^{-1} y = \pi and x = ky, x = ky, then find the value of 39^{2k} + 5^k 39^{2k} + 5^k

\sin ^{ -1 }{ \left( \dfrac { 2\sec { x } }{ 1+\sec ^{ 2 }{ x } } \right) =y }\sin ^{ -1 }{ \left( \dfrac { 2\sec { x } }{ 1+\sec ^{ 2 }{ x } } \right) =y }

Solve for x: \cos { \left( \sin ^{ -1 }{ x } \right) } =\dfrac{ 1 }{ 7 }x: \cos { \left( \sin ^{ -1 }{ x } \right) } =\dfrac{ 1 }{ 7 }.

Solve: \tan^{-1}2x+\tan^{-1}3x=\displaystyle\frac{\pi}{4}\tan^{-1}2x+\tan^{-1}3x=\displaystyle\frac{\pi}{4}.

Solve: 3\tan^{-1}x+\cot^{-1}x=\pi3\tan^{-1}x+\cot^{-1}x=\pi.

Solve $\displaystyle \tan^{-1} \left ( \frac{1-x}{1+x} \right ) = \frac{1}{2} \tan^{-1} x, \: \: \left( 0<x<1 \right)$

Solve for $\displaystyle x$ and $\displaystyle y$ ; $\displaystyle \sin^{-1} x + \sin^{-1} y = \frac{2 \pi}{3}$ and $\displaystyle \cos^{-1} x - \cos^{-1} y = \frac{\pi}{3}$

Solve $\displaystyle \tan x< 2$

Find the inverse of the following functions:
$\displaystyle f(x)=\sin ^{-1}\left(\frac{x}{3}\right),x\in [-3,3]$
then $f^{-1}(\pi/2)$

Prove: $\displaystyle { \cos }^{ -1 }\frac { 4 }{ 5 } +{ \cos }^{ -1 }\frac { 12 }{ 13 } ={ \cos }^{ -1 }\frac { 33 }{ 65 }$

$\dfrac {1}{2}\tan^{-1} x = \cos^{1} \left \{\dfrac {1 + \sqrt {1 + x^{2}}}{2\sqrt {1 + x^{2}}} \right \}^{\dfrac {1}{2}}$ .

$\displaystyle\, \tan^{-1}\frac{2}{11} + \tan^{-1}\frac{7}{24} = \tan^{-1}\frac{1}{2}$

Find the value of $\sin\left\{2\sin^{-1}\dfrac{3}{5}\right\}$

The range of $arc\sin { x } +arc\cos { x } +arc\tan { x }$ is

Prove that $\displaystyle\, \tan^{-1}\frac{\sqrt{1 + x^2} - 1}{x}=\dfrac{1}{2}\tan^{-1}x, x \neq 0$

Evaluate $\sin ^{ -1 }{ \left( \cos { x } \right) }$

Write the range of $\sin^{-1}x$ .

Solve for x :
${\left( {{{\tan }^{ - 1}}x} \right)^2} + {\left( {{{\cos }^{ - 1}}x} \right)^2} = \dfrac{{5{\pi ^2}}}{8}$

If $y=$ ${\cot ^{ - 1}}\,\left( {\sqrt {\cos x} } \right) - {\tan ^{ - 1}}\,\left( {\sqrt {\cos x} } \right)$ , then prove that $\sin y = {\tan ^2}\dfrac{x}{2}.$

Simplify: $\tan^{-1}\left(\dfrac{a - x}{1 + ax}\right)$

Write the function in simplest form : $\tan^{-1} \left ( \dfrac{x}{\sqrt{a^2-x^2}} \right ) where, |x|<a$ .

Calculating the principal value, find the value of $\cos\left[\sin^{-1}\left(\dfrac{3}{5}\right)\right]$ .

Solve for x : $\cos^{-1} x + \sin^{-1} \left(\dfrac{x}{2} \right) = \dfrac{\pi}{6}$

Prove that: $\cot \left(\dfrac {\pi}{2}-2\ \cot^{-1}3\right)=\dfrac{3}{4}$

Evaluate: $sec^{-1}(-2)$

Solve ${\tan ^{ - 1}}\left( {\tan \frac{{2\pi }}{3}} \right)$

Evaluate
${\cos ^{ - 1}}\dfrac{1}{2} + 2{\sin ^{ - 1}}\dfrac{1}{2}$

Solve: ${\sin ^{ - 1}}\left( {\frac{{1 - {x^2}}}{{1 + {x^2}}}} \right)$

Solve:-
${\cos ^{ - 1}}\left( {\frac{1}{2}} \right) - 2{\sin ^{ - 1}}\left( { - \frac{1}{2}} \right)$

Differentiate $\tan^{-1}\left(\dfrac{a\cos x-b\sin x}{b\cos x+a\sin x}\right)$ .

$\sin\left(2\tan^{-1}\sqrt{\dfrac{1-x}{1+x}}\right)$ .

Solve:
${\sin ^{ - 1}}(\cos x)$

$sin^{-1}(cosx)$

Solve:
${\sin ^{ - 1}}(\cos x)$

$sin^{-1}sin15+cos^{-1}cos20+tan^{-1}tan 25=$

Prove $\tan ^ { - 1 } \dfrac { 1 } { 2 } + \tan ^ { - 1 } \dfrac { 2 } { 11 } = \tan ^ { - 1 } \dfrac { 3 } { 4 }$

$\sin ^ { - 1 } \left( \dfrac { 2 x } { 1 + x ^ { 2 } } \right)$

Find the value of $\cot ^ { - 1 } ( - \sqrt { 3 } )$

${\tan ^{ - 1}}\left( 2 \right) + {\tan ^{ - 1}}\left( 3 \right) =$

Solve:
${\sin ^{ - 1}}x + {\sin ^{ - 1}}\sqrt {1 - {x^2}}$

Prove:
$\tan^{-1}\sqrt{x}=\dfrac{1}{2}\cos^{-1}\left (\dfrac{1-x}{1+x}\right),x\epsilon [0,1]$

$tan^{-1}(tan\,5)$

Solve:
${ \cos }^{ -1 }\left( \dfrac { 3\cos x-4\sin x }{ 5 } \right)$

Evaluate :
$\cos(2\cos^{-1}x+\sin^{-1}x)$ at $x=\dfrac{1}{5}$ .

Simplify ${\sin ^{ - 1}}\left( {\sin \dfrac{{2\pi }}{3}} \right)$

Prove that : ${ cos }^{ -1 }\left( \dfrac { 3 }{ 5 } \right) +{ cos }^{ -1 }\left( \dfrac { 4 }{ 5 } \right) =\dfrac { \pi }{ 2 }$

${\cos ^{ - 1}}\left( { - \cfrac{{\sqrt 3 }}{2}} \right)$

Simplify: $\sin.{ \cot }^{ -1 }{ \cot x }$

Solve for $x$ :
$4\sin^{-1}x+\cos^{-1}x=\pi$ .

If $\sin^{-1}x=\tan^{-1}y$ then prove that $\dfrac{1}{x^2}-\dfrac{1}{y^2}=1$ .

Prove that 3 $sin^{-1}=sin^{-1} (3x-4x^{3}),x\epsilon[\frac{-1}{2},\frac{1}{2}]$

Find the value of $\tan^{-1}{\left(\tan{\dfrac{2\pi}{3}}\right)}$

Solve:
$3\tan ^{ -1 }{ x } =\tan ^{ -1 }{ \left( \dfrac { 3x-{ x }^{ 3 } }{ 1-3{ x }^{ 2 } } \right) }$

Evaluate the following :
$\sin^{-1} (\sin 10)$

if $\sin x=1$ then find $\sin 2x$

$y = \sin ^ { - 1 } \left( \frac { 2 n } { 1 + n ^ { 2 } } \right) + \sec ^ { - 1 } \left( \frac { 1 + n ^ { 2 } } { 2 n } \right)$

If ${\left( {{{\tan }^{ - 1}}x} \right)^2} + {\left( {{{\cot }^{ - 1}}x} \right)^2} = \dfrac{{5{\pi ^2}}}{8}$ , then find $x.$

Prove that :
$\cos^{-1}\left(\dfrac{12}{13}\right)+\sin^{-1}\left(\dfrac{3}{5}\right)=\sin^{-1}\left(\dfrac{56}{65}\right)$ .

Find the value of $\sin^{-1}\left (\sin \dfrac{3\pi}{5}\right)$ .

Write the value of $\cos^{-1} (\cos 6)$ .

Prove that :
$\tan^{-1} 1 +\tan^{-1} 2 +\tan^{-1} 3=\pi$

If $\tan^{-1} 2 +\tan^{-1} 3 +\theta =\pi$ , find the value of $\theta$ .

Prove that :
$\tan^{-1} 2 +\tan^{-1}3=\dfrac{3\pi}{4}$

Solve
${\sin }^{ -1 }(\cos x)$ .

Evaluate
$\tan (\tan^{-1}(-4))$

Evaluate $\cos \left[\cos^{-1}\left (\dfrac {-\sqrt 3}{2}\right) +\dfrac {\pi}{6}\right]$

Find the value of $\tan^{-1}\left(\tan \dfrac {5\pi}{6}\right)+ \cos^{-1} \left(\cos \dfrac {13\pi}{6}\right)$ .

Prove that $\cos \left(\dfrac {\pi}{4}-2\cot^{-1} 3\right)=7$ .

If $\displaystyle x > y > 0$ then find the value of $\displaystyle \tan^{-1} \frac{x}{y} + \tan^{-1} \left [ \frac{x + y}{x - y} \right ]$ ,

If $\displaystyle x + y + z = xyz$ , and $\displaystyle x, \: y, \: z > 0$ , then find the value of $\displaystyle \tan^{-1}x + \tan^{-1} y + \tan^{-1} z$

Prove: $\displaystyle { \tan }^{ -1 }\sqrt { x } =\frac { 1 }{ 2 } { \cos }^{ -1 }\left( \frac { 1-x }{ 1+x } \right) ,x\in \left[ 0,1 \right]$

Write the function in the simplest form:
$\displaystyle { \tan }^{ -1 }\frac { \sqrt { 1+{ x }^{ 2 } } -1 }{ x } ,x\neq 0$

If $y = \sin (\cos^{-1} x)$ and $x = 99$ , then $1/y^2$ is equal to

Write the function in the simplest form:
$\displaystyle { \tan }^{ -1 }\left( \sqrt { \frac { 1-\cos { x } }{ 1+\cos { x } } } \right) ,x<\pi$

Prove that : $\displaystyle { \sin }^{ -1 }\frac { 5 }{ 13 }+{ \cos }^{ -1 }\frac { 3 }{ 5 }={ \tan }^{ -1 }\frac { 63 }{ 16 }$

Prove the following:
$\cos^{-1}\left (\dfrac {12}{13}\right )+ \sin^{-1}\left (\dfrac {3}{5}\right ) = \sin^{-1}\left (\dfrac {56}{65}\right )$

If $\tan^{-1}x + \tan^{-1} y = \dfrac {\pi}{4}, xy < 1$ , then write the value of $x + y + xy.$

Write the principal value of $\cos^{-1}\left (\dfrac {1}{2}\right )-2 \sin^{-1} \left (-\dfrac {1}{2}\right ).$

Prove that: $\tan^{-1} \dfrac {1}{5} + \tan^{-1} \dfrac {1}{7} + \tan^{-1} \dfrac {1}{3} + \tan^{-1} \dfrac {1}{8} = \dfrac {\pi}{4}$

If $\sin^{-1}x + \sin^{-1} y = \pi$ and $x = ky,$ then find the value of $39^{2k} + 5^k$

$\sin ^{ -1 }{ \left( \dfrac { 2\sec { x } }{ 1+\sec ^{ 2 }{ x } } \right) =y }$

Solve for $x: \cos { \left( \sin ^{ -1 }{ x } \right) } =\dfrac{ 1 }{ 7 }$ .

Solve: $\tan^{-1}2x+\tan^{-1}3x=\displaystyle\frac{\pi}{4}$ .

Solve: $3\tan^{-1}x+\cot^{-1}x=\pi$ .

Prove that $\cos ^{ -1 }{ \left( -x \right) } =\pi -\cos ^{ -1 }{ \left( x \right) }$ , $-1\le x\le 1$ .