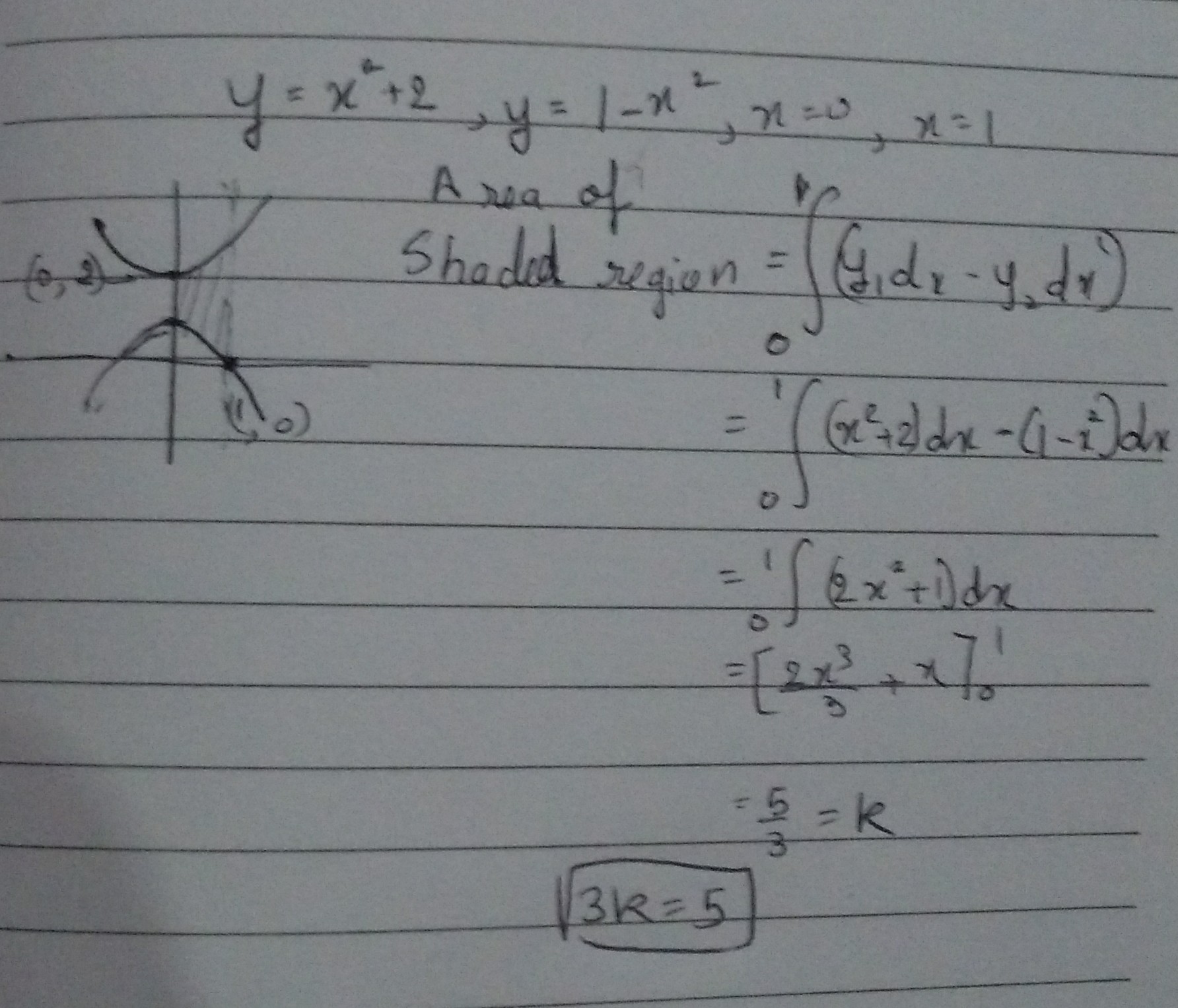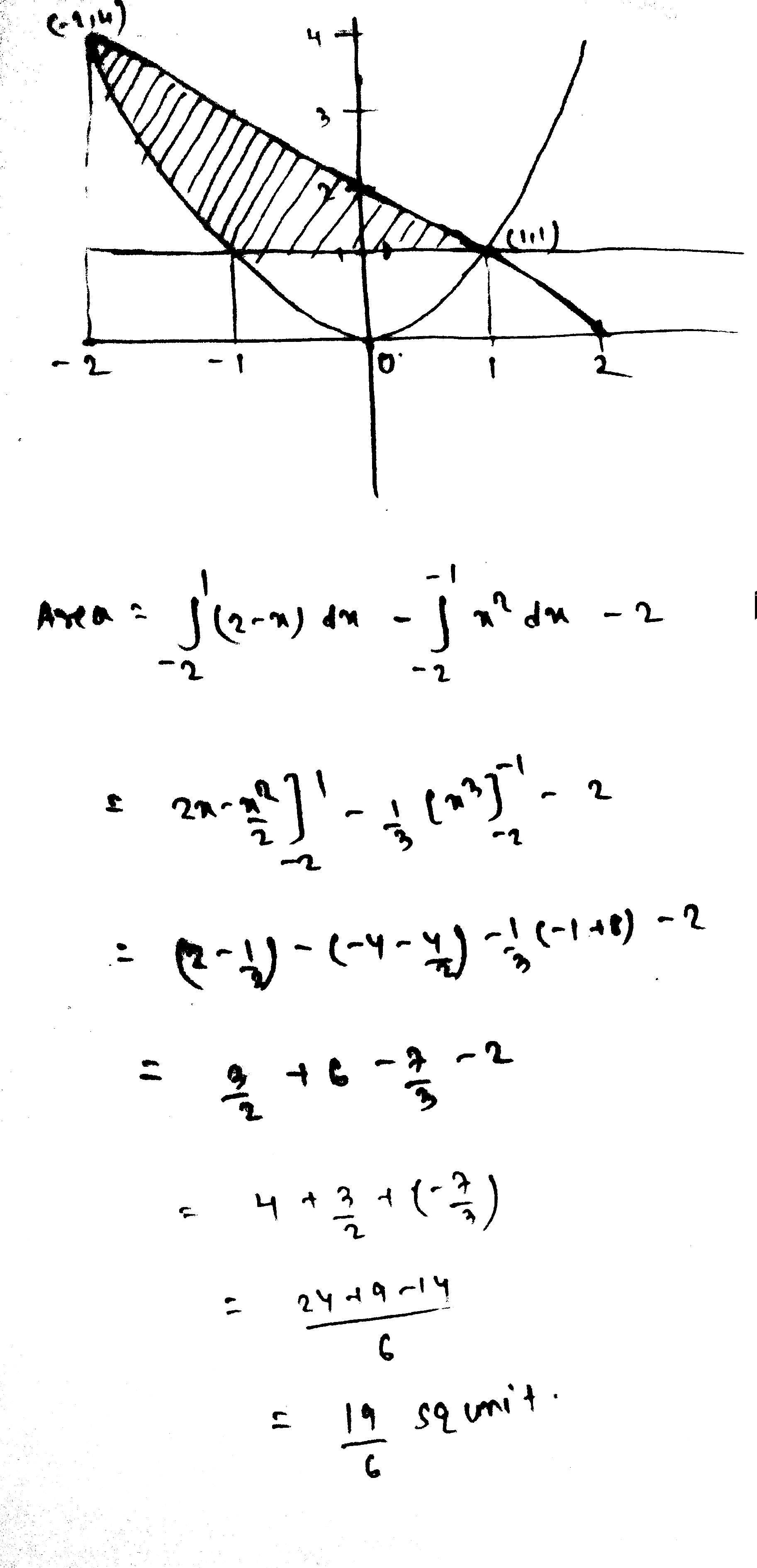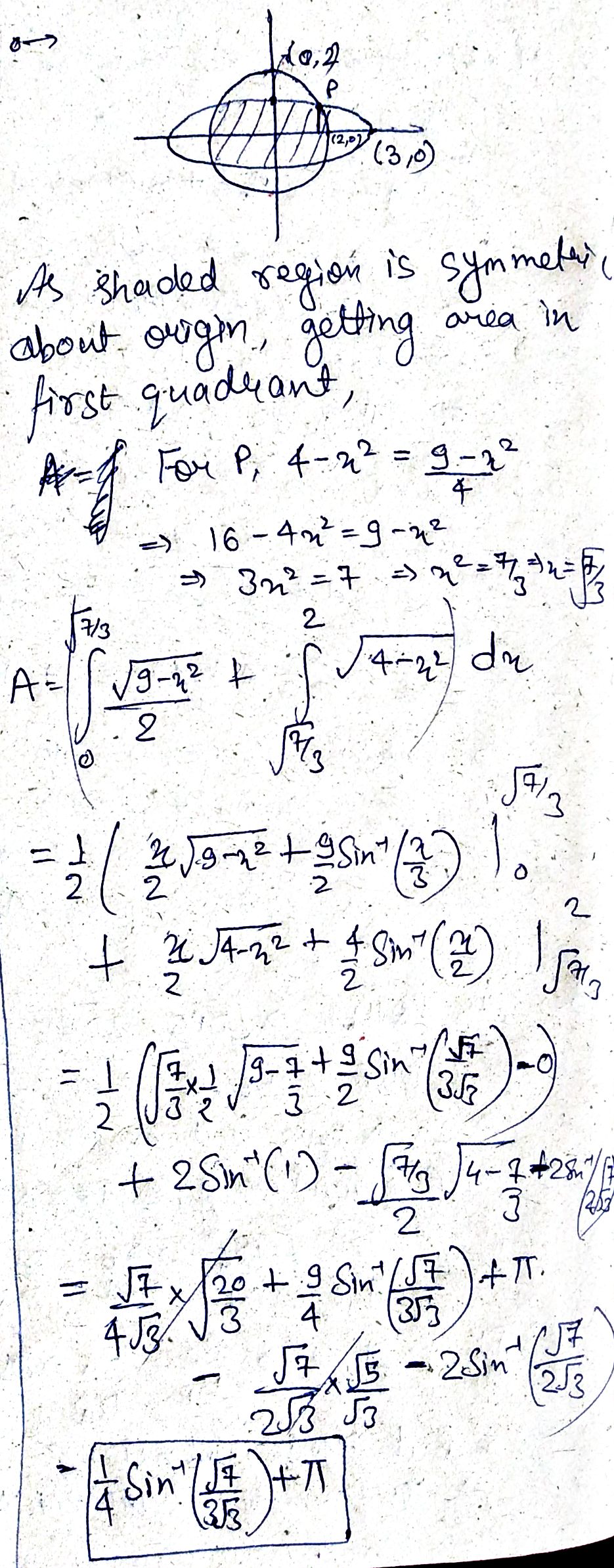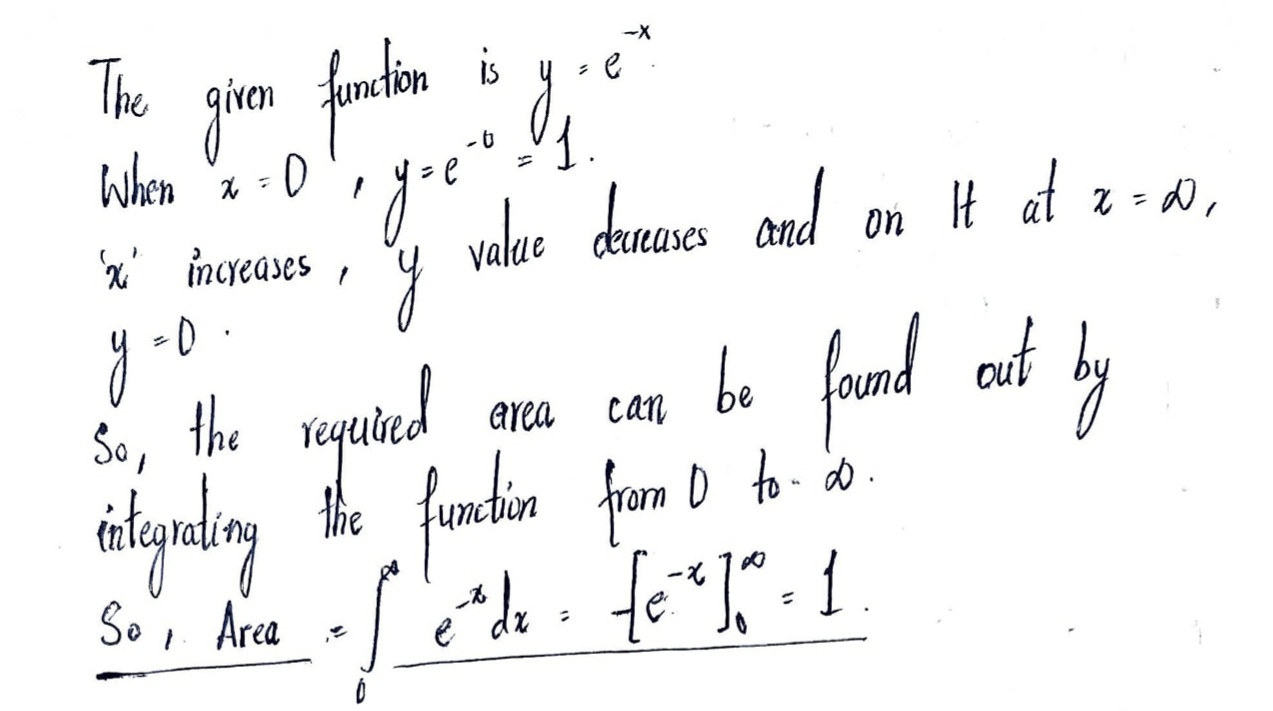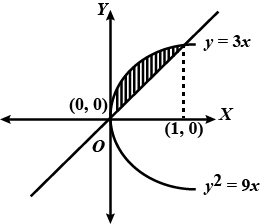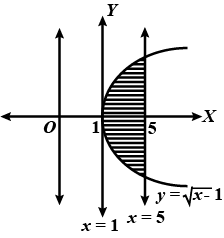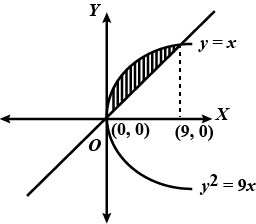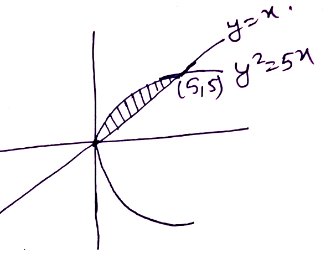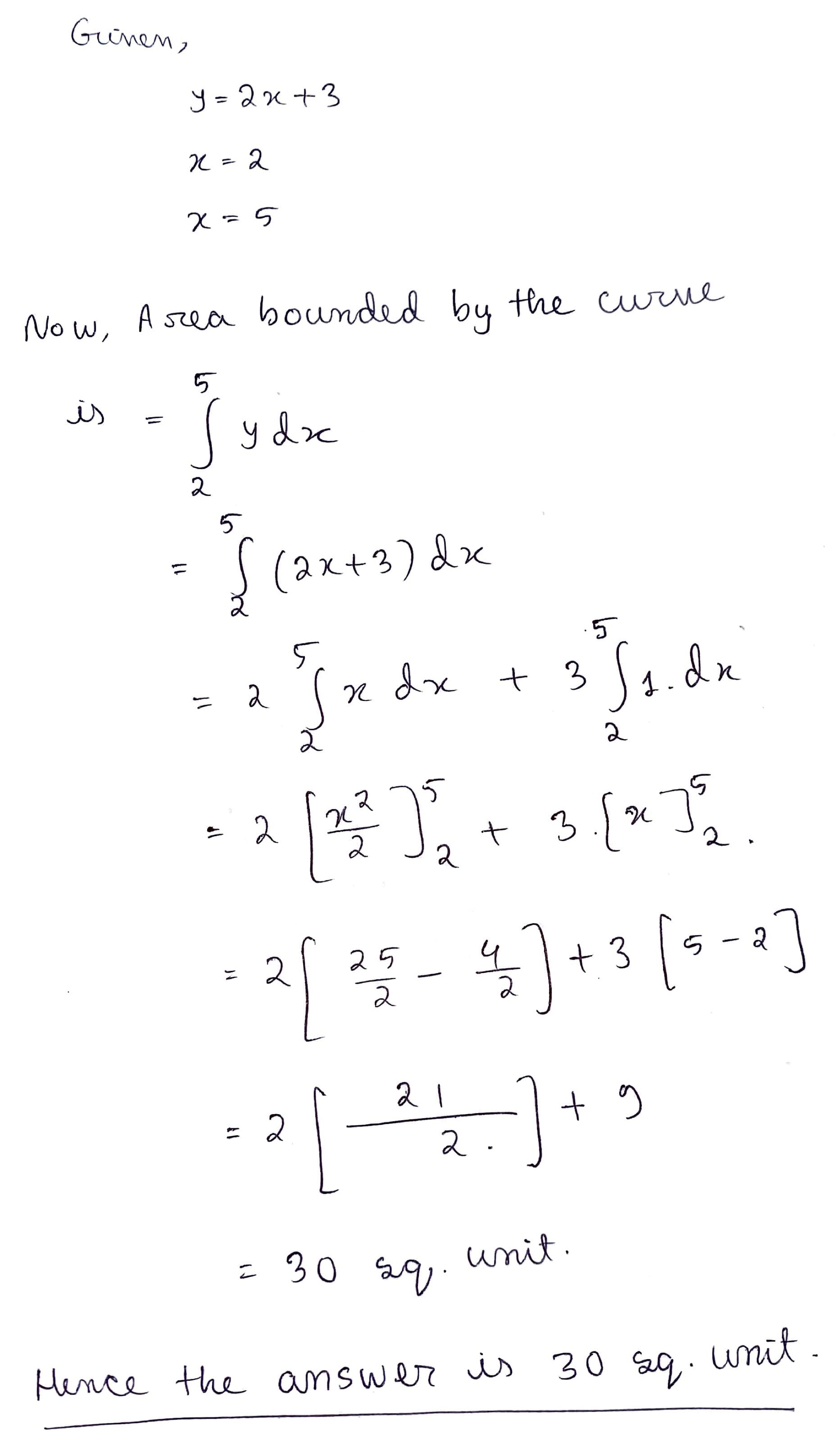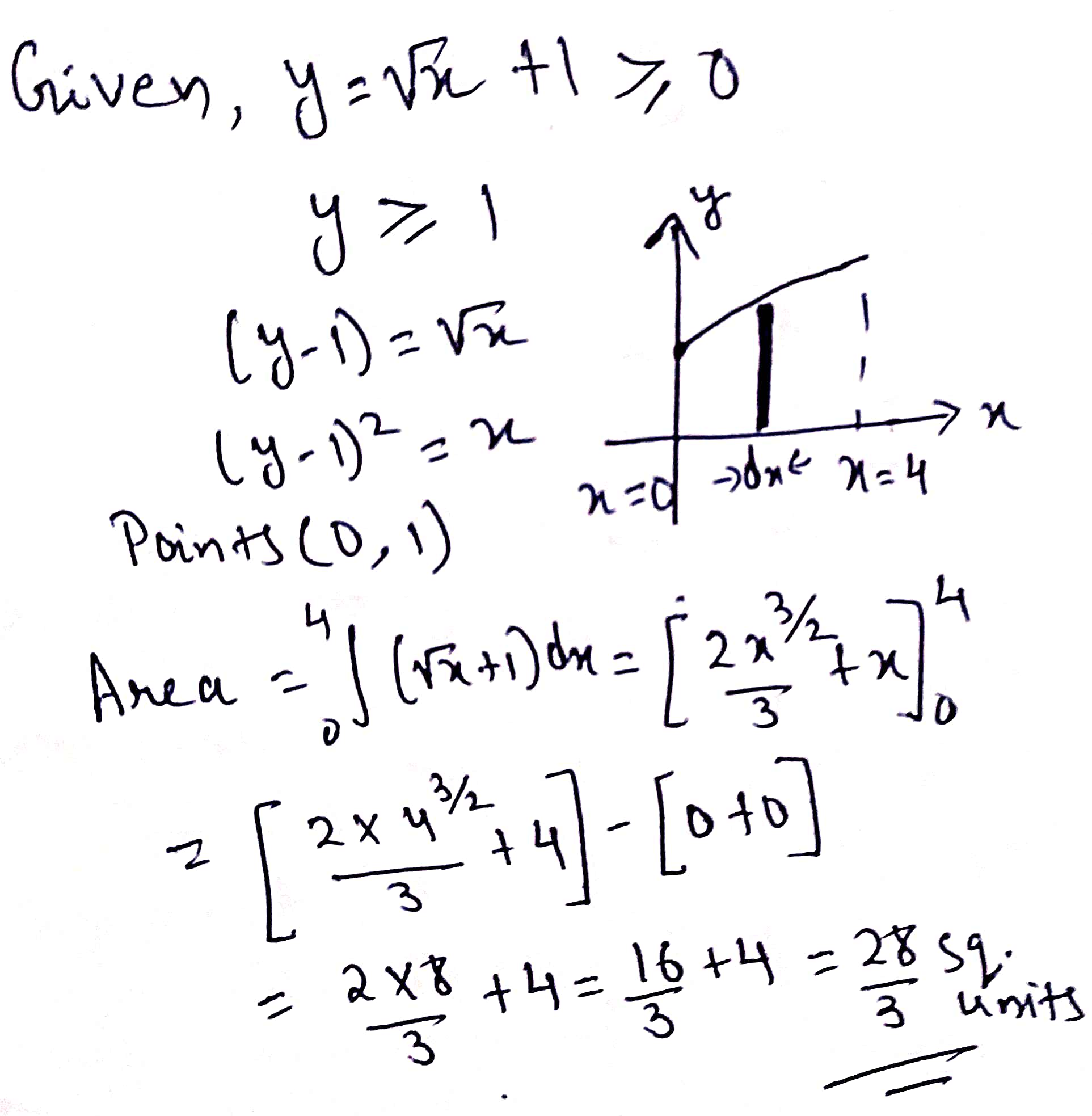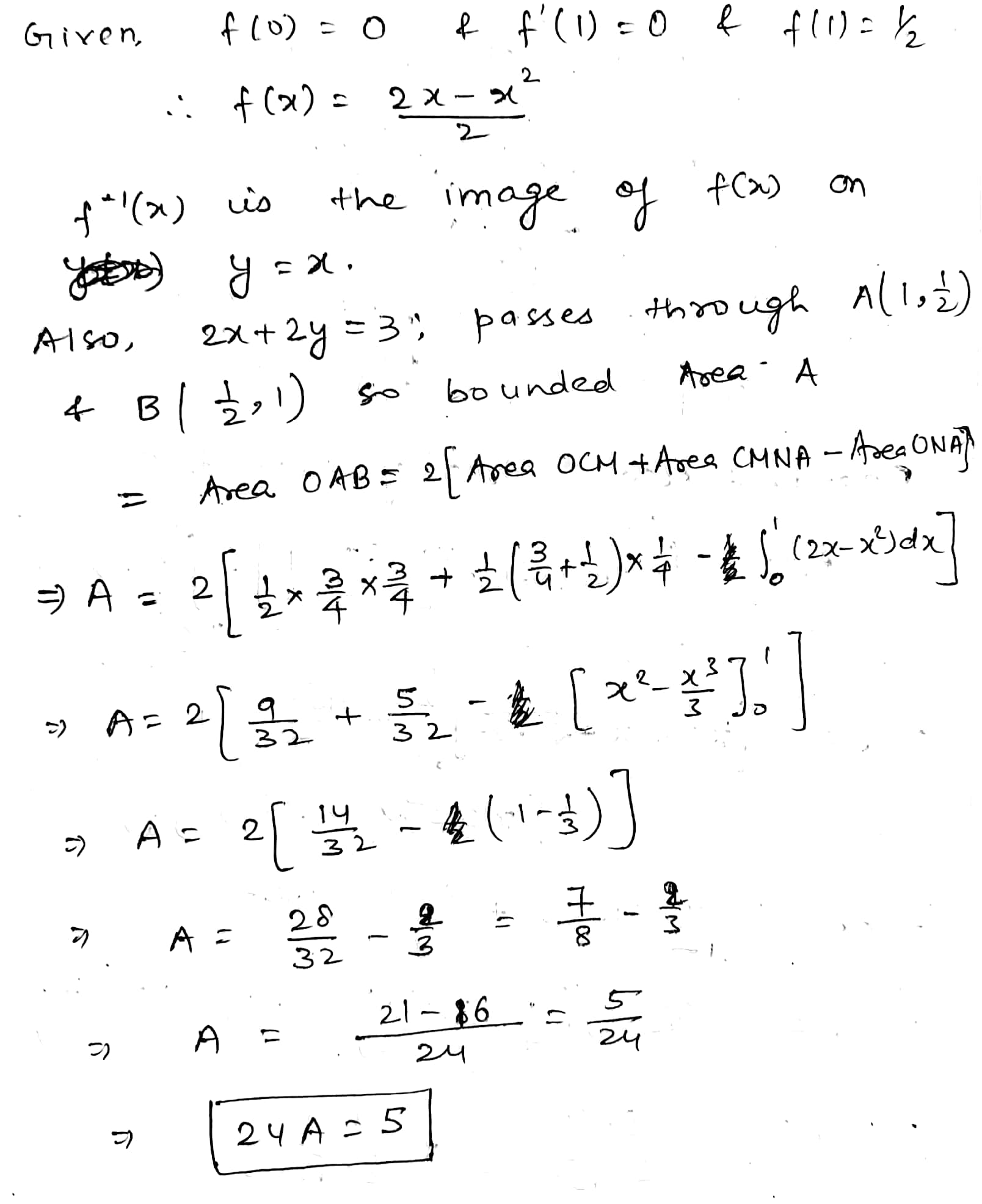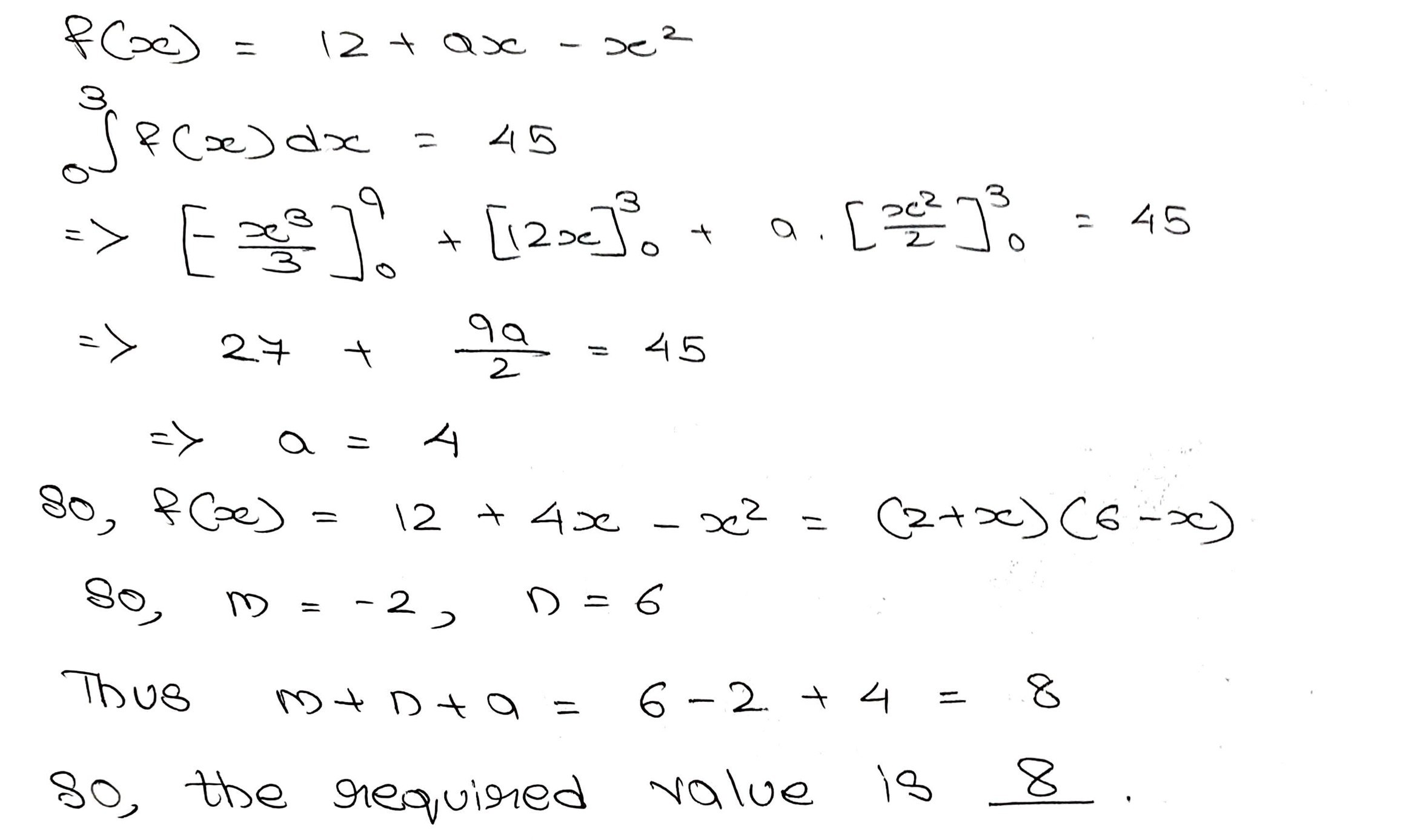Application Of Integrals - Class 12 Commerce Maths - Extra Questions
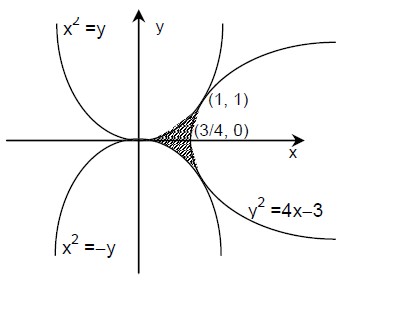
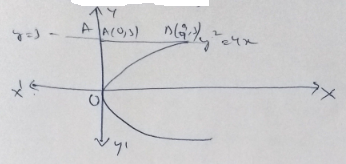
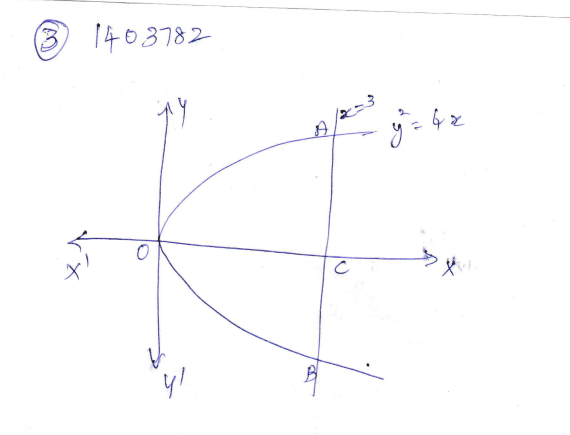
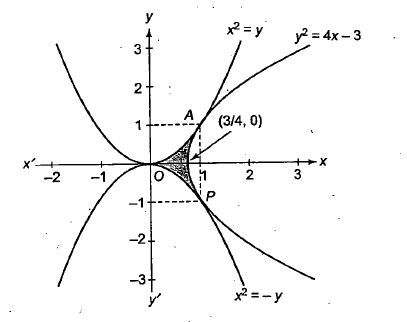
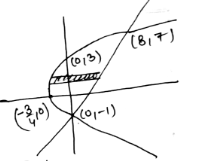
Find the area bounded by the curves $$x^{2}=y,x^{2}=-y\, \,$$ and $$y^{2}=4x-3$$
Find the area of the region bounded by the lines $$2y+x=8,x=2$$ and $$x=4$$
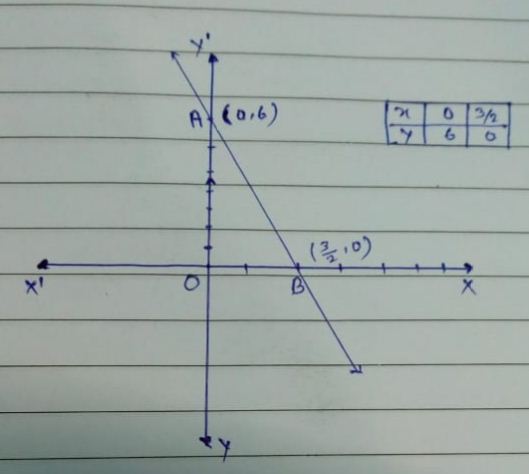
Draw the graph of the linear equation 4x+y=6 . At what points the graph of the equation cuts the x-axis and the y-axis ? Find area bounded by this line and coordinate axes.
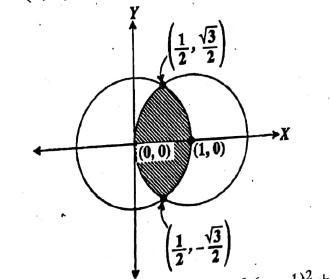
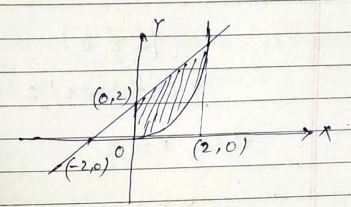
Find the are of the region enclosed by two circles $${ x }^{ 2 }+{ y }^{ 2 }=1$$ and $${ \left( x-1 \right) }^{ 2 }+{ y }^{ 2 }=1$$
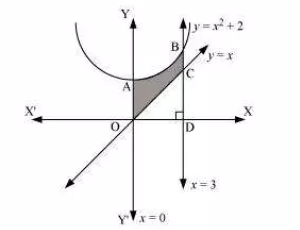
Find the area of the region enclosed by parabola $$y={ x }^{ 2 }+2$$ and lines $$y=x, x=3$$ and $$x=0$$
The area of the region bounded by the curve at $$y = \tan x$$ tangent drawn to curve at $$x = \dfrac{\pi }{4}$$
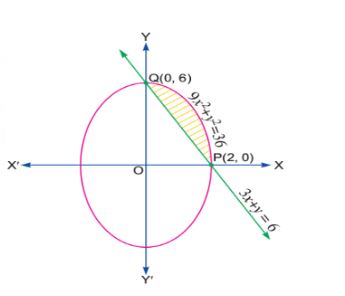
Find the area lying in first quadrant and included between the circle $${ x }^{ 2 }+{ y }^{ 2 }=8$$ and $$x$$ axis.
Find the area between the parabolas $${y^2} = 7x$$ and $${x^2} = 7y$$.
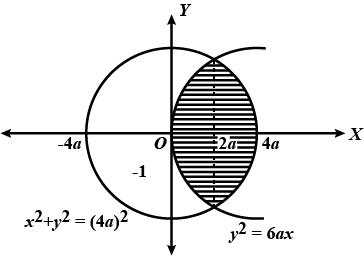
Find the area of the region common to the circle $${x^2} + {y^2} = 9$$ and the parabola $${y^2} = 8x$$.
Find the area of the region bounded by the curves
$$x^{2}+y^{2}=36$$ and $$y^{2}=9x$$
Find area between:
$$x=2y-y^{2}$$ $$and$$ $$y=2+x.$$
Find the area of the region bounded by
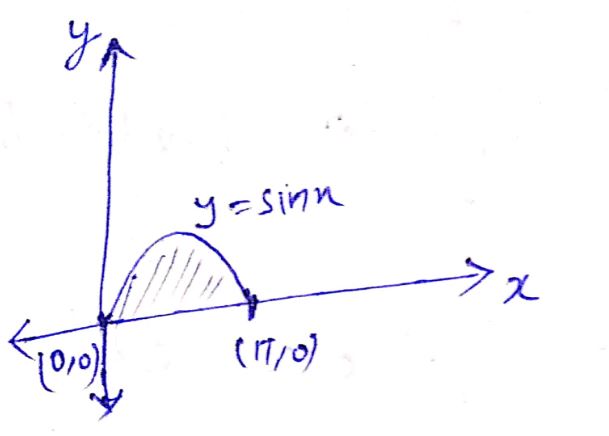
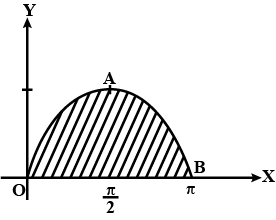
$$a)\,\,y = \sin x,\,\,y = 0,\,\,x = 0$$ and $$x = \pi $$
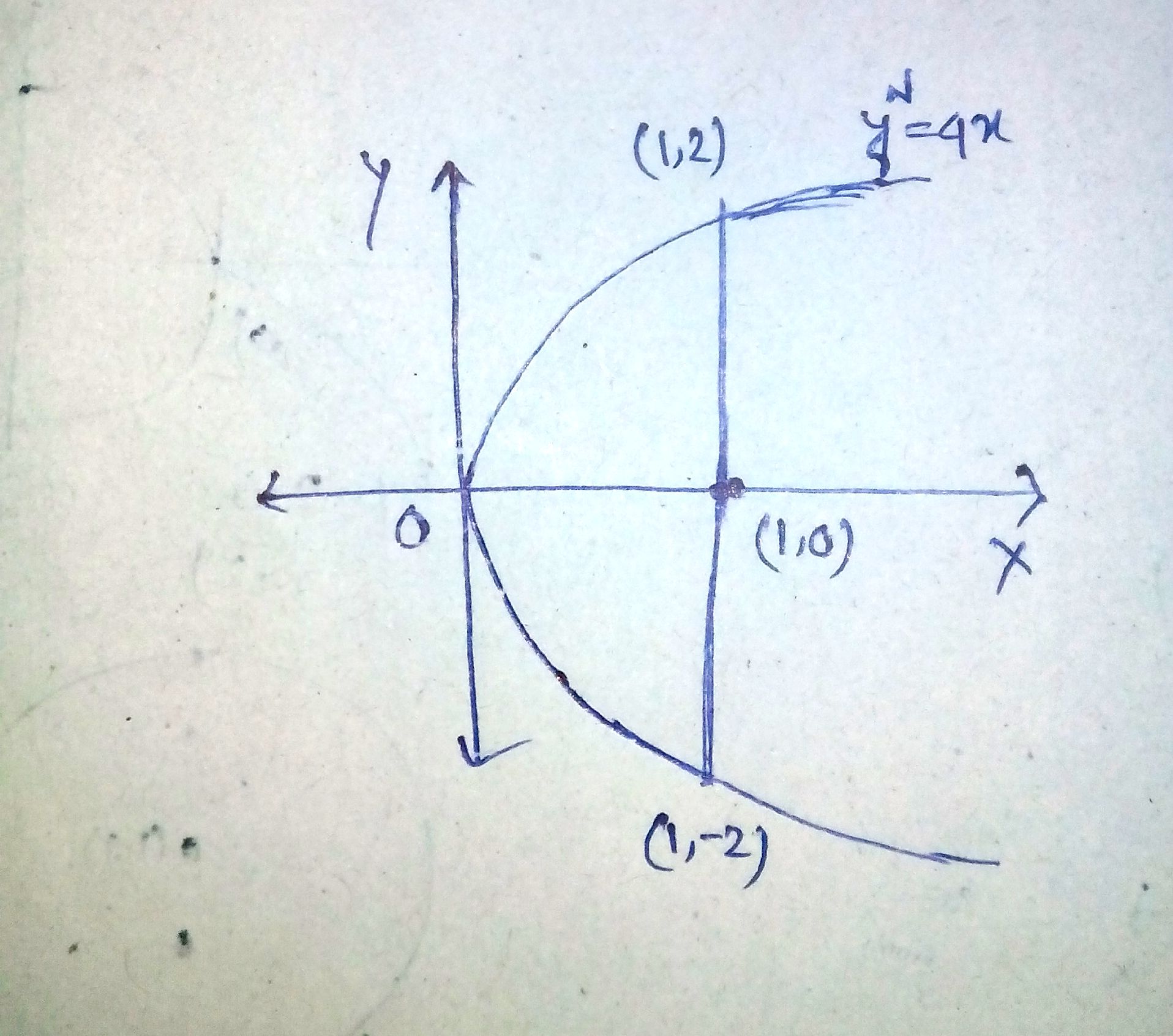
Find the area of the region bounded by the curve $$y^{2}=4x, y-axis$$ & the line $$y=3$$.
Find the area between $$x=0$$ and $$x=4-y^2$$.
Find the area of the region bounded by
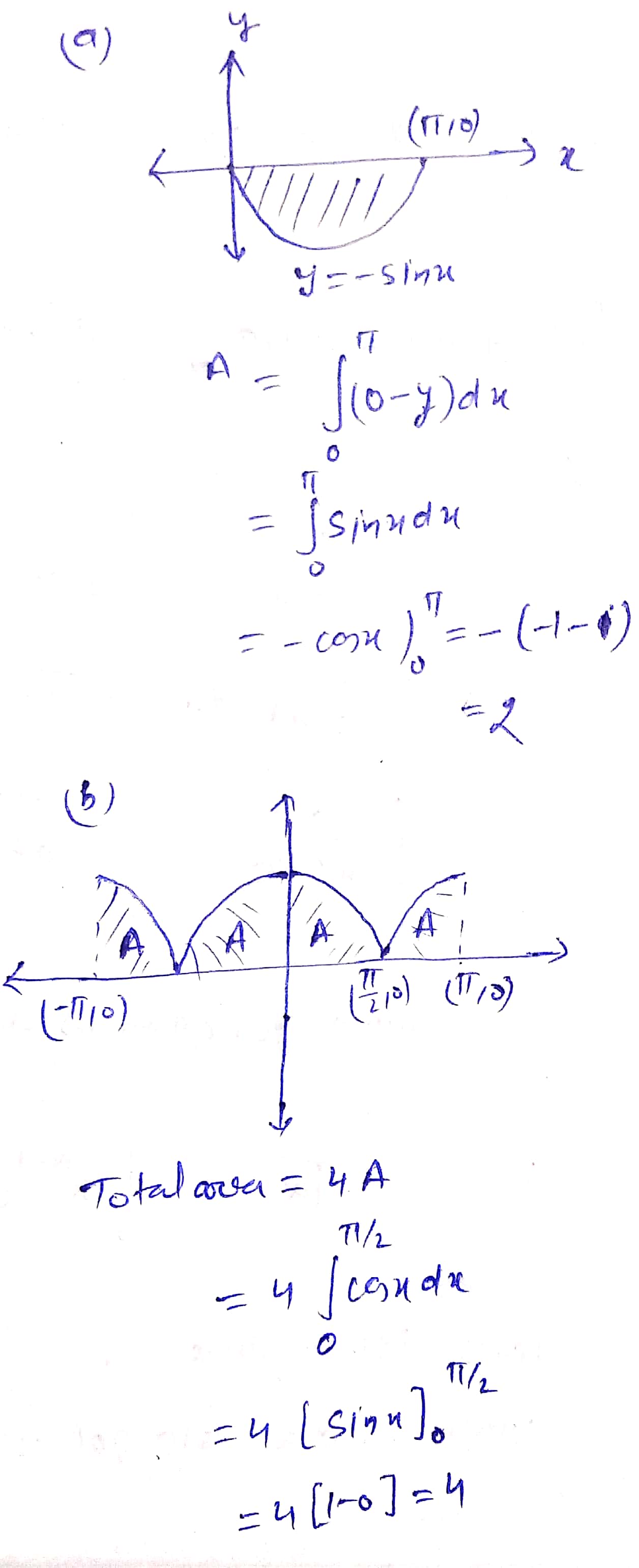
$$a)\,\,y =-\sin x,\,y = 0,\,x = 0$$ and $$x = \pi $$
$$b)\,\,y = \left| {\cos x} \right|,\,y = 0,\,x = - \pi $$ and $$x = \pi $$
Find the area of the region included between
the parabola $$y=x^{2}+3$$ and the line $$y=x+3$$
A 2 m wide verandah runs all around outside a hall of size 20 m by 8 m . Find the area of the verandah .
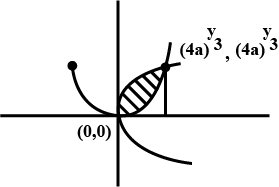
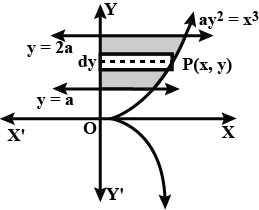
Find the area of the region bounded by the curve $$ay^{2}=x^{3}$$, the $$y-axis$$ and the lines $$y=a$$ and $$y=2a$$.
Calculate the area of shaded part of the figure given below
Find the area of the region bounded by the parabola $$y^{2}=4ax$$ and its latus rectum.
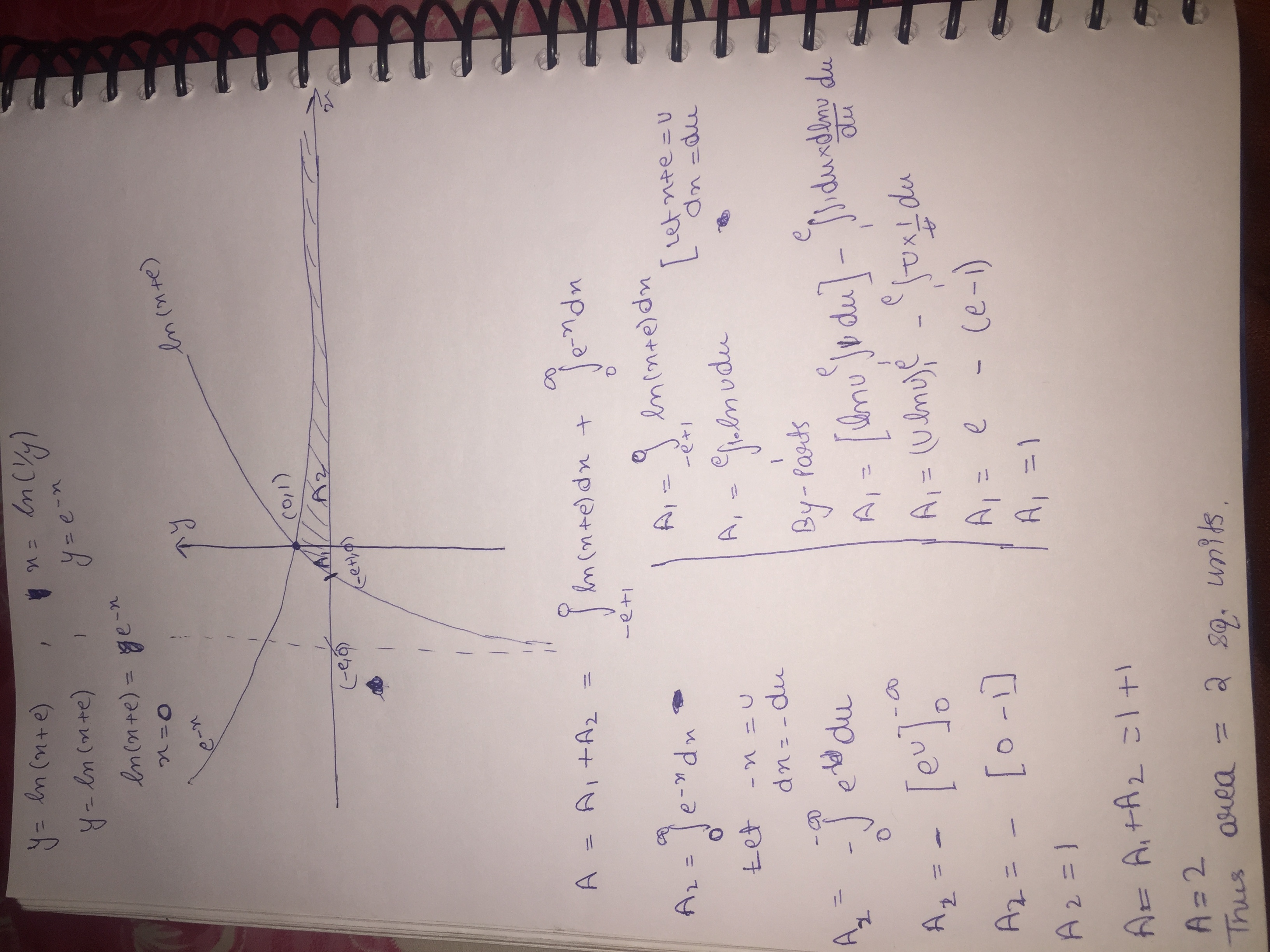
Compute the area of the region bounded by the curves $$y=ex\log { x } $$ and $$\displaystyle y=\frac { \log { x } }{ ex } $$, where $$\log{e}=1$$ is
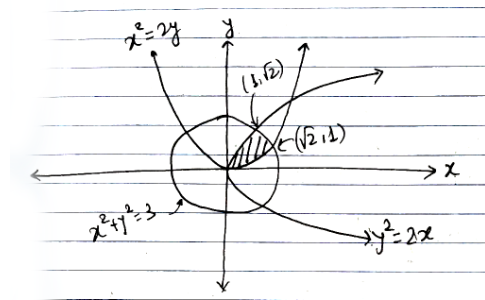
Compute the area of the figure which lies in the first quadrant inside the curve $$x^2+y^2=3a^2$$ & is bounded by the parabola $$x^2=2\ ay$$ & $$y^2=2 ax (a> 0)$$.
The area bounded by the curves $$ x= y^{2} $$ and $$ x=3-2y^{2} $$ is:
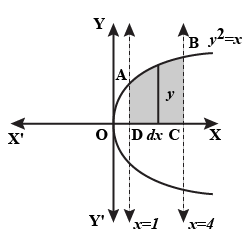
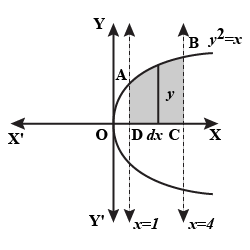
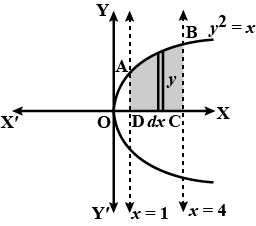
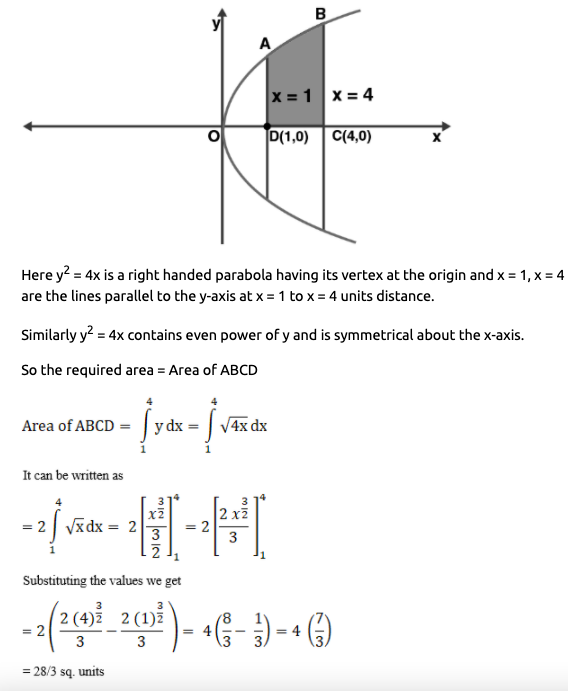
Find the area of the region bounded by the curve $$y^2 = x$$ and the lines $$x = 1, x = 4$$ and the x-axis in the first quadrant.
Find the area of the region bounded by $$y^2 = 9x, x = 2, x = 4$$ and the $$x$$-axis in the first quadrant.
The positive value of parameter '$$a$$' for which the area bounded by parabolas $$y = x - ax^2$$ & $$ay = x^2$$ attains its the maximum value is
The area between $$x = y^2$$ and $$x = 4$$ is divided into two equal parts by the line $$x=a$$, find the value of $$a$$.
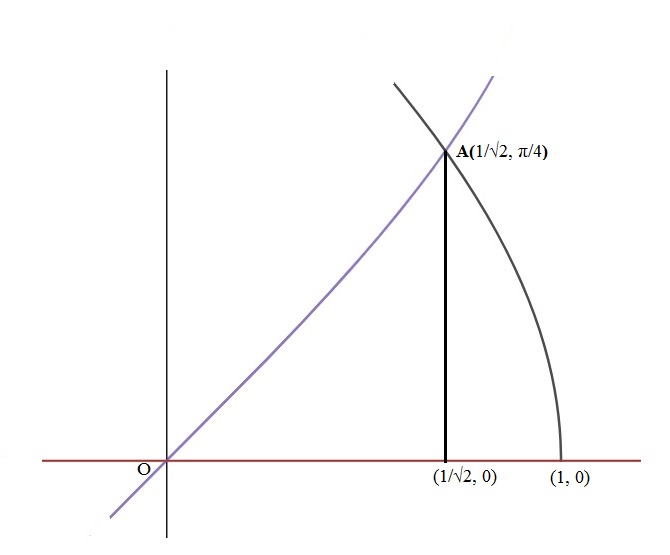
Find the area of the smaller part of the circle $$x^2 + y^2 = a^2$$ cut off by the line $$x=\dfrac {a}{\sqrt 2}$$.
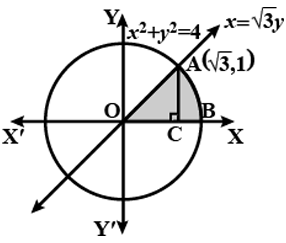
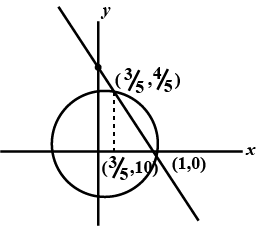
Find the area of the region in the first quadrant enclosed by $$x$$-axis, line $$x = \sqrt 3 y$$ and the circle $$x^2 + y^2 = 4$$.
Find the area of the region bounded by $$x^2 = 4y, y = 2, y = 4$$ and the $$y$$-axis in the first quadrant.
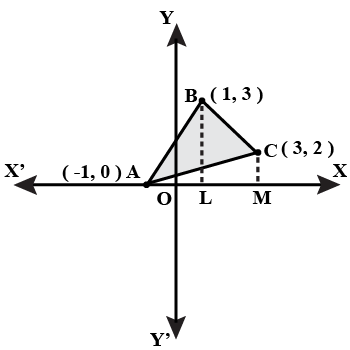
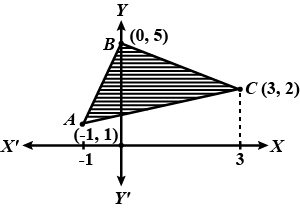
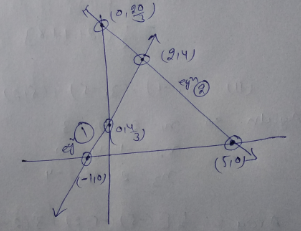
Using integration find the area of the region bounded by the triangle whose vertices are $$(-1, 0), (1,3)$$ and $$(3,2)$$.
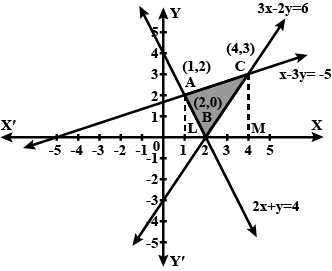
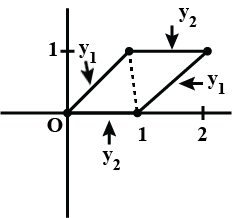
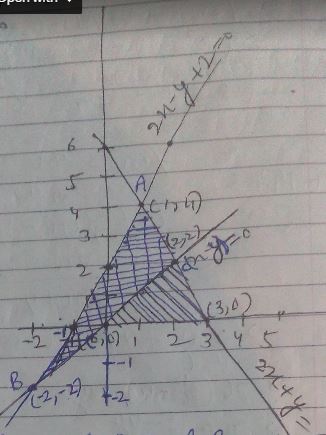
Using the method of integraton find the area of the region bounded by lines: $$2x+y=4, 3x-2y=6$$ and $$x-3y+5=0$$
Find the area of the circle $$4x^2 + 4y^2 = 9$$ which is interior to the parabola $$x^2 = 4y$$.
Find the area bounded by the curve $$y =\sin {x}$$ between $$x = 0$$ and $$x = 2\pi$$
Find the area of the region lying in the first quadrant and bounded by
$$y= 4 x^2, x=0, y=1$$ and $$y=4$$.
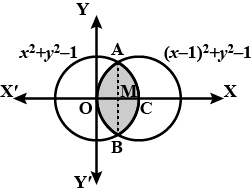
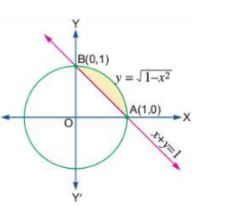
Find the area bounded by curves $$(x - 1)^2 + y^2 = 1$$ and $$x^2 + y^2 = 1$$.
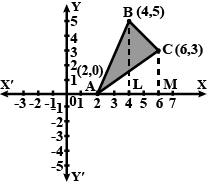
Using the method of integration find the area of the triangle $$ABC$$, coordinates of whose vertices are $$A (2,\ 0),\ B (4,\ 5)$$ and $$C (6,\ 3)$$
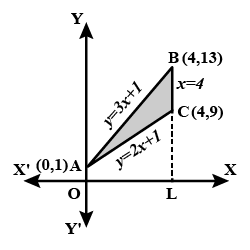
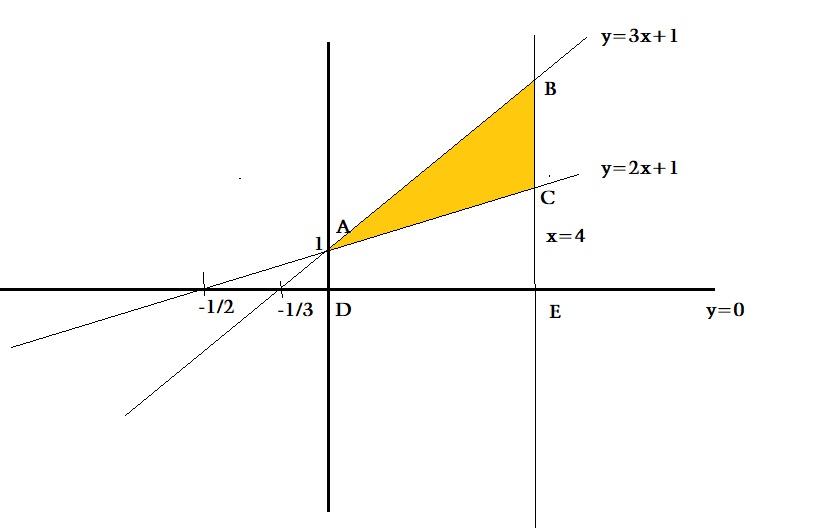
Using integration find the area of the triangular region whose sides have the equations $$y=2x+1, y=3x+1$$ and $$x=4$$
Find the area under the given curves and given lines:
(i) $$y=x^2, x=1, x=2$$ and $$x$$-axis
(ii) $$y=x^4, x=1, x=5$$ and $$x$$-axis
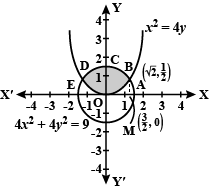
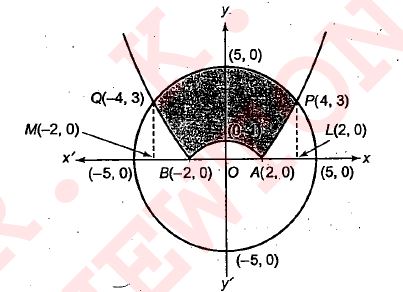
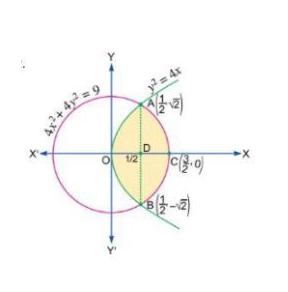
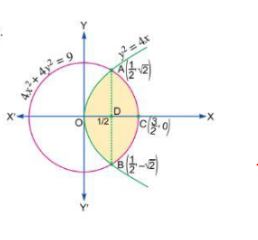
Find the area of the region $$\{ \left( x,y \right) :{ y }^{ 2 }\le 4x,4{ x }^{ 2 }+4{ y }^{ 2 }=9. $$
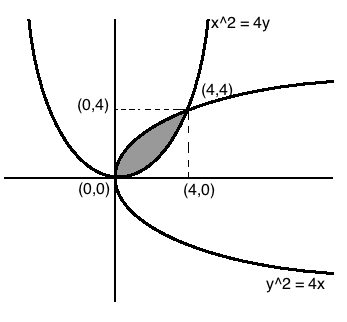
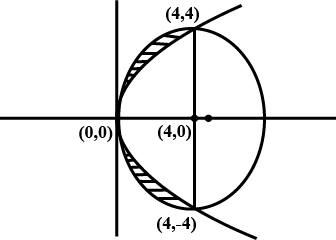
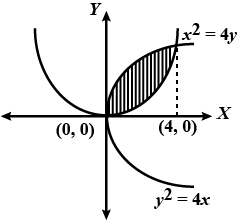
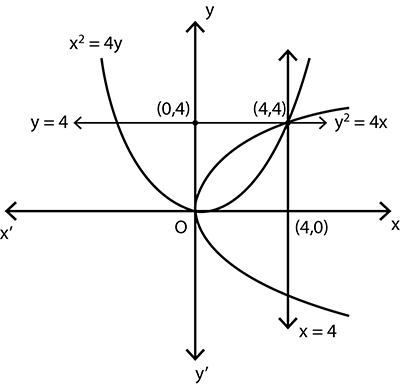
Find the area of the region bounded by the two parabolas $$x^{2} = 4y$$ and $$y^{2} = 4x$$. (Draw the figure in answer-book)
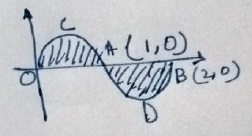
Find the area of the region enclosed by the curves $$y = 4x - x^2, y = 5 - 2x$$
Consider the functions :
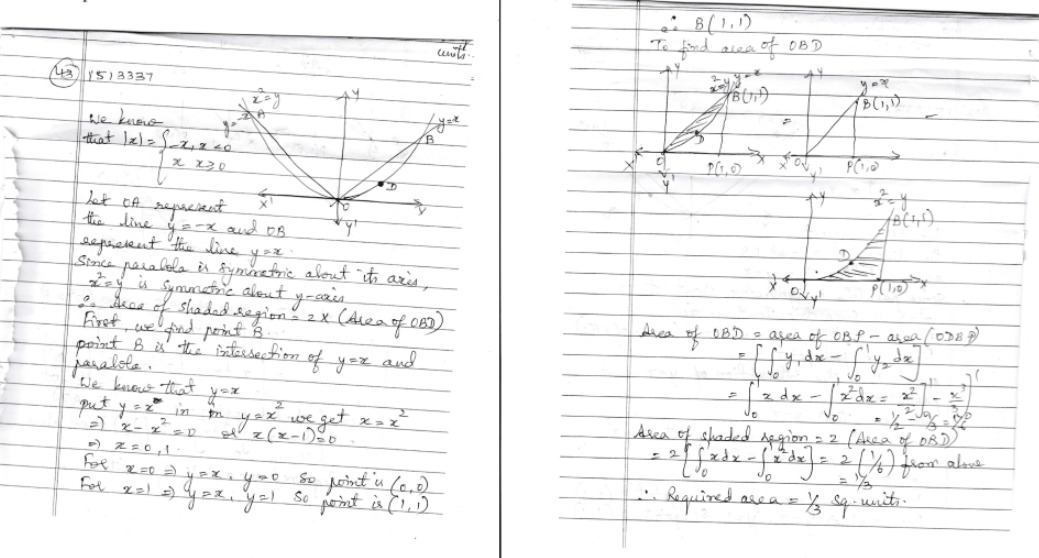
$$f(x)=|x|-1$$ and $$g(x)=1-|x|$$
(a) Sketch their graphs and shade the closed region between them.
(b) Find the area of their shaded region.
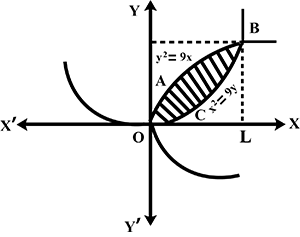
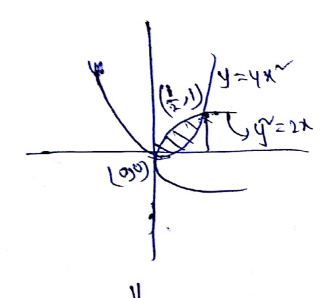
Find the area included between the two curves $${ y }^{ 2 }=9x$$ and $${ x }^{ 2 }=9y$$
Find the area of the region lying between the parabolas $$y^{2} = 4ax$$ and $$x^{2} = 4ay$$
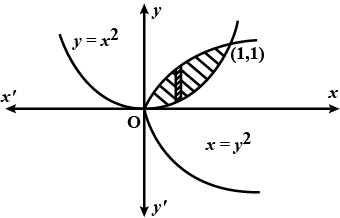
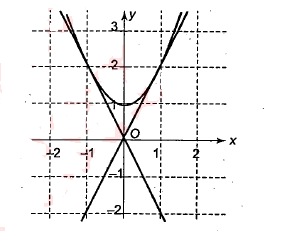
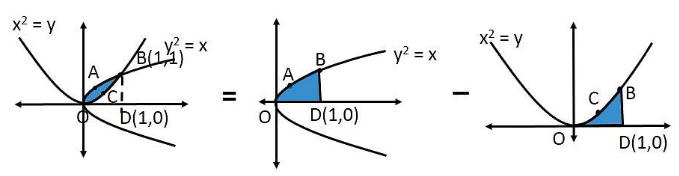
Find the area of the region bounded by the two parabolas $$y=x^2$$ and $$y^2=x$$.
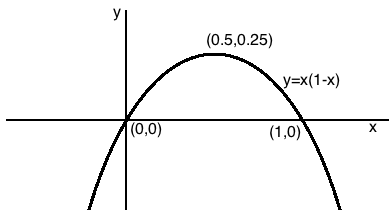
(i) Find the area bounded by the curve $$y=x(1-x)$$ between the points where it crosses the x-axis.
(ii) Find the area between the curves $$y=x$$ and $$y={x}^{3}$$.
Find a continuous function $$f$$, where $$(x^4-4x^2) \le f(x) \le (2x^2-x^3)$$ such that the area bounded by $$y=f(x), y=x^4-4x^2$$, y-axis, and the line $$x=t$$, where $$(0 \le t \le 2)$$ is $$k$$ times the area bounded by $$y=f(x), y=2x^2-x^3$$, y-axis, and line $$x=t$$ (where $$0\le t \le 2)$$.
Differentiate the following function with respect to x.If $$y=\left(\sin \dfrac{x}{2}+\cos \dfrac{x}{2}\right)$$, find $$\dfrac{dy}{dx}$$ at $$x=\dfrac{\pi}{3}$$.
Find the area of the region enclosed by the parabola $$y^{2} = 5x + 6$$ and $$x^{2} = y$$.
A curve passing through point $$\left( 1,2 \right)$$ possessing the following property; the segment of the tangent between the point of tangency & the x-axis is bisected at the point of intersection with the y-axis. If $$A$$ is area bounded by the curve & line $$x=1$$ then $$9{ A }^{ 2 }$$ is equal to
Find the area enclosed by the curves $$y=mod(x-1)$$ and $$y=mod(x-1)+1$$
Prove that the area enclosed between two parabolas $$y^{2} = 4ax$$ and $$x^{2} = 4ay$$ is $$\dfrac{16a^{2}}{3}$$
Find all possible value of $$b$$ so that area bounded between $$y = x - bx^{2}$$ and $$y = \dfrac {x^{2}}{b}$$ is maximum.
Find the area of the closed figure bounded by the following curve
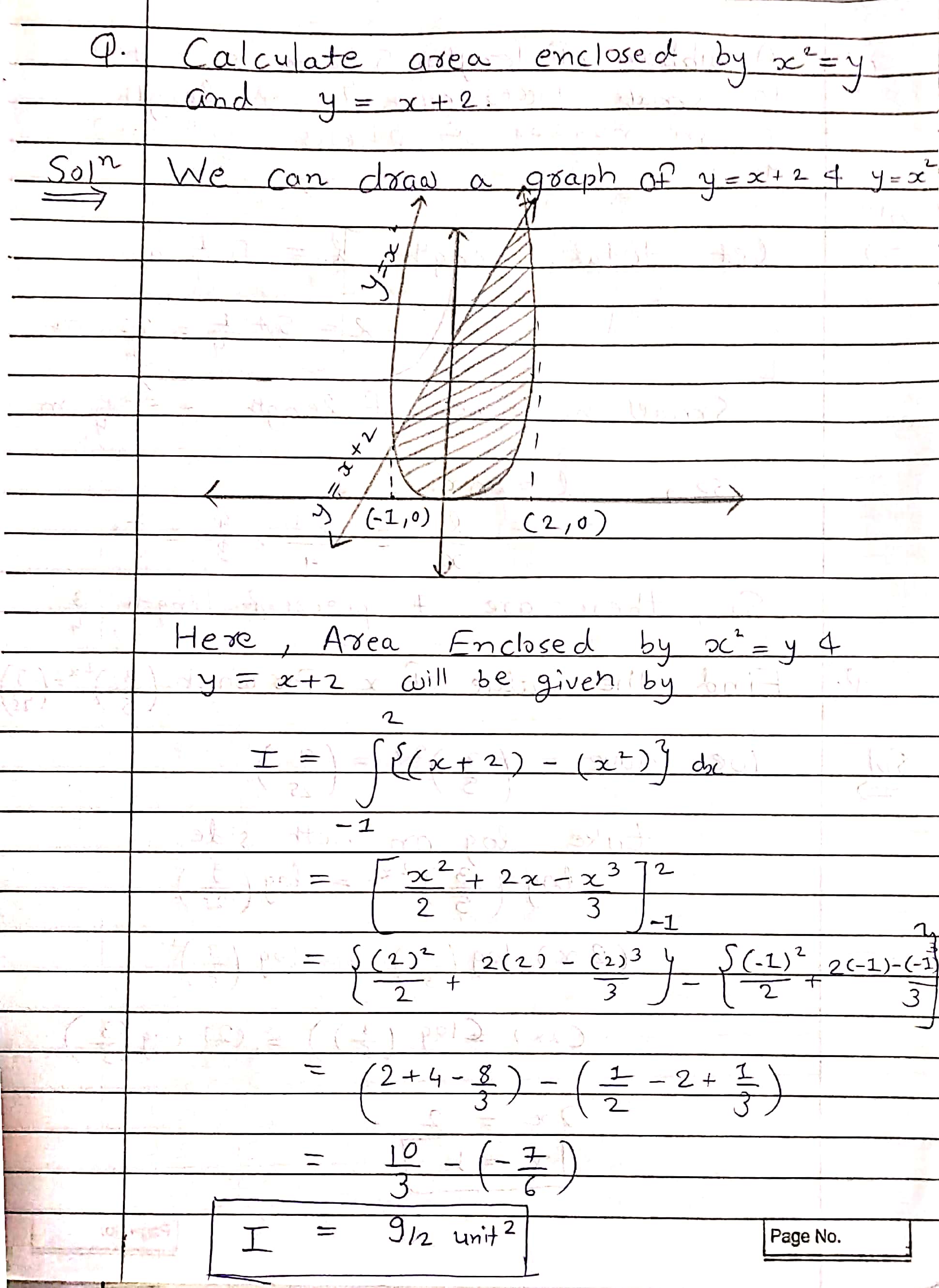
$$y = x^2$$, $$y = x + 2$$.
Find the area bounded by the curve y=4x(x-1)(x-2) and the x axis.
Find the area of the closed figure bounded by the following curve
$$y$$ = $$x^2$$ - $$2x + 2, y = 2 + 4x$$ - $$x^2$$.
If the area of the closed figure bounded by the following curves $$y =$$ $$x^2$$ $$+ 2, y = 1 - $$$$x^2$$, $$x = 0, x = 1$$ is k. Find 3k
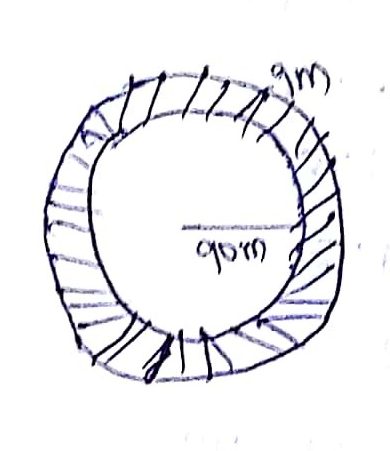
The radius of a circular garden is 90 m. There is a road 9 m wide around it. Find total area of the road and the cost of levelling the road at Rs.5 per sq.m.
Find the area of the closed figure bounded by the following curve
$$y$$ = $$x^2, y \, = \, 2x \, - \, x^2$$.
Find the area of the closed figure bounded by the following curve
$$y = x^2 - 2x + 3, y = 3x - 1$$.
Find the area of the closed figure bounded by the following curves
$$y$$ = $$x^2, y \, =\, 1 \, +\, \frac{1}{4}\, x^2$$.
The area of the region lying inside $$x^2+(y-1)^2=1$$ and out side $$c^2x^2+y^2=c^2$$, where $$c=(\sqrt{2}-1)$$ is
If $$f\left( x \right) = \sin x\forall x \in \left[ {0,x/2} \right]$$, $$f\left( x \right) + f\left( {\pi - x} \right) = 2\forall x \in \left[ {x/2,\pi } \right]$$ and $$f\left( x \right) = f\left( {2\pi - x} \right)\forall x \in \left[ {\pi ,2\pi } \right]$$ then find the area bounded by $$y=f(x)$$ and the $$x-$$ axis.
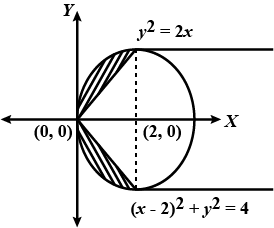
Find the area lying above x-axis and included between the circle $$x^2+y^2= 8x $$ and inside of the parabola $$y^2= 4x.$$ is $$m\pi+\dfrac{32}{3}$$.Find the value of $$m$$
If area enclosed by the curve $$|x| + |y| \le k$$ is $$f(k)$$ sq.unit, Then what will be the value of $$\frac{{f(10)}}{{100}}$$.
Using integration, find the area of the region bounded by the curves $${y}^{2}=4ax$$ and $${x}^{2}=4ay$$, where $$a>0$$.
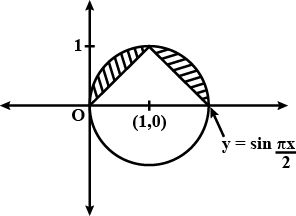
Find the area bounded by $$x^{2} +y^{2} -2x =0$$ and $$y= \sin\dfrac{\pi x}{2}$$ in the upper half of the circle is $$\dfrac{{\pi}^2-a}{a\pi}$$. Find a.
The area enclosed between the curve $${y^2} = x$$ and $${x^2} = y$$ is equal to
If the area of the region bounded by the curve $$y =ex \ln x$$ and $$y = \dfrac{(\ln x)}{ex}$$ is $$\dfrac{e^2-m}{4e}$$.Find $$m$$
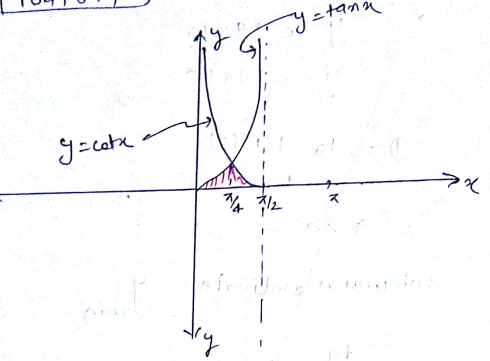
Area laying between the curves $$y = \tan \,x,\,y = \cot x\,and\,x - axis,\,x\left[ {o,\frac{\pi }{2}} \right]\,\,is$$
Given below are Matching Type Questions,with two columns(each having some items) each.Each item of column $$I$$ has to be matched with the items of column $$II$$, by encircling the correct match(es):
The area of the region bounded by the curve $$y={x}^{2}$$ and $$y={\sec}^{-1}\left[-{\sin}^{2}x\right],$$ (where $$\left[.\right]$$ denotes the greatest integer function), is $$\dfrac{4\pi\sqrt{\pi}}{n}$$ sq. unit. Find the value of $$n$$.
Find the area bounded by the curve $$y = \sqrt {x}, x = 2y + 3$$ in the first quadrant and x-axis.
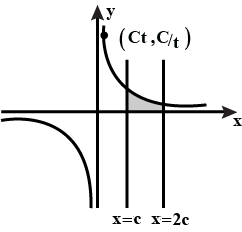
Find the area of the region bounded by the curve $$xy = {c^2}$$, the X-axis, and the lines $$x = c$$, $$x = 2c$$
Find the area of the region bounded by $$y = 2x + 1\ y = 3x + 1$$ and $$x = 4$$.
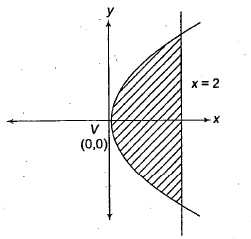
Find the area of region bounded by the line $$x = 2$$ and the parabola $$y^{2} = 8x$$.
$$x^2=y$$ and $$y=x+2$$.
Calculate the area between two curves:$$y=x^2$$
$$y=x+1$$.
$$y=x+1$$.
Area bounded by $${x^2} = 4ay$$ and $$y = \dfrac{{8{a^3}}}{{{x^2} + 4{a^2}}}$$ is :
Find the area bounded by $${x^2} + {y^2} + 4x + 6y - 3 = 0$$ and $${x^2} + 4x = 6y + 14$$.
The area of the square is $$(4x^2-2x-6)$$ square units. A triangle inside the square has an area $$(x^2-4x+5)$$ square units. Find the area of the shaded portion.
Find the area bounded on the right by the line $$x+y=2,$$ on the left by the parabola $$y=x^{2}$$ and below by the $$x-$$axis.
The area ( in square units) of the region bounded by the curves $$y + 2{x^2} = 0$$ and $$y + 3{x^2} = 1$$, is equal to:
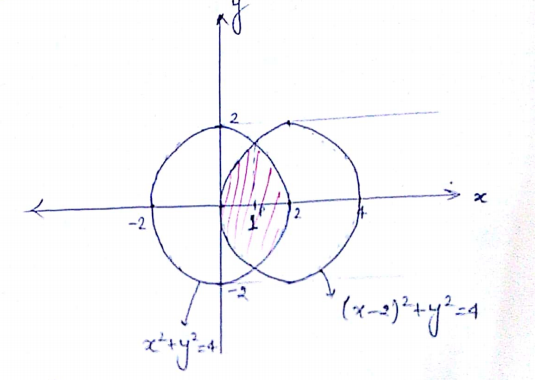
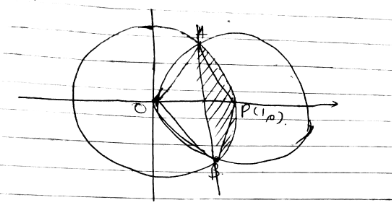
Find the area of the region enclosed between the two circles $$x^{2}+y^{2}=4$$ and $${ \left( x-2 \right) }^{ 2 }+{ y }^{ 2 }=4.$$
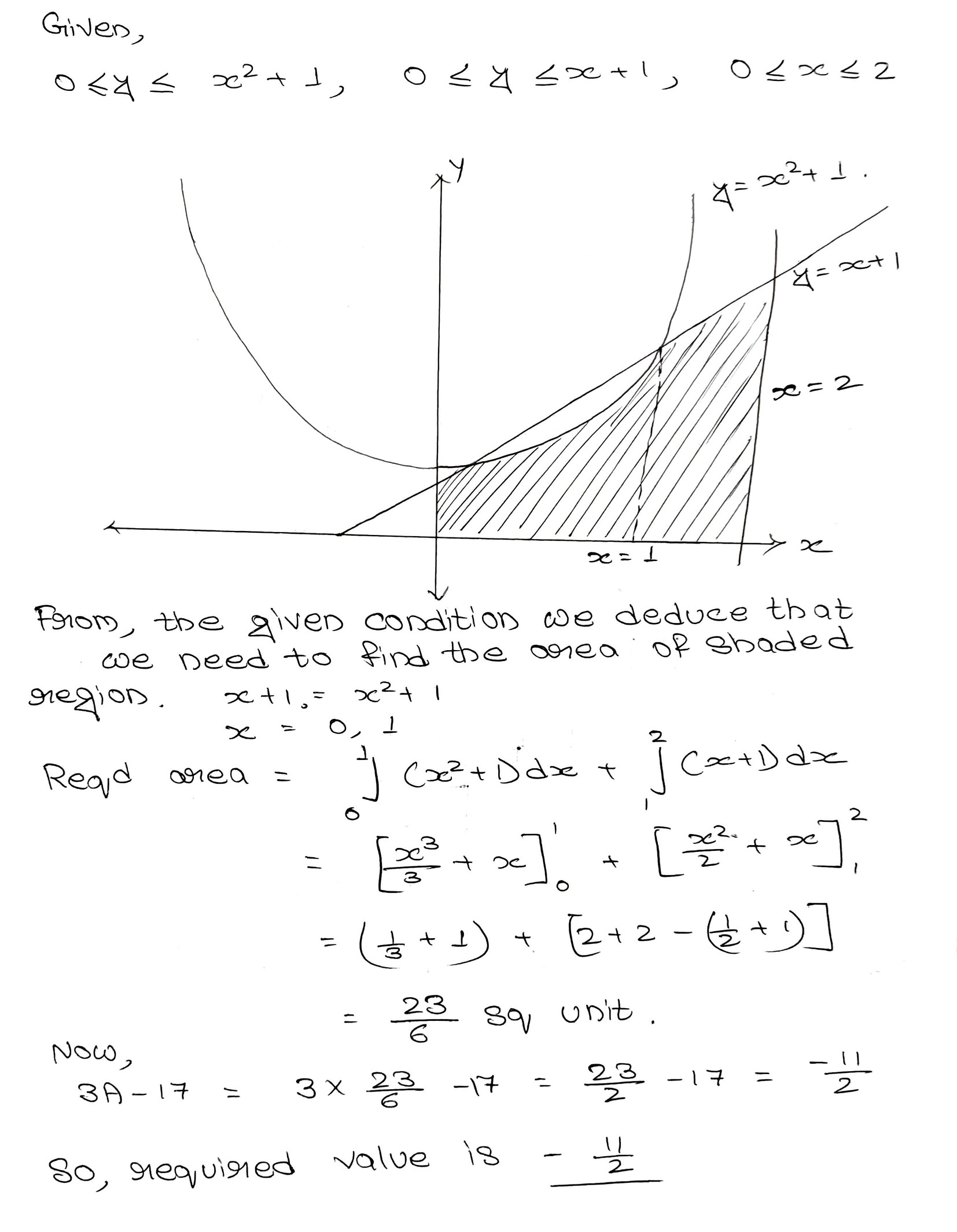
Find the area of the region $$\{(x, y): 0 \le y x^2 + 1, 0 \le y \le x + 1, 0 \le x \le 2\}$$
Find the area bounded by the curves $${x^2} + {y^2} = 4,{x^2} = - \sqrt 2 \,y$$ and $$x=y$$
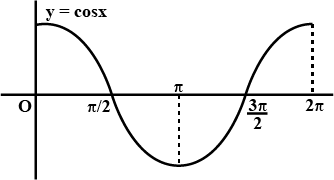
Find the area bounded by the curve $$y=\cos {x}$$ between $$x=0$$ and $$x=2\pi$$
Find the area enclosed between the parabola $${y^2} = z$$ and $${x^2} = y$$.
Find the area of the region bounded by the parabola $$x^2=4y$$ and the line $$x=4y-2$$.
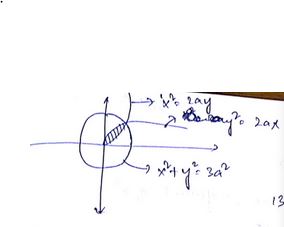
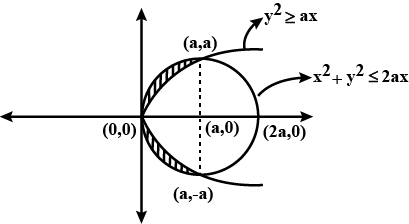
Find area bounded by $$x^{2}+y^{2}\le 2ax,\ y^{2}\ge ax$$, $$x\ge 0$$, $$y\le 0$$
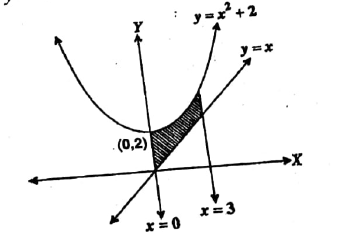
Find the area of the region bounded by the curves $$y=x^2+2, y=x, x=0$$ and $$x=3$$.
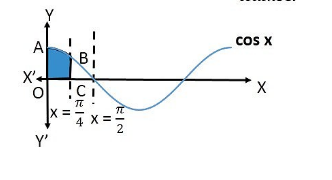
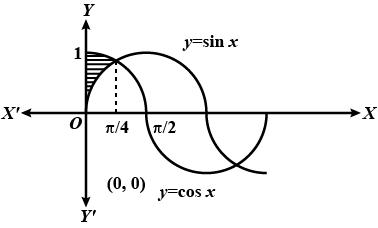
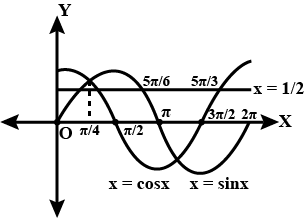
Find the area bounded by the curve $$y=\cos{x},\ y=\sin{x}$$, y-axis and $$0\le\ x\ \le\ \dfrac{\pi}{4}$$
Find area of common region of circle $$x^{2}+y^{2}=2$$ and parabola $$y^{2}=x$$
Find the area of region:
$$ {(x,y):x^{2}+y^{2}\leq 1,\leq x+\frac{y}{2}}$$
Find the area of a quadrilateral constructed by lines $$|x|+|y|=1$$
Find the area of region lying between parabolas $${y^2} = 4ax\& {x^2} =
4ay$$ where $$a > 0$$
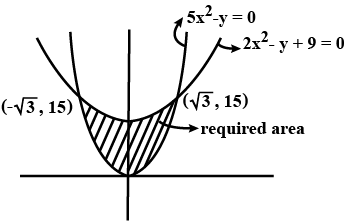
The area inside the parabola $$5{x}^{2}-y=0$$ but outside the parabola $$2{x}^{2}-y+9=0$$ is
Find the area between the two parabolas $$y^{2}$$=$$x ,X^{2}$$=$$y$$.
Find the area bonded by the curves
$$x^2 + y^2 = 25, 4y = |4 - x^2|$$ and $$x = 0$$ above the X-axis.
Find area bounded by $$x^{2} + y^{2} - 2x = 0$$ and $$y = \sin \dfrac {\pi x}{2}$$ in the upper half of the circle.
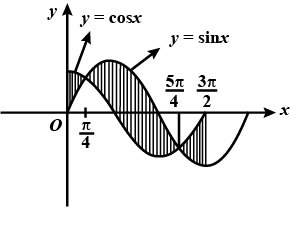
The area bounded by the curve $$y = \cos x$$ and $$y = \sin x$$ between the ordinates $$x = 0$$ and $$x = \dfrac { 3 \pi } { 2 }$$ is
Find the area of that part of the circle $${x}^{2}+{y}^{2}=16$$ which is exterior to the parabola $${y}^{2}=6x$$.
Find the areas included between the parabolas
(i) $${y}^{2}=4ax$$ and $${x}^{2}=4ay$$
(ii) $${y}^{2}=4ax$$ and $${x}^{2}=4by$$
The area bounded by the parabola $${y}^{2}=5x+6$$ and $${x}^{2}=y$$
The area in the first quadrant bounded by the curves $${x^2} = 2y,{y^2} = 2x$$ and $${x^2} + {y^2} = 3$$ is
The area below the line $$y = x + 1$$ and bounded by the curve $${x^2} + {y^2} - 4x - 6y - 19 = 0$$ is
Find area of triangle between the coordination axis of line $$3x-4y-12=0$$
Find the area of the region enclosed by $${y^2} = 8x$$ and $$x + y = 0$$.
Find the area of the region bounded by the curves $$y=x^2$$,$$y=2-x$$ and $$y=1$$
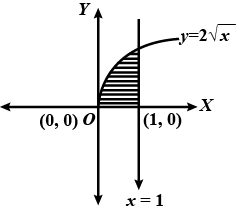
Calculate the area under the curve $$y = 2\sqrt {x}$$ included between the lines $$x = 0$$ and $$x = 1$$.
Find the area of the region bounded by $${ x }^{ 2 }=4y$$, the y-axis and the abscissae y=2 and y=4, in the first quadrant.
Find the area enclosed by the curve $$x = 3\cos t, y = 2\sin t$$.
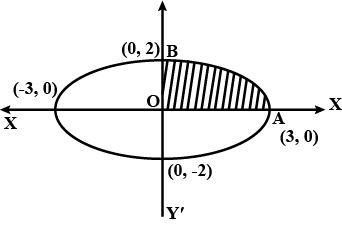
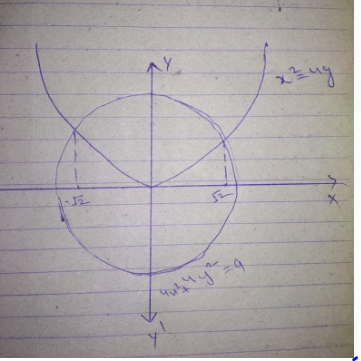
Find area of circle $$4{x}^{2}+4{y}^{2}=9$$ which is interior to the parabola $${x}^{2}=4y$$
Find the area enclosed by the curves $$y=4x^{2}$$ and $$y^{2}=2x$$.
Find the area enclosed between $$y^{2}=4ax$$ and $$x^{2}=y$$.
Find the area of the region common between the curve $${x^2} + {y^2} = 4$$ and $${x^2} + 4{y^2} = 9$$.
Find the area of the region bounded by the parabola $$y^{2} = 2x$$ and the straight line $$x - y = 4$$.
Find the area of the region bounded by the following curves, the $$X-$$axis and the given lines.
$$y=x^{4}, x=1, x=5$$
Find the area of the region bounded by the following curves, the $$X-$$axis and the given lines.
$$y=\sqrt {6x+4}, x=0, x=2$$
Find the area of one of the curvilinear triangles formed by $$y=sin\:x,y=cos\:x$$ and x axis
Find the area of the region bounded by the curve y = x$$^2$$ and the line y = $$2$$.
Find the area lying above $$x-$$axis and included between the circle $$x^{2}+y^{2}=8x$$ and inside of the parabola $$y^{2}=4x$$.
Draw the rough sketch of the parabolas $$y=5x^{2}-3$$ and $$y=3x^{2}+5$$, using integration, find the area ( in square unit)between them to the nearest integer
Find the area of the region bounded by the curve $$ay^{2} = x^{3}$$, the $$y-axis$$ and the line $$y = a$$ and $$y = 2a$$.
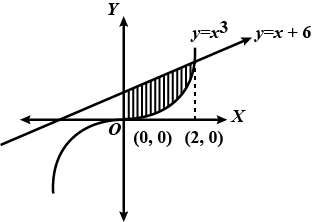
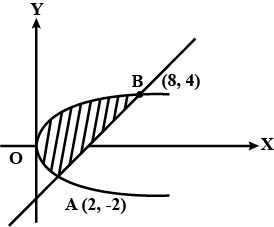
Find the area of the region bounded by the curve $$y = x^{3}$$ and $$y = x + 6$$ and $$x = 0$$.
Find the area of the region bounded by the curve $${ y }^{ 2 }=4x\quad $$ and the line x=3
Find the area bounded by the curve $$x ^ { 2 } = 4 y$$ and the line $$x = 4 y - 2$$. If the answer is $$\dfrac a8$$. what is the value of $$a$$?
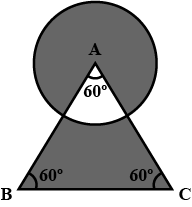
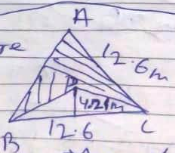
Circular arc of radius $$7$$ cm has been drawn with vertex A of an equilateral triangle ABC of side $$14$$ cm at center. Find the area of shaded region.
Find the area of the region bounded by the $$y-$$axis, $$y=\cos x$$ and $$y=\sin x,\ 0\le x\le \pi /2$$
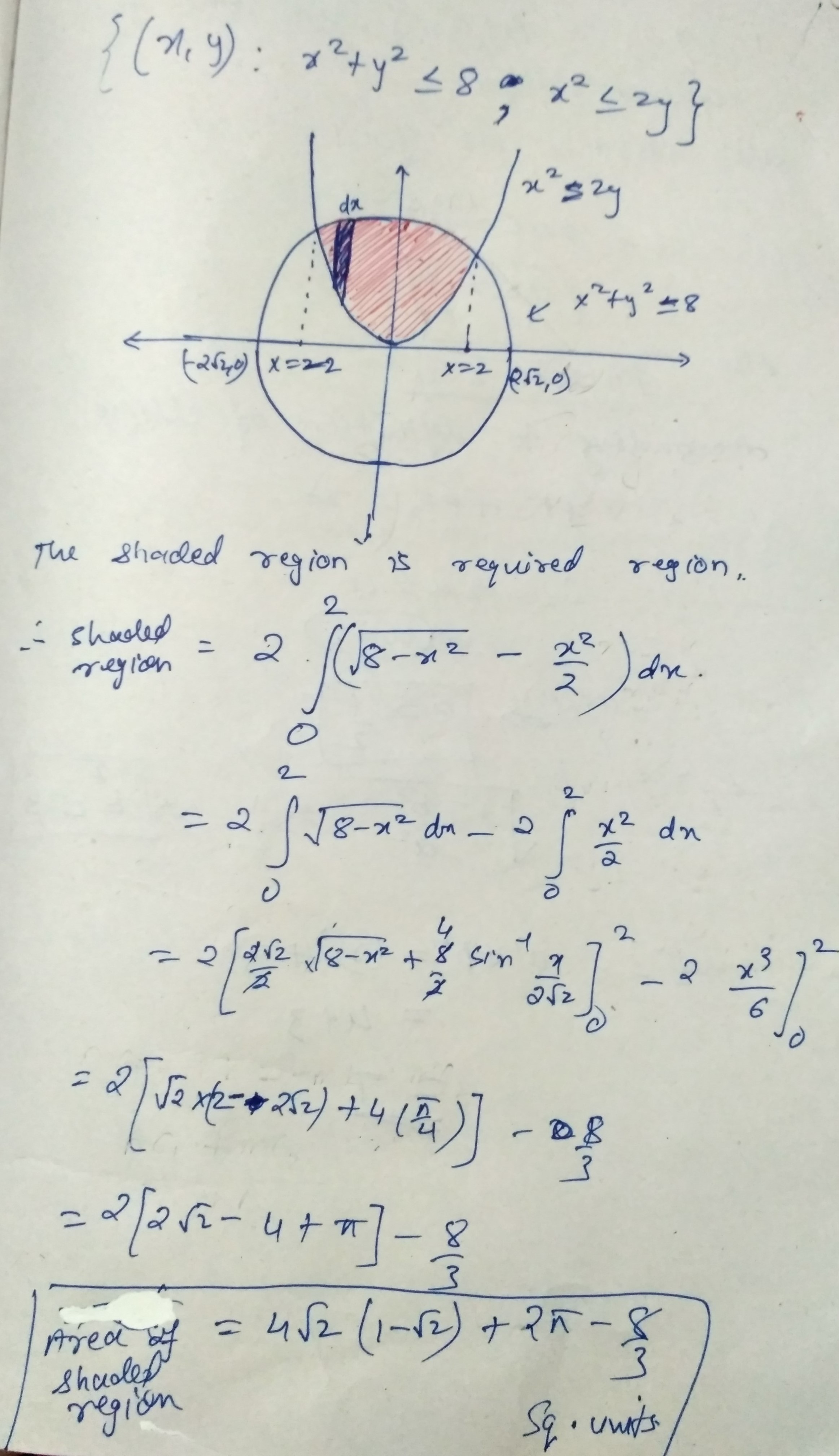
Find the area of the region.
$$\{(x, y):x^2+y^2\leq 8, x^2\leq 2y\}$$.
Find the area of the region bounded by the parabola $$y = x ^ { 2 }$$ and the line $$y = x$$ in the first quadrant.
Find the area bounded by the curve $$y = 2\cos x$$ and the x-axis from $$x = 0$$ to $$x = 2\pi$$.
Find the area bounded by the curve $$y=4-x^{2}$$ and the lines $$y=0,y=3$$.
Find the area of the region enclosed by the curves $$y=\sin\pi x, y=x^2-x, x=2$$.
Compute the area of the region bounded by the curves $$y=tanx$$ and $$y=tan^{ 2 } \left(\dfrac{ -\pi }{2}<x<\dfrac{\pi }{2 }\right) .$$
Find the area of the shaded region
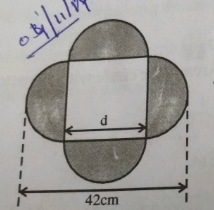
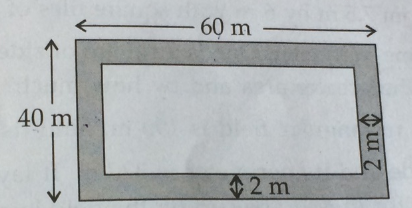
In the given figure, find the area of the path (shaded portion) which is $$2\ m$$ wide all round.
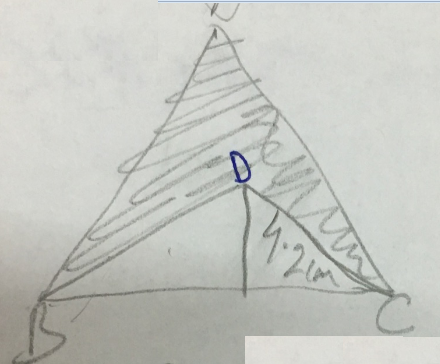
Area of $$\triangle ABC=68.2 sqm$$. Find the area of shaded region
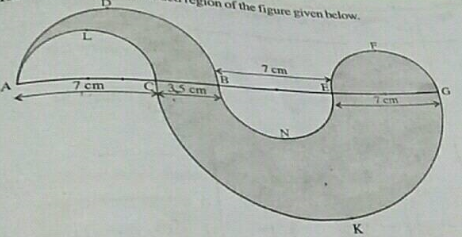
Find the area of the region bounded by the curves
$$x^{2}+y^{2}=16$$ and $$x^{2}=6y$$.
Find the area of shaded region of the figure given below.
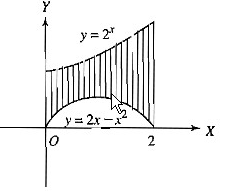
Compute the area of the figure bounded by the straight lines $$x=0, x=2$$ and the curves $$y=2^x$$ and $$y=2x-x^2$$.
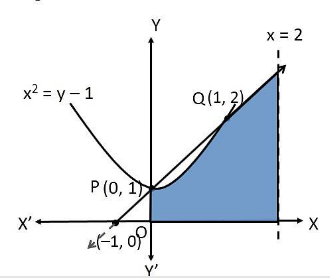
Using integration, find the area of the region bounded by the line. $$x - y + 2 = 0 ,$$ the curve $$x = \sqrt { y }$$ and $$y$$-axis.
Using integration, find the area of the region bounded by the line $$x + 2 = y ,$$ the curve $$x = \sqrt { y }$$ and $$y$$ -axis.
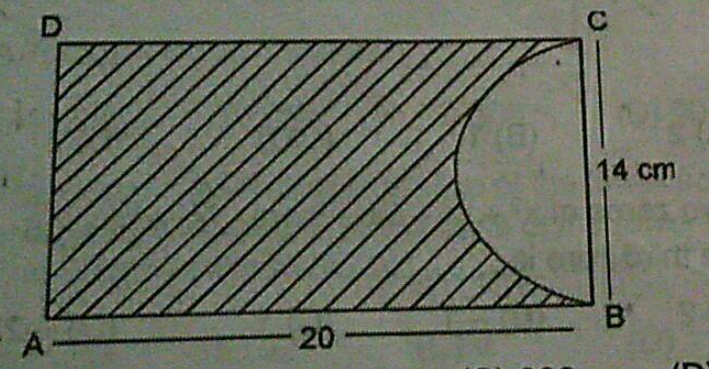
In the diagram $$\square A B C D$$ is the rectangular paper. If $$A B= 20 \mathrm { cm }$$ and $$B C = 14 \mathrm { cm }$$ then what is the area of the shaded region if the semicircle with diameter $$B C$$ is cut from the paper.
Find the area of the region enclosed by curves $$2x+y^2
=48$$ and $$x=y$$ .
$$AO=OB$$ perimeter $$=47 =cm$$
find the area of shaded region
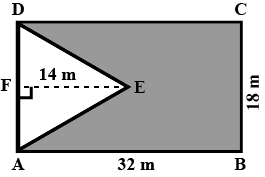
In Fig $$31$$ $$ABCD$$ is a rectangle with diameter $$32\ m$$ by $$18\ m$$. $$ADE$$ is a triangle such that $$EF \bot AD$$ and $$EF=14\ cm$$. Calculate the area of the shaded region.
Find the area bounded by line $$y=3x+2$$, x-axis and ordinates $$x=-1$$ and $$x=1$$.
Find the area bounded by $$y=x^2+x$$ from $$x=4$$ to $$x=6$$
Find the area of the region bounded by $$y^{2}=2x$$ and the line $$x-y=4$$
Form the differential equation of the family of curves represented by the equation(a being the parameter).$$(x-a)^2+2y^2=a^2$$.
In the figure, $$PQRS$$ is a square with side $$10 cm$$. The sectors drawn with P and R as centres from the shaded figure. Find the area of the shaded figure $$(\pi=3.14)$$
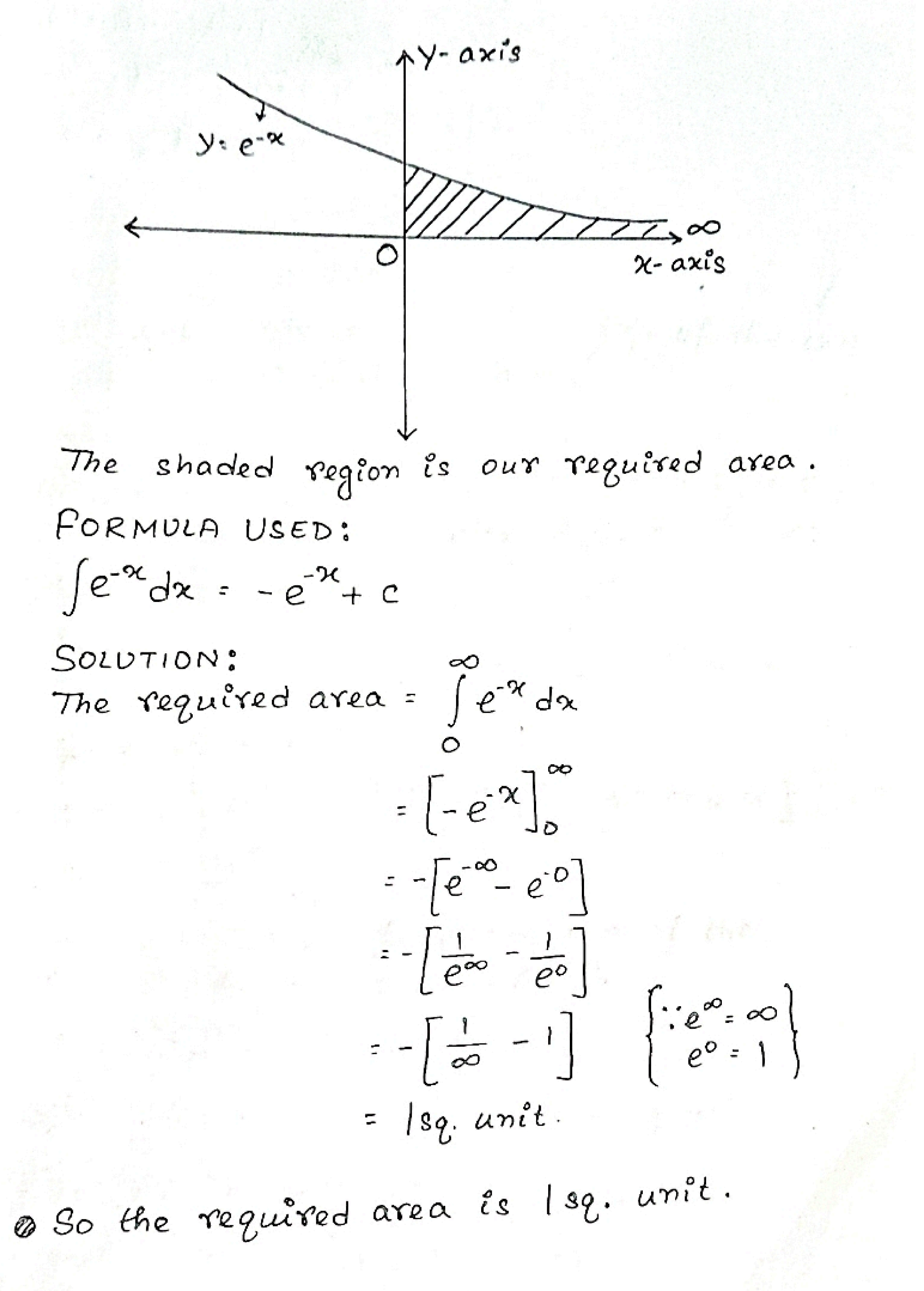
Find the area bounded by the curve y =$${ e }^{ -x }$$ the, X axis and the Y- axis
Find the area of region $$y=x^3-2x^2 $$ from $$x=6$$ to $$x=12$$
Find the area of region bounded.
$${ y }^{ 2 }=4x$$ and the line $$x=3$$
Find the area bounded by $$y=x^2+3$$ from $$x=3$$ to $$x=6$$
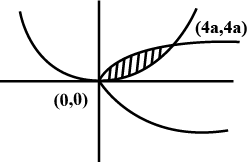
Find the area of the region bounded by the parabolas $$y^2=4x$$ and $$x^2=4y$$.
Find the area of the region bounded by the curve $$y=x^2, y=|2-x^2|$$ and $$y=2$$, whuch lies to the right of the line $$x=1$$
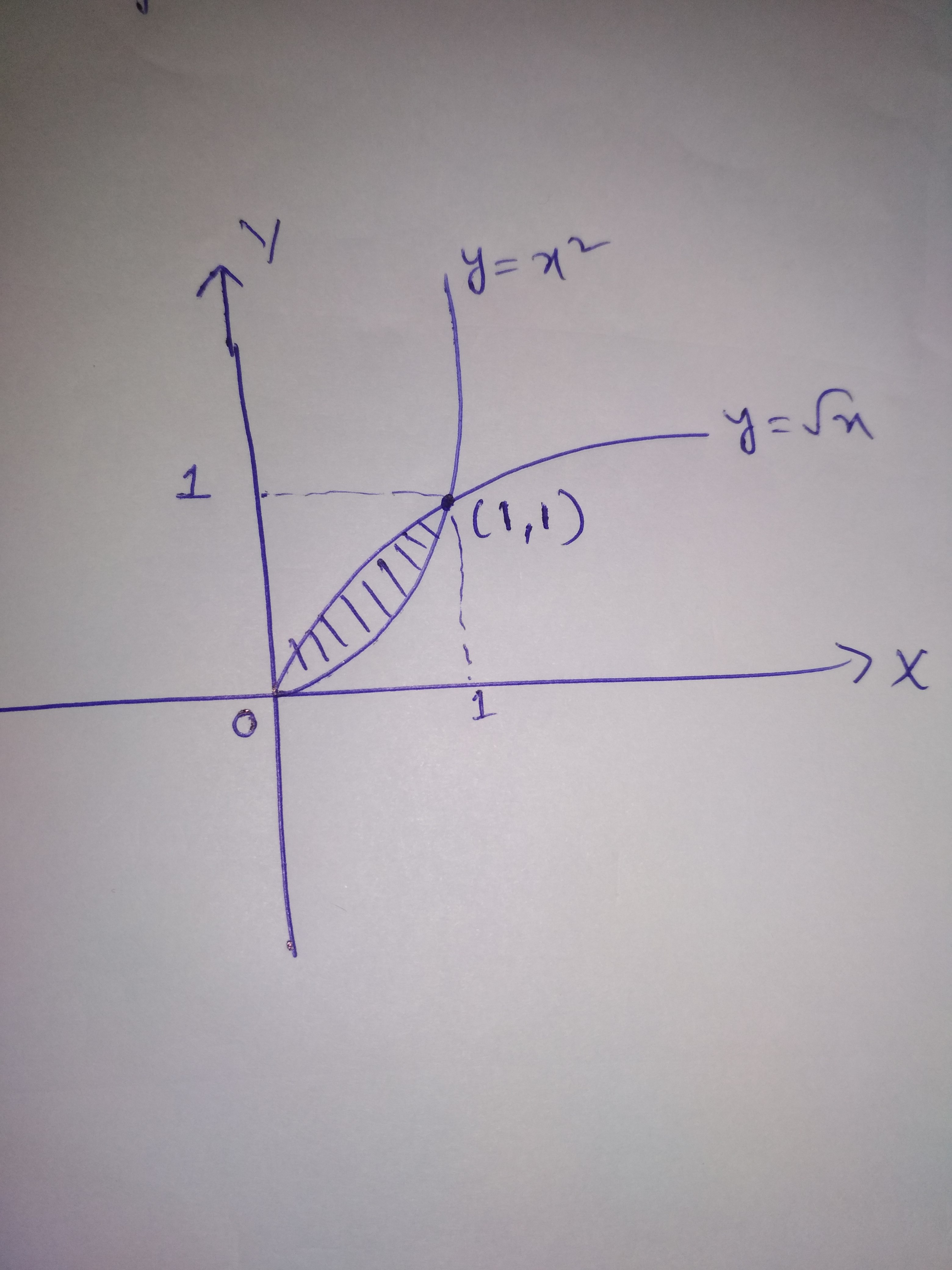
Find the area bounded between the curves $$y = x^2, y = \sqrt{x}$$.
Find the area of the region bounded by the curve $$x^{2}=4y$$ and the line $$x=4y-2$$.
Find the area of the region bounded by the parabola$$y = x^2$$ and $$y = |x|$$.
Find the area of region bounded by the triangle whose vertices are $$(-1, 1), (0, 5)$$ and $$(3, 2)$$, using integration.
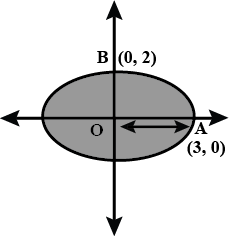
Find the area of the region bounded by ellipse $$\dfrac { { x }^{ 2 } }{ 4 } +\dfrac { { y }^{ 2 } }{ 9 } =1$$
Find the area of the region bounded by the curves $$y^{2} = 4x, x^{2} = 4y$$.
Find the area cut off from the parabola $$4y = 3x^{2}$$ with the line $$2y = 3x + 12$$.
Find the area bounded by the curve $$y=\cos x, x-$$ axis and the ordinates $$x=0$$ and $$x=2\pi$$.
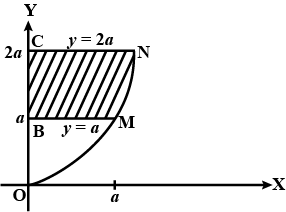
Find the area of the region bounded by the curve $$ay^{2}=x^{3}$$, the $$y$$-axis and the lines $$y=a$$ and $$y=2a$$.
Find the area bounded by the curve $$y=\cos, x-$$ axis and the ordinates $$x=0$$ and $$x=2\pi$$.
Find the area bounded by the ellipse $$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$$ and the ordinates $$x=0$$ and $$x=ae$$, where $$b^{2}=a^{2}(1-e^{2})$$ and $$e<1$$
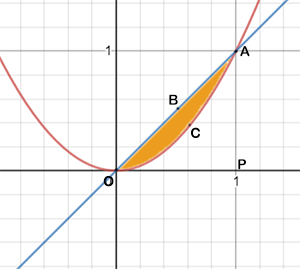
Find the area of the region bounded by the curve $$y=\sqrt{x}$$ and the line $$y=x$$.
Find the area of the region included between the parabola $$y^2=4x$$ and the circle $$x^2+y^2-8x=0$$, lying in the first quadrant.
Find the area of the region bounded by the parabola $$y^2=2x+1$$ and the line $$x-y=1$$.
Find the area of the region bounded by the parabola $$y^2=4x$$, the x-axis, and the lines $$x=1$$ and $$x=4$$.
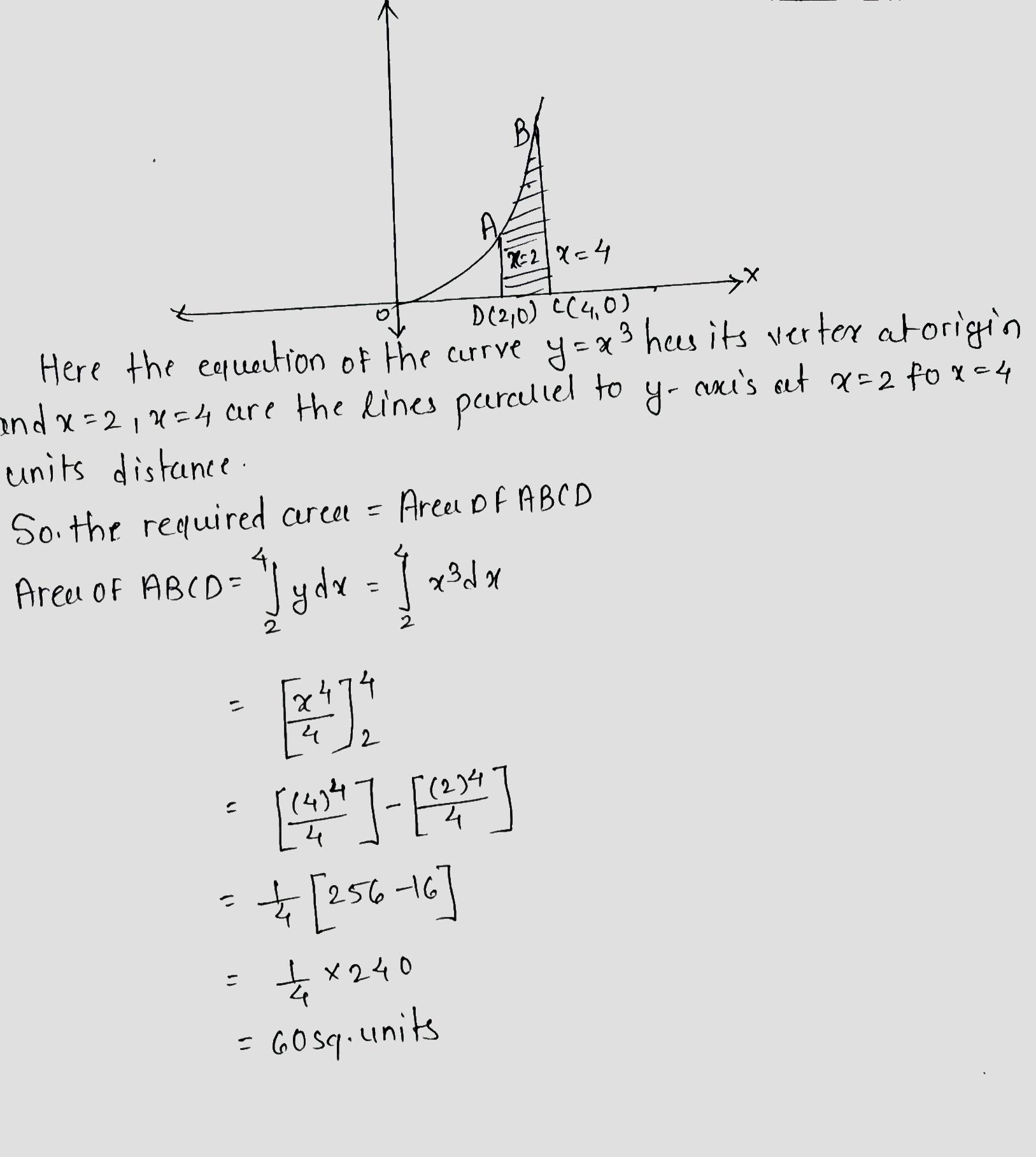
Determine the area enclosed by the curve $$y=x^3$$, and the lines $$y=0, x=2$$ and $$x=4$$.
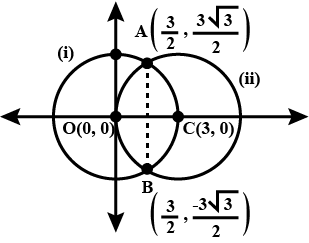
Using integration find the area of the region bounded between the two circles $$x^2 + y^2 = 9$$ and $$(x - 3)^2 + y^2 = 9$$
Find the area of the region $$\{(x, y):x^2\leq y\leq x\}$$.
Determine the area under the curve $$y=\sqrt{a^2-x^2}$$, included between the lines $$x=0$$ and $$x=a$$.
Find the area bounded by the curve $$y=(4-x^2)$$, the y-axis and the lines $$y=0, y=3$$.
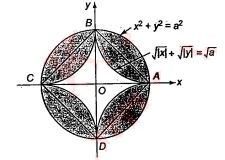
a. Sketch and find the area bounded by the curve $$\sqrt {|x|}\,+\sqrt{|y|}\,=\sqrt{a}$$ and $$ x^2+y^2=a^2$$ (where $$a>0$$).
b. If curve $$|x|+|y|=a$$ divides the area in two parts, then fiind their ratio in the first quadrant only.
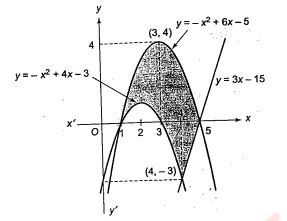
Find the area bounded by the curves $$y=-x^2+6x-5,\, y=-x^2+4x-3$$ and the straight line $$ y=3x-15$$ and lying right to $$x=1$$.
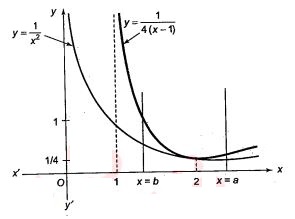
Find the value of $$a$$ where $$(a>2)$$ for which the reciprocal of the area enclosed between $$y=\dfrac{1}{x^2}\,;\, y+\dfrac{1}{4(x-1)}\,;\, x=2$$ and $$x=a$$ is $$a$$ itself and for what value of $$b \in (1,2),$$ the area of the figure bounded by the lines $$x=b$$ and $$x=2$$ is $$1-\dfrac{1}{b}$$.
If the area bounded by $$y=x^2+2x-3$$ and the line $$y=kx+1$$ is the least, find $$k$$ and also the least area.
Find the area of that part of the circle $$x^2 + y^2= 16$$, which is exterior to the parabola $$y^2= 6\,x$$.
Find the area of the region included between the parabolas $$y^2 = 4\,ax$$ and $$x^2 = 4\,ay$$, where $$a > 0$$.
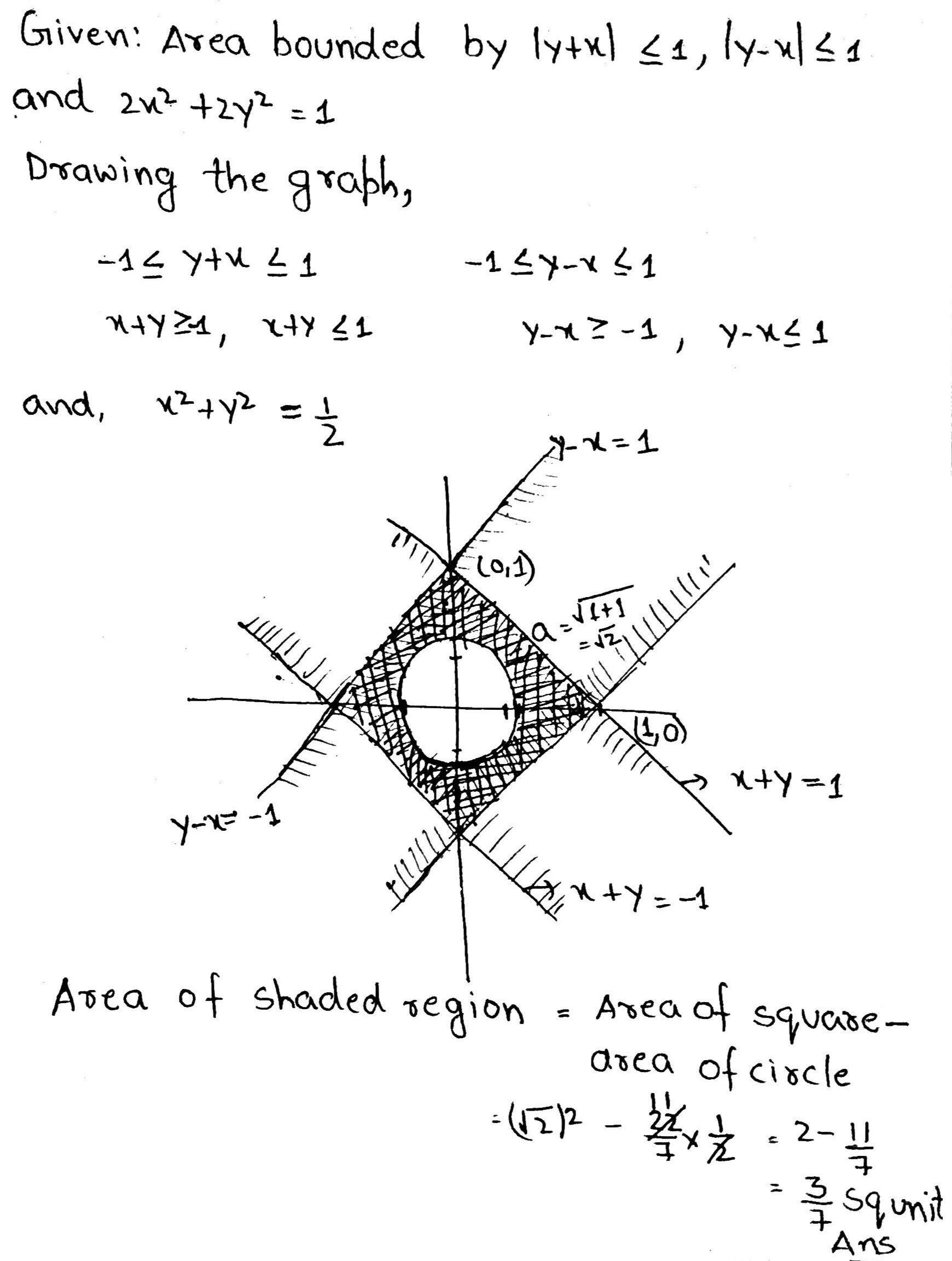
Sketch the region and find the area bounded by the curves $$ \mid y+ x \mid \leq 1, \ \mid y-x \mid \leq 1$$ and $$2x^2 +2y^2 =1$$.
The value of $$c+2$$ for which the area of the figure bounded by the curve $$y=8x^2 - x^5$$; the straight lines $$x=1$$ and $$x=c$$ and $$X-$$axis is equal to $$\dfrac{16}{3}$$, is...........
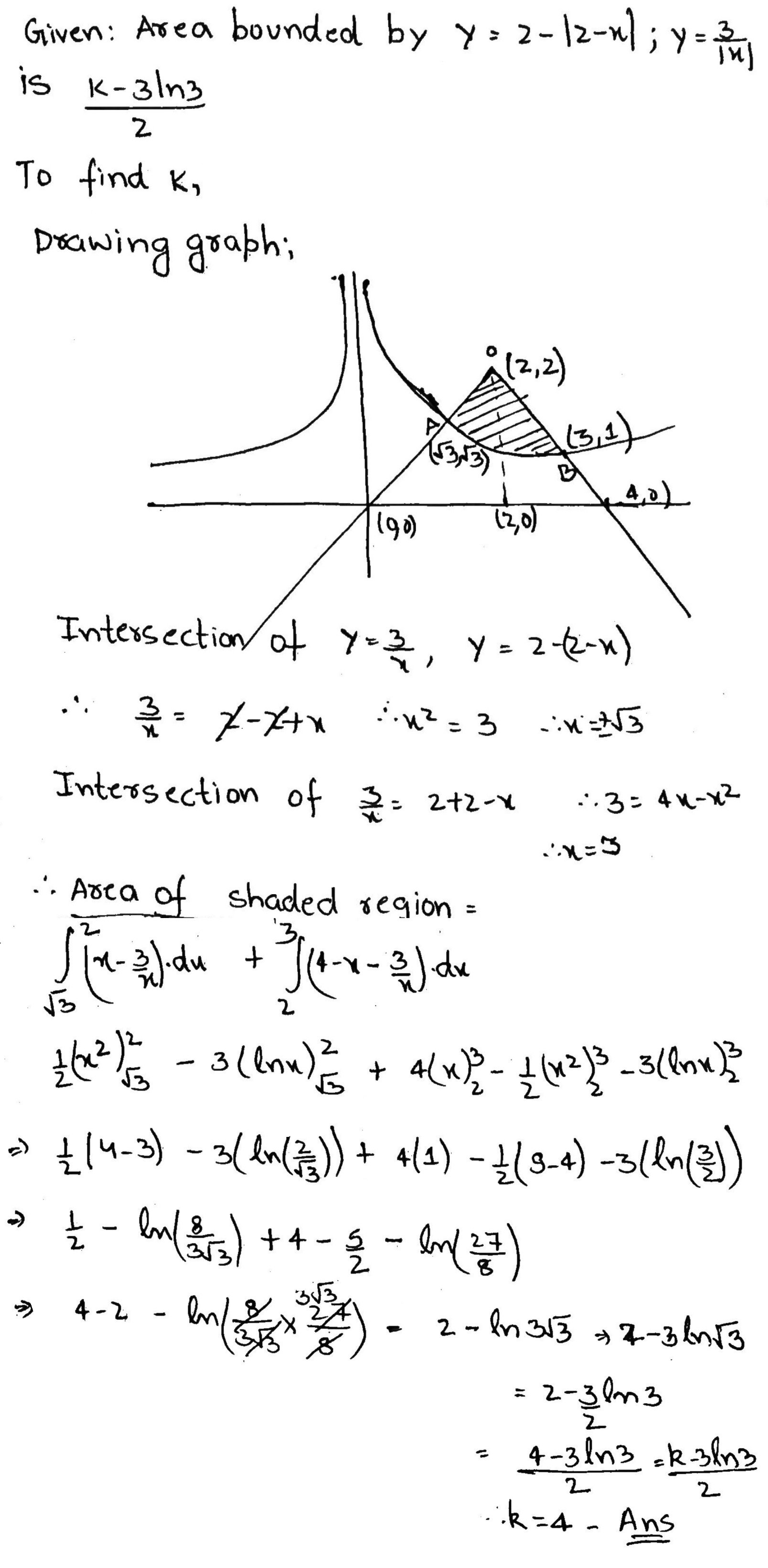
The area bounded by $$y=2- \mid 2-x \mid; \ y= \dfrac{3}{\mid x \mid}$$ is $$\dfrac{k-3 \ ln\ 3}{2},$$ then $$k$$ is equal to........
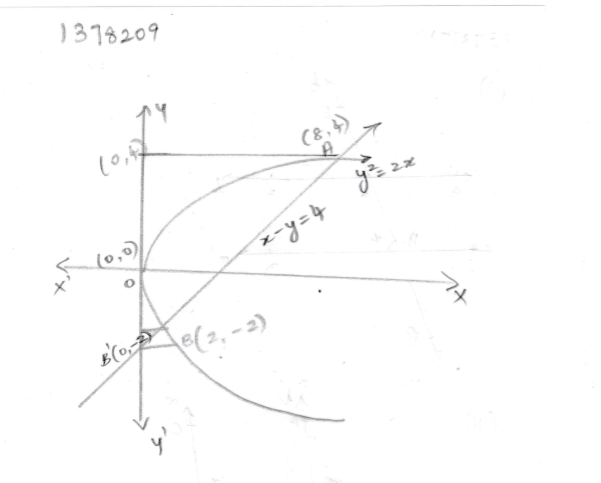
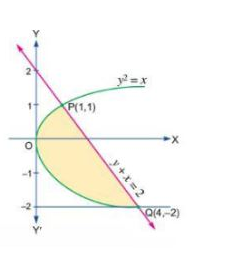
Find the area enclosed by the parabola $$y^2 = x$$ and line $$y+ x = 2$$.
A point $$P$$ moves in $$XY-$$plane in such a way that $$[ \mid x \mid ] + [ \mid y \mid ]=1,$$ where $$[.]$$ denotes the greatest integer function. Area of the region representing all possible of the point $$P$$ is equal to..............
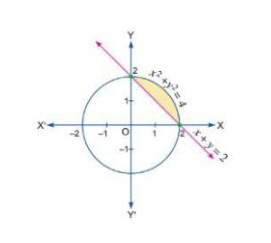
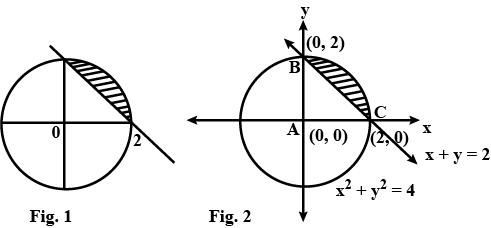
Find the area of the region $${(x, y): x^2 +y^2 \leq 4, x + y \geq 2}$$.
Let $$C$$ be a curve passing through $$M(2,2)$$ such that the slope of the tangent at any point to the curve is reciprocal of the ordinate of the point. If the area bounded by curve $$C$$ and line $$x=2$$ is $$A$$, then find the value of $$\dfrac{3A}{2}$$
Find the area enclosed by the curve $$C:y=x\sqrt{9-x^2}(x\ge 0)$$ and the x-axis.
If the area bounded by the curve $$y=x^2+1$$ and the tangents to it drawn from the origin is $$A$$, then find the value of $$3A$$.
Find the area of the region $$\left \{ (x, y): x^2 + y^2 \leq16, y^2\leq6x\right\} $$
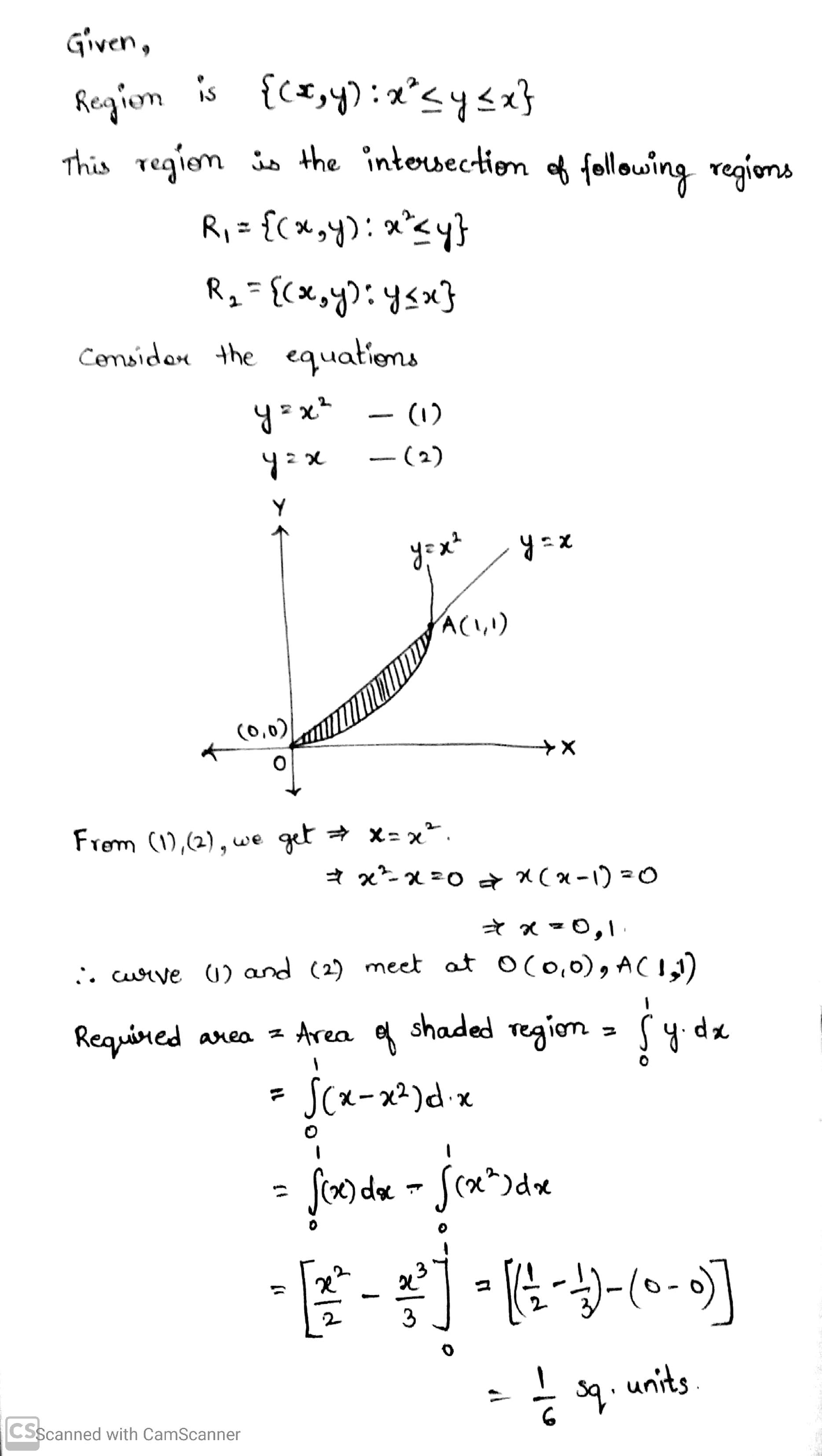
Find the area of the region $$ \left \{ (x, y): x^2 \leq y \leq x \right \}$$
Using integration, find the area of the region $$\{(x, y) : 9x^2 + y^2 \leq 36 $$ and $$3x + y \geq 6\}$$.
Find the area of the region $$\left \{ (x, y): x^2 + y^2 \leq 1 \leq x + y \right \} $$
In what ratio does the x-axis divide the area of the region bounded by the parabolas $$y = 4x - x^2$$ and $$y = x^2 - x$$?
Find all the possible values of $$b > 0$$, so that the area of the bounded region enclosed between the parabolas $$y = x - bx^2 $$ and $$y = \dfrac{x^2}{b}$$ is maximum.
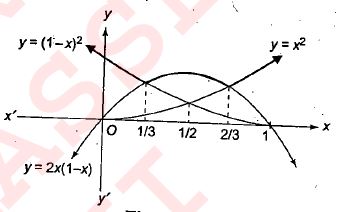
Let $$f(x) =$$ Maximum $$\{x^2, (1 - x)^2 , 2x(1 - x)\}$$, where $$0 \le x \le 1$$. Determine the area of the region bounded by the curves $$y = f(x)$$, x - axis , $$x = 0$$ and $$x = 1$$.
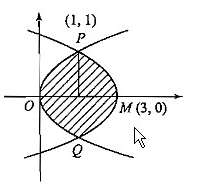
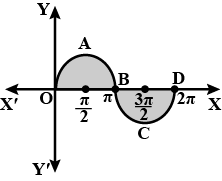
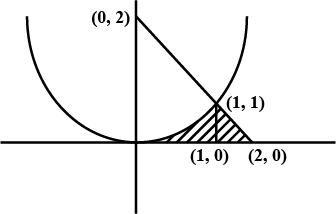
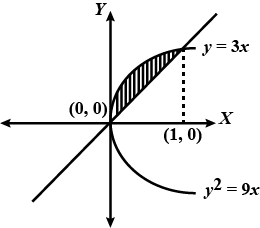
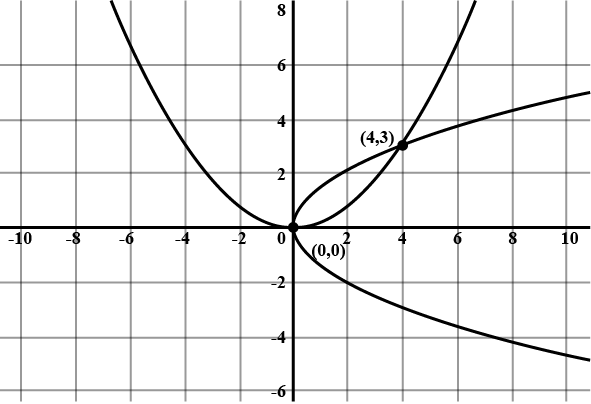
Find the area bounded by the curve $$x^2 = y, x^2 = -y$$ and $$y^2 = 4x -3$$.
Compute the area of the region bounded by the curves $$y = ex \log_ex$$ and $$y = \dfrac{\log x}{ex}$$
Let $$f(x)$$ be a continuous function given by $$f(x) = \begin{Bmatrix} 2x, & |x| \le 1 \\ x^2 + ax + b, & |x| > 1 \end{Bmatrix}$$. Find the area of the region in the third quadrant bounded by the curves $$x = -2y^2$$ and $$y = f(x)$$ lying on the left of the line $$8x + 1 = 0$$.
Sketch the curves and identify the region bounded by $$x = \dfrac{1}{2}, x = 2 , y = \ln x$$ and $$y = 2^x$$. Find the area of this region.
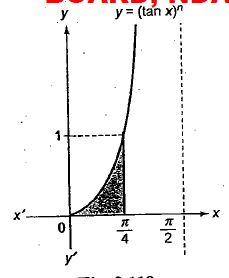
Let $$A_n$$ be the area bounded by the curve $$y = (\tan x)^n$$ and the lines $$x = 0 , y = 0$$ and $$x = \dfrac{\pi}{4}$$. Prove that for $$n > 2 , A_n + A_{n - 2} = \dfrac{1}{n - 1}$$ and deduce $$\dfrac{1}{2n + 2} < A_n < \dfrac{1}{2n - 2}$$.
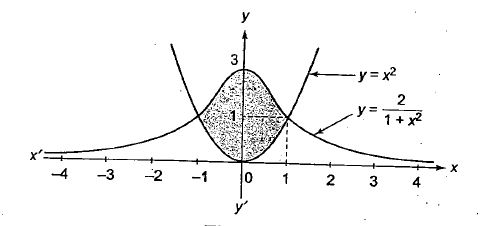
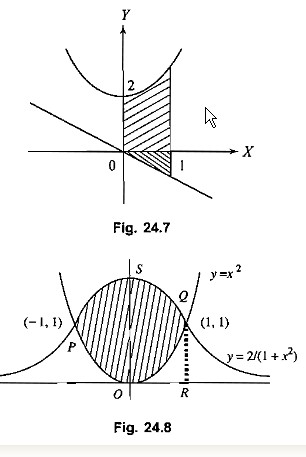
Sketch the region bounded by the curves $$y = x^2$$ and $$y = \dfrac{2}{1 + x^2}$$. Find the area.
Find the area of the region bounded by the parabola $$y^{2} = 2px, x^{2} = 2py$$.
Find the area of the curve $$y = \sin x$$ between $$0$$ and $$\pi$$.
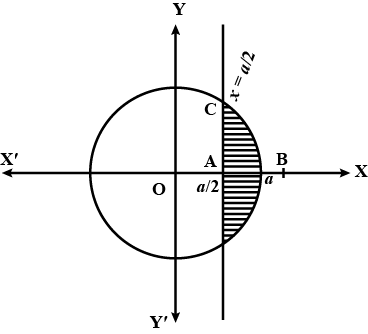
Find the area of minor segment of the circle $$x^{2} + y^{2} = a^{2}$$ cut off by the line $$x = \dfrac {a}{2}$$.
Fill in the blanks in each of the Examples:
The area of the region bounded by the curve $$x = y^{2}, y-axis$$ and the line $$y = 3$$ and $$y = 4$$ is ______.
Fill in the blanks in each of the Examples:
The area of the region bounded by the curve $$y = x^{2} + x, x - axis$$ and the line $$x = 2$$ and $$x = 5$$ is equal to ______.
Find the area of the region bounded by the curves $$y^{2} = 9x, y = 3x$$.
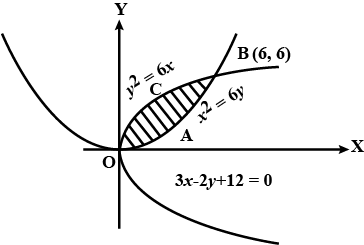
Find the area of region bounded by the parabolas $$y^{2} = 6x$$ and $$x^{2} = 6y$$.
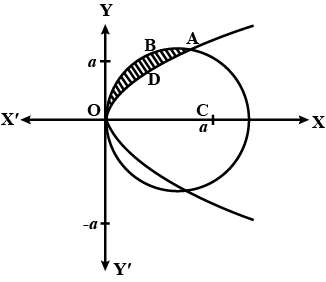
Find the area of the region above the x-axis, included between the parabola $$y^{2} = ax$$ and the circle $$x^{2} + y^{2} = 2ax$$.
Find the area enclosed by the curve $$y = -x^{2}$$ and the straight line $$x + y + 2 = 0$$.
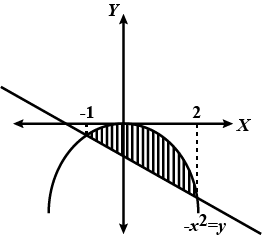
Draw a rough sketch of the curve $$y = \sqrt {x -1}$$ in the interval $$[1, 5]$$. Find the area under the curve and between the lines $$x = 1$$ and $$x = 5$$.
Find the area of the region included between $$y^{2} = 9x$$ and $$y = x$$.
Find the area of the region bounded by the curve $$y^{2} = 2x$$ and $$x^{2} + y^{2} = 4x$$.
Sketch the region $$\left \{(x, 0) : y = \sqrt {4 - x^{2}}\right \}$$ and x-axis. Find the area of the region using integration.
Determine the area under the curve $$y = \sqrt {a^{2} - x^{2}}$$ included between the lines $$x = 0$$ and $$x = a$$.
Find the area of the region bounded by $$y = \sqrt {x}$$ and $$y = x$$.
Draw a rough sketch of the region $$\left \{(x, y) : y^{2} \leq 6ax\ and\ x^{2} + y^{2} \leq 16a^{2}\right \}$$. Also, find the area of the region sketched using method of integration.
Draw a rough sketch of the given curve $$y = 1 + |x + 1|, x = -3, y = 0$$ and find the area of the region bounded by them, using integration.
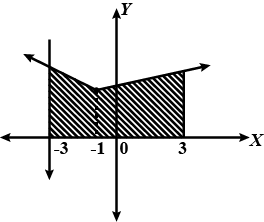
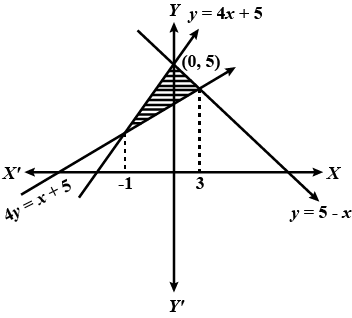
Find the area bounded by the lines $$y = 4x + 5, y = 5 - x$$ and $$4y = x + 5$$.
Find the area between the curve $$y=\sin x $$ and $$y=\cos x$$ and the lines $$x=0$$ and $$x=\pi$$
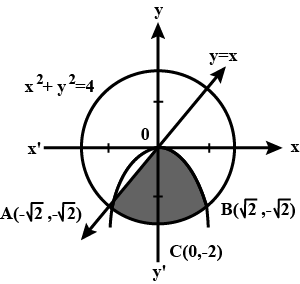
Find the area of the region $${(x,y):x^2+y^2=4,x+y\ge 2}$$
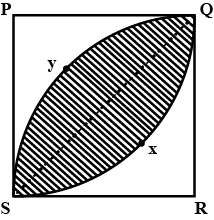
Prove that the curves $$y^2 = 4x $$ and $$x^2 = 4y$$ divide the area of square bounded by $$x = 0, x = 4, y = 4$$ and $$y = 0$$ into three equal parts.
If the area of the region bounded by point (x, y) satisfying the condition $$\left \{ (x,y);0 \leq y \leq x^2 + 1,0 \leq y \leq x + 1,x = 0,x = 2,y = 0 \right \}\: is\: A (unit)^2 \: then\: \left [ \frac{23}{A} \right ]\: equals\: to$$
Consider two curves $$C_{1} : y=\dfrac{1}{x}$$ and $$C_{2} : y=lnx$$ on the $$xy$$ plane. Let $$D_{1}$$ denotes the region surrounded by $$C_{1}, C_{2}$$ and the line $$x = 1$$ and $$D_{2}$$ denotes the region surrounded by $$C_{1}, C_{2}$$ and the line $$x = a.$$ If $$D_{1}=D_{2},$$ then the sum of logarithm of possible values of $$a$$ is:
If the x-axis divide the area of the region bounded by the parabolas $$ y = 4x - x^{2} $$ and $$ y = x^{2} - x $$ in the ratio of $$ a : b $$ then $$ ab $$ is equal to
If $$A$$ is the area of the figure bounded by the straight lines $$ x =0$$ and $$ x=2,$$ and the curves $$ y=2 ^{x}$$ and $$ y=2x-x^{2}$$ then the value of $$\displaystyle 672 \left( \dfrac{3}{\log 2}-A\right) $$ is
The area bounded by curves
The area of the region bounded by the curves $$y=\left| x-1 \right| $$ and $$y=3-\left| x \right| $$ in square units is
Using integration, prove that the curves $$y^2=4x$$ and $$x^2=4y$$ divide the area of the square bounded by $$x=0, x=4, y=0$$ and $$y=4$$ into three equal parts.
Find the area of the region bound by the curves $$y=6x-{x}^{2}$$ and $$y={x}^{2}-2x$$.
Find the area of the region common to be circle $$x^{2} + y^{2} = 9$$ and the parabola $$y^{2} = 8x$$.
Find the common area (in sq. units) enclosed by the parabolas $$4{y}^{2}=9x$$ and $$3{x}^{2}=16y$$.
Let $$f(x)=\max \left \{sin x , cos x, \dfrac{1}{2}\right\}$$ then determine the area of region bounded by curves y=f(x),x-axis,y-axis and $$ x=2\pi$$
Find the area enclosed between the curves $$\displaystyle y=\log _{ e }{ \left( x+e \right) }, x=\log _{ e }{ \left( \dfrac { 1 }{ y } \right) }$$ and $$x-axis$$
Make a rough sketch of the graph of y=$$sin^2x$$,0<x<x/2 then find the area
enclosed between the curve,x axis and the line
The area of the region bounded by $$y= x-[x] , y= [x], x\epsilon[ 0,2]$$ is $$\dfrac{1}{m}$$.Find the value of $$m$$
On the coordinates plane XOY hatch a set of points whose coordinates satisfy the following inequalities in two variables x and y (show the boundary belonging to the set by a solid line and that not belonging to the set by a dash line).
$$| y| + 2 |x| \leqslant x^2 + 1$$
Find the area bounded by the parabola $${y}^{2}=5x$$ and the line $$y=x$$.
Given a square and, a circle of the same area. What is larger, the length of the circle or. the perimeter of the square?
Find the area between the region of parabola $${y}^{2}=2x$$ and circle $${x}^{2}+{y}^{2}=8$$.
Area common to the curve $$y = \sqrt{9 - x^2}$$ and $$x^{2} + y^{2} = 6x$$ is $$\dfrac{9\sqrt{3}}{2}+n\pi$$. Find $$n$$
Draw the graph of the linear equations $$4x-3y+4=0$$ and $$4x+3y-20=0$$. Find the area bounded by these lines and x-axis.
Find the area (sq.units) bounded by $$y = {\sin ^{ - 1}}x$$ and $$y={\cos ^{ - 1}}x$$ and x-axis.
(Find answer correct upto two decimal places)
The area of the region described by $$A=\{(x, y): x^2+y^2\leq 1$$ and $$y^2\leq 1-x\}$$ is-
Find the area of the region bounded by the curve $${(y - 1)^2} = 4(x + 1)$$ and the line $$y = x - 1$$.
Find the area of the region $$\left\{ \left( x,y \right) :0\le y\le { x }^{ 2 }+1,0\le y\le x+1,0\le x\le 2 \right\} $$.
Using integration find the area of the following region $$(x, y):|x+2|\leq y\leq \sqrt{20-x^2}$$.
Find the area bounded by curves $$(x-1)^{2}+y^{2}=1$$ and $$x^{2}+y^{2}=1$$
The area (in square units) bounded by the curves $$y = \sqrt {x} $$, $$ 2y - x + 3 = 0$$, and lying in the first quadrant is
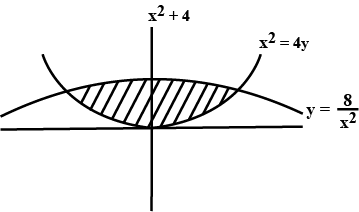
Find the area of the figure contained between the parabola $$x^{2}=4y$$ and the curve $$y=\dfrac{8}{x^{2}+4}$$
Find the area bounded by curves $${\left( {x - 1} \right)^2} + {y^2} = 1$$ and $${x^2} + {y^2} = 1$$
Find the area of the region in the first quadrant enclosed by x-axis, the line $$x=\sqrt{3} y$$ and the circle $$x^2+y^2=4$$
Find the area of the region bounded by the following curves, the $$X-$$axis and the given lines.A
$$y=\sqrt {16x+x^{2}}, x=0, x=4$$
ARB represents a semicircular plate where AB = 14 cm. A semicircle ASO is cut away. (O is the mid-point pf AB). What is the area of the remaining portion ? (Take $$\pi =\dfrac { 22 }{ 7 }).$$
Draw the graph of $$2x+y=6$$ and $$2x-y+2=0$$. Shade the region bounded by these lines and $$x-y$$. Find the area of the shaded region.
Find the area of the shaded region in fig:- if $$ABCD$$ is a square of side $$14\ cm$$ and $$APD \times BPC$$ are semi circles.
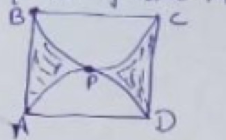
Find the common area enclosed by the parabolas $$y^{2}=x$$ and $$x^{2}=y$$
Find the area bounded by the curve $$y= { e }^{ -x }$$, the X-axis and the Y-axis.
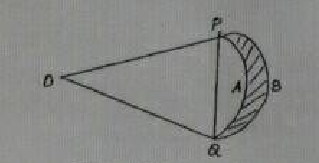
Adjoining figure two arcs $$PAQ$$ and $$PBQ$$ is a part of a circle with center $$O$$ and radius $$OP$$ while arcs $$PBQ$$ is a semicircle drawn on $$PQ$$ as diameter, If $$OP=PQ=10\ cm$$. Show that the area of the shaded region is $$25\left( \sqrt {3}-\dfrac {\pi}{6}\right)cm^ {2}$$
To find the area of the region bounded by the line, y=2 x+3, the x-axis and the lines y=2 and x=5.
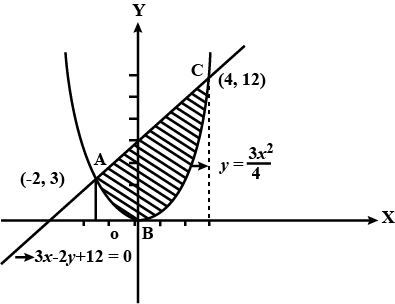
Using intergration find the area of the region included between the parabola $$4y={ 3x }^{ 2 }$$ and the line 3x=2y+12=0.
Draw a rough sketch of the region $$ \left\{ ( x , y ) : y ^ { 2 } \leq 3 x , 3 x ^ { 2 } + 3 y ^ { 2 } \leq 16 \right\} $$ and find the area enclosed by the region, using the method of integration.
Sketch the graph of $$y=\sqrt{x}+1$$ in $$[0,4]$$ and determine the area of the region enclosed by the curve, the axis of $$X$$ and the lines $$x=0, \ x=4$$.
Find a continuous function $$'f'$$, where $$(x^4-4x^2)\leq f(x)\leq (2x^2-x^3)$$ such that the area bounded by $$y=f(x),\,y+x^4-4x^2,$$ the $$y-axis$$ and the line $$x=t$$, where $$(0\leq t\leq 2)$$ is $$k$$ times the area bounded by $$y=f(x),\,y=2x^2-x^3,\,y-axis$$ and the line $$x=t$$ (where $$0\leq t\leq 2$$).
Find the area of the region bounded by the curve $$(y-1)^2=4(x+1)$$ and the line $$y=x-1$$.
If the area enclosed by the curves $$f (x)=con^{-1}(cosx) \,\,and\, \, g(x)={ sin }^{ -1 }\left( cosx \right)\, in\, x\in \left[ \dfrac { 9\pi }{ 4 } ,\dfrac { 15\pi }{ 4 } \right]\,is\,a\pi^2/b$$ (where a and b are coprime), then the value of (a - b) is
Consider $$f(x) = x^2 - 3x +2$$. The area bounded by $$\mid y \mid = f( \mid x \mid), \ x \geq 1$$ is $$A$$, then find the value of $$3A+2$$.
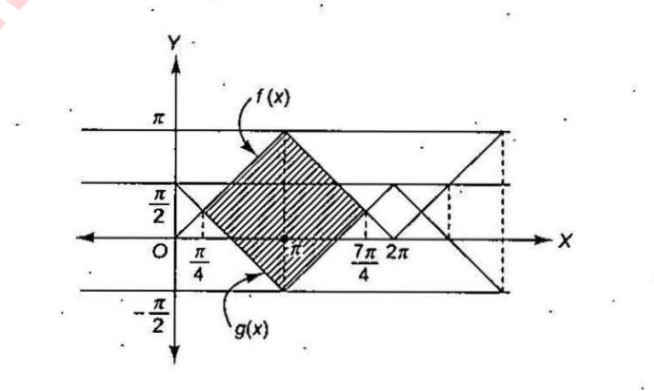
Let $$ f:[0,1] \rightarrow \bigg[ 0, \dfrac{1}{2} \bigg] $$ be a function such that $$f(x)$$ is a polynomial of $$2nd$$ degree, satisfy the following condition :
(a) $$f(0) =0$$
(b) has a maximum value of $$\dfrac{1}{2}$$ at $$x=1$$.
If $$A$$ is the area bounded by $$y= f(x); \ y=f^{-1}(x)$$ and the line $$2x +2y-3=0$$ in $$1st$$ quadrant, then the value of $$24A$$ is equal to .............
Let $$f(x) = minimum \{ e^x , \ \dfrac{3}{2}, \ 1+e^{-x} \}, \ 0 \leq x \leq 1$$. Find the area bounded by $$y=f(x), \ X-$$axis, $$Y-$$axis and the line $$x=1$$
Match the statements of List 1 with values of List 2.
Let $$f(x)=min \bigg\{ sin^{-1} x, \ cos^{-1} x, \ \dfrac{\pi}{6} \bigg\}, \ x \epsilon [0,1]$$. If area bounded by $$y=f(x)$$ and $$X-$$axis, between the lines $$x=0$$ and $$x=1$$ is $$\dfrac{a-x}{b(\sqrt{3} +1)}$$. Then, $$(a-b)$$ is...........
Find the area of curve enclosed by :
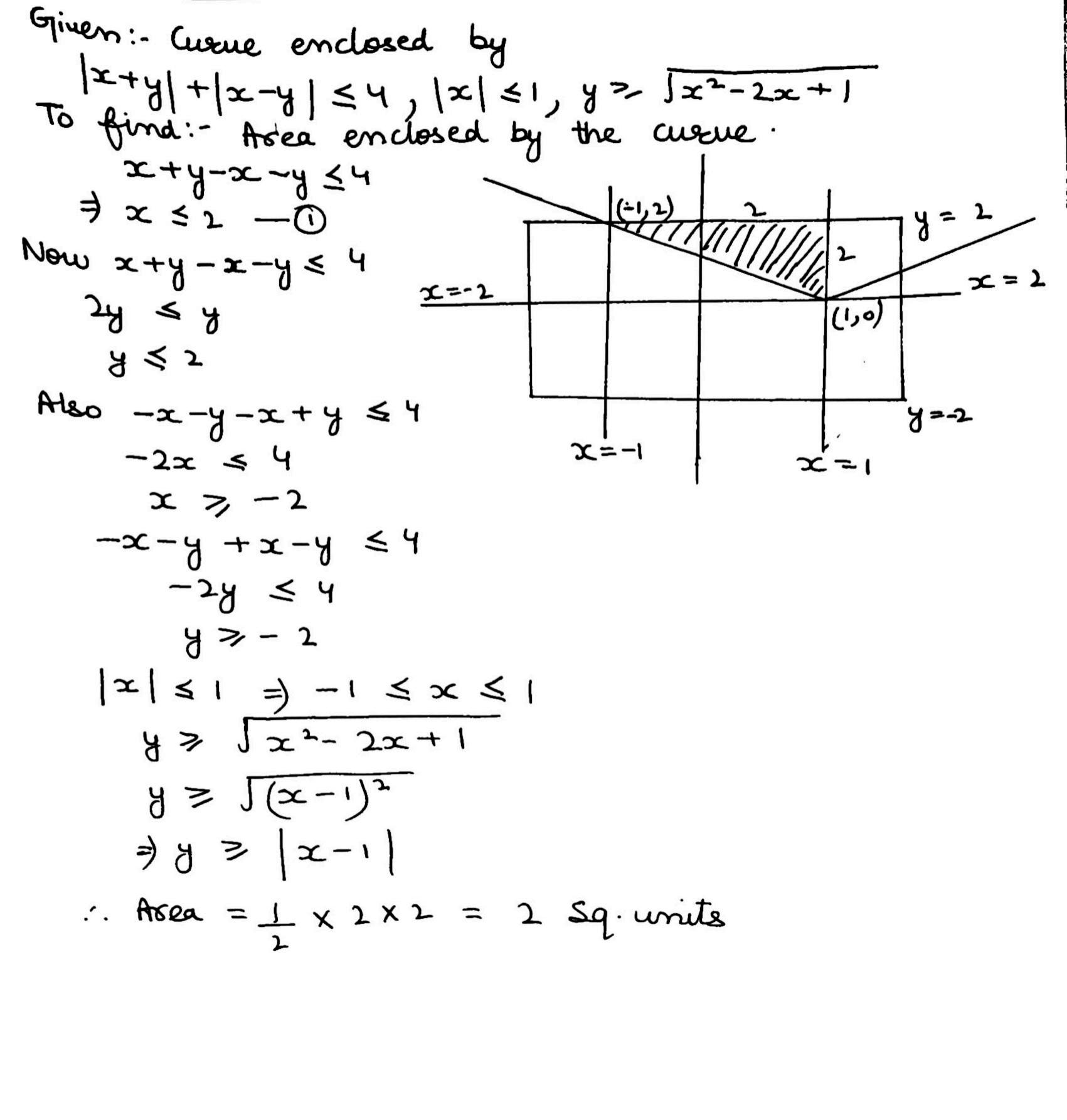
$$ \mid x+ y \mid + \mid x-y \mid \leq 4, \ \mid x \mid \leq 1, \ y \geq \sqrt{x^2 -2x +1} $$.
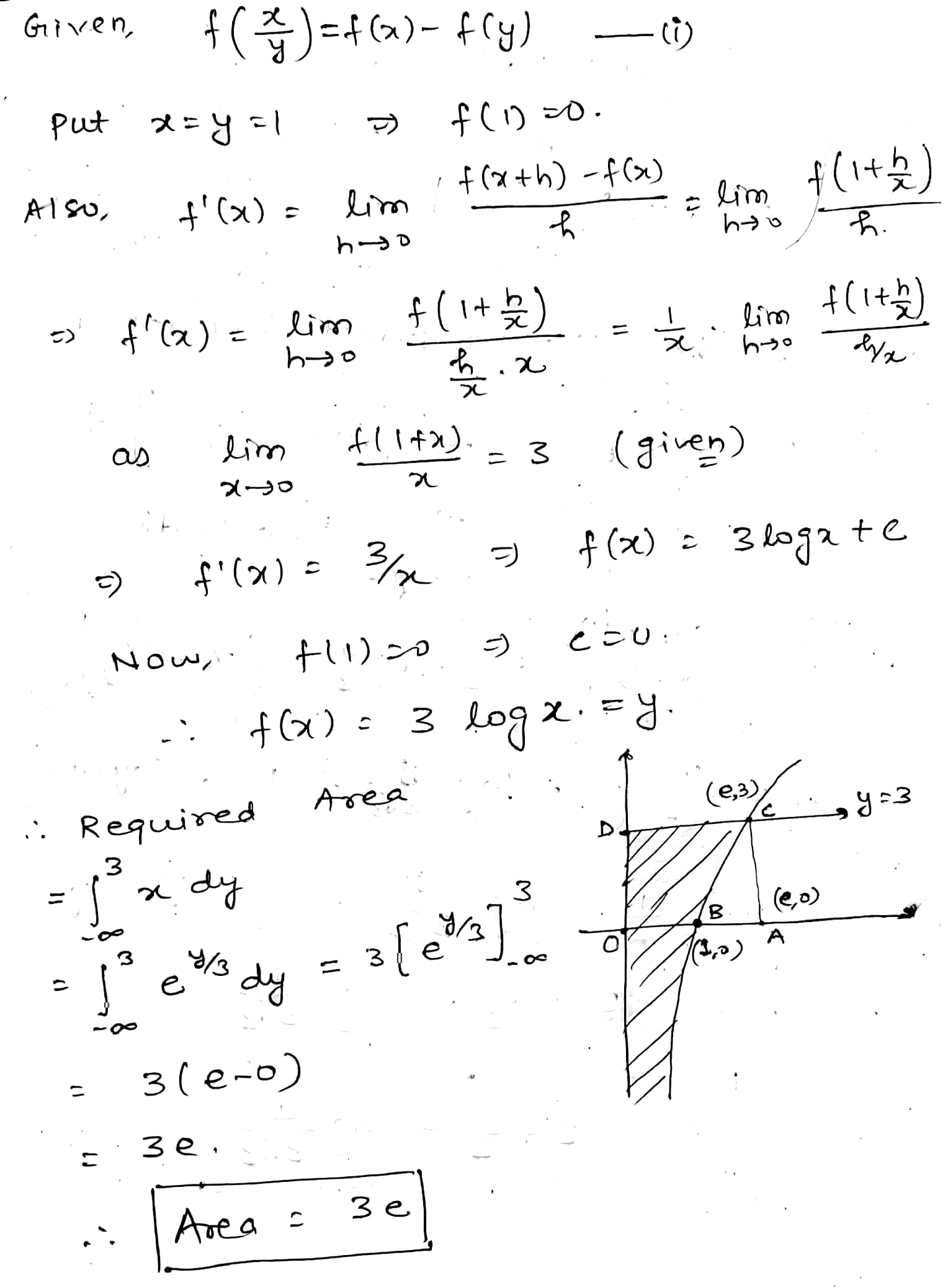
Let $$f$$ be a real valued function satisfying $$f \bigg( \dfrac{x}{y} \bigg) = f(x) -f(y)$$ and $$\underset{x \rightarrow 0}{lim} \ \dfrac{f(1+x)}{x} =3$$. Find the area bounded by the curve $$y=f(x)$$, the $$Y-$$axis and the line $$y=3$$, where $$x, \ y \epsilon R^+$$.
If the area enclosed by the curve $$y=\sqrt{x}$$ and $$x=-\sqrt{y}$$, the circle $$x^2+y^2=2$$ above the x-axis, is A then the value of $$\dfrac{16}{\pi}A$$ is
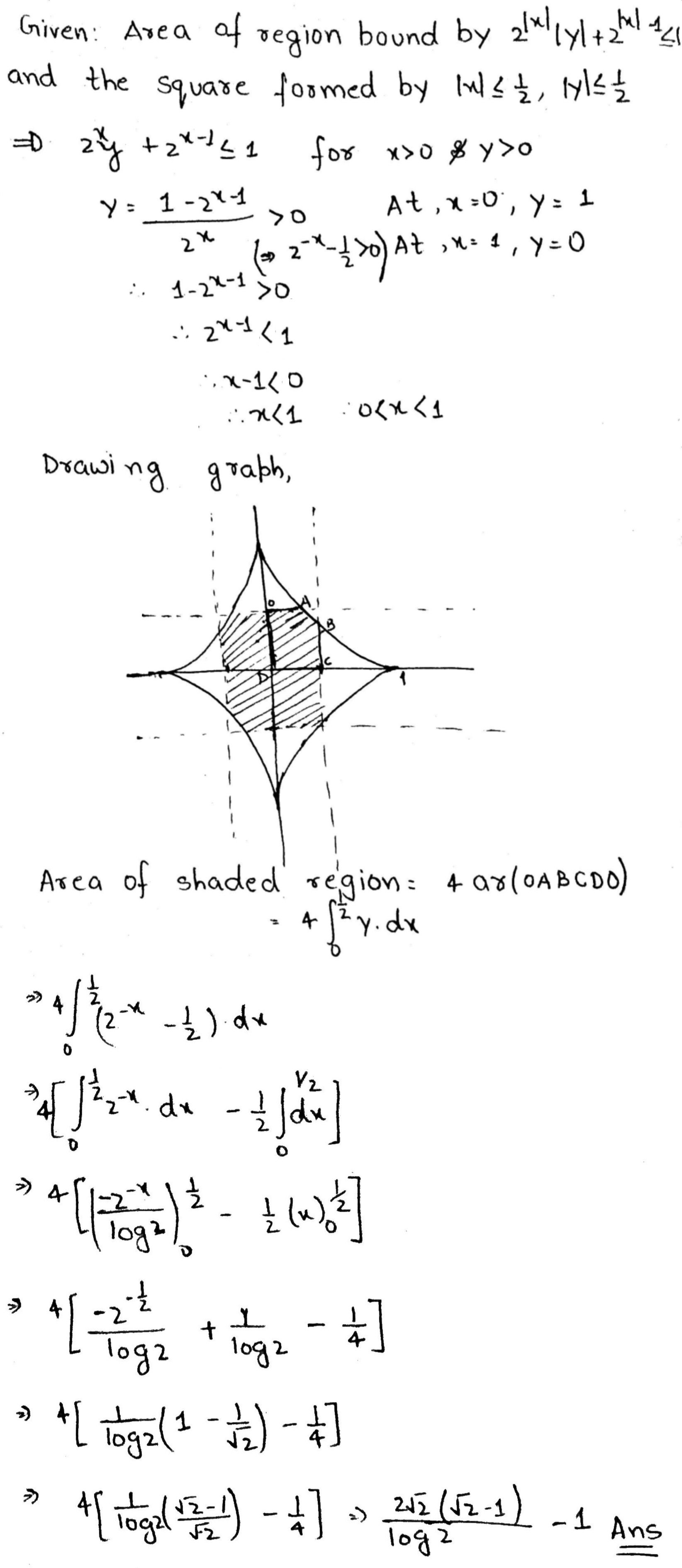
Find the area of the region bounded by the curve, $$2^{\mid x \mid} \mid y \mid + 2^{\mid x \mid -1} \leq 1$$, with in the square formed by the lines $$\mid x \mid \leq \dfrac{1}{2}, \ \mid y \mid \leq \dfrac{1}{2}$$
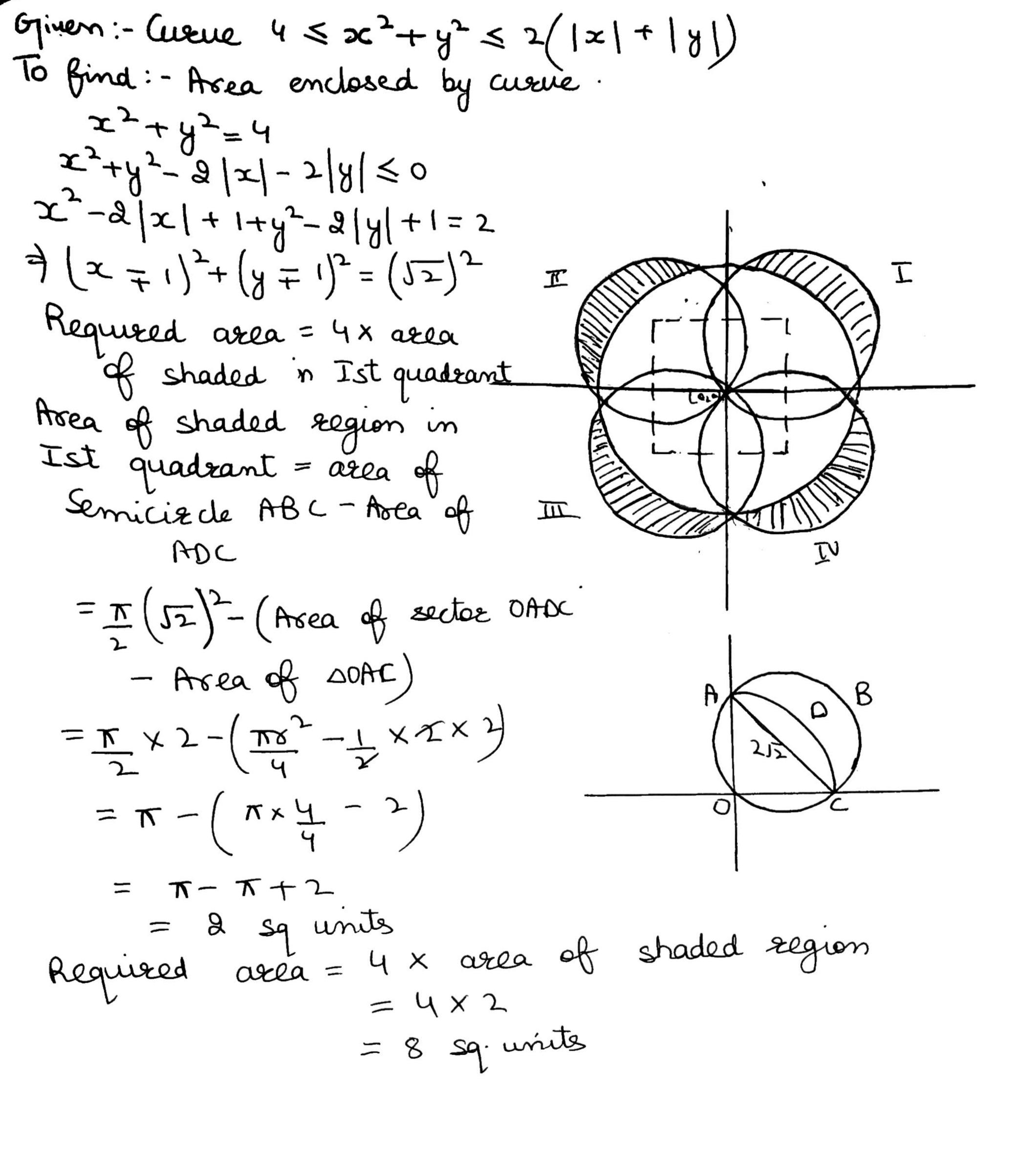
Calculate the area enclosed by the curve
$$ 4 \leq x^2+y^2 \leq 2(\mid x \mid + \mid y \mid) $$.
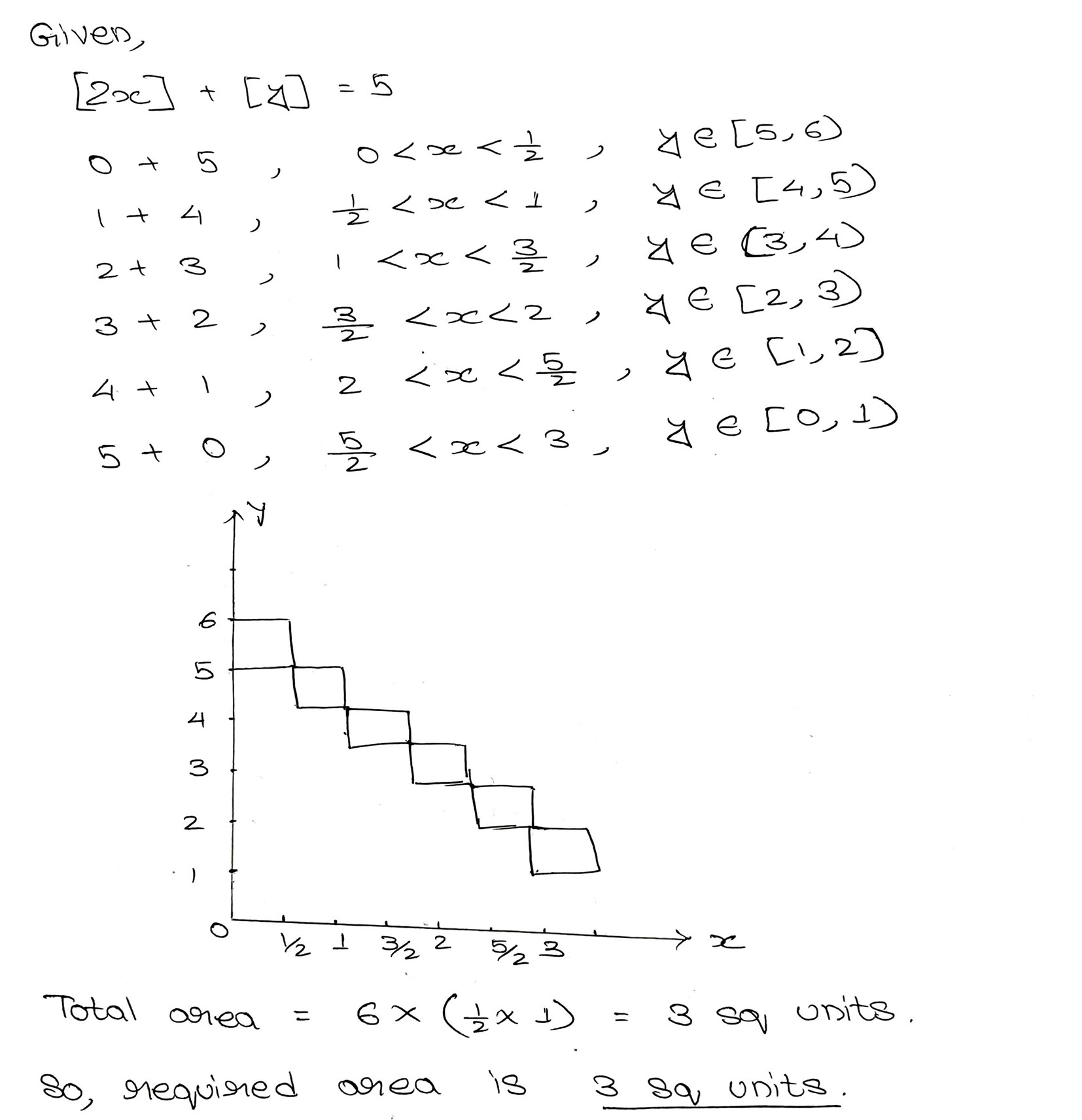
Area bounded by the relation $$[2x]$$ + $$[y]=5,x,y>0$$ is (where [.]) represents greatest integer function
If the area of the region $$\{(x,y):0\le y\le x^2+1,0\le y\le x+1,0\le x\le 2\}$$ is A, then the value of $$3A-17$$ is
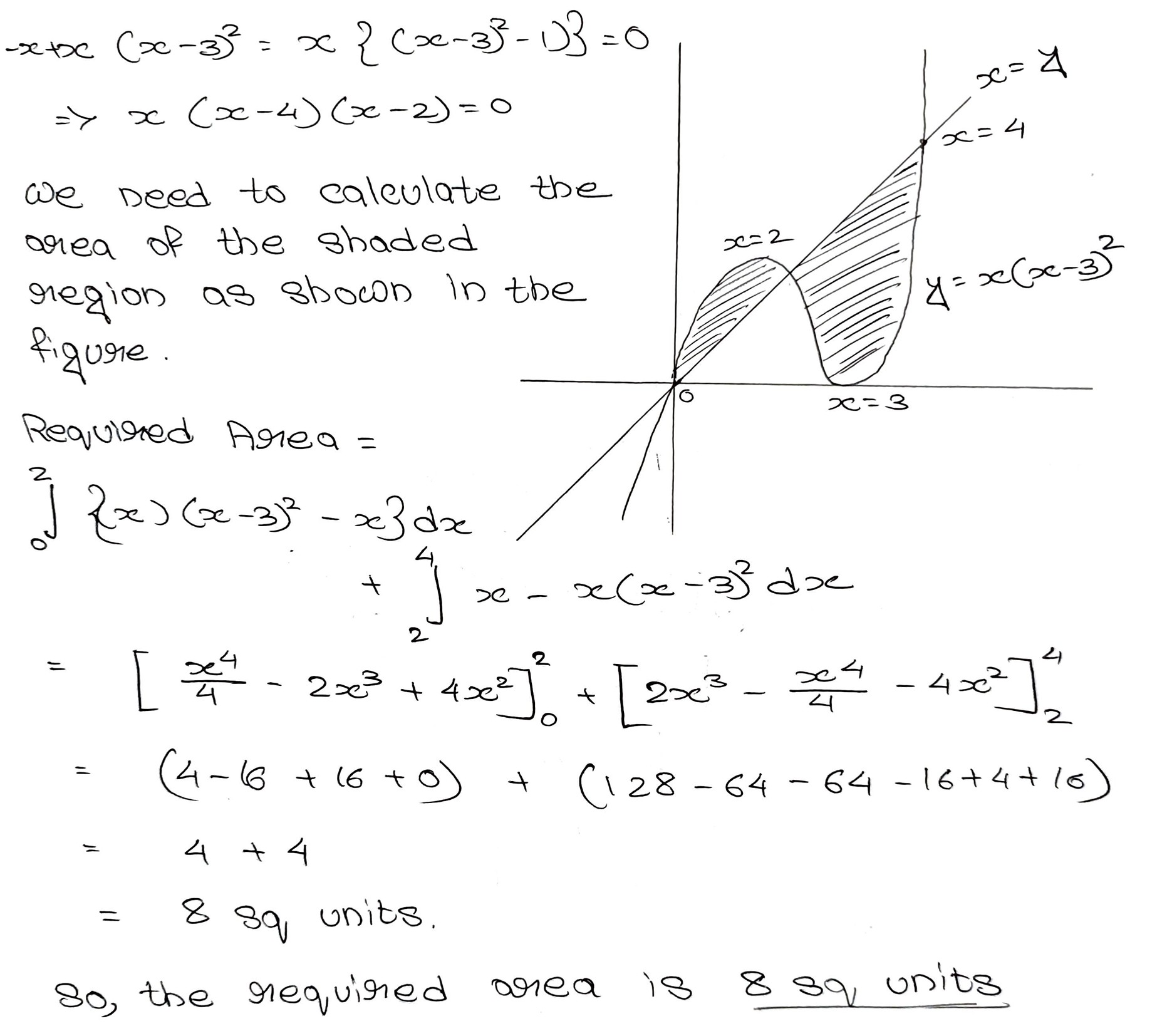
The area bounded by the curves $$y=x(x-3)^2$$ and $$y=x$$ is (in.sq.units)
The area enclosed by $$f(x)=12+ax+\,-x^2$$ coordinates axes and the ordinates at $$x=3(f(3)>0)$$ is $$45$$ square units. If $$m$$ and $$n$$ are the x-axis intercept of the graph of $$y=f(x)$$ then the value of $$
(m+n+a)$$ is
Find all the values of the parameter $$a(a \leq 1)$$ for which the area of the figure bounded by the pair of straight lines $$y^2 -3y +2 =0$$ and the curves $$y=[a]x^2, \ y=\dfrac{1}{2}[a]x^2$$ is the greatest, where $$[.]$$ denotes the greatest integer function.
Find the area of the region included between the parabola $$y = \dfrac {3x}{4}$$ and the line $$3x - 2y + 12 = 0$$.
Class 12 Commerce Maths Extra Questions
- Application Of Derivatives Extra Questions
- Application Of Integrals Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Linear Programming Extra Questions
- Matrices Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions