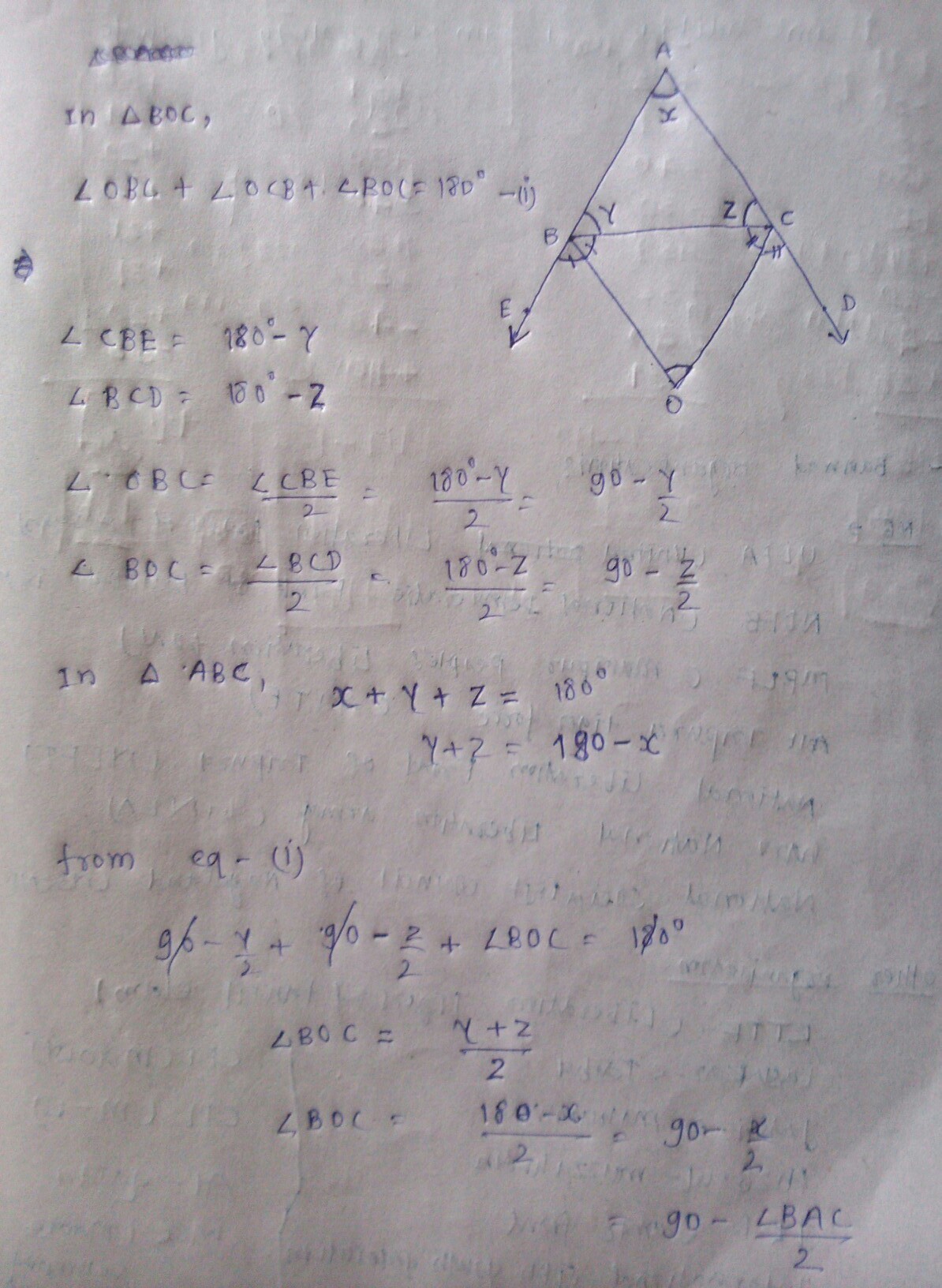Basic Geometrical Ideas - Class 6 Maths - Extra Questions
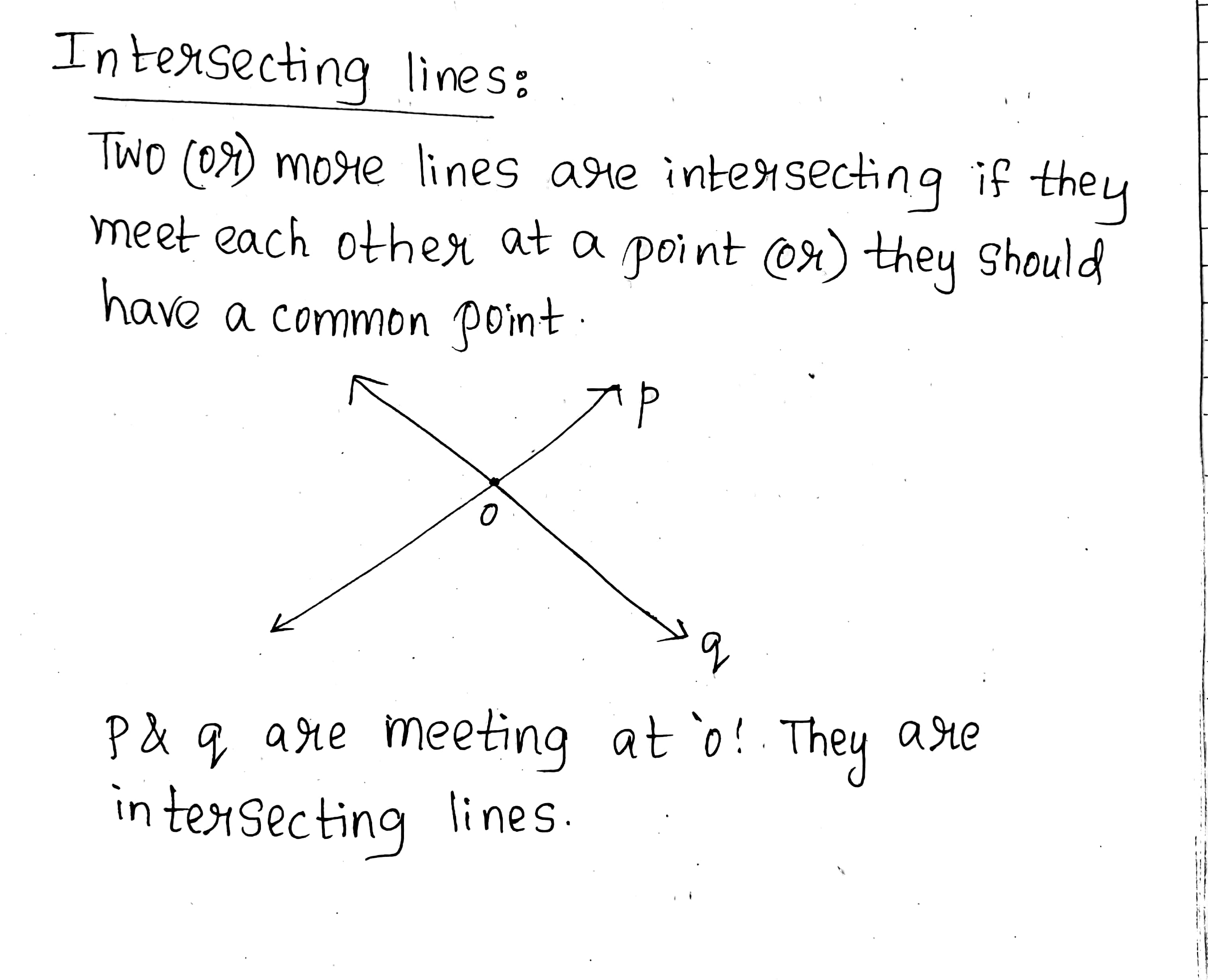
Define the following terms: Intersecting lines
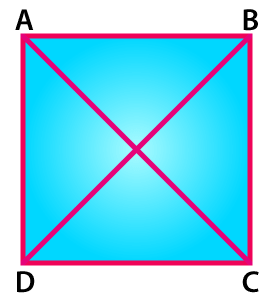
Explain how a square is:
(i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle
Identify all the quadrilaterals that have
(a) four sides of equal length (b) four right angles
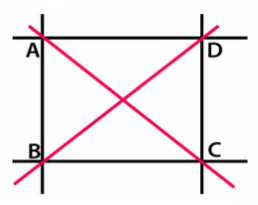
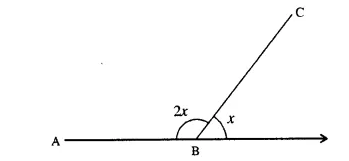
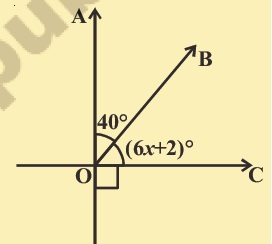
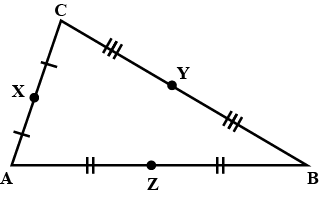
Find the value of x in the following figure.
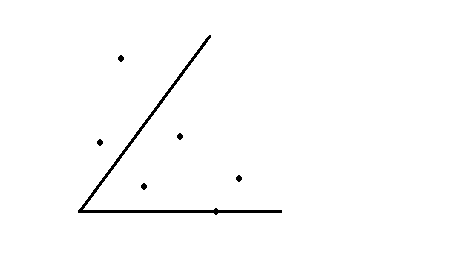
Identify the positions of the given $$6$$ points with respect to the angle. How many of the shown points lie in the interior of the angle?
How many vertices does an angle have?
How many arms does an angle have?
Identify the positions of the given $$6$$ points with respect to the angle. How many of the shown points lie in the exterior of the angle?

Prove that the sum of the three angles of a triangle is two right angles. If in a right angles triangle an acute angle is 1/4th the other, find the acute angles.
If one of the angles of triangle is $${50^ \circ }$$ and the other two angle are equal, find the measure of each of equal angles
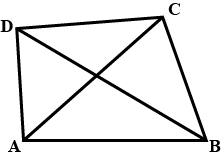
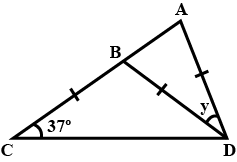
In the figure $$ABCD , BD= BC = AD $$ and $$\angle ACD = {37^ \circ }$$. find $$\angle ADB$$
What are distinct intersecting lines?
Prove that the two lines that are respectively perpendicular to two intersecting lines intersect each other.
Two angles form a linear pair, the measure of one angle is twice the measure of the other angle. Find the measure of both these angles.
The product of two consecutive positive integers isFormulate the quadratic equation whose roots are these integers.
How many lines can pass through two distinct points.
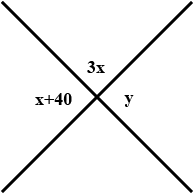
Find the value of $$x$$ and $$y$$.
Find the 'x'
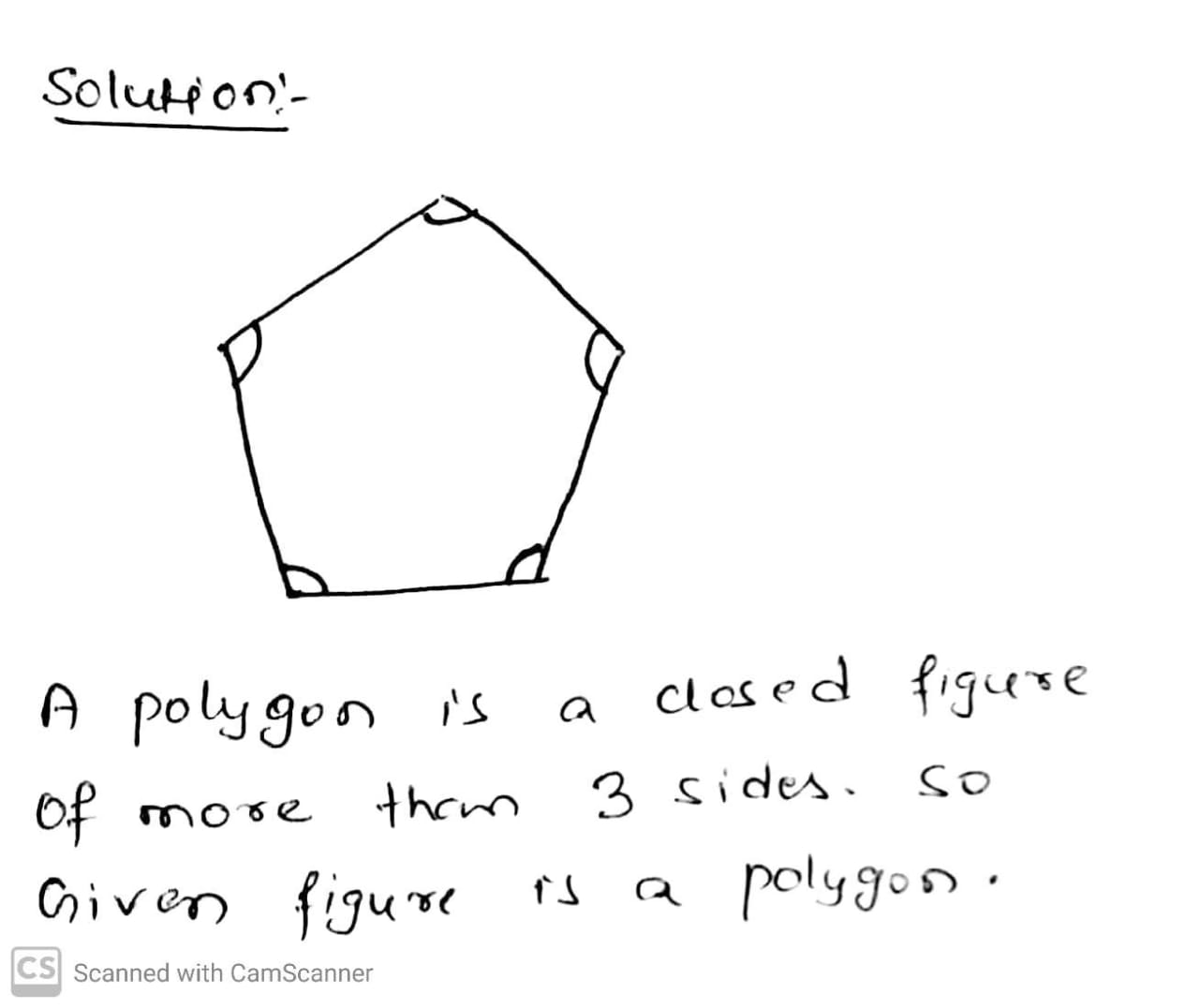
What is polygon ?
The supplement of an angle is one-third of itself. Determine the angle and its supplement.
Fill in the blanks:
A four sided polygon is called a ____
Define the following term : Intersecting lines
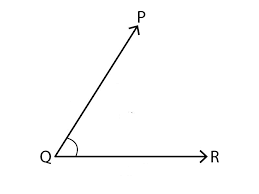
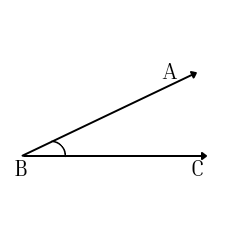
Name the vertex and the arms of $$\angle ABC$$ given in the figure.
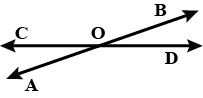
Use the figure to name two pairs of intersecting lines.
Draw any line segment $$\overline{AB}$$. Mark any point M on it. Through M, draw a perpendicular to $$\overline{AB}$$. (Use ruler and compasses)
Draw rough diagram to illustrate the following.
Closed curve.
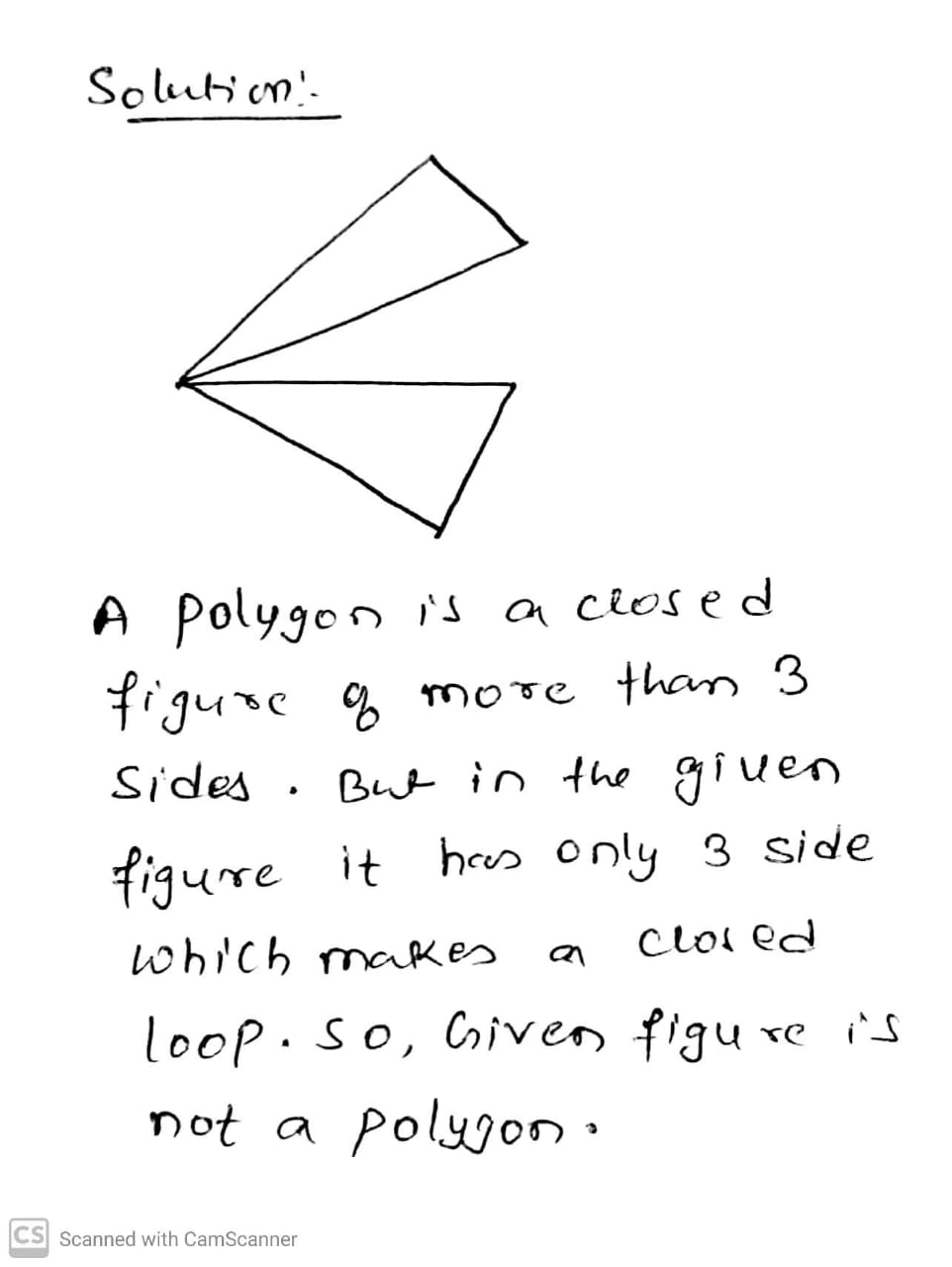
Examine whether the following is a polygon or not. If not, say why?
In how many points can two distinct lines at the most intersect ?
From the given figure, write line whose point of intersection is $$E$$.
If one of four angles formed by two intersecting lines is a right angle, then show that each of the four angles is a right angle.
In the given figure. Name concurrent lines.
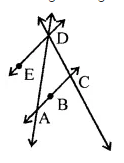
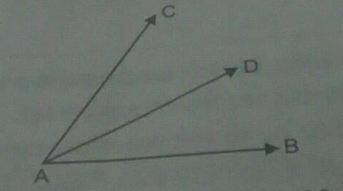
Use the figure to name
Line passing through A.
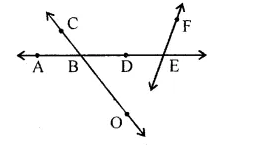
In Fig., name the following :
Two pairs of non-intersecting line segments.
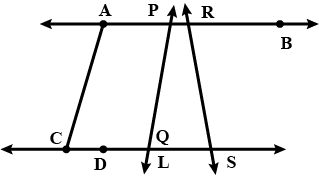
Define the following term :
Interesting Lines
Fill in the blanks in each of the following to make the statement true:
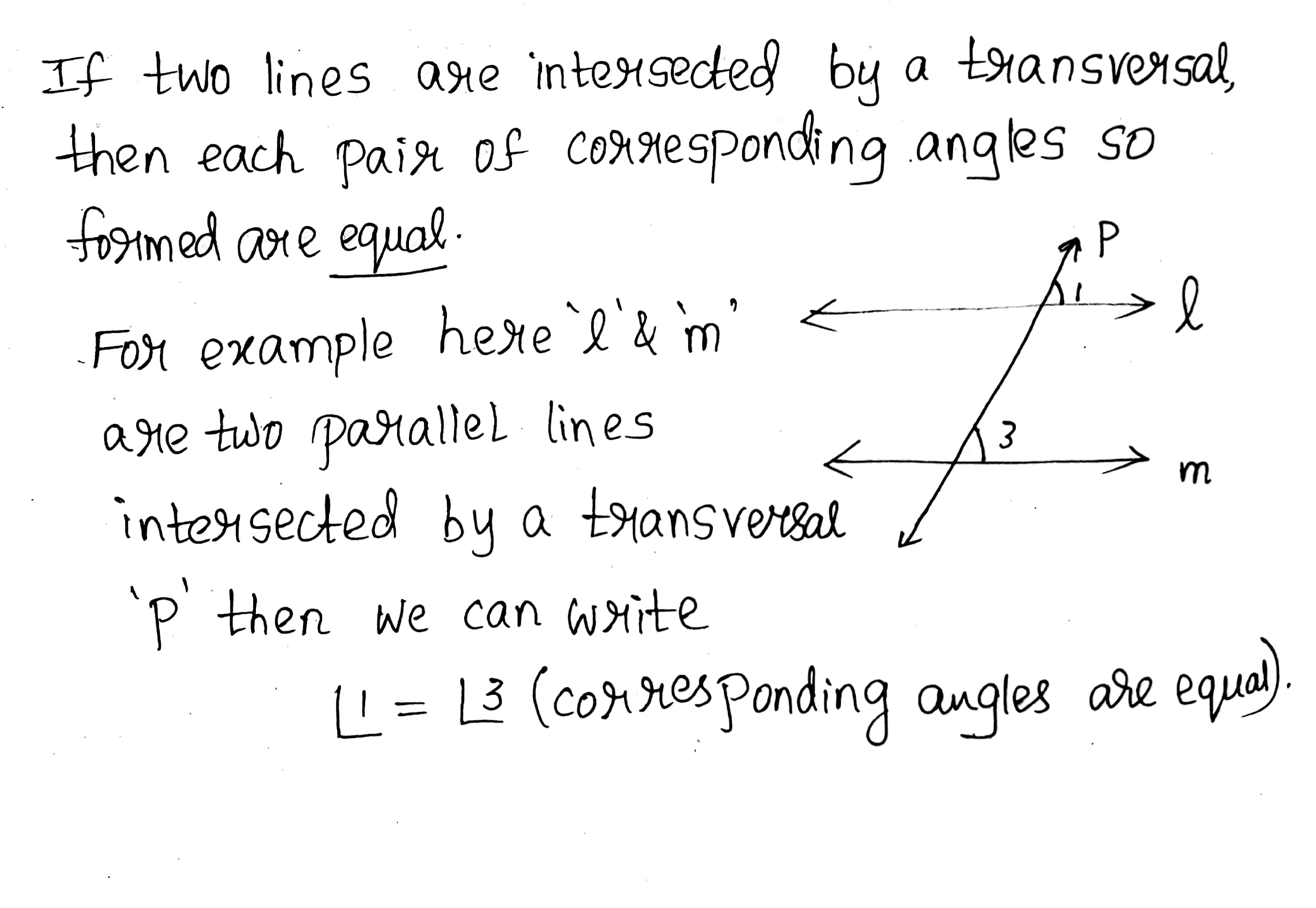
If two parallel lines are intersected by a transversal, then each pair of corresponding angles are _______
How many lines can be drawn through two distinct given point?
Use the figure to name:
A line
Fill in the blanks:
There is exactly one line passing through _____ distinct points in a plane.
Fill in the blank:
A curve which does not cross itself at any point is called a ....... curve.
Fill in the blank:
A simple closed curve made up entirely of line segments is called a _____.
In figure, how many points are marked? Name them.
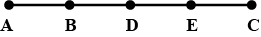
How many line segments are there in figure?

The distance around a circle is its _____ .
State the midpoints of all the sides of figure.
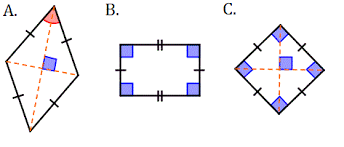
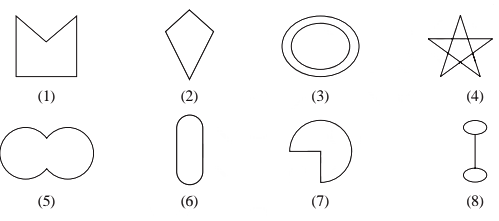
Can you identify the regular quadrilateral?
How many lines can pass through
(a) one given point ?
(b) two given points ?
State whether True or False.
(a) All rectangles are squares.
(b) All rhombuses are parallelograms.
(c) All squares are rhombuses and also rectangles.
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
Name the quadrilaterals whose diagonals.
(i) bisect each other (ii) are perpendicular bisectors of each other (iii) are equal
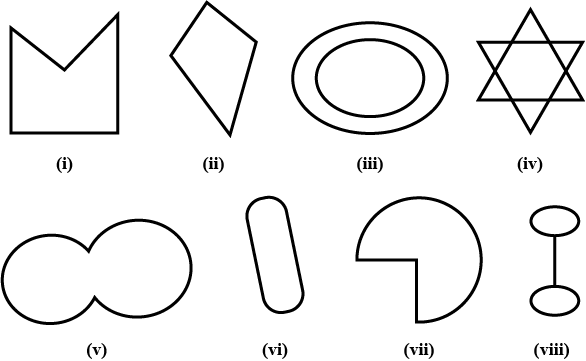
Given here are some figures:
Classify each of them on the basis of the following
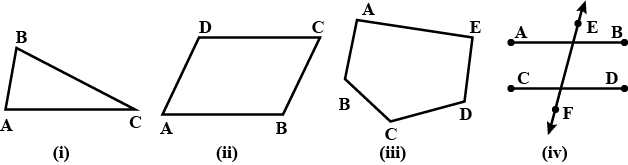
(a) Simple curve (b) Simple closed curve (c) Polygon (d) Convex polygon (e) Concave polygon
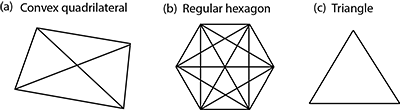
How many diagonals does each of the following have?
(a) A convex quadrilateral (b) A regular hexagon (c) A triangle
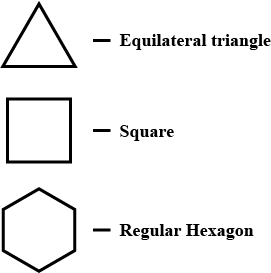
What is a regular polygon?
State the name of a regular polygon of
(i) $$3$$ sides (ii) $$4$$ sides (iii) $$6$$ sides
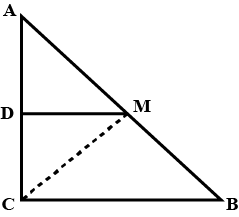
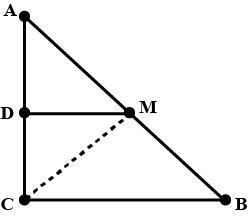
$$ABC$$ is a triangle right angled at $$C$$. A line through the midpoint $$M$$ of hypotenuse $$AB$$ and Parallel to $$BC$$ intersects $$AC$$ and $$D$$. Show that $$MD\perp AC$$.
$$PQ,QR$$ and $$RS$$ are three consecutive sides of a regular polygon. If <$$QPR=20^o$$ find the number of side in the polygon.
An angle is greater thanIs its complementary angle greater than 45 or equal to 45 or less than 45?
Find the ratio in which the line joining $$(-2, 5)$$ and $$(-5, -6)$$ is divided by the line $$y=-3$$. Hence find the point of intersection.
Fill in the blanks using the correct word given in brackets:
Two polygons of the same number of sides are similar, if (a) their corresponding angles are and (b) their corresponding sides are ..........(equal, proportional).
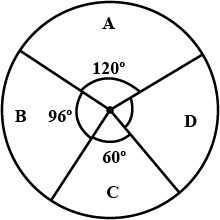
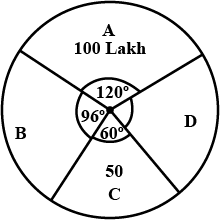
A pie chart representing the population of four cities is shown here. Read the pie chart and find the population of the city $$D$$.
What is a regular polygon?
In given figure, the AB and AC of$$\Delta \,ABC$$ are produced to point E and D respectively. If bisectors BO and Co of $$\angle CBE$$ and $$\angle BCD$$ recspectively meet at point O.

In the given figures, lines $$AB$$ and $$CD$$ intersect at point $$O$$ such that $$\angle A O D+\angle B O D+\angle B O C = 300 ^ { \circ }$$. Find $$\angle A O C$$
Find the measure of each exterior angle of a regular pentagon, hexagon, heptagon, polygon of 15 sides.
If any straight line be drawn from the vertex of a triangle to its opposite side. prove that it will be intersected by the straight line which joints the mid-points of the opposite sides.
$$AD$$ bisects $$\angle {CAD} = {(8x + 6)^ \circ}$$ and $$\angle {DAB} = {(x + 20)^ \circ}$$, what is the value of x?
Four angles of a polygon are $$120^o$$ each and the remaining angles are all equal to $$160^o$$ each. Find the number of sides
Determine the number of sides of a polygon whose exterior and interior angles are in the ratio $$1 : 5$$.
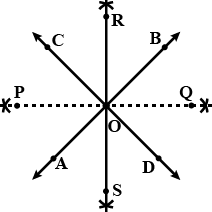
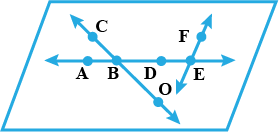
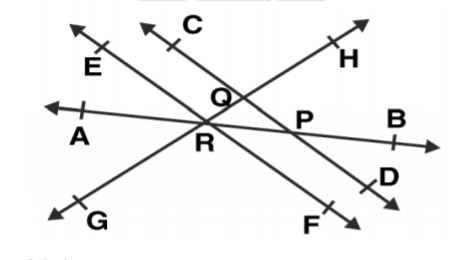
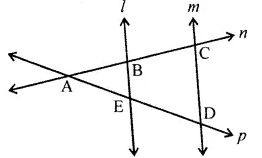
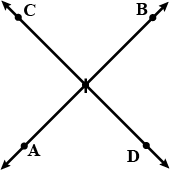
Name the interesting pairs of lines and points of intersection in the given
Name the intersecting pairs of lines and points of intersection in the given figure
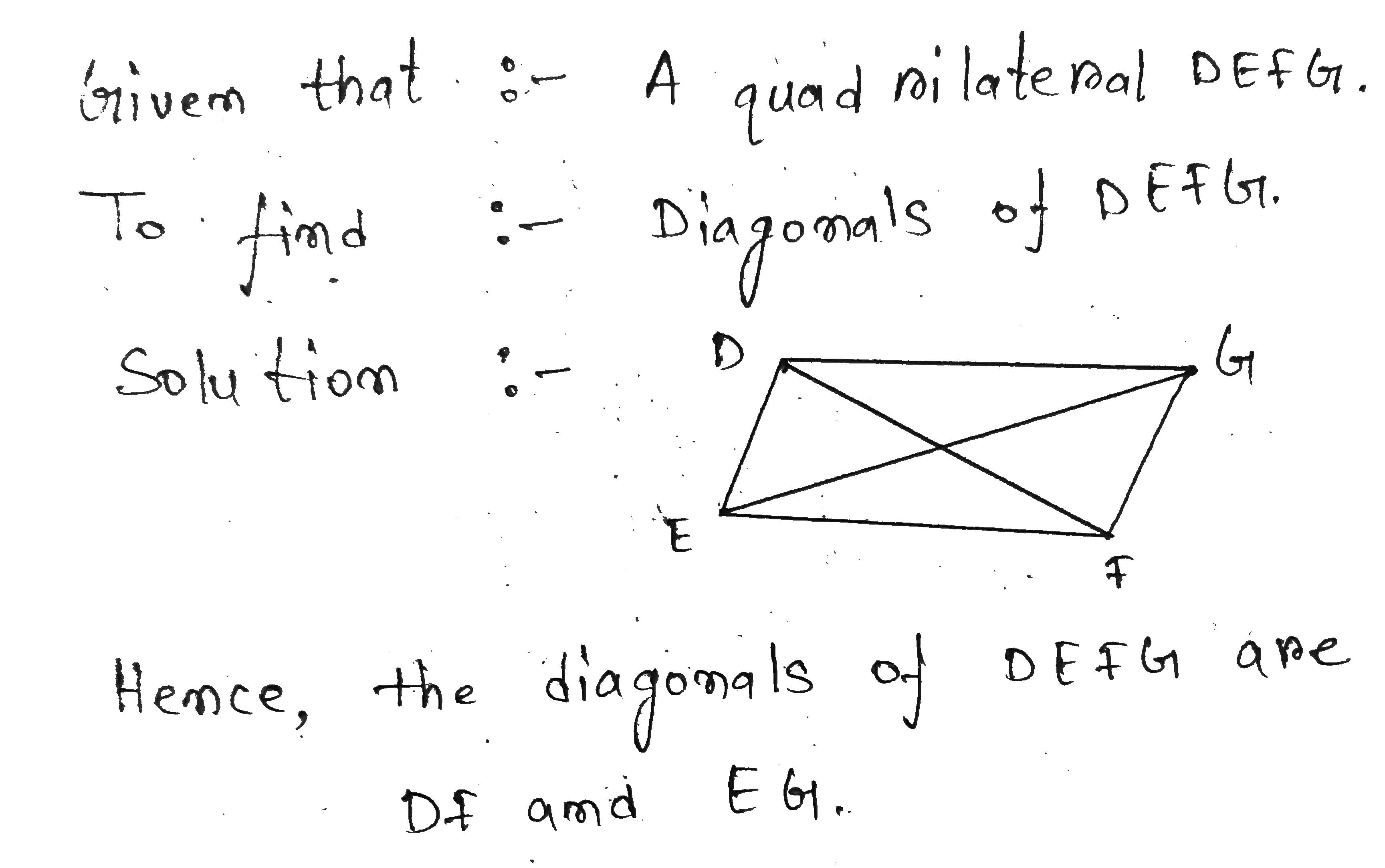
Fill in the blank.The diagonals of the quadrilateral DEFG are ____ and ____.
How many vertices and sides do these polygons have?
Octagon.
How many vertices and sides do these polygons have?
Hexagon.
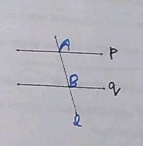
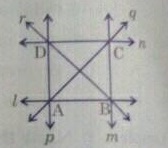
In fig., name:
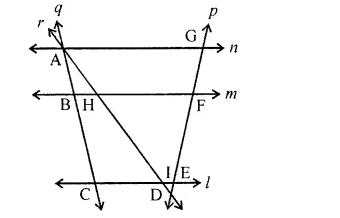
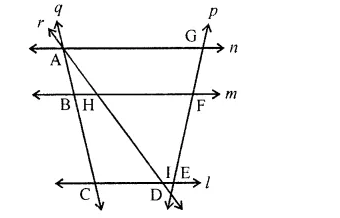
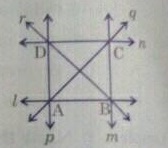
Point of intersection of the lines $$q$$ and $$n$$.
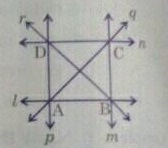
In fig., name:
Point of intersection of the lines $$p$$ and $$q$$.
Name any four polygons along with their number of sides.
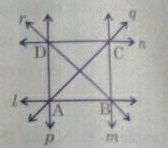
In fig., name:
Point of intersection of the lines $$r$$ and $$n$$.
How many vertices and sides do these polygons have?
Pentagon.
The perimeter of a regular pentagon is $$100$$ cm. How long is its each side?
Draw a rough figure and label suitably in the following case.
$$\overleftrightarrow{XY}$$ and $$\overleftrightarrow{PQ}$$ intersect at M.
Explain why a circle is not a polygon.
Define a polygon.
Convert $$x=\dfrac{7y+10}{4}$$ in the form of $$y=mx+c$$
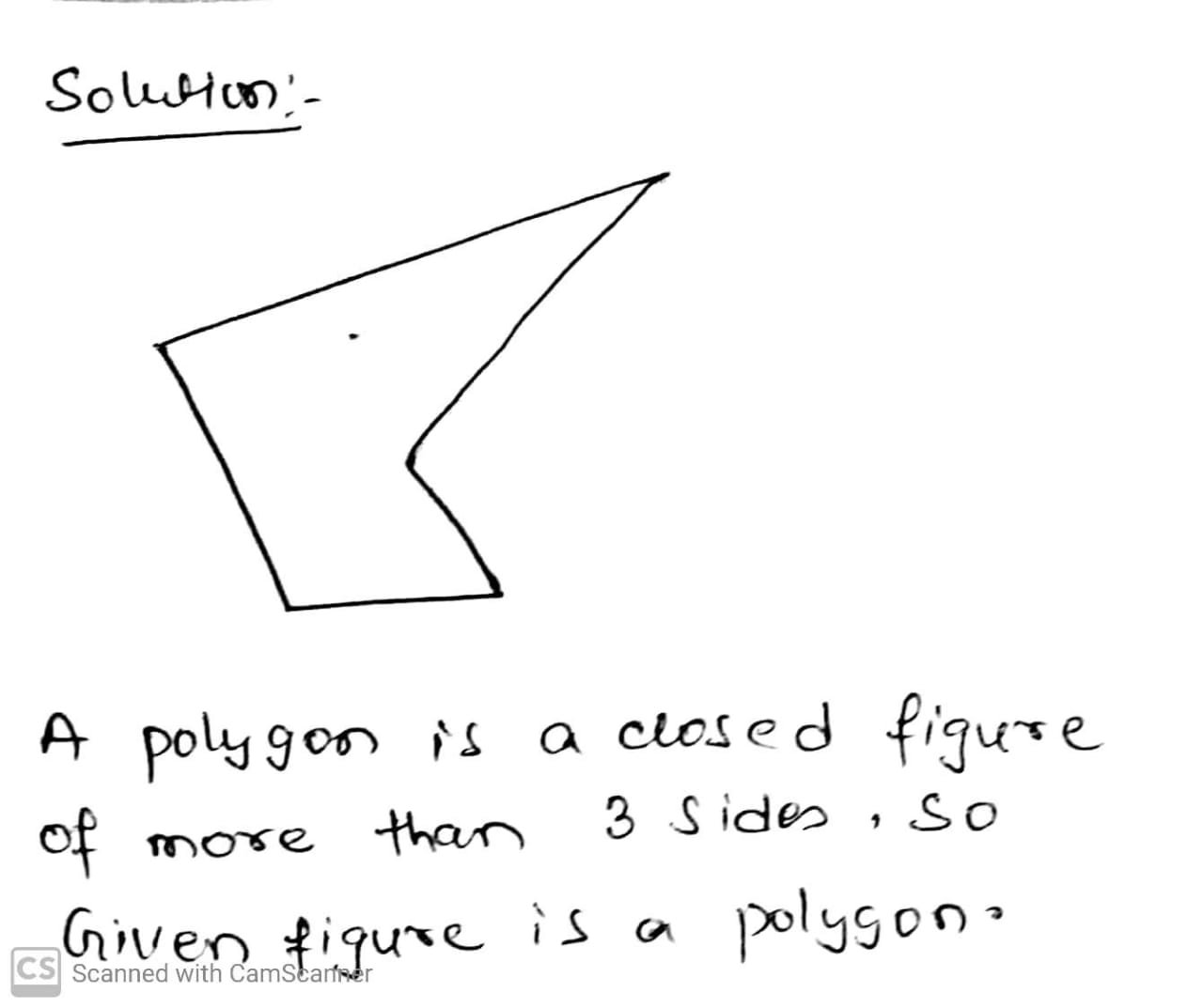
Examine whether the following is a polygon or not. If not, say why?

Draw rough diagram to illustrate the following.
Open curve.
Give reasons for the following.
Squares, rectangles, parallelograms are all quadrilaterals.
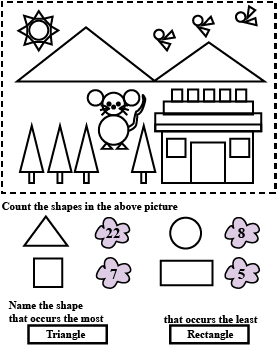
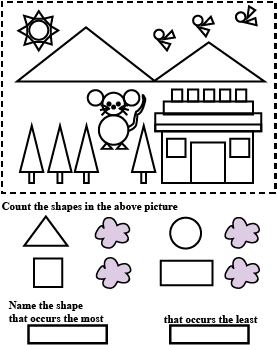
Count the shapes in the above pictures.
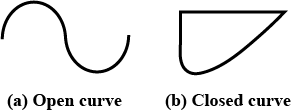
Classify the given curves as (i) Open or (ii) Closed.
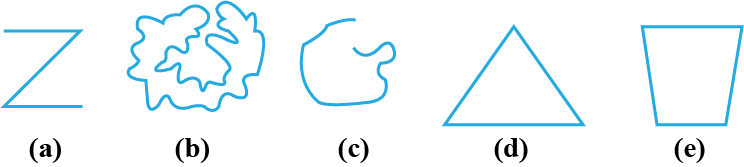
Name the polygon shown in the figure. Make two more examples of same type.
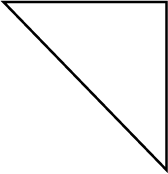
Name the polygon. Make two more examples of same type.
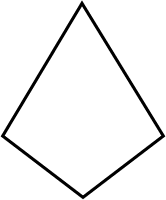
Consider the given figure and answer the question is it a curve?

Consider the given figure and answer whether is it closed or not?

Examine whether the following is a polygon or not. If not, say why?
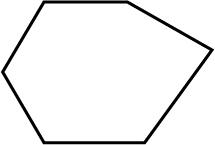
Draw a line l and a point X on it. Through X, draw a line segment $$\overline{XY}$$ perpendicular to l.
Now draw a perpendicular to $$\overline{XY}$$ at Y.(use ruler and compasses).
Classify the following curve as open or closed:

Classify the following curve as open or closed:

Draw rough diagrams to illustrate the following:
(a) Open curve
(b) Closed curve
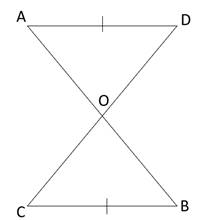
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Classify the following curve as open or closed:

Classify the following curve as open or closed:

A polygon has $$44$$ diagonals. Find the number of its sides.
Given two points $$P $$ and $$Q,$$ find how many line segments do they determine?
Classify the following curve as open or closed:

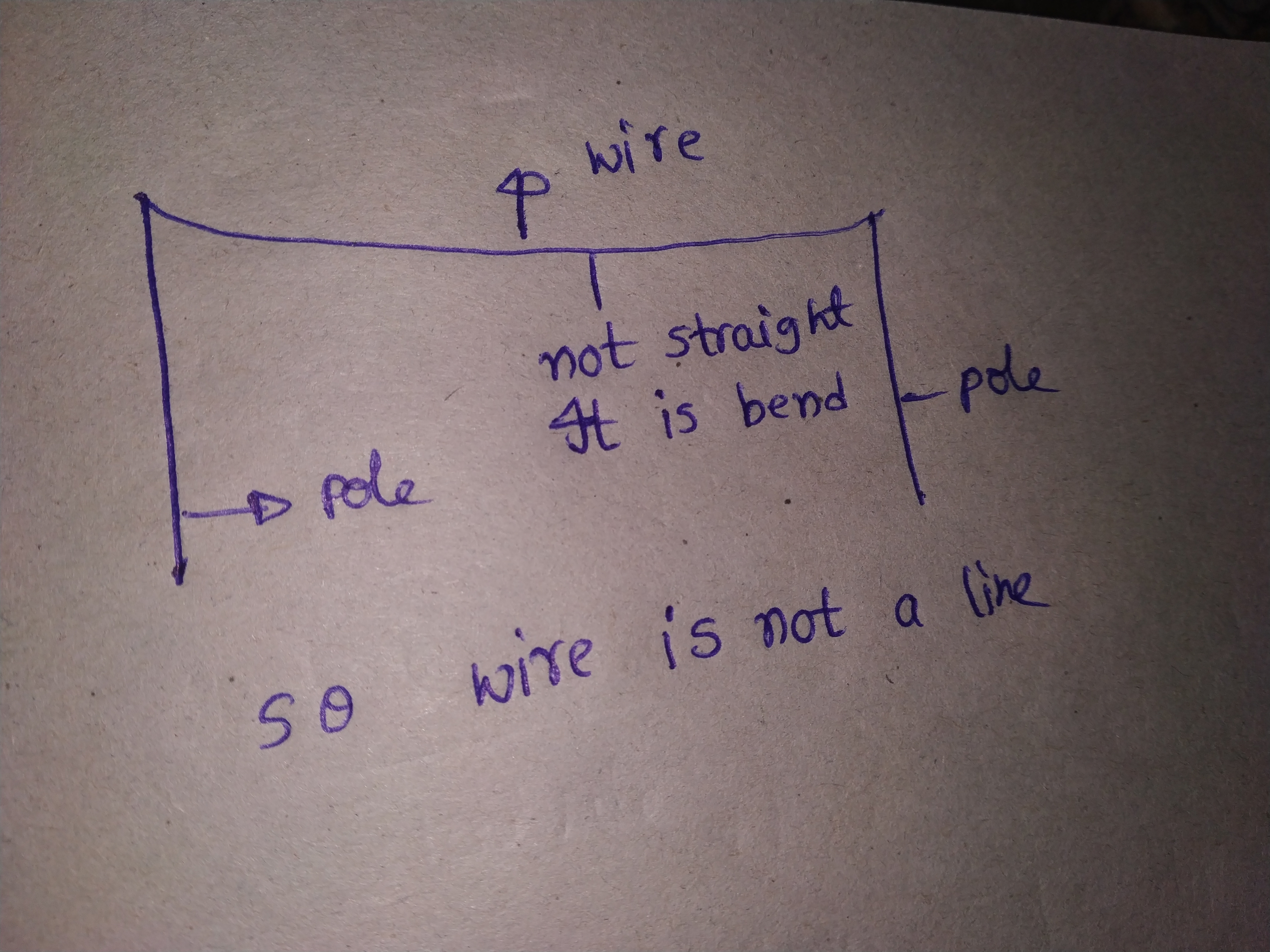
There are a number of ways by which we can visualize a portion of a line. Type 1 if the following statement represents a portion of a line otherwise 0.
Wire between two electric poles.
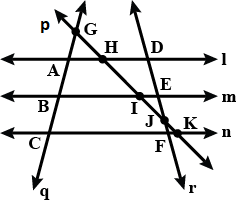
From figure, write lines whose point of intersection is D.
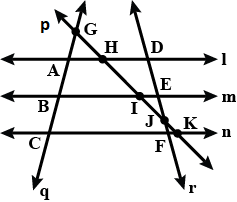
From figure, write lines whose point of intersection is E.
Complete the following, so as to make a true statement:
A diagonal of a quadrilateral is a line segment that joins two ____ vertices of the quadrilateral.
Illustrate, if possible the following with a rough diagram:
A polygon with two sides.
Illustrate, if possible the following with a rough diagram:
An open curve made up entirely of line segments
Given are some figures. Classify each of these figures on the basis of the following:
(i) simple curve (ii) simple closed curve (iii) polygon (iv) Convex polygon (iv) convex polygon (v) concave polygon (vi) Not a curve
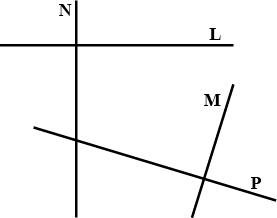
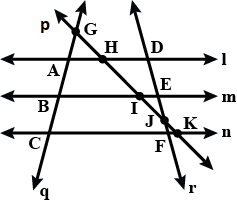
From figure, write all pairs of intersecting lines.
What is a regular polygon? State the name of a regular polygon of
(i) 3 sides (ii) 4 sides (iii) 6 sides
From figure, write lines whose point of intersection is $$I$$.
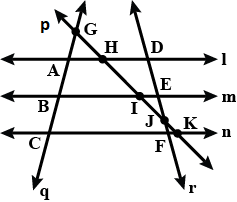
Write the names of these lines.
Name the lines which are concurrent at A.
From figure, write lines whose point of intersection is A.
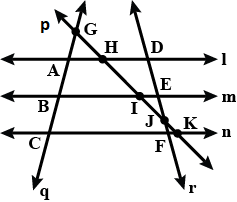
Classify the following curve as open or closed.

Count the number of line segments in figure.
Draw a polygon and shade its interior. Also draw its diagonals, if any.
Write the arms and the vertex of $$\angle LMP$$ given in figure.

Is it a closed curve?

Is it a closed curve?

Is it a closed curve?

Is it a closed curve?
Is it a closed curve?
How many angles are formed in the figure. Name them.
Is it a closed curve?

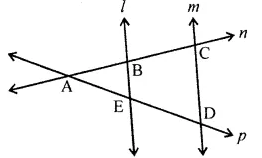
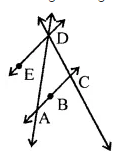
In the adjoining figure, name:
Three lines, whose point of intersecting is $$P$$
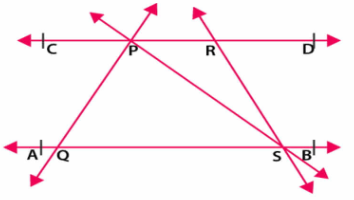
In the adjoining figure, name :
(i) Two pairs of intersecting lines and their corresponding points of intersection.
(ii) Three concurrent lines and their points of intersection
(iii) three rays
(iv) Two line segments
Define the following term : Half-line
Fill in the blank:
The curves which have different beginning and end points are called ____ curves.
From the given figure, write all pairs of intersection lines.
Draw rough diagram to illustrate the following:
open simple curve
In the given figure. Name all pairs of intersecting lines.
In the given figure, write all pairs of intersecting lines.
In the given figure, write the name of concurrent lines.
Examine whether the following figures are polygons. Give reasons.
Examine whether the following figures are polygons. Give reasons.
Name each of the following polygons:
Name each of the following polygons:
Name each of the following polygons:
Examine whether the following figures are polygons. Give reasons.
Name each of the following polygons:
Examine whether the following figures are polygons. Give reasons.
The common part between the two angles $$BAC$$ and $$DAB$$ in figure is ______
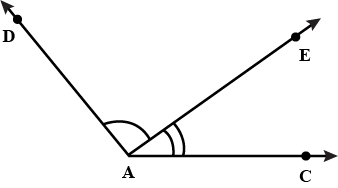
The number of common points in the two angles marked in figure is _____.
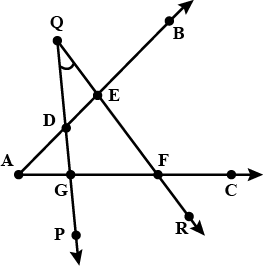
The number of diagonals in a hexagon is ______
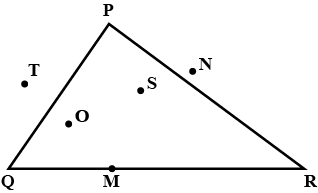
In figure, points lying in the interior of the triangle $$PQR$$ are ____, that in the exterior are ______ and that on the triangle itself are _______
The number of common points in the two angles marked in figure _____

The number of common points in the two angles marked in figure is _____
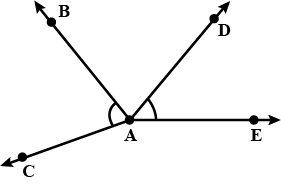
The number of common points in the two angles marked in figure is ____
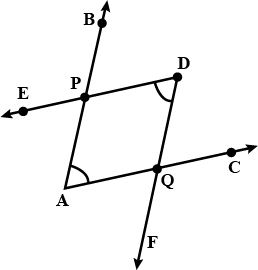
Name the following angles of figure, using three letters:
(a) $$\angle 1$$ (b) $$\angle 2$$ (c) $$\angle 3$$ (d) $$\angle 1+\angle 1=2$$ (e) $$\angle 2+\angle 3$$ (f) $$\angle 1+\angle 2+\angle 3$$ (g) $$\angle CBA-\angle 1$$

Name the line segments shown in figure.
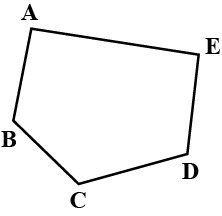
Name the points and then the line segments in each of the given figures.
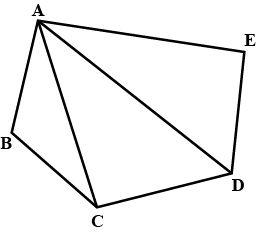
Name the vertices and the line segments in figure.
Write down fifteen angles (less than $${180}^{o}$$) involved in figure.
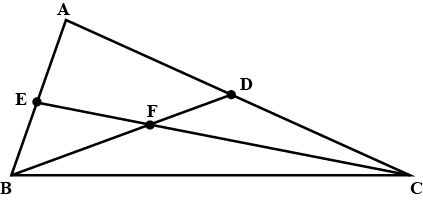
Name all the line segments in figure.
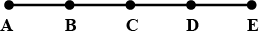
Will the measure of $$\angle ABC$$ and of $$\angle CBD$$ make measure of $$\angle ABD$$ in figure?

If two rays intersect, will their point of intersection be the vertex of an angle of which the rays are the two sides?
In figure,
(a) What is $$AE+EC$$?
(b) What is $$AC-EC$$?
(c) What is $$BD-BE$$?
(d) what is $$BD-DE$$?
How many points are marked in figure?

Will the lengths of line segment $$AB$$ and line segment $$BC$$ make the length of line segment $$AC$$ in figure?
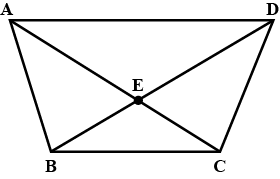
Which points in figure appear to be mid-points of the line segments? When you locate a mid-point, name te two equal line segments formed by it
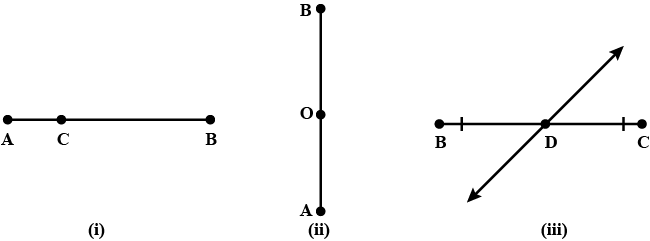
Is it possible for the same
(a) Line segment to have two different lengths?
(b) Angle to have two different measures?
Find out the incorrect statement, if any, in the following:
An angle is formed when we have
(a) Two rays with a common end-point
(b) Two line segments with a common end-point
(c) A ray and a line segment with a common end-point
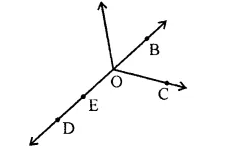
Look at figure and mark a point
(a) $$A$$ which is in the interior of both $$\angle 1$$ and $$\angle 2$$
(b) $$B$$ which is in the interior of only $$\angle 1$$
(c) Point $$C$$ in the interior of $$\angle 1$$
Now, state whether points $$B$$ and $$C$$ lie in the interior of $$\angle 2$$ also

In figure
(a) Is $$AC+CB=AB$$?
(b) Is $$AB+AC=CB$$?
(c) Is $$AB+BC=CA$$?

Draw all the diagonals of a pentagon $$ABCDE$$ and name them.
How many line segments are there in figure? Name them

In figure, how many line segments are there? Name them

In figure how many points are marked? Name them.

In figure, how many line segments are there? Name them.
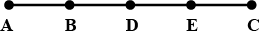
In figure, how many points are marked? Name them

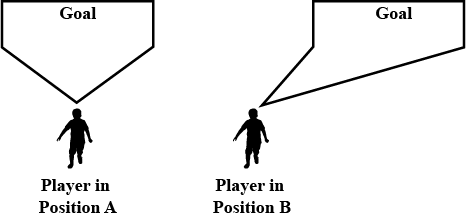
The drawing below Fig., show angles formed by the goalposts at different positions of a football player.The greater the angle, the better chance the player has of scoring a goal. For example, the player has a better chance of scoring a goal from Position $$A$$ than from Position $$B$$.
In Parts (a) and (b) given below it may help to trace the diagram and draw and measure angles.
Seven football players are practicing their kicks. They are lined up in a straight line in front of the goalpost Fig. Which player has the best (the greatest) kicking angle?
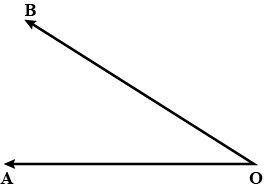
For each angle given below, write the name of the vertex, the names of the arms and the name of the angle.
Solve the following :
The ratio between exterior angle and interior angle of a regular polygon is $$ 1 : 5 $$. Find the number of sides of the polygon.
Fill in the blanks to make the statements true.
A polygon is a simple closed curve made up of only ________ .
Fill in the blanks to make the statement true.
A nonagon has _______ sides .
Fill in the blank to make the statement true.
The name of three-sided regular polygon is _____ .
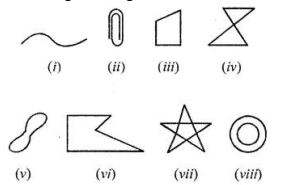
Some of the figures are given:
Classify each of them on the basis of the following:
(a) Simple curve
(b) simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Fill in the blanks to make the statements true.
Is a closed curve made up of line segments ? The name for this shape is ______ .
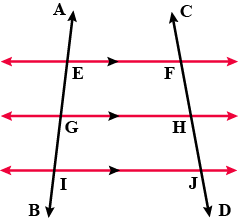
From the adjoining figure, write all the lines which intersect $$EF$$.
Give two examples from your surroundings for the following:
intersecting lines
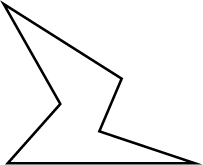
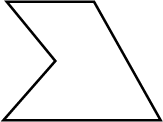
State, if the following is polygon:
For the angle given below, write the name of the vertex, the names of the arms and the name of the angle.
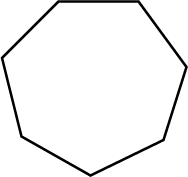
State, if the following is polygon:
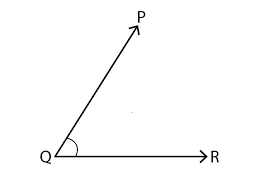
For each angle given below, write the name of the vertex, the names of the arms and the name of the angle.
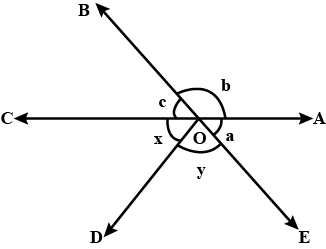
Name the angles marked by letters $$a, b, c, x$$ and $$y$$
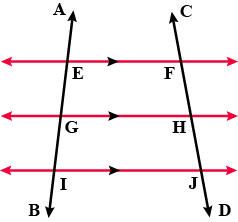
From the adjoining figure, write lines whose point of intersection is $$G$$.
For each angle given below, write the name of the vertex, the names of the arms and the name of the angle.
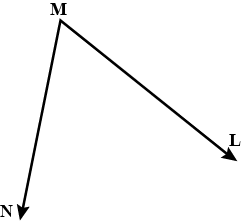
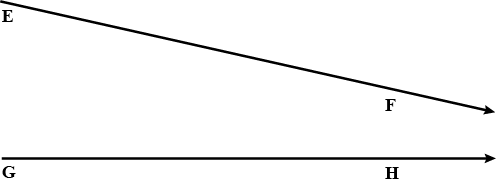
State, whether the above pairs of lines or rays appear to be parallel or intersecting.
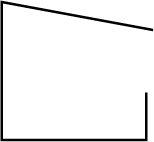
State, if the following is polygon:
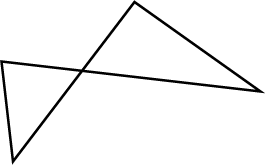
State, if the following is polygon:
The ratio between the interior angle and the exterior angle of a regular polygon is $$2:1$$. Find:
number of sides in the polygon.
State which of the following are polygons:
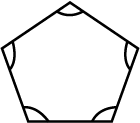
State which of the following are polygons:
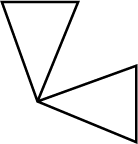
State which of the following are polygons:
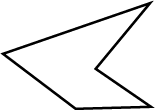
State, if the following is polygon:
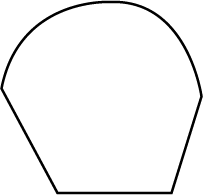
Fill in the blanks:
In case of regular polygon, with
| Number of sides | Each exterior angle | Each interior angle |
| $$6$$ | ........... | .......... |
State which of the following are polygons:

State whether the given figure is polygon or not.
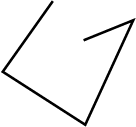
Consider the given figure and answer the questions :
a) Is it a curve ?
b) Is it closed ?

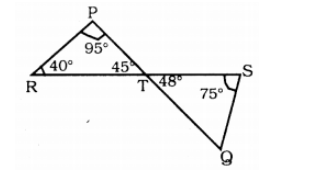
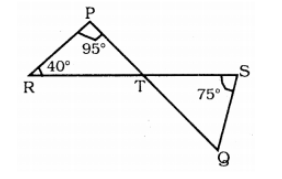
In fif 3.42 , if lines PQ and RS intersect at point T such , that $$\angle PRT = 40 , \angle RPT = 95^{\circ} $$ and $$\angle TSQ = 75^{\circ} $$ , find $$\angle SQT $$
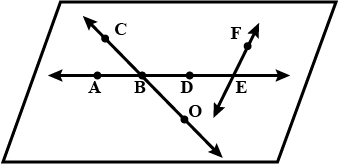
Use the figure to name:
a) Line containing point E
b) Line passing through A.
c) Line on which O lies.
d) Two pairs of intersecting lines
Illustrate, if possible, each one of the following with a rough diagram :
a) A closed curve that is not a polygon
b) An open curve made up entirely of line segments
c) A polygon with two sides.
Name each polygon.
Make two more examples of each of these.
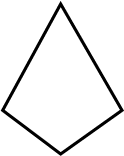
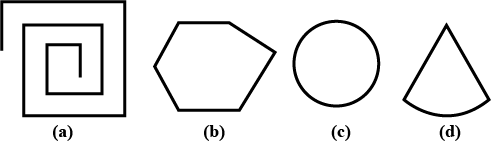
Examine whether the following are polygons. If any one among them is no, say why?
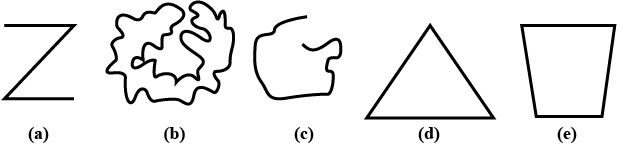
Classify the following curves as
(i) open or
(ii) closed
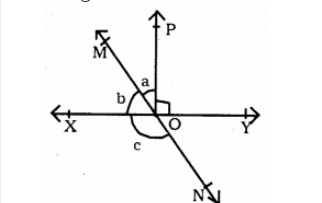
In fig 3.14 , lines XY and MN intersects at O . If $$\angle POY = 90^{\circ} $$ and $$a : b = 2:3 , $$ find c
Write the answer of each of the following questions:
(iii) Write the name of the point where these two lines intrsect.
Name each polygon.
Make two more examples of each of these.
Write the name of the point where these two lines intersect.
The straight roads intersects each other at O. A testing center have to formed such that its distance from O be 1 km and equidistant from two roads, Show the possible cases of testing center by figure.
Find the number of sides of a regular polygon if each exterior angle is equal to its adjacent interior angle
Find the number of sides of a regular polygon if each exterior angle is equal to half its adjacent interior angle
Find the number of sides of a regular polygon if each exterior angle is equal to one third of its adjacent interior angle.
A triangle is a closed planar shape with
A variable straight line of slope $$4$$ intersects the hyperbola $$xy = 1$$ at two points. Find the locus of the point which divides the line segment between these two points in the ratio $$1:9$$.
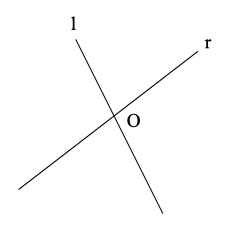
In fig., name:
Point of intersection of the lines $$l$$ and $$m$$.
Is it possible to have a regular polygon whose each interior angle is :
$$138^{o}$$
Show that the lines $$\vec{r} = (3\hat{i} + 2\hat{j} - 4\hat{k})$$ + $$\lambda(\hat{i} + 2\hat{j} + 2\hat{k})$$ and $$\vec{r} = (5\hat{i} - 2\hat{j})$$ + $$\mu(3\hat{i} + 2\hat{j} + 6\hat{k})$$ are intersecting and find their point of intersection.
Classify the following curve as open or closed.

Which of the following are closed curves? Which of them are simple?
Class 6 Maths Extra Questions
- Algebra Extra Questions
- Basic Geometrical Ideas Extra Questions
- Data Handling Extra Questions
- Decimals Extra Questions
- Fractions Extra Questions
- Integers Extra Questions
- Knowing Our Numbers Extra Questions
- Mensuration Extra Questions
- Playing With Numbers Extra Questions
- Practical Geometry Extra Questions
- Ratio And Proportion Extra Questions
- Symmetry Extra Questions
- Understanding Elementary Shapes Extra Questions
- Whole Numbers Extra Questions