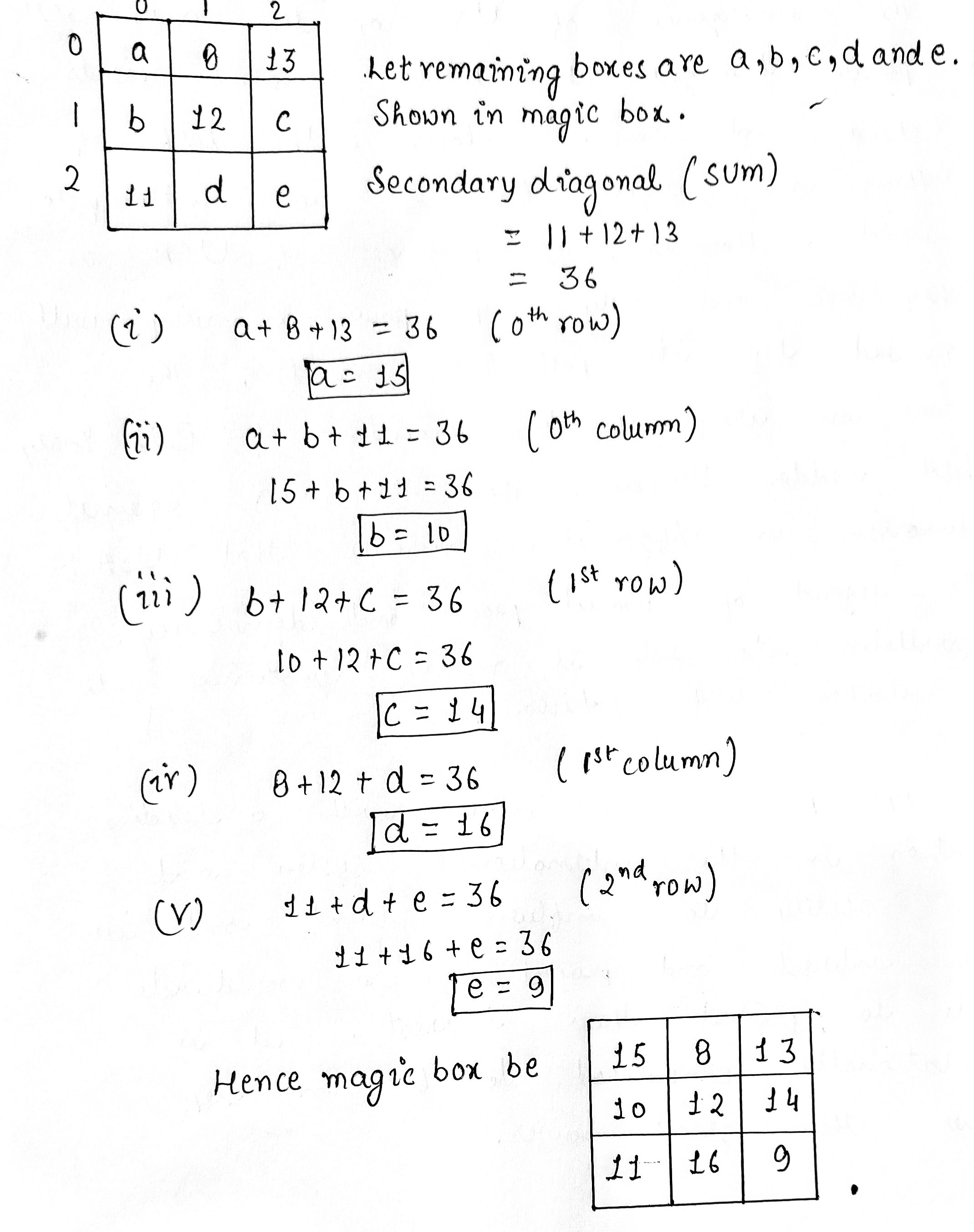Can You See The Pattern - Class 5 Maths - Extra Questions
Solve the magic square.
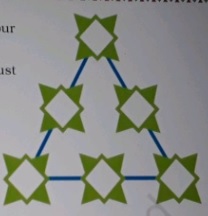
Draw a magic triangle whose magic number's sum is $$11$$.
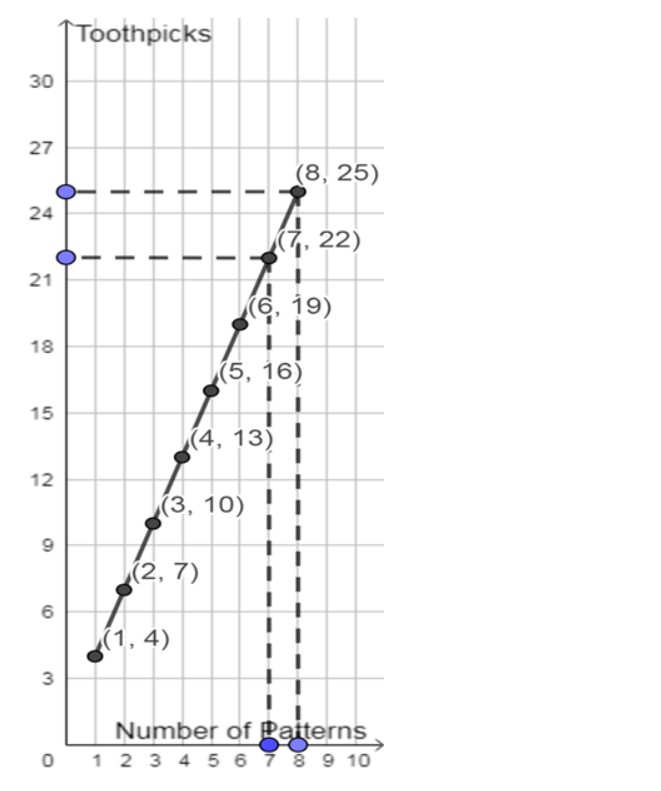
Observe the toothpick pattern given below:
Would make sense to join the points on this graph Explain.

Fill in the blank spaces by integers of the given magic square so that the sum of the integers in each row, each column and each diagonal is $$-6$$.
| $$-1$$ | ||
| $$3$$ | $$-2$$ | |
Using the numbers from $$9$$ to $$17$$, construct a $$3\times 3$$ magic square. What is the magic sum here? What relation is there between the magic sum and the number in the central cell?
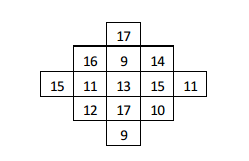
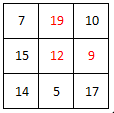
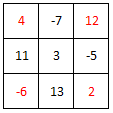
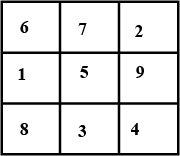
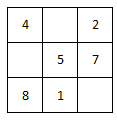
Find the value of magic square.
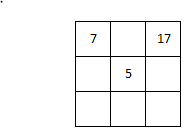
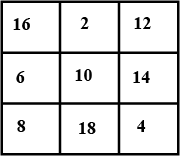
Solve the magic square.
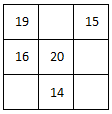
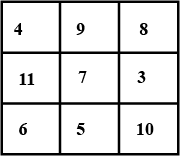
Solve the magic square.
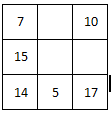
Complete the magic square.
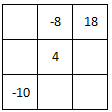
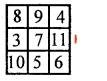
Solve the magic square.
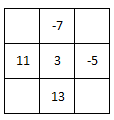
In a row of boys, Srinath is $${7}^{th}$$ from the left and Venkat is $${12}^{th}$$ from the right. If they interchange their positions, Srinath becomes $${22}^{nd}$$ from the left. How many boys are there in the row?
In a row of plants, a plant is $$16^{th}$$ from either end of the row. How many trees are there in the row ?
$$\square +\square +\square =30$$
Fill the boxes using $$(1, 3, 5, 7, 9, 11, 13, 15)$$ You can also repeat the numbers.
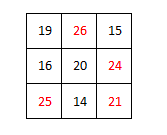
In a "magic square", the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?
| $$\dfrac {4}{11}$$ | $$\dfrac {9}{11}$$ | $$\dfrac {2}{11}$$ |
| $$\dfrac {3}{11}$$ | $$\dfrac {5}{11}$$ | $$\dfrac {7}{11}$$ |
| $$\dfrac {8}{11}$$ | $$\dfrac {1}{11}$$ | $$\dfrac {6}{11}$$ |
In a "magic square", the sum of the numbers in each row, in each column and along the diagonal is the same. Is this a magic square ?
| $$\dfrac{4}{11}$$ | $$\dfrac{9}{11}$$ | $$\dfrac{2}{11}$$ |
| $$\dfrac{3}{11}$$ | $$\dfrac{5}{11}$$ | $$\dfrac{7}{11}$$ |
| $$\dfrac{8}{11}$$ | $$\dfrac{1}{11}$$ | $$\dfrac{6}{11}$$ |
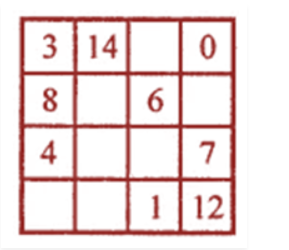
Complete the following magic square by supplying the missing numbers:
| 2 | 15 | 16 | |
| 9 | 12 | ||
| 7 | 10 | ||
| 14 | 17 |
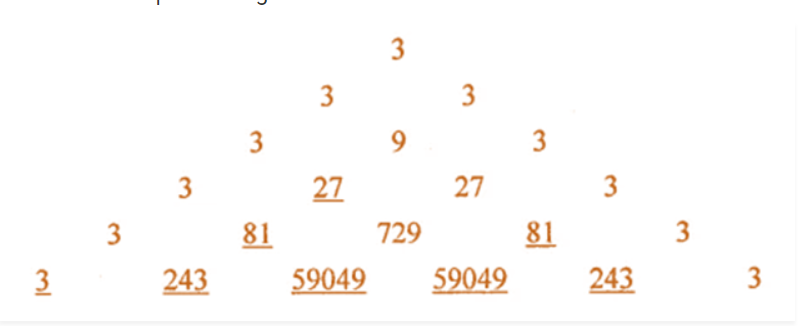
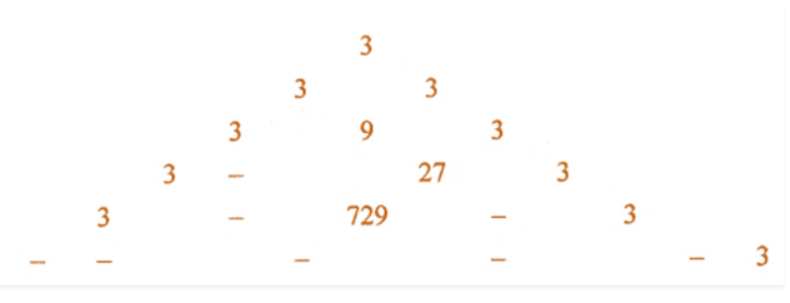
Fill in the blanks to complete the following number triangle:
In two-digit numbers, how many times does the digit $$5$$ occur in the unit's place?
A magic square is an array of numbers having the same number of rows and columns and the sum of numbers in each row, column or diagonal being the same. Fill in the blank cells of the following magic squares:
| 22 | 6 | 13 | 20 | |
| 10 | 12 | 19 | ||
| 9 | 11 | 18 | 25 | |
| 15 | 17 | 24 | 26 | |
| 16 | 7 | 14 |
A magic square is an array of numbers having the same number of rows and columns and the sum of numbers in each row, column or diagonal being the same. Fill in the blank cells of the following magic squares:
| 8 | 13 | |
| 12 | ||
| 11 |
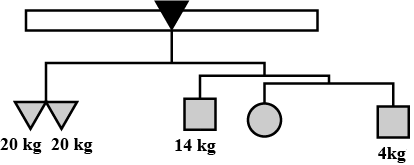
The given figure represents a weighing balance. The weights of some objects in the balance are given.
Find the weight of each square and the circle.
Observe the toothpick pattern given below:
Imagine that this pattern continues. Complete the table to show the number of toothpicks in the first six terms.

Complete the magic square given alongside using number $$ 0,1,2,3,........,15 $$ (only once),so that sum along each row, column and diagonal is $$ 30.$$
In two-digit numbers, how many times does the digit $$5$$ occur in the ten's place.
Solve the following riddles, you may yourself construct such riddles.
Who am I?
Go round a square counting every corner Thrice and no more! Add the count to me To get exactly thirty-four!
Complete the following magic squares:
Using the numbers from 9 to 17 construct a $$ 3 \times 3 $$ magic square. What is the Magic sum here? What relation is there between the magic sum and the number in the central cell?
Construct a $$ 3 \times 3 $$ magic square using all odd numbers from 1 to 17.
Starting with the middle cell in the bottom row of the square and "using numbers from 1 to 9 construct a $$ 3 \times 3 $$ magic square.
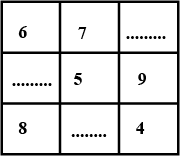
Complete the following magic square:
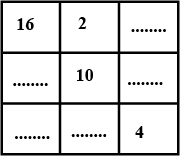
Complete the following magic square:
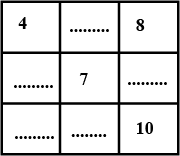
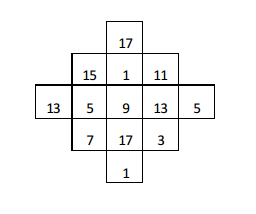
Complete the adjoining magic square (Hint. In a $$ 3 \times 3 $$ magic square the magic sum is $$$$ times the central number)
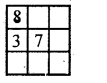
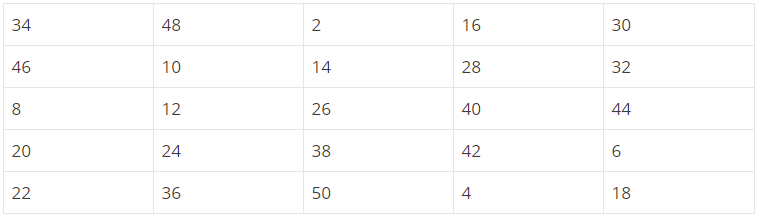
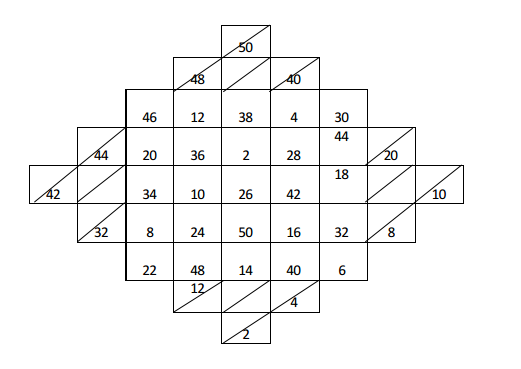
Construct a $$ 5 \times 5 $$ magic square using all even numbers from 1 to 50.
What relation is there between the magic sum and the number in the central cell?
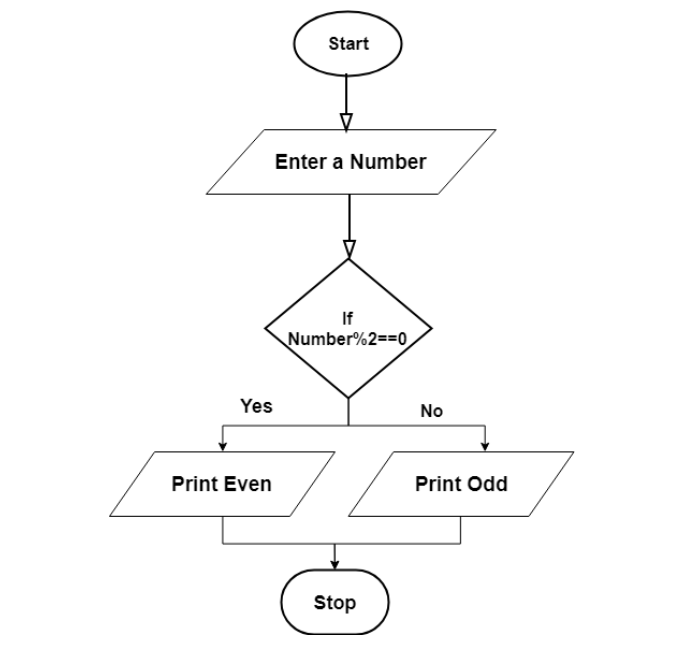
Write an algorithm to check if a number is even or odd, using both pseudocode and flowchart.
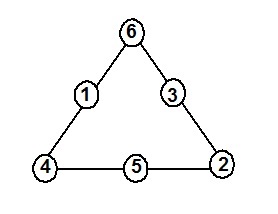
Now use number $$1 - 6$$ to make your own magic triangle.
Rule : Numbers on each side must add up to $$10$$.
Starting with the middle cell in the bottom row of the square and using numbers from $$1$$ to $$9$$, construct a $$3\times 3$$ magic square
Construct a $$3\times 3$$ magic square using all odd number from $$1$$ to $$17$$
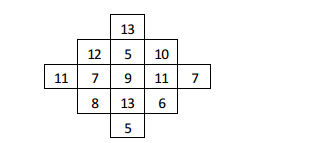
Using the numbers from $$5$$ to $$13$$, construct a $$3\times 3$$ magic square. What is the magic sum here? What relation is there between the magic sum and the number in the central cell?
Construct a $$5\times 5$$ magic square using all even number from $$1$$ to $$50$$
Replace each $$\ast$$ by the correct digit of the above:
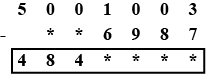
Replace each $$\ast$$ by the correct digit of the above:

Class 5 Maths Extra Questions
- Area And Its Boundary Extra Questions
- Be My Multiple I Will Be Your Factor Extra Questions
- Boxes And Sketches Extra Questions
- Can You See The Pattern Extra Questions
- Does It Look The Same Extra Questions
- How Big How Heavy Extra Questions
- How Many Squares Extra Questions
- Mapping Your Way Extra Questions
- Parts And Whole Extra Questions
- Shapes And Angles Extra Questions
- Smart Charts Extra Questions
- Tenths And Hundreths Extra Questions
- The Fish Tale Extra Questions
- Ways To Multiply And Divide Extra Questions