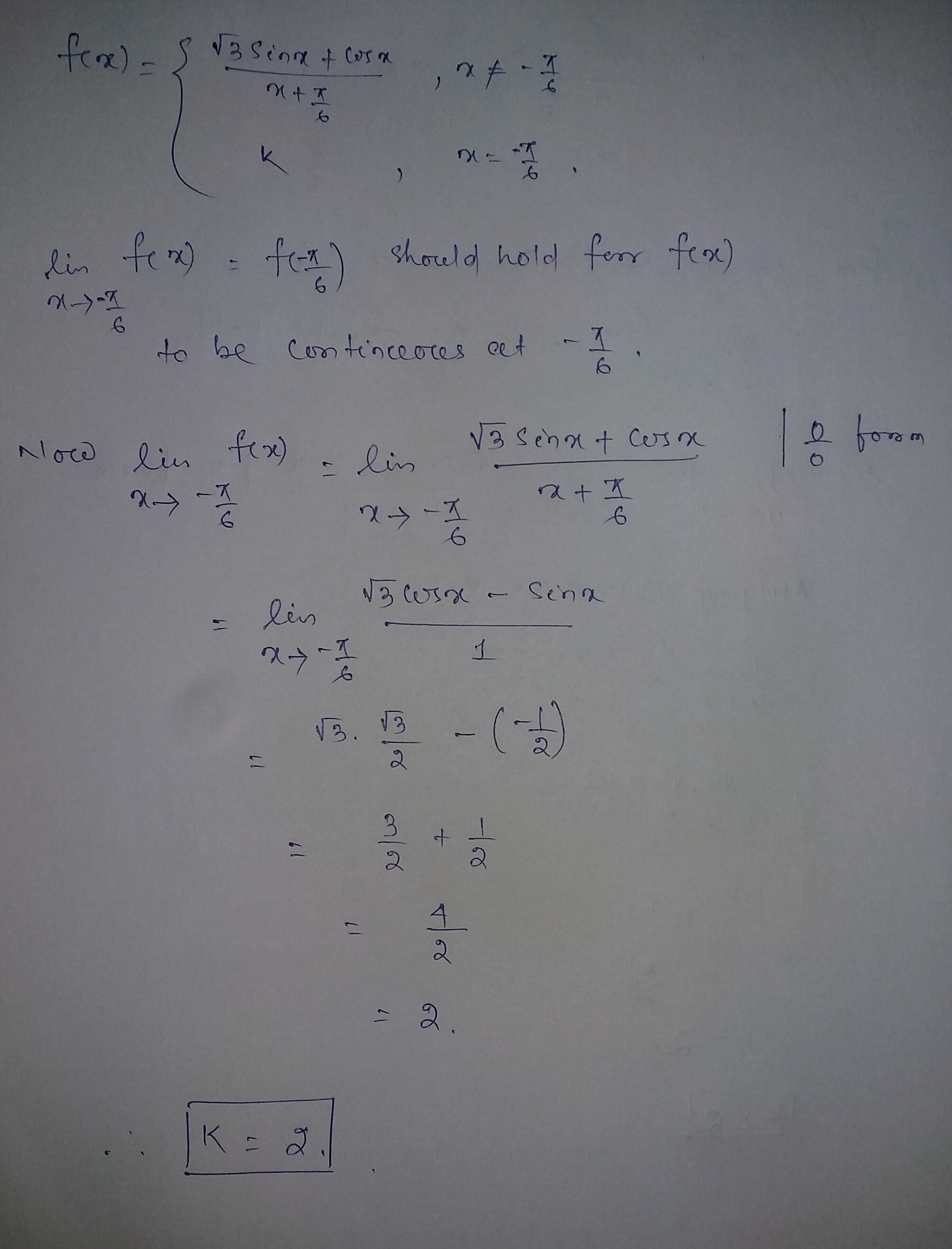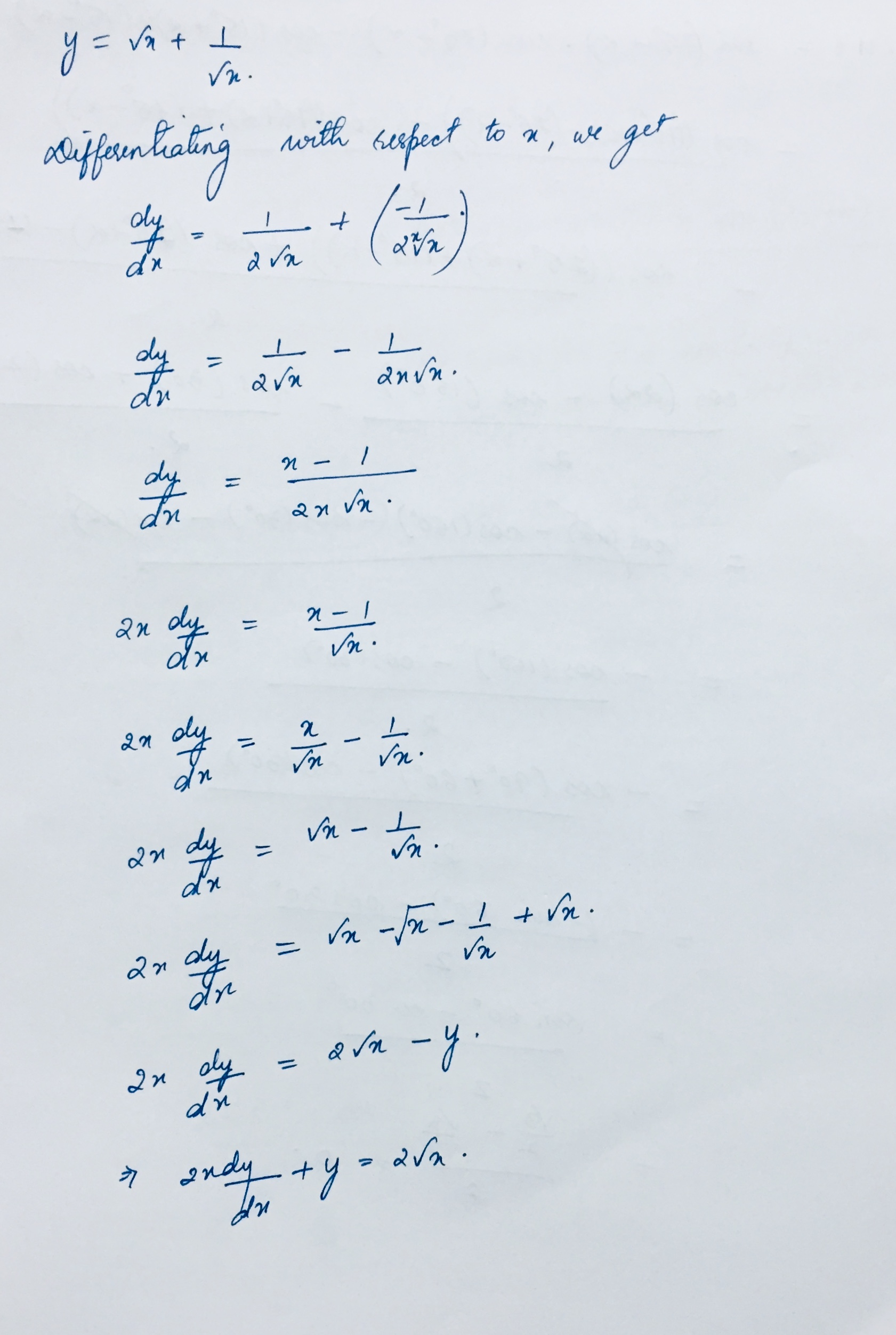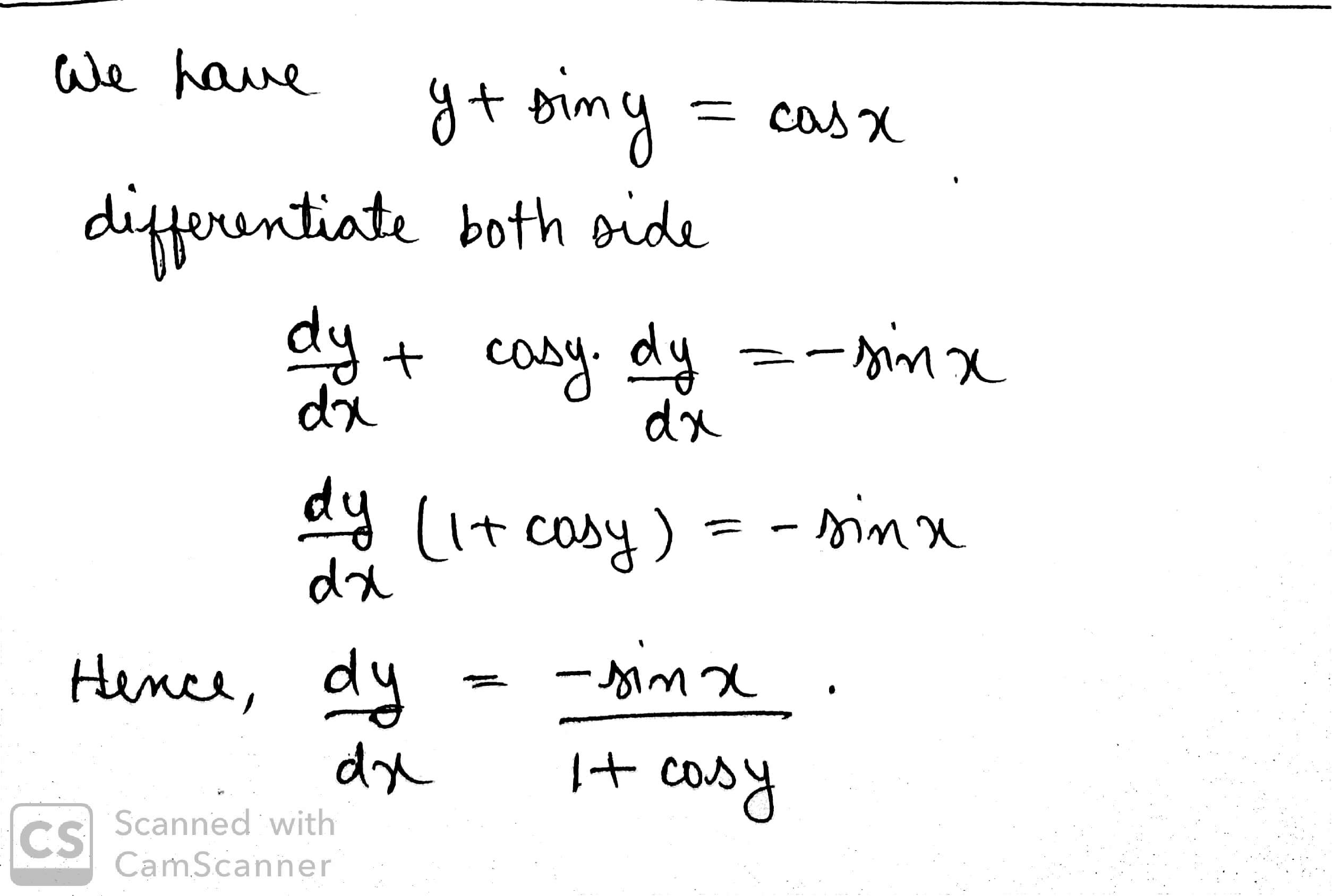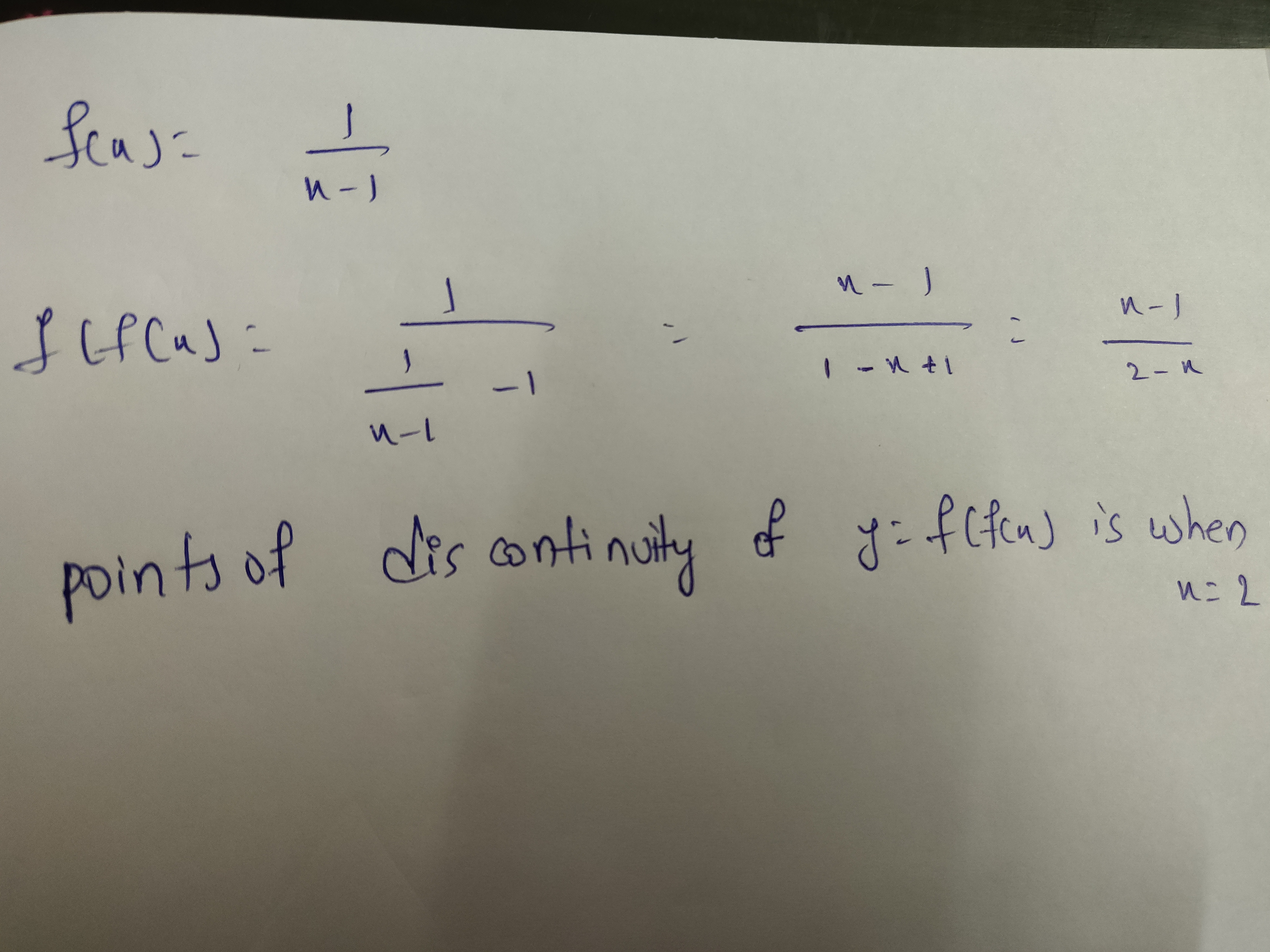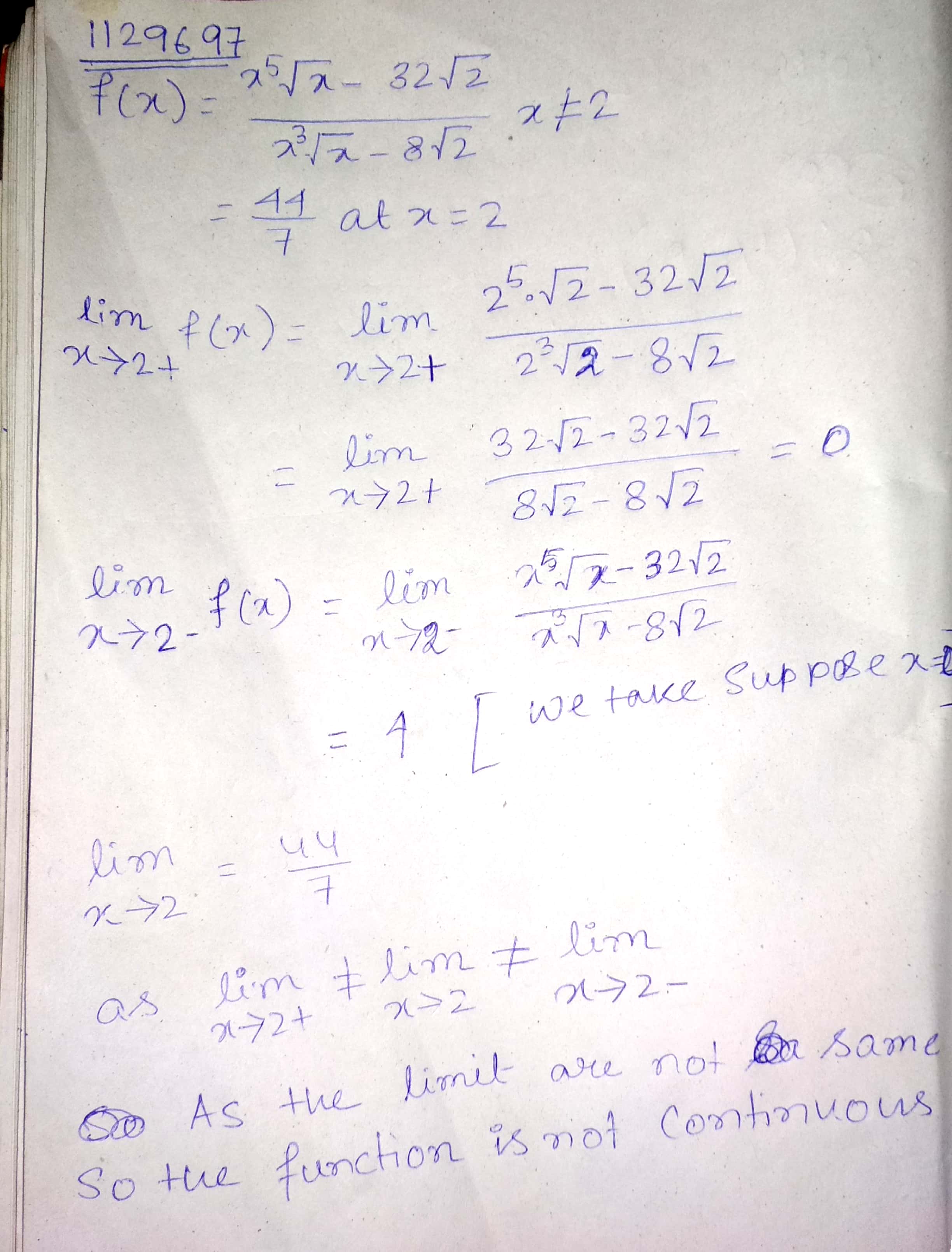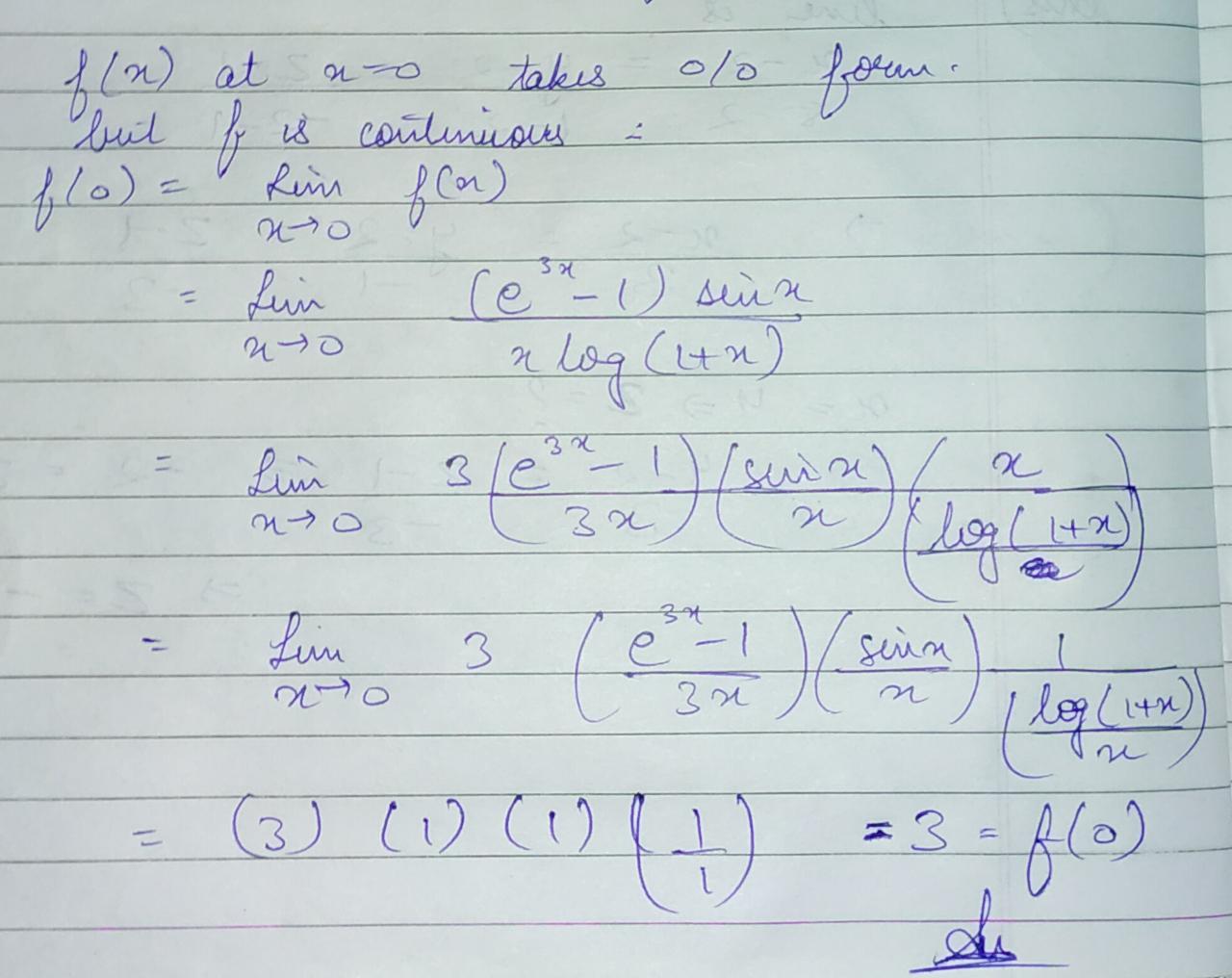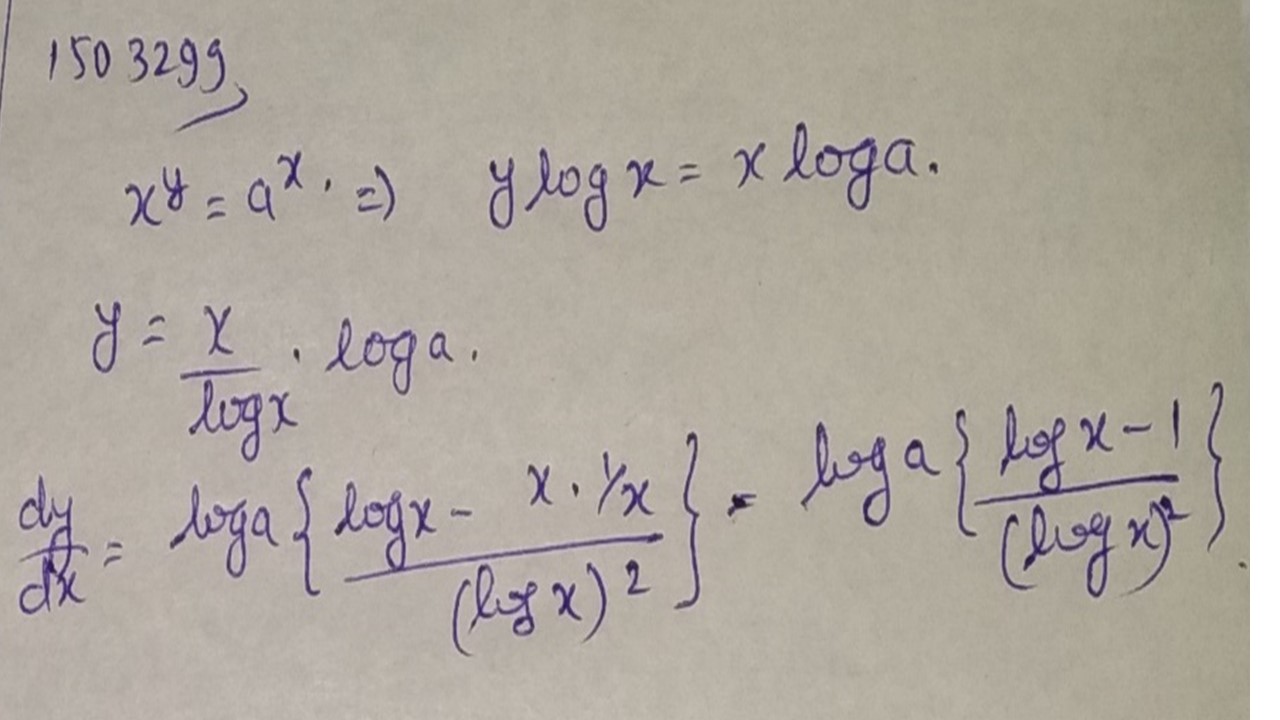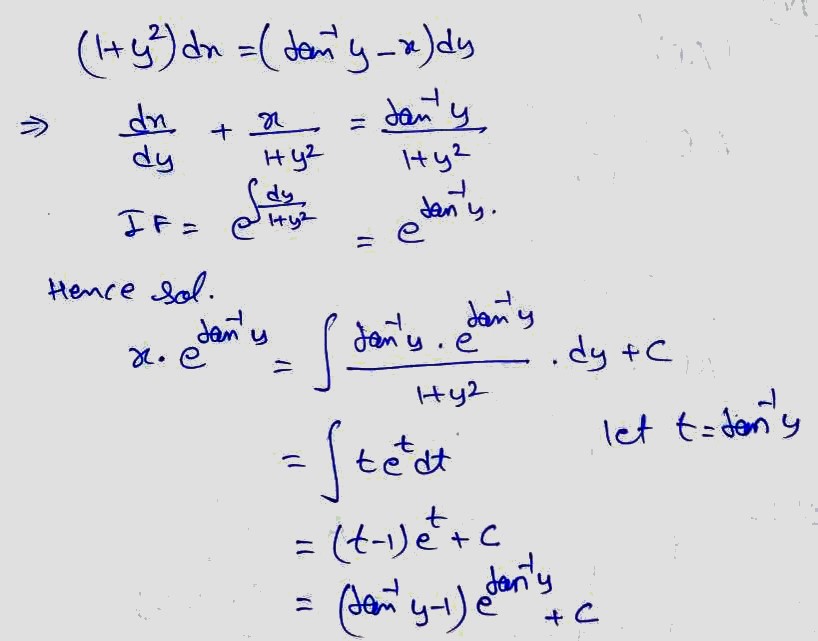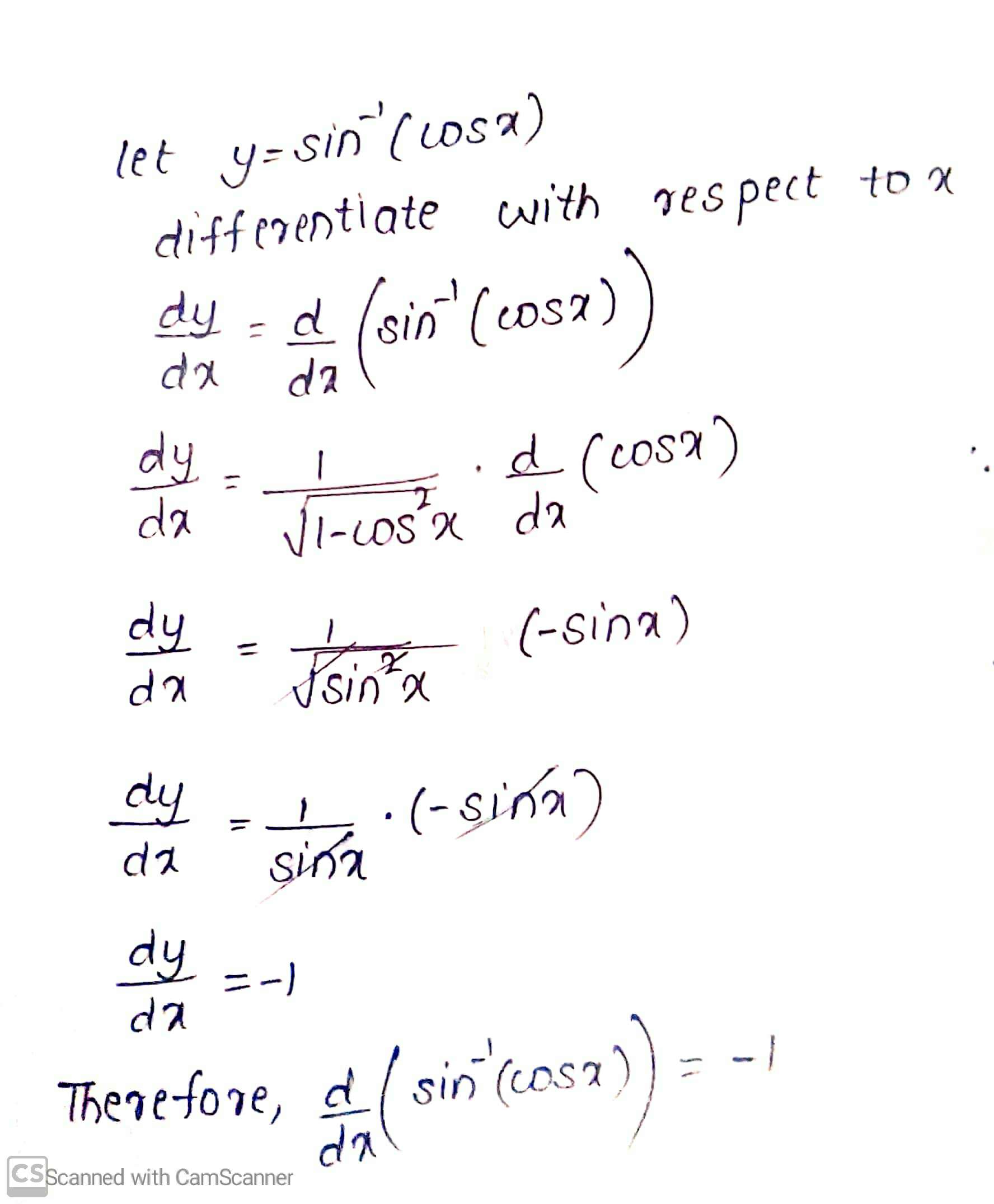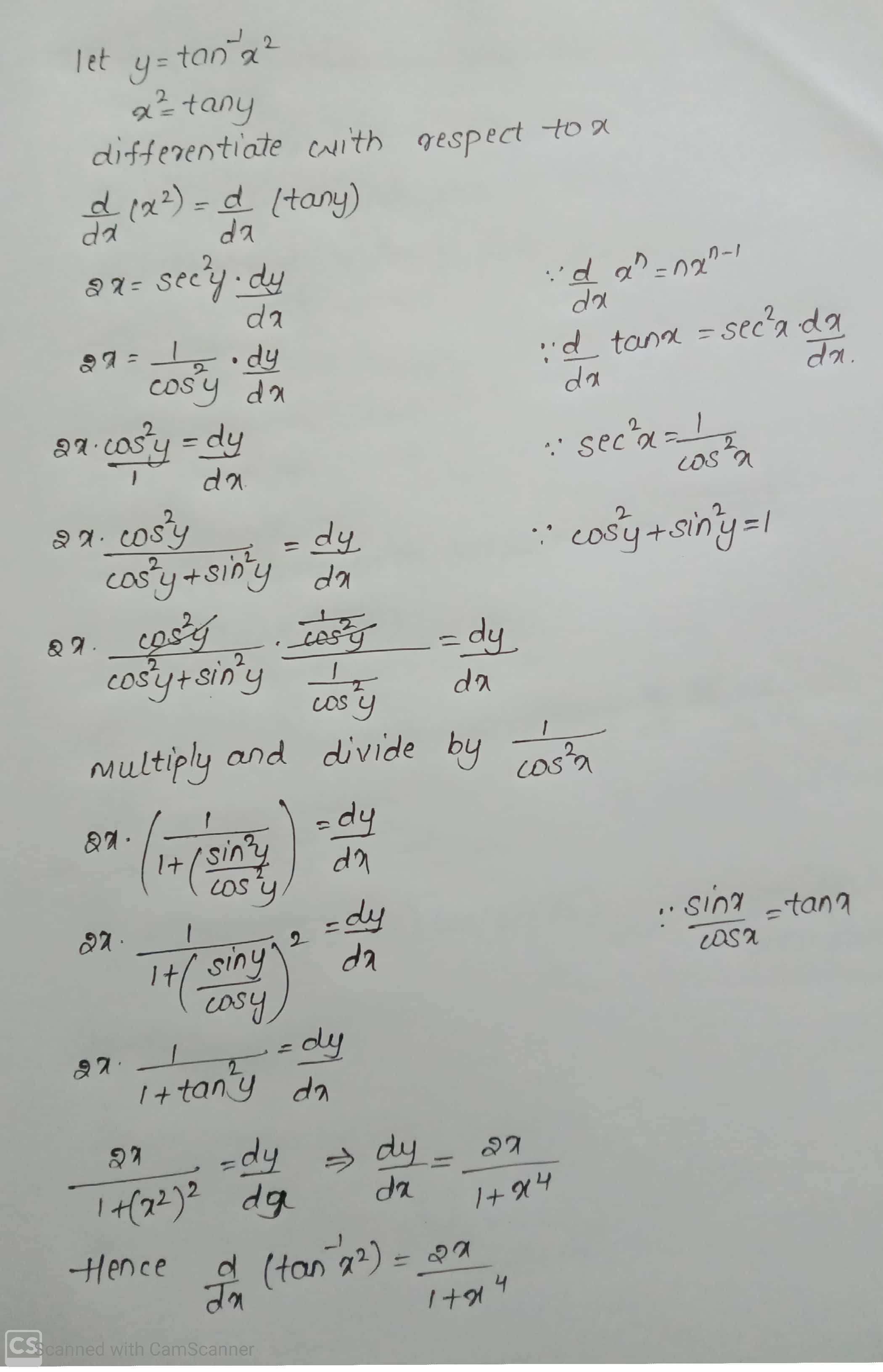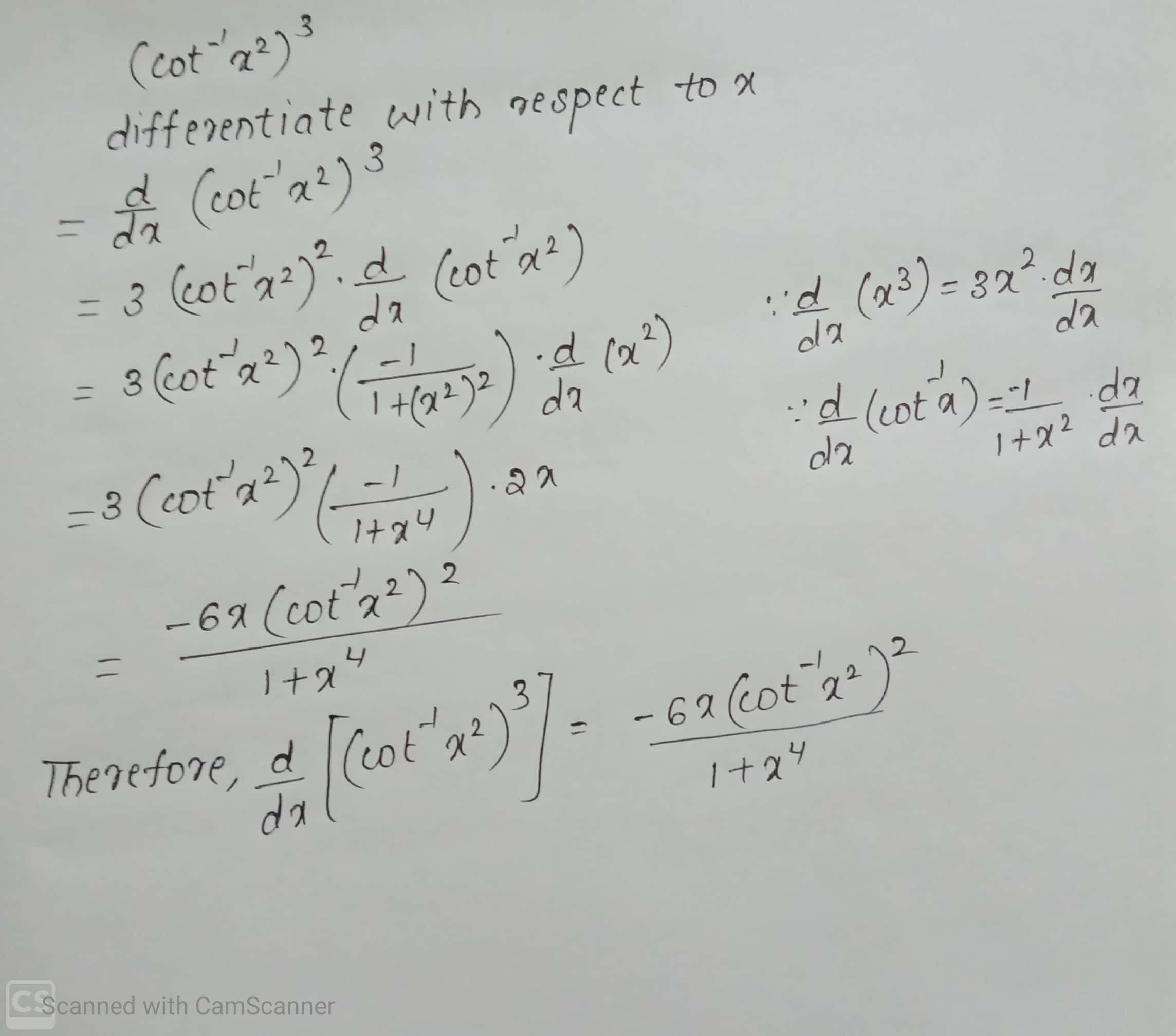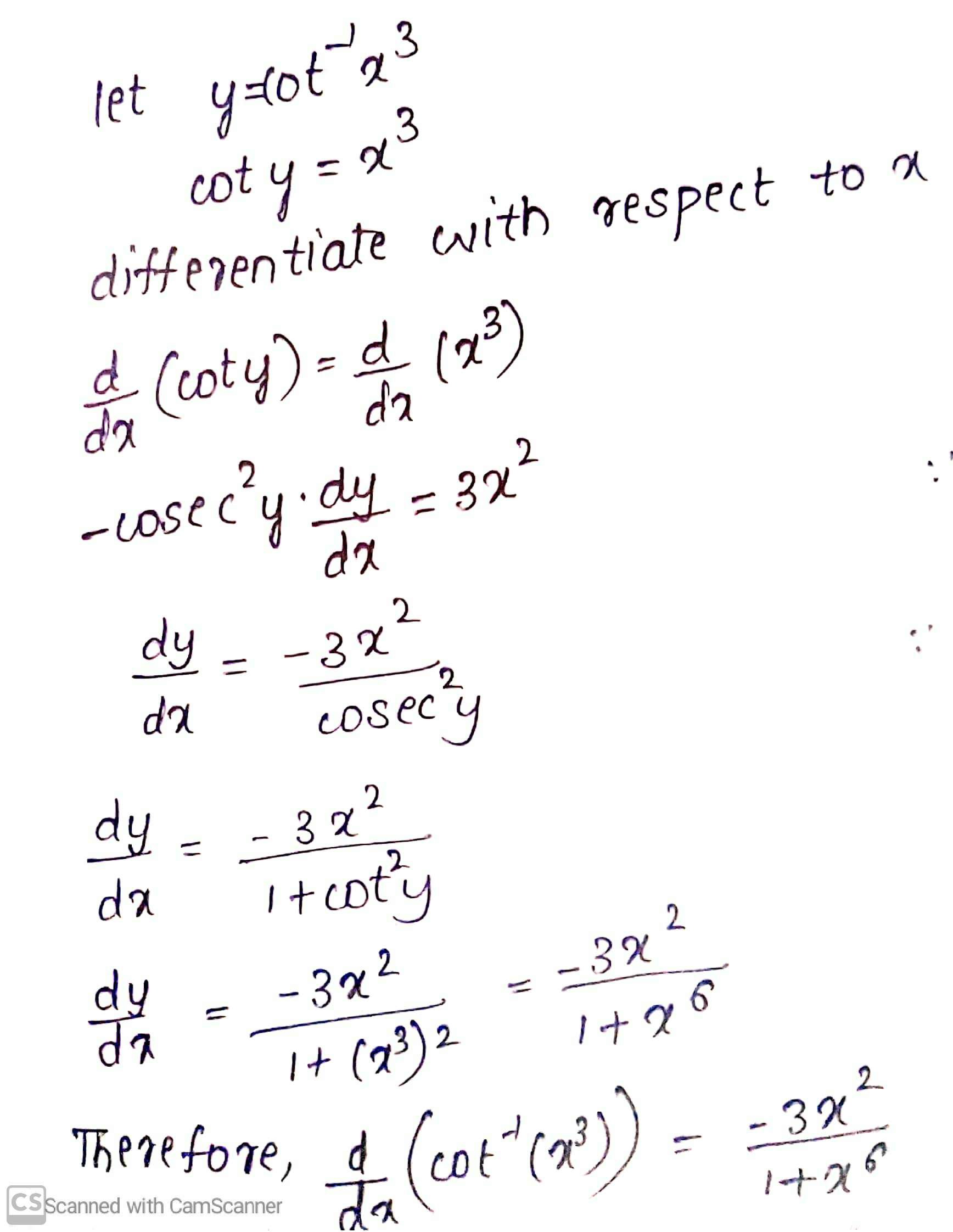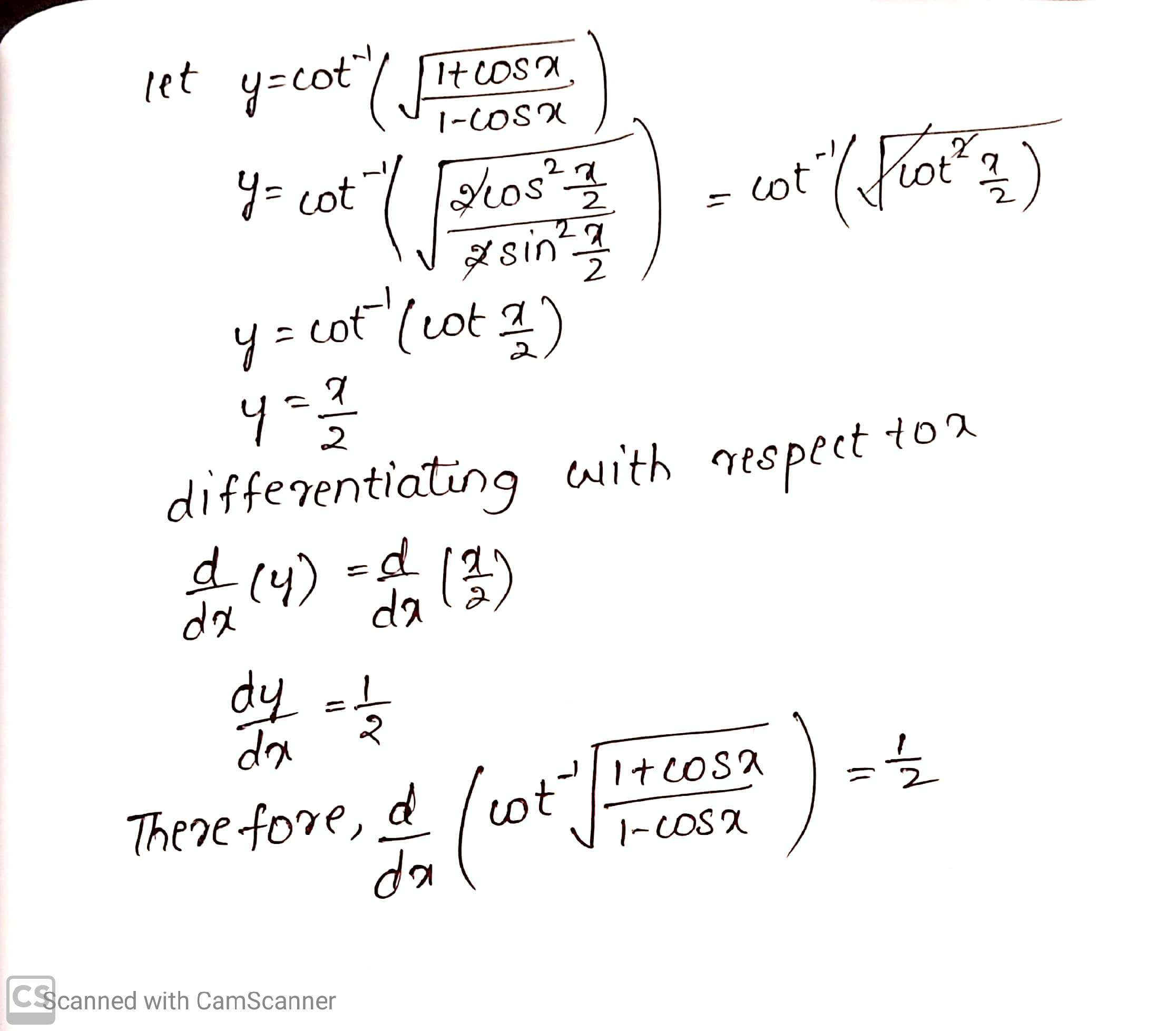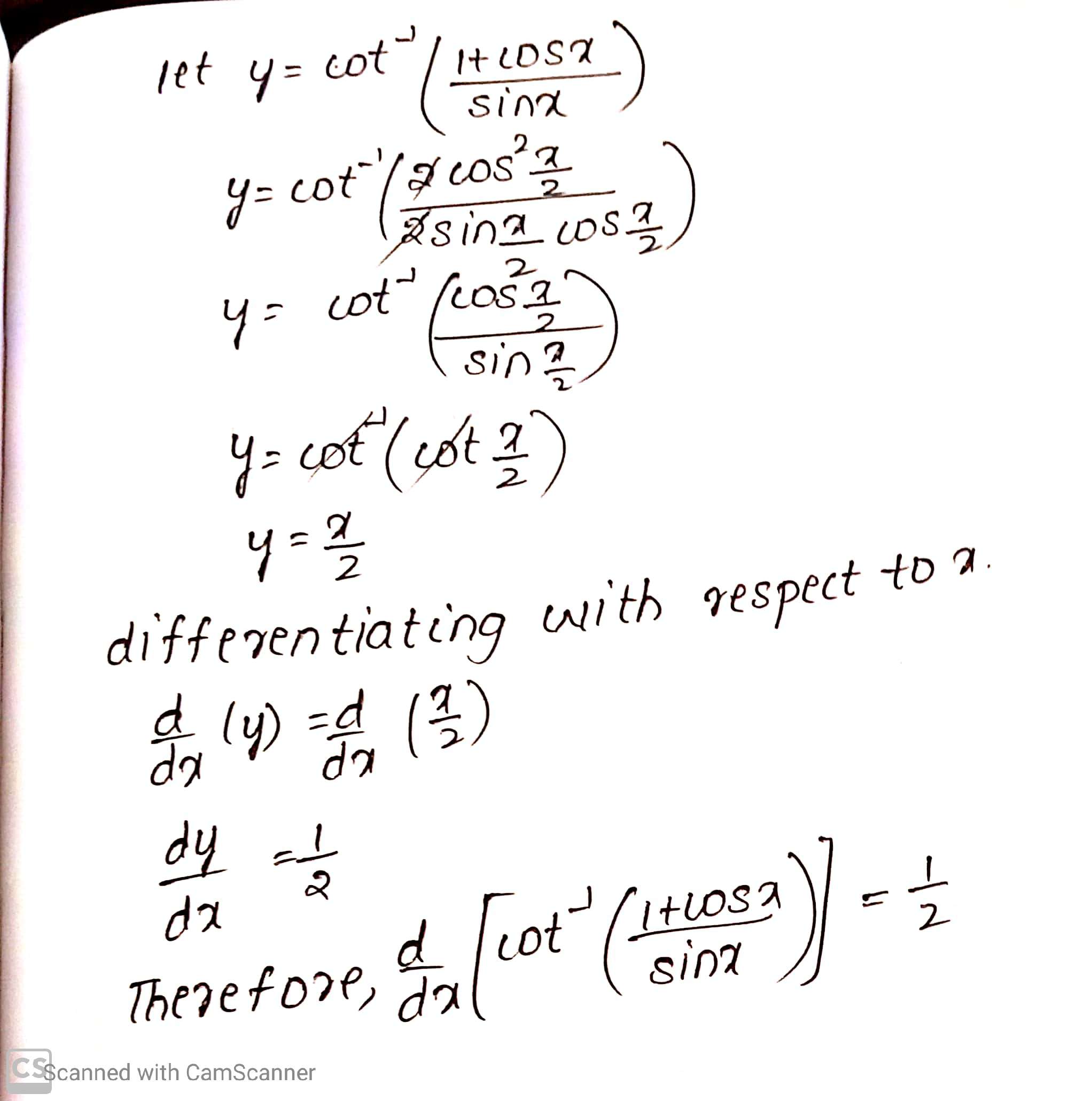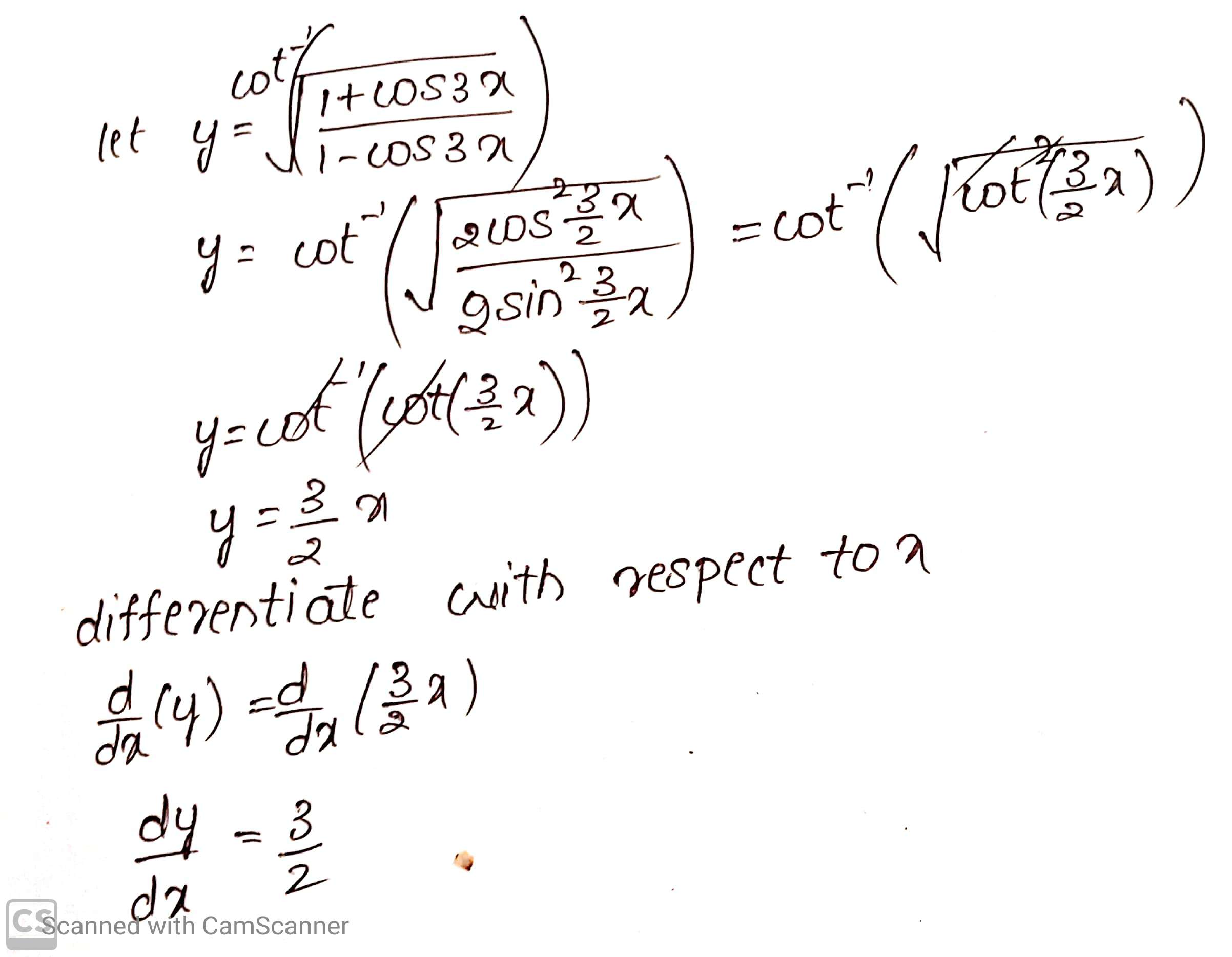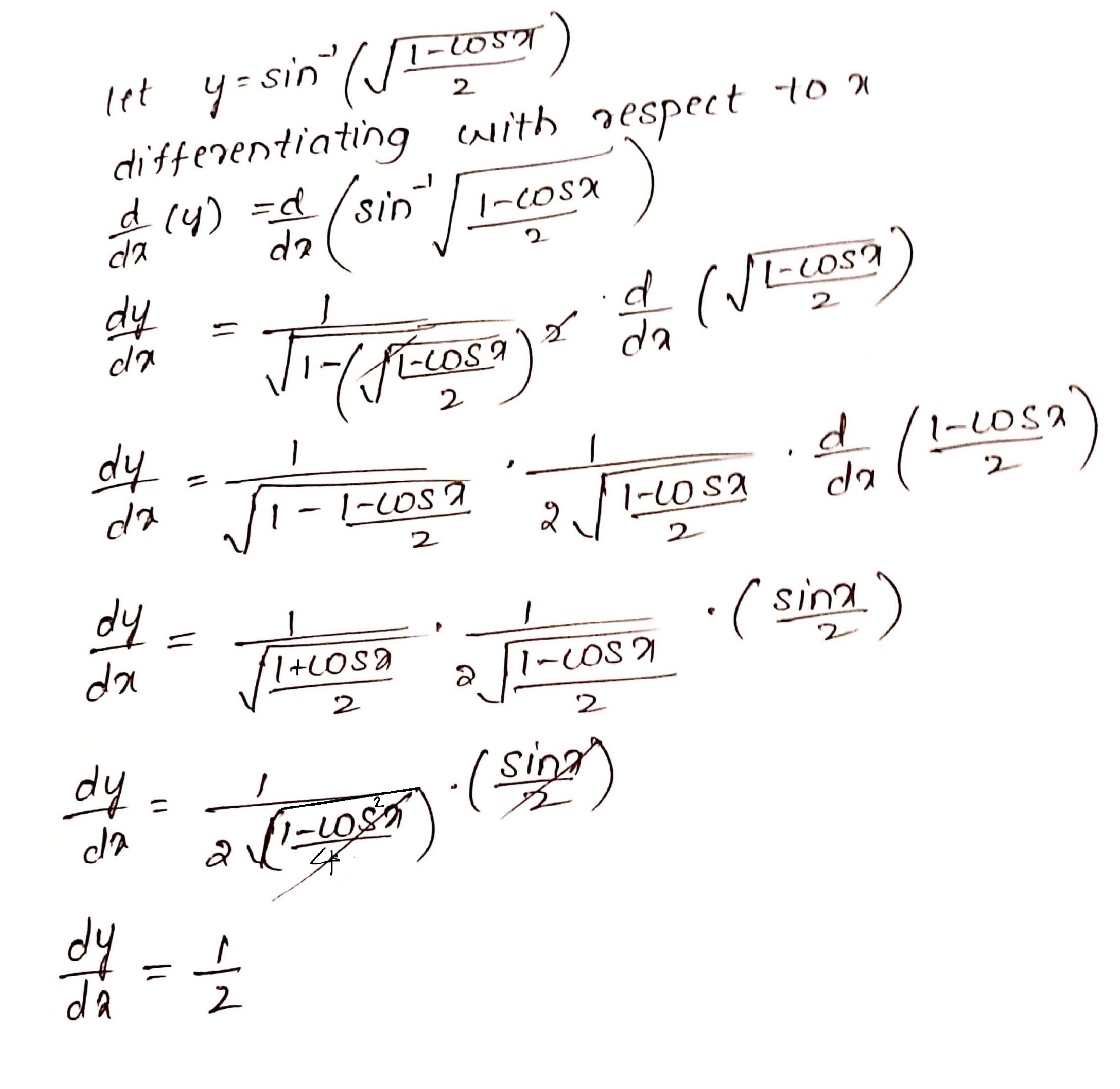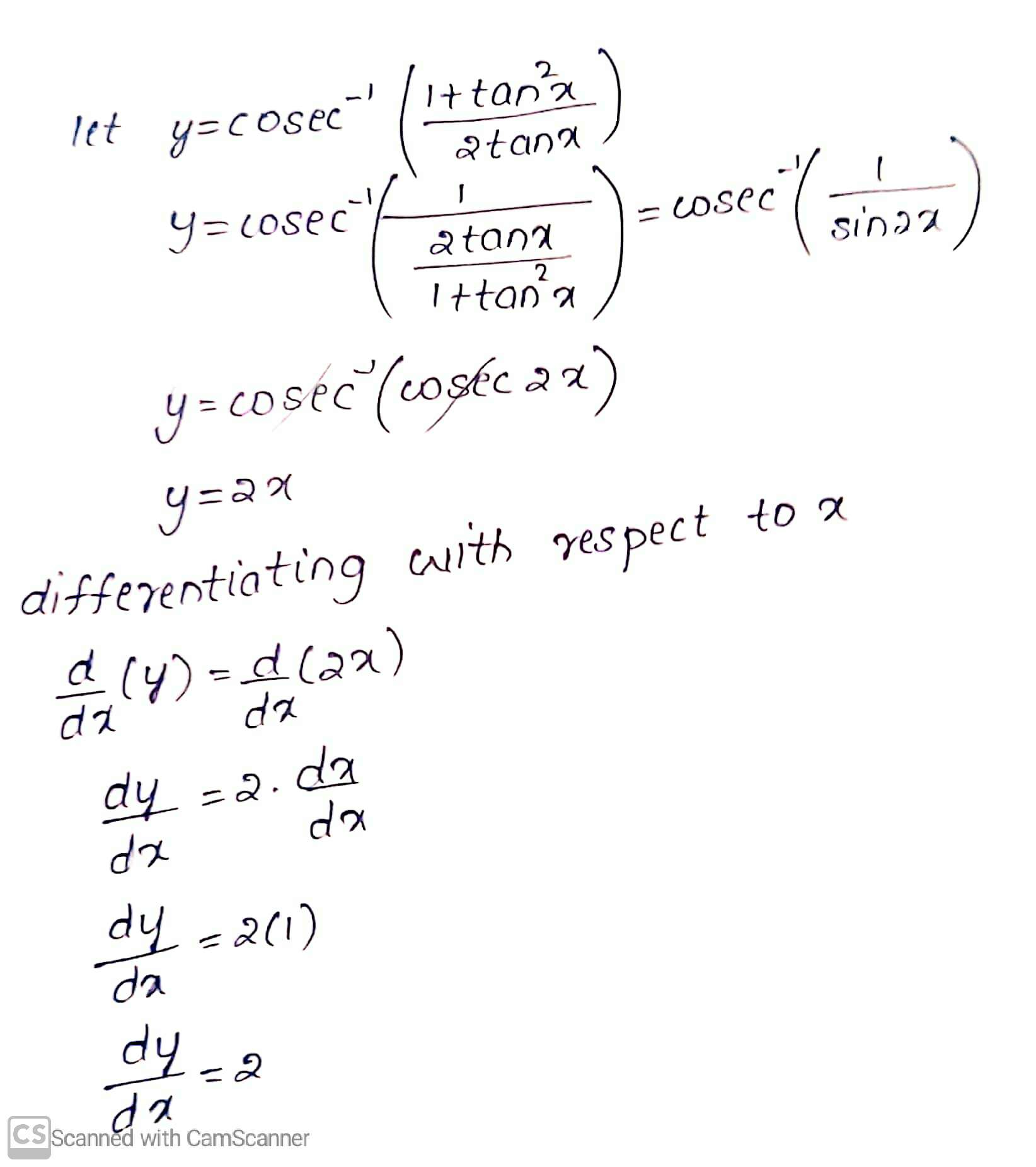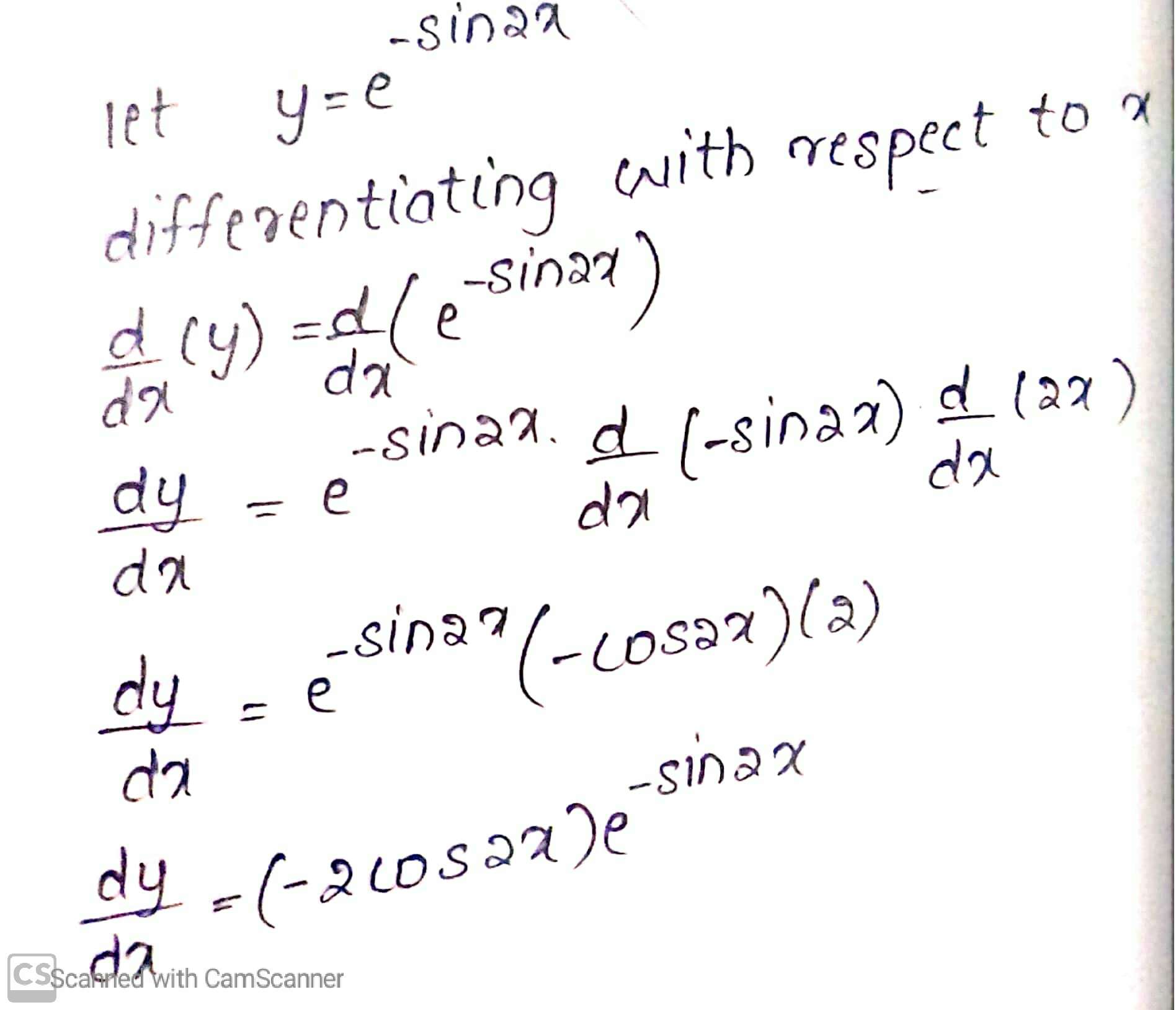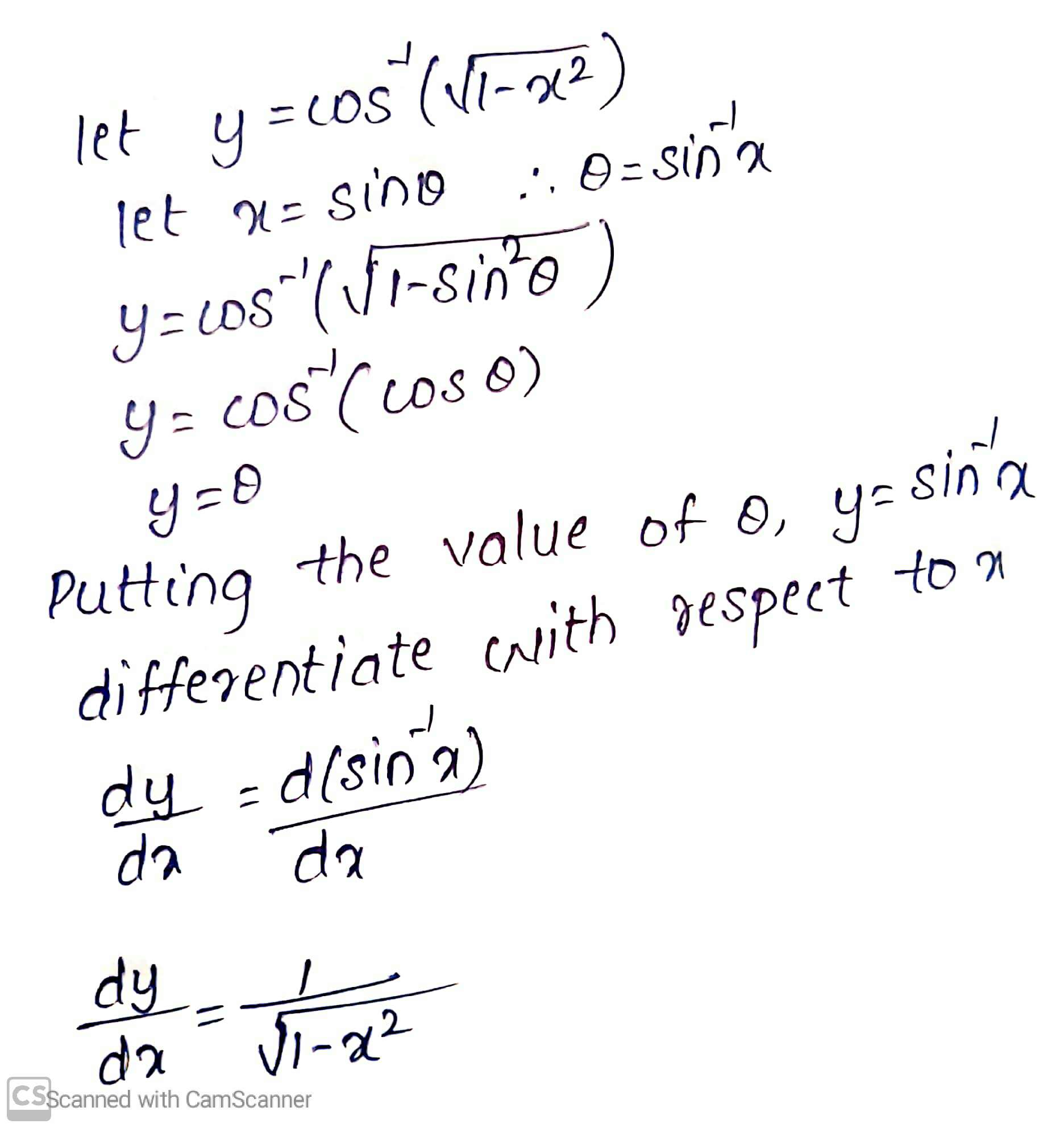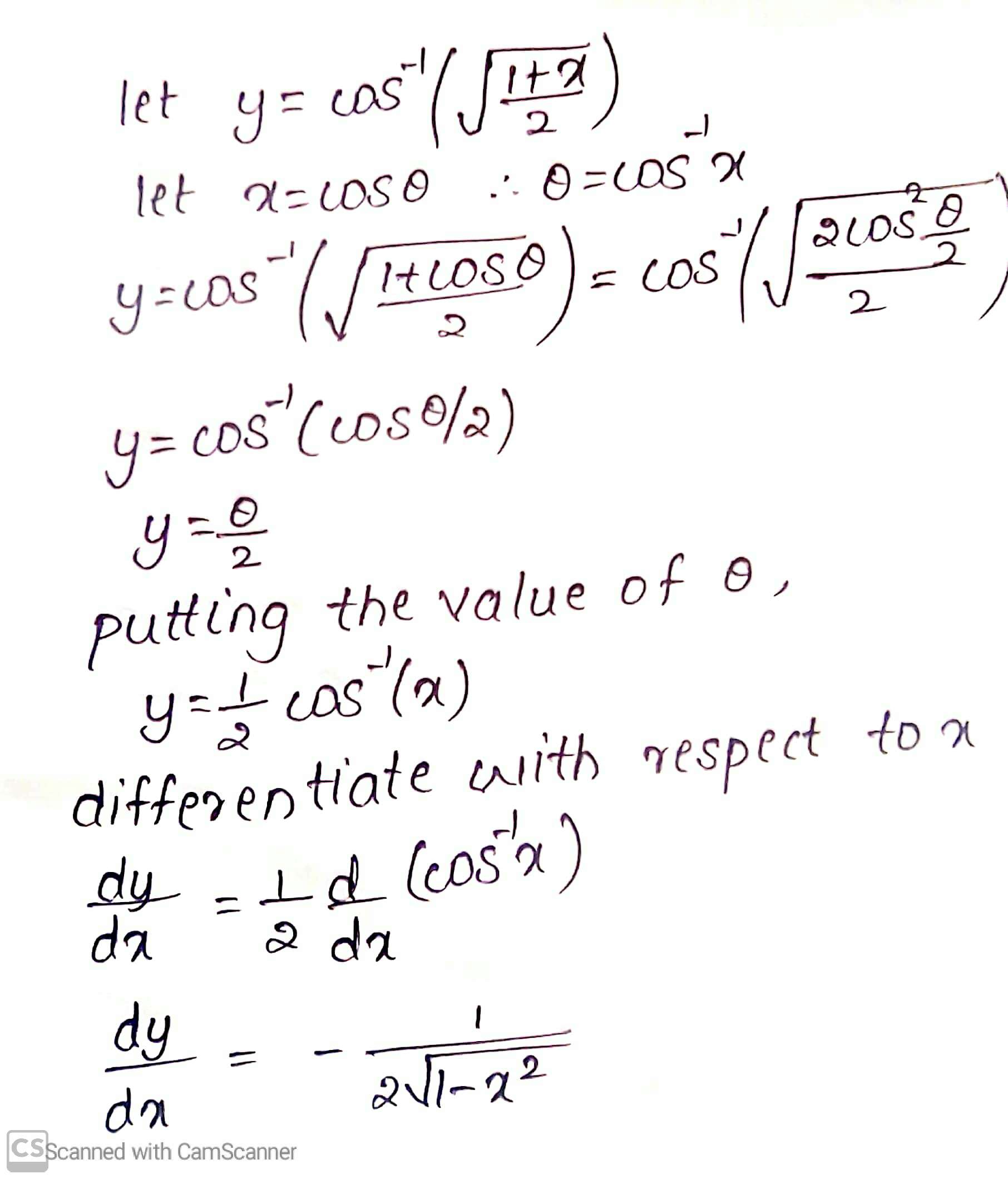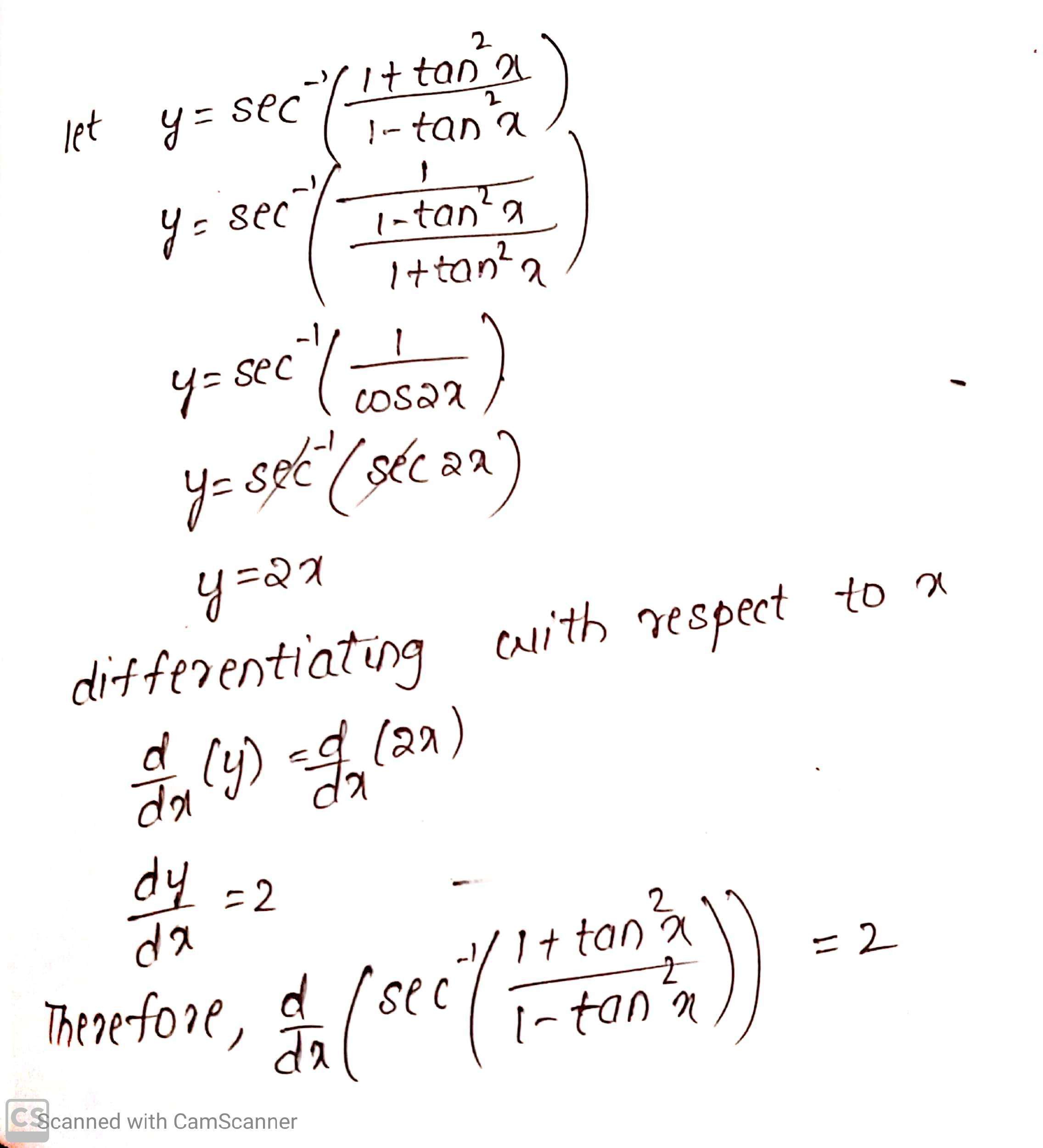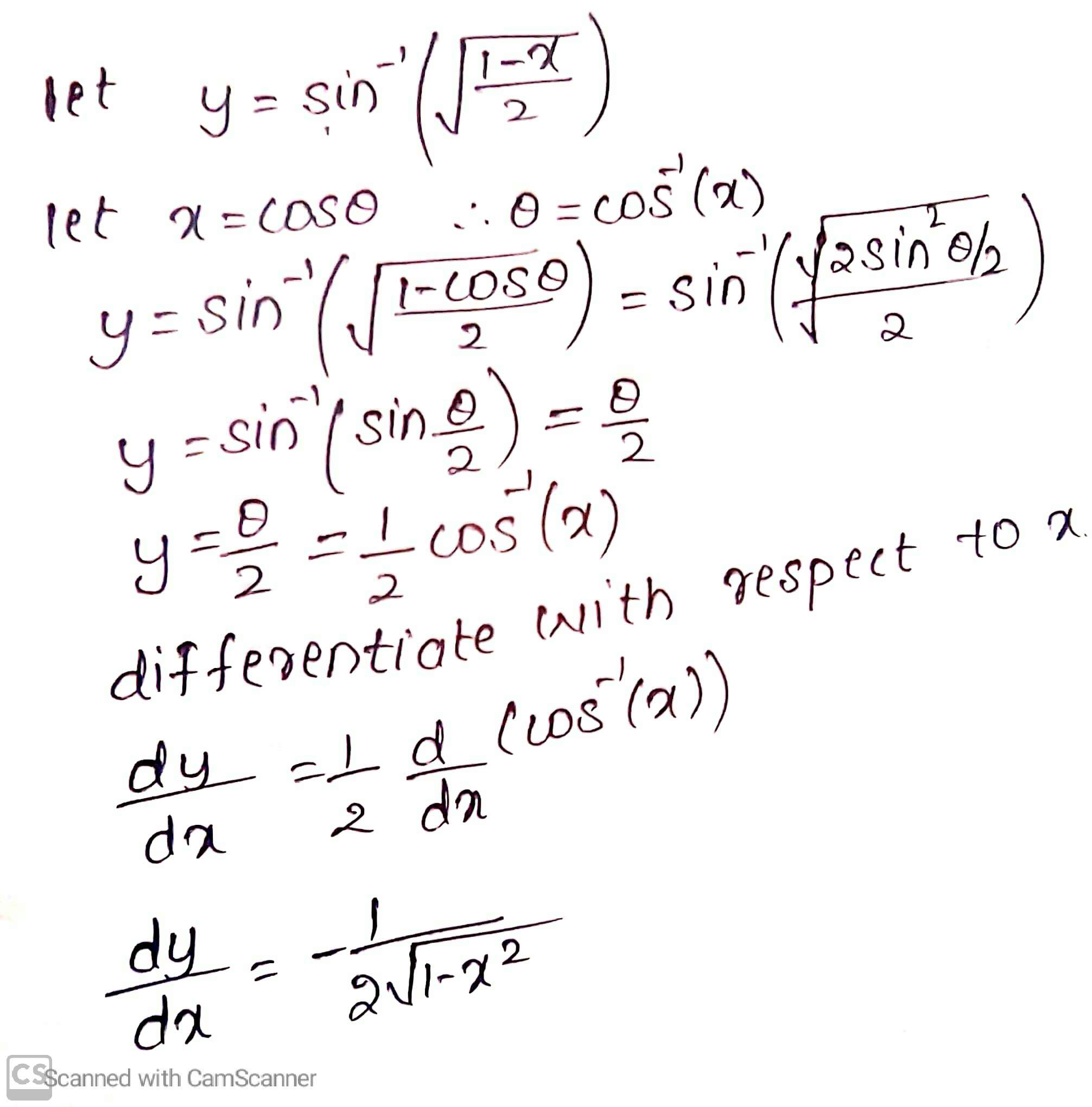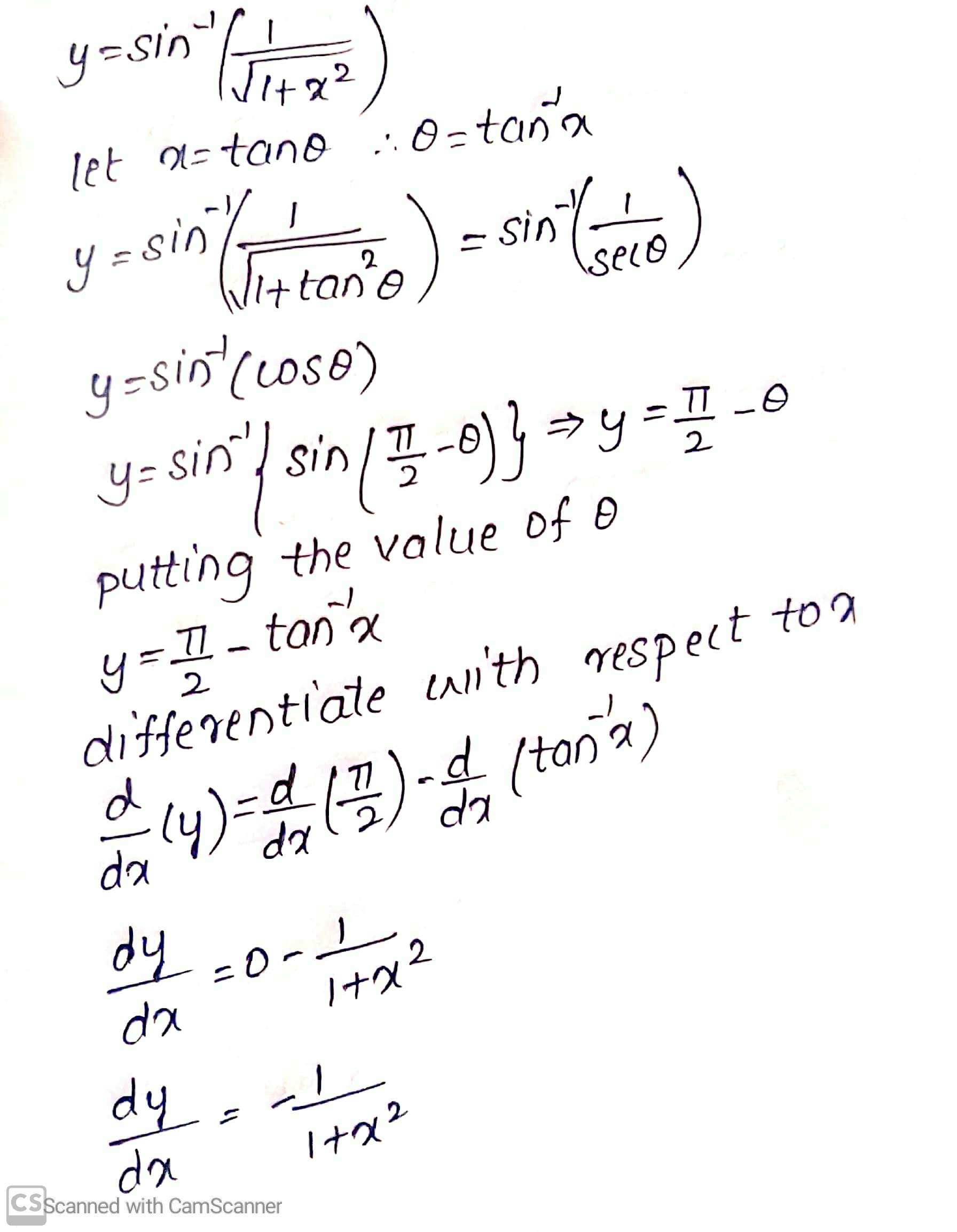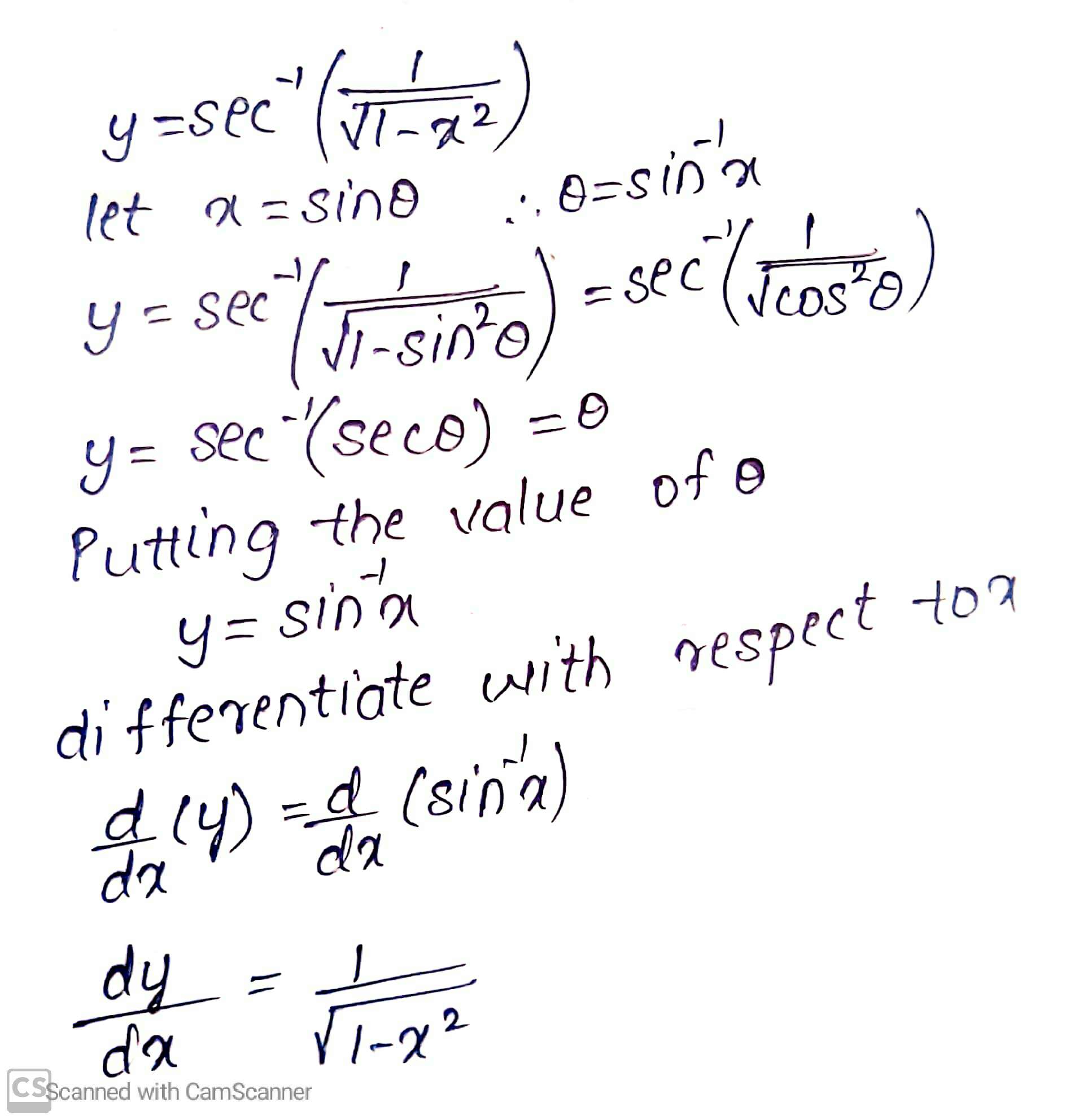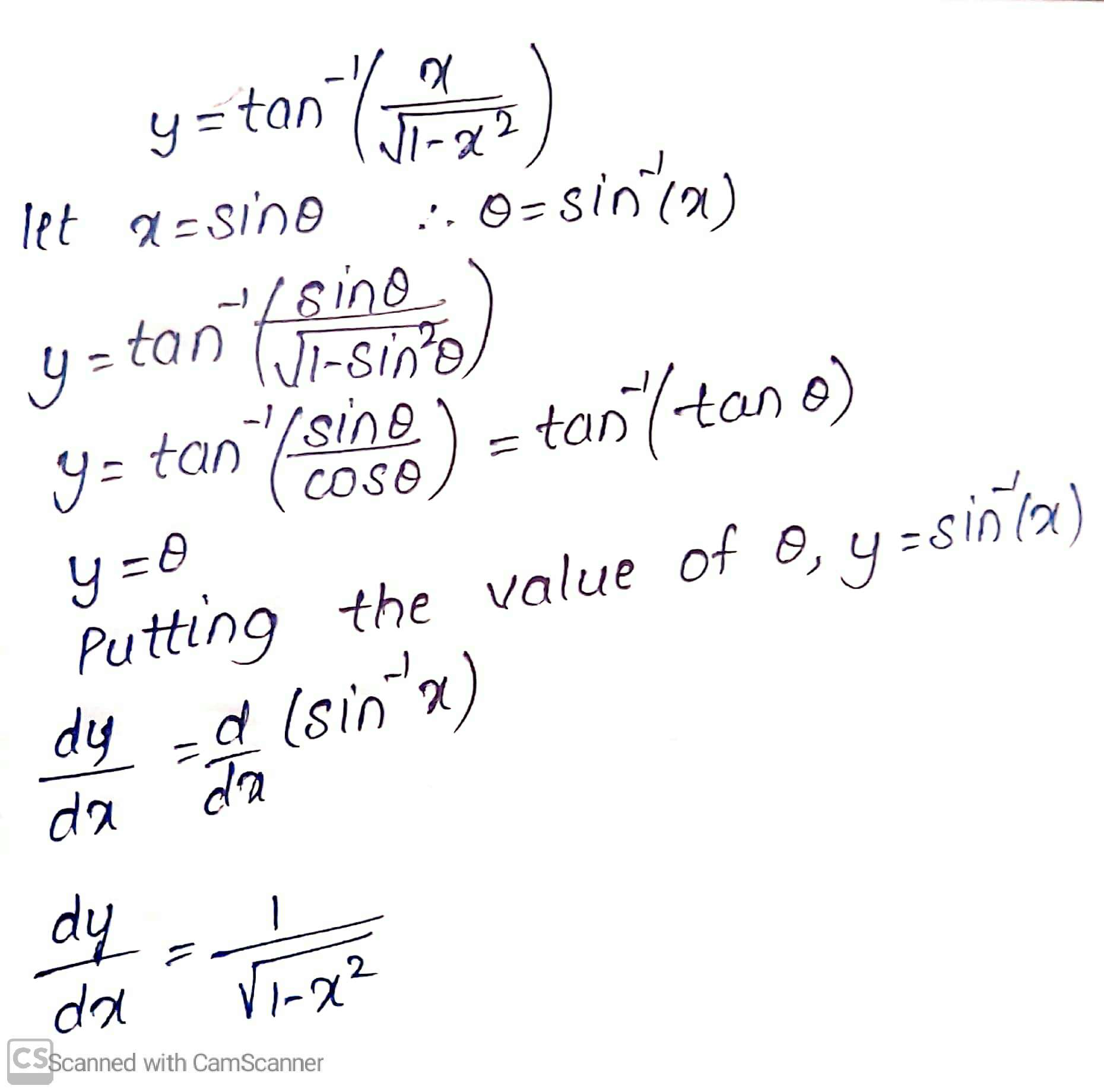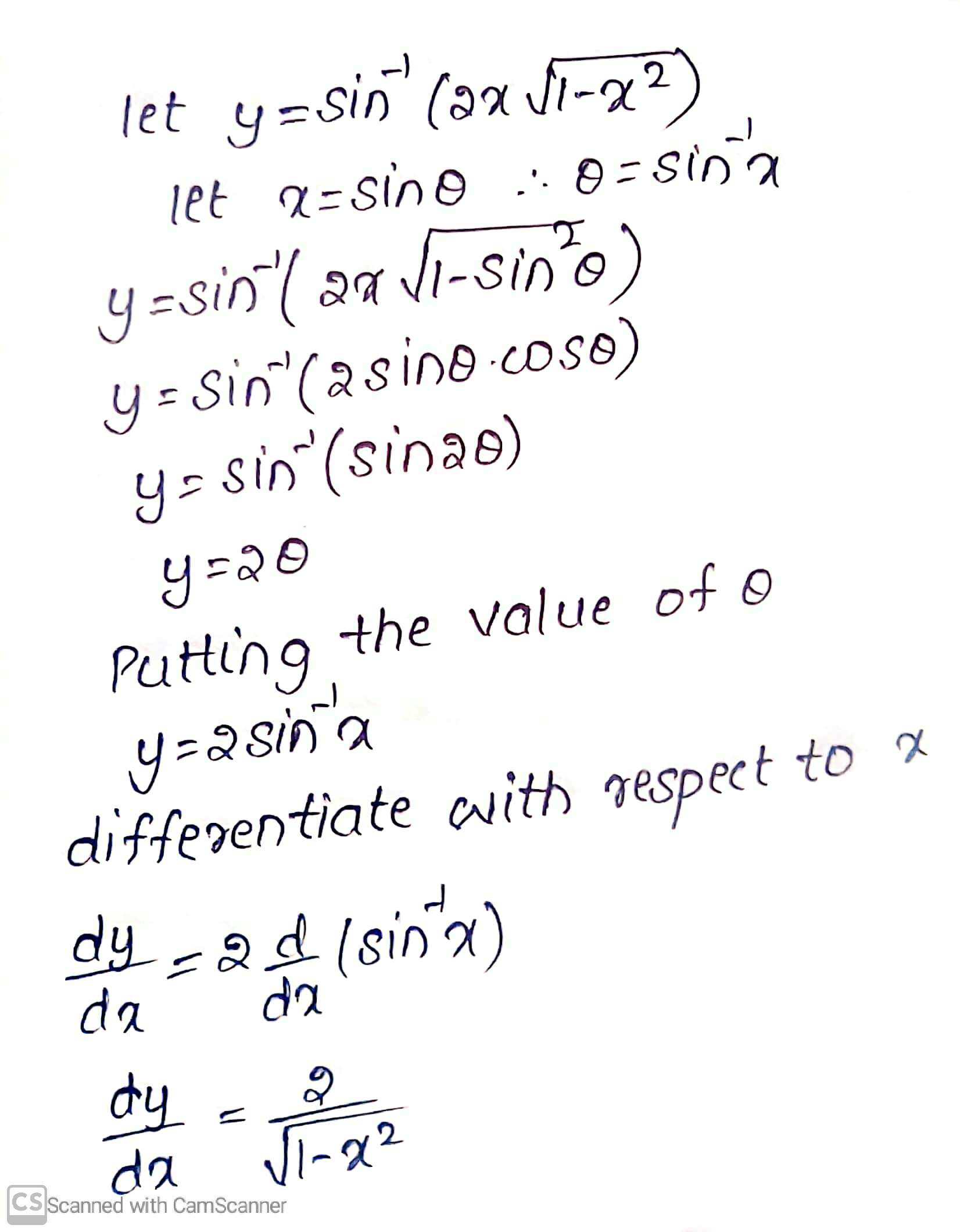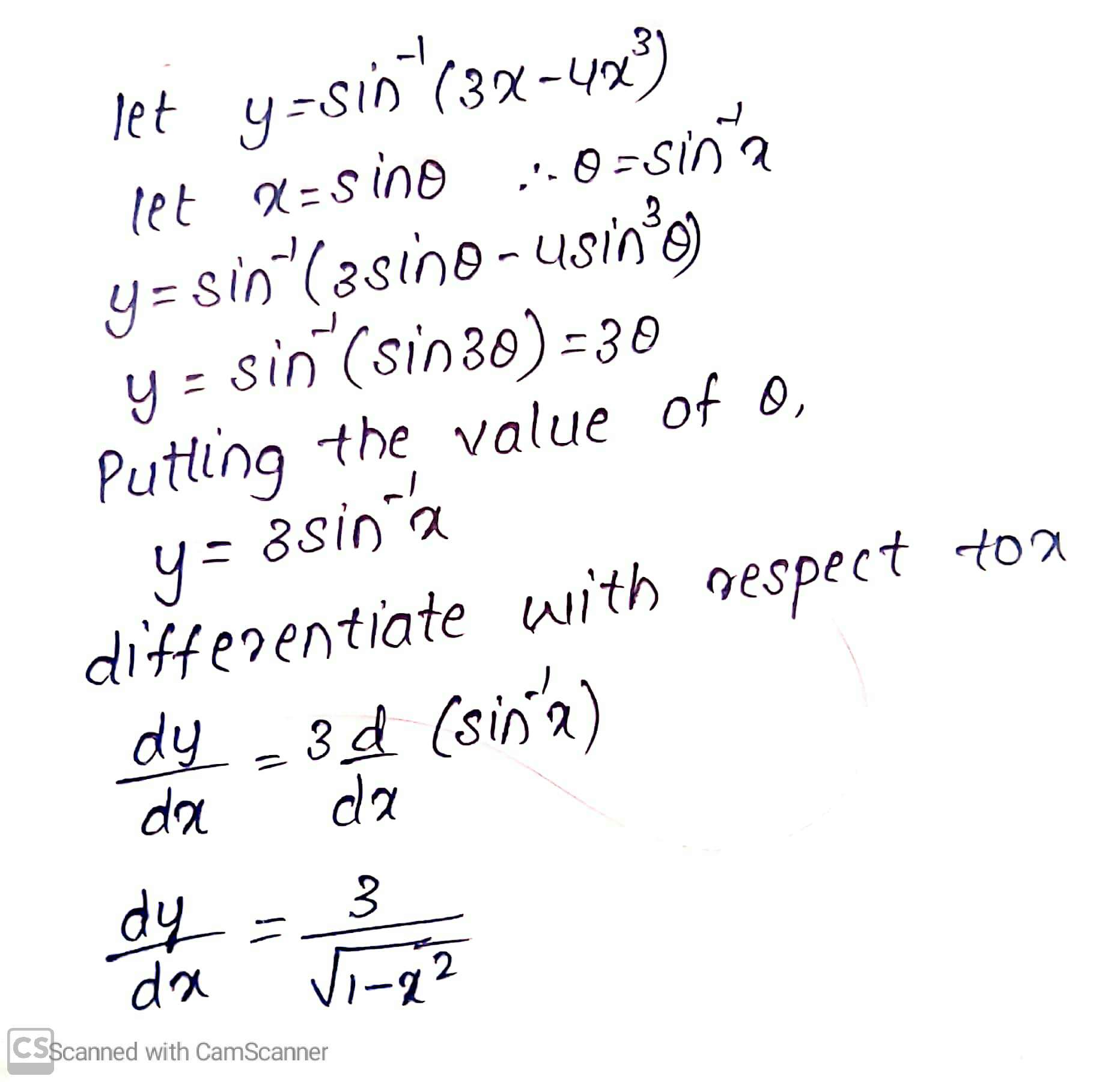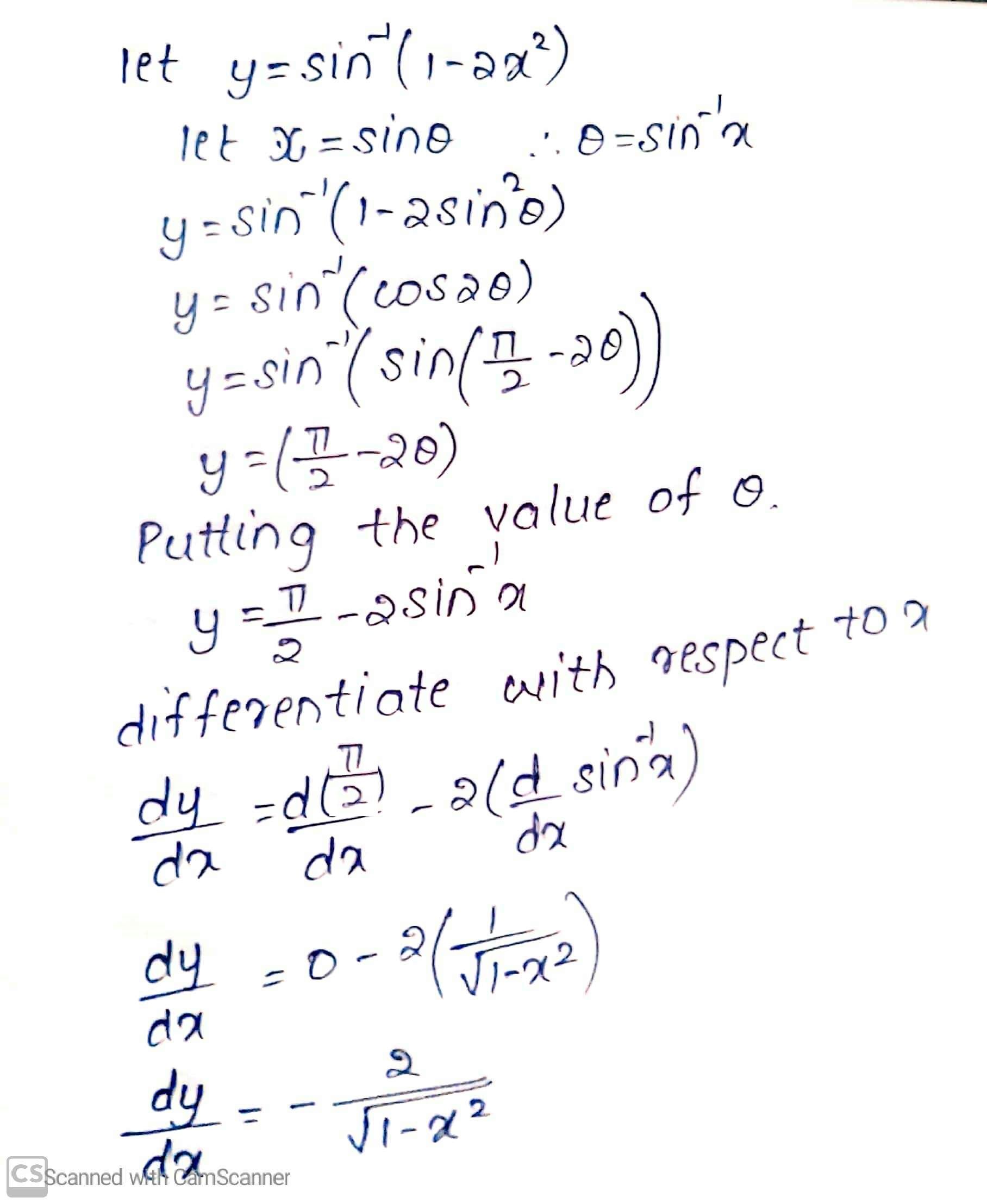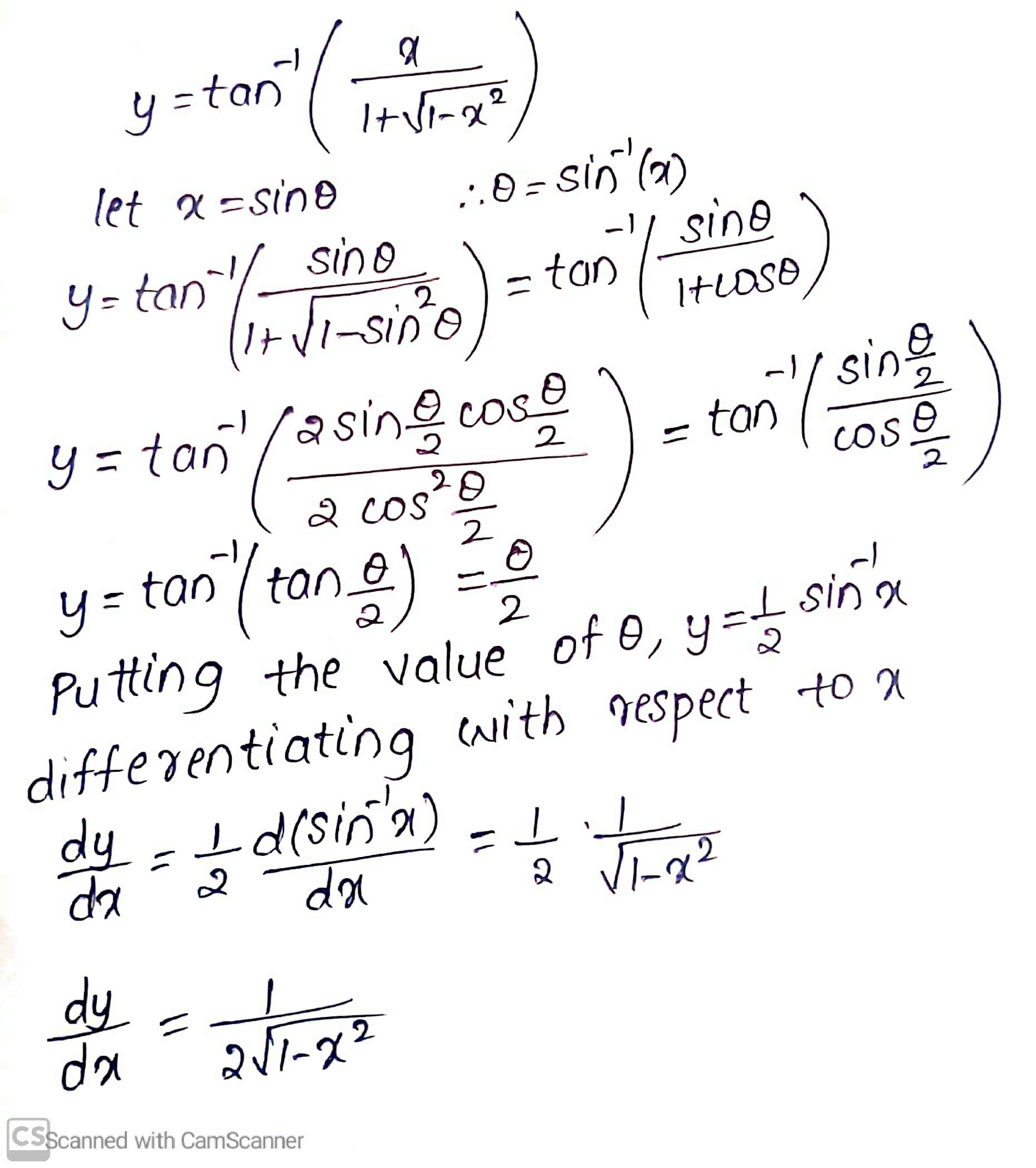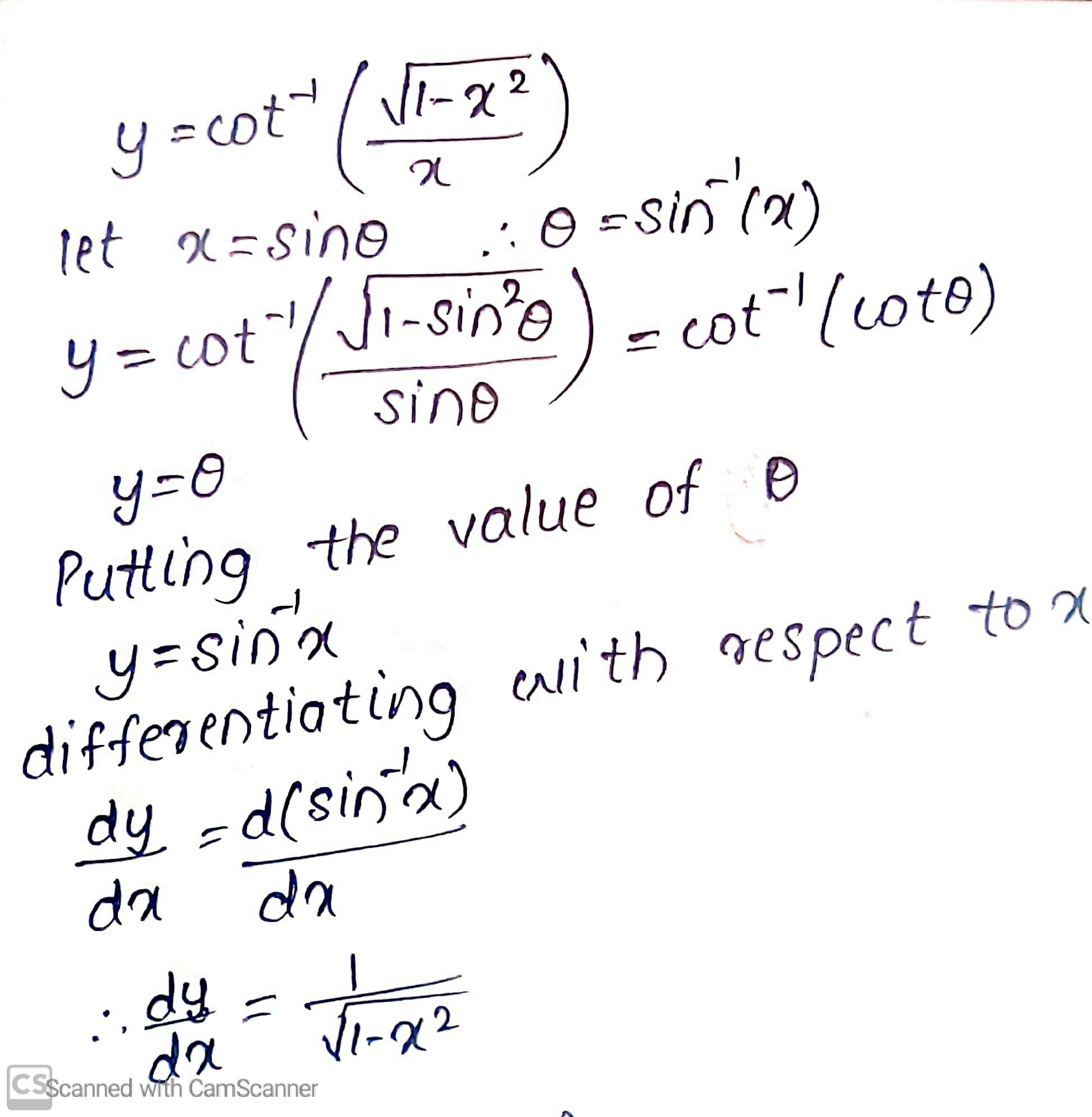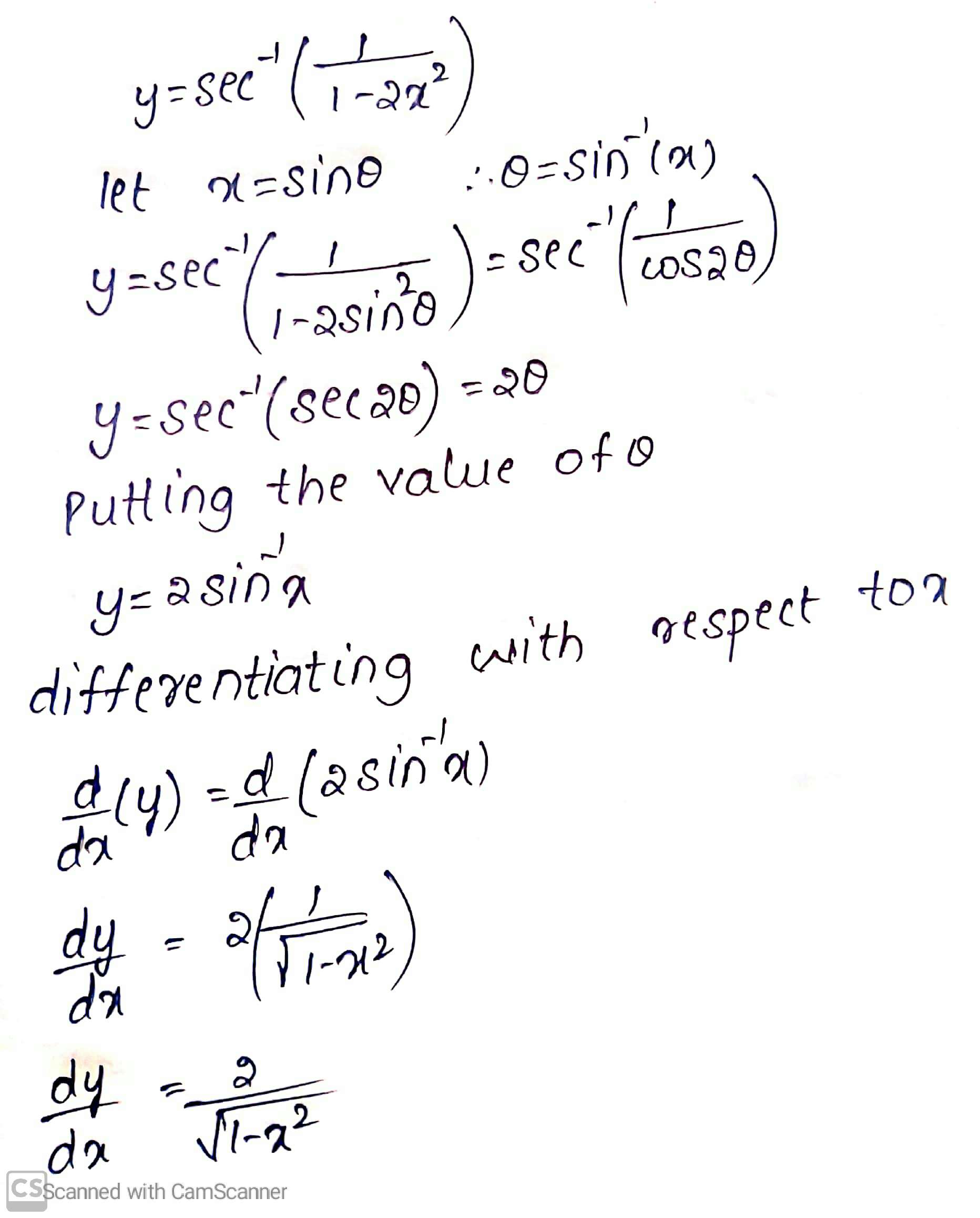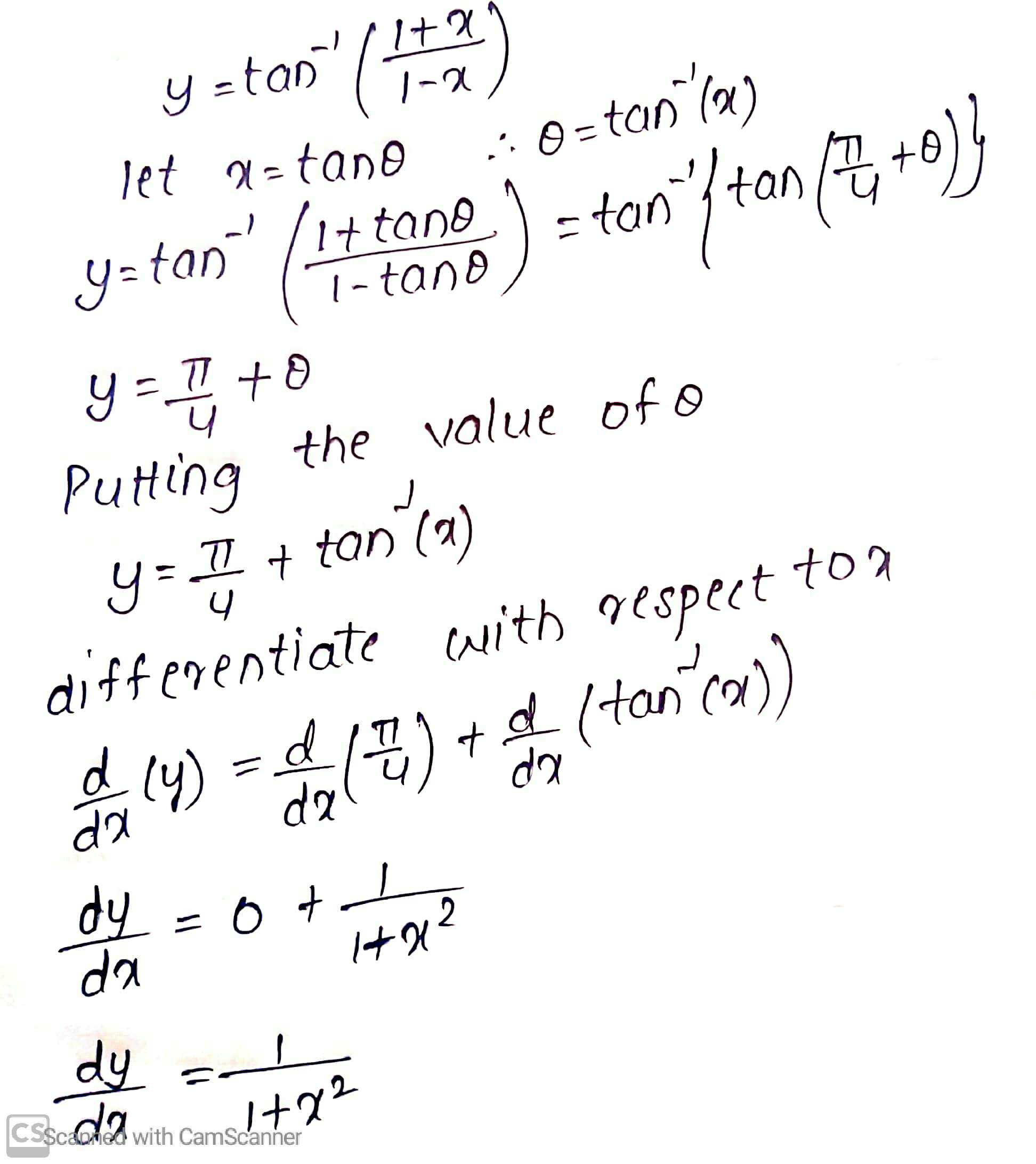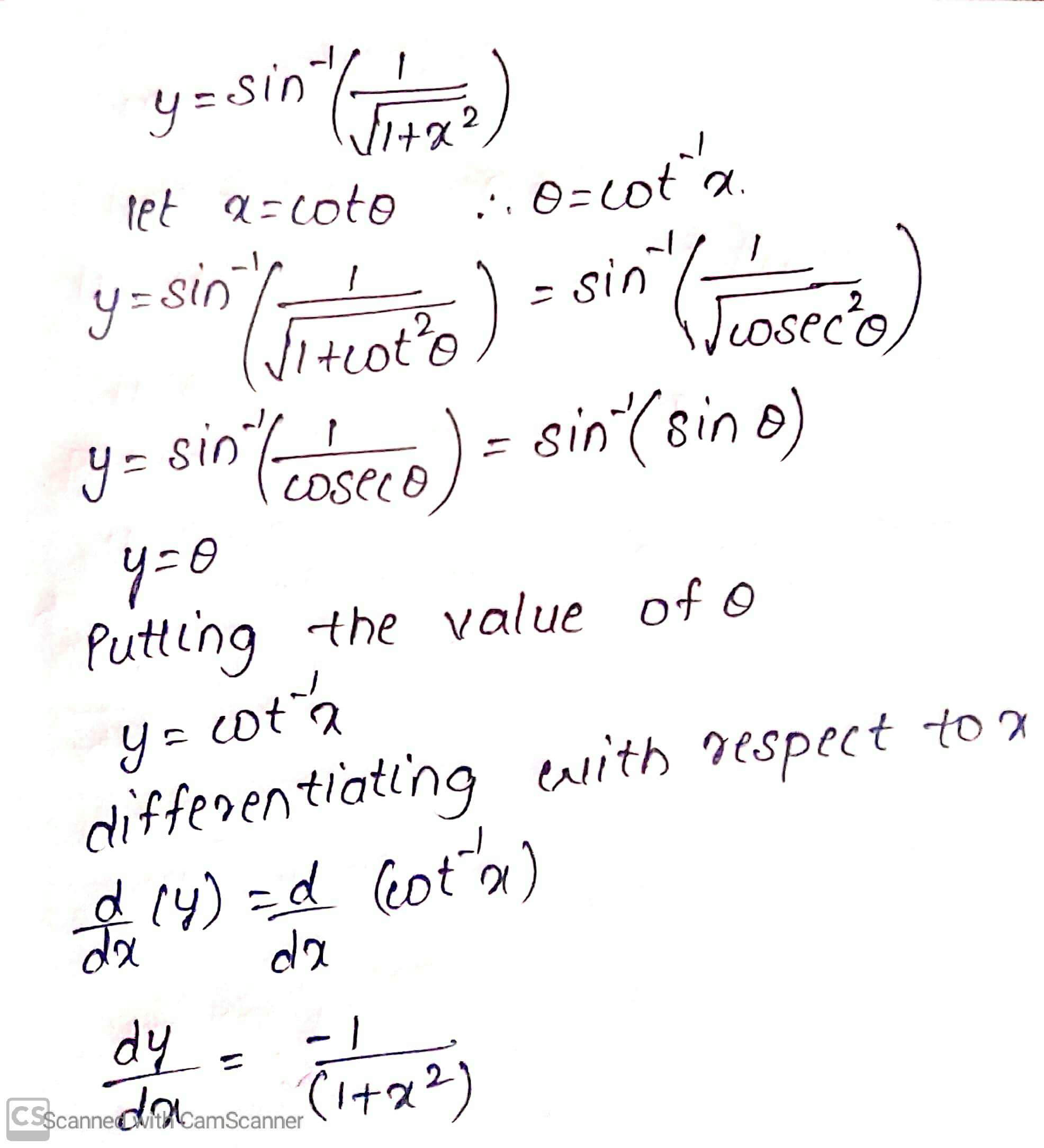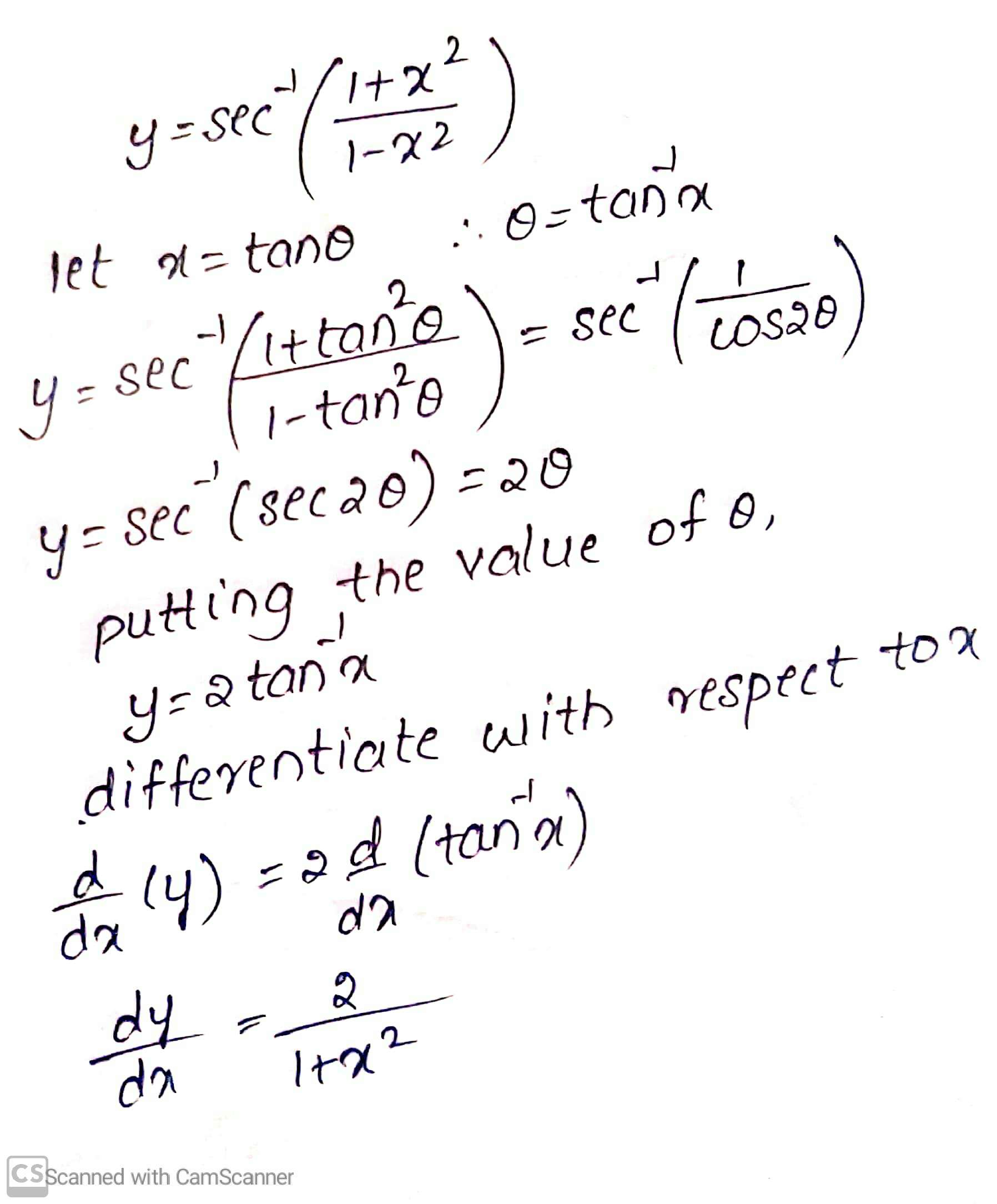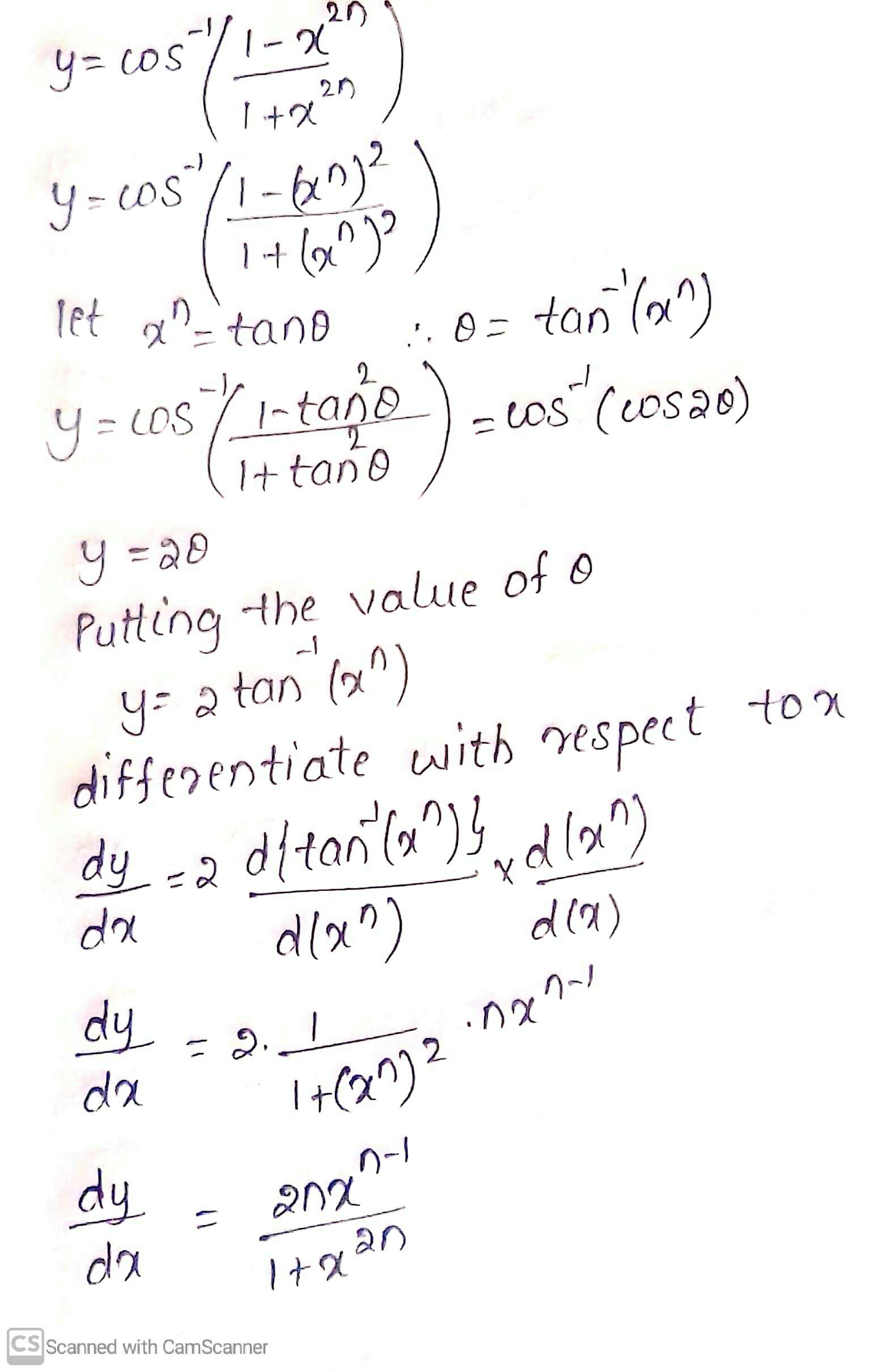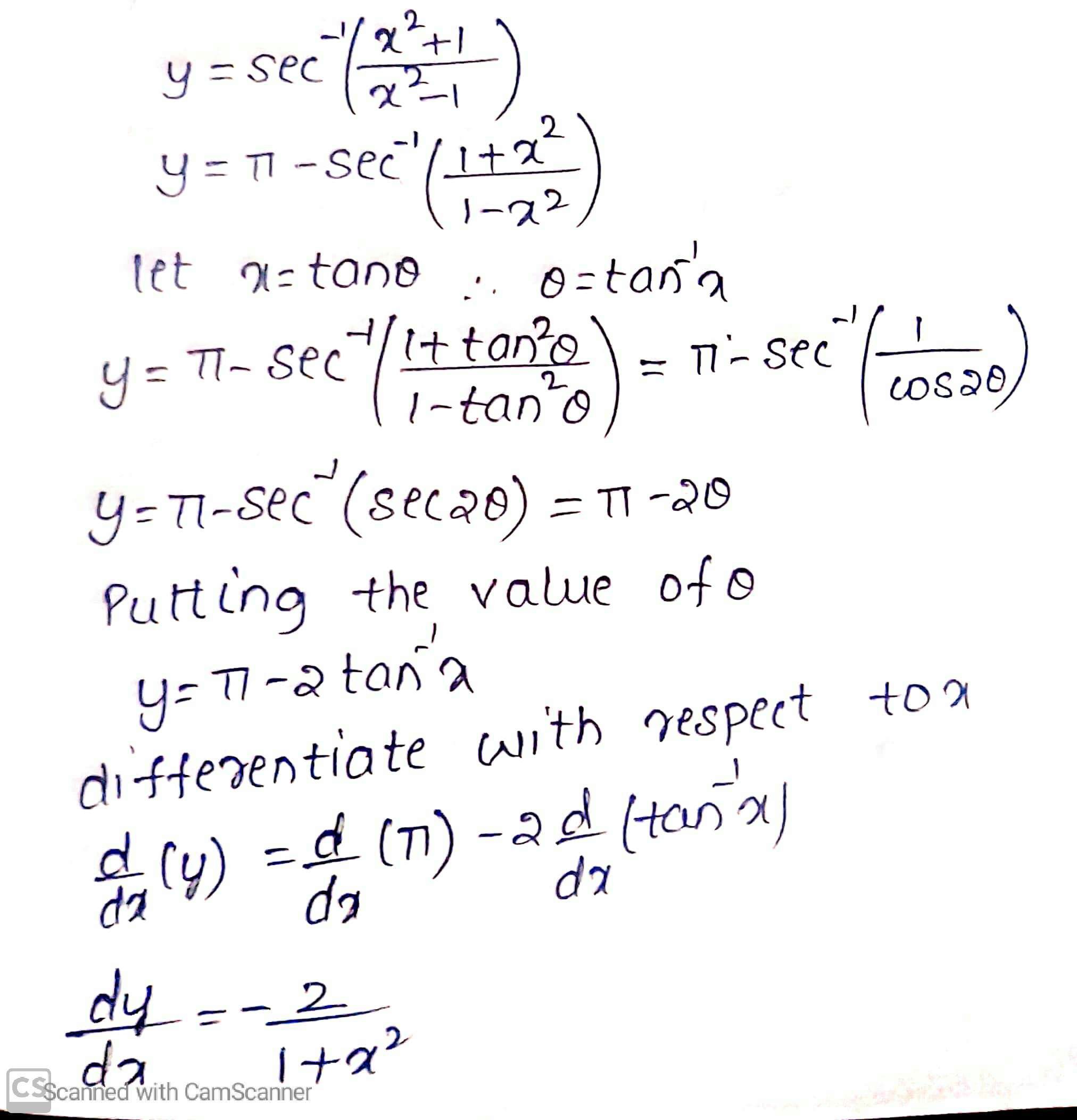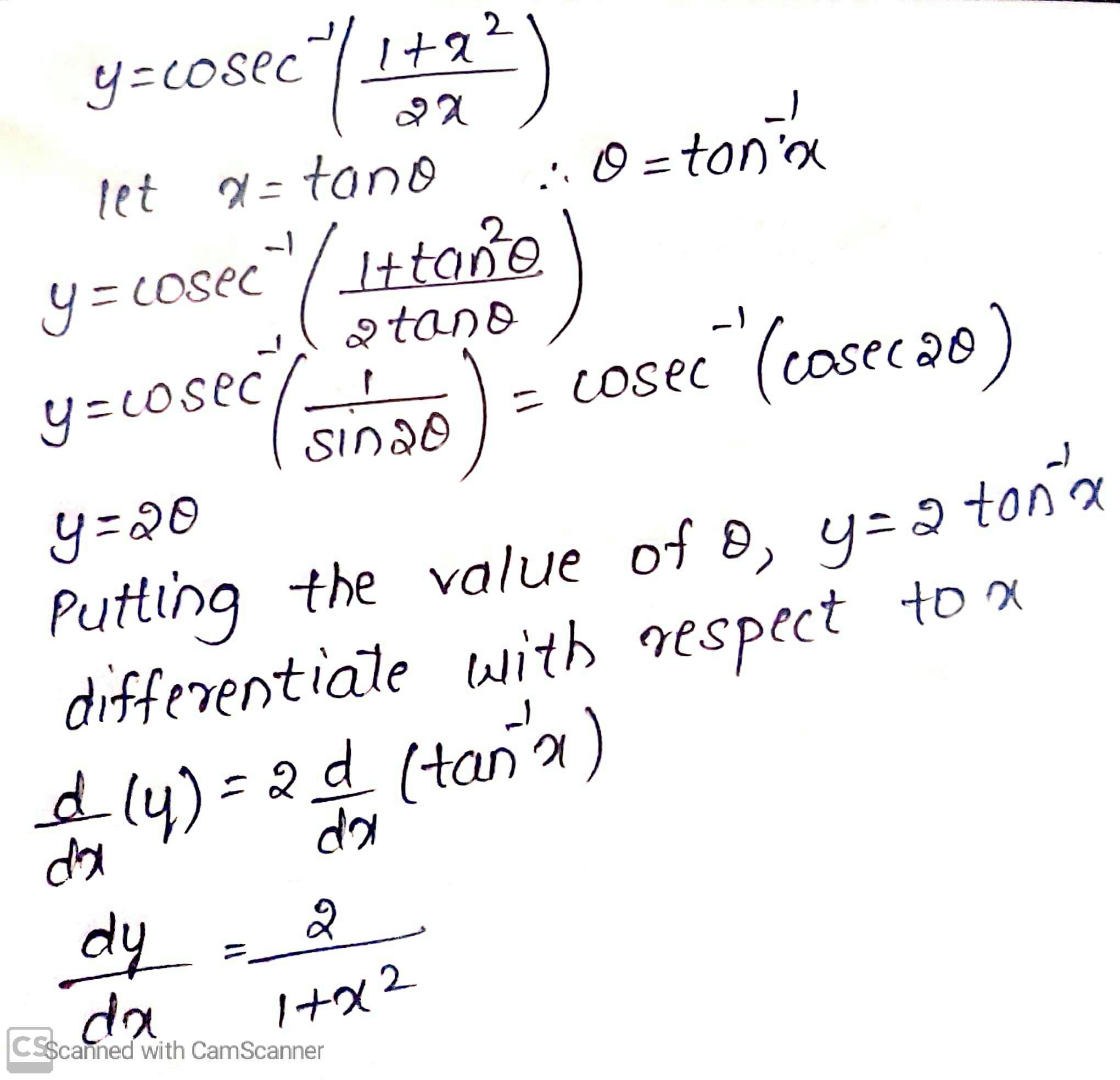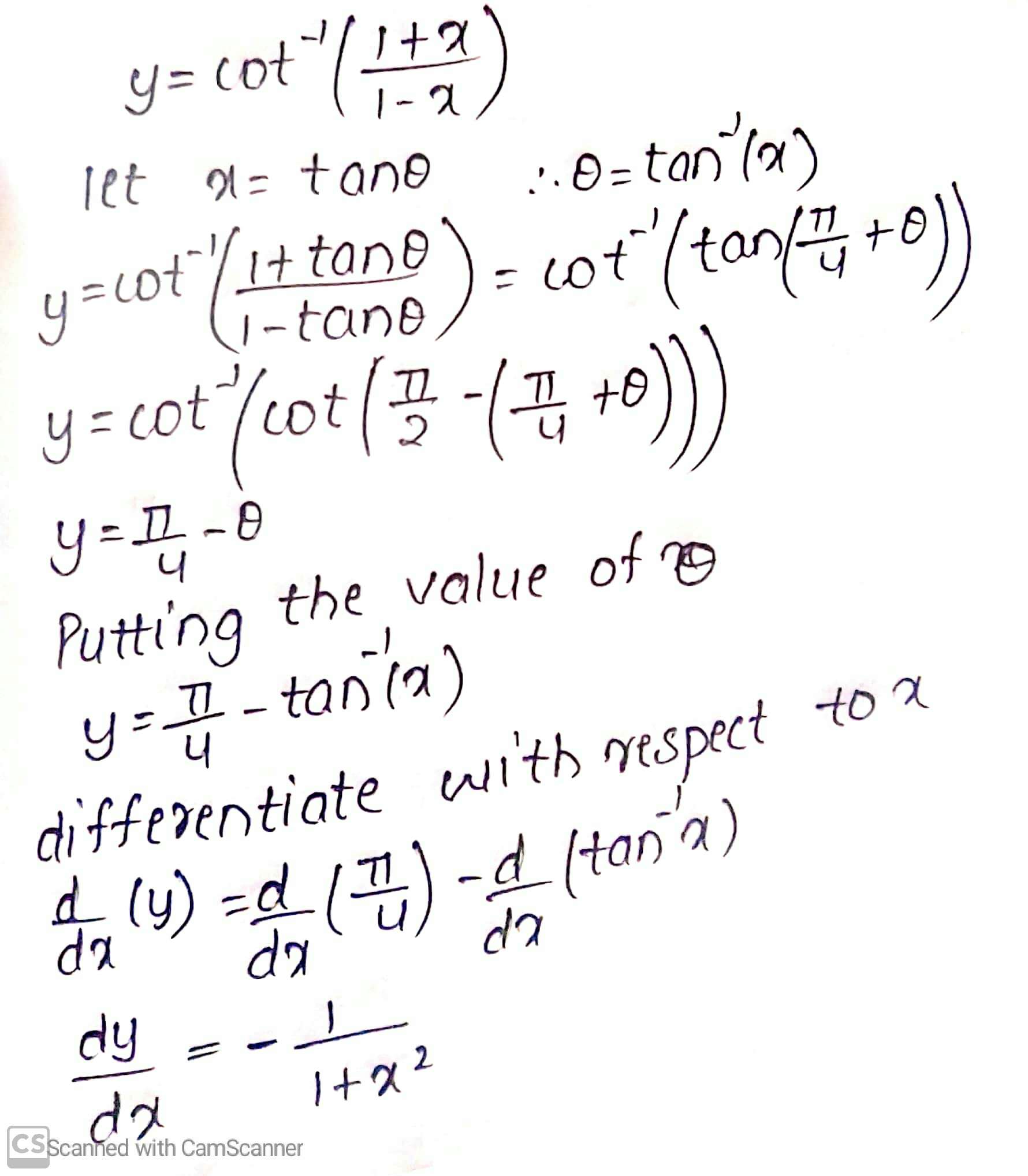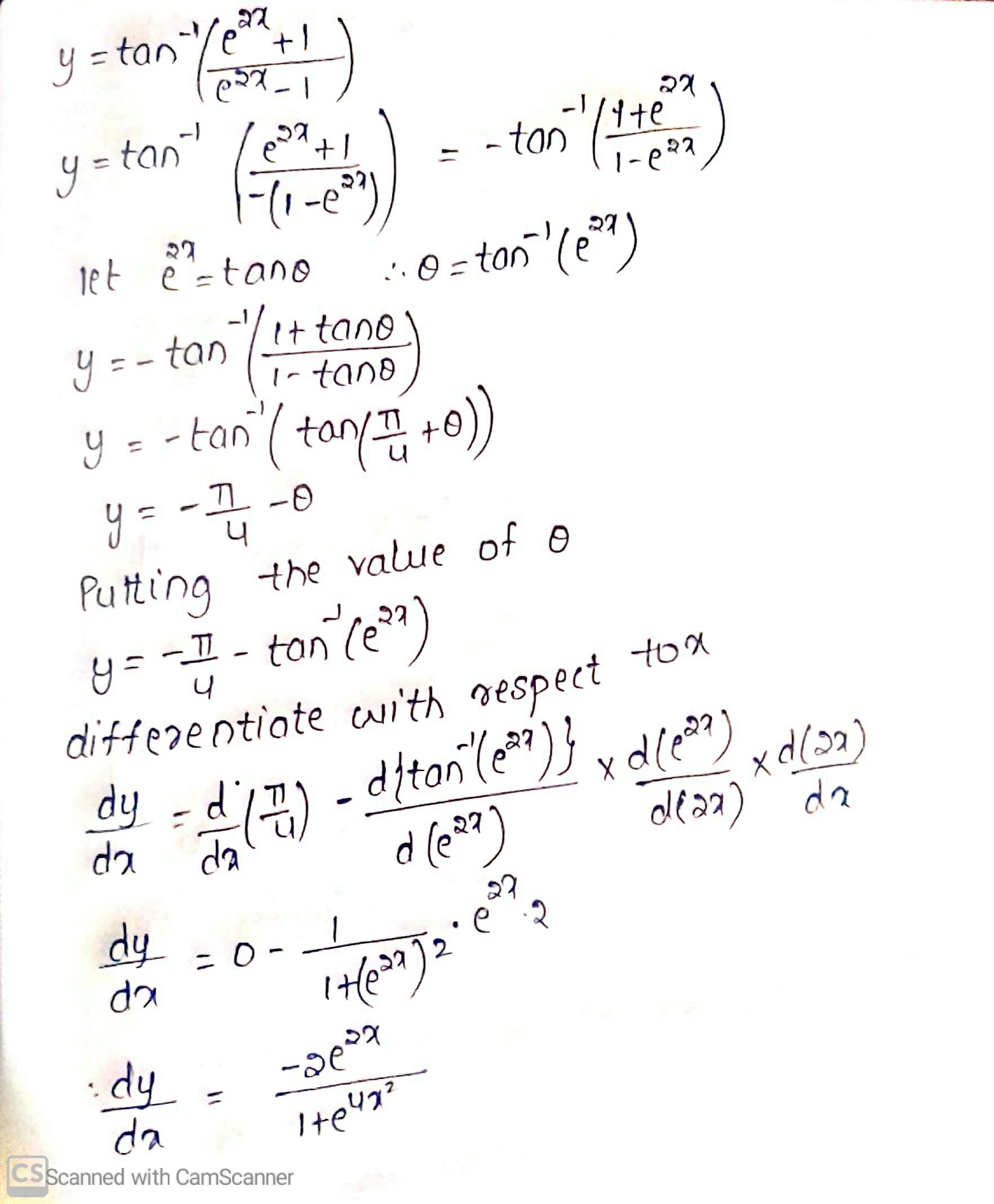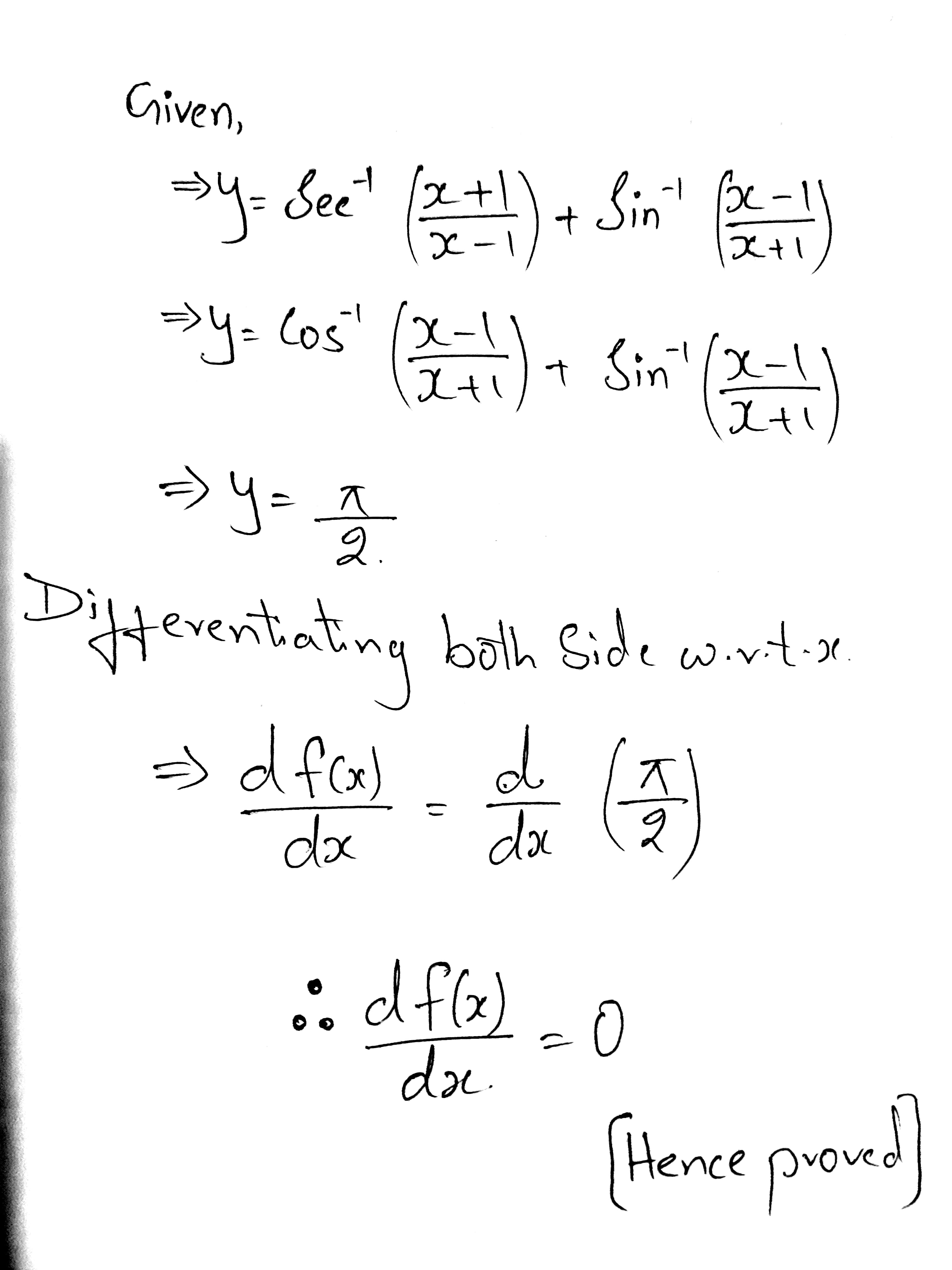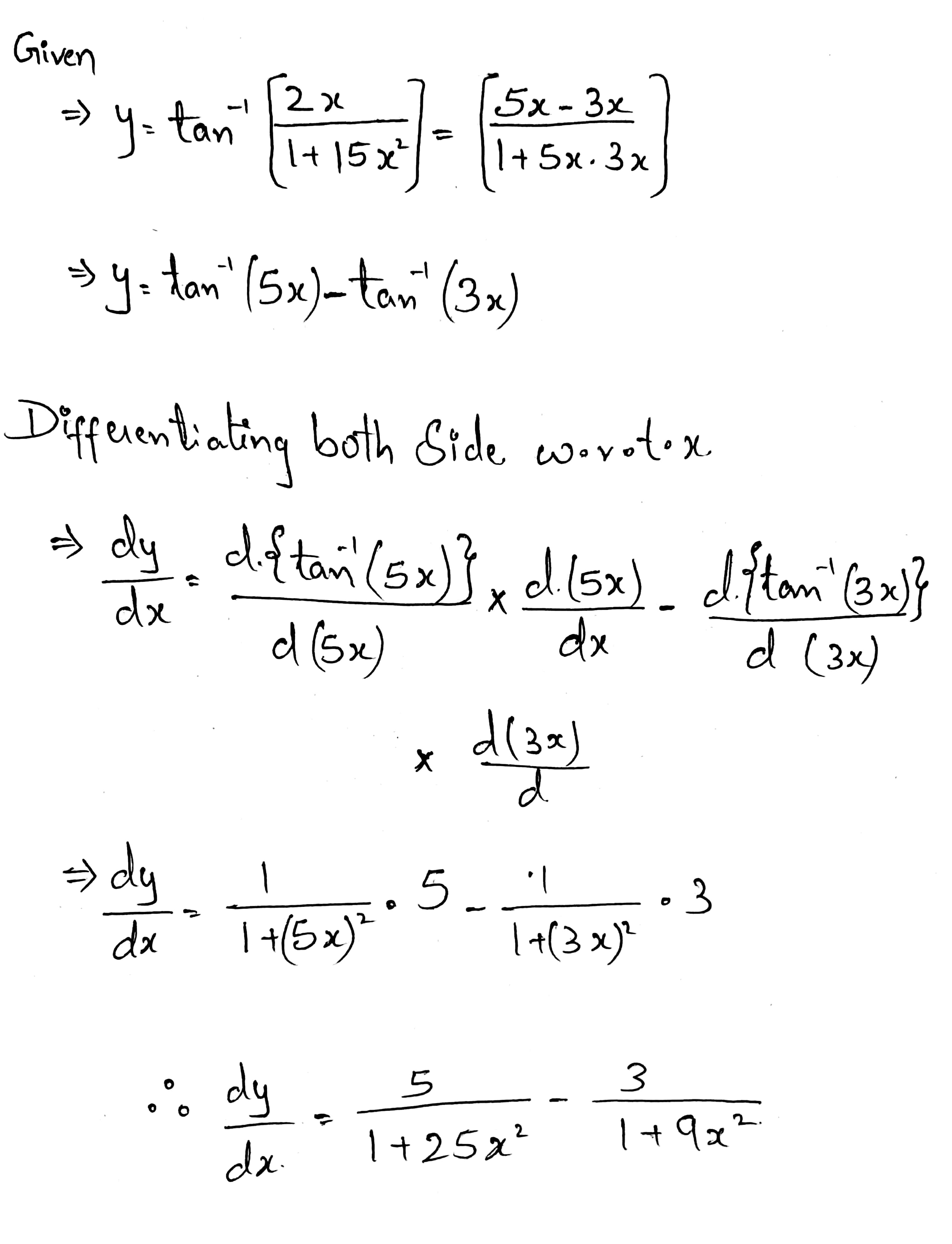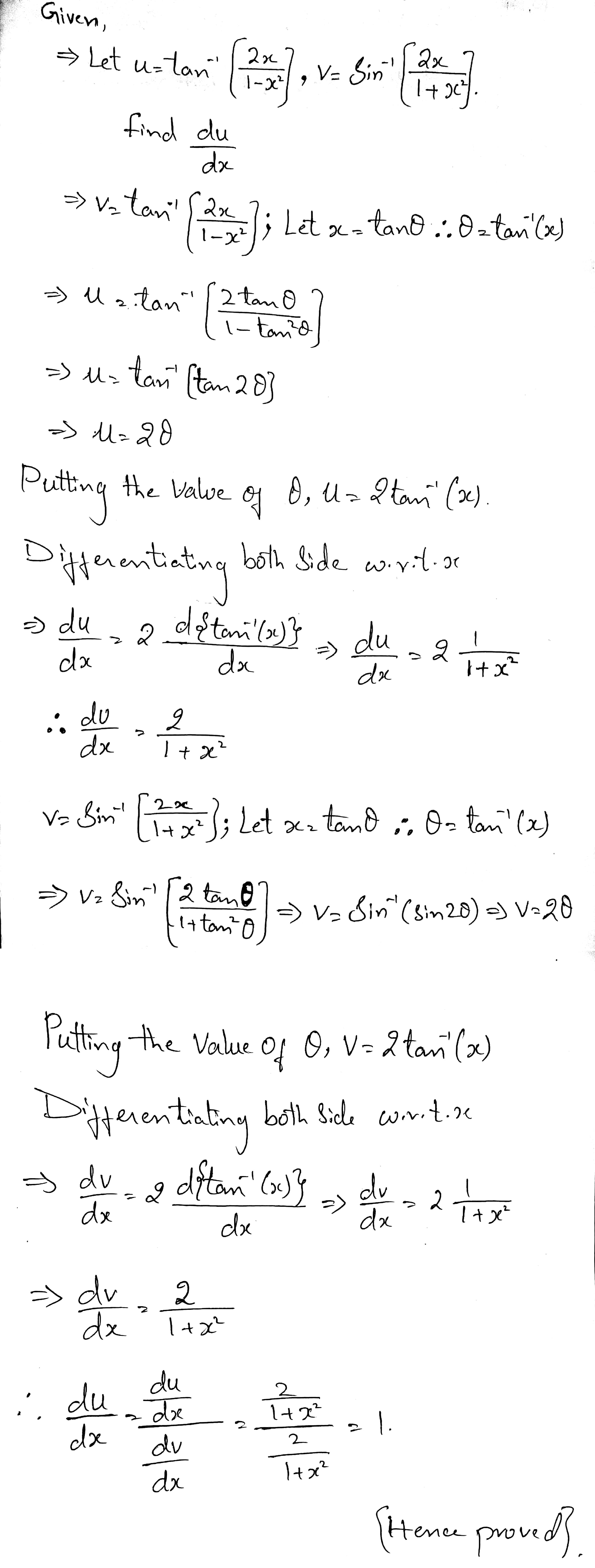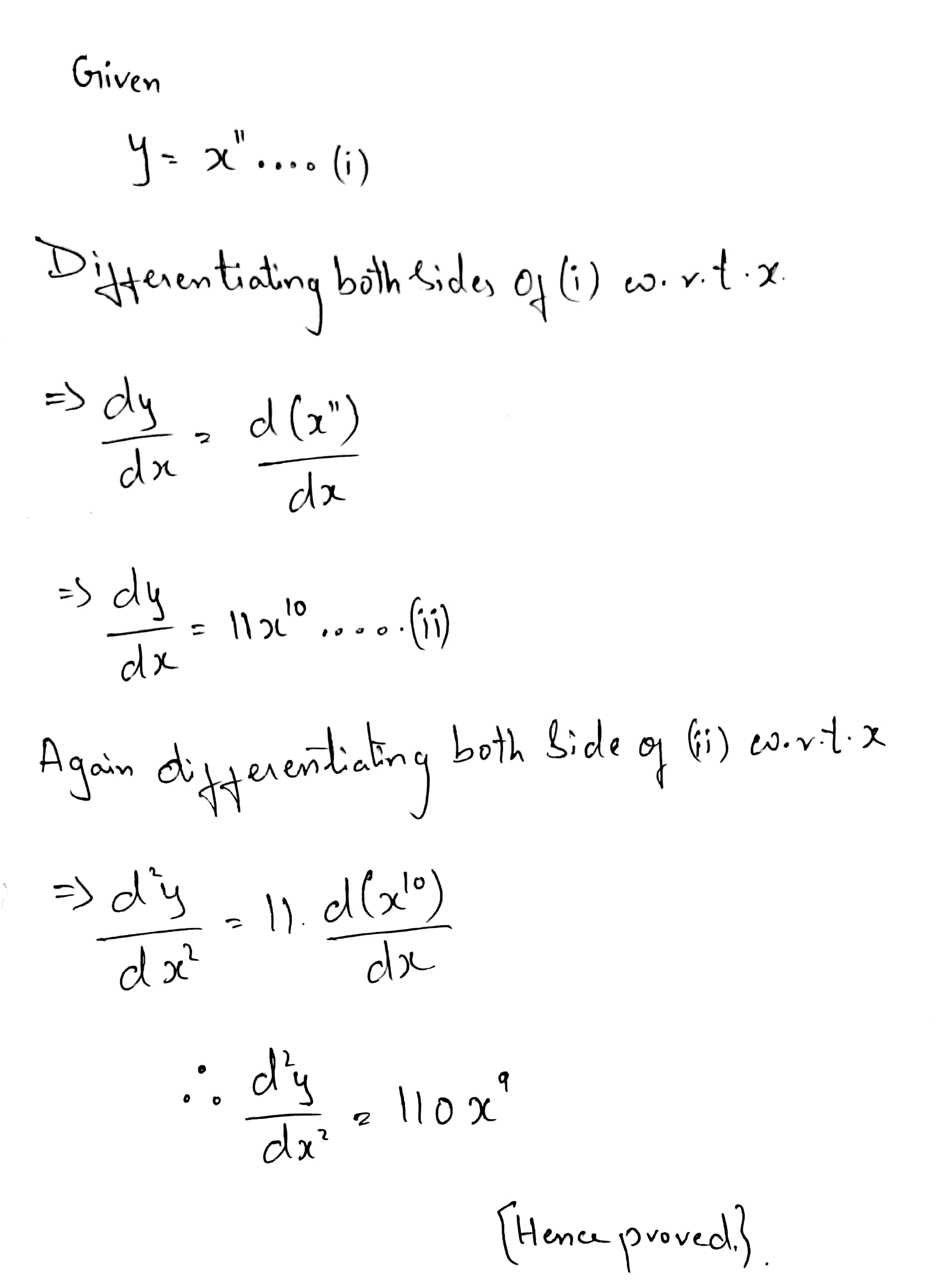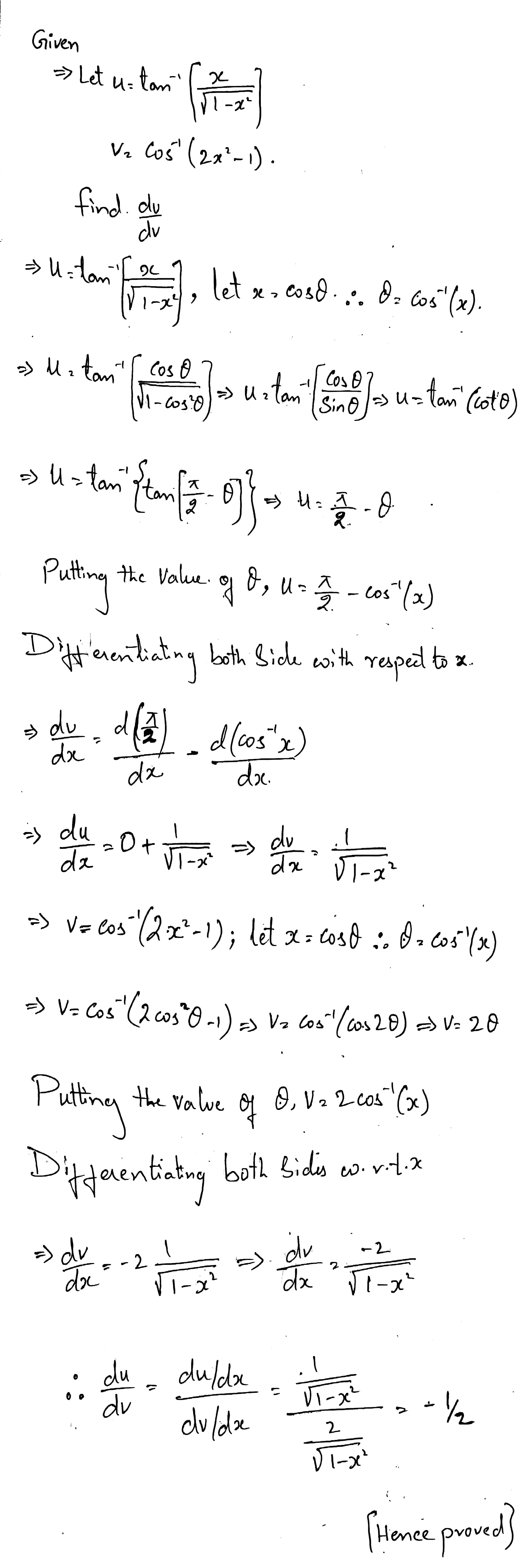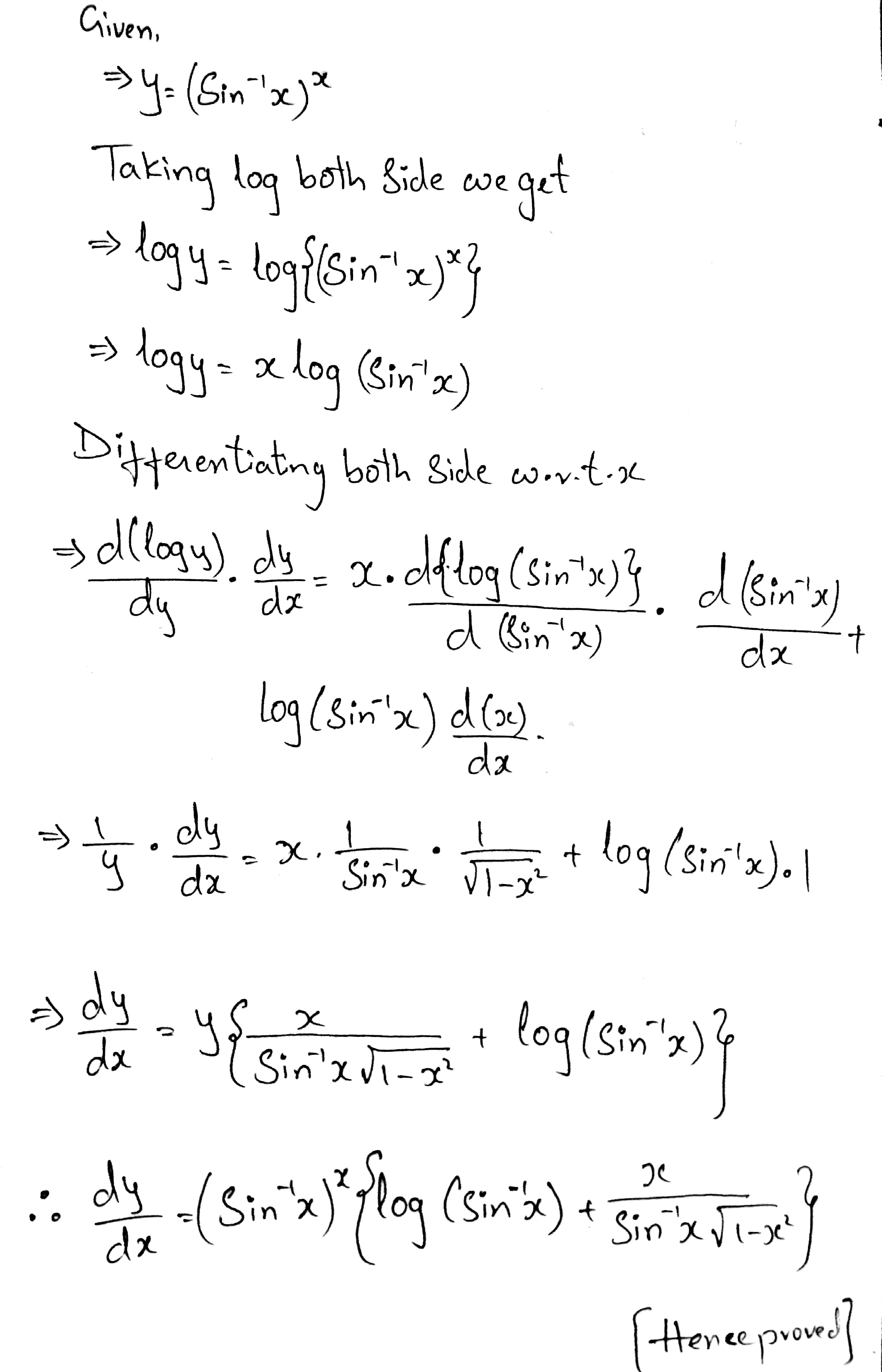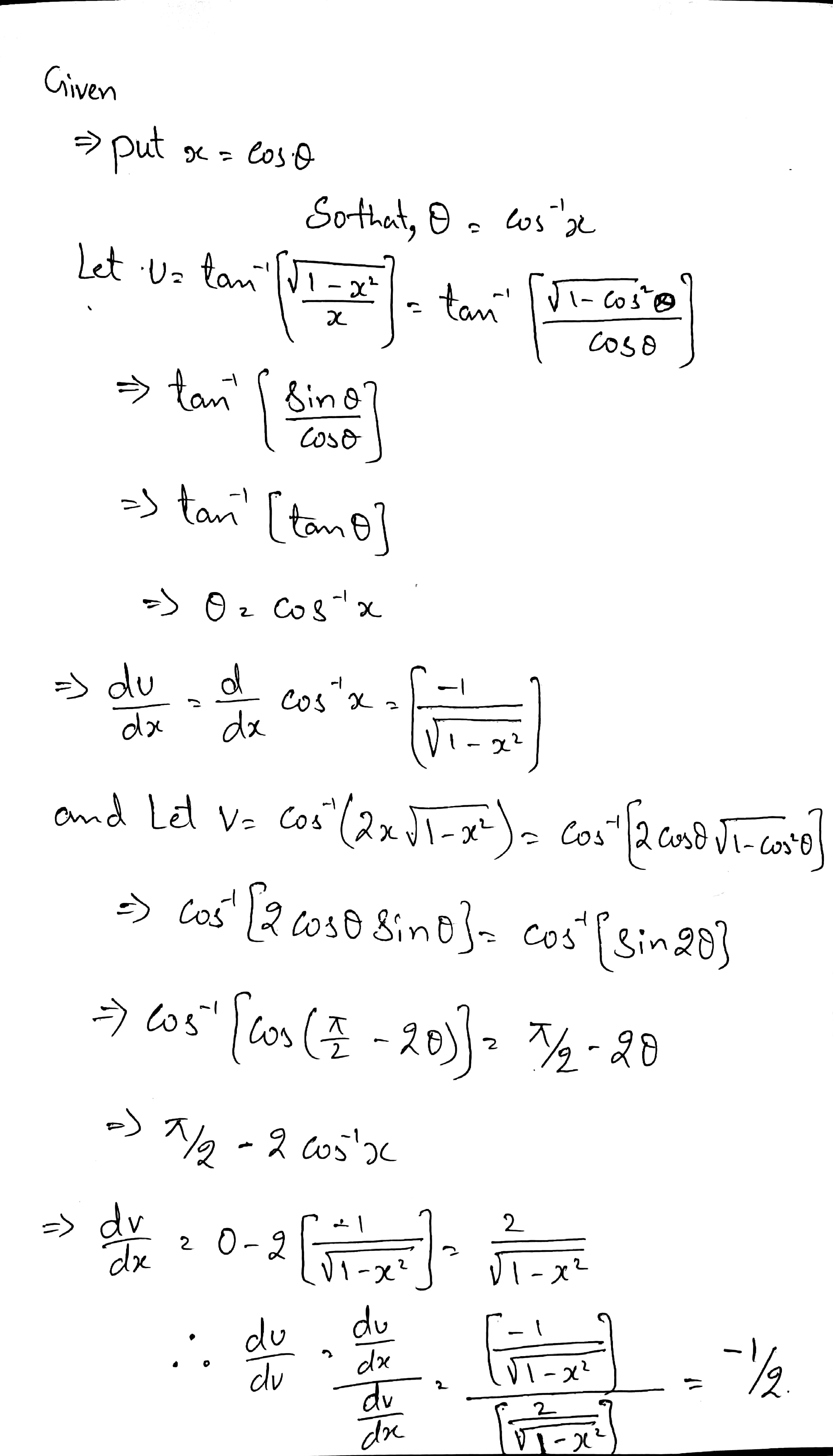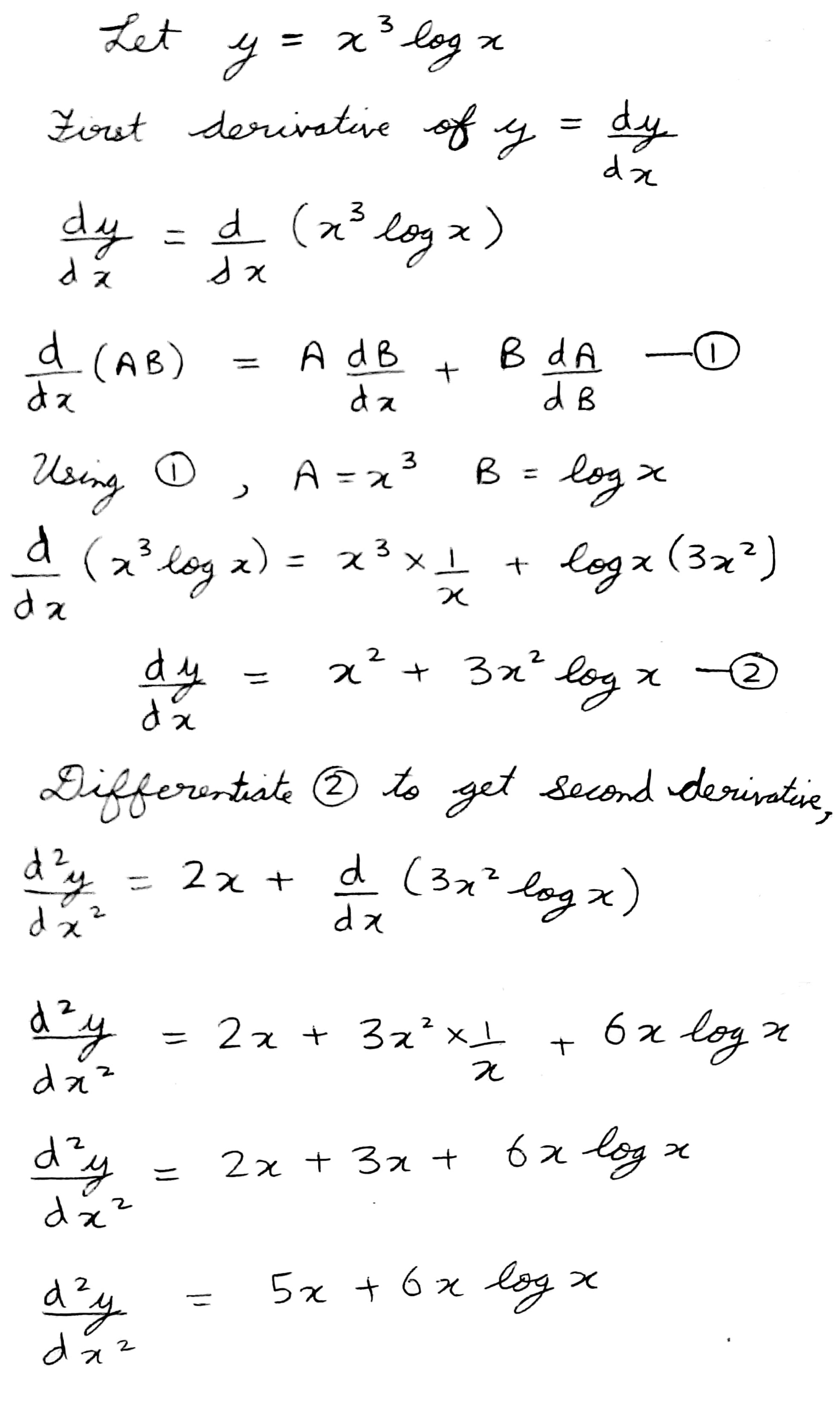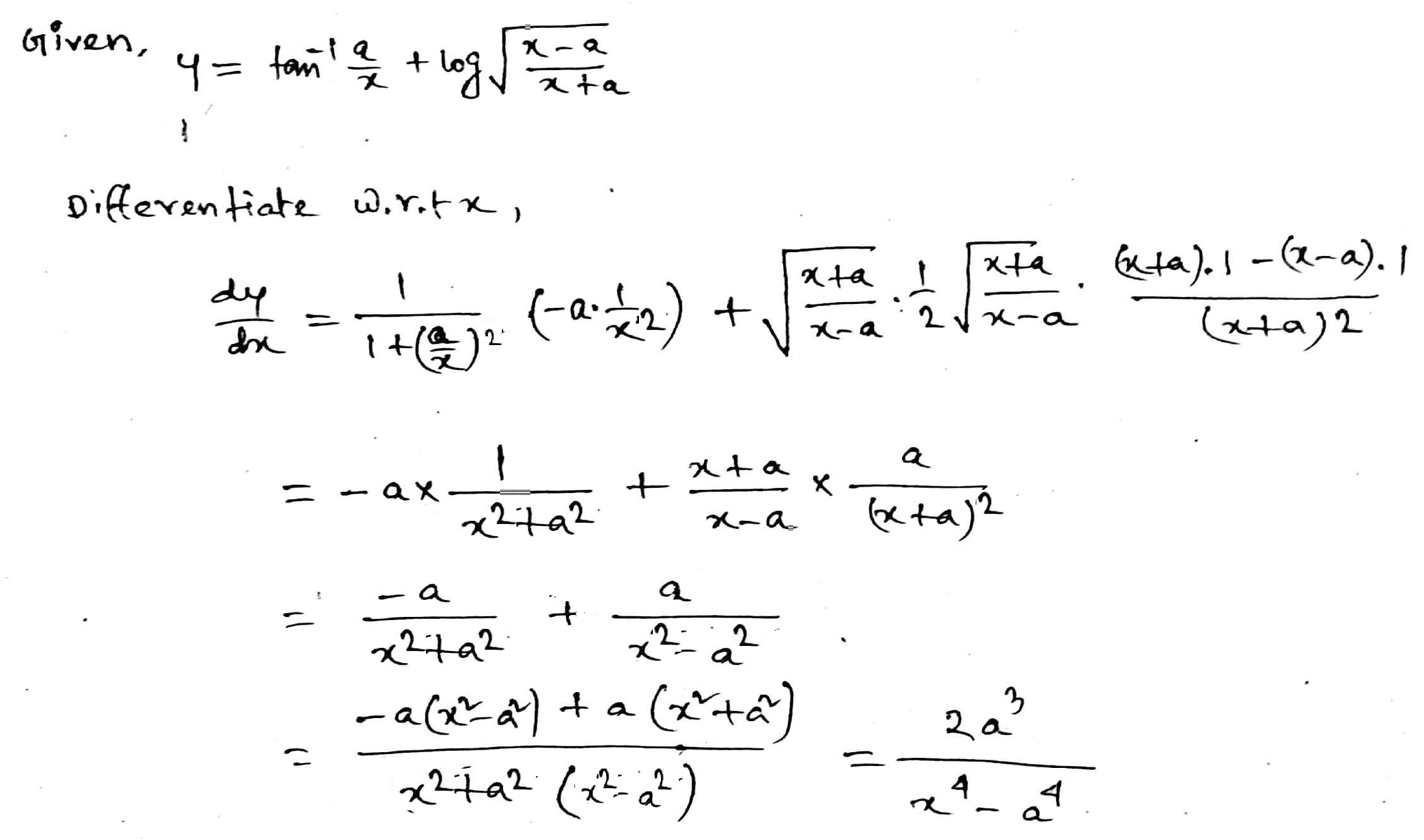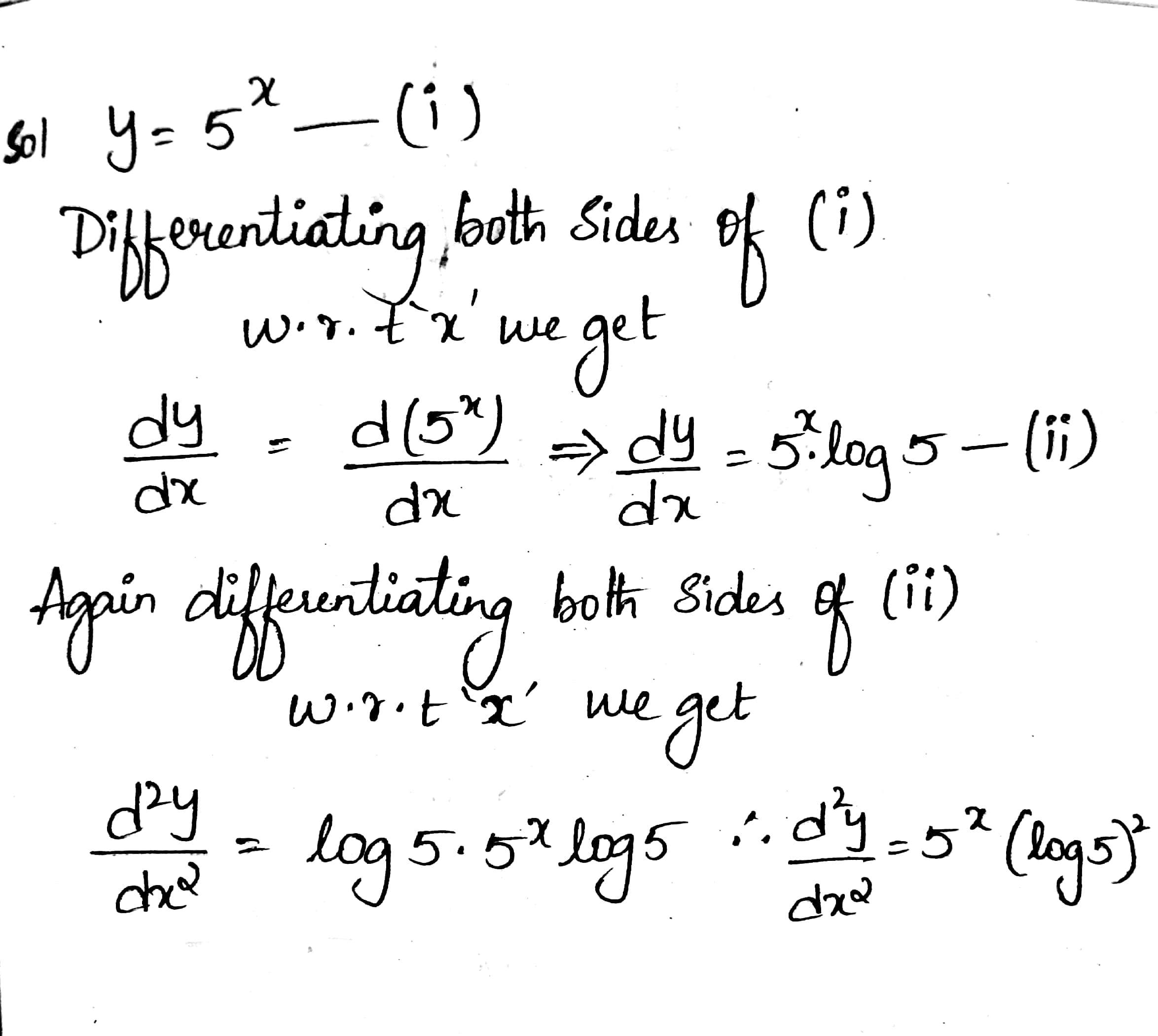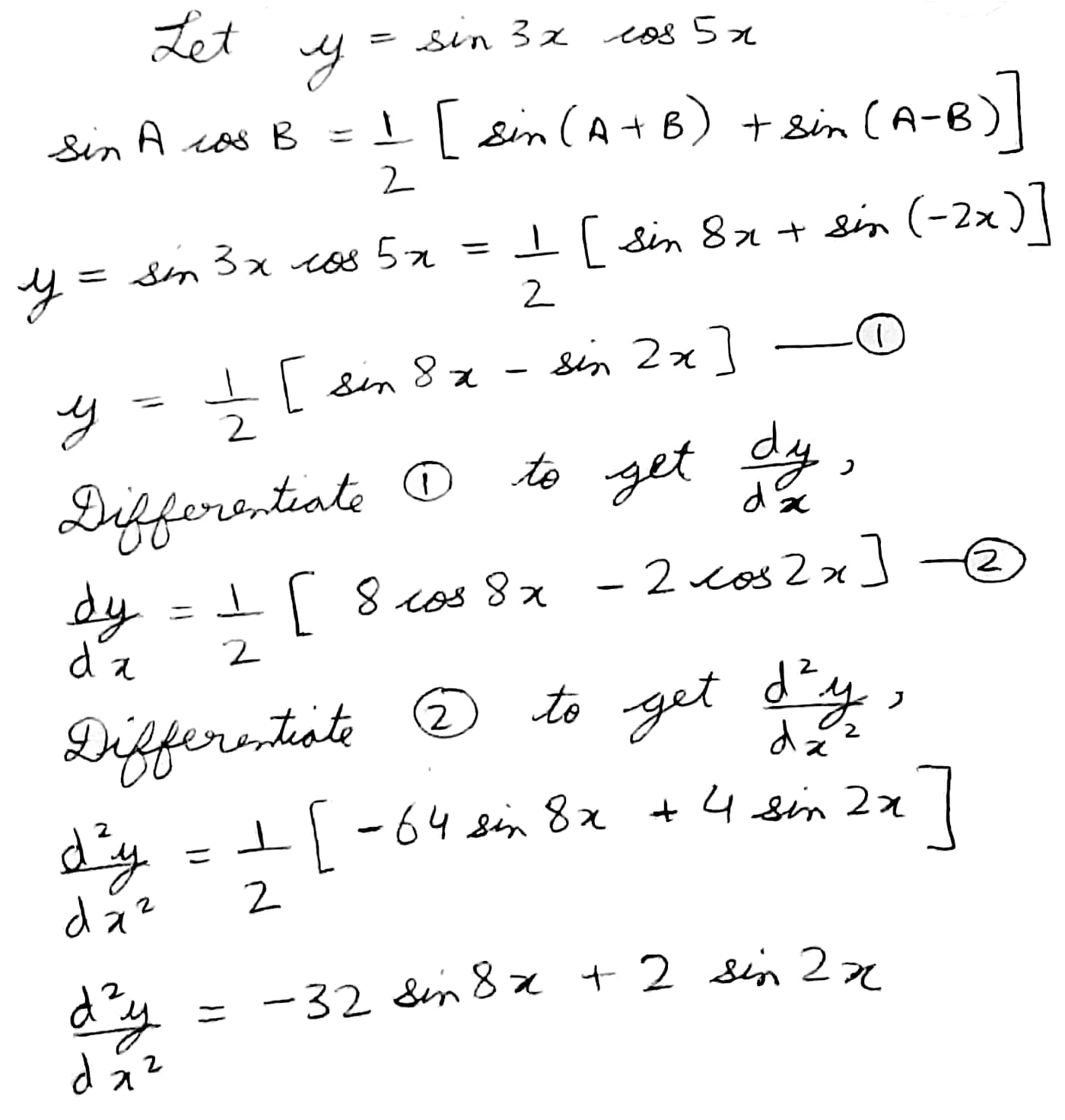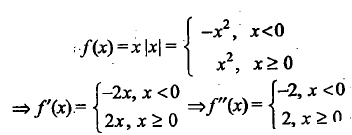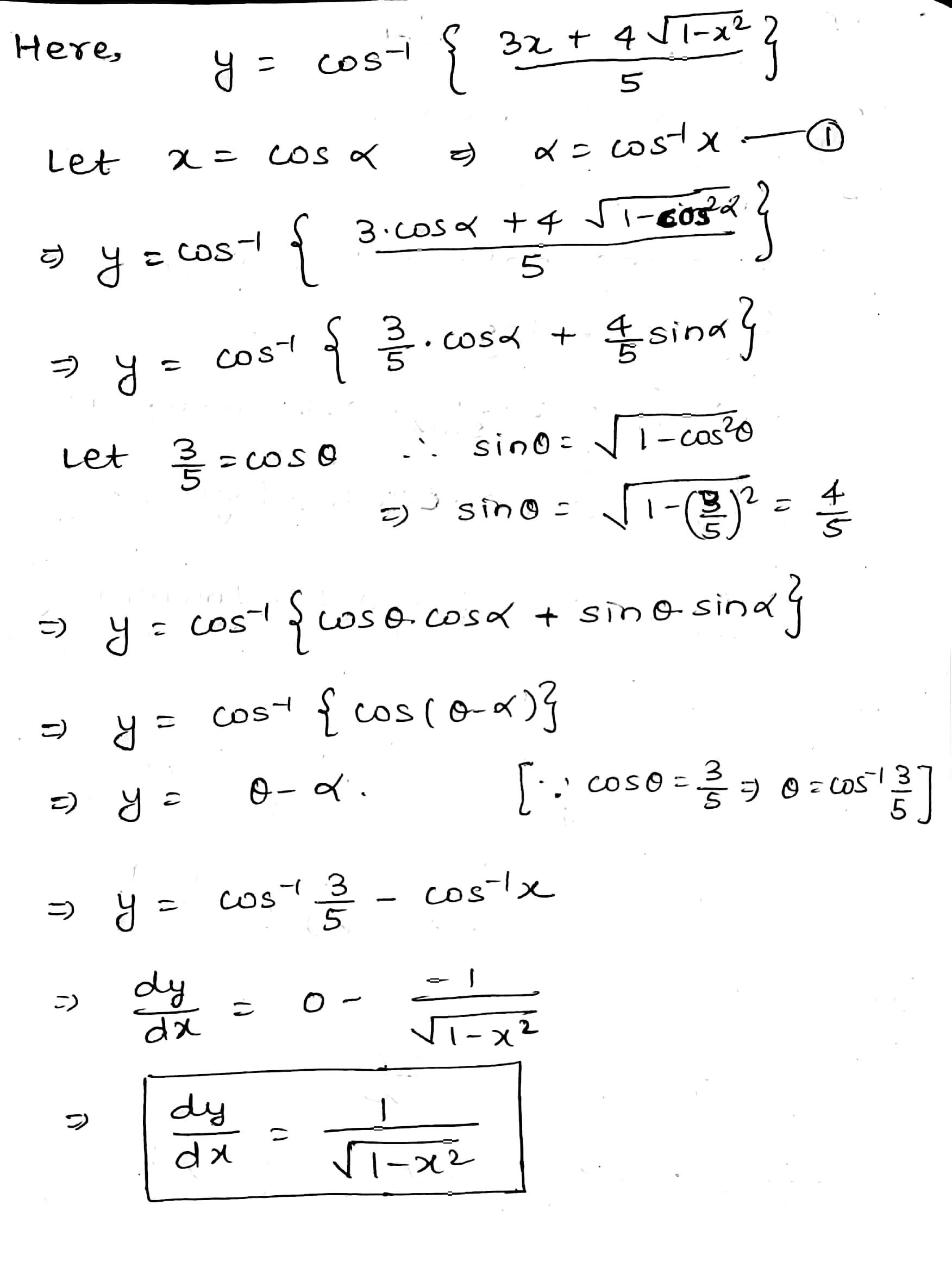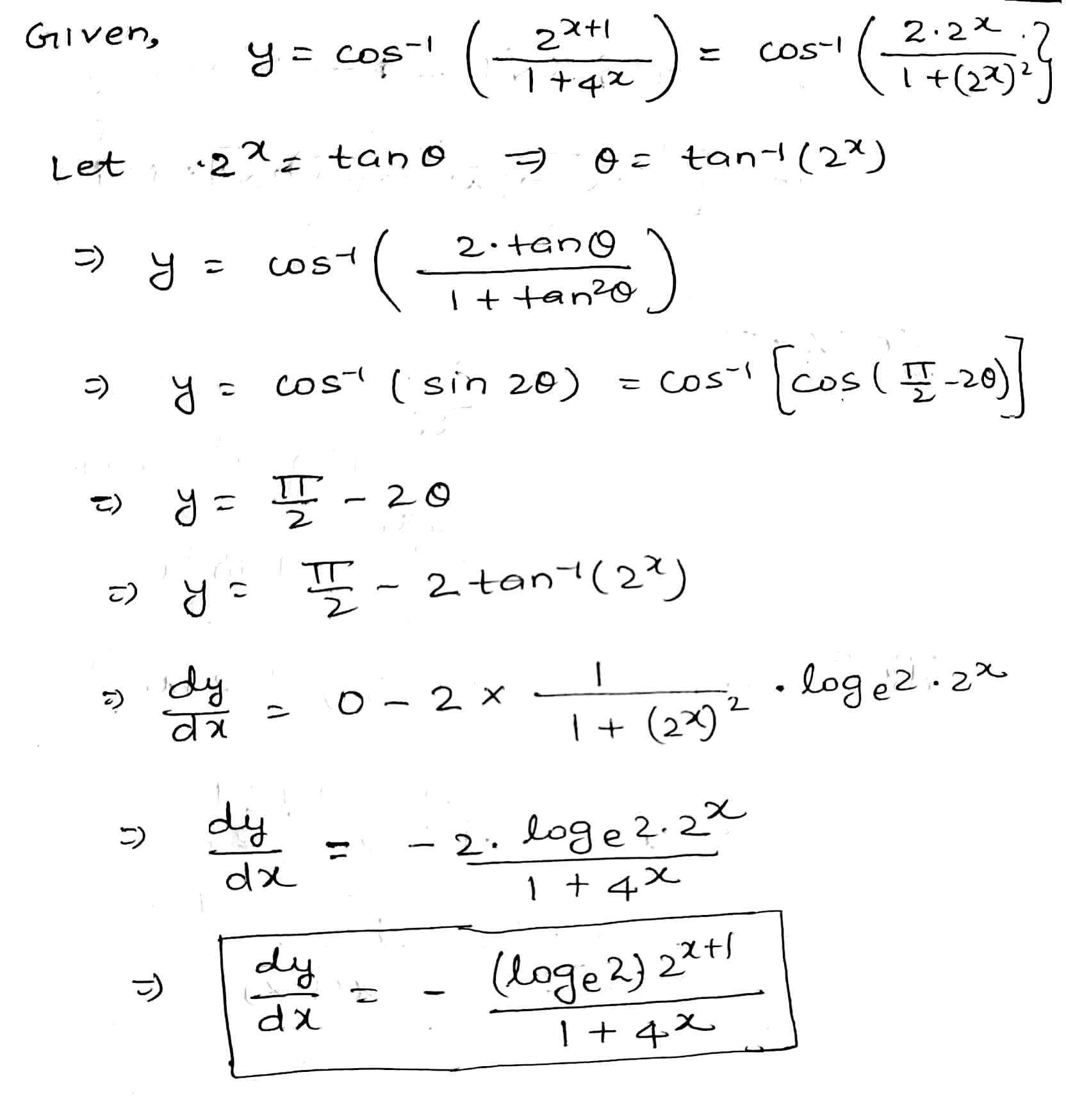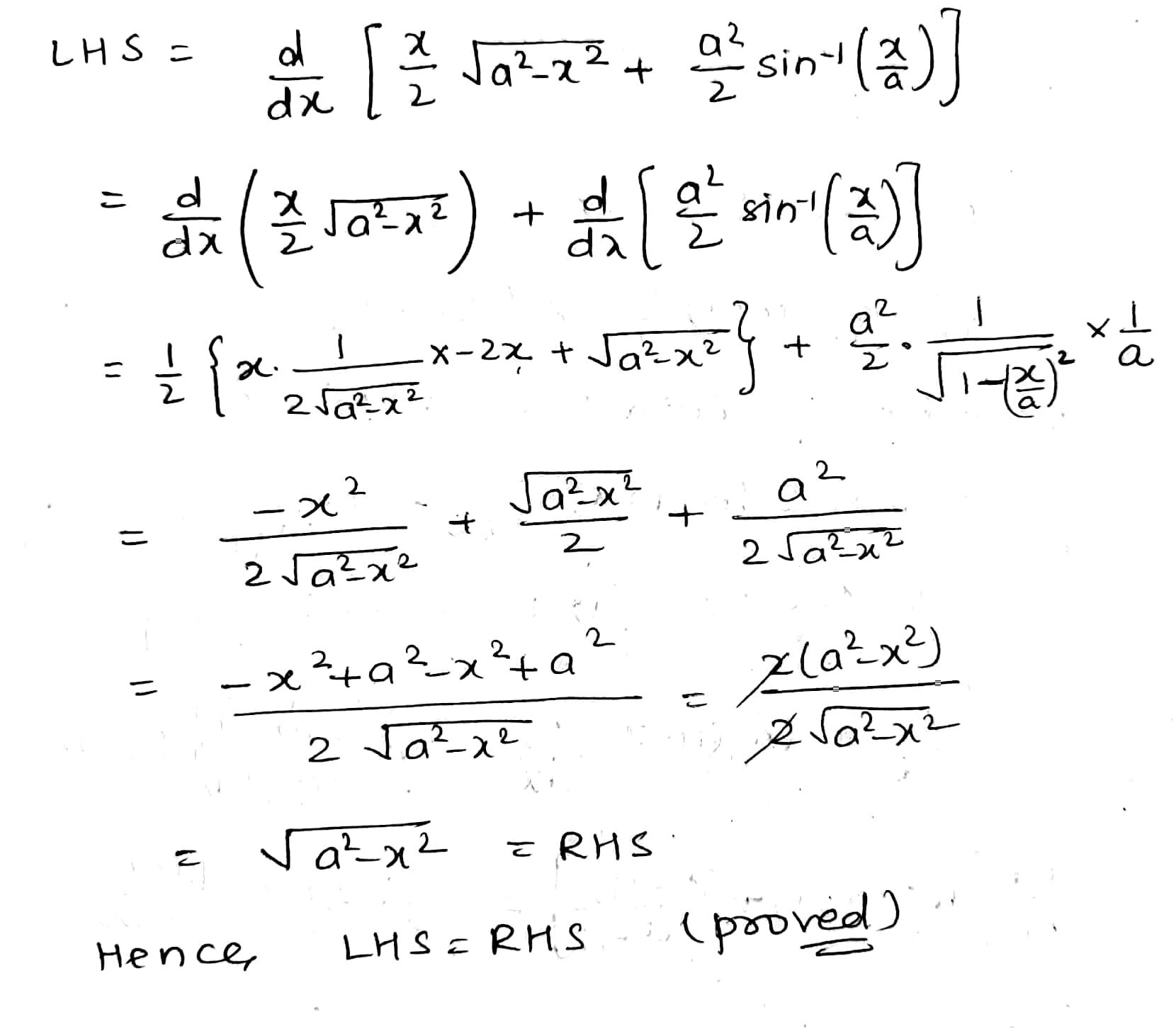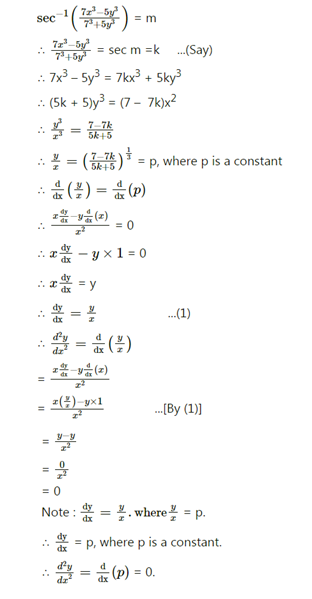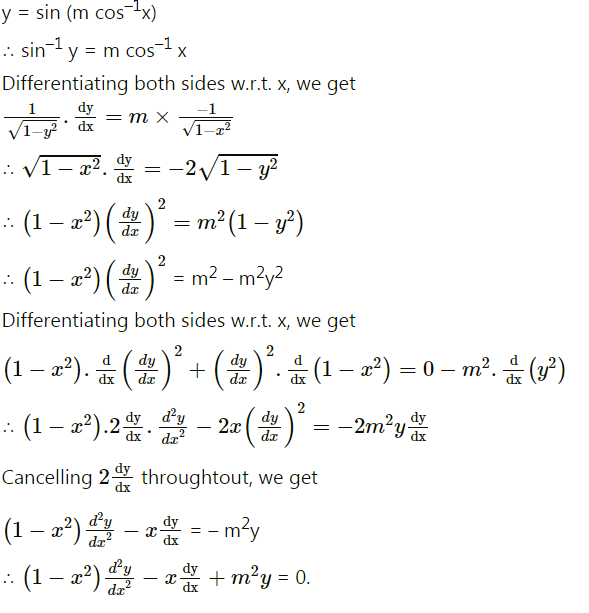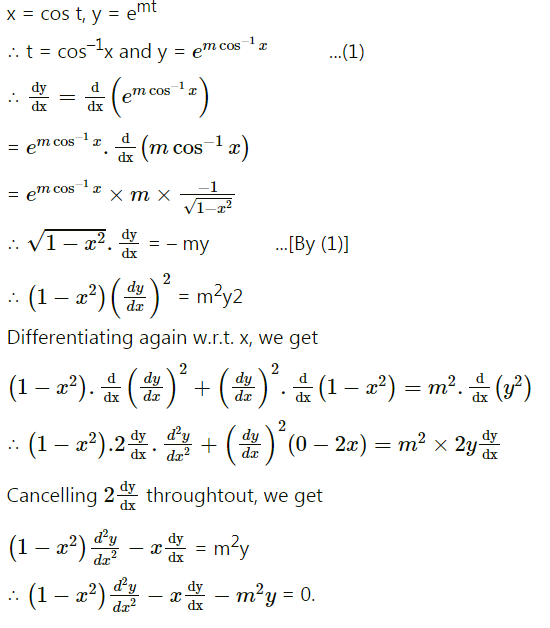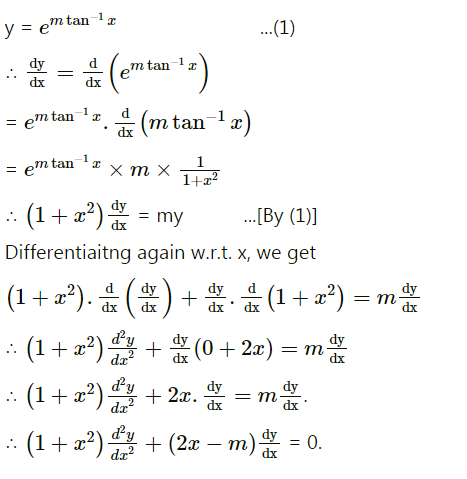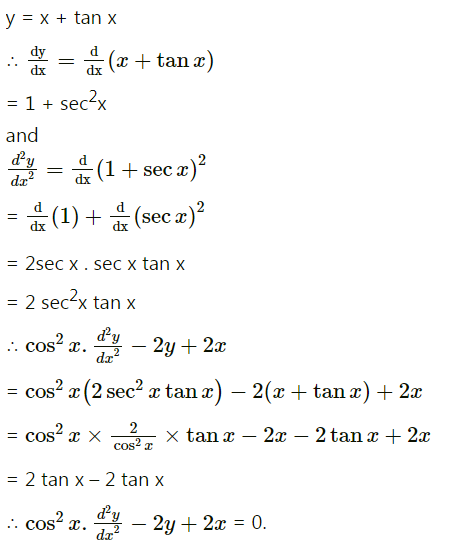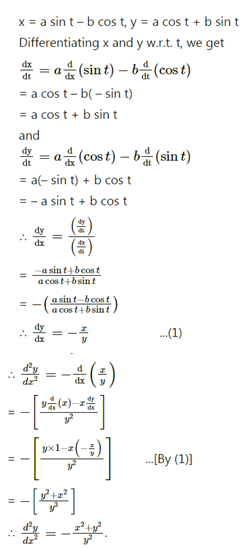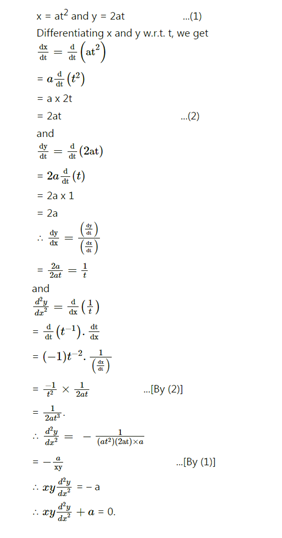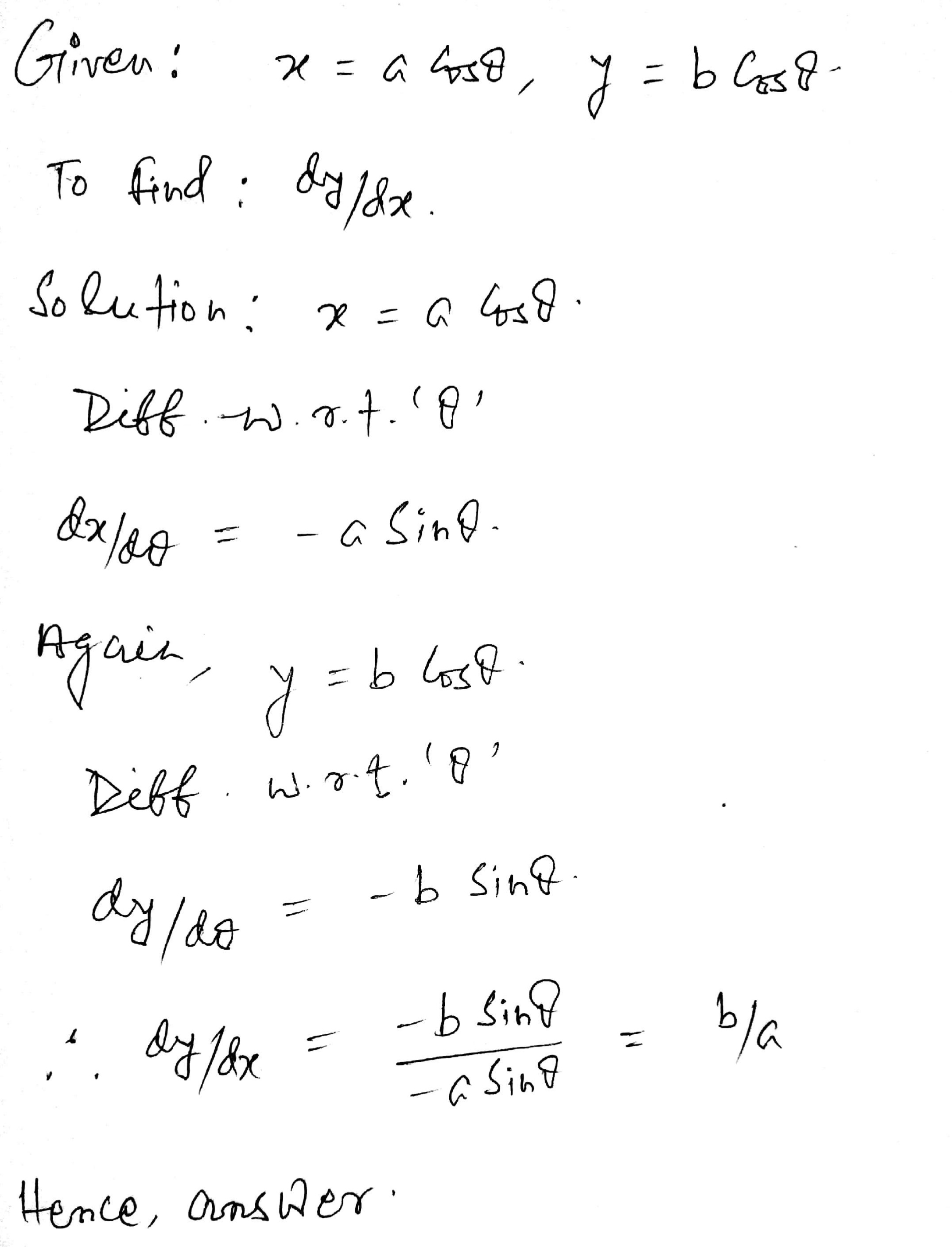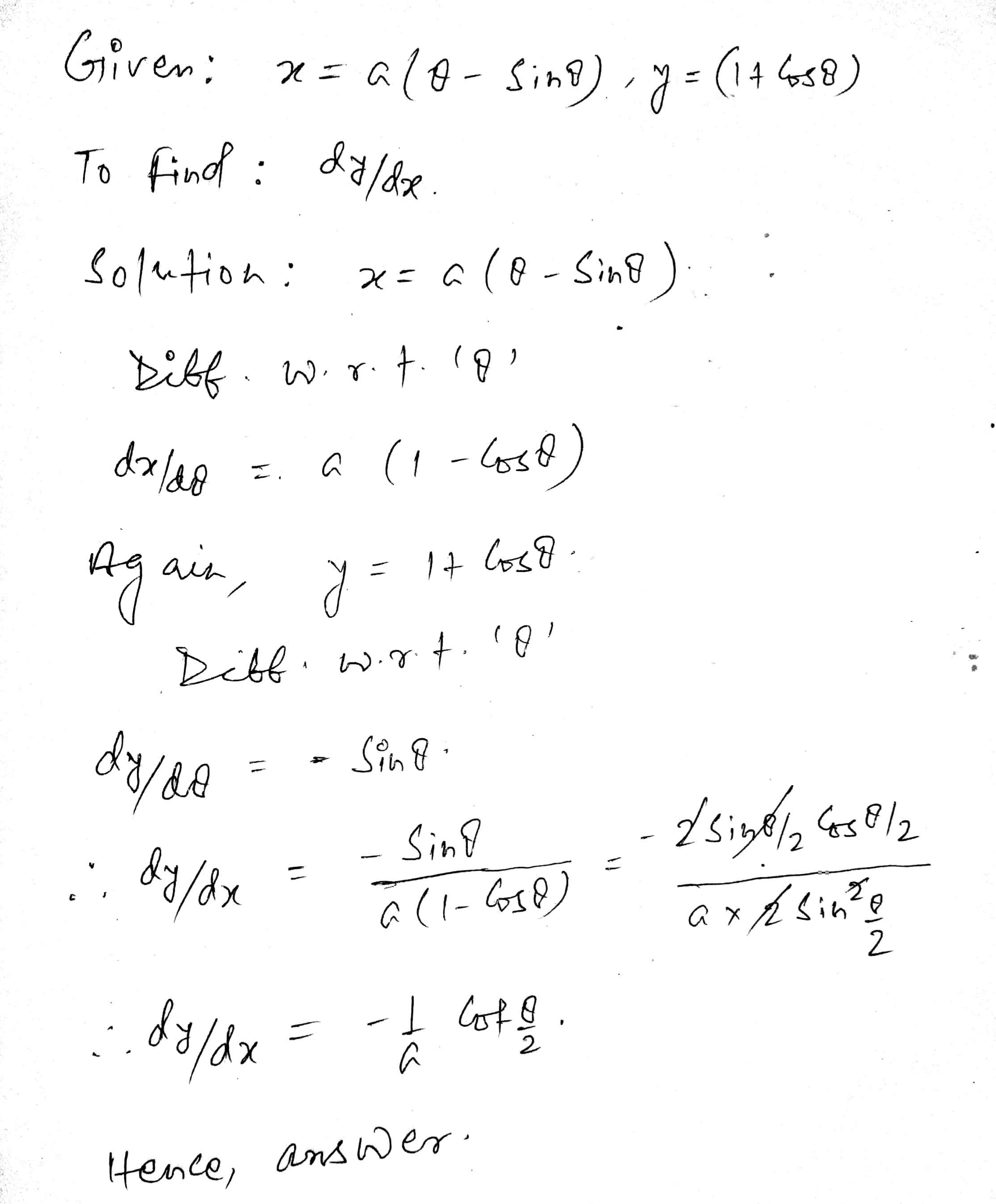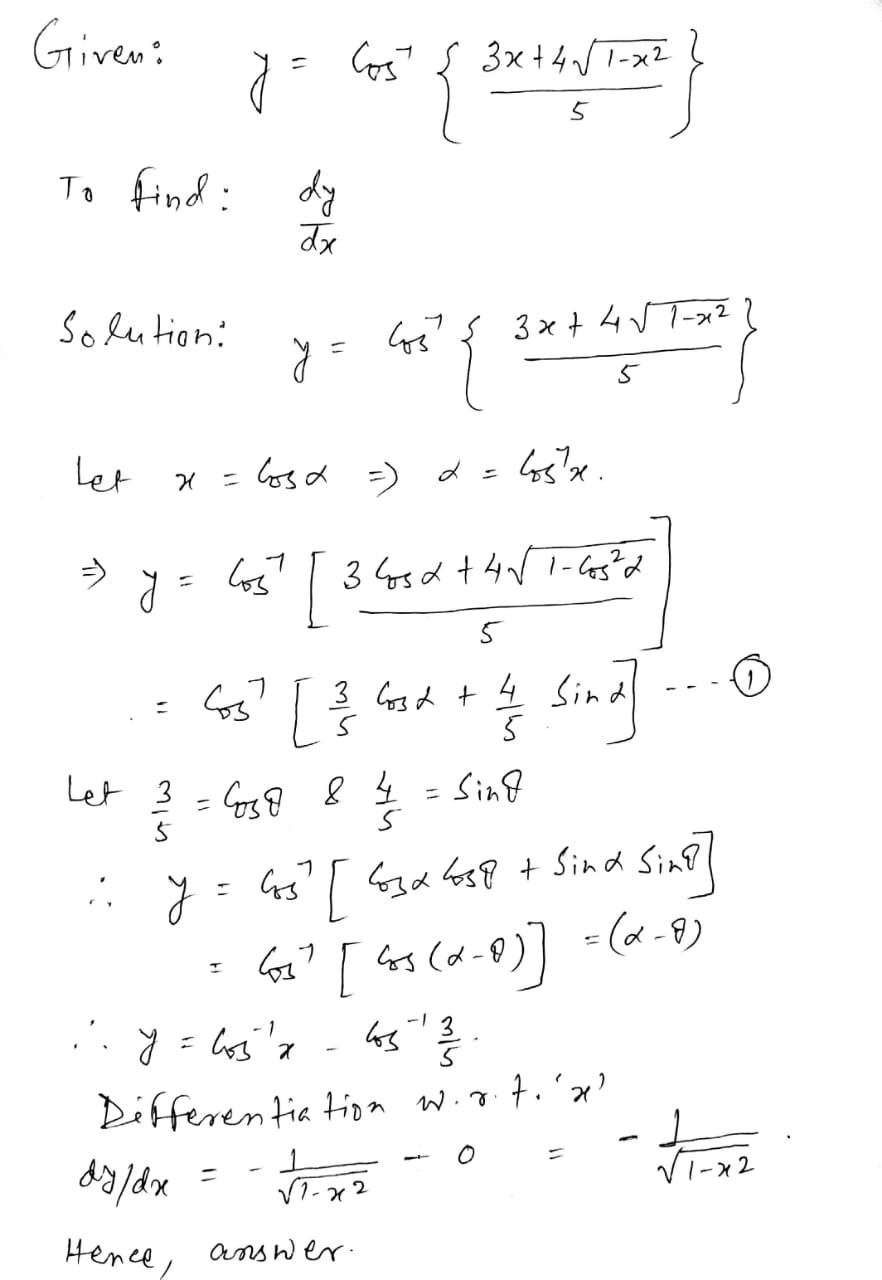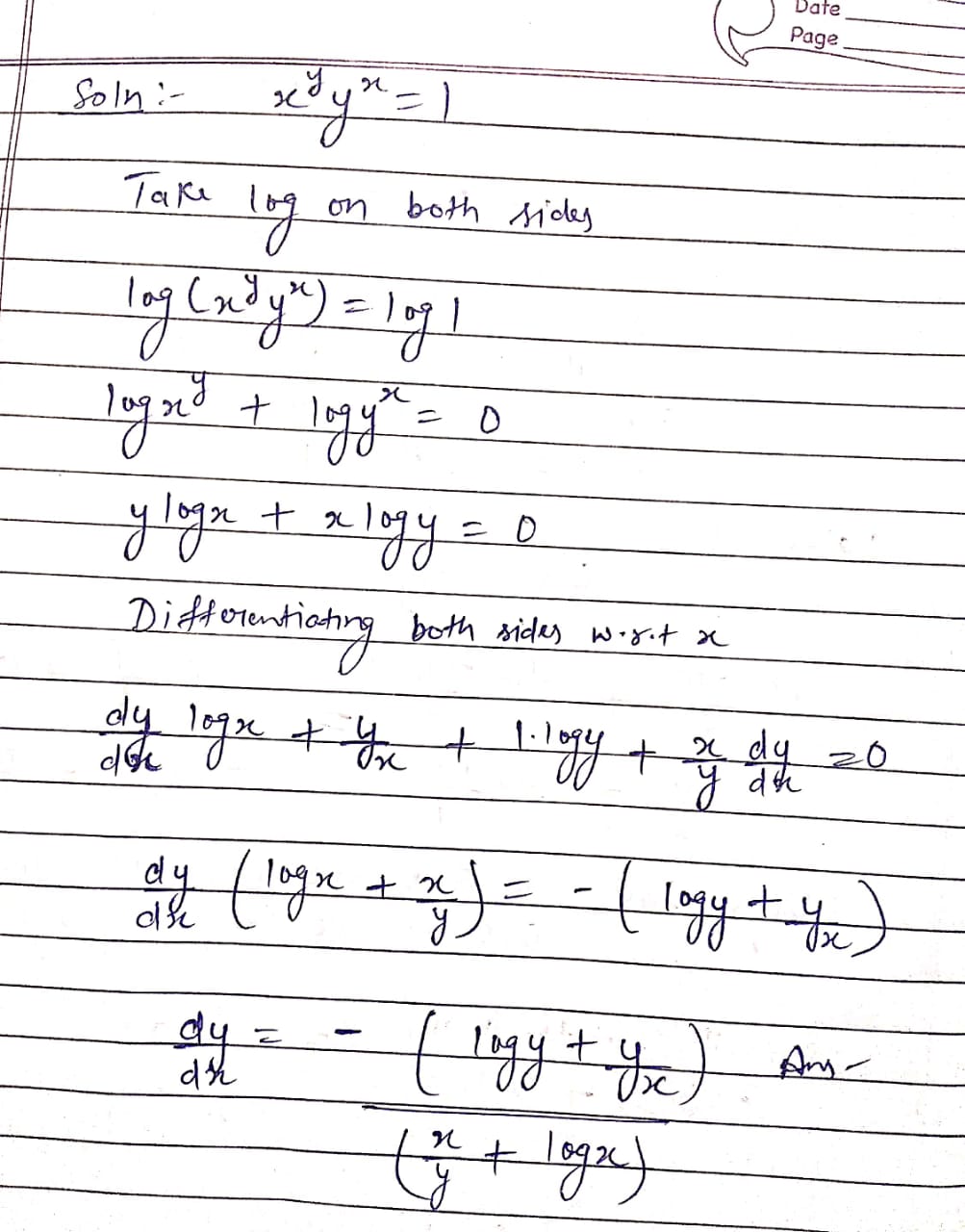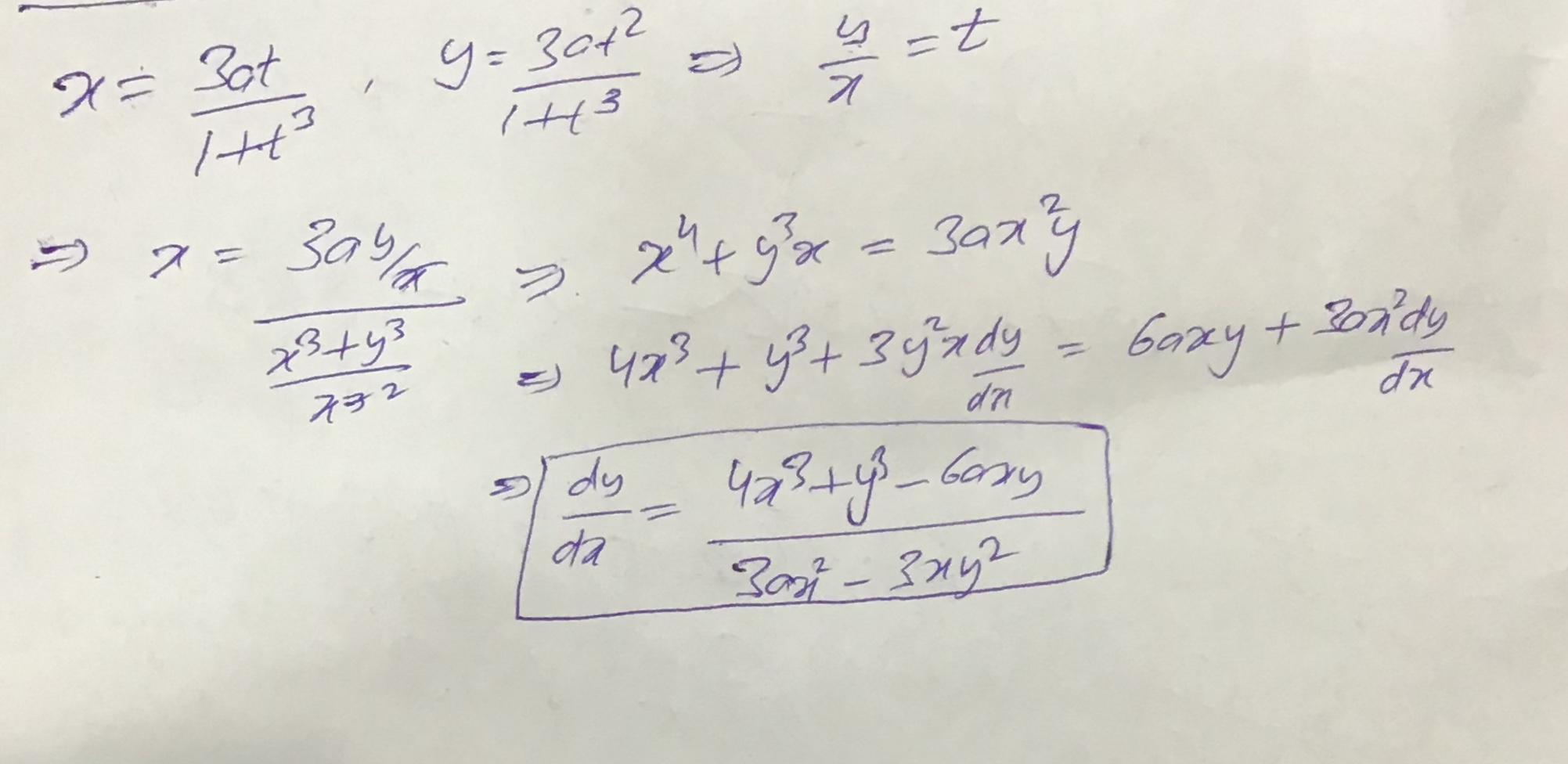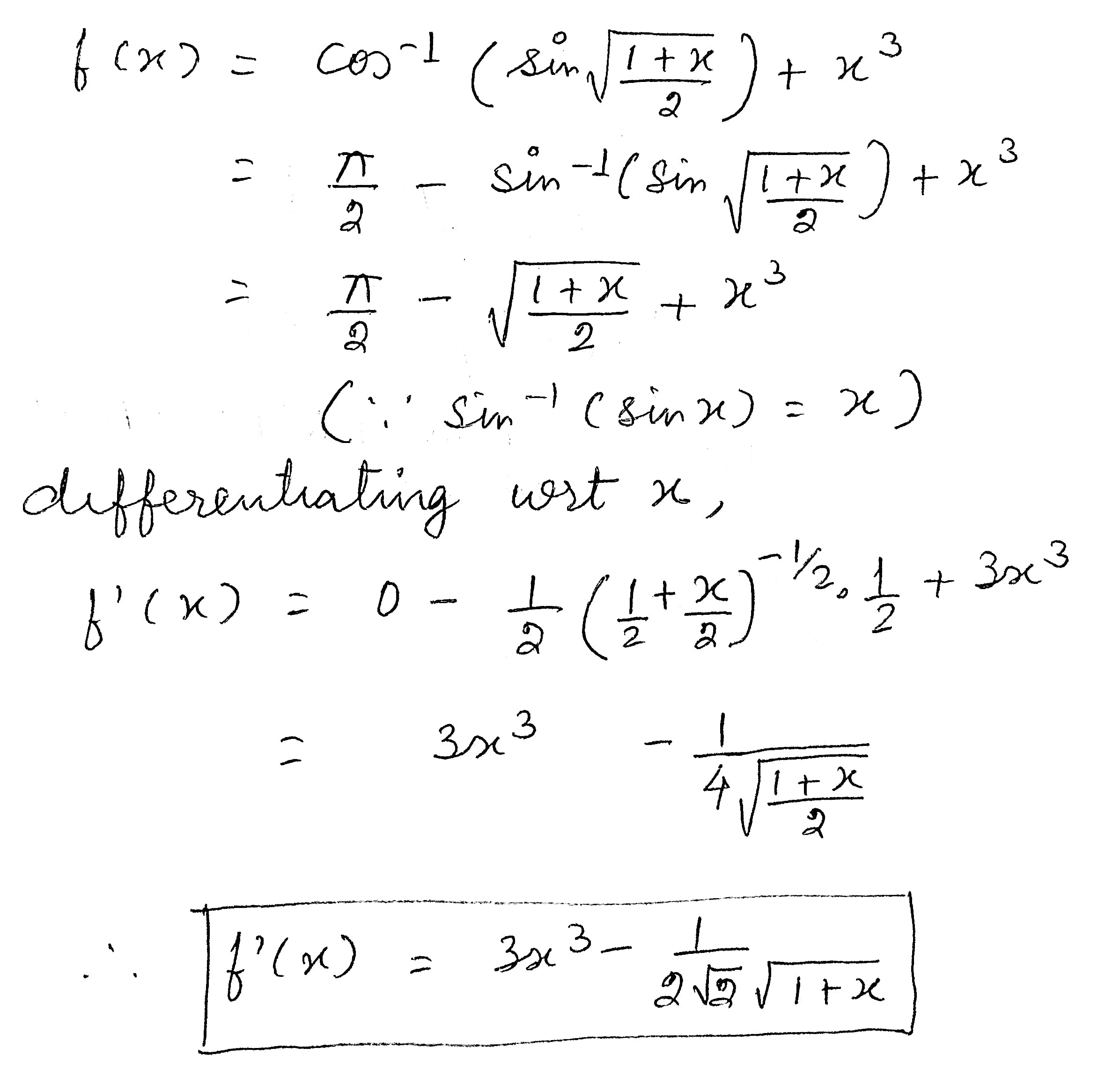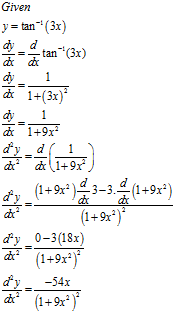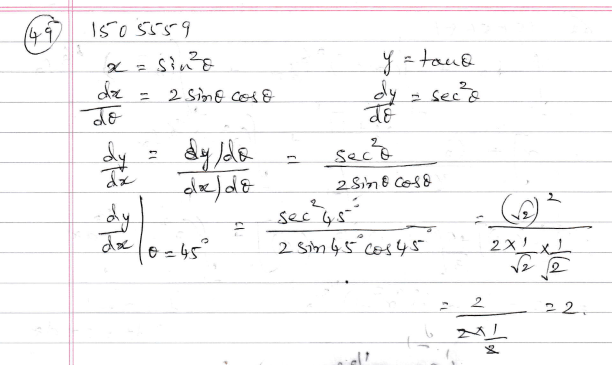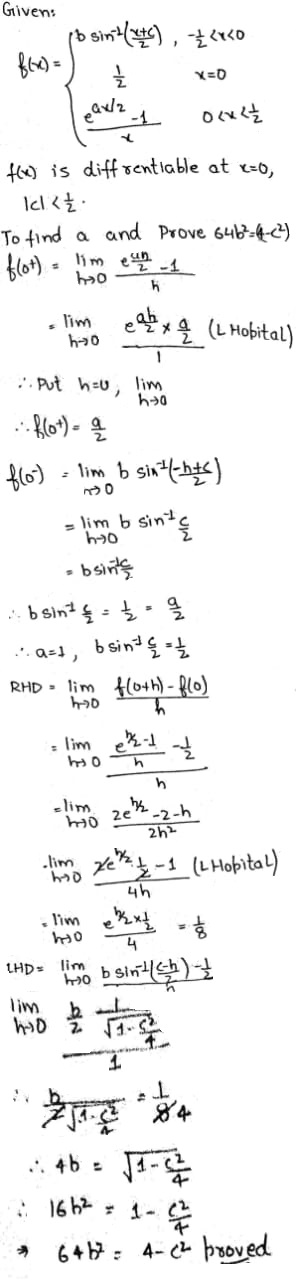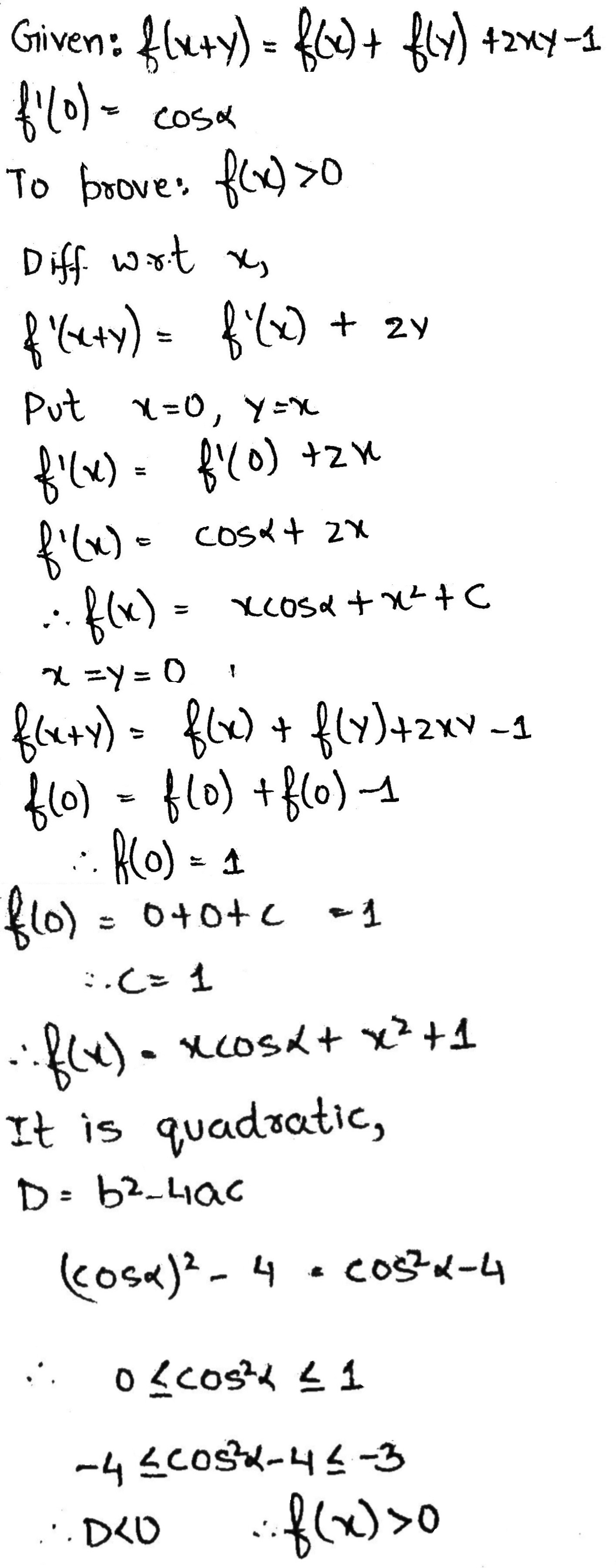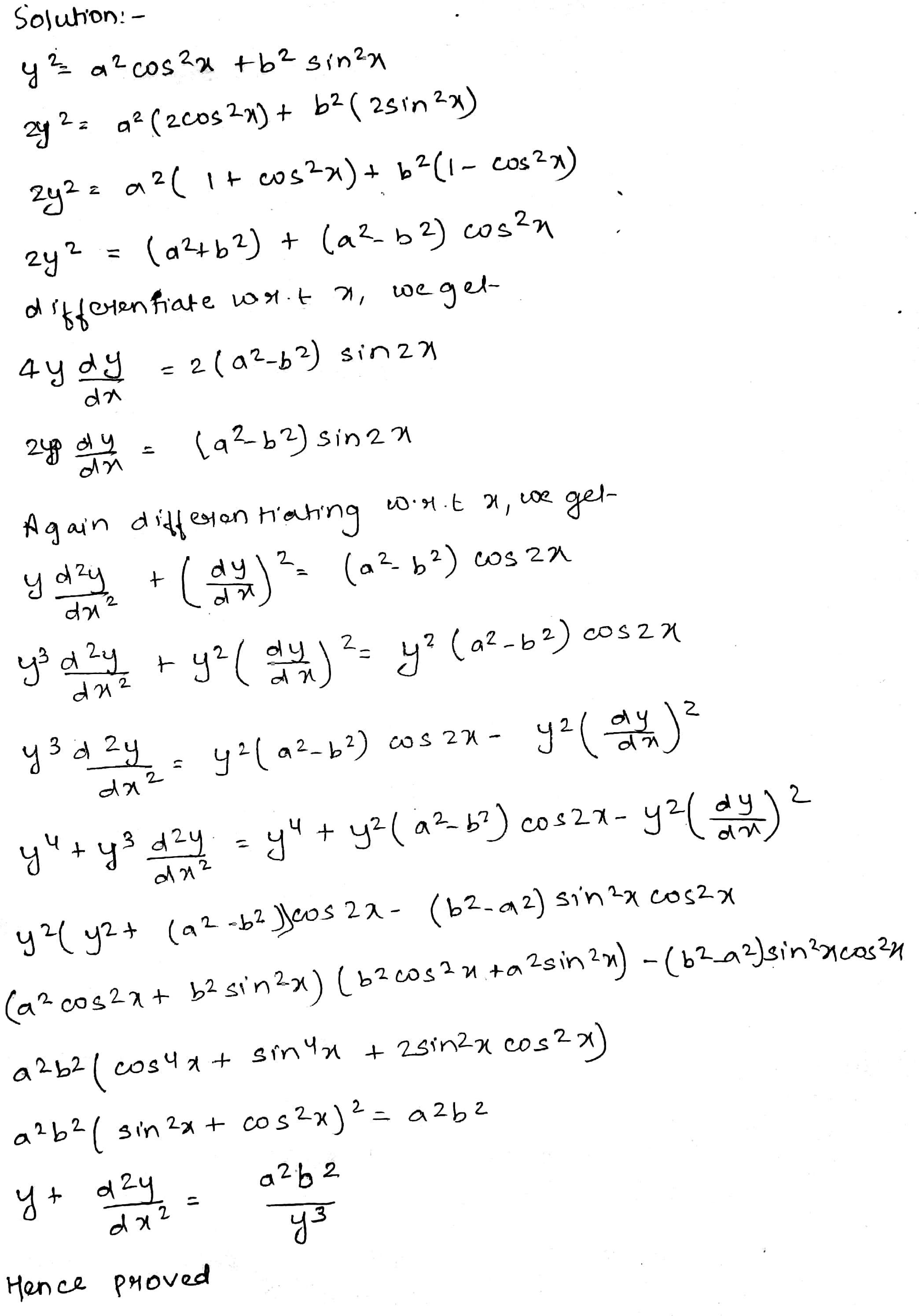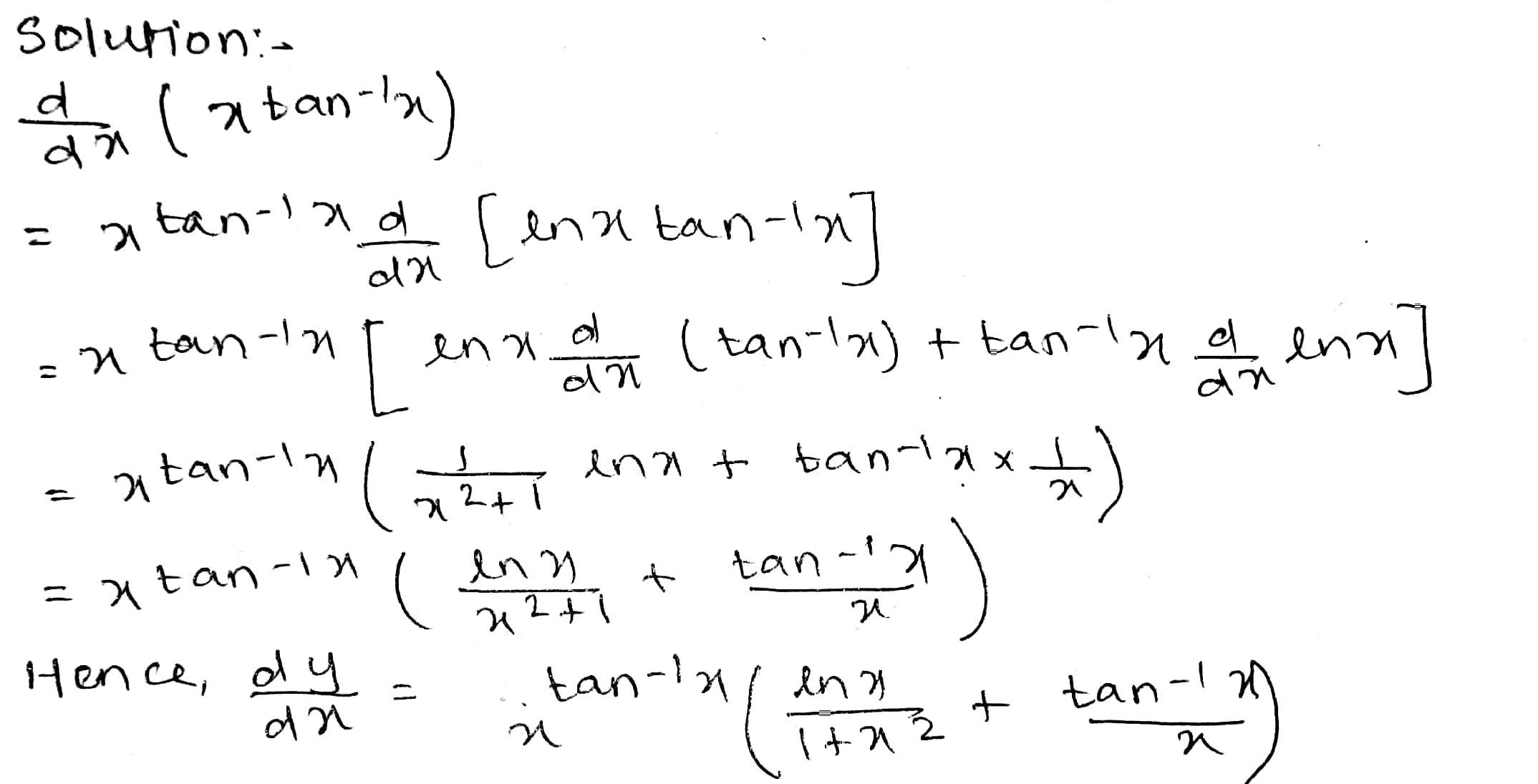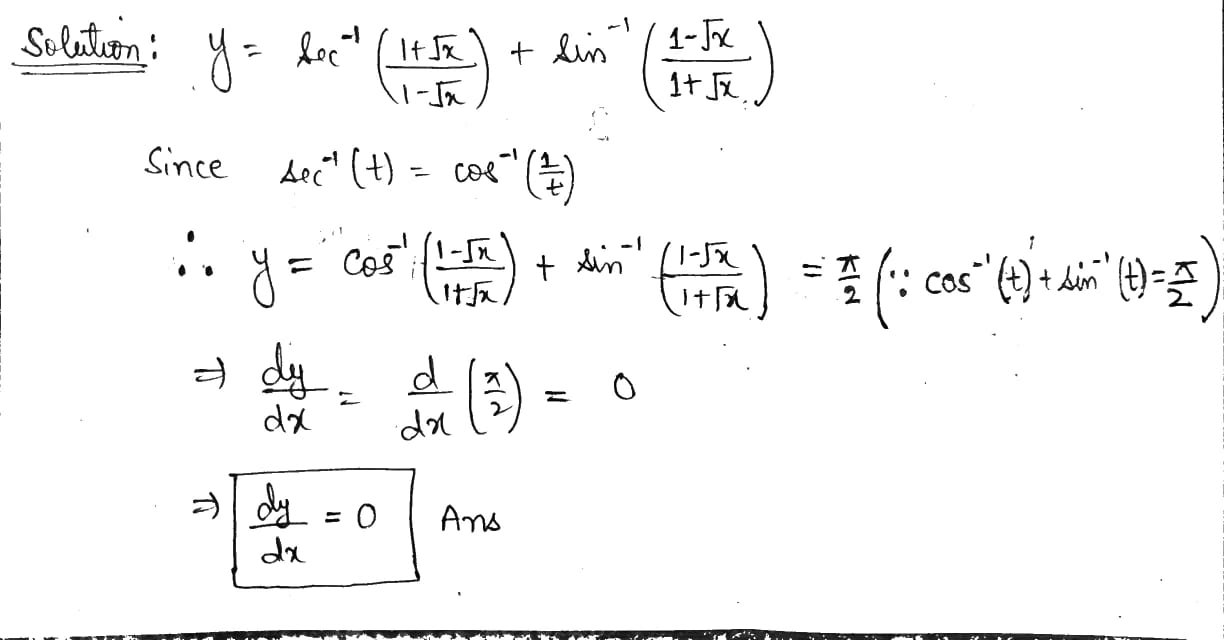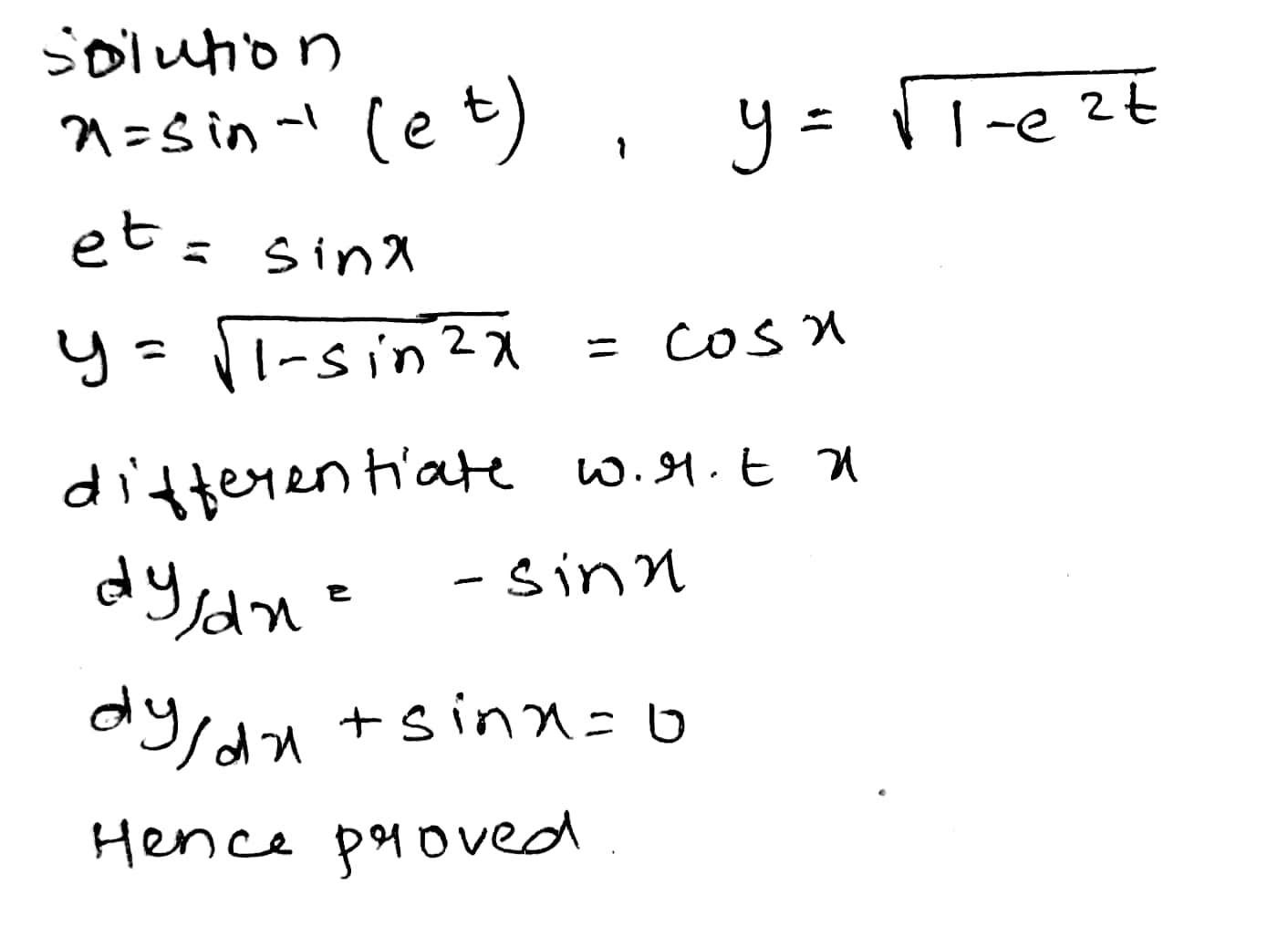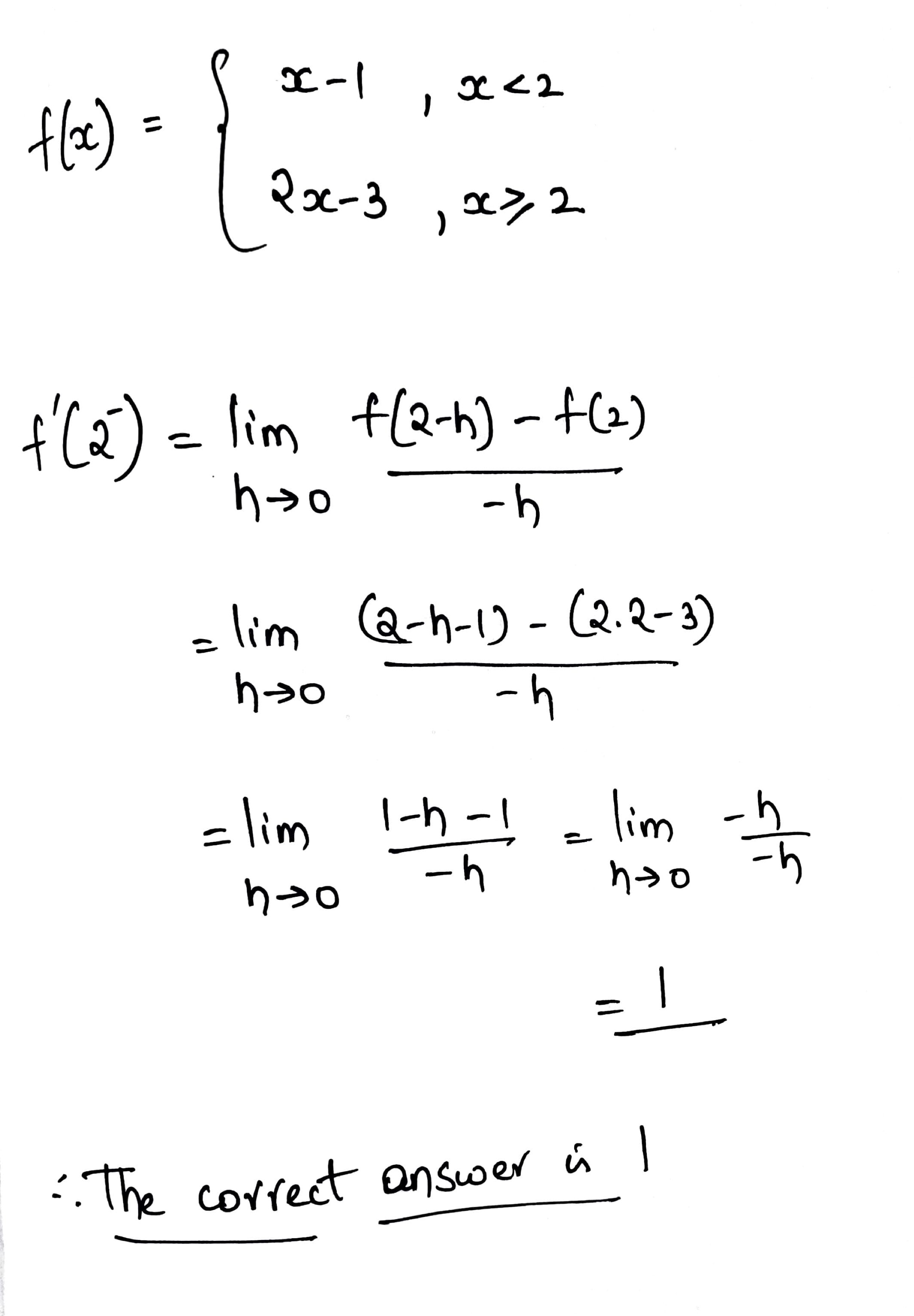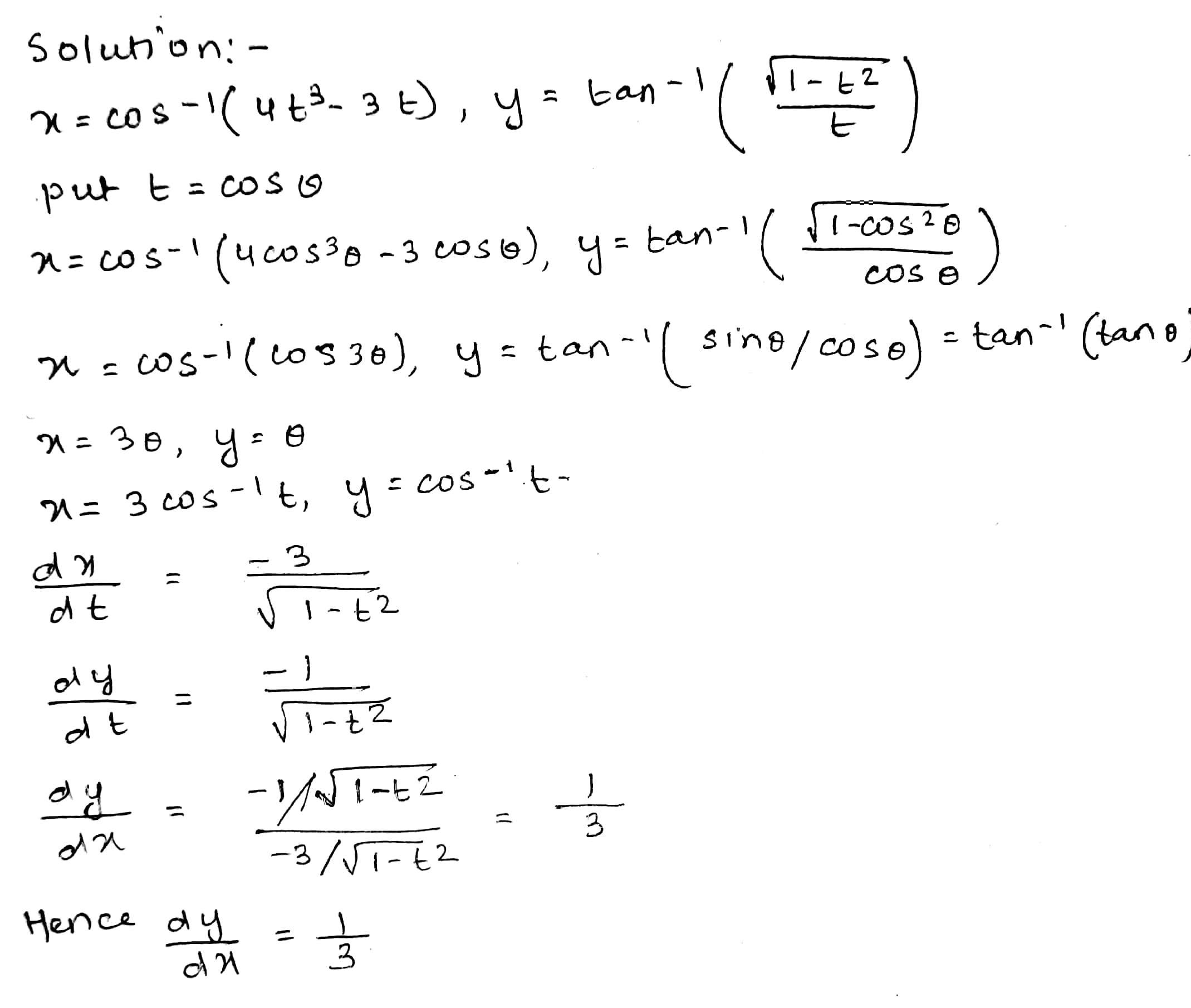Continuity And Differentiability - Class 12 Commerce Maths - Extra Questions
Find $$\dfrac{dy}{dx}$$, if $$x^2+xy+y^2=100$$.
Differentiate the given function w.r.t. $$x$$.
$$\displaystyle e^{\sin^{-1} x}$$
If $$y=3e^{2x}+2e^{3x}.$$prove that $$\dfrac{d^2y}{dx^2}-5\dfrac{dy}{dx}+6y=0$$.
Differentiate $$\begin{pmatrix}x+\dfrac{1}{x}\end{pmatrix}^x$$ with respect to $$x$$.
Solve $$\displaystyle \lim_{x\rightarrow -2}\dfrac{(\dfrac{1}{x}+\dfrac{1}{2})}{x+2}$$
Let $$f (x) = \left\{\begin{matrix} \sin x,& for \ x \geq 0\\ 1 - \cos x, & for \ x < 0\end{matrix}\right.$$ and $$g(x) = e^x$$. Then $$(g of)' (0)$$ is
Differentiate $$\sin { { h }^{ -1 }\left( \cfrac { x }{ 3 } \right) } $$ with respect to $$x$$. Find out the solution of the integration $$\int { \cfrac { 1 }{ \left( { x }^{ 2 }+9 \right) } dx } $$ Further find out the value of the integral $$\int { \cfrac { 1 }{ \left( { x }^{ 2 }+49 \right) } dx } $$ ?
Show that $$\cfrac { d }{ dx } \left( \tan { { h }^{ -1 }x } \right) =\cfrac { 1 }{ 1-{ x }^{ 2 } } $$
Differentiate the following function with respect to $$x$$
$$\tan { { h }^{ -1 }\left( 3x+1 \right) } $$
Differentiate the following function w.r.t.$$x$$
$$\sqrt [3] {(2x^{2}-7x-4)^{5}}$$
Show that $$\cfrac { d }{ dx } \left( \cos { { h }^{ -1 }x } \right) =\cfrac { 1 }{\sqrt{ { x }^{ 2 }-1 } } $$
Prove that
$$\cfrac { d }{ dx } \left( \cot { { h }^{ -1 }x } \right) =\cfrac { -1 }{ \left( { x }^{ 2 }-1 \right) } $$
Differentiate $${X}^{\log{x}}+{(\log{x})}^{x}$$ w.r.t.x.
Find $$\dfrac{{dy}}{{dx}}$$ if $$f(x)=\cos 3x.6{e^{6x}}$$
Find $$k$$ such that function is continuous at $$x=0$$$$f(x)=\dfrac{x^3-3x}{sinx}$$ for $$x\neq0$$ $$=k$$ for $$x=0$$
Differentiate the following function w.r.t.x.
$$\dfrac{1}{(x^{2}+3^{2})}$$
Differentiate: $$f\left( x \right) = {\left[ {\log \left( {7x + 3} \right)} \right]^5}$$ with respect to $$x$$.
Differentiate $$ \sec {x^{\tan x}}$$ with respect to $$x$$
If $$x = a\left( {\cos t + t\sin t} \right)$$ and $$y = a\left( {\sin t - t\cos t} \right)$$, find $$\dfrac{{{d^2}y}}{{d{x^2}}}$$
Show that $$f(x)=|x-2|+|x-3|$$ is not differentiable at $$x=2$$.
If $$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$$, find $$\dfrac{dy}{dx}$$.
Find $$\dfrac {d^{2}y}{dx^{2}}$$, of the following functions: $$x=at^{2},y=2at$$.
For a positive constant 'a' find $$\dfrac{{dy}}{{dx}}$$, where
$$y = {a^{t + \frac{1}{t}}},\,and\,x = {\left( {t + \frac{1}{t}} \right)^a}$$
If $$x = 2 \,at^2, y = at^4$$ find $$\dfrac{dy}{dx}$$.
Let $$y=x^2-2x+1$$ then find the value of $$y$$ for which $$\dfrac{dy}{dx}=-2$$.
Differentiate $$\dfrac{\tan x}{x}\left(\log\dfrac{e^x}{x^x}\right)$$.
Let $$y=2^x+x^2+2$$ then find $$\dfrac{dy}{dx}$$.
Let $$y=x^{10}+10^x+10$$ then find $$\dfrac{dy}{dx}$$
Find $$\dfrac {dy}{dx}$$ in$$x = a (\theta - \sin \theta)$$
$$y = b (1 - \cos \theta)$$
$$y = b (1 - \cos \theta)$$
Given that $${\left( {f\left( x \right)} \right)^{g\left( y \right)}} = {e^{f\left( x \right) - g\left( y \right)}}$$. Find $$\dfrac{{d f(x)}}{{d g(x)}}$$
$$f ( x ) = \dfrac { 2 x ^ { 2 } - 5 x + 7 } { ( x - 1 ) ( x - 2 ) ( x - 3 ) }$$ is continuous or not?
Differentiate w.r.t. $$x$$ in $$\tan^{-1} \left(\dfrac{5x}{1 - 6x^2} \right)$$
Differentiate $${ x }^{ { x }^{ 2 } }$$ w.r.t. $$x$$
$$x=a(\cos 2t+2t\ \sin 2t)$$ and $$y=a(\sin 2t-2t \cos 2t)$$ find second order derivative.
If $$x=2\cos{\theta}-\cos{2\theta}$$ and $$y=2\sin{\theta}-\sin{2\theta}$$, then prove that $$\cfrac{dy}{dx}=\tan{(\cfrac{3\theta}{2})}$$
If $$x = a \left (t - \dfrac {1}{t}\right ), y = a\left (t + \dfrac {1}{t}\right )$$
Show that: $$ \dfrac {dy}{dx} = \dfrac {x}{y}$$.
For what values $$k$$ is the following function continuous at $$x=-\dfrac{\pi}{6}$$ ?
$$f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt 3 \sin x + \cos x}}{{x + \dfrac{\pi }{6}}}\,,\,x \ne - \dfrac{\pi }{6}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,k\,\,\,\,\,\,\,\,\,\,\,\,\,\,,x = - \dfrac{\pi }{6}\end{array} \right.$$
$$y=x^2+x$$ then Find $$\dfrac {dy}{dx}$$.
If $$x=\dfrac {\sin^{3}t}{\sqrt {\cos 2t}},y=\dfrac {\cos^{3}t}{\sqrt {\cos 2t}}$$, then find $$\dfrac {dy}{dx}$$.
Evaluate : $$\displaystyle \lim_{x\rightarrow 2}{\dfrac{x^{3}-8}{x^{2}-4}}$$
Find the derivative of $$\tan^{-1} \left(\dfrac{\sin x}{1+\cos x}\right)$$ with respect to $$\tan^{-1}\left(\dfrac{\cos x}{1+\sin x}\right)$$.
Determine the value of 'k' for which the following function is continuous at $$ x = 3 ,$$$$\, f (x)= \begin {cases}\dfrac{(x+3)^2-36}{x-3} , & x \neq 3\\ k , & x =3\end {cases}$$
If $$y=\sqrt { x } +\dfrac { 1 }{ \sqrt { x } } $$, show that $$2x\dfrac { dy }{ dx } +y=2\sqrt { x } . $$
$$ y = \sqrt{x} + \frac{1}{\sqrt{x}}$$
Differentiating with respect to x, we get
$$ \frac{dy}{dx} = \frac{1}{2\sqrt{x}} + (\frac{-1}{2\sqrt[x]{x}})$$
$$ \frac{dy}{dx} = \frac{1}{2\sqrt{x}} - \frac{1}{2x\sqrt{x}}.$$
$$ \frac{dy}{dx} = \frac{x-1}{2x\sqrt{x}}$$
$$ 2x\frac{dy}{dx} = \frac{x-1}{\sqrt{x}}$$
$$ 2x\frac{dy}{dx} = \frac{x}{\sqrt{x}} - \frac{1}{\sqrt{x}}.$$
$$ 2x\frac{dy}{dx} =\sqrt{x}-\frac{1}{\sqrt{x}}$$
$$ 2x\frac{dy}{dx} = \sqrt{x}-\sqrt{x}-\frac{1}{\sqrt{x}}+\sqrt{x}$$
$$ 2x\frac{dy}{dx} = 2\sqrt{x}-y$$
$$\Rightarrow 2x\frac{dy}{dx} +y = 2\sqrt{x}$$
If $$r=at^2, y=2at$$, then find $$\dfrac{dy}{dx}$$.
Sol x=$$at^{2}$$, y=2 at find $$\frac{dy}{dx}$$
$$x=at^{2}$$ y=2at
$$\frac{dx}{dt}=2at $$ $$ \frac{dy}{at}=2a$$
$$\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$$ $$=\frac{2a}{2at}$$
$$\frac{dy}{dx}=\frac{1}{t}$$
Find $$\dfrac{dy}{dx}$$ :$$6x-9+8y=0$$
Find $$\dfrac {dy}{dx}$$, if $$y+\sin{y}=\cos{x}$$.
Find $$\dfrac{dy}{dx}$$ :
$$\sin x +y = 5x-10x^{2}$$
Differentiate the following functions
$${\left[ {{{\left( {\tan \,x} \right)}^{\tan \,x}}} \right]^{\tan \,x}}$$ at $$x = \frac{\pi }{4}$$.
Find $$\dfrac{dy}{dx}$$ :$$x^{2}+5x+2y^{2}=2$$
$$ y = 2\tan x$$ Find $$\dfrac{dy}{dx}$$ at $$x=\dfrac{\pi}{4}$$
Find $$\dfrac{dy}{dx}$$ :$$2y^{2}+6x=5$$
Find $$\dfrac{dy}{dx}$$ if $$y=\dfrac 1{\sqrt x}$$
$$y={ sinx }^{ }$$ find $$\dfrac{d^2y}{dx^2}$$
Show that $$f(x)=\left\{\begin{matrix}12x-13, & if & x\leq 3\\ 2x^2+5, & if & x > 3\end{matrix}\right.$$ is differentiable at $$x=3$$. Also, find $$f'(3)$$.
Define differentiability of a function at a point.
Find whether the following function is differentiable at $$x=1$$ and $$x=2$$ or not:
$$f(x)=\left\{\begin{matrix} x, & x\leq 1\\ 2-x, & 1\leq x\leq 2\\ -2+3x-x^2, & x > 2\end{matrix}\right.$$.
Is every differentiable function continuous?
If $$f(x)$$ is differentiable at $$x=c$$, then write the value of $$\displaystyle\lim_{x\rightarrow c}f(x)$$.
Show that $$f(x)=\left\{\begin{matrix}12x-13, & if & x\leq 3\\ 2x^2+5, & if & x > 3\end{matrix}\right.$$ is differentiable at $$x=3$$. Also, find $$f'(3)$$.
If $$\tan (x+y)+ \tan (x-y)=1,$$ then find $$\dfrac{dy}{dx}$$.
Is every continuous function differentiable?
If $$f(x)=|x-2|$$ write whether $$f'(2)$$ exists or not.
If $$y=x^x$$, then find $$\dfrac{dy}{dx}$$.
Differentiate with respect to $$x$$:
$$(x^x)$$
Find $$\dfrac{dy}{dx}$$, when
If $$x=\cos t$$ and $$y=\sin t$$, prove that $$\dfrac {dy}{dx}=\dfrac{1}{\sqrt{3}}$$ at $$t=\dfrac {2 \pi}{3}$$
If $$x=10(t-\sin t),\ y=12(1-\cos t),$$ find $$\dfrac {dy}{dx}.$$
If $$x=\sin t$$ and $$y=\cos t$$, then find $$\dfrac{dy}{dx}$$.
If $$x=3\sin {t} ,\ y=3\cos {t} ,$$ then find $$\dfrac {dy}{dx}$$ at $$t=\dfrac { \pi }{ 3 } $$.
If $$x=4t^2,y=6t$$, then find $$\dfrac{dy}{dx}$$.
Find $$\dfrac {dy}{dx}$$, when $$x= {2t}$$ and $$y={1-t^{2}}$$.
Find $$\dfrac{dy}{dx}$$, when $$x=4t, y=\dfrac{4}{t}$$.
Find $$\dfrac{dy}{dx}$$, when
$$x=3at^2$$ and $$y=2at$$.
Differentiate the following w.r.t. $$ x: \operatorname{cosec}^{-1}\left(\dfrac{1}{4 \cos ^{3} 2 x-3 \cos 2 x}\right) $$
Find the second order derivative of $$y=$$ $$ x^{20} $$
Find $$\dfrac{dy}{dx}$$, if $$x=2at^2$$ and $$y=at^4$$.
If $$x=\sin t$$ and $$y=\cos t$$, find $$\dfrac{dy}{dx}$$.
If $$x=e^t \cos t$$ and $$y=e^{-t} \sin t$$, find $$\dfrac{dy}{dx}$$.
Differentiate the following w.r.t. $$ x: \cot ^{-1}\left(x^{3}\right) $$
Find $$\dfrac{dy}{dx}$$, if $$x=a\cos \theta, y=b\cos \theta$$.
Find $$\dfrac{dy}{dx}$$, if $$x=\sin t, y=\cos 2t$$.
Find derivative of $$y=x^2+e^x+x^x$$.
If $$f(x)$$ is a twice differentiable function such that $$f(a) = 0, f(b) = 2, f(c) = 1, f(d) = 2, f(e) = 0,$$ where $$a < b < c < d < e,$$ then the minimum number of zeroes of $$g(x) = (f'(x))^{2}+f''(x)f(x))$$ in the interval $$[a, e]$$ is
If $$f(x)$$ is a twice differentiable function such that $$\displaystyle f\left ( a \right )= 0,$$ $$f\left ( b \right )= 2,$$ $$f\left ( c \right )=-1,$$ $$f\left ( d \right )=2$$ and $$\displaystyle f\left ( e \right )=0,$$ where $$\displaystyle a< b< c< d< e, $$ then the minimum number of zeros of $$\displaystyle g(x)={f'(x)}^{2}+f"(x)\cdot f\left ( x \right )$$ in the interval $$[a,c]$$ is
Let $$\displaystyle f\left ( x \right )=\frac{x^{3}+x^{2}-16x+20}{\left ( x-2 \right )^{2}}if x\neq 2,=k,ifx=2.$$ If $$\displaystyle f\left ( x \right )$$ is continuous for all x,then $$k=b \times7$$ Find b
If $$\displaystyle y=\frac{(x+1)^{2}\sqrt{x-1}}{(x+4)^{2}e^{x}}$$, then show that $$\displaystyle \frac{dy}{dx}=\frac{x+1^{2}\sqrt{(x-1)}}{(x+4)e^{x}}\left [ \frac{5x-3}{2(x^{2}-1)}+\frac{x+6}{x+4} \right ]$$
If $$f(x)$$ and $$g(x)$$ both are discontinuous at any point, then show that their composition may be differentiable at that point.
Solve $$\displaystyle \lim_{x\rightarrow \pi /2}\frac{\sin x-\left ( \sin x \right )^{\sin x}}{1-\sin x+\log \sin x}$$
Differentiate the function w.r.t. $$x$$.
$$\displaystyle x^{x \cos x} + \frac{x^2 + 1}{x^2 - 1}$$
Differentiate the function w.r.t. $$x$$.
$$(\log x)^x + x^{\log x}$$
Differentiate the function w.r.t. $$x$$.
$$\displaystyle \left( x + \frac{1}{x} \right)^x + x^{\left( 1 + \tfrac{1}{x} \right) }$$
Differentiate the function w.r.t. $$x$$.
$$(\log x)^{\cos x}$$
Differentiate the function w.r.t. $$x$$.
$$\displaystyle x^{\sin x} + (\sin x)^{\cos x}$$
Differentiate the given function w.r.t. $$x$$:
$$(\sin x - \cos x)^{(\sin x - \cos x)}$$, $$\displaystyle{\frac{\pi}{4} < x < \frac{3\pi}{4}}$$
Differentiate the given function w.r.t. $$x$$:
$$x^{x^{2} - 3} + (x - 3)^{x^{2}}$$, for $$x > 3$$
If $$x$$ and $$y$$ are connected parametrically by the given equation, then without eliminating the parameter, find $$\displaystyle \frac{dy}{dx} $$
$$x = 2at^2, y = at^4$$
Discuss the continuity of the following function :
$$f(x)=\sin { x } +\cos { x } $$.
If $$x=\sqrt { { a }^{ \sin ^{ -1 }{ t } } } ,\quad y=\sqrt { { a }^{ \cos ^{ -1 }{ t } } } $$, show that $$\cfrac{dy}{dx}=-\cfrac{y}{x}$$
If $$u, v$$ and $$w$$ are functions of $$x$$, then show that
$$\cfrac { d }{ dx } \left( u,v,w \right) =\cfrac { du }{ dx } v.w+u.\cfrac { dv }{ dx } .w+u.v\cfrac { dw }{ dx } $$
in two ways- first by repeated application of product rule, second by logarithmic differentiation.
If $$x$$ and $$y$$ are connected parametrically by the given equation, then without eliminating the parameter, find $$\displaystyle \frac{dy}{dx} $$.$$x = a(\cos \theta + \theta \sin \theta)$$ and $$y = a(\sin \theta - \theta \cos \theta)$$
Differentiate w.r.t $$x$$.
$$\sin^{-1} \left (\dfrac {a\cos x + b\sin x}{\sqrt {a^{2} + b^{2}}}\right )$$
If $$x = a\left (t - \dfrac {1}{t}\right ), y = a\left (t + \dfrac {1}{t}\right )$$, then show that $$\dfrac {dy}{dx} = \dfrac {x}{y}$$
If $$x = at^{2}, y = 2at$$, then find $$\dfrac {dy}{dx}$$.
Find $$\cfrac { dy }{ dx } $$ where $$ { x }^{ y }={ y }^{ x };x>0,y>0$$.
If $$x^{y} = e^{x - y}$$, then show that $$\dfrac {dy}{dx} = \dfrac {\log x}{(1 + \log x)^{2}}$$
Show that the function $$f(x) = \left\{\begin{matrix} 3 - x, & if &x < 1 \\ 2, & if & x = 1\\ 1 + x, & if & x > 1\end{matrix}\right.$$ is continuous at $$x = 1$$
If $$x=a \sin^3\theta$$ and $$y=a \cos^3\theta$$, then find the value of $$\displaystyle\frac{dy}{dx}$$.
Find the differential coefficient of $$\tan ^{ -1 }{ x } $$
If $$y = x^x$$, find $$\dfrac{dy}{dx}$$.
Determine the value of 'k' for which the following function is continuous at $$x = 3$$:
$$f(x) = \left\{\begin{matrix} \dfrac{(x + 3)^2 - 36}{x - 3}& , x \neq 3 \\ k & , x = 3\end{matrix}\right.$$
If a curve is represented parametrically by the equations.
$$x=\sin\left(t+\dfrac{7\pi}{12}\right)+$$$$\sin\left(t-\dfrac{\pi}{12}\right)+\sin\left(t+\dfrac{3\pi}{12}\right),$$ $$y = \cos\left(t+\dfrac{7\pi}{12}\right)+\cos\left(t-\dfrac{\pi}{12}\right)+\cos\left(t+\dfrac{3\pi}{12}\right)$$ then find the value of $$\dfrac{d}{dt}\left(\dfrac{x}{y}-\dfrac{y}{x}\right)$$ at $$t = \dfrac{\pi}{8}$$
If $$y=$$ $$\sec x + \tan x$$, then prove that $$\displaystyle \frac{d^2y}{dx^2} = \frac{\cos x}{(1 - \sin x)^2}$$
Suppose f is continuous $$f(0)=0, f(1)=1, f'(x)> 0$$ and $$\displaystyle\int_{0}^{1}f(x)dx=\frac{1}{3}$$. Find the value of the definite integral $$\displaystyle\int_{0}^{1}f^{-1}(y)dy$$.
Differentiate $$sec^{-1}x$$ w.r.to x by first principle.
Differentiate the function $$\tan^{-1} \dfrac{2x}{1 - x^{2}}$$ w.r.to $$\cos^{-1}(\dfrac{1 - x^{2}}{1 + x^{2}})$$
Differentiate $$\tan ^{ -1 }{ \left( \dfrac { x }{ \sqrt { 1-{ x }^{ 2 } } } \right) }$$ w.r.t $$\sin ^{ -1 }{ \left( 2x\sqrt { 1-{ x }^{ 2 } } \right) }$$.
Differentiate the following function with respect to $$x$$
$$\cos { { h }^{ -1 }(4+3x) } $$
Differentiate the following function with respect to $$x$$:
$$\sin { { h }^{ -1 }\left( \sqrt { x } \right) } $$
Differentiate the following $$\displaystyle\frac{e^x}{\sin x}$$.
If $$x=a(2\theta -\sin 2\theta)$$ and $$y=a(1-\cos 2\theta)$$, find $$\displaystyle\frac{dy}{dx}$$ when $$\theta =\displaystyle\frac{\pi}{3}$$.
Evaluate: $$y={ \left( \sin { x } \right) }^{ \tan { x } }+{ \left( \cos { x } \right) }^{ \sec { x } }$$
For $$ x = \sqrt { { a }^{ \tan ^{ -1 }{ t } } } ,y=\sqrt { { a }^{ \cot ^{ -1 }{ t } } } ,t\in R$$, find $$\cfrac { dy }{ dx } $$.
Let $$f(x)$$ be differentiable function in $$ \left[ \left. -1,\infty \right)\right.$$ and $$f(0)=1$$ such that $$\lim\limits_{t \to x+1}\large{\frac{t^2f(x+1)-(x+1)^2 f(t)}{f(t)-f(x+1)}}=1$$. Find the value of $$\lim\limits_{x \to 1}\large{\frac{\ln \left(f(x)\right)- \ln 2}{x-1}}$$
Find $$\dfrac{dy}{dx}$$, when
i) $$x=at^2$$ and $$y=2at$$
ii) $$x=a(\theta+\sin \theta)$$ and $$y=a(1-\cos \theta)$$.
If $$x = \sin t, y = \cos 2t$$ then prove that $$\dfrac {dy}{dx} = -4\sin t$$.
Find the derivative with respect to $$x$$ of the function:
$$(\log_{\cos x}\sin x)(\log_{\sin x} \cos x)^{-1}+\sin ^{-1}\dfrac{2x}{1+x^2}$$ at $$x=\dfrac{\pi}{4}$$.
Differentiate: $$\sqrt {e^{\sqrt {x}}},x>0$$
Find $$\dfrac{dy}{dx}$$, if $$ y = x^{\sin \, x} + (\sin \, x)^{\cos \, x}$$
If $$y = {\cos ^{ - 1}}\left\{ {\dfrac{{2x - 3\sqrt {1 - {x^2}} }}{{\sqrt {13} }}} \right\}.$$ Find $$\dfrac{{dy}}{{dx}}$$.
If $$y = {\left( {{{\cot }^{ - 1}}x} \right)^2}$$, then show that $$\left( {1 + {x^2}} \right)^2{{{d^2}y} \over {d{x^2}}} + 2x\left( {1 + {x^2}} \right){{dy} \over {dx}} = 2.$$
If $$Y=\cot ^{ -1 }{ \left[ \dfrac { \sqrt { 1+\sin { x } } +\sqrt { 1-\sin { x } } }{ \sqrt { 1+\sin { x } } -\sqrt { 1-\sin { x } } } \right] } $$. Prove that $$\dfrac {dy}{dx}$$ is independent of $$x$$.
Find the derivative of $$\tan {\sqrt {x}}$$ w.r.t. $$x$$., using first principle
If $${y^x} = {e^{y - x}}$$ then prove that $$\frac{{dy}}{{dx}} = \frac{{{{\left( {1 + \log y} \right)}^2}}}{{\log y}}$$.
Differentiate w.r.t. x :$$f(x) = \sqrt {\sin \left( {\cos x} \right)} $$
Solve : $$y = \sin^{-1} \left(\dfrac{1 - x^2}{1 + x^2} \right) , 0 < x < 1$$
If $$x=a(\cos t+log \tan \dfrac{t}{2})$$ and $$y=a\sin t$$, then find $$\dfrac{d^2y}{dx^2}$$ at $$t=\dfrac{\pi}{3}$$.
If $$x=a\sec^3\theta$$, $$y=a\tan^3\theta$$ find $$\dfrac{dy}{dx}$$ at $$\theta =\dfrac{\pi}{4}$$.
Differentiate $$y=\left[ \sin ^{ -1 }{ \left( x-\dfrac { 4{ x }^{ 3 } }{ 27 } \right) } \right]$$ w.r.t $$x$$
Find $$\dfrac{dy}{dx}$$ when $$y=\dfrac{1+\sin 2x-\cos 2x}{1+\sin 2x+\cos 2x}$$.
Find $$\dfrac{{dy}}{{dx}}$$:
$$x = \dfrac{{{e^t} + {e^{ - t}}}}{2}\,and\,y = \dfrac{{{e^t} - {e^{ - t}}}}{2}$$
If $$x = a{\cos ^3}\theta $$ and $$y = a{\sin ^3}\theta $$ , then find the value of $$\,\dfrac{{{d^2}y}}{{d{x^{2\,\,}}}}$$ at $$\theta = \dfrac{n}{6}$$
f(x)=x cosx
Find $$f'(\pi)$$
Formula: cos(A+B)= cosA cosB- sinA sinB.
Find $$\dfrac{dy}{dx}$$ for $$2x^2+5xy+3y^2=1$$.
If $$f(x)=\begin{cases} \dfrac { { 2 }^{ x+2 }-16 }{ { 4 }^{ x }-16 }\ ,\ if x\neq 2 \\ k \quad \quad \quad \quad, \ if x = 2 \end{cases}$$ is continuous at $$x=2$$, find $$k$$
Let $$y=e^x.\sin(ax^2+bx+c)$$ then find $$\dfrac{dy}{dx}$$.
If $$x=3\sin \theta-\sin 3\theta \\ y=3 \cos \theta-\cos \theta$$
Find $$\dfrac {dy}{dx}$$ at $$x=\dfrac {\pi}{3}$$
Find $$\frac{dy}{dx}=sin^{-1}x$$
Diffrentiate w.r.t $$x$$
$$\tan^{-1}x$$
Find the derivative w.r.t to $$x$$ $$i)x^y$$
Find the derivative of $$x^x - 2^{\sin x}$$ w.r.t. x
Find $$d=\dfrac{dy}{dx}$$ if $$x=\dfrac{\sin^3t}{\sqrt{\cos 2t}}$$
$$y=\dfrac{\cos^3t}{\sqrt{\cos 2t}}$$
If the function $$f(x)=\dfrac {(4^{\sin x}-1)^{2}}{x\log (1+2x)}$$ for $$x \neq 0$$ is continuous at $$x=0$$, Find $$f(0)$$
Let $$y=3x^2+5x$$ find $$\dfrac{dy}{dx}$$
If $$y$$ is a differentiable function of $$u$$ and $$u$$ is a differentiable function of $$x$$, then prove that $$\dfrac { dy }{ dx } =\dfrac { dy }{ du } .\dfrac { du }{ dx } .$$
Given $$f\left( x \right) = \dfrac{1}{{x - 1}}$$ . Find the points of discontinuity of the composite function $$y =[ f\left\{ {f\left( x \right)} \right\}]$$
$$f(x)=\dfrac{1}{x-1}$$
$$f(f(x))=\dfrac{1}{\dfrac{1}{x-1}-1}=\dfrac{x-1}{1-x+1}=\dfrac{x-1}{2-x}$$
Points of discontinuity of $$y=f(f(x))$$ is when $$x=2$$.
Show that $$f(x)=\left\{\begin{matrix} \dfrac{\cos ax-\cos bx}{x^2} & if & x\neq 0\\ \dfrac{1}{2}\left(b^2-a^2\right) & if & x=0\end{matrix}\right.$$ where a and b are real constants, is continuous at $$0$$.
Let $$f(x) = 1 + 4x - x^{2}, \forall x\epsilon R$$
$$g(x) = \left\{\begin{matrix} max.&\left \{f(t); x \leq t\leq (x + 1); 0\leq x < 3\right \} \\ min. & \left \{(x + 3); (3\leq x \leq 5\right \}\end{matrix}\right.$$
Discuss the continuity and differentiability of $$g(x)$$ for all $$x\epsilon [0, 5]$$.
If $$x=a\sin 2t(1+\cos 2t)$$ and $$y=b2t(1-\cos 2t)$$, find the values of $$\dfrac{dy}{dx}$$ at $$t=\dfrac{\pi}{4}$$ and $$t=\dfrac{\pi}{3}$$.
Differentiate $$x\ \cos^{-1} x$$.
Discuss the continuity of $$f(x)$$
$$= \dfrac {x^{5}\sqrt {x} - 32\sqrt {2}}{x^{3}\sqrt {x} - 8\sqrt {2}} x\neq 2$$
$$= \dfrac {44}{7}$$, at $$x = 2$$.
Verify Rolle's Theorem for the function $$f\left( x \right) = {x^2} + 2x - 8,x \in \left[ { - 4,2} \right]$$
Prove that given function is not continuous$$f(x) = \left.\begin{matrix} \dfrac {\log x - \log 7}{x - 7},& for\ x\neq 7\\ = 7, & for\ x = 7\end{matrix}\right\}$$ at $$x = 7$$.
A function $$7(x)$$ is said to be continuous at a point $$x=0$$, in its domain if the following three conditions are satisfied:
$$\rightarrow f(a)$$ exists (i.e., the value of $$f(a)$$ is finite)
$$\rightarrow \displaystyle\lim_{x\rightarrow a}f(x)$$ exists (i.e. the right hand limit equal to left hand limit & both are finite).
$$\rightarrow \displaystyle\lim_{x\rightarrow a}f(x)=f(a)$$
LHL for $$x=7$$
$$f(x)=\left[\dfrac{log(7-h)-log 7}{7-h-7}\right]$$ [$$h > 0$$ and limit h tending to zero]
$$=\dfrac{log\left(\dfrac{7-h}{7}\right)}{-h}$$
$$=\dfrac{log\left[1+\left(-\dfrac{h}{7}\right)\right]}{7\left(-\dfrac{h}{7}\right)}=\dfrac{1}{7}$$ $$\left[\displaystyle\lim_{x\rightarrow 0}\dfrac{log(1+x)}{x}=1\right]$$
RHL for $$x=7$$
$$f(x)=\left[\dfrac{log(7+h)-log 7}{7+h-7}\right]$$ [$$h > 0$$ & limit h tending to zero]
$$=\dfrac{log\left(\dfrac{7+h}{h}\right)}{h}$$
$$=\dfrac{log\left[1+\displaystyle\left(\dfrac{h}{7}\right)\right]}{7\left(\dfrac{h}{7}\right)}$$
$$=\dfrac{1}{7}$$
for $$x=7$$, $$f(x)$$ is given as $$7$$
Hence, LHL$$=$$RHL but not equal to $$f(x)$$
$$\therefore f(x)$$ is conti at $$x=7$$.
Use Rolle's theorem to prove that equation $$ax^{2}+bx=\dfrac{a}{3}+\dfrac{b}{2}$$ has a root between 0 and 1.
If $$y = {x^x},{\text{ then prove that }}{{{d^2}y} \over {d{x^2}}} - {1 \over y}{\left( {{{dy} \over {dx}}} \right)^2} - {y \over x} = 0$$.
If $${\left( {{x^2} + {y^2}} \right)^2} = xy,$$ find $$\frac{{dy}}{{dx}}$$.
If $$x=asin2t(1+cos2t)$$ and $$y=bcos2t(1-cos2t),$$ then find the values of $$\frac { dy }{ dx } $$ at $$t=\frac { \pi }{ 4 } $$ and $$t=\frac { \pi }{ 3 } .$$
Differentiate $$\tan^{-1}\left(\dfrac{3a^2x-x^3}{a^3-3ax^2}\right)$$, $$-\dfrac{1}{\sqrt{3}}<\dfrac{x}{a}<\dfrac{1}{\sqrt{3}}$$
Differentiate $${ \left( x+\dfrac { 1 }{ x } \right) }^{ x }$$ $$w.r.t$$ $$x$$.
Solve :
$$y = {x^{{x^{{x^{....\infty }}}}}}$$ ,then $$\frac{{dy}}{{dx}}$$
If $$y = ( \log x ) ^ { x } - x ^ { \log x } $$ then find $$\dfrac { d y } { d x }$$.
If $$y=(\sin x)^{\log x}$$ then find $$\dfrac{dy}{dx}$$.
Find $$\dfrac{dy}{dx}$$ of the function $$(\cos x)^y=(\cos y)^x$$ w.r.t.$$x$$.
If $$x^2 + 2xy + y^2 = 42$$, then find $$\dfrac{dy}{dx}$$
If $$y = x ^ { x }$$, find $$\frac { d y } { d x }$$.
$$f(x)\begin{matrix} =2,\quad for\quad x<1 \\ =ax+b,\quad for\quad 1\le x<3 \\ =3,\quad for\quad x\ge 3 \end{matrix}$$ is continuous at $$x=1$$ and $$x=3$$, find $$a$$ and $$b$$.
$$f(x)\begin{matrix} =\cfrac { { x }^{ 2 }-16 }{ x-4 } +a\quad for\quad x<4 \\ =2,\quad for\quad x=4 \\ =3{ x }^{ 2 }+4x+b,\quad for\quad x>4 \end{matrix}$$ is continuous at $$x=4$$, find $$a$$ and $$b$$.
Extend the definition of the following by continuity $$f(x)=\cfrac{1-\cos{7(x-\pi)}}{5{(x-\pi)}^{2}}$$ at the point $$x=\pi$$.
Check whether the function $$|x|$$ is continuous at $$x=0$$.
Verify that y = $$ae^{-x}$$ is a solution of
$$\dfrac{d^2y}{dx^2}=\dfrac{1}{y}\left(\dfrac{dy}{dx}\right)^2$$
Find $$\dfrac{{dy}}{{dx}}\ if\,\,\,y = \,\,\,\,\,{\tan ^{ - 1}}\left[ {\dfrac{{\sqrt {1 + \sin x} + \sqrt {1 - \sin x} }}{{\sqrt {1 + \sin x} - \sqrt {1 - \sin x} }}} \right]$$
R.E.F image
Solution -
$$ y = tan^{-1} [\frac{\sqrt{1+sin\,x}+\sqrt{1-sin\,x}}{\sqrt{1+sin\,x}-\sqrt{1-sin\,x}}] $$
$$ tan\,y = \frac{(\sqrt{1+sin\,x}+\sqrt{1-sin\,x})(\sqrt{1+sin\,x}+\sqrt{1-sin\,x})}{\sqrt{1+sin\,x}-\sqrt{1-sin\,x}(\sqrt{1+sin\,x}+\sqrt{1-sin\,x})} $$
$$ tan\,y = \frac{1+cos\,x}{sin\,x} $$
$$ sec\,y = \frac{\sqrt{2+2\,cos\,x}}{sin^{2}x} $$
$$ sec^{2}\frac{dy}{dx} = \frac{-sin^{2}x-(1+cos\,x)cos\,x}{sin^{2}x} $$
$$ \frac{2+2cos\,x}{sin^{2}x} \frac{dy}{dx} = \frac{-sin^{2}x-cos\,x-cos^{2}x}{sin^{2}x} $$
$$ \frac{dy}{dx} = \frac{-cosx-1}{2+2cos\,x} = \frac{-1/2(2+2\,cos\,x)}{(2+2\,cos\,x)} $$
$$ \frac{dy}{dx} = \frac{-1}{2} $$
If $$x ^ { 2 } + y ^ { 2 } = 1 - \frac { 1 } { t }$$ and $$x ^ { 4 } + y ^ { 4 } = t ^ { 2 } + \frac { 1 } { t ^ { 2 } }$$. Show that $$\frac { d y } { d x } = \frac { 1 } { x ^ { 3 } y }$$.
If $$x = a\left( {\theta - \sin \theta } \right)\,and\,y = a\left( {1 + \cos \theta } \right)$$ then prove that $$\frac{{dy}}{{dx}} = - \cot \left( {\frac{\theta }{2}} \right)$$.
$$\frac { d ^ { 2 } } { d x } \left( \tan ^ { - 1 } \left( \frac { \sqrt { 1 + x } - \sqrt { 1 - x } } { \sqrt { 1 + x } + \sqrt { 1 - x } } \right) \right) = \dots \dots$$ $$\dfrac {x}{p \sqrt {({1-x^2})^3}}$$ $$( \left| x \right| > 1)$$ then p =
If $$f ( x ) = \dfrac { 4 ^ { x } - 2 ^ { x + 1 } + 1 } { 1 - \cos x } , \text { for } x \neq 0$$ is continuous at $$x = 0$$, find $$f(0)$$
Find $$\dfrac {dy}{dx }$$, if $$x=a(1+\cos\theta) ,y=a(\theta+\sin\theta$$)
Let $$f(x+y)=f(x)+f(y)$$ for all $$x,\ y\in R$$. If $$f(x)$$ is continue at $$x=0$$ show that $$f(x)$$ is continuous at all $$x$$
Differentiate the following w.r.t. $$ x$$ :
$$\cos^{-1}\left (\dfrac{3\cos x - 4\sin x}{5}\right)$$
Find the derivative of $$(\sin x) ^{\cos^{-1}x}$$ with respect to $$x$$.
If $$y=\sin^{-1}x$$ then find $$y"$$.
Find the values of $$a$$ and $$b$$ so that the function $$f(x)=\left\{\begin{matrix} x^2+3x+a, & if & x\leq 1\\ bx+2, & if & x > 1\end{matrix}\right.$$ is differentiable at each $$x\in R$$.
$$f(x)=\left\{\begin{matrix} x^2+3x+a, & if & x\leq 1\\ bx+2, & if & x > 1\end{matrix}\right.$$
$$f(x)$$ is differentiable
$$\Rightarrow \displaystyle\underset{x\rightarrow 1^-}{lt}f^1(x)=\underset{x\rightarrow 1^+}{lt}f^1(x)$$
$$\Rightarrow \underset{x\rightarrow 1^-}{lt}(2x+3)=b$$
$$\therefore b=2+3=5$$
$$\therefore f(x)$$ is continuous as it is differentiable
$$\Rightarrow \underset{x\rightarrow 1^-}{lt}f(x)=\underset{x\rightarrow 1^+}{lt}f(x)$$
$$\Rightarrow \underset{x\rightarrow 1^-}{lt}(x^2+3x+a)=\underset{x\rightarrow 1^+}{lt}(bx+2)$$
$$\Rightarrow 1+3+a=\underset{x\rightarrow 1^+}{lt}(5x+2)$$
$$\therefore a=7-4=3$$.
Let $$y=\sin^{-1}(\cos x)$$ then find $$\dfrac{dy}{dx}$$.
If $$x=\left(t+\dfrac{1}{t}\right)^{a},\ y=a^{t+\tfrac{1}{t}}$$, then find $$\dfrac{dy}{dx}$$.
Find $$f'(1)$$ for $$f(x)=e^{5x+3}$$.
Find the derivative of $$f(x)=2x^{2}+3x-5$$ at $$x=-1$$ Also prove that $$f'(0)+3f'(-1)=0$$
If $$y=\dfrac{x\sin^{-1}{x}}{\sqrt{1-x^{2}}}$$, find $$\dfrac{dy}{dx}$$
If $$x= a \cos ^3 \theta,\, y= a \sin ^3 \theta$$, then find $$\dfrac{{{d^2}y}}{{d{x^2}}}$$ at $$\theta = \dfrac {\pi}{4}$$.
If $$ax+by^{2}=\cos y$$, then find $$\dfrac{dy}{dx}$$.
Prove that : $$\dfrac{d{(x^x)} }{{dx}}= {x^x}(1 + \log x)$$
The equation $$x=\dfrac{2a\theta }{1+\theta ^{2}},y=\dfrac{a(1-\theta ^{2})}{1+\theta ^{2}}$$ (where 'a' is a constant) is the parametric equation of the curve.Find $$\dfrac{dy}{dx}$$
If $$x=\cos \theta $$ and $$y=\tan \theta$$ find $$\dfrac{dy}{dx}$$
Differentiate $$\tan ^ { - 1 } \left( \dfrac { 2 ^ { x + 1 } } { 1 - 4 ^ { x } } \right)$$ w.r.t. $$x.$$
If $$ { ax }^{ 2 }+2xy+{ by }^{ 2 } =0$$ then find $$\dfrac { dy }{ dx } .$$
If $$f(x)$$ is continuous at $$f\left( x \right) =\begin{matrix} \dfrac { 1-\cos { kx } }{ { x }^{ 2 } } , \\ =\dfrac { 1 }{ 2 } , \end{matrix}\begin{matrix} for\ x\neq 0 \\ for\ x=0 \end{matrix}$$
Find $$k$$.
If $$\cos{x}=\cfrac{t}{\sqrt{1+t^2}}$$ and $$\sin{y}=\cfrac{1}{\sqrt{1+t^2}}$$ then prove that $$\cfrac{dy}{dx}=1$$
Find $$\dfrac{dy}{dx}$$ :
$$3x^{2}+tanx+secx=y+6$$
$$y=\sin x$$ find $$\dfrac{d^2y}{dx^2}$$
Let $$y=\log \dfrac{1+x}{1-x}$$ then find $$\dfrac{dy}{dx}$$.
Find
$$\dfrac { dy}{ dx } $$, If $$x=4t$$ and $$y=\dfrac { 4 }{ t } $$
Find $$\dfrac{dy}{dx}$$ at $$t=\dfrac{\pi}{4}$$If $$x=cost$$ and $$y=sin t$$
If $${x^y} = {y^x}$$, then find $$\dfrac {dy}{dx}$$.
$$x^{y}=y^{x}.$$
Taking $$log$$ on both sides
$$y \log x= x \log y.$$
Differentiating both the sides by $$uv$$ rule
$$ y.\dfrac{1}{x}+logx.\dfrac{dy}{dx}=x.\dfrac{1}{y}\dfrac{dy}{dx}+\log y$$
$$\Rightarrow \dfrac{y}{x}-logy =\dfrac{x}{y}.\dfrac{dy}{dx}-logx\dfrac{dy}{dx}$$
$$\Rightarrow \dfrac{y-xlogy}{x}=\dfrac{dy}{dx}(\dfrac{x-ylogx}{y})$$
$$\Rightarrow \dfrac{dy}{dx}=\dfrac{\dfrac{y-xlogy}{x}}{\dfrac{x-ylogx}{y}}$$
$$\Rightarrow \dfrac{dy}{dx}=\dfrac{y}{x}(\dfrac{y-xlogy}{x-ylogx}).$$
If $$x=\dfrac { a }{ 1+{ t }^{ 3 } } ,y=\dfrac { at }{ 1+{ t }^{ 3 } } $$ then show that $$\dfrac { dy }{ dx }$$ at $$t=1$$ is $$ \dfrac{1}{p}$$ then $$p =$$
If $$f\left( x \right)$$ is continuous at x=0 where $$f\left( x \right) = {{\left( {{e^{3x}} - 1} \right)\sin x} \over {x\log \left( {1 + x} \right)}}$$ for $$x \ne 0$$ find $$f\left( 0 \right)$$
Differentiate $$x=y+\dfrac{1}{y+\dfrac{1}{y+\dfrac{1}{y+\dfrac{1}{y+\dfrac{1}{y+...\infty}}}}}$$ w.r.t $$x$$
If $$x=a \cos \theta +b\sin\theta $$, $$y=a \sin \theta -b \cos \theta $$, then show that $${ y }^{ 2 }\dfrac { d^{ 2 }{ y } }{ { dx }^{ 2 } } -x\dfrac { dy }{ dx } +y=0$$.
If $$\displaystyle \int{\dfrac{\sin{x}}{\sin{\left(x-\alpha\right)}}dx}=Ax+B\log{\sin{\left(x-\alpha\right)}}+c$$ then find the value of $$\left(A,B\right)$$
If $$x ^ { y } = a ^ { x } ,$$ prove that $$\dfrac { d y } { d x } =\dfrac {\log a(\log x-1)}{(\log x)^2}$$.
$$x^{y}=a^{x}\Rightarrow y log x= x log a$$
$$y=\frac{x}{log x}log a$$
$$\frac{dy}{dx}= log a \left \{ \frac{log x-x.\frac{1}{x}}{(log x)^{2}} \right \}= log a\left \{ \frac{log x-1}{(log x)^{2}} \right \}$$
If $${ x }^{ 2 }=c^{ x-y },$$ then find $$\dfrac{ dy }{ dx } $$
Differentiate $$y={ 3 }^{ x },(x>0)$$ w.r.t $$x$$
The parametric equations of a curve are $$x = 2t - \sin 2t, y = 5t + \cos 2t$$, for $$0\leq t \leq \dfrac {1}{2}\pi$$. At the point $$P$$ on the curve, the gradient of the curve is $$2$$.
Show that the value of the parameter at $$P$$ satisfies the equation $$2 \sin 2t - 4 \cos 2t = 1$$.
Solve the differential equation
$$(tan^{-1}y-x)dy=(1+y^{2})dx$$
Show that $$f(x)=|x-3|$$ is continuous but not differentiable at $$x=3$$.
Show that the function $$f(x)=\left\{\begin{matrix} x^m\sin\left(\dfrac{1}{x}\right), & x\neq 0\\ 0, & x=0\end{matrix}\right.$$ is continuous but not differentiable at $$x=0$$, if $$0 < m < 1$$.
If $$f(x)=\left\{\begin{matrix} ax^2-b & , & if & |x| <1 \\ \dfrac{1}{|x|} & , & if & |x| \geq 1\end{matrix}\right.$$ is differentiable at $$x=1$$, find a, b.
Find the values of a and b, if the function $$f(x)$$ defined by $$f(x)=\left\{\begin{matrix} x^2+3x+a, & x\leq 1\\ bx+2, & x >1\end{matrix}\right.$$ is differentiable at $$x=1$$.
Find the values of a and b so that the function $$f(x)=\left\{\begin{matrix} x^2+3x+a, & if & x\leq 1\\ bx+2, & if & x > 1\end{matrix}\right.$$ is differentiable at each $$x\in R$$.
Find $$\dfrac{dy}{dx}$$ in $$xy=c^{2}$$.
Show that the function $$f(x)=\left\{\begin{matrix} x^m\sin\left(\dfrac{1}{x}\right), & x\neq 0\\ 0 &, x=0\end{matrix}\right.$$ is differentiable at $$x=0$$, if $$m > 1$$.
Show that the function $$f(x)=\left\{\begin{matrix} |2x-3|[x], & x \geq 1\\ \sin\left(\dfrac{\pi x}{2}\right), & x < 1\end{matrix}\right.$$ is continuous but not differentiable at $$x=1$$.
Show that the function $$f(x)=\left\{\begin{matrix} x^m\sin\left(\dfrac{1}{x}\right), & x\neq 0\\ 0, & x=0\end{matrix}\right.$$ is neither continuous nor differentiable, if $$m\leq 0$$.
Show that the function f defined as follows
$$f(x)=\left\{\begin{matrix} 3x^2-2, & 0 < x\leq 1\\ 2x^2-x, & 1 < x\leq 2\\ 5x-4, & x > 2 \end{matrix}\right.$$
is continuous but not differentiable at $$x=2$$.
Examine the differentiability of the function f defined by $$f(x)=\left\{\begin{matrix} 2x+3, & if & -3\leq x < -2\\ x+1, & if & -2\leq x < 0\\ x+2, & if & 0\leq x\leq 1\end{matrix}\right.$$.
Find whether the following function is differentiable at $$x=1$$ or not:
$$f(x)=\left\{\begin{matrix} x, & x\leq 1\\ 2-x, & 1\leq x\leq 2\\ -2+3x-x^2, & x > 2\end{matrix}\right.$$.
Find $$ \dfrac{dy}{dx},$$, if $$x=at^{2}$$ and $$y=2\ at$$.
Discuss the continuity and differentiability of $$f(x)=e^{|x|}$$.
Find whether the following function is differentiable at $$x=1,2$$:
$$f(x)=\left\{\begin{matrix} x, & x\leq 1\\ 2-x, & 1\leq x\leq 2\\ -2+3x-x^2, & x > 2\end{matrix}\right.$$.
Differentiate the following functions with respect to $$x$$
$$(\log x)^{\log x}$$
Discuss the continuity and differentiability of $$f(x)=|\log |x||$$.
Consider the given function.
$$f(x)=|\log |x||$$
Since, it is an absolute function. So, it a continuous function.
Let see the graph of the given function,
From the graph, it is clear that the function $$f(x)$$ is not differentiable at $$x=-1$$ and $$x=1$$ but continuous for all $$x$$.
Write an example of a function which is everywhere continuous but fails to be differentiable exactly at five points.
Differentiate w.r.t. $$x$$:$$y=e^x +10^x+x^x$$
If $$x=\sin 3t$$ and $$y=5t^2$$, find $$\dfrac{dy}{dx}$$.
Find $$\dfrac {dy}{dx},$$ if $$x= {3at}$$ and $$y={3at^{2}}$$.
Find $$\dfrac{dy}{dx}$$, when $$x=e^t-3$$ and $$y=e^t+5$$.
Find $$\dfrac{dy}{dx}$$, if $$x=\sin 3t$$ and $$y=4t^3$$.
Find $$ \dfrac{dy}{dx},$$ if $$x=a\left( \theta +\sin { \theta } \right) $$ and $$y=a\left( 1-\cos { \theta } \right) $$.
Find $$ \dfrac{dy}{dx},$$ when
$$x=a \cos {\theta} $$ and $$y=b \sin {\theta} $$
$$x^{x^{2}-3}+(x-3)^{x^2}$$
Find $$\dfrac {dy}{dx},$$ if $$x=b \sin^{2} {\theta}$$ and $$y=a \cos^{2} {\theta}$$.
Find $$\dfrac{dy}{dx}$$, when
If $$x=e^t\sin t $$ and $$y=e^{-t}$$
Differentiate the following function with respect to x.
$$\dfrac{x^n}{\sin x}$$.
Let $$S$$ be the set of points where the function, $$f(x)=|2-|x-3||,x\epsilon R$$, is not differentiable.
Then $$\displaystyle \sum_{x\epsilon S}\,f(f(x))$$ is equal to ______.
$$f(x)= \begin{cases} \,\,\,\,\,\,1-x\,\,\,\,\,\,x<1 \\ \,\,\,\,\,\,x- 1\,\,\,\,\,\,\,1\le x< 3\\ { \begin{matrix} \,\,\,\,5-x \,\,\,3\le x< 5\\x-5\,\,x\ge 5 \end{matrix} } \end{cases}$$
Given $$f(x)=|2-|x-3||$$So here $$f(x) $$ is not differentiable
at $$x=1,3,5$$
$$S=\{1,3,5\}$$
$$S=\{1,3,5\}$$
$$\displaystyle \therefore \sum_{x\in s}f(x)=f(f(1))+f(f(3))+f(f(5))$$
$$=f(0)+f(2)+f(0)$$
$$=1+1+1$$
$$=3$$
Let $$f$$ defined on $$[0,1]$$ be twice differentiable such that $$\left| f''(x) \right| \le 1$$ for all $$x\in [0,1]$$. If $$f(0)=f(1)$$, then show that $$\left| f'(x) \right| <1$$ for all $$x\in [0,1]$$
Differentiate w.r.t. $$x$$:$$y=x^n+n^x +x^x +n^n$$
Show that a constant function is always differentiable.
Differentiate each of the following $$w.r.t.x:$$
$$\cos^{-1}2x$$
Differentiate each of the following $$w.r.t.x:$$
$$\tan^{-1}(\cos x)$$
Differentiate each of the following $$w.r.t.x:$$
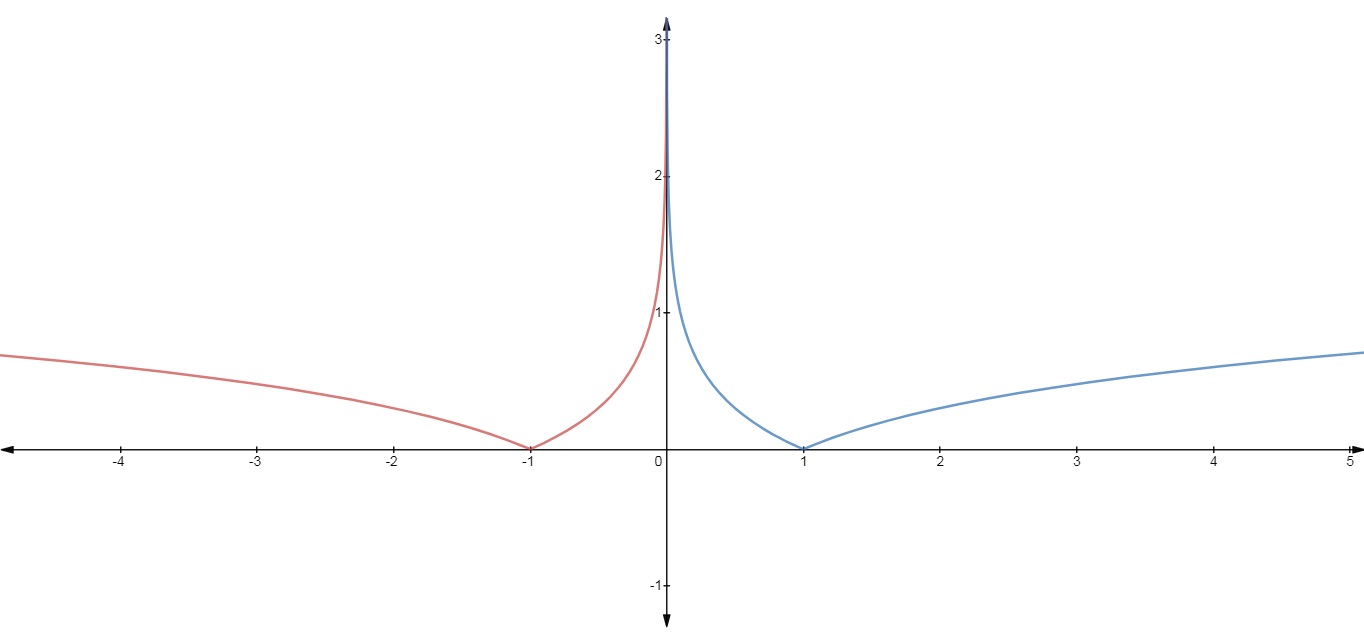
$$\sin^{-1}(\cos x)$$
Differentiate each of the following $$w.r.t.x:$$
$$\tan^{-1}x^{2}$$
Differentiate each of the following $$w.r.t.x:$$
$$\sec^{-1}\sqrt{x}$$
Differentiate each of the following $$w.r.t.x:$$
$$(1+x^{2})\tan^{-1}x$$
Differentiate each of the following $$w.r.t.x:$$
$$(\cot^{-1}x^{2})^{3}$$
Differentiate each of the following $$w.r.t.x:$$
$$\cot^{-1}(e^{x})$$
Differentiate each of the following $$w.r.t.x:$$
$$\cot^{-1}x^{3}$$
Differentiate each of the following $$w.r.t.x:$$
$$\sin^{-1}\dfrac{x}{a}$$
Differentiate the following $$w.r.t.x:$$
$$\cot^{-1}\left(\sqrt{\dfrac{1+\cos x}{1-\cos x}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{\sin x}{1+\cos x}\right)$$
Differentiate each of the following $$w.r.t.x:$$
$$\tan(\sin^{-1}x)$$
Differentiate the following $$w.r.t.x:$$
$$\cot^{-1}\left(\dfrac{1+\cos x}{\sin x}\right)$$
Differentiate each of the following $$w.r.t.x:$$
$$\tan^{-1}(\cos\sqrt{x})$$
Differentiate each of the following $$w.r.t.x:$$
$$\sqrt{\sin^{-1}x^{2}}$$
Differentiate each of the following $$w.r.t.x:$$
$$\cot^{-1}\left(\sqrt{\dfrac{1+\cos 3x}{1-\cos 3x}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\cot^{-1}\left(\dfrac{\cos x-\sin x}{\cos x+\sin x}\right)$$
Differentiate each of the following $$w.r.t.x:$$
$$\sin^{-1}\left\{\sqrt{\dfrac{1-\cos x}{2}}\right\}$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{\cos x+\sin x}{\cos x-\sin x}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}(\cot x)+\cot^{-1}(\tan x)$$
Differentiate the following $$w.r.t.x:$$
$$\csc^{-1}\left(\dfrac{1+\tan^{2}x}{2\tan x}\right)$$
Differentiate the following w.r.t.$$x$$:
$$e^{-\sin 2x}$$
Differentiate the following $$w.r.t.x:$$
$$\cos^{-1}(\sqrt{1-x^{2}})$$
Differentiate the following $$w.r.t.x:$$
$$\cos^{-1}\left\{\sqrt{\dfrac{1+x}{2}}\right\}$$
Differentiate each of the following $$w.r.t.x:$$
$$\sin^{-1}\left\{\sqrt{1-x^{2}}\right\}$$
Differentiate the following $$w.r.t.x:$$
$$\sin^{-1}\left(\dfrac{1-\tan^{2}x}{1+\tan^{2}x}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\sec^{-1}\left(\dfrac{1+\tan^{2}x}{1-\tan^{2}x}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\sin^{-1}\left(\sqrt{\dfrac{{1-x}}{2}}\right)$$
Differentiate each of the following $$w.r.t.x:$$
$$\cot^{-1}(\text cosec x+\cot x)$$
Differentiate the following $$w.r.t.x:$$
$$\sin^{-1}\left\{\dfrac{1}{\sqrt{1+x^{2}}}\right\}$$
Differentiate the following $$w.r.t.x:$$
$$\sec^{-1}\left(\dfrac{1}{\sqrt{1-x^{2}}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{x}{\sqrt{1-x^{2}}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\sin^{-1}\left\{2x\sqrt{1-x^{2}}\right\}$$
Differentiate the following $$w.r.t.x:$$
$$\sin^{-1}(3x-4x^{3})$$
Differentiate the following $$w.r.t.x:$$
$$\sin^{-1}(1-2x^{2})$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{x}{1+\sqrt{1-x^{2}}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\cot^{-1}\left(\dfrac{\sqrt{1-x^{2}}}{x}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\sec^{-1}\left(\dfrac{1}{1-2x^{2}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{1+x}{1-x}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left\{\dfrac{\sqrt{1+a^{2}x^{2}}-1}{ax}\right\}$$
Differentiate the following $$w.r.t.x:$$
$$\sin^{-1}\left\{2ax\sqrt{1-a^{2}x^{2}}\right\}$$
Differentiate the following $$w.r.t.x:$$
$$\sin^{-1}\left(\dfrac{1}{\sqrt{1+x^{2}}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\sec^{-1}\left(\dfrac{1+x^{2}}{1-x^{2}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\cos^{-1}\left(\dfrac{1-x^{2n}}{1+x^{2n}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-}\left\{\dfrac{x}{\sqrt{a^{2}-x^{2}}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{3x-x^{3}}{1-3x^{2}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\sec^{-1}\left(\dfrac{x^{2}+1}{x^{2}-1}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\text cosec^{-1}\left(\dfrac{1+x^{2}}{2x}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\cot^{-1}\left(\dfrac{1+x}{1-x}\right)$$
If $$y=\sin^{-1}\left(\dfrac{2x}{1+x^{2}}\right)+\sec^{-1}\left(\dfrac{1+x^{2}}{1-x^{2}}\right)$$, show that $$\dfrac{dy}{dx}=\dfrac{4}{(1+x^{2})}$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{e^{2x}+1}{e^{2x}-1}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{5x}{1-6x^{2}}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{3-2x}{1+6x}\right)$$
Differentiate the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{\sqrt{a}+\sqrt{x}}{1-\sqrt{ax}}\right)$$
If $$y=\sec^{-1}\left(\dfrac{x+1}{x-1}\right)+\sin^{-1}\left(\dfrac{x-1}{x+1}\right)$$, show that $$\dfrac{dy}{dx}=0$$.
If $$y=\tan^{-1}\left(\dfrac{ax-b}{bx-a}\right)$$, prove that $$\dfrac{dy}{dx}=\dfrac{1}{(1+x^{2})}$$
Differentiate $$\sin^{-1}\left(\dfrac{2^{x+1}}{1+4^{x}}\right)$$ w.r.t.x.
Differentiate the following $$w.r.t.x:$$
$$\sin^{-1}\left\{\dfrac{x^{2}}{\sqrt{x^{4}+a^{4}}}\right\}$$
Differentiate each of the following $$w.r.t.x:$$
$$\tan^{-1}\left(\dfrac{2x}{1+15x^{2}}\right)$$
Differentiate $$\tan^{-1}\left(\dfrac{2x}{1-x^2}\right)$$ with respect to $$\sin^{-1}\left(\dfrac{2x}{1+x^2}\right)$$
Differentiate $$\cos^{-1}\left(\dfrac{1-x^2}{1+x^2}\right)$$ with respect to $$\tan^{-1}\left(\dfrac{3x-x^3}{1-3x^2}\right)$$.
Find the second derivation of:
$$x^{11}$$
Differentiate $$\tan^{-1}\left(\dfrac{x}{\sqrt{1-x^2}}\right)$$ with respect to $$\cos^{-1}(2x^2-1)$$
Find $$\dfrac {dy}{dx}$$, when $$y=\dfrac {x\cos^{-1}x}{\sqrt {1-x^2}}$$.
Find $$\dfrac {dy}{dx}$$, when $$y=(\sin^{-1}x)^{x}$$.
If $$y=\dfrac {\sin ^{-1}x}{\sqrt {1-x^2}}$$, prove that $$(1-x^2)\dfrac {dy}{dx}=(xy+1)$$
Differentiate $$\tan^{-1}\left(\dfrac{\sqrt{1-x^2}}{x}\right)$$ w.r.t. $$\cos^{-1}(2x\sqrt{1-x^2})$$, when $$x\neq 0$$.
Find $$\dfrac{dy}{dx}$$, when $$x=\cos^{-1}\dfrac{1}{\sqrt{1+t^2}}, y=\sin^{-1}\dfrac{t}{\sqrt{1+t^2}}$$.
Find $$\dfrac {dy}{dx}$$, when $$y=x^{(\cos^{-1}x)}$$.
Find the second derivation of:
$$x^{3}\log x$$
If $$y=\tan^{-1}\dfrac {a}{x}+\log \sqrt {\dfrac {x-a}{x+a}}$$, prove that $$\dfrac {dy}{dx}=\dfrac {2a^3}{(x^4 - a^4)}$$
Find the second derivation of:
$$\tan x$$
Find the second derivation of:
$$5^{x}$$
Find the second derivation of $$\sin\ 3x\cos 5x$$.
Find the second derivation of:
$$e^{2x}\cos 3x$$
Find the second derivative of $$e^{3x}\sin 4x$$.
Fill in the blanks
Let $$f(x)=x\left | x \right |.$$ The set of points Where f(x) is twice differentiable is ...
We have Clearly f'' (x) exists at every point except except x=0 Thus f(x) is twice differentiable on R-{0}
If $$ f(x)=\cos ^{-1} \dfrac{1}{\sqrt{13}}(2 \cos x-3 \sin x) $$
$$+\sin ^{-1} \dfrac{1}{\sqrt{13}} \times(2 \cos x+3 \sin x) \text { w.r.t. } \sqrt{1+x^{2}}$$
then find $$\dfrac { d f(x)} {d x} $$ at $$ x=3 / 4 $$
If $$ x \in\left(0, \dfrac{\pi}{2}\right), $$ then show that $$ \dfrac{d}{d x} \cos ^{-1}\left\{\dfrac{7}{2}(1+\cos 2 x)+\sqrt{\left(\sin ^{2} x-48 \cos ^{2} x\right)} \sin x\right\} $$
$$ =1+\dfrac{7 \sin x}{\sqrt{\sin ^{2} x-48 \cos ^{2} x}} $$
A function is represented parametrically by the equations $$x = \dfrac{1 + t}{t^3} ; y = \dfrac{3}{2t^2} + \dfrac{2}{t}$$, then the value of $$\left|{\dfrac{dy}{dx} - x{\left(\dfrac{dy}{dx}\right)^3}}\right|$$ is.
The derivative of $$\sec^{-1} \left ( \frac{1} {2x^{2} - 1} \right )$$, then $$f^{'}(x)$$ at $$x = e$$ is ________________. (IIT-JEE, 1985)
$$\operatorname{Let} g(x)$$ be differentiable on $$R$$ and $$\int_{\sin t}^{1} x^{2} g(x) d x\\$$$$=(1-\sin t),$$ where $$t \in\left(0, \dfrac{\pi}{2}\right) .$$ Then the value of $$g\left(\dfrac{1}{\sqrt{2}}\right)$$is
Let $$ u(x) $$ and $$ v(x) $$ are differentiable function such that $$ \dfrac{u(x)}{v(x)}=7 $$. If $$ \dfrac{u^{\prime}(x)}{v^{\prime}(x)}=p $$ and $$ \left(\dfrac{u(x)}{v(x)}\right)^{\prime}=q, $$ then $$ \dfrac{p+q}{p-q} $$ has the value equal to $$\cdots$$
Let $$F(x) = f(x) g(x) h(x)$$ for all real $$x$$, where $$f(x), g(x)$$ and $$h(x)$$ are differentiable functions. At some point $$x_0$$, $$F'(x_0) = 21F(x_0), f'(x_0) = 4f(x_0), g'(x_0) = -7g(x_0)$$ and $$h'(x_0) = kh(x_0)$$. Then $$k$$= _______________. (IIT-JEE, 1997)
Differentiate $$\tan ^{-1} \left ( \dfrac{\sqrt{1 - x^{2}}}{x} \right )$$ with respect to $$\cos ^{-1} (2x \sqrt{1 - x^{2}})$$, when $$x \neq 0$$.
Differentiate $$\tan ^{-1} \dfrac{x}{\sqrt{1 - x^{2}}}$$ with respect to $$\sin ^{-1} (2x \sqrt{1 - x^{2}})$$
If $$ y = \cos ^{-1} \left \{ \dfrac{3x + 4\sqrt{1 - x^{2}}}{5} \right \}$$ then find $$\dfrac{dy}{dx}$$
Find $$\dfrac{dy}{dx}$$ if $$y = \sin ^{-1} \left [ x\sqrt{1 - x} - \sqrt{x} \sqrt{1 - x^{2}} \right ]$$
Differentiate the following function with respect to $$x$$
$$ f(x) = \tan ^{-1} \left ( \dfrac{1 - x}{1 + z} \right )- \tan ^{-1} \left ( \dfrac{x + 2}{1 - 2x} \right )$$.
If $$y = \cos ^{-1} \left ( \dfrac{2^{x+1}}{1 + 4^{x}} \right )$$, then find $$\dfrac{dy}{dx}$$
Differentiate the following with respect to :
$$\tan ^{-1} \left ( \dfrac{\sqrt{1 + x} - \sqrt{1 - x}}{\sqrt{1 + x} + \sqrt{1 - x}} \right )$$
Differentiate $$\tan ^{-1} \left [ \dfrac{\sqrt{1 + x^{2}} - 1}{x} \right ]$$ with respect to $$x.$$
Prove that : $$\dfrac{d}{dx} \left [ \dfrac{x}{2}\sqrt{a^{2} - x^{2}} + \dfrac{a^{2}}{2} \sin ^{-1} \left ( \dfrac{x}{a} \right ) \right ] = \sqrt{a^{2} - x^{2}}$$
Differentiate the following w.r.t. $$ x: \tan ^{-1}(\log x) $$
If $$f(x)$$ be a differentiable function such that $$f'(x) = g(x) , g"(x)$$ exists, $$|f(x)| < 1$$ and $$(f(0))^2 + (g(0))^2 = 9$$. Prove that there is a point c where $$c \in (-3, 3)$$ such that $$g(c). g"(c) < 0$$
Differentiate with respect to x:
$$\sin ^{-1} \left ( \dfrac{2^{x + 1}. 3^x}{1 + (36)^{x}} \right )$$
Using derivative, prove that: $$ \sec ^{-1} x+\operatorname{cosec}^{-1} x=\dfrac{\pi}{2} \quad \ldots $$ [for $$ \left.|x| \geq 1\right] $$
Differentiate $$\tan ^{-1} \left ( \dfrac{\sqrt{1 + x^{2}} - 1}{x} \right )$$ with respect to $$\tan ^{-1} x$$, when $$x \neq 0.$$
Using derivative, prove that: $$ \tan ^{-1} x+\cot ^{-1} x=\dfrac{\pi}{2} $$
Differentiate the following w.r.t. $$ x: \sin ^{-1}\left(\sqrt{\dfrac{1+x^{2}}{2}}\right) $$
Differentiate the following w.r.t. $$ x: \operatorname{cosec}^{-1}\left(e^{-x}\right) $$
Differentiate the following w.r.t. $$ \mathrm{x}: \operatorname{cosec}^{-1}\left[\dfrac{1}{\cos \left(5^{x}\right)}\right] $$
Differentiate the following w.r.t. $$ x: \cos ^{-1}\left(\sqrt{\dfrac{1+\cos x}{2}}\right) $$
Differentiate the following w.r.t. $$ x: \cot ^{-1}\left[\cot \left(e^{x^{2}}\right)\right] $$
Differentiate the following w.r.t. $$ x: \tan ^{-1}(\sqrt{x}) $$
Differentiate the following w.r.t. $$ x: \cos ^{-1}\left(1-x^{2}\right) $$
Differentiate the following w.r.t. $$ x: \cos ^{-1}\left(\dfrac{\sqrt{1-\cos \left(x^{2}\right)}}{2}\right) $$
Differentiate the following w.r.t. $$ x: \sin ^{-1}\left(x^{\frac{3}{2}}\right) $$
Differentiate the following w.r.t. $$ x: \cot ^{-1}\left(4^{x}\right) $$
Find the second order derivatives of the following :
$$2x^{5} - 4x^{3} - \frac{2} {x^{2}} - 9$$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left[\dfrac{1-\tan \left(\dfrac{x}{2}\right)}{1+\tan \left(\dfrac{x}{2}\right)}\right] $$
Differentiate the following w.r.t $$x : \sin \left [ 2 \tan^{-1} \left( \sqrt{\frac{1 - x}{1 + x}} \right ) \right ]$$
Differentiate the following w.r.t $$x : \tan^{-1} \left( \frac{ \sqrt{x}(3 - x)}{1 - 3x} \right ) $$
Differentiate the following w.r.t $$x : \tan^{-1} \left[ \sqrt{ \frac{ \sqrt{1 + x^2} + x}{\sqrt{1 + x^2} - x}} \right ] $$
Differentiate the following w.r.t $$x : \cos^{-1} \left( \frac{ \sqrt{1 + x} - \sqrt{1 - x}}{2} \right ) $$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left(\sqrt{\dfrac{1+\cos x}{1-\cos x}}\right) $$
Find second order derivatives of the following :
$$e^{2x} \cdot \tan x$$
Find the second order derivatives of the following:
$$\log \left(\log x \right)$$
Find the second order derivatives of the following :
$$x^{3} \cdot \log x$$
Find the second order derivatives of the following :
$$x^{x}$$
Differentiate the following w.r.t. $$ x: \cot ^{-1}\left(\dfrac{\sin 3 x}{1+\cos 3 x}\right) $$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left(\dfrac{\cos 7 x}{1+\sin 7 x}\right) $$
Find the second order derivatives of the following :
$$e^{4x} \cdot \cos 5x$$
Differentiate the following w.r.t. $$ x: \tan ^{-1}(\operatorname{cosec} x+\cot x) $$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left[\dfrac{1+\cos \left(\dfrac{x}{3}\right)}{\sin \left(\dfrac{x}{3}\right)}\right] $$
Differentiate the following w.r.t. $$ x: \cos ^{-1}\left(\dfrac{\sqrt{3} \cos x-\sin x}{2}\right) $$
Differentiate the following w.r.t. $$ x: \operatorname{cosec}^{-1}\left[\dfrac{10}{6 \sin \left(2^{x}\right)-8 \cos \left(2^{x}\right)}\right] $$
Differentiate the following w.r.t. $$ x: \sin ^{-1}\left(\dfrac{4 \sin x+5 \cos x}{\sqrt{41}}\right) $$
Differentiate the following w.r.t. $$ \mathrm{x}: \cos ^{-1}\left[\dfrac{3 \cos \left(e^{x}\right)+2 \sin \left(e^{x}\right)}{\sqrt{13}}\right] $$
Differentiate the following w.r.t. $$ x: \sin ^{-1}\left(\dfrac{1-x^{2}}{1+x^{2}}\right) $$
Differentiate the following w.r.t. $$ x: \cot ^{-1}\left[\dfrac{\sqrt{1+\sin \left(\dfrac{4x}{3}\right)}+\sqrt{1-\sin \left(\dfrac{4 x}{3}\right)}}{\sqrt{1+\sin \left(\dfrac{4 x}{3}\right)}-\sqrt{1-\sin \left(\dfrac{4 x}{3}\right)}}\right] $$
Differentiate the following w.r.t. $$ x: \sin ^{-1}\left(\dfrac{\cos \sqrt{x}+\sin \sqrt{x}}{\sqrt{2}}\right) $$
Differentiate the following w.r.t. $$ x: \cos ^{-1}\left(\dfrac{3 \cos 3 x-4 \sin 3 x}{5}\right) $$
Differentiate the following w.r.t. $$ x: \cos ^{-1}\left(\dfrac{1-x^{2}}{1+x^{2}}\right) $$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left(\dfrac{2 x}{1-x^{2}}\right) $$
Differentiate the following w.r.t. $$ x: \sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right) $$
Differentiate the following w.r.t. $$ x: \sin ^{-1}\left(\dfrac{1-25 x^{2}}{1+25 x^{2}}\right) $$
Differentiate the following w.r.t. $$ x: \sin ^{-1}\left(\dfrac{4^{x+\frac{1}{2}}}{1+2^{4 x}}\right) $$
Differentiate the following w.r.t. $$ x: \cos ^{-1} \dfrac{\left(1-9^{x}\right)}{\left(1+9^{x}\right)} $$
Differentiate the following w.r.t. $$ x: \cot ^{-1}\left(\dfrac{1-\sqrt{x}}{1+\sqrt{x}}\right) $$
Differentiate the following w.r.t. $$ x: \sin ^{-1}\left(\dfrac{1-x^{3}}{1+x^{3}}\right) $$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left(\dfrac{2 x^{\tfrac{5}{2}}}{1-x^{5}}\right) $$
Differentiate the following w.r.t. $$ x: \cos ^{-1}\left(\dfrac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\right) $$
Find $$\dfrac{d^{2}y} {dx^{2}}$$ of the following :
$$x = a \left(\theta - \sin \theta\right), y = a \left(1 - \cos \theta\right)$$
Differentiate the following w.r.t. $$ x: \cos ^{-1}\left(3 x-4 x^{3}\right) $$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left[\dfrac{2^{x}+2}{1-3\left(4^{x}\right)}\right] $$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left(\dfrac{2^{x}}{1+2^{2 x+1}}\right) $$
Differentiate the following w.r.t. $$ \mathrm{x}: \cot ^{-1}\left(\dfrac{a^{2}-6 x^{2}}{5 a x}\right) $$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left(\dfrac{2 \sqrt{x}}{1+3 x}\right) $$
Differentiate the following w.r.t. $$ \mathrm{x}: \tan ^{-1}\left(\dfrac{a+b \tan x}{b-a \tan x}\right) $$
Differentiate the following w.r.t. $$ x: \cot ^{-1}\left(\dfrac{1+35 x^{2}}{2 x}\right) $$
Find $$\dfrac{d^{2}y} {dx^{2}} $$ of the following:
$$x = 2at^{2}, y= 4at$$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left(\dfrac{5-x}{6 x^{2}-5 x-3}\right) $$
Differentiate the following w.r.t. $$ x: \tan ^{-1}\left(\dfrac{8 x}{1-15 x^{2}}\right) $$
Differentiate the following w.r.t. $$ x: \cot ^{-1}\left(\dfrac{4-x-2 x^{2}}{3 x+2}\right) $$
If $$sec^{-1} \left(\frac{7x^{3} - 5y^{3}} {7^{3} + 5y^{3}} \right) = m$$, show $$\frac{d^{2}y} {dx^{2}} = 0$$.
If $$y= \sin \left(m \cos^{-1}x \right)$$, then show that $$\left(1 - x^{2}\right) \frac{d^{2}y} {dx^{2}} - x\frac{dy} {dx} + m^{2}y = 0$$
If $$x = \cos t, y = e^{mt}$$, show that $$\left(1 - x^{2} \right) \frac{d^{2}y} {dx^{2}} - x \frac{dy} {dx} - m^{2}y = 0$$
If $$y = e^{m \tan^{-1} x}$$, show that $$\left(a + x^{2} \right) \frac{d^{2}y} {dx^{2}} + \left(2x - m\right) \frac{dy} {dx} = 0$$
If $$x^{2} + 6xy + y^{2} = 10$$, show that $$\frac{d^{2}} {dx^{2}} = \frac{80} {\left(3x + y \right)^{3}}$$
Find $$\frac{d^{2}y} {dx^{2}} $$ of the following:
$$x = a \cos \theta, y = b \sin \theta $$ at $$\theta = \frac{\pi} {4}$$
Find $$\frac{d^{2}y} {dx^{2}} $$ of the following :
$$x = \sin \theta, y = \sin^{3} \theta$$ at $$\theta = \frac{\pi} {2}$$
If $$y = x + \tan x$$, show that $$\cos^{2}x \cdot \frac{d^{2}y} {dx^{2}} - 2y + 2x = 0 $$
If $$x = a \sin t - b \cos t, y = a \cos t + b \sin t$$, show that $$\frac{d^{2}y} {dx^{2}} = - \frac{x^{3} + y^{2}} {y^{3}}$$
If $$x = at^{2} $$ and $$ y = 2at$$, then show that $$xy \frac{d^{2}y} {dx^{2}} + a = 0$$
Differentiate w.r.t .x.
$$ (\sin x)^{x} + \sin ^{-1} \sqrt{x}$$
Differentiate $$ \tan ^{-1}\left(\dfrac{\cos x}{1+\sin x}\right) w . r . t . \sec ^{-1} x $$
Differentiable the functions given in Exercises 1 to 11 w.r.t .x.
$$ y = \sqrt{\dfrac{(x - 1)(x -2)}{(x - 3)(x - 4) (x - 5)}} $$
$$Differentiable \space the \space following \space wrt\space x:$$ $$ y = \dfrac{\cos x}{\log x} $$
If a and y connected parametrically by the equation given in Exercise 1 to 10 , without eliminating the parameter ,find $$ \dfrac{dy}{dx}$$
$$ x = 2 at^{2} , y = at^{4}$$
Differentiate the following w.r.t. $$x$$:
$$ e^{\sin^{-1}} x $$
Differentiate the following w.r.t. x:
$$ y = \dfrac{e^{x}}{\sin x} $$
$$Differentiate$$ $$the$$ $$following$$ $$wrt$$ $$x$$:
$$ \sin ( \tan^{-1}e^{-x}) $$
Differentiate w.r.t .x.
$$ y = x^{x \cos x} + \dfrac{x^{2}+1}{x^{2}- 1}$$
Differentiate $$ \tan ^{-1}\left(\dfrac{\sqrt{1+x^{2}}-1}{x}\right) w \cdot r \cdot t \tan ^{-1}\left(\dfrac{2 x \sqrt{1-x^{2}}}{1-2 x^{2}}\right) $$
If a and y connected parametrically by the equation given in Exercise 1 to 10 , without eliminating the parameter ,find $$ \dfrac{dy}{dx}$$
Undefined control sequence /cfrac
If a and y connected parametrically by the equation given in Exercise 1 to 10 , without eliminating the parameter ,find $$ \dfrac{dy}{dx}$$
$$ x = a \sec \theta , y = b \tan \theta $$
If a and y connected parametrically by the equation given in Exercise 1 to 10 , without eliminating the parameter ,find $$ \dfrac{dy}{dx}$$
$$ x = \cos \theta - \cos 2 \theta y = \sin \theta - \sin 2 \theta $$
If a and y connected parametrically by the equation given in Exercise 1 to 10 , without eliminating the parameter ,find $$ \dfrac{dy}{dx}$$
$$ x = a \cos \theta , y = b \cos \theta $$
If a and y connected parametrically by the equation given in Exercise 1 to 10 , without eliminating the parameter ,find $$ \dfrac{dy}{dx}$$
$$ x = \sin t , y \cos 2t $$
If a and y connected parametrically by the equation given in Exercise 1 to 10 , without eliminating the parameter ,find $$ \dfrac{dy}{dx}$$
$$ x = a (\theta - \sin \theta), y = ( 1 + \cos \theta) $$
If a and y connected parametrically by the equation given in Exercise 1 to 10 , without eliminating the parameter ,find $$ \dfrac{dy}{dx}$$
$$ x = 4t , y = \dfrac{4}{t}$$
If a and y connected parametrically by the equation given in Exercise 1 to 10 , without eliminating the parameter ,find $$ \dfrac{dy}{dx}$$
$$ x = a (\cos t + \log \tan \dfrac{t}{2}) , y = a \sin t $$
If a and y connected parametrically by the equation given in Exercise 1 to 10 , without eliminating the parameter ,find $$ \dfrac{dy}{dx}$$
$$ x = a ( \cos \theta + \sin \theta) , y = a ( \sin \theta - \theta \cos \theta )$$
Find the second order derivatives of the function $$ x^{3} \log x $$
Find the second order derivatives of the function given in Exercise 1 to 10 .
$$ \sin (\log x)$$
Find the second order derivatives of the function given function:
$$ x^{2} + 3x + 2 $$
Find the second order derivatives of the function given below:
$$ \tan^{-1} x $$
Find the second order derivatives of the function given in Exercise 1 to 10 .
$$ x . \cos x $$
Find the second order derivatives of the function given in Exercise 1 to 10 .
$$ e^{6x}cos 3 x $$
Find the second order derivatives of the function given below.
$$ e^{x} \sin 5x $$
If $$ y = \cos^{-1} x $$ find $$\dfrac {dy}{dx}$$
Find the second order derivatives of the function given in Exercise 1 to 10 .
$$ \log (\log x)$$
Find the second order derivatives of the function given below:
$$ \log x $$
If $$ y = \cos^{-1} \left \{ \dfrac{3x +4\sqrt{1 - x^{2}}}{5} \right \} $$ Find $$ \dfrac{dy}{dx} $$
Differentiate
If $$ y = \sin^{-1} \left [ \dfrac{1 - \sqrt{x}}{1 +\sqrt{x}} \right ] + \cos^{-1}\left [ \dfrac{1 + \sqrt{x}}{1 - \sqrt{x}} \right ] $$ , find $$ \dfrac{dy}{dx}$$
Differentiate $$ sin^{-1}\left ( \dfrac{t}{\sqrt{1 + t^{2}}} \right ) $$ w .r.t.x
$$ \cos^{-1}\left ( \dfrac{1}{\sqrt{1 + t^{2}}} \right )$$
Show that following functions are differentiable for every value of $$x$$:
Constant function, $$f(x)=c$$, where $$c$$ is a constant
Differentiate w.r.t.x the function in Exercise 1 to 11 .
$$ \sin^{-1} (x\sqrt{x}) , 0 \leq x \leq 1 $$
If $$ f : [-5 , 5] \rightarrow R $$ is differentiable function if f (x) does not vanish anywhere , then prove that $$ f (-5) \neq f (5). $$
Show that following functions are differentiable for every value of $$x$$:
Identify functions, $$f(x)=x$$
Find $$\dfrac{dy}{dx}$$ if $$ y = 12 ( 1 - \cos t) ; x = 10 ( t - \sin t) $$
If $$ y = 500 e ^{7x} + 600^{-7x} $$ show that$$ \dfrac{d^{2}y}{dx^{2}} = 49 y $$
Show that following functions are differentiable for every value of $$x$$:
$$f(x)=e^x$$
Examine the function $$f(x)=\begin{cases} |x-3|;\ x \ge 1 \\ \dfrac{x^2}{4}-\dfrac{3x}{2}+\dfrac{13}{4};\ x < 1 \end{cases}$$ for continuity at $$x=1$$ and $$3$$
Examine the function $$f(x)=\begin{cases} \dfrac{\tan x}{\sin x};\ x \ne 0 \\ 1;\ x=0 \end{cases}$$ for continuity at $$x=0$$
Examine the function fix) for continuity at $$x=0$$. If $$f(x)=\begin{cases} \dfrac{e^{1/x}-1}{e^{-1/x}+1},\ x \ne 0 \\ 1,\ \ x=0 \end{cases}$$
Examine the function for differentiability at
$$x=0; f(x)=\begin{cases} \begin{matrix} x \tan^{-1} x; & x \ne 0 \end{matrix} \\ \begin{matrix} 0; & x=0 \end{matrix} \\ \begin{matrix} & \end{matrix} \end{cases}$$
Test the continuity of the function $$f(x)=\dfrac{|3x-4|}{3x-4}$$ at $$x=\dfrac{4}{3}$$
If function $$f(x)=\begin{cases} \begin{matrix} \dfrac{\sin (m+1x+ \sin x)}{x} & x < 0 \end{matrix} \\ \begin{matrix} \dfrac{1}{2}; & x=0 \end{matrix} \\ \begin{matrix} \dfrac{x^{3/2}+1}{2}; & x < 0 \end{matrix} \end{cases}$$ is continuous at $$x=0$$, then find $$m$$
Find the derivative of following functions w.r.t. $$x$$:
$$\sin^{-1} \left\{ 2x \sqrt{1-x^2}\right\}, -\dfrac{1}{2} < x < \dfrac{1}{2}$$
Find the derivative of following functions w.r.t. $$x$$:
$$\cos^{-1} \left( \dfrac{1-x^2}{1+x^2} \right), x \in (0,\infty)$$
Find the derivative of following functions w.r.t. $$x$$:
$$\sin^{-1} (3x-4x^3), x \in \left( \dfrac{-1}{2},\dfrac{1}{2} \right)$$
Find the derivative of following functions w.r.t. $$x$$:
$$\tan^{-1} \left( \dfrac{a+x}{1-ax}\right)$$ (Hint : Put $$x= \tan \theta, a= \tan \alpha$$)
Find the derivative of following functions w.r.t. $$x$$:
$$\cos^{-1} \left( \dfrac{1-x^2}{1+x^2} \right), x \in (0,1)$$
Find the derivative of following functions w.r.t. $$x$$:
$$\cos^{-1} (2x)+2 \cos^{-1} (\sqrt{1-4x^2})$$ (Hint : Put $$2x= \cos \theta$$)
Find the derivative of following functions w.r.t. $$x$$:
$$\sin^{-1} \left( \dfrac{1+x^2}{1-x^2}\right)+\cos^{-1}\left( \dfrac{1+x^2}{1-x^2}\right)$$ [Hint: $$\sin^{-1} \theta+\cos^{-1}\theta=\dfrac{\pi}{2}$$]
Find the derivative of following functions w.r.t. $$x$$:
$$\cos^{-1} \left( \sqrt{\dfrac{1+x}{2}} \right)$$ (Hint $$x= \cos \theta$$)
Find the derivative of following functions w.r.t. $$x$$:
$$\cos^{-1} (4x^3-3x), x \in \left( \dfrac{1}{2} , 1 \right)$$
Find the derivative of following functions w.r.t. $$x$$:
$$sec^{-1} \left( \dfrac{1}{2x^2-1} \right), x \in \left(0, \dfrac{1}{2}\right)$$
Find the derivative of following functions w.r.t. $$x$$:
$$\tan^{-1} \left( \dfrac{2^x+1}{1-4^x}\right)$$ (Hint : Put $$2^x= \tan \theta, $$)
If $$y=a \sin x+ b \cos x$$, then prove that:
$$\dfrac{d^2y}{dx^2}+y=0$$
Find $$\dfrac{d^2y}{dx^2}$$, when :
$$y=x^3+ \tan x$$
Find $$\dfrac{d^2y}{dx^2}$$, when :
$$y=x^2+3x+2$$
Find the derivative of following functions w.r.t. $$x$$:
$$\sin \left\{ 2 \tan^{-1} \left( \sqrt{\dfrac{1-x}{1+x}}\right) \right\}$$ (Hint : Put $$x= \cos \theta$$)
Find $$\dfrac{dy}{dx}$$ of following functions:
$$ y \sqrt{1-x^2}=\sin^{-1}x$$
Find $$\dfrac{d^2y}{dx^2}$$, when :
$$y=x \cos x$$
Find $$\dfrac{d^2y}{dx^2}$$, when :
$$y=e^{-x} \cos x$$
Find the derivative of following functions w.r.t. $$x$$:
$$\cos^{-1} (\sqrt{1+x^2+x}) $$ (Hint : Put $$x= \cos \theta$$)
Find $$\dfrac{d^2y}{dx^2}$$, when :
$$y=a \sin x- b \cos x$$
Find $$\dfrac{d^2y}{dx^2}$$, when :
$$y=2 \sin x+3 \cos x$$
If $$y=(\sin^{-1}x)^2$$, then prove that:
$$(1-x^2) \dfrac{d^2 y}{dx^2}-x \dfrac{dy}{dx}-2=0$$
Differentiate given functions w.r.t. $$x$$:
$$\sin^{-1} x+ \sin^{-1} \sqrt{1-x^2}$$
If $$y=\sec x+ \tan x$$, then prove that:
$$\dfrac{d^2 y}{dx^2}=\dfrac{\cos x}{(1- \sin x)^2}$$
Differentiate given functions w.r.t. $$x$$:
$$\dfrac{\cos^{-1} \dfrac{x}{2}}{\sqrt{2x+7}}, -2 < x < 2$$
Find whether function is increasing or decreasing in given domain$$ f(x) = tan^{-1} X - X, X \epsilon R$$
Solve the following differential equation$$x+y=\sin^{-1} \left(\dfrac {dy}{dx}\right)$$
Solve:
$$\sin^{-1}\left[\dfrac{dy}{dx}+\dfrac{2}{x}y\right]=x$$
Match the columns
Derivatives of function
If $$x = \cos t (3 - 2\cos^{2}t)$$ and $$y =\sin t (3 - 2\sin^{2} t)$$, find the value of $$\dfrac {dy}{dx}$$ at $$t = \dfrac {\pi}{4}$$
If $$x$$ and $$y$$ are differentiable functions of $$t$$, then show that
$$\dfrac {dy}{dx} = \dfrac {\dfrac {dy}{dt}}{\dfrac {dx}{dt}}$$ if $$\dfrac {dx}{dt}\neq 0$$
Differentiate the function w.r.t. $$x$$.
$$\displaystyle (x \cos x)^x + (x \sin x)^{\tfrac{1}{x}}$$
Prove that the difference of the infinite continued fractions $$\displaystyle\frac{1}{a+}\frac{1}{b+}\frac{1}{c+}..., \frac{1}{b+}\frac{1}{a+}\frac{1}{c+}.....,$$ is equal to $$\displaystyle\frac{a-b}{1+ab}$$.
Show that $$\left(\displaystyle\frac{1}{a+}\frac{1}{b+}\frac{1}{c+}....\right)\left(c+\displaystyle\frac{1}{b+}\frac{1}{a+}\frac{1}{c_1}....\right)=\displaystyle \frac{1+bc}{1+ab}$$.
Solve:
If $$x^yy^x=1$$,Find $$\dfrac{dy}{dx}$$
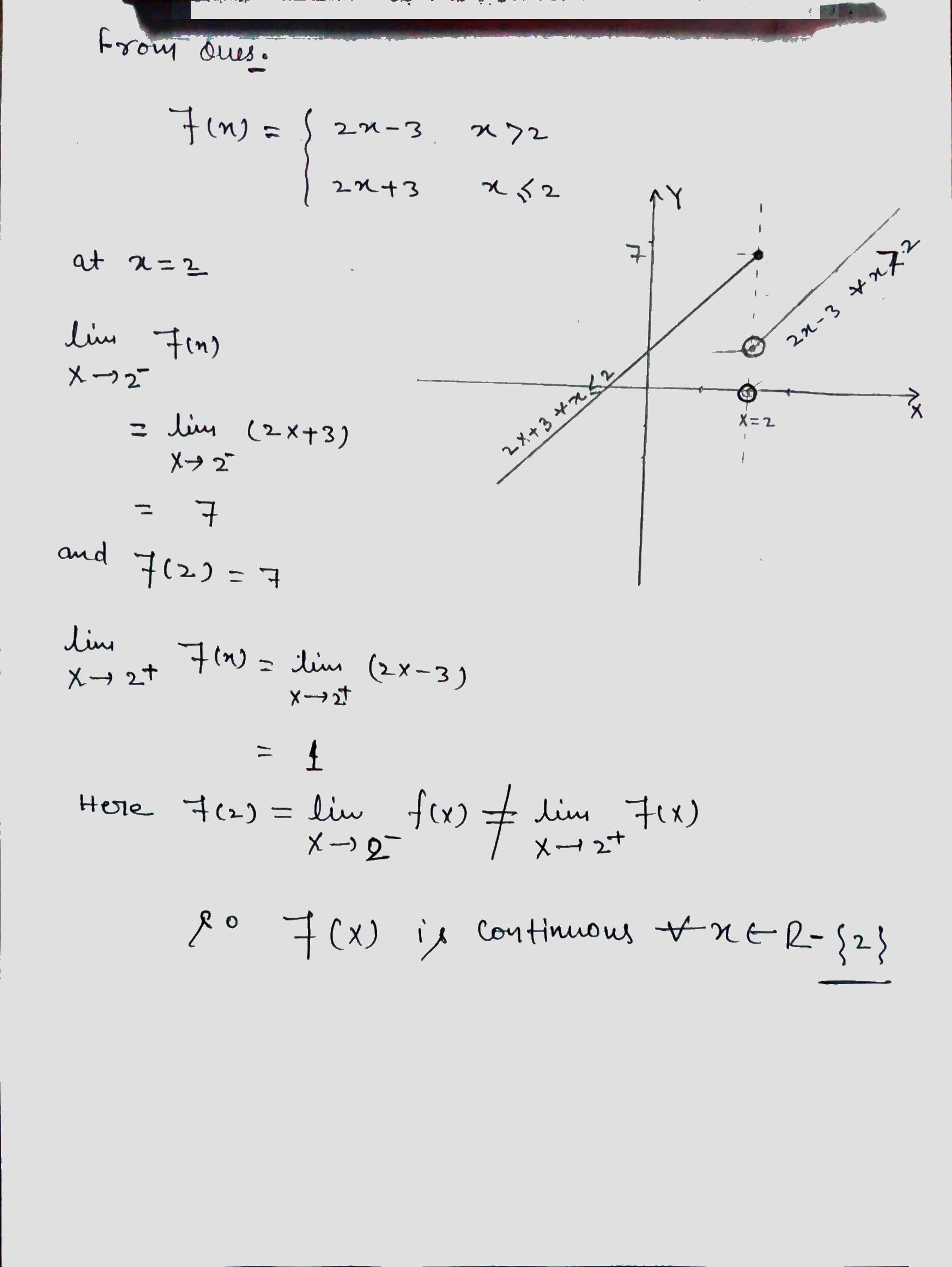
When $$x \leq 2, f(x) = 2x +3 $$ here $$f(x)$$ is a polynomial function, therefore it is continuous on $$R$$, in particular it is continuous when $$x\leq2$$
When $$x> 2, f(x) = 2x -3 $$ here $$f(x)$$ is a polynomial function, therefore it is continuous on $$R$$, in particular it is continuous when $$x>2$$ at $$x=2$$
$$x = \cfrac{{{{\sin }^3}t}}{{\sqrt {\cos 2t} }},\,y = \cfrac{{{{\cos }^3}t}}{{\sqrt {\cos 2t} }}$$ then find $$\dfrac{dy}{dx}$$
Differentiate the following function w.r.t. x :$${\cos}^{-1}{(1-2{\sin}^{2}{x})}$$
If $$x=4t^{2}+5,y=6t^{2}+7t+3$$, find $$\dfrac{d^{2}y}{dx^{2}}$$.
If $$y=(\sin x)^{x}+x^{x}$$ then find $$\dfrac{dy}{dx}$$
Find$$ \dfrac{dy}{dx}$$, where $$ x=\dfrac{3at}{1+t^3}, y=\dfrac{3at^2}{1+t^3}$$
$$x=\dfrac{3at}{1+t^{3}}, y=\dfrac{3at^{2}}{1+t^{3}}\Rightarrow \dfrac{y}{x}=t$$
$$\Rightarrow x=\dfrac{3ay/x}{\dfrac{x^{3}+y^{3}}{x+2}}\Rightarrow x^{4}+y^{3}x= 3ax^{2}y$$
$$\Rightarrow 4x^{3}+y^{3}+3y^{2}x\dfrac{dy}{dx}= 6axy+3ax^{2}\dfrac{dy}{dx}$$
$$\Rightarrow \dfrac{dy}{dx}=\dfrac{4x^{3}+y^{3}-6axy}{3ax^{2}-3xy^{2}}$$
$$log\left(\dfrac{dy}{dx}\right)=3x+4y; y=0$$ when $$x=0$$.
Find $$\frac { d y } { d x }$$ for
If $$x = \dfrac { \sin ^ { 3 } t } { \sqrt { \cos 2 t } } , y = \dfrac { \cos ^ { 3 } t } { \sqrt { \cos 2 t } }$$ then find $$\dfrac { d y } { d x }$$
If for $$x\epsilon \left( 0,\frac { 1 }{ 4 } \right) $$, the derivative of $${ tan }^{ -1 }\left( \frac { 6x\sqrt { x } }{ 1-9{ x }^{ 3 } } \right) $$ is $$\sqrt { x } \cdot g\left( x \right) $$, then g(x)= $$\dfrac {1-kx^3}{(1+9x^3)^2}$$ then k =
if $$y={ b\tan }^{ -1 }\left( \frac { x }{ a } +{ \tan }^{ -1 }\left( \frac { y }{ x } \right) \right) ,\quad find\quad \frac { dy }{ dx } $$
if $$x\sqrt { 1+y } +y\sqrt { 1+x } =0,-1<x<1,x\neq y$$ then prove that $$\frac { dy }{ dx } =-\frac { 1 }{ { \left( 1+x \right) }^{ 2 } } $$
Find:
$$\dfrac { dy }{ dx } =sin(x+y)+cos(x+y)$$
Find the deivative of f $$(x)={ cos }^{ 1 }\left( sin\sqrt { \dfrac { 1+x }{ 2 } } \quad \right) +{ x }^{ 3 }$$
If $$x^{y}+y^{x}=a^{b}$$, then show that $$\dfrac{dy}{dx}=-\left (\dfrac{yx^{y-1}+y^{x}\log y}{x^{y}\log x+xy^{x-1}}\right)$$
If $$y=\tan^{-1}(3x)$$, then find $$\dfrac{d^{2}y}{dx^{2}}$$.
Given
$$y=tan^{-1}(3x)$$
$$\frac{dy}{dx}=\frac{d}{dx}tan^{-1}(3x)$$
$$ \frac{dy}{dx}=\frac{1}{1+(3x)^{2}}$$
$$\frac{dy}{dx}=\frac{1}{1+9x^{2}}$$
$$\frac{d^{2}y}{dx^{2}}=\frac{d}{dx}(\frac{1}{(1+9x^{2})})$$
$$\frac{d^{2}y}{dx^{2}}=\frac{(1+9x^{2})\frac{d}{dx}3-3\frac{d}{dx}(1+9x^{2})}{(1+9x^{2})^{2}}$$
$$\frac{d^{2}y}{dx^{2}}=\frac{0-3(18x)}{(1+9x^{2})^{2}}$$
$$\frac{d^{2}y}{dx^{2}}=\frac{-54x}{(1+9x^{2})^{2}}$$
If $$x=\sin^{2}\theta ,y=\tan \theta $$, then find $$\dfrac{dy}{dx}$$ at $$\theta ={45}^{\circ}$$.
If $$x=a\left( \cos { t } +\log { \tan { \dfrac { t }{ 2 } } } \right) ,y=a\sin { t } $$, then show that $$\dfrac { dy }{ dx } =\tan { t } $$.
Differentiate the following functions with respect to $$x$$
$$\sqrt {\dfrac {1+\sin x}{1-\sin x}}$$
If $$\cos^{-1}\left (\dfrac {x^2 - y^2}{x^2 + y^2}\right)=\tan^{-1}\ a$$, prove that $$\dfrac {dy}{dx}=\dfrac {y}{x}$$.
If $$y=x \sin y,$$ prove that $$ \dfrac {dy}{dx}= \dfrac{\sin y}{(1-x \cos y)}$$.
Differentiate the following function from first principle:
$$\sin^{-1} (2x+3)$$
$$f(x) = \left\{\begin{matrix} x^2 + ax + 1,& x \ \text{is rational} \\ ax^2+2x+b, & x \ \text{is irrational} \end{matrix}\right.$$
A function $$f(x)$$ defined as is continuous at $$x=1$$ and $$2$$ then the values of $$a$$ and $$b$$
If $$ f\left(\dfrac{x+y}{3}\right)=\dfrac{2+f(x)+f(y)}{3} $$ for all real $$ x $$ and $$ y $$ and $$ f^{\prime}(2)=2, $$ then determine $$ y=f(x) $$
$$f(x) = \left\{\begin{matrix} b\sin^{-1} \left(\dfrac{c+x}{2}\right), & -\dfrac{1}{2} < x < 0 \\ \dfrac{1}{2}, & x = 0 \\ \dfrac{e^{ax/2}-1}{x}, & 0 < x < \dfrac{1}{2} \end{matrix}\right.$$if $$\left | C \right |\leq \dfrac{1}{2}$$ and f(x) is a differentiable function at x=0 given Find the value of a and prove that 64 $$b^{2}=4-c^{2}$$
Let $$ f(x+y)=f(x)+f(y)+2 x y-1 $$ for all real $$ x $$ and $$ y $$ and $$ f(x) $$ be differentiable function.
If $$ f^{\prime}(0)=\cos \alpha, $$ then prove that $$ f(x)>0 \forall x \in R $$
If $$y^{2} = a^{2} cos^{2} x + b^{2} sin^{2} x$$, show that $$ y + \dfrac{d^{2}}{dx^{2}} = \dfrac{a^{2}b^{2}}{y^{3}}$$
Differentiate the following w.r.t. $$ x: x^{\tan ^{-1} x} $$
If $$y=\sec^{-1}\Bigg(\dfrac{1+\sqrt{x}}{1-\sqrt{x}}\Bigg)+\sin^{-1}\Bigg(\dfrac{1-\sqrt{x}}{1+\sqrt{x}}\Bigg)$$, then $$\dfrac{dy}{dx}$$ is equal to ___________.
If $$ \sin ^{-1}\left(\dfrac{x^{5}-y^{5}}{x^{5}+y^{5}}\right)=\dfrac{\pi}{6}, $$ show that $$ \dfrac{d y}{d x}=\dfrac{x^{4}}{3 y^{4}} $$
Let the function ln $$(f(x))$$ is defined where $$f(x)$$ exists for $$x \le 2$$ and $$k$$ is fixed positive real number. Prove that if $$\dfrac{d}{dx} (x\ f (x)) \ge -k\ f(x)$$, then $$f(x) \ge Ax^{k-1}$$ where $$A$$ is independent of $$x$$.
If $$ x=\sin ^{-1}\left(e^{t}\right), y=\sqrt{1-e^{2 t}}, $$ show that $$ \sin x+\dfrac{d y}{d x}=0 $$
If $$f(x)=\begin{cases} x-1;x<2 \\ 2x-3; x \ge 2 \end{cases}$$ then find $$f^{'}(2-0)$$
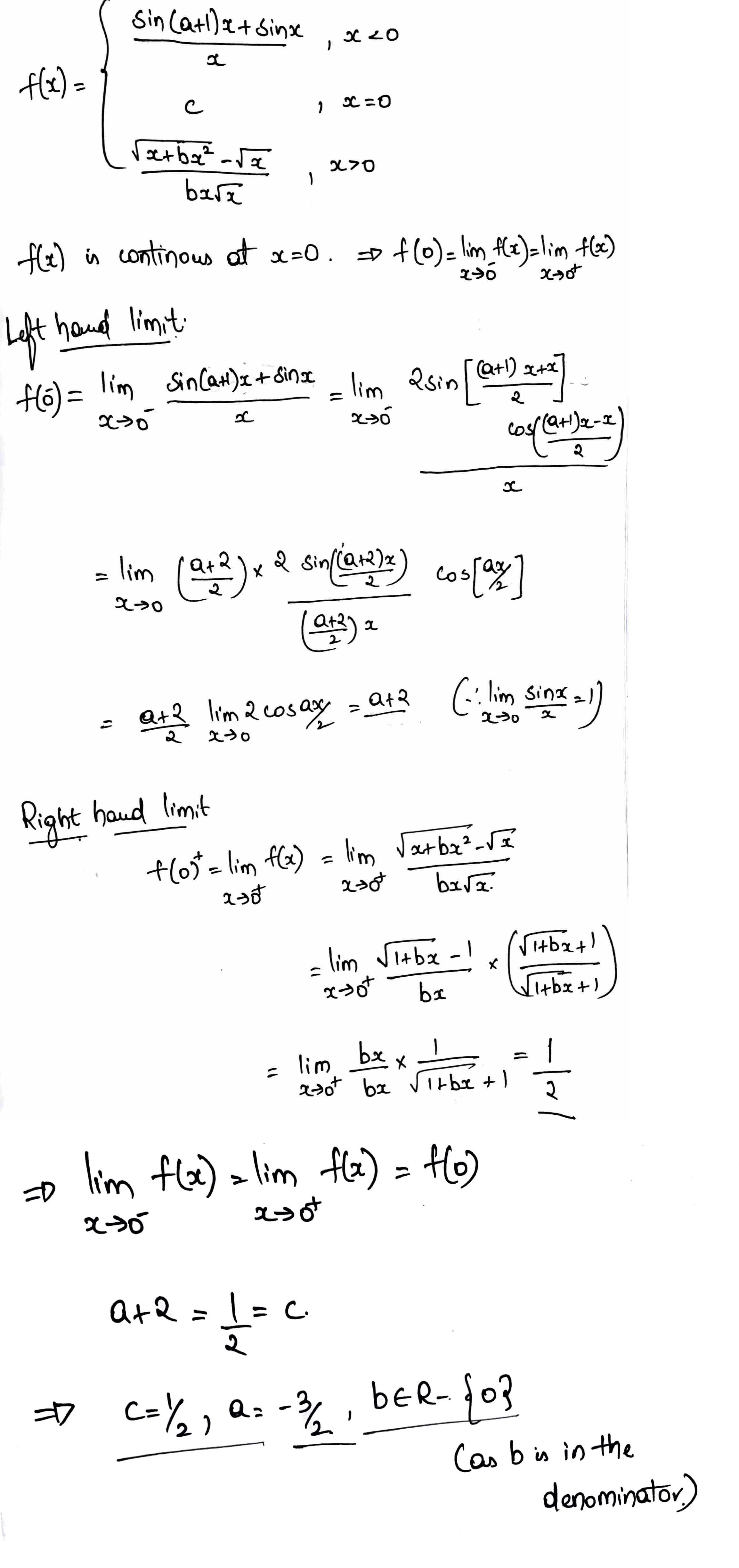
Find $$a,b,c$$ if the function $$f(x)=\begin{cases} \begin{matrix} \dfrac{\sin (a+1)x+\sin x}{x} & x< 0 \end{matrix} \\ \begin{matrix} c, & x=0 \end{matrix} \\ \begin{matrix} \dfrac{\sqrt{x+bx^2}-\sqrt x}{bx \sqrt x} & x > 0 \end{matrix} \end{cases}$$ is continuous at $$x=0$$
Differentiate $$ \sin ^{-1}\left(\dfrac{2 x}{1+x^{2}}\right) w . r . t . \cos ^{-1}\left(\dfrac{1-x^{2}}{1+x^{2}}\right) $$
Find $$ \dfrac{d y}{d x}, $$ if $$ : x=\cos ^{-1}\left(\dfrac{2 t}{1+t^{2}}\right), y=\sec ^{-1}\left(\sqrt{1+t^{2}}\right) $$
Find $$ \dfrac{\mathrm{dy}}{\mathrm{dx}}, $$ if $$ : x=\cos ^{-1}\left(4 t^{3}-3 t\right), y=\tan ^{-1}\left(\dfrac{\sqrt{1-t^{2}}}{t}\right) $$
Differentiate $$ \tan ^{-1}\left(\dfrac{x}{\sqrt{1-x^{2}}}\right) w . r . t . \sec ^{-1}\left(\dfrac{1}{2 x^{2}-1}\right) $$
Class 12 Commerce Maths Extra Questions
- Application Of Derivatives Extra Questions
- Application Of Integrals Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Linear Programming Extra Questions
- Matrices Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions