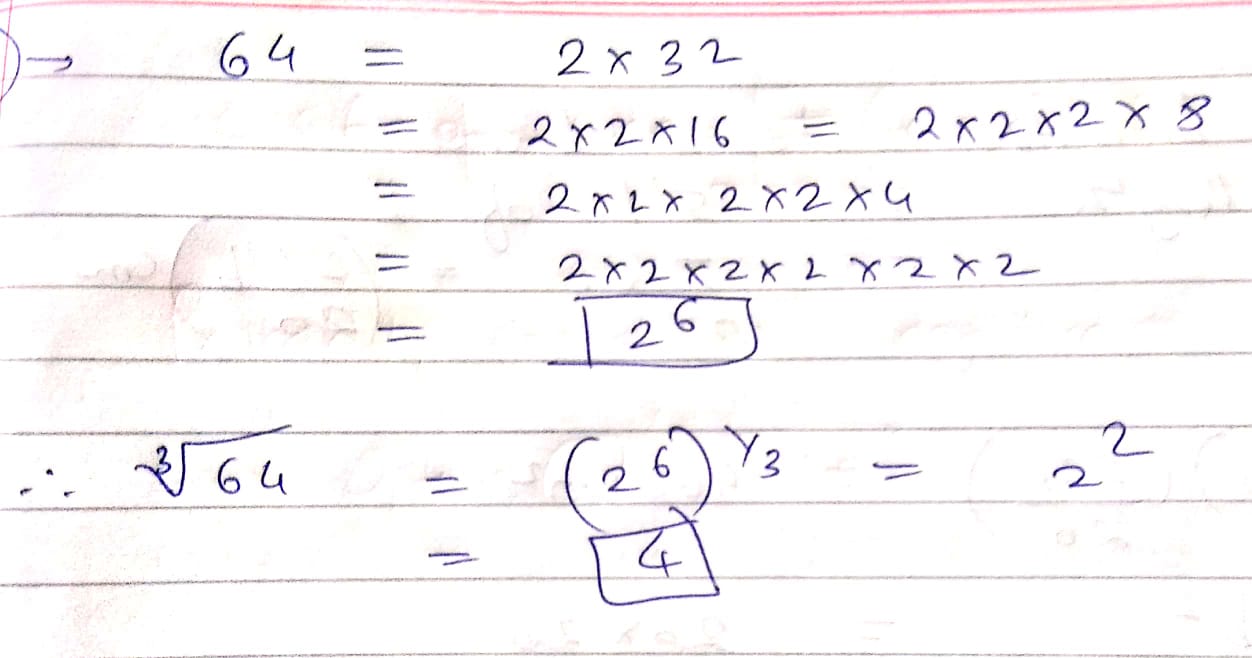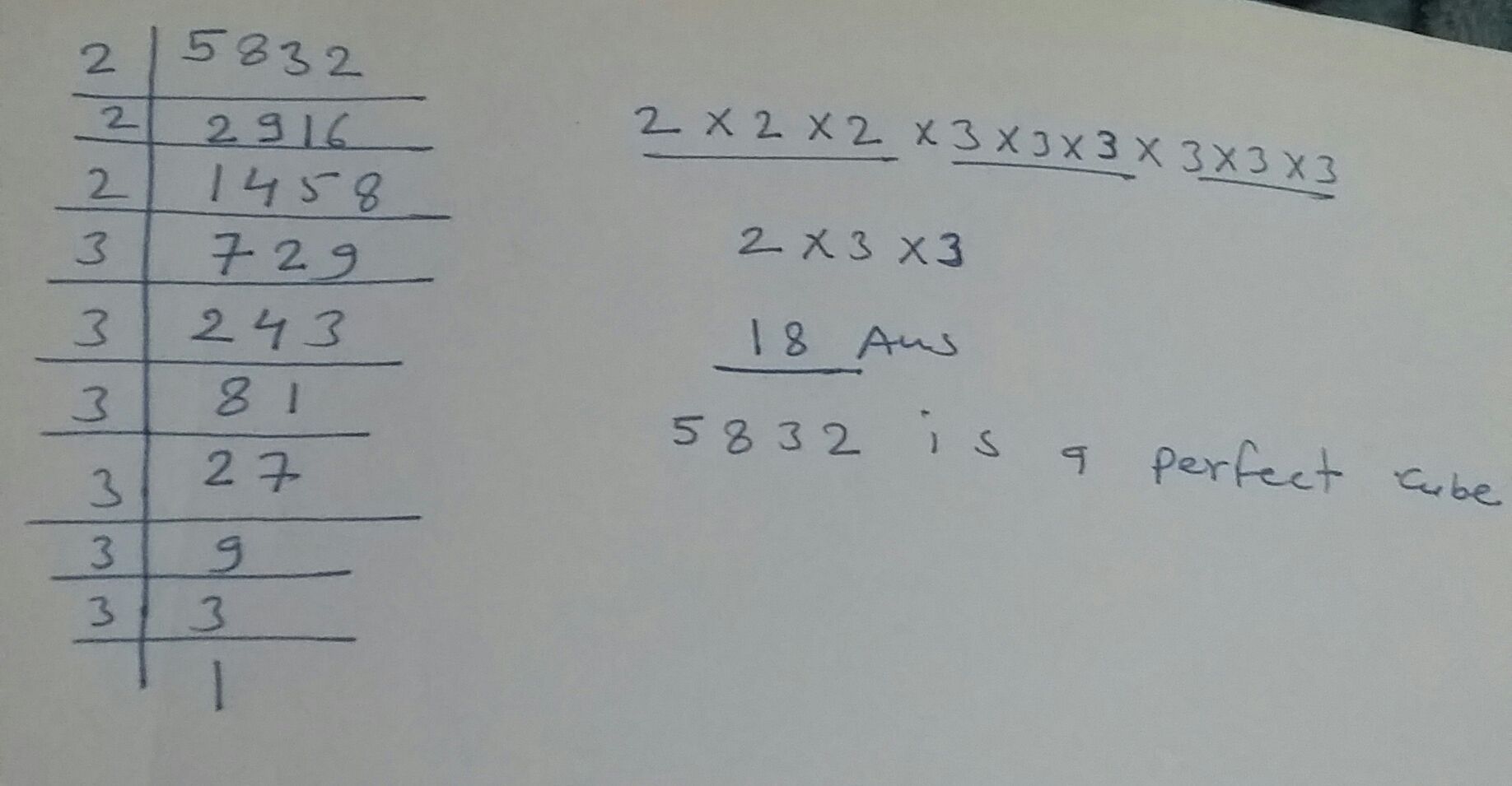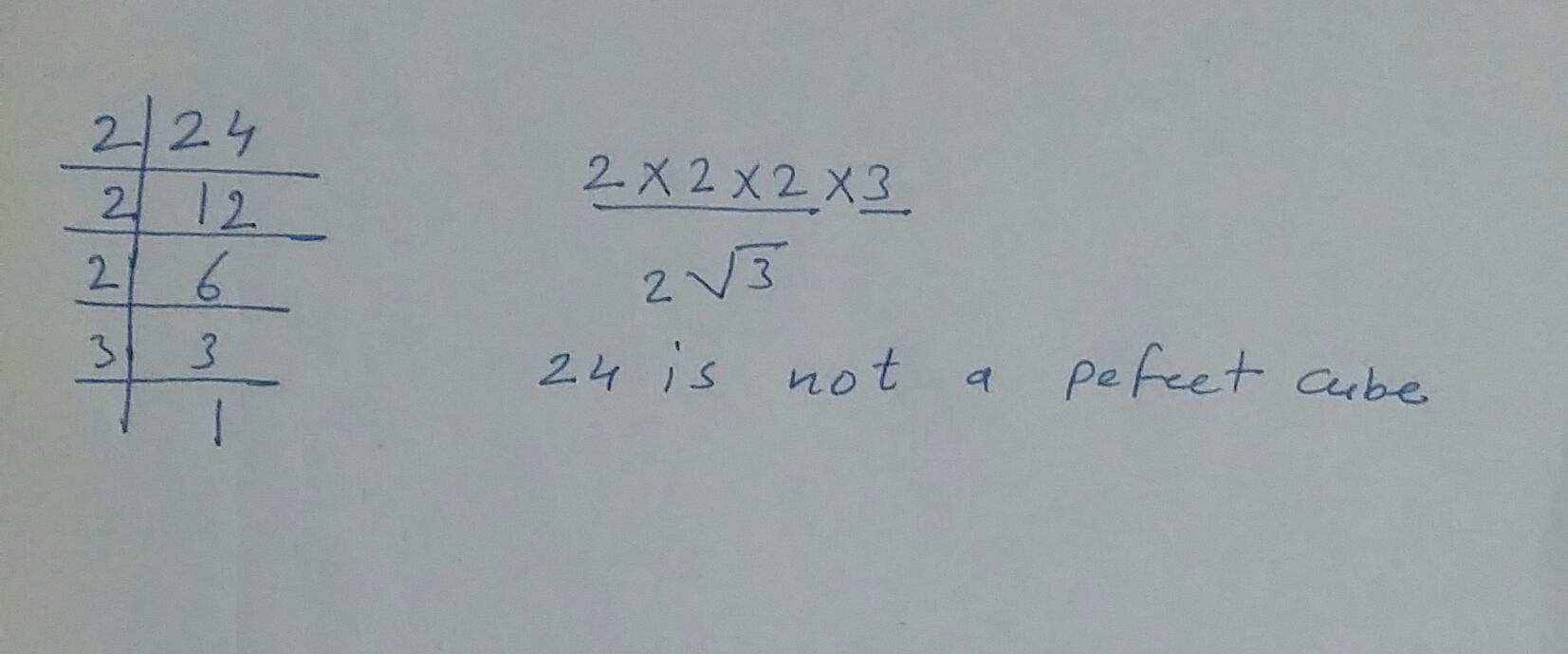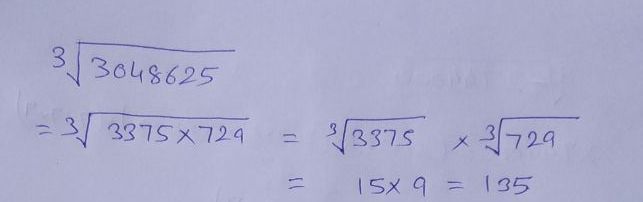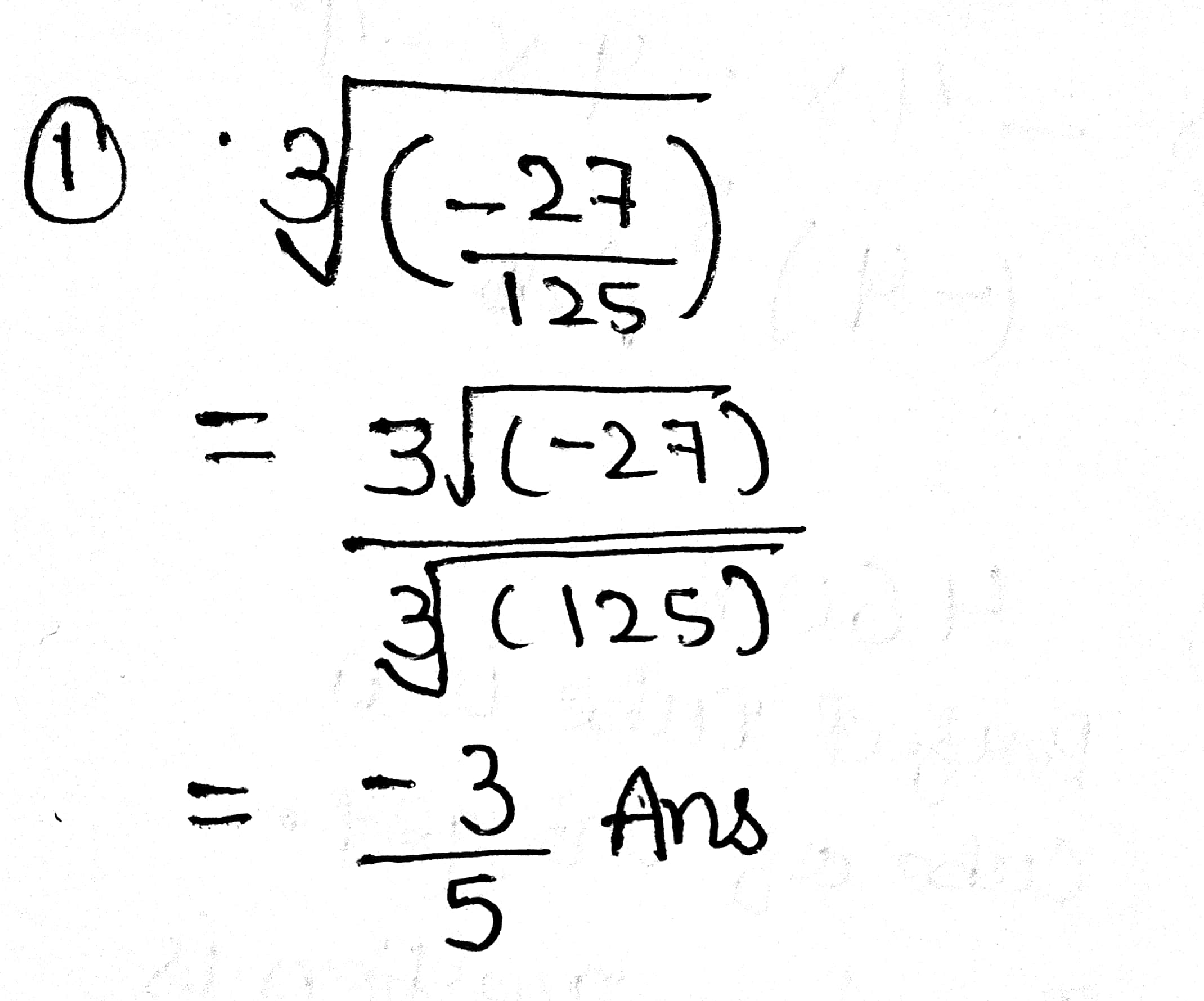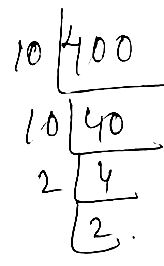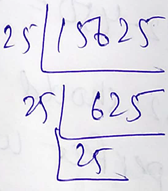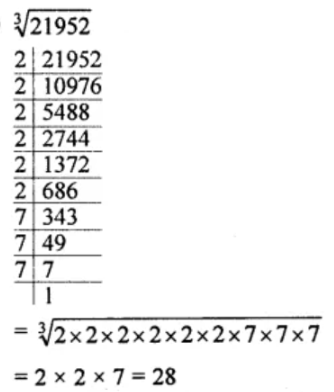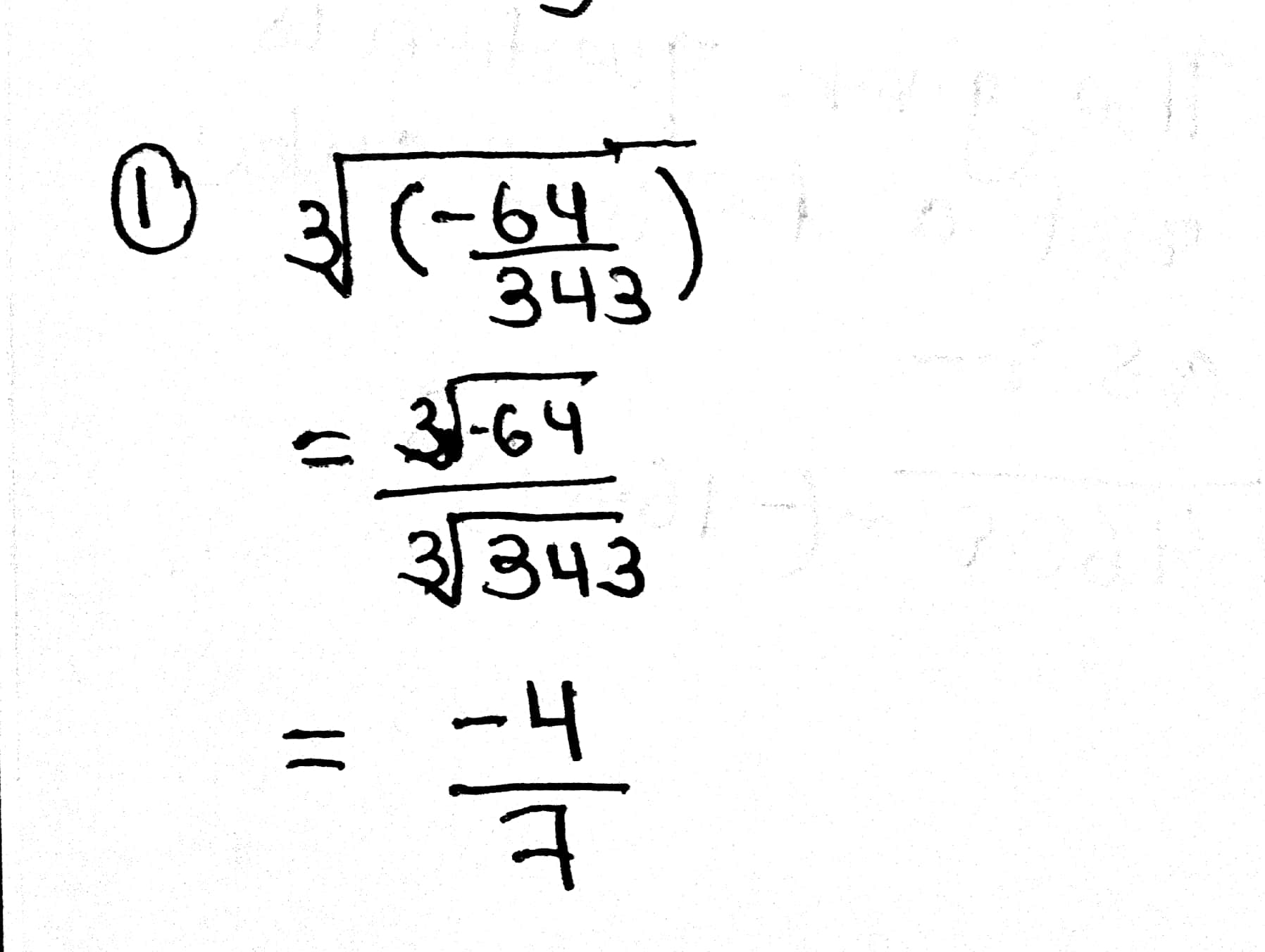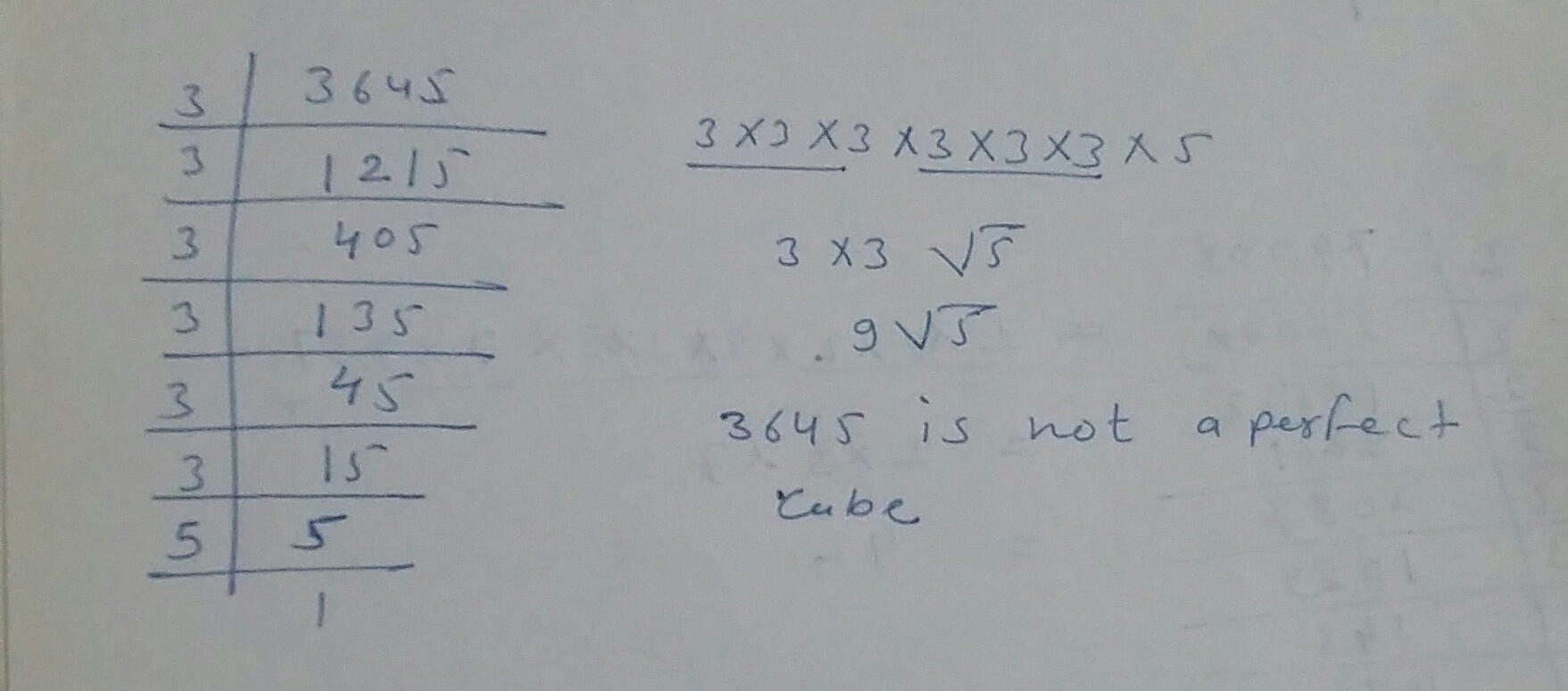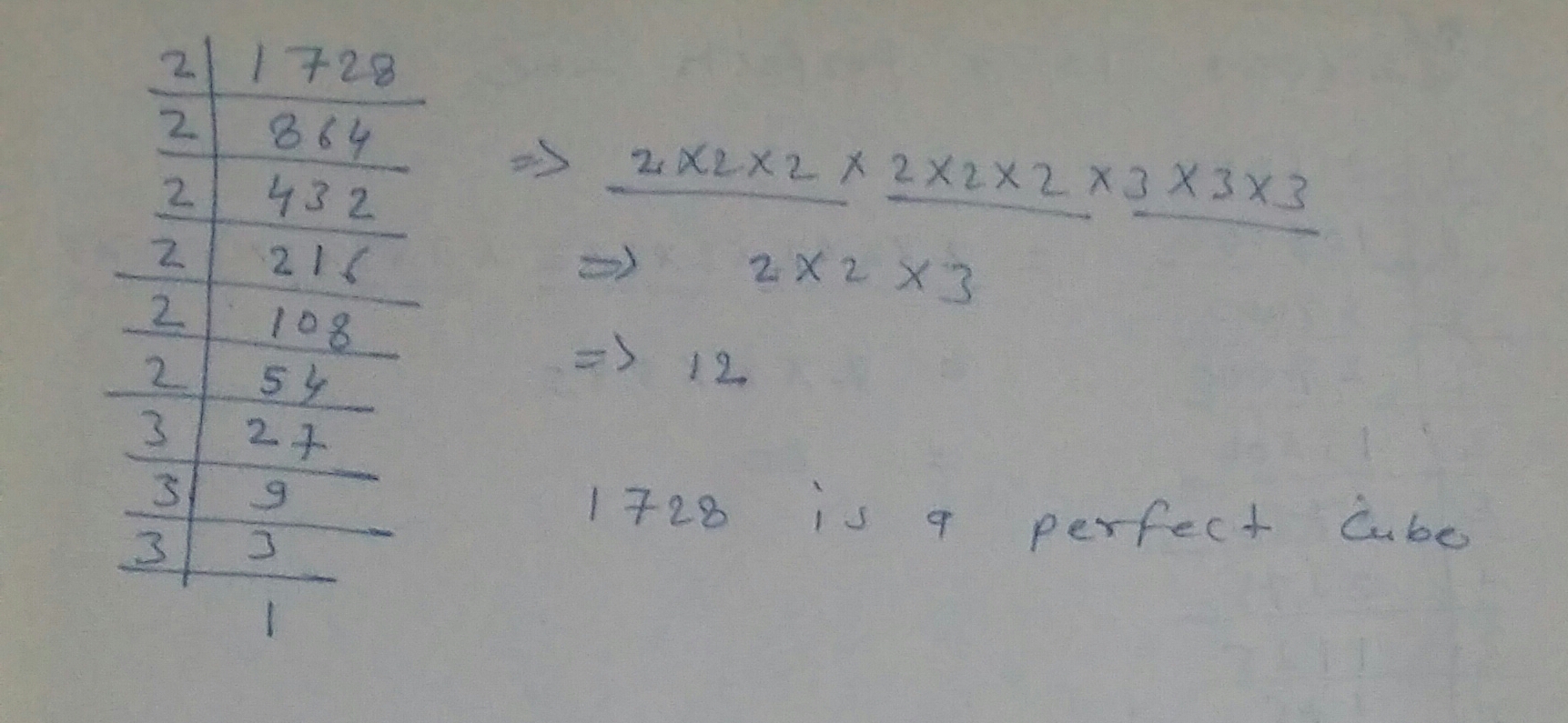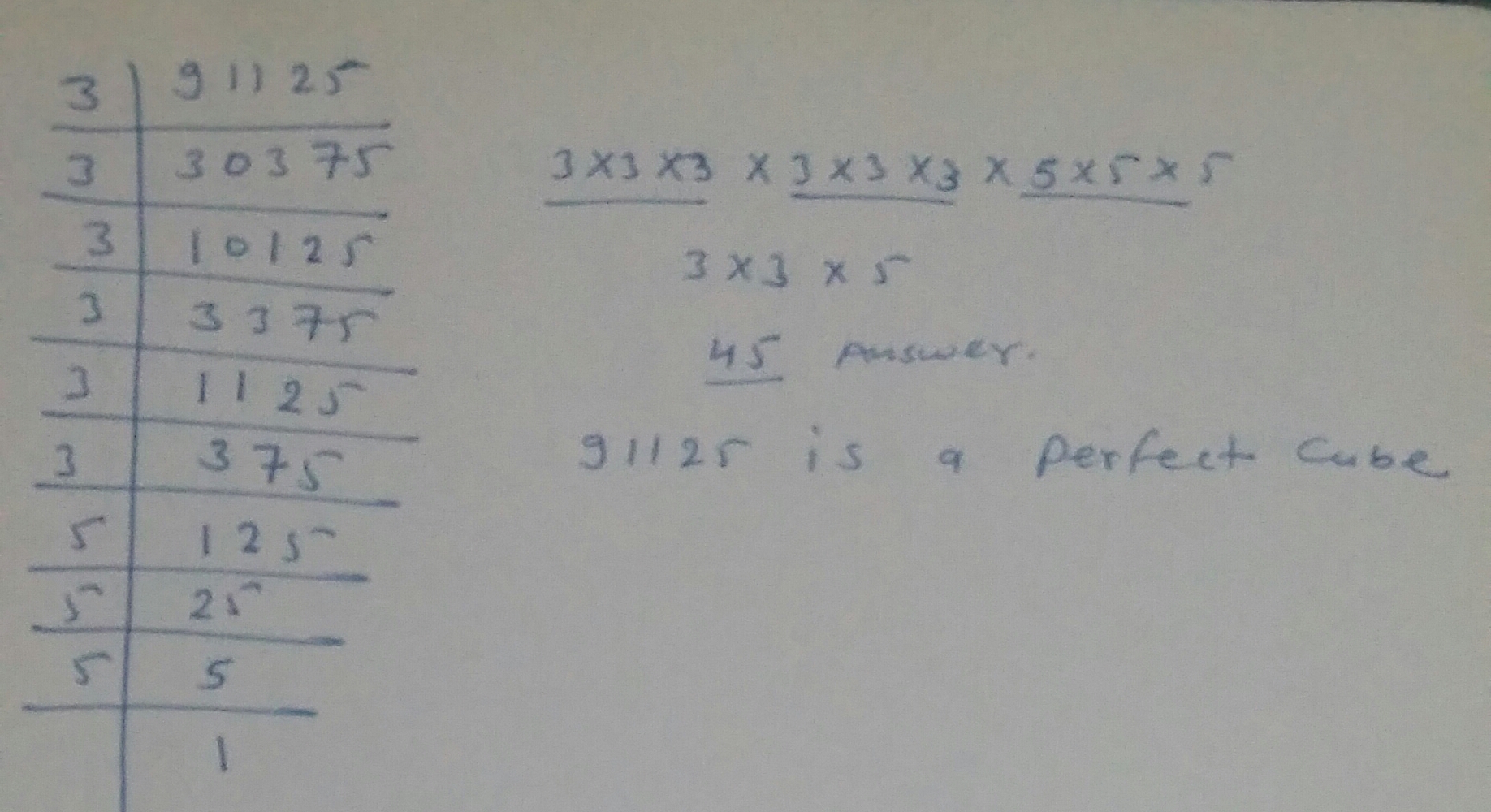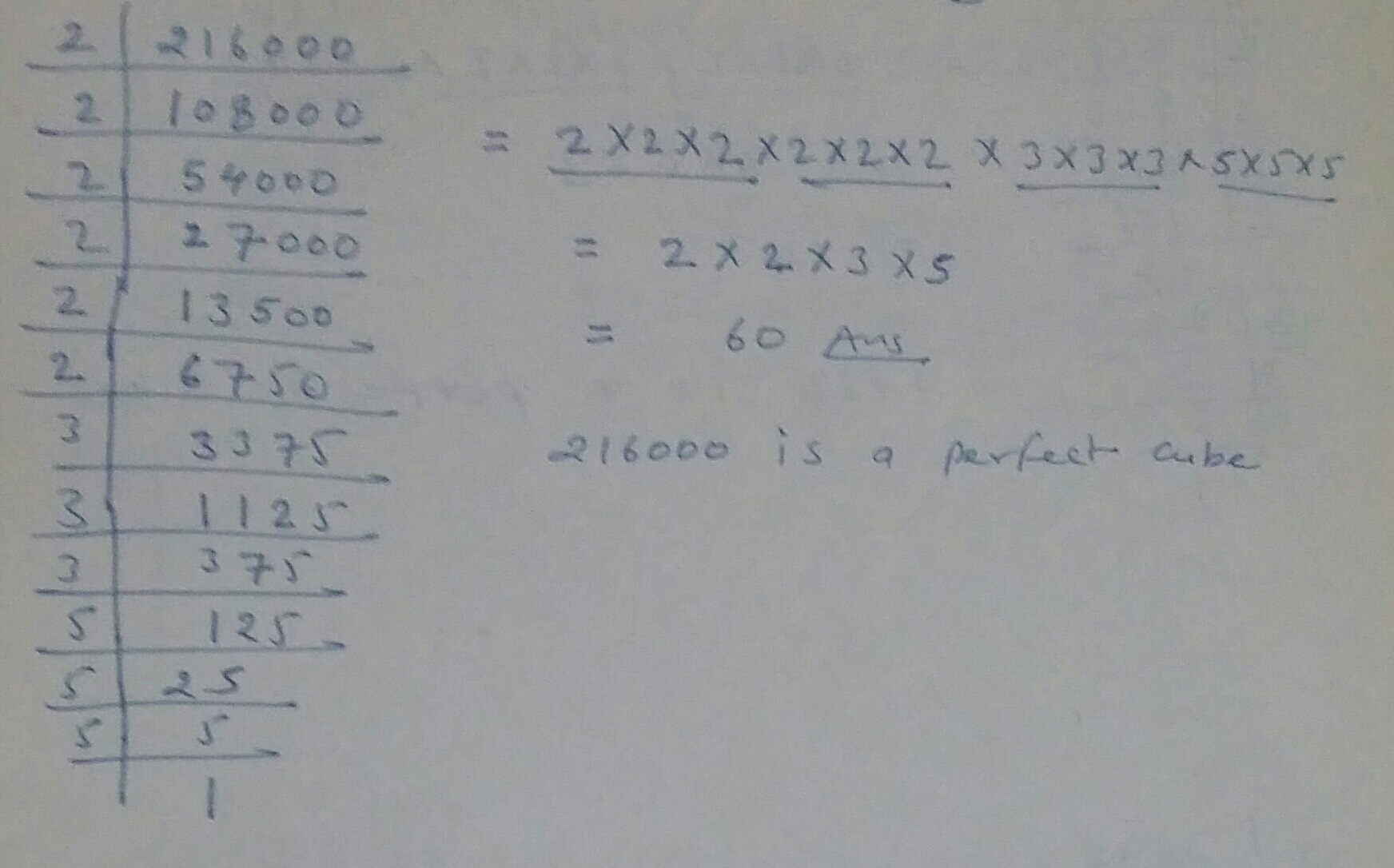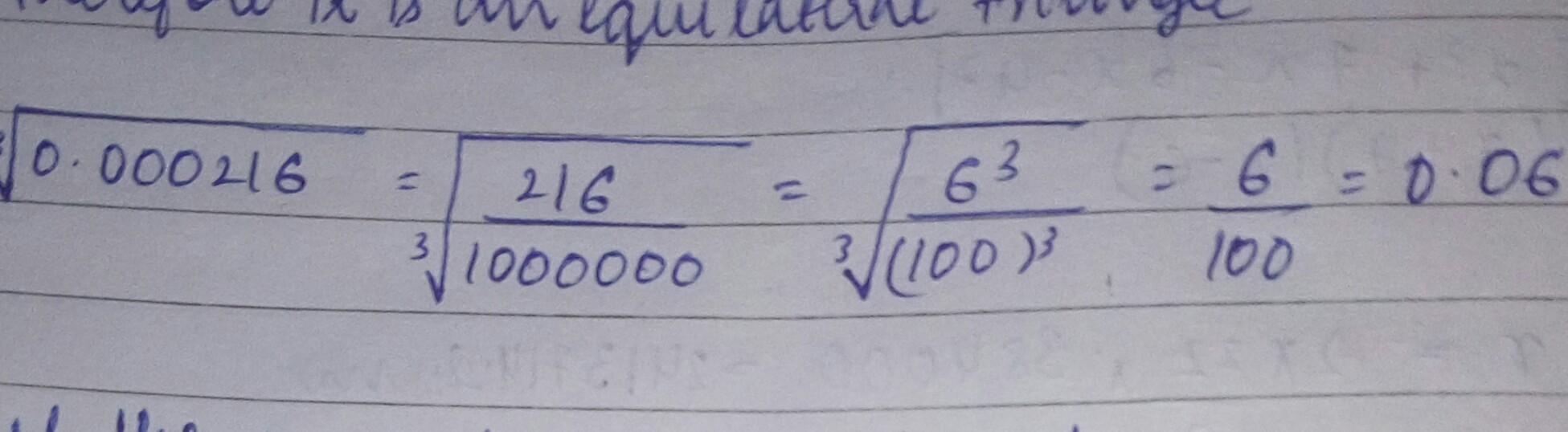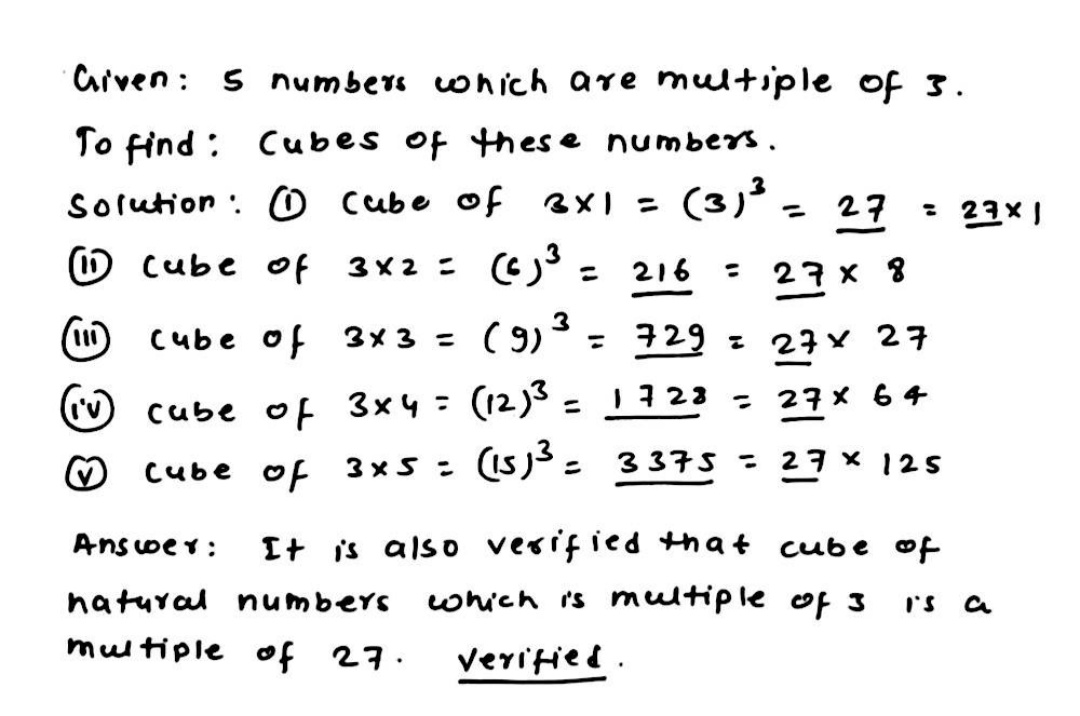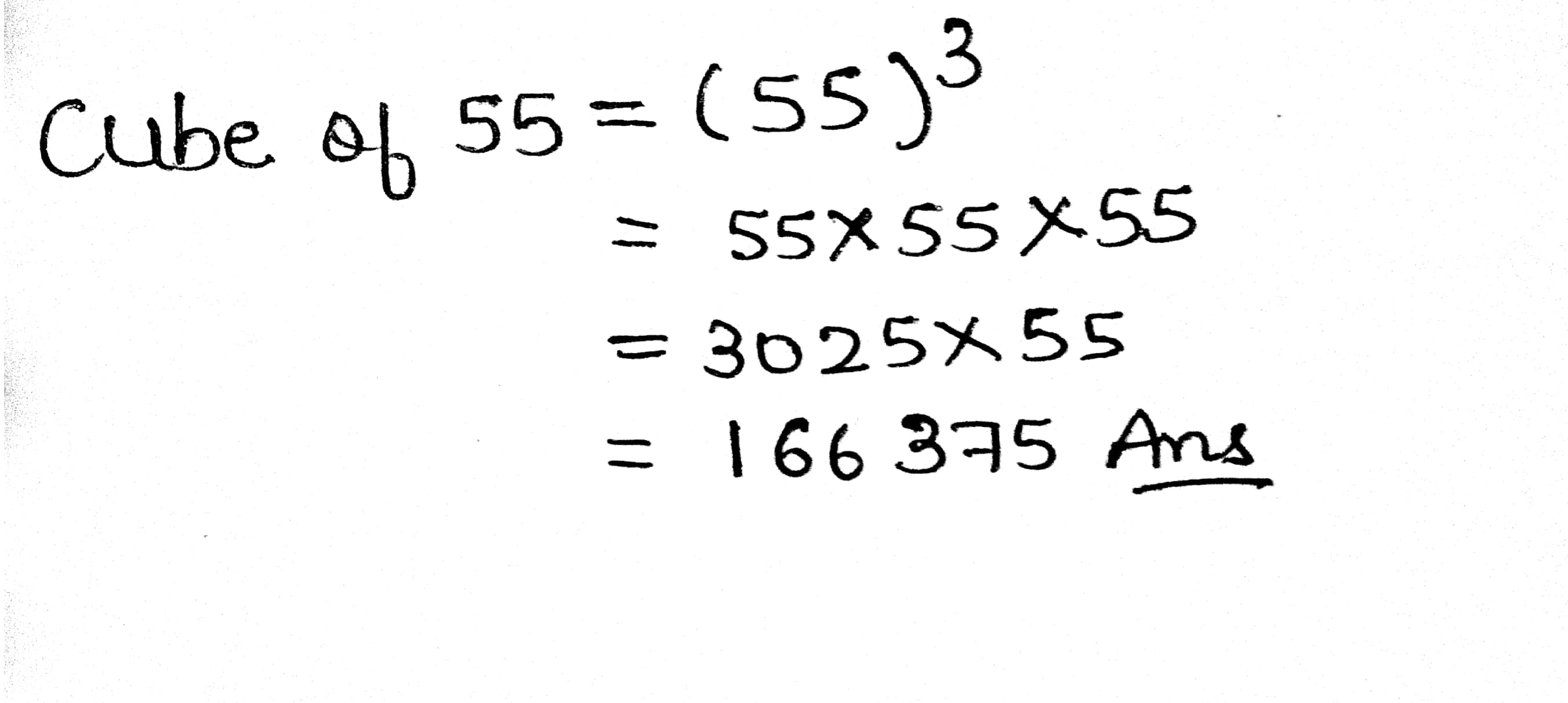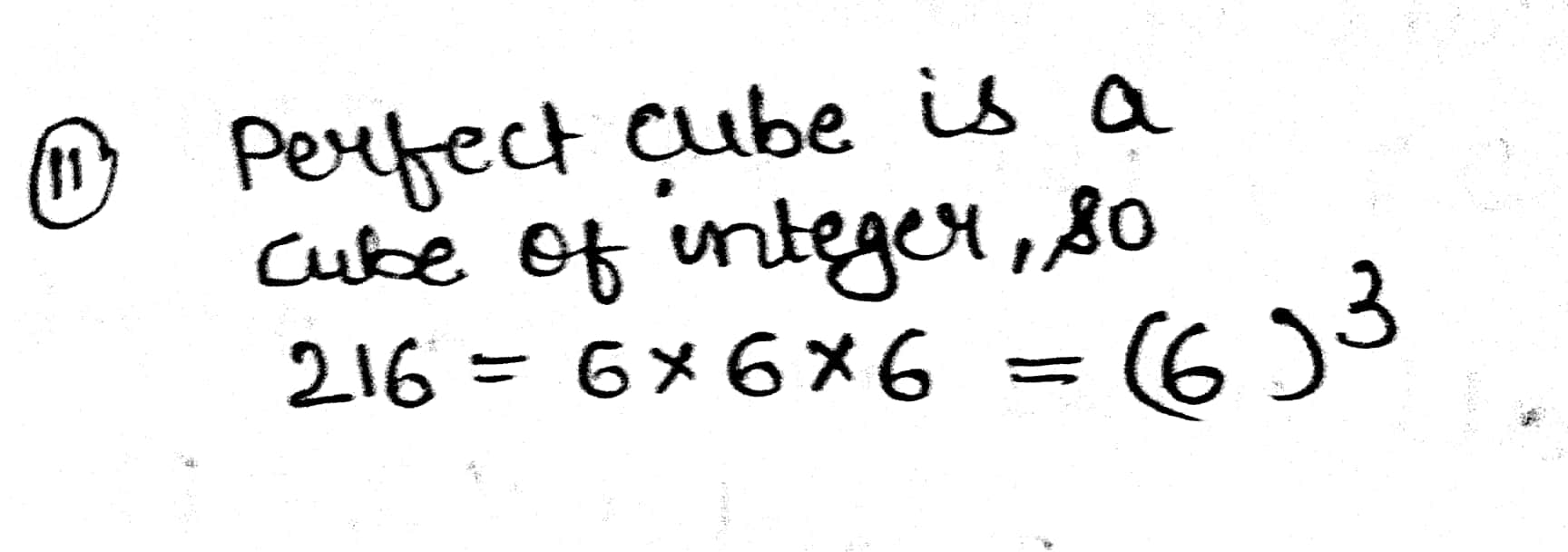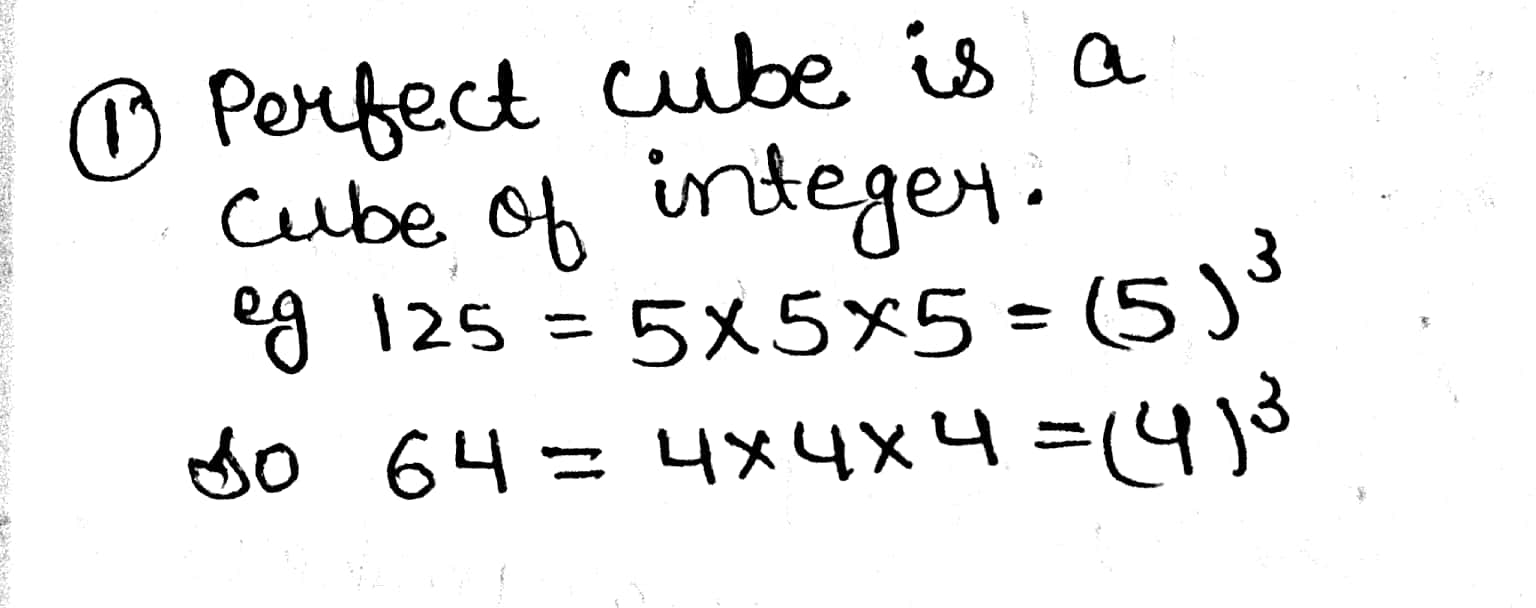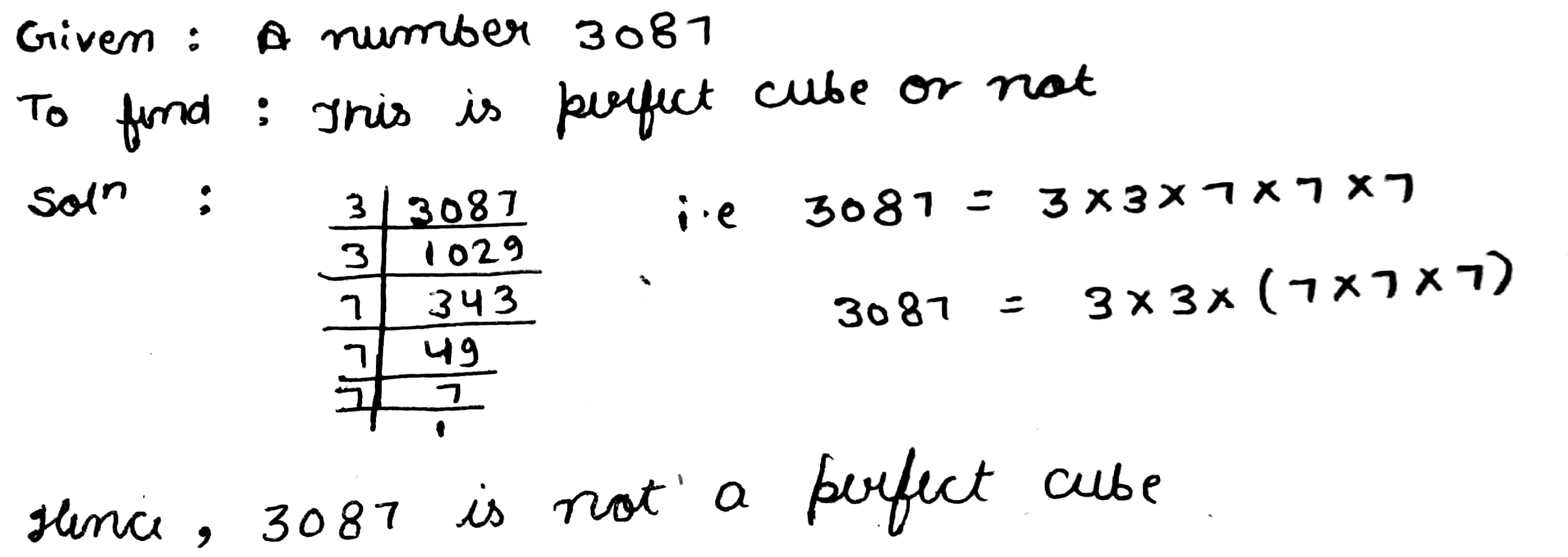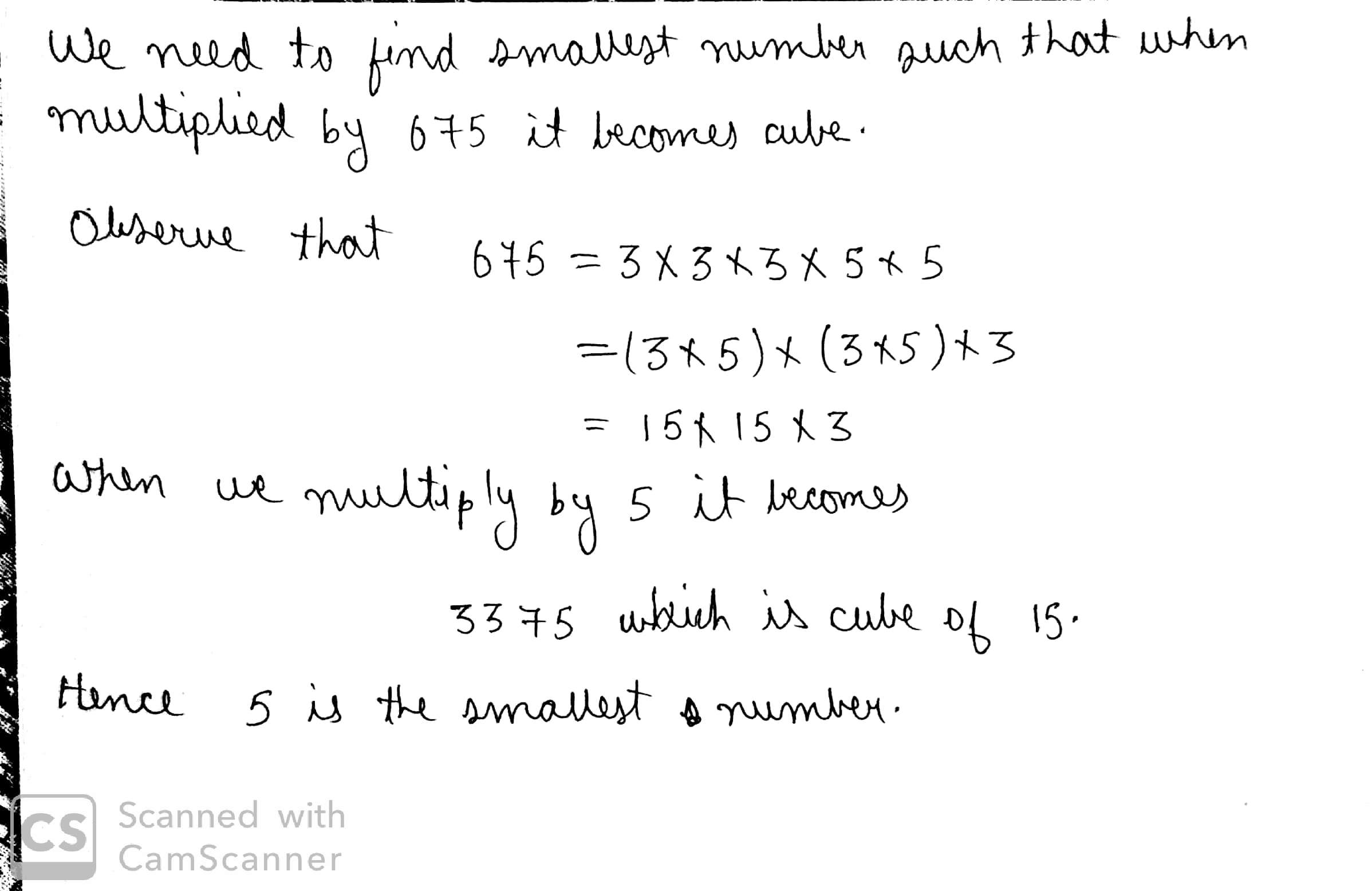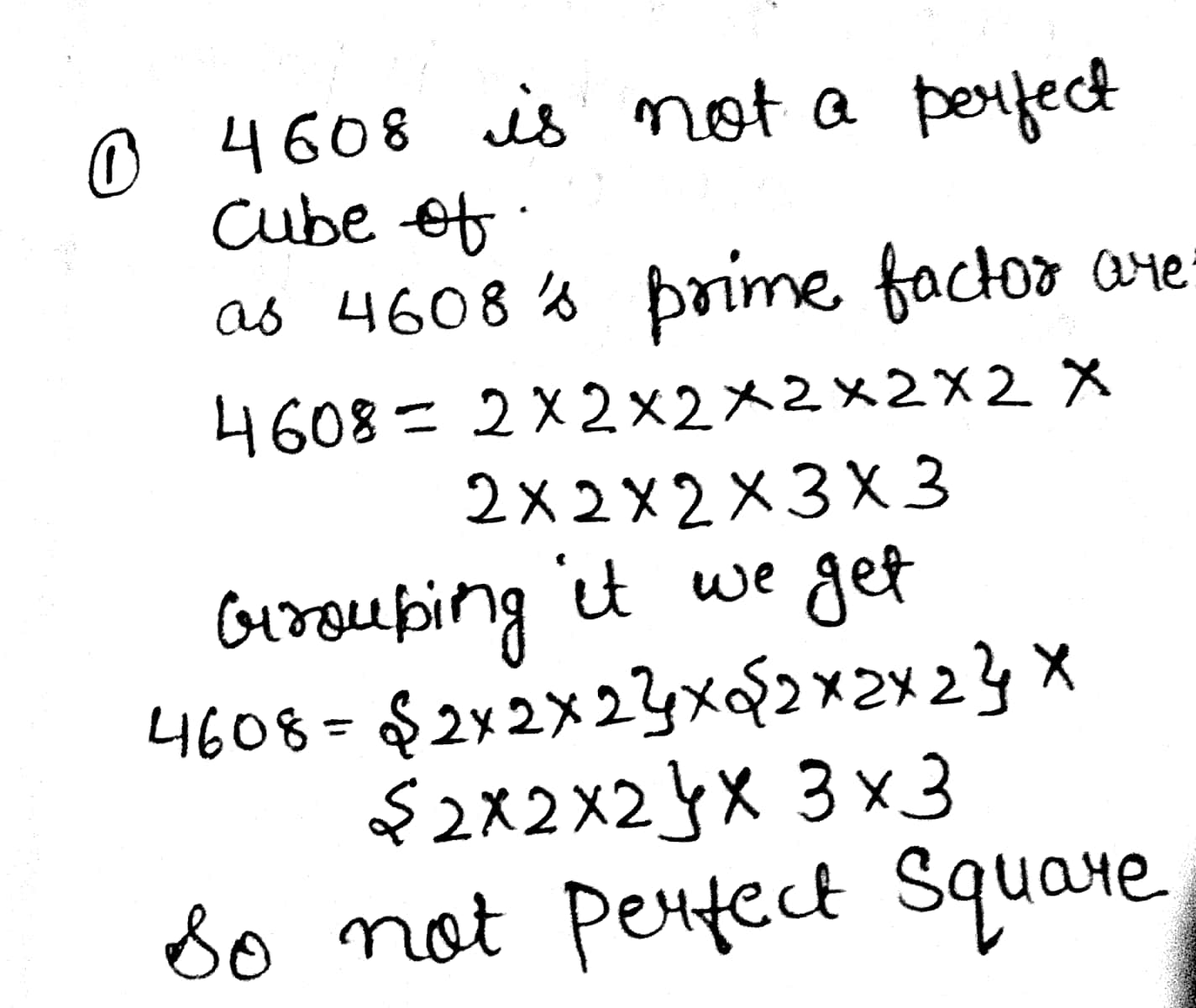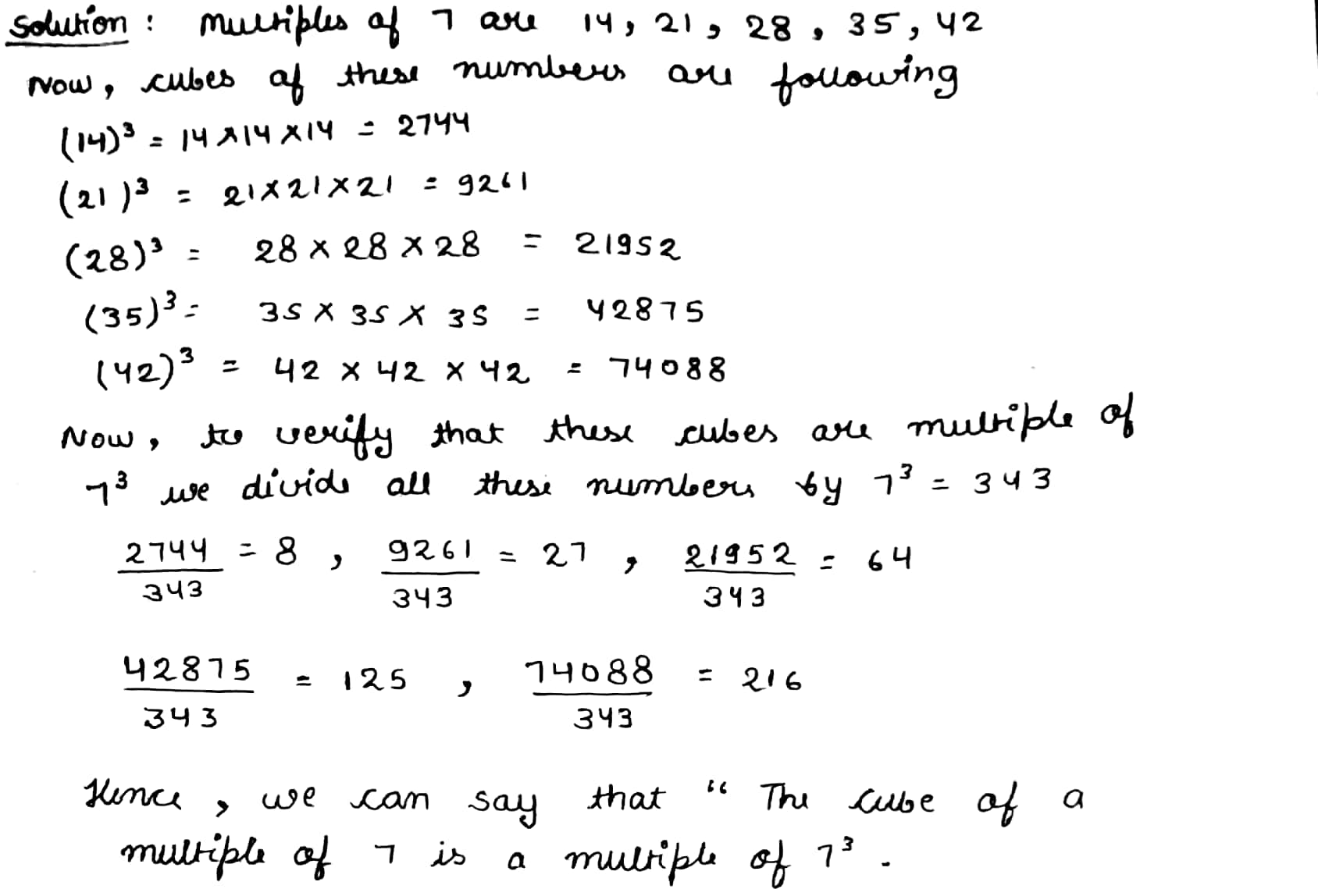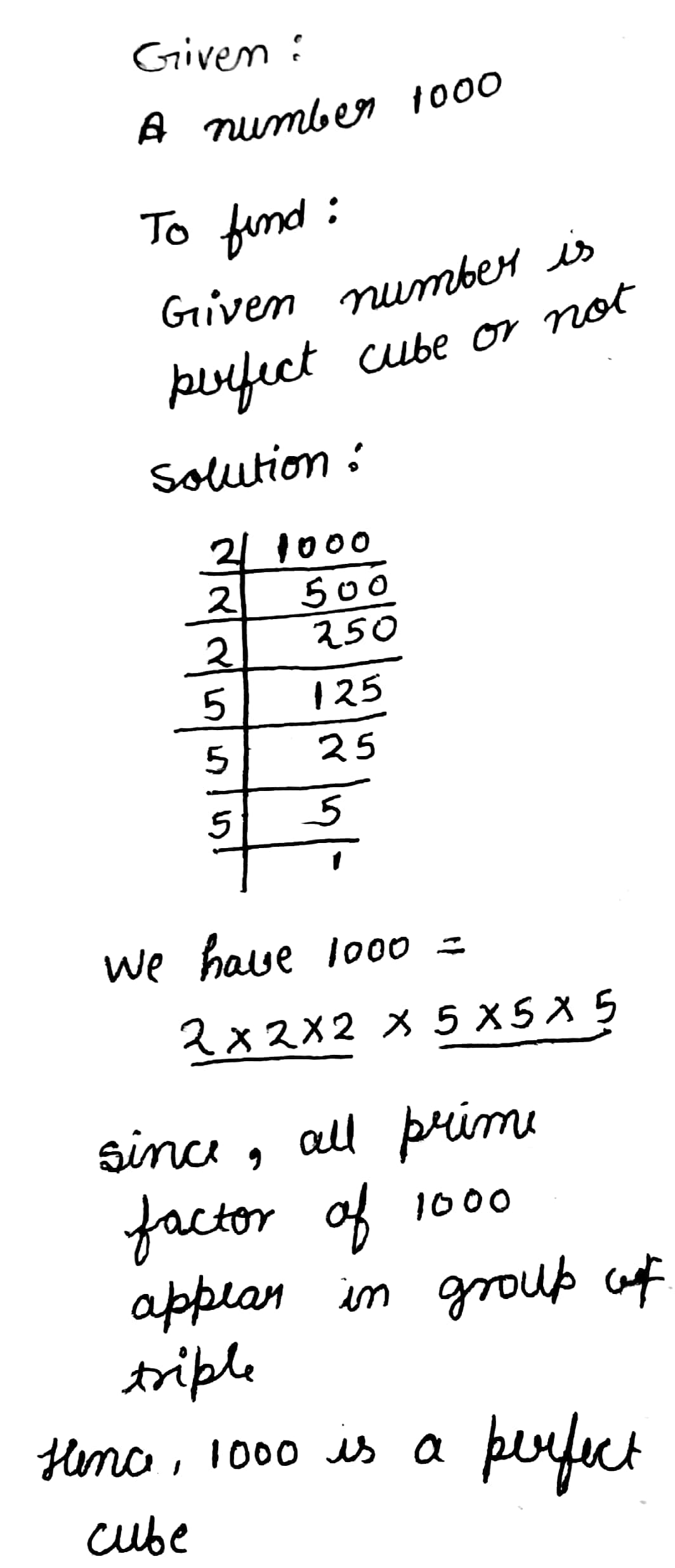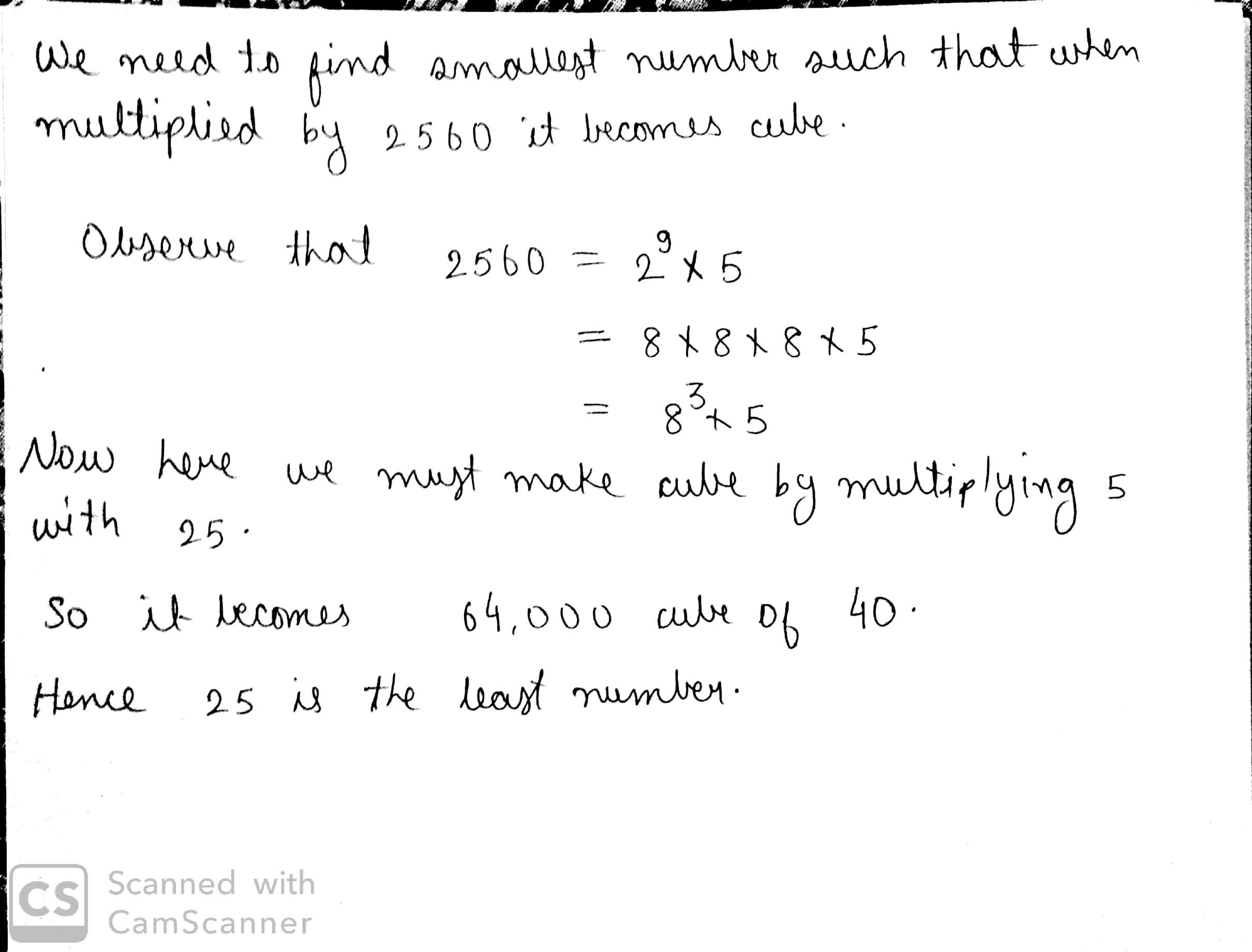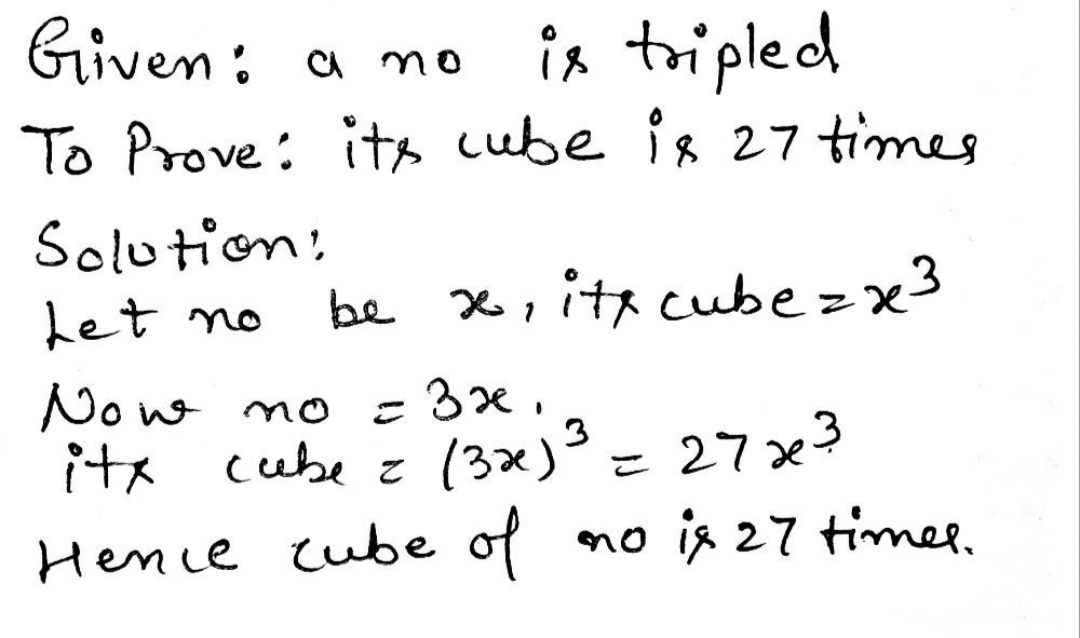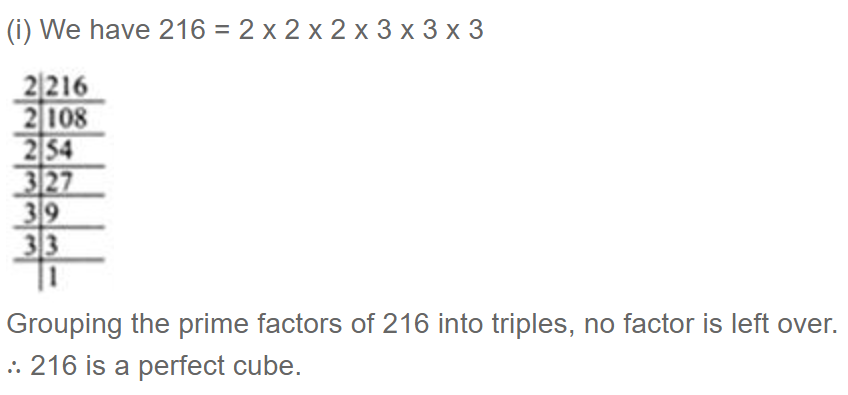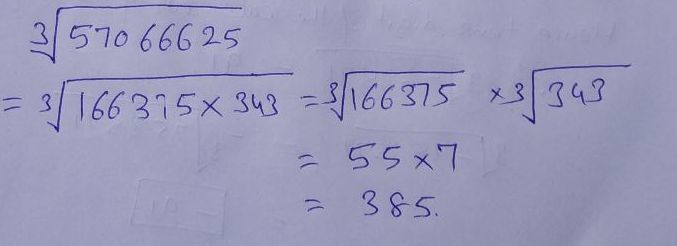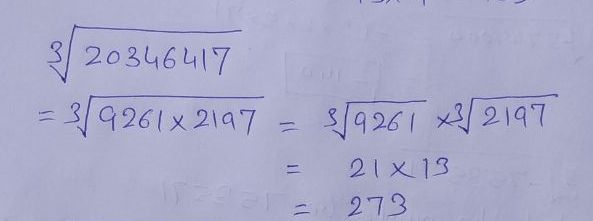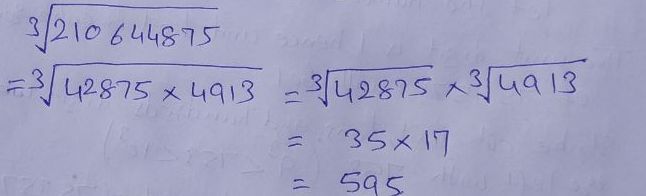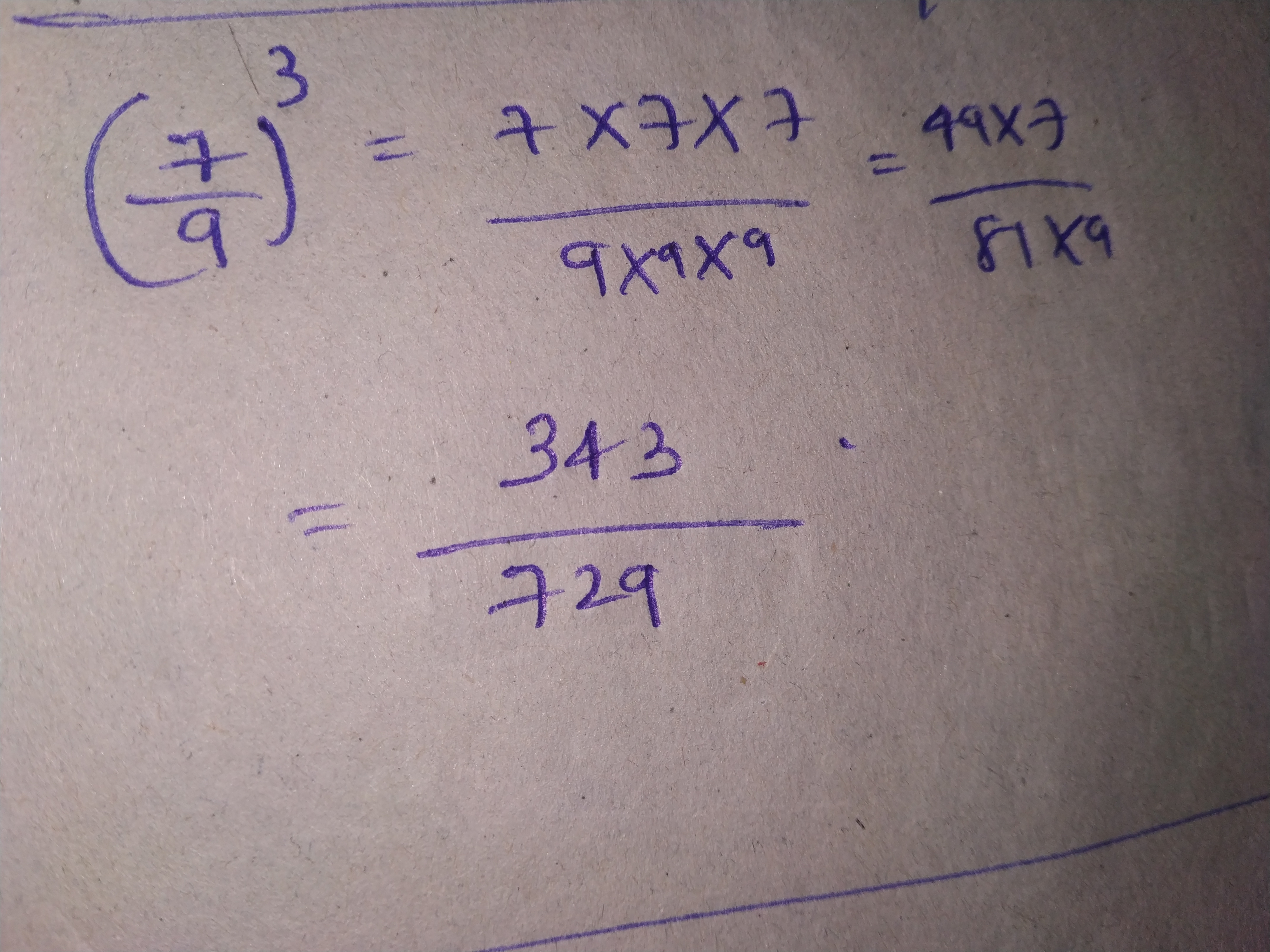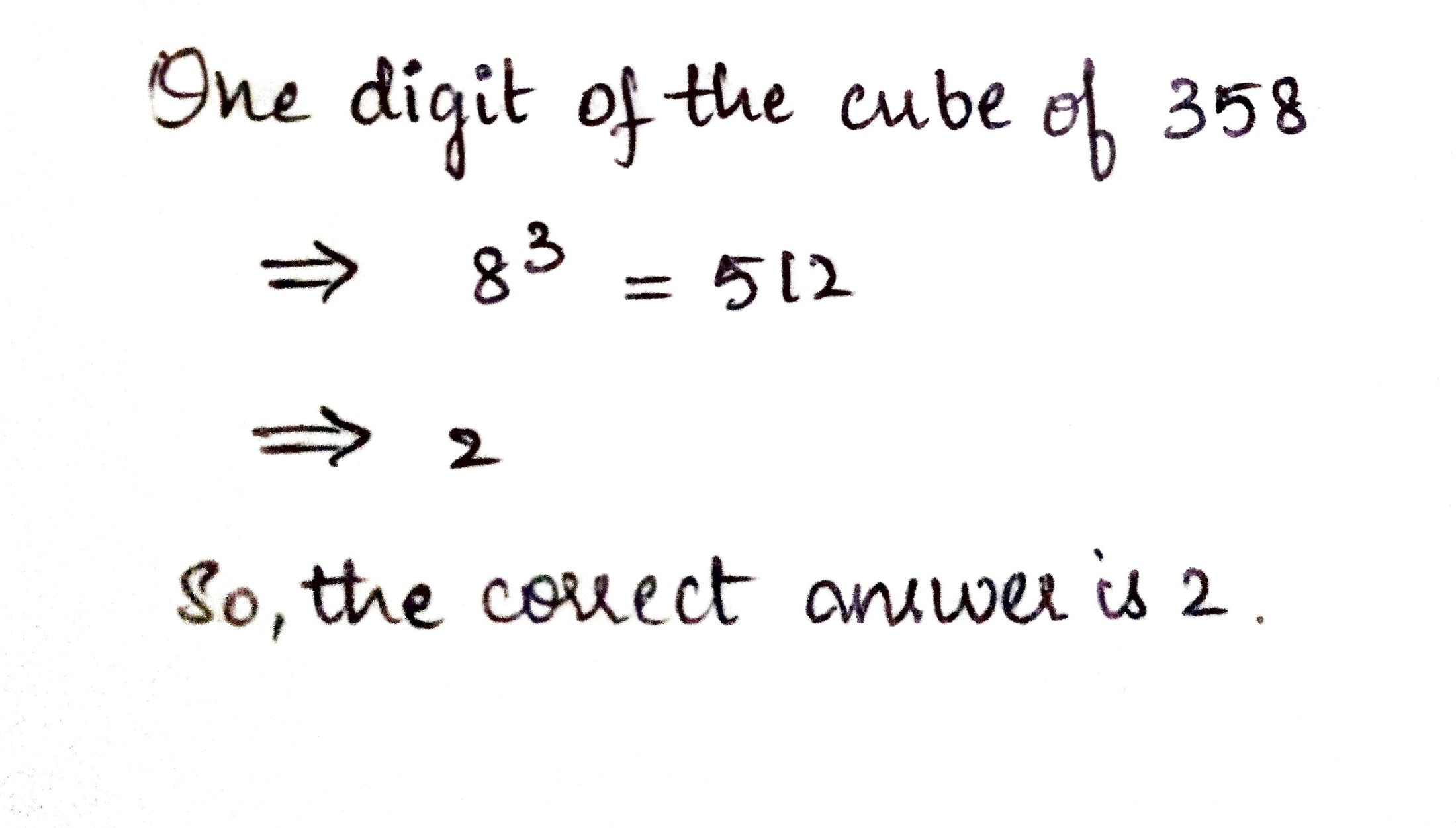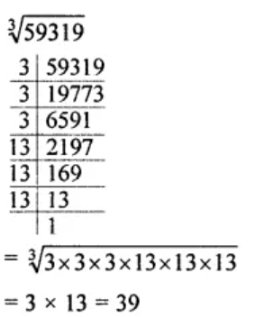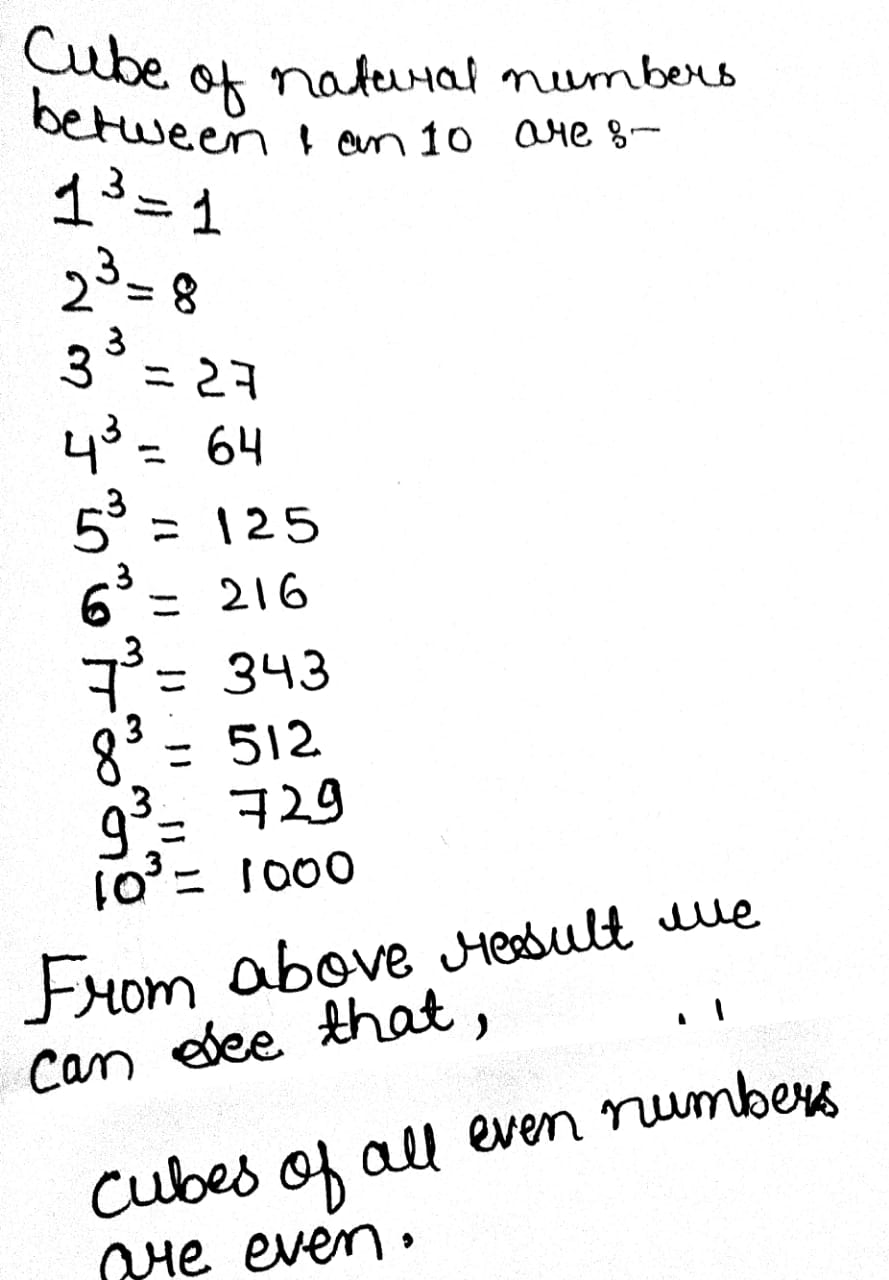Cubes And Cube Roots - Class 8 Maths - Extra Questions
Find the value of: $$\displaystyle \sqrt[3]{729}$$.
Cube root of $$185193$$ is:
Find the cube root of the following numbers by prime factorization:
$$157464$$
Fill in the blanks to make the statements true.
Ones digit in the cube of 38 is ______.
Find the cube root of each of the following numbers by prime factorization method.
$$64$$
Find the cube root of the following numbers by prime factorization:
$$32768$$
Find the cube root of $$9a{ b }^{ 2 }+\left( { b }^{ 2 }+24{ a }^{ 2 } \right) \sqrt { { b }^{ 2 }-3a^{ 2 } } $$.
Find the cube of following decimal numbers:
(a) $$0.7$$
(b) $$0.09$$
(c) $$1.1$$
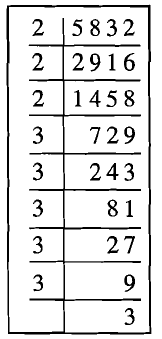
Are the following number perfect cubes?If yes,then find the number whose cube is the given numbers:$$5832$$
Are the following number perfect cubes?If yes,then find the number whose cube is the given numbers:$$24$$ ?
Find the cube of $$-12$$.
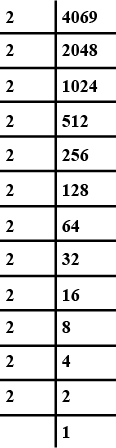
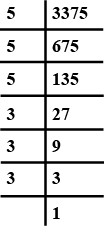
Find the cube roots of the number $$3048625$$ using the fact that
$$3048625=3375\times 729$$.
Evaluate: $$(1.2)^{3}$$
Evaluate: $$(21)^{3}$$
Evaluate: $$(15)^{3}$$
Evaluate the cube root of :
$$\displaystyle \sqrt [ 3 ]{ \left (\dfrac{-27}{125} \right ) } $$
Find the cube root of
$$135\sqrt { 3 } -87\sqrt { 6 } $$
Find the cube root of
$$38+17\sqrt { 5 } $$
Find the given number is a perfect cube or not.
$$540$$
Find the number is perfect cube or not?
$$620$$
Find the cube root of each of the following cube numbers through estimation.
$$148877$$
Find the cubes of:
$$-30$$
Evaluate $$\sqrt[3]{64}$$
Which of the following numbers are not perfect cubes?
$$1728$$
Find the cube root of the given number through estimation:$$1512$$
Evaluate: $$\sqrt[3] {8\times 17\times 17\times 17}$$.
The natural number whose cube is equal to itself is ____ .
Evaluate :
(i) (1.2)$$ \displaystyle ^{3}$$
(ii) (3.5)$$ \displaystyle ^{3}$$
(iii) (0.8)$$ \displaystyle ^{3}$$
(iv) (0.5)$$ \displaystyle ^{3}$$
If $$a+b+c=0$$ then prove that $$a^3+b^3+c^3=3abc$$.
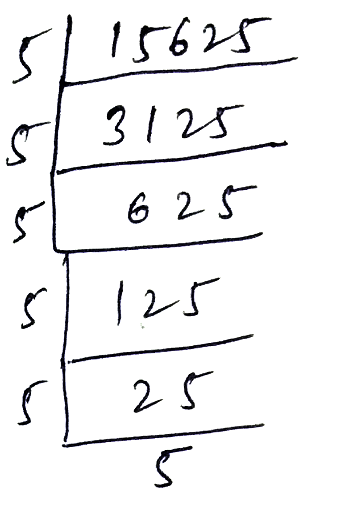
Find the cube root of $$15625$$ by prime factorization method.
Find the smallest number by which $$243$$ must be multiplied to obtain a perfect cube.
Find the smallest number by which $$72$$ must be multiplied to obtain a perfect cube.
Find the smallest number by which $$675$$ must be multiplied to obtain a perfect cube.
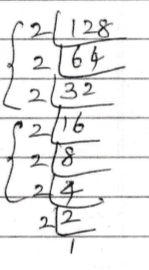
Find the smallest number by which the following number must be divided to obtain a perfect cube:$$128$$
Find the cubic root of the following number by prime factorisation method:
$$13824$$
Find the smallest number by which $$256$$ must be multiplied to obtain a perfect cube.
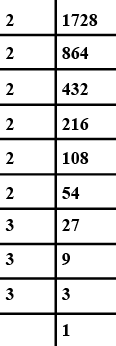
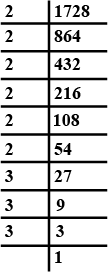
Find the cube roots of $$1728$$ by prime factorization:
Find the cube of $$133$$.
Evaluate: $$\sqrt [3]{8\times 125}$$.
Find the cube root of $$474552$$:
By what smallest number $$3645$$ be multiplied so that the product becomes a perfect cube?
Find the negative of cube root of $$-2744000$$.
Find the smallest number by which $$1323$$ must be multiplied so that the product is a perfect cube.
Show that $$\sqrt [3]{125\times 64}=\sqrt [3]{125}\times \sqrt [3]{64}$$
Find the value of $$\displaystyle (28)^{3}-(78)^{3}+(50)^{3}$$
Show that $$\sqrt [3]{216\times (-343)}=\sqrt [3]{216}\times \sqrt [3]{-343}$$
Evaluate: $$\sqrt [ 3 ]{ 27\times 64 } $$.
Evaluate $$(96)^3$$
Evaluate $$\sqrt [ 3 ]{ 125\times 64 } $$.
Find the cube root of the following number by prime factorisation method
175616
Find the cube root of the following number by the prime factorization method.
91125
Evaluate the following:$$\sqrt [3] { 512\times 729 }$$
Find the negative of cube root of $$-512$$.
Find the cube root of: $$8$$
Find $$(7)^3=$$?
The value of $$(21)^3$$ is?
Find $$(12)^3=$$?
Using the method of successive subtraction of numbers $$1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397,..........$$
Examine if the following number is a perfect cube or not
792
Find $$(100)^3$$.
Multiply $$137592$$ by the smallest number so that the product is a perfect cube.
Find the value of $$(302)^3$$?
Write cubes of $$5$$ natural numbers which are multiples of $$3$$ and verify the following:
'The cube of natural number, which is a multiple of $$3$$ is a multiple of $$27$$.
Find the cube root of $$74088$$.
Find the cube root of a given number through estimation: $$5832$$.
By the method of finding unit digit and tens digit of cube root, find the cube root of $$-68921.$$
State true or false.
(i) Cube of any odd number is even.
(ii) A perfect cube does not end with two zeros.
(iii) If square of a number ends with $$5$$, then its cube ends with $$25$$.
(iv) There is no perfect cube which ends with $$8$$.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
Looking at the pattern, fill in the gaps in the following
| $$2$$ | $$3$$ | $$4$$ | $$-5$$ | __ | $$8$$ | __ |
| $$2^3 = 8$$ | $$3^3 = ......$$ | $$.... = 64$$ | $$..... = .....$$ | $$6^3 = .....$$ | $$..... = ....$$ | $$.... = -729$$ |
How many perfect cubes you can find from $$1$$ to $$100$$? How many from $$-100$$ to $$100$$?
Find the cube root by prime factorisation: $$46656$$
Find the cube root by prime factorization $$10648$$
What is the least positive integer k for which 15k is the cube of a number?
Find the cube root by prime factorisation $$15625$$
Find the cube of $$6$$.
What is the least positive integer with which you have to multiply $$243$$ to get a perfect cube?
Find the cube root of
$$99-70\sqrt { 2 } $$
$$Evaluate\,\sqrt[3]{{0.000343}} + \sqrt[3]{{0.729}} + \sqrt[3]{{1.331}}$$
Find the cube root of a given number through estimation: $$2197$$.
Factorise $$8{x^3} + 27{y^3} + 36{x^3}y + 54x{y^2}$$
Find the cube roots of $$64$$
Which of the following numbers are perfect cubes? In case of perfect cube find the number with cube is the given number.
$$21952$$
Find the cube of the following:
$$0.4$$.
Cube of $$\left(2-\dfrac{1}{3}\right)$$ is
Find that the number is a perfect cube or not?
$$588$$
Among the following, the correct statement isi) $$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$$ii) $$(a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3$$
$$\sqrt[3]{{8 \times 125}}$$
Find following is a perfect cubes or not ?
$$9000$$
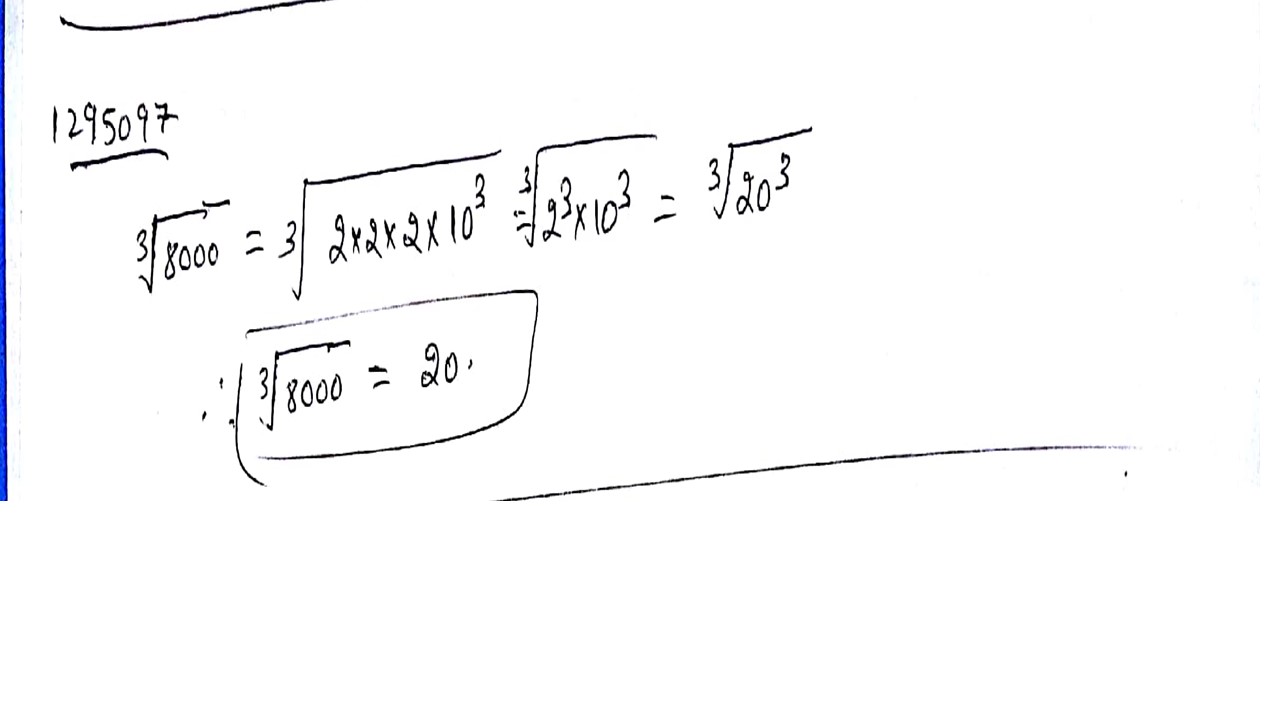
Find $$8000$$ is a perfect cubes or not ?
Find if the given number is a perfect cube or not?
$$3375$$
Find it is a perfect cubes or not ?
$$400$$
Find the given number is a perfect cube or not.
$$13824$$
Find following is a perfect cubes or not ?
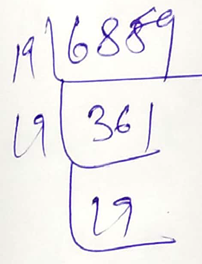
$$6859$$
State whether $$10648$$ is a perfect cube or not?
By multiplying an integer convert number to a perfect cube,Find the number?
$$2025$$
Find it is a perfect cubes or not ?
1562515625
If the square of a number ends with $$5$$, then its cube ends with $$25$$. True or false? Give reason.
Find which of the following are perfect cubes?
(i) $$243$$ (ii) $$588$$ (iii) $$1331$$ (iv) $$24000$$ (v) $$1728$$ (vi) $$1938$$
Test whether the numbers $$243, 516, 729, 8000$$ are perfect cubes or not
Is $$51123$$ a perfect cube?
Find the Cube Using Identity (i) $$105$$ (ii) $$27$$ (iii) $$45$$
Solve $$12x^{7}+x^{7}+x$$ for if $$x=7$$?
Which of the following numbers are not perfect cubes?
$$216$$
Evaluate $$\sqrt [3]{343}$$.
Find the value of $$64^{\frac{1}{3}}$$.
Solve $$(-10)^{3}+(7)^{3}+(3)^{3}$$
Classify as linear, cubic or quadratic.
$$y+y^3+y^2$$.
Find the cube of the number $$8$$.
Is $$128$$ a perfect cube?Find its cube root.
Find the cube root of each of the following cube numbers through estimation.
$$59319$$
Evaluate:$${\left(103\right)}^{3}$$
Evaluate $${ 46 }^{ 3 }+{ 34 }^{ 3 }$$
Find the cube root of each of the following numbers:
$$-250047$$
Calculate cube root:
$$8000$$
Find the unit's digit of the cube of $$5022$$.
Which of the following numbers are not perfect cubes?
$$ 1000$$
Evaluate $$\sqrt[3] {(-1331) \times 3375}$$
Find the cube root of the following numbers by prime factorization:
$$35937$$
Find the cubes of the following number:
$$-13$$
Solved:
$$\sqrt [ 3 ]{ 64 } $$
Find the cubes of the following number:
$$3 \dfrac{1}{5}$$
Find the cubes of the following number:
$$-5 \dfrac{1}{7}$$
Find the cube of :
$$54$$
Find the cube of :
$$31$$
Find the cubes of :
$$1.6$$
Find the side of a cube whose volume is $$4096 \,m^3.$$
Find the cube root of the following numbers by prime factorisation:
$$21952$$
Find the cube of :
$$42$$
Find the cube of the following number:
$$-3 \dfrac{4}{9}$$
Find the cube of the following number:
$$-17$$
Find the value of:
$$7^3$$
Find the cube of :
$$11$$
Find the cubes of:
$$-3$$
Find the cubes of:
$$-25$$
Find the cubes of :
$$0.12$$
Find the cubes of:
$$-50$$
Find the cubes of:
$$-7$$
Find the cube of :
$$0.02$$
Find the cube of $$-18$$
Find the cube of :
$$0.8$$
Find the cubic root of the following number by prime factorisation method:
$$15625$$
Find the cubic root of the following number by prime factorisation method:$$10648$$
Find the smallest number by which a given number must be divided to obtain a perfect cube:$$192$$
Find the cube root of $$46656$$ by prime factorisation method.
Find the smallest number by which a given number must be divided to obtain a perfect cube:
$$704$$
Find the smallest number by which a given number must be divided to obtain a perfect cube:
$$135$$
You are told that $$1,331$$ is a perfect cube. Can you guess without factorisation what is its cube root?
Find the cubic root of the following number by prime factorisation method:
$$27000$$
Find the smallest number by which the given number must be divided to obtain a perfect cube:
$$81$$
What is the smallest number by which $$243$$ should be multiplied to get a perfect cube?
Simplify: $$\displaystyle \frac{\sqrt[3]{512}-\sqrt[3]{216}}{\sqrt[3]{125}-\sqrt[3]{64}}$$.
Find the cube root of $$5832$$ by prime factorisation method.
What is the smallest number by which $$18522$$ must be divided so that the quotient is a perfect cube?
What is the smallest number by which 675 must be multiplied so that the product is a perfect cube?
What is the smallest number by which $$675$$ must be multiplied so that the product is a perfect cube?
Find the smallest number by which $$68600$$ must be multiplied to get a perfect cube.
Evaluate
(i) $$\displaystyle (1005)^{3}$$ (ii) $$\displaystyle (997)^{3}$$
You are told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root?Similarly, guess the cube roots of 4913, 12167, 32768
Find the smallest number by which $$72$$ must be multiplied to obtain a perfect cube.
Find the smallest number by which $$256$$ must be multiplied to obtain a perfect cube.
Find the smallest number which should be multiplied to $$2916$$ to get a perfect cube.
Find the smallest number which should be multiplied to $$36125$$ to get a perfect cube.
Find the smallest number which should be multiplied to $$432$$ to get a perfect cube.
Find the smallest number which should be multiplied to $$100$$ to get a perfect cube.
Find the smallest number which should be multiplied to $$10976$$ to get a perfect cube.
Find the smallest number which should be multiplied to $$1323$$ to get a perfect cube.
Find the smallest number which should be multiplied to $$10584$$ to get a perfect cube.
Find the smallest number which should be multiplied to $$15625$$ to get a perfect cube.
Evaluate :
(i) (8)$$ \displaystyle ^{3}$$
(ii) (15)$$ \displaystyle ^{3}$$
(iii) (21)$$ \displaystyle ^{3}$$
(iv) (60)$$ \displaystyle ^{3}$$
Evaluate the cube root of :
$$\displaystyle \sqrt [ 3 ]{ \left ( \dfrac{-64}{343} \right )} $$
Find cube root of $$1331$$
Find the smallest number by which $$2808$$ must be multiplied so that the product is a perfect cube.
Find the smallest number by which $$33275$$ must be multiplied so that the product is a perfect cube.
What is the smallest number by which $$392$$ must be multiplied so that the product is a perfect cube?
Is the following number a perfect cube or not? If it is perfect cube then answer $$1$$, otherwise answer $$0$$.$$106480$$
Find the cube root of $$8000$$.
What is the smallest number by which $$8640$$ must be divided so that the quotient is a perfect cube?
Divide the number $$26244$$ by the smallest number so that the quotient is a perfect cube.
Find the cube root of $$2744$$.
Write cubes of all natural numbers between 1 and 20 and verify the following statement. If the statement is true then answer is $$1$$ if not then the answer is $$0$$
Statement: Cubes of all even natural numbers are even.
Find the cube root of $$512$$
Write cubes of $$5$$ natural numbers which are of the form $$\displaystyle 3n+1$$ (e.g. 4,7,10,....) and verify the following:
'The cube of a natural number of the form $$\displaystyle 3n+1$$ is a natural number of the same form'.
Find the cube root of 125.
Find cube root of the following numbers by prime factorisation method.
(i) $$64$$
(ii) $$512$$
(iii) $$10648$$
(iv) $$27000$$
(v) $$15625$$
(vi) $$13824$$
(vii) $$110592$$
(viii) $$46656$$
(ix) $$175616$$
(x) $$91125$$
You are told that $$1331$$ is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube root of $$4913, 12167, 32768$$.
Which of the following are not perfect cubes?
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656
How many perfect cubes are there from $$1$$ to $$500$$? How many are perfect squares among these cubes?
Find the smallest square no. which is divisible by each of the numbers $$8,15 $$ and $$20$$.
If $$18^{3}=5832$$ then $$3\sqrt{0.005832}=?$$
Find the smallest no. by which each of the following no. must be divided to obtain a perfect cube.
(i) $$81$$
(ii) $$128$$
(iii) $$135$$
(iv) $$192$$
(v) $$704$$
Find the cubes of the first five odd natural numbers and the cube of the first five even natural numbers. What can we say about the parity of the odd cubes and even cubes?
Write an equivalent exponential form for radical expression.
$$\sqrt [ 3 ]{ 13 } $$
What is a smallest number by which $$2560$$ is to be multiplied so that the product is a perfect cube?
If a cube has side-length $$10$$ cm, what is its volume?
What is the smallest number by which $$1600$$ is to be divided, so that the quotient is a perfect cube?
Show that $$6$$ is not a perfect cube.
Find the cube root of $$103823$$.
What are the digits in the unit's place of the cubes of $$1, 2, 3, 4, 5, 6, 7, 8, 9, 10$$? Is it possible to say that a number is not a perfect cube by looking at the digit in unit's place of the given number, just like we did for squares?
Find the cubes of $$10$$, $$30$$, $$100$$, $$1000$$. What can we say about the zeros at the end?
Find the cube root of $$-17576$$ using factorization.
What is the cube of $$20$$?
Find the cube root of $$216$$ by factorisation.
Find the smallest number that should be multiplied with $$7803$$ so that the product becomes a perfect cube.
Find the cube of $$16$$.
Find the cube of $$21$$.
Test whether the given number is perfect cube or not: $$243$$
Test whether the given number is perfect cube or not: $$2700$$
Find the cube of $$8$$.
Find the smallest number by which $$8640$$ must be divided so that the quotient is a perfect cube.
Find the cube root of the given number through estimation: $$3375$$
Find the smallest number by which $$8788$$ must be multiplied to obtain a perfect cube.
Find the cube of $$30$$.
Find the smallest number by which each of the following number must be multiplied to obtain a perfect cube.
(i) $$243$$ (ii) $$256$$ (iii) $$72$$ (iv) $$675$$ (v) $$100$$
Which of the following numbers are not perfect cubes?
(i) $$128$$ (ii) $$100$$ (iii) $$64$$ (iv) $$125$$ (v) $$72$$ (vi) $$625$$
Find the value of the following:
(i) $$15^{3}$$ (ii) $$(-4)^{3}$$ (iii) $$(1.2)^{3}$$ (iv) $$\left (\dfrac {-3}{4}\right )^{3}$$
Find the smallest number by which each of the following number must be divided to obtain a perfect cube:
(i) $$81$$ (ii) $$128$$ (iii) $$135$$ (iv) $$192$$ (v) $$704$$ (vi) $$625$$
Is $$243$$ a perfect cube? If not, find the smallest number by which $$243$$ must be multiplied to get a perfect cube.
Find the cube root of $$27\times 64$$.
Find the cube root of each of the following numbers by prime Factorization method:
(i) $$729$$ (ii) $$343$$ (iii) $$512$$ (iv) $$0.064$$ (v) $$0.216$$ (vi) $$5\dfrac{23}{64}$$ (vii) $$-1.331$$ (viii) $$-27000$$
Is $$64$$ a perfect cube?
Check whether the following are perfect cubes?
(i) $$400$$ (ii) $$216$$ (iii) $$729$$ (iv) $$250$$ (v) $$1000$$ (vi) $$900$$
Find the cube root of $$\dfrac {125}{216}$$
$$512$$
Is $$250$$ a perfect cube? If not, then by which smallest natural number should $$250$$ be divided so that the quotient is a perfect cube?
Find the factors of $$(a + b + c)^{3} - (b + c - a)^{3} - (c + a - b)^{3} - (a + b - c)^{3}$$.
Use Euclid's division lemma to show that the cube of any positive integer is of the form $$9m,9m+1$$ or $$ 9m+8$$
Write ones digit of the cube of each of the following numbers:$$231$$
$$358$$
$$419$$
$$725$$
$$854$$
$$987$$
$$752$$
$$893$$
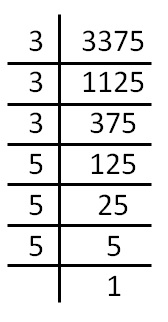
$$3375$$
Find the value of $$4^3$$
$${x}^{3}+7{x}^{2}+x=$$?
If $$x=7$$
Find the cube of $$-1$$.
$$\sqrt[3]{5832}\times \sqrt[3]{15625}=\sqrt[3]{(18)^3\times ()^3}$$.
Find $$\left(\dfrac{2}{3}\right)^{3}$$.
Write the ones digit of the cube of each of the following numbersA) $$231$$
B) $$358$$
C) $$491$$
D) $$854$$
E) $$987$$
F) $$752$$
If $$7 ^ { 3 } = 343$$ then $$ \sqrt [3]{ 343 } = ?$$
Find the cube root of $$-17576$$ using factorisation.
Simplify :
$$\sqrt [4]{81} - 8\sqrt [3]{216} + 15\sqrt [3]{32} + \sqrt {225}$$.
Evaluate $$\sqrt[3]{{0.000343}} + \sqrt[3]{{0.729}} + \sqrt[3]{{1.331}}$$
Express $$15^3$$ as the sum of consecutive odd numbers.
Simplify : $$\dfrac{\sqrt[3]{8} - \sqrt[3]{125}}{1 - 5\sqrt{2}}$$
If $$2a + 3b + c = 0$$ then show that:
$$8{a^3} + 27{b^3} + {c^3} = 18abc$$
The radius of a nuleus of mass number $$'A'$$ is given by $$R=1.3\ \times 10^{-16}\times A^{1/3}$$. Find the order of magnetude of radius for a nucles with $$A=216$$.
Find the cube of the following:
$$2.5$$.
Factorize:$$125x^3+27y^3+8z^3-90xyz$$
Find the cube root of $$5832$$.
Find the cube root of the following by prime factorization method
$$5832$$ $$and$$ $$21952$$$$ ?$$
Is $$53240$$ a perfect cube? If not then by which smallest natural numbers should be divided so that the quotient is a perfect cube?
Are the following number perfect cubes?If yes,then find the number whose cube is the given numbers:$$3645$$
Is $$392$$ a perfect cube? If not find the smallest natural number by which $$392$$ must be multiplied, so that the product is a perfect cube.
Find the smallest number which when multiplied with $$53240$$ will make the product a perfect cube.
Are the following number perfect cubes?If yes,then find the number whose cube is the given numbers:$$1728$$
Are the following number perfect cubes?If yes,then find the number whose cube is the given numbers:$$175616$$
Are the following number perfect cubes?If yes,then find the number whose cube is the given numbers:$$91125$$
Find the cube root of the following numbers by prime fractorisaiton method.$$343$$
$$4096$$
$$5832$$
$$125000$$
$${ (3\times x) }^{ 3 }=1728$$.
What is the value of x.
Evaluate $$\sqrt{6+}\sqrt [ 3 ]{ 27 } $$
Find the value of:
$$9^{3}$$
Are the following number perfect cubes?If yes,then find the number whose cube is the given numbers:$$74088$$
Are the following number perfect cubes?If yes,then find the number whose cube is the given numbers:$$216000$$
$${\left( { - 5} \right)^a} = - 125$$
Find the value of $${x^3} + {\dfrac {1} {x^3}}$$ if $$x + \dfrac { 1} {x} = 2$$
Solve : $$\sqrt[3]{1.331} + \sqrt[3]{0.027} + \sqrt[3]{0.008}$$
Find the value of the following.
$$5^{3}$$
What is the least number by which $$13720$$ must be divide so that the quotient is a perfect cube ?
Find the cube root of each of the following cube numbers through estimation.
$$85184$$
Find the cube root of the number by prime factorization method: 54872.
Factorise: $$27{a^3} + \dfrac{1}{{64{b^3}}} + \dfrac{{27{a^2}}}{{4b}} + \dfrac{{9a}}{{16b^2}}$$.
Find the smallest number by which the given number must be multiplied to obtain a perfect cube:- 8192
Find the cube root of each of the following cube numbers through estimation.
$$19683$$
Find the following
$$\sqrt [3]{0.000216}$$
Find the cube root of each of the following numbers:
$$5^{1182}$$
Find the cube of the number $$100$$.
Write the cubes of $$5$$ natural numbers which are multiples of $$3$$ and verify the followings:
The cube of a natural which is a multiple of $$3$$ is a multiple of $$27$$'
Find the cube of the following number:
$$55$$
Find the cube of the following number $$12$$.
Find $$\dfrac { \sqrt [ 3 ]{ 729 } +\sqrt [ 3 ]{ 343 } }{ \sqrt [ 3 ]{ 512 } } $$
Find the cube of the number $$40$$.
Find the cubes of the following number $$7$$.
Show that cube of any positive integer is of the form $$4 m , 4 m + 1$$ or $$4 m +3$$ , for some integer $$m$$ .
Which is the smallest number that must be multiplied to $$77175$$ to make it a perfect cube?
Which of the following are perfect cubes?
$$216$$
Which of the following are perfect cubes?
$$64$$
Check whether the following number is perfect cube or not.$$3087$$
What is the smallest number by which the following numbers must be multiplied, so that the products are perfect cubes?
$$675$$
Check whether the following number is perfect cube or not.$$106480$$
Check whether the following number is perfect cube or not.$$456533$$
Check whether the following number is perfect cube or not.$$166375$$
Which of the following are perfect cubes?
$$4608$$
Write the cubes of $$5$$ natural numbers of which are multiples of $$7$$ and verify the following:
The cube of a multiple of $$7$$ is a multiple of $$7^{3}$$.
Check whether the following number is perfect cube or not.
$$1000$$
What is the smallest number by which the following numbers must be multiplied, so that the products are perfect cubes?
$$7803$$
What is the smallest number by which the following numbers must be multiplied, so that the products are perfect cubes?
$$107811$$
By which smallest number must the following number be divided so that the quotient is a perfect cube?
$$7803$$
What is the smallest number by which the following numbers must be multiplied, so that the products are perfect cubes?
$$35721$$
What is the smallest number by which the following numbers must be multiplied, so that the products are perfect cubes?
$$2560$$
By which smallest number must the following number be divided so that the quotient is a perfect cube?
$$108711$$
By which smallest number must the following numbers be divided so that the quotient is a perfect cube?
$$8788$$
By which smallest number must the following number be divided so that the quotient is a perfect cube?
$$8640$$
By which smallest number must the following numbers be divided so that the quotient is a perfect cube?
$$675$$
What is the smallest number by which the following numbers must be multiplied, so that the products are perfect cubes?
$$1323$$
By which smallest number must the following number be divided so that the quotient is a perfect cube?
$$243000$$
Check whether the following number is a perfect cube or not.
$$64$$
Show that:
$$\sqrt[3]{64\times 729}=\sqrt[3]{64}\times \sqrt[3]{729}$$
Find the cube of $$-11$$.
Prove that if a number is tripled then its cube is $$27$$ times the cube of the given number.
Find the cube of $$-21$$.
Show that:
$$\sqrt[3]{27}\times \sqrt[3]{64}=\sqrt[3]{27\times 64}$$
Which of the following numbers are not perfect cubes?
$$216$$
By which smallest number must the following numbers be divided so that the quotient is a perfect cube?
$$35721$$
Evaluate: $$(3.5)^{3}$$
Fill in the blanks:
$$\sqrt[3]{480}=\sqrt[3]{3}\times 2\times \sqrt[3]{\text{___}}$$.
Fill in the blanks:
$$\sqrt[3]{1728}=4\times $$_____.
Find the cube roots of the numbers $$57066625$$ using the fact that
$$57066625=166375\times 343$$.
Fill in the blanks:
$$\sqrt[3]{\text{_____}}=\sqrt[3]{4}\times \sqrt[3]{5}\times \sqrt[3]{6}$$
Find the cube roots of the numbers $$20346417$$ using the fact that
$$20346417=9261\times 2197$$.
Fill in the blanks:
$$\sqrt[3]{\text{___}}=\sqrt[3]{7}\times \sqrt[3]{8}$$.
Find the cube roots of the numbers $$ 210644875$$ using the fact that
$$210644875=42875\times 4913$$.
Express each of the following as a rational number of the from $$ \dfrac{p}{q}$$:$$ \left ( \dfrac{7}{9} \right )^3 $$
Fill in the blanks:
$$\sqrt[3]{125\times 27}=3\times $$ ______.
Evaluate: $$(8)^{3}$$
Evaluate: $$\left(\cfrac{10}{11}\right)^{3}$$
Evaluate: $$(60)^{3}$$
Evaluate: $$\left(\cfrac4{7}\right)^{3}$$
Evaluate: $$(0.05)^{3}$$
Evaluate: $$(0.8)^{3}$$
Is $$8000$$ a perfect cube? In case of perfect cube, find the number whose cube it is.
Evaluate: $$\left(\cfrac{1}{15}\right)^{3}$$
Is $$3375$$ a perfect cube? In case of perfect cube, find the number whose cube it is.
Is $$125$$ a perfect cube? In case of perfect cube, find the number whose cube it is.
Evaluate: $$\left(\cfrac{13}{15}\right)^{3}$$
Is $$5324$$ a perfect cube? In case of perfect cube, find the number whose cube it is.
Is $$9261$$ a perfect cube? In case of perfect cube, find the number whose cube it is.
Is $$243$$ a perfect cube? In case of perfect cube, find the number whose cube it is.
Is $$343$$ a perfect cube? In case of perfect cube, find the number whose cube it is.
Evaluate $$\sqrt[3]{343}$$
Evaluate $$\sqrt[3]{1728}$$
Evaluate $$\sqrt[3]{9261}$$
Evaluate $$\sqrt[3]{8000}$$
Evaluate $$\sqrt[3]{3375}$$
Evaluate $$\sqrt[3]{4096}$$
Evaluate $$\sqrt[3]{729}$$
Evaluate:
$$ (1.5)^3 $$
Evaluate:
$$ ( 0.05)^3 $$
Fill in the blanks to make the statements true.
There are ________ perfect cubes between 1 and 1000.
Evaluate:
$$ ( 0.3)^3 $$
Fill in the blanks to make the statements true.
The cube of 100 will have _______ zeroes.
Fill in the blanks to make the statements true.
The least number by which 72 be divided to make it a perfect cube is _________.
Fill in the blanks to make the statements true.
The least number by which 72 be multiplied to make it a perfect cube is __________.
Fill in the blanks to make the statements true.
Cube of a number ending in $$7$$ will end in the digit _________.
Write cubes of first three multiples of 3.
Find the product of the cube of $$(-2)$$ and the square of $$(+4)$$.
$$\Big \{\Big[5^2 + (12^2)^{\frac{1}{2}}\Big]\Big \}^3$$
Is 9720 a perfect cube? If not, find the smallest number by which it should be divided to get a perfect cube.
Difference of two perfect cubes isIf the cube root of the smaller of the two numbers is 3, find the cube root of the larger number.
Find the smallest number by which the following number must be divided to obtain a perfect cube:
$$1536$$
Using prime factorisation, find the cube roots of
a) 512
b) 2197
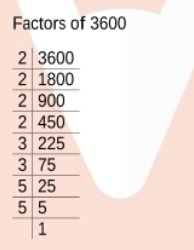
By what smallest number should 3600 be multiplied so that the quotient is a perfect cube? Also find the cube root of the quotient.
Find the smallest number by which the following number must be multiplied to obtain a perfect cube:
$$3072$$
Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube:
$$19652$$
Using prime factorization, find which of the following are perfect cubes.
a) $$128$$
b) $$343$$
c) $$729$$
d) $$1331$$
Find the smallest number by which the following number must be divided to obtain a perfect cube:
$$28672$$
Find the smallest number by which the following number must be divided to obtain a perfect cube:
$$10985$$
Write the one's digit of the cube of the following number:
$$419$$
Write the one's digit of the cube of the following number:
$$987$$
Write the one's digit of the cube of the following number:
$$231$$
Which of the following are cubes of even natural numbers or odd natural numbers:
(i) $$125$$
(ii) $$512$$
(iii) $$1000$$
(iv) $$2197$$
(v) $$4096$$
(vi) $$6859$$
Write the one's digit of the cube of the following number:
$$854$$854$$
Write the one's digit of the cube of the following number:
$$358$$
Find the smallest number by which the following number must be divided to obtain a perfect cube:
$$13718$$
Write the one's digit of the cube of the following number:
$$725$$
Find the cube root of the following numbers by prime factorization:
$$42875$$
Write the one's digit of the cube of the following number:
$$752$$
Find the cube root of the following numbers by prime factorization:
$$262144$$
Find the cube root of the following numbers by prime factorization:
$$21952$$
Find the cube root of the following numbers by prime factorization:
$$373248$$
Multiply $$6561$$ by the smallest number so that product is a perfect cube. Also, find the cube root of the product.
Find the cube of :
$$7$$
Find the cube root of the following numbers by prime factorisation:
$$59319$$
Find the cube root of the following numbers by prime factorization:
$$12167$$
Write the one's digit of the cube of the following number:
$$893$$
Find the cube roots of:
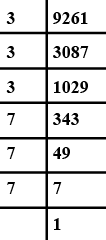
$$ 9261 $$
Find the cube-roots of:
$$ 64 \times 729$$
Find the cube roots of:
$$ 4096$$
Find the cube roots of:
$$729$$
Find that the number is a perfect cube or not ?
$$1331$$
Find that the number is a perfect cube or not ?
$$1938$$
Find the cube roots of:
$$1728$$
Find the cube roots of:
$$ 3375 $$
Find that the number is a perfect cube or not ?
$$1728$$
Find that the number is a perfect cube or not ?
$$24000$$
What is the cube of 8?
Which of the following are cubes of ?
(i) An even number
(ii) An odd number
$$ 216 , 729 , 3375 , 8000 , 125 , 343 , 4096 $$ and $$ 9261$$
Find the smallest number by which $$ 8768$$ must be divided so that the quotient is a perfect cube.
Find the cube root of $$355045312441$$ perfect cube number, by division method.
Find the cube root by prime factorization.
$$3375$$
Find the cube-roots of:
$$ 3375 \times 512 $$
Find the cube-roots of:
$$ 729 \times 8000$$
Find the cube-roots of:
$$ -125 \times 1000$$
Find the cube root of the following number by prime factorization method:$$729$$
Find the cube root of the following number by prime factorization method:
Find the cube root of the following number by prime factorization method:$$1331$$
Find the cube root of the following number by prime factorization method:
Find the cube root of $$4096.$$
Test whether the given number is perfect cube or not: $$516$$
Test whether the given number is perfect cube or not: $$729$$
Test whether the given number is perfect cube or not: $$8000$$
Find the cube root of the given number through estimation: $$5832$$
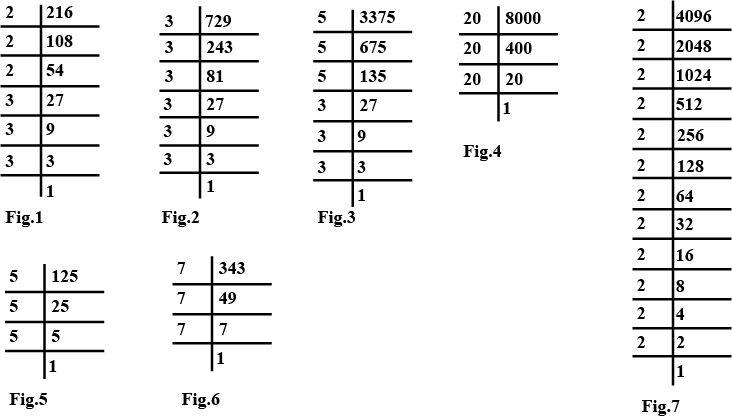
Write the cubes of all natural numbers between $$1$$ and $$10$$ and verify the following statements:
Cubes of all even natural numbers are even.
Find the cube root of the given number through estimation:$$2197$$
for all cuboids with square base and given volume prove that cube has minimum surface area.
You are told that $$1,331$$ is a perfect cube. Can you guess without factorization what is its cube root? Similarly, guess the cube roots of $$4913,12167,32768$$.
By taking three different values of $$n$$ verify the truth of the following statements:
If $$n$$ is even, then $$n^{3}$$ is also even.
By taking three different values of $$n$$ verify the truth of the following statements:
If $$n$$ is odd, then $$n^{3}$$ is also odd.
$$571787$$ is a perfect cube.
Find the cube root of the following number.
By taking three different values of $$n$$ verify the truth of the following statements:
If a natural number $$n$$ is of the form $$3p+2$$ then $$n^{3}$$ also a number of the same type.
Class 8 Maths Extra Questions
- Algebraic Expressions And Identities Extra Questions
- Comparing Quantities Extra Questions
- Cubes And Cube Roots Extra Questions
- Data Handling Extra Questions
- Direct And Inverse Proportions Extra Questions
- Exponents And Powers Extra Questions
- Factorisation Extra Questions
- Introduction To Graphs Extra Questions
- Linear Equations In One Variable Extra Questions
- Mensuration Extra Questions
- Playing With Numbers Extra Questions
- Practical Geometry Extra Questions
- Rational Numbers Extra Questions
- Squares And Square Roots Extra Questions
- Understanding Quadrilaterals Extra Questions
- Visualising Solid Shapes Extra Questions