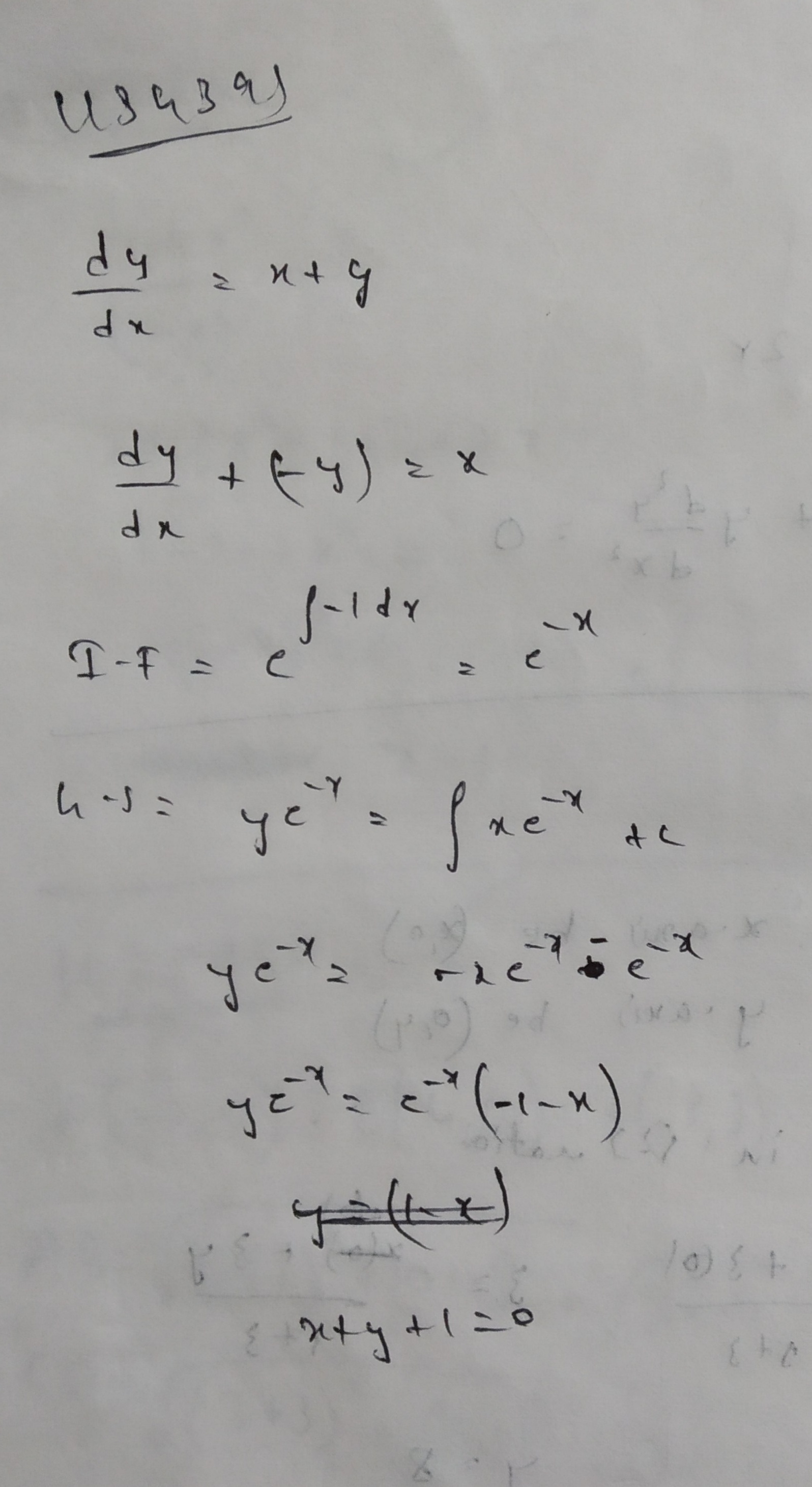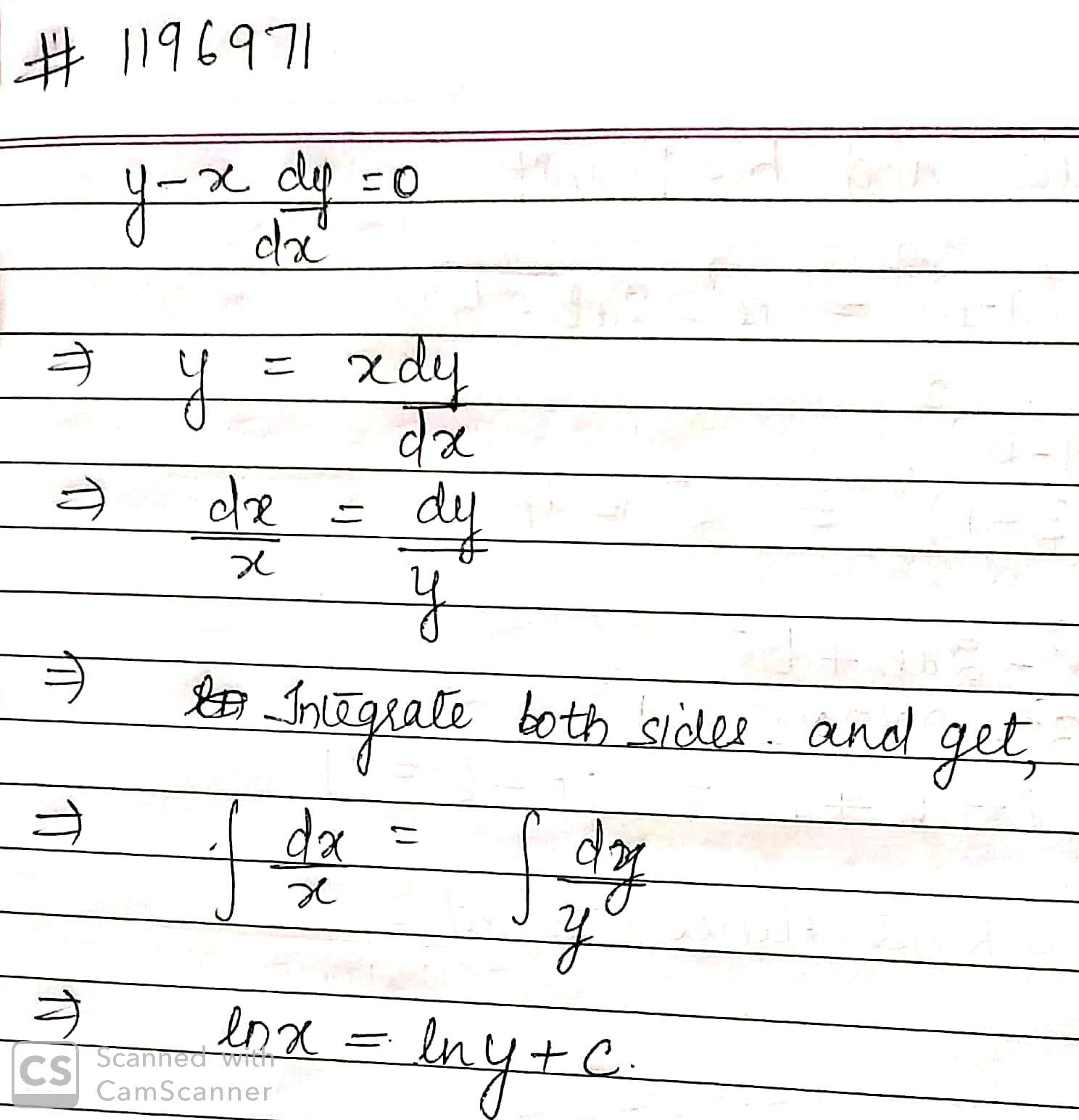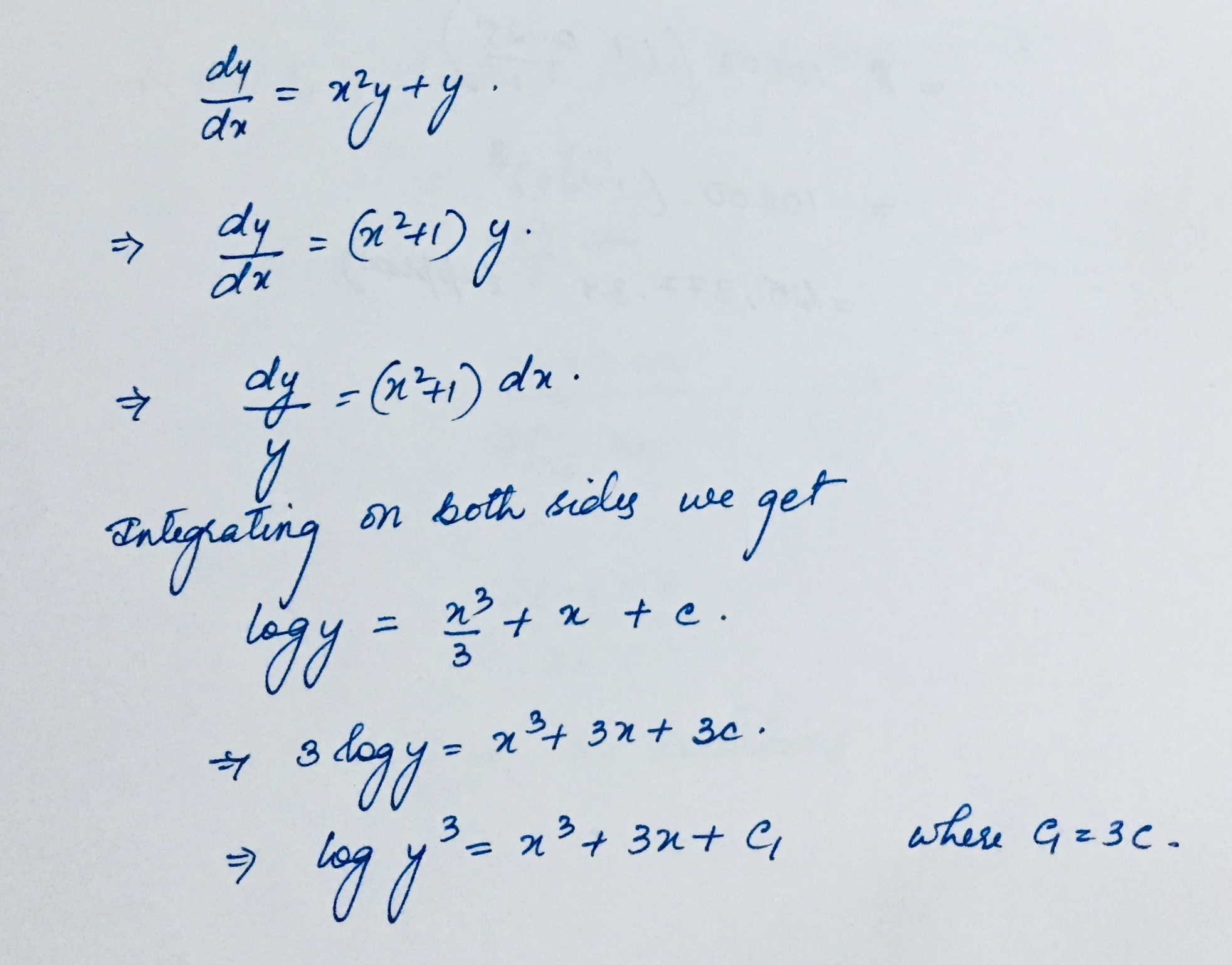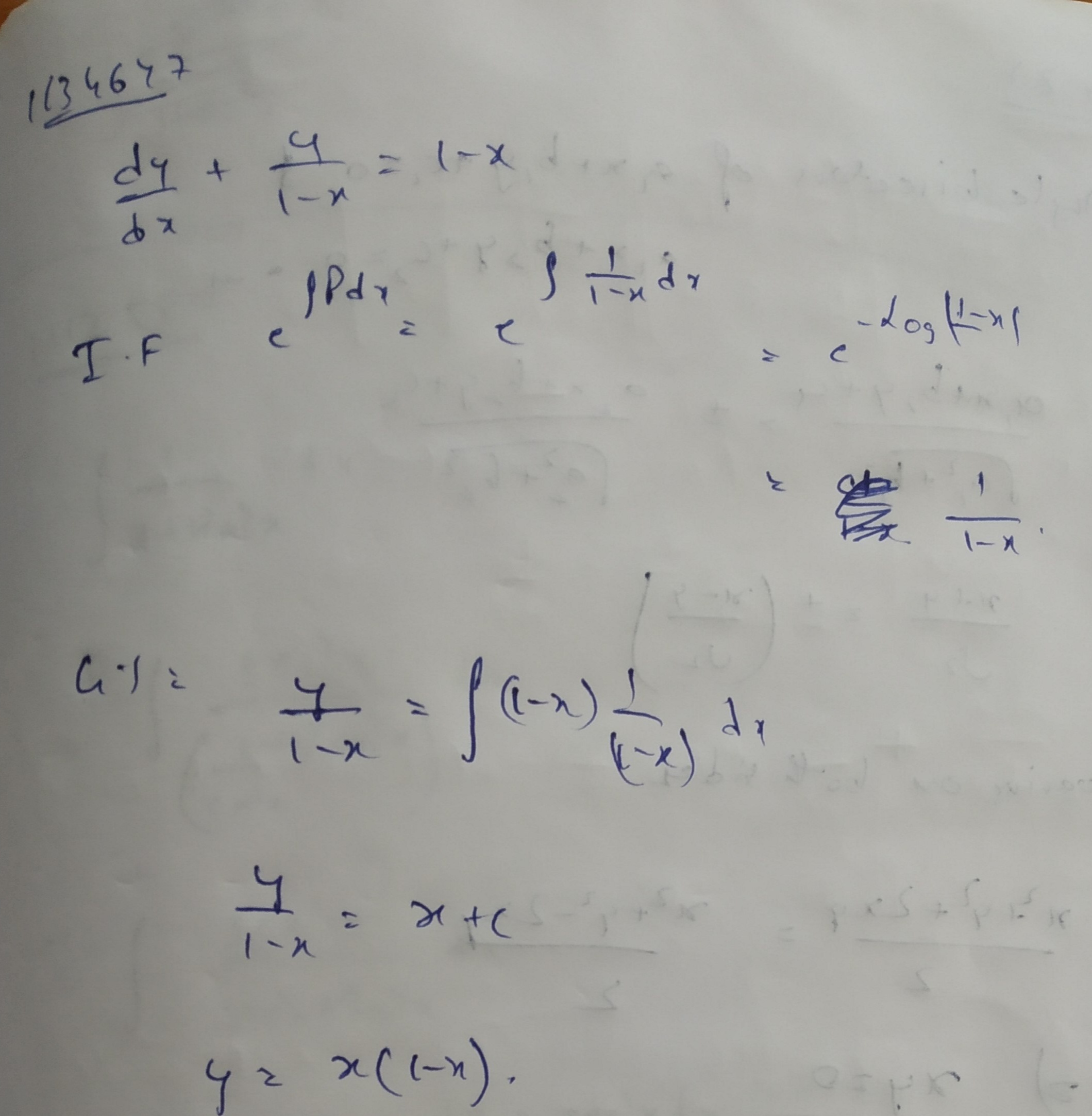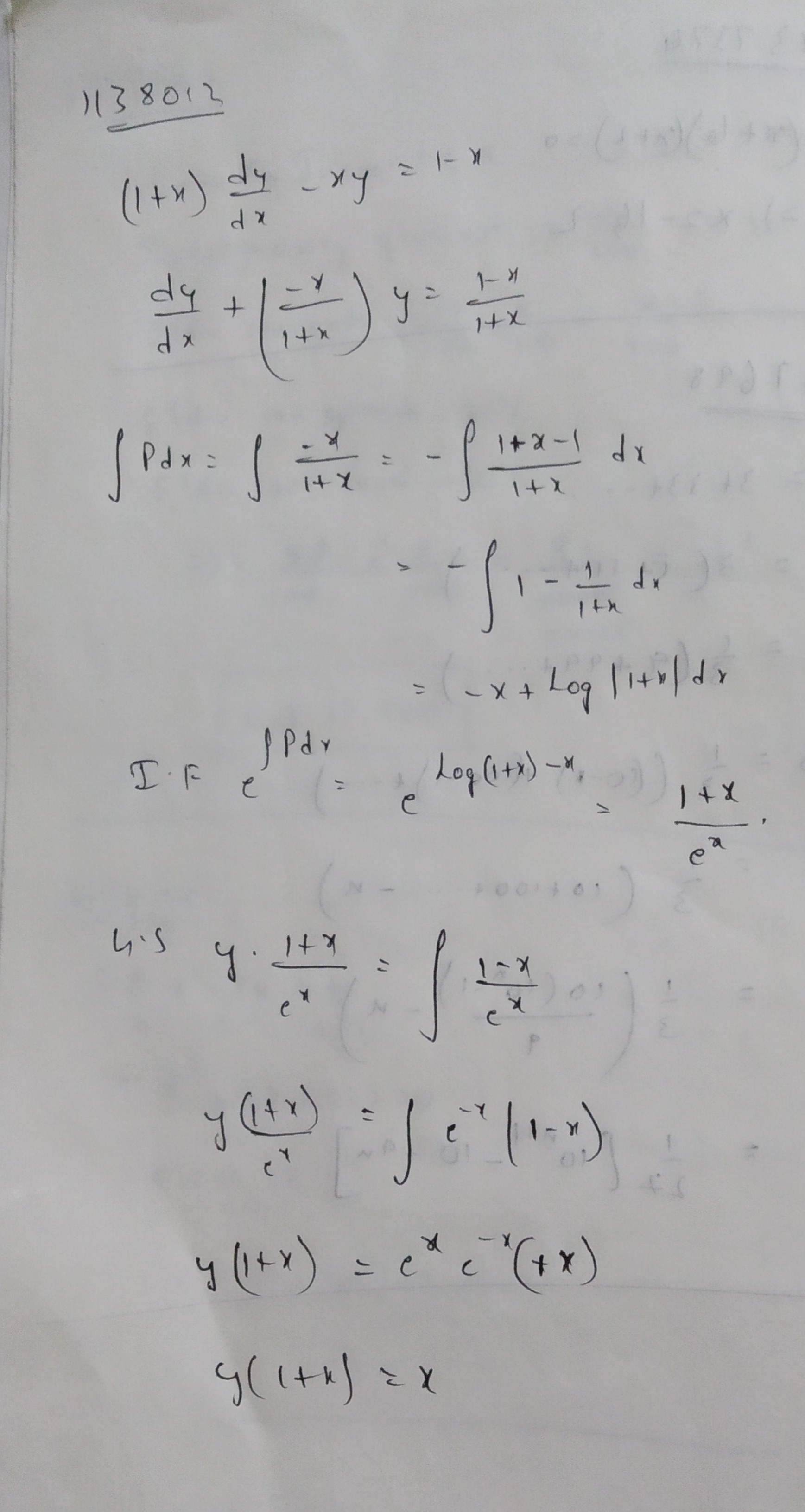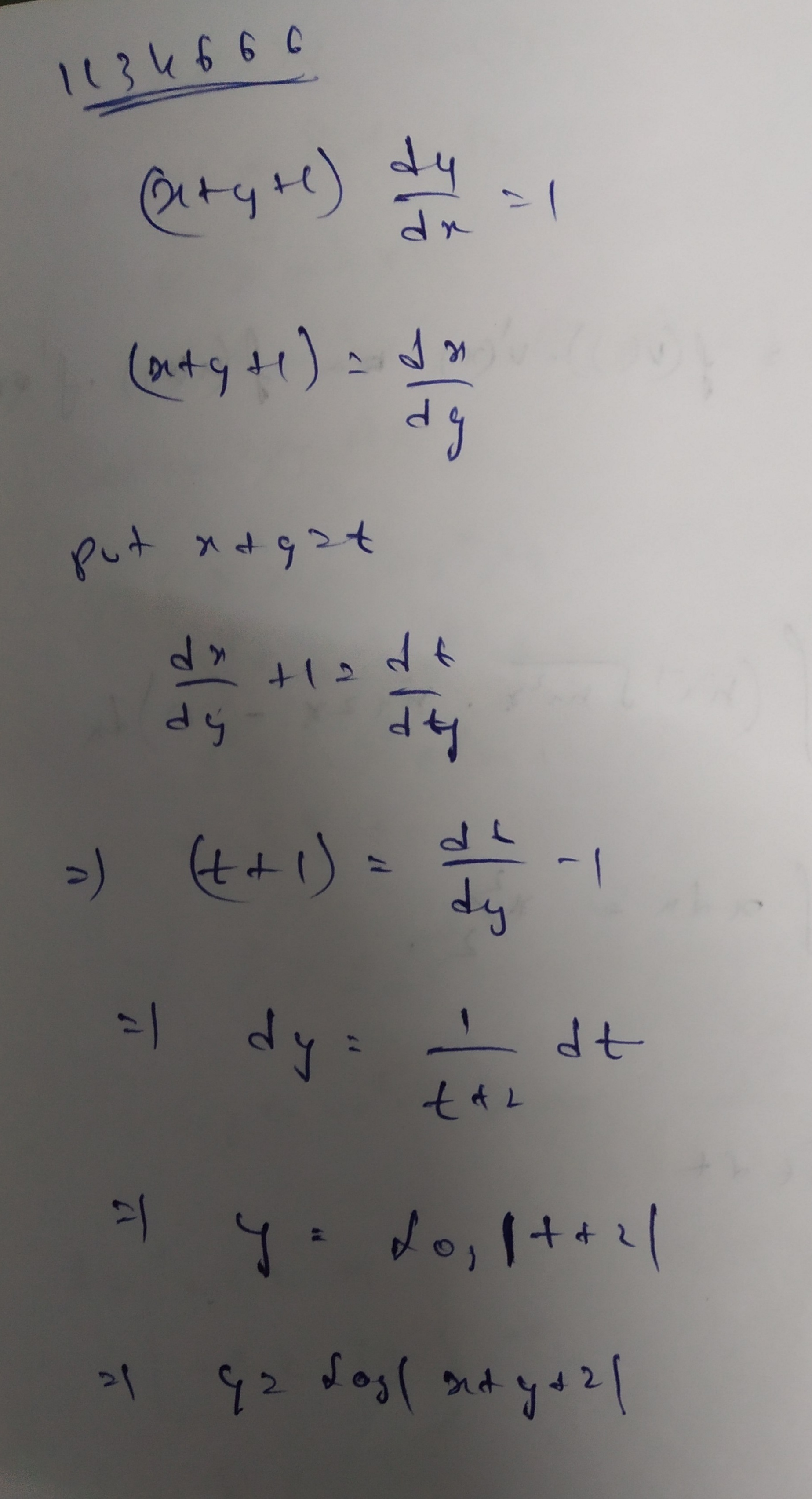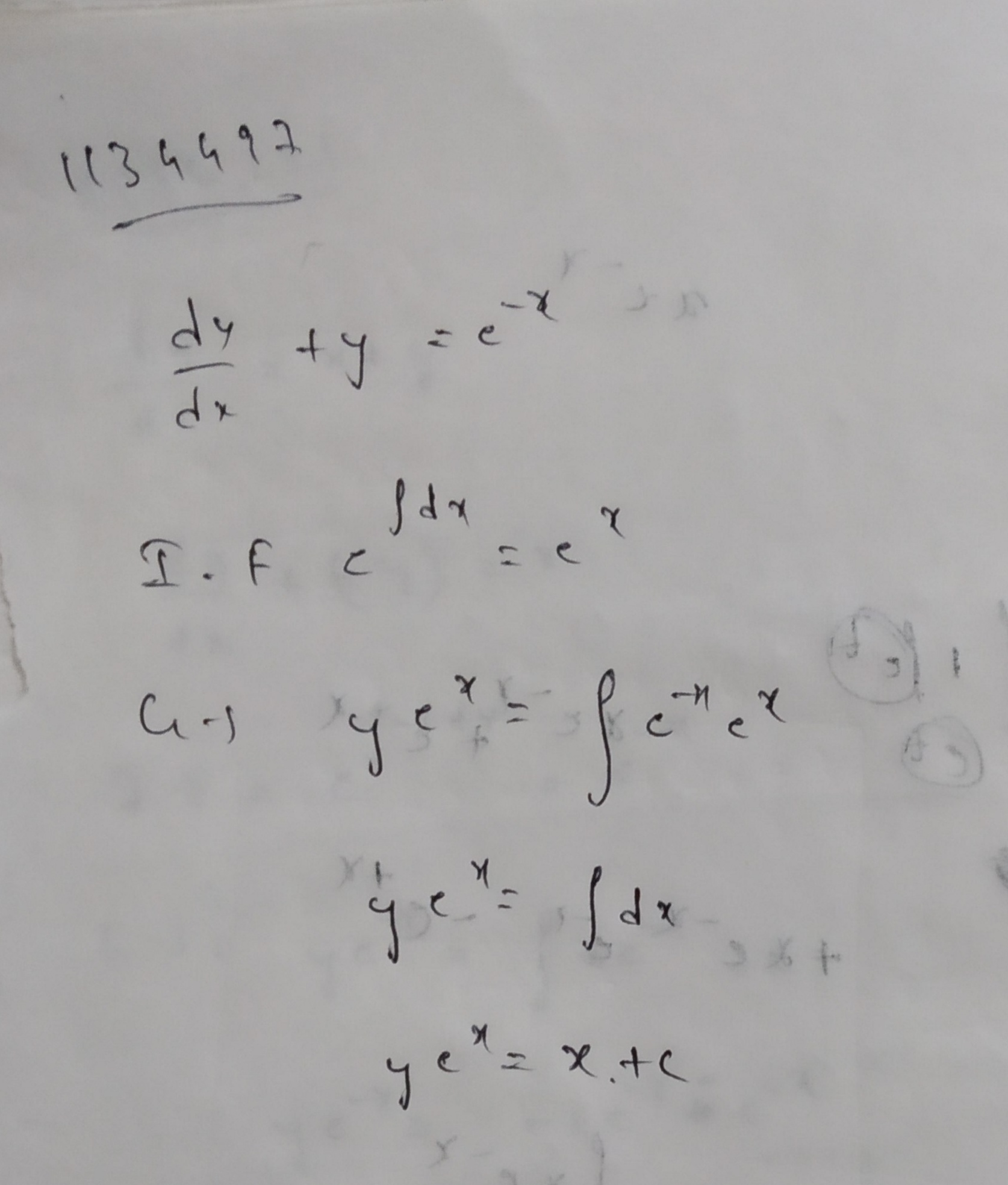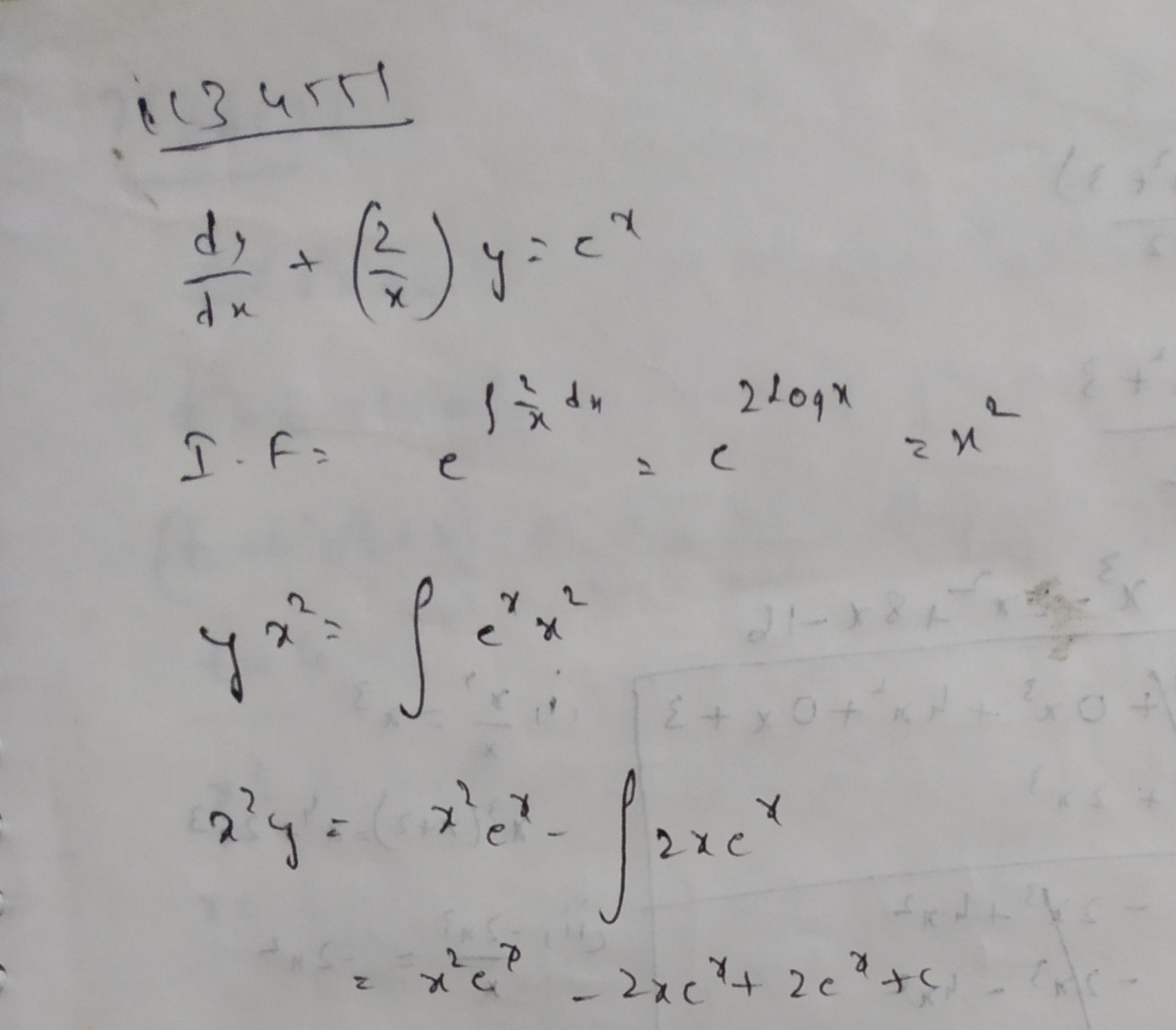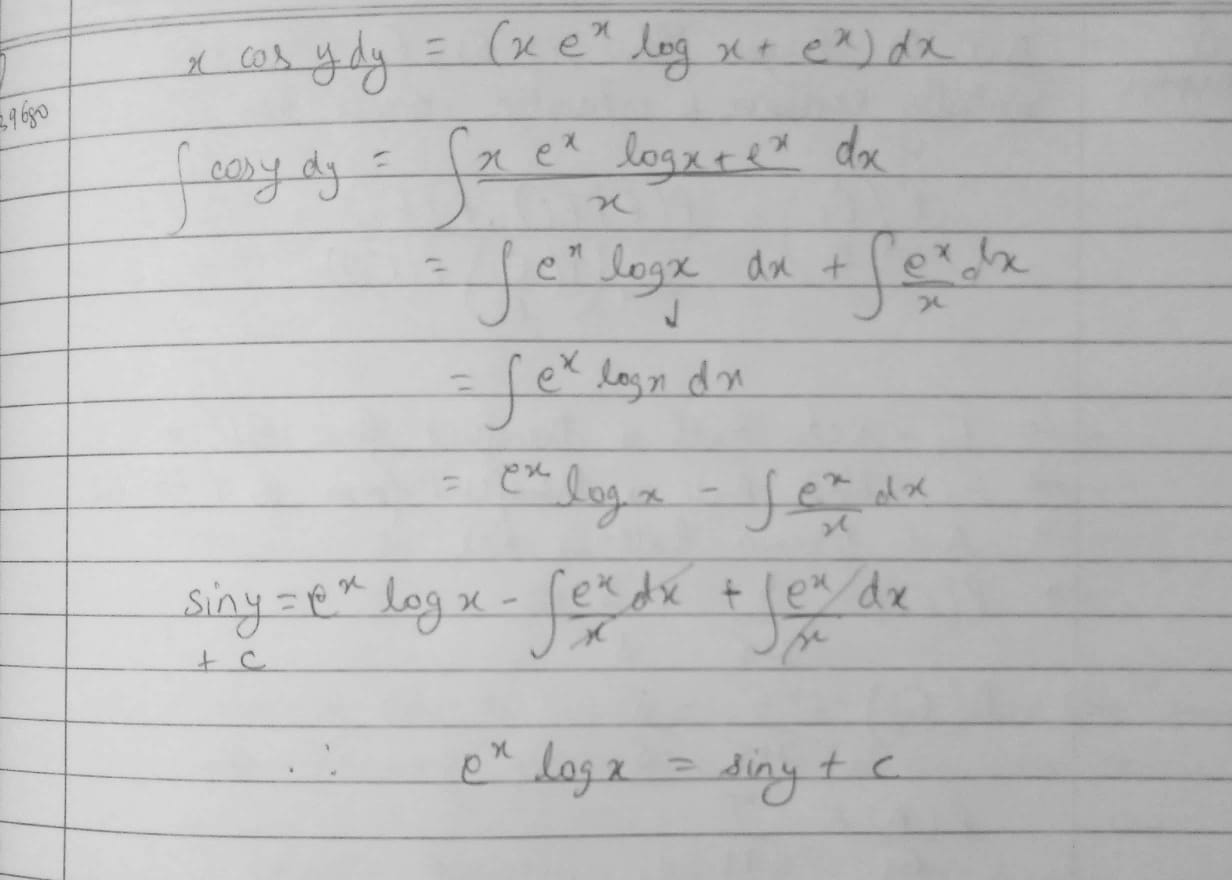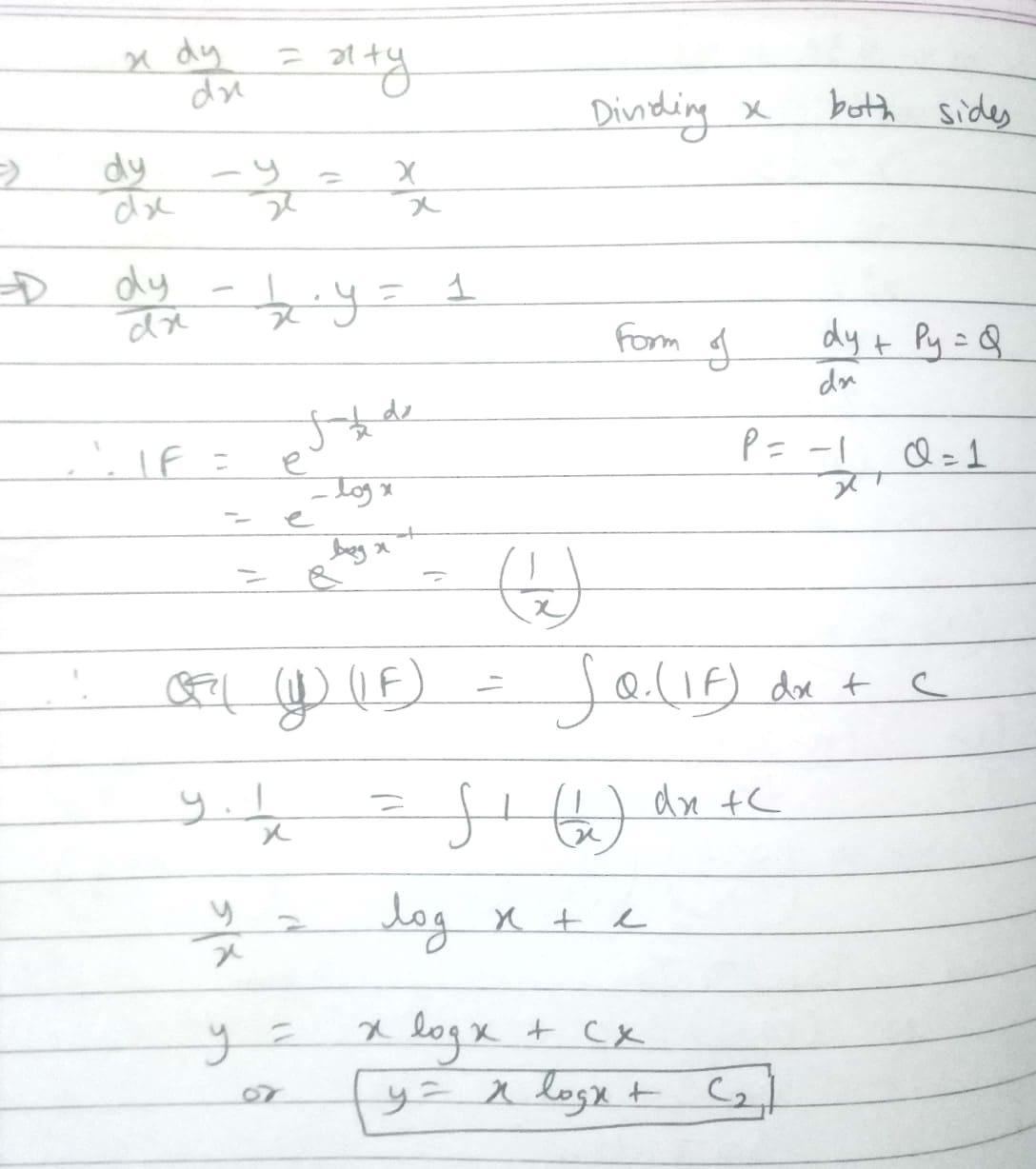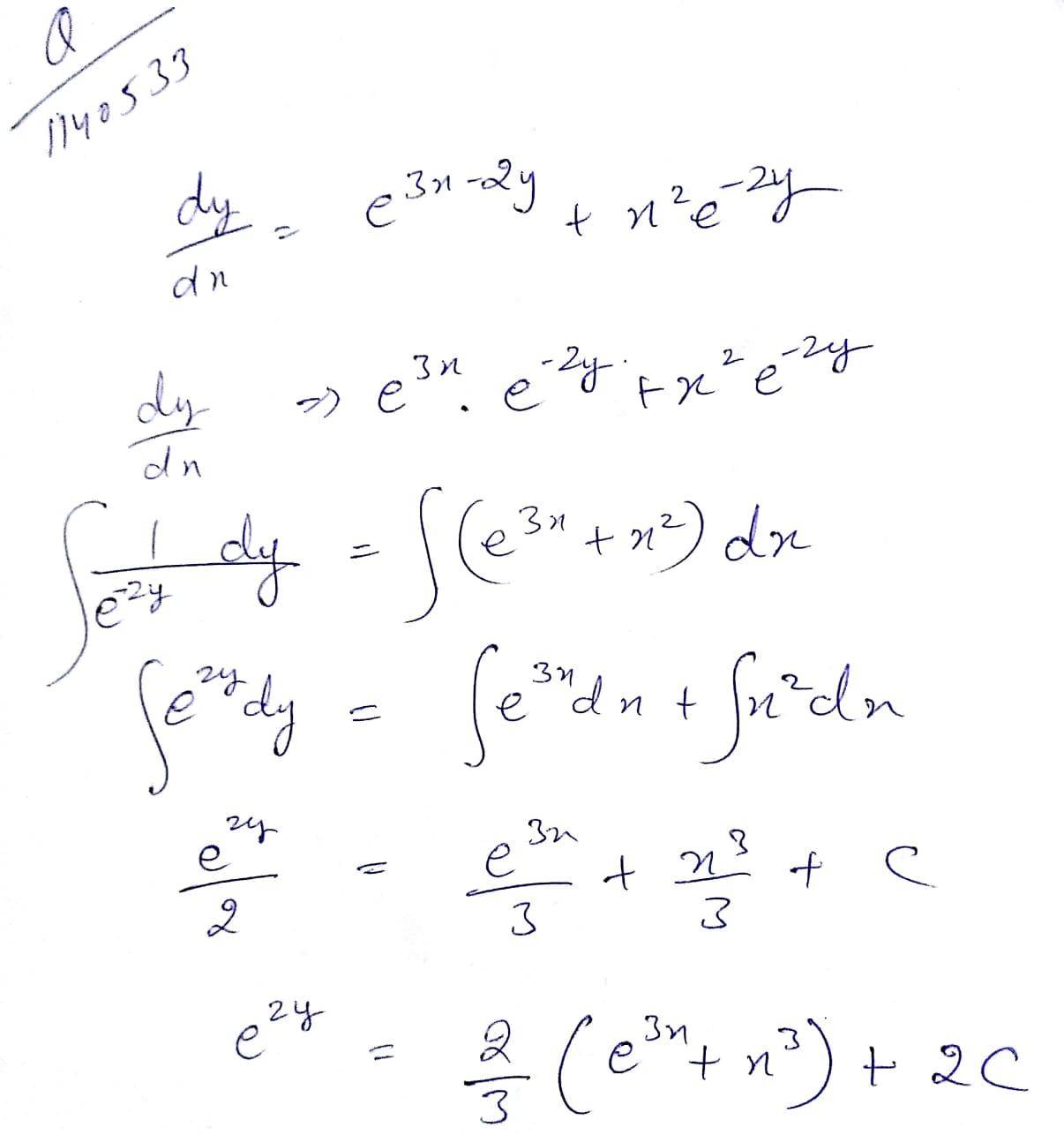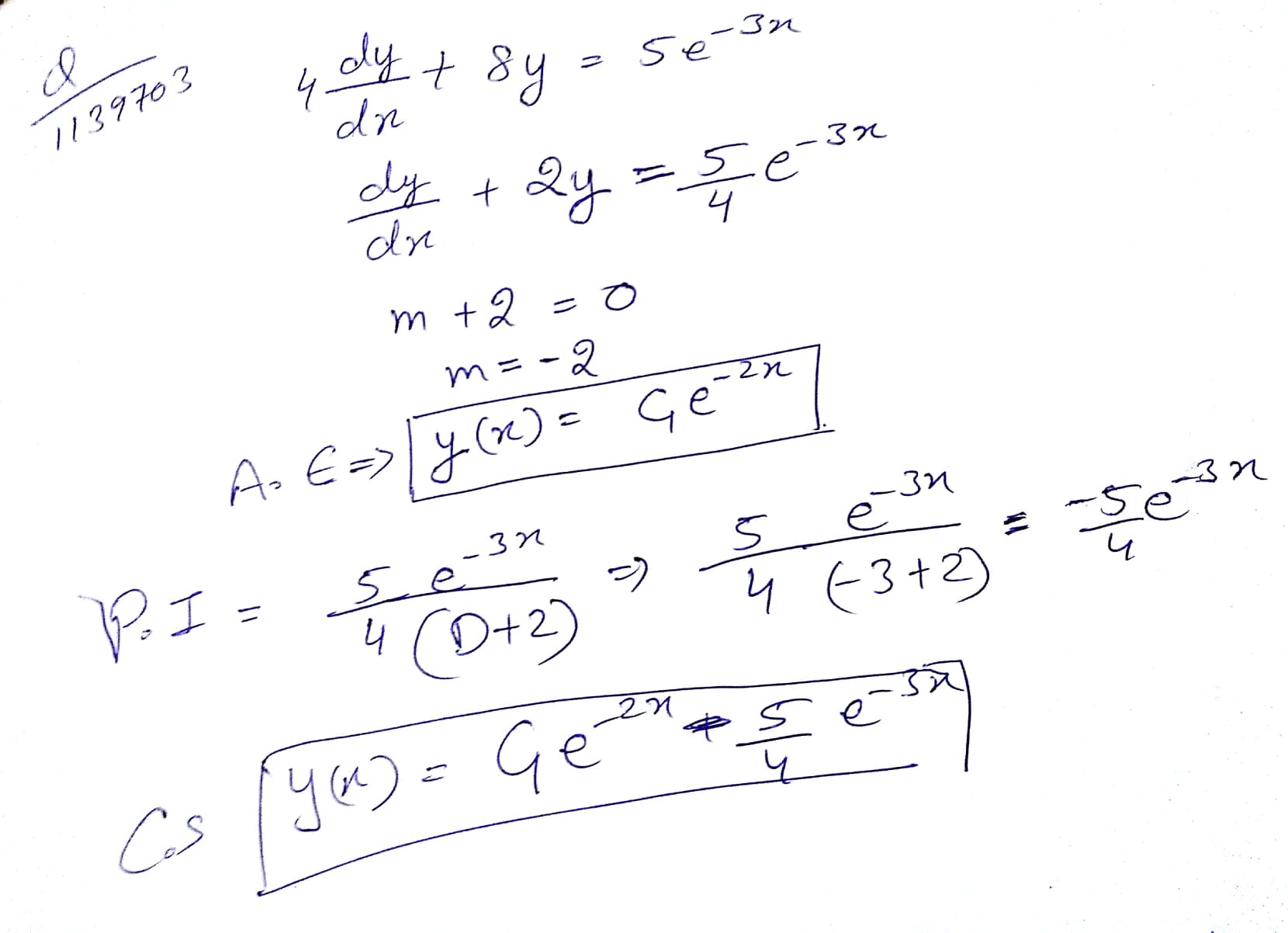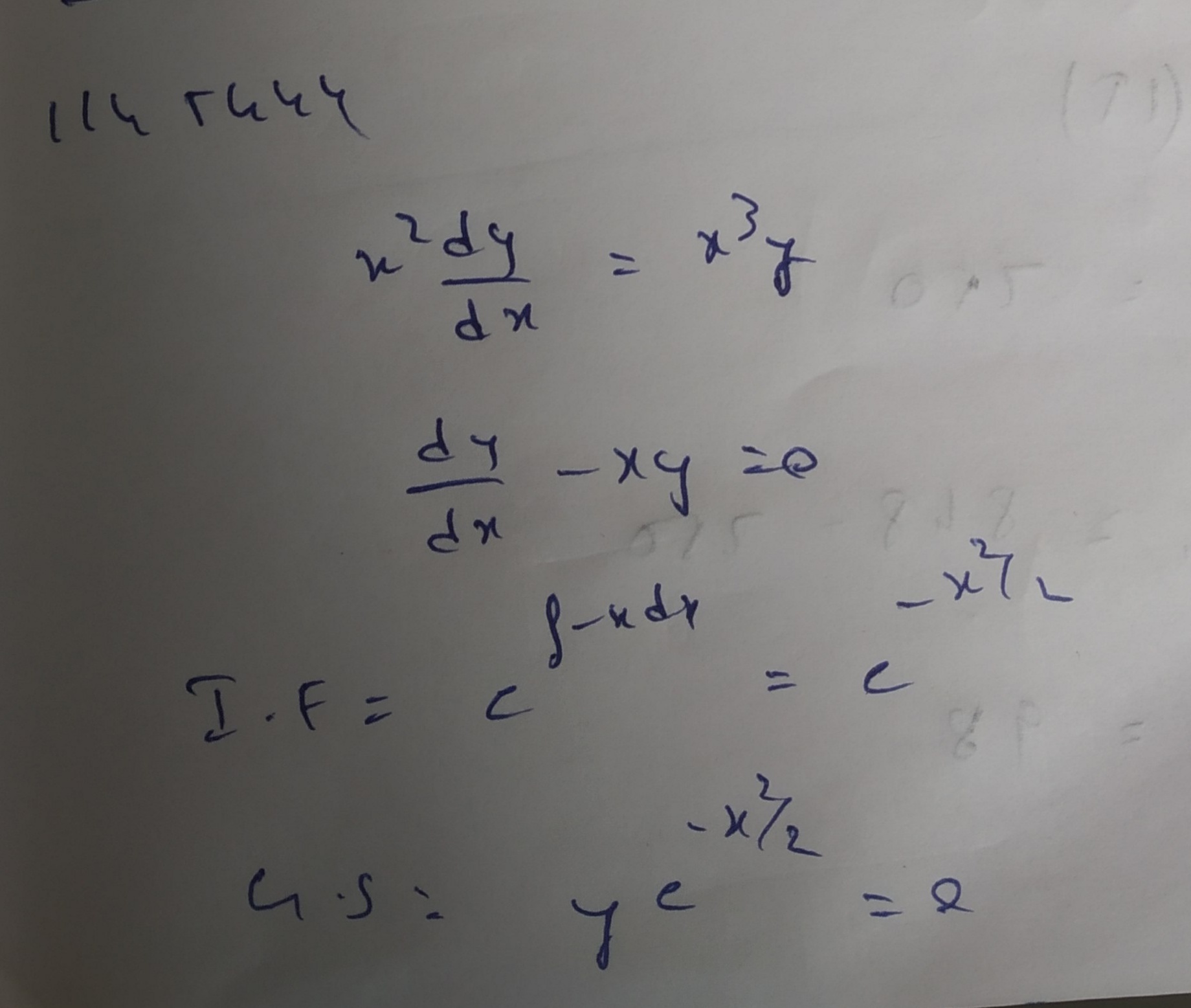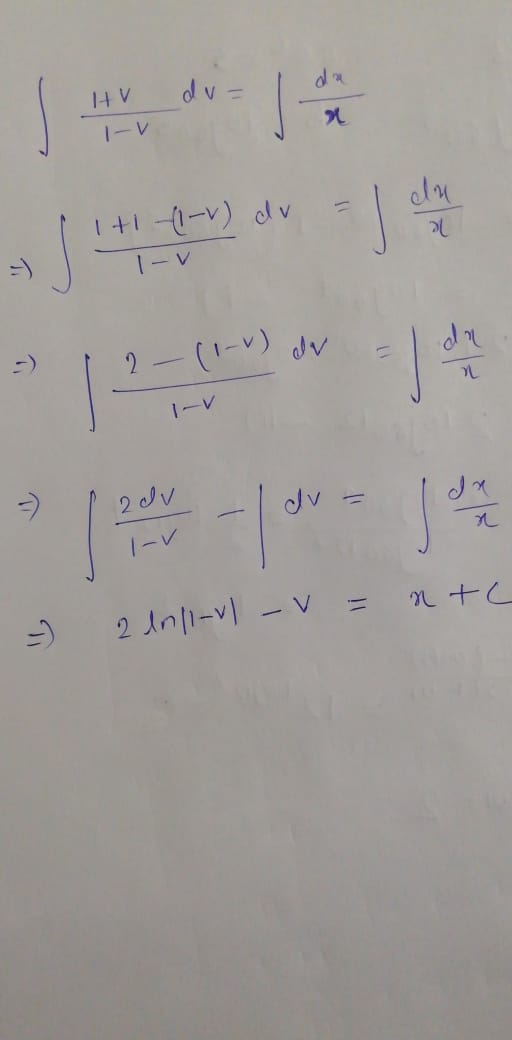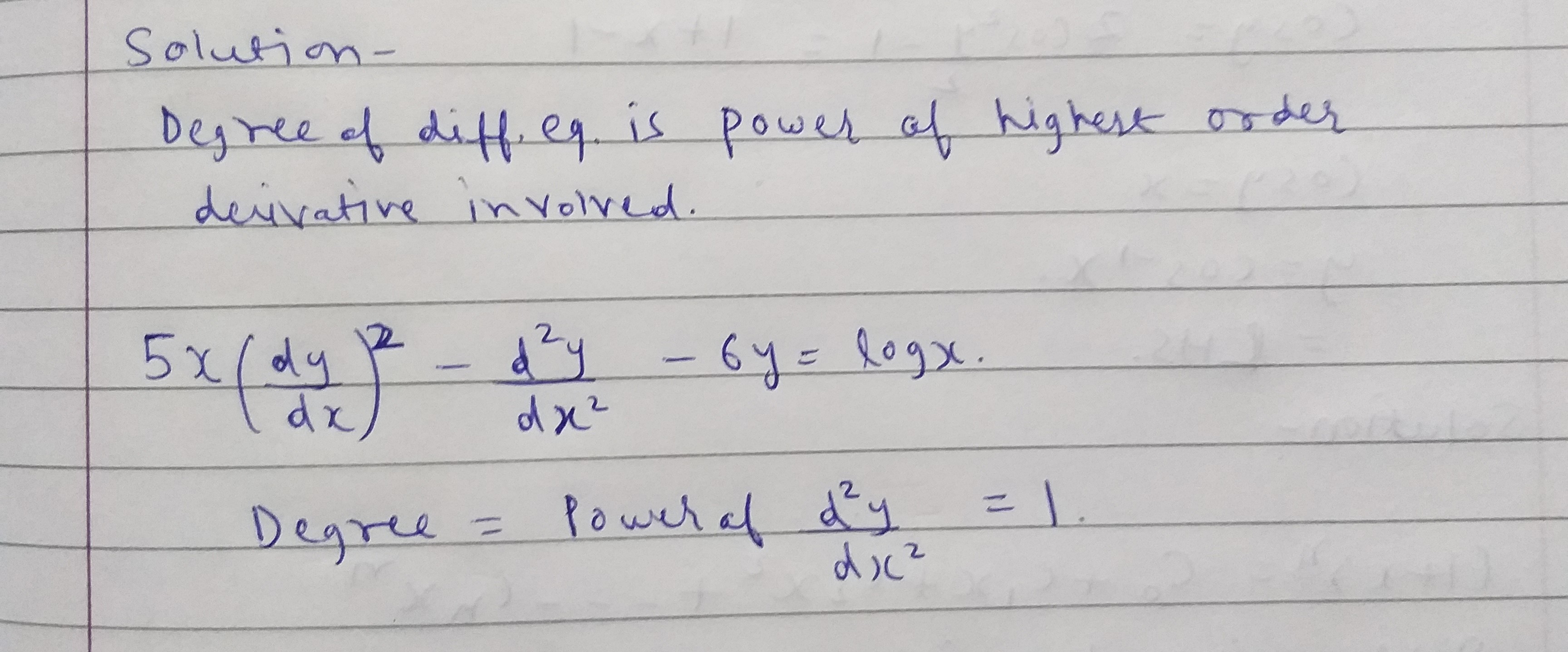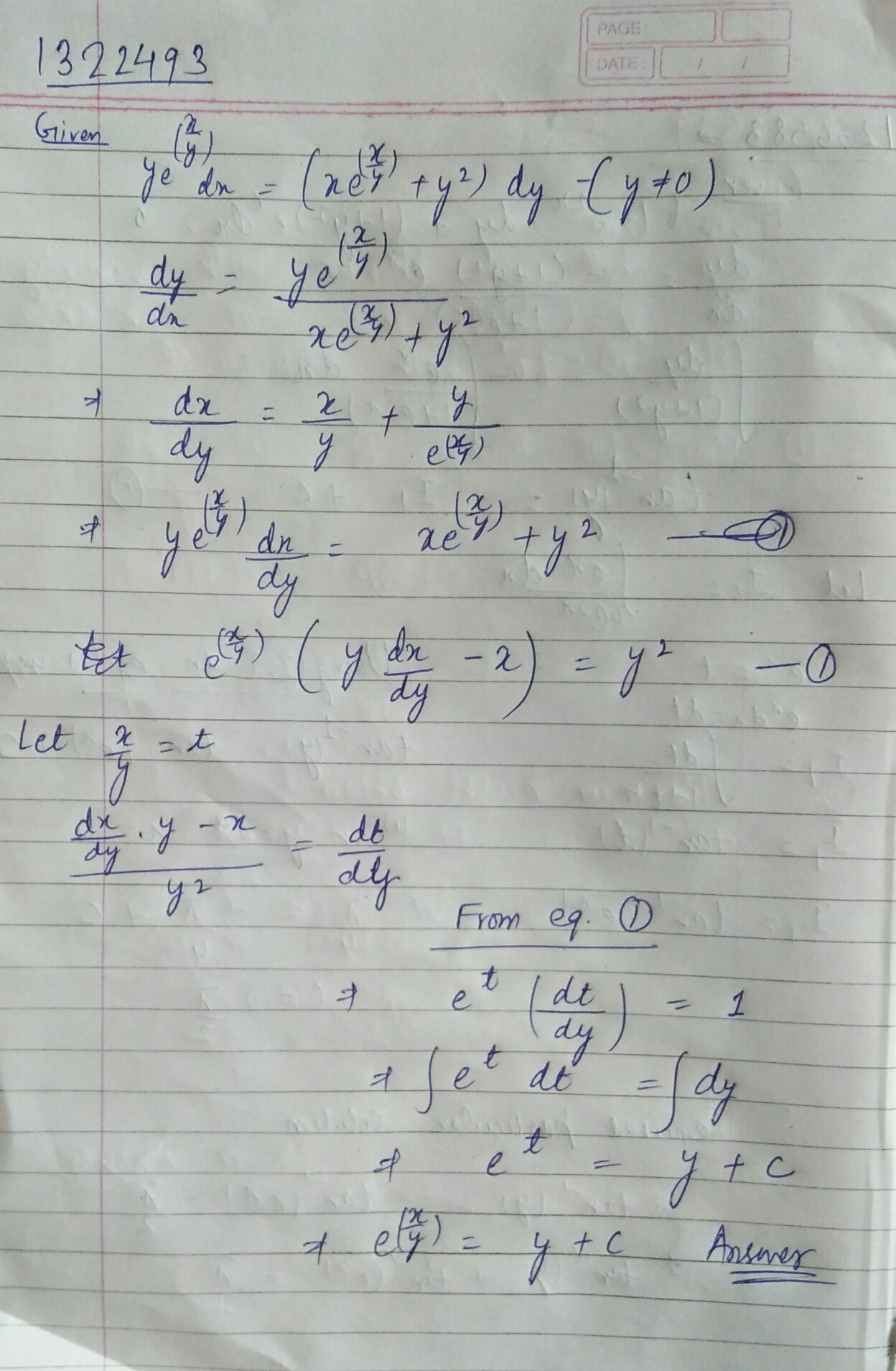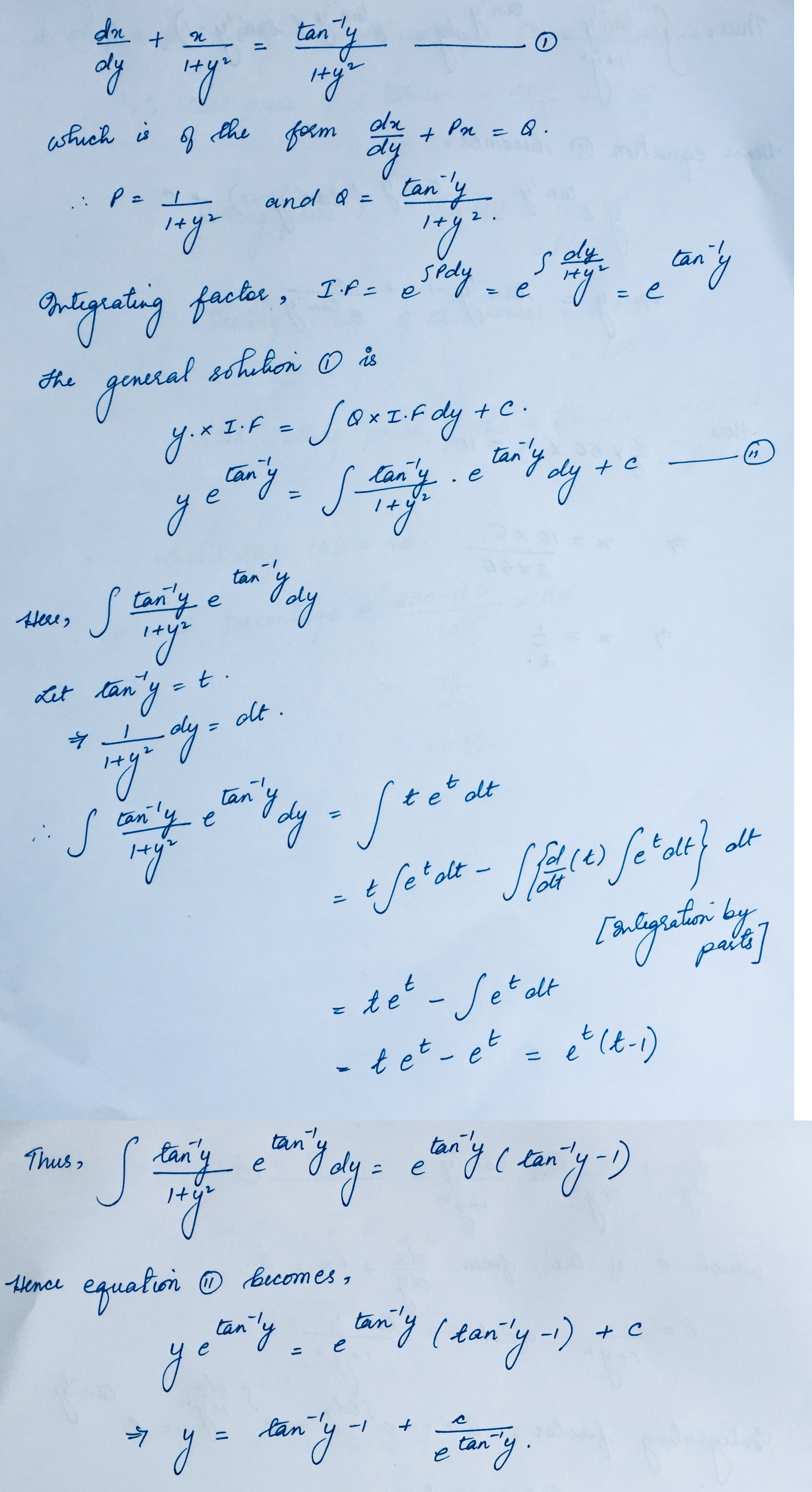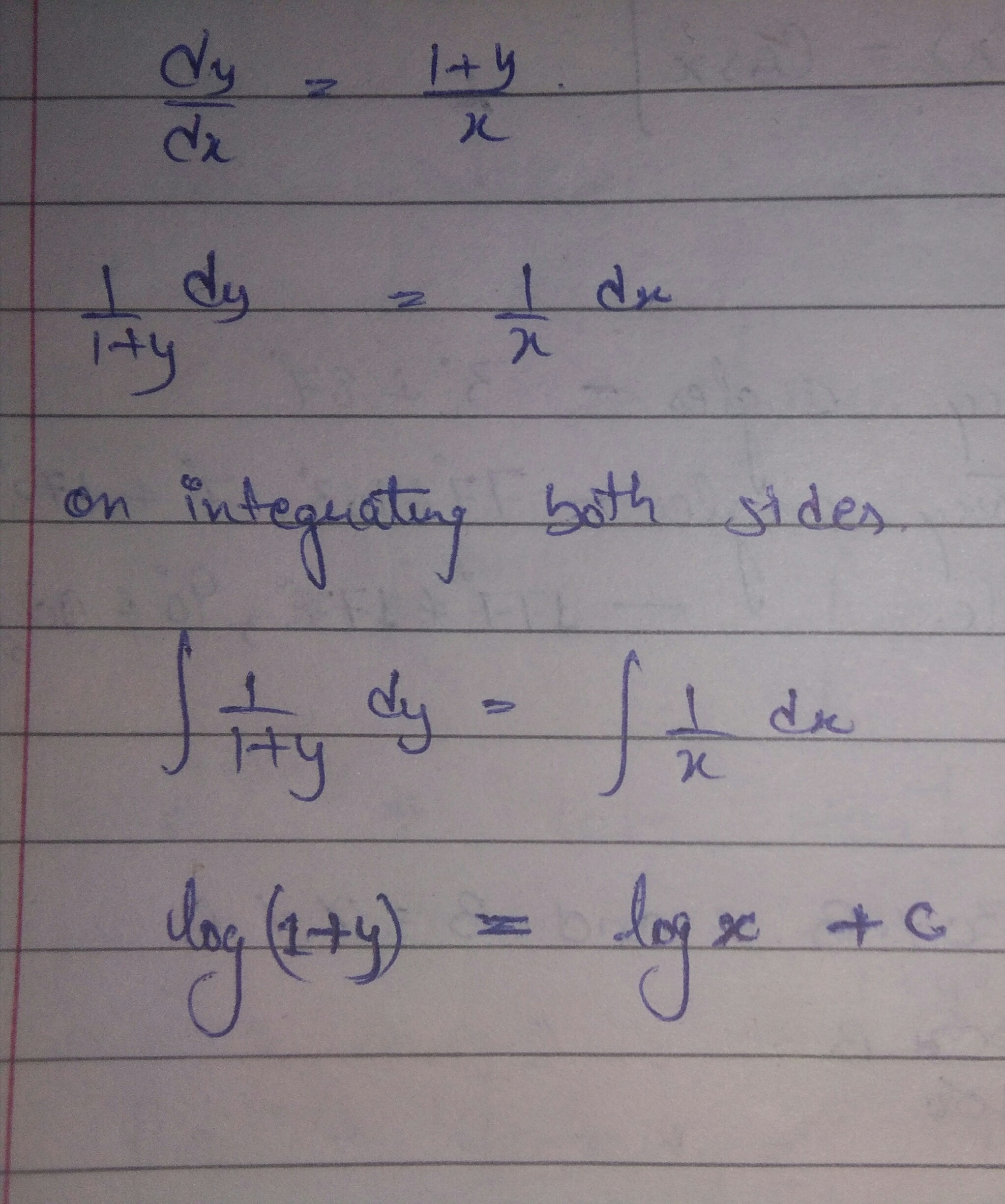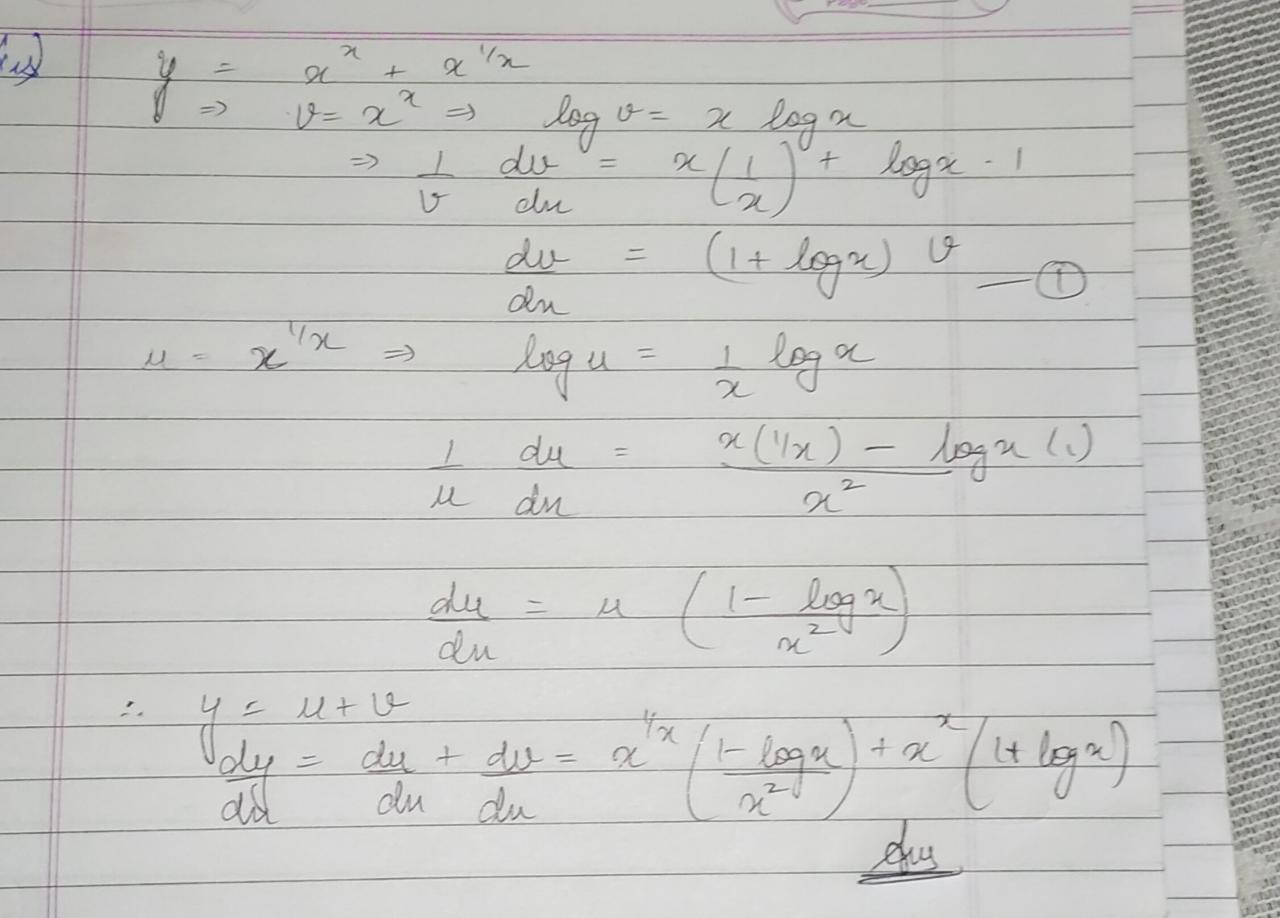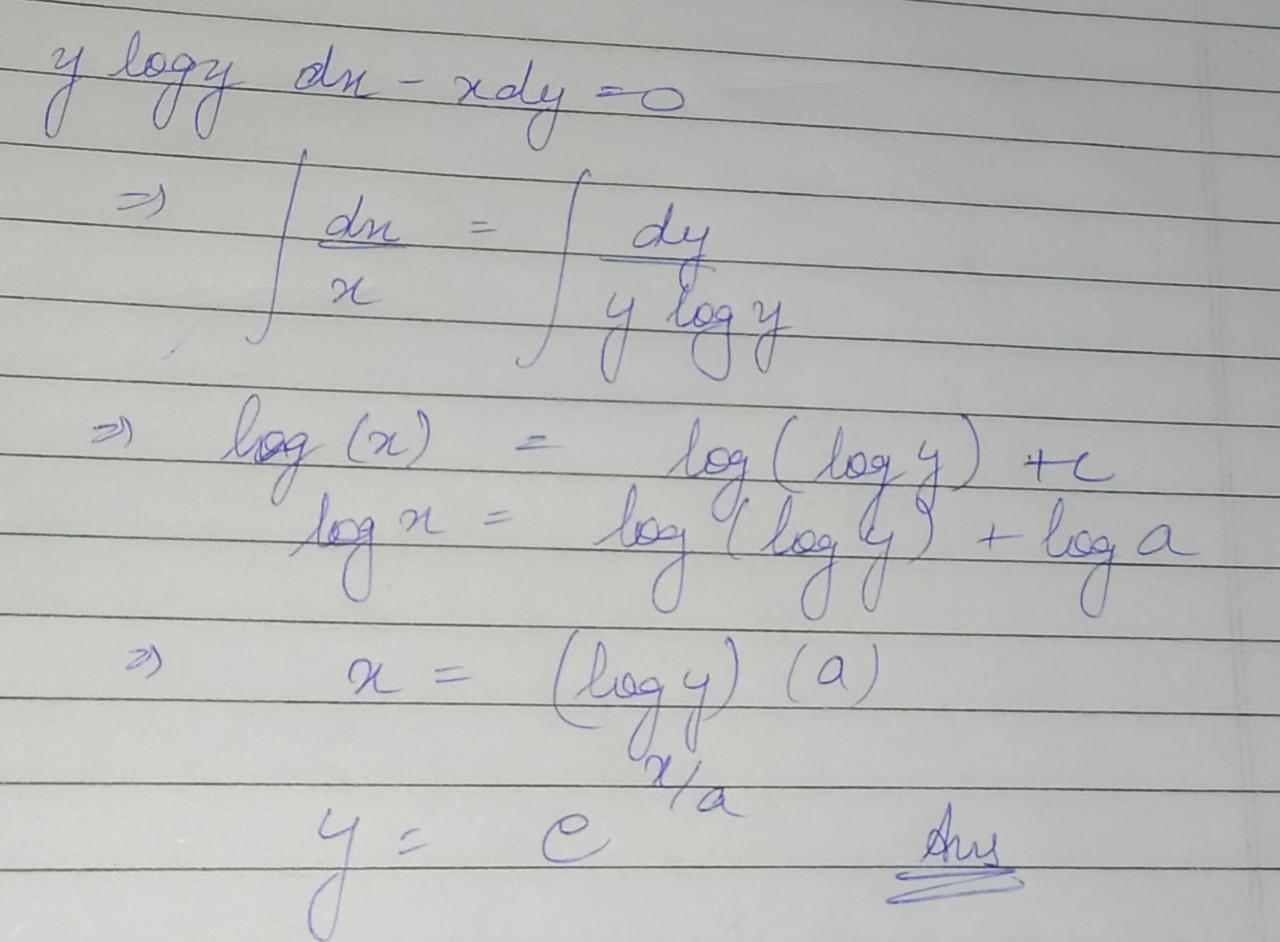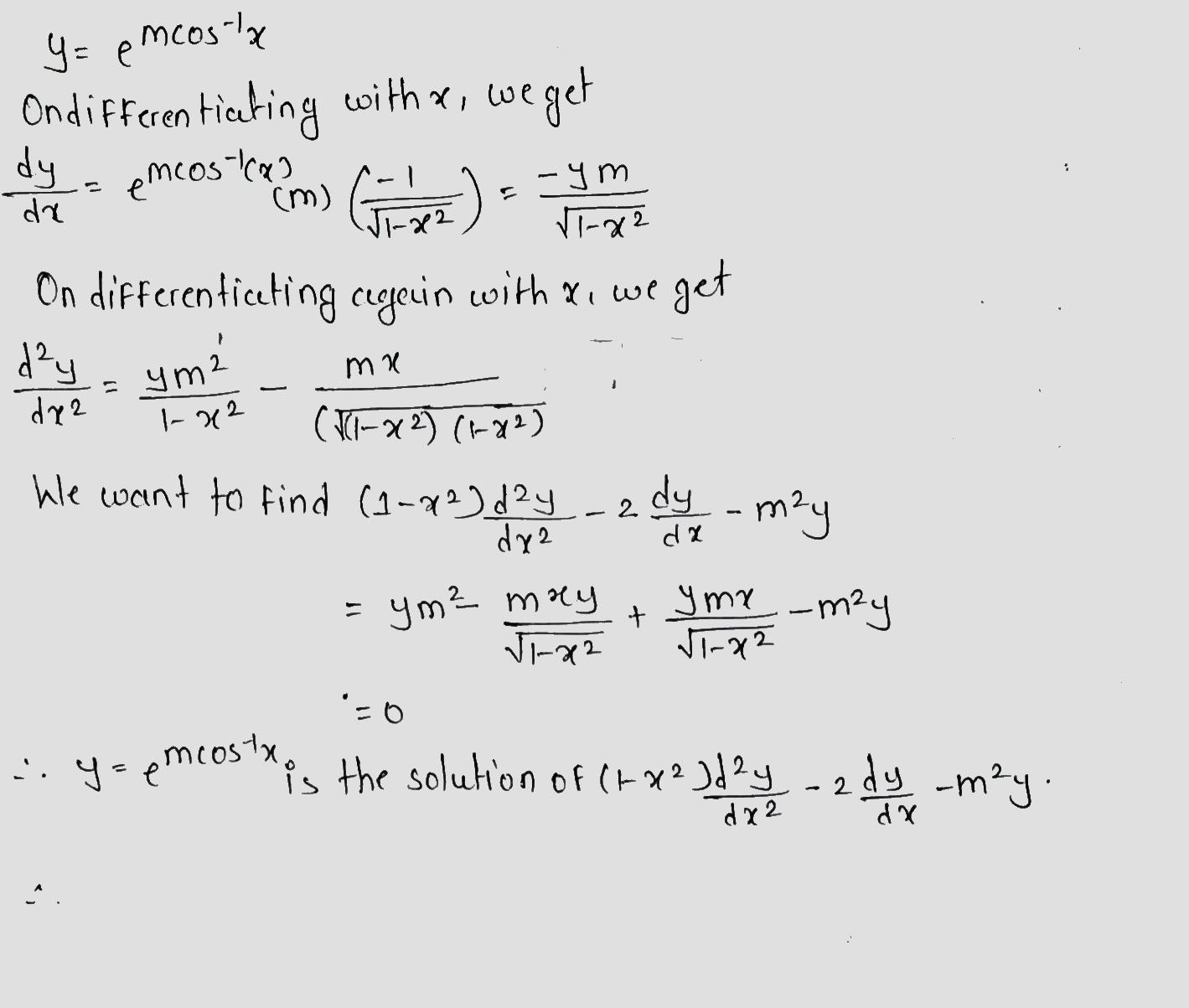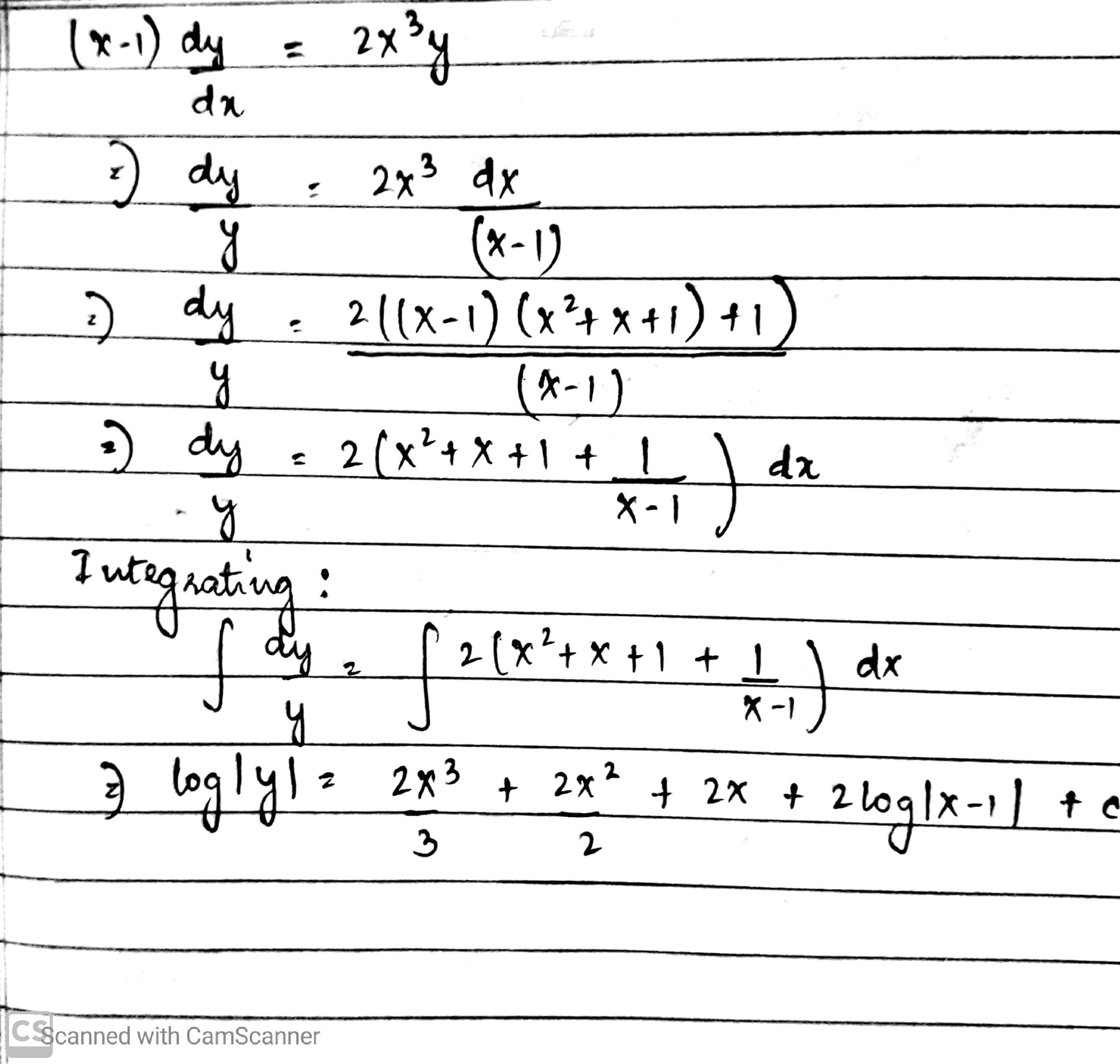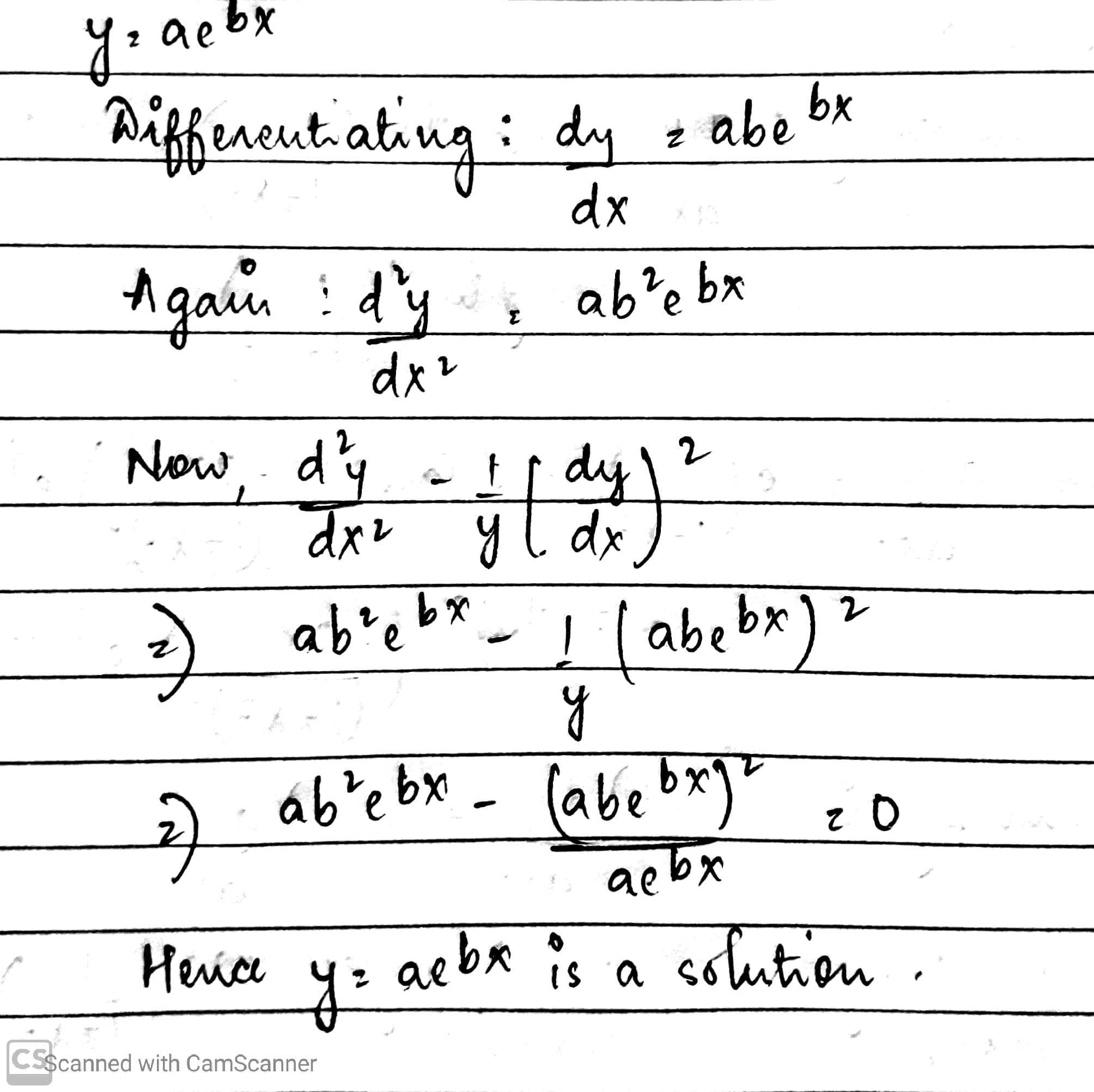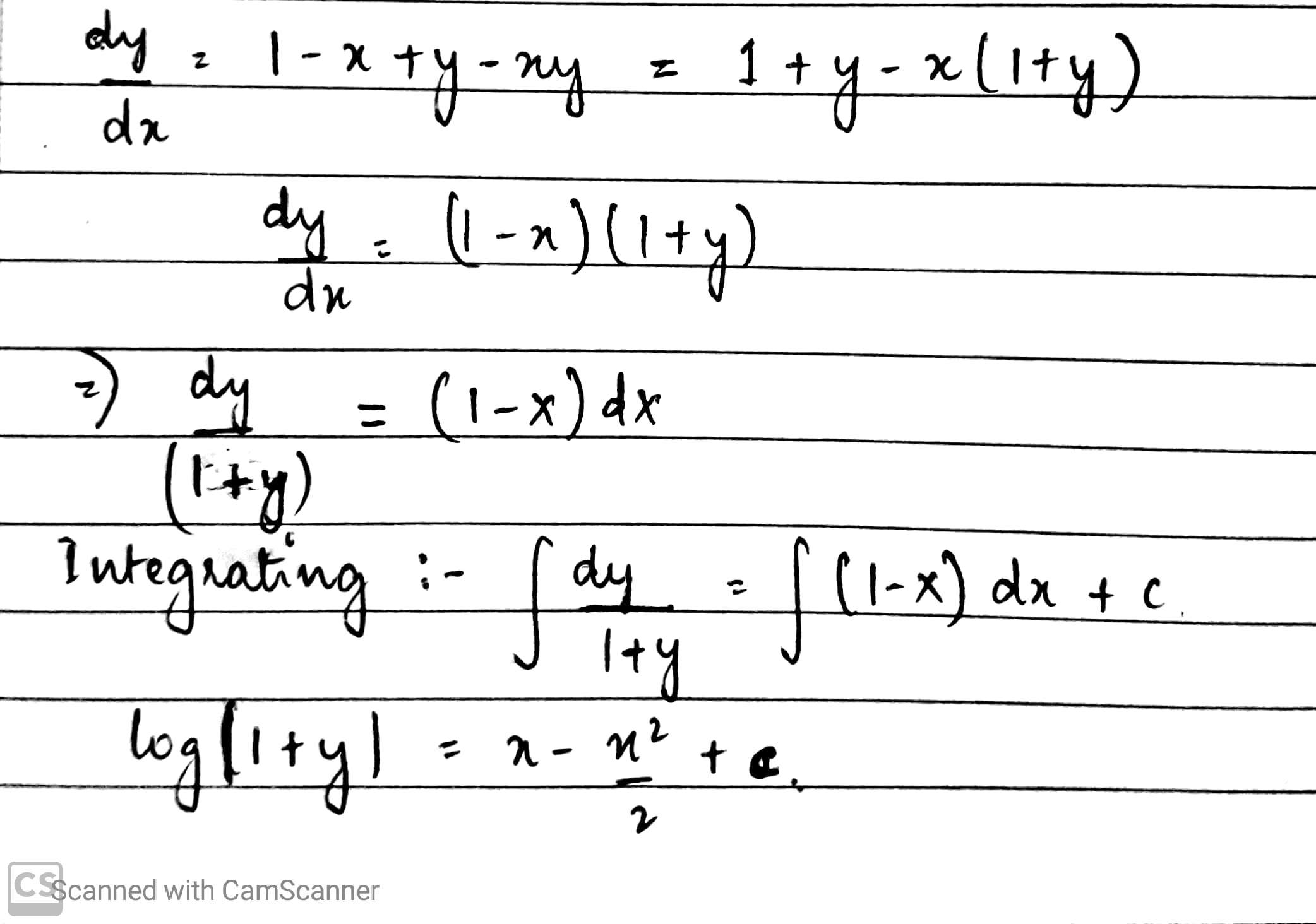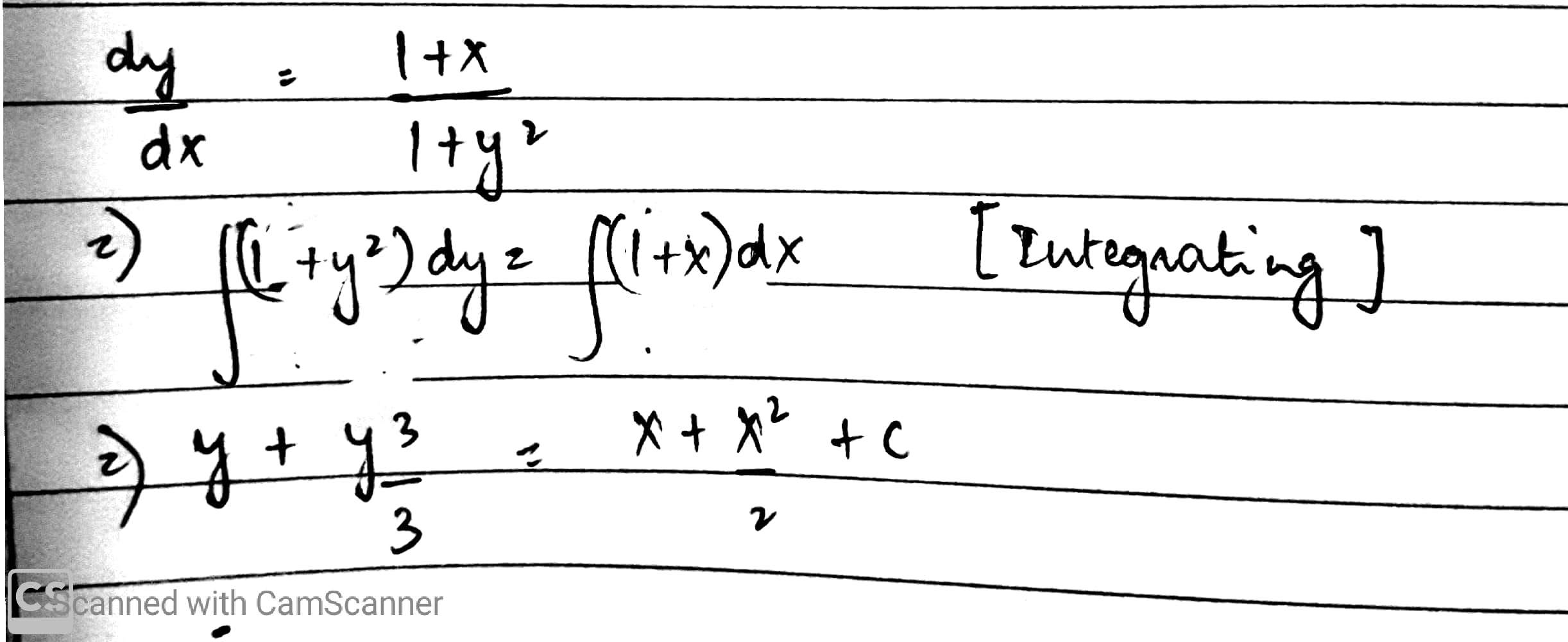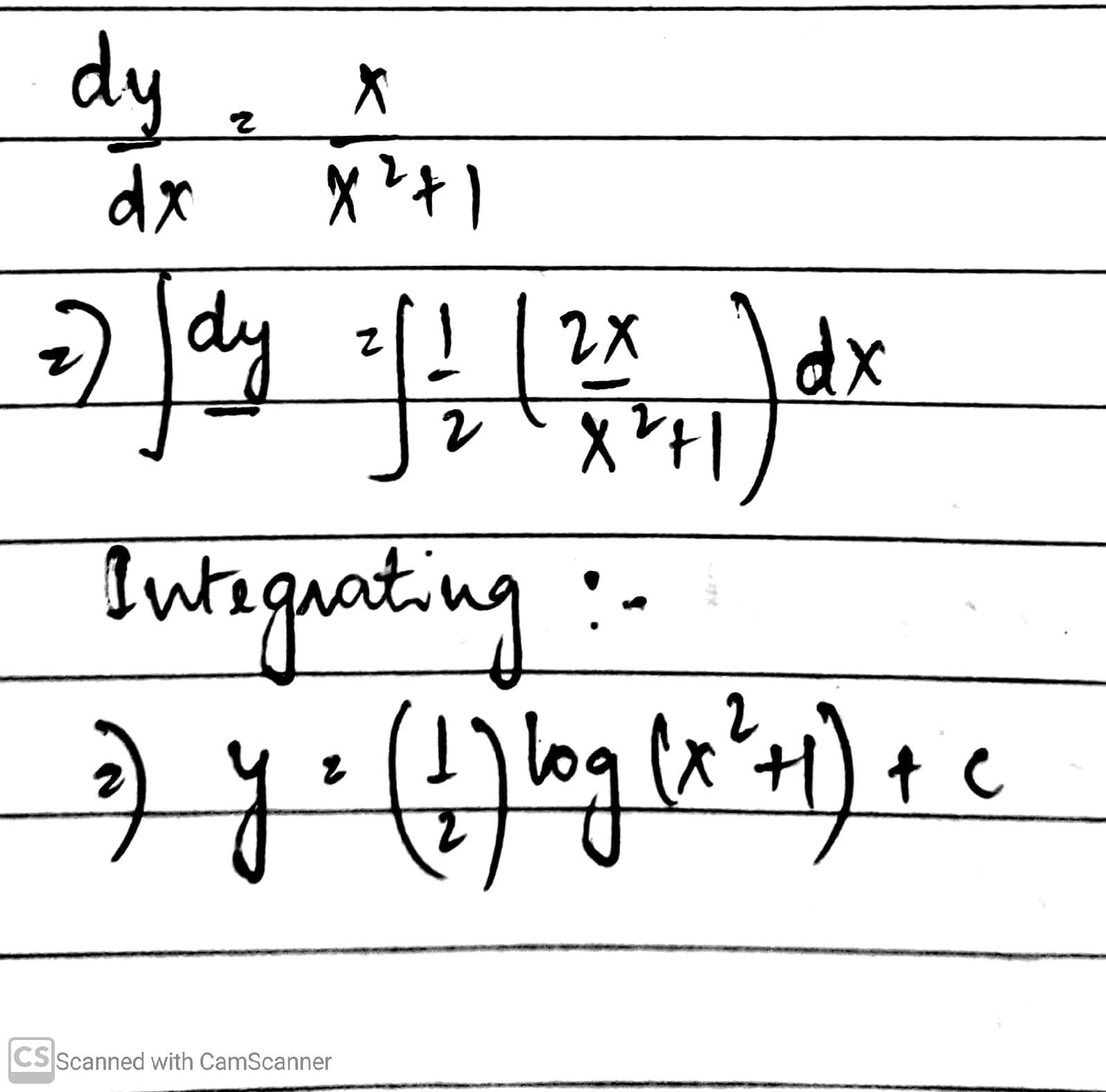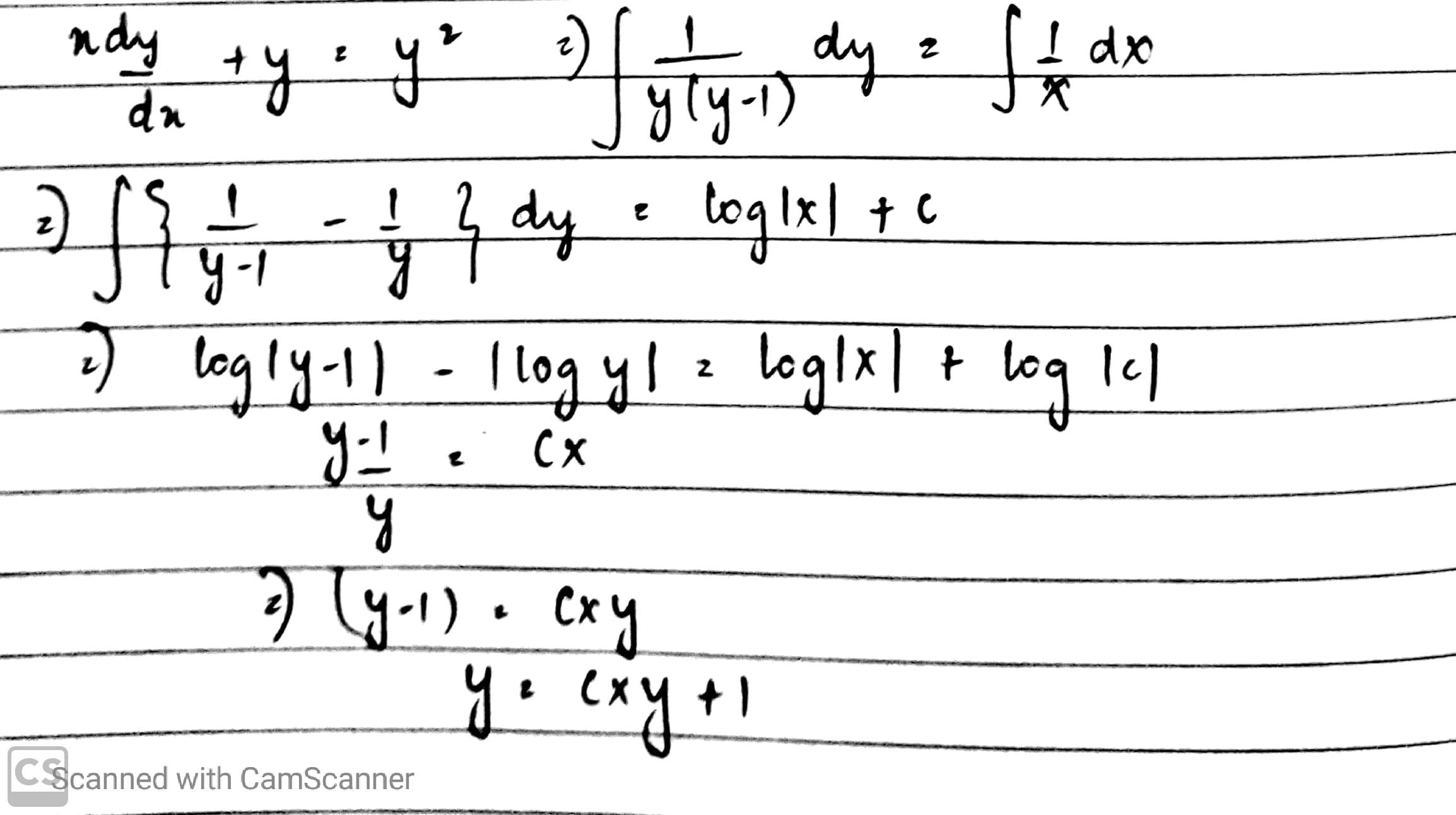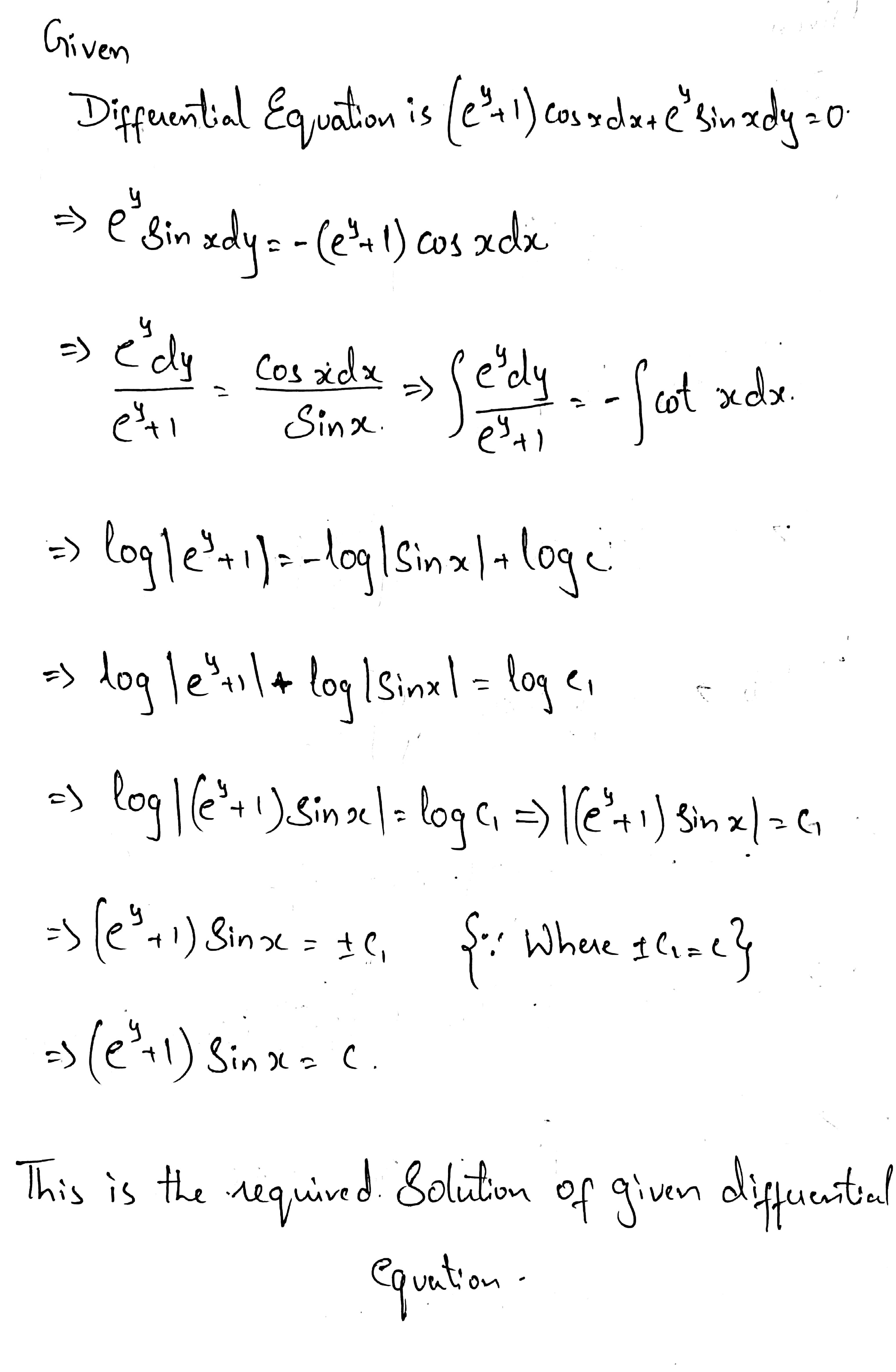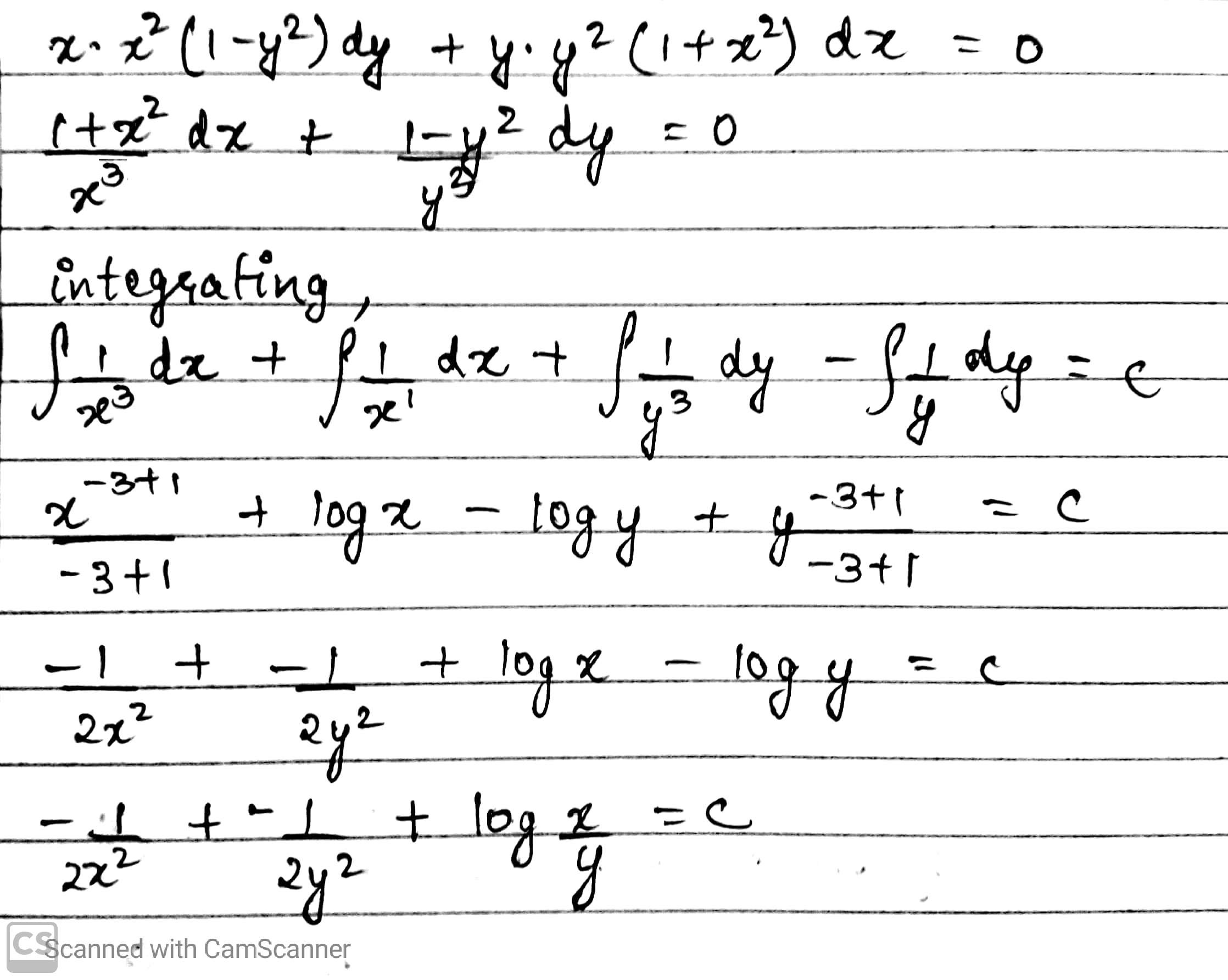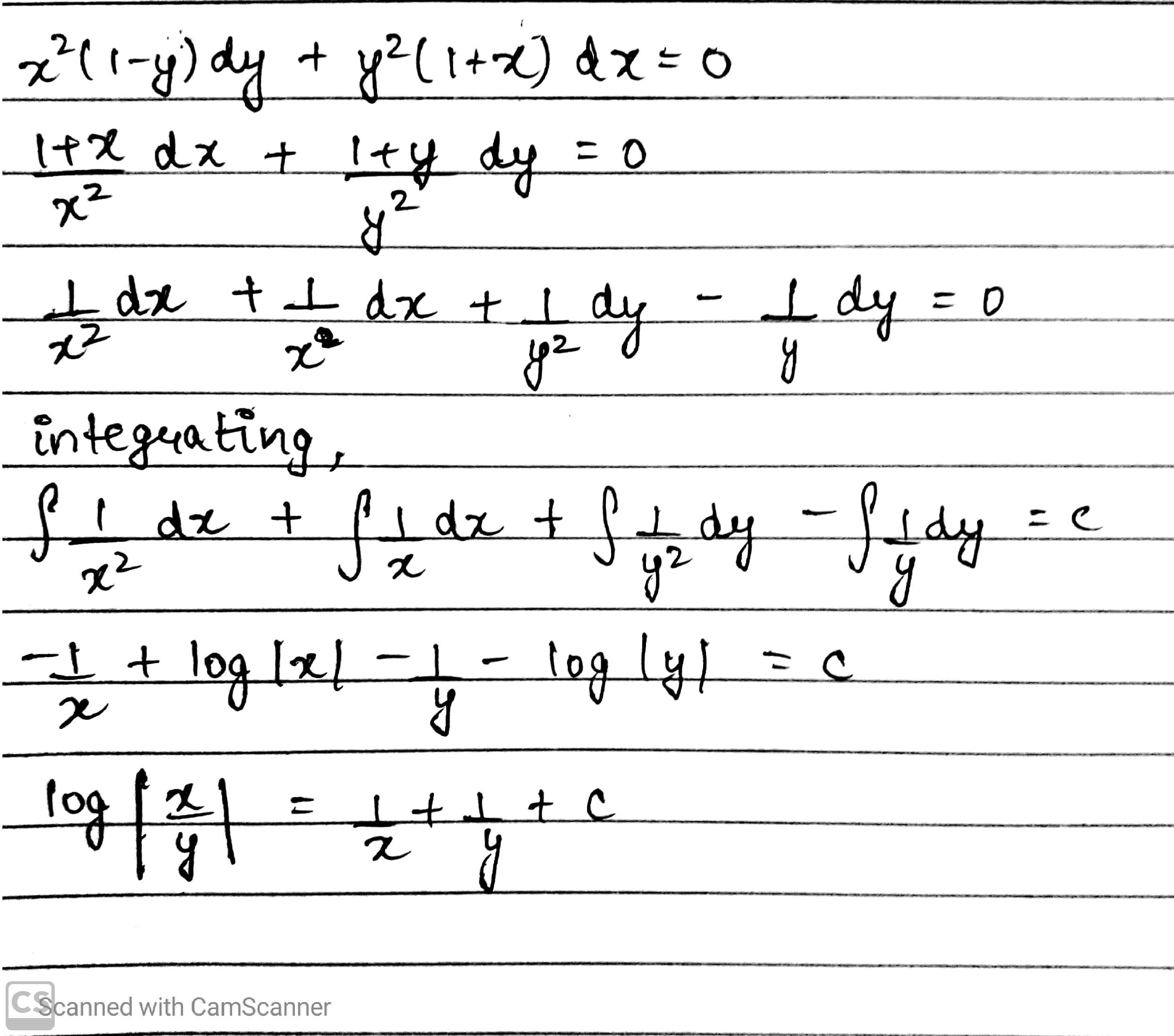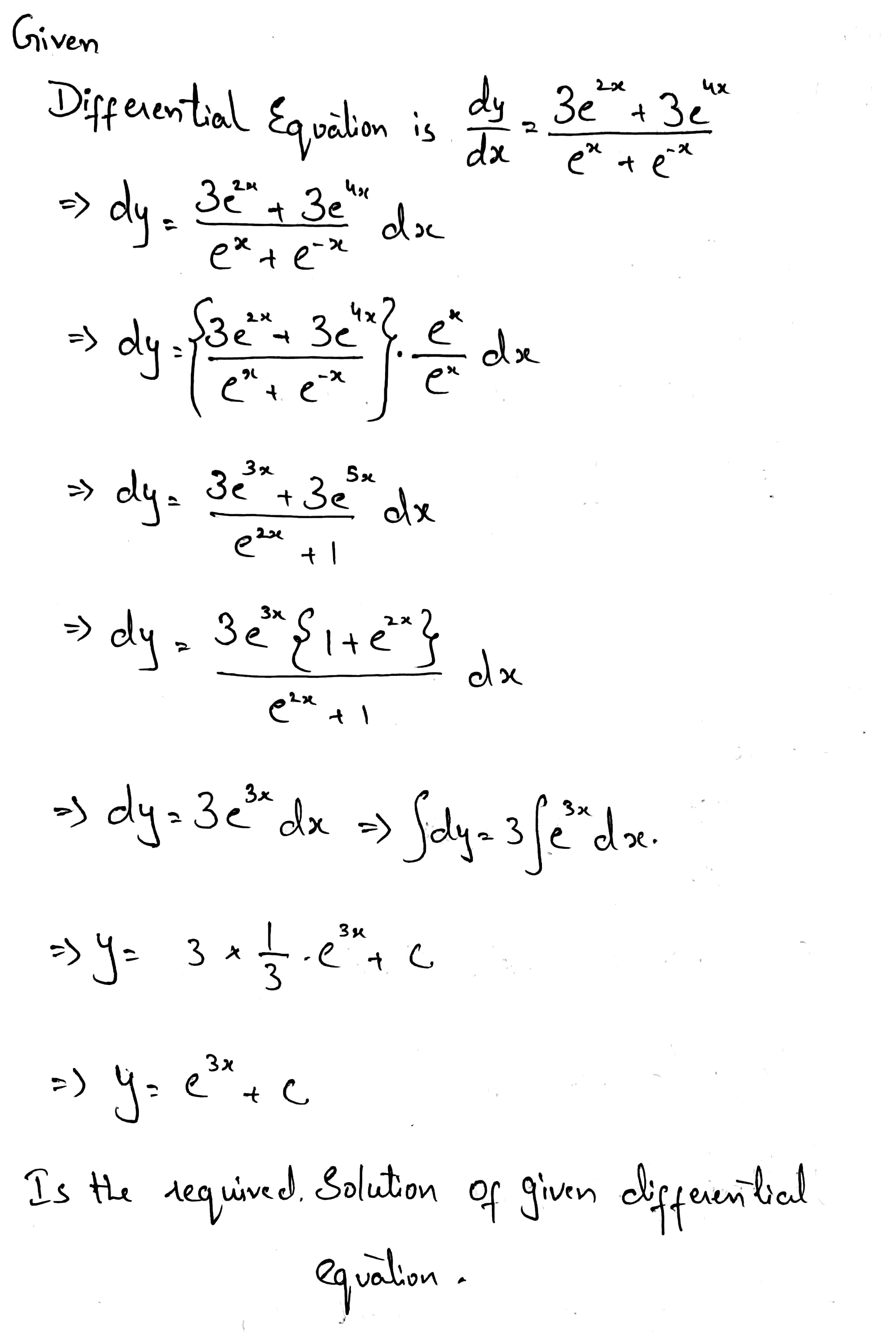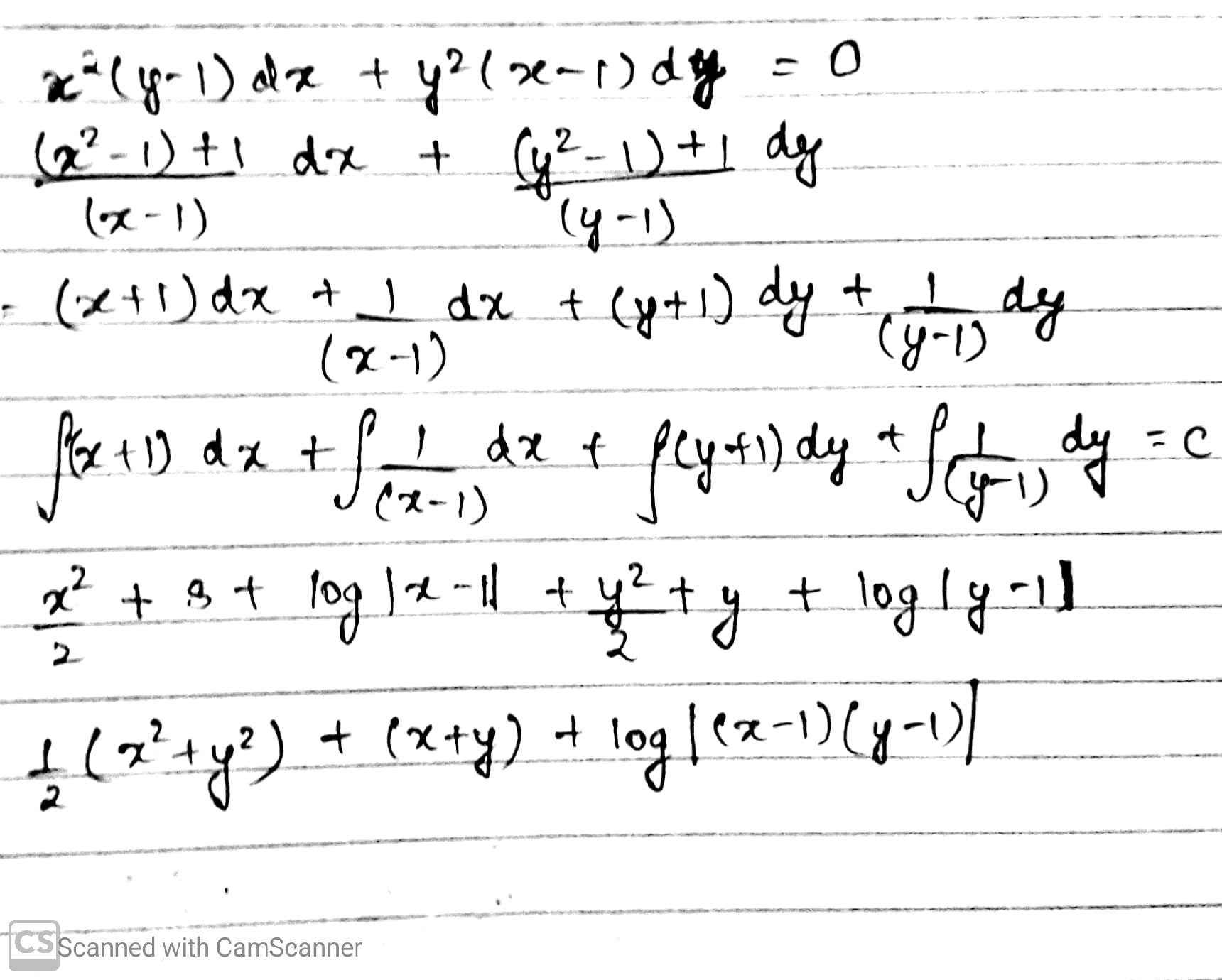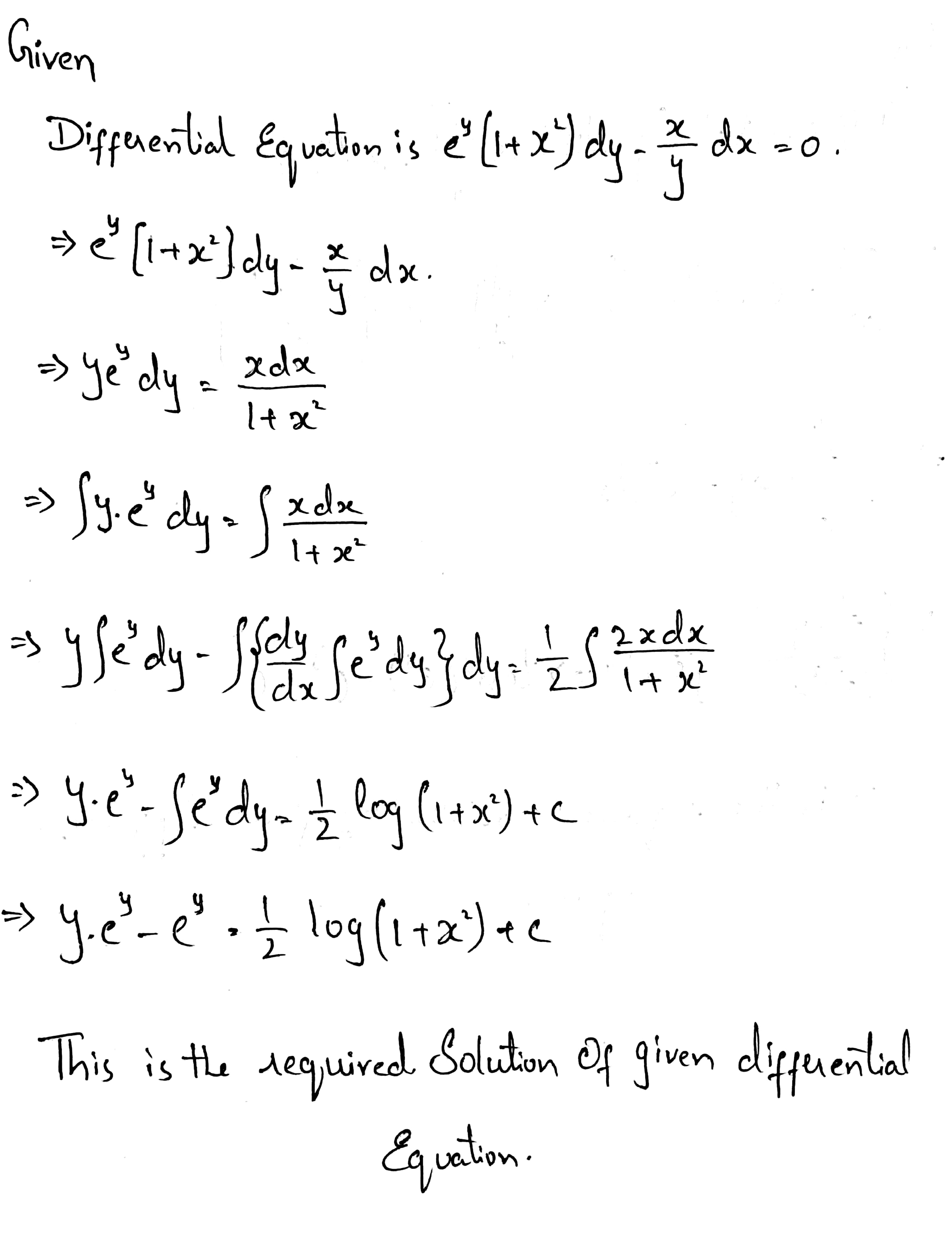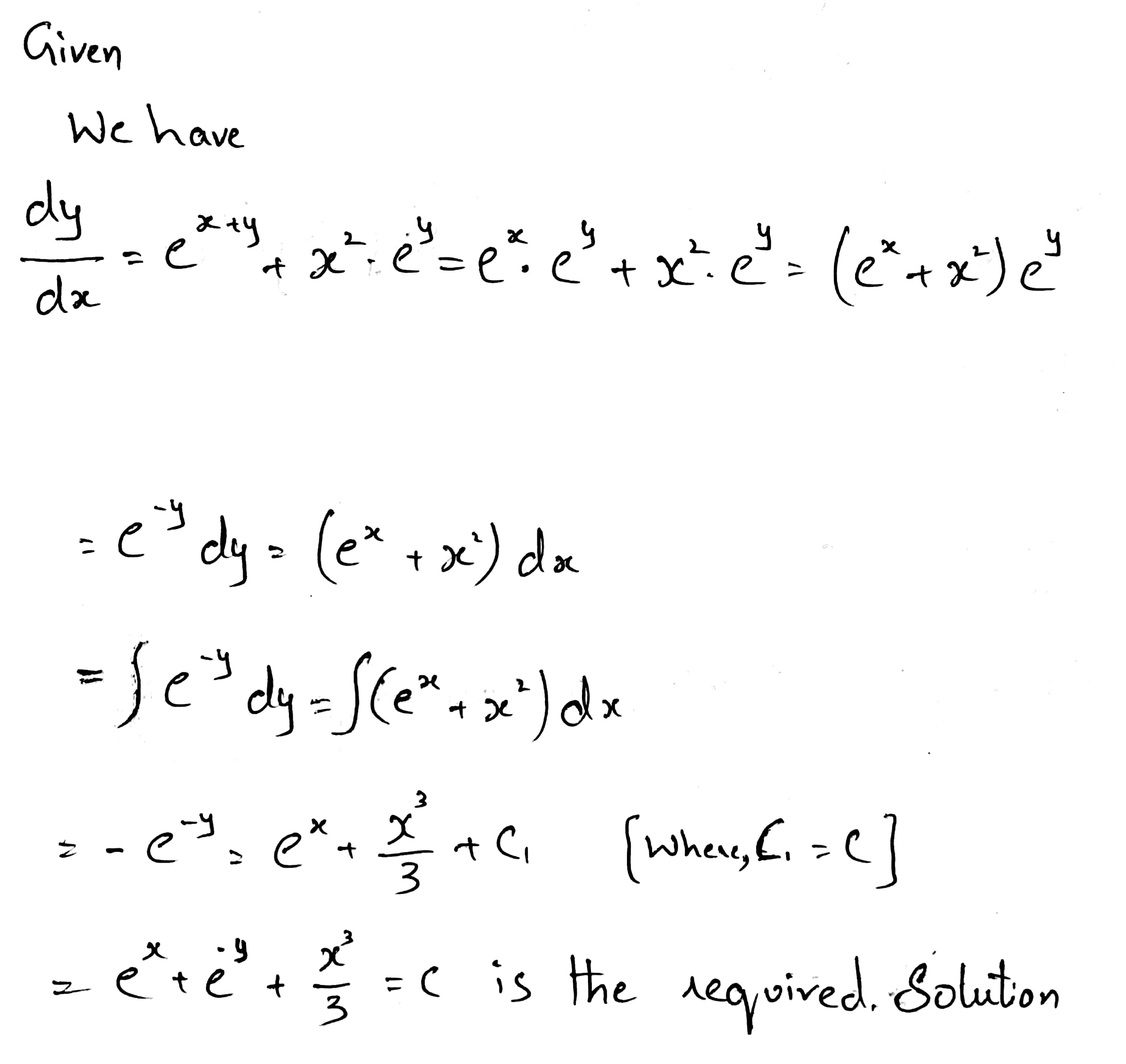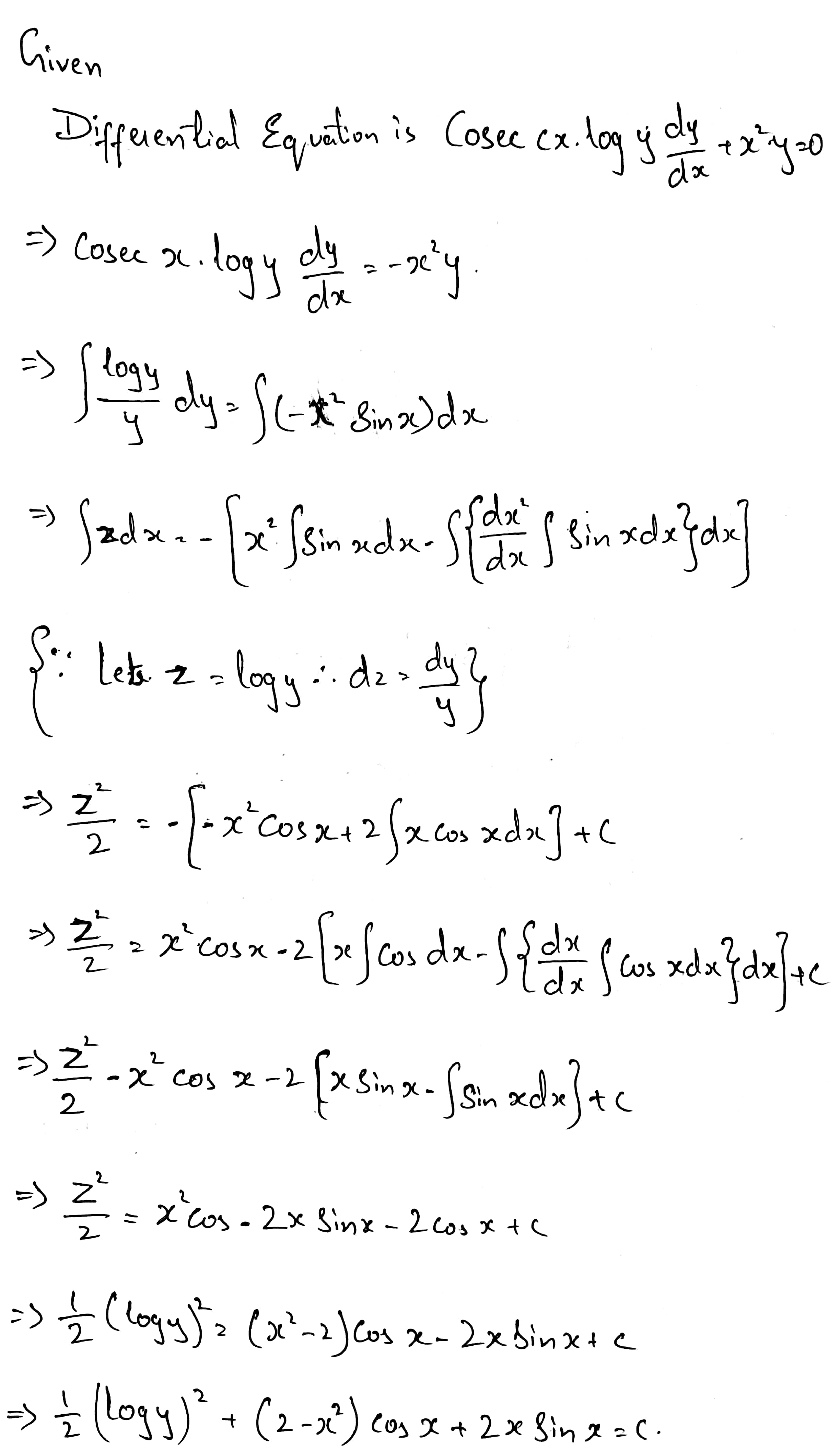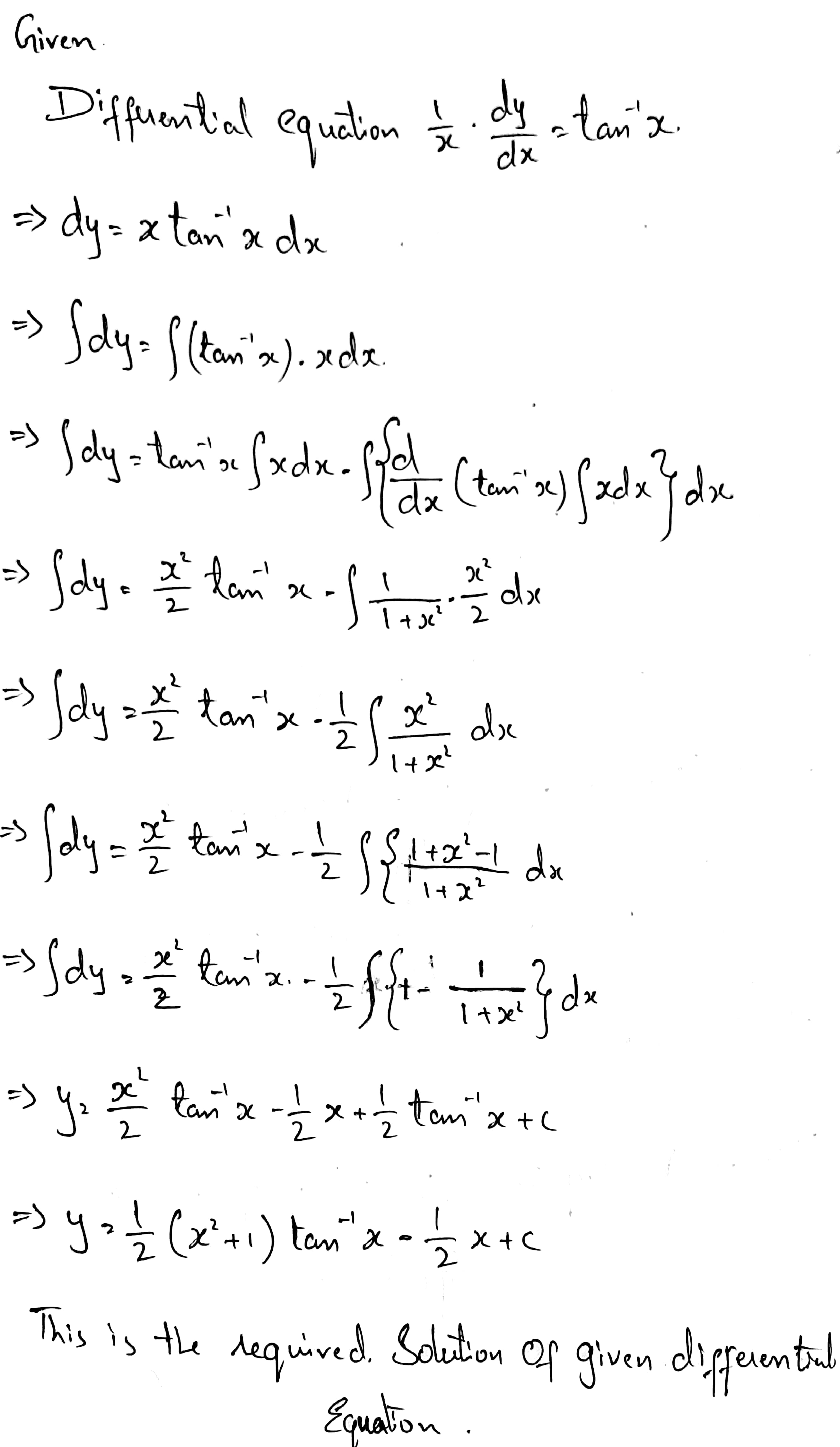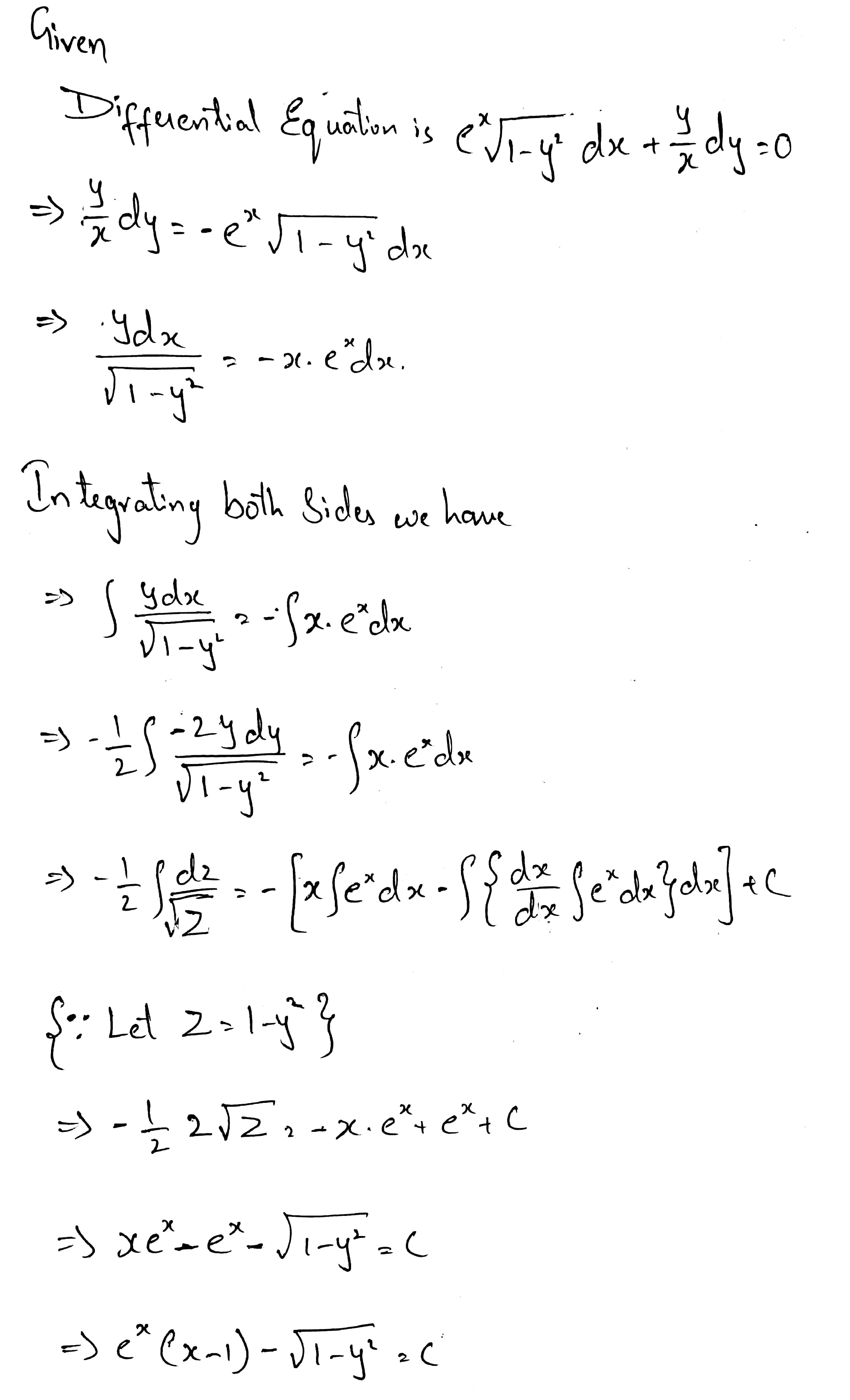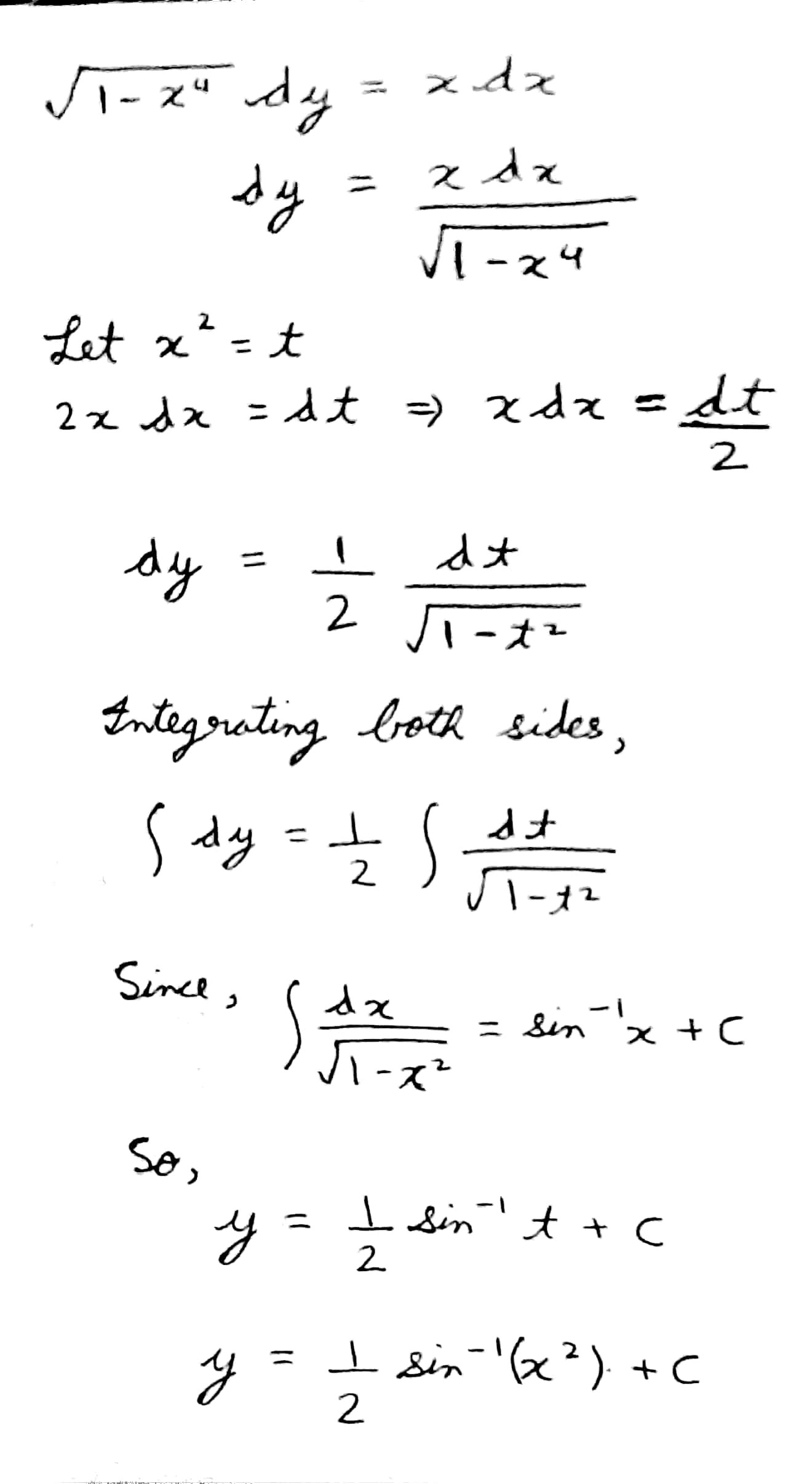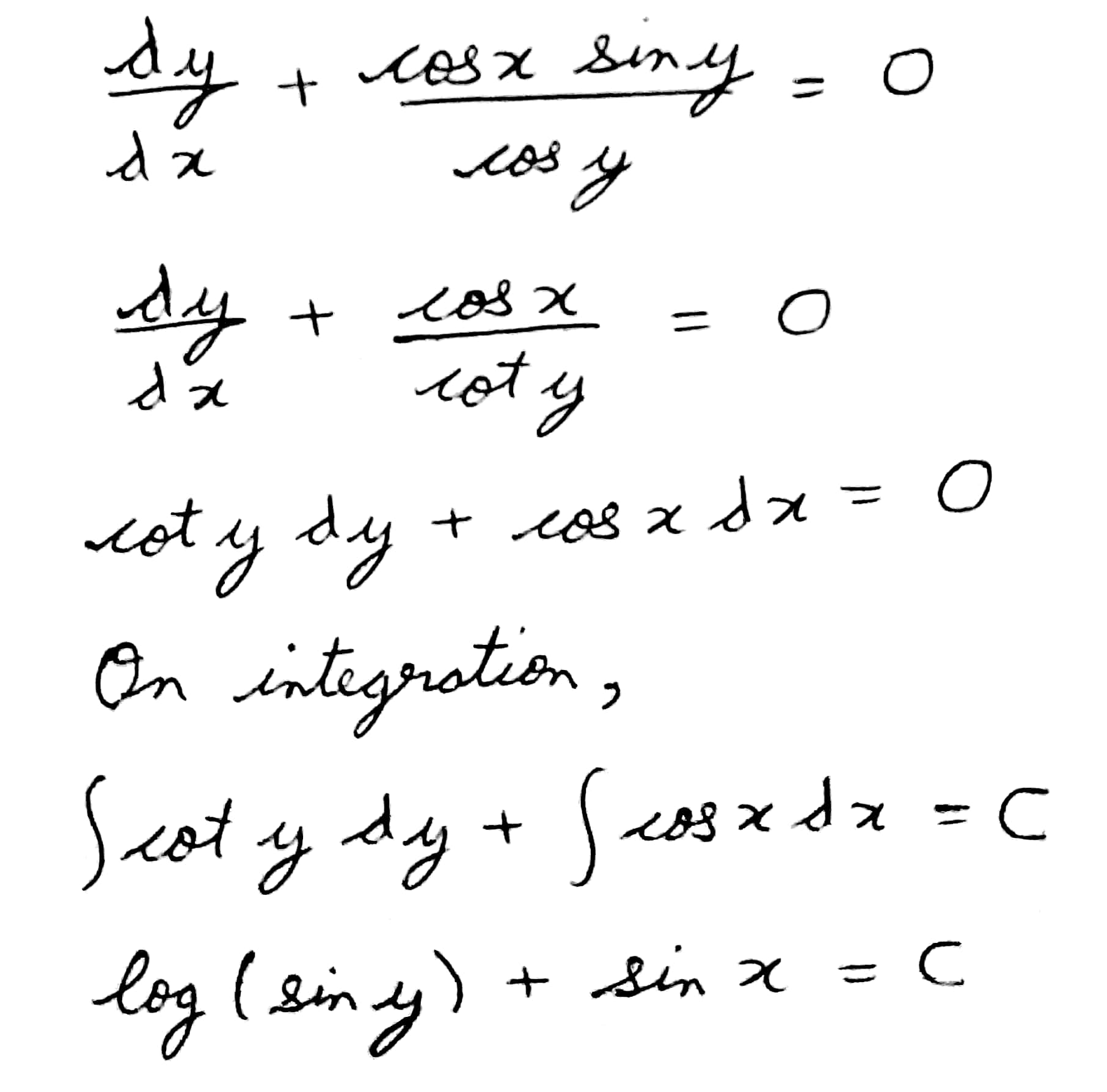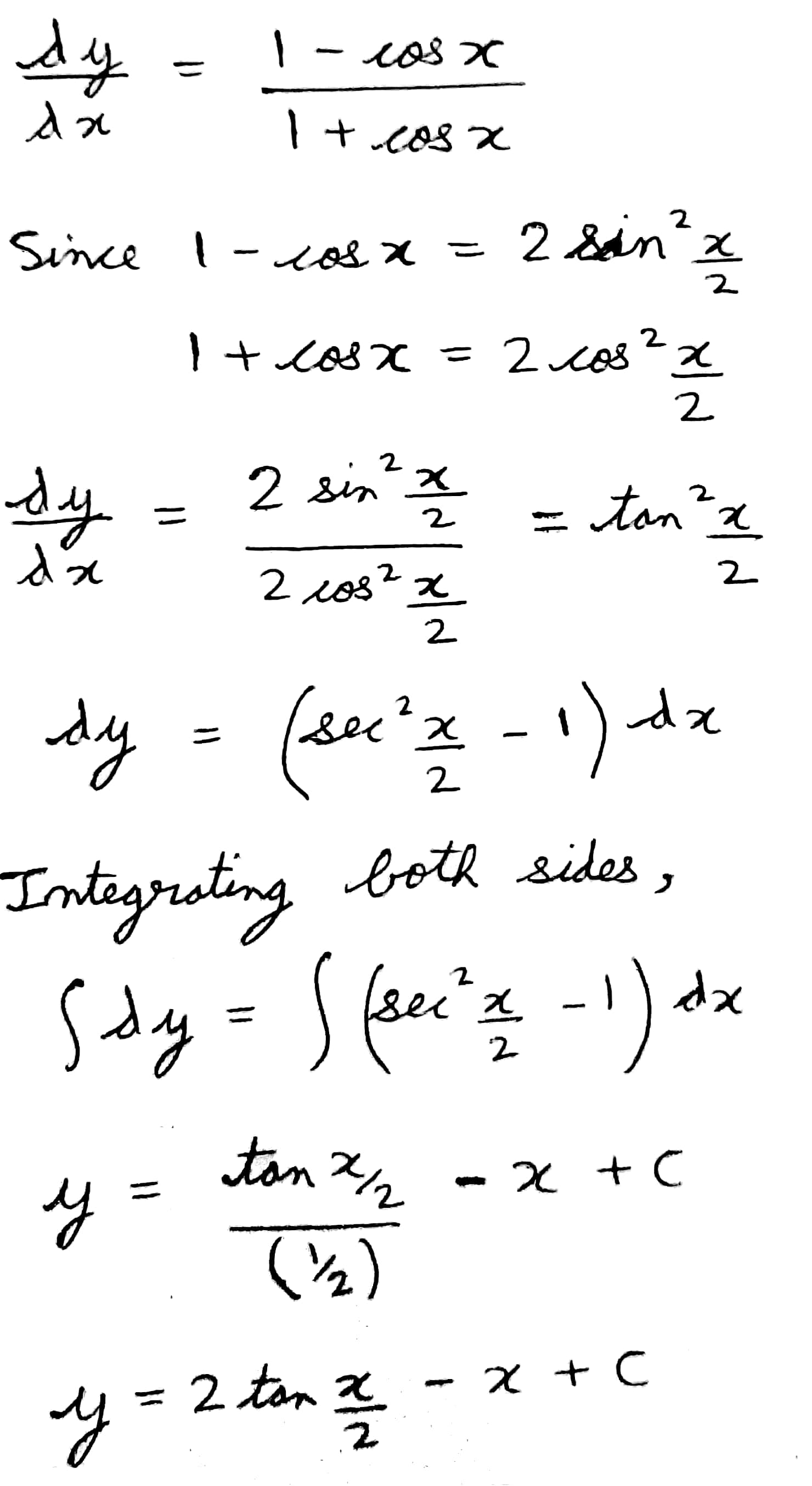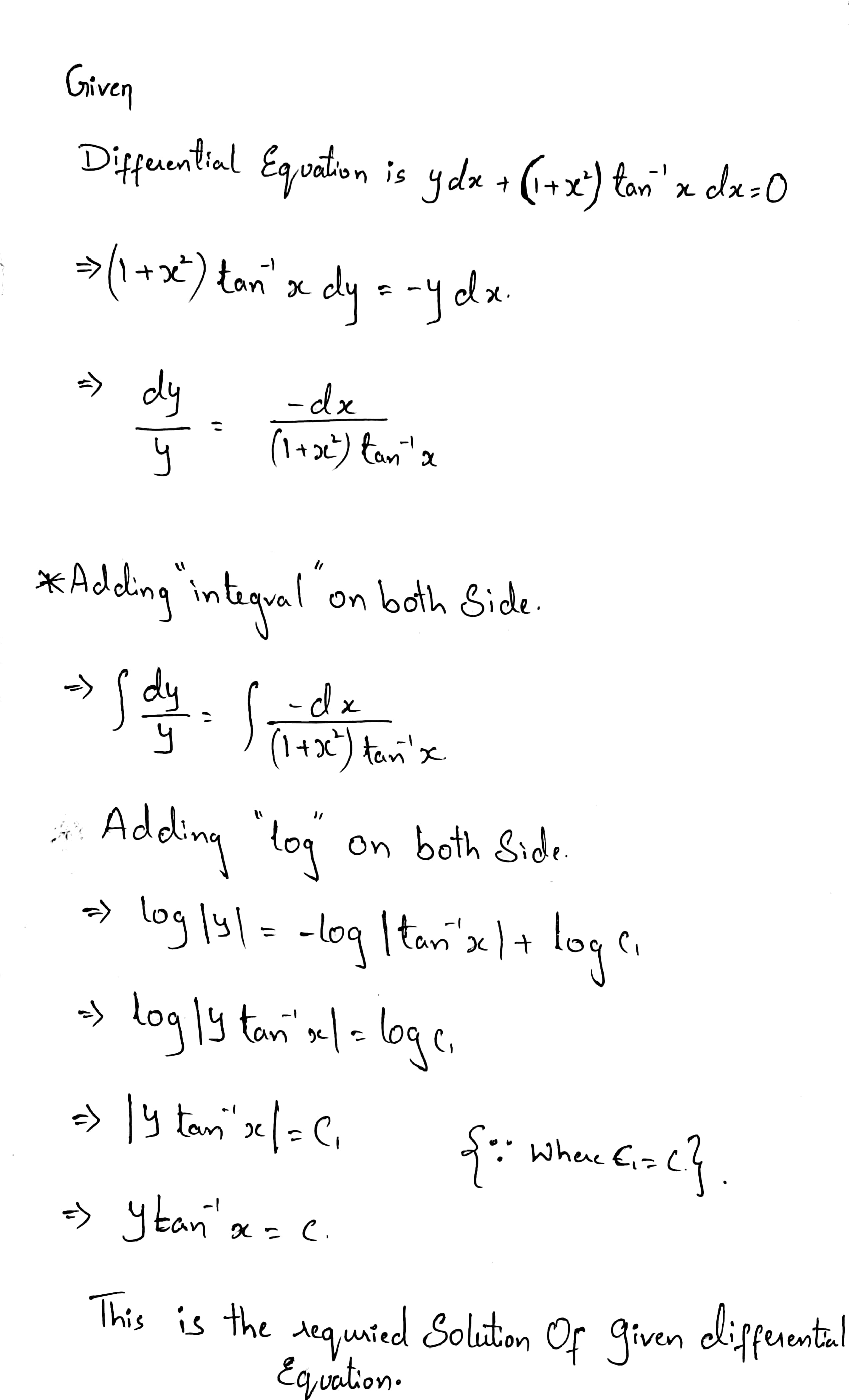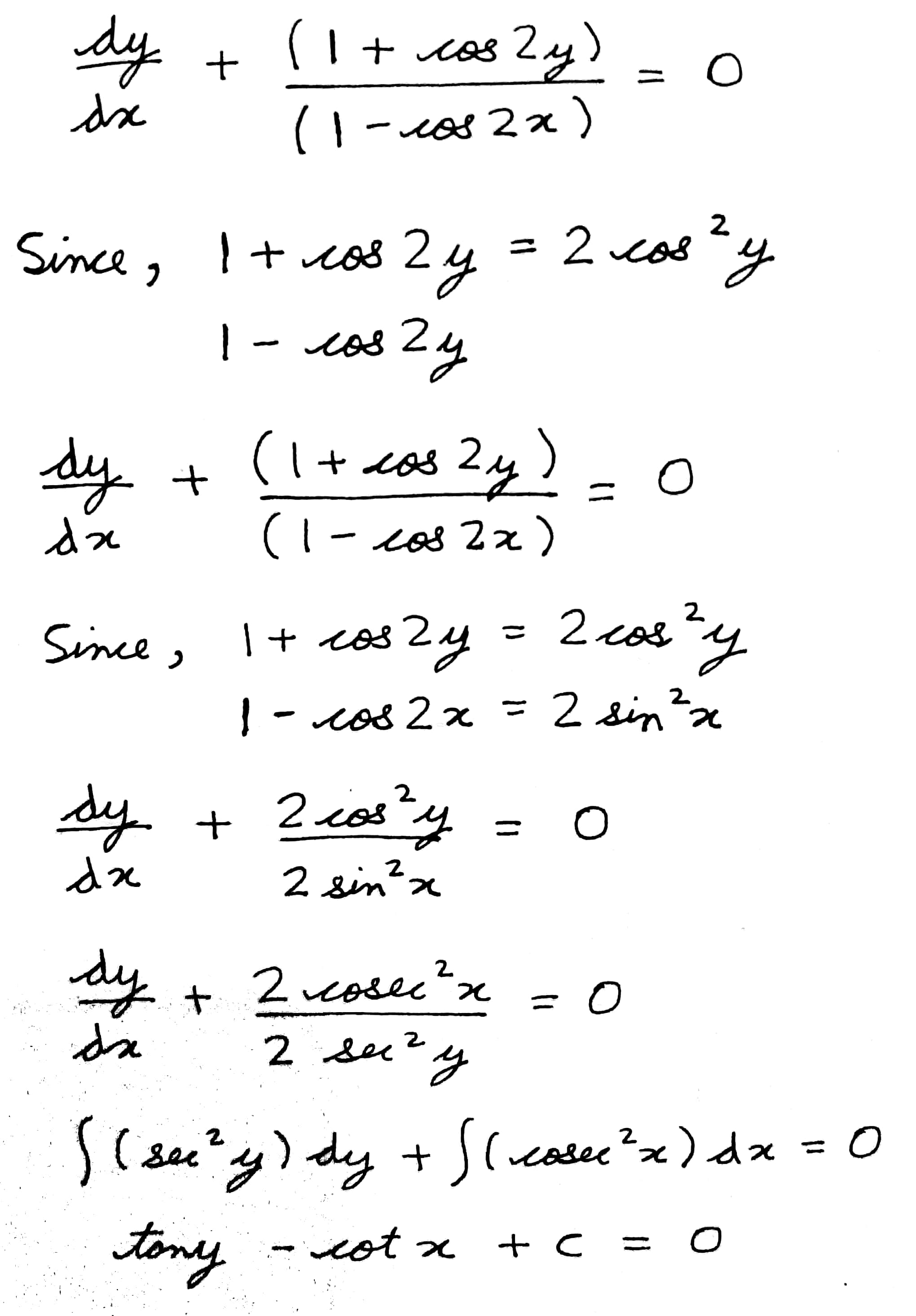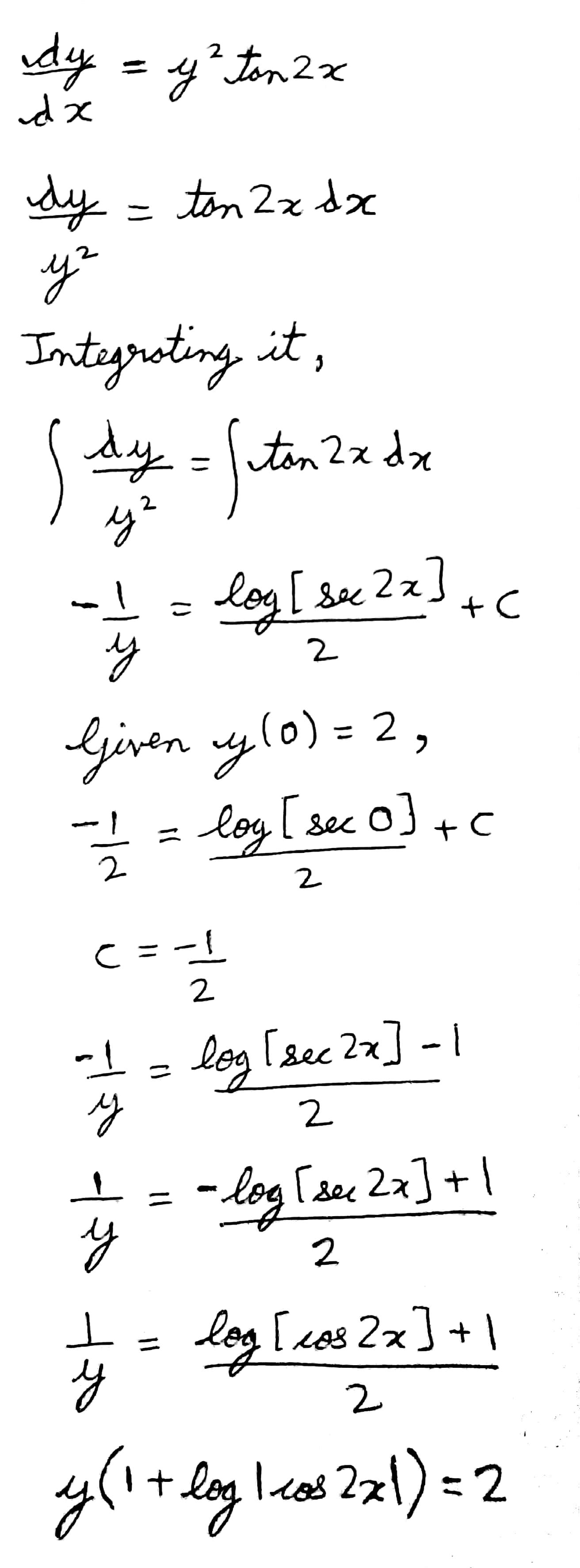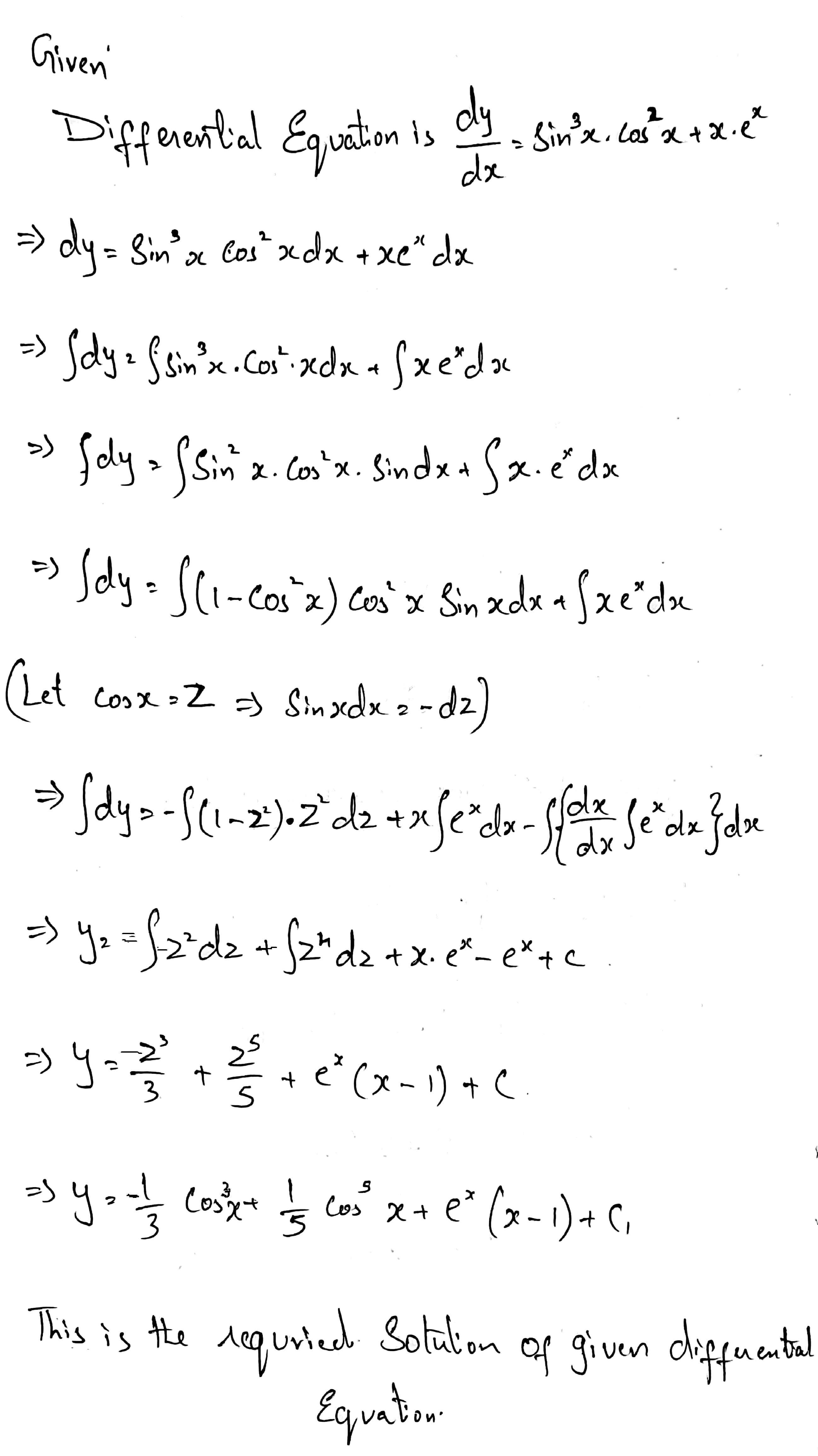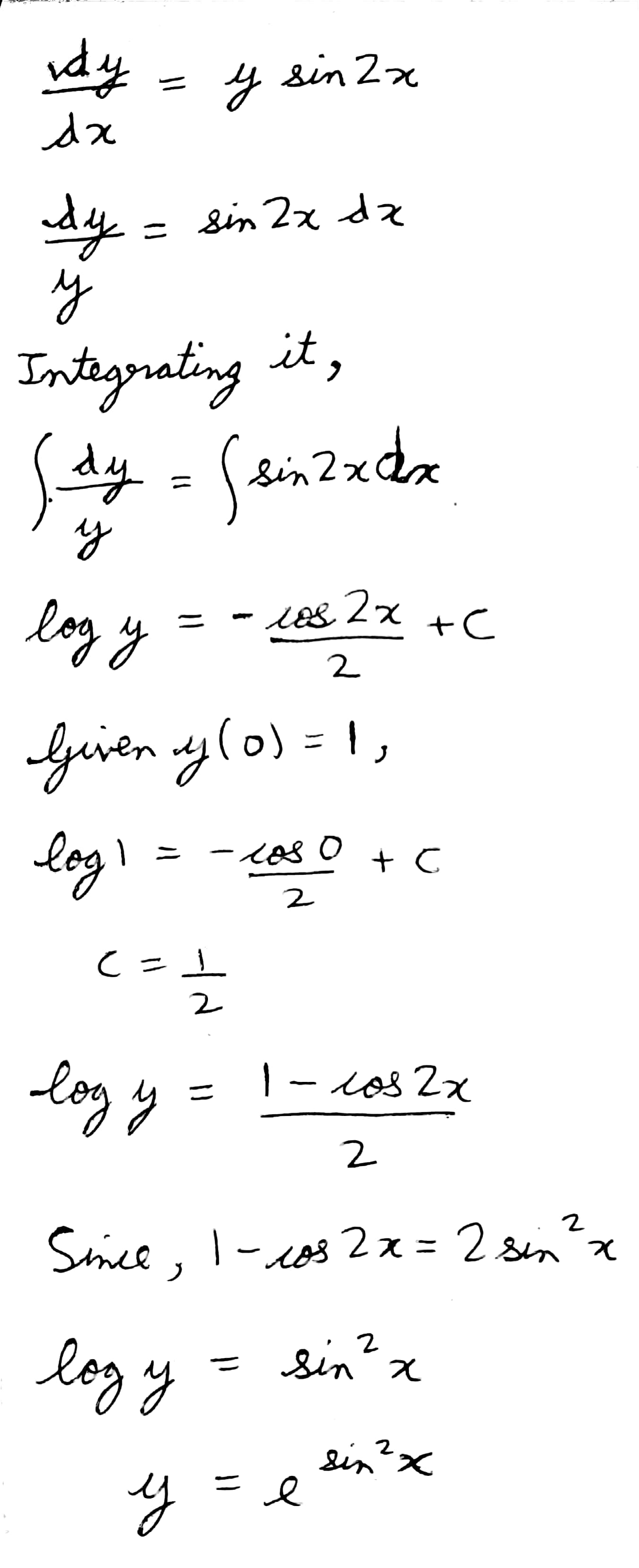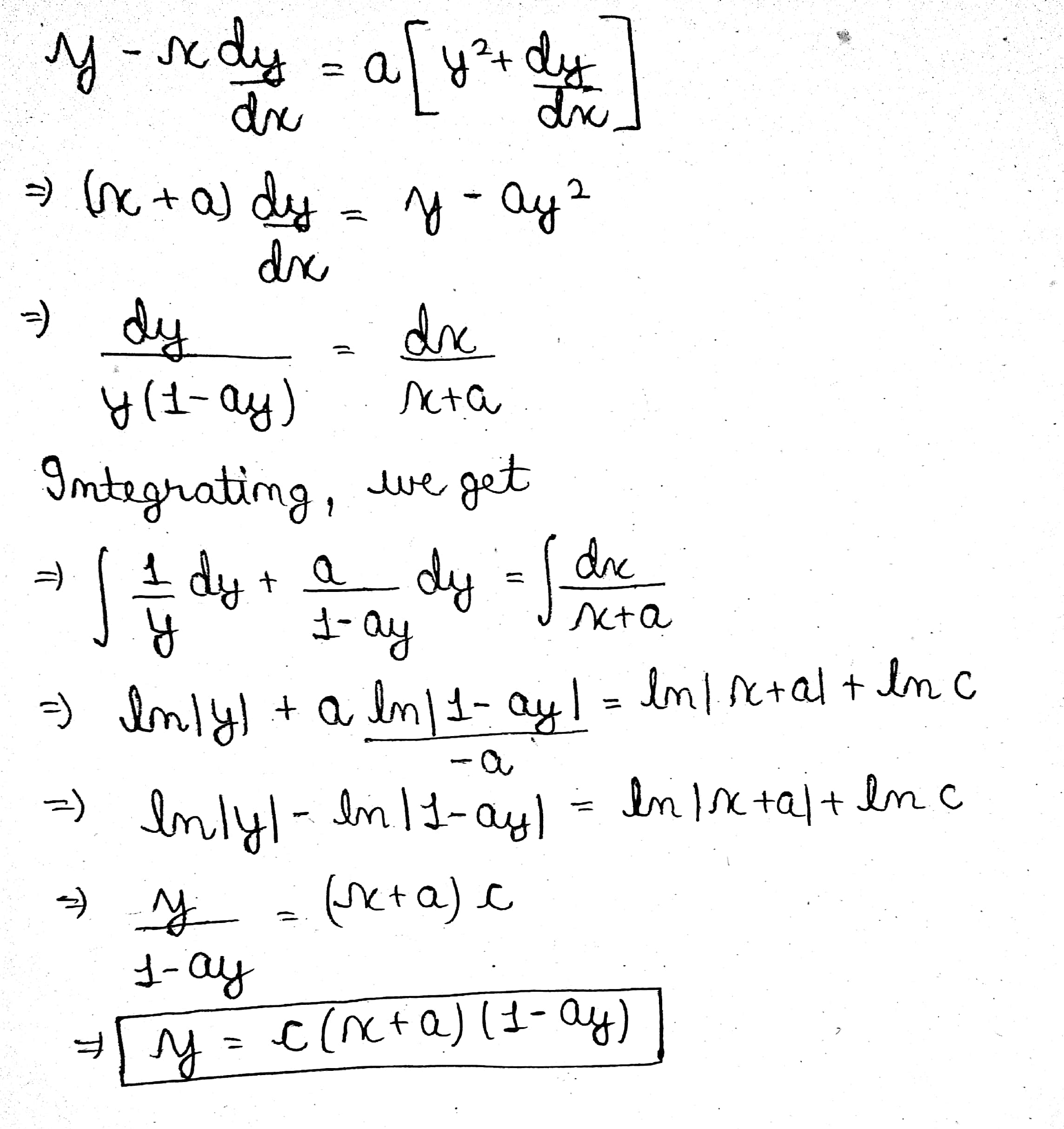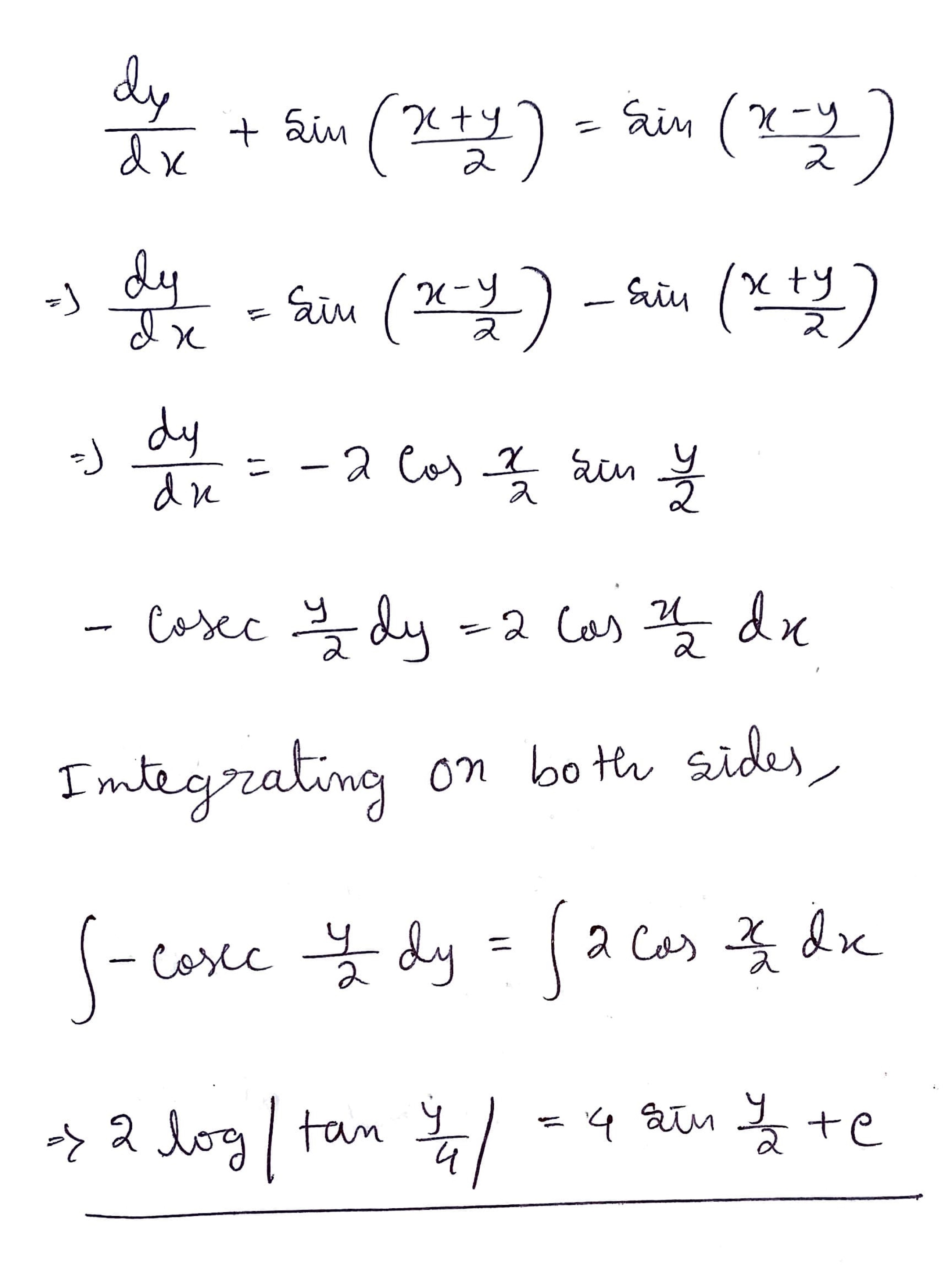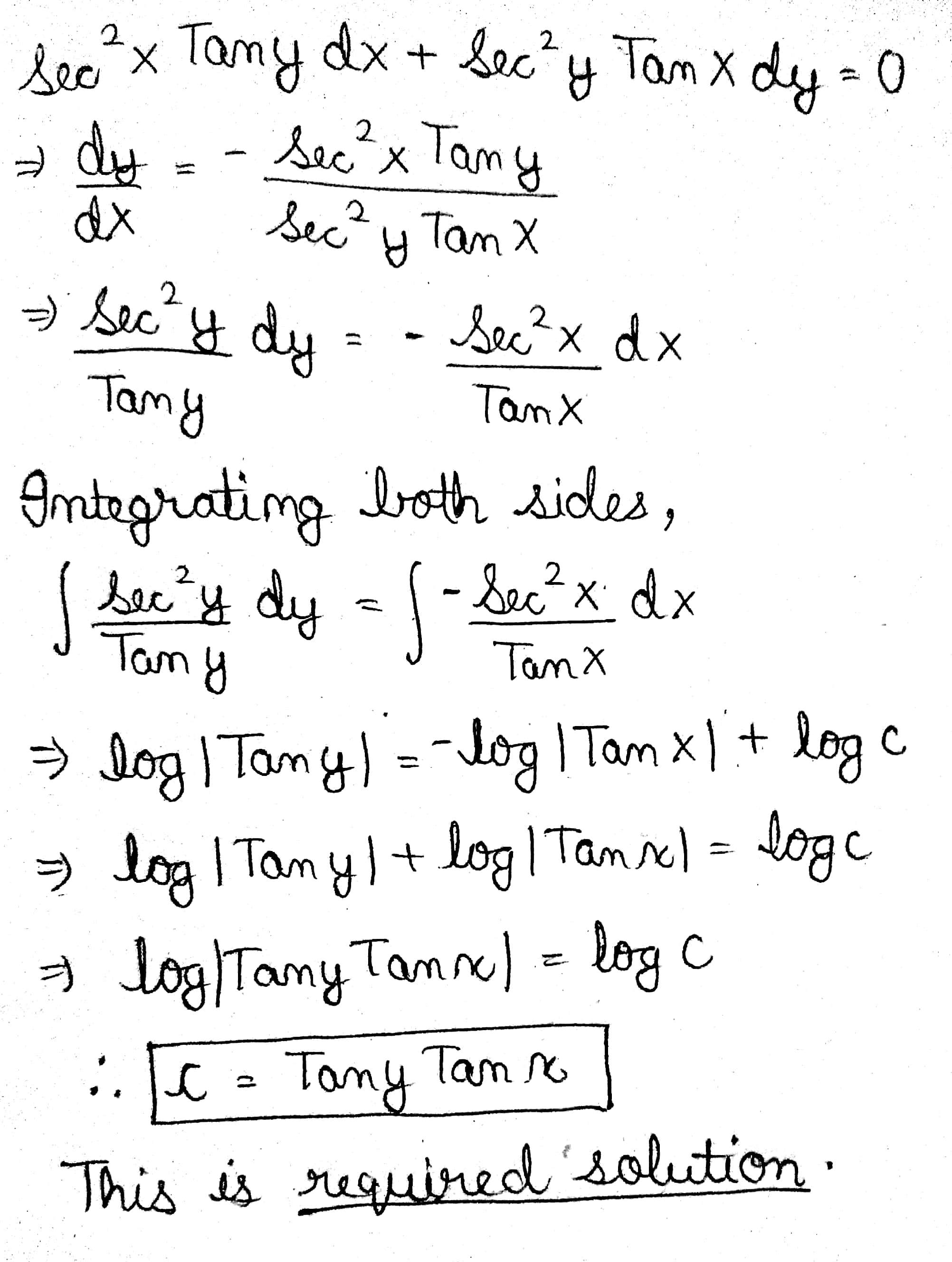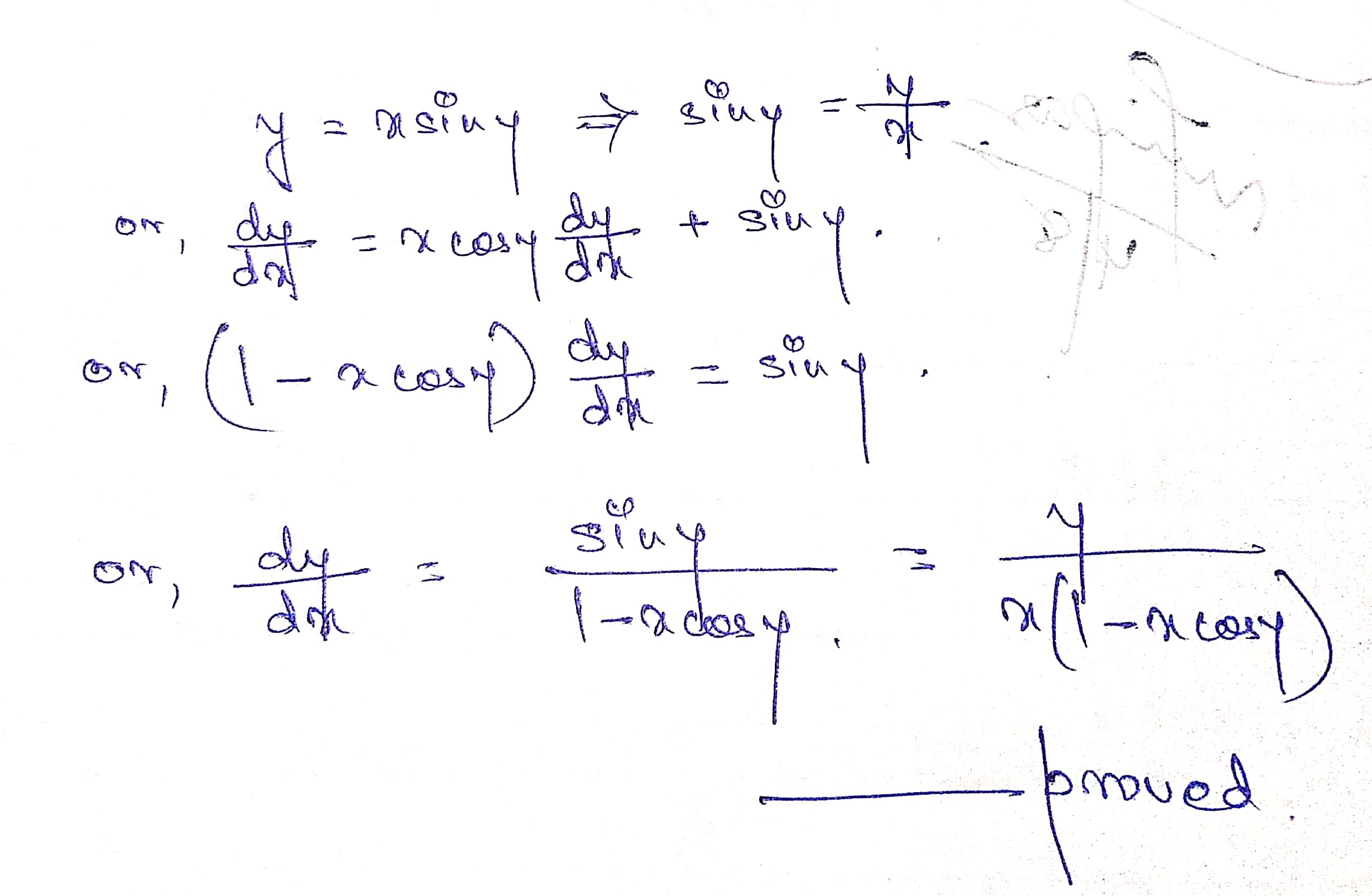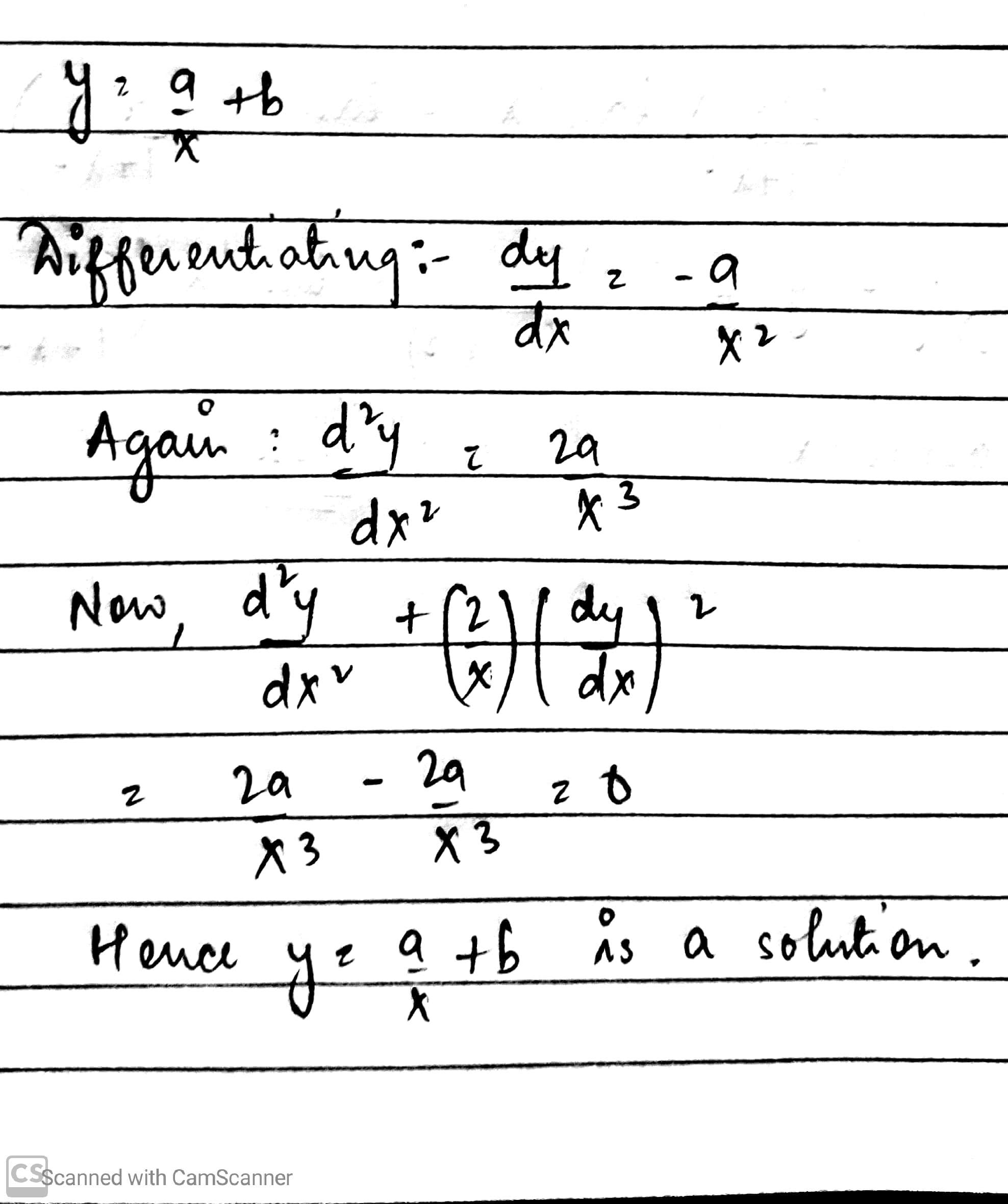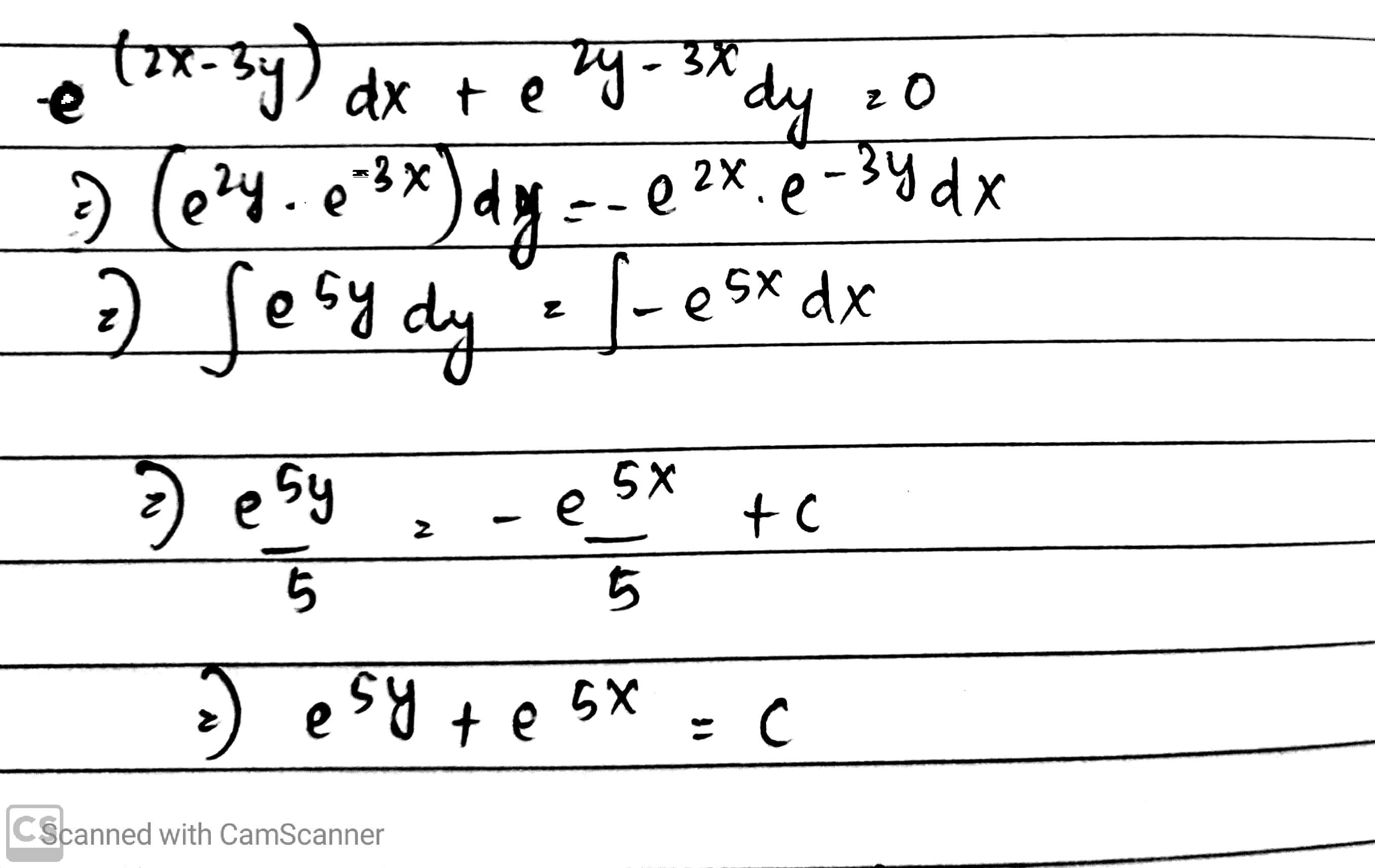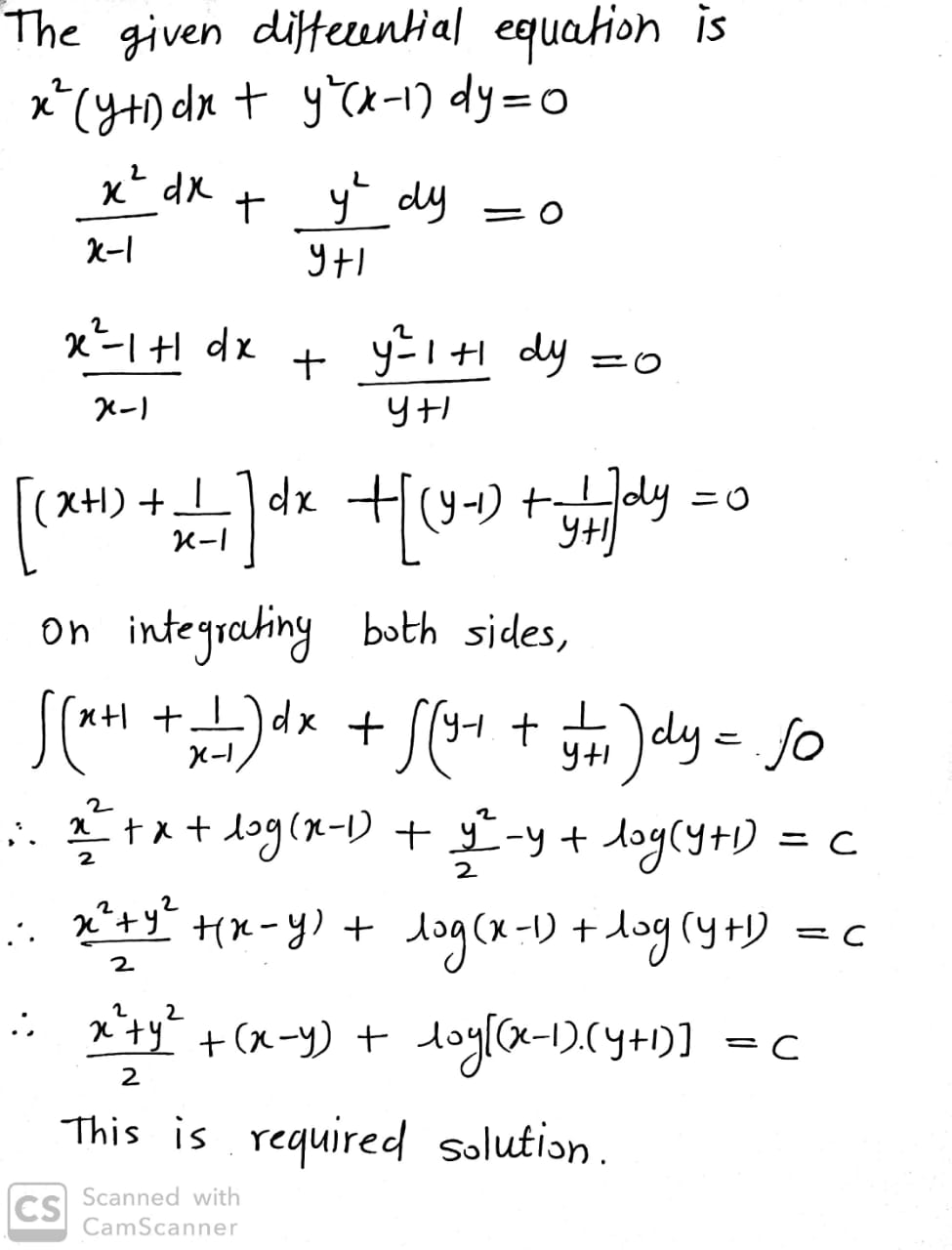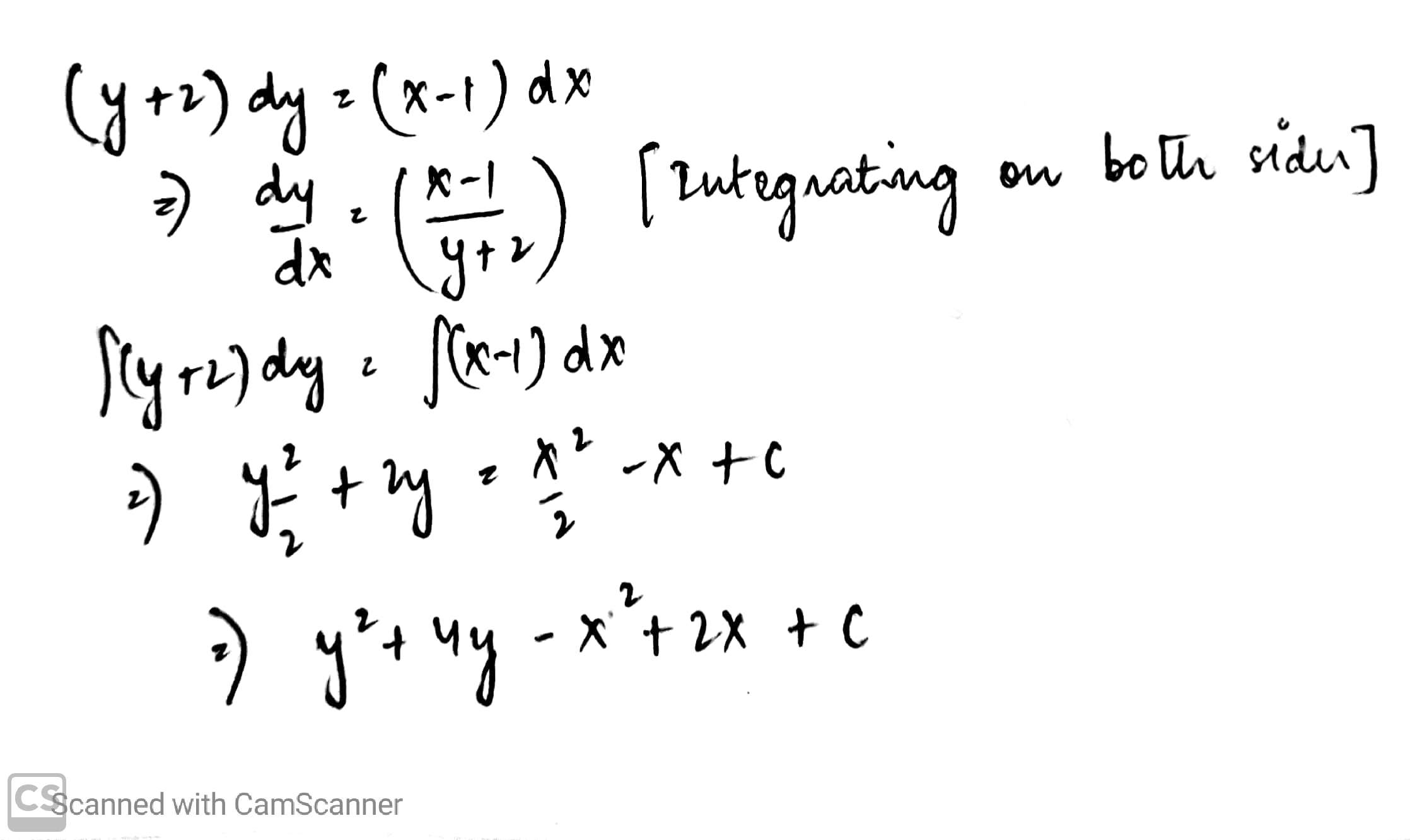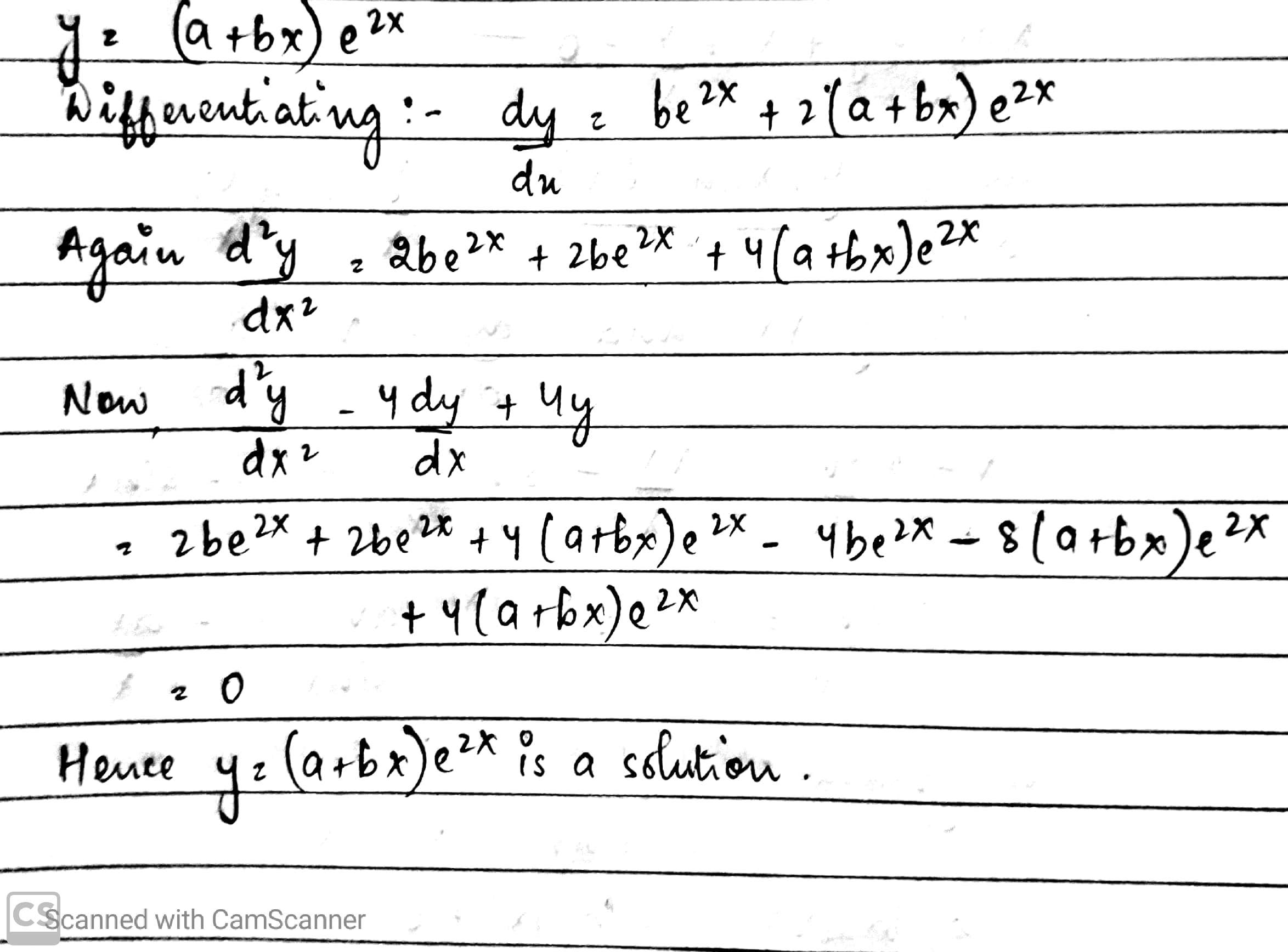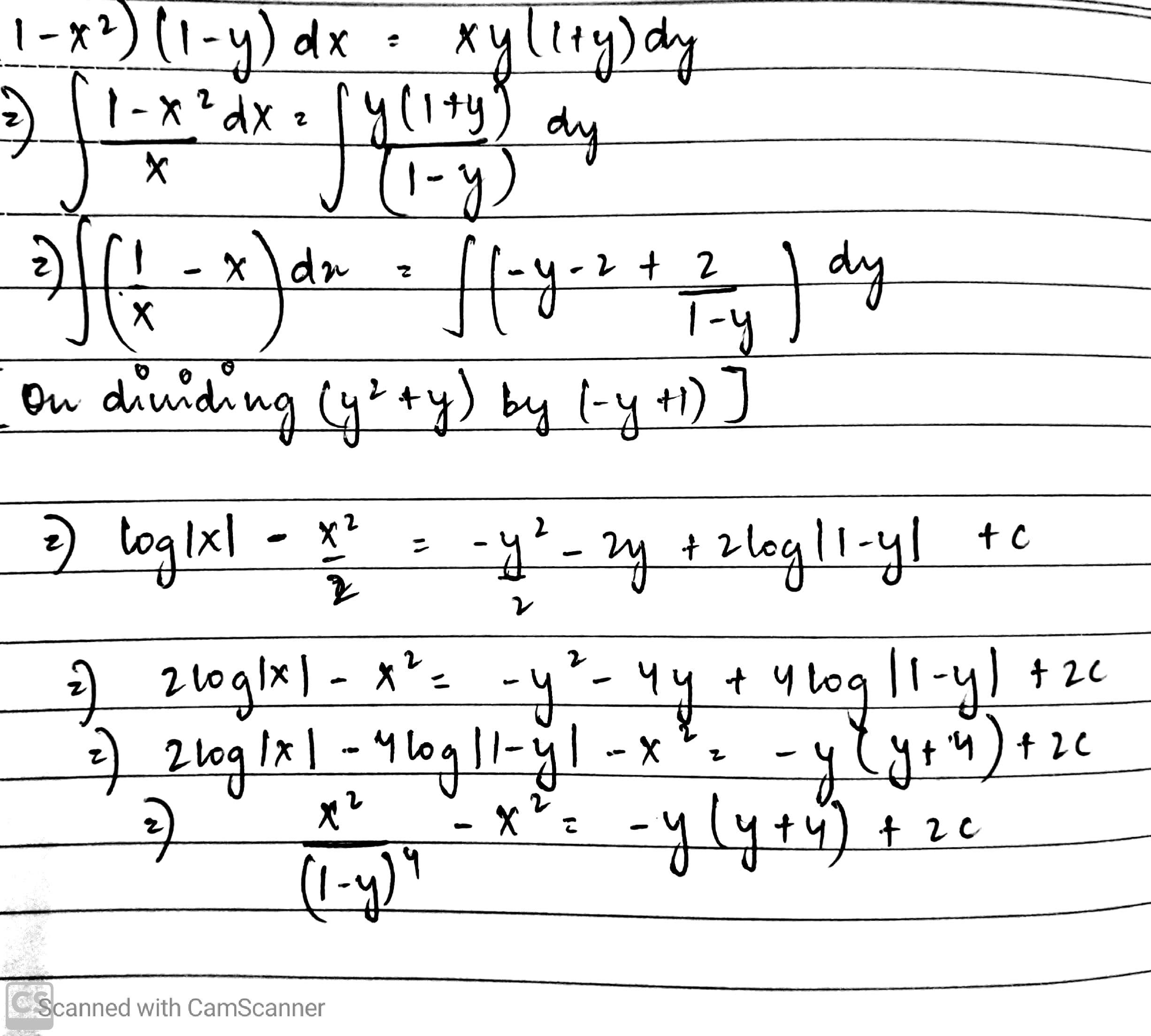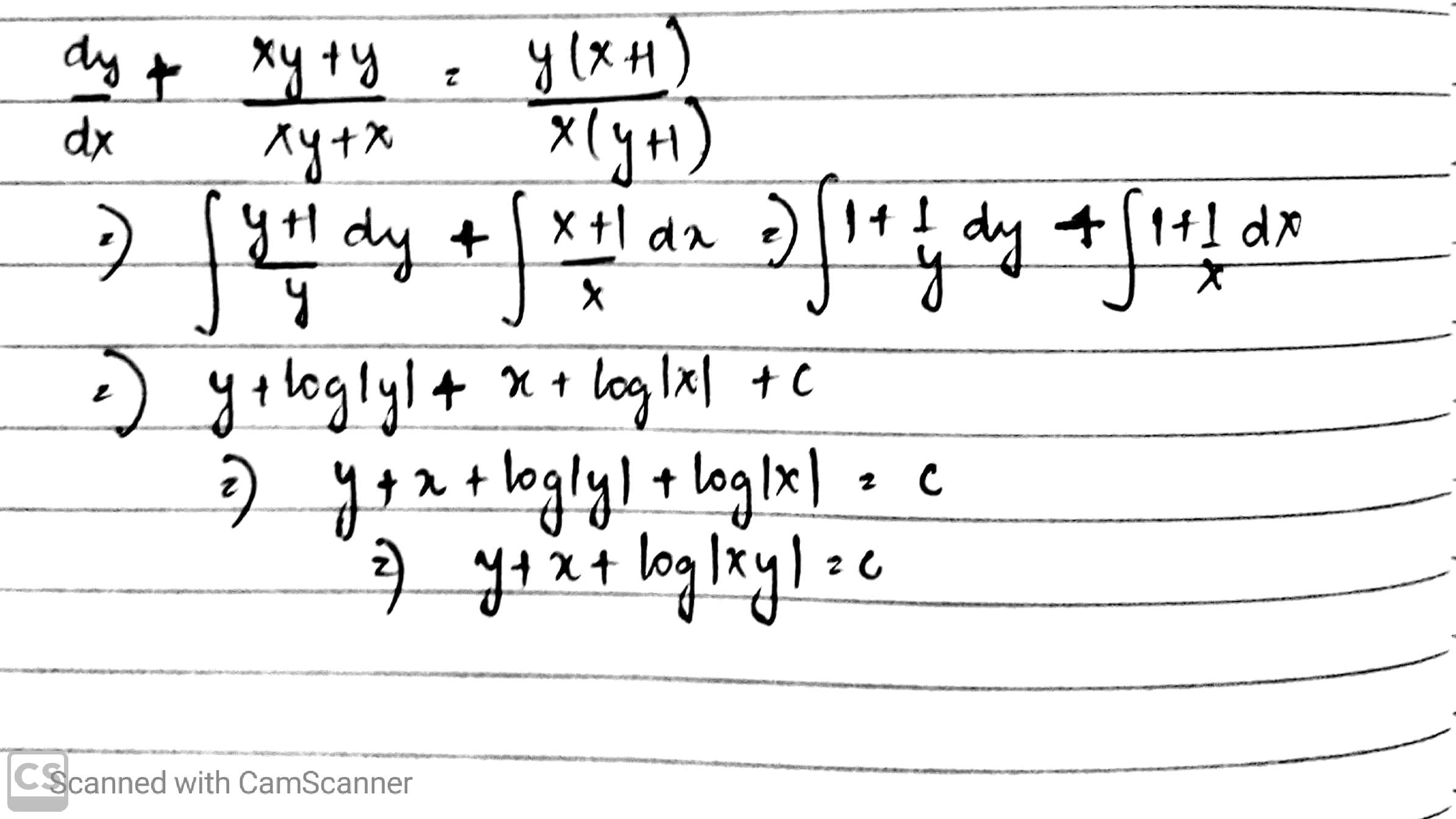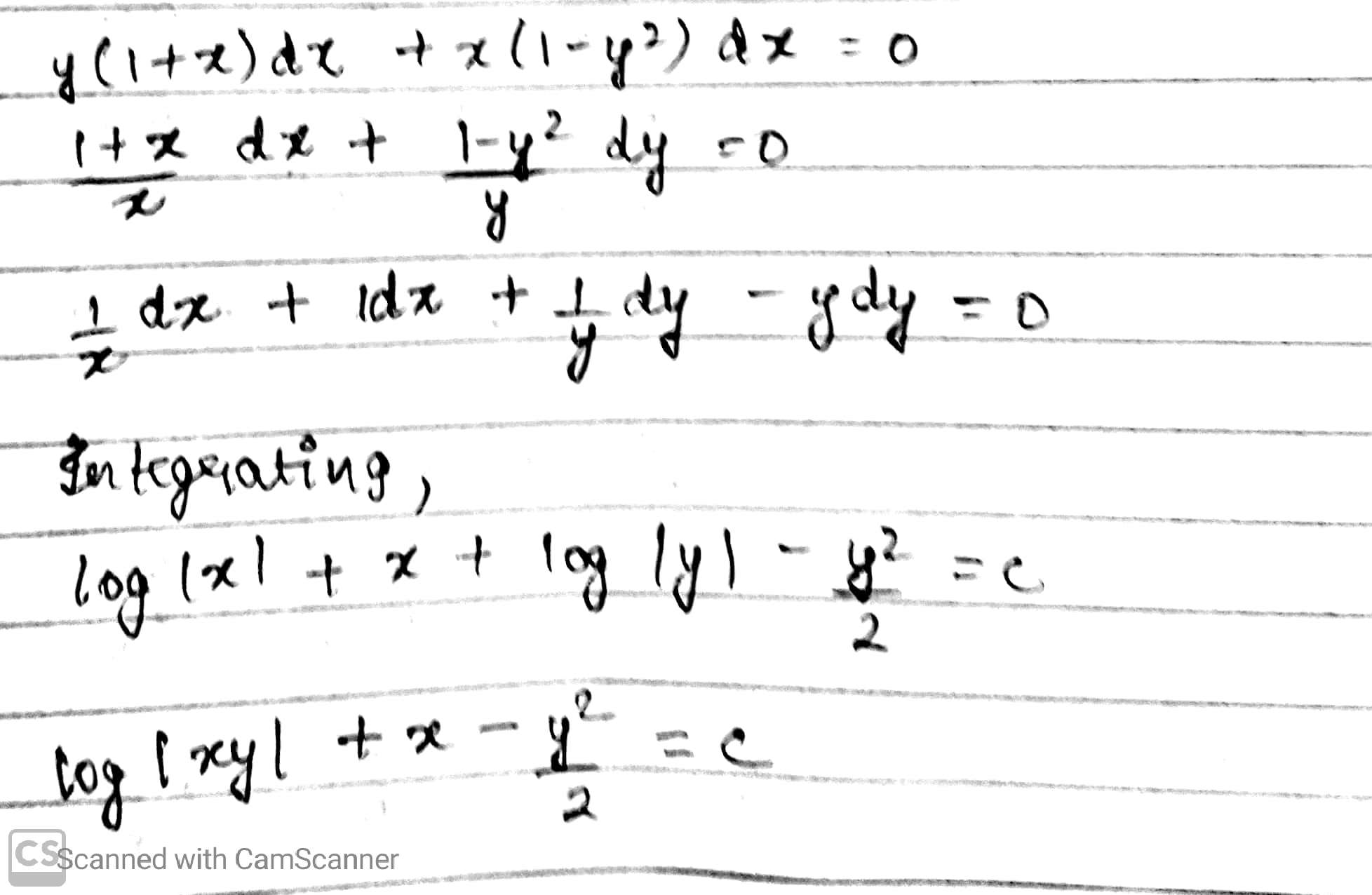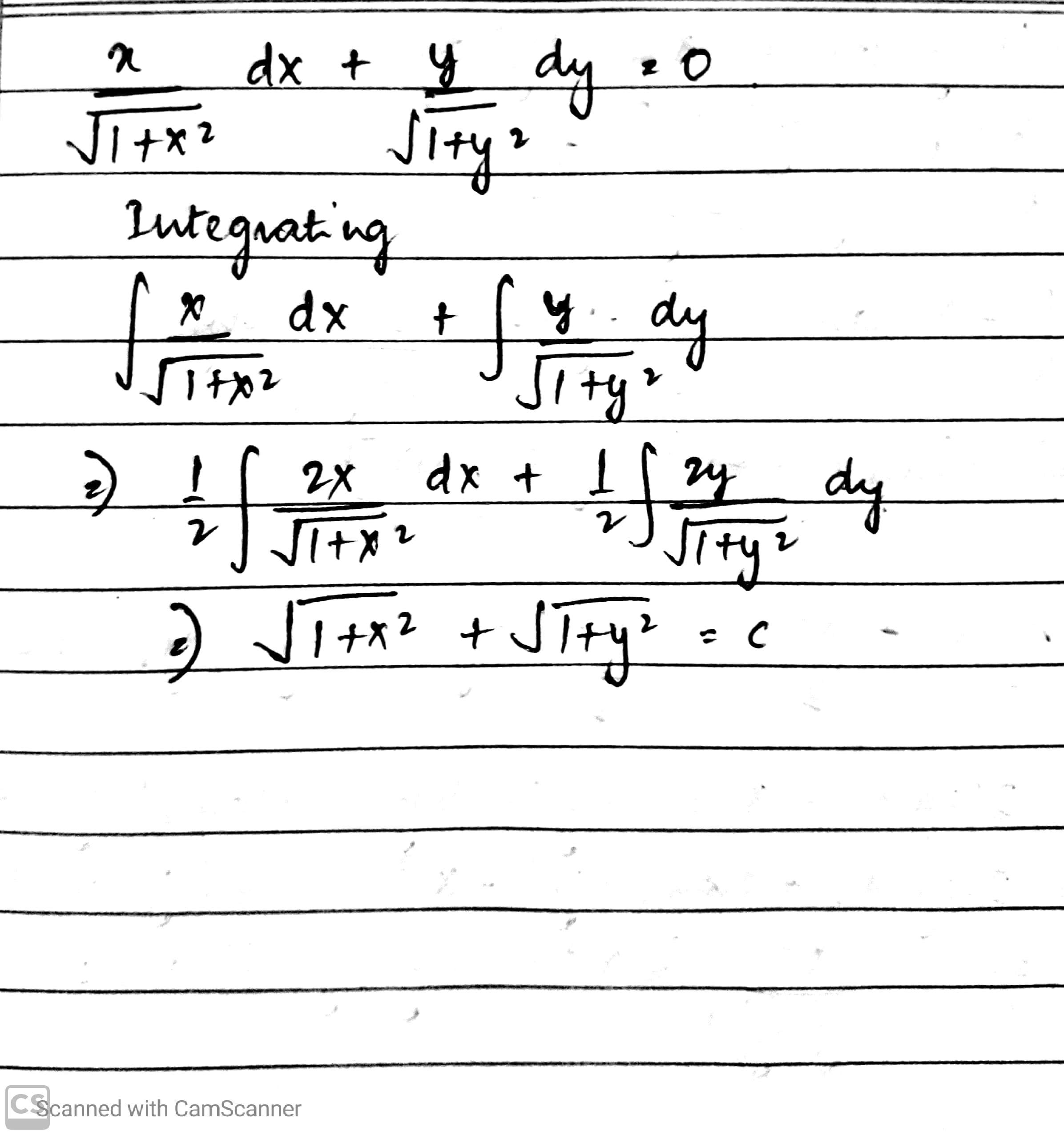Differential Equations - Class 12 Commerce Maths - Extra Questions
Find the order of the differential equations of all circles in the plane XOY which have their centres on x-axis and have give radius.
Order of differential equation of $$y=mx+c$$
Order of differential equation of $$y=mx$$
Solve the differential equation: $$(1+x^2)dy=(1+y^2)dx$$.
Solve : $$\dfrac{dy}{dx} = 1 + x + y + xy$$
The integrating factor of the differential equation $$\dfrac { dy }{ dx } -y\tan { x } =\cos { x } $$ is :
Find the particular solution of the differential equation:
$$y(1 + \log x) \dfrac {dx}{dy} - x\log x = 0$$
when $$y = e^{2}$$ and $$x = e$$.
Distinguish which one is initial valued ordinary differential equation and boundary valued ordinary differential equation:i) $$y''+2y=e^x, y(\pi)=1; y'(\pi)= 2$$i) $$y''+2y=e^x, y(0)=1; y'(1)= 1$$
Solve the following differential equation:
$$\dfrac{dy}{dx} = e^{x-y}+ x^2 e^{-y}$$
A particle is moving along the X-axis. Its acceleration at time $$t$$ is proportional to its velocity at that time. Find the differential equation of the motion of the particle.
Solve:
$$\cos y\dfrac{dy}{dx} = \sin x$$.
Solve: $$(x+y)(dx-dy)=dx+dy$$
Solve the following differential equation:
$$\log \left(\dfrac{dy}{dx}\right)= ax + by$$
Verify $$y=cx+\dfrac{1}{x}$$ is a solution of the differential equations $$y\dfrac{dy}{dx}=x\left(\dfrac{dy}{dx}\right)^2+1$$, where c is arbitrary constant.
Solve:-$$\sin x\frac{{dy}}{{dx}} + 3y = \cos x$$
Find the value of $$dy/dx$$,
$${y}^{2}=4ax$$
Solve the following Differential equation :
$$\frac{dy}{dx}=(y-4x^2)^2$$
The $$D\cdot E $$ is $$\left( \dfrac { { d }^{ 3 }y }{ d{ x }^{ 3 } } \right) ^{ \dfrac { 1 }{ 6 } }\cdot \left( \dfrac { { d }y }{ d{ x } } \right) ^{ \dfrac { 1 }{ 3 } }=5$$ Prove that: $$ \left( \dfrac { { d }^{ 3 }y }{ d{ x }^{ 3 } } \right) \cdot \left( \dfrac { { d }y }{ d{ x } } \right) ^{ 2 }=5^{ 6 }$$
find the solution of $$(e^{x}+e^{-x})\dfrac {dy}{dx}=e^{x}-e^{-x}$$
Prove that
$$y = 2e^x + 3e^2x$$ is not g.s. of differential equation $$y^2 - 3y + 2y = 0$$
If $$e^x+e^y=e^{x+y}$$, prove that $$\dfrac{dy}{dx}+e^{y-x}=0$$.
The soultion of $$3e^x \cos^2 ydx + (1- e^x)\cot ydy = 0$$ is
$$\cos{x}\dfrac{dy}{dx}-\cos{2x}=\cos{3x}$$
Find the particular sol of $$D.E. \dfrac {dy}{dx} = y\tan x;\ y = 1\ x = 0$$.
Solve $$\dfrac{dy}{dx}=x+y$$.
$$\displaystyle \frac{dy}{dx} = x+y $$
$$\displaystyle \frac{dy}{dx}+(-y) = x $$
$$\displaystyle I-F = e^{\displaystyle \int -1dx} = e^{-x} $$
$$\displaystyle h-s = ye^{-x} = \int xe^{-x}+c $$
$$\displaystyle ye^{-x} = -xe^{-x}-e^{-x} $$
$$\displaystyle ye^{-x} = e^{-x}(-1-x) $$
$$\displaystyle x+y+1 = 0 $$
(1+$$y^{2}$$ ) dx=2xy dyBy simplifying get the below expression:
$$\int \dfrac{2y}{1+y^{2}}dy=\int \dfrac{1}{x}dx$$
$$\int \dfrac{2y}{1+y^{2}}dy=\int \dfrac{1}{x}dx$$
Solve the following differentiate:
$$x (x - y)dy + y^{2}dx = 0$$.
Solve: $$ \dfrac { d y } { d x } = 1 +\dfrac {1}{ y ^ { 2 }}$$
$$F(x, y) = x^3 + y^3 + 3x^2y + 3 xy^2$$. Is this homogeneous function.
$$y-x\dfrac{dy}{dx}=0$$
$$\dfrac{dy}{dx} + y = x^{-2}$$
Verify that $$y=2\sin{3x}$$ is the solution of the D.E $$\cfrac{{d}^{2}y}{d{x}^{2}}+9y=0$$
Solve
$$\cos x \cdot \cos y\ dy-\sin x \cdot \sin y\ dx=0$$
Find the Particular solution of the differential equations
$${ x }^{ 2 }dy+\left( xy+{ y }^{ 2 } \right) dx=0;y=1$$ when ,$$x=1$$
Define particular solution of a differential equation
Solve the following differential equations.
$$y - x \dfrac{dy}{dx} = 0$$
Find $$\dfrac {dy}{dx}$$
$$\left( x ^ { 3 } - 2 y ^ { 3 } \right) d x + 3 x y ^ { 2 } d y = 0$$
Consider the differential equation,$$\dfrac{dy}{dx}+\sin y=\cos x$$.Find the order of the differential equation.
Find solution of $$e ^ { x } \tan y dx+ \left( 1 - e ^ { x } \right) \sec ^ { 2 } y d y = 0$$.
Find general solution of
$$\dfrac {dy}{dx} = 1 + x + y + xy$$
Solve the differential equation by variable separable method:$$ \left( { e }^{ y }+1 \right) \cos { x } dx+{ e }^{ y }\sin { x } dy=0.$$
Solve:$$\dfrac{dy}{dx}=1+y^2$$.
Find an expression for y given $$\dfrac{dy}{dx}=7x^{5}$$
$$\frac{dy}{dx}= 7x^{5}\Rightarrow dy = 7x^{5}dx$$
Integrating both sides, we have
$$\int dy= \int 7x^{5}dx\Rightarrow y=\frac{7x^{6}}{6}+c$$
Solve :$$\dfrac{dy}{dx}=(1+x^2)(1+y^2)$$
If $$( 2 + \sin x ) \dfrac { d y } { d x } + ( y + 1 ) \cos x =0$$ and $$y ( 0 ) = 1,$$ then $$y \left( \dfrac { \pi } { 2 } \right)$$ is equal to :
Find the general solution of the following differential equation.$$\dfrac{{dy}}{{dx}} = 1 + x + y + xy$$
Solve$$\dfrac { dy }{ dx } ={ x }^{ 2 }y+y$$
$$\dfrac{dy}{dx}=x^2y+y$$
$$\Rightarrow \dfrac{dy}{dx}=(x^2+1)y$$
$$\Rightarrow \dfrac{dy}{y}=(x^2+1)dx$$
Integrating on both sides we get
$$log y=\dfrac{x^3}{3}+x+c$$
$$\Rightarrow 3 log y=x^3+3x+3c$$
$$\Rightarrow log y^3=x^3+3x+c_1$$
where $$c_1=3c$$.
Solve :$$(x+y)^2\dfrac{dy}{dx}=a^2$$
Find the particular solution of the differential equation $$\left( 1 + x ^ { 2 } \right) \dfrac { d y } { d x } + 2 x y = \dfrac { 1 } { 1 + x ^ { 2 } }$$ given that at $$x = 1 , y = 0$$
Solve :$$\sin^{-1}\left (\dfrac{dy}{dx}\right )=x+y$$
Find general solution of D.E
$$\dfrac{{dy}}{{dx}} = {x^2}y + y$$
Solve the differential equation:$$\dfrac{d^2y}{dx^2}-y=0$$.
Solve :$$\dfrac{dy}{dx}=(1+x^2)(1+y^2)$$
Find the general solution of $$\dfrac{dy}{dx} = e^{x + y}$$.
Define a ordinary differential equation.
Solve the differential equation :$$y \log y dx-xdy=0$$
Solve :$$\dfrac{dy}{dx}=e^{x+y}$$
Solve the following differential equation.$$\dfrac{dy}{dx}=x-1$$.
Solve:
$$\dfrac{{dy}}{{dx}} = \sin x - x$$
Find the solution of $$\dfrac{dy}{dx}=2^{y-x}$$.
Define a differential equation.
Solve $$\dfrac{dy}{dx}=e^{x+y}$$
Solve the following differential equation:
$$y^2dy-x^2dx=0$$.
For the following differential equation, find the general solution.$$\dfrac{dy}{dx}=\sin x$$
Solve the following differential equation.$$\dfrac{dy}{dx}=e^x$$
For the following differential equation, find the general solution.$$x dy=dx $$.
Solve the differential equation :$$\dfrac{dy}{dx}=3x$$
Solve the following differential equation.$$\dfrac{dy}{dx}+2x=e^{3x}$$.
Solve the following differential equation.$$\dfrac{dy}{dx}+1=\sin x$$.
Show that $$y=e^x(A\cos x+B\sin x)$$ is the solution of the differential equation $$\dfrac{d^2y}{dx^2}-2\dfrac{dy}{dx}+2y=0$$.
Answer the following question in one word or one sentence or as per exact requirement of the question.
How many arbitrary constants are there in the general solution of the differential equation of order $$3$$.
Solve the following differential eqauton.$$y^2dy-x^2dx=0$$.
Find the area of the triangle with vertices at the points :
$$(-1,-8),(-2,-3) \ and \ (3,2)$$
Write the order of the differential equation associated with the primitive $$y=C_1+C_2e^x+C_3e^{-2x+C_4}$$, where $$C_1, C_2, C_3, C_4$$ are arbitrary constants.
Show that the function $$y=A\cos x+B\sin x$$ is a solution of the differential equation $$\dfrac{d^2y}{dx^2}+y=0$$.
Show that the function $$y=A\cos x+B\sin x$$ is a solution of the differential equation $$\dfrac{d^2y}{dx^2}+y=0$$.
Solve the following systems of linear equations $$ x+y= 5 $$$$y+z = 3$$$$ x+z = 4$$
Solve $$\dfrac{\ln \left ( \sec x+\tan x \right )}{\cos x}dx=\dfrac{\ln \left ( \sec y+\tan y \right )}{\cos y}dy$$
Determine whether or not the following function is homogeneous: $$f(x, y) = \sqrt{x^{2} + 2xy + 3y^{2}}$$
If homogeneous enter 1 else enter 0.
If $$y_1\, \&\, y_2$$ be solutions of the differential equation $$\displaystyle \frac{dy}{dx}\, +\, Py\, +\, Q$$, where $$P$$ & $$Q$$ are functions of $$x$$ alone and $$y_2\, =\, y_1 z$$, then $$z\, =\, 1\, -\, a\, e^{-\displaystyle {\int \frac{Q}{y_1} dx}}$$, '$$a$$' being an arbitrary constant. If you think this is true write 1 otherwise write 0.
For each of the differential equations given, find a particular solution satisfying the given condition.
1. $$\cfrac{dy}{dx}+2y\,\tan\,x=\sin x:y=0$$ when $$x=\cfrac{\pi}{3}$$
$$(1+x^2)\cfrac{dy}{dx}+2xy=\cfrac{1}{1+x^2};y=0$$ when $$x=1$$
$$\cfrac{dy}{dx}-3\,y\cot\,x=\sin\,2x; y=2$$ when $$x=\cfrac{\pi}{2}$$
Find a particular solution of the differential equation $$(x-y)(dx+dy)=dx-dy$$, given that $$y=-1$$ when $$x=0$$.
Find the equation of a curve passing through the point (0,-2) given that at any point (x, y) on the curve, the product of the slope of its tangent and $$y$$ coordinate of the point is equal to the $$x$$ coordinate of the point.
Find the particular solution of the differential equation
$$(1+e^{2x})dy+(1+y^2)e^xdx=0$$, given that $$y=1$$ when $$x=0$$.
The general solution of the differential equation $$\dfrac{dy}{dx}=e^{x+y}$$ is
Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:
$$y = e^x + 1$$ : $$y''- y = 0$$
$$y = x^2 + 2x + C$$ : $$y'- 2x -2 = 0$$
$$y = \cos \,x + C$$ : $$y' + \sin \,x = 0$$
$$y = \sqrt{1+ x^2}$$ : $$y' = \cfrac{xy}{1+x^2}$$
$$y = Ax$$ : $$xy = y (x \neq 0)$$
$$y = x\, \sin\, x$$ : $$xy = y + x \sqrt{x^2 y^2} (x \neq 0 \,and\, x > y \,or\, x < y)$$
$$xy = \log \,y + C$$ : $$y'=\cfrac{y^2}{1-xy}(xy\neq 1)$$
$$y-\cos \,y =x$$ : $$(y\, \sin \, y+\cos\, y+x)y'=y$$
$$x+y=\tan^{-1}y$$ : $$y^2y'+y^2+1=0$$
$$y=\sqrt{a^2-x^2} x \epsilon (-a, a)$$ : $$x+y\cfrac{dy}{dx} = 0(y\neq 0)$$
$$y = e^x + 1$$ : $$y''- y = 0$$
$$y = x^2 + 2x + C$$ : $$y'- 2x -2 = 0$$
$$y = \cos \,x + C$$ : $$y' + \sin \,x = 0$$
$$y = \sqrt{1+ x^2}$$ : $$y' = \cfrac{xy}{1+x^2}$$
$$y = Ax$$ : $$xy = y (x \neq 0)$$
$$y = x\, \sin\, x$$ : $$xy = y + x \sqrt{x^2 y^2} (x \neq 0 \,and\, x > y \,or\, x < y)$$
$$xy = \log \,y + C$$ : $$y'=\cfrac{y^2}{1-xy}(xy\neq 1)$$
$$y-\cos \,y =x$$ : $$(y\, \sin \, y+\cos\, y+x)y'=y$$
$$x+y=\tan^{-1}y$$ : $$y^2y'+y^2+1=0$$
$$y=\sqrt{a^2-x^2} x \epsilon (-a, a)$$ : $$x+y\cfrac{dy}{dx} = 0(y\neq 0)$$
Find the general solution of the differential equation $$\dfrac {dy}{dx} + \sqrt {\dfrac {1 - y^{2}}{1 - x^{2}}} = 0$$.
Find a particular solution of the differential equation $$(x+1)\cfrac{dy}{dx}=2\,e^{-y}-1$$, given that $$y=0$$ when $$x=0$$.
Solve the differential equation:
$$(\tan^{-1}y-x)dy = (1+y^2)dx$$.
Find a particular solution of the differential equation $$\dfrac{dy}{dx}+y\, \cot\,x=4x\, \text{cosec } x(x\neq 0)$$, given that $$y = 0$$ when $$x=\dfrac{\pi}{2}$$
If $$y = e^{m.{\cos}^{-1}x}$$, prove that :
$$(1-x^2)\dfrac{d^2y}{dx^2}-x\dfrac{dy}{dx}=m^2y$$
Solve the differential equation:
$$\log \left (\dfrac{dy}{dx} \right ) = 2x - 3y$$
Find general solution of differential equation $$\dfrac {dy}{dx} = \dfrac {1 + y^{2}}{1 + x^{2}}$$
Find general solution of differential equation $$\dfrac {dy}{dx} + y = 1 (y\neq 1)$$.
Solve the differential equation: $$y \dfrac {dy}{dx} = \dfrac {x}{e^{y}}$$
Find the general solution of differential equation $$\cfrac { dy }{ dx } +\sqrt { \cfrac { 1-{ y }^{ 2 } }{ 1-{ x }^{ 2 } } } =0$$; $$x\ne 1$$.
Find $$y = (sin^{-1} x)^2$$, then show that $$(1- x^2) \dfrac{d^2 y}{dx^2} - x \dfrac{dy}{dx} = 2$$.
Find the general solution of the differential equation $$\dfrac{dy}{dx} - \dfrac{y}{x} = 0$$.
Solve the differential equation $$x\ dy = y\ dx + \sqrt {x^{2} + y^{2}}dx$$
Solve: $$(x^2 + y^2)dx + (2xy)dy = 0$$
Find a particular solution of the differential equation $$\left( 1+{ x }^{ 2 } \right) dy+2xydx=\cot { x } dx$$, given that $$y=0$$ if $$x=\cfrac { \pi }{ 2 } $$
Solve the differential equation: $$(xy^{2} + x)dx + (yx^{2} + y)dy = 0$$
If $$y=\sin(2\sin^{-1}x)$$, then prove that: $$\displaystyle\frac{dy}{dx}=2\sqrt{\displaystyle\frac{1-y^2}{1-x^2}}$$.
Solve the Differential Equation, $$(1 + x) y dx + (1 - y) x dy = 0$$.
Solve the differential equation $$\left( 1+{ x }^{ 2 } \right) \dfrac { dy }{ dx } +y={ e }^{ \tan ^{ -1 }{ x } }$$.
Find the general solution of the differential equation
$$e^{x} \tan y dx + (1 - e^{x}) \sec^{2} y\ dy = 0$$.
Solve: $$\dfrac {dy}{dx} =1-xy +y -x$$
Solve: $$\displaystyle \frac{dy}{dx} = \cos^3 x \sin^2 x + x \sqrt{2x + 1}$$
Find the particular solution of the differential equation $$\displaystyle\dfrac{dy}{dx}+2y\tan x=\sin x$$, given that $$y=0$$ when $$x=\displaystyle\dfrac{\pi}{3}$$.
Solve the differential equation $$\cfrac { dy }{ dx } =\cfrac { y+\sqrt { { x }^{ 2 }+{ y }^{ 2 } } }{ x } $$
Solve the differential equation:
$$(1 + e^{2x})dy + (1 + y^{2})e^{x}dx = 0$$.
Solve the differential equation $${ (x+y) }^{ 2 }\cfrac { dy }{ dx } ={ a }^{ 2 }\quad $$
Find the general solution of the differential equation $$x\dfrac {dy}{dx} + 2y = x^{2}\log x$$.
Solve the differential equation $$\cos ^{ 2 }{ x } \cfrac { dy }{ dx } +y=\tan { x } $$
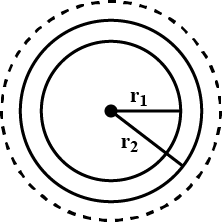
Find the order of the differential equation of the family of all the circles with their centres at the origin.
$$ \rightarrow $$ For the family of circle general equation is $$ (x-h)^2 + (y-k)^2 = r^2 $$
Here, $$(h,k) = (0,0)$$ as their centres are at origin.
$$ \cdot $$ For circle $$1$$ lets assume radius$$r_1$$ and we know centre is $$(0,0).$$
$$ \rightarrow $$ Let us assume another circle $$2$$ with radius $$r_2$$ and which has center $$(0,0)$$
$$ \cdot $$ Similarly many concentric circles will be formed.
(Refer the image)
For circle $$1$$ , $$x^2 + y^2 = r_1^2 $$
For circle $$2 , x^2 + y^2 = r_2^2 $$
$$ \rightarrow $$ The differential equation we will find after differentiating any above equation w.r.t. $$x$$ so we get :
$$ \therefore x^2 + y^2 = r_1^2 $$
$$ \therefore 2x + 2y = \dfrac {dy}{dx} = 0 $$
$$ \therefore \dfrac {dy}{dx} = \left( \dfrac {-x}{y} \right) $$
Therefore, the order of differential equation is $$1.$$
Show that $$3e^x \tan y \ dx + (1 - e^x) \sec^2 y \ dy = 0$$
The general solution of differential equation $$\dfrac{dy}{dx}=\dfrac{x+y}{x-y} $$is
Form the different equations of all concentric circles at the origin.
Solve $$x\cos ydy=(xe^x In x+e^x)dx$$
Solve:$$\dfrac{dy}{dx}=\dfrac{y+x}{y-x}$$.
Solve: $$x\left( x-1 \right) \cfrac { dy }{ dx } -\left( x-2 \right) y={ x }^{ 3 }\left( 2x-1 \right)$$
Solve:
$$y-x\dfrac{dy}{dx}=a\left(y^2+\dfrac{dy}{dx}\right)$$
Solve:$$\dfrac{dy}{dx}=\dfrac{x^2+2}{y}$$.
Solve:$$\dfrac{dy}{dx}=\dfrac{x-y}{x+1}$$.
Solve: $$\frac{dy}{dx} = \frac{x(2y -x)}{x(2y +x)}$$, if $$y =1$$ when $$x= 1$$
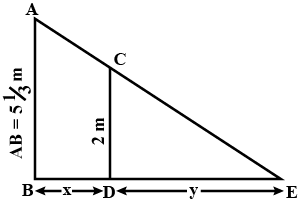
A man, $$2m$$ tall, walks ar the rate of $$1\frac{2}{3}m/s$$ towards a street light which is $$5\frac{1}{3}m$$ above the ground. At what rates is the tip of his shadow moving ? At what is the length of the shadow changing when he is $$3\dfrac{1}{3}m$$ from the base of the light?
$$\dfrac{dx}{dt}=1\dfrac{2}{3}m/s$$
From figure it is clear $$\triangle ABE$$ and $$\triangle CDE$$ are similar
$$\therefore$$ $$\dfrac{AB}{CD}=\dfrac{BE}{DE}=\dfrac{AE}{CE}$$ ----- ( 1 )
$$AB=5\dfrac{1}{3}m$$ and $$CD=2m$$ [ Given ]
Let $$BD=x$$ and $$DE=y$$
$$\Rightarrow$$ $$AE=x+y$$
Now, substituting the values we get,
$$\dfrac{5\dfrac{1}{3}}{2}=\dfrac{x+y}{y}$$
$$\Rightarrow$$ $$\dfrac{16}{6}=\dfrac{x+y}{y}$$
$$\Rightarrow$$ $$16y=6x+6y$$
$$\Rightarrow$$ $$10y=6x$$ ------ ( 2 )
Differentiating w.r.t we get,
$$10\dfrac{dy}{dt}=6\dfrac{dx}{dt},$$ but $$\dfrac{dx}{dt}=1\dfrac{2}{3}=\dfrac{5}{3}$$
$$\Rightarrow$$ $$\dfrac{dy}{dx}=\dfrac{6}{10}\times \dfrac{5}{3}$$
$$\Rightarrow$$ $$\dfrac{dy}{dx}=1$$
Hence, the shadow increases at the rate of $$1m/s.$$
$$AB=5\dfrac{1}{3}m$$ and $$CD=2m$$
To find the rate at which the tip of the shadow $$E$$ moves,
we have to find the rate at which $$BE=x+y$$ moves.
Let $$BE=x+y=p$$
From ( 1 ),
$$\dfrac{AB}{CD}=\dfrac{BE}{DE}$$
$$\Rightarrow$$ $$\dfrac{8}{3}=\dfrac{x+y}{y}=\dfrac{p}{y}$$
$$\Rightarrow$$ $$\dfrac{8}{3}y=p$$
Differentiating w.r.t $$t$$ bothe sides we get,
$$\Rightarrow$$ $$\dfrac{8}{3}\dfrac{dy}{dt}=\dfrac{dp}{dt}$$
But $$\dfrac{dy}{dt}=1$$
$$\therefore$$ $$\dfrac{dp}{dt}=\dfrac{8}{3}$$
The rate at which the tip of the shadow moves is $$\dfrac{8}{3}m/s$$
The solution of the differential equation $$x\dfrac{{dy}}{{dx}} = - \dfrac{y}{2} - \dfrac{{\sin 2x}}{{2y}}$$ is given by
$$x\sqrt {1+y} +y\sqrt {1+x}=0$$, prove that $$\dfrac { dy }{ dx } =\dfrac { -1 }{ { \left( 1+x \right) }^{ 2 } }$$
Solve $$e^{y}(x+1)=1$$
Find the solution of $$\dfrac{dy}{dx} = 1 +y $$.
$$y - x\frac{{dy}}{{dx}} = 5\left( {{y^2} + \frac{{dy}}{{dx}}} \right)$$
$$\dfrac{dy}{dx} + \dfrac{y}{x} = xy^2\sin x$$
Solve:
$$x^{e}+e^{x}+e^{e}$$
Find the general solution of the differential equation $$\left( {1 + {y^2}} \right)+\left( {x - {e^{\text{tan} ^{ - 1}y}}} \right)\frac{{dy}}{{dx}} = 0$$
Solve $$(x^{3} + x^{2} + x + 1)\dfrac {dy}{dx} = 2x^{2} + x$$ if the value of $$y = 1$$ when $$x = 0$$.
Find the order and degree of
$$y''' + y^2 + e^{y^1} = 0$$
Integrate for y :$$(x^3+x^2+x+1)\dfrac{dy}{dx}=2x^2+x$$.
Solve: $$ydx-xdy=xydx$$.
$$x^2(y+1)dx+y^2(x-1)dy=0$$.
If $$y=y(x)$$ and $$\cfrac { 2+\sin { x } }{ y+1 } \left( \cfrac { dy }{ dx } \right) =-\cos { x } ,y(0)=1$$, then $$y\left( \cfrac { \pi }{ 2 } \right) $$ equals:
The solution of the equation $$(2y-1)dx-(2x+3)dy=0$$ is
Solve : $$\dfrac{dy}{dx} + \dfrac{3x^2}{1 + x^3} y = \dfrac{1 + x^2}{1 + x^3}$$
Solve: $$(1+y^2)\dfrac{dx}{dy}+x =e^{-\tan^{-1}}y$$
$$\dfrac{{dy}}{{dx}} = {x^2}\left( {x - 2} \right)$$Given $$y=2$$; when $$x=0$$.
Solve the differential equation $$({e^x} + 1)ydy + (y + 1)dx = 0$$
Solve: $$\dfrac{{dy}}{{dx}} + 2y = \sin x$$
The solution of $$\left( {1 + {x^2}} \right)\frac{{dy}}{{dx}} + xy = 5x$$
If $$dx + dy = (x+y)(dx-dy) \Rightarrow y+ \log (x+y)=x+C$$ is the solution of differential equation
Show that the function $$y=e^{3x}(A+Bx)$$ is a solution of the differential equation $$\dfrac{d^2y}{dx^2}-6\dfrac{dy}{dx}+9y=0$$.
Show that the function $$y=Ax+\dfrac{B}{x}$$ is a solution of the differential equation $$x^2\dfrac{d^2y}{dx^2}+x\dfrac{dy}{dx}-y=0$$.
$$(x^3+x^2+x+1)\dfrac{dy}{dx}=2x^2+x; y=1$$ when $$x=0$$.
Solve:
$$\left( {2xy + {y^2}} \right)dx + \left( {{x^2} + xy} \right)dy = 0,y\left( 1 \right) = 1$$
For each of the differential equations, find the general solution:
1.$$\dfrac{dy}{dx} = \dfrac{1- cos x}{1 + cos x}$$
2.$$\dfrac{dy}{dx} = \sqrt{4 - y^2} (-2 < y < 2)$$
Solve the differential equation
$$xy\dfrac { dy }{ dx } =\dfrac { 1+{ y }^{ 2 } }{ 1+{ x }^{ 2 } } \left( 1+x+{ x }^{ 2 } \right) $$
Verify that $$xy = \log y + c$$ is a solution of the differential equation $$(xy - 1) \dfrac {dy}{dx} + y^{2} = 0$$.
Solve:
$$\dfrac{\mathrm{d} y}{\mathrm{d} x}=1+e^{x-y}$$
Solve $$(x+y)^{2}\dfrac {dy}{dx}=a^{2}$$
Solve the following differential equation :$$(1+y+x^2y)dx+(x+x^3)dy=0$$
Find $$\dfrac {dy}{dx}$$ if $$y = x^{2} - 2^{\sin x}$$.
$$\dfrac{dy}{dx} + \dfrac{y}{(1-x)} = 1 - x$$
$$\displaystyle \frac{dy}{dx}+\frac{y}{1-x} = 1-x $$
$$\displaystyle I.F e^{\int pdx} = e^{\int \dfrac{1}{1-x}}dx = e^{log|1-x|} $$
$$\displaystyle = \frac{1}{1-x} $$
G.1 $$\displaystyle = \frac{y}{1-x} = \int (1-x)\frac{1}{(1-x)}dx $$
$$\displaystyle \frac{y}{1-x} = x+c $$
$$\displaystyle y = x(1-x) $$
$$x(x-1) \dfrac{dy}{dx} - (x-2)y = x^2 (2x - 1)$$
Solve: $$(1 +x) \dfrac{dy}{dx} - xy = 1 - x$$
$$\displaystyle (1 +x) \dfrac{dy}{dx} - xy = 1 - x$$
$$\displaystyle \frac{dy}{dx}+(\frac{-x}{1+x})y = \frac{1-x}{1+x} $$
$$\displaystyle \int pdx = \int \frac{-x}{1+x} = -\int \frac{1+x-1}{1+x}dx $$
$$\displaystyle = -\int 1-\frac{1}{1+x}dx $$
$$\displaystyle = -x+log|1+x|dx $$
$$\displaystyle I.F e^{\int pdx} = e^{log(1+x)-x} = \frac{1+x}{e^{x}} $$
$$\displaystyle 4.5 y .\frac{1+x}{e^{x}} = \int \frac{1-x}{e^{x}} $$
$$\displaystyle y\frac{(1+x)}{e^{x}} = \int e^{-x}(1-x) $$
$$\displaystyle y(1+x) = e^{x}c^{-x}(+x) $$
$$\displaystyle y (1+x) = x $$
$$(x+y+1)\dfrac{dy}{dx} = 1$$
$$(x+y+1)\dfrac{dy}{dx} = 1$$
$$(x+y+1) = \dfrac{dx}{dy} $$
Put $$ x+y = t $$
$$ \dfrac{dx}{dy}+1 = \dfrac{dt}{dy} $$
$$ \Rightarrow (t+1) = \dfrac{dt}{dy}-1 $$
$$ \Rightarrow dy = \dfrac{1}{t+2}dt $$
$$ \Rightarrow y = log|1+2| $$
$$ \Rightarrow y = log|x+y+2| $$
$$x(1-x^2) dy + (2x^2y - y -ax^3) dx = 0$$
Solve:
$$x\dfrac{dy}{dx}=y-x\tan\dfrac{y}{x}$$
Show that the differential equation is homogenous & solve it $$ydx+xlog\left(\dfrac{y}{x}\right)dy-2xdy=0$$.
Solve the following differential equations
(i)$$\dfrac{dy}{dx}+y=e^{-x}$$
$$\displaystyle \frac{dy}{dx}+y = e^{-x} $$
$$\displaystyle I.F e^{\displaystyle\int dx} = e^{x} $$
G-1 $$\displaystyle ye^{x} = \int e^{-x}e^{x} $$
$$\displaystyle ye^{x} =\int dx $$
$$\displaystyle ye^{x}=x+c $$
Solve $$\dfrac{dy}{dx}+\dfrac{2y}{x}=e^x$$.
$$\displaystyle \frac{dy}{dx}+(\dfrac{2}{x})y = e^{x} $$
$$\displaystyle I.F = e^{\displaystyle \int \dfrac{2}{x}}dx = e^{2logx} = x^{2} $$
$$\displaystyle yx^{2} = \int e^{x}x^{2} $$
$$\displaystyle x^{2}y = x^{2}e^{x}-\int 2xe^{x} $$
$$\displaystyle = x^{2}e^{x}-2xe^{x}+2e^{x}+c $$
$$2\ xy\dfrac {dy}{dx}={x}^{2}+{y}^{2}$$
Find the particular solution of the differential equation $$\left( x-y \right) \frac { dy }{ dx } =\left( x+2y \right) $$, Given that $$y=0$$ when $$x=1$$.
Solve the following differential equation:
$$x\cos { ydy } =\left( { xe }^{ x }\log { x+{ e }^{ x } } \right) dx$$
$$ x\, cos\, y \,dy = (xe^x logx+e^x) dx $$
$$ \displaystyle \int cos\,y\, dy = \int \dfrac{xe^{x}logx+e^{x}}{x}dx$$
$$ \displaystyle = \int e^{x}logx dx+\int \dfrac{e^{x}dx}{x}$$
$$ \displaystyle = \int e^{x} logx dx$$
$$ \displaystyle = e^{x}logx = \int \dfrac{e^{x}}{x}dx$$
$$ \displaystyle siny = e^{x} log x - \int \dfrac{e^x}{x}dx+\int \dfrac{e^x}{x} dx $$
$$ \therefore e^x logx = siny+c $$
$$x\dfrac {dy}{dx}=x+y$$
$$x\dfrac{dy}{dx}= x+y$$
Dividing x both sides
$$\Rightarrow \dfrac{dy}{dx}-\dfrac{y}{x}= \dfrac{x}{x}$$
$$\Rightarrow \dfrac{dy}{dx}-\dfrac{1}{x}.y=1$$
From of $$\dfrac{dy}{dx}+P_{y}=Q$$
$$P=\dfrac{-1}{x},Q=1$$
$$\therefore 1F= e^{\displaystyle -\dfrac{1}{2}d}$$
$$=e^{-log x}$$
$$=(\dfrac{1}{x})$$
$$\displaystyle \therefore (y)(1F)= \int Q.(1F)dx+c$$
$$\displaystyle y. \frac{1}{x} = \int 1(\dfrac{1}{x})dx+c$$
$$\dfrac{y}{x}= log\,x+e$$
$$y = xlogx+cx$$
or $$y= x\, log x+c_{2}$$
Solve:$$\left( { 3x }^{ 2 }+{ y }^{ 2 } \right) dy+\left( { x }^{ 2 }+{ 3y }^{ 2 } \right) dx=0$$
Solve the following differential equation.
$$\dfrac{dy}{dx}=e^{3x-2y}+x^{2}e^{-2y}$$
Show that $$y=e^{m\sin^{-1}x}$$ is a solution of the differential equation $$(1-x^{2})y_{2}-xy_{1}-m^{2}y=0$$.
$$ \displaystyle y = e^{m\,sin^{1}x} $$
$$ \displaystyle {y}' = m\,sin^{1}x $$ $$ e^{m\,sin^{-1}x} $$ $$ -\frac{1}{\sqrt{1-x^{2}}} $$
$$ \displaystyle {y}''= \frac{(\sqrt{1-x^{2}})(\frac{m^{2}e^{m\,sin^{-1}x}}{\sqrt{1-x^{2}}})-me^{m\,sin^{-1}}(\frac{1}{2})(1-x^{2})^{-1/2}(-2x)}{(\sqrt{1-x^{2}})^{2}} $$
$$ \displaystyle = \frac{m^{2}e^{m\,sin^{-1}x}+\frac{m\,x\,e^{sin^{-1}x}}{\sqrt{1-x^{2}}}}{1-x^{2}} $$
$$\displaystyle = \frac{m^{2}y+n{y}'}{1-x^{2}} $$
$$ \displaystyle (1-x^{2}){y}''= m^{2}y+x{y}' $$
$$ \displaystyle (1-x^{2}){y}''-m^{2}y-xy = 0 $$
Find solution for $$DE \Rightarrow \left (\dfrac {dy}{dx}\right )^{2} - y \dfrac {dy}{dx} + x = 0$$.
Solve the following differential equation:
$$4\frac { dy }{ dx } +8y={ 5e }^{ -3x }$$
$$ 4\dfrac{dy}{dx}+8y = 5e^{-3x}$$
$$ \dfrac{dy}{dx}+2y = \dfrac{5}{4}e^{-3x}$$
$$ m+2 = 0$$
$$ m = -2 $$
$$ A.E \Rightarrow y(x) = C_1 e^{-2x}$$
$$ P.I = \dfrac{5e^{-3x}}{4(D+2)} \Rightarrow \dfrac{5e^{-3x}}{4(-3+2)} = \dfrac{-5e^{-3x}}{4}$$
C.S $$ y(x) = C_1 e^{-2x}-\dfrac{5}{4}e^{-3x}$$
For each the differential equations given, find the general solution :
$$ \dfrac {dy}{dx} + 2y \sin x $$
$${ye}^{x/y}dx=\left ( { {xe}^{x/y}+{y}^{2} }\right)\ dy$$.
$$ye^{x/y}dx= (xe^{x/y}+y^{2})dy$$
$$\dfrac{dx}{dy}= \dfrac{xe^{x/y}+y^{2}}{ye^{x/y}}$$
$$=\dfrac{x}{y}e^{x/y}+y/e^{x/y}$$
$$x= vy$$
$$\dfrac{dx}{dy}= v+y\dfrac{dv}{dy}$$
$$v+y\dfrac{dv}{dy}= ve^{v}+y/e^{v}$$
$$y\dfrac{dy}{dy}= \dfrac{ve^{v}}{e^{v}}-v+\dfrac{y}{ev}$$
$$y\dfrac{dv}{dy}= v-v+\dfrac{y}{e^{v}}$$
$$\displaystyle \int e^{v}dv= \int \dfrac{y}{y}dy$$
$$e^{v}+e=y$$
$$\Rightarrow y=e^{x/y}+e$$
$$xy\dfrac {dy}{dx}={x}^{2}-{y}^{2}$$
$$y = 2\dfrac {dy}{dx} + \left (\dfrac {dy}{dx}\right )^{2} y$$.
Solve $$x^{2}\dfrac {dy}{dx}=x^{3}y$$
$$ x^{2}\dfrac{dy}{dx} = x^{3}y $$
$$ \dfrac{dy}{dx}-xy = 0 $$
$$ I.F = C^{f-xdy} = C^{-x^{2}/2} $$
$$ G.S : ye^{-x^{2}/2} = 0 $$
Find the solution of the differential equation $$\left( x\log { x } \right) \frac { dy }{ dx } +y=2x\log { x,\left( x\ge 1 \right) }$$.
Solve the following rational equations
$$2(y+3)-xy\dfrac {dy}{dx}=0$$ given that $$y(1)=-2$$
Find the differential equation of the family of all the circles.
(A) touching X-axis at the origin.
(B) touching Y-axis at the origin.
$$e^{x}\tan y dx+(1-e^{x})\sec^{2}y dy=0$$
Find the $$I.F$$ of the differential equation: $$\cos^{2}x\dfrac {dy}{dx}+y=\tan x$$
Find the solution of $$(\sqrt{a+x})\left(\dfrac{dy}{dx}\right)+x=0$$.
Solve : $$ \dfrac{dy}{dx} = \dfrac{y^2 - x}{2y (x + 1)}$$
The solution of $$\dfrac{dy}{dx}=\dfrac{\sqrt{x^2-y^2}+y}{x}$$.
Find the differential equation of all ellipse $$\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$$, where $$a$$ and $$b$$ are constant.
If $$f\left( x \right) = x\sin \,x,\,$$ find $$f'\left( \pi \right)$$, using first principle.
solve. $$xdy - (4 + 2{x^2})dx = 0$$
Solve $$ydx-xdy=x^{2}ydx$$
Prove that $$y = \frac{A}{x} + B$$ is the solution of the differential equation $$\frac{{{d^2}y}}{{d{x^2}}} + \frac{2}{x}\frac{{dy}}{{dx}} = 0$$.
Simplify: $$\frac{1}{{{x^2} - 5x + 6}} - \frac{1}{{{x^2} - 3x + 2}}$$
If $$y = \log \left( {1 + 2{t^2} + {t^4}} \right),\,\,x = {\tan ^{ - 1}}t,$$ find $$\dfrac{{{d^2}y}}{{d{x^2}}}$$
Can $$y=ax+\cfrac{b}{a}$$ be a solution of the following differential equation?
$$y=x\cfrac{dy}{dx}+\cfrac{b}{\cfrac{dy}{dx}}$$.......($$^{\ast}$$)
If no, find the solution of the D.E ($$^{\ast}$$).
If $$dy = (4t^3+3t^2+4t) dt$$ find the value of y.
Evaluate: $$\int \frac { 1 + v } { 1 - v } d v = \int \frac { d x } { x }$$
Find $$\frac{{dy}}{{dx}}$$when $$y = {e^{\sqrt x + \sin x}}$$
$$y=e^{\sqrt{x}+\sin x}$$
$$\dfrac{dy}{dx}=e^{\sqrt{x}+\sin x}\left(\dfrac{1}{2\sqrt{x}+\cos x}\right)$$
$$\dfrac{dy}{dx}=e^{\sqrt{x}+\sin x\left(\dfrac{1+2\sqrt{x}\cos x}{2\sqrt{x}}\right)}$$
$$\dfrac{dy}{dx}=\dfrac{e^{\sqrt{x}+\sin x}(1+2\sqrt{x}\cos x}{2\sqrt{x}}$$
What is the degree of the following differential equation ?
$$5x{\left( {\frac{{dy}}{{dx}}} \right)^2} - \frac{{{d^2}y}}{{d{x^2}}} - 6y = \log x.$$
solution -
Degree of diff.eg. is power of highest order
derivative involved.
$$5x{\left( {\frac{{dy}}{{dx}}} \right)^2} - \frac{{{d^2}y}}{{d{x^2}}} - 6y = \log x.$$
Degree = power of $$ \frac{d^{2}y}{dx^{2}} = 1 $$
Let $$y=a\cos(\log x)+b\sin(\log x)$$ is a solution of the differential equation $${x^2}\frac{{{d^2}y}}{{d{x^2}}} + x\frac{{dy}}{{dx}} + y = 0$$.Prove.
solve the differential equation : $$\dfrac{{dy}}{{dx}} + y {\,\sec ^2}\,x = \tan x\,{\sec ^{2\,}}y;\,y\,(0) = 1$$
$$\dfrac{dy}{dx}=\dfrac{1-cos\:x}{1+cos\:x}$$
Find the order and degree of : $$\sqrt[3]{\dfrac{d^2y}{dx^2}} = \sqrt{\dfrac{dy}{dx}}$$.
Evaluate:
$$( 1 + \cos x ) d y = ( 1 - \cos x ) d x$$
Solve: $$\dfrac{dy}{dx} + \dfrac{4}{\left(\dfrac{dy}{dx}\right)} = 5$$
Evaluate: $$\frac { d y } { d x } = \sin ( x + y ) + \cos ( x + y )$$
Solve: $$\sqrt { 1 + x ^ { 2 } } \sqrt { 1 + y ^ { 2 } } \ d x + x y d y = 0$$
Solve: $$\dfrac{d^2 y}{dx^2} + \dfrac{dy}{dx} + e^x = 0$$
Solve the differential equation $$\cfrac{dy}{dx}=\cfrac{\sqrt{1-{y}^{2}}}{\sqrt{1-{x}^{2}}}$$.
Solve : $$\left( e ^ { 3 } + 1 \right) \cos x d x + e ^ { y } \sin x d y = 0$$
Show that the given differential equation is homogeneous
$$({x^2} + xy)dy = ({x^2} + {y^2})dx$$
Solve $$\dfrac{dy}{dx}=cos\:\left(x+y\right)$$
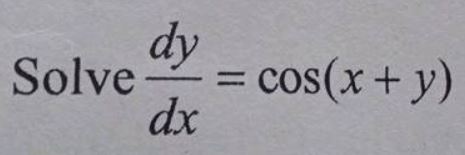
$$\dfrac{dy}{dx} = (1 + x^2) (1 + y^2)$$
For differential equation $$\left(\dfrac{dy}{dx}\right)^{2}-x\left(\dfrac{dy}{dx}\right)+y=0$$,find the solution
Solve
$$(1+e^{x/y})dx+e^{x/y} \left(1-\dfrac{x}{y}\right)dy=0$$
$$x + y \dfrac { d y } { d x } = \sec \left( x ^ { 2 } + y ^ { 2 } \right)$$
Solve $$\dfrac{dy}{dx}=1+x+y+xy$$
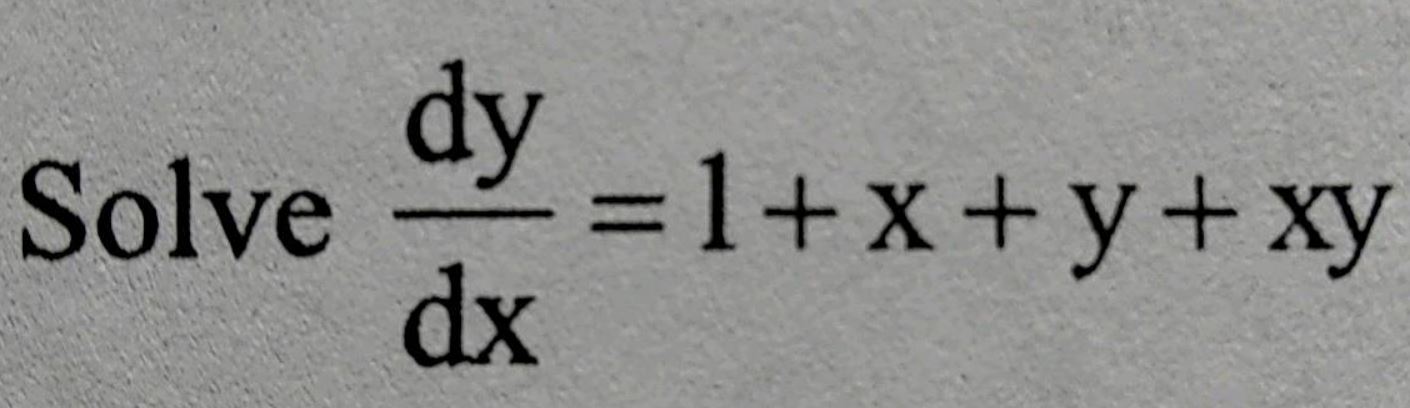
Find the general solution of the equation given by $$\dfrac {dy}{dx}+\dfrac {1+y^{2}}{1+x^{2}}=0$$.
solve xdy - ydx =$$\sqrt{x^2 + y^2dx}$$
Solve:$$\dfrac{dy}{dx}=x+e^x$$.
Solve:$$\dfrac{dy}{dx}=\sqrt{4-y^{2}}(-2 < y < 2)$$.
Solve the differential equation $$\left( 1+e^{ 2x } \right) dy+(1+y^{ 2 }){ e }^{ x }dx=0$$ given that $$y=1$$ when $$x=0$$.
Solve:$$\cos ( x + y ) d y = d x$$
If $$x = \sin t,y = \sin pt$$ then prove that $$(1 - {x^2}){d^2}y - xdy + {p^2}y = 0$$
Solve the differential equation :$$y\log { y } \dfrac { dx }{ dy } +x-\log { y=0 }$$.
Solve: $$(x+y)\dfrac{dy}{dx}= 1$$
The general solution of the differential equation $$\dfrac{dy}{dx}=(1+x^2)(1+y^2)$$.
Find the general solution of the differential equation.
$$(1+\tan y)(dx-dy)+2xdy=0$$.
Solve the differential equation $$(1+y^2)(1+log{\,}x)dx+x{\,}dy=0$$, given that when $$x=1$$ then $$y=1$$.
Solve $$y$$ $$ dx-(x+2y^2)dy = 0$$
Solve : $$y^{2}dx+(x^{2}+xy)dy=0$$
Solve the differential equation $$\cos\left(\dfrac{dy}{dx}\right)=a, (a\in R)$$.
Solve the differential equation $$(x^{2}-y^{2})dx+2xydy=0$$.
Prove that $$y={ ae }^{ -2x }+{ be }^{ x }$$ is the solution of differential equation $$\dfrac { { d }^{ 2 }y }{ { dx }^{ 2 } } +\dfrac { dy }{ dx } -2y=0$$
Construct a differential equation by eliminating the arbitrary constants $$a,b$$ from the equation:$$y=(ax+b)e^x$$.
Reduce the following differential equation to the variables separable form and hence solve.
$$(x-y)^2\dfrac{dy}{dx}=a^2$$.
Solve the following differential equation.
$$y-x\dfrac{dy}{dx}=0$$.
Solve the differential equation $$ye^{ { \dfrac { x }{ y } } }dx=\left( xe^{ { \dfrac { x }{ y } } }+y^{ { 2 } } \right) dy(y\neq 0).$$
$$\dfrac { dx }{ dy } +\dfrac { x }{ 1+{ y }^{ 2 } } =\dfrac { { tan }^{ -1 }y }{ 1+{ y }^{ 2 } } $$
The solution of differential equation $$(sinx + cosx)dy$$ + $$(cosx - sinx)dx=0$$ is
$$(\sin x+\cos x)dy+(\cos x-\sin x)dx=0$$
$$(\sin x+\cos x)dy=-(\cos x-\sin x)dx$$
$$\dfrac{dy}{dx}=-\dfrac{(\cos x-\sin x)}{(\sin x+\cos x)}$$
$$dy=-\dfrac{(\cos x-\sin x)}{(\sin x+\cos x)}dx$$
$$\displaystyle\int dy=-\displaystyle\int \dfrac{\cos x-\sin x}{\sin x+\cos x}dx$$
$$\sin x+\cos x=t$$
$$(\cos x-\sin x)dx=dt$$
$$(\sin x-\cos x)dx=-dt$$
$$y=\displaystyle\int -\dfrac{dt}{t}+c$$
$$=-log |t|+c$$
$$y=-log|\sin x+\cos x|+c$$.
Solve:$$y - x\dfrac{{dy}}{{dx}} = a\left( {{y^2} + \dfrac{{dy}}{{dx}}} \right)$$
Solve the differential equation: $${ x }dy-ydx=\sqrt { { x }^{ 2 }+{ y }^{ 2 } } dx$$
Solve :$$\dfrac{dy}{dx}=\dfrac{1}{y^2+\sin y}, y\neq 0$$
Solve the differential equation $$\dfrac{dy}{dx}=\dfrac{1+y}{x}$$
$$\frac{dy}{dx}=\frac{1+y}{x}$$
$$\frac{1}{1+y}dy=\frac{1}{x}dx$$
on integerating both sides.
$$\int \frac{1}{1+y}dy=\int \frac{1}{x}dx$$
$$log (1+y)= log x+c$$
Find the differential equation whose solution represents the family: $$y = a e ^ { 3 x } + b e ^ { x }$$
Find the differential equation of the family of curve $$y=A{e}^{2x}+B{e}^{-2x}$$ for different values of $$A$$ and $$B$$.
Verify whether $$y=\sqrt{1+x^{2}}$$ is a solution of the differential equation $$y'=\dfrac{x}{\sqrt{1+x^{2}}}$$
Solve:
$$\dfrac { d y } { d x } = x+1 ; $$ find $$y $$ when $$x = 2$$
Solve:
$$ \dfrac { d y } { d x } = 2 x ^ { 2 } + x ; $$ find $$y $$ when $$x = 0$$
Solve $$ x \frac { d y } { d x } + 2 x = x ^ { 2 } \log x $$
Find the general solution for the following differential equation:
$$x^{2}dy+y(x+y)dx=0$$
Let $$y=\sin^{-1}x$$ then prove that $$(1-x^2)y_2-xy_1=0$$. Where $$y_1$$ and $$y_2$$ are first and second order derivatives of $$y$$ with respect to $$x$$ respectively.
Find $$\dfrac{dy}{dx}$$ for $$y=\sqrt{x+\sqrt{x+\sqrt{x+.....}}}$$.
Write the order of the differential equation: $$ \left(\dfrac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{d} x^{2}}\right)=\left(\dfrac{\mathrm{dy}}{\mathrm{dx}}\right)^{3}+\mathrm{x} $$
For each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
$$y=ae^x+be^{-x}+x^2$$ : $$x\frac {d^2y}{dx^2}+2\frac {dy}{dx}-xy+x^2-2=0$$
$$xdy + (y - x^{3})dx = 0$$
Solve: $$\displaystyle y - x\frac{{dy}}{{dx}} = a\left( {{y^2}+\frac{{dy}}{{dx}}} \right)$$
or, $$\ln |y|-\ln|1-ay|=\ln |(a+x)|+\ln c$$ [ Where $$c$$ is integrating constant]
or, $$\dfrac{y}{1-ay}=c(a+x)$$.
If $$ x=at^{ 2 },\ \ y= 2at,$$ then find $$ y\dfrac { dy }{ dx } $$
Solve the differential equation :
$$(xdy - ydx)\,y\,sin\left( {\frac{y}{x}} \right) = (ydx + xdy)X\,\cos \,\left( {\frac{y}{x}} \right)$$
Solve:$$\left(y+3{x}^{2}\right)\dfrac{dx}{dy}=x$$
Solve: $$\dfrac{dy}{dx} + 1 = e^{x + y}$$.
Find the particular solution of differential equal $$x\left( {{x^2} - 1} \right)\dfrac{{dy}}{{dx}} = 1;y = 0$$ and $$x = 2.$$
$$x(x^2-1)dy=dx$$
$$dy=\dfrac{dx}{x(x^2-1)}$$
Integrating on both sides
$$\displaystyle\int dy=\displaystyle\int \dfrac{dx}{x(x^2-1)}$$
$$y=\displaystyle\int \dfrac{dx}{x(x+1)(x-1)}$$ …………..$$(1)$$
We can write
$$\dfrac{1}{x(x+1)(x-1)}=\dfrac{A}{x}+\dfrac{B}{(x+1)}+\dfrac{C}{(x-1)}$$
$$
By cancelling the denominators
$$1=A(x-1)(x+1)+Bx(x-1)+C(x+1).x$$
Putting $$x=0$$
$$1=A(0-1)(0+1)+B.0(0-1)+C.0(0+1)$$
$$1=-A$$
$$A=-1$$
Similarly putting $$x=-1$$
$$1=A(-1-1)(-1+1)+B(-1)(-1-1)+C(-1)(-1+1)$$
$$1=A(-2)(0)+B(-1)(-2)+C:0$$
$$1=0+2B+0$$
$$2B=1$$
$$B1/2$$
Putting $$x=1$$
$$1=A(1-1)(1+1)+B(1)(1-1)+C.1(1+1)$$
$$1=20.A+0.B+2C$$
$$1=2C$$
$$C=1/2$$
Therefore $$\dfrac{1}{x(x+1)(x-1)}=\dfrac{-1}{x}+\dfrac{1/2}{(x+1)}-\dfrac{1/2}{(x-1)}$$
Now, from $$(1)$$
$$y=\displaystyle\int \dfrac{1}{(x(x+1)(x-1)}\cdot dx$$
$$=\displaystyle\int \dfrac{1}{x}+dx+1/2\displaystyle\int \dfrac{dx}{x+1}+\dfrac{1}{2}\displaystyle\int \dfrac{dx}{x-1}$$
$$=log |x|+\dfrac{1}{2}.log |x+1|+\dfrac{1}{2}log|x-1|+c$$
$$=\dfrac{-2}{2}log |x|+\dfrac{1}{2} log |x+1|+\dfrac{1}{2}log|x-1|+c$$
$$=\dfrac{1}{2}\left[-2log |x|-2+log |(x+1)(x-1)|\right]+c$$
$$=\dfrac{1}{2}\left[ log x^{-2}log|(x+1)(x-1)|\right]+c$$
$$=\dfrac{1}{2}\left[log |x^{-2}(x^2-1)|\right]+c$$ $$[\because log a+log b-log ab]$$
$$=\dfrac{1}{2}log \left|\dfrac{x^2-1}{x^2}\right|+c$$
$$\therefore y=\dfrac{1}{2}log\left|\dfrac{x^2-1}{x^2}\right|+c$$ …………..$$(1)$$
Given that
$$x=2; y=0$$
Substituting values in $$(1)$$, we get
$$0=\dfrac{1}{2}log\left|\dfrac{2^2-1}{2^2}\right|+c$$
$$0=\dfrac{1}{2}log\dfrac{3}{4}+c$$
$$c=-\dfrac{1}{2}log \dfrac{3}{4}$$
Putting value of c in $$(1)$$
$$y=\dfrac{1}{2}log \left|\dfrac{x^2-1}{x^2}\right|-\dfrac{1}{2}log 3/4$$.
If y = sec $$\sqrt { x } $$, Then find $$\dfrac { dy }{ dx } $$
If $$y={ x }^{ x }+{ x }^{ 1/x }$$, then find $$\dfrac { dy }{ dx } $$.
Find the differential equation representing the family of curves $$y=ae^{bx+5}$$ where a and b are arbitrary constants.
Find the differential equation of the family of curves, $$x = A \cos nt + B \sin nt$$, where $$A$$ and $$B$$ are arbitrary constants.
Solve the differential equation :
$$ y \ \log y \ dx-xdy=0$$
Solve the differential equation $$(x -1 ) \dfrac{dy}{dx} = 2x^3y$$
$$ (x-1) \frac{dy}{dx} = 2x^{3}y.$$
$$ \frac{dy}{y} = \frac{2x^{3} dx}{x-1}$$
$$ \frac{dy}{y} = \frac{2(x^{3} - 1 + 1)}{x-1} dx $$
$$ \frac{dy}{y} = \left \{ 2 \frac{(x-1)(x^{2}+x+1)}{x-1} + \frac{2}{x-1}\right \} dx$$
$$ \int \frac{dy}{y} = \int 2(x^{2} + x + 1) dx + \int \frac{2dx}{(x-1)}$$
$$ \Rightarrow log y = 2 \left \{ \frac{x^{3}}{3} + \frac{x^{2}}{2} + 2 log (x-1) + c \right \}$$
$$ \Rightarrow log y = log(x-1)^{2} + \frac{2x^{3}}{3} + x^{2} 2x+c.$$
Solve the following differential equation.
$$(1+x^2)\dfrac{dy}{dx}-x=2\tan^{-1}x$$
Show that $$y=e^x(A\cos x+B\sin x)$$ is the solution of the differential equation $$\dfrac{d^2y}{dx^2}-2\dfrac{dy}{dx}+2y=0$$.
Show that the function $$y=A\cos x+B\sin x$$ is a solution of the differential equation $$\dfrac{d^2y}{dx^2}+y=0$$.
Solve the following differential equation.
$$\cos x\dfrac{dy}{dx}-\cos 2x=\cos 3x$$
Write the order of the differential equation of the family of circles touching $$Y$$-axis at the origin.
Write the order of the differential equation of all non-horizontal lines in a plane.
Solve the following differential equation.$$(x^3+x^2+x+1)\dfrac{dy}{dx}=2x^2+x$$
Write the order of the differential equation of the family of circles touching $$X$$-axis at the origin.
Solve the following differential equation.
$$\dfrac{dy}{dx}=\sec^2x$$.
Solve the following differential equation.
$$\dfrac{dy}{dx}=x-1$$
Solve the following differential equation.$$\dfrac{dy}{dx}+1=\sin x$$
Show that $$y = e^{x} (A\cos x + B\sin x)$$ is the solution of the differential equation $$\dfrac {d^{2}y}{dx^{2}} - 2 \dfrac {dy}{dx} + 2y = 0$$.
Write the order of the differential equation whose solution is $$y=a\cos x+b\sin x+ce^{-x}$$.
Differentiate the following function$$(x+2)(x+3)$$.
Find the solution of the differential equation $$\dfrac{dy}{dx}=\log x$$,
Find the area of the triangle with vertices at the points :
$$(0,0),(6,0) \ and \ (4,3)$$
If $$\sin x$$ is an integrating factor of the differential equation $$\dfrac{dy}{dx}+Py=Q$$, then write the value of $$P$$.
For the following differential equation, find the general solution.$$\dfrac{dy}{dx}+x=1$$.
Form the differential equation from the following primitive where constant is arbitrary.$$xy=a^2$$.
Represent the following families of curves by forming the corresponding differential equation(a, b being parameters).$$x^2+y^2=a^2$$.
Solve the following differential equation.
$$x dy=(-y+2x^4+x^2)dx$$.
Solve the following differential equation.$$(x^3+x^2+x+1)\dfrac{dy}{dx}=2x^2+x$$.
Form the differential equation from the following primitives where constant is arbitrary.$$y=ax^2+bx+c$$.
Show that $$y=ax^3+bx^2+c$$ is a solution of the differential equation $$\dfrac{d^3y}{dx^3}=6a$$.
$$\displaystyle \int _0^{\pi/2} \sin x \cos x dx $$ is equal to:
$$\displaystyle \int _0^{\pi/2} \sin x \cos x dx $$ is equal to:
Represent the following families of curves by forming the corresponding differential equation.(a, b being parameters).$$x^2-y^2=a^2$$.
Show that $$y=e^x(A\cos x+B\sin x)$$ is the solution of the differential equation $$\dfrac{d^2y}{dx^2}-2\dfrac{dy}{dx}+2y=0$$.
Solve the following differential equation.
$$\dfrac{dy}{dx}+y\tan x=\cos x$$.
Answer the following question in one word or one sentence or as per exact requirement of the question.Write the differential equal obtained eliminating the arbitrary constant C in the equation $$xy=C^2$$.
Solve the following differential equation.$$\dfrac{dy}{dx}=x^2$$.
Solve the following differential equation.$$\dfrac{dy}{dx}=\sec^2x$$.
Show that $$y = e^{x} (A \cos x + B \sin x)$$ is the solution of the differential equation $$\dfrac {d^{2}y}{dx^{2}} - 2 \dfrac {dy}{dx} + 2y = 0$$.
Solve the following differential equation.
$$(x^3+x^2+x+1)\dfrac{dy}{dx}=2x^2+x$$.
Form the differential equation of the family of curves represented by $$y^2=(x-c)^3$$.
Show that $$y=\dfrac1x$$ is a solution of the differential equation $$\dfrac{dy}{dx}=\log x$$
Show that the function $$y=A\cos x+B\sin x$$ is a solution of the differential equation $$\dfrac{d^2y}{dx^2}+y=0$$.
Solve the following differential equation.$$\dfrac{dy}{dx}=x^5+x^2-\dfrac{2}{x}, x\neq 0$$.
Solve the following differential equation.
$$\dfrac{dy}{dx}+2x=e^{3x}$$.
Show that $$y=\dfrac1x$$ is a solution of the differential equation $$\dfrac{dy}{dx}=\log x$$
Solve the following differential equation.$$\dfrac{dy}{dx}={1-\cos x}$$
Show that $$y=ax^3+bx^2+c$$ is a solution of the differential equation $$\dfrac{d^3y}{dx^3}=6a$$.
Solve the following differential equation.
$$(x^3-2y^3)dy+3x^2ydx=0$$.
Solve the following differential equation.$$\dfrac{dy}{dx}=x^2+x-\dfrac{1}{x}, x\neq 0$$.
Solve the following differential equation.$$(x^2+1)\dfrac{dy}{dx}=1$$.
Solve the following differential equation.
$$\dfrac{dy}{dx}=x^2+3x+7$$.
For the following differential equation, find the general solution.
$$x dy=dx $$.
For the following differential equation, find the general solution.
$$\dfrac{dy}{dx}=\sin x$$.
Form the differential equation corresponding to $$y^2-2ay+x^2=a^2$$ by eliminating a.
Differentiate the following function with respect to x.$$\dfrac{x^2\cos \dfrac{\pi}{4}}{\sin x}$$.
Show that $$y=ax^3+bx^2+c$$ is a solution of the differential equation $$\dfrac{d^3y}{dx^3}=6a$$.
Solve the following differential equation.
$$\dfrac{dy}{dx}={1-\cos x}$$
For the following differential equation, find the general solution.$$\dfrac{dy}{dx}=\sin x$$.
For the following differential equation, find the general solution.
$$x dy=dx $$.
Verify that $$y = e^{m \cos^{-1} x}$$ is a solution of the differential equation $$(1 - x^{2}) \dfrac {d^{2}y}{dx^{2}} - x\dfrac {dy}{dx} - m^{2}y = 0$$.
Verify that $$Ax^{2} + By^{2} = 1$$ is a solution of the differential equation $$x\left \{y \dfrac {d^{2} y}{dx^{2}} + \left (\dfrac {dy}{dx}\right )^{2} \right \} = y \dfrac {dy}{dx}$$.
Find the general solution of each of the following differential equations:
$$(x - 1) \dfrac {dy}{dx} = 2x^{3}y$$.
Verify that $$y = ae^{bx}$$ is a solution of the differential equation $$\dfrac {d^{2}y}{dx^{2}} = \dfrac {1}{y} \left (\dfrac {dy}{dx}\right )^{2}$$.
Find the general solution of each of the following differential equations:
$$x^{4} \dfrac {dy}{dx} = -y^{4}$$.
Verify that $$y = \dfrac {c - x}{1 + cx}$$ is a solution of the differential equation $$(1 + x^{2}) \dfrac {dy}{dx} + (1 + y^{2}) = 0$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} = (1 + x^{2})(1 + y^{2})$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} = 1 - x + y - xy$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} = e^{x + y}$$.
Find the general solution of the following differential equations:
$$\dfrac {dy}{dx} = \dfrac {1 + x}{1 + y^{2}}$$.
Find the general solution of each of the following differential equations:
$$(e^{x} + e^{-x}) dy - (e^{x} - e^{-x}) dx = 0$$.
Find the general solution of each of the following differential equations:
$$y\log y\ dx - x\ dy = 0$$.
Find the general solution of each of the following differential equations:
$$(1 + x^{2}) \dfrac {dy}{dx} = xy$$.
Find the general solution of each of the following differential equations:
$$\cos x (1 + \cos y)dx - \sin y(1 + \sin x)dy = 0$$.
Find the general solution of the following differential equations:
$$\dfrac {dy}{dx} = \dfrac {x}{x^{2} + 1}$$
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} = e^{x - y} + x^{2} e^{-y}$$.
Find the general solution of each of the following differential equations:
$$\sec^{2} x \tan y \ dx + \sec^{2} y\tan x\ dy = 0$$.
Find the general solution of each of the following differential equations:
$$x\dfrac {dy}{dx} + y = y^{2}$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} = e^{x + y} + e^{x - y}$$.
Find the general solution of each of the following differential equations:
$$(1 - x^{2}) dy + xy (1 - y)dx = 0$$.
Find the general solution of each of the following differential equations:
$$(e^{y} + 1)\cos x\ dx + e^{y}\sin x\ dy = 0$$.
Find the general solution of each of the following differential equations:
$$x(x^{2} - x^{2}y^{2}) dy + y(y^{2} + x^{2}y^{2}) dx = 0$$.
Find the general solution of the following differential equations:
$$(x^{2} - xy^{2}) dy + (y^{2} + xy^{2}) dx = 0$$.
Find the general solution of the following differential equations:
$$3e^{x} \tan y\ dx + (1 - e^{x})\sec^{2} y\ dy = 0$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} = \dfrac {3e^{2x} + 3e^{4x}}{e^{x} + e^{-x}}$$.
Find the general solution of each of the following differential equations:
$$(x^{2}y - x^{2}) dx + (xy^{2} - y^{2}) dy = 0$$.
Find the general solution of each of the following differential equations:
$$e^{y}(1 + x^{2}) dy - \dfrac {x}{y}dx = 0$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} = e^{x + y} + x^{2}e^{y}$$.
Find the general solution of each of the following differential equations:
$$cosec x\log y \dfrac {dy}{dx} + x^{2} y = 0$$.
Find the general solution of each of the following differential equations:
$$\dfrac {1}{x} \cdot \dfrac {dy}{dx} = \tan^{-1} x$$.
Find the general solution of the following differential equations:
$$e^{x} \sqrt {1 - y^{2}} dx + \dfrac {y}{x} dy = 0$$.
Find the general solution of each of the following differential equations:
$$\sqrt {1 - x^{4}} dy = xdx$$.
Find the general solution of each of the following differential equations:
$$(\cos x) \dfrac {dy}{dx} + \cos 2x = \cos 3x$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} + \dfrac {\cos x \sin y}{\cos y} = 0$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} = \dfrac {1 - \cos x}{1 + \cos x}$$.
Find the general solution of each of the following differential equations:
$$ydx + (1 + x^{2}) \tan^{-1} x\ dy = 0$$.
Find the general solution of the following differential equations:
$$\cos x (1 + \cos y) dx - \sin y(1 + \sin x)dy = 0$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} + \dfrac {(1 + \cos 2y)}{(1 - \cos 2x)} = 0$$.
Find the general solution of each of the following differential equations:
$$\dfrac {1}{x}\cos^{2}y dy + \dfrac {1}{y}\cos^{2} x dx = 0$$.
Find the general solution of each of the following differential equations:
$$\sin^{3} x dx - \sin y\ dy = 0$$.
Solve $$\dfrac {dy}{dx} = y^{2}\tan 2x$$, given that $$y = 2$$ when $$x = 0$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} + \sin (x + y) = \sin (x - y)$$.
Find the general solution of each of the following differential equations:
$$\dfrac {dy}{dx} = \sin^{3}x\cos^{2} x + xe^{x}$$.
Solve the differential equation $$\dfrac {dy}{dx} = y\sin 2x$$, given that $$y(0) = 1$$.
Solve the differential equation $$(x + 1)\dfrac {dy}{dx} = 2xy$$, given that $$y(2) = 3$$.
Solve $$\dfrac {dy}{dx} = y\tan x$$, given that $$y = 1$$ when $$x = 0$$.
Solve $$\dfrac {dy}{dx} = y\cot 2x$$, given that $$y = 2$$ when $$x = \dfrac {\pi}{4}$$.
If $$ y=\left(1 / 2^{n-1}\right) \cos \left(n \cos ^{-1} x\right) $$, then prove that $$ y $$ satisfies the differential equation $$ \left(1-x^{2}\right) \dfrac{d^{2} y}{d x^{2}}-x \dfrac{d y}{d x}+n^{2} y=0 $$
The integrating factor of $$\dfrac {dy}{dx}+y=\dfrac {1+y}{x}$$ is _______ .
If the dependent variable y is changed to $$'z'$$ by the substitution $$y = \tan z$$ and the differential equation $$\dfrac{d^2 y}{dx^2} = 1 + \dfrac{2 (1 + y)}{1 + y^2} \left(\dfrac{dy}{dx}\right)^2$$ is changed to $$\dfrac{d^2z}{dx^2} = \cos^2 z + k \left(\dfrac{dz}{dx}\right)^2$$, then the value of k equals.
General solution of the differential equation of the type
$$\dfrac {dy}{dx}+P_1x=Q_1$$ is given by _______ .
If the independent variable x is changed to y, then the differential equation $$x \dfrac{d^2 y}{dx^2} + \left(\dfrac{dy}{dx}\right)^3 - \dfrac{dy}{dx} = 0$$ is changed to $$x \dfrac{d^2 x}{dy^2} + \left(\dfrac{dx}{dy}\right)^2 = k$$ where k equals
Integrating factor of the differential equation $$x\dfrac {dy}{dx}-y=\sin x$$ is _________.
The number pf arbitrary constants in a particular solution of the differential equation $$\tan xdx +\tan y dy=0$$ is __________.
Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:
$$y = \cos x + C : y’+ \sin x = 0$$
For each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
$$y=e^x(a\, \cos\,x+b\, sin\, x)$$ : $$\cfrac{d^2y}{dx^2}-2\cfrac{dy}{dx}+2y=0$$
Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:
$$y= x^2 + 2x + C : y' - 2x - 2 = 0$$
In each of the Exercises 1 to 10 verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:
$$(\begin{aligned}y=\& \sqrt{a^{2}-x^{2}}, &\,x \in(-a, a): x+y \frac{d y}{d x}=0(y \neq 0)\end{aligned})$$
Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:
$$y = e^x + 1 : y’’- y’ = 0$$
In each of the Exercises 1 to 10 verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:
$$y = Ax : xy = y (x \neq 0)$$
For each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
$$y = x \,\sin 3x$$ : $$\cfrac{d^2y}{dx^2}+9y-6\,\cos\,3x=0$$
Match the statements/expressions in List 1 with the open intervals in List 2.
List 1 contains different functions and List 2 contains differential equations. Match options in List 1 with corresponding differential equation from List 2
For each of the differential equations, find the general solution:
$$\cfrac{dy}{dx}+2y=\sin\,x$$ 2. $$\cfrac{dy}{dx}+3y=e^{-2x}$$$$\cfrac{dy}{dx}+\cfrac{y}{x}=x^{2}$$
4. $$\cfrac{dy}{dx}+(\sec\,x)y=\tan\,x$$ ...$$\left(0\le x < \cfrac{\pi}{2}\right)$$
5. $$\cos^2x\cfrac{dy}{dx}+y=\tan\,x$$ ...$$\left(0\le x < \cfrac{\pi}{2}\right)$$
$$x\cfrac{dy}{dx}+2y=x^2\log\, x$$$$x\, \log\, x\cfrac{dy}{dx}+y = \cfrac{2}{x} \log x$$
$$(1+x^2)dy + 2xy dx = \cot x dx$$ ...$$ (x \neq 0)$$
$$x\cfrac{dy}{dx}+y-x+xy\, \cot\, x=0$$ ...$$(x\neq 0)$$$$(x+y)\cfrac{dx}{dy}=1$$
$$y\, dx+(x-y^2)dy=0$$12. $$(x+3y^2)\cfrac{dy}{dx}=y$$ ...$$(y > 0)$$
4. $$\cfrac{dy}{dx}+(\sec\,x)y=\tan\,x$$ ...$$\left(0\le x < \cfrac{\pi}{2}\right)$$
5. $$\cos^2x\cfrac{dy}{dx}+y=\tan\,x$$ ...$$\left(0\le x < \cfrac{\pi}{2}\right)$$
$$x\cfrac{dy}{dx}+2y=x^2\log\, x$$
$$(1+x^2)dy + 2xy dx = \cot x dx$$ ...$$ (x \neq 0)$$
$$x\cfrac{dy}{dx}+y-x+xy\, \cot\, x=0$$ ...$$(x\neq 0)$$
$$y\, dx+(x-y^2)dy=0$$
For each of the differential equations, find the general solution:
$$\cfrac{dy}{dx} = \cfrac{1-\cos\, x}{1+\cos\, x}$$
$$\cfrac{dy}{dx} = \sqrt{4-y^2}(-2 < y < 2)$$
$$\cfrac{dy}{dx} = 1(y\neq 1)$$
$$\sec^2x\, \tan \,y\, dx+\sec^2\, y\, \tan \, x\, dy = 0$$
5. $$(e^x + e^{-x}) dy- (e^x -e^{-x}) dx = 0$$
$$\cfrac{dy}{dx} = (1+x^2)(1+y^2)$$
$$y\, \log\, y\, dx- x \,dy = 0$$
$$x^4\cfrac{dy}{dx} = -y^5$$
$$\cfrac{dy}{dx}=\sin^{-1}x$$
$$e^x \,\tan \,y \,dx + (1 -e^x) \sec^2\, y\, dy = 0$$
Find the particular solution of the differential equation $$\dfrac {dy}{dx} = \dfrac {x(2\log x + 1)}{\sin y + y\cos y}$$ given that $$y = \dfrac {\pi}{2}$$ when $$x = 1$$.
Find the particular solution of the differential equation $$\dfrac {dy}{dx} = 1 + x + y + xy$$, given that $$y = 0$$, when $$x = 1$$.
Show that the general solution of the differential equation $$\dfrac{dy}{dx}+\dfrac{y^2+y+1}{x^2+x+1}=0$$ is given by $$(x+y+1)=A(1-x-y-2xy)$$, where $$A$$ is parameter.
Verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
(i) $$y=e^x(a\, \cos\,x+b\, sin\, x)$$ : $$\cfrac{d^2y}{dx^2}-2\cfrac{dy}{dx}+2y=0$$
(ii) $$y = x \,\sin 3x$$ : $$\cfrac{d^2y}{dx^2}+9y-6\,\cos\,3x=0$$
(iii) $$x^2 = 2y^2 \,\log\, y$$ : $$(x^2+ y^2 ) \cfrac{dy}{dx}-xy= 0$$
Find the particular solution of the differential equation $$\dfrac {dy}{dx} + 2y\cot x = 4x\ cosec x (x\neq 0)$$, given that $$y = 0$$, when $$x = \dfrac {\pi}{2}$$
Solve the differential equation $$2xy + y^2 - 2x^2 \dfrac{dy}{dx} = 0$$.
Solve the differential equation:
$$(x + 1)dy - 2 xy\ dx = 0$$
Solve: $$(x^2-yx^2)dy+(y^2+xy^2)dx=0$$
Verify that $$y^{2} = 4a (x + a)$$ is a solution of the differential equation $$y \left \{1 - \left (\dfrac {dy}{dx} \right )^{2} \right \} = 2x \dfrac {dy}{dx}$$.
Solve: $$\left( { D }^{ 2 }-4D+1 \right) y={x}^{2}$$
The solution of $$x^{2}y^{2}_{1} + xy\ y_{1} - 6y^{2} = 0$$ are (here $$y_{1} = dy/ dx)$$ ?
Let $$f : \mathbb {R} \rightarrow \mathbb {R}$$ be a differentiable function with $$f(0) = 0$$. If $$y = f(x)$$ satisfies the differential equation $$\dfrac {dy}{dx} = (2 + 5y)(5y - 2)$$, then the value of $$\displaystyle \lim_{x\rightarrow -\infty} f(x)$$ is $$k$$. Then what is the value of $$5k\,?$$
Solve$$\int { \frac { dy }{ y } } =\int { \frac { dx }{ x } } $$
Show that $$y = ae^{2x} + be^{-x}$$ is a solution of the differential equation $$\dfrac {d^{2}y}{dx^{2}} - \dfrac {dy}{dx} - 2y = 0$$.
$$\sec^{2} x\tan{y}\ dy+\sec^{2} y\tan x\ dx=0$$
Solve:
$$(x-y)^{2}\dfrac {dy}{dx}=a^{2}$$
Solve the following differential equation:
$$\left( { x }^{ 2 }+1 \right) \frac { dy }{ dx } +2xy=\sqrt { { x }^{ 2 }+4 }.$$
Solve : $$(x^2 D^2 + 3xD + 1) y = \dfrac{1}{(1 - x)^2}$$
Solve $$(D^2+4D+3)y=e^{-x}\sin x+x e^{3x}$$.
Solve the differential equation $$(\tan^{-1} x-y)dx = (1+x^2)dy$$.
Consider the differential equation $$y^2dx+\left(x-\dfrac{1}{y}\right)dy=0$$. It $$y(1)=1$$, then x is given by?
Prove that $${x}^{2}-{y}^{2}=c\left({x}^{2}+{y}^{2}\right)^{2}$$ is the general solution of differential equation $$\left({x}^{3}-3x{y}^{2}\right)dx=\left({y}^{3}-{3x}^{2}y\right)dy$$, where $$c$$ is a parameter.
$$\dfrac{dy}{dx}= \dfrac{x^{3}-3xy^{2}}{y^{3}-3x^{2}y}$$
Let $$\dfrac{y}{x}= v\Rightarrow y= vx$$
$$y^{1}= v+xv^{1}$$
$$v+xv^{1}= \dfrac{1-3v^{2}}{v^{3}-3v}$$
$$xv^{1}= \dfrac{1-3v^{2}-v}{v^{3}-3v}\Rightarrow xv^{1}=\dfrac{1-v^{4}}{v^{3}-3v}$$
$$\displaystyle = \int \dfrac{v^{3}-3v}{1-v^{4}}dv= \int \dfrac{1}{x}dx$$
$$\displaystyle \dfrac{-1}{4}\int \dfrac{v^{3}}{1-v^{4}}dv-\int \dfrac{3v}{1-v^{4}}dv= \int \dfrac{1}{x}dx$$
$$\displaystyle [\dfrac{-1}{4}log(1-v^{4})-\dfrac{1}{4}log(\dfrac{1+v^{2}}{1-v^{2}})]= logx+ log C$$
$$\displaystyle \dfrac{-1}{4}log[\dfrac{(1+v^{2})^{4}}{(1-v^{2})^{2}}]= log\: Cx$$
$$log[\dfrac{(1-v^{2})^{2}}{(1+v^{2})^{4}}]^{1/4}= log\: Cx$$
$$Cx= [\dfrac{(1-v^{2})^{2}}{(1+v^{2})^{4}}]^{1/4}= \dfrac{(1-v^{2})^{1/2}}{(1+v^{2})}$$
$$xC(1+v^{2})= (1-v^{2})^{1/2}$$
$$C(\dfrac{x^{2}+y^{2}}{x^{2}})x= (\dfrac{x^{2}-y^{2}}{x^{2}})^{1/2}$$
$$C(\dfrac{x^{2}+y^{2}}{x})=\dfrac{\sqrt{x^{2}-y^{2}}}{x}$$
squaring both sides, we get,
$$(x^{2}-y^{2})= C(x^{2}+y^{2})^{2}$$
Which is the required solution.
Solve $$y''=5y'+5(y'-5y)$$.
Evaluate : $$( x + y ) ( d x - d y ) = d x + d y$$
Solve:$$\dfrac { d y } { d x } + \dfrac { \sqrt { \left( x ^ { 2 } - 1 \right) \left( y ^ { 2 } - 1 \right) } } { x y } = 0$$
$$\dfrac { d y } { d x } + \dfrac { \sqrt { \left( x ^ { 2 } - 1 \right) \left( y ^ { 2 } - 1 \right) } } { x y } = 0$$
Solve: $$\left( 1+\tan { y } \right) \left( dx-dy \right) +2xdy=0$$
Solve the differential equation : $$(y-x\frac{dy}{dx}-a(y^{2}+\frac{dy}{dx})$$ ) =0
Solve that
$$x \left( 1 + y ^ { 2 } \right) d x + y \left( 1 + x ^ { 2 } \right) d y = 0$$
For each of the differential equations in Exercises from $$11$$ to $$15$$, find the particular solutions satisfying the given condition:
$$(x+y)dy+(x-y)dx=0; y=1$$ when $$x=1$$
Find the general solution of the differential equation $$x\dfrac{dy}{dx}+y-x+xy$$ $$\cot$$ $$x=0,$$ $$(x\neq 0)$$
Solve the differential equation $$y-x\dfrac{dy}{dx}=a\{ { y }^{ 2 }+\dfrac { dy }{ dx } \} $$
Solve the following differential equation :
$$(\cot^{-1}y+x)dy=(1+y^{2})dx$$
The general solution of the differential equation $$\dfrac{dy}{dx}+sin\dfrac{x+y}{2}= sin\dfrac{x-y}{2}$$ is
Find the general solution of the $$\left( { y }^{ 2 }-{ x }^{ 2 } \right) dy=3xy\ dx$$.If the general solution is $$y^2(\alpha x^2-y^2)^3=c$$ then find the value of $$\alpha$$.
the solution of the differential equation $${ sec }^{ 2 }xtan\quad y\quad dx+{ sec }^{ 2 }ytan\quad x\quad dy=0\quad is$$
Solve the differential equation $$\dfrac{dy}{dx} = x^5tan^{-1}(x^3)$$.
Find the general solution of the differential equation $$\dfrac{dy}{dx} +y.cot x = 2x+x^cot x.$$
Verify that $$x^{2} = 2y^{2} \log {y}$$ is a solution of the differential equation $$\left (x^{2} + y^{2} \right ) \dfrac {dy}{dx} - xy = 0$$.
The general solution of differential equation $$ \frac{d y}{d x}=\frac{x+y}{x-y} $$ is
Verify that $$y = e^{x} \cos bx$$ is a solution of the differential equation $$\dfrac {d^{2}y}{dx^{2}} - 2 \dfrac {dy}{dx} + 2y = 0$$.
If $$y=x\sin y$$, show that $$\dfrac{dy}{dx}=\dfrac{y}{x(1-x\cos y)}$$.
Find the general solution of the differential equation $$\dfrac{dy}{dx}-y=\cos x$$.
Verify that $$y = \dfrac {a}{x} + b$$ is a solution of the differential equation $$\dfrac {d^{2}y}{dx^{2}} + \dfrac {2}{x}\left (\dfrac {dy}{dx}\right ) = 0$$.
Find the general solution of the following differential equations:
$$e^{2x - 3y}dx + e^{2y - 3x}dy = 0$$.
Find the general solution of each of the following differential equations:
$$x^{2} (y + 1) dx + y^{2} (x - 1) dy = 0$$.
Find the general solution of the following differential equations:
$$\dfrac {dy}{dx} = \dfrac {x - 1}{y + 2}$$
Verify that $$y = (a + bx)e^{2x}$$ is the general solution of the differential equation $$\dfrac {d^{2}y}{dx^{2}} - 4\dfrac {dy}{dx} + 4y = 0$$.
Find the general solution of each of the following differential equations:
$$y(1 - x)^{2} \dfrac {dy}{dx} = x(1 + y^{2})$$.
Verify whether that $$y = \log (x + \sqrt {x^{2} + a^{2}})$$ satisfies the differential equation $$\dfrac {d^{2}y}{dx^{2}} + x\dfrac {dy}{dx} = 0$$.
Verify that $$y = e^{-3x}$$ is a solution of the differential equation $$\dfrac {d^{2}y}{dx^{2}} + \dfrac {dy}{dx} - 6y = 0$$.
Solve: $$(x+y)(dx-dy)=dxdy$$.[Hint: Substitute $$x+y=z$$ after separating $$dx$$ and $$dy$$]
Find the general solution of each of the following differential equations:
$$(1 - x^{2}) (1 - y) dx = xy (1 + y)dy$$.
Find the general solution of the following differential equations:
$$\dfrac {dy}{dx} + \dfrac {xy + y}{xy + x} = 0$$.
Find the general solution of the following differential equations:
$$(y + xy) dx + (x - xy^{2}) dy = 0$$.
Find the general solution of each of the following differential equations:
$$x\sqrt {1 + y^{2}} dx + y \sqrt {1 + x^{2}} dy = 0$$.
Find the integrating factor of differential equation
$$\dfrac{dy}{dx} + \dfrac{1}{\sin x} y = e^x$$
Find the integrating factor of differential equation $$\dfrac{dy}{dx} + y \tan x = \sin x$$
Class 12 Commerce Maths Extra Questions
- Application Of Derivatives Extra Questions
- Application Of Integrals Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Linear Programming Extra Questions
- Matrices Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions