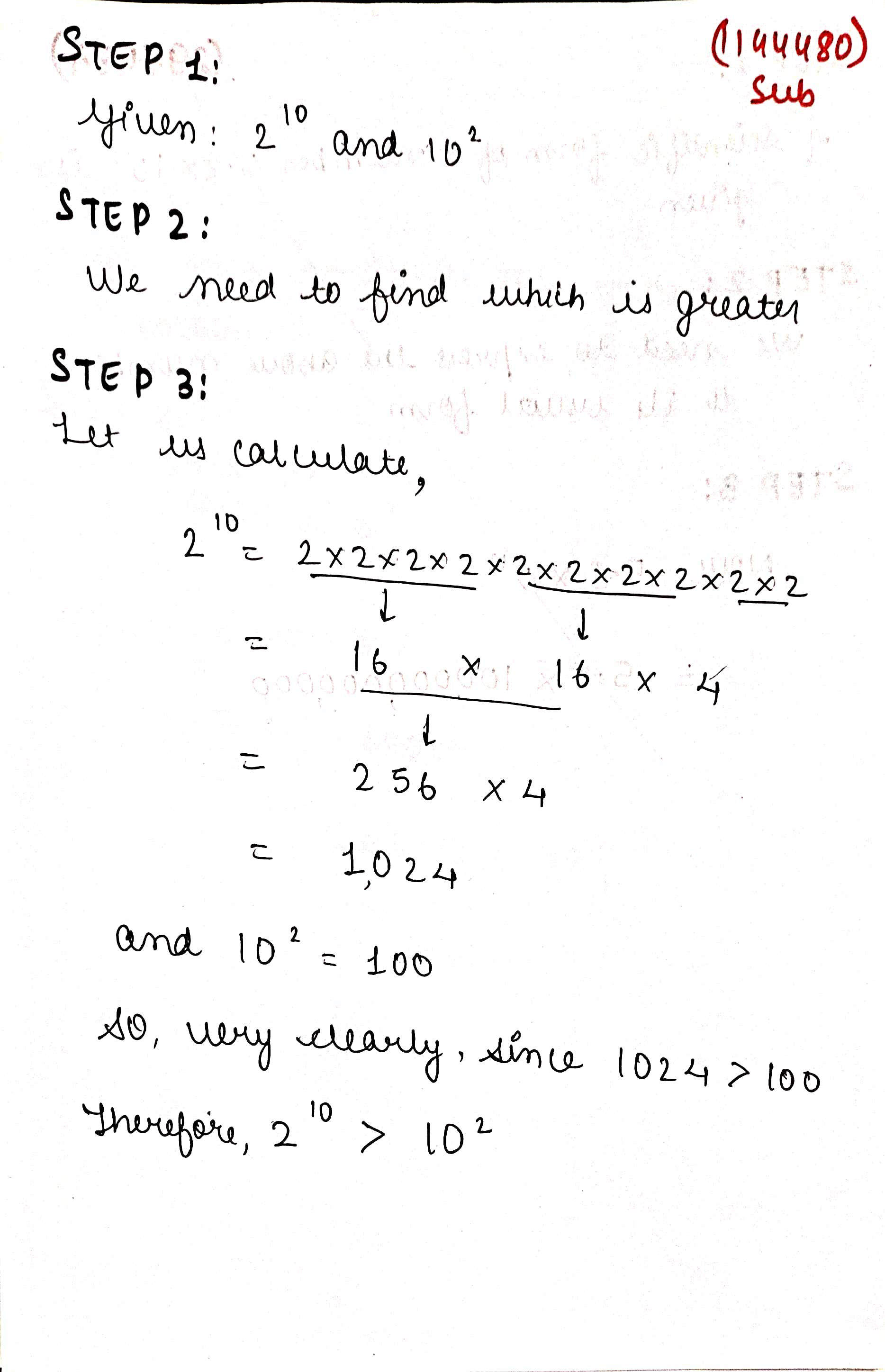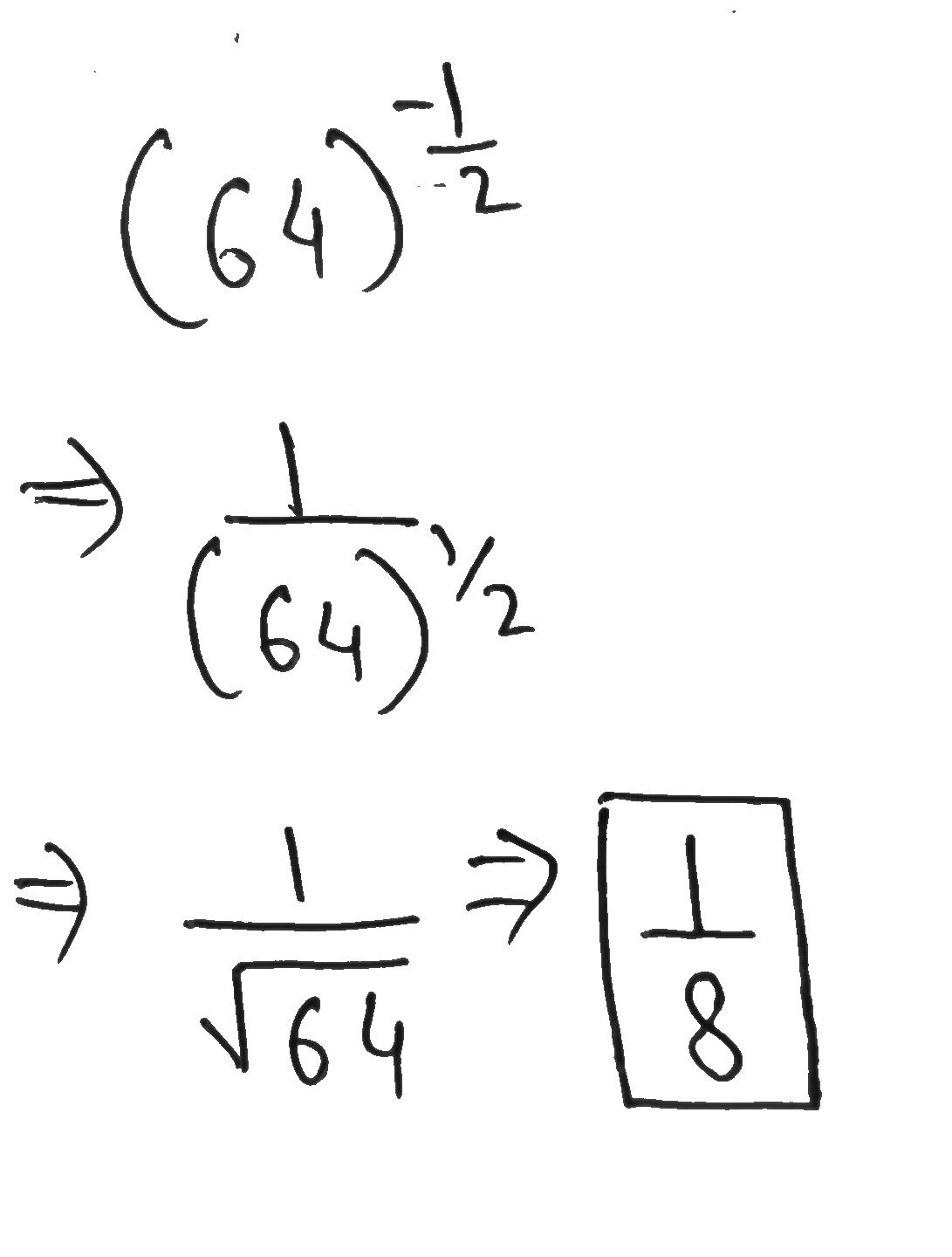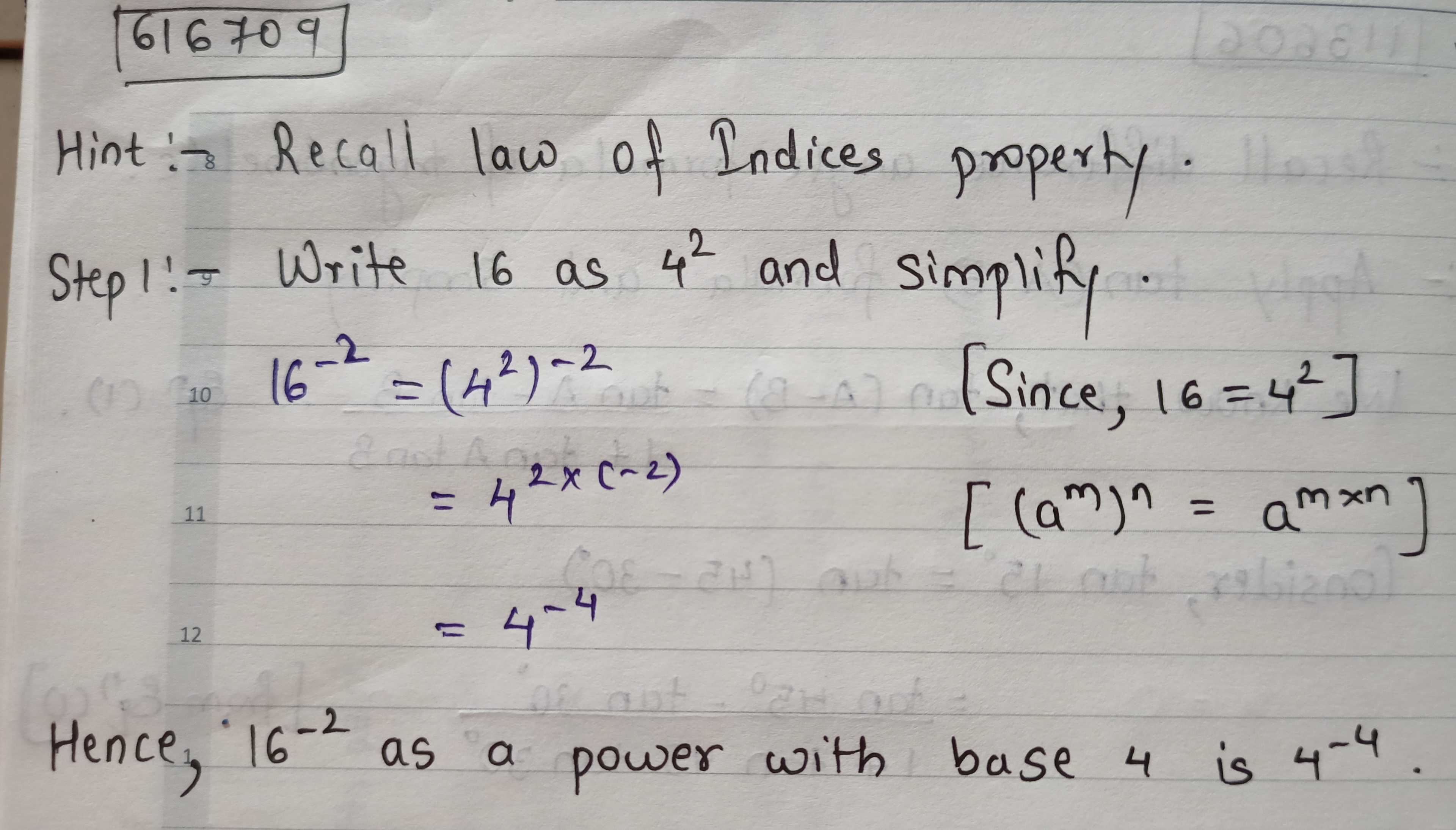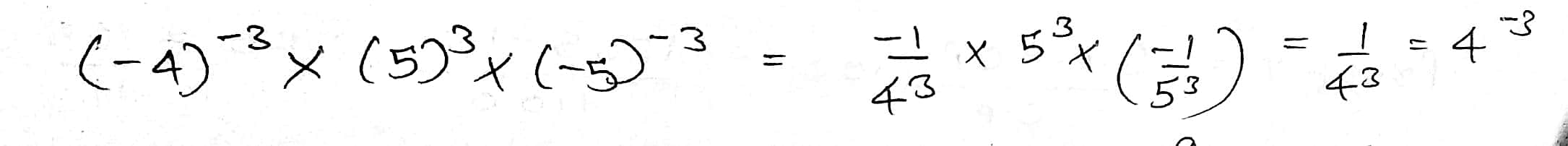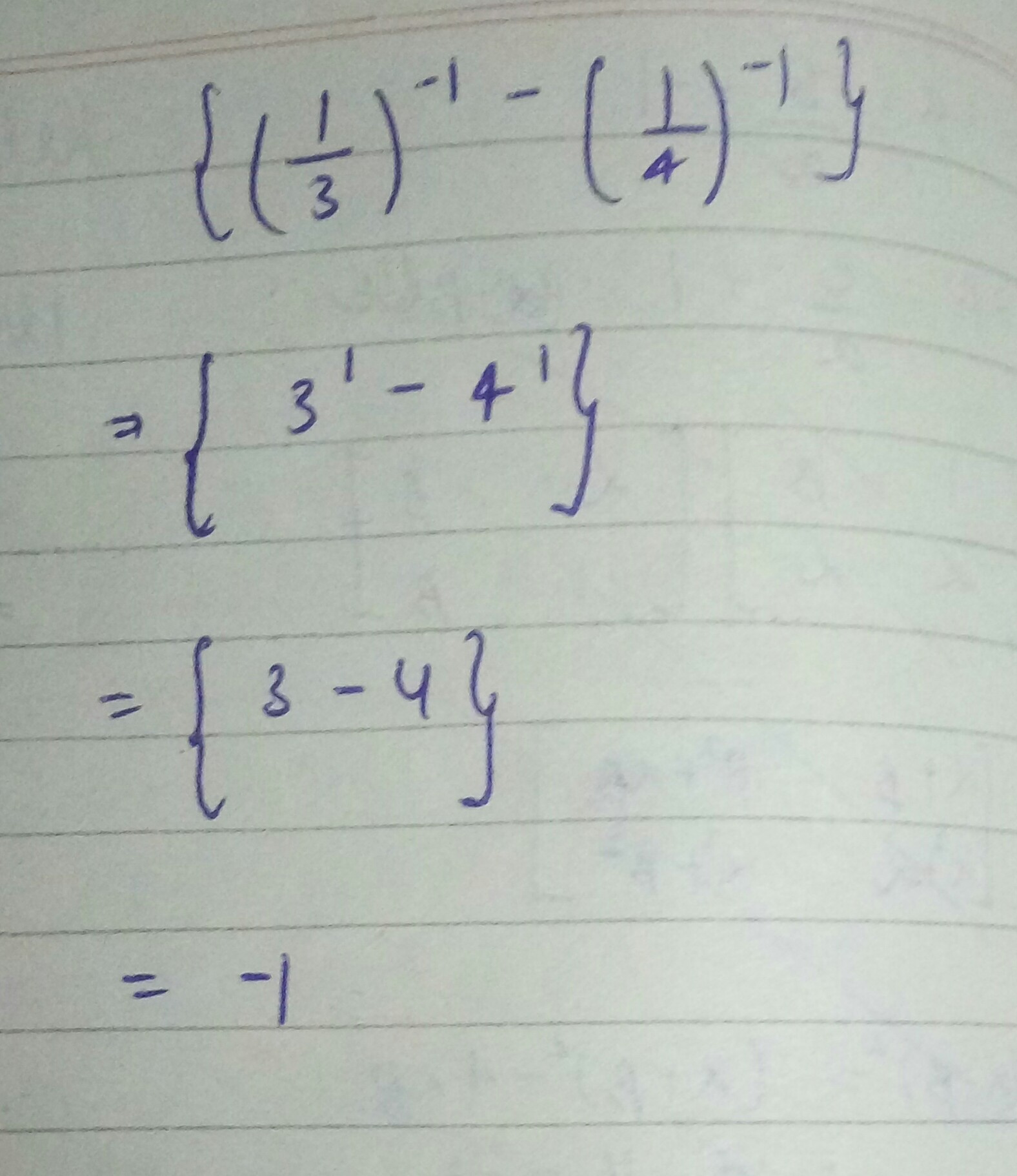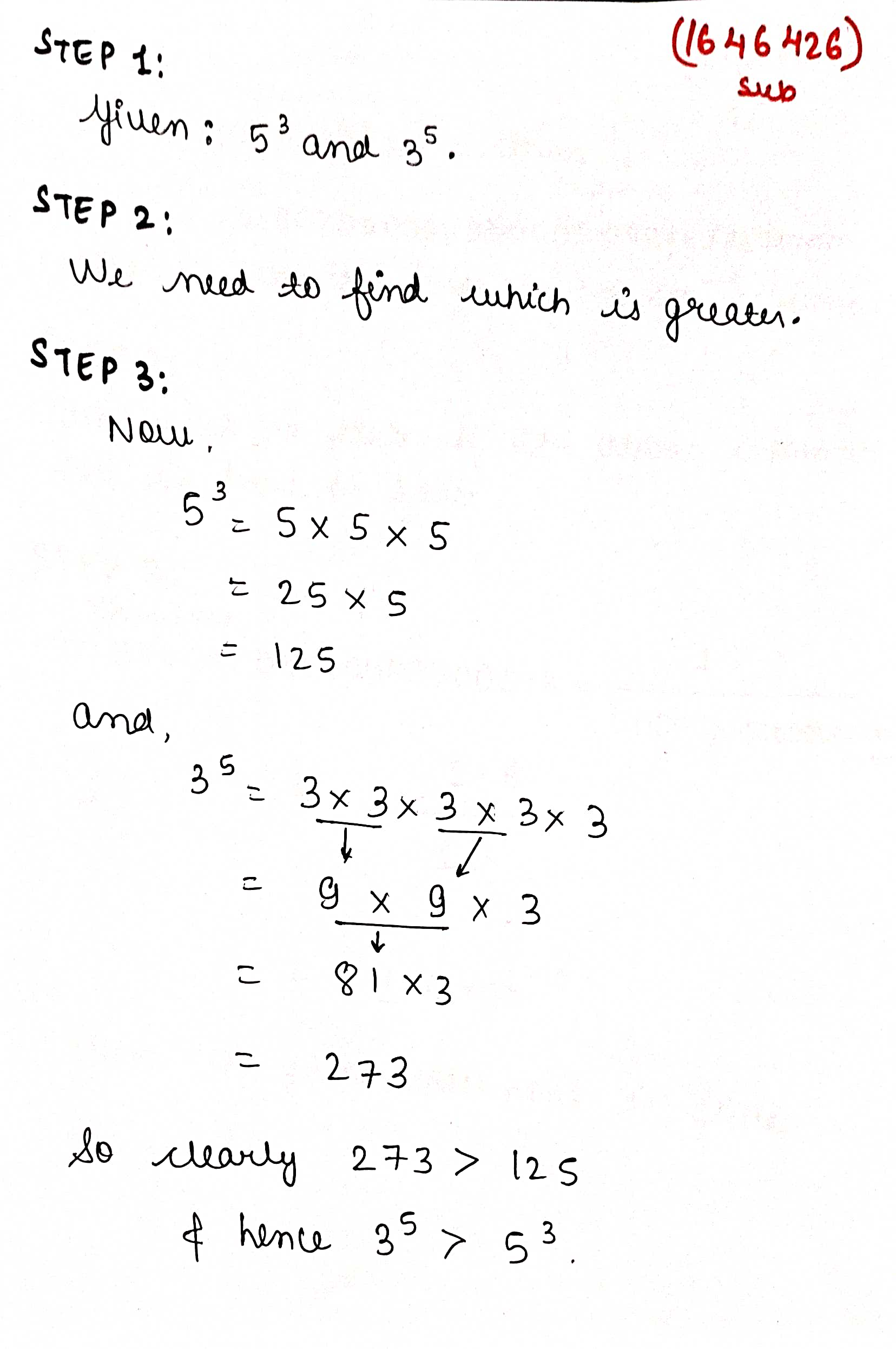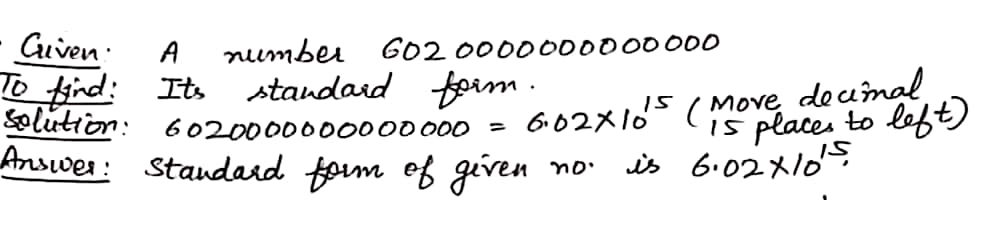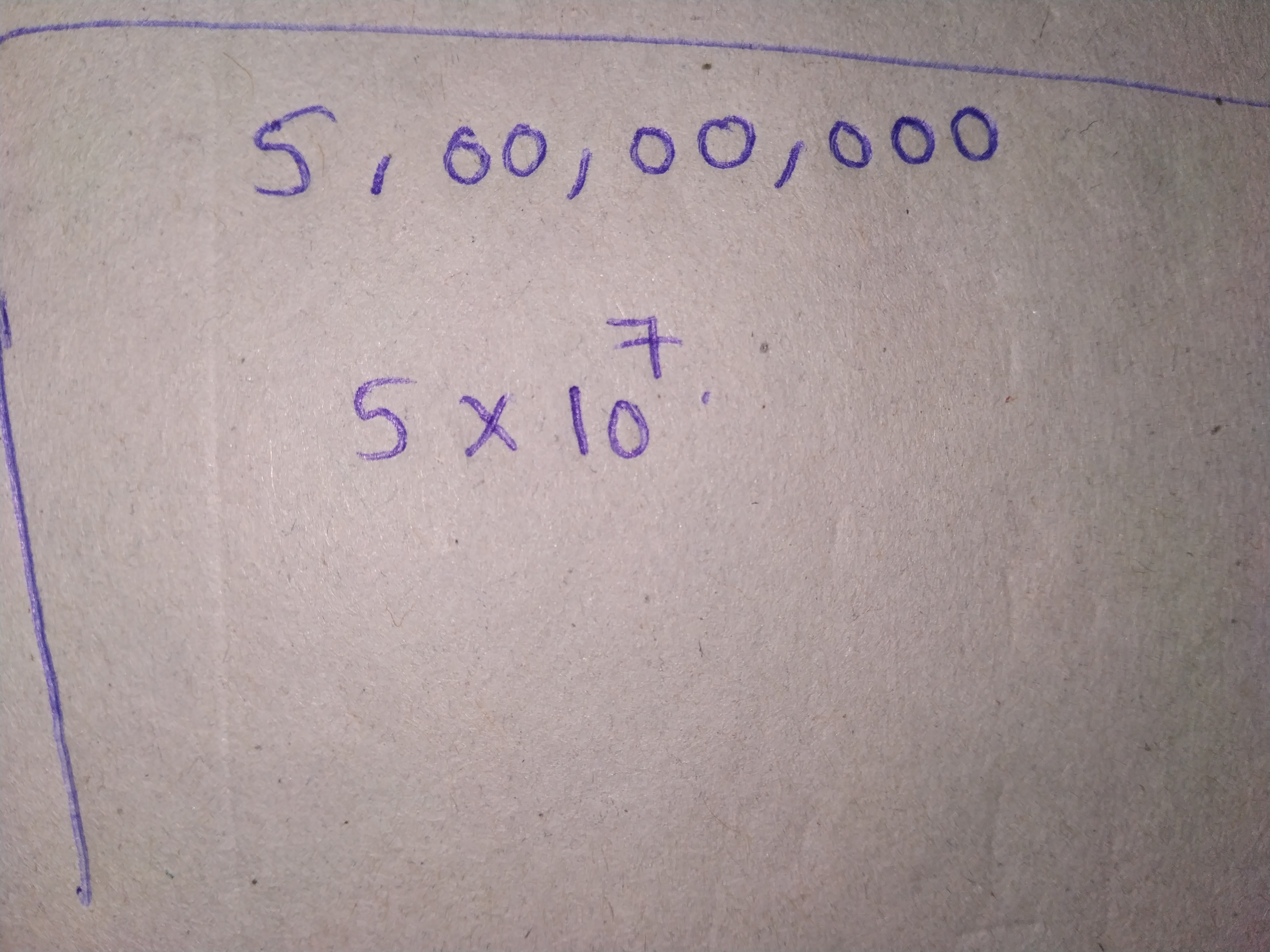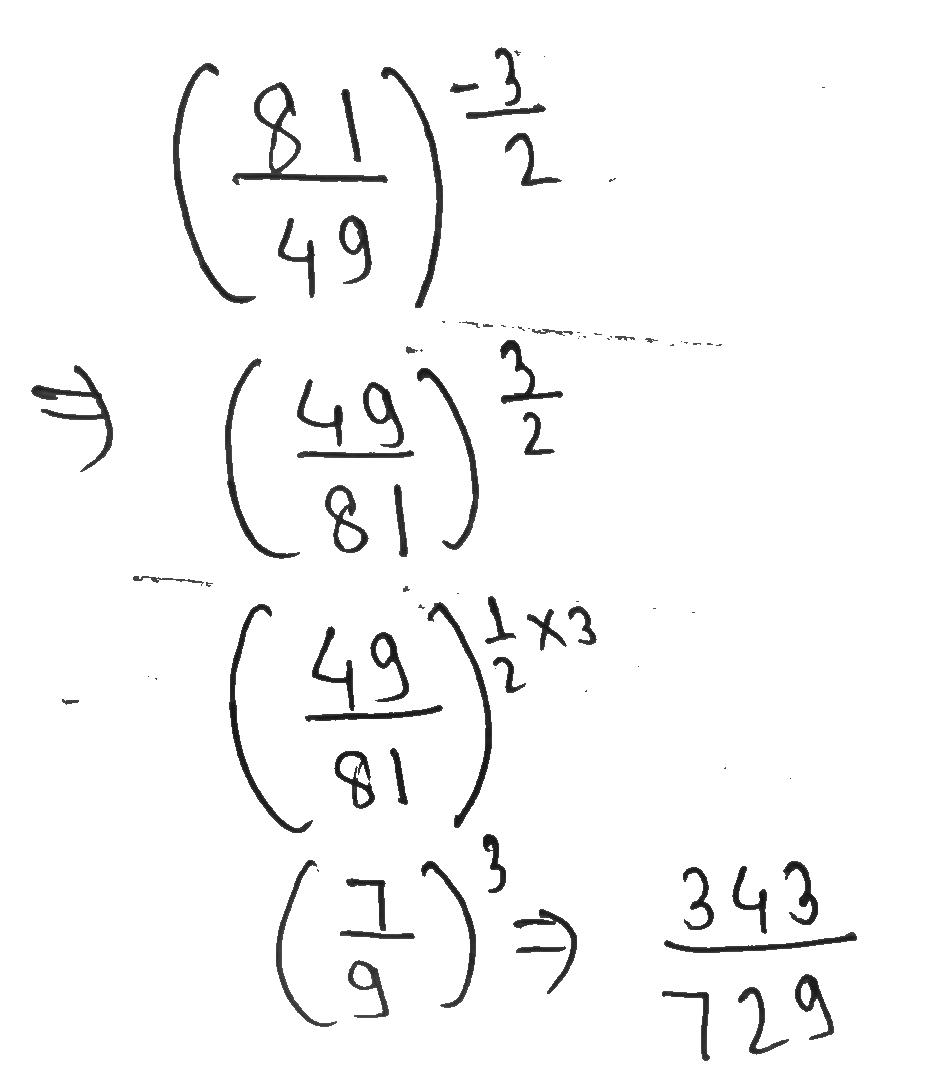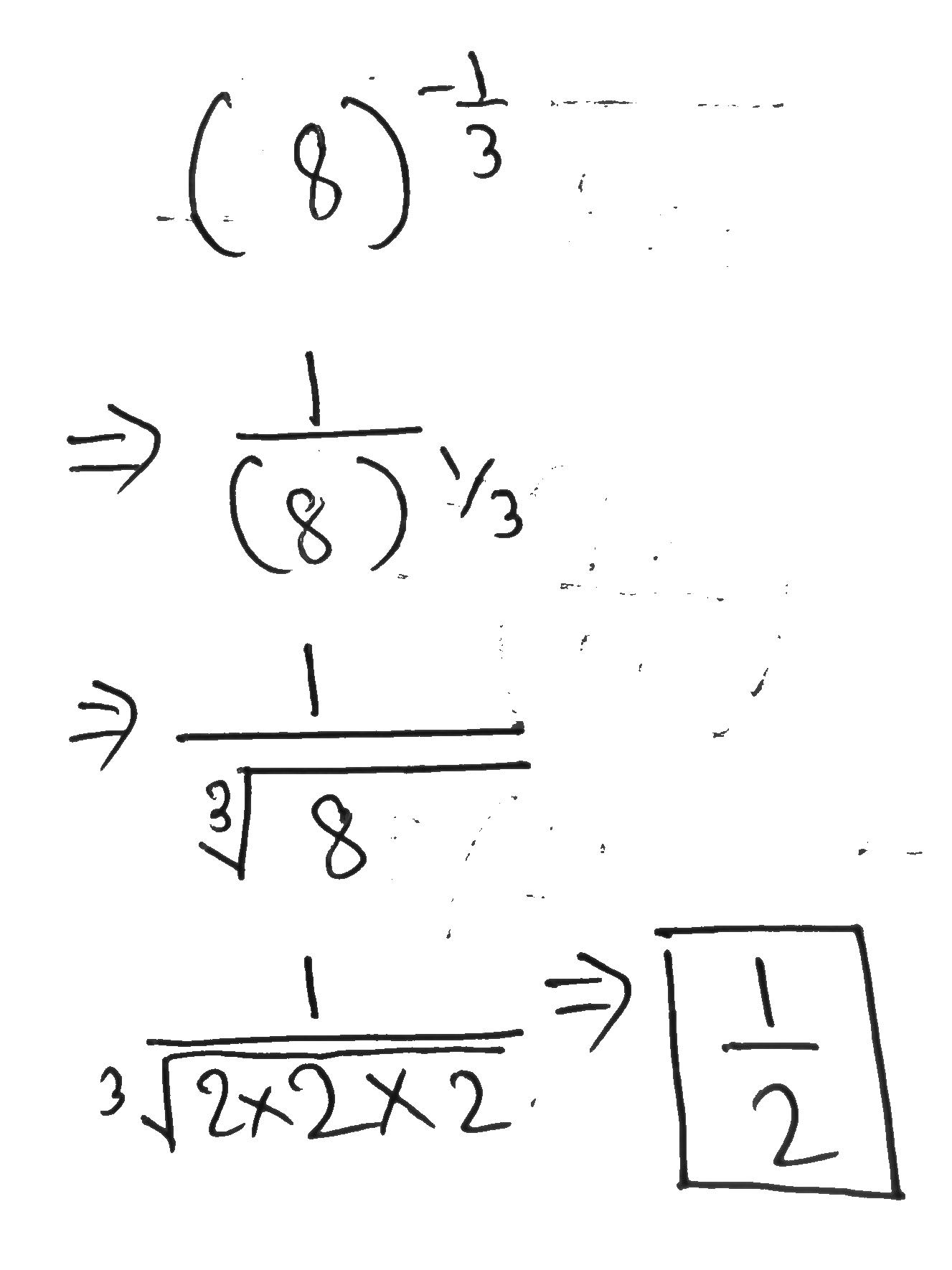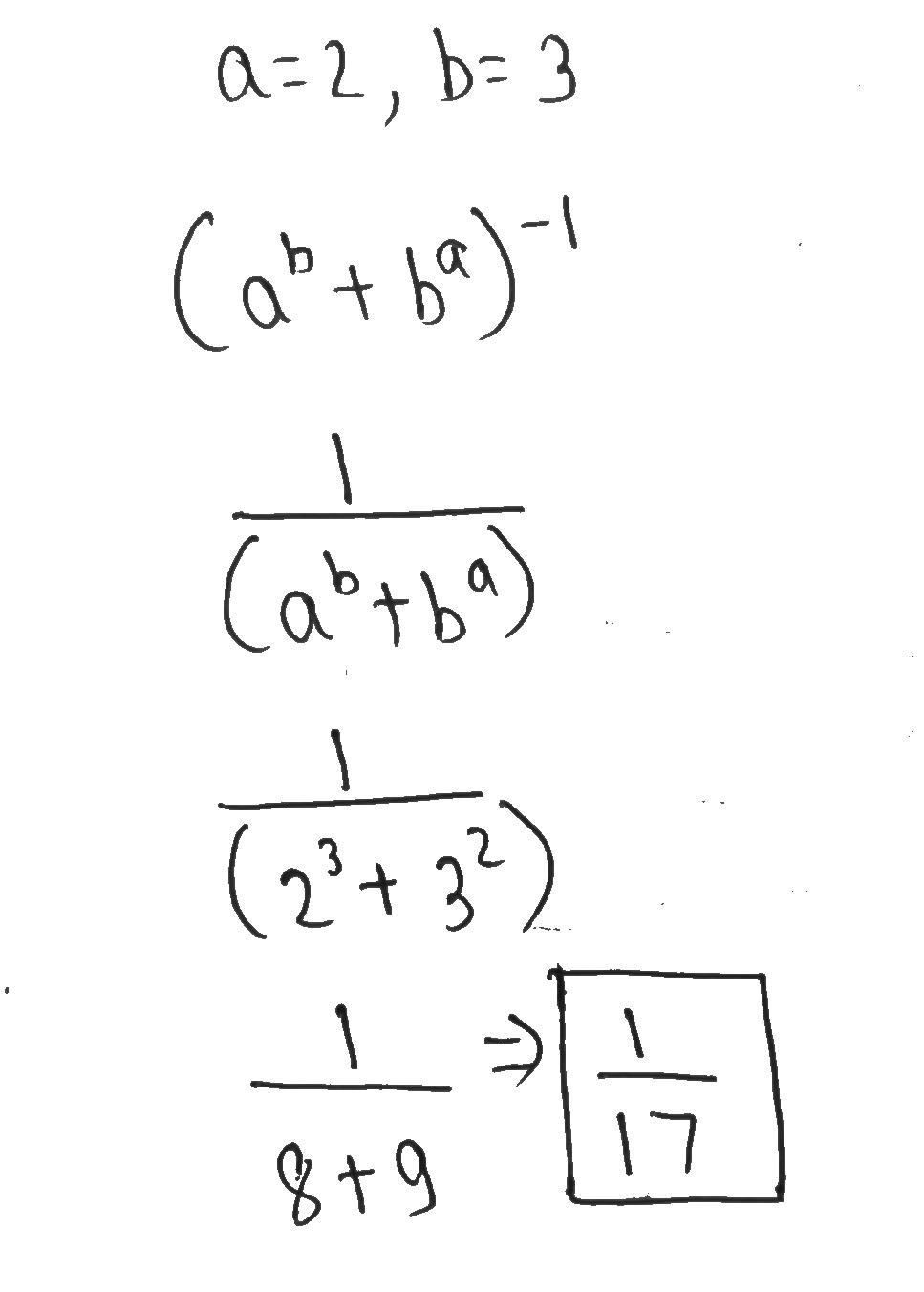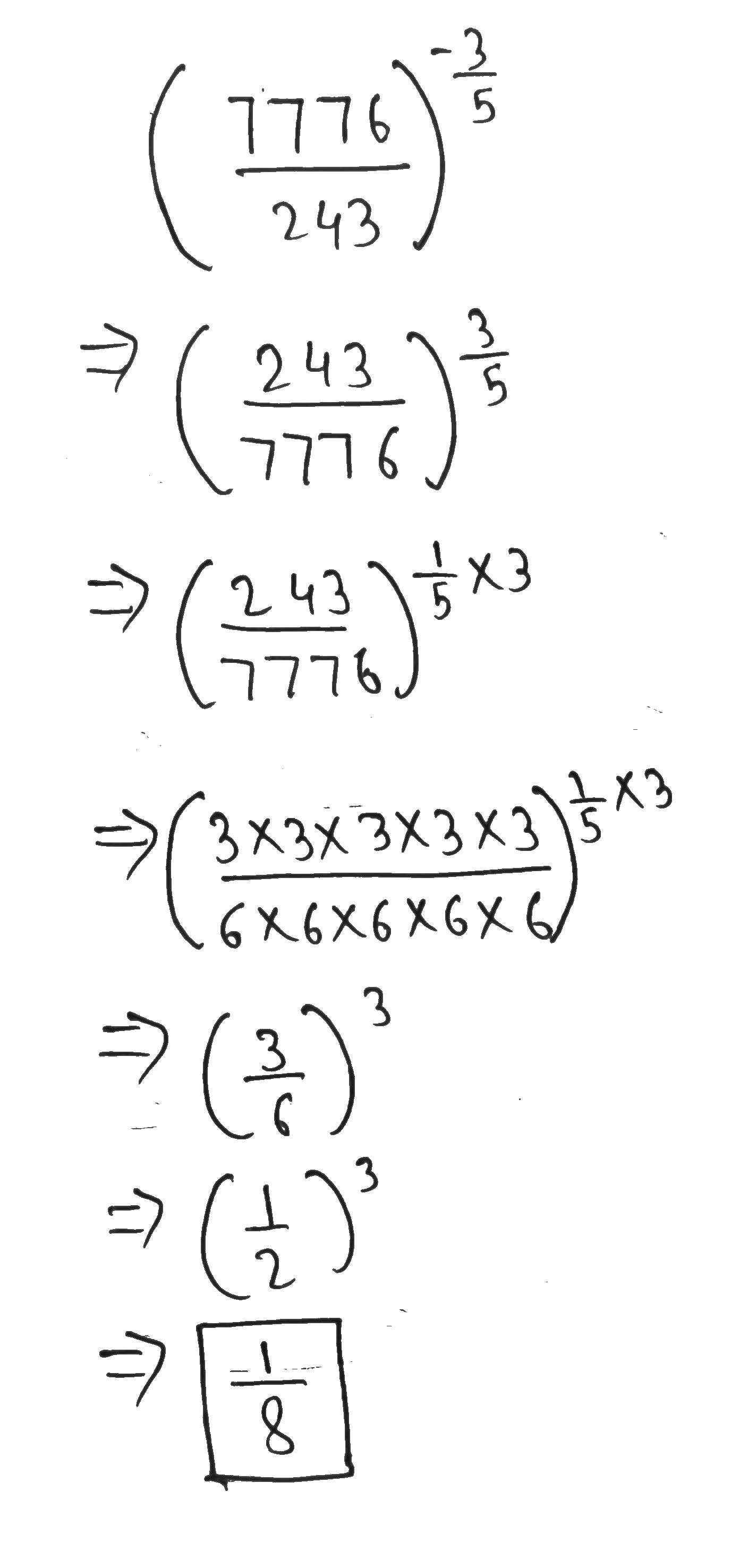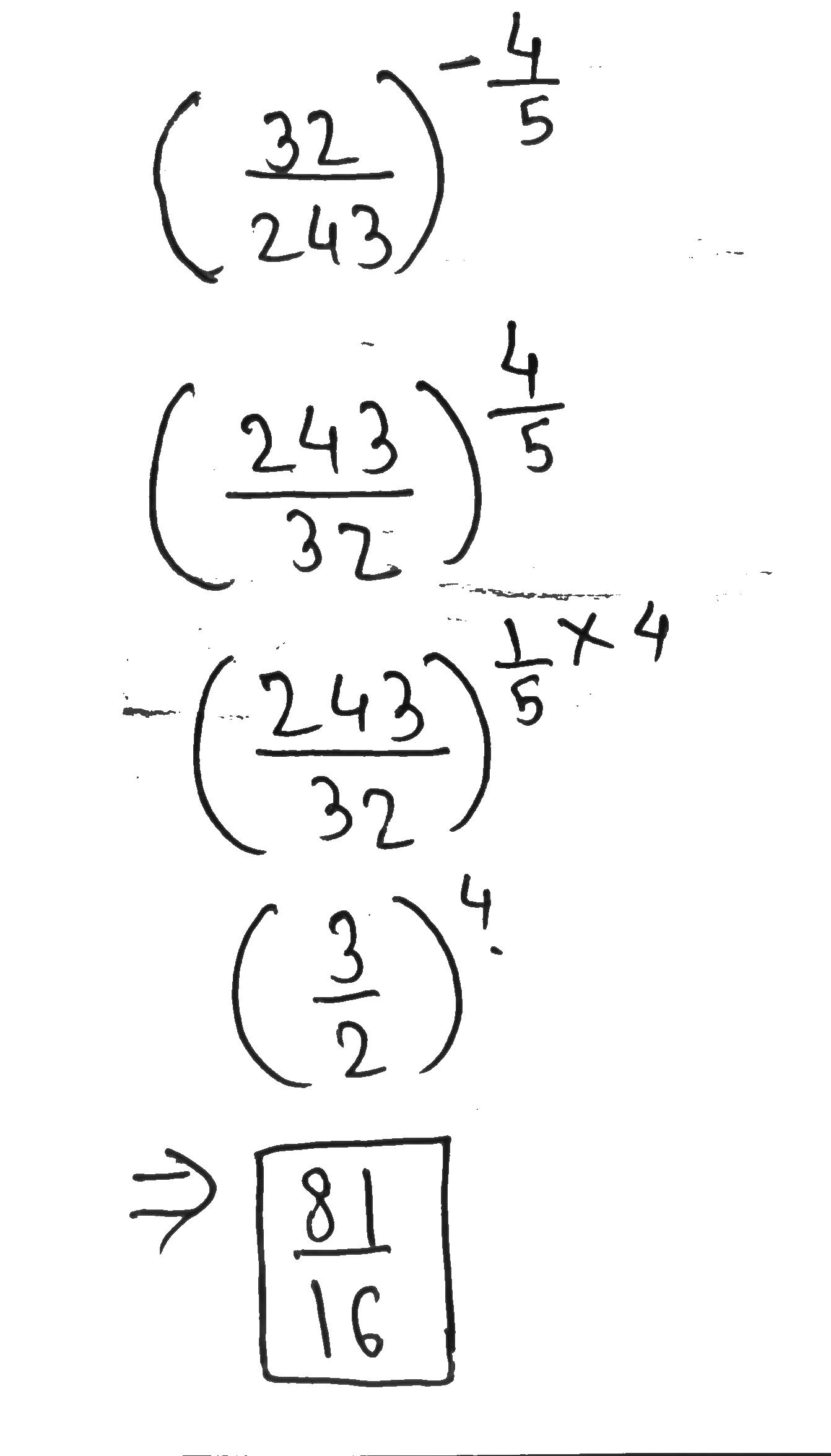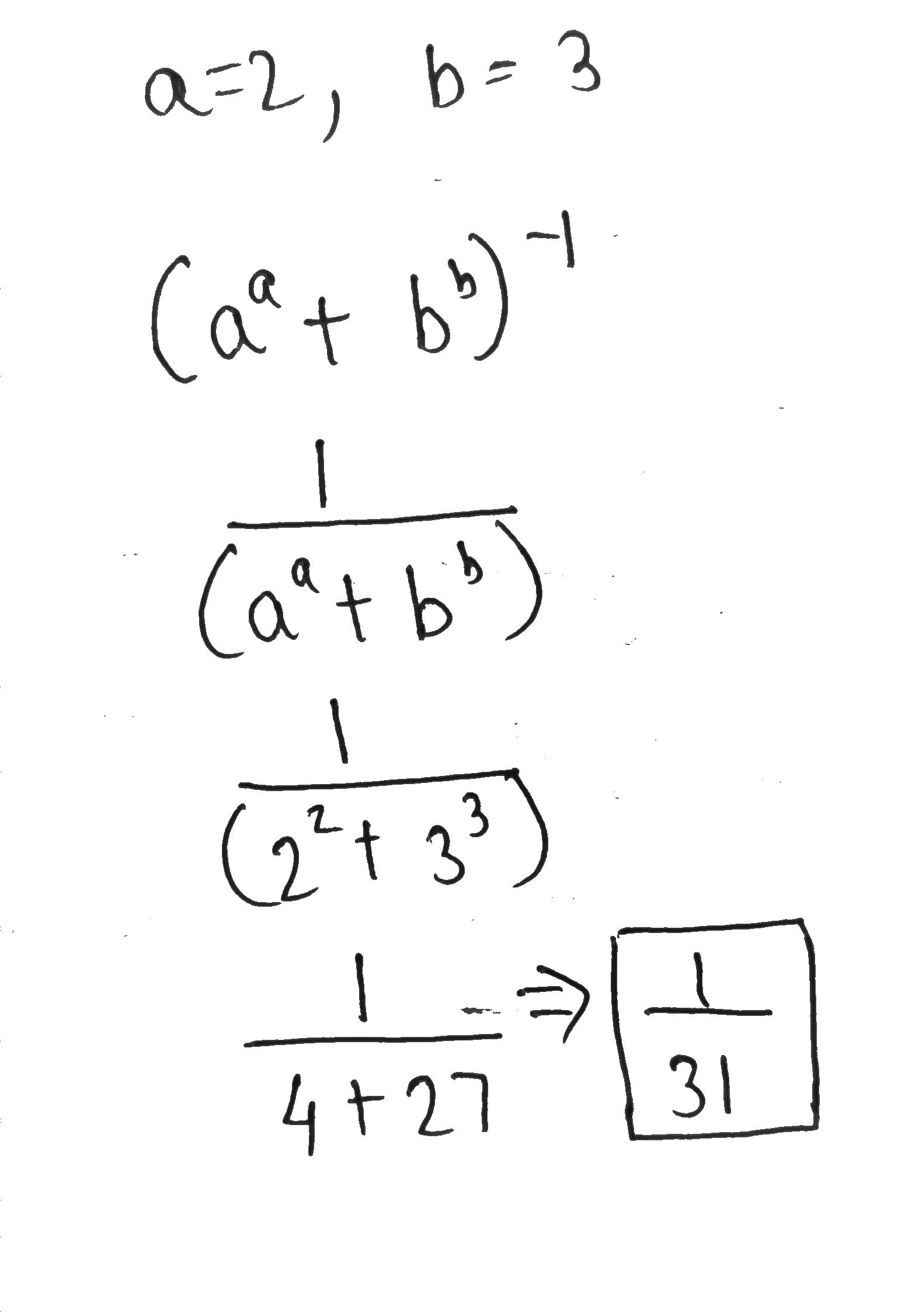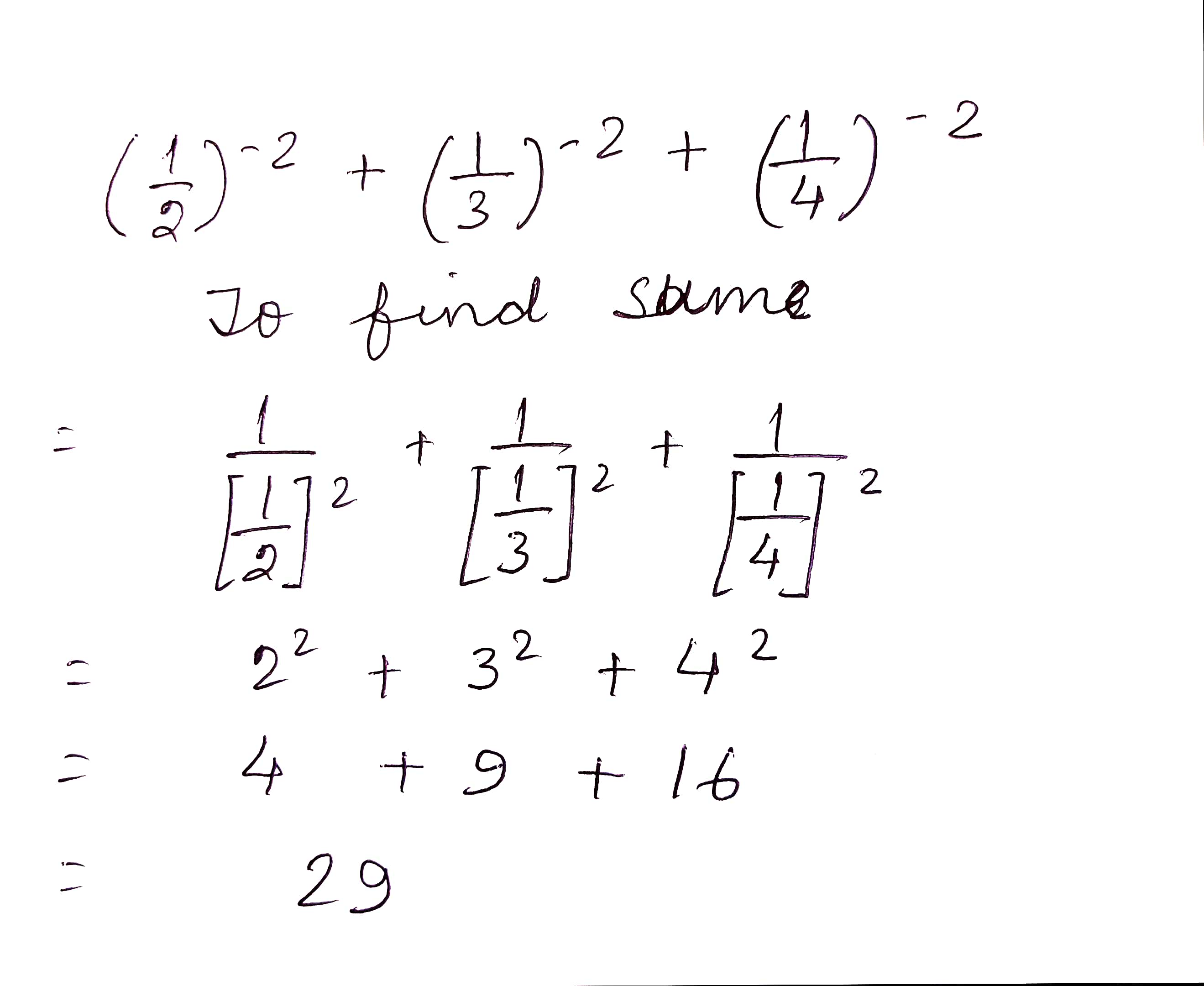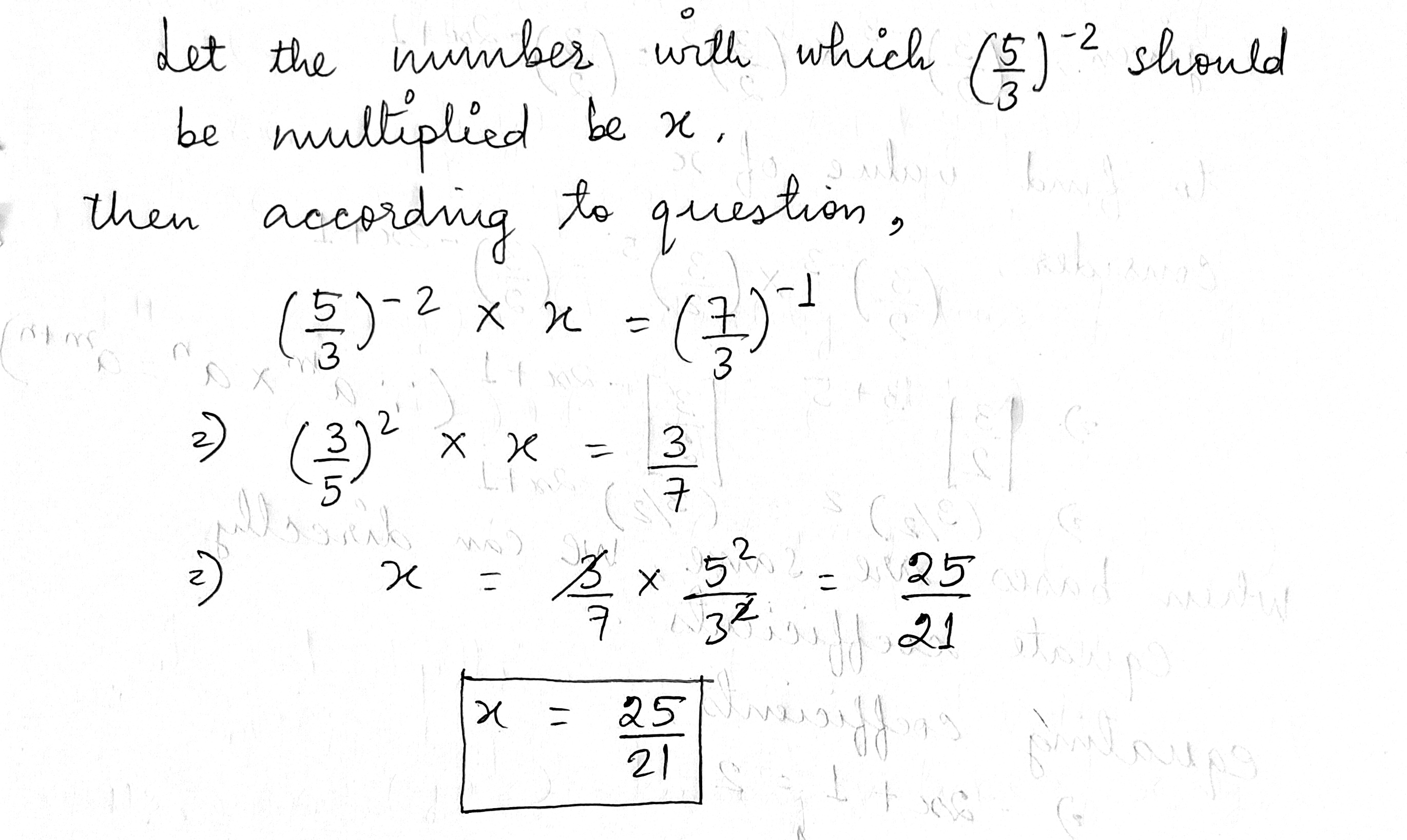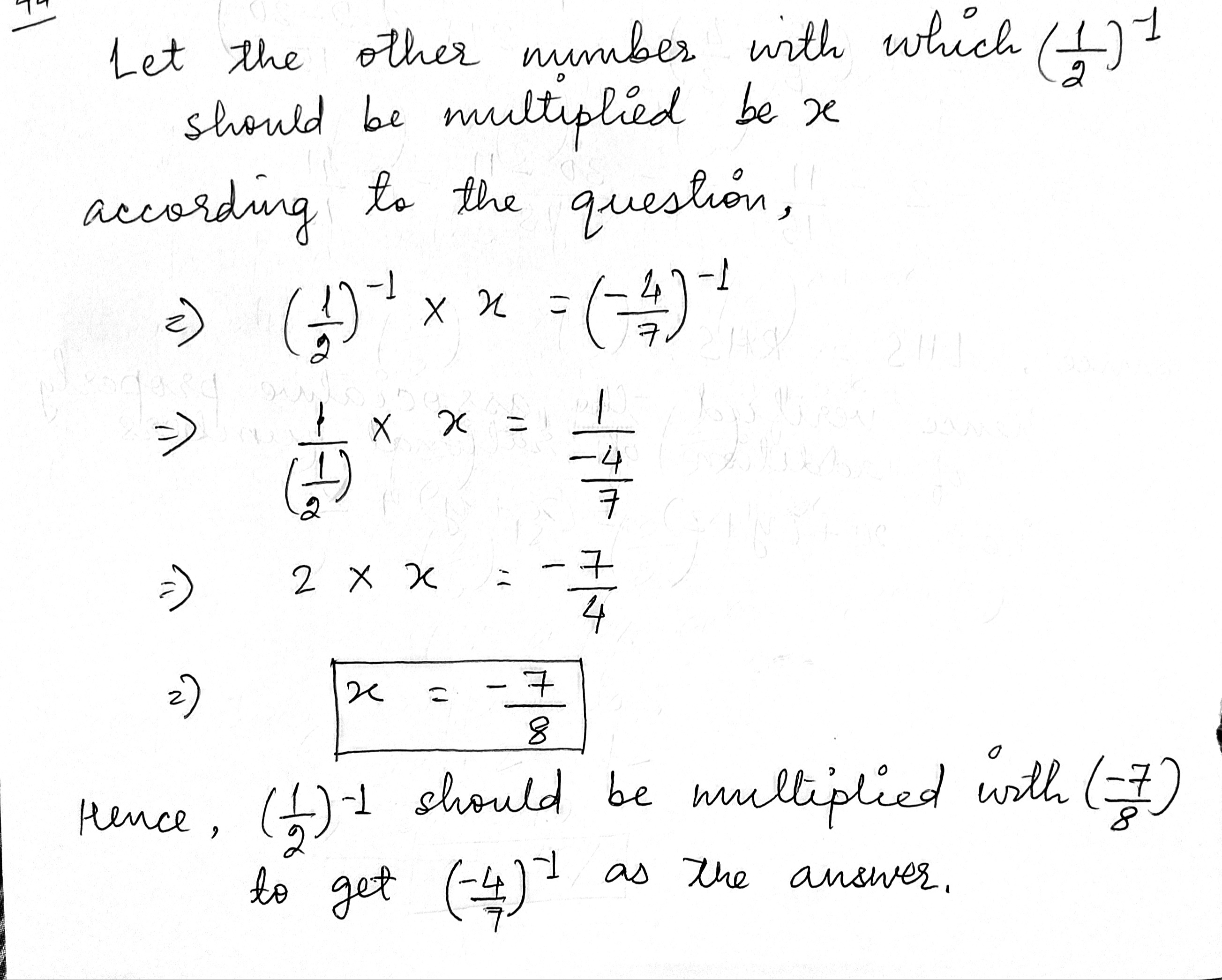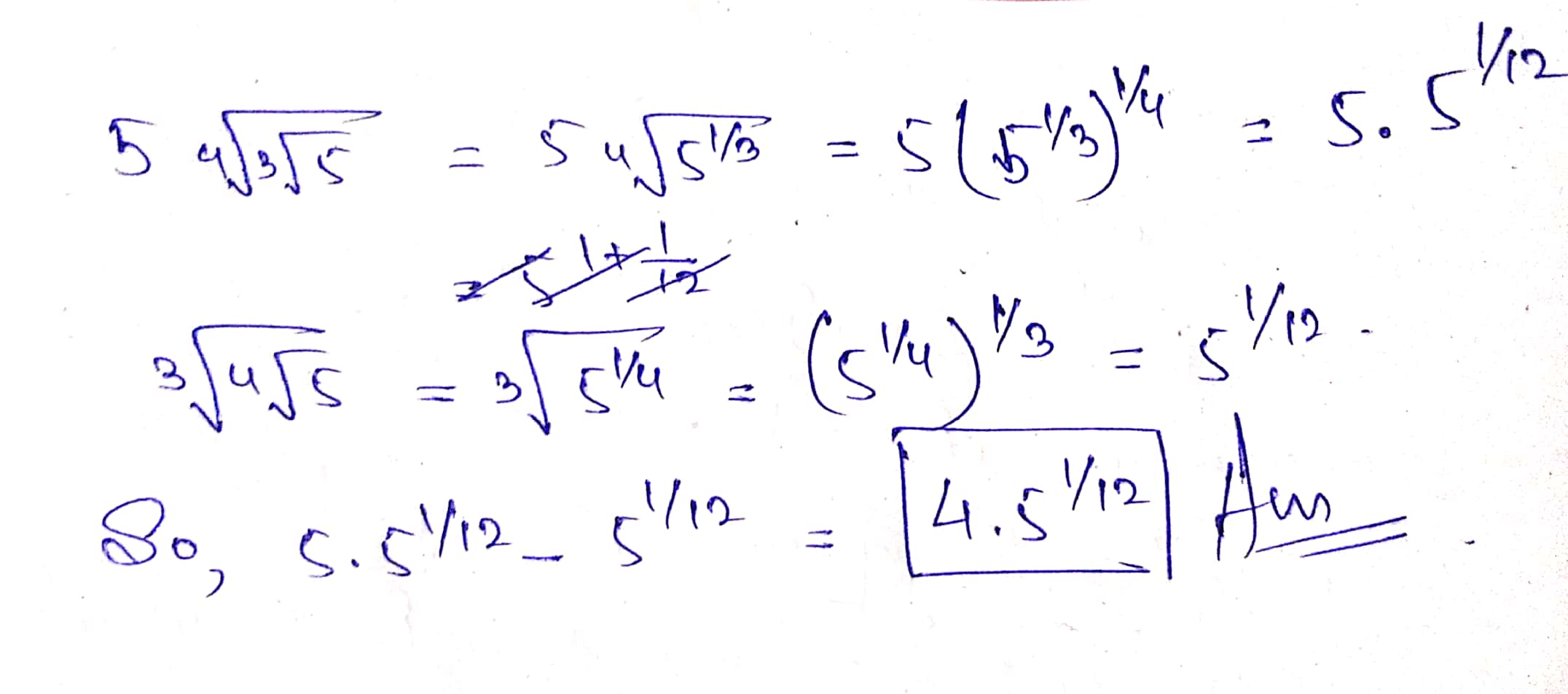Exponents And Powers - Class 8 Maths - Extra Questions

Evaluate : $$\left (\dfrac 8{125}  \right )^{-\tfrac13}$$

Here we have,
$$\ \left (\dfrac8{125}  \right )^{-1/3}$$
$$= \left [ \dfrac{\left (2 \times 2 \times 2 \right )}{ \left (5 \times 5 \times 5  \right )} \right ]^{-1/3}$$
$$= \left (\dfrac{2^{3}}{5^{3}}  \right )^{-1/3}$$
$$= \left (\dfrac 25  \right )^{3 \times -1/3}$$
$$= \left (\dfrac 25  \right )^{-1}$$
$$= \dfrac 52 = 2\space  \dfrac12$$


$$\left ( \dfrac{-1}{27} \right )^{-2/3}$$

Here we have,
$$\left ( \dfrac {-1}{27} \right )^{-2/3}\\= \left (\dfrac{-1^3}{3^{3}} \right)^{-2/3}\\ = \left (\dfrac{-1}3  \right )^{3 \times -\tfrac23}\\ = \left (-\dfrac 13  \right )^{-2}\\ = \left (-3  \right )^{2}= 9$$


Identify the greater number, wherever possible, in the following.
$$2^{10}$$ or $$10^{2}$$.


2122891_1144480_ans_898579562ac04c1980ccc9b701f5c14d.jpeg


Express the number appearing in the following statement in standard form.
The earth has $$1,535,000,000$$ cubic $$km$$ of seawater.


2123007_1218720_ans_fe29b06c11134310a6251f197ae8dd8d.jpg


Express the number appearing in the following statement in standard form.
Diameter of the Earth is $$1,27,56,000$$ meters.


2123515_1218696_ans_ddd2b0b7e55e4974b91f442c260c6e31.jpg


Express the the mean distance between Earth and moon is $$384,000,000\ m$$ in standard from.

Standard form of $$3,84,000,000$$ is $$3.84 \times 10^{8}$$


Express the number appearing in the following statement in standard from.
The univers is estimated to be $$12,000,000,000$$ years old.


1350213_1218703_ans_a44627f6ee9e4af5acbbfed813f261fa.jpeg


Express the number appearing in the following statement in standard from:
The distance between Sun and Saturn is $$1,433,000,000,000\ m\ .$$

Standard form of $$1,433,000,000$$ is $$1.433 \times 10^{9}$$.


Write the given product in exponential form.
$$7\times a\times a\times a..... 8$$ times $$\times b\times b\times b\times … 5$$ times.


2123423_1674302_ans_6de19f5186e54a87a74abc123a874919.jpeg


Write the given expression in the product form.
$$30x^4y^4z^5$$


2124214_1674308_ans_6e6b2279fdc7437983ffd5a735544304.jpg


Write the given product in exponential form.
$$4\times a\times a\times ….. 5\text{ times }\times b\times b\times ….. 12\text{ times }\times c\times c..... 15\text{ times }$$.


2123533_1674303_ans_d2635ba01f2349309412d4e5fa1323d7.jpg


Express the numbers appearing in the following statements in the standard form:
The universe is estimated to be about 12,000,000,000 years old.


2122955_1676692_ans_4c1140f67e1d4fb1bff948998632a0cb.jpeg


Express the numbers appearing in the following statements in the standard form:
Diameter of the Earth is 1,27,56,000 metres.


2124528_1676679_ans_da939a44b95e4ed5b5478b91e785f928.jpeg


Evaluate $$64^{\tfrac{-1}{2}}$$.


1680411_1715586_ans_1a74c1f3d6494ecbb0c5c800c8a44936.jpg


Identify the greater number, wherever possible, in the following?
$$100^2$$ or $$2^{100}$$.

$$ { 100^{ 2 } }\, \, or\, \, { 2^{ 100 } } \\ \Rightarrow { 100^{ 2 } }=100\times 100=10,000 \\ \Rightarrow { 2^{ 100 } }=2\, \, hundred\, \, times \\ \Rightarrow kb{ 2^{ 10 } }=1024 \\ \Rightarrow { 2^{ 20 } }=1024\times 1024>10,000 \\ \therefore { 2^{ 100 } }\, \, is\, \, greater\, \, than\, \, { 100^{ 2 } }\, \, \, \, Ans.$$


Identify the greater number in the following.
$$2^8$$ or $$8^2$$.


2123516_1144474_ans_e1c342d88e694a79b4f9e17172c91f65.jpg


Write the following number in standard form:
$$\dfrac{1}{1000000}$$.


2124203_1395270_ans_b0daf7548e1f4a7b965013d63f9abdca.jpg


Evaluate
$$\left(\dfrac 3 5\right)^{-2}$$

Let us evaluate the given expression,
By using the formula $$\left(a^{-n}=1/a^n\right)$$
So, $$\left(\dfrac 35\right)^{-2}=\left(\dfrac 53\right)^2$$
$$=\left(\dfrac 53\right)\times \left(\dfrac 53\right)$$
$$=\dfrac{25}9$$


Express the number appearing in the following statement in standard from.
$$60,230,000,000,000,000,000,000$$ molecules are present in a drop of water weighing $$1.8\ gm$$.




1190355_1218710_ans_6354ef79abb74059935d975cd6a6ffdb.jpeg


Which is greater?
$$\left (\dfrac{1}{2}  \right )^{\frac{1}{2}}$$ or $$\left (\dfrac{2}{3}  \right )^{\frac{1}
{3}}$$ 

L.C.M of $$2$$ and $$3$$ is $$6$$.
$$\therefore \left (\cfrac{1}{2}  \right )^{\tfrac{1}{2}}=\sqrt[2]{\cfrac{1}{2}}=\sqrt[2\times 3]{\left (\cfrac{1}{2}  \right )^{3}}=\sqrt[6]{\cfrac{1}{8}}$$

and  $$\left (\cfrac{2}{3}  \right )^{\tfrac{1}{3}}=\sqrt[3]{\cfrac{2}{3}}=\sqrt[3\times 2]{\left (\cfrac{2}{3}  \right )^{2}}=\sqrt[6]{\cfrac{4}{9}}$$

But $$\cfrac{4}{9}> \cfrac{1}{8}$$

$$\therefore \sqrt[3]{\cfrac{2}{3}} >\sqrt[2]{\cfrac{1}{2}}$$


Prove that:
$$(\sqrt{3 \times 5^{-3}} \div \sqrt [ 3 ]{ 3^{ -1} } \sqrt{5}) \times \sqrt [ 6 ]{ 3 \times 5^6 } = \dfrac{3}{5}$$

Given,
$$\dfrac{\sqrt{3\times 5^{-3}}}{\sqrt[3]{3}^{-1}\sqrt{5}} \times \sqrt[6]{3\times 5^6}$$

$$=\dfrac {3^{\dfrac{1}{2}}\times 5^{\dfrac{-3}{2}}} {3^{\dfrac{-1}{3}} \times 5^{\dfrac{1}{2}}} \times 3^{\dfrac{1}{6}}\times 5^{\dfrac{6}{6}}$$

$$=3^{\dfrac{5}{6}}\times 5^{-2} \times 3^{\dfrac{1}{6}}\times 5^{1} $$

$$=3\times 5^{-1}$$

$$=\dfrac{3}{5}$$

$$\dfrac{\sqrt{3\times 5^{-3}}}{\sqrt[3]{3}^{-1}\sqrt{5}} \times \sqrt[6]{3\times 5^6}=\dfrac{3}{5}$$



Express $$16^{-2}$$ as a power with base $$4$$


2159639_616709_ans_4d8fdf1b49b243d2804be657a8b774a5.jpg


Which is greater $$7^{92}$$ or $$8^{91}$$?

$$\dfrac{(7^{92})}{(8^{91})} $$

$$=(\dfrac{7}{8})^{91}\times 7 $$

 Now, $$\dfrac{ 7}{8} =0.875$$

As we know that,  $$0.875\times0.875 \approx 0.75 (0.9 \times 0 .9 =0.81) $$

$$0.875\times0.75 \approx 0.6 $$

Next, $$0.875 \times 0.6 \approx 0.5 $$

The point is every subsequent multiplication of $$0.875$$ reduces the numerator by digit

clearly after 4 more such multiplication, we land at 0.1

Therefore, the total numerator$$=0.1\times7=0.7$$

Which is already less than 1

Hence $$(8)^{91} > 7^{92}$$



Which is larger: $${ \left( 100 \right)  }^{ 4 }$$ or $$ { \left( 125 \right)  }^{ 3 }$$?


2122809_557988_ans_aed082783d43409aaf6eb5440ab31bbb.jpg


Simplify and give reasons
$$\left(\dfrac{3}{4}\right)^{-3}$$

$$\left(\dfrac 34\right)^{-3}\\ a^{-n}=\dfrac 1{a^n}\\\implies\left( \dfrac43 \right) ^3\\\left(\dfrac ab\right)^n=\dfrac {a^n}{b^n}\\\implies \dfrac {4^3}{3^3}=\dfrac{64}{27}$$


Express the following in standard from:
i) $$76854000\times 10^{8}$$
ii) $$0.000089\times 10^{6}$$

$$(i)$$ $$76854000 \times {10^8} \Rightarrow 7.6854 \times {10^{15}}$$
$$(ii)$$ $$0.000089 \times {10^6} \Rightarrow 8.9 \times {10^1}$$


Simplify $$\displaystyle \frac { \left( 5 ^ { - 3 } \right) ^ { 2 } \times 3 ^ { 4 } } { \left( 3 ^ { - 2 } \right) ^ { - 3 } \times \left( 5 ^ { 3 } \right) ^ { - 2 } }$$

Let  $$a\displaystyle=\frac{(5^{-3})^2\times 3^4}{(3^{-2})^{-3}\times (5^3)^{-2}}$$

$$a\displaystyle=\frac{(5^{-3})^2\times 3^4}{(3^{-2})^{-3}\times (5^3)^{-2}}=\frac{5^{-6}\times 3^4}{3^6\times 5^{-6}}$$

$$a\displaystyle=\dfrac{3^4}{3^6}$$

$$a=\dfrac {1}{3^2}$$

$$a=\dfrac{1}{9}$$

$$\displaystyle \therefore \frac{(5^{-3})^2\times 3^4}{(3^{-2})^{-3}\times (5^3)^{-2}}=\dfrac{1}{9}$$


Compare the following numbers:
$$2.7\times{10}^{12};1.5\times{10}^{8}$$

$$\textbf{Step 1: Given}$$

Two numbers in standard form are $$2.7\times 10^{12}$$ and $$1.5\times 10^8.$$

$$\textbf{Step 2: To Find}$$
To compare the given numbers.
$$\textbf{Step 3: Calculation}$$
Let us make the powers of $$ 10$$ equal in both the numbers to compare
$$2.7\times 10^{12}=2.7\times 10^4\times 10^8$$
                    $$=27000\times 10^8$$

Now, as the exponent of 10 in the two numbers is same we hve,
$$\begin{array}{l}27000 > 1.5\\ \Rightarrow 27000 \times {10^8} > 1.5 \times {10^8}\\ \Rightarrow 2.7 \times {10^{12}} > 1.5 \times {10^8}\end{array}$$

$$\textbf{Step 4: Conclusion}$$
$$2.7 \times 10^{12} >1.5 \times 10^{8}$$


Simplify and write the answer in exponential form
$${ \left( -4 \right)  }^{ -3 }\times { \left( 5 \right)  }^{ 3 }\times { \left( -5 \right)  }^{ -3 }$$

$$(-4)^{=3} \times (5)^3 \times (-5)^{-3}= \dfrac{-1}{4^3} \times 5^3 \times \left(\dfrac{-1}{5^3}\right) = \dfrac{1}{4^3} = 4$$
1226991_1398609_ans_02a29b2290324b8a803c276acfce6692.jpg


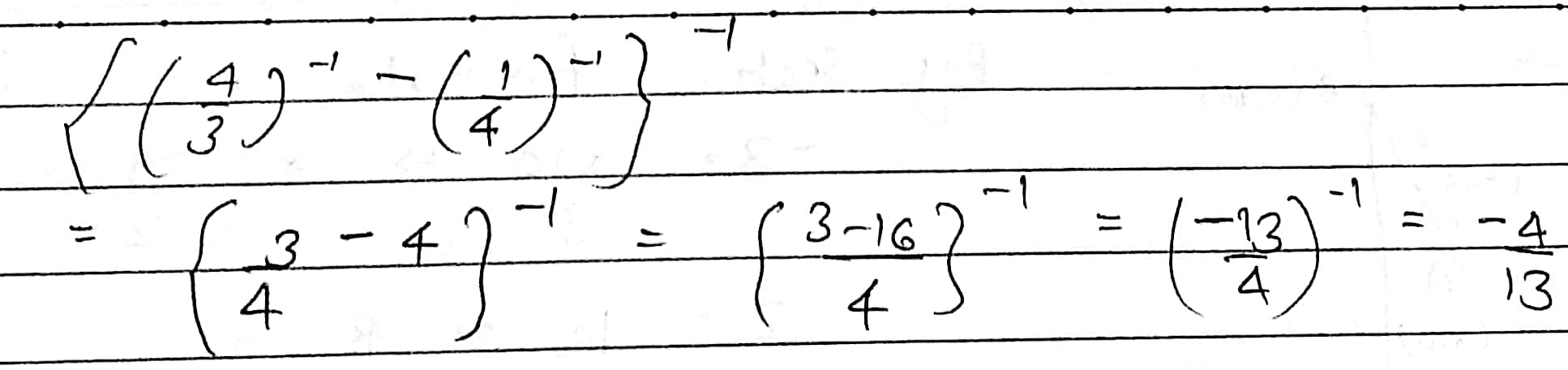
Evaluate $$\left\{\left(\dfrac{4}{3}\right)^{-1}-\left(\dfrac{1}{4}\right)^{-1}\right\}^{-1}$$

$$\left\{\left(\dfrac{4}{3}\right)^{-1}-\left(\dfrac{1}{4}\right)^{-1}\right\}^{-1}$$
$$=\left\{\dfrac{3}{4}-4\right\}^{-1}=\left\{\dfrac{3-16}{4}\right\}^{-1}=\left(\dfrac{-13}{4}\right)^{-1}=\dfrac{-4}{13}$$.

1208062_1395391_ans_7f39573d691b42b28b75eea553506c6a.jpg


Express $$512$$ in power notation.


2124179_1456674_ans_053a5e0db7304575956d2f06dce65c1d.jpg


Prove that:
$${ \left\{ { \left( \dfrac { 1 }{ 3 }  \right)  }^{ -1 }-{ \left( \dfrac { 1 }{ 4 }  \right)  }^{ -1 } \right\}  }^{ -1 } = -1$$

$$\left\{\left(\dfrac{1}{3}\right)^{-1} -\left(\dfrac{1}{4}\right)^{-1}\right\}$$
$$=\left\{ 3^{1}- 4^{1}\right\}$$
$$=\left\{3- 4\right\}$$
$$=-1$$.

1210359_1349936_ans_5dee9575fa4e41f3bc9b328e2b542976.jpg


Say true or false and justify your answer:
$${2}^{3}> {5}^{2}$$

$$\textbf{Step 1: Given}$$

$$2^3>5^2$$

$$\textbf{Step 2: To do}$$

To check if $$2^3>5^2$$ is true or false

$$\textbf{Step 3: Calcualtion}$$ $$\textbf{The exponent of a number says how many times to use the number in a multiplication.}$$

$$ LHS$$

$$2^3=2\times 2\times 2$$

     $$=8$$

$$RHS$$

$$5^2=5\times 5$$

     $$=25$$

We know that $$8<25$$

i.e., $$2^3<5^2$$

Hence the given statement is false.

$$\textbf{Step 4: Conclusion}$$

Statement $$2^3>5^2$$ is false.


Evaluate:
$$\left[\left(-\dfrac{2}{3}\right)^{-2}\right]^3\times \left(\dfrac{1}{3}\right)^{-4}\times 3^{-1}\times \dfrac{1}{6}$$

$$\left[\left(-\dfrac{2}{3}\right)^{-2}\right]^3\times \left(\dfrac{1}{3}\right)^{-4}\times 3^{-1}\times \dfrac{1}{6}$$
$$\left[\left(-\dfrac{3}{2}\right)^{2}\right]^3\times 3^{4}\times \dfrac{1}{3}\times \dfrac{1}{3\times 2}$$
$$\left(-\dfrac{3}{2}\right)^6\times (3)^2\times \dfrac{1}{2}$$
$$=\dfrac{3^{6+2}}{2^{6+1}}$$
$$=\dfrac{3^8}{2^7}$$


Find:
$$125^{\frac{-1}{3}}$$

$$125^{\frac{-1}{3}} = \frac{1}{125^{\frac{1}{3}}}$$
$$=\dfrac{1}{(5 \times 5 \times 5)^{\frac{1}{3}}} =\dfrac{1}{(5^3)^{\frac{1}{3}}}$$
$$=\dfrac{1}{5^{3 \times \frac{1}{3}}} =\dfrac{1}{5}$$


Evaluate
$$(-3)^{-3}$$

Let us evaluate the given expression,
By using the formula $$(a^{-n}=1/a^n)$$
So, 
$$(-3)^{-3}=(-1/3)^3$$
$$=(-1/3)\times (-1/3)\times (-1/3)$$
$$=-1/27$$


Evaluate:
(i) $${\left (\dfrac{1}{3}\right )^{-1} - \left (\dfrac{1}{4}\right )^{-1}} $$
(ii) $$\left (\dfrac{5}{8}\right )^{-7}\times \left (\dfrac{8}{5}\right )^{-4} $$

(i) $${\left (\dfrac{1}{3}\right )^{-1} - \left (\dfrac{1}{4}\right )^{-1}} $$

     $$  = [3-4]^{-1} = (-1) $$

(ii) $$\left (\dfrac{5}{8}\right )^{-7}\times \left (\dfrac{8}{5}\right )^{-4} $$

      $$ = \left (\dfrac{8}{5}\right )^{7}\times \left (\dfrac{5}{8}\right )^{4} $$

     $$  = \dfrac{512}{125} $$


Which is greater $$(150)^{300}$$ or $$(20000)^{100}\times (100)^{100}$$?

$$(20000)^{100}\times (100)^{100}=2^{100}\times (100)^{200}\times (100)^{200}\times (100)^{100}=(2^{1/3})^{300}\times (100)^{300}$$ 
$$\Rightarrow (20000)^{100}\times (100)^{100}=(100\sqrt[3]{2})^{300}$$ 
As $$100(\sqrt[3]{2})< 150$$
$$\therefore \boxed{(150)^{300}}$$ is greater.


Evaluate:
(i) $$3^{-2}$$
(ii) $$(-4)^{-2}$$
(iii) $$\left (\dfrac{1}{2}\right)^{-5}$$

(i) To evaluate: $$3^{-2}$$

Now,
$$ 3^{-2} = \dfrac{1}{3^{2}} =\dfrac{1}{9} $$

Hence, the required value is $$\dfrac{1}{9}$$ .

(ii)  To evaluate: $$(-4)^{-2}$$

Now,
$$ (-4)^{-2} = \dfrac{1}{(-4)^{2}} =\dfrac1{4^2} = \dfrac{1}{16} $$

Hence, the required value is $$\dfrac{1}{16}$$ .

(iii) To evaluate: $$\left(\dfrac{1}{2}\right)^{-5}$$

Now,
$$ \left ( \dfrac{1}{2}\right )^{-5} = \dfrac{1}{(2)^{-5}} = 2^5 = 32 $$

Hence, the required value is $$32$$ .


Show that $$(1.1)^{10000} > 1000$$

Lets take log on both sides,  since the values $$1.01$$ & $$1000$$ are greater than 1 the inequality remains same.

$$\implies \log{1.01^{1000}} > \log{1000}$$
$$\implies 1000\times \log 1.01 > 3$$
$$ \implies 1000\times 0.0043 > 3$$
$$ \implies 4.3 >3$$

Which is true and therefore we can say that $$(1.01)^{1000}>1000$$


Find $$x$$ in the expression $$(18)^{3.5}\div (27)^{3.5}\times 6^{3.5}=2^{x}$$

$$\dfrac{18^{3.5}}{27^{3.5}}\times 6^{3.5}=(\dfrac{18\times 6}{27})^{3.5}= (4)^{3.5}= 2^7=2^x$$
                         $$x=7$$


Mass of the earth is $$5.97\times {10}^{24}\ kg$$ and mass of the moon is $$7.35\times {10}^{22}\ kg$$. What is the difference of their masses?

Mass of Earth = $$ = 5.97 \times {10^{24}}\,Kg$$
Mass of the moon $$ = 7.35 \times {10^{22}}\,Kg$$
Difference of their masses in $$Kg$$  $$ = 5.97 \times {10^{24}} - 7.35 \times {10^{22}}$$
                                                     $$= \left( {5.97 \times {{10}^2} - 7.35} \right){10^{22}}$$
                                                     $$ = \left( {597 - 7.35} \right) \times {10^{22}}$$
                                                     $$ = 589.65 \times {10^{22}}$$
                                                     $$ = 589.65 \times {10^{24}}$$
                                                     $$ = 5.89 \times {10^{24}}$$


Compare $$7 \times 10^{-6}$$ and $$129 \times 10^{-7}.$$

First we will rewrite $$129\times10^{-7},$$
$$\begin{aligned}{}129 \times {10^{ - 7}} &= \frac{{129}}{{10}} \times {10^{ - 6}}\\ &= 12.9 \times {10^{ - 6}}\end{aligned}$$

Now, on comparing $$12.9\times10^{-6}$$ and $$7\times10^{-6}$$ we get that $$10^{-6}$$ is common in both and $$12.9>7.$$

Hence, $$12.9\times10^{-6}>7\times10^{-6}$$ or $$129\times10^{-7}>7\times10^{-6}$$


Which one is greater between $$31^{14}$$ and $$17^{18}$$?

$$We\quad know\quad that\quad 32>31\\ \rightarrow { \left( 2 \right)  }^{ 5 }>31\\ Raising\quad both\quad sides\quad to\quad power\quad of\quad 14\\ \therefore \left( { \left( 2 \right)  }^{ 5 } \right) ^{ 14 }>{ 31 }^{ 14 }\\ \rightarrow { 2 }^{ 70 }>{ 31 }^{ 12 }.....\left( 1 \right) \\ Now\quad consider\quad 17>16\\ \rightarrow 17>{ \left( 2 \right)  }^{ 4 }\\ Raising\quad both\quad sides\quad to\quad power\quad of\quad 18\\ \therefore { 17 }^{ 18 }>\left( { \left( 2 \right)  }^{ 4 } \right) ^{ 18 }\\ \rightarrow { 17 }^{ 18 }>{ 2 }^{ 72 }.....\left( 2 \right) \\ Now\quad { 2 }^{ 72 }>{ 2 }^{ 70 }....\left( 3 \right) \quad \\ From\quad points\quad 1,2\quad and\quad 3\\ { 17 }^{ 18 }>{ 31 }^{ 14 }$$


Express the following in the decimal form:
$$4.67\times {10}^{4}$$


2123526_566960_ans_a5d002adf3a047e38ff5459cd17f7d68.jpg


Simplify: $$\left(\dfrac{81}{16}\right)^{-3/4} \times \left(\dfrac{25}{9}\right)^{-3/2} \times \left(\dfrac{2}{5}\right)^{-3}$$

$$\left(\dfrac{81}{16}\right)^{-3/4} \times \left(\dfrac{25}{9}\right)^{-3/2} \times \left(\dfrac{2}{5}\right)^{-3}$$
$$=\left(\dfrac{3^4}{2^4}\right)^{-3/4} \times \left(\dfrac{5^2}{3^2}\right)^{-3/2} \times \left(\dfrac{2}{5}\right)^{-3}$$
$$=\left(\dfrac{3}{2}\right)^{4\times-3/4} \times \left(\dfrac{5}{3}\right)^{2\times-3/2} \times \left(\dfrac{2}{5}\right)^{-3}$$
$$=\left(\dfrac{3}{2}\right)^{-3} \times \left(\dfrac{5}{3}\right)^{-3} \times \left(\dfrac{2}{5}\right)^{-3}$$
$$=\left(\dfrac{30}{30}\right)^{-3}$$
$$=1$$.


Find the value of $$x$$ for which$${ \left\{ { \left( \dfrac { -2 }{ 7 }  \right)  }^{ 2 } \right\}  }^{ x }\times { \left( \dfrac { -7 }{ 2 }  \right)  }^{ -1 }=\dfrac { -8 }{ 343 }$$.

$${\left\{ {{{\left( {\dfrac{{ - 2}}{7}} \right)}^2}} \right\}^x} + {\left( {\dfrac{{ - 7}}{2}} \right)^{ - 1}} = \dfrac{{ - 8}}{{343}}$$

$$ \Rightarrow {\left( {\dfrac{{ - 2}}{7}} \right)^{2x}} + \left( {\dfrac{{ - 2}}{7}} \right) = {\left( {\dfrac{{ - 2}}{7}} \right)^3}$$

$$ \Rightarrow {\left( {\dfrac{{ - 2}}{7}} \right)^{2x + 1}} = {\left( {\dfrac{{ - 2}}{7}} \right)^3}$$

$$ \Rightarrow 2x + 1 = 3$$

$$ \Rightarrow 2x =  - 2$$

$$ \Rightarrow x =  - 1$$



If $$9^{x} \times 3^{2}\times \left(3^{\left(\tfrac{-x}{2}\right)}\right)^{-2}=\dfrac{1}{27}$$, then find the value of $$x$$.

The given equation is :
$${ 9 }^{ x }\times 3^{ 2 }\times { \left( { 3 }^{ \frac { -x }{ 2 }  } \right)  }^{ -2 }=\frac { 1 }{ 27 } $$
It can be written as:
$$3^{ 2x }\times 3^{ 2 }\times 3^{ x }=3^{ -3 }$$
$${ 3 }^{ 2x+2+x }={ 3 }^{ -3 }$$ 
$${ 3 }^{ 3x+2 }={ 3 }^{ -3 }$$
Now,since the bases are same,then comparing the powers,we get $$3x+2=-3$$
$$x=\frac { -5 }{ 3 } $$


If $$\left(\dfrac{5}{3}\right)^{-15} \times \left(\dfrac{5}{3}\right)^{11} =\left(\dfrac{5}{3}\right)^{8x}$$, then $$x$$ =?


2122857_1042806_ans_4923d2cbb2294fc8808fac0f39a99bed.jpeg


If the standard form of $$12,000,000,000$$ is $$1.2\times 10^{m}$$ then find the value of $$m$$.


2127672_705091_ans_322afb99a2754aefa8e9b45c9d39ea16.jpg


If $${ \left( 64 \right)  }^{ x }=\cfrac { 1 }{ { \left( 256 \right)  }^{ y } } =2\sqrt { 2 } $$; then show that $$3x+4y=0$$.

Given $${(64)}^x=2^{1.5}$$
$$\Rightarrow { { (2 }^{ 6 }) }^{ x }={ 2 }^{ 1.5 }\\ $$
Exponent and bases should be equal
$$\Rightarrow 6x=1.5$$
$$\Rightarrow x=0.25$$

Given $${(256)}^{-y}=2^{1.5}$$
$$\Rightarrow { { (2 }^{ 8 }) }^{ -y }={ 2 }^{ 1.5 }\\ $$
Exponent and bases should be equal
$$\Rightarrow -8y=1.5$$
$$\Rightarrow y=-\dfrac3{16}$$

Now $$3x+4y=3(0.25)+4\left(-\dfrac3{16}\right) = \dfrac34 - \dfrac34$$ $$=0$$


If $$2^{x-1}+2^{x+1}=1280$$, then find the value of $$x$$.


2123420_1115507_ans_e0e108a761864d62a1b0f2ec56d3e2c2.jpeg


Identify the greater number, wherever possible, in the following?
$$5^3$$ or $$3^5$$.

$${ 5^{ 3 } }\, \, or\, \, { 3^{ 5 } } \\ \Rightarrow { 5^{ 3 } }=5\times 5\times 5=125 \\ \Rightarrow { 3^{ 5 } }=3\times 3\times 3\times 3\times 3=243 \\ \therefore { 3^{ 5 } }\, \, >\, \, \, { 5^{ 3 } }\, \, \,$$


If $$x^{1/p} = y^{1/q} = z^{1/r}$$ and $$xyz = 1, $$ then the value of $$p+q+r = ? $$

$$x^{1/p}=y^{1/q}=z^{1/r}=k$$ (say)
$$\Rightarrow x=k^p, y=k^q, z=k^r$$
$$xyz=1$$ (given)
$$k^p.k^q.k^r=1$$
$$k^{(p+q+r)}=1$$.
$$\boxed{\Rightarrow (p+q+r)=0}$$.


Identify the greater number between the following:
$$4^3$$ or $$3^4$$

$$ { 4^{ 3 } }\, \, or\, \, { 3^{ 4 } } \\ \Rightarrow { 4^{ 3 } }=4\times 4\times 4=164 \\ \Rightarrow { 3^{ 4 } }=3\times 3\times 3\times 3=81 \\ \therefore { 3^{ 4 } }\, \, >\, \, \, { 4^{ 3 } }\, \, \,$$


Which is greater among the following?
$$\sqrt{2}, \sqrt[3]{4}$$ and $$ \sqrt[4]{3}$$

$$\sqrt 2, (4)1/3, \Rightarrow LCM\ (2, 3, 4)=12$$
$$(i)\ \sqrt 2=(2)^{1/2}=2^{(6/12)}=(2^6)^{1/12}=(64)^{1/12}$$
$$(ii)\ 4^{1/3}=(4)^{4/12}=(256)^{1/12}$$
$$(iii)\ 3^{1/4}=3^{3/12}=(3^3)^{1/12}= (27)^{1/12}$$
$$(4)^{1/3} > (2)^{1/2} > 3^{1/4}$$



$$\begin{array}{l} If\, \, { e^{ \left( { { { \sin   }^{ 2 } }x+{ { \sin   }^{ 2 } }x+{ { \sin   }^{ 6 } }x......\infty  } \right) \log { e^{ 2 } }  } }\, and\, { y^{ 2 } }-5y+4=0\, satisfy\, the\, equation\, then\, find\, the\,  \\ value\, of\, \frac { { \sin  x } }{ { \cos  x-\sin  x } }  \end{array}$$

$$\begin{array}{l} Given \\ { e^{ \left( { { { \sin   }^{ 2 } }x+{ { \sin   }^{ 2 } }x+{ { \sin   }^{ 6 } }x......\infty  } \right) \log { e^{ 2 } }  } } \\ ={ e^{ \log  2\left( { \frac { 1 }{ { 1-{ { \sin   }^{ 2 } }x } }  } \right)  } } \\ ={ 2^{ \left( { \frac { 1 }{ { 1-2{ { \sin   }^{ 2 } }x } }  } \right)  } }={ 2^{ { { \sec   }^{ 2 } }x } }=y \\ Now, \\ { y^{ 2 } }-5y+4=0 \\ \Rightarrow { y^{ 2 } }-4y-y+4=0 \\ \Rightarrow y\left( { y-4 } \right) -1\left( { y-4 } \right) =0 \\ \Rightarrow \left( { y-4 } \right) \left( { y-1 } \right) =0 \\ \therefore y=4\, and\, y=1 \\ If\, { 2^{ { { \sec   }^{ 2 } }x } }=1 \\ { \sec ^{ 2 }  }x=0\, \, \left( { not\, possible\, as\, { { secx } }\ge 1 } \right)  \\ else, \\ { 2^{ { { \sec   }^{ 2 } }x } }=4 \\ { \sec ^{ 2 }  }x=2 \\ \cos  x=\frac { 1 }{ { \sqrt { 2 }  } }  \\ Thus,\, the\, value\, of\, \frac { { \sin  x } }{ { \cos  x-\sin  x } } =\frac { { \frac { 1 }{ { \sqrt { 2 }  } }  } }{ { \frac { 1 }{ { \sqrt { 2 }  } } -\frac { 1 }{ { \sqrt { 2 }  } }  } } \, \Rightarrow Not\, defined. \\  \end{array}$$


Write the base and the exponent of $$(7x)^{2}$$

Given the number is $$(7x)^2$$.
So the base is $$7x$$ and the exponent is $$2$$.


Change the given number into it's standard form
$$128000000$$

$$128000000$$
$$=128\times {10}^{6}$$
$$=12.8\times 10\times {10}^{6}$$
$$=1.28\times 10\times 10\times {10}^{6}$$
$$=1.28\times {10}^{8}$$


$$(\sqrt [ 5 ]{ 8 } )^{\dfrac{5}{2}}\times (16)^{\dfrac{-3}{2}}$$

We have,

$$ {{\left( \sqrt[5]{8} \right)}^{\frac{5}{2}}}\times {{\left( 16 \right)}^{\frac{-3}{2}}} $$

$$ \Rightarrow {{\left( 8 \right)}^{\frac{1}{5}\times \frac{5}{2}}}\times {{\left( {{2}^{4}} \right)}^{\frac{-3}{2}}} $$

$$ \Rightarrow {{\left( {{2}^{3}} \right)}^{\frac{1}{2}}}\times {{\left( 2 \right)}^{-6}} $$

$$ \Rightarrow {{2}^{\frac{3}{2}-6}} $$

$$ \Rightarrow {{2}^{\frac{-9}{2}}} $$


Hence, this is the answer.



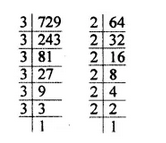
Express the following as a product of prime factors in exponential form : 
$$729\times 64$$

$$729 \times 64$$

$$=3\times 3\times 3\times 3\times 3\times 3  \times 2\times 2\times 2\times 2\times 2\times 2$$

$$=3^6 \times 2^6$$

1771764_1595758_ans_c465ce418c2040b89989981cad8105d9.PNG


Identify the greater number in each of the following numbers:
$${2}^{8}$$ or $${8}^{2}$$

We have : (1) $${2}^{8}=2\times 2\times 2\times 2\times 2\times 2\times 2\times 2=64\times 4 = 256$$ 
                 (2) $${8}^{2}=8\times 8=64$$                 
                     Since $$256> 64$$
                     Thus, $${2}^{8}$$ is greater than $${8}^{2}$$.


Identify the greater number among the two numbers:
$${2}^{10}$$ or $${10}^{2}$$

$${2}^{10}=2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 2=1,024$$
$${10}^{2}=10\times 10=100$$
Since, $$1,024> 100$$
Thus, $${2}^{10}> {10}^{2}$$


Identify the greater number in the following numbers:
$${100}^{2}$$ or $${2}^{100}$$



1338811_1646428_ans_3c7233746012489e9a8b2dcd3b668158.jpeg


Express the number appearing in the following statements in standard form:
$$602,300,000,000,000,000,000,000$$ molecules are contained in a drop of water weighing $$1.8gm$$.


2126821_1646517_ans_ea3db53a20c043c69f1af917034bdeb5.jpg


Write $$629000$$ in standard form.

$$629000=6.29\times 100000$$
            $$=6.29\times 10^5$$


Express the number appearing in the following statement in standard form:
The Earth has $$1,353,000,000$$ cubic km of seawater.


2122806_1646518_ans_fb0b6e61ae2b41a783b41499d03451a4.jpg


Identify the greater number, wherever possible, in each of the following:
$${5}^{3}$$ and $${3}^{5}$$


2122871_1646426_ans_2b650dc0f38040eaa539be9867cb9e2a.jpeg


On solving the equation $$ 7^{2x+3} = 1 $$, we get $$x=\dfrac{-3}{b}$$ then find the value of $$b$$.

Given, $$7^{2x+3}=1$$

The above equation can also be written as:  $$7^{2x+3}=7^0$$

By comparing powers we get;

$$2x+3=0$$

$$\therefore x=-\dfrac{3}{2}$$

Comparing the value of x with the question we got $$\Rightarrow b=2$$


Standard from of $$6020000000000000$$ is $$6.02\times 10^{16}$$.
Enter 1 if it is True or 0 if it is False

The correct answer is 0

1872099_1671200_ans_d4909c69cdc4466a866e80cb6f06376c.jpg


Express the following numbers in standard from:
$$4 \div 100000$$


2123374_1671229_ans_e593e15fb433482d8aaf8580f7e5b141.jpeg


Write the given expression in the product form.
$$43p^{10}q^5r^{15}$$


2126813_1674309_ans_e97f13578e0942e9b4d8ef927820584d.jpg


Write the given product in exponential form.
$$8\times b\times b\times b\times a\times a\times a\times a$$.

We know that if a number say $$b$$ is multiplied three times. That is, $$b\times b\times b$$ can be written as $$b^{3}$$.
Similarly,
$$8\times b\times b\times b =$$ $$ 8^{1} \times$$ $$ b^{3}$$.
Thus 
$$8\times b\times b\times b\times a\times a\times a\times a =$$ $$ 8^{1} \times$$ $$ b^{3}$$ $$\times a^{4}$$.
                                                     $$=8^{1}b^{3}a^{4}$$.


Write the expression $$5xy\times 3x^2y\times 7y^2$$ in exponential form.

We know that if a number say $$b$$ is multiplied three times. That is, $$b\times b\times b$$ can be written as $$b^3$$.
=> $$b^3$$ = $$b\times b\times b$$
Similarly,
$$ 5xy = 5\times x \times y$$.
$$3x^{2}y = 3\times x\times x\times y$$.
$$ 7y^{2} = 7 \times y \times y$$.
Thus, 
$$ 5xy \times 3 x^{2} y \times 7y^{2} = 5 \times x \times y \times 3 \times x \times x \times y \times 7 \times y \times y $$
                                 $$= 5 \times 3 \times 7 \times x \times y \times x \times x \times y \times y \times y $$.
                                 $$ = 105 \times x^{3} \times y^{4} $$.
                                 $$ = 105 x^{3}y^{4} $$.


Write the given expression in the product form.
$$a^2b^5$$.

We know that if a number say $$b$$ is multiplied three times. That is, $$b\times b\times b$$ can be written as $$b^3$$.
$$\implies b^3$$  $$=b\times b\times b$$
So,
$$ a^{2} = a \times a $$
$$ b^{5} = b \times b \times b \times b \times b $$
Thus,
$$a^{2}b^{5} = a \times a\times b\times b\times b\times b\times b$$.                                                


Write the given expression in the product form.
$$17p^{12}q^{20}$$.

Let, $$a$$ number is multiplied three times. 
That is, $$ a^{3}$$ $$ = a\times a \times a $$.
So,
$$p^{12} =  p \times p \times p \times p \times p \times p \times p \times p \times p \times p\times p\times p $$.
$$q^{20} =  q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q$$.
Thus,
$$17p^{12}q^{20}= 17 \times p \times p \times p \times p \times p \times p \times p \times p \times p \times p\times p\times p \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times q \times $$
                    $$  q \times q \times q \times q \times q \times q \times q \times q $$.


Express the following number in standard form:
$$0.00000000000942$$


2124178_1671204_ans_22f1f76dd4bf4ec4bbe9905191e67eaa.jpg


Express the following Number in the standard form:
$$ 846 \times 10^7 $$


2126809_1676660_ans_2a2955078ad64291944c7f6c55344d91.jpg


find the product of
$$a^3\times 3ab^2\times 2a^2b^2$$.

We know that if a number say $$b$$ is multiplied three times. That is, $$b\times b\times b$$ can be written as $$b^3$$.
=> $$b^3$$ = $$b\times b\times b$$
Similarly,
$$ a^{3} = a\times a \times a$$.
$$3ab^{2} = 3\times a\times b\times b$$.
$$ 2a^{2}b^{2} = 2 \times a \times a \times b \times b$$.
Thus, 
$$ a^{3} \times 3 ab^{2}\times 2a^{2}b^{2} = a\times a \times a \times 3\times a\times b\times b \times 2  \times a \times a \times b \times b  $$.
                                 $$ = 6 \times a\times a \times a \times a\times b\times b \times a \times a \times b \times b $$.
                                 $$ = 6 \times a\times a \times a \times a\times a \times a \times b \times b \times b\times b $$.
                                 $$ = 6 \times a^{6} \times b^{4} $$
                                 $$ = 6 a^{6}b^{4} $$.


Express the number $$5,00,00,000$$ in the standard from.


1517375_1676654_ans_c18af6997fcc4e5cbda50a6db554d66e.jpg


Write the given statement in the product form.
$$x^3y^4$$.

We know that, 
$$b^{3}$$ = $$b\times b\times b$$.
Similarly,
$$x^{3}= x\times x\times x$$.
$$y^{4} = y \times y\times y\times y$$.
Thus,
$$x^{3}y^{4}= x\times x\times x \times  y \times y\times y\times y$$.


Write the following number in the usual form: 
$$ 4.83 \times 10^7 $$

Now,
$$4.83\times 10^7$$

$$=\dfrac{483}{10^2}\times 10^7$$

$$=483\times 10^{(7-2)}$$

$$=483\times 10^5$$

$$=4,83,00,000$$


Express the following Numbers in the standard from: $$ 723 \times 10^9 $$


1518033_1676661_ans_5c44db87ccd540b69b813e1345778905.jpeg


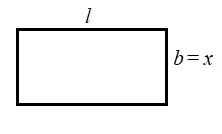
The area of a rectangle is given by the product of its length and breadth. The length of a rectangle is two-third of its breadth. Find its area, if its breadth is x cm.

Let,
The length of the rectangle =$$l$$.
 The breadth of the rectangle = $$b$$.   
Given, 
The breadth of a rectangle ($$b$$) = $$x$$ ---- (1)
The length of the rectangle ($$l$$)= $$\dfrac{2}{3} $$ of breadth of rectangle.
                                               $$l$$ = $$\dfrac{2}{3} \times b$$   --- (2)
Area of a rectangle = Product of length and breadth
                                  = $$ l \times b$$.                         
                                  = $$\dfrac{2}{3} \times b \times b$$.        [From (2)]
                                  = $$\dfrac{2}{3} x^{2}$$.                  [From (1)]                                          
                            

1409231_1674315_ans_eab502b3f28e4aaaa603a1cf1eea0b5e.png


Simplify $$\left(\dfrac{81}{49}\right)^{-\tfrac{3}{2}}$$.


1680419_1715594_ans_fbec276dc041422bab362920a1dd2723.jpg


Write the following in ascending order of magnitude.
$$\sqrt[6]{6}, \sqrt[3]{7}, \sqrt[4]{8}$$.


1886511_1715630_ans_6e627ebfbc73456d9f99b4eddd7abba6.jpg


Evaluate $$8^{\tfrac{-1}{3}}$$.


1680413_1715588_ans_9f3d599e3ea34e54a7d7eb8c5b4d7e86.jpg


If $$a=2, b=3$$ find the value of $$(a^b+b^a)^{-1}$$.


1680414_1715591_ans_79a781da72a342b38617dfa4ae6f1c4a.jpg


Simplify $$\left(\dfrac{7776}{243}\right)^{-\dfrac{3}{5}}$$.


1680456_1715598_ans_1df053908a894225807522960a3e8f77.jpg


Evaluate:
$$\left(\dfrac{1}{2}\right)^{-5}$$

Given $$\left(\dfrac{1}{2}\right)^{-5}$$

According to law of exponents, we can write $$\left(\dfrac{1}{2}\right)^{-5}$$ as
$$\left(\dfrac{1}{2}\right)^{-5}=2^{5}\left[\because a^{-m}=\left(\dfrac{1}{a^{m}}\right)\right]$$

But we know that $$2^{5}$$ is $$32, \left(\dfrac{1}{2}\right)^{-5}=32$$


Evaluate:
$$4^{-3}$$

Given: $$4^{-3}$$

According to law of exponents we can write $$4^{-3}$$

$$4^{-3}=\left(\dfrac{1}{4^{3}}\right) \left[\because a^{-m}=\left(\dfrac{1}{a^{m}}\right)\right]$$

But we know that $$4^{3}$$ is $$64$$
Hence $$4^{-3}=\dfrac{1}{64}$$


Evaluate:
$$\left(\dfrac{4}{3}\right)^{-3}$$

Given: $$\left(\dfrac{4}{3}\right)^{-3}$$

According to law of exponents, we can write $$\left(\dfrac{4}{3}\right)^{-3}$$ as

$$\left(\dfrac{4}{3}\right)^{-3}=\left(\dfrac{3}{4}\right)^{3}$$

$$\left[\because \left(\dfrac{a}{b}\right)^{-m}=\left(\dfrac{b}{a}\right)^{m}\right]$$

But we know that $$3^{3}$$ is $$27$$ and $$4^{3}$$ is $$64$$, now substitute this in above

We get $$\left(\dfrac{3}{4}\right)^{3}=\dfrac{3^{3}}{4^{3}}$$

$$\therefore \dfrac{3^{3}}{4^{3}}=\dfrac{27}{64}$$


Simplify $$\left(\dfrac{32}{243}\right)^{-\tfrac{4}{5}}$$.


1680452_1715597_ans_03464b450a1d4c9892a1bbc6d927a85d.jpg


If $$a=2, b=3$$ find the value of $$(a^a+b^b)^{-1}$$.


1680417_1715592_ans_8eaf5d3b5bb5464387e3857d6b069b19.jpg


Evaluate:
$$\left\{\left(\dfrac{3}{2}\right)^{-2}\right\}^{2}$$

Given that $$\left\{\left(\dfrac{3}{2}\right)^{-2}\right\}^{2}$$

According to third law of exponents i.e., $$\left\{\left(\dfrac{a}{b}\right)^{m}\right\}^{n}=\left(\dfrac{a}{b}\right)^{m\times n}$$

We can apply this law in above equation we get $$\left\{\left(\dfrac{3}{2}\right)^{-2}\right\}^{2}=\left(\dfrac{3}{2}\right)^{-4}$$

Again apply the third law of exponents,

Now $$\left(\dfrac{3}{2}\right)^{-4}=\left(\dfrac{2}{3}\right)^{4}=\dfrac{16}{81}$$            $$\left[\because \left(\dfrac{a}{b}\right)^{-m}=\left(\dfrac{b}{a}\right)^{m}\right]$$

We know that $$3^{4}$$ is $$81$$ and $$2^{4}$$ is $$16$$
On substituting we get $$\left(\dfrac{2}{3}\right)^{4}=\dfrac{16}{81}$$


Evaluate $$\left\{\left(\dfrac{1}{3}\right)^{-3}-\left(\dfrac{1}{2}\right)^{-3}\right\}\div \left(\dfrac{1}{4}\right)^{-3}$$

Given that $$\left\{\left(\dfrac{1}{3}\right)^{-3}-\left(\dfrac{1}{2}\right)^{-3}\right\}\div \left(\dfrac{1}{4}\right)^{-3}$$

The above equation is in the form of $$\left(\dfrac{a}{b}\right)^{-m}=\left(\dfrac{b}{a}\right)^{m}$$

By applying the law we get $$\left\{\left(\dfrac{1}{3}\right)^{-3}-\left(\dfrac{1}{2}\right)^{-3}\right\}\div \left(\dfrac{1}{4}\right)^{-3}= [3^{3}-2^{3}]\div (4^{3})$$

On simplifying above equation by substituting the $$2^{3}$$ is $$8,3^{3}$$ is $$27$$ and $$4^{3}$$ is $$64$$

We get $$\left\{3^{2}-2^{3}\right\}\div (4^{3})=(27-8)\div 64=\dfrac{19}{64}$$


Evaluate : $$\left (1 \dfrac{61} {64}\right )^{-\tfrac{2} {3}}$$

Here we have
$$\left (1 \dfrac{61} {64}\right )^{-\tfrac{2} {3}} = \left ( \dfrac{125} {64}\right )^{-\tfrac{2} {3}}\\ = \left ( \dfrac{5^{3}} {4^{3}}\right )^{-\tfrac{2} {3}}\\  = \left (\dfrac 54  \right )^{3 \times -\tfrac23}\\  = \left (\dfrac 54  \right )^{-2}\\  = \left (\dfrac45  \right )^{2}\\ =\dfrac{ 16}{25}$$


Evaluate:
$$\left(\dfrac{2}{3}\right)^{-3}\times \left(\dfrac{2}{3}\right)^{-2}$$

Given $$\left(\dfrac{2}{3}\right)^{-3}\times \left(\dfrac{2}{3}\right)^{-2}$$

According to first law of exponents, $$\left(\dfrac{a}{b}\right)^{m}\times \left(\dfrac{a}{b}\right)^{n}=\left(\dfrac{a}{b}\right)^{m+n}$$

We can write above equation as $$\left(\dfrac{2}{3}\right)^{-3}\times \left(\dfrac{2}{3}\right)^{-2}=\left(\dfrac{2}{3}\right)^{-3+(-2)}= \left(\dfrac{2}{3}\right)^{-5}$$

Now we have $$\left(\dfrac{2}{3}\right)^{-5}$$, this can be written in the form of $$a^{m}=\left(\dfrac{1}{a^{m}}\right)$$

Then above equation becomes, $$\left(\dfrac{2}{3}\right)^{-5}= \left(\dfrac{3}{2}\right)^{5}$$

But we know that $$3^{5}$$ is $$243$$ and the value of $$2^{5}$$ is $$32$$,

Substituting these in above equation, we get $$\left(\dfrac{3}{2}\right)^{5}=\left(\dfrac{243}{32}\right)$$


Evaluate:
$$\left\{\left(\dfrac{-2}{3}\right)^{2}\right\}^{-2}$$

Given $$\left\{\left(\dfrac{-2}{3}\right)^{2}\right\}^{-2}$$

According to third law of exponents i.e. $$\left\{\left(\dfrac{a}{b}\right)^{m}\right\}^{n}=\left(\dfrac{a}{b}\right)^{m\times n}$$

We can apply this law in above equation we get $$\left\{\left(\dfrac{-2}{3}\right)^{2}\right\}^{-2}=\left(\dfrac{-2}{3}\right)^{2\times (-2)}$$

Again apply the third law of exponents we get, $$\left(\dfrac{-2}{3}\right)^{2\times (-2)}=\left(\dfrac{-2}{3}\right)^{-4}$$

Now above equation is in the form of $$\left(\dfrac{a}{b}\right)^{-m}=\left(\dfrac{b}{a}\right)^{m}$$

So we get $$\left(\dfrac{-2}{3}\right)^{-4}=\left(\dfrac{3}{-2}\right)^{4}$$

But we know that $$3^{4}$$ is $$81$$ and $$2^{4}$$ is $$16$$
$$\therefore \left(\dfrac{3}{-2}\right)^{4}=\dfrac{81}{16}$$


Evaluate:
$$\left(\dfrac{-2}{3}\right)^{-5}$$

Given $$\left(\dfrac{-2}{3}\right)^{-5}$$

According to law of exponents,we can write $$\left(\dfrac{-2}{3}\right)^{-5}$$ as

$$\left(\dfrac{-2}{3}\right)^{-5}=\left(\dfrac{3}{-2}\right)^{5}$$

$$\left[\because \left(\dfrac{a}{b}\right)^{-m}=\left(\dfrac{b}{a}\right)^{m}\right]$$

But we know that $$3^{5}$$ is $$243$$ and the value of $$2^{o}$$ is $$32$$ 

Now substituting these value in above equation,
We get $$\left(\dfrac{3}{-2}\right)^{5}=\left(\dfrac{3^{5}}{-2^{5}}\right)=\left(\dfrac{243}{-32}\right)$$

$$\therefore \left(\dfrac{3}{-2}\right)^{5}=-\dfrac{243}{32}$$


Evaluate:
$$\left(\dfrac{-2}{3}\right)^{-3}\times \left(\dfrac{-2}{3}\right)^{-2}$$

Given $$\left(\dfrac{-2}{3}\right)^{-3}\times \left(\dfrac{-2}{3}\right)^{-2}$$

According to $$a^{-m}=\left(\dfrac{1}{a^{m}}\right)$$ we can write above equation as

$$\left(\dfrac{-2}{3}\right)^{-3}\times \left(\dfrac{-2}{3}\right)^{-2}=\left(\dfrac{3}{-2}\right)^{3}\times \left(\dfrac{3}{-2}\right)^{2}$$

Now apply the first law of exponents i.e. $$\left(\dfrac{a}{b}\right)^{m}\times \left(\dfrac{a}{b}\right)^{n}=\left(\dfrac{a}{b}\right)^{m+n}$$

[$$\because$$ Base in same in above equation]

We get $$\left(\dfrac{3}{-2}\right)^{3}\times \left(\dfrac{3}{-2}\right)^{-2}=\left(\dfrac{3}{-2}\right)^{3+2}=\left(\dfrac{3}{-2}\right)^{5}$$

But we know that $$3^{5}$$ is $$243$$ and $$2^{5}$$ is $$32$$
$$\therefore \left(\dfrac{3}{-2}\right)^{5}=\dfrac{243}{-32}$$


Evaluate:
$$\left[\left\{\left(\dfrac{-1}{3}\right)^{2}\right\}^{-2}\right]^{-1}$$

Given $$\left[\left\{\left(\dfrac{-1}{3}\right)^{2}\right\}^{-2}\right]^{-1}$$

According to third law of exponents i.e. $$\left\{\left(\dfrac{a}{b}\right)^{m}\right\}^{n}=\left(\dfrac{a}{b}\right)^{m\times n}$$

We can apply this law in above equation we get $$\left\{\left(\dfrac{-2}{3}\right)^{2}\right\}^{-2}=\left(\dfrac{-2}{3}\right)^{2\times (-2)}$$

Again apply the third law of exponents,

Now, $$\left\{\left(\dfrac{-1}{3}\right)^{2}\right\}^{2}=\left(\dfrac{-1}{3}\right)^{4}$$
But we know that $$3^{4}=81$$, on substituting We get $$\left(\dfrac{-1}{3}\right)^{4}=\dfrac{1}{81}$$


Evaluate $$[\{(5^{-1})\times (3^{-1})\}^{-1}\div 6^{-1}]$$

Given $$[\{(5^{-1})\times (3^{-1})\}^{-1}\div 6^{-1}]$$

The above equation is in the form of $$\left(\dfrac{a}{b}\right)^{-m}=\left(\dfrac{b}{a}\right)^{m}$$

By applying the law we get $$[\{(5^{-1})\times (3^{-1})\}^{-1}\div 6^{-1}]=\left[\left\{\left(\dfrac{1}{5}\right)\times \left(\dfrac{1}{3}\right)\right\}^{-1}\div \left(\dfrac{1}{6}\right)\right]$$

On simplifying the above equation, we get:
$$\left[\left\{\left(\dfrac{1}{5}\right)\times \left(\dfrac{1}{3}\right)\right\}^{-1}\div \left(\dfrac{1}{6}\right)\right]=\left[\left(\dfrac{1}{15}\right)^{-1}\div \left(\dfrac{1}{6}\right)\right]=\left(15\div \left(\dfrac{1}{6}\right)\right)$$
$$\Rightarrow \left(15 \times \dfrac{6}{1}\right)=90\quad \quad \left[\because \ \dfrac{a}{b} \div \dfrac{c}{d}=\dfrac{a}{b} \times \dfrac{d}{c}\right]$$

Hence, $$[\{(5^{-1})\times (3^{-1})\}^{-1}\div 6^{-1}]=90$$.


Find the value of:
$$\left(\dfrac{1}{2}\right)^{-1}+\left(\dfrac{1}{3}\right)^{-2}+\left(\dfrac{1}{4}\right)^{-2}$$

Given that $$\left(\dfrac{1}{2}\right)^{-1}+\left(\dfrac{1}{3}\right)^{-2}+\left(\dfrac{1}{4}\right)^{-2}$$

The above equation is in the form of $$a^{-m}=\left(\dfrac{1}{a^{m}}\right)$$

By applying this law, we get:
$$\left(\dfrac{1}{2}\right)^{-1}+\left(\dfrac{1}{3}\right)^{-2}+\left(\dfrac{1}{4}\right)^{-2}=2+3^{2}+4^{2}$$

On simplifying, we get:
$$2+3^{2}+4^{2}=2+9+16$$
$$=27$$

Hence, $$\left(\dfrac{1}{2}\right)^{-1}+\left(\dfrac{1}{3}\right)^{-2}+\left(\dfrac{1}{4}\right)^{-2}=27$$.


Solve the following:
$$100^{-10}$$

Use $$x^{-m}=\dfrac{1}{x^m}$$
$$=100^{-10}=\dfrac{1}{100^{10}}$$


Simplify :
$$\left( \dfrac{1}{4}\right)^{-2}+\left( \dfrac 12\right)^{-2}+\left( \dfrac 13\right)^{-2}$$

Use, $$a^{m}=\left(\dfrac{1}{a}\right)^{-m}$$
$$\therefore \left( \dfrac {1}{4}\right)^{-2}+\left( \dfrac {1}{2}\right)^{-2}+\left( \dfrac {1}{3}\right)^{-2}=(4)^2+(2)^2+(3)^2=16+4+9=29$$


Simplify :
$$\left[ \left( \dfrac{-2}{3}\right)^{-2}\right]^{3}\times \left( \dfrac{1}{3}\right)^{-4}\times 3^{-1}\times \dfrac 16$$

Use, $$(a^m)^n=(a)^{mn}, a^{-m}=\dfrac{1}{a^m}, a^m \times a^n =a^{m+n}$$ and $$a^m \div a^n =(a)^{m-n}$$
Therefore,
$$\left( \left( \dfrac{-2}{3}\right)^{-2}\right)^3\times \left( \dfrac{1}{3}\right)^{-4}\times 3^{-1}\times \dfrac 16=\left( \dfrac{-2}{3}\right)^{(-2)\times 3}\times (3)^4\times \dfrac 13 \times \dfrac 16$$
$$=\left( \dfrac {-2}{3}\right)^6 \times 3^4 \times \dfrac{1}{3}\times \dfrac{1}{2\times 3}$$
$$=\left( \dfrac{3}{-2}\right)^6 \times 3^4 \times \dfrac{1}{3\times 2\times 3}=\dfrac{(3)^6}{(2)^6}\times 3^4 \times \dfrac{1}{2^1 \times 3^2}$$
$$=\dfrac{(3)^{6+4}}{(2)^{6+1}\times 3^2}$$
$$=\dfrac{(3)^{10}}{2^7 \times 3^2}=\dfrac{3^{10-2}}{2^7}=\dfrac{3^8}{2^7}$$


Simplify :
$$\dfrac{49\times z^{-3}}{7^{-3}\times 10\times z^{-5}}( z\neq 0)$$

Use $$a^m \div a^n =(a)^{m-n}$$
$$\Rightarrow \dfrac{49\times z^{-3}}{7^{-3}\times 10\times z^{-5}}=\dfrac{(7)^2\times z^{-3}}{7^{-3}\times 10\times z^{-5}}=\dfrac{(7)^{2+3 }\times z^{-3+5}}{10}$$
$$\Rightarrow \dfrac{49\times z^{-3}}{7^{-3}\times 10\times z^{-5}}=\dfrac{(7)^5 \times z^2}{10}=\dfrac{7^5}{10}z^2$$


Express as a power of a rational number with negative exponent.
$$\left[ \left( \dfrac{-3}{2}\right)^{-2}\right]^{-3}$$

Use $$(a^m)^n =(a)^{mn}$$ and $$a^{-m}=\dfrac{1}{a^m}$$
We have, $$\left( \left( \dfrac{-3}{2}\right)^{-2}\right)^{-3}=\left( \dfrac{-3}{2}\right)^{-2\times (-3)}=\left( \dfrac{-3}{2}\right)^6=\left( \dfrac{3}{2}\right)^{6}$$
$$\therefore \left( \left( \dfrac{-3}{2}\right)^{-2}\right)^{-3}=\left( \dfrac{3}{2}\right)^{6}$$


Find the value of $$[4^{-1}+3^{-1}+6^{-2}]^{-1}$$

$$x^{-x}=\dfrac{1}{x^m}$$
$$\Rightarrow [4^{-1}+3^{-1}+6^{-2}]^{-1} $$
$${ \left[ \dfrac { 1 }{ 4 } +\dfrac { 1 }{ 3 } +\dfrac { 1 }{ { 6 }^{ 2 } }  \right]  }^{ -1 }={ \left[ \dfrac { 1 }{ 4 } +\dfrac { 1 }{ 3 } +\dfrac { 1 }{ 36 }  \right]  }^{ -1 }$$
$$\Rightarrow [4^{-1}+3^{-1}+6^{-2}]^{-1} == { \left[ \dfrac { 9+12+1 }{ 36 }  \right]  }^{ -1 }$$
$$\Rightarrow [4^{-1}+3^{-1}+6^{-2}]^{-1} ={ \left[ \dfrac { 22 }{ 36 }  \right]  }^{ -1 }$$
$$\Rightarrow [4^{-1}+3^{-1}+6^{-2}]^{-1} ={ \left[ \dfrac { 36 }{ 22 }  \right]  }= \dfrac{18}{11}$$


If $$36=6 \times 6=6^2$$, then $$\dfrac{1}{36}$$ expressed as a power with base $$6$$ is ______.

$$x^{-m}=\dfrac{1}{x^m}$$
$$\Rightarrow 36=6 \times 6=6^2$$
$$\therefore \dfrac{1}{36} =\dfrac{1}{6 \times 6}$$ 
$$\Rightarrow \dfrac{1}{36} = \dfrac{1}{6 \times 6} $$
$$\Rightarrow \dfrac{1}{36} = \dfrac{1}{6 ^2} $$
$$\Rightarrow \dfrac{1}{36} = 6^{-2}$$


The value of $$[3^{-1} \times \  4^{-1}]^2$$ is _______.

$$[3^{-1} \times \  4^{-1}]^2 =\dfrac{1}{(3 \times 4)^2} =\dfrac{1}{(12)^2} =\dfrac{1}{(4 \times 3)^2} =\dfrac{1}{(4^2 \times 3)^2}$$


If $$\dfrac{5^m \times 5^3 \times 5^{-2}}{5^{-5}}=5^{12}$$. Find $$m$$.

Using, laws of exponents, $$a^m \div a^n =(a)^{m-n}$$ and $$a^{-m}=\dfrac{1}{a^m}$$
Then, equation becomes
$$5^m \times 5^3 \times 5^{-2}\times 5^5=5^{12}$$
Now using, $$a^m \times a^n =a^{m+n}$$
$$\Rightarrow 5^m \times 5^8 \times 5^{-2}=5^{12}$$
$$\Rightarrow 5^m \times 5^6=5^{12}$$
$$\Rightarrow 5^{m+6}=5^{12}$$
Comparing both sides
$$\Rightarrow m+6=12$$
$$\Rightarrow m=6$$


Evaluate
$$(2/7)^{-4}$$

Let us evaluate the given expression,
By using the formula $$(a^{-n}=1/a^n)$$
So, 
$$(2/7)^{-4}=(7/2)^4$$
$$=(7/2)\times (7/2)\times (7/2)\times (7/2)$$
$$=2401/16$$


Consider a quantity of a radioactive substance. The fraction of this quantity that remains after $$t$$ half - lives can be found by using the expression $$3^{-t}$$.
What fraction of substance remains after $$7$$ half-lives?

Since, $$3^{-t}$$ is the expression used for finding the fraction of the quantity that remains after $$t$$ half-lives.
Hence, the fraction of substance remains after $$7$$ half-lives will be equal to $$3^{-7}$$ i.e. $$\dfrac{1}{3^7}$$.


In a shrinking machine, a piece of stick is compressed to reduce its length. If $$9\ cm$$ long sandwich is put into the shrinking machine below, how many $$cm$$ long will it be when it emerges?
1793339_eb4f53aba018449798bf5ae8032549b9.png


In given machine $$\cfrac13$$ is base because $$(\times \cfrac13)$$ is given and $$-1$$ is power of base.
So, machine will shrink the object by $$\left(\times\left(\cfrac13\right)^{-1}=\times3\right)$$

So, if we put a $$9\ cm$$ long sandwich into the shrinking machine then the length of sandwich would become $$=9\times \dfrac{1}{3^{-1}}=9\times 3=27\ cm$$


What happens when $$1\ cm$$ worms are sent through these hook-ups?
1793341_5f8d91854bfb42e799cbcaa84af7f12b.png

If $$a$$ is input to $$\times x^y$$ machine then output will be $$a\times x^y$$
When two such machines are hooked up, output of one is input to other.
So, for overall output their stretching power multiplies.
So,
If you put $$1\ cm$$ worms through $$( \times 2^1 )$$ and $$(\times 2^{-1})$$ machine,
the result will be $$=1\times 2\times2^{-1}=1\times 2\times \dfrac 12=1\ cm$$.
That is worm will remain as it is, after going through both machines.


Find the value of
$$\dfrac{6^n}{6^{-2}}=6^3$$

Given, $$\dfrac{6^n}{6^{-2}}=6^3$$
$$a^m \div a^n=(a)^{m-n}$$
Using law of exponent 
$$\Rightarrow 6^{n-(-2)}=6^3$$
On comparing both sides-
$$n+2=3$$
$$n=1$$
Therefore the value of $$n$$ is $$1$$.


Simplify
$$[(2)^{-1}+(4)^{-1}+(3)^{-1}]^{-1}$$

Let us simplify the given expression
$$[(2)^{-1}+(4)^{-1}+(3)^{-1}]^{-1}=[(1/2)+(1/4)+(1/3)]^{-1}$$
$$=[(6+3+4)/12]^{-1}$$
$$=[13/12]^{-1}$$
$$=12/13$$


Evaluate:
$$(0.25)^{-1}$$.

$$(0.25)^{-1}=\dfrac1{0.25}=\dfrac{100}{25}=4$$


Evaluate:
$$5^{-4} \times (125)^{\dfrac {5}{3}}- (25)^{-\dfrac 12}$$

$$5^{-4} \times (125)^{\dfrac {5}{3}}- (25)^{-\dfrac 12}=5^{-4}\times (5\times 5\times 5)^{\dfrac 53}\div (5\times 5)^{-\dfrac 12}$$
$$=5^{-4}\times (5^{3})^{\dfrac 53}\div (5^2)^{-\dfrac 12}$$
$$=5^{-4}\times \left(5^{3+\dfrac 53}\right) \div \left(5^{2\left(-\dfrac 12 \right)}\right)$$
$$=\dfrac {5^{-4}\times 5^{3}}{5^{-1}}$$
$$=\dfrac {5^{5-4}}{5^{-1}}$$
$$=\dfrac {5^{-1}}{5^{-1}}$$
$$=5^{1-(-1)}$$
$$=5^{2}$$
$$=5\times 5$$
$$=25$$


Simplify:
$$(a+b)^{-1}, (a^{-1}+b^{-1})$$

$$(a+b)^{-1}, (a^{-1}+b^{-1})=\dfrac {1}{(a+b)}\times \left(\dfrac {1}{a}+\dfrac {1}{b}\right)$$
$$=\dfrac {1}{a+b}\times \left(\dfrac {b+a}{ab}\right)$$
$$=\dfrac {1}{a+b}\times \dfrac {(a+b)}{ab}$$
$$=\dfrac {1}{ab}$$


Evaluate : $$\left (0.027  \right )^{-1/3}$$

Here we have,
$$\ \left (0.027\right )^{-1/3}\\ = \left (\dfrac{27}{1000  }\right )^{-1/3}\\ = \left [ \dfrac{\left (3 \times 3 \times 3 \right )}{ \left (10 \times 10 \times 10  \right )} \right ]^{-1/3}\\ = \left (\dfrac{3^{3}}{10^{3} } \right )^{-1/3}\\ = \left (\dfrac 3{10}  \right )^{3 \times -\tfrac13}\\ = \left (\dfrac 3{10}  \right )^{-1}\\ = \dfrac{10}3 $$



$$(m+n)^{-1}(m^{-1}+n^{-1}) =(mn)^{-1}$$

L.H.S $$(m+n)^{-1}(m^{-1}+n^{-1}) $$
$$=\dfrac{1}{m+n}(\dfrac{1}{m}+\dfrac{1}{n})\\=\dfrac{1}{m+n}\times\dfrac{n+m}{mn}=\dfrac{1}{mn}$$
$$=(mn)^{-1}$$
=R.H.S.
Hence proved.


Evaluate: $$\left ( \dfrac{81}{16} \right )^{-3/4}$$

Here we have,
$$\ \ \left ( \dfrac{81}{16} \right )^{-3/4} = \left ( \dfrac{3^{4}}{2^{4} }\right ) ^{-3/4}$$
$$\quad = \left [\left ( \dfrac 32 \right )^{4} \right ]^{-3/4}\\ \quad =  \left ( \dfrac 32 \right )^{(-3/4) \times 4}$$
$$\quad= \left ( \dfrac 32 \right )^{-3} \\ \quad= \left ( \dfrac23 \right )^{3}\\ \quad= \dfrac{2^{3}}{3^{3}} \\ \quad= \dfrac{\left (2 \times 2 \times 2  \right )}{\left ( 3 \times 3 \times 3  \right )}\\ \quad=\dfrac 8{27}$$


$$\left (1\frac{61} {64}  \right )^{-\frac{2} {3}}$$

$$\left (1\frac{61} {64}  \right )^{-\frac{2} {3}} = \left (\frac{125} {64}  \right )^{-\frac{2} {3}} = \left (\frac{5^{3}} {4^{3}}  \right )^{-\frac{2} {3}} $$
$$= \left ( 5/4 \right )^{3 \times -2/3}$$
$$= \left ( 5/4 \right )^{-2}$$
$$ = \left (4/5  \right )^{2}$$
$$= 16/25$$


Prove that :
$$\dfrac{a^{-1}}{a^{-1}+b^{-1}}+\dfrac{a^{-1}}{a^{-1}-b^{-1}}=\dfrac{2b^2}{b^2-a^2}$$

$$\dfrac{a^{-1}}{a^{-1}+b^{-1}}+\dfrac{a^{-1}}{a^{-1}-b^{-1}}=\dfrac{2b^2}{b^2-a^2}$$
$$L.H.S=\dfrac{a^{-1}}{a^{-1}+b^{-1}}+\dfrac{a^{-1}}{a^{-1}-b^{-1}}$$
$$=\dfrac{\dfrac{1}{a}}{\dfrac{1}{a}+\dfrac{1}{b}}+\dfrac{\dfrac{1}{a}}{\dfrac{1}{a}-\dfrac{1}{b}}$$
$$=\dfrac {\dfrac{1}{a}}{\dfrac{b+a}{ab}}+\dfrac{\dfrac{1}{a}}{\dfrac{b-a}{ab}}$$
$$=\dfrac{1}{a}\times \dfrac{ab}{b+a}+\dfrac{1}{a}\times \dfrac{ab}{b-a}$$
$$=\dfrac{b}{b+a}+\dfrac{b}{b-a}$$
$$=\dfrac{b^2-ab+b^2+ab}{b^2-a^2}$$
$$=\dfrac{2b^2}{b^2-a^2}$$
$$=R.H.S.$$


Simplify each of the following and express with positive index:
$$[1-(1-(1-n)^{-1})^{-1}]^{-1}$$

$$[1-(1-(1-n)^{-1})^{-1}]^{-1} =\dfrac {1}{[1-(1-(1-n)^{-1})^{-1}]^{-1}}$$
$$=\dfrac {1}{1-\dfrac {1}{1-(1-n)^{-1}}}$$
$$=\dfrac {1}{1-\dfrac {1}{(1-n)}}$$
$$=\dfrac {1}{1-\dfrac {1}{\dfrac {1(1-n)-1}{(1-n)}}}$$
$$=\dfrac {1}{1-\dfrac {1}{\dfrac {1-n-1}{(1-n)}}}$$
$$=\dfrac {1}{1-\dfrac {1}{\dfrac {-n}{(1-n)}}}$$
$$=\dfrac {1}{1-\dfrac {(1-n)}{-n}}$$
$$=\dfrac {1}{1+\dfrac {(1-n)}n{}}$$
$$=\dfrac {1}{\dfrac {n+(1-n)}{n}}$$
$$=\dfrac {1}{\dfrac {n+1-n}{n}}$$
$$=\dfrac {n}{1}$$


$${ \left( \frac { 1 }{ 2 }  \right)  }^{ -2 }+{ \left( \frac { 1 }{ 3 }  \right)  }^{ -2 }+{ \left( \frac { 1 }{ 4 }  \right)  }^{ -2 }=?$$


2040779_1327564_ans_8b316d0538f5408993659280aa7bcd05.jpg


Express the number appearing in the following statement in standard from.
Diameter of the sun is $$1,400,000,000 \text{ m}$$

Diameter of sun $$=1,400,000,000 \text{ m}$$
In standard form, 
$$\Rightarrow$$ Diameter of sun $$=\left( 1.4\times 10^9\right) \text{ m}$$



By what a number should $$\left (\dfrac {5}{3}\right)^{-2}$$ be multiplied so that the product may be equal to $$\left (\dfrac {7}{3}\right)^{-1}$$?  


2039750_1671150_ans_014d188d26484118b43d6b2f5db1573d.jpg


By what a number should $$\left (\dfrac {1}{2}\right)^{-1}$$ be multiplied so that the product may be equal to $$\left (\dfrac {-4}{7}\right)^{-1}$$?  


2039749_1671144_ans_34dce122f7d944c2867033ca8780e8b5.jpg


Express the number appearing in the following statement in standard from.
Mass of Uranus is $$86,800,000,000,000,000,000,000,000\ kg$$


2122819_1218733_ans_cc6f8801a2da4b93ae665a033d1f7530.jpg


The value of $$5\sqrt[4]{\sqrt[3]{5}}-\sqrt[3]{\sqrt[4]{5}}$$ is?


1328855_1587682_ans_2aacf8a670ef41dbba41c0e4ed3a0c8c.jpg


Class 8 Maths Extra Questions