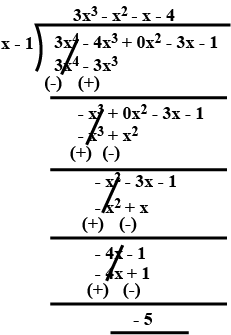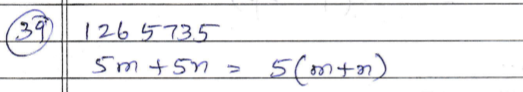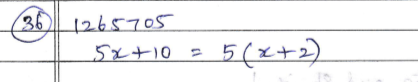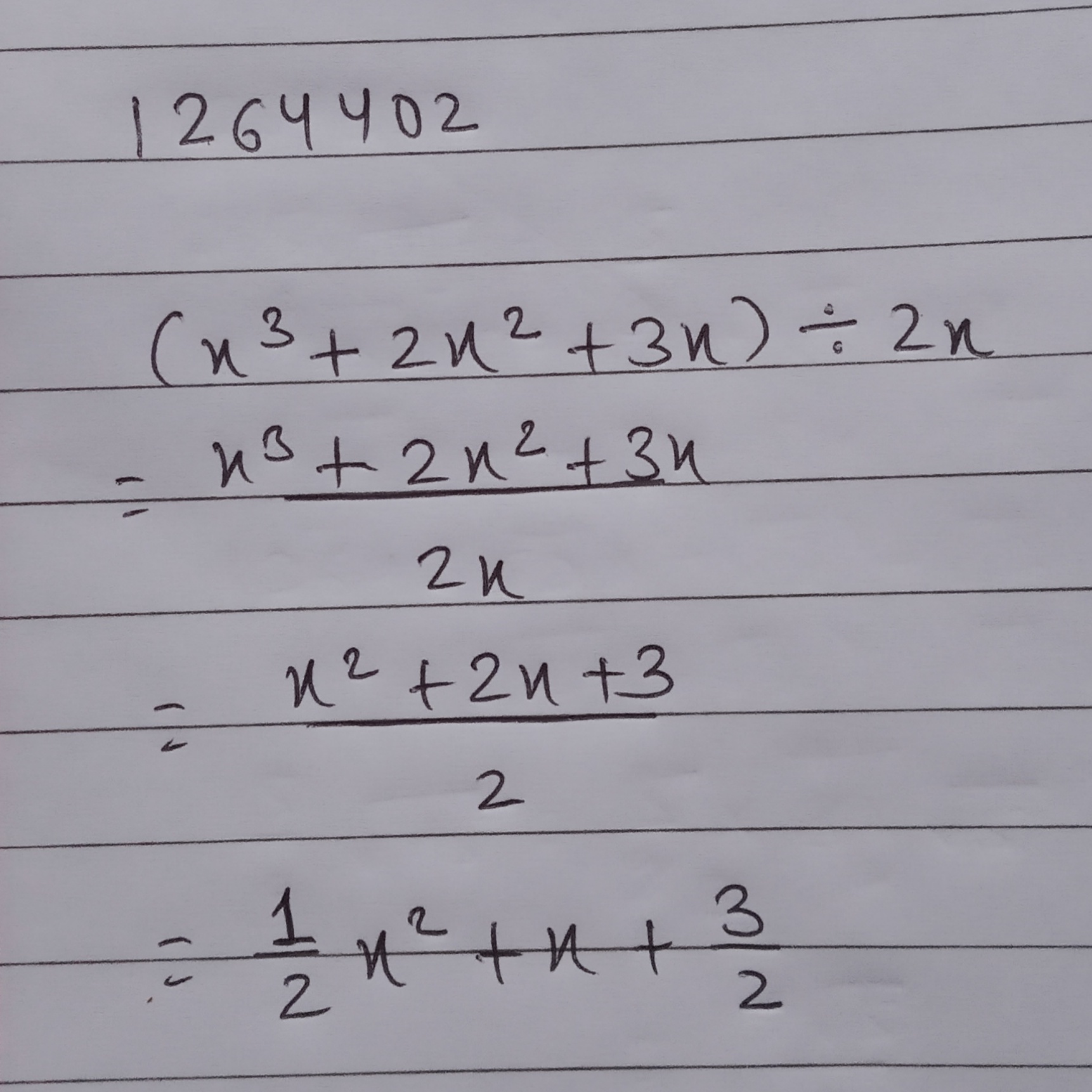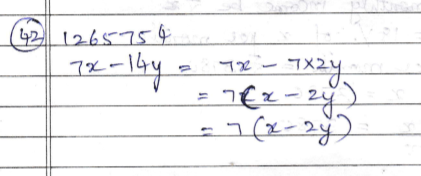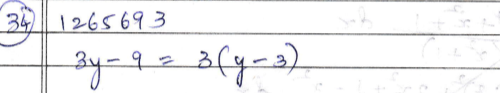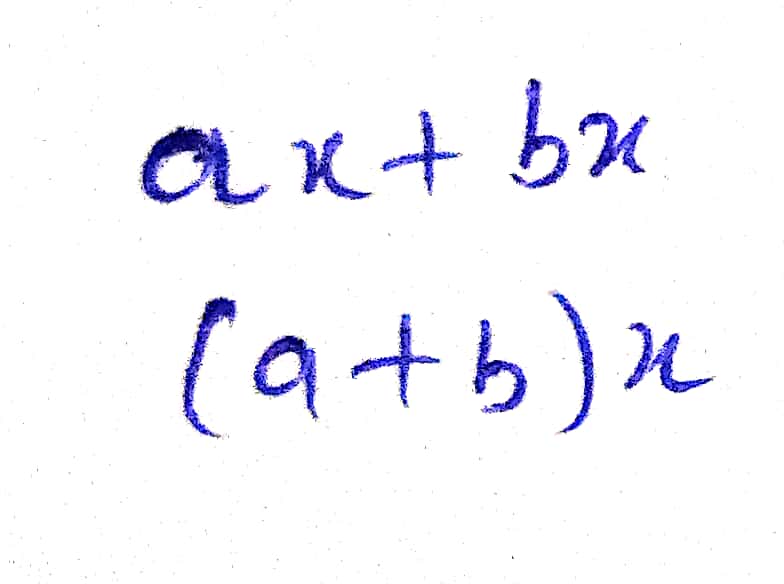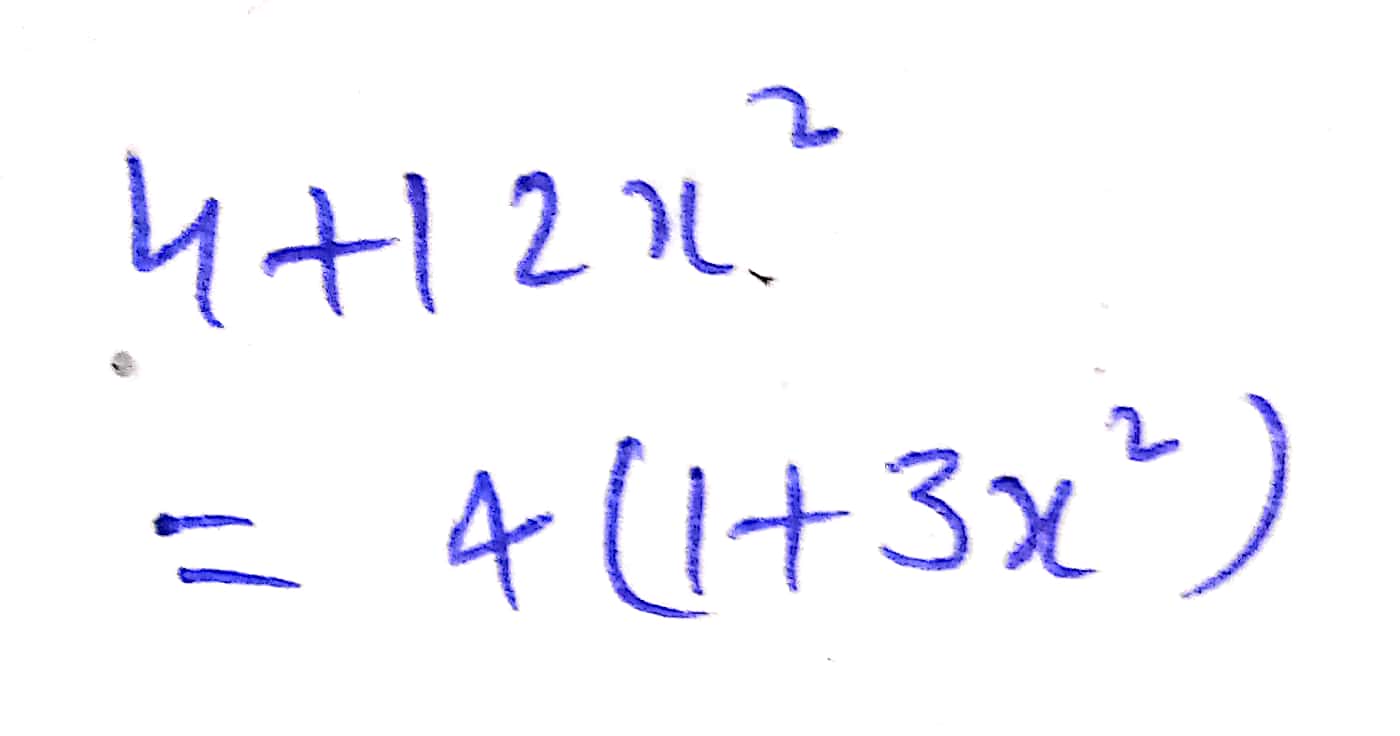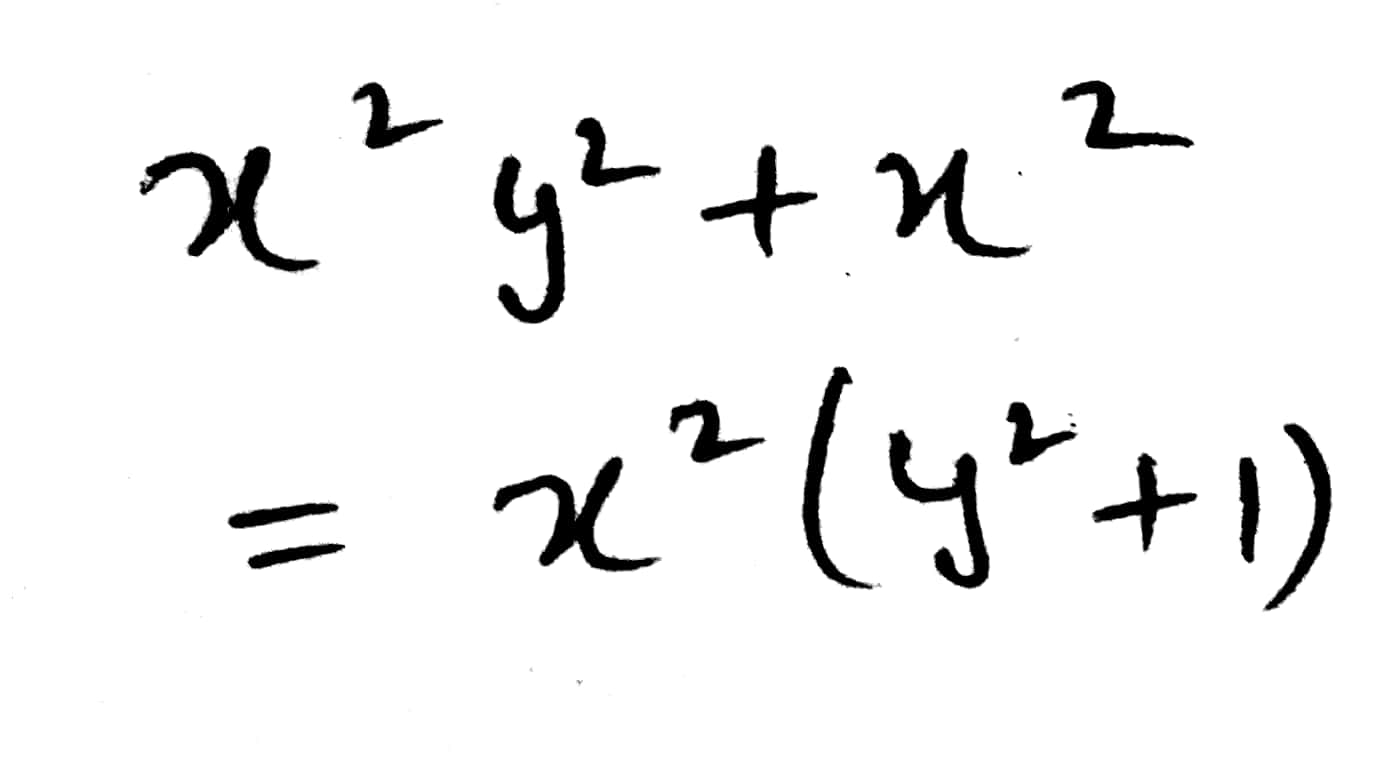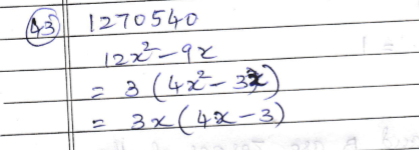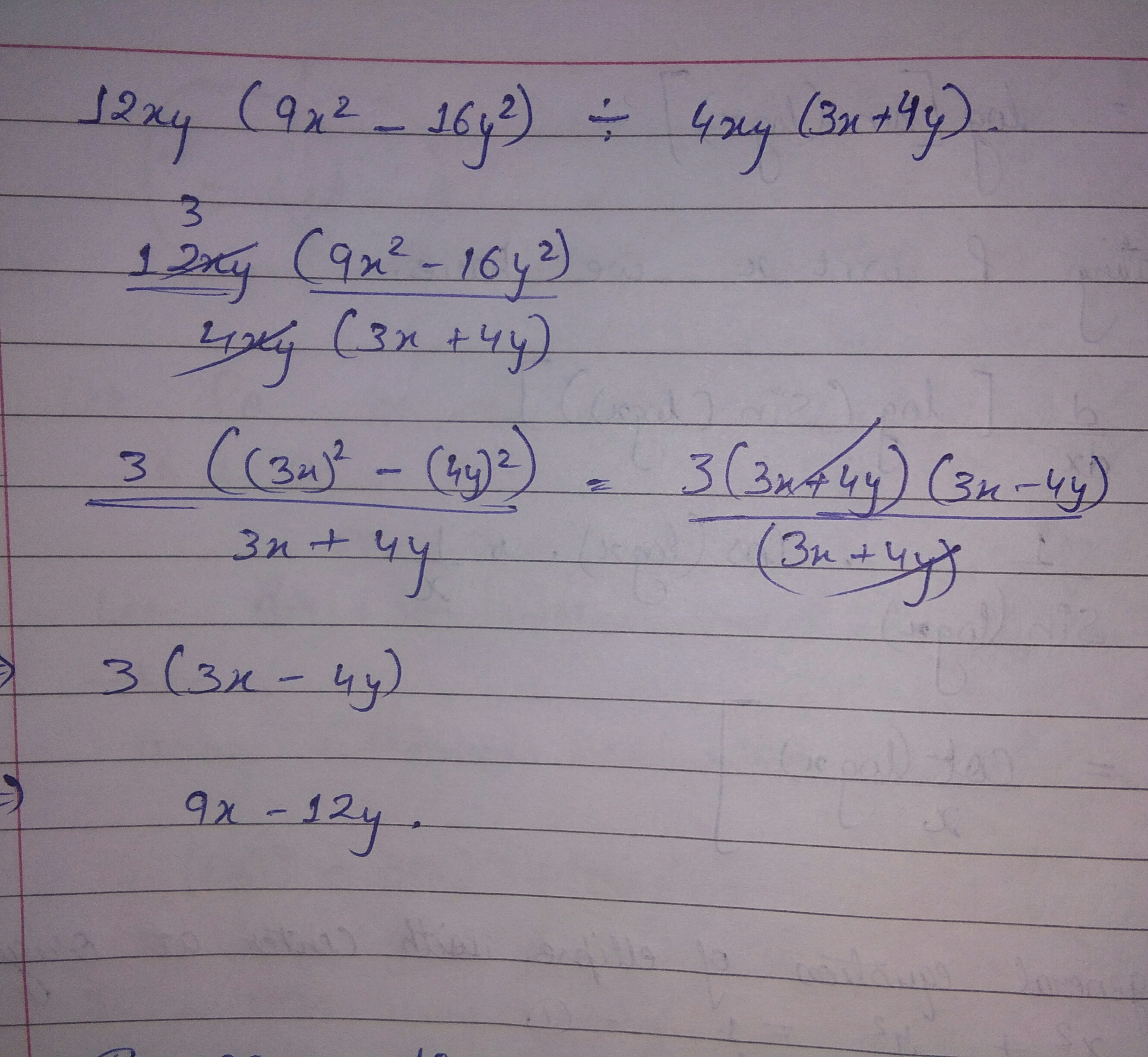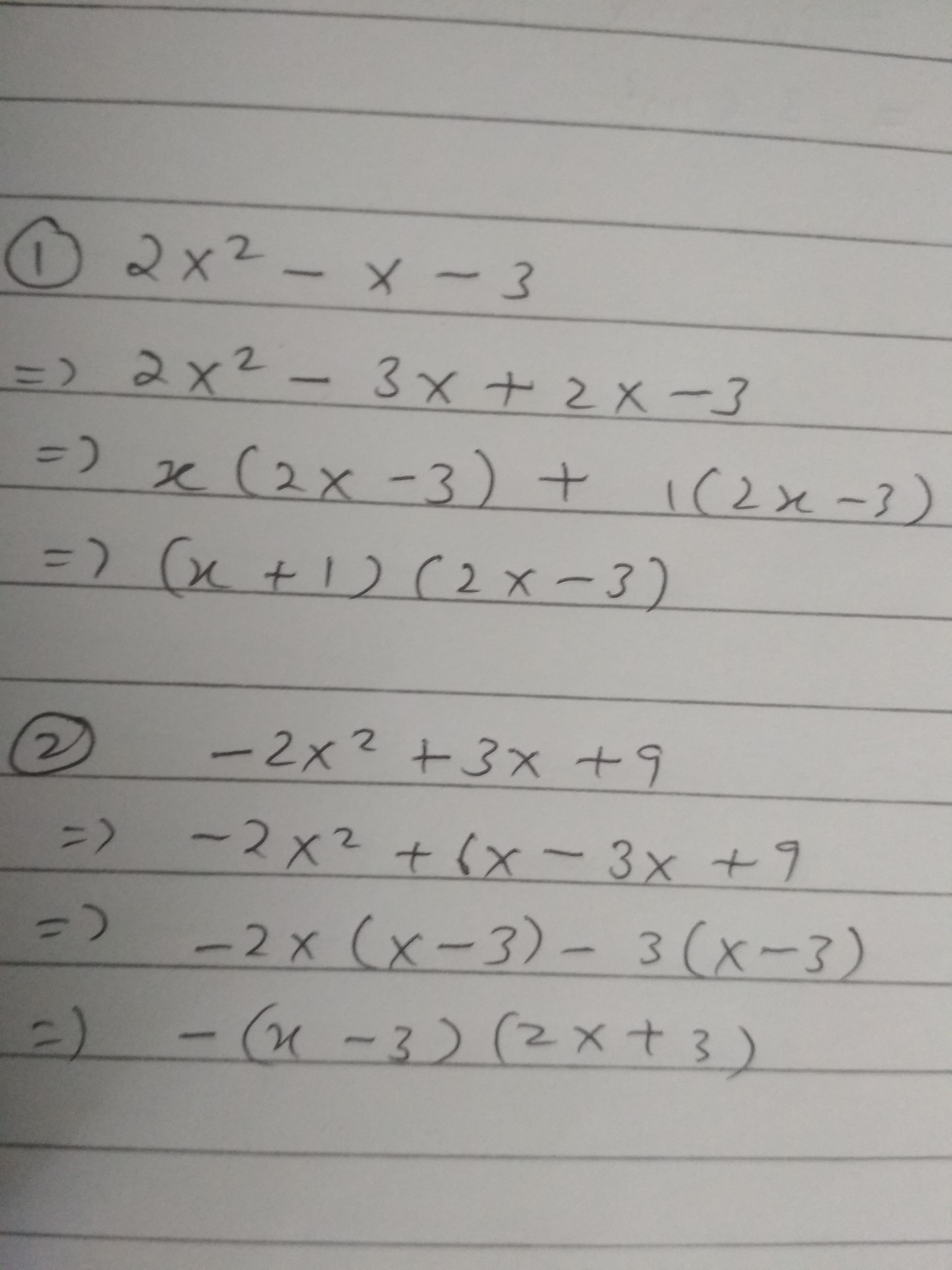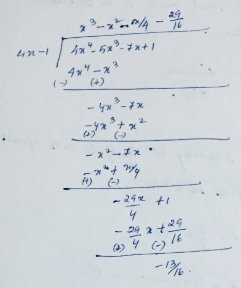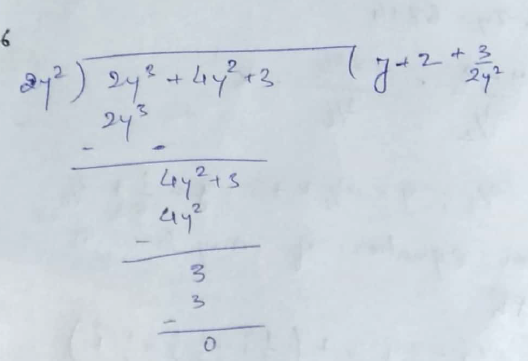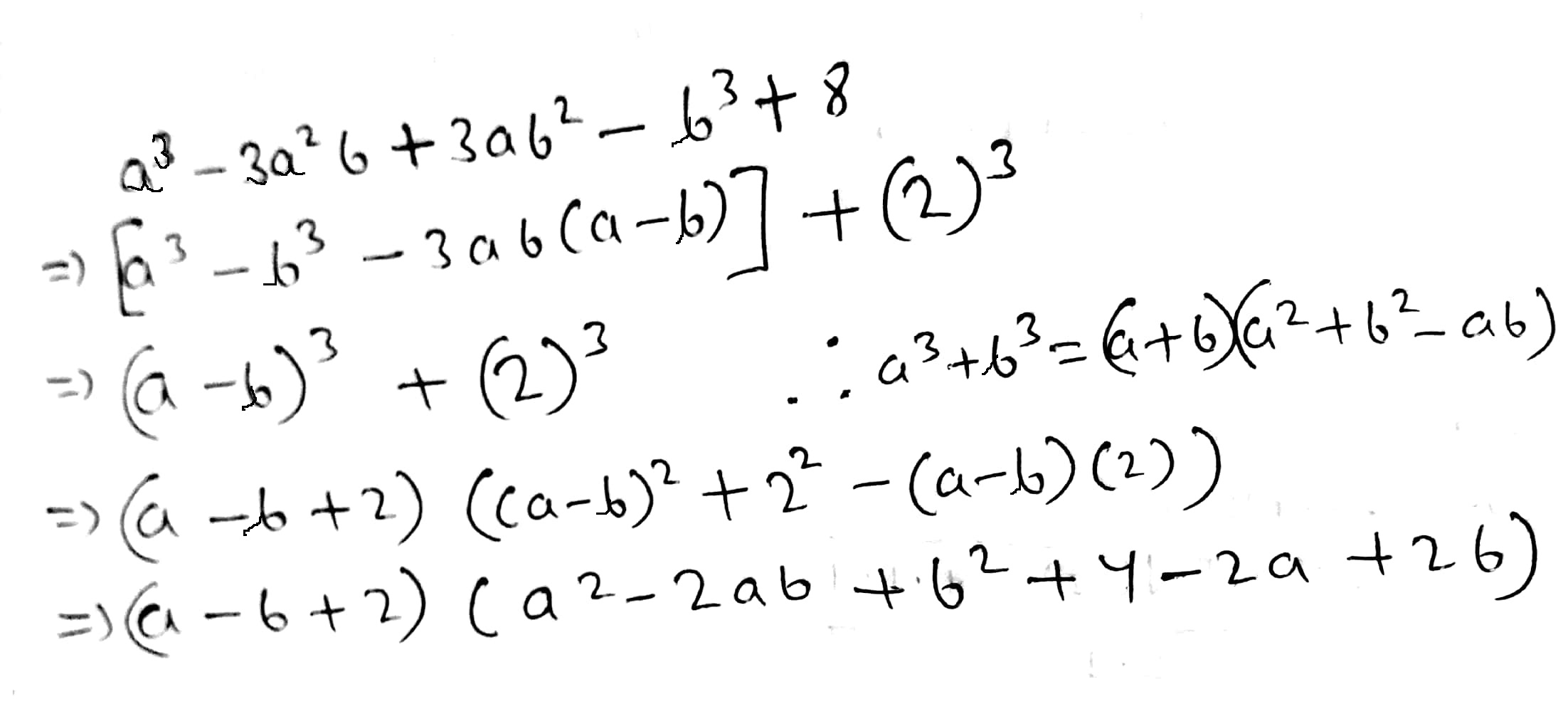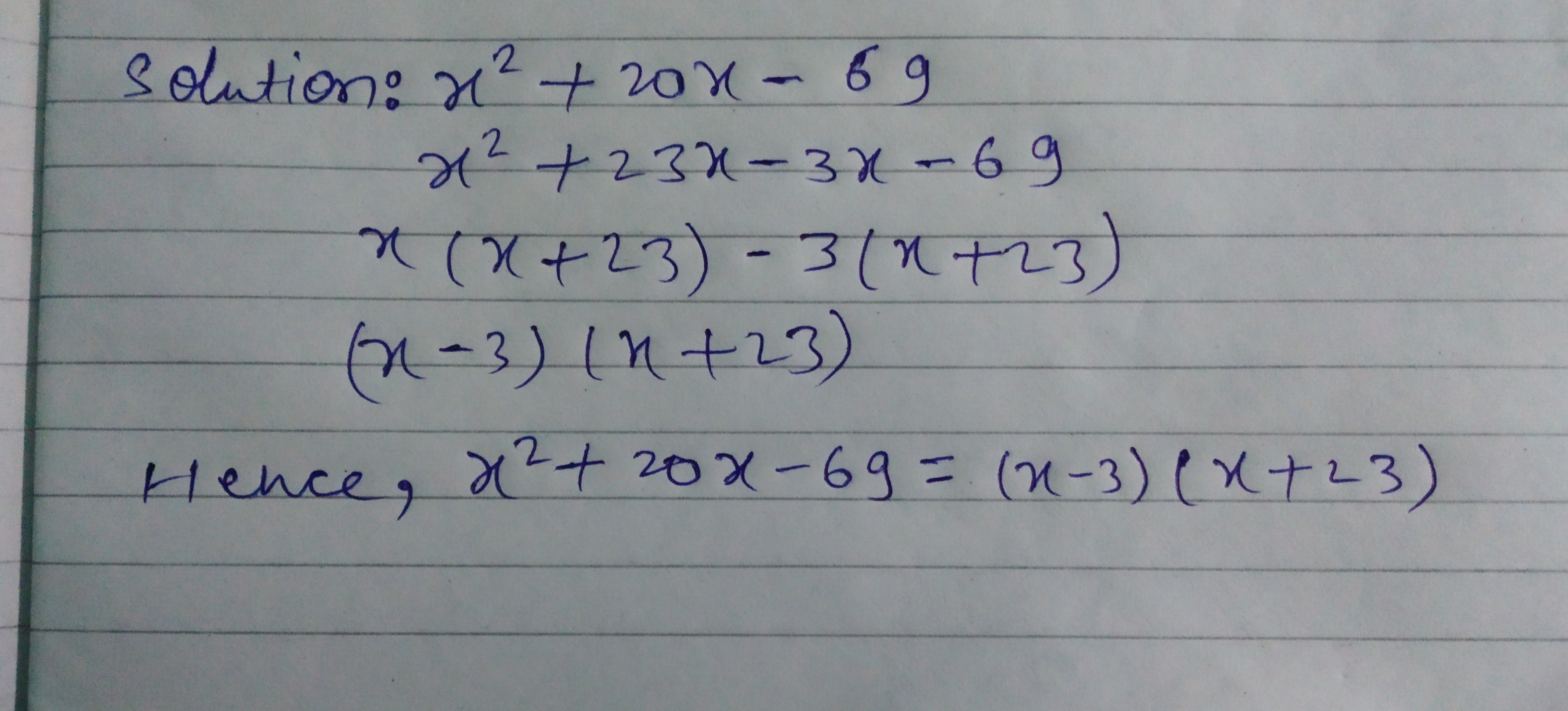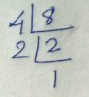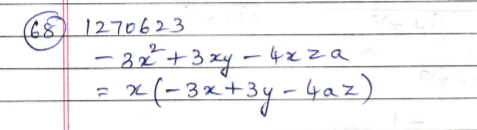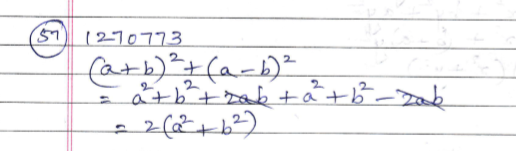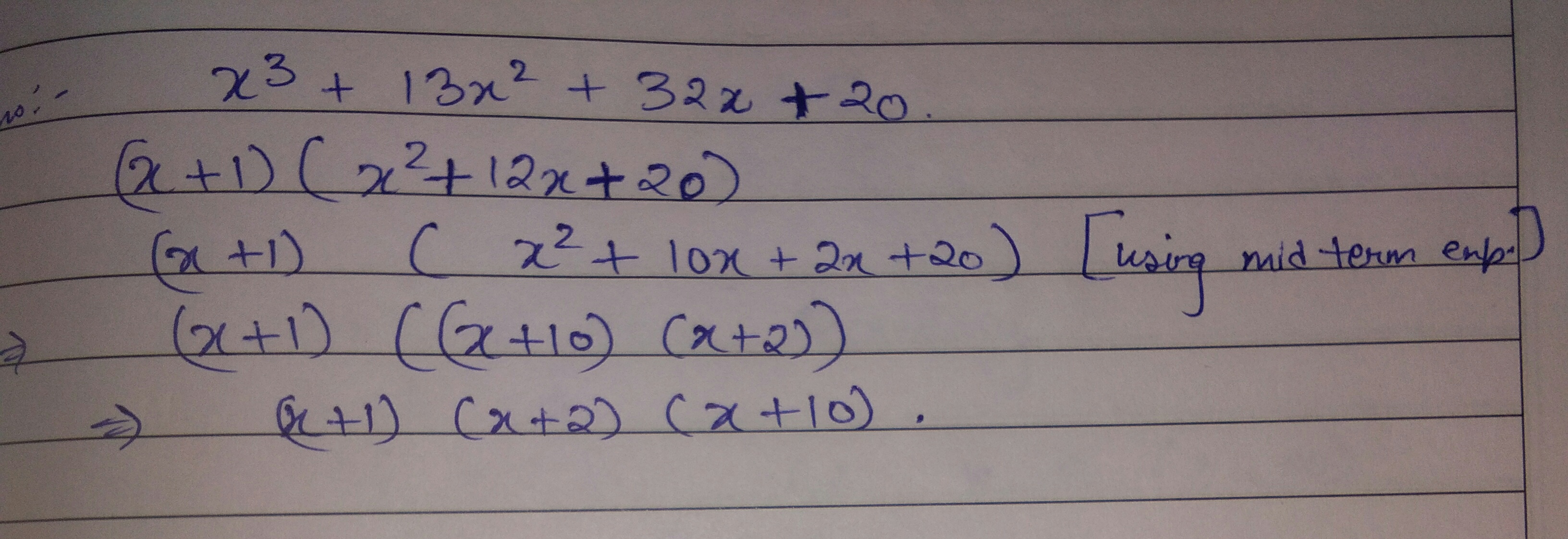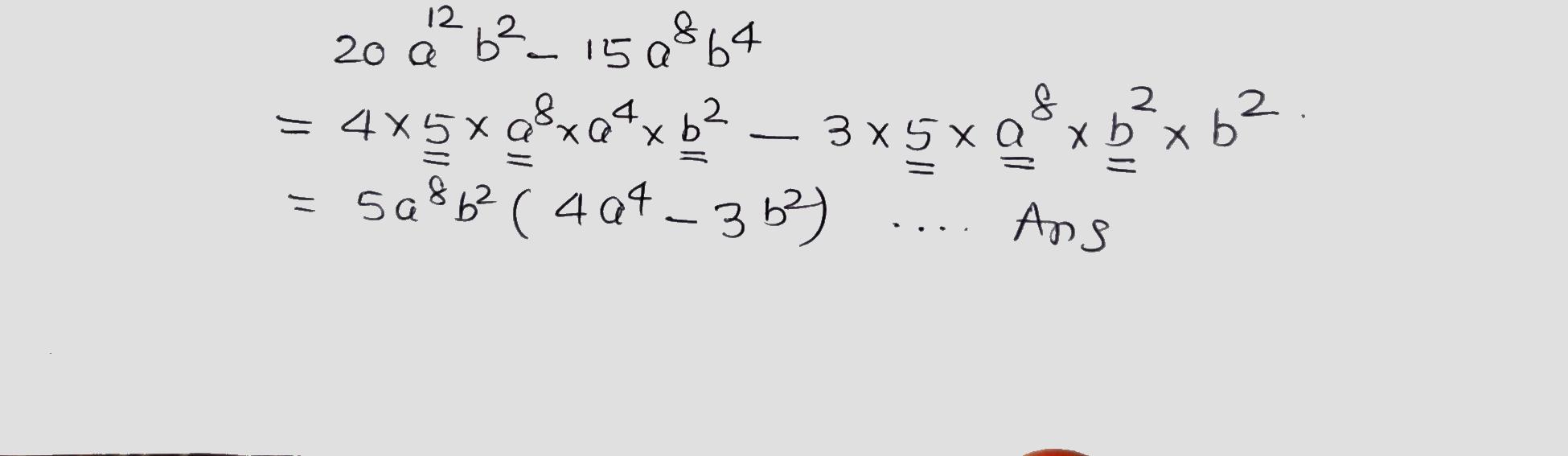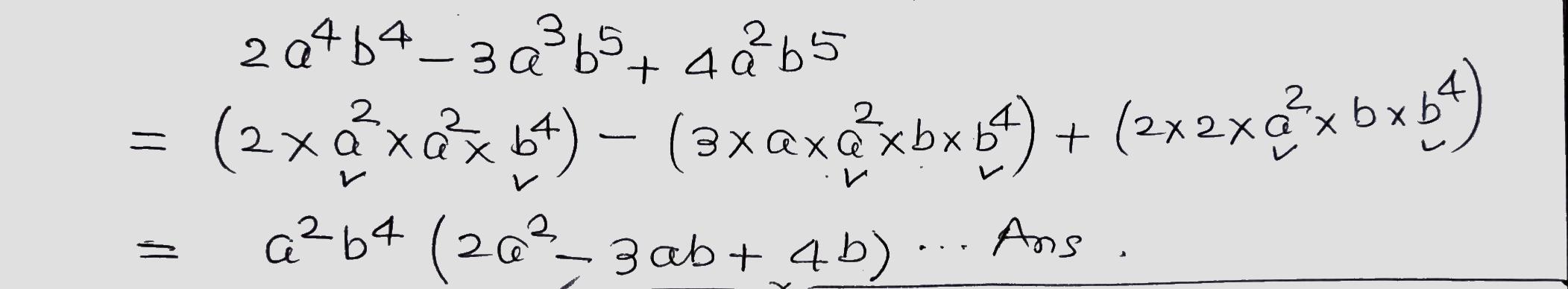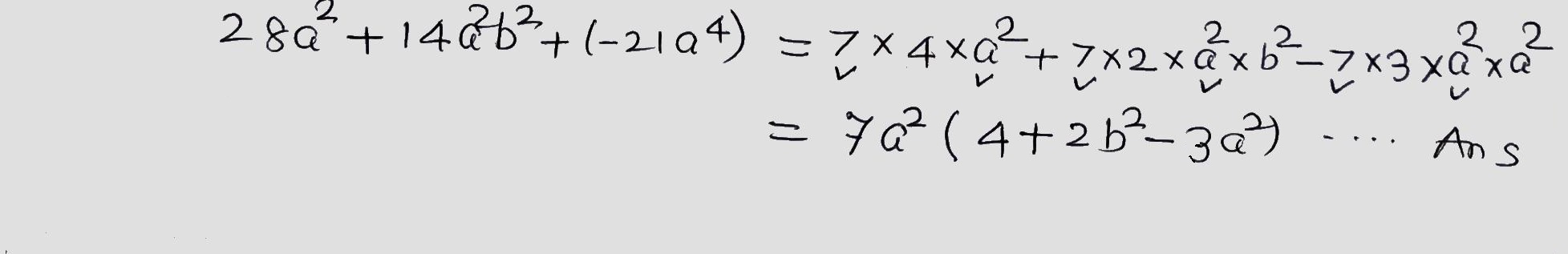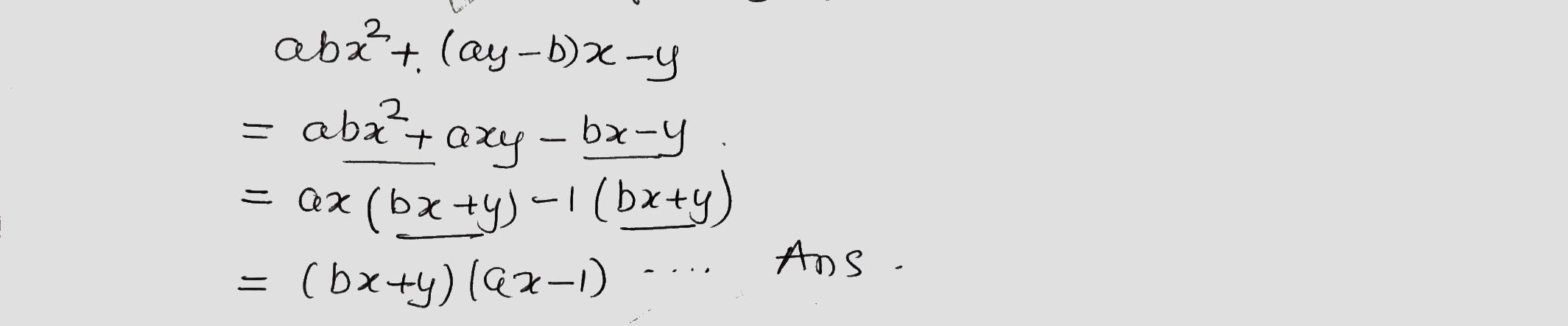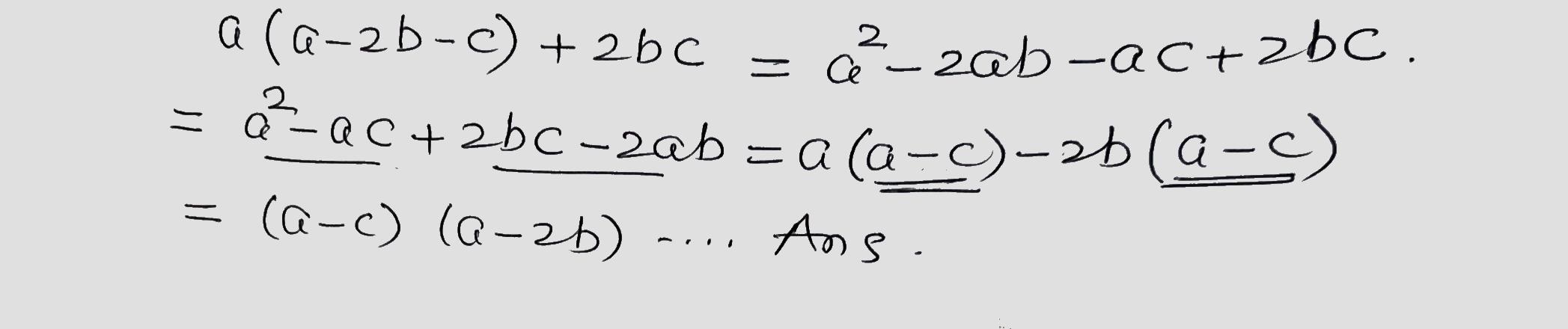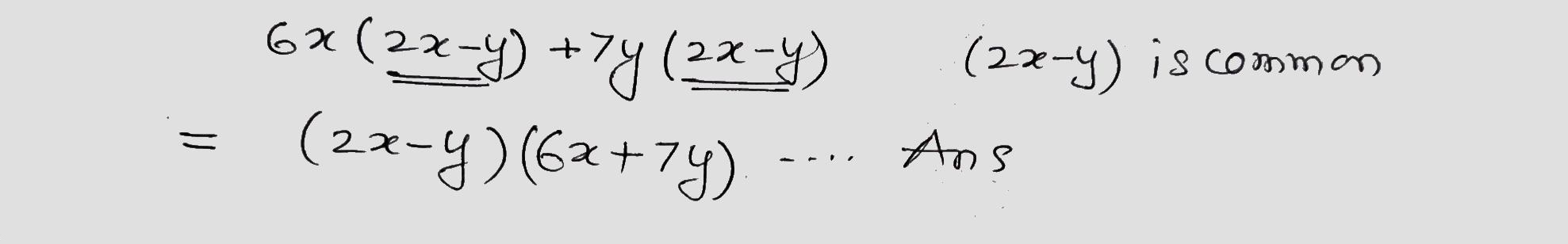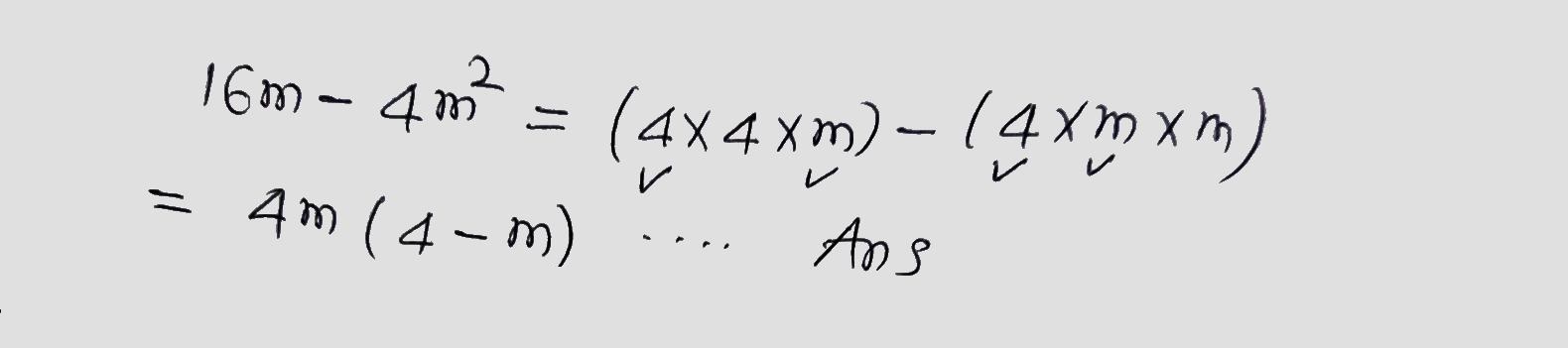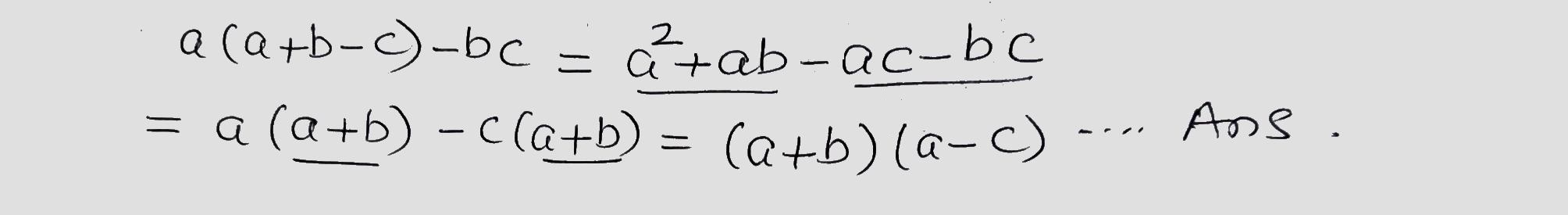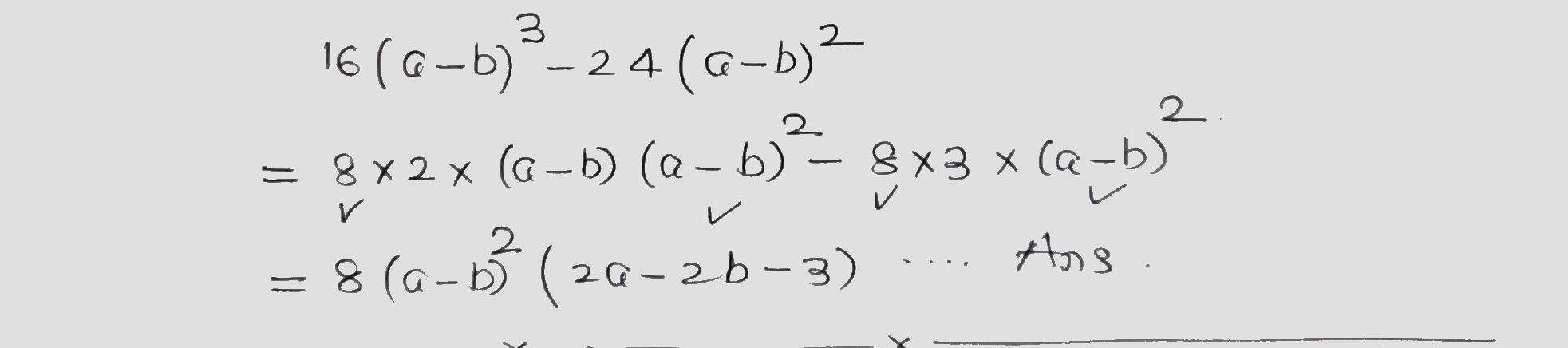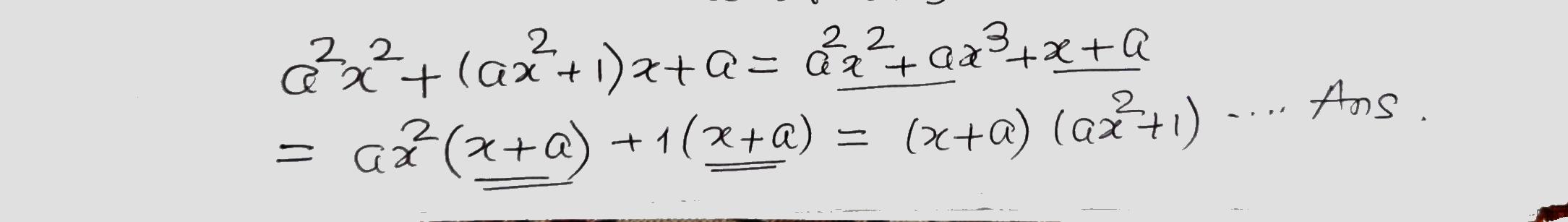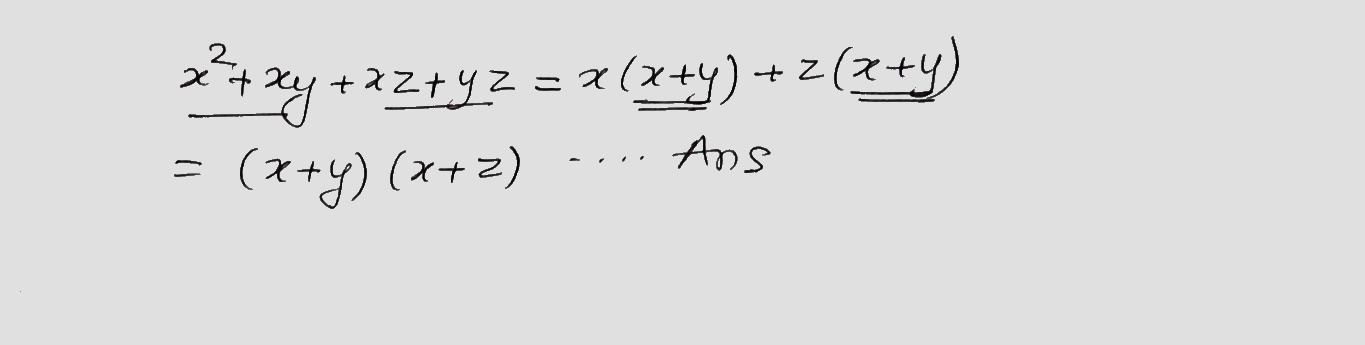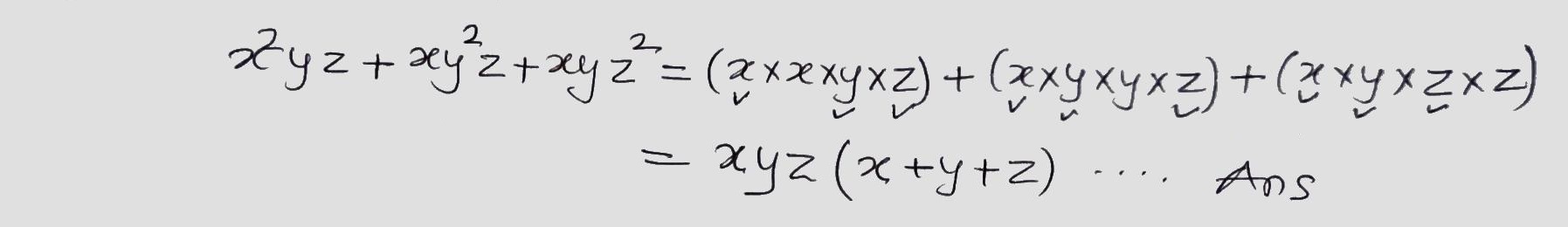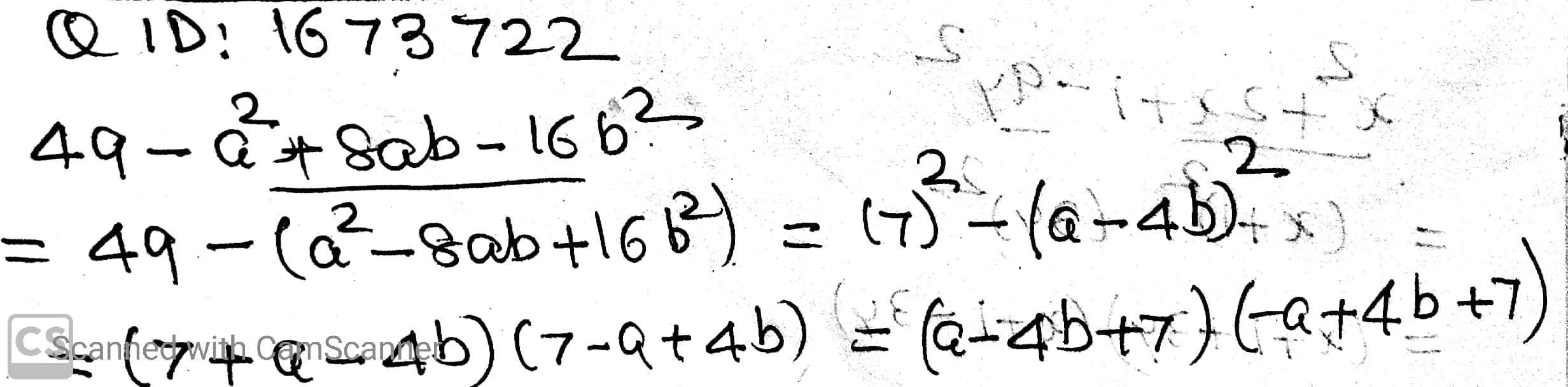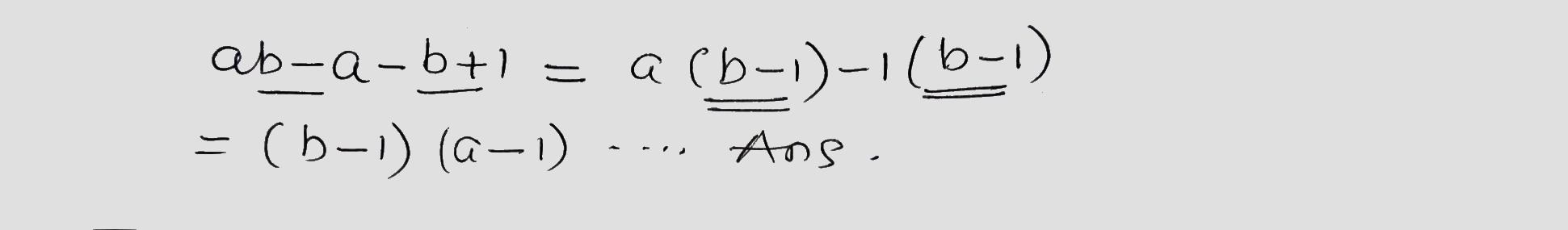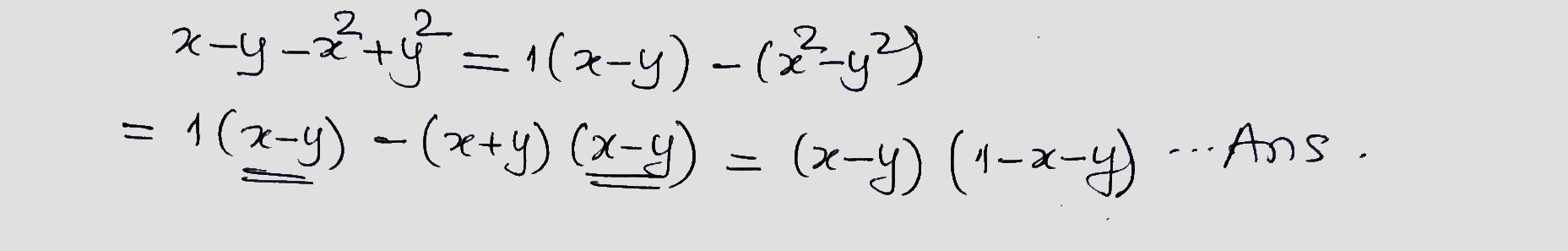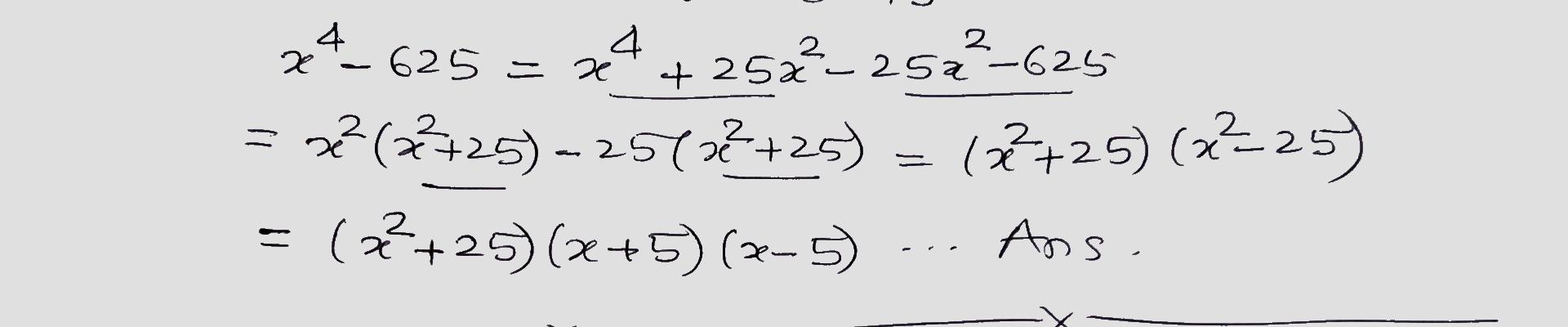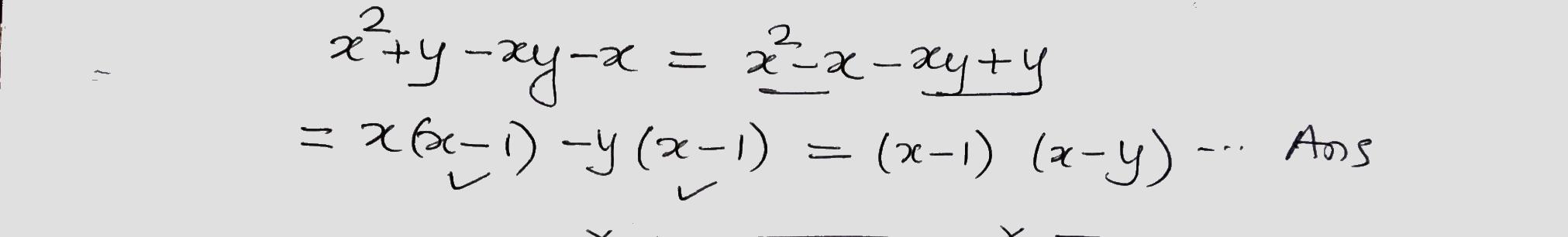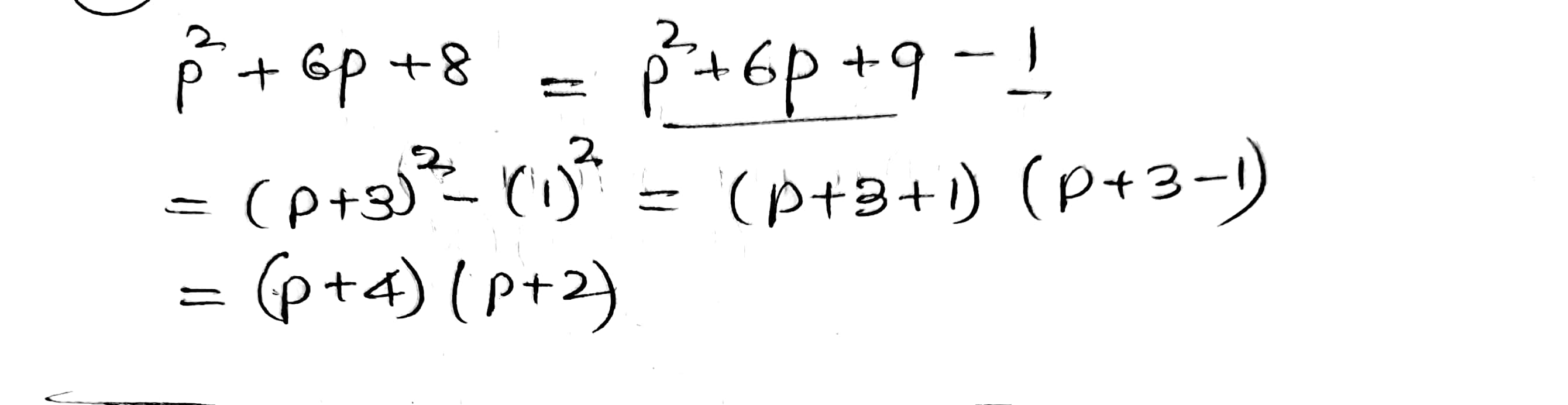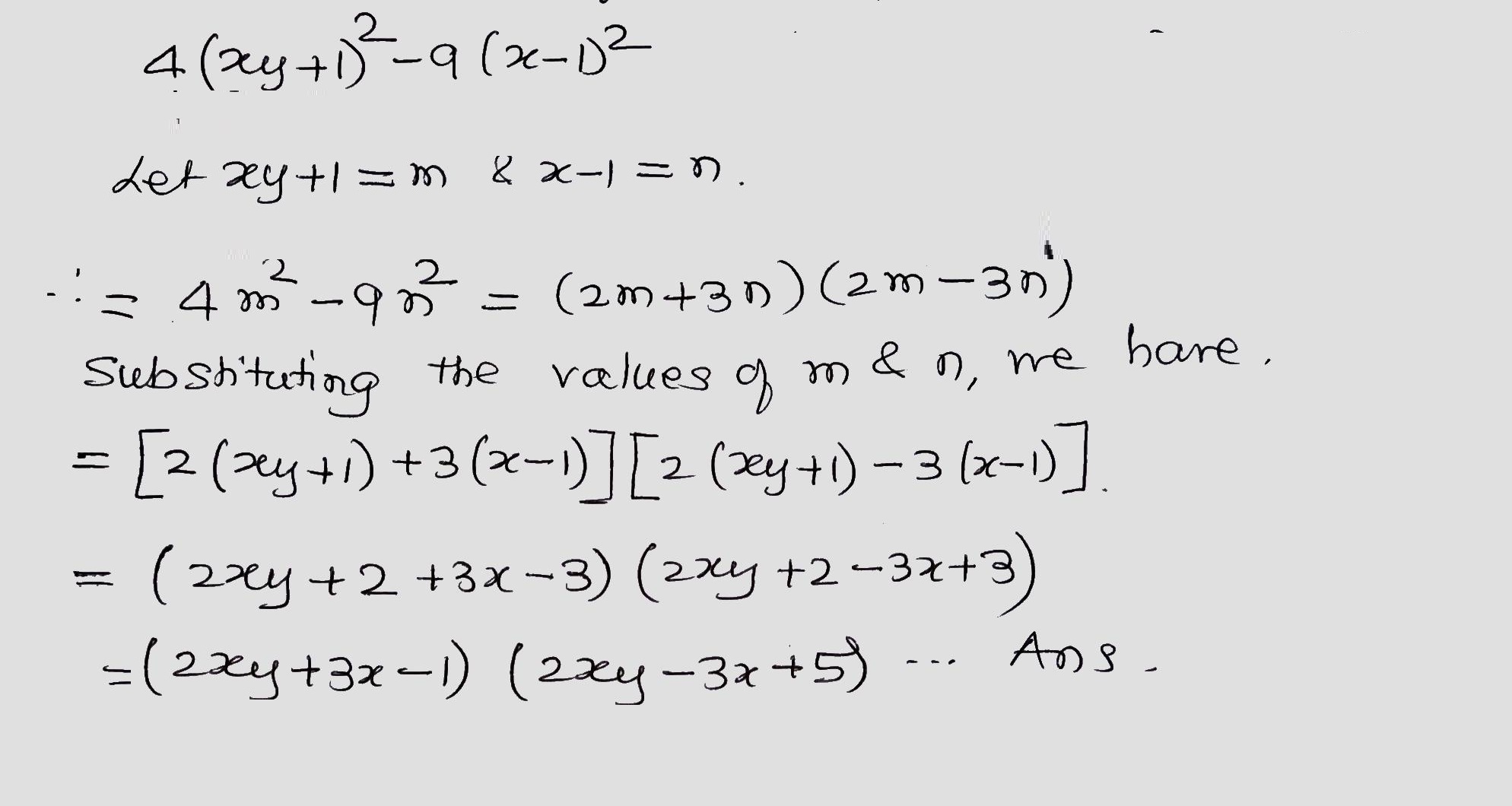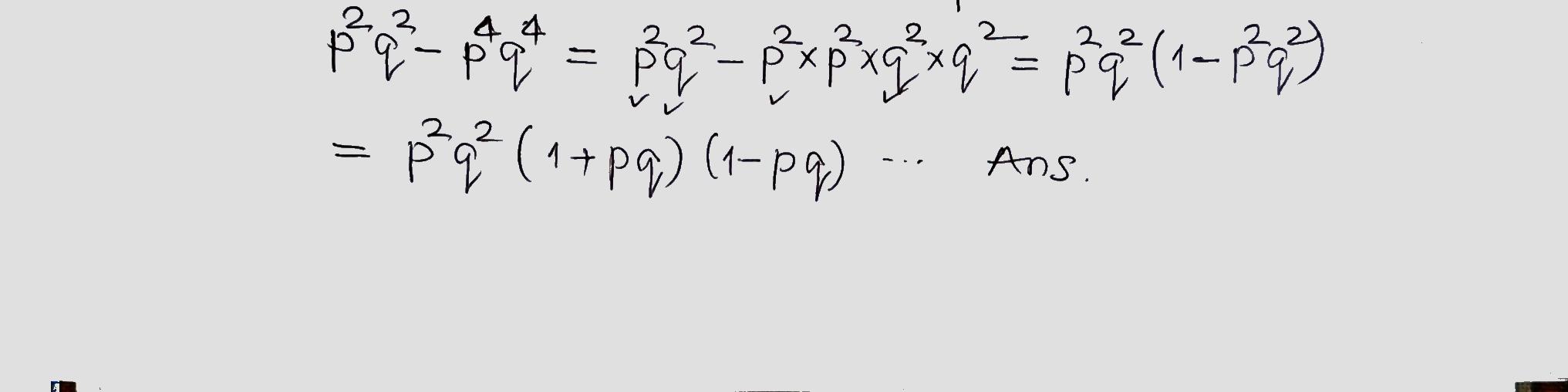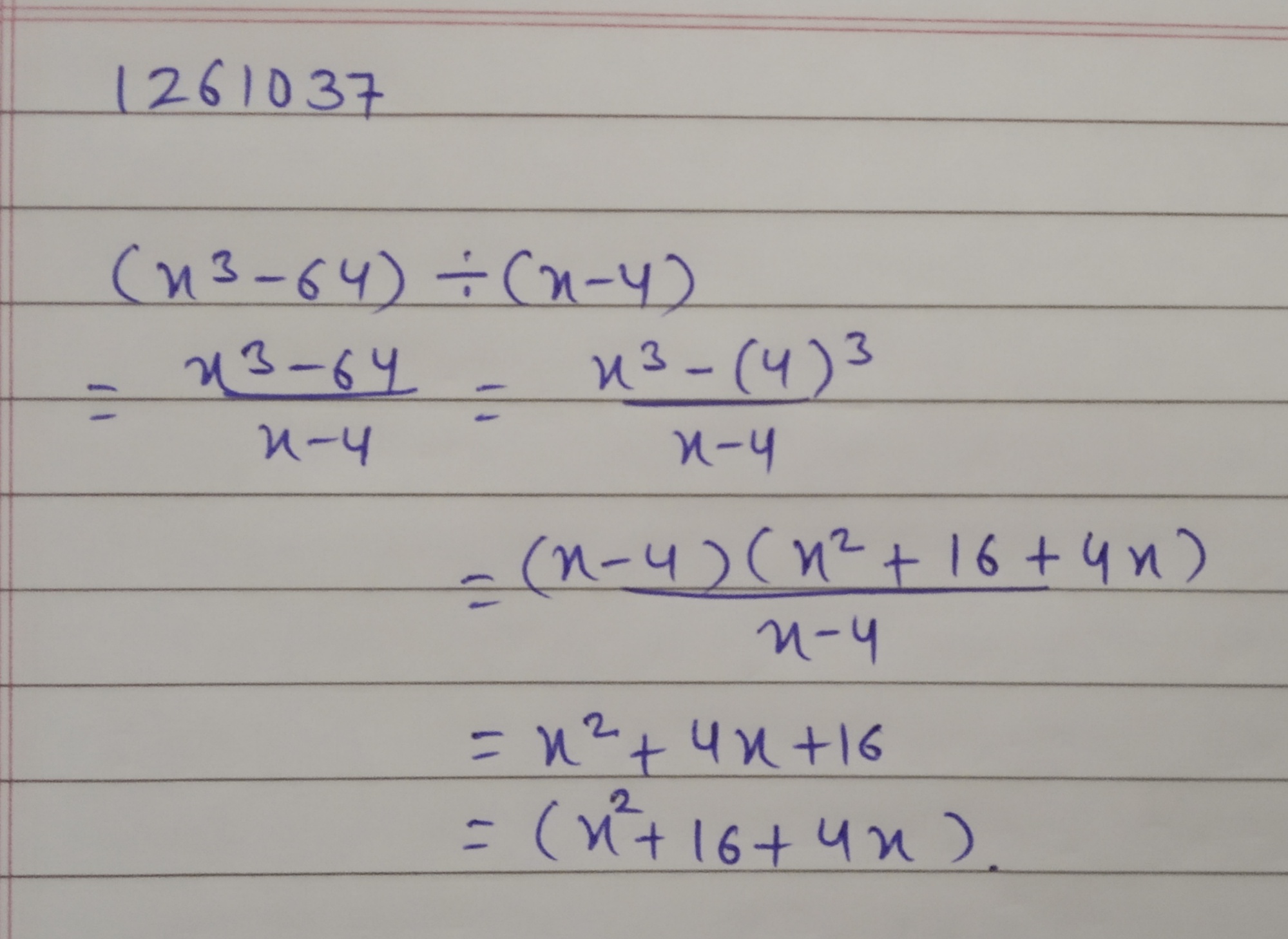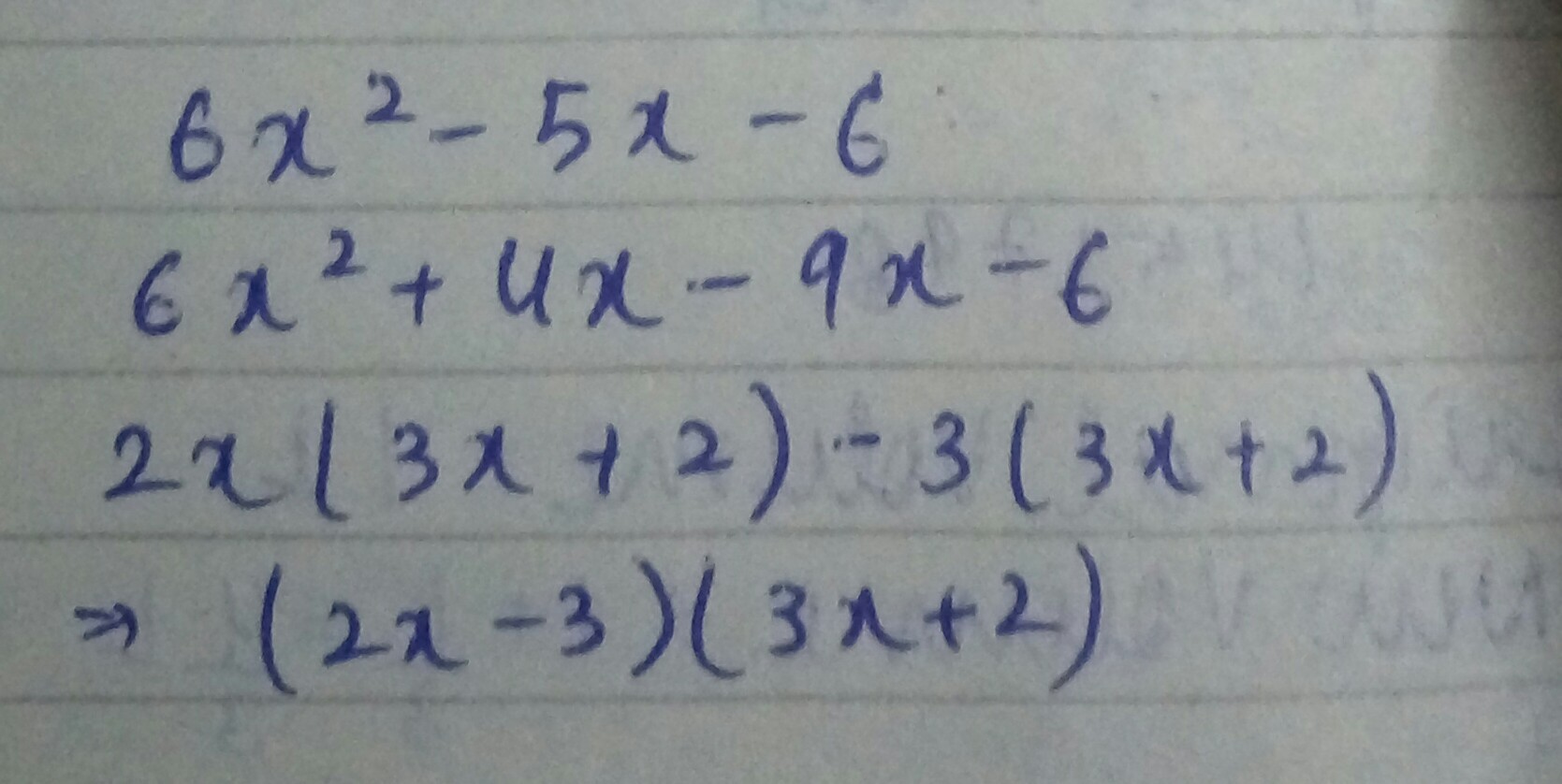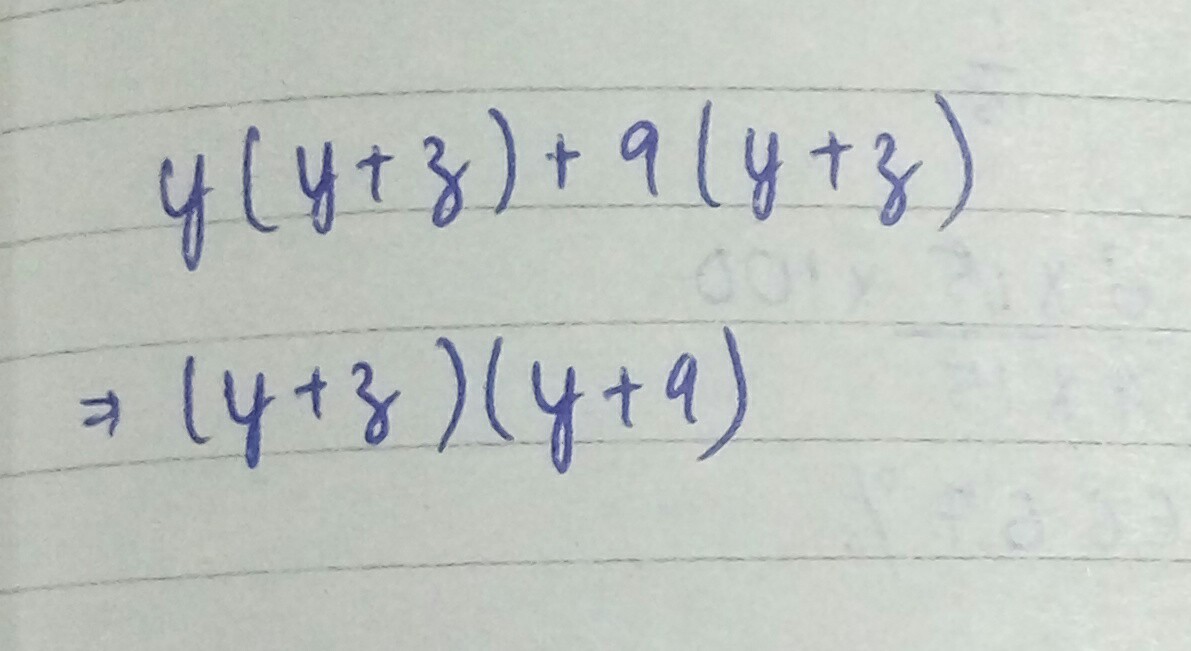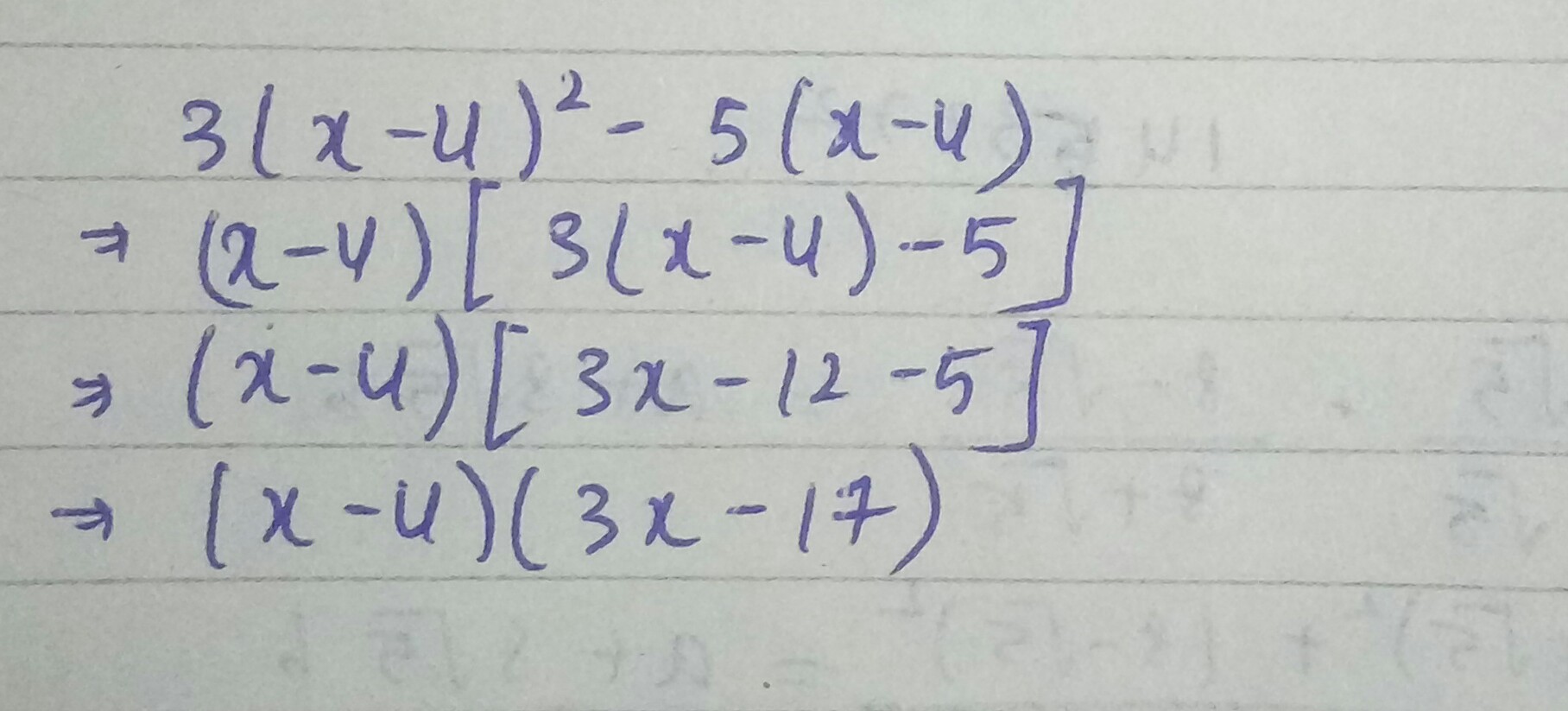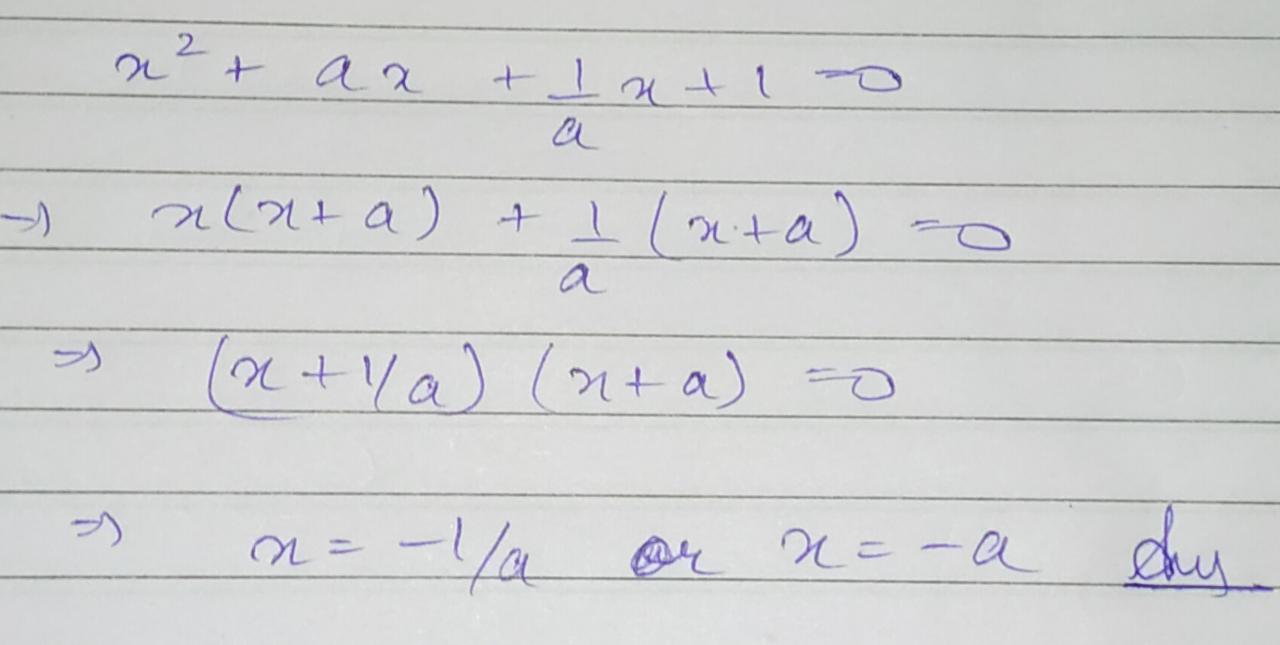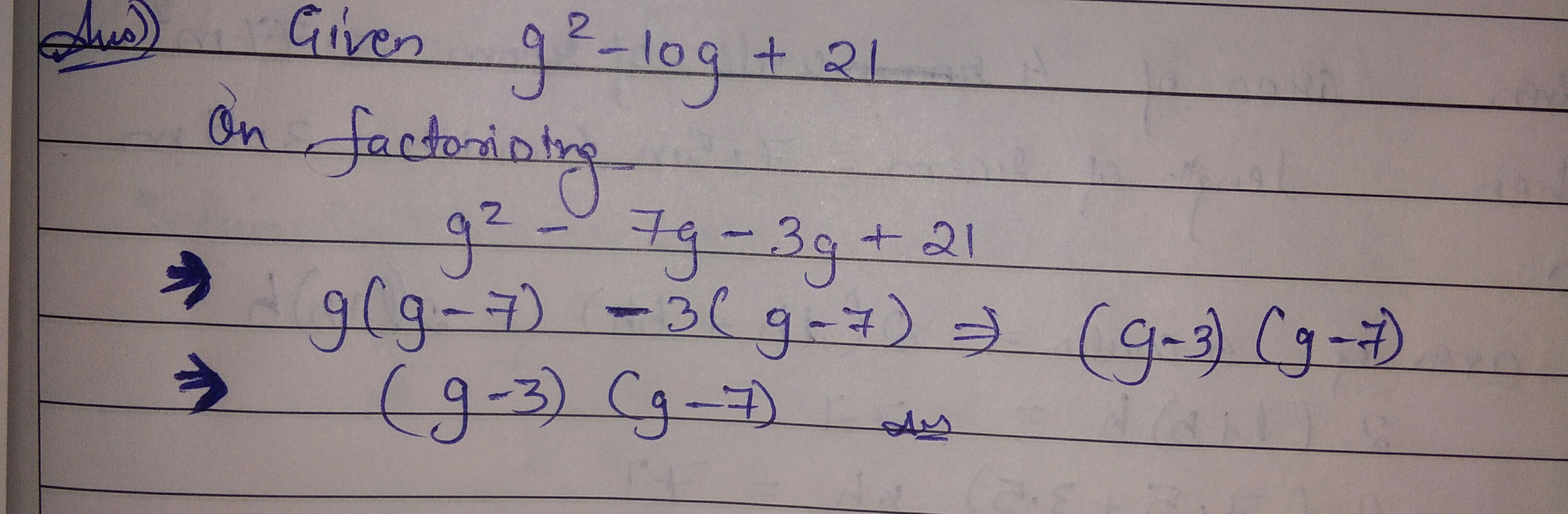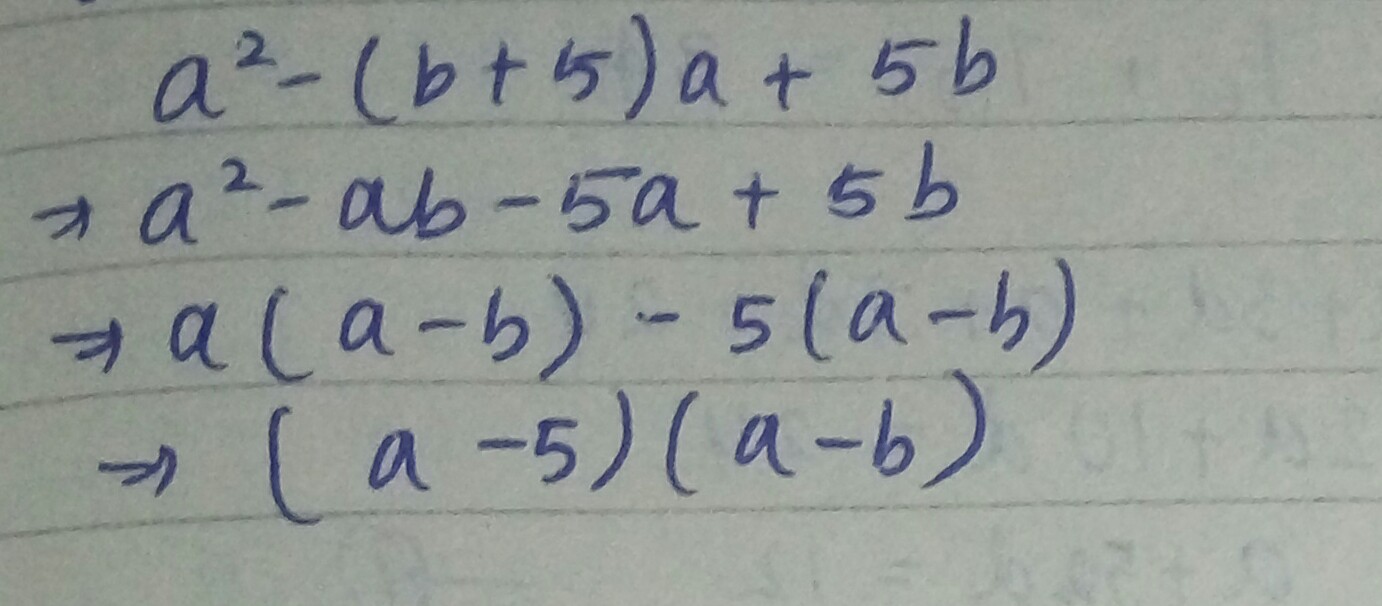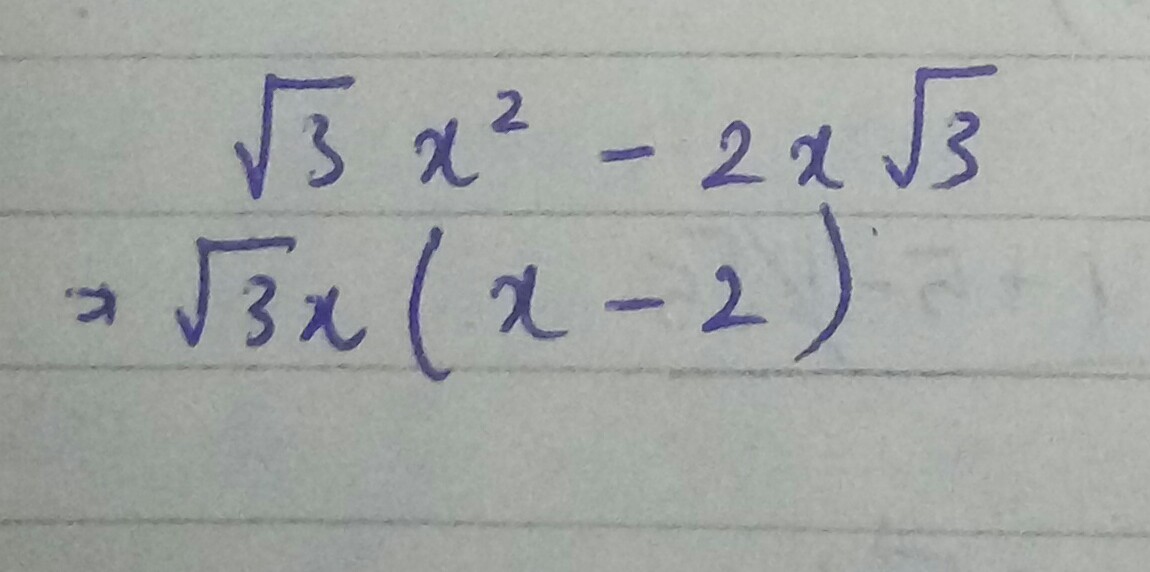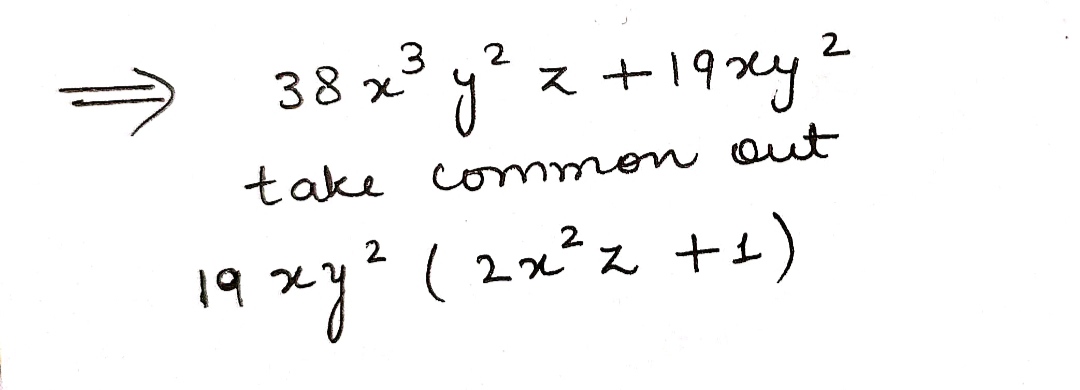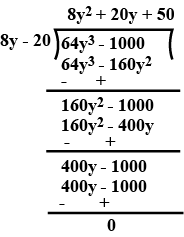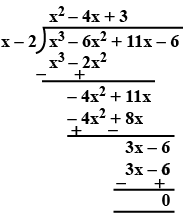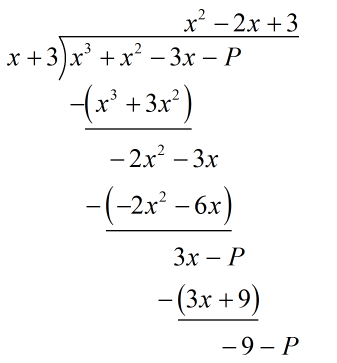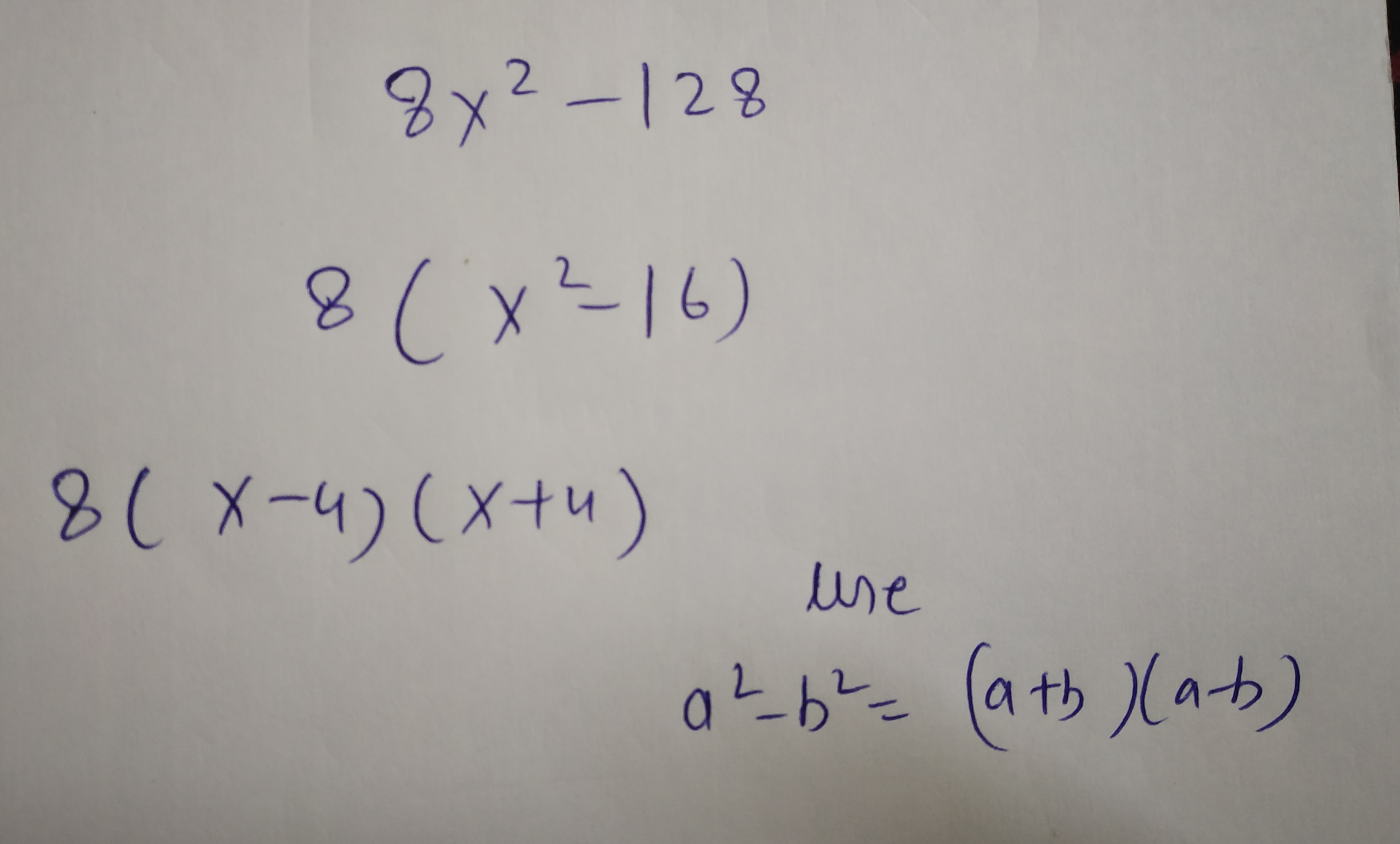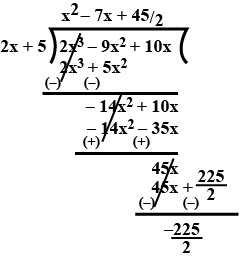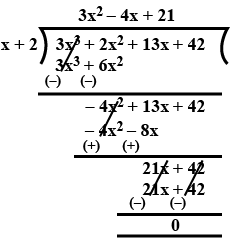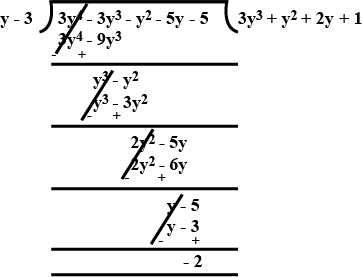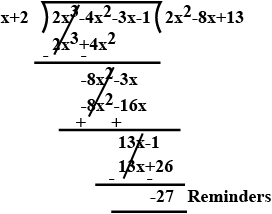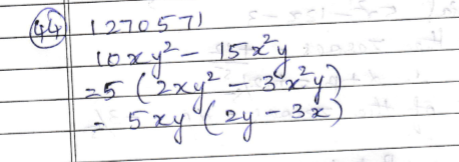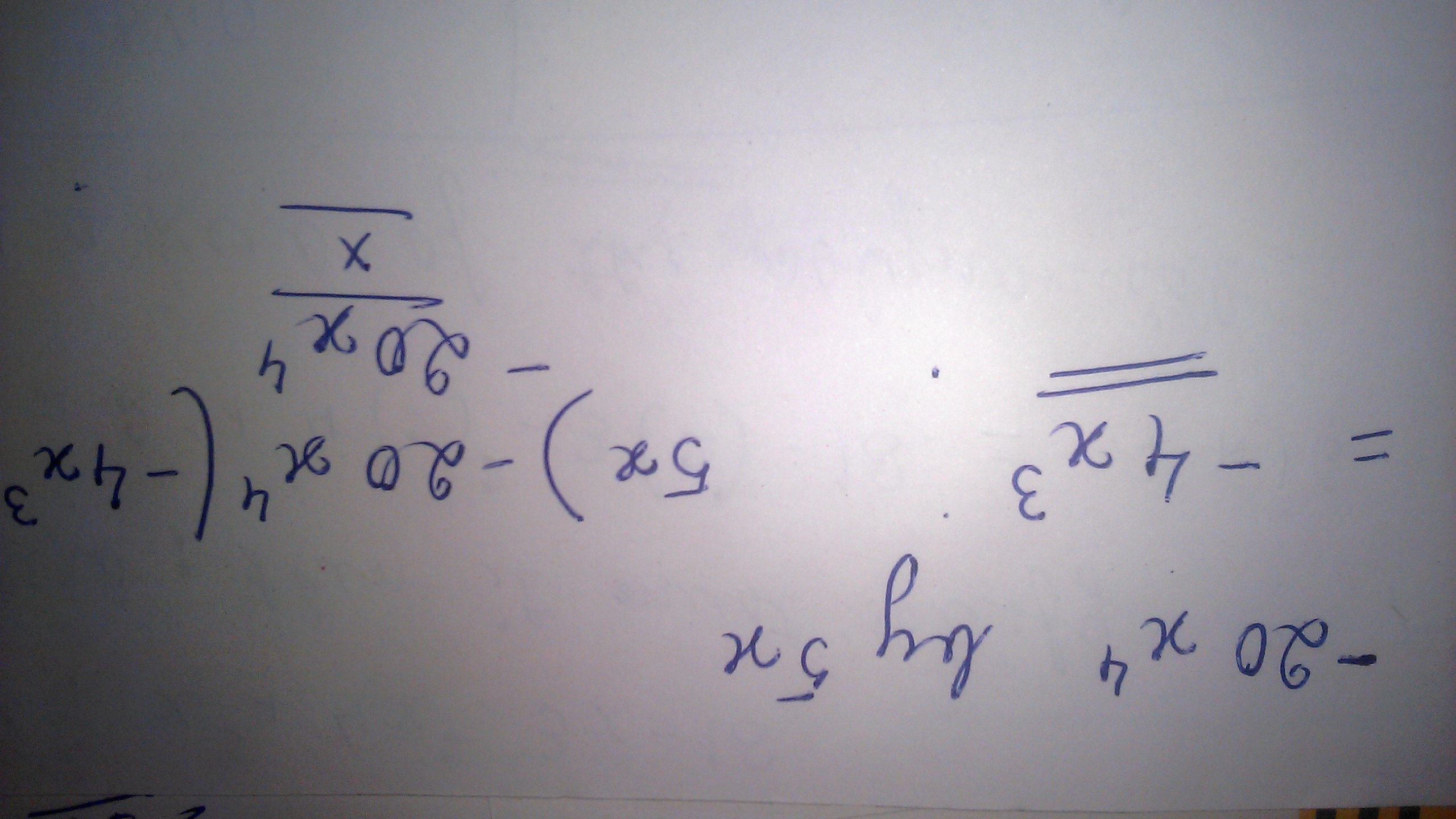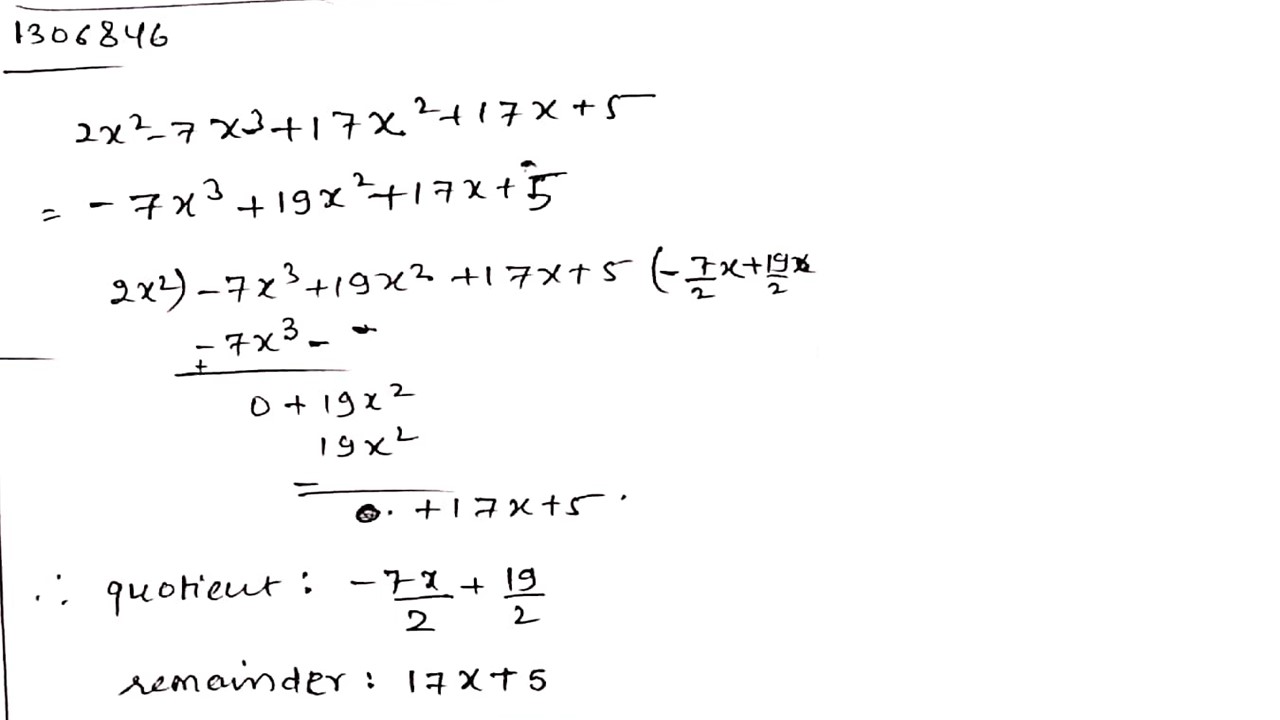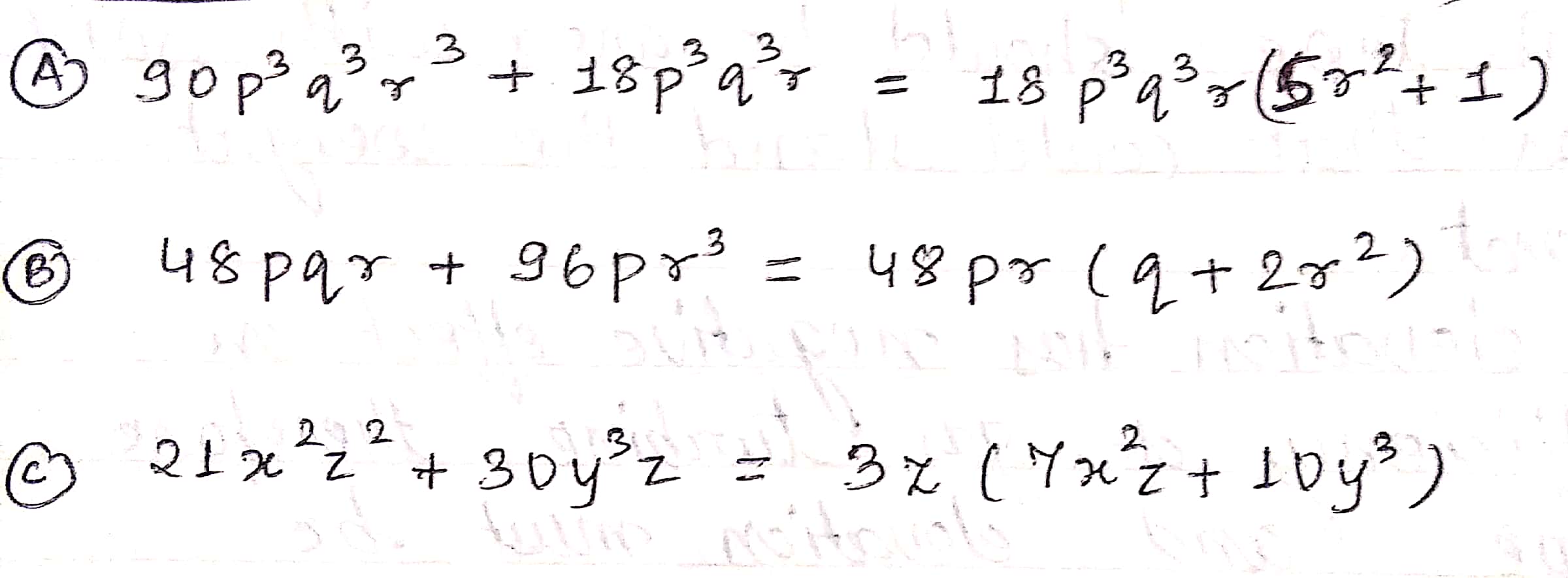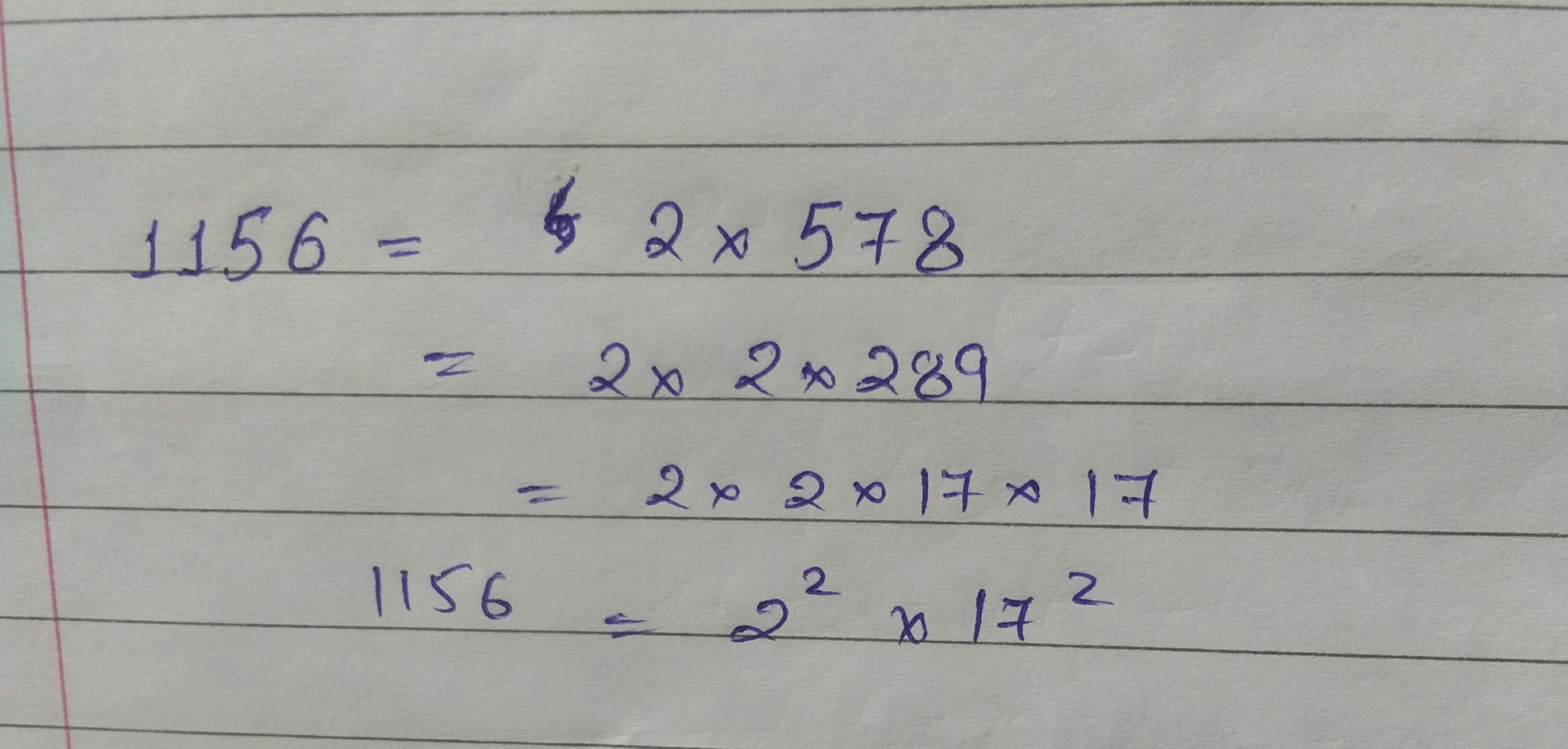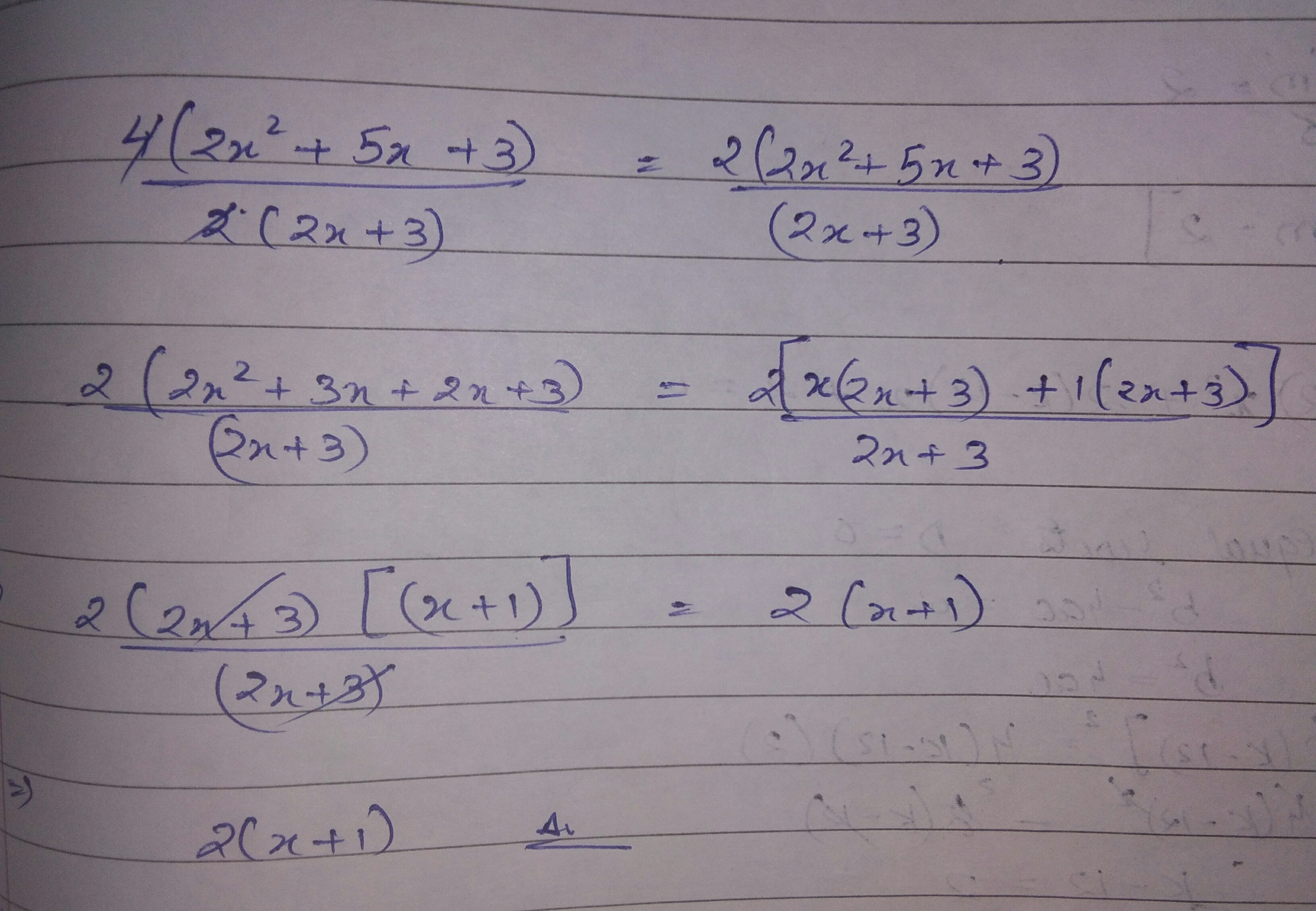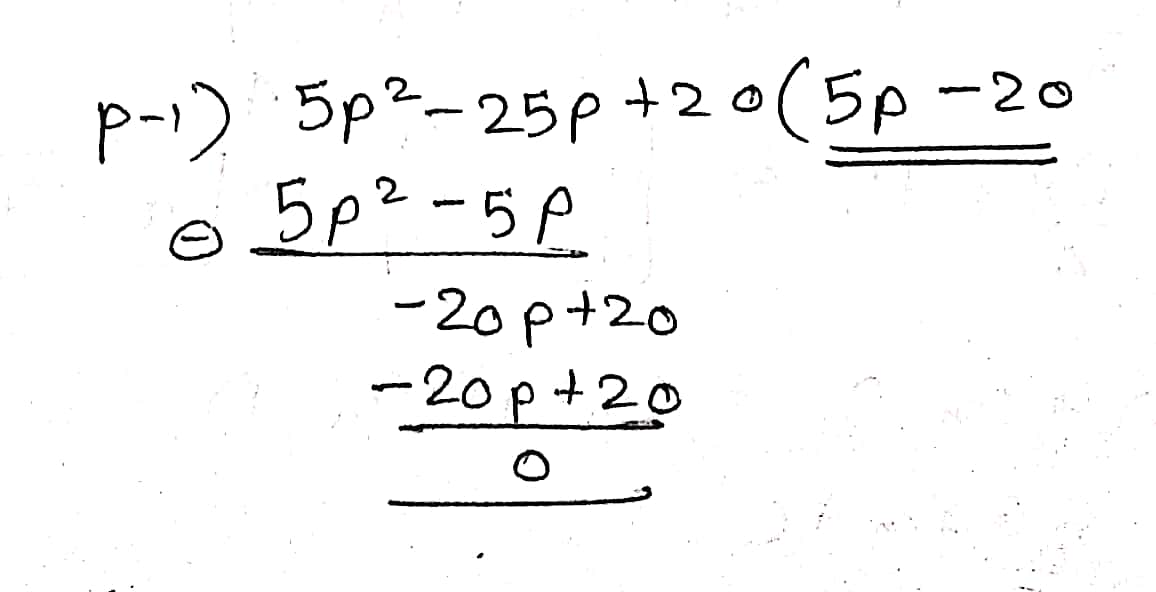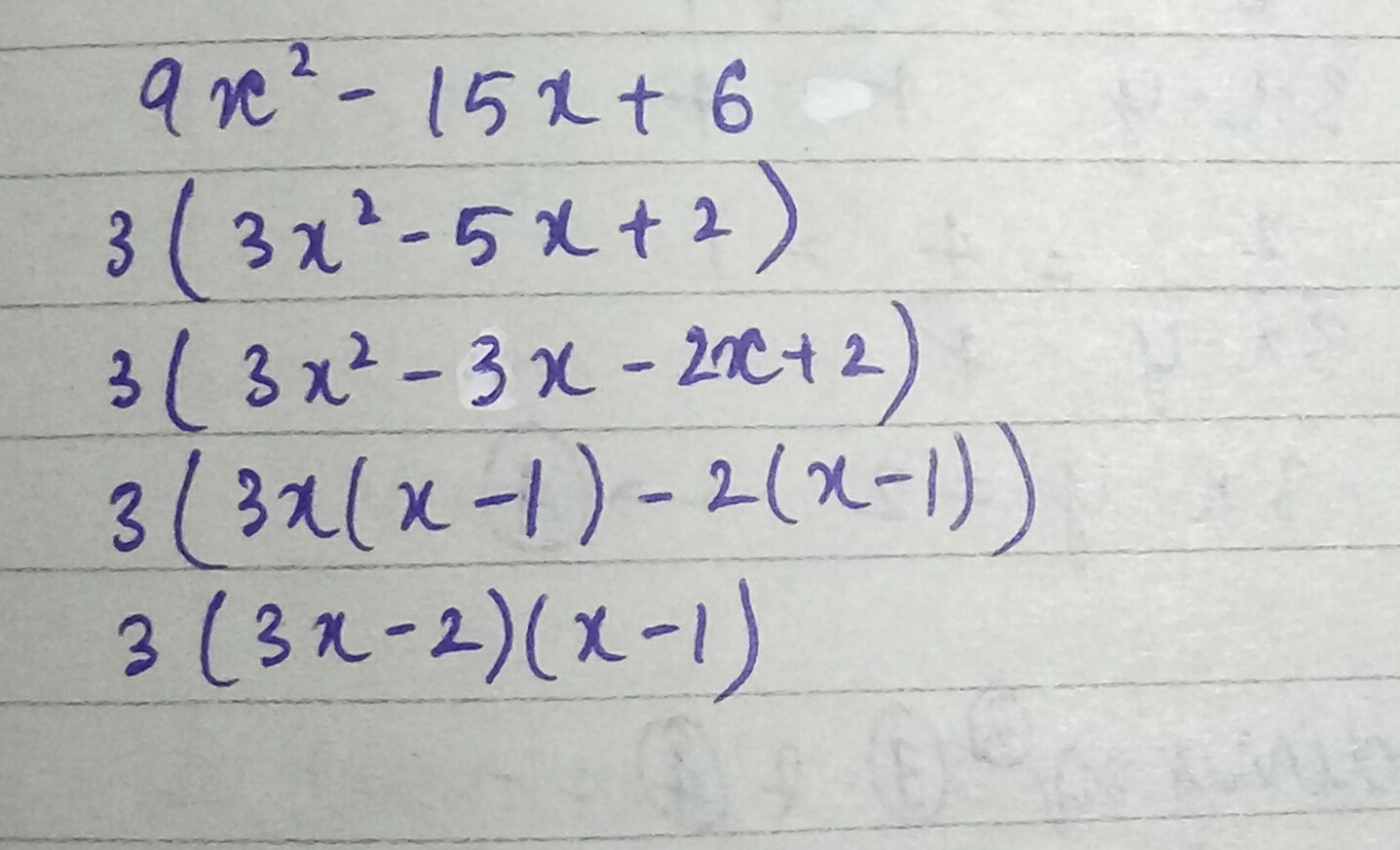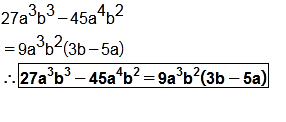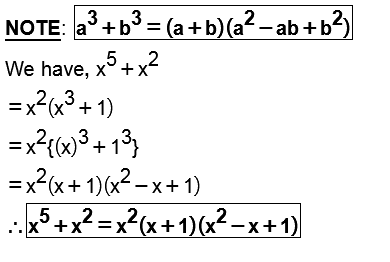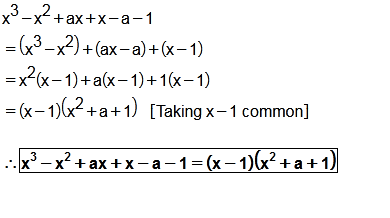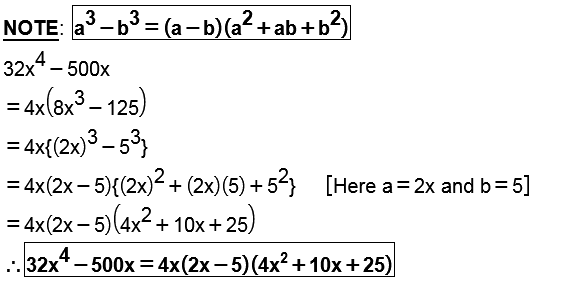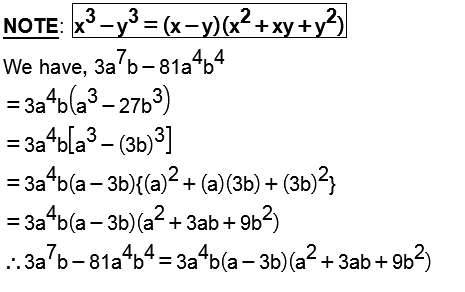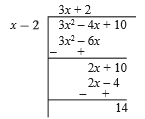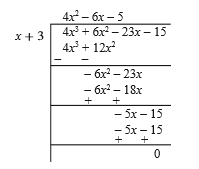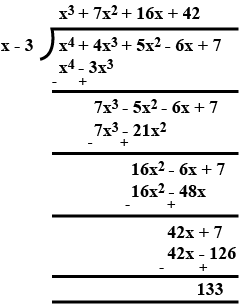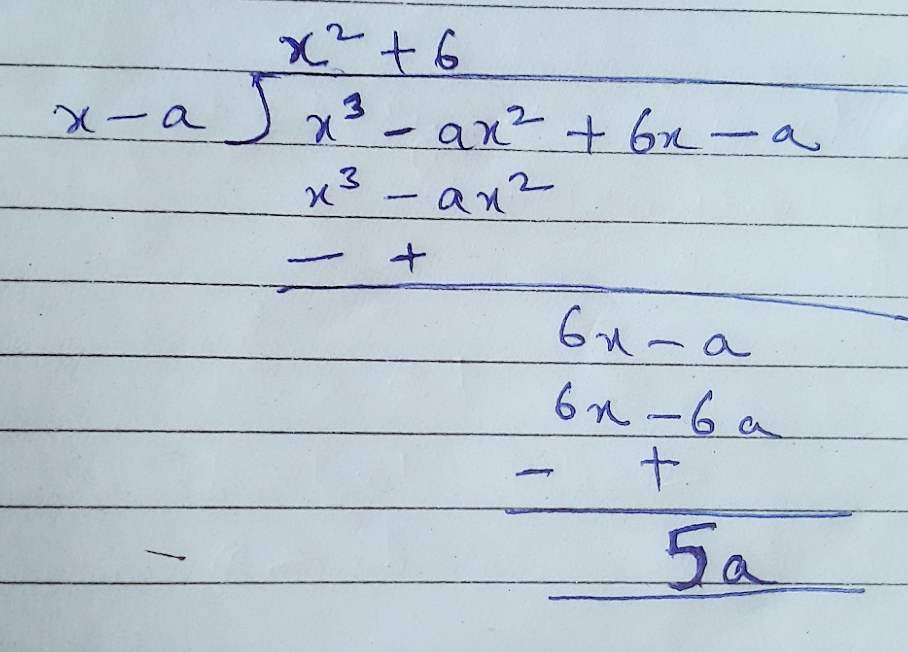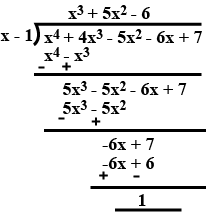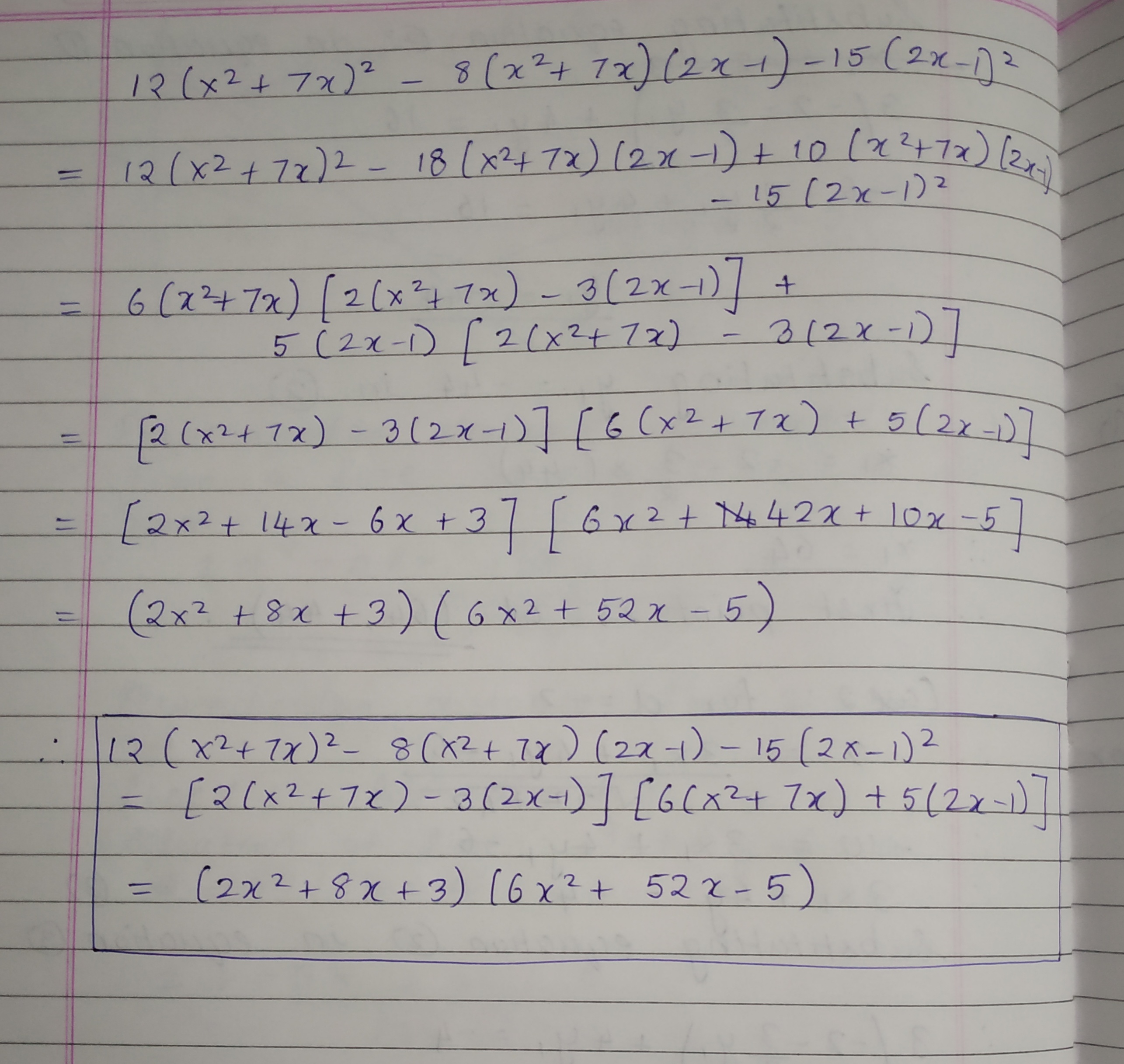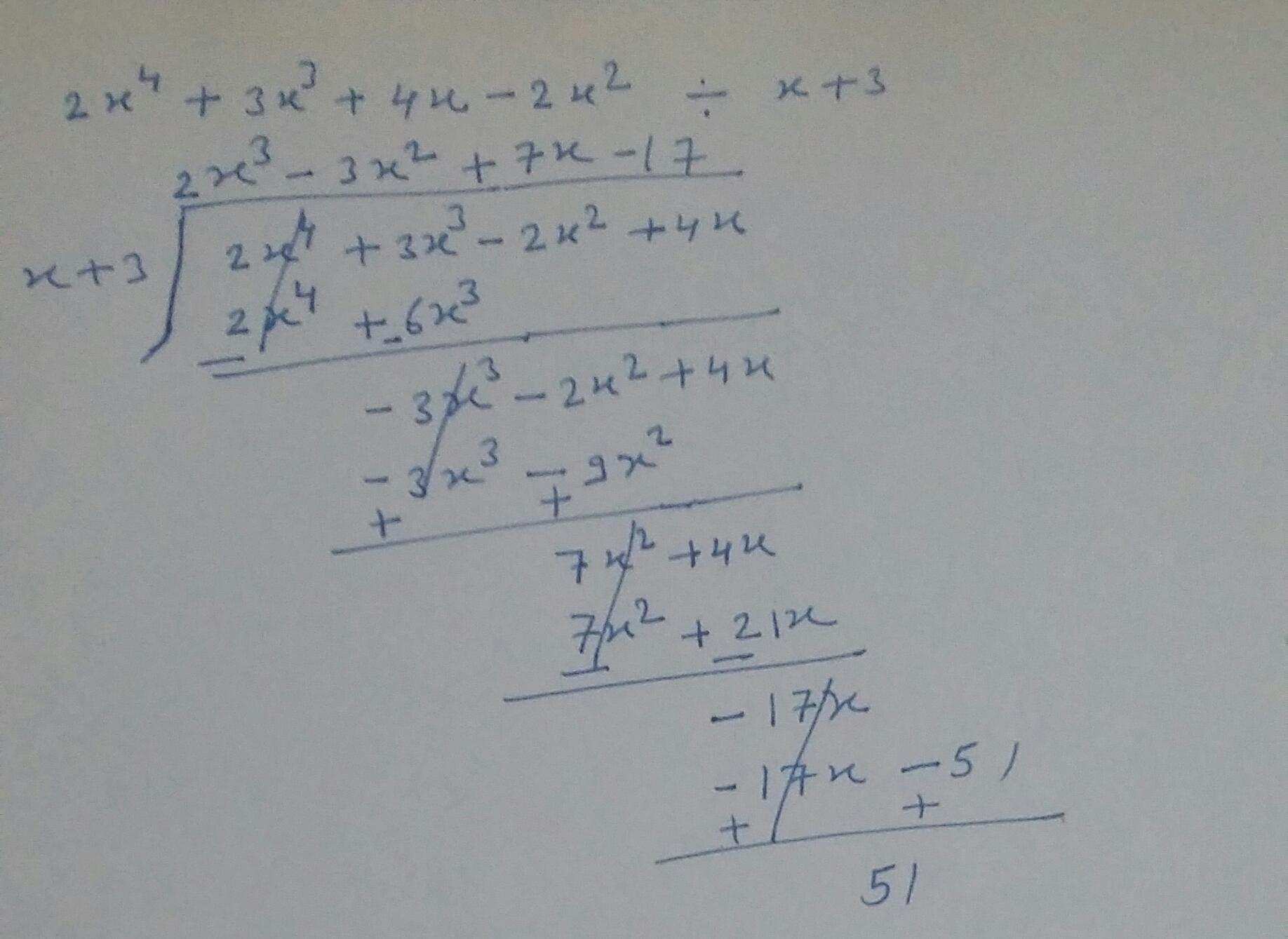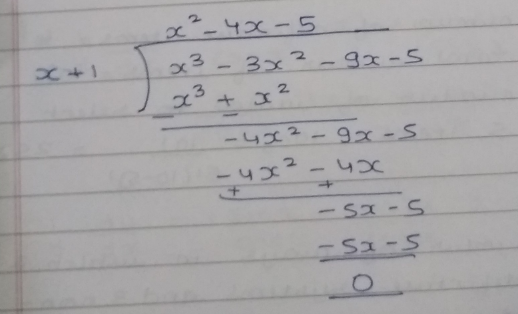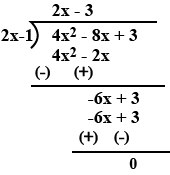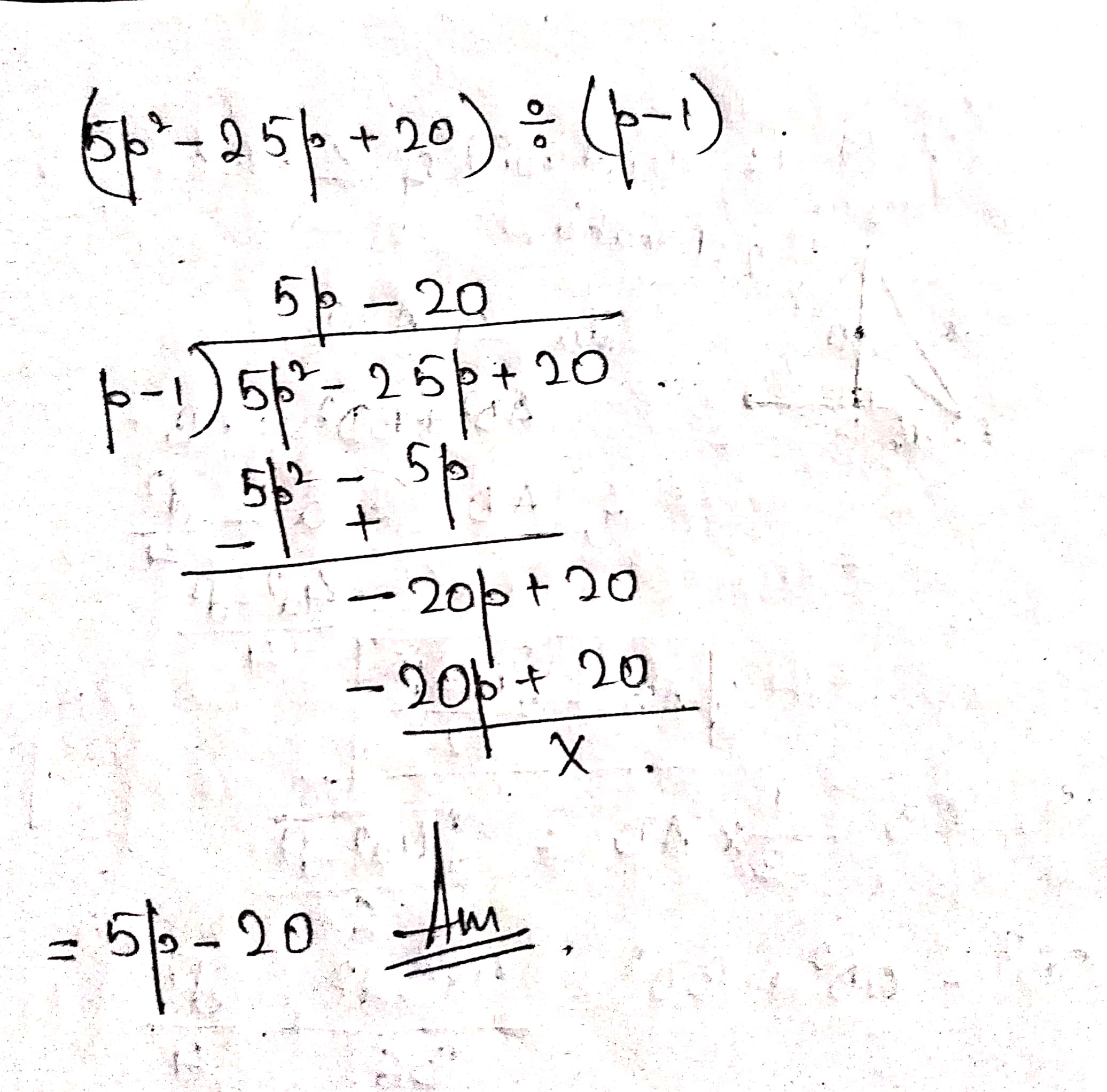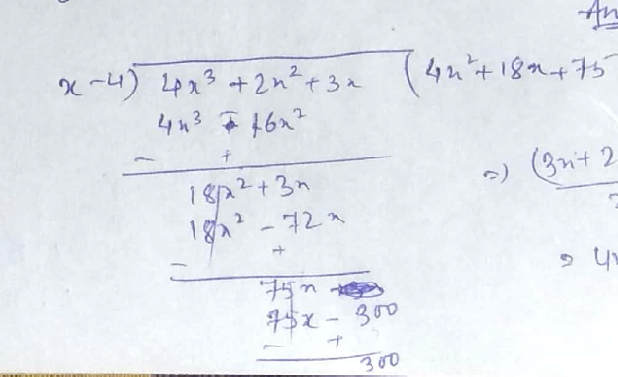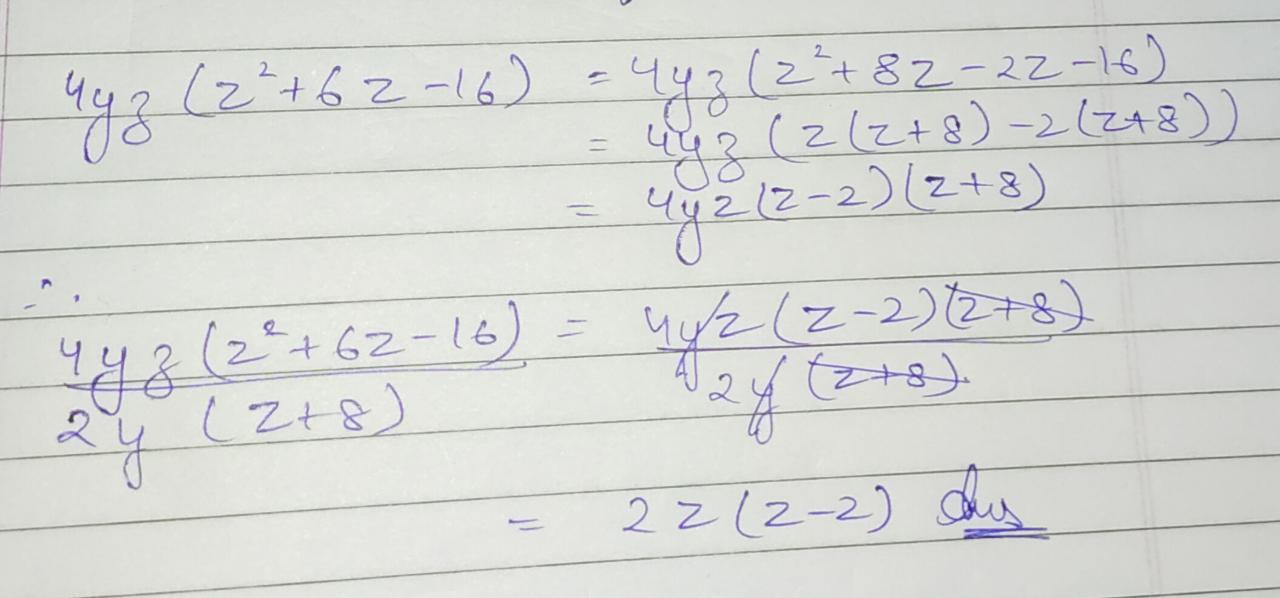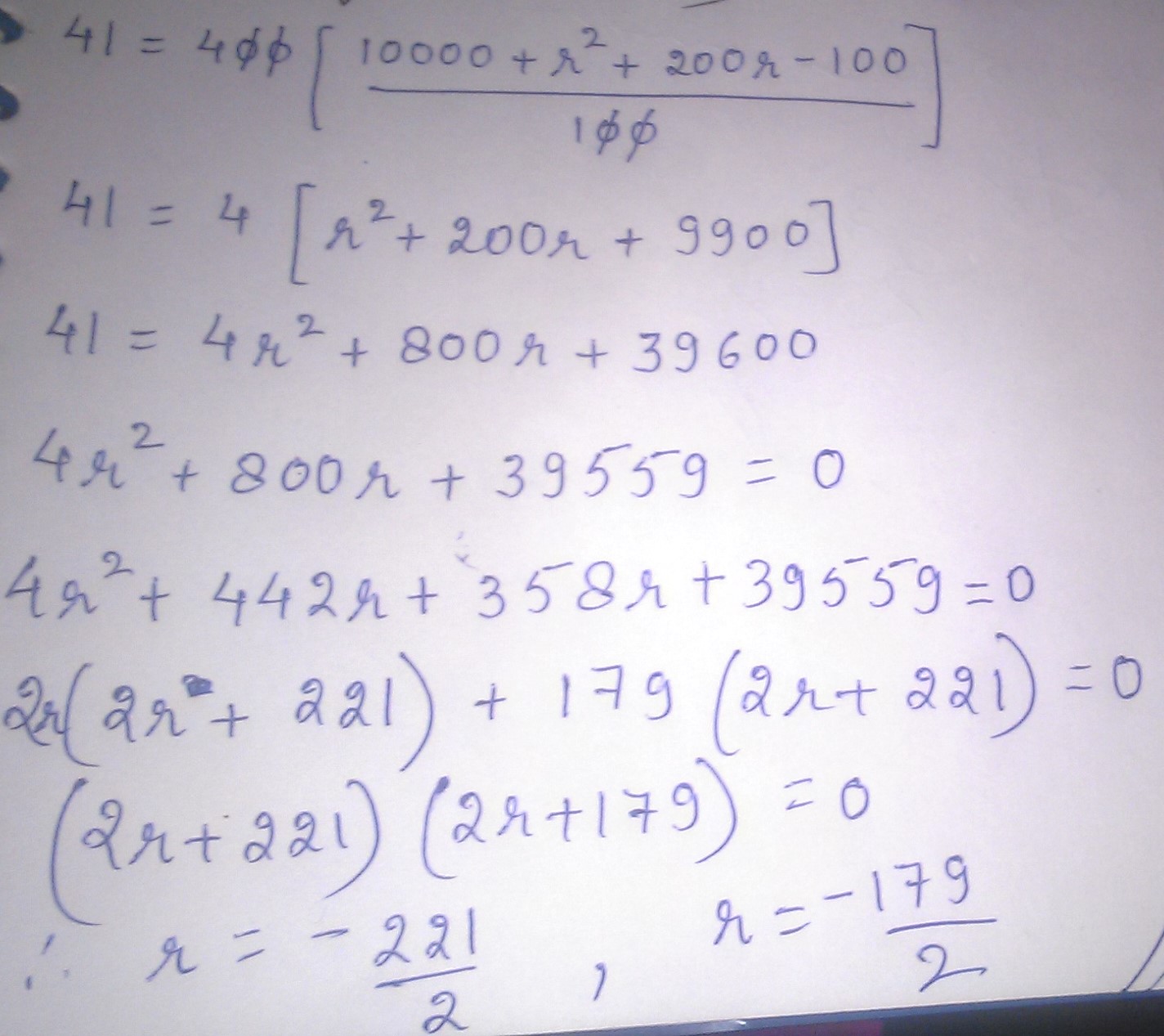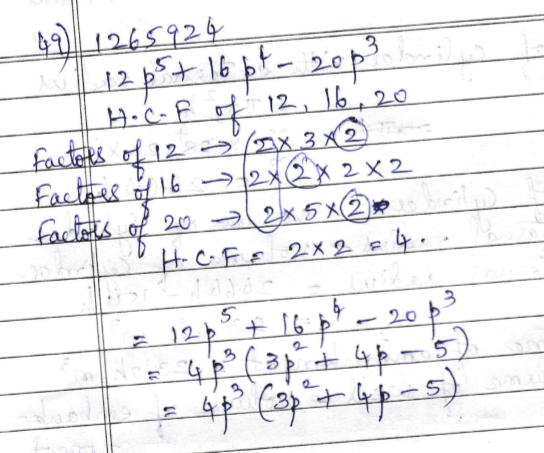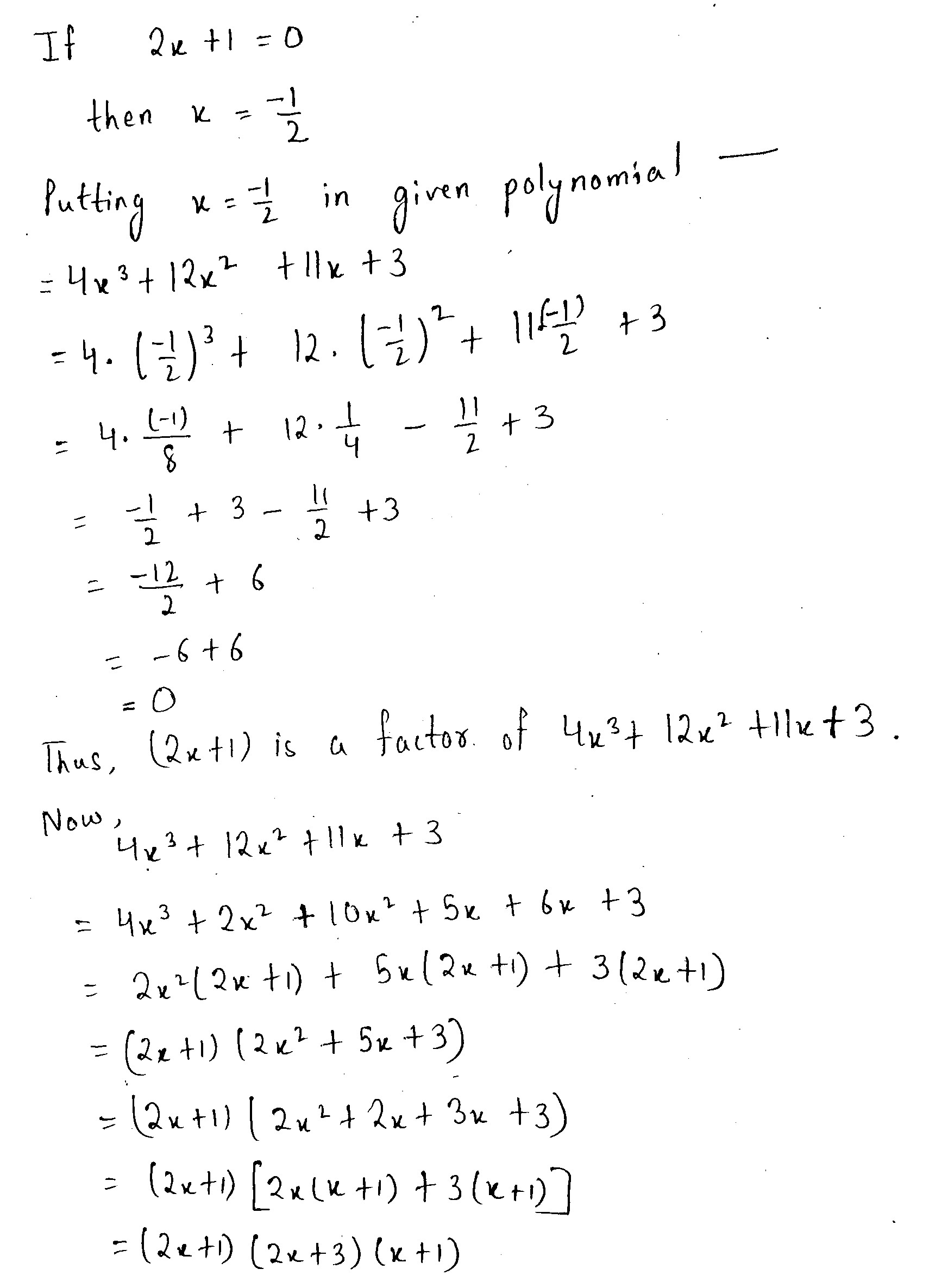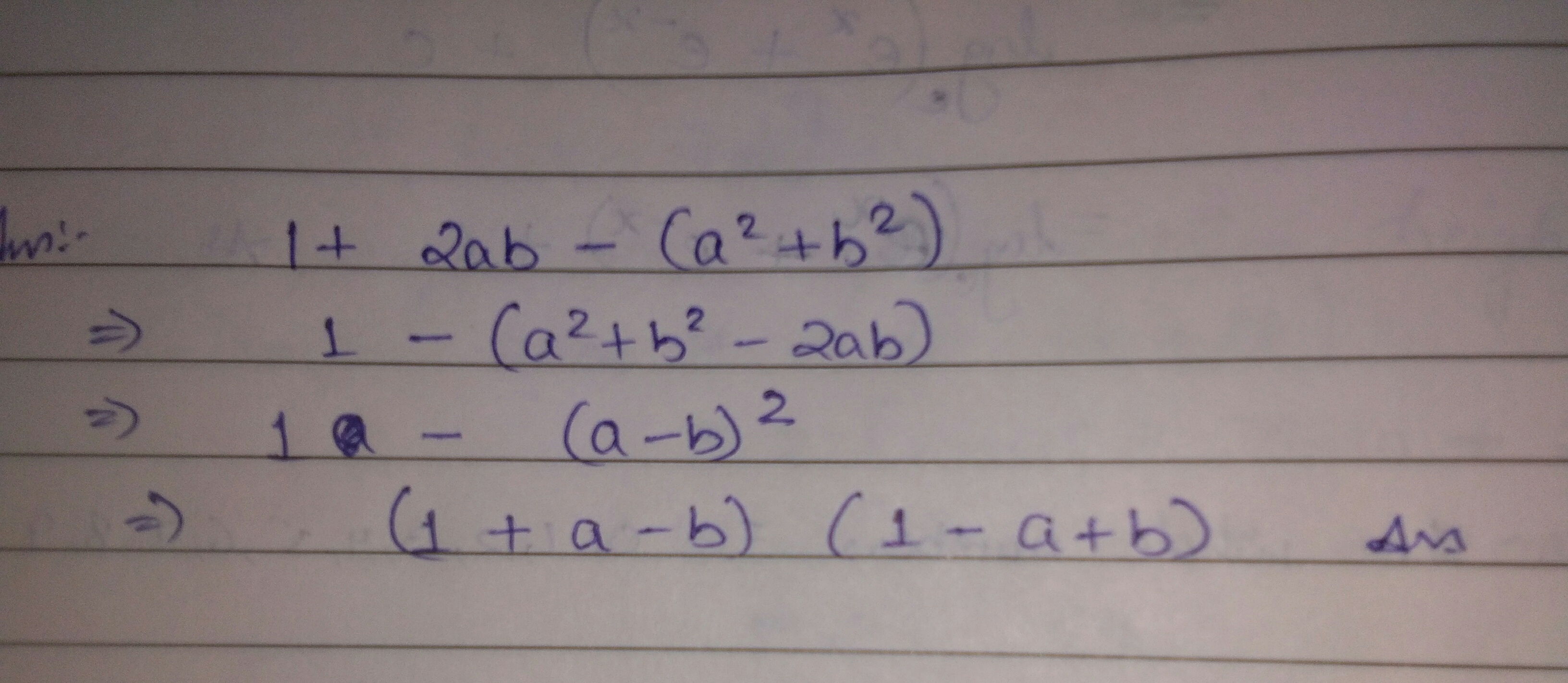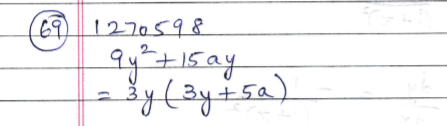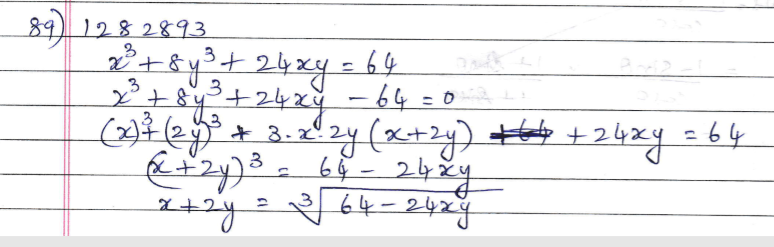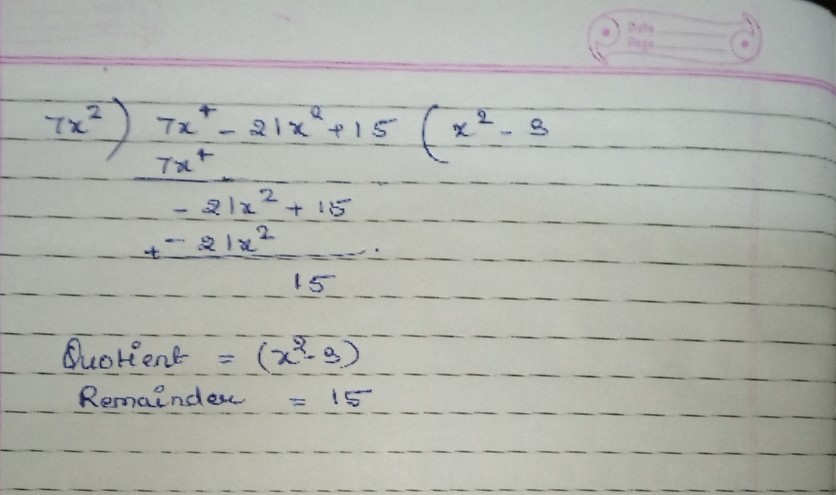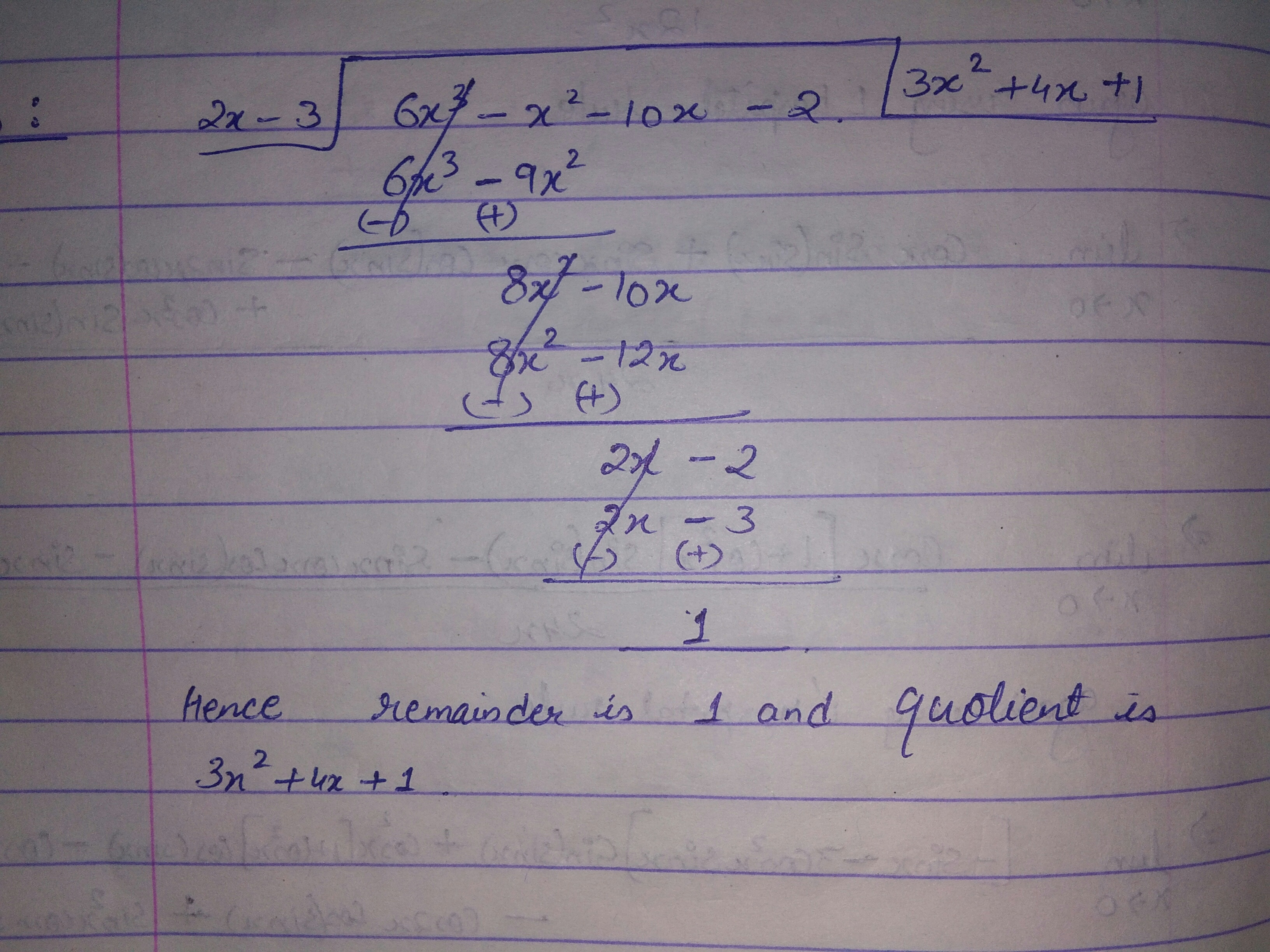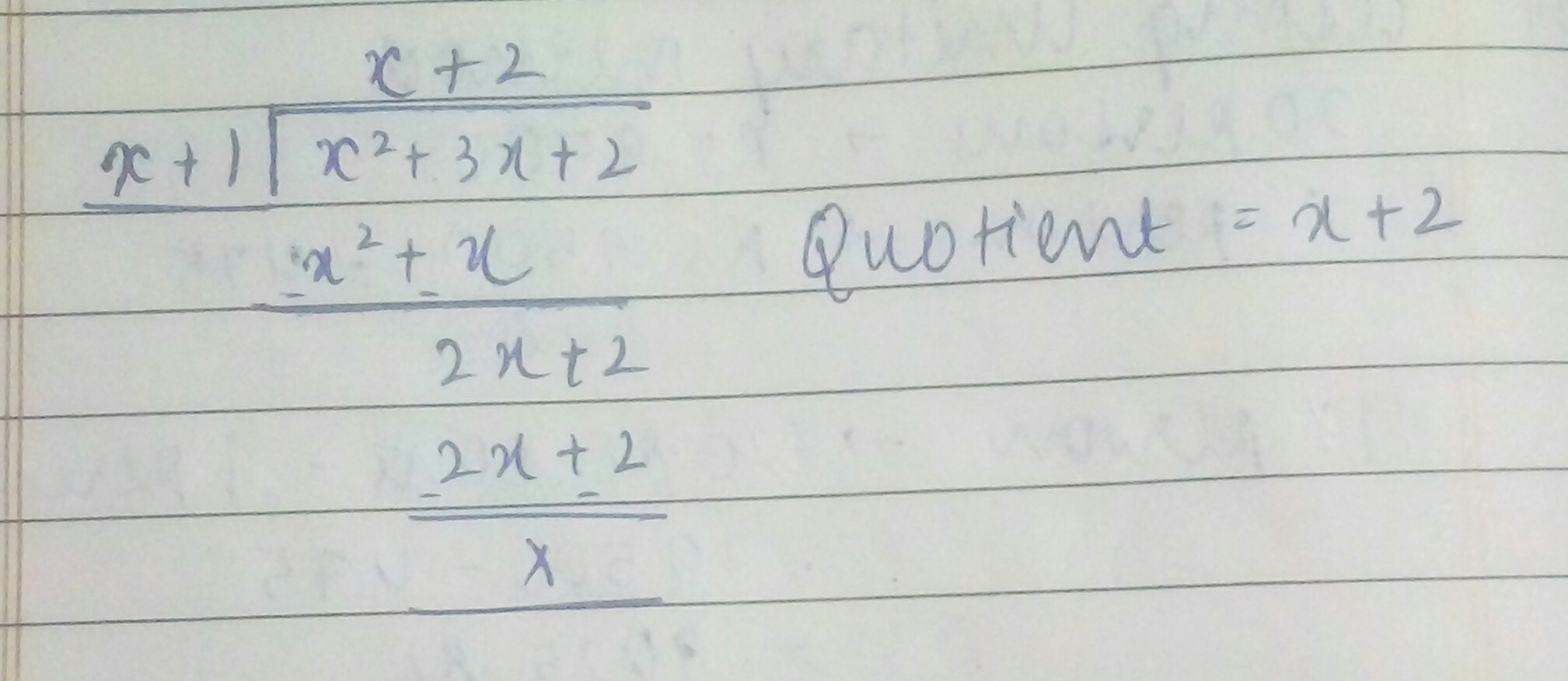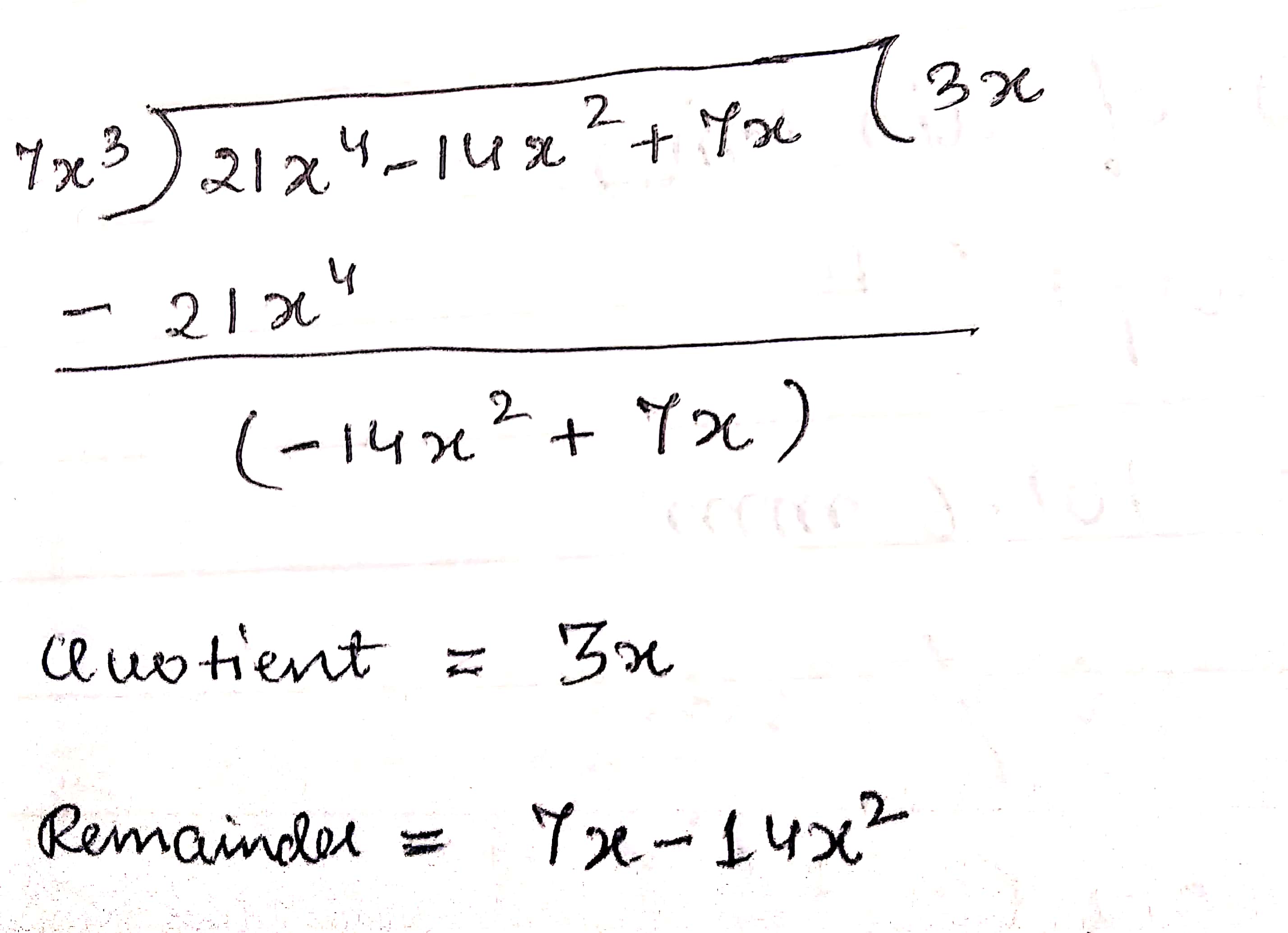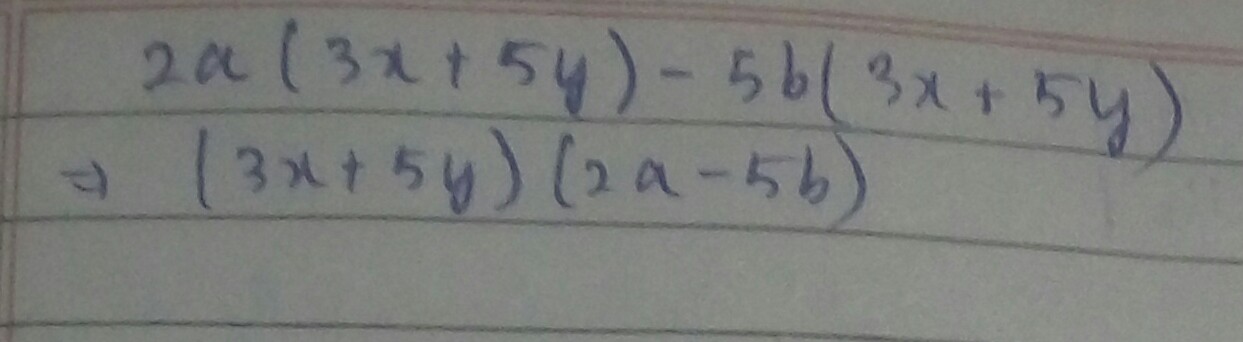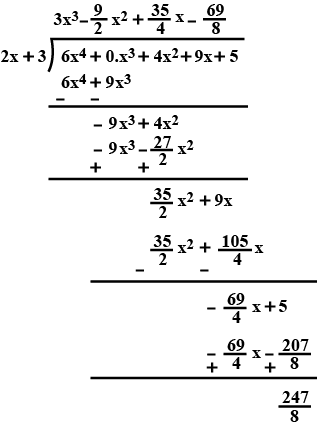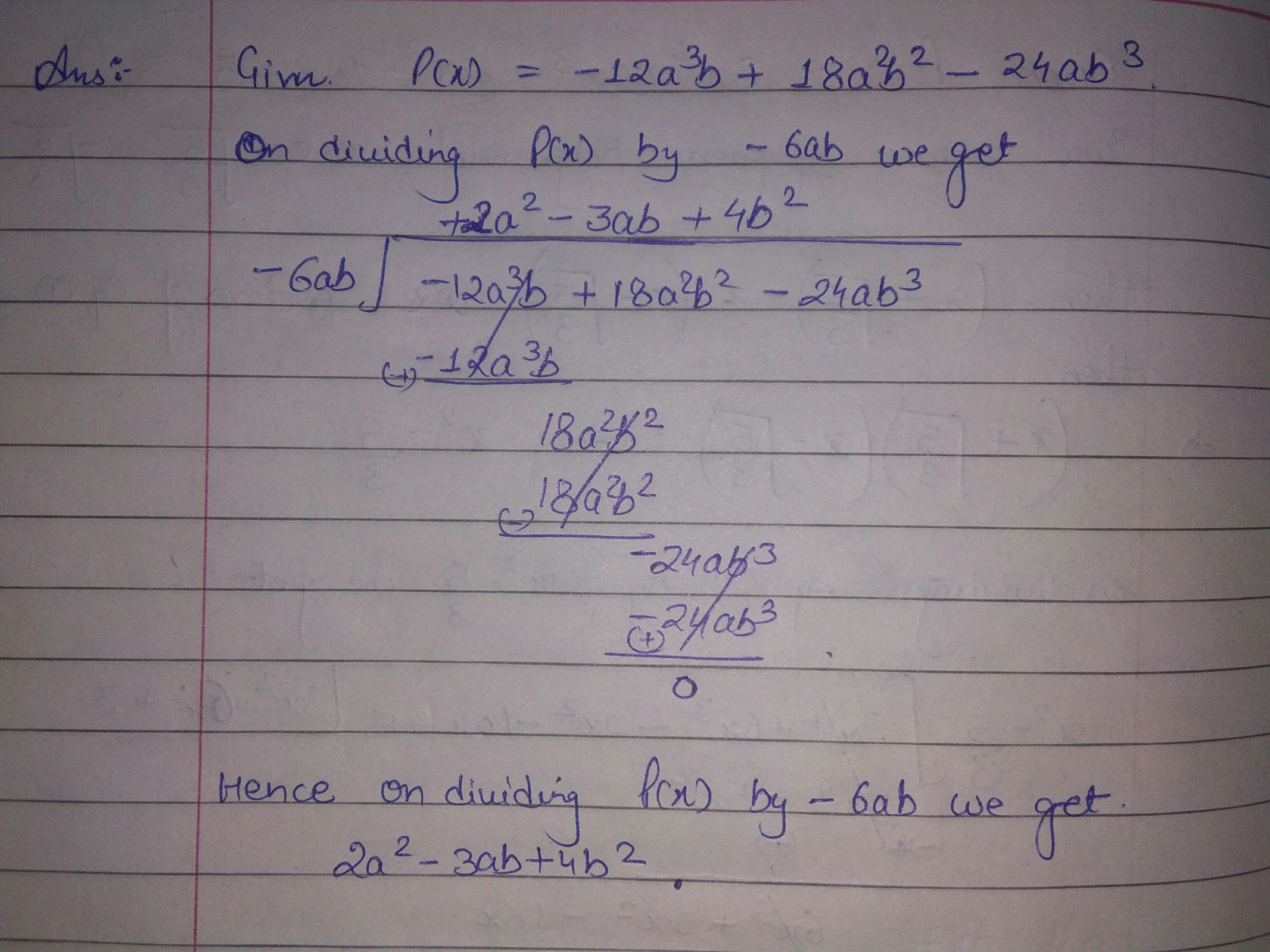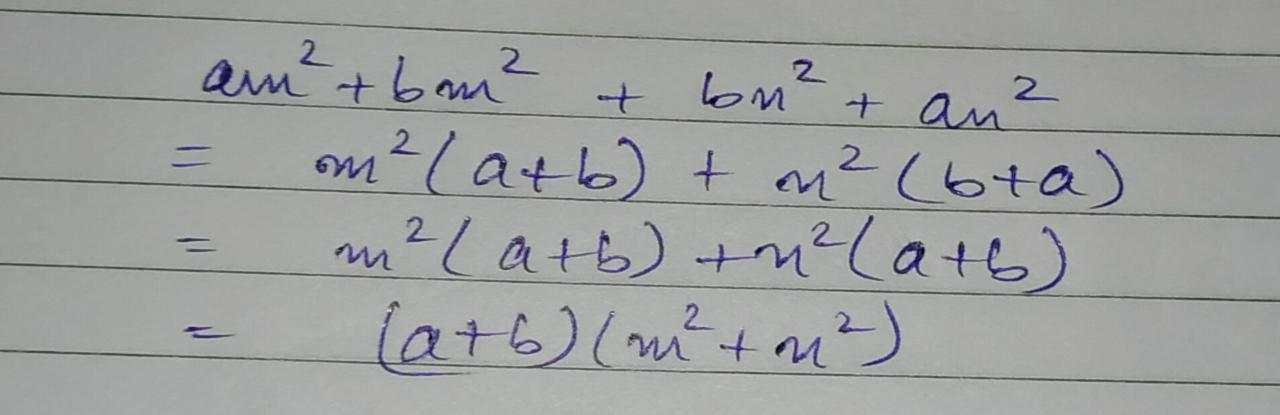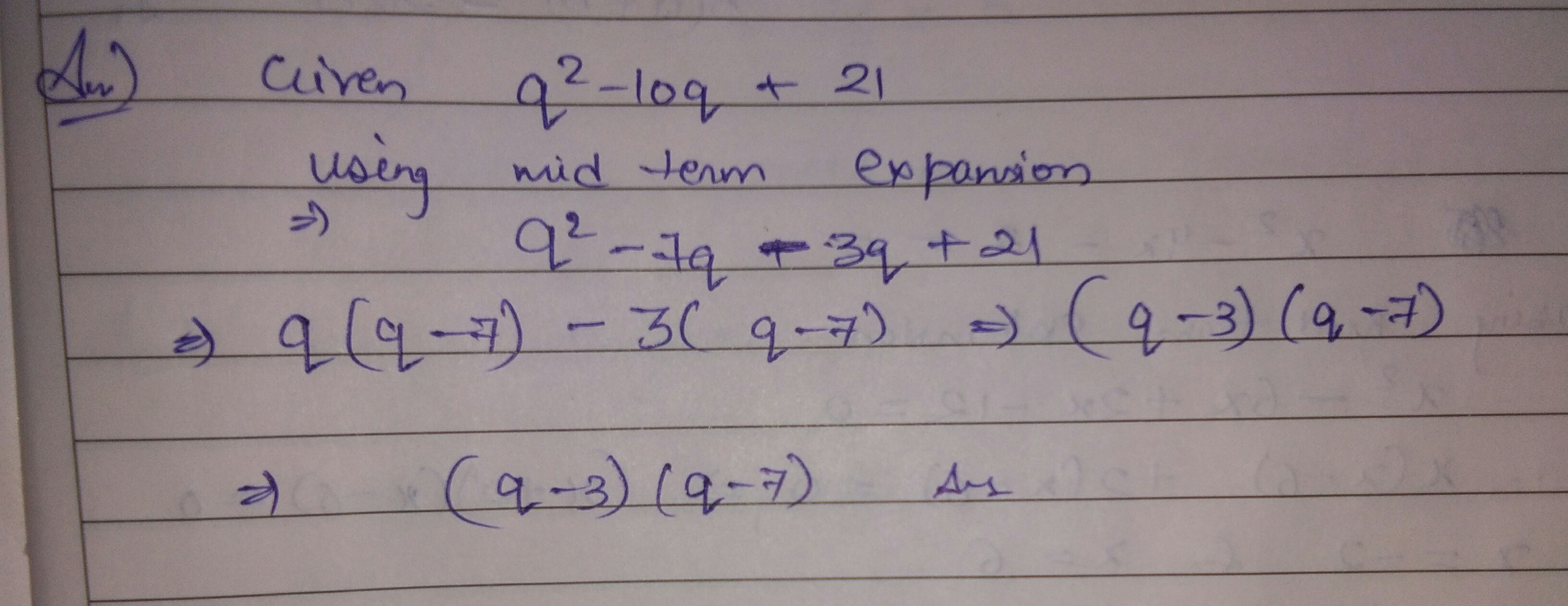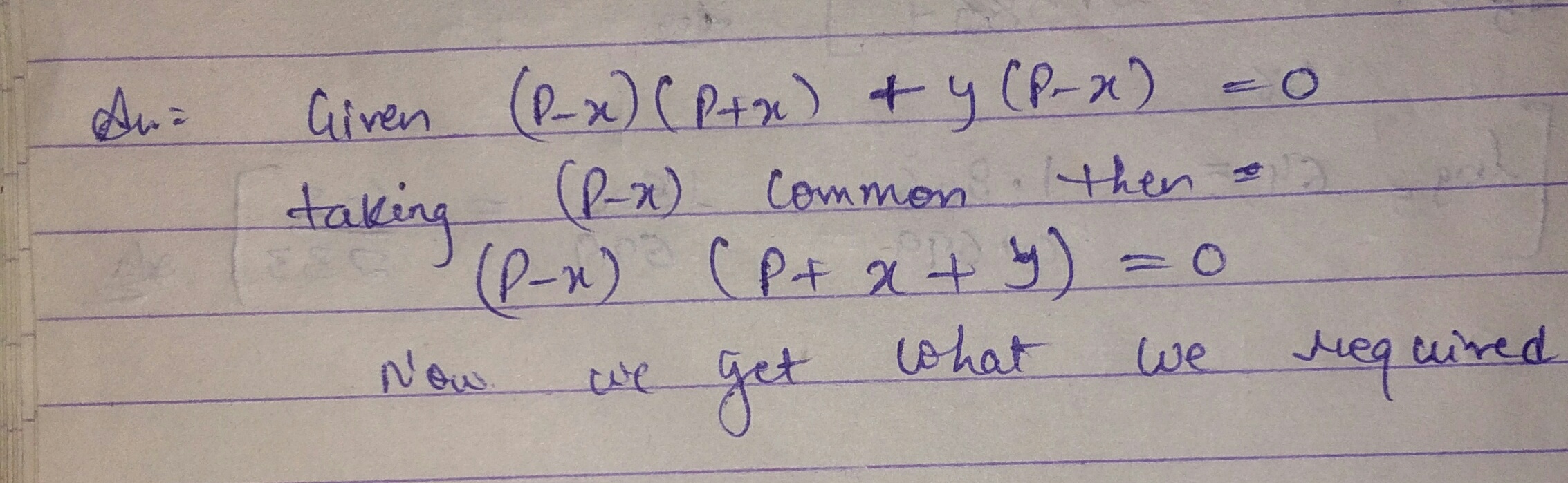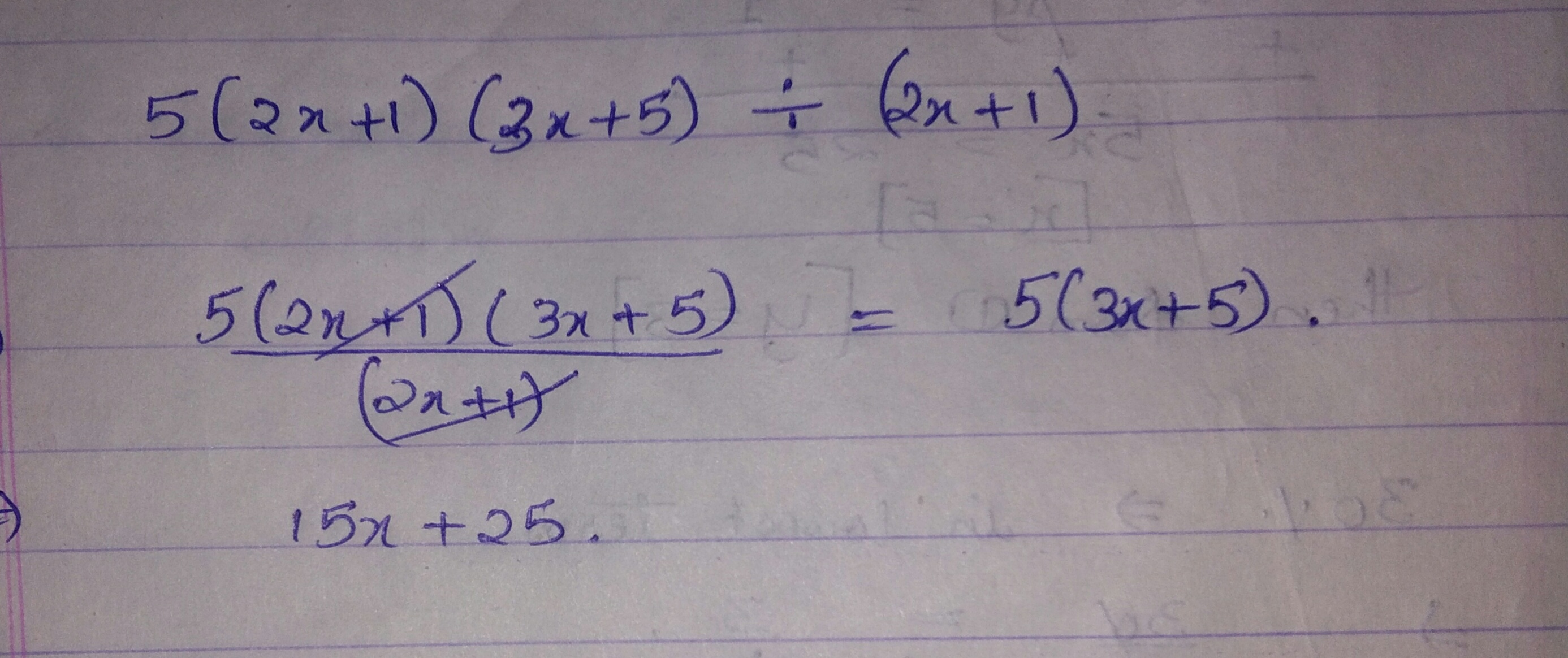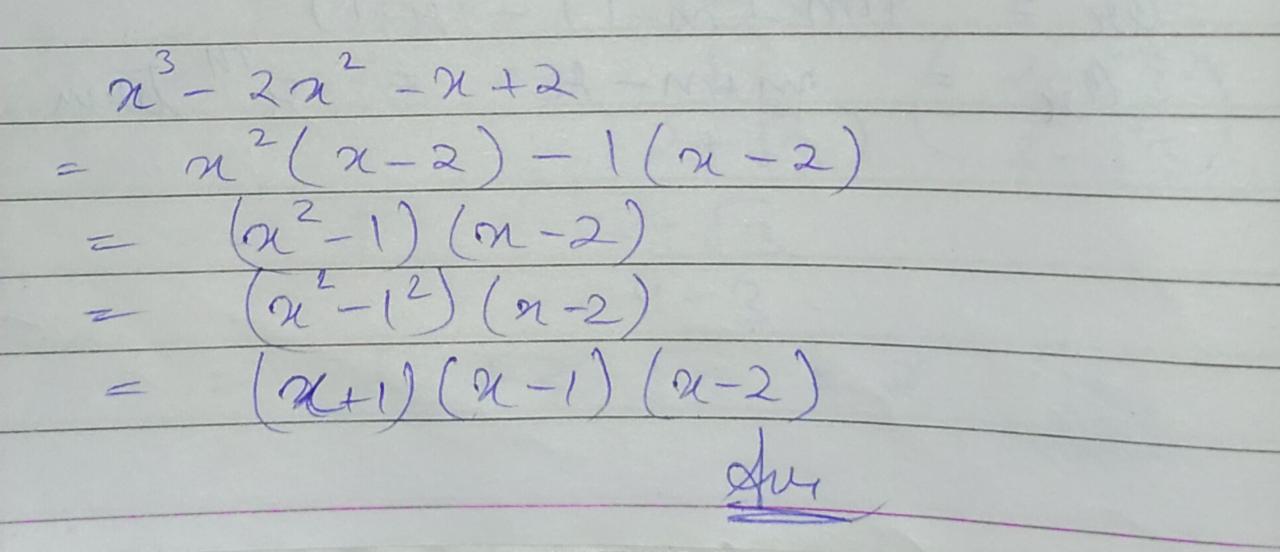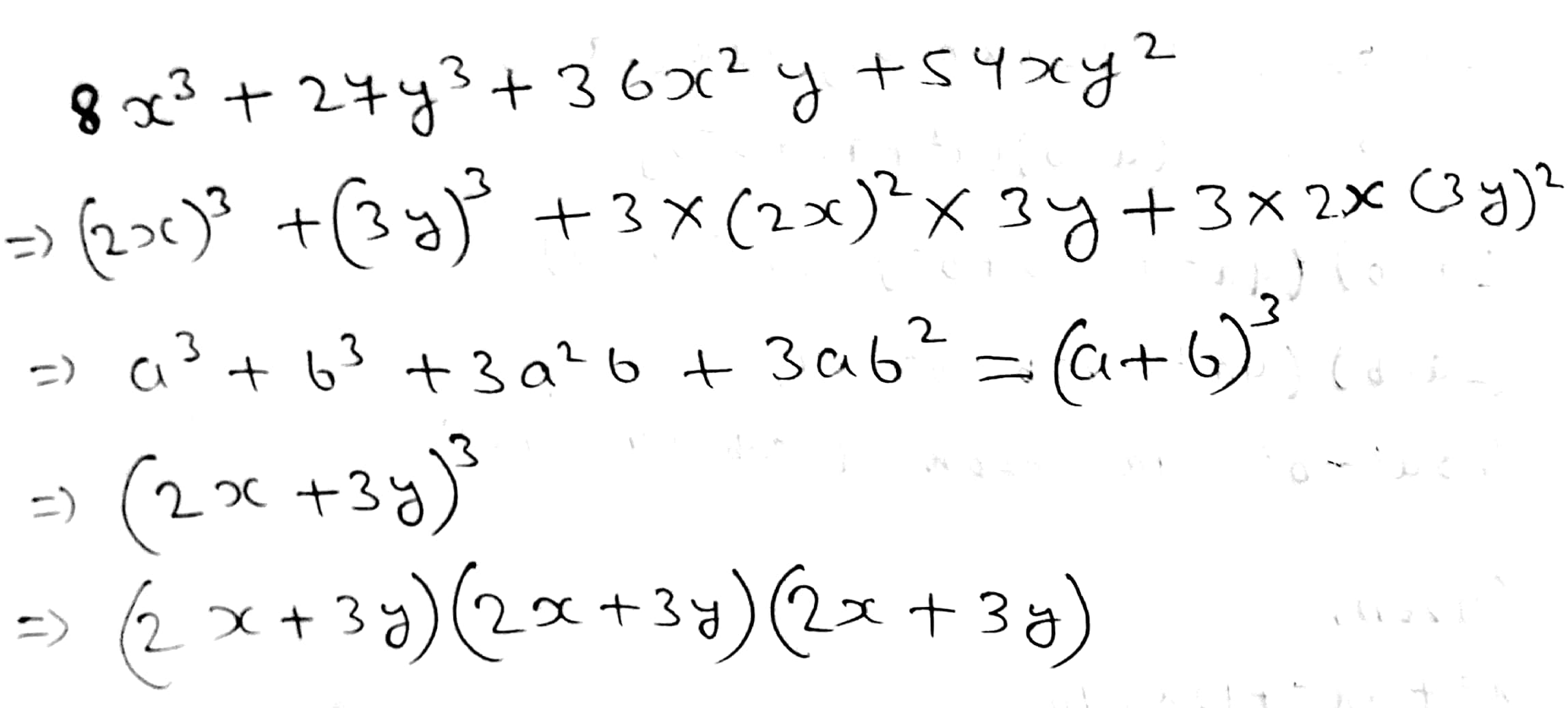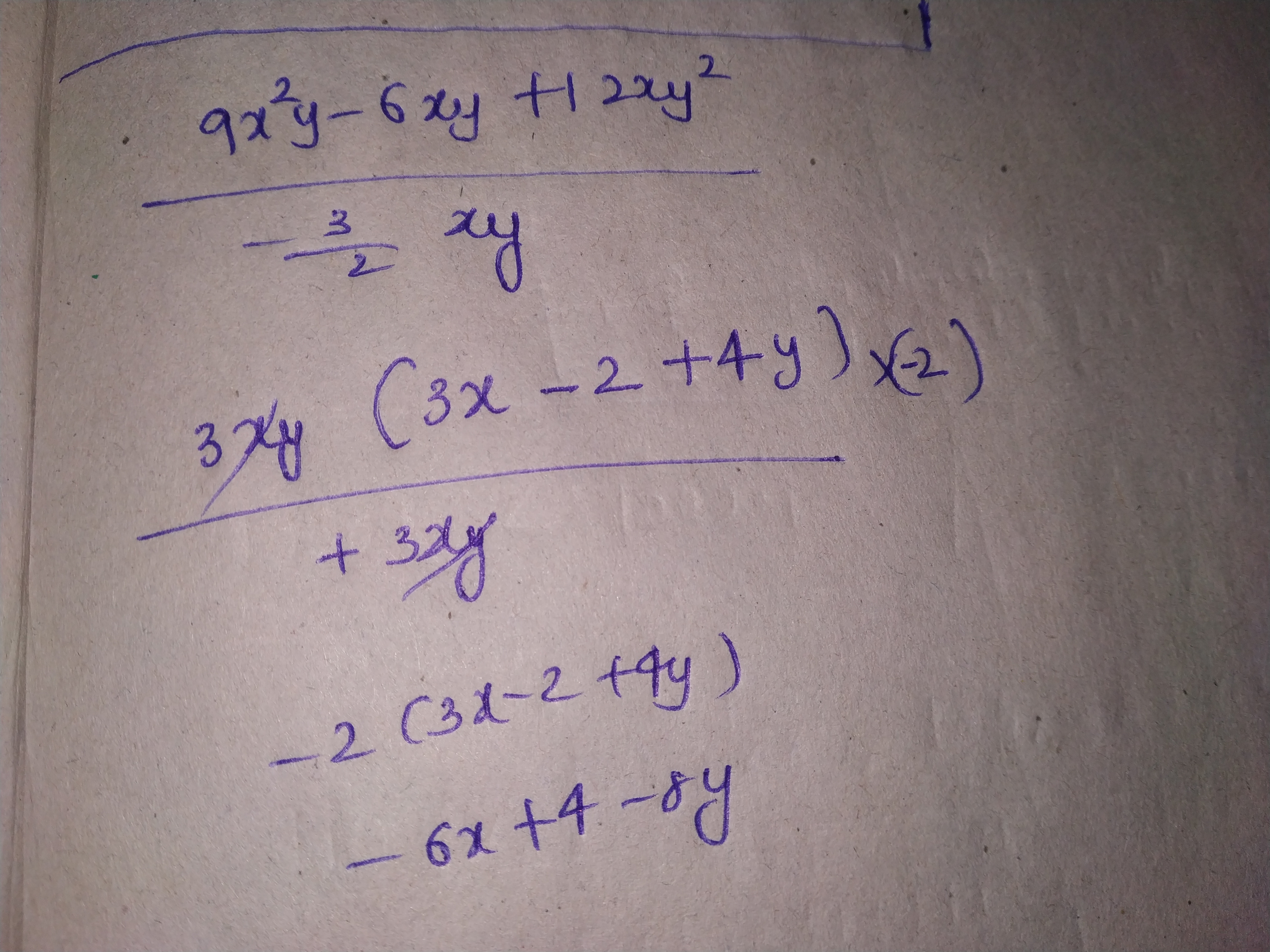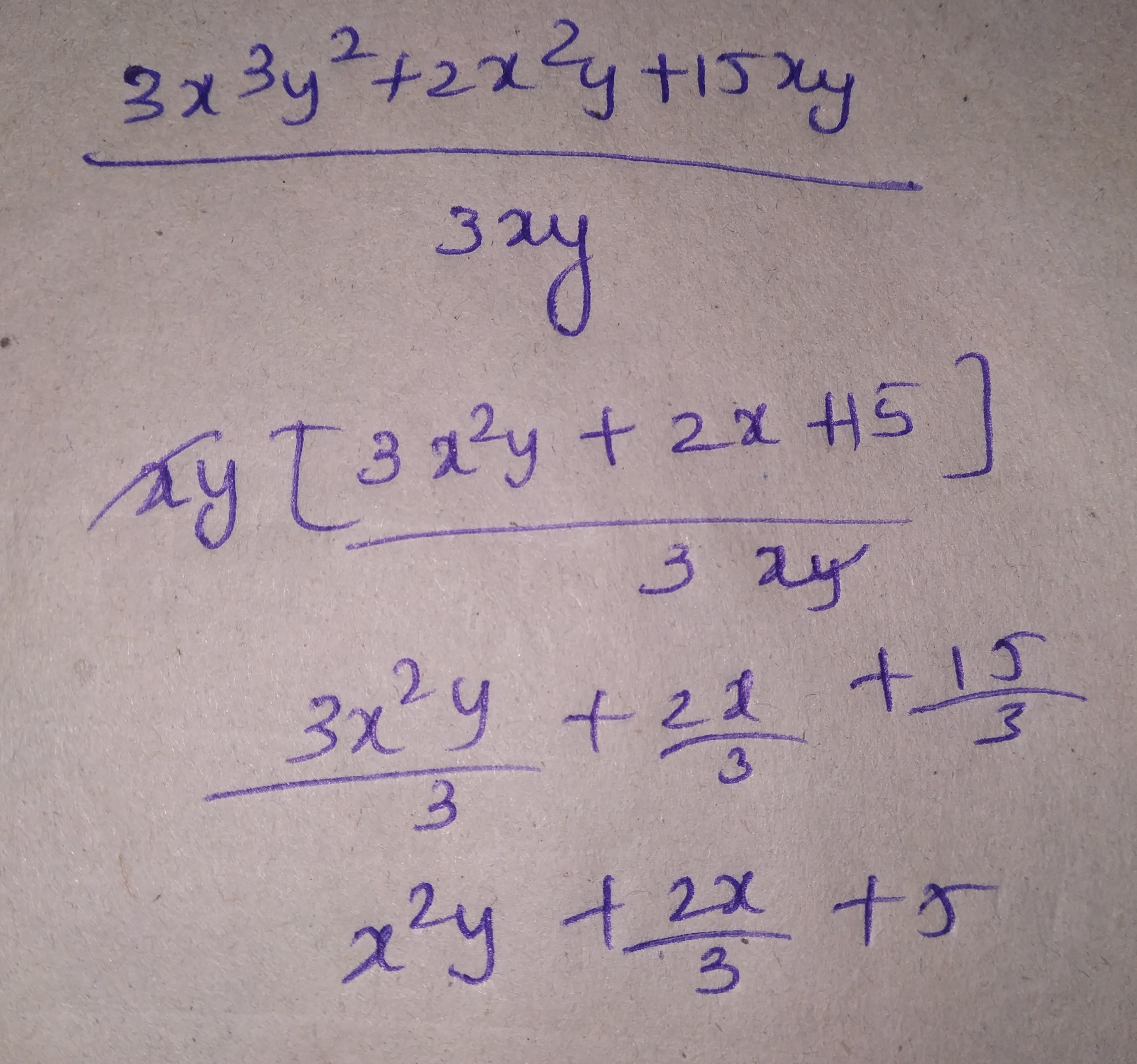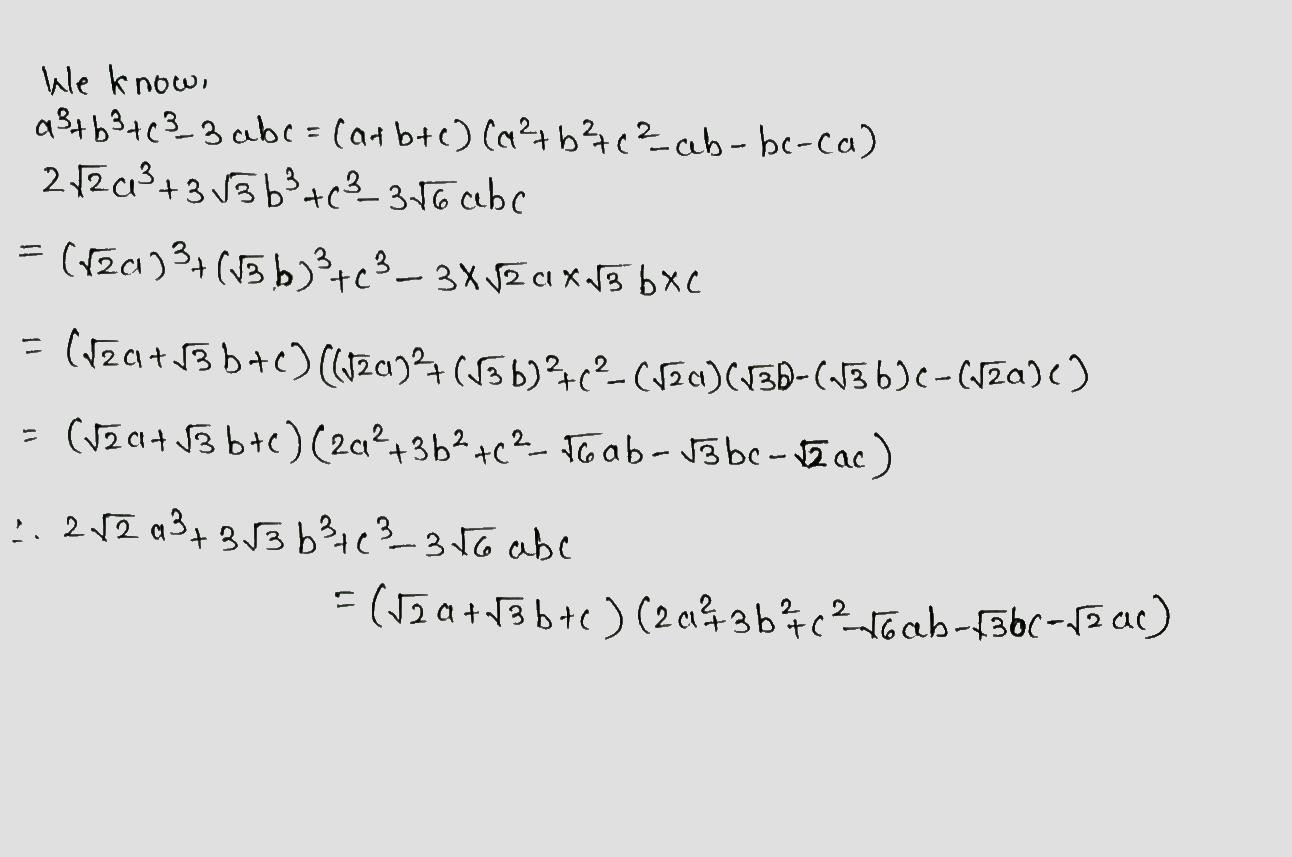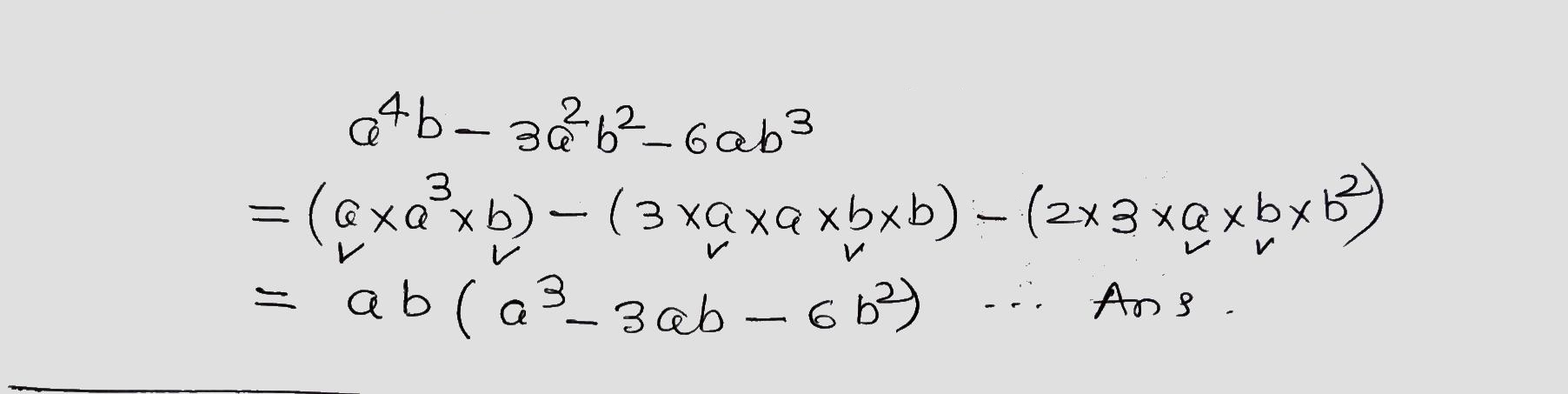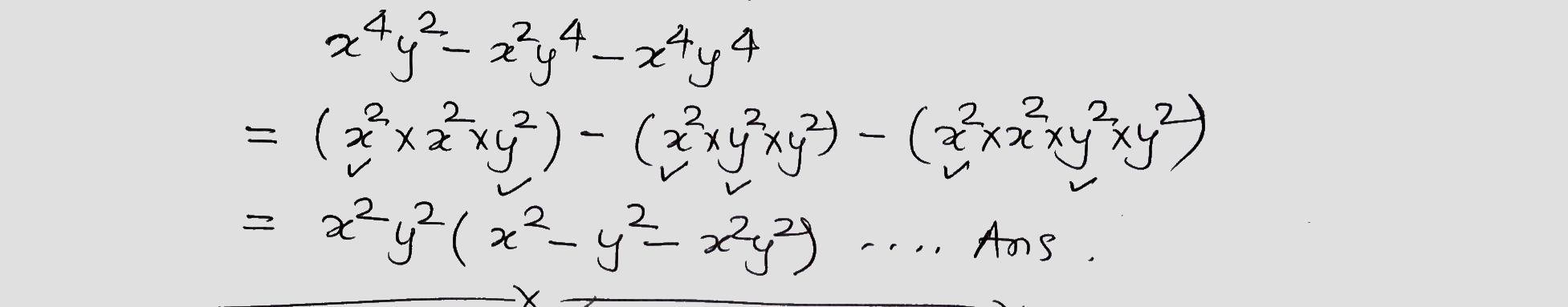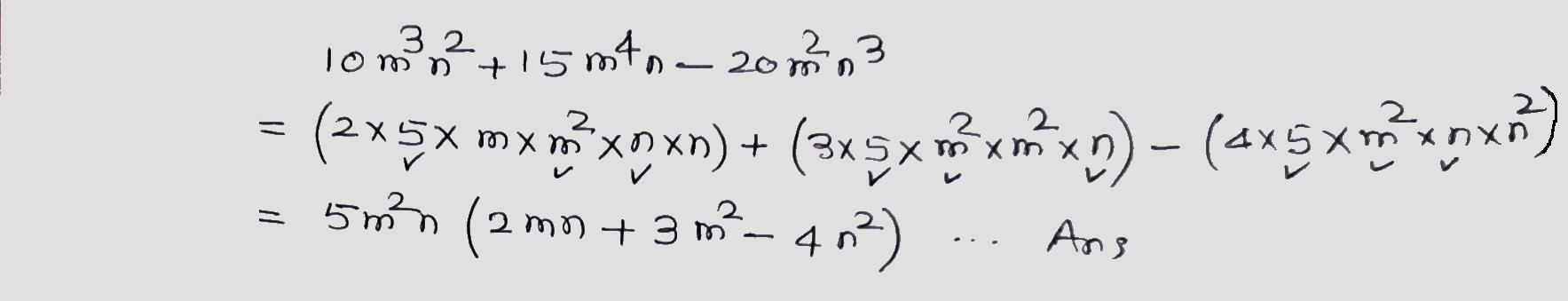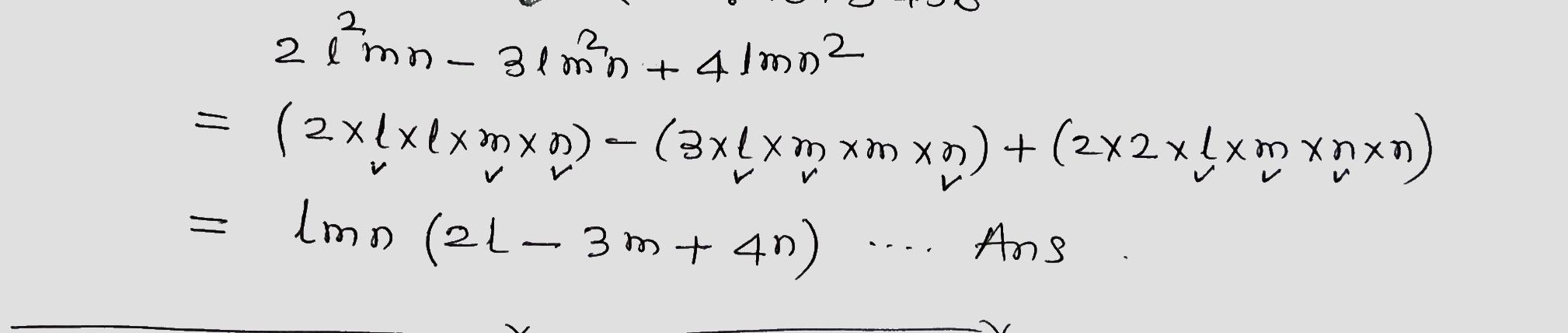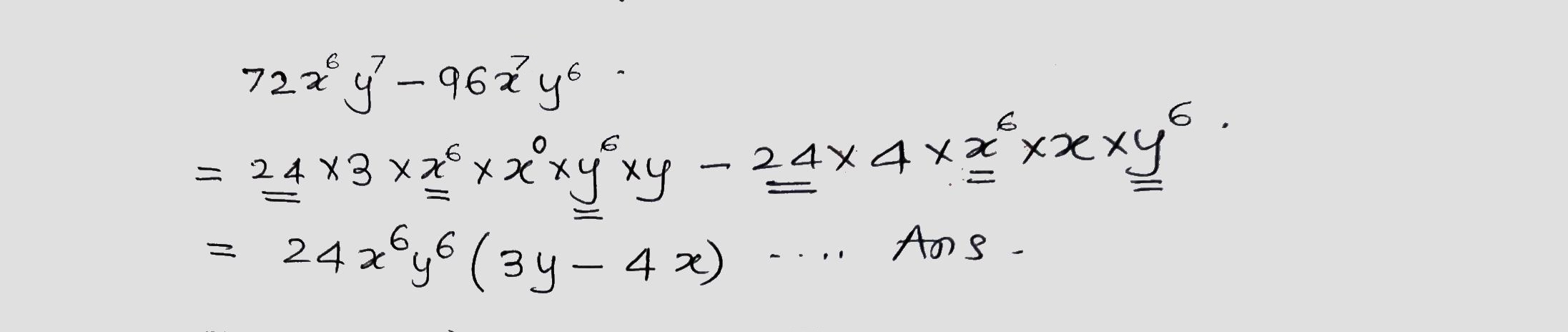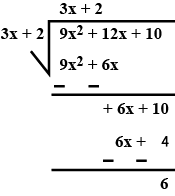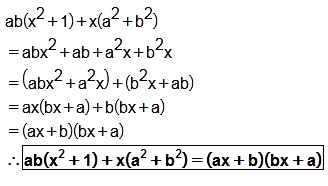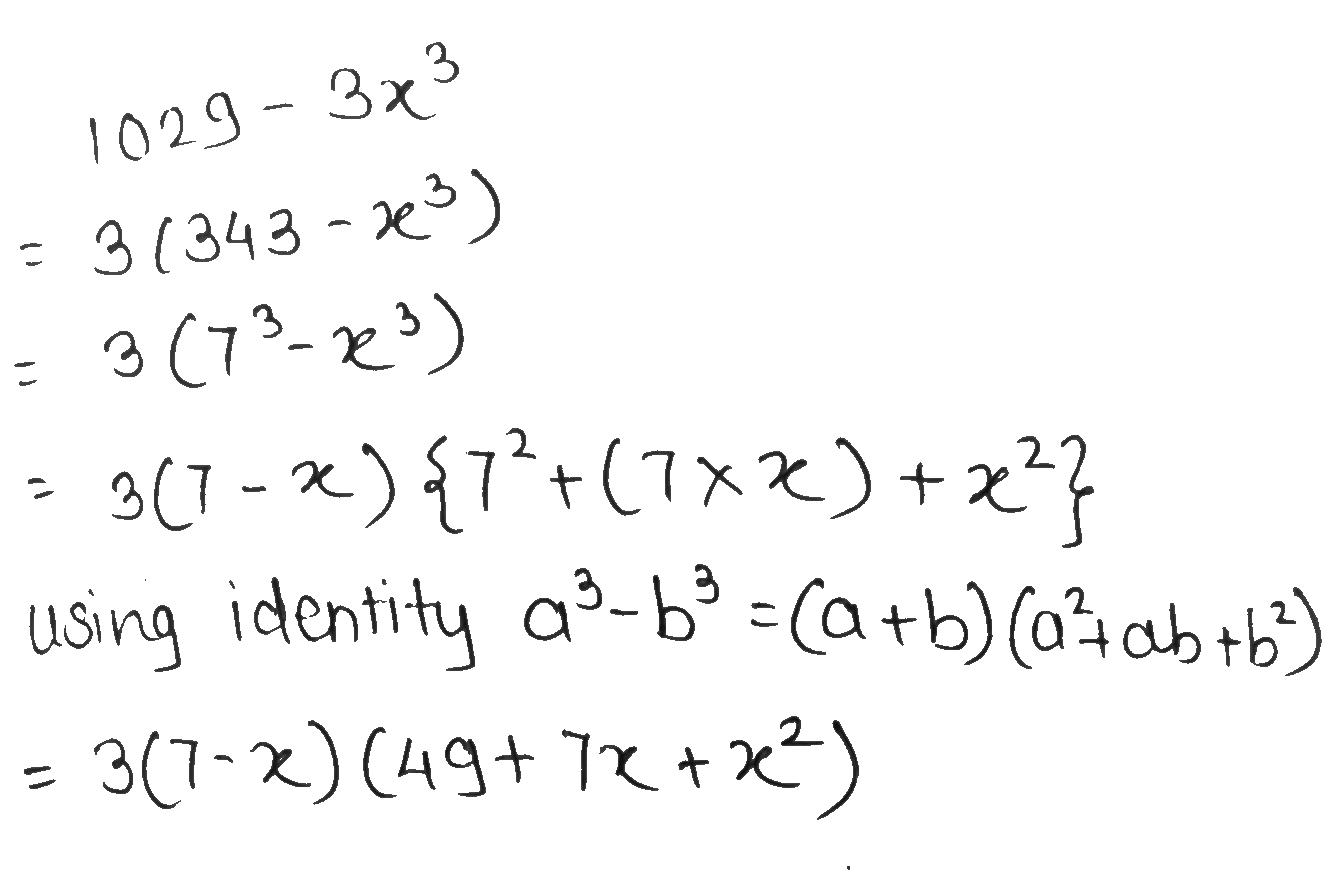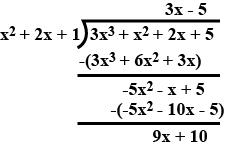Class 8 Maths - Factorisation

Factorise $$ab({x^2} + {y^2}) - xy({a^2} + {b^2})$$.

$$ab( x^2 + y^2) – xy (a^2 +b^2)$$

$$= ab x^2 + aby^2 – xya^2 – xy b^2$$

$$= ( abx^2 – xya^2) + ( aby^2 – xyb^2)$$

$$= ax( bx – ay) + by (ay – bx)$$

$$ = (bx-ay) ( ax-by)$$

Divide the polynomial $$3x^{4} -4x^{3} -3x - 1$$ by $$x -1$$.

Quotient $$= 3x^3 - x^2 - x - 4$$

Remainder $$ = -5$$

973215_1053628_ans_e934a9a41f4d4850b16e41929b78ef00.png

Find the root of given equation $${x}^{2}+6x+5$$

$$\begin{array}{l} { x^{ 2 } }+6x+5 \\ ={ x^{ 2 } }x+5x+5 \\ =x\left( { x+1 } \right) +5\left( { x+1 } \right) \\ =\left( { x+1 } \right) \left( { x+5 } \right) \end{array}$$

Factorize $$x\left( {x + z} \right) - y\left( {y + z} \right)$$

$$\begin{aligned}x\left( {x + z} \right) - y\left( {y + z} \right) &= {x^2} + xz - {y^2} - yz\\& = {x^2} - {y^2} + xz - yz\\& = \left( {x - y} \right)\left( {x + y} \right) + z\left( {x - y} \right)\\& = \left( {x - y} \right)\left( {x + y + z} \right)\end{aligned}$$

Factorise the expression and divide them as directed.
$$(5p^2-25p+20)\div (p-1)$$.

$$5{p^2}-25{p}+20$$

$$=5{p^2}-5{p}-20{p}+20$$

$$=5{p}(p-1)-20(p-1)$$

$$=(p-1)(5p-20)$$

Now, $$ (5 p^2-25{p}+20)\div (p-1)$$

$$=\dfrac{(p-1)(5{p}-20)}{(p-1)}$$

$$=5{p}-20$$

$$=5\left(p-4\right)$$

Factousation, $$16{p^2}{q^2}{r^3} - 24{p^3}{q^2}{r^2} + 8{p^3}{q^2}{r^2}$$

1336581_1245237_ans_80325eea4f54452abd3d6d89d0f8039b.PNG

factorise
$$3 x ^ { 2 } + 6 x ^ { 3 }$$

$$3x^2+6x^3\\=3x^2(1+2x)$$

Factorise:
$$ab^{2}+b(a-1)-1$$

Factorise

$$ab^2+b(a-1)-1$$

$$\Rightarrow ab^2+ba-b-1$$

$$\Rightarrow ab(b+1)-1(b+1)$$

$$\Rightarrow (b+1)(ab-1)$$

Hence, this is answer.

1195706_1242172_ans_78c118dcb49c4c4f86fc18637cf54694.png

Factorize:
$$4 a ^ { 2 } - 8 a b$$

$$4a^2-8ab\\=4a(a-2b)$$

Factorize
$$x ^ { 2 } + 7 x + 12 = 0$$

$$x^2+7x+12\\=x^2+4x+3x+12\\=x(x+4)+3(x+4)\\=(x+4)(x+3)$$

Factorize:
$$2 x ^ { 3 } b ^ { 2 } - 4 x ^ { 5 } b ^ { 4 }$$

$$2x^3b^2-4x^5b^4\\=2x^3b^2(1-2x^2b^2)$$

Factorize: $$15 x ^ { 4 } y ^ { 3 } - 20 x ^ { 3 } y$$

$$15x^4y^3-20x^3y\\=5x^3y(3xy^2-4)$$

Factorize:.$$15 x + 5$$

15x+5=5(3x+1)

Factorise completely by removing a monomial factor.
5m+5n

1334600_1265735_ans_8ba6814cf19c4d938122423d07cb7437.PNG

Factorise completely by removing a monomial factor.
5a+8b

1334589_1265746_ans_151bf29c82d041f08554eb54d969cb69.PNG

Factorise completely by removing a monomial factor.
2x-4

1334598_1265726_ans_aae4c4f1ebc54b7c917ee790e3404c96.PNG

Factorize:
$$a ^ { 3 } b - a ^ { 2 } b ^ { 2 } - b ^ { 3 }$$

$$a^3b-a^2b^2-b^3\\=b(a^3-a^2b-b^2)$$

Factorise completely by removing a monomial factor.
5x+10

1334594_1265705_ans_00f5b24ac65043a2ba88d85b82d60b28.PNG

Solve : $$(x^3+2x^2+3x) \div 2x$$

1338767_1264402_ans_9df468182216446db192fe24e9dffe8c.jpg

Factorise completely by removing a monomial factor.
-3m-15n

1334591_1265764_ans_82528a8c281e45fbb70a9617a606e2c4.PNG

Factorise completely by removing a monomial factor.
7x-14y

1334590_1265754_ans_24d904e859674039933f4ec5e8d991e9.PNG

Factorise completely by removing a monomial factor.
$$3y-9$$

1334587_1265693_ans_dc0e90f81d1b4efa9c25c459f153bca5.PNG

Factorize:
$$6 x ^ { 2 } y + 9 x y ^ { 2 } + 4 y ^ { 3 }$$

$$6x^2y+9xy^2+4y^3\\=y(6x^2+9xy+4y^2)$$

Factorise completely by removing a monomial factor.
-7p-14q

1334592_1265772_ans_24d31c5518ba484c9036735eca2ee9ed.PNG

Factorise completely by removing a monomial factor.
ax+bx

$$ax+bx$$

$$(a+b)x$$.

1200452_1265820_ans_356bc57c39ce46fe887d1a072db2b1b0.jpg

Factorise completely by removing a monomial factor.
$$4 + 12{x^2}$$

$$4+12x^2=4(1+3x^2)$$.
1209973_1265838_ans_48d4b63120994163be433c9505f9d88a.jpg

Factorise completely by removing a monomial factor.
$${x^2}{y^{}} + x{y^2}$$

Given binomial is $$x^2y+xy^2$$

Taking $$xy$$ common from both terms, we get:

$$xy(x+y)$$

$$\Rightarrow (xy)(x+y)$$

Hence, the given binomial can be represented as the product of a monomial and a binomial as: $$x^2y+xy^2=(xy)(x+y)$$.

Factorize:
$$6{x^2} - 11x$$

$$6x^2-11x$$

$$=x(6x-11)$$.

Factorise :
$$a{x^2} + a{b^3}$$

$$ax^2+ab^3=a(x^2+b^3)$$.

Factorise completely by removing a monomial factor
$${x^2}{y^2} + {x^2}$$

$$x^2y^2+x^2=x^2(y^2+1)$$.
1209979_1265886_ans_11d8734964ff4a889cbf380588d2f98d.jpg

divide
$$({y^2} + 10y + 24) \div (y + 4)$$

$$(y^2+10y+24)/(y+4)=[(y+4)(y+6)]/(y+4)=y+6$$

Factorise completely by removing a monomial factor
ax+ay+az

1334607_1265863_ans_6139a9ceb549424492beba18921d6448.PNG

Factories:-
$$6n+12n^2$$

We have,

$$6n+12^2$$

On factorization we get,

$$6n(1+2n)$$

Hence, this is the answer.

Factories:-
$$6n+12n^2+21n$$

We have,

$$6n+12n^2+21n$$

$$=12n^2+27n$$

On factorization we have,

$$=3n(4n+9)$$

Hence, this is the answer.

Factorize $$x^3+13x^2+32x+20$$, if it is given that $$x+2$$ is its factor.

$$x^3 + 13x^2 + 32x + 20$$

$$=x^3+2x^2+11x^2+22x+10x+20$$

$$=x^2(x+2)+11x(x+2)+10(x+2)$$

$$= (x+2)(x^2+11x+10)$$

$$= (x+2)[x^2+x+10x+10]$$

$$= (x+2)[x(x+1)+10(x+1)]$$

$$=(x+2)(x+1)(x+10)$$

Factorise
$$12{x^2} - 9x$$

1335914_1270540_ans_b145de79cbe04b019d74961005a75935.PNG

$$12xy(9x^{2}-16y^{2})\div 4xy(3x+4y)$$

$$12xy(9x^2-16y^2)\div 4xy(3x+4y)$$

$$\dfrac{12xy(9x^2-16y^2)}{4y(3x+4y)}$$

$$\dfrac{3((3x)^2-(4y)^2)}{3x+4y}=\dfrac{3(3x+4y)(3x-4y)}{(3x+4y)}$$

$$\Rightarrow 3(3x-4y)$$

$$\Rightarrow 9x-12y$$.

1204164_1393810_ans_410bf84426b84c64a1c8a1e7cee38bcd.JPG

Factorize: $${x^3} + 6{x^2}y + 9x{y^2}$$.

Now,

$${x^3} + 6{x^2}y + 9x{y^2}$$

$$=x(x^2+6xy+9y^2)$$

$$=x(x+3y)^2$$.

Factorize:
$$(a^2-b^2)x^2+2ax+1$$.

Now,

$$(a^2-b^2)x^2+2ax+1$$

$$=(a^2x^2+2ax+1-b^2x^2$$

$$=(ax+1)^2-(bx)^2$$

$$=(ax+bx+1)(ax-bx+1)$$.

Factorise :
1. $$2x^{2}-x-3$$
2. $$-2x^{2}+3x+9$$

$$(1)$$ $$2x^2-x-3$$

$$\Rightarrow 2x^2-3x+2x-3$$

$$\Rightarrow x(2x-3)+1(2x-3)$$

$$\Rightarrow (x+1)(2x-3)$$

$$(2)$$ $$-2x^2+3x+9$$

$$\Rightarrow -2x^2+6x-3x+9$$

$$\Rightarrow -2x(x-3)-3(x-3)$$

$$\Rightarrow -(x-3)(2x+3)$$.

1222818_1394245_ans_3b8ed597284147e7bdb8440260cd3b63.jpg

Solve:
$$z^2-16z+55=0$$.

Now,

$$z^2-16z+55=0$$

or, $$z^2-11z-5z+55=0$$

or, $$(z-5)(z-11)=0$$

or, $$z=5,11$$.

Factorize: $${x}^{2}+10x+24$$

Given, $${x}^{2}+10x+24$$

$$={x}^{2}+6x+4x+24$$

$$=x\left(x+6\right)+4\left(x+6\right)$$

$$=\left(x+6\right)\left(x+4\right)$$

$$(4x^4-5x^3-7x+1)\div (4x-1)$$.

quotient $$={x}^{3}-{x}^{2}-\cfrac{x}{4}-\cfrac{29}{16}$$

remainder $$=\cfrac{-13}{16}$$

We know , $$dividend=divisor\times quotient +remainder

$$4{x}^{4}-5{x}^{3}-7x+!=(4x-1)({x}^{3}-{x}^{2}-\cfrac{x}{4}-\cfrac{29}{16}-\cfrac{13}{16}$$

1343488_1251168_ans_b4a4a9fbbc3e4b06a1c866fa66192d47.PNG

Divide $$\left( { 2y }^{ 3 }+{ 4y }^{ 2 }+3 \right) \div { 2y }^{ 2 }$$

$$\therefore (2y^{3}+4y^{2}+3)\div 2y^{2}$$

$$=y+2+\cfrac{3}{2y^{2}}$$

1380961_1240116_ans_0c667084a1004e5fb21044fa041463e7.png

Factorise : $$ 150 -6x^2 $$

Given : $$ 150 -6x^2 $$

By taking $$6$$ as common
$$ 150 -6x^2 $$ $$= 6 (25 -x^2 ) $$

We can write it as
$$ 150 -6x^2 $$ $$ =6 (5^2 -x^2 ) $$

Based on equation $$ a^2 -b^2 = (a+b)(a-b) $$

We get,
$$ 150 -6x^2 $$ $$ = 6 (5+x)(5-x) $$

Factorise : $$ 8ab^2 - 18a^3 $$

Given : $$ 8ab^2 -18 a^3 $$

By taking $$2a$$ as common
$$ 8ab^2 -18 a^3 $$$$= 2a ( 4b^2 -9a^2)$$

We can write it as
$$ 8ab^2 -18 a^3 $$$$ =2a[ (2b)^2 -(3a)^2]$$

Based on equation $$ a^2 -b^2 = (a+b)(a-b) $$

We get,
$$ 8ab^2 -18 a^3 $$$$ = 2a(2b+3a)(2b-3a) $$

Factorise : $$ x^2 +\dfrac {1}{x^2} - 2 -3x +\dfrac {3}{x} $$

Given : $$ x^2 +\dfrac {1}{x^2} - 2 -3x +\dfrac {3}{x} $$

We can further write it as
$$ x^2 +\dfrac {1}{x^2} - 2 -3x +\dfrac {3}{x} $$$$ = \left( x -\dfrac {1}{x}\right)^2 - 3\left(x - \dfrac {1}{x} \right) $$

By taking the common terms out

$$ x^2 +\dfrac {1}{x^2} - 2 -3x +\dfrac {3}{x} $$$$ = \left( x -\dfrac {1}{x} \right)\left(x - \dfrac {1}{x} -3\right) $$

Factorise : $$ a (a-2b-c) +2bc $$

Given : $$ a (a-2b-c) +2bc $$

By multiplying the terms
$$ a (a-2b-c) +2bc $$ $$ =a^2 -2ab-ac +2bc $$

By taking the common terms out
$$ a (a-2b-c) +2bc $$ $$= a(a-2b) -c(a-2b) $$

So we get,
$$ a (a-2b-c) +2bc $$ $$= (a-c)(a-2b) $$

Factorise : $$ 4a^2 -9b-2bc -c^2 $$

Given : $$ 4a^2 -9b-2a -3b $$

We can write it as
$$ 4a^2 -9b-2a -3b $$$$ = (2a)^2 -(3b)^2 -(2a+3b) $$

Based on the equation $$ a^2 -b^2 = (a+b)(a-b) $$

We get,
$$ 4a^2 -9b-2a -3b $$$$= ( 2a+3b)(2a-3b)-(2a+3b) $$

By taking $$( 2a+ 3b)$$ as common

$$ 4a^2 -9b-2a -3b $$$$ = (2a +3b)(2a-3b -1 ) $$

Factorise the following expressions:
(i) $$ 32a^2b - 72b^3 $$
(ii) $$ 9 (a +b)^3 - 25 ( a+b) $$

$$ (i) 32a^2b-72b^3 $$

$$=8b(4a^2-9b^2)$$

$$=8b[(2a)^2-(3b)^2] $$

$$=8b(2a+3b)(2a-3b) $$

$$ (ii) 9(a+b)^3-25(a+b) $$

$$=(a+b)[9(a+b)^2-25] $$

$$=(a+b)[{ \{ 3(a+b) }\} ^{ 2 }-(5)^{ 2 }] $$

$$=(a+b)[(3a+3b)^2-(5)^2] $$

$$=(a+b)[(3a+3b+5)(3a+3b-5)] $$

$$=(a+b)(3a+3b+5)(3a+3b-5) $$

$$ 18 m +16 n $$

$${\textbf{Step - 1: Perform factorisation using suitable method}}{\text{.}}$$

$${\text{We have to find the factorisation of 18m + 16n}}{\text{.}}$$

$${\text{So let's factorise 18m and 16n first}}{\text{.}}$$

$${\text{18m}} = 2 \times 3 \times 3 \times {\text{m}}{\text{.}}$$

$${\text{16n}} = 2 \times 2 \times 2 \times 2 \times {\text{n}}{\text{.}}$$

$${\textbf{Step - 2: Find the factors of given, using common factor method}}{\text{.}}$$

$${\text{So here the common factors is only 2}}{\text{.}}$$

$${\text{The factorised form of 18m + 16n is like , }}2 \times \left( {9{\text{m}} + 8{\text{n}}} \right).$$

$$\mathbf{{\textbf{Hence, the required factorised form is 2}} \left( {9{\textbf{m + 8n}}} \right).}$$

$$ 20x^2 -45y^2 $$

$$ 20x^2 -45y^2 $$
take out common in all terms,
$$ 5(4x^2 -9y^2) $$
$$ 5( (2x)^2 - (3y)^2) $$
we know that $$ a^2 -b^2 = (a+b)(a-b) $$
$$ 5(2x +3y)(2x -3y) $$

$$ x^3 -25x $$

$$ x^3 -25x $$
Take out common in all terms
$$ x(x^2 -25) $$
Above terms can be written as,
$$ x(x^2 -5^2) $$
We know that $$ a^2 -b^2 = (a+b)(a-b) $$
$$ x(x +5)(x-5) $$

$$ 14 (a-3b)^3 - 21p (a -3b) $$

$$ 14 (a-3b)^3 - 21p (a -3b) $$
Take out common in all terms,
Then,$$ 7(a-3b)[2(a-3b)^2-3p]$$
Therefore, HCF of $$14 (a-3b)^3$$ and $$ 21p(a-3b)$$ is $$ 7(a-3b). $$

Factorise $$ 27a^3b^3 - 18 a^2b^3 + 75a^3b^2 $$

$$ 27a^3b^3 - 18 a^2b^3 + 75a^3b^2 $$

Minimum power of $$a$$ in every term is $$2$$

Minimum power of $$b$$ in every term is $$2$$

$$3$$ can be taken common from $$27,18\ \& \ 75$$.

Taking out common factor in all the terms, we get:

$$ 3a^2b^2(9a-6b+25a) $$

$$ 10 (2p +q)^3 -15b( 2p +q)^2 + 35(2p +q) $$

$$ 10 (2p +q)^3 -15b( 2p +q)^2 + 35(2p +q) $$
Take out common in all terms,
Then, $$ 5(2p+q)[2a(2p+q)^2-3b(2p+q)+7] $$
Therefore,HCF of $$ 10a(2p+q)^3,15b(2p+q)^2 $$ and $$ 35(2p+q) $$ is $$ 5(2p+q).$$

$$ 150 -6a^2 $$

$$ 150 -6a^2 $$
Take out common in all terms,
$$ 6( 25 - a^2 ) $$
$$ 6 ( 5^2 -a^2) $$
We know that $$ a^2 -b^2 = (a+b)(a-b) $$
So $$ 6 ( 5+a)(5-a) $$

$$ 32x^2 -18y^2 $$

$$ 32x^2 -18y^2 $$
take out common in all terms
$$ 2( 16x^2 -9y^2 ) $$
$$ 2( (4x)^2 - (3y)^2) $$
We know that $$ a^2 -b^2 = (a+b)(a-b) $$
$$ 2 (4x +3y)(4x-3y) $$

$$ 3a(x^2 +y^2) +6b ( x^2 +y^2 ) $$

$$ 3a(x^2 +y^2) +6b ( x^2 +y^2 ) $$
Take out common in both terms,
Then, $$ 3(x^2+y^2)(a+2b)$$
Therefore,HCF of $$ 3a(x^2+y^2) \quad and \quad 6b(x^2+y^2) \quad is \quad 3(x^2+y^2) $$.

$$ x(x^2+y^2-x^2) +y(-x^2-y^2 +z^2) -z (x^2 +y -z^2) $$

$$ x(x^2+y^2-x^2) +y(-x^2-y^2 +z^2) -z (x^2 +y -z^2) $$
Take out common in all terms,
Then,$$ (x^2+y^2-z^2)[x-y-z] $$
Therefore,HCF of $$ x(x^2+y^2-z^2),y(-x^2-y^2+z^2) $$ and $$ z(x^2+y-z^2) $$ is $$ (x^2+y^2-z^2) $$.

$$ \pi a^5 - \pi^3 ab^2 $$

$$ \pi a^5 - \pi^3 ab^2 $$
Take out common in all terms,
$$ \pi a ( a^4 - \pi^2 b^2) $$
$$ \pi a(a^2)^2 - ( \pi b)^2 ) $$
We know that $$ a^2 -b^2 = (a+b)(a-b) $$
$$ \pi a(a^2 +\pi b) (a^2 - \pi b ) $$

Factorise $$m^2+m+1=0$$.

$$ { m^{ 2 } }+m+1=0 \\ factorise\, \, this\, \, quadratic\, \, equation\, \, by\, \, \\ { { Discriminant\ method } }{ { . } } \\ { { D=1-4 } }\times { { 1=-3 } } \\ \Rightarrow { { Roots } }\, \, { { = } }\frac { { { { -1 } }\pm \sqrt { -3 } } }{ { 2\times 1 } } \, \, \, \, \, \, \left[ { \because \sqrt { -1 } =i } \right] \\ \Rightarrow m=\frac { { -1\pm \sqrt { -3 } } }{ 2 } \\ \Rightarrow m=-1\pm \sqrt { 3 } i \\ \therefore m=\sqrt { 3 } i-1\, \, or\, \, \left( { -\sqrt { 3 } i-1 } \right) \, \, $$

Factorize:
$${a}^{3}-3{a}^{2}b+3a{b}^{2}-{b}^{3}+8$$

1650984_1669429_ans_29a85c9886c74b66a2a906a89366445e.jpg

Factorise:
$$x^{2}+20x-69$$

1295051_1255879_ans_329b2e2a32cf4f4dbdd33e82a05cf50b.jpg

Divide $$\sqrt{2}a^3+3\sqrt{2}a^2+6a$$ by $$2a$$.

1304522_1581637_ans_07b39c834ab04dad9cfc4e9426a7e30c.jpg

Factorize $$\dfrac {1}{6}a^{2}-a+\dfrac {4}{3}$$.

$$\dfrac { 1 }{ 6 } { a }^{ 2 }-a+\dfrac { 4 }{ 3 } $$

$$=\dfrac{a^2-6a+8}{6}$$

$$=\dfrac{a^2-4a-2a+8}{6}$$

$$=\dfrac{a\left( a-4\right) -2\left( a-4\right)}{6}$$

$$=\dfrac{\left( a-2\right) \left( a-4\right)}{6}$$

Hence, the answer is $$\dfrac{\left(a-2\right)\left( a-4\right)}{6}.$$

1187413_1218545_ans_7b253e6b9e484f098194b69e7558583f.png

Factorise:
$$4u^2+8u$$

1338070_1278097_ans_0b238c44bb1c4ed3b9bc0c403212231d.PNG

Factorise
$$ - 3{x^2} + 3xy - 4xza$$

1353301_1270623_ans_0421011b480c4972b03f8c21606a6e42.PNG

Factorise:
$$\left( {a - b} \right) + {\left( {a - b} \right)^2}$$

1352016_1270773_ans_0a2ae66120d2411c8aef37c3f7ad8a98.PNG

Factorise:
$$ - 5{a^2} + 4a + 5\left( { - {a^2} + 5} \right)$$

1338039_1276519_ans_95828ee1c2394ca49b7ded58097f372c.PNG

Factorize $$x^{3}+13x^{2}+32x+20$$

1304726_1271480_ans_298e5677f6d44260ba4634e1a64a2ad7.JPG

Resolve $$2{b}^{2}-5b-3$$ in to factors.

Given, $$2{b}^{2}-5b-3$$

$$=2{b}^{2}-6b+b-3$$

$$=2b\left(b-3\right)+1\left(b-3\right)$$

$$=\left(b-3\right)\left(2b+1\right)$$

Factorise: $${ 7x }^{ 3 }z-{ 21x }z^{ 2 }$$

$$7{x}^{3}z-21x{z}^{2}$$

$$=7xz\left({x}^{2}-3z\right)$$

$${ ab }^{ 2 }+(a-1)b-1$$

$${ ab }^{ 2 }+(a-1)b-1$$
Above qyestion can be written as,
$$ ab^2+ab-b-1 $$
Take out common in all terms,
$$ ab(b+1)-1(b+1) $$
$$ (b+1)(ab-1) $$

Factorise: $${ x }^{ 2 }+18x+45$$

$$\begin{array}{l} { x^{ 2 } }+18x+45 \\ ={ x^{ 2 } }+15x+3x+45 \\ =x\left( { x+15 } \right) +3\left( { x+15 } \right) \\ =\left( { x+15 } \right) \left( { x+3 } \right) \end{array}$$

Factorize $$p^2+1.5p+0.5$$.

1318507_1586943_ans_5b3cd5e8ed1e413396cedf2dd2244eaf.jpg

Find the quotient and remainder on dividing the polynomials $$a{x^2} + \left( {b + ac} \right)x + bc\;by\;x + c$$

1211384_1505694_ans_4c8eb1a5af14450680717dfab468f453.jpg

Resolve into factors $$3x^2-6x$$

Given that: $$3x^2-6x$$

$$ = 3\times x\times x-2\times 3\times x $$, factor each monomial

$$=3x(x-2)$$, factor out common factor $$3x$$

The factors form of $$3x^2-6x$$ is $$3x.(x -2)$$

Divide : $$a^2 + 7a +12$$ by $$(a+4)$$.

$$a^2+7a+12 = a^2+4a+3a+12 $$

$$=a(a+4)+3(a+4)$$

Now dividing it by $$(a+4)$$:

$$\Rightarrow \dfrac{a(a+4)+3(a+4)}{(a+4)} = a+3$$

Find the quotient and remainder.
$$(2p^{2}+7p-9)\div (p-6)$$

1294378_1609041_ans_0bae36a272094f2992519bf3b42ba931.jpg

Factorise

$$18a^3b^3−27a^2b^3+36a^3b^2$$

let’s take HCF of above equationBy taking $$9a^2b^2$$ as a common factor for the above equation we get$$18a^3b^3-27a^2b^3+36a^3b^2=9a^2b^2(2ab - 3b +4a)$$

Factorise

$$12x^2y^3 - 21 x^3y^2$$

let’s take HCF of above equationBy taking $$3x^2y^2$$ as a common factor for the above equation we get,
$$12x^2y^3$$ - $$21x^3y^2 = 3x^2y^2(4y-7x)$$

Factorise

$$15ab^2 – 20a^2b$$

let’s take HCF of above equationBy taking 5ab as a common factor for the above equation we get,
$$15ab^2 - 20a^2b =5ab(3b - 4a)$$

Factorise the following:
$$27 - 125x^{3} - 135x + 225x^{2}$$

$$27 - 125x^{3} - 135x + 225x^{2}$$

$$= (3)^{3} - (5x)^{3} - 3(3)(5x)[3 - 5x]$$

$$= (3 - 5x)^{3}$$

$$[\because (a - b)^{3} = a^{3} - b^{3} - 3ab(a - b)]$$

Resolve in to factors $$x^2+xy$$

Given that: $$x^2+xy$$

$$=x\cdot x+x\cdot y$$, factor each terms

$$=x(x+y)$$, factor out common factor $$x$$

Hence the factorisation of $$x^2+xy$$ is $$x(x+y)$$

Factorise $$9{x}^{2}+12xy$$.

We write $$9{x}^{2}+12xy=(3x)(3x)+(3x)(4y)$$
Here $$3x$$ is the common to both the terms. Hence
$$(3x)(3x)+(3x)(4y)=3x(x+4y)$$
Thus $$3,x$$ and $$(3x+4y)$$ are the factors of $$9{x}^{2}+12xy$$

Factorise the following:
$$125x^{3} + 64y^{3} - 300x^{2}y + 240xy^{2}$$

$$125x^{3} - 64y^{3} - 300x^{2}y + 240xy^{2}$$
$$= (5x)^{3} - (4y)^{3} - 3(5x)(4y) [5x - 4y]$$
$$= (5x - 4y)^{3}$$
$$[\because (a - b) = a^{3} - b^{3} - 3ab(a - b)]$$

$$5x^2-10x$$

We can see that $$5x$$ is the HCF of $$5x^2$$ and $$10x$$.

We can remove them from both the terms.

Thus we get,
$$5x^2 - 10x$$

$$ = (5x)(x) - (5x) \times 2$$

$$ = (5x)(x - 2)$$.

Factorise $$6xy + 9y^2$$

Factor out $$3y$$ from the expression,

$$6xy+9y^2=3y(2x+3y)$$

So, the factors of the given expression are equal to $$3,y$$ and $$(2x+3y).$$

Divide $$-8x^{9}$$ by $$2x^{7}$$

We divide $$-8$$ by $$2$$ and $$x^{9}$$ by $$x^{7}$$. Thus
$$\dfrac {-8x^{9}}{2x^{7}} = \left (\dfrac {-8}{2}\right )\left (\dfrac {x^{9}}{x^{7}}\right ) = -4x^{9 - 7} = -4x^{2}$$.

Find the common factors of the terms $$8x$$ and $$24$$.

We need to find common factors of $$8x$$ and $$24$$.

The factor of $$8x=2\times 2\times 2\times x$$

and that of $$24=3\times 2\times 2\times 2$$

Therefore, the common factors are $$2\times 2\times 2=8$$.

Factorise: $$25-50p-100q$$.

We observe that $$25-50p-100q=25(1-2p-4q)$$. Hence $$25$$ and $$(1-2p-4q)$$ are the factors of $$25-50p-100q$$.

Factorise: $$2p(a-b)+3q(5a-5b)+4r(2b-2a)$$.

$$2p(a-b)+3q(5a-5b)+4r(2b-2a)$$
$$=2p(a-b)+3q\times 5(a-b)-4\times r\times 2(a-b)$$
$$=(a-b)(2p+15q-8r)$$
Thus $$(a-b)$$ and $$(p+15p-8r)$$ are the factors of the given expression.

Factorise $$25a^2 b + 35ab^2$$

Given expression is $$25a^2b+35ab^2$$

It can be factorized as $$25a^2b+35ab^2=5ab(5a+7b)$$.

Factorise the following:
$$64a^{3} + 21b^{3}$$

$$64a^{3} + 27b^{3}$$
$$= (4a)^{3} + (3b)^{3}$$
$$= (4a + 3b)[(4a)^2 - 4a.3b + (3b)^2]$$
$$[\because a^{3} + b^{3} = (a + b)(a^{2} - ab + b^{2})]$$
$$= (4a + 3b)[16a^{2} - 12ab + 9b^{2}]$$

Factorise $$6ab - b^2 - 2bc + 12 ac$$

Given expression is $$6ab-b^2-2bc+12ac$$

It can be factorised as,

$$6ab-b^2-2bc+12ac$$

$$=6ab-b^2+12ac-2bc$$

$$=b(6a-b)+2c(6a-b)$$

$$=(6a-b)(b+2c)$$

Thus factors are $$(6a-b)$$ and $$(b+2c)$$.

Factorise: $$7p^2 + 49pq$$

We need to factorise $$7p^2+49pq$$

We can write it as $$7p^2+49pq=7p(p+7q)$$
Thus factors are $$7,p,(p+7q)$$.

Factorise:
$$a^4-343a$$

$$a^4-343a$$

$$=a(a^3-343)$$

Using,

$$a^3-b^3=(a-b)(a^2+b^2+ab)$$

$$=a(a^3-7^3)$$

$$=a(a-7)(a^2+7^2+7a)$$

$$=a(a-7)(a^2+49+7a)$$

Factorise: $$4ab{ x }^{ 2 }+8abx+12aby$$

Since in the equation $$4abx^2+8abx+12aby$$, $$4ab$$ is the common term, therefore, can be factorised as follows:

$$4abx^2+8abx+12aby=4ab(x^2+2x+3y)$$

factorise : $${ 27p }^{ 3 }\left( { 4q-2r }^{ 3 } \right) +{ 64q }^{ 3 }\left( { 2r-3p }^{ 3 } \right) +{ 8r }^{ 3 }\left( { 3p-4q }^{ 3 } \right)$$

2039421_1285022_ans_5e387b322e074cfa9f92d7f2c53e6829.jpg

Find the factors of $$y^{2}-7y+12$$.

$${y}^{2}-7y+12$$

$$y^2-3y-4y+12$$

$$y(y-3)-y(y-3)$$

$$(y-3)(y-4)$$

$$\therefore$$ $$y=3,4$$

$$(p^{2}+5p+4)\div(p+1)$$

2045403_1571400_ans_bfcdb54b8ac743a7af3c90e91a76e44e.jpg

Factorise: $$36a^2b - 60a^2bc$$

We need to factorise $$36a^2b-60a^2bc$$

$$=36a^2b-60a^2bc$$
$$=3\times 4a^2b(3-5c)$$

Factorise the following:
$$2x^3y^2-4x^2y^3+8xy^4$$

To factorise:

$$2x^3y^2-4x^2y^3+8xy^4$$

Now,

$$2x^3y^2-4x^2y^3+8xy^4$$

$$=2xy^2\times x^2-2xy^2\times 2xy+2xy^2\times 4y^2$$

$$=2xy^2(x^2-2xy+4y^2)$$

Hence, this is the answer.

Factorize the following.
$$20a^{12}b^2-15a^8b^4$$.

1682352_1673422_ans_2c352bbee4b14e13b2078f9882583616.jpg

Find the common factors of the given terms: $$4m^2, 6m^2, 8m^3$$

We need to find common factors of $$4m^2, 6m^2, 8m^3$$

The factor of $$4m^2=2\times 2\times m\times m$$,

$$6m^2=3\times 2\times m\times m$$

and that of $$8m^3=2\times 2\times 2\times m\times m\times m$$

Therefore, the common factors are $$2\times m\times m=2m^2$$.

Factorize the following.
$$2a^4b^4-3a^3b^5+4a^2b^5$$.

1682457_1673431_ans_7551428d0779489eb4f2871342b9dcd4.jpg

Factorize the following.
$$28a^2+14a^2b^2-21a^4$$.

1682468_1673432_ans_d304553947514524a92c5de4de5e17b2.jpg

Factorize the following expression.
$$abx^2+(ay-b)x-y$$.

1687283_1673560_ans_0acb2b358e8c4d53af9f1007295eee66.jpg

Factorize the following expression.
$$a(a-2b-c)+2bc$$.

1687341_1673573_ans_b9a879aa9e0d4c4fa55912e91815c2c9.jpg

Factorize the following algebraic expression.
$$6x(2x-y)+7y(2x-y)$$.

1686882_1673450_ans_d38cd98cf31646439fd9ea37bba3aff8.jpg

Factorize the following.
$$16m-4m^2$$.

1682608_1673440_ans_3d4d426f4f184777a831733064261b01.jpg

Factorize the following.
$$9x^2y+3axy$$.

Take $$3xy$$ common from both the terms

$$9x^2y+3axy=3xy(3x+a)$$

Factorize the following expression.
$$a(a+b-c)-bc$$.

1687344_1673576_ans_fe906399bb12496799c2fe5870406fa5.jpg

Factorize the following expression.
$$16(a-b)^3-24(a-b)^2$$.

1687300_1673567_ans_251ffb479d21482683be0eb6460cb541.jpg

Find the common factors of the given terms: $$7xy, 35x^2y^3$$

We need to find common factors of $$7xy, 35x^2y^3$$

The factor of $$7xy=7\times x\times y$$

and that of $$35x^2y^3=7\times 5\times x\times x\times y\times y\times y$$

Therefore, the common factors are $$7\times y\times x=7xy$$.

Factorise the polynomial: $$3ax - 6xy + 8by - 4bx$$

$$3ax-6xy+8by-4bx$$

$$=3x(a-2y)-2b(a-2y)$$

$$=(3x-2b)(a-2y)$$

Thus the factors are $$(3x-2b),(a-2y)$$

Factorise: $$5x^2 - 25xy$$

We need to factorise $$5x^2-25xy$$

We can write it as $$5x^2-25xy=5x(x-5y)$$
Thus factors are $$5,x,(x-5y)$$.

Factorize the following expression.
$$a^2x^2+(ax^2+1)x+a$$.

1687315_1673570_ans_ece42bbd75e140438f82834d3a3027e2.jpg

Factorize the following expression.
$$x^2+xy+xz+yz$$.

1687179_1673533_ans_0d79d5a4c3b74e06a6e0e08bcb9e1230.jpg

Factorize the following.
$$x^2yz+xy^2z+xyz^2$$.

1682622_1673444_ans_406ab5a59e684d6e963930d513e68763.jpg

Factorize the following algebraic expression.
$$49-a^2+8ab-16b^2$$.

1588648_1673722_ans_02bda3f37c004635b1c2a39b6cb0edc4.jpg

Factorize the following expression.
$$ab-a-b+1$$.

1687366_1673581_ans_12c15203e26049a7969b6323ec86d3ab.jpg

Factorize the following expression.
$$x-y-x^2+y^2$$.

1694019_1673649_ans_9bbc40d6abe74b9fb88ff11f0b41513a.jpg

Factorize the following expression.
$$x^4-625$$.

1694015_1673643_ans_3861a4b50fc34493878f234dcb2b4117.jpg

Factorize the following expression.
$$x^2+y-xy-x$$.

1687369_1673584_ans_e93d217eec404dbc8dc0611d996ee4e1.jpg

Find the common factors of the given terms: $$12x^2y, 18xy^2$$

The expansion of $$12x^2y$$ is $$3\times 2\times 2\times x\times x\times y$$

And that of $$18xy^2$$ is $$3\times 3\times 2\times x\times y\times y$$

By factorization, we see that the term $$2,3,x,y$$ are common to both.

Hence, the common factors of the given terms is $$6xy$$.

Find the common factors of the given terms: $$15p, 20qr, 25rp$$.

The factor of $$15p=3\times 5\times p$$

$$20qr=4\times 5\times q\times r$$

$$25pr=5\times 5\times p\times r$$

The common factors is $$5$$

Factorise: $$ut + at^2$$

We need to factorise $$ut+at^2$$

We can write it as $$ut+at^2=t(u+at)$$
Thus factors are $$t,(at+u)$$.

Factorise the polynomial: $$x^3 + 2x^2 + 5x + 10$$

$$x^3+2x^2+5x+10$$

$$=x^2(x+2)+5(x+2)$$

$$=(x^2+5)(x+2)$$
the factors are $$(x^2+5),(x+2)$$

Factorise: $$25x^2 + 9y^2 - 30xy$$

Using the identity $$(a^2+b^2-2ab)=(a-b)^2$$

We can write, $$(25x^2+9y^2-30xy)$$ as

$$=(5x)^2+(3y)^2-2\times 5x\times 3y$$

$$=(5x-3y)^2$$

Hence, factors are$$(5x-3y)(5x-3y)$$.

Factorize the following quadratic polynomial by using the method of completing the square.
$$p^2+6p+8$$.

1590495_1673866_ans_5d747843cf3c4b2095b94c7e913f0717.jpg

Factorize the following expressions:
$$17l^{2} + 85m^{2}$$

Given polynomial is $$17l^2+85m^2$$

Here we can take $$17$$ common form both the terms.

Thus we have $$17l^2+85m^2=17(l^2+5m^2)$$

Hence, factors are $$17,(l^2+5m^2)$$.

Factorize the following expression.
$$4(xy+1)^2-9(x-1)^2$$.

1694026_1673654_ans_9d6e4fdad620439c8c35217dcd6af907.jpg

Factorize the following expression.
$$p^2q^2-p^4q^4$$.

1694008_1673639_ans_d53c1bd5f02e425ba03f23765f801bef.jpg

Factorize the following expressions:
$$-12y + 20y^{3}$$

Given polynomial is $$-12y+20y^3$$

Here we can take $$-4y$$ common from both the terms.

Thus we have $$-12y+20y^3=-4y(3-5y^2)$$

Hence, factors are $$-4y,(3-5y^2)$$

Factorize the following expressions:
$$5a^{2} + 35a$$

Given polynomial is $$5a^2+35a$$

Here we can take $$5a$$ common form both the terms.

Thus we have $$5a^2+35a=5a(a+7)$$

Hence, factors are $$5,a,(a+7)$$.

Factorize the following expressions:
$$pq - pqr$$

Given polynomial is $$pq-pqr$$

Here we will take $$pq$$ common from both the terms.

Thus we have $$pq-pqr=pq(1-r)$$

Hence, factors are $$p,q,(1-r)$$.

Factorize: $$6xy - 4y + 6 - 9x$$

Given polynomial is $$6xy-4y+6-9x$$

It can be factorised as

$$6xy-4y+6-9x=2y(3x-2)-3(3x-2)$$

$$=(3x-2)(2y-3)$$

Thus factors are $$(3x-2),(2y-3)$$.

Factorize the following expressions:
$$18m^{3} - 45mn^{2}$$

Given polynomial is $$18m^3-45mn^2$$

Here we can take $$9m$$ common form both the terms.

Thus we have $$18m^3-45mn^2=9m(2m^2-5n^2)$$

Hence, factors are $$3,3m,(2m^2-5n^2)$$

Factorize:
$$mx - my - nx + ny$$

We need to factorise $$mx-my-nx+ny$$

Thus we have $$mx-my-nx+ny=m(x-y)-n(x-y)$$
Factor out the term $$x-y$$, we get

$$=(x-y)(m-n)$$

Factorize:
$$ax^{3} - bx^{2} + ax - b$$

Given polynomial is $$ax^3-bx^2+ax-b$$

It can be factorised as

$$ax^3-bx^2+ax-b=x^2(ax-b)+1(ax-b)$$

$$=(ax-b)(x^2+1)$$

Thus factors are$$(ax-b),(x^2+1)$$.

Factorize:
$$2m^{3} + 3m - 2m^{2} - 3$$

Given polynomial is $$2m^3+3m-2m^2-3$$

It can be factorised as

$$2m^3+3m-2m^2-3=m(2m^2+3)-1(2m^2+3)$$

$$=(m-1)(2m^2+3)$$

Thus factors are $$(m-1),(2m^2+3)$$.

Factorize:
$$2x + 3xy + 2y + 3y^{2}$$

Given polynomial is $$2x+3xy+2y+3y^2$$

It can be factorised as

$$2x+3xy+2y+3y^2=x(2+3y)+y(2+3y)=(x+y)(2+3y)$$

Thus factors are $$(x+y),(2+3y)$$.

Factorize:
$$p^{2} - 6p + 8$$

We need to factorise $$p^2-6p+8$$

It can be written as $$p^2-6p+8=p^2-4p-2p+8$$

$$=p(p-4)-2(p-4)$$

$$=(p-4)(p-2)$$

Factorize the polynomial:
$$a^{2} + 13a + 12$$

$$a^2+13a+12$$

$$=a^2+12a+a+12$$

$$=a(a+12)+1(m+12)$$

$$=(a+12)(a+1)$$
factors are $$(a+12),(a+1)$$

Factorize:
$$a^{2} + 11b + 11ab + a$$

Given polynomial is $$a^2+11b+11ab+a$$

It can be rearranged as $$a^2+11ab+a+11b$$

It can be factorised as

$$a^2+11ab+a+11b=a(a+11b)+1(a+11b)$$

$$=(a+11b)(a+1)$$

Thus the factors are $$(a+11b)(a+1)$$.

Factorize:
$$15b^{2} - 3bx^{2} - 5b + x^{2}$$

Given polynomial is $$15b^2-3bx^2-5b+x^2$$

It can be factorised as

$$15b^{2} - 3bx^{2} - 5b + x^{2}=3b(5b-x^2)-1(5b-x^2)$$

$$=(3b-1)(5b-x^2)$$

Thus factors are $$(3b-1),(5b-x^2)$$.

Factorize:
$$169p^{2} - 625q^{2}$$

Given expression is $$169p^2-625q^2$$

We know $$a^2-b^2=(a-b)(a+b)$$

By using this identity, we have

$$169p^2-625q^2=(13p)^2-(25q)^2$$

$$=(13p-25q)(13p+25q)$$
Thus factors are $$(13p-25q),(13p+25q)$$.

Factorize:
$$a^{2}x^{2} + axy + abx + by$$

Given polynomial is $$a^2x^2+axy +abx+by$$

It can be factorised as

$$a^2x^2+axy+abx+by=ax(ax+y)+b(ax+y)$$

$$=(ax+y)(ax+b)$$

Thus factors are $$(ax+y),(ax+b)$$.

Work out the following divisions:
$$(9x^{5} - 15x^{4} - 21x^{2}) \div (3x^{2})$$

$$(9x^{5} - 15x^{4} - 21x^{2}) \div (3x^{2})$$

$$=\dfrac{9x^5-15x^4-21x^2}{3x^2}$$

$$=\dfrac{9x^5}{3x^2}-\dfrac{15x^4}{3x^2}-\dfrac{21x^2}{3x^2}$$

$$=3x^3-5x^2-7$$

Work out the following divisions:
$$(5x^{3} - 4x^{2} + 3x) \div (2x)$$

$$\dfrac{5x^3-4x^2+3x}{2x}$$

$$=\dfrac{5x^3}{2x}-\dfrac{4x^2}{2x}+\dfrac{3x}{2x}$$

$$=\dfrac{5}{2}x^2-2x+\dfrac{3}{2}$$

Factorize the polynomial:
$$x^{2} - 14xy + 24y^{2}$$

$$x^2-12xy+24y^2$$

$$=x^2-12xy-2xy+24y^2$$

$$=x(x-12y)-2y(x-12y)$$

$$=(x-2y)(x-12y)$$
factor are,$$(x-2y),(x-12y)$$

Factorize the polynomial:
$$m^{2} - 21m - 72$$

$$m^2-21m-72=m^2-24m+3m-72=(m-24)(m+3)$$
factors are $$(m-24),(m+3)$$

Work out the following divisions:
$$(8x^{4}yz - 4xy^{3}z + 3x^{2}yz^{4})\div (xyz)$$

$$\dfrac{8x^4yz-4xy^3z+3x^2yz^4}{xyz}$$

$$=\dfrac{8x^4yz}{xyz}-\dfrac{4xy^3z}{xyz}+\dfrac{3x^2yz^4}{xyz}$$

$$=8x^3-4y^2+3xz^3$$

Simplify the following expressions:
$$(x^{2} + 7x + 10)\div (x + 2)$$

$$=\dfrac{x^2+7x+10}{x+2}$$

$$=\dfrac{x^2+5x+2x+10}{x+2}$$

$$=\dfrac{x(x+5)+2(x+5)}{x+2}$$

$$=\dfrac{(x+5)(x+2)}{x+2}$$

$$=x+5$$

Work out the following divisions:
$$4x^{2}y - 28xy + 4xy^{2} \div (4xy)$$

$$\dfrac{4x^2y-28xy+4xy^2}{-4xy}$$

$$=\dfrac{4x^2y}{-4xy}-\dfrac{28xy}{-4xy}+\dfrac{4xy^2}{-4xy}$$

$$=-x+7-y$$

$$=7-x-y$$

Work out the following divisions:
$$5y^{3} - 4y^{2} + 3y \div y$$

$$\dfrac{5y^3-4y^2+3y}{y}$$

$$=\dfrac{5y^3}{y}-\dfrac{4y^2}{y}+\dfrac{3y}{y}$$

$$=5y^2-4y+3$$

Simplify:
$$(7m^{2} - 6m)\div m$$

$$\dfrac{7m^2-6m}{m}$$

$$=\dfrac{7m^2}{m}-\dfrac{6m}{m}$$

$$=7m-6$$

Factorize the polynomial:
$$x^{2} - 5x + 6$$

$$x^2-5x+6$$

$$=x^2-3x-2x+6$$

$$=x(x-3)-2(x-3)$$

$$=(x-2)(x-3)$$

factors are $$(x-3),(x-2)$$

Factorize the following:
$$2m^{2} - 10mn - 2m + 10n$$

We need to factorise $$2m^2-10mn-2m+10n$$

It can be written as $$2m^2-10mn-2m+10n=2m(m-5n)-2(m-5n)$$

$$=(m-5n)(2m-2)$$

$$=2(m-5n)(m-1)$$

Factorise:
$$4a - 8b + 5ax - 10 bx$$

$$4a - 8b + 5ax - 10bx $$

$$= (4a - 8b) + (5ax - 10 bx)$$

$$= 4(a - 2b) + 5x(a - 2b) $$

$$= (a - 2b) (4 + 5x)$$

Resolved into factor
$$ap+ap^{2}$$

$$\begin{array}{l} ap+a{ p^{ 2 } }=a\left( { p+{ p^{ 2 } } } \right) \\ =ap\left( { 1+p } \right) \end{array}$$

Hence, the factor is $$ap\left( { 1+p } \right) $$

Solve $$2x^2 - 5x =0 $$

Given: $$2x^{2}-5x=0$$

$$=x\left (2x-5\right )=0$$

Case 1: $$x=0$$

Case 2: $$2x-5=0$$

$$x=\dfrac 52$$

Therefore $$x=0, \dfrac 52$$

Factorize:
$$ { ab }^{ 2 }-ab-{ a }^{ 2 }b+{ a }^{ 2 }$$

$$a{ b }^{ 2 }-ab-{ a }^{ 2 }b+{ a }^{ 2 }\\ \Rightarrow ab(b-1)-{ a }^{ 2 }(b-1)\\ \Rightarrow (ab-{ a }^{ 2 })(b-1)=a(b-a)(b-1)$$

Factorisation of 721 ?

Factorization of $$721$$

$$\Rightarrow 7\times 103$$

Hence, this is the answer.

Factorize of $$a^{2}+10\ a+24$$

$$ a^{2}+10a+24$$

Split $$24$$ as such that sum or difference of factor is equal to $$10 $$

$$ 24 = 6\times 4 $$

$$ = 6+4 = 10 $$

$$ a^{2}+6a+4a+24 $$

$$ a(a+6)+4(a+6) $$

$$ = (a+6)(a+4) $$

Divide the following:
$$({ x }^{ 3 }-64)\div (x-4)$$

1339265_1261037_ans_6903b396b56f448eac1c1479323011f8.jpg

Divide, Write the quotient and the remainder.
$$40a^{3}\div (-10a)$$

$$40{a}^{3}\div\left(-10a\right)$$

$$=\dfrac{40{a}^{3}}{-10a}$$

$$=-4{a}^{2}$$

Divide: $$3{a}^{3}-9{a}^{2}b-6a{b}^{2}$$ by $$-3a$$

given, $$3{a}^{3}-9{a}^{2}b-6a{b}^{2}\div\,-3a$$

$$=\dfrac{3{a}^{3}-9{a}^{2}b-6a{b}^{2}}{-3a}$$

$$=\dfrac{-3a\left(-{a}^{2}+3ab+2{b}^{2}\right)}{-3a}$$

$$=-{a}^{2}+3ab+2{b}^{2}$$

$$=2{b}^{2}+3ab-{a}^{2}$$

Factorize:
$$99x^2-202xy+99y^2$$.

Now,

$$99x^2-202xy+99y^2$$

$$=100x^2-200xy+100y^2-(x^2+2xy+y^2)$$

$$=(10x-10y)^2-(x+y)^2$$

$$=(9x-11y)(11x-9y)$$.

Simplify :
$$3x(2+5x)-6(1-2x)$$

$$3x(2+5x)-6(1-2x)$$

$$=6x+15x^2-6+12x$$

$$=15x^2+18x-6$$

Factorise
$$6{ x }^{ 2 }-5x-6$$

$$6x^2-5x-6$$

$$6x^2+4x-9x-6$$

$$2x(3x+2)-3(3x+2)$$

$$\Rightarrow (2x-3)(3x+2)$$.

1205708_1453800_ans_ef8af3a9acd34aad93dc09b943533306.jpg

Factories the expressions.
$$y(y+z)+9(y+z)$$

$$y(y+z)+9(y+z)$$

$$\Rightarrow (y+z)(y+9)$$.

1199969_1445638_ans_01ed311dfe4842c88af8a74e3c05e289.jpg

Factorize:
$$x ^ { 2 } - 23 x + 132$$

$$\begin{aligned}{}{x^2} - 23x + 132 &= {x^2} - 12x - 11x + 132\\& = x(x - 12) - 11(x - 12)\\ &= (x - 11)(x - 12)\end{aligned}$$

Factorise :
$$6x^{2}+5x-6$$

$$6 x^2+5 x-6=6 x^2+9 x-4 x-6=3 x(2 x+3)-2(2 x+3)=(3 x-2)(2 x+3)$$

Factorise the following expression.
$${q^2} - 10q + 21$$

Now,

$${q^2} - 10q + 21$$

$$=q^2-7q-3q+21$$

$$=(q-3)(q-7)$$.

Factorise the expression
$$ax^{2}+bx$$

$$a {x}^{2} + bc$$

$$= x \left( ax + b \right)$$

Hence $$a {x}^{2} + bx = x \left( ax + b \right)$$.

Factorise:
$$q^2-10q+21$$

$${q}^{2} - 10q + 21$$

$$= {q}^{2} - 7q - 3q + 21$$

$$= q \left( q - 7 \right) - 3 \left( q - 7 \right)$$

$$= \left( q - 3 \right) \left( q - 7 \right)$$

Solve : $$3\left( x-4 \right) ^{ 2 }-5\left( x-4 \right) $$

$$3(x-4)^2-5(x-4)$$

$$\Rightarrow (x-4)[3(x-4)-5]$$

$$\Rightarrow (x-4)[3x-12-5]$$

$$\Rightarrow (x-4)(3x-17)$$.

1205728_1453886_ans_f1003bf30f19400e828a6bdb64743200.jpg

Solve it :-
$$x^2 + (a + \frac{1}{a}) x + 1 = 0$$

1326044_1566063_ans_3c035f1fbe2045ecaf5004792501a7f5.jpeg

Factorize;$${ g }^{ 2 }-10 g+21.$$

1318684_1490219_ans_1a3a655a0e954885b812e03e347fdd96.JPG

Factorise:
$$\sqrt {2}x-\sqrt {3}x^{2}$$

$$\sqrt{2}{x} - \sqrt{3} {x}^{2}$$

$$= x \left( \sqrt{2} - \sqrt{3} x \right)$$

Hence $$\sqrt{2}{x} - \sqrt{3} {x}^{2} = x \left( \sqrt{2} - \sqrt{3} x \right)$$

Factorise : $${ a }^{ 2 }-\left( b+5 \right) a+5b$$

$$a^2-(b+5)a+5b$$

$$\Rightarrow a^2-ab-5a+5b$$

$$\Rightarrow a(a-b)-5(a-b)$$

$$\Rightarrow (a-5)(a-b)$$.

1205718_1453810_ans_e457d2820f2342dca2bd9275f97af0a9.jpg

Find
$$\sqrt { 3} { x }^{ 2 } -2x\sqrt { 3 } $$

$$\sqrt{3}x^2-2x\sqrt{3}$$

$$\Rightarrow \sqrt{3}x(x-2)$$.

1205730_1453890_ans_74bd55cc5dc841c8959b3bd280f712c8.jpg

Factorize
$$ 21 py^2 -56py $$

$$ 21 py^2 -56py $$
Take $$7py$$ common in both terms,
Thus, $$ 7py(3y-8) $$

Divide :
$$x^{5} - 15x^{4} - 10x^{2}$$ by $$-5x^{2}$$

$$x^{5} - 15x^{4} - 10x^{2}$$ by $$-5x^{2}$$
It can be written as
$$= (x^{5} - 15x^{4} - 10x^{2}) / -5x^{2}$$
Separating the terms
$$= x^{5} / - 5x^{2} - 15x^{4} / -5x^{2} - 10x^{2} / -5x^{2}$$
$$= -1 / 5x^{3} + 3x^{2} + 2$$

Divide :
$$8m - 16$$ by $$-8$$

$$8m - 16$$ by $$-8$$
We can write it as
$$= (8m - 16) / -8$$
Separating the terms

$$= \dfrac{8m}{-8}-\dfrac{16}{-8}$$

$$=-m+2$$

Divide :
$$4a^{2} - a$$ by $$-a$$

$$4a^{2} - a$$ by $$-a$$
We can write it as
$$= (4a^{2} - a) / - a$$
Separating the trms
$$= 4a^{2} / -a - a. -a$$
$$= -4a + 1$$

Divide :
$$3y^{3} - 9ay^{2} - 6ab^{2}y$$ by $$- 3y$$

$$3y^{3} - 9ay^{2} - 6ab^{2}y$$ by $$- 3y$$
It can be written as
$$= 3y^{3} / -3y - 9ay^{2} / - 3y - 6ab^{2}y / -3y$$
$$= - y^{2} + 3ay^{2} + 2ab^{2}$$

Divide :
$$10x^{3}y - 9xy^{2} - 4x^{2}y^{2}$$ by $$xy$$

$$10x^{3}y - 9xy^{2} - 4x^{2}y^{2}$$ by $$xy$$
It can be written as
$$= (10x^{3}y - 9xy^{2} - 4x^{2}y^{2}) / xy$$
Separating the terms
$$= 10x^{3}y / xy - 9xy^{2} / xy - 4x^{2}y^{2} / xy$$
$$= 10x^{2} - 9y - 4xy$$

Divide :
$$8x + 24$$ by $$4$$

$$8x + 24$$ by $$4$$
We can write it as
$$= (8x + 24) / 4$$
Separing the terms
$$= 8x / 4 + 24 / 4$$
$$= 2x + 6$$

$$ 4x^3 -6 x^2 $$

$$ 4x^3 -6 x^2 $$
Take out common in both terms,
Then, $$ 2x^2(2x-3) $$
Therefore,HCF of $$ 4x^3\quad and \quad 6x^2 \quad is \quad 2x^2.$$

Factorise the expression $$m^2 - 4m - 21$$

Comaring $$m^2 - 4m - 21$$ with the identity $$x^2 + (a + b) x + ab$$ we not that ab = - 21, and a + b = - 4. So, (-7) + 3 = 4 and (-7)(3) = -21
Hence, $$m^2 - 4m - 21 = m^2 - 7m + 3m - 21$$
$$= m(m - 7) + 3(m - 7)$$
$$= (m - 7)(m + 3)$$
Therefore $$m^2 - 4m - 21 = (m - 7)(m + 3)$$

Factorise : $$14{x^2} + 9x + 1$$

$$14x^2+7x+2x+1$$

$$\Rightarrow 7x\left( { 2x+1 } \right) +1\left( { 2x+1 } \right) $$

$$\Rightarrow \left( { 7x+1 } \right) \left( { 2x+1 } \right) $$

Hence, the answer is $$\left( { 7x+1 } \right) \left( { 2x+1 } \right). $$

Solve
$$3x^{4}-4x^{3}$$

$$3{ x }^{ 4 }-4{ x }^{ 3 }={ x }^{ 3 }\left( 3x-4 \right) $$

Facrorise $$m(m-1)-n(n-1)$$

$$m(m-1)-n(n-1)$$

$${ m }^{ 2 }-m-{ n }^{ 2 }+n$$

$$\left( { m }^{ 2 }-{ n }^{ 2 } \right) -\left( m-n \right) $$

$$\left( m+n \right) \left( m-n \right) -\left( m-n \right) $$

$$=\left( m-n \right) \left( m+n-1 \right) $$

Identify the terms and factors in the following expression.
i) $$5ab^2 + 7a^2b$$
ii) $$12xyz - 6xy$$

i) $$5ab^2 + 7a^2b$$

$$=ab(5b+7a)$$.

ii) $$12xyz - 6xy$$

$$=xy(12z-6)$$.

Divide $$(4{x}^{2}-17xy+4{y}^{2} ) by ( x-4y)$$

$$\begin{array}{l} 4{ x^{ 2 } }-17xy+4{ y^{ 2 } }=4{ x^{ 2 } }-16xy-xy+4{ y^{ 2 } } \\ \Rightarrow 4x\left( { x-4y } \right) -y\left( { x-4y } \right) \\ \Rightarrow \left( { x-4y } \right) \left( { 4x-y } \right) \\ =\left( { 4x-y } \right) \end{array}$$

Factorize:
$$p^2+p-(a+2)(a+1)$$.

Now,

$$p^2+p-(a+2)(a+1)$$

$$=p^2+p\{(a+2)-(a+1)\}-(a+2)(a+1)$$

$$=p(p+a+2)-(a+1)(p+a+2)$$

$$=(p+a+2)(p-a-1)$$.

Factorize:
$$6(x-y)^2-(x-y)-15$$.

Now,

$$6(x-y)^2-(x-y)-15$$

$$=6(x-y)^2-10(x-y)+9(x-y)-15$$

$$=2(x-y)(3x-3y-5)+3(3x-3y-5)$$

$$=(3x-3y-5)(2x-2y+3)$$.

Factorise
$$5y^{2}+5y-10$$

Consider $$5y^2+5y-10$$

$$5y^2+5y-10=5(y^2+y-2)$$

$$=5(y-1)(y+2)$$

$$\therefore 5y^2+5y-10=5(y-1)(y+2)$$

Factorise $$64xy+8xy^{2}$$

Simplifying $$64xy + 8x{y^2}$$

$$\Rightarrow 64xy + 8x{y^2} = 8xy\left( {8 + y} \right)$$

Divided $$(32{x}^{4}{y}^{3}-16{x}^{3}{y}^{4})$$ by $$(-8{x}^{2}y)$$

$$\dfrac{32x^4y^3 - 16x^3y^4}{-8x^2y}$$

Taking $$16x^3y^3$$ common from numerator,

$$\Rightarrow \dfrac{16x^3y^3(2x - y)}{-8x^2y}$$

$$\Rightarrow$$ $$2xy^2(y - 2x)$$

$$\Rightarrow 2xy^3 - 4x^2y^2$$

Factorise:
$$24x^3 – 36x^2y$$

Let’s take HCF of the equation $$24x^3 - 36x^2y

By taking $$12x^2$$ as a common factor for the above equation we get,

$$24x^3 - 36x^2y = 12x^2(2x - 3y)$$

$$38x^{3}y^{2}z + 19xy^{2}$$ is equal to __________ .

1975368_1792776_ans_a1e08ab85c07496c8c91bdd016eb669c.jpg

Factorise
$$12x^2-27$$

By simplifying further the above equation is $$3(4x^2 - 9)$$
By using the formula $$a^2 - b^2 = (a+b) (a-b)$$
Now solving for the above equation
$$ 3(4x^2 - 9) = 3 ((2x)^2 - (3)^2 = 3(2x+3) (2x - 3)$$

Factorise

$$x(a-3) + y(3-a)$$

$$x(a-3) +y(a-3)$$

By taking $$(a-3)$$ as a common factor for the above equation we get,

$$x(a-3) +y(a-3) = (a-3) (x+y)$$

Factorise

$$x^3(2a-b) + x^2(2a-b)$$

By taking $$2a-b$$ as a common factor for the above equation we get,
$$x^3(2a-b) + x^2(2a-b)=(2a-b)(x^3+x^2)$$

Factorise
$$ 16p^3-4p $$

$$16p^3-4p$$ can be written as $$4p (4p^2 -1)$$
By using the formula $$a^2 - b^2 = (a +b) (a -b) $$
Now solving for the above equation
$$ (4p^2 - 1) =4p((2p)^2-(1)^2)$$

$$=4p (2p +1)(2p -1)$$

$$9+6z+9a^2$$

we rewrite it as $$z^2 + 6z + 9$$

We solve by using the formula $$(a +b)^2 = a^2 + b^2 + 2ab$$

We get,

$$z^2 +(3)^2 + 2(z) (3) = (z + 3)^2$$

Factorise
$$3x^5-48x^3$$

$$3x^5-48x^3$$ can be written as $$3x^3(x^2-16)$$
By using the formula $$a^2 - b^2 = (a + b) (a - b) $$
Now solving for the above equation
$$ 3x^3(x^2 - 16) = 3x^3((x)^2 - (4)^2) = 3x^3(x + 4) (x - 4)$$

Factorise
$$20a^2-45b^2$$

By simplifying further the above equation is $$5(4a^2 - 9b^2)$$
By using the formula $$a^2 - b^2 = (a + b)$$
Now solving for the above equation
$$ 5 (4a^2 - 9b^2) = 5((2a)^2 - (3b)^2)=5(2a +3b) (2a -3b)$$

Perform the following division:
$$(ax^{3}-bx^{2}+cx) \div (-dx)$$

$$\dfrac{ax^{3}-bx^{2}+cx}{-dx}$$

$$=\dfrac{ax^{3}}{(-dx)}+\dfrac{bx^{2}}{dx}+\dfrac{cx}{(-dx)}$$

$$=-\dfrac{a}{d}x^{2}+\dfrac{b}{d}x-\dfrac{c}{d}$$

Factorise the following polynomials :
(i) $$ a^2b+ab^2 -abc - b^2c +axy +bxy $$
(ii) $$ ax^2 -bx^2 + ay^2 -by^2 + az^2 - bz^2 $$

$$ (i) a^2b+ab^2-abc-b^2c+axy+bxy $$

=$$ab(a+b)-bc(a+b)+xy(a+b) $$

=$$ (a+b)(ab-bc+xy) $$

$$(ii) ax^2-bx^2+ay^2-by^2+az^2-bz^2 $$

=$$x^2(a-b)+y^2(a-b)+z^2(a-b) $$

=$$(a-b)(x^2+y^2+z^2) $$

$$ 8x^2 - 6x^2 + 10x $$

$$ 8x^2 - 6x^2 + 10x $$
Tke out common in both terms,
Then,$$ 2x(4x^2-3x+5) $$
Therefore,HCF of $$ 8x^3,6x^2 \quad and \quad 10x \quad is \quad 2x.$$

Divide:
$$14p^2q^3 - 32p^3q^2 + 15pq^2 - 22p + 18q$$ by $$-2p^2q$$.

$$\frac{14p^2q^3 - 32p^3q^2 + 15pq^2 - 22p + 18q}{-2p^2q}$$
= $$\frac{14p^2q^3}{-2p^2q} - \frac{32p^3q^2}{-2p^2q} + \frac{15pq^2}{-2p^2q} - \frac{22p}{-2p^2q} + \frac{18q}{-2p^2q}$$
= $$7q^2 + 16pq - \frac{15q}{2p} + \frac{11}{pq} - \frac{9}{p^2}$$

$$ 28 p^2q^2 r - 42 pq^2r^2 $$

$$ 28 p^2q^2 r - 42 pq^2r^2 $$
Tke out common in both terms,
Then, $$ 14pq^2r(2p-3r) $$
Therefore, HCF of $$ 28p^2q^2r \quad and \quad 42 pq^2r^2 \quad is \quad 14pq^2r $$

Factorise the following :
$$ 12x^3 -14x^2 -10x $$

$$ 12x^3 -14x^2 -10x $$

=$$ 2x(6x^2-7x-5)$$........[ Now,as $$ 6 \times (-5)=-30 \Rightarrow -30=-10 \times 3 \quad and \quad -7=-10+3] $$

=$$ 2x(6x^2+3x-10x-5) $$

=$$ 2x \{3x (2x+1)-5(2x+1)\} $$

=$$2x(2x+1)(3x-5) $$

Factorise the following :
$$ 10x^2 -18x^3 +14x^4 $$

$$ 10x^2 -18x^3 +14x^4 $$

HCF of $$ 10,18,14=2 $$

So,$$ 10x^2-18x^3+14x^4 $$

=$$ 2x^2(5-9x+7x^2) $$

Factorise by taking out the common factors:
$$2(2x - 5y)( 3x + 4y) - 6(2x - 5y) (x - y)$$

$$2(2x - 5y)( 3x + 4y) - 6(2x - 5y) (x - y)$$

Taking $$(2x - 5y)$$ common from both terms

$$= (2x - 5y)[2(3x + 4y) - 6(x - y)]$$

$$=(2x - 5y)(6x + 8y - 6x + 6y)$$

$$=(2x - 5y)(8y + 6y)$$

$$=(2x - 5y)(14y)$$

$$=(2x - 5y) 14y$$

Solve:
$$x^2(a-b)-y^2(a-b)+z^2(a-b)$$

Simplifying we get

$$x^2(a-b)-y^2(a-b)+z^2(a-b)=(a-b)(x^2-y^2+z^2)$$

Factorise:
$$3a^5-108a^3$$

$$3a^5-108a^3=3a^3(a^2-36)$$

$$3a^5-108a^3=3a^3(a^2-6^2)$$

$$3a^5-108a^3=3a^3(a-6)(a+6)$$ $$[\therefore a^2-b^2=(a+b)(a-b)]$$

Factorise:
$$50a^3-2a$$

$$50a^3-2a=2a(25a^2-1)$$

$$50a^3-2a=2a((5a)^2-1^2)$$

$$50a^3-2a=2a(5a+1)(5a-1)$$

Resolve in to factors: $$5 - 10m - 20n.$$

Given expression is $$5-10m-20n$$.

We can rewrite it as:

$$5-5\times 2\times m-5\times 4\times n$$

$$=5-5(2m)-5(4m)$$

Taking $$5$$ common from all the terms, we get:

$$5(1-2m-4n)$$

Hence, $$5-10m-20n=5(1-2m-4n)$$.

Factorise :
$$4x^2+\dfrac{1}{4x^2}+1$$

$$4x^2+\dfrac{1}{4x^2}+1$$
$$=4x^2+\dfrac{1}{4x^2}+2-1$$
$$=4x^2+\dfrac{1}{4x^2}+2 \times 2x \times \dfrac{1}{2x}-1$$
$$=(2x + \dfrac{1}{2x})^2-(1)^2$$
$$=(2x + \dfrac{1}{2x}-1)(2x + \dfrac{1}{2x}+1)$$

Solve:
$$4x(3x-2y)-2y(3x-2y)$$

Simplifying we get

$$4x(3x-2y)-2y(3x-2y)=(3x-2y)(4x-2y)$$

$$=(3x-2y)\times 2(2x-y)$$

$$=2(3x-2y)(2x-y)$$

Factorise :
$$24a^3-37a^2-5a$$

$$24a^{3} + 37a^{2} - 5a$$

$$=a[24a^2+37a-5]$$

$$=a[24a^2-3a+40a-5]$$

$$=a[3a(8a-1)+5(8a-1)]$$

$$=a(3a+5)(8a-1)$$

Find and correct errors of the following mathematical expressions:
$$ \dfrac{3x^{2}+1}{3x^{2}} =1+1 =2 $$

The given statement is incorrect.
After separating the denominators, we get
$$ \dfrac{3x^{2}+1}{3x^{2}} =1+\dfrac{1}{3x^{2}} $$

The above statement is the correct one.

Resolve in to factors:$$(1.6)a^2 - (0.8)a$$

Given that : $$(1.6)a^2-(0.8)a$$

$$=(0.8\cdot 2)(a\cdot a)-(0.8)a$$, factor each monomial

$$=(0.8a)(2a)-(0.8a)$$

$$=0.8a(2a-1)$$, factor out common factor $$(0.8)a$$

Factors of $$(1.6)a^2-(0.8)a$$ are $$0.8a , (2a - 1)$$

Resolve in to factors : $$x^2+xy$$

Given that: $$x^2+xy$$

$$= x\times x+x\times y$$, factor each monomial

$$=x(x+y)$$, take out common factor $$x$$

Factors of $$x^2+xy$$ are $$x, (x+y)$$

Divide the given polynomial by the given monomial : $$(5x^2 - 6x)\div 3x$$

Given polynomial is $$(5x^{ 2 }-6x)$$ and the given monomial is $$3x$$

The required division is

$$=\dfrac{(5x^{ 2 }-6x)}{3x}$$
$$=\dfrac{x(5x-6)}{3x}$$
$$=\dfrac{(5x-6)}{3}$$

Factorise the expression: $$5y^2 -20y - 8z+ 2yz$$

$$5y^2-20y -8z+2yz$$
$$=5y^2-20y+2yz-8z$$
$$=5y(y-4)+2z(y-4)$$
$$=(y-4)(5y+2z)$$

Factorise the expression: $$6xy-4y+6 -9x$$

$$6xy-4y+6 -9x$$
$$=6xy-9x-4y+6$$
$$=3x(2y-3)-2(2y-3)$$
$$=(2y-3)(3x-2)$$

Factorise the expression: $$y(y + z)+ 9(y + z)$$

$$y(y + z)+ 9(y + z)$$
$$=(y + z)(y + 9)$$

Divide $$64y^3-1000$$ by $$8y -20$$.

Here, Dividend $$= 64{ y }^{ 3 }1000$$

Divisor $$= 8y-2$$

Hence, quotient $$= 8{ y }^{ 2 }+20y+50$$

Write down all possible factors of $$3x^2y$$

We have, $$3x^2y= 1 \times 3 \times xy =3 \times x^2y = 3x \times xy$$
$$=3xy \times x = x^2 \times 3y = y \times 3x^2$$
Thus, the possible factors of $$3x^2y$$ are $$1, 3, x, y, 3x, 3y, xy, 3xy, x^2y, 3x^2y$$

$$(n^{3} - n)$$ is divisible by $$3$$. Explain the reason

$$n^3 - n = n (n^2 - 1) = n (n - 1) (n + 1) $$

Whenever a number is divided by 3, the remainder obtained is either $$0$$ or $$1$$ or $$2$$.
∴ $$n = 3p$$ or $$3p + 1$$ or $$3p + 2,$$ where $$p$$ is some integer.
If $$n = 3p$$, then $$n$$ is divisible by $$3$$.
If $$n = 3p + 1,$$ then $$n – 1 = 3p + 1 –1 = 3p$$ is divisible by $$3$$.
If $$n = 3p + 2, $$then $$n + 1 = 3p + 2 + 1 = 3p + 3 = 3(p + 1) $$is divisible by $$3$$.
So, we can say that one of the numbers among $$n, n – 1 $$and $$n + 1 $$ is always divisible by $$3$$.
⇒$$ n (n – 1) (n + 1)$$ is divisible by $$3$$.

Factorise the polynomial: $$m^2 - mn + 4m - 4n$$

$$m^2-mn+4m-4n$$

$$=m(m-n)+4(m-n)$$

$$=(m+4)(m-n)$$
The factors are $$(m+4),(m-n)$$

Factorise: $$x^2 - 36$$

We need to factorise $$x^2-36$$

The given expression can be factorised by using property $$(a^2-b^2)=(a+b)(a-b)$$

It can be written as $$x^2-36=x^2-6^2$$

Here $$a=x, b=6$$

Hence, $$(x^2-36)=(x+6)(x-6)$$

Factorise: $$x^2 - 81$$

We have to factorise $$x^2-81$$

We will use identity $$a^2-b^2=(a-b)(a+b)$$

It can be written as $$x^2-81=(x+9)(x-9)$$

Thus factors are $$(x+9),(x-9)$$.

Factorise: $$36x^2 + 96xy + 64y^2$$

Using identity,$$a^2+b^2-2ab=(a-b)^2$$

$$36x^2+96xy+64y^2=(6x)^2+2\times 6x\times 8y+(8y)^2 $$

$$=(6x+8y)^2$$

$$=(6x+8y)(6x+8y)$$

Hence, the factors are $$(6x+8y)(6x+8y)$$.

Factorise: $$m^2 - 121$$

We have the identity $$(a-b)(a+b)=a^2-b^2$$

We need to simplify by using identity $$m^2-121=(m-11)(m+11)$$

The factors are $$m-11,m+11$$.

Factorise: $$25m^2 - 40mn + 16n^2$$

Using the identity $$(a^2+b^2-2ab)=(a-b)^2$$

We can write it as $$(25m^2+16n^2-40mn)$$ as

$$=(5m)^2+(4n)^2-2\times 5m\times 4n$$

$$=(5m-4n)^2$$

Hence, the factors are$$(5m-4n)(5m-4n)$$.

Factorise: $$a^2 + 10 a + 25$$

By using identity $$(a+b)^2=a^2+b^2+2ab$$

It can be written as $$a^2+10a+25$$

$$a^2+5^2+2\times a\times 10=(a+5)^2=(a+5)(a+5) $$

Hence, factors are $$(a+5)(a+5)$$.

Factorise: $$49x^2 - 25y^2$$

We need to factorise $$49x^2-25y^2$$

The given expression can be factorised by using property $$(a^2-b^2)=(a+b)(a-b)$$

It can be written as $$49x^2-25y^2=(7x)^2-(5y)^2$$

Here $$a=7x, b=5y$$

Hence, $$(49x^2-25y^2)=(7x+5y)(7x-5y)$$

Factorise: $$x^4 - y^4$$

We need to factorise $$x^4-y^4$$

The given expression can be factorised by using property $$(a^2-b^2)=(a+b)(a-b)$$

It can be written as $$x^4-y^4=(x^2)^2-(y^2)^2$$

Here $$a=x^2, b=y^2$$

Hence, $$(x^4-y^4)=(x^2+y^2)(x^2-y^2)=(x^2+y^2)(x+y)(x-y)$$

Find the errors in the following mathematical sentence:
$$(3x + 2) \div 3x = \dfrac{2}{3x}$$

$$\dfrac{(3x + 2)}{3x} = 1 + \dfrac{2}{3x}$$ is the correct division of the given mathematical sentence not $$\dfrac{2}{3x}$$.

Factorise: $$x^2 -ax - bx + ab$$

We need to factorise $$x^2-ax-bx+ab$$

It can be written as $$(x^2-ax-bx+ab)=x(x-a)-b(x-a)=(x-b)(x-a)$$

Thus, the factors are $$x-a$$ and $$x-b$$

Factorise: $$x(y + z) - 5(y + z)$$

Given expression is $$x(y+z)-5(y+z)$$

We can take $$(y+z)$$ common from the given expression.

Hence, we get $$x(y+z)-5(y+z)=(x-5)(y+z)$$.

Factorise: $$mn + m + n + 1$$

We can factorise it $$mn+m+n+1$$ as

$$=m(n+1)+1(n+1)$$

$$=(m+1)(n+1)$$

Therefore, factors are $$(m+1)(n+1)$$.

Factorise the polynomial: $$lx^2 + mx$$

We need to factorise $$lx^2+mx$$

It can be written as $$lx^2+mx=x(lx+m)$$

Thus factors are $$x,(lx+m)$$.

Check whether the given expression is correct?
$$\dfrac{4x + 3}{3} =x + 1$$

The given mathematical expression is incorrect, the correct division of the same would be:

$$\dfrac{4x + 3}{3} = \dfrac{4}{3} x + 1$$

Factorise: $$7y^2 + 35z^2$$

We need to factorise $$7y^2+35z^2$$

It can be written as $$7y^2+35z^2=7(y^2+5z^2)$$

Thus factors are $$7,(y^2+5z^2)$$.

Verify whether the given mathematical statement is correct?
$$3x + 5 \div 3 = 5$$

The given mathematical statement is incorrect.

Correct statement is:$$(3x + 5) \div 3 = x + \dfrac{5}{3}$$

Factorise: $$a^4 - (b + c)^4$$

We need to factorise $$a^4-(b+c)^4$$

The given expression can be factorised by using property $$(x^2-y^2)=(x+y)(x-y)$$

It can be written as $$a^4-(b+c)^4=(a^2)^2-[(b+c)^2]^2$$

Here $$x=a^2, y=(b+c)^2$$

Hence, $$(a^4-(b+c)^4)=(a^2+(b+c)^2)(a^2-(b+c)^2)=(a^2+(b+c)^2)(a+b+c)(a-b-c)$$

Hence, the factors are $$(a^2+(b+c)^2),(a+b+c),(a-b-c)$$.

Factorize the following expressions:
$$15a^{2}b + 35ab$$

Given polynomial is $$15a^2b+35ab$$

Here we can take $$5ab $$ common form both the terms.

Thus w ehave $$15a^2b+35ab=5ab(3a+7)$$

Hence, factors are $$5,a,b,(3a+7)$$.

Factorize the following expressions:
$$7x - 14y$$

Given expression is $$7x-14y$$

Here we have to take $$7$$ common from both the terms.

Thus we have $$7x-14y=7x-(7\times 2y)=7(x-2y)$$

Factors are $$7,(x-2y)$$.

Factorize the following expressions:
$$3x - 45$$

Given expression is $$3x-45$$

We can factorised it as $$3x-45=3x-(3\times 15)=3(x-15)$$

Thus factors are $$3,(x-15)$$.

Simplify:-
$$2ab + 2b + 3a$$

1713811_618137_ans_c360bf3962ac49b398e41218e00891ec.jpg

Solve: $$(x^{6} - 3x^{4} + 2x^{2})\div 3x^{2}$$

$$(x^{6} - 3x^{2} + 2x^{2}) \div 3x^{2}$$
$$= \dfrac {x^{6} - 3x^{4} + 2x^{2}}{3x^{2}}$$
$$= \dfrac {x^{6}}{3x^{2}} - \dfrac {3x^{4}}{3x^{2}} + \dfrac {2x^{2}}{3x^{2}}$$
$$= \dfrac {1}{3}x^{4} - x^{2} + \dfrac {2}{3}$$
Alternative Method:
We can find the common factor $$x^{2}$$ and simplify it as
$$\dfrac {x^{6} - 3x^{4} + 2x^{2}}{3x^{2}} = \dfrac {x^{2}(x^{4} - 3x^{2} + 2)}{3x^{2}}$$
$$= \dfrac {1}{3} (x^{4} - 3x^{2} + 2)$$
$$= \dfrac {x^{4}}{3} - x^{2} + \dfrac {2}{3}$$

Factorize the following expressions:
$$2x + 6$$

Given expression is $$2x+6$$

Here we can take $$2$$ common.

Then we have $$2x+6=2(x+3)$$

Factorize the following:
$$x^{3} - 3x^{2} + x - 3$$

We need to factorise $$x^3-3x^2+x-3$$

Here we will apply method of taking common terms.

Thus $$x^3-3x^2+x-3=x^2(x-3)+1(x-3)=(x-3)(x^2+1)$$

Thus factors are $$(x-3)(x^2+1)$$.

Factorize the following:
$$2xy - 3ab + 2bx - 3ay$$

We need to factorise $$2xy-3ab+2bc-3ay$$

It can be factorised by taking common factors from two terms at a time.

It can be written as $$2xy-3ay+2bx-3ab=y(2x-3a)+b(2x-3a)$$ $$=(2x-3a)(y+b)$$

Factorize the following expressions:
$$4x^{2} + 20xy$$

We need to factorise $$4x^2+20xy$$

Here we will take $$4x$$ common.

Thus $$4x^2+20xy=4x(x+5y)$$

Hence, factors are $$4x, (x+5y)$$.

Simplify: $$3(5y^{2} - 3y + 2)$$

We need to simplify $$3(5y^2-3y+2)$$

Here $$3$$ is getting multiplied with the whole bracket.

Lets solve $$3(5y^2-3y+2)=3\times 5y^2-3\times 3y+3\times 2$$

$$=15y^2-9y+6$$

Factorize the following expressions:
$$3x^{2} - 12xy$$

We need to factorise $$3x^2-12xy$$

Here we can take $$3x$$ common.

Thus we have $$3x^2-12xy=3x(x-4y)$$

Hence, factors are $$3x, (x-4y)$$.

Solve: $$(8x^{3} - 5x^{2} + 6x) \div 2x$$

$$(8x^{3} - 5x^{2} + 6x)\div 2x$$
$$= \dfrac {8x^{3} - 5x^{2} + 6x}{2x}$$
$$= \dfrac {8x^{3}}{2x} - \dfrac {5x^{2}}{2x} + \dfrac {6x}{2x}$$
$$= 4x^{2} - \dfrac {5}{2} x + 3$$
Alternative Method
For $$8x^{3} - 5x^{2} + 6x$$, separating $$2x$$ from each term we get,
$$8x^{3} - 5x^{2} + 6x = 2x(4x^{2}) - 2x\left (\dfrac {5}{2}x\right ) + 2x(3)$$
$$= 2x\left (4x^{2} - \dfrac {5}{2}x + 3\right )$$
$$\dfrac {8x^{3} - 5x^{2} + 6x}{2x} = \dfrac {2x(4x^{2} - \dfrac {5}{2}x + 3)}{2x}$$
$$= 4x^{2} - \dfrac {5}{2}x + 3$$

Solve: $$(7x^{2} - 5x)\div x$$

$$(7x^{2} - 5x) \div x = \dfrac {7x^{2} - 5x}{x}$$
$$= \dfrac {7x^{2}}{x} - \dfrac {5x}{x}$$
$$= \dfrac {7\times x\times x}{x} - \dfrac {5\times x}{x}$$
$$= 7x - 5$$
Alternative Method:
$$\dfrac {7x^{2} - 5x}{x} = 7x^{2 - 1} - 5x^{1 - 1}$$
$$= 7x^{1} - 5x^{0} = 7x - 5 (1)$$
$$[\because a^{0} = 1]$$
$$= 7x - 5$$

Factorise the following:
$$6a^5 - 18a^3 + 42a^2$$

$$6a^5 - 18a^3 + 42a^2$$

Highest common factor is $$6a^2$$

$$\therefore 6a^5 - 18a^3 + 42 a^2 $$

$$= 6a^2(a^3 - 3a + 7)$$

Factorise:
$$2a^3 + 4a^2$$

$$2a^3 + 4a^2$$

Highest common factor is $$2a^2$$

$$\therefore 2a^3 + 4a^2 $$

$$= 2a^2 (a + 2)$$.

Find the remainder using remainder theorem, when:
$$3x^3+4x^2-5x+8$$ is divided by $$x-1$$

According to remainder theorem, when $$f(x) $$ is divided by $$(x-1)$$, Remainder $$=f(1)$$

$$f(x) = 3x^3+4x^2-5x+8$$

$$f(1)=3(1)^3+4(1)^2-5(1)+8$$

$$=3+4-5+8=10$$

$$\therefore $$ Remainder$$=10$$

Find the remainder using remainder theorem, when:
$$8x^4+12x^3-2x^2-18x+14$$ is divided by $$x+1$$

According to remainder theorem when $$f(x) $$ is divided by $$(x+1)$$, Remainder $$=f(-1)$$

$$f(x)=8x^4+12x^3-2x^2-18x+14$$

$$f(-1)=8(-1)^4+12(-1)^3-2(-1)^2-18(-1)+14$$

$$=8-12-2+18+14=26$$

$$\therefore$$ Remainder $$=26$$

Find the factors of $$a(b - c)^{3} + b(c - a)^{3} + c(a - b)^{3}$$.

Given equation can be written as

$$a{ \left( b-c \right) }^{ 3 }+b{ \left( c-a \right) }^{ 3 }+c{ \left( a-b \right) }^{ 3 }$$

$$=a(b-c)^3-b(b-c+a-b)^3+c(a-b)^3$$
$$=a(b-c)^3-b(b-c)^3-b(a-b)^3-3b(b-c)(a-b)(a-c)+c(a-b)^3$$
$$=(b-c)^3(a-b)+(a-b)^3(c-b)-3b(b-c)(a-b)(a-c)$$
$$=(a-b)(b-c)((b-c)^2-(a-b)^2-3b(a-c))$$
$$=(a-b)(b-c)((b-c+a-b)(b-c-(a-b))-3b(a-c))$$
$$=(a-b)(b-c)((a-c)(2b-c-a)-3b(a-c))$$
$$=(a-b)(b-c)(a-c)(2b-c-a-3b)$$
$$=(a-b)(b-c)(c-a)(a+b+c)$$

Find the remainder using remainder theorem, when:
$$4x^3-12x^2+11x-5$$ is divided by $$2x-1$$

According to remainder theorem, when $$f(x)$$ is divided by $$(2x-1)$$, Remainder $$=f(\dfrac{1}{2})$$

$$f(x)=4x^3-12x^2+11x-5$$

$$f(\dfrac{1}{2})=4(\dfrac{1}{2})^3-12 (\dfrac{1}{2})^2+11(\dfrac{1}{2})-5$$

$$=4\times \dfrac{1}{8}-12 \times \dfrac{1}{4}+11\times \dfrac{1}{2}-5$$

$$=\dfrac{1}{2}-3+\dfrac{11}{2}-5$$

$$=\dfrac{12}{2}-8$$

$$=6-8=-2$$

$$\therefore$$ Remainder =$$=-2$$

Determine whether $$(x+1)$$ is a factor of the polynomial:
$$6x^4+7x^3-5x-4$$

According to factor theorem, when $$f(x)$$ is divided by $$(x+1)$$, $$f(-1)=0$$

$$f(x)=6x^4+7x^3-5x-4$$

$$f(-1)=6(-1)^4+7(-1)^3-5(-1)-4$$

$$=6-7+5-4=0$$

$$\because f(-1)=0$$, we can say that $$(x+1)$$ is a factor of the given polynomial

Determine whether $$(x+1)$$ is a factor of the polynomial:
$$2x^4+9x^3+2x^2+10x+15$$

According to factor theorem, when $$f(x)$$ is divided by $$(x+1)$$, $$f(-1)=0$$

$$f(x)=2x^4+9x^3+2x^2+10x+15$$

$$f(-1)=2(-1)^4+9(-1)^3+2(-1)^2+10(-1)+15$$

$$=2-9+2-10+15=0$$

$$\because f(-1)=0, (x+1) $$ is a factor of the given polynomial.

Find the factors of $$a^{4} (b^{2} - c^{2}) + b^{4}(c^{2} - a^{2}) + c^{4} (a^{2} - b^{2})$$.

The given equation is $$a^4(b^2-c^2)+b^4(c^2-a^2)+c^4(a^2-b^2)$$
We can write the above equation as
$$a^4(b^2-c^2)-b^4(b^2-c^2+a^2-b^2)+c^4(a^2-b^2)$$
$$=a^4(b^2-c^2)-b^4(b^2-c^2)-b^4(a^2-b^2)+c^4(a^2-b^2)$$
$$=(b^2-c^2)(a^4-b^4)-(a^2-b^2)(b^4-c^4)$$
$$=(b^2-c^2)(a^2-b^2)(a^2+b^2)-(a^2-b^2)(b^2-c^2)(b^2+c^2)$$
$$=(b^2-c^2)(a^2-b^2)(a^2+b^2-b^2-c^2)$$
$$=(b^2-c^2)(a^2-b^2)(a^2-c^2)$$
$$=-(b^2-c^2)(a^2-b^2)(c^2-a^2)$$
$$=-(b+c)(b-c)(a+b)(a-b)(c+a)(c-a)$$

Factorise: $${x^2} + 7x - 18$$

$$x^{2}+7x-18$$

$$=x^{2}-2x+9x-18$$

$$=x(x-2)+9(x-2)$$

$$=(x-2)(x+9)$$

$$\therefore x^{2}+7x-18=(x-2)(x+9)$$

Factorize:
$$m^3-m$$.

Now,

$$m^3-m$$

$$=m(m^2-1)$$

$$=m(m+1)(m-1)$$.

Simplify:
$$2\left(a^2+\dfrac{1}{a^2}\right)-\left(a-\dfrac{1}{a}\right)-7$$.

Now,

$$2\left(a^2+\dfrac{1}{a^2}\right)-\left(a-\dfrac{1}{a}\right)-7$$

$$=2\left(a-\dfrac{1}{a}\right)^2+4-\left(a-\dfrac{1}{a}\right)-7$$ [ Since $$(a^2+b^2)=(a-b)^2+2ab$$]

$$=2\left(a-\dfrac{1}{a}\right)^2-\left(a-\dfrac{1}{a}\right)-3$$

$$=2\left(a-\dfrac{1}{a}\right)^2-3\left(a-\dfrac{1}{a}\right)+2\left(a-\dfrac{1}{a}\right)-3$$

$$=\left(2a-\dfrac{2}{a}-3\right)\left(a-\dfrac{1}{a}+1\right)$$

Factorize $${(y - (b - a))^2}$$

$$(y-(b-a))^2$$

$$y^2+(b-a)^2-2(b-a)y$$

$$\implies y^2-2(b-a)y+(b-a)^2$$

Simplify:
$$x(x-4)-y(y-4)$$.

Now,

$$x(x-4)-y(y-4)$$

$$=x^2-y^2+4y-4x$$

$$=(x+y)(x-y)+4(y-x)$$

$$=(x-y)(x+y-4)$$

Factorize
$${x^2} - x + 10$$

Let $$x^{2}-x+10=0\implies x=\dfrac{1\pm\sqrt{1+40}}{2}=\dfrac{1\pm\sqrt{41}}{2}$$

$$x^{2}-x+10=\bigg(x-\dfrac{1-\sqrt{41}}{2}\bigg)\bigg(x-\dfrac{1+\sqrt{41}}{2}\bigg)$$

Simplify:
$$x^6+6x^3+8$$.

Now,

$$x^6+6x^3+8$$

$$=$$$$x^6+4x^3+2x^3+8$$

$$=$$$$x^3(x^3+4)+2(x^3+4)$$

$$=(x^3+4)(x^3+2)$$

Simplify:
$$a^2-3b^2-c^2-2ab+4bc$$.

Now,

$$a^2-3b^2-c^2-2ab+4bc$$

$$=(a^2-2ab+b^2)-4b^2-c^2+4bc$$

$$=(a-b)^2-(2b-c)^2$$

$$=(a+b-c)(a-b+c)$$.

Divide $${x}^{3}-6{x}^{2}+11x-6$$ by $$x-2$$ and verify the division algorithm

Let $$f(x)={ x }^{ 3 }-6{ x }^{ 2 }+11x-6$$

and $$ p(x)=x-2$$

Dividing $$f(x)$$ by $$p(x)$$ we get

Quotient $$q(x)={ x }^{ 2 }-4x+3$$ and Remainder $$r(x)=0$$

$$p(x)q(x)=(x-2)({ x }^{ 2 }-4x+3)\\ p(x)q(x)={ x }^{ 3 }-4{ x }^{ 2 }+3x-2{ x }^{ 2 }+8x-6\\ p(x)q(x)={ x }^{ 3 }-6{ x }^{ 2 }+11x-6$$

$$\Rightarrow p(x)q(x)=f(x)$$

$$\Rightarrow p(x)q(x)+0=f(x)$$

$$\Rightarrow p(x)q(x)+r(x)=f(x)$$

Hence division algorithm verified.

Factorise: $$12ax - 4ab + 18bx - 6b^2=0$$

$$12ax - 4ab + 18bx - 6b^2=0$$

$$ = 4a(3x-b) + 6b(3x-b) \\ = (4a+6b)(3x-b) \\ = 2(2a +3b)(3x-b)$$

Factorise $$x^4-5x^2+6$$.

Now,

$$x^4-5x^2+6$$

$$=x^4-3x^2-2x^2+6$$

$$=x^2(x^2-3)-2(x^2-3)$$

$$=(x^2-2)(x^2-3)$$.

Factorise
$$6x^{2}+11x+6$$

Let

$$6x^2+11x+6$$

Let us consider the

$$a=6,\;b=11,\;c=6$$

and, $$b^2-4ac$$

$$=11^2-4 \times 6 \times 6$$

$$=121-144$$

$$=-23$$

Since $$b^2-4ac<0 $$,

Therefore,

the equation $$6x^2+11x+6$$ has no real roots.

Factorise $$8a^{2}-22ab+15b^{2}$$.

$$8{a^2} - 22ab + 15{b^2}$$

$$ = 8{a^2} - 12ab - 10ab + 15{b^2}$$

$$ = 4a\left( {2a - 3b} \right) - 5b\left( {2b - 3a} \right)$$

$$ = \left( {2a - 3b} \right)\left( {4a - 5b} \right)$$

If a polynomial $$f(x)$$ is divided by $${x}^{2}-16$$ then remainder is $$5x+3$$, what will be the remainder when the same polynomial is divided by $$(x+4)$$?

Let the quotient be $$q(x)$$

$$f(x)=(x^2-16)+(5x+3)$$

$$\dfrac{f(x)}{(x+4)}=\dfrac{(x+4)(x-4)}{x+4}q(x)+\dfrac{5x+3}{x+4}$$

Remainder=Remainder when $$5x+3$$ is divided by $$x+4$$

$$=5(-4)+3=-17$$

Factorize $$125a^{3}+343b^{3}$$.

given, $$125{a^3} + 343{b^3}$$

$$=(5a)^3+(7b)^3$$

Using identity,

$${a^3} + {b^3} = (a + b)({a^2} - ab + {b^2})$$

$$(5a)^3+(7b)^3=(5x+7y)(25x^2-35x+49y^2)$$

$$p(x)=x^{3}+3x^{2}+3x+1$$ is divided by $$x=-\dfrac{1}{2}$$
$$p(a) x=-\dfrac{1}{2}=0$$
$$x=\dfrac{1}{2}$$
$$p\left(\dfrac{1}{2}\right)= \left(\dfrac{1}{2}\right)^{3}+3\left(\dfrac{1}{2}\right)^{2}+3\left(\dfrac{1}{2}\right)+1$$

$$p(x)=x^3+3x^2+3x+1$$

$$g(x)=x-\frac{1}{2}$$

$$g(x)=0,x=\frac{1}{2}$$

by factor theorem when $$p(x)$$ is divided by $$g(x)$$

Remainder $$=p(\frac{1}{2})$$

$$(\dfrac{1}{2})^3+3(\dfrac{1}{2})^2+3(\dfrac{1}{2})+1=\dfrac{27}{8}$$

Factorize $$4x^{2}-3x-7$$

$$4{x^2} - 3x - 7$$

$$ = 4{x^2} + 4x - 7x - 7$$

$$ = 4x\left( {x + 1} \right) - 7\left( {x + 1} \right)$$

$$ = \left( {4x - 7} \right)\left( {x + 1} \right)$$

Simplify:
$$a^2y^2+ay-(a+2)(a+1)$$.

Now,

$$a^2y^2+ay-(a+2)(a+1)$$

$$=a^2y^2+ay\{(a+2)-(a+1)\}-(a+2)(a+1)$$

$$=ay(ay+a+2)-(a+1)(ay+a+2)$$

$$=(ay+a+2)(ay-a-1)$$.

Answer any two of the following:
factorize $$4{ \left( a-1 \right) }^{ 2 }-4\left( a-1 \right) =3$$

Let $$a-1=x$$

$$4x^2-4x=3$$

$$4x^2+2x-6x-3=0$$

$$2x(2x+1)-3(2x+1)=0$$

$$(2x+1)(2x-3)=0$$

Put $$x=a-1$$

$$(2a-1)(2a-5)=0$$

Find the value of $$P$$ for which polynomial $$x^{3}+x^{2}-3x-P$$ is exactly divisible by polynomial $$(x+3)$$.

Consider the given polynomial.

$$\Rightarrow {{x}^{3}}+{{x}^{2}}-3x-P$$

Therefore, consider the division shown below.

If $$\left( x+3 \right)$$ completely divides $${{x}^{3}}+{{x}^{2}}-3x-P$$, then

$$ -9-P=0 $$

$$ P=-9 $$

Hence, the required value of $$P$$ is $$-9$$.
1025066_1057300_ans_a873b77698234e408229692ec36ae57f.PNG

Divide $$4x^3 + 3x^2 - 2x + 8 $$ by $$ x - 2$$

$$x-2$$ $$\bigg )\ 4x^3+3x^2-2x+8\bigg($$ $$4x^2+11x+20$$

$$4x^3-8x^2 $$

-------------------------------

$$11x^2-2x$$

$$11x^2-22x$$

--------------------------------

$$20x+8$$

$$20x-40$$

-----------------------------------------

$$48$$

$$\Rightarrow \dfrac{4x^3+3x^2-2x+8}{x-2}=4x^2+11x+20+\dfrac{48}{x-2}$$

Divide $$6{a}^{4}-2{a}^{2}-a$$ by $${a}^{2}$$

$$=\dfrac{6{a}^{4}-2{a}^{2}-a}{{a}^{2}}$$

$$=\dfrac{6{a}^{4}}{{a}^{2}}-\dfrac{2{a}^{2}}{{a}^{2}}-\dfrac{a}{{a}^{2}}$$

$$=6{a}^{2}-2-\dfrac{1}{a}$$

Factorise: $${x}^{2}+6x+5$$ $$= 0$$

$${x^2} + 6x + 5$$

$$ = {x^2} + 1x + 5x + 5$$

$$ = x\left( {x + 1} \right) + 5\left( {x + 1} \right)$$

$$ = \left( {x + 1} \right)\left( {x + 5} \right) = 0$$

$$x = - 1, - 5$$

Factorise $$ab\left( {{x^2} + {y^2}} \right) - xy\left( {{a^2} + {b^2}} \right)$$

$$ab(x^2+y^2)-xy(a^2+b^2)$$

$$\Rightarrow$$ $$abx^2+aby^2- a^2xy-b^2xy$$

$$\Rightarrow$$ $$abx^2+b^2xy+aby^2-a^2xy$$

$$\Rightarrow$$ $$bx(ax-by)-ay(ax-by)$$

$$\Rightarrow$$ $$(ax-by)(bx-ay)$$

Factorize $${x^2} - 2x - 8$$

$$x^2-2x-8$$

We can Split the Middle Term of this expression to factorize it.

$$\Rightarrow$$ $$x^2-4x+2x-8$$

$$\Rightarrow$$ $$x(x-4)+2(x-4)$$

$$\Rightarrow$$ $$(x-4)(x+2)$$

$$\therefore$$ $$x=4$$ or $$x=-2$$

Simplify:
$$(a^2-b^2)(x^2-y^2)+4abxy$$

Now,

$$(a^2-b^2)(x^2-y^2)+4abxy$$

$$=(ax)^2+(by)^2+2abxy-(ay)^2+2abxy-(bx)^2$$

$$=\{(ax)^2+(by)^2+2abxy\}-\{(ay)^2-2abxy+(bx)^2\}$$

$$=(ax+by)^2-(ay-bx)^2$$

$$=(ax+by+ay-bx)(ax+by-ay+bx)$$

Factorize $$8x^2-128$$.

1317525_1064843_ans_a627f61655a3424690c4949031e3d968.jpg

Simplify:
$$p^2+p-(a+1)(a+2)$$.

Now,

$$p^2+p-(3a+1)(3a+2)$$

$$=p^2+\{(3a+2)-(3a+1)\}p-(3a+1)(3a+2)$$

$$=p(p+3a+2)-(3a+1)(p+3a+2)$$

$$=(p+3a+2)(p-3a-1)$$

Divide $$2x^3-9x^2+10x$$ by $$(2x+5)$$ and also verify the result.

From the fig. we get,

Quotient $$=x^2-7x+\dfrac{45}{2}$$

Remainder$$=-\dfrac{225}{2}$$

Verify;-

$$2x+5=0$$

$$x=-\dfrac{5}{2}$$ satisfy the equation,

$$=2x^3-9x^2+10x$$

$$=2\left ( \dfrac{-5}{2} \right )^{3}-9\left ( \dfrac{-5}{2} \right )^2+10\left ( \dfrac{-5}{2} \right )$$

$$=2\left ( \dfrac{-125}{8} \right )-9\left ( \dfrac{25}{4} \right )+10\left ( \dfrac{-5}{2} \right )$$

$$=\left ( \dfrac{-125}{4} \right )-9\left ( \dfrac{25}{4} \right )+10\left ( \dfrac{-5}{2} \right )$$

$$=\dfrac{-125}{4} - \dfrac{225}{4} -\dfrac{50}{2}$$

$$=-\dfrac{225}{2}$$

Therefore, $$x=-\dfrac{5}{2}$$ satisfy the equation.

994752_1072144_ans_f5da2c8a7bc84f7d98c13c4ef6349720.png

Simplify:
$$x^2+4x-y^2+4y$$

Now,

$$x^2+4x-y^2+4y$$

$$=x^2-y^2+4(x+y)$$

$$=(x-y)(x+y)+4(x+y)$$

$$=(x+y)(x-y+4)$$.

Simplify: $$\cfrac{\cfrac{y}{6} + \cfrac{2y}{3}}{y +\cfrac{2y-1}{3}}$$.

$$=\cfrac{\cfrac{y}{6} + \cfrac{2y}{3}}{y +\cfrac{2y-1}{3}}$$

$$=\cfrac{\cfrac{5y}{6}}{\cfrac{5y-1}{3}}$$

$$=\cfrac{5y}{10y-2}$$

Divide $$3x^3+2x^2+13x+42$$ by $$(x+2)$$ and also verify the result.

From the figure,

Quotient $$=3x^2-4x+21$$

Remainder$$=0$$

Verify;-

$$x+2=0$$

$$\ x= -2$$ , satisfy the given equation,

$$3x^3+2x^2+13x+42$$

$$=3\left (-2\right )^3+2\left ( -2 \right )^2+13\left ( -2 \right )+42$$

$$=3\left (-8\right )+2\left ( 4\right )+13\left ( -2 \right )+42$$

$$=-24+8-26+42$$

$$=0$$

Therefore, $$x=-2$$ satisfy the given equation.

994767_1072132_ans_39faa3767bfb4d9da748c096f6151a73.png

Factorize:
$$a^2+b^2$$

Now,

$$a^2+b^2$$

$$=a^2-(ib)^2$$ [ Since $$i^2=-1$$]

$$=(a+ib)(a-ib)$$.

Simplify: $$x^2 + 6x + 9 - 4y^2$$.

We have,

$$x^2 + 6x + 9 - 4y^2$$

$$=(x+3)^2-(2y)^2$$

Now use $$(a^2-b^2)=(a-b)(a+b)$$

$$=(x+2y+3)(x-2y+3)$$.

Factorize : $$ (x+y) (2x+3y)- (x+y) (x+1) $$

Given that:

$$(x+y)(2x+3y)-(x+y)(x+1)$$

$$=(x+y)\ [(2x+3y)-(x+1)]$$ [ Taking $$(x+y)$$ common]

$$=(x+y)\ [2x+3y-x-1]$$

$$=(x+y)\ [x+3y-1].$$

This is the required solution.

Simplify: $$\left(n^2 + \dfrac{1}{n^2}\right) - 4\left(n + \dfrac{1}{n}\right) + 6$$

Now,

$$\left(n^2 + \dfrac{1}{n^2}\right) - 4\left(n + \dfrac{1}{n}\right) + 6$$

$$=\left(n + \dfrac{1}{n}\right)^2-2.n.\dfrac{1}{n} - 4\left(n + \dfrac{1}{n}\right) + 6$$ [ Since $$a^2+b^2=(a+b)^2-2ab$$]

$$=\left(n + \dfrac{1}{n}\right)^2- 4\left(n + \dfrac{1}{n}\right) + 4$$

$$=\left(n + \dfrac{1}{n}-2\right)^2$$

Factorise: $$8{y^2} - y$$

We have

$$8{{y}^{2}}-y$$

$$y\left( 8y-1 \right)$$

Hence, this is the answer.

Factorize $$6{ x }^{ 2 }+17x+5$$ by using the Factor Theorem.

Let $$p(x)=6x^{2}+17x+5 = 6(x^2+\dfrac{17}{6}+\dfrac{5}{6})$$

The term $$\dfrac{5}{6} $$ can be written as a multiple of many terms. For example, one would be $$(\pm\dfrac{5}{2},\pm\dfrac{1}{3}),(\pm\dfrac{5}{6},\pm1),...……...$$.

Let $$p(\frac{-1}{3})=0$$ then by factor theorem $$\dfrac{-1}{3}$$ is the factor of $$P(x)$$ then the other factor will be $$\dfrac{-5}{2}$$;

Thus $$6x^{2}+17x+5$$ can be factorized as $$(2x+5)(3x+1)$$

Or,

$$p(x)=6x^{2}+17x+5 = 6x^2+15x+2x+5$$

$$= 2x(3x+1)+5(3x+1)$$

$$ = (2x+5)(3x+1)$$

Divide $$3{y^4} - 8{y^3} - {y^2} - 5y - 5$$ by $$y-3$$ and find the quotient and the reminder.

Consider the given polynomial.

$$3{{y}^{4}}-8{{y}^{3}}-{{y}^{2}}-5y-5$$

So, quotient and remainder shown in figure.

Hence, quotient is $$3{{y}^{3}}+{{y}^{2}}+2y+1$$ and remainder is $$-2$$.

996101_1074821_ans_8b3d673c75b64a19a5f19df3185e4fd6.png

Factorise.
$$m^2-23m+120$$.

Consider the given expression.

$$ \Rightarrow {{m}^{2}}-23m+120 $$

$$ \Rightarrow {{m}^{2}}-15m-8m+120 $$

$$ \Rightarrow m\left( m-15 \right)-8\left( m-15 \right) $$

$$ \Rightarrow \left( m-15 \right)\left( m-8 \right) $$

Hence, this is the required factorization.

Factorise:
$${x^2} + 8x + 16$$

$$x^{2}+8x+16$$

$$=x^{2}+4x+4x+16$$

$$=x(x+4)+4(x+4)$$

$$=(x+4)(x+4)$$

$$=(x+4)^{2}$$

Solve: $$16a^{2}-b^{2}+4a+b$$

We have,

$$ 16{{a}^{2}}-{{b}^{2}}+4a+b $$

$$ ={{\left( 4a \right)}^{2}}-{{b}^{2}}+\left( 4a+b \right) $$

$$ =\left( 4a+b \right)\left( 4a-b \right)+\left( 4a+b \right) $$

$$ =\left( 4a+b \right)\left( 4a-b+1 \right) $$

Hence, this is the answer.

Find the remainder when $$x^3+3x^2+3x+1$$ is divided by $$x+1$$

Dividend$$={x}^{3}+3{x}^{2}+3x+1$$

and Divisor$$=x+1$$

Thus, remainder$$=0$$

1263970_1089283_ans_24743e8eccbd4a5ebd5fb4647f59b1c6.PNG

Factorize by factorisation method $$15x^5y^2+3x^3y+19$$

To factorize by common factor method, we need to take out the common factor from each term of the expression.

$$15x^5y^2+3x^3y+19=5\times3\times x^5\times y^2+3\times x^3\times y+19=3x^3y(5x^2y+1)+19$$

Find the remainder when $$x^3 + x^2 + x + 1$$ is divided by $$x - \frac{1}{2}$$, by using remainder theorem.

Now using reminder theorem,

$$ D=d\times Q+r $$

$$ \left( {{x}^{3}}+{{x}^{2}}+x+1 \right)=\left( {{x}^{2}}+\dfrac{3}{2}x+\dfrac{7}{4} \right)\left( x-\dfrac{1}{2} \right)+\dfrac{15}{8} $$

Hence, this is the answer.
1025068_1098781_ans_7541a7e02c07418fba500b4ae2ff2b2c.png

Factorise:
$$c+bc^2-ba^2-a$$.

To factorise:

$$c+bc^2-ba^2-a$$

Now,

$$c+bc^2-ba^2-a$$

$$=c-a+b(c^2-a^2)$$

$$=(c-a)+b(c+a)(c-a)$$

$$=(c-a)[1+b(c+a)]$$

$$=(c-a)(1+bc+ab)$$

Hence, factorised.

Factorise: $$27{x^3} - 21{x^2} + 15{x^4}$$

$$27 x ^ { 3 } - 21 x ^ { 2 } + 15 x ^ { 4 }$$

$$= 15 x ^ { 4 } + 27 x ^ { 3 } - 21 x ^ { 2 }$$

$$= 3 x ^ { 2 } \left( 5 x ^ { 2 } + 9 x - 21 \right)$$

Solve:
$$8{a^2}b - 3ab + 5{b^2} \ by \ 6ab$$

$$\dfrac{8{a}^{2}b-3ab+5{b}^{2}}{6ab}$$

$$=\dfrac{b\left(8{a}^{2}-3a+5b\right)}{6ab}$$

$$=\dfrac{8{a}^{2}-3a+5b}{6a}$$

Evaluate
$$(5x^{3}-3x^{2})\div x^{2}$$

Given

$$(5x^3-3x^2)\div x^2=\dfrac{5x^3-3x^2}{x^2}$$

$$=\dfrac{5x^3}{x^2}-\dfrac{3x^2}{x^2}$$

$$=5x^2-3$$

Simplify
$$\left( {5{a^3}b - 7a{b^3}} \right) \div ab$$

$$\dfrac{(5a^{3}b-7ab^{3})}{ab}=5a^{2}-7b^{2}$$

Simplify $${x^4} + 2{x^3}y - 2x{y^3} - {y^4}$$

We have,

$$ {{x}^{4}}+2{{x}^{3}}y-2x{{y}^{3}}-{{y}^{4}} $$

$$ ={{x}^{4}}-{{y}^{4}}+2{{x}^{3}}y-2x{{y}^{3}} $$

$$ ={{\left( {{x}^{2}} \right)}^{2}}-{{\left( {{y}^{2}} \right)}^{2}}+2xy\left( {{x}^{2}}-{{y}^{2}} \right) $$

$$ =\left( {{x}^{2}}-{{y}^{2}} \right)\left( {{x}^{2}}+{{y}^{2}} \right)+2xy\left( {{x}^{2}}-{{y}^{2}} \right) $$

$$ =\left( {{x}^{2}}-{{y}^{2}} \right)\left( {{x}^{2}}+{{y}^{2}}+2xy \right) $$

$$ =\left( {{x}^{2}}-{{y}^{2}} \right){{\left( x+y \right)}^{2}} $$

$$ =\left( x+y \right)\left( x-y \right){{\left( x+y \right)}^{2}} $$

$$ ={{\left( x+y \right)}^{3}}\left( x-y \right) $$

Hence, this is the answer.

$$24a^{3}b^{2} + 8a^{2}b^{2} + 12ab$$ by $$6ab$$.

$$4{ a }^{ 2 }b+\cfrac { 4 }{ 3 } ab+2$$

Divide $${2{x^3} - 4{x^2} - 3x - 1}$$ by $${x + 2}$$

Hence, this is the answer.
1161513_1100539_ans_03672181104d450cb5adaea5aba167a6.png

Divide $$3x^{4}+2x^{2}-3$$ by $$(x+1)$$ and find quotient and remainder.

We, know that

$$P(x)=g(x).Q(x)+R(x)$$

$$\implies 3x^4+2x^2-3=(x+1)(3x^3-3x^2+5x-5)+2$$

Hence, Quotient $$Q(x)=3x^3-3x^2+5x-5$$

And, Remainder $$=2$$

The volume of a cuboid is given by the expression $$3x^{3}-12x$$. Find the possible expression for its dimensions.

Let us factorize the given expression,

$$ 3{x}^{3}-12x =3x\left({x}^{2}-4\right)$$

$$=3x \left(x-2\right) \left(x+2\right)$$

On comparing the above factorized form with the formula for volume of cuboid $$l\times b\times h.$$ We can conclude that, the possible dimensions are,

$$\left(3x\right), \left(x-2\right)$$ and $$\left(x+2\right)$$

Factorize: $$12x^{2}-7x+1$$

$$12x^{2}-7x+1$$

$$=12x^{2}-4x-3x+1$$

$$=4x(3x-1) -1(3x-1)$$

$$=(4x-1)(3x-1)$$

$$\therefore (12x^{2}-7x+1)$$=$$(4x-1)(3x-1)$$

Convert into factorials:
$$3 \times 6 \times 9 \times 12 \times 15 \times 18$$

$$3\times 6\times 9\times 12\times 15\times 18=3^{6}(1\times 2\times 3\times 4\times 5\times 6)=3^{6}\times 6!$$

Solve:-
$$a^{2}-11a+30$$ by $$(a-5)$$

$$\dfrac{{a}^{2}-11a+30}{a-5}$$

$$=\dfrac{{a}^{2}-6a-5a+30}{a-5}$$

$$=\dfrac{a\left(a-6\right)-5\left(a-6\right)}{a-5}$$

$$=\dfrac{\left(a-6\right)\left(a-5\right)}{a-5}$$

$$=a-6$$

Divide :
$$15{p^3} \div 3p$$

$$\dfrac{15{p}^{3}}{3p}=\dfrac{5\times 3\times}{3p}=5\times{p}^{3-1}=5{p}^{2}$$

$$\left( { m }^{ 2 }-14m-32 \right) \div \left( m+2 \right) $$

$$(m^2-14m-32) \div (m+2)$$

$$=\dfrac{m^2-14m-32}{m+2}$$

$$=\dfrac{m^2-16m+2m-32}{m+2}$$

$$=\dfrac{m(m-16)+2(m-16)}{m+2}$$

$$=\dfrac{(m-16)(m+2)}{m+2}=m-16$$

Factorise the expressions using the common factor method.
$$8x^2y + 4x$$

$$8 {x}^{2} y + 4x$$

$$= \left( 4x \times 2xy \right) + 4x$$

$$= 4x \left( 2xy + 1 \right)$$

Therefore,

$$8 {x}^{2} y + 4x = 4x \left( 1 + 2xy \right)$$

Solve :-
$$\left( {3{x^2} + 5x - 9} \right) \times \left( {3x - 5} \right)$$

$$=(3x^{2}+5x-9)\times (3x-5)$$

$$=9x^{3}+15x^{2}-27x-15x^{2}-25x+45$$

$$=9x^{3}-52x+45$$

Solve: $$21 m ^ { 2 } \div 7 m$$

$$21m^2 \div 7m = \dfrac{21m^2}{7m} = 3m$$

Divide. Write the quotient and the remainder.
(a) $$21{m}^{2}\div 7m$$
(b) $$40{a}^{3}\div (-10a)$$

$$(i)$$

$$\left. 7m \right) \overline { 21{ m }^{ 2 } } \left( 3m \right. \\ \\ \quad -21{ m }^{ 2 }\\ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \\ \qquad \quad 0$$

$$(ii)$$

$$\left. -10a \right) \overline { 40{ a }^{ 3 } } \left( -4a^{2} \right. \\ \\ \quad \quad-40{ a }^{ 3 }\\ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \\ \qquad \quad 0$$

Factories : $$2xy+2y+3x+3$$

Consider the given expression.

$$2xy+2y+3x+3$$

$$\Rightarrow 2y(x+1)+3(x+1)$$

$$\Rightarrow (2y+3)(x+1)$$

Hence, this is the answer.

Factorise:
$$6{x}^{2}{y}^{3}-12{x}^{2}{y}^{2}+18{x}^{3}y$$

$$6x^2y(y^2-2y+3x)$$

$$=6x^2y(y(y-2)+3x)$$

This $$x^2, y; (y^2-2y+3x)$$ are its factors.

Divide the given polynomial by the given monomial.
$$(p^{3}q^{6}-p^{6}q^{3})\div p^{3}q^{3}$$

$$(p^3 q^6 - p^6 q^3) \div p^3 q^3$$

$$ = \dfrac{p^3 q^6}{p^3 q^3} - \dfrac{p^6 q^3} {p^3 q^3 }$$

$$ = q^3 - p^3$$ (Ans)

Factorize :
$$7x(3x-y)+7y(3x-y)$$

To factorise $$ \rightarrow 7x(3x-y)+7y(3x-y)$$

Take $$(3x-y)$$ as common

$$ = (3x-y)(7x+7y)$$

$$ = (3x-y).7(x+y) = 7(3x-y)(x+y)$$

the product of two polynomials is $$7.5{ a }^{ 3 }{ b }^{ 2 }-2.5ab+10{ a }^{ 2 }{ b }^{ 2 } $$. if one of them is 2.5ab,find the other polynomial.

Product$$(P)=7.5a^3b^2-2.5ab+10a^2b^2$$

$$P_1=2.5ab$$

$$P_2=$$$$\cfrac{7.5a^3b^2-2.5ab+10a^2b^2}{2.5ab}\\ =3a^2b-1+4ab$$

Solve $$18a^{3}b-27a^{2}b$$

$$18a^3b-27a^2b\\=9a^2b(2a-3)$$

Solve by factorization method: $$\sqrt{3}x^2+10x+7 \sqrt{3}=0$$

$$\quad \sqrt { 3 } { x }^{ 2 }+10x+7\sqrt { 3 } =0\\ \Rightarrow \sqrt { 3 } { x }^{ 2 }+3x+7x+7\sqrt { 3 } =0\\ \Rightarrow \sqrt { 3 } x\left( x+\sqrt { 3 } \right) +7\left( x+\sqrt { 3 } \right) =0\\ \Rightarrow \left( x+\sqrt { 3 } \right) \left( \sqrt { 3 } x+7 \right) =0\\ \Rightarrow x=-\sqrt { 3 } \quad or\quad x=\frac { -7 }{ \sqrt { 3 } } $$

Divide the polynomial $${x^3} - 2{x^2} - 4x - 1$$ by $$x - 1$$ and find the
remainder.

$$x^2-x-5$$

______________

$$x-1)x^3-2x^2-4x-1$$

$$x^3-x^2$$

___________

$$-x^2-4x$$

$$-x^2+x$$

____________

$$-5x-1$$

$$-5x+5$$

___________

$$-6$$

___________

Remainder$$=-6$$.

Factorise
$$10x{y^2} - 15{x^2}y$$

1335917_1270571_ans_3f81b89490ba4555bc63cfbd8e34079e.PNG

Facrtorise
$$9x^2-6x+1=0$$

A] $$9x^{2}-6x+1=0$$

$$\Rightarrow 9x^{2}-3x-3x+1=0$$

$$\Rightarrow 3x(3x-1)-1(3x-1)=0$$

$$\therefore (3x-1)^{2}=0$$

so, $$x=\frac{1}{3},\frac{1}{3}$$

1188926_1294174_ans_83c8a372380f453cae5d6f2f33aaca33.jpg

Factorise

$$3x(5a - 6b) - 12{a^2}(5{a^{}} - 6b)$$

1352020_1270743_ans_addcc164a41e4ba79fc5077d776ac59a.PNG

$$-20 x^{4} $$ by $$5x$$

$$-20x^4$$ by $$5x$$

$$=-4x^3$$.

$$5x)-20x^4(-4x^3$$

$$-20x^4$$

__________

$$x$$

__________

1144342_1269671_ans_85ac2e1d8b45414caa3ddc36f4ff2d58.jpg

Factorise $$\left( {a - b} \right) + {\left( {a - b} \right)^2}$$

$$(a-b)+(a-b)^2=(a-b)[1+(a-b)]$$

$$=(a-b)(1+a-b)$$

Factorize:-
$$2x^2-7x-15$$

We have,

$$\begin{array}{l} 2{ x^{ 2 } }-7x-15 \\ =2{ x^{ 2 } }-10x+3x-15 \\ =2x\left( { x-5 } \right) +3\left( { x-5 } \right) \\ =\left( { x-5 } \right) \left( { 2x+3 } \right) \end{array}$$

Hence, this is the answer.

Divide : $$-36x^{4}/(-9x)$$

$$-36x^{ 4 }\div (-9x)$$

$$=4x^3$$

Divide $$2{x^2} - 7{x^3} + 17{x^2}+17x +5 $$ by $$2{x^2}$$

1213397_1306846_ans_c993135c41dc48e3894b059e5fac831f.JPG

Find the value of a, if $${\text{x}}\;{\text{ - }}\;{\text{a}}$$ is factor of $${x^3} - {a^2}x + x + 2$$.

We have,

$$p(x)=x^3-a^2x+x+2$$

Since, $$(x-a)$$ is the factor of this polynomial.

So,

$$p(a)=0$$

Therefore,

$$a^3-a^2(a)+a+2=0$$

$$a^3-a^3+a+2=0$$

$$a+2=0$$

$$a=-2$$

Hence, this is the answer.

$${ 2x }^{ 2 }-5x-2xy+5y$$

We have,

$$ 2{{x}^{2}}-5x-2xy+5y $$

$$ \Rightarrow x\left( 2x-5 \right)-y\left( 2x-5 \right) $$

$$ \Rightarrow \left( 2x-5 \right)\left( x-y \right) $$

Hence, this is the answer.

Factorise the following expression :
$$7x-42$$

$$7x - 42$$

$$= 7\times(x - 6)$$

Factorize:
$$x^2-9x+20$$

Now,

$$x^2-9x+20$$

$$=x^2-4x-5x+20$$

$$=(x-4)(x-5)$$.

Find the factors of the polynomial given below.
$$2m^{2}+5m+3$$

$$ 2m^{2} + 5m + 3 $$

$$ = 2m^{2} + 2m +3m +3$$

$$ = 2m(m+1) + 3 (m+1)$$

$$ = (2m+3) (m+1)$$

$$\therefore$$ The factors are $$(2m+3)$$ and $$(m+1)$$

Solve the equation : $$3 n ^ { 3 } + 4 n ^ { 2 } + n=0$$

$$3n^{3}+4n^{2}+n=0$$

$$\Rightarrow n[3n^{2}+4n+1]=0$$

$$\Rightarrow 3n^{2}+4n+1=0$$ n=0

$$\Rightarrow 3n^{2}+3n+n+1=0$$

$$\Rightarrow 3n[n+1]+1[n+1]=0$$

$$\Rightarrow (n+1)(3n+1)=0$$

$$\Rightarrow $$ n=-1 or 3n=-1

$$\Rightarrow $$ n=-1 or $$n=-\frac{1}{3}$$

$$\therefore n=0, -1, -\frac{1}{3}$$

1191059_1306801_ans_82bd6f07b5c94b7894c73485725406d8.jpeg

Find the product using the distributive law of multiplication.
$$( x + 7 ) ( x - 2 )$$

$$(x+7)(x-2)$$

$$=x(x-2)+7(x-2)$$

By distributive law

$$=x^2-2x+7x-14$$

$$=x^2+5x-14$$.

Factorize:
$$(2x^{3}+54)$$

$$\left( 2 {x}^{3} + 54 \right)$$

$$= 2 \left( {x}^{3} + 27 \right)$$

$$= 2 \left( {\left( x \right)}^{3} + {\left( 3 \right)}^{3} \right)$$

$$= 2 \left( x + 3 \right) \left( {x}^{2} - 3x + {3}^{2} \right) \quad \left( \because {a}^{3} + {b}^{3} = \left( a + b \right) \left( {a}^{2} - ab + {b}^{2} \right) \right)$$

$$\therefore \left( 2 {x}^{3} + 54 \right) = 2 \left( x + 3 \right) \left( {x}^{2} - 3x + 9 \right)$$

Factories
$$x^{2}+11x+18$$

$${x}^{2} + 11x + 18$$

$$= {x}^{2} + 9x + 2x + 18 \quad \left( \because 18 = 9 \times 2 \right)$$

$$= x \left( x + 9 \right) + 2 \left( x + 9 \right)$$

$$= \left( x + 2 \right) \left( x + 9 \right)$$

Therefore,

$${x}^{2} + 11x + 18 = \left( x + 9 \right) \left( x + 2 \right)$$

Define factorisation.

Factorisation $$\rightarrow$$ Factorisation means to find two or more expressions whose product is equal to the given expression.

Write the following polynomials in factored from:
(i) $$90p^{3}q^{3}r^{3}+18p^{3}q^{3}r$$
(ii) $$48pqr+96qr^{3}$$
(iii) $$21x^{2}z^{2}+30y^{3}z$$
(iv) $$36x^{2}y^{3}z^{2}+72x^{2}y^{3}z^{3}$$

(A) $$90 p^3 q^3 r^3 + 18 p^3 q^3 r = 18 p^3 q^3 r (5 r^2+1)$$

(B) $$ 48 pqr + 96 pr^3 = 48 pr (q+2r^2)$$

1172977_1346875_ans_2cc4f86e4526453ea33b579ab38019d2.jpg

Solve :
$$6xy-4y+6-9x$$

Given, $$6xy - 4y + 6 - 9x$$

$$= 6xy - 9x - 4y + 6$$

$$= 3x \left( 2y - 3 \right) - 2 \left( 2y - 3 \right)$$

$$= \left( 2y - 3 \right) \left( 3x - 2 \right)$$

Therefore,

$$6xy - 4y + 6 - 9x = \left( 2y - 3 \right) \left( 3x - 2 \right)$$

Carry out the following division :
$$28 x ^ { 4 } \div 56 x$$

$$28{x^4}\div 56{x}=\dfrac{28}{56}\times \dfrac{x^4}{x}=\dfrac{x^3}{2}$$

Simplify
$$21b-60+7b-20b$$

$$21b-60+7b-20b$$

$$\Rightarrow 21b+7b-20b-60$$

$$\Rightarrow 28b-20b-60$$

$$\Rightarrow 8b-60$$

$$\Rightarrow 4[2b-15]$$

Factorise : $$16w^{3}-u^{4}w^{3}$$

$$16w^{3}-u^{4}w^{3}$$

$$=w^{3}(16-u^{4})$$

$$=w^{3}(4^{2}-(u^{2})^{2})$$

$$=w^{3}(4+u^{2})(4-u^{2})$$

$$=w^{3}(4+u^{2})(2^{2}-u^{2})$$

$$=w^{3}(4+u^{2})(2+u)(2-u)$$

Factorize : $$\dfrac { 36{m}^{2} } { 289 } - 81$$

$$\begin{array}{l} We\, have \\ \dfrac { { 36 {m}^{2}} }{ { 289 } } { }-81 \\ ={\left( { \dfrac { 6m }{ { 17 } } } \right) }^{2}-{ \left( 9 \right) ^{ 2 } } \\ =\left( { \dfrac { 6 m}{ { 17 } } +9 } \right) \left( { \dfrac { 6m }{ { 17 } } -9 } \right) \\ =\left( { \dfrac { { 6m+153 } }{ { 17 } } } \right) \left( { \dfrac { { 6m-153 } }{ { 17 } } } \right) \\ Which\, is\, the\, required\, answer. \end{array}$$

Factories : $$p ^ { 2 } + 6 p + 8$$

We have,

$$\begin{array}{l} { p^{ 2 } }+6p+8 \\ ={ p^{ 2 } }+4p+2p+8 \\ =p\left( { p+4 } \right) +2\left( { p+4 } \right) \\ =\left( { p+4 } \right) \left( { p+2 } \right) \end{array}$$

Hence, this is the answer.

Factorize:
$$x^{1}+x^{2}\times 25$$

$$x+25{x}^{2}=x\left(1+25x\right)$$

Factorise.
$$4a^{2}+7a-2$$

$$4{a}^{2}+7a-2$$

$$=4{a}^{2}+8a-a-2$$

$$=4a\left(a+2\right)-1\left(a+2\right)$$

$$=\left(a+2\right)\left(4a-1\right)$$

Hence the factors are $$\left(a+2\right)\left(4a-1\right)$$

Express the following as the product of exponent through prism factorization
$$1156$$

1156$$=2\times 578$$

$$=2\times2\times289$$

$$=2\times2\times17\times17$$

1156=$$2^{2}\times17^{2}$$

1211658_1362857_ans_8827674e579743bab84c1ffbb7327f4f.JPG

Factorize :
$$a^{2}-b^{2}-a-b$$

given, $$a^{2}-b^{2}-a-b$$

$$=(a^{2}-b^{2})-(a+b)$$

$$=(a+b)[(a-b)-1]$$

$$=(a+b)(a-b-1)$$

Factorise.
$$11{x}^{2}+17x+6$$

$$11{x}^{2}+17x+6$$

$$=11{x}^{2}+11x+6x+6$$

$$=11x\left(x+1\right)+6\left(x+1\right)$$

$$=\left(x+1\right)\left(11x+6\right)$$

Hence the factors are $$\left(x+1\right)\left(11x+6\right)$$

Factorise:$$25m^{2}-70mn+49n^{2}$$

$$25{m}^{2}-70mn+49{n}^{2}$$

$$={\left(5m\right)}^{2}-2\times 5m\times 7n+{\left(7n\right)}^{2}$$ is of the form $${a}^{2}-2ab+{b}^{2}={\left(a-b\right)}^{2}$$

$$={\left(5m-7n\right)}^{2}$$

Factorise.
$$4x^{2}+3x-7$$

$$4{x}^{2}+3x-7$$

$$=4{x}^{2}+7x-4x-7$$

$$=x\left(4x+7\right)-1\left(4x+7\right)$$

$$=\left(4x+7\right)\left(x-1\right)$$

Hence the factors are $$\left(4x+7\right)\left(x-1\right)$$

Factorise: $$2x^{2}-3x+1$$.

Given: a quadratic equation; $$2{x}^{2}-3x+1$$

$$=2{x}^{2}-2x-x+1$$

$$=2x\left(x-1\right)-1\left(x-1\right)$$

$$=\left(2x-1\right)\left(x-1\right)$$

Factorise.
$$9x^{2}-6x+1$$

$$9{x}^{2}-6x+1$$

$$=9{x}^{2}-3x-3x+1$$

$$=3x\left(3x-1\right)-1\left(3x-1\right)$$

$$=\left(3x-1\right)\left(3x-1\right)$$

Factos of $$9{x}^{2}-6x+1=\left(3x-1\right)\left(3x-1\right)$$

Factorise:
$$8xy+yz$$

$$8xy+yz$$

$$=y\left(8x+z\right)$$

$$(6x^{3}+11x^{2}-10x-7)\div (2x+1)$$

1199865_1381949_ans_853fe51c8e7a44a1a45c279a5c7a4531.JPG

Factorise.
$$9x^{2}-8x-1$$

$$9{x}^{2}-8x-1$$

$$=9{x}^{2}-9x+x-1$$

$$=9x\left(x-1\right)-1\left(x-1\right)$$

$$=\left(9x-1\right)\left(x-1\right)$$

Factos of $$9{x}^{2}-6x+1=\left(9x-1\right)\left(x-1\right)$$

Divide $$4(2x^{2}+5x+3)$$ by $$2(2x+3)$$

$$\frac{4(2x^{2}+5x+3)}{2(2x+3)} =\frac{2(2x^{2}+5x+3)}{2x+3}$$

$$\frac{2(2x^{2}+3x+2x+3)}{(2x+3)} =\frac{2\left [ x(2x+3)+1(2x+3) \right ]}{2x+3}$$

$$\frac{2(2x+3)\left [ (x+1) \right ]}{(2x+3)} =2(x+1)$$

$$\Rightarrow 2(x+1)$$

1202398_1390054_ans_f6088bb5896a4309be5769419c4b1b87.JPG

Factorise the expression
$$am^{2}+bm^{2}+bn^{2}+an^{2}$$

$$am^{2}+bm^{2}+bn^{2}+an^{2}$$

$$\Rightarrow m^{2}(a+b)+n^{2}(b+a)$$

$$\Rightarrow m^{2}(a+b)+n^{2}(a+b)$$

$$\Rightarrow (m^{2}+n^{2})(a+b)$$

Factorize the following:
$$3x-9$$

$$3x-9$$

$$=3\left(x-3\right)$$

Factorise:$$14m-21$$

$$14m-21$$

$$=7\left(2m-3\right)$$

Factorise: $$15ab^{2}-20a^{2}b$$

$$15a{b}^{2}-20{a}^{2}b$$

$$=5ab\left(3b-4a\right)$$

Factorise the expression
$$(xy+y)+x+1$$

$$\left(xy+y\right)+x+1$$

$$=y\left(x+1\right)+\left(x+1\right)$$

$$=\left(x+1\right)\left(y+1\right)$$

Solve: $$(5p^{2}-25p+20)\div (p-1)$$

$$p-1) 5p^2-25p+20(5p-20$$

$$5p^2-5p$$

_______________

$$-20p+20$$

________________

$$0$$.

1214882_1396662_ans_8308a1dd715a4fd28dc5642d779906d5.jpg

Divide.
(a) $$12{ x }^{ 3 }\quad by\quad 3x$$

$$\mathrm{(a)} 12{x^3}\div 3{x}=\dfrac{12 x^3}{3{x}}=\dfrac{12}{3}\times \dfrac{x^3}{x}=4{x^2}$$

Carry out the following divisions
$$-54l^{4}m^{3}n^{2}$$ by $$9l^{2}m^{2}n^{2}$$

Now,

$$\dfrac{-54l^4m^3n^2}{9l^2m^2n^2}$$

$$=-6l^2m$$.

Solve the following when $$x^{3}+3x^{2}+3x+1$$ is divisible by
$$x$$

$$(x^3+3 x^2+3 x+1)\div x=\dfrac{x^3+3{x^2}+3 x+1}{x}$$

$$=\dfrac{x(x^2+3 x+3)}{x}+\dfrac{1}{x}$$

$$=x^2+3{x}+3+\dfrac{1}{x}$$

Factorise: $$16(2p-3q)^{2}-4(2p-3q)$$

$$16(2 p-3 q)^2-4(2{p}-3{q})=4(2{p}-3{q})(4(2{p}-3{q})-1)$$

$$=(8{p}-12{q})(8{p}-12{q}-1)$$

Factorise the following expression by finding common factor.
$$p^{3}-16p^{2}=0$$

$$p^3-16p^2\\p^2(p-16)=0\\p^2=0\\p-16=0\\p=16$$

Factorise $${ x }^{ 2 }+x-2$$

$${\textbf{Step - 1: Breaking the middle term of the quadratic equation}}{\text{.}}$$

$${\text{We have the expression as }}{x^2} + x - 2,{\text{so the middle term is }}x.$$

$${\text{We can write }}x{\text{ as }}2x - x.$$

$${\text{Now we have the expression as }}{x^2+x-2 = x^2} + 2x - x - 2$$

$${\textbf{Step - 2: Factorizing}}{\text{.}}$$

$${\text{On taking common from first two terms and common from last two term, we get}}$$

$$x^2+x-2 = x(x - 2) - (x - 2) $$

$$\Rightarrow x^2+x-2 = (x - 1)(x - 2) $$

$${\textbf{Therefore, }}\mathbf{{x^2} + x - 2 = 0{\text{ can be factorized into }}(x - 1)(x - 2) = 0.}$$

Factorise:
$$4x^{2}+9y^{2}+25z^{2}+12xy+30yz+20zx$$

Now,

$$4x^{2}+9y^{2}+25z^{2}+12xy+30yz+20zx$$

$$=4x^{2}+12xy+9y^{2}+25z^{2}+30yz+20zx$$

$$=(2x+3y)^2+(5z)^{2}+30yz+20zx$$

$$=(2x+3y)^2+(5z)^{2}+2\times 5z(3y+2x)$$

$$=(2x+3y+5z)^2$$.

Simplify:
$$3{\left( {a - 2b} \right)^2} - 5\left( {a - 2b} \right)$$

Now,

$$3{\left( {a - 2b} \right)^2} - 5\left( {a - 2b} \right)$$

$$=(a-2b)\{3(a-2b)-5\}$$

$$=(a-2b)(3a-6b-5)$$.

Factorise
$${ 5 b }^{ 2 }-6b+1$$

$$5{b}^{2}-6b+1$$

$$=5{b}^{2}-5b-b+1$$

$$=5b\left(b-1\right)-\left(b-1\right)$$

$$=\left(5b-1\right)\left(b-1\right)$$

Factorise:$${ a }^{ 2 }{ x }^{ 2 }+\left( { ax }^{ 2 }+1 \right) x+a$$

$${a}^{2}{x}^{2}+\left(a{x}^{2}+1\right)x+a$$

$$={a}^{2}{x}^{2}+a{x}^{3}+x+a$$

$$=a{x}^{2}\left(a+x\right)+1\left(x+a\right)$$

$$=\left(x+a\right)\left(a{x}^{2}+1\right)$$

Simplify:
$$(x^2-5)(x+5)+25$$

Now,

$$(x^2-5)(x+5)+25$$

$$=x^3+5x^2-5x-25+25$$

$$=x^3+5x^2-5x$$

$$=x(x^2+5x-5)$$.

Simplify:$$\left(3{x}^{2}-x\right)\div\left(-x\right)$$.

$$=\dfrac{3{x}^{2}-x}{-x}$$

$$=\dfrac{x\left(3x-1\right)}{-x}$$

$$=\dfrac{3x-1}{-1}$$

$$=-\left(3x-1\right)$$

$$=-3x+1=1-3x$$

Factorise the following expression.
$${p^2} + 6p + 8$$

Now,

$$p^2+6p+8$$

$$=p^2+4p+2p+8$$

$$=(p+2)(p+4)$$.

Factorise:
2a+36c

$$2a+36c=2\left(a+18c\right)$$

On dividing $$ p\left(4 p^{2}-16\right) $$ by $$ 4 p(p-2), $$ we get (a) $$ 2 p+4 $$ (b) $$ p+2 $$

$$p(4 p^2 - 16)=4 p(p^2- 4)=4 p(p^2-2^2)=4 p(p-2)(p+2)$$

$$p(4 p^2-16) \div 4 p(p-2)=\dfrac{p(4 p^2-16)}{4 p(p-2)}=\dfrac{4 p(p-2)(p+2)}{4 p(p-2)}=p+2$$

The answer is $$(b)$$

Find :
$${ 9x }^{ 2 }-15x+6=?$$

$$9x^2-15x+6$$

$$3(3x^2-5x+2)$$

$$3(3x^2-3x-2x+2)$$

$$3(3x(x-1)-2(x-1))$$

$$3(3x-2)(x-1)$$.

1199875_1445106_ans_05fa614c45e745108cb2d6cbc370bb85.jpg

$$36\left( x+4 \right) \left( { x }^{ 2 }+7x+10 \right) \div 9\left( x+4 \right) $$

We need to divide the polynomial $$36(x+4)(x^2+7x+10)$$ by the binomial $$9(x+4)$$.

Hence, $$\dfrac{36(x+4)(x^2+7x+10)}{9(x+4)}$$

$$=\dfrac{9(x+4)}{9(x+4)}\times 4(x^2+7x+10)$$

$$=4(x^2+7x+10)$$

$$=4(x^2+5x+2x+10)$$

$$=4[x(x+5)+2(x+5)]$$

$$=4[(x+2)(x+5)]$$

$$=4(x+2)(x+5)$$

Hence, $$36(x+4)(x^2+7x+10)\div 9(x+4)=4(x+2)(x+5)$$.

In the division algorithm of polynomials the divisor is $$(x+2)$$, quotient is $$(x+1)$$ and the remainder is $$4$$ . Find the dividend?

Given$$:b=x+2,q=x+1,r=4$$

By Euclid's division lemma,$$a=bq+r$$

$$\Rightarrow a=\left(x+2\right)\left(x+1\right)+4$$

$$\Rightarrow a={x}^{2}+\left(2+4\right)x+2\times 1+4$$

$$\Rightarrow a={x}^{2}+6x+6$$

$$\therefore$$ Dividend $$={x}^{2}+6x+6$$

Factorise the given polynomial expression:
$${a}^{2}{x}^{2}+(a{x}^{2}+1)x+a$$

Given,

$${a}^{2}{x}^{2}+(a{x}^{2}+1)x+a$$

By Rearranging the terms we get,

$${a}^{2}{x}^{2}+a+(a{x}^{2}+1)x$$

$$=a(a{x}^{2}+1)+(a{x}^{2}+1)x$$

$$=(x+a)(a{x}^{2}+1)$$

$$\therefore {a}^2{x}^2+(ax^2+1)+a=(x+a)(a{x}^{2}+1)$$

Factorise : $$ 27 a^3b^3 - 45 a^4 b^2 $$

1563616_1714930_ans_c138989cd4eb418d8061937fdee378f3.png

Factorise $$14p^{2} + 21pq$$.

$$14p^2+21pq\\7p (2p + 3q)$$.

Factorise the quadratic expression:
$${x}^{2}+y-xy-x$$

Given,

$$x^2+y-xy-x$$

By Rearranging the terms we get,

$$x^2-x+y-xy$$

$$=x(x-1)-y(x-1)$$

$$=(x-1)(x-y)$$

$$\therefore x^2=y-xy-x=(x-1)(x-y)$$

Factorise : $$x^5 +x^2 $$

1563346_1715257_ans_8b093a2a9b9d496c816b202a5f581ca4.png

Factorise the given polynomial expression:
$${x}^{3}+x-3{x}^{2}-3$$

Given $$x^3+x-3x^2-3$$

$$=x^3-3x+x^2-3$$

$$=x^2(x-3)+1(x-3)$$

$$=(x-3)({x}^{2}+1)$$

$$\therefore x^3+x-3x^2-3=(x-3)(x^2+1)$$

Factorise completely:
$$18{x}^{2}-24x$$

$$18x^{2}-24x$$=$$6x(3x-4)$$

Factorise : $$ x^3-x^2+ax+x-a-1 $$

1563619_1714964_ans_1cc80fd7c32b4b78b0b5661f96d2e1e0.png

Factorise : $$ 32x^4 -500 x $$

1563359_1715273_ans_6ba60cd1b04f40898a65cd3e918fb145.png

Factorise:
$$6d^2e-9e^2$$.

Given expression: $$6d^2e-9e^2$$

$$= 3e(2d^2)-3e(3e)$$ {Taking $$3e$$ as common factor}

$$=3e(2d^2-3e)$$

Divide $$5m^{3}-30m^{2}+45m$$ by $$5m$$

$$5m^3-30m^2+45m$$ by $$5m$$

On dividing polynomial by a monomial we have divide every variables of polynomial.

$$\Rightarrow$$ $$\dfrac{5m^2-30m^2+45m}{5m}$$ $$=\dfrac{5m^3}{5m}-\dfrac{30m^2}{5m}+\dfrac{45m}{5m}$$

$$=\dfrac{5}{5}m^{3-1}-\dfrac{30}{5}m^{2-1}+\dfrac{45}{5}m^{1-1}$$

$$=m^2-6m+9$$

Write the greatest common factor of the following terms $$2xy$$, $$-y^{2}$$, $$2xy$$

$$y(2x, -y, 2x^{2})$$

Greatest common factor is $$y$$

Common factor of $$ax^{2} + bx$$ is _____ .

Factors of $$ax^{2} = a\times x \times x$$

Factors of $$bx = b \times x$$

Hence, the common factor of $$ax^2+bx$$ is $$x$$.

Factorise the following expressions: $$-xy - ay$$

$$—xy — ay$$
$$= y(-x-a)$$

Factorise : $$ 3a^7 b - 81 a^4b^4 $$

1563362_1715274_ans_2258f06443bc4b69a6c29be16f0a60cc.png

Factorise the following expressions: $$ ax^{2} - bx^{2} + cx$$

$$ax^{2} — bx^{2} + cx$$
$$=x(ax^{2}-bx+c)$$

Factorise the following expressions: $$6ab + 12bc$$

$$6ab + 12bc$$
$$= 6b(a+2c)$$

$$ 15ax^3 -9ax^2 $$

$$ 15ax^3 -9ax^2 $$
Take out common in both terms,
Then, $$ 3ax^2(5x-3) $$
Therefore,HCF of $$ 15 ax^3\quad and \quad 9ax^2 is \quad 3ax^2.$$

If factorised form of $$18mn + 10mnp$$ is $$amn (b + 5p)$$. Then product of $$a$$ and $$b$$ is

We have,

$$18mn + 10mnp$$

Factoring $$2mn$$ out,

$$=2mn(9+5p)$$

$$\therefore 18mn+10mnp =2mn(9+5p)$$

comparing with $$a=2, b=9$$
$$ab=18.$$

Factorise the following expressions: $$l^{2}m^{2}n - lm^{2}n^{2} l^{2}mn^{2}$$

Given expession: $$l^2m^2n-lm^2n^2l^2mn^2$$

taking $$l^2m^2n$$ common from the expression

$$\Rightarrow l^2m^2n(1-lmn^3)$$

the given expression can be factorised as $$l^2m^2n(1-lmn^3)$$

Divide:
$$5x^{2} - 3x$$ by $$x$$

$$\begin{aligned}{}\left( {5{x^2} - 3x} \right) \div x& = \frac{{5{x^2} - 3x}}{x}\\ &= \frac{{5{x^2}}}{x} - \frac{{3x}}{x}\\& = 5x - 3\end{aligned}$$

Factorize : $$a^{2}(b+c)^{2}+b^{2}(c+a)^{2}+c^{2}(a+b)+abc(a+b+c)+(a^{2}+b^{2}+c^{2})(bc+ca+ab)$$

$$f(a)=a^{2}(b+c)^{2}+b^{2}(c+a)^{2}+c^{2}(a+b)^{2}+abc(a+b+c)+(a^{2}+b^{2}+c^{2})(bc+ca+ab)$$
$$f(-b)=b^{2}(b+c)^{2}+b^{2}(c-b)^{2}-b^{2}c^{2}+(2b^{2}+c^{2})(bc-bc-b^{2})$$
$$=b^{2}(b^{2}+c^{2}+2b^{4}c^{2}+b^{2}-2bc)$$
$$=b^{2}\left [ 2b^{2}+2c^{2} \right ]$$
$$=2b^{4}+| 2b^{2}c^{2}-b^{2}c^{2}-2b^{4}-b^{2}c^{2}=0$$
$$\therefore (a+b)$$ is a factor
Since the expression is cyclic,
$$(a+b)(b+c)(c+a)$$ are factors.
$$\therefore k(a+b+c)(a+b)(b+c)(c+a)$$
By putting $$a=0, b=1, c=2,$$ we get
$$k=1$$
$$\therefore (a+b+c)(a+b)(b+c)(c+a)$$ are the factors.

Factorise $$xy^2 - xz^2$$, Hence, find the value of
$$40 \times 5.5^2 - 40 \times 4.5^2$$

$$Factorizing\quad xy^{ 2 }-xz^{ 2 }\\ =x(y^{ 2 }-z^{ 2 })\\ =x(y+z)(y-z),\\ i.e\quad value\quad of\quad 40\times 5.5^{ 2 }-40\times 4.5^{ 2 }\\ =40(5.5+4.5)(5.5-4.5)\\ =400$$

What are the possible expressions for the dimension of the cuboids whose volumes are given as in image?

(i)

$$3x^{2}-12x=3x(x-4)$$

$$=3\times x\times (x-4)$$,

The possible values of dimensions are $$3,\ x$$ and $$x-4.$$

(ii)

$$12ky^{2}+8ky-20k$$

$$=4k(3y^{2}+2y-5)$$

$$=4k(3y^{2}+5y-3y+5)$$

$$=4k\left \{ y(3y+5)-1(3y+5)\right \}$$

$$=4k(3y+5)(y-1)$$

The possible values of dimensions are $$4k$$, $$(3y+5)$$ and $$(y-1).$$

Factorise the following using appropriate identities:
(i) $$9x^2+6xy+y^2$$
(ii) $$4y^2-4y+1$$
(iii) $$x^2-\displaystyle\frac{y^2}{100}$$

(i) $$9x^{2}+6xy+y^{2}=(3x)^{2}+2(3x)(y)+(y)^{2}=(3x+y)^{2}$$

(ii) $$4y^{2}-4y+1=(2y)^{2}-2(2y)(1)+1=(2y-1)^{2}$$

(iii) $$x^{2}-\dfrac{y^{2}}{100}=(x)^{2}-\left ( \dfrac{y}{10} \right )^{2}=\left ( x-\dfrac{y}{10} \right )\left ( x+\dfrac{y}{10} \right )$$

Find the common factors of the given terms.
(i) $$12x, 36$$

(ii) $$2y, 22xy$$

(iii) $$14 pq, 28 p^{2}q^{2} $$

(iv) $$2x, 3x^{2}, 4 $$

(v) $$6abc , 24 ab^{2} , 12a^{2}b $$

(vi) $$ 16x^{3}, -4x^{2}, 32x $$

(vii) $$10 pq, 20qr, 30rp$$

(viii) $$ 3x^{2}y^{3}, 10x^{3}y^{2}, 6x^{2}y^{2}z $$

(i) $$12x = 2\times 2\times 3\times x$$
$$36 = 2\times 2\times 3\times 3$$
Common factor $$= 2\times 3 =6$$

(ii) $$2y = 2\times y$$
$$22y = 2\times 11\times y$$
Common factor $$=2$$

(iii) $$14 pq= 2\times 7\times p\times q$$
$$28 p^{2}q^{2} = 2\times 2\times 7\times p\times p\times q\times q$$
Common factor $$= 14 pq$$

(iv) $$2x = 2\times x$$
$$ 3x^{2} = 3\times x\times x $$
$$4 = 2\times 2$$
Common factor $$= 1$$

(v) $$6abc = 6\times a\times b\times c$$
$$ 24ab^{2} = 2\times 2\times 2\times 3\times a\times b\times b $$
$$ 12a^{2}b = 2\times 2\times 3\times a\times a\times b$$
Common factor $$= 6ab$$

(vi) $$ 16x^{3} = 2\times 2\times 2\times 2\times x\times x\times x $$
$$ -4x^{2} = -2\times 2\times x\times x $$
$$32 x = 2\times 2\times 2\times 2\times 2\times x $$
Common factor $$= 2x$$

(vii) $$ 10pq = 2\times 5\times p\times q $$
$$20qr = 2\times 2\times 5\times q\times r$$
$$30rp = 2\times 3\times 5$$
Common factor $$= 2\times 5 = 10$$

(viii) $$ 3x^{2}y^{3} = 3\times x\times x\times y\times y\times y $$
$$ 10x^{3}y^{2} = 2\times 5\times x\times x\times x\times y\times y $$
$$ 6x^{2}y^{2} z = 2\times 3\times x\times x\times y\times y\times z $$
Common factor = $$ x^{2}y^{2} $$

Factorise: $${ x }^{ 2 }+14x+45$$

$$x^2+14x+45$$

$$= x^2+9x+5x+45$$

$$= (x^2+9x) +(5x+45)$$

$$= x(x+9)+5(x+9)$$

$$=(x+9)(x+5) $$

Factorise: $$36{ x }^{ 2 }+25+60x$$

$$36x^2+25+60x$$ or , $$36x^2+60x +25$$

$$= 36x^2+30x +30x+25$$

$$= (36x^2+30x) +(30x+25)$$

$$= 6x(6x+5)+5(6x+5)$$

$$=(6x+5)(6x+5) = (6x+5)^2$$

Find and correct errors of the following mathematical expressions:
$$ \dfrac{4x+5}{4x} =5 $$

The given statement is incorrect.
After separating the denominators, we get

$$ \dfrac{4x+5}{4x} = 1+ \dfrac{5}{4x} $$ which is the correct statement.

Factorise
(i) $$x^{2}+xy +8x+8y $$
(ii) $$15xy-6x+5y-2 $$
(iii) $$ax+by-ay-by$$
(iv) $$15pq+15+9q+25p$$
(v) $$z-7+7xy-xyz$$

(i) $$x^{2}+xy +8x+8y $$
$$= x(x+y)+8(x+y)$$
$$= (x+8)(x+y)$$

(ii) $$15xy-6x+5y-2$$
$$= 3x(5y-2)+1(5y-2)$$
$$ = (3x+1)(5y-2)$$

(iii) $$ax+by-ay-by $$
$$= x(a+b) -y(a+b) $$
$$= (x-y) (a+b)$$

(iv) $$15pq+15+9q+25p $$
$$= 3q (5p+3)+5(5p+3) $$
$$= (3q+5)(5p+3)$$

(v) $$z-7+7xy-xyz$$
$$= z(1-xy)-7(1-xy)$$
$$= (z-7) (1-xy)$$

Factorise
(i) $$4p^{2} - 9q^{2} $$
(ii) $$63a^{2}-112b^{2} $$
(iii) $$49x^{2}-36 $$
(iv) $$16x^{5}-144x^{3} $$
(v) $$(l+m)^{2}-(l-m)^{2}$$
(vi) $$9x^{2}y^{2}-16 $$
(vii) $$(x^{2}-2xy+y^{2})-z^{2} $$
(viii) $$25a^{2}-4b^{2}+28bc-49c^{2} $$

(i) $$4p^{2} - 9q^{2} $$

$$= (2p)^{2} - (3q)^{2} $$
$$= (2p+3q) (2p-3q)$$

(ii) $$63a^{2}-112b^{2} $$

$$=7[ (3a)^{2} - (4b)^{2} ] $$
$$ = 7(3a+4b) (3a-4b)$$

(iii) $$49x^{2}-36 $$

$$= [(7x)^{2} - (6)^{2}] $$
$$= (7x-6) (7x+6 )$$

(iv) $$16x^{5}-144x^{3}$$

$$ = 16 x^{3} [ x^{2} - 3^{2} ] $$
$$ = 16 x^{3} (x-3)(x+3)$$

(v) $$(l+m)^{2}-(l-m)^{2}$$

$$= 2m\times 2l = 4lm$$

(vi) $$9x^{2}y^{2}-16 $$

$$= [ (3xy)^{2} - 4^{2} ]$$
$$=(3xy-4) (3xy+4)$$

(vii) $$(x^{2}-2xy+y^{2})-z^{2} $$

$$= [(x-y)^{2} - z^{2} ] $$
$$= (x-y+z) (x-y-z)$$

(viii) $$25a^{2}-4b^{2}+28bc-49c^{2}$$

$$ = (5a)^{2}- [(2b-7c)^{2}] $$
$$ = (5a+2b-7c) (5a-2b+7c) $$

Factorise: $$2a\left( x-y \right) +3b\left( 5x-5y \right) +4c\left( 2y-2x \right) $$

$$2a(x−y)+3b(5x−5y)+4c(2y−2x)$$

$$ = 2a(x−y)+3b\times {5(x−y)}+4.2(x-yc)$$

$$ = 2a(x−y)+15b(x−y)-8c(x-y)$$

$$ = (2a+15b-8c)(x-y)$$

Find and correct errors of the following mathematical expressions:
$$ \dfrac{7x+5}{5} =7x $$

The given statement is incorrect.
We will get correct statement by separating denominators, which is
$$ \dfrac{7x+5}{5} = 1+ \dfrac{7x}{5} $$

Divide the polynomial by the given monomial
(i) $$(5x^{2}-6x) \div 3x $$
(ii) $$(3y^{8}-4y^{6}+5y^{4})\div y^{4} $$
(iii) $$8(x^{3}y^{2}z^{2}+x^{2}y^{3}z^{2} +x^{2}y^{2}z^{3})\div 4x^{2}y^{2}z^{2} $$
(iv) $$(x^{3}+2x^{2}+3x) \div 2x $$
(v) $$(p^{3}q^{6}-p^{6}q^{3}) \div p^{3}q^{3} $$

(i) $$(5x^{2}-6x) \div 3x $$
$$= \dfrac{1}{3}(5x-6)$$

(ii) $$(3y^{8}-4y^{6}+5y^{4})\div y^{4}$$

$$ = 3y^{4}-4y^{2}+5 $$

(iii) $$8(x^{3}y^{2}z^{2}+x^{2}y^{3}z^{2} +x^{2}y^{2}z^{3})\div 4x^{2}y^{2}z^{2} $$

$$ =2(x+y+z) $$

(iv) $$(x^{3}+2x^{2}+3x) \div 2x $$

$$=\dfrac{1}{2}(x^{2}+2x+3) $$

(v) $$(p^{3}q^{6}-p^{6}q^{3}) \div p^{3}q^{3}$$

$$ = q^{3}- p^{3} $$

Find the remiander if we divide $$\left( 15{ y }^{ 4 }-16{ y }^{ 3 }+9{ y }^{ 2 }-\dfrac { 1 }{ 3 } y-\dfrac { 50 }{ 9 } \right) $$ by $$\left( 3y-2 \right) $$

$$\left(15 y^4 - 16 y^3 + 9y^2 - \dfrac{1}{3} y - \dfrac{50}{9} \right) = (3y - 2) y + R$$

Put $$y = 2/3$$ in the above equation we get

$$D + R = \dfrac{-32}{9} \Rightarrow R = -\dfrac{-32}{9}$$

Factorise: $$7xa-70xb$$

Since in the expression $$7xa-70xb$$, $$7x$$ is the common term, therefore, can be factorised as follows:

$$7xa-70xb=7x(a-10b)$$

Find the common factor of the given terms: $$4x^2, \ 6xy, \ 8y^2x$$

The given terms are $$4x^2, 6xy$$ and $$8y^2x$$

To find out: The common factor of the given terms.

We can factorise each of the given terms as:

$$4x^2=2\times 2\times x\times x$$

$$6xy=3\times 2\times x\times y$$

$$8y^2x=2\times 2\times 2\times y\times y\times x$$

We see $$2$$ and $$x$$ common in each terms.

Hence, common factor $$=2\times x=2x$$

Therefore, the common factor of the given terms is $$2x$$.

Factorise: $$\sqrt { 3 } { y }^{ 2 }+11y+6\sqrt { 3 } $$

$$\sqrt{3}y^2+11y+6\sqrt{3}$$

$$= \sqrt{3}y^2+9y+2y+6\sqrt{3}$$

$$= (\sqrt{3}y^2+9y) +(2y+6\sqrt{3})$$

$$= \sqrt{3}y(y+3\sqrt{3})+2(y+3\sqrt{3})$$

$$=( y+3\sqrt{3})( \sqrt{3}y +2) $$

Factorise: $$13{ m }^{ 2 }+156{ n }^{ 2 }$$

Since in the expression $$13m^2+156n^2$$, $$13$$ is the common term, therefore, can be factorised as follows:

$$13m^2+156n^2=13(m^2+12n^2)$$

Factorise: $$a^3 - a^2 b^2 - ab + b^3$$

We need to factorise $$a^3-a^2b^2-ab+b^3$$

Writing terms with common factors aside,

$$(a^3-a^2b^2)-(ab-b^3)$$

$$a^2(a-b^2)-b(a-b^2)$$

$$=(a^2-b)(a-b^2)$$
Thus factors are $$(a^2-b),(a-b^2)$$.

Factorise the expression $$x^2 + 10 x + 25$$

The given expression contains three terms and the first and third terms are perfect squares. That is $$x^2$$ and 25 $$(5^2)$$. Also the middle term contains the positive sign. This suggests that it can be written in the form of $$a^2 + 2ab + b^2$$, so $$x^2 + 10 x + 25 = (x)^2 + 2 (x) (5) + (5)^2$$
We can compare it with $$a^2 + 2ab + b^2$$ which in turn is equal to the LHS of the identity ie. $$(a + b)^2 $$. Here a = x and b = 5
We have $$x^2 + 10 x + 25 = (x + 5)^2 = (x + 5)(x + 5)$$

Factorise: $$12{ \left( { a }^{ 2 }+7a \right) }^{ 2 }-8\left( { a }^{ 2 }+7a \right) \left( 2a-1 \right) -15{ \left( 2a-1 \right) }^{ 2 }$$

$$12(a^2+7a)^2−8(a^2+7a)(2a−1)−15(2a−1)^2$$

Let $$ (a^2+7a)=x$$ and $$(2a-1) =y$$

Then the previous equation becomes:

$$12x^2-8xy-15y^2$$

$$= 12x^2-18xy+10xy-15y^2$$

$$= (12x^2-18xy)+(10xy-15y^2)$$

$$= 6x(2x-3y)+5y(2x-3y)$$

$$ = (6x+5y)(2x-3y)$$

Substituting the values of x and y:

$$ = {6(a^2+7a)+5(2a-1)}{2(a^2+7a)-3(2a-1)}$$

$$= (12a^2+42a+10a-5)(2a^2+14a-6a+3)$$

$$(12a^2+52a-5)(2a^2+8a+3)$$

Factorise $$48a^2 - 243b^2$$

We see that the two terms are not perfect squares. But both has '3' as common factor.
That is $$48a^2 - 243 b^2 = 3[16a^2 - 81b^2]$$
$$= 3[(4a)^2 - (9b)^2]$$ Again $$a^2 - b^2 = (a + b)(a - b)$$
$$= 3 [(4a + 9b)(4a - 9b)]$$
$$= 3(4a + 9b) (4a - 9b)$$

Factorise the expression $$4x^2 + 20x - 96$$

We notice that 4 is the common factor of all the terms.
Thus $$4x^2 + 20x - 96 = 4[x^2 + 5x - 24]$$
Now consider $$x^2 + 5x - 24$$
$$= x^2 + 8x - 3x - 24$$
$$= x(x + 8) - 3(x + 8)$$
$$=(x + 8)(x - 3)$$
Therefore $$4x^2 + 20x - 96 = 4 (x + 8) (x - 3)$$

Factorise:
$$16z^2 - 48z + 36$$

Taking common numerical factor from the given expression we get

$$16z^2 - 48z + 36 = (4 \times 4z^2) - (4 \times 12z) + (4 \times 9) = 4(4z^2 - 12z + 9)$$

Note that $$4z^2 = (2z)^2 ; 9 = (3)^2$$ and $$12z = 2(2z) (3)$$

as, $$a^2 - 2ab + b^2 = (a - b)^2$$

$$\therefore$$ $$4z^2 - 12z + 9 = (2z)^2 - 2(2z) (3) + (3)^2$$

$$ = (2z - 3)^2$$

By comparison,

$$16z^2 - 48z + 36 = 4(4z^2 - 12z + 9) = 4(2z - 3)^2$$

$$= 4(2z - 3) (2z - 3)$$

Factorise the expression $$p^4 - 256$$

$$p^4 = (p^2)^2$$ and $$256 = (16)^2$$
Thus $$p^4 - 256 = (p^2)^2 - (16)^2$$
$$= (p^2 - 16)(p^2 + 16)$$ $$[\because p^2 - 16 = (p + 4)(p - 4)]$$
$$= (p + 4)(p - 4)(p^2 + 16)$$

Divide $$30(a^2bc + ab^2 c + abc^2) $$ by $$6abc$$

$$30(a^2bc + ab^2c + abc^2)$$
$$= 2 \times 3 \times 5 [(a \times a \times b \times c)+ (a \times b \times b \times c)+ (a\times b \times c \times c)]$$
$$= 2\times 3 \times 5 \times a\times b\times c (a + b + c)$$
Thus $$30(a^2 bc + ab^2c + abc^2) \div 6abc$$
$$= \dfrac{2 \times 3 \times 5 \times abc (a + b + c)}{2 \times 3 \times abc}$$
$$= 5(a + b+ c)$$
Alternatively $$30(a^2 bc + ab^2 c + abc^2) \div 6abc$$
$$= \dfrac{30 a^2 bc}{6abc} + \dfrac{30 ab^2c}{6abc} + \dfrac{30abc^2}{6abc}$$
$$= 5a + 5b + 5c$$
$$=5(a + b + c)$$

Factorise: $$81x^2 - 198xy + 121y^2$$

The given polynomial $$81x^2-198xy+121y^2$$ can be factorized as follows:

$$81x^{ 2 }-198xy+121y^{ 2 }\\ =(9x)^{ 2 }-(2\times 9x\times 11y)+(11y)^{ 2 }\\ =(9x-11y)^{ 2 }\quad \quad \quad \quad \quad \quad \quad \quad \quad (\because \quad (a-b)^{ 2 }=a^{ 2 }+b^{ 2 }-2ab)$$

Hence, $$81x^{ 2 }-198xy+121y^{ 2 }=(9x-11y)^{ 2 }$$.

Factorise the expression $$x^2 + 2xy + y^2 - 4z^2$$

The first three terms of the expression is in the form $$(x + y)^2$$ and the fourth term is a perfect square.
Hence, $$x^2 + 2xy + y^2 - 4z^2 = (x + y)^2 - (2z)^2$$
$$=[(x + y) + 2z][(x + y) - 2z]$$
$$= (x + y + 2z) (x + y - 2z)$$

Find out the quotient and the remainder when
$$P(x) = x^{3} + 4x^{2} - 5x + 6$$ is divided by $$g(x) = x + 1$$

$$x + 1)\overset {x^{2} + 3x - 8}{\overline {x^{3} + 4x^{2} - 5x + 6}}$$
$$\underset {(-)}{x^{3}} \underset {(-)}{+} 1x^{2}$$
$$+ 3x^{2} - 5x + 6$$
$$\underset {(-)}{+} 3x^{2} \underset {(-)}{+} 3x$$
$$-8x + 6$$
$$\underset {(+)} 8x \underset {(+)}{-} 8$$
$$14$$
Therefore, $$q(x) = x^{2} + 3x - 8$$ and $$R(x) = 14$$.

Divide $$3y^{3} + 2y^{2} + y$$ by $$y$$.

Given polynomial is $$3y^{3}+2y^{2}+y$$.

Dividing it by $$y$$:

$$(3y^{3}+2y^{2}+y)\div y$$

Taking $$y$$ common from all the terms of the given polynomial,

$$\Rightarrow y(3y^2+2y+1)\times \cfrac{1}{y}$$

$$\Rightarrow 3y^2+2y+1$$

Hence, $$3y^{3}+2y^{2}+y$$ divided by $$y$$ is $$ 3y^2+2y+1$$.

Divide $$4p^{2} + 2p + 2$$ by $$'2p'$$ .

Given polynomial $$4P^{2}+2P+2$$ divided by $$2p$$

$$4p^{2}+2p+2\div 2p$$

$$\Rightarrow 4p^{2}+2p+2\times \cfrac{1}{2p}$$

$$\Rightarrow 2(2p^{2}+p+1)\times \cfrac{1}{2p}$$

$$\Rightarrow \cfrac{2p^{2}+p+1}{p}$$

Laxmi does not want to disclose the length, breadth and height of a cuboid of her project. She has constructed a polynomial $${ x }^{ 3 }-6{ x }^{ 2 }+11x-6$$ by taking the values of length, breadth and height as its zeroes. Can you open the secret [i.e., find the measures of length, breadth and height]?

Solution:

Given polynomial whose zeroes are length, breadth and height respectively is $$x^3-6x^2+11x-6.$$

$$x^3-6x^2+11x-6=0$$

0r, $$x^3-x^2-5x^2+5x+6x-6=0$$

or, $$x^2(x-1)-5x(x-1)+6(x-1)=0$$

or, $$(x-1)(x^2-5x+6)=0$$

or, $$(x-1)(x^2-3x-2x+6)=0$$

or, $$(x-1)\left\{x(x-3)-2(x-3)\right\}=0$$

or, $$(x-1(x-2)(x-3))=0$$

or, $$x=1$$ or $$x=2$$ or $$x=3$$

Therefore, length, breadth and height of cuboid are $$3units,2units$$ and $$1unit$$ respectively.

Factorise $$3{ x }^{ 4 }-10{ x }^{ 3 }+5{ x }^{ 2 }+10x-8$$

Factorisation:

$$3x^4-10x^3+5x^2+10x-8$$

$$=3x^4-3x^3-7x^3+7x^2-2x^2+2x+8x-8$$

$$=3x^3(x-1)-7x^2(x-1)-2x(x-1)+8(x-1)$$

$$=(x-1)(3x^3-7x^2-2x+8)$$

$$=(x-1)(3x^3+3x^2-10x^2-10x+8x+8)$$

$$=(x-1)\left\{3x^2(x+1)-10x(x+1)+8(x+1)\right\}$$

$$=(x-1)(x+1)(3x^2-10x+8)$$

$$=(x-1)(x+1)(3x^2-6x-4x+8)$$

$$=(x-1)(x+1)\left\{3x(x-2)-4(x-2)\right\}$$

$$=(x-1)(x+1)(x-2)(3x-4)$$

Factorize:
$$a^{2}x + abx + ac + aby + b^{2}y + bc$$

Using common factor method :

$$=a^2x+abx+aby+b^2y+ac+bc$$

$$=ax\left( { a+b } \right) +by\left( { a+b } \right) +c\left( { a+b } \right) $$

$$=\left( { a+b } \right) \left[ { ax+by+c } \right] $$

Hence, the answer is $$\left( { a+b } \right) \left[ { ax+by+c } \right].$$

Factorize:
$$x^{2} + \dfrac {2}{3}x + \dfrac {1}{9}$$

$$x^2+\dfrac{2}{3}x+\dfrac{1}{9}$$

$$=x^2+\dfrac{1}{3}x+\dfrac{1}{3}x+\dfrac{1}{9}$$

$$=x\left( { x+\dfrac { 1 }{ { 3 } } } \right) +\dfrac { 1 }{ { 3 } }\left( { x+\dfrac { 1 }{ { 3 } } } \right) $$

$$=\left( { x+\dfrac { 1 }{ { 3 } } } \right) \left( { x+\dfrac { 1 }{ { 3 } } } \right) $$

$$=\left( { x+\dfrac { 1 }{ { 3 } } } \right)^2.$$

Hence, the answer is $$\left( { x+\dfrac { 1 }{ { 3 } } } \right)^2.$$

Factorize the following expressions:
$$2a^{5}b^{3} - 14a^{2}b^{2} + 4a^{3}b$$

Let us first find the HCF of all the terms of the given polynomial $$2a^5b^3-14a^2b^2+4a^3b$$ by factoring the terms as follows:

$$2a^{ 5 }b^{ 3 }=2\times a\times a\times a\times a\times a\times b\times b\times b\\ 14a^{ 2 }b^{ 2 }=2\times 7\times a\times a\times b\times b\\ 4a^{ 3 }b=2\times 2\times a\times a\times a\times b$$

Therefore, $$HCF=2\times a\times a\times b=2a^{ 2 }b$$

Now, we factor out the HCF from each term of the polynomial $$2a^5b^3-14a^2b^2+4a^3b$$ as shown below:

$$2a^{ 5 }b^{ 3 }-14a^{ 2 }b^{ 2 }+4a^{ 3 }b=2a^{ 2 }b(a^{ 3 }b^{ 2 }-7b+2a)$$

Hence, $$2a^{ 5 }b^{ 3 }-14a^{ 2 }b^{ 2 }+4a^{ 3 }b=2a^{ 2 }b(a^{ 3 }b^{ 2 }-7b+2a)$$.

Factorise : $$2x^{2}+7x+3$$.

$$2{x^2} + 7x + 3$$

$$ = 2{x^2} + 6x + x + 3$$

$$ = 2x\left( {x + 3} \right) + 1\left( {x + 3} \right)$$

$$ = \left( {2x + 1} \right)\left( {x + 3} \right)$$

Rearrange the like terms:
$$7l^{3}m^{2} - 21lm^{2}n + 28lm$$

The given terms $$7l^3m^2,21lm^2n$$ and $$28lm$$ can be rewritten as follows:

$$7l^{ 3 }m^{ 2 }=7\times l\times l\times l\times m\times m\\ 21lm^{ 2 }n=7\times 3\times l\times m\times m\times n\\ 28lm=7\times 4\times l\times m$$

These terms have $$7,l$$ and $$m$$ as common factors, therefore,

$$7l^{ 3 }m^{ 2 }-21lm^{ 2 }n+28lm\\ =(7\times l\times l\times l\times m\times m)-(7\times 3\times l\times m\times m\times n)+(7\times 4\times l\times m)\\ =7\times l\times m[(l\times l\times m)-(3\times m\times n)+(4)]\quad \quad \quad \quad \quad \quad \quad (Combining\quad like\quad terms)\\ =7lm(l^{ 2 }m-3mn+4)$$

Hence, $$7l^{ 3 }m^{ 2 }-21lm^{ 2 }n+28lm=7lm(l^{ 2 }m-3mn+4)$$.

Factorize the following expressions:
$$3x^{3} - 5x^{2} + 6x$$

Factorize : $$3x^3-5x^2+6x.$$

We can take $$x$$ common,

$$x\left( 3x^2-5x+6 \right) $$

Hence, the answer is $$x\left( 3x^2-5x+6 \right). $$

Factorize the following:
$$ab(x^{2} + 1) + x (a^{2} + b^{2})$$

$$ab\left( { x }^{ 2 }+1 \right) +x\left( { a }^{ 2 }+{ b }^{ 2 } \right) $$

$$\Rightarrow abx^2+a^2x+b^2x+ab$$

$$\Rightarrow ax\left( bx+a \right) +b\left( bx+a \right) $$

$$\Rightarrow \left( ax+b \right) \left( bx+a \right) $$

Hence, the answer is $$\left( ax+b \right) \left( bx+a \right).$$

Find the remainder using remainder theorem, when:
$$2x^3-4x^2+7x+6$$ is divided by $$x-2$$

According to remainder theorem when $$f(x) $$ is divided by $$(x-2)$$, Remainder $$=f(2)$$

$$f(x)=2x^3-4x^2+7x+6$$

$$f(2)=2(2)^3-4(2)^2+7(2)+6$$

$$=16-8+14+6=28$$

$$\therefore $$ Remainder $$=28$$

If the polynomials $$mx^3-2x^2+25x-26$$ and $$2x^3-mx+9$$ leave the same remainder when they are divided by $$(x-2)$$, find the value of m. Also find the remainder.

Let, $$f(x)=mx^3-2x^2+25x-26$$

$$f(2)=m(2)^3-2(2)^2+25(2)-26$$

$$=8m-8+50-26$$

$$=8m+16$$

Let,$$p(x)=2x^3-mx+9$$

$$p(2)=2(2)^3-2m+9$$

$$=16+9-2m=25-2m$$

Given: $$ f(x)$$ and $$p(x) $$ leave the same remainder, when they are divided by $$(x-2)$$,

$$\therefore f(2)=p(2)$$

$$\implies 8m+16=25-2m$$

$$\implies 8m+2m=25-16$$

$$\implies 10m=9$$

$$\implies m=\dfrac{9}{10}$$

Now,

Remainder$$=f(2)=8m+16$$

$$=8\times \dfrac{9}{10}+16$$

$$=7.2+16=23.2$$

When the polynomial $$2x^3-ax^2+9x-8$$ is divided by$$x-3$$ the remainder is Find the value of a.

According to remainder theorem, when $$f(x)$$ is divided by $$(x-3)$$,Remanider $$=f(3)=28$$(given).

$$f(x)=2x^3-ax^2+9x-8$$

$$\implies f(3)=2(3)^3-a(3)^2+9(3)-8$$

$$\implies 28=54-9a+27-8$$

$$\implies 9a=73-28=45$$

$$\implies a=\dfrac{45}{9}=5$$

Find the value of m if $$x^3-6x^2+mx+60$$ leaves the remainder 2 when divided by $$(x+2)$$.

According to remainder theorem, when $$f(x)$$ is divided by $$(x+2)$$,Remanider $$=f(-2)=2$$(given).

$$f(x)=x^3-6x^2+mx+60$$

$$f(-2)=(-2)^3-6(-2)^2+(-2)m+60$$

$$\implies 2=-8-24-2m+60$$

$$\implies 2m=28-2=26$$

$$\implies m=\dfrac{26}{2}=13$$

Determine whether $$(x+1)$$ is a factor of the polynomial:
$$x^3-14x^2+3x+12$$

According to factor theorem, when $$f(x)$$ is divided by $$(x+1)$$,$$f(-1)=0$$

$$f(x)=x^3-14x^2+3x+12$$

$$f(-1)=(-1)^3-14(-1)^2+3(-1)+12$$

$$=-1-14-3+12=-6$$

$$\because f(-1) \neq 0 , (x+1)$$ is not a factor of the polynomial.

If $$(x-1)$$ divides $$mx^3-2x^2+25x-26$$ with remainder $$0$$, find the value of $$m$$.

According to remainder theorem, when $$f(x)$$ is divided by $$(x-1)$$

Remainder $$=f(1)=0$$(given).

$$f(x)=mx^3-2x^2+25x-26$$

$$f(1)=m(1)^3-2(1)^2+25(1)-26$$

$$\implies 0=m-2+25-26$$

$$\implies m-3=0$$

$$\implies m=3$$

Find the remainder using remainder theorem, when:
$$x^3-ax^2-5x+2a$$ is divided by $$x-a$$

According to remainder theorem, when $$f(x)$$ is divided by $$(x-a)$$, Remainder $$ =f(a)$$

$$f(x)=x^3-ax^2-5x+2a$$

$$f(a)=a^3-a(a)^2-5(a)+2a$$

$$=a^3-a^3-5a+2a$$

$$-3a$$

$$\therefore$$ Remanider$$=-3a$$

Determine whether $$(x+1)$$ is a factor of the polynomial:
$$3x^3+8x^2-6x-5$$

According to factor theorem, when $$f(x) $$ is divided by $$(x+1), f(-1)=0$$

$$f(x)=3x^3+8x^2-6x-5$$

$$f(-1)=3(-1)^3+8(-1)^2-6(-1)-5$$

$$=-3+8+6-5=6$$

$$\because f(-1) \neq 0, (x+1) $$is not a factor of the given polynomial.

Determine whether $$(x+4)$$ is a factor of $$x^3+3x^2-5x+36$$.

According to factor theorem, when $$f(x) $$ is divided by $$(x+4), f(-4)=0$$

$$f(x)=x^3+3x^2-5x+36$$

$$f(-4)=(-4)^3+3(-4)^2-5(-4)+36$$

$$=-64+48+20+36=40 $$

$$\because f(-4) \neq 0, (x+4) $$ is not a factor of the given polynomial.

Find the remainder using remainder theorem, when:
$$4x^3-3x^2+2x-4$$ is divided by $$x+3$$

According to remainder theorem when $$f(x) $$ is divided by $$(x+3)$$, Remainder $$=f(-3)$$

$$f(x)=4x^3-3x^2+2x-4$$

$$f(-3)=4(-3)^3-3(-3)^2+2(-3)-4$$

$$=4\times -27-3\times 9-6-4=-108-27-10=-145$$

$$\therefore$$ Remainder $$=-145$$

Determine whether $$(2x+1)$$ is a factor of $$4x^3+4x^2-x-1$$.

According to factor theorem, when $$f(x) $$ is divided by $$(2x+1)$$, $$f(\dfrac{-1}{2})=0$$

$$f(x)=4x^3+4x^2-x-1$$

$$f(\dfrac{-1}{2})=4(\dfrac{-1}{2})^3+4(\dfrac{-1}{2})^2-(\dfrac{-1}{2})-1$$

$$=4 \times \dfrac{-1}{8}+4 \times \dfrac{1}{4}+\dfrac{1}{2}-1$$

$$=\dfrac{-1}{2}+1+\dfrac{1}{2}-1=0$$

$$\because f(\dfrac{-1}{2})=0, (2x+1) $$ is a factor of the polynomial.

Give possible expressions for the length and breadth of the following rectangles, in which their areas are given:
Area: $$35{y}^{2}+13y-12$$

$$= 35y^{2}+13y-12$$

$$=35y^{2}+35y-12y-12$$

$$=35y(y+1)-12(y+1)$$

$$=(35y-12)(y+1)$$

$$l=35y-12$$ ,$$b=y+1$$

$$y+1$$ ,$$b = 35y-12$$

Factorize $$x^3 + 3x^2 - x - 3$$

Let $$p(x) = x^3 + 3x^2 - x - 3$$

p(x) is a cubic polynomial, so it may have three linear factors.

The constant term is -3. The factors of -3 are -1, 1, -3 and 3.

$$p(-1) = (-1)^3 + 3 (-1)^2 - (-1) - 3 = -1 + 3 + 1 -3 = 0$$

$$\therefore (x + 1)$$ is a factor of p(x).

$$p(1) = (1)^3 + 3(1)^2 - 1 - 3 = 1 + 3 - 1 - 3 = 0$$

$$\therefore (x - 1)$$ is a factor of p(x).

$$p(-3) = (-3)^3 + 3(-3)^2 - (-3) - 3 = - 27 + 27 + 3 - 3 = 0$$

$$\therefore (x + 3)$$ is a factor of p(x).

The three factors of p(x) are (x + 1), (x - 1) and (x - 3)

$$\therefore x^3 + 3x^2 - x - 3 = (x + 1) (x - 1) (x + 3)$$.

Find the remainder when $$x^3-7x^2-x+6$$ is divided by $$(x+2)$$.

According to remainder theorem, when$$ f(x) $$ is divided by $$(x+2)$$, Remainder $$=f(-2)$$

$$f(x)=x^3-7x^2-x+6$$

$$f(-2)=(-2)^3-7(-2)^2-(-2)+6$$

$$=-8-7\times 4+2+6$$

$$=-8-28+8=-28$$

$$\therefore$$ Remainder $$=-28$$

Using factor theorem show that $$(x- 1)$$ is factor of $$4x^3-6x^2+9x-7$$.

According to factor theorem, when $$f(x) $$ is divided by $$(x-1), f(1)=0$$

$$f(x)=4x^3-6x^2+9x-7$$

$$f(1)=4(1)^3-6(1)^2+9(1)-7$$

$$=4-6+9-7=0$$

$$\because f(1)=0, (x-1)$$ is a factor of the given polynomial

Find the value of a if $$2x^3-6x^2+5ax-9$$ leaves the remainder 13 when it is divided by x-2.

Let $$p(x)=2x^3-6x^2+5ax-9$$
When p(x) is divided by (x -2) the remainder is p(2).
Given that p(2)=13
$$\rightarrow 2(2)^3-6(2)^2+5a(2)-9=13$$
$$2(8)-6(4)+10a-9=13$$
$$16-24+10a-9=13$$
$$10a-17=13$$
$$10a=30$$
$$\therefore a=3$$

Factorize the following
$$2x^2 - 15x + 27$$

$$2x^2 - 15 x + 27$$

Coefficient of $$x^2 = 2$$; constant term $$= 27$$

Their product $$= 2 \times 27 = 54$$

Coefficient of $$x = -15$$

$$\therefore$$ product $$= 54$$; sum $$= -15$$

$$2x^2 - 15x + 27 $$

$$= 2x^2 - 6x - 9x + 27$$

$$= 2x(x - 3) - 9 (x - 3)$$

$$= (x - 3)(2x - 9)$$

$$\therefore 2x^2 - 15x + 27 = (x - 3)(2x - 9) $$

Find the remainder when $$x^3+ax^2-3x+a$$ is divided by x+a.

Let $$p(x)=x^3+ax^2-3x+a$$
When p(x) is divided by (x+a) the remainder is p(-a).
$$p(-a)=(-a)^3+a(-a)^2-3(-a)+a=-a^3+a^3+4a=4a$$
$$\therefore$$ The remainder is 4a.

Find the quotient and the remainder when $$10-4x+3x^2$$ is divided by$$x-2$$.

Let us first write the terms of each polynomial in descending order ( or ascending order). thus, the given problem becomes $$93x^2-4x+10) \div (x-2)$$
(i) $$\frac{3x^2}{x}=3x$$
(ii) $$3x(x-2)=3x^2-6x$$
(iii) $$\frac{2x}{2}=2$$
(iv) $$2(x-2)=2x-4$$
$$\therefore$$ Quotient$$=3x+2$$ and Remainders=14
$$(i.e. 3x^2-4x+10=(x-2)(3x+2)+14$$ and is in form
$$Divided =(Divisor \times quotient +Remainder)$$

Find the quotient and the remainder $$(4x^3+6x^2-23x-15)\div (3+x)$$

Write the given polynomials in ascending or decending order.
$$(4x^3+6x^2-23x-15)\div (3+x)$$
(i)$$\frac{4x^3}{x}=4x^2$$
(ii) $$4x^2(x+3)=4x^3+12x^2$$
(iii) $$\frac{-6x^2}{x}=6x$$
(iv) $$-6x(x+3)=-6x^2-18x$$
(v) $$\frac{-5x}{x}=-5$$
(vi) $$-5(x+3)=-5x-15$$
$$\therefore$$ Quotient $$=4x^2-6x-5$$
Remainder =0

Determine the value of $$p$$ if $$(x+3)$$ is a factor of $$x^3-3x^2-px+24$$.

According to factor theorem, when $$f(x)$$ is divided by $$(x+3), f(-3)=0$$

$$f(x)=x^3-3x^2-px+24$$

$$f(-3)=(-3)^3-3(-3)^2-p(-3)+24$$

$$\implies 0=-27-27+3p+24$$

$$\implies 0=3p-30$$

$$\implies 3p=30$$

$$\implies p=\dfrac{30}{3}=10$$

If the polynomials $$2x^3+ax^2+4x-12$$ and $$x^3+x^2-2x+a$$ leave the same remainder when divided by (x-3), find the value of a. Also find the remainder.

Let $$p(x)=2x^3+ax^2+4x-12$$,
$$q(x)=x^3+x^2-2x+a$$
When p(x) is divided by (x-3) the remainder is p(3). Now,
$$p(3)=2(3)^3+a(3)^2+4(3)-12$$
$$2(27)+a(9)+12-12$$
$$54+9a$$ ....(1)
When q(x) is divided by (x-3) the remainder is q(3). Now,
$$q(3)=2(3)^3+(3)^2+2(3)+a$$
$$(27)+(9)-6+a$$
$$30+a$$ ......(2)
Given that p(3)=q(3). That is,
$$54+9a=30+a$$ (By (1) and (2))
$$9a-a=30-54$$
$$8a=-24$$
$$\therefore a=-\frac{24}{8}=-3$$
Substituting a=-3 in p(3), we get
$$p(3) =54+9(-3) =54 -27=27$$
$$\therefore$$ The remainder is 27.

Find the remainder when $$f(x)=12x^3-13x^2-5x+7$$ is divided by $$(3x+2).$$

$$f(x)=12x^3-13x^2-5x+7$$
When f(x) is divided by (3x+2) the remainder is $$f\left ( -\frac{2}{3} \right )$$. Now,
$$f\left ( -\frac{2}{3} \right )=12\left ( -\frac{2}{3} \right )^3-13\left ( -\frac{2}{3} \right )^2-5\left ( -\frac{2}{3} \right )+7$$
$$=12\left ( -\frac{8}{27} \right )-13\left ( \frac{4}{9} \right )+\frac{10}{3}+7$$
$$-\frac{32}{9}-\frac{52}{9}+\frac{10}{3}+7=\frac{9}{9}=1$$
$$\therefore$$ The remainder is 1.

Factorize:
$$6x^{2}+11x-10$$

$$6{x^2} + 11x - 10$$

$$ = 6{x^2} + 15x - 4x - 10$$

$$ = 3x\left( {2x + 5} \right) - 2\left( {2x + 5} \right)$$

$$ = \left( {3x - 2} \right)\left( {2x + 5} \right)$$

If $$a+b+c=0$$, show that $$6\left( { a }^{ 5 }+{ b }^{ 5 }+{ c }^{ 5 } \right) =5\left( { a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 } \right) \left( { a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 } \right) $$.

We have identically
$$\left( 1+ax \right) \left( 1+bx \right) \left( 1+cx \right) =1+px+q{ x }^{ 2 }+r{ x }^{ 3 }$$,
where $$p=a+b+c$$, $$q=bc+ca+ab$$, $$r=abc$$.
Hence, using the condition given,
$$\left( 1+ax \right) \left( 1+bx \right) \left( 1+cx \right) =1+q{ x }^{ 2 }+r{ x }^{ 3 }$$.
Taking logarithms and equating the coefficients of $${ x }^{ n }$$, we have $$\dfrac { { \left( -1 \right) }^{ n-1 } }{ n } \left( { a }^{ n }+{ b }^{ n }+{ c }^{ n } \right) =$$ coefficient of $${ x }^{ n }$$ in the expansion of $$\log { \left( 1+q{ x }^{ 2 }+r{ x }^{ 3 } \right) } =$$ coefficient of $${ x }^{ n }$$ in $$\left( q{ x }^{ 2 }+r{ x }^{ 3 } \right) -\dfrac { 1 }{ 2 } { \left( q{ x }^{ 2 }+r{ x }^{ 3 } \right) }^{ 2 }+\dfrac { 1 }{ 3 } { \left( q{ x }^{ 2 }+r{ x }^{ 3 } \right) }^{ 3 }-\cdots $$
By putting $$n=2,3,5$$ we obtain
$$-\dfrac { { a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 } }{ 2 } =q$$, $$\dfrac { { a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 } }{ 3 } =r$$, $$\dfrac { { a }^{ 5 }+{ b }^{ 5 }+{ c }^{ 5 } }{ 5 } =-qr$$;
whence $$\dfrac { { a }^{ 5 }+{ b }^{ 5 }+{ c }^{ 5 } }{ 5 } =\dfrac { { a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 } }{ 3 } \cdot \dfrac { { a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 } }{ 2 }$$,
and the required result at once follows.
If $$a=\beta -\gamma ,b=\gamma -\alpha ,c=\alpha -\beta $$, the given condition is satisfied; hence we have identically for all values of $$\alpha ,\beta ,\gamma $$
$$6\left\{ { \left( \beta -\gamma \right) }^{ 5 }+{ \left( \gamma -\alpha \right) }^{ 5 }+{ \left( \alpha -\beta \right) }^{ 5 } \right\} =5\left\{ { \left( \beta -\gamma \right) }^{ 3 }+{ \left( \gamma -\alpha \right) }^{ 3 }+{ \left( \alpha -\beta \right) }^{ 3 } \right\} \left\{ { \left( \beta -\gamma \right) }^{ 2 }+{ \left( \gamma -\alpha \right) }^{ 2 }+{ \left( \alpha -\beta \right) }^{ 2 } \right\} $$
that is,
$$6\left\{ \left( \beta -\gamma \right)^{ 5 }+{ \left( \gamma -\alpha \right) }^{ 5 }+{ \left( \alpha -\beta \right) }^{ 5 }\right\}=5\left( \beta -\gamma \right) \left( \gamma -\alpha \right) \left( \alpha -\beta \right) \left( { \alpha }^{ 2 }+{ \beta }^{ 2 }+{ \gamma }^{ 2 }-\beta \gamma -\gamma \alpha -\alpha \beta \right) $$;

$$ 6\left ( a^{5}+b^{5}+c^{5} \right )=5\left ( {a^{3}+b^{3}+c^{3}}\right )\left (a^{2}+b^{2}+c^{2} \right ) $$

Hence proved.

Prove that $${ \left( a+b \right) }^{ 5 }-{ a }^{ 5 }-{ b }^{ 5 }=5ab\left( a+b \right) \left( { a }^{ 2 }+ab+{ b }^{ 2 } \right) $$.

L.H.S$$=(a+b)^5-a^5-b^5$$

$$=a^5+5ab^4+10a^2b^3+10a^3b^2+5a^4b+b^5-a^5-b^5$$

$$=5ab^4+10a^2b^3+10a^3b^2+5a^4b$$

$$=5ab(b^3+2ab^2+2a^{2}b+a^3)$$

$$=5ab\{(a+b)(a^2-ab+b^2)+2ab(a+b)\}$$

$$=5ab(a+b)(a^2-ab+b^2+2ab)$$

$$=5ab(a+b)(a^2+ab+b^2)$$

$$=$$R.H.S

Alternate Method

Denote the expression on the left by $$E$$; then $$E$$ is a function of $$a$$ which vanishes when $$a=0$$; hence $$a$$ is a factor of $$E$$; similarly $$b$$ is a factor of $$E$$. Again $$E$$ vanishes when $$a=-b$$, that is $$a+b$$ is a factor of $$E$$; and therefore $$E$$ contains $$ab\left( a+b \right) $$ as a factor. The remaining factor must be of two dimensions, and, since it is symmetrical with respect to $$a$$ and $$b$$, it must be of the form $$A{ a }^{ 2 }+Bab+A{ b }^{ 2 }$$; thus
$${ \left( a+b \right) }^{ 5 }-{ a }^{ 5 }-{ b }^{ 5 }=ab\left( a+b \right) \left( A{ a }^{ 2 }+Bab+A{ b }^{ 2 } \right) $$,
where $$A$$ and $$B$$ are independent of $$a$$ and $$b$$.
Putting $$a=1$$, $$b=1$$, we have $$15=2A+B$$;
putting $$a=2$$, $$b=-1$$, we have $$15=5A-2B$$;
Hence $$A=5$$, $$B=5$$; and thus the required result at once follows.

Show that $${ \left( x+y \right) }^{ 7 }-{ x }^{ 7 }-{ y }^{ 7 }=7xy\left( x+y \right) { \left( { x }^{ 2 }+xy+{ y }^{ 2 } \right) }^{ 2 }$$.

The expression, $$E$$, on the left vanishes when $$x=0$$, $$y=0$$, $$x+y=0$$; hence it must contain $$xy\left( x+y \right) $$ as a factor.
Putting $$x=\omega y$$, we have
$$E=\left\{ { \left( 1+\omega \right) }^{ 7 }-{ \omega }^{ 7 }-1 \right\} { y }^{ 7 }=\left\{ { \left( -{ \omega }^{ 2 } \right) }^{ 7 }-{ \omega }^{ 7 }-1 \right\} { y }^{ 7 }$$
$$=\left( -{ \omega }^{ 2 }-\omega -1 \right) { y }^{ 7 }=0$$;
hence $$E$$ contains $$x-\omega y$$ as a factor; and similarly we may show that it contains $$x-{ \omega }^{ 2 }y$$ as a factor; that is, $$E$$ is divisible by
$$\left( x-\omega y \right) \left( x-{ \omega }^{ 2 }y \right) $$, or $${ x }^{ 2 }+xy+{ y }^{ 2 }$$.
Further, $$E$$ being of degree seven, and $$xy\left( x+y \right) \left( { x }^{ 2 }+xy+{ y }^{ 2 } \right) $$ of five dimensions, the remaining factor must e of the form $$A\left( { x }^{ 2 }+{ y }^{ 2 } \right) +Bxy$$; thus
$${ \left( x+y \right) }^{ 7 }-{ x }^{ 7 }-{ y }^{ 7 }=xy\left( x+y \right) \left( { x }^{ 2 }+xy+{ y }^{ 2 } \right) \left( A{ x }^{ 2 }+Bxy+A{ y }^{ 2 } \right)$$.
Putting $$ x=1$$, $$y=1$$, we have $$21=2A+B$$;
pitting $$x=2$$, $$y=-1$$, we have $$21=5A-2B$$;
whence $$A=7$$, $$B=7$$;
$$\therefore { \left( x+y \right) }^{ 7 }-{ x }^{ 7 }-{ y }^{ 7 }=7xy\left( x+y \right) { \left( { x }^{ 2 }+xy+{ y }^{ 2 } \right) }^{ 2 }$$.

Factorise : $${y^2} - 4y + 3$$

$$y^2-4y+3$$

$$=y^2-y-3y+3$$

$$=y\left( y-1 \right)-3 \left( y-1 \right)$$

$$=\left( y-1 \right) \left( y-3 \right)$$

Hence, the answer is $$\left( y-1 \right) \left( y-3 \right).$$

Factorise: $$2{x^2} + 11x - 21$$

$$2x^2+11x-21$$

$$\Rightarrow 2x^2+14x-3x-21$$

$$\Rightarrow 2x\left( { x+7 } \right) -3\left( { x+7 } \right) $$

$$\Rightarrow \left( { 2x-3 } \right) \left( { x+7 } \right) $$

Hence, the answer is $$ \left( { 2x-3 } \right) \left( { x+7 } \right).$$

The expression $$2{ x }^{ 3 }+b{ x }^{ 2 }-cx+d\quad $$ leaves the same remainder, when divided by $$x+1$$ or $$x-2$$ or $$2x-1$$. Find $$b$$ and $$c$$.

$$\left(x+1\right)\left(x-2\right)\left(2x-1\right)=2{x}^{3}+b{x}^{2}-cx+d$$

$$\Rightarrow\,\left({x}^{2}-2x+x-2\right)\left(2x-1\right)=2{x}^{3}+b{x}^{2}-cx+d$$

$$\Rightarrow\,\left({x}^{2}-x-2\right)\left(2x-1\right)=2{x}^{3}+b{x}^{2}-cx+d$$

$$\Rightarrow\,2{x}^{3}-{x}^{2}-2{x}^{2}+x-4x+2=2{x}^{3}+b{x}^{2}-cx+d$$

$$\Rightarrow\,2{x}^{3}-3{x}^{2}-3x+2=2{x}^{3}+b{x}^{2}-cx+d$$

Comparing the coefficients, we get

$$b=-3,c=3,d=2$$

$$\therefore\,b=-3,c=3,d=2$$

Factorize : $$x^2-24x-180$$

$$x^2-24x-180$$

$$=x^2-30x+6x-180$$

$$=x(x-30)+6(x-30)$$

$$=(x-30)(x+6)$$

Factorise : $$6 - x - {x^2}$$

$$\textbf{Step 1: Factorizing}$$

$$\text{We have }6-x-x^2$$$$= 6-3x+2x-x^2$$

$$= (6-3x)+(2x-x^2)$$

$$= 3(2-x)+x(2-x)$$

$$= (3+x)(2-x)$$

$$\mathbf{\textbf{Hence, }6-x-x^2 \textbf{ can be factorised to }(3+x)(2-x)}$$

Factorise : $${x^2} - 11x - 80$$

$$x^2-11x-80$$

$$=x^2-16x+5x-80$$

$$=x\left( x-16 \right) +5\left( x-16 \right) $$

$$=\left( x-16 \right) \left( x+5 \right) $$

Hence, the answer is $$\left( x-16 \right) \left( x+5 \right).$$

Simplify :
i) $$\cfrac{-14x^8y^5+21x^{10}y-28x^7y^6}{7x^7y^8}$$
ii) $$\cfrac{15a^4x^8-30a^{7}x^5-45a^6x^6}{20a^{14}x^5}$$
iii) $$\cfrac{-60x^4a^5-75x^{3}a^6+8x^5a^4}{-20x^8a^4}$$

i) $$\cfrac{-14x^8y^5+21x^{10}y-28x^7y^6}{7x^7y^8}$$ $$=-\cfrac{2x}{y^3}+\cfrac{3x^3}{y^7}-\cfrac{4}{y^2}$$

$$=\cfrac{1}{y^2}\left(\cfrac{-2x}{y}+\cfrac{3x^3}{y^5}-\small{4}\right)$$

ii) $$\cfrac {15a^4x^8-30a^{7}x^5-45a^6x^6}{20a^{14}x^5}$$$$=\cfrac {3x^3}{4a^{10}}-\cfrac{6}{4a^7}-\cfrac{9x}{4a^8}$$

$$=\cfrac {3}{4a^7}\left(\cfrac{x^3}{a^3}-\small{2}-\cfrac{3x}{a}\right)$$

iii) $$\cfrac{-60x^4a^5-75x^{3}a^6+8x^5a^4}{-20x^8a^4}$$$$=\left(\cfrac{3a}{x^4}+\cfrac{15a^2}{4x^5}-\cfrac{2}{5x^3}\right)$$

Factorise : $${z^2} - 32z - 105$$

$$z^2-32z-105$$

$$=z^2-35z+3z-105$$

$$=z\left( z-35 \right) +3\left( z-35 \right) $$

$$=\left( z+3 \right) \left( z-35 \right) $$

Hence, the answer is $$\left( z+3 \right) \left( z-35 \right). $$

Factorise : $$6{x^2} + 17x + 12$$

Factorise : $$6x^2+17x+12$$ using common method.

$$6x^2+17x+12$$

The coefficient of $$x^2$$ is $$6$$ and constant is $$12.$$ The product of two coefficients $$=6\times 12=72$$

Now, the coefficient of middle term $$=17$$

We know, that the factors of $$72$$ such that the sum of these factors is $$17$$ are $$8\;\&\;9 \left(8\times 9=72,\; 8+9=17\right)$$

So, $$6x^2+8x+9x+12$$

$$\Rightarrow 2x\left( { 3x+4 } \right) +3\left( { 3x+4 } \right) $$

$$\Rightarrow \left( { 2x+3 } \right) \left( { 3x+4 } \right). $$

Hence, the answer is $$\left( { 2x+3 } \right) \left( { 3x+4 } \right). $$

Resolve into factors of $$4{x^2} - 25{y^2} + 2x + 5y$$

$$(2x)^2 - (5y)^2 +2x+5y$$

$$=(2x-5y)(2x+5y)+1(2x+5y)$$

$$=(2x+5y)(2x-5y+1)$$

Factorise
$$x^3 - 2x^2 - x + 2$$

$$x^3 - 2x^2 - x + 2$$

$$=x^2(x - 2)- 1(x - 2)$$

$$=(x^2-1)(x-2)$$

$$=(x+1)(x-1)(x-2)$$

Express in standard form
$$(x-a) (x-b)$$

$$\left( x-a \right) \left( x-b \right) $$

$$=x^2-\left( a+b \right) x+ab$$

Hence, the answer is $$x^2-\left( a+b \right) x+ab.$$

Factorise: $$6{x^2} + 11x - 10$$

$$6x^2+11x-10$$

$$\Rightarrow 6x^2+15x-4x-10$$

$$\Rightarrow 3x\left( { 2x+5 } \right) -2\left( { 2x+5 } \right) $$

$$\Rightarrow \left( { 3x-2 } \right) \left( { 2x+5 } \right) $$

Hence, the answer is $$\left( { 3x-2 } \right) \left( { 2x+5 } \right).$$

Factorise: $$18{x^2} + 3x - 10$$

$$18x^2+3x-10$$

$$\Rightarrow 18x^2+15x-12x-10$$

$$\Rightarrow 3x\left( { 6x+5 } \right) -2\left( { 6x+5 } \right) $$

$$\Rightarrow \left( { 3x-2 } \right) \left( { 6x+5 } \right) $$

Hence, the answer is $$\left( { 3x-2 } \right) \left( { 6x+5 } \right).$$

Factorize $$y^2-( a+ b) y + ab$$

$$\textbf{Step 1: Open the bracket and simplify.}$$

$$y^2-(a+b)y + ab= $$$$ y^2-ay-by+ab$$

$$= y(y-a)-b(y-a)$$

$$= (y-a) (y-b)$$

$$\textbf{Hence, (y-a) (y-b) are the two factors.}$$

Factorize:
$$x^2+3\sqrt{2}x+4=0$$

$$x^2+3\sqrt2 x+4=0$$

$$\implies x^2+2\sqrt2 x +\sqrt2 x+4=0$$

$$\implies x(x+2\sqrt2)+\sqrt2(x+2\sqrt2)=0$$

$$\implies (x+\sqrt2)(x+2\sqrt2)=0$$

Divide P(x) by g(x)
P(x) $$={x^4} - 3{x^2} - 4$$
g(x)$$ = x + 2$$

$$p\left( x \right) =x^4-3x^2-4$$

$$g\left( x \right) =x+2$$

Since divisor, we can divide the polynomial by synthetic division.

$$\therefore$$ Quotient $$:x^3-2x^2+x-2.$$

Hence, the answer is $$x^3-2x^2+x-2.$$

Factorize:
$$(i)\ \ \ {x^2} + 9x + 18$$
$$(ii)\ \ 6{x^2} + 7x - 3$$
$$(iii)\ 2{x^2} - 7x - 15$$
$$(iv)\ \ 84 - 2r - 2{r^2}$$

$$(i). $$

$$x^2+9x+18 = x^2+3x+6x+18$$

$$=x{ \left( x+3 \right) }+6{ \left( x+3 \right) }$$

$$={ \left( x+3 \right) }{ \left( x+6 \right) }$$

$$(ii).$$

$$ 6x^2+7x-3= 6x^2+9x-2x-3$$

$$=3x{ \left( 2x+3 \right) }-1{ \left( 2x+3 \right) }$$

$$={ \left( 3x-1 \right) }{ \left( 2x+3 \right) }$$

$$(iii).$$

$$ 2x^2-7x-15=2x^2-10x+3x-15$$

$$=2x{ \left( x-5 \right) }+3{ \left( x-5 \right) }$$

$$={ \left( x-5 \right) }{ \left( 2x+3 \right) }$$

$$(iv).$$

$$ 84-2r-2r^2=-\left( 2r^2+2r-84 \right) $$

$$=-\left(2r^2+14r+12r-84\right) $$

$$=-\left( 2r\left( r+7 \right) -12\left( r+7 \right) \right) $$

$$=-\left( r+7 \right) \left( 2r-12 \right)$$

If you divide $$f\left( x \right) = {x^3} + 3{x^2} - kx - 12$$ by $$\left( {x - 3} \right)$$, you get remainder $$30$$. Find $$k$$ and also find the quotient.

$$f(x)=x^3+3x^2-kx-12$$$

According to remainder theorem

$$f(3)=30$$

$$\implies (3)^2+3(3)^3-k(3)-12=30$$

$$\implies 27+27-3k-12=30 \implies 3k=54-12-30=12$$

$$\implies k=4$$

$$f(x)=x^3+3x^2-4x-12$$

$$\implies \cfrac{x^3+3x^2-4x-12}{x-3} = x^2+6x+14$$

So, Quotient $$=x^2+6x+14$$

Simplify $$\dfrac {{x}^{2}}{9}-\dfrac {{y}^{2}}{4}$$

$$\begin{array}{l} \dfrac { { { x^{ 2 } } } }{ 9 } -\dfrac { { { y^{ 2 } } } }{ 4 } \\ ={ \left( { \dfrac { x }{ 3 } } \right) ^{ 2 } }-{ \left( { \dfrac { y }{ 2 } } \right) ^{ 2 } } \\ =\left( { \dfrac { x }{ 3 } -\dfrac { y }{ 2 } } \right) \left( { \dfrac { x }{ 3 } +\dfrac { x }{ 2 } } \right) \, \, \, \left[ { { a^{ 2 } }-{ b^{ 2 } }=\left( { a-b } \right) \left( { a+b } \right) } \right] \end{array}$$

Let $$p(x) = x^{4}-3x^{2}+2x + 5$$. Find the remainder when $$p(x)$$ is divided by $$(x-1)$$.

We know that the remainder when a polynomial $$p(x)$$ is divided by $$(x - a)$$ is $$p(a)$$.

Given that,

$$p(x) = x^4 -3x^2 +2x +5$$

Divisor $$=(x-1)$$

So, The Remainder $$= p(1)$$

$$= (1)^4 - 3(1)^2 + 2(1) + 5$$

$$= 1 - 3 +2 +5$$

$$= 5$$

factorise
$$9x^{2}+12xy$$

$$9{ x }^{ 2 }+12xy$$

$$=\left( 3 \right) \left( 3x^2+4xy \right) $$

$$=\left( 3x \right) \left( 3x+4y \right) $$

Divide $$({x^2} + 5x + 6 )$$ by $$( x + 2)$$.

We divide the given polynomial $$x^2+5x+6$$ by the monomial $$x+2$$ as shown below:

$$\dfrac { x^{ 2 }+5x+6 }{ x+2 } \\ =\dfrac { x^{ 2 }+3x+2x+6 }{ x+2 } \\ =\dfrac { x(x+3)+2(x+3) }{ x+2 } \\ =\dfrac { (x+2)(x+3) }{ x+2 } \\ =x+3$$

Hence, $$\dfrac { x^{ 2 }+5x+6 }{ x+2 } =x+3$$.

Factorize: $$2x^{2}-7x-15$$

Simplifying the equation,

$$2{x^2} - 7x - 15$$

$$ = 2{x^2} - 10x + 3x - 15$$

$$ = 2x\left( {x - 5} \right) + 3\left( {x - 5} \right)$$

$$ = \left( {2x + 3} \right)\left( {x - 5} \right)$$

Factorise:$$15x+5$$

Simplifying $$15x + 5$$.

$$15x + 5 = 5\left( {3x + 1} \right)$$

Factorize the following:$$8{x}^{2}-14x+8x-14$$

Simplifying $$8{x^2} - 14x + 8x - 14$$.

$$8{x^2} - 14x + 8x - 14$$

$$ = 2x\left( {4x - 7} \right) + 2\left( {4x - 7} \right)$$

$$ = \left( {2x + 2} \right)\left( {4x - 7} \right)$$

$$ = 2\left( {x + 1} \right)\left( {4x - 7} \right)$$

Factorise $${X}^{2}-7X+10=0$$

Simplifying $${X^2} - 7X + 10 = 0$$

$${X^2} - 5X - 2X + 10 = 0$$

$$X\left( {X - 5} \right) - 2\left( {X - 5} \right) = 0$$

$$\left( {X - 5} \right)\left( {X - 2} \right) = 0$$

Factorize the following:
$$(16-81{x}^{2})$$

Simplifying $$16 - 81{x^2}$$

$$16 - 81{x^2}$$

$$ = {\left( 4 \right)^2} - {\left( {9x} \right)^2}$$

$$ = \left( {4 + 9x} \right)\left( {4 - 9x} \right)$$

Find the remainder when $${x^2}\, - \,a{x^2}\, + \,8x\, + \,a$$ is divided by $$(x - a)$$

Here the concept of reminder theorem can be used.

this theorem states that the reminder when f(x) is divided by (x-a) is f(a).

let

$$ f(x)$$= $$x^2$$- $$ax^2$$+$$8x$$+$$a$$

We can find f(a) by substituting '$$a$$' in the replace of $$x$$ in the above equation.

$$ f(a)$$= $$a^2$$- $$a \times a^2$$+$$8a$$+$$a$$

$$ f(a)$$= $$a^2$$- $$a^3$$+$$9a$$

Hence the reminder is $$a^2$$- $$a^3$$+$$9a$$

Divide $$p(x) = 2x^3 - 11x^2 + 19x - 10$$ by g(x) = 2x -Find the quotient and remainder.

Given,

$$p(x)=2x^3-11x^2+19x-10$$

$$g(x)=2x-5$$

$$\underline {\ \ \ x^2-3x+2\ \ \ \ \quad \quad \quad \quad }$$

$$2x-5)2x^3-11x^2+19x-10$$

$$2x^3-5x^2$$

$$(-)$$ $$(+)$$

____________________

$$-6x^2+19x$$

$$-6x^2+15x$$

$$(+)$$ $$(-)$$

____________________

$$+4x-10$$

$$(-)$$ $$(+)$$

_________________

$$0$$

$$\Rightarrow 2x^3-11x^2+19x-10=(2x-5)(x^2-3x+2)$$

$$\therefore$$ Quotient $$=x^2-3x+2$$ and remainder $$=0$$.

Factorize the following:$$3x-{3}^{2}$$

Simplifying $$3x - {3^2}$$

$$=3x - {3^2}$$

Taking 3 common from both the terms:

$$ = 3\left( {x - 3} \right)$$

Factorize:
$$3x^{2}-14x+18$$

$$3{x^2} - 14x + 18$$

Factor with discriminant method,

$$x = \dfrac{{14 \pm \sqrt {{{\left( { - 14} \right)}^2} - 4 \times 3 \times 18} }}{{2 \times 3}}$$

$$x = \dfrac{{14 \pm \sqrt {20} i}}{6}$$

$$ = \left( {x - \left( {\dfrac{{14 - \sqrt {20} i}}{6}} \right)} \right)\left( {x - \left( {\dfrac{{14 + \sqrt {20} i}}{6}} \right)} \right)$$

Factorize $$y^{2}-10y+25$$

Simplifying $${y^2} - 10y + 25$$.

$${y^2} - 10y + 25$$

$$ = {y^2} - 5y - 5y + 25$$

$$ = y\left( {y - 5} \right) - 5\left( {y - 5} \right)$$

$$ = \left( {y - 5} \right)\left( {y - 5} \right)$$

Factorise $$(i) x^{2}+3\sqrt{3}x+6$$
$$(ii) 6x^{2}+\sqrt{5}x-10$$

(i)$$x^2+3\sqrt 3x+6$$

This can be written as

$$\Rightarrow x^2+\sqrt 3x+2\sqrt 3x+6$$

$$\Rightarrow x(x+\sqrt 3)+2\sqrt 3(x+\sqrt 3)$$

$$\Rightarrow (x+\sqrt 3)(x+2\sqrt 3)$$

Therefore, $$\Rightarrow x^2+3\sqrt3x+6= (x+\sqrt 3)(x+2\sqrt 3)$$

(ii)$$6x^2+\sqrt 5x-10$$

This can be written as

$$\Rightarrow 6(x^2+\dfrac{\sqrt 5}{6}x-\dfrac{5}{3})$$

$$\Rightarrow 6(x^2-\dfrac{\sqrt 5}{2}x+\dfrac{2\sqrt 5}{3}x-\dfrac{5}{3})$$

$$\Rightarrow 6[x(x-\dfrac{\sqrt 5}{2})+\dfrac{2\sqrt 5}{3}(x-\dfrac{\sqrt 5}{2})]$$

$$\Rightarrow 6(x+\dfrac{2\sqrt 5}{3})(x-\dfrac{\sqrt 5}{2})$$

Therefore, $$\Rightarrow 6x^2+\sqrt5x-10= 6(x+\dfrac{2\sqrt 5}{3})(x-\dfrac{\sqrt 5}{2})$$

Factorise : $$x^{2}+3\sqrt{3}x+6$$

$$x^2+3\sqrt 3x+6$$

This can be written as

$$\Rightarrow x^2+\sqrt 3x+2\sqrt 3x+6$$

$$\Rightarrow x(x+\sqrt 3)+2\sqrt 3(x+\sqrt 3)$$

$$\Rightarrow (x+\sqrt 3)(x+2\sqrt 3)$$

Therefore, $$\Rightarrow x^2+3\sqrt3x+6= (x+\sqrt 3)(x+2\sqrt 3)$$

Find the remainder when the polynomial $$4y^3 - 3y^2 - 5y + 1$$ is divided by $$2y + 3$$.

$$2y+3$$ $$)4y^3-3y^2-5y+1($$ $$2y^2-\dfrac{9}{2}y+\dfrac{17}{4}$$

$$4y^3+6y^2$$

$$(-)$$

----------------------------------------

$$-9y^2-5y$$

$$-9y^2-\dfrac{27}{2}y$$

$$(-)$$

----------------------------------------

$$\dfrac{17}{2}y+1$$

$$\dfrac{17}{2}y+\dfrac{51}{4}$$

$$(-)$$

---------------------------------------------

$$-\dfrac{47}{4}$$

$$\dfrac{4y^3-3y^2-5y+1}{2y+3} = 2y^2-\dfrac{9}{2}y+\dfrac{17}{4} - \dfrac {47}{4(2y+3)}$$

Express in the product of two polynomial$$x^4+y^4+x^2y^2$$.

Let us add and subtract $$x^2y^2$$ in the given expression $$x^4+y^4+x^2y^2$$ and then solve as shown below:

$$(x^{ 4 }+y^{ 4 }+x^{ 2 }y^{ 2 }+x^{ 2 }y^{ 2 })-x^{ 2 }y^{ 2 }\\ =[(x^{ 2 })^{ 2 }+(y^{ 2 })^{ 2 }+2x^{ 2 }y^{ 2 }]-x^{ 2 }y^{ 2 }\\ =[(x^{ 2 }+y^{ 2 })^{ 2 }]-x^{ 2 }y^{ 2 }\quad \quad \quad \quad \left( \because \quad (a+b)^{ 2 }=a^{ 2 }+b^{ 2 }+2ab \right) \\ =(x^{ 2 }+y^{ 2 })^{ 2 }-(xy)^{ 2 }\\ =(x^{ 2 }+y^{ 2 }-xy)(x^{ 2 }+y^{ 2 }+xy)\quad \quad (\because \quad a^{ 2 }-b^{ 2 }=(a-b)(a+b))$$

Hence, $$x^{ 4 }+y^{ 4 }+x^{ 2 }y^{ 2 }=(x^{ 2 }+y^{ 2 }-xy)(x^{ 2 }+y^{ 2 }+xy)$$.

Factorize:
$$(1){ \quad x }^{ 3 }-{ 2x }^{ 2 }-x+2\\ (2)\quad { x }^{ 3 }-{ 3x }^{ 2 }-9x-5\\ (3)\quad { x }^{ 3 }+{ 13x }^{ 2 }+32x+20\\ (4)\quad { y }^{ 3 }+{ y }^{ 2 }-y-1$$

(1) $$x^{3}-2x^{2}-x+2$$

$$=x^{2}(x-2)-1(x-2)$$

$$=(x-2)(x^{2}-1)$$

$$=(x-2)(x-1)(x+1)$$

(2) $$x^{3}-3x^{2}-9x-5$$

$$=x^{3}+(x^{2}-4x^{2})-(4x+5x)-5$$

$$=(x^{3}+x^{2})-(4x^{2}+4x)-(5x+5)$$

$$=x^{2}(x+1)-4x(x+1)-5(x+1)$$

$$=(x^{2}-4x-5)(x+1)-5(x+1)$$

$$=(x^{2}-4x-5)(x+1)$$

$$=(x^{2}-5x+x-5)(x+1)$$

$$=(x-5)(x+1)^{2}$$

(3) $$x^{3}+13x^{2}+32x+20$$

$$=(x^{3}+x^{2})+(12x^{2}+12x)+(20x+20)$$

$$=(x^{2}+12x+20)(x+1)$$

$$=(x+1)(x+2)(x+10)$$

(4) $$y^{3}+y^{2}-y-1=y^{2}(y+1)-1(y+1)$$

$$=(y^{2}-1)(y+1)$$

$$=(y-1)(y+1)^{2}$$

Find the remainder when $$x^4+4x^3-5x^2-6x+7$$ is divisible by $$x-3$$.

We divide $$x^4+4x^3-5x^2-6x+7$$ by $$(x-3)$$ as shown in the above image:

From the division, we observe that the quotient is $$x^3+7x^2+16x+42$$ and the remainder is $$133$$.

Hence, the remainder is $$133$$.

1231014_1074148_ans_ec2bb7f3465e48e9b87658d8ef85c084.png

Factorise $$x^2-3x+2$$.

In the given polynomial $$x^2-3x+2$$,

The first term is $$x^2$$ and its coefficient is $$1$$.

The middle term is $$-3x$$ and its coefficient is $$-3$$.

The last term is a constant term $$2$$.

Multiply the coefficient of the first term by the constant $$2\times 1=2$$.

We now find the factor of $$2$$ whose sum equals the coefficient of the middle term, which is $$-3$$ and then factorize the polynomial $$x^2-3x+2$$ as shown below:

$$x^{ 2 }-3x+2\\ =x^{ 2 }-x-2x+2\\ =x(x-1)-2(x-1)\\ =(x-1)(x-2)$$

Hence, $$x^{ 2 }-3x+2=(x-1)(x-2)$$.

Divide :
$${2x}^{3}-{5x}^{2}-{3x}\ by (x-1)$$ ?

$$\begin{array}{c}2{x^3} - 5{x^2} - 3x = x\left( {2{x^2} - 5x - 3} \right)\\ = x\left( {2{x^2} - 6x + x - 3} \right)\\ = x\left( {2x\left( {x - 3} \right) + 1\left( {x - 3} \right)} \right)\\ = x\left( {2x + 1} \right)\left( {x - 3} \right)\end{array}$$

So,

$$2{x^3} - 5{x^2} - 3x$$ by x-1 is ,

$$\frac{{x\left( {2x + 1} \right)\left( {x - 3} \right)}}{{x - 1}}$$

Factorise the following:
$$27a^{3} - 8b^{3} - 54a^{2}b + 36ab^{2}$$

$$27a^{3} - 8b^{3} - 54a^{2}b + 36ab^{2}$$
$$= (3a)^{3} - (2b)^{3} - 3(3a)(2b) [3a - 2b]$$
$$= (3a - 2b)^{3}$$
$$[\because (a - b)^{3} = a^{3} - b^{3} - 3ab (a - b)]$$

Find the remainder when $$x^4+4x^3-5x^2-6x+7$$ is divided by $$x+1$$.

We have, $$P(x)=x^{4}+4x^{3}-5x^{2}-6x+7$$

here Divisor is $$x+1$$

$$\qquad \qquad { x }^{ 3 }+{ 3x }^{ 2 }-8x+1\\ (x+1)\sqrt { { x }^{ 4 }+{ 4x }^{ 3 }-{ 5x }^{ 2 }-6x+7\\ { x }^{ 3 }+{ x }^{ 3 } } \\ \qquad \quad \quad -\quad \quad -\\ \qquad \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \\ \qquad \qquad \qquad { 3x }^{ 3 }-{ 5x }^{ 2 }\\ \qquad \qquad \qquad { 3x }^{ 3 }+{ 3x }^{ 2 }\\ \qquad \qquad \qquad -\quad \quad -\\ \qquad \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \\ \qquad \qquad \qquad \qquad -{ 8x }^{ 2 }-6x\\ \qquad \qquad \qquad \qquad -{ 8x }^{ 2 }-8x\\ \qquad \qquad \qquad \qquad +\quad \quad +\\ \qquad \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \\ \quad \quad \quad \quad \qquad \qquad \qquad \quad 2x+7\\ \qquad \qquad \qquad \qquad \qquad \quad 2x+2\\ \qquad \qquad \qquad \qquad \qquad -\quad -\\ \qquad \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 5$$

We get $$5$$ as remainder.

Find the remainder when $$x^4+4x^3-5x^2-6x+7$$ is divided by $$x-2$$.

We divide $$x^4+4x^3-5x^2-6x+7$$ by $$(x-2)$$ as shown in the above image:

From the division, we observe that the quotient is $$x^3+6x^2+7x+8$$ and the remainder is $$23$$.

Hence, the remainder is $$23$$.

1231017_1074154_ans_c9883a455f0f4673bf98eaec94d990e2.png

Find the remainder when $$x^3-ax^2+6x-a$$ is divided by $$x-a$$.

We divide $$x^3-ax^2+6x-a$$ by $$(x-a)$$ as shown in the above image:

From the division, we observe that the quotient is $$x^2+6$$ and the remainder is $$5a$$.

Hence, the remainder is $$5a$$.

1232059_1075288_ans_93b8c98ba38b48d3ba54bb7b427e5567.jpg

Find the remainder when $$x^4+4x^3-5x^2-6x+7$$ is divided by $$x+2$$.

We divide $$x^4+4x^3-5x^2-6x+7$$ by $$(x+2)$$ as shown in the above image:

From the division, we observe that the quotient is $$x^3+2x^2-7x+8$$ and the remainder is $$-9$$.

Hence, the remainder is $$-9$$.

1231020_1074157_ans_757c0fe2ba854ec1abd12436f597f7ce.png

Find the remainder when $$x^4+4x^3-5x^2-6x+7$$ is divided by $$x-1$$.

We divide $$x^4+4x^3-5x^2-6x+7$$ by $$(x-1)$$ as shown in the above image:

From the division, we observe that the quotient is $$x^3+5x^2-6$$ and the remainder is $$1$$.

Hence, the remainder is $$1$$.

1231023_1074159_ans_7286b11cc4c74e3c8999c9b07be39f9d.png

Solve:
$$x^2+9x+18$$.

In the given polynomial $$x^2+9x+18$$,

The first term is $$x^2$$ and its coefficient is $$1$$.

The middle term is $$9x$$ and its coefficient is $$9$$.

The last term is a constant term $$18$$.

Multiply the coefficient of the first term by the constant $$1\times 18=18$$.

We now find the factor of $$18$$ whose sum equals the coefficient of the middle term, which is $$9$$ and then factorize the polynomial $$x^2+9x+18$$ as shown below:

$$x^{ 2 }+9x+18\\ =x^{ 2 }+3x+6x+18\\ =x(x+3)+6(x+3)\\ =(x+3)(x+6)$$

Hence, $$x^{ 2 }+9x+18=(x+3)(x+6)$$.

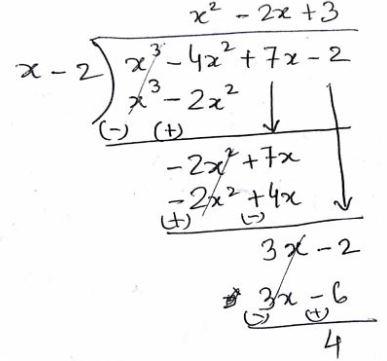
Find the remainder:
$$\left( {{x^3} - 4{x^2} + 7x - 2} \right) \div \left( {x - 2} \right)$$.

$$(x^3 -4x^2+7cx-2)\div (x-2)$$

$$[\because \ x^3=x.x^2]$$

$$[\because \ -2x^2=x.(-2x)]$$

$$[\because \ 3x^x.(3)]$$

1420330_1078364_ans_874d970176274dcdb254d86889594463.png

Evaluate:
$$\dfrac{1}{2}x^2-3x+4$$.

$$\dfrac { 1 }{ 2 } { x }^{ 2 }-3x+4$$

$$=\dfrac { 1 }{ 2 } { x }^{ 2 }-2x-x+4$$

$$=1/2x\left( x-4 \right) -1\left( x-4 \right) $$

$$=\left( x-4 \right) \left( 1/2x-1 \right) $$

Factorise $$a^3-36a$$.

\begin{array}{l} a\left( { { a^{ 2 } }-36 } \right) \\ a\left( { a-b } \right) \left( { a+b } \right) \end{array}

Factorise
$$12x +15$$

$$=12x+15$$

$$=3×4×x+3×5$$

$$=3(4x+5)$$

$$3x^2-x-4$$.

In the given polynomial $$3x^2-x-4$$,

The first term is $$3x^2$$ and its coefficient is $$3$$.

The middle term is $$-x$$ and its coefficient is $$-1$$.

The last term is a constant term $$-4$$.

Multiply the coefficient of the first term by the constant $$3\times -4=-12$$.

We now find the factor of $$-12$$ whose sum equals the coefficient of the middle term, which is $$-1$$ and then factorize the polynomial $$3x^2-x-4$$ as shown below:

$$3x^{ 2 }-x-4\\ =3x^{ 2 }+3x-4x-4\\ =3x(x+1)-4(x+1)\\ =(3x-4)(x+1)$$

Hence, $$3x^{ 2 }-x-4=(3x-4)(x+1)$$.

Solve:
$$5{x^2} - 22x - 15 = 0$$

By using middle term split method,

$$5{ x }^{ 2 }-22x-15=0$$

$$\Rightarrow 5{ x }^{ 2 }-25x+3x-15=0$$

$$\Rightarrow 5x(x -5)+3(x-5)=0$$

$$\Rightarrow (x-5)(5x+3)=0$$

Either $$x-5=0 \Rightarrow x = 5$$ or $$5x+3=0 \Rightarrow x=-\dfrac{3}{5}$$

Factorize - $${x^2} + \dfrac{1}{{{x^2}}} - 2x - \dfrac{2}{x} + 2$$

We have,

$${{x}^{2}}+\dfrac{1}{{{x}^{2}}}-2x-\dfrac{2}{x}+2$$

$$ {{x}^{2}}+\dfrac{1}{{{x}^{2}}}+2-2\left( x+\dfrac{1}{x} \right) $$

$$ {{\left( x+\dfrac{1}{x} \right)}^{2}}-2\left( x+\dfrac{1}{x} \right) $$

$$ \left( x+\dfrac{1}{x} \right)\left( x+\dfrac{1}{x}-2 \right) $$

Hence, this is the answer.

Give possible expressions for the length and breadth of the following rectangles, in which their areas are given:
Area: $$25{a}^{2}-35a+12$$

$$=25a^2-35a+12$$

$$=25a^2-25a-12a+12$$

$$=25a(a-1)-12(a-1)$$

$$=(25a-12)(a-1)$$

Area $$=l.b =$$ length $$\times $$ breath

1. $$l=25a-12,b=a-1$$

2. $$l=a-1,b=25a-12$$

$$4x^2+4\sqrt{3}x+3=0$$.

In the given quadratic polynomial $$4x^{ 2 }+4\sqrt { 3 } x+3=0$$,

The first term is $$4x^2$$ and its coefficient is $$4$$.

The middle term is $$4\sqrt { 3 } x$$ and its coefficient is $$4\sqrt { 3 } $$.

The last term is a constant term $$3$$.

Multiply the coefficient of the first term by the constant $$4\times 3=12$$.

We now find the factor of $$12$$ whose sum equals the coefficient of the middle term, which is $$4\sqrt { 3 } $$ and then factorize the quadratic polynomial $$4x^{ 2 }+4\sqrt { 3 } x+3=0$$ as shown below:

$$4x^{ 2 }+4\sqrt { 3 } x+3=0\\ \Rightarrow 4x^{ 2 }+2\sqrt { 3 } x+2\sqrt { 3 } x+3=0\\ \Rightarrow 2x(2x+\sqrt { 3 } )+\sqrt { 3 } (2x+\sqrt { 3 } )=0\\ \Rightarrow (2x+\sqrt { 3 } )(2x+\sqrt { 3 } )=0\\ \Rightarrow (2x+\sqrt { 3 } )=0,\quad (2x+\sqrt { 3 } )=0\\ \Rightarrow 2x=-\sqrt { 3 } ,\quad 2x=-\sqrt { 3 } \\ \Rightarrow x=-\dfrac { \sqrt { 3 } }{ 2 } ,\quad x=-\dfrac { \sqrt { 3 } }{ 2 }$$

Hence, $$x=-\dfrac { \sqrt { 3 } }{ 2 } ,-\dfrac { \sqrt { 3 } }{ 2 } $$.

Factorise:
$$a^2 + 12a+32$$

In the given polynomial $$a^2+12a+32$$,

The first term is $$a^2$$ and its coefficient is $$1$$.

The middle term is $$12a$$ and its coefficient is $$12$$.

The last term is a constant term $$32$$.

Multiply the coefficient of the first term by the constant $$1\times 32=32$$.

We now find the factor of $$32$$ whose sum equals the coefficient of the middle term, which is $$12$$ and then factorize the polynomial $$a^2+12a+32$$ as shown below:

$$a^{ 2 }+12a+32\\ =a^{ 2 }+4a+8a+32\\ =a(a+4)+8(a+4)\\ =(a+4)(a+8)$$

Hence, $$a^{ 2 }+12a+32=(a+4)(a+8)$$.

Factorise:
$$z^2+13z+40$$

In the given polynomial $$z^2+13z+40$$,

The first term is $$z^2$$ and its coefficient is $$1$$.

The middle term is $$13z$$ and its coefficient is $$13$$.

The last term is a constant term $$40$$.

Multiply the coefficient of the first term by the constant $$1\times 40=40$$.

We now find the factor of $$40$$ whose sum equals the coefficient of the middle term, which is $$13$$ and then factorize the polynomial $$z^2+13z+40$$ as shown below:

$$z^{ 2 }+13z+40\\ =z^{ 2 }+8z+5z+40\\ =z(z+8)+5(z+8)\\ =(z+5)(z+8)$$

Hence, $$z^{ 2 }+13z+40=(z+5)(z+8)$$.

Factorise:
$$s^2+12s+27$$

In the given polynomial $$s^2+12s+27$$,

The first term is $$s^2$$ and its coefficient is $$1$$.

The middle term is $$12s$$ and its coefficient is $$12$$.

The last term is a constant term $$27$$.

Multiply the coefficient of the first term by the constant $$1\times 27=27$$.

We now find the factor of $$27$$ whose sum equals the coefficient of the middle term, which is $$12$$ and then factorize the polynomial $$s^2+12s+27$$ as shown below:

$$s^{ 2 }+12s+27\\ =s^{ 2 }+9s+3s+27\\ =s(s+9)+3(s+9)\\ =(s+3)(s+9)$$

Hence, $$s^{ 2 }+12s+27=(s+3)(s+9)$$.

Factorize $$1+2p + p^2$$

$${p}^{2}+2p+1$$

$${p}^{2}+p+p+1$$

$$p\left(p+1\right)+1\left(p+1\right)$$

$$\left(p+1\right) \left(p+1\right)={ \left(p+1\right)}^{2}$$

Factorise
$$a^2+4b^2-4ab-4c^2$$.

$${ a }^{ 2 }+{ (2b) }^{ 2 }-2(2b)(a)-{ (2c) }^{ 2 }$$

using $${ x }^{ 2 }+{ y }^{ 2 }-2xy={ (x-y) }^{ 2 }$$ we get ,

$${ (a-2b) }^{ 2 }-{ (2c) }^{ 2 }$$

using $${ x }^{ 2 }-{ y }^{ 2 }=(x+y)(x-y)$$ , we get

$$(a-2b+2c).(a-2b-2c)$$

Factories the given algebraic expression by taking out the common terms. Also, write the common term
$$8ab+14a^{2}b-2a^{3}-12ab^{2}$$

We first factorize each term of the given expression $$8ab+14a^2b−2a^3−12ab^2$$ as shown below:

$$8ab=2\times 2\times 2\times a\times b\\ 14a^{ 2 }b=2\times 7\times a\times a\times b\\ 2a^{ 3 }=2\times a\times a\times a\\ 12ab^{ 2 }=2\times 2\times 3\times a\times b\times b$$

The common factors are $$2$$ and $$a$$, therefore, the HCF is $$2\times a=2a$$.

Now, by taking out the common term(HCF), we have:

$$8ab+14a^{ 2 }b−2a^{ 3 }−12ab^{ 2 }=2a(4b+7ab-2a^{ 2 }-6b^{ 2 })$$

Hence, the common term is $$2a$$.

Factorise each of the following:
$$9x^2-6x+1$$

In the given polynomial $$9x^2-6x+1$$,

The first term is $$9x^2$$ and its coefficient is $$9$$.

The middle term is $$-6x$$ and its coefficient is $$-6$$.

The last term is a constant term $$1$$.

Multiplication of the coefficient of the first term by the constant is 9$$.

We now find the factor of $$9$$ whose sum equals the coefficient of the middle term, which is $$-6$$ and then factorize the polynomial $$9x^2-6x+1$$ as shown below:

$$9x^{ 2 }-6x+1\\ =9x^{ 2 }-3x-3x+1\\ =3x(3x-1)-1(3x-1)\\ =(3x-1)(3x-1)\\ =(3x-1)^{ 2 }$$

Hence, $$9x^{ 2 }-6x+1=(3x-1)^{ 2 }$$.

Factorise:
$$p^2 + p - 132$$

In the given polynomial $$p^2+p-132$$,

The first term is $$p^2$$ and its coefficient is $$1$$.

The middle term is $$p$$ and its coefficient is $$1$$.

The last term is a constant term $$-132$$.

Multiply the coefficient of the first term by the constant $$1\times -132=-132$$.

We now find the factor of $$-132$$ whose sum equals the coefficient of the middle term, which is $$1$$ and then factorize the polynomial $$p^2+p-132$$ as shown below:

$$p^{ 2 }+p-132\\ =p^{ 2 }+12p-11p-132\\ =p(p+12)-11(p+12)\\ =(p-11)(p+12)$$

Hence, $$p^{ 2 }+p-132=(p-11)(p+12)$$.

$$\frac{{10{x^2} + 15x + 63}}{{5{x^2} - 25x + 12}} = \frac{{2x + 3}}{{x - 5}}$$

$$\begin{array}{l} \frac { { 10{ x^{ 2 } }+15x+63 } }{ { 5{ x^{ 2 } }-25x+12 } } =\frac { { 2x+3 } }{ { \left( { x-5 } \right) } } \\ \Rightarrow 10{ x^{ 3 } }-50{ x^{ 2 } }+15{ x^{ 2 } }-75x+63x-315=\left( { 10{ x^{ 3 } }-50{ x^{ 2 } }+24x+15{ x^{ 2 } }-75x+36 } \right) \\ \Rightarrow 10{ x^{ 3 } }-10{ x^{ 3 } }-50{ x^{ 2 } }+50{ x^{ 2 } }+15{ x^{ 2 } }-15{ x^{ 2 } }-75x+75x+63x-24x=351 \\ \Rightarrow 39x=351 \\ \therefore x=9 \end{array}$$

Factorise:
$$a^2+5a-104$$

In the given polynomial $$a^2+5a-104$$,

The first term is $$a^2$$ and its coefficient is $$1$$.

The middle term is $$5a$$ and its coefficient is $$5$$.

The last term is a constant term $$-104$$.

Multiply the coefficient of the first term by the constant $$1\times -104=-104$$.

We now find the factor of $$-104$$ whose sum equals the coefficient of the middle term, which is $$5$$ and then factorize the polynomial $$a^2+5a-104$$ as shown below:

$$a^{ 2 }+5a-104\\ =a^{ 2 }+13a-8a-104\\ =a(a+13)-8(a+13)\\ =(a-8)(a+13)$$

Hence, $$a^{ 2 }+5a-104=(a-8)(a+13)$$.

Factorize $$2x^2+x-4=0$$.

$$\begin{matrix} 2{ x^{ 2 } }+x-4=0\, \, factorise \\ \to It\, \, is\, \, not\, \, factor\, \, by\, \, common\, \, factorisation. \\ \end{matrix}$$

Find the common factor of the given term.
$$3a, 21ab$$.

$$3a,\, \, 21ab $$

$$3a=3\times a $$

$$21ab=3\times 7\times a\times b$$

common factor is $$=3a\, $$

Solve the factorisation method:$$x + \frac{1}{x} = 11\frac{1}{{11}}$$

$$x+\dfrac{1}{x}=11\dfrac{1}{11}$$

$$\Rightarrow \dfrac{x^{2}+1}{x}=\dfrac{(11\times 11+1)}{11}$$

$$\Rightarrow 11x^{2}+11=122x$$

$$\Rightarrow 11x^{2}-122x+11=0$$

$$\Rightarrow 11x^{2}-121x-x+11=0$$

$$\Rightarrow 11x(x-11)-(x-11)=0$$

$$\Rightarrow (11x-1)(x-11)=0$$

$$\Rightarrow 11x-1=0$$ or $$x-11=0$$

$$\Rightarrow x=\dfrac{1}{11}$$ or $$x=11$$

Enter 1 if it is true else 0.
$$(25m^{4}-15m^{3}+10m+8)\div5m^{3}$$ $$=5m-3+\dfrac {2}{m^2}+\dfrac {8}{5m^3}$$

$$\dfrac{25{m}^{4}-15{m}^{3}+10m+8}{5{m}^{3}}$$

$$=\dfrac{25{m}^{4}}{5{m}^{3}}-\dfrac{15{m}^{3}}{5{m}^{3}}+\dfrac{10m}{5{m}^{3}}+\dfrac{8}{5{m}^{3}}$$

$$=5m-3+\dfrac{2}{{m}^{2}}+\dfrac{8}{5{m}^{3}}$$

Find the common factor of the given term : $$8x, 24$$

$$8x,\, \, 24 \\ \Rightarrow 8x=2\times 2\times 2\times x \\ \Rightarrow 24=2\times 2\times 2\times 3$$

Common factor is $$=2\times 2\times 2=8\, \,$$

Factorize: $$ 3 a ^ { 2 } b - 12 a ^ { 2 } - 9 b + 36 $$

Let us factorize the given expression $$3a^2-12a^2-9b+36$$ as shown below:

$$3a^{ 2 }b-12a^{ 2 }-9b+36\\ =3a^{ 2 }(b-4)-9(b-4)\\ =(b-4)(3a^{ 2 }-9)\\ =(b-4)3(a^{ 2 }-3)\\ =3(b-4)(a^{ 2 }-3)\\ =3(b-4)(a-3)(a+3)\quad \quad \quad \quad (\because \quad x^{ 2 }-y^{ 2 }=(x-y)(x+y))$$

Hence, $$3a^{ 2 }b-12a^{ 2 }-9b+36=3(b-4)(a-3)(a+3)$$.

Factors : $$\left(5x-\dfrac{1}{x}\right)^2 + 5 \left(5x- \dfrac{1}{x}\right)+6$$

Let $$(5x-\dfrac1x)=k$$

So, $$k^2+5k+6=k^2+3k+2k+6=k(k+3)+2(k+3)=(k+2)(k+3)\\=(5x-\dfrac1x+2)(5x-\dfrac1x+3)$$

Divide the polynomial $$3x^{4}-4x^{3}-3x-1$$ by $$x-1$$. B using long division method only. Also check whether $$x+1$$ is a factor or not.

$$3x^3-x^2-x-4$$

__________________

$$x-1$$$$) 3x^4-4x^3+0x^2-3x-1$$

$$3x^4-3x^3$$

__________________

$$-x^3+0x^2-3x$$

$$-x^3+x^2$$

________________

$$-x^2-3x-1$$

$$-x^2+x$$

_______________

$$-4x-1$$

$$-4x+4$$

_______________

$$-5$$

$$\therefore \dfrac{3x^4-4x^3-3x-1}{x-1}=3x^3-x^2-x-4$$

Remainder$$=-5$$

Now to check whether $$x+1$$ is factor or not,

$$x+1=0$$

$$x=-1$$

Put $$x=-1$$ in $$3x^4-4x^3-3x-1$$

$$3(-1)^4-4(-1)^3-3(-1)-1$$

$$=3+4+3-1$$

$$=9\neq 0$$

$$\therefore$$ By Remainder theorem, we conclude $$(x+1)$$ is not a factor.

1069164_1159958_ans_e1e1895c86a045afad35d8464fe50d00.png

If $$x+a$$ is a common factor of $$f\left( x \right) = {x^2} + x - 6$$ and $$g\left( x \right) = {x^2} + 3x - 18$$ Then find the value of a

$$f\left(x\right)={x}^{2}+x-6$$

$$={x}^{2}+3x-2x-6$$

$$=x\left(x+3\right)-2\left(x+3\right)$$

$$=\left(x+3\right)\left(x-2\right)$$

$$g\left(x\right)={x}^{2}+3x-18$$

$$={x}^{2}+6x-3x-18$$

$$=x\left(x+6\right)-3\left(x+6\right)$$

$$=\left(x-3\right)\left(x+6\right)$$

There is no Common factor between $$\left(x+3\right)\left(x-2\right)$$ and $$\left(x-3\right)\left(x+6\right)$$

Hence value of $$a$$ is unknown.

Divide $${4x}^{3}+{20x}^{2}+33x+18\ by \left (x+2\right)$$

1118050_1163955_ans_0ccba4765f8a4d309166df77592cd0c5.jpeg

Factorize using identities
$$t^{4}-625$$

$${t}^{4}-256$$

$$={t}^{4}-{16}^{2}$$

$$=\left({t}^{2}-16\right)\left({t}^{2}+16\right)$$

$$=\left({t}^{2}-{4}^{2}\right)\left({t}^{2}+16\right)$$

$$=\left(t-4\right)\left(t+4\right)\left({t}^{2}+16\right)$$

Find the remainder when $$f(x) = 2{x^3} - 6{x^2} + 4x - 2$$ is divided by $$g(x)=2x - 1$$

When $$f(x)$$ is divisible by $$(x-a)$$ then the remainder is $$f(a)$$

We have $$g(x)=2x-1=2\left(x-\dfrac{1}{2}\right)$$

Therefore $$a=\dfrac{1}{2}$$

$$f\left(\dfrac{1}{2}\right)=2\left(\dfrac{1}{2}\right)^3-6\left(\dfrac{1}{2}\right)^2+4\left(\dfrac{1}{2}\right)-2$$

$$=2\cdot \dfrac{1}{8}-6\cdot \dfrac{1}{4}+4\cdot \dfrac{1}{2}-2$$

$$=\dfrac{1}{4}-\dfrac{3}{2}+2-2$$

$$=\dfrac{1}{4}-\dfrac{3}{2}$$

$$f\left(\dfrac{1}{2}\right)=-\dfrac{5}{4}$$

Thus the remainder is $$-\dfrac{5}{4}$$

Simplify:
$$\left(1+\dfrac{x^2-y^2-z^2}{2yz}\right)\left(\dfrac{1}{x+y-z}+\dfrac{1}{z+x-y}\right)$$

$$\bullet$$ Now,

$$\left (1+\dfrac {x^2+y^2+z^2}{2yz}\right) \left (\dfrac {1}{x+y+z}+\dfrac {1}{z+x-y}\right)$$

$$=\left (\dfrac {x^2-(y^2-2yz+z^2)}{2yz}\right) \left (\dfrac {z+x-y+x+y-z}{(x+y-z)(z+x-y)}\right)$$

$$=\dfrac {x^2-(y-z)^2}{2yz}, \dfrac {2x}{(x+y-z)(z+x-y)}$$

$$=\dfrac {(x-y+z)(x+y-z)}{2yz}, \dfrac {2x}{(x+y-z)(z+x-y)}$$

$$=\left (\dfrac {2x}{2yz}\right)=\left (\dfrac {x}{yz}\right)$$

Divide. Write the quotient and the remainder.
$$(5x^{3}-3x^{2}) \div x^{2}$$

1146929_1214694_ans_ed5674a074a74c9d9a4091c6aae79b56.jpg

Divide : $$(6x^{5}-4x^{4}+8x^{3}+2x^{3})\div 2x^{2}$$

$$(6x^5-4x^4+8x^3+2x^3)+2x^2$$

$$=(6x^5-4x^4+10x^3)\div 2x^2$$

Taking $$x^2$$ common

$$\dfrac{x^2(6x^3-4x+0)}{2x^2}=\dfrac{6x^3-4x+10}{2}$$

$$=3x^3-2x+5$$.

factorise :
$$12(x^2 + 7x )^2 - 8(x^2 + 7x)(2x - 1) -15 (2x - 1)^2$$

$$ 12(x^{2}+7x)^{2}-8(x^{2}+7x)(2x-1)-15(2x-1)^{2} $$

$$ = 12(x^{2}+7x)^{2}-18(x^{2}+7x)(2x-1)+10(x^{2}+7x)(2x-1)$$

$$-15(2x-1)^{2} $$

$$ = 6(x^{2}+7x)[2(x^{2}+7x)-3(2x-1)]+$$

$$5(2x-1)[2(x^{2}+7x)+3(2x-1)] $$

$$ = [2(x^{2}+7x)-3(2x-1)][6(x^{2}+7x)+5(2x-1)] $$

$$ = [2x^{2}+14x-6x+3][6x^{2}+42x+10x-5] $$

$$ = (2x^{2}+8x+3)(6x^{2}+52x-5) $$

$$ \therefore 12(x^{2}+7x^{2})^{2}-8(x^{2}+7x)(2x-1)-15(2x-1)^{2} $$

$$ = [2(x^{2}+7x)-3(2x-1)][6(x^{2}+7x)+5(2x-1)] $$

$$ = (2x^{2}+8x+3)(6x^{2}+52x-5) $$

1176067_1203561_ans_d13d9313be394c378e3034319d7d034b.jpg

Factorise
$$2 a ^ { 2 } + 10 a - 28 = 0$$

$$\begin{matrix} 2{ a^{ 2 } }+10a-28=0 \\ 2{ a^{ 2 } }+14a-3a-28=0 \\ 2a\left( { a+7 } \right) -4\left( { a+7 } \right) =0 \\ \left( { 2a-4 } \right) \left( { a+7 } \right) =0 \\ \left( { 2a-4 } \right) \left( { a+7 } \right) =0 \\ 2a-4=0 \\ a=2\, \, \, or\, \, a=7\, \, \, Ans. \\ \end{matrix}$$

Factorise :$$x^{4}+5x^{3}+5x^{2}-5x-6.$$

1115646_1201953_ans_d68413c5bf5b48ba889af926891d9a0e.jpg

Solve :$$(2x^4+3x^3+4x-2x^2)\div (x+3)$$

1148427_1186784_ans_4c43ebc730bf456784201b2d4632bbbc.jpg

Solve:$$6x-3y$$

Consider the given expression,

$$ \Rightarrow 6x-3y $$

$$ \Rightarrow 3\left( 2x-y \right) $$

Hence, this is the answer.

Simplify:
$${a^2} + 4{b^2} - 4a -8b +4ab$$

Now,

$$a^2+4b^2-4a-8b+4ab$$

$$=(a^2+4ab+4b^2)-4(a+2b)$$

$$=(a+2b)^2-4(a+2b)$$

$$=(a+2b)(a+2b-4)$$.

Simplify:
$$a{x^2}y - bxyz - a{x^2}z + bx{y^2}$$

Given,

$$ax^{2}y-bxyz- ax^{2} z+ bxy^{2}$$

$$=xy (ax+ by) - xz (by+ ax)$$

$$= (ax+by) (xy-xz)$$

$$= (ax+by)x(y-z)$$

Factorize the given polynomial
$$x^{3}-3x^{2}-9x-5$$

Given $$x^3-3x^2-9x-5$$

Let $$x=1$$

So, $$x^3-3x^2-9x-5$$

$$=(1)^3-3(1)^2-9(1)-5$$

$$=1-3-9-5$$

$$=-16\neq 0$$

So, $$1$$ is not a factor

Let $$x=-1$$

So, $$x^3-3x^2-9x-5$$

$$=(-1)^3-3(-1)^2-9(-1)-5$$

$$=-1-3+9-5$$

$$=0$$

So, $$-1$$ is a factor

Divide $$x^3-3x^2-9x-5$$ by $$(x+1)$$

(Refer image)

$$\therefore x^2-4x-5=x^2-5x+x-5$$

$$=x(x-5)+1(x-5)$$

$$=(x-5)(x+1)$$

So, factors are $$(x+1)(x-5)(x+1)$$.

1381355_1211123_ans_2dde85e2aa7643238b72596424ef2b17.PNG

Factories $${p}^{2}-36p+99$$

$$p^2-36p+99$$

$$p^2-33p-3p-99$$

$$p(p-33)-3(p-33)$$

$$(p-33)(p-3)$$

$$p-33=0$$ $$p-3=0$$

$$p=33$$ $$p=3$$.

Factorise the following :
$$\begin{array} { l } { (i)6 a + 6 b } \\ { (ii)a x + b x } \\ { (iii)3 x ^ { 2 } - 6 a ^ { 6 } } \end{array}$$
$$\begin{array} { l } {(iv) 9 x ^ { 2 } + 3 x } \\ { (v)12 x ^ { 3 } y - 4 x y ^ { 2 } } \end{array}$$
$$\begin{array} { l } {(vi) \dfrac { 1 } { 2 } x + \dfrac { 1 } { 2 } } \\ (vii){ c d m + c d t } \\ (viii){ 36 a ^ { 2 } b ^ { 3 } - 18 a ^ { 3 } b ^ { 2 } } \\(ix) { 25 m ^ { 2 } n ^ { 3 } - 5 m n } \\(x) { 3 a y + 3 a z } \end{array}$$
$$\begin{array} { l } { (xi)185 a + 185 b } \\(xii) { 28 x - 14 y } \\ (xiii){ a x - a y } \\ (xiv){ 12 y ^ { 3 } + 6 a ^ { 3 } } \\ (xv){ 3 x + 9 y } \end{array}$$

(i) $$6a+6b=6(a+b)$$

(ii) $$ax+bx=(a+b)x$$

(iii) $$3{x}^{2}-6{a}^{6}=3({x}^{2}-2{a}^{6})=3(x-\sqrt 2{a}^{3})(x+\sqrt{2}{a}^{3})$$

(iv) $$9{x}^{2}+3x=3x(3x+1)$$

(v) $$12{x}^{3}y-4x{y}^{2}=4xy(3{x}^{2}-y)$$

(vi) $$\cfrac{1}{2}x+\cfrac{1}{2}=\cfrac{1}{2}(x+1)$$

(vii) $$cdm+cdt=cd(m+t)$$

(viii) $$36{a}^{2}{b}^{3}-18{a}^{3}{b}^{2}=18{a}^{2}{b}^{2}(2b-a)$$

(ix) $$25{m}^{2}{n}^{3}-5mn=5mn(5m{n}^{2}-1)$$

(x) $$3ay+3az=3a(y+z)$$

(xi) $$185a+185b=185(a+b)$$

(xii) $$28x-14y=14(2x-y)$$

(xiii) $$ax-ay=a(x-y)$$

xiv) $$12{y}^{3}+6{a}^{3}=6(2{y}^{3}+{a}^{3})$$

(xv) $$3x+9y=3(x+3y)$$

Divide $$4{x^2} - 8x + 3$$ by $$2x - 1$$.

We can do this by long division method.

i) $$\cfrac{4x^{2}}{2x}=2x$$

ii) $$\cfrac{-6x}{2x}=-3$$

$$\therefore 4x^{2}-8x+3=(2x-1)(2x-3)$$

1185470_1220362_ans_8c03905c5e294e58a3b01e27d5f27e2a.png

What is the remainder if $${ p }^{ 11 }+{ p }^{ 9 }+{ p }^{ 7 }+{ p }^{ 5 }+{ p }^{ 3 }+{ p }^{ 2 }$$ divided by p + 1

Let $$P^{11}+P^7+P^3+P^2=f(P)$$

Using remainder theorem, get

Remainder $$=f(P)=f(-1)=(-1)^{11}+(-1)^9+(-1)^7+(-1)^5+(-1)^3+(-1)^2=-4$$

$$(5p^2-25p+20)\div (p-1)$$.

1299215_1225931_ans_89e79bf8c71f42e89d0db0b5033e6d7b.jpg

Divide the given polynomial by the given monomial:
(i) $$\left( 5 x ^ { 2 } - 6 x \right) \div 3 x$$
(ii) $$8$$ $$\left( x ^ { 3 } y ^ { 2 } z ^ { 2 } + x ^ { 2 } y ^ { 3 } z ^ { 2 } + x ^ { 2 } y ^ { 2 } z ^ { 3 } \right) \div 4 x ^ { 2 } y ^ { 2 } z ^ { 2 }$$

1193571_1223883_ans_8c17d9953d054e1ca5d94f16017bd511.jpeg

Solve $$\dfrac{x^2+5x+6}{x+3}$$.

$$\dfrac{x^2+5x+6}{x+3}$$

$$=\dfrac{x^2+3x+2x+6}{x+3}$$

$$=\dfrac{(x+3)(x+2)}{x+3}$$

$$=x+2$$

Factories : $$am^2+bm^2+bn^2+an^2$$

Consider the given expression,

$$ \Rightarrow a{{m}^{2}}+b{{m}^{2}}+b{{n}^{2}}+a{{n}^{2}} $$

$$ \Rightarrow m\left( a+b \right)+{{n}^{2}}\left( b+a \right) $$

$$ \Rightarrow \left( a+b \right)\left( m+n \right) $$

Hence, this is the answer.

Solve:
$$x^{2}-2x-8=0$$

$$x^2-2x-8=0$$

$$\Rightarrow x^2-4x+2x-8=0$$

$$\Rightarrow x(x-4)+2(x-4)=0$$

$$\Rightarrow (x-4)(x+2)=0$$

$$\Rightarrow x=4, \ x=-2$$

Factorise
$$x^{2}+19x-150$$

$$x^2+19x-150=x^2+25x-6x-150$$

$$x^2+19x-150=x(x+25)-6(x+25)$$

$$x^2+19x-150=(x+25)(x-6)$$

Show that $$\frac { x ^ { 2 } + 2 x y + y ^ { 2 } - a ^ { 2 } + 2 a b - b ^ { 2 } } { ( x + y - a + b ) } = ( x + y + a - b )$$

$$\dfrac{x^2 + 2 xy + y^2 - (a^2 + 2ab + b^2)}{(x + y - a + b)}$$

$$\dfrac{(x + y)^2 - (a - b)^2}{x + y - (a + b)} = \dfrac{(x + y - (a - )) (x + y + (a - b))}{[x + y - (a - b)]}$$

$$[ \because a^2 - b^2 = (a + b) (a - b)]$$

$$= x + y + a - b$$ Hence, proved

$$(3x+2x^2+4x^3)\div (x-4)$$.

$$\Rightarrow \cfrac{(3x+2x^{2}+4x^{3})}{x-4}=4x^{2}+18x+75+\cfrac{300}{x-4}$$
1380627_1240098_ans_20ccd1f8d46b47959591a6016280edb2.png

Factorize the expression and divide them as directed.
$$4yz(z^2+6z-16)\div 2y(z+8)$$.

1302540_1242750_ans_2e43f484199f4e958cc06f308a4b0a0a.jpeg

Solve for r:
$$41=400$$ $$[\big[\frac{100+r}{100}\big]^{2}-1]$$

$$41=400\left[\dfrac{10000+r^2+200r-100}{100}\right]$$

$$41=4[r^2+200r+9900]$$

$$41=4r^2+800r+39600$$

$$4r^2+800r+39559=0$$

$$4r^2+442r+358r+39559=0$$

$$2r(2r+221)+179(2r+221)=0$$

$$(2r+221)(2r+179)=0$$

$$\therefore r=\dfrac{-221}{2}, r=\dfrac{-179}{2}$$.

1127992_1244741_ans_e2e3f88fd24c49dbbb142723b3f61fda.jpg

Factorise
$$4 u ^ { 2 } + 8 u$$

$$4{u}^{2}+8u$$

$$=4u(u+2)$$

Factorise:
$$12{p^5} + 16{p^4} - 20{p^3}$$

1334611_1265924_ans_4b2bece38f6c469f84cc948ecbe50362.PNG

Factorize:$$x ^ { 2 } - m ^ { 2 } + 6 m n - 9 n ^ { 2 }$$

$$x^2-(m^2-6mn+9n^2)\\=x^2-[m^2-2(m)(3n)+(3n)^2]\\=x^2-(m-3n)^2\\=[x-(m-3n)][x+(m-3n)]\\=(x-m+3n)(x+m-3n)$$

Factorise:
$${p^3} - 3pq + p{q^2}$$

1335835_1265893_ans_3db0186d86d04f6e82ce535517c0e69b.PNG

Prove that $${n} ^ { 7 } - 7{ n} ^ { 5 } + 14 {n} ^ { 3 } - 8 n$$ is divisible by $$840$$ for all $$n \in N$$

$$n^7-7n^5+14n^3-8^n$$

$$=n(n-1)(n+1)(n^4-6n^2+8)$$

$$=n(n-1)(n+1)(n^2-2)(n^2-4)$$

$$=(n-2)(n-1)(n)(n+1)(n+2)(n^2-2)$$

This expression is a product of $$5$$ consecutive terms. Hence the given expression is divisible by $$5!=120$$

We need further to prove that the given expression is divisible by $$7$$.

Let $$n=7a+k$$ where $$k=0, 1, 2, 3, 4, 5, 6$$

$$n=7a+0$$

$$\implies n$$ is divisible by $$7$$

$$n=7a+1$$

$$\implies n-1$$ is divisible by $$7$$

$$n=7a+2$$

$$\implies n-2$$ is divisible by $$7$$

$$n=7a+5$$

$$\implies n+2$$ is divisible by $$7$$

$$n=7a+6$$

$$\implies n+1$$ is divisible by $$7$$

$$n=7a+3$$

$$n^2-2=(7a+3)^2-2$$

$$=7p+q-2=7q$$

$$n=7a+4$$

$$n^2-2=(7a+4)^2-2$$

$$=7r+16-2=7r$$

Hence, the given expression is divisible by $$120\times 7=840$$.

Factorise :
$$6x^{2}+7x-3$$

In order to factorise $$6x^2 + 7x - 3$$, we have to find two numbers p and q such that $$p + q = 7$$ and $$pq = -18$$.

Clearly, $$9 + (-2) = 7$$ and $$9 \times (-2) = -18$$.

So, we write the middle term $$7x$$ as $$9x + (-2x ),$$ i.e., $$9x -2x$$.

$$\therefore 6x^2 + 7x - 3 = 6x^2 + 9x - 2x - 3$$

$$= 3x (2x + 3) - 1 (2x + 3)$$

$$= (2x + 3)(3x - 1)$$

Show that (2x+1) is a factor of $${ 4x }^{ 3 }+{ 12x }^{ 2 }+11x+3$$. Hence, factories $${ 4x }^{ 3 }+{ 12x }^{ 2 }+11x+3$$.

1867727_1270301_ans_15c0e3d5f0274861ba8d05ade681073d.jpg

The polynomial $$6{x^4} + 8{x^3} - 5{x^2} + ax + b$$ is exactly divisible by polynomial $$2x-5$$ then find the value of $$2b-a$$

1335858_1266279_ans_1556e951f09f46b5b98b13c5b8769140.PNG

Factorise completely by removing a monomial factor
$$7{x^3} - 5{y^2}$$

1335837_1265900_ans_c93d58c3f2664d57a508ebb5371a2e8b.PNG

Factorise: $$1+2ab-\left( { a }^{ 2 }{ +b }^{ 2 } \right) $$

1304729_1269240_ans_abb423da52f44bad87a7f3f95d43dc77.JPG

Factorise:
$$2a{b^2} - 6bc + 8abc$$

$$2ab^2-6bc+8abc$$

$$=2b(ab-3c+4bc)$$

factorise
$$9{y^2} + 15ya$$

1353302_1270598_ans_2f260dd416a145a8bd8f3a2be645c7b8.PNG

If $$x^{3}+8y^{3}+24xy=64$$ then $$x+2y=$$

1353322_1282893_ans_d0737bd49da640a484f55df70774312b.PNG

Factorise completely: $$2{x^3} + {x^2} - 2x - 1$$

given, $$2x^{3}+x^{2}-2x-1$$

$$=x^{2}(2x+1)-1(2x+1)$$

$$=(x^{2}-1)(2x+1)$$

$$=(x+1)(x-1)(2x+1)$$

Factorise the following expressions.
$$\left( i \right)\,\,\,\,{p^2} + 6p + 8\,\,\,\,\left( {ii} \right)\,\,\,{q^2} - 10q + 21\,\,\,\,\left( {iii} \right)\,\,\,{p^2} + 6p - 16$$

$$(i)$$

$$\begin{aligned}{}{p^2} + 6p + 8& = {p^2} + 4p + 2p + 8\\ &= p\left( {p + 4} \right) + 2\left( {p + 4} \right)\\& = \left( {p + 2} \right)\left( {p + 4} \right)\end{aligned}$$

$$(ii)$$

$$\begin{aligned}{}{q^2} -10q +21& = {q^2} -7q- 3q +21\\ &= q\left( {q -7} \right) - 3\left( {q -7} \right)\\& = \left( {q - 3} \right)\left( {q -7} \right)\end{aligned}$$

$$(iii)$$

$$\begin{aligned}{}{p^2} + 6p -16& = {p^2} + 8p - 2p -16\\ &= p\left( {p + 8} \right) - 2\left( {p + 8} \right)\\& = \left( {p - 2} \right)\left( {p + 8} \right)\end{aligned}$$

factorize
$$a^{2}-5b+ab-25$$

$$\begin{array}{l} { a^{ 2 } }-5b+ab-25 \\ \Rightarrow { a^{ 2 } }-{ 5^{ 2 } }+ab-5b \\ \Rightarrow { a^{ 2 } }-{ 5^{ 2 } }+b\left( { a-5 } \right) \\ \Rightarrow \left( { a-5 } \right) \left( { a+5 } \right) +b\left( { a-5 } \right) \\ \Rightarrow \left( { a-5 } \right) \left[ { a+5+b } \right] \\ \Rightarrow \left( { a-5 } \right) \left( { a+b+5 } \right) \end{array}$$

Factorise the following
(i) $$p^2 +6p+8$$

$$p^2+6p+8$$ [By splitting the middle term]

$$\Rightarrow p^2+2p+4p+8$$

$$\Rightarrow p(p+2)+4(p+2)$$

$$\Rightarrow (p+4)(p+2)$$.

Factorise
$$49a^{2}b^{4}-4a^{2}b^{6}$$

$$\begin{array}{l} 49{ a^{ 2 } }{ b^{ 4 } }-4{ a^{ 2 } }{ b^{ 6 } } \\ { \left( { 7a{ b^{ 2 } } } \right) ^{ 2 } }-{ \left( { 4a{ b^{ 3 } } } \right) ^{ 2 } }\, \, \left[ { { a^{ 2 } }-{ b^{ 2 } }=\left( { a-b } \right) \left( { a+b } \right) } \right] \\ \left( { 7a{ b^{ 2 } }-4a{ b^{ 3 } } } \right) \left( { 7a{ b^{ 2 } }+4a{ b^{ 3 } } } \right) \end{array}$$

Find, in each case, the remainder when: $$x^{4}-3x^{2}+2x+1$$ is divided by $$x-1$$.

From remainder theorem, we know that when a polynomial $$f (x)$$ is divided by $$(x – a)$$, then the remainder is $$f(a).$$

Given, $$f(x) = x^4 – 3x^2 + 2x + 1$$ is divided by $$x – 1$$

So, remainder $$= f(1) = (1)^4 – 3(1)^2 + 2(1) + 1 = 1 – 3 + 2 + 1 = 1$$

Factorise using
$$12x+75x^{5}-60x^{8}$$

$$\begin{array}{l} 12x+75{ x^{ 5 } }-60{ x^{ 8 } } \\ \Rightarrow 3x\left( { 4+25{ x^{ 4 } }-20{ x^{ 7 } } } \right) \\ 3x\left\{ { 4+5{ x^{ 4 } }\left( { 5-4{ x^{ 3 } } } \right) } \right\} \end{array}$$

Factorise
(i) $$a^4 -b^4$$ (ii) $$p^4 -81$$ (iii) $$x^4 -(y+z)^4$$ (iv) $$x^4 -(x-z)^4$$ (v) $$a^4 -2a^2 b^2 +b^4$$

$$i){ a }^{ 4 }-{ b }^{ 4 }=({ a }^{ 2 }-{ b }^{ 2 })({ a }^{ 2 }+{ b }^{ 2 })=(a+b)(a-b)({ a }^{ 2 }+{ b }^{ 2 })\\ =(a+b)({ a }^{ 2 }+{ b }^{ 2 })(a-b)\\ii){ p }^{ 4 }-81\\ =(p^{ 2 }-9)({ p }^{ 2 }+9)\\ =(p+3)(p-3)({ p }^{ 2 }+9)\\iii){ x }^{ 4 }-{ (y+z) }^{ 4 }=({ x }^{ 2 }-{ (y+z) }^{ 2 })({ x }^{ 2 }+{ (y+z) }^{ 2 })\\ =(x+y+z)(x-y-z)({ x }^{ 2 }+{ (y+z) }^{ 2 })\\ iv){ x }^{ 4 }-{ (x-z) }^{ 4 }=({ x }^{ 2 }-{ (x-z) }^{ 2 })({ x }^{ 2 }+{ (x-z) }^{ 2 })\\ =(x+x-z)(x-x+z)({ x }^{ 2 }+{ (x-z) }^{ 2 })\\ =(2x-z)(z)({ x }^{ 2 }+{ (x-z) }^{ 2 })\\v){ a }^{ 4 }-2{ a }^{ 2 }{ b }^{ 2 }+{ b }^{ 4 }={ a }^{ 4 }-{ a }^{ 2 }{ b }^{ 2 }-{ a }^{ 2 }{ b }^{ 2 }+{ b }^{ 4 }\\ ={ a }^{ 2 }({ a }^{ 2 }-{ b }^{ 2 })-{ b }^{ 2 }({ a }^{ 2 }-{ b }^{ 2 })\\ ={ ({ a }^{ 2 }-{ b }^{ 2 }) }^{ 2 }\\ ={ (a+b) }^{ 2 }{ (a-b) }^{ 2 }$$

Factorise :
$$x^{2}+5x+1$$

$$x^{2}+5x+1=0$$

$$=x^{2}+5x+1-1=0-1$$

$$=1-1+5x+x^{2}=0-1$$

$$=5x+x^{2}=0-1$$

$$=x^{2}+5x=-1$$

coeff of x is 5. Take $$\frac{5}{2}$$, square it & add it on both sides

$$=5x+6.25+x^{2}=-1+6.25$$

$$=6.25+5x+x^{2}=5.25$$

$$=(x+2.5)(x+2.5)= 5.25$$

$$\therefore x+2.5=2.29$$

$$x=-0.208$$

$$x+2.5=-2.29$$

$$x=-4.79$$

1186831_1292447_ans_b4d478d5d6f94825991cc68258a2bedc.jpg

$$\left( {{x^2} + 7x + 12} \right)/\left( {x + 3} \right)$$

$$\begin{array}{l} \dfrac { { { x^{ 2 } }+7x+12 } }{ { x+3 } } \\ \dfrac { { { x^{ 2 } }+4x+3x+12 } }{ { x+3 } } \\ \dfrac { { x\left( { x+4 } \right) +3\left( { x+4 } \right) } }{ { \left( { x+3 } \right) } } \\ \dfrac { { \left( { x+3 } \right) \left( { x+4 } \right) } }{ { \left( { x+3 } \right) } } \\ =x+4 \end{array}$$

Solve the following.
$$\dfrac{{x - 1}}{{x - 2}} + \dfrac{{x - 3}}{{x - 4}} = 3\dfrac{1}{3}(x \ne 2,4)$$

$$ \frac{(x-1)(x-4)+(x-3)(x-2)}{(x-2)(x-4)} = \frac{10}{2}$$

$$ 3[(x^{2}-5x+4)+(x^{2}-5x+6)] = 10[x^{2}-6x+8]$$

$$ 3[2x^{2}-10x+10] = 10x^{2}-60x+80$$

$$ 6x^{2}-30x+30=10x^{2}-60x+80$$

$$ 4x^{2}-30x+50=0.$$

$$ 2x^{2}-15x+25=0.$$

$$ 2x^{2}-10x-5x+25=0.$$

$$ \Rightarrow 2x(x-5)-5(x-5)=0$$

$$ (2x-5)(x-5)=0$$

$$ (2x-5)=0$$ or $$ x-5=0$$

$$ x=5/2$$ or $$ x=5$$

1212361_1298478_ans_49956c3427ff49c7ba59faa31e3fd34c.JPG

Factorise
$$18x^{2}+48x+32$$

$$18{x^2} + 48x + 32 = 18{x^2} + 24x + 24x + 32$$

$$ = 6x\left( {3x + 4} \right) + 8\left( {3x + 4} \right)$$

$$ = \left( {6x + 8} \right)\left( {3x + 4} \right) $$

Solve: $$(7x^4 - 21x^2 + 15) \div 7x^2$$.

1181567_1292949_ans_8f4267053909499ab5889f454196cd95.jpg

Divides and write the quotient and the remainder.
$$\left( { 6x }^{ 5 }-{ 4x }^{ 4 }+{ 8x }^{ 3 }+{ 2x }^{ 2 } \right) \div { 2x }^{ 2 }$$

$$=\dfrac{6{x}^{5}-4{x}^{4}+8{x}^{3}+2{x}^{2}}{2{x}^{2}}$$

$$=\dfrac{2{x}^{2}\left(3{x}^{3}-2{x}^{2}+4x+1\right)}{2{x}^{2}}$$

$$=3{x}^{3}-2{x}^{2}+4x+1$$

$$\therefore$$ Quotient$$=3{x}^{3}-2{x}^{2}+4x+1$$

and Remainder$$=0$$

Divide $$6{x}^{3}-{x}^{2}-10x-2$$ by $$2x-3$$

img

1194073_1367941_ans_a3fcf33657a34cd8939543172a12d26e.JPG

If $${x}^{3}+a{x}^{2}+bx+6$$ is divisible by $$\left(x-2\right)$$ and leaves remainder $$3$$ when divided by $$\left(x-3\right)$$ then find the value of $$a$$ and $$b$$.

Let the given polynomial be $$p\left(x\right) ={x}^{3}+a{x}^{2}+ bx + 6$$

Given $$p\left(x\right)$$ is divisible by $$\left(x – 2\right)$$, hence $$p\left(2\right)= 0$$

Put $$x = 2$$ in $$p\left(x\right)$$

$$p(2) = {2}^{3}+ a{\left(2\right)}^{2}+ b(2) + 6$$

$$\Rightarrow 0 = 8 + 4a + 2b + 6$$

$$\Rightarrow 4a + 2b = – 14$$

$$\Rightarrow 2a + b = – 7 $$ .........$$ (1)$$

It is also given that when $$p\left(x\right)$$ is divided by $$\left(x – 3\right)$$ the remainder is $$3$$

That $$p\left(3\right)= 3$$

Put $$x = 3$$ in $$p\left(x\right)$$

$$p\left(3\right) = {3}^{3}+ a{\left(3\right)}^{2}+ b(3) + 6$$

$$\Rightarrow 3 = 27 + 9a + 3b + 6$$

$$\Rightarrow 9a + 3b = – 30$$

$$\Rightarrow 3a + b = – 10 $$ .....$$(2)$$

Subtract $$(2)$$ from $$(1)$$

$$\Rightarrow 3a+b-2a-b= -10+7$$

$$\therefore a = – 3$$

Substitute $$a = – 3$$ in $$(1)$$, we get

$$2\left(– 3\right) + b = –7$$

$$\therefore b = –1$$

Divide $$x^{2}+3x+2$$ by $$x+1$$

$$x+2$$

___________

$$x+1)x^2+3x+2$$

$$x^2+x$$

___________

$$2x+2$$

___________

$$x$$

___________

Quotient$$=x+2$$.

1185909_1349745_ans_555d44c90019460d847f3d0d2f2f90ab.jpg

Simplify : $$\dfrac { a ^ { 3 } - 27 } { 5 a ^ { 2 } - 16 a + 3 } \div \dfrac { a ^ { 2 } + 3 a + 9 } { 25 a ^ { 2 } - 1 }$$

$$\begin{array}{l} \dfrac { { { a^{ 3 } }-27 } }{ { 5{ a^{ 2 } }-16a+3 } } \div \dfrac { { { a^{ 2 } }+3a+9 } }{ { 25{ a^{ 2 } }-1 } } \\ =\dfrac { { \left( { a-3 } \right) \left( { { a^{ 2 } }+9+3a } \right) } }{ { \left( { 5{ a^{ 2 } }-15a-a+3 } \right) } } \times \dfrac { { \left( { 5a-1 } \right) \left( { 5a+1 } \right) } }{ { \left( { { a^{ 2 } }+3a+9 } \right) } } \\ =\dfrac { { \left( { a-3 } \right) \times \left( { 5a-1 } \right) \times \left( { 5a+1 } \right) } }{ { \left( { 5a-1 } \right) \left( { a-3 } \right) } } \\ =5a+1 \end{array}$$

simplify : $$a^{3}-12a-16$$

Let $$f{\left( a \right)} = {a}^{3} - 12a - 16$$

$$f{\left( -2 \right)} = {\left( -2 \right)}^{3} - 12 \left( -2 \right) - 16 = 0$$

Thus,

$$\left( a + 2 \right)$$ is a factor of $${a}^{3} - 12a - 16$$.

Now dividing $$f{\left( a \right)}$$ by $$\left( a + 2 \right)$$, we get

$$\left( {a}^{3} - 12a - 16 \right) \div \left( a + 2 \right) = {a}^{2} - 2a - 8$$

Now,

$${a}^{2} - 2a - 8$$

$$= {a}^{2} - 4a + 2a - 8$$

$$= \left( a - 4 \right) \left( a + 2 \right)$$

Therefore,

$${a}^{3} - 12a - 16 = \left( a + 2 \right) \left( a - 4 \right) \left( a + 2 \right)$$

$$\Rightarrow {a}^{3} - 12a - 16 = {\left( a + 2 \right)}^{2} \left( a - 4 \right)$$

Divide and write the quotient and the remainder
$$(21x^{4}-14x^{2}+7x)\div 7x^{3}$$

1172941_1338693_ans_afcb9ead1dd6475a9b8752c91e90ef2f.jpg

factorize
$$4x+8$$

Here, 4 is the common factor

Now,

$$4(x+4)$$ are the factor.

Solve:
$$2a(3x+5y)-5b(3x+5y)$$

$$ 2a (3x + 5y) - 5b (3x + 5y)$$

$$ \Rightarrow (3x + 5y) (2a - 5b)$$

1185853_1348760_ans_2c154516fb2342909b288275afa3ab30.jpg

Divide the given polynomial by the given monomial
8$$\left( x ^ { 3 } y ^ { 2 } z ^ { 2 } + x ^ { 2 } y ^ { 3 } z ^ { 2 } + x ^ { 2 } y ^ { 2 } z ^ { 3 } \right) \div 4 x ^ { 2 } y ^ { 2 } z ^ { 2 }$$

given, $$8(x^3y^2z^2+x^2y^3z^2+x^2y^2z^3)\div 4x^2y^2z^2$$

$$=8x^2y^2z^2(x+y+z)\div 4x^2y^2z^2$$

$$=\dfrac{8x^2y^2z^2}{4x^2y^2z^2}(x+y+z)$$

$$=2(x+y+z)$$.

Factorize:
$$3+2a-a^{2}$$

$$3 + 2a - {a}^{2}$$

$$= 3 + 3a - a - {a}^{2}$$

$$= 3 \left( 1 + a \right) - a \left( 1 + a \right)$$

$$= \left( 3 - a \right) \left( 1 + a \right)$$

Therefore

$$3 + 2a - {a}^{2} = \left( 3 - a \right) \left( 1 + a \right)$$

Solve the following
$$(6x^{4}+4x^{2}+9x+5) \div (2x+3)$$

$$\left( 6 {x}^{4} + 4 {x}^{2} + 9x + 5 \right) \div \left( 2x + 3 \right)$$

Quotient $$= \left( 3 {x}^{3} - \cfrac{9}{2} {x}^{2} + \cfrac{35}{4} x - \cfrac{69}{8} \right)$$

Remainder $$= \cfrac{247}{8}$$

1289188_1337743_ans_c56a883a5b824769a1f583f8ada2c045.png

Divide and write the equation $$\left( {{y^2}+10y + 24} \right) \div \left( {y + 4} \right)$$

We have,

$$\left( {{y^2}+10y + 24} \right) \div \left( {y + 4} \right)$$

$$\Rightarrow \dfrac{\left( {{y^2}+10y + 24} \right)}{\left( {y + 4} \right)}$$

$$\Rightarrow \dfrac{\left( y+6 \right) \left( y+4 \right) }{\left( {y + 4} \right)}$$

$$\Rightarrow y+6$$

Hence, this is the answer.

Factorise:$${x}^{4}+{x}^{2}+1$$

$$={x}^{4}+2\times {x}^{2}+1-{x}^{2}$$

$$={\left({x}^{2}+1\right)}^{2}-{x}^{2}$$

$$=\left({x}^{2}+1+x\right)\left({x}^{2}+1-x\right)$$

$$=\left({x}^{2}+x+1\right)\left({x}^{2}-x+1\right)$$

Factorize -
$${ ax }^{ 2 }+{ bx }^{ 2 }-{ ay }^{ 2 }-{ by }^{ 2 }$$

$$a{x}^{2}+b{x}^{2}-a{y}^{2}-b{y}^{2}$$

$$=\left(a+b\right){x}^{2}-\left(a+b\right){y}^{2}$$

$$=\left(a+b\right)\left({x}^{2}-{y}^{2}\right)$$

$$=\left(a+b\right)\left(x+y\right)\left(x-y\right)$$

Find the factorss of $$x^{4}+3x^{3}-7x^{2}-27x-18$$

If $$x = a$$ is a zero, then $$x – a$$ is a factor

$$f\left(x\right)=x^4+3x^3−7x^2−27x−18$$

$$f\left(-1\right)=1-3−7+27−18=0$$

$$\left(x+1\right)$$ is a factor of $$f\left(x\right)$$

The other factors are calculated by using synthetic division.

$$\left(x+1\right)\left(x^3+2x^2-9x-18\right)$$

$$=\left(x+1\right)\left(x^2\left(x+2\right)-9\left(x+2\right)\right)$$

$$=\left(x+1\right)\left(x+2\right)\left({x}^{2}-9\right)$$

$$=\left(x+1\right)\left(x+2\right)\left(x-3\right)\left(x+3\right)$$

Factorise:
$$(x^{3}-2x^{2}-5x+6)$$

Let $$f\left(x\right)={x}^{3}-2{x}^{2}-5x+6$$

$$\Rightarrow f\left(1\right)={1}^{3}-2{1}^{2}-5\times 1+6=1-2-5+6=0$$

Using synthetic division, we have

$${x}^{2}-x-6=0$$ is the other factor

$$\left(x-1\right)\left({x}^{2}-x-6\right)=0$$

$$=\left(x-1\right)\left({x}^{2}-3x+2x-6\right)=0$$

$$=\left(x-1\right)\left(x\left(x-3\right)+2\left(x-3\right)\right)=0$$

$$=\left(x-1\right)\left(x+2\right)\left(x-3\right)$$ are the factors of $$f\left(x\right)$$

Divide $$15{x}^{3}-20{x}^{2}+13x-12$$ by $$ 3x-6$$

img

1188892_1367917_ans_c4d60b68fd4d4b0cabf911ce45e827a6.jpg

Verify whether $$2y-5$$ is a factor of $$4{y}^{4}-10{y}^{3}-10{x}^{2}+30y-15$$

1194072_1367932_ans_448f493289a7423093ef489dc66da470.PNG

Write the factors of
$$15xy-6x+5y-2$$

$$=15xy-6x+5y-2$$

$$=3x\left(5y-2\right)+1\left(5y-2\right)$$

$$=\left(3x+1\right)\left(5y-2\right)$$

Work out the following divisions
(i) $$\left(11x-121\right)\div 11$$
(ii) $$\left(15x-25\right)\div \left(3x-5\right)$$
(iii) $$10y\left(9y+21\right)\div 2\left(3y+7\right)$$
(iv)$$9{p}^{2}{q}^{2}(3z-12)\div 27pq\left(z-4\right)$$

$$(i) (11x-121) \div 11$$

$$=\dfrac{11(x-11)}{11} = x-11$$

$$(ii) (15x-25) \div (3x-5)$$

$$=\dfrac{5(3x-5)}{3x-5} = 5$$

$$(iii) 10y(9y+21) \div 2(3y+7)$$

$$=\dfrac{5y(9y+21)}{3y+7} = 5y \times 3 = 15y$$

$$(iv) 9p^{2}q^{2}(3z-12) \div 27pq(z-4)$$

$$=\dfrac{pq(3z-12)}{3(z-4)}$$

$$=pq$$

Find the value of $$a$$ and $$b$$, if the zeros of the polynomial. $$x^{3}-3x^{2}+x+1$$ are $$a-b,\ a,\ a+b$$

1302719_1370313_ans_ac72039910b24ae1bdbfbb2c7f94a66c.jpg

$$({ y }^{ 2 }+10y+24)\div (y+4)$$

$$({ y }^{ 2 }+10y+24)\div (y+4)$$ = $$\dfrac{y^{2}+10y+24}{y+4}$$

= $$\dfrac{y^{2}+4y+6y+24}{y+4}$$

= $$\dfrac{(y+6)(y+4)}{y+4}$$

= $$y+6$$

Factorise.
$$6a^{2}+7a-5$$

$$6{a}^{2}+7a-5$$

$$=6{a}^{2}+10a-3a-5$$

$$=2a\left(3a+5\right)-1\left(3a+5\right)$$

$$=\left(2a-1\right)\left(3a+5\right)$$

Hence the factors are $$\left(2a-1\right)\left(3a+5\right)$$

Factorise $$ { \left( x-2y \right) }^{ 2 }+7\left( x-2y \right) +12$$

Let $$\alpha=x-2y$$ then

$$={\alpha}^{2}+7\alpha+12$$

$$={\alpha}^{2}+4\alpha+3\alpha+12$$

$$=\left(\alpha+4\right)\left(\alpha+3\right)$$

$$=\left(x-2y+4\right)\left(x-2y+3\right)$$ where $$\alpha=x-2y$$

Divide $$-12a^{3}b+18a^{2b^{2}}-24ab^{3}$$ by $$-6ab$$

1194617_1374769_ans_2fefbaa8b98147369208245cda0519a6.JPG

Factorise.
$$6x^{2}-11xy-10y^{2}$$

$$6{x}^{2}-11xy-10{y}^{2}$$

$$=6{x}^{2}-15xy+4xy-10{y}^{2}$$

$$=3x\left(2x-5y\right)-2y\left(2x-5y\right)$$

$$=\left(2x-5y\right)\left(3x-2y\right)$$

Hence the factors are $$\left(2x-5y\right)\left(3x-2y\right)$$

Factorize :
$$8(a+1)^{2}+2(a+1)(b+2)-15(b+2)^{2}$$

$$8(a+1)^{2}+2(a+1)(b+2)-15(b+2)^{2}$$

Let $$a+1=x$$ and $$b+2=y$$. Then,

$$8x^{2}+2xy-15y^{2}$$

$$=8x^{2}+12xy-10xy-15y^{2}$$

$$=4x(2x+3y)-5y(2x+3y)$$

$$=(2x+3y)(4x-5y)$$

$$=(2a+3b+8)(4a-5b-6)$$

Factorise.
$$3x^{2}+11xy+6y^{2}$$

$$3{x}^{2}+11xy+6{y}^{2}$$

$$=3{x}^{2}+9xy+2xy+6{y}^{2}$$

$$=3x\left(x+3y\right)+2y\left(x+3y\right)$$

$$=\left(3x+2y\right)\left(x+3y\right)$$

Hence the factors are $$\left(3x+2y\right)\left(x+3y\right)$$

Factorize the following:
$$20a^{12}b^{2}-15a^{8}b^{4}$$

$$20{a}^{12}{b}^{2}-15{a}^{8}{b}^{4}$$

$$=5{a}^{8}{b}^{2}\left(4{a}^{4}-3{b}^{2}\right)$$

$$=5{a}^{8}{b}^{2}\left({\left(\sqrt{2}a\right)}^{4}-{\left(\sqrt{3}b\right)}^{2}\right)$$

$$=5{a}^{8}{b}^{2}\left({\left(\sqrt{2}a\right)}^{2}+{\left(\sqrt{3}b\right)}^{2}\right)\left({\left(\sqrt{2}a\right)}^{2}-{\left(\sqrt{3}b\right)}^{2}\right)$$

$$=5{a}^{8}{b}^{2}\left({\left(\sqrt{2}a\right)}^{2}+{\left(\sqrt{3}b\right)}^{2}\right)\left(\sqrt{2}a-\sqrt{3}b\right)\left(\sqrt{2}a+\sqrt{3}b\right)$$

Simplify: $$30a^{3}b^{3}c^{3}+45abc$$

$$30{a}^{3}{b}^{3}{c}^{3}+45abc$$

$$=15abc\left(2{a}^{2}{b}^{2}{c}^{2}+3\right)$$

Factorise:$$4xy - x + 12y -3$$

$$4xy-x+12y-3$$

$$=x\left(4y-1\right)+3\left(4y-1\right)$$

$$=\left(4y-1\right)\left(x+3\right)$$

Write the common factors of :$${ 4a }^{ 2 }b$$ and $$3ab$$

Factors of $$4{a}^{2}b=2\times 2\times a\times a\times b$$

Factors of $$3ab=3\times a\times b$$

Common factor$$=a\times b=ab$$

Factorize: $${x}^{2}-15x+56$$

Given, $${x}^{2}-15x+56$$

$$={x}^{2}-7x-8x+56$$

$$=x\left(x-7\right)-8\left(x-7\right)$$

$$=\left(x-7\right)\left(x-8\right)$$

Resolve $${x}^{8}+{x}^{4}+1$$ in to factors.

$${x}^{8}+{x}^{4}+1$$

$$={\left({x}^{4}\right)}^{2}+2{x}^{4}+1-{x}^{4}$$

$$={\left({x}^{4}+1\right)}^{2}-{\left({x}^{2}\right)}^{2}$$

$$=\left({x}^{4}+1+{x}^{2}\right)\left({x}^{4}+1-{x}^{2}\right)$$

$$=\left({x}^{4}+{x}^{2}+1\right)\left({x}^{4}-{x}^{2}+1\right)$$

$$=\left({\left({x}^{2}\right)}^{2}+2{x}^{2}+1-{x}^{2}\right)\left({\left({x}^{2}\right)}^{2}-2{x}^{2}+1+{x}^{2}\right)$$

$$=\left({\left({x}^{2}+1\right)}^{2}-{x}^{2}\right)\left({\left({x}^{2}-1\right)}^{2}+{x}^{2}\right)$$

$$=\left({x}^{2}+x+1\right)\left({x}^{2}-x+1\right)\left({\left({x}^{2}-1\right)}^{2}+{x}^{2}\right)$$

Solve
$$\left(x^ {4}+x^ {3}+3x^ {2}+3x+12\right)\div \left(x^ {2}+2\right)$$

Remainder$$=x+10$$
1336488_1385299_ans_d02dcdbbcbe840cfad8c8d9104dffee7.PNG

Factorize:
$$pqr-{ p }^{ 2 }q+{ pq }^{ 2 }r$$

$$pqr-{p}^{2}q+p{q}^{2}r$$

$$=pq\left(r-p+qr\right)$$

Solve:
$$x^{3}-x^{2}-14x+14$$

$${x}^{3}-{x}^{2}-14x+14$$

$$={x}^{2}\left(x-1\right)-14\left(x-1\right)$$

$$=\left(x-1\right)\left({x}^{2}-14\right)$$

$$=\left(x-1\right)\left({x}^{2}-{\left(\sqrt{14}\right)}^{2}\right)$$

$$=\left(x-1\right)\left(x-\sqrt{14}\right)\left(x+\sqrt{14}\right)$$

Factorize:
$$4x^2-12xy+9y^2+2x-3y$$

Now,

$$4x^2-12xy+9y^2+2x-3y$$

$$=(2x-3y)^2+(2x-3y)$$

$$=(2x-3y)(2x-3y+1)$$.

write the quotient and the remainder.
$$\left( { 2x }^{ 4 }+{ 3x }^{ 3 }+4x-2\right) \div \left( x+2 \right) $$

Remainder$$=2$$

Quotient$$=2{x}^{3}-{x}^{2}+2x$$

1327202_1414059_ans_2fe6c7fba82a4ad1b8e6b881b349cc51.PNG

Divide $$(-x^6+2x^4+4x^3+2x^2)$$ by $$(2\sqrt2 x^2)$$

$$(-x^6+2x^4+4x^3+2x^2)\div $$$$(2\sqrt2 x^2)=\dfrac{-x^6+2 x^4+4 x^3+2 x^2}{2\sqrt{2}x^2}=\dfrac{x^2(-x^4+2 x^2+4 x+2)}{2 \sqrt{2} x^2}$$

$$=\dfrac{1}{2\sqrt{2}}(-x^4+2 x^2+4 x+2)$$

Factorize:
$$x^2-7x+10$$.

Now,

$$x^2-7x+10$$

$$=x^2-5x-2x+10$$

$$=(x-2)(x-5)$$.

Solve the following
$$8x^{3}-6x^{2}+x=0$$

Now,

$$8x^{3}-6x^{2}+x=0$$

or, $$x(8x^2-6x+1)=0$$

or, $$x(8x^2-4x-2x+1)=0$$

or, $$x\{4x(2x-1)-1(2x-1)\}=0$$

or, $$x(4x-1)(2x-1)=0$$

or, $$x=0,\dfrac{1}{4},\dfrac{1}{2}$$.

Factorise.
$$x^{ 2 } + xy + 8x + 8y$$

$$x^2+x{y}+8 x+8 y$$

$$=x(x+y)+8(x+y)$$

$$=(x+8)(x+y)$$

Divide $$(5{p^2} - 25p + 20) \div (p-1)$$

$$(5p^2-25p+20)\div 5(p-4)$$

$$\Rightarrow 5p^2-25p+20=5(p^2-5p+4)$$

$$=5[p^2-4p-p+4]$$

$$=5[p(p-1)-4(p-1)]$$

$$=5[(p-1)(p-4)]$$

$$\therefore$$ $$(5p^2-25p+20)\div (p-1)=\dfrac{5(p-1)(p-4)}{(p-1)}$$

$$=5(p-4)$$.

$$\therefore (5p^2-25p+20)\div (p-1)=5(p-4)$$.

1196717_1394116_ans_824b363c1bac4cf7bdbc6dde910ea286.jpg

Solve :
$$15x + 5$$

$$15x + 5$$

Simplifying we get

$$15x+5=5(3x+1)$$

Factorise :-
$${a^4} - 2{a^2}{b^2} + {b^4}$$

$$a^4-2 a^2 b^2+b^4=a^4-a^2 b^2-a^2 b^2+b^4=a^2(a^2-b^2)- b^2(a^2-b^2)=(a^2-b^2)^2$$

As we know that

$$x^2-y^2=(x+y)(x-y)$$

$$\implies a^4-2 a^2 b^2+b^4=(a^2-b^2)^2=(a-b)^2(a+b)^2$$

Factorise:$$\sqrt{3} x^{2}+4x-7\sqrt{3}$$

The given expression is $$\sqrt{3}{x}^{2}+4x-7\sqrt{3}$$

We are asked to factorise the given expression.

We can factorise the given expression by rewriting it and taking out common terms.

$$\sqrt{3}{x}^{2}+4x-7\sqrt{3}$$

The expression can be written as:

$$\sqrt{3}{x}^{2}-3x+7x-7\sqrt{3}$$

$$\Rightarrow \sqrt{3}{x}^{2}-\sqrt3 \times \sqrt3 x+7x-7\sqrt{3}$$

Taking out $$\sqrt3 x$$ common from the first two terms and $$7$$ from the last two.

$$\Rightarrow \sqrt{3}x\left(x-\sqrt{3}\right)+7\left(x-\sqrt{3}\right)$$

$$\Rightarrow \left(\sqrt{3}x+7\right)\left(x-\sqrt{3}\right)$$

Thus, $$\left(\sqrt{3}x+7\right)\ and \ \left(x-\sqrt{3}\right)$$ are the factors of the given expression.

Hence, $$\sqrt{3}{x}^{2}+4x-7\sqrt{3}=\left(\sqrt{3}x+7\right)\left(x-\sqrt{3}\right)$$

Factorise: $$x^2+2x+1$$

Given $$ x^{2}+2x+1$$

$$\Rightarrow x^{2}+x+x+1$$

$$\Rightarrow x (x+1)+1(x+1)$$

$$\Rightarrow (x+1)(x+1)$$

Simplify :-
$$\dfrac{8({x^3}{y^2}{z^2} + {x^2}{y^3}{z^2} + {x^2}{y^2}{z^3})}{4{x^2}{y^2}{z^2}}$$

$$\dfrac{8(x^3y^2z^2+x^2y^3z^2+x^2y^2z^3)}{4x^2y^2z^2}$$

$$=\dfrac{8x^3y^2z^2+8x^2y^3z^2+8x^2y^2z^3}{4x^2y^2z^2}$$

$$=\dfrac{8x^2y^2z^2(x+y+z)}{4x^2y^2z^2}$$

$$=2(x+y+z)$$.

Factorise : $$ a^2x^2 +(ax^2 +1)x +a $$

Given : $$ a^2x^2 +(ax^2 +1)x +a $$

By multiplying the terms
$$ a^2x^2 +(ax^2 +1)x +a $$$$ =a^2x^2 +ax^3 +x+a $$

By taking the common terms out
$$ a^2x^2 +(ax^2 +1)x +a $$$$ = ax^2 (a+x) +1(x+a) $$

So we get,
$$ a^2x^2 +(ax^2 +1)x +a $$$$ =(a+x)(ax^2 +1) $$

Solve:
$$49(x^4-5x^3-24x^2)\div 11x(x-8)$$

$${x}^{4} - 5{x}^{3} - 24 {x}^{2}$$

$$= {x}^{2} \left( {x}^{2} - 5x - 24 \right)$$

$$= {x}^{2} \left[ {x}^{2} - 8x + 3x - 24 \right]$$

$$= {x}^{2} \left( x - 8 \right) \left( x + 3 \right)$$

Therefore,

$$49 \left( {x}^{4} - 5 {x}^{3} - 24 {x}^{2} \right) \div 11x \left( x - 8 \right)$$

$$= \cfrac{49 \left( {x}^{4} - 5{x}^{3} - 24{x}^{2} \right)}{11x \left( x - 8 \right)}$$

$$= \cfrac{49 {x}^{2} \left( x - 8 \right) \left( x + 3 \right)}{11x \left( x - 8 \right)}$$

$$= \cfrac{49}{11} x \left( x + 3 \right)$$

Hence $$49 \left( {x}^{4} - 5 {x}^{3} - 24 {x}^{2} \right) \div 11x \left( x - 8 \right) = \cfrac{49}{11} x \left( x + 3 \right)$$

Solve:
$$(m^2-14m-32)\div (m+2)$$

$${m}^{2} - 14m - 32$$

$$= {m}^{2} - 16m + 2m - 32$$

$$= \left( m - 16 \right) \left( m + 2 \right)$$

Therefore,

$$\left( {m}^{2} - 14m - 32 \right) \div \left( m + 2 \right)$$

$$= \cfrac{\left( m - 1 6 \right) \left( m + 2 \right)}{\left( m + 2 \right)}$$

$$= \left( m - 16 \right)$$

Simplify:
$$z - 7 + 7xy - xyz$$

Given:

$$z-7+7xy-xyz$$

$$=z-xyz-7+7xy$$

$$= z(1-xy)-7(1-xy)$$

$$= (1-xy)(z-7)$$

Factorise the following expressions.
$$\left(1\right){p}^{2}+6p+8$$
$$\left(2\right){q}^{2}-10q+21$$
$$\left(3\right){p}^{2}+6p-16$$

$$1) p^{2}+6p+8$$

$$=p^{2}+4p+2p+8$$

$$=p(p+4)+2(p+4)$$

$$=(p+4)(p+2)$$

$$2)q^{2}-10q+21$$

$$=q^{2}3q-7q+21$$

$$=q(q-3)-7(q-3)$$

$$=(q-3)(q-7)$$

$$3)p^{2}+6p-16$$

$$=p^{2}-2p+8p-16$$

$$=p(p-2)+8(p-2)$$

$$=(p+8)(p-2)$$

Simplify:
$$15xy-6x+5y-2$$

Given expression is $$ 15xy-6x+5y-2 $$.

Simplifying the given expression by combining the like terms or taking out common parts:

$$ = (15xy+5y)-(6x+2) $$

$$ = 5y(3x+1)-2(3x+1) $$

$$ =( 5y-2)(3x+1) $$

$$ = (3x+1)(5y-2) $$

Hence, $$15xy-6x+5y-2=(3x+1)(5y-2)$$.

Factorize:
$$x^2-100x+99$$

Now,

$$x^2-100x+99$$

$$=x^2-99x-x+99$$

$$=(x-99)(x-1)$$.

Factorise the expression
$$am^{2}+bm^{2}+bn^{2}+an^{2}$$

1306769_1457760_ans_fd3576e8e2514d339ec14fd82376ad85.jpeg

Factorise:
$$z-7+7xy-xyz$$

$$z - 7 + 7xy - xyz$$

$$= z - xyz - 7 + 7xy$$

$$= z \left( 1 - xy \right) - 7 \left( 1 - xy \right)$$

$$= \left( 1 - xy \right) \left( z - 7 \right)$$

Hence $$z - 7 + 7xy - xyz = \left( 1 - xy \right) \left( z - 7 \right)$$.

Factorize:$${ q }^{ 2 }-10 q+21.$$

1318647_1490386_ans_5a852de0d51b48a5b332fac6c6b372c3.JPG

Factorise:
$$6xy(a^2+b^2)+8yz(a^2+b^2)-10xz(a^2+b^2)$$

$$6xy \left( {a}^{2} + {b}^{2} \right) + 8yz \left( {a}^{2} + {b}^{2} \right) - 10xz v$$

$$= \left( {a}^{2} + {b}^{2} \right) \left( 6xy + 8yx - 10xz \right)$$

$$= 2 \left( {a}^{2} + {b}^{2} \right) \left( 3xy + 4 yz - 5 xz \right)$$

Factorise:
$$6xy(a^2+b^2)+8yz(a^2+b^2)-10xz(a^2+b^2)$$

$$6xy \left( {a}^{2} + {b}^{2} \right) + 8yz \left( {a}^{2} + {b}^{2} \right) - 10xz \left( {a}^{2} + {b}^{2} \right)$$

$$= \left( {a}^{2} + {b}^{2} \right) \left( 6xy + 8yz - 10xz \right)$$

$$= 2 \left( {a}^{2} + {b}^{2} \right) \left( 3xy + 4yz - 5xz \right)$$

Factorise:
$$36a^{2}+12abc-15b^{2}c^{2}$$

$$36 {a}^{2} + 12abc - 15 {b}^{2} {c}^{2}$$

$$= 3 \left( 12 {a}^{2} + 4 abc - 5 {b}^{2} {c}^{2} \right)$$

$$= 3 \left( 12 {a}^{2} + 10abc - 6 abc - 5 {b}^{2} {c}^{2} \right)$$

$$= 3 \left( 2a \left( 6a + 5bc \right) - bc \left( 6a - 5bc \right) \right)$$

$$= 3 \left( 2a - bc \right) \left( 6a + 5bc \right)$$

Divide 48a$$^{3}$$ by 6a

1318686_1490209_ans_2f0ed174750149d7a09968bc0b2345ec.JPG

Factorize: $$(p - x) (p + x) + y (p - x) = 0$$

1323535_1491306_ans_b69fa613584642708fa22c18ff93ebae.JPG

Simplify:
$$[4{ y }^{ 3 }+5{ y }^{ 2 }+6y]\div 2y$$

Given: $$\dfrac{4{y}^{3}+5{y}^{2}+6y}{2y}$$

$$=\dfrac{4{y}^{3}}{2y}+\dfrac{5{y}^{2}}{2y}+\dfrac{6y}{2y}$$

$$=2{y}^{2}+\dfrac{5y}{2}+3$$

Simplify:
$$x^2-33x+90$$

Now,

$$x^2-33x+90$$

$$=x^2-30x-3x+90$$

$$=(x-30)(x-3)$$.

Factorize $$y^2 + 10y + 24 $$

1894545_1473447_ans_923fe8a9e5c8441bbf70e8aeca29b1e6.jpg

Divide as directed.
5$$ ( 2 x + 1 ) ( 3 x + 5 ) \div ( 2 x + 1 ) $$

1326365_1494319_ans_447df0bea48043d6aa997407ed85c51b.JPG

Factorise the expression $${ 2a }^{ 3 }-{ 3a }^{ 2 }b+{ 5ab }^{ 2 }-ab$$

Given: $$2a^{3}-3a^{2}b+5ab^{2}-ab$$

$$=a(2a^{2}-3ab+5b^{2}-b)$$

Factorise $$x^3-2x^2-x+2$$

1311064_1535009_ans_22a361e1b29646c4b6db6bcdd6681caa.jpeg

Look at several examples of rational numbers in the form $$\dfrac{p}{q}(q\neq 0)$$, where $$p$$ and $$q$$ are integers with no common factors other than $$1$$ and having terminating decimal representations. Can you guess what property $$q$$ must satisfy?

Prime factorization of $$q$$ must have only powers of $$2$$ or $$5$$ or both.

Consider the following rational numbers:

$$(i)\dfrac{7}{8}=\dfrac{7}{2^{3}}=\dfrac{7\times 5^{3}}{2^{3}\times 5^{3}}=\dfrac{875}{(2\times 5)^{3}}=\dfrac{875}{10^{3}}=\dfrac{875}{1000}=0.875$$

$$(ii) \dfrac{3}{40}=\dfrac{3}{2^{3}\times 5}=\dfrac{3\times 5^{2}}{2^{3}\times 5^{3}}=\dfrac{75}{(2\times 5)^{3}}=\dfrac{75}{1000}=0.075$$

$$(iii)\dfrac{4}{25}=\dfrac{4\times 2^{2}}{5^{2}\times 2^{2}}=\dfrac{4\times 4}{(5\times 2)^{2}}=\dfrac{16}{100}=0.16$$

We observe that the denominators of all the above rational numbers are of the form $$2^{m}\times 5^{n}$$ i.e., the prime factorizations of denominators have only powers of $$2$$ or powers of $$5$$ or both.

Factorise : $$ax^{3}y^{2} + bx^{2}y^{3} + cx^{2}y^{2}z$$.

$$ax^3y^2+bx^2y^3+cx^2y^2z$$

Minimum power of $$x$$ and $$y$$ present in each term is 2. Hence $$x^2y^2$$ can be taken common.

$$ax^3y^2+bx^2y^3+cx^2y^2z=x^2y^2(ax+by+cz)$$

Divide :
$$x + 2x^{2} + 3x^{4} - x^{5}$$ by $$2x$$.

$$\dfrac{x+2x^2+3x^4-x^5}{2x}$$

$$\Rightarrow \dfrac{x}{2x}+\dfrac{2x^2}{2x}+\dfrac{3x^4}{2x}-\dfrac{x^5}{2x}$$

$$\Rightarrow \dfrac{1}{2}+x+\dfrac{3}{2}x^3-\dfrac{1}{2}x^4$$

Factorize:
$$8{x}^{3}+27{y}^{3}+36{x}^{2}y+54x{y}^{2}$$

1650964_1669428_ans_df813793b78f4c7eadce4e664522f0d5.jpg

Divide :
$$9x^{2} y - 6xy + 12xy^{2}$$ by $$-\dfrac {3}{2} xy$$.

1507708_1672529_ans_75305cf7be9744e48497a11e04f54164.jpg

Divide :
$$3x^{3}y^{2} + 2x^{2}y + 15xy$$ by $$3xy$$.

1507710_1672530_ans_1190e19e7a124ebfa351252b9d4ce0bc.jpg

Divide :
$$5z^{3} - 6z^{2} + 7z$$ by $$2z$$.

$$\dfrac{5z^3-6z^2+7z}{2z}$$

$$=\dfrac{5z^3}{2z}-\dfrac{6z^2}{2z}+\dfrac{7z}{2z}$$

$$=\dfrac{5}{2}z^2-\dfrac{6}{2}z+\dfrac{7}{2}$$

$$=\dfrac{5}{2}z^2-\dfrac{2\times 3}{2}z+\dfrac{7}{2}$$

$$=\dfrac{5}{2}z^2-3z+\dfrac{7}{2}$$

Divide :
$$y^{4} - 3y^{3} + \dfrac {1}{2} y^{2}$$ by $$3y$$.

$$\dfrac{y^4-3y^3+\dfrac{1}{2}y^2}{3y}$$

$$=\dfrac{y^4}{3y}$$$$-\dfrac{3y^3}{3y}$$$$+\dfrac{1}{2\times 3y}y^2$$

$$=\dfrac{1}{3}y^3-y^2+\dfrac{1}{6}y$$

Divide :
$$-4a^{3} + 4a^{2} + a$$ by $$2a$$.

$$\dfrac{-4a^3+4a^2+a}{2a}$$

$$\Rightarrow \dfrac{-4a^3}{2a}+\dfrac{4a^2}{2a}+\dfrac{a}{2a}$$

$$\Rightarrow \dfrac{-2\times 2a\times a^2}{2a}+\dfrac{2\times 2a\times a}{2a}+\dfrac{a}{2a}$$

$$\Rightarrow -2a^2+2a+\dfrac{1}{2}$$

$$2\sqrt 2{a}^{3}+3\sqrt 3{b}^{3}+{c}^{3}-3\sqrt 6abc$$

1652202_1669523_ans_4abee9e24c0543c78d63beb9b5cac089.jpeg

Divide :
$$4z^{3} + 6z^{2} - z$$ by $$-\dfrac {1}{2}z$$.

To divide $$(4z^{3} + 6z^{2} - z)$$ by $$-\dfrac {1}{2}z$$

Now

$$\dfrac{4z^{3} + 6z^{2} - z}{-\dfrac {1}{2}z}$$

$$=-\dfrac{2(4z^{3} + 6z^{2} - z)}{z}$$

$$=-\dfrac{2z(4z^{2} + 6z - 1)}{z}$$

$$=-2(4z^{2} + 6z - 1)$$

Hence, the answer is $$=-2(4z^{2} + 6z - 1)$$

Divide :
$$\sqrt {3}a^{4} + 2\sqrt {3} a^{3} + 3a^{2} - 6a$$ by $$3a$$.

Given expressions are $$\sqrt{3} a^4 + 2\sqrt{3} a^3 + 3a^2 - 6a$$ and $$3a$$.

On dividing $$\sqrt{3} a^4 + 2\sqrt{3} a^3 + 3a^2 - 6a$$ by $$3a$$, we get:

$$\dfrac{\sqrt{3} a^4 + 2\sqrt{3} a^3 + 3a^2 - 6a}{3a}$$

$$=\dfrac{\sqrt{3} a^4}{3a} + \dfrac{2\sqrt{3} a^3}{3a} + \dfrac{3a^2}{3a} - \dfrac{6a}{3a}$$

$$=\dfrac{\sqrt{3} a^4}{\sqrt{3} \times \sqrt{3} a} + \dfrac{2 \sqrt{3} a^3}{\sqrt{3} \times \sqrt{3}a} + \dfrac{3a^2}{3a} - \dfrac{6a}{3a}$$

$$=\dfrac{1}{\sqrt{3}} a^3 + \dfrac{2}{\sqrt{3}} a^2 + a - 2$$

Hence, $$\dfrac{\sqrt{3} a^4 + 2\sqrt{3} a^3 + 3a^2 - 6a}{3a}=\dfrac{1}{\sqrt{3}} a^3 + \dfrac{2}{\sqrt{3}} a^2 + a - 2$$.

Factorize the following.
$$a^4b-3a^2b^2-6ab^3$$.

1682590_1673434_ans_6cd9410b98c5458fbe7a7680b91d4595.jpg

Factorize the following.
$$x^4y^2-x^2y^4-x^4y^4$$.

1682601_1673437_ans_609c288551984d13a8081b35ffc0f225.jpg

Factorize the following.
$$20x^3-40x^2+80x$$.

$$\textbf{Step-1: Take greatest common factor common }$$

$$\text{Given polynomial :}$$ $$20x^3−40x^2+80x$$

$$\Rightarrow 20x(x^2-2x+4)$$

$$\textbf{Hence , 20x and }\boldsymbol{x^2 - 2x + 4}\textbf{ is the factors }$$

Factorize the following.
$$10m^3n^2+15m^4n-20m^2n^3$$.

1682453_1673429_ans_5fabf1fc58d1450a8b9ebdada4efb00b.jpg

Factorize the following.
$$2l^2mn-3lm^2n+4lmn^2$$.

1682596_1673436_ans_e1a4e711cd71456a8ea56f94ca482462.jpg

Factorize the following.
$$72x^6y^7-96x^7y^6$$.

1682372_1673424_ans_73175d5718934290999d9b32cbc8b3d1.jpg

Factorize the following expression.
$$3x^3y-243xy^3$$.

$$\textbf{Step 1: Factorize the given expression by using known identities.}$$

$$\text{Given expression,}$$

$$3x^3y-243xy^3$$

$$=3xy(x^2-81y^2)$$

$$=3xy[x^2-(9y)^2]$$

$$=3xy(x-9y)(x+9y)$$ $$[\because\boldsymbol{x^2-y^2=(x-y)(x+y)}]$$

$$\textbf{Hence, }\boldsymbol{3x^3y-243xy^3=3xy(x-9y)(x+9y).}$$

Factorize the following expression.
$$16(2x-1)^2-25y^2$$.

$$\textbf{Step 1: Factorize the given expression by using known identities.}$$

$$\text{Given expression,}$$

$$16(2x-1)^2-25y^2$$

$$=4^2(2x-1)^2-5^2y^2$$

$$=[4(2x-1)]^2-[5y]^2$$

$$=[4(2x-1)-5y][4(2x-1)+5y]$$ $$[\because\boldsymbol{a^2-b^2=(a-b)(a+b)}]$$

$$=(8x-5y-4)(8x+5y-4)$$

$$\textbf{Hence, }\boldsymbol{16(2x-1)^2-25y^2=(8x-5y-4)(8x+5y-4).}$$

Divide the polynomial $$(9x^2 + 12x + 10) $$ by $$(3x + 2)$$ and write the quotient and the remainder.

Divide $$(9x^2+12x+10)$$ by $$(3x+2)$$

Refer image.

So Quotient is $$3x+2$$ and Remainder is $$6$$.

1501124_1700912_ans_31d3e45869a34ba38cb8b0704898c6f4.png

Factorise : $$ 9x^2 + 12 xy $$

Given : $$ 9x^ 2 + 12 xy $$

Consider $$ 9x^ 2 + 12 xy $$

Now by taking $$3x$$ as common,

$$ 9x^ 2 + 12 xy $$ $$= 3x(3x +4y) $$

Factorise : $$ 18x^2 y -24xyz $$

Given : $$ 18x^2 y -24xyz $$

Considering $$ 18x^2 y -24xyz $$

Now by taking $$6xy$$ as common in the equation
we get,

$$ 18x^2 y -24xyz $$ $$ = 6xy ( 3x -4z) $$

Factorise : $$ a^3 +a -3a^2 -3 $$

Given : $$ a^3 +a -3a^2 -3 $$

We can further write it as

$$ a^3 +a -3a^2 -3 $$ $$= a(a^2 +1)-3(a^2 +1) $$

So we get,

$$ a^3 +a -3a^2 -3 $$ $$=(a-3)(a^2 +1 ) $$

Factorise : $$ 2x+4y-8xy-1 $$

Given : $$ 2x+4y-8xy-1 $$

We can further write it as
$$ 2x+4y-8xy-1 $$$$ = 2x-1 -8xy +4y $$

By taking common terms out
$$ 2x+4y-8xy-1 $$$$ =(2x-1)-4y(2x-1) $$

So we get,
$$ 2x+4y-8xy-1 $$$$ =(2x-1)(1-4y) $$

Factorise : $$ x^2 +y-xy -x $$

Given : $$ x^2 +y -xy -x $$

By taking $$x$$ as common in the first and $$1$$ as common in the second term

$$ x^2 +y -xy -x $$ $$ = x(x-y)-1(x-y) $$

So we get,

$$ x^2 +y -xy -x $$ $$ = (x-1)(x-y) $$

Factorise : $$ abx^2+a^2x+b^2x+ab $$

Given : $$ abx^2+a^2x+b^2x+ab $$

We can further write it as

$$ abx^2+a^2x+b^2x+ab $$$$ =ax(bx +a) +b(bx+a) $$

So we get,

$$ abx^2+a^2x+b^2x+ab $$$$=(ax+b)(bx+a) $$

Factorise : $$ 2a^2 + bc-2ab- ac $$

Given : $$ 2a^2 + bc-2ab- ac $$

We can further write it as
$$ 2a^2 + bc-2ab- ac $$ $$ =2a^2 -2ab -ac+ bc $$

By taking the common terms out
$$ 2a^2 + bc-2ab- ac $$ $$ = 2a(a-b) -c(a-b) $$

So we get,
$$ 2a^2 + bc-2ab- ac $$ $$= (a-b) (2a-c) $$

Factorise : $$ ab(x^2+y^2) -xy(a^2+b^2)$$

Given : $$ ab (x^2 +y^2) - xy (a^2 +b^2 ) $$

By multiplying the terms
$$ ab (x^2 +y^2) - xy (a^2 +b^2 ) $$$$ = abx^2 +aby^2 -a^2xy -b^2 xy $$

We can further write it as
$$ ab (x^2 +y^2) - xy (a^2 +b^2 ) $$$$ = abx^2 -a^2xy +aby^2 -b^2xy $$

By taking out the common terms out
$$ ab (x^2 +y^2) - xy (a^2 +b^2 ) $$$$ =ax(bx-ay) +by(ay-bx) $$

By taking the negative sign out
$$ ab (x^2 +y^2) - xy (a^2 +b^2 ) $$ $$=ax(bx-ay) -by(bx -ay) $$

So we get ,
$$ ab (x^2 +y^2) - xy (a^2 +b^2 ) $$$$= ( ax-by)(bx-ay) $$

Factorise : $$ a^2 +ab(b+1)+b^3 $$

Given : $$ a^2 +ab(b+1)+b^3 $$

By multiplying the terms
$$ a^2 +ab(b+1)+b^3 $$$$ =a^2 +ab^2 +ab+b^3 $$

We can further write it as
$$ a^2 +ab(b+1)+b^3 $$$$= a^2 + ab+ab^2+ b^3 $$

By taking the common terms out
$$ a^2 +ab(b+1)+b^3 $$$$= a(a+b) +b^2 (a+b) $$

So we get,
$$ a^2 +ab(b+1)+b^3 $$$$= (a+b^2)(a+b) $$

Factorise : $$ 20x^2 -45 $$

Given : $$ 20x^2 -45 $$

By taking $$5$$ as common
$$ 20x^2 -45 $$$$ = 5(4x^2 -9) $$

We can write it as
$$ 20x^2 -45 $$$$ = 5((2x)^2 -3^2 )$$

Based on the equation $$ a^2 -b^2 =(a+b)(a-b) $$

We get,
$$ 20x^2 -45 $$$$ = 5(2x+3)(2x-3)$$

Factorise : $$ a(a+b-c)-bc $$

Given : $$ a(a+b-c)-bc $$

We can further write it as
$$ a(a+b-c)-bc $$$$=a^2 +ab -ac-bc $$

By taking the common terms out
$$ a(a+b-c)-bc $$$$ = a(a+b) -c(a+b) $$

So we get,
$$ a(a+b-c)-bc $$ $$ =(a+b)(a-c) $$

Factorise : $$ ab(x^2+ 1) +x(a^2 +b^2 ) $$

1563622_1714984_ans_b3970a533e9341cdb5e919c384fba9e4.png

Factorise : $$ a^2 -b^2 -a -b $$

$$\textbf{Step 1 : Simplify the form}$$

$$\text{Consider } a^2 - b^2 - a - b\space $$$$=(a - b)(a + b) - a - b $$$$\quad \quad \quad \mathbf{[(x^2-y^2) = (x-y)(x+y)]}$$

$$=(a + b ){(a - b - 1 )}$$$$\quad \textbf{[Take (a-b) common from both the terms]}$$

$$\textbf{Hence , }\boldsymbol{a^2 - b^2 - a - b} \textbf{ is equal to } \boldsymbol{(a + b)(a - b - 1)}$$

Factorise : $$ 9a^2 +6a+ 1 -36b^2 $$

Given : $$ 9a^2 +6a+ 1-36b^2 $$

We can further write its as
$$ 9a^2 +6a+ 1-36b^2 $$$$ = (9a^2 +6a +1 )-36b^2 $$

So we get
$$ 9a^2 +6a+ 1-36b^2 $$$$ = [(3a)^2 +2 \times 3 \times 1 +1^2 ]-(6b)^2 $$
$$ 9a^2 +6a+ 1-36b^2 $$$$ = (3a+1)^2 -(6b)^2 $$

Based on the equation $$ a^2 -b^2= (a+b)(a-b) $$

We get,
$$ 9a^2 +6a+ 1-36b^2 $$$$ =(3a+1+6b)(3a+1-6b) $$

Factorise : $$ 4a^2 -4b^2 +4a +1 $$

Given : $$ 4a^2 -ab^2 +4a +1 $$

We can write it as

$$ 4a^2 -ab^2 +4a +1 $$$$ =(4a^2 +4a +1 )-4b^2 $$

We get,
$$ 4a^2 -ab^2 +4a +1 $$$$= [(2a)^2 +2 \times 2a \times 1 +1^2]-(2b)^2 $$

On further calculation
$$ 4a^2 -ab^2 +4a +1 $$$$ =(2a +1)^2 -(2b)^2 $$

Based on the equation $$ a^2 -b^2 = (a+b)(a-b) $$

Using the formula
$$ 4a^2 -ab^2 +4a +1 $$ $$ =(2a +1+ 2b)(2a+1-2b)$$

So we get
$$ 4a^2 -ab^2 +4a +1 $$$$ = ( 2a+ 2b+1)(2a-2b +1 )$$

Factorise : $$ a^2 -b^2 -4ac +4c^2 $$

Given : $$ a^2 -b^2-4ac +4c^2 $$

We can write it as
$$ a^2 -b^2-4ac +4c^2 $$$$ = a^2 -4ac +4c^2 -b^2 $$

So we get
$$ a^2 -b^2-4ac +4c^2 $$$$ =a^2 -2 \times a \times 2x + 2c^2 -b^2 $$
$$ a^2 -b^2-4ac +4c^2 $$$$ = (a-2c)^2 -b^2 $$

Based on the equation $$ a^2 -b^2= (a+b)(a-b) $$

We get,
$$ a^2 -b^2-4ac +4c^2 $$$$ =(a-2c +b)(a-2c-b) $$

Factorise : $$ 5x^2 -16x -21 $$

Given : $$ 5x^2 -16x-21 $$

We can further write it as
$$ 5x^2 -16x-21 $$$$ =5x^2 +5x -21x -21 $$

by taking out the common terms
$$ 5x^2 -16x-21 $$$$ = 5x(x+1)-21(x+1) $$

So we get,
$$ 5x^2 -16x-21 $$$$ =(5x-21)(x+1) $$

Factorise : $$ 18x^2 + 3x -10 $$

Given : $$ 18x^2 +3x -10 $$

We can further write it as:
$$ 18x^2 +3x -10 $$$$ = 18x^2 -12 x+ 15x -10 $$

By taking out the common terms:
$$ 18x^2 +3x -10 $$$$ = 6x(3x-2) +5(3x-2) $$

So we get,
$$ 18x^2 +3x -10 $$$$ =(6x+5)(3x-2) $$

Factorise : $$ 25x^2 -10x+ 1-36y^2 $$

Given : $$ 25x^2 -10 x+ 1-36y^2 $$

We can further write the given question as
$$ 25x^2 -10 x+ 1-36y^2 $$$$ =(25x^2 -10 x+ 1)-36y^2 $$

So we get
$$ 25x^2 -10 x+ 1-36y^2 $$$$=[(5x)^2 -2 \times 5x \times 1 +1^2]-(6y)^2 $$
$$ 25x^2 -10 x+ 1-36y^2 $$$$ =(5x -1)^2 -(6y)^2 $$

Based on the equation $$ a^2 -b^2 =(a+b)(a-b) $$

We get,
$$ 25x^2 -10 x+ 1-36y^2 $$$$ =(5x-1 +6y)(5x-1-6y) $$

Factorise : $$ a^2 +2ab +b^2 -9c^2 $$

Given : $$ a^2 +2ab +b^2 -9c^2 $$

We can write the given question as
$$ a^2 +2ab +b^2 -9c^2 $$$$ =(a +b)^2 -(3c)^2 $$

Based on the equation $$ a^2 -b^2 =(a+b)(a-b) $$

We get,

$$ a^2 +2ab +b^2 -9c^2 $$$$ =( a+ b+ 3c)(a+b-3c) $$

Factorise : $$ x^3 - 5x^2 -x+5 $$

Given : $$ x^3 -5x^2 -x+5 $$

By taking common terms
$$ x^3 -5x^2 -x+5 $$$$ =x^2 (x-5)-1(x-5) $$

So we get
$$ x^3 -5x^2 -x+5 $$$$ =(x-5)(x^2 -1) $$

Based on the equation $$ a^2 -b^2= (a+b)(a-b) $$

We get,
$$ x^3 -5x^2 -x+5 $$$$ =(x-5)(x+1)(x-1) $$

Factorise : $$ a^2 -b^2 +2bc - c^2$$

Given : $$ a^2-b^2+2bc-c^2$$

We can write it as
$$ a^2-b^2+2bc-c^2$$$$ = a^2 -(b^2 -2bc +c^2 ) $$

We know that, $$(a-b)^2=a^2-2ab+b^2$$

$$ a^2-(b^2-2bc+c^2)$$$$= a^2 -(b-c)^2 $$

Based on the identity, $$ a^2 -b^2 = (a+b)(a-b) $$

We get,
$$ a^2-(b-c)^2$$$$ = [a + (b-c)[a- (b-c)] $$
$$ \implies a^2-(b-c)^2$$$$ =( a+b-c)(a-b+c) $$
$$\therefore$$ $$a^2-b^2+2bc-c^2=(a+b-c)(a-b+c)$$

Factorise : $$ x^2 +y^2 -z^2 -2xy $$

Given : $$ x^2 +y^2 -z^2 -2xy $$

We can write it as
$$ x^2 +y^2 -z^2 -2xy $$ $$ =(x^2 +y^2 -2xy)-z^2 $$

So we get
$$ x^2 +y^2 -z^2 -2xy $$ $$ = ( x-y)^2 -z^2 $$

Based on the equation $$ a^2 -b^2 =(a+b)(a-b) $$

We get ,
$$ x^2 +y^2 -z^2 -2xy $$ $$ =(x-y+z)(x-y-z) $$

Divide:
$$8x^{2}y^{2}-6xy^{2}+10 x^{2}y^{3}$$ by $$2xy$$

$$8x^2y^2-6xy^2+10x^2y^3$$ by $$2xy$$

On dividing polynomial by a monomial we have divide every variables of polynomial.

$$\Rightarrow$$ $$\dfrac{8x^2y^2-6xy^2+10x^2y^3}{2xy}$$ $$=\dfrac{8x^2y^2}{2xy}-\dfrac{6xy^2}{2xy}+\dfrac{10x^2y^3}{2xy}$$

$$=\dfrac{8}{2}x^{2-1}y^{2-1}-\dfrac{6}{2}x^{1-1}y^{2-1}+\dfrac{10}{2}x^{2-1}y^{3-1}$$

$$=4xy-3y+5xy^2$$

Factorise: $$36x^3y –60x^2y^3z$$

Given: $$36x^3y - 60x^2y^3z $$

By taking $$12x^2y$$ as a common factor for the above equation we get,

$$36x^3y - 60x^2y^3z = 12x^2y(3x - 5y^2z)$$

Factorise : $$ x^4y^4 - xy $$

Given expression is $$x^4y^4-xy$$

We can take out $$xy$$ as common.

Hence, the expression becomes:

$$xy \left(x^3y^3-1\right)$$

$$\Rightarrow xy \left[(xy)^3-1^3\right]$$

We know that, $$a^3-b^3=(a-b)(a^2+b^2+ab)$$

Hence, the expression becomes:

$$xy\left[(xy-1)((xy)^2+1^2+1(xy))\right]$$

$$\Rightarrow xy\left[(xy-1)(x^2y^2+1+xy)\right]$$

$$\Rightarrow xy(xy-1)(x^2y^2+xy+1)$$

Hence, $$x^4y^4-xy=xy(xy-1)(x^2y^2+xy+1)$$.

Divide $$12x^{4}+8x^{3}-6x^{2}$$ by $$-2x^{2}$$

While dividing a polynomial by a monomial, we have to divide every variables of polynomial.

$$\Rightarrow$$ $$\dfrac{12x^4+8x^3-6x^2}{-2x^2}=\dfrac{12x^4}{-2x^2}+\dfrac{8x^3}{-2x^2}-\dfrac{6x^2}{-2x^2}$$

$$=-\dfrac{12}{2}x^{4-2}-\dfrac{8}{2}x^{3-2}+\dfrac{6}{2}x^{2-2}$$

$$=-6x^2-4x+3$$

Factorise : $$ 16x^4 +54 x $$

Given : $$ 16x^4+54x $$

We can write the given question as,

$$ 16x^4+54x=2x(8x^3+27) $$

According to the equation,
$$ a^3+b^3=(a+b)(a^2-ab+b^2) $$

So we get,
$$ 2x(8x^3+27) $$$$ =2x((2x)^3+3^3) $$

Using the equation,
$$ =2x((2x)+3)((2x)^2-(2x)(3)+(3)^2) $$

$$ 16x^4+54x $$$$ = 2x(2x+3)(4x^2-6x+9) $$

Factorise : $$ x - 8xy^3 $$

Given : $$ x-8xy^3 $$

We can write the given question as,
$$ x-8xy^3=x(1-8y^3) $$

According to the equation,
$$ a^3-b^3=(a-b)(a^2+ab+b^2) $$

So we get,
$$ x(1-8y^3) $$$$ =x(1^3-(2y)^3) $$

using the equation,

$$=x[(1-2y)(1^2+2y+(2y)^2)] $$

$$ x-8xy^3 $$$$=x(1-2y)(1+2y+4y^2) $$

Divide:
$$9x^{2}y-6xy+12xy^{2}$$ by $$-3xy$$

$${\textbf{Step - 1: Write the equivalent expression by diving each term of polynomial }}$$

$${\textbf{by the monomial}}{\text{.}}$$

$${\text{Dividing each term by the monomial we get, }}\\\Rightarrow\dfrac{{{\text{9}}{{\text{x}}^{\text{2}}}{\text{y}}}}{{{\text{ - 3xy}}}}{\text{ - }}\dfrac{{{\text{6xy}}}}{{{\text{ - 3xy}}}}{\text{ + }}\dfrac{{{\text{12x}}{{\text{y}}^{\text{2}}}}}{{{\text{ - 3xy}}}}$$

$${\text{= ( - 3}}{{\text{x}}^{{\text{2 - 1}}}}{{\text{y}}^{{\text{1 - 1}}}}{\text{ + 2}}{{\text{x}}^{{\text{1 - 1}}}}{{\text{y}}^{{\text{1 - 1}}}}{\text{ - 4}}{{\text{x}}^{{\text{1 - 1}}}}{{\text{y}}^{{\text{2 - 1}}}}{\text{)}}{\text{.}}$$

$${\text{= - 3x + 2 - 4y}}$$

$${\textbf{Hence, the required answer is }}{\mathbf{ - 3x + 2 - 4y}}{\text{.}}$$

Find the values of a and b so that the polynomial $$(x^4+ax^3-7x^2+8x+b)$$ is exactly divisible by $$(x+2)$$ as well as $$(x+3)$$.

We are given that polynomial $$(x^4+ax^3-7x^2+8x+b)$$ is exactly divisible by $$(x+2)$$ as well as $$(x+3)$$.

The two divisors in the question are $$(x + 2)$$ and $$(x + 3)$$. As it is given that the given polynomial is divisible by both these divisors, that means;

$$x + 2 = 0$$ and $$x + 3 = 0$$

So, $$x = -2$$ and $$x = -3$$ will make the remainder zero when these values of x are substituted in the given polynomial.

$$f(x) = x^{4}+ax^{3} -7x^{2} +8x+b$$

So, $$f(-2)$$ and $$f(-3)$$ will be equal to zero.

$$f(-2) = (-2)^{4}+a(-2)^{3} -7(-2)^{2} +8(-2)+b =0$$

$$f(-3) = (-3)^{4}+a(-3)^{3} -7(-3)^{2} +8(-3)+b =0$$

$$f(-2) = 16-8a -28 -16+b =0 $$

$$\Rightarrow -8a+b-28=0\quad \quad ....(1)$$

$$f(-3) = 81-27a -63 -24+b =0$$

$$\Rightarrow -27a+b -6 =0 \quad \quad ....(2)$$

Now, subtracting $$(2)$$ from $$(1)$$:

$$-8a+b -28 =0$$

$$-27a+b -6 =0$$

+ - + -

$$\overline{\ \ 19a - \ \ 22 \ \ =\ \ 0}$$

$$\Rightarrow a = \dfrac{22}{19}$$

Putting the value of $$a$$ in $$(1)$$, we get;

$$-8a+b -28 =0$$

$$-8\left(\dfrac{22}{19}\right) +b -28 =0$$

$$\Rightarrow b = 28 + \dfrac{176}{19}$$

$$\Rightarrow b = \dfrac{708}{19}$$

Hence, the value of $$a$$ is $$\dfrac{22}{19}$$ and the value of $$ b $$ is $$ \dfrac{708}{19}$$.

Find the value of 'a' for which the polynomial $$(x^4-x^3-11x^2-x+a)$$ is divisible by $$(x+3)$$.

$$P(x) = x^4-x^3-11x-x+a$$

$$= x^4-x^3-12x + a$$

$$P(-3) = 81+27+36+a =0$$

So, $$a = -144.$$

Factorise : $$ 1029 - 3x^3 $$

1673382_1715284_ans_973915ff2da440409cdb2e60fd174cf3.jpg

Factorise:
$$16a^2 – 24ab$$

Given: $$16a^2$$ $$ – 24ab$$

By taking $$8a$$ as a common factor for the above equation we get,

$$16a^2$$ $$– 24ab = 8a (2a – 3b)$$

Factorise :
$$14x^3+21x^4y-28x^2y^2$$

let’s take HCF of above equationBy taking $$7x^2$$ as a common factor for the above equation we get, $$14x^3+21x^4y-28x^2y^2 = 7x^2(2x + 3x^2y- 4y^2)$$

Factorise

$$9x^3 – 6x^2 + 12x$$

let’s take HCF of above equationBy taking $$3x$$ as a common factor for the above equation we get,
$$9x^3 -6x^2 + 12x = 3x(3x^2 - 2x + 4)$$

Factorise

$$6a(a-2b) + 5b(a-2b)$$

By taking $$a-2b$$ as a common factor for the above equation we get,
$$6a (a-2b) + 5b (a-2b) = (a-2b) (6a + 5b)$$

Factorise

$$10x^3 -15x^2$$

let’s take HCF of above equationBy taking $$5x^2$$ as a common factor for the above equation we get,
$$10x^3 - 15x^2 = 5x^2(2x-3)$$

Factorise

$$2m(1-n) + 3(1-n)$$

By taking $$(1-n)$$ as a common factor for the above equation we get
$$\Rightarrow 2m (1-n) + 3(1-n) = (1-n) (2m + 3)$$

The sum of first $$n$$ natural numbers is given by the expression $$\dfrac{n^{2}}{2} + \dfrac{n}{2}$$. Factorise this expression.

Given,

Sum of first $$n$$ natural numbers $$=\dfrac{n^{2}}{2} + \dfrac{n}{2}$$

Factorizing the given expression, we get,

$$\dfrac{n^{2}}{2} + \dfrac{n}{2}$$ $$= \dfrac{1}{2}(n^{2}+n) $$

$$= \dfrac{1}{2} n(n +1)$$

$$\therefore \dfrac{n^{2}}{2} + \dfrac{n}{2}= \dfrac{1}{2} n(n +1)$$

Perform the following division:
$$(3pqr-6p^{2}q^{2}r^{2}) \div 3pq$$

The dividion is carried out as follows :

$$\dfrac{3pqr-6p^{2}q^{2}r^{2}}{3pq}$$

$$\\=\dfrac{3pqr}{3pq} -\dfrac{6p^{2}q^{2}r^{2}}{3pq}$$

$$=\dfrac {3\cdot p\cdot q\cdot r}{3\cdot p\cdot q}-\dfrac{2\cdot3\cdot p\cdot p\cdot q\cdot r\cdot r}{3\cdot p\cdot q}$$

Cancelling out the common factors in numerator and denominator,

$$=r-2\cdot p\cdot q\cdot r\cdot r$$

$$=r-2pqr^2$$

Write the greatest common factor of the following terms $$-18a^{2}$$, $$108a$$

We have

$$-18a^2=(-1)\times 18\times a\times a$$

$$108a=18\times 6\times a$$

$$\therefore$$ Greatest common factor is $$18a$$

Write the greatest common factor of the following terms $$3x^{2}y$$, $$18xy^{2}$$, $$-6xy$$

We have

$$3x^2y=3\times x\times x\times y$$

$$18xy^2=3\times 6\times x \times y\times y$$

$$-6xy=(-1)\times 6\times x \times y$$

$$\therefore$$ Greatest common factor is $$3xy$$

The common factor method of factorisation for a polynomial is based on __________ property.

1974136_1792827_ans_8a98965c4b0b45f48214d05f730d17ed.jpg

The factorisation of 2x + 4y is __________ .

We have,

$$2x + 4y$$

Factoring $$2$$ out, we get

$$= 2(x+2y)$$

Hence $$2x + 4y= 2(x+2y)$$

Factorise the following polynomials :
(i) $$ 25 abc^2 - 15a^2b^2c $$
(ii) $$ x^2yz + xy^2z + xyz^2 $$

$$ (i) 25abc^2-15a^2b^2c=5abc(5c-3ab) $$

$$ (ii) x^2yz+xy^2z+xyz^2=xyz(x+y+z) $$

Factorise the following polynomials :
(i) $$ 8xy^3 + 12x^2 y^2 $$
(ii) $$ 15ax^3 - 9ax^2 $$

$$ (i) 8xy^3 + 12x^2y^2=4xy^2(2y+3x) $$

$$ (ii) 15 ax^3-9ax^2=3ax^2(5x-3) $$

Factorise the following polynomials :
$$ 10a( 2p +q)^3 - 15b ( 2p +q)^2 + 35 ( 2p + q) $$

$$ 10a(2p+q)^3-15b(2p+q)^2+35(2p+q) $$

=$$ 5[2a(2p+q)]^3-3b(2p+q)^2+7(2p+q)] $$

=$$5(2p+q)[2a(2p+q)^2-3b(2p+q)+7 ] $$

Factorise the following polynomials :
(i) $$ 21 py^2 - 56 py$$
(ii) $$ 4x^3 - 6x^2 $$

$$ (i) 21py^2-56py=7py(3y-8) $$

$$ (ii) 4x^3-6x^2=2x^2(2x-3) $$

Factorise the following polynomials :
(i) $$ 8x^3 - 6x^2 + 10 x $$
(ii) $$ 14mn + 22m -62 p $$

$$ (i) 8x^3-6x^2+10x=2x(4x^2-3x+5) $$

(Take $$2x$$ common from each term)

$$(ii) 14mn +22 m-62p=2(7mn+11m-31p)$$

(Take $$2$$ common from each term)

Factorise the following polynomials :
(i) $$ 6(x+2y)^3 + 8 ( x+ 2 y)^2 $$
(ii) $$ 14 (a -3b)^3 - 21 p(a -3b) $$

$$ (i) \ 6(x+2y)^3+8(x+2y)^2 $$

Taking $$(x+2y)^2$$ common, we get:

$$(x+2y)^2[6(x+2y)+8] $$

$$= (x+2y)^2[6x+12y+8] $$

$$=(x+2y)^2(2)(3x+6y+4) $$

$$=2(x+2y)^2(3x+6y+4) $$

Hence, $$6(x+2y)^3+8(x+2y)^2 =2(x+2y)^2(3x+6y+4) $$

$$ (ii) \ 14(a-3b)^3-21p(a-3b) $$

Taking $$7$$ common, we get:

$$ 7[2(a-3b)^3-3p(a-3b)] $$

$$= 7(a-3b)\{2(a-3b)^2-3p\} $$

Hence, $$14(a-3b)^3-21p(a-3b) = 7(a-3b)\{2(a-3b)^2-3p\}$$

Factorise the following polynomials:
(i) $$ 18p^2q^2 -24pq^2 +30p^2q $$
(ii) $$ 27a^3b^3 - 18a^2 b^3 + 75 a^3 b^2 $$

$$(i)$$ Factor out $$6pq$$ from the given expression,

$$18{p^2}{q^2} - 24p{q^2} + 30{p^2}q = 6pq(3pq - 4q + 5p)$$

$$ (ii)$$ Factor out $$3 a^2b^2$$ from the given expression.

$$ 27a^3b^3-18a^2b^3+75a^3b^2= 3a^2b^2(9ab-6b+25a) $$

Find the quotient and the remainder when $$ P(x)=3 x^{3}+x^{2}+2 x+5 $$ is divided by
$$g(x)=x^{2}+2 x+1 \qquad\qquad$$

The quotient and remainder when $$ P(x)=3 x^{3}+x^{2}+2 x+5 \quad $$ is divided by $$ g(x)=x^{2}+2 x+1 $$ are $$ 3 x-5 $$ and $$ 9 x+10 $$ respectively.
1679202_1803908_ans_f7d0011ac1884947b3d124d9d6a43d64.png

1679202_1803908_ans_f7d0011ac1884947b3d124d9d6a43d64.png

Factorise the expressions and divide them as directed:
$$(x^{2}-22x+117) \div (x-13)$$

Factorising the dividend,

$$x^2-22x+117$$

$$=x^2-13x-9x+117\qquad$$[Splitting the middle term]

$$=x(x-13)-9(x-13)$$

$$=(x-13)(x-9)$$

$$\therefore (x^{2}-22x+117) \div (x-13)$$

$$=\dfrac{x^{2}-22x+117}{x-13}$$

$$=\dfrac{(x-13)(x-9)}{x-13}$$

Cancelling out the common factor,

$$=x-9$$

Factorise the following polynomials :
(i) $$ 15a( 2p - 3p) - 10b ( 2 p - 3q) $$
(ii) $$ 3a(x^2 +y^2) + 6b ( x^2 +y^2 ) $$

$$ (i) 15a(2p-3q)-10b(2p-3q) $$

=$$ (2p-3q)(15a-10b) $$

=$$(2p-3q)(5)(3a-2b) $$

=$$5(2p-3q)(3a-2b) $$

$$ (ii) 3a(x^2+y^2)+6b(x^2+y^2) $$

=$$(x^2+y^2)(3a+6b)$$

=$$(x^2+y^2)(3)(a+2b) $$

=$$3(x^2+y^2)(a+2b) $$

Divide:
$$9x^4 - 8x^3 - 12x + 3$$ by $$3x$$

$$\frac{9x^4 - - 8x^3 - 12x + 3}{3x}$$
= $$\frac{9x^4}{3x} - \frac{8x^3}{3x} - \frac{12x}{3x} + \frac{3}{3x}$$
= $$3x^3 - \frac{8}{3}x^2 - 4 + \frac{1}{x}$$

$$ 2 \pi r^2 - 4 \pi r $$

$$2 \pi r^2-4 \pi r$$
Take out common in both terms,
Then, $$ 2 \pi r (r-2) $$
Therefore,HCF of $$ 2\pi r^2 \quad and \quad 4 \pi r \quad is \quad 2 \pi r..$$

$$\text{Factorise } x^3 +x +2 $$

$$ {\textbf{Step -1: Simplification}} $$

$$ {\text{As we know that }}{{\text{x}}^3} + {1} = (x + 1)({x^2} - x + 1) $$

$$ {\text{Given, }}{{\text{x}}^3} + 1 + x + 1 $$

$$ = (x + 1)({x^2} - x + 1) + x + 1 $$

$$ = (x + 1)({x^2} - x + 1) + (x + 1) $$

$$ = (x + 1)({x^2} - x + 1 + 1) $$

$$ = (x + 1)({x^2} - x + 2) $$

$$ {\textbf{Hence, the answer is }}\mathbf{(x + 1)({x^2} - x + 2)} $$

$$ 32x^4 -500 x $$

$$ 32x^4 -500 x $$
Take out common in all terms we get,
$$ 4x(8x^3-125)$$
Above terms can be written as,
$$ 4x((2x)^3-5^3)$$
We know that,$$ a^3-b^3=(a-b)(a^2+ab+b^2)$$
Where,$$ a=2x,b=5 $$
=$$4x(2x-5)((2x)^2+(2x \times 5)+5^2)$$
=$$4x(2x-5)(4x^2+10x+25)$$

$$ (x^6 / 343) +( 343 / x^6 ) $$

$$ (x^6 / 343) +( 343 / x^6 ) $$
Above terms can be written as,
$$(x^2/7)^3+(7/x^2)^3 $$
We know that, $$ a^3+b^3=(a+b)(a^2-ab+b^2)$$
Where,$$a=(x^2/7),b=(7/x^2)$$
Then,$$(x^2/7)^3+(7/x^2)^3=[(x^2/7)+(7/x^2)][(x^2/7)^2-((x^2/7)\times (7/x^2))+(7/x^2)^2]$$
=$$[(x^2/7)+(7/x^2)][(x^4/49)-1+(49/x^4)] $$

$$ x^2 +x^5 $$

$$ x^2 +x^5 $$
Take out common in all terms we get,
$$ x^2(1+x^3)$$
$$x^2(1^3+x^3)$$
We know that,$$a^3+b^3=(a+b)(a^2-ab+b^2)$$
Where,$$a=1,b=x $$
=$$x^2[(1+x)(1^2-(1\times x)+x^2)]$$
=$$ x^2(1+x)(1-x+x^2)$$

$$ a^3 - a -120 $$

$$ a^3 - a -120 $$
Above terms can be written as,
$$ a^3-a-125+5 $$
Rearranging the above terms,we get
$$ a^3-125-a+5 $$
$$(a^3-125)-(a-5)$$
$$(a^3-5^3)-(a-5)$$
We know that,$$ a^3-b^3=(a-b)(a^2+ab+b^2)$$
$$[(a-5)(a^2+5a+5^2)]-(a-b)$$
$$(a-5)(a^2+5a+25)-(a-5)$$
$$(a-5)(a^2+5a+25-1)$$
$$(a-5)(a^2+5a+24)$$

$$ a^2(b+c) - ( b+c)^3 $$

$$ a^2(b+c) - ( b+c)^3 $$
Take out common in all terms,
$$ (b+c)(a^2 - (b+c)^2) $$
We know that $$ a^2 -b^2 = (a+b)(a- b) $$
$$ ( b+c)(a+b+c) (a-b-c) $$

$$ x^4 +5x^2 + 9 $$

$$ x^4 + 5x^2 + 9 $$
$$ x^4 + 6x^2 – x^2 + 9 $$
$$ (x^4 + 6x^2 + 9) – x^2 $$
$$ ((x^2)2 + (2 \times x^2 \times 3) + 3^2)$$
We know that,$$ (a + b)^2 = a^2 + 2ab + b^2 $$,
$$ ((x^2)^2 + (2 \times x^2 \times 3) + 3^2) $$
So, $$ (x^2 + 3)^2 – x^2 $$
We know that, $$ a^2 – b^2 = (a + b) (a – b) $$
$$ (x^2 + 3 + x) (x^2 + 3 – x) $$

$$ 2x^4 -32 $$

$$ 2x^4 -32 $$
Take out common in all terms,
$$ 2(x^4 -16) $$
Above terms can be written as,
$$ 2((x^2)^2 - 4^2 ) $$
We know that $$ a^2 -b^2 =(a +b)(a-b) $$
$$ 2(x^2 + 4)(x^2 -4) $$
$$ 2(x^2 +4)(x^2 -2^2) $$
$$ 2(x^2 +4)(x+2)(x-2) $$

$$ x^4 - 1/ x^4 $$

$$ x^4 - 1/x^4 =(x^2 +1/x^2)(x^2 -1/x^2) $$
$$ = ( x^2 +1/x^2)(x+1/x)(x-1/x) $$
From $$ (i), (ii) $$ and $$ (iii) $$ substitute the values we get,
$$ = ( 97 /36) \times ( 13 / 6) \times ( 5/ 6) $$
$$ = 6305 / 1296 $$

$$ a^4 +b^4 - 7a^2b^2 $$

$$ a^4 +b^4- 7a^2b^2 $$
Above terms can be written as
$$ a^4 +b^4 +2a^2 b62 -9a^2 b^2 $$
we know that $$ (a+b)^2 =a^2 +2ab +b^2 $$
$$ [ (a^2)^2 + (b^2)^2 +( 2 \times a^2 \times b^2)] - (3ab)^2 $$
$$ ( a^2 +b^2)^2 -(3ab)^2 $$
we know that $$ (a+b)^2 =a^2 +2ab +b^2 $$
$$ [(a^2)^2 +(b^2)^2 + ( 2 \times a^2 \times b^2 ) ] -(3ab)^2 $$
$$ (a^2 +b^2)^2 - (3ab)^2 $$
We know that $$ a^2 -b^2 = ( a+b)(a-b) $$
$$ (a^2 +b^2 +3ab)(a^2 +b^2 -3ab) $$

Divide:
$$ 9 x^3 - 6x^2\,\, by\,\, 3x$$

We have to divide $$9x^3 - 6x^2\,\, by\,\, 3x$$

$$9x^3 - 6x^2 \div 3x = \dfrac{(9 \times x^3 - 6 \times x^2) }{ (3 \times x)}$$

Separating the terms, we get

$$=\dfrac{ (9 \times x^3) }{ (3 \times x)} - \dfrac{(6 \times x^2) }{ (3 \times x)}$$

We get,

$$= 3 \times x^{3-1} - 2 \times x^{2-1}$$

$$= 3x^2 - 2x$$

Hence, $$9x^3 - 6x^2 \div 3x = 3x^2 - 2x$$

$$ 5a^4 - 5a^3 +30a^2 -30 a $$

$$ 5a^4 - 5a^3 +30a^2 -30 a $$
Take out common in both terms,
$$ 5a(a^3-a^2+6a-6) $$
$$ 5a[a^2(a-1)+6(a-1)]$$
$$ 5a(a-1)(a^2+6)$$

$$ 15(2x-3)^3 - 10 (2x-3 ) $$

$$ 15(2x-3)^3 - 10 (2x-3 ) $$
Take out common in both terms,
Then, $$ 5(2x-3)[3(2x-3)^2-2]$$

Factorize the following
$$a^{12}x^{4} - a^{4} x^{12} $$

$$ [(a^6)^2 (x^2)^2 - (a^2)^2 (x^6)^2]$$

$$ = [(a^6x^2)^2 - (a^2 x^6)^2] $$

$$ = (a^6 x^2 + a^2x^6)(a^6 x^2 - a^2 x^6) $$

$$ = a^2x^2 (a^4 + x^4) [(a^3)^2 x^2 - a^2(x^3)^2] $$

$$ = a^2x^2 (a^4 + x^4) [(a^3x)^2 - (ax^3)^2] $$

$$= a^2x^2 (a^4 + x^4)[(a^3x + ax^3) (a^3x - ax^3)] $$

$$ =a^2x^2 (a^4 + x^4) [ax(a^2 + x^2). ax(a^2 - x^2)] $$

$$ = a^2x^2 (a^4 + x^4)[a^2x^2 (a^2 + x^2)(a^2 - x^2)]$$

$$ = a^4 x^4 (a^4 + x^4)(a^2 + x^2)(a + x)(a - x) $$

Divide:
$$ 15x^3y^2 + 25x^2y^3 - 36x^4y^4 \,\,by\,\, 5x^2y^2$$

We have to devide $$15x^3y^2 + 25x^2y^3 - 36x^4y^4 \,\,by\,\, 5x^2y^2$$

$$15x^3y^2 + 25x^2y^3 - 36x^4y^4 \div 5x^2y^2 \\= \dfrac{(15x^3y^2 + 25x^2y^3 - 36x^4y^4) }{ (5x^2y^2)}$$

$$= \dfrac{(15 \times x^3 \times y^3)} {(5 \times x^2 \times y^2)} +\dfrac{ (25 \times x^2 \times y^3) }{ (5 \times x^2 \times y^2)} - \dfrac{(36 \times x^4 \times y^4) }{ (5 \times x^2 \times y^2)}$$

On further calculation, we get

$$= 3 \times x^{3-2} \times y^{2-2} + 5 \times x^{2-2} \times y^{3-2} -\dfrac{ (36 \times x^{4-2} \times y^{4-2})} 5$$

$$= 3 \times x^1 \times y^0 + 5 \times x^0 \times y^1 - \dfrac{(36 \times x^2 \times y^2) } 5$$

$$= 3x + 5y - \dfrac{(36x^2y^2) }5$$

Hence, $$15x^3y^2 + 25x^2y^3 - 36x^4y^4 \div 5x^2y^2 = 3x + 5y - \dfrac{(36x^2y^2) }5$$

$$ a^3 - ( 1/a^3) -2a +2/a$$

$$ a^{12}x^4 - a^4 x^{12} $$

$$ a^{12}x^4 - a^4 x^{12} $$
Take out common in both terms,
$$ a^4x^4(a^8-x^8)$$
$$ a^4x^4((a^4)^2-(x^4)^2)$$
We know that,$$ (a^2-b^2)=(a+b)(a-b)$$
$$ a^4x^4(a^4+x^4)(a^4-x^4)$$
$$ a^4x^4(a^4+x^4)((a^2)^2-(x^2)^2) $$
$$ a^4x^4(a^4+x^4)(a^2+x^2)(a^2-x^2)$$
$$a^4x^4(a^4+x^2)(a+x)(a-x)$$

$$ x^3 -(8 /x) $$

Above terms can be written as,

$$ (1/x)(x^3-8) $$

$$(1/x)[(x)^3-(2)^3]$$

We know that,$$ a^3-b^3=(a-b)(a^2+ab+b^2)$$

So, $$ a=x,b=2 $$

$$(1/x)(x-2)(x^2+2x+4)$$

Carry out the following divisions:
$$(x^3 + 2x^2 + 3x) \div 2x$$

$$\begin{aligned}{}\left( {{x^3} + 2{x^2} + 3x} \right) \div 2x &= \frac{{{x^3} + 2{x^2} + 3x}}{{2x}}\\ &= \frac{{{x^3}}}{{2x}} + \frac{{2{x^2}}}{{2x}} + \frac{{3x}}{{2x}}\\ &= \frac{1}{2}{x^2} + x + \frac{3}{2}\end{aligned}$$

$$ 9x^3y +41x^2y^2 +20xy^3 $$

$$ 9x^3y +41x^2y^2 +20xy^3 $$
Take out common in all terms,
$$ xy(9x^2+41xy+y^2)$$
Above terms can be written as,
$$ xy(9x^2+36xy+5xy+20y^2)$$
$$xy[9x(x+4y)+5y(x+4y)]$$
$$ xy(x+4y)(9x+5y)$$

Divide:
$$ 6m^2 - 16 m^3 + 10 m^4\,\, by\,\, - 2m$$

We have to divide $$6 m^2 - 16m^3 + 10m^4 \,\,by\,\, - 2m$$

$$6m^2 - 16m^3 + 10 m^4 \div - 2m\\ = \dfrac{(6 \times m^2- 16 \times m^3 + 10 \times m^4) }{ - 2 \times m}\\$$

Separating the terms, we get

$$= \dfrac{(6 \times m^2)}{ (- 2 \times m)} - \dfrac{(16 \times m^3)}{ (- 2 \times m)} +\dfrac{ (10 \times m^4) }{ (- 2 \times m)}$$

$$= - 3 \times m^{2-1} + 8 \times m^{3-1} - 5 \times m^{4-1}$$

$$= - 3 \times m + 8 \times m^2 - 5 \times m^3$$

$$= - 3m + 8m^2 - 5m^3$$

Hence, $$6m^2 - 16m^3 + 10m^4 \div - 2m = - 3m + 8m^2 - 5m^3$$

Solve:
$$17a^6b^8-34a^4b^6+51a^2b^4$$

$$17a^6b^8-34a^4b^6+51a^2b^4$$

Simplifying we get

$$17a^2b^6(a^4b^4-2a^2b^2+3)$$

Solve:
$$4a^2-8ab$$

Simplifying we get

$$4a^2-8ab=4a(a-2b)$$

Divide:
$$ 36a^3x^5 - 24a^4x^4 + 18a^5x^3\,\, by\,\, - 6a^3x^3$$

We have to divide $$36a^3x^5 - 24a^4x^4 + 18a^5x^3 \,\,by\,\, - 6a^3x^3$$

$$36a^3x^5 - 24a^4x^4 + 18a^5x^3 \div (- 6a^3x^3)\\ =\dfrac{ (36a^3x^5 - 24a^4x^4 + 18a^5x^3)}{ - 6a^3x^3}\\= \dfrac{(36.a^3.x^5) }{ (-6.a^3.x^3)} - \dfrac{(24.a^4.x^4) }{ (-6.a^3.x^3)} + \dfrac{(18.a^5.x^3) }{ (-6.a^3.x^3)}$$

We get,

$$= - 6.x^{5-3} + 4.a^{4-3}.x^{4-3} - 3.a^{5-3}$$

$$= -6x^2 + 4ax - 3a^2$$

Hence, $$36a^3x^5 24a^4x^4 + 18a^5x^3 \div (- 6a^3x^3) = - 6x^2 + 4ax - 3a^2$$

Simplify:
$$a^3b-a^2b^2-b^3$$

Given: $$a^3b-a^2b^2-b^3$$

Taking $$b$$ as a common factor we get,

$$a^3b-a^2b^2-b^3$$ $$=b(a^3-a^2b-b^2)$$

Solve:
$$3x^2+6x^3$$

Simplifying we get

$$3x^2+6x^3=3x^2(1+2x)$$

Solve:
$$a^3-a^2+a$$

Simplifying we get

$$a^3-a^2+a=a(a^2-a+1)$$

Solve:
$$3x^5y-27x^4y^2+12x^3y^3$$

Simplifying we get

$$3x^5y-27x^4y^2+12x^3y^3=3x^3y(x^2-9xy+4y^2)$$

Solve:
$$6x^2y+9xy^2+4y^3$$

Simplifying we get $$6x^2y+9xy^2+4y^3=y(6x^2+9xy+4y^2)$$

Solve:
$$2x^3b^2-4x^5b^4$$

Simplifying we get

$$2x^3b^2-4x^5b^4=2x^3b^2(1-2x^2b^2)$$

Solve:
$$15x^4y^3-20x^3y$$

Simplifying we get

$$15x^4y^3-20x^3y=5x^3y(3xy^2-4)$$

Solve:
$$12abc-6a^2b^2c^2+3a^3b^3c^3$$

Simplifying we get

$$12abc-6a^2b^2c^2+3a^3b^3c^3=3abc(4-2abc+a^2b^2c^2)$$

Factorise by taking out the common factors :
$$ab(a^2 + b^2- c^2) - bc(c^2- a^2- b^2) + ca(a^2 + b^2- c^2)$$

$$ab(a^2 + b^2- c^2) - bc(c^2- a^2- b^2) + ca(a^2 + b^2- c^2)$$

$$=ab(a^2 + b^2- c^2) + bc(-c^2+ a^2+ b^2) + ca(a^2 + b^2- c^2)$$

$$=(a^2+b^2-c^2)[ab+bc+ca]$$

Factorise by taking out the common factors:
$$2x(a - b) + 3y(5a - 5b) + 4z(2b - 2a)$$

$$2x(a - b) + 3y(5a - 5b) + 4z(2b - 2a)$$
$$=2x(a - b) + 15y(a - b) + 8z(b - a)$$
$$=(a-b)[2x+15y-8z]$$

Factorise :
$$3x^7y-81x^4y^4$$

$$3x^7y-81x^4y^4=3xy(x^6-27x^3y^3)$$

$$3x^7y-81x^4y^4=3xy((x^2)^3-(3xy)^3)$$

$$3x^7y-81x^4y^4=3xy(x^2-3xy)[x^4+3x^3y+9x^2y^2]$$

$$3x^7y-81x^4y^4=3xy(x (x-3y)x^2[x^2+3xy+9y^2])$$

$$3x^7y-81x^4y^4=3x^4y((x-3y)[x^2+3xy+9y^2])$$

$$3x^7y-81x^4y^4=3x^4y(x-3y)[x^2+3xy+9y^2]$$

Find the prime factorisation of the following numbers:
$${ 85 }^{ 3 }-{ 68 }^{ 3 }+{ 5 }^{ 3 }-{ 22 }^{ 3 }$$

Let us consider $$68-5+22=85$$, therefore, the given problem can be rewritten as:

$$[(68)+(-5)+(22)]^3-(68)^3-(-5)^3-(22)^3$$

We know the identity: $$(a+b+c)^3-a^{ 3 }-b^{ 3 }-c^3=3(a+b)(b+c)(c+a)$$

Using the above identity taking $$a=68$$, $$b=-5$$ and $$c=22$$, the equation

$$[(68)+(-5)+(22)]^3-(68)^3-(-5)^3-(22)^3$$ can be factorised as follows:

$$[(68)+(-5)+(22)]^{ 3 }-(68)^{ 3 }-(-5)^{ 3 }-(22)^{ 3 }=3\left( 68-5 \right) \left( -5+22 \right) \left( 22+68 \right) =3\times 63\times 17\times 90$$

$$=2\times (3\times 3\times 3\times 3\times 3)\times 5\times 7\times 17=2\times 3^{ 5 }\times 5\times 7\times 17$$

Hence, $$85^3-68^3+5^3-22^3=2\times 3^{ 5 }\times 5\times 7\times 17$$

Find the prime factorisation of the following numbers:
$${ 100 }^{ 3 }-{ 49 }^{ 3 }+{ 10 }^{ 3 }-{ 61 }^{ 3 } $$

Let us consider $$49-10+61=100$$, therefore, the given problem can be rewritten as:

$$[(49)+(-10)+(61)]^3-(49)^3-(-10)^3-(61)^3$$

We know the identity: $$(a+b+c)^3-a^{ 3 }-b^{ 3 }-c^3=3(a+b)(b+c)(c+a)$$

Using the above identity taking $$a=49$$, $$b=-10$$ and $$c=61$$, the equation

$$[(49)+(-10)+(61)]^3-(49)^3-(-10)^3-(61)^3$$ can be factorised as follows:

$$[(49)+(-10)+(61)]^{ 3 }-(49)^{ 3 }-(-10)^{ 3 }-(61)^{ 3 }=3\left( 49-10 \right) \left( -10+61 \right) \left( 61+49 \right) =3\times 39\times 51\times 110$$

$$=2\times (3\times 3\times 3)\times 5\times 11\times 13\times 17=2\times 3^{ 3 }\times 5\times 11\times 13\times 17$$

Hence, $$100^3-49^3+10^3-61^3=2\times 3^{ 3 }\times 5\times 11\times 13\times 17$$

Find the prime factoristion of the following numbers:
$${ 30 }^{ 3 }-{ 12 }^{ 3 }-{ 10 }^{ 3 }-{ 8 }^{ 3 }$$

Let us consider $$12+10+8=30$$, therefore, the given problem can be rewritten as:

$$[(12)+(10)+(8)]^3-(12)^3-(10)^3-(8)^3$$

We know the identity: $$(a+b+c)^3-a^{ 3 }-b^{ 3 }-c^3=3(a+b)(b+c)(c+a)$$

Using the above identity taking $$a=12$$, $$b=10$$ and $$c=8$$, the equation

$$[(12)+(10)+(8)]^3-(12)^3-(10)^3-(8)^3$$ can be factorised as follows:

$$[(12)+(10)+(8)]^{ 3 }-(12)^{ 3 }-(10)^{ 3 }-(8)^{ 3 }=3\left( 12+10 \right) \left( 10+8 \right) \left( 8+12 \right) =3\times 22\times 18\times 20$$

$$=(2\times 2\times 2\times 2)\times (3\times 3\times 3)\times 5\times 11=2^{ 4 }\times 3^{ 3 }\times 5\times 11$$

Hence, $$30^3-12^3-10^3-8^3=2^{ 4 }\times 3^{ 3 }\times 5\times 11$$

Factorise: $$3{ x }^{ 2 }+6x+6$$

Since in the equation $$3x^2+6x+6$$, $$3$$ is the common term, therefore, can be factorised as follows:

$$3x^2+6x+6=3(x^2+2x+2)$$

Factorise: $$2p(x+y)-3q(x+y)$$

Since in the expression $$2p(x+y)-3q(x+y)$$, $$(x+y)$$ is the common term, therefore, can be factorised as follows:

$$2p(x+y)-3q(x+y)=(x+y)(2p-3q)$$

Factorise: $$18{ x }^{ 2 }y=24xyz$$

Since in the expression $$18x^2y-24xyz$$, $$6xy$$ is the common term, therefore, can be factorised as follows:

$$18x^2y-24xyz=6xy(3x-4z)$$

Factorise: $$5{ x }^{ 2 }-20xy$$

Since in the expression $$5x^2-20xy$$, $$5x$$ is the common term, therefore, can be factorized as follows:

$$5x^2-20xy=5x(x-4y)$$

Factorize: $$4{ (a+b) }^{ 2 }-6(a+b)$$

Since in the expression $$4(a+b)^2-6(a+b)$$, $$2(a+b)$$ is the common in both the terms,

therefore, the given expression can be factorised as follows:

$$4(a+b)^2-6(a+b)$$

$$=2(a+b)[2(a+b)-3]$$

$$=2(a+b)(2a+2b-3)$$

Factorise: $$3x^4 + 6x^3y + 9x^z$$

Let us first find the HCF of all the terms of the given polynomial $$3x^4+6x^3y+9x^2$$ by factoring the terms as follows:

$$3x^{ 4 }=3\times x\times x\times x\times x\\ 6x^{ 3 }y=2\times 3\times x\times x\times x\times y\\ 9x^{ 2 }=3\times 3\times x\times x$$

Therefore, $$HCF=3\times x\times x=3x^{ 2 }$$

Now, we factor out the HCF from each term of the polynomial $$3x^4+6x^3y+9x^2$$ as shown below:

$$3x^{ 4 }+6x^{ 3 }y+9x^{ 2 }=3x^{ 2 }(x^{ 2 }+2xy+3)$$

Hence, $$3x^{ 4 }+6x^{ 3 }y+9x^{ 2 }=3x^{ 2 }(x^{ 2 }+2xy+3)$$.

Solve: $$8x^{2}-72xy+12x$$

We first factorize each term of the given polynomial $$8x^2-72xy+12x$$ as shown below:

$$8x^{ 2 }=2\times 2\times 2\times x\times x\\ 72xy=2\times 2\times 2\times 3\times 3\times x\times y\\ 12x=2\times 2\times 3\times x$$

The common factors of $$8x^2,72xy$$ and $$12x$$ are $$2,2$$ and $$x$$, therefore, the HCF is:

$$2\times 2\times x=4x$$

Thus, taking out the HCF, we have:

$$8x^{ 2 }-72xy+12x=4x(2x-18y+3)$$

Hence, $$8x^{ 2 }-72xy+12x=4x(2x-18y+3)$$.

Factories the given algebraic expression by taking out the common terms. Also, write the common term
$$5pq+20p^{3}q^{3}-15p^{2}q$$

We first factorize each term of the given expression $$5pq+20p^3q^3−15p^2q$$ as shown below:

$$5pq=5\times p\times q\\ 20p^{ 3 }q^{ 3 }=2\times 2\times 5\times p\times p\times p\times q\times q\times q\\ 15p^{ 2 }q=3\times 5\times p\times p\times q$$

The common factors are $$5,p$$ and $$q$$, therefore, the HCF is $$5\times p\times q=5pq$$.

Now, by taking out the common term(HCF), we have:

$$5pq+20p^{ 3 }q^{ 3 }−15p^{ 2 }q=5pq(1+4p^{ 2 }q^{ 2 }-3p)$$

Hence, the common term is $$5pq$$.

Factorise: $$3a^2bc + 6ab^2c + 9abc^2$$

Let us first find the HCF of all the terms of the given polynomial $$3a^2bc+6ab^2c+9abc^2$$ by factoring the terms as follows:

$$3a^{ 2 }bc=3\times a\times a\times b\times c\\ 6ab^{ 2 }c=3\times 2\times a\times b\times b\times c\\ 9abc^{ 2 }=3\times 3\times a\times b\times c\times c$$

Therefore, $$HCF=3\times a\times b\times c=3abc$$

Now, we factor out the HCF from each term of the polynomial $$3a^2bc+6ab^2c+9abc^2$$ as shown below:

$$3a^{ 2 }bc+6ab^{ 2 }c+9abc^{ 2 }=3abc(a+2b+3c)$$

Hence, $$3a^{ 2 }bc+6ab^{ 2 }c+9abc^{ 2 }=3abc(a+2b+3c)$$.

Factorise: $$4p^2 + 5pq - 6pq^2$$

Let us first find the HCF of all the terms of the given polynomial $$4p^2+5pq-6pq^2$$ by factoring the terms as follows:

$$4p^{ 2 }=2\times 2\times p\times p\\ 5pq=5\times p\times q\\ 6pq^{ 2 }=2\times 3\times p\times q\times q$$

Therefore, $$HCF=p$$

Now, we factor out the HCF from each term of the polynomial $$4p^2+5pq-6pq^2$$ as shown below:

$$4p^{ 2 }+5pq-6pq^{ 2 }=p(4p+5q-6q^{ 2 })$$

Hence, $$4p^{ 2 }+5pq-6pq^{ 2 }=p(4p+5q-6q^{ 2 })$$.

Factorise $$3x^2 + 6x^2 y + 9xy^2$$

Let us first find the HCF of all the terms of the given polynomial $$3x^2+6x^2y+9xy^2$$ by factoring the terms as follows:

$$3x^{ 2 }=3\times x\times x\\ 6x^{ 2 }y=3\times 2\times x\times x\times y\\ 9xy^{ 2 }=3\times 3\times x\times y\times y$$

Therefore, $$HCF=3\times x=3x$$

Now, we factor out the HCF from each term of the polynomial $$3x^2+6x^2y+9xy^2$$ as shown below:

$$3x^{ 2 }+6x^{ 2 }y+9xy^{ 2 }=3x(x+2xy+3y^{ 2 })$$

Hence, $$3x^{ 2 }+6x^{ 2 }y+9xy^{ 2 }=3x(x+2xy+3y^{ 2 })$$.

Factorize the following expressions:
$$6x^{3}y - 12x^{2}y + 15x^{4}$$

Let us first find the HCF of all the terms of the given polynomial $$6x^3y-12x^2y+15x^4$$ by factoring the terms as follows:

$$6x^{ 3 }y=2\times 3\times x\times x\times x\times y\\ 12x^{ 2 }y=2\times 2\times 3\times x\times x\times y\\ 15x^{ 4 }=3\times 5\times x\times x\times x\times x$$

Therefore, $$HCF=3\times x\times x=3x^{ 2 }$$

Now, we factor out the HCF from each term of the polynomial $$6x^3y-12x^2y+15x^4$$ as shown below:

$$6x^{ 3 }y-12x^{ 2 }y+15x^{ 4 }=3x^{ 2 }(2xy-4y+5x^{ 2 })$$

Hence, $$6x^{ 3 }y-12x^{ 2 }y+15x^{ 4 }=3x^{ 2 }(2xy-4y+5x^{ 2 })$$.

Factorise:
$$x^2-17x+60$$

In the given polynomial $$x^2-17x+60$$,

The first term is $$x^2$$ and its coefficient is $$1$$.

The middle term is $$-17x$$ and its coefficient is $$-17$$.

The last term is a constant term $$60$$.

Multiply the coefficient of the first term by the constant $$1\times 60=60$$.

We now find the factor of $$60$$ whose sum equals the coefficient of the middle term, which is $$-17$$ and then factorize the polynomial $$x^2-17x+60$$ as shown below:

$$x^{ 2 }-17x+60\\ =x^{ 2 }-12x-5x+60\\ =x(x-12)-5(x-12)\\ =(x-5)(x-12)$$

Hence, $$x^{ 2 }-17x+60=(x-5)(x-12)$$.

Find integers 'a' and 'b' such that $$(x^{2} - x- 1)$$ divides $$ax^{17} + bx^{16} + 1$$.

Let $$f(x)=a\cdot x^{17}+b\cdot x^{16}+1$$

Given that $$x^2-x-1$$ divides $$f(x)$$, hence we can represent $$f(x)$$ as

$$f(x)=(x^2-x-1)\cdot p(x)$$ Eq.$$(1)$$

where $$p(x)=c_1.x^{15}+c_2.x^{14}+ ...........c_{15}.x+c_{16}$$ in which $$c_1,c_2,...c_{16}$$ are constant coefficients.

On comparing both sides of Eq.$$(1)$$, we see that $$f(x)$$ has its constant term as $$+1$$, which can only be achieved via multiplication of $$x^2-x-1$$ and $$p(x)$$, if and only if constant term $$c_{16}=-1$$

Now, $$f(x)=(x^2-x-1)(c_1.x^{15}+c_2.x^{14}+ ...........c_{15}.x-1)$$

As, $$f(x)$$ has no terms of $$x$$, we can say $$c_{15}=1$$

Similarly, on comparing the coefficients of $$f(x)$$ and the resultant from the multiplcation of $$p(x)$$ with $$x^2-x-1$$, we can easily evaluate coefficients $$c_{14}, c_{13}.....b , a$$

On solving , we see that $$c_{14}=-2, c_{13}=3,c_{12}=-5$$ and so on

which gives a pattern with alternate + and - signs and with each next terms magnitude is equal to the sum of magnitude of last two terms. whiuch is the property for Fibbonaci series.

Therefore, for magnitude

$$a=c_1=F_{17}$$ and $$b=c_1+c_2 =-F_{16}$$

where $$F_{16} $$ and $$ F_{17}$$ are the sixteenth and seventeenth Fibbonaci numbers.

And sign we can adjust accordingly as the alternate sign is changing.

$$\Rightarrow$$ $$a=F_{17}= 1597$$ and $$b=-F_{16}=-987 $$

Factorise $$4x^2+4\sqrt{3}x+3=0$$.

$$\begin{matrix} 4{ x^{ 2 } }+4\sqrt { 3 } x+3=0 \\ Factor\, \, of\, 12\, \, is: \\ 4\times 3=12=2\sqrt { 3 } \times 2\sqrt { 3 } \\ Then,\, \, \, \\ 4{ x^{ 2 } }+2\sqrt { 3 } x+2\sqrt { 3 } x+3=0 \\ 2x\left( { 2x+\sqrt { 3 } } \right) +\sqrt { 3 } \left( { 2x+\sqrt { 3 } } \right) =0 \\ \left( { 2x+\sqrt { 3 } } \right) \, \, \, \left( { 2x+\sqrt { 3 } } \right) \\ { \left( { 2x+\sqrt { 3 } } \right) ^{ 2 } }=0 \\ \therefore \left( { 2x+\sqrt { 3 } } \right) =0 \\ x=\sqrt { \frac { 3 }{ 2 } } \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, Ans. \\ \end{matrix}$$

Factorisation - Class 8 Maths - Extra Questions

Factorise $$ab({x^2} + {y^2}) - xy({a^2} + {b^2})$$.

Divide the polynomial $$3x^{4} -4x^{3} -3x - 1$$ by $$x -1$$.

Find the root of given equation $${x}^{2}+6x+5$$

Factorize $$x\left( {x + z} \right) - y\left( {y + z} \right)$$

Factorise the expression and divide them as directed.$$(5p^2-25p+20)\div (p-1)$$.

Factousation, $$16{p^2}{q^2}{r^3} - 24{p^3}{q^2}{r^2} + 8{p^3}{q^2}{r^2}$$

factorise $$3 x ^ { 2 } + 6 x ^ { 3 }$$

Factorise:$$ab^{2}+b(a-1)-1$$

Factorize:$$4 a ^ { 2 } - 8 a b$$

Factorize $$x ^ { 2 } + 7 x + 12 = 0$$

Factorize:$$2 x ^ { 3 } b ^ { 2 } - 4 x ^ { 5 } b ^ { 4 }$$

Factorize: $$15 x ^ { 4 } y ^ { 3 } - 20 x ^ { 3 } y$$

Factorize:.$$15 x + 5$$

Factorise completely by removing a monomial factor.5m+5n

Factorise completely by removing a monomial factor.5a+8b

Factorise completely by removing a monomial factor.2x-4

Factorize: $$a ^ { 3 } b - a ^ { 2 } b ^ { 2 } - b ^ { 3 }$$

Factorise completely by removing a monomial factor.5x+10

Solve : $$(x^3+2x^2+3x) \div 2x$$

Factorise completely by removing a monomial factor.-3m-15n

Factorise completely by removing a monomial factor.7x-14y

Factorise completely by removing a monomial factor.$$3y-9$$

Factorize:$$6 x ^ { 2 } y + 9 x y ^ { 2 } + 4 y ^ { 3 }$$

Factorise completely by removing a monomial factor.-7p-14q

Factorise completely by removing a monomial factor.ax+bx

Factorise completely by removing a monomial factor.$$4 + 12{x^2}$$

Factorise completely by removing a monomial factor.$${x^2}{y^{}} + x{y^2}$$

Factorize:$$6{x^2} - 11x$$

Factorise :$$a{x^2} + a{b^3}$$

Factorise completely by removing a monomial factor$${x^2}{y^2} + {x^2}$$

divide$$({y^2} + 10y + 24) \div (y + 4)$$

Factorise completely by removing a monomial factorax+ay+az

Factories:-$$6n+12n^2$$

Factories:-$$6n+12n^2+21n$$

Factorize $$x^3+13x^2+32x+20$$, if it is given that $$x+2$$ is its factor.

Factorise$$12{x^2} - 9x$$

$$12xy(9x^{2}-16y^{2})\div 4xy(3x+4y)$$

Factorize: $${x^3} + 6{x^2}y + 9x{y^2}$$.

Factorize:$$(a^2-b^2)x^2+2ax+1$$.

Factorise : 1. $$2x^{2}-x-3$$2. $$-2x^{2}+3x+9$$

Solve:$$z^2-16z+55=0$$.

Factorize: $${x}^{2}+10x+24$$

$$(4x^4-5x^3-7x+1)\div (4x-1)$$.

Divide $$\left( { 2y }^{ 3 }+{ 4y }^{ 2 }+3 \right) \div { 2y }^{ 2 }$$

Factorise : $$ 150 -6x^2 $$

Factorise : $$ 8ab^2 - 18a^3 $$

Factorise : $$ x^2 +\dfrac {1}{x^2} - 2 -3x +\dfrac {3}{x} $$

Factorise : $$ a (a-2b-c) +2bc $$

Factorise : $$ 4a^2 -9b-2bc -c^2 $$

Factorise the following expressions:(i) $$ 32a^2b - 72b^3 $$(ii) $$ 9 (a +b)^3 - 25 ( a+b) $$

$$ 18 m +16 n $$

$$ 20x^2 -45y^2 $$

$$ x^3 -25x $$

$$ 14 (a-3b)^3 - 21p (a -3b) $$

Factorise $$ 27a^3b^3 - 18 a^2b^3 + 75a^3b^2 $$

$$ 10 (2p +q)^3 -15b( 2p +q)^2 + 35(2p +q) $$

$$ 150 -6a^2 $$

$$ 32x^2 -18y^2 $$

$$ 3a(x^2 +y^2) +6b ( x^2 +y^2 ) $$

$$ x(x^2+y^2-x^2) +y(-x^2-y^2 +z^2) -z (x^2 +y -z^2) $$

$$ \pi a^5 - \pi^3 ab^2 $$

Factorise $$m^2+m+1=0$$.

Factorize:$${a}^{3}-3{a}^{2}b+3a{b}^{2}-{b}^{3}+8$$

Factorise:$$x^{2}+20x-69$$

Divide $$\sqrt{2}a^3+3\sqrt{2}a^2+6a$$ by $$2a$$.

Factorize $$\dfrac {1}{6}a^{2}-a+\dfrac {4}{3}$$.

Factorise:$$4u^2+8u$$

Factorise$$ - 3{x^2} + 3xy - 4xza$$

Factorise:$$\left( {a - b} \right) + {\left( {a - b} \right)^2}$$

Factorise:$$ - 5{a^2} + 4a + 5\left( { - {a^2} + 5} \right)$$

Factorize $$x^{3}+13x^{2}+32x+20$$

Resolve $$2{b}^{2}-5b-3$$ in to factors.

Factorise: $${ 7x }^{ 3 }z-{ 21x }z^{ 2 }$$

$${ ab }^{ 2 }+(a-1)b-1$$

Factorise: $${ x }^{ 2 }+18x+45$$

Factorize $$p^2+1.5p+0.5$$.

Find the quotient and remainder on dividing the polynomials $$a{x^2} + \left( {b + ac} \right)x + bc\;by\;x + c$$

Resolve into factors $$3x^2-6x$$

Divide : $$a^2 + 7a +12$$ by $$(a+4)$$.

Factorise the expression and divide them as directed.
$$(5p^2-25p+20)\div (p-1)$$.

factorise
$$3 x ^ { 2 } + 6 x ^ { 3 }$$

Factorise:
$$ab^{2}+b(a-1)-1$$

Factorize:
$$4 a ^ { 2 } - 8 a b$$

Factorize
$$x ^ { 2 } + 7 x + 12 = 0$$

Factorize:
$$2 x ^ { 3 } b ^ { 2 } - 4 x ^ { 5 } b ^ { 4 }$$

Factorise completely by removing a monomial factor.
5m+5n

Factorise completely by removing a monomial factor.
5a+8b

Factorise completely by removing a monomial factor.
2x-4

Factorize:
$$a ^ { 3 } b - a ^ { 2 } b ^ { 2 } - b ^ { 3 }$$

Factorise completely by removing a monomial factor.
5x+10

Factorise completely by removing a monomial factor.
-3m-15n

Factorise completely by removing a monomial factor.
7x-14y

Factorise completely by removing a monomial factor.
$$3y-9$$

Factorize:
$$6 x ^ { 2 } y + 9 x y ^ { 2 } + 4 y ^ { 3 }$$

Factorise completely by removing a monomial factor.
-7p-14q

Factorise completely by removing a monomial factor.
ax+bx

Factorise completely by removing a monomial factor.
$$4 + 12{x^2}$$

Factorise completely by removing a monomial factor.
$${x^2}{y^{}} + x{y^2}$$

Factorize:
$$6{x^2} - 11x$$

Factorise :
$$a{x^2} + a{b^3}$$

Factorise completely by removing a monomial factor
$${x^2}{y^2} + {x^2}$$

divide
$$({y^2} + 10y + 24) \div (y + 4)$$

Factorise completely by removing a monomial factor
ax+ay+az

Factories:-
$$6n+12n^2$$

Factories:-
$$6n+12n^2+21n$$

Factorise
$$12{x^2} - 9x$$

Factorize:
$$(a^2-b^2)x^2+2ax+1$$.

Factorise :
1. $$2x^{2}-x-3$$
2. $$-2x^{2}+3x+9$$

Solve:
$$z^2-16z+55=0$$.

Factorise the following expressions:
(i) $$ 32a^2b - 72b^3 $$
(ii) $$ 9 (a +b)^3 - 25 ( a+b) $$

Factorize:
$${a}^{3}-3{a}^{2}b+3a{b}^{2}-{b}^{3}+8$$

Factorise:
$$x^{2}+20x-69$$

Factorise:
$$4u^2+8u$$

Factorise
$$ - 3{x^2} + 3xy - 4xza$$

Factorise:
$$\left( {a - b} \right) + {\left( {a - b} \right)^2}$$

Factorise:
$$ - 5{a^2} + 4a + 5\left( { - {a^2} + 5} \right)$$

Find the quotient and remainder.
$$(2p^{2}+7p-9)\div (p-6)$$

Factorise

$$18a^3b^3−27a^2b^3+36a^3b^2$$

Factorise

$$12x^2y^3 - 21 x^3y^2$$

Factorise

$$15ab^2 – 20a^2b$$

Factorise the following:
$$27 - 125x^{3} - 135x + 225x^{2}$$

Factorise the following:
$$125x^{3} + 64y^{3} - 300x^{2}y + 240xy^{2}$$

Factorise the following:
$$64a^{3} + 21b^{3}$$

Factorise:
$$a^4-343a$$

Factorise the following:
$$2x^3y^2-4x^2y^3+8xy^4$$

Factorize the following.
$$20a^{12}b^2-15a^8b^4$$.

Factorize the following.
$$2a^4b^4-3a^3b^5+4a^2b^5$$.

Factorize the following.
$$28a^2+14a^2b^2-21a^4$$.

Factorize the following expression.
$$abx^2+(ay-b)x-y$$.

Factorize the following expression.
$$a(a-2b-c)+2bc$$.

Factorize the following algebraic expression.
$$6x(2x-y)+7y(2x-y)$$.

Factorize the following.
$$16m-4m^2$$.

Factorize the following.
$$9x^2y+3axy$$.

Factorize the following expression.
$$a(a+b-c)-bc$$.

Factorize the following expression.
$$16(a-b)^3-24(a-b)^2$$.

Factorize the following expression.
$$a^2x^2+(ax^2+1)x+a$$.

Factorize the following expression.
$$x^2+xy+xz+yz$$.

Factorize the following.
$$x^2yz+xy^2z+xyz^2$$.

Factorize the following algebraic expression.
$$49-a^2+8ab-16b^2$$.

Factorize the following expression.
$$ab-a-b+1$$.

Factorize the following expression.
$$x-y-x^2+y^2$$.

Factorize the following expression.
$$x^4-625$$.

Factorize the following expression.
$$x^2+y-xy-x$$.

Factorize the following quadratic polynomial by using the method of completing the square.
$$p^2+6p+8$$.

Factorize the following expressions:
$$17l^{2} + 85m^{2}$$

Factorize the following expression.
$$4(xy+1)^2-9(x-1)^2$$.

Factorize the following expression.
$$p^2q^2-p^4q^4$$.

Factorize the following expressions:
$$-12y + 20y^{3}$$

Factorize the following expressions:
$$5a^{2} + 35a$$

Factorize the following expressions:
$$pq - pqr$$

Factorize the following expressions:
$$18m^{3} - 45mn^{2}$$

Factorize:
$$mx - my - nx + ny$$

Factorize:
$$ax^{3} - bx^{2} + ax - b$$

Factorize:
$$2m^{3} + 3m - 2m^{2} - 3$$

Factorize:
$$2x + 3xy + 2y + 3y^{2}$$

Factorize:
$$p^{2} - 6p + 8$$

Factorize the polynomial:
$$a^{2} + 13a + 12$$

Factorize:
$$a^{2} + 11b + 11ab + a$$

Factorize:
$$15b^{2} - 3bx^{2} - 5b + x^{2}$$