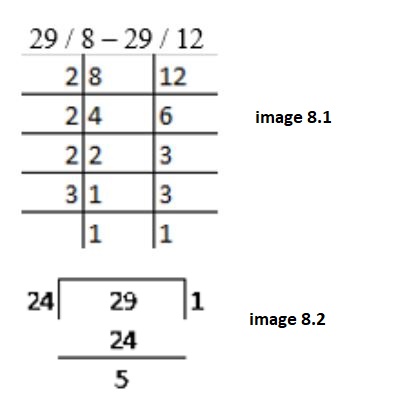
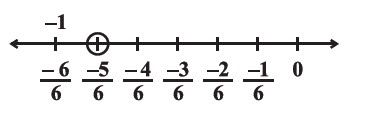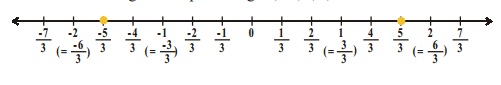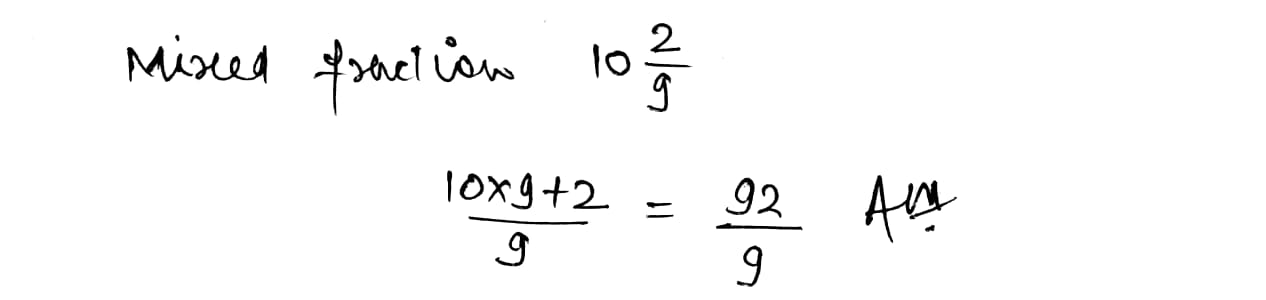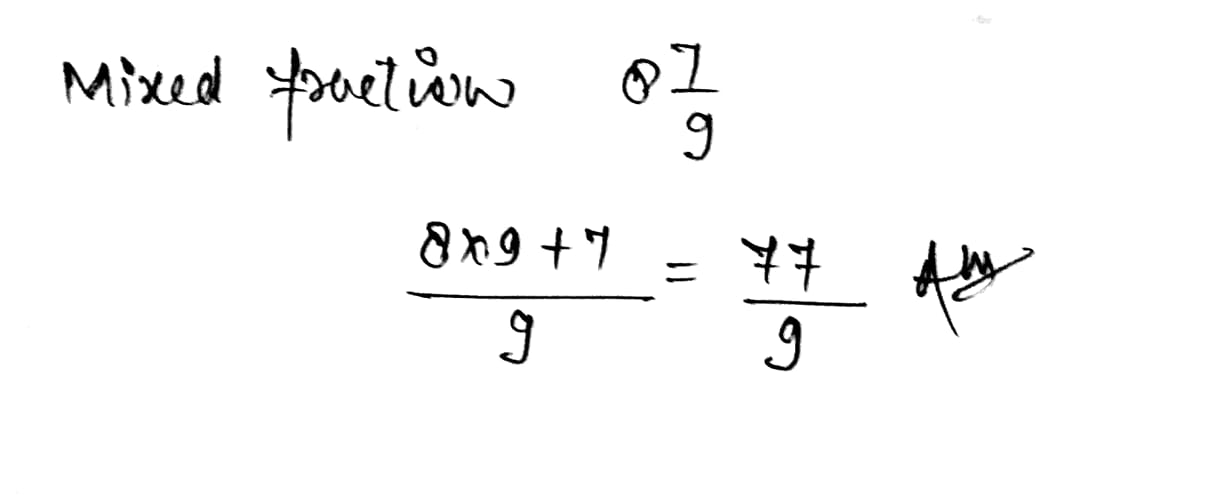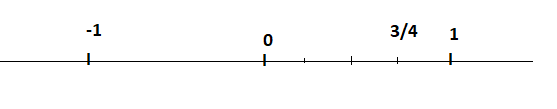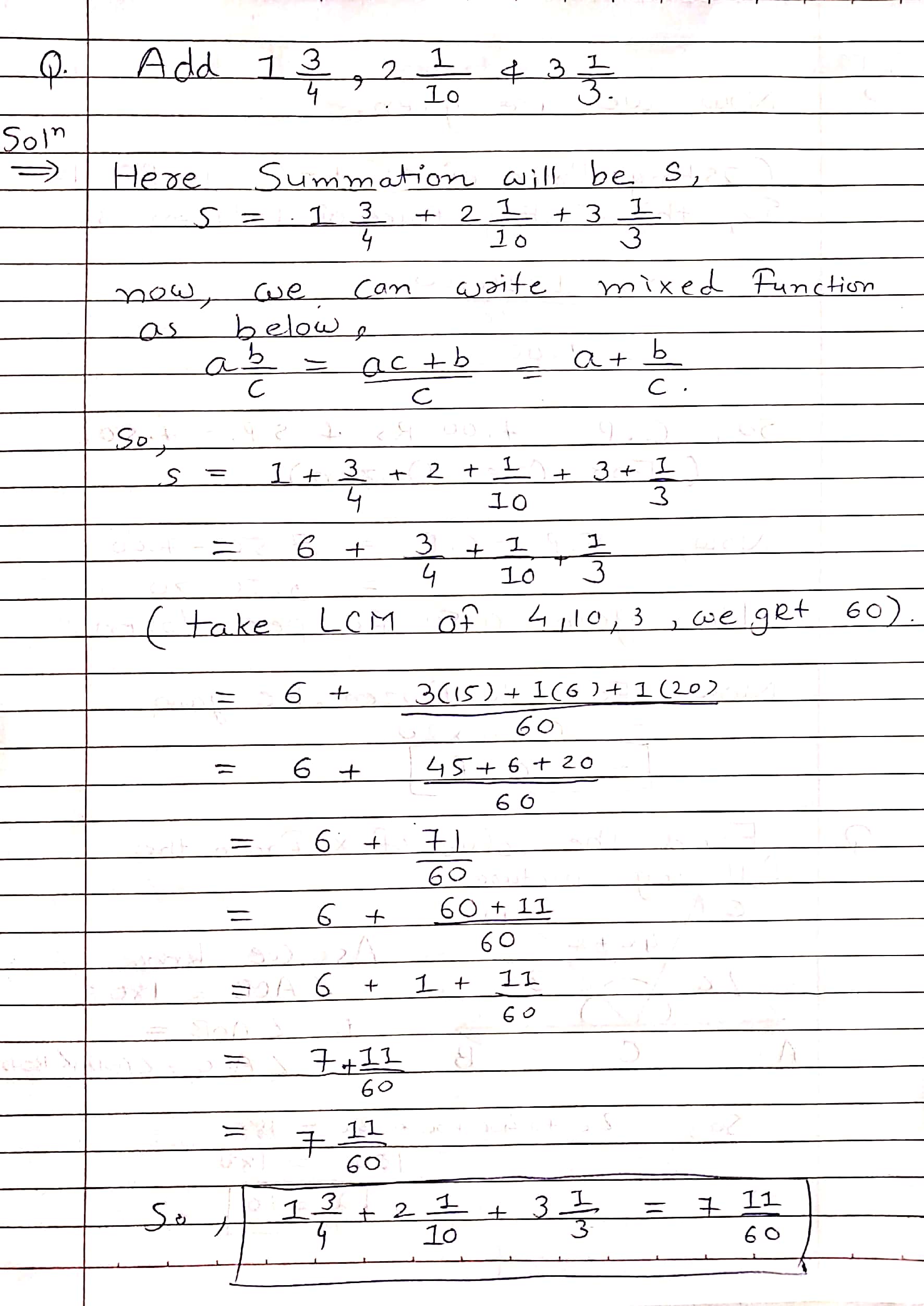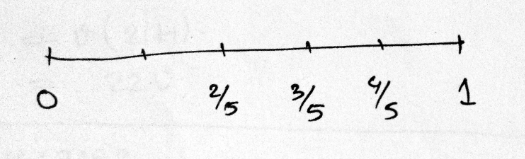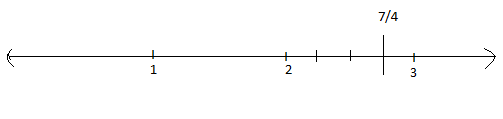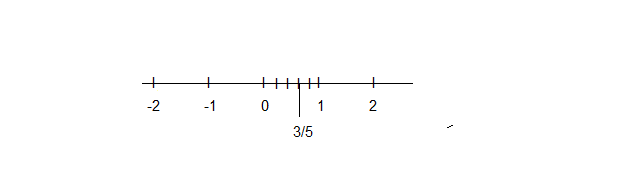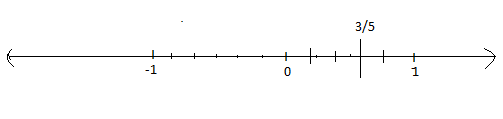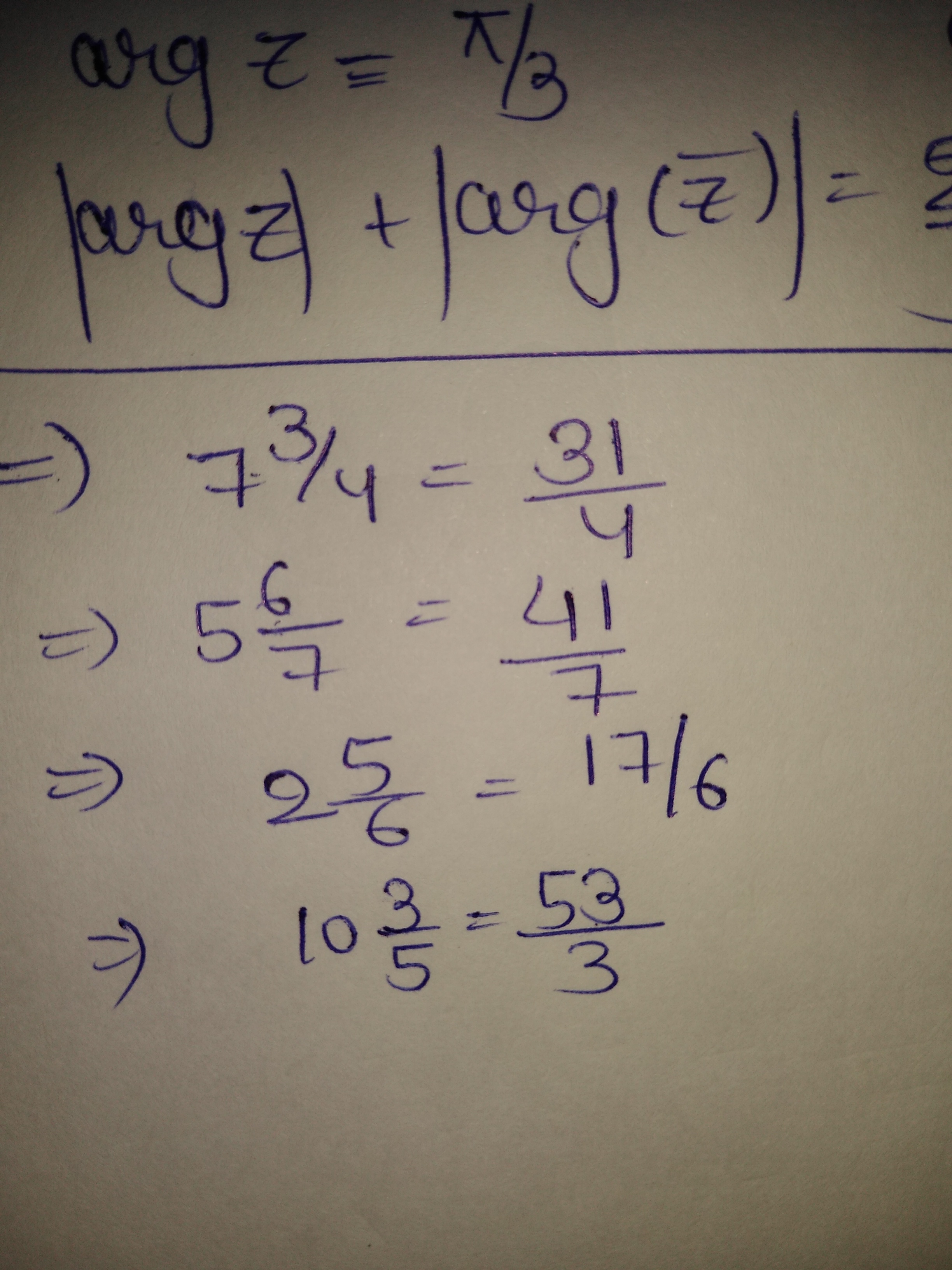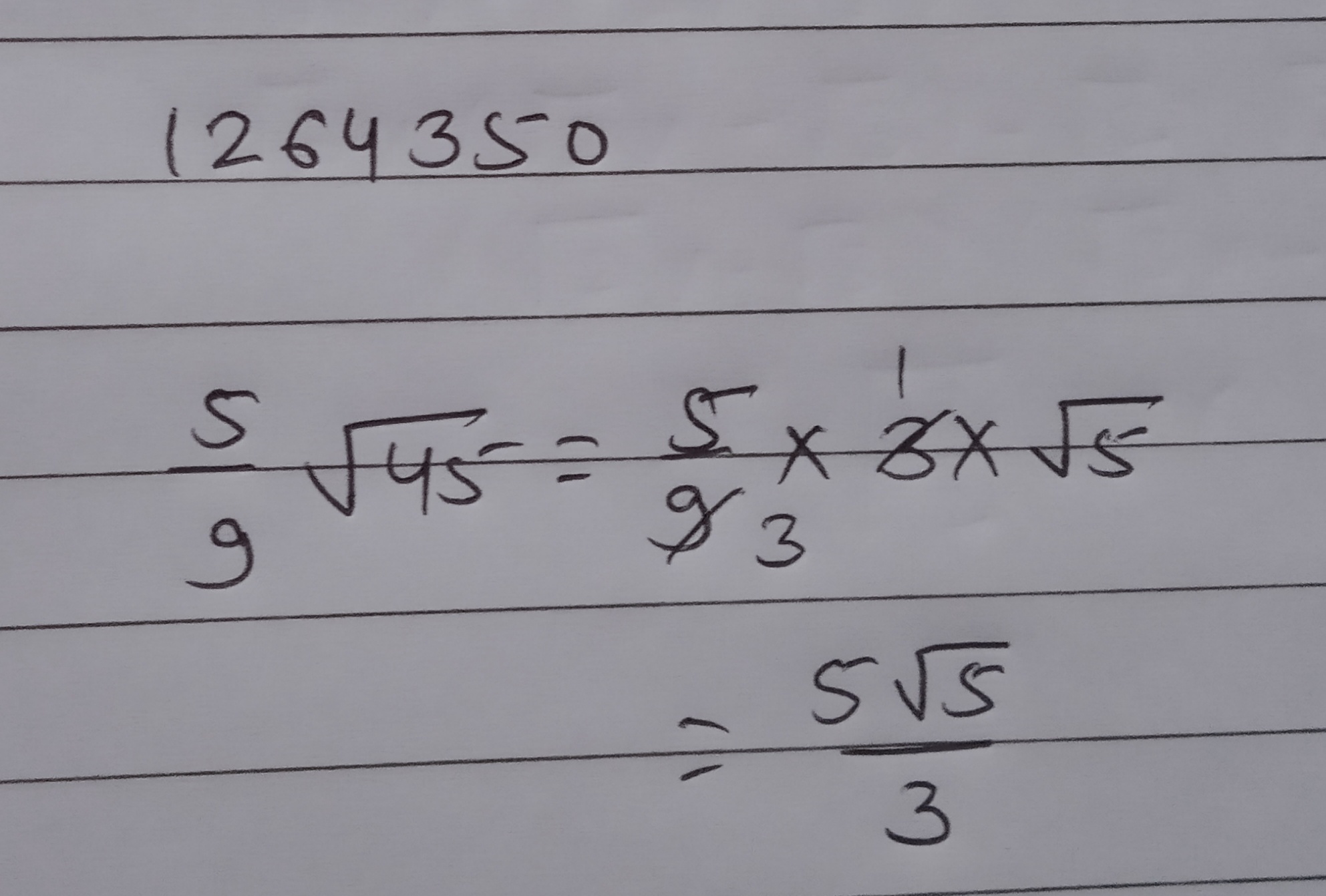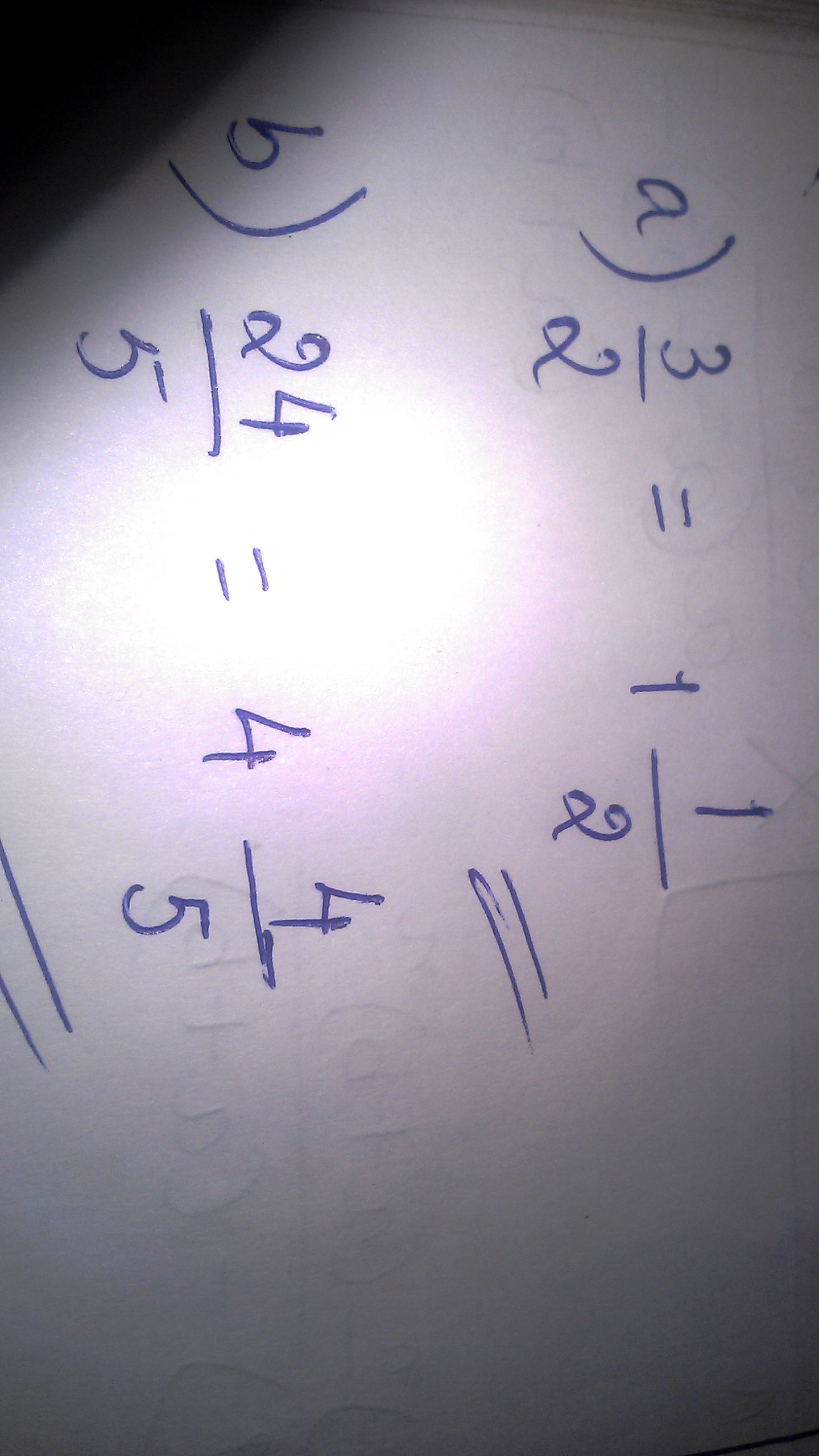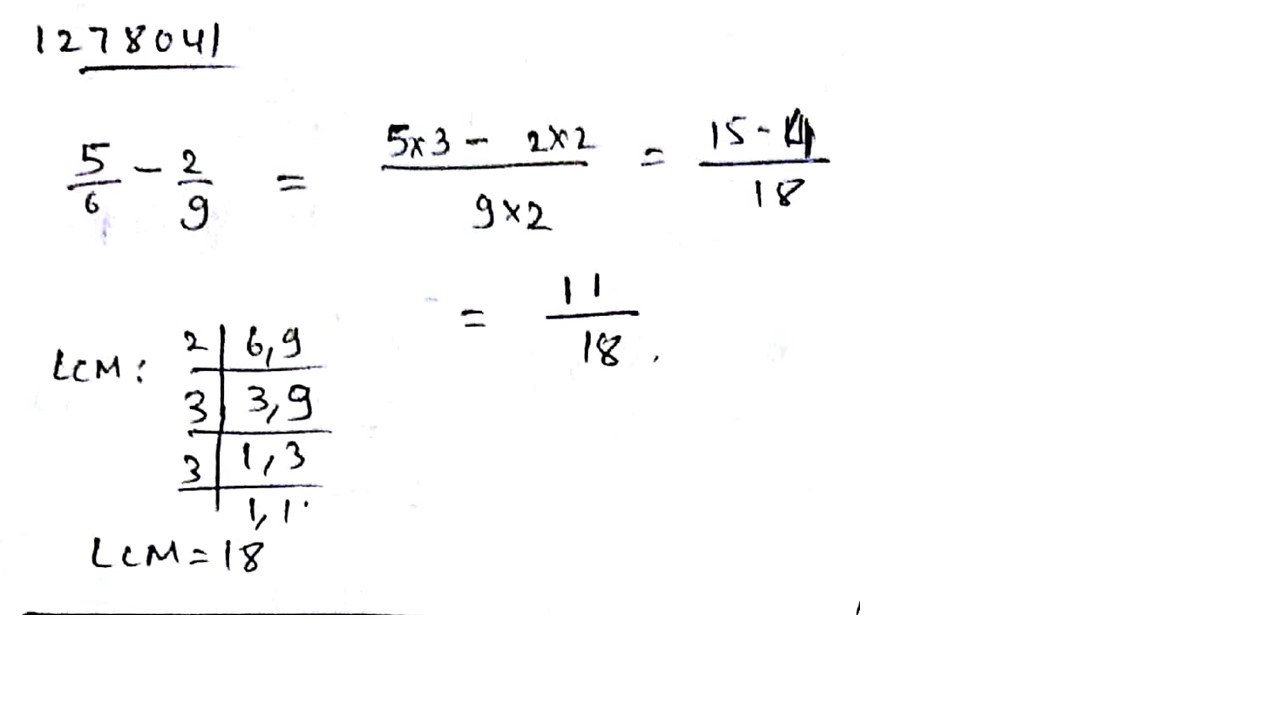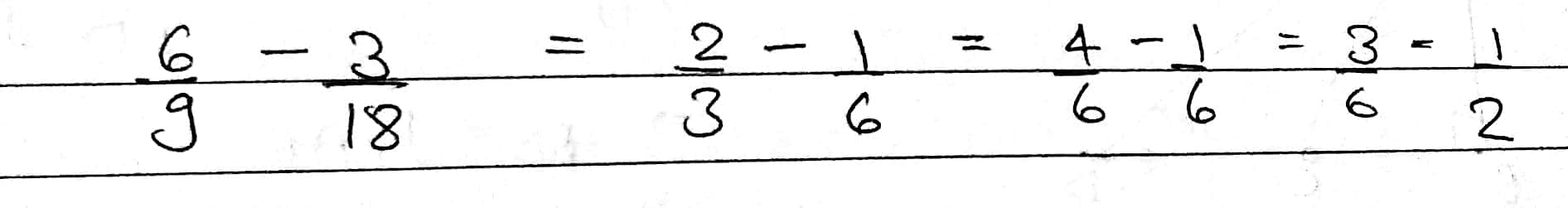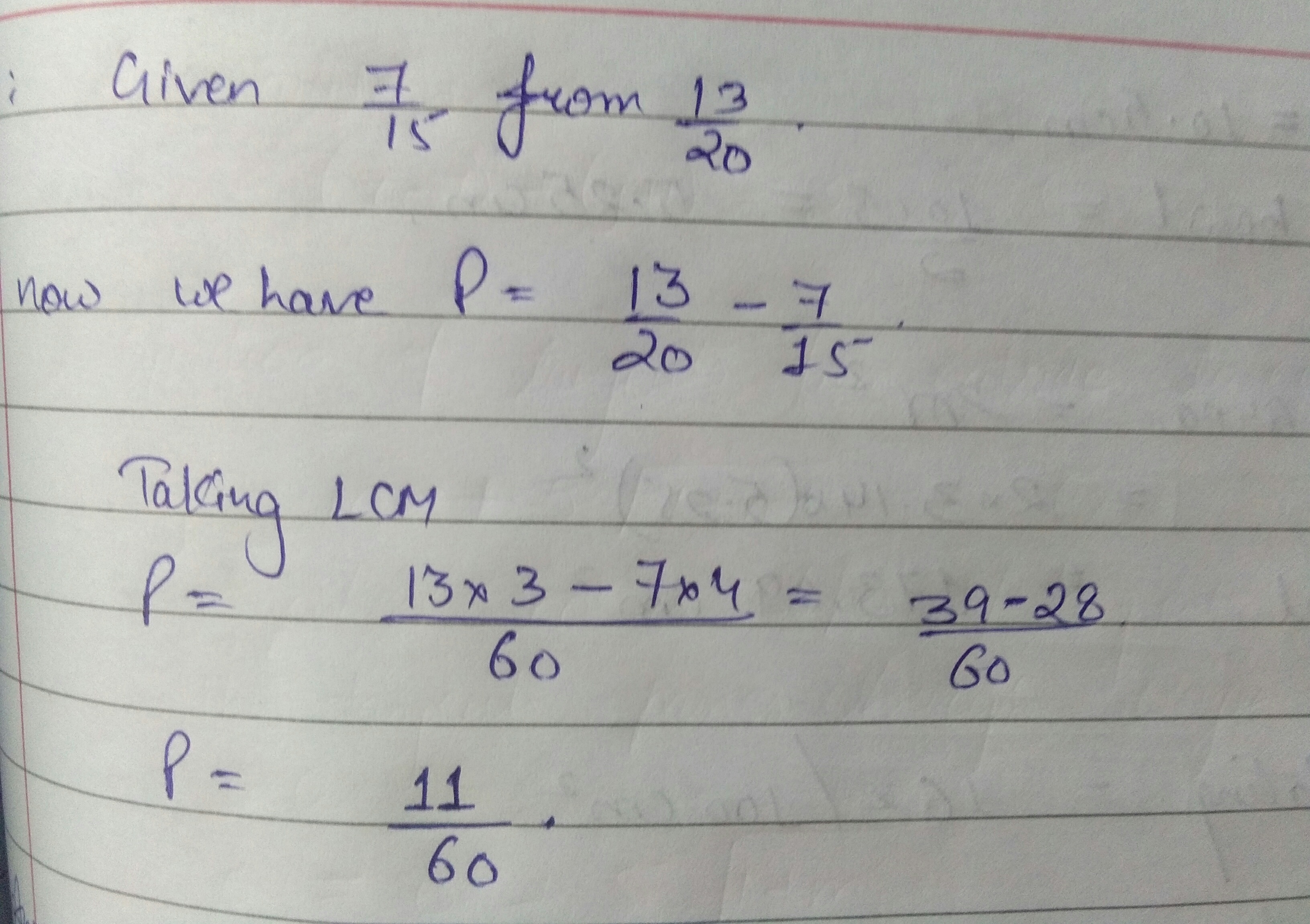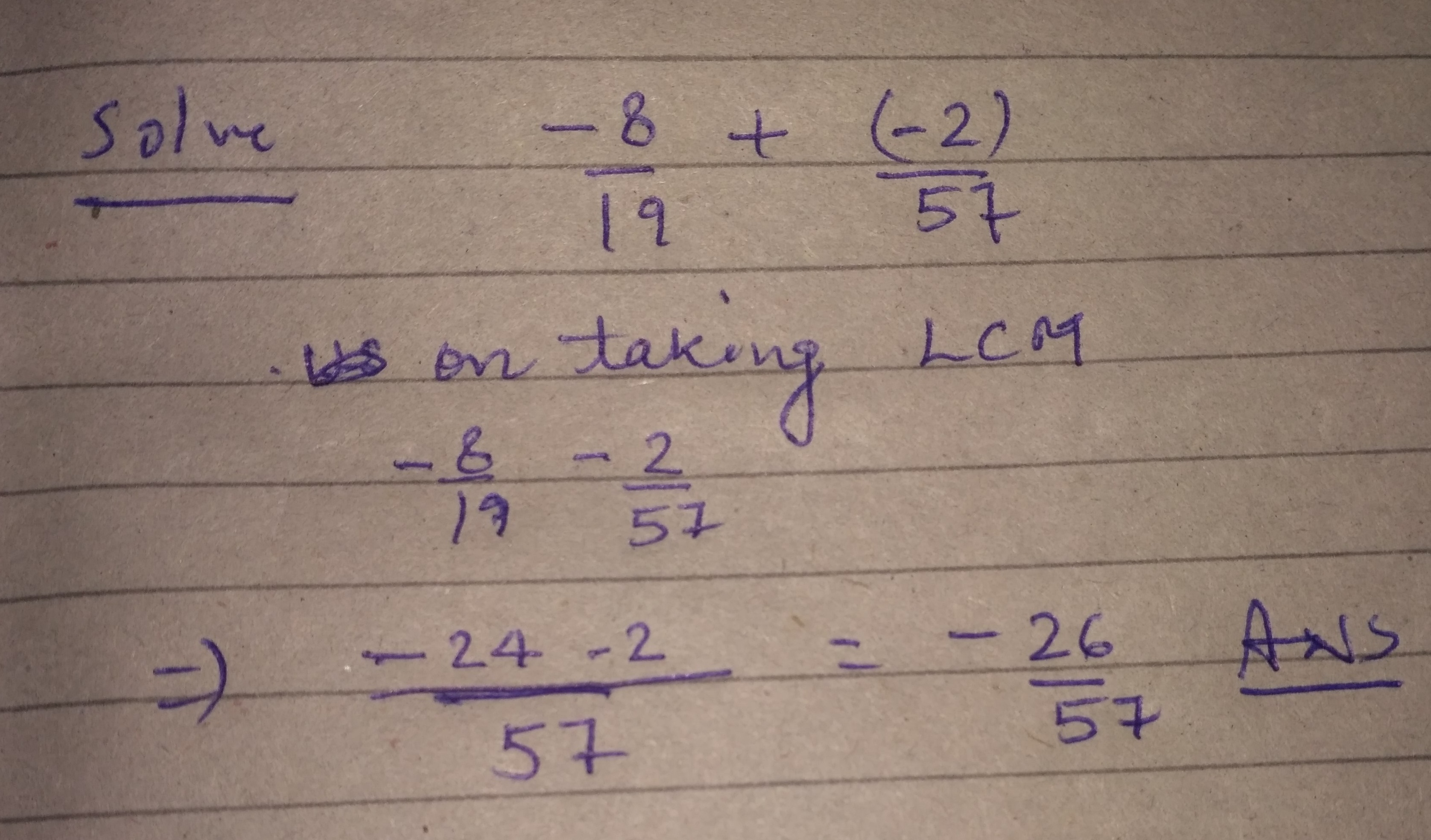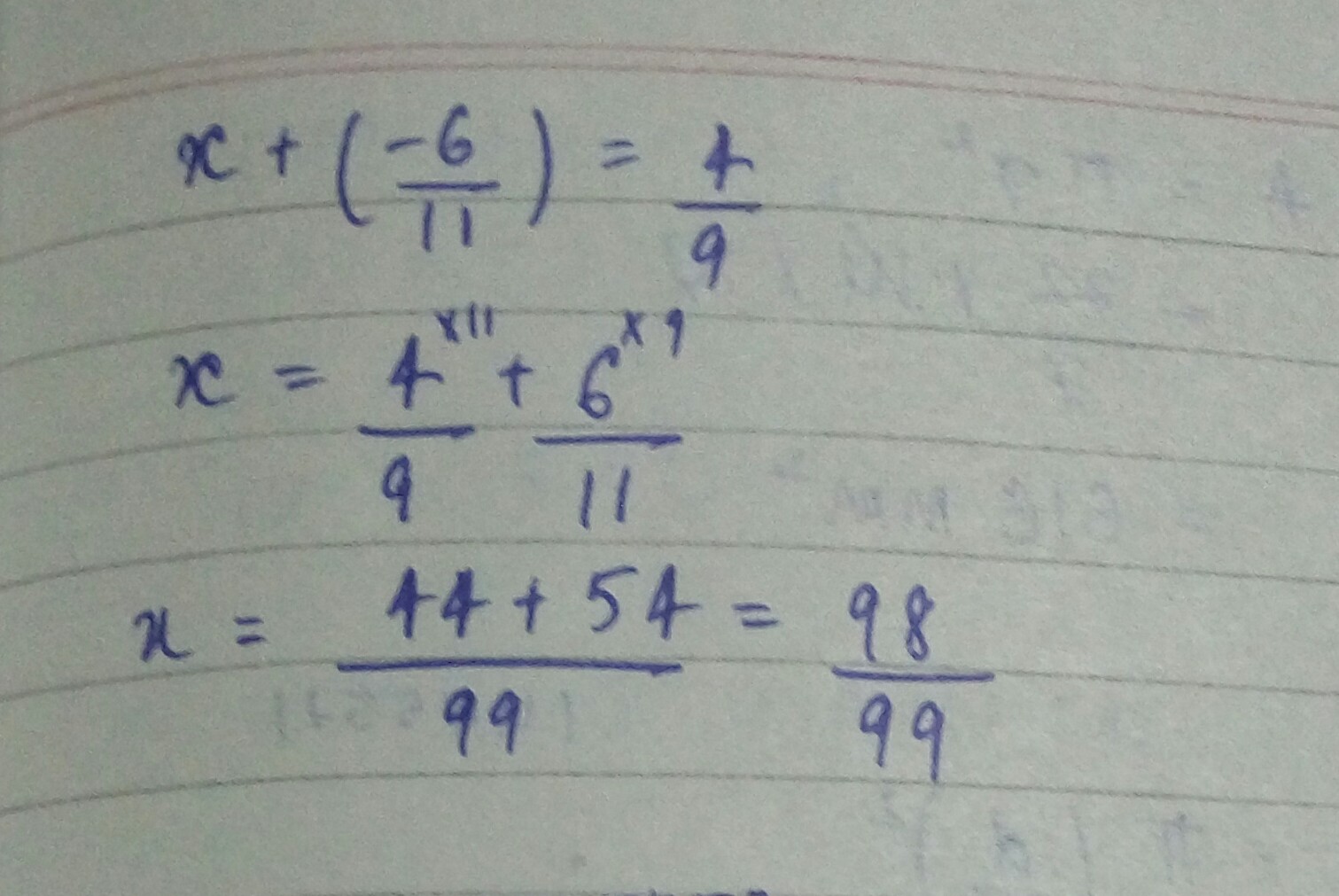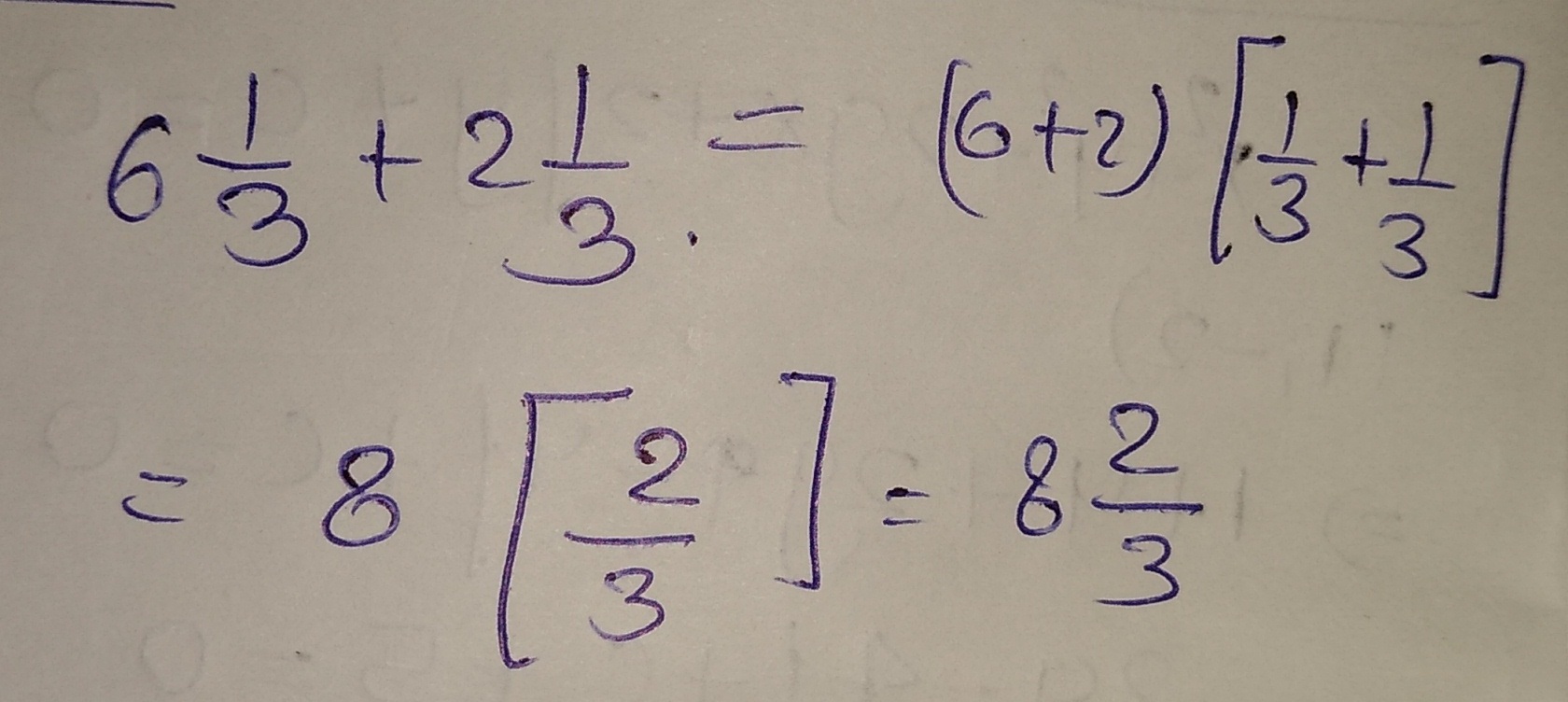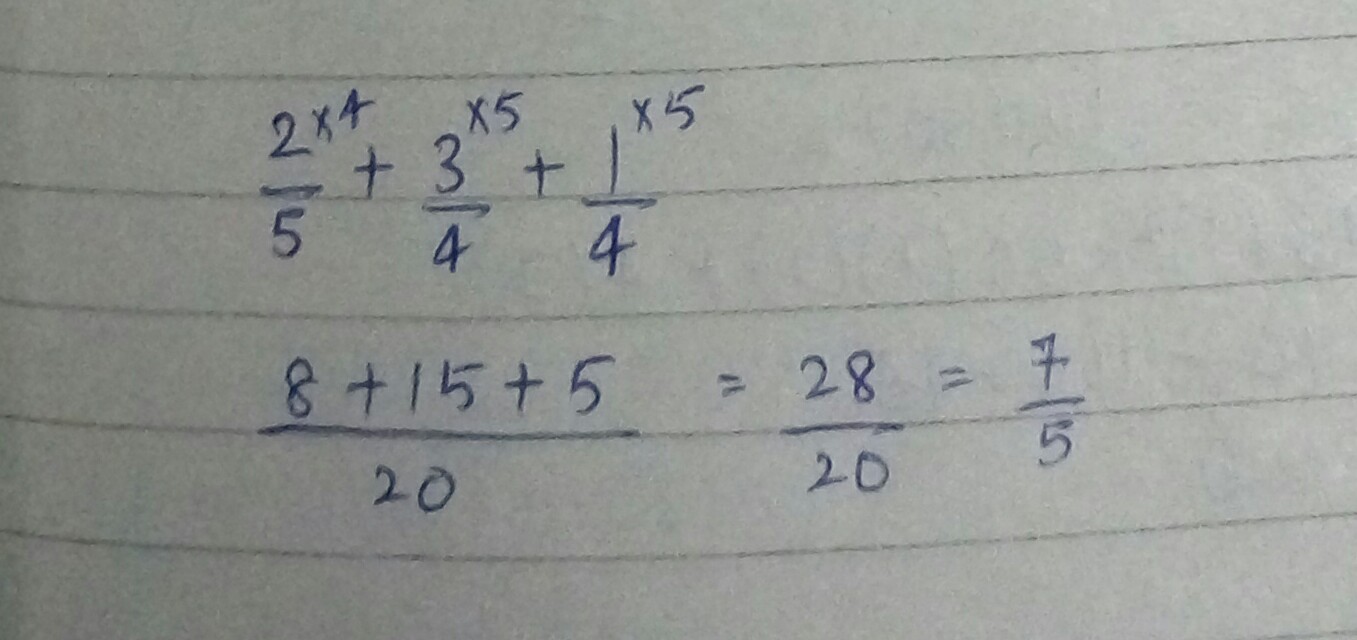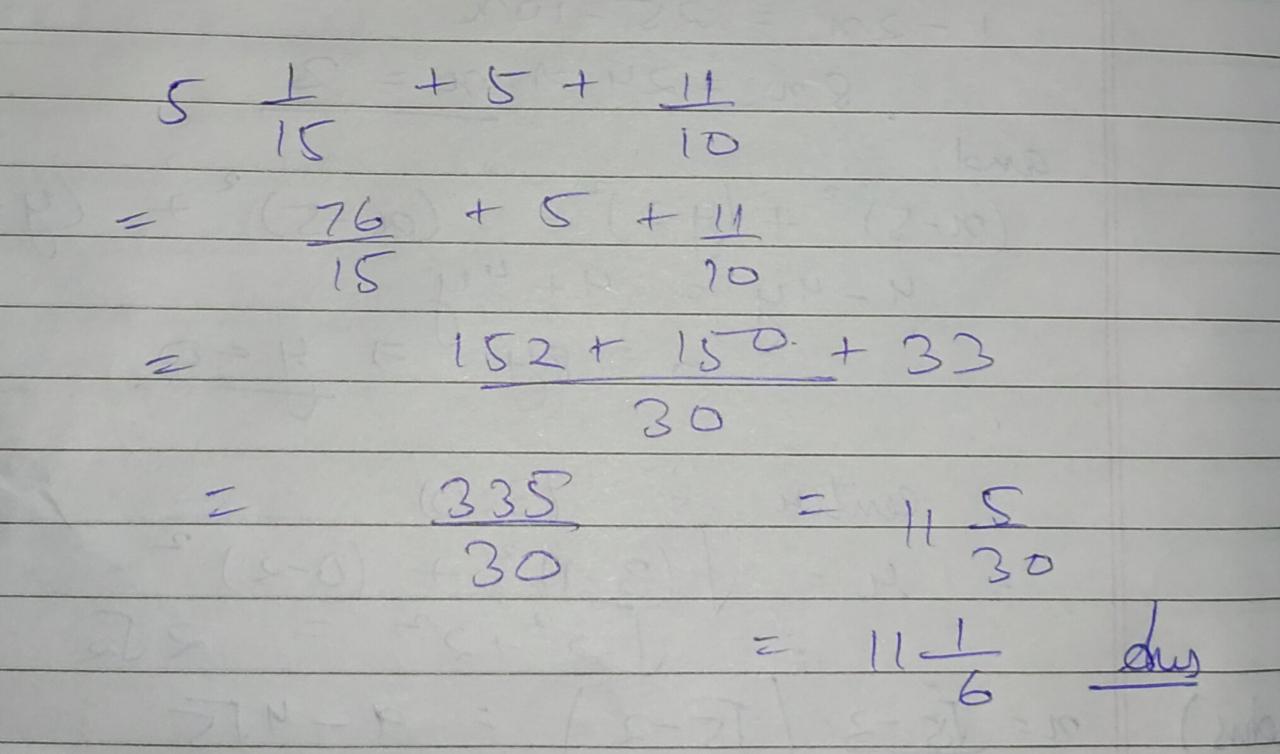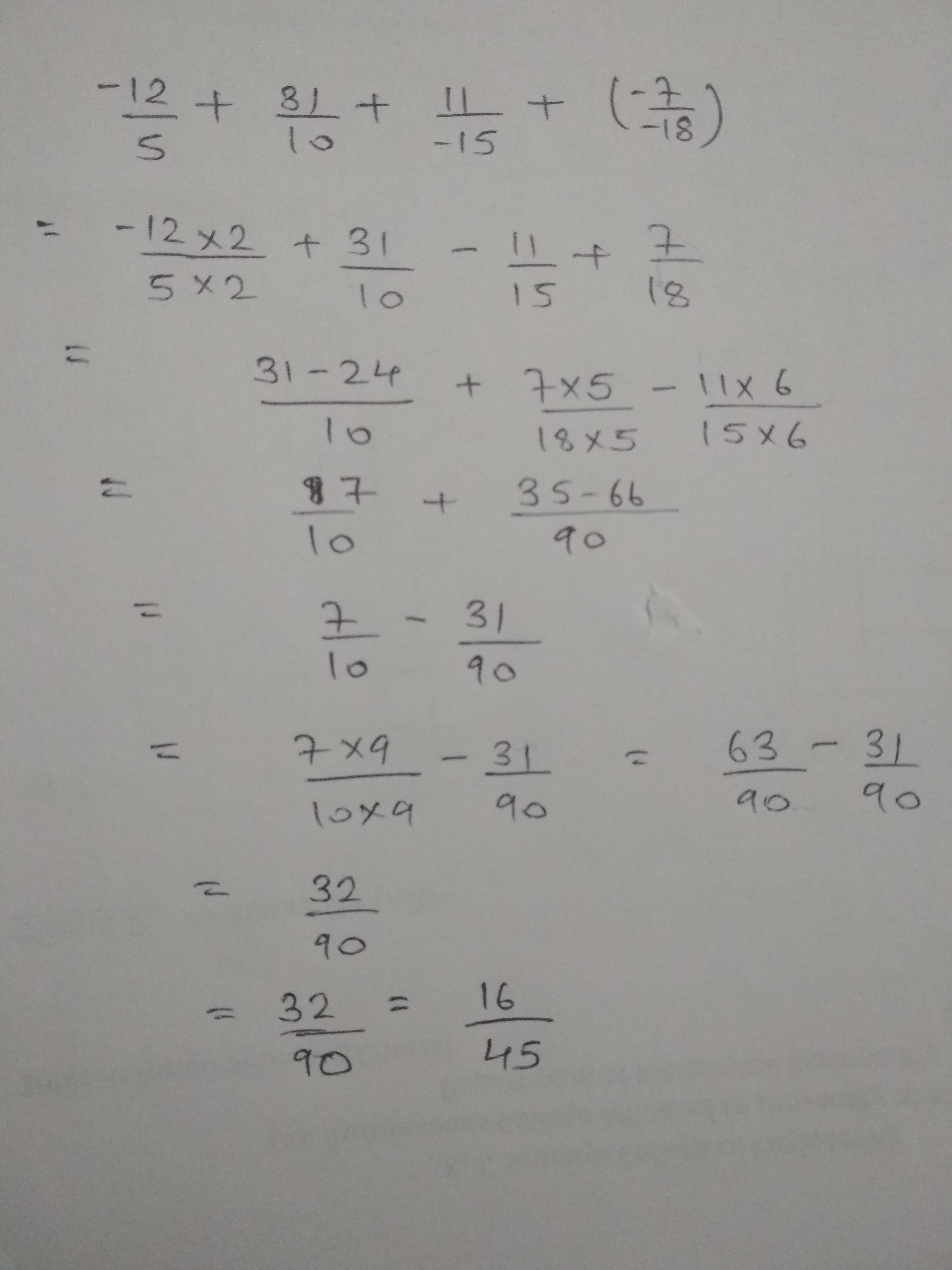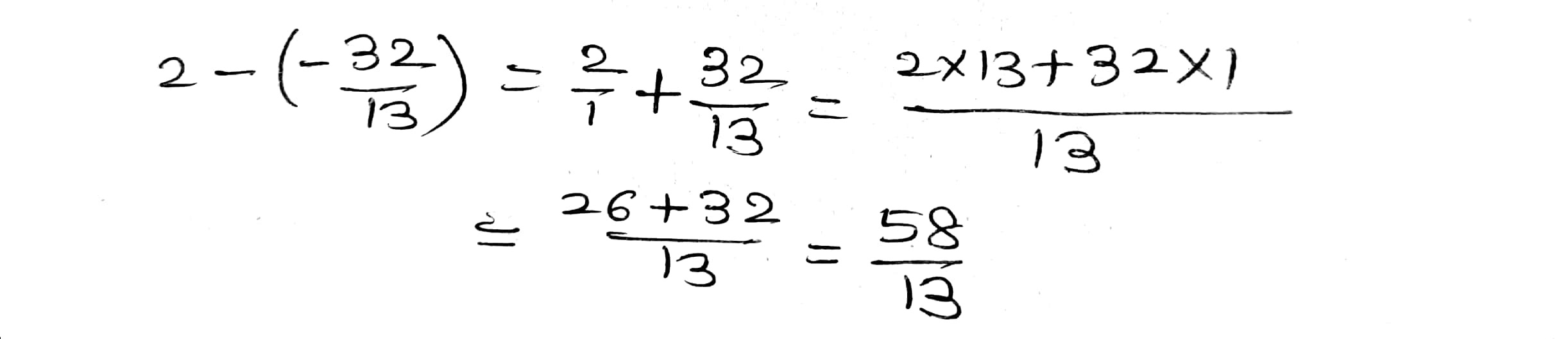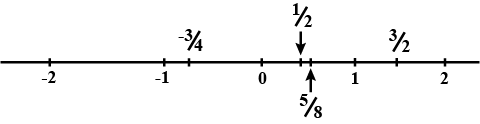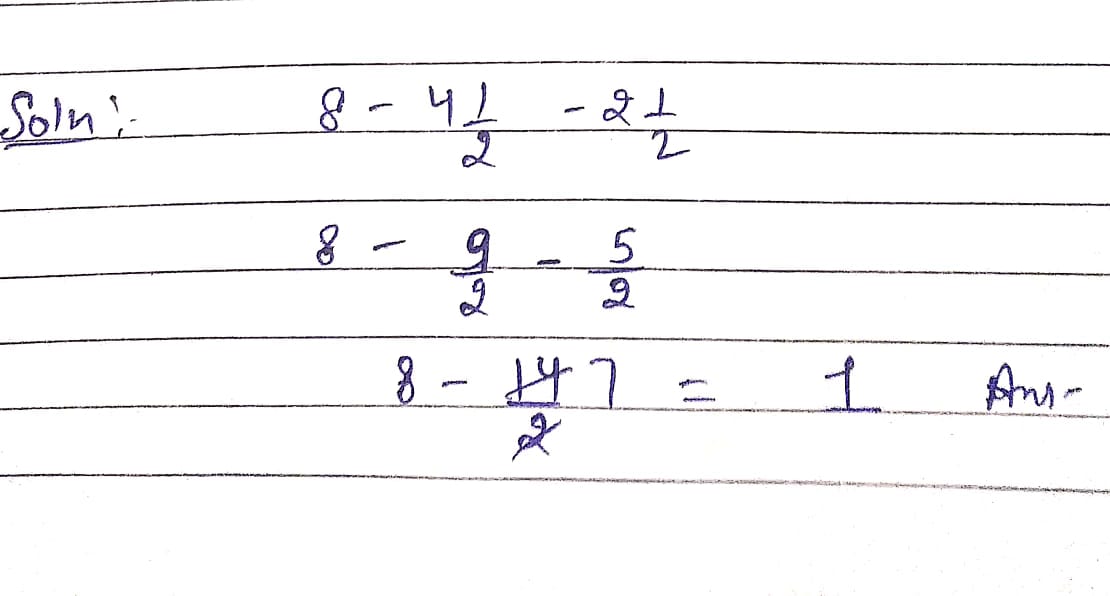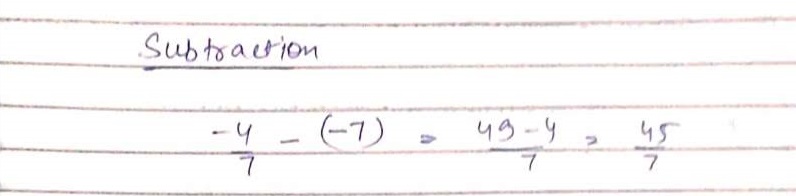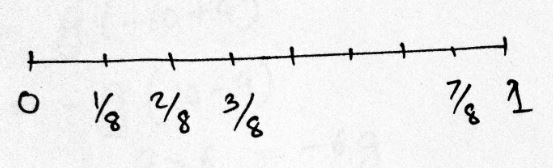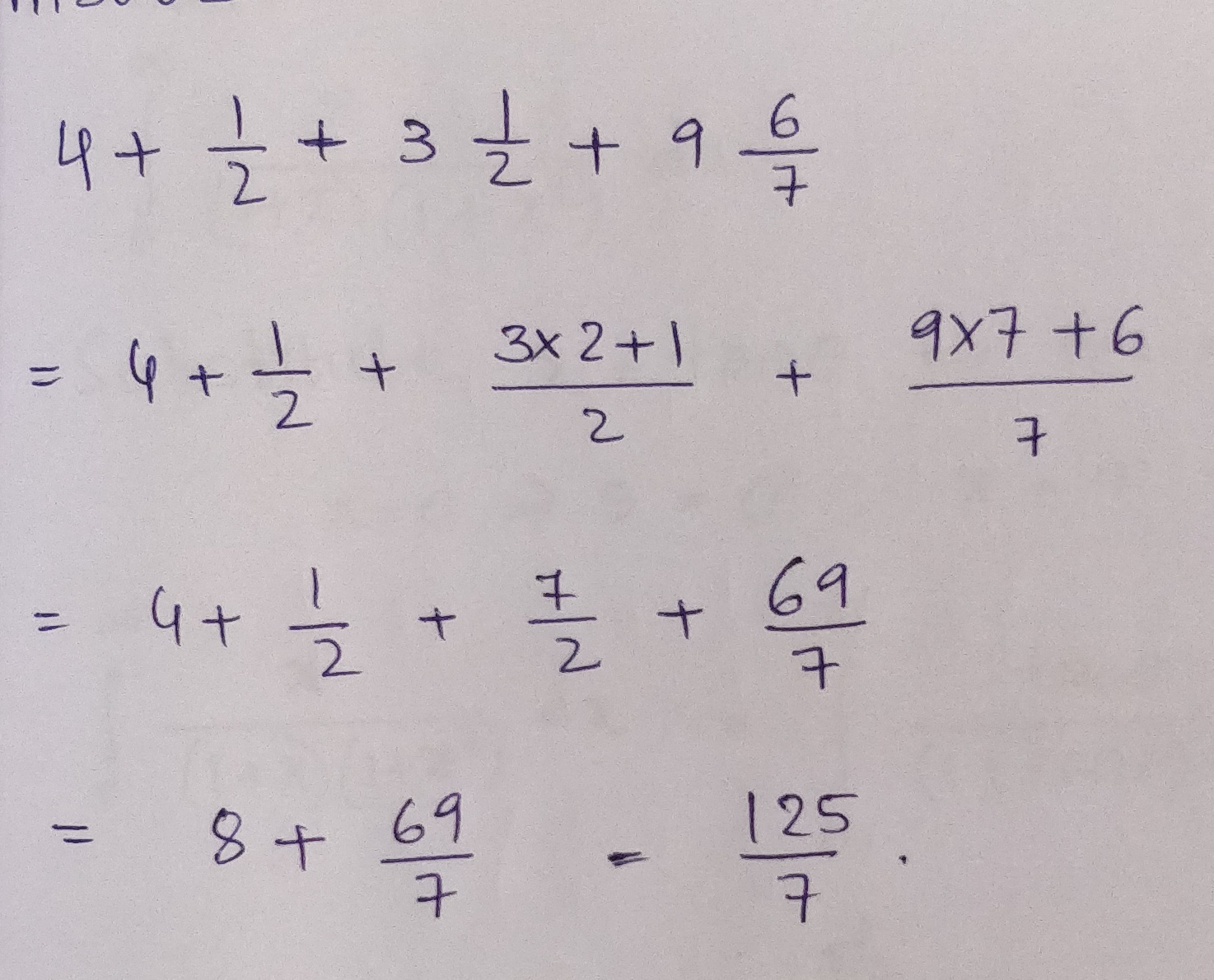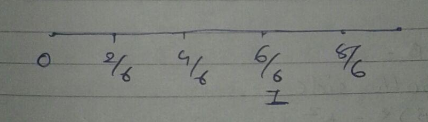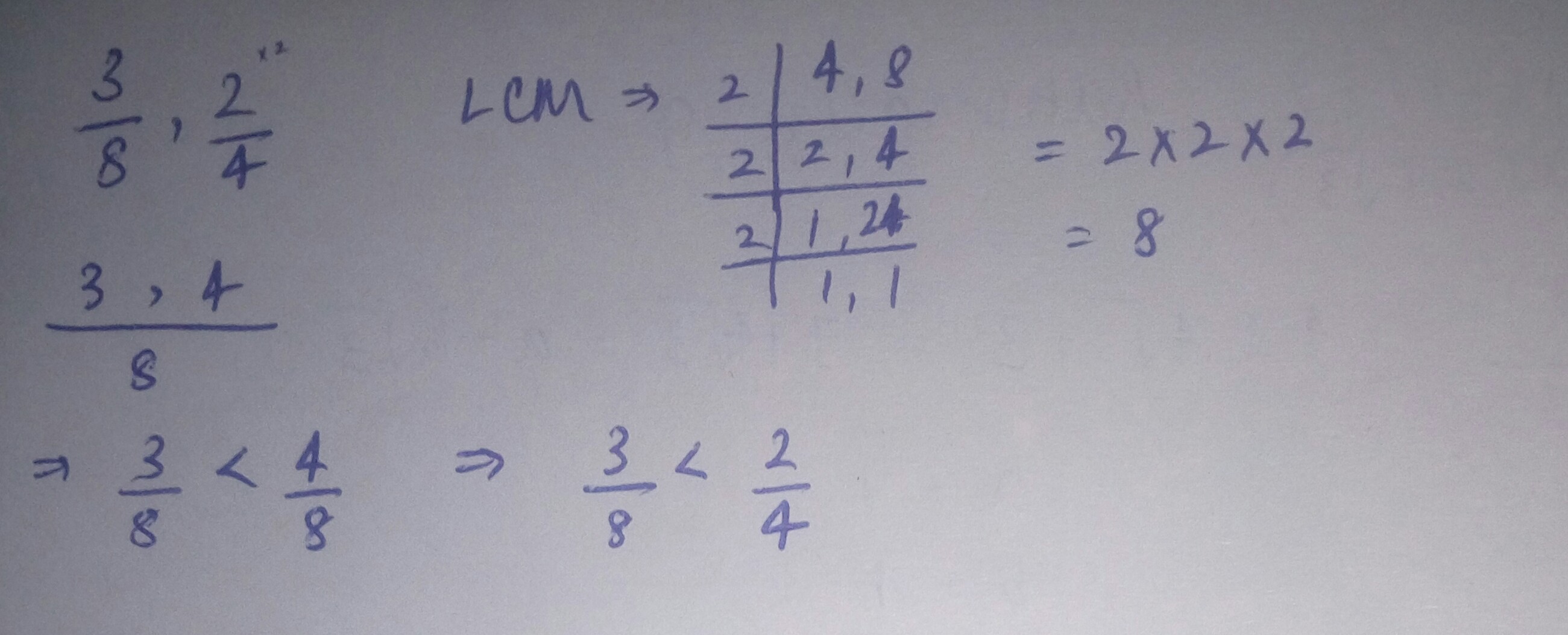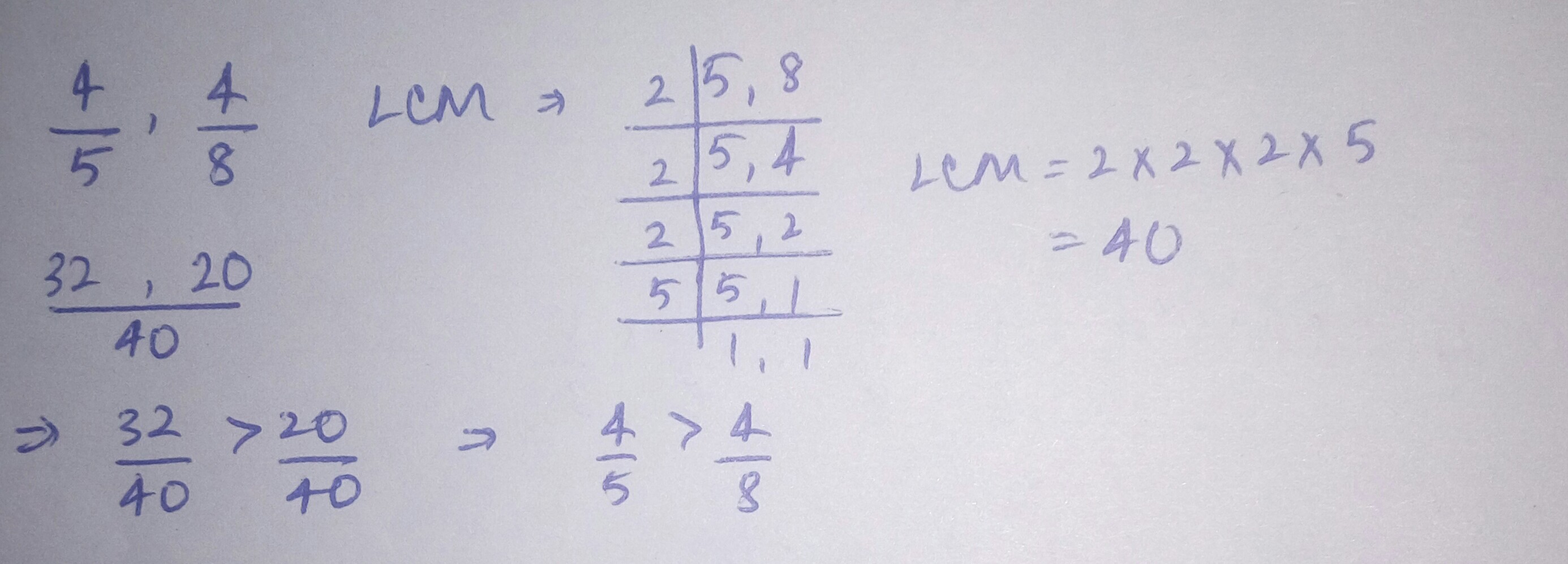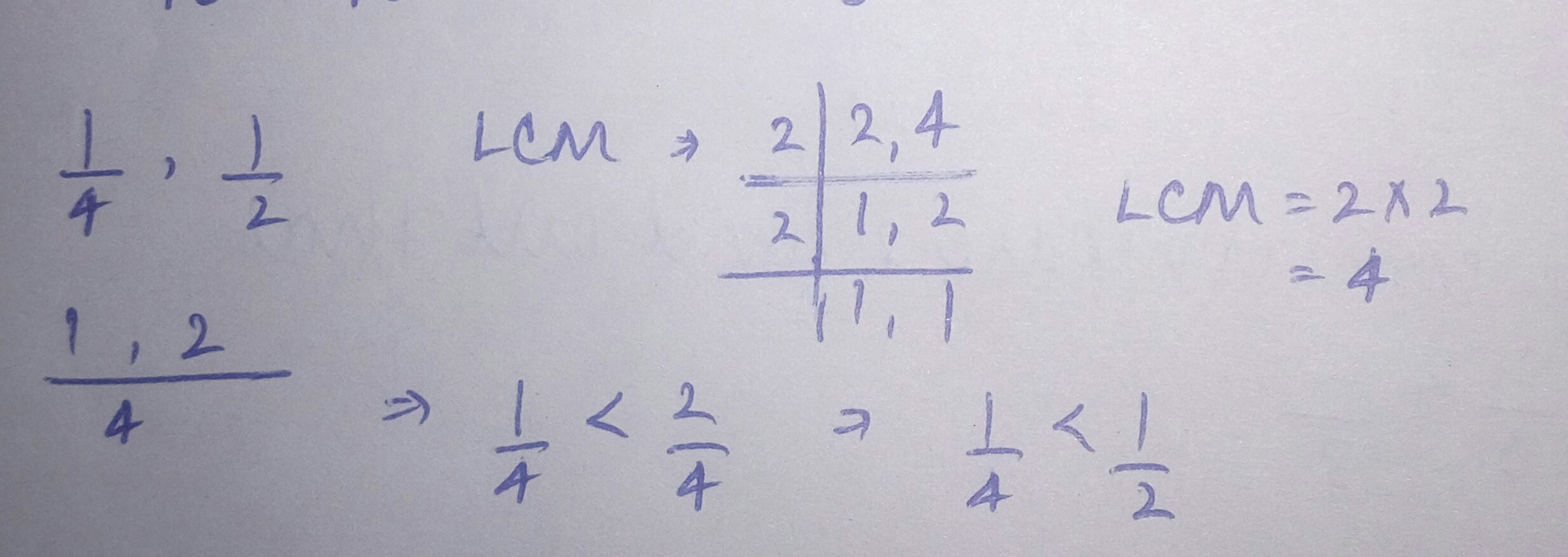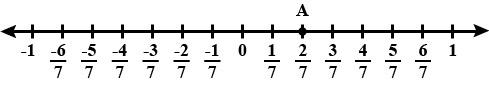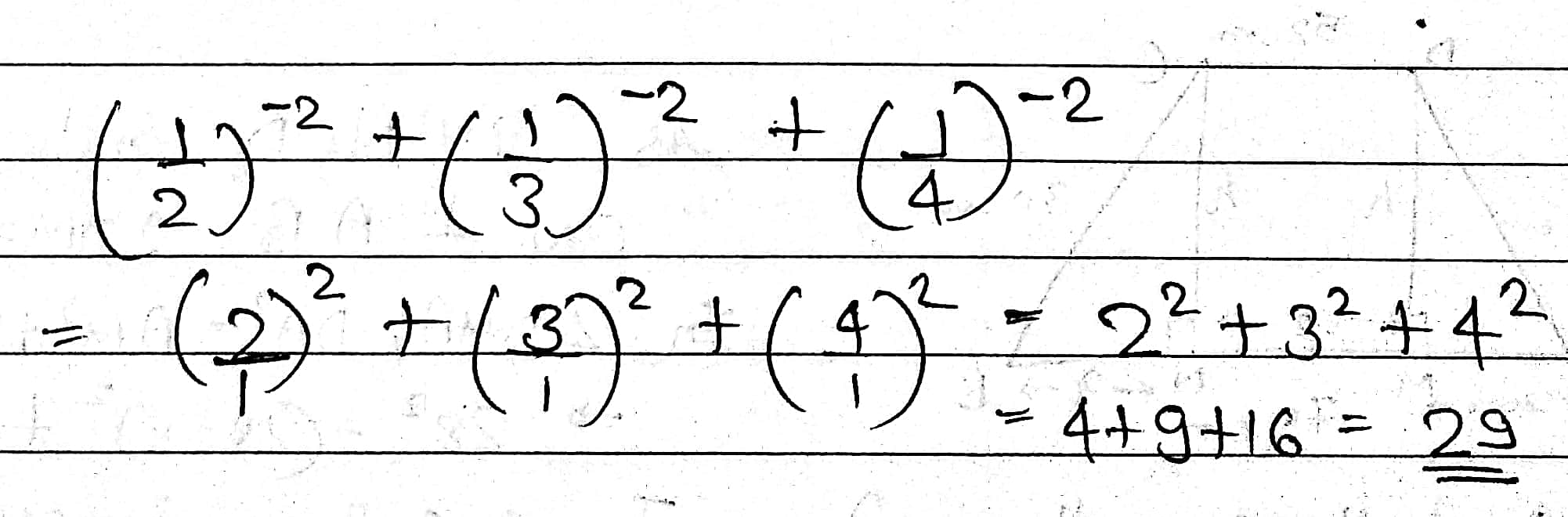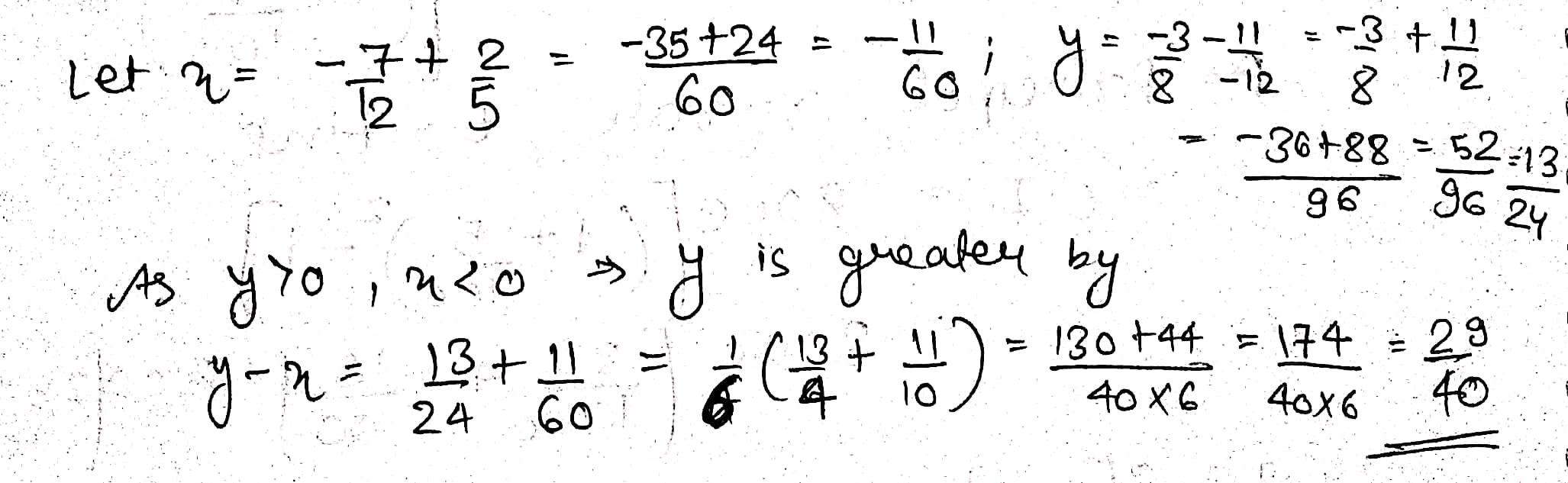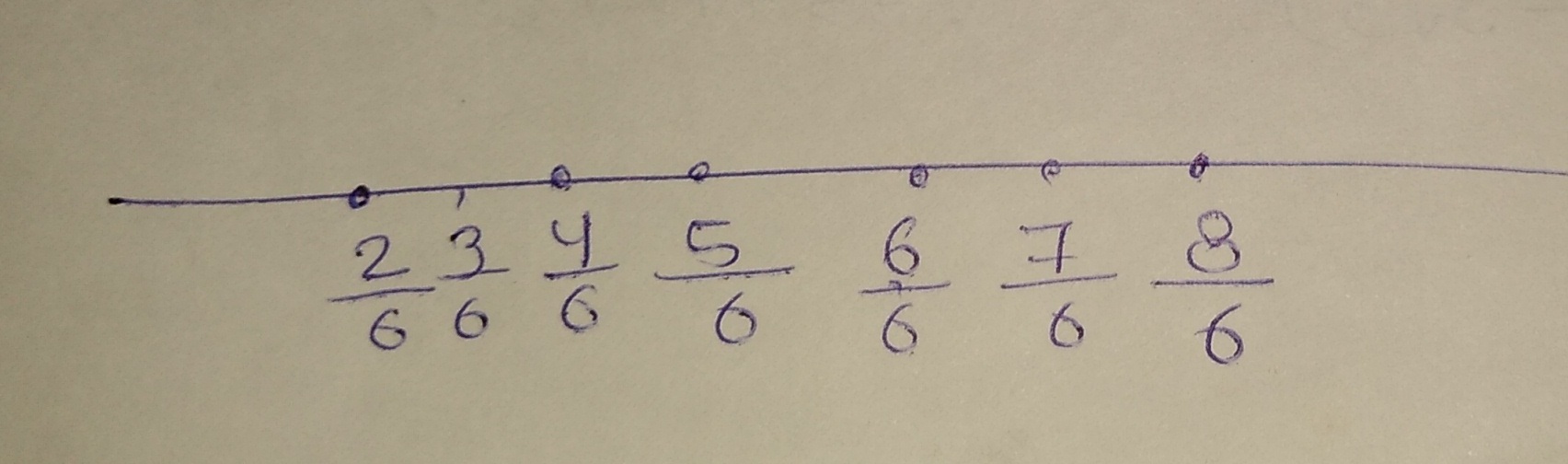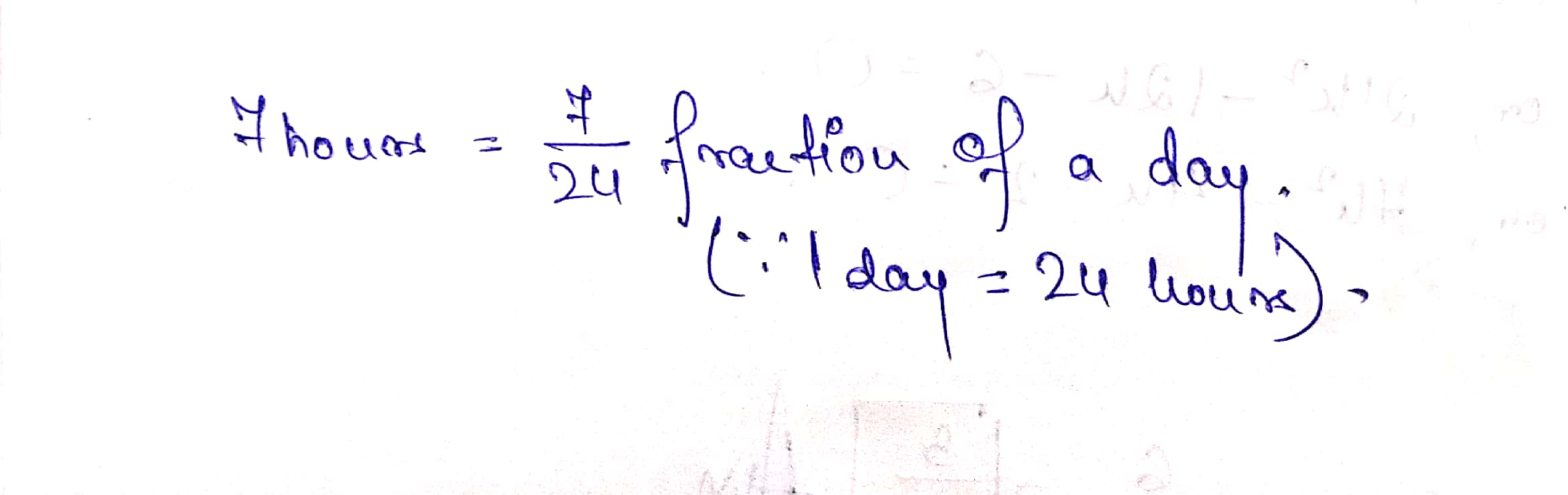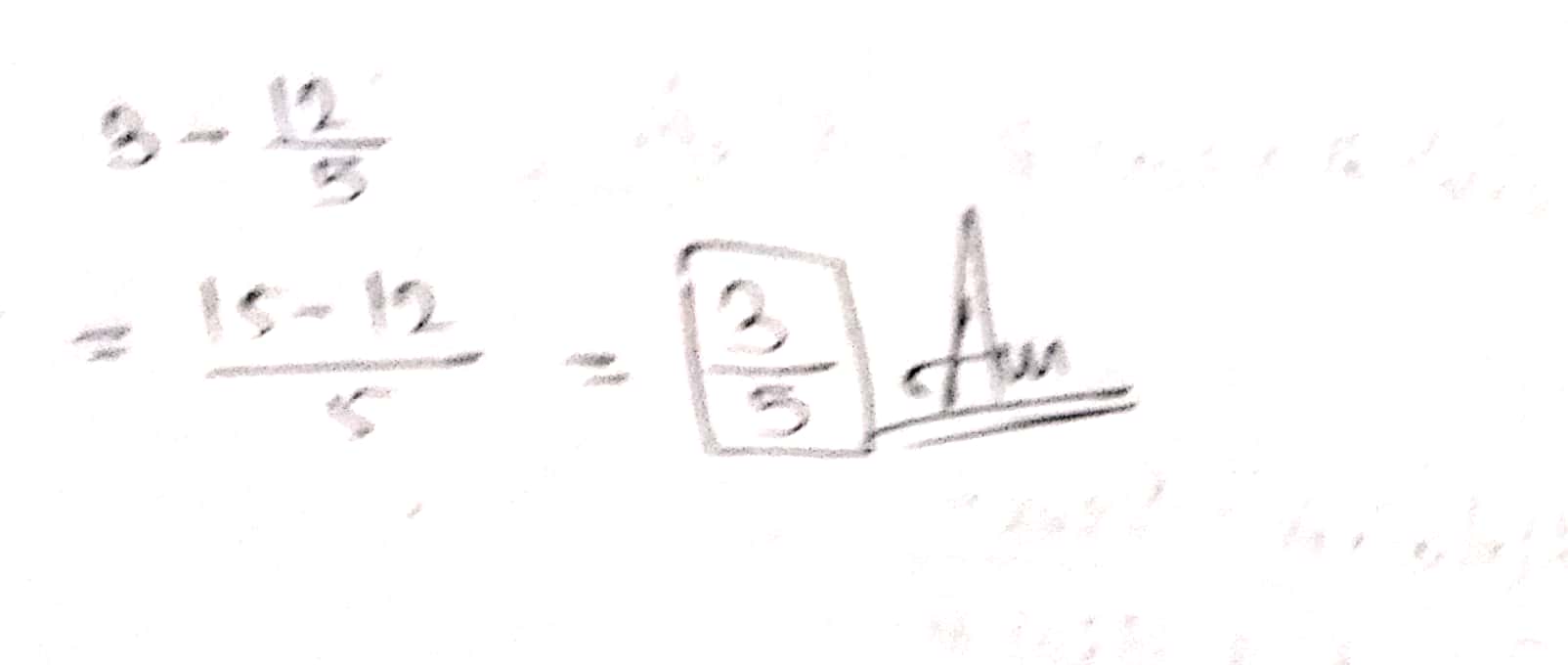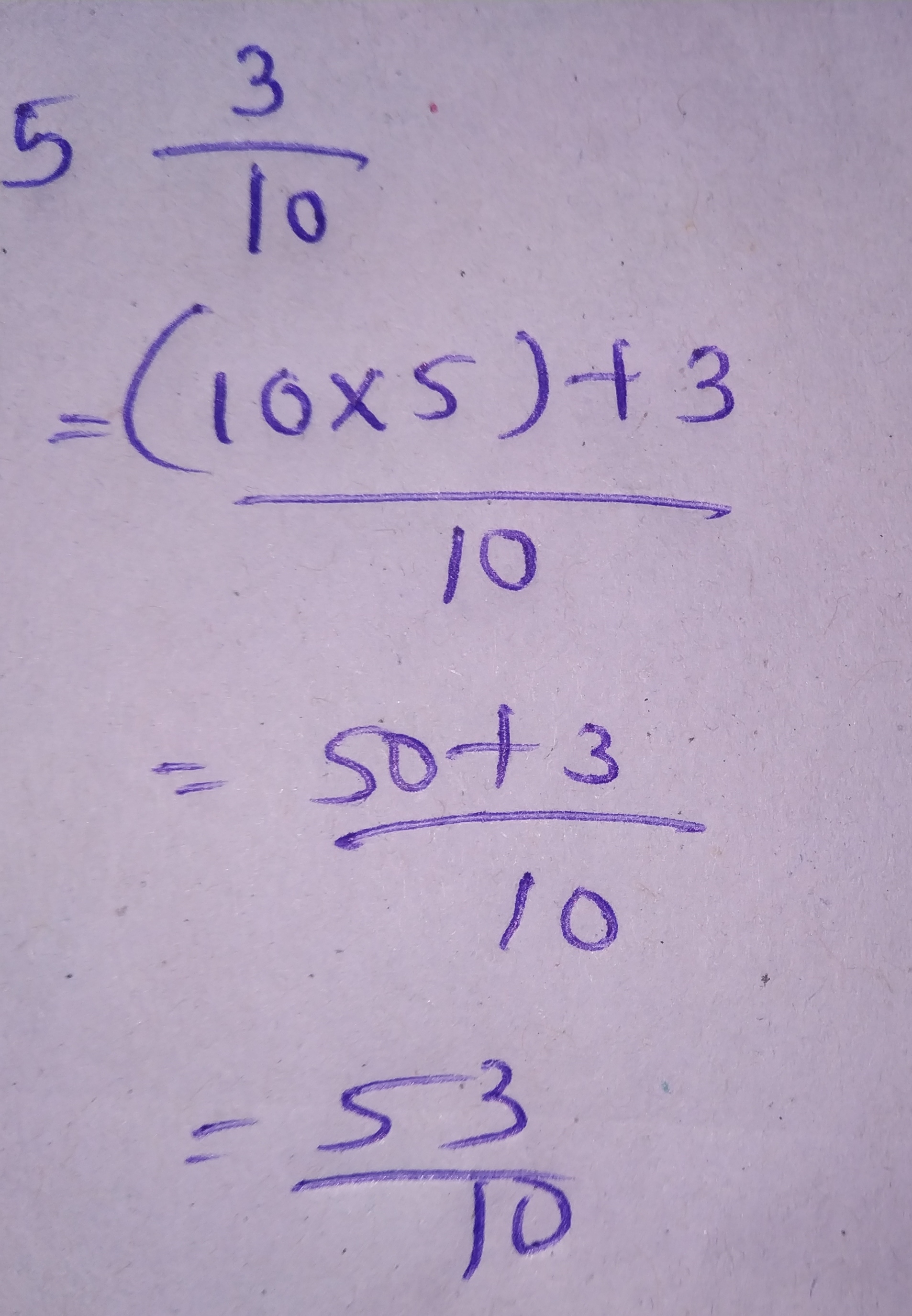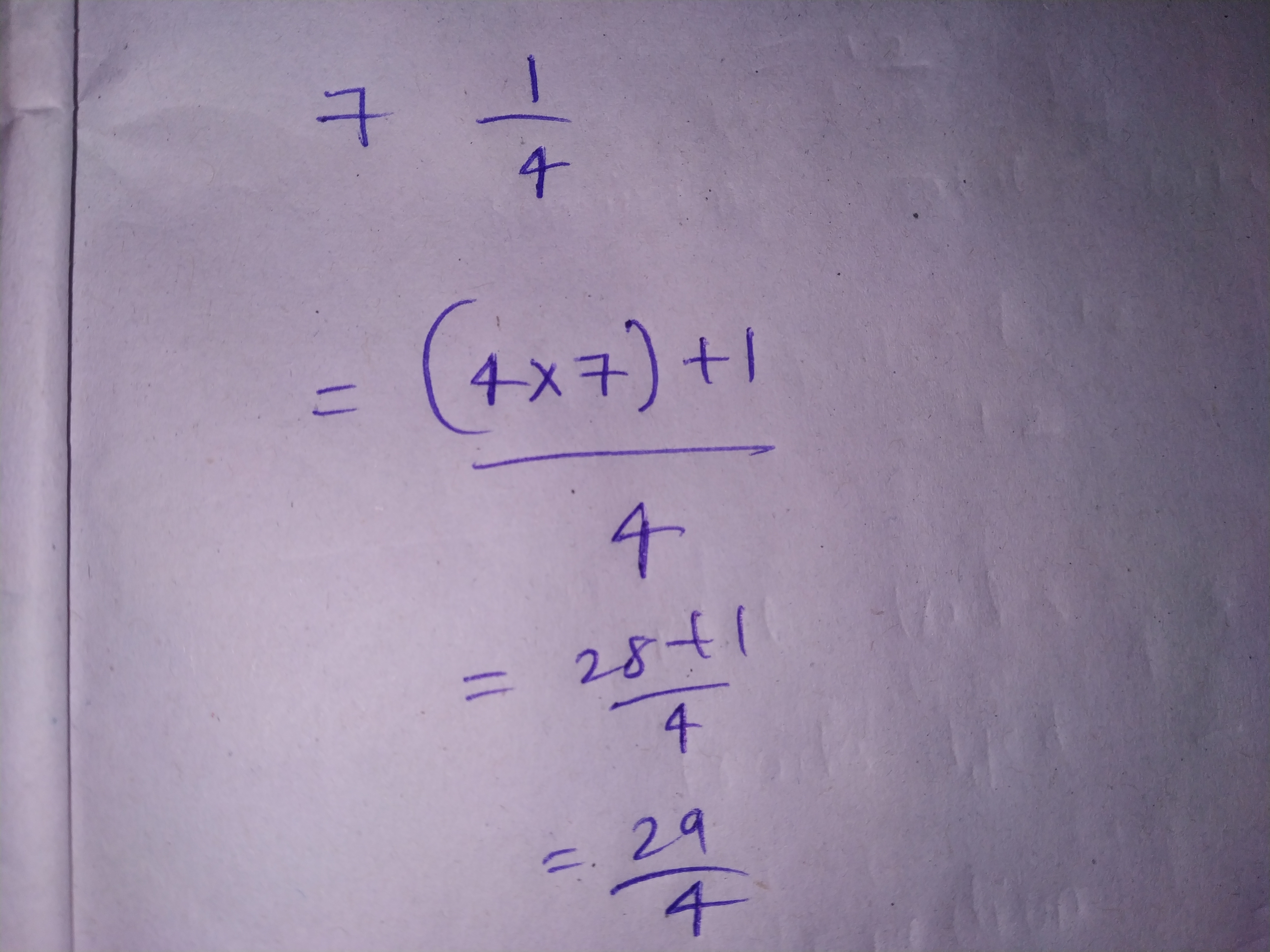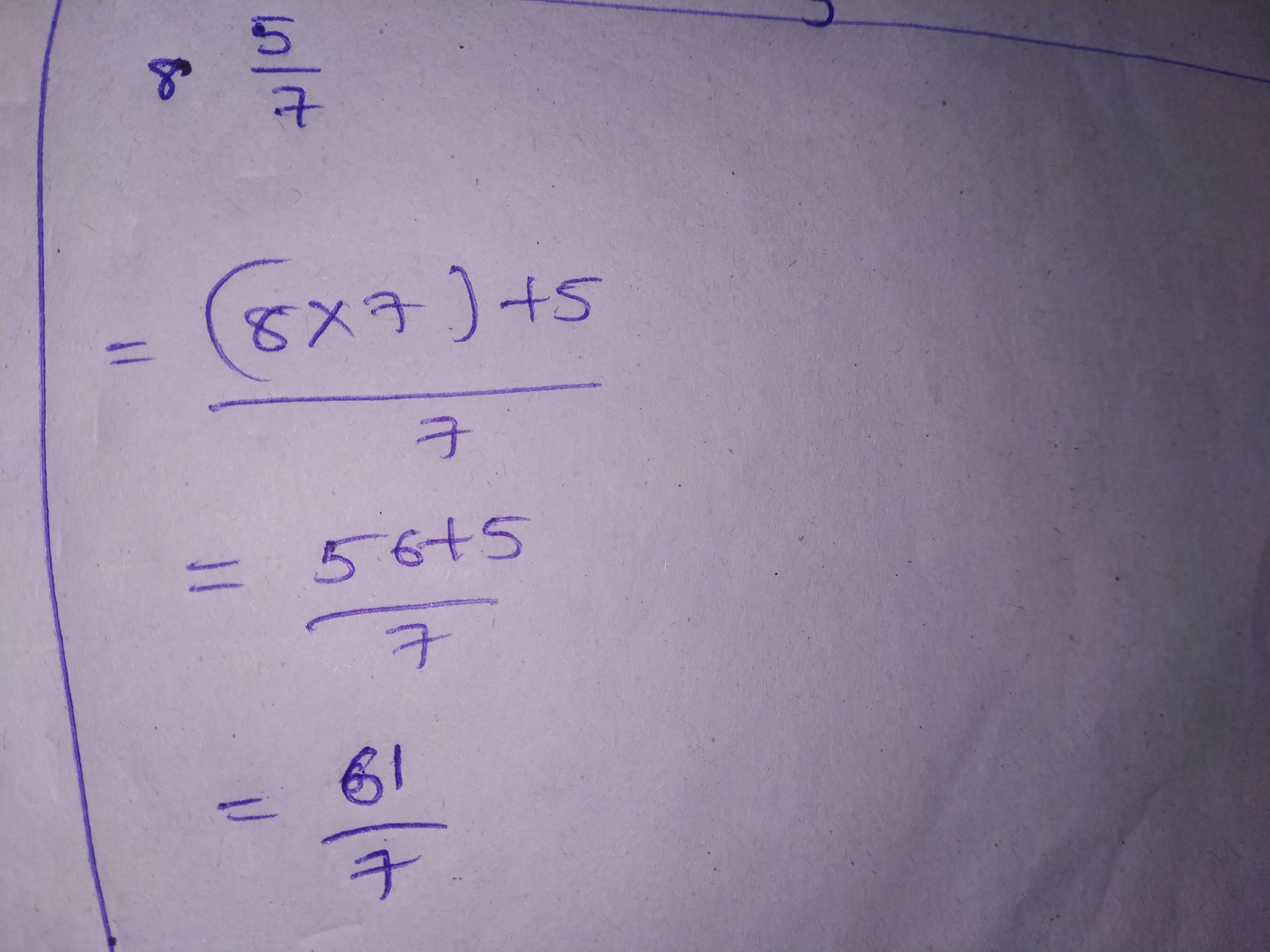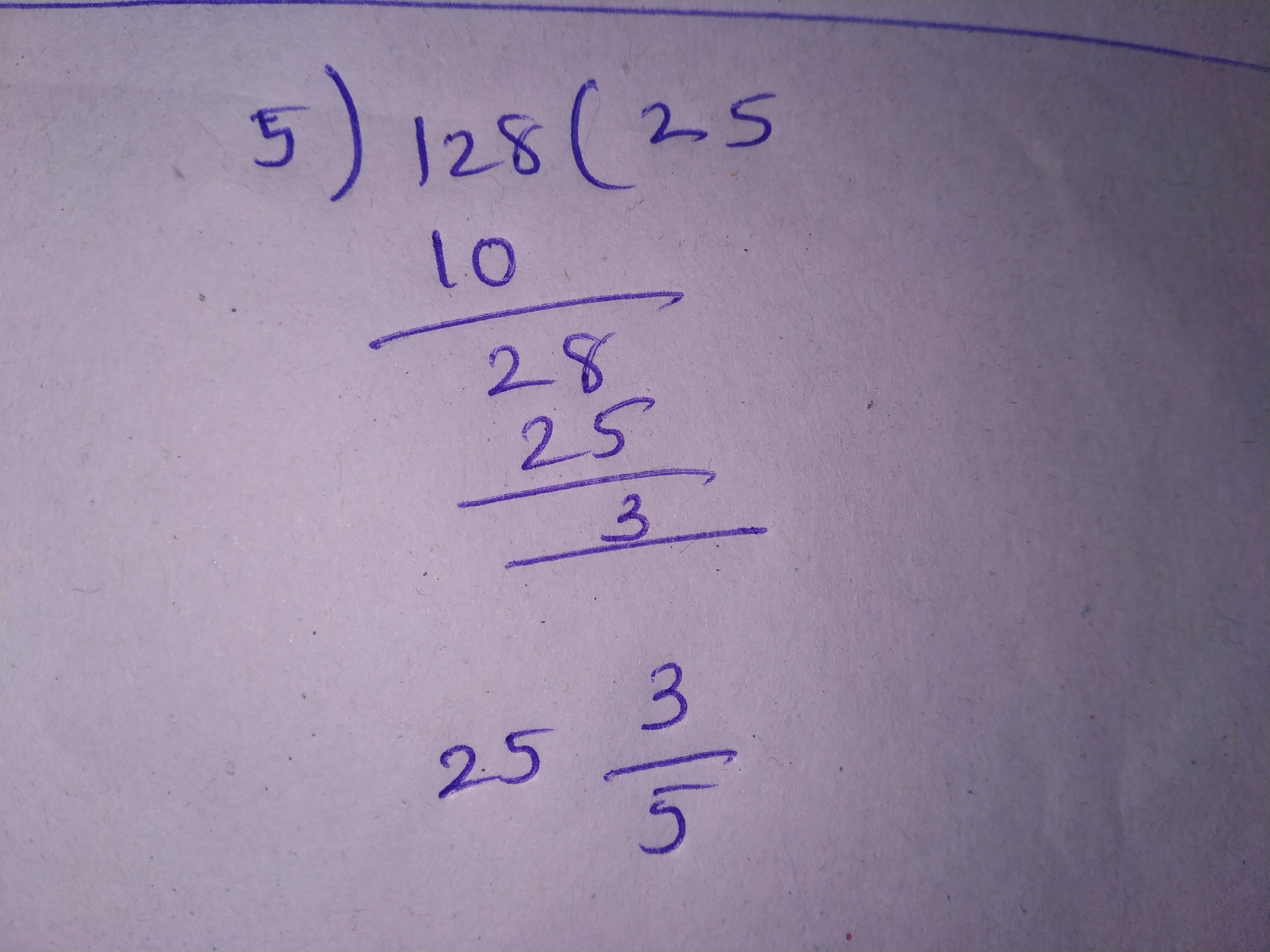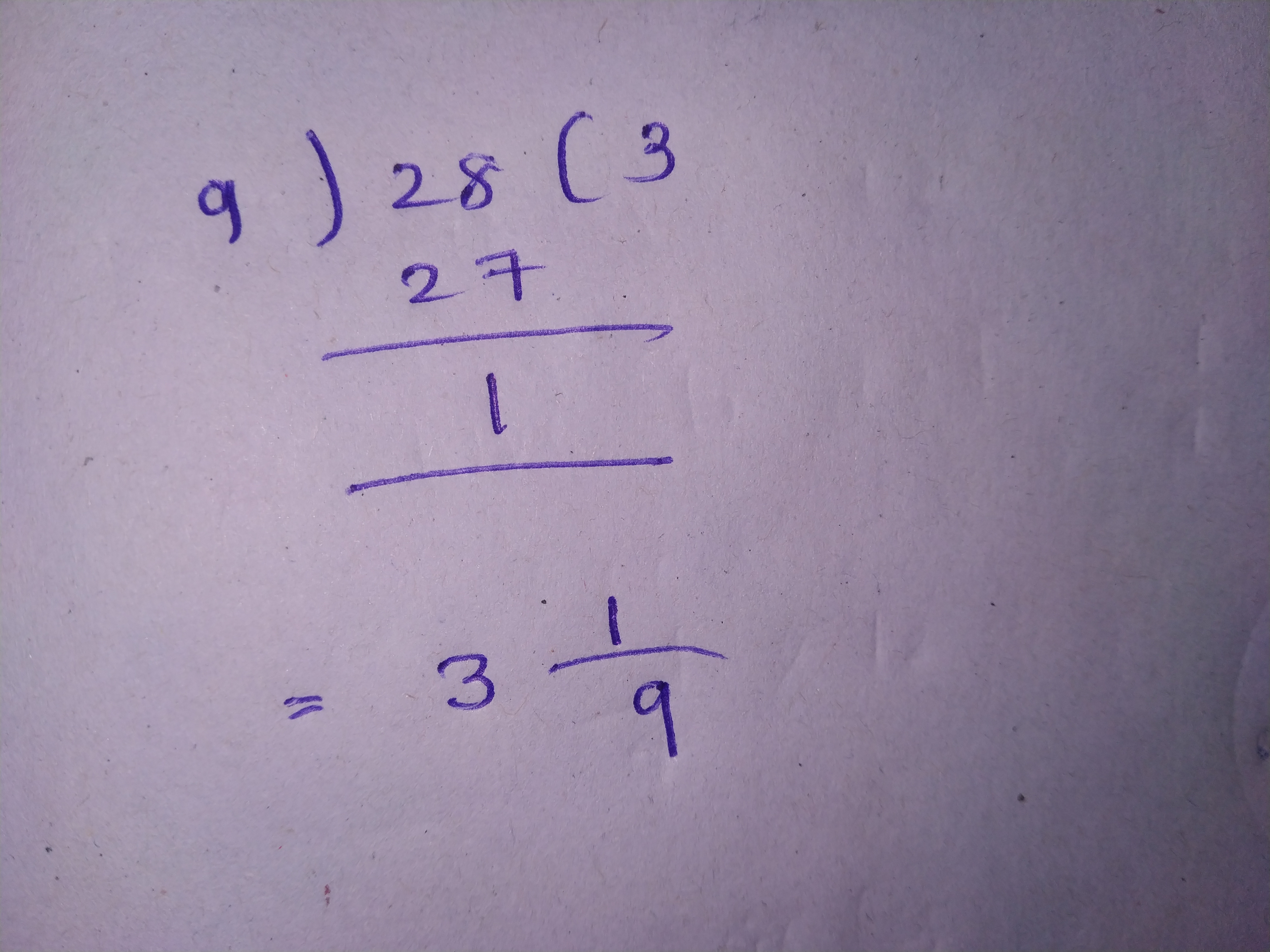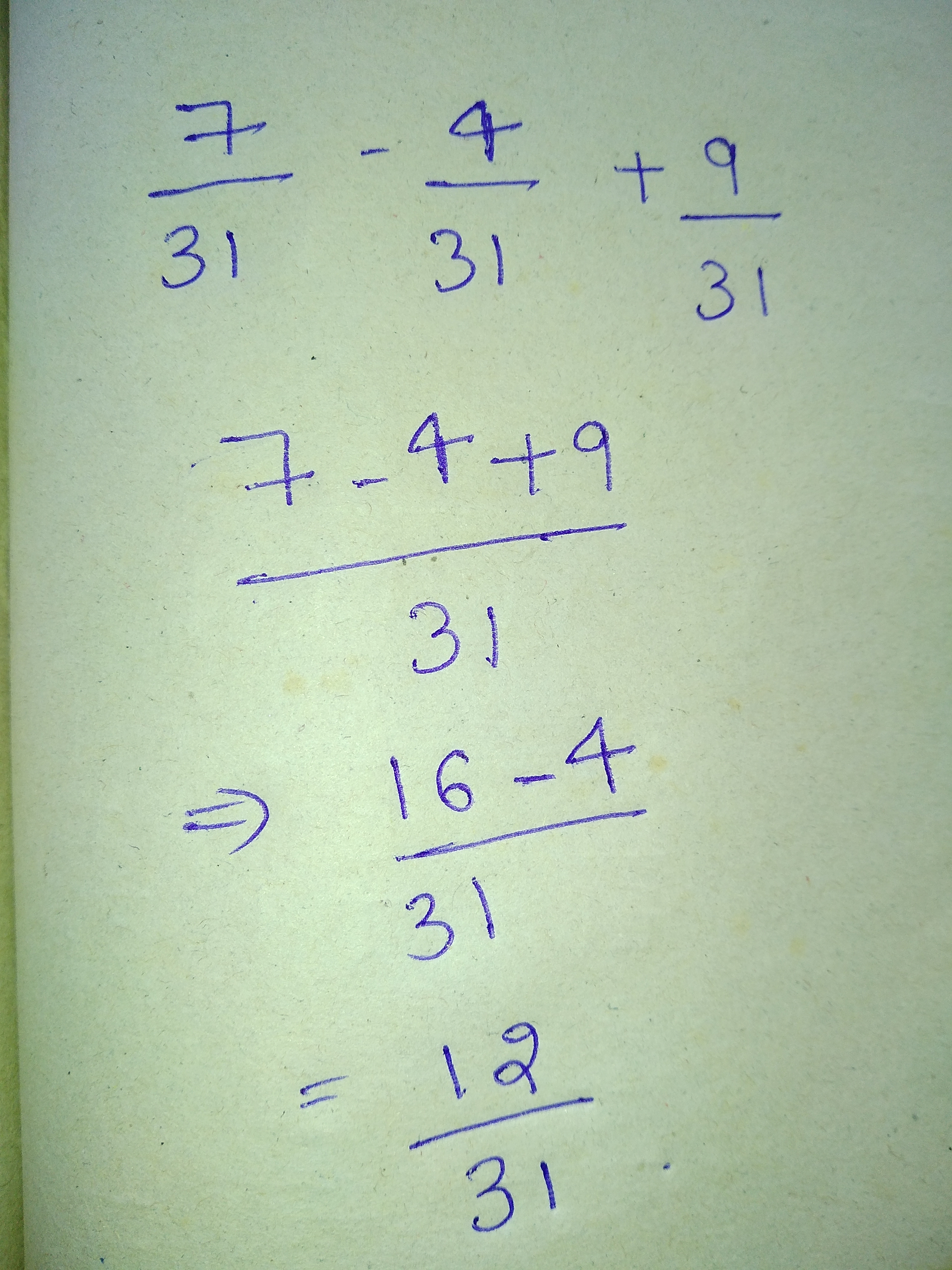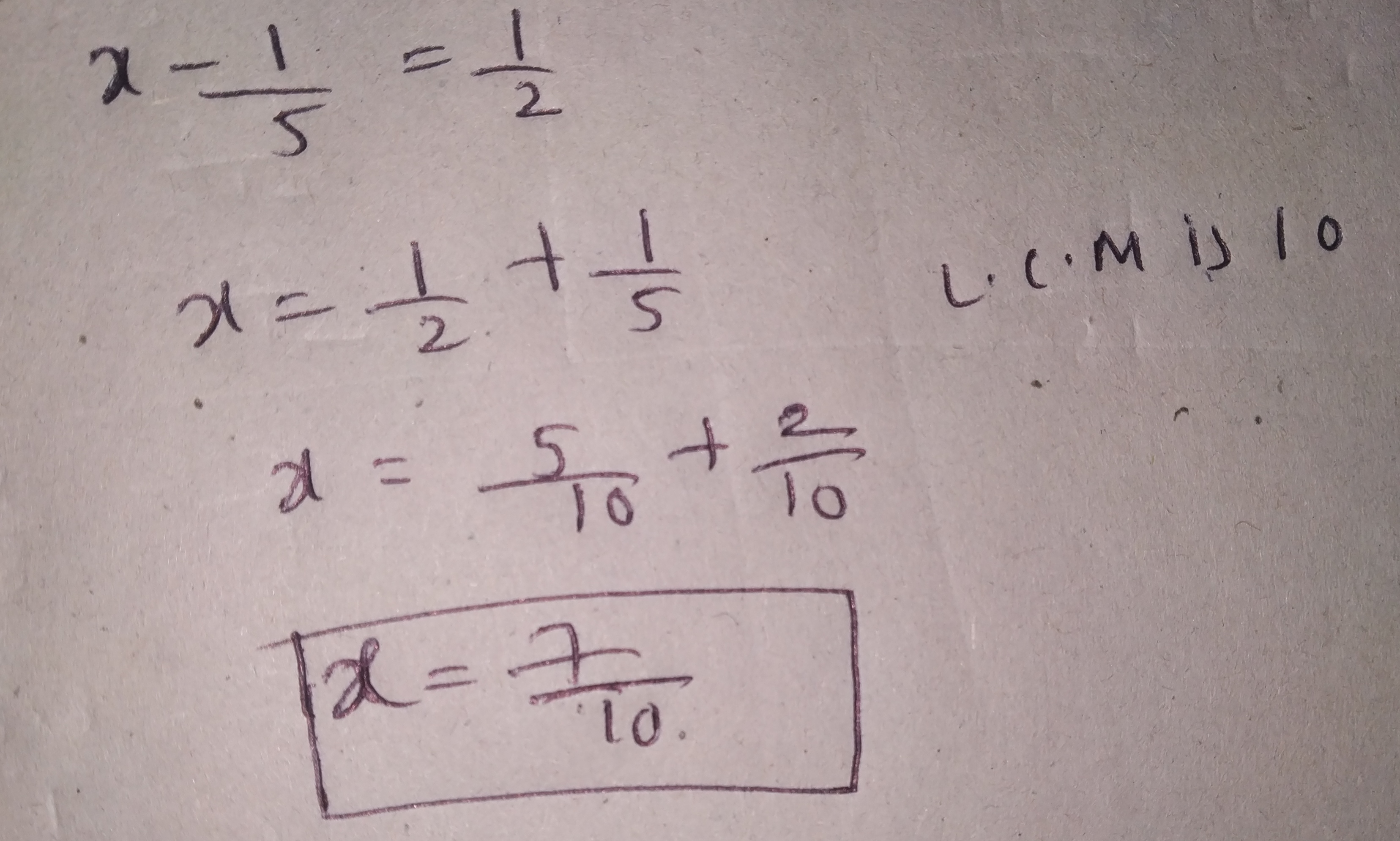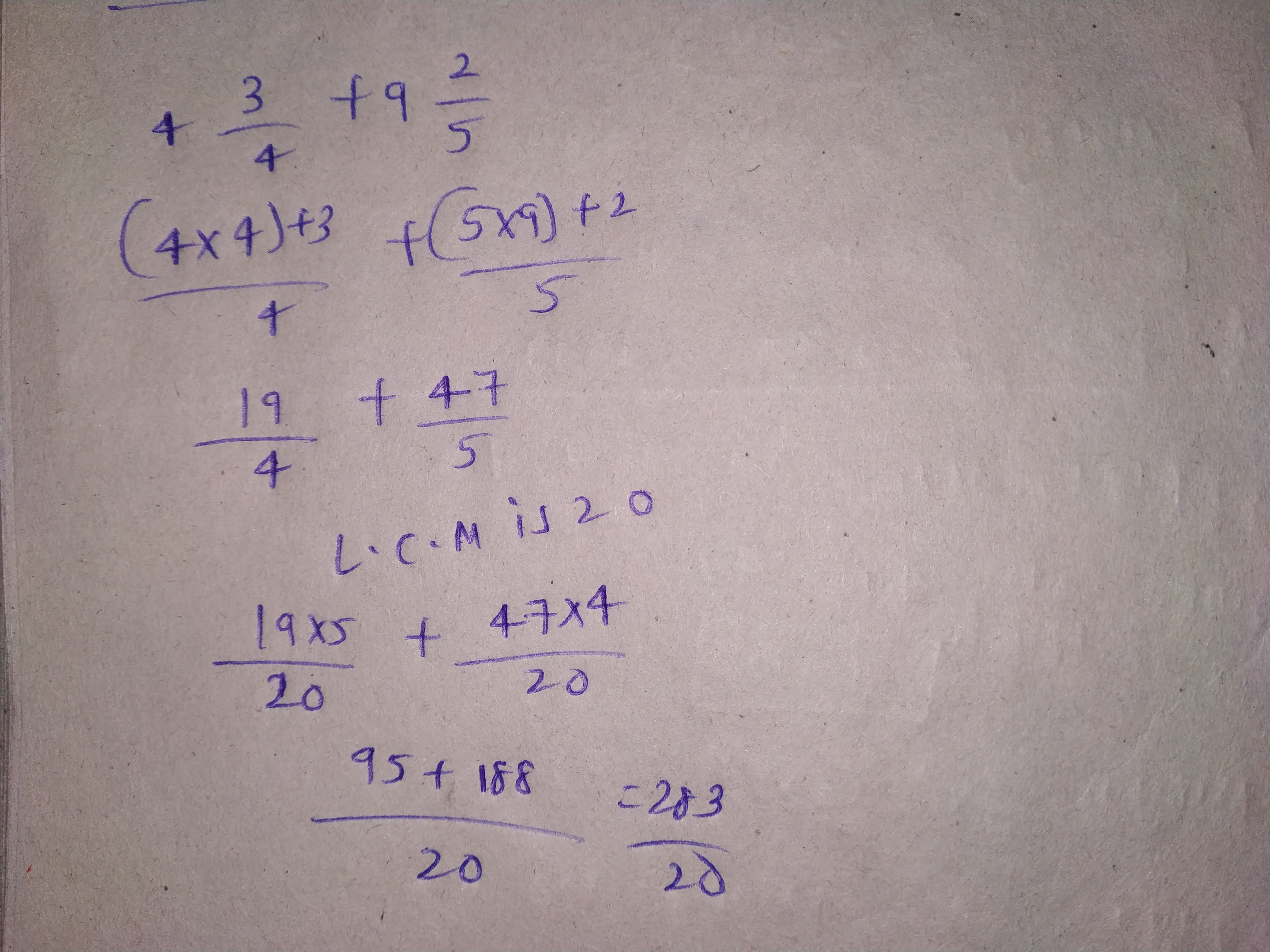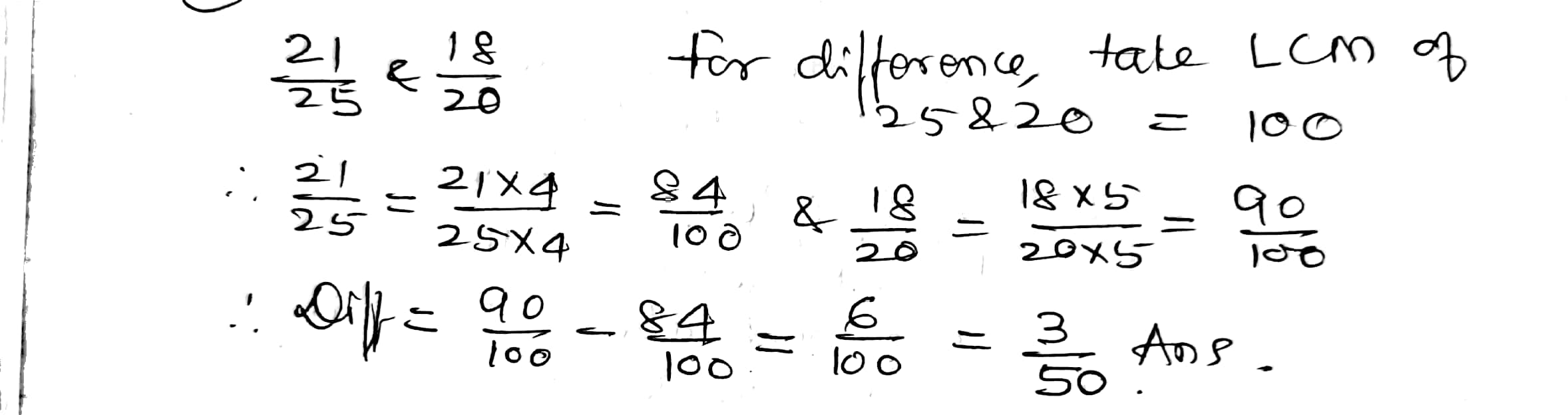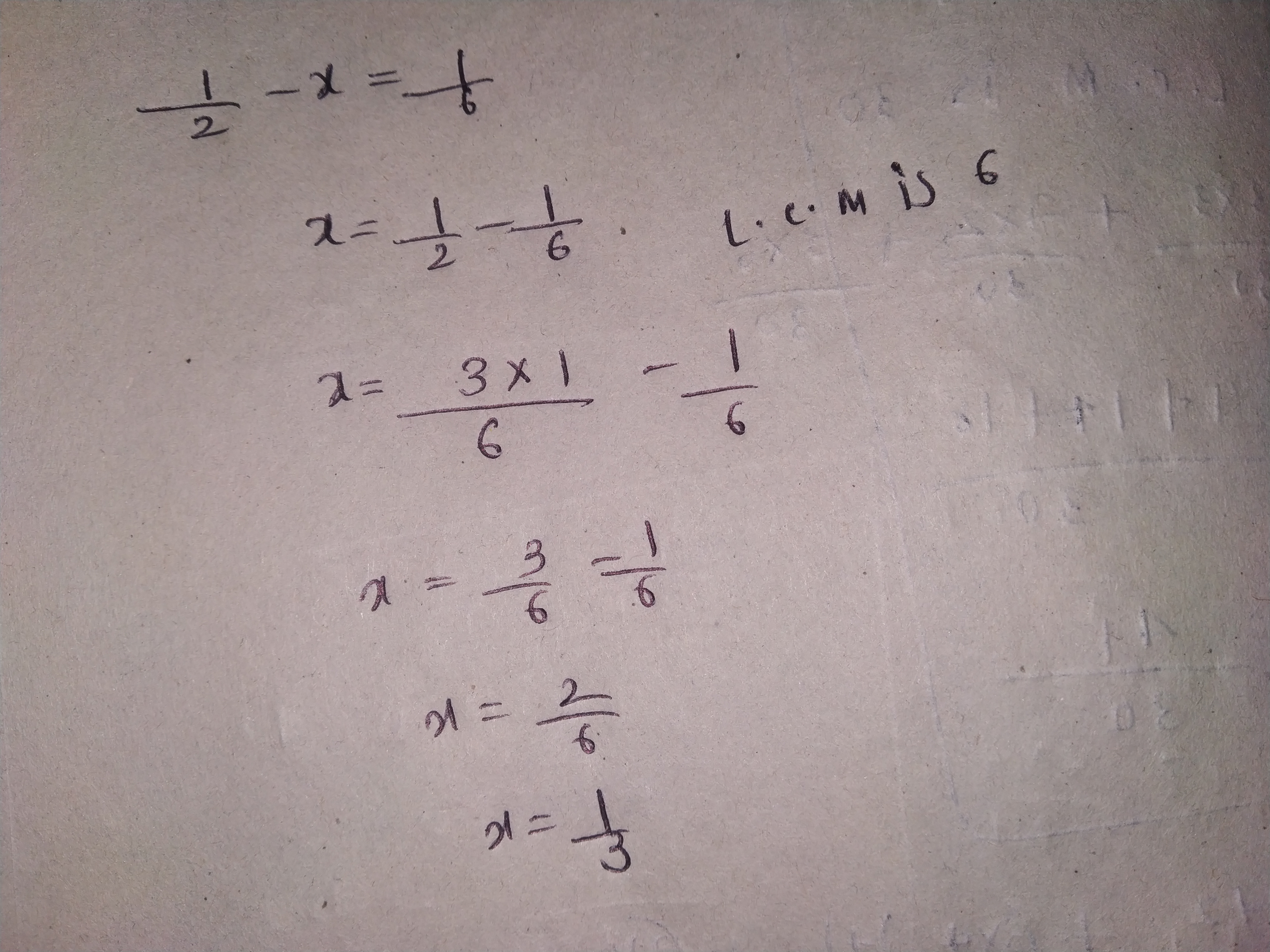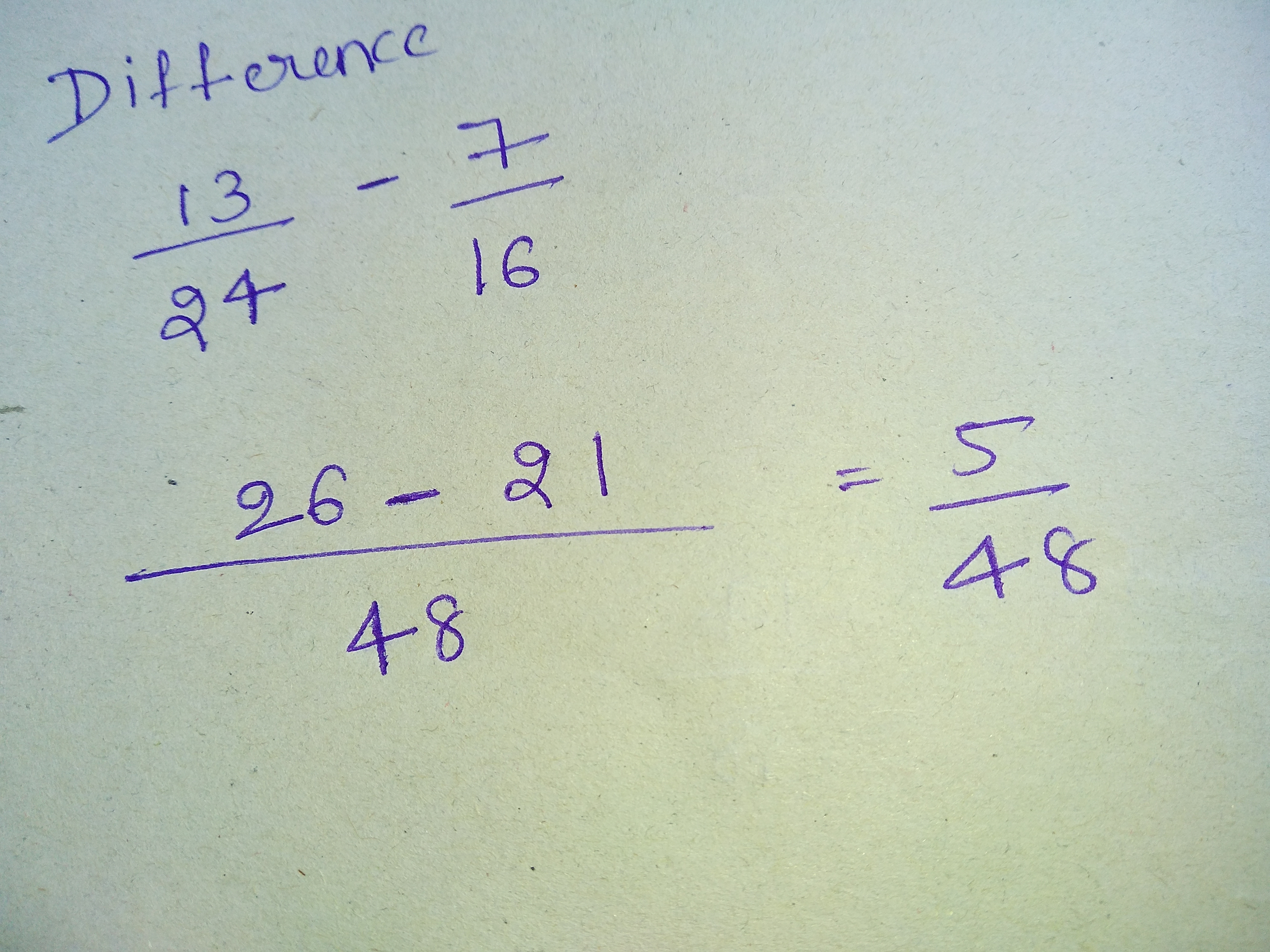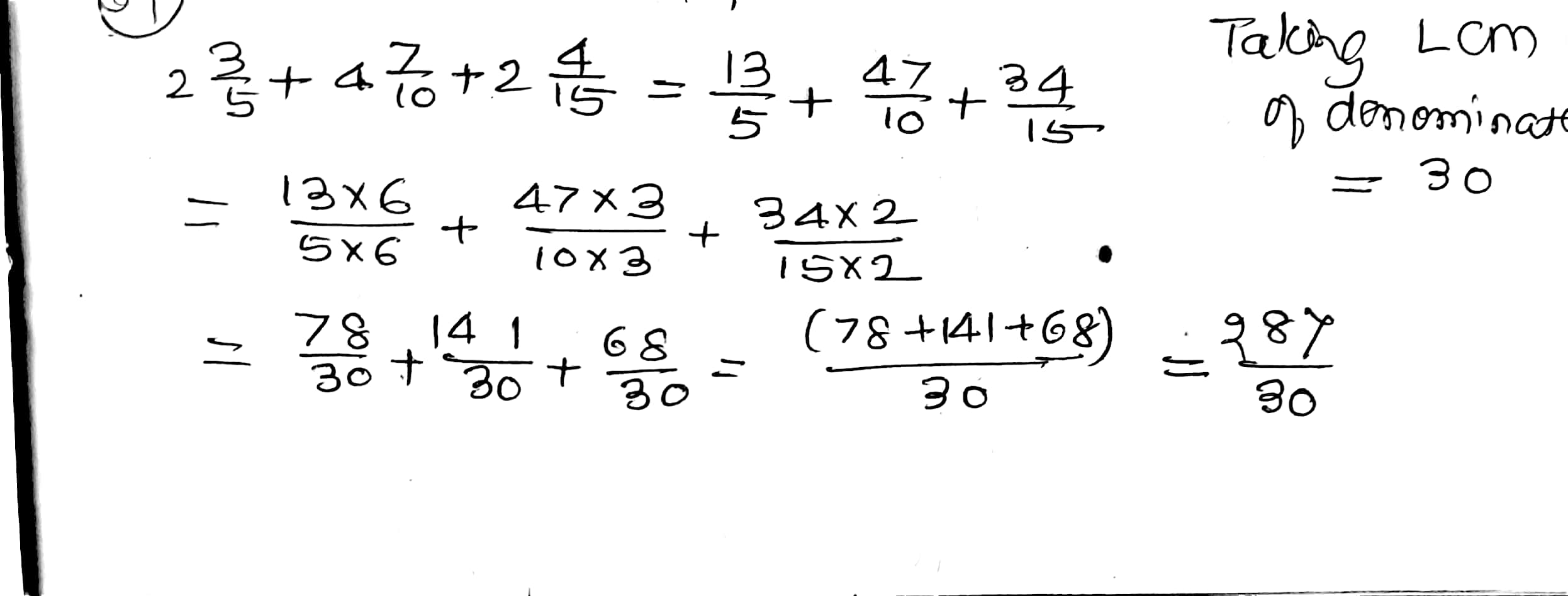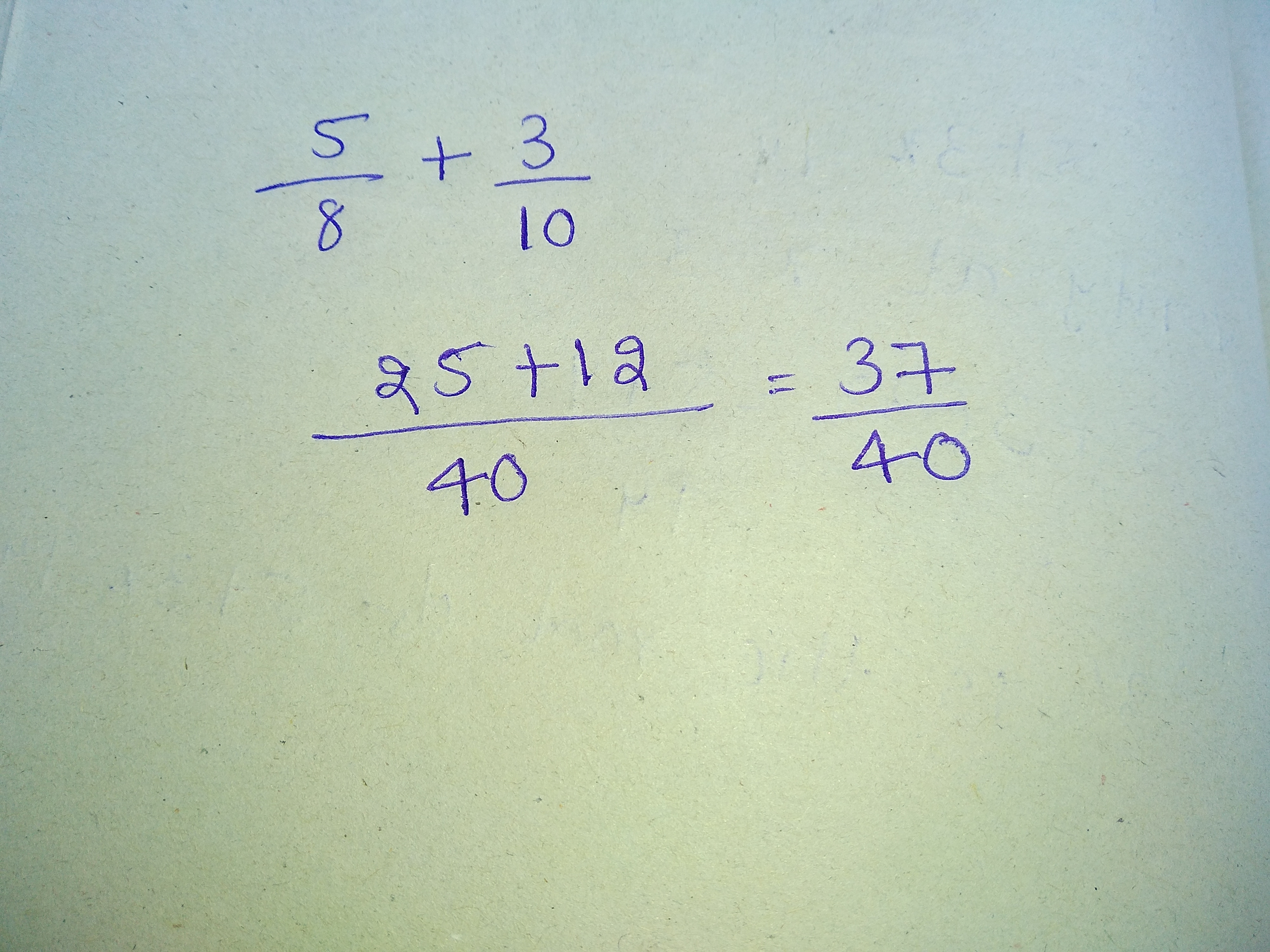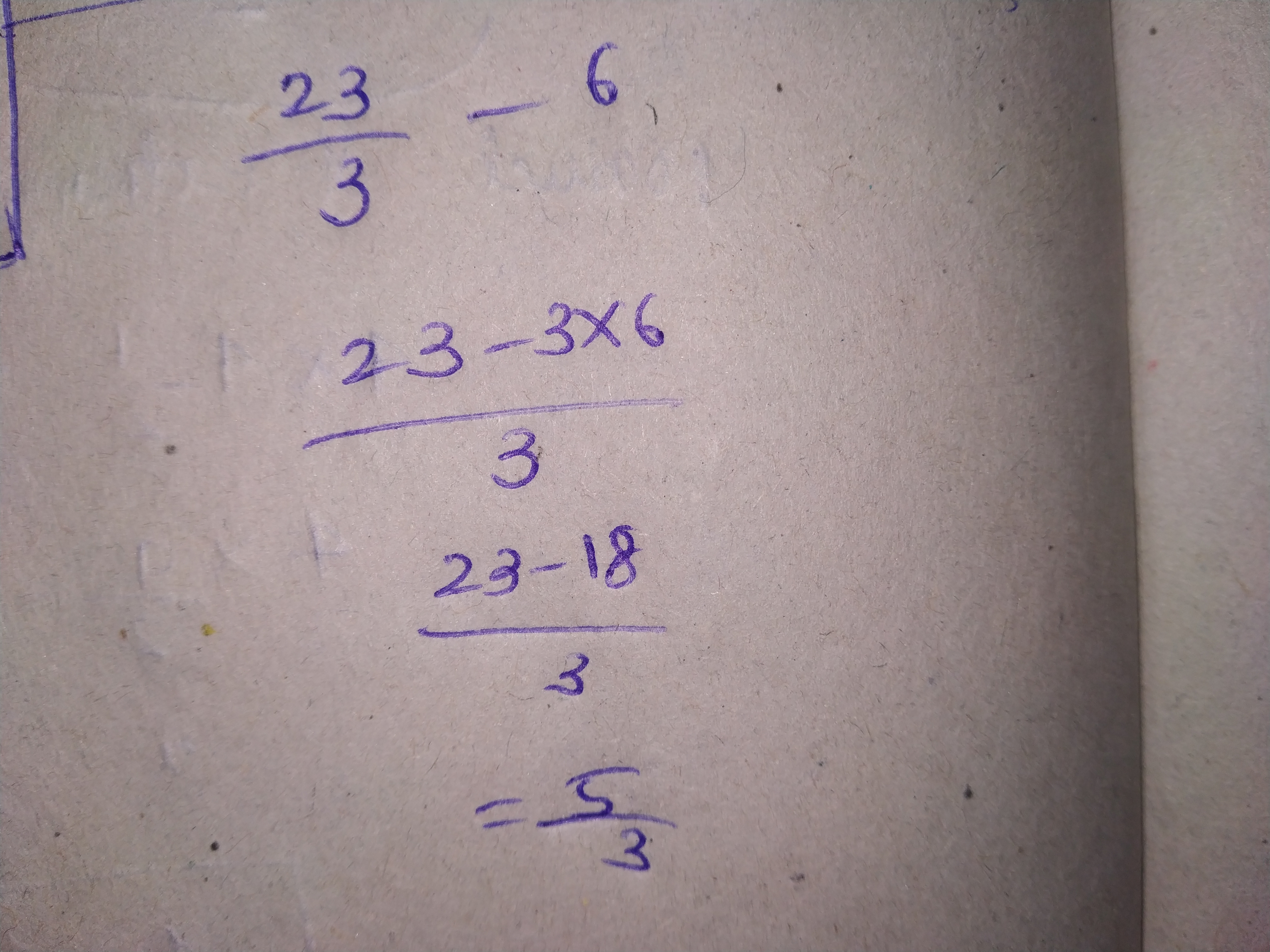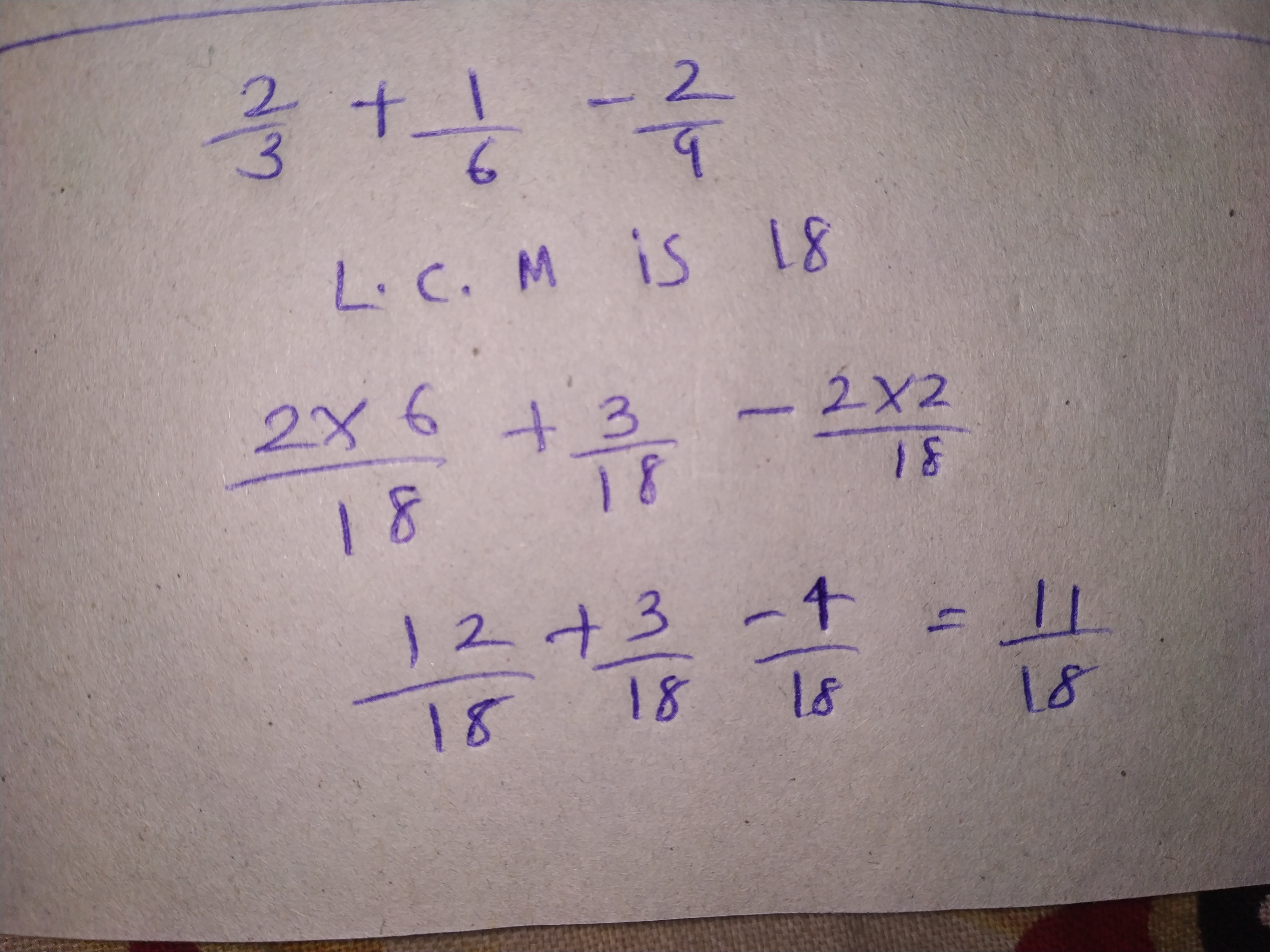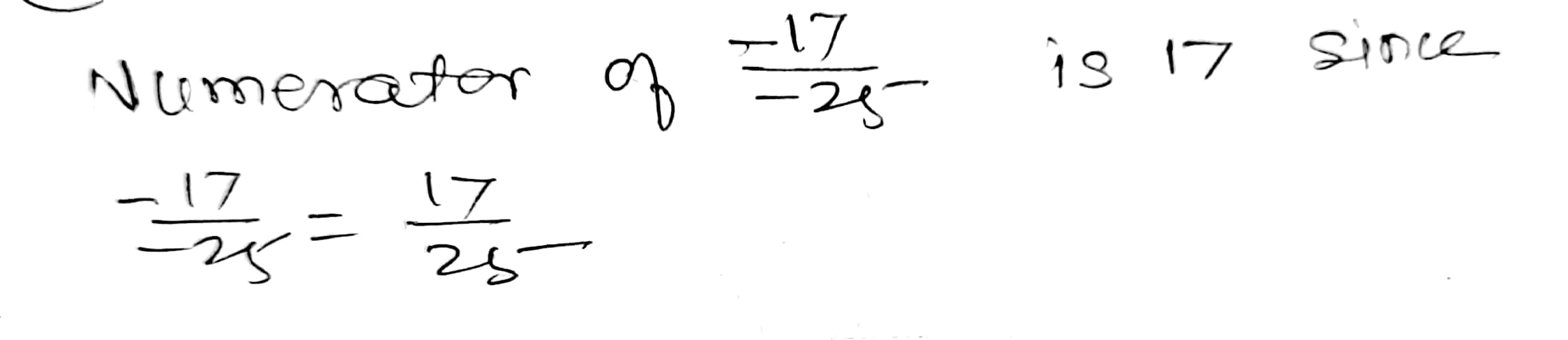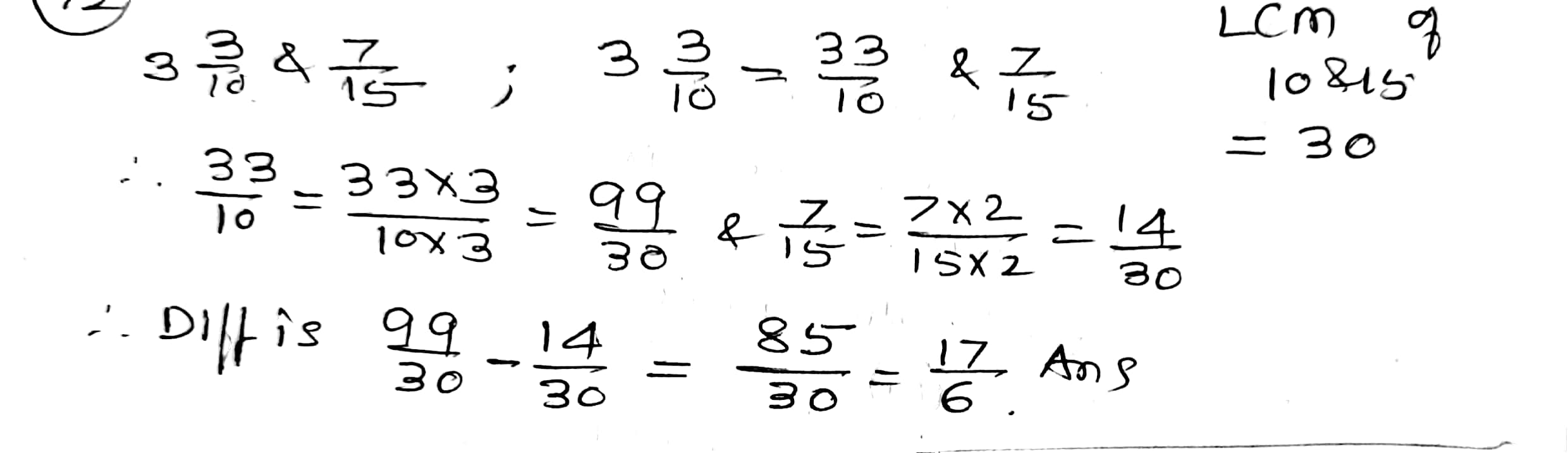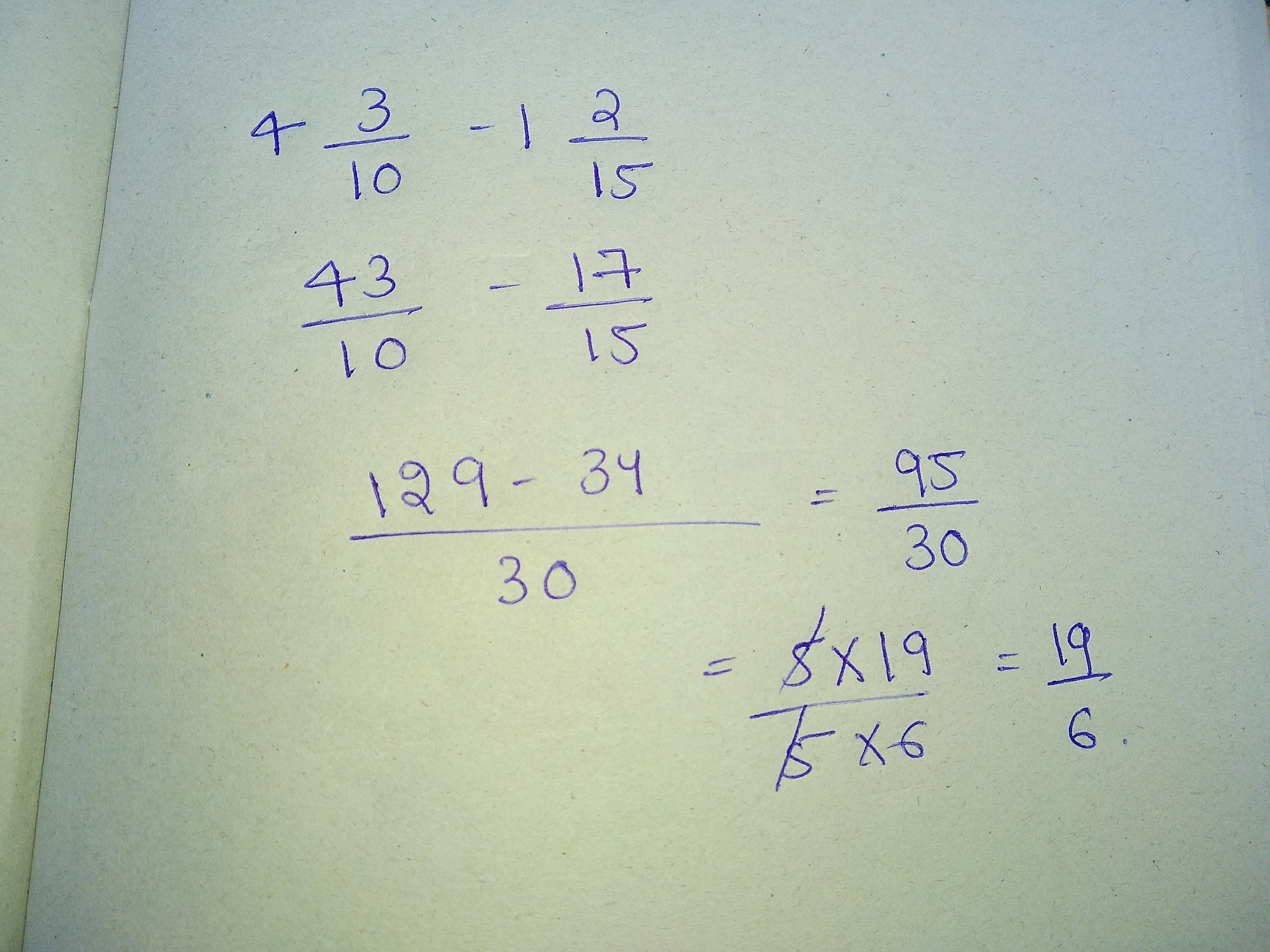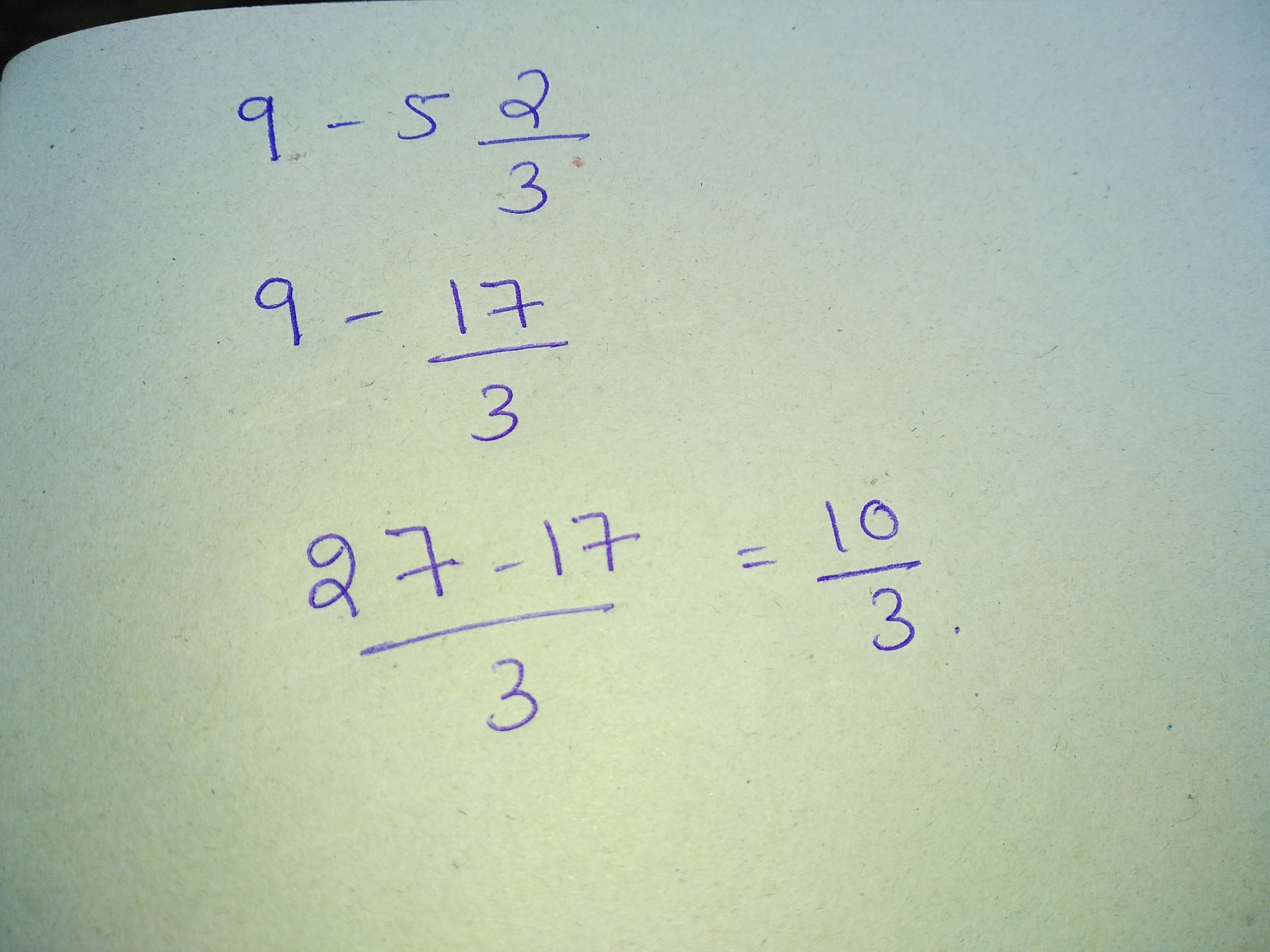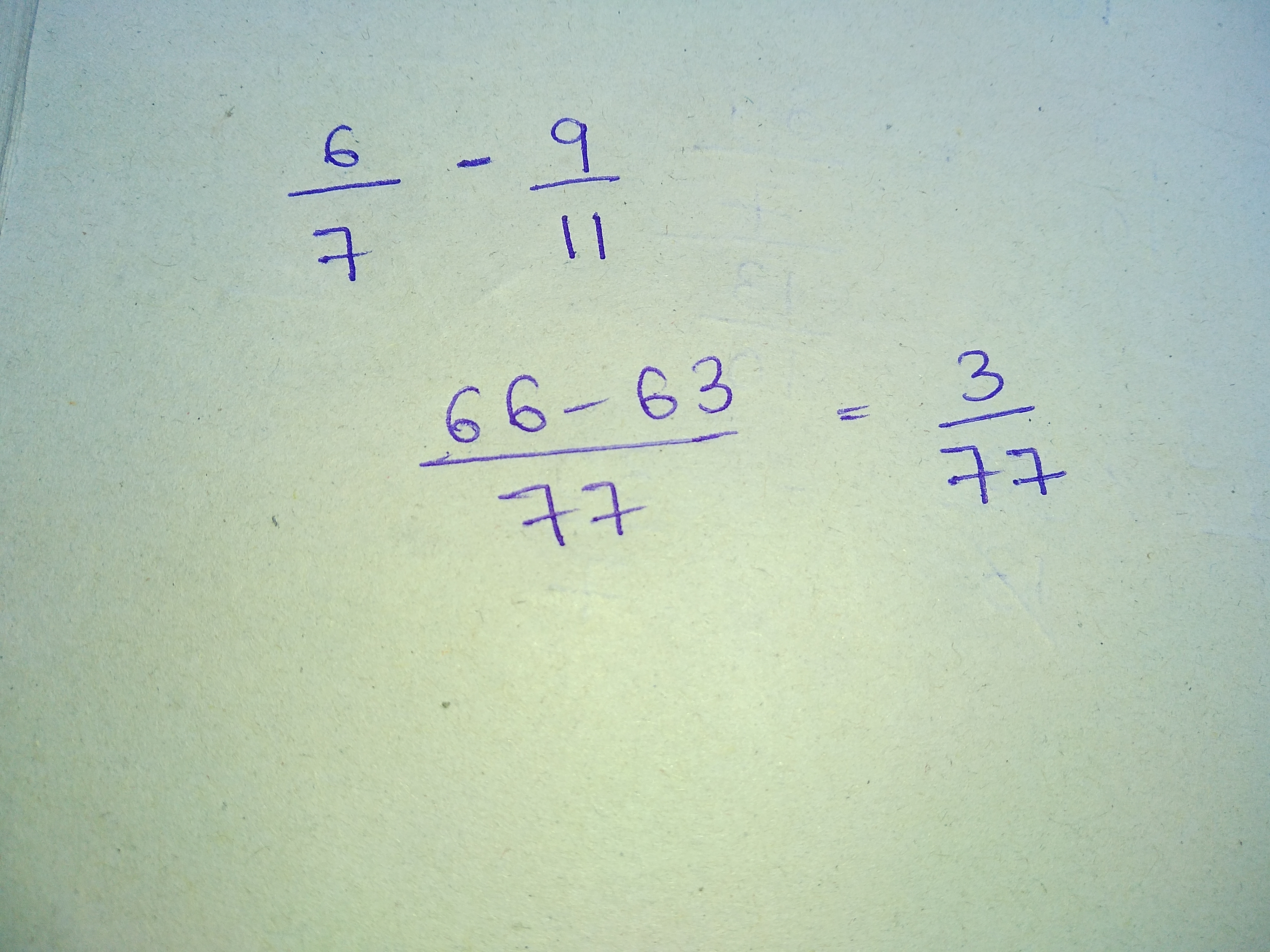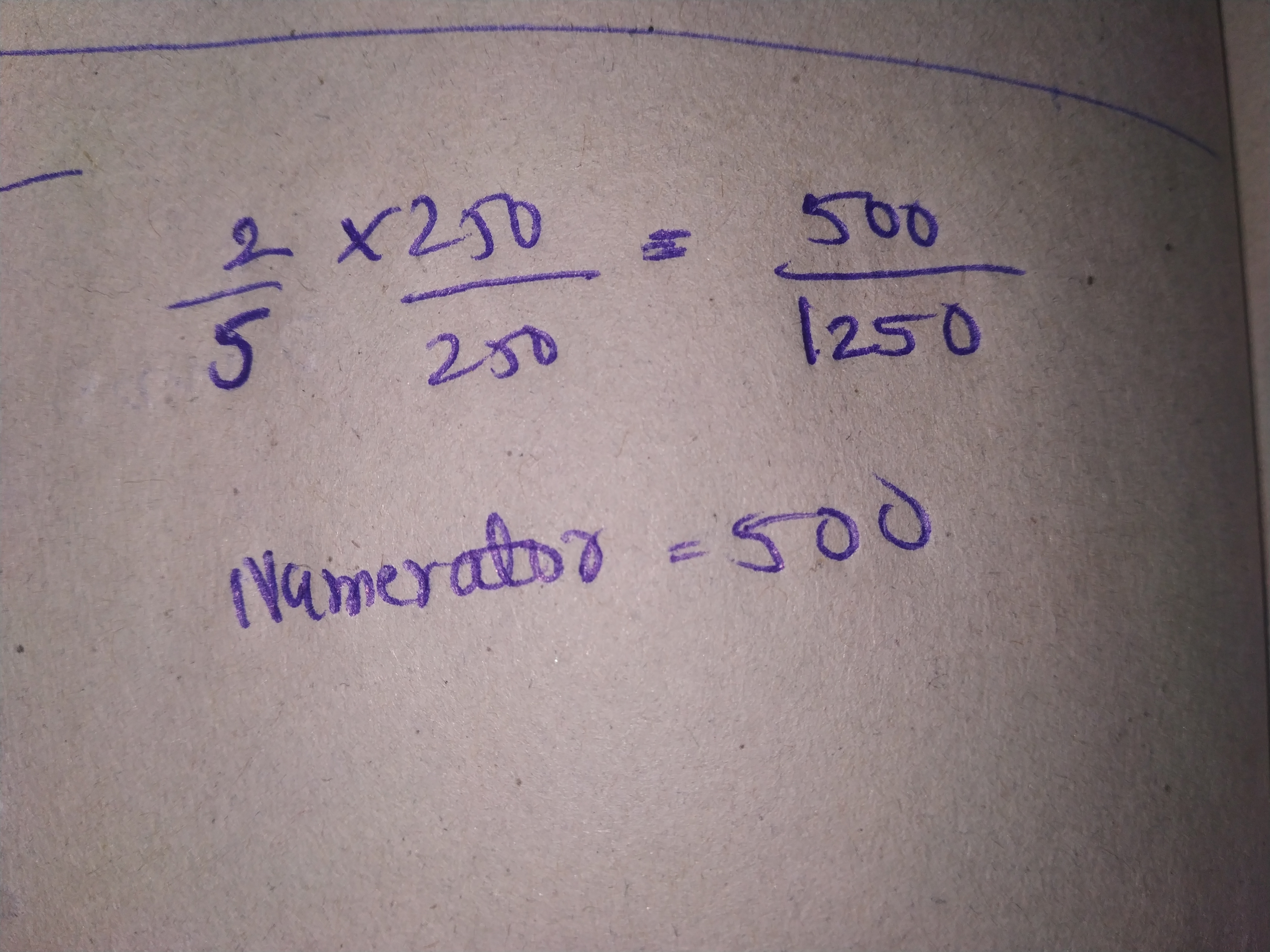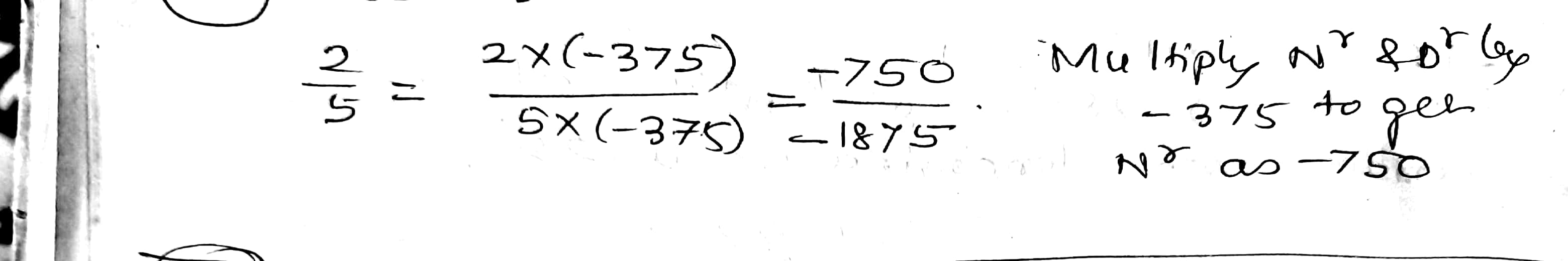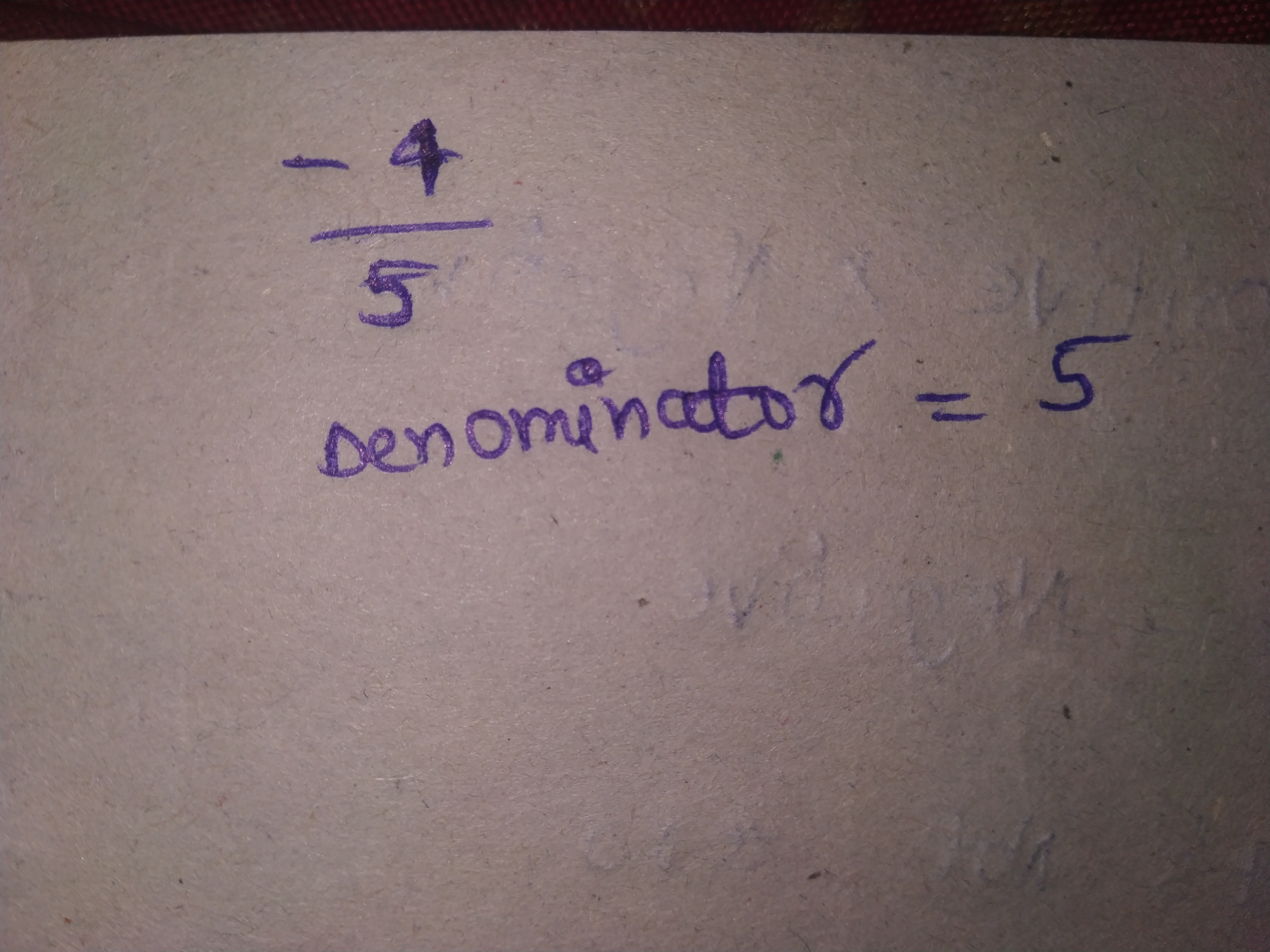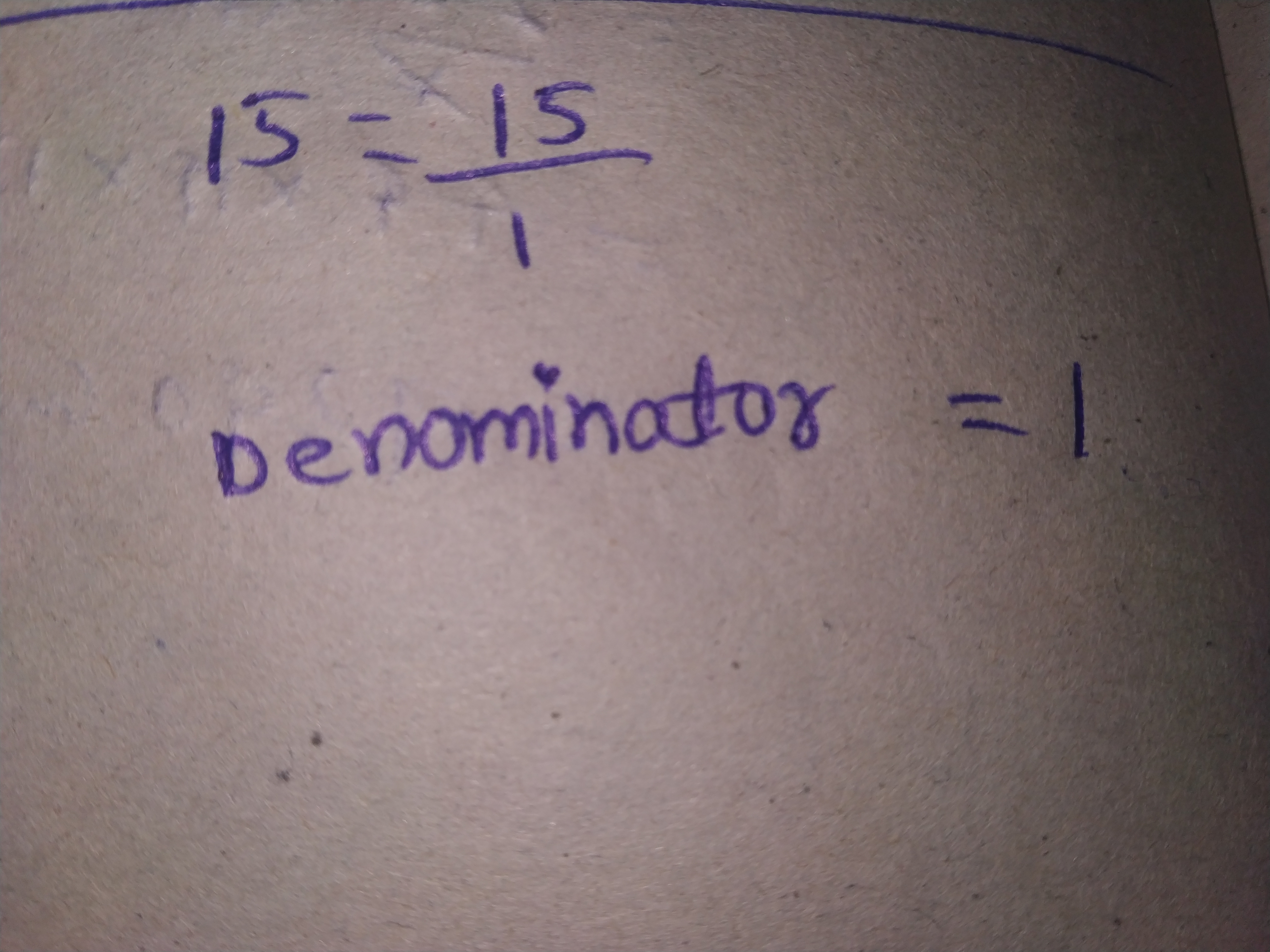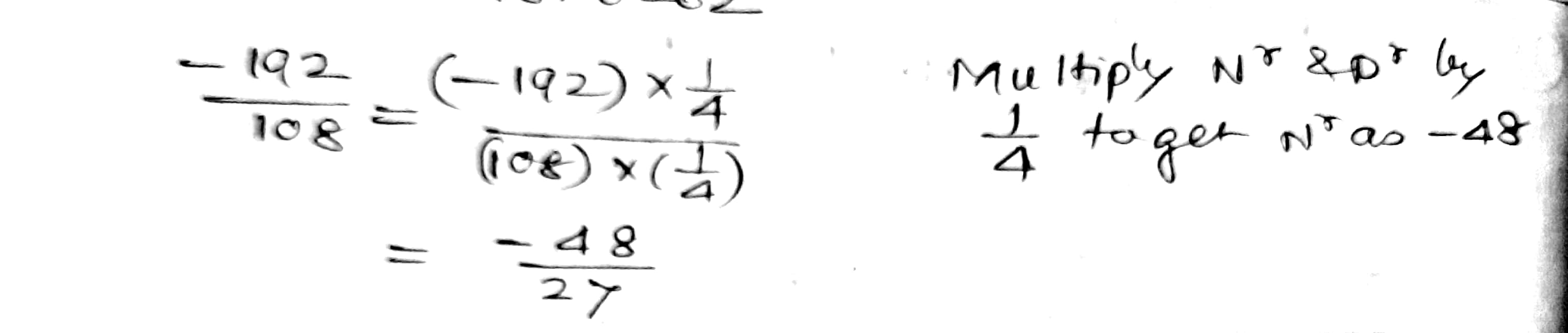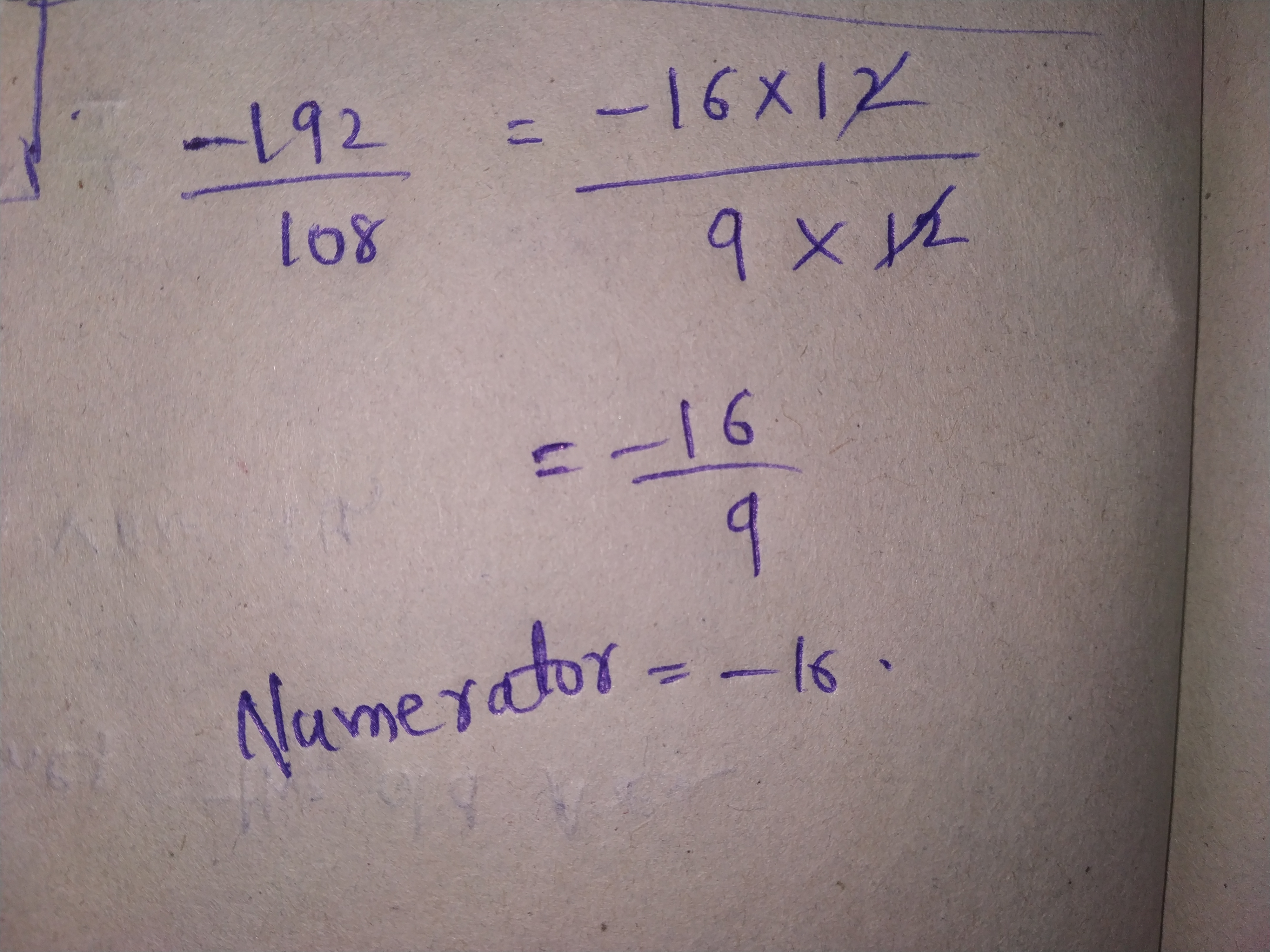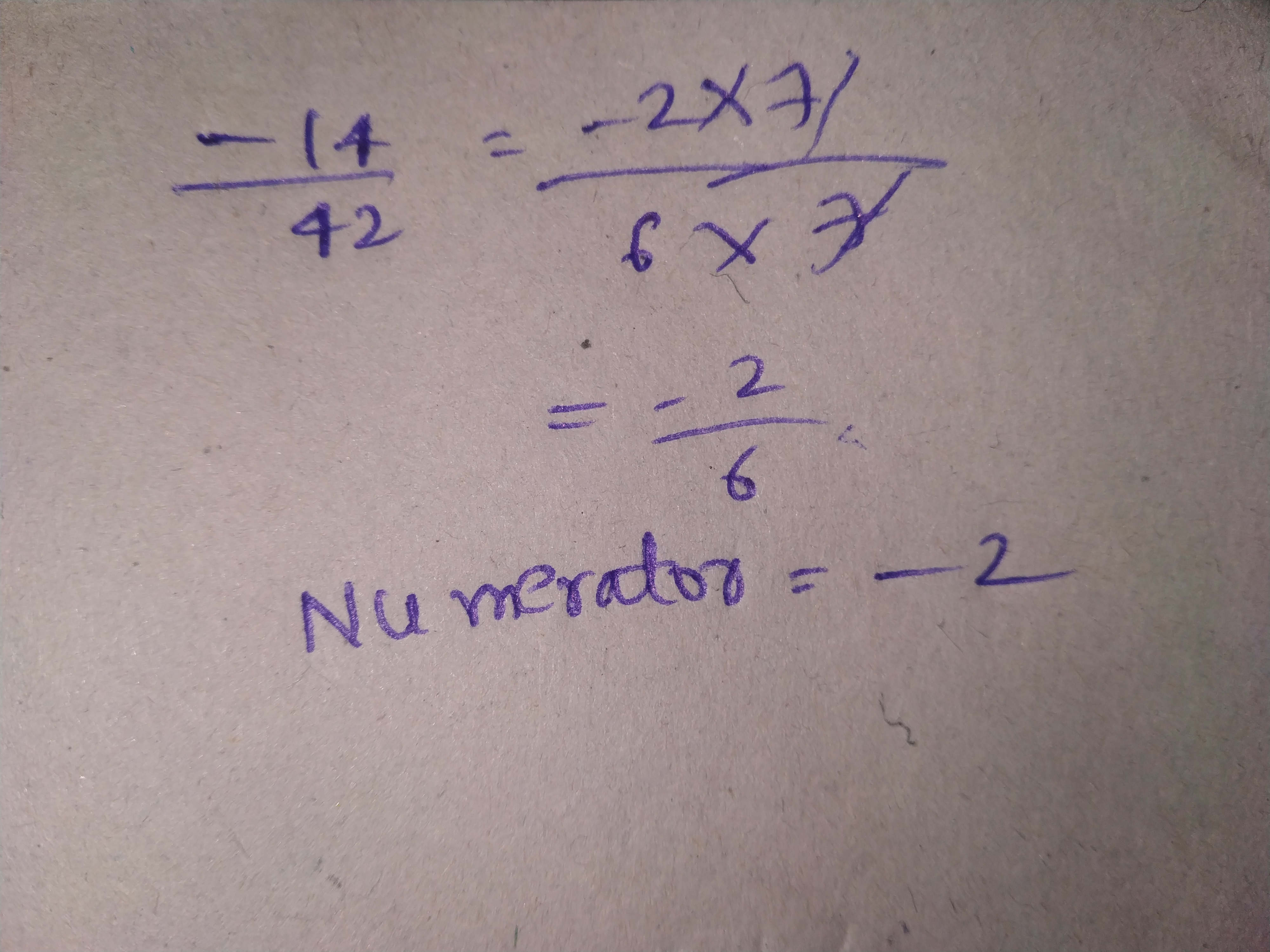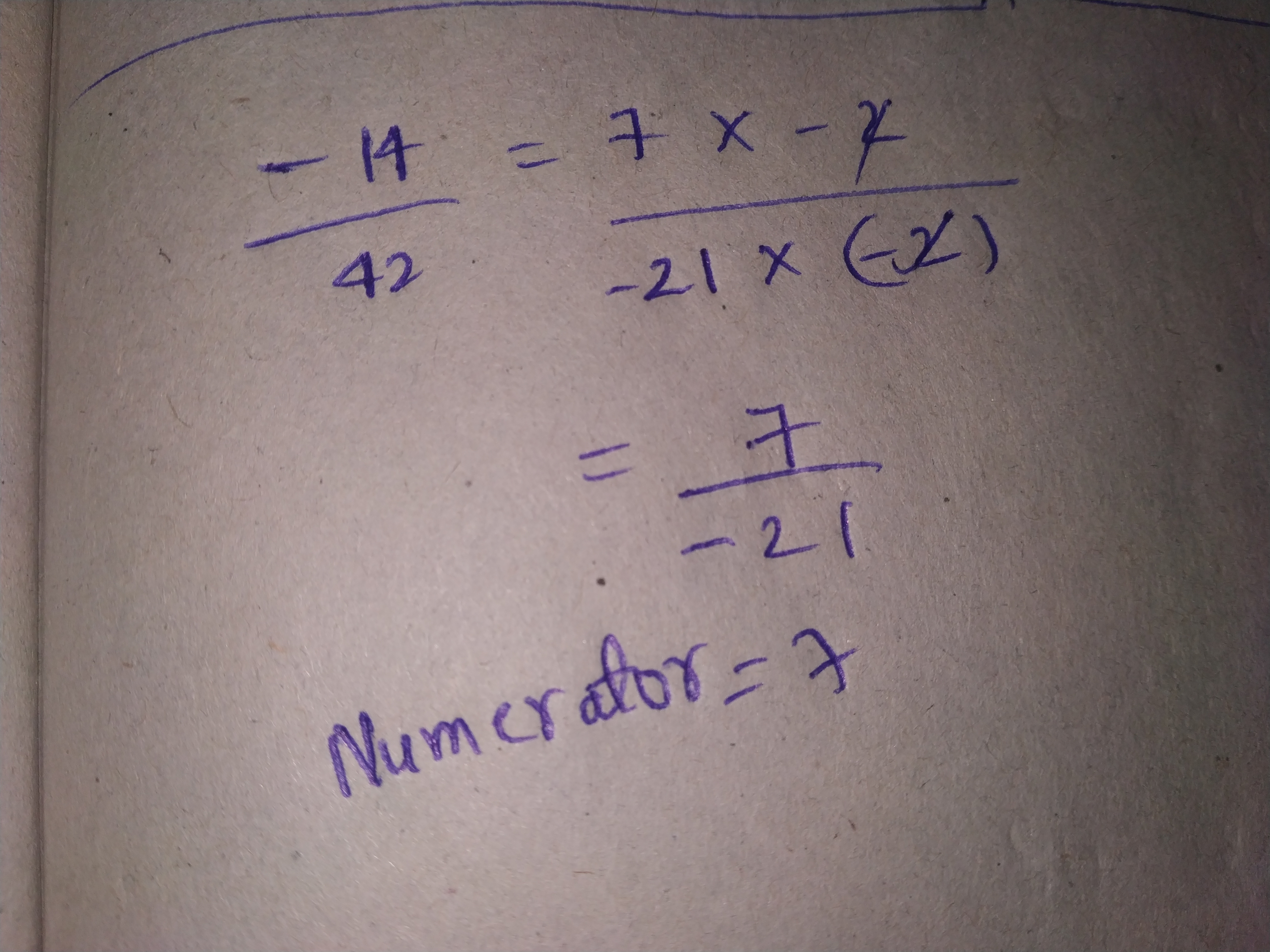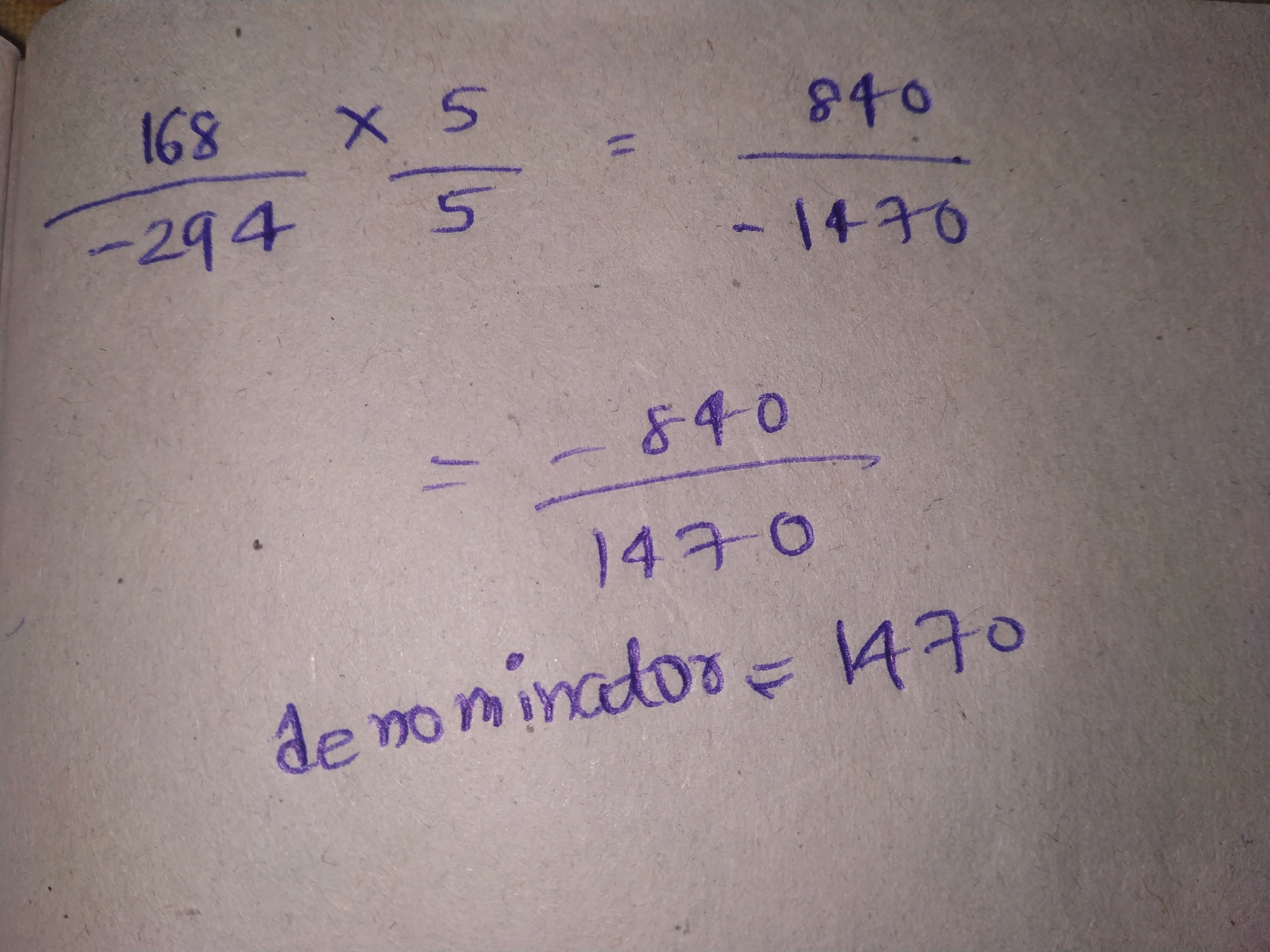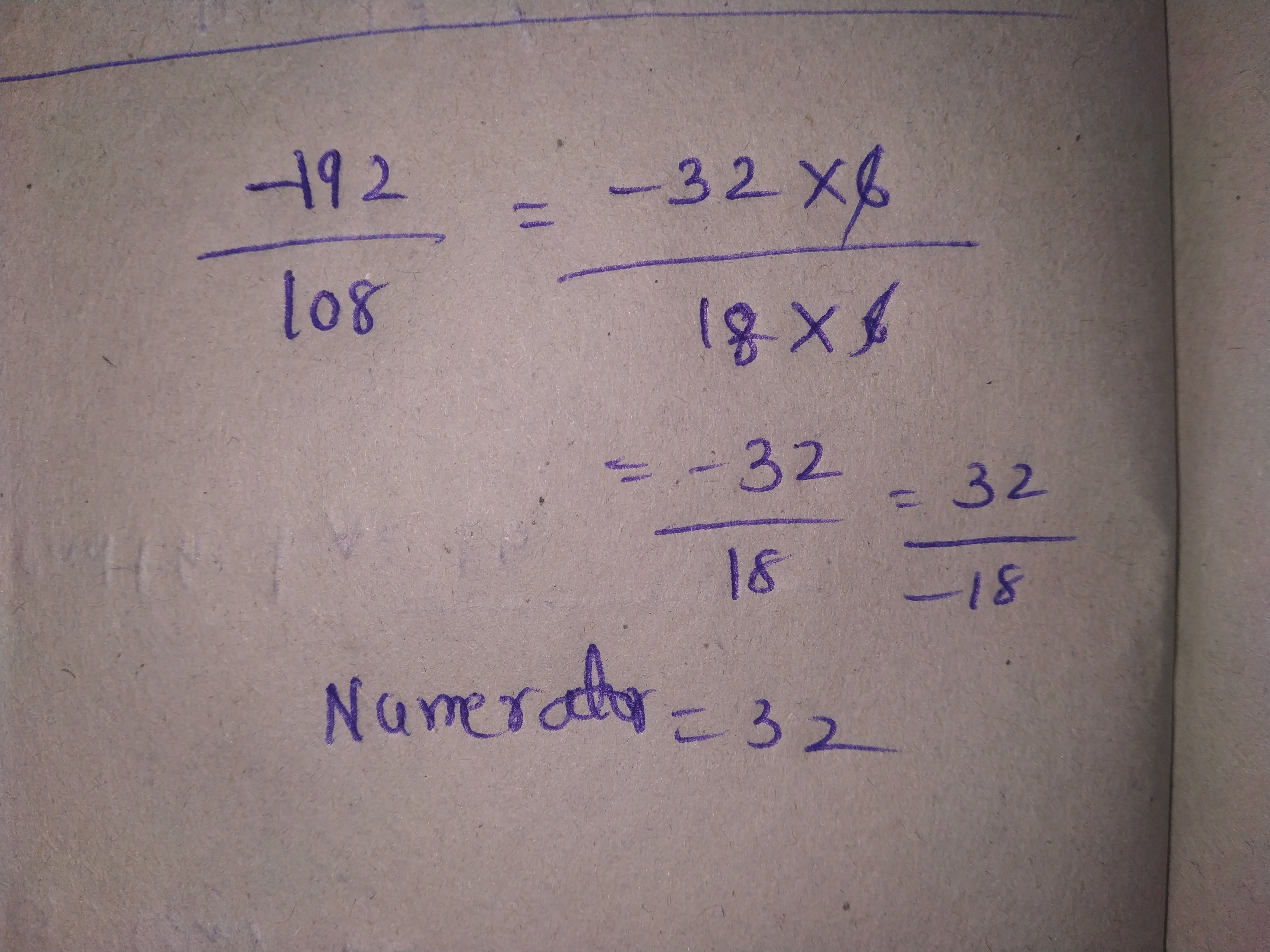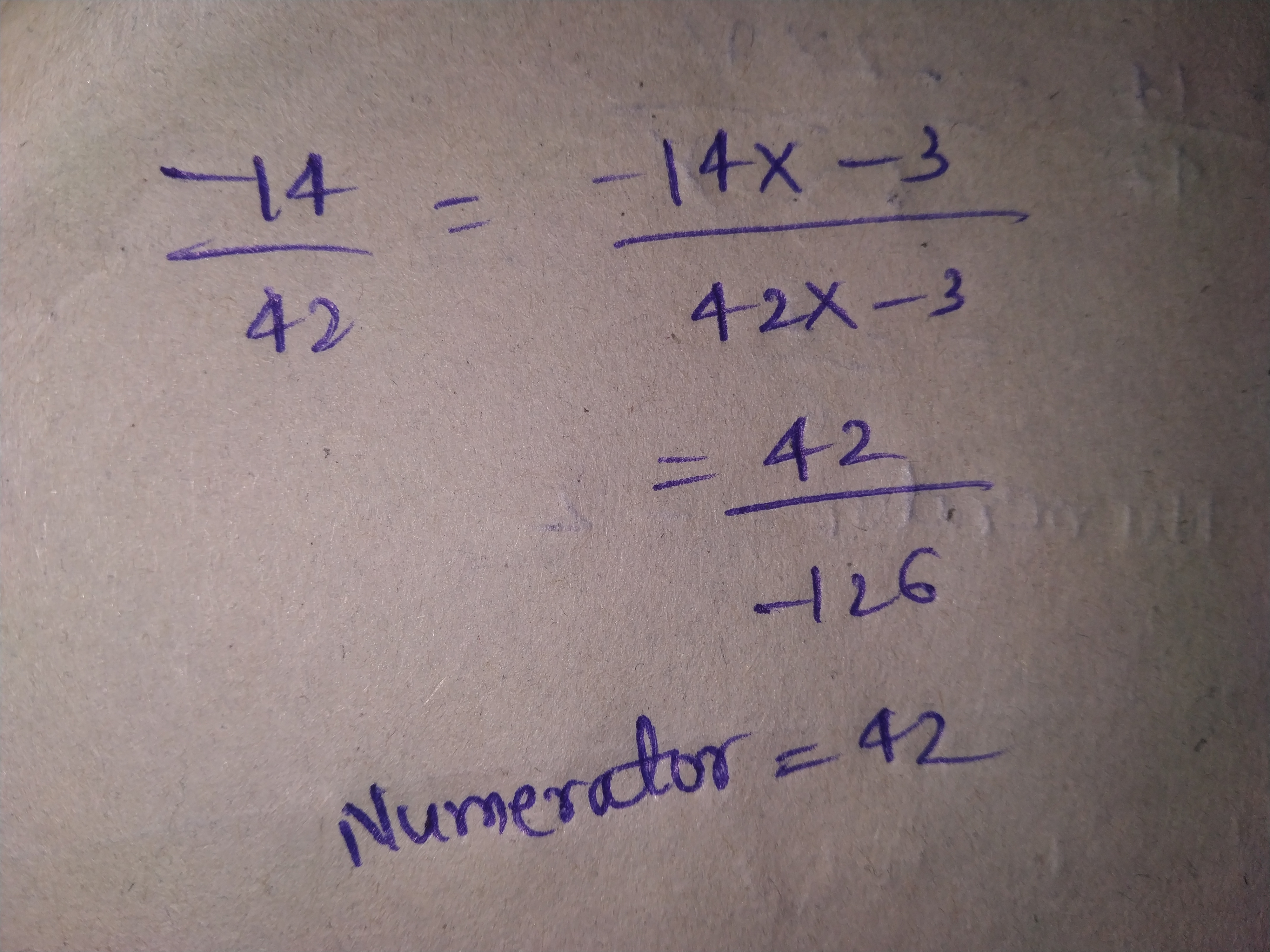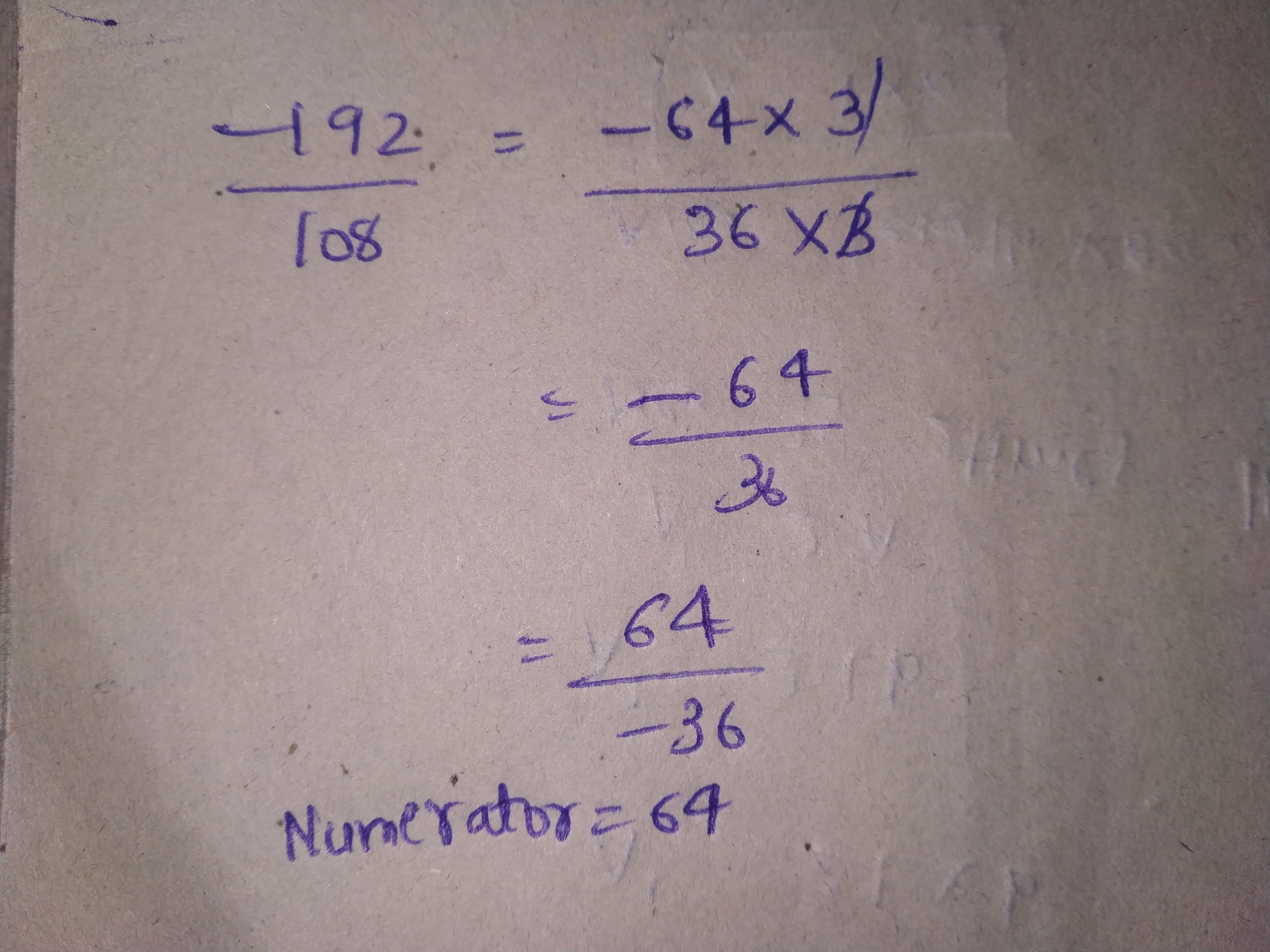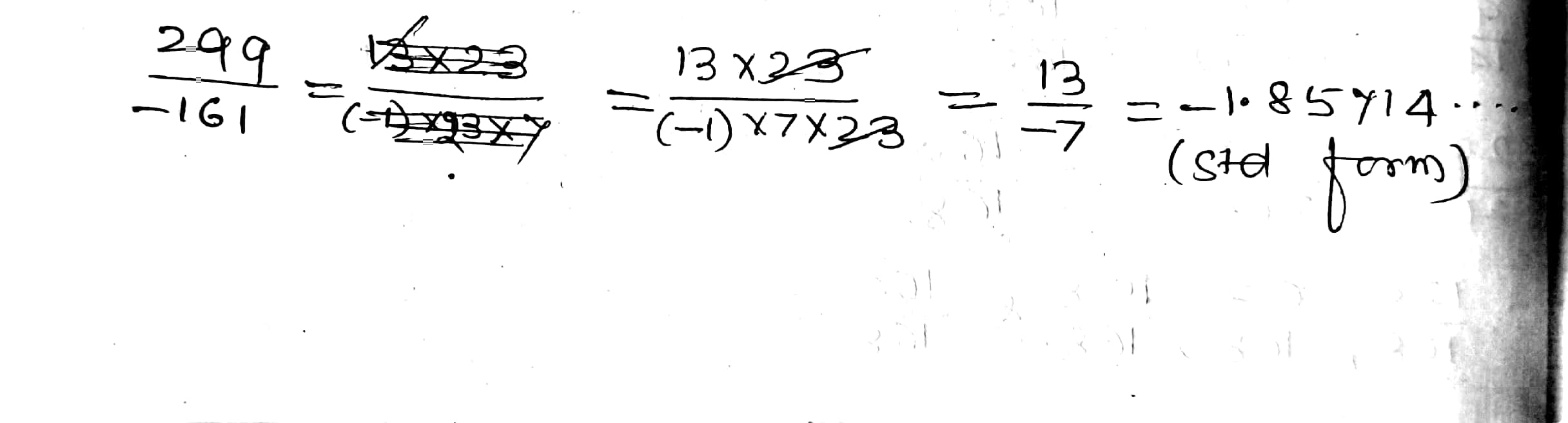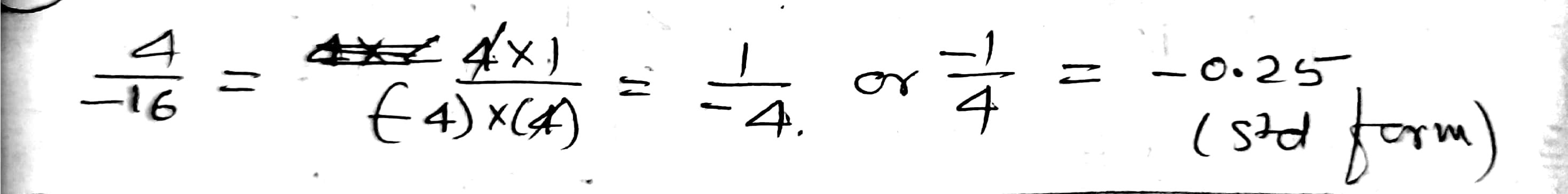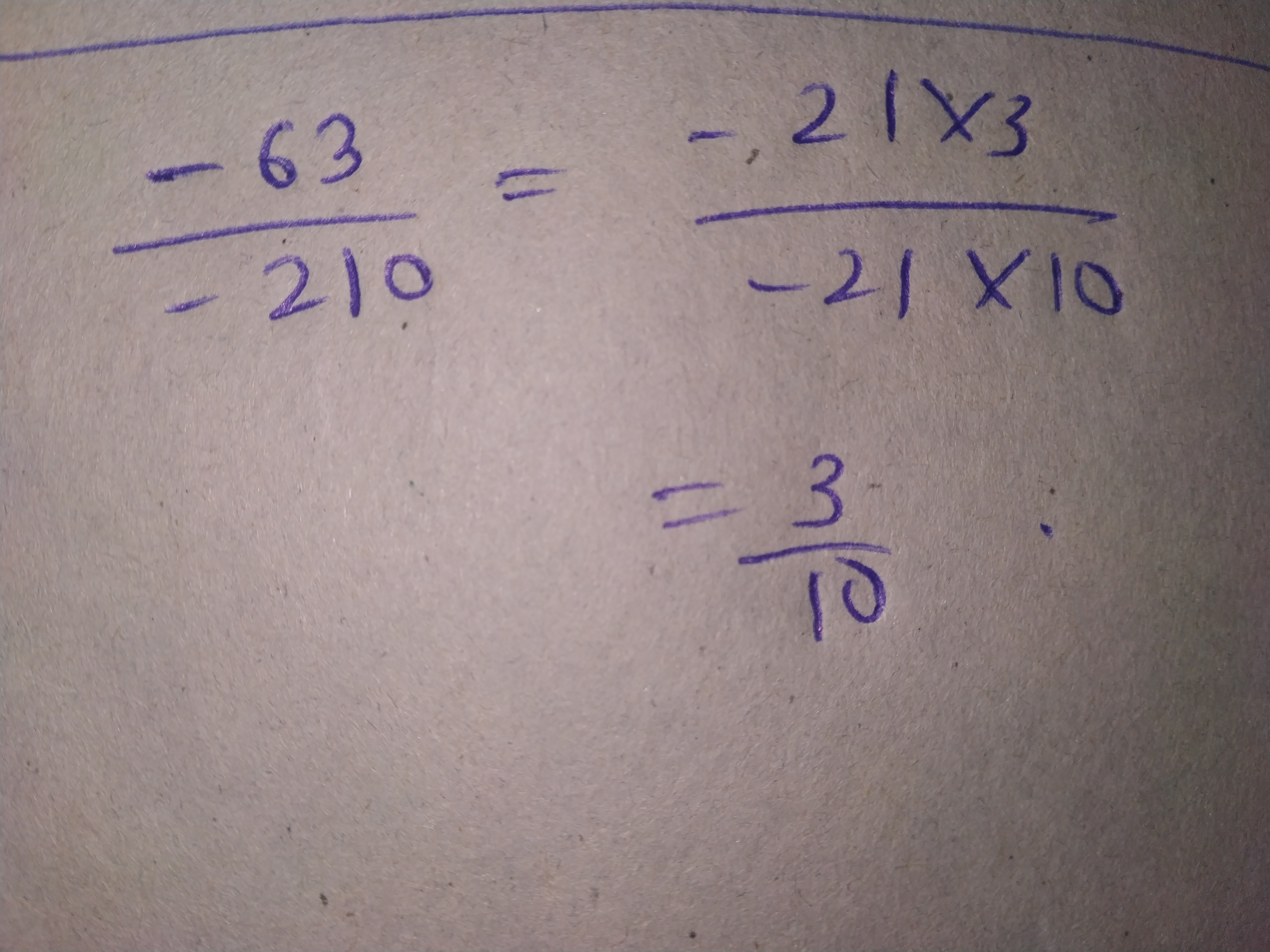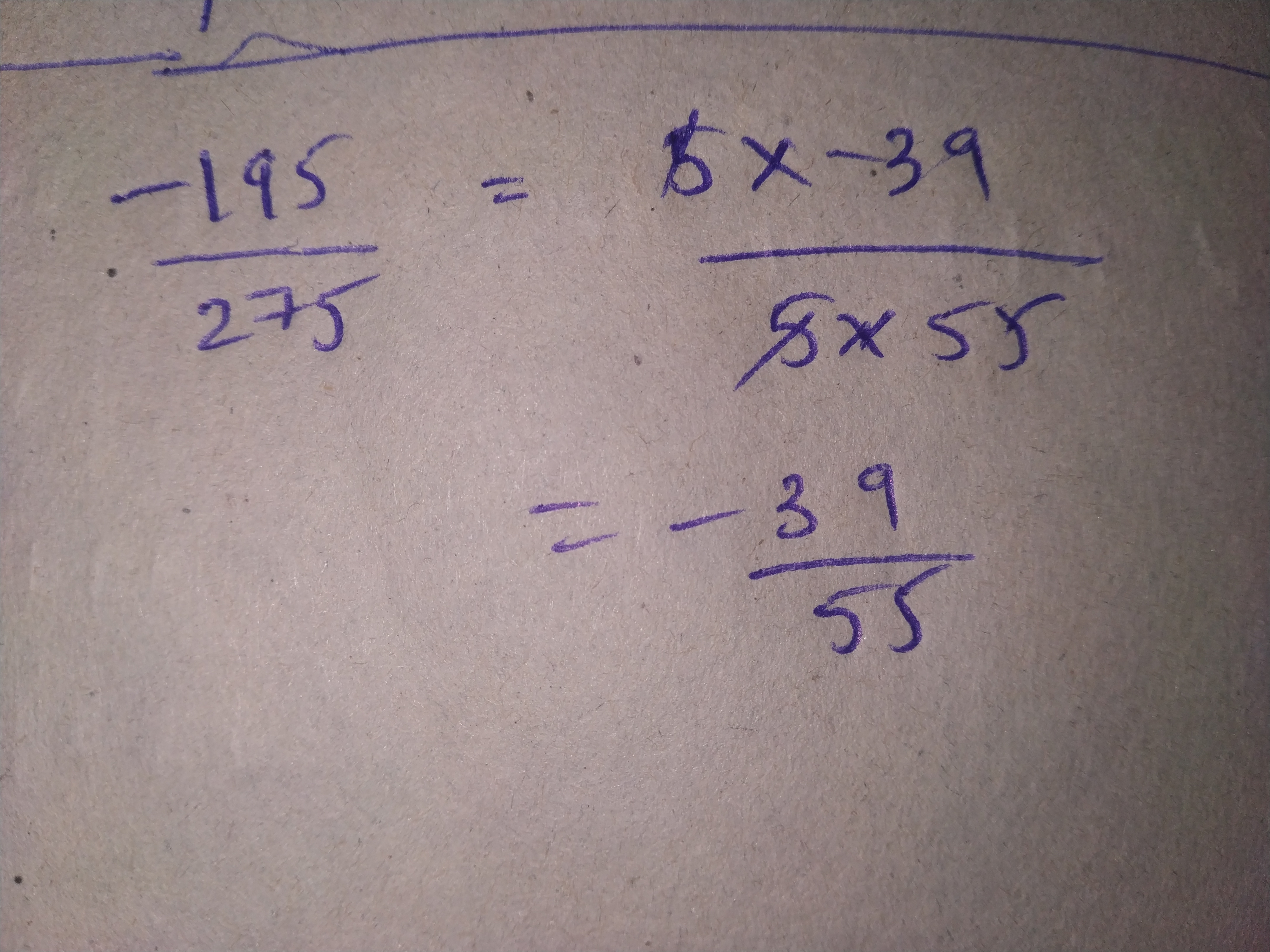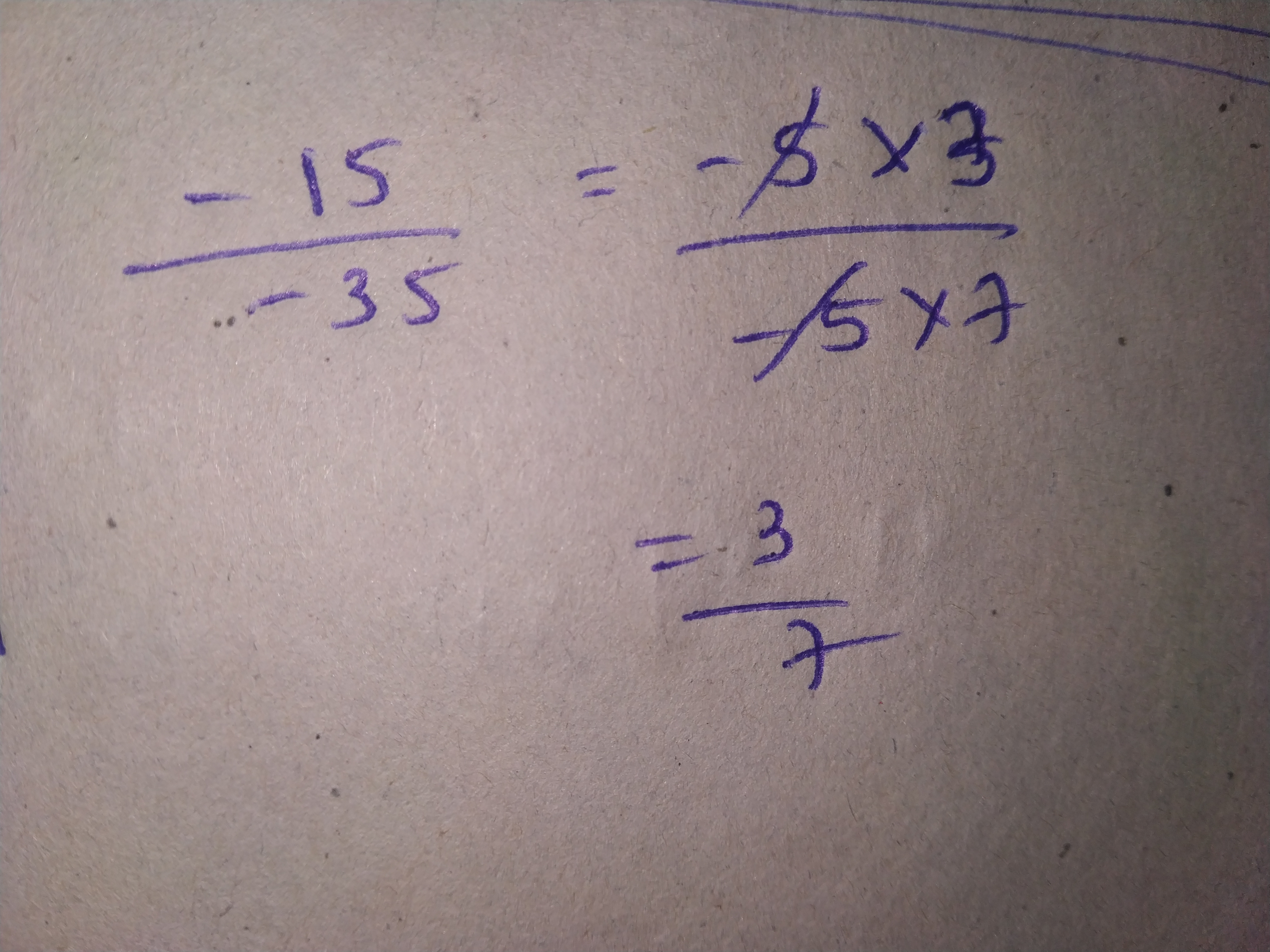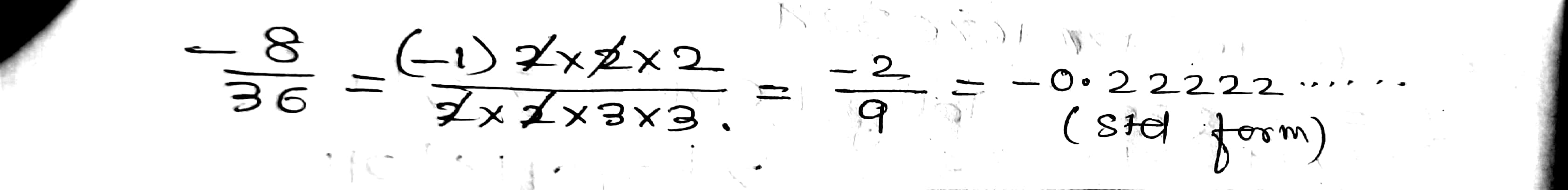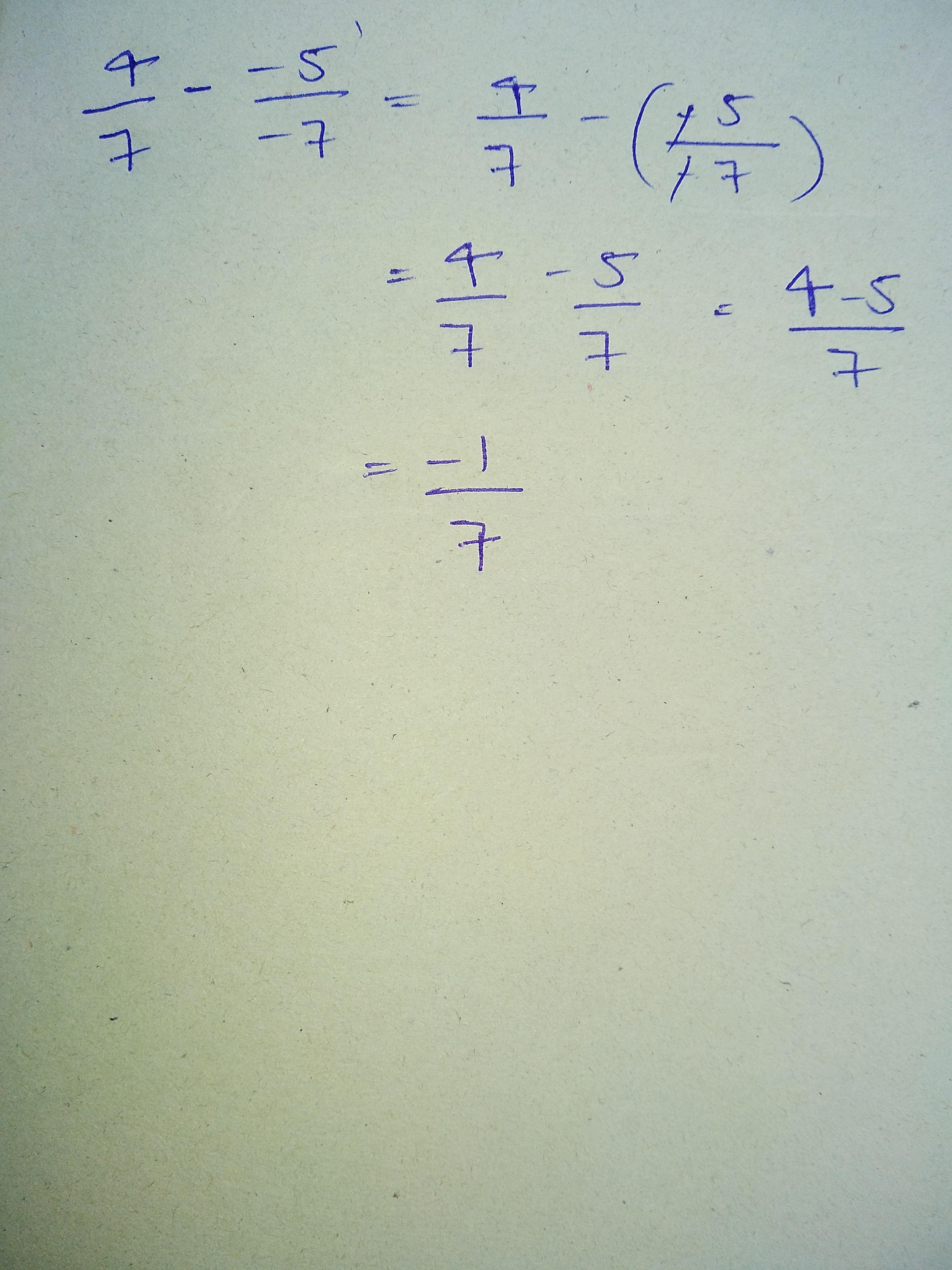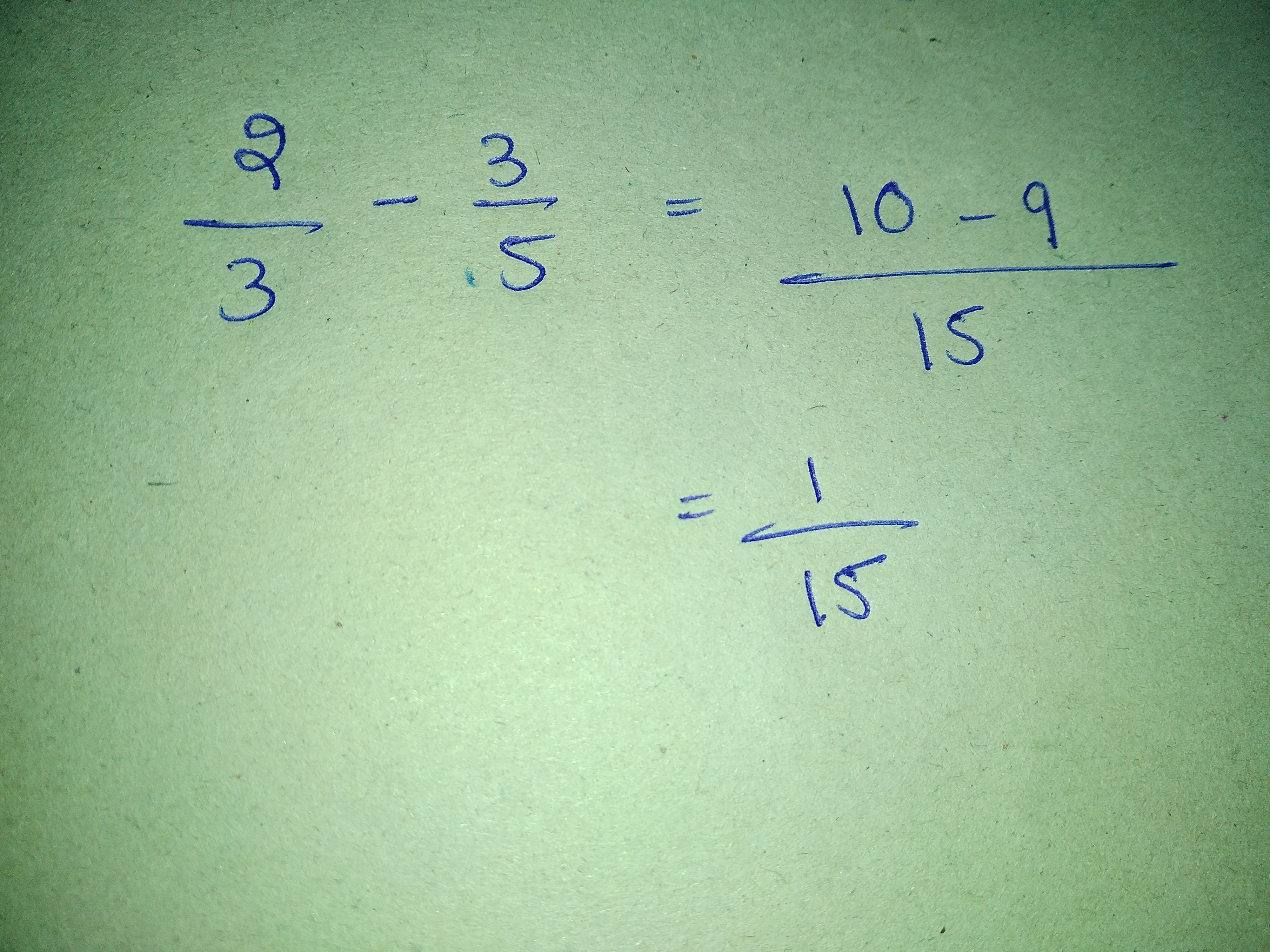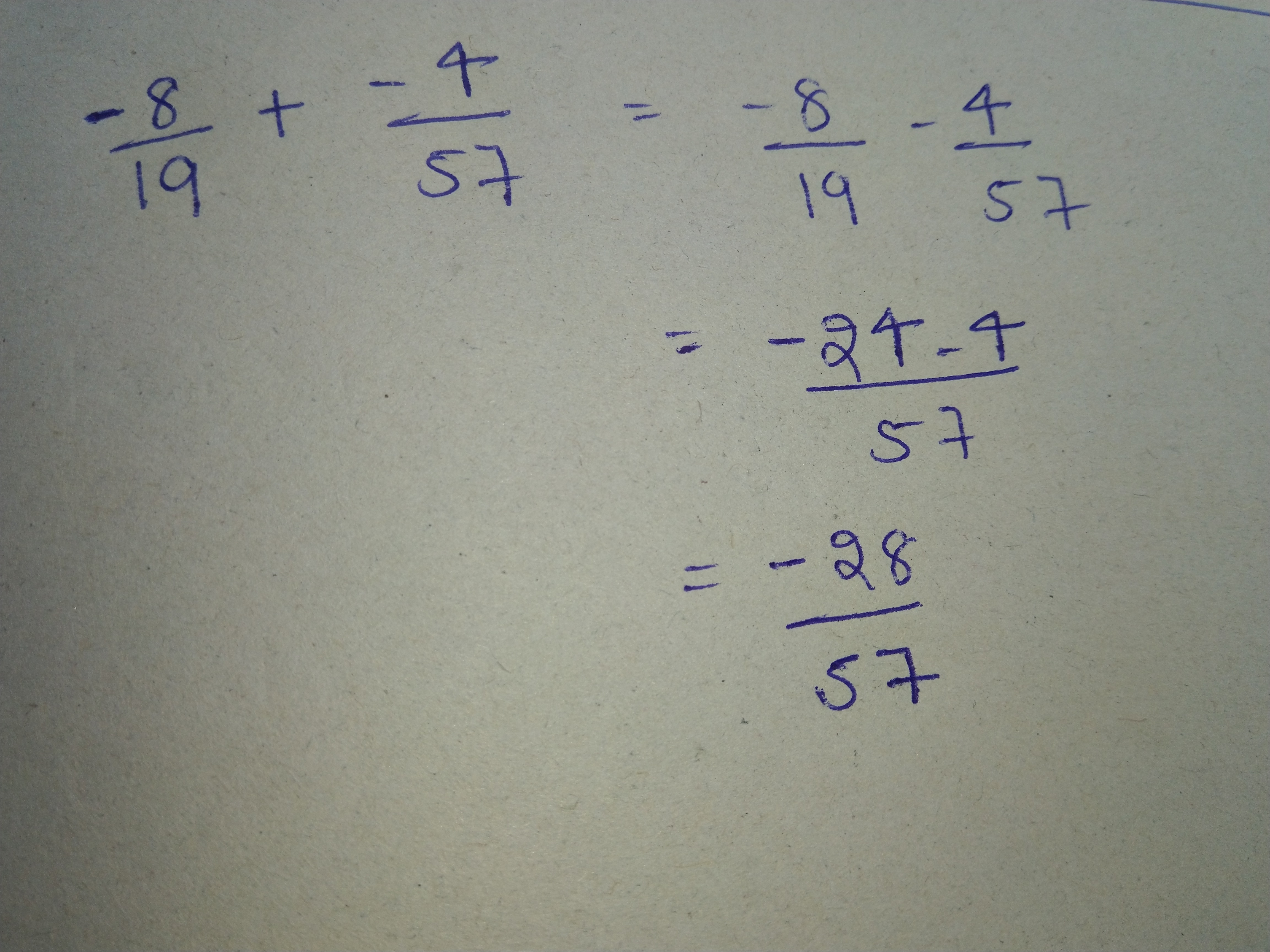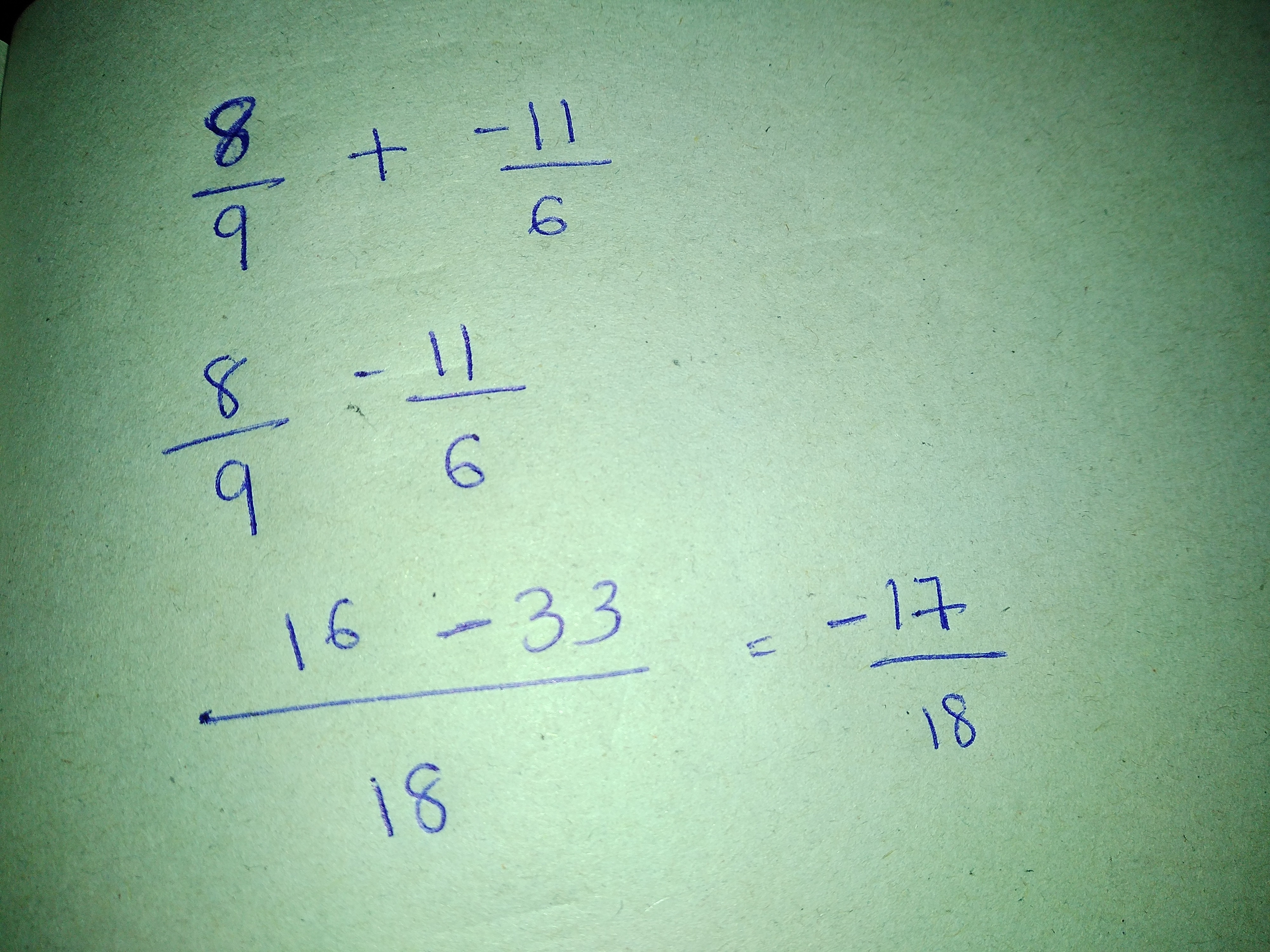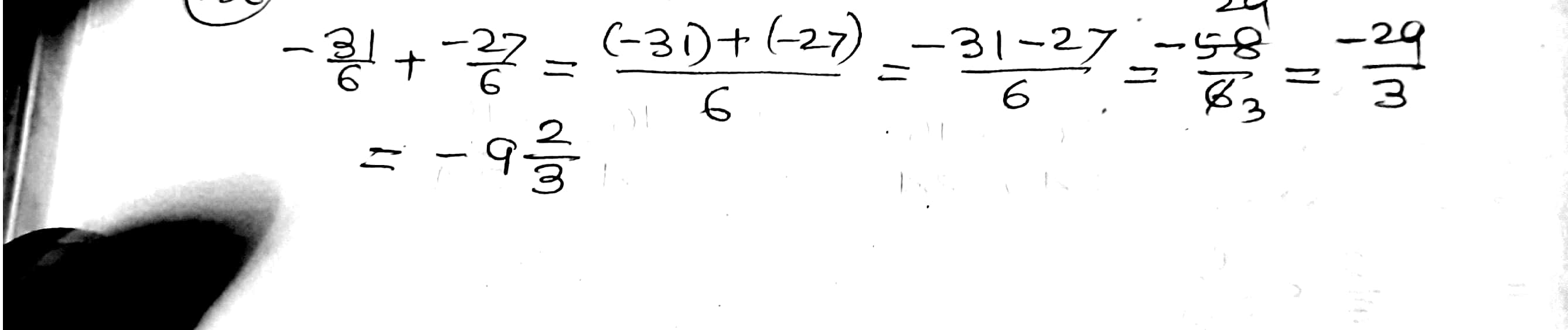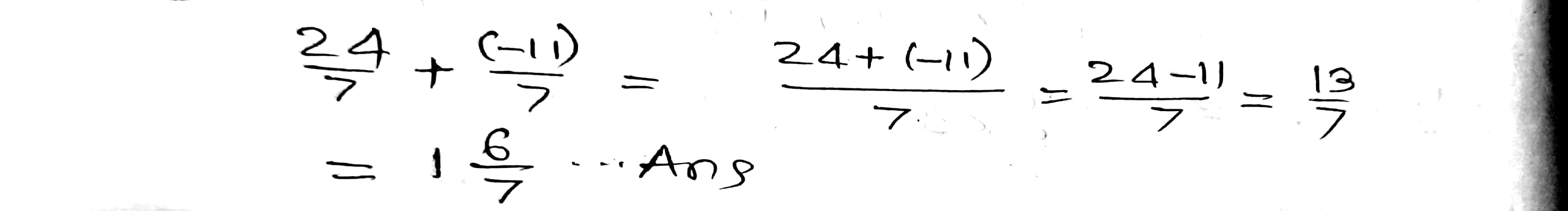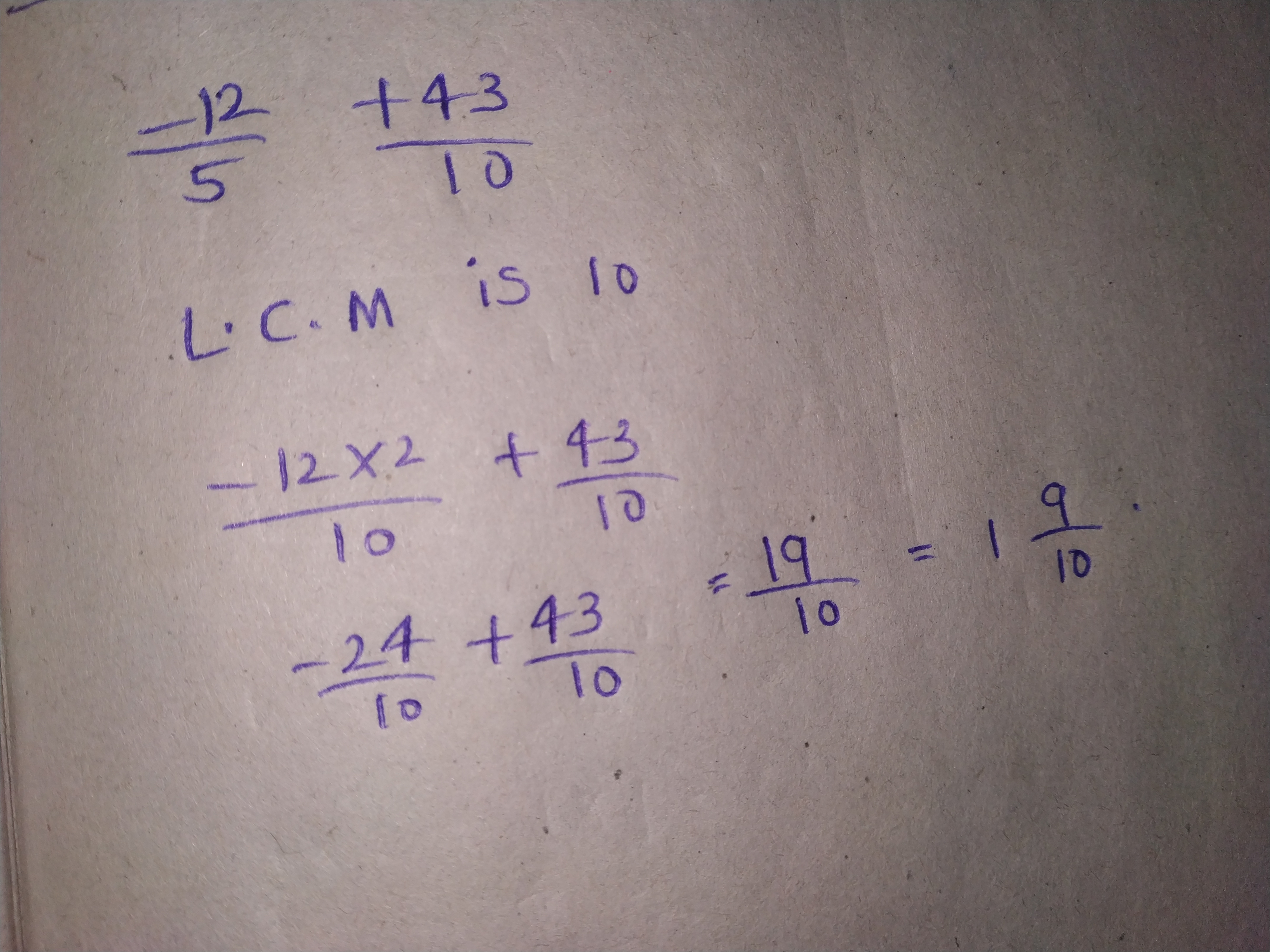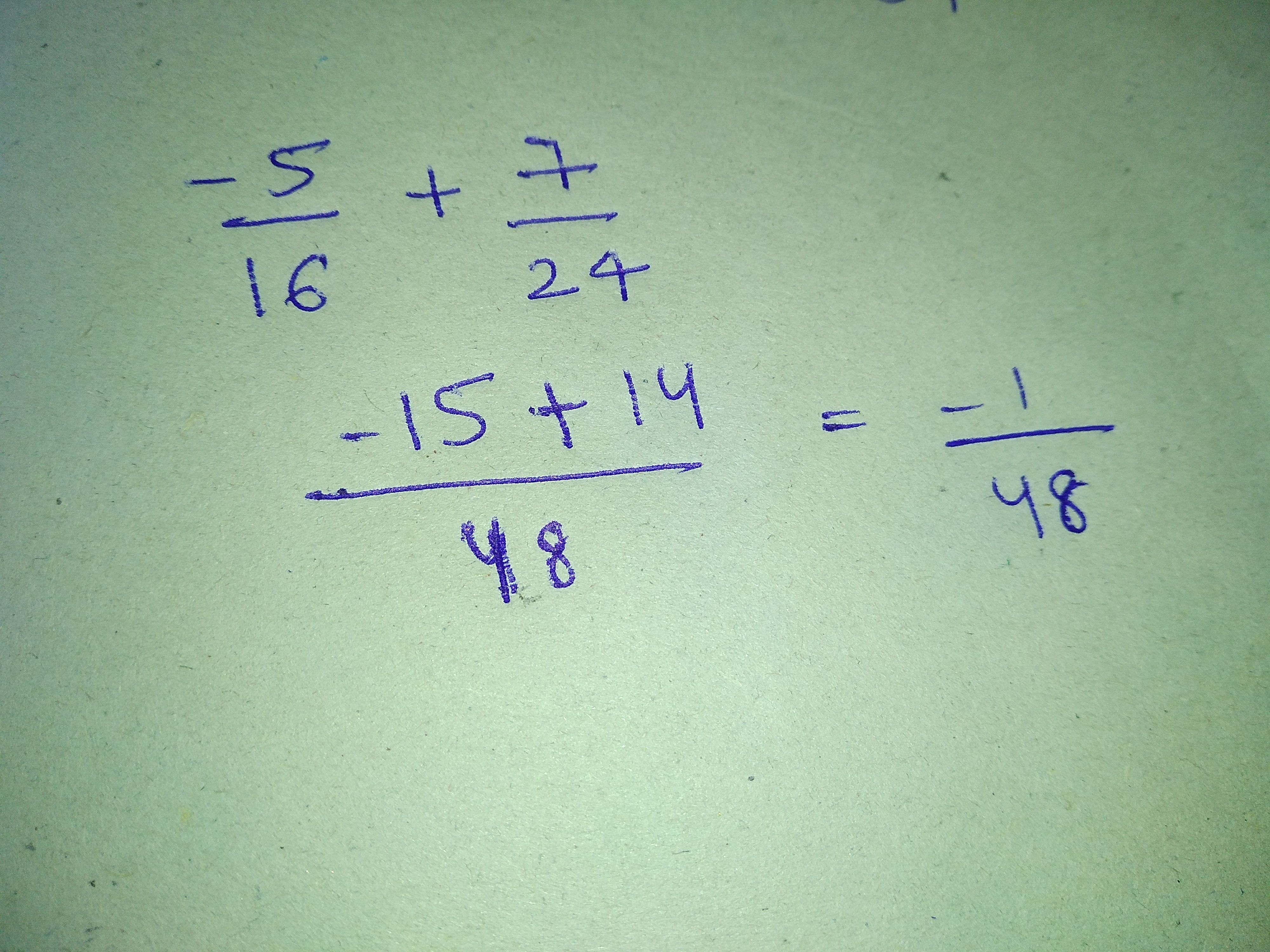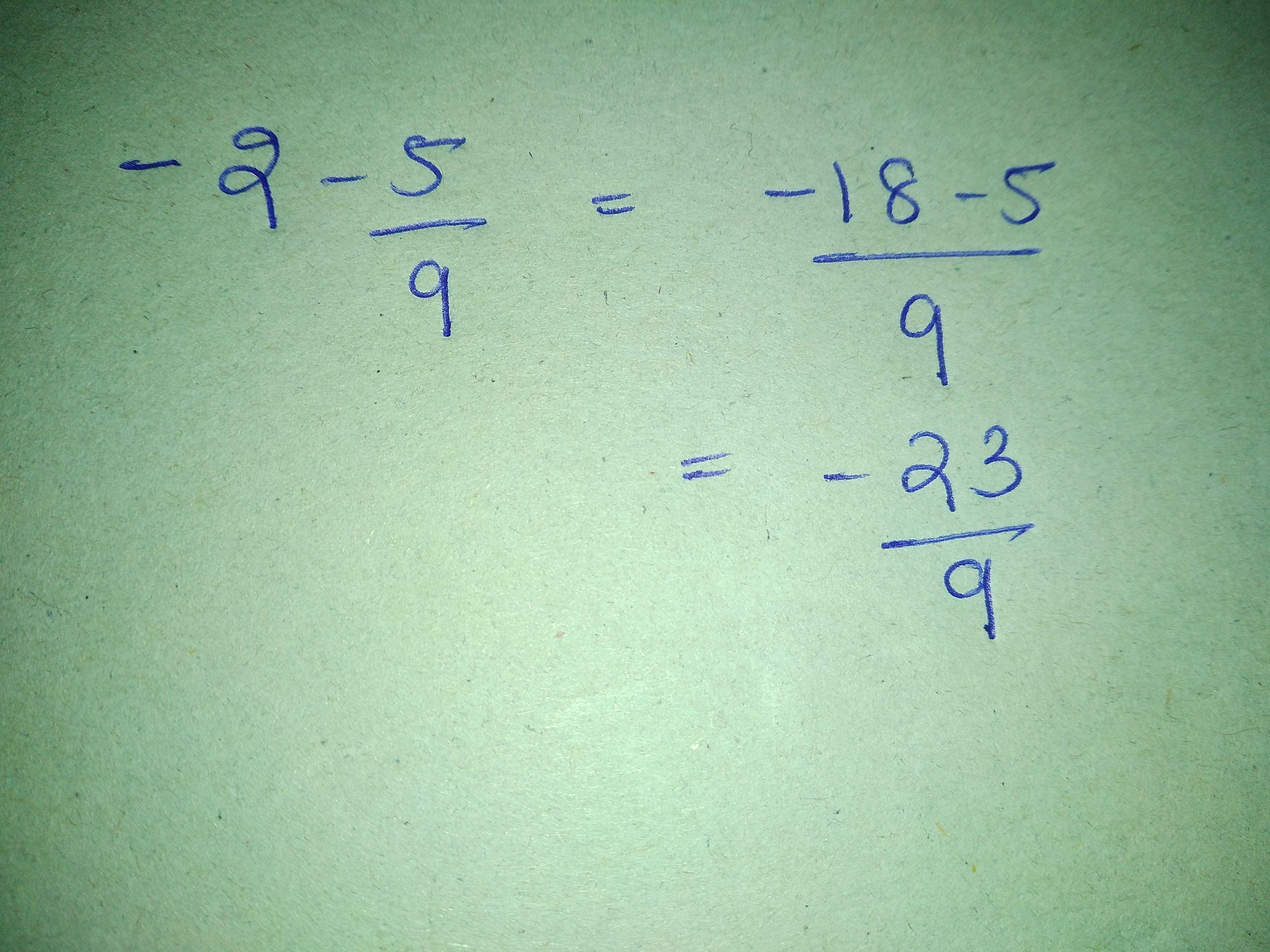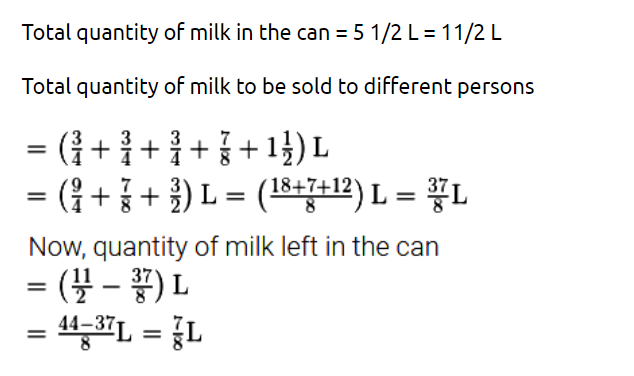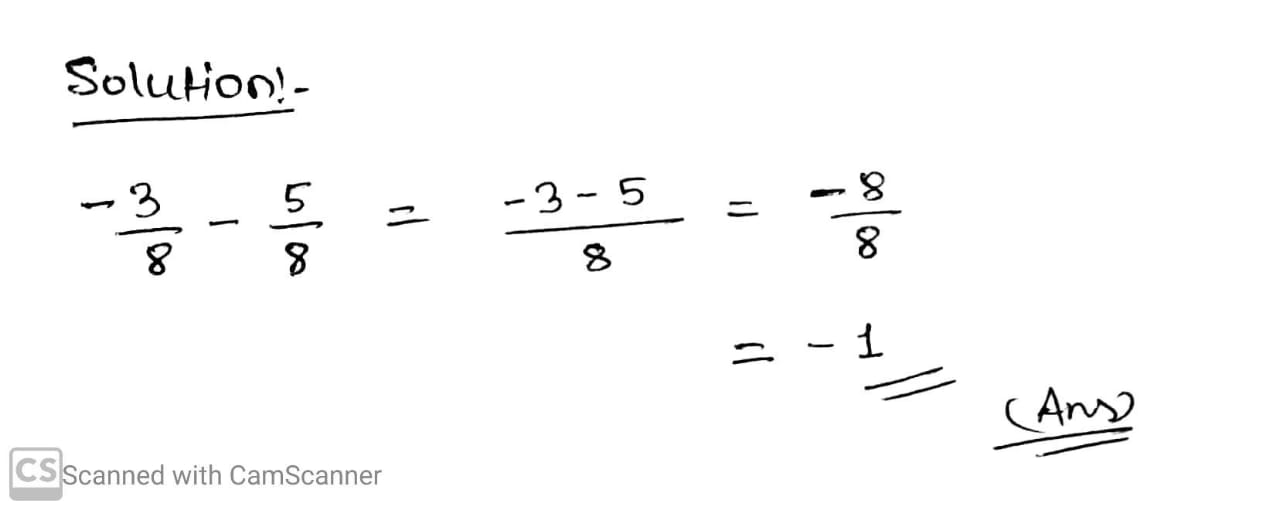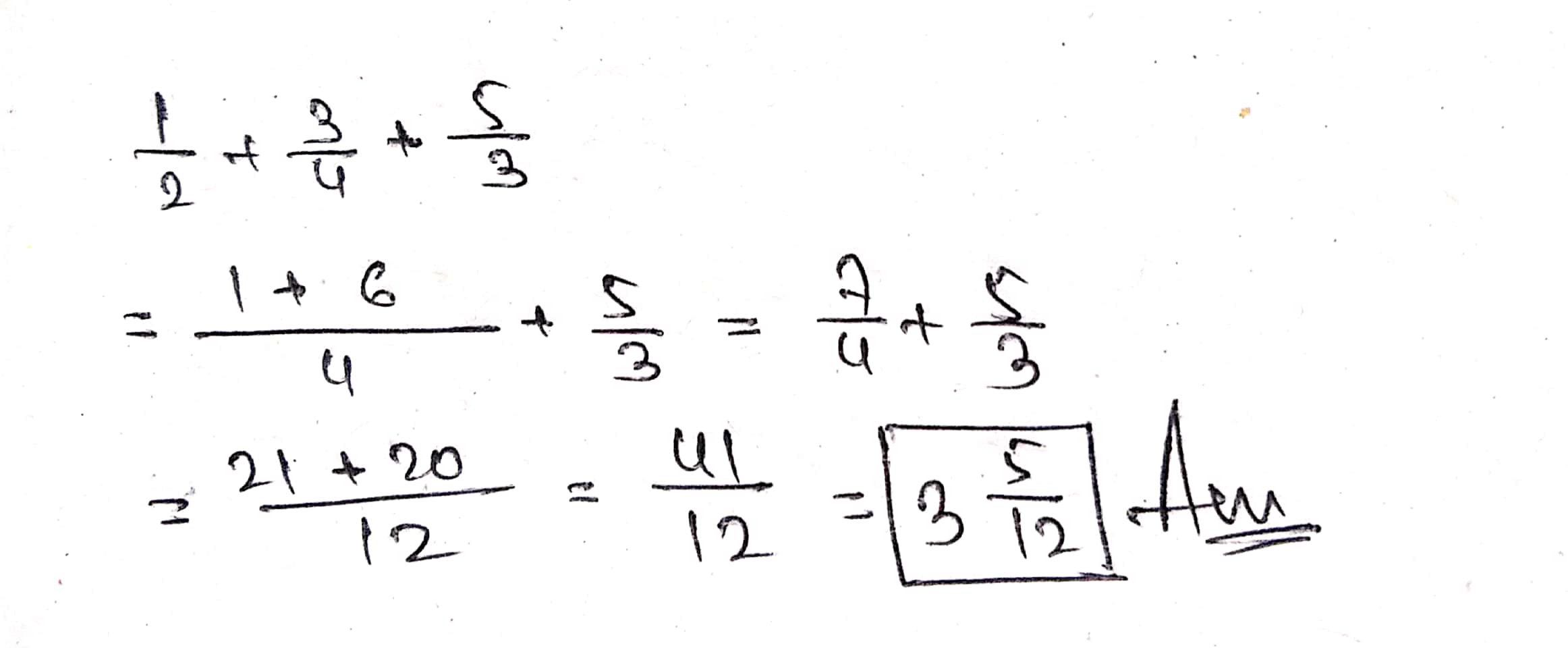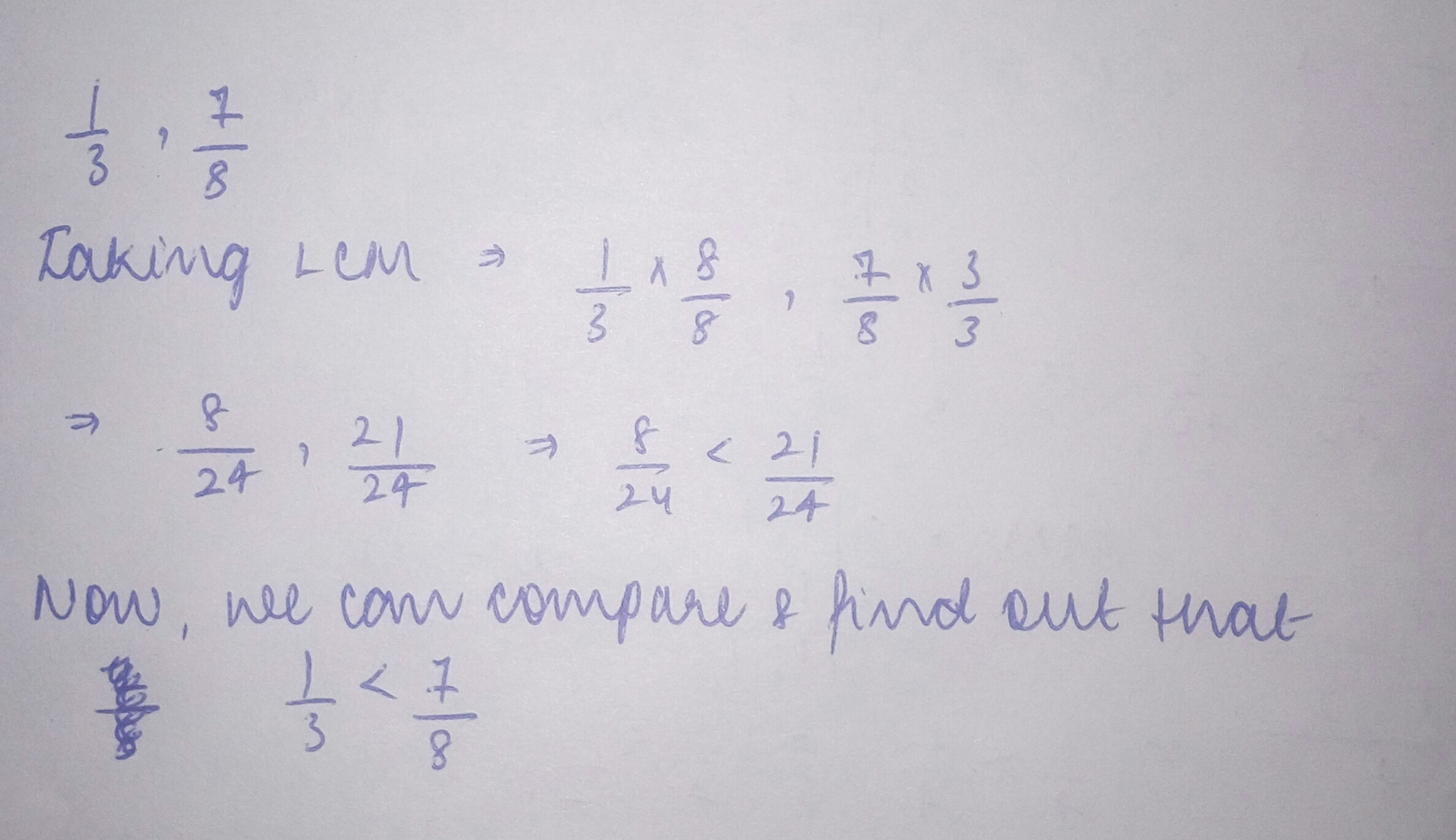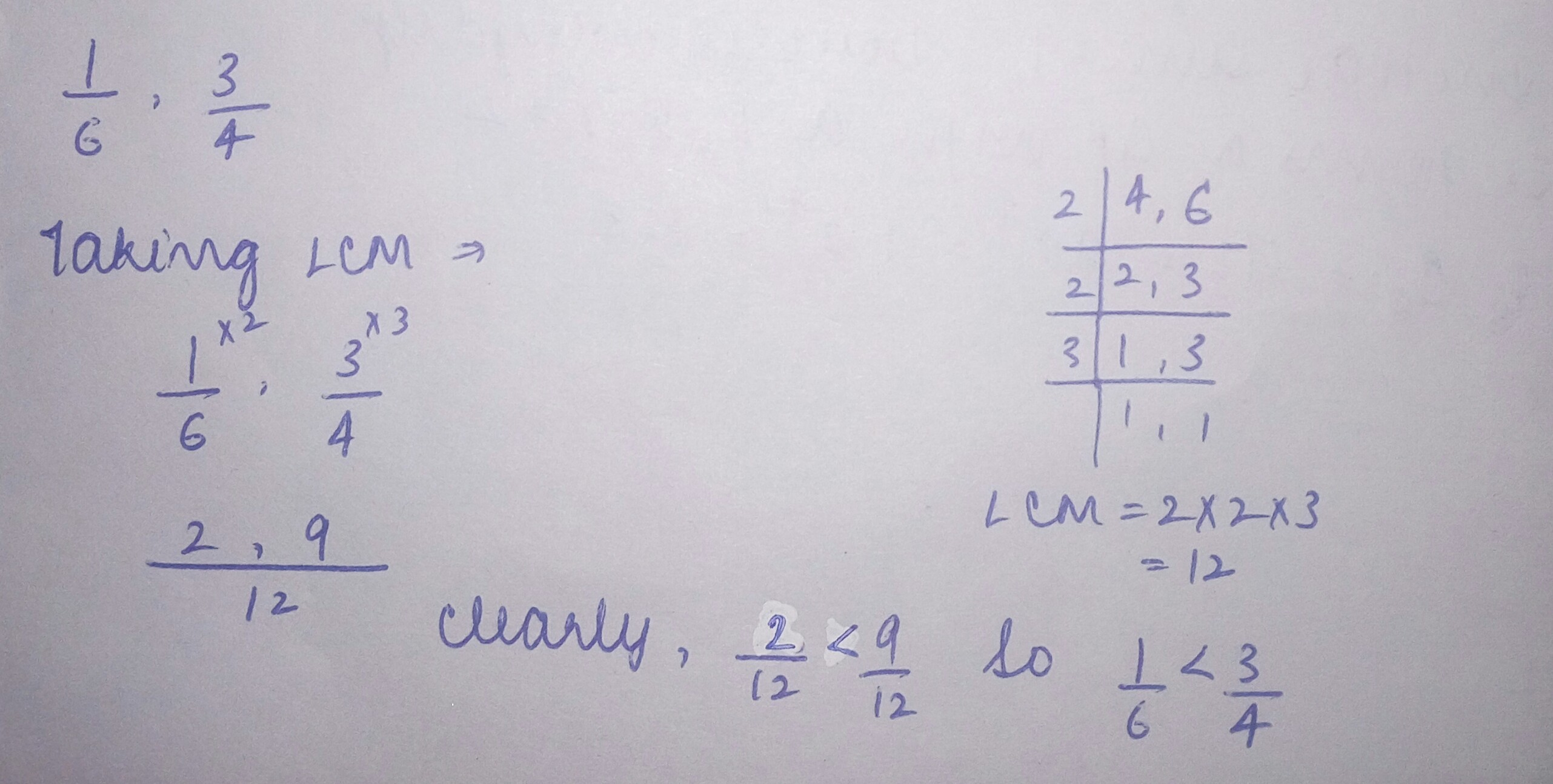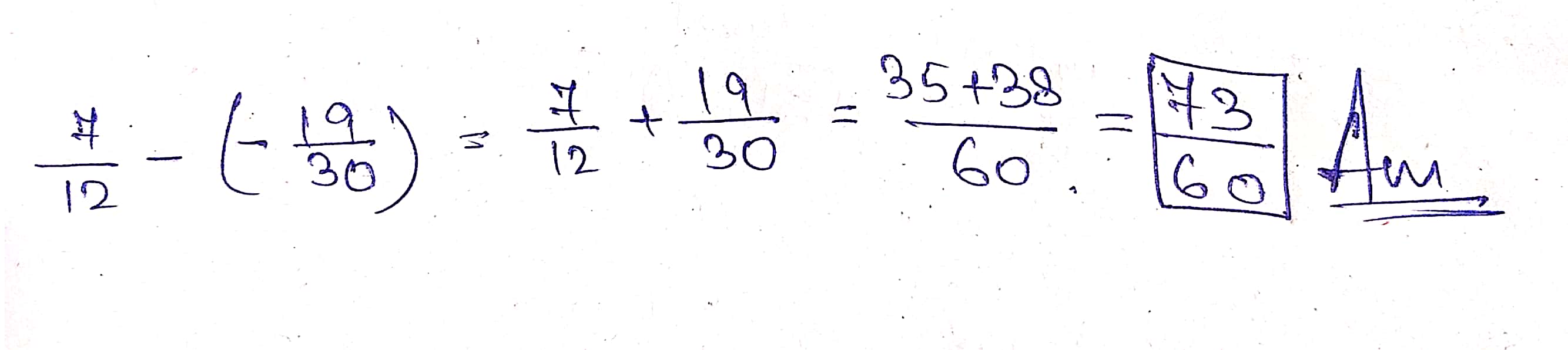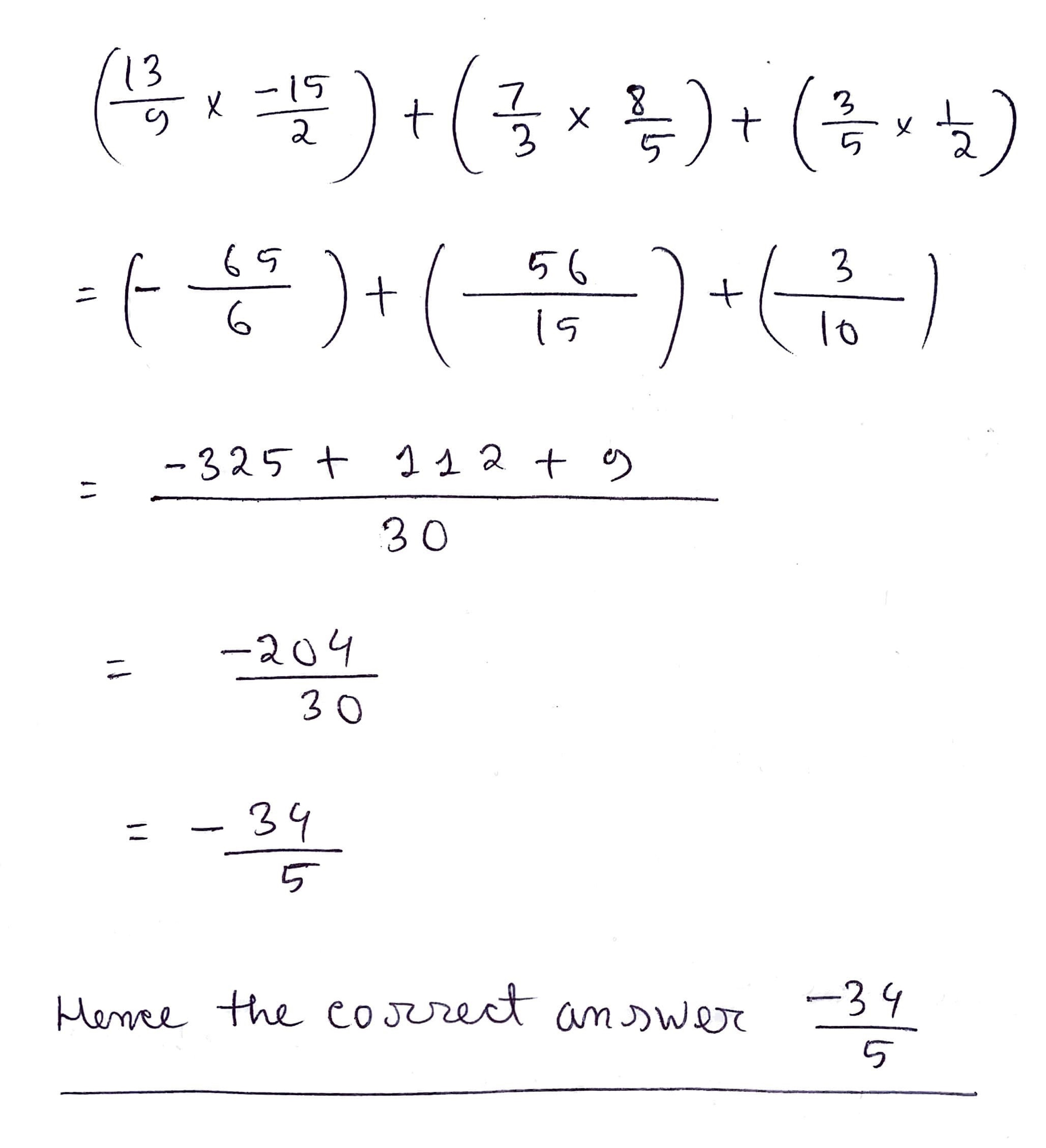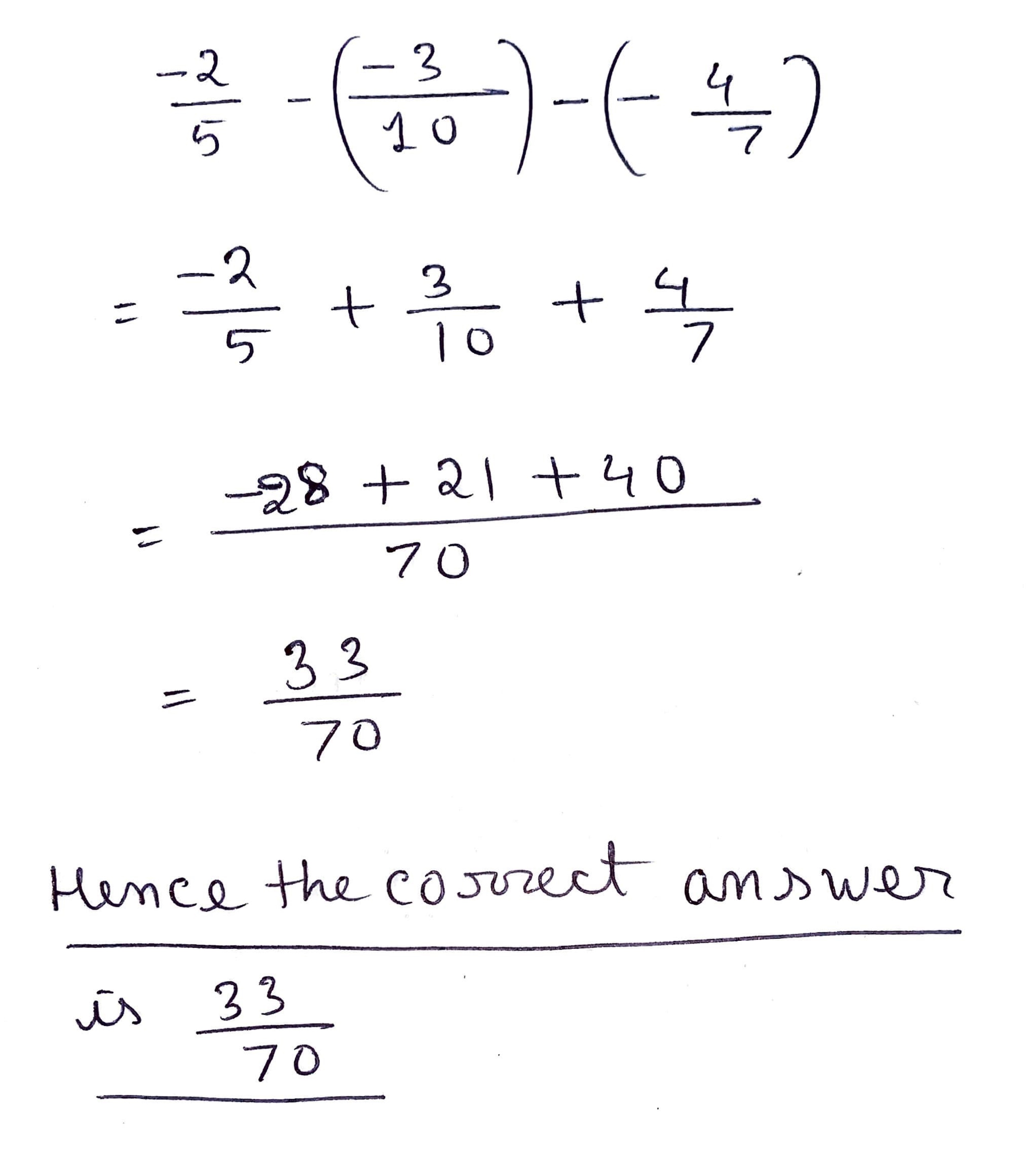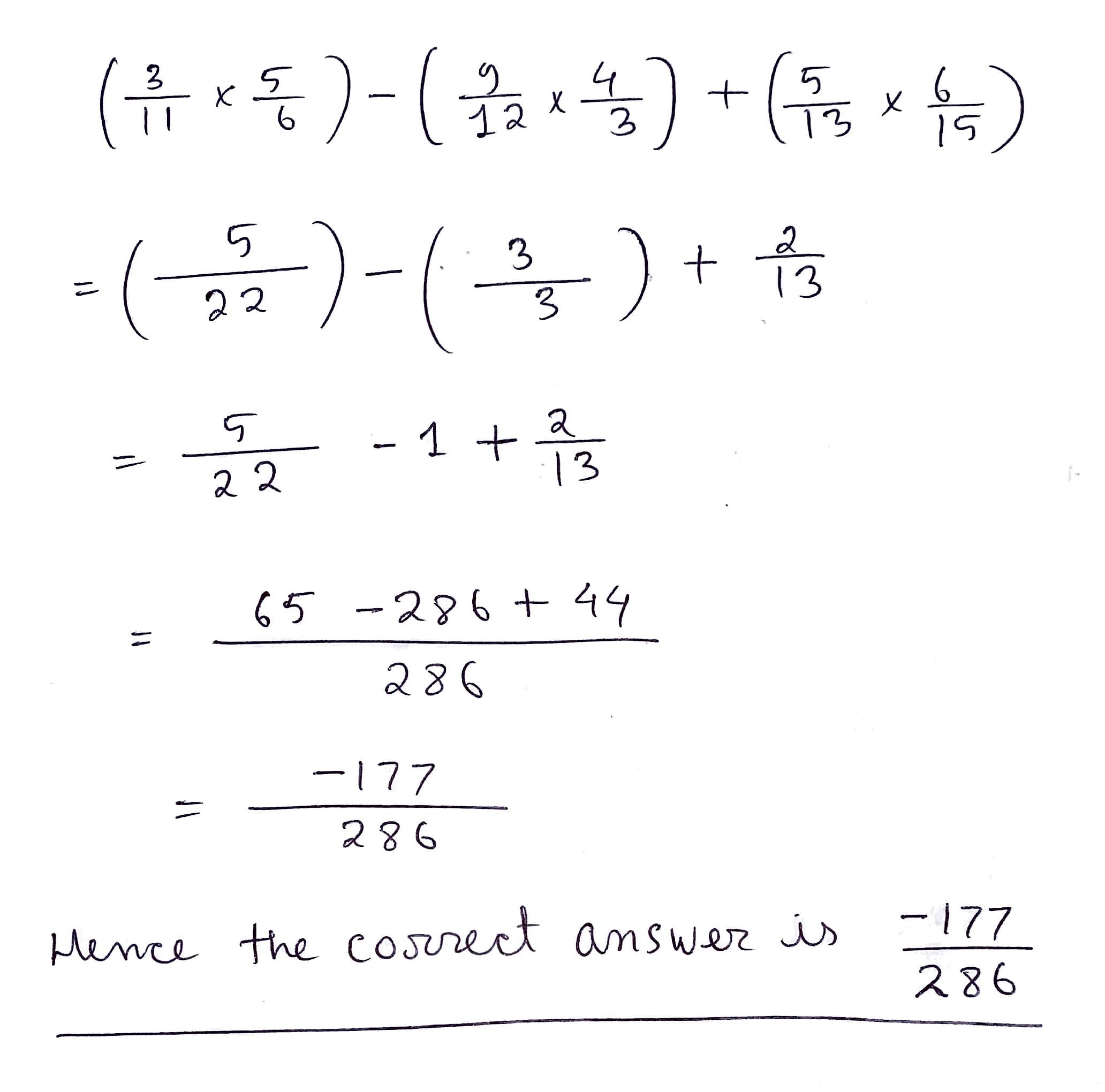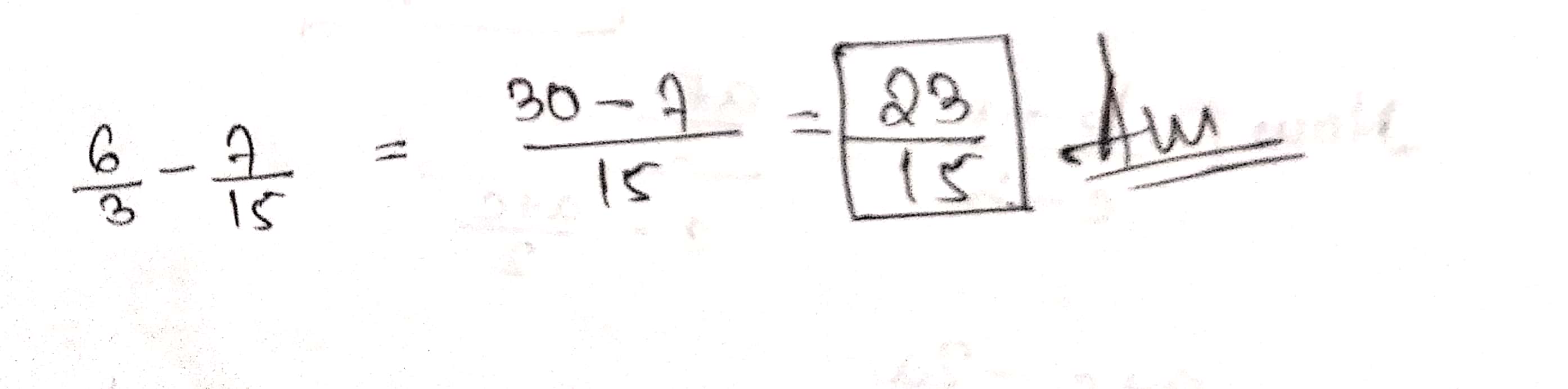Fractions - Class 6 Maths - Extra Questions
Represent $$\dfrac{-5}{6}$$ on the number line.
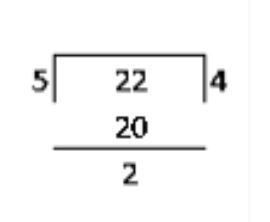
Convert the fraction in its simplest form.$$108 : 100$$ is $$\displaystyle \frac{27}{25}$$
if true then enter $$1$$ and if false then enter $$0$$.
if true then enter $$1$$ and if false then enter $$0$$.
The simplest form of the ratio $$25:100$$ is ____
Reduce to standard form $$ \displaystyle \frac{36}{-24}$$
Satypal walks $$ \displaystyle \frac{2}{3} $$km from a place P towards east and then there $$ \displaystyle 1\frac{5}{7} $$km towards west Where will he be now from P ?
Verify the following
$$\left( \dfrac{5}{4} + \dfrac{-1}{2} \right) + \dfrac{-3}{2} = \dfrac{5}{4} + \left( \dfrac{-1}{2} + \dfrac{-3}{2} \right)$$
Represent $$\dfrac {5}{3}$$ and $$-\dfrac {5}{3}$$ on the number line
Simplify $$\dfrac{2}{5} + \dfrac{3}{7} + \left(\dfrac{-6}{5} \right ) + \left( \dfrac{-13}{7}\right )$$
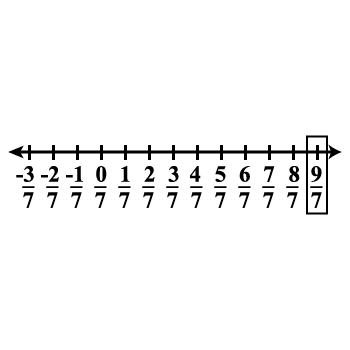
Represent the given number on the number line: $$\dfrac{9}{7}$$
If $$\displaystyle\frac{x}{b+c-a}=\displaystyle\frac{y}{c+a-b}=\frac{x}{a+b-c}$$, then rove that $$\displaystyle\frac{x+y+z}{a+b+c}=\displaystyle\frac{x(y+z)+y(z+x)+z(x+y)}{2(ax+by+cz)}$$.
Find the factor which will rationalise:
$$\sqrt [ 3 ]{ 3 } -\sqrt { 2 } $$
Find the factor which will rationalise:
$$\sqrt [ 3 ]{ 3 } -1$$
Find two proper fractions in their lowest terms having $$12$$ and $$8$$ for their denominators and such that their difference is $$\dfrac{1}{24}$$.
Find the factor which will rationalise:
$$\sqrt [ 6 ]{ 5 } +\sqrt [ 3 ]{ 2 } $$
Find two fractions having $$7$$ and $$9$$ for their denominators, and such that their sum is $$1\dfrac{10}{63}$$.
Convert the following mixed fraction into improper fraction.
$$\displaystyle 10\frac{2}{9}$$.
Convert the following mixed fraction into improper fraction.
$$\displaystyle 1\frac{2}{7}$$.
Convert the following mixed fraction into improper fraction.
$$\displaystyle 8\frac{7}{9}$$.
Convert the following improper fraction into mixed fraction.
$$\displaystyle\frac{9}{4}$$.
Convert the following improper fraction into mixed fraction.
$$\displaystyle\frac{27}{4}$$.
Solve the following:
$$\cfrac { 5 }{ 8 } +\cfrac { 1 }{ 6 } $$ = $$\dfrac ab$$ . Find a + b
Fill in the blank, with appropriate answer by doing addition and subtraction.
Which rational number should be subtracted from $$\dfrac{-5}{6}$$ to get $$\dfrac{4}{9} $$?
Using suitable rearrangement and find the sum,
$${4 \over 7} + \left( {{{ - 4} \over 9}} \right) + {3 \over 7} + \left( {{{ - 13} \over 9}} \right)$$
Solve$${\left( {{1 \over 2}} \right)^3} + {\left( {{1 \over 3}} \right)^3} - {\left( {{5 \over 6}} \right)^3}$$
If $$\dfrac{9}{5}$$ + $$\dfrac{11}{6}$$ is $$\dfrac{m}{30}$$ then m equals to:
Add the following rational numbers:
$$\dfrac{1}{2}+\dfrac{4}{5}$$
Add$${3 \over 5}{\rm{ and }}{2 \over 3}$$
What should be subtracted from $$-2$$ to get $$\frac{3}{8} $$?
Add$${\rm{2 and - 1}}{1 \over 2}$$
If $$\left[ \frac{-2}{5} +\frac{1}{5} \right] - \frac{2}{3}=\dfrac{-m}{15}$$.Find $$m$$
Find$${{53} \over {14}} - {{201} \over {196}}$$
Rationalise the denominator of $$\dfrac{5}{\sqrt{3}-\sqrt{5}}$$
What should be added to $$-2$$ to get $$\frac{3}{8} $$?
Evaluate:
$$(i) \dfrac{3}{7} + \dfrac{-4}{9} - \dfrac{-11}{7} - \dfrac{7}{9} $$
$$(ii) \dfrac{2}{3} + \dfrac{-4}{5} - \dfrac{1}{3} - \dfrac{2}{5} $$
$$(iii) \dfrac{4}{7} -\dfrac{-8}{9} - \dfrac{-13}{7} + \dfrac{17}{9} $$
Convert it to improper fraction $$3\frac{3}{4}$$
solve $$\left(2 - \dfrac{3}{ 5}\right)$$
Show the fraction $$\dfrac{2}{5},\dfrac{3}{5},\dfrac{4}{5}$$ and $$\dfrac{5}{5}$$ on a number line.
Add: $$\dfrac{5}{12} +\dfrac{3}{8}$$
Write the additive inverse of each of $$\dfrac{2}{8}$$ and $$\dfrac{-5}{9}$$
Express $$\dfrac {17}{7}$$ as mixed fraction.
Find (i) $$5-3\dfrac {1}{4}=$$...............
Convert it to mixed fraction $$\frac{34}{5}$$
Solve :$$21+\dfrac {7}{8}$$
What is : $$\dfrac{3}{20}-\dfrac{5}{8}$$ ?
$$7-3\dfrac{1}{2}=$$_______
Solve :$$36+\dfrac {12}{5}$$
Solve :$$9+\dfrac {3}{2}$$
Solve: $$\dfrac{3}{5} + \dfrac{2}{7}$$
Add $$\dfrac{-2}{5}$$ and its multiplicative inverse.
Solve $$8\dfrac{x}{6} + 3\dfrac{3}{8} = 12\dfrac{5}{4}$$
Solve :$$15+\dfrac {5}{7}$$
If $$\dfrac {16}{17}+\dfrac {2}{17}=\dfrac{m}{17}$$.Find $$m$$
Add the following
$$\dfrac{4}{7}$$ and $$\dfrac{5}{7}$$
Solve
$$2-\dfrac{3}{5}$$
Simplify: $$1\dfrac{7}{8}\times 3\dfrac{1}{5}$$
Write the following rational number in decimal form
$$\dfrac {23}{2^{3}\cdot 5^{2}}$$
The sum of two rational numbers is $$\dfrac { 4 }{ 21}$$. If one of them is $$\dfrac { 5 }{ 7 }$$, find the other.
Express each of the following as a fraction in simplest form:
$$66\dfrac { 2 }{ 3 }\%$$
Simplify $$\dfrac {23}{16}$$
Simplify $$\dfrac{1}{2} + \dfrac{5}{2} + \dfrac{3}{{10}}$$
Solve $$2\dfrac{1}{2} - 1\dfrac{4}{5}$$
Write the additive inverse of $$\dfrac{{43}}{9}\,$$
Soham poured some water in two fish bowls. He poured $$4\dfrac{5}{8}$$ liters of water in the first dish bowl and $$2\dfrac{5}{6}$$ liters in the second bowl. How much water Soham pour in the first bowls altogether?
Work out :$$4\dfrac{9}{8} - 2\dfrac{4}{5}$$
Express each of the following as a fraction in simplest form:
$$33\dfrac { 1 }{ 2 }\%$$
Subtract: $$\dfrac { 31 }{ 2 } -\dfrac { 2 }{ 3 }$$
How do represent fraction on number line
$$\dfrac{3}{4}$$
Add the following fractions.
(a) $$\dfrac{7}{12}$$ and $$\dfrac{3}{8}$$ (b) $$\dfrac{9}{16}$$ and $$\dfrac{7}{12}$$.
Add.
$$6\dfrac{1}{3}+2\dfrac{1}{3}$$
If $$\dfrac{5}{7}+\dfrac{9}{11}=\dfrac{118}{11a}$$. Find $$a$$
What number should be added in $$\dfrac{-7}{8}$$ to get $$\dfrac{4}{9}$$
Evaluate $$\dfrac{6}{{96}} + \dfrac{4}{{192}}$$
In a camp, there are $$420$$ boys and $$180$$ girls. Find the ratio of boys to girls:
Add $$\dfrac{6}{{96}} + \dfrac{4}{{92}}$$
What fraction is $$270g$$ of $$3 kg$$.
Subtract $$\dfrac {2}{5}-5$$
Simplify$$:\,8\dfrac{5}{6} - 3\dfrac{3}{8} + 1\dfrac{7}{2}$$.
Simplify: $$ 2\dfrac{2}{3} +3\dfrac{1}{2} $$
Mother bought two chickens. One weight $$1\dfrac{3}{4}\ kg$$ and the other $$1\dfrac{1}{2}\ kg$$. How much did they both weigh together?
How much less is $$28$$km than $$42.6$$km?
Solve : $$4\dfrac{1}{2} - \dfrac{1}{4} + \dfrac{1}{5} + \dfrac{3}{5}$$
$$ - \frac{2}{{21}} + \frac{3}{7}$$
Solve $$4\dfrac{2}{3} - 1\dfrac{{11}}{{12}}$$
Add $$1\dfrac{3}{4}, 2\dfrac{1}{10}, 3\dfrac{1}{3}$$.
Prove that : $$\dfrac{a^{-1}}{a^{-1} + b^{-1}} + \dfrac{a^{-1}}{a^{-1} - b^{-1}} = \dfrac{-2b^2}{b^2 - a^2}$$
A family eats $$1\dfrac{2}{3}$$ breads at a meal. Will $$3$$ breads be enough for $$2$$ meals?
List five rational numbers between
1) -1 and 0
2) -2 and -1
3) $$\dfrac{-4}{5}$$ and $$\dfrac{-2}{3}$$
4) $$\dfrac{1}{2}$$ and $$\dfrac{2}{3}$$
Convert the following into proper fraction: $$4\dfrac{3}{5}$$
Add $$-2 + \dfrac{15}{2} + \dfrac{11}{4} =$$
Draw number lines and locate the points on them:
$$\frac{2}{5}, \frac{3}{5}, 1, \frac{4}{5}$$
Solve:
$$\dfrac{16}{9}-{{x}^{2}}=0$$
Simplify: $$\dfrac{3}{7} + \left( {\dfrac{{ - 6}}{{11}}} \right) + \left( {\dfrac{{ - 8}}{{21}}} \right) + \left( {\dfrac{5}{{22}}} \right)$$
Solve: $$\dfrac{3}{8}-\dfrac{1}{12}$$
Draw number lines and locate the points on them:
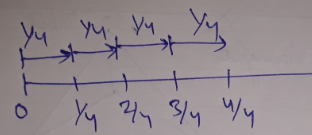
$$\dfrac{1}{4}, \dfrac{2}{4}, \dfrac{3}{4}, \dfrac{4}{4}$$
$$\left(2\frac{1}{2}+3\frac{1}{3}\right)+\frac{2}{9}\left(3\frac{1}{8}-2\frac{1}{12}\right)$$
Evaluate: $$\frac{1}{-15}+\frac{5}{-12}$$
Is $$\dfrac{3}{4}$$ is a proper fraction?
Evaluate: $$\frac{-8}{9}+\frac{-5}{12}$$
Evaluate: $$4+\frac{3}{-5}$$
Evaluate: $$\frac{5}{9}+\frac{3}{-4}$$
What numbers should be added to $$\cfrac { -5 }{ 8 } $$ so as to get $$\cfrac { -3 }{ 2 } ?$$
Evaluate: $$0+\frac{-2}{7}$$
Evaluate: $$\frac{5}{-11}+0$$
Evaluate: $$2+\frac{-3}{5}$$
Evaluate: $$\frac{4}{-9}+1$$
Find:
$$\dfrac{3}{5} + \dfrac{2}{7}$$
Represent the following number on the number line
$$\dfrac {7}{4}$$
Convert into improper fractions.
$$8\frac{1}{2}$$
Convert into improper fractions.
$$4\dfrac{5}{6}$$
Represents these number on number line
$$\dfrac {3}{5}$$
Represent the following number on the number line
$$\dfrac {3}{5}$$
Evaluates : $$\left(\dfrac{1}{3}\right)^{-1} + \left(\dfrac{1}{5}\right)^{-1} - \left(\dfrac{1}{6}\right)^{-1}$$
Solve: $$9\dfrac{1}{9}-3\dfrac{4}{7}$$
Add $$1\dfrac{2}{3} + 2\dfrac{4}{5}$$
Add $$\cfrac{8}{6} + \cfrac{5}{3}$$
Find $$\dfrac{{\sqrt 3 }}{2} \times \dfrac{{\sqrt 3 }}{2} + \dfrac{1}{2} \times \dfrac{1}{2} $$
$$a=\dfrac{1}{6}$$ and $$\dfrac{6}{7}=\dfrac{5}{b}$$, what is the value of $$a+b$$?
What should be added to $$\left[ {\dfrac{{ - 3}}{5} + \dfrac{{ - 5}}{3}} \right]$$ to get $$1$$?
Add $$\cfrac{5}{4} + \left( {\cfrac{{ - 11}}{4}} \right)$$
Which of the following are proper fractions?$$\dfrac{1}{8},\dfrac{2}{5},\dfrac{{16}}{{21}},\dfrac{{23}}{{10}},3,\dfrac{8}{{17}}$$
Solve :$$2+\dfrac {3}{4}$$
What number should be added to $$\dfrac {-6}{5}$$ as so to get $$\dfrac {1}{3}$$?
Solve
$$\dfrac {1}{18}+\dfrac {1}{18}$$
Solve
$$\dfrac {5}{8}+\dfrac {3}{8}$$
In a bag, there are $$20 kg$$ of fruits. If $$7\dfrac {1}{6} kg$$ of these fruits be oranges and $$8\dfrac {2}{3} kg$$ of these are apples and rest are grapes. Find the mass of the grapes in the bag.
Show $$\dfrac{1}{2}$$ on a number line.
Solve:
$$\frac{2}{{21}} + \frac{3}{7}$$
$$\frac{2}{5} + \frac{1}{3}$$
Express as a mixed fraction
(i) $$\dfrac{37}{8}$$
(ii) $$\dfrac{28}{5}$$
(i) $$\dfrac{37}{8}$$
(ii) $$\dfrac{28}{5}$$
Find: $$ - \dfrac{6}{{11}} - \left( { - \dfrac{7}{{15}}} \right)$$
Find the sum $$\dfrac{5}{3}+\dfrac{3}{5}$$
Find the sum $$\dfrac{-2}{3}+0$$
Add and express sum of the following rational numbers: $$\dfrac{-11}{4}$$ and $$\dfrac{24}{7}$$
Solve:-
$$3\frac{3}{4} + 5\frac{1}{6} + 4\frac{1}{3}$$
The sum of a fraction and its reciprocal is $$1{\frac{1}{2}}$$ more than the fraction. Find the fraction.
What should be added to $$5\dfrac{1}{5}$$ to get $$7\dfrac{3}{7}$$?
Solve: $$\dfrac{5}{12}+\dfrac{7}{16}$$
Solve the
$$\dfrac{7}{9}-\dfrac{2}{5}$$
Solve: $$\dfrac{56}{8}-2\dfrac{3}{7}$$.
Solve:
$$\dfrac{19}{5}+\dfrac{-7}{5}$$
Write the fraction whose numerator is one and equivalent to $$\dfrac{9}{36}$$?
Solve the
$$\dfrac{-3}{7}+\dfrac{2}{3}$$
Solve $$3\dfrac{2}{5}-2\dfrac{1}{4}$$.
Solve
$$\dfrac{-5}{6}+\dfrac{3}{11}$$
Find $$17-12\dfrac{2}{8}$$.
Solve the
$$\dfrac{-13}{7}+\dfrac{6}{7}$$
Solve :
$$ \dfrac {5}{3} + \dfrac {3}{5} $$=?
Covert $$\dfrac{2}{3}, \dfrac{5}{7}$$ pair of fraction into like fractions?
Simplify: $$ \dfrac {7}{24} - \dfrac {17}{36} $$
Find equivalent fraction $$\dfrac{3}{14}$$ having
a) numerator $$42$$ b) denominator $$132$$
Convert $$1\dfrac{4}{11}$$ into improper fraction?
Substact the sum of $$\dfrac{1}{2}$$ and $$-\dfrac{1}{4}$$ from the sum of $$\dfrac{3}{8}$$ and $$\dfrac{1}{4}$$
Solve :
$$ \dfrac {-2}{3} + 0 $$
Find $$\dfrac{3}{7} + \left(\dfrac{-6}{11} \right) + \left(\dfrac{-8}{21} \right) + \dfrac{5}{22}$$
Find :
$$ \dfrac {-3}{8} - \dfrac {7}{11} $$
Find :
$$ -2\dfrac {1}{3} + 4 \dfrac {3}{5} $$
Add$$\dfrac{\left ( -447 \right )}{495}+\dfrac{745}{\left ( 990 \right )}$$
Solve : $$\dfrac{(1.3)^2}{6 \times 0.315} + \dfrac{0.315}{2}$$
Solve:
(i) $$1 \dfrac{2}{3} - 3\dfrac{5}{6}$$ (ii) $$4 \dfrac{1}{2} - 3\dfrac{1}{3}$$
Express the following as improper fractions:
$$7\dfrac{3}{4}$$
$$5\dfrac{6}{7}$$
$$2\dfrac{5}{6}$$
$$10\dfrac{3}{5}$$
$$75 \ paise$$ is ________ part of a rupee
Solve: $$1 \dfrac{2}{3} + 2\dfrac{4}{5}$$
Solve:
$$ \dfrac {5}{4} + \left( \dfrac {-11}{4} \right) $$
Verify the following equality
$$\left(\dfrac{-3}{5}+\dfrac{1}{6}\right)+\dfrac{9}{10}=\dfrac{-3}{5}+\left(\dfrac{1}{6}+\dfrac{9}{10}\right)$$
Solve $$\dfrac{7}{18}+\dfrac{11}{18}-1$$
Find the sum:
(i) $$\frac { 5 }{ 4 } +\left( \frac { -11 }{ 4 } \right) $$
$$1\dfrac{1}{2}$$ .convert to mix fraction.
Solve : $$\left[\dfrac{4}{5} +\left\{\dfrac{3}{5} + \left(\dfrac{2}{5} - \dfrac{1}{6} \right) \right\} + \dfrac{1}{2}\right] - \dfrac{2}{3}$$
Find the value.
$$\dfrac{-3}{7}=\dfrac{...}{14}=\dfrac{9}{...}=\dfrac{-6}{...}$$
Fractions:-
(ii) $$\dfrac{9}{5}-\dfrac{6}{7}+\dfrac{3}{2}-\dfrac{5}{4}.$$
Solve $$\dfrac{2}{3} - \dfrac{1}{9}$$
Fractions:-
(i) $$\dfrac{3}{5}+\dfrac{6}{4}.$$
Work out the following. Simplify your answers where possible.
a) $$7 + \frac{7}{8} = \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_$$
b) $$14 + \frac{7}{9} = \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_$$
What is the fraction of Rs. $$1$$ to $$50$$ paise
If $$\dfrac{1}{5}$$ of a number is subtracted from $$\dfrac{1}{3}$$ of that number, the result is $$6$$. Find the number.
Fill $$>, <$$ or $$=$$ sign
$$\cfrac{15}{42}$$ $$\square$$ $$\cfrac{15}{19}$$
Find the value:-
$$\frac{3}{{13}} + \frac{2}{7}$$
Find the sum :
$$\dfrac{-3}{-11}+\dfrac{5}{9}$$
Solve:-
$$\left ( \dfrac{1}{2} \right )^{3}+\left ( \dfrac{1}{3} \right )^{3}-\left ( \dfrac{5}{6} \right )^{3}$$
Add:$$\dfrac{5}{3} + \dfrac{3}{5}$$
Solve:
$$\frac{{ - 2}}{3} + 0$$
Solve :
$$\dfrac{-9}{10}+\dfrac{22}{15}$$
Fill in the boxes with the symbols '<' or '>' to make the given statements true:- $$\dfrac{5}{11} \Box \dfrac{3}{7}$$
- $$\dfrac{8}{15} \Box \dfrac{3}{5}$$
- $$\dfrac{11}{14} \Box \dfrac{29}{35}$$
- $$\dfrac{13}{27} \Box \dfrac{15}{48}$$
- $$\dfrac{5}{11} \Box \dfrac{3}{7}$$
- $$\dfrac{8}{15} \Box \dfrac{3}{5}$$
- $$\dfrac{11}{14} \Box \dfrac{29}{35}$$
- $$\dfrac{13}{27} \Box \dfrac{15}{48}$$
Arrange the following rational number in descending order
$$\frac{17}{-30},\frac{11}{-15},\frac{-7}{10},\frac{3}{5}.$$
Solve:
$$\frac{{ - 9}}{{10}} + \frac{{32}}{{15}}$$
$$7\frac{1}{2} - \left[ {2\frac{1}{4} + \left\{ {1\frac{1}{4} - \frac{1}{2}\left( {\frac{3}{2} - \frac{1}{3} - \frac{1}{6}} \right)} \right\}} \right]$$
Evaluate : (i) $$\dfrac{6}{(-25)}$$ - $$\dfrac{4}{(-15)}$$
Substract: $$\dfrac{-4}{15}$$ from$$ \dfrac{-7}{15}$$
Substract: $$\dfrac{-3}{8}$$ from$$ \dfrac{5}{8}$$
Solve: $$4+\dfrac{7}{8}.$$
Substract: $$\dfrac{2}{5}$$ from $$\dfrac{3}{5}$$
Solve: $$2\dfrac{2}{3}+3\dfrac{1}{2}.$$
Solve: $$\dfrac{7}{10}+\dfrac{2}{5}+\dfrac{3}{2}.$$
Simi's book is $$\frac{3}{5}$$ kg and Soma's book is $$\frac{3}{8}$$ kg in weight. Whose book is heavier and by how much?
The value of $$\left( \cfrac { 3 }{ 5 } +\cfrac { 4 }{ 7 } \right) -\cfrac { 3 }{ 7 } $$
Find out the reciprocal of $$\left( \frac { - 1 } { 8 } \right) ^ { 6 } .$$
What should be added to $$\dfrac{-7}{12}$$ as to get $$\dfrac{9}{16}$$
Solve $$1 + \frac{1}{8} - \frac{{27}}{8}$$
Substract: $$\dfrac{-3}{7}$$ from $$\dfrac{5}{4}$$
$$2\dfrac{3}{11}+4\dfrac{1}{9}+\dfrac{1}{3}$$
Mixed numbers always represent a -----------------.
Simplify: $$\dfrac{8}{-15}+\dfrac{4}{-3}$$
Evaluate
$$\dfrac{1}{2}+6\dfrac{2}{7}+\dfrac{2}{5}=$$
Write the following surd in simplest from .
$$\dfrac {5}{9} \sqrt {45}$$
Express 1 day as a fraction of 1 week.
Solve:
$$3\frac{2}{5} - 2\frac {1}{4}$$
Convert into mixed fractions.
(a) $$\frac{3}{2}$$
(b)$$\frac{24}{5}$$
Solve: $$\dfrac{4}{9} + \dfrac{2}{7}$$
Solve: $$\dfrac{5}{6} - \dfrac{2}{9}$$
Solve: $$\dfrac{3}{4} - \dfrac{1}{2}$$
Express 20 seconds as a fraction of 1 minute.
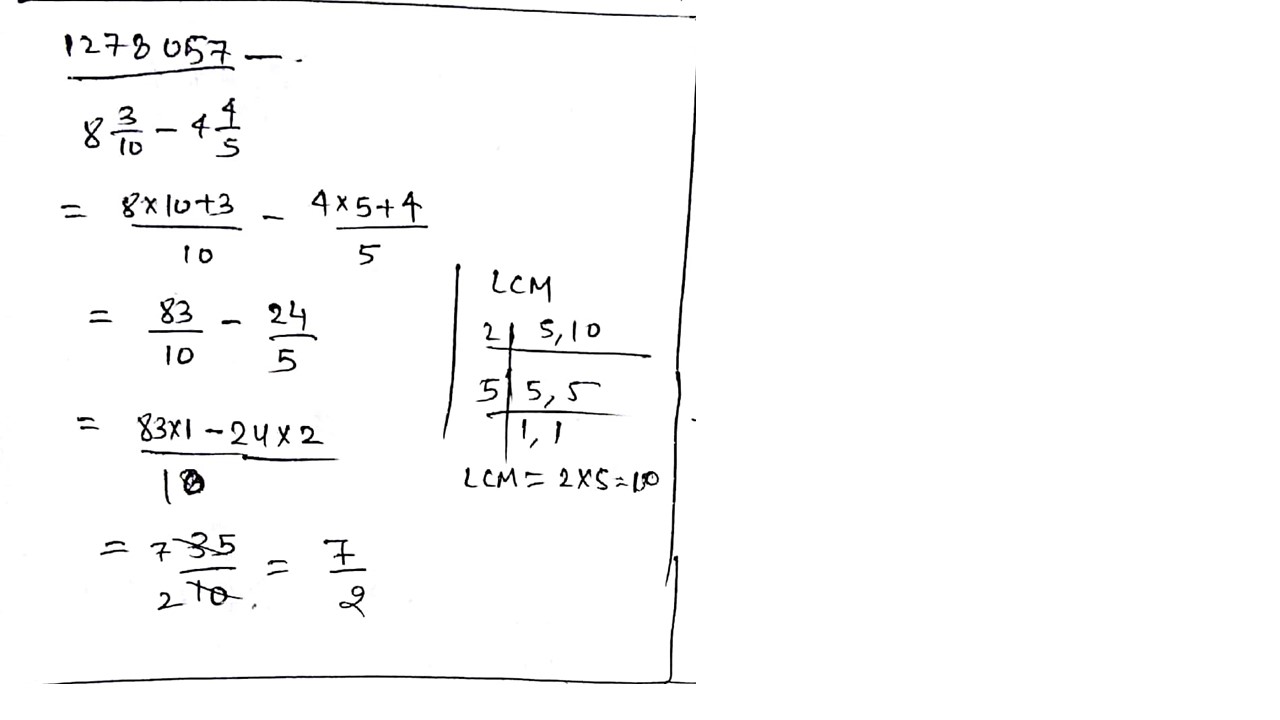
Solve: $$8\dfrac{3}{10} - 4\dfrac{4}{5}$$
Draw number lines and locate the point on them :
$$\dfrac {2}{5},\dfrac {3}{5},\dfrac {8}{5},\dfrac {4}{5}$$
$$\dfrac{2}{3}$$ + $$\dfrac{2}{4}$$
Subtract $$\dfrac {-5}{6}$$ from $$\dfrac {1}{3}$$.
Solve: $$2\dfrac{3}{4}+4\dfrac{2}{3}+1$$
Wrote the following as mixed fraction
$$\dfrac { 7 }{ 2 } ,\dfrac { 8 }{ 5 } $$
simplify :
$$2\dfrac{3}{5}+1\dfrac{3}{10}-3\dfrac{2}{15}$$
Express $$10$$ months as a fraction of $$1$$ year.
Javed was given $$\dfrac{5}{7}$$ of a basket of oranges. What fraction of oranges was left in the basket.
Subtract: $$\dfrac {-18}{11}$$ from $$\dfrac {1}{1}$$.
$$\dfrac { 9 }{ 11 } -\dfrac { 4 }{ 15 } $$
$$\dfrac{1}{22}+\dfrac{21}{22}$$.
Simplify:$$\dfrac{6}{9}-\dfrac{3}{18}$$
Reduce the following fractions to simplest from:
(i) $$\dfrac{48}{60}$$
(ii) $$\dfrac{150}{60}$$
Solve:(a)$$\dfrac { 2 }{ 3 } +\dfrac { 1 }{ 7 }$$ (b)$$\dfrac { 3 }{ 10 } +\dfrac { 7 }{ 15 } $$ (c)$$\dfrac { 4 }{ 9 } +\dfrac { 2 }{ 7 } $$ (d)$$\dfrac { 5 }{ 7 } +\dfrac { 1 }{ 3 } $$
(e)$$\dfrac { 4 }{ 5 } +\dfrac { 2 }{ 3 } $$ (f)$$\dfrac { 3 }{ 4 } -\dfrac { 1 }{ 3 } $$ (g)$$\dfrac { 5 }{ 6 } -\dfrac { 1 }{ 3 } $$
Solve
$$\dfrac {-8}{19}+\dfrac {(-2)}{57}$$
Solve : $$\dfrac{3}{4} - \dfrac{1}{3}$$
Represent each of the following number on the number line:
$$\dfrac {1}{3}$$.
Simplify:$$\dfrac{16}{39}+\dfrac{9}{-26}$$
Subtract the following fraction and reduce to the lowest term $$\dfrac{7}{15}$$ from $$\dfrac{13}{20}$$
Add:$$\dfrac{3}{4}{a}^{2}b,\,\dfrac{2}{3}{a}^{2}b$$
Add the following
$$\dfrac {4}{7}\ and\ \dfrac {5}{7}$$
Add: $$\dfrac{3}{5}x \ \ ,\,\dfrac{2}{3}x \ \ \ \ ,\dfrac{-4}{5}x$$
$$5\dfrac {1}{3}-3\dfrac {1}{2}=$$_______
Add:$$\dfrac{5}{-11}$$ and $$\dfrac{8}{11}$$
Simplify :$$6+\{ \frac { 4 }{ 3 } +(\frac { 3 }{ 4 } -\frac { 1 }{ 3 } )\} $$
Raju plucked two papayas. One of them weighed $$\dfrac{1}{4}$$kg, and the other weighed $$\dfrac{1}{2}$$kg, so what is their total weight.
Solve:
$$\dfrac {-8}{19}+\dfrac {(-2)}{57}$$
Add : $$\dfrac{5}{6}$$ & $$\dfrac{13}{15}$$
Add the following.
$$\dfrac { -5 }{ 3 } ,\dfrac { -4 }{ 3 } ,\dfrac { -3 }{ 3 } $$
Multiply and write your answer in the lowest form.
$$\dfrac{4}{5} \times 2$$
Find the interval between $$7:15$$ am and $$12:15$$ pm.
The sum of two fraction is $$5\cfrac { 3 }{ 9 } $$. If one of the fractions is $$2\cfrac { 3 }{ 4 } $$, find the other fraction.
Convert $$4\dfrac{5}{6} $$ in to improper fraction
Simplify:
$$\dfrac {8}{10}+\dfrac {9}{10}$$
Add the following.
$$a)\dfrac{3}{24}+\dfrac{11}{24}$$
$$ b)\dfrac{3}{10}+\dfrac{2}{10}+\dfrac{7}{10}$$
Simplify:
$$3\dfrac {1}{4}+4\dfrac {5}{6}$$
Convert $$3\dfrac{5}{6}$$ into an improper fraction.
Find the sum of $$9\dfrac { 3 }{ 8 } +10\dfrac { 5 }{ 8 } $$
Add.
$$\dfrac {1}{3}+\dfrac {3}{4}+\dfrac {2}{5}$$
Add $$\dfrac { 3 }{ 7 }$$ and $$\dfrac { 2 }{ 3 } $$.
What number should be added to $$\dfrac { -6 }{ 11 } $$ so as to get $$\dfrac { 4 }{ 9 } $$?
Find the sum of $$\dfrac { 1 } { 3 } + \dfrac { 1 } { 4 }$$.
Solve: $$6{1 \over 3} + 2{1 \over 3}$$
Compare: $$\dfrac { 3 }{ 7 } $$ and $$\dfrac { 2 }{ 3 } $$
The sum of two numbers is $$11$$ and the sum of their reciprocals is $$\dfrac{{11}}{{28}}$$ Find the numbers.
simplify:
$$ 1 \frac{1}{2}+\frac{4}{9}+13 \frac{1}{2} $$
Find :
$$\dfrac { 2 }{ 5 } +\dfrac { 3 }{ 4 } +\dfrac { 1 }{ 4 } $$
Add $$\dfrac { 16 }{ 5 } ,\dfrac { 3 }{ 5 } $$.
What should be added to $$(\frac{1}{3}+\frac{3}{5})$$ to get $$\frac{-6}{20}?$$
Write the following in order of size, starting with the smallest
$$0.239$$ $$\sqrt{0.057}$$ $$\cfrac{11}{46}$$
Convert into proper fractions: $$8\dfrac { 3 }{ 4 } $$
Add
$$ 5 \frac{1}{15}+5+\frac{11}{10} $$
$$100+50+5+\frac{1}{100}$$
Write each of the following as decimals.
$$20 + 9 + \dfrac {4}{10} + \dfrac {1}{100}$$
Solve $$\displaystyle 5\frac { 2 }{ 7 } -\frac { 8 }{ 9 } +\left( \frac { -3 }{ 14 } \right) -21\frac { 3 }{ 19 } .$$
Evaluate $$\displaystyle \frac{{ - 12}}{5} + \frac{{31}}{{10}} + \frac{{11}}{{ - 15}} + \frac{{ - 7}}{{ - 18}}$$
Simplify: $$\dfrac{3}{5} - \dfrac{7}{{20}}$$
Evaluate $$\dfrac{1}{9}+\dfrac{2}{9}$$.
Find the difference:
$$1 / 2 - 3 / 8$$
Find the difference:
$$3\dfrac{5}{8}-2\dfrac{5}{12}$$
Find the difference:
$$2\dfrac{3}{10}=1\dfrac{7}{15}$$
Find the difference:
$$\dfrac{7 }{ 12} - \dfrac{5 }{ 12}$$
Find the difference:
$$2\dfrac{7}{9}-1\dfrac{8}{15}$$
Find the difference:
$$\dfrac{5}{6}-\dfrac{4}{9}$$
Without using you calculator, work out $$1\cfrac{7}{12}+\cfrac{13}{20}$$
You must show all your working and give your answer as a mixed number in its simplest form.
Find the difference:
$$5 / 8 1 / 8$$
Find the difference:
$$4\dfrac{3}{7}-2\dfrac{4}{7}$$
Write down the numerator and the denominator of the fraction given below:
$$6/11$$
Write down the numerator and the denominator of the fraction given below:
$$8/15$$
Find the difference:
$$6\dfrac{2}{3}-3\dfrac{3}{4}$$
Find the difference:
$$7-5\dfrac{2}{3}$$
Write down the numerator and the denominator of the fraction given below:
$$4/9$$
Write a fraction for the following:
Three - tenths
Solve: $$2+\dfrac{11}{15} - \dfrac{5}{9}$$
Find the difference:
$$10-6\dfrac{3}{8}$$
Find the difference:
$$5/8 + 3/4 - 7/12$$
Write a fraction for the following:
Four- sevenths
Write down the fraction in which
numerator $$= 7$$, denominator $$= 16$$
Find the sum:
$$\dfrac{5}{8} +\dfrac{ 1}{8}$$
Write down the numerator and the denominator of the fraction given below:
$$5/1$$
Write down the fraction in which
numerator $$= 8$$, denominator $$= 15$$
Write down the fraction in which
numerator $$= 5$$, denominator $$= 12$$
Write down the fraction in which
numerator $$= 3$$, denominator $$= 8$$
Find the sum:
$$\dfrac{4}{9} + \dfrac{8}{9}$$
Write down the numerator and the denominator of the fraction given below:
$$12/17$$
Which of the following are improper fractions?
$$3 / 2, 5 / 6, 9 / 4, 8 / 8, 3, 27 / 16, 23 / 31, 19 / 18, 10 / 13, 26 / 26$$
Which of the following are proper fractions?
$$1/2,3/5,10/7,7/4,2,15 /8,16/16,10/11,23/ 10$$
Find the sum:
$$1\dfrac{3}{5}+2\dfrac{4}{5}$$
Find the sum:
$$3\dfrac{2}{3}+1\dfrac{5}{6}+2$$
Find the sum:
$$\dfrac{2}{9} + \dfrac{5}{6}$$
Find the sum:
$$3\dfrac{1}{8}+1\dfrac{5}{12}$$
Find the sum:
$$2\dfrac{3}{4}+5\dfrac{5}{6}$$
Find the sum:
$$\dfrac{4}{15} + \dfrac{17}{20}$$
Find the sum:
$$9\dfrac{7}{10}+3\dfrac{8}{15}$$
Find the sum:
$$\dfrac{7}{12} + \dfrac{9}{16}$$
Write down the numerator and the denominator of the following rational number:
$$\cfrac5{-8}$$
Write six improper fractions with numerator $$13.$$
Write six improper fractions with denominator $$5$$
Write the following fractions in number form :
(i) One - sixth
(ii) Three - eleventh,
(iii) Seven - fortieth
(iv) Thirteen - one hundred twenty fifth
Simplify the following :
$$(i) 1 \dfrac{2}{3} + 2 \dfrac{1}{2} + \dfrac{3}{4}$$
$$(ii) 3 \dfrac{2}{9} + 2 \dfrac{1}{3} +2 \dfrac{7}{12}$$
$$(iii) \dfrac{7}{12} + \dfrac{8}{9} - \dfrac{5}{6}$$
$$(iv) 1 \dfrac{3}{25} + \dfrac{7}{20} - \dfrac{2}{5}$$
$$(v) 1 \dfrac{13}{14} - 2 \dfrac{5}{6} + 1\dfrac{6}{7}$$
Work out the following :
$$(i)\ \dfrac{2}{3} + \dfrac{3}{4}$$
$$(ii)\ \dfrac{5}{7} - \dfrac{4}{9} $$
$$(iii)\ \dfrac{1}{2} + \dfrac{3}{5} $$
$$(iv)\ 1 \dfrac{4}{9} + 3 \dfrac{5}{12}$$
Convert $$ 2435\ m $$ to $$ km $$ and express the result as a mixed fraction.
Find in the missing fractions :
$$(i) \dfrac{7}{10} - \Box = \dfrac{3}{10}$$
$$(ii) \Box + \dfrac{5}{27} = \dfrac{12}{27}$$
$$(iii) \Box - \dfrac{5}{7} = \dfrac{2}{7}$$.
Simplify: $$[8(5/6)]-[3(3/8)]+[1(7/12)]$$
Fill in the blanks.
$$7 \dfrac{2}{5} + ........ = 12$$
Fill in the blanks
A proper fraction lies between $$0 $$ and .......
Fill in the blanks.
A mixed fraction can be converted into ......... fraction.
Sarita bought $$\dfrac{2}{5}$$ metre of ribbon and Lalita $$\dfrac{3}{4}$$ metre of ribbon.
What is the total length of the ribbon they bought?
The weight of three packets are $$2 \dfrac{3}{4} kg $$. $$3 \dfrac{1}{3} kg. $$ and $$5\dfrac{2}{5} kg.$$ Find total weight of all the three packets.
Evaluate :
$$ 3 \dfrac{5}{12} - 1 \dfrac{2}{3} $$
The reciprocal of an improper fraction is an
improper fraction.
Evaluate :
$$ 3 \dfrac{5}{12} + 1 \dfrac{2}{3} $$
The reciprocal of a proper fraction is a proper fraction.
Enter 1 if it is true else enter 0.The standard form of the rational number $$\dfrac{14}{12}$$ is $$\dfrac{7}{6}$$
Enter 1 if true else enter 0.
The rational number $$\dfrac{-81}{15}$$ reduced to simplest form is $$\dfrac{-7}{13}$$.
Subtract $$\left(2/7 - 5/21 \right)$$ from the sum of 3/4, 5/7 and 7/12.
Simplify : $$2 \dfrac{1}{2} - 3 \dfrac{1}{4} + 5\dfrac{5}{6}$$
Put the $$(\checkmark),$$ wherever applicable
Number | Natural Number | Whole Number | Integer | Fraction | Rational Number |
$$-19\dfrac{3}{4}$$ |
Evaluate :
$$ \dfrac{7}{26} + 2 + \dfrac{-11}{13} $$
Evaluate :
$$ \dfrac{-5}{9} + \dfrac{-7}{12} + \dfrac{11}{18} $$
Evaluate :
$$ \dfrac{7}{-27} + \dfrac{11}{18} $$
Evaluate :
$$ \dfrac{9}{-16} + \dfrac{-5}{-12} $$
Reduce to a single fraction:
$$2 \dfrac{1}{2} + 2 \dfrac{1}{3} - 1 \dfrac{1}{4}$$
Evaluate :
$$ \dfrac{-3}{8} + \dfrac{-5}{12} $$
Evaluate :
$$ \dfrac{-2}{3} + \dfrac{3}{4} $$
Evaluate :
$$ \dfrac{-5}{7} - \left (\dfrac{-3}{8} \right ) $$
Evaluate :
$$ \dfrac{7}{-26} + \dfrac{16}{39} $$
Reduce to a single fraction:
1/2 + 2/3
Reduce to a single fraction:
$$2 \dfrac{5}{8} - 2 \dfrac{1}{6} + 4 \dfrac{3}{4}$$
Subtract:
$$ 3/7$$ and $$3/7$$
Subtract:
$$2$$ form $$2/3$$
Evaluate :
$$ \dfrac{5}{9} + \dfrac{-7}{6} $$
Subtract:
$$1/8$$ from $$5/8$$
Subtract:
$$-4/7$$ from $$-6/11$$
Subtract:
$$-2/5$$ and $$2/5$$
Subtract:
$$0$$ and $$-4/5$$
What number should be added to $$8 \dfrac{2}{3}$$ to get $$12 \dfrac{5}{6}$$?
What should be subtracted from $$8 \dfrac{3}{4}$$ to get $$2 \dfrac{2}{3}$$?
Evaluate :
$$ \dfrac{-4}{9} - \dfrac{2}{-3} $$
Evaluate :
$$ \dfrac{-5}{18} - \dfrac{-2}{9} $$
Subtract :
$$ \dfrac{-5}{8} From \dfrac{-13}{16}$$
Subtract :
$$ \dfrac{1}{4} From \dfrac{-3}{8}$$
Evaluate :
$$ \dfrac{2}{3} - \dfrac{4}{5} $$
Evaluate :
$$ - 1 - \dfrac{4}{9} $$
Subtract :
$$ \dfrac{4}{9} From \dfrac{-5}{9}$$
Evaluate :
$$ \dfrac{-2}{7} - \dfrac{3}{-14}$$
Subtract :
$$ \dfrac{-8}{11} From \dfrac{4}{11}$$
Evaluate :
$$ \dfrac{5}{21} - \dfrac{-13}{42}$$
Subtract :
$$ \dfrac{-9}{22} From \dfrac{5}{33}$$
Solve:
$$\frac{4}{9} + \frac{2}{7}$$
Solve:
$$\displaystyle \frac{3}{4} - \frac{1}{3}$$
On the basis of given number line, answer the following.
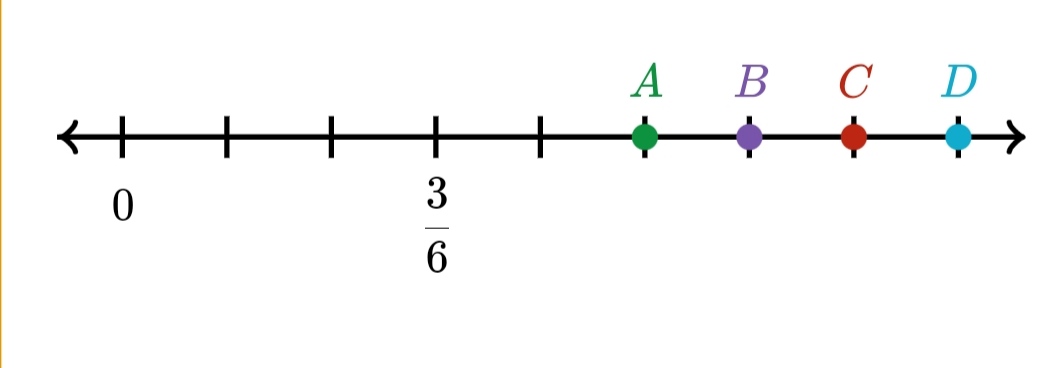
Consider the following number line and match each point to its value.
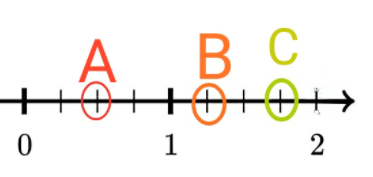
The given number line represents the fraction ____.
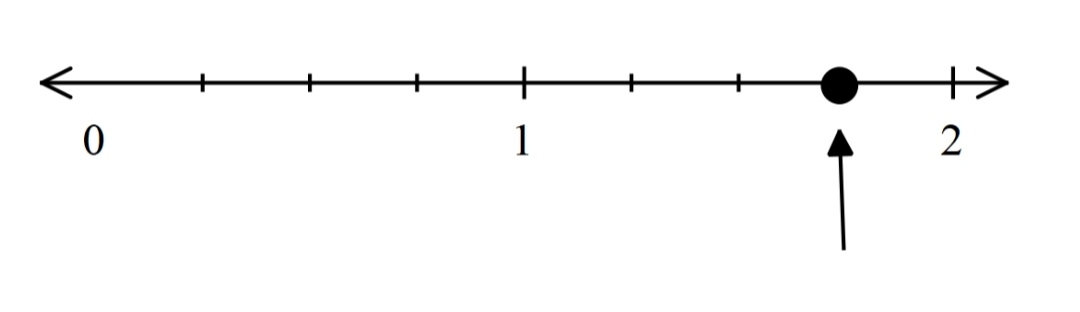
Subtract: $$\dfrac {3}{4}$$ from $$\dfrac {1}{3}$$.
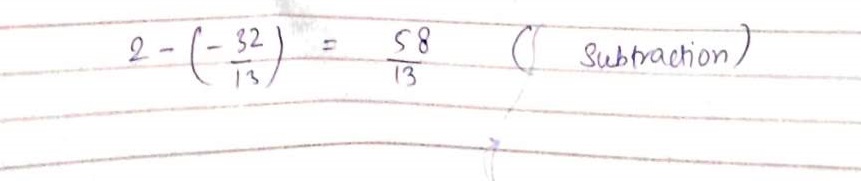
Subtract: $$\dfrac{-32}{13}$$ from 2
Solve the following:
$$\cfrac { 7 }{ 9 } +\cfrac { 1 }{ 3 } $$ =K. Find 9K
Fill in the missing fraction.
$$\displaystyle \square -\frac{3}{21}=\frac{5}{21}$$.
Convert the following mixed fraction into improper fraction.
$$\displaystyle 3\frac{2}{8}$$.
Represent the given number on the number line: $$-\dfrac{7}{5}$$
Fill in the missing fraction.
$$\displaystyle \square +\frac{5}{27}=\frac{12}{27}$$.
If x is a proper fraction, show that $$\displaystyle\frac{x}{1-x^2}-\frac{x^3}{1-x^6}+\frac{x^5}{1-x^{10}}-.......=\displaystyle \frac{x}{1+x^2}+\frac{x^3}{1+x^6}+\frac{x^5}{1+x^{10}}+.....$$
Solve the following:
$$1-\cfrac { 4 }{ 7 } =K.$$ Find $$14K$$
Convert the following improper fraction into mixed fraction.
$$\displaystyle\frac{11}{2}$$.
Solve the following:
$$2+\cfrac { 3 }{ 4 } $$ = K. Find 4K
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, (2^{3/2} + 27y^{3/5}) : \left ( \left ( \frac{1}{2} \right )^{-1/2} + 3 y^{1/5} \right )$$
$$\dfrac{3}{7}+\bigg(\dfrac{-6}{11}\bigg)+\bigg(\dfrac{-8}{21}\bigg)+\bigg(\dfrac{5}{22}\bigg)$$=$$\bigg(\dfrac{-125}{462}\bigg)$$.If true enter $$1$$ else $$0$$.
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \frac{\frac{x - y}{\sqrt{x} - \sqrt{y}} - \frac{x - y}{\sqrt{x} + \sqrt{y}}}{\frac{\sqrt{x} - \sqrt{y}}{x - y} + \frac{\sqrt{x} + \sqrt{y}}{x - y}} \cdot \frac{2 \sqrt{xy}}{y -x}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
Simplify the following expressions.
$$\displaystyle\left ( \left ( \frac{y}{y - x} \right )^{-2} - \frac{(x + y)^2 - 4xy}{x^2 -xy}\right ) \frac{x^4}{x^2 y^2 - y^4}$$
Using suitable rearrangement and find the sum,
$$ - 5 + {7 \over {10}} + ( - 3) + {3 \over 7} + \left( {{{ - 4} \over 5}} \right) + {5 \over {14}}$$
What is the value of $$2 + {1 \over {2 + {2 \over {5 + {2 \over 3}}}}}?$$
If 1 is added in the numerator and denominator, then fraction becomes $${\dfrac 3 4}$$ and if we substract 1 from both numerator and denominator then becomes $${\dfrac 2 3}$$, then find the fraction.
Find the multiplicative inverse of the following.
(i) $$-13$$ (ii) $$\dfrac{-13}{19}$$ (iii) $$\dfrac{1}{5}$$
Subtract 3 kg 765 g from 9 kg 401g
Represent the rational numbers $$\dfrac{1 }{ 2},\dfrac{ - 3} {4},\dfrac{3 }{ 2}$$ and $$\dfrac{5 }{ 8}$$ on the number line.
What should be added to $$\dfrac{4} {5}$$ to get $$\dfrac{49}{30}?$$
Add the following rational numbers:
(a) $$\dfrac{2}{7}$$ and $$\dfrac{3}{7}$$
(b) $$\dfrac{-4}{11}$$ and $$\dfrac{7}{11}$$
The value of $$\left ({\dfrac {3} {5}}\right )$$ + $$\left (\dfrac {1} {2}\right )$$ is
Simplify :
$$8-4\dfrac{1}{2}-2\dfrac{1}{4}$$
Subtract:
$$2\dfrac {3}{5}$$ from $$-3/7$$.
A bag contains $$20$$ balls of which $$3$$ balls are green, $$10$$ balls are red and the remaining are blue. What fraction of the ball represent red, blue and green balls?
$$\displaystyle 2\dfrac{3}{11}+1\dfrac{3}{77}$$.
Dhriti,s house is $$\dfrac{9}{10}\ km$$ from her school. She walked some distance and then took a bus for $$\dfrac{1}{2}\ km$$ to reach the school. How far did she walk ?
Convert $$\displaystyle 3\dfrac{920}{1331}$$ into improper fraction.
Express the following as mixed fraction
$$\dfrac{17}{7}$$.
If the numerator of a fraction is multiplied by $$2$$ and its denominator is increasing by $$1$$, it becomes $$1$$.However if the numerator is increasing by $$4$$ and denominator is multiplied by $$2$$, the fraction becomes $$\dfrac {1}{2}$$. Find the fraction.
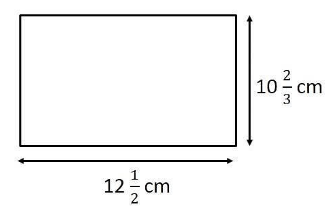
A rectangle sheet of paper is $$12\dfrac {1}{2}\ cm$$ long and $$10\dfrac {2}{3}\ cm$$ wide Find the perimeter of the rectangle.
Find the area of rectangular park which is $$18\dfrac{3}{5}$$m long and $$8\dfrac{2}{3}$$m breadth.
Express the following as mixed fraction
$$\dfrac{11}{5}$$.
How many pieces of $$\dfrac{3}{2}$$ m each can be cut from a lace measuring 15 m?
Evaluate the following:
$$\dfrac {3}{10}+\dfrac {2}{5}$$
$$2\dfrac {3}{4}-\dfrac {1}{4}$$
Sneha can complete a work in $$36$$ days. Rashmi can complete the same work in $$24$$ days. If both work together, then they will be able to complete the work approximately.
Evaluate $$\left[ \dfrac { 5 }{ 4 } +\dfrac { -1 }{ 2 } \right] +\dfrac { -3 }{ 2 } \dfrac { -5 }{ 4 } +\left( \dfrac { 1 }{ 2 } +\dfrac { -3 }{ 2 } \right) $$
Solve $$\dfrac {5}{6}+\dfrac {(-3)}{21}$$
Simplify $$ \left(2\dfrac{4}{5}-\dfrac{7}{10}\right)$$
Simplify $$3\dfrac{4}{7}\times 2\dfrac{2}{5}\times 1\dfrac{3}{4}$$.
Convert into single fraction$$\dfrac{25}{11}+\dfrac{80}{77}$$.
What should be subtracted from $$8\dfrac{3}{10}$$ to get $$2\dfrac{2}{3}$$?
Honey baked a cake. She used $$4\cfrac{5}{8}$$ cups of flour and $$3\cfrac{1}{8}$$ cups of sugar. How much more flour than sugar did Honey use?
Subtract $$\dfrac{3}{4}$$ from $$\dfrac{1}{3}$$.
Subtract $$-7$$ from $$\dfrac{-4}{7}$$.
Bunty walked $$1\cfrac{5}{8}km$$. Then he took a bus and travelled another $$3\cfrac{1}{6}km$$. After that he took a taxi and travelled $$\cfrac{11}{4}km$$. How much distance did he travel in all?
Solve : $$\dfrac{7}{10} + \dfrac{2}{5} + \dfrac{3}{2}$$
The sum of a fraction and its reciprocal is $$\dfrac{13}{6}$$. Find the fraction if its numerator is $$1$$ less than the denominator.
Subtract $$\dfrac{-32}{13}$$ from $$2$$.
Draw number lines and locate the points on them:
$$\dfrac{1}{8}, \dfrac{2}{8}, \dfrac{3}{8}, \dfrac{7}{8}$$
Evaluate $$2+\dfrac{1}{1-\dfrac{1}{1-\dfrac{1}{3}}}$$
Solve : $$3 + \dfrac{6}{14} + 4 \dfrac{1}{4}$$
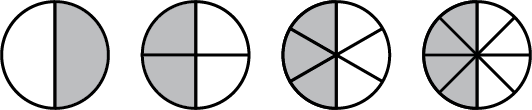
Write the fractions representing each of the shaded regions. Are all these fractions equivalent?
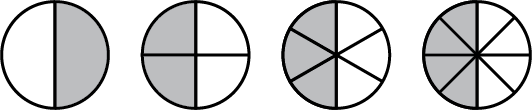
Solve : $$8 \dfrac{7}{10} - 3 \dfrac{5}{11}$$
Solve
$$\dfrac{-7}{10} + \dfrac{13}{15} + \dfrac{27}{20}$$
Solve:
$$\dfrac { 5 }{ 12 } +\dfrac { 7 }{ 16 }$$= ?
Simplify: $$\dfrac { 8 }{ 5 } +\left[ \dfrac { 3 }{ 4 } +\dfrac { 5 }{ 6 } \right]$$
Simplify: $$\dfrac{4}{5}+\dfrac{1}{5}$$
$$4+\dfrac{1}{2}+3\dfrac{1}{2}+9\dfrac{6}{7}$$.
Add $$2\dfrac { 5 }{ 6 } +1\dfrac { 11 }{ 12 }$$
Solve: $$4\dfrac{3}{8}-\dfrac{25}{18}$$.
Sarita bought $$\dfrac{2}{5}$$ meter of ribbon and Lalita $$\dfrac{3}{4}$$ meter of ribbon. What is the total length of the ribbon they bought?
Simplify:
$$\dfrac{8}{{ - 13}} + \dfrac{6}{{ - 3}} - \dfrac{1}{2}$$
From a $$20\ m$$ roll of cloth, three pieces of lengths $$2\dfrac{5}{8}m, 3\dfrac{1}{3}m$$ and $$3\dfrac{2}{5}m$$ are cut out. What length of the cloth is left?
Solve
$$4 \frac { 1 } { 8 } - 8 \frac { 1 } { 3 }$$
Rakaesh had $$1$$ rope of $$7\dfrac{1}{4}$$ length and another $$6\dfrac{3}{7}$$ meters length. How much length of rope did rakesh have in all?
Find the value of the following
$$\dfrac{3}{5}+\dfrac{7}{10}+\left ( \dfrac{-8}{12} \right )+\dfrac{4}{3}$$
Find the sum of following.
(a) $$\dfrac{3}{7},\dfrac{5}{7}$$ (b) $$\dfrac{4}{5},\dfrac{3}{6}$$
Change the following groups of fractions to like fractions:
(i)$$\dfrac{1}{3},\dfrac{2}{5},\dfrac{3}{4},\dfrac{1}{6}$$
(ii)$$\dfrac{5}{6},\dfrac{7}{8},\dfrac{11}{12},\dfrac{3}{10}$$
(iii) $$\dfrac{2}{7},\dfrac{7}{8},\dfrac{5}{14},\dfrac{9}{16}$$
(i)$$\dfrac{1}{3},\dfrac{2}{5},\dfrac{3}{4},\dfrac{1}{6}$$
(iii) $$\dfrac{2}{7},\dfrac{7}{8},\dfrac{5}{14},\dfrac{9}{16}$$
From a rope $$10 \dfrac {1}{2} m $$ long, $$ 4 \dfrac {5}{8} m $$ is cut off. Find the length of the remaining rope.
What should be added to $$ - \dfrac{{17}}{{15}}$$ to get $$ - \dfrac{{8}}{{21}}.$$
Solve:
$${\left(6\dfrac {4}{11}\right)}^{2}-{\left(4\dfrac {7}{11}\right)}^{2}$$
Solve:$$\dfrac{1}{2} + \dfrac{1}{3}$$
Solve $$\dfrac{2}{3}+\dfrac{1}{7}$$
solve : $${(5 + 2\sqrt 6 )^{x2 - 3}} + {(5 - 2\sqrt 6 )^{x2 - 3}} = 10$$
Simplify: $$\dfrac{2}{3}+\left(\dfrac{-4}{5}\right)+\dfrac{1}{4}+\left(\dfrac{-2}{3}\right)+\left(\dfrac{-11}{5}\right)$$
Solve:
$$\dfrac{3}{5} + \dfrac{1}{4}$$
Solve:$$\dfrac{1}{5} + \dfrac{1}{6}$$
Simplify:
$$4 \dfrac { 1 } { 3 } - 2 \dfrac { 2 } { 3 }$$
Find the value of the equation
$$\displaystyle 20 + 3 + {1 \over {10}} + {3 \over {100}} + {4 \over {1000}}$$
$$\displaystyle 20 + 3 + {1 \over {10}} + {3 \over {100}} + {4 \over {1000}}$$
Replace and $$mnsq^2$$ in each of the following by the correct number :
(a) $$\dfrac{2}{7}=\dfrac{8}{\Box }$$ (b) $$\dfrac{5}{8}=\dfrac{10}{\Box }$$
(c) $$\dfrac{3}{5}=\dfrac{\Box}{20}$$ (d) $$\dfrac{45}{60}=\dfrac{15}{\Box}$$
(e) $$\dfrac{18}{24}=\dfrac{\Box}{4}$$
Convert into improper fraction :
$$2\dfrac{3}{4}$$
$$4\dfrac{1}{2} + 2\dfrac{5}{7} \times \dfrac{7}{{19}} - \dfrac{7}{{19}} \div 2$$
Add the following rational numbers-
$$\dfrac{3}{4},\dfrac{-2}{5}$$
Add the following rational numbers-
$$\dfrac{3}{7},\dfrac{13}{17}$$
Convert the following into improper fraction:
$$5\dfrac{3}{4}$$
Convert into improper fraction :
$$3\dfrac{2}{5}$$
Add the following rational numbers-
$$\dfrac{-7}{9},\dfrac{-3}{4}$$
Find the value of $$\left[ {{1^3} + {2^3} + {3^3} + {8^2}} \right] -\displaystyle {5 \over {2.}}$$
Solve the following equation :-
$$\dfrac {2}{3}+\dfrac {5}{3}$$
Find the value of 4 + $$\dfrac{1}{2} -\dfrac{1}{2}+ 2 +\dfrac{1}{2}\left(2\dfrac{1}{2}\right)$$
Shubham painted $$\dfrac{2}{3}$$ of the wall space in his room. His sister Madhavi helps and painted $$\dfrac{1}{3}$$ of the wall space. How much did they paint together.
Naina was given $$1\dfrac { 1 } { 2 }$$ piece of cake and Najma was given $$1\dfrac { 1 } { 3 }$$ piece of cake. Find the total amount of cake was given to both of them.
Find the proportionality constant between $$3:4$$ and $$2:5$$
Show $$\dfrac {2}{6},\ \dfrac {4}{6},\ \dfrac {8}{6}$$ and $$\dfrac {6}{6}$$ on the number line.
Simplify
$$\dfrac{4}{7}-\dfrac{8}{9}-\dfrac{13}{7}+\dfrac{17}{21}$$.
$$\dfrac {8}{2^{2}+1}+\dfrac {16}{2^{6}+1}+\dfrac {32}{2^{14}+1}+\dfrac {64}{2^{14}+1}+\dfrac {128}{2^{18}+1}=$$ ?
If $$1 \dfrac { 1 } { 4 } : 2 \dfrac { 1 } { 3 } = p : q$$ and $$q : r = 4 \dfrac { 1 } { 2 } : 5 \dfrac { 1 } { 4 } ,$$ find $$p : r$$
Compare the fractions.
$$\dfrac{3}{8}\square \dfrac{2}{4}$$.
Rahul studied science for $$\dfrac{1}{3}$$ hour and English for $$\dfrac{1}{3}$$ hour? How long did he study?
Compare the fractions.
$$\dfrac{4}{5}\square \dfrac{4}{8}$$.
Compare the fractions.
$$\dfrac{1}{4}\square \dfrac{1}{2}$$.
Simplify:$$1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{7}{5}}}$$
$$\left( -\dfrac { 2 }{ 3 } \right) ^{ 4 }-\left( -\dfrac { 3 }{ 4 } \right) ^{ 3 }$$
Verify$$\dfrac { 2 }{ 5 } +\dfrac { 1 }{ 3 } =\dfrac { 1 }{ 3 } +\dfrac { 2 }{ 5 } $$
Solve
$$5-\left(\dfrac {8}{11}-3\dfrac {3}{11}\right)$$
Simplify : $$\left[ \dfrac { 5 } { 6 } - \dfrac { 2 } { 12 } \right] - \left[ \dfrac { 6 } { 12 } - \dfrac { 1 } { 3 } \right]$$
Find the value of c if $$\dfrac1c=\dfrac23+\dfrac35$$
$$[3\frac { 1 }{ 4 } \div \{ 1\frac { 1 }{ 4 } -\frac { 1 }{ 2 } (2\frac { 1 }{ 2 } -{ \frac { 1 }{ 4 } -\frac { 1 }{ 6 } } )\} ]$$
Represent the following number on the number line:
$$\dfrac {2}{7}$$
Solve:
$$\dfrac{-5}{10}+\dfrac{6}{13}+8$$
Simplify:$$\dfrac{5}{3}+\dfrac{11}{2}+\dfrac{-9}{4}+\dfrac{-8}{3}+\dfrac{-7}{2}$$
A person earns $$Rs. 100$$ in a day. If he spents $$Rs. 14\dfrac {2}{7}$$ on food and $$Rs. 30\dfrac {2}{3}$$ on petrol. How much did he save on that day?
Simplify : $$\dfrac{2}{3}+3\dfrac{1}{6}+4\dfrac{2}{9}+2\dfrac{5}{18}$$
Subtract $$\dfrac{-3}{8}$$ from $$\dfrac{-5}{7}$$
Verify the following:$$\dfrac{-5}{8}+\dfrac{3}{5}=\dfrac{3}{5}+\dfrac{-5}{8}$$
I bought one dozen bananas and ate five of them.What fraction of the total number of bananas was left?
Solve
$$\left(\dfrac{1}{2}\right)^{-2}+\left(\dfrac{1}{3}\right)^{-2}+\left(\dfrac{1}{4}\right)^{-2}$$
Simplify:$$\dfrac{1}{3}+\dfrac{1}{6}$$
Anita put $$\dfrac{1}{4}$$ cup of flour in a bowl.Meena mixed $$\dfrac{1}{6}$$ cup of flour in it.How much more flour should Arti mix in it equal to $$1$$ cup of flour?
Solve:
$$\displaystyle \frac{5}{2} - \frac{3}{5} \times \frac{7}{2} + \frac{3}{5} \times \left( {\frac{{ - 2}}{3}} \right)$$
Steve is planning to bake 3 loaves of bread. Each loaf calls for $$5\frac{1}{4}$$ cups of flour. He knows he has 20 cups on hand . Will he have enough flour left for a cake recipe that requires $$3\frac{3}{4}$$ cups?
Simplify $$1\dfrac { 2 }{ 75 } -\dfrac { 3 }{ 8 } +\dfrac { 1 }{ 4 } $$.
Which is greater, the sum of $$\dfrac {-7}{12} $$ and $$\dfrac {2}{5}$$ of the sum of $$\dfrac {-3}{8}$$ and $$\dfrac {-11}{-12}$$, and by how much?
Show that $$\dfrac{3}{7}$$ lies between $$\dfrac{2}{5}$$ and $$\dfrac{5}{7}$$
Evaluate $$1\cfrac{2}{5} - \cfrac{3}{8} + \cfrac{1}{4} $$.
Solve:$$\dfrac{x+35}{6}-\dfrac{x+7}{9}=\dfrac{x+21}{4}$$
Evaluate $$
2 \dfrac{3}{4}+2 \dfrac{2}{3}
$$.
Simplify :- $$\dfrac { -2 }{ 3 } +\dfrac { 5 }{ 7 } + \dfrac { 14 }{ 11 } $$
(a)
| $$\dfrac{2}{3}$$ | $$\dfrac{4}{3}$$ | |
| $$\dfrac{1}{3}$$ | $$\dfrac{2}{3}$$ | |
| $$\dfrac{1}{2}$$ | $$\dfrac{1}{3}$$ | |
| $$\dfrac{1}{3}$$ | $$\dfrac{1}{4}$$ | |
Express $$\dfrac{-11}{9}$$ as a rational number with denominator $$-99$$
Simplify
$$\dfrac { 1 }{ 2 } \times\dfrac{1}{4}$$
Simplify $$\dfrac { 1 }{ 2 } -\dfrac { 1 }{ 3 } $$.
Simplify:$$3\dfrac{1}{5}$$ + $$\dfrac{6}{8}$$
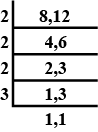
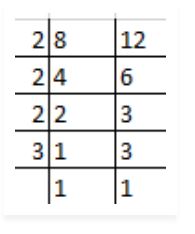
Find the reduced form of ratio $$\dfrac {38}{57}$$.
Express $$\dfrac{-11}{9}$$ as a rational number with denominator $$-18$$
Show $$\dfrac{2}{6}, \dfrac{4}{6}, \dfrac{8}{6}, \dfrac{5}{6}$$ and $$\dfrac{6}{6}$$ on the number line also arrange them in ascending order.
Solve: $$\dfrac{4}{5} + \dfrac{2}{3}$$
Solve: $$\dfrac{3}{10} + \dfrac{7}{15}$$
Find the reciprocal of $$\displaystyle {3 \over 5}$$, $$\displaystyle{9 \over {10}}$$, $$\displaystyle{3 \over 9}$$,$$\displaystyle{7 \over 4}$$ and $$\displaystyle{9 \over 2}$$ also classify them as proper and improper fractions.
Simplify $$\dfrac { 3 }{ 4 } +\dfrac { -2 }{ 5 } $$.
What can you say about the prime factorisation of the denominator of $$27.\overline {142857} $$
Mary bought $$3\dfrac { 1 }{ 2 } $$ m of lace. show used $$1\dfrac { 3 }{ 4} $$ m of lace for her new dress How much lace in left with her?
Asha and Samuel have bookshelves of the same size partly filled with books. Asha's shelf is $$\dfrac { 5 }{ 6 } $$th full and Samuel's shelf is $$\dfrac { 2 }{ 5 } $$th full. Whose bookshelf is more full? By what fraction?
Add the following fractions.
$$\dfrac { 3 }{ 2 } ,\dfrac { 13 }{ 17 } $$
Add the following fractions.
$$\dfrac { -7 }{ 9 } ,\dfrac { -3 }{ 4 } $$
Jaidev takes $$2\dfrac { 1 }{ 5 } $$ minutes to walk across the school ground. Rahul takes $$\dfrac { 7 }{ 4 } $$ minutes to do the same. who takes less time and by what fraction?
$$7$$ hours $$=$$ ________ fraction of a day.
subract 2 from 6
Write these fractions appropriately as additions or subtractions:
Simplify : $$6+\left \{ \frac{4}{3} (\frac{3}{4}-\frac{1}{3}) \right \}$$
$$3-\dfrac{12}{5}$$.
Find the sum : $$\dfrac{3}{4}+\dfrac{5}{6}+\dfrac{11}{8}$$
Solve:
$$\dfrac {8}{15} + \dfrac {3}{15}$$
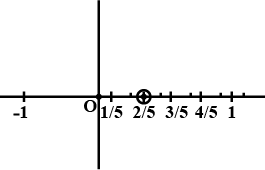
Represent $$\dfrac {2}{5}$$ on a number line.
Solve :
$$\dfrac { 1 }{ 4 } +\dfrac { 0 }{ 4 } $$
Express the following as improper fractions:
$$7\dfrac {3}{4}$$
Represent $$\dfrac {0}{8}$$ and $$\dfrac {8}{8}$$ on a number line.
Convert each of the following into a mixed fractions:
$$\dfrac {145}{9}$$
Convert each of the following into an improper fraction:
$$5\dfrac {3}{10}$$
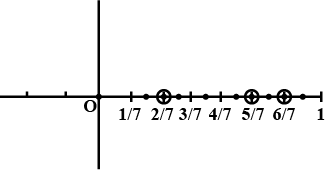
Represent $$\dfrac {2}{7}, \dfrac {5}{7}$$ and $$\dfrac {6}{7}$$ on a number line.
Convert each of the following into an improper fraction:
$$7\dfrac {1}{4}$$
Convert each of the following into a mixed fractions:
$$\dfrac {226}{15}$$
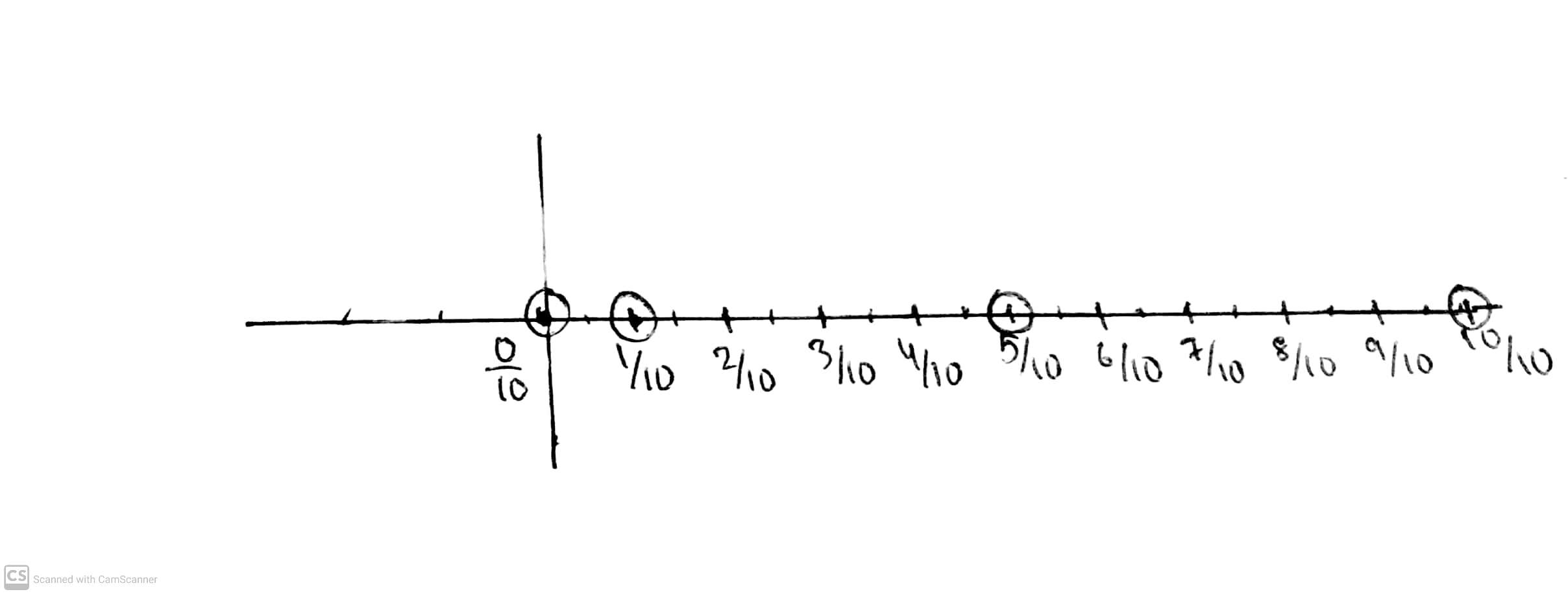
Represent $$\dfrac {0}{10}, \dfrac {1}{10}, \dfrac {5}{10}$$ and $$\dfrac {10}{10}$$ on a number line.
Convert each of the following into an improper fraction:
$$8\dfrac {5}{7}$$
Convert each of the following into a mixed fractions:
$$\dfrac {128}{5}$$
Convert each of the following into a mixed fractions:
$$\dfrac {28}{9}$$
Solve :
$$\dfrac {7}{31} - \dfrac {4}{31} + \dfrac {9}{31}$$
Solve:
$$\dfrac {3}{22} + \dfrac {7}{22}$$
Write these fractions appropriately as addition or subtractions.

Solve:
$$\dfrac {0}{15} + \dfrac {2}{15} +\dfrac {1}{15}$$
Convert each of the following into an improper fraction:
$$12\dfrac {7}{15}$$
Solve :
$$\dfrac {4}{13} + \dfrac {2}{13} + \dfrac {1}{13}$$
Arrange the following fractions in the ascending order:
$$\dfrac {3}{5}, \dfrac {1}{5}, \dfrac {4}{5}, \dfrac {2}{5}$$
Arrange the following fractions in the ascending order:
$$\dfrac {37}{47}, \dfrac {37}{50}, \dfrac {37}{100}, \dfrac {37}{1000}, \dfrac {37}{85}, \dfrac {37}{41}$$
Find the equivalent fraction of $$\dfrac {3}{5}$$, having:
numerator $$9$$
Solve:
$$\dfrac {1}{4} + \dfrac {0}{4}$$
Replace $$\square$$ by the correct number.
$$\square - \dfrac {1}{5} = \dfrac {1}{2}$$
Find the sum:
$$4\dfrac{3}{4}+9\dfrac{2}{5}$$
Find the sum:
$$\dfrac{5}{6}+3+\dfrac{3}{4}$$
Find the difference of
$$\dfrac{21}{25}$$ and $$\dfrac{18}{20}$$
Replace $$\square$$ by the correct number :
$$\dfrac {1}{2} - \square = \dfrac {1}{6}$$.
Replace $$\square$$ by the correct number.
$$\square - \dfrac {5}{8} = \dfrac {1}{4}$$
Find the difference of
$$\dfrac{13}{24}$$ and $$\dfrac{7}{16}$$
Find the sum:
$$2\dfrac{3}{5}+4\dfrac{7}{10}+2\dfrac{4}{15}$$
Find the sum:
$$\dfrac{5}{8}+\dfrac{3}{10}$$
Find the difference of
$$6$$ and $$\dfrac{23}{3}$$
Simplify:
$$\dfrac{2}{3}+\dfrac{1}{6}-\dfrac{2}{9}$$
Write down the numerator of each of the following rational numbers:
$$\dfrac{-17}{-25}$$
Write down the numerator of each of the following rational numbers:
$$\dfrac{15}{-4}$$
Find the difference of
$$8-\dfrac{5}{9}$$
Find the difference of
$$3\dfrac{3}{10}$$ and $$\dfrac{7}{15}$$
Find the difference of
$$4\dfrac{3}{10}-1\dfrac{2}{15}$$
Simplify:
$$7\dfrac{5}{6}-4\dfrac{3}{8}+2\dfrac{7}{12}$$
Find the difference of
$$9-5\dfrac{2}{3}$$
Write down the numerator of each of the following rational numbers:
$$\dfrac{-7}{5}$$
Find the difference of
$$\dfrac{6}{7}-\dfrac{9}{11}$$
Write the following rational numbers as integers:
$$\dfrac{95}{1}$$
Write down the denominator of the following rational number:
$$\dfrac{-15}{-82}$$
Express $$\dfrac{2}{5}$$ as a rational number with numerator :
$$500$$
Write the following rational numbers as integers:
$$\dfrac{34}{1}$$
Express $$\dfrac{2}{5}$$ as a rational number with numerator :
$$-750$$
Write the following rational numbers as integers:
$$\dfrac{-73}{1}$$
Write down the numerator of each of the following rational numbers:
$$\dfrac{8}{9}$$
Write down the denominator of each of the following rational numbers:
$$\dfrac{-4}{5}$$
Write down the denominator of each of the following rational numbers:
$$15$$
Write the following integers as rational numbers with denominator $$1$$:
$$-15$$
Express $$\dfrac{-192}{108}$$ as a rational number with numerator:
$$-48$$
Express $$\dfrac{168}{-294}$$ as a rational number with denominator:
$$-49$$
Express $$\dfrac{-192}{108}$$ as a rational number with numerator:
$$-16$$
Write $$\dfrac{-14}{42}$$ in a form so that the numerator is equal to:
$$-2$$
Write $$\dfrac{-14}{42}$$ in a form so that the numerator is equal to:
$$7$$
Express $$\dfrac{168}{-294}$$ as a rational number with denominator:
$$1470$$
Express $$\dfrac{-192}{108}$$ as a rational number with numerator:
$$32$$
Write $$\dfrac{-14}{42}$$ in a form so that the numerator is equal to:
$$-70$$
Write $$\dfrac{-14}{42}$$ in a form so that the numerator is equal to:
$$42$$
Express $$\dfrac{-192}{108}$$ as a rational number with numerator:
$$64$$
Write each of the following rational numbers in the standard form:
$$\dfrac{299}{-161}$$
Write each of the following rational numbers in the standard form:
$$\dfrac{68}{-119}$$
Write each of the following rational numbers in the standard form:
$$\dfrac{4}{-16}$$
Write each of the following rational numbers in the standard form:
$$\dfrac{-63}{-210}$$
Write each of the following rational numbers in the standard form:
$$\dfrac{-195}{275}$$
Write each of the following rational numbers in the standard form:
$$\dfrac{2}{10}$$
Write each of the following rational numbers in the standard form:
$$\dfrac{-15}{-35}$$
Fill in the blanks so as to make the statement true:
The standard form of $$-1$$ is ______
Write each of the following rational numbers in the standard form:
$$\dfrac{-8}{36}$$
Evaluate each of the following:
$$-\dfrac{4}{7} - \dfrac{2}{-3}$$
Evaluate each of the following:
$$\dfrac{4}{7} - \dfrac{-5}{-7}$$
Evaluate each of the following:
$$\dfrac{2}{3} - \dfrac{3}{5}$$
Simplify:
$$\dfrac{-8}{19} + \dfrac{-4}{57}$$
Simplify:
$$\dfrac{8}{9} + \dfrac{-11}{6}$$
Add and express the sum as a mixed fraction :
$$\dfrac{-31}{6}$$ and $$\dfrac{-27}{6}$$
Add and express the sum as a mixed fraction :
$$\dfrac{24}{7} + \dfrac{-11}{7}$$
Add and express the sum as a mixed fraction :
$$\dfrac{-12}{5} + \dfrac{43}{10}$$
Simplify:
$$\dfrac{-5}{16} + \dfrac{7}{24}$$
Simplify:
$$\dfrac{1}{-12} + \dfrac{2}{-15}$$
What number should be subtracted from $$\dfrac{3}{7}$$ to get $$\dfrac{5}{4}$$ ?
Evaluate each of the following:
$$-2 - \dfrac{5}{9}$$
What should be added to $$\displaystyle \left(\frac{1}{2} + \frac{1}{3} + \frac{1}{5}\right)$$ to get $$3$$?
What should be added to $$\left(\dfrac{2}{3} + \dfrac{3}{5}\right)$$ to get $$\dfrac{-2}{15}$$?
What number should be added to $$\dfrac{-5}{11}$$ so as to get $$\dfrac{26}{33}$$?
Simplify:
$$\displaystyle \frac{-3}{2} + \frac{5}{4} -\frac{7}{4}$$
What should be subtracted from $$\left(\dfrac{3}{4} - \dfrac{2}{3} \right)$$ to get $$\dfrac{-1}{6}$$?
Simplify:
$$\displaystyle \frac{5}{4} -\frac{7}{6} -\frac{-2}{3}$$
Simplify:
$$\displaystyle \frac{5}{3} - \frac{7}{6} + \frac{(-2)}{3}$$
What number should be added to $$\dfrac{-5}{7}$$ to get $$\dfrac{-2}{3}$$?
Subtract : $$\dfrac {-13}{9}$$ from $$0$$.
Simplify:
$$\displaystyle \left(\frac{-9}{4} \times \frac{5}{3}\right) + \left(\frac{13}{2} \times \frac{5}{6}\right)$$
Fill in the blanks:
$$\dfrac{-4}{13} - \dfrac{-3}{26} = ...$$
Fill in the blanks:
$$\dfrac{-7}{9} + ... = 3$$
Fill in the blanks:
$$\dfrac{-9}{14}+.... = -1$$
Subtract :
$$\dfrac {-7}{1}$$ from $$\dfrac {-4}{7}$$.
Subtract :
$$\dfrac {-32}{13}$$ from $$\dfrac {-6}{5}$$.
Subtract :
$$\dfrac {-8}{9}$$ from $$\dfrac {-3}{5}$$.
Fill in the blanks:
$$.... + \dfrac{15}{23} = 4$$
Subtract :
$$\dfrac {-9}{7}$$ from $$\dfrac {-1}{1}$$.
Find the following ratio in the simplest form:
$$24$$ to $$56$$
Using the rearrangement property find the sum:
$$\dfrac {4}{3} + \dfrac {3}{5} + \dfrac {-2}{3} + \dfrac {-11}{5}$$.
On one day a rickshaw puller earned $$Rs. 160$$. Out of his earnings he spent $$Rs. 26 \dfrac 35$$ on tea and snacks. $$Rs. 50 \dfrac {1}{2}$$ on food and $$Rs. 16 \dfrac 25$$ on repairs of the rickshaw. How much did he save on that day?
What number should be added to $$\dfrac {-5}{8}$$ so as to get $$\dfrac {-3}{2}$$?
What number should be added to $$-1$$ so as to get $$\dfrac {5}{7}$$?
Find the following ratio in the simplest form:
$$84$$ paise to Rupees $$3$$
Using the rearrangement property find the sum:
$$\dfrac {-6}{7} + \dfrac {-5}{6} + \dfrac {-4}{9} + \dfrac {-15}{7}$$.
Using the rearrangement property find the sum:
$$\dfrac {-8}{3} + \dfrac {-1}{4} + \dfrac {-11}{6} + \dfrac {3}{8}$$.
Using the rearrangement property find the sum:
$$\dfrac {-13}{20} + \dfrac {11}{14} + \dfrac {-5}{7} + \dfrac {7}{10}$$.
What number should be subtracted from $$\dfrac {-2}{3}$$ to get $$\dfrac {-1}{6}$$?
Find the each of the following ratios in the simplest form:
$$2.4\ km$$ to $$900\ m$$
Find the following ratio in the simplest form:
$$4\ kg$$ to $$750\ g$$
Find the following ratio in the simplest form:
$$1.8\ kg$$ to $$6\ kg$$
Express the following ratio in simplest form:
$$85:561$$
Express the following ratio in simplest form:
$$36:90$$
Express the following ratio in simplest form:
$$480:384$$
Express each of the following ratio in the simplest form:
$$777:1147$$
Express the following ratio in the simplest form:
$$186:403$$
Express the following ratio in simplest form:
$$324:144$$
Find the following ratio in the simplest form:
$$48$$ Minutes to $$1$$ Hour
Write the following ratio in the simplest form:
$$3$$ weeks: $$30$$ days
Write the following ratio in the simplest form:
$$48\ min:2\ hrs\ 40\ min$$
Write the following ratio in the simplest form:
$$1\ L\ 35\ mL: 270\ mL$$
Find the difference:
$$\dfrac58-\dfrac7{12}$$
Write the following ratio in the simplest form:
$$4\ kg : 2\ kg\ 500\ g$$
Write the following ratio in the simplest form:
Rupees $$6.30$$: Rupees $$16.80$$
Write the following ratio in the simplest form:
$$3\ m\ 5\ cm : 35\ cm$$
Find the sum
$$3\dfrac{4}{5}+2\dfrac{3}{10}+1\dfrac{1}{15}$$
Find the difference
$$3\dfrac{1}{5}-\dfrac{7}{10}$$
Divide the sum of $$(65/12)$$ and $$(8/3)$$ by their difference.
Find the sum
$$\cfrac{5}{9} + \cfrac{3}{9}$$
Find the difference
[2(5/9)]-[1(7/15)]
Find the sum
(8/9)+(7/12)
Find the difference
$$\left( {\dfrac{5}{7}} \right) - \left( {\dfrac{2}{7}} \right)$$
Find the difference
(5/6)-(3/4)
Find the difference
$$7-\left[4\left(\cfrac{2}{3}\right)\right]$$
Find the difference
$$3\dfrac{3}{10}-1\dfrac{7}{15}$$
Simplify: $$8-[4(1/2)]-[2(1/4)]$$
What number must be added to each term of the ratio $$9:16$$ to make the ratio $$2:3$$
Simplify: (2/3)+(5/6)-(1/9)
Aneeta bought $$3\dfrac{3}{4}$$ kg apples and $$4\dfrac{1}{2}$$ kg guava. What is the total weight of fruits purchased by her?
What number must be subtracted from each term of the ratio $$17:33$$ so that the ratio becomes $$7:15$$?
A number representing a part of a _____ is called a fraction.
$$ 13 \dfrac{5}{18} $$ Is a _____ fraction.
$$ \dfrac{7}{19} $$ Is a _____ fraction.
$$ \dfrac{18}{8} $$ Is a _____ fraction.
A fraction with denominator greater than the numerator is called a _____ fraction.
$$ \dfrac{67}{14} - \dfrac{24}{14} $$=_____.
$$ \dfrac{17}{9} + \dfrac{41}{9} $$=_____.
$$ \dfrac{11}{16}.....\dfrac{14}{15} $$
The fraction $$ \frac{6}{15} $$ in simplest form is _____.
The fraction $$ \dfrac{17}{34} $$ in simplest form is _____.
$$ \dfrac{12}{75}.....\dfrac{32}{200} $$
Express $$ 6 \dfrac{2}{3} $$ as an improper fraction.
Katrina rode her bicycle $$ 6\dfrac{1}{2} km $$ in the morning and $$ 8\dfrac{3}{4} km $$ in the evening. Find the distance traveled by her altogether on that day.
Add $$ 1 \dfrac{1}{4} $$ and $$ 6 \dfrac{1}{2} $$.
Add the fractions $$ \dfrac{3}{8} $$ and $$ \dfrac{2}{3} $$.
(i) What number should be added to $$\dfrac{5}{12} $$ to get $$2 \dfrac{2}{8}$$ ?
(ii) What number should be subtracted from $$5$$ to get $$1 \dfrac{5}{13}$$ ?
$$ \dfrac{18}{15}.....1.3 $$
Subtract $$ 1 \dfrac{1}{4} $$ from $$ 6 \dfrac{1}{2} $$.
$$ \dfrac{8}{15}.....\dfrac{95}{14} $$
Subtract $$ \dfrac{1}{6} $$ from $$ \dfrac{1}{2}. $$
On an average $$ \frac{ 1}{10} $$ the food eaten is turned into organism's own body and is available for the next level of the consumer in a food chain. What fraction of the food eaten is not available for the next level?
Sunil purchased $$ 12 \dfrac {1}{2} $$ litres of juice on Monday and $$ 14 \dfrac {3}{4} $$ litres of juice on Tuesday . How many litres of juice did he purchase together in two days?
Nasir travelled $$ 3 \frac {1}{2} $$ km in a bus and then walked $$ 1 \frac {1}{8} km $$ to reach a town . How much did he travel to reach the town ?
The fish caught by neetu was of weight $$ 3 \frac {3}{4} Kg $$ and the fish caught by Narendra was of weight $$ 2 \frac {1}{2} kg $$
How much more did Neetu's fish weigh than that of Narendra ?
Write a pair of fractions whose sum is $$ \frac {7}{11} $$ and difference is $$ \frac {2}{11} $$.
A bamboo of length $$2 \dfrac{3}{4} $$ metre broke into two pieces. One piece was $$\dfrac{7}{8}$$ metre long. How long is the other pieces ?
When Sunita weighted herself on monday. She found that she had gained $$ 1 \dfrac {1}{4} $$ kg. earlier her weight was $$ 46 \dfrac {3}{8} kg $$ What was her weight on monday ?
What is wrong in the following additions ?
Nazima gave $$ 2 \frac {3}{4} $$litres out of $$ 5 \frac {1}{2} litres $$ of juice she purchased to her friends.how many litres of juice is left with her ?
Neelam's father needs $$ 1 \dfrac {3}{4}m $$ of cloth for the skirt of neelam's new dress and $$ \dfrac {1}{2} m $$ for the scarf. How much cloth must he but in all?
Asha and Samuel have bookshelves of the same size partly filled with books. Asha's shelf is $$\dfrac{5}{6}$$ full and Samuel's shelf is $$\dfrac{3}{5}$$ full. Whose bookshelf is more full and by what fraction?
Will be quotient
$$7\frac{1}{6} +3\frac{2}{3}$$ be a fraction greater
than 1.5 or less than 1.5? Explain.
Reemu read $$\dfrac{1}{5}th$$ pages of a book. If she reads further $$40$$ pages, she would have read $$\dfrac{7}{10} $$th pages of the book. How many pages are left to be read?
Using suitable rearrangement and find the sum:
$$-5 + \dfrac{7}{10} + \dfrac{3}{7} + (-3) + \dfrac{5}{14} + \dfrac{-4}{5}$$
In the morning, a milkman filled $$5\frac{1}{5}$$L of milk in his can. He sold to Renu, Kamla and Renuka $$\frac{3}{4 }L$$ each; to Shadma he sold $$\frac{7}{8}$$L; and to Jassi he gave $$1\frac{1}{2}L$$. How much milk is left in the can?
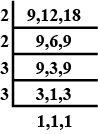
Four friends had a competition to see how far they could hop on one foot. the table given shows the distance covered by each.
| Name | Seema | Nancy | Megha | Soni |
| Distance covered (km) | $$\dfrac{1}{25}$$ | $$\dfrac{1}{32}$$ | $$\dfrac{1}{40}$$ | $$\dfrac{1}{20}$$ |
(b) What is the total distance covered by Seema and Megha?
(c) Who walked farther, Nancy or Megha?
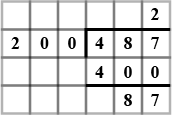
The diagram shows the wingspans of different species of birds. Use the diagram to answer the question given below:
(a) How much longer is the wingspan of an Albatross than the wingspan of a Sea gull ?
(b) How much longer is the wingspan of a Golden eagle than the wingspan of a Blue jay ?

From the following fractions, separate:
(i) Proper fractions
(ii) Improper fractions:
2 / 9, 4 / 3, 7 / 15, 11 / 20, 20 / 11, 18 / 23 and 27 / 35
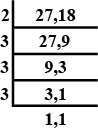
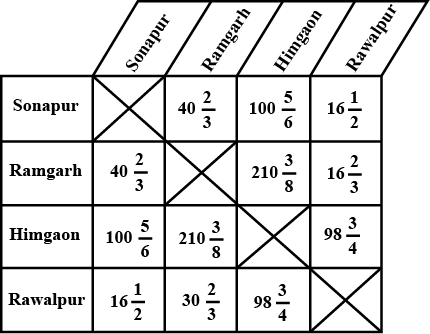
The table given below shows the distances, in kilometres, between four villages of a state. To find the distance between two villages, locate the square where the roe for one village and the column for the other village intersect.
(a) Compare the distance between Himgaon and Rawalpur to Sonapur and Ramgarh ?
(b) If you drove from Himgaon to Sonapur and then from Sonapur to Rawalpur, how far would you drive ?
Simplify-
$$\dfrac{3}{7} + \dfrac{-2}{21} \times \dfrac{-5}{6}$$
Evaluate the following:
(i) $$\dfrac{4}{3} + \dfrac{7}{8}$$ (ii) $$8 \dfrac{1}{2} - 3 \dfrac{5}{8}$$
(ii) $$\dfrac{5}{12}+ \dfrac{1}{18}- \dfrac{2}{9}$$
Add the following fractions:
(i) $$1\dfrac { 3 }{ 4} $$ and $$\dfrac{3 }{ 8}$$
(ii) $$\dfrac{2}{ 5}$$, $$2\dfrac { 3 }{ 15} $$ and $$\dfrac{7} { 10}$$
(iii) $$1\dfrac { 7 }{ 8} $$, $$1\dfrac { 1 }{ 2} $$ and $$1\dfrac { 3 }{ 4} $$
(iv) $$3\dfrac { 3 }{ 4} $$, $$2\dfrac { 1 }{ 6} $$, and $$1\dfrac { 5 }{ 8} $$
(v)$$2\dfrac { 8 }{ 11} $$ , $$\dfrac{11}{ 18}$$ and $$3\dfrac { 5 }{ 6} $$
A skirt that is $$35\dfrac{7}{8}\,cm$$ long has a hem of $$3\dfrac{1}{8} \,cm.$$ How long will the skirt be if the hem is let down ?
Classify each fraction given below as decimal or vulgar fraction, proper or improper fraction and mixed faction
11/10
Simplify the following:
(i) $$7 \dfrac{3}{4} - 3 \dfrac{5}{6} + \dfrac{7}{8}$$
(ii) $$6 \dfrac{1}{8} - 2 \dfrac{1}{12} - 5 \dfrac{1}{10} + 3 \dfrac{7}{25}$$
Convert given fractions into fractions with equal numerators:
6/13, 15/23 and 12/17
Convert given fractions into fractions with equal numerators:
15/19, 25/28, 9/11 and 45/47
Classify each fraction given below as decimal or vulgar fraction, proper or improper fraction and mixed faction
$$3 \dfrac{2}{9}$$
Classify each fraction given below as decimal or vulgar fraction, proper or improper fraction and mixed faction
18/7
Convert given fractions into fractions with equal denominators:
5/6 and 7/9
Put the given fractions in ascending order by making denominators equal:
$$1/3, 2/5, 3/4$$ and $$1/6$$
Convert given fractions into fractions with equal denominators:
$$4/5, 17/20, 23/20$$ and $$11/16$$
Convert given fractions into fractions with equal numerators:
8/9 and 12/17
Convert given fractions into fractions with equal denominators:
2/3, 5/6 and 7/12
Classify each fraction given below as decimal or vulgar fraction, proper or improper fraction and mixed faction
13/20
The heights of two vertical poles, above the earth's surface, are $$14 \dfrac{1}{2}$$ m and $$22 \dfrac{1}{3}$$ m respectively. How much higher is the second pole as compared with the height of the first pole?
Arrange the given fractions in descending order by making numerators equal :
$$3/7, 4/9, 5/7$$ and $$8/11$$
A student bought $$4 \dfrac{1}{3}$$ m of yellow ribbon, $$6 \dfrac{1}{6}$$ m of red ribbon and $$3 \dfrac{2}{9}$$ m of blue ribbon decorating a room. How many meters of ribbon did he buy?
Arrange the given fractions in descending order by making numerators equal:
$$1/10, 6/11, 8/11$$ and $$3/5$$
Put the given fractions in ascending order by making denominators equal:
$$5/6, 7/8, 11/12$$ and $$3/10$$
From a sack of potatoes weighing 120 kg, a merchant sells portions weighing $$6 kg, 5 \dfrac{1}{4} kg, 9 \dfrac{1}{2} kg$$ and $$9 \dfrac{3}{4}$$ kg respectively.
(i) How many kg did he sell?
(ii) How many kg are still left in the sack?
Reduce to a single fraction:
$$2/3 - 1/6$$
Arrange the given fractions in descending order by making numerators equal:
$$5/6, 4/15, 8/9$$ and $$1/3$$
Put the given fractions in ascending order by making denominators equal:
$$5/7, 3/8, 9/14$$ and $$20/21$$
Reduce to a single fraction:
$$3/5 - 1/10$$
Subtract :
$$ \dfrac{5}{8} From \dfrac{-3}{8}$$
A rectangular field is $$ 16 \dfrac{1}{2} m$$ long and $$ 12 \dfrac{2}{5} m$$ wide. Find the perimeter of the field.
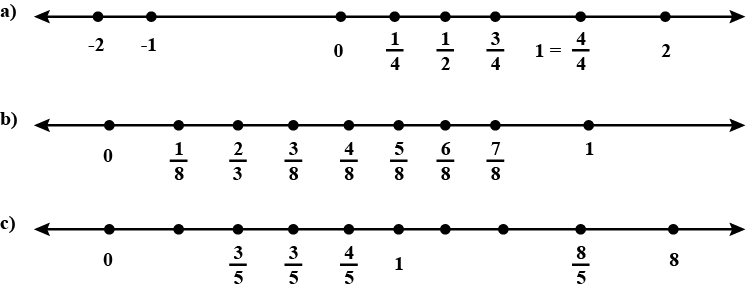
Draw number lines and locate the points on them:
a) $$\frac{1}{2}, \frac{1}{4}, \frac{3}{4},\frac{4}{4}$$
b) $$\frac{2}{5}, \frac{3}{5}, \frac{8}{5},\frac{4}{5}$$
c) $$\frac{2}{5}, \frac{3}{5}, \frac{8}{5},\frac{4}{5}$$
Which is greater, 3/5 or 7/10 and by how much?
Subtract:
2/9 from 4/5
A bought $$3 \dfrac{3}{4}$$ kg of wheat and $$2 \dfrac{1}{2}$$ kg of rice. Find the total weight wheat and rice bought.
Solve:
$$\frac{5}{7} + \frac{1}{3}$$
Reduce to a single fraction:
$$2/3 - 3/5 + 3 - 1/5$$
Reduce to a single fraction:
$$2/3 - 1/5 + 1/10$$
Reduce to a single fraction:
1/4 + 5/6 - 1/12
Fill in the missing fraction
(a) $$\frac{7}{10} - \Box = \frac{3}{10}$$
(b) $$\Box - \frac{3}{21} = \frac{5}{21}$$
(c) $$\Box - \frac{3}{6} = \frac{3}{6}$$
(d) $$\Box + \frac{5}{27} = \frac{12}{27}$$
Solve:
$$4 \frac{2}{3} + 3 \frac{1}{4}$$
Solve:
$$\frac{4}{3} - \frac{1}{2}$$
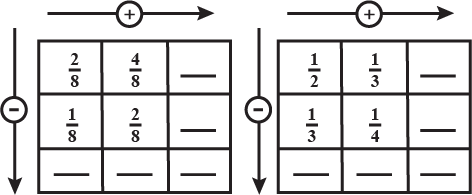
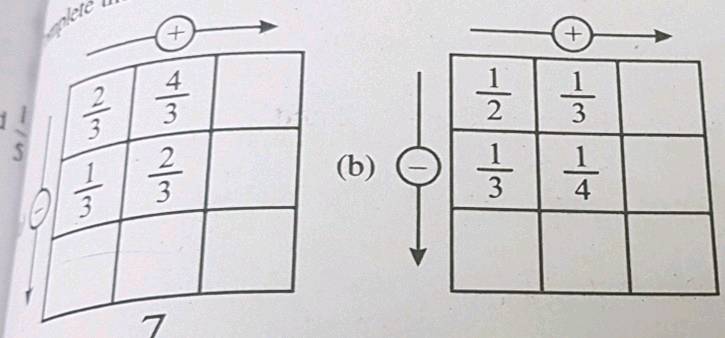
Complete the addition - subtraction box.

Solve:
$$\frac{16}{5} - \frac{7}{5}$$
Fill in the blanks:
$$\Box - \frac{1}{5} = \frac{1}{2}$$
Fill in the blanks:
$$\frac{1}{2} - \Box = \frac{1}{6}$$
Solve
(a) $$\frac{1}{18} + \frac{1}{18}$$
(b) $$\frac{8}{15} + \frac{3}{15}$$
(c) $$\frac{7}{7} - \frac{5}{7}$$
(d) $$\frac{1}{22}+ \frac{21}{22}$$
(e) $$\frac{12}{15} - \frac{7}{15}$$
(f) $$\frac{5}{8} + \frac{3}{8}$$
(g) $$1 - \frac{2}{3} \Big( 1 = \frac{3}{3}\Big)$$
(h) $$\frac{1}{4} + \frac{0}{4}$$
Fill in the blanks:
$$\Box - \frac{5}{8} = \frac{1}{4}$$
Complete the addition - subtraction box.
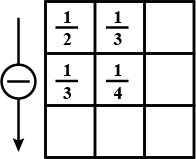
Simply the following :
(i) $$\left( \frac { 25 }{ 9 } +\frac { 12 }{ 3 } \right) +\frac { 3 }{ 5 } $$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\dfrac{2^{-2} + 2^{0}}{\left(\dfrac{1}{2}\right)^{-2} - 5 \cdot (-2)^{-2} + \left(\dfrac{2}{3}\right)^{-2}}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\dfrac{(0. 6)^{0} - (0.1)^{-1}}{\left(\dfrac{3}{2^3}\right)^{-1} \cdot \left(\dfrac{3}{2}\right)^3 + \left(-\dfrac{1}{3}\right)^{-1}}$$
Solve the following:
$$\displaystyle\frac{x - 1}{x^{3/4} + x^{1/2}}\, \cdot \frac{x^{1/2} + x^{1/4}}{x^{1/2}+ 1}\, \cdot x^{1/4} + 1$$ for $$x = 16$$
Solve the following:
$$\displaystyle\dfrac{a^3 - a - 2b - \dfrac{b^2}{a}}{\left ( 1 - \sqrt{\dfrac{1}{a} + \dfrac{b}{a^2}} \right )(a + \sqrt{a + b})}: \left ( \dfrac{a^3 + a^2 + ab + a^2b}{a^2 - b^2} + \dfrac{b}{a - b} \right )$$ for $$a =23, b = 22$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\frac{3\dfrac{1}{3} \sqrt{\dfrac{9}{80}} - \dfrac{5}{4} \sqrt{\dfrac{4}{5}} + 5 \sqrt{\dfrac{1}{5}} + \sqrt{20} - 10\sqrt{0.2}} {3\dfrac{1}{2} \sqrt{32} - \sqrt{4\dfrac{1}{2}} + 2 \sqrt{\dfrac{1}{8}} + 6\sqrt{\dfrac{2}{9}} - 140\sqrt{0.02}} \, \sqrt{\dfrac{2}{3}}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
Find $$x$$ if $$\displaystyle\frac{0.1 (6) + 0.(3)}{0.(3) + 1.1 (6)} \, x = 10$$ Calculate (5 31)
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \left ( \frac{1}{(a^{1/2} + b^{1/2})^{-2}} \right ) - \left ( \frac{\sqrt{a} - \sqrt{b}}{a^{3/2} - b^{3/2}} \right )^{-1} (ab)^{-1/2}$$
Subtract:
$$\dfrac{4}{5}$$ from $$\dfrac{1}{2}$$
$$\dfrac{1}{2}+\dfrac{3}{4}+\dfrac{5}{3}$$.
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, 2(a + b)^{-1} (ab)^{1/2}\left ( 1 + \frac{1}{4}\left ( \sqrt{\frac{a}{b}} - \sqrt{\frac{b}{a}} \right )^2 \right )^{1/2}$$
Can a mixed fraction have the form $$2 \dfrac{5}{2}$$?
Compare the fractions.
$$\dfrac{1}{3}\square \dfrac{7}{8}$$.
Compare the fractions.
$$\dfrac{1}{6}\square \dfrac{3}{4}$$.
Find the difference of $$\frac{7}{12}$$ and $$-\frac{19}{30}$$
Simplify:
$$\displaystyle \left(\frac{13}{9} \times \frac{-15}{2}\right) + \left(\frac{7}{3} \times \frac{8}{5}\right) + \left(\frac{3}{5} \times \frac{1}{2}\right)$$
Simplify:
$$\displaystyle \frac{-2}{5} - \frac{-3}{10} - \frac{-4}{7}$$
Simplify:
$$\displaystyle \left(\frac{3}{11} \times \frac{5}{6}\right) - \left(\frac{9}{12} \times \frac{4}{3}\right) + \left(\frac{5}{13} \times \frac{6}{15}\right)$$
$$\dfrac{6}{3}-\left(\dfrac{7}{15}\right)$$.
Class 6 Maths Extra Questions
- Algebra Extra Questions
- Basic Geometrical Ideas Extra Questions
- Data Handling Extra Questions
- Decimals Extra Questions
- Fractions Extra Questions
- Integers Extra Questions
- Knowing Our Numbers Extra Questions
- Mensuration Extra Questions
- Playing With Numbers Extra Questions
- Practical Geometry Extra Questions
- Ratio And Proportion Extra Questions
- Symmetry Extra Questions
- Understanding Elementary Shapes Extra Questions
- Whole Numbers Extra Questions