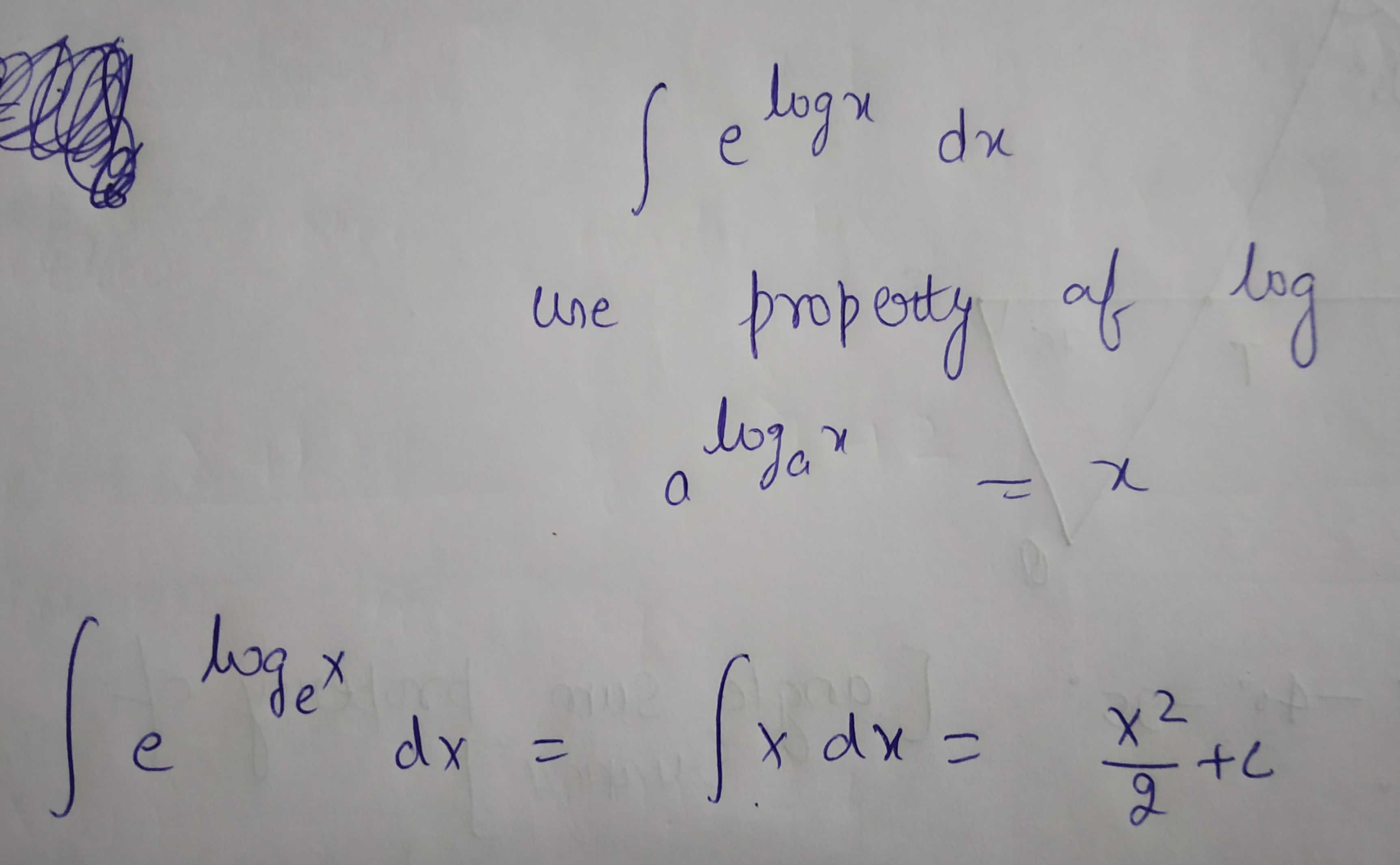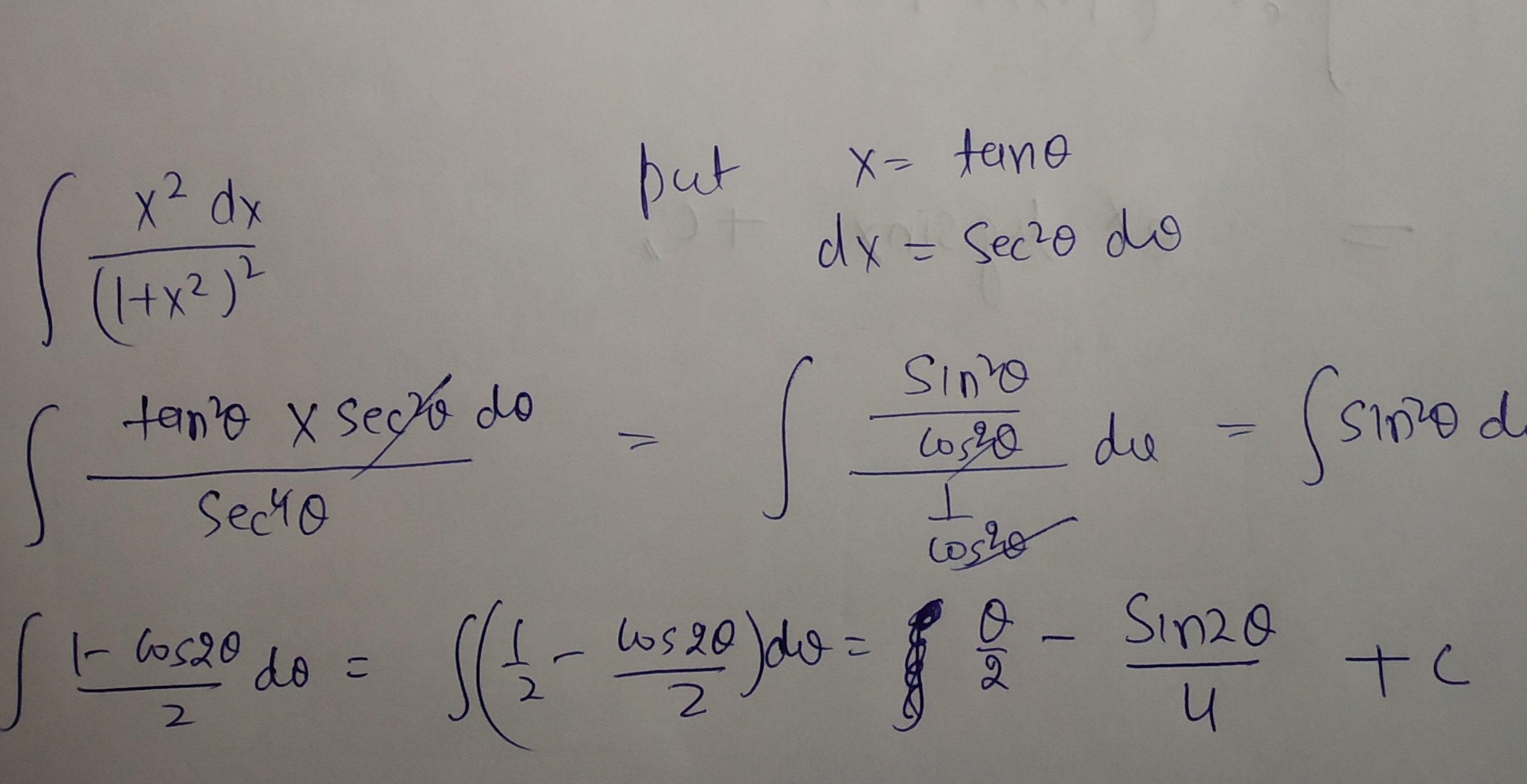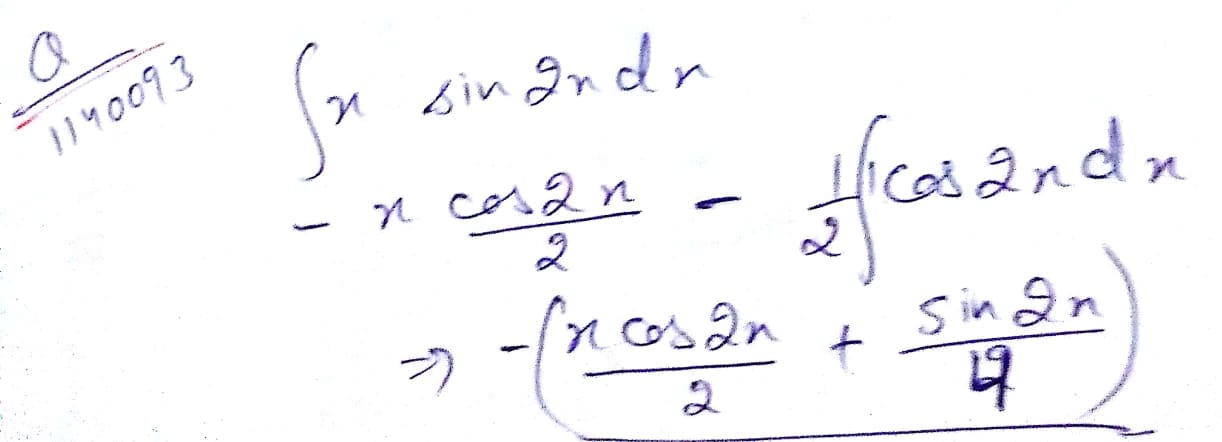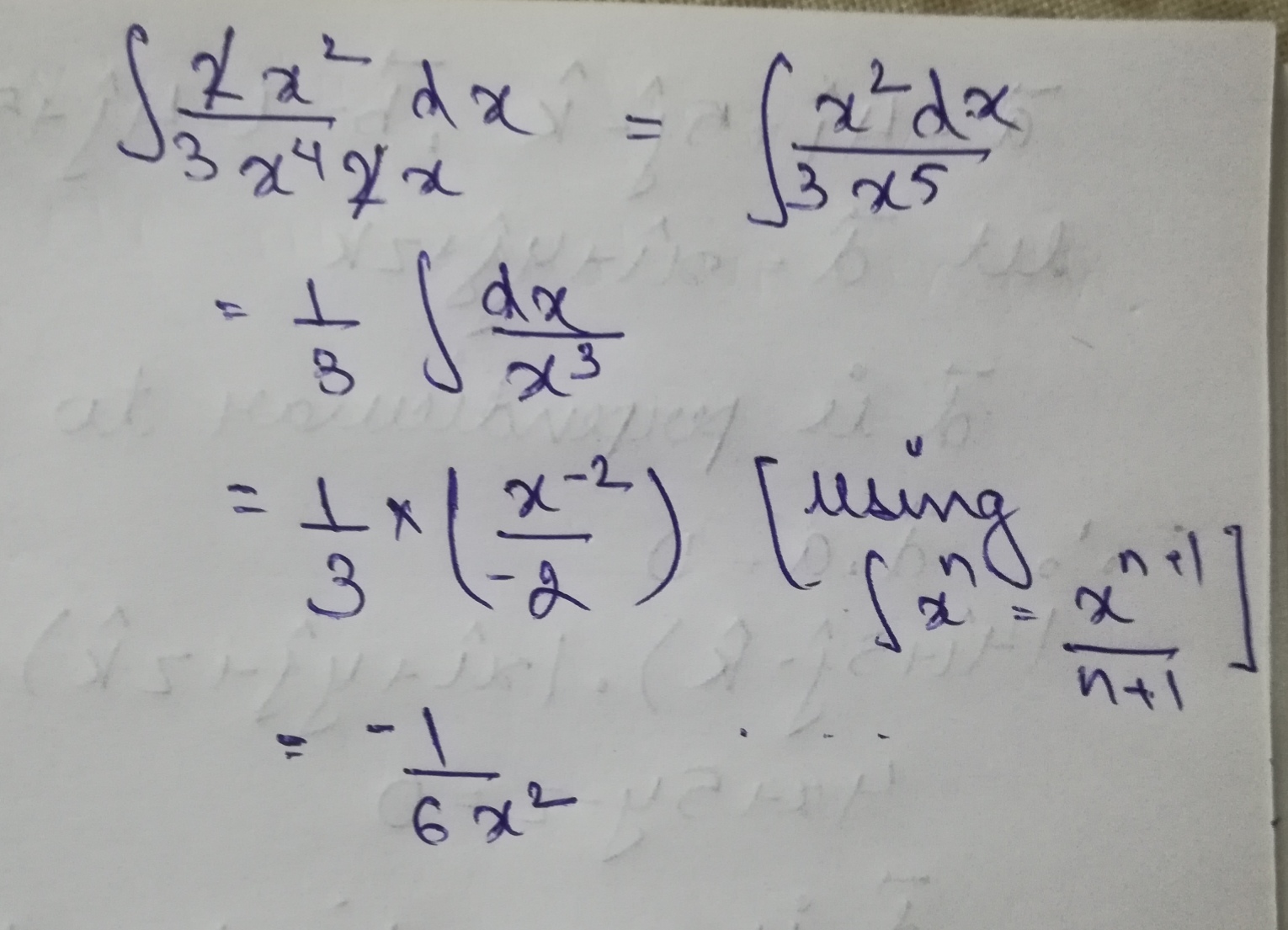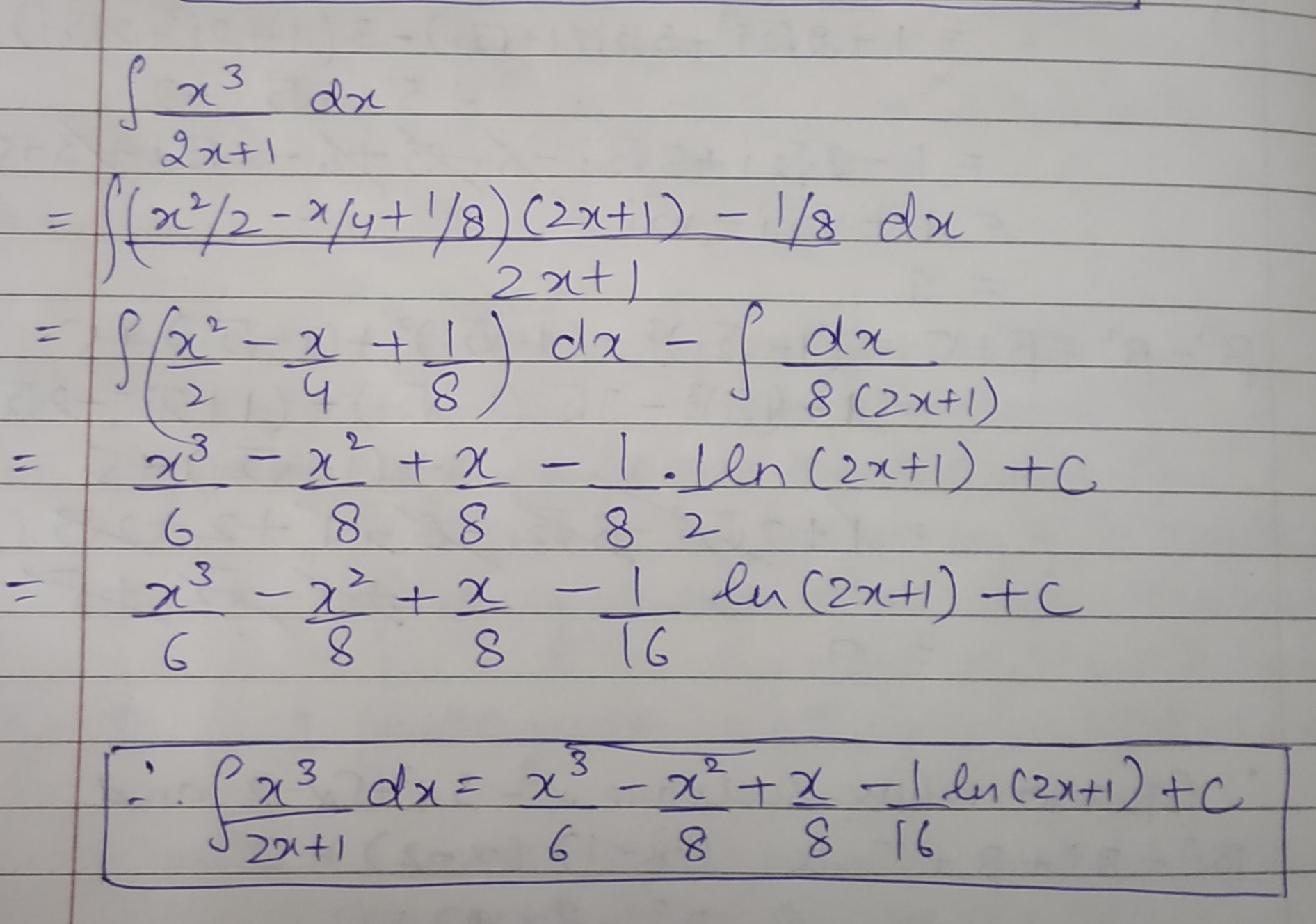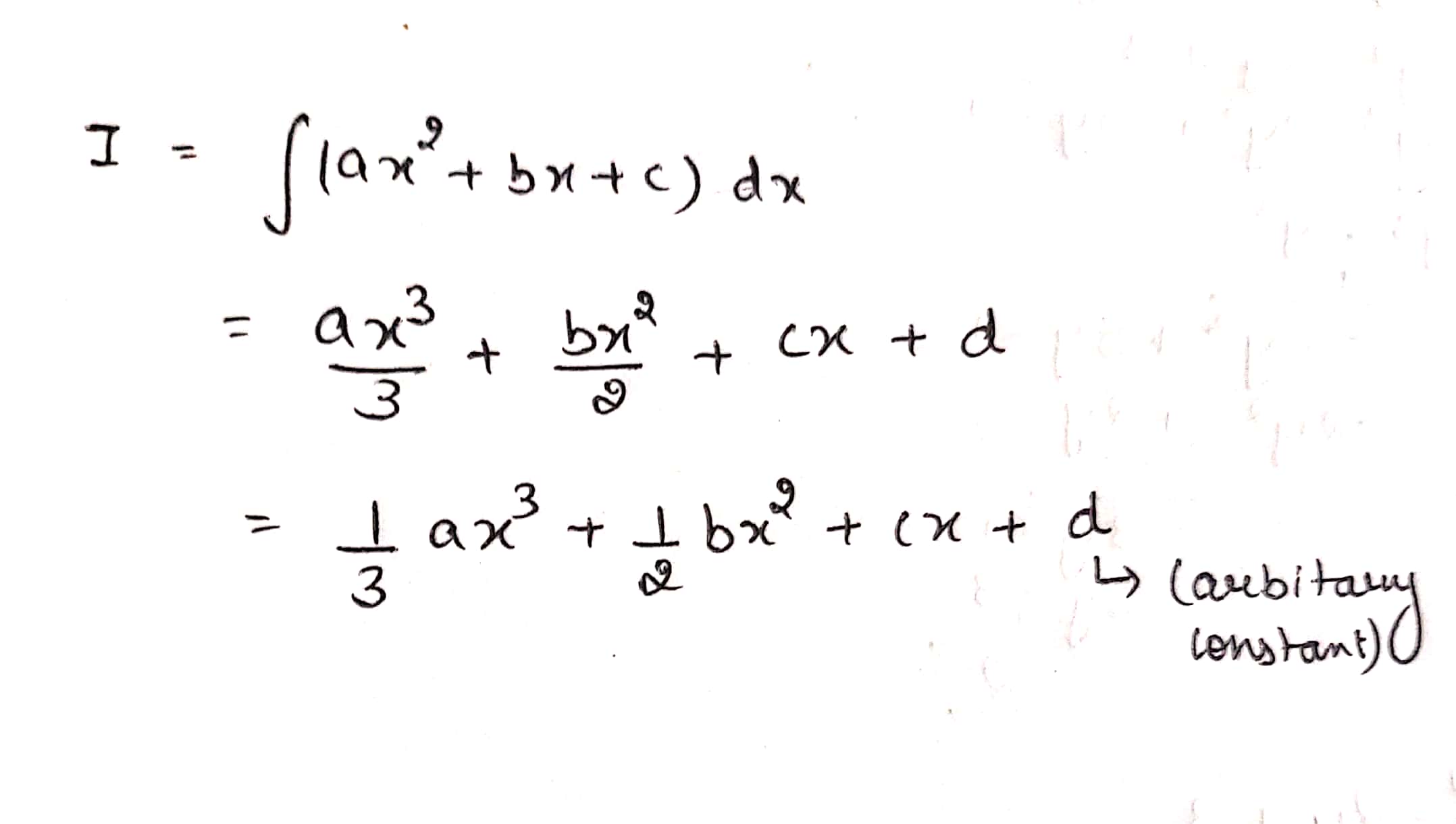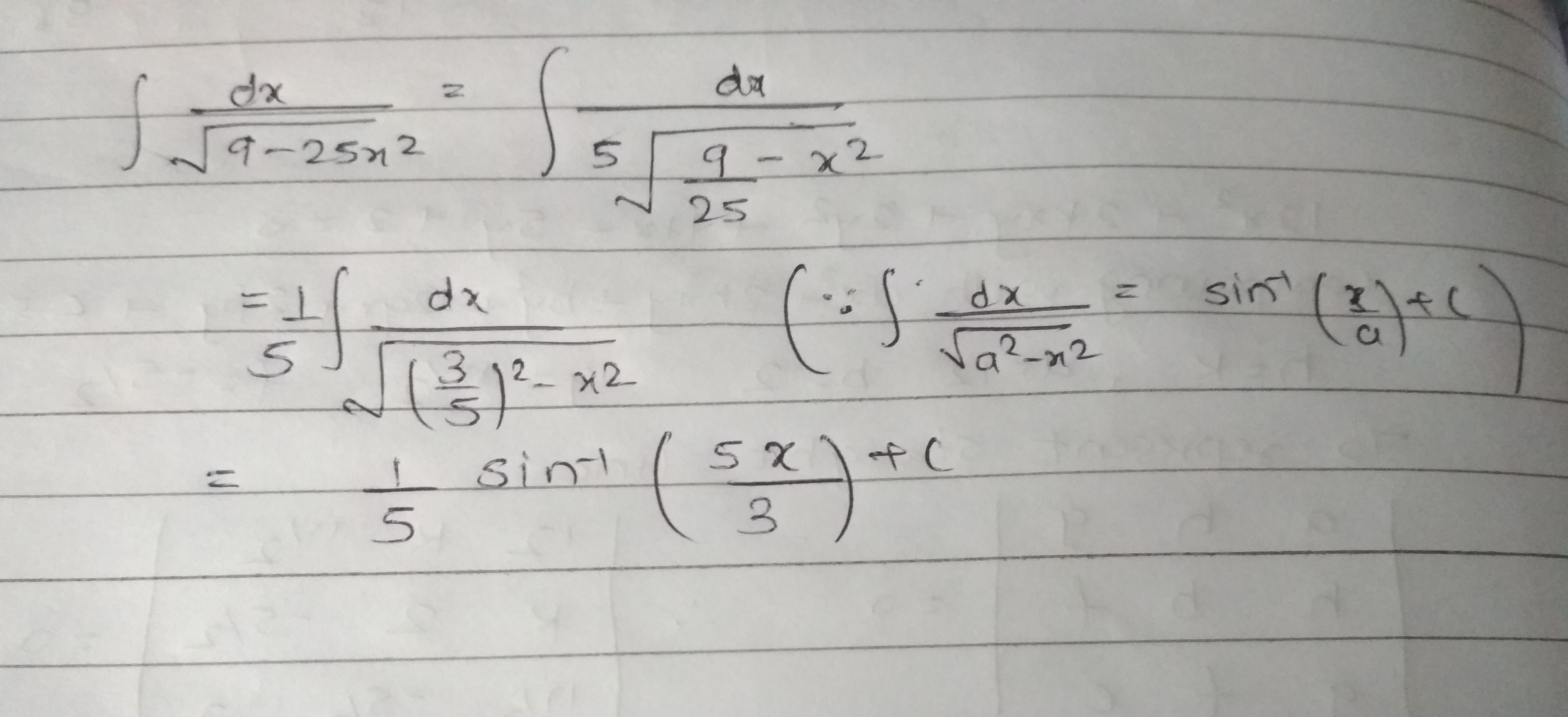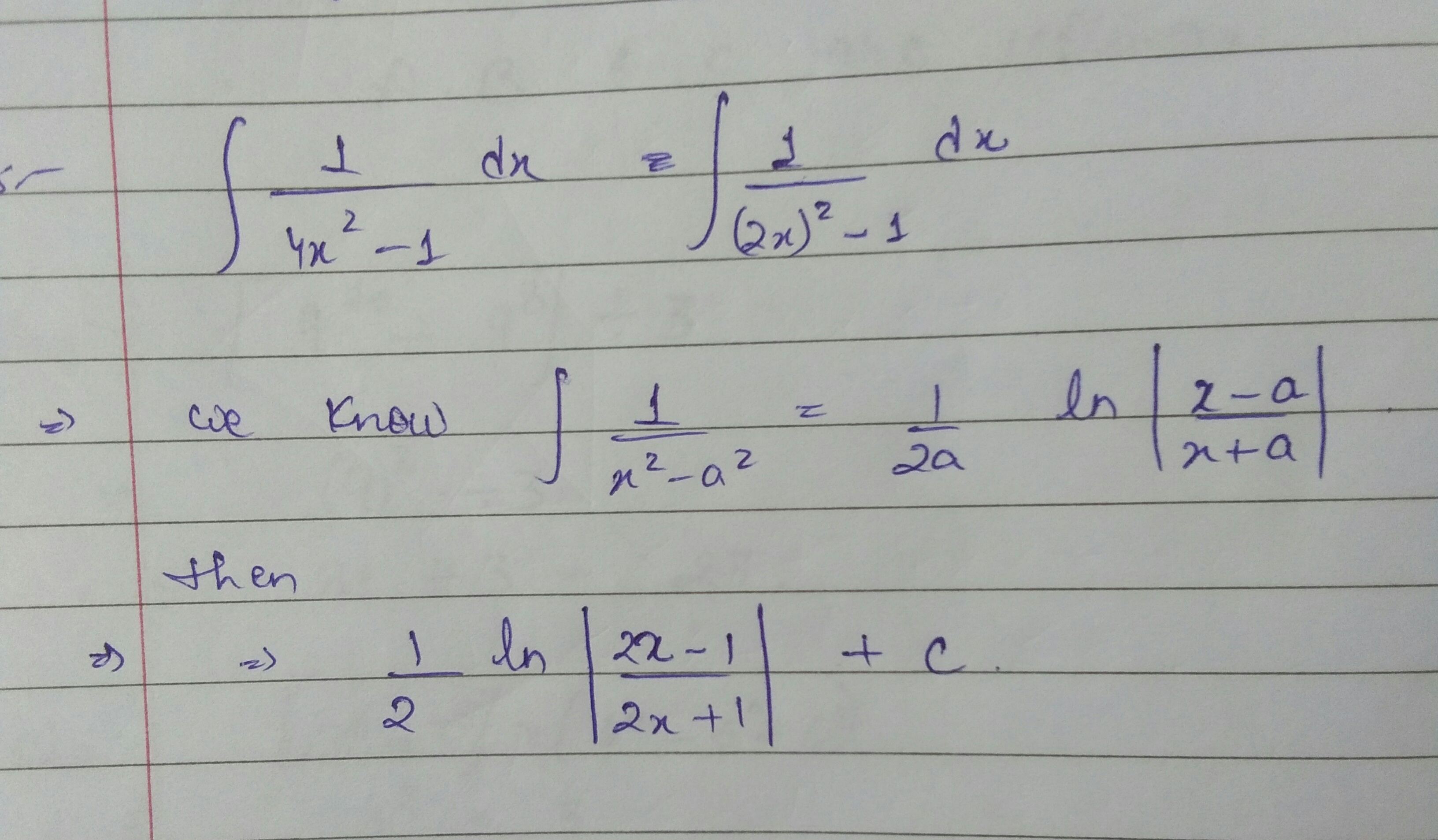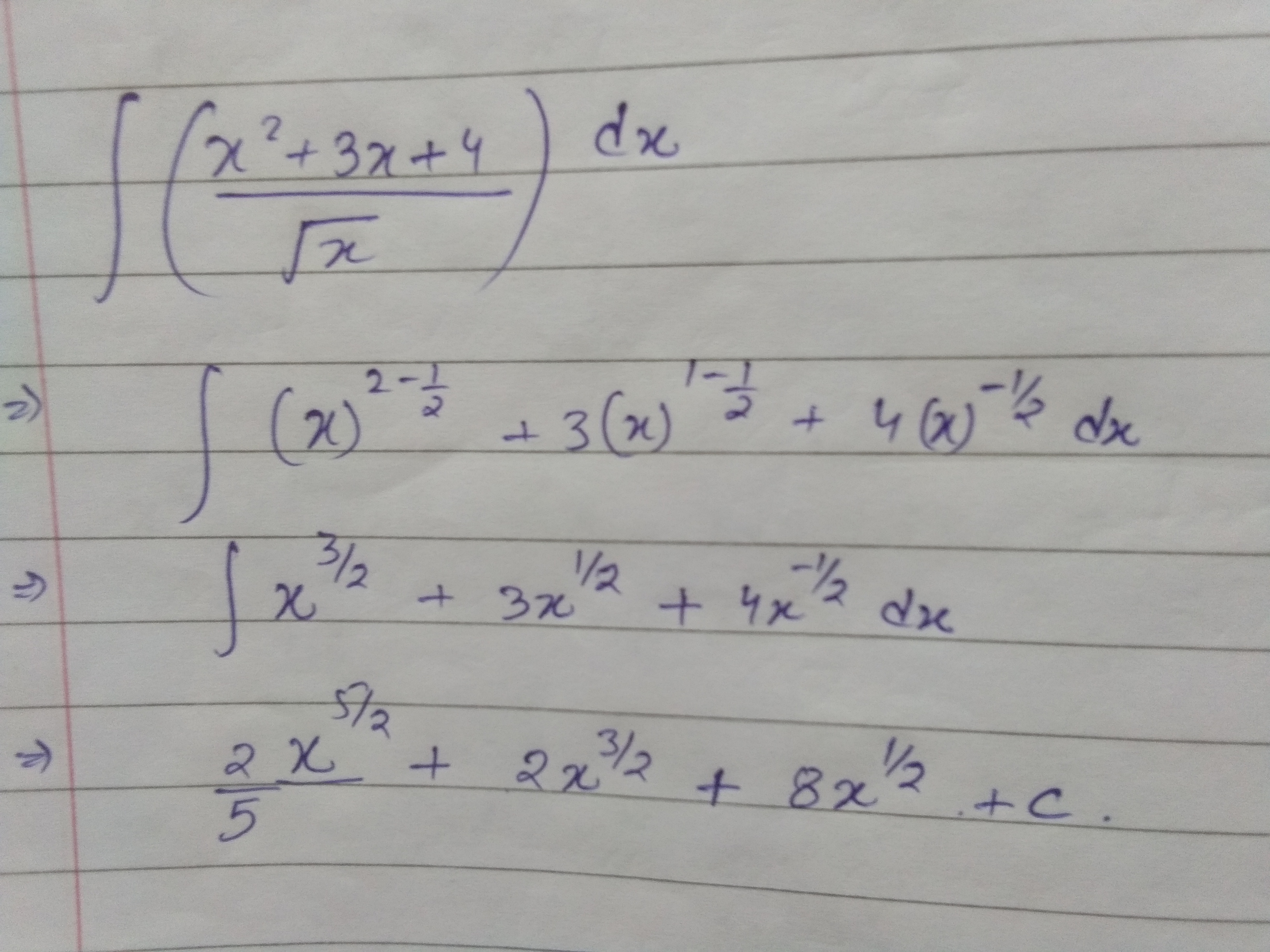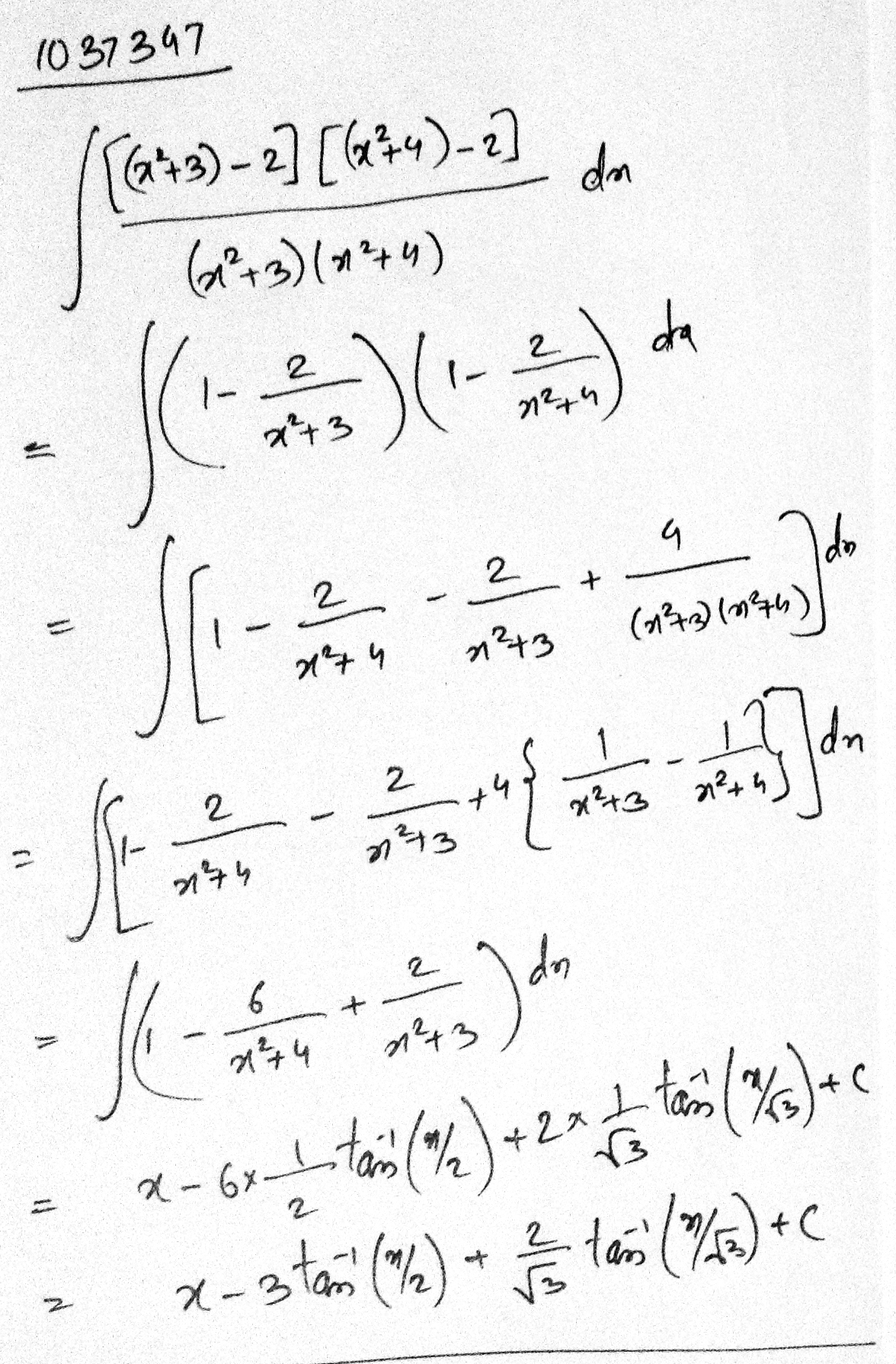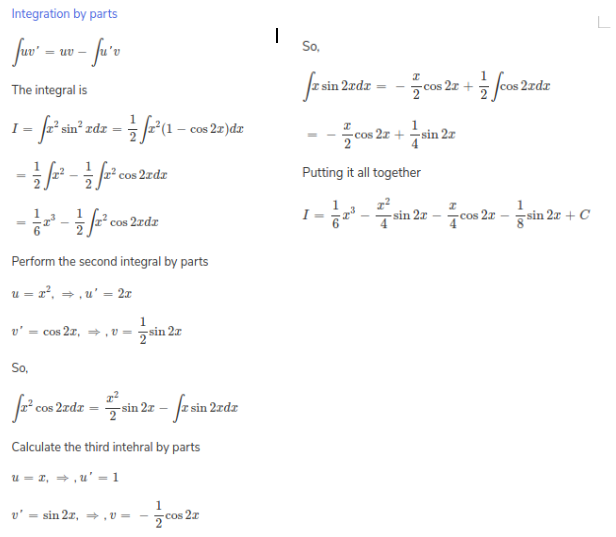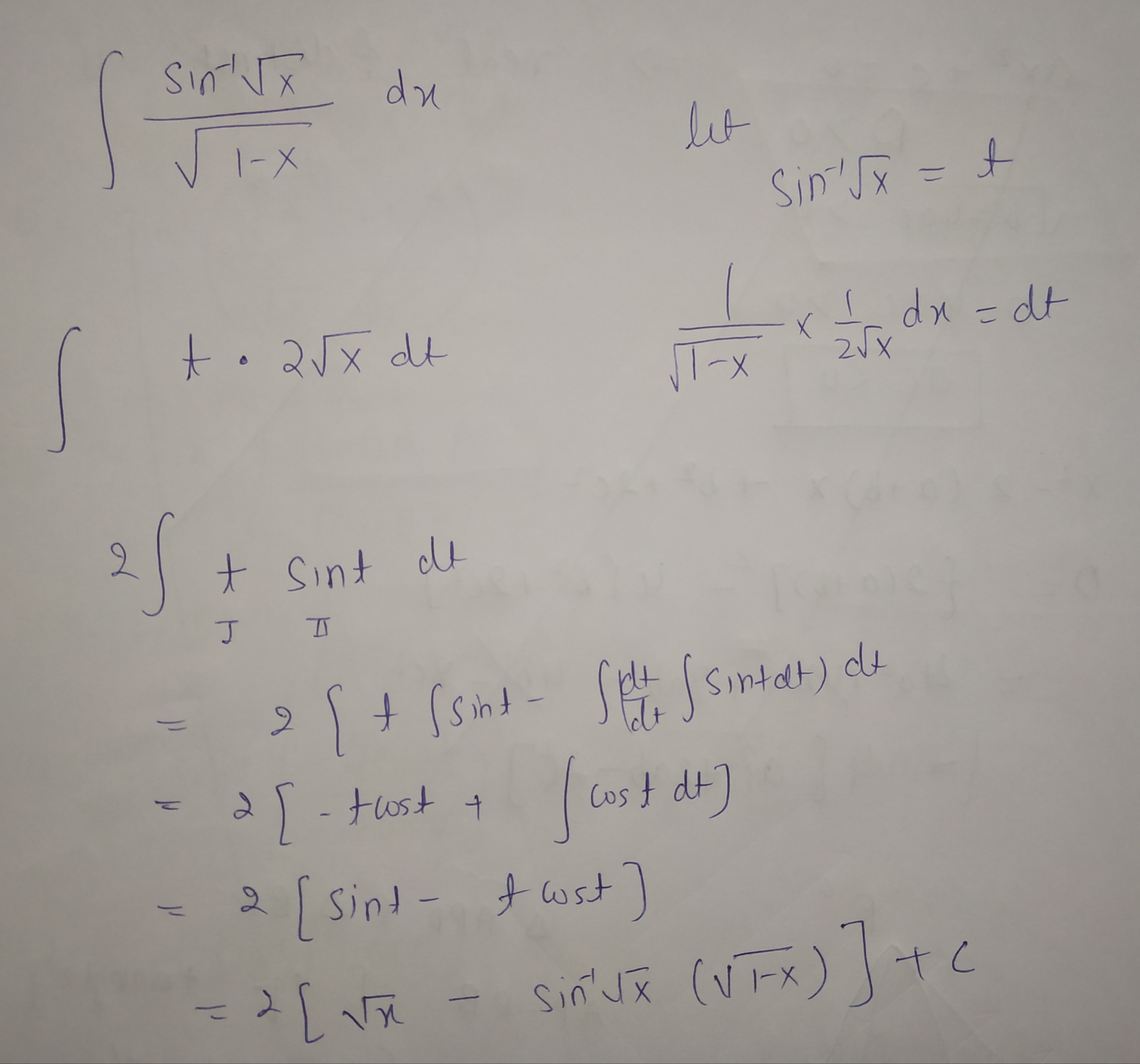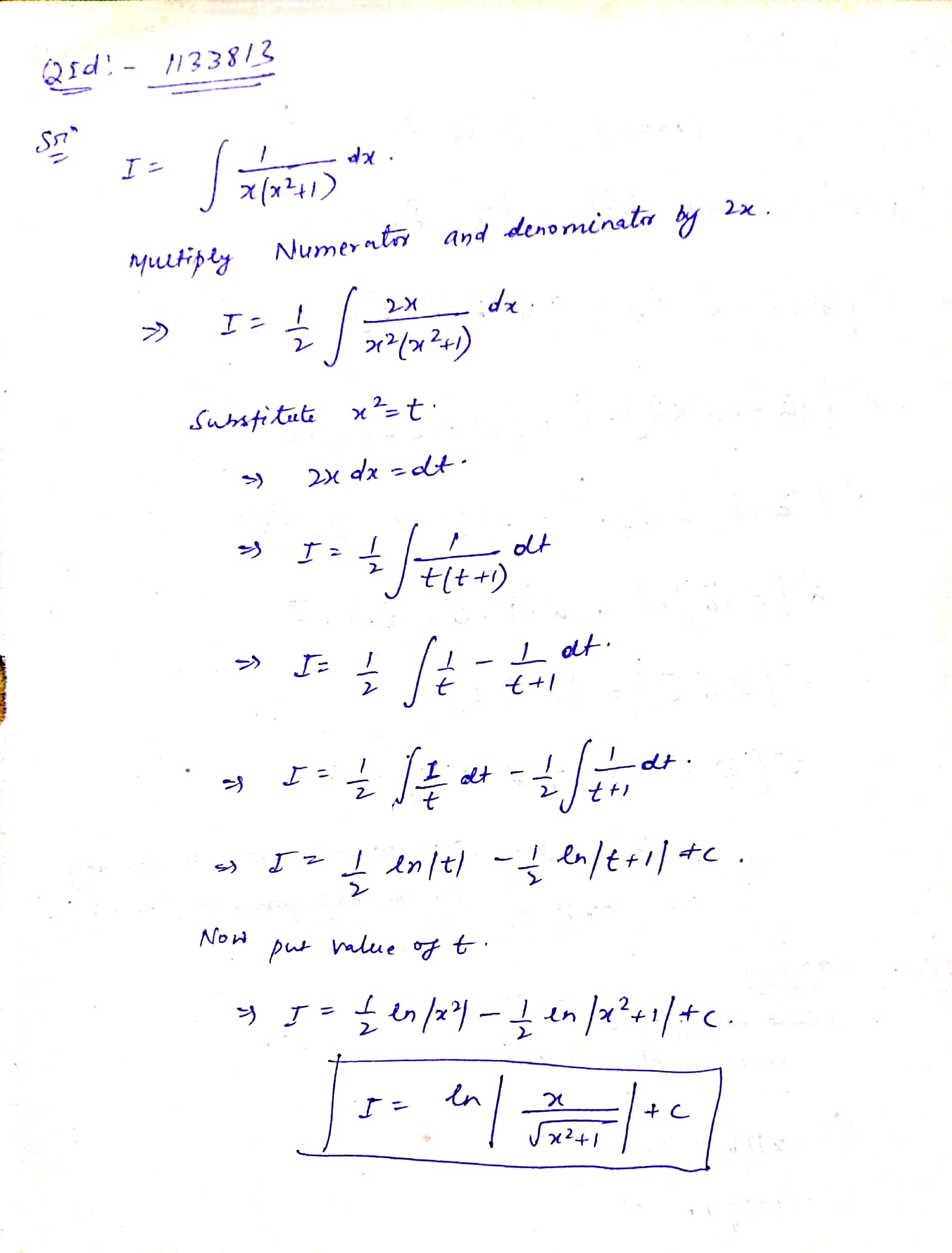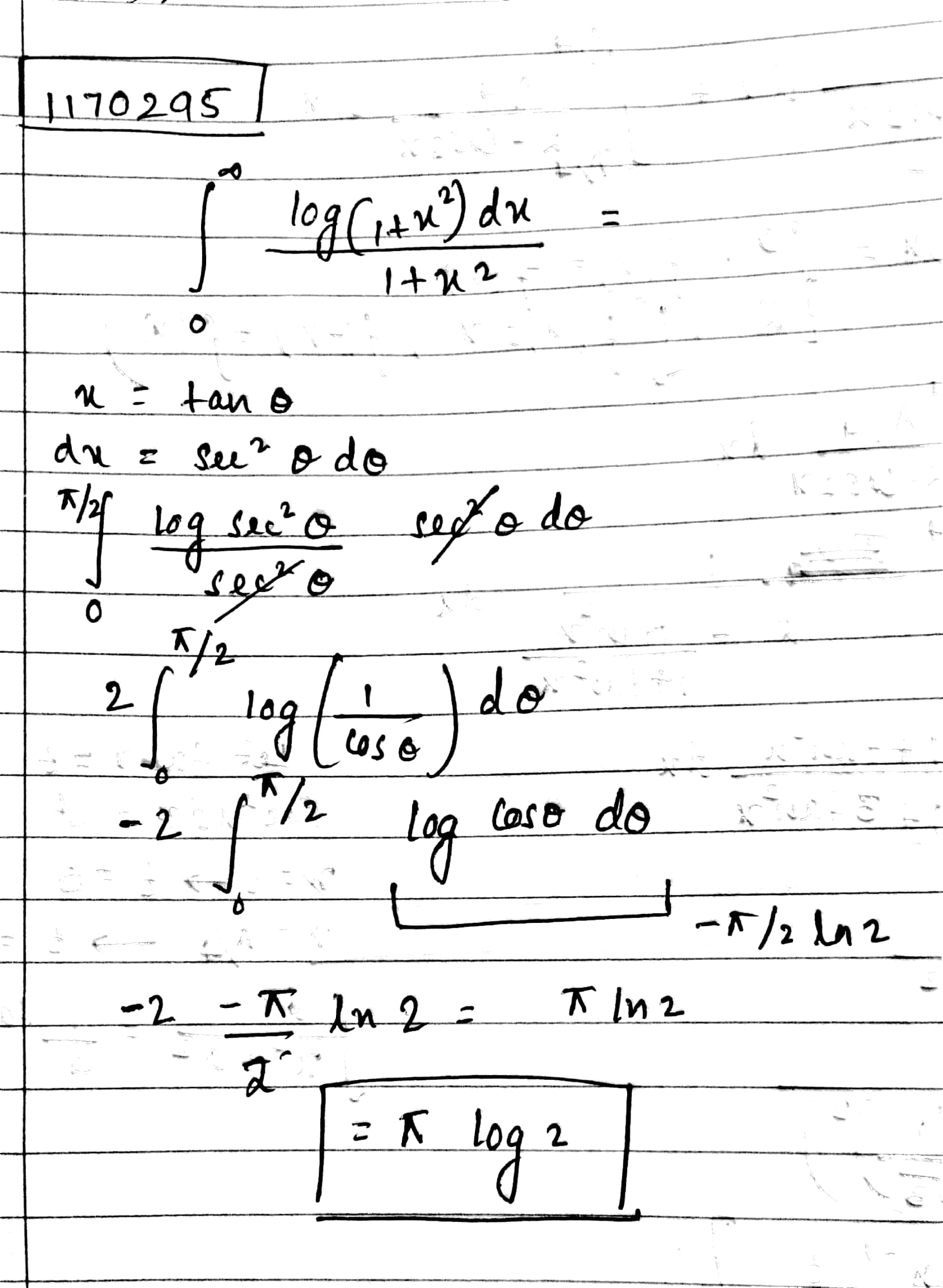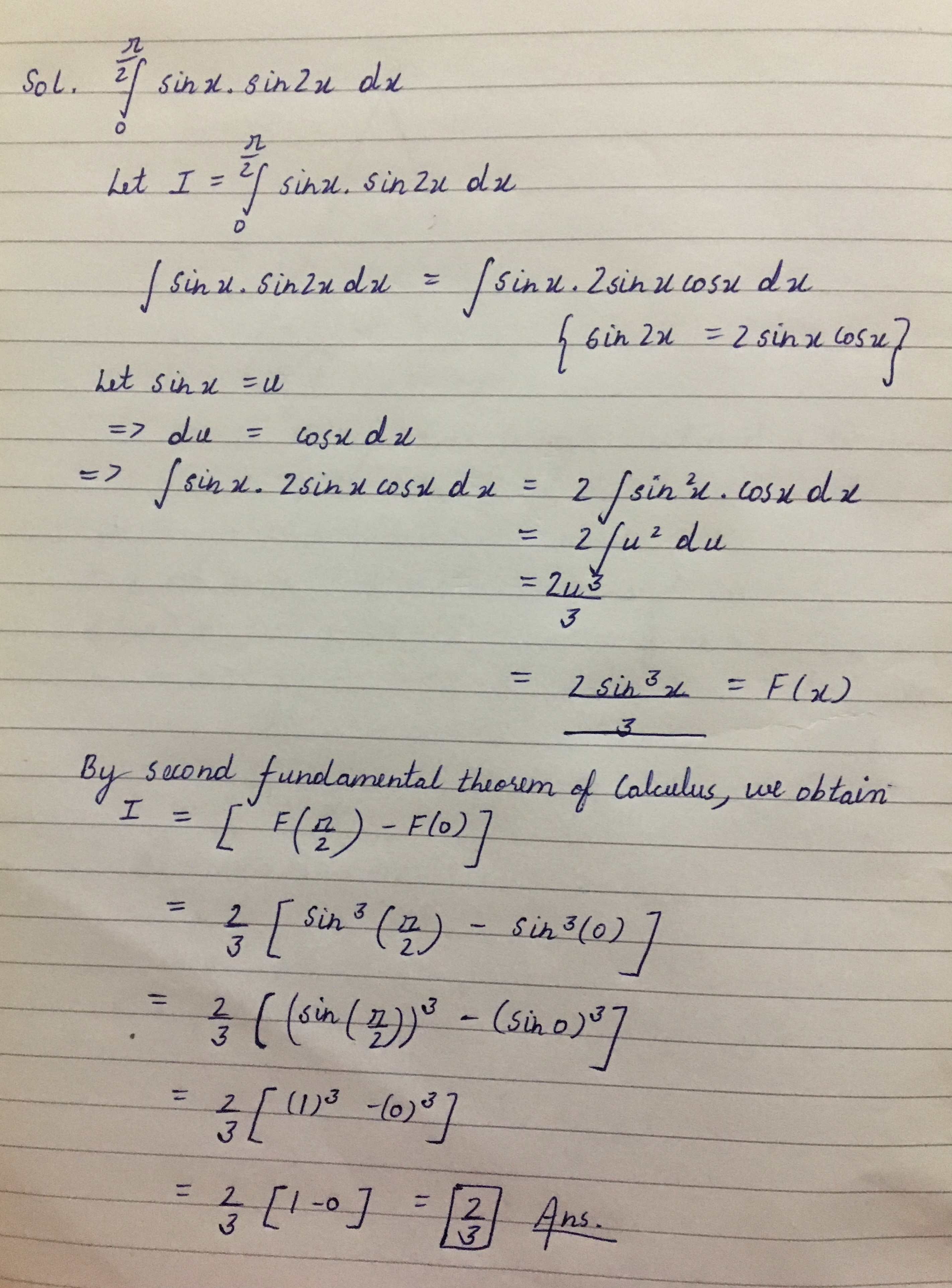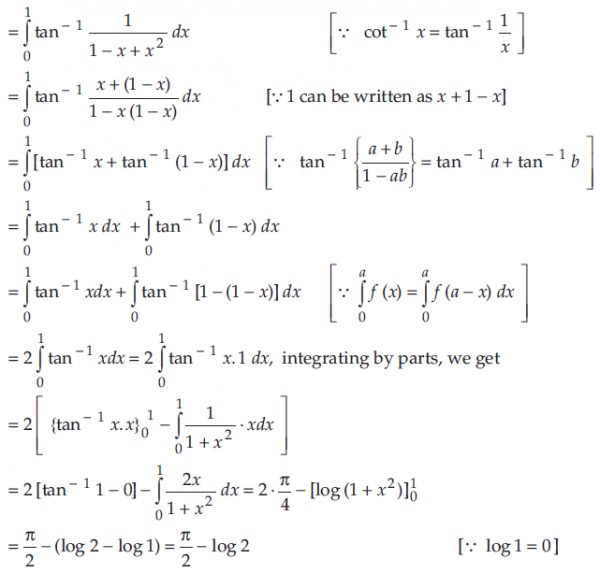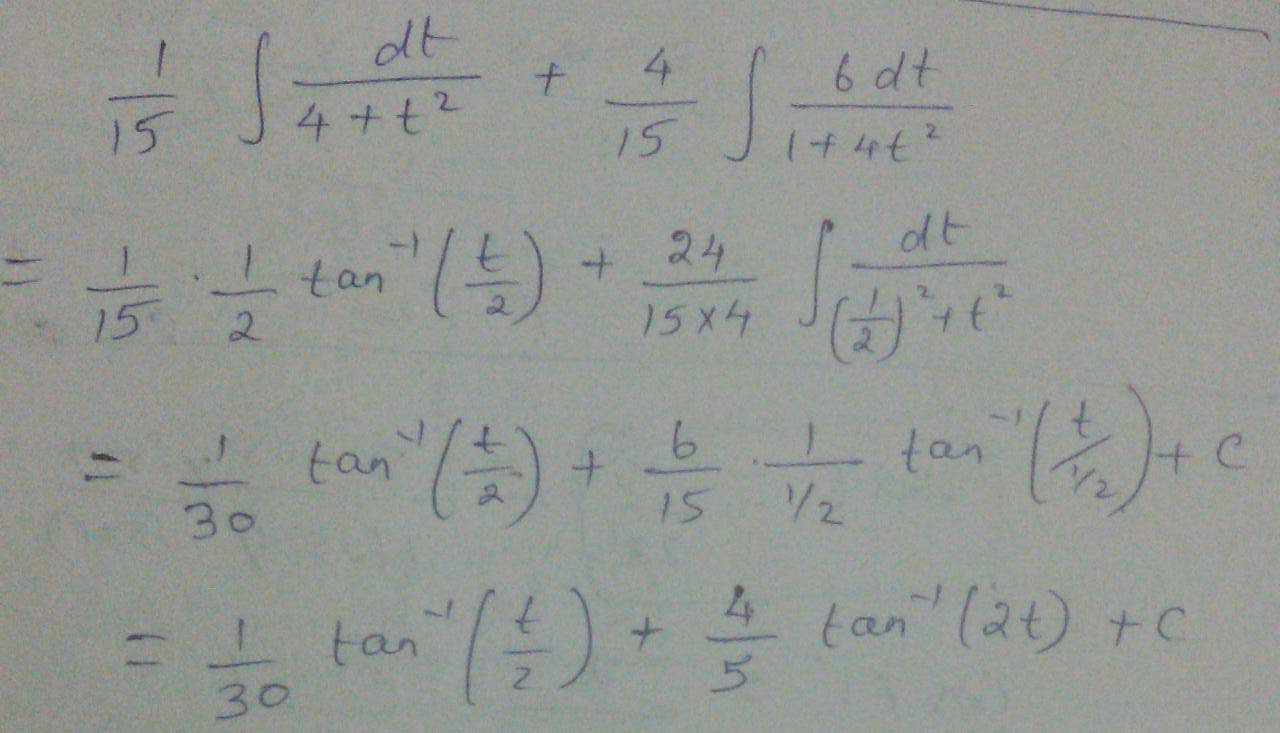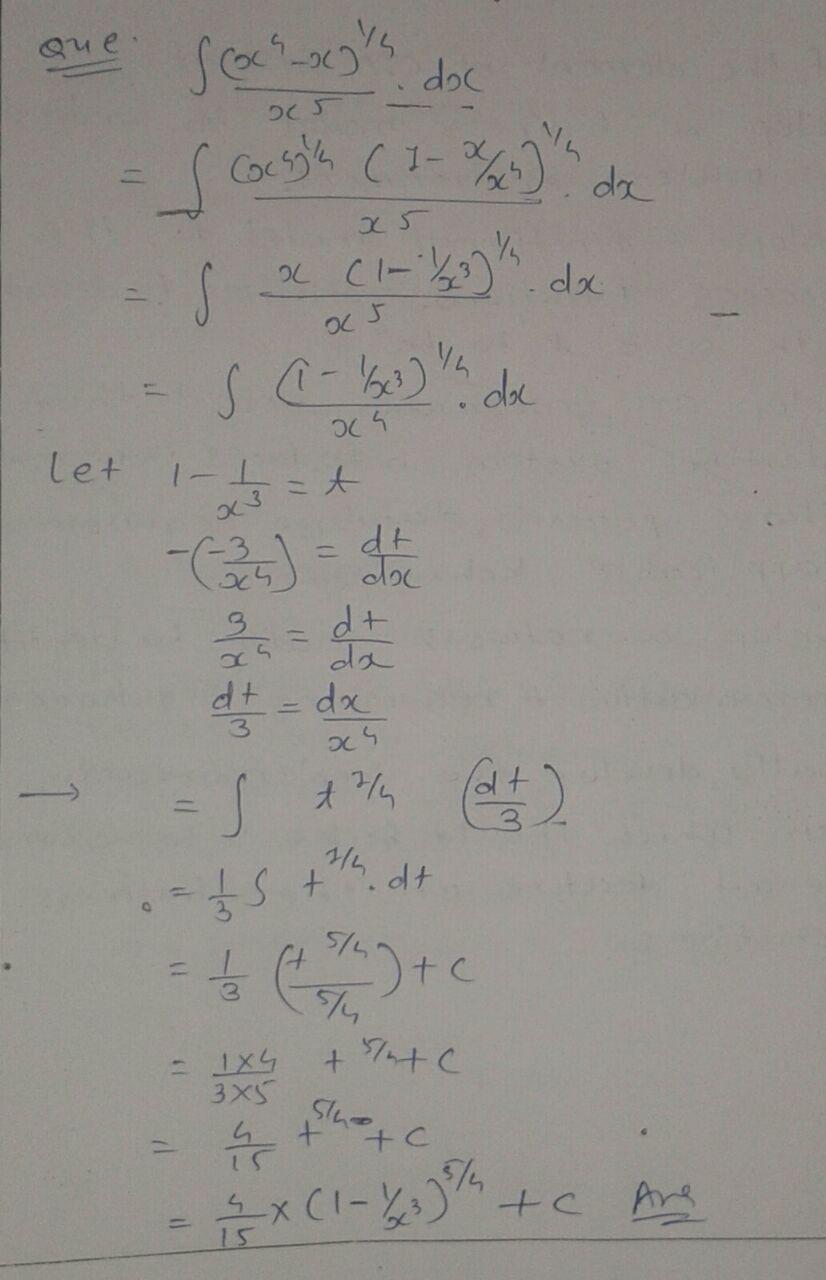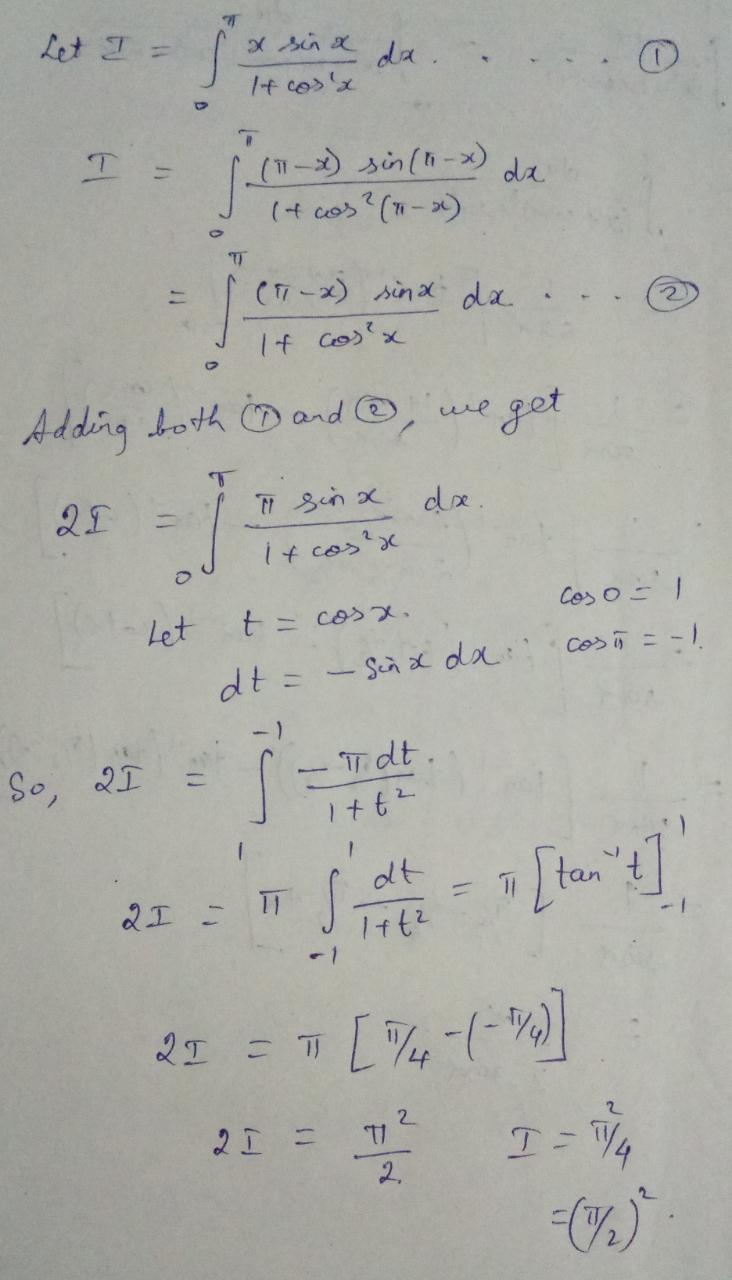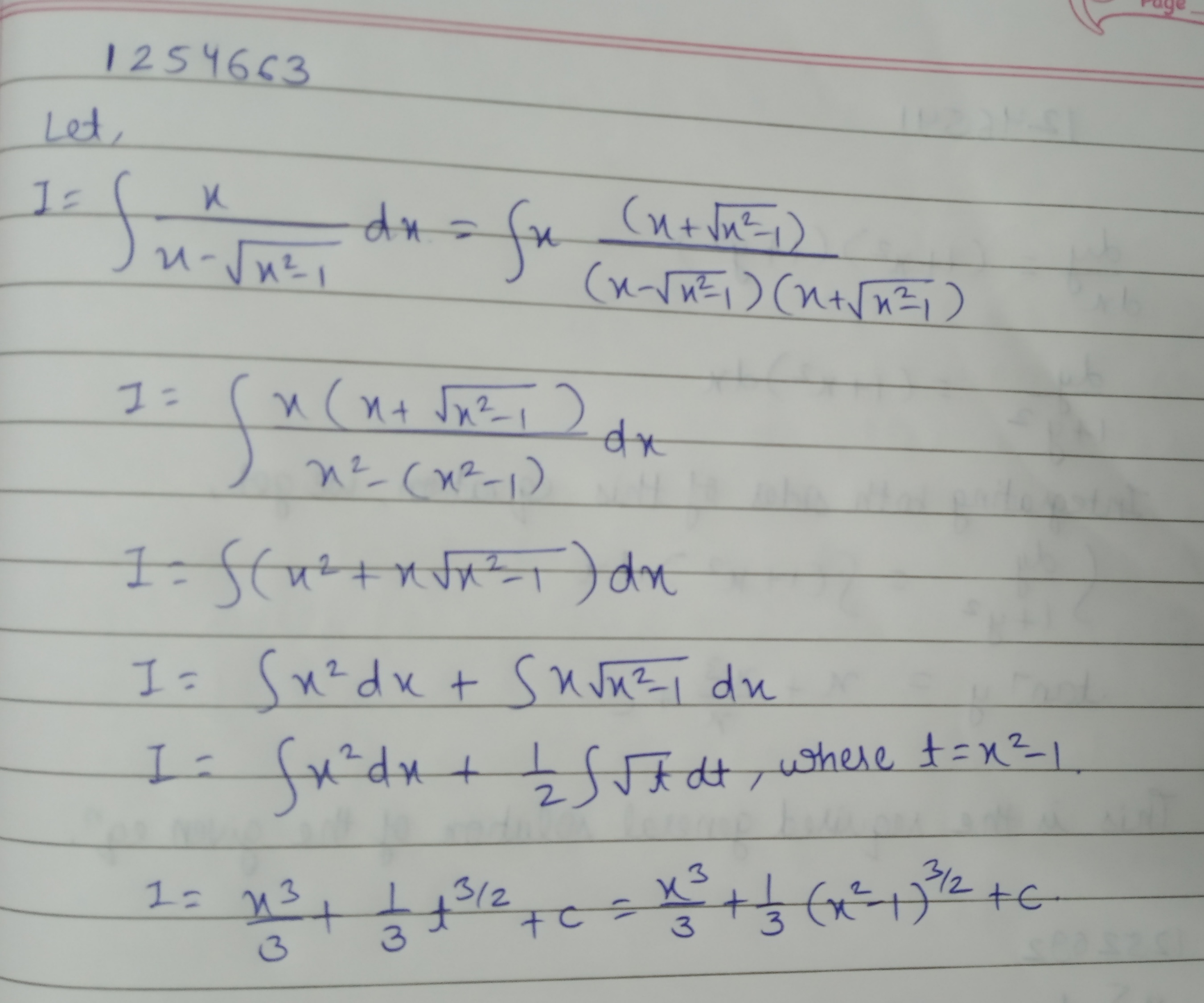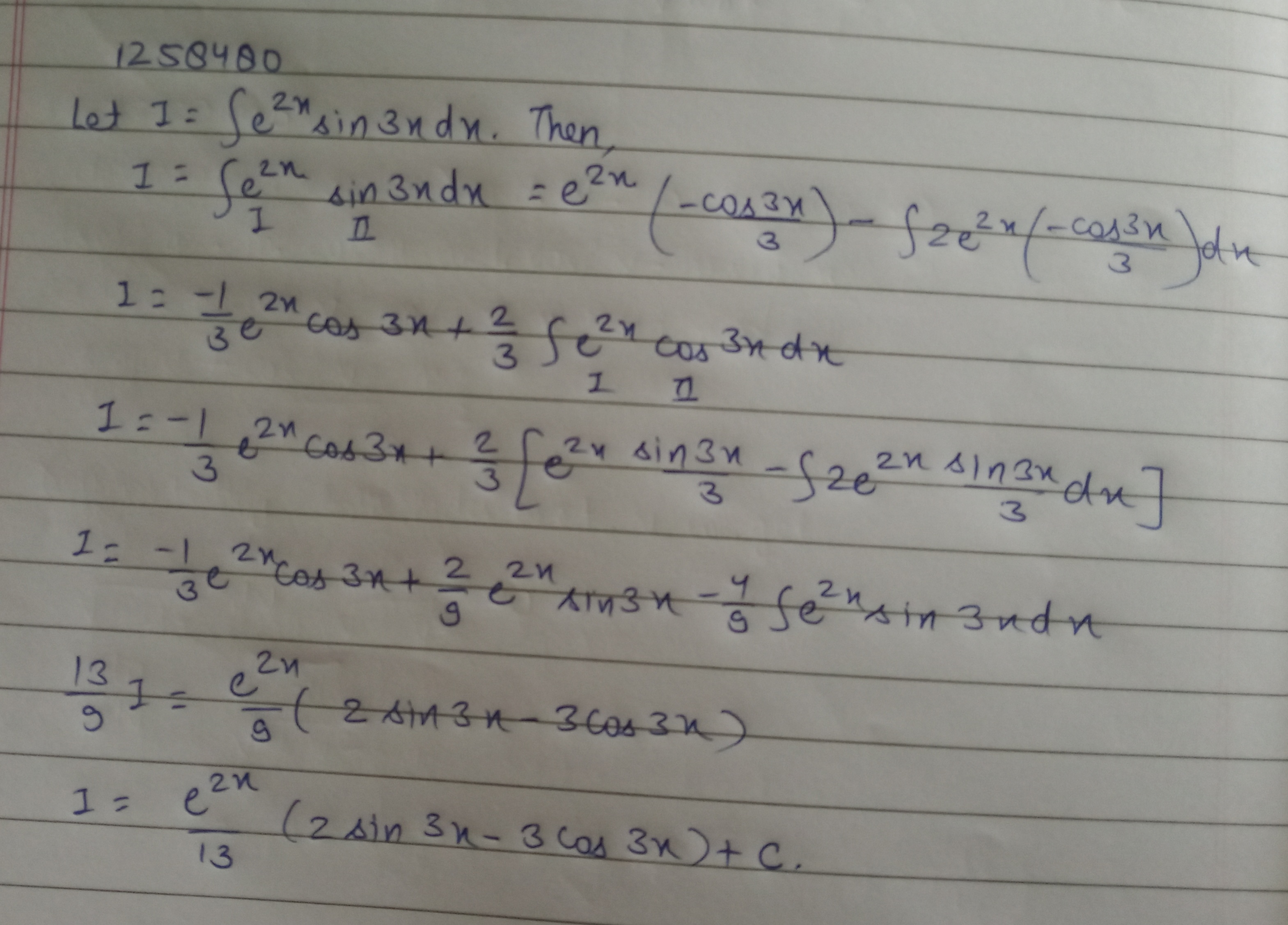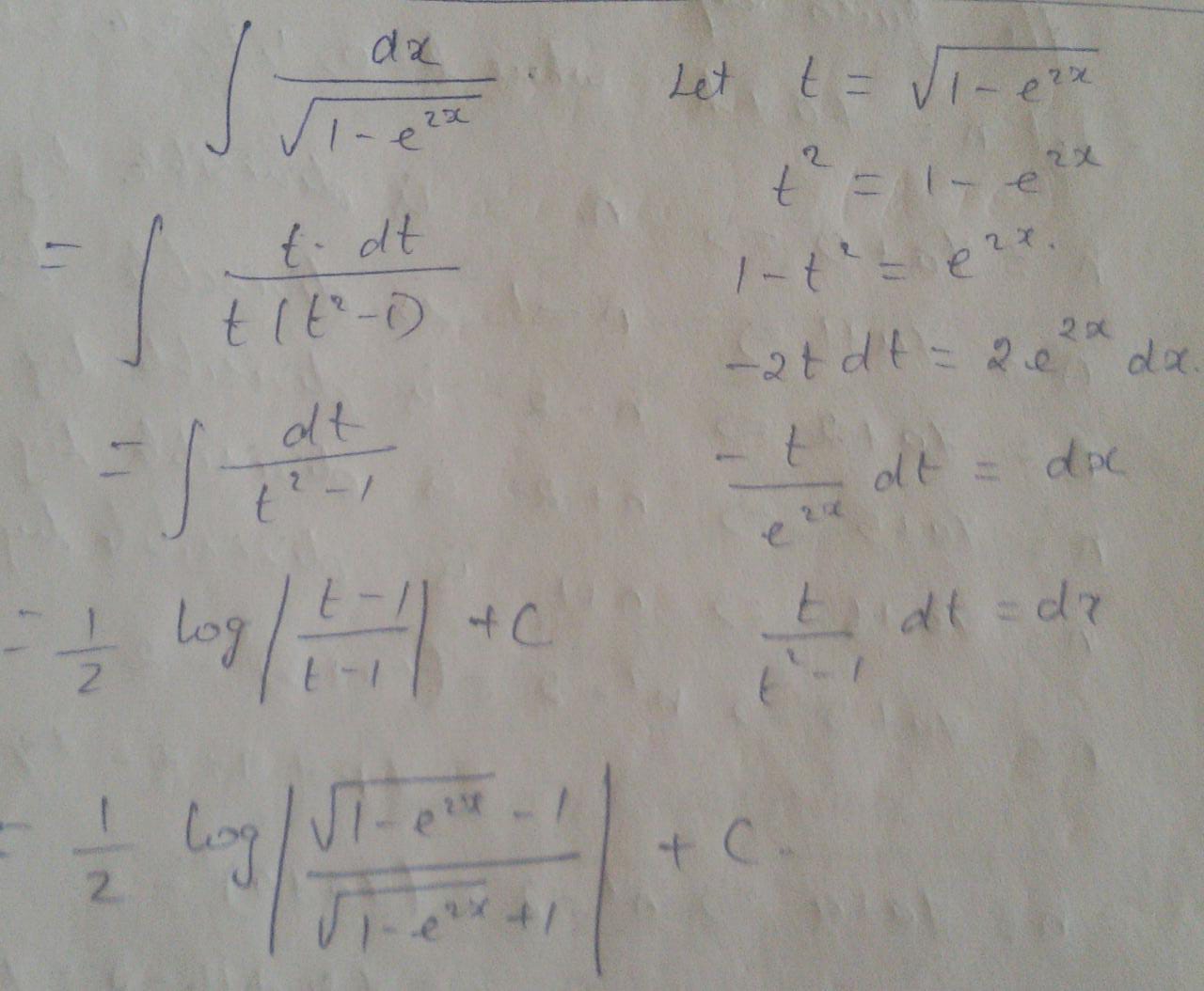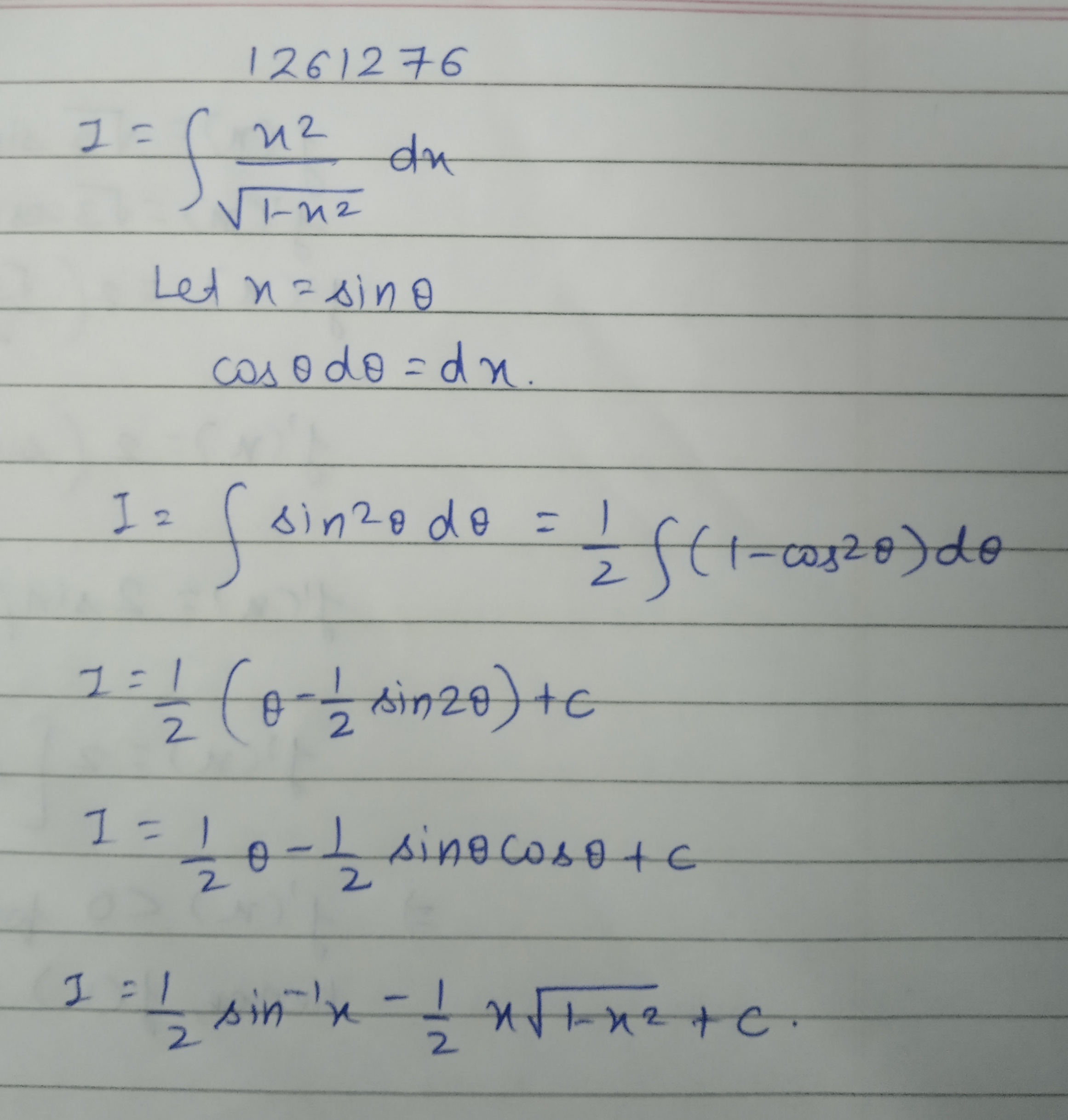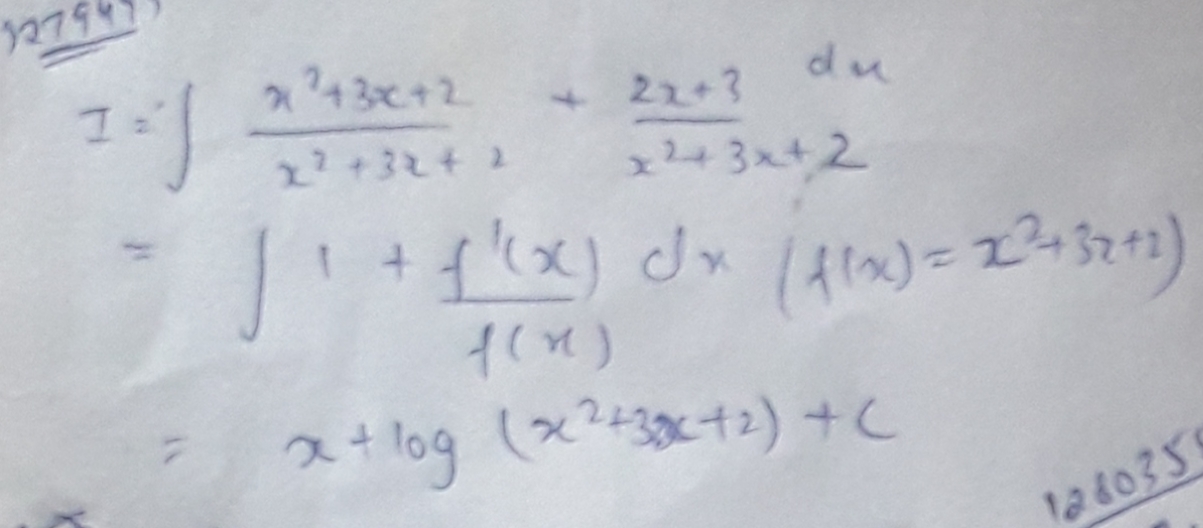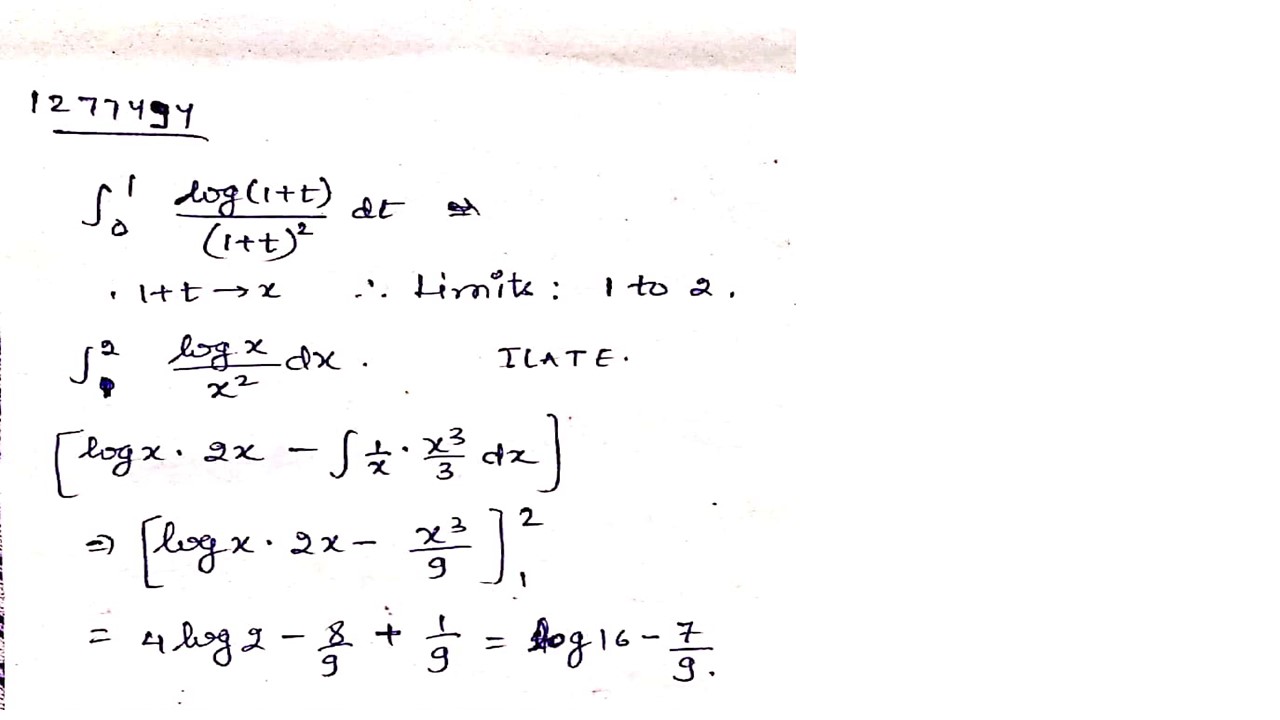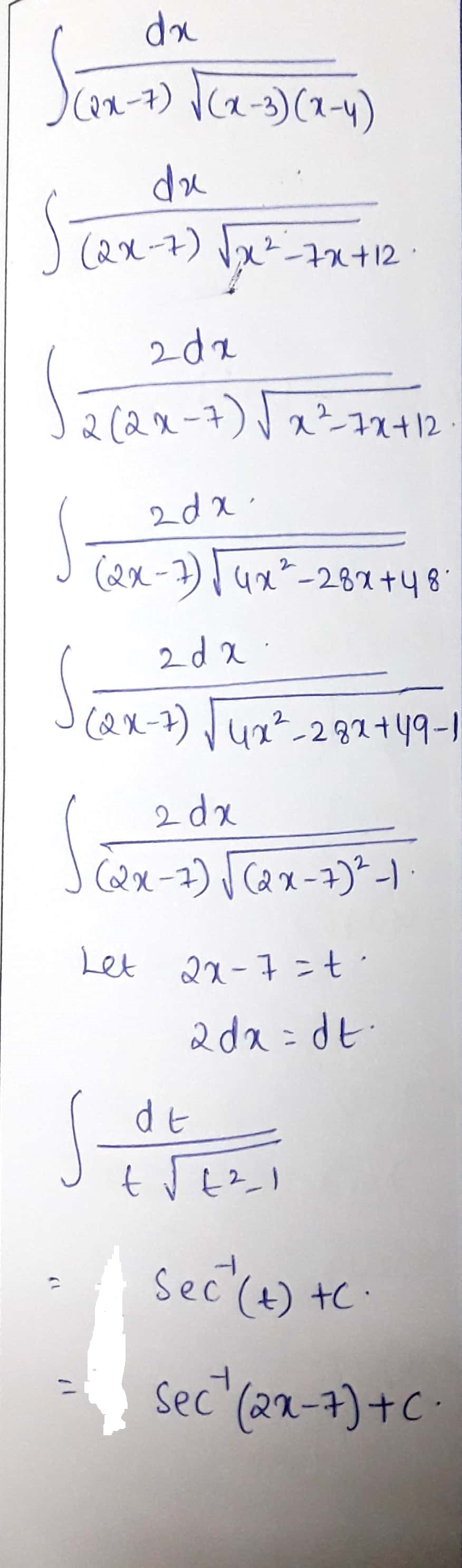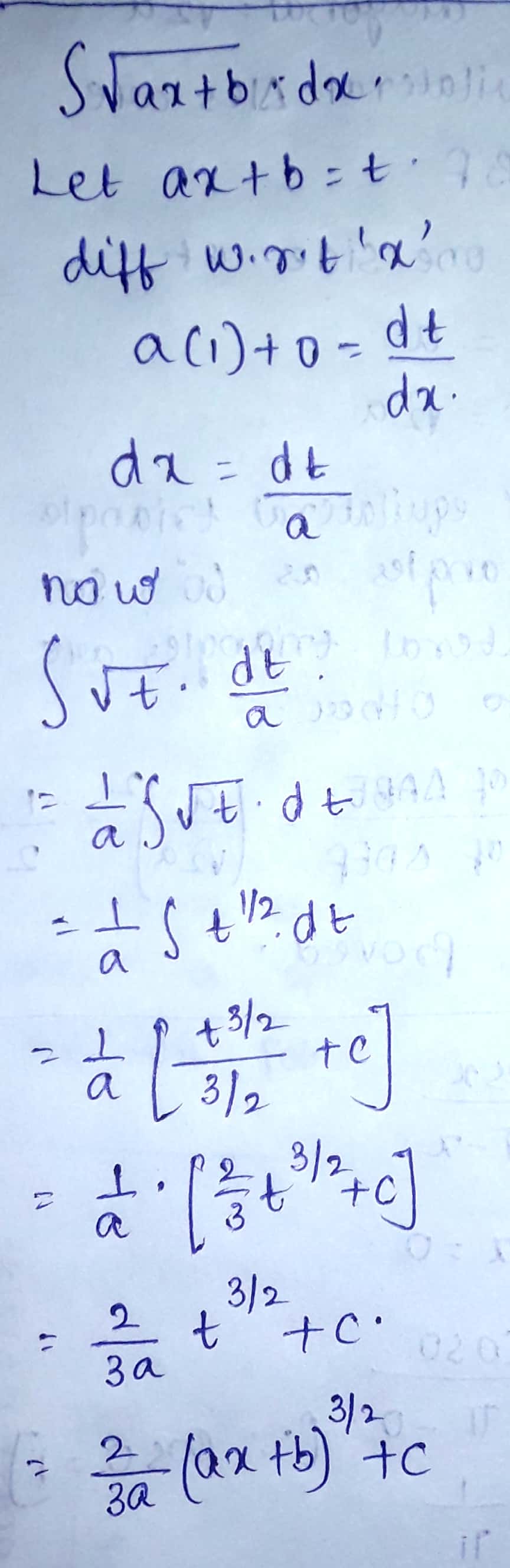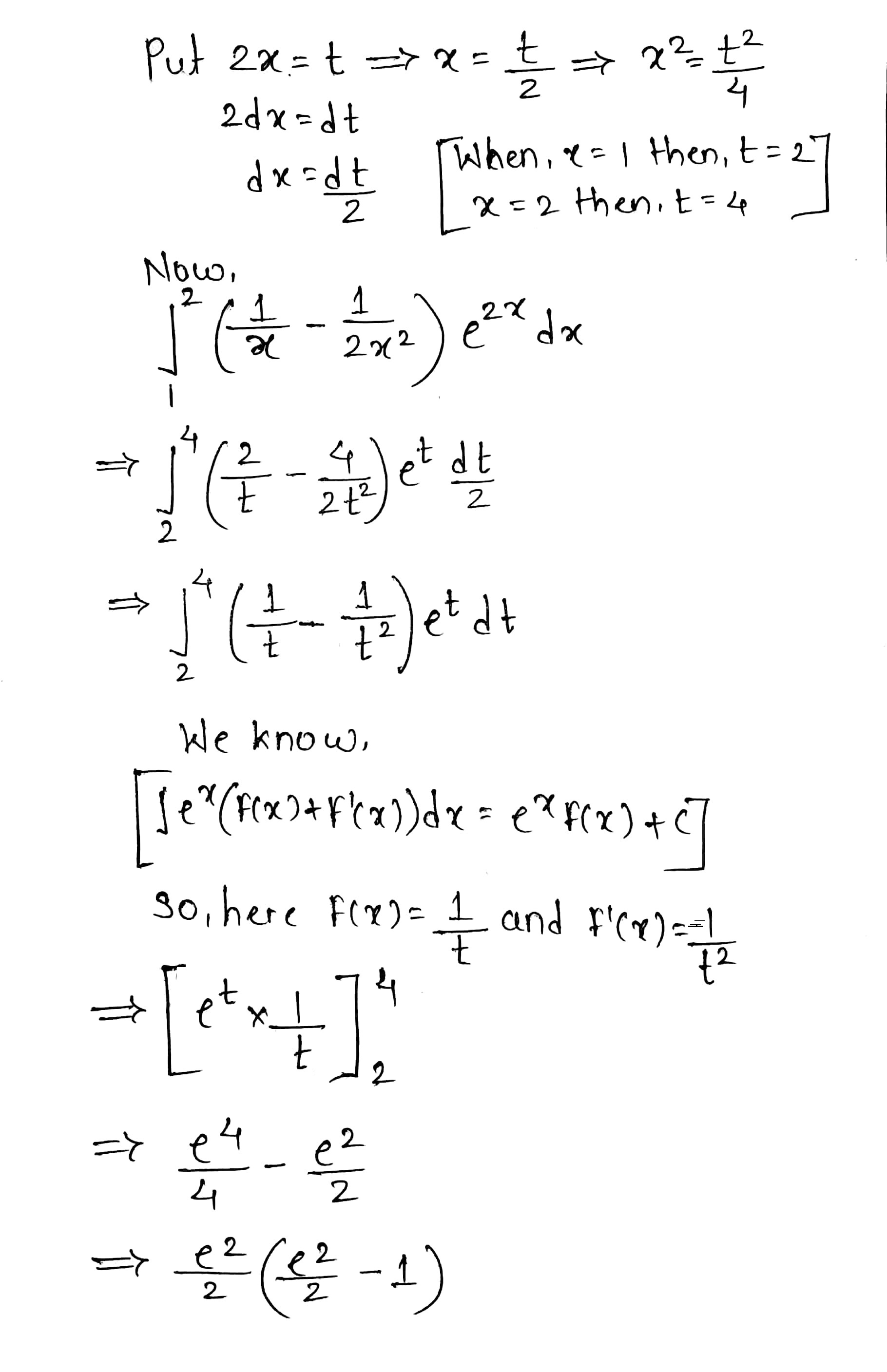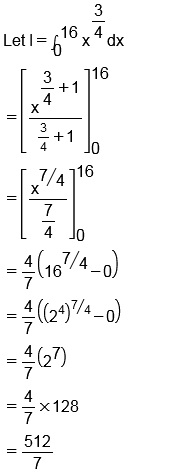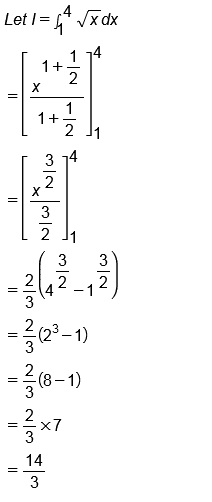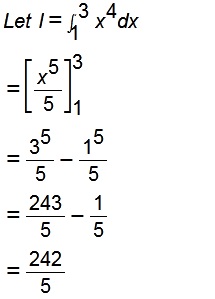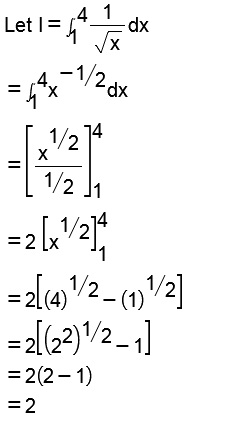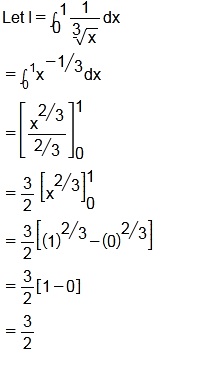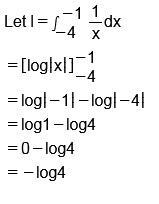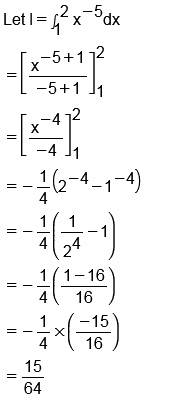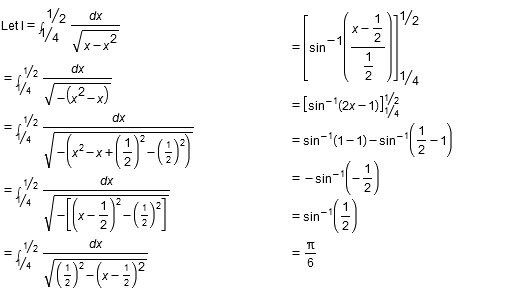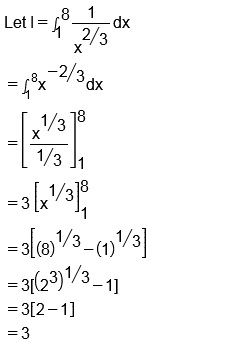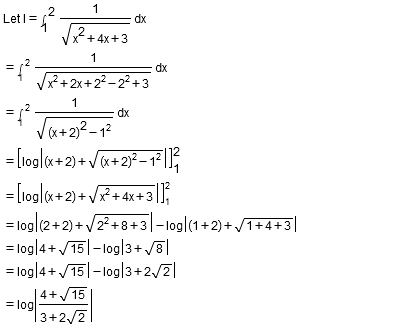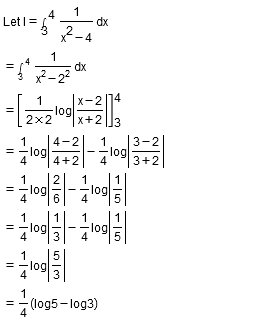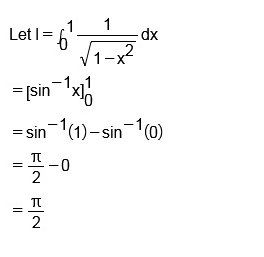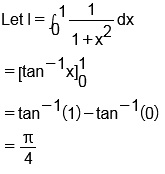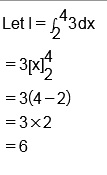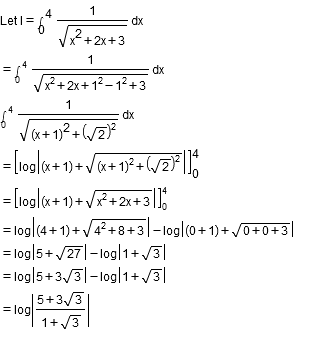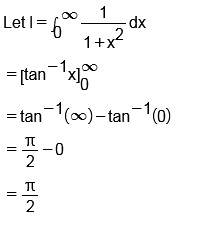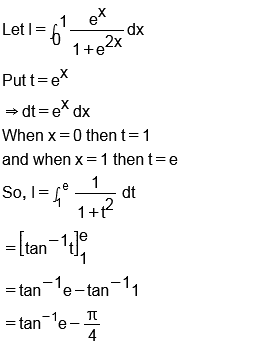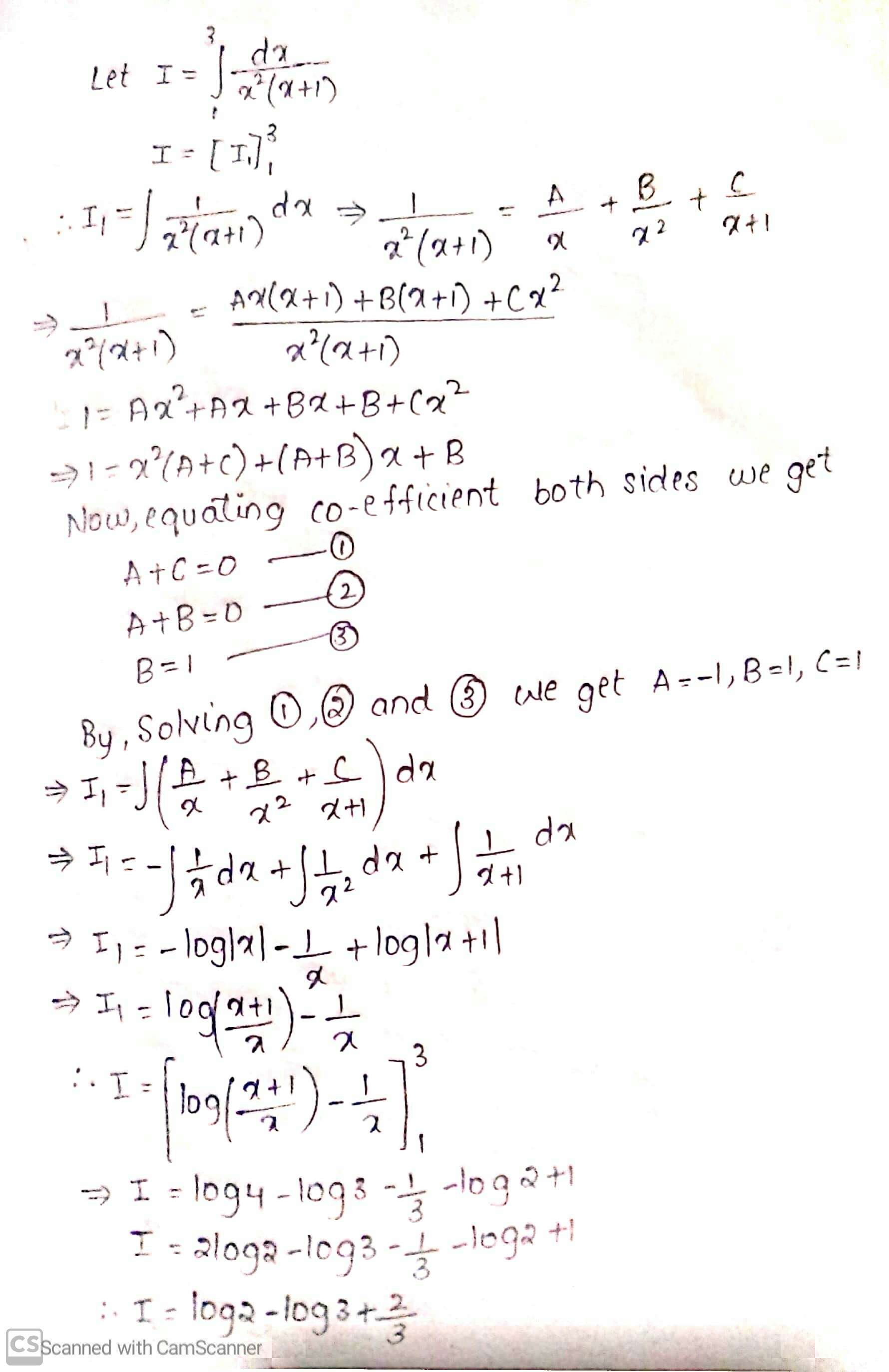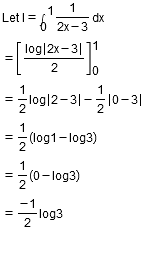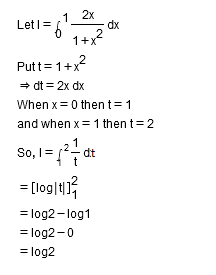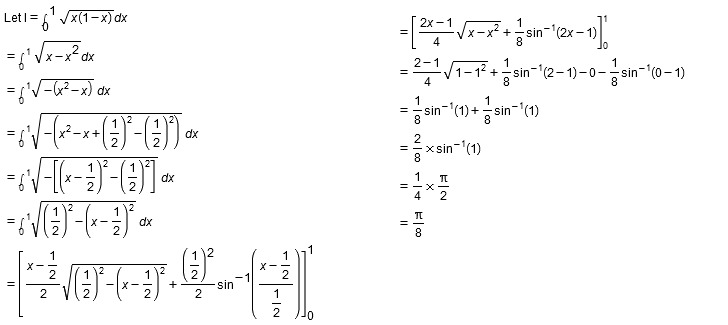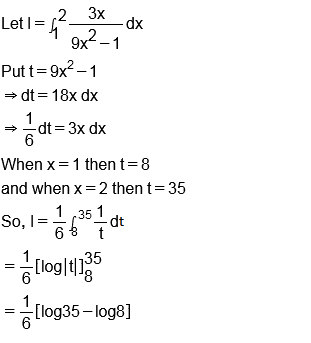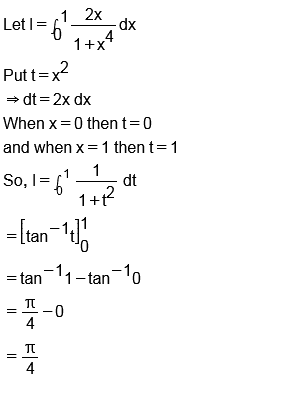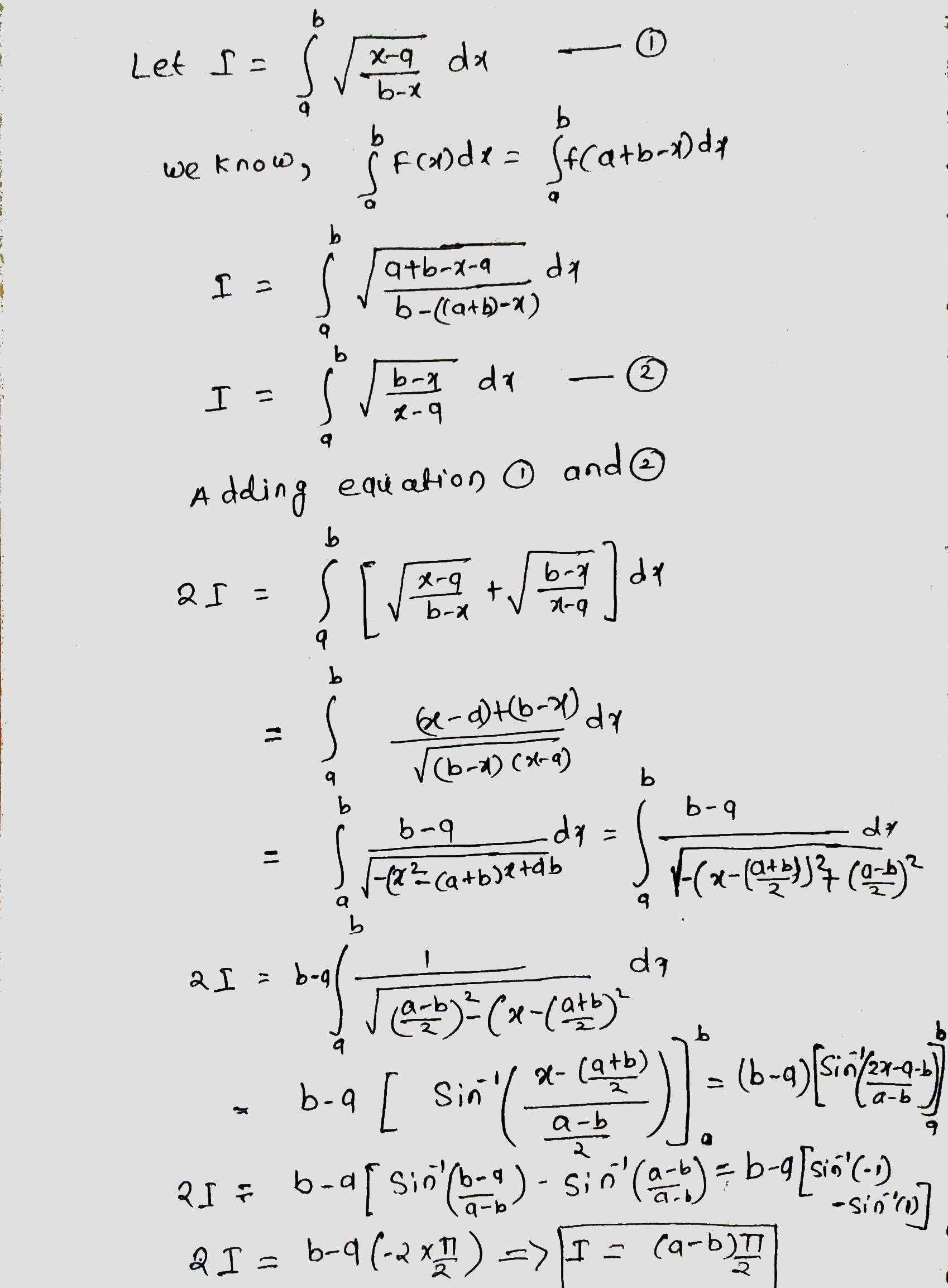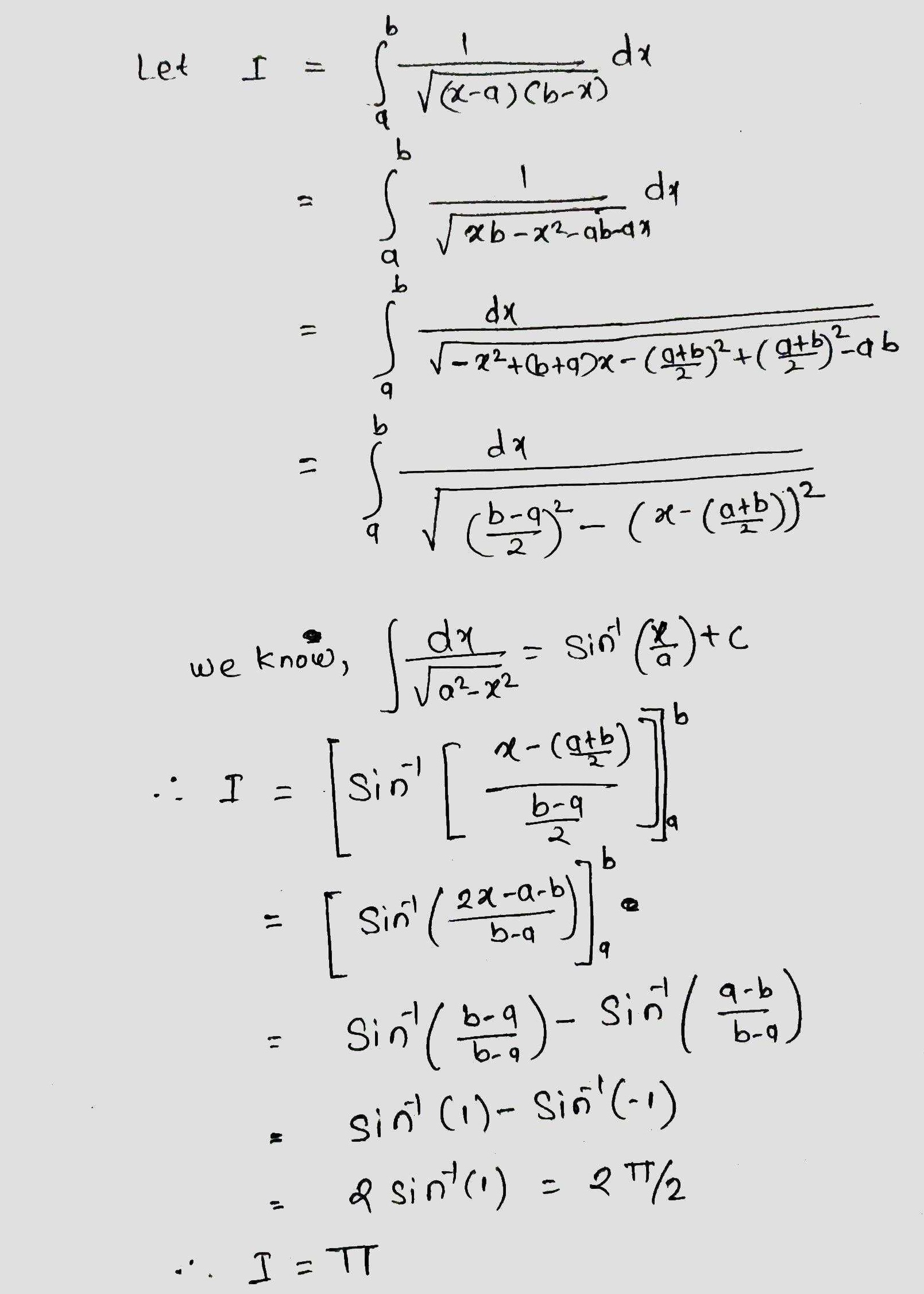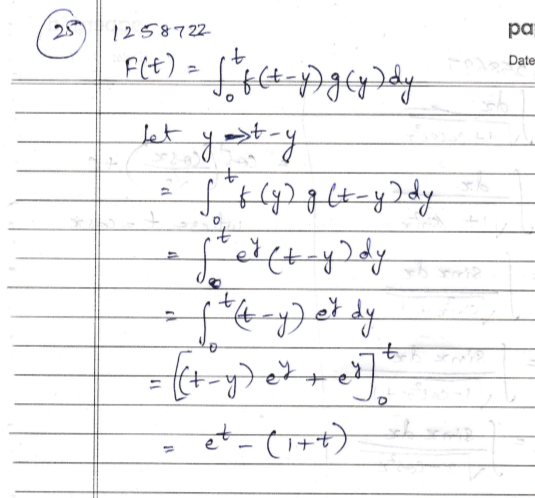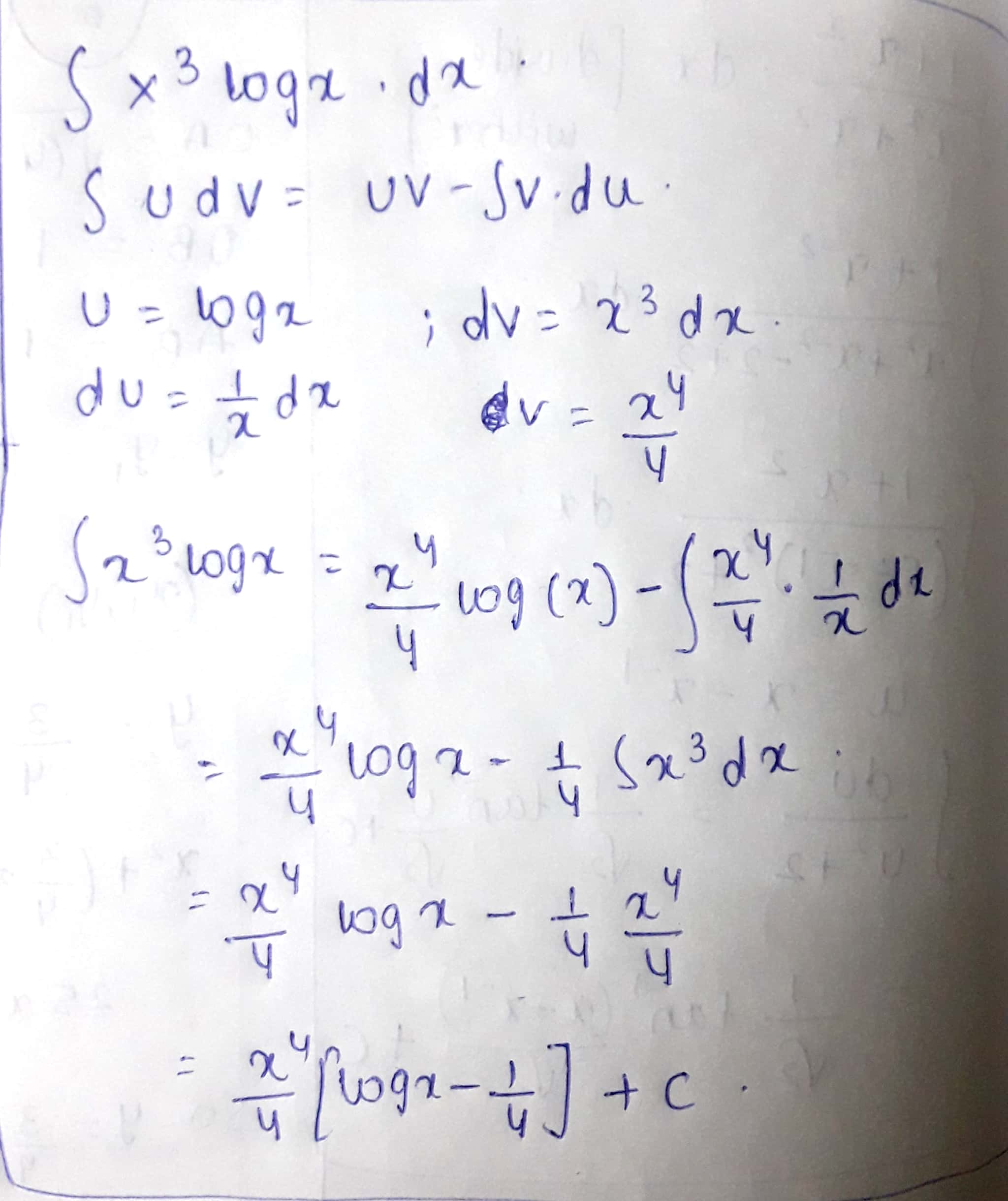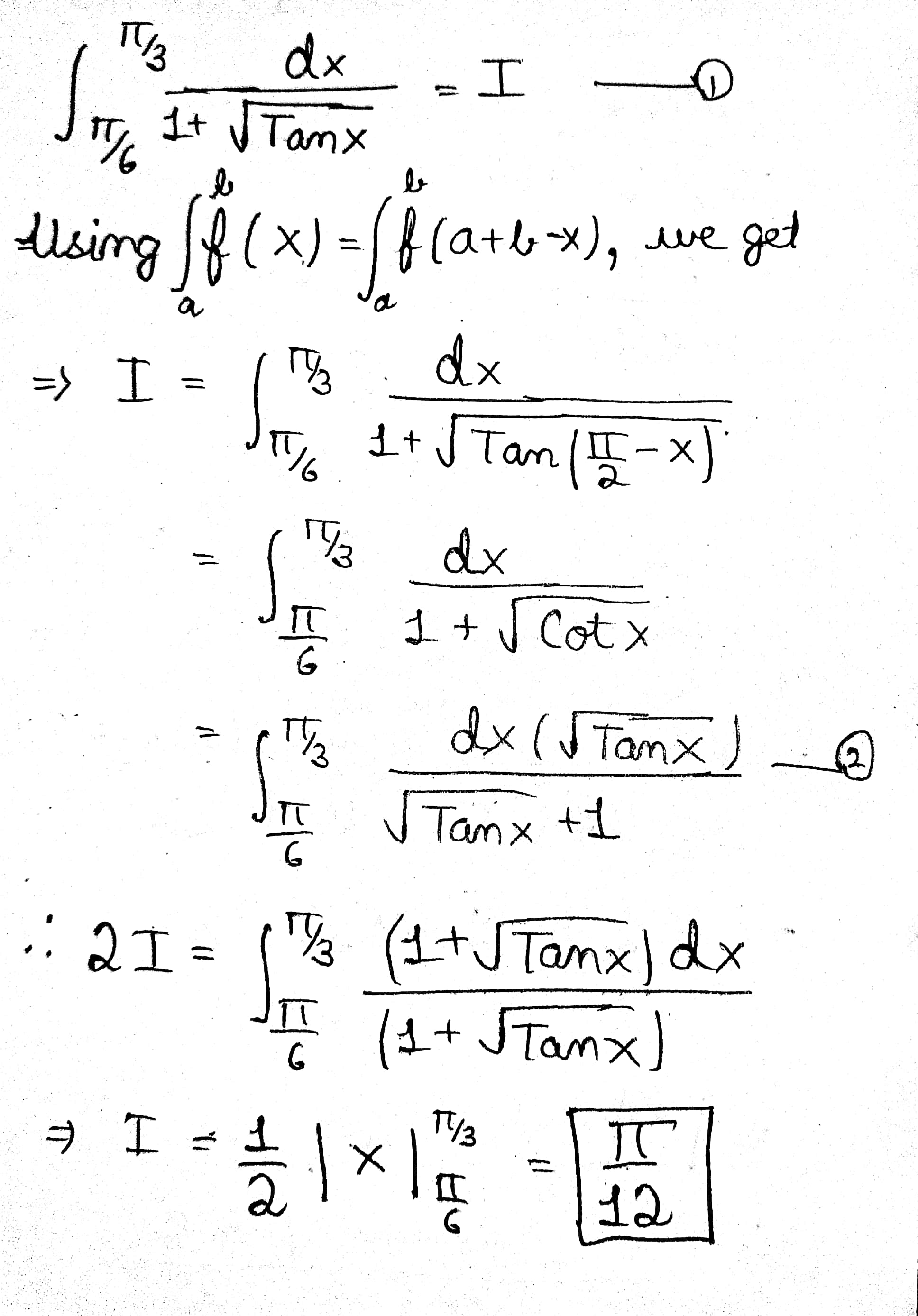Integrals - Class 12 Commerce Maths - Extra Questions
Evaluate :$$\displaystyle\int \sqrt{\dfrac{1-\cos 2x}{1+\cos 2x}}dx$$
Evaluate : $$\int_{-1}^{0} (e^{3x}+7x-5)dx$$.
$$\int_{0}^{1} \dfrac {xe^{x}}{(1 + x)^{2}}dx$$.
Find $$\displaystyle\int \dfrac{\sin^6x}{\cos^8x} \ dx$$
Evaluate the integrals
$$\int _{ 0 }^{ 2 }{ \cfrac { 1 }{ \left( { x }^{ 2 }+1 \right) } dx } $$
Evaluate : $$\displaystyle \int_{0}^{1}\dfrac {2x + 3}{5x^{2} + 1} dx$$
Evaluate :$$\int \dfrac{2\cos x}{3 \sin^2x} \ dx$$
Evaluate :$$\displaystyle\int \dfrac{x^3-x^2+x-1}{x-1}dx$$
$$\int { \dfrac { 3x }{ 3x-1 } dx } $$
Evaluate :$$\int \dfrac{dx}{x(x^5+3)}$$
Find the following integrals:
i) $$\displaystyle \int { \dfrac { { x }^{ 3 }-1 }{ { x }^{ 2 } } dx }$$
ii) $$\displaystyle \int { \left( { x }^{ \cfrac { 2 }{ 3 } }+1 \right) dx }$$
iii) $$\displaystyle \int { \left( { x }^{ \cfrac { 3 }{ 2 } }+2{ e }^{ x }-\dfrac { 1 }{ x } \right) dx }$$
The acceleration of a motorcycle is given by $$a_{x}(t) = At - Br^{2}$$, where $$A = 1.50\ ms^{-2}$$ and $$B = 0.120\ ms^{-4}$$. The motorcycle is at rest at the origin at time $$t = 0$$.
Find its position and velocity as functions of time.
$$\displaystyle _{0}^{5}\int \dfrac{4\sqrt{x+4}}{4\sqrt{x+4}+4\sqrt{9-x}}$$
Evaluate $$\int {x\ln \sqrt {xdx} } $$
Solve: $$\displaystyle\int\limits_{-\dfrac{\pi}{2}}^{\dfrac{\pi}{2}} \sin^5 x.\cos^{100} x \,dx $$
$$\int_1^{\sqrt 3 } {\dfrac{{dx}}{{1 + {x^2}}}} $$
$$\int \dfrac {1}{\sqrt {3x+5}-\sqrt {3x+2}}dx$$
Solve $$\displaystyle \int { \dfrac { 1 }{ \log _{ x }{ e } } dx }$$
$$\displaystyle \int_{0}^\cfrac{\pi}{4} \sin 3x \sin 2x\ dx$$
Evaluate $$\int {\dfrac {\sin x}{\sin (x+a)}}dx$$
$$\displaystyle\int e^{log x}dx$$.
Integrate with respect to $$x$$:
$$\displaystyle \int \dfrac {1}{x^{6}{(1+x^{-5})}^{\frac {1}{5}}}dx$$
Solve $$\displaystyle\int\limits_0^x {\dfrac{{\sqrt x }}{{\sqrt x + \sqrt {8 - x} }}dx} $$
Solve : $$\int \dfrac{dx}{x(n + 1) (n + 2)}$$
Solve:
$$\int {\dfrac{1}{{{a^2} - {x^2}}} = \dfrac{1}{{2a}}\log \left| {\dfrac{{a + x}}{{a - x}}} \right|} $$
Evaluate $$\int \dfrac {1}{a^{x}b^{x}}dx$$
Solve
$$\displaystyle \int \dfrac {1-x^{2}}{x(1-2x)} = $$
Solve $$\displaystyle \overset{4}{\underset{2}{\int}} 2^x dx$$.
The value of $$\int _{ 0 }^{ { \pi }/{ 2 } }{ \cfrac { dx }{ 1+\tan ^{ 3 }{ x } } } $$ is
$$\int {x^2}{e^x} dx$$ =
Solve:
$$\frac{1}{2}\int {\frac{{2x}}{{{{\left( {1 + x} \right)}^2}}}dx} $$
$$\int{\dfrac{{x}^{2}dx}{{(1+{x}^{2})}^{2}}}$$.
Integerate:
$$\int {x\,\cos \,x\,dx} $$
$$\int \dfrac {\cos 2x}{\cos^{2}x.\sin^{2}x}dx$$
Solve $$\displaystyle\int_{}^{} {\dfrac{{\left( {3{{\tan }^2}x + 2} \right){{\sec }^2}x}}{{{{\left( {{{\tan }^3}x + 2\tan x + 5} \right)}^2}}}dx} $$
Solve $$\displaystyle\int\limits_b^a {\frac{x}{{\sqrt {{a^2} + {x^2}} }}dx} $$
$$\int x{\sin ^{ - 1}}x$$
Evalute $$\int\limits_0^a x {\left( {{a^2} - {x^2}} \right)^{\frac{7}{2}}}dx$$
Evaluate: $$\int \,lnx \cdot \dfrac{1}{(x + 1)^2}dx$$ equals
$$\displaystyle \int x\dfrac{1}{(x+1)^2}dx$$
Using Integration by parts,we get
$$=\displaystyle ln x\int \dfrac{1}{(x+1)^2}dx-\int\left(\dfrac{d}{dx}lnx\int\dfrac{1}{(x+1)^2}dx\right)dx$$
$$\displaystyle =ln x\left(\dfrac{-1}{x+1}\right)-\int \dfrac{1}{x}\left(\dfrac{-1}{x+1}\right)dx$$
$$=\dfrac{-lnx}{x+1}+\int \dfrac{dx}{x(x+1)}$$
$$=\dfrac{1}{x(x+1)}=\dfrac{A}{x}+\dfrac{B}{x+1}$$ (Partial fraction)
$$1=A(x+1)+Bx$$
put $$x=0$$ we get $$A=1$$
put $$x=-1$$ ,we get $$B=-1$$
$$\displaystyle =\dfrac{-ln x}{x+1}+\int \dfrac{dx}{x}-\int \dfrac{dx}{x+1}$$
$$=\dfrac{-ln x}{x+1}+ln x -ln (x+1)$$
$$=\dfrac{-ln x}{x+1}+ln \left(\dfrac{x}{x+1}\right)+C$$
$$\boxed{\displaystyle \int \dfrac{ln x}{(x+1)^2}dx=\dfrac{-ln x}{x+1}+ln \left(\dfrac{x}{x+1}\right)+C}$$
The value of $$\displaystyle\int_1^{37\pi } {\dfrac{{\pi \sin \left( {\pi \log x} \right)}}{x}} \,dx$$
$$\int \cot^{2}xdx = $$
$$\displaystyle\int 2x\sqrt{x} dx$$.
$$\displaystyle\int \left(\dfrac{e^x+e^{-x}}{e^x-e^{-x}}\right)^2dx$$.
$$\displaystyle\int \dfrac{1}{1+\cot}dx$$.
Solve : $$\displaystyle \int \dfrac{x^2}{(4 + x)^{3/2}} dx$$
Evaluate :$$\displaystyle \int x.(\log x)^2 \ dx$$
Solve : $$\displaystyle \int\limits_{-\pi/2}^{\pi/2} \sin^7x \ dx$$
Evaluate :$$\displaystyle \int\limits_{0}^{\pi/2} \dfrac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}dx$$
Evaluate : $$\displaystyle \int\limits_{0}^{\pi/4} \log(1+\tan x)dx$$
Evaluate :$$\displaystyle \int x \ \sin x \ dx$$
Solve :-$$I = \displaystyle \int_0^{\infty}\dfrac{dx}{e^x+e^{-x}}$$
$$\displaystyle\int x\left(\dfrac{\sec 2x-1}{\sec 2x+1}\right)dx$$.
Evaluate:
$$\int x.\sin{2x}dx$$
$$ \displaystyle \int x sin2xdx $$
$$ \displaystyle \dfrac{-x cos2x}{2}-\dfrac{1}{2}\int cos 2x dx $$
$$ \Rightarrow -(\dfrac{xcos2x}{2}+\dfrac{sin2x}{4})$$
Evaluate :
$$\displaystyle\int_{0}^{\pi} \dfrac{1}{1+\sin x} dx$$
$$\displaystyle \int_{0}^{\pi } \frac{1}{1+sinx}dx $$
$$\displaystyle = \int_{0}^{\pi } \frac{1-sinx}{1-sin^{2}x}dx $$ Raticnaising the devotion
$$\displaystyle = \int_{0}^{\pi } \frac{1-sinx}{cos^{2}x}dx $$
$$\displaystyle = \int_{0}^{\pi } (sec^{2}x-tan\,x sec\,x) dx $$
$$\displaystyle | tan x - sec\,x |_{0}^{\pi } $$
$$\displaystyle = tan \pi -tan\,0 - sec\pi +sec\,0 $$
$$\displaystyle = 0-0-(-1)+1 $$
$$ \Rightarrow 1+1 = 2 $$
$$\displaystyle\int e^x\left(\dfrac{x-1}{x^2}\right)dx$$.
$$\displaystyle\int (x+1)e^xlog (xe^x)dx$$.
$$\displaystyle\int x \sin^3x dx$$.
Solve:
$$ \int_0^1 x^3 \sqrt{1 +3x^4 } dx $$
Integrate:
$$\int \sin^4xdx$$
$$\int \frac{2x^{2}}{3x^{4}2x} dx$$
$$ \int \frac{2x^{2}}{3x^{4}2x}dx = \int \frac{x^{2}dx}{3x^{5}}$$
$$ = \frac{1}{3}\int \frac{dx}{x^{3}}$$
$$ = \frac{1}{3}\times (\frac{x^{-2}}{-2})$$ [using $$ \int x^{n}= \frac{x^{n+1}}{n+1}]$$
$$ = \frac{-1}{6x^{2}}$$
$$\int {\dfrac{{{e^x}dx}}{{\left( {1 + {e^{2x}}} \right)}}} $$
Evaluate :$$\displaystyle \int e^{ax} \cos(bx+c) \ dx$$
Evaluate; $$\int {\left( {\frac{{3{x^4} - 5{x^3} + 4{x^2} - x + 2}}{{{x^3}}}} \right)dx} $$
$$I = \int\limits_0^1 {\frac{{\left( {1 - x} \right)dx}}{{\left( {1 + x} \right)}}} $$
Calculate $$\int \frac{x}{x^{2}+1}dx$$
Solve: $$\displaystyle \int \dfrac{x^3}{2x + 1}dx$$.
$$\displaystyle\int \dfrac{x^3}{2x+1}dx$$
$$=\displaystyle\int \dfrac{(x^2/2-x/3+1/8)(2x+1)-1/8}{2x+1}dx$$
$$=\displaystyle\int \left(\dfrac{x^2}{2}-\dfrac{x}{4}+\dfrac{1}{8}\right)dx-\displaystyle\int \dfrac{dx}{8(2x+1)}$$
$$=\dfrac{x^3}{6}-\dfrac{x^2}{8}+\dfrac{x}{8}-\dfrac{1}{8}\dfrac{1}{2}ln(2x+1)+c$$
$$=\dfrac{x^3}{6}-\dfrac{x^2}{8}+\dfrac{x}{8}-\dfrac{1}{16}ln(2x+1)+c$$
$$\therefore \displaystyle\int \dfrac{x^3}{2x+1}dx=\dfrac{x^3}{6}-\dfrac{x^2}{8}+\dfrac{x}{8}-\dfrac{1}{16}ln(2x+1)+c$$.
Evaluate: $$ \displaystyle\int \dfrac { \dfrac{- 1} 6 } { ( x + 3 ) } d x + \int \dfrac { \dfrac1 6 } { ( x - 3 ) } d x$$
Find the following integrals:
$$\int (ax^{2} + bx + c) dx$$.
$$I=\displaystyle\int (ax^2+bx+c)dx$$
$$=\dfrac{ax^3}{3}+\dfrac{bx^2}{2}+cx+d$$
$$=\dfrac{1}{3}ax^3+\dfrac{1}{2}bx^2+cx+d$$ (arbitrary constant).
Evaluate
$$\int \sqrt{1+t^{3}} dt$$
Solve:
$$\int\limits_0^1 {{{\tan }^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)dx} $$
$$\int_{0}^{1}tan^{-1}(\frac{2x}{1-x^{2}})dx$$
$$\int_{0}^{1}tan^{-1}(tan x)dx$$
$$\int_{0}^{1} 2x dx = [2\frac{x^{2}}{2}]_{0}^{1}=1$$
Evaluate $$\displaystyle\int_{0}^{\pi/2}\dfrac{\cos^{2}x}{1+3\sin^{2}x}\ dx$$
Evaluate $$\int_0^n { xdx} $$.
$$\displaystyle \int { \dfrac { 1 }{ \sqrt { 9-25{ x }^{ 2 } } } } dx$$
$$\int \frac{dx}{\sqrt{9-25x^{2}}}=\int \frac{dx}{5\sqrt{\frac{9}{25}-x^{2}}}$$
$$=\frac{1}{5}\int \frac{dx}{\sqrt{(\frac{3}{5})^{2}-x^{2}}}$$ $$(\because \int \frac{dx}{\sqrt{a^{2-x^{2}}}}=sin^{-1}(\frac{x}{a})+c)$$
$$=\frac{1}{5}sin^{-1}(\frac{5x}{3})+c$$
Evaluate:
$$\int \dfrac{\sqrt{x^{2}-a^{2}}}{x}dx$$
Prove that:
$$\displaystyle \int x^5(x+7)dx$$
Evaluate $$\displaystyle\int_{0}^{\pi/4}\sin^{3}2t\cos 2t\ dt$$
Evaluate $$\displaystyle\int_{0}^{\pi/4}\sin^{3}2t\cos 2t\ dt$$
Evaluate : $$\int _{ 0 }^{ \pi /2 }{ sinxdx } $$.
Solve $$\int _ { 0 } ^ { \frac { \pi } { 2 } } \cos ^ { 2 } x d x$$
Solve it
$$2I=\int _{ O }^{ Q }{ dx } $$
Evaluate:$$\displaystyle\int\limits_{0}^{1} \dfrac{dx}{1+x^2}$$
Prove that:
$$\displaystyle \int \dfrac {1}{4x^{2}-1}dx$$
$$\int \frac{1}{4x^{2}-1}dx=\int \frac{1}{(2x)^{2}-1}dx$$
$$\Rightarrow$$ we know $$\int \frac{1}{x^{2}-a^{2}}=\frac{1}{2a}In \left | \frac{x-a}{x+a} \right |$$
then
$$\Rightarrow \frac{1}{2} in \left | \frac{2x-1}{2x+1} \right |+c$$
Evaluate $$\displaystyle\int { \left( \dfrac { { x }^{ 2 }+3x+4 }{ \sqrt { x } } \right) } dx$$
$$\int (\frac{x^{2}+3x+4}{\sqrt{x}})dx$$
$$\Rightarrow \int (x)^{2-\frac{1}{2}}+3(x)^{1-\frac{1}{2}}+4(x)\frac{-1}{2}$$
$$\Rightarrow \int x^{3/2}+3x^{1/2}+4x^{-1/2}dx$$
$$\Rightarrow \frac{2}{5}x^{5/2}+2x^{3/2}+8x^{1/2}+c.$$
Evaluate:
$$\displaystyle \int _{0}^\dfrac {\pi}{2}{}(2\log \sin x-\log \sin 2x)dx$$
$$I=\displaystyle\int\dfrac{\pi}{2}(2log\sin x -log\sin 2x )dx$$
$$I=\displaystyle\dfrac{\pi}{2}\displaystyle\int_0^{\dfrac {\pi}{2}}[2log\sin x-log (2\sin x\cos x)]dx$$
$$I=\dfrac{\pi}{2}\displaystyle\int_0^{\dfrac{\pi}{2}}[2log\sin x-log\sin x - log\cos x-log 2]dx$$
$$I=\dfrac{\pi}{2}\displaystyle\int_0^{\dfrac{\pi}{2}}(2log\sin x-2log \sin x-log 2)dx$$
$$I=\dfrac{\pi^2}{2}\displaystyle\int^{\dfrac{\pi}{2}}_0(-log 2)dx$$
$$I=-\dfrac{\pi^2}{4}(log 2)$$.
Evaluate : $$\displaystyle I = \int {\cfrac{{{{\sin }^{ - 1}}x}}{{\sqrt {\,1 - {x^2}} }}} dx$$
Evaluate the following definite integrals :
$$\displaystyle \int _{0}^{\pi /2} \cos^2 x\ dx$$
Evaluate $$\displaystyle\int_{0}^{\pi/3}\dfrac{\cos x}{3+4\sin x}dx$$
Evaluate the definite integral :
$$\displaystyle \int_{0}^{5}x^4\ dx$$
Evaluate the definite integral:
$$\displaystyle \int_{0}^{\pi /2} \cos x\ dx$$
Evaluate: $$\displaystyle\int_{0}^{1}\dfrac{\sqrt{\tan^{-1}x}}{1+x^{2}}dx$$
Evaluate $$\displaystyle\int_{0}^{1}\dfrac{\tan^{-1}x}{1+x^{2}} \ dx$$
Evaluate $$\displaystyle\int_{4}^{12}x\ dx$$
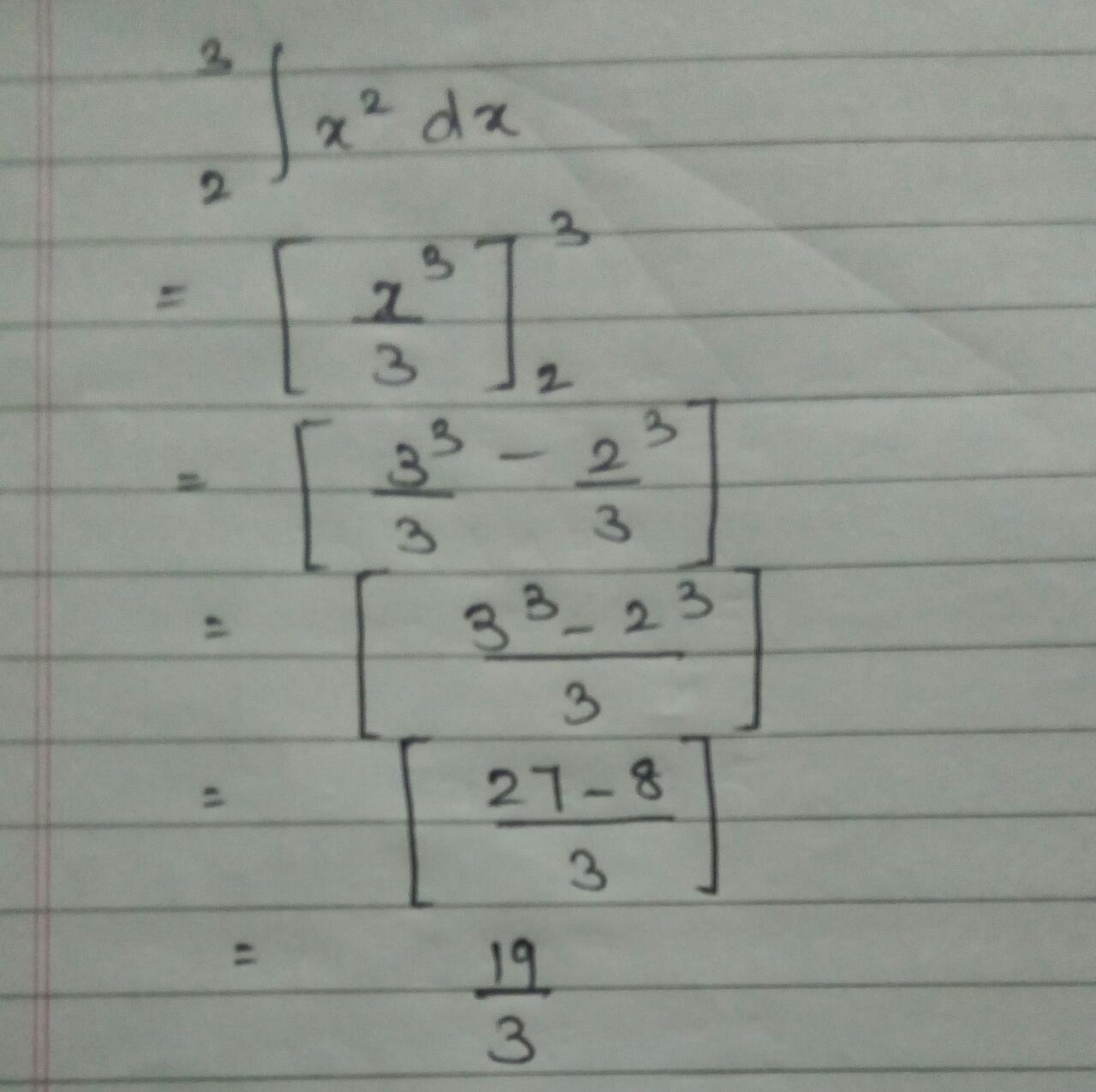
Evaluate $$\displaystyle \int_{2}^{3}x^{2}dx$$
$$\displaystyle^{3}_{2}\int x^2dx$$
$$=\left[\dfrac{x^3}{3}\right]^3_2$$
$$=\left[\dfrac{3^3}{3}-\dfrac{2^3}{3}\right]$$
$$=\left[\dfrac{3^3-2^3}{3}\right]$$
$$=\left[\dfrac{27-8}{3}\right]$$
$$=\dfrac{19}{3}$$.
$$\int \dfrac{1}{1-cos\dfrac{x}{2}}$$ dx
Evaluate:$$\displaystyle\int \dfrac{1}{2x+3}dx$$
Evaluate the following definite integrals :
$$\displaystyle \int_{0}^{\frac {\pi} {2}}\sin^3 x\cos x\ dx$$
Evaluate:$$\displaystyle\int_{2}^{1}|x-3|\ dx$$
Evaluate the definite integral:$$\displaystyle\int_{-1}^{1}5x^{4}\sqrt{x^{5}+1}\ dx$$
Evaluate the definite integral :
$$\displaystyle \int_{0}^{\pi /2} \sin x \ dx$$
Evaluate $$\displaystyle\int_{0}^{1}\sqrt x \ dx$$
Evaluate the definite integral:$$\displaystyle\int_{0}^{\pi/2}\dfrac{\cos^{2}x}{1+3\sin^{2}x}\ dx$$
Evaluate the definite integral:$$\displaystyle \int_{0}^{\pi /2} \sin 2x\ dx$$
$$\displaystyle \int _0^{\pi/2} \sin x \cos x dx $$ is equal to:
Evaluate $$\displaystyle\int_{0}^{\pi/4}\sin^{3}2t\cdot \cos 2t\ dt$$
Evaluate the following integral :
$$\displaystyle\int_{0}^{\pi}x\sin x\cos^{4}x\ dx$$
Evaluate the following definite integral:
$$\displaystyle\int_{0}^{2}x\sqrt{x+2}dx$$
Evaluate the following definite integral :$$\displaystyle \int _{0}^{\pi /2} \cos^2 x\ dx$$
Evaluate $$\displaystyle \int_{0}^{1} \dfrac {1}{\sqrt {1+x}-\sqrt {x}} \, dx$$
Evaluate the given integral: $$\displaystyle \int_{0}^{1} (1+x)^5 dx$$
Solve $$\displaystyle \int_{0}^{\pi} {1+ \dfrac {x}{2}}dx$$
Evaluate the following integral :$$\displaystyle\int_{0}^{\pi} ({1+\sin x})\ dx$$
Evaluate the following definite integral:$$\displaystyle \int_{0}^{1} \dfrac {1}{\sqrt {1+x-\sqrt x}}dx$$
Evaluate the following integral:
$$\displaystyle \int_{0}^{1} \ x+x^2 dx$$
Evaluate $$\displaystyle\int_{0}^{1}\dfrac{\tan^{-1}x}{1+x^{2}}dx$$
Evaluate the following definite integral:$$\displaystyle \int_{1}^{2}\dfrac {1}{\sqrt {(x-1) (2-x)}}dx$$
Evaluate the following definite integral:
$$\displaystyle\int_{0}^{1}\sqrt x \ dx$$
Evaluate the following definite integral:
Evaluate $$\displaystyle \int_{1}^{2} \dfrac {x}{(x+1)(x+2)}dx$$
$$\displaystyle \int_{0}^{\pi /2}\frac{\cos ^{2}x\sin x}{\sqrt{(1+\cos ^{2}x)}}dx=\frac{1}{n}[\sqrt{k}-log(\sqrt{m}+1)]$$.Find $$k+m+n$$ ?
$$\displaystyle \int_{-1}^{1}\frac{x\sin ^{-1}x}{\sqrt{\left ( 1-x^{2} \right )}}dx= ??$$
The value of $$ \displaystyle 3\int _{ 0 }^{ \pi/2 }{ \sqrt { \cos x-\cos ^{ 3 } x } dx } $$ is
The value of $$\displaystyle \int_{0}^{1/2}\frac{dx}{\sqrt{\left ( x-x^{2} \right )}}$$is $$\displaystyle \frac{\pi }{k}.$$ Find the value of $$k$$.
$$\displaystyle \int_{0}^{\pi. }\frac{dx}{1+2\sin ^{2}x}= \frac{\pi }{\sqrt{\left ( k \right )}}$$
what is k?
Solve $$\displaystyle \int_{0}^{\infty }\log \left ( x+\frac{1}{x} \right )\frac{dx}{1+x^{2}}$$
Prove that $$\displaystyle \int_{0}^{\infty }\frac{\log \left ( 1+x^{2} \right )}{1+x^{2}}dx= {\pi} \log 2$$
$$\displaystyle I= \int_{0}^{\pi }\frac{x\tan x}{\sec x+\tan x}dx= \frac{\pi }{C}\left ( \pi -2 \right ).$$
What is C?
Evaluate: $$\int_{2}^{4} \dfrac {x}{x^{2} + 1}dx$$
Evaluate $$\displaystyle\int _{ 0 }^{ \pi }{ \log { \left( 1-\cos { x } \right) } dx } $$.
If $$\int (x^6+x^4+x^2)\sqrt{2x^4+3x^2+6}dx=\dfrac{(\alpha x^6+\beta x^4+\gamma x^2)^{3/2}}{18}+C$$ where C is constant then find the value of $$(\beta + \gamma-\alpha).$$
Evaluate:$$\displaystyle \int _{ 1 }^{ e }{ \left( \frac{1}{\sqrt{x \ln x}} + \sqrt{\frac{\ln x}{x}} \right) dx }$$
Solve $$ \int {r^5} {e^x} dx $$:(Given $$r$$ is constant)
Evaluate: $$\displaystyle \int_{2}^{3} \dfrac {x\ dx}{x^{2} + 1}$$.
Prove that $$\displaystyle \int_{0}^{a}f(x)dx = \int_{0}^{a} f(a - x)dx$$ and hence evaluate $$\displaystyle \int_{0}^{a} \dfrac {\sqrt {x}}{\sqrt {x} + \sqrt {a - x}} dx$$.
Solve:$$\displaystyle \int { \dfrac { \sqrt { 1+{ x }^{ 2 } } }{ { x }^4 } } dx$$
For what $$a < 0$$ does the inequality $$\displaystyle\, \int_{a}^{0}(3^{-2x} \, \, 2.3^{-x})dx \geqslant 0$$ hold true?
Calculate the following integrals.
$$\displaystyle \int_{0}^{2e} \, \frac{dx}{0.5x \, + \, 1}.$$
Evaluate $$\int_{0}^{1} x \tan^{-1} x\ dx$$.
Evaluate: $$\int_{0}^{\pi/2} \dfrac {x}{a^{2}\cos^{2} x + b^{2}\sin^{2}x} dx$$.
Evaluate: $$\int { \tan ^{ -1 }{ x } } dx$$
Sita is driving along a straight highway in her car. At time $$t = 0$$, when Sita is moving at $$10\ ms^{-1}$$ in the positive x-direction, she passes a signpost at $$x = 50\ m$$. Here acceleration is a function of time:
$$a = 2.0\ ms^{-2} - \left (\dfrac {1}{10} ms^{-3}\right )t$$
Derive expressions for her velocity and position as functions of time.
$$\int\limits_0^{\pi /2} {{1 \over {{a^2}{{\sin }^2}x + {b^2}{{\cos }^2}x}}dx} $$
Evaluate the integral:$$\displaystyle \int e^x\left(\frac{1+sinx}{1+cosx}\right) dx$$
Find $$ \int { \dfrac { ({ x }^{ 2 }+1)({ { x }^{ 2 } }+2) }{ ({ { x }^{ 2 } }+3)({ { x }^{ 2 } }+4) } dx }$$
Integrate:
$$\int { \dfrac { 2+\sin { 2x } }{ 1+\cos { 2x } } } { e }^{ 2 }dx$$
$$ \displaystyle \int\left [\frac{2+\sin 2 x}{1 + (2\cos^2 2x -1)}\right]e^2 = \left[\frac{2 + \sin 2x}{2\cos^2 x}\right] \quad \because (\cos 2x = 2\cos^2 x-1) $$
$$ \displaystyle \int \left[\frac{2(1+\cos x\sin x)}{2 \cos^2 x}\right] \quad \because \sin 2x = \sin x \cos x $$
$$ \displaystyle \int \left[\frac{1}{\cos^2 x}+\frac{\cos x\sin x}{ \cos^2 x}\right] =\int [\sec^2 x + \tan x] dx $$
$$ \displaystyle = \int \sec^2 x \,dx + \int \tan x \, dx $$
$$ \displaystyle = e^2 [\tan x - ln |\cos x | + c] $$
Integrate:
$$\int { \dfrac { \left( x-3 \right) { e }^{ x } }{ { \left( x-1 \right) }^{ 3 } } dx }$$
$$ \displaystyle \int \dfrac{(x-3)e^{x}}{(x-1)^{3}}dx $$ (By ILATE)
let $$x-1 = m$$ or $$m+1 = x $$
$$ dx =dm$$
$$ \Rightarrow \displaystyle \int \dfrac{(m-2)e^{m+1}}{m^{3}}dm$$
Here (1) $$ u = (m-2)e^{m+1}, V = \dfrac{1}{m^{3}}$$
$$ (\because \displaystyle \int uv \, dx = u \int v dx - \int \left [ \dfrac{dv}{dx} \int v \,dx \right ])$$
$$ \Rightarrow \dfrac{-e^{m+1}(m-2)}{2m^{2}} - \displaystyle \int -\frac{e^{m+1}+e^{m+1}m}{2m^{2}}dm $$
$$ \displaystyle -\dfrac{1}{2} \int \dfrac{-e^{m+1}+e^{m+1}m}{m^{2}}dm $$
Here (2)$$ m = e^{m+1}+e^{m+1} m , v = \dfrac{1}{m^{2}}$$
$$ \Rightarrow \frac{-1}{2} \left [ -\left ( \dfrac{-e^{m+1}+e^{m+1}m}{m} \right )-e^{m+1} dn \right ]$$
$$ (-e^{m+1})$$
$$ \Rightarrow \dfrac{-1}{2} \left ( -\dfrac{e^{m+1}+e^{m+1}m}{m} -(-e^{1+m})\right )$$
$$ \dfrac{-e^{m+1}}{2m}$$
$$ \Rightarrow \dfrac{-e^{m+1}(m-2)}{2m^{2}} + \dfrac{e^{m+1}}{2m}+c $$
or
$$ \Rightarrow \boxed{ \dfrac{e^{x}(x-3)}{2(x-1)^{2}}+ \dfrac{e^{x}}{2(x-1)}+c}$$
Evaluate :
$$e^{2x}\left(\dfrac{1-\sin 2x}{1-\cos 2x}\right)dx$$
Evaluate : $$\int\limits_0^{\pi /2} {\dfrac{{\cos x\,dx}}{{\left( {\,\cos \,x\, + \,\sin x} \right)}}} $$
$$\displaystyle\int\limits_0^{\frac{\pi }{2}} {\left( {2\log \sin x - \log \sin 2x} \right)dx} $$
$$\int \sin^{-1} \ (\dfrac{2x +2}{\sqrt{4x^{2} +8x +13}}\ )dx$$ =
Integrate $$\int x\log 2x \, dx$$
$$\displaystyle\int^{1/2}_0\dfrac{x\ dx}{(y^2+x^2)^{3/2}}$$
$$\displaystyle \int_{0}^{2}2x dx=$$
$$\int (\log x)^{2}dx$$
Solve $$\displaystyle\int { \left[ \dfrac { \sqrt { { x }^{ 2 }+1 } \left[ \ln { \left( { x }^{ 2 }+1 \right) -2\ln { x } } \right] }{ { x }^{ 4 } } \right] } dx$$
$$\int { \sqrt { \left( \dfrac { x-1 }{ x+1 } \right) } } dx$$
Find the value of $$\displaystyle\int { \dfrac { d\left( { x }^{ 2 }+1 \right) }{ \sqrt { \left( { x }^{ 2 }+2 \right) } } }$$
$$\int_{0}^{\frac{\pi}{2}}\dfrac{\sin\ x-\cos\ x}{1+\sin x\ \cos\ x}dx$$
Solve:
$$\displaystyle \int x^{2} \sin^{2}x dx$$
Integrate with respect to $$x$$.:
$$e^{x}(\text{sec}^2 {x}+\tan x)$$
$$\int { x\left( \dfrac { \sec { 2x } -1 }{ \sec { 2x } +1 } \right) dx } $$
Evaluate:$$\displaystyle\int{{(\ln x)}^{4}dx}$$
$$ \int { \dfrac { arc\sin { \sqrt { x } } }{ \sqrt { 1-x } } dx }$$
$$\displaystyle\int x\cos^3x\sin x dx$$.
$$\int {x{{\sin }^2} x\times dx} $$
$$\int {x\sin 3xdx} $$
Solve $$\displaystyle\int x\sin^{-1} xdx$$.
Let $$f:\left[ -2,3 \right] \rightarrow \left[ 0,\infty \right) $$ be a continuous function such that $$f\left( 1-x \right) -f\left( x \right) $$ for all $$x\epsilon \left[ -2,3 \right] $$.If $${ R }_{ 1 }$$ is the numerical value of the area of the region bounded by $$y=f\left( x \right) ,x=-2,x=3$$ and the axis of x and $${ R }_{ 2 }=\int _{ 2 }^{ 3 }{ xf\left( x \right) dx } $$, then:-
Evaluate $$\displaystyle\int\limits_4^9 {\dfrac{{dx}}{{\sqrt {\left( {9 - x} \right)\left( {x - 4} \right)} }}} $$
Integrate:$$\displaystyle \int \dfrac{2}{(x^{2}+1)^{2}}dx$$
$$\displaystyle\int \dfrac{dx}{3x^2+13x -10}$$
Integrate
$$\int_0^1 {\frac{{{x^3}}}{{{x^2} + 1}}dx} $$
$$\int_{0}^{\pi/2}\dfrac {\sin x \cos x}{1+\sin^{4}x}dx$$
Solve $$\int\sin 4x\sin 8xdx$$
Solve : $$\displaystyle \underset{0}{\overset{\infty}{\int}} \dfrac{x \, \ln \, x}{(1 + x^2)^2}$$
Solve :$$\displaystyle \int_0^{\pi}\dfrac{1}{a^2-2a \cos x+1}dx$$
Evaluate:$$\displaystyle \int _{ 0 }^{ 1 } x^2+ 2x $$ dx
Solve$$\displaystyle\int\dfrac{{\cos x}}{{1 + \cos x}}dx$$
Solve : $$\displaystyle \int \, \dfrac{dx}{\sqrt{2x - x^2}}$$
Evaluate the integrals using substitution.
$$\displaystyle\int^1_0\dfrac{x^2}{x^2+1}dx$$.
$$\int x\log (1-x^{2})dx =$$
Solve:
$$\int {\sin x\left( {2 + 5x} \right)} dx$$
Solve:
$$\int {{e^x}} \left( {\frac{{x - 1}}{{{x^2}}}} \right)dx$$
$$\displaystyle\int^1_0\tan^{-1}(1-x+x^2)dx$$.
Solve : $$\int \dfrac{t^4 - 3 t^2 + 2}{t^2 (1 + t^2)} , dt$$
Solve : $$\displaystyle2 \underset{0}{\overset{\pi / 2}{\int}} x \, sin \, x \, dx$$
Solve: $$\displaystyle \int_0^{\pi}(\sqrt{1+\sin t}).dt$$
$$\displaystyle\int^2_1\left(\dfrac{1}{x}-\dfrac{1}{2x^2}\right)e^{2x}dx$$.
$$\displaystyle\int x^2\sin^{-1}x dx$$.
$$\displaystyle \int { \dfrac { 1 }{ 2 } \cos ^{ -1 }{ x } dx } $$
Evaluate:$$\displaystyle\int\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2dx$$.
Evaluate: $$\displaystyle\int \dfrac {dx}{x(1 + x^{2})}$$.
Evaluate :
$$\displaystyle\int _{0}^{\pi/2} x\cos{2x}dx$$
$$\displaystyle\int _{0}^{\pi/2} x\cos{2x}dx$$
Solve:$$\displaystyle \int_0^1 \dfrac{x\tan^{-1}x}{(1+x^2)^{3/2}}dx$$
$$I=\int_{0}^{1}{\tan^{-1}(\frac{2x-1}{1+x-x^{2}})}$$
Evaluate $$ \int x ^ { 3 } \log 2 x d x $$
Solve: $$\displaystyle \overset{\frac{\pi}{2}}{\underset{0}{\int}} \sqrt{\cos \theta}\cdot \sin^3 \theta d\theta$$
$$\int _{ -1 }^{ 1 }{ \frac { dx }{ { x }^{ 2 }+2x+5 } }$$
$$\int x\sqrt{3x-2}dx$$
Find the following integral.
$$\displaystyle\int (x^{\frac{2}{3}}+1)dx$$.
Evaluate $$\displaystyle \int { \frac { 1 }{(1-2x) } }dx $$
If $$ g(x) =\displaystyle \int _{ 0 }^{ x }{ \cos { 4t\ dt, } } $$ then $$g(x+\pi)$$ equals
$$\int\limits_0^{\pi /2} {\dfrac{{\cos x}}{{1 + \cos x + \sin x}}dx} $$
Evaluate
$$\int\limits_0^\infty {\frac{{\log \left( {1 + {x^2}} \right)dx}}{{1 + {x^2}}}} = $$
$$\displaystyle\int_{\frac{1}{9}}^{\frac{1}{4}} {\dfrac{{dx}}{{(1 - x)\sqrt x }}} = \,\log \dfrac{3}{2}$$
Evaluate:$$\displaystyle \int { { \left( a\tan { x+b\cot { x } } \right) }^{ 2 }dx }$$
Evaluate :$$\int { { 2x }^{ 3 }{ e }^{ { x }^{ 2 } } } dx$$
Integrate $$\int x.sin2xdx$$
$$\int_{\frac{\pi }{6}}^{\frac{\pi }{6}}\frac{sin x +cos x}{\sqrt{sin 2x}}dx$$
Integrate $$\int_{-\dfrac {\pi}{4}}^{\dfrac {\pi}{4}} \dfrac {1}{1 - \sin x} dx$$.
Solve:$$\displaystyle \int_0^{2\pi}\dfrac{\cos x }{1+\sin^2 x} dx$$
Evaluate
$$\int {x\,{e^{ - x}}} \,\,dx$$
Solve:$$\int \dfrac{1}{\sqrt{1-e^{2x}}}dx$$
If $$f(x)=\displaystyle \int_{0}^{x}{t(\sin x-\sin t)dt}$$ then $$f'(x)$$?
$$\int\limits_0^{\pi /2} {\dfrac{{a\sin x + b\cos x}}{{\sin x + \cos x}}dx} $$
Solve:$$\displaystyle \int_1^2 \dfrac{1}{x(1+x^2)}dx$$
$$\displaystyle \int \left(\dfrac{1-\tan{x}}{1-\tan{x}}\right)^{2}dx$$
$$\int\limits_0^1 {{{\sin }^{ - 1}}\left( {\frac{{2x}}{{1 + {x^2}}}} \right)dx} $$
Evaluate; $$\displaystyle\int _ { 0 } ^ { \pi/2 } \log \sin { 2 } x d x$$
Integrate : $$\displaystyle\int _ { 1 } ^ { 2 } \frac { \ln x } { x ^ { 2 } } d x$$
Prove:
$$\int _ { 0 } ^ { \pi } \dfrac { x \sin x } { 1 + \cos ^ { 2 } x } d x = \dfrac { \pi ^ { 2 } } { 4 }$$
Evaluate: $$\displaystyle \int^{\frac{\pi}{2}}_{0} log \,\sin x \,dx$$
Evaluate $$\int _ { 0 } ^ { 1 } \frac { 2 x + 3 } { 5 x ^ { 2 } + 1 } d x$$
Evaluate : $$\displaystyle \int _{0}^{\pi/2}2\sin{x}\cos{x}\tan^{-1}{(\sin{x})}dx$$
Solve
$$\int\dfrac{\cos 5x+\cos 4x}{1-2 \cos 3x} dx$$
If $$\int \frac { 1 } { 5 + 4 \cos 2 \theta } d \theta = A \tan ^ { - 1 } ( B \tan \theta ) + c$$ then $$( A , B ) =$$
Evaluate:-
$$\int\limits_0^{\pi /2} {\operatorname{\sin x} .\sin 2xdx} $$
$$\displaystyle \int _{0}^{1}\cot^{-1}{(1-x+x^{2})}dx$$
Integrate: $$\dfrac { 3 x ^ { 2 } } { x ^ { 6 } + 1 }$$
Solve:$$\displaystyle \int \dfrac { \sin ^ { 3 } x + \cos ^ { 3 } x } { \sin ^ { 2 } x \cos ^ { 2 } x } d x$$
Evaluate:$$\displaystyle\frac { 1 } { 15 } \int \frac { d t } { 4 + t ^ { 2 } } + \frac { 4 } { 15 } \int \frac { 6 d t } { 1 + 4 t ^ { 2 } }$$
$$\dfrac{1}{15}\displaystyle\int \dfrac{dt}{4+t^2}+\dfrac{4}{15}\displaystyle\int \dfrac{6dt}{1+4t^2}$$
$$=\dfrac{1}{15}\cdot \dfrac{1}{2}\tan^{-1}\left(\dfrac{t}{2}\right)+\dfrac{24}{15\times 4}\displaystyle\int \dfrac{dt}{\left(\dfrac{1}{2}\right)^2+t^2}$$
$$=\dfrac{1}{30}\tan^{-1}\left(\dfrac{t}{2}\right)+\dfrac{6}{15}\cdot\dfrac{1}{1/2}\tan^{-1}\left(\dfrac{t}{\dfrac{1}{2}}\right)+c$$
$$=\dfrac{1}{30}\tan^{-1}\left(\dfrac{t}{2}\right)+\dfrac{4}{5}\tan^{-1}(2t)+c$$.
Prove that
$$\displaystyle \int _ { 0 } ^ { 1 } \cfrac { 2 n + 3 } { 5 n ^ { 2 } + 1 } d x$$
$$ \int_{0}^{1} \frac{2n+3}{5n^{2}+1} dn$$
$$ = \frac{1}{5} \int_{0}^{1} \frac{10n}{5n^{2}+1} dn+\frac{1}{5}\int \frac{3}{n^{2}+\frac{1}{5}}dn$$
$$5n^{2}+1=t$$
10n dn = dt
$$ = \frac{1}{5} \int_{0}^{1}\frac{1}{t} dt + \frac{3}{5} \int \frac{1}{n^{2} + \left ( \frac{1}{\sqrt{5}} \right )^{2}}dn$$
$$ = \frac{1}{5}\left [ log(5n^{2} + 1) \right ]_{0}^{1} + \frac{3}{5} (\sqrt{5})\left [ tan^{-1}n\sqrt{5} \right ]_{0}^{1}$$
$$ = \frac{log6}{5} + \frac{3}{\sqrt{5}} tan^{-1}\sqrt{5}$$
Evaluate : $$\int \frac{dx}{a+be^{cx}}$$
$$I=\displaystyle\int \dfrac{dx}{a+be^{cx}}$$
$$I=\displaystyle\int\dfrac{dx}{e^{cx}[ae^{-cx}+b]}$$
$$I=\displaystyle\int \dfrac{e^{-cx}dx}{ae^{-cx}+b}$$ $$[$$Let $$ae^{-cx}+b=u$$ $$a(-c)e^{-cx}dx=du, e^{-cx}dx=\dfrac{du}{-ac}]$$
$$=\displaystyle\int \dfrac{du/-ac}{u}$$
$$I=\dfrac{-1}{ac}\displaystyle\int \dfrac{du}{u}$$
$$I=\dfrac{-1}{ac}(ln u+\alpha)$$
$$I=\dfrac{-1}{ac}(ln (ae^{-cx}+b)+\alpha)$$
Constant of integration.
Evaluate :
$$\int \dfrac{(x^{4}-x)^{1/4}}{x^{5}}dx$$
$$\int \dfrac{(x^{4}-x)^{1/4}}{x^{5}}dx$$
$$ = \int \frac{(x^{4})^{1/4}(1-\frac{x}{x^{4}})^{1/4}}{x^{5}}.dx$$
$$ = \int \frac{x(1-\frac{1}{x^{3}})^{1/4}}{x^{5}}.dx$$
$$ = \int \frac{(1-\frac{1}{x^{3}})^{1/4}}{x^{4}}. dx$$
Let $$ 1-\frac{1}{x^{3}} = t$$
$$ -(\frac{-3}{x^{4}}) = \frac{dt}{dx}$$
$$ \frac{3}{x^{4}} = \frac{dt}{dx}$$
$$ \frac{dt}{3}= \frac{dx}{x^{4}}$$
$$ \rightarrow = \int t^{2/4} (\frac{dt}{3})$$
$$ = \frac{1}{3}\int t^{\frac{1}{4}}.dt$$
$$ = \frac{1}{3}(\frac{t^{5/4}}{5/4})+C$$
$$ = \frac{1\times 4}{3\times 5}t^{5/4}+C$$
$$ = \frac{4}{15}t^{5/4}+C$$
$$ = \frac{4}{15}\times (1-\frac{1}{x^{3}})^{5/4}+C$$
Evaluate:$$\displaystyle\int_{0}^{\frac{\pi}{4}}{\ln{\left(1+\tan{x}\right)}dx}$$
Evaluate:$$\displaystyle\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}}{\dfrac{x\,dx}{1+\sin{x}}}$$
Evaluate: $$\int _ { 0 } ^ { \pi } \dfrac { x \sin x } { 1 + \cos ^ { 2 } x } d x$$
Let $$I=\displaystyle\int^{\pi}_0\dfrac{x\sin x}{1+\cos^2x}dx$$ ………$$(1)$$
$$I=\displaystyle\int^{\pi}_0\dfrac{(\pi -x)\sin(\pi-x)}{1+\cos^2(\pi-x)}dx$$
$$=\displaystyle\int^{\pi}_0\dfrac{(\pi -x)\sin x}{1+\cos^2x}dx$$ ……..$$(2)$$
Adding both $$(1)$$ and $$(2)$$, we get
$$2I=\displaystyle\int^{\pi}_0\dfrac{\pi\sin x}{1+\cos^2x}dx$$
Let $$t=\cos x$$ $$\cos 0=1$$
$$dt=-\sin xdx$$ $$\cos\pi =-1$$
So, $$2I=\displaystyle\int^{-1}_1\dfrac{-\pi dt}{1+t^2}$$
$$2I=\pi\displaystyle\int^1_{-1}\dfrac{dt}{1+t^2}=\pi\left[\tan^{-1}t\right]^1_{-1}$$
$$2I=\pi\left[\dfrac{\pi}{4}-\left(-\dfrac{\pi}{4}\right)\right]$$
$$2I=\dfrac{\pi^2}{2}$$
$$I=\dfrac{\pi^2}{4}$$
$$I=\left(\dfrac{\pi}{2}\right)^2$$.
Evaluate : $$\displaystyle \int \dfrac{x}{x-\sqrt{x^2-1}}dx$$
Evaluate: $$\displaystyle \int e^{2x} \sin 3x \ dx $$
Evaluate:
$$\displaystyle \int_{0}^{\dfrac {\pi}{4}}\dfrac {\sin x+\cos x}{9+16\sin 2x}dx$$
Evaluate: $$\displaystyle\int \dfrac { 1 } { 7 + 5 \cos x } d x =$$
Evaluate:$$\displaystyle\int_{-\pi}^{\pi}{\dfrac{{\cos}^{2}{x}}{1+{a}^{x}}dx}$$ where $$a>0$$
$$\int \sqrt { \sec x - 1 } d x$$ is equal to
Integrate:
$$\frac { 1 } { \sqrt { 16 - 9 x ^ { 2 } } }$$
Solve:
$$\displaystyle \int_{0}^{T/2}{I_{0}\sin(wt)dt}$$
$$\int_{0}^{T/2}I_{0} sin(wt).dt$$
$$=I_{0}\int_{0}^{T/2} sin (wt).dt$$
$$=I_{0}[\frac{-cos\, wt}{w}]_{0}^{T/2}$$
$$= \frac{I_{0}}{w}[- cos\, w.\frac{T}{2}-(-cos 0)]$$
$$= \frac{I_{0}}{w}[-cos(\frac{2\pi }{T}.\frac{T}{2})+cos 0]$$
$$= \frac{I_{0}}{w}[- cos\pi + cos0]$$
$$= \frac{I_{0}}{w}[I+1]$$
$$= \frac{2I_{0}}{w}$$
$$= \frac{2I_{0}}{(\frac{2\pi }{T})}$$
$$= \frac{T.I_{0}}{\pi }$$
Evaluate: $$\displaystyle\int \dfrac { \cos ^ { 3 } x } { \sin ^ { 2 } x + \sin x }$$
Evaluate:$$\displaystyle\int{\dfrac{\left(x+1\right)dx}{x{\left(1+x{e}^{x}\right)}^{2}}}$$
Evaluate:
$$\displaystyle\int { x\log { \left( x+1 \right) } dx } $$
Evaluate: $$\displaystyle \int {\dfrac {dx } { \sqrt { 1 - {e} ^ { 2 x } } } }$$
$$\displaystyle\int \dfrac{dx}{\sqrt{1-e^{2x}}}$$
$$=\displaystyle\int \dfrac{t\cdot dt}{t(t^2-1)}$$
$$=\displaystyle\int \dfrac{dt}{t^2-1}$$
$$=\dfrac{1}{2}log\left|\dfrac{t-1}{t-1}\right|+c$$
$$=\dfrac{1}{2}log\left|\dfrac{\sqrt{1-e^{2x}}-1}{\sqrt{1-e^{2x}}+1}\right|+c$$
Let $$t=\sqrt{1-e^{2x}}$$
$$t^2=1-e^{2x}$$
$$1-t^2=e^{2x}$$
$$-2tdt=2e^{2x}dx$$
$$\dfrac{-t}{e^{2x}}=dx$$
$$\dfrac{t}{t^2-1}dt=dx$$.
Integrate: $$\sin ^ { 3 } x \cos ^ { 3 } x$$
Evaluate:$$\displaystyle\int{\left({e}^{\ln{x}}+\sin{x}\right)\cos{x}dx}$$
Evaluate the following:
$$\displaystyle\int \dfrac { 2 x + 7 } { ( x - 4 ) ^ { 2 } } d x$$
Evaluate:$$\displaystyle\int{\sqrt{1+\csc{x}}dx}$$
Evaluate :$$\displaystyle \int \dfrac{x^2}{\sqrt{1-x^2}}dx$$.
Evaluate the following definite integral:$$\displaystyle \int _{\pi /6}^{\pi /4} \csc x \ dx$$
Integrate $$\dfrac{x^{2}+5x+5}{x^{2}+3x+2}$$ with respect to $$x$$.
$$I=\int \frac{x^{2}+3x+2}{x^{2}+3x+2}+\frac{2x+3}{x^{2}+3x+2}dx$$
$$= \int 1+\frac{f'(x)}{f(x)}dx(f(x)=x^{2}+3x+2)$$
$$ = x+log (x^{2}+3x+2)+c$$
solve the following.
$$\int\limits_0^1 {\frac{{\log (1 + t)}}{{(1 + {t})^2}}} dt$$
Evaluate $$\int {\dfrac{{{{\cos }^2}x}}{{{{\sin }^3}x{{\left( {{{\sin }^5}x + {{\cos }^5}x} \right)}^{\frac{3}{5}}}}}dx} $$
$$\int_0^{\pi /2} {\dfrac{1}{{1 + {{\tan }^3}x}}} dx$$
Evaluate :
$$\displaystyle\int { \dfrac { \sin { \left( x-a \right) } }{ \sin { \left( x+a \right) } } dx } $$
$$ \int \frac{sin (x-a)}{sin (x+a)}dx $$
Let $$ x+a = \theta $$
$$ dx = d\theta $$
so $$ x-a = \theta -2a $$
$$ \int \frac{sin (\theta -2a)}{sin \theta }d\theta $$
$$ \int \frac{sin \theta cos2a-sin2a cos\theta }{sin \theta }d\theta $$
$$ \int (cos2a-sin2a . tan\theta )d\theta $$
$$ = \int cos2a d\theta -\int sin2a . tan\theta .d\theta $$
$$ = \theta cos2a-sin2a\int tan\theta\, d\theta $$
$$ = \theta cos2a-sin2a (-log \,cos\theta )+c $$
$$ = \theta cos2a+sin2a . log\, cos\theta $$
$$ = (x+a)cos2a+sin2a\, log\, cos(x+a)$$
+c
Evaluate: $$\displaystyle \int{\dfrac{dx}{(2x-7)\sqrt{(x-3)(x-4)}}}$$.
$$\displaystyle\int \dfrac{dx}{(2x-7)\sqrt{(x-3)(x-4)}}$$
$$\displaystyle\int \dfrac{dx}{(2x-7)\sqrt{x^2-7x+12}}$$
$$\displaystyle\int \dfrac{dx}{2(2x-7)\sqrt{x^2-7x+12}}$$
$$\displaystyle\int \dfrac{2dx}{(2x-7)\sqrt{4x^2-28x+48}}$$
$$\displaystyle\int \dfrac{2dx}{(2x-7)\sqrt{4x^2-28x+49-1}}$$
$$\displaystyle\int \dfrac{2dx}{(2x-7)\sqrt{(2x-7)^2-1}}$$
Let $$2x-7=t$$
$$2dx=dt$$
$$\displaystyle\int \dfrac{dt}{t\sqrt{t^2-1}}$$
$$=\sec^{-1}(t)+c$$
$$=\sec^{-1}(2x-7)+c$$.
Prove that
$$\displaystyle \int \dfrac {x^{2}}{x^{6}+1}dx$$
Solve:
$$\displaystyle \int{\dfrac{dx}{\cos(x-a)\cos (x-b)}}$$
$$\int \frac{dx}{cos (x-a)cos (x-b)}$$
$$\int \frac{sin (a-b)}{sin (a-b)}\times \frac{1}{cos (x-a)cos (x-b)}dx$$
$$=\frac{1}{sin (a-b)}\int \frac{sin (a-b)}{cos (x-a)cos (x-b)}dx$$
$$=\frac{1}{sin (a-b)}\int \frac{sin a-b+x-x}{cos (x-a)cos (x-b)}dx$$
$$=\frac{1}{sin (a-b)}\int \frac{sin (x-b)+(a-x)}{cos (x-a)cos (x-b)}dx$$
$$=\frac{1}{sin (a-b)}\int \frac{sin (x-b)-(x-a)}{cos (x-a)cos (x-b)}dx$$
$$ =\frac{1}{sin (a-b)}\int \frac{sin (x-b)cos (x-a)-cos (x-b)sin(x-a)}{cos (x-a)cos (x-b)}dx$$
$$=\frac{1}{sin (a-b)}\int \frac{sin(x-b)cos (x-a)}{cos (x-a)cos (x-b)}-\frac{cos (x-b)sin (x-a)}{cos (x-a) cos (x-b)}dx$$
$$=\frac{1}{sin (a-b)}[\int tan (x-b).dx-\int tan (x-a).dx]$$
$$=\frac{1}{sin (a-b)}[-log \left | cos (x-b) \right |+log\left | cos (x-a) \right |]+c$$
$$=\frac{1}{sin (a-b)}[log\left | cos (x-a) \right |-log\left | cos (x-b) \right |]+c$$
$$=\frac{1}{sin (a-b)}log[\frac{cos (x-a)}{cos (x-b)}]+c$$
Solve:
$$\displaystyle\int { \sqrt { ax+b } } dx$$
$$\int \sqrt{ax+b}.dx$$
Let $$ax+b = t$$
diff w.r.t 'x'
$$a(1)+0=\frac{dt}{dx}$$
$$dx=\frac{dt}{a}$$
now
$$\int \sqrt{t}.\frac{dt}{a}$$
= $$\frac{1}{a}\int \sqrt{t}.dt$$
= $$\frac{1}{a}\int t^{1/2}.dt$$
= $$\frac{1}{a}[\frac{t^{3/2}}{3/2}+C]$$
= $$\frac{1}{a}.[\frac{2}{3}t^{3/2}+C]$$
= $$\frac{2}{3a}t^{3/2}+C$$
= $$\frac{2}{3a}(ax+b)^{3/2}+C$$
Evaluate the integral $$\displaystyle\int_{0}^{2}x\sqrt{x+2}dx$$.
$$\int _{ 0 }^{{ \pi /2 } }{ { x }^{ 2 } } { cos }^{ 2 }$$ x dx
Evaluate : $$\displaystyle \int \dfrac{\tan^{ - 1}x}{1+x^2}\ dx $$
Integrate $$\int {({{\sin }^{ - 1}}} x{)^2}dx$$
$$\displaystyle\int ^{\pi/2}_{\pi/4} \sqrt{1-\sin 2 x} d x=?$$
$$\displaystyle\int\dfrac{1}{3\sin x-4\sin^3x}dx$$.
Solve $$\int \dfrac{cos^{9}x}{sin x} dx $$
Evaluate $$\displaystyle\int \dfrac {x^3+4x^2+9x}{x^2+4x+9} dx$$
Using integration, find the area of the triangle formed by negative $$x - axis$$ and tangent and normal to the circle $${x^2} + {y^2} = 9$$ at $$( - 1,2\sqrt 2 )$$.
Evaluate: $$\displaystyle \int{\dfrac{(2x+3)dx}{x^2+3x+6}}$$
$$\displaystyle \int{ \sin }^{ 4 }x \cos x dx$$
$$\int _{ 0 }^{ 1 }{ \frac { x }{ \sqrt { 1+{ x }^{ 2 } } } } dx$$
Evaluate :$$\int x^2 (1-\dfrac{1}{x^2})dx$$
Evaluate $$\displaystyle\int^\pi_0 \dfrac{x}{a^2cos^2x+ b^2sin^2x} dx$$
Evaluate: $$\displaystyle \int (x^3+5x^2+6)(3x^2+5x)d x $$
Evaluate: $$\displaystyle \int (x^2+5x+6)(2x+5)d x $$
Find:
$$\int _{ 1 }^{ 2 }{ \dfrac { \ell nx }{ { x }^{ 2 } } } dx$$
Integrate:$$\displaystyle\int{{\tan}^{3}{x}dx}$$
Find :
$$\int { xsinxdx } $$.
Evaluate: $$ \displaystyle \int \dfrac{2 x}{\left(x^{2}+4\right)} d x $$
Simplify:
$$\int { \dfrac { secx }{ secx+tanx } } $$
$$\int _{ -5 }^{ 5 }{ \left(x+2\right)} dx$$
$$\int _{ 1 }^{ 3 }{ a^{ x } } dx$$
Evaluate: $$I =\displaystyle \int \log \sin x dx$$
Evaluate :
$$\int { \log x } dx$$
Find :
$$\int { \dfrac { { sec }^{ 2 }x }{ { tan }^{ 2 }x+4 } dx } $$
Find :
$$\int { xcosxdx } $$.
Evaluate : $$\int sin4x . sin8x dx$$.
Evaluate:
$$\int { { x }^{ 2 }.{ e }^{ -2 } } dx$$
Evaluate: $$\displaystyle \int_{0}^{\frac{\pi}{4}}\dfrac{dx}{5+4 cos x}$$
$$\displaystyle\int^{\pi/4}_0\dfrac{dx}{5+4\cos x}=\displaystyle\int^{\pi/4}_0\dfrac{dx}{5+4\left(\dfrac{1-\tan^2x/2}{1+\tan^2x/2}\right)}$$
$$=\displaystyle\int^{\pi/4}_0\dfrac{dx(1+\tan^2x/2)}{5+5\tan^2x/2+4-4\tan^2x/2}$$
$$=\displaystyle\int^{\pi/4}_0\dfrac{\sec^2x/2dx}{9+\tan^2x/2}$$ Let $$t=\tan x/2$$ $$dt=\dfrac{1}{2}\sec^2x/2dx$$
$$=\displaystyle\int^{\pi/4}_0\dfrac{2dt}{9+t^2}$$
When $$x/2=0, t=0$$; when $$x/2=\pi/4$$ $$\Rightarrow t=1$$
$$=\displaystyle\int^1_0\dfrac{2dt}{9+t^2}$$
$$=\left.2\times \dfrac{1}{3}\tan^{-1}\left(\dfrac{t}{3}\right)\right]^1_0$$
$$=\dfrac{2}{3}\left[\tan^{-1}\left(1/3\right)-\tan^{-1}(0)\right]$$
$$=\dfrac{2}{3}\left[\tan^{-1}\left(1/3\right)-0\right]$$
$$=\dfrac{2}{3}\tan^{-1}\left(1/3\right)$$.
Evaluate :$$\displaystyle \int { \log } x{dx}$$
Evaluate the following definite integrals:
$$\displaystyle \int _{0}^{1/3} \dfrac {1}{\sqrt {1-x^2}}dx$$
Evaluate $$\displaystyle\int_{1}^{2}\dfrac{3x}{9x^{2}-1}dx$$
Solve : $$\displaystyle \int _{ 0 }^{ \pi }{ \dfrac { x\tan{ x } }{ \sec { x } +\tan { x } } } dx$$
Evaluate the following definite integrals :
$$\displaystyle \int _{0}^1 \dfrac {1}{1+x^2}dx$$
$$\displaystyle\int_{0}^{1}\dfrac{e^{x}}{1+e^{2x}}dx$$
Find the value of $$\int x \tan^2x \, dx$$.
Evaluate $$\displaystyle\int_{2}^{4}\dfrac{x}{x^{2}+1}dx$$
Evaluate $$\displaystyle\int_{0}^{\pi/2}\dfrac{\cos x}{1+\sin^{2}x}dx$$
Evaluate:
$$\displaystyle\int_{0}^{\pi/2}\dfrac{\sin\theta}{\sqrt{1+\cos\theta}}d\theta$$
Evaluate the following definite integrals:
$$\displaystyle \int _{\pi /6}^{\pi /4} cosec \ x \ dx$$
Evaluate $$\displaystyle\int_{0}^{a}\sqrt{a^{2}-x^{2}}dx$$
Evaluate the following definite integrals :
$$\displaystyle \int _{0}^{\pi} \dfrac {1}{1+\sin x}dx$$
Evaluate the integral $$\displaystyle\int_{0}^{1/2}\dfrac{x\sin^{-1}x}{\sqrt{1-x^{2}}}dx$$.
Evaluate $$\displaystyle\int_{0}^{\pi/4}(\sqrt{\tan}x+\sqrt{\cot}x)dx$$
Evaluate $$\displaystyle\int_{0}^{2}x\sqrt{x+2} \ dx$$
Evaluate the following definite integral.
$$\displaystyle \int _{2}^3 \dfrac {x}{x^2+1}dx$$
Evaluate $$\displaystyle\int_{0}^{1}\dfrac{2x}{1+x^{4}}dx$$
Evaluate the definite integral :
$$\displaystyle \int_{0}^{1} \dfrac {2x+3}{5x^2 +1}dx$$
Evaluate the definite integral :
$$\displaystyle \int_{0}^{1} (1+x)^5 dx$$
Evaluate the definite integral:$$\displaystyle\int_{0}^{\pi/4}\sin^{3}2t\cos 2t\ dt$$
Evaluate: $$\displaystyle\int_{0}^{\pi/4}\sin^{3}2t\cos 2t\ dt$$.
Evaluate:$$\displaystyle\int \sec x\tan x dx$$
Evaluate the following definite integral:$$\displaystyle \int_{1}^{2} e^{2x} \left (\dfrac {1}{x}-\dfrac {1}{2x^2}\right)dx$$
Evaluate:$$\displaystyle\int_{0}^{\pi}\log (1-\cos x)\ dx$$
$$\displaystyle \int \dfrac 1{\sqrt {3-x^2}}dx$$
Evaluate $$\displaystyle\int_{0}^{\pi/2}\dfrac{\sin x+\cos x}{3+\sin 2x}dx$$
Evaluate:$$\displaystyle\int_{0}^{\pi/4}\dfrac{\tan^{3}x}{1+\cos 2x}dx$$
Evaluate the following integral :
$$\displaystyle\int_{0}^{\pi/2}\dfrac{x\sin x\cos x}{\sin^{4}x+\cos^{4}x}\ dx$$
Evaluate the definite integral :
$$\displaystyle \int_{1}^{2}\dfrac {1}{\sqrt {(x-1) (2-x)}}dx$$
Evaluate the integral $$\displaystyle\int_{0}^{\pi/4}\sin^{3}2t\cos 2t\ dt$$.
$$\displaystyle\int_{0}^{\pi/4}\sec ^2 x \ dx$$
Evaluate $$\displaystyle\int_{0}^{1}\dfrac{\tan^{-1}x}{1+x^{2}}dx$$
Evaluate the following definite integral:
$$\displaystyle \int_{-1}^{1}\dfrac {1}{x^2 +2x+5}dx$$
$$\displaystyle\int_{0}^{1}\dfrac{1-x^{2}}{(1+x^{2})^{2}}dx$$
Evaluate the following definite integrals :$$\displaystyle \int _{0}^{\pi /2} \cos^2 x\ dx$$
Evaluate the integral $$\displaystyle\int_{-1}^{1}5x^{4}\sqrt{x^{5}+1}\ dx$$.
Evaluate the following definite integral:$$\displaystyle \int_{e}^{e^2} \left\{\dfrac {1}{\log x} -\dfrac {1}{(\log x)^2}\right\} dx$$
Evaluate the following integral:
$$\displaystyle\int { \cfrac { \cos { x } }{ \cos { 3x } } } dx$$
Evaluate the following definite integral:
$$\displaystyle\int_{4}^{9}\dfrac{\sqrt{x}}{(30-x^{3/2})^{2}}\ dx$$
Evaluate the following integral:
$$\displaystyle \int { \cfrac { 1 }{ 2{ x }^{ 2 }-x-1 } } dx\quad $$
Evaluate $$\displaystyle \int_{0}^{3}(2x^2+3x +5)dx$$
Solve :$$\displaystyle \int { \left( x+2 \right) \sqrt { 3x+5 } } dx$$
Evaluate the following integral:
$$\displaystyle \int { \cfrac { 1 }{ \left( \sin { x } -2\cos { x } \right) \left( 2\sin { x } +\cos { x } \right) } } dx$$
Evaluate the following integrals:
$$\displaystyle\int { \cfrac { 1 }{ 4\sin ^{ 2 }{ x } +5\cos ^{ 2 }{ x } } } dx$$
Evaluate the following integral:
$$\displaystyle\int { \cfrac { 1 }{ 3+2\cos ^{ 2 }{ x } } } dx\quad $$
Evaluate the following integrals:
$$\displaystyle \int { \cfrac { 2 }{ 2+\sin { 2x } } } dx\quad $$
Evaluate the following definite integral:
$$\displaystyle \int_{e}^{e^2} \left\{\dfrac {1}{\log x} -\dfrac {1}{(\log x)^2}\right\} dx$$
Evaluate the following integrals:
$$\int { \cfrac { 1 }{ 5-4\sin { x } } } dx\quad $$
Evaluate the following integral:
$$\displaystyle \int { \cfrac { 1 }{ \sin ^{ 2 }{ x } +\sin { 2x } } } dx\quad $$
Evaluate the following integrals:
$$\int { \cfrac { 1 }{ 1-2\sin { x } } } dx\quad $$
Evaluate the following integral:
$$\displaystyle\int { \cfrac { 1 }{ \cos { 2x } +3\sin ^{ 2 }{ x } } } dx$$
Evaluate $$\displaystyle \int_{1}^{3}(2x^2+5x)dx$$
Evaluate the following integrals
$$\int { \cfrac { 1 }{ \sin { x } -\sqrt { 3 } \cos { x } } } dx\quad $$
Evaluate the following integrals
$$\int { \cfrac { 1 }{ 5+7\cos { x } +\sin { x } } } dx$$
Evaluate the following integrals
$$\int { \cfrac { 1 }{ 1-\cot { x } } } dx\quad $$
Evaluate the following integrals
$$\int { \cfrac { 1 }{ \sin { x } +\cos { x } } } dx$$
Evaluate the following integrals:
$$\int { \cfrac { 1 }{ 4\cos { x } -1 } } dx\quad $$
Evaluate the given integral.
$$\displaystyle \int { \cfrac { \log { \left( \log { x } \right) } }{ x } } dx$$
Evaluate the following integrals
$$\int { \cfrac { 2\sin { x } +3\cos { x } }{ 3\sin { x } +4\cos { x } } } dx\quad $$
Evaluate the following integrals
$$\int { \cfrac { 1 }{ 3+4\cot { x } } } dx\quad $$
Evaluate the following integral:
$$\displaystyle \int { \cfrac { { x }^{ 2 } }{ { x }^{ 4 }-{ x }^{ 2 }-12 } } dx$$
Evaluate the given integral.
$$\int { \log { (x+1) } } dx$$
$$\displaystyle\int_{0}^{\pi/4}\sin^{3}2t\cos 2t\ dt$$.
Evaluate the following integrals
$$\int { \cfrac { 1 }{ p+q\tan { x } } } dx\quad $$
Evaluate the given integral.
$$\int { { x }^{ 3 }\log { x } } dx$$
Evaluate the following integrals
$$\int { \cfrac { 1 }{ 1-\tan { x } } } dx\quad $$
Evaluate: $$\displaystyle\int \dfrac{-\sin x }{5+\cos x}dx$$
Evaluate: $$\displaystyle\int \sec x\tan x dx$$
Evaluate: $$\displaystyle \int \cot x dx$$.
Solve : $$\displaystyle\int_{0}^{3}|3x-1|\ dx$$
Evaluate the following definite integral:
$$\displaystyle\int_{0}^{\pi/2}\dfrac{\sin^{3/2} x}{\sin^{3/2}x+\cos^{3/2} x}\ dx$$
Evaluate the following definite integral:
Evaluate the following definite integral:
$$\displaystyle\int_{-1}^{1}5x^{4}\sqrt{x^{5}+1}\ dx$$
Evaluate the following integrals :$$\displaystyle\int_{0}^{\pi} x\ dx$$
Solve : $$\displaystyle\int_{-2}^{2}|2x+3|\ dx$$
Evaluate $$\displaystyle \int _0^2 \dfrac x 3 \, dx $$
Evaluate the following integrals $$\displaystyle\int_{0}^{\pi/2}\dfrac{\sin^{3/2} x}{\sin^{3/2}x+\cos^{3/2} x}\, dx$$
Evaluate $$\displaystyle\int^{16}_0x^{3/4}dx$$.
Evaluate $$\displaystyle\int^4_1\sqrt{x}dx$$.
Evaluate $$\displaystyle\int^3_1x^4dx$$.
Evaluate $$\displaystyle\int^4_1\dfrac{dx}{\sqrt{x}}$$.
Evaluate : $$\displaystyle \int \dfrac{dx}{x^2+4x+8}$$
Evaluate $$\displaystyle\int^1_0\dfrac{dx}{\sqrt [3]{x}}$$.
Evaluate $$\displaystyle\int^{-1}_{-4}\dfrac{dx}{x}$$.
Evaluate $$\displaystyle\int^2_1x^{-5}dx$$.
Evaluate $$\displaystyle\int^{1/2}_{1/4}\dfrac{dx}{\sqrt{x-x^2}}$$.
Evaluate $$\displaystyle\int^8_1\dfrac{dx}{x^{2/3}}$$.
Evaluate $$\displaystyle\int^2_1\dfrac{dx}{\sqrt{x^2+4x+3}}$$.
Evaluate $$\displaystyle\int^4_3\dfrac{dx}{(x^2-4)}$$.
Evaluate $$\displaystyle\int^1_0\dfrac{dx}{\sqrt{1-x^2}}$$.
Evaluate $$\displaystyle\int^1_0\dfrac{dx}{(1+x^2)}$$.
Evaluate $$\displaystyle\int^4_23dx$$.
Evaluate $$\displaystyle\int^1_0\dfrac{dx}{(1+x+2x^2)}$$.
Evaluate $$\displaystyle\int^4_0\dfrac{dx}{\sqrt{x^2+2x+3}}$$.
Evaluate $$\displaystyle\int^{\infty}_0\dfrac{dx}{(1+x^2)}$$.
Evaluate the following integral:
$$\displaystyle\int^1_0\dfrac{e^x}{(1+e^{2x})}dx$$.
Evaluate $$\displaystyle\int^2_1\dfrac{5x^2}{(x^2+4x+3)}dx$$.
Evaluate $$\displaystyle\int^3_1\dfrac{dx}{x^2(x+1)}$$.
Evaluate the following integral:
$$\displaystyle\int^1_0\dfrac{dx}{(2x-3)}$$.
Evaluate the following integral:
$$\displaystyle\int^1_0\dfrac{2x}{(1+x^2)}dx$$.
Evaluate $$\displaystyle\int^1_0\sqrt{x(1-x)}dx$$.
Evaluate the following integral:
$$\displaystyle\int^2_1\dfrac{3x}{(9x^2-1)}dx$$.
Evaluate $$\displaystyle\int^2_1\dfrac{dx}{x(1+2x)^2}$$.
Evaluate the following integral:
$$\displaystyle\int^1_0\dfrac{2x}{(1+x^4)}dx$$.
Evaluate $$\displaystyle \int_{a}^{b} \sqrt{\dfrac{x-a}{b-x}}dx$$
$$\text { Evaluate: } \displaystyle \int_{0}^{1} \dfrac{d x}{1+x^{2}}$$
$$\text { Evaluate: } \displaystyle \int_{0}^{1 / \sqrt{2}} \dfrac{\mathrm{d} \mathrm{x}}{\sqrt{1-x^{2}}}$$
Evaluate $$\displaystyle \int_{a}^{b} \dfrac{1}{\sqrt{(x-a)(b-x)}}dx,b>a$$
$$\displaystyle \int_{1}^{2}\dfrac{dx}{\sqrt{x}-\sqrt{x-1}}$$
$$\text { Evaluate: } \displaystyle \int \dfrac{d x}{x+x \log x}$$
If $$\int_{0}^{1}\left(3 x^{2}+2 x+k\right) \mathrm{dx}=0,$$ then find the value of $$k$$.
Find the value of the following integrals:
$$\displaystyle \int^{1}_{0} \frac{x^2}{1 + x^2} dx$$
$$\text { Evaluate: } \displaystyle \int_{0}^{1} \dfrac{d x}{\sqrt{2 x+3}} d x$$
$$\displaystyle \int_{0}^{\pi} log \;(1 - cos \;x) dx $$
Find the value of the following integrals:
$$\displaystyle \int^{3}_{0} \sqrt{\frac{x}{3 - x}} dx$$
If $$\displaystyle \int _a^x t \ y (t)dt = x^2 + y(x)$$, then find $$y(x)$$.
$$\text { Evaluate: } \int x \sin ^{-1} x d x$$
$$\text { Evaluate: } \displaystyle \int_{2}^{3} \dfrac{1}{x} \mathrm{d} \mathrm{x}$$
Find the value of the following integrals:
$$\displaystyle \int^{2}_{1} \frac{dx}{(x + 1)(x + 2)}$$
If $$f(x)$$ is a function satisfying, $$\displaystyle f\left(\frac{1}{x}\right)+x^2f(x)=0$$ for all non-zero $$x$$, then evaluate $$\displaystyle\int_{\displaystyle\sin{\theta}}^{\displaystyle\csc{\theta}}{f(x)dx}$$.
If $$\displaystyle\int_{0}^{\pi /2}\frac{dx}{3+4\sin x}dx=\frac{1}{\sqrt{\left ( k \right )}}\log \left ( \frac{4+\sqrt{7}}{3} \right )$$ then find the value of $$k$$.
For $$ x > 0 $$ , let $$ f\left ( x \right )= \displaystyle \int_{1}^{x}\displaystyle \frac{\log t}{t+1}dt $$. The value of $$ 98\left ( f\left ( e \right )+f\left ( 1/e \right ) \right ) $$ is
Let $$\displaystyle I= \int_{3n\pi }^{\left ( n+\frac{1}{n} \right )3\pi }\frac{4x dx}{\left [ \left ( a^{2}+b^{2} \right )+\left ( a^{2}-b^{2} \right )\cos \frac{2nx}{3} \right ]^{2}}$$ (where a,b>0)
prove that $$\displaystyle I=\frac{9\left ( 2n^{2}+1 \right )\pi }{n^{2}}\frac{a^{2}-b^{2}}{a^{3}b^{3}}$$
If $$\displaystyle \int_{0}^{1}\frac{dx}{(1+x)(2+x)\sqrt{x(1-x)}}=\frac{\pi A}{\sqrt{6}(\sqrt{3}+1) (157)} $$, then $$A$$ is equal to
Evaluate: $$\displaystyle\int_{0}^{\dfrac{\pi}{2}}\sqrt{sin\,\phi} \, cos^5\,\phi\,d\,\phi$$
Evaluate $$\int_{0}^{\pi}e^{|\cos x|}\left (2\sin \left (\dfrac {1}{2}\cos x\right ) + 3\cos \left (\dfrac {1}{2}\cos x\right )\right )\sin x dx$$.
Evaluate: $$\displaystyle\int \dfrac{tan\,x}{(a^2+b^2tan^2x)}dx$$
The value of $$\displaystyle \int_{1/3}^{3}\dfrac {\tan \left (x^{2} + \dfrac {1}{x^{2}}\right )}{\sin \left (x + \dfrac {1}{x}\right )} \dfrac {dx}{x}$$ is
Evaluate $$\displaystyle \int { \dfrac { \left( \cos { 5x+\cos { 4x } } \right) }{ 1-2\cos { 3x } } } dx$$
Solve $$\displaystyle\int \dfrac {dx}{\sin x+\sec x}$$
Evaluate $$\int\limits_0^{\frac{\pi }{4}} {{{\cos }^{\frac{3}{2}}}\left( {2x} \right)cos\left( x \right)dx} $$
Solve : $$\displaystyle\int sec^{-1} \sqrt{x} \, dx$$
Solve $$\int_0^1 {{{\cot }^{ - 1}}} (1 - x + {x^2})dx$$.
Evaluate $$ \ \int _{ 0 }^{ \pi }{ \dfrac { xdx }{ 1+\cos ^{ 2 }{ x } } }$$
Evaluate:
$$\displaystyle \int^{\frac{\pi}{4}}_{0}e^{\sin x}(1 + \tan x \sec x)dx$$
$$\int {x{{\sin }^{ - 1}}xdx} $$
If $$f\left( x \right) =\int { \dfrac { ({ x }^{ 2 }+\sin ^{ 2 }{ x } ) }{ 1+{ x }^{ 2 } } } \sec ^{ 2 }{ x } dx$$ and $$f\left( 0 \right)=0$$, then $$ f\left( 1 \right)$$ is equal to
Evaluate:$$\displaystyle \int_0^1 \dfrac {2x}{x^2+1}dx $$
Find solution in terms of indefinite integration, using substitution
$$\int_0^1 {x\cos \left( {{{\tan }^{ - 1}}x} \right)} \,dx$$
Evaluate: $$\displaystyle {\int {\left( {\dfrac{{1 - x}}{{1 + {x^2}}}} \right)} ^2}{e^x}\,dx$$
$$\int (\sec^{2} x+\csc^{2} x)dx$$
Find the following integral.
$$\displaystyle\int \dfrac{x^3-1}{x^2}dx$$.
Find the following integral.
$$\displaystyle\int (x^{\frac{1}{2}}+2e^x-\frac{1}{x})dx$$.
$$\displaystyle\int^{\pi/2}_0\dfrac{\sin 8xlog (\cot x)dx}{\cos 2x}$$.
Find : $$\int {\log
x.dx} $$
Sol
$$ \displaystyle \int (logx)dx $$
$$ \displaystyle =\int (logx).1dx $$
Now, we know that
$$ \displaystyle \int uv dx = u\int vdx -\int ({u}' \int v dx)dx ...(1)$$
Here, u = logx
v = 1
putting values in eq (1), we get
$$ \displaystyle \int (logx).1dx = logx \int 1.dx-\int (\dfrac{d(logx)}{dx}.\int 1.dx)dx $$
$$ = (logx)x-\int 1/x . 2 dx $$
$$ = x log x- \int 1.dx $$
$$ \boxed{\int logx dx = xlogx-x+c}$$
Evaluate: $$\int\limits_0^{\pi /2} {\dfrac{{\left( {\sin x + \cos x} \right)dx}}{{9 + 16\,\sin 2x}}} $$
Integrate $$\dfrac{1}{x(x^n+1)}$$ with respect to x.
Evaluate:$$\displaystyle\int_{\tfrac{-3\pi}{2}}^{\tfrac{-\pi}{2}}{\left[{\left(x+\pi\right)}^{3}+{\cos}^{2}{\left(x+3\pi\right)}\right]dx}$$
Evaluate
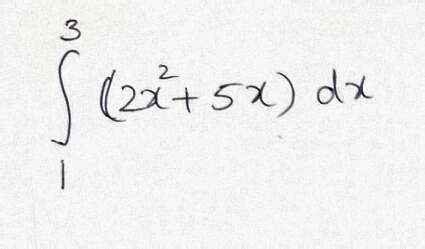
Find $$\displaystyle \int \dfrac{x^{4}dx}{(x-1)(x^{2}+1)}$$
Let $$f\left(y\right)={e}^{y},\,\,g\left(y\right)=y,\,\,y>0$$ then $$F\left(t\right)=\displaystyle\int_{0}^{t}{f\left(t-y\right)g\left(y\right)dy}=$$
Integrate:$$\int { \frac { dx }{ 3cosx+4sinx+6 } } $$
$$I=\displaystyle \int x^{3}\log{x}\ dx$$
$$\displaystyle\int x^3log x\cdot dx$$
$$\displaystyle\int udv=uv-\displaystyle\int v.du$$
$$u=log x$$; $$dv=x^3dx$$
$$du=\dfrac{1}{x}dx$$ $$v=\dfrac{x^4}{4}$$
$$\displaystyle\int x^3 log x=\dfrac{x^4}{4}log(x)-\displaystyle\int \dfrac{x^4}{4}\cdot \dfrac{1}{x}dx$$
$$=\dfrac{x^4}{4}log x-\dfrac{1}{4}\displaystyle\int x^3dx$$
$$=\dfrac{x^4}{4}log x-\dfrac{1}{4}\dfrac{x^4}{4}$$
$$=\dfrac{x^4}{4}[log x-\dfrac{1}{4}]+c$$.
$$\int\dfrac{dx}x({x^{3/2}+1})$$ Solve it.
Evaluate $$\int (\log x)^{2}dx$$.
Evaluate:
$$\displaystyle\int \dfrac {\sin x\ dx}{\sin^{3}x+\cos^{3}x}$$
$$ \int _ { - 5 } ^ { 5 } | x + 2 | d x $$
Prove that $$\displaystyle \int^b_a f(x)dx = \int^b_a f(a + b - x) dx$$ and evaluate $$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\dfrac{dx}{1+\sqrt{\tan x}}$$
Evaluate: $$\displaystyle \int \sqrt{4-3x-2x^{2}} dx$$
Evaluate the following:
$$\displaystyle \int e^{-3x} \,cos^3 \,xdx$$
Evaluate the following integrals:
$$\int { \cfrac { 1 }{ 5+4\cos { x } } } dx$$
If f(x) is a function satisfying $$f\left( \dfrac{1}{x}\right)+x^2f(x)=0$$ for all non-zero x, then $$\displaystyle \int_{sin\Theta}^{cosec\Theta}f(x)dx$$ is equal to
Evaluate : $$\int_0^{\pi/2}{\cfrac{x}{\sin{x}+\cos{x}}}dx$$
Class 12 Commerce Maths Extra Questions
- Application Of Derivatives Extra Questions
- Application Of Integrals Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Linear Programming Extra Questions
- Matrices Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions